Abstract
Two kinds of automata are presented, for recognising new classes of regular and context-free nominal languages. We compare their expressive power with analogous proposals in the literature, showing that they express novel classes of languages. Although many properties of classical languages hold no longer in the nominal case, we design a slight restriction of our models that preserve some interesting ones. In particular, we prove the emptiness problem decidable and we construct the intersection between (restricted) regular and context-free automata. By examples and walking through their properties we argue the relevance of our models in the context of the verification of resource usage patterns.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Describing resources and reasoning about their usages is a difficult task that emerges in all scenarios where effective mechanisms are strongly required to control how possibly unboundedly many computational resources are granted to multiple and heterogeneous entities. A paradigmatic example are Cloud systems [24], that support network access to a shared pool of dynamically configurable computing resources with elastic usage requirements. Similarly, in the so-called Internet of Things [23], mobile devices are capable to dynamically discover, acquire and interact with multiple heterogeneous resources. The ability of dealing with unboundedly many resources also underpins the manipulation of XML schemata [39]; the orchestration of Web-services [41]; the development of security protocols (e.g. nonces and time-stamps) [1, 20].
Abstract models are needed for describing the behaviour of programs involving a potentially unbounded number of computational resources, for detecting bugs and verifying properties of their usage. In this paper we will contribute to the definition of an abstract model based on languages over infinite alphabets, aka nominal languages. In particular, we will propose two new kind of automata that recognise a class of regular and of context-free languages with an infinite alphabet, through which one can abstractly represent several complex patterns of resource usages, as illustrated below.
In the context of programming languages, the term resource refers to software or operating system entities, such as graphic devices, file handles, network and database connections, as well as concurrent objects like locks. The following recursive function \(\mathtt {updateFiles}\), written in an F#-like syntax, abstractly implements a resource usage pattern, typical of many applications, e.g. for updating and synchronizing a storage service available on the cloud—this programming pattern is known in the programming language community under the name of Resource Acquisition Is Initialization Footnote 1 idiom. Intuitively, the code below monitors the changes to a certain number of files of interest. We omit the actual operations on the resources in order to focus on the control flow pattern followed for acquiring and releasing them.
In reaction to a change notification (here encoded in the info parameter) the routine updates the files if certain conditions are met (represented by the updatable condition). We assume that the metadata of the files of interest are stored into a suitable data structure, i.e. a collection, and that an iterator (itCollection) steps through the collection of files. Notice that the routine uses a fresh file r at each iteration. The use construct defines the scope of a resource usage: it binds similarly to let, but it additionally take care of disposing the resource when the it leaves its scope.

Since we are only interested in how the routine above operates over its resources, we can abstractly represent a computation by only recording resource activations and disposals (within the scope). Intuitively, a run-time monitor can extract information from a run and represent it as the following trace
where \(r1,r2,\dots , rn\) correspond to the fresh files created by new and disposed by rel. In the trace, the files appear following a pattern that has the same structure of the words in the context-free language \(\{ww^R\}\), where \(w^R\) stands for the reverse of w. Additionally, the file resources \(r1,r2,\dots , rn\) are pairwise distinct because of the freshness constraint (granted by the invocations to new), and because resource disposal adheres to the scope imposed by the use construct. Note also that there are unboundedly many fresh file resources because the value of n depends on the actual size of the collection which is unknown a priori; we call this property unbound freshness.
It is worth noting that calculi for concurrent and distributed systems faced the similar problem of handling unboundedly many fresh (or restricted) names, in the development of the so called nominal calculi [12, 25, 31, 36, 44].
We now consider another aspect of resource usage, on a simple Java-like programming example. Consider a basic service for managing resources with the try-with- resources Footnote 2 statement that declares one or more resources, and that ensures each declared resource to be closed (disposed or released in our terms) at the end of the statement. Recall that only Java objects that implement the interface java.lang.AutoCloseable are resources.

The client is granted access to all the services associated with the objects including the getInfo() method that handles the service metadata. After the invocations of doIt, the client gets and stores inside a local object (here String) a (meta) property of the whole object, i.e. of the whole resource. When try-with-resources is completed the object resource is disposed. However, the client can still access and operate with the metadata of the resource. The following trace abstractly represents the creation of fresh resources and access to any of their public parts in a run.
The last action represents what we call a late access to myObj, performed through the last statement on metaDataInfo. Through such a late access, the client can acquire possibly confidential (meta)data, leading to an unwanted information flow from the service to the client. Expressing and detecting at a suitable abstraction level the correct flow of information requires then the ability of tracking in exact terms how and when resources are accessed.
Although the Java program above may appear artificial, it is an instance of the well-known programming pattern for Object Oriented programming, called object-pool,Footnote 3 where the object kept is still accessible after its release. Note that nominal techniques are needed because pools are not necessarily finite. A paradigmatic example is the Cached Thread Pools of Java,Footnote 4 which can spawn an unbound number of threads, while reusing the ones that have been released. Late usage of resources also occurs in the composition of web services [21].
The examples above and the programming pragmatics show the importance of devising expressive and flexible abstractions to control the usage of resources. The problem becomes crucial by the current programming practice, where it is common to pick from the Web some scripts, or plugins, or code snippets, and assemble them into a bigger program, with little or no control about the correctness (e.g. security) of the whole program. Verifying properties may be cumbersome even for small programs, and it may also lead to rather complex checking machineries. Correctness properties are typically expressed in terms of formalisms which predicate over execution traces of, e.g., finite state machines, regular expressions, context-free grammars, linear temporal logics, and their extensions. The encoding of resource usage properties like unbound freshness and late usage discussed above cannot be directly expressed in standard specification formalisms, because it is crucial to deal with freshness of resources and their scope.
The literature has many proposals for statically abstracting program behaviour, as done in the simple traces given above (see [6, 9, 16, 40, 46], just to cite a few). Along this line, two of the authors of this paper introduced a framework to statically compute sound over-approximations of the possible run-time traces of a program [3–6]. This approximations are then model-checked [8] to guarantee that prescribed policies will hold at runtime. The over-approximations can be seen as context-free languages, and the present work aims at extending that approach also to nominal languages [34].
In summary, the contribution of this paper are the following. We introduce an abstract model for modelling resource usage that takes care of (i) expressing context-free behaviour, as well as regular ones (ii) handling unboundedly many resources, with (iii) unbound freshness, and (iv) late usage of resources.
We express context-free traces of resource usage through Pushdown Nominal Automata (\({\text {PDNA}}_{\pm }\)), that extend classical pushdown automata. The alphabet of \({\text {PDNA}}_{\pm }\) is infinite, so we can undertake item (ii) above in the style of nominal techniques [22].
To guarantee freshness of resources (i.e. of the symbols of the alphabet), the \({\text {PDNA}}_{\pm }\) exploit (finitely many) additional structures, called m-registers, that store resources in a stack-like fashion. A resource is fresh if no m-register contains it. Since m-registers have unbounded capacity, unbounded freshness, as stated in (iii), is guaranteed. As expected, when a resource is released, it is removed from the m-register that stores it, and so it can be re-used as fresh later on. Finally, we grant late usage allowing a resource to be mentioned after it has been disposed, as in item (iv). The stack of \({\text {PDNA}}_{\pm }\) plays a crucial role in this mechanism: a resource in use, i.e. occurring in a m-register, say N, can be saved in the stack and can remain there after it has been removed from N, ready to be recalled once occurring again on top of the stack. In the over-simplified example above, the metadata will be recorded in a m-register N, and a mention to it pushed on the stack. After disposing the object, one can still access its metadata through the hook stored in the stack.
Here we also investigate the problem of handling unboundedly many resources and of unbounded freshness in regular languages. To do that, we introduce the new model of Finite State Nominal Automata (\({\text {FSNA}}_{\pm }\)), that are finite state automata enriched with a finite number of m-registers.
We then prove that the languages recognised by both \({\text {FSNA}}_{\pm }\) and \({\text {PDNA}}_{\pm }\) are closed under union, and the first ones are also closed under intersection, provided that symbols are not released. The intersection of a language accepted by a \({\text {FSNA}}_{\pm }\) with that of a \({\text {PDNA}}_{\pm }\) is recognised by a \({\text {PDNA}}_{\pm }\), provided that neither automata release resources. Neither the \({\text {FSNA}}_{\pm }\) and \({\text {PDNA}}_{\pm }\) languages, instead, are closed under complement.
We also establish the decidability of the emptiness for \({\text {FSNA}}_{\pm }\) and for the subclass of \({\text {PDNA}}_{\pm }\) in which symbols are not released. Consequently, it is feasible to model-check a property expressed as a (restricted) \({\text {FSNA}}_{\pm }\) against a model expressed as a (restricted) \({\text {PDNA}}_{\pm }\), by verifying the emptiness of their intersection, in the style of [49].
We also compare the expressiveness and some properties of our models with other proposals in the literature, that will be briefly surveyed. In particular, we consider the regular languages over infinite alphabet and their recognisers investigated in [7, 14, 18, 27, 29, 31, 33, 47, 48], as well as the context-free languages over infinite alphabet of [7, 12, 15, 17, 39, 42, 43].
The paper is organised as follows. Notation and abbreviations are summarised in Table 1. In Sect. 2 we introduce \({\text {FSNA}}_{\pm }\); we study their language theoretical properties in Sect. 3; and we compare their expressiveness and their properties with those of other models in the literature in Sect. 4. Section 5 introduces \({\text {PDNA}}_{\pm }\); investigates their properties in Sect. 6; and compares them with other proposals in Sect. 7.
2 Finite State Nominal Automata
As anticipated in the introduction, our automata abstractly model traces of software systems, with the focus on the pattern they follow when manipulating resources. A common pattern is that programs can only request a fresh resource, and not a specific one: think of object references, server mirrors, nonces, etc. Resources are often manipulated opaquely: the program is only allowed to test them for equality. Hence, fresh resources are interchangeable: the set of traces that a program can generate does not depend on the specific identity of the resources involved, but only on their relative equality and inequality. In the literature this property is called language equivariance [12].
To keep our presentation simple, we almost always consider languages over resources, disregarding actions on them. Occasionally, we shall consider actions on resources as well (known as data-words [11] and briefly surveyed before Example 2), to illustrate the minor changes needed to deal with them (see e.g. Fig. 2). To account for freshness, resources are abstractly represented by symbols of an infinite alphabet \(a \in {\varSigma }\), that we assume partitioned in a finite set of static symbols \({\varSigma }_s\) and an infinite set of dynamic symbols \({\varSigma }_d\). The first is intended to represent the finite amount of resources known before program execution, while \({\varSigma }_d\) contains the resources that may be acquired or generated at run-time.
Our automata use special data structures to record the dynamic symbols appearing in a recognised string, called mindful registers (m-registers for short). An m-register N is actually a stack S of symbols in \({\varSigma }_d\) and an activation state (\(x \in \{1,0\}\)). An empty stack makes the m-register empty, as well, and we denote it by \(\boxtimes {}\). When the tag x is 1 then the m-register is active, otherwise the m-register is inactive. The operations on an m-register N are built on the standard \(\mathtt {push}\), \(\mathtt {top}\) and \(\mathtt {pop}\) operations as follows:
An s-push operation makes an m-register active, regardless of its activation state. The operation s-top yields a value only if the m-register is active and not empty, otherwise it is undefined. Finally, after a s-pop, the m-register N becomes inactive. Note that s-popping an empty m-register results in a no-operation, so making it impossible to discern an inactive m-register from an empty one.
A symbol is fresh with respect to an m-register when it does not appear in its stack.
Before formally defining Finite State Nominal Automata (FSNA\(_{\pm }\) for short) we intuitively illustrate their recognising mechanisms through the automaton \(R_0\) in Fig. 1. A run on \(R_0\) recognising a word w is a sequence of configurations leading from its initial state \(q_0\) to its final state \(q_2\). We assume that \(R_0\) has two m-registers that will be part of configurations. In the initial configuration the two m-registers are empty and we render them as \(\big [\boxtimes {}, \boxtimes {} \big ]\).
The leftmost edge is  , and following it the automaton reads no symbol (recorded by \(\varepsilon \)) and goes from the configuration \(\langle q_0, \big [\boxtimes {}, \boxtimes {} \big ]\rangle \) to a configuration of the form
, and following it the automaton reads no symbol (recorded by \(\varepsilon \)) and goes from the configuration \(\langle q_0, \big [\boxtimes {}, \boxtimes {} \big ]\rangle \) to a configuration of the form  where a symbol \(a \in {\varSigma }_d\) is s-pushed in the m-register number 2, as dictated by the label \(2+\), provided a is fresh w.r.t. both the m-registers of \(R_0\). By using the edge
where a symbol \(a \in {\varSigma }_d\) is s-pushed in the m-register number 2, as dictated by the label \(2+\), provided a is fresh w.r.t. both the m-registers of \(R_0\). By using the edge  the automaton reaches the configuration
the automaton reaches the configuration  and reads a, i.e. the s-top symbol of the m-register number 2, while nothing is done on the m-registers because of the label \(\varepsilon \).
and reads a, i.e. the s-top symbol of the m-register number 2, while nothing is done on the m-registers because of the label \(\varepsilon \).
There are three edges looping in state \(q_2\). The edge  s-pushes a fresh symbol in the m-register number 1 and reads no symbol;
s-pushes a fresh symbol in the m-register number 1 and reads no symbol;  recognises the s-top symbol of m-register number 1 and leaves the m-registers untouched. Slightly differently, the edge labelled
recognises the s-top symbol of m-register number 1 and leaves the m-registers untouched. Slightly differently, the edge labelled  s-pops a symbol from the m-register number 1 (because the label is \(1-\)) and recognises no symbol. After following it the m-register number 1 becomes inactive and the edge
s-pops a symbol from the m-register number 1 (because the label is \(1-\)) and recognises no symbol. After following it the m-register number 1 becomes inactive and the edge  can not be followed.
can not be followed.
A run on \(R_0\) is  .
.
The reader may convince himself that the language recognised by \(R_0\) is \(\{aw \mid a \in {\varSigma }_d, w \in {\varSigma }_d^* , a \notin ||w||\}\).
In the formal definition and hereafter we use some notation and abbreviations collected in Table 1. We denote the set of the natural numbers by \({\mathbb {N}}\), \(\underline{\mathtt {k}}\) is the segment of the natural numbers \(\{ i \mid 1 \le i \le k\}\), w is a word in \({\varSigma }^*\) with length |w| and i-th symbol w[i], \(\Vert {w} \Vert \) denotes the set of symbols used in w, \(\varepsilon \) is the empty word.
Definition 1
(Finite State Nominal Automata)
A finite state nominal automaton (\({\text {FSNA}}_{\pm }\)) is the tuple \(R=\langle Q, q_{0},{\varSigma }, \delta , r, F \rangle \) where:
-
Q is a finite set of states, \(q,q_1,q',\ldots \in Q\)
-
\(q_0 \in Q\) is the initial state
-
\({\varSigma }={\varSigma }_{s} \cup {\varSigma }_{d}\) is the infinite alphabet (\({\varSigma }_{s}\) is finite, \({\varSigma }_{d}\) denumerable, \({\varSigma }_s \cap {\varSigma }_d = \emptyset \))
-
\(r \in {\mathbb {N}}\) is the number m-registers
-
\(\delta \) is the transition relation: \((q,\sigma , q',{\varDelta }) \in \delta \) with \(\sigma \in {\varSigma }_s \cup \underline{\mathtt {r}} \cup \{\varepsilon \}, {\varDelta } \in \{i+,i- \mid i \in \underline{\mathtt {r}}\} \cup \{\varepsilon \}\) We call a transition new when \({\varDelta }=i+\); delete when \({\varDelta }=i-\); update when \({\varDelta } \ne \varepsilon \). For brevity, we write
 whenever \((q,\sigma ,q',{\varDelta }) \in \delta \)
whenever \((q,\sigma ,q',{\varDelta }) \in \delta \)
-
\(F \subseteq Q\) is the set of final states
A configuration is a tuple \(C=\langle q , w , [N_{1},\dots ,N_{r}] \rangle \) where q is the current state, \(w \in {\varSigma }^*\) is the word to be recognised and \([N_{1},\dots ,N_{r}]\) is an array of r m-registers with symbols in \({\varSigma }_d\). The configurations \(\langle q_{f} \in F, \varepsilon , [N_{1},\dots , N_{r}] \rangle \) are final.
The application of a transition is detailed by the following definition:
Definition 2
(Recognising step) Given an \({\text {FSNA}}_{\pm }\ R\), a step \(\langle q , w , [N_{1},\dots ,N_{r}] \rangle \rightarrow \langle q' , w' , [N_{1}',\dots ,N_{r}'] \rangle \) occurs if and only if there exists a transition  such that both conditions hold:
such that both conditions hold:
-
1.
\({\left\{ \begin{array}{ll} \sigma = \varepsilon &{}\Rightarrow w = w' \quad \text { and} \\ \sigma = i &{}\Rightarrow w = \text {s-top}(N_{i})w' \quad \text { and}\\ \sigma \in {\varSigma }_{s} &{}\Rightarrow w = \sigma w' \end{array}\right. }\)
-
2.
\( {\left\{ \begin{array}{ll} {\varDelta } \!=\! i+ &{}\Rightarrow \exists b \!\in \! {\varSigma }_d. N_{i}'\! =\! \text {s-push}(b,N_{i}) \wedge \forall j . b \notin \Vert {N_{j}} \Vert \wedge \forall j \ (j \ne i). N_{j} = N_{j}' \text { and} \\ {\varDelta } = i- &{}\Rightarrow N_{i}' = \text {s-pop}(N_{i}) \quad \wedge \quad \forall j \ (j \ne i). N_{j} = N_{j}' \quad \text { and} \\ {\varDelta } = \varepsilon &{}\Rightarrow \forall j . N_{j} = N_{j}' \end{array}\right. } \)
Finally, the language accepted by an FSNA\(_{\pm }\) R, which we call (nominal) regular, is
where \(\rightarrow ^*\) denotes the reflexive and transitive closure of the \(\rightarrow \) relation.
A couple of examples follow.
Example 1
The \({\text {FSNA}}_{\pm }\ R_{1}\) in Fig. 2 recognises \({\varSigma }^{*}\). The run \(\rho _1\) recognises the word aax, where x can be any symbol in \({\varSigma }\), even a itself, because the m-registers are empty when a fresh symbol is required by the edge labeled \(1+\).
By removing the edge  from \(R_1\) we obtain the automaton \(R_2\) in Fig. 2. Without that deletion edge, there is no way to forget a symbol from the m-registers. Hence all the issued symbols are recorded in the m-registers stack, and when a new symbol is s-pushed it must be fresh with respect to all of them. The language accepted by the \({\text {FSNA}}_{\pm }\ R_{2}\) is \(L_0=\{w \in {\varSigma }_d^{*} \mid \forall i,j\, (i \ne j).\, w[i]\ne w[j]\}\). The run \(\rho _2\) recognises the string abc.
from \(R_1\) we obtain the automaton \(R_2\) in Fig. 2. Without that deletion edge, there is no way to forget a symbol from the m-registers. Hence all the issued symbols are recorded in the m-registers stack, and when a new symbol is s-pushed it must be fresh with respect to all of them. The language accepted by the \({\text {FSNA}}_{\pm }\ R_{2}\) is \(L_0=\{w \in {\varSigma }_d^{*} \mid \forall i,j\, (i \ne j).\, w[i]\ne w[j]\}\). The run \(\rho _2\) recognises the string abc.
The next example considers traces of data-words [38]. A data-word is a finite sequence of positions each having a label which either represents an action and is taken from a finite alphabet, or data and is taken from an infinite alphabet. We feel free to use data-words to ease the development of our examples, indeed only minor variations of our automata definitions are required to handle a finite number of actions acting on both static and dynamic resources.
Example 2
Consider again the first example in the introduction showing the recursive function updateFiles. In the abstraction of a run, we actually considered traces in the form of data-words, where the actions new and rel operate on files. The \({\text {FSNA}}_{\pm }\ R_{3}\) in Fig. 2 accepts the unwanted traces where the resource that was picked second-last (new(1)) is released (rel(1)) before the release of the resource that was picked last (new(2)). Note that the (data-word) symbols \(\sigma \) assume the form \(\texttt {new(u)}, \texttt {rel(u)}, u \in \underline{\mathtt {2}} \cup {\varSigma }_s\).
Note that the constraint on \(\text {s-pop}{}\) to deactivate the affected m-register limits the expressiveness of FSNA\(_{\pm }\). Indeed, by relaxing that condition, we would be able to count on each m-register, by performing a new transition to increment, a delete to decrement and using the active/inactive status of m-registers to discern whether it is zero or not. These mechanisms are very similar to the ones of r-counter machines [35].
Three examples of \({\text {FSNA}}_{\pm }\ R_i\) and of their runs \(\rho _i\). The automaton \(R_{1}\) accepts \({\varSigma }^{*}\); note that the dynamic symbol x can be any symbol in \({\varSigma }_d\), even a, because the m-register is empty when x is s-pushed and there is no restriction on its freshness. The automaton \(R_{2}\) accepts \(L_{0}\) in Example 1; and \(R_{3}\) accepts strings \(\mathtt {new}(a)\mathtt {new}(b)\mathtt {rel}(a)\) (\(a \ne b\))
We introduce now a sub-class of \({\text {FSNA}}_{\pm }\) where no delete transitions are allowed, as it is the case for the automaton \(R_2\) in Fig. 2. As expected, this restriction reduces the expressiveness of FSNA\(_{\pm }\), e.g. none of this restricted automata can accept \({\varSigma }^{*}\).
Definition 3
(\({\text {FSNA}}_{+}\)) An \({\text {FSNA}}_{+}\) is a \({\text {FSNA}}_{\pm }\) with no delete transition  .
.
In the statement below \({\mathcal {L}}({\text {FSNA}}_{+}),{\mathcal {L}}({\text {FSNA}}_{\pm })\) denote the classes of language of \({\text {FSNA}}_{+},{\text {FSNA}}_{\pm }\), respectively.
Property 1
\({\mathcal {L}}({\text {FSNA}}_{+}) \subsetneq {\mathcal {L}}({\text {FSNA}}_{\pm })\)
Proof
By contradiction, assume there exists a \({\text {FSNA}}_{+}\) with r m-registers that accepts \({\varSigma }^*\). Consider a string of the form ww with \(|w| = |\Vert {w} \Vert | = r+1\) and let \(b \in \Vert {w} \Vert \) be such that \(b \ne \text {s-top}(N_i)\) after w has been scanned; note that such a b always exists. However, ww can not be accepted because b still occurs in one of the r m-registers and thus can not be s-pushed again. \(\square \)
We present now a variation of the \({\text {FSNA}}_{+}\)s which can update more than one m-register in a single transition. This variation will be useful in the proof of Theorem 6, as expected, this parallelization does not extend the expressiveness of the \({\text {FSNA}}_{\pm }\). For simplicity, we permit below to update two m-registers only, the extension to any finite number being straightforward.
Definition 4
(Finite Nominal Automata 2) A finite state nominal automaton 2 (\({\text {FSNA}}_{+}\)2) is a tuple \(R=\langle Q, q_{0},{\varSigma }, \delta 2 , r, F \rangle \) where:
-
\(Q, q_{0}, {\varSigma }, r \text { and } F\) are as in Definition 1
-
\(\delta 2\) is the transition relation: \((q,\sigma , q',\left( {\varDelta }_{1},{\varDelta }_{2}) \right) \in \delta 2\) with \(q,q' \in Q, \sigma \in {\varSigma }_s \cup \underline{\mathtt {r}} \cup \{\varepsilon \}, {\varDelta }_1,{\varDelta }_2 \in \{i+ \mid i \in \underline{\mathtt {r}}\} \cup \{\varepsilon \}\), such that \(\forall i \in \underline{\mathtt {r}}.\, ({\varDelta }_1,{\varDelta }_2 \ne i-)\) and \(({\varDelta }_{1} = {\varDelta }_{2} \Rightarrow {\varDelta }_{1} = {\varDelta }_{2} = \varepsilon )\)
Definition 5
(Recognising step)
A step \(\langle q , w , [N_{1},\dots ,N_{r}]\rangle \rightarrow \langle q' , w' , [N_{1}',\dots ,N_{r}'] \rangle \) occurs iff there exists  such that
such that
-
1.
As in Definition 2
-
2.
\({\left\{ \begin{array}{ll} \forall j \in \mathtt {{\underline{r}}}\ (j \ne {\varDelta }_{1},{\varDelta }_{2}).\,N_{j} = N_{j}' \text { and}\\ {\varDelta }_{1} = i+ \Rightarrow \exists b_1 \in {\varSigma }_d . N_{i}' = \text {s-push}(b_{1},N_{i}) \quad \wedge \quad \forall j \in \mathtt {{\underline{r}}}.\, b_{1} \notin \Vert {N_{j}} \Vert \\ \quad \qquad \wedge \quad b_{1} \ne \text {s-top}(N_{i}) \quad \text { and}\\ {\varDelta }_{2} = i+ \Rightarrow \exists b_2 \in {\varSigma }_d . N_{i}' = \text {s-push}(b_{2},N_{i}) \quad \\ \qquad \quad \wedge \quad \forall j \in \mathtt {{\underline{r}}}.\, b_{2} \notin \Vert {N_{j}} \Vert \quad \wedge \quad b_{2} \ne \text {s-top}(N_{i}) \end{array}\right. } \)
As anticipated, the \({\text {FSNA}}_{+}\)2 have the same expressive power of \({\text {FSNA}}_{+}\).
Theorem 1
Given a \({\text {FSNA}}_{+}\)2 A there exists an \({\text {FSNA}}_{+}\ A'\) accepting the same language.
Proof
Let \(A=\langle Q,q_{0},{\varSigma },\delta 2,r,F\rangle \) and define \(A'=\langle Q \cup Q' ,q_{0},{\varSigma },\delta ,r,F\rangle \) where \(Q'\) is a set of fresh states \(q_p\), one for each transition \(p \in \delta 2\) and \(\delta \) is such that  we have that
we have that  . It is now immediate proving the equality of the accepted languages. \(\square \)
. It is now immediate proving the equality of the accepted languages. \(\square \)
3 Properties of the \({\text {FSNA}}_{\pm }{}\)
This section studies some language theoretical properties of the two classes of automata \({\text {FSNA}}_{\pm }\) and \({\text {FSNA}}_{+}\) introduced so far. The following property is immediate:
Property 2
Increasing the number of m-registers increases the expressive power of FSNA\(_{\pm }\).
Any finite number of m-registers is not sufficient for breaking the barrier between regular and context-free languages, because m-registers are not full-fledged stacks: they become inactive after an s-pop and empty registers can not be distinguished from inactive ones. This is shown by the following “classical” example, showing a Dyck-like language that is not regular.
Example 3
Let \(L_r=\{ww^R \in {\varSigma }_{d}^{*} \mid \left| w \right| = r \text { and } \forall i,j \, (i \ne j).\, w[i]\ne w[j] \}\) then no \({\text {FSNA}}_{\pm }\ R\) with less that r states and r m-registers accepts \(L_r\). Indeed, a standard argument on FSA proves that r states are required. Assume now that R has less than r registers \(N_i\) and accepts \(ww^R\). By the pigeonhole principle, there is at least a symbol of w, say a, such that \(\forall i . a \ne \text {s-top}(N_i)\) when w has been read. Since \(a \in \Vert {w} \Vert \), a needs to be s-pushed while traversing \(w^R\), but it is fresh so it can be replaced by any other (fresh) different symbol, which makes R to accept also \(ww'^R\), where \(w'^R \ne w^R\): contradiction.
We establish now a few closure properties w.r.t. standard language operations: union (\(\cup \)), intersection (\(\cap \)), complementation (\(\overline{\phantom {x}.\phantom {x}}\)), concatenation (\(\cdot \)) and Kleene star (\(*\)). To simplify and structure the proofs of these properties we need some auxiliary technical definitions.
In order to support the definition of the intersection automaton R, we will use the standard construction, that builds the product of two automata \(R_1\) and \(R_2\). As usual, a state of R is a pair of states of \(R_1\) and \(R_2\), but it has an additional component: the merge function defined below, that describes how the m-registers of the two automata to intersect are mapped into those of the intersection automaton. Given that Definition 6-8 aim to support the proof of the closure by intersection of \({\text {FSNA}}_{+}\) (and later \({\text {PDNA}}_{+}\)), we assume all the mentioned m-registers to be active.
Definition 6
(Merge function) Let \(m: \{1,2\} \times \underline{\mathtt {r}} \rightarrow \underline{\mathtt {2r}}\) be a function. Stipulating \(m_{1}(x)=m(1,x),m_{2}(x)=m(2,x)\), m is a merge iff \(m_{1}\) and \(m_{2}\) are injective.
The m-registers i, j are merged by m, in symbols  , when \(m_{1}(i)=m_{2}(j)\), we write
, when \(m_{1}(i)=m_{2}(j)\), we write  when they are not merged or, by abuse of notation, whenever \(i=\varepsilon \) or \(j=\varepsilon \).
when they are not merged or, by abuse of notation, whenever \(i=\varepsilon \) or \(j=\varepsilon \).
We stipulate that m extends to a relation between active m-registers such that
and \(\forall i,j \in \underline{\mathtt {r}}\)
-
1.
\(\text {s-top}(N_{i}^{1})=\text {s-top}(M_{m_{1}(i)})\) and \(\text {s-top}(N_{i}^{2})=\text {s-top}(M_{m_{2}(i)})\)
-
2.

-
3.
\(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{1}} \Vert \cup \bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{2}} \Vert = \bigcup _{i \in \mathtt {{\underline{2r}}}} \Vert {M_{i}} \Vert \)
The \(m_1\) (resp. \(m_2\)) component of m associates the state of the m-registers of the \(R_1\) automaton (resp. \(R_2\)) with the ones of R. As we will show afterwards, the extension of the merge to a relation between m-registers can be used to develop an invariant between the states of the m-registers of \(R_1,R_2\) and the states of the m-registers of R along a recognising run of a word w.
Definition 7
(Effective Update) Given two merge functions \(m,m'\), the effective update
 of \({\varDelta }_{1},{\varDelta }_{2} \in \{i+ \mid i \in \underline{\mathtt {r}}\} \cup \{\varepsilon \}\) is the pair \((\overline{{\varDelta }_{1}},\overline{{\varDelta }_{2}})\) where:
of \({\varDelta }_{1},{\varDelta }_{2} \in \{i+ \mid i \in \underline{\mathtt {r}}\} \cup \{\varepsilon \}\) is the pair \((\overline{{\varDelta }_{1}},\overline{{\varDelta }_{2}})\) where:
if  then \(\overline{{\varDelta }_{1}}=m'_{1}({\varDelta }_{1})\) and \(\overline{{\varDelta }_{2}}=\varepsilon \);
then \(\overline{{\varDelta }_{1}}=m'_{1}({\varDelta }_{1})\) and \(\overline{{\varDelta }_{2}}=\varepsilon \);
if  then
then
-
\(\overline{{\varDelta }_{1}}\) is such that:
- –:
-
if \({\varDelta }_{1}=\varepsilon \) then \(\overline{{\varDelta }_{1}}=\varepsilon \) else if \(m_1({\varDelta }_{1})\ne m_1'({\varDelta }_{1}) \) then \(\overline{{\varDelta }_{1}} = \varepsilon \) else \(\overline{{\varDelta }_{1}}=m'_{1}({\varDelta }_{1})\)
-
\(\overline{{\varDelta }_{2}}\) is such that:
- –:
-
if \({\varDelta }_{2}=\varepsilon \) then \(\overline{{\varDelta }_{2}}=\varepsilon \) else if \(m_2({\varDelta }_{2})\ne m_2'({\varDelta }_{2}) \) then \(\overline{{\varDelta }_{2}} = \varepsilon \) else \(\overline{{\varDelta }_{2}}=m'_{2}({\varDelta }_{2})\)
Definition 8
(Evolution) Given a merge m we say that a merge \(m'\) is an evolution of m with respect to \({\varDelta }_{1},{\varDelta }_{2}\), in symbols  , iff
, iff
-
1.
\(\forall i \in \{1,2\}, j \in \underline{\mathtt {r}}\ (j \ne {\varDelta }_{1},{\varDelta }_{2}).\;m_{i}(j) = m_{i}'(j)\)
-
2.
if
 then
then 
-
3.
if
 then
then 
To intuitively illustrate the definitions above, in Fig. 3 we show a portion of the automaton \(R=R_1 \cap R_2\) recognising the intersection of the two \({\text {FSNA}}_{+}\ R_1\) and \(R_2\).
The intersection automaton R is obtained by the standard construction that builds the new states as the product of the old ones. Additionally, each pair \(\langle q^1, q^2 \rangle \) (\(q^1,q^2 \in R_1,R_2\) resp.) is enriched with a merge function m. The m describes how the m-registers of the two automata are mapped into those of R
The idea underlying m is to guarantee the following invariant \({\mathcal {I}}\) along the runs: if \(R_1\) and \(R_2\) are in configurations \(\langle q_{0}^1, w, [\fbox {y}]\rangle \) and \(\langle q_{0}^2, w, [\fbox {x}]\rangle \) then (i) R will be in configuration \(\langle \langle q_{0}^1,q_{0}^2,m \rangle , w, [\fbox {h},\fbox {z}] \rangle \) and (ii) if two m-registers have the same s-tops then they are merged by m (and vice versa). This is illustrated in the left-most configurations of Fig. 4: if \(x=y=a\) then m maps the two registers to one register of R (here the second one), and \(z=a\). The edges of the automaton are also defined in the standard way. However, the m-register mentioned in \(\sigma \) of R is the one merged by m, provided that \(R_1\) and \(R_2\) agree on \(\sigma \). Also the updates \(({\overline{{\varDelta }}},\overline{{\varDelta }'})\) in R are determined by the updates \({\varDelta }_1\) of \(R_1\) and \({\varDelta }_2\) of \(R_2\) under the merge m, and form an effective update (see Definition 7).
Consider again Fig. 3. The transition  is present because there are
is present because there are  and
and  and m maps the first m-register of \(R_1\) and that of \(R_2\) to the second of R. Instead, the state \(\langle \langle q_{0}^1,q_{0}^2 \rangle , m' \rangle \) (omitted in the figure) has no outgoing edges, because the symbols read by \(R_1\) and \(R_2\) are kept apart by \(m'\).
and m maps the first m-register of \(R_1\) and that of \(R_2\) to the second of R. Instead, the state \(\langle \langle q_{0}^1,q_{0}^2 \rangle , m' \rangle \) (omitted in the figure) has no outgoing edges, because the symbols read by \(R_1\) and \(R_2\) are kept apart by \(m'\).
There are transitions that only differ for the merge function in their target state. Not all the possible merges respect however the invariant \({\mathcal {I}}\) mentioned above. Indeed, we only keep those that are evolution (in the sense of Definition 8) of the merge in the source state, according to the updates \({\varDelta }_1,{\varDelta }_2\) of \(R_1,R_2\) respectively. For example, the transition  permits the recognising step
permits the recognising step  , where the m-register of \(R_1\) now has got a d, while that of \(R_2\) has got c, and \(m'\) keeps them apart.
, where the m-register of \(R_1\) now has got a d, while that of \(R_2\) has got c, and \(m'\) keeps them apart.
Instead, if both m-registers store the same dynamic symbol c, the merge is still m, and the transition t above enables the step  and guarantees the invariant.
and guarantees the invariant.
We are now ready to state and prove some closure properties of \({\text {FSNA}}_{\pm }\) and \({\text {FSNA}}_{+}\):
Theorem 2
(Closure properties)
\(\cup \) | \(\cap \) |
|
| \(*\) | ||
|---|---|---|---|---|---|---|
\({\mathcal {L}}({\text {FSNA}}_{\pm })\) | \(\checkmark \) | \(\times \) | \(\times \) | \(\checkmark \) | \(\checkmark \) | |
\({\mathcal {L}}({\text {FSNA}}_{+})\) | \(\checkmark \) | \(\checkmark \) | \(\times \) | \(\times \) | \(\times \) |
Proof
Union: it suffices a new initial state with two outgoing \(\varepsilon \)-transition to the old initial states.
Concatenation (and Kleene star) for \({\text {FSNA}}_{\pm }\): a sequence of transitions from the final states of the first \({\text {FSNA}}_{\pm }\) make inactive all the m-registers, leading to a state, call it \(q^r\), having loops that can empty them all (see Fig. 5a; note that the m-registers may not be emptied in the state \(q^r\)). Then an \(\varepsilon \)-transition goes from \(q^r\) to the initial state of the second automaton.
Complement of \({\text {FSNA}}_{\pm }\): Consider \(L=\{w \mid \exists a \in {\varSigma }_d, n \in {\mathbb {N}} . a \hbox { appears } 2n+1\hbox { times in }w \}\) that is recognised by the \({\text {FSNA}}_{\pm }\) in Fig. 5b. Assume that its complement \({\overline{L}}=\{ w \mid \forall a \in {\varSigma }_d.\ \exists n \in {\mathbb {N}}.\ a\hbox { appears }2n\hbox { times in }w\}\) is recognised by an automaton R with r m-registers. This automaton also accepts ww, where \(w=a_{1},\dots ,a_{r+1}, \forall i,j \, (i \ne j) .a_{i} \ne a_{j}\). However, after recognising w, there exists some \(a_{i}\) that is not s-top of any m-register. The word \(ww'\) where \(w'\) is obtained by w by replacing \(a_{i}\) with a fresh symbol b is accepted by R, as well: contradiction because \(L \ni ww' \notin {\overline{L}}\).
Complement for \({\text {FSNA}}_{+}\): Property 1 (\({\varSigma }^*\) is the complement of \(\emptyset \)) suffices.
Concatenation (and Kleene star) for \({\text {FSNA}}_{+}{}\): Consider \(L=\{ww' \mid w \in L \text { and } w' \in L'\}\), with \(L,L'\) languages of two \({\text {FSNA}}_{+}\ R,R'\). If R accepts a string w such that \(a \in w,a \in w'\) but \(a \ne \text {s-top}(N_{i})\) for all the m-registers in the final configuration of all accepting runs, then we obtain a contradiction because a can not be s-pushed since not fresh.
Intersection of \({\text {FSNA}}_{\pm }\) Let \(L_1 = \{ a p^n q^m a\}\), with \(a \in {\varSigma }_d\) and p, q be chosen symbols in \({\varSigma }_s\). Clearly, \(L_1\) is regular. Consider the language recognised by the automaton in Fig. 6: \(L_2 = \{ a p^n q^m b \mid a \in {\varSigma }_d, a=b \Rightarrow m > n \}\). Now, the language \(L_1 \cap L_2 = \{a p^n q^m a \mid m > n \}\) can not be recognised by any \({\text {FSNA}}_{\pm }\).
Intersection of \({\text {FSNA}}_{+}\) We formalise here the intuitive construction given in Fig. 3, the proof uses Definition 9 and Lemmas 1 and 2 given below. Given two automata \(R_1\) and \(R_2\), we construct the intersection automaton \(R_1 \cap R_2\) recognising \({\mathcal {L}}(R_1) \cap {\mathcal {L}}(R_2)\).
The proof of the equivalence \({\mathcal {L}}(R_1 \cap R_2) = {\mathcal {L}}(R_1) \cap {\mathcal {L}}(R_2)\) can be obtained by induction on the length of the runs by using Lemmas 1 and 2. Without loss of generality, we consider the simplifying assumption that all the registers are active in the initial configuration. Indeed all the m-registers can be initialised by initial \(\varepsilon \)-transitions, without modifying the recognised language.
a The concatenation automaton of two automata \(R_1\) and \(R_2\) has the states and the transition of both of them, as initial state the one of \(R_1\), as final states the ones of \(R_2\). The final states of \(R_1\) are connected to \(q^{r}\), \(q^{r}\) is connected to the initial state of \(R_2\). The self-loops in \(q^r\) are used to empty the r m-registers. b An automaton recognising \(L=\{w \mid \exists a . w[i]=a \text { and }a\hbox { appears }2n+1\hbox { times in }w\}\)
Definition 9
(Intersection Automaton) The intersection automaton of two \({\text {FSNA}}_{+}\)s \(R_{1}=\langle Q_{1},q_{0}^{1},{\varSigma },\delta _{1},r,F_{1}\rangle \) and \(R_{2}=\langle Q_{2},q_{0}^{2},{\varSigma },\delta _{2},r,F_{2}\rangle \) is the following \({\text {FSNA}}_{+}\)2:
-
\({\overline{Q}} = Q_{1} \times M \times Q_{2}\) where M is a set of merge functions for m-registers
-
\(\overline{q_{0}}=\langle q_{0}^{1},m^{*},q_{0}^{2}\rangle \), with \(m^{*}\) s.t. \(m^{*}_{1},m^{*}_{2}\) are the identity functions (i.e. the r registers of the two intersecting automata are merged onto the first r registers of \(R_1 \cap R_2\))
-
\({\overline{F}} = \{\langle q_{1},m,q_{2}\rangle \mid q_{1} \in F_{1}, q_{2} \in F_{2}, m \in M\}\)
-
 iff
iff  and
and 
- or:
-
 and
and - –:
-
\({\overline{\sigma }} = \varepsilon \) and
- –:
-
\(q_{2}'=q_{2}\) and
- –:
-

- or:
-
 symmetric to the previous case.
symmetric to the previous case.
Now we prove the two lemmata used before for proving that \(R_{1} \cap R_{2}\) accepts \(L(R_{1}) \cap L(R_{2})\). Intuitively, the first states that whenever two automata \(R_1,R_2\) make a step with the same label, also the automaton \(R_1 \cap R_2\) can perform the very same step.
Lemma 1
Let \(R_{1}\) and \(R_{2}\) be two \({\text {FSNA}}_{+}\), let \(a \ne \varepsilon \) and
\(\text {step}_{1}: \langle q_{1}, aw ,[N_{1}^{1},\dots ,N_{r}^{1}]\rangle \longrightarrow \langle q_{1}' , w, [N_{1}^{'1}, \dots , N_{r}^{'1}] \rangle \) and
\(\text {step}_{2}: \langle q_{2}, aw, [N_{1}^{2},\dots ,N_{r}^{2}]\rangle \longrightarrow \langle q_{2}' ,w, [N_{1}^{'2}, \dots , N_{r}^{'2}] \rangle \) be steps of \(R_1\) and \(R_2\), respectively.
Then for any merge m and \([M_{1}\dots ,M_{2r}]\) m-registers of \(R_{1} \cap R_{2}\) such that
there exists the step of \(R_{1} \cap R_{2}\)
\(\overline{\text {step}}:\,\langle \langle q_{1}, m , q_{2} \rangle , aw, [M_{1},\dots ,M_{2r}] \rangle \longrightarrow \langle \langle q_{1}', m' , q_{2}' \rangle , w,[M_{1}',\dots ,M_{2r}'] \rangle \) with
Proof
Assume that  and
and  justify step\(_1\) and step\(_2\). Then we have the following cases, depending on the labels of these transition.
justify step\(_1\) and step\(_2\). Then we have the following cases, depending on the labels of these transition.
-
\(\sigma _{1},\sigma _{2} \in \mathtt {{\underline{r}}}\) Define \(m'\) such that \(\forall i,j \in \underline{\mathtt {r}}\, ( i \ne {\varDelta }_1, j \ne {\varDelta }_2).\, m_{1}'(i)=m_{1}(i),m_{2}'(j)=m_{2}(j)\). If \(\text {s-top}(N_{{\varDelta }_{1}}^{'1})=\text {s-top}(N_{{\varDelta }_{2}}^{'2})\) \(({\varDelta }_{1},{\varDelta }_{2} \ne \varepsilon )\)
-
if
 then let \(m_{1}'({\varDelta }_{1})=m_{2}({\varDelta }_{2})\) and \(m_{2}'({\varDelta }_{2})=m_{2}({\varDelta }_{2})\).
then let \(m_{1}'({\varDelta }_{1})=m_{2}({\varDelta }_{2})\) and \(m_{2}'({\varDelta }_{2})=m_{2}({\varDelta }_{2})\). -
Otherwise if
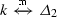 or
or  then let \(m_{1}'({\varDelta }_{1})=m_{2}'({\varDelta }_{2})=h \notin \text {Img}(m)\).
then let \(m_{1}'({\varDelta }_{1})=m_{2}'({\varDelta }_{2})=h \notin \text {Img}(m)\).
If
 but
but-
\(m_{1}'({\varDelta }_{1})\) (resp. \(m_{2}'({\varDelta }_{2})\)) is such that \(\text {s-top}(N_{{\varDelta }_{1}}^{'1})=\text {s-top}(N_{k}^{'2}),{\varDelta }_{1} \ne \varepsilon \) for some \(k\ne {\varDelta }_{2}\) then let \(m_{1}'({\varDelta }_{1})=m_{2}(k)\).
-
Otherwise,
-
if
 for some \(k \ne {\varDelta }_{2}\), then let \(m_{1}'({\varDelta }_{1})= h \notin \text {Img}(m)\).
for some \(k \ne {\varDelta }_{2}\), then let \(m_{1}'({\varDelta }_{1})= h \notin \text {Img}(m)\). -
Otherwise, if
 for all \(k \ne {\varDelta }_{2}\) then let \(m_{1}'({\varDelta }_{1}) \in \{h\} \cup m({\varDelta }_{1})\), with \(h \notin \text {Img}(m)\).
for all \(k \ne {\varDelta }_{2}\) then let \(m_{1}'({\varDelta }_{1}) \in \{h\} \cup m({\varDelta }_{1})\), with \(h \notin \text {Img}(m)\).
-
Recall that m is a merge and note that \(m, m'\) may possibly differ in \({\varDelta }_{1},{\varDelta }_{2}\). Now we show that also \(m'\) is a merge, by showing its projections are injective. By contradiction, assume \(m'\) is not injective, then if \(m'({\varDelta }_{1})\ne m({\varDelta }_{1})\) (resp. for \({\varDelta }_{2}\)), by construction, it is only the case that \(m_{1}'({\varDelta }_{1})=m_{2}'(k)\) for some k. If \(k={\varDelta }_{2}\) then \(m_{1}'({\varDelta }_{1})=m_{2}'(k) \notin \text {Img}(m)\), contradiction because \(m_{1}',m_{2}'\) are injective since there is no k s.t. \(m_{1}'(k)=m_{1}'({\varDelta }_{1})\) or \(m_{2}'(k)=m_{2}'({\varDelta }_{2})\). If \(k\ne {\varDelta }_{2}\) then we have that only \(m_{2}'\) can be non-injective, but this requires \(m_{2}'({\varDelta }_{2}) = m_{2}'(k), k \ne {\varDelta }_{2}\) but this is not possible by construction.
We show that
 : condition (1) is trivially satisfied by construction, conditions (2–3) are taken explicitly into account in the construction.
: condition (1) is trivially satisfied by construction, conditions (2–3) are taken explicitly into account in the construction.Since \(\text {step}_{1}\) and \(\text {step}_{2}\) fulfil the hypothesis, by condition 1.2 of Definition 2, it turns out that both \(N^{1}_{\sigma _{1}},N^{2}_{\sigma _{2}}\) are active and \(a=\text {s-top}(N^{1}_{\sigma _{1}})=\text {s-top}(N^{2}_{\sigma _{2}})\). This last fact implies that \(m_{1}(\sigma )=m_{2}(\sigma )\) since m is merge. By letting \({\overline{\sigma }}=m_{1}(\sigma )\), conditions (1) and (2) imply that \(\text {s-top}(M_{{\overline{\sigma }}})=a\).
By construction of \(A_{1} \cap A_{2}\) we then have the transition

where
 .
.Next we shall prove that \(m'\) is a merge of m-registers through which \([M_{1}',\dots ,M_{2r}']\) can be obtained from \([M_{1}, \dots , M_{2r}]\) and \(\overline{\text {step}}\) is justified by \({\overline{t}}\).
First, \(\forall i \in \underline{\mathtt {r}} (i\ne \overline{{\varDelta }_{1}}, \overline{{\varDelta }_{2}}). M_{i}=M_{i}'\). If \(\overline{{\varDelta }_{1}} \ne \varepsilon \wedge m({\varDelta }_{1})=m'({\varDelta }_{1})\) then let \(M_{\overline{{\varDelta }_{1}}}'=\text {s-push}(b_1,M_{\overline{{\varDelta }_{1}}})\) with \(b_{1}=\text {s-top}(N_{{\varDelta }_{1}}^{'1})\) otherwise let \(M_{\overline{{\varDelta }_{1}}}' = M_{\overline{{\varDelta }_{1}}}\). Symmetrically for \(M_{\overline{{\varDelta }_{2}}}'\) (note that \(\overline{{\varDelta }_{1}}\ne \overline{{\varDelta }_{2}}\)).
We prove now that \(m'([N_{1}^{'1},\dots ,N_{r}^{'1},N_{1}^{'2},\dots ,N_{r}^{'2}])=[M_{1}'\dots ,M_{2r}']\). The conditions (1) and (2) are satisfied because for all \(i,j \in \underline{\mathtt {r}}\) s.t. \(i \ne {\varDelta }_{1},j \ne {\varDelta }_{2}\) we have \(m_{1}'(i)=m_{1}(i), m_{2}'(j)=m_{2}(j)\), the involved m-register are left untouched and m is a merge of m-registers. By construction of \(M_{m'({\varDelta }_{1})}'\) (resp. \(M_{m'({\varDelta }_{2})}'\)) we also have that \(\text {s-top}(M_{m'({\varDelta }_{1})}')=\text {s-top}(N_{{\varDelta }_{1}}')\). The condition (3) is implied by the construction of \(m'\), condition (4) holds because \(b_{1},b_{2}\) are in \(\bigcup _{i \in \mathtt {{\underline{2r}}}} \Vert {M_{i}'} \Vert \) only if they are in \(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{'1}} \Vert \) or \(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{'2}} \Vert \) respectively.
We now show that the condition 2 of Definition 5 is satisfied. With the construction above \(\bigcup _{i \in \mathtt {{\underline{2r}}}} \Vert {M_{i}} \Vert =\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {M_{i}'} \Vert {\setminus } \{b_{1},b_{2}\}\). Since \(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{1}} \Vert \cup \bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{2}} \Vert = \bigcup _{i \in \mathtt {{\underline{2r}}}} \Vert {M_{i}} \Vert \), if \(b_{1} \in \bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{2}} \Vert \) then \( b_{1} \in \bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {M_{i}} \Vert \), otherwise, by condition 2 of Definition 2 for \(\text {step}_{1}\), \(b_{1} \notin \bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{1}} \Vert \). This holds symmetrically for \(b_{2}\). Then if \(b_{1},b_{2}\) are pushed on top of \(M_{\overline{{\varDelta }_{1}}},M_{\overline{{\varDelta }_{2}}}\) then they are fresh, i.e. \(b_{1},b_{2} \notin \bigcup _{i \in \mathtt {{\underline{r}}}}\Vert {M_{i}} \Vert \). Also, when both are pushed on top of \(M_{\overline{{\varDelta }_{1}}},M_{\overline{{\varDelta }_{2}}}\) we have \(b_{1} \ne b_{2}\), so satisfying condition 2 of Definition 5.
Since a satisfies condition 1 of Definition 5 for \({\overline{t}}\), the following step exists:

-
-
if \(\sigma _{1},\sigma _{2}\in {\varSigma }_{s}\), the proof is analogous to that of the previous case: take \(m'\) as above, then by construction of \(R_{1} \cap R_{2}\) we have the following transition, where \({\overline{\sigma }}=\sigma _{1}=\sigma _{2}\)

With the same construction of \([M_{1}',\dots ,M_{r}']\) above, we obtain
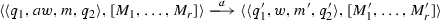
-
\(\sigma _{1}=\varepsilon \) or \(\sigma _{2}=\varepsilon \), trivial. \(\square \)
The following lemma states that whenever the automaton \(R_1 \cap R_2\) makes a step, also the automata \(R_1\) and \(R_2\) can perform the very same step.
Lemma 2
Let \(R_{1}\) and \(R_{2}\) be two \({\text {FSNA}}_{+}\), let \(a \ne \varepsilon \) and let \(\overline{\text {step}} : \langle \langle q_{1}, m , q_{2} \rangle , aw, [M_{1},\dots ,M_{2r}] \rangle \longrightarrow \langle \langle q_{1}', m' , q_{2}' \rangle , w,[M_{1}',\dots ,M_{2r}'] \rangle \) be a step of \(R_{1} \cap R_{2}\) then for any \([N_{1}^{1}\dots ,N_{r}^{1}],[N_{1}^{2}\dots ,N_{r}^{2}]\) such that
there exist two steps of \(R_{1}\) and \(R_{2}\)
\(\text {step}_{1} : \langle q_{1}, aw ,[N_{1}^{1},\dots ,N_{r}^{1}]\rangle \longrightarrow \langle q_{1}' , w, [N_{1}^{'1}, \dots , N_{r}^{'1}] \rangle \) and
\(\text {step}_{2} : \langle q_{2}, aw, [N_{1}^{2},\dots ,N_{r}^{2}]\rangle \longrightarrow \langle q_{2}' ,w, [N_{1}^{'2}, \dots , N_{r}^{'2}] \rangle \) and
Proof
Assume that  justifies \(\overline{\text {step}}\).
justifies \(\overline{\text {step}}\).
-
if \({\overline{\sigma }} \ne \varepsilon \) then by construction of \(R_{1} \cap R_{2}\) we have that
 and
and  . We only prove the case \({\overline{\sigma }} \in \mathtt {{\underline{r}}}\); the others follow from a similar argument.
. We only prove the case \({\overline{\sigma }} \in \mathtt {{\underline{r}}}\); the others follow from a similar argument. - –:
-
if \({\overline{\sigma }} \in \mathtt {{\underline{r}}}\): let \([N_{1}^{'1},\dots ,N_{r}^{'1}]\) (resp. \([N_{1}^{'2},\dots ,N_{r}^{'2}]\)) be such that \(\forall i \in \underline{\mathtt {r}} \,(m_{1}'(i) \ne \overline{{\varDelta }_{1}} \wedge m_{1}'(i)=m_{1}(i)) . N_{i}^{'1} = N_{i}^{1}\). If \({\varDelta }_{1} \ne \varepsilon \) then take
$$\begin{aligned} N_{{\varDelta }_{1}}^{'1} = \text {s-push}(\text {s-top}(M_{m_{1}'({\varDelta }_{1})}'),N_{{\varDelta }_{1}}^{1}) \end{aligned}$$Condition 1 of Definition 2 is satisfied for the transition \(t_{1}\) because \(\text {s-top}(M_{{\overline{\sigma }}}) = \text {s-top}(N_{\sigma _{1}})= a\) since \({\overline{\sigma }}=m_{1}(\sigma _{1})\) by construction and m is a merge of m-registers. We prove now condition 2 of Definition 2. For \(b = \text {s-top}(M_{m_{1}'({\varDelta }_{1})}')\) we consider the two cases: \(\overline{{\varDelta }_{1}} \ne \varepsilon \) and \(\overline{{\varDelta }_{1}}=\varepsilon \). In the first case the condition is guaranteed by the fact that \(b \not \in \bigcup _{j \in \underline{\mathtt {2r}}} \Vert {M_{j}} \Vert \), hence, since m is a merge of m-registers (condition 3) \(b \not \in \bigcup _{j \in \underline{\mathtt {r}}} \Vert {N_{j}^1} \Vert \). When \(\overline{{\varDelta }_{1}}=\varepsilon \) then we have \(m_1'({\varDelta }_1)\ne m_2'({\varDelta }_2)\), in this case \(m_1'({\varDelta }_1)\ne m_1({\varDelta }_1)\), by injectivity of \(m_1'\), by the fact that m is a merge of m-registers and by the fact that \(m_1'\) only differs from \(m_1\) in \({\varDelta }_1\) we have that \(\forall i \in \underline{\mathtt {r}} . \text {s-top}(M_{m_1'({\varDelta }_1)}) \ne \text {s-top}(N_{i}^1)\). For \(c = \text {s-top}(M_{m_{2}'({\varDelta }_{2})}')\). We consider two cases: \(\overline{{\varDelta }_{2}} \ne \varepsilon \) and \(\overline{{\varDelta }_{2}}=\varepsilon \). In the first case the condition is guaranteed by the fact that \(c \not \in \bigcup _{j \in \underline{\mathtt {2r}}} \Vert {M_{j}} \Vert \), hence, since m is a merge of m-registers (condition 3) \(c \not \in \bigcup _{j \in \underline{\mathtt {r}}} \Vert {N_{j}^2} \Vert \). When \(\overline{{\varDelta }_{2}}=\varepsilon \) then we have two cases: \(m_2'({\varDelta }_2)=m_1'({\varDelta }_1)=\overline{{\varDelta }_1}\) or \(m_2'({\varDelta }_2)\ne m_1'({\varDelta }_1)\). In the first case the condition is satisfied by the same reasoning above because \(c = \text {s-top}(M_{\overline{{\varDelta }_1}}')\), the second case is verified only when \(m_2'({\varDelta }_2)\ne m_2({\varDelta }_2)\), in this case, by injectivity of \(m_2'\), by the fact that m is a merge of m-registers and by the fact that \(m_2'\) only differs from \(m_2\) in \({\varDelta }_2\) we have that \(\forall i \in \underline{\mathtt {r}} . \text {s-top}(M_{m_2'({\varDelta }_2)}) \ne \text {s-top}(N_{i}^2)\). Hence all the conditions for \(t_1,t_2\) are satisfied, so both step\(_1\) and step\(_2\) exist. We are left to prove that \(m'([N_{1}^{'1},\dots ,N_{r}^{'1},N_{1}^{'2},\dots ,N_{r}^{'2}])=\) \([M_{1}'\dots ,M_{2r}']\). The conditions (1) and (2) are satisfied because for all \(i,j \in \underline{\mathtt {r}}\) s.t. \(i \ne {\varDelta }_{1},j \ne {\varDelta }_{2}\) we have \(m_{1}'(i)=m_{1}(i), m_{2}'(j)=m_{2}(j)\), the involved m-register are left untouched and m is a merge of m-registers. By construction of \(N_{{\varDelta }_{1}}'\) (resp. \(N_{{\varDelta }_{2}}'\)) we also have that \(\text {s-top}(M_{m'({\varDelta }_{1})}')=\text {s-top}(N_{{\varDelta }_{1}}')\). The condition (3) is implied by the construction of \(N_{{\varDelta }_{1}}'\) because (for some j) \(m_1'({\varDelta }_1)=m_2'(j)\) implies \(\text {s-top}(N_{{\varDelta }_{1}}^{'1})=\text {s-top}(M_{m'({\varDelta }_{1})}')=\text {s-top}(N_{j}^{'2})\), condition (4) holds because b, c are in \(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{'1}} \Vert \) or \(\bigcup _{i \in \mathtt {{\underline{r}}}} \Vert {N_{i}^{'2}} \Vert \) only if they are in \(\bigcup _{i \in \mathtt {{\underline{2r}}}} \Vert {M_{i}'} \Vert \) respectively. \(\square \)
Having proved both Lemmas 1 and 2, we conclude the proof of the whole theorem. \(\square \)
Note that the same argument used in the proof of the intersection between two \({\text {FSNA}}_{\pm }\) suffices to establish the following property.
Property 3
There exists languages \(L_1\) and \(L_2\), accepted by \({\text {FSNA}}_{\pm }\) and \({\text {FSNA}}_{+}\), respectively such that \(L_1 \cap L_2\) is not a regular nominal language.
We now study the decidability of some typical problems in automata theory, namely those of membership, universality and emptiness. Given an automaton R, the first and the second problems amount to check if a word w and \({\varSigma }^*\) are accepted by R; the third if \({\mathcal {L}}(R) = \emptyset \).
Theorem 3
-
1.
The membership problem for \({\text {FSNA}}_{\pm }\) is decidable
-
2.
The universality problem is undecidable for \({\text {FSNA}}_{\pm }\), while for \({\text {FSNA}}_{+}\) it is decidable, and the answer is always negative
-
3.
The emptiness problem is decidable for \({\text {FSNA}}_{\pm }\)
Proof
-
1.
A trivial linear non-deterministic procedure suffices.
-
2.
Theorem 4 proved in the next sub-section guarantees that \({\text {FSNA}}_{\pm }\) are more expressive than \({\text {FMA}}\). Now the statement follows because universality is undecidable for \({\text {FMA}}\) [39]. Since \({\text {FSNA}}_{+}\) can not generate \({\varSigma }^*\), the second claim is proved.
-
3.
The actual content of the m-registers is negligible when reasoning about emptiness, only their activation states are important because a step can be inhibited by an inactive m-register. So, we can abstract a configuration \(\langle q , w , [N_{1},\dots ,N_{r}]\rangle \) as a pair \(\langle q, [x_{1},\dots ,x_{r}]\rangle \), where \(x_i\) is the activation state of \(N_i\). Suppose now that there exist an accepting run for w. The problem is now reduced to verify the emptiness of a non-nominal finite state automaton. \(\square \)
4 Expressiveness of FSNA\(_{\pm }\)
In the literature there are many nominal languages, working on infinite alphabets or on data-words. We consider here only those that are intuitively regular, in that they can not express Dyck-like languages, e.g. the language \(\{ww^R\}\) when |w| is not bounded (see Example 3). An incomplete list of the regular languages in the literature includes variable finite automata (\({\text {VFA}}\)) [27], finite memory automata (\({\text {FMA}}\)) [29] and their extension with non-deterministic reassignment (NFMA) [30], Usage Automata (\({\text {UA}}\)) [7], fresh-register automata (FRA) [47] and their evolution history register automata (HRA) [48], class register automata (CRA) [14], Data Walking Automata (DWA) [33], the variant of HD-automata in [18] and the \({\texttt {fp-automata}}\) [31].
A notion similar to the one of the m-register can be found in HRA [48] and in the chronicles of the chronicle deallocating automata [32].
Table 2 recalls the closure properties of \({\text {FSNA}}_{\pm }\) and \({\text {FSNA}}_{+}\) and of those models above for which the literature provides these results.
The next theorem investigates the relationship among our models and the (regular) ones in the literature in terms of expressiveness. When considering data-words, we assume for simplicity that there is a single action \(\alpha \) on resources, that will be omitted in words, i.e. we write a instead of \(\alpha (a)\). We write  when two sets A, B are incomparable, i.e. \(A \nsubseteq B,B \nsubseteq A\).
when two sets A, B are incomparable, i.e. \(A \nsubseteq B,B \nsubseteq A\).
Theorem 4
(Expressiveness comparison)
-
1.
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {VFA}}) \supsetneq {\mathcal {L}}({\text {UA}}) \)
-
2.
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {FMA}})\)
-
3.
\({\mathcal {L}}({\text {FSNA}}_{+})\supsetneq {\mathcal {L}}({\text {UA}})\)
-
4.

-
5.

-
6.

-
7.

-
8.
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supseteq {\mathcal {L}}({\texttt {fp-automata}})\)
Proof
Sketch:
-
1.
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {VFA}}) \supsetneq {\mathcal {L}}({\text {UA}}) \) The \({\text {VFA}}\) have been proved more expressive than \({\text {UA}}\) in [19]. A \({\text {FSNA}}_{\pm }\) simulates a \({\text {VFA}}\) by using m-registers associated to each variable (and never s-popping them), the distinguished free variable y of VFA can be mapped to a m-register that is always s-popped after being used. The last condition matches the one of \({\text {VFA}}\) requiring the symbols associated to each occurrence of y in the witnessing pattern to be different from the other variables, but possibly equal to another symbol associated with y. The language \(L_{0}\) in the Example 1 belongs to \({\mathcal {L}}({\text {FSNA}}_{\pm })\) but not to \({\mathcal {L}}({\text {VFA}})\).
-
2.
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {FMA}})\) The main differences between the two models are the following. The registers of \({\text {FMA}}\) have an initial assignment, while \({\text {FSNA}}_{\pm }\) have static resources playing the same role (and initialisation can anyway be done by initial \(\varepsilon \)-transitions that \({\text {FMA}}\) have not). \({\text {FMA}}\) associate the reassignment function \(\rho \) with states rather than with edges; the same effects can be obtained by \({\text {FSNA}}_{\pm }\) when all the edges starting from a state q have the same \({\varDelta }\). Additionally, \(\rho \) reassigns a register using the input symbol, while \({\text {FSNA}}_{\pm }\) update an m-register (through an \(\varepsilon \)-transition) and then recognize the fresh symbol in it. In \({\text {FMA}}\), all the registers have to be different, and a reassignment may update a register with the same symbol it already contains; the \({\text {FSNA}}_{\pm }\) can simulate this behaviour using two edges with \({\varDelta } = i+\) and \({\varDelta }=\varepsilon \), accounting for the cases a new symbol is assigned or the same one is reassigned, respectively. So, \({\mathcal {L}}({\text {FSNA}}_{\pm }) \supseteq {\mathcal {L}}({\text {FMA}})\) and the language \(L_{0}\) in Example 1 shows that inclusion is strict.
-
3.
\({\mathcal {L}}({\text {FSNA}}_{+}) \supsetneq {\mathcal {L}}({\text {UA}}) \) The expressiveness of \({\text {UA}}\) is the same of \({\text {VFA}}\) without the y (see [34]), so the construction in item 1 suffices (note that there will be no delete transitions).
-
4.
 and 5.
and 5.  Consider \(L_0=\{w \in {\varSigma }_d^{*} \mid \forall i,j.\, w[i]\ne w[j]\}\) of Example 1. We have that \(L_{0} \in {\mathcal {L}}({\text {FSNA}}_{+})\) but \(L_{0} \notin {\mathcal {L}}({\text {VFA}}) \cup {\mathcal {L}}({\text {FMA}}) \). Also \({\varSigma }^{*} \in {\mathcal {L}}({\text {FMA}})\cap {\mathcal {L}}({\text {VFA}})\) but \({\varSigma }^{*} \notin {\mathcal {L}}({\text {FSNA}}_{+})\).
Consider \(L_0=\{w \in {\varSigma }_d^{*} \mid \forall i,j.\, w[i]\ne w[j]\}\) of Example 1. We have that \(L_{0} \in {\mathcal {L}}({\text {FSNA}}_{+})\) but \(L_{0} \notin {\mathcal {L}}({\text {VFA}}) \cup {\mathcal {L}}({\text {FMA}}) \). Also \({\varSigma }^{*} \in {\mathcal {L}}({\text {FMA}})\cap {\mathcal {L}}({\text {VFA}})\) but \({\varSigma }^{*} \notin {\mathcal {L}}({\text {FSNA}}_{+})\). -
5.
 Consider the language \(L=\{ a_0 b_0 \dots a_n b_n \mid \forall i,j.\, i \ne j \Rightarrow a_i \ne a_j , b_i \ne b_j \}\), L is not recognised by any FSNA\(_{\pm }\) but it is recognised by an HRA because of the capability of using multiple stories. On the other hand the language \(L' = \{ a_1 \dots a_n b_1 \dots b_n \mid \forall i,j.\, i \ne j \Rightarrow a_i \ne a_j \wedge b_i \ne b_j, n-i \ge j \Rightarrow b_i \ne a_j \}\) is in \({\mathcal {L}}({\text {FSNA}}_{\pm })\) but not in \({\mathcal {L}}({\text {HRA}})\). This is because m-registers are stacks while places are sets.
Consider the language \(L=\{ a_0 b_0 \dots a_n b_n \mid \forall i,j.\, i \ne j \Rightarrow a_i \ne a_j , b_i \ne b_j \}\), L is not recognised by any FSNA\(_{\pm }\) but it is recognised by an HRA because of the capability of using multiple stories. On the other hand the language \(L' = \{ a_1 \dots a_n b_1 \dots b_n \mid \forall i,j.\, i \ne j \Rightarrow a_i \ne a_j \wedge b_i \ne b_j, n-i \ge j \Rightarrow b_i \ne a_j \}\) is in \({\mathcal {L}}({\text {FSNA}}_{\pm })\) but not in \({\mathcal {L}}({\text {HRA}})\). This is because m-registers are stacks while places are sets. -
6.
 and \({\mathcal {L}}({\text {FSNA}}_{\pm }) \supseteq {\mathcal {L}}({\texttt {fp-automata}})\) Both \({\text {FSNA}}_{\pm },{\text {FSNA}}_{+}\) recognise the language \(\{a_1\dots a_n \mid i\ne j \Rightarrow a_i \ne a_j \}\), that instead is not by any \({\texttt {fp-automata}}\). However \({\text {FSNA}}_{+}\) can not recognise \({\varSigma }^*\), a language in \({\mathcal {L}}({\texttt {fp-automata}})\). \(\square \)
and \({\mathcal {L}}({\text {FSNA}}_{\pm }) \supseteq {\mathcal {L}}({\texttt {fp-automata}})\) Both \({\text {FSNA}}_{\pm },{\text {FSNA}}_{+}\) recognise the language \(\{a_1\dots a_n \mid i\ne j \Rightarrow a_i \ne a_j \}\), that instead is not by any \({\texttt {fp-automata}}\). However \({\text {FSNA}}_{+}\) can not recognise \({\varSigma }^*\), a language in \({\mathcal {L}}({\texttt {fp-automata}})\). \(\square \)
5 Pushdown Nominal Automata
The introduction discusses a simple program that picks up and releases unboundedly many resources. The behaviour of this program was conveniently abstracted as the Dyck-like context-free nominal language of words
where \(r1,r2,\dots , rn\) are pairwise distinct resources. Various kinds of recognisers for these context-free nominal languages have been recently proposed and justified by their theoretical and practical relevance [12, 13, 17, 37, 42].
Below, we extend \({\text {FSNA}}_{\pm }\) with a stack, so obtaining our version of nominal, push-down automata. Of course, the nominal language \(\{ ww^R \}\) of Example 3 is accepted by one of them.
We store elements of the infinite alphabet \({\varSigma }\) in the stack of a \({\text {PDNA}}_{\pm }\), and we can push on it strings of symbols in \({\varSigma }\), possibly retrieved through the indexes of m-registers. By pushing, e.g., the string \(a\,3\,b\) one actually pushes \(a\,\text {s-top}(N_3)\,b\). A preliminary definition is in order to handle these cases.
Definition 10
Let \(\zeta \in ({\varSigma }_s \cup \underline{\mathtt {r}})^*\) and let S be a stack. Then, \(Pushreg(\zeta ,S)\) extends the standard push operation as follows
Definition 11
(Pushdown Nominal Automata) A Pushdown Nominal Automata (PDNA\(_{\pm }\)) is \(A = \langle Q, q_{0},{\varSigma }, \delta , r, F \rangle \) where:
-
\(Q,q_{0},r,F\) are as in \({\text {FSNA}}_{\pm }\) (Definition 1)
-
\(\delta \) is the transition relation: \((q,\sigma ,Z, q',{\varDelta },\zeta ) \in \delta \) with \(\sigma \in {\varSigma }_s \cup \underline{\mathtt {r}} \cup \{\varepsilon ,\top \}, Z \in {\varSigma }_s \cup \underline{\mathtt {r}} \cup \{\varepsilon ,?\}, {\varDelta } \in \{ i+,i- \mid i \in \underline{\mathtt {r}}\} \cup \{\varepsilon \}, \zeta \in ({\varSigma }_s \cup \underline{\mathtt {r}})^*\). For \((q,\sigma ,Z,q',{\varDelta },\zeta ) \in \delta \) we use the notation

A configuration is a tuple \(C=\langle q , w , [N_{1},\dots ,N_{r}], S \rangle \) where \(q,w,[N_{1},\dots ,N_{r}]\) are as in \({\text {FSNA}}_{\pm }\) and S is a stack with symbols in \({\varSigma }\).
A configuration \(\langle q_{f} \in F, \varepsilon , [N_{1},\dots , N_{r}] , \boxtimes {} \rangle \) is final (\(\boxtimes {}\) is the empty stack).
As defined below, \({\text {PDNA}}_{\pm }\) may use in a richer way than standard pushdown automata the top of the stack, call it a. First, we can compare the current symbol in the input with a, if the symbol \(\sigma \) in the transition to be applied is \(\top \). Also, if \(Z = \varepsilon \) the string obtained from \(\zeta \) is pushed on the stack, as explained above. Instead, if \(Z = i\) the top a is popped from the stack, provided that the s-top of the \(i^{th}\) m-register is a. Finally, if \(Z = ?\) a pop occurs, with no further constraints.
Definition 12
(Recognising Step) Given a \({\text {PDNA}}_{\pm }\ A\), the step \(\langle q , w , [N_{1},\dots ,N_{r}],S \rangle \rightarrow \langle q' , w' , [N_{1}',\dots ,N_{r}'], S' \rangle \) occurs iff  and the following hold
and the following hold
-
1.
condition 1 of Definition 2 and \( \sigma = \top \Rightarrow w = top(S) w' \text { and} \)
-
2.
condition 2 of Definition 2 and
-
3.
\( {\left\{ \begin{array}{ll} Z = \varepsilon \Rightarrow S' = Pushreg(\zeta ,S) \text { and} \\ Z = i \Rightarrow S' = {Pushreg}(\zeta ,pop(S)) \wedge top(S)=\text {s-top}(N_{i}) \text { and} \\ Z = ? \Rightarrow S' = Pushreg(\zeta ,pop(S)) \end{array}\right. } \)
Finally, the language accepted by a PDNA\(_{\pm }\) A, which we call (nominal) context-free, is
The following example shows that \({\text {PDNA}}_{\pm }{}\) are able to express the above new-rel language on data-words (1).
Example 4
The \({\text {PDNA}}_{+}\) accepting (1) is in Fig. 7b. The labels of transitions, but \({\varDelta }\), contain \(\mathtt {new}(u), \mathtt {rel}(u), u \in \underline{\mathtt {r}} \cup {\varSigma }_s\). Figure 7b also shows the run for \(\mathtt {new}(a)\, \mathtt {new}(b)\, \mathtt {rel}(b) \mathtt {rel}(a)\); also here we omit the strings in configurations and we only mention the symbols in the m-registers. Note that, only keeping the names of the resources, we get \(\bigcup _{r \in {\mathbb {N}}}L_{r} = \{ww^{R} \mid w \in {\varSigma }_{d}^{*}\}\), for \(L_{r}\) of Example 3.
The late usage pattern discussed in the introduction can be expressed by \({\text {PDNA}}_{\pm }\). This comes with the ability of recognising symbols on the stack, while they have been deleted from the m-registers. The following example witnesses this feature.
Example 5
Figure 7a shows a \({\text {PDNA}}_{\pm }\) accepting \(L_{p}=\{ww^{R} \mid w \in {\varSigma }_{d}^{*}\}\), and a run accepting aabbaa (for brevity, we do not write the strings to be recognised in the configurations, as the current symbols label the steps). The automaton behaves just as a FSNA\(_{\pm }\) in the 1st, 3rd, 5th and 7th steps of \(\rho _1\). Additionally, in this initial part of the run, the stack is involved in the 2nd, 4th and 6th steps. They all occur because of edge  , that causes the symbol in the m-register 1 to be pushed on the stack. In steps 8th,9th,10th the edge
, that causes the symbol in the m-register 1 to be pushed on the stack. In steps 8th,9th,10th the edge  causes the top of the stack to be (successfully) matched with the current symbol (as dictated by the label \(\top \)) and popped (because of ?).
causes the top of the stack to be (successfully) matched with the current symbol (as dictated by the label \(\top \)) and popped (because of ?).
As done for \({\text {FSNA}}_{\pm }\) we introduce the class of automata that update two m-registers at the same time, and the sub-class of \({\text {PDNA}}_{\pm }\) without delete transitions.
Definition 13
( \({\text {PDNA}}_{+}\) and \({\text {PDNA}}_{+}\)2)
-
A \({\text {PDNA}}_{+}\) is a \({\text {PDNA}}_{\pm }\) with no edges
 .
. -
A \({\text {PDNA}}_{+}\)2 is a \({\text {PDNA}}_{+}\) with transitions of the form
 (cf. Definition 4)
(cf. Definition 4)
As expected, the class of languages accepted by \({\text {PDNA}}_{\pm }\) strictly includes that accepted by \({\text {PDNA}}_{+}\). Indeed, the same proof of Property 1 applies here. Just as done for \({\text {FSNA}}_{+}\)2, we can prove that \({\text {PDNA}}_{+}\)2 and \({\text {PDNA}}_{+}\) have the same expressive power. In spite of the reduced expressiveness, \({\text {PDNA}}_{+}\) can accept a wide class of (Dyck-like) context-free languages, for instance the automaton in Example 4 is a \({\text {PDNA}}_{+}\).
6 Properties of \({\text {PDNA}}_{\pm }{}\)
Obviously, the class of pushdown nominal languages includes the regular ones.
Property 4
\({\mathcal {L}}({\text {FSNA}}_{\pm }) \subsetneq {\mathcal {L}}({\text {PDNA}}_{\pm })\)
Proof
Inclusion is trivially proved: from a given \({\text {FSNA}}_{\pm }\) obtain the equivalent \({\text {PDNA}}_{\pm }\) by adding labels \(\zeta =\varepsilon ,Z=\varepsilon \) to each edge. Example 3 suffices to prove that the inclusion is strict. \(\square \)
We now study under which operators the classes of languages accepted by \({\text {PDNA}}_{\pm }\) and \({\text {PDNA}}_{+}\) are closed.
Theorem 5
(Closure properties)
\(\cup \) | \(\cap \) |
|
| \(*\) | |
|---|---|---|---|---|---|
\({\mathcal {L}}({\text {PDNA}}_{\pm })\) | \(\checkmark \) | \(\times \) | \(\times \) | \(\checkmark \) | \(\checkmark \) |
\({\mathcal {L}}({\text {PDNA}}_{+})\) | \(\checkmark \) | \(\times \) | \(\times \) | \(\times \) | \(\times \) |
Proof
Union:
The construction is the same of Theorem 2 in both cases; of course the initial \(\varepsilon \)-transitions do not alter the stack (\(\zeta = Z = \varepsilon \)).
Intersection and complement:
Follows from the classical results on context-free languages, the same languages of the classical counterexamples can be used in our case.
Concatenation and Kleene star:
The proof in Theorem 2 applies here as well; note that the stack is empty in the initial and final configurations. \(\square \)
A classical result in automata theory is that the class of context-free languages is closed by intersection with the class of regular ones. We investigate the same property in the nominal case, and we find that only the intersection of \({\text {FSNA}}_{+}\) and \({\text {PDNA}}_{+}\) is a \({\text {PDNA}}_{+}\) (hence a \({\text {PDNA}}_{\pm }\)).
Theorem 6
(Intersection)
is a | \({\text {FSNA}}_{\pm }\cap {\text {PDNA}}_{\pm }\) | \({\text {FSNA}}_{\pm }\cap {\text {PDNA}}_{+}\) | \({\text {FSNA}}_{+}\cap {\text {PDNA}}_{\pm }\) | \({\text {FSNA}}_{+}\cap {\text {PDNA}}_{+}\) |
|---|---|---|---|---|
\({\text {PDNA}}_{\pm }\) | \(\times \) | \(\times \) | \(\times \) | \(\checkmark \) |
\({\text {PDNA}}_{+}\) | \(\times \) | \(\times \) | \(\times \) | \(\checkmark \) |
Proof
Consider the \({\text {FSNA}}_{\pm }\) language \(L_1 = \{ a p^n b q^m r^{n'} c s^{m'} d \mid a=c \Rightarrow n' > n, b=d \Rightarrow m' > m , a \ne b, c \ne d \}\) in Fig. 8 and the \({\text {PDNA}}_{+}\) language \(L_2 = a \{p\}^* b \{q\}^* \{r\}^* a \{s\}^* b\). The language \(L_1 \cap L_2 = \{ a p^n b q^m r^{n'} c s^{m'} d \mid n' > n , m' > m, a \ne b\}\), by classical reasoning on context-free languages, is not recognised by any \({\text {PDNA}}_{+}\) nor \({\text {PDNA}}_{\pm }\). Note that \(L_1\) can be recognised by the \({\text {PDNA}}_{\pm }\) obtained by adding \(Z=\varepsilon ,\zeta =\varepsilon \) to all the edges in Fig. 8 and \(L_2\) is a nominal regular language recognised by both a \({\text {FSNA}}_{+}\) and a \({\text {FSNA}}_{\pm }\). This justifies the entries \(\times \) of the statement.
We prove now that \({\text {PDNA}}_{+}\cap {\text {FSNA}}_{+}\) is a \({\text {PDNA}}_{+}\):
The proof follows step by step that of Theorem 2, with additional care to manage the stack, which however is only determined by how the \({\text {PDNA}}_{+}\) handles it. The detailed construction follows.
Given the \({\text {PDNA}}_{+}\ \langle Q_{1},q_{0}^{1},{\varSigma },\delta _{1},r,F_{1}\rangle \) and the \({\text {FSNA}}_{+}\ \langle Q_{2},q_{0}^{2},{\varSigma },\delta _{2},r,F_{2}\rangle \), their intersection automaton (of type \({\text {PDNA}}_{+}\)2) is \( \langle {\overline{Q}}, {\overline{q_{0}}}, {\varSigma }, {\overline{\delta }}, 2r, {\overline{F}} \rangle \), where
-
\({\overline{Q}} = Q_{1} \times M \times Q_{2}\), with M set of merge functions
-
\({\overline{q_{0}}}=\langle q_{0}^{1}, m^* ,q_{0}^{2}\rangle \) where \(m^*\) is a merge such that \(m^*_1,m^*_2\) are the identity functions (i.e. the m-registers of the two intersecting automata are initially merged onto the firsts r register of the intersection automaton)
-
\({\overline{F}} = \{\langle q_{1},m,q_{2}\rangle \mid q_{1} \in F_{1}, q_{2} \in F_{2},m\in M\}\)
-
 iff
iff  and
and and
and  and \( (\sigma _{1},\sigma _{2} \in \underline{\mathtt {r}} \) or \(\sigma _{1},\sigma _{2} \in {\varSigma }_{s})\) and
and \( (\sigma _{1},\sigma _{2} \in \underline{\mathtt {r}} \) or \(\sigma _{1},\sigma _{2} \in {\varSigma }_{s})\) and - –:
-
if \(\sigma _{1}, \sigma _{2} \in \underline{\mathtt {r}}\) then \({\overline{\sigma }}=m_{1}(\sigma _{1})=m_{2}(\sigma _{2})\) and
- –:
-
if \(\sigma _{1}, \sigma _{2} \in {\varSigma }_{s}\) then \({\overline{\sigma }}=\sigma _{1}=\sigma _{2}\) and
- –:
-
 , \({\overline{Z}}=m_{1}(Z), {\overline{\zeta }}=m_{1}(\zeta )\)
, \({\overline{Z}}=m_{1}(Z), {\overline{\zeta }}=m_{1}(\zeta )\)
or  and
and  and
and  and \({\overline{\zeta }}=m_{1}(\zeta )\)
and \({\overline{\zeta }}=m_{1}(\zeta )\)
and either  implies
implies  , \({\overline{Z}}=m_{2}(\sigma _{2})\),
, \({\overline{Z}}=m_{2}(\sigma _{2})\),  ,
,
or \(Z = ?\) implies 
or  and \({\overline{\sigma }} = \varepsilon \),
and \({\overline{\sigma }} = \varepsilon \),  , \({\overline{Z}}=m_{1}(Z), {\overline{\zeta }}=m_{1}(\zeta )\)
, \({\overline{Z}}=m_{1}(Z), {\overline{\zeta }}=m_{1}(\zeta )\)
or  ,
,  , \({\overline{Z}}=\varepsilon , {\overline{\zeta }}=\varepsilon \ \ \square \)
, \({\overline{Z}}=\varepsilon , {\overline{\zeta }}=\varepsilon \ \ \square \)
We finally prove that the emptiness problem is decidable for \({\text {PDNA}}_{+}\). The proof relies on a variant of the classical pumping lemma. Roughly it says that, given a language L recognised by a  , there exists a constant n, such that any string \(w \in L,|w| > n\) can be decomposed as \(w=uvxyz\), such that also \(w'=u'x'z'\) belongs to L with \(u',x',z'\) obtained from u, x, z by carefully substituting (distinguished) dynamic symbols and erasing v and y. Before proving it, we need some auxiliary definitions and lemmata.
, there exists a constant n, such that any string \(w \in L,|w| > n\) can be decomposed as \(w=uvxyz\), such that also \(w'=u'x'z'\) belongs to L with \(u',x',z'\) obtained from u, x, z by carefully substituting (distinguished) dynamic symbols and erasing v and y. Before proving it, we need some auxiliary definitions and lemmata.
Since we focus on the emptiness problem, we are interested in the existence of a word, rather than in its actual shape. Therefore, whenever immaterial, we feel free to omit from now onwards the word in configurations and the input symbol in transitions.Footnote 5
Notation
From now onwards, assume as given a \({\text {PDNA}}_{+}\) and let \(C=\langle q,[N_{1},\dots , N_{r}],S \rangle \) be a configuration; \(\rho =C_{1} \rightarrow ^{*} C_{k}, C_{i}=\langle q_{i}, w_{i}, [N_{1}^{i}, \dots , N_{r}^{i}] , S_{i}\rangle \) be a run; \(B=[B[1],\dots ,B[n]]\) denote an array, and let \(B[i,\dots ,j], i \le j\) denote the portion of the array between the i-th and j-th positions. We will also use the array notation for stacks, assuming that the leftmost item S[1] is the bottom and S[i] is the i-th element in it, the height of a stack S will be denoted |S|.
Also, call swap f an injective partial function \(f: {\varSigma }_{d} \rightharpoonup {\varSigma }_{d}\), and its homomorphic extensions to strings, tuples, array and stacks.
What follows extends similar definitions and proofs of [2].
Definition 14
( C-rep) Let \(E_{S}\) be the set of symbols occurring in the stack S of a configuration C such that \(e \in E_{S}\) iff \(\forall i. top(N_{i})\ne e\). Let

Let \(f_{S}:E_{S} \rightarrow \{1, \dots , \left| S \right| \}\) to be such that \(f_{S}(e)=first(e,S)\) (note that \(f_{S}\) is injective).
The function C-rep(S) that returns a stack of symbols in \({\varSigma }_{s} \cup \{ i \mid 1 \le i \le r \} \cup \{{\underline{i}} \mid 1 \le i \le \left| S \right| \}\) is defined by:
-
\(C\hbox {-rep}([])=[]\)
-
\(C\hbox {-rep}( b::S')=a::C\text {-rep}(S')\hbox { iff}\)
- –:
-
\(b \in {\varSigma }_{s},a=b\) or
- –:
-
\(b \in {\varSigma }_{d}, \exists i . b = top(N_{i}), a=i\) or
- –:
-
\(b \in {\varSigma }_{d}, \forall i . b \ne top(N_{i}), a=\underline{f_{S}(b)}\)
Definition 15
(Activation state) The activation state of the m-registers of a configuration C is an array \(m=[m[1],\dots ,m[r]]\) where \(m[i]=1\) iff \(N_{i}\) is active, \(m[i]=0\) otherwise.
Definition 16
(Representative state) The representative state of a configuration C is the triple (q, m, R) where m is the activation state of the m-registers and \(R = C\)-rep(S), i.e. R represents S on C. We write \(C \sim C'\) to indicate that C has the same representative state of \(C'\).
Lemma 3
Let \(C_{1} \rightarrow C_{1}'\) then for any configuration \(C_{2}\) such that \(C_{2} \sim C_{1}\) there exists \(C_{2}'\) such that \(C_{2} \rightarrow C_{2}'\) and \(C_{2}' \sim C_{1}'\).
Proof
Let \(t=(q,\sigma ,Z,q',{\varDelta },\zeta ) \in \delta \) be used for justifying the transition \(C_{1} \rightarrow C_{1}'\). We first show that t justifies also \(C_{2} \rightarrow C_{2}'\) by constructing a suitable \(C_{2}'=\langle q', [M_{1}', \dots , M_{r}'], T' \rangle \). First of all, note that, being \(C_{1} \sim C_{2}\), the main stacks S and T have the same depth and the m-registers \(N_{i}\) and \(M_{i}\) have the same activation state. Therefore, since \(C_{1}\) satisfies (1m), also \(C_{2}\) does, i.e. :
For the same reason, in condition (3), the operations pop(T), top(T) and \(\text {s-top}(M_{i})\) are defined and so are the arguments of the operation \(\text {Pushreg}\). Note that \(\zeta \) may contain a reference to a register j and again we have that the required \(\text {s-top}(M_{j})\) is defined, because the activation state of \(M_{j}\) is the same of \(N_{j}\).
We are left to prove that condition (2) can be fulfilled by the \(M_{j}'\) and to prove that \(C_{1}' \sim C_{2}'\). We proceed by cases on \({\varDelta }\).
- Case \({\varDelta } = i+\)):
-
Let \(\forall j (j \ne i). M_{j}' = M_{j}\), \(M_{i}' = \text {s-push}(c,M_{i})\) with c to be \(T[first(c,M_{i})]\) if \(c \in S\) to preserve the representative state, that requires to relate \(T'\) with \(S'\). Otherwise we choose \(c \notin M_{j}\), \(\forall j \in \mathtt {{\underline{r}}}\) and \(c \notin T\). We are left to prove that \(C_{2}' \sim C_{1}'\). Trivially \(C_{2}'\) and \(C_{1}'\) have the same state \(q'\). The activation state of the m-registers is also the same, because in both configurations only the i-th is affected (if active it is left such as well it becomes active because of the \(\text {s-push}\)), while the activation state of the others is the same in \(C_{1}'\) and \(C_{2}'\) because \(C_{1} \sim C_{2}\). Also \(E_{S}=E_{T}\) and the same \(\zeta \) is pushed on both stacks, so \(E_{S'}=E_{T'}\). Now \(f_{S'}(\text {s-top}(N_{i}))=f_{T'}(\text {s-top}(M_{i}))\), that proves \(C_{1}' \sim C_{2}'\).
- Case \({\varDelta } = i-\)):
-
Let \(M_{j}'=M_{j}, \forall j (j \ne i)\) and \(M_{i}'=\text {s-pop}(M_{i})\) which is defined because \(C_{1}\sim C_{2}\). The proof that the tuple \((q',{\varDelta },\zeta ) \in \delta (q,\sigma ,Z)\) justifies \(C_{2} \rightarrow C_{2}'\) is similar to the case above. Only the \(i-th\) m-register is affected, if active it gets deactivated, it is left deactivated otherwise.
- Case \({\varDelta } = \varepsilon \)):
-
Letting \(M_{j}'=M_{j}, \forall j \in \mathtt {{\underline{r}}}\) suffices to fulfil condition (2). The proof that the transition \((q,\sigma ,Z,q',{\varDelta },\zeta )\) belongs to \(\delta \) justifies \(C_{2} \rightarrow C_{2}'\) is similar to the case above. Only the i-th m-register is affected, if active it gets deactivated, it is left deactivated otherwise. \(\square \)
Definition 17
(Level) A level \(G=(i,j,h)\) with height l on \(\rho \) is a triple (i, j, h) such that \(1 \le i < j < h \le k\) and
-
\(\left| S_{i} \right| = \left| S_{h} \right| , \left| S_{j} \right| = \left| S_{i} \right| + l\)
-
\(\left| S_{i} \right| \le \left| S_{u} \right| \le \left| S_{j} \right| \) for all \(u. i \le u \le j\).
-
\(\left| S_{h} \right| \le \left| S_{u} \right| \le \left| S_{j} \right| \) for all \(u. j \le u \le h\)
Given a level G on \(\rho \), define two indices \(l_\downarrow ^{G},f_\uparrow ^{G}\), called respectively last-push and first-pop of G.
Figure 9 shows an example of levels, \(l_\downarrow \) and \(f_\uparrow \).
Property 5
Given a level (i, j, h) with height l on \(\rho \), for each \(k < l\) there exists a level (u, j, v) for some u, v with height k.
Definition 18
(Full state) Let G be a level on \(\rho \) and let \(C_{l_\downarrow ^{G}}=\langle q,[N_{1},\dots ,N_{r}],a::S\rangle ,C_{f_\uparrow ^{G}}=\langle q',[N_{1}',\dots ,N_{r}'],S'\rangle \).
The full state of a level G on \(\rho \) is the tuple \((c,q,m,q',m')\) such that:
-
If \(a \in {\varSigma }_{s}\) then \(c=a\), if \(a \in {\varSigma }_{d}\) and \(\exists i . top(N_{i})=a\) then \(c = i\), if \(a \in {\varSigma }_{d}\) and \(\forall i . top(N_{i})\ne a\) then \(c = \star \).
-
\(m,m'\) are the activation states of the m-registers in \(C_{l_\downarrow ^{G}},C_{f_\uparrow ^{G}}\), respectively.
Property 6
Let \(C_{1}=\langle q_{1},[N_{1}^{1},\dots ,N_{r}^{1}],S_{1}\rangle \rightarrow ^{n} C_{n}=\langle q_{n},[N_{1}^{n},\dots ,N_{r}^{n}],S_{n}\rangle \) and let \(G=(1,j,n)\) be a level on the above run with height l, for some j. Then there exists a cutoff run \(D_{l_\downarrow ^{G}},\dots ,D_{f_\uparrow ^{G}}\) with \(D_{i}=\langle q_{i}, [N_{1}^{i},\dots ,N_{r}^{i}],S_{i}'\rangle \), \(S_{i}' = T::S_{i}[1,\dots ,\left| S_{i} \right| - l]\) for any stack T with \(top(T)=top(S_{l_\downarrow ^{G}})\).
Proof
Sketch: by definition of level the transitions does not depend on the content of the stack below the height of \( S_{l_\downarrow ^{G}}\) \(\square \)
We now prove our restricted pumping lemma: a de-pumping lemma.
Lemma 4
(De-Pumping Lemma) Let \(A = \langle Q, q_{0}, \delta , r, {\varSigma }_{s} \cup {\varSigma }_{d}, F \rangle \) be a \({\text {PDNA}}_{+}\) and let \(p' = 2^{r}\left| Q \right| ^{2}(\left| {\varSigma }_{s} \right| +r+1)\) and \(p = 2^{r} \left| Q \right| (\left| {\varSigma }_{s} \right| +r+p'+1)^{p'} + 1\). For each word \(w \in L(A)\) such that \(\left| w \right| > p\) and \(\rho \) is (one of) the shortest among its accepting runs, we can construct a word \(w' \in L(A)\) with a strictly shorter accepting run.
Proof
Let \(w \in L(A)\) such that \(\left| w \right| > p\); take \(\rho =C_{1} \rightarrow \dots \rightarrow C_{k}\), \(C_{i}=\langle q_{i}, w_{i}, [N_{1}^{i}, \dots , N_{r}^{i}] , S_{i}\rangle \) out of the set of the shortest accepting runs; and let l be the maximum height of the stack in \(\rho \).
- Case \(l \le p'\)):
-
Recall that \(\left| w \right| > p\), hence \(\rho \) contains at least p configurations. There are at most \(2^{r} \left| Q \right| (\left| {\varSigma }_{s} \right| +r+l+1)^{l}<p\) different representative states of the configurations of \(\rho \). Hence there are at least two configurations \(C_{x},C_{y}, x < y\) with the same representative state. By applying Lemma 3, from the run \(C_{y} \rightarrow ^{*} C_{k}\) we obtain that also \(C_{x} \rightarrow ^{*} F\) for some F with the same representative state of \(C_{k}\). Therefore, also F is a final configuration. The thesis follows because the run \(\rho ' = C_{1} \rightarrow ^{*} C_{x} \rightarrow ^{*} F\) is shorter than \(\rho \).
- Case \(l > p'\)):
-
Note that there is a level on \(\rho \) with height l, say \(G = (i,j,h)\). By Property 5, there exist at least l levels (u, j, v) with different heights that are levels on \(\rho \). There are only \(p' < l\) different full states that can be associated with these levels, hence there exist two levels, say \(U=(u_{1},j,v_{1})\) and \(V=(u_{2},j,v_{2})\) with the same full state. Assume w.l.o.g. \(n_{U} = \left| S_{u_{1}} \right| =\left| S_{v_{1}} \right| < \left| S_{u_{2}} \right| =\left| S_{v_{2}} \right| =n_{V}\). Let \(C_{l_\downarrow ^{U}},C_{l_\downarrow ^{V}}\) be the configuration with index last-push and let \(C_{f_\uparrow ^{U}},C_{f_\uparrow ^{V}}\) be the configuration with index first-pop of level U and V respectively (see Fig. 9). By Lemma 6, from the run \(C_{l_\downarrow ^{V}} \rightarrow ^{*} C_{f_\uparrow ^{V}}\) it is possible to obtain a cut off run \( D_{l_\downarrow ^{V}}=\langle q_{l_\downarrow ^{V}},w_{l_\downarrow ^{V}},[N_{1}^{l_\downarrow ^{V}},\dots ,N_{r}^{l_\downarrow ^{V}}],T_{l_\downarrow ^{V}} \rangle \rightarrow ^{*} \) \(\qquad \qquad \qquad \qquad D_{f_\uparrow ^{V}} = \langle q_{f_\uparrow ^{V}},w_{f_\uparrow ^{V}},[N_{1}^{f_\uparrow ^{V}},\dots ,N_{r}^{f_\uparrow ^{V}}],T_{f_\uparrow ^{V}} \rangle \) where \(T_{i} = S_{l_\downarrow ^{U}}::S_{i}[n_{V},\dots ,\left| S_{i} \right| ]\). Since \(T_{l_\downarrow ^{V}}=T_{f_\uparrow ^{V}}=S_{l_\downarrow ^{U}}=S_{f_\uparrow ^{U}}\) and \(C_{l_\downarrow ^{U}},C_{f_\uparrow ^{U}}\) have the same full state of \(C_{l_\downarrow ^{V}},C_{f_\uparrow ^{V}}\), respectively, it follows that \(D_{l_\downarrow ^{V}}\sim C_{l_\downarrow ^{U}}\) and \(D_{f_\uparrow ^{V}}\sim C_{f_\uparrow ^{U}}\). Consequently, by Lemma 3, from the run \(D_{l_\downarrow ^{V}}\rightarrow ^{*}D_{f_\uparrow ^{V}}\) we obtain the run \(C_{l_\downarrow ^{U}} \rightarrow ^{*} H\) for some \(H \sim D_{f_\uparrow ^{V}}\sim C_{f_\uparrow ^{U}} \). By the same lemma, from the run \(C_{f_\uparrow ^{U}} \rightarrow ^{*} C_{k}\) we obtain a run \(H \rightarrow ^{*} F\), where F has the same representative state of \(C_{k}\), hence it is final. The thesis follows because the run \(C_{1} \rightarrow ^{*} C_{l_\downarrow ^{U}} \rightarrow ^{*} H \rightarrow ^{*} F\) is shorter than \(\rho \). \(\square \)
We eventually prove the decidability of the emptiness problem for our push-down nominal automata with no delete transitions; we conjecture that it is instead undecidable for \({\text {PDNA}}_{\pm }\).
Theorem 7
Given a \({\text {PDNA}}_{+}\ A\), it is decidable whether \(L(A) = \emptyset \).
Proof
(Sketch) By repeatedly applying the De-Pumping Theorem 4, L(A) is non empty if it contains a word \(w'\), made of distinguished symbols, and such that \(|w'| \le p\), where p is the constant in Theorem 4. \(\square \)
7 Expressiveness of \({\text {PDNA}}_{\pm }{}\)
To the best of our knowledge, the literature has different notions of nominal context-free languages, i.e. able to express Dyck-like languages: quasi context-free languages (QCFL) [17], \({\text {Usages}}\) introduced in [7], the context-free automata (that we call here NPA) in [13], DMPA [15], HOPAD [42], Pebble automata [39], and the pushdown r-register system (r-PDRS) [37].
Below we compare the properties and the expressive power of \({\text {PDNA}}_{\pm }\) with that of above models for different notions of nominal context-free languages.
Table 3 shows some closure properties of our automata with those of the other models, when presented in the literature. To the best of our knowledge, the closure of a context-free nominal language with a regular one has not been investigated explicitly for other nominal models, even if it is folklore that intersecting a \({\text {QCFL}}\) with a \({\text {FMA}}\) automaton can be done mimicking the construction of the intersection between \({\text {FMA}}\). Remarkably, we have constructed the \({\text {PDNA}}_{+}\) resulting from the intersection of a \({\text {PDNA}}_{+}\) with a \({\text {FSNA}}_{+}\) (see Theorem 6).
The decidability and the complexity of the emptiness problem has been investigated for \({\text {QCFL}}, {\text {Usages}}\), DMPA, Pebble automata because of the relevance of this problem in verification. In [37] the authors shows the decidability of reachability on r-PDRS automata, which implies the decidability of their emptiness. In Table 4 we summarise the decidability results of the emptiness problem for the above models and for ours.
We now compare the expressiveness of \({\text {PDNA}}_{\pm }\) and \({\text {PDNA}}_{+}\) with that of other models in the literature. Also here, we assume that data-words have a single action, not displayed in words (see Theorem 4).
Theorem 8
(Expressivness Comparison)
-

-
\({\mathcal {L}}({\text {PDNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {QCFL}})\)
-
\({\mathcal {L}}({\text {PDNA}}_{+}) = {\mathcal {L}}({\text {Usages}})\)
-
\({\mathcal {L}}({\text {PDNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {Usages}})\)
-

Proof
-
\({\mathcal {L}}({\text {PDNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {QCFL}} )\) We consider the infinite alphabet pushdown automata (IAPA) that recognise \({\mathcal {L}}({\text {QCFL}} )\) [17]. The same argument in Theorem 4, item 2 (\({\mathcal {L}}({\text {FSNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {FMA}} )\)) suffices for showing the inclusion, which is strict, because \(L_0\) in the Example 1 is not recognised by any IAPA.
-
\({\mathcal {L}}({\text {PDNA}}_{+}) = {\mathcal {L}}({\text {Usages}})\) \({\text {Usages}}\) are built from (static and dynamic) symbols n (actually \(\alpha (n)\), where \(\alpha \) is an action on n) with operation of sequentialization \(\cdot \), nondeterminism \(+\), recursion and creation of a new dynamic symbol, through \(\nu n\) (see Table 5). When sequentialising two processes, the second can not use any dynamic symbol used by the first one, just as it happens when two \({\text {PDNA}}_{+}\) are sequentialised by connecting the final states of the first with the initial one of the second. Since there is no deletion, the m-registers monotonically grow. Nondeterministic choice \(+\) directly corresponds to the union of two automata. Recursion can be dealt with as done in [6] by transforming an expression in a BPA, that has an immediate counterpart as a \({\text {PDNA}}_{+}\). For each occurrence of a \(\nu n\) in the usage at hand we associate an m-register. Creation of a new symbol, i.e. reducing the \(\nu n\), corresponds to updating the corresponding m-register. When a \(\nu n\) occurs within a recursive expression, a renaming occurs to guarantee freshness of the dynamic symbol to be generated. Note that only a finite number of m-registers is necessary, as the number of \(\nu n\) occurring in a usage is fixed and Property 7 holds.
-
\({\mathcal {L}}({\text {PDNA}}_{\pm }) \supsetneq {\mathcal {L}}({\text {Usages}})\) \({\varSigma }^{*} \in {\mathcal {L}}({\text {PDNA}}_{\pm })\), while \({\varSigma }^{*} \notin {\mathcal {L}}({\text {Usages}})\) by Theorem 9.
-
 The proof of Theorem 8, item 5 suffices (\({\text {FSNA}}_{+}\supsetneq {\text {FMA}}\)).
The proof of Theorem 8, item 5 suffices (\({\text {FSNA}}_{+}\supsetneq {\text {FMA}}\)). -
 Using their multiple stacks, the DMPA can express the language (of patterns) \(\{ a^nb^nc^n \}\), that can not be recognised by a \({\text {PDNA}}_{\pm }\). However, their notion of freshness also requires that a new symbol can not occur in the stacks, which is not the case for \({\text {PDNA}}_{\pm }\). \(\square \)
Using their multiple stacks, the DMPA can express the language (of patterns) \(\{ a^nb^nc^n \}\), that can not be recognised by a \({\text {PDNA}}_{\pm }\). However, their notion of freshness also requires that a new symbol can not occur in the stacks, which is not the case for \({\text {PDNA}}_{\pm }\). \(\square \)
Note in passing that the expressiveness of \({\texttt {fp-automata}}\) does not go beyond the one of \({\text {PDNA}}_{\pm }\), deallocation of \({\texttt {fp-automata}}\) can be reproduced in \({\text {PDNA}}_{\pm }\) by delete transitions; swapping the contents of two registers in \({\texttt {fp-automata}}\) via a permutation (there are only a finite number of them) can be done by \({\text {PDNA}}_{\pm }\) by suitably mentioning/updating/deleting the corresponding registers in the next states.
A detailed comparison between the expressiveness of \({\text {PDNA}}_{\pm }{}\) and r-PDRS [37] is out of the scope of this paper, mainly because recognising languages with an unbound number of fresh resources (unbound/global freshness), or with late usage, were not an issue for r-PDRS. Extending their main result on the decidability of reachability on r-PDRS in these cases does not seem straightforward. Indeed, the original result in [37] is based on the limited distinguishability lemma (Lemma 5.), which states that for any recognising run there exists an equally long run where only 3r symbols are used. This lemma would be false for e.g. \(L = \{ w \mid \forall i,j \, (i \ne j). w[i] \ne w[j]\}\) (accepted by a \({\text {FSNA}}_{+}{}\)), because the length of any recognizing run of \(w \in L\) is at least \(| \Vert {w} \Vert | = |w|\), and it suffices to take a run longer than 3r.
8 Conclusions
We modelled two new aspects of resource usage arising in current programming languages and paradigms, namely unbound freshness, i.e. the possibility of having unboundedly many fresh resources, and late usage, i.e. the possibility of referring to a resource even after it has been disposed. We do that through novel classes of automata for nominal languages, that read from the input unboundedly many fresh symbols. These symbols can explicitly be released, and re-used later on, as if they were fresh. We intuitively classify our automata as context-free \({\text {PDNA}}_{\pm }\), and regular \({\text {FSNA}}_{\pm }\), respectively, because they can recognise Dyck-like languages, and can not, respectively. We also considered a sensible restriction of them, \({\text {PDNA}}_{+}\) and \({\text {FSNA}}_{+}\), that can not release and re-use as fresh symbols already seen.
We studied some closure properties of our models: union, intersection, complementation, concatenation and Kleene star. We related the expressive power of our nominal automata to that of some analogous models in the literature and we investigated the decidability of the problems of emptiness and universality for them.
The decidability of the emptiness, in particular in the context-free case, is important because it provides foundations to some verification techniques. To the best of our knowledge, no class of nominal languages proposed so far is closed under complementation.
Lack of closure under complementation affects, for example, the standard automata-based model-checking procedure [49]. This wide-spread verification technique requires to represent both the model and the properties as languages L (typically context-free) and \(L'\) (typically regular) and to verify the emptiness of the intersection of L with the complement of \(L'\). Indeed, an element of a non-empty intersection is a counterexample to the property in hand. However, this problem is mitigated when the property, i.e. a regular language, is not specified as the set of the accepted words, rather by the set of non accepted words, following the so-called default-accept paradigm [45]. In other words, one specifies the unwanted behaviour, so making complementation unnecessary at all. This is typically the case some properties arising in static analysis [26, 40] and for security policies [4, 45], that define behaviour that are deemed unacceptable. The specification of the property in the default-accept approach is usually done through an automaton (e.g. a security automaton), the language of which contains the unwanted behaviour. Operationally, one then builds a run-time execution monitor based on this automaton, that watches programs and performs a transition in correspondence with an execution step that possibly affects the property under monitoring. Right before the automaton reaches a final state, the program run is aborted, because it is about to violate some requirement. Following a static approach, one typically extracts an abstract behaviour from a program and model-checks it against the required property, expressed by an automaton where complementation is built-in (for security properties, see e.g. [6, 8, 28]).
The connection between nominal automata and program verification has been also investigated in [26]. The authors introduce a programmer-friendly language (TOPL) which can be used to express temporal properties of objects. A TOPL formula can be transformed to obtain a register automaton, which in turn can be used to monitor the execution of a Java program, seeking for violation of the property expressed by the formula, in a default-accept manner.
This paper contributes to this line of research, characterising a large class for which the automata based model-checking is feasible, when default-accept properties are of interest. We proposed \({\text {PDNA}}_{+}\) to express the model and \({\text {FSNA}}_{+}\) for the property, the intersection of which is again a \({\text {PDNA}}_{+}\). We also proved the decidability of emptiness problem for \({\text {PDNA}}_{+}\). These two results guarantee that model-checking is effective in the nominal setting, within the default-accept paradigm. Further investigation is required on understanding the impact the disposal mechanism has on the feasibility of this verification technique.
A different approach to verification has been recently proposed in [9]: compliance of a model with respect to a property is checked through a notion of simulation between automata. In [10], the same authors propose a logic with variables ranging over an infinite domain and establish a correspondence with a parametrised transition system. We can easily adapt their verification technique to our case, even though decidability of simulation is presently an open issue for our models.
Further research is needed to fill in the gap between our foundational results and prototypical implementations of our abstract model-checking procedure. Languages and logics which match the expressiveness of our models are also needed to make nominal technique easier to use for developers, in the style of [10, 26].
Notes
Consequently, we have that \(\langle q, [N_{1},\dots ,N_{r}],S\rangle \rightarrow \langle q', [N_{1}',\dots ,N_{r}'],S'\rangle \) iff there exists
 satisfying the conditions \((2-3)\) of Definition 12 and the following holds:
satisfying the conditions \((2-3)\) of Definition 12 and the following holds: - (1m):
-
\( {\left\{ \begin{array}{ll} \sigma = \top \Rightarrow top(S) \text { is defined}\\ \sigma = i \Rightarrow \text {s-top}(N_{i}) \text { is defined} \end{array}\right. }\)
If \(\langle q, [N_{1},\dots ,N_{r}],S\rangle \rightarrow \langle q', [N_{1}',\dots ,N_{r}'],S'\rangle \) because there exists
 satisfying the conditions (1m, 2, 3) then by setting for any \(w'\) the word w such that$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma &{}= \varepsilon \Rightarrow w = w' \\ \sigma &{}= \top \Rightarrow w = aw' \\ \sigma &{}= i \Rightarrow w = aw' \end{array}\right. } \end{aligned}$$
satisfying the conditions (1m, 2, 3) then by setting for any \(w'\) the word w such that$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma &{}= \varepsilon \Rightarrow w = w' \\ \sigma &{}= \top \Rightarrow w = aw' \\ \sigma &{}= i \Rightarrow w = aw' \end{array}\right. } \end{aligned}$$we have that also \(\langle q,w, [N_{1},\dots ,N_{r}],S\rangle \rightarrow \langle q', w',[N_{1}',\dots ,N_{r}'],S'\rangle \). By induction, if \(\langle q, [N_{1},\dots ,N_{r}],S \rangle \rightarrow ^{*} \langle q', [N_{1}',\dots ,N_{r}'],S' \rangle \) then for any word \(w'\) there exists a word w such that \(\langle q,w, [N_{1},\dots ,N_{r}],S \rangle \rightarrow ^{*} \langle q',w', [N_{1}',\dots ,N_{r}'],S' \rangle \).
References
Abadi, M., Needham, R.M.: Prudent engineering practice for cryptographic protocols. IEEE Trans. Softw. Eng. 22(1), 6–15 (1996). doi:10.1109/32.481513
Amarilli, A., Jeanmougin, M.: A proof of the pumping lemma for context-free languages through pushdown automata (2012). arXiv:1207.2819
Bartoletti, M., Costa, G., Degano, P., Martinelli, F., Zunino, R.: Securing Java with local policies. JOT 8(4), 5–32 (2009)
Bartoletti, M., Degano, P., Ferrari, G.L.: Planning and verifying service composition. JCS 17(5), 799–837 (2009)
Bartoletti, M., Degano, P., Ferrari, G.L., Zunino, R.: Semantics-based design for secure web services. IEEE Trans. Softw. Eng. 34(1), 33–49 (2008)
Bartoletti, M., Degano, P., Ferrari, G.L., Zunino, R.: Local policies for resource usage analysis. ACM Trans. Program. Lang. Syst. 31(6), 23 (2009)
Bartoletti, M., Degano, P., Ferrari, G.L., Zunino, R.: Model checking usage policies. Math. Struct. Comput. Sci. 25(3), 710–763 (2015)
Bartoletti, M., Zunino, R.: LocUsT: a tool for checking usage policies. Tech. Rep. TR08-07, University of Pisa (2008)
Belkhir, W., Chevalier, Y., Rusinowitch, M.: Guarded variable automata over infinite alphabets (2013). arXiv:1304.6297
Belkhir, W., Rossi, G., Rusinowitch, M.: A parametrized propositional dynamic logic with application to service synthesis. In: Advances in Modal Logic 10, invited and Contributed Papers from the Tenth Conference on “Advances in Modal Logic, Groningen, The Netherlands, 5–8 August 2014, pp. 34–53 (2014). http://www.aiml.net/volumes/volume10/Belkhir-Rossi-Rusinowitch.pdf
Benedikt, M., Ley, C., Puppis, G.: Automata vs. logics on data words. In: Dawar, A., Veith, H. (eds.) CSL, LNCS, vol. 6247, pp. 110–124. Springer, Berlin (2010)
Bojańczyk, M., Klin, B., Lasota, S.: Automata theory in nominal sets (2011). http://www.mimuw.edu.pl/sl/PAPERS/lics11full.pdf
Bojanczyk, M., Klin, B., Lasota, S.: Automata with group actions. In: LICS, pp. 355–364. IEEE Computer Society, Washington, DC, USA (2011). doi:10.1109/LICS.2011.48
Bollig, B.: An automaton over data words that captures EMSO logic. In: Katoen, J.P. , König, B. (eds.) CONCUR 2011, LNCS, vol. 6901, pp. 171–186. Springer, Berlin (2011)
Bollig, B., Cyriac, A., Gastin, P., Kumar, K.N.: Model checking languages of data words. In: Birkedal, L. (ed.) FOSSACS 2012, LNCS, vol. 7213, pp. 391–405. Springer, Berlin (2012)
Chaki, S., Rajamani, S.K., Rehof, J.: Types as models: model checking message-passing programs. In: Conference Record of POPL 2002: The 29th SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Portland, OR, USA, January 16–18, 2002, pp. 45–57 (2002)
Cheng, E.Y.C., Kaminski, M.: Context-free languages over infinite alphabets. Acta Inf. 35(3), 245–267 (1998)
Ciancia, V., Tuosto, E.: A novel class of automata for languages on infinite alphabets. Tech. rep., CS-09-003, University of Leicester, UK (2009)
Degano, P., Ferrari, G.L., Mezzetti, G.: Nominal automata for resource usage control. In: Moreira, N., Reis, R. (eds.) CIAA 2012, LNCS, vol. 7381, pp. 125–137. Springer, Berlin (2012)
Dierks, T., Rescorla, E.: RFC 5246: The Transport Layer Security (TLS) Protocol Version 1.2 (2008). http://tools.ietf.org/html/rfc5246
Ferris, C., Farrell, J.: What are web services? Commun. ACM 46(6), 31 (2003). doi:10.1145/777313.777335
Gabbay, M., Pitts, A.: A new approach to abstract syntax with variable binding. Form. Asp. Comput. 13(3), 341–363 (2002)
Gershenfeld, N., Krikorian, R., Cohen, D.: The internet of things. Sci. Am. 291(4), 76 (2004)
Gong, Z., Gu, X., Wilkes, J.: PRESS: predictive elastic resource scaling for cloud systems. In: Proceedings of the 6th International Conference on Network and Service Management, CNSM 2010, Niagara Falls, Canada, October 25–29, 2010, pp. 9–16 (2010). doi:10.1109/CNSM.2010.5691343
Gordon, A.D.: Notes on nominal calculi for security and mobility. In: Focardi, R., Gorrieri, R. (eds.) FOSAD 2000, LNCS, vol. 2171, pp. 262–330. Springer, Berlin (2001)
Grigore, R., Distefano, D., Petersen, R.L., Tzevelekos, N.: Runtime verification based on register automata. In: Tools and Algorithms for the Construction and Analysis of Systems—19th International Conference, TACAS 2013, Lecture Notes in Computer Science, vol. 7795, pp. 260–276. Springer, Berlin (2013)
Grumberg, O., Kupferman, O., Sheinvald, S.: Variable automata over infinite alphabets. In: Dediu, A.H., Fernau, H., Martín-Vide, C. (eds.) LATA, LNCS, vol. 6031, pp. 561–572. Springer, Berlin (2010)
Jensen, T.P., Métayer, D.L., Thorn, T.: Verification of control flow based security properties. In: 1999 IEEE Symposium on Security and Privacy, Oakland, California, USA, May 9–12, 1999, pp. 89–103 (1999)
Kaminski, M., Francez, N.: Finite-memory automata. TCS 134(2), 329–363 (1994)
Kaminski, M., Zeitlin, D.: Finite-memory automata with non-deterministic reassignment. Int. J. Found. Comput. Sci. 21(5), 741–760 (2010)
Kurz, A., Suzuki, T., Tuosto, E.: On nominal regular languages with binders. In: Birkedal, L., (ed.) FOSSACS 2012, LNCS, vol. 7213, pp. 255–269. Springer, Berlin (2012)
Kurz, A., Suzuki, T., Tuosto, E.: Nominal regular expressions for languages over infinite alphabets. Extended abstract (2013). arXiv:1310.7093
Manuel, A., Muscholl, A., Puppis, G.: Walking on data words. In: Mogens, N., Branislav, R. (eds.) Computer Science-Theory and Applications, pp. 64–75. Springer, Berlin (2013)
Mezzetti, G.: Nominal context-free behaviour. Ph.D. thesis, University of Pisa (2014)
Minsky, M.L.: Computation: Finite and Infinite Machines. Prentice-Hall, Englewood Cliffs, NJ (1967)
Montanari, U., Pistore, M.: \(\pi \)-calculus, structured coalgebras, and minimal hd-automata. In: Mogens, N., Branislav, R. (eds.) MFCS 2000, LNCS, vol. 1893, pp. 569–578. Springer, Berlin (2000)
Murawski, A.S., Ramsay, S.J., Tzevelekos, N.: Reachability in pushdown register automata. In: Csuhaj-Varjú, E., Dietzfelbinger, M., Ésik, Z. (eds.) Mathematical Foundations of Computer Science 2014 - 39th International Symposium, MFCS 2014, Budapest, Hungary, August 25–29, 2014. Proceedings, Part I, Lecture Notes in Computer Science, vol. 8634, pp. 464–473. Springer, Berlin (2014). doi:10.1007/978-3-662-44522-8_39
Neven, F., Schwentick, T., Vianu, V.: Towards regular languages over infinite alphabets. Math. Found. Comput. Sci. 2001, 560–572 (2001)
Neven, F., Schwentick, T., Vianu, V.: Finite state machines for strings over infinite alphabets. ACM Trans. Comput. Log. (TOCL) 5(3), 403–435 (2004)
Nielson, F., Nielson, H.R., Hankin, C.: Principles of Program Analysis, 1st ed. 1999. corr. 2nd printing, 1999 edn. Springer, Berlin (2005)
Papazoglou, M.P.: Web Services—Principles and Technology. Prentice Hall, Englewood Cliffs (2008). http://vig.pearsoned.com/store/product/1%2C1207%2Cstore-12521_isbn-0321155556%2C00.html
Parys, P.: Higher-order pushdown systems with data. In: Faella, M., Murano, A. (eds.) GandALF, EPTCS, vol. 96, pp. 210–223 (2012)
Perrin, D., Pin, J.: Infinite words: automata, semigroups, logic and games. Pure Appl. Math. 141 (2004)
Pitts, A.M., Stark, I.D.B.: Observable properties of higher order functions that dynamically create local names, or what’s new? In: Andrzej, M.B., Stefan, S. (eds.) MFCS 1993, LNCS, vol. 711, pp. 122–141. Springer, Berlin (1993)
Schneider, F.B.: Enforceable security policies. ACM Trans. Inf. Syst. Secur. (TISSEC) 3(1), 30–50 (2000)
Skalka, C., Smith, S.F., Horn, D.V.: Types and trace effects of higher order programs. J. Funct. Program. 18(2), 179–249 (2008)
Tzevelekos, N.: Fresh-register automata. ACM SIGPLAN Not. 46(1), 295–306 (2011)
Tzevelekos, N., Grigore, R.: History-register automata. In: Pfenning, F. (ed.) Foundations of Software Science and Computation Structures - 16th International Conference, FOSSACS 2013, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2013, Rome, Italy, March 16–24, 2013. Proceedings, vol. 7794, pp. 17–33. Springer, Berlin (2013)
Vardi, M.Y., Wolper, P.: An automata-theoretic approach to automatic program verification. In: LICS, pp. 332–344. IEEE Computer Society (1986)
Acknowledgments
We thank Lillo Galletta, Alexander Kurz, Matteo Sammartino and Nikos Tzevelekos for many helpful discussions and the anonymouos referees for their suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been partially supported by the MIUR PRIN project Security Horizons.
Appendix: Usages
Appendix: Usages
To compare the expressive power of \({\text {PDNA}}_{\pm }\) against \({\text {Usages}}\) we need to extend the expressiveness theorems about \({\text {Usages}}\).
Theorem 9
The language \({\varSigma }^{*}\) is not generated by any \({\text {Usages}}\).
Proof
The proof has the following structure: a new transition system for \({\text {Usages}}\) is given, this is provably equivalent to the original one [7]. Then a few lemmata are proved to provide support for the final argument.
In the following we will use the word redex to identify the source of a transition deduced by only applying an (instance of an) axiom.
Lemma 5
If  and \(\mu h. U\) is its redex, then
and \(\mu h. U\) is its redex, then  .
.
Proof
(By induction on the depth of the proof)
There are two exhaustive cases:
-
Base case: \(U_{0} = \mu h. U \) and the thesis follows easily.
-
Inductive case:
 has been proved by
has been proved by 
by rule (seq) as last step. By the inductive hypothesis we have that
 and the thesis follows easily.
and the thesis follows easily.
\(\square \)
Lemma 6
If  and k is the least index such that \(\mu h . U\) is the redex of
and k is the least index such that \(\mu h . U\) is the redex of  and rule (rec) is never used in reducing \(U_{i}, i < k\) then \(U_{i} = C_{i}[\mu h. U]\) for some \(C_{i}\) and \(a_{k}=\varepsilon \).
and rule (rec) is never used in reducing \(U_{i}, i < k\) then \(U_{i} = C_{i}[\mu h. U]\) for some \(C_{i}\) and \(a_{k}=\varepsilon \).
Lemma 7
Let  be a computation and let k be the least index such that \(\mu h . U\) is the redex of
be a computation and let k be the least index such that \(\mu h . U\) is the redex of  and rule (rec) is never used in reducing \(U_{i}, i < k\) then \(\exists U_{i}' \equiv U_{i}, i < k\) such that
and rule (rec) is never used in reducing \(U_{i}, i < k\) then \(\exists U_{i}' \equiv U_{i}, i < k\) such that  and (rec) is never used reducing \(U_{i}, 0 \le i \le k\).
and (rec) is never used reducing \(U_{i}, 0 \le i \le k\).
Proof
By Lemma 6
\(U_{i} = C_{i}[\mu h . U], i \le k\), also \(\mu h . U\) is never the redex of \(U_{i}, i < k\), hence also  . By Lemma 5
. By Lemma 5
 . \(\square \)
. \(\square \)
Lemma 8
Let  such that
such that  such that
such that  is deduced using (rec) rule.
is deduced using (rec) rule.
Proof
By repeated application of Lemma 7. \(\square \)
Property 7
(of capture avoiding substitutions) Given \(\mu h . U\), if n occurs in the scope of \(\nu n\), then  contains a term \(\nu n'. U', n' \ne n\) and n does not occur in \(U'\).
contains a term \(\nu n'. U', n' \ne n\) and n does not occur in \(U'\).
Proof
Follows because unfolding a recursion is capture-avoiding and all the bound names are different. \(\square \)
For simplicity , we write \(a_{n}\) for the dynamic resource replacing a name n in U when the rule (new) is applied.
Let U with k occurrences of \(\nu n_{i}\) be such that \(\llbracket U \rrbracket = {\varSigma }^{*}\) and let \(s = a_{n_{1}}a_{n_{2}}\dots a_{n_{k+1}}a_{n_{1}}a_{n_{2}}\dots a_{n_{k+1}}\). By Lemma 8, there exists \(U' \equiv U\) such that  with no transition deduced using rule (rec).
with no transition deduced using rule (rec).
Since \(\nu .n_{k+1}\) does not occur in U, then there exists a subterm of U of the form \(\mu h. {\overline{U}}\), with \(\nu n_{i}. U'', (0 < i \le k)\) in \({\overline{U}}\). Therefore, \(U' = U\{\mu h . {\overline{U}} /h\}\) and the replacing term contains \(\nu n_{k+1}. U''\{n_{k+1}/n_{i}\}, n_{k+1}\ne n_{i}\) for some i because our assumption of keeping bound names apart.
Therefore \(\nu n_{k+1}. U''\{n_{k+1}/n_{i}\}\) occurs in \(U'\) for some \(U''\) (by Lemma 8) and \(n_{i}\) does not occur in \(U''\{n_{k+1}/n_{i}\}\). Also \(n_{k+1}\) must occur at least twice in \(U''\{n_{k+1}/n_{i}\}\) and nowhere else. Since \(U''\{n_{k+1}/n_{i}\}\) can not generate \(a_{n_{i}}\), it can not generate \(a_{n_{k+1}}a_{n_{1}}\dots a_{n_{k}}a_{n_{k+1}}\). \(\square \)
Rights and permissions
About this article
Cite this article
Degano, P., Ferrari, GL. & Mezzetti, G. Regular and context-free nominal traces. Acta Informatica 54, 399–433 (2017). https://doi.org/10.1007/s00236-016-0261-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-016-0261-6






 whenever
whenever 

 then
then 
 then
then 


 simultaneously updates two m-registers. In the figure the second component of the configurations, i.e. the word that might be recognised, is omitted for clarity
simultaneously updates two m-registers. In the figure the second component of the configurations, i.e. the word that might be recognised, is omitted for clarity



 iff
iff  and
and 
 and
and 
 symmetric to the previous case.
symmetric to the previous case. then let
then let 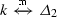 or
or  then let
then let  but
but for some
for some  for all
for all  : condition (1) is trivially satisfied by construction, conditions (2–3) are taken explicitly into account in the construction.
: condition (1) is trivially satisfied by construction, conditions (2–3) are taken explicitly into account in the construction.
 .
.

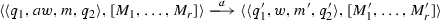
 and
and  . We only prove the case
. We only prove the case 



 and 5.
and 5.  Consider
Consider  Consider the language
Consider the language  and
and 

 .
. (cf. Definition
(cf. Definition 

 iff
iff  and
and and
and  and
and  ,
, 



 The proof of Theorem 8, item 5 suffices (
The proof of Theorem 8, item 5 suffices ( Using their multiple stacks, the DMPA can express the language (of patterns)
Using their multiple stacks, the DMPA can express the language (of patterns)  satisfying the conditions
satisfying the conditions  satisfying the conditions (1m, 2, 3) then by setting for any
satisfying the conditions (1m, 2, 3) then by setting for any  has been proved by
has been proved by 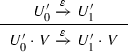
 and the thesis follows easily.
and the thesis follows easily.