Moving from interface theories to assembly theories

Abstract

We show how interface theories supporting pairwise component analysis can be extended in a generic way to a multi-component environment. This leads to the abstract framework of an assembly theory which captures notions of assembly refinement and communication-safety in assemblies of interacting components. An assembly theory supports also encapsulation of assemblies into interfaces and hence hierarchical constructions. We propose general rules that should be satisfied by any concrete assembly theory, like compositional construction and refinement of communication-safe assemblies. We discuss general procedures how to construct an assembly theory on top of a given interface theory such that (some of) the laws of an assembly theory are automatically guaranteed by the properties of an underlying interface theory. As a proof of concept we consider two instances of our approach. The first one starts from the (optimistic) interface theory of interface automata proposed by de Alfaro and Henzinger, and the second one from the (pessimistic) interface theory of modal I/O-interfaces. In the latter case, we propose a new notion of modal assembly refinement which has all the required properties, in particular it preserves modal communication-safety of assemblies. A small case-study illustrates how our concepts can be methodologically applied.

1 Introduction

Reactive software components are commonly understood as encapsulated units which communicate with their environment via well-defined interfaces. Interface specifications provide a means to describe the visible (i.e. black-box) behaviour of a component. They serve, on the one hand, to express what is expected from the environment for a correct functioning of a component, and, on the other hand, to specify what is offered by a component. For the development of component systems on the basis of interfaces we can identify three key issues: the ability to build larger specifications from smaller ones (by composition), the (stepwise) refinement of interface specifications, and compatibility requirements ensuring safe communication of components. Of course, it is important that the different aspects fit properly together, i.e., that refinement is preserved by composition and that compatibility of interfaces is preserved by refinement, thus guaranteeing independent implementability of components. These crucial requirements, that any concrete interface theory should obey, are nicely formulated by the rules of an “interface language” by de Alfaro and Henzinger [16]. It assumes a domain ${\mathcal {F}}$ of interfaces, a (partial) composition operator ${\mathbin {\otimes }} : {\mathcal {F}}\times {\mathcal {F}}\mathrel {\rightharpoonup }{\mathcal {F}}$, a refinement relation ${\mathrel {\preccurlyeq }} \subseteq {\mathcal {F}}\times {\mathcal {F}}$ relating concrete and abstract interface specifications, and a binary compatibility relation ${\sim } \subseteq {\mathcal {F}}\times {\mathcal {F}}$. On this basis, [16] defines the principle of independent implementability as follows:

• Independent implementability:  For all $F_1, F_2, G_1, G_2 \in {\mathcal {F}}$,

•       if $G_1 \sim G_2$ and $F_1 \mathrel {\preccurlyeq }G_1$, $F_2 \mathrel {\preccurlyeq }G_2$,

•       then $F_1 \sim F_2$ and $(F_1 \mathbin {\otimes }F_2) \mathrel {\preccurlyeq }(G_1 \mathbin {\otimes }G_2)$.¹

Particular frameworks satisfying these requirements are formulated for interface automata in [14] and for modal I/O-transition systems in [6, 24]. Some approaches go beyond that and study further operators like conjunction and quotient. For instance, [29] considers conjunction and quotient for modal languages. Lüttgen and Vogler introduce modal interface automata in [27] allowing disjunctive must-transitions. They define parallel composition following the optimistic approach to compatibility of [14], they define conjunction and disjunction and establish compositionality results (which improve shortcomings of other approaches). They also study the pessimistic case to compatibility in [28]. Other papers consider interface theories with relational interfaces and show compositionality results for different kinds of composition, like serial, parallel and feedback compositions; see [31].

Interface theories support the pairwise construction and analysis of components but they do not consider $n$-ary component assemblies which is the standard case in practice. As a consequence, complex systems can only be described by composing interfaces of their constituent parts pairwise, one after the other, to larger interfaces. But this procedure does not lead to a sufficiently rich representation of a component assembly. First, since interfaces are supposed to describe the black-box behaviour of components, we lose architectural information when interfaces are composed. Even more importantly, it is not clear whether a pairwise analysis of components can lead to reliable results for $n$-ary component assemblies. Indeed we will show, that for analysing compatibility of components this is in general not the case. Concerning refinement of a component assembly, the pairwise approach leaves only one option: Each single interface of an assembly must be separately refined and the single refinements must be (successively) composed to obtain a refinement of the whole system. This is guaranteed by the principle of independent implementability stated above. Though independent implementability is clearly an important requirement, it should not be the only way to construct a refinement of an interface assembly. For instance, it is also important that an implementation, say $F$, of a local interface $G$ occurring in an assembly can be correctly substituted by another local implementation, say $F'$, even if $F'$ is not an isolated refinement of $G$, but works well in the context of the rest of the assembly. Such kinds of assembly refinement are more flexible than interface-wise refinement and should also be supported.

In this paper we are interested in a rigorous method for extending the binary, two-component approach of interface theories to a multi-component approach for assemblies. We propose to do this in a generic way that is applicable to any concrete instantiation of an interface theory. For that purpose we first set up general assumptions on interface theories much in the line of the work of de Alfaro and Henzinger; cf. [15, 16]. Then we show how an assembly theory can be constructed on top of a given interface theory such that assemblies are represented by families of interfaces. An assembly theory formalises basic requirements for systems of interacting components. It comprises a communication-safety predicate for expressing the absence of communication errors, a refinement relation for assemblies, and a packing operation for encapsulating assemblies into components thus supporting hierarchical system constructions. Any assembly theory must satisfy compositionality and compatibility laws for communication safety, encapsulation and refinement. We consider canonical assemblies whose communication-safety predicate is uniquely determined by the underlying compatibility relation for interfaces. We show that pairwise compatibility of the interfaces belonging to an assembly is in general not sufficient. Therefore we define communication safety of an assembly in a way which guarantees that any member, say $F_j$, of an assembly $\langle F_i\rangle _{i \in I}$ can communicate in a proper way with the rest of the assembly $\langle F_i\rangle _{i \in I{\setminus } \{j\}}$ forming the environment of $F_j$. This idea has been spelled out already by Liu et al. in [26]: “When we connect a set of components in a network, we need to check whether the types of inputs match the types of outputs connected to them and whether each component’s assumptions about the rest of the system have been met.” Formally, we use the interface compatibility relation to require compatibility of each $F_j$ with the rest of the assembly. We also consider a simple variant of canonical assemblies where the assembly refinement notion is simply obtained from interface-wise refinement of the members of an assembly. The disadvantage of this simple approach is, however, that it does not support context-dependent substitution of interface implementations. Therefore, when building up an assembly theory, we suggest to use the communication-safety notion derived from interface compatibility and to use an individual refinement notion for assemblies.

As a concrete instance of this approach we consider a canonical assembly theory for modal I/O-interfaces and we define the behaviour of an assembly by a modal transition system with distinguished communication labels (representing synchronous communication) and with explicit error states representing erroneous communication. We show that any refinement of an error-free assembly is error-free, which is similarly to Bujtor and Vogler [10] who make error states explicit and require error-freeness for refinements of error-free interface specifications. In our example we consider the so-called pessimistic approach to interaction compatibility where communication safety must be ensured in any environment. As another instance of our framework we consider interface automata which use an optimistic compatibility notion where two communicating partners can rely on a helpful environment that avoids components to run into a communication error.

Relationship to [20] and  [21]. Foundational ideas of this work have been developed in [20] and [21]. In [20] we have studied the concrete case of modal assemblies with a simple form of interface-wise assembly refinement. This has been improved in [21] to support context-dependent refinement. Moreover, [21] proposes an abstract notion of an assembly theory and shows that modal assemblies are an instance. The new approach presented here is a significant enhancement since it describes a method how to construct an assembly theory on top of a given interface theory. It is driven by the idea that certain properties of an assembly theory, like compositionality of communication safety, can be obtained for free from corresponding properties of their underlying interface theory. The key for this development is the notion of a canonical assembly theory. We consider also a default construction leading automatically to a “simple” assembly theory on top of any existing instance of an interface theory.

Synopsis. In Sect. 2 we define the abstract notion of an interface theory and in Sect. 3 we consider two instances: interface automata and modal interfaces. Then, in Sect. 4, we introduce the abstract notion of an assembly theory and we provide guidelines how to derive an assembly theory from an arbitrary interface theory. How this works for interface automata and for modal interfaces is shown in Sect. 5, where we also consider an assembly refinement not based on component-wise refinement. A small case-study is presented in Sect. 6 showing how our concepts can be methodologically applied. In Sect. 7 we discuss related work and in Sect. 8 we finish with some concluding remarks pointing out future research directions.

Dedication. This piece of work is dedicated to Walter Vogler as an appreciation of his extraordinary scientific achievements in the broad field of concurrency theory and distributed systems. We would like to express our thanks to Walter for many, often intensive discussions which brought new insights and led to scientific progress. We are sure that the scientific communication with Walter will continue and we are looking forward to this. Congratulations to your 60th birthday, Walter!

2 Interface theories

The abstract concept of an interface theory defines rudimentary properties that should be satisfied by any formal framework for interface specifications. We assume a class ${\mathcal {F}}$ of interface specifications (interfaces for short). Each interface is supposed to provide a black box specification of a component which shows the functionality of the component for its users. Interface theories provide typically a composition operator $\mathbin {\otimes }$ that allows to combine interfaces to larger ones. For two interfaces $F$ and $G$, their composition $F \mathbin {\otimes }G$ is again an interface and therefore represents a black-box behaviour, more precisely it represents the black-box behaviour of the composition of the two components specified by $F$ and $G$.

The composition operator is, in general, a partial function since it is not always meaningful to compose specifications. We say that two interfaces $F$ and $G$ are composable, if $F \mathbin {\otimes }G$ is defined. Composability is often of syntactic nature. More interesting is the semantic compatibility of two components (concerning, e.g., their interaction behaviour) which is expressed by a binary compatibility predicate $cp$. The compatibility relation is not necessarily symmetric. Thus it is possible to express by $cp (F, G)$, when the communication requirements of one interface $F$ are met by another interface $G$.

An interface theory should support incremental design of compatible systems which is expressed by property (F1) below. It is motivated by the following question: If an interface $F$ is compatible with an interface $G$, can we compose $G$ with another interface, say $H$, such that $F$ is still compatible now with the larger context $G \mathbin {\otimes }H$? The property of incremental design requires that this should indeed be possible, provided that the composition of $F$ and $G$ is compatible with the additional interface $H$. We will show in Sect. 4, Theorem. 2, that this property is crucial for the compositional construction of communication-safe assemblies.

Finally, an interface theory should support stepwise refinement of interfaces. For this purpose we require a reflexive and transitive refinement relation $\mathrel {\preccurlyeq }$ which relates “concrete” and “abstract” specifications. $F \mathrel {\preccurlyeq }G$ means that interface $F$ is a refinement of interface $G$. For compatible interfaces, compatibility of interfaces must be preserved by refinement (property (F2)) and refinement must be compositional, i.e., it must be preserved by the composition operator (property (F3)).

Definition 1

(Interface theory) An interface theory ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ consists of

• a class ${\mathcal {F}}$ of interface specifications;

• a partial composition operator $\mathbin {\otimes }: {\mathcal {F}}\times {\mathcal {F}}\mathrel {\rightharpoonup }{\mathcal {F}}$ which is commutative² and associative³; we call $F$ and $G$ composable if $F \mathbin {\otimes }G$ is defined;

• a compatibility predicate ${ cp } \subseteq {\mathcal {F}}\times {\mathcal {F}}$ such that $cp (F, G)$ implies $F \mathbin {\otimes }G$ defined;

• a reflexive and transitive refinement relation ${\mathrel {\preccurlyeq }} \subseteq {\mathcal {F}}\times {\mathcal {F}}$,

such that for all $F, G, H, F_1, F_2, G_1, G_2 \in {\mathcal {F}}$ the following properties are satisfied:

• F1. Incremental design: If $cp (F, G)$ and $cp (F \mathbin {\otimes }G, H)$, then $cp (F, G \mathbin {\otimes }H)$;

• F2. Preservation of compatibility: If $cp (G_1, G_2)$, $F_1 \mathrel {\preccurlyeq }G_1$, and $F_2 \mathrel {\preccurlyeq }G_2$, then $cp (F_1, F_2)$;

• F3. Compositional refinement for compatible interfaces: If $cp (G_1, G_2)$, $F_1 \mathrel {\preccurlyeq }G_1$, and $F_2 \mathrel {\preccurlyeq }G_2$, then $F_1 \mathbin {\otimes }F_2 \mathrel {\preccurlyeq }G_1 \mathbin {\otimes }G_2$.

Two interfaces $F$ and $G$ are equivalent, written $F \mathrel {\approx }G$, if $F \mathrel {\preccurlyeq }G$ and $G \mathrel {\preccurlyeq }F$.

Preservation of compatibility (F2) together with compositional refinement for compatible interfaces (F3) yield the law of independent implementability; see Sect. 1.

Some interface theories satisfy a stronger version of requirement (F3) such that refinement is preserved by composition even without the assumption that the abstract interfaces are compatible.

Definition 2

(Compositional refinement) An interface theory $({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ supports compositional refinement if for all $F_1, F_2, G_1, G_2 \in {\mathcal {F}}$, if $G_1 \mathbin {\otimes }G_2$ is defined, $F_1 \mathrel {\preccurlyeq }G_1$, and $F_2 \mathrel {\preccurlyeq }G_2$, then $F_1 \mathbin {\otimes }F_2$ is defined and $F_1 \mathbin {\otimes }F_2 \mathrel {\preccurlyeq }G_1 \mathbin {\otimes }G_2$.

Incremental design considers the situation in which larger systems are built from smaller ones. But one may also consider the reverse direction and ask, whether compatibility of an interface with an environment⁴ remains valid when the environment is reduced? This means that the compatibility of an interface $F$ with an environment $G$ is ensured, i.e., $cp (F, G)$, if one can find an interface, say $H$, such that $F$ is compatible with the larger environment $G \mathbin {\otimes }H$, i.e., $cp (F, G \mathbin {\otimes }H)$. Interface theories which satisfy this property are called optimistic. They rely on the existence of a “helpful” environment.

Definition 3

(Optimistic interface theory) An interface theory $({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ is optimistic if for all composable $F, G\in {\mathcal {F}}$ the following holds: If there exists an interface $H \in {\mathcal {F}}$, which is composable with $F$ and with $G$, such that $cp (F, G \mathbin {\otimes }H)$, then $cp (F, G)$.

2.1 Interface theories by de Alfaro and Henzinger

A formal notion of an interface theory was, to our knowledge, first proposed by de Alfaro and Henzinger in [15]. In their work, an interface theory consists of an interface algebra together with a component algebra thus distinguishing between interface specifications and component implementations. Later, in [16], the authors have introduced the term interface language which simplifies the approach by considering just interfaces with the requirements that independent implementability and incremental design are supported. Our notion of an interface theory is very close to an interface language in the sense of [16]. The differences are the following: (1) We require that interface composition is commutative and associative for pairwise composable interfaces. (2) Our compatibility predicate is not required to be symmetric. Hence it can express the communication requirements from the perspective of a single component and it is also applicable for serial compositions, like in [31], where symmetry of compatibility is also not required. (3) Our notion of incremental design is looser than the one of an interface language. This is possible since we can rely on commutativity and associativity of interface composition. Finally, we introduce the notion of an optimistic interface theory. It is inspired by the discussions in [16], based on the idea that compatibility of interfaces should rely on the existence of a helpful environment.

3 Instances of interface theories

3.1 Interface automata

We show that the interface automata by de Alfaro and Henzinger [14, 16] form an interface theory that is optimistic. We first briefly recall the definition of interface automata, their composition, and their refinement in terms of alternating simulation. We follow [16] requiring input determinism for interface automata which ensures associativity and compositionality of alternating simulation for compatible interfaces. However, to distinguish syntactic composability from semantic compatibility, we prefer the approach of [14], in which interface compositions are always defined when they are composable. The composition of composable but not compatible interfaces is empty.

3.1.1 Interface automata, products, and refinement

An interface automaton labelling $L = (I, O, T)$, or IA-labelling for short, consists of pairwise disjoint sets of input labels $I$, output labels $O$, and internal labels $T$. We write ${\bigcup }L$ for the set $I \cup O \cup T$ of all labels of $L$.

An interface automaton ${P = (L, S, V_{0}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}})}$ consists of an IA-labelling $L = (I, O, T)$, a set of states $S$, a set $V_{0} \subseteq S$ of initial states with $|V_{0}| \le 1$, and a transition relation ${{\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}} \subseteq S \times {\bigcup }L \times S}$ that is input-deterministic, i.e., if ${(s, l, s_1) \in {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}}$ and ${(s, l, s_2) \in {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}}$ for $l \in I$, then $s_1 = s_2$. The interface automaton $P$ is empty if $V_{0} = \emptyset$. For an $l \in {\bigcup }L$, we write ${s \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'}$ for ${(s, l, s') \in {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}}$. More generally, for an $X \subseteq {\bigcup }L$, we write $s \mathrel {{\overset{X}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ if either $s = s'$ or there are $s_0, \ldots , s_n \in S$ and $l_0, \ldots , l_{n-1} \in X$ such that $s_0 = s$, $s_n = s'$, and $s_k \mathrel {{\overset{l_k}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s_{k+1}$ for all $0 \le k \le n-1$.

Two IA-labellings $L_1 = (I_1, O_1, T_1)$ and $L_2 = (I_2, O_2, T_2)$ are composable if they overlap only on complementary types, i.e. ${\bigcup }L_1 \cap {\bigcup }L_2 = (I_1 \cap O_2) \cup (I_2 \cap O_1)$; these labels are called shared. The product of two composable IA-labellings $L_1 = (I_1, O_1, T_1)$ and $L_2 = (I_2, O_2, T_2)$ is given by the IA-labelling $L_1 \mathrel {\otimes ^{\mathrm {ia}}}L_2 = ((I_1 {\setminus } O_2) \cup (I_2 {\setminus } O_1), (O_1 {\setminus } I_2) \cup (O_2 {\setminus } I_1), T_1 \cup T_2 \cup ({\bigcup }L_1 \cap {\bigcup }L_2))$. Two interface automata are composable if their IA-labellings are composable.

The product $P \mathrel {\otimes ^{\mathrm {ia}}}Q$ of two composable interface automata interleaves unshared and internal labels and synchronises on shared labels [16, Def. 6]. Formally, the product of ${P = (L_P, S_P, V_{0, P}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}}})}$ and ${Q = (L_Q, S_Q, V_{0, Q}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}}})}$, where $P$ and $Q$ are composable, is given by the interface automaton ${P \mathrel {\otimes ^{\mathrm {ia}}}Q = (L_P \mathrel {\otimes ^{\mathrm {ia}}}L_Q, S_P \times S_Q, V_{0, P} \times V_{0, Q}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}})}$ with ${((s_P, s_Q), l, (s_P', s_Q')) \in {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}}$ if, and only if

• $l \in (I_P {\setminus } O_Q) \cup (O_P {\setminus } I_Q) \cup T_P$ and $s_P \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P'$ and $s_Q = s_Q'$; or

• $l \in (I_Q {\setminus } O_P) \cup (O_Q {\setminus } I_P) \cup T_Q$ and $s_Q \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} s_Q'$ and $s_P = s_P'$; or

• $l \in {\bigcup }L_P \cap {\bigcup }L_Q$ and $s_P \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P'$ and $s_Q \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} s_Q'$.

The refinement $P \mathrel {\preccurlyeq ^{\mathrm {ia}}}Q$ of an interface automaton $Q$ by an interface automaton $P$ is defined by means of an alternating simulation relation from $P$ to $Q$ which relates the initial states of $P$ and $Q$ [16, Def. 11]. An alternating simulation relation from $P$ to $Q$ requires that an input of $Q$ is immediately matched by $P$; an output of $P$ has to be matched by an output in $Q$, but only after an arbitrary number of internal actions from $Q$; and an internal action of $P$ has to be matched by an arbitrary number of internal actions of $Q$. Formally, for ${P = ((I_P, O_P, T_P), S_P, V_{0, P}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}}})}$ and ${Q = ((I_Q, O_Q, T_Q), S_Q, V_{0, Q}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}}})}$ a binary relation $R \subseteq S_P \times S_Q$ is an alternating simulation relation from $P$ to $Q$ if for all $(s_P, s_Q) \in R$

• ${s_Q \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} s_Q' \wedge l \in I_Q \Rightarrow \exists s_P' \in S_P \,.\, s_P \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P' \wedge (s_P', s_Q') \in R}$;

• ${s_P \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P' \wedge l \in O_P \Rightarrow \exists s_Q' \in S_Q \,.\, s_Q \mathrel {{\overset{T_Q}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} {\cdot } \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} s_Q' \wedge (s_P', s_Q') \in R}$;

• ${s_P \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P' \wedge l \in T_P \Rightarrow \exists s_Q' \in S_Q \,.\, s_Q \mathrel {{\overset{T_Q}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{Q}}}} s_Q' \wedge (s_P', s_Q') \in R}$.

$P \mathrel {\preccurlyeq ^{\mathrm {ia}}}Q$ holds if $I_Q \subseteq I_P$ and $O_P \subseteq O_Q$ and there is an alternating simulation relation $R$ from $P$ to $Q$ such that there are $s_{0, P} \in V_{0, P}$ and $s_{0, Q} \in V_{0, Q}$ with $(s_{0, P}, s_{0, Q}) \in R$.

3.1.2 An optimistic interface theory of interface automata

Two composable, non-empty interface automata $P$ and $Q$ are compatible [16, Def. 8], written as $P \mathrel {\sim ^{\mathrm {ia}}}Q$, if no error state of $P \mathrel {\otimes ^{\mathrm {ia}}}Q$ can be reached autonomously from the initial state of $P \mathrel {\otimes ^{\mathrm {ia}}}Q$: An error state of $P \mathrel {\otimes ^{\mathrm {ia}}}Q$ is a state $(s_P, s_Q)$ of the product where $P$ offers an output label in $s_P$ to $Q$ or $Q$ offers an output label in $s_Q$ to $P$, but the other interface automaton does not provide a corresponding input label in $s_Q$ or $s_P$, respectively; a state $(s_P', s_Q')$ is autonomously reachable from a state $(s_P, s_Q)$ if there is a path from $(s_P, s_Q)$ to $(s_P', s_Q')$ using only internal labels and unshared output labels. Obviously, $\mathrel {\sim ^{\mathrm {ia}}}$ is a symmetric relation.

The composition $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q$ [14, Def. 10] of $P$ and $Q$ is defined by restricting the product $P \mathrel {\otimes ^{\mathrm {ia}}}Q$ to the set of those states from which no error state can be reached autonomously (in [16, Def. 9], composition is restricted to compatible interface automata); in particular, if an error state of the product is autonomously reachable from the initial state the composition is an empty interface automaton.

Example 1

Consider the composition of the following two interface automata where the input and output labels of each interface automaton are shown on the surrounding borders and we use a ${\mathsf{! }}$ to indicate that a label is used as an output and a $\mathsf{? }$ to indicate input uses:

After receiving the unshared label $\mathsf{a }$, the interface automaton $\mathsf{P }$ would send out the shared label $\mathsf{b }$ to $\mathsf{Q }$, but $\mathsf{Q }$ will not accept this input. But there exists a helpful environment, which does not send $\mathsf{a }$, such that the error state is not reachable in this environment. Therefore $\mathsf{P }$ and $\mathsf{Q }$ are compatible and their composition $\mathsf{P } \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}\mathsf{Q }$ just consists of an initial state without any transitions. This example also shows that interface automata compatibility does not imply deadlock freedom.

Composition of interface automata is obviously commutative (up to a bijection between states). De Alfaro and Henzinger claim [14, Thm. 1] that composition is also associative, i.e., $(P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q) \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R = P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$ for pairwise composable interface automata $P$, $Q$, and $R$. However, as has been observed by Bujtor and Vogler [10], this only holds for the input-deterministic variant which we consider here and which is also considered in [16].

Moreover, de Alfaro and Henzinger show the properties of preservation of compatibility and compositional refinement for compatible interfaces [16, Thm. 4]. Our notion of incremental design (F1) follows from the associativity of composition: If $P \mathrel {\sim ^{\mathrm {ia}}}Q$ and $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q \mathrel {\sim ^{\mathrm {ia}}}R$, then $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q$ and $R$ are non-empty interface automata, since otherwise compatibility cannot hold. By $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q \mathrel {\sim ^{\mathrm {ia}}}R$, $(P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q) \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$ is also not empty. From associativity, $(P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q) \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R = P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$, we get that $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$ is not empty, and hence $P \mathrel {\sim ^{\mathrm {ia}}}Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$ , since otherwise an error state of $P \mathrel {\otimes ^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$ would be autonomously reachable from its initial state and thus $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$ would be empty (cf. [16, Thm. 3, fn. 2]).

Proposition 1

${\fancyscript{F}}^{\mathrm {ia}}= ({\mathcal {F}}^{\mathrm {ia}}, {\mathbin {\mathbin {\Vert }^{\mathrm {ia}}}}, {\mathrel {\sim ^{\mathrm {ia}}}}, {\mathrel {\preccurlyeq ^{\mathrm {ia}}}})$ with ${\mathcal {F}}^{\mathrm {ia}}$ the class of interface automata⁵ is an interface theory.

Moreover, this interface theory ${\fancyscript{F}}^{\mathrm {ia}}$ of interface automata is also optimistic: Let $P$, $Q$, and $R$ be pairwise composable interface automata with $P \mathrel {\sim ^{\mathrm {ia}}}Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$. Then $P$ and $Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$ are both not empty. Moreover, $P \mathrel {\sim ^{\mathrm {ia}}}Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$ implies that $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R)$ is not empty. From associativity, $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}(Q \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R) = (P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q) \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$, we get that $(P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q) \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}R$ is not empty, and thus, in particular, that $P \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}Q$ is not empty. Hence, $P \mathrel {\sim ^{\mathrm {ia}}}Q$.

3.2 Modal interfaces

We show that a notion of modal interfaces, based on the modal transition systems by Hüttel and Larsen [24, 25], give rise to an interface theory. In contrast to interface automata, modal interface distinguish between transitions which are optional (may) or mandatory (must) and thus yield proper support for loose specifications and refinements.

3.2.1 Modal interfaces, products, and refinement

A modal interface labelling $L = (I, O)$, or MI-labelling for short, consists of two disjoint sets of input labels $I$ and output labels $O$, such that the invisible action $\tau$ is not an element of $I \cup O$. We write ${\bigcup }L$ for the set $I \cup O$ of all labels of $L$.

A modal interface $M = (L, S, s_{0},{\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}},{\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}})$ consists of an MI-labelling $L = (I, O)$, a set of states $S$, an initial state $s_{0} \in S$, a may-transition relation ${\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}} \subseteq S \times ({\bigcup }L \cup \{ \tau \}) \times S$, and a must-transition relation ${\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}} \subseteq {\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}$, i.e., any must-transition is also a may-transition. For $l \in {\bigcup }L \cup \{\tau \}$, we write $s \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ for $(s, l, s') \in {\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}$ and $s \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ for ${(s, l, s') \in {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}}}$. For denoting sequences of transitions that abstract from silent transitions, we use the following notation:

• 1. We write $s \mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ if there is a (possibly empty) sequence of may-transitions from $s$ to $s'$ all labelled by $\tau$, and likewise for must-transitions. For $l \in {\bigcup }L$, we write $s \mathrel {{\overset{\widehat{l}}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ for $s \mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} {\cdot } \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} {\cdot } \mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$, and likewise for must-transitions.

• 2. To express that a sequence of transitions is obtained by an arbitrary order of single transitions involving only labels of a given set $X \subseteq {\bigcup }L$ or the invisible action $\tau$, we write $s \mathrel {{\overset{\widehat{X}}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ for $s \mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} {\cdot } \mathrel {{\overset{\widehat{l}_1}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} \cdots \mathrel {{\overset{\widehat{l}_n}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} {\cdot } \mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}} s'$ with $n \ge 0$ and $l_1, \dots , l_n \in X$, and likewise for must-transitions.

The set of states that are reachable from the initial state $s_{0}$ is denoted by ${\fancyscript{R}}(M)$.

Two MI-labellings $L_1 = (I_1, O_1)$ and $L_2 = (I_2, O_2)$ are composable if $I_1 \cap I_2 = \emptyset = O_1 \cap O_2$. The labels in ${\bigcup }L_1 \cap {\bigcup }L_2 = (I_1 \cap O_2) \cup (I_2 \cap O_1)$ are called shared. The product of two composable MI-labellings $L_1 = (I_1, O_1)$ and $L_2 = (I_2, O_2)$ is given by the MI-labelling $L_1 \mathrel {\otimes ^{\mathrm {mi}}}L_2 = ((I_1 {\setminus } O_2) \cup (I_2 {\setminus } O_1), (O_1 {\setminus } I_2) \cup (O_2 {\setminus } I_1))$. Two modal interfaces are composable if their MI-labellings are composable.

The product $M \mathrel {\otimes ^{\mathrm {mi}}}N$ of two composable modal interfaces $M$ and $N$ is defined analogous to the product of interface automata (see Sect. 3.1) such that transitions with shared actions are performed (only) simultaneously, but here after composition the shared labels become $\tau$. Additionally, a synchronisation transition in $M \mathrel {\otimes ^{\mathrm {mi}}}N$ is a must-transition only if both of the single synchronising transitions are must-transitions. This product of composable modal interfaces is commutative and associative (up to a bijection between states).

The refinement $M \mathrel {\preccurlyeq ^{\mathrm {mi}}}N$ of a modal interface $N$ by a modal interface $M$ expresses that required (must) transitions of the abstract specification $N$ must also occur in the concrete specification $M$, and, conversely, that allowed (may) transitions of the concrete specification $M$ must be allowed by the abstract specification $N$, but can be omitted in the concrete one [23]. Formally, for $M = (L_M, S_M, s_{0, M}, {\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}}}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}}})$ and $N = (L_N, S_N, s_{0, N},{\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}}, {\mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}} )$ a binary relation $R \subseteq S_M \times S_N$ is a weak modal simulation relation from $M$ to $N$ if for all $(s_M, s_N) \in R$ and for all $l_M \in {\bigcup }L_M$ and $l_N \in {\bigcup }L_N$ the following holds:

$$\begin{aligned}&\text {R1.}\qquad \qquad s_N \mathrel {{\overset{l_N}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N' \Rightarrow \exists s_M' \in S_M \,.\,s_M \mathrel {{\mathrel {{\overset{\widehat{l_N}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}}}} s_M' \wedge (s_M', s_N') \in R;\\&\text {R2.}\qquad \qquad s_N \mathrel {{\overset{\tau }{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{A}}}} s_N' \Rightarrow \exists s_M' \in S_M \,.\, s_M\mathrel {{\mathrel {{\overset{\widehat{\tau }}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}}}} s_M' \wedge (s_M', s_N')\in R;\\&\text {R3.}\qquad \qquad s_M \mathrel {{\overset{l_M}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}} s_M' \Rightarrow \exists s_N' \in S_N \,.\, s_N \mathrel {{\mathrel {{\overset{\widehat{l_M}}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}}} s_N' \wedge (s_M', s_N') \in R;\\&\text {R4.}\qquad \qquad s_M \mathrel {{\overset{\tau }{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}} s_M' \Rightarrow \exists s_N' \in S_N \,.\, s_N \mathrel {{\mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}}} s_N' \wedge (s_M', s_N') \in R. \end{aligned}$$

$M \mathrel {\preccurlyeq ^{\mathrm {mi}}}N$ holds if $L_M = L_N$ and there is a weak modal simulation relation $R$ from $M$ to $N$ such that $(s_{0, M}, s_{0, N}) \in R$. $M$ and $N$ are equivalent, written as $M \mathrel {\approx ^{\mathrm {mi}}}N$ if both $M \mathrel {\preccurlyeq ^{\mathrm {mi}}}N$ and $N \mathrel {\preccurlyeq ^{\mathrm {mi}}}M$ hold.

Fig. 1

Product and refinement of modal interfaces

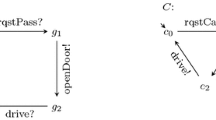
An example of the product and the refinement of modal interfaces is shown in Fig. 1: The shared labels $\mathsf{x }$ and $\mathsf{y }$ are turned into $\tau$ in the product, which in this case can be skipped yielding an equivalent modal interface.

The refinement of modal interfaces is reflexive and transitive, and it is preserved by the product of modal interfaces [20]: For $i \in \{ 1, 2 \}$, let $M_i, N_i$ be modal interfaces such that $M_i \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_i$ and let $M_1$ and $M_2$ be composable. Then $M_1 \mathrel {\otimes ^{\mathrm {mi}}}M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1 \mathrel {\otimes ^{\mathrm {mi}}}N_2$. In fact, this refinement is witnessed by the weak modal simulation relation⁶ $\{ ((s_{1}, s_{2}), (t_{1}, t_{2})) \in (S_{M_1} \times S_{M_2}) \times (S_{N_1} \times S_{N_2}) \mid (s_{1}, t_{1}) \in R_1 \wedge (s_2, t_2) \in R_2 \}$ for weak modal simulation relations $R_i$ from $M_i$ to $N_i$ witnessing $M_i \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_i$ for $i \in \{ 1, 2 \}$ [20, Lem. 2].

3.2.2 An interface theory of modal interfaces

For modal interfaces, we use a notion of compatibility inspired by weak modal compatibility in [6]. This compatibility notion, as well as the (strong) compatibility notions in [14, 16] and [24], are based on the idea that outputs are autonomous and must be accepted by a communication partner while inputs are subject to external choice and need not to be served. Hence, outputs express assumptions of an interface that must be satisfied by corresponding inputs of the environment. For instance, the modal interface $\mathsf{M }_1$ shown in Fig. 2a assumes that the output $\mathsf{x! }$ will always be accepted by the modal interface $\mathsf{M }_2$. This is indeed the case and therefore $\mathsf{M }_1$ is compatible with its environment $\mathsf{M }_2$. In Fig. 2b, however, the interface $\mathsf{M }_2'$ does not match the assumptions of $\mathsf{M }_1'$, since $\mathsf{M }_1'$ can autonomously decide to output $\mathsf{y! }$ which cannot be accepted by the interface $\mathsf{M }_2'$. In both figures we have directly connected the labellings of the modal interfaces to exhibit shared labels.

Fig. 2

Autonomy of outputs. a Compatible modal interfaces. b Incompatible modal interfaces

Strong modal compatibility, pursued by [14, 16] and [24], is based on the idea that whenever one component wants to send an output it finds the communication partner in a state, in which it must take the corresponding input immediately. Weak modal compatibility [6] is more liberal since it is sufficient if the communication partner must accept the message possibly after performing first some silent must-transitions. But simple examples show, see e.g. Example 2 below, that this requirement is still too strong and would fail in many practical applications. Therefore we generalise weak compatibility further and allow the communication partner to take the input only after performing silent must-transitions and/or mandatory open (i.e. non-shared) outputs. This works well because these open outputs are again guaranteed to be taken (possibly after a delay) when further interfaces, meeting the assumptions of the open outputs, are added. A formal justification of this fact will be given in the proof of Theorem 1 below.

Definition 4

(Modal compatibility) Let $M$ and $N$ be composable modal interfaces. $M$ is modally compatible with $N$, written as $cp ^{\mathrm {mi}}(M, N)$, if for each $(s_M, s_N) \in {\fancyscript{R}}(M \mathrel {\otimes ^{\mathrm {mi}}}N)$ and each $l \in O_M \cap I_N$ the following holds with $X = O_N {\setminus } I_M$:

$$\begin{aligned} {\exists s_M' \in S_M \,.\, s_M \mathrel {{\mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}}}} s_M'\ \Rightarrow \ \exists s_N' \in S_N \,.\, s_N \mathrel {{\mathrel {{\overset{\widehat{X}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}}} \cdot \mathrel {{\mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}}}} s_N'.} \end{aligned}$$

Note that modal compatibility is in general not symmetric; e.g., in Fig. 2b, $\lnot cp ^{\mathrm {mi}}(\mathsf{M }_1', \mathsf{M }_2')$ but $cp ^{\mathrm {mi}}(\mathsf{M }_2', \mathsf{M }_1')$.

Example 2

The two interfaces on top of Fig. 1 are modally compatible in both directions. For instance, if the right-hand-side interface is in the state in which it wants to issue $\mathsf{y! }$, it finds the other interface either in the state before it must issue $\mathsf{z! }$ or before it must accept $\mathsf{y? }$. In the latter case, the communication assumptions of the right-hand-side interface are immediately met. But also in the first case, the left-hand-side interface must accept $\mathsf{y? }$ after it has sent the open output $\mathsf{z! }$ (which cannot be dropped in any refinement, since it is a must-transition). This situation would neither be captured by strong nor by weak compatibility.

Modal compatibility is not the same as deadlock-freedom. Indeed deadlock-freedom is neither necessary nor sufficient. For instance, the interfaces in Fig. 2b are not compatible but their composition is deadlock-free. Deadlock-freedom does not take into account here the violation of the communication assumptions of $\mathsf{M }_1'$. In this case, deadlock analysis would not suffice to detect the communication error. On the other hand, the two interfaces in Fig. 3 are trivially compatible. Due to lacking outputs none of the two interfaces has proper assumptions on its environment. There is, however, an immediate deadlock in the composition of the two interfaces, since none of the inputs is served. (Of course one can also imagine other variants of communication correctness where inputs must be served.) As a conclusion, deadlock behaviour of a composed system can, in general, not be identified with the satisfaction of local communication assumptions (of the single components within the system).

Theorem 1

${\fancyscript{F}}^{\mathrm {mi}}= ({{\mathcal {F}}^{\mathrm {mi}}}, {\mathrel {\otimes ^{\mathrm {mi}}}}, { cp ^{\mathrm {mi}}}, {\mathrel {\preccurlyeq ^{\mathrm {mi}}}})$ with ${\mathcal {F}}^{\mathrm {mi}}$ the class of modal interfaces⁷ is an interface theory supporting compositional refinement.

Proof

We have to prove conditions (F1) and (F2) of interface theories and that ${\fancyscript{F}}^{\mathrm {mi}}$ supports compositional refinement, since support for compositional refinement implies condition (F3) and all other requirements, like transitivity of refinement, are obvious. The preservation of refinement by the product of modal interfaces, i.e., that $M_1 \mathrel {\otimes ^{\mathrm {mi}}}M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1 \mathrel {\otimes ^{\mathrm {mi}}}N_2$ is implied by $M_1 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1$ and $M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_2$ for composable modal interfaces $N_1$ and $N_2$, corresponds to the support of compositional refinement in ${\fancyscript{F}}^{\mathrm {mi}}$.

For (F1), incremental design, let $M$, $N$, and $P$ be pairwise composable modal interfaces, let $cp ^{\mathrm {mi}}(M, N)$, and let $cp ^{\mathrm {mi}}(M \mathrel {\otimes ^{\mathrm {mi}}}N, P)$. We have to show that $cp ^{\mathrm {mi}}(M, N \mathrel {\otimes ^{\mathrm {mi}}}P)$. Let $l \in O_M \cap I_{N \mathrel {\otimes ^{\mathrm {mi}}}P}$ and let $(s_M, (s_N, s_P)) \in {\fancyscript{R}}(M \mathrel {\otimes ^{\mathrm {mi}}}(N \mathrel {\otimes ^{\mathrm {mi}}}P))$ such that ${s_M \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M}}}} s_M'}$. We have to prove that there are $(s_N', s_P'), (s_N'', s_P'') \in S_{N \mathrel {\otimes ^{\mathrm {mi}}}P}$ such that

$$\begin{aligned} \textstyle (s_N, s_P) \mathrel {{\overset{{\widehat{X}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N'', s_P'') \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N', s_P'), \end{aligned}$$

with $X = O_{N \mathrel {\otimes ^{\mathrm {mi}}}P} {\setminus } I_M$. Since $M$, $N$, and $P$ are pairwise composable, $l$ is either an input of $N$ or of $P$.

Let $l$ be an input of $N$. We have $(s_M, s_N) \in {\fancyscript{R}}(M \mathrel {\otimes ^{\mathrm {mi}}}N)$ by disregarding communication with $P$. Since $cp ^{\mathrm {mi}}(M, N)$, there is an $s_N' \in S_N$ with ${s_N \mathrel {{\overset{\widehat{Y}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N'' \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N'}$ for some $s_N'' \in S_N$ where $Y = O_N {\setminus } I_M$ which, in particular, does not show any labels for communication with $M$. Using $cp ^{\mathrm {mi}}(M \mathrel {\otimes ^{\mathrm {mi}}}N, P)$, we demonstrate by induction on the length $n$ of the path for ${s_N \mathrel {{\overset{\widehat{Y}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N''}$ that also

$$\begin{aligned} \textstyle (s_N, s_P) \mathrel {{\overset{{\widehat{X}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N'', s_P') \end{aligned}$$

for some $s_P' \in S_P$ from which the claim follows since $l$ is an input of $N$.

Fig. 3

Deadlocking modal interfaces

If $n = 0$, we may choose $s_P' = s_P$. Now let ${s_N\mathrel {{\overset{{\widehat{Y}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N''' \mathrel {{\overset{m}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N}}}} s_N''}$ be a path of length $n+1$ with $m \in Y \cup \{ \tau \}$. By the induction hypothesis, there is an $s_P'' \in S_P$ with

$$\begin{aligned} {\textstyle (s_N, s_P) \mathrel {{\overset{{\widehat{X}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N''', s_P'').} \end{aligned}$$

If $m \in \{ \tau \} \cup (O_N {\setminus } (I_M \cup I_P))$, then the claim is obvious by choosing $s_P' = s_P''$. If $m \in O_N \cap I_P$, then by $cp ^{\mathrm {mi}}(M \mathrel {\otimes ^{\mathrm {mi}}}N, P)$ it follows that there are $s_P', s_P''' \in S_P$ such that ${s_P'' \mathrel {{\overset{{\widehat{Z}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P''' \mathrel {{\overset{m}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P'}$ with $Z = O_P {\setminus } I_{M \mathrel {\otimes ^{\mathrm {mi}}}N}$, that is, without communication to $M \mathrel {\otimes ^{\mathrm {mi}}}N$, and thus

$$\begin{aligned} {\textstyle (s_N''', s_P'') \mathrel {{\overset{{\widehat{X}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N''', s_P''') \mathrel {{\overset{\tau }{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N'', s_P'),} \end{aligned}$$

since $Z \subseteq X$ and $m \in O_N \cap I_P$, and we have established the inductive claim.

Let now $l$ be an input of $P$. By that ${s_P \mathrel {{\overset{{\widehat{Z}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P'' \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}} s_P'}$ with $Z = O_P {\setminus } I_{M \mathrel {\otimes ^{\mathrm {mi}}}N}$, that is, without communication to $M \mathrel {\otimes ^{\mathrm {mi}}}N$. Thus also

$$\begin{aligned} {(s_N, s_P) \mathrel {{\overset{{\widehat{Z}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N, s_P'') \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N \mathrel {\otimes ^{\mathrm {mi}}}P}}}} (s_N, s_P')} \end{aligned}$$

establishing the claim since $Z \subseteq X$.

For condition (F2), preservation of compatibility, let $M_1$, $M_2$, $N_1$, $N_2$ be modal interfaces with $cp ^{\mathrm {mi}}(N_1, N_2)$ and $M_1 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1$, $M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_2$. Let $(s_1, s_2) \in {\fancyscript{R}}(M_1 \mathrel {\otimes ^{\mathrm {mi}}}M_2)$ and $l \in O_{M_1} \cap I_{M_2}$ with ${s_1 \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M_1}}}} s_1'}$ for some $s_1' \in S_{M_1}$. Since $M_1 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1$ and $M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_2$, compositional refinement implies $M_1 \mathrel {\otimes ^{\mathrm {mi}}}M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1 \mathrel {\otimes ^{\mathrm {mi}}}N_2$. Thus there is a $(t_1, t_2) \in {\fancyscript{R}}(N_1 \mathrel {\otimes ^{\mathrm {mi}}}N_2)$ such that $s_1$ and $t_1$ are related by the weak modal simulation relation from $M_1$ to $N_1$. Since ${s_1 \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M_1}}}} s_1'}$ and $M_1 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_1$, using (R3) of weak modal simulation, there are transitions ${ t_1 \mathrel {{\mathrel {{\overset{\widehat{\tau }}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N_1}}}}}} t_1'}$ and ${t_1' \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N_1}}}} t_1''}$ for some $t_1', t_1'' \in S_{N_1}$. In particular, $(t_1', t_2) \in {\fancyscript{R}}(N_1 \mathrel {\otimes ^{\mathrm {mi}}}N_2)$. Since $cp ^{\mathrm {mi}}(N_1, N_2)$, there is a $t_2' \in S_{N_2}$ with ${t_2 \mathrel {{\overset{\widehat{Y}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N_2}}}} \cdot \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{N_2}}}} t_2'}$ with $Y = O_{N_2} {\setminus } I_{N_1}$. But this path of must-transitions is preserved, up to silent must-transitions, under the weak modal simulation relation for $M_2 \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_2$ using (R1) and (R2). Hence $cp ^{\mathrm {mi}}(M_1, M_2)$. $\square$

The modal interface theory is not optimistic; cf. Definition 3. A counter example is given in Fig. 4. Obviously, $cp ^{\mathrm {mi}}(\mathsf{M }, \mathsf{N } \mathrel {\otimes ^{\mathrm {mi}}}\mathsf{P })$, since in the composition of the three interfaces $\mathsf{M }$ will never reach the state in which it wants to send $\mathsf{y! }$, because $\mathsf{P }$ will never send $\mathsf{x! }$ to $\mathsf{M }$. Also $cp ^{\mathrm {mi}}(\mathsf{N }, \mathsf{M } \mathrel {\otimes ^{\mathrm {mi}}}\mathsf{P })$, since $\mathsf{N }$ does not show any requirements. However, if we omit $\mathsf{P }$ and want to check $cp ^{\mathrm {mi}}(\mathsf{M }, \mathsf{N })$, then $\mathsf{x? }$ is an open input in the composition of $\mathsf{M }$ and $\mathsf{N }$ and therefore $\mathsf{M }$ will reach the state in which it wants to send $\mathsf{y! }$. But $\mathsf{N }$ does not accept $\mathsf{y? }$; thus $\mathsf{M }$ is not compatible with $\mathsf{N }$ and $cp ^{\mathrm {mi}}(\mathsf{M }, \mathsf{N })$ does not hold.

Fig. 4

Counter example to optimistic modal interface theory

4 From interface theories to assembly theories

4.1 Assembly theories

We extend the abstract concept of an interface theory ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ by introducing, additionally to the domain ${\mathcal {F}}$ of interfaces, a domain ${\mathcal {A}}$ of assemblies. For this purpose, we assume that each assembly $A \in {\mathcal {A}}$ consists of a family $A = \langle F_i\rangle _{i \in I}$ of pairwise composable interfaces $F_i \in {\mathcal {F}}$ with $I$ finite.

To address behavioural compatibility of the (interacting) components which constitute an assembly, we introduce a communication-safety predicate $cs \subseteq {\mathcal {A}}$ on assemblies. We require that an assembly theory must offer a (partial) packing operation $pack : {\mathcal {A}}\mathrel {\rightharpoonup }{\mathcal {F}}$, which allows us to encapsulate a communication-safe assembly into a component interface by hiding the internals of the assembly. Thus hierarchical assemblies can be constructed by using packed assemblies as their components. Finally, we distinguish between interface and assembly refinement, expressed by the binary relations ${\mathrel {\preccurlyeq }} \subseteq {\mathcal {F}}\times {\mathcal {F}}$ for interfaces and ${\mathrel {\sqsubseteq }} \subseteq {\mathcal {A}}\times {\mathcal {A}}$ for assemblies.

Some crucial properties relating the formation of assemblies, encapsulation, communication safety, and refinement are required for any concrete assembly theory. Property (A1) below requires that assemblies can be constructed hierarchically by packing sub-assemblies into interfaces. (A2) deals with compositionality of communication-safety. If an assembly $A$ is formed by the union of several sub-assemblies, then we can check the communication safety of $A$ by showing (i) that each sub-assembly is itself communication-safe, and (ii) that on the boundaries between the sub-assemblies no communication errors can occur. (The latter is formally expressed by requiring communication safety for the assembly obtained by the packed sub-assemblies). Hence, once the sub-assemblies are locally “fine”, it only remains to consider the interactions on the boundaries between them. This important property supports also efficient communication-safety checking, since in concrete applications it is often possible to consider minimised versions of the packed sub-assemblies. Property (A3) implies that such efficient strategies can also be applied for packing assemblies in a compositional way. Another important property is expressed by (A4) guaranteeing that refinements of communication-safe assemblies are communication-safe. (A5) is straightforward requiring that encapsulation of communication-safe assemblies which are in the assembly refinement relation leads to interfaces which are in interface refinement relation. Finally, (A6) formulates a compositionality requirement for the refinement of communication-safe assemblies. It says that under the same assumptions used for (A2), local refinements of sub-assemblies propagate to global assembly refinement.

Definition 5

(Assembly theory) Let ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ be an interface theory. An assembly theory $({\mathcal {A}}, { cs }, { pack }, {\mathrel {\sqsubseteq }})$ over ${\fancyscript{F}}$ consists of

• the class ${\mathcal {A}}= \{ \langle F_i\rangle _{i \in I} \mid 0 < |I| < \infty \hbox { and }F_i, F_j \in {\mathcal {F}}\hbox { composable for }i \ne j \in I\}$ ⁸ of assemblies;

• a communication-safety predicate $cs \subseteq {\mathcal {A}}$ such that $\langle F \rangle \in cs$ for all $F \in {\mathcal {F}}$; we write $cs (A)$ for $A \in cs$;

• a partial encapsulation operation $pack : {\mathcal {A}}\mathrel {\rightharpoonup }{\mathcal {F}}$, such that $pack (A)$ is defined if $cs (A)$ holds, and $pack (\langle F\rangle ) = F$ for all $F \in {\mathcal {F}}$;

• a reflexive and transitive assembly refinement relation ${\mathrel {\sqsubseteq }} \subseteq {\mathcal {A}}\times {\mathcal {A}}$ with $\langle F\rangle \mathrel {\sqsubseteq }\langle G\rangle$ if $F \mathrel {\preccurlyeq }G$, for all $F, G \in {\mathcal {F}}$,

such that for all $A, B, A_1, \ldots , A_n, B_1, \ldots , B_n \in {\mathcal {A}}$ the following conditions are satisfied:

• A1. Hierarchical construction: if $A = A_1 \uplus \ldots \uplus A_n$ and $cs (A_k)$ for all $k \in \{ 1, \ldots , n \}$, then $\langle pack (A_1), \ldots , pack (A_n) \rangle \in {\mathcal {A}}$.

• A2. Compositionality of communication-safety: if $A = A_1 \uplus \ldots \uplus A_n$, $cs (A_k)$ for all $k \in \{ 1, \ldots , n \}$, and $cs (\langle pack (A_1), \ldots , pack (A_n) \rangle )$, then $cs (A)$.

• A3. Compositionality of encapsulation: if $A = A_1 \uplus \ldots \uplus A_n$, $cs (A_k)$ for all $k \in \{ 1, \ldots , n \}$, and $cs (\langle pack (A_1), \ldots , pack (A_n) \rangle )$, then $pack (A) = pack (\langle pack (A_1), \ldots , pack (A_n) \rangle )$.

• A4. Preservation of communication-safety by refinement: If $A \mathrel {\sqsubseteq }B$ and $cs (B)$, then $cs (A)$.

• A5. Preservation of refinement by encapsulation: If $A \mathrel {\sqsubseteq }B$ and $cs (B)$, then $pack (A) \mathrel {\preccurlyeq } pack (B)$.

• A6. Compositional refinement of communication-safe assemblies: if $A = A_1 \uplus \ldots \uplus A_n$, $B = B_1 \uplus \ldots \uplus B_n$, $cs (\langle pack (B_1), \ldots , pack (B_n) \rangle )$, and $cs (B_k)$ and $A_k \mathrel {\sqsubseteq }B_k$ for all $k \in \{ 1, \ldots , n \}$, then $A \mathrel {\sqsubseteq }B$.

Two assemblies $A$ and $B$ are equivalent, written $A \mathrel {\equiv }B$, if $A \mathrel {\sqsubseteq }B$ and $B \mathrel {\sqsubseteq }A$.

From the laws of an assembly theory it follows that communication-safe assemblies can be constructed in an incremental manner, i.e., by enlarging the assembly by one interface at a time, each time checking that the packed assembly up to now is communication-safe with the additional interface. In fact, we get from (A2):

• Incremental design: Let $A \in {\mathcal {A}}$ be an assembly and let $F \in {\mathcal {F}}$ such that $A \cup \langle F\rangle \in {\mathcal {A}}$. If $cs (A)$ and $cs (\langle pack (A),F \rangle )$, then $cs (A \cup \langle F \rangle )$.

Similarly, the following law of independent implementability is also a consequence of the properties (A5) and (A6) of an assembly theory.

• Independent implementability: Let $A, B \in {\mathcal {A}}$ such that $A \mathrel {\sqsubseteq }B$ and let $F, G \in {\mathcal {F}}$ such that $F \mathrel {\preccurlyeq }G$ and $B \cup \langle G \rangle \in {\mathcal {A}}$. If $cs (B)$ and $cs (\langle pack (B),G \rangle )$, then $A \cup \langle F \rangle \mathrel {\sqsubseteq }B \cup \langle G\rangle$.

Moreover, in each assembly theory interface-wise refinement induces an assembly refinement:

Lemma 1

Let $({\mathcal {A}}, cs , pack , {\mathrel {\sqsubseteq }})$ be an assembly theory over the interface theory $({\mathcal {F}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$. Let $\langle F_i\rangle _{i \in I}, \langle G_i\rangle _{i \in I} \in {\mathcal {A}}$, $cs (\langle G_i\rangle _{i \in I})$, and $F_i \mathrel {\preccurlyeq }G_i$ for all $i \in I$. Then $\langle F_i\rangle _{i \in I} \mathrel {\sqsubseteq }\langle G_i\rangle _{i \in I}$.

Proof

We can apply (A6) since $cs (\langle G_i\rangle )$, $pack (\langle G_i\rangle ) = G_i$, and $\langle F_i\rangle \mathrel {\sqsubseteq }\langle G_i\rangle$ for each $i \in I$.

$\square$

In correspondence with optimistic interface theories, we may also consider optimistic assembly theories.

Definition 6

(Optimistic assembly theory) An assembly theory $({\mathcal {A}}, cs , pack , {\mathrel {\sqsubseteq }})$ over an interface theory $({\mathcal {F}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ is optimistic, if $cs (\langle F_i\rangle _{i \in I})$ implies $cs (\langle F_i\rangle _{i \in J})$ for each $\emptyset \ne J \subseteq I$.

4.2 Canonical assembly theories

To state the general requirements for an assembly theory over a given interface theory ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$, we have used in Def. 5 the underlying class ${\mathcal {F}}$ of interfaces to define assemblies and the interface refinement notion $\mathrel {\preccurlyeq }$ to formulate the requirement (A5). In this section we show that we can use the interface composition operator $\mathbin {\otimes }$ and the interface compatibility relation $cp$, first to derive a communication-safety predicate for assemblies, and then to define an encapsulation operator for packing communication-safe assemblies. For this purpose, we extend the binary operator for interface composition to an $n$-ary composition operator on non-empty, finite families $\langle F_i\rangle _{i \in I}$ of pairwise composable interfaces, i.e., to a composition operator on assemblies, by the following inductive definition:

• $\bigotimes \langle F \rangle = F$,

• $\bigotimes \langle F_i\rangle _{i \in I \uplus \{ j \}} = \bigotimes \langle F_i\rangle _{i \in I} \mathbin {\otimes }F_{j}$.

The order of the composition is irrelevant, since the binary composition of interfaces is commutative and also associative for pairwise composable interfaces.

We are now interested in the definition of an appropriate communication-safety predicate for assemblies by using the compatibility relation $cp$ for interfaces. A first obvious idea would be to consider an assembly $A = \langle F_i\rangle _{i \in I}$ communication-safe if all pairs of interfaces in $A$ are compatible, i.e., if $cp (F_i ,F_j)$ holds for all $i \ne j$. While this may work for some particular compatibility notions, the next two examples show that this idea is in general not applicable.

Example 3

Consider the following assembly of interface automata:

Then (trivially) $\mathsf{P } \mathrel {\sim ^{\mathrm {ia}}}\mathsf{Q }$, $\mathsf{Q } \mathrel {\sim ^{\mathrm {ia}}}\mathsf{R }$ (since interface automata compatibility is optimistic), and also (trivially) $\mathsf{P } \mathrel {\sim ^{\mathrm {ia}}}\mathsf{R }$. But and and also . Hence, for $\mathsf{P }$, the composition $\mathsf{Q } \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}\mathsf{R }$ of the rest of the assembly is not a valid environment since it does not satisfy the environment assumptions of $\mathsf{P }$. (Note that, as illustrated in Example 1, $\mathsf{Q } \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}\mathsf{R }$ consists only of the initial state without any transitions.) Similarly, also for the other interfaces the rest of the assembly is not a valid environment. Thus the assembly $\mathsf{I }$ should be rejected because it is not communication-safe.

Fig. 5

An assembly of modal interfaces which is not communication-safe

Example 4

Consider the assembly $\mathsf{A }'$ of modal interfaces in Fig. 5. The modal interfaces $\mathsf{M }_1$, $\mathsf{M }_2$, and $\mathsf{M }_3'$ are pairwise compatible (in each direction). For instance, $cp ^{\mathrm {mi}}(\mathsf{M }_2, \mathsf{M }_3')$ holds since $\mathsf{M }_3'$ will accept the output $\mathsf{y! }$ of $\mathsf{M }_2$ after it has issued its own open output $\mathsf{z! }$. But $\lnot cp ^{\mathrm {mi}}(\mathsf{M }_2, \mathsf{M }_1 \mathrel {\otimes ^{\mathrm {mi}}}\mathsf{M }_3')$, since there is a circular wait. Hence, $\mathsf{M }_1 \mathrel {\otimes ^{\mathrm {mi}}}\mathsf{M }_3'$ is not a valid environment for $\mathsf{M }_2$ and therefore the assembly $\mathsf{A }'$ cannot be considered communication-safe. Again pairwise checking of compatibility does not suffice to show the communication safety of the assembly.

Another attempt for the definition of communication-safe assemblies could use the incremental construction idea. For instance, one could say that an assembly $A = \langle F,G,H\rangle$ is communication-safe if it can be constructed by first forming a communication-safe sub-assembly of $A$ and then checking that the remaining interface is compatible with the sub-assembly. This definition would, however, not work for pessimistic compatibility as illustrated by the next example. The example shows that there can be communication-safe assemblies for which no incremental construction is possible. Therefore, incremental design should just be a sufficient condition to obtain communication safety but not a necessary one.

Example 5

Let us consider the following assembly of modal interfaces:

Following the idea of modal compatibility, this assembly is communication-safe since for each of its members the rest of the assembly satisfies the communication requirements. For instance, $\mathsf{P }$ wants to issue $\mathsf{y! }$ which is accepted by the rest of the assembly, since after a communication $\mathsf{x }$ between $\mathsf{M }$ and $\mathsf{N }$, $\mathsf{M }$ is ready to receive $\mathsf{y? }$. Similarly the communication requirements of $\mathsf{N }$ are fulfilled by the rest of the assembly (and $\mathsf{M }$ has anyway no output). Now let us try to construct the assembly incrementally. We cannot start with $\mathsf{N }$ and $\mathsf{M }$ since $\lnot cp ^{\mathrm {mi}}(\mathsf{N }, \mathsf{M })$ and therefore the sub-assembly $\langle \mathsf{N }, \mathsf{M }\rangle$ cannot be considered communication-safe. Similarly, we can also not start with $\mathsf{P }$ and $\mathsf{M }$ since $\lnot cp ^{\mathrm {mi}}(\mathsf{P }, \mathsf{M })$. However, we could start with $\langle \mathsf{N }, \mathsf{P }\rangle$ since their labels are disjoint and therefore no communication error can occur. Incremental design would then require to check that the sub-assembly $\langle \mathsf{N }, \mathsf{P }\rangle$ works well with $\mathsf{M }$. But $\langle \mathsf{N }, \mathsf{P }\rangle$ might issue $\mathsf{y! }$ and $\mathsf{M }$ is not able to receive $\mathsf{y? }$ after performing autonomous actions.

We will follow now the idea of Liu et al. [26] stated in the introduction: “When we connect a set of components in a network, we need to check [...] whether each component’s assumptions about the rest of the system have been met.” In our setting this means: For each interface $F_j$ occurring in an assembly $\langle F_i\rangle _{i \in I}$ the rest of the assembly, given by $E_j = \langle F_i\rangle _{i \in I {\setminus } \{ j \}}$, plays the role of the environment for $F_j$. An assembly is communication-safe if each $F_j$ is compatible with its environment $E_j$. For the representation of the behaviour of the environment $E_j$, which is relevant for the communication with $F_j$, we use the $n$-ary composition of the interfaces in $E_j$ and require that $F_j$ is compatible with $\bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}}$. This leads to the following definition of communication safety:

• C1. $cs (\langle F_i \rangle _{i \in I})$ if, and only if, for all $j \in I$, $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{j \}})$.

For an assembly $A = \langle F_i\rangle _{i \in I}$, the composition $\bigotimes \langle F_i\rangle _{i \in I}$ is an interface. For communication-safe assemblies it represents the black box behaviour of the composition of the members of the assembly. Therefore the $n$-ary composition is well-suited to define the encapsulation of communication-safe assemblies into interfaces:

• C2. $pack (\langle F_i\rangle _{i \in I}) = \bigotimes \langle F_i\rangle _{i \in I}$, if ${ cs }(\langle F_i\rangle _{i \in I})$, and undefined otherwise.

Theorem 2

(Canonical assembly theory) Let ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ be an interface theory. Let ${\fancyscript{A}}= ({\mathcal {A}}, { cs }, { pack }, {\mathrel {\sqsubseteq }})$ such that ${\mathcal {A}}$ is defined as in Def. 5, $cs$ is defined by (C1), $pack$ is defined by (C2) and ${\mathrel {\sqsubseteq }} \subseteq {\mathcal {A}}\times {\mathcal {A}}$ is an assembly refinement relation according to Def. 5. Then ${\fancyscript{A}}$ is an assembly theory over ${\fancyscript{F}}$ which we call a canonical assembly theory over ${\fancyscript{F}}$.

Proof

We have to show that the conditions (A1), (A2), and (A3) in Definition 5 follow from the definitions of $cs$ and $pack$. Let $A = \langle F_i\rangle _{i \in I}$, $I = I_1 \uplus \ldots \uplus I_n$, $A_k = \langle F_i \rangle _{i \in I_k}$ and $cs (A_k)$ for $k \in \{ 1, \ldots , n \}$.

For (A1), hierarchical construction, we obviously have

$$\begin{aligned} \textstyle \langle pack (A_1), \ldots , pack (A_n) \rangle = \langle \bigotimes \langle F_i \rangle _{i \in I_1}, \ldots , \bigotimes \langle F_i \rangle _{i \in I_n} \rangle \in {\mathcal {A}}. \end{aligned}$$

For (A2), compositionality of communication-safety, let also $cs (\langle pack (A_1), \ldots , pack (A_n) \rangle )$ hold. We have to prove $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$. Without loss of generality let $j \in I_1$. By definition of $cs$, $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I_1 {\setminus } \{ j \}})$ and $cp ( pack (A_1), \bigotimes \langle pack (A_2), \ldots , pack (A_n) \rangle )$ hold. Since $pack (A_1) = \bigotimes \langle F_i\rangle _{i \in I_1}$, we get $cp (F_j, \langle F_i \rangle _{i \in I_1 {\setminus } \{ j \}} \mathbin {\otimes }\bigotimes \langle pack (A_2), \ldots , pack (A_n) \rangle )$, i.e., $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}})$ by incremental design (F1).

For (A3), compositionality of encapsulation, let again also $cs (\langle pack (A_1), \ldots , pack (A_n) \rangle )$ hold. Then by (A2) $cs (A)$ also holds and we have

$$\begin{aligned}&\textstyle pack (\langle pack (A_1), \ldots , pack (A_n) \rangle ) = pack (\langle \bigotimes \langle F_i \rangle _{i \in I_1}, \ldots , \bigotimes \langle F_i \rangle _{i \in I_n} \rangle )\\&\quad =\textstyle \bigotimes \langle \bigotimes \langle F_i \rangle _{i \in I_1}, \ldots , \bigotimes \langle F_i \rangle _{i \in I_n} \rangle = \bigotimes \langle F_i \rangle _{i \in \bigcup _{1 \le k \le n} I_k} = pack (\langle F_i \rangle _{i \in I}). \end{aligned}$$

$\square$

Proposition 2

Let ${\fancyscript{F}}= ({\mathcal {F}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ be an optimistic interface theory and ${\fancyscript{A}}= ({\mathcal {A}}, cs , pack , {\mathrel {\sqsubseteq }})$ a canonical assembly theory over ${\fancyscript{F}}$. Then ${\fancyscript{A}}$ is optimistic.

Proof

Let $cs (\langle F_i\rangle _{i \in I})$ hold, i.e., $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$, and let $\emptyset \ne J \subseteq I$. If $|J| = 1$, then $cs (\langle F_i\rangle _{i \in J})$ holds, since ${\fancyscript{A}}$ is an assembly theory. Let thus $|J| > 1$ and $j \in J$. Then $cp (F_j, \bigotimes \langle F_i\rangle _{i \in J {\setminus } \{ j \}})$ by the definition of $\bigotimes$ and the optimism of ${\fancyscript{F}}$. $\square$

4.3 Simple assembly theories

Let us now turn to assembly refinement. The question is whether we can also derive a meaningful assembly refinement relation $\mathrel {\sqsubseteq }$ from the interface refinement relation $\mathrel {\preccurlyeq }$. There are two obvious options. The first one is to define assembly refinement $A \mathrel {\sqsubseteq }B$ by requiring $cs (A)$, $cs (B)$, and that $pack (A) \mathrel {\preccurlyeq } pack (B)$ is an interface refinement between the packed assemblies. We consider this option not as meaningful, because packaging assemblies abstracts away all architectural and interaction information that is relevant for an assembly and therefore should be taken into account by an assembly refinement. Another option is to require component-wise refinement of the interfaces of assemblies, i.e., for two assemblies $A = \langle F_i\rangle _{i \in I}$ and $B = \langle G_j\rangle _{j \in J}$ we define:

• C3. $A \mathrel {\sqsubseteq }B \iff I = J \wedge \forall i \in I \,.\, F_i \mathrel {\preccurlyeq }G_i$.

This definition works, see Theorem 3 below, but, in general, it is not flexible enough. The reason is that within the context of an assembly $A$, a single interface $F$ may be replaced by another interface $F'$ and the resulting assembly can still be a valid refinement of the former one, even if $F'$ is not an interface refinement of $F$. This is not surprising since interfaces considered in isolation may substantially differ, but in certain contexts this may be resolved. This observation was, e.g., the motivation for studying component substitutability in component-interaction automata in [13].

Example 6

Consider the following automata $\mathsf{F }$, $\mathsf{G }$ and $\mathsf{G }'$ which may either be interpreted as interface automata or as modal interfaces:

In fact, since the product in both interpretations is closed, ${\mathbin {\mathbin {\Vert }^{\mathrm {ia}}}} = {\mathrel {\otimes ^{\mathrm {mi}}}}$. Obviously, $\mathsf{F } \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}\mathsf{G }' \le \mathsf{F } \mathbin {\mathbin {\Vert }^{\mathrm {ia}}}\mathsf{G }$ with $\le$ either interface automata or modal refinement. But $\mathsf{G }'$ is neither an interface automata refinement of $\mathsf{G }$ nor a modal refinement of $\mathsf{G }$.

As a consequence of these considerations we are interested in assembly refinement relations which do not require component-wise refinement. Following the general rules of an assembly theory we must, however, respect a range in which assembly refinement must be located: Let $({\mathcal {A}}, { cs }, { pack }, {\mathrel {\sqsubseteq }})$ be a canonical assembly theory over the interface theory $({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$. Then for any assemblies $\langle F_i\rangle _{i \in I}$ and $\langle G_i\rangle _{i \in I}$ in ${\mathcal {A}}$ with $cs (\langle G_i\rangle _{i \in I})$ we have the following chain of implications:

$$\begin{aligned} \textstyle (\forall i \in I \,.\, F_i \mathrel {\preccurlyeq }G_i)\ \Rightarrow \ \langle F_i\rangle _{i \in I} \mathrel {\sqsubseteq }\langle G_i\rangle _{i \in I}\ \Rightarrow \ \bigotimes \langle F_i\rangle _{i \in I} \mathrel {\preccurlyeq }\bigotimes \langle G_i\rangle _{i \in I}. \end{aligned}$$

In fact, the upper bound for the assembly refinement $\langle F_i\rangle _{i \in I} \mathrel {\sqsubseteq }\langle G_i\rangle _{i \in I}$ in the implication to the left is the proposition of Lem. 1. The lower bound in the implication to the right follows from property (A5) in Definition 5 and from property (C2) using transitivity of interface refinement.

Finally, let us point out that definition (C3) would indeed always lead to an assembly theory provided that the underlying interface theory supports compositional refinement or is optimistic.

Theorem 3

(Simple assembly theory) Let ${\fancyscript{F}}= ({{\mathcal {F}}}, {\mathbin {\otimes }}, { cp }, {\mathrel {\preccurlyeq }})$ be an interface theory which either supports compositional refinement or is optimistic (or both). Let ${\fancyscript{A}}= ({\mathcal {A}}, { cs }, { pack }, {\mathrel {\sqsubseteq }})$ be a canonical assembly theory over ${\fancyscript{F}}$ such that ${\mathrel {\sqsubseteq }}$ is defined by (C3). Then ${\fancyscript{A}}$ is an assembly theory over ${\fancyscript{F}}$ which we call the simple assembly theory over ${\fancyscript{F}}$.

Proof

We have to show that $\mathrel {\sqsubseteq }$ is a reflexive and transitive assembly refinement relation with $\langle F\rangle \mathrel {\sqsubseteq }\langle G\rangle$ if $F \mathrel {\preccurlyeq }G$ and satisfying (A4), (A5), and (A6) of Definition 5. Reflexivity and transitivity follow from the corresponding assumptions for $\mathrel {\preccurlyeq }$, and that $F \mathrel {\preccurlyeq }G$ implies $\langle F\rangle \mathrel {\sqsubseteq }\langle G\rangle$ holds by definition.

For the requirements of preservation of communication-safety (A4) and refinement encapsulation (A5), let $A = \langle F_i\rangle _{i \in I}$ and $B = \langle G_j\rangle _{j \in J}$ be assemblies with $A \mathrel {\sqsubseteq }B$, i.e., $I = J$ and $F_i \mathrel {\preccurlyeq }G_i$ for all $i \in I$, and let $cs (B)$ hold, i.e., $cp (G_j, \bigotimes \langle G_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$. We have to prove $cs (A)$, i.e., $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$ in order to obtain (A4), and $pack (A) \mathrel {\preccurlyeq } pack (B)$, i.e., $\bigotimes \langle F_i\rangle _{i \in I} \mathrel {\preccurlyeq }\bigotimes \langle G_i\rangle _{i \in I}$ for (A5).

If ${\fancyscript{F}}$ supports compositional refinement, then $\bigotimes \langle F_i\rangle _{i \in I} \mathrel {\preccurlyeq }\bigotimes \langle G_i\rangle _{i \in I}$ immediately follows. If ${\fancyscript{F}}$ is optimistic, then $cs (B)$ implies $cp (G_i, \bigotimes \langle G_j\rangle _{j \in J})$ for all $i \in I$ and $\emptyset \ne J \subseteq I {\setminus } \{ j \}$, and thus inductively $\bigotimes \langle F_i\rangle _{i \in I} \mathrel {\preccurlyeq }\bigotimes \langle G_i\rangle _{i \in I}$ by compositional refinement of compatible interfaces (F3). Hence, in both cases we get (A5). We also have in both cases $\bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}} \mathrel {\preccurlyeq }\bigotimes \langle G_i\rangle _{i \in I {\setminus } \{ j \}}$ for all $j \in I$. Since $cp (G_j, \bigotimes \langle G_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$, preservation of compatibility (F2) induces $cp (F_j, \bigotimes \langle F_i\rangle _{i \in I {\setminus } \{ j \}})$. Hence, we obtain (A4) in both cases.

For compositional refinement of communication-safe assemblies (A6), let $A = \langle F_i\rangle _{i \in I}$, $I = I_1 \uplus \ldots \uplus I_n$, let $B = \langle G_j\rangle _{j \in J}$, $J = J_1 \uplus \ldots \uplus J_n$, $cs (\langle pack (\langle G_j\rangle _{j \in J_1}, \ldots , \langle G_j\rangle _{j \in J_n})\rangle )$, and $cs (\langle G_j\rangle _{j \in J_k})$ and $\langle F_i\rangle _{i \in I_k} \mathrel {\sqsubseteq }\langle G_j\rangle _{j \in J_k}$ for all $k \in \{ 1, \ldots , n \}$. Then $I_k = J_k$ for all $k \in \{ 1, \ldots , n \}$ and $F_j \mathrel {\preccurlyeq }G_j$ for all $j \in J = J_1 \cup \ldots \cup J_n$. Hence $I = J$ and $F_j \mathrel {\preccurlyeq }G_j$ for all $j \in J$ follows. $\square$

5 Instances of assembly theories

5.1 The simple assembly theories of interface automata and modal interfaces

According to Theorem 3, we get immediately a simple assembly theory ${\fancyscript{A}}^{{\mathrm {ia}}}$ of interface automata over the interface theory ${\fancyscript{F}}^{\mathrm {ia}}= ({\mathcal {F}}^{\mathrm {ia}}, {\mathbin {\mathbin {\Vert }^{\mathrm {ia}}}}, {\mathrel {\sim ^{\mathrm {ia}}}}, {\mathrel {\preccurlyeq ^{\mathrm {ia}}}})$, since this interface theory is optimistic, cf. Sect. 3.1. In detail, this simple assembly theory ${\fancyscript{A}}^{{\mathrm {ia}}}= ({\mathcal {A}}^{{\mathrm {ia}}}, { cs ^{{\mathrm {ia}}}}, { pack ^{{\mathrm {ia}}}}, {\mathrel {\mathrel {\sqsubseteq }^{{\mathrm {ia}}}}})$ reads as follows:

• ${\mathcal {A}}^{{\mathrm {ia}}}= \{ \langle P_i\rangle _{i \in I} \mid 0 < |I| < \infty \hbox { and }P_i, P_j \in {\mathcal {F}}^{\mathrm {mi}}\hbox { composable for }i \ne j \in I \}$

• $cs ^{{\mathrm {ia}}}(\langle P_i\rangle _{i \in I})$ if, and only if, $P_j \mathrel {\sim ^{\mathrm {ia}}}\big \Vert ^{\mathrm {ia}}\langle P_i\rangle _{i \in I {\setminus } \{ j \}}$ for all $j \in I$

• $pack ^{{\mathrm {ia}}}(\langle P_i\rangle _{i \in I}) = \big \Vert ^{\mathrm {ia}}\langle P_i\rangle _{i \in I}$

• $\langle P_i\rangle _{i \in I} \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {ia}}}}\langle Q_j\rangle _{j \in J}$ if, and only if, $I = J$ and $P_i \mathrel {\preccurlyeq ^{\mathrm {ia}}}Q_i$ for all $i \in I$

The assembly theory ${\fancyscript{A}}^{{\mathrm {ia}}}$ is optimistic by Proposition 2.

We also can construct a simple assembly theory ${\fancyscript{A}}^{{\mathrm {mi}}}$ of modal interfaces over the modal interface theory ${\fancyscript{F}}^{\mathrm {mi}}= ({\mathcal {F}}^{\mathrm {mi}}, {\mathrel {\otimes ^{\mathrm {mi}}}}, { cp ^{\mathrm {mi}}}, {\mathrel {\preccurlyeq ^{\mathrm {mi}}}})$, since this interface theory supports compositional refinement, cf. Theorem 1. Spelled out, this simple assembly theory ${\fancyscript{A}}^{{\mathrm {mi}}}= ({\mathcal {A}}^{{\mathrm {mi}}}, { cs ^{{\mathrm {mi}}}}, { pack ^{{\mathrm {mi}}}}, {\mathrel {\mathrel {\sqsubseteq }^{{\mathrm {mi}}}}})$ consists of

• ${\mathcal {A}}^{{\mathrm {mi}}}= \{ \langle M_i\rangle _{i \in I} \mid 0 < |I| < \infty \hbox { and }M_i, M_j \in {\mathcal {F}}^{\mathrm {mi}}\hbox { composable for }i \ne j \in I \}$

• $cs ^{{\mathrm {mi}}}(\langle M_i\rangle _{i \in I})$ if, and only if, $cp ^{\mathrm {mi}}(M_j, \bigotimes ^{\mathrm {mi}}\langle M_i\rangle _{i \in I {\setminus } \{ j \}})$ for all $j \in I$

• $pack ^{{\mathrm {mi}}}(\langle M_i\rangle _{i \in I}) = \bigotimes ^{\mathrm {mi}}\langle M_i\rangle _{i \in I}$

• $\langle M_i\rangle _{i \in I} \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {mi}}}}\langle N_j\rangle _{j \in J}$ if, and only if, $I = J$ and $M_i \mathrel {\preccurlyeq ^{\mathrm {mi}}}N_i$ for all $i \in I$

Figure 6 shows the pictorial representation of a modal assembly consisting of three pairwise composable modal interfaces $\mathsf{M }_1$, $\mathsf{M }_2$, and $\mathsf{M }_3$ which is modally communication-safe, i.e., $cs ^{{\mathrm {mi}}}(\langle \mathsf{M }_1, \mathsf{M }_2, \mathsf{M }_3\rangle )$.

Fig. 6

A communication-safe modal assembly

The assembly $\mathsf{A }'$ in Fig. 5, which is a slight variant of the assembly in Fig. 6 such that the order of the input $\mathsf{y? }$ and output $\mathsf{z! }$ in $\mathsf{M }_3$ is reversed, is not communication-safe, since $\lnot cp ^{\mathrm {mi}}(\mathsf{M }_2, \mathsf{M }_1 \mathrel {\otimes ^{\mathrm {mi}}}\mathsf{M }_3')$, cf. Example 4. The product $\bigotimes ^{\mathrm {mi}}\mathsf{A }'$ would just consist of the initial state without transitions. This shows, that if an assembly $A$ is not (modally) communication-safe, the product $\bigotimes ^{\mathrm {mi}}A$ does not reflect this serious issue, as dangling outputs are simply ignored. In this sense, the product $\bigotimes ^{\mathrm {mi}}A$ is not a proper representation of the full behaviour of the assembly. Also communications within members of the assembly are not shown in $\bigotimes ^{\mathrm {mi}}A$, since the product turns communication labels into the silent, invisible action $\tau$. For understanding the semantics of an assembly we need, however, a faithful behaviour representation with visible communications which will be considered in the next section.

5.2 A modal assembly theory based on assembly behaviours

We now build another canonical assembly theory over the interface theory $({\mathcal {F}}^{\mathrm {mi}}, {\mathrel {\otimes ^{\mathrm {mi}}}}, { cp ^{\mathrm {mi}}}, {\mathrel {\preccurlyeq ^{\mathrm {mi}}}})$ of modal interfaces, which keeps the notion of assemblies ${\mathcal {A}}^{{\mathrm {mi}}}$, communication-safety $cs ^{{\mathrm {mi}}}$, and encapsulation $pack ^{{\mathrm {mi}}}$ of the simple modal assembly theory ${\fancyscript{A}}^{{\mathrm {mi}}}$, but replaces the refinement relation $\mathrel {\mathrel {\sqsubseteq }^{{\mathrm {mi}}}}$ by a more flexible notion based on an explicit definition of the behaviour of modal assemblies. This notion of behaviour on the one hand indeed shows communication errors and also keeps communication labels separated from the silent action $\tau$.

5.2.1 Modal I/O-transition systems

Modal I/O-transition systems, or MIOs for short, slightly generalise the notion of modal interfaces in Sect. 3.2 by extending the possible labellings to include communication labels.

Thus a MIO-labelling $L = (I, O, C)$ consists of pairwise disjoint sets of input labels $I$, output labels $O$, and communication labels $C$ such that the invisible action $\tau$ is not an element of $I \cup O \cup C$. The definition of a MIO is the same as the one of a modal interface only changing the labellings. Two MIO-labellings are composable if they are composable in the sense of IA-labellings the communication labels playing the role of internal labels. The product $M \otimes ^{\mathrm {m}}N$ of two composable MIOs is the same as the product of modal interfaces, but, like in interface automata, shared labels are not turned into $\tau$ but become communication labels. Also the refinement $M \mathrel {\preccurlyeq ^{\mathrm {m}}}N$ of a MIO $N$ by a MIO $M$ is defined just as the refinement of modal interfaces; in particular, and in contrast to interface automata, communication labels are not abstracted away in the refinement, but have to be preserved. Finally, we introduce a hiding operator $\xi$ from MIO-labellings to MI-labellings that forgets the communication labels, i.e., $(I, O, C)\xi = (I, O)$, and lift this hiding to an operator from MIOs to modal interfaces such that $M\xi$ has $L_M\xi$ as its labelling and all communication labels occurring in the MIO $M$ are turned into $\tau$. Obviously, $M \mathrel {\preccurlyeq ^{\mathrm {m}}}N$ implies $M\xi \mathrel {\preccurlyeq ^{\mathrm {mi}}}N\xi$.

5.2.2 Communication errors in modal assemblies

Based on MIOs, we consider an explicit notion of communication errors in a modal assembly. We extend MIOs by error states and define the behaviour of a modal assembly as such a MIO with error states which record these communication errors. For a modal assembly $A$ we define $\bigotimes ^{\mathrm {m}}A$ inductively by $\bigotimes ^{\mathrm {m}}\langle M\rangle = M$ ⁹ and $\bigotimes ^{\mathrm {m}}\langle M_i\rangle _{i \in I \uplus \{ j \}} = \bigotimes ^{\mathrm {m}}\langle M_i\rangle _{i \in I} \otimes ^{\mathrm {m}}M_j$.

Definition 7

(Communication errors) Let $A = \langle M_i\rangle _{i \in I}$ be a modal assembly. If $|I| = 1$, then the set of communication errors ${\fancyscript{E}}(A) = \emptyset$. Otherwise, for each $j \in I$, let $E_j = \bigotimes ^{\mathrm {m}}\langle M_i\rangle _{i \in I {\setminus } \{ j \}}$. Then the communication errors ${\fancyscript{E}}(A)$ are given by the set of pairs $((s_i)_{i \in I}, l)$ such that $(s_i)_{i \in I} \in {\fancyscript{R}}(\bigotimes ^{\mathrm {m}}A)$ and there is $j \in I$ with $l \in O_{M_j} \cap I_{E_j}$, a state $s_j' \in S_{M_j}$ with ${s_j \mathrel {{\overset{l}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{M_j}}}} s_j'}$ but there are no transitions

$$\begin{aligned} {\textstyle (s_i)_{i \in I \setminus \{ j \}} \mathrel {{\overset{{\widehat{X_j}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{E_j}}}} \cdot \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{E_j}}}} (s_i')_{i \in I \setminus \{ j \}}} \end{aligned}$$

with $X_{j} = C_{E_j} \cup (O_{E_j} {\setminus } I_{M_j})$.¹⁰

A communication error shows two pieces of information: in which state and for which output an offered communication has no corresponding input. Note that only communication errors occurring in the reachable part of $\bigotimes ^{\mathrm {m}}A$ are considered.

Comparing the definition of communication errors of a modal assembly with the definition of the communication-safety predicate for modal assemblies in Sect. 5.1, we immediately get.

Lemma 2

Let $A \in {\mathcal {A}}^{{\mathrm {mi}}}$. Then $cs ^{{\mathrm {mi}}}(A)$ if, and only if, ${\fancyscript{E}}(A) = \emptyset$.

Definition 8

(MIOs with error states) A MIO with error states (EMIO) is a pair $(M, E)$ consisting of a MIO $M$ and a set of error states $E \subseteq S_M$. The reachable states of $(M,E)$ are the reachable states of $M$, i.e. ${\fancyscript{R}}(M,E) = {\fancyscript{R}}(M)$.

The error composition of MIOs is obtained by taking their product enriched by error states (if there are any) which are then reached by the unsuccessful communication labels $l$. The idea is similar to the consent operator introduced in [1] to compose languages by indicating communication errors in traces.

Definition 9

(Error composition of MIOs) Let $A = \langle M_i\rangle _{i \in I}$ be a modal assembly and let $P = \bigotimes ^{\mathrm {m}}A$. The error composition of $A$ is given by the EMIO

$$\begin{aligned} {\textstyle \bigotimes ^{\mathrm {err}}A = ((L_P, S_P \cup {\fancyscript{E}}(A), s_{0, P}, \mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}, \mathrel {{\overset{}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}}), {\fancyscript{E}}(A))} \end{aligned}$$

with may-transition relation ${{\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{}}}}} = {\mathrel {{\overset{}{\dashrightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{P}}}}} \cup \{(p, l, (p, l)) \mid (p, l) \in {\fancyscript{E}}(A) \}}$.

The behaviour of a modal assembly is given by the error composition of the modal interfaces of the assembly. It may also be considered as the semantics of the assembly. If no communication error is reachable in the assembly behaviour, the assembly is communication-safe.

Definition 10

(Behaviour of a modal assembly) The behaviour of a modal assembly $A \in {\mathcal {A}}^{{\mathrm {mi}}}$ is given by ${ beh }(A) = \bigotimes ^{\mathrm {err}}A$.

As an example, consider the assembly $\mathsf{A }$ in Fig. 6 and its (reachable) behaviour shown in Fig. 7, where we indicate communication labels at the lower border. The assembly is communication-safe since there is no reachable error state. In fact all interfaces will be able to send their messages, possibly after a delay. For instance, $\mathsf{M }_1$ can send $\mathsf{x }$ to $\mathsf{M }_2$ after $\mathsf{M }_2$ has communicated the message $\mathsf{y }$ to $\mathsf{M }_3$.

Fig. 7

Behaviour of the assembly $\mathsf{A }$ in Fig. 6

Reconsider now the assembly $\mathsf{A }'$ of Fig. 5. The EMIO representing the (reachable) behaviour of $\mathsf{A }'$ is shown in Fig. 8; it contains three reachable error states. These are induced by the cyclic wait of the single interfaces in $\mathsf{A }'$. Hence the assembly $\mathsf{A }'$ is not communication-safe.

Fig. 8

Behaviour of the assembly $\mathsf{A }'$ in Fig. 5

The encapsulation of a modal assembly $A$ that shows no communication errors amounts to hiding the communication labels in the behaviour of $A$.

Lemma 3

Let $A \in {\mathcal {A}}^{{\mathrm {mi}}}$ be a modal assembly and $(M, E) = { beh }(A)$. Then $E = \emptyset$ implies $pack ^{{\mathrm {mi}}}(A) = M\xi$.

Let us demonstrate how the principle of incremental design (see Sect. 4), which is a consequence of (A2), works for the example assembly $\mathsf{A }$ in Fig. 6 in terms of behaviours. We start with the assembly $\bar{\mathsf{A }} = \langle \mathsf{M }_1, \mathsf{M }_2 \rangle$. The behaviour of this assembly is shown in Fig. 9a. Obviously, $\bar{\mathsf{A }}$ is communication-safe. We now want to add the interface $\mathsf{M }_3$ to $\bar{\mathsf{A }}$. First, we pack the assembly $\bar{\mathsf{A }}$ which yields the modal interface $pack ^{{\mathrm {mi}}}(\bar{\mathsf{A }})$ shown in Fig. 9b. Then we consider the assembly $\bar{\mathsf{C }} = \langle pack ^{{\mathrm {mi}}}(\bar{\mathsf{A }}), \mathsf{M }_3 \rangle$ whose behaviour is shown in Fig. 9c. Obviously $\bar{\mathsf{C }}$ is communication-safe and therefore, by the law of incremental design, the assembly $\mathsf{A } = \langle \mathsf{M }_1, \mathsf{M }_2, \mathsf{M }_3 \rangle$ is also communication-safe. The incremental communication-safety check would, in general, be much more efficient if we would minimise packed assemblies w.r.t. silent transitions. This would be sound due to the laws for (weak) modal assembly refinement considered below.

Fig. 9

Modal behaviours for assembly $\mathsf{A }$ in Fig. 6. a Behaviour of assembly $\bar{\mathsf{A }}$. b Modal interface $pack ^{{\mathrm {mi}}}(\bar{\mathsf{A }})$. c Behaviour of assembly $\bar{\mathsf{C }}$

Consider once more the assembly $\mathsf{A }'$ in Fig. 5 and assume that we want to construct it in an incremental way. Then we could start again with the assembly $\bar{\mathsf{A }} = \langle \mathsf{M }_1, \mathsf{M }_2 \rangle$ which is communication-safe. But now, for adding the interface $\mathsf{M }_3'$, we have to consider the assembly $\bar{\mathsf{C }}' = \langle pack ^{{\mathrm {mi}}}(\bar{\mathsf{A }}), \mathsf{M }_3' \rangle$ and to check communication-safety. The behaviour of $\bar{\mathsf{C }}'$ is shown in Fig. 10; it has two error states. Hence, the incremental design step would not succeed and anyway, as we know from before, the assembly $\mathsf{A }'$ is not communication-safe.

Fig. 10

Behaviour of assembly $\bar{\mathsf{C }}'$

Conversely, we cannot deduce from the communication safety of an assembly $A \cup B$ that (i) $\langle pack ^{{\mathrm {mi}}}(A), pack ^{{\mathrm {mi}}}(B) \rangle$ is communication-safe and we can also not deduce that (ii) the sub-assemblies $A$, $B$ are communication-safe. Hence the converse direction of (A2) does not hold. A counter-example for (i) is shown in Fig. 11a. We can observe that the assembly $\mathsf{C }_1$ is communication-safe; its (reachable) behaviour, see Fig. 11b, contains no reachable error states. If we pack the sub-assembly $\langle \mathsf{N }, \mathsf{P } \rangle$ we obtain the modal interface shown in Fig. 11c. But the assembly $\langle \mathsf{M }, pack ^{{\mathrm {mi}}}(\langle \mathsf{N }, \mathsf{P } \rangle ) \rangle$ is not communication-safe. The reason is that $pack ^{{\mathrm {mi}}}(\langle \mathsf{N }, \mathsf{P } \rangle )$ has an output $\mathsf{y! }$ in its initial state, but the interface $\mathsf{M }$ can never accept this particular output as an input. It can only perform an $\mathsf{x }$-communication with $pack ^{{\mathrm {mi}}}(\langle \mathsf{N }, \mathsf{P } \rangle )$ and then accept “another” $\mathsf{y! }$ output of $pack ^{{\mathrm {mi}}}(\langle \mathsf{N }, \mathsf{P } \rangle )$ issued in another state.

Fig. 11

Counter-example for (i). a Modal assembly $\mathsf{C }_1$. b Behaviour of assembly $\mathsf{C }_1$. c Modal interface $pack ^{{\mathrm {mi}}}(\langle \mathsf{N }, \mathsf{P }\rangle )$

A counter-example for (ii) is shown in Fig. 12. The whole assembly $\mathsf{C }_2$ is communication-safe, but the sub-assembly $\langle \mathsf{N }, \mathsf{M }' \rangle$ is not. The reason is that $\mathsf{N }$ has an output $\mathsf{y! }$ in its initial state, but $\mathsf{M }'$ has an open input $\mathsf{x? }$ before it can accept $\mathsf{y? }$ which is not allowed. (Inputs are not subject to internal choice and we cannot be sure that an environment will serve this input.)

Fig. 12

Counter-example for (ii)

5.2.3 Behaviour refinement of modal assemblies

For the refinement of modal assemblies we compare their behaviours. Since assembly behaviours are MIOs with error states, we first extend the refinement notion for MIOs to EMIOs, such that error states are respected by the refinement relation.

Definition 11

(Refinement of MIOs with error states) Let $(M_A, E_A)$ and $(M_B, E_B)$ be two EMIOs. $(M_A, E_A)$ is a refinement of $(M_B, E_B)$, if $M_A \mathrel {\preccurlyeq ^{\mathrm {m}}}M_B$ witnessed by a weak modal simulation relation $R \subseteq ((S_{M_A} {\setminus } E_A) \times (S_{M_B} {\setminus } E_B)) \cup (E_A \times E_B)$ with $(s_{0, M_A}, s_{0, M_B}) \in R$.

Definition 12

(Behaviour refinement of modal assemblies) A modal assembly $A$ behaviourally refines a modal assembly $B$, written as $A \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}B$, if ${ beh }(A)$ is a refinement of ${ beh }(B)$.

This behavioural refinement of modal assemblies is not restricted to interface-wise refinement, as motivated in Ex. 6. Still, it yields a canonical assembly theory over the modal interface theory:

Theorem 4

$({\mathcal {A}}^{{\mathrm {mi}}}, { cs ^{{\mathrm {mi}}}}, { pack ^{{\mathrm {mi}}}}, {\mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}})$ is a canonical assembly theory over ${\fancyscript{F}}^{\mathrm {mi}}$.

Proof

It remains to check that the conditions (A4), (A5) and (A6) of an assembly theory are satisfied, since that $M \mathrel {\preccurlyeq ^{\mathrm {mi}}}N$ implies $\langle M\rangle \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}\langle N\rangle$ is obvious.

(A4): Let $A \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}B$ and $cs ^{{\mathrm {mi}}}(B)$. Let $(M_A, E_A) = { beh }(A) = \bigotimes ^{\mathrm {err}}A$ and $(M_B, E_B) = { beh }(B) = \bigotimes ^{\mathrm {err}}B$. If an error state in $E_A$ would be reachable in $M_A$, then $A \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}B$ would imply that some error state in $E_B$ is also reachable in $M_B$ since error states must be related to error states by a refinement. Thus $cs ^{{\mathrm {mi}}}(A)$ holds by Lemma 2.

(A5): Let $A \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}B$ and $cs ^{{\mathrm {mi}}}(B)$. Let $(M_A, E_A) = { beh }(A)$ and $(M_B, E_B) = { beh }(B)$. Then $cs ^{{\mathrm {mi}}}(B)$ implies $E_B = \emptyset$, and thus $E_A = \emptyset$ since $A \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}B$. Furthermore, $M_A \mathrel {\preccurlyeq ^{\mathrm {m}}}M_B$ implies $M_A\xi \mathrel {\preccurlyeq ^{\mathrm {mi}}}M_B\xi$, i.e., $pack ^{{\mathrm {mi}}}(A) \mathrel {\preccurlyeq ^{\mathrm {mi}}} pack ^{{\mathrm {mi}}}(B)$ by Lemma 3.

(A6): By Lemma 2, Lemma 3, and (A2) it suffices to prove the following: Let $A = \langle M_i\rangle _{i \in I}$ and $B = \langle N_j\rangle _{j \in J}$ be modal assemblies. Let $I = I_1 \uplus \ldots \uplus I_n$ and $J = J_1 \uplus \ldots \uplus J_n$. Let $A_k = \langle M_i\rangle _{i \in I_k}$, $B_k = \langle N_j\rangle _{j \in J_k}$, ${\fancyscript{E}}(A_k) = \emptyset$, ${\fancyscript{E}}(B_k) = \emptyset$ for all $k \in \{ 1, \ldots , n \}$. Let $P_k = \bigotimes ^{\mathrm {m}}A_k$, $Q_k = \bigotimes ^{\mathrm {m}}B_k$, and $P_k \mathrel {\preccurlyeq ^{\mathrm {m}}}Q_k$ for $k \in \{ 1, \ldots , n \}$. Let ${\fancyscript{E}}(\langle Q_1\xi , \ldots , Q_n\xi \rangle ) = \emptyset$. Then ${\fancyscript{E}}(\langle P_1\xi , \ldots , P_n\xi \rangle ) = \emptyset$.

Let $j \in \{ 1, \ldots , n \}$. Assume for a contradiction that there is a communication error $((p_k)_{1 \le k \le n}, l) \in {\fancyscript{E}}(\langle P_1\xi , \ldots , P_n\xi \rangle )$ with $l \in O_{P_j\xi } \cap I_{E_j}$ with $E_j = \bigotimes ^{\mathrm {m}}\langle P_k\xi \rangle _{1 \le k \ne j \le n}$. Let $X_j = C_{E_j} \cup (O_{E_j} {\setminus } I_{P_j\xi })$. Without loss of generality, we can assume that $j = 1$. By $P_k \mathrel {\preccurlyeq ^{\mathrm {m}}}Q_k$ and consequently $P_k\xi \mathrel {\preccurlyeq ^{\mathrm {mi}}}Q_k\xi$ for all $k \in \{ 1, \ldots , n \}$, we have that $\bigotimes ^{\mathrm {m}}\langle P_k\xi \rangle _{1 \le k \le n} \mathrel {\preccurlyeq ^{\mathrm {m}}}\bigotimes ^{\mathrm {m}}\langle Q_k\xi \rangle _{1 \le k \le n}$ and thus there is a state $(q_k)_{1 \le k \le n} \in S_{\bigotimes ^{\mathrm {m}}\langle Q_k\xi \rangle _{1 \le k \le n}}$ which is related to $(p_k)_{1 \le k \le n}$ in the weak modal simulation relation. In particular, the may-output $l$ is also present at $(q_k)_{1 \le k \le n}$ and thus ${(q_k)_{2 \le k \le n} \mathrel {{\overset{{\widehat{Y_j}}}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{F_{j}}}}} \cdot \mathrel {{\overset{l}{\rightarrow }\!\!\!{\genfrac{}{}{0.0pt}1{}{F_{j}}}}} (q_k')_{2 \le k \le n}}$ with $F_j = \bigotimes ^{\mathrm {m}}\langle Q_k\xi \rangle _{2 \le k \le n}$ and $Y_j = C_{F_j} \cup (O_{F_j} {\setminus } I_{Q_j\xi })$. But this series of must-transitions is also available in $E_1$. $\square$

6 Case-study: a modal cash desk assembly

We illustrate how our techniques for modal interfaces and modal assemblies work for the development of a (small) component system. We consider a simple cash desk application, inspired by [30]: At a cash desk, all the sale items of a customer are registered and their data printed out on the cash register roll; afterwards the grand total is printed and the customer may pay in cash or by credit card.

Fig. 13

Overview of top-down development of the cash desk application

Figure 13 gives an overview of the different steps in a top-down development of such a cash desk system. We first capture the abstract requirements of the whole system in a modal interface CashDesk. In the next step, we develop an architecture as a modal assembly CashDeskAssembly and show its modal communication-safety. In order to verify the correctness of the chosen architecture w.r.t. the requirements we have to prove that its encapsulated modal interface refines the modal interface CashDesk (proof obligation (1) in Fig. 13). Now we replace two of the modal interfaces inside of CashDeskAssembly, namely CashDeskController by CashDeskController’ and ClearingCompany by ClearingCompany’, and prove that the resulting modal assembly CashDeskAssemblyRef is a refinement of CashDeskAssembly (proof obligation (2)). From this we infer two properties: First, since assembly refinement preserves communication-safety, CashDeskAssemblyRef is also communication-safe. Secondly, by preservation of refinement by encapsulation, the modal interface obtained by packing CashDeskAssemblyRef is a modal interface refinement of the packed original assembly, i.e. (3) holds. By transitivity of refinement, (1) and (3) compose to a refinement of CashDesk by the packed assembly CashDeskAssemblyRef.

Requirements specification. We start by an abstract requirements specification of the whole system which is given by the modal interface CashDesk in Fig. 14. The specification is rather loose having only a single must-transition requiring cash payment to be possible in any system implementation whenever a printTotal! has been performed before. The other transitions are may-transitions. At the start of a sale arbitrarily many items may be taken and printed; note that only as many printItem!s should be performed as item?s have been taken before, but this cannot be specified with finite state. Also a saleFinish? request may be accepted, possibly followed by printing items (that have not been printed yet) and then printing the total. As an alternative to cash payment, also payment by credit card may be offered by an implementation.

Fig. 14

Interface CashDesk

Fig. 15

Cash desk assembly with contained interfaces

System architecture. In the next step, we specify an architecture for the intended system, which is given by the modal assembly CashDeskAssembly in Fig. 15. The assembly CashDeskAssembly consists of three interfaces, CashDeskGUI, CashDeskController and ClearingCompany. The CashDeskGUI interface behaviour waits for a newSale?from the environment, then reacts to incoming item?s by issuing corresponding itemReady!s until a saleFinish? arrives, upon which it signals finish!. The CashDeskController interface behaviour starts each sale by issuing newSale! and then answers each itemReady? by printItem! until a finish? arrives, upon which a printTotal! is issued and either cash? or creditCard? is accepted. Only creditCard? is a may-transition, such that in a refinement of CashDeskController it may be absent or turned into a must-transition. The ClearingCompany waits for a verify? and then reacts with a verified!. For simplicity of presentation we have only specified the positive case where a credit card is validated. The interface ClearingCompany is input-enabled. The input verify? is always accepted but no reaction is performed if it occurs directly after a previous verify?.

Fig. 16

Behaviour of CashDeskAssembly in Fig. 15

Communication-safety. We now want to check that CashDeskAssembly is modally communication-safe. For this purpose we compute the behaviour of the assembly which is given by the EMIO in Fig. 16. It shows not only the possible inputs and outputs, but also the communications happening in the assembly. If there would be an output request of one component to another component in the assembly which can not be taken (even after a delay with autonomous must-transitions of the rest of the assembly), an error state would be reachable in the EMIO which is not the case here. Hence, by Lem. 2, CashDeskAssembly is modally communication-safe. Let us convince ourselves that indeed no output possible in one of the assembly’s modal interfaces is lost. Crucial states are the states A and B. In state A the CashDeskGUI has reached its lowest state in Fig. 15 where it wants to send out itemReady! and has already communicated an itemReady to the CashDeskController before. In the assembly state A the CashDeskController has also reached its lowest state in Fig. 15 where it can perform an open output printItem!. Only after this output it can input, as requested, itemReady?. But this is fine with our liberal notion of communication-safety which allows to delay a reception after performing first some autonomous must-transitions. A similar situation occurs in state B of the assembly, where the CashDeskController accepts an output finish! of the CashDeskGUI only if it has performed an output of printItem! before.

Alternatively, we could also check the communication-safety of CashDeskAssembly by incremental design; see Sect. 4.

Packing the assembly. As the result of assembly encapsulation yields an interface, packing an assembly is a decisive step for hierarchical system development. Packing the modal assembly CashDeskAssembly results in the modal interface shown in Fig. 17. Figure 18 shows an equivalent but “smaller” interface¹¹.

Fig. 17

Packed CashDeskAssembly

Fig. 18

Interface equivalent to the one in Fig. 17

Correctness of the assembly. We now want to show that the visible behaviour of CashDeskAssembly fits to the abstract requirements specification of the system given by the interface CashDesk. This means that we must verify the proof obligation (1) in Fig. 13. Due to the equivalence of the modal interfaces in Figs. 17 and 18, it suffices to prove $min ( pack ^{{\mathrm {mi}}}(\mathsf{CashDeskAssembly})) \mathrel {\preccurlyeq ^{\mathrm {mi}}}\mathsf{CashDesk}$. We have verified this statement with the MIO-Workbench [6].

Fig. 19

Cash desk assembly refinement with contained interfaces

Assembly refinement. CashDeskAssembly introduces architectural and behavioural requirements, the latter given by the assembly behaviour in Fig. 16. In the next step we refine CashDeskAssembly by the assembly CashDeskAssemblyRef where the interface CashDeskController is replaced by the interface CashDeskController’ and the interface ClearingCompany is replaced by ClearingCompany’; see Fig. 19. In the interface CashDeskController’ the previous may-transition for creditCard? is turned into a must-transition such that any implementation must support credit card payment as an alternative to cash payment. In contrast to ClearingCompany, the new interface ClearingCompany’ is not input-enabled. The behaviour of the new assembly is simply obtained from the EMIO in Fig. 16 by turning the may-transition with label creditCard? into a must-transition which yields obviously an EMIO refinement. Hence, by Definition 12, $\mathsf{CashDeskAssemblyRef} \mathrel {\mathrel {\sqsubseteq }^{{\mathrm {m}}}}\mathsf{CashDeskAssembly}$, i.e., we have verified proof obligation (2). Since CashDeskAssembly is communication-safe, preservation of communication-safety by assembly refinement implies that CashDeskAssemblyRef is communication-safe as well. Moreover, encapsulation of assemblies turns assembly refinement into interface refinement, and therefore we obtain proof obligation (3) in Fig. 13. Now we can utilise that interface refinement is transitive to be sure that the visible behaviour of the encapsulated assembly CashDeskAssemblyRef is conform to the system’s interface specification.

Let us point out that the interface ClearingCompany’ is not a modal interface refinement of ClearingCompany since the (looping) must-transition for the input verifyPin? in the second state of ClearingCompany is not preserved by ClearingCompany’. Hence component-wise refinement would not work in this case. On the other hand the assembly refinement is intuitively correct since the cash desk controller is a context for the clearing company which never sends verifyPin! twice, one after the other.

7 Related work

Several examples in the literature show that the transition from theories considering only two components at a time to a multi-component environment is not trivial. Such transformations have been studied, e.g., when moving from binary session types to multi-party (asynchronous) session types in [22], or when moving from pairwise system analysis in [11] to team automata considered in [12]. We are, however, not aware of any approach that does the transformation in a generic way on the basis of abstract laws for interface and assembly theories.

The idea to consider assemblies as sets of components, automata, or interfaces is obviously present in many approaches in the literature; see e.g. CFSMs [9], the BIP framework [4, 17], team automata [12], component-interaction automata [13], and modal assemblies [20]. So it is an interesting question to what extent our concepts and laws for assembly theories appear in the different frameworks. In [9] communication protocols are studied based on collections of communicating finite state machines. Communication is asynchronous via queues and the focus there is particularly on communication properties, like specified reception (and how to check this), which could be used as a communication-safety predicate in our sense. In the BIP framework systems of components are considered together with particular interaction models, which are not incorporated into our notion of an assembly. BIP provides, as required for an assembly theory, a composition operator, it deals with certain properties of systems, like interaction safety, and focuses on compositionality results much in the spirit of an assembly theory. Compositionality results are also studied in [12] for systems of reactive transition systems (playing the role of interfaces). Our notion of an assembly could be instantiated by the concept of a composable system, and communication-safety by the notion of a compatible system in [12]. Different synchronisation strategies are applicable and interpreted via team automata. For the case of the synchronous product, Cor. 9 in [12] states a compositionality result, which is very similar to compositionality of communication-safety required for assembly theories in property (A2). Also the notion of a compatible system in [12] follows the suggestion of Liu et al. explained in Sect. 1. In [13] systems of composable component-interaction automata are used as assemblies. [13] focuses merely on substitutability of components which is also a motivation for our notion of behavioural refinement of modal assemblies. Another possibility to obtain a liberal refinement notion (taking into account contexts) is the use of contracts specifying environment assumptions such that refinement can be relativised accordingly; see [7] and [5].

8 Conclusions

Interface theories consider component interfaces pairwise while assemblies follow a multi-component approach. One might think that the extension of an interface theory to a theory of component assemblies is straightforward and rather trivial. We have shown that this is not the case, neither for obtaining a sound notion of communication-safety for assemblies nor for obtaining a powerful assembly refinement relation. Therefore, we have introduced an explicit notion of an assembly theory and we have studied, on a generic basis, how an assembly theory can be built over a given interface theory. We have considered the notion of a canonical assembly theory, whose communication-safety predicate is derived from the underlying (binary) interface compatibility relation, and a restricted version of it, called simple assembly theory, which fixes assembly refinement to be pairwise interface refinement. A simple assembly theory does, however, not support context-dependent component substitutions. As an instance of a simple assembly theory we have considered assemblies of interface automata and as an instance of a canonical assembly theory we have studied assemblies of modal I/O-interfaces. The modal assembly theory offers a powerful assembly refinement relation respecting inter-component communications. It relies on a formal notion for assembly behaviours which makes communication errors explicit.

Future directions. The definitions of an interface theory and of an assembly theory were guided by two goals: (1) to be abstract and hence instantiable by concrete formalisms, and (2) to capture kernel requirements for systems of communicating components.

Concerning (1) we are interested in studying more instantiations of assembly theories, in particular assemblies which rely on different communication styles, like asynchronous and/or multi-cast communication. An assembly theory using modal I/O-Petri nets as interfaces and asynchronous communication via channel places could already be easily derived from the results in [18]. This approach supports infinite state systems keeping the properties of communication-safety and refinement decidable. Other interesting instantiations of assembly theories could be studied for interface theories using relational interfaces; see [31] and [5, Sect. 7]. It would be interesting to see to what extent the interface diagrams in [31] could be considered as assemblies and how the binary compatibility notion for relational interfaces could be extended to assemblies.

As stated in point (2) above, the focus of our work lies on rudimentary properties of component systems and not on providing convenient syntactic means to specify system architectures. For the latter architecture description languages (ADLs), like e.g. PADL [2, 8] and WRIGHT [3], have been designed. We believe, however, that assembly theories can provide a useful semantic layer for the interpretation of ADLs. How such an interpretation could look like can be seen in [19] where we have designed a graphical (and algebraic) component model supporting components with ports, connectors and assemblies (formed by local component and connector declarations), as well as assembly encapsulation into composite components. [19] uses I/O-transition systems for local behaviours on the specification level and their parallel composition (involving relabelling), as well as hiding, for the interpretation of composite components on the semantic level. We think that similarly we could provide an interpretation of the PADL constructs in an assembly theory, whose interfaces would be given by CSP processes equipped with an I/O-alphabet, and the outcome should be equivalent to the current PADL semantics (at least if we restrict to synchronous communication). Then it would be interesting to study which properties of PADL architectures would correspond to communication-safety and assembly refinement. Currently PADL does not have a proper refinement notion for architectures but it considers behavioural conformity of architectures which relies on pairwise behavioural conformity of their underlying architectural elements. Hence, using behavioural conformity for refinement, an assembly interpretation of PADL would probably lead to a simple assembly theory in the sense of Sect. 4.3. Since our notion of an assembly theory is generic, it could also be interesting to investigate a generic ADL such that architectural concepts are fixed and interpreted in a generic assembly theory while concrete formalisms for behavioural specifications can be injected later.