On the structure of semigroups whose regular elements are completely regular

Abstract

We study the structure of strongly 2-chained semigroups, which can be defined alternatively as semigroups whose regular elements are completely regular. The main result is a semilattice decomposition of these semigroups in terms of ideal extensions of completely simple semigroups by poor semigroups and idempotent-free semigroups.

1 Introduction and notations

This article proposes a study of semigroups whose regular elements are completely regular. These semigroups can also be defined by means of E-chains of idempotents of size 2. Due to this property, they are called strongly 2-chained semigroups. Commutative semigroups and semigroups with central idempotents are strongly 2-chained semigroups. Strongly 2-chained semigroups also appear naturally in the study of variant semigroups (Theorem 1.3), free idempotent-generated semigroups (Example 2.10), or in ring theory [37,38,39, 46, 48, 49]. Our main result is a semilattice decomposition of strongly 2-chained semigroups into poor ideal extensions of completely simple semigroups and idempotent-free semigroups. This result can be seen as the non-regular analog of Clifford’s theorem [14], which decomposes completely regular semigroups into semilattices of completely simple semigroups. Up to now, such a semilattice decomposition had only been extended to non-regular semigroups under the additional assumption of $\pi$-regularity (where every element has a power that is regular) [7, 9, 68,69,70, 74, 79, 80, 87]. Our decomposition is also applied to certain subclasses defined by E-chains of idempotents of size 1.

We first recall the main notions of semigroup theory that will be used throughout the article. In this paper, S denotes a semigroup, and E(S) denotes the set of idempotents of S. By $S^1$ we mean the monoid generated by S.

Let a be an element of a semigroup S. An element x of S that is a solution to the equation $axa=a$ is called an inner inverse of a, and an element x of S that is a solution to $xax=x$ is called an outer inverse of a. If both equations $axa=a$ and $xax=x$ hold, then x is called a reflexive inverse of a. The element $a\in S$ is regular if it has an inner inverse x. In this case, $b=xax$ is a reflexive inverse of a. A particular solution to $axa=a, xax=x, ax=xa$ is unique if it exists and is usually called the group inverse of a, denoted by $a^\#$. We denote the set of regular elements of S by ${{\,\textrm{reg}\,}}(S)$ and the set of group invertible elements (also called completely regular elements) by ${{\,\textrm{Gr}\,}}(S)$. A semigroup S is (completely) regular if all its elements are (completely) regular.

Green’s preorders and relations [35] have proved fundamental in the early development of semigroup theory, notably in the study of regular semigroups. They are defined upon principal (left, right, two-sided) ideals—or divisibility—as follows. For elements a and b of S,

$$\begin{aligned}{} & {} a \le _{{\mathcal {L}}} b\quad \quad \Longleftrightarrow \quad \quad S^1 a\subseteq S^1 b\;\quad \qquad \Longleftrightarrow \;\quad \;\quad (\exists x\in S^1)\; a = xb;\\{} & {} a \le _{{\mathcal {R}}} b\quad \!\quad \Longleftrightarrow \quad \quad aS^1\subseteq bS^1\;\qquad \quad \Longleftrightarrow \;\quad \;\quad (\exists x\in S^1)\; a = bx;\\{} & {} a \le _{{\mathcal {J}}} b\quad \!\quad \Longleftrightarrow \quad S^1aS^1\subseteq S^1bS^1\;\,\,\quad \Longleftrightarrow \;\quad (\exists x,y\in S^1)\; a = xby. \end{aligned}$$

Observe that

$$\begin{aligned}\displaystyle \le _{{\mathcal {J}}}\;=\;\le _{{\mathcal {L}}}\circ \le _{{\mathcal {R}}}\;=\;\le _{{\mathcal {R}}}\circ \le _{{\mathcal {L}}}\;=\;\le _{{\mathcal {L}}}\vee \le _{{\mathcal {R}}}. \end{aligned}$$

When $a\le _{{\mathcal {J}}} b$, we also say that b divides a and we denote $b\mathrel {\vert } a$. The intersection of the preorders $\le _{{\mathcal {L}}}$ and $\le _{{\mathcal {R}}}$ is also a preorder, denoted by $\le _{{\mathcal {H}}}$. If $\le _{{\mathcal {K}}}$ is any of these preorders, then $a{\,{\mathcal {K}}\,}b$ if $a\le _{{\mathcal {K}}}b$ and $b\le _{{\mathcal {K}}}a$, and $K_a=\{b\in S\mathrel {\vert } b{\,{\mathcal {K}}\,}a\}$ denotes the ${\mathcal {K}}$-class of a. The relations ${\mathcal {L}}$ and ${\mathcal {R}}$ commute, so that their join equals their product

$$\begin{aligned}{\mathcal {D}}={\mathcal {L}}\vee {\mathcal {R}}={\mathcal {R}}\circ {\mathcal {L}}={\mathcal {L}}\circ {\mathcal {R}}. \end{aligned}$$

This enables us to describe ${\mathcal {D}}$-classes as egg-boxes, each row (respectively column) corresponding to an ${\mathcal {R}}$-class (respectively ${\mathcal {L}}$-class), and each case to an ${\mathcal {H}}$-class. By Green’s lemma [35], any two ${\mathcal {H}}$-classes within a single ${\mathcal {D}}$-class are isomorphic. If a ${\mathcal {D}}$-class contains a regular element, then all elements of the class are regular. In the following figures of egg-box diagrams of ${\mathcal {D}}$-classes, gray boxes will denote group ${\mathcal {H}}$-classes, and idempotents will be bold. As an illustration, the Fig. 1 depicts the ${\mathcal {D}}$-class of a regular element $a\in S$ with reflexive inverse $b\in S$ (so that $ab,ba\in E(S)$).

Fig. 1

${\mathcal {D}}$-class of a with reflexive inverse b

The following result will be fundamental in the sequel.

Lemma 1.1

([35, Theorem 7], [52, Theorem 3]) Let $a,b\in S$. Then $ab\in R_a\cap L_b$ if and only if $R_b\cap L_a$ contains an idempotent. In this case

$$\begin{aligned}aH_b=H_a b=H_a H_b=H_{ab}=R_a\cap L_b. \end{aligned}$$

In particular, $a{\,{\mathcal {H}}\,}a^2$ (a is completely regular) if and only if $H_a$ contains an idempotent, in which case $H_a$ is a group.

The first part of Lemma 1.1 is usually known as Miller and Clifford’s theorem, whereas its last part is known as Green’s theorem. If $ab\in R_a\cap L_b$, then one says that ab is a trace product. Miller and Clifford’s theorem is related to the question of stability. We refer the reader to [1, 24, 41] for a more detailled discussion regarding stable semigroups. According to [24], an element x of a semigroup S is right-stable (respectively left-stable) if, for all $y\in S$, $x {\,{\mathcal {J}}\,}xy$ implies $x {\,{\mathcal {R}}\,}xy$ (respectively $x {\,{\mathcal {J}}\,}yx$ implies $x {\,{\mathcal {L}}\,}yx$). An element is stable if it is both left and right-stable, and a semigroup is (left, right) stable if each of its elements is (left, right) stable. In a stable semigroup, ${\mathcal {D}}={\mathcal {J}}$. In general, only the inclusion ${\mathcal {D}}\subseteq {\mathcal {J}}$ holds.

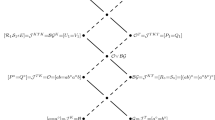
Green’s preorders and relations take interesting forms when applied to idempotents, and are a crucial notion regarding biordered sets [23, 60,61,62, 66]. In turn, biordered sets are essential to study idempotent-generated semigroups, in particular the free ones. Since 1980, numerous authors have focused on investigating these free idempotent-generated semigroups, with a particular emphasis on their maximal subgroups [10, 33, 34, 50, 63]. More recently, the word problem on such semigroups has also been explored [17, 18, 21]. Given $e,f\in E(S)$, it is well-known that $e\le _{{\mathcal {L}}} f$ if and only if $ef=e$, in which case we also denote $e\mathrel {\omega ^{\ell }} f$. Dually, $e\le _{{\mathcal {R}}} f$ if and only if $fe=e$, in which case we also denote $e\mathrel {\omega ^r} f$. The notation comes from the fact that the natural partial order $\omega$ on the set of idempotents of a semigroup is defined by $e\mathrel {\omega } f\iff e\mathrel {\omega ^{\ell }} f$ and $e\mathrel {\omega ^r} f$. Nambooripad [60] noticed that, for all $e\in E(S)$, $\tau ^{\ell }(e):f\mapsto ef$ (respectively $\tau ^r(e):f\mapsto fe$), defined whenever $f\mathrel {\omega ^{\ell }} e$ (respectively $f\mathrel {\omega ^{r}} e$), is a partially defined idempotent transformation on the set E(S) that respects the partial orders $\omega ^{\ell }$ and $\omega ^r$. Let $\tau =\{\left( \tau ^{\ell }(e),\tau ^r(e)\right) | e\in E(S)\}$ be this set of partial transformations. The quadruple ${\mathcal {E}}=\left( E\left( S\right) ,\omega ^{\ell },\omega ^r,\tau \right)$ is precisely the biordered set of the semigroup S. Biordered sets can also be defined abstractly as certain quadruples ${\mathcal {E}}=\left( E,\omega ^{\ell },\omega ^r,\tau \right)$ satisfying certain axioms [60]. Shortly after their introduction as such quadruples by Nambooripad, Clifford has shown that the two preorders and the associated partial transformations induce naturally and in a one-to-one fashion a partial product $*$ on the set E that satisfies further axioms. It is now more common to call this partial algebra ${\mathcal {E}}= \left( E, *\right)$ a biordered set [16, 23, 61]. We will say that e and f are left associates, and write $e\mathrel {\sim _{\ell }} f$, if $e\mathrel {\omega ^{\ell }} f$ and $f\mathrel {\omega ^{\ell }} e$ (that is $ef=e$ and $fe=f$). This is equivalent to $e{\,{\mathcal {L}}\,}f$. The term “associates” traces back to Clifford [15], who called two elements $a,b\in S$ left associates if they are ${\mathcal {L}}$-related. It was (re)introduced by Nielsen [65] for idempotents only in the context of ring theory. Nielsen used the notation $\sim _{\ell }$ because, in the case of a ring R, $e\mathrel {\sim _{\ell }} f$ if and only if $f=ue$ for some invertible element $u\in R$. And, classically, two idempotents e, f of R are conjugate, denoted $e\sim f$, if $f=ueu^{-1}$ for some invertible element $u\in R$. Back to the semigroup case, we will say that two idempotents $e,f\in E(S)$ are right associates, denoted $e\mathrel {\sim _{r}} f$, if $e\mathrel {\omega ^r} f$ and $f\mathrel {\omega ^r} e$. The main reason for keeping two distinct notations ${\mathcal {L}}$ and $\sim _{\ell }$ is the following: whereas ${\mathcal {L}}$ and ${\mathcal {R}}$ commute, this is not the case for $\sim _{\ell }$ and $\sim _{r}$. We will denote by $\sim _{r\ell }$ the product $\sim _{r}\circ \sim _{\ell }$; that is $e\mathrel {\sim _{r\ell }} f$ if there exists $h\in E(S)$ such that $e\mathrel {\sim _{r}} h\mathrel {\sim _{\ell }} f$. Dually $\sim _{\ell r}= \sim _{\ell }\circ \sim _{r}$, that is $e\mathrel {\sim _{\ell r}} f$ if there exists $h\in E(S)$ such that $e\mathrel {\sim _{\ell }} h\mathrel {\sim _{r}} f$.

Composition of left and right association leads to the notions of E-paths and E-chains, introduced by Nambooripad [61] (see also [51, 57]), and of chains of associate idempotents [39, 48], which are of great importance in ring theory. An E-path in S is a sequence of idempotents $(e_1, e_2, \ldots , e_n)$ of S such that $e_i\,(\sim _{r}\cup \sim _{\ell })\,e_{i+1}$ for all $i = 1, \ldots , n - 1$. An equivalence relation is introduced on the set of E-paths by adding or removing inessential idempotents, where an idempotent $e_i$ of a path $(e_1, e_2, \ldots , e_n)$ is inessential if $e_{i-1}\mathrel {\sim _{r}} e_i \mathrel {\sim _{r}} e_{i+1}$ or $e_{i-1}\mathrel {\sim _{\ell }} e_i \mathrel {\sim _{\ell }} e_{i+1}$. An E-chain is then the equivalence class of an E-path relative to this equivalence relation. It is proved in [61] that each E-chain $(f_1, f_2, \ldots , f_m)$ has a unique canonical representative of the form $(e_1, e_2, \ldots , e_n)$, where every vertex is essential. Such a sequence is called an n-chain of associate idempotents in [39]. More precisely, if the chain starts with left associates, then $e_1\mathrel {\sim _{\ell }} e_2\mathrel {\sim _{r}} \ldots {\textrm{e}}_n$ where the symbols alternate between left and right association, and it is called a left n-chain. Dually, a chain of size n starting with $\mathrel {\sim _{r}}$ is a right n-chain. Chains of associated idempotents have gained interest in ring theory, notably because of two properties. Firstly, in the case of rings, the relation of left association admits various interesting forms, see [39, Lemma 3.1] and [44, Section 21]. It follows that chains of idempotents of a ring are easier to handle than in the semigroup case. For instance, they can be characterized using some “generalized Euclidean algorithm” [38]. Secondly, they relate to properties of direct summands of modules. Let M be a module, and let A, B be any two direct summands of M. Then $A=eM$ and $B=fM$ for some e, f idempotents of $R={{\,\textrm{End}\,}}(M)$, ring of endomorphisms of M. By definition, $A=eM$ and $B=fM$ are perspective if they have a common complementary summand ($A\oplus C=M=B\oplus C$ for some submodule C of M). This holds precisely when e and f are right 3-chained [39, 48]. Along similar lines, $e\sim _{\ell r} f$ and $e\sim _{r\ell } f$ if and only if A and B “share all their complements” [39], meaning that for any submodule C of M, $A\oplus C=M\iff B\oplus C=M$.

In the sequel, we will also need the notion of primitive idempotents. An idempotent $e\in E(S)$ is primitive if $f\mathrel {\omega } e$ ($ef=f=fe$) for some $f\in E(S)$ implies $e=f$. A semigroup is primitive if all its idempotents are primitive. Recall that a semigroup with no proper two-sided ideal is called simple. Equivalently, S is simple if and only if ${\mathcal {J}}$ is the universal relation on S. A simple semigroup with a primitive idempotent is actually a primitive semigroup and termed completely simple. Equivalently, completely simple semigroups are the completely regular and simple semigroups. In terms of stability, completely simple semigroups are the stable and simple semigroups.

As is well-known, two idempotents $e,f\in E(S)$ are ${\mathcal {D}}$-related if and only if the left (equivalently right) S-acts Se and Sf are isomorphic. This is also equivalent to the existence of $a,b\in S$ such that $ab=e$ and $ba=f$. In this case, $a'=aba$ and $b'=bab$ are reflexive inverses ($a'b'a'=a', b'a'b'=b'$) such that $e=a'b'$ and $f=b'a'$. If $e{\,{\mathcal {D}}\,}f$ we say that e and f are isomorphic idempotents, and write $e\simeq f$. Unlike association, which depends only on the biordered set of idempotents, isomorphism depends on the ambient semigroup in general.¹ As previously noted, this implies, by Green’s lemma, that the subgroups $H_e$ and $H_f$ are isomorphic.

In this paper, we will focus on semigroups in which the regular elements are completely regular. By Lemma 1.1, this condition is equivalent to the following property: for any two isomorphic idempotents $e,f\in E(S)$, $e\mathrel {\sim _{r\ell }} f$ and $e\mathrel {\sim _{\ell r}} f$. Following the ring definition of Khurana and Nielsen [39, Definition 3.7], we refer to such semigroups as strongly 2-chained semigroups, meaning that any two isomorphic idempotents are related by a left 2-chain and a right 2-chain. More precisely, we deduce from Lemma 1.1 the following result (also stated in [48, Corollary 4.10]).

Corollary 1.2

Let S be a semigroup. The following statements are equivalent:

• (1) S is strongly 2-chained;

• (2) ${{\,\textrm{reg}\,}}(S)={{\,\textrm{Gr}\,}}(S)$ (regular elements are completely regular);

• (3) Regular ${\mathcal {D}}$-classes of S are completely simple subsemigroups of S.

Proof

$(1)\Rightarrow (2):$ Assume (1) and let $a\in {{\,\textrm{reg}\,}}(S)$, with reflexive inverse b. Then ab, ba are isomorphic idempotents. By (1), $ab\mathrel {\sim _{r}} e\mathrel {\sim _{\ell }} ba$ for some idempotent $e\in E(S)$. Since also $a{\,{\mathcal {R}}\,}ab$ and $a{\,{\mathcal {L}}\,}ba$, we have that $a,e\in R_{ab}\cap L_{ba}$. It follows that $a{\,{\mathcal {H}}\,}e$. By Lemma 1.1, a is completely regular. Figure 2 depicts the ${\mathcal {D}}$-class of a.

Fig. 2

Egg-box diagram showing that a is completely regular

$(2)\Rightarrow (3):$ Assume (2) and consider a regular ${\mathcal {D}}$-class D. Let $a,b\in D$. Then $a{\,{\mathcal {L}}\,}x{\,{\mathcal {R}}\,}b$ for some $x\in D$. As x is regular it is completely regular by (2), and $H_x=L_a\cap R_b$ contains an idempotent by Lemma 1.1. It follows that $ab\in R_a\cap L_b\subseteq D$ by Lemma 1.1 (Fig. 3), and D is a semigroup. As in any semigroup ${\mathcal {D}}\subseteq {\mathcal {J}}$, the semigroup D is simple. As it is also completely regular by (2), it is completely simple.

Fig. 3

Egg-box diagram showing that ab is a trace product

$(3)\Rightarrow (1):$ Finally, assume (3) and let e, f be isomorphic idempotents of S. Consider the regular ${\mathcal {D}}$-class $D=D_e$. By assumption, D is a completely simple semigroup. As $e{\,{\mathcal {D}}\,}f$, we have that $e{\,{\mathcal {R}}\,}x{\,{\mathcal {L}}\,}f$ for some $x\in D$. But D is completely simple, hence x is completely regular. By Lemma 1.1, it follows that $x{\,{\mathcal {H}}\,}g$ for some $g\in E(S)$. Consequently, $e\mathrel {\sim _{r}} g \mathrel {\sim _{\ell }} f$ and $e\mathrel {\sim _{r\ell }} f$ (Fig. 4).

Fig. 4

Egg-box diagram showing that $e\sim _{r\ell } f$

Fig. 5

Variant semigroups $T^a_4$, $a = [1, 1, 2, 2]$ (top) and $a = [1, 2, 2, 2]$ (bottom)

By dual arguments, $e\mathrel {\sim _{\ell r}} f$, and S is strongly 2-chained. $\square$

Strong 2-chaining can thus easily be read on the egg-box diagram of the semigroup. Recall that for a semigroup (S, .), the variant semigroup S at $a\in S$ is $S^a=(S,._a)$ with sandwich operation $x._a y=xay$. Figure 5 (see [19, Figure 3]) presents the egg-box diagram of the variant semigroups $T^a_4$ of the full transformation semigroup $T_4$, with $a = [1, 1, 2, 2]$ and $a = [1, 2, 2, 2]$. As previously, on the figure, the group ${\mathcal {H}}$-classes (those that contain an idempotent) are the gray boxes. One observes two regular ${\mathcal {D}}$-classes, whose ${\mathcal {H}}$-classes all contain an idempotent. Thus, $T^a_4$ is strongly 2-chained.

By the same arguments, ${\mathcal {M}}_{32}^{J_{231}}({\mathbb {Z}}_2)$ (semigroup of 3-by-2 rectangular matrices over the two-element field ${\mathbb {Z}}_2$ under a certain sandwich operation) is also strongly 2-chained (Fig. 6, see [20, Figure 4]). For a precise definition of ${\mathcal {M}}_{32}^{J_{231}}({\mathbb {Z}}_2)$, we refer to [20, Section 4].

Fig. 6

${\mathcal {M}}_{32}^{J_{231}}({\mathbb {Z}}_2)$

That the three previous variant semigroups are strongly 2-chained actually results from a general phenomenon. Indeed, in each case, they are variant semigroups at idempotent elements $e\in E(S)$ such that eSe is completely regular. The following theorem was suggested to the author by J. East.

Theorem 1.3

Let S be a semigroup, and let $e\in E(S)$. Then the variant semigroup $S^e=(S,._e)$, with sandwich operation $x._e y=xey$, is strongly 2-chained iff the local submonoid eSe of S is strongly 2-chained.

Proof

We denote any of Green’s relations ${\mathcal {K}}$ in $S^e$ with a superscript: $a\,{\mathcal {K}}^e\, b$ if and only if a and b are ${\mathcal {K}}$-related in $S^e$. First, suppose that the local submonoid eSe is strongly 2-chained. Let $x\in {{\,\textrm{reg}\,}}(S^e)$ be a regular element with inner inverse $x'\in S^e$. We prove that x is completely regular in $S^e$. By Lemma 1.1, it is sufficient to prove that $x\,{\mathcal {H}}^e\, x$. As $x=x._ex'._ex=xex'ex$, we see that $x{\,{\mathcal {R}}\,}xe$ and $x{\,{\mathcal {L}}\,}ex$. We also observe that $ex=exex'ex$, so that $ex{\,{\mathcal {R}}\,}exe$. Dually, $xe{\,{\mathcal {L}}\,}exe$. And $exe=(exe)(ex'e)(exe)$, so that $exe\in {{\,\textrm{reg}\,}}(eSe)$. By Corollary 1.2, we have that exe is completely regular in eSe, hence in S. We deduce from Lemma 1.1 that $H_{exe}=R_{ex}\cap L_{xe}$ contains an idempotent. Still by Lemma 1.1, $(xe)(ex)=xex\in R_{xe}\cap L_{ex}=H_x$ (Fig. 7).

Fig. 7

Egg-box diagram showing that $xex{\,{\mathcal {H}}\,}x$

Thus, $x=xexs$ for some $s\in S^1$, so that $x=xe(xexs)s=x._e x._e (xs^2)$. Therefore, it holds that $x\,{\mathcal {R}}^e\, x._e x$. Dually, we can prove that $x\,{\mathcal {L}}^e\, x._e x$, thereby showing that $x._e x\,{\mathcal {H}}^e\, x$. It follows that x is completely regular in $S^e$, and we conclude by Corollary 1.2.

Conversely, suppose that $S^e$ is strongly 2-chained, and let $x\in {{\,\textrm{reg}\,}}(eSe)$. Then $x=xx'x$ for some $x'=ex'e\in eSe$, and $x=xex'ex$. Thus, we see that $x=x._e x'._e x\in {{\,\textrm{reg}\,}}(S^e)$. By Corollary 1.2, we have that $x\in {{\,\textrm{Gr}\,}}(S^e)$. Therefore, there exists $x^\#\in S^e$ such that $x._e x^\#._e x=x$, $x^\#._e x._e x^\#=x^\#$ and $x._e x^\#=x^\#._e x$. Equivalently, we have that $x=xex^\#ex$, $x^\#exe x^\#=x^\#$ and $xex^\#=x^\#ex$. Also, as $x=exe$, we have that $ex=xe=x$. Let $x''=ex^\#e\in eSe$.² We have that $x=xex^\#ex=xx''x$, $x''=ex^\#e=ex^\#exex^\#e=x''xx''$ and $xx''=exex^\#e=ex^\#exe=x''x$. This proves that $x''$ is the group inverse of x in eSe. We conclude by Corollary 1.2 that eSe is strongly 2-chained. $\square$

In the sequel, we may consider certain standard constructions: direct products, 0-direct unions, Rees quotients or Rees matrix semigroups with sandwich matrix $P=(1)$. We leave the proof of the following results as an exercise for the reader.

Lemma 1.4

Direct products (respectively 0-direct unions, Rees quotients, Rees matrix semigroups with $P=(1)$) of strongly 2-chained semigroups are strongly 2-chained.

If every two isomorphic idempotents of a semigroup S are related by either a left or a right 2-chain (that is, for all $e,f\in E(S), e\simeq f$ implies $e\mathrel {\sim _{\ell r}} f$ or $e\mathrel {\sim _{r \ell }} f$) then we say that S is weakly 2-chained. We will also consider the subclasses of strongly (respectively weakly, respectively left, respectively right) 1-chained semigroups. A semigroup is strongly (respectively weakly, respectively left, respectively right) 1-chained if any two isomorphic idempotents $e\simeq f$ satisfy $e\mathrel {\sim _{\ell }} f$ and $e\mathrel {\sim _{r}} f$ (respectively $e\mathrel {\sim _{\ell }} f$ or $e\mathrel {\sim _{r}} f$, respectively $e\mathrel {\sim _{\ell }} f$, respectively $e\mathrel {\sim _{r}} f$). The definition of chained semigroups extends to larger chains. Results on these semigroups can be found in [48], which also discusses ring theoretical aspects. In fact, many recent results have been proved regarding 2, 3 and 4-chained rings [30, 38, 39, 43, 46, 48, 49].

The rest of the paper is divided as follows. In Sect. 2, we expose succinctly the general theory of semilattice decompositions, and describe the finest semilattice congruence on a semigroup. We also recall the main results obtained so far for completely regular and completely $\pi$-regular semigroups (whose definition is recalled in Sect. 2). Then, in a second time, we characterize semilattice indecomposable strongly 2-chained semigroups. We thereby obtain a semilattice decomposition of strongly 2-chained semigroups into poor ideal extensions of completely simple semigroups and idempotent-free semigroups. In Sect. 3, we apply the results obtained in Sect. 2 to derive the structure of weakly and strongly 1-chained semigroups. The case of strongly 2-chained semigroups with the additional property that (certain) products of idempotents are idempotents is also considered.

2 Semilattices decomposition of strongly 2-chained semigroups

Decomposition of mathematical objects into smaller “simple” pieces has profoundly irrigated all mathematical fields. In the context of semigroup theory, semilattices decompositions play a prominent role³. By definition, a semilattice decomposition of a semigroup S is a decomposition $S = \bigcup _{\alpha \in Y} S_{\alpha }$, where Y is a semilattice (commutative semigroup of idempotents), the $S_{\alpha }$ are pairwise disjoint semigroups, and $S_{\alpha } S_{\beta }\subseteq S_{\alpha \beta } \;(\forall \alpha ,\beta \in Y)$. In this direction, the case of completely regular semigroups can surely be considered as one of the first (after the Rees–Sushkevich theorem on completely simple semigroups [72, 76]) and one of the most elegant results in the realm of pure semigroup theory.

Theorem 2.1

([14, Theorems 1 and 2]) Let S be a semigroup. Then the following statements are equivalent:

• (1) S is a completely regular semigroup ($S={{\,\textrm{Gr}\,}}(S)$);

• (2) S is a union of groups;

• (3) S is a semilattice of completely simple semigroups.

This fundamental structure theorem has been inspiring the community for decades. In 1955, Tamura and Kimura [82] proved that every semigroup has a greatest semilattice decomposition. And one year later, Tamura [78, Theorem 7] proved that each component of the greatest semilattice decomposition is semilattice indecomposable, where a semigroup S is semilattice indecomposable if every semilattice homomorphic image of S is trivial. Equivalently, S is semilattice indecomposable if the finest semilattice congruence is the universal relation on S. The finest semilattice congruence was first described by Yamada [88], and then refined by Tamura in 1972 [79]. The power divisibility relation $\rightarrow$ is defined as follows: $a\rightarrow b \iff b^n\in S^1aS^1$ for some $n>0$. We also define $\rightarrow ^{\infty }$ as the transitive closure of $\rightarrow$. The main result of [79] is that the finest semilattice congruence $\sigma$ on a semigroup S is the symmetric closure of $\rightarrow ^{\infty }$:

$$\begin{aligned}a\mathrel {\sigma } b\iff a\mathrel {\rightarrow ^{\infty }}b \text { and } b\mathrel {\rightarrow ^{\infty }}a. \end{aligned}$$

Interestingly, Putcha proved in 1974 that one can permute transitive closure and symmetric closure in Tamura’s construction of $\sigma$. Define - as the symmetric closure of $\rightarrow$:

$$\begin{aligned}a{-}b\iff a\mathrel {\rightarrow } b \text { and }b\mathrel {\rightarrow } a. \end{aligned}$$

Then $\sigma$ is the transitive closure ${-}^{\infty }$ of the relation - [70, Theorem 1.1]. Other characterizations exist. In [67], Petrich describes $\sigma$ in terms of completely prime ideals and filters, while in [13], Bogdanović and Ćirić describe $\mathrel {\sigma }$ by means of principal radicals.

Some special semilattice decompositions have also been investigated by the aforementioned authors [8, 12, 68,69,70, 80, 81, 83, 84]. Their decompositions rely on the Archimedean condition, where a semigroup S is Archimedean if, for any $a,b\in S$, there exists $n\in {\mathbb {N}}$ such that $a^n\in S^1bS^1$. Equivalently, S is Archimedean if and only if $\rightarrow$ is the universal relation on S. Putcha [69, Theorem 2.2] proved in particular that a semigroup S is a semilattice of Archimedean semigroups if and only if it satisfies condition (P): for any $a,b\in S$, if $a\mathrel {\vert }b$ then $a^2\mathrel {\vert }b^m$ for some $m\in {\mathbb {N}}$. The proof was completed by Tamura [80, Theorem 1]. In the same article, Tamura also proved two important results. Firstly, Archimedean semigroups are semilattice indecomposable [80, Proposition 4]. Secondly, the condition (P) is equivalent with transitivity of $\rightarrow$ [80, Proposition 7]. Semilattices of Archimedean semigroups are now called Putcha semigroups [59]. An interested reader can consult [53] for a survey of the topic.

Several more decompositions have been discovered by Shevrin [74], Galbiati and Veronesi [29, 87], and Bogdanović and Ćirić [7], which apply to semigroups satisfying a power regularity condition. A semigroup S in which every element has a power that is regular is known as a quasi-regular semigroup, an eventually regular semigroup, or a $\pi$-regular semigroup (where $\pi$ stands for “power”). Similarly, semigroups in which every element has a power that lies in a subgroup go by a variety of names, including epigroups, group-bound semigroups, quasi-periodic semigroups, or completely $\pi$-regular semigroups. We shall use the terminology “(completely) $\pi$-regular semigroups” in the sequel. Semigroups that are both completely $\pi$-regular and Archimedean are called completely Archimedean semigroups. The next theorem subsumes the results obtained by the aforementioned authors under the $\pi$-regularity condition. For a comprehensive survey of the topic, we refer the reader to [9].

Theorem 2.2

([9, Theorem 5.7]) Let S be a semigroup. Then the following statements are equivalent:

• (1) S is $\pi$-regular and ${{\,\textrm{reg}\,}}(S)={{\,\textrm{Gr}\,}}(S)$;

• (2) S is completely $\pi$-regular and a semilattice of Archimedean semigroups;

• (3) S is a semilattice of completely Archimedean semigroups.

Theorem 2.2 and the classes of semigroups therein need some comments.

• The semigroups of Theorem 2.2 are sometimes called Galbiati–Veronesi–Shevrin semigroups [5] or uniformly $\pi$-regular semigroups [9].

• $\pi$-regularity is a very general finiteness condition on semigroups, originally introduced by Arens and Kaplansky [3] in the context of rings. An important result due to Edwards [25] is that Lallement’s lemma⁴ [42] holds in $\pi$-regular semigroups. Completely $\pi$-regular semigroups are a natural extension of finite and periodic semigroups (since any finite semigroup is periodic, and any element in a periodic semigroup has a power that is idempotent). They are largely studied in semigroup theory [22, 36, 45, 58, 68, 74, 75]. By [24, Proposition 7], completely $\pi$-regular semigroups are stable. They also appear naturally in module and ring theory ([2, 4, 11, 40, 64, 86]. Algebraic algebras over a field, Artinian rings (in particular the simple ones, that are the full matrix rings over a division ring) and perfect rings are completely $\pi$-regular. A module satisfies Fitting’s lemma if and only if its endomorphism ring is completely $\pi$-regular. And among commutative rings, the completely $\pi$-regular ones are those with Krull dimension 0.

• Most proofs of Theorem 2.2 rely on the various characterizations of the finest semilattice congruence $\sigma$. Another approach, used in [87], is to study directly extensions of Green’s relations in the special case of $\pi$-regular semigroups, and then prove a semilattice congruence property. This approach aligns more closely with Clifford’s original approach, but tailored to $\pi$-regular semigroups. It has also been successfully applied in other contexts, resulting in the identification of numerous additional semilattice decompositions through the analysis of other extended Green’s relations [27, 47, 73].

In the following, our purpose is to improve Theorems 2.1 and 2.2 by removing the regularity and $\pi$-regularity assumptions. To prove our semilattice decomposition theorem, we first need the following stability result.

Lemma 2.3

Let S be a strongly 2-chained semigroup, and let $x\in {{\,\textrm{reg}\,}}(S)$ and $y\in S$. Then:

• (1) if $x{\,{\mathcal {J}}\,}xy$ then $x{\,{\mathcal {R}}\,}xy$;

• (1’) if $x{\,{\mathcal {J}}\,}yx$ then $x{\,{\mathcal {L}}\,}yx$.

In particular, x is stable and $D_x=J_x$.

Proof

We prove (1); the proof of $(1')$ is dual. Let $x\in {{\,\textrm{reg}\,}}(S)$ and $y\in S$. The semigroup S is strongly 2-chained by assumption, so that $x\in {{\,\textrm{reg}\,}}(S)$ is completely regular by Corollary 1.2. Therefore x admits a group inverse $x^\#$. Suppose that $x{\,{\mathcal {J}}\,}xy$. Then $x=uxyv$ for some $u,v\in S^1$. Let $e=xx^\#, f=(x^\#xyv)(x^\#ux)$. We have that $x=uxyv=x x^\#x$ and $x^\#=x^\#xx^\#$. Thus,

$$\begin{aligned} f^2&=(x^\#xyv)(x^\#ux)(x^\#xyv)(x^\#ux)=(x^\#xyv)(x^\#uxyv)(x^\#ux)\\&=(x^\#xyv)(x^\#x x^\#ux)=(x^\#xyv)(x^\#ux)=f, \end{aligned}$$

and f is idempotent. Let $a=(ux)$ and $b=(x^\#x yv x^\#)$. Then

$$\begin{aligned}e=xx^\#=(uxyv) x^\#=(ux x^\#x yv) x^\#=(ux) (x^\#x yv x^\#)=ab. \end{aligned}$$

Since also

$$\begin{aligned}f=(x^\#xyv)(x^\#ux) =(x^\#x yv x^\#)(ux)=ba, \end{aligned}$$

we have that e, f are isomorphic idempotents. As $ab=e$, $ba=f$ and $bab=fb=be=b$, it follows that $L_x\cap R_f=L_e\cap R_f$ contains the regular element b. But, by Corollary 1.2, regular elements are completely regular. It follows that b is completely regular. Thus, by Lemma 1.1, we deduce that $H_{b}=L_x\cap R_f$ contains an idempotent. By Lemma 1.1 again, we have that $xf\in R_x\cap L_f$. But $xf=(xy)(vx^\#ux)$, so that $xf\le _{{\mathcal {R}}} xy$. Finally, we observe that $x\le _{{\mathcal {R}}} xf \le _{{\mathcal {R}}} xy \le _{{\mathcal {R}}} x$, so that $x{\,{\mathcal {R}}\,}xy$ (Fig. 8).

As a consequence of (1) and $(1')$, we see that the element x is stable. By [24, Theorem 8], we deduce that $D_x=J_x$. $\square$

Fig. 8

Egg-box diagram showing that $x\in reg(S)$ is left stable

Next, we consider divisibility. Recall that $a\mathrel {\vert }b$ if $b\in S^1aS^1$, that is $b=yaz$ for some $y,z\in S^1$.

Lemma 2.4

Let S be a semigroup, and let $x\in S$ and $e\in E(S)$ be such that $x\mathrel {\vert }e$. Then:

(1):

there exists $f{\,{\mathcal {D}}\,}e$ such that $f\le _{{\mathcal {R}}} x$;

(1’):

there exists $g{\,{\mathcal {D}}\,}e$ such that $g\le _{{\mathcal {L}}} x$.

Proof

We prove (1). The second result $(1')$ is dual. Let $x\in S$ and $e\in E(S)$ be such that $x\mathrel {\vert }e$. Then $e=yxz$ for some $y, z\in S^1$. Let $a=(yxz)y=ey$ and $b=(xz)(yxz)=xze$. Then $ab=(yxz)^3=e^3=e$. Let $f=ba=xzey$. Then $f\le _{{\mathcal {R}}} x$. Also

$$\begin{aligned} f^2=xzeyxzey=xze^3y=xzey=f, \end{aligned}$$

so that $f\in E(S)$. It follows that $e=ab$ and $f=ba$ are isomorphic idempotents, that is $f{\,{\mathcal {D}}\,}e$. $\square$

Lemma 2.5

Let S be a strongly 2-chained semigroup, and let $e\in E(S)$ and $x\in S$ be such that $x\mathrel {\vert }e$. Then $x^n\mathrel {\vert }e$ for any $n\ge 1$.

Proof

We prove the lemma by induction on n. For $n=1$ there is nothing to prove. For $n=2$, by Lemma 2.4, there exists $e'\in E(S)$ such that $e'{\,{\mathcal {D}}\,}e$ and $e'\le _{{\mathcal {R}}} x$. Choose such $e'$. By definition of the preorder $\le _{{\mathcal {R}}}$, it holds that $e'=xy$ for some $y\in S^1$. Let $a=x$, $b=yxy$ and $f=ba=(yx)^2=ye'x$. Then

$$\begin{aligned} f^2=(yx)^4=y(xy)^3x=ye'x=f, \end{aligned}$$

so that f is an idempotent. Since $e'=e'^2=ab$, we deduce that $e'$ and f are isomorphic idempotents. By assumption, S is strongly 2-chained, and it follows that $e'\mathrel {\sim _{\ell r}} f$ and $e'\mathrel {\sim _{r\ell }} f$. Therefore, there exist $g,h\in E(S)$ such that $e'\mathrel {\sim _{\ell }} g\mathrel {\sim _{r}} f$ and $e'\mathrel {\sim _{r}} h\mathrel {\sim _{\ell }} f$. It follows that $R_f\cap L_{e'}$ and $R_{e'}\cap L_f$ both contain idempotents (respectively the idempotents g and h). Consider the product $fe'=(yx)^2(xy)=(yxy)x^2y$. By Clifford and Miller’s theorem (Lemma 1.1), $fe'\in R_f\cap L_{e'}$ since $R_{e'}\cap L_f$ contains the idempotent h. It follows that $e'=ufe'$ for some $u\in S^1$. Now $e'{\,{\mathcal {D}}\,}e$ so that $e=vw$, $e'=wv$ for some $v,w\in S^1$. In particular, $e=e^2=vwvw=ve'w$. Finally, $e=ve'w=v(ufe')w=(vuyxy)x^2(yw)$ and $x^2\mathrel {\vert }e$ (Fig. 9).

We finally prove the induction step. Let $n\ge 1$, and suppose that $x^n\mathrel {\vert }e$. By applying the previous result to $x'=x^n$, we obtain that $(x')^2=x^{2n}\mathrel {\vert }e$, so that $e=yx^{2n}z$ for some $y,z\in S^1$. It follows that $e=yx^{n+1}x^{n-1}z$ and $x^{n+1}\mathrel {\vert }e$. $\square$

Fig. 9

Egg-box diagram showing that $x^2|e$

Corollary 2.6

Let S be a strongly 2-chained semigroup, and let $x\in S$ and $e\in E(S)$ be such that $x\mathrel {\rightarrow ^{\infty }} e$. Then $x\mathrel {\vert }e$.

Proof

We first prove a reduction step. Let $x,y\in S$ be such that $x\rightarrow y \rightarrow e$. Then $x\mathrel {\vert }y^n$ for some $n\ge 1$, and $y\mathrel {\vert }e$ since e is idempotent. By Lemma 2.5, $y^n\mathrel {\vert }e$. It follows that $x\mathrel {\vert }y^n\mathrel {\vert }e$. But divisibility is a transitive relation, so that $x\mathrel {\vert }e$.

Assume now that $x\mathrel {\rightarrow ^{\infty }} e$. Then there exist $p\ge 1$ and $x_1,\cdots , x_p\in S$ such that

$$\begin{aligned} x\rightarrow x_1\rightarrow \cdots \rightarrow x_p\rightarrow e. \end{aligned}$$

By applying the reduction step p times from the right, we obtain that $x\mathrel {\vert }e$. $\square$

We are now almost in a position to state and prove our main result. But first, we have to consider the structure of a strongly 2-chained, semilattice indecomposable semigroup. Recall that a minimal two-sided ideal of S is unique if it exists and is called the kernel of S.

Proposition 2.7

Let S be a strongly 2-chained, semilattice indecomposable semigroup with an idempotent $e\in E(S)$. Then $D_e$ is the completely simple kernel of S. Also, any two idempotents of S are isomorphic.

Proof

Consider the finest semilattice congruence $\mathrel {\sigma }$ on S. By [79], this congruence is the reflexive closure of $\mathrel {\rightarrow ^{\infty }}$: $(\forall a,b\in S)\,a\mathrel {\sigma } b\iff a\mathrel {\rightarrow ^{\infty }}b \text { and } b\mathrel {\rightarrow ^{\infty }}a$.

Since S is semilattice indecomposable, we have that $\mathrel {\sigma }$ is the universal relation. Consider the regular ${\mathcal {D}}$-class $D=D_e$ of e. We prove that D is the kernel of S. To this end, let $s,t\in S^1$, $d{\,{\mathcal {D}}\,}e$ and let $x=sdt$. Then $d\mathrel {\vert }x$ by construction. Also, we have that $e\mathrel {\vert }d$. Thus, it holds that $e\mathrel {\vert }x$. On the other hand, it follows from universality of $\mathrel {\sigma }$ that $x\mathrel {\rightarrow ^{\infty }} e$. Thus, $x\mathrel {\vert }e$ by Corollary 2.6. We proved that $e\mathrel {\vert }x$ and $x\mathrel {\vert }e$, that is $x{\,{\mathcal {J}}\,}e$. But S is strongly 2-chained and e is regular, so that $D_e=J_e$ by Lemma 2.3. Thus, $x\in D$, and D is an ideal of S. It is completely simple by Corollary 1.2. Consequently, D is a minimal two-sided ideal of S, that is the kernel if S.

Finally, since a kernel is unique if it exists, any two ${\mathcal {D}}$-classes of idempotents coincide. It follows that any two idempotents of S are ${\mathcal {D}}$-related (isomorphic). $\square$

The final ingredient to our next result is the following theorem due to Tamura.

Theorem 2.8

[78, Theorem 7] If a semilattice decomposition of a semigroup S, $S=\bigcup _{\alpha \in Y} S_{\alpha }$, is greatest, then each class $S_{\alpha }$ is a semilattice indecomposable semigroup. Conversely if each $S_{\alpha }$ is semilattice indecomposable, then such a semilattice decomposition of S is greatest.

Now we have all the prerequisites to prove the main theorem of the paper, that describes the greatest semilattice decomposition of a strongly 2-chained semigroup.

Theorem 2.9

Let S be a semigroup. Then the following statements are equivalent:

• (1) S is strongly 2-chained;

• (2) S is a semilattice of semilattice indecomposable semigroups $S_{\alpha }$ with the following property: each $S_{\alpha }$ has at most one regular ${\mathcal {D}}$-class $D_{\alpha }$, that is the completely simple kernel of the component $S_{\alpha }$;

• (3) S is a semilattice of semigroups $S_{\alpha }$ with the following property: each $S_{\alpha }$ has at most one regular ${\mathcal {D}}$-class $D_{\alpha }$, that is a completely simple semigroup;

• (4) Regular elements of S are completely regular.

Proof

$(1)\Rightarrow (2):$ Consider the finest semilattice congruence $\mathrel {\sigma }$ on S, and its associated greatest semilattice decomposition. By Theorem 2.8, the components of the decomposition (the $\sigma$-classes) are semilattice indecomposable. Since ${\mathcal {D}}\subseteq \sigma$, the components of the semilattice either contain no regular elements, or they contain at least one regular ${\mathcal {D}}$-class. In the latter case, they contain at least one idempotent (recall that any regular ${\mathcal {D}}$-class contains at least one idempotent).

Therefore, we consider hereafter a component $T=\sigma _e$ of the semilattice that contains an idempotent $e\in E(S)$. We first prove that T is a strongly 2-chained semigroup. Let f, g be isomorphic idempotents in T. Then $e=ab, f=ba$ for some $a,b\in T$. Thus, since $T\subseteq S$, we have that e and f are isomorphic in S. By strong 2-chaining, there exist $h,k\in E(S)$ such that $f\mathrel {\sim _{\ell }} h\mathrel {\sim _{r}} g$ and $f\mathrel {\sim _{r}} k \mathrel {\sim _{\ell }} g$. In particular, $f=fh$ and $h=hf$. Since $\sigma$ is a semilattice congruence, we deduce that $f=fh\mathrel {\sigma } hf=h$. Dually, $f=k f \mathrel {\sigma } fk=k$. Finally, $h,k\in T=\sigma _e=\sigma _f$ and T is strongly 2-chained.

We have proved that T is a strongly 2-chained, semilattice indecomposable semigroup with an idempotent $e\in E(S)$. By Proposition 2.7, $D_e$ is the completely simple kernel of T. Consider a second regular ${\mathcal {D}}$-class $D'$ of T. Then it contains an idempotent f and $D'=D_f$. But all idempotents of T are isomorphic by Proposition 2.7, so that $f{\,{\mathcal {D}}\,}e$. Thus $D_f=D_e$ is the only regular class of T.

$(2)\Rightarrow (3):$ Straightforward.

$(3)\Rightarrow (4):$ Let $a\in S$ be a regular element. Then a belongs to the unique regular ${\mathcal {D}}$-class D of $\mathrel {\sigma }_a$. By assumption, D is a completely simple semigroup, and, in particular, it is completely regular. Consequently, a is completely regular.

$(4)\Rightarrow (1):$ This is Corollary 1.2. $\square$

Example 2.10

Let S be an idempotent-generated, completely regular semigroup. We let $E=E(S)$ be its set of idempotents, and ${\mathcal {E}}=(E,\omega ^{\ell },\omega ^r,\tau )$ be its biordered set. It is known that the free idempotent-generated semigroup $IG({\mathcal {E}})$ has the following properties (see for instance [34]):

• (1) its set of idempotents $E\left( IG\left( {\mathcal {E}}\right) \right)$, usually denoted by $\bar{E}$, is in one-to-one correspondence with E (via a map $\phi$). We denote by $\bar{e}\in \bar{E}$ the preimage of $e\in E$ by $\phi$;

• (2) the bijective map $\phi :\bar{E}\rightarrow E$ can be uniquely extended to a surjective⁵ semigroup homomorphism $\psi : IG({\mathcal {E}}) \twoheadrightarrow S$;

• (3) any two idempotents $\bar{e}, \bar{f}\in \bar{E}$ are left (respectively right) associates if and only if $e,f\in E$ are left (respectively right) associates in S;

• (4) any two idempotents $\bar{e},\bar{f}\in \bar{E}$ are isomorphic in $IG({\mathcal {E}})$ if and only if e, f are isomorphic in S.

As S is strongly 2-chained by Corollary 1.2, it follows from (3) and (4) that $IG({\mathcal {E}})$ is strongly 2-chained. By Theorem 2.1, S admits a semilattice decomposition $S= \bigcup _{\alpha \in Y} S_{\alpha }$, with all the $S_{\alpha }$ completely simple semigroups. Also, $\sigma ={\mathcal {J}}={\mathcal {D}}$ in this case, so that the components $S_{\alpha }$ are the ${\mathcal {D}}$-classes of S, and the decomposition is the greatest one.

Consider the canonical quotient map $q:S\twoheadrightarrow S/\sigma =Y$. Then $q\circ \psi :IG({\mathcal {E}})\twoheadrightarrow S\twoheadrightarrow Y$ provides us with a semilattice decomposition of $IG({\mathcal {E}})$. Denote by $\rho$ the kernel of $q\circ \psi$. By construction, it is a semilattice congruence, and any $\rho$-class is of the form

$$\begin{aligned}T_{\alpha }=(q\circ \psi )^{-1}(\alpha )=\psi ^{-1}(S_{\alpha }). \end{aligned}$$

As $S_{\alpha }$ is completely simple, it contains an idempotent $e\in E$. By (1) and (2), $\bar{e}\in T_{\alpha }$. Now, let $\bar{f}\in \bar{E}$ be a second idempotent in $T_{\alpha }$. Then $f\in S_{\alpha }$ and f, e are isomorphic in E. By (4), $\bar{e}$ and $\bar{f}$ belong to the same ${\mathcal {D}}$-class in $IG({\mathcal {E}})$.

Finally, all components $T_{\alpha }$ induced by the semilattice congruence $\rho$ contain a unique regular ${\mathcal {D}}$-class, that is a completely simple semigroup by Corollary 1.2. This proves that $\rho$ induces a semilattice decomposition that satisfies the assumption (3) of Theorem 2.9.

Example 2.11

We specialize Example 2.10, and consider the setting of Example 2 in [10]. Let Y be the three-element semilattice (free semilattice generated by two elements e, f, the last element being $ef=fe=\star$, zero of the semilattice). Y is trivially a completely regular, idempotent-generated semigroup, with greatest semilattice decomposition $Y=\bigcup _{\alpha \in Y} \{\alpha \}$. Let ${\mathcal {E}}$ be the associated biordered set. Then $IG({\mathcal {E}})=<\bar{e},\bar{f}|\bar{e}^2=\bar{e}, \bar{f}^2=\bar{f}>^{\bar{\star }}$, whose elements are words over the alphabet $\{\bar{e},\bar{f}\}$ alternating the symbols $\bar{e}$ and $\bar{f}$, with a zero $\bar{\star }$ adjoined. The semilattice Y induces the semilattice decomposition $IG({\mathcal {E}})=\bigcup _{\alpha \in Y} T_{\alpha }$ (Fig. 10), where: $T_{e}=\{\bar{e}\}$ and $T_{f}=\{\bar{f}\}$ are completely simple semigroups; $T_{\star }=\{\bar{\star },\bar{e}\bar{f}, \bar{f}\bar{e}, \bar{e}\bar{f}\bar{e}, \bar{f}\bar{e}\bar{f}, \cdots \}$ has a unique regular ${\mathcal {D}}$-class, the idempotent $\bar{\star }$.

Fig. 10

$IG({\mathcal {E}})=\bigcup _{\alpha \in Y} T_{\alpha }$

This is, however, not the greatest semilattice decomposition of $IG({\mathcal {E}})$. Indeed, $T_{\star }$ is not semilattice indecomposable. The greatest semilattice decomposition is $IG({\mathcal {E}})=\bigcup _{\alpha \in Y^{0}} T_{\alpha }$ (Fig. 11), where: $Y^{0}$ is the semilattice Y with a new zero 0 adjoined; $U_{e}=\{\bar{e}\}$, $U_{f}=\{\bar{f}\}$ and $U_{0}=\{\bar{\star }\}$ are completely simple semigroups; $U_{\star }=\{\bar{e}\bar{f}, \bar{f}\bar{e}, \bar{e}\bar{f}\bar{e}, \bar{f}\bar{e}\bar{f}, \cdots \}$ has no regular element.

Fig. 11

$IG({\mathcal {E}})=\bigcup _{\alpha \in Y^0} U_{\alpha }$ (Greatest semilattice decomposition)

Theorem 2.9 has other formulations, but we need to introduce more definitions. A semigroup with a single idempotent is called unipotent, and poor if this unique idempotent is a zero of the semigroup. A semigroup without idempotents is idempotent-free, or simply an IF-semigroup. The semigroup S is E-inversive [85] (or E-dense [28]) if, for every $a \in S$, $ax \in E(S)$ for some $x\in S$. Equivalently, by [55, Theorem 3.1], S is E-inversive if any element a has an outer inverse ($bab=b$ for some $b\in S$). Semigroups with 0 and $\pi$-regular semigroups are E-inversive. Indeed, if $a^nba^n=a^n$ for some $n\ge 1$, then $a(a^{n-1}b)\in E(S)$. When a semigroup S contains a two-sided ideal I, one can form the Rees quotient S/I, and we say that S is an ideal extension of the semigroup I by the semigroup S/I. According to Theorem 2.9, a strongly 2-chained semigroup S admits a greatest semilattice decomposition $S=\bigcup _{\alpha \in Y} S_{\alpha }$, where each component $S_{\alpha }$ contains either no regular ${\mathcal {D}}$-class or a single one $D_{\alpha }$, that is the completely simple kernel of $S_{\alpha }$. Thus, the semigroups $S_{\alpha }$ are either IF-semigroups, or they are ideal extensions of the completely simple semigroup $D_{\alpha }$ by the poor semigroup $S_{\alpha }/D_{\alpha }$. Such ideal extensions (by poor semigroups) are also called poor extensions. Poor extensions of completely simple semigroups have been characterized by [56, Theorem 4.2] as primitive E-inversive semigroups. Therefore, we obtain the following corollary.

Corollary 2.12

Let S be a semigroup. Then the following statements are equivalent:

• (1) S is strongly 2-chained (equivalently ${{\,\textrm{reg}\,}}(S)={{\,\textrm{Gr}\,}}(S)$);

• (2) S is a semilattice of IF-semigroups and primitive E-inversive semigroups;

• (3) m S is a semilattice of IF-semigroups and poor extensions of completely simple semigroups.

Moreover, we can choose the components in the previous decompositions to be semilattice indecomposable.

Example 2.13

Let T be a poor semigroup. Let also $I,\Lambda$ be two sets, and consider $S={\mathcal {M}}(I,T,\Lambda )$, the associated Rees matrix semigroup with sandwich matrix $P=(1)$. Then the following equality holds: ${{\,\textrm{reg}\,}}(S)=(I,0,\Lambda )=E(S)$. It follows that $K={{\,\textrm{reg}\,}}(S)$ is the completely simple kernel of S, and a rectangular band. In particular, S is strongly 2-chained. As the Rees quotient S/K is a poor semigroup, we have that S is a poor extension of the completely simple semigroup K. Consider $T=\bigcup _{\alpha \in Y} T_{\alpha }$ any semilattice decomposition of T, with $T_0$ the component of 0. Then $S=\bigcup _{\alpha \in Y} {\mathcal {M}}(I,T_{\alpha },\Lambda )$ is a semilattice decomposition of S, where the components are idempotent-free except ${\mathcal {M}}(I,T_{0},\Lambda )$, which is a poor extension of the completely simple semigroup K. If we start with the greatest semilattice decomposition of T, then we obtain the greatest semilattice decomposition of S.

Example 2.14

We specialize Example 2.13 as follows. Let A and B be semilattice indecomposable IF-semigroups (for instance disjoint copies of the free monogenic semigroup), and let $T=A\mathrel {\dot{\cup }} B\mathrel {\dot{\cup }} 0$ be the 0-direct union of A and B. Let also $I,\Lambda$ be two sets and $S={\mathcal {M}}(I,T,\Lambda )$ be the associated Rees matrix semigroup with sandwich matrix $P=(1)$. Then S is a poor extension of the completely simple semigroup ${\mathcal {M}}(I,0,\Lambda )$ by the 0-direct union ${\mathcal {M}}(I,A,\Lambda )\mathrel {\dot{\cup }} {\mathcal {M}}(I,B,\Lambda )\mathrel {\dot{\cup }} \{0\}$. As A and B are semilattice indecomposable, we finally deduce that the greatest semilattice decomposition of S is given by Fig. 12.

The semigroups ${\mathcal {M}}(I,A,\Lambda )$ and ${\mathcal {M}}(I,B,\Lambda )$ are semilattice indecomposable IF-semigroups, while ${\mathcal {M}}(I,0,\Lambda )$ is a completely simple semigroup.

Fig. 12

Greatest semilattice decomposition of ${\mathcal {M}}(I,A\mathrel {\dot{\cup }} B\mathrel {\dot{\cup }} 0,\Lambda )$

3 Semilattices decomposition of strongly and weakly 1-chained semigroups

In this final section, we turn our attention to certain subclasses of strongly 2-chained semigroups. Indeed, by using Theorem 2.9 and Corollary 2.12, we will be able to obtain a semilattice decomposition of certain strongly 2-chained semigroups enjoying additional properties. We will first address the case of strongly and weakly 1-chained semigroups. Then, at the end of the section, strongly 2-chained semigroups where (certain) products of idempotents are idempotents will be studied.

Recall that, by definition, S is strongly 1-chained if isomorphic idempotents are left and right associates. But ${\mathcal {H}}$-classes contain at most one idempotent. Therefore, S is strongly 1-chained if and only if isomorphic idempotents are equal. These semigroups have appeared in the literature under the name viable semigroups [71]. We also recall the following definitions. A homogroup is a semigroup that has a kernel which is a group. An ideal I of S is a retract of S if there exists an homomorphism of S onto I which leaves each element of I fixed. In this case, we also say that the extension S of I is retractive (or a retract extension). By [32, Theorem 2.10], a homogroup is the same as a retract extension of a group. Unipotent homogroups have been characterized by [56, Theorem 3.1] (see also [54, Theorem 4.1 and Theorem 4.3]).

Theorem 3.1

Let S be a semigroup. Then the following statements are equivalent:

• (1) S is E-inversive and has a single idempotent;

• (2) S is a poor (retract) extension of a group;

• (3) S is an unipotent homogroup.

The following corollary characterizes strongly 1-chained semigroups in terms of certain semilattice decompositions. The equivalences $(3)\iff (5)\iff (7)$ were obtained directly by Putcha and Weissglass [71, Theorem 6].

Corollary 3.2

Let S be a semigroup. Then the following statements are equivalent:

• (1) S is strongly 1-chained;

• (2) S is a semilattice of IF-semigroups and unipotent homogroups;

• (3) S is a semilattice of IF-semigroups and unipotent semigroups;

• (4) S is a semilattice of IF-semigroups and unipotent E-inversive semigroups;

• (5) S is a semilattice of IF-semigroups and poor (retract) extensions of groups;

• (6) Inner inverses are commuting inverses ($aba=a\Rightarrow ab=ba \;(\forall a,b\in S)$);

• (7) S is viable ($ab,ba\in E(S)\Rightarrow ab=ba \;(\forall a,b\in S)$).

Moreover, we can choose the components in the previous decompositions to be semilattice indecomposable.

Proof

By Theorem 3.1, $(5)\Leftrightarrow (4)\Leftrightarrow (2)\Rightarrow (3)$. We prove the remaining chain of implications $(3)\Rightarrow (6)\Rightarrow (7)\Rightarrow (1)\Rightarrow (5)$.

$(3)\Rightarrow (6):$ Supppose (3), and let $a,b\in S$ be such that $aba=a$. Since S a semilattice of IF-semigroups and unipotent semigroups, it follows that the isomorphic idempotents $e=ab$ and $f=ba$ are in the same component. But this component is unipotent, hence $e=f$.

$(6)\Rightarrow (7):$ Suppose (6) and let $a,b\in S$ be such that $ab,ba\in E(S)$. Let $a'=aba$. Then $a'ba'=a'$. It follows from (6) that $a'b=ba'$. But $a'b=abab=(ab)^2=ab$ and dually, $ba'=ba$; thus, $ab=ba$.

$(7)\Rightarrow (1):$ Suppose (7) and let e, f be isomorphic idempotents. Then $e=ab$ and $f=ba$ for some $a,b\in S$; thus, $e=ab=ba=f$. In particular, $e\mathrel {\sim _{r}} f$ and $e\sim _{\ell } f$.

$(1)\Rightarrow (5):$ Suppose (1). Then S is strongly 2-chained, hence a semilattice of IF-semigroups and poor extensions of completely simple semigroups by Corollary 2.12. But, by (1), isomorphic idempotents of S are equal. Thus, each completely simple semigroup in the decomposition is unipotent, hence a group. $\square$

Example 3.3

Consider the setting of Example 2.11. The semilattice $Y=\{e,f,\star \}$ is strongly 1-chained; Therefore, so is $IG({\mathcal {E}})$. The first semilattice decomposition obtained in Example 2.11 is $IG({\mathcal {E}})=\bigcup _{\alpha \in Y} T_{\alpha }$ where: $T_{e}=\{\bar{e}\}$ and $T_{f}=\{\bar{f}\}$ are groups; $T_{\star }=\{\bar{\star },\bar{e}\bar{f}, \bar{f}\bar{e}, \bar{e}\bar{f}\bar{e}, \bar{f}\bar{e}\bar{f}, \cdots \}$ is a unipotent homogroup.

Its greatest semilattice decomposition is $IG({\mathcal {E}})=\bigcup _{\alpha \in Y^{0}} U_{\alpha }$, where: $U_{e}=\{\bar{e}\}$, $U_{f}=\{\bar{f}\}$ and $U_{0}=\{\bar{\star }\}$ are groups; $U_{\star }=\{\bar{e}\bar{f}, \bar{f}\bar{e}, \bar{e}\bar{f}\bar{e}, \bar{f}\bar{e}\bar{f}, \cdots \}$ is an IF-semigroup.

By similar arguments, we obtain the structure of weakly 1-chained semigroups. A left group is a left simple semigroup (a semigroup with no proper left ideal) that contains an idempotent. Equivalently, it is the direct product of a left zero semigroup (where $ab=a$ for all a, b in S) and a group. The notion of a right group is dual to that of a left group.

Corollary 3.4

Let S be a semigroup. Then the following statements are equivalent:

• (1) S is weakly 1-chained;

• (2) S is a semilattice of IF-semigroups and poor extensions of left and right groups;

• (3) S satisfies the quasi-identity:

  $$\begin{aligned}aba=a\Rightarrow \{ab^2a^2=a=a^2b \text { or } a^2b^2a=a=ba^2\} \;(\forall a,b\in S).\end{aligned}$$

Proof

$(1)\Rightarrow (2):$ Assume that S is weakly 1-chained. Then S is strongly 2-chained, hence a semilattice of IF-semigroups and poor extensions of completely simple semigroups. Let T be one of these completely simple semigroups. It contains an idempotent, so that we have to prove that it is left or right simple. If S is unipotent, it is a group. So, suppose that it contains at least two distinct idempotents e, f. By weak 1-chaining, either $e\mathrel {\sim _{\ell }} f$ or $e\mathrel {\sim _{r}} f$, but not both (otherwise $e=f$). Suppose that $e\mathrel {\sim _{\ell }} f$, and let $a\in T$. Since T is completely simple, a is completely regular. By Lemma 1.1, $a{\mathcal {H}}g$ for some idempotent $g\in E(T)$. As T is a completely simple, we have that e and g are isomorphic, so that $e\mathrel {\sim _{\ell }} g$ or $e\mathrel {\sim _{r}} g$ by weak 1-chaining. Symmetrically $f\mathrel {\sim _{\ell }} g$ or $f\mathrel {\sim _{r}} g$. Suppose that $f\sim _{\ell } g$. Then $e\mathrel {\sim _{\ell }} f\mathrel {\sim _{\ell }} g$ and $e \mathrel {\sim _{\ell }} g$. Alternatively, suppose that $f\mathrel {\sim _{r}} g$. Since f and e are not right associates, we have that e and g are not right associates. Thus, $e\mathrel {\sim _{\ell }} g$. It follows that, in both cases, $e\mathrel {\sim _{\ell }} g$, and $a{\,{\mathcal {L}}\,}g{\,{\mathcal {L}}\,}e$. Finally, all elements of T are ${\mathcal {L}}$-related to e, and T is left simple. In the second case $e\mathrel {\sim _{r}} f$, then T would be right simple. This proves (2).

$(2)\Rightarrow (3):$ Assume (2) and let $a,b\in S$ be such that $aba=a$. Then the isomorphic idempotents $e=ab$, $f=ba$ are in the same component, hence either ${\mathcal {L}}$ or ${\mathcal {R}}$-related. In the first case, $ef=e$ and $fe=f$, that is $ab^2a=ab$ and $ba^2b=ba$. Multiplying the first equation on the right by a yields $ab^2a^2=aba=a$. Multiplying the second equation on the left by a yields $a^2b=a$. The second case is dual.

$(3)\Rightarrow (1):$ Assume (3) and let $e,f\in E(S)$ be isomorphic idempotents. Then $e=ab$ and $f=ba$ for some $a\in {{\,\textrm{reg}\,}}(S)$ and some reflexive inverse b of a. By (3), either $ab^2a^2=a=a^2b$ or $a^2b^2a=a=ba^2$. In the first case, we have that $a=ab^2a^2$ and $a^2b=a$. Therefore, $ab=ab^2a^2b=ab^2a$. Equivalently $e=ef$. Also, $fe=ba^2b=ba=f$. Thus, $e\sim _{\ell } f$. The second case is dual. $\square$

Fig. 13

Semilattice Y

The same arguments yield that S is left 1-chained if and only if S is a semilattice of IF-semigroups and poor extensions of left groups, if and only if S satisfies the quasi-identity:

$$\begin{aligned} aba=a\Rightarrow ab^2a^2=a=a^2b\;(\forall a,b\in S). \end{aligned}$$

The right case is dual.

Example 3.5

Consider the matrix semigroup

$$\begin{aligned}S=\begin{pmatrix} \{0,1\} &{} {\mathbb {N}}\\ 0&{} \{0,1\}\end{pmatrix}=\left\{ \begin{pmatrix} e &{} n\\ 0&{} f\end{pmatrix}\mathrel {|}e,f\in \{0,1\}, n\in {\mathbb {N}}\right\} . \end{aligned}$$

Let $A\notin \{\begin{pmatrix} 1 &{} 0\\ 0&{} 1\end{pmatrix}, \begin{pmatrix} 0 &{} 0\\ 0&{} 0\end{pmatrix}\}$ be a regular element of S. Then $A=\begin{pmatrix} 1 &{} n\\ 0&{} 0\end{pmatrix}$ or $A=\begin{pmatrix} 0 &{} n\\ 0&{} 1\end{pmatrix}$ for some $n\in {\mathbb {N}}$. In particular, ${{\,\textrm{reg}\,}}(S)=E(S)$. In the first case, A is idempotent and its inner inverses are of the form $B=\begin{pmatrix} 1 &{} p\\ 0&{} f\end{pmatrix}$ for some $p\in {\mathbb {N}}$ and $f\in \{0,1\}$. It then holds that $BA=A=A^2$, so that

$$\begin{aligned}A^2B^2A=ABBA=ABA=A \text { and }BA^2=BA=A. \end{aligned}$$

The second case is dual, and the cases $A=\begin{pmatrix} 1 &{} 0\\ 0&{} 1\end{pmatrix}$ or $A=\begin{pmatrix} 0 &{} 0\\ 0&{} 0\end{pmatrix}$ are straightforward. We thus deduce from Corollary 3.4 that S is weakly 1-chained.

We now produce a semilattice decomposition of the form of Corollary 3.4. We let Y be the semilattice shown in Fig. 13.

We let also

$$\begin{aligned}S_1=\left\{ \begin{pmatrix} 1 &{} 0\\ 0&{} 1\end{pmatrix}\right\} , \qquad S_*=\begin{pmatrix} 1 &{} {\mathbb {N}}^*\\ 0&{} 1\end{pmatrix}=\left\langle \begin{pmatrix} 1 &{} 1\\ 0&{} 1\end{pmatrix}\right\rangle , \end{aligned}$$

$$\begin{aligned}S_{\ell }=\begin{pmatrix} 0 &{} {\mathbb {N}}\\ 0&{} 1\end{pmatrix},\qquad S_r=\begin{pmatrix} 1 &{} {\mathbb {N}}\\ 0&{} 0\end{pmatrix},\qquad S_0=\begin{pmatrix} 0 &{} {\mathbb {N}}\\ 0&{} 0\end{pmatrix}. \end{aligned}$$

Then $S=\bigcup _{\alpha \in Y} S_{\alpha }$ is a semilattice decomposition of S with $S_1$ a group, $S_*$ a monogenic IF-semigroup, $S_{\ell }$ a left zero semigroup, $S_r$ a right zero semigroup and $S_0$ a poor semigroup (precisely a nilsemigroup); see Fig. 14. As all the components are semilattice indecomposable, the decomposition is actually the greatest semilattice decomposition of S.

Fig. 14

Greatest semilattice decomposition of $S=\begin{pmatrix} \{0,1\} &{} {\mathbb {N}}\\ 0&{} \{0,1\}\end{pmatrix}$

In case the semigroup is additionally $\pi$-regular, then there are no IF-components, and the ideal extensions are nil-extensions. We notably recover with Corollary 3.2 the semilattice decomposition of uniformly-$\pi$-inverse semigroups (strongly 1-chained $\pi$-regular semigroups in our terminology) into nil-extensions of groups of Bogdanović et al. [9, Theorem 5.10]. We also derive from Corollary 3.4 that weakly 1-chained $\pi$-regular semigroups are semilattices of nil-extensions of left and right groups. If the semigroup is regular, we recover the celebrated result of Clifford that a completely regular semigroup with commuting idempotents (also known as a Clifford semigroup) is a semilattice of groups. Also, weakly 1-chained regular semigroups are semilattices of left and right groups. Some more characterizations of these semigroups are the content of [6, Theorem 3.3]. Left (respectively right) 1-chained regular semigroups are semilattices of left (respectively right) groups.

We finally consider some other specific subclasses of strongly 2-chained semigroups. Recall that a rectangular band B is a semigroup satisfying the identity $aba=a$ for all a, b in B. Rectangular groups, which are direct products of a rectangular band and a group, lie between completely simple semigroups and (left, right) groups. It is well-known that rectangular groups are precisely the completely simple semigroups that are also orthodox, meaning they are regular and their product of idempotents are idempotents [31, Theorem 1.6]. This characterization allows us to describe semilattices of IF-semigroups and poor extensions of rectangular groups.

Corollary 3.6

Let S be a semigroup. Then the following statements are equivalent:

(1):

S is strongly 2-chained, and satisfies the quasi-identity:

$$\begin{aligned}aba=a \Rightarrow a^2b^2a^2=a^2\, (\forall a,b\in S); \end{aligned}$$

(2):

S is a semilattice of IF-semigroups and poor extensions of rectangular groups;

(3):

S satisfies the quasi-identity:

$$\begin{aligned}aba=a \Rightarrow ab^2a^2=a\, (\forall a,b\in S); \end{aligned}$$

(3’):

S satisfies the quasi-identity:

$$\begin{aligned}aba=a \Rightarrow a^2b^2a=a\, (\forall a,b\in S). \end{aligned}$$

Proof

$(1)\Rightarrow (2):$ Assume (1). By assumption, S is strongly 2-chained, so that S is a semilattice of semigroups without idempotents and poor extensions of completely simple semigroups by Corollary 2.12. Consider one of these completely simple semigroups T, and let $e,f\in E(T)$. As T is completely simple, it holds that ${\mathcal {D}}={\mathcal {J}}=T\times T$. Thus, $e{\,{\mathcal {D}}\,}f$. It follows that e, f are isomorphic in T, meaning that $e=ab, f=ba$ for some $a,b\in T$ with b being a reflexive inverse of a. In particular, it holds that $aba=a$, so that $a^2b^2a^2=a^2$ by (1). By multiplying both sides by b on the left and on the right, we obtain that $ba^2b^2a^2b=ba^2b$, which is equivalent to $(fe)(fe)=fe$. Hence, T is an orthodox semigroup.

$(2)\Rightarrow (3):$ Assume (2) and let $a,b\in S$ be such that $aba=a$. Firstly, as rectangular groups are completely simple, S is strongly 2-chained by Corollary 2.12. By Corollary 1.2, the regular element a is then group invertible, with group inverse $a^\#$. Secondly, the isomorphic idempotents ab and ba are in the same component since ${\mathcal {D}}\subseteq {\mathcal {J}}\subseteq \sigma$, finest semilattice congruence. Finally, since rectangular groups are orthodox, the product (ba)(ab) is idempotent; therefore, $ba^2b^2a^2b=ba^2b$. Multiplying both sides by a on the left and on the right yields $a^2b^2a^2=a^2$. Multiplying on the left by $a^\#$ yields $ab^2a^2=a$.

$(3)\Rightarrow (1):$ Assume (3) and let $a,b\in S$ be such that $aba=a$. Then $ab^2a^2=a$ by (3), and multiplying on the left by a yields $a^2b^2a^2=a^2$. We now prove that the regular element a of S is completely regular. Since $ab^2a^2=a$, it follows that $a{\,{\mathcal {L}}\,}a^2$. Let $b'=bab$. Then $b'ab'=b'$, and we deduce that $b'a^2b'^2=b'$ by (3). Multiplying both sides by a on the left and on the right yields $a^2b'^2a=ab'a=a$ and $a{\,{\mathcal {R}}\,}a^2$. Finally, $a{\,{\mathcal {H}}\,}a^2$. It follows that a is completely regular by Green’s theorem (Lemma 1.1). We conclude by Corollary 1.2 that S is strongly 2-chained.

Finally, observe that (1) and (2) are self-dual statements. Thus they are also equivalent to the dual statement $(3')$ of (3). $\square$

Example 3.7

Consider the semigroup of Example 2.13. We observed that $S={\mathcal {M}}(I,T,\Lambda )$ is a poor extension of the completely simple semigroup $K={\mathcal {M}}(I,0,\Lambda )$, with K a rectangular band. Thus statement (2) of Corollary 3.6 is valid, and (3) should also be valid. We prove directly that the quasi-identity $aba=a \Rightarrow ab^2a^2=a$ is satisfied. So, let $a,b\in S$ be such that $aba=a$. Then a is regular, hence $a\in K={{\,\textrm{reg}\,}}(S)$. As K is an ideal of S, we have that $ba\in K$. Finally, we deduce that $ab^2a^2=a(ba)a=a$ since K is a rectangular band.

More specifically, it may happen that the whole of E(S) is closed under product (one says that S is an E-semigroup), or even a commutative set (S is E-commutative).

Proposition 3.8

Let S be a semigroup. Then:

• (1) S is strongly 2-chained and an E-semigroup if and only if ${{\,\textrm{reg}\,}}(S)$ is a completely regular and orthodox subsemigroup of S;

• (2) S is strongly 2-chained and E-commutative if and only if ${{\,\textrm{reg}\,}}(S)$ is a Clifford subsemigroup of S, if and only if S is strongly 1-chained and an E-semigroup.

Proof

If S is E-commutative or an E-semigroup, then products of idempotents are idempotents hence regular. As is well known, this implies that products of regular elements are regular.

• (1) Suppose that S is strongly 2-chained and an E-semigroup. Then ${{\,\textrm{reg}\,}}(S)$ is a subsemigroup of S. It is completely regular by Corollary 1.2. It is orthodox as a regular E-semigroup. The converse implication is straightforward by Corollary 1.2.

• (2) To prove (2), we prove a chain of implications. Firstly, suppose that S is strongly 2-chained and E-commutative. Then ${{\,\textrm{reg}\,}}(S)$ is a subsemigroup of S. It is completely regular by Corollary 1.2. As it is also E-commutative, it is a Clifford semigroup.

  Secondly, suppose that ${{\,\textrm{reg}\,}}(S)$ is a Clifford semigroup. Then it is a semilattice of groups. Let $e=ab$ and $f=ba$ be isomorphic idempotents. Then e, f are idempotents in the same group, hence they are equal. It follows that S is strongly 1-chained and E-commutative, let alone an E-semigroup.

  Finally, suppose that S is strongly 1-chained and an E-semigroup. Then S is trivially strongly 2-chained. Let e and f be idempotents of S. As S is an E-semigroup, we have that ef and fe are idempotents. They are isomorphic by construction, hence equal by strong 1-chaining. $\square$