Keywords

1 Introduction

The study of laminar mixed convection flow in the lid-driven cavity has been the interest among a number of engineering applications, such as cooling microelectronics devices, nuclear reactors, HVAC systems, food processing, and many others [1,2,3,4,5,6]. According to our bibliographic research, among the studies carried out in the context of this framework, we cite the numerical investigation of mixed convective heat transfer in a lid-driven cavity with rotating cylinders analyzed by Shubham et al.[7] for different Grashof numbers and various rotating speeds of the inner cylinders. Keya et al.[8] presented a numerical study of mixed convection inside a lid-driven enclosure with a double-pipe heat exchanger. The authors present the influence of several values of Richardson, Reynolds, and Prandtl numbers on heat transfer rate. They concluded that the rate of heat transfer is maximum for high values of Ri and Re, and low values of Pr. Another work recently published was fulfilled by Kashyap et al. [9], the authors used the lattice Boltzmann method to investigate the influence of the cavity inclination on mixed convection in a two-sided lid-driven cavity with a hot porous block. They concluded that tilting the cavity increases the rate of heat transfer and entropy generation. The numerical study of MHD mixed convection in a lid-driven square enclosure filled with nanofluid was studied by Selimefendigil and Öztop [10] who used the Richardson and Hartmann numbers, cylinder's angular rotational speed, and solid volume fraction of the nanoparticles as governing parameters.

To the best of our knowledge, no research have been carried out about laminar mixed convection flow in a lid-driven cavity with two rotating embedded cylinders and insulated vertical walls. In this study, we aim to use the lattice Boltzmann method with BGK approximation coupled with immersed boundary method (IBM) as a numerical tool to simulate laminar mixed convection in a lid-driven cavity with insulated vertical walls in the presence of two rotating hot cylinders. The governing parameters of this study are the Richardson number and different configurations related to the direction of rotation of the cylinders.

2 Problem Geometry and Numerical Method

2.1 Problem Geometry

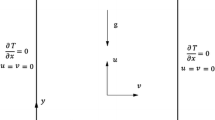
Figure 1 presents the physical domain used in this work; it is composed of two inner cylinders of radii R1 and R2 inside a rectangular cavity. The two cylinders are uniformly heated to high temperature Th, and the bottom and upper walls of the cavity are maintained at low temperature Tc, the vertical walls are insulated and air (Pr = 0.7) is the working fluid.

Fig. 1.
figure 1

Schematic diagram of the physical problem with boundary conditions

Full size image

The Richardson number (Ri), Prandtl number (Pr), and Nusselt number (Nuav) are the dimensionless numbers taken into consideration in this study and are defined as:

$$ {\text{Ri}} = \frac{Ra}{{Re^{2} Pr}} $$
(1)
$$ Nu_{av} = \frac{L}{{\left( {T_{h} - T_{c} } \right)S}}\int {\frac{\partial T}{{\partial n}}ds} $$
(2)

with S is the perimeter of the each cylinder, L is the characteristic length. Re and Ra refer to the Reynolds number and Rayleigh number respectively.

2.2 Numerical Method

In most cases, computational fluid dynamics (CFD), which is based on the Navier-Stokes equations, is used to simulate fluids behavior. Recently, the lattice Boltzmann approach stands out as an alternative to the conventional methods in the field of simulation of fluid flow and heat transfer. For this method, the fluid is presented by particles, which are located at lattice sites at time \(t,\) the particles are presented by a distribution function \(f\) and move in set directions as illustrated in Fig. 2.

The distribution functions are calculated by solving the Lattice Boltzmann Equation (LBE) (Eq. 3). Chen's simple relaxation time lattice Boltzmann method (SRT-LBM) [11] is adopted for this study.

$$ \frac{\partial f}{{\partial t}} + {\varvec{c}}.\Delta f = - \frac{1}{{\tau_{f} }}\left( {f - f^{eq} } \right) + F_{ext} $$
(3)

The parameter \({\varvec{c}}\) is the particle velocity vector, \(f_{i}^{eq}\) the equilibrium distribution function, \(\tau_{f}\) represents the relaxation time and \(F_{ext}\) the external force term representing the buoyancy force \(F_{ext} = 3\omega_{i} g_{y} \beta \Delta T\) taking into consideration the Boussinesq approximation [12].

The discretized version of the LBE equation Eq. (3) is presented in Eq. (4);

$$ \frac{{\partial f_{i} }}{\partial t} + c_{i} .\Delta f_{i} = - \frac{1}{{\tau_{f} }}\left( {f_{i} - f_{i}^{eq} } \right) + F_{ext} $$
(4)

where i ϵ {0,8} and \(f_{i}\) stands the associated distribution function in direction i. This discretization conserves the mass, momentum, and energy of the fluid particles (conservation laws). The parameter \(c_{i}\) denotes the discrete velocity and \(f_{i}^{eq}\) the equilibrium distribution function.

The lattice-Boltzmann method solves Eq. (3) in two steps: collision and steaming.

  • Collision:

    $$ f_{i} \left( {x,t + \Delta t} \right) = f_{i} \left( {x,t} \right) + \frac{\Delta t}{{\tau_{f} }}\left( {f_{i}^{eq} \left( {x,t} \right) - f_{i} \left( {x,t} \right)} \right) $$
    (5)

  • Streaming:

    $$ f_{i} \left( {x + \Delta x,t + \Delta t} \right) = f_{i} \left( {x,t + \Delta t} \right) $$
    (6)

where ∆t and ∆x are the time step and lattice spacing, respectively.

According to [13], the equilibrium distribution function is represented in Eq. (7).

$$ f_{i}^{eq} = \omega_{i} \left( {1 + \frac{3}{{c^{2} }}{\varvec{c}}_{i} .{\varvec{u}} + \frac{9}{{2c^{4} }}\left( {{\varvec{c}}_{i} .{\varvec{u}}} \right)^{2} - \frac{3}{{2c^{2} }}\left( {{\varvec{u}}.{\varvec{u}}} \right)} \right) $$
(7)

where \(\omega_{i}\) is the weight of the equilibrium distribution in the direction i.

$$ \omega_{i = } \left\{ {\begin{array}{*{20}c} {4/9\,i = 0} \\ {1/9\,i = 1,2,3,4} \\ {1/36\,i = 5,6,7,8} \\ \end{array} } \right. $$
(8)
$$ {\varvec{c}}_{i = } \left\{ {\begin{array}{*{20}c} {\left( {0.0} \right)\,i = 0} \\ {c\left( {{\text{cos}}\left( {\frac{i - 1}{2}\pi } \right),{\text{sin}}\left( {\frac{i - 1}{2}\pi } \right)} \right){ }\,i = 1,2,3,4} \\ {c\sqrt 2 \left( {{\text{cos}}\left( {\frac{2i - 1}{4}\pi } \right),{\text{sin}}\left( {\frac{2i - 1}{4}\pi } \right)} \right){ }\,i = 5,6,7,8} \\ \end{array} } \right. $$
(9)

Equations (10) and (11) are used to calculate the macroscopic quantities such as fluid velocity and density.

$$ \rho = \mathop \sum \limits_{i = 0}^{i = 8} f_{i} $$
(10)
$$ \rho {\varvec{u}} = \mathop \sum \limits_{i = 0}^{i = 8} {\varvec{c}}_{{\varvec{i}}} f_{i} $$
(11)

The macroscopic temperature T is obtained by:

$$ T\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{i = 8} g_{i} \left( {x,t} \right) $$
(12)

where \(g_{i}\) are the internal energy distribution functions. In this study, the two-dimensional nine-velocity (D2Q9) model is used for both density and energy distribution functions as shown in Fig. 2.

Fig. 2.
figure 2

The D2Q9 model's lattice arrangement for 2D LBM.

Full size image

2.3 Boundary Conditions

To deal with the boundary conditions, Guo et al.[14] propose the split-forcing method coupled with lattice-Boltzmann method to apply the effect of the immersed body force on a non-Newtonian flow field [15]. For this case, the density distribution function \(f_{i}\) and the internal energy density distribution \(g_{i}\) associated with the velocity and temperature fields are given respectively by:

$$ f_{i} \left( {x + \Delta x,t + \Delta t} \right) = f_{i} \left( {x,t} \right) + \frac{\Delta t}{{\tau_{f} }}\left( {f_{i}^{eq} \left( {x,t} \right) - f_{i} \left( {x,t} \right)} \right) + F_{i} \left( {x,t} \right)\Delta t $$
(13)
$$ g_{i} \left( {x + \Delta x,t + \Delta t} \right) = g_{i} \left( {x,t} \right) + \frac{\Delta t}{{\tau_{g} }}\left( {g_{i}^{eq} \left( {x,t} \right) - g_{i} \left( {x,t} \right)} \right) + Q_{i} \left( {x,t} \right)\Delta t $$
(14)

The quantities \(F_{i} \left( {{\text{x}},{\text{t}}} \right)\) and \(Q_{i} \left( {{\text{x}},{\text{t}}} \right)\) denote the discrete external force and the discrete energy source term, respectively, which are given by:

$$ F_{i} \left( {x,t} \right) = \left( {1 - \frac{1}{{2\tau_{f} }}} \right)w_{i} \left( {3\frac{{{\varvec{c}}_{i} - {\varvec{u}}\left( {x,t} \right)}}{{c^{2} }} + 9\frac{{{\varvec{c}}_{i} {\varvec{u}}\left( {x,t} \right)}}{{c^{4} }}{\varvec{c}}_{i} } \right).F\left( {x,t} \right) $$
(15)
$$ Q_{i} \left( {x,t} \right) = \left( {1 - \frac{1}{{2\tau_{g} }}} \right)w_{i} Q\left( {x,t} \right) $$
(16)

In the Eqs. (15) and (16), the terms \({\text{F}}\left( {{\text{x}},{\text{t}}} \right)\) and \({\text{Q}}\left( {{\text{x}},{\text{t}}} \right)\) refer to the body force and energy source density, respectively. They are expressed by Eqs. (17) and (18) as follow:

$$ F\left( {x,t} \right) = 2{\rho}\left( {x,t} \right)\frac{{U^{d} - U^{noF} \left( {x,t} \right)}}{{\Delta t{ }}} $$
(17)

where \(U^{d}\) is the desired velocity of the immersed boundary and \(U^{noF} \left( {x,t} \right)\) is the unforced velocity at the forcing point.

$$ Q\left( {x,t} \right) = 2{\rho}\left( {x,t} \right)\frac{{c^{2} }}{{3T_{0} }}\frac{{T^{d} - T^{noF} \left( {x,t} \right)}}{{\Delta t{ }}} $$
(18)

In the Eq. (18), \(T^{d}\) and \(T^{noF} \left( {x,t} \right)\) refer to the desired temperature of the immersed boundary and the unforced temperature at the interpolation point, respectively. It is to be noted that the steep boundary conditions given above are applied in the calculation algorithm between streaming and collision steps as referred in [16].

2.4 Code Validation

In order to validate the computer code, a verification has been carried out by comparing the results with certain results published in the literature in terms of isotherms and streamlines as illustrated in the Fig. 3.

Fig. 3.
figure 3

Comparison of isotherms and streamlines with the results by Tao et al. [17] (a) and (c), and present work (b) and (d) respectively for \(Ri = 10\) and \(Pr = 0.7\).

Full size image

A second validation has been carried out quantitatively in the case of free convection heat transfer generated between a heated imbedded cylinder and a square cavity studied by Shu et al. [18]. The comparative results presented in Table 1 in terms averaged values of Nusselt number \(\overline{Nu}\), show a good agreement.

Table 1. Comparison of the average Nusselt number \(\overline{Nu}\) with previous results.
Full size table

3 Results and Discussion

To investigate the Richardson’s number effect for different rotational configurations of the cylinders on the isotherms and streamlines, the study is carried out using the grid 200 × 200 for two values of the Richardson number (Ri = 0.5 and 100), and four rotational configurations as indicated in Table 2.

Table 2. Configurations of rotational directions of the cylinders.
Full size table
Fig. 4.
figure 4

Contours of isotherms (a)–(c) and streamlines (b)–(d) for Ri = 0.5 (left) and Ri = 100 (right) for the configuration 1.

Full size image
Fig. 5.
figure 5

Contours of isotherms (a)–(c) and streamlines (b)–(d) for Ri = 0.5 (left) and Ri = 100 (right) for the configuration 2.

Full size image
Fig. 6.
figure 6

Contours of isotherms (a)–(c) and streamlines (b)–(d) for Ri = 0.5 (left) and Ri = 100 (right) for the configuration 3.

Full size image
Fig. 7.
figure 7

Contours of isotherms (a)–(c) and streamlines (b)–(d) for Ri = 0.5 (left) and Ri = 100 (right) for the configuration 4.

Full size image

The mixed convection flow in a lid-rectangular cavity with two embedded rotating hot cylinders is numerically carried out in this work. The impact of the Richardson number on the streamlines and isotherms is analyzed for two values of this parameter (Ri = 0.5, Ri = 100) and the four configurations as described in Table 2. It is to be remembered that the top wall of the cavity is moving at a constant velocity \(u_{w}\).

Figures 4(c), 5(c), 6(c), and 7(c) illustrate the isotherms corresponding to Ri = 100 for the four configurations. The appearance of the plume patterns in the isotherms indicates the dominance of the natural convection mode Ri*Re >> 1. In addition to that, the corresponding streamlines show complex structures generally dominated by two main cells. In the case of Ri = 0.5, illustrated in Figs. 4(a), 5(a), 6(a), and 7(a), the temperature field is strongly affected owing to the top wall motion and cylinders rotation, which means that the magnitude of the forced convection becomes strong enough to affect the temperature field.

For the first configuration 1 (the two cylinders are counter-clockwise rotating). In Fig. 4(b), the flow structure at Ri = 0.5 is characterized by the appearance of a large clockwise eddy in the upper part of the cavity, which prevents the appearance of the plume in the isotherms as in Fig. 4(c). Moreover, a large cell encompassing the cylinders and extending to the lower cold wall is formed. As a result, the thermal effect of the heating cylinders reaches the bottom zone of the cavity, whereas for Ri = 100, the corresponding isotherms illustrated in Fig. 4(d) show a cold zone in the lower part of the cavity and the area adjacent to the upper wall. This means that for Ri = 100, the effect of the heating cylinders is more apparent in the area above the cylinders due to the prevailing role of natural convection for this value of Ri.

Concerning configuration 2 (the cylinder 1 is counter-clockwise rotating and the cylinder 2 is clockwise rotating), the flow at Ri = 0.5 consists of a large cell that covers the main part of the cavity and the inner cells formed around the rotating cylinders, as depicted in Fig. 5(b). This cell is due to the motion of the top wall of the cavity and supported the second cylinder that rotates clockwise. This configuration favors the appearance of two small vortices near the lower corners of the cavity and the extension of the zone heated by the cylinders above them even for this small value of Ri for which the shear force effect prevails.

The patterns of streamlines and isotherms corresponding to the configuration 3 (the first cylinder rotates clockwise and the second cylinder rotate counter-clockwise) are illustrated for Ri = 0.5 and Ri = 100 respectively in Fig. 6(a), (b), (c), (d). For this configuration where the two cylinders rotate in opposite directions, the aiding role between the moving wall and the left cylinder leads to a complex flow structure where the main formed cells rotate clockwise at Ri = 0.5 as it can be seen in Fig. 6(b). The corresponding isotherms exemplified in Fig. 6(a) show the presence of a thermal plume pointing downward and an extension of the space affected by the heating of the cylinders up to the vicinity of the cold walls. At Ri = 100, the dominant effect of natural convection outweighs the forced convection, which favors the formation of two vertical cells around the cylinders (Fig. 6(d)) and modifies the orientation of the thermal plumes that all point upwards (Fig. 6(c)).

For the fourth configuration where the two cylinders rotate clockwise, the latter play an aiding role with the upper moving wall. Thus, at Ri = 0.5, the forced convection role is dominant and Figs.7(b) shows that the flow is mainly unicellular. The cell covers the whole space in the cavity and its inner lines surround the cylinders. As a result, the corresponding isotherms form contours enclosing the two cylinders while their open lines are mainly located in the areas not affected by the heating cylinders; i.e. near the cooled horizontal walls.

The results presented in Table 3 in terms of mean Nusselt number \(\overline{Nu}\), show a better contribution of each cylinder to the heat transfer at Ri = 0.5 for the configurations 1 to 3 since \(\overline{Nu}\) recorded at Ri = 100 is noticeably lower for these configurations due to the fact that the mixed convection overcomes the natural convection. For the fourth configuration, the maximum stream function in Fig. 7(b) is located near the cavity wall, i.e. away from the two cylinders, which explains the exception of this configuration characterized by a mean Nusselt number obtained with Ri = 100 higher than that corresponding to Ri = 0.5.

Table 3. Average Nusselt number \(\overline{Nu}\) for both cylinders and all configurations.
Full size table

4 Conclusion

A numerical study of mixed convection heat transfer in lid-driven cavity with two embedded rotating cylinders and insulated vertical walls has been conducted. To achieve this problem, the immersed boundary-lattice Boltzmann based on the D2Q9 model with the BGK collision operator was used. Four configurations corresponding to different rotational directions of the cylinders were considered. Based on the preliminary results, the forced convection mode prevails over natural convection at Ri = 0.5. In addition, the rate of heat exchange decrease was found globally attenuated by increasing the Richardson number for all configurations except the fourth one for which the tendency is reverted. These findings should be extended by considering more values of the governing parameters to arrive at more objective conclusions.