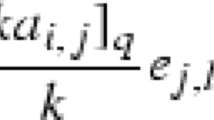Poisson commutative subalgebras associated with a Cartan subalgebra

Abstract

Let ${\mathfrak g}$ be a reductive Lie algebra and $\mathfrak t\subset \mathfrak g$ a Cartan subalgebra. The $\mathfrak t$-stable decomposition ${\mathfrak g}=\mathfrak t\oplus {\mathfrak m}$ yields a bi-grading of the symmetric algebra ${\mathcal {S}}({\mathfrak g})$. The subalgebra ${\mathcal {Z}}_{({\mathfrak g},\mathfrak t)}$ generated by the bi-homogenous components of the symmetric invariants $F\in {\mathcal {S}}({\mathfrak g})^{\mathfrak g}$ is known to be Poisson commutative. Furthermore the algebra ${\tilde{{\mathcal {Z}}}}=\textsf{alg}\langle {\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})},{\mathfrak t}\rangle$ is also Poisson commutative. We investigate relations between ${\tilde{{\mathcal {Z}}}}$ and Mishchenko–Fomenko subalgebras. In type A, we construct a quantisation of ${\tilde{{\mathcal {Z}}}}$ making use of quantum Mishchenko–Fomenko algebras.

1 Introduction

Let ${\mathfrak g}$ be a finite-dimensional reductive Lie algebra over an algebraically closed field $\Bbbk$ of characteristic zero. The symmetric algebra ${\mathcal {S}}({\mathfrak g})\cong \Bbbk [\mathfrak g^*]$ of ${\mathfrak g}$ is equipped with the standard Poisson structure, i.e., the Lie–Poisson bracket $\{\,\,,\,\}$. A subalgebra $A\subset {\mathcal {S}}({\mathfrak g})$ is Poisson commutative if $\{A,A\}=0$. Poisson commutative subalgebras attract a great deal of attention, because of their relationship to integrable systems and geometric representation theory. If $\{A,A\}=0$, then ${\mathrm {tr.deg\,}}A\leqslant {\varvec{b}}({\mathfrak g})$, where ${\varvec{b}}({\mathfrak g}):=\frac{1}{2}(\dim {\mathfrak g}+{\mathsf {rk\,}}{\mathfrak g})$ is the dimension of a Borel subalgebra of ${\mathfrak g}$.

The celebrated “argument shift method”, which goes back to Mishchenko–Fomenko [7], produces interesting Poisson commutative subalgebras. Namely, to any $\gamma \in {\mathfrak g}^*$, one associates the subalgebra $(\mathcal{M}\mathcal{F})_\gamma \subset {\mathcal {S}}({\mathfrak g})$. Following Vinberg [19], we say that $(\mathcal{M}\mathcal{F})_\gamma$ is the Mishchenko–Fomenko subalgebra associated with $\gamma$. This algebra can be described as follows. Let ${\mathcal {S}}({\mathfrak g})^{\mathfrak g}$ be the Poisson centre of $({\mathcal {S}}({\mathfrak g}), \{\,\,,\,\})$, i.e.,

$$\begin{aligned} {\mathcal {S}}({\mathfrak g})^{\mathfrak g}=\{H\in {\mathcal {S}}({\mathfrak g})\mid \{H,x\}=0 \ \ \forall x\in {\mathfrak g}\}. \end{aligned}$$

For $F\in {\mathcal {S}}({\mathfrak g})$, let $\partial _{\gamma } F$ be the directional derivative of F with respect to $\gamma \in {\mathfrak g}^*$, i.e.,

$$\begin{aligned} \partial _{\gamma }F(x)=\frac{\textit{d}}{\textit{d}t} F(x+t\gamma )\Big |_{t=0}. \end{aligned}$$

By definition, the algebra $(\mathcal{M}\mathcal{F})_\gamma$ is generated by all $\partial _\gamma ^k F$ with $k\geqslant 0$ and $F\in {\mathcal {S}}({\mathfrak g})^{{\mathfrak g}}$. Clearly, $(\mathcal{M}\mathcal{F})_\gamma$ is a graded subalgebra of ${\mathcal {S}}({\mathfrak g})$. The importance of these subalgebras and their quantum counterparts is demonstrated e.g. in [3, 4, 8, 19]. Suppose that $\gamma$ is regular. Then $(\mathcal{M}\mathcal{F})_\gamma$ is a maximal Poisson commutative subalgebra of ${\mathcal {S}}({\mathfrak g})$ [11]. For regular semisimple elements, this has been earlier proved by Tarasov [17]. Furthermore, $(\mathcal{M}\mathcal{F})_\gamma$ is freely generated by ${\varvec{b}}({\mathfrak g})$ homogeneous elements, see e.g. [11].

Let ${\mathfrak f}$ be a subalgebra of ${\mathfrak g}$. Suppose that there is an ${\mathfrak f}$-stable decomposition ${\mathfrak g}={\mathfrak f}\oplus {\mathfrak m}$, i.e., $[{\mathfrak f},{\mathfrak m}]\subset {\mathfrak m}$. This yields a bi-homogeneous decomposition of ${\mathcal {S}}({\mathfrak g})$:

$$\begin{aligned} {\mathcal {S}}({\mathfrak g})=\bigoplus _{i,j \geqslant 0} {\mathcal {S}}^i({\mathfrak f})\otimes {\mathcal {S}}^j({\mathfrak m}) \end{aligned}$$

and for any $F\in {\mathcal {S}}({\mathfrak g})$ we get the decomposition $F=\sum _{i,j}F_{i,j}$, where $F_{i,j}\in {\mathcal {S}}^i({\mathfrak f})\otimes {\mathcal {S}}^j({\mathfrak m})$.

Let ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak f})}$ be the subalgebra of ${\mathcal {S}}({\mathfrak g})$ generated by the bi-homogeneous components $H_{i,j}$ of all $H\in {\mathcal {S}}({\mathfrak g})^{{\mathfrak g}}$. Since H is ${\mathfrak g}$-invariant, each $H_{i,j}$ is ${\mathfrak f}$-invariant, hence ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak f})}\subset {\mathcal {S}}({\mathfrak g})^{{\mathfrak f}}$. The subalgebras ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak f})}$ are not necessarily Poisson commutative [13, Example 2.3]. However, it is proved in loc. cit. that ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak f})}$ is Poisson commutative whenever $[{\mathfrak f},{\mathfrak f}]=0$. In particular, if ${\mathfrak f}={\mathfrak t}$ is a Cartan subalgebra of ${\mathfrak g}$, then ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})}$ is Poisson commutative. Since ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})}\subset {\mathcal {S}}({\mathfrak g})^{\mathfrak t}$ and ${\mathfrak t}$ is commutative, the subalgebra generated by ${\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})}$ and ${\mathfrak t}$ is still Poisson commutative. We denote it by ${\tilde{{\mathcal {Z}}}}=\textsf{alg}\langle {\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})},{\mathfrak t}\rangle$. By [13, Theorem 3.2], ${\tilde{{\mathcal {Z}}}}$ is a polynomial algebra, it is a maximal Poisson commutative subalgebra and ${\mathrm {tr.deg\,}}{\tilde{{\mathcal {Z}}}}={\varvec{b}}({\mathfrak g})$. Results of Section 3 in [13] demonstrate that ${\tilde{{\mathcal {Z}}}}$ is closely related to Mishchenko–Fomenko subalgebras. One of the goals of this paper is to further elaborate on these relations.

Let ${\mathfrak m}\subset {\mathfrak g}$ be the ${\mathfrak t}$-stable complement of ${\mathfrak t}$ in ${\mathfrak g}$. Then ${\mathfrak t}^*$ (resp. ${\mathfrak m}^*$) is identified with the annihilator ${\mathrm {Ann\,}}\!({\mathfrak m})\subset {\mathfrak g}^*$ (resp. ${\mathrm {Ann\,}}\!({\mathfrak t})\subset {\mathfrak g}^*$). Our first result is that, for any $\gamma \in {\mathfrak t}^*$, the restrictions of ${\tilde{{\mathcal {Z}}}}$ and $(\mathcal{M}\mathcal{F})_\gamma$ to $\gamma +{\mathfrak m}^*$ coincide, see Theorem 2.1.

There is a Poisson bracket $\{\,\,,\,\}_{(\gamma )}$ on $\Bbbk [\gamma +{\mathfrak m}^*]^{\mathfrak t}\cong {\mathcal {S}}({\mathfrak m})^{\mathfrak t}$, inherited from ${\mathcal {S}}({\mathfrak g})$. The rank of this bracket is equal to $\dim {\mathfrak g}-3{\mathsf {rk\,}}{\mathfrak g}$ and if $\mathcal {B}$ is a Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{{\mathfrak t}},\{\,\,,\,\}_{(\gamma )})$, then ${\mathrm {tr.deg\,}}\mathcal {B}\leqslant \frac{1}{2}(\dim {\mathfrak g}-{\mathsf {rk\,}}{\mathfrak g})$, see Sect. 2.1. We show that if $\gamma$ is a regular point of ${\mathfrak g}^*$, then ${\tilde{{\mathcal {Z}}}}|_{\gamma +{\mathfrak m}^*}$ is a maximal Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{\mathfrak t},\{\,\,,\,\}_{(\gamma )})$ of transcendence degree $\frac{1}{2}(\dim {\mathfrak g}-{\mathsf {rk\,}}{\mathfrak g})$.

If $\mu \in {\mathfrak t}^*$ is regular in ${\mathfrak g}^*$, then $(\mathcal{M}\mathcal{F})_\mu \subset {\mathcal {S}}({\mathfrak g})^{\mathfrak t}$ and the component of grade 2 in $(\mathcal{M}\mathcal{F})_\mu$ equals ${\mathcal {S}}^2({\mathfrak t})\oplus {\mathbb V}(\mu )$, where ${\mathbb V}(\mu )$ is a certain subspace of dimension ${\mathsf {rk\,}}\![{\mathfrak g},{\mathfrak g}]$. There is a natural choice for such a ${\mathbb V}(\mu )$, which is explicitly described by Vinberg [19]. We recall it in Sect. 2. In [14], Rybnikov proved that if $\mu$ is generic enough, then $(\mathcal{M}\mathcal{F})_{\mu }$ is equal to the Poisson centraliser of ${\mathbb V}(\mu )$ in ${\mathcal {S}}({\mathfrak g})^{\mathfrak t}$. His proof goes through for all simple types, but does not apply to all regular points. We prove that in type A, the centraliser description holds for all regular $\mu$, see Proposition 2.8.

An interesting task is to produce a quantisation of ${\tilde{{\mathcal {Z}}}}$, i.e., a commutative subalgebra $\mathscr {Z}$ of the enveloping algebra ${\mathcal {U}}({\mathfrak g})$ such that ${\mathrm {gr\,}}\!(\mathscr {Z}) \subset {\mathcal {S}}({\mathfrak g})$ coincides with ${\tilde{{\mathcal {Z}}}}$. In case of $(\mathcal{M}\mathcal{F})_{\mu }$, the quantisation problem was raised in [19]. A solution, the quantum Mishchenko–Fomenko subalgebra $\mathcal {F}_\mu \subset {\mathcal {U}}({\mathfrak g})$, is obtained in [15] and [4]. These subalgebras are studied in [3, 4, 8, 16, 18]. For ${\mathfrak g}=\mathfrak {gl}_n$, we quantise ${\tilde{{\mathcal {Z}}}}$ in Sect. 3, see Theorem 3.2. For any ${\mathfrak g}$, we can lift quadratic in ${\mathfrak m}$ elements of ${\tilde{{\mathcal {Z}}}}$ to commuting elements of ${\mathcal {U}}({\mathfrak g})$. In the context of Sect. 3, we have found many similarities with quantum counterparts of Mishchenko–Fomenko subalgebras. This may be an indication that the algebra ${\tilde{{\mathcal {Z}}}}$ always has a quantisation.

2 Preliminaries on the coadjoint action and Poisson-commutativity

Let ${\mathfrak q}$ be a Lie algebra over $\Bbbk$. Let ${\mathfrak q}^\xi$ denote the stabiliser in ${\mathfrak q}$ of $\xi \in {\mathfrak q}^*$. The index of ${\mathfrak q}$, ${\mathrm {ind\,}}{\mathfrak q}$, is defined by ${\mathrm {ind\,}}{\mathfrak q}=\min _{\xi \in {\mathfrak q}^*} \dim {\mathfrak q}^\xi$. The set of regular elements of ${\mathfrak q}^*$ is

$$\begin{aligned} {\mathfrak q}^*_\textsf{reg}=\{\eta \in {\mathfrak q}^*\mid \dim {\mathfrak q}^\eta ={\mathrm {ind\,}}{\mathfrak q}\} . \end{aligned}$$

(1.1)

Then ${\mathfrak q}^*_\textsf{sing}={\mathfrak q}^*\setminus {\mathfrak q}^*_\textsf{reg}$. Set further ${\varvec{b}}(\mathfrak q)=(\dim {\mathfrak q}+{\mathrm {ind\,}}{\mathfrak q})/2$. If $\mathfrak q=\mathfrak g$ is reductive, then ${\mathrm {ind\,}}\mathfrak g={\mathsf {rk\,}}\mathfrak g$ and ${\varvec{b}}(\mathfrak g)$ is the dimension of a Borel subalgebra of $\mathfrak g$.

For any $\gamma \in {\mathfrak q}^*$, one defines the Poisson bracket $\{\,,\,\}_{\gamma }$ on ${\mathfrak q}^*$ by $\{\xi ,\eta \}_{\gamma }=\gamma ([\xi ,\eta ])$ for $\xi ,\eta \in {\mathfrak q}$. This new bracket is compatible with the standard Lie–Poisson bracket $\{\,\,,\,\}$ on ${\mathcal {S}}(\mathfrak q)$, i.e., any linear combination of $\{\,\,,\,\}$ and $\{\,\,,\,\}_{\gamma }$ is again a Poisson brackets. For more details, see [2, Sect. 1.8.3]. There is a well-known method, the Lenard–Magri scheme, for constructing “large” Poisson commutative subalgebras of ${\mathcal {S}}({\mathfrak q})$, which is related to compatible brackets, see e.g. [5]. In this way, one obtains $(\mathcal{M}\mathcal{F})_\gamma$ from the pair $(\{\,\,,\,\},\{\,\,,\,\}_{\gamma })$.

In [13], starting form an $\mathfrak f$-stable decomposition $\mathfrak q=\mathfrak f\oplus \mathfrak m$ with $[\mathfrak f,\mathfrak f]=0$, a Poisson commutative subalgebra ${\mathcal {Z}}_{({\mathfrak q},{\mathfrak f})}\subset {\mathcal {S}}({\mathfrak q})$ was constructed. From now on, we consider a particularly interesting case, where $\mathfrak q=\mathfrak g={\mathsf {Lie\,}}G$ is a reductive Lie algebra and $\mathfrak f={\mathfrak t}$ is a Cartan subalgebra. Set $l={\mathsf {rk\,}}{\mathfrak g}$.

The algebra ${\mathcal {S}}({\mathfrak g})^{\mathfrak g}$ is a polynomial ring. Let $\{H_1,\dots ,H_l\}$ be a set of homogeneous algebraically independent generators of ${\mathcal {S}}({\mathfrak g})^{\mathfrak g}$ with $\deg H_j=d_j$. We have $\sum _{j=1}^l d_j={\varvec{b}}({\mathfrak g})$. Let ${\mathfrak g}={\mathfrak u}\oplus {\mathfrak t}\oplus {\mathfrak u}^-$ be a fixed triangular decomposition. Set ${\mathfrak m}={\mathfrak u}\oplus {\mathfrak u}^-$. The vector space decomposition ${\mathfrak g}={\mathfrak t}\oplus {\mathfrak m}$ provides the bi-homogeneous decomposition of each $H_j$:

$$\begin{aligned} H_j=\sum _{i=0}^{\textit{d}_j} (H_j)_{(i,\textit{d}_j-i)}, \end{aligned}$$

where $(H_j)_{(i,\textit{d}_j-i)}\in {\mathcal {S}}^i({\mathfrak t})\otimes {\mathcal {S}}^{\textit{d}_j-i}({\mathfrak m})\subset {\mathcal {S}}^{d_j}({\mathfrak g})$. Then we say that $d_j-i$ is the ${\mathfrak m}$-degree of $(H_j)_{(i,d_j-i)}$. Now, ${\mathcal {Z}}:={\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})}$ is the algebra generated by

$$\begin{aligned} \{ (H_j)_{(i,d_j-i)} \mid j=1,\dots ,l; i=0,1,\dots , d_j-3, d_j-2, d_j\}, \end{aligned}$$

see [13]. The total number of functions in this family equals $\sum _{j=1}^l (d_j+1) - l={\varvec{b}}(\mathfrak g)$ and they are algebraically independent [13]. Replacing the elements $(H_j)_{(d_j,0)}\in {\mathcal {S}}^{d_j}({\mathfrak t})$ with a basis of ${\mathfrak t}$, we obtain a larger subalgebra, denoted ${\tilde{{\mathcal {Z}}}}$, which is still polynomial and Poisson commutative.

2.1 Notation and conventions

For a subalgebra $A\subset {\mathcal {S}}({\mathfrak g})$ and $\gamma \in {\mathfrak g}^*$, we set $\textit{d}_\gamma A=\{\textit{d}_\gamma F \mid F\in A\}$.

Given a Poisson algebra $\mathcal {A}$ and $a\in \mathcal {A}$, let $\mathcal {Z}_a\mathcal {A}=\{F\in \mathcal {A}\mid \{a,F\}=0\}$ denote the Poisson centraliser of a in $\mathcal {A}$.

Let $\mathfrak l\subset \mathfrak g$ be a Lie subalgebra. Then ${\mathcal {S}}(\mathfrak g)^{\mathfrak l}=\{F\in {\mathcal {S}}(\mathfrak g)\mid \{\xi ,F\}=0 \ \forall \xi \in \mathfrak l\}$ and ${\mathcal {U}}(\mathfrak g)^{\mathfrak l}$ stands for the centraliser $\{X\in {\mathcal {U}}(\mathfrak g)\mid [\xi ,X]=0 \ \forall \xi \in \mathfrak l\}$ of $\mathfrak l$ in ${\mathcal {U}}(\mathfrak g)$.

For an irreducible affine variety Y over $\Bbbk$, we let $\Bbbk [Y]$ stand for the ring of regular functions on Y and $\Bbbk (Y)={\textrm{Quot}\,}\Bbbk [Y]$ for the field of rational functions on Y. A statement that a certain assertion holds for generic points of Y (or for generic orbits on Y) means that this assertion holds for all points of a nonempty open subset $U\subset Y$ (for all orbits intersecting U).

If ${\mathfrak g}={\mathfrak f}\oplus {\mathfrak m}$ and $\xi \in {\mathfrak g}$, then $\xi =\xi _{\mathfrak f}+\xi _{{\mathfrak m}}$, where $\xi _{\mathfrak f}\in \mathfrak f$ and $\xi _{{\mathfrak m}}\in {\mathfrak m}$.

Let $\Delta$ be the set of roots of $({\mathfrak g},{\mathfrak t})$ and $\Delta ^+\subset \Delta$ the subset of positive roots corresponding to ${\mathfrak u}$. For $\alpha \in \Delta$, let $e_\alpha \in \mathfrak g_{\alpha }$ be a nonzero root vector. We let $h_\alpha \in [{\mathfrak g}_\alpha ,{\mathfrak g}_{-\alpha }]\subset {\mathfrak t}$ be such that $\alpha (h_\alpha )=2$.

We say that ${\mathfrak g}$ is of type A, if ${\mathfrak g}=\mathfrak {sl}_{l+1}$. In that case, we fix ${\mathfrak t}$ as the subspace of diagonal matrices and use the standard linear functions $\varepsilon _i\in {\mathfrak t}^*$ such that $\varepsilon _i(\textrm{diag}(a_1,\ldots ,a_{l+1}))=a_i$. We fix the standard triangular decomposition with $\Delta ^+=\{\varepsilon _i-\varepsilon _j\mid i<j\}$. For $1\leqslant i,j\leqslant n$, let $E_{ij}\in \mathfrak {gl}_n$ be a matrix unit (elementary matrix).

If ${\mathfrak g}$ is semisimple, then ${\mathfrak g}$ is identified with ${\mathfrak g}^*$ via the Killing form $\kappa$.

3 Partial localisations and reductions by the action of ${\mathfrak t}$

Results of [13] show that ${\tilde{{\mathcal {Z}}}}=\textsf{alg}\langle {\mathcal {Z}}_{({\mathfrak g},{\mathfrak t})},{\mathfrak t}\rangle$ is closely related to Mishchenko–Fomenko subalgebras. Our goal now is to elaborate on this relation.

Recall that ${\mathfrak m}=\mathfrak u\oplus \mathfrak u^-$. Consider $\mathcal {A}={\mathcal {S}}({\mathfrak g})^{\mathfrak t}\otimes _{{\mathcal {S}}({\mathfrak t})}\Bbbk ({\mathfrak t}^*)\subset \Bbbk ({\mathfrak g}^*)^{{\mathfrak t}}$ as a ring of ${\mathcal {S}}({\mathfrak m})^{\mathfrak t}$-valued rational functions on ${\mathfrak t}^*$; here $FM\otimes {\tilde{F}}=M\otimes F{\tilde{F}}$ for $M\in {\mathcal {S}}({\mathfrak m})^{\mathfrak t}, F\in {\mathcal {S}}({\mathfrak t})\cong \Bbbk [{\mathfrak t}^*], {\tilde{F}}\in \Bbbk ({\mathfrak t}^*)$ and $(FM\otimes {\tilde{F}})(\mu )=F(\mu ){\tilde{F}}(\mu ) M$, if $\mu \in {\mathfrak t}^*$. Since $\{{\mathcal {S}}({\mathfrak g})^{\mathfrak t},{\mathcal {S}}({\mathfrak g})^{\mathfrak t}\}\subset {\mathcal {S}}({\mathfrak g})^{\mathfrak t}$ and $\{{\mathcal {S}}({\mathfrak g})^{\mathfrak t},{\mathfrak t}\}=0$, the ring $\mathcal {A}$ inherits a Poisson structure from ${\mathcal {S}}({\mathfrak g})$ and this Poisson structure is $\Bbbk ({\mathfrak t}^*)$-linear. For $\mu \in {\mathfrak t}^*$, set

$$\begin{aligned} \mathcal {A}_\mu =\{ A\in \mathcal {A}\mid A(\mu ) \,\text { is well-defined}\,\}. \end{aligned}$$

Let $\psi _\mu \!: \mathcal {A}_\mu \rightarrow {\mathcal {S}}(\mathfrak m)^{\mathfrak t}$ be the evaluation homomorphism. Then ${\mathcal {S}}({\mathfrak g})^{\mathfrak t}\subset \mathcal {A}_\mu$ for each $\mu$ and on ${\mathcal {S}}({\mathfrak g})^{{\mathfrak t}}\cong \Bbbk [{\mathfrak g}^*]^{\mathfrak t}$, the map $\psi _\mu$ coincides with the restriction homomorphism

$$\begin{aligned} \Bbbk [{\mathfrak g}^*]^{\mathfrak t}\rightarrow \Bbbk [\mu +{\mathfrak m}^*]^{\mathfrak t}\cong {\mathcal {S}}({\mathfrak m})^{\mathfrak t}. \end{aligned}$$

We define a bi-linear map $\{\,\,,\,\}_{(\mu )}\!: {\mathfrak m}\times {\mathfrak m}\rightarrow {\mathfrak m}\oplus \Bbbk$ by

$$\begin{aligned} \{x,y\}_{(\mu )}:=\psi _\mu ([x,y])=[x,y]_{\mathfrak m}+\mu ([x,y]_{{\mathfrak t}}) \ \text { for } \ x,y\in {\mathfrak m}\end{aligned}$$

and then extend it to a bi-linear operation on ${\mathcal {S}}(\mathfrak m)^{\mathfrak t}$ using the Leibniz rule. For X, Y in ${\mathcal {S}}(\mathfrak m)^{\mathfrak t}\subset \mathcal {A}$, we have

$$\begin{aligned} \psi _{\mu }(\{X,Y\})=\{X,Y\}_{(\mu )}=\{\psi _\mu (X),\psi _\mu (Y)\}_{(\mu )}. \end{aligned}$$

Using the $\Bbbk ({\mathfrak t}^*)$-linearity of the Poisson bracket on $\mathcal {A}$, we conclude that $\{\,\,,\,\}_{(\mu )}$ is a Poisson structure on ${\mathcal {S}}(\mathfrak m)^{\mathfrak t}$ and $\psi _\mu$ is a Poisson homomorphism with respect to $\{\,\,,\,\}_{(\mu )}$.

The ring $\mathcal {A}=\bigoplus _{N\geqslant 0}\mathcal {A}_N$ is graded by the degree in ${\mathfrak m}$ with $\mathcal {A}_N={\mathcal {S}}^N({\mathfrak m})^{\mathfrak t}\otimes _{\Bbbk }\Bbbk ({\mathfrak t}^*)$ and $\psi _\mu (\mathcal {A}_\mu \cap \mathcal {A}_N)={\mathcal {S}}^N({\mathfrak m})^{\mathfrak t}$. Since the Poisson bracket on $\mathcal {A}$ is $\Bbbk ({\mathfrak t}^*)$-linear, for any $A\in {\mathcal {S}}({\mathfrak g})^{{\mathfrak t}}$ and any $N\geqslant 0$, the subset $\mathcal {Z}_A(\mathcal {A}_{\leqslant N})=\mathcal {Z}_A\mathcal {A}\cap (\bigoplus _{i=0}^N \mathcal {A}_{i})$ is a vector space over $\Bbbk ({\mathfrak t}^*)$. It is a subspace of a finite-dimensional $\Bbbk ({\mathfrak t}^*)$-space $\mathcal {A}_{\leqslant N}$. Evaluating the defining equations of the centraliser $\mathcal {Z}_A (\mathcal {A}_{\leqslant N})$ at $\mu \in {\mathfrak t}^*$, we obtain

$$\begin{aligned} \dim _{\Bbbk ({\mathfrak t}^*)} \mathcal {Z}_A (\mathcal {A}_{\leqslant N}) = \dim \left( \mathcal {Z}_{\psi _\mu (A)}({\mathcal {S}}({\mathfrak m})^{\mathfrak t},\{\,\,,\,\}_{(\mu )})\cap {\mathcal {S}}^{\leqslant N}({\mathfrak m})\right) , \end{aligned}$$

(2.1)

whenever $\mu$ is generic enough.

Recall that we identify ${\mathfrak t}^*$ with ${\mathrm {Ann\,}}\!({\mathfrak m})\subset {\mathfrak g}^*$.

Theorem 2.1

If $\mu \in {\mathfrak t}^*$, then $\psi _\mu ({\tilde{{\mathcal {Z}}}})=\psi _\mu ((\mathcal{M}\mathcal{F})_{\mu })$.

Proof

Suppose first that $\mu \ne 0$. We fix $h\in {\mathfrak t}$ such that $\mu (h)=1$ and write $\mathfrak g =\Bbbk h\oplus \ker \mu$, where ${\mathfrak m}\subset \ker \mu$. Let $H\in {\mathcal {S}}({\mathfrak g})^{{\mathfrak g}}$ be homogeneous with $\deg H=d$. We decompose H as a sum

$$\begin{aligned} H=H_{0} h^{d} + H_{1}h^{d-1}+\cdots + H_{k}h^k +\cdots + H_{d}, \end{aligned}$$

where $H_{k}\in {\mathcal {S}}^k(\ker \mu )$. By the choice of h, we have

$$\begin{aligned} \partial _\mu ^k H=\sum _{r=k}^{d} r(r-1)\ldots (r-k+1)h^{r-k}H_{d-r} \end{aligned}$$

and

$$\begin{aligned} \psi _\mu (\partial _\mu ^k H)= \sum _{r=k}^{d} r(r-1)\ldots (r-k+1) \psi _\mu (H_{d-r}). \end{aligned}$$

Therefore $\psi _\mu ((\mathcal {M}\mathcal {F})_{\mu })=\textsf {alg}\langle \psi _\mu (H_{d-r}) \mid d\geqslant 1, H\in {\mathcal {S}}^d({\mathfrak g})^{\mathfrak g}, 0\leqslant r < d \rangle$.

Let $M_{d-i}\in {\mathcal {S}}^{d-i}({\mathfrak m})$ be such that the bi-homogeneous component $H_{i,d-i}\in {\mathcal {S}}^i({\mathfrak t})\otimes {\mathcal {S}}^{d-i}({\mathfrak m})$ of H lies in $h^i M_{d-i} + (\ker \mu \cap {\mathfrak t}){\mathcal {S}}({\mathfrak g})$. Then

$$\begin{aligned} \psi _\mu (H_{i,d-i})= M_{d-i} =\psi _\mu (h^i H_{d-i})=\psi _\mu (H_{d-i}) \end{aligned}$$

for all i. Since ${\tilde{{\mathcal {Z}}}}$ is generated by ${\mathfrak t}$ and $H_{i,d-i}$ with $H\in {\mathcal {S}}^d({\mathfrak g})^{\mathfrak g}$, we are done for $\mu \ne 0$.

If $\mu =0$, then $(\mathcal{M}\mathcal{F})_{0}={\mathcal {S}}(\mathfrak g)^{\mathfrak g}$ and $\psi _0(H)=\psi _0(H_{0,d})$. For other generators of ${\tilde{{\mathcal {Z}}}}$, we have $\psi _0({\mathfrak t})=0$ and $\psi _0(H_{i,d-i})=0$, whenever $i>0$. $\square$

A Mishchenko–Fomenko subalgebra is Poisson commutative and $\psi _\mu$ is a Poisson homomorphism; hence

$$\begin{aligned} 0\!= & {} \!\psi _\mu (\{ (\mathcal{M}\mathcal{F})_{\mu }, (\mathcal{M}\mathcal{F})_{\mu } \})\! =\!\{ \psi _\mu ((\mathcal{M}\mathcal{F})_{\mu }),\psi _\mu ( (\mathcal{M}\mathcal{F})_{\mu }) \}_{(\mu )}\\= & {} \{\psi _{\mu } ({\tilde{{\mathcal {Z}}}}),\psi _\mu ({\tilde{{\mathcal {Z}}}})\}_{(\mu )}\!=\!\psi _\mu (\{{\tilde{{\mathcal {Z}}}},{\tilde{{\mathcal {Z}}}}\}) \end{aligned}$$

for each $\mu \in {\mathfrak t}^*$. Since for any $A\in \mathcal {A}\setminus \{0\}$, the image $\psi _\mu (A)$ is well-defined and nonzero for almost all $\mu$, Theorem 2.1 provides a new proof for the fact that $\{{\tilde{{\mathcal {Z}}}},{\tilde{{\mathcal {Z}}}}\}=0$.

Assume that $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$. Then the polynomials $\partial _\mu ^k H_j$ with $1\leqslant j\leqslant l$ and $0\leqslant k<d_j$ are algebraically independent, cf. [11]. In particular, $\{\partial _\mu ^{d_j-1}H_j \mid 1\leqslant j\leqslant l\}$ is a basis of ${\mathfrak t}$ and ${\mathfrak t}\subset (\mathcal{M}\mathcal{F})_{\mu }$. This fact follows also from the Kostant regularity criterion for ${\mathfrak g}$ [6, Theorem 9],

$$\begin{aligned} \langle \textit{d}_\xi H_j \mid 1\leqslant j\leqslant l\rangle _{\Bbbk }={\mathfrak g}^\xi \ \text { if and only if }\ \xi \in {\mathfrak g}^*_\textsf{reg}, \end{aligned}$$

(2.2)

since $\textit{d}_\mu H_j=\frac{1}{(d_j-1)!}\partial _{\mu }^{d_j-1}H_j$.

Quadratic elements of $(\mathcal{M}\mathcal{F})_{\mu }$ are of particular importance. If not stated otherwise, assume that ${\mathfrak g}$ is semisimple. Set $\varvec{f}_j:=\varvec{f}_j(\mu ):=\psi _\mu ((H_j)_{(d_j-2,2)})$. Then

$$\begin{aligned} \partial _{\mu }^{d_j-2} H_j \in (d_j-2)!\varvec{f}_j +{\mathcal {S}}^2({\mathfrak t}). \end{aligned}$$

(2.3)

Since ${\mathfrak t}\subset (\mathcal{M}\mathcal{F})_{\mu }$, we have $\varvec{f}_j \in (\mathcal{M}\mathcal{F})_{\mu }$ for all j. Furthermore, the component of grade 2 in $(\mathcal{M}\mathcal{F})_{\mu }$ is equal to ${\mathcal {S}}^2({\mathfrak t})\oplus {\mathbb V}(\mu )$, where ${\mathbb V}(\mu )=\langle \varvec{f}_j \mid 1\leqslant j\leqslant l\rangle _{\Bbbk }$. If $\mu$ is generic enough, then $(\mathcal{M}\mathcal{F})_{\mu }$ is equal to the Poisson centraliser

$$\begin{aligned} \mathcal {Z}_{{\mathbb V}(\mu )}:=\{F\in {\mathcal {S}}({\mathfrak g})^{\mathfrak t}\mid \{F,\varvec{f}_j\}=0 \ \forall j\} \end{aligned}$$

by [14, Theorem 1].

Remark 2.2

An explicit description of the elements $\varvec{f}_j$ is crucial for the considerations in [14, 19] and many others. We present a quick elementary argument that produces such a description. Set $h_j=\textit{d}_\mu H_j$. Similar to the proof of Theorem 2.1, write $\mathfrak g=\Bbbk h\oplus \ker \mu$, where $\mu (h)=1$. Then

$$\begin{aligned} H_j=c h^{d_j}+h^{d_j-1}h' + h^{d_j-2} H'+\sum _{\alpha \in \Delta ^+} C_\alpha h^{d_j-2} e_\alpha e_{-\alpha } +\sum _{k=3}^{d_j} h^{d_j-k} H_{j,k}, \end{aligned}$$

where $c,C_\alpha$ are scalars, $h',H',H_{j,k}\in {\mathcal {S}}(\ker \mu )$, and $h'\in {\mathfrak t}$, $H'\in {\mathcal {S}}^2({\mathfrak t})$. In this notation, $h_j=c d_j h+h'$. Since $H_j\in {\mathcal {S}}({\mathfrak g})^{\mathfrak g}$, we have $\{e_\alpha ,H_j\}=0$ for each $\alpha \in \Delta ^+$. Note that $\{e_\alpha ,e_{-\alpha }\}=\mu (h_\alpha )h+h''$, where $h''\in (\ker \mu \cap {\mathfrak t})$. Considering the terms of $\{e_\alpha ,H_j\}$ that lie in $\Bbbk h^{d_j-1} {\mathfrak m}$, and then necessarily in $\Bbbk h^{d_j-1} e_{\alpha }$, we obtain

$$\begin{aligned} -\alpha (c d_j h+h') + C_\alpha \mu (h_\alpha )=0 \end{aligned}$$

for each positive root $\alpha$. Since $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$, we have $\mu (h_\alpha )\ne 0$ for each $\alpha \in \Delta ^+$. Hence $C_\alpha =\dfrac{\alpha (h_j)}{\mu (h_\alpha )}$. Here $\varvec{f}_j=\sum _{\alpha \in \Delta ^+} C_\alpha e_\alpha e_{-\alpha }$.

The discussion in Remark 2.2 confirms the description obtained by Vinberg in [19] :

$$\begin{aligned} {{\mathbb V}(\mu )} = \left\{ \sum _{\alpha \in \Delta ^+} \frac{\alpha (h)}{\mu (h_\alpha )} e_\alpha e_{-\alpha } \mid h\in {\mathfrak t}\right\} , \end{aligned}$$

(2.4)

whenever $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$.

3.1 Bi-linear operations $\{\,\,,\,\}_{(\gamma )}$ and $\{\,\,,\,\}_{\mathfrak m}$

For any $\gamma \in {\mathfrak t}^*$, we have defined a Poisson bracket $\{\,\,,\,\}_{(\gamma )}=\{\,\,,\,\}_{\mathfrak m}+\{\,\,,\,\}_\gamma$ on ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$ as a sum of two bi-linear operations. The second summand is the restriction to ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$ of the Poisson bracket “with frozen argument” $\{\,\,,\,\}_\gamma$, which is defined on ${\mathcal {S}}(\mathfrak g)$. Note that the operation $\{\,\,,\,\}_{\mathfrak m}$ is not a Poisson bracket on ${\mathcal {S}}({\mathfrak m})$, because it does not satisfy the Jacobi identity. However, in case $\gamma =0$, we obtain $\{\,\,,\,\}_{\mathfrak m}=\{\,\,,\,\}_{(0)}$, which is a Poisson bracket on ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$.

Let $\widehat{x}$ be a skew-symmetric form on $\mathfrak g$ associated with $x\in \mathfrak g^*$, i.e., $\widehat{x}(\xi ,\eta )=x([\xi ,\eta ])$ if $\xi ,\eta \in \mathfrak g$. For a Poisson structure, one defines its Poisson tensor (bivector) $\pi$ by the property that $\{F,H\}=\pi (\textit{d}F\wedge \textit{d}H)$ for functions F and H. In this terms, $\widehat{x}=\pi (x)$, if $\pi$ is the Poisson tensor of $\{\,,\,\}$. In general, one says that the rank of the Poisson structure is equal to the rank ${\mathsf {rk\,}}\pi$ of its Poisson tensor. Then ${\mathsf {rk\,}}\pi$ is the maximal dimension of a symplectic leave of $\pi$, see e.g. [2, Chapter 1].

Proposition 2.3

Let $\mathcal {B}$ be a Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{{\mathfrak t}},\{\,\,,\,\}_{(\gamma )})$. Then for any $\gamma$, we have ${\mathrm {tr.deg\,}}\mathcal {B}\leqslant \dim \mathfrak u$.

Proof

We identify ${\mathcal {S}}({\mathfrak m})$ with $\Bbbk [\gamma +{\mathfrak m}^*]$. Then

$$\begin{aligned} \{F,H\}_{(\gamma )}(x) =x([\textit{d}_x F,\textit{d}_x H])=\widehat{x}(\textit{d}_x F,\textit{d}_x H) \ \ \text { for all } \ \ x\in \gamma +{\mathfrak m}^*, \, F,H\in {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}. \end{aligned}$$

Since $\{\mathcal {B},\mathcal {B}\}_{(\gamma )}=0$, the subspace $\textit{d}_x \mathcal {B}$ is isotropic w.r.t. $\widehat{x}$ for any $x\in \gamma +{\mathfrak m}^*$. Furthermore $\widehat{x}(\textit{d}_x {\mathcal {S}}({\mathfrak g})^{{\mathfrak t}},\mathfrak t)=0$.

Let $T\subset G$ be the torus with ${\mathsf {Lie\,}}T={\mathfrak t}$. Generic T-orbits on $\gamma +{\mathfrak m}^*$ are closed, hence they are separated by the regular T-invariants $\Bbbk [\gamma +{\mathfrak m}^*]^T\cong {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$. Thus $\textit{d}_x{\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}\subset \textit{T}_x^{\,*}(\gamma +{\mathfrak m}^*)$ is the annihilator of the tangent space $\textit{T}_x(Tx)={\textrm{ad}}^*({\mathfrak t})x$ of the orbit Tx for a generic $x\in \gamma +{\mathfrak m}^*$. The orthogonal complement ${\mathfrak t}^{\perp _{\widehat{x}}}$ of ${\mathfrak t}$ in ${\mathfrak g}$ w.r.t. $\widehat{x}$ is the subset

$$\begin{aligned} \{\xi \in \mathfrak g \mid x([\xi ,{\mathfrak t}])=0\}=\{\xi \in \mathfrak g\mid {\textrm{ad}}^*({\mathfrak t})x \ \hbox { annihilates \,}\ \xi \}. \end{aligned}$$

Here we have ${\mathfrak t}^{\perp _{\widehat{x}}}={\mathfrak t}\oplus \textit{d}_x {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}=\textit{d}_x{\mathcal {S}}(\mathfrak g)^{{\mathfrak t}}$. Note that ${\mathsf {rk\,}}\widehat{x}=\dim {\mathfrak g}- l$.

Keeping the assumption that x is generic, we have ${\mathfrak t}\cap \ker \widehat{x}=0$. Since $\widehat{x}({\mathfrak t},{\mathfrak t})=0$, the rank of  $\widehat{x}|_{{\mathfrak t}^{\perp _{\widehat{x}}}}$ is equal to ${\mathsf {rk\,}}\widehat{x} -2\dim {\mathfrak t}$. Thus

$$\begin{aligned} {\mathsf {rk\,}}\!(\widehat{x}|_{\textit{d}_x {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}})={\mathsf {rk\,}}\!(\widehat{x}|_{\textit{d}_x {\mathcal {S}}({\mathfrak g})^{{\mathfrak t}}})=\dim \mathfrak g-3l=2(\dim \mathfrak u-l). \end{aligned}$$

(2.5)

Since $\dim \textit{d}_x {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}=\dim {\mathfrak g}-2l$, we obtain $\dim \textit{d}_x\mathcal {B}\leqslant (\dim \mathfrak u-l) + (\dim {\mathfrak g}-2\,l - (\dim \mathfrak g-3\,l))= \dim \mathfrak u.$ Thus, ${\mathrm {tr.deg\,}}\mathcal {B}\leqslant \dim \mathfrak u$. $\square$

The equality (2.5) shows that the rank of the Poisson bracket $\{\,\,,\,\}_{(\gamma )}$ on ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$ is equal to $2(\dim \mathfrak u-l)=\dim {\mathfrak m}-2\,l$.

Remark 2.4

Set $Y_\gamma :=\gamma +{\mathfrak m}^*$. The algebra ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}\cong \Bbbk [Y_\gamma ]^T$ is the algebra of regular functions on the affine variety $Y_\gamma /\!\!/T$  and the bracket $\{\,,\,\}_{(\gamma )}$ on ${\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$ is obtained by the Hamiltonian reduction w.r.t. the restriction ${\mathfrak g}^*\rightarrow {\mathfrak t}^*$. We have $\dim Y_\gamma /\!\!/T={\mathrm {tr.deg\,}}{\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}=\dim {\mathfrak g}-2 l$. The bound for ${\mathrm {tr.deg\,}}\mathcal {B}$ given by Proposition 2.3 is of the form $\dim Y_\gamma /\!\!/T -\frac{1}{2} (\dim {\mathfrak m}-2l)$, where $\dim {\mathfrak m}-2l$ is the rank of the Poisson structure in question. This is a general upper bound, existing for any Poisson algebra. The equality (2.5) can be deduced from the fact that generic symplectic leaves of $Y_\gamma /\!\!/T$ are of the form $(Gx\cap Y_\gamma )/\!\!/T$ with $\dim (Gx\cap Y_\gamma )/\!\!/T = \dim {\mathfrak g}-3\dim {\mathfrak t}$.

Theorem 2.5

Suppose that $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$. Then for any $\gamma \in {\mathfrak t}^*$, we have ${\mathrm {tr.deg\,}}\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })=\dim \mathfrak u$, and $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$ is a maximal Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{\mathfrak t},\{\,\,,\,\}_{(\gamma )})$.

Proof

Let $\{e,h,f\}\subset \mathfrak g$ be a principal $\mathfrak {sl}_2$-triple such that $h\in {\mathfrak t}$, $e\in \mathfrak u$, $f\in \mathfrak u^-$. Set $\chi _+=\kappa (e,.\,), \chi _-=\kappa (f,.\,)\in \mathfrak g^*$. Since $e+({\mathfrak t}\oplus \mathfrak u^-)$ and $f+({\mathfrak t}\oplus \mathfrak u)$ consist of regular elements [6], we have $(\Bbbk \chi _+\oplus \Bbbk \chi _-\oplus \Bbbk \mu ) \cap \mathfrak g^*_\textsf{sing}=0$. Therefore $\dim \textit{d}_{x}(\mathcal{M}\mathcal{F})_{\mu }={\varvec{b}}(\mathfrak g)$ for any nonzero $x\in \Bbbk \chi _+\oplus \Bbbk \chi _-$, see e.g. [12, Cor. 1.6  & Lemma 2.1].

For any $F\in {\mathcal {S}}(\mathfrak g)$ and $y\in \mathfrak m^*$, we have $\textit{d}_y F \in \textit{d}_y(\psi _0(F))+{\mathfrak t}$. Hence $\dim \textit{d}_x \psi _0((\mathcal{M}\mathcal{F})_{\mu })$ is equal to $\dim \mathfrak u$. Each $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$ is a Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{{\mathfrak t}},\{\,,\,\}_{(\gamma )})$, thereby ${\mathrm {tr.deg\,}}\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })\leqslant \dim \mathfrak u$ by Proposition 2.3. Thus, ${\mathrm {tr.deg\,}}\psi _0((\mathcal{M}\mathcal{F})_{\mu })=\dim \mathfrak u$.

The differentials $\textit{d}_x(\psi _0(\partial _\mu ^k H_j))$ with $k<d_j-1$ and $1\leqslant j\leqslant l$ are linearly independent for each $x\in (\Bbbk \chi _+ \oplus \Bbbk \chi _-){\setminus }\{0\}$. Thus, ${\mathcal J}\cap (\Bbbk \chi _+ \oplus \Bbbk \chi _-)\subset \{0\}$ for the Jacobian subset

$$\begin{aligned} \mathcal {J}=\{y\in {\mathfrak m}^* \mid \bigwedge _{0\leqslant k<d_j-1,\, 1\leqslant j\leqslant l} \textit{d}_y (\psi _0(\partial _\mu ^k H_j))=0\}. \end{aligned}$$

If $F\in {\mathcal {S}}(\mathfrak g)$ is homogeneous, then $\psi _0(F)$ is also homogeneous. This applies to each $\partial _\mu ^k H_j$ and leads to the conclusion that $\mathcal {J}$ does not contain divisors. By [10, Theorem 1.1], $\psi _0((\mathcal{M}\mathcal{F})_{\mu })$ is an algebraically closed subalgebra of ${\mathcal {S}}({\mathfrak m})$, i.e., if $F\in {\mathcal {S}}({\mathfrak m})$ is algebraic over the quotient field ${\textrm{Quot}\,}\psi _0((\mathcal{M}\mathcal{F})_{\mu })$, then $F\in \psi _0((\mathcal{M}\mathcal{F})_{\mu })$.

Suppose $\psi _0((\mathcal{M}\mathcal{F})_{\mu })\subset \mathcal {B}\subset ({\mathcal {S}}({\mathfrak m})^{{\mathfrak t}},\{\,\,,\,\}_{(\gamma )})$, where $\mathcal {B}$ is a Poisson commutative subalgebra. Then ${\mathrm {tr.deg\,}}\mathcal {B}\leqslant \dim \mathfrak u$ by Proposition 2.3. Thereby the inclusion $\psi _0((\mathcal{M}\mathcal{F})_{\mu })\subset \mathcal {B}$ is an algebraic extension and $\psi _0((\mathcal{M}\mathcal{F})_{\mu })=\mathcal {B}$. The argument shows also that $\psi _0((\mathcal{M}\mathcal{F})_{\mu })$ coincides with its Poisson centraliser in ${\mathcal {S}}({\mathfrak m})^{\mathfrak t}$ w.r.t. $\{\,,\,\}_{{\mathfrak m}}$ and finishes the case $\gamma =0$.

For any homogeneous $F\in {\mathcal {S}}(\mathfrak g)\setminus {\mathfrak t}{\mathcal {S}}({\mathfrak g})$, the image $\psi _0(F)$ is the highest degree component of any $\psi _\gamma (F)$. In particular, the equality ${\mathrm {tr.deg\,}}\psi _0((\mathcal{M}\mathcal{F})_{\mu })=\dim \mathfrak u$ leads to ${\mathrm {tr.deg\,}}\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })\geqslant \dim \mathfrak u$, thereby ${\mathrm {tr.deg\,}}\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })=\dim \mathfrak u$. Assume that $F\in {\mathcal {S}}({\mathfrak m})^{\mathfrak t}$ commutes with $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$ w.r.t. $\{\,\,,\,\}_{(\gamma )}$ and does not lie in $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$. Then the highest degree component of F commutes with $\psi _0((\mathcal{M}\mathcal{F})_{\mu })$ w.r.t. $\{\,\,,\,\}_{{\mathfrak m}}$, which means that this component lies in $\psi _0((\mathcal{M}\mathcal{F})_{\mu })$. Then we can reduce the degree of F by subtracting a suitable element of $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$. This standard reduction argument proves that $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })$ is a maximal Poisson commutative subalgebra of $({\mathcal {S}}({\mathfrak m})^{\mathfrak t},\{\,\,,\,\}_{(\gamma )})$ for each $\gamma \in {\mathfrak t}^*$. $\square$

Corollary 2.6

Both, $\mathcal {B}_1=(\mathcal{M}\mathcal{F})_{\mu }\otimes _{{\mathcal {S}}({\mathfrak t})}\Bbbk ({\mathfrak t}^*)$ and $\mathcal {B}_2={\tilde{{\mathcal {Z}}}}\otimes _{{\mathcal {S}}({\mathfrak t})}\Bbbk ({\mathfrak t}^*)$, are maximal Poisson commutative subalgebras of $\mathcal {A}$.

Proof

By the construction, $\{\mathcal {B}_i,\mathcal {B}_i\}=0$ for both i. Assume that $\mathcal {B}_i$ is not maximal. Then there is $a\in \mathcal {A}\setminus \mathcal {B}_i$ such that $\{a,\mathcal {B}_i\}=0$. For each $\gamma \in {\mathfrak t}^*$, we have $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })\subset \psi _\gamma (\mathcal {B}_1)$ and $\psi _\gamma ({\tilde{{\mathcal {Z}}}})\subset \psi _\gamma (\mathcal {B}_2)$. For any $\gamma \in {\mathfrak t}^*$ such that $a(\gamma )$ is well-defined, $\{\psi _\gamma (a),\psi _\gamma (\mathcal {B}_i)\}_{(\gamma )}$ is zero. If $\gamma$ is regular in ${\mathfrak g}^*$, then $\psi _\gamma ((\mathcal{M}\mathcal{F})_{\mu })=\psi _\gamma (\mathcal {B}_1)$,  $\psi _\gamma ({\tilde{{\mathcal {Z}}}})=\psi _\gamma ((\mathcal{M}\mathcal{F})_{\gamma })=\psi _\gamma (\mathcal {B}_2)$, and $\psi _\gamma (a)\in \psi _\gamma (\mathcal {B}_i)$ by Theorems 2.5, 2.1.

There is $N\geqslant 0$ such that $a\in \mathcal {A}_{\leqslant N}$. Here $\mathcal {A}_{\leqslant N}$ is a finite-dimensional vector space over $\Bbbk ({\mathfrak t}^*)$ and $a\not \in \mathcal {A}_{\leqslant N}\cap \mathcal {B}_i$. Then for almost all $\gamma$, we have $\psi _\gamma (a)\not \in \psi _\gamma ( \mathcal {A}_{\leqslant N}\cap \mathcal {B}_i)$. The algebra ${\tilde{{\mathcal {Z}}}}$ is generated by bi-homogeneous elements. Hence it is graded by the ${\mathfrak m}$-degree, ${\tilde{{\mathcal {Z}}}}=\bigoplus _{k\geqslant 0} (\mathcal {A}_k\cap {\tilde{{\mathcal {Z}}}})$. Recall that $\psi _\gamma (\mathcal {A}_k)={\mathcal {S}}^k({\mathfrak m})^{\mathfrak t}$. Thus, in case $i=2$,

$$\begin{aligned} \psi _\gamma (\mathcal {B}_2)=\psi _\gamma ({\tilde{{\mathcal {Z}}}})=\bigoplus _{k\geqslant 0} \psi _\gamma (\mathcal {A}_k\cap {\tilde{{\mathcal {Z}}}}), \end{aligned}$$

and we can conclude that $\psi _\gamma (a)\not \in \psi _\gamma (\mathcal {B}_2)$ for generic $\gamma$, which is a contradiction.

The algebra $(\mathcal{M}\mathcal{F})_{\mu }$ is not homogeneous in ${\mathfrak m}$. However, the highest ${\mathfrak m}$-degree components of the generators $\partial ^k_\mu H_j$ with $k<d_j-1$ lie in ${\mathcal {S}}({\mathfrak m})$ and are algebraically independent by Theorem 2.5. Therefore, if $\psi _\gamma (a)\not \in \psi _\gamma ( \mathcal {A}_{\leqslant N}\cap \mathcal {B}_1)$, then $\psi _\gamma (a)\not \in \psi _\gamma (\mathcal {B}_1)$. $\square$

3.2 Poisson centraliser of the quadratic part

For any $F\in {\mathcal {S}}({\mathfrak g})$, let $F_\bullet$ be the component of F of the highest degree in ${\mathfrak t}$. If $F\in {\mathcal {S}}({\mathfrak g})$ is homogeneous and $\psi _\gamma (F_\bullet )\ne 0$ for $\gamma \in \mathfrak t^*$, then $\psi _\gamma (F_\bullet )$ is the lowest degree component of $\psi _\gamma (F)$. Let $F\in \mathcal {Z}_{{\mathbb V}(\mu )}$ be homogeneous. Since $\varvec{f}_j=\varvec{f}_j(\mu )\in {\mathcal {S}}({\mathfrak m})$ for each j, we may write $\psi _\gamma (\varvec{f}_j)=\varvec{f}_j$. Then $\{\varvec{f}_j,\psi _\gamma (F)\}_{(\gamma )}=0$ and $\{\varvec{f}_j,\psi _\gamma (F_\bullet )\}_{\gamma }=0$. A computation of $\{\varvec{f}_j,\psi _\gamma (F_\bullet )\}_{\gamma }$ is not difficult, cf. [14], because

$$\begin{aligned} \{e_\beta e_{-\beta },\prod _{\alpha \in \Delta ^+} (e_\alpha ^{r_\alpha } e_{-\alpha }^{r_\alpha ^-})\}_{\gamma } = \gamma (h_\beta )(r^-_{\beta }-r_{\beta })\prod _{\alpha \in \Delta ^+} (e_\alpha ^{r_\alpha } e_{-\alpha }^{r_\alpha ^-}), \end{aligned}$$

if $\beta \in \Delta ^+$. Note that the centraliser $\mathcal {Z}_{{\mathbb V}(\mu )}$ is a homogeneous subalgebra of ${\mathcal {S}}({\mathfrak g})$.

We write $\psi _\gamma (F_\bullet )$ in the basis $\{e_{\pm \alpha }\mid \alpha \in \Delta ^+\}$. Let $M=c_{{\bar{r}},\gamma } \prod _{\alpha \in \Delta ^+} (e_\alpha ^{r_\alpha } e_{-\alpha }^{r_\alpha ^-})$ be a summand of $\psi _\gamma (F_\bullet )$ with $c_{{\bar{r}},\gamma }\ne 0$. Then the explicit description of ${\mathbb V}(\mu )$, see (2.4), implies that

$$\begin{aligned} \sum _{\alpha \in \Delta ^+} \frac{\alpha ({\tilde{h}})}{\mu (h_\alpha )} (r_\alpha -r_\alpha ^-)\gamma (h_\alpha )=0 \end{aligned}$$

(2.6)

for each ${\tilde{h}}\in {\mathfrak t}$. The equality holds for all points $\gamma$ such that $c_{{\bar{r}},\gamma }\ne 0$. These points form a dense open subset of ${\mathfrak t}^*$. Thereby

$$\begin{aligned} \sum _{\alpha \in \Delta ^+} \frac{\alpha ({\tilde{h}})}{\mu (h_\alpha )} (r_\alpha -r_\alpha ^-) h_\alpha =0. \end{aligned}$$

(2.7)

If the numbers $\frac{1}{\mu (h_\alpha )}$ are linearly independent over $\mathbb Q$, then $r_\alpha =r_\alpha ^-$ for each positive root $\alpha$ [14]. In the same paper, it is shown that indeed the numbers $\frac{1}{\mu (h_\alpha )}$ are linearly independent over $\mathbb Q$ for generic $\mu \in {\mathfrak t}^*$. We keep the assumption $\mu \in {\mathfrak g}^*_\textsf{reg}$.

Lemma 2.7

(cf. [14]) Suppose that $\psi _\gamma (F_\bullet )$ lies in $\Bbbk [e_{\alpha } e_{-\alpha } \mid \alpha \in \Delta ^+]$ for any $F\in \mathcal {Z}_{{\mathbb V}(\mu )}$ and any $\gamma \in {\mathfrak t}^*$. Then $\mathcal {Z}_{{\mathbb V}(\mu )}=(\mathcal{M}\mathcal{F})_{\mu }$.

Proof

If $F_\bullet$ does not lie in $\Bbbk [{\mathfrak t}, e_\alpha e_{-\alpha }\mid \alpha \in \Delta ^+]$ for some $F\in \mathcal {Z}_{{\mathbb V}(\mu )}$, then there is $\gamma \in {\mathfrak t}^*$, such that $\psi _\gamma (F_\bullet )\not \in \Bbbk [e_{\alpha } e_{-\alpha } \mid \alpha \in \Delta ^+]$, a contradiction. Thus $F_\bullet \in \Bbbk [{\mathfrak t}, e_\alpha e_{-\alpha }\mid \alpha \in \Delta ^+]$ for each $F\in \mathcal {Z}_{{\mathbb V}(\mu )}$ and ${\mathrm {tr.deg\,}}\Bbbk [F_\bullet \mid F\in \mathcal {Z}_{{\mathbb V}(\mu )}]\leqslant |\Delta ^+|+l={\varvec{b}}(\mathfrak g)$. The algebras $\mathcal {Z}_{{\mathbb V}(\mu )}$ and $\Bbbk [F_\bullet \mid F\in \mathcal {Z}_{{\mathbb V}(\mu )}]$ are homogeneous and their Poincaré series coinside. Hence they have one and the same transcendence degree by [1, Satz 4.5]. Thus ${\mathrm {tr.deg\,}}\mathcal {Z}_{{\mathbb V}(\mu )}\leqslant {\varvec{b}}(\mathfrak g)$. By the construction, $(\mathcal{M}\mathcal{F})_{\mu }\subset \mathcal {Z}_{{\mathbb V}(\mu )}$. Moreover, ${\mathrm {tr.deg\,}}(\mathcal{M}\mathcal{F})_{\mu }={\varvec{b}}(\mathfrak g)$ and the algebra $(\mathcal{M}\mathcal{F})_{\mu }$ is algebraically closed in ${\mathcal {S}}(\mathfrak g)$ [11, Sect. 3]. Since $(\mathcal{M}\mathcal{F})_{\mu }\subset \mathcal {Z}_{{\mathbb V}(\mu )}$ is an algebraic extension, we have $(\mathcal{M}\mathcal{F})_{\mu }=\mathcal {Z}_{{\mathbb V}(\mu )}$. $\square$

Proposition 2.8

Suppose that ${\mathfrak g}$ is of type A$_{n-1}$. Then $(\mathcal{M}\mathcal{F})_{\mu }=\mathcal {Z}_{{\mathbb V}(\mu )}$ for any $\mu \in {\mathfrak t}^*\cap {\mathfrak g}^*_\textsf{reg}$.

Proof

Let $M=c_{{\bar{r}},\gamma } \prod _{\alpha \in \Delta ^+} (e_\alpha ^{r_\alpha } e_{-\alpha }^{r_\alpha ^-})$ be a summand of $\psi _\gamma (F_\bullet )$ with $c_{{\bar{r}},\gamma }\ne 0$ for some homogeneous element $F\in \mathcal {Z}_{{\mathbb V}(\mu )}$ and some $\gamma \in {\mathfrak t}^*$. For ${\tilde{h}}=\frac{1}{n}\textrm{diag}(n{-}1,-1,\ldots ,-1)$, the equality (2.7) reads

$$\begin{aligned} \sum _{k=2}^n \frac{1}{\mu (E_{11}-E_{kk})} (r_{\varepsilon _1-\varepsilon _k}-r_{\varepsilon _1-\varepsilon _k}^-) (E_{11}-E_{kk})=0. \end{aligned}$$

Since the matrices $E_{11}-E_{kk}$ with $2\leqslant k\leqslant n$ are linearly independent, we conclude that $r_{\varepsilon _1-\varepsilon _k}=r_{\varepsilon _1-\varepsilon _k}^-$ for each k. Then inserting $\frac{1}{n-1}\textrm{diag}(0,n{-}2,-1,\ldots ,-1)$ as ${\tilde{h}}$ brings $r_{\varepsilon _2-\varepsilon _k}=r_{\varepsilon _2-\varepsilon _k}^-$ for all $k\geqslant 3$. Continuing in this way, we prove that the assumptions of Lemma 2.7 are satisfied for F and hence also for all elements of $\mathcal {Z}_{{\mathbb V}(\mu )}$. $\square$

4 Remarks on quantisation

A commutative subalgebra $\mathcal {Q}\subset {\mathcal {U}}({\mathfrak g})$ is a quantisation of a Poisson commutative subalgebra $\mathcal {B}\subset {\mathcal {S}}({\mathfrak g})$, if ${\mathrm {gr\,}}\!(\mathcal {Q})=\langle {\mathrm {gr\,}}\!(a) \mid a\in \mathcal {Q}\rangle _{\Bbbk }$ coincides with $\mathcal {B}$.

Keep the assumption $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$. Then ${\mathfrak t}\subset (\mathcal{M}\mathcal{F})_{\mu }$. Assume that $\mathcal {Q}\subset {\mathcal {U}}({\mathfrak g})$ is a quantisation of $(\mathcal{M}\mathcal{F})_{\mu }$. Then ${\mathfrak t}\subset \mathcal {Q}$ and $\mathcal {Q}\subset {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$. We regard $\varvec{f}_j=\sum _{\alpha \in \Delta ^+} C_\alpha e_{\alpha }e_{-\alpha }$ as an element of ${\mathcal {U}}(\mathfrak g)$ without adding new summands or changing the order of the factors. Since $\mathfrak g^{{\mathfrak t}}={\mathfrak t}$, the subalgebra $\mathcal {Q}$ must contain all $\varvec{f}_j\in {\mathcal {U}}({\mathfrak g})$. In [19], it is shown that $[\varvec{f}_j,\varvec{f}_i]=0$ in ${\mathcal {U}}({\mathfrak g})$ for all i, j. Set $\widetilde{{\mathbb V}}(\mu )=\langle \varvec{f}_j\mid 1\leqslant j\leqslant l\rangle _{\Bbbk }\subset {\mathcal {U}}({\mathfrak g})$.

If $\mu$ is generic enough, then $(\mathcal{M}\mathcal{F})_{\mu }$ is equal to the Poisson centraliser $\mathcal {Z}_{{\mathbb V}(\mu )}$ [14]. Therefore $\mathcal {Q}$ is the centraliser of $\widetilde{{\mathbb V}}(\mu )$ in ${\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$. The quantisation of this $(\mathcal{M}\mathcal{F})_{\mu }$ is unique. In type A, it was shown earlier in [18], that the quantisation of $(\mathcal{M}\mathcal{F})_{\mu }$ is unique for any $\mu \in {\mathfrak t}^* \cap {\mathfrak g}^*_\textsf{reg}$. Proposition 2.8 provides a new proof for the uniqueness result in case ${\mathfrak g}=\mathfrak {sl}_{n}$.

The existence of $\mathcal {Q}$ is proven in [9] for classical ${\mathfrak g}$, in [17] for type A, and in [4, 15] for any ${\mathfrak g}$. Let $\mathcal {F}_\gamma \subset {\mathcal {U}}({\mathfrak g})$ with $\gamma \in {\mathfrak g}^*$ be the quantum Mishchenko–Fomenko subalgebra, which is a commutative algebra constructed in [15] and [4]. Then ${\mathrm {gr\,}}\!(\mathcal {F}_\gamma )=(\mathcal{M}\mathcal{F})_{\gamma }$ for any $\gamma \in {\mathfrak g}^*_\textsf{reg}$ [4, 15] and for any $\gamma \in {\mathfrak g}^*$ in case ${\mathfrak g}$ is of type A or C [8].

Now we lift elements $F_j=(H_j)_{(d_j-2,2)}\in {\tilde{{\mathcal {Z}}}}$ to ${\mathcal {U}}({\mathfrak g})$. Write $F_j=\sum _{\alpha \in \Delta ^+} F_{j,\alpha } e_\alpha e_{-\alpha }$, where $F_{j,\alpha }\in {\mathcal {S}}^{d_j-2}({\mathfrak t})$, and regard this sum as an element of ${\mathcal {U}}(\mathfrak g)$. Recall that in ${\mathcal {S}}({\mathfrak g})$, we have $\varvec{f}_j\in (\mathcal{M}\mathcal{F})_{\mu }$ and $\psi _\mu (F_j)=\psi _\mu (\varvec{f}_j)=\varvec{f}_j$.

We work with ${\mathcal {C}}={\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}\otimes _{{\mathcal {S}}({\mathfrak t})}\Bbbk ({\mathfrak t}^*)$ as with a non-commutative algebra over $\Bbbk ({\mathfrak t}^*)$ generated by the monomials

$$\begin{aligned} M=e_{\alpha _1}^{r_1}\ldots e_{\alpha _N}^{r_N}e_{-\alpha _N}^{r_N^-}\ldots e_{-\alpha _1}^{r_1^-}, \end{aligned}$$

(3.1)

where $N=|\Delta ^+|$, some numbering of the positive roots is fixed, and $\sum \nolimits _{i=1}^N(r_i-r_i^-)\alpha _i=0$. These monomials form a basis of ${\mathcal {S}}(\mathfrak m)^{\mathfrak t}$. We say that $\sum _{i=1}^N(r_i+r_i^-)=:\deg _{\mathfrak m}M$ is the degree (or the $\mathfrak m$-degree) of M. The algebra structure of ${\mathcal {C}}$ is given by the coefficients $Q_M^{M',M''}\in \Bbbk ({\mathfrak t}^*)$ of $M' M''= \sum _{M} Q_M^{M',M''} M$, where $M,M',M''$ are of the form (3.1). In these terms, one can extend the map $\psi _\mu \!:\mathcal {A}_\mu \rightarrow {\mathcal {S}}({\mathfrak m})^{{\mathfrak t}}$ to a rational map from ${\mathcal {C}}$ by evaluating at $\mu$ the coefficients $Q_M^{M',M''}$. Formally, set ${\mathcal {C}}_\mu =\{ A\in {\mathcal {C}}\mid A(\mu ) \,\text { is well-defined}\,\}$. As a vector space, the image $\psi _\mu ({\mathcal {C}}_\mu )=:{\tilde{{\mathcal {U}}}}({\mathfrak m})^{{\mathfrak t}}$ is isomorphic to ${\mathcal {S}}({\mathfrak m})^{\mathfrak t}$. We let $[\,\,,\,]_{(\mu )}$ stand for the Lie algebra structure on it. The algebra $({\tilde{{\mathcal {U}}}}({\mathfrak m})^{{\mathfrak t}},[\,,\,]_{(\mu )})$ should not be regarded as a subset of ${\mathcal {U}}({\mathfrak m})^{\mathfrak t}$ in whatever sense! Note that a similar construction exists for any $\Bbbk ({\mathfrak t}^*)$-basis of ${\mathcal {C}}$.

Example 3.1

We check that $[F_j,F_s]=0$ in ${\mathcal {U}}(\mathfrak g)$ for all j and s. By definition

$$\begin{aligned}{}[F_j,F_s]{} & {} =\sum \limits _{\alpha ,\beta \in \Delta ^+} F_{j,\alpha }F_{s,\beta } e_\alpha e_{-\alpha } e_{\beta }e_{-\beta } - \sum \limits _{\alpha ,\beta \in \Delta ^+} F_{j,\alpha }F_{s,\beta } e_\beta e_{-\beta } e_{\alpha }e_{-\alpha } \\{} & {} \quad = \sum _{\alpha \ne \beta } F_{j,\alpha }F_{s,\beta } (e_\alpha e_{-\alpha } e_{\beta }e_{-\beta }- e_\beta e_{-\beta } e_{\alpha }e_{-\alpha }) \\{} & {} \quad = \sum _{\alpha \ne \beta } F_{j,\alpha }F_{s,\beta } ( [e_{\alpha },e_\beta ] e_{-\alpha } e_{-\beta }+e_\alpha [e_{-\alpha }, e_{\beta }] e_{-\beta } + e_{\beta } [e_{\alpha }, e_{-\beta }] e_{-\alpha }\\{} & {} \qquad + e_\beta e_\alpha [e_{-\alpha }, e_{-\beta }]). \end{aligned}$$

In this particular case, further straightening of the sums in brackets does not involve elements of ${\mathfrak t}$. For each $\gamma \in {\mathfrak t}^*\cap \mathfrak g^*_\textsf{reg}$, the elements $\psi _\gamma (F_j)$ and $\psi _\gamma (F_s)$ belong to the quantum Mishchenko–Fomenko subalgebra $\mathcal {F}_\gamma \subset {\mathcal {U}}({\mathfrak g})$ associated with $\gamma$. If we replace each $F_{j,\alpha }F_{s,\beta }$ with $\psi _\gamma (F_{j,\alpha }), \psi _{\gamma }(F_{s,\beta })$, then the total sum is zero for each $\gamma \in {\mathfrak t}^*\cap \mathfrak g^*_\textsf{reg}$. This implies that the initial sum is zero in ${\mathcal {U}}(\mathfrak g)$.

The algebra ${\mathcal {C}}=\bigcup _{N\geqslant 0}{\mathcal {C}}_N$ is filtered by the degree in ${\mathfrak m}$. Here ${\mathcal {C}}_0={\mathcal {C}}_1=\Bbbk ({\mathfrak t}^*)$ and the $\Bbbk ({\mathfrak t}^*)$-space ${\mathcal {C}}_2$ has a basis $\{1, e_\alpha e_{-\alpha } \mid \alpha \in \Delta ^+\}$. More generally, any ${\mathcal {C}}_N$ has a monomial basis consisting of the monomials M, of the form (3.1), with $\deg _{\mathfrak m}M\leqslant N$. Since the commutator in ${\mathcal {C}}$ is $\Bbbk ({\mathfrak t}^*)$-linear, for any $A\in {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$ and any $N\geqslant 0$, the centraliser $\mathcal {Z}_A({\mathcal {C}}_{N})=\mathcal {Z}_A {\mathcal {C}}\cap {\mathcal {C}}_N$ is a vector space over $\Bbbk ({\mathfrak t}^*)$. It is a subspace of the finite-dimensional space ${\mathcal {C}}_N$. Evaluating the defining equations of $\mathcal {Z}_A({\mathcal {C}}_{N})$ at $\mu \in {\mathfrak t}^*$, we obtain

$$\begin{aligned} \dim _{\Bbbk ({\mathfrak t}^*)} \mathcal {Z}_A ({\mathcal {C}}_{N}) = \dim \left( \mathcal {Z}_{\psi _\mu (A)}({\tilde{{\mathcal {U}}}}({\mathfrak m})^{\mathfrak t},[\,\,,\,]_{(\mu )})\cap {\tilde{{\mathcal {U}}}}_{N}({\mathfrak m})\right) , \end{aligned}$$

(3.2)

whenever $\mu$ is generic enough. This applies also to centralisers of finite subsets of elements. Since $\psi _\mu (\mathcal {F}_\mu )$ commutes with all $\psi _{\mu }(\varvec{f}_j)=\psi _\mu (F_j)$ w.r.t. $[\,,\,]_{(\mu )}$, the equality (3.2) shows that the coefficients of the Poincaré series of the centraliser

$$\begin{aligned} \mathcal {Z}_{\widetilde{{\mathbb V}}(\mu )}{\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}=\{ \Xi \in {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}} \mid [\Xi ,F_j]=0 \ \forall j\} \end{aligned}$$

are large, $\dim _{\Bbbk ({\mathfrak t}^*)} \mathcal {Z}_{\widetilde{{\mathbb V}}(\mu )}({\mathcal {C}}_N)\geqslant D_N$, where

$$\begin{aligned} D_N=\dim ({\mathcal {S}}^{\leqslant N}({\mathfrak m}){\mathcal {S}}({\mathfrak t})\cap \Bbbk [\partial _\mu ^k H_j \mid 1\leqslant j\leqslant l, 0\leqslant k<d_j-1]). \end{aligned}$$

In other words, enough elements of ${\mathcal {U}}({\mathfrak g})^{\mathfrak t}$ commute with $\widetilde{{\mathbb V}}(\mu )$. It is not known, whether the centraliser $\mathcal {Z}_{\widetilde{{\mathbb V}}(\mu )}{\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$ is commutative or not. In order to solve the quantisation problem for ${\tilde{{\mathcal {Z}}}}$, one may try to obtain upper bounds for dimensions related to $\mathcal {Z}_{\widetilde{{\mathbb V}}(\mu )}{\mathcal {U}}({\mathfrak g})^{\mathfrak t}$ or to $\mathcal {Z}_{\widetilde{{\mathbb V}}(\mu )}{\mathcal {C}}$.

Let $\textsf{symm}\!:{\mathcal {S}}({\mathfrak g})\rightarrow {\mathcal {U}}({\mathfrak g})$ be the canonical symmetrisation map.

Theorem 3.2

Suppose that ${\mathfrak g}$ is of type A$_l$. Then there is a commutative subalgebra $\mathscr {Z}\subset {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$ such that ${\mathrm {gr\,}}\!(\mathscr {Z})={\tilde{{\mathcal {Z}}}}$ and $F_j=\sum _{\alpha \in \Delta ^+} F_{j,\alpha } e_\alpha e_{-\alpha }\in \mathscr {Z}$ for each $1\leqslant j\leqslant l$.

Proof

For convenience, we work with ${\mathfrak g}=\mathfrak {gl}_n$ instead of $\mathfrak {sl}_{l+1}$. Let $H_j=\Delta _j$ be coefficients of the characteristic polynomial, here $\deg \Delta _j=j$. We write $\Delta _j$ in the basis $\{E_{ik}\mid i,k\leqslant n\}$. Let X be a monomial appearing in $\Delta _j$ with a nonzero coefficient. If $E_{ii}$ is a factor of X, then for all other factors $E_{sk}$ of X, we have $i\not \in \{s,k\}$. For ${\mathfrak t}=\langle E_{ii}\mid 1\leqslant i\leqslant n\rangle _{\Bbbk }$, the ${\mathfrak t}$-factors of X commute with all factors of X. Another feature of the set $\{\Delta _j\mid 1\leqslant j\leqslant n\}$ is that

$$\begin{aligned} \mathcal {F}_\xi =\textsf {alg}\langle \textsf {symm}(\partial _\xi ^k \Delta _j) \mid 1\leqslant j\leqslant n, 0\leqslant k< j\rangle \ \text{ for } \text{ any } \ \xi \in {\mathfrak g}^*, \end{aligned}$$

see [16, 18] and [8, Theorem 3.1]. Set

$$\begin{aligned} \mathscr {Z}=\textsf {alg}\langle {\mathfrak t}, \textsf {symm}((\Delta _j)_{(i,j-i)}) \mid 1\leqslant j\leqslant n, 0\leqslant i\leqslant j-2\rangle \subset {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}. \end{aligned}$$

We have ${\mathrm {gr\,}}\!(\mathscr {Z})={\tilde{{\mathcal {Z}}}}$, because a basis of ${\mathfrak t}$ and the elements $(\Delta _j)_{(i,j-i)}$ form an algebraically independent set of generators of ${\tilde{{\mathcal {Z}}}}$. In order to prove that $\mathscr {Z}$ is commutative, we use maps $\psi _\mu \!:{\mathcal {C}}_\mu \rightarrow {\tilde{{\mathcal {U}}}}({\mathfrak m})^{{\mathfrak t}}$ with $\mu \in {\mathfrak t}^*$, working now with the $\Bbbk ({\mathfrak t}^*)$-basis

$$\begin{aligned} \{\textsf{symm}(M) \mid M\in {\mathcal {S}}({\mathfrak m})^{\mathfrak t}\text { monomial in } E_{ij} \text { with } i,j\leqslant n\} \end{aligned}$$

of ${\mathcal {C}}$.

We decompose $(\Delta _j)_{(i,j-i)}=\sum _s P_{j,i}^{(s)}M_{j,j-i}^{(s)}$, where $P_{j,i}^{(s)}\in {\mathcal {S}}^{i}({\mathfrak t})$ are pairwise different monomials in elements $E_{kk}$ and $M_{j,u}^{(s)}\in {\mathcal {S}}^u({\mathfrak m})$ are nonzero. Since the factors of $P_{j,i}^{(s)}$ commute with $M_{j,j-i}^{(s)}$, we have

$$\begin{aligned} \textsf{symm}(P_{j,i}^{(s)}M_{j,j-i}^{(s)})=P_{j,i}^{(s)} \textsf{symm}(M_{j,j-i}^{(s)}) \end{aligned}$$

for each s. Furthermore, $\partial _\mu ^k (P_{j,i}^{(s)}M_{j,j-i}^{(s)})=(\partial _\mu ^k P_{j,i}^{(s)})M_{j,j-i}^{(s)}$ and

$$\begin{aligned} \textsf{symm}(\partial _\mu ^k (P_{j,i}^{(s)}M_{j,j-i}^{(s)}))=(\partial _\mu ^k P_{j,i}^{(s)})\textsf{symm}(M_{j,j-i}^{(s)}). \end{aligned}$$

Finally $\psi _\mu {\circ }\textsf{symm}(\partial _\mu ^k (P_{j,i}^{(s)}M_{j,j-i}^{(s)}))=i(i-1)\ldots (i-k+1)P_{j,i}^{(s)}\!(\mu )\textsf{symm}(M_{j,j-i}^{(s)})$. Therefore $\psi _\mu (\mathcal {F}_\mu )$ is generated by $\sum _{s} P_{i,j}^{(s)}\!(\mu )\textsf{symm}(M_{j,j-i}^{(s)})$ with $1\leqslant j\leqslant n$ and $0\leqslant i \leqslant j-2$. Recall that $\psi _\mu (\mathcal {F}_\mu )$ is a commutative subalgebra of $({\tilde{{\mathcal {U}}}}({\mathfrak m})^{{\mathfrak t}},[\,\,,\,]_{(\mu )})$ by the construction.

Next we observe that $\psi _\mu {\circ }\textsf{symm}((\Delta _j)_{(i,j-i)})=\sum _s P_{j,i}^{(s)}\!(\mu )\textsf{symm}(M_{j,j-i}^{(s)})\in \psi _\mu (\mathcal {F}_\mu )$. Thus, $\psi _\mu (\mathscr {Z})$ is commutative for any $\mu \in {\mathfrak t}^*$. By a general principle already used in Sect. 2, this implies $[\mathscr {Z},\mathscr {Z}]=0$. In case of

$$\begin{aligned} F_j=(\Delta _j)_{(j-2,2)}=\sum _{\alpha \in \Delta ^+} F_{j,\alpha } e_\alpha e_{-\alpha } \ \text { with } \ j\geqslant 2, \end{aligned}$$

the coefficients $F_{j,\alpha }$ are monomials in $E_{kk}$ and $\textsf{symm}(F_j)=\sum _{\alpha \in \Delta ^+} F_{j,\alpha } (e_\alpha e_{-\alpha } - \frac{1}{2}h_\alpha )\in \mathscr {Z}$. Therefore also $\sum _{\alpha \in \Delta ^+} F_{j,\alpha } e_\alpha e_{-\alpha }\in \mathscr {Z}$.

In order to return from $\mathfrak {gl}_n$ to $\mathfrak {sl}_{l+1}$ with $l+1=n$, we restrict the invariants $\Delta _j$ to $\mathfrak {sl}_n^*$. This can be achieved by writing first $E_{ii}={\tilde{E}}_{ii}+z$ for each i with $z=\frac{1}{n}{\textrm{diag}}(1,\ldots ,1)$ and then by setting $z=0$. If ${\tilde{\Delta }}_j=\Delta _j|_{\mathfrak {sl}_n^*}$ and ${\tilde{\mathscr {Z}}}\subset {\mathcal {U}}(\mathfrak {sl}_n)$ is generated by ${\mathfrak t}$ together with the elements $\textsf{symm}( ({\tilde{\Delta }}_j)_{(i,j-i)})$, where $j\geqslant 2$, then ${\tilde{\mathscr {Z}}}$ is a required commutative subalgebra. $\square$

The quantisation $\mathscr {Z}\subset {\mathcal {U}}({\mathfrak g})^{{\mathfrak t}}$ of ${\tilde{{\mathcal {Z}}}}$ described in the proof of Theorem 3.2 is a curious subalgebra. Let $V_\lambda$ be an irreducible finite-dimensional ${\mathfrak g}$-module with ${\mathfrak g}=\mathfrak {sl}_n$ and $(V_\lambda )_{\mu }$ the subspace of $V_\lambda$ corresponding to a ${\mathfrak t}$-weight $\mu$. Then $\mathscr {Z}$ acts on $(V_\lambda )_{\mu }$ as $\mathcal {F}_\mu$. In particular, the action of $\mathscr {Z}$ on $V_\lambda$ is diagonalisable, since $\mu$ takes real values on the standard real form of ${\mathfrak t}$, see [3]. Furthermore, if $\mu \in {\mathfrak t}^*\cap {\mathfrak g}^*_\textsf{reg}$, then also by results of [3], $\mathcal {F}_\mu$, and hence $\mathscr {Z}$, acts on $(V_\lambda )_{\mu }$ with a simple spectrum. However, the action of $\mathscr {Z}$ on $(V_\lambda )_{\mu }$ may not have a simple spectrum if $\mu \not \in {\mathfrak t}^*\cap {\mathfrak g}^*_\textsf{reg}$. For instance, $\mathscr {Z}$ acts via scalars on the zero weight subspace $V_\lambda ^{\mathfrak t}$.

Example 3.3

Suppose that $\mathfrak g=\mathfrak {sl}_3$. Then ${\tilde{{\mathcal {Z}}}}$ is generated by a basis of ${\mathfrak t}$, two invariants $H_1,H_2$, and $F_2=(H_2)_{(1,2)}=\sum _{\alpha \in \Delta ^+} F_{2,\alpha } e_\alpha e_{-\alpha }$. Here $F_{2,\alpha } \in {\mathfrak t}$ for each $\alpha$. We regard $F_2$ as an element of ${\mathcal {U}}(\mathfrak g)$. Then $\mathscr {Z}$ is generated by ${\mathfrak t}$, $F_2$, and ${\tilde{H}}_1,{\tilde{H}}_2$, where $\tilde{H}_1,{\tilde{H}}_2\in {\mathcal {U}}({\mathfrak g})$ are independent central elements. On an irreducible finite-dimensional $\mathfrak g$-module $V_\lambda$, the last two generators act via scalar multiplication. The actions of ${\mathfrak t}$ and $F_2$ annihilate $V_\lambda ^{{\mathfrak t}}$.