On Riemannian polyhedra with non-obtuse dihedral angles in 3-manifolds with positive scalar curvature

Abstract

We determine the combinatorial types of all the 3-dimensional simple convex polytopes in ${\mathbb {R}}^3$ that can be realized as mean curvature convex (or totally geodesic) Riemannian polyhedra with non-obtuse dihedral angles in Riemannian 3-manifolds with positive scalar curvature. This result can be considered as an analogue of Andreev’s theorem on 3-dimensional hyperbolic polyhedra with non-obtuse dihedral angles. In addition, we construct many examples of such kind of simple convex polytopes in higher dimensions.

1 Introduction

A Riemannian polyhedron of dimension n is a polyhedral domain W with faces in an n-dimensional Riemannian manifold (M, g) with the induced Riemannian metric $g(W)=g|_W$ (see Gromov [12, § 1]). Moreover, each codimension-one face (or facet) $F_i$ of W is contained in a smooth hypersurface $\Sigma _i$ of M such that

• Whenever two facets $F_i$ and $F_j$ of W are adjacent, the corresponding hypersurfaces $\Sigma _i$ and $\Sigma _j$ intersect transversely in M.

• The boundary $\partial F_i$ of each facet $F_i$ consists of $F_i\cap F_j$ where $F_j$ ranges over all the facets adjacent to $F_i$, and the decomposition $\partial F_i= \bigcup _j F_i\cap F_j$ gives an $(n-1)$-dimensional Riemannian polyhedron structure to $F_i$.

Note that the ambient manifold M here is not necessarily compact or closed. Typical examples of Riemannian polyhedra are the intersections of finitely many domains with smooth mutually transversal boundaries in a Riemannian manifold (e.g. convex polytopes in the Euclidean space ${\mathbb {R}}^n$).

Definition 1.1

Let $W_i$ be a Riemannian polyhedron in $(M_i,g_i)$, $i=1,2$. We call $W_1$ and $W_2$ combinatorially equivalent if there is a bijection between their faces that preserves the inclusion relation. We call $W_1$ and $W_2$ pseudo-diffeomorphic if there exists a homeomorphism $\varphi : W_1\rightarrow W_2$ which is the restriction of a diffeomorphism from an open neighborhood of $W_1$ in $M_1$ to an open neighborhood of $W_2$ in $M_2$, and we call $\varphi$ a pseudo-diffeomorphism from $W_1$ to $W_2$. If, moreover, $\varphi$ is face-preserving (i.e. $\varphi$ maps every face of $W_1$ homeomorphically onto a face of $W_2$), we call $\varphi$ a diffeomorphism from $W_1$ to $W_2$. In this case, we also say that $W_2$ is a realization of $W_1$ in $(M_2,g_2)$. It is clear that a diffeomorphism from $W_1$ to $W_2$ induces a combinatorial equivalence.

By Wiemeler [24, Corollary 5.3] (also see Davis [8, Corollary 1.3]), two simple convex polytopes in ${\mathbb {R}}^n$ are diffeomorphic (as Riemannian polyhedra) if and only if they are combinatorially equivalent. Recall that a convex polytope P in ${\mathbb {R}}^n$ is called simple if every codimension-k face of P is contained in exactly k different facets of P. The reader is referred to [27] for the basic notions of convex polytopes.

Definition 1.2

Let W be a Riemannian polyhedron.

• We say that W has acute or non-obtuse dihedral angles if the dihedral angle function on every codimension-two face of W ranges in $(0, \pi /2)$ or $(0, \pi /2]$. Especially, we call W right-angled if the dihedral angle function on every codimension-two face of W is constantly $\pi /2$.

• We call W mean curvature convex if every facet of W has non-negative mean curvature in the ambient Riemannian manifold. Especially, we call W totally geodesic if every facet of W is a totally geodesic submanifold.

Convention In this paper, the mean curvature of a boundary point of a domain in a Riemannian manifold is always taken with respect to the inward unit normal vector.

The main purpose of this paper is to study the combinatorial types of all the 3-dimensional simple convex polytopes in ${\mathbb {R}}^3$ that can be realized as mean curvature convex (or totally geodesic) Riemannian polyhedra with non-obtuse dihedral angles in Riemannian 3-manifolds with positive scalar curvature.

For $n\ge 1$, let $\Delta ^n$ and $[0,1]^n$ denote the standard n-simplex and n-cube in ${\mathbb {R}}^n$, respectively. The following is the main theorem of this paper.

Theorem 1.3

Suppose P is a 3-dimensional simple convex polytope in ${\mathbb {R}}^3$. Then P can be realized as a mean curvature convex Riemannian polyhedron with non-obtuse dihedral angles in a Riemannian 3-manifold with positive scalar curvature if and only if P is combinatorially equivalent to a convex polytope that can be obtained from $\Delta ^3$ by a sequence of vertex-cuts.

Definition 1.4

(Vertex-Cut) Let P be an n-dimensional simple convex polytope in ${\mathbb {R}}^n$ and v a vertex of P. Choose a plane H in ${\mathbb {R}}^n$ such that H separates v from the other vertices of P. Let $H_{\ge }$ and $H_{\le }$ be the two half spaces determined by H and assume that v belongs to $H_{\ge }$. Then $P\cap H_{\ge }$ is an $(n-1)$-simplex, and $P\cap H_{\le }$ is a simple convex polytope which we refer to as a vertex-cut of P. For example, a vertex-cut of $\Delta ^3$ is combinatorially equivalent to $\Delta ^2\times [0,1]$ (the triangular prism).

The simplicial polytope dual to a convex polytope that is obtained from $\Delta ^3$ by a sequence of vertex-cuts is known as a stacked 3-polytope. By definition, a stacked n-polytope is a polytope obtained from $\Delta ^n$ by repeatedly gluing another n-simplex onto one of its facets (see [18]). One reason for the significance of stacked polytopes is that, among all simplicial n-polytopes with a given number of vertices, the stacked polytopes have the fewest possible higher-dimensional faces.

A well known special case of Theorem 1.3 is: if a 3-dimensional simple convex polytope P can be realized as a totally geodesic polyhedron with non-obtuse dihedral angles in the standard unit 3-sphere $S^3$, then combinatorially P must be a 3-simplex (see [7, Sec. 6.3]).

Corollary 1.5

Suppose P is a 3-dimensional simple convex polytope in ${\mathbb {R}}^3$. Then P can be realized as a right-angled totally geodesic Riemannian polyhedron in a Riemannian 3-manifold with positive scalar curvature if and only if P is combinatorially equivalent to a convex polytope that can be obtained from $\Delta ^3$ by a sequence of vertex-cuts.

Note that Theorem 1.3 and Corollary 1.5 still hold if we assume the scalar curvature of the ambient Riemannian 3-manifold to be positive constant (see Corollary 3.2).

Theorem 1.3 can be thought of as an analogue of Andreev’s theorem (see [1, 2]) on totally geodesic polyhedra with non-obtuse dihedral angles in the 3-dimensional hyperbolic space ${\mathbb {H}}^3$ (see [20] for a new proof). Andreev’s theorem is essential for proving Thurston’s Hyperbolization theorem for Haken 3-manifolds. Especially, Andreev’s theorem tells us that a simple convex 3-polytope P can be realized as a right-angled totally geodesic hyperbolic polyhedron in ${\mathbb {H}}^3$ if and only if P has no prismatic 3-circuits or prismatic 4-circuits (this result was also obtained by A. V. Pogorelov in an earlier paper [19]).

In addition, the following question proposed by Gromov in [12] is related to our study.

Question (Gromov [12, §1.7]): What are the possible combinatorial types of mean curvature convex Riemannian polyhedra W with acute dihedral angles in a Riemannian manifold with non-negative scalar curvature?

If W in the above question is the realization of 3-dimensional simple convex polytope in a Riemannian 3-manifold with positive scalar curvature, then the combinatorial type of W must belong to the cases described in Theorem 1.3. But conversely, it is not clear whether we can construct a Riemannian polyhedron with acute dihedral angles for every combinatorial type described in Theorem 1.3. Indeed, the Riemannian polyhedra constructed in the proof of Theorem 1.3 are all right-angled.

The paper is organized as follows. In Sect. 2, we review the definition of real moment-angle manifold associated to a simple convex polytope. Besides, we quote a result from Wu and Yu [25] on when a 3-dimensional real moment-angle manifold can admit a Riemannian metric with positive scalar curvature. In Sect. 3, we give a proof of Theorem 1.3 using the idea of “doubling-smoothing” of Riemannian manifolds described in [12, §2.1] along with the result from [25]. In Sect. 4, we construct some examples of totally geodesic non-obtuse Riemannian polyhedra with positive scalar curvature in higher dimensions and propose a question.‘

2 Real moment-angle manifolds

Suppose P is an n-dimensional simple convex polytope in Euclidean space ${\mathbb {R}}^n$. Let ${\mathcal {F}}(P)=\{F_1,\ldots , F_m\}$ be the set of all facets of P. Let ${\mathbb {Z}}_2={\mathbb {Z}}/2{\mathbb {Z}}$ and let $e_1,\ldots , e_m$ be a basis of $({\mathbb {Z}}_2)^m$. Define a function $\lambda _0: {\mathcal {F}}(P) \rightarrow ({\mathbb {Z}}_2)^m$ by

$$\begin{aligned} \lambda _0(F_i) = e_i, \ 1\le i \le m. \end{aligned}$$

(1)

For any proper face f of P, let $G_f$ denote the subgroup of $({\mathbb {Z}}_2)^m$ generated by the set $\{ \lambda _0(F_i) \, |\, f\subset F_i \}$. For any point $p\in P$, let f(p) denote the unique face of P that contains p in its relative interior. In [6, Construction 4.1], the real moment-angle manifold ${\mathbb {R}}{\mathcal {Z}}_{P}$ of P is a closed orientable n-manifold defined by the following quotient construction

$$\begin{aligned} {\mathbb {R}}{\mathcal {Z}}_{P}:= P\times ({\mathbb {Z}}_2)^m /\sim \end{aligned}$$

(2)

where $(p,g) \sim (p',g')$ if and only if $p=p'$ and $g^{-1}g' \in G_{f(p)}$. So at every vertex of P, $2^n$ copies of P are glued together so that locally they look like the $2^n$ cones of ${\mathbb {R}}^n$ bounded by the n coordinate hyperplanes meeting at the origin. Let

$$\begin{aligned} \eta : P\times ({\mathbb {Z}}_2)^m \rightarrow {\mathbb {R}}{\mathcal {Z}}_{P} \end{aligned}$$

(3)

be the quotient map. There is a canonical action of $({\mathbb {Z}}_2)^m$ on ${\mathbb {R}}{\mathcal {Z}}_{P}$ defined by

$$\begin{aligned} g'\cdot [(p,g)] = [(p,g'+g)],\ \forall \, p\in P, \, \forall \, g,g'\in ({\mathbb {Z}}_2)^m, \end{aligned}$$

whose orbit space can be identified with P. Let

$$\begin{aligned} \Theta _P: {\mathbb {R}}{\mathcal {Z}}_{P} \rightarrow P \end{aligned}$$

be the orbit map. Note that each facet F of P is also a simple convex polytope and, $\Theta ^{-1}_P(F)$ is a disjoint union of several copies of ${\mathbb {R}}{\mathcal {Z}}_F$ embedded in ${\mathbb {R}}{\mathcal {Z}}_{P}$ with trivial normal bundles.

The study of real moment-angle manifolds is an important subject in toric topology. The reader is referred to Davis and Januszkiewicz [6], Buchstaber and Panov [5], Kuroki et al. [15] and Wu and Yu [25] for more information of the topological and geometric properties of real moment-angle manifolds. The construction of ${\mathbb {R}}{\mathcal {Z}}_P$ in (2) also makes sense for any smooth nice manifold with corners. The topology of such generalized spaces are studied in a recent paper Yu [26].

In addition, we can realize ${\mathbb {R}}{\mathcal {Z}}_{P}$ as a non-degenerate intersection of $m-n$ real quadrics (quadric hypersurfaces) in ${\mathbb {R}}^m$, which induces a $({\mathbb {Z}}_2)^m$-invariant smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ (see [5, §6]). Consider a presentation of P as follows:

$$\begin{aligned} P = P(A,b)=\{ x\in {\mathbb {R}}^n\,|\, \langle a_i,x\rangle + b_i\ge 0, \, i=1,\ldots ,m\} \end{aligned}$$

(4)

where $A=(a_1,\ldots ,a_m)$ is an $n\times m$ real matrix. Since P has a vertex, the rank of A is equal to n. Define a map

$$\begin{aligned} i_{A,b}: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m, \ \ i_{A,b}(x)=A^tx+b \end{aligned}$$

(5)

where $b=(b_1,\ldots ,b_m)^t \in {\mathbb {R}}^m$. So the map $i_{A,b}$ embeds P into the positive cone ${\mathbb {R}}^m_{\ge 0}=\{ (x_1,\ldots ,x_m)\in {\mathbb {R}}^m\,|\, x_i\ge 0, i=1,\ldots ,m \}$. We can define a space ${\mathbb {R}}{\mathcal {Z}}_{A,b}$ by the following commutative diagram

where $\mu (x_1,\ldots , x_m)=(x^2_1,\ldots , x^2_m)$. Clearly $({\mathbb {Z}}_2)^m$ acts on ${\mathbb {R}}{\mathcal {Z}}_{A,b}$ with quotient space P and $i_{{\mathcal {Z}}}$ is a $({\mathbb {Z}}_2)^m$-equivariant embedding. It is easy to see that ${\mathbb {R}}{\mathcal {Z}}_{A,b}$ is homeomorphic to ${\mathbb {R}}{\mathcal {Z}}_P$. In addition, the image of ${\mathbb {R}}^n$ under $i_{A,b}$ is an affine plane of dimension n in ${\mathbb {R}}^m$, which we can specify by $m-n$ linear equations:

$$\begin{aligned} i_{A,b}({\mathbb {R}}^n)&=\{ y\in {\mathbb {R}}^m \,|\, y=A^tx+b, x\in {\mathbb {R}}^n\} \\&=\{y\in {\mathbb {R}}^m\,|\, \Gamma y =\Gamma b\} \end{aligned}$$

where $\Gamma =(\gamma _{jk})$ is an $(m-n)\times m$ matrix of rank $m-n$ so that $\Gamma A^t=0$. In other words, the rows of $\Gamma$ form a basis of all the linear relations among $a_1,\ldots ,a_m$. Then we can write the image of ${\mathbb {R}}{\mathcal {Z}}_{A,b}$ under $i_{{\mathcal {Z}}}$ explicitly as the common zeros of $m-n$ real quadratic equations in ${\mathbb {R}}^m$:

$$\begin{aligned} i_{{\mathcal {Z}}} ({\mathbb {R}}{\mathcal {Z}}_{A,b})= \left\{ (y_1,\ldots ,y_m)^t\in {\mathbb {R}}^m \,|\, \sum ^m_{k=1} \gamma _{jk} y^2_k = \sum ^m_{k=1} \gamma _{jk} b_k, \, 1\le j \le m-n \right\} .\nonumber \\ \end{aligned}$$

(6)

The above intersection of real quadrics is non-degenerate (i.e. the gradients of these quadrics are linearly independent everywhere in their intersection). This implies that ${\mathbb {R}}{\mathcal {Z}}_{A,b}$ is embedded as an n-dimensional smooth submanifold in ${\mathbb {R}}^m$ where $({\mathbb {Z}}_2)^m$ acts smoothly. So P is embedded as a Riemannian polyhedron in $i_{{\mathcal {Z}}}({\mathbb {R}}{\mathcal {Z}}_{A,b})$ with the induced metric from ${\mathbb {R}}^m$.

Example 2.1

The standard simplex $\Delta ^n \subset {\mathbb {R}}^n$ is defined by

$$\begin{aligned} \Delta ^n =\{ (x_1,\ldots , x_n)\in {\mathbb {R}}^n\,|\, x_1+\cdots + x_n\le 1, \, x_i\ge 0, \, i=1,\ldots , n. \} \end{aligned}$$

By the notation in (4), we have $\Delta ^n= P(A,b)$ where

$$\begin{aligned} A_{n\times (n+1)}= \begin{pmatrix} 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad -\,1 \\ 0 &{}\quad 1 &{}\quad \cdots &{}\quad 0 &{}\quad -\,1 \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 &{}\quad -\,1 \end{pmatrix}, \ \ \ b= (0,0,\ldots ,0,1)^t \in {\mathbb {R}}^{n+1}. \end{aligned}$$

So the image of the embedding $i_{A,b}:\Delta ^n\hookrightarrow {\mathbb {R}}^{n+1}$ [see (5)] is given by

$$\begin{aligned} \{ (x_1,\ldots , x_{n+1})\in {\mathbb {R}}^{n+1}\,|\, x_1+\cdots +x_{n+1}=1, \, x_i\ge 0,\, i=1,\ldots ,n+1 \}. \end{aligned}$$

Then by (6), $i_{{\mathcal {Z}}}({\mathbb {R}}{\mathcal {Z}}_{A,b}) \subset {\mathbb {R}}^{n+1}$ is given by the following equation

$$\begin{aligned} y^2_1 + \cdots + y^2_{n+1}=1, \ (y_1,\ldots , y_{n+1})^t \in {\mathbb {R}}^{n+1} \end{aligned}$$

which is exactly the standard unit sphere $S^n$ in ${\mathbb {R}}^{n+1}$. Moreover, the canonical $({\mathbb {Z}}_2)^{n+1}$-action on ${\mathbb {R}}{\mathcal {Z}}_{\Delta ^n}$ is equivalent to the action of $({\mathbb {Z}}_2)^{n+1}$ on $S^n$ by the reflections about the coordinate hyperplanes of ${\mathbb {R}}^{n+1}$. More precisely, for each $1\le i \le n+1$, the ith generator of $({\mathbb {Z}}_2)^{n+1}$ acts on $S^n$ by

$$\begin{aligned} (y_1,\ldots , y_{i-1}, y_i, y_{i+1}, \ldots , y_{n+1} ) \longrightarrow (y_1,\ldots , y_{i-1}, -y_i, y_{i+1}, \ldots , y_{n+1} ). \end{aligned}$$

In the following, we think of ${\mathbb {R}}{\mathcal {Z}}_{\Delta ^n}$ as $S^n$ equipped with the above $({\mathbb {Z}}_2)^{n+1}$-action.

The theorem below tells us what kind of 3-dimensional real moment-angle manifolds can admit a Riemannian metric with positive scalar curvature.

Theorem 2.2

(Proposition 4.8 and Corollary 4.10 in Wu-Yu [25]) Let P be a 3-dimensional simple convex polytope in ${\mathbb {R}}^3$ with m facets. Then ${\mathbb {R}}{\mathcal {Z}}_P$ admits a Riemannian metric with positive scalar curvature if and only if P is combinatorially equivalent to a convex polytope that can be obtained from $\Delta ^3$ by a sequence of vertex-cuts. Moreover, we can choose the Riemannian metric with positive scalar curvature on ${\mathbb {R}}{\mathcal {Z}}_P$ to be invariant with respect to the canonical $({\mathbb {Z}}_2)^m$-action on ${\mathbb {R}}{\mathcal {Z}}_P$.

3 Proof of Theorem 1.3

Our proof of Theorem 1.3 is inspired by Gromov’s proof of the dihedral rigidity of the n-cube in [12]. Gromov’s proof is based on the idea of doubling the cube n times and uses the well-known fact that the n-dimensional torus admits no metric with positive scalar curvature. Here we observe that for a simple convex polytope P with m facets, doubling P m times gives the real moment-angle manifold ${\mathbb {R}}{\mathcal {Z}}_P$. Then starting from a Riemannian metric with positive scalar curvature on P that satisfies certain conditions on the boundary of P as stated in Theorem 1.3, we can construct an invariant Riemannian metric on ${\mathbb {R}}{\mathcal {Z}}_P$ with positive scalar curvature by the procedure of “doubling-smoothing” of metrics described in [12]. So the combinatorial type of P is restricted by Theorem 2.2. But the description of the “doubling-smoothing” of Riemannian metrics in [12] is very sketchy, we will give more detailed exposition in our proof of Theorem 1.3 below. Our proof slightly generalizes the argument in Gromov and Lawson [10, Theorem 5.7].

Let A be a subspace of a topological space X. The double of X along A is the quotient space of the disjoint union of two copies of X by identifying each point of A in one copy of X to the same point in the other copy.

Suppose F and $F'$ are two facets of a Riemannian polyhedron W which intersect transversely at a codimension-two face $F\cap F'$.

• Let $\angle (F,F')_x$ denote the dihedral angle of W at a point $x\in F\cap F'$.

• Let $\angle (F,F')$ denote the dihedral angle of W at an arbitrary point of $F\cap F'$.

Proof of Theorem 1.3

Let P be a simple convex 3-polytope in ${\mathbb {R}}^3$ whose facets are $F_1,\ldots , F_m$. Let $\Theta _P: {\mathbb {R}}{\mathcal {Z}}_P\rightarrow P$ be the orbit map of the canonical $({\mathbb {Z}}_2)^m$-action on ${\mathbb {R}}{\mathcal {Z}}_P$. So each $\Theta ^{-1}_P(F_i)$, $1\le i \le m$, consists of some closed connected 2-manifolds that intersect transversely in ${\mathbb {R}}{\mathcal {Z}}_P$. Since we are working in dimension 3, we do not need to worry about the existence or uniqueness of the smooth structures in our manifolds.

We first prove the “if” part. Suppose P is combinatorially equivalent to a convex polytope that can be obtained from $\Delta ^3$ by a sequence of vertex-cuts. Then by Theorem 2.2, there exists a $({\mathbb {Z}}_2)^m$-invariant Riemannian metric $g_0$ with positive scalar curvature on ${\mathbb {R}}{\mathcal {Z}}_P$. Note that P is realized as the fundamental domain of the canonical $({\mathbb {Z}}_2)^m$-action on ${\mathbb {R}}{\mathcal {Z}}_P$ which is bounded by the submanifolds $\Theta ^{-1}_P(F_i)$, $1\le i \le m$. Moreover, by definition each $\Theta ^{-1}_P(F_i)$ is the fixed point set of the generator $e_i\in ({\mathbb {Z}}_2)^m$ under the canonical $({\mathbb {Z}}_2)^m$-action [see (1)]. It is a standard fact that every connected component of the fixed point set (with the induced Riemannian metric) of an isometry on a Riemannian manifold is a totally geodesic submanifold (see [14, Theorem 1.10.15]). So each $\Theta ^{-1}_P(F_i)$ consists of totally geodesic submanifolds of $({\mathbb {R}}{\mathcal {Z}}_P,g_0)$. In addition, the dihedral angles between any components of $\Theta ^{-1}_P(F_i)$ and $\Theta ^{-1}_P(F_j)$ (whenever they intersect) are always equal to $\pi /2$ since the $({\mathbb {Z}}_2)^m$-action on $({\mathbb {R}}{\mathcal {Z}}_P,g_0)$ is isometric. Therefore, P is realized as a right-angled totally geodesic Riemannian polyhedron in $({\mathbb {R}}{\mathcal {Z}}_P,g_0)$. The “if” part is proved.

Next, we prove the “only if” part. We can obtain ${\mathbb {R}}{\mathcal {Z}}_P$ by iterated doubling of P as follows. By the notation in the definition of ${\mathbb {R}}{\mathcal {Z}}_P$ [see (1) and (3)], define

$$\begin{aligned} H_j:=\hbox {the subgroup of} {\mathbb {Z}}^n_2 \hbox {generated by} e_1,\ldots , e_j,\ 1\le j \le m, \ \text {and} \ H_0:=\{0\}; \end{aligned}$$

Then let

$$\begin{aligned} Y^{(j)}:= \eta (P\times H_j),\ \ F^{(j)}_i:=\eta (F_i\times H_{j}), \ 1\le i,j \le m. \end{aligned}$$

So $Y^{(j)}$ is the gluing of $2^j$ copies of P under $\eta$ whose boundary is

$$\begin{aligned} \partial Y^{(j)} = \bigcup _{i > j} F^{(j)}_i. \end{aligned}$$

In addition, for any facet $F_i$ of P and any element $g\in {\mathbb {Z}}^m_2$, let

$$\begin{aligned} F_{i,g}:= \eta (F_i\times \{g\}), \ 1\le i \le m. \end{aligned}$$

Then we have

$$\begin{aligned} F^{(j)}_i = \bigcup _{g\in H_j} F_{i,g}, \ 1\le i,j\le m. \end{aligned}$$

So $Y^{(j)}$ is a Riemannian polyhedron in ${\mathbb {R}}{\mathcal {Z}}_P$ whose facets are $\{ F_{i,g} \,|\, i>j, g\in H_{j}\}$.

Fig. 1

The filtration of ${\mathbb {R}}{\mathcal {Z}}_{\Delta ^2} = S^2$

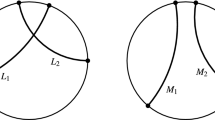
By identifying P with $Y^{(0)}$, we have a filtration (see Fig. 1 for example)

$$\begin{aligned} P= Y^{(0)} \subset Y^{(1)} \subset \cdots \subset Y^{(m)} = {\mathbb {R}}{\mathcal {Z}}_P. \end{aligned}$$

Clearly, $Y^{(j+1)}$ is the double of $Y^{(j)}$ along $F^{(j)}_{j+1}$ for each $0\le j \le m-1$. Note that $F^{(j)}_{j+1}$ may not be connected.

In the following, we do induction on j and assume that:

• (a) There exists a pseudo-diffeomorphism $\varphi _j: Y^{(j)}\rightarrow W_j$ where $W_j$ is a mean curvature convex Riemannian polyhedron in a Riemannian 3-manifold $(M_{j},g_{j})$ with positive scalar curvature, and $\varphi _j$ maps every $F^{(j)}_i$ on $\partial Y^{(j)}$ to be a union of facets of $W_j$.

Note that here we cannot require $\varphi _j$ to be face-preserving when $j\ge 1$ since $W_j$ may have more facets than $Y^{(j)}$ (see Fig. 2 for example).

We say that a facet E of $W_j$ comes from the facet $F_i$ of P if

$$\begin{aligned} \Theta _P(\varphi _j^{-1}(E))\subset F_i \ \text {or equivalently}\ E\subset \varphi _j(F^{(j)}_i)\ \text {where} \ j< i \le m. \end{aligned}$$

There are two types of edges (codimension-two faces) on $\partial W_j$ (see Fig. 2):

Type-I The intersection of two facets that come from different facets of P.

Type-II The intersection of two facets that come from the same facet of P.

Moreover, we assume $W_j$ to satisfy the following two conditions in our induction hypothesis.

• (b) The dihedral angles of $W_j$ are non-obtuse at every Type-I edge on $\partial W_j$.

• (c) The dihedral angles of $W_j$ range in $(0,\pi ]$ at every Type-II edge on $\partial W_j$.

Fig. 2

Two types of edges on the boundary of $W_1$

From the above assumptions, we will construct a pseudo-diffeomorphism $\varphi _{j+1}$ from $Y^{(j+1)}$ to a mean curvature convex Riemannian polyhedron in a Riemannian 3-manifold with positive scalar curvature that satisfies (a),(b) and (c). First of all, let

$$\begin{aligned} V_j:= \{ x\in M_j ;\, \textrm{dist}(x, W_j) \le \delta \},\ \delta \ll 1; \end{aligned}$$

By [9, Theorem 1.1], we can multiply a smooth function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ to some components of the metric $g_j|_{W_{j}}$ and obtain a new metric $g'_j$ with positive scalar curvature on $W_j$ so that the mean curvature of $g'_j$ at every facet of $W_j$ is positive. So without loss of generality, we can just assume that the mean curvature of $g_j$ at every facet of $W_j$ is positive at the beginning. Then for a sufficiently small $\delta$, it is not hard to show that $V_j$ is a mean curvature convex domain in $(M_j,g_j)$.

Fig. 3

A domain $U_j$ containing $W_j$

Let e be an edge on boundary of $\varphi _j ( F^{(j)}_{j+1} )$. We can write $e=G_e\cap \varphi _j ( F^{(j)}_{j+1})$ where $G_e$ is a facet of $W_j$. Let $F_e$ be the union of the geodesic segments in $V_j$ emanating from the points of e that are orthogonal to $G_e$ (see Fig. 3). Then the dihedral angles between $F_e$ and the facets in $\varphi _j ( F^{(j)}_{j+1})$ and $\partial V_j$ are all less than $\pi$.

If we cut off an open subset from $V_j$ along $\varphi _j ( F^{(j)}_{j+1} )$ and these $F_e$’s, we obtain a compact polyhedral domain $U_{j}$ containing $W_j$ where $\partial U_j\cap \partial W_j = \varphi _j ( F^{(j)}_{j+1} )$ (see Fig. 3). Clearly, $U_j$ is also mean curvature convex. Moreover, define

$$\begin{aligned}{} & {} {\widehat{U}}_j:= \{ x\in M_j ;\, \textrm{dist}(x, U_j) \le \delta \},\ \delta \ll 1; \\{} & {} \quad {\widehat{W}}_j:= W_j \, \cup \, \big \{\text {geodesic segments in }{\widehat{U}}_j \text { emanating orthogonally} \\{} & {} \quad \text { from faces in}\ \varphi _j ( F^{(j)}_{j+1} )\big \}. \end{aligned}$$

So ${\widehat{U}}_j\backslash U_j$ is a thin collar of $\partial {\widehat{U}}_j$. Then consider

$$\begin{aligned} D(U_j)&:= \big \{ p\in {\widehat{U}}_j\times [-1,1]\,;\, \textrm{dist}\big (p, U_j \times \{ 0\}\big ) =\varepsilon \big \}, \ 0<\varepsilon < \delta /2, \end{aligned}$$

(7)

$$\begin{aligned} D(W_j)&:= \big \{ p\in {\widehat{W}}_j\times [-1,1]\,;\, \textrm{dist}\big (p, W_j \times \{ 0\}\big ) =\varepsilon \big \}, \ 0<\varepsilon < \delta /2. \end{aligned}$$

(8)

It is easy to see that $D(U_j)$ is homeomorphic to the double of $U_j$ along $\partial U_j$, and $D(W_j)$ is homeomorphic to the double of $W_j$ along $\varphi _j(F^{(j)}_{j+1})$ (see Fig. 4). Hence $D(W_j)$ is homeomorphic to $Y^{(j+1)}$. More precisely, there exists a homeomorphism

$$\begin{aligned} \varphi _{j+1}: Y^{(j+1)}\rightarrow D(W_j) \end{aligned}$$

which maps a normal neighborhood $N(F^{(j+1)}_{j+1})$ of $F^{(j+1)}_{j+1}$ in $Y^{(j+1)}$ onto the bending region of $D(W_j)$ and maps the two components of $Y^{(j+1)}\backslash N(F^{(j+1)}_{j+1})$ onto the two copies of $W_j$ in $D(W_j)$ that are parallel to $W_j\times \{0\}$. Moreover, by our assumption that $\varphi _j: Y^{(j)}\rightarrow W_j$ is a pseudo-diffeomorphism, we can extend $\varphi _{j+1}$ to a diffeomorphism from an open neighborhood of $Y^{(j+1)}$ in ${\mathbb {R}}{\mathcal {Z}}_P$ to an open neighborhood of $D(W_j)$ in $D(U_j)$. So $\varphi _{j+1}$ is also a pseudo-diffeomorphism.

We remark that here if the dihedral angles of $W_j$ were greater than $\pi$ at an edge in $\varphi _j(F^{(j)}_{j+1})$, then $D(U_j)$ and $D(W_j)$ would have some holes in the bending region. This is the reason why we need to assume $W_j$ to satisfy the condition (c).

Geometrically, $D(U_j)$ and $D(W_j)$ will have some codimension-one creases where the induced metric from ${\widehat{U}}_j\times [0,1]$ is not smooth. In addition, the facets in $\varphi _j(F^{(j)}_{j+1})\subset \partial W_j$ may have different types of local configurations which will cause different shapes of $D(W_j)$ in the bending region (see Fig. 4). In particular in dimension 3, there are possibly three types of local configurations of facets in $\varphi _j(F^{(j)}_{j+1})$ and $\partial U_j$ (see Fig. 5).

Fig. 4

$D(U_j)$ and $D(W_j)$

Fig. 5

Local configurations of facets of $W_j$ in dimension 3

Next, we use the (slightly generalized) argument in [10, Theorem 5.7] to obtain a Riemannian metric on $D(U_j)$ with positive scalar curvature. Let

• $M_{j+1}= D(U_j)$ with the creases smoothed out;

• $g_{j+1}=$ the metric on $M_{j+1}$ induced from the product metric $g_j \times g_{[-1,1]}$       on $U_j\times [-1,1]$.

Using [9, Theorem 1.1] again, we can assume that the mean curvature of $g_j$ at every facet of $U_j$ is positive. Then similarly to the proof of [10, Theorem 5.7], we can compute the scalar curvature of $g_{j+1}$ by estimating the principal curvatures of $D(U_j)$ in $U_j\times [-1,1]$ as follows.

On the region parallel to $U_j\times \{0\}$ in ${\widehat{U}}_j\times [-1,1]$, the scalar curvature of $g_{j+1}$ on $D(U_j)$ is clearly positive. So the difficulty comes from the bending region of $D(U_j)$. The following argument is parallel to the argument in the proof of Gromov-Lawson [10, Theorem 5.7]. Let x be an arbitrary point on $\partial U_j$. We have the following three cases according to where x lies.

• (i) If x is the relative interior of a facet E on $\partial U_j$, then there is a unique normal direction of $\partial U_j$ at x. Let $\sigma _x$ be the geodesic segment in ${\widehat{U}}_j$ emanating orthogonally from $\partial U_j$ at x. Then $\sigma _x \times [-1,1]$ is totally geodesic in ${\widehat{U}}_j \times [-1,1]$. The intersection of $\sigma _x \times [-1,1]$ with $D(U_j)$ is of the form shown in Fig. 6. Let $\mu _1,\mu _2$ be the principal curvatures of $\partial U_j$ at x. Then at a point p corresponding to the angle $\theta \in (-\pi /2, \pi /2)$, the principal curvatures of $D(U_j)$ will be of the form

  $$\begin{aligned}&\lambda _0 = \frac{1}{\varepsilon } \cos \theta + O(\varepsilon ), \ \ \lambda _1= \big (\mu _1+O(\varepsilon )\big )\cos \theta + O(\varepsilon ^2), \\&\lambda _2= \big (\mu _2+O(\varepsilon )\big )\cos \theta + O(\varepsilon ^2). \end{aligned}$$

  Let ${\widehat{\kappa }}$ be the scalar curvature function of ${\widehat{U}}_j$ (and ${\widehat{U}}_j\times [-1,1]$). The by the Gauss equation, the scalar curvature $\kappa$ of $g_{j+1}$ at p is of the form

  $$\begin{aligned} \kappa = {\widehat{\kappa }} + \Big ( \frac{2}{\varepsilon } H + O(1) \Big ) \cos ^2\theta + O(\varepsilon ) \end{aligned}$$

  where $H=\mu _1+\mu _2$ is the mean curvature of $\partial U_j$ at x. By our assumption of $g_j$, we have ${\widehat{\kappa }}>0$ and $H>0$. So we have $\kappa >0$ when $\varepsilon$ is sufficiently small.

• (ii) If x is the relative interior of an edge $E \cap E'$ where E and $E'$ are two facets on $\partial U_j$, the normal direction of $\partial U_j$ at x in ${\widehat{U}}_j$ is not unique. Let $\sigma _x$ and $\sigma '_x$ be the geodesic segments orthogonal to E and $E'$ at x, respectively. Let $\Sigma ^{(E,E')}_x$ be the union of the geodesic segments in ${\widehat{U}}_j$ orthogonal to $E\cap E'$ at x which is bounded $\sigma _x$ and $\sigma '_x$. So $\Sigma ^{(E,E')}_x$ looks like a fan with fan angle $\pi -\angle (E,E')_x$. Note that $\angle (E,E')_x \in (0,\pi ]$ by the condition (b) and (c) of $W_j$. Moreover, x determines an oval-shaped patch (see Fig. 7) in the intersection of $\Sigma ^{(E,E')}_x \times [-1,1]$ and $D(U_j)$. Let $\mu _1,\mu _2$ be the principal curvatures of E at x. At a point p corresponding to the angles $\phi \in [0, \pi -\angle (E,E')_x]$ and $\theta \in (-a_{\phi }, a_{\phi })$ where $0<a_{\phi } \le \pi /2$ is determined by $\phi$, the principal curvatures of $D(U_j)$ will be of the form (see Fig. 7):

  $$\begin{aligned}&\lambda _0 = \frac{1}{\varepsilon } \cos \phi \cos \, \theta + O(\varepsilon ), \ \ \lambda _1= \big (\mu _1+O(\varepsilon )\big )\cos \phi \cos \theta + O(\varepsilon ^2), \\&\lambda _2= \big (\mu _2+O(\varepsilon )\big )\cos \phi \cos \theta + O(\varepsilon ^2). \end{aligned}$$

  So we have

  $$\begin{aligned} \kappa = {\widehat{\kappa }} + \Big ( \frac{2}{\varepsilon } H + O(1) \Big ) \cos ^2\phi \cos ^2\theta + O(\varepsilon ). \end{aligned}$$

  By our assumption of ${\widehat{\kappa }}$ and H, we have $\kappa >0$ when $\varepsilon$ is sufficiently small.

• (iii) If $x=E \cap E' \cap E''\cap E'''$ is a vertex where E, $E'$, $E''$ and $E'''$ are four facets on $\partial U_j$, the geodesic segments in ${\widehat{U}}_j$ emanating from x determine a cone $C_x$ which is bounded by the fans $\Sigma ^{(E,E')}_x$, $\Sigma ^{(E',E'')}_x$, $\Sigma ^{(E'',E''')}_x$ and $\Sigma ^{(E''',E)}_x$ (see Fig. 8). Moreover, x determines a football-shaped region in the intersection of $C_x\times [-1,1]$ and $D(U_j)$ which is parametrized by three angles $\phi _1,\phi _2$ and $\theta$, where $\phi _1 \in [0, \pi -\angle (E,E')_x]$, $\phi _2 \in [0, \pi -\angle (E,E'')_x]$ and $\theta \in (-a_{\phi _1,\phi _2}, a_{\phi _1,\phi _2})$, where $0<a_{\phi _1,\phi _2}\le \pi /2$ is determined by $\phi _1$ and $\phi _2$. Similarly to the previous cases, for a point corresponding to $\phi _1,\phi _2$ and $\theta$, we obtain

  $$\begin{aligned}\quad \kappa = {\widehat{\kappa }} + \Big ( \frac{2}{\varepsilon } H + O(1) \Big ) \cos ^2\phi _1\cos ^2\phi _2\cos ^2\theta + O(\varepsilon ).\end{aligned}$$

  By our assumption of ${\widehat{\kappa }}$ and H, we have $\kappa >0$ when $\varepsilon$ is sufficiently small.

Fig. 6

The bending region of $D(U_j)$ parametrized by one angle

Fig. 7

The bending region of $D(U_j)$ parametrized by two angles

Fig. 8

The bending region of $D(U_j)$ parametrized by three angles

So in all cases, we have $\kappa >0$. By the above discussion, the bending region of $D(U_j)$ can be written as $A_1\cup A_2\cup A_3$ where $A_1$, $A_2$ and $A_3$ consist of the points parametrized by one, two and three angles, respectively. Besides, let $A_0$ be the region of $D(U_j)$ that is parallel to $U_j\times \{0\}$. There are some obvious creases at the intersections of $A_0$, $A_1$, $A_2$ and $A_3$ where the metric $g_{j+1}$ does not have continuous second derivatives. But by some small perturbations of $D(U_j)$, we can smooth out these creases so that the condition $\kappa >0$ still holds. The local model of the smoothing is given by the Cartesian product of an open subset of the quadrant ${\mathbb {R}}^2_{\ge 0}$ with the curve $\gamma$ shown in Fig. 9 where $\gamma$ is smooth except at $t=0$. For every point $x\in {\mathbb {R}}^2_{\ge 0}$, we deform $\{x\}\times \gamma$ to be $\{x\}\times {\widetilde{\gamma }}$, where ${\widetilde{\gamma }}$ is an everywhere smooth curve that differs from $\gamma$ only in a small interval $0< t < \delta$ for some $\delta \ll 1$ (see Fig. 9). After smoothing the creases, $D(W_j)$ becomes a Riemannian polyhedron in $(M_{j+1},g_{j+1})$ that we desire.

Fig. 9

Smoothing a curve $\gamma$ near $t=0$

Next, let us verify that $D(W_j)$ satisfies the conditions (b) and (c). By the definition of ${\widehat{W}}_j$ and $D(W_j)$, any facet G of $D(W_j)$ in the bending region is of the following form:

$$\begin{aligned} G= \big ( I_{E\cap F}\times [-1,1] \big ) \cap D(W_j) \end{aligned}$$

where E, F are two facets of $W_j$ with $E\subseteq \varphi _j(F^{(j)}_{j+1})$ and $F \nsubseteq \varphi _j(F^{(j)}_{j+1})$, and $I_{E\cap F}$ is union of the geodesic segments in ${\widehat{U}}_j$ orthogonal to E that emanate from points in $E\cap F$ (see Fig. 10). This implies:

• G is a totally geodesic facet of $D(W_j)$.

• $\angle ({\widetilde{E}}_{\pm \varepsilon },G) =\pi /2$ where ${\widetilde{E}}_{\pm \varepsilon }$ is the parallel copy of E in $W_j\times \{\pm \varepsilon \}$.

Fig. 10

Facets of $D(W_j)$ in the bending region

Let ${\widetilde{F}}_{\pm \varepsilon }$ be the parallel copy of F in $W_j\times \{\pm \varepsilon \}$. By the condition (b) of $W_j$, the dihedral angles $\angle ({\widetilde{E}}_{\varepsilon },{\widetilde{F}}_{\varepsilon })$ and $\angle ({\widetilde{E}}_{- \varepsilon },{\widetilde{F}}_{- \varepsilon })$ are both non-obtuse. So

$$\begin{aligned} \angle (G,{\widetilde{F}}_{\pm \varepsilon }) \in (0,\pi ]. \end{aligned}$$

(9)

If an edge L of $D(W_j)$ is not contained in the two parallel copies of $\varphi _j(F^{(j)}_{j+1})$ in $W_j\times \{\pm 1\}$, the dihedral angles of $D(W_j)$ at L will agree with the dihedral angles of the counterpart of L in $W_j\times \{0\}$. These include all the Type-I edges of $D(W_j)$. Then since $W_j$ satisfies the condition (b), so does $D(W_j)$.

All the Type-II edges of $D(W_j)$ that lie in the two parallel copies of $\varphi _j(F^{(j)}_{j+1})$ in $W_j\times \{\pm \varepsilon \}$ are:

$$\begin{aligned} \big \{ G\cap {\widetilde{F}}_{\pm \varepsilon };\, F \nsubseteq \varphi _j(F^{(j)}_{j+1}),\, G\ \text {is a facet of}\ D(W_j) \ \text {in the bending region} \big \}. \end{aligned}$$

It follows from (9) that $D(W_j)$ satisfies the condition (c) at these edges. At other Type-II edges, $D(W_j)$ also satisfies the condition (c) by our assumption of $W_j$.

Moreover, the conditions (b) and (c) still hold for $D(W_j)$ after we smooth the creases of $D(U_j)$ since the smoothing does not change the tangent spaces of the facets of $D(U_j)$ incident to the creases.

In addition, $D(W_j)$ is mean curvature convex in $(M_{j+1},g_{j+1})$ since its facets in the bending region are all totally geodesic while its facets outside the bending region have the same mean curvatures as their counterparts in $W_j\times \{0\}$.

So from the above arguments, we obtain a pseudo-diffeomorphism $\varphi _{j+1}$ from $Y^{(j+1)}$ to $W_{j+1}:=D(W_j)$ where $W_{j+1}$ is a mean curvature convex Riemannian polyhedron in $(M_{j+1},g_{j+1})$ with positive scalar curvature and $W_{j+1}$ satisfies the conditions (b) and (c). This finishes the induction.

Observe that when $j=m-1$, $\partial U_{m-1} = \partial W_{m-1} =\varphi _{m-1}(F^{(m-1)}_{m})$. This implies $W_{m-1}=U_{m-1}$. So by our doubling construction (8), the pseudo-diffeomorphism $\varphi _m: Y^{(m)} = {\mathbb {R}}{\mathcal {Z}}_P \rightarrow W_m = D(W_{m-1})$ is actually a diffeomorphism, where $W_m$ is a compact Riemannian 3-manifold with positive scalar curvature. Then by Theorem 2.2, P must be combinatorially equivalent to a convex polytope that can be obtained from $\Delta ^3$ by a sequence of vertex cuts. So we finish the proof of the “only if” part and hence the whole theorem. $\square$

Remark 3.1

In the proof of the “only if” part of Theorem 1.3, there is a canonical action of $H_j\cong ({\mathbb {Z}}_2)^j$ on both $Y^{(j)}$ and $W_j$, $1\le j \le m$. Indeed, we can define the action of $H_j$ on $W_j$ inductively through the doubling construction $D(W_{j-1})$. From our definition of the pseudo-diffeomorphism $\varphi _j: Y^{(j)}\rightarrow W_j$, it is easy to see that $\varphi _j$ is equivariant with respect to the canonical $H_j$-actions for all $1\le j \le m$.

Proof of Corollary 1.5

If P is combinatorially equivalent to a convex polytope obtained from $\Delta ^3$ by a sequence of vertex-cuts, it follows from the proof of the “if” part of Theorem 1.3 that P is realized as a right-angled totally geodesic Riemannian polyhedron in $({\mathbb {R}}{\mathcal {Z}}_P,g_0)$. The reverse direction also follows from Theorem 1.3 immediately. $\square$

Corollary 3.2

The statements of Theorem 1.3 and Corollary 1.5 still hold if we assume that the ambient Riemannian 3-manifold in these two theorems has positive constant scalar curvature.

Proof

By the solution of the equivariant Yamabe problem in Hebey and Vaugon [13], if ${\mathbb {R}}{\mathcal {Z}}_P$ has a $({\mathbb {Z}}_2)^m$-invariant Riemannian metric $g_0$ with positive scalar curvature, then there exists a $({\mathbb {Z}}_2)^m$-invariant Riemannian metric ${\overline{g}}_0$ conformal to $g_0$ on ${\mathbb {R}}{\mathcal {Z}}_P$ which has positive constant scalar curvature. So we can prove this corollary by applying the same proof of the “if” part of Theorem 1.3 to $({\mathbb {R}}{\mathcal {Z}}_P,{\overline{g}}_0)$.

$\square$

4 Examples in higher dimensions

The argument of “doubling-smoothing” of Riemannian polyhedra in the proof of Theorem 1.3 can be generalized to any dimension $n\ge 2$ (also see [12, §2.1]). Indeed, the only new ingredient in the proof of the higher dimensions is: there are more types of local configurations of facets on the boundary of the polyhedra in our iterated doubling construction. So if an n-dimensional simple convex polytope P in ${\mathbb {R}}^n$ can be realized as a mean curvature convex Riemannian polyhedron with non-obtuse dihedral angles in a Riemannian n-manifold with positive scalar curvature, then we can construct a Riemannian metric on ${\mathbb {R}}{\mathcal {Z}}_P$ with positive scalar curvature. Note that the iterated doubling construction induces a smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ from P which is equivariant with respect to the canonical $({\mathbb {Z}}_2)^m$-action. Then since the equivariant smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ is known to be unique up to equivariant diffeomorphisms (see [15, Proposition 3.8]), this smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ should agree with the smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ determined by the embedding $i_{{\mathcal {Z}}}: {\mathbb {R}}{\mathcal {Z}}_P\rightarrow {\mathbb {R}}^m$ (see Sect. 2). But unfortunately, we do not have the analogue of Theorem 2.2 for ${\mathbb {R}}{\mathcal {Z}}_P$ in higher dimensions. So we cannot determine all possible combinatorial types of P in dimension greater than 3.

On the other hand, we can construct many examples of such kind of simple convex polytopes P in arbitrarily high dimensions as follows. Let us first quote some well known results on the existence of Riemannian metrics with positive scalar curvature.

Theorem 4.1

(see Gromov and Lawson [11] and Schoen and Yau [21]) Let N be a closed manifold which admits a Riemannian metric with positive scalar curvature. If M is a manifold that is obtained from N by surgery in codimension $\ge 3$, then M also admits a Riemannian metric with positive scalar curvature.

Moreover, there is an equivariant version of Theorem 4.1 for manifolds equipped with a compact Lie group action as follows.

Theorem 4.2

(Theorem 11.1 in [3]) Let M and N be G-manifolds where G is a compact Lie group. Assume that N admits an G-invariant metric of positive scalar curvature. If M is obtained from N by equivariant surgeries of codimension at least three, then M admits a G-invariant metric of positive scalar curvature.

It is shown in Bosio and Meersseman [4, Lemma 2.3] that up to combinatorial equivalence any n-dimensional simple convex polytope P can be obtained from the n-simplex by a finite number of flips at some proper faces. Let f be a proper face of P which is combinatorially equivalent to the k-simplex $\Delta ^k$. Roughly speaking, the flip of P at f gives us a new polytope, denoted by $\textrm{flip}_{f}(P)$, which is obtained by cutting off a small neighborhood N(f) of f from P and a neighborhood $N(\Delta ^k)$ of $\Delta ^k$ from $\Delta ^n$, and then gluing $P\backslash N(f)$ and $\Delta ^n\backslash N(\Delta ^k)$ together along their cutting sections and merging the nearby facets (see [17, 23] or [4] for the precise definition). For example, Fig. 11 shows the flip of a 3-dimensional simple convex polytope at a vertex and at an edge, respectively. Note that doing a flip on P at a vertex v is equivalent to cutting off v from P, which will increase the number of facets by one. But whenever $\dim (f)>0$, the number of facets of $\textrm{flip}_{f}(P)$ will be equal to that of P. In addition, a flip of P at a face corresponds to a bistellar move on $\partial P^*$ where $P^*$ is the dual simplicial polytope of P (see [4, 17]).

Fig. 11

Flip of a simple convex polytope P at a face f

From the viewpoint of the construction of real moment-angle manifolds, a flip of P at a codimension-k face f corresponds to an equivariant surgery on ${\mathbb {R}}{\mathcal {Z}}_P$ at some codimension-k submanifolds. More specifically, it is a $({\mathbb {Z}}_2)^m$-equivariant surgery on ${\mathbb {R}}{\mathcal {Z}}_P$ if $\dim (f)>0$ or a $({\mathbb {Z}}_2)^{m+1}$-equivariant surgery on ${\mathbb {R}}{\mathcal {Z}}_P \times {\mathbb {Z}}_2$ if $\dim (f)=0$, where m is the number of facets of P (see [16, §4]). Then it follows from [4, Lemma 2.3] that we can obtain ${\mathbb {R}}{\mathcal {Z}}_P$ from ${\mathbb {R}}{\mathcal {Z}}_{\Delta ^n}= S^n$ (see Example 2.1) by a sequence of equivariant surgeries for any n-dimensional simple convex polytope P. Moreover, the sequence of equivariant surgeries induce an (unique) equivariant smooth structure on ${\mathbb {R}}{\mathcal {Z}}_P$ step by step from the standard smooth structure on $S^n$.

Proposition 4.3

Suppose P is an n-dimensional simple convex polytope in ${\mathbb {R}}^n$ with $n\ge 3$. If P is combinatorially equivalent to a convex polytope that can be obtained from the n-simplex $\Delta ^n$ by a sequence of flips at faces of codimension at least three, then P can be realized as a right-angled totally geodesic Riemannian polyhedron in a Riemannian n-manifold with positive scalar curvature.

Proof

By our assumption of P, ${\mathbb {R}}{\mathcal {Z}}_P$ can be obtained from ${\mathbb {R}}{\mathcal {Z}}_{\Delta ^n}= S^n$ by a sequence of equivariant surgeries at some submanifolds with codimension at least three. Note that the induced Riemannian metric $g_0$ on $S^n$ from ${\mathbb {R}}^{n+1}$ has positive constant scalar (sectional) curvature, and $g_0$ is invariant with respect to the canonical action of $({\mathbb {Z}}_2)^{n+1}$ on $S^n$ (see Example 2.1). Then it follows from Theorem 4.2 that ${\mathbb {R}}{\mathcal {Z}}_P$ has a $({\mathbb {Z}}_2)^m$-invariant Riemannian metric $g_1$ with positive scalar curvature where m is the number of facets of P. Finally, by applying the proof of the “if” part of Theorem 1.3 to $({\mathbb {R}}{\mathcal {Z}}_P,g_1)$, we can deduce that P is realized as a right-angled totally geodesic Riemannian polyhedron in $({\mathbb {R}}{\mathcal {Z}}_P,g_1)$. $\square$

To explore the generalization of Theorem 1.3 to higher dimensions, it is natural for us to ask the following question.

Question::

Is it true that the examples given in Proposition 4.3 are exactly all the n-dimensional simple convex polytopes in ${\mathbb {R}}^n$ ($n\ge 3$) that can be realized as mean curvature convex (or totally geodesic) Riemannian polyhedra with non-obtuse dihedral angles in Riemannian n-manifolds with positive scalar curvature?

To answer the above question, we need to understand for what simple convex polytope P the manifold ${\mathbb {R}}{\mathcal {Z}}_P$ can admit a Riemannian metric with positive scalar curvature. It is well known that in dimension $\ge 5$, such kind of problems are related to the existence of spin structures, ${\widehat{A}}$-genus and $\alpha$-invariant defined by index theory (see [22]). In dimension 4, the existence of Riemannian metrics with positive scalar curvature implies the vanishing of Seiberg-Witten invariants. But the calculations of these invariants for ${\mathbb {R}}{\mathcal {Z}}_P$ are very difficult in general.