Brasselet number and Newton polygons

Abstract

We present a formula to compute the Brasselet number of $f:(Y,0)\rightarrow (\mathbb {C}, 0)$ where $Y\subset X$ is a non-degenerate complete intersection in a toric variety X. As applications we establish several results concerning invariance of the Brasselet number for families of non-degenerate complete intersections. Moreover, when $(X,0) = (\mathbb {C}^n,0)$ we derive sufficient conditions to obtain the invariance of the Euler obstruction for families of complete intersections with an isolated singularity which are contained in X.

1 Introduction

Given a germ of an analytic function $f:(\mathbb {C}^{n},0) \rightarrow (\mathbb {C},0)$ with an isolated critical point at the origin, an important invariant of this germ is its Milnor number [28], denoted by $\mu (f)$. The Milnor number is considered as a central invariant, since it provides algebraic, topological and geometric information about the germ f. For instance, the Milnor number coincides with the number of Morse points of a morsefication of f.

Initially the Milnor number was associated to germs of analytic functions $f : (\mathbb {C}^n, 0) \rightarrow (\mathbb {C}, 0)$ with an isolated critical point, and consequently it was used to study isolated hypersurface singularities. However this invariant is well defined in many others contexts, for example curves [9], isolated complete intersection singularities (ICIS) [21], and determinantal varieties of codimension two [39], to name just a few.

The local Euler obstruction was defined by MacPherson in [23] for the construction of characteristic classes of singular complex algebraic varieties. Thereafter, it has been deeply investigated by many authors such as Brasselet and Schwartz [7], Dutertre [13], Gaffney et al. [15], Gonzalez-Sprinberg [20], Lê and Teissier [22], Matsui and Takeuchi [26], among others. We denote by (X, 0) a germ of an analytic singular space embedded in $\mathbb {C}^n$ and by $f:(X,0) \rightarrow (\mathbb {C},0)$ a germ of an analytic function with an isolated critical point at the origin. Brasselet, Massey, Parameswaran and Seade [4] introduced an invariant associated to f called the Euler obstruction of f and denoted by $\mathrm{Eu}_{f,X}(0)$. Roughly speaking, $\mathrm{Eu}_{f,X}(0)$ is the obstruction to extending a lifting of the conjugate of the gradient vector field of f as a section of the Nash bundle of (X, 0). This invariant is closed related with the local Euler obstruction of X, what explains its name.

An important consequence of the definition given by MacPherson, is that the local Euler obstruction does not depend on the Whitney stratification of X. Moreover, it was proved in [7] that the local Euler obstruction is a constructible function, which means that, it is constant along the strata of a Whitney stratification of X. This is essentially a consequence of the topological triviality of X on the Whitney strata. The following Lefschetz-type formula was proved by Brasselet, Lê and Seade [2].

Theorem 1.1

Let $(X,0) \subset (\mathbb {C}^n,0)$ be an equidimensional complex analytic singularity germ with a Whitney stratification $\{V_{i}\}$, then given a generic linear form L, there exists $\varepsilon _0$ such that for any $\varepsilon$ with $0<\varepsilon < \varepsilon _0$, we have

$$\begin{aligned} \mathrm{Eu}_X(0)=\sum _{i}\chi \big (V_i\cap B_\varepsilon \cap L^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X}(V_i), \end{aligned}$$

where $\chi$ is the Euler–Poincaré characteristic, $B_\varepsilon :=B_\varepsilon (0)$ is the ball with center the origin and radius $\varepsilon$, $\mathrm{Eu}_{X}(V_i)$ is the value of the local Euler obstruction of X at any point of the stratum $V_i$, and $0 < \vert \delta \vert \ll \varepsilon \ll 1$.

The previous theorem says that the local Euler obstruction, as a constructible function on X, satisfies the Euler condition relatively to a generic linear function.

For the Euler obstruction of an analytic function $f:(X,0) \rightarrow (\mathbb {C},0)$ with an isolated critical point at the origin, there is also a Lefschetz-type formula. This formula was proved in [4]. The purpose of the authors was to understand what prevents the local Euler obstruction from satisfying the local Euler condition with respect to functions which are singular at the origin.

Theorem 1.2

Let $(X,0) \subset (\mathbb {C}^n,0)$ be an equidimensional complex analytic singularity germ with a Whitney stratification $\{V_{i}\}$, and let $f : (X,0) \rightarrow ({\mathbb {C}},0)$ be a function with an isolated singularity at 0. Then,

$$\begin{aligned} \mathrm{Eu}_{f,X}(0)=\mathrm{Eu}_X(0) \,- \,\left( \sum _{i} \chi \big (V_i\cap B_\varepsilon \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_X(V_i) \right) , \end{aligned}$$

where $0 < \vert \delta \vert \ll \varepsilon \ll 1$.

The last equation presents the relation between the local Euler obstruction of X and the Euler obstruction of f.

Seade, Tibăr and Verjovsky continued the study of the properties of $\mathrm{Eu}_{f,X}(0)$ in [40]. The authors proved that the Euler obstruction of f is closely related to the number of Morse points of a morsefication of f, as follows.

Proposition 1.3

Let (X, 0) be an equidimensional complex analytic singularity germ of dimension d and $f: (X,0) \rightarrow (\mathbb {C},0)$ a germ of an analytic function with an isolated critical point at the origin. Then

$$\begin{aligned} \mathrm{Eu}_{f,X}(0) = (-1)^{d} n_\mathrm{reg}, \end{aligned}$$

where $n_\mathrm{reg}$ is the number of Morse points in the regular part of X appearing in a stratified morsefication of f.

Therefore, the Euler obstruction of f is the number of Morse points of a morsefication of f on the regular part of X, up to the sign. Hence this invariant can be seen as a generalization of the Milnor number of f.

Another invariant associated with a germ of an analytic function $f:(X,0) \rightarrow (\mathbb {C},0)$ is the Brasselet number introduced by Dutertre and Grulha in [12]. We will denote this number by $\mathrm{B}_{f,X}(0)$. If f has an isolated critical point, then the Brasselet number satisfies the equality

$$\begin{aligned} \mathrm{B}_{f,X}(0) = \mathrm{Eu}_{X}(0) - \mathrm{Eu}_{f,X}(0). \end{aligned}$$

If f is linear and generic, then $\mathrm{B}_{f,X}(0)=\mathrm{Eu}_X(0)$, hence it can be viewed as a generalization of the local Euler obstruction. Moreover, even if f has a non-isolated singularity it provides interesting results. For example, the Brasselet number satisfies a Lê-Greuel type formula (see [12, Theorem 4.4] or Theorem 2.5 below), i.e., the difference of the Brasselet numbers $\mathrm{B}_{f,X}(0)$ and $\mathrm{B}_{f,X^{g}}(0)$ is measured by the number of Morse critical points on the top stratum of the Milnor fiber of f appearing in a morsefication of g, where $g: (X,0) \rightarrow (\mathbb {C},0)$ is a prepolar function (see Definition 2.4) and $X^{g}=X \cap g^{-1}(0)$.

Although they are important, the invariants mentioned above are not easily computed using their definition. In the literature there are formulas which make the computation easier, see [2, 4, 13, 22]. Some authors worked on more specific situations. In the special case of toric surfaces, an interesting formula for the local Euler obstruction was proved by Gonzalez-Sprinberg [20]. This formula was generalized by Matsui and Takeuchi [26] for normal toric varieties of any dimension.

Toric varieties are particularly interesting objects, since they have a strong relation with elementary convex geometry. On these varieties we have an action of the algebraic torus $(\mathbb {C}^{*})^n$ that induces a finite decomposition of the variety into orbits, all of which are homeomorphic to a torus.

In [41], Varchenko described the topology of the Milnor fiber of a function $f:(\mathbb {C}^n,0) \rightarrow (\mathbb {C},0)$ using the geometry of the Newton polygon of f, and consequently, the Milnor number can be expressed by volumes of polytopes related to the Newton polygon of f. In his proof, he constructed a toric modification of $\mathbb {C}^n$ on which the pull-back of f defines a hypersurface with only normal crossing singularities. While $\mathbb {C}^n$ is a very special smooth toric variety, it seems natural to generalize his formula to Milnor fibers over general singular toric varieties. This was done by Matsui and Takeuchi in [27].

We use [27] to establish several combinatorial formulas for the computation of the Brasselet number of $f:(Y,0)\rightarrow (\mathbb {C}, 0)$ where $Y\subset X$ is a non-degenerate complete intersection in a toric variety X. These formulas will be given in terms of volumes of Newton polygons associated to f.

This paper is organized as follows. In Sect. 2, we present some background material concerning the Brasselet number and toric varieties, which will be used in the entire work. In Sect. 3, we compute the Brasselet number of a polynomial function $f : (X, 0) \rightarrow (\mathbb {C}, 0)$, where $X \subset \mathbb {C}^n$ is a toric variety. Moreover, we compute this invariant for functions defined on $X^{g} = X\cap g^{-1}(0)$, where $g: X \rightarrow \mathbb {C}^k$ is a non-degenerate complete intersection. As a consequence, assuming that g has an isolated critical point on X and on $X^f$, we also obtain a formula for the number of stratified Morse critical points on the top stratum of the Milnor fiber of f appearing in a morsefication of $g: X \cap f^{-1}(\delta ) \cap B_{\varepsilon } \rightarrow \mathbb {C}$. As applications we establish several results concerning constancy of these invariants. In Sect. 4, we consider the case where $(X,0) = (\mathbb {C}^n,0)$ and we derive sufficient conditions to obtain the constancy of the Euler obstruction for families of complete intersections with an isolated singularity which are contained on X. We use this result to study the invariance of the Bruce–Roberts’ Milnor number for families of functions defined on hypersurfaces. In Sect. 5, we work in the case of surfaces, i.e., in the case where X is a 2-dimensional toric variety. In this situation, we present a characterization of a polynomial function $g: X \rightarrow \mathbb {C}$ which has a stratified isolated singularity at the origin. We use this characterization to present some examples for a class of toric surface that is also determinantal. In Sect. 6, we study the GSV-index on non-degenerated complete intersection in toric varieties.

2 Generalities: stratifications, Brasselet number and toric varieties

For the convenience of the reader and to fix the notation we present some general facts in order to establish our results.

2.1 Stratifications and Brasselet number

In order to introduce the definition and the properties of the Brasselet number, we need some notions about stratifications. For more details, we refer to Massey [24, 25]. Let $A \subset \mathbb {C}^n$, $B\subset \mathbb {C}^m$ and $f : A \rightarrow B$ be a function with $n, m\in \mathbb {N}$. We will fix the notation, $A^{f}:=A\cap f^{-1}(0)$.

Consider $X\subset \mathbb {C}^n$ a reduced complex analytic set of dimension d which is included in an open set U. Let $F : U \rightarrow \mathbb {C}$ be a holomorphic function and $f : X \rightarrow \mathbb {C}$ be the restriction of F to X, i.e., $f:=F|_X$.

Definition 2.1

A good stratification of X relative to f is a stratification $\mathcal {V}$ of X which is adapted to $X^{f}$, such that $\left\{ V_i \in \mathcal {V}; \ \ V_i \not \subset X^{f}\right\}$ is a Whitney stratification of $X \setminus X^{f}$, and for any pair of strata $(V_{\alpha },V_{\beta })$ such that $V_{\alpha } \not \subset X^{f}$ and $V_{\beta } \subset X^{f}$, the $(a_f)$-Thom condition is satisfied. We call the strata included in $X^{f}$ the good strata.

By [17], given a stratification $\mathcal {S}$ of X one can refine $\mathcal {S}$ to obtain a Whitney stratification $\mathcal {V}$ of X which is adapted to $X^{f}$. By [3, 36] the refinement $\mathcal {V}$ satisfies the $(a_f)$-Thom condition, i.e., good stratifications always exist.

Definition 2.2

Consider X and f as before. Let $\mathcal {V}=\{V_i\}$ be a stratification of X. The critical locus of f relative to $\mathcal {V}$, denoted by $\Sigma _{\mathcal {V}} f$, is the union of the critical locus of f restricted to each of the strata, i.e., $\Sigma _{\mathcal {V}} f = \bigcup _{i} \Sigma (f|_{V_i})$.

A critical point offrelative to $\mathcal {V}$ is a point $p \in \Sigma _{\mathcal {V}} f$. If the stratification $\mathcal {V}$ is clear, we will refer to the elements of $\Sigma _{\mathcal {V}} f$ simply as stratified critical points of f. If p is an isolated point of $\Sigma _{\mathcal {V}} f$, we call p a stratified isolated critical point of f (with respect to $\mathcal {V}$). If $\mathcal {V}$ is a Whitney stratification of X and $f : X \rightarrow \mathbb {C}$ has a stratified isolated critical point at the origin, then

$$\begin{aligned} \left\{ V_{\alpha } \setminus X^{f}, V_{\alpha } \cap X^{f} \setminus \left\{ 0 \right\} , \left\{ 0\right\} ; \ \ V_{\alpha } \in \mathcal {V} \right\} , \end{aligned}$$

is a good stratification for f. We call it the good stratification induced by f.

Definition 2.3

Suppose that X is equidimensional. Let $\mathcal {V} = \left\{ V_i \right\} _{i=0}^{q}$ be a good stratification of X relative to f. The Brasselet number is defined by

$$\begin{aligned} \mathrm{B}_{f,X}(0) := \sum _{i =1}^q\chi \big (V_i\cap B_{\varepsilon }(0) \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X}(V_i), \end{aligned}$$

where $0< \left| \delta \right| \ll \varepsilon \ll 1$.

If f has a stratified isolated critical point at the origin and X is equidimensional, Theorem 1.2 implies that

$$\begin{aligned} \mathrm{B}_{f,X}(0) = \mathrm{Eu}_X(0) - \mathrm{Eu}_{f,X}(0). \end{aligned}$$

(2.1)

The Brasselet number has many interesting properties, e.g., it satisfies several multiplicity formulas, which enable the authors to establish in [12] a relative version of the local index formula and a Gauss–Bonnet formula for $\mathrm{B}_{f,X}(0)$. However, one of the most important properties of this invariant is the Lê-Greuel type formula (Theorem 2.5). To present this result we need to impose some conditions on the functions to ensure that $X^{g}$ meets $X^{f}$ in a nice way. So it is necessary to define:

Definition 2.4

Let $\mathcal {V}$ be a good stratification of X relative to f. We say that $g : (X,0) \rightarrow (\mathbb {C}, 0)$ is prepolar with respect to $\mathcal {V}$ at the origin if the origin is an isolated critical point of g.

The condition that g is prepolar means that g has an isolated critical point (in the stratified sense), both on X and on $X^{f}$, and that $X^g$ intersects transversely each stratum of $\mathcal {V}$ in a neighborhood of the origin, except perhaps at the origin itself. However, it is important to note that, while $X^g$ meets $X^f$ in a nice way, $X^f$ may have arbitrarily bad singularities when restricted to $X^g$. The $(a_f)$-Thom condition in Definition 2.3 together with the hypothesis that g is prepolar ensure that $g:X \cap f^{-1}(\delta ) \cap B_{\varepsilon } \rightarrow \mathbb {C}$ has no critical points on $g^{-1}(0)$ [24, Proposition 1.12]. Therefore, the number of stratified Morse critical points on the top stratum $V_q \cap f^{-1}(\delta )\cap B_{\varepsilon }(0)$, in a morsefication of $g : X \cap f^{-1}(\delta ) \cap B_{\varepsilon }(0) \rightarrow \mathbb {C}$, does not depend on the morsefication.

The next theorem shows that the Brasselet number satisfies a Lê-Greuel type formula [12, Theorem 4.4].

Theorem 2.5

Suppose that X is equidimensional and that g is prepolar with respect to $\mathcal {V}$ at the origin. Then,

$$\begin{aligned} \mathrm{B}_{f,X}(0) - \mathrm{B}_{f,X^{g}}(0) = (-1)^{d-1}n_q, \end{aligned}$$

where $n_q$ is the number of stratified Morse critical points on the top stratum $V_q \cap f^{-1}(\delta )\cap B_{\varepsilon }(0)$ appearing in a morsefication of $g : X \cap f^{-1}(\delta ) \cap B_{\varepsilon }(0) \rightarrow \mathbb {C}$, and $0 < \left| \delta \right| \ll \varepsilon \ll 1$. In particular, this number is independent on the morsefication.

2.2 Toric varieties

The theory of toric varieties can be seen as a cornerstone for the interaction between combinatorics and algebraic geometry, which relates the combinatorial study of convex polytopes to algebraic torus actions. Moreover, for polynomial functions defined on such varieties, it is possible to obtain a combinatorial description of the topology of their Milnor fibers in terms of Newton polygons (see [27, 34]). The reader may consult [14, 32] for an overview about toric varieties.

Let $N \cong \mathbb {Z}^d$ be a $\mathbb {Z}$-lattice of rank d and $\sigma$ a strongly convex rational polyhedral cone in $N_{\mathbb {R}} = \mathbb {R} \otimes _{\mathbb {Z}} N$. We denote by M the dual lattice of N and the polar cone $\check{\sigma }$ of $\sigma$ in $M_{\mathbb {R}} = \mathbb {R} \otimes _{\mathbb {Z}} M$ by

$$\begin{aligned} \check{\sigma } = \left\{ v \in M_{\mathbb {R}}; \ \ \left\langle u,v\right\rangle \ge 0 \ \ \text {for any} \ \ u \in \sigma \right\} , \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ is the usual inner product in $\mathbb {R}^d$. Then the dimension of $\check{\sigma }$ is d and we obtain a semigroup $S_{\sigma }:= \check{\sigma } \cap M$.

Definition 2.6

A d-dimensional affine toric variety $X_{\sigma }$ is defined by the spectrum of $\mathbb {C}[S_{\sigma }]$, i.e., $X=\mathrm {Spec}(\mathbb {C}[S_{\sigma }])$.

The algebraic torus $T = \mathrm{{Spec}}(\mathbb {C}[M])\cong (\mathbb {C}^{*})^d$ acts naturally on $X_{\sigma }$ and the T-orbits in $X_{\sigma }$ are indexed by the faces $\Delta$ of $\check{\sigma }$ ($\Delta \prec \check{\sigma }$). We denote by $\mathbb {L}(\Delta )$ the smallest linear subspace of $M_{\mathbb {R}}$ containing $\Delta$. For a face $\Delta$ of $\check{\sigma }$, denote by $T_{\Delta }$ the T-orbit in $\mathrm {Spec}(\mathbb {C}[M \cap \mathbb {L}(\Delta )])$ which corresponds to $\Delta$. We observe that the d-dimensional affine toric varieties are exactly those d-dimensional affine, normal varieties admitting a $(\mathbb {C}^{*})^d$-action with an open, dense orbit homeomorphic to $(\mathbb {C}^{*})^d$. Moreover, each T-orbit $T_{\Delta }$ is homeomorphic to $(\mathbb {C}^{*})^{r}$, where r is the dimension of $\mathbb {L}(\Delta )$.

Therefore we obtain a decomposition $X_{\sigma } = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta }$ into T-orbits, which are homeomorphic to algebraic torus $(\mathbb {C}^{*})^{r}$. Due to this fact, and also the informations coming from the combinatorial residing in these varieties, many questions that were originally studied for functions defined on $\mathbb {C}^d$ can be extended to functions defined on toric varieties.

Consider $f: X_{\sigma } \rightarrow \mathbb {C}$ a polynomial function on $X_{\sigma }$, i.e., a function that corresponds to an element $f=\sum _{v\in S_{\sigma }}{a_v \cdot v}$ of $\mathbb {C}[S_{\sigma }]$, where $a_v \in \mathbb {C}$.

Definition 2.7

Let $f=\sum _{v\in S_{\sigma }}{a_v \cdot v}$ be a polynomial function on $X_{\sigma }$.

• (a) The set $\left\{ v \in S_{\sigma }; \ \ a_v \ne 0 \right\} \subset S_{\sigma }$ is called the support of f and we denote it by ${{\,\mathrm{supp}\,}}f$;

• (b) The Newton polygon $\Gamma _{+}(f)$ of f is the convex hull of

  $$\begin{aligned} \bigcup _{v \in {{\,\mathrm{supp}\,}}f} (v+ \check{\sigma }) \subset \check{\sigma }. \end{aligned}$$

Now let us fix a function $f \in \mathbb {C}[S_{\sigma }]$ such that $0 \notin {{\,\mathrm{supp}\,}}f$, i.e., $f: X_{\sigma } \rightarrow \mathbb {C}$ vanishes at the T-fixed point 0. Considering $M(S_{\sigma })$ the $\mathbb {Z}$-sublattice of rank d in M generated by $S_{\sigma }$, we have that each element v of $S_{\sigma } \subset M(S_{\sigma })$ is identified with a $\mathbb {Z}$-vector $v=(v_1,\ldots ,v_d)$. Then for $g = \sum _{v \in S_{\sigma }} b_v \cdot v \in \mathbb {C}[S_{\sigma }]$ we can associate a Laurent polynomial $L(g) = \sum _{v \in S_{\sigma }} b_v \cdot x^{v}$ on $T = (\mathbb {C}^*)^d$, where $x^{v}:=x_1^{v_1}\cdot x_2^{v_2} \ldots \; x_d^{v_d}$.

Definition 2.8

We say that $f=\sum _{v\in S_{\sigma }}{a_v\cdot v} \in \mathbb {C}[S_{\sigma }]$ is non-degenerate if for any compact face $\gamma$ of $\Gamma _{+}(f)$ the complex hypersurface

$$\begin{aligned} \bigl \{ x=(x_1,\ldots ,x_d) \in (\mathbb {C}^*)^d \,\bigm |\, L(f_{\gamma })(x) = 0\bigr \} \end{aligned}$$

in $(\mathbb {C}^*)^d$ is smooth and reduced, where $f_{\gamma } := \sum _{v \in \gamma \cap S_{\sigma }} a_v \cdot v$.

We can also study non-degeneracy in case of complete intersections defined on $X_{\sigma }$. Let $f_1,f_2, \ldots , f_k \in \mathbb {C}[S_{\sigma }]$$(1 \le k \le d = \dim X_{\sigma })$ and consider the following subvarieties of $X_{\sigma }$:

$$\begin{aligned} V:= \left\{ f_1=\ldots =f_{k-1} = f_k =0 \right\} \subset W:= \left\{ f_1=\ldots =f_{k-1} =0 \right\} . \end{aligned}$$

Assume that $0 \in V$. For each face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$, we set

$$\begin{aligned} I(\Delta )= \bigl \{ j=1,2,\ldots , k-1 \,\bigm |\, \Gamma _{+}(f_j) \cap \Delta \ne \emptyset \bigr \} \subset \left\{ 1,2,\ldots ,k-1 \right\} \end{aligned}$$

and $m(\Delta )= \# I(\Delta ) + 1$.

Let $\mathbb {L}(\Delta )$ and $M(S_{\sigma } \cap \Delta )$ be as before and $\mathbb {L}(\Delta )^{*}$ the dual vector space of $\mathbb {L}(\Delta )$. Then $M(S_{\sigma } \cap \Delta )^{*}$ is naturally identified with a subset of $\mathbb {L}(\Delta )^{*}$ and the polar cone $\check{\Delta }= \bigl \{ u \in \mathbb {L}(\Delta )^{*} \,\bigm |\, \left\langle u, v\right\rangle \ge 0 \ \ for any \ \ v\in \Delta \bigr \}$ of $\Delta$ in $\mathbb {L}(\Delta )^{*}$ is a rational polyhedral convex cone with respect to the lattice $M(S_{\sigma } \cap \Delta )^{*}$ in $\mathbb {L}(\Delta )^{*}$.

Definition 2.9

(i) For a function $f ={ \sum \nolimits _{v\in \Gamma _{+}(f)}} a_v \cdot v \in \mathbb {C}[S_{\sigma }]$ on $X_{\sigma }$ and $u \in \check{\Delta }$, we set $f|_{\Delta } = \sum _{v\in \Gamma _{+}(f) \cap \Delta } a_v \cdot v \in \mathbb {C}[S_{\sigma } \cap \Delta ]$ and

$$\begin{aligned} \Gamma (f|_{\Delta };u) = \bigl \{ v \in \Gamma _{+}(f)\cap \Delta \,\bigm |\, \left\langle u, v\right\rangle = \mathrm{min} \left\langle u,w\right\rangle , \ \ \text {for} \ \ w \in \Gamma _{+}(f) \cap \Delta \bigr \}. \end{aligned}$$

We call $\Gamma (f|_{\Delta };u)$ the supporting face of u in $\Gamma _{+}(f) \cap \Delta$.

(ii) For $j \in I(\Delta ) \cup \left\{ k \right\}$ and $u \in \check{\Delta }$, we define the u-part $f_{j}^{u} \in \mathbb {C}[S_{\sigma } \cap \Delta ]$ of $f_j$ by

$$\begin{aligned} f_{j}^{u} = \displaystyle {\sum _{v\in \Gamma (f_{j}|_{\Delta };u)} a_v \cdot v} \in \mathbb {C}[S_{\sigma } \cap \Delta ], \end{aligned}$$

where $f_j = \displaystyle {\sum _{v\in \Gamma _{+}(f_j)} a_v \cdot v} \in \mathbb {C}[S_{\sigma }]$.

By taking a $\mathbb {Z}$-basis of $M(S_{\sigma })$ and identifying the u-parts $f_{j}^{u}$ with Laurent polynomials $L(f_{j}^{u})$ on $T = (\mathbb {C}^{*})^d$ as before, we have that the following definition does not depend on the choice of the $\mathbb {Z}$-basis of $M(S_{\sigma })$.

Definition 2.10

We say that $(f_1,\ldots ,f_k)$ is non-degenerate if for any face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$ (including the case where $\Delta = \check{\sigma }$) and any $u \in \mathrm{Int}(\check{\Delta }) \cap M(S_{\sigma } \cap \Delta )^{*}$ the following two subvarieties of $(\mathbb {C}^{*})^d$ are non-degenerate complete intersections

$$\begin{aligned}&\bigl \{ x \in (\mathbb {C}^{*})^d \,\bigm |\, L(f_{j}^{u})(x)=0, \ \forall j \in I(\Delta ) \bigr \}; \\&\quad \bigl \{ x \in (\mathbb {C}^{*})^d \,\bigm |\, L(f_{j}^{u})(x)=0, \forall j \in I(\Delta ) \cup \left\{ k\right\} \bigr \}, \end{aligned}$$

i.e., if they are reduced smooth complete intersections varieties in the torus $(\mathbb {C}^{*})^{d}$.

This last definition is presented in [27] and it is a generalization of the one in [34].

For these non-degenerate singularities, it is possible to describe their geometrical and topological properties using the combinatorics of the Newton polygon. This is done in [27] using mixed volume as follows. For each face $\Delta \prec \check{\sigma }$ of $\check{\sigma }$ such that $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$, we set

$$\begin{aligned} f_{\Delta } = \Bigl (\displaystyle {\prod _{j\in I(\Delta )}} f_j\Bigr )\cdot f_k \in \mathbb {C}[S_{\sigma }] \end{aligned}$$

and consider its Newton polygon $\Gamma _{+}(f_{\Delta }) = \left\{ \sum _{j \in I(\Delta )} \Gamma _{+}(f_j) \right\} + \Gamma _{+}(f_k) \subset \check{\sigma }$. Let $\gamma _{1}^{\Delta },\ldots , \gamma _{\nu (\Delta )}^{\Delta }$ be the compact faces of $\Gamma _{+}(f_{\Delta }) \cap \Delta (\ne \emptyset )$ such that $\dim \gamma _{i}^{\Delta } = \dim \Delta -1$. Then for each $1\le i \le \nu (\Delta )$ there exists a unique primitive vector $u_{i}^{\Delta } \in \mathrm{Int}(\check{\Delta }) \cap M(S_{\sigma } \cap \Delta )^{*}$ which takes its minimal value in $\Gamma _{+}(f_{\Delta }) \cap \Delta$ exactly on $\gamma _{i}^{\Delta }$.

For $j \in I(\Delta ) \cup \left\{ k \right\}$, set $\gamma (f_j)_{i}^{\Delta } := \Gamma (f_{j}|_{\Delta };u_{i}^{\Delta })$ and $d_{i}^{\Delta }:= \mathrm{min}_{w\in \Gamma _{+}(f_k) \cap \Delta } \left\langle u_{i}^{\Delta },w\right\rangle$. Note that we have

$$\begin{aligned} \gamma _{i}^{\Delta } = \displaystyle {\sum _{j \in I(\Delta ) \cup \left\{ k \right\} }} \gamma (f_j)_{i}^{\Delta } \end{aligned}$$

for any face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$ and $1 \le i \le \nu (\Delta )$. For each face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$, $\dim \Delta \ge \mathrm{m}(\Delta )$ and $1 \le i \le \nu (\Delta )$, we set $I(\Delta ) \cup \left\{ k\right\} = \left\{ j_1,j_2,\ldots ,j_{\mathrm{m}(\Delta )-1},k=j_{\mathrm{m}(\Delta )} \right\}$ and

$$\begin{aligned} K_{i}^{\Delta } := \sum _{{{ \alpha _1+\ldots +\alpha _{\mathrm{m}(\Delta )} = \dim \Delta -1} \atop {\alpha _q \ge 1 \ \ \text {for} \ \ q\le \mathrm{m}(\Delta )-1}} \atop {\alpha _{\mathrm{m}(\Delta )} \ge 0}}^{} \mathrm{Vol}_{\mathbb {Z}}(\underbrace{\gamma (f_{j_1})_{i}^{\Delta },\ldots , \gamma (f_{j_1})_{i}^{\Delta }}_{\alpha _1-\text {times}},\ldots ,\underbrace{ \gamma (f_{j_{\mathrm{m}(\Delta )}})_{i}^{\Delta },\ldots ,\gamma (f_{j_{\mathrm{m}(\Delta )}})_{i}^{\Delta }}_{\alpha _{\mathrm{m}(\Delta )}-\text {times}}). \end{aligned}$$

Here

$$\begin{aligned} \mathrm{Vol}_{\mathbb {Z}}(\underbrace{\gamma (f_{j_1})_{i}^{\Delta },\ldots , \gamma (f_{j_1})_{i}^{\Delta }}_{\alpha _1-\text {times}},\ldots ,\underbrace{ \gamma (f_{j_{\mathrm{m}(\Delta )}})_{i}^{\Delta },\ldots ,\gamma (f_{j_{\mathrm{m}(\Delta )}})_{i}^{\Delta }}_{\alpha _{\mathrm{m}(\Delta )}-\text {times}}) \end{aligned}$$

is the normalized $(\dim \Delta -1)$-dimensional mixed volume with respect to the lattice $M(S_{\sigma } \cap \Delta ) \cap L(\gamma _{i}^{\Delta })$ (see Definition 2.6, pg 205 from [16]). For $\Delta$ such that $\dim \Delta -1 =0$, we set

$$\begin{aligned} K_{i}^{\Delta } = \mathrm{Vol}_{\mathbb {Z}}(\underbrace{\gamma (f_{k})_{i}^{\Delta },\ldots , \gamma (f_{k})_{i}^{\Delta }}_{0-\text {times}}) := 1 \end{aligned}$$

(in this case $\gamma (f_k)_{i}^{\Delta }$ is a point).

3 The Brasselet number and torus actions

We present formulas for the computation of the Brasselet number of a function defined on a non-degenerate complete intersection contained in a toric variety using Newton polygons. As applications we establish several results concerning its invariance for families of non-degenerate complete intersections.

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(f_1,\ldots ,f_k): (X_{\sigma },0) \rightarrow (\mathbb {C}^k,0)$ a non-degenerate complete intersection, with $1\le k \le d$. From now on we will denote by g the complete intersection $(f_1,\ldots ,f_{k-1})$ and by f the function $f_k$. Let $\mathcal {T}$ be the decomposition of $X_{\sigma } = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta }$ into T-orbits, and $\mathcal {T}_{g}$ the decomposition of $X_{\sigma }^{g} = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta } \cap X_{\sigma }^{g}$. Since g is a non-degenerate complete intersection, $\mathcal {T}_g$ is a decomposition of $X_\sigma ^g$ into smooth subvarieties [27, Lemma 4.1]. We are interested in the situation where $\mathcal {T}_g$ is a Whitney stratification.

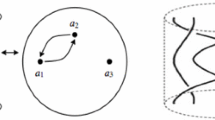
Example 3.1

Let $S_{\sigma } = \mathbb {Z}_{+}^3$ and let $X_{\sigma } = \mathbb {C}^3$ be the smooth 3-dimensional toric variety. Consider $(g,f):(X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ a non-degenerate complete intersection, where

$$\begin{aligned} g(z_1,z_2,z_3) = z_2^2 - z_1^3 -z_1^2z_3^2. \end{aligned}$$

Fig. 1

Real illustration to $X_{\sigma }^{g}$

The decomposition $\mathcal {V} = \{V_{0}=\{0\}, \ \ V_{1}=\{\text {axis} - z_3\} \setminus \{0\}, \ \ V_{2} = (X_{\sigma }^{g})_\mathrm{{reg}}\}$ is a Whitney stratification of the non-degenerate complete intersection $X_{\sigma }^{g}$, where $(X_{\sigma }^{g})_\mathrm{{reg}}$ is the regular part of $X_{\sigma }^{g}$ (see Fig. 1). For a subset $I \subset \{1,2,3\}$ we denote the face $\sum _{i \in I} {\mathbb {R}_{+}}{e_{i}}^{*}$ of $\check{\sigma } = (\mathbb {R}_{+}^{3})^{*}$ by $\Delta _{I}$ and by $\Delta _0$ the face $\{0\}$, where ${e_i}^*$ denotes the elements of the canonical basis of $(\mathbb {R}^{3})^{*}$. The Whitney stratification $\mathcal {T}$ of $X_{\sigma }$ is given by the following T-orbits: $T_{\Delta _{0}} = \{0\}$, $T_{\Delta _{1}} = \mathbb {C}^{*} \times \{0\} \times \{0\}$, $T_{\Delta _{2}} = \{0\} \times \mathbb {C}^{*} \times \{0\}$, $T_{\Delta _{3}} = \{0\} \times \{0\} \times \mathbb {C}^{*}$, $T_{\Delta _{12}} = \mathbb {C}^{*} \times \mathbb {C}^{*} \times \{0\}$, $T_{\Delta _{13}} = \mathbb {C}^{*} \times \{0\} \times \mathbb {C}^{*}$, $T_{\Delta _{23}} = \{0\} \times \mathbb {C}^{*} \times \mathbb {C}^{*}$, $T_{\Delta _{123}} = \mathbb {C}^{*} \times \mathbb {C}^{*} \times \mathbb {C}^{*}$. Now, observe that $T_{\Delta _{3}} \cap X_{\sigma }^{g} = T_{\Delta _{3}} = V_{1}$, then the stratification

$$\begin{aligned} \mathcal {T}_g = \left\{ T_{\Delta _{I}} \cap X_{\sigma }^{g}, \ \ \Delta _{0} \right\} _{\Delta _{I} \prec \check{\sigma }} \end{aligned}$$

is a Whitney stratification of $X_{\sigma }^{g}$.

In Sect. 5 we will provide others examples where the stratification $\mathcal {T}_{g}$ is Whitney (see [33, Section 9] for more examples). We observe that in general $\mathcal {T}_g$ is not a Whitney stratification (see [33, Example 9.5]).

Theorem 3.2

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^k,0)$ a non-degenerate complete intersection. If $\mathcal {T}_g$ is a Whitney stratification, then

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }^{g}}(0) = \sum _{{\Gamma _{+} (f) \cap \Delta \ne \emptyset } \atop {\dim \Delta \ \ge \ m(\Delta )}} (-1)^{\dim \Delta \ - \ m(\Delta )} \left( \sum _{i=1}^{\nu (\Delta )} d_{i}^{\Delta } \cdot K_{i}^{\Delta } \right) \cdot \mathrm {Eu_{X_{\sigma }^{g}}}(T_{\Delta } \cap X_{\sigma }^g). \end{aligned}$$

Proof

Let $(X_\sigma ^g)^f := X^g_\sigma \cap X^f_\sigma$ be the zero set of f in $X^g_\sigma$. By [17, Section 1.7], there exists a refinement of $\mathcal {T}_g$, denoted by $\mathcal {T}_{(g,f)} = \{W_i\}$, such that $\mathcal {T}_{(g,f)}$ is adapted to $(X_\sigma ^g)^f$ and it is a Whitney stratification. Moreover, this stratification satisfies the $(a_f)$-Thom condition (see [3, 36]), and then it is a good stratification of $X^g_\sigma$ related to f. By definition, the Brasselet number reads

$$\begin{aligned} \mathrm{B}_{f,X_\sigma ^g}(0) = \sum _{i}\chi \big (W_i\cap B_{\varepsilon }(0) \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X_\sigma ^g}(W_i), \end{aligned}$$

where $0< \left| \delta \right| \ll \varepsilon \ll 1$.

As $\mathcal {T}_{(g,f)}$ is a refinement of $\mathcal {T}_g$, each $T_\Delta \cap X^g_\sigma$ is a disjoint union of $W_i$, i.e.,

$$\begin{aligned} T_\Delta \cap X^g_\sigma = \bigsqcup _{W_i \cap T_\Delta \cap X^g_\sigma \not = \emptyset } W_{i}, \end{aligned}$$

and since $\mathcal {T}_g$ is a Whitney stratification,

$$\begin{aligned} \mathrm{Eu}_{X_\sigma ^g}(T_\Delta \cap X^g_\sigma ) = \mathrm{Eu}_{X_\sigma ^g}(W_i), \end{aligned}$$

for any $W_i$ that meets $T_\Delta \cap X^g_\sigma$. Then

$$\begin{aligned} \mathrm{B}_{f,X_\sigma ^g}(0) = \sum _{\Delta }\chi \big (T_\Delta \cap X^g_\sigma \cap B_{\varepsilon } \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X_\sigma ^g}(T_\Delta \cap X^g_\sigma ). \end{aligned}$$

(3.1)

Note that $f:X_{\sigma } \rightarrow \mathbb {C}$ has an isolated stratified critical value at $0 \in \mathbb {C}$ by [24, Proposition 1.3]. Thus the integers $\chi (T_\Delta \cap X^g_\sigma \cap B_{\varepsilon } \cap f^{-1}(\delta ) \big )$ can be calculated by the nearby cycle functor ${\psi }_{f}$ [26, Eq. (4.2)], i.e.,

$$\begin{aligned} \chi \big ( T_\Delta \cap X^g_\sigma \cap B_{\varepsilon } \cap f^{-1}(\delta ) \big ) = \chi (\psi _{f}(\mathbb {C}_{T_{\Delta } \cap X_{\sigma }^{g}})_{0}), \end{aligned}$$

(3.2)

since $X_{\sigma }^{g}\cap B_\varepsilon \cap f^{-1}(\delta ) = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta } \cap B_\varepsilon \cap X_{\sigma }^{g} \cap f^{-1}(\delta )$ is a Whitney stratification of the Milnor fiber $X_{\sigma }^{g}\cap B_\varepsilon \cap f^{-1}(\delta )$. By the proof of Theorem 3.12 in [27] and by equations (52), (77), (78), we have that

$$\begin{aligned} \chi (\psi _{f}(\mathbb {C}_{T_{\Delta } \cap X_{\sigma }^{g}})_{0}) = (-1)^{\dim \Delta \ - \ m(\Delta )} \left( \sum _{i=1}^{\nu (\Delta )} d_{i}^{\Delta } \cdot K_{i}^{\Delta } \right) . \end{aligned}$$

(3.3)

To complete the proof, we observe that $f\equiv 0$ on $T_{\Delta }$ for any face $\Delta$ such that $\Gamma _{+}(f) \cap \Delta = \emptyset$, then we can neglect those faces. $\square$

If $f: X_{\sigma }^{g} \rightarrow \mathbb {C}$ has a stratified isolated critical point, then Eq. (2.1) holds. Altogether, we have:

Corollary 3.3

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^k,0)$ a non-degenerate complete intersection. If $\mathcal {T}_g$ is a Whitney stratification and $f: X_{\sigma }^{g} \rightarrow \mathbb {C}$ has an isolated singularity at the origin, then the difference $\mathrm{Eu}_{X_{\sigma }^{g}}(0) - \mathrm{Eu}_{f,X_{\sigma }^{g}}(0)$ is equal to

$$\begin{aligned} \sum _{{\Gamma _{+} (f) \cap \Delta \ne \emptyset } \atop {\dim \Delta \ \ge \ m(\Delta )}} (-1)^{\dim \Delta \ - \ m(\Delta )} \left( \sum _{i=1}^{\nu (\Delta )} d_{i}^{\Delta } \cdot K_{i}^{\Delta } \right) \cdot \mathrm {Eu_{X_{\sigma }^{g}}}(T_{\Delta } \cap X_{\sigma }^g). \end{aligned}$$

When $k=1$, using an argument similar to the one used in Theorem 3.2, we obtain $\mathrm{B}_{f,X_{\sigma }}(0)$. In fact, using again [3, 17, 36] we can pass to a refinement of $\mathcal {T}$ to obtain a good stratification of $X_\sigma$ relative to f. Thus we can use the same argument as in the proof of Theorem 3.2 to obtain

$$\begin{aligned} \mathrm{B}_{f,X_\sigma }(0) = \sum _{\Delta }\chi \big (T_\Delta \cap B_{\varepsilon }(0) \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X_\sigma }(T_\Delta ). \end{aligned}$$

Now for each face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f) \cap \Delta \ne \emptyset$, let $\beta _{1}^{\Delta }$, $\beta _{2}^{\Delta }$, $\ldots ,\beta _{\mu (\Delta )}^{\Delta }$ be the compact faces of $\Gamma _{+}(f) \cap \Delta$ such that $\mathrm {dim}\beta _{i}^{\Delta } = \dim \Delta -1$. Let $\Gamma _{i}^{\Delta }$ be the convex hull of $\beta _{i}^{\Delta } \sqcup \left\{ 0\right\}$ in $\mathbb {L}(\Delta )$ and consider the normalized $(\dim \Delta )$-dimensional volume of $\Gamma _{i}^{\Delta }$, $\mathrm {Vol}_{\mathbb {Z}}(\Gamma _{i}^{\Delta }) \in \mathbb {Z}$, with respect to the lattice $M(S_{\sigma } \cap \Delta )$. Here $M(S_{\sigma } \cap \Delta )$ denotes the sublattice of $M(S_{\sigma })$ generated by $S_{\sigma } \cap \Delta$. Then we have the following result.

Proposition 3.4

Assume that $f = \sum _{v\in S_{\sigma }} a_v \cdot v \in \mathbb {C}[S_{\sigma }]$ is non-degenerate. Then

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }}(0)= \sum _{\Gamma _{+} (f) \cap \Delta \ne \emptyset }(-1)^{\dim \Delta - 1} \big ( \sum _{i=1}^{\mu (\Delta )}\mathrm{{Vol_{\mathbb {Z}}}}(\Gamma _{i}^{\Delta }) \big )\cdot \mathrm {Eu_{X_{\sigma }}}(T_{\Delta }). \end{aligned}$$

Proof

For each $(\dim \Delta -1)$-compact face $\beta _{i}^{\Delta }$ of $\Gamma _{+}(f) \cap \Delta \ne \emptyset$, with $1\le i \le \mu (\Delta )$ we have

$$\begin{aligned} K_{i}^{\Delta } := \mathrm{Vol}_{\mathbb {Z}}(\underbrace{\beta _{i}^{\Delta },\ldots ,\beta _{i}^{\Delta }}_{{(\mathrm{dim}\Delta -1})-\text {times}}), \end{aligned}$$

and from [16, Proposition 2.7] we now that

$$\begin{aligned} \mathrm{Vol}_{\mathbb {Z}}(\underbrace{\beta _{i}^{\Delta },\ldots , \beta _{i}^{\Delta }}_{{(\dim \Delta \ -\ 1})-\text {times}}) = \mathrm{Vol}_{\mathbb {Z}}(\beta _{i}^{\Delta }). \end{aligned}$$

Therefore, the result follows from the fact that

$$\begin{aligned} \mathrm{{Vol_{\mathbb {Z}}}}(\Gamma _{i}^{\Delta }) = d_{i}^{\Delta }\cdot K_{i}^{\Delta }, \end{aligned}$$

(3.4)

for $1\le i \le \mu (\Delta )$. $\square$

We will apply Theorem 3.2 in order to show that the Brasselet number is invariant for some families of complete intersections. We need some new concepts and notations.

Definition 3.5

A deformation of a map germ $f : (X, 0) \rightarrow (\mathbb {C}^{k}, 0)$ is another map germ $F : (\mathbb {C}\times X) \rightarrow (\mathbb {C}^{k}, 0)$ such that $F(0, x) = f(x)$, for all $x \in X$.

We assume that F is origin preserving, that is, $F(t, 0) = 0$ for all $t \in \mathbb {C}$, so we have a 1-parameter family of map germs $f_t : (X, 0) \rightarrow (\mathbb {C}^{k}, 0)$ given by $f_t(x) = F(t, x)$. Moreover, associated to the family $f_t : (X, 0) \rightarrow (\mathbb {C}^{k}, 0)$ we have the family $X^{f_t} = X \cap f_{t}^{-1}(0)$ of subvarieties of X. In the particular case of a polynomial function $f : (X, 0) \rightarrow (\mathbb {C}, 0)$, any polynomial deformation $f_t$ can be written as:

$$\begin{aligned} f_t(x) = f(x)+ \sum _{i=1}^{r} \theta _{i}(t) \cdot h_{i}(x) \end{aligned}$$

(3.5)

for some polynomials $h_{i}: (X,0) \rightarrow (\mathbb {C},0)$ and $\theta _{i}:(\mathbb {C},0) \rightarrow (\mathbb {C},0)$, where $\theta _{i}(0)=0$, for all $i=1,\ldots ,r$.

Suppose that $f: X_{\sigma } \rightarrow \mathbb {C}$ is a polynomial function defined on a toric variety $X_{\sigma }$. Consider a family as in Eq. (3.5) with $\Gamma _{+}(h_i) \subset \Gamma _{+}(f)$, for all $i=1,\ldots ,r$. Let $\gamma _{i_1}^{\Delta },\gamma _{i_2}^{\Delta },\ldots , \gamma _{i_{\nu (\Delta )}}^{\Delta }$ and $\beta _{1}^{\Delta },\beta _{2}^{\Delta },\ldots ,\beta _{\mu (\Delta )}^{\Delta }$ be the compact faces of $\Gamma _{+}(h_i) \cap \Delta$ and of $\Gamma _{+}(f) \cap \Delta$, respectively, such that $\dim \gamma _{l}^{\Delta }=\dim \beta _{j}^{\Delta } = \dim \Delta -1$. If for each face $\Delta \prec \check{\sigma }$, with $\Gamma _{+}(h_i) \cap \Delta \ne \emptyset$, we have that $\gamma _{i_l}^{\Delta } \cap \beta _{j}^{\Delta } = \emptyset$, for all $l=1,\ldots ,i_{\nu (\Delta )}$ and $j=1,\ldots ,\mu (\Delta )$, then

$$\begin{aligned} \Gamma _+(f_t) = \Gamma _+(f), \ \ \text {for all} \ \ t\in \mathbb {C}. \end{aligned}$$

In this case, we fix the notation

$$\begin{aligned} \Gamma _{+}(h_i) \subsetneqq \Gamma _{+}(f), \end{aligned}$$

(3.6)

for all $i=1,\ldots ,r$.

In the sequel, we present some applications of Theorem 3.2.

Corollary 3.6

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety. Suppose that $(g,f_t): (X_{\sigma },0) \rightarrow (\mathbb {C}^k,0)$ is a non-degenerate complete intersection for each $t\in \mathbb {C}$ with

$$\begin{aligned} f_t(x) = f(x)+\sum _{i=1}^{r} \theta _{i}(t) \cdot h_{i}(x) \end{aligned}$$

being a polynomial function on $X_{\sigma }$ with $h_i$ satisfying the condition (3.6) for all $i=1,\ldots ,r$. If $\mathcal {T}_g$ is a Whitney stratification and $(g,f_t)$ is a family of non-degenerate complete intersections, then $\mathrm{B}_{f_t,X_{\sigma }^g}(0)$ is constant for the family.

Proof

As we have already noted, for each face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f) \cap \Delta \ne \emptyset$, the Newton polygon $\Gamma _{+}(f_{\Delta })$ of the function

$$\begin{aligned} f_{\Delta } = \Bigl ({\prod _{j\in I(\Delta )}} f_j\Bigr )\cdot f \in \mathbb {C}[S_{\sigma }] \end{aligned}$$

is $\left\{ \sum _{j \in I(\Delta )} \Gamma _{+}(f_j) \right\} + \Gamma _{+}(f) \subset \check{\sigma }$. Therefore, $\Gamma _{+}(f_\Delta ) = \Gamma _{+}(({f_t})_\Delta )$, for all $t \in \mathbb {C}$, where

$$\begin{aligned} (f_{t})_{\Delta } = \Bigl (\displaystyle {\prod _{j\in I(\Delta )}} f_j\Bigr )\cdot f_t, \end{aligned}$$

since $\Gamma _{+}(f) = \Gamma _{+}(f_t)$. Then the result follows by Theorem 3.2. $\square$

Roughly speaking the Brasselet number depends only on the monomials of smallest degree in each variable.

Given $f: (X_{\sigma },0) \rightarrow (\mathbb {C},0)$ a non-degenerate function, as before, we denote by $\mathcal {T}_{f}$ the decomposition

$$\begin{aligned} X_{\sigma }^{f}= \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta } \cap X_{\sigma }^{f} \end{aligned}$$

of $X_{\sigma }^{f}$, and by $\mathcal {T}^{f}$ the decomposition $\left\{ T_{\Delta } \cap X_{\sigma }^{f}, \ \ T_{\Delta } \setminus X_{\sigma }^{f}, \ \ \left\{ 0\right\} \right\} _{\Delta \prec \check{\sigma }}$ of $X_{\sigma }$. If $\mathcal {T}_{f}$ is a Whitney stratification of $X_{\sigma }^{f}$, then $\mathcal {T}^{f}$ is a Whitney stratification of $X_{\sigma }$ which is adapted to $X_{\sigma }^{f}$. In fact, this follows from the fact that $\mathcal {T}$ is a Whitney stratification of $X_{\sigma }$. Consequently, $\mathcal {T}^f$ is a good stratification of $X_{\sigma }$ relative to f.

Let g and f be non-degenerate polynomial functions on $X_{\sigma }$. In general we have no way to relate the local Euler obstructions $\mathrm{Eu}_{X_{\sigma }^{g}}(T_{\Delta } \cap X_{\sigma }^{g})$ to $\mathrm{Eu}_{X_{\sigma }}(T_{\Delta })$. However, if we assume the additional hypothesis that g has an isolated critical point at 0 both in $X_{\sigma }$ and in $X_{\sigma }^f$ (in stratified sense), the following result holds.

Theorem 3.7

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ a non-degenerate complete intersection. Suppose that $\mathcal {T}^{f}$ is a good stratification of $X_{\sigma }$ relative to f and that g is prepolar with respect to $\mathcal {T}^{f}$, then

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }^{g}}(0) = \sum _{{\Gamma _{+} (f) \cap \Delta \ne \emptyset } \atop {\dim \Delta \ \ge \ 2}} (-1)^{\dim \Delta \ - \ {2}} \left( \sum _{i=1}^{\nu (\Delta )} d_{i}^{\Delta } \cdot K_{i}^{\Delta } \right) \cdot \mathrm {Eu_{X_{\sigma }}}(T_{\Delta }). \end{aligned}$$

Proof

Consider $\mathcal {T}_{g} = \left\{ T_{\Delta } \cap X_{\sigma }^{g} \right\} _{\Delta \prec \check{\sigma }}$ the stratification of $X_{\sigma }^{g}$. Using the same argument as in the proof of Theorem 3.2 we can pass to a refinement $\mathcal {T}_{(g,f)}$ and we obtain a good stratification of $X_{\sigma }^{g}$ relative to f. Then

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }^{g}}(0) = \sum _{\Gamma _{+}(f)\cap \Delta \ne \emptyset }\chi \big (W_{\Delta }\cap B_{\varepsilon } \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X_{\sigma }^{g}}(W_{\Delta }), \end{aligned}$$

where $W_{\Delta }$ are the strata of $\mathcal {T}_{(g,f)}$ which are not contained in $\left\{ f = 0 \right\}$, and $0 < \left| \delta \right| \ll \varepsilon \ll 1$. Moreover, for $\Delta \prec \check{\sigma }$, we have $\mathrm{Eu}_{X_{\sigma }}(T_{\Delta }) = \mathrm{Eu}_{X_{\sigma }^{g}}(W_{\Delta })$, since $X_{\sigma }^g$ intersects the strata of $\mathcal {T}^f$ transversally (see [11, Proposition IV. 4.1.1]). Hence,

$$\begin{aligned} \begin{aligned}&\mathrm{B}_{f,X_{\sigma }^{g}}(0)= & {} \displaystyle { \sum _{\Gamma _{+}(f)\cap \Delta \ne \emptyset } }\chi \big (X_{\sigma }^{g} \cap T_{\Delta } \cap B_{\varepsilon } \cap f^{-1}(\delta ) \big ) \cdot \mathrm{Eu}_{X_{\sigma }}(T_{\Delta }).&\end{aligned} \end{aligned}$$

Finally, as $\Gamma _{+}(g) \cap \Delta \ne \emptyset$ for any face $0\precneqq \Delta \prec \check{\sigma }$, then $m(\Delta ) = 2$, for all face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f) \cap \Delta \ne \emptyset$. Since g is prepolar,

$$\begin{aligned} X_{\sigma }^{g}\cap B_\varepsilon \cap f^{-1}(\delta ) = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta } \cap B_\varepsilon \cap X_{\sigma }^{g} \cap f^{-1}(\delta ) \end{aligned}$$

is a Whitney stratification of the Milnor fiber $X_{\sigma }^{g}\cap B_\varepsilon \cap f^{-1}(\delta )$. Therefore, we obtain the result by Eqs. (3.2) and (3.3). $\square$

Therefore, if $\mathcal {T}^f$ is a good stratification of $X_{\sigma }$ relative to f and g is prepolar with respect to $\mathcal {T}^f$, we can obtain a more general version of Corollary 3.6, since we can relate the local Euler obstructions $\mathrm{Eu}_{X_{\sigma }^{g}}(T_{\Delta } \cap X_{\sigma }^{g})$ to the Euler local obstructions $\mathrm{Eu}_{X_{\sigma }}(T_{\Delta })$.

Corollary 3.8

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ a non-degenerate complete intersection. Suppose that

$$\begin{aligned} \Bigl (g_s(x),f_t(x) \Bigr )= \Bigl (g(x) + \sum _{i=1}^{m}\xi _{i}(s)\cdot l_i(x), f(x)+\sum _{j=1}^{r} \theta _{j}(t)\cdot h_j(x) \Bigr )\end{aligned}$$

is a family of non-degenerate complete intersections with $l_i$ and $h_j$ satisfying the condition (3.6) for all $i=1,\ldots ,m$ and $j=1,\ldots ,r$. If $\mathcal {T}^{f_t}$ is a good stratification of $X_{\sigma }$ relative to $f_t$ and $g_s$ is prepolar with respect to $\mathcal {T}^{f_t}$ at the origin, for all $s,t \in \mathbb {C}$, then, $\mathrm{B}_{f_t,X_{\sigma }^{g_s}}(0)$ is constant for all $t,s \in \mathbb {C}$.

Proof

Since $\Gamma _{+}(l_i) \subset \Gamma _{+}(g) \ \ \text {and} \ \ \Gamma _{+}(h_j) \subset \Gamma _{+}(f)$, for each face $\Delta \prec \check{\sigma }$ such that $\Gamma _{+}(f) \cap \Delta \ne \emptyset$, the Newton polygon $\Gamma _{+}(f_{\Delta })$ of the function

$$\begin{aligned} f_{\Delta } = \Bigl (\displaystyle {\prod _{\Gamma _{+}(f) \cap \Delta \ne \emptyset }} g \Bigr )\cdot f \in \mathbb {C}[S_{\sigma }] \end{aligned}$$

is equal to $\Gamma _{+}(({f_{t})}^{s}_{\Delta } )$, where

$$\begin{aligned} {(f_{t})}^{s}_{\Delta } = \Bigl (\displaystyle {\prod _{\Gamma _{+}(f_t) \cap \Delta \ne \emptyset }} g_s \Bigr )\cdot f_t \in \mathbb {C}[S_{\sigma }]. \end{aligned}$$

Then by Eqs. (3.2) and (3.3), we can conclude that the Euler characteristic

$$\begin{aligned} \chi \Bigl (X_{\sigma }^{g_s} \cap T_{\Delta } \cap B_{\varepsilon } \cap f_{t}^{-1}(\delta ) \Bigr )\end{aligned}$$

is constant for all $s,t \in \mathbb {C}$. Moreover, as $g_s$ is prepolar with respect to $\mathcal {T}^{f_t}$, then we can proceed exactly in the same way as in Theorem 3.7 to obtain

$$\begin{aligned} \mathrm{Eu}_{X_{\sigma }}(T_{\Delta }) = \mathrm{Eu}_{X_{\sigma }^{g_s}}(T_{\Delta } \cap X_{\sigma }^{g_s}), \end{aligned}$$

and this concludes the proof. $\square$

As a consequence of Proposition 3.4 and Theorem 3.7, we have that if $\mathcal {T}^f$ is a good stratification of $X_{\sigma }$ relative to f and if $g: X_{\sigma } \rightarrow \mathbb {C}$ is prepolar with respect to $\mathcal {T}^f$, we can express the number of stratified Morse critical points on the stratum of maximal dimension appearing in a morsefication of $g : X_{\sigma } \cap f^{-1}(\delta ) \cap B_{\varepsilon } \rightarrow \mathbb {C}$ in terms of volumes of convex polytopes. More precisely, by Theorem 2.5, we have

$$\begin{aligned} \begin{array}{lllll} (-1)^{d-1}n_d &{} = \displaystyle { \sum _{{\Gamma _{+} (f) \cap \Delta \ne \emptyset }}}(-1)^{\dim \Delta - 1} \big ( \sum _{i=1}^{\mu (\Delta )}\mathrm{{Vol_{\mathbb {Z}}}}(\Gamma _{i}^{\Delta }) \big )\cdot \mathrm {Eu_{X_{\sigma }}}(T_{\Delta }) &{} \\ &{}\quad -\,\displaystyle \sum _{{\Gamma _{+} (f) \cap \Delta \ne \emptyset } \atop {\dim \Delta \ge 2}} (-1)^{\dim \Delta - {2}} \big ( \sum _{i=1}^{\nu (\Delta )} d_{i}^{\Delta } \cdot K_{i}^{\Delta } \big )\cdot \mathrm {Eu_{X_{\sigma }}}(T_{\Delta }) &{} \\ \end{array} \end{aligned}$$

where $n_d$ is the number of stratified Morse critical points on the top stratum $T_{\Delta _d} \cap f^{-1}(\delta )\cap B_{\varepsilon }$ appearing in a morsefication of $g : X_{\sigma } \cap f^{-1}(\delta ) \cap B_{\varepsilon } \rightarrow \mathbb {C}$. Therefore, if $f_t(x)= f(x)+\sum _{j=1}^{r} \theta _j(t) \cdot h_j(x)$ is a family of non-degenerate polynomial functions on $X_{\sigma }$ and if $(g_s,f_t): (X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ is a family of non-degenerate complete intersections which satisfy the same hypotheses as Corollary 3.8, then

$$\begin{aligned} (-1)^{d-1}n_d = \mathrm{B}_{f_t,X_{\sigma }}(0) - \mathrm{B}_{f_t,{X_{\sigma }^{g_s}}}(0) \end{aligned}$$

is constant for all $s,t \in \mathbb {C}$. More precisely, we can state the following result.

Corollary 3.9

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and $(g,f):(X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ a non-degenerate complete intersection. Suppose that

$$\begin{aligned} \Bigl (g_s(x),f_t(x) \Bigr )= \Bigl (g(x) + \sum _{i=1}^{m}\xi _{i}(s)\cdot l_i(x), f(x)+\sum _{j=1}^{r} \theta _{j}(t)\cdot h_j(x) \Bigr )\end{aligned}$$

is a family of non-degenerate complete intersections with $l_i$ and $h_j$ satisfying the condition (3.6) for all $i=1,\ldots ,m$ and $j=1,\ldots ,r$. If $\mathcal {T}^{f_t}$ is a good stratification of $X_{\sigma }$ relative to $f_t$ and $g_s$ is prepolar with respect to $\mathcal {T}^{f_t}$ at the origin, for all $s,t \in \mathbb {C}$, then $(-1)^{d-1}n_d$ is constant for all $s, t \in \mathbb {C}$.

We will present some applications of the results presented before in the next section and some examples in Sect. 5.

4 The local Euler obstruction and Bruce–Roberts’ Milnor number

In this section, we derive sufficient conditions to obtain the invariance of the local Euler obstruction for families of complete intersections which are contained in $X_{\sigma } \subset \mathbb {C}^n$. As an application, we study the invariance of the Bruce–Roberts’ Milnor number for families of functions defined on hypersurfaces.

4.1 Local Euler obstruction of non-degenerate complete intersections

As observed in [5, Remark 2.5] the local Euler obstruction is not a topological invariant. However, for non-degenerate complete intersections we have the following result.

Theorem 4.1

Let $X_{\sigma } \subset \mathbb {C}^n$ be a d-dimensional toric variety and k a positive integer in $\{2,\ldots ,d\}$. Consider $g=(f_1,\ldots ,f_{k-1}): (X_{\sigma },0) \rightarrow (\mathbb {C}^{k-1},0)$ a non-degenerate complete intersection, such that $\mathcal {T}_g$ is a Whitney stratification. Suppose that

$$\begin{aligned} g_s(x) = \Bigl (f_1(x) + \sum _{{i_1}=1}^{m_1} \theta _{i_1}(s) \cdot h_{i_1}(x),\ldots ,f_{k-1}(x) + \sum _{{i_{k-1}}=1}^{m_{k-1}} \theta _{i_{k-1}}(s) \cdot h_{i_{k-1}}(x) \Bigr )\end{aligned}$$

is a family of non-degenerate complete intersections, such that $\mathcal {T}_{g_s}$ is a Whitney stratification and $h_{i_p}$ satisfies the condition (3.6) for all $p \in \left\{ 1,\ldots ,k-1 \right\}$ and $i_p \in \left\{ 1, \ldots , m_p\right\}$. If there exists $L: \mathbb {C}^n \rightarrow \mathbb {C}$ a linear form which is generic with respect to $X_{\sigma }^{g_s}$ for all $s \in \mathbb {C}$ and such that $(g_s,L)$ is a non-degenerate complete intersection, then $\mathrm{Eu}_{X_{\sigma }^{g_s}}(0)$ is invariant for the family $\{g_s\}_{s\in \mathbb {C}}$.

Proof

As $L: \mathbb {C}^n \rightarrow \mathbb {C}$ is a linear form which is generic with respect to $X_{\sigma }^{g_s}$, for all $s \in \mathbb {C}$,

$$\begin{aligned} \mathrm{Eu}_{X_{\sigma }^{g_s}}(0) = \mathrm{B}_{L,X_{\sigma }^{g_{s}}}(0). \end{aligned}$$

Moreover, $T_\Delta \cap X^{g_{s}}_\sigma \cap B_{\varepsilon } \cap L^{-1}(\delta )$ induces a Whitney stratification on the Milnor fiber $X^{g_{s}}_\sigma \cap B_{\varepsilon } \cap L^{-1}(\delta )$. Therefore, the result follows from Theorem 3.2, and from the fact that for all face $\Delta \ne \left\{ 0\right\}$ of $\check{\sigma }$, the Newton polygon $\Gamma _{+}(L_{\Delta })$ of the function

$$\begin{aligned} L_{\Delta } = \Bigl (\displaystyle {\prod _{j\in I(\Delta )}} f_j \Bigr )\cdot L \in \mathbb {C}[S_{\sigma }] \end{aligned}$$

is equal to $\Gamma _{+}({L_{\Delta }^{s}})$. Here,

$$\begin{aligned} {L_{\Delta }^{s}} = \Bigl (\displaystyle {\prod _{p\in I(\Delta )}} f_p + \sum _{{i_p}=1}^{m_p} \theta _{i_p} \cdot h_{i_p} \Bigr )\cdot L \in \mathbb {C}[S_{\sigma }]. \end{aligned}$$

$\square$

Corollary 4.2

Let $S_{\sigma } = \mathbb {Z}_{+}^n$ and let $X_{\sigma } = \mathbb {C}^n$ be the smooth n-dimensional toric variety. Consider $g=(f_1,\ldots ,f_{k-1}): \mathbb {C}^n \rightarrow \mathbb {C}^{k-1}$ a non-degenerate complete intersection with an isolated singularity at 0, where $2\le k \le n$. Suppose that

$$\begin{aligned} g_s(x) = \Bigl (f_1(x) + \sum _{{i_1}=1}^{m_1} \theta _{i_1}(s) \cdot h_{i_1}(x),\ldots ,f_{k-1}(x) + \sum _{{i_{k-1}}=1}^{m_{k-1}} \theta _{i_{k-1}}(s) \cdot h_{i_{k-1}}(x) \Bigr )\end{aligned}$$

is a family of non-degenerate complete intersections with an isolated singularity at 0, where $h_{i_p}$ satisfies the condition (3.6) for all $p \in \left\{ 1,\ldots ,k-1 \right\}$ and $i_p \in \left\{ 1, \ldots , m_p\right\}$. If there exists $L: \mathbb {C}^n \rightarrow \mathbb {C}$ a linear form which is generic with respect to $X_{\sigma }^{g_s}$, for all $s \in \mathbb {C}$ and such that $(g_s,L)$ is a non-degenerate complete intersection, then $\mathrm{Eu}_{X_{\sigma }^{g_s}}(0)$ is invariant for the family $\{g_s\}_{s\in \mathbb {C}}$.

Proof

As $g_s$ is a family of complete intersections with an isolated singularity at 0, the decomposition $\mathcal {T}_{g_{s}}$ of $X_{\sigma }^{g_{s}} = \bigsqcup _{\Delta \prec \check{\sigma }} T_{\Delta } \cap X_{\sigma }^{g_{s}}$ is a Whitney stratification, once $\mathcal {T}$ is a Whitney stratification of $X_{\sigma }$. Therefore, the result follows from Theorem 4.1. $\square$

With the same assumptions as in Theorem 4.1, suppose that $f_t(x) = f_k(x)+\sum _{{i_k}=1}^{m_k} \theta _{i_k}(t)\cdot h_{i_k}(x)$ is a family of polynomial functions such that $(g_s,f_t)$ is a family of non-degenerate complete intersections where $h_{i_k}$ satisfies the condition (3.6), i.e.,

$$\begin{aligned} \Gamma _{+}(h_{i_k}) \subsetneqq \Gamma _{+}(f_k), \ \ \text {for all} \ \ i_k=1,\ldots ,m_k. \end{aligned}$$

Moreover, assume that $f_t: X_{\sigma }^{g_s} \rightarrow \mathbb {C}$ has a stratified isolated critical point at 0. For each face $\Delta \prec \check{\sigma }$ satisfying $\Gamma _{+}(f_k) \cap \Delta \ne \emptyset$, the Newton polygon $\Gamma _{+}(f_{\Delta })$ of the function

$$\begin{aligned} f_{\Delta } = \big (\displaystyle {\prod _{j\in I(\Delta )}} f_j \big )\cdot f_k \in \mathbb {C}[S_{\sigma }] \end{aligned}$$

is equals to $\Gamma _{+}((f_{t})^{s}_{\Delta } )$, where

$$\begin{aligned} (f_{t})^{s}_{\Delta } = \Bigl (\displaystyle {\prod _{p\in I(\Delta )}} f_p + \sum _{{i_p}=1}^{m_p} \theta _{i_p} \cdot h_{i_p} \Bigr )\cdot \Bigl (f_t = f_k+\sum _{i_{k}=1}^{m_k} \theta _{i_k}\cdot h_{i_k} \Bigr )\in \mathbb {C}[S_{\sigma }]. \end{aligned}$$

By Theorem 3.2 we conclude that the Euler characteristic of the Milnor fiber of $f_t: X_{\sigma }^{g_s} \rightarrow \mathbb {C}$ is invariant for all $s,t\in \mathbb {C}$. Therefore, $\mathrm{Eu}_{f_t, X_{\sigma }^{g_s}}(0)$ is invariant for the family.

4.2 Bruce–Roberts’ Milnor number

In [6], Bruce and Roberts introduced a Milnor number for functions germs on singular varieties.

Let X be a sufficiently small representative of the germ (X, 0) and let I(X) denote the ideal in $\mathcal {O}_{n,0}$ consisting of the germs of functions vanishing on X. We say that two germs f and g in $\mathcal {O}_{n,0}$ are $\mathcal {R}_X$- equivalent if there exists a germ of diffeomorphism $\phi : (\mathbb {C}^n,0)\rightarrow (\mathbb {C}^n,0)$ such that $\phi (X)=X$ and $f\circ \phi =g$. Let $\theta _n$ denote the $\mathcal {O}_{n,0}$- module of germs of vector fields on $(\mathbb {C}^n,0).$ Each vector field $\xi \in \theta _n$ can be seen as a derivation $\xi :\mathcal {O}_{n,0}\rightarrow \mathcal {O}_{n,0}$. We denote by $\theta _X$ those vector fields that are tangent to X, i.e.,

$$\begin{aligned} \theta _X:=\bigl \{ \xi \in \theta _n \,\bigm |\, dg(\xi )=\xi g\in I(X), \forall g\in I(X)\bigr \}. \end{aligned}$$

Definition 4.3

Let f be a function in $\mathcal {O}_{n,0}$ and let $df(\theta _X)$ be the ideal $\{\xi f: \xi \in \theta _X\}$ in $\mathcal {O}_{n,0}$. The number

$$\begin{aligned} \mu _{BR}(X,f)=\dim _{\mathbb {C}}\frac{\mathcal {O}_{n,0}}{df(\theta _X)} \end{aligned}$$

is called the Bruce–Roberts number of f with respect to X.

We refer to [6] for more details about $\mu _{BR}(X,f)$. In particular, $\mu _{BR}(X,f)$ is finite if and only if f is $\mathcal {R}_X$-finitely determined.

An interesting open problem is to know whether the Bruce–Roberts number is a topological invariant or not. In [18, 19, Corollary 5.19] Grulha gave a partial answer. The author proved that, if (X, 0) is a hypersurface whose logarithmic characteristic variety $\mathrm{LC}(X)$ [6, Definition 1.13], is Cohen-Macaulay and if $f_t$ is a $C^0$- $R_X$-trivial deformation of f, then $\mu _{BR}(f_t,X)$ is constant.

For any hypersurface X the problem of $\mathrm{LC}(X)$ being Cohen-Macaulay remains open. When X is a weighted homogeneous hypersurface with an isolated singularity, $\mathrm{LC}(X)$ is Cohen-Macaulay by [31, Theorem 4.2].

Let us recall that $\mu (f)$ denotes the Milnor number [28] of a germ of an analytic function $f : (\mathbb {C}^n,0) \rightarrow (\mathbb {C}, 0)$ with an isolated critical point at the origin and it is defined as

$$\begin{aligned} \mu (f) = \dim _{\mathbb {C}} \frac{\mathcal {O}_{n,0}}{J (f )}, \end{aligned}$$

where $\mathcal {O}_{n,0}$ is the ring of germs of analytic functions at the origin, and J(f) is the Jacobian ideal of f.

Using [31, Theorem 4.2], and assuming that there exists L satisfying the hypotheses of Corollary 4.2 we prove the following result.

Proposition 4.4

Let $S_{\sigma } = \mathbb {Z}_{+}^n$ and let $X_{\sigma } = \mathbb {C}^n$ be the smooth n-dimensional toric variety. Consider $(g,f):(X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ a non-degenerate complete intersection, and

$$\begin{aligned} \Bigl (g_s(x),f_t(x) \Bigr )= \Bigl (g(x) + \sum _{i=1}^{m}\xi _{i}(s)\cdot l_i(x), f(x)+\sum _{j=1}^{r} \theta _{j}(t)\cdot h_j(x) \Bigr )\end{aligned}$$

a family of non-degenerate complete intersections with $h_j$ and $l_i$ satisfying the condition (3.6). Suppose that, for all $s,t \in \mathbb {C}$, $X_{\sigma }^{g_s} \subset \mathbb {C}^n$ is a weighted homogeneous hypersurface with an isolated singularity at the origin. If $f_t: \mathbb {C}^n \rightarrow \mathbb {C}$ is a polynomial function with an isolated singularity at the origin such that $f_t: X_{\sigma }^{g_s} \rightarrow \mathbb {C}$ has also a stratified isolated singularity at the origin, then $\mu _{BR}(f_t,X_{\sigma }^{g_s})$ is constant to all $s,t \in \mathbb {C}$.

Proof

From [35, Corollary 2.38] we have

$$\begin{aligned} \mu _{BR}(f_t,X_{\sigma }^{g_s}) = \mu (f_t) + \mathrm{Eu}_{X_{\sigma }^{g_s}}(0) + (-1)^{n-1}(\mathrm{Eu}_{f_t,{X_{\sigma }}^{g_s}}(0) + 1). \end{aligned}$$

By the hypothesis $X_\sigma = \mathbb {C}^n$, then $L(g^{\mu })(x) = g_\mu (x)$, for all $\mu \in \mathrm{Int}(\check{\Delta }) \cap M(S_{\sigma } \cap \Delta )^{*}$. From Definitions 2.8 and 2.10, we can conclude that $f_t:\mathbb {C}^n \rightarrow \mathbb {C}$ is a family of non-degenerate polynomial functions. Furthermore,

$$\begin{aligned} \Gamma _{+}(f) = \Gamma _{+}(f_t), \ \ \text {for all} \ \ t \in \mathbb {C}, \end{aligned}$$

since $h_j$ satisfies the condition (3.6). Then, by [27, Corollary 3.5]

$$\begin{aligned} \chi (f^{-1}(\delta ) \cap B_{\varepsilon }) = \chi (f_{t}^{-1}(\delta ) \cap B_{\varepsilon }), \ \ \text {for all} \ \ t \in \mathbb {C}, \end{aligned}$$

where $0 < \left| \delta \right| \ll \varepsilon \ll 1$. Consequently, $\mu (f_t)$ is constant, once $\chi (f^{-1}(\delta ) \cap B_{\varepsilon })= 1 + (-1)^{n-1} \mu (f)$. Therefore the result follows from Corollary 4.2 and the remark that follows Corollary 4.2. $\square$

We observe that this result is a kind of generalization of [30, Theorem 3.6].

5 Toric surfaces

Let f be a polynomial function defined on a 2-dimensional toric variety $X_{\sigma } \subset \mathbb {C}^{n}$. In this section, we present a characterization of the polynomial functions $g: X_{\sigma } \rightarrow \mathbb {C}$ which are prepolar with respect to $\mathcal {T}^f$ at the origin. Using this characterization and the results of the last sections we present some examples of computation of the Brasselet number $\mathrm{B}_{f,X_{\sigma }}(0)$, for a class of toric surfaces $X_{\sigma }$ that are also determinantal.

Let us remember that a strongly convex cone in $\mathbb {R}^2$ has the following normal form.

Proposition 5.1

([14]) Let $\sigma \subset \mathbb {R}^2$ be a strongly convex cone, then $\sigma$ is isomorphic to the cone generated by the vectors $v_1 = pe_1 - qe_2$ and $v_2 = e_2$, for some integers $p,q \in \mathbb {Z}_{>0}$ such that $0<q<p$ and p, q are coprime.

Given a cone $\sigma \subset \mathbb {R}^2$, Riemenschneider [37, 38] proved that the binomials which generate the ideal $I_{\sigma }$ are given by the quasiminors of a quasimatrix, where $X_{\sigma } = V(I_{\sigma })$. In the following we recall the definition of quasimatrix.

Definition 5.2

Given $A_{i}, B_{i}, C_{l,l+1} \in \mathbb {C}$ with $i=1,\ldots ,n$ and $l=1,\ldots ,n-1$, a quasimatrix with entries $A_{i}, B_{i}, C_{l,l+1}$ is written as

The quasiminors of the quasimatrix A are defined by

$$\begin{aligned} A_i \cdot B_j - B_i\cdot (C_{i,i+1}\cdot C_{i+1,i_2} \cdots C_{j-1,j})\cdot A_j \end{aligned}$$

for $1 \le i < j \le n$.

Given $\sigma \subset \mathbb {R}^2$ generated by $v_1 = p e_{1} - q e_{2}$ and $v_{2} = e_{2}$, with p and q as above, let us consider the Hirzebruch–Jung continued fraction

$$\begin{aligned} \frac{p}{p-q} = a_2 - \frac{1}{a_3 - \frac{1}{\ldots - \frac{1}{a_{n-1}}}} = [[a_2, a_3, \ldots ,a_{n-1}]] \end{aligned}$$

where the integers $a_2, \ldots , a_{n-1}$ satisfies $a_i \ge 2$, for $i=2,\ldots ,n-1$. By [38] we have:

Proposition 5.3

The ideal $I_{\sigma }$ is generated by the quasiminors of the quasimatrix

where the $a_i$ are given by the Hirzebruch–Jung continued fraction of $\frac{p}{p-q}$. Moreover, this set of generators is minimal.

Then, if $a_i = 2$ for $i=3,\ldots , n-2$, we have that $X_{\sigma }$ is a determinantal surface [15, 29, 39], in particular if the minimal dimension of embedding of $X_{\sigma }$ is 4, i.e., if

$$\begin{aligned} \frac{p}{p-q} = a_2 - \frac{1}{a_3} \end{aligned}$$

then $X_{\sigma }$ is always determinantal and the ideal $I_{\sigma }$ is generated by the $2 \times 2$ minors of the matrix

We will consider $\sigma$ as in Proposition 5.1. Taking $a_2,\ldots , a_{n-1}$ the integers coming from the Hirzebruch–Jung continued fraction of $\frac{p}{p-q}$, we will denote by

$$\begin{aligned} \mu _1 = (\mu _1^{1},\mu _1^{2})=(1,0), \ \ \mu _2 = (\mu _2^{1},\mu _2^{2})=(1,1), \ \ \mu _{i+1}^{j}=a_i \cdot \mu _{i}^{j} - \mu _{i-1}^{j}, \end{aligned}$$

the minimal set of generators of $S_{\sigma }$, with $i=2,\ldots ,n-1$; $j=1,2$. We note that it is possible to show that $\mu _n =(\mu _n^{1},\mu _n^{2})=(q,p)$ (see [37, 38]). Thus $\varphi : (\mathbb {C}^*)^2 \times X_{\sigma } \rightarrow X_{\sigma }$ given by

$$\begin{aligned} \varphi ((t_1,t_2),(z_1,\ldots ,z_n)) = (t_1 \cdot z_1,t_1 \cdot t_2 \cdot z_2,t_1^{\mu _3^{1}} \cdot t_2^{\mu _3^{2}} \cdot z_3,\ldots , t_1^{q} \cdot t_2^{p} \cdot z_n) \end{aligned}$$

is an action of $(\mathbb {C}^{*})^2$ in $X_{\sigma }$. Each orbit of $\varphi$ is an embedding of a d-dimensional torus, $0\le d \le 2$, in $X_{\sigma }$. The action $\varphi$ has 4 orbits, that are

$$\begin{aligned} \begin{array}{lrl} T_{\Delta _0} &{} = &{}\{(0,\ldots ,0) \} \\ T_{\Delta _1} &{} = &{} \bigl \{ (t_1,0,\ldots ,0) \,\bigm |\, t_1 \in \mathbb {C}^* \bigr \} \cong \mathbb {C}^* \\ T_{\Delta _2} &{} = &{}\bigl \{ (0,\ldots ,0,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \} \cong \mathbb {C}^* \\ T_{\Delta _3} &{} = &{} \bigl \{ (t_1,t_1 \cdot t_2,t_1^{\mu _3^{1}} \cdot t_2^{\mu _3^{2}},\ldots ,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \} \cong (\mathbb {C}^*)^2 \end{array}. \end{aligned}$$

Moreover, as in Sect. 3,

$$\begin{aligned} X_{\sigma } = \bigsqcup _{\Delta _i \prec \check{\sigma }} T_{\Delta _i}, \end{aligned}$$

with $i=0,1,2,3$, is a decomposition of $X_{\sigma }$ in strata satisfying the Whitney conditions.

The toric surfaces obtained in Proposition 5.3 are normal toric surfaces, then they are smooth or they have isolated singularity at the origin. Therefore, if $f =\sum _{v\in S_{\sigma }} a_v \cdot v \in \mathbb {C}[S_{\sigma }]$ is a non-degenerate polynomial function on $X_{\sigma }$, then

$$\begin{aligned} \mathcal {T}_f=\bigl \{ T_{\Delta _i} \cap X_{\sigma }^{f} \,\bigm |\, i=0,1,2,3\bigr \}, \end{aligned}$$

is a Whitney stratification of $X_{\sigma }^{f}$, since $T_{\Delta _{1}}$ and $T_{\Delta _{2}}$ are smooth subvarieties of $\overline{T}_{\Delta _{3}} = X_{\sigma }$ which satisfy $\overline{T}_{\Delta _{1}} \cap \overline{T}_{\Delta _{2}} = \{ (0,\ldots ,0)\}$. As a consequence,

$$\begin{aligned} \mathcal {T}^{f}=\bigl \{ T_{\Delta _i} \setminus X_{\sigma }^{f}, \ \ T_{\Delta _i} \cap X_{\sigma }^{f}, \ \ \left\{ 0 \right\} \,\bigm |\, i=0,1,2,3\bigr \}, \end{aligned}$$

is a good stratification of $X_{\sigma }$ relative to f.

Next, we characterize the polynomial functions which have a stratified isolated singularity at the origin.

Lemma 5.4

Let $\sigma \subset \mathbb {R}^2$ be a strongly convex cone and $\mathcal {T}$ the Whitney stratification of $X_{\sigma } \subset \mathbb {C}^n$ whose strata are $T_{\Delta _0}$, $T_{\Delta _1}$, $T_{\Delta _2}$ and $T_{\Delta _3}$. Then, a non-degenerate polynomial function $g: (X_{\sigma },0) \rightarrow (\mathbb {C},0)$ has an isolated singularity at the origin (in the stratified sense) if, and only if,

$$\begin{aligned} g(z_1,\ldots ,z_n) = c_1z_1^{p_1} + h(z_1,\ldots ,z_n) + c_nz_n^{p_n}, \end{aligned}$$

where h is a polynomial function on $X_{\sigma }$, $c_1,c_n \in \mathbb {C}^{*}$ and $p_1,p_n \in \mathbb {Z}^*_+$.

Proof

Let us write g as follows

$$\begin{aligned} g(z_1,\ldots ,z_{n}) = \displaystyle {\sum _{l=1}^{m} c_lz_1^{p_1^l} z_2^{p_2^l} \ldots z_{n}^{p_{n}^l}}, \end{aligned}$$

where $l=1,\ldots ,m$, $p_i^{l} \in \mathbb {Z}^*_+$ and $c_l \in \mathbb {C}$.

Suppose that g has a stratified isolated singularity at the origin $0 \in \mathbb {C}^n$, with respect to the stratification $\mathcal {T}$, then there must be $l_1,l_n \in \left\{ 1,\ldots ,m \right\}$ such that

$$\begin{aligned} \begin{array}{lrl} c_{l_1} \in \mathbb {C}^*, \ \ &{} p_1^{l_1} \ne 0 \ \ \text {and} \ \ &{} p_{i}^{l_1} = 0, \ \ \text {for} \ \ i \in \left\{ 2,\ldots ,n\right\} \\ c_{l_n} \in \mathbb {C}^*, \ \ &{} p_n^{l_n} \ne 0 \ \ \text {and} \ \ &{} p_{i}^{l_n} = 0, \ \ \text {for} \ \ i \in \left\{ 1,\ldots ,n-1\right\} \end{array}, \end{aligned}$$

otherwise $T_{\Delta _1}, T_{\Delta _2} \subset \Sigma _{\mathcal {T}} g$, since

$$\begin{aligned} T_{\Delta _1} = \bigl \{ (t_1,0,\ldots ,0) \,\bigm |\, t_1 \in \mathbb {C}^*\bigr \},\ and \ T_{\Delta _2} = \bigl \{ (0,\ldots ,0,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \}. \end{aligned}$$

In other words, g must contain monomials of the form $c_1z_1^{p_1}$ and $c_nz_n^{p_n}$.

Now, suppose that g has the form mentioned above, then $\Gamma _{+}(g) \cap \Delta _1 \ne \emptyset$, $\Gamma _{+}(g) \cap \Delta _2\ne \emptyset$ and $\Gamma _{+}(g) \cap \Delta _3 \ne \emptyset$. By the proof of [27, Lemma 4.1] we can conclude that $g|_{T_{\Delta _{1}}}: T_{\Delta _{1}} \rightarrow \mathbb {C}$ and $g|_{T_{\Delta _{2}}}: T_{\Delta _{2}} \rightarrow \mathbb {C}$ are non-degenerate polynomial functions. Moreover,

$$\begin{aligned} \begin{array}{lrl} T_{\Delta _1} &{} = &{} \bigl \{ (t_1,0,\ldots ,0) \,\bigm |\, t_1 \in \mathbb {C}^* \bigr \} \cong \mathbb {C}^*,\\ T_{\Delta _2} &{} = &{}\bigl \{ (0,\ldots ,0,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \} \cong \mathbb {C}^*, \\ T_{\Delta _3} &{} = &{} \bigl \{ (t_1,t_1 \cdot t_2,t_1^{\mu _3^{1}} \cdot t_2^{\mu _3^{2}},\ldots ,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \} \cong (\mathbb {C}^*)^2. \end{array} \end{aligned}$$

Then by [34, Lemma 78] there exists an $\varepsilon >0$ such that $g|_{T_{\Delta _{1}}}$, $g|_{T_{\Delta _{2}}}$ and $g|_{T_{\Delta _{3}}}$ have no singularities in ${T_{\Delta _{1}}} \cap B_{\varepsilon }$, ${T_{\Delta _{2}}} \cap B_{\varepsilon }$ and ${T_{\Delta _{3}}} \cap B_{\varepsilon }$, respectively. $\square$

As a consequence of Lemma 5.4 we obtain information about the singular set of g just by looking at its Newton polygon $\Gamma _{+}(g)$. More precisely, a non-degenerate polynomial function $g: (X_{\sigma },0) \rightarrow (\mathbb {C},0)$ has an isolated singularity at the origin (in the stratified sense) if, and only if, $\Gamma _{+}(g)$ intersects $\Delta _1$ and $\Delta _2$, exactly in the same way as the classic case, i.e., in the case where $X_{\sigma } = \mathbb {C}^2$.

Proposition 5.5

Let $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ be a non-degenerate complete intersection, such that f and g have no irreducible components in common. The polynomial function g is prepolar with respect to $\mathcal {T}^f$ if, and only if,

$$\begin{aligned} g(z_1,\ldots ,z_n) = c_1z_1^{p_1} + h(z_1,\ldots ,z_n) + c_nz_n^{p_n}, \end{aligned}$$

where h is a polynomial function on $X_{\sigma }$, $c_1,c_n \in \mathbb {C}^{*}$ and $p_1,p_n \in \mathbb {Z}_{+}^*$.

Proof

Consider the good stratification

$$\begin{aligned} \mathcal {T}^f = \bigl \{ T_{\Delta _i} \setminus X_{\sigma }^{f}, \ \ T_{\Delta _i} \cap X_{\sigma }^{f}, \ \ \left\{ 0 \right\} \,\bigm |\, i=0,1,2,3\bigr \}, \end{aligned}$$

of $X_{\sigma }$ relative to f. The sets $T_{\Delta _1}$ and $T_{\Delta _2}$ are given by

$$\begin{aligned} T_{\Delta _1} = \bigl \{ (t_1,0,\ldots ,0) \,\bigm |\, t_1 \in \mathbb {C}^*\bigr \}\ and \ T_{\Delta _2} = \bigl \{ (0,\ldots ,0,t_1^{q} \cdot t_2^{p}) \,\bigm |\, t_1,t_2 \in \mathbb {C}^*\bigr \}. \end{aligned}$$

From the fact that f is a non-degenerate polynomial function, there are only two possibilities for each stratum $T_{\Delta _i} \cap X_{\sigma }^{f}$. Either $T_{\Delta _i} \cap X_{\sigma }^{f}$ is a finite set or $T_{\Delta _i} \cap X_{\sigma }^{f} = T_{\Delta _i}$. Therefore, if g is prepolar with respect to $\mathcal {T}^f$, then $\Gamma _{+}(g) \cap \Delta _{1} \ne \emptyset$ and $\Gamma _{+}(g) \cap \Delta _{2} \ne \emptyset$, otherwise $T_{\Delta _i} \cap X_{\sigma }^{f} \subset \Sigma _{\mathcal {T}^f} g$ or $T_{\Delta _i} \setminus X_{\sigma }^{f} \subset \Sigma _{\mathcal {T}^f} g$, for $i=1,2$.

Now, suppose that g have the form mentioned above, then the result follows from Lemma 5.4 and from the fact that, as f and g have no irreducible components in common, i.e., $X_{\sigma }^{g} \cap X_{\sigma }^{f}$ is a finite set. $\square$

Example 5.6

Let $\sigma \subset \mathbb {R}^2$ be the cone generated by the vectors $v_1 = e_2$ and $v_2 = ne_1 - e_2$. The toric surface associated to $\sigma$ is $X_{\sigma } = V(I_{\sigma }) \subset \mathbb {C}^{n+1}$, where $I_{\sigma }$ is the ideal generated by the $2 \times 2$ minors of the matrix

i.e., $X_{\sigma }$ is a determinantal surface with codimension $n-1$. Consider $f: X_{\sigma } \rightarrow \mathbb {C}$ the function given by $f(z_1,\ldots ,z_{n+1})=z_1^d + z_{n+1}^{d} + tg(z_1,\ldots ,z_{n+1})$, where

$$\begin{aligned} g(z_1,\ldots ,z_{n+1}) = \displaystyle {\sum _{l=1}^{m} z_1^{p_1^l} z_2^{p_2^l} \ldots z_{n+1}^{p_{n+1}^l}} \end{aligned}$$

is a polynomial function on $X_{\sigma }$ satisfying $p_1^{l} + p_2^{l} + \ldots + p_{n+1}^{l} > d$ for every $l=1,\ldots ,m$. If f is a non-degenerate polynomial function then

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }}(0)= 2d -nd^2. \end{aligned}$$

Indeed, consider $h:X_{\sigma } \rightarrow \mathbb {C}$ the function given by $h(z_1,\ldots ,z_{n+1}) = z_1^d + z_{n+1}^d$. The Newton polygon $\Gamma _+(h)$ has a unique 1-dimensional compact face $\beta _1$, that is the straight line segment connecting the points (d, 0) and (d, nd) in $\check{\sigma }$. Using the notation of Proposition 3.4, we have that $\Gamma _1^{\Delta _1}$ is the straight line segment connecting the points (0, 0) and (d, 0), $\Gamma _1^{\Delta _2}$ is the straight line segment connecting the points (0, 0) and (d, nd) and $\Gamma _1^{\Delta _3}$ is the triangle with vertices (0, 0), (d, 0) and (d, nd). Therefore,

$$\begin{aligned} {\mathrm{Vol}}_{\mathbb {Z}}(\Gamma _{1}^{\Delta _1})=\mathrm {Vol_{\mathbb {Z}}}(\Gamma _{1}^{\Delta _2}) = d \ \ \text {and} \ \ {\mathrm{Vol}}_{\mathbb {Z}}(\Gamma _{1}^{\Delta _3})=nd^2. \end{aligned}$$

By Proposition 3.4,

$$\begin{aligned} \mathrm{B}_{h,X_{\sigma }}(0)=2d-nd^2, \end{aligned}$$

since $X_{\sigma }$ has an isolated singularity at the origin, and consequently $\mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{1}}) = \mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{2}}) = \mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{3}}) = 1$. Now, $S_{\sigma }$ is the semigroup generated by

$$\begin{aligned} \left\{ (1,0),(1,1),(1,2)\ldots ,(1,n) \right\} , \end{aligned}$$

and then $\Gamma _+(g) \subset \Gamma _+(h)$. Moreover, by Lemma 5.4, f has an isolated singularity at the origin, thus

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }}(0)= \mathrm{Eu}_{X_{\sigma }}(0) - \mathrm{Eu}_{f,X_{\sigma }}(0). \end{aligned}$$

However, González-Sprinberg [20] proved that $\mathrm{Eu}_{X_{\sigma }}(0) = 3-(n+1)$. Hence,

$$\begin{aligned} \mathrm{Eu}_{f,X_{\sigma }}(0) = 3-(n+1)-2d+nd^2. \end{aligned}$$

Therefore, a morsefication of f has $3-(n+1)-2d+nd^2$ Morse points on the regular part of $X_{\sigma }$.

Example 5.7

Let $\sigma \subset \mathbb {R}^2$ be the cone generated by the vectors $v_1 = e_2$ and $v_2 = 2e_1 - e_2$. The toric surface associated to $\sigma$ is $X_{\sigma } = V(I_{\sigma }) \subset \mathbb {C}^3$, with $I_{\sigma }$ the ideal generated by $z_1z_3 - z_2^{2}$. Consider $f: X_{\sigma } \rightarrow \mathbb {C}$ the function given by $f(z_1,z_2,z_3)=z_2^2 - z_1^3$, which is a non-degenerate polynomial function, whose singular set is

$$\begin{aligned} \Sigma f = \bigl \{ (0,0,z_3) \,\bigm |\, z_3 \in \mathbb {C}\bigr \} \subset X_{\sigma }. \end{aligned}$$

Moreover, $\Gamma _+(f)$ has a unique 1-dimensional compact face $\beta _1$, which is the straight line segment connecting the points (3, 0) and (2, 2) in $\check{\sigma }$. Thus, $\Gamma _1^{\Delta _1}$ is the straight line segment connecting the points (0, 0) and (3, 0), $\Gamma _1^{\Delta _3}$ is the triangle with vertices (0, 0), (3, 0) and (2, 2), and $\Gamma _1^{\Delta _2} = \emptyset$. Therefore, by Proposition 3.4,

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }}(0)=3-6=-3 \end{aligned}$$

since $X_{\sigma }$ has an isolated singularity at the origin, and consequently

$$\begin{aligned} \mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{1}}) = \mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{2}}) = \mathrm{Eu}_{X_{\sigma }}(T_{\Delta _{3}}) = 1. \end{aligned}$$

Now let $g: X_{\sigma } \rightarrow \mathbb {C}$ be the non-degenerate polynomial function given by

$$\begin{aligned} g(z_1,z_2,z_3)= z_1 - z_3^2, \end{aligned}$$

which is prepolar with respect to $\mathcal {T}^f$. Moreover, (g, f) is a non-degenerated complete intersection. The Newton polygon $\Gamma _{+}(g\cdot f)$ has two 1-dimensional compact faces $\gamma _1$ and $\gamma _2$, which are the straight line segment connecting the points (4, 0) and (3, 2) and the straight line segment connecting the points (3, 2) and (4, 6), respectively. Thus, the primitive vectors

$$\begin{aligned} u_{1}^{\Delta _3}, u_{2}^{\Delta _3} \in \mathrm{Int}(\check{\Delta _3}) \cap M(S_{\sigma } \cap \Delta _3)^{*} \end{aligned}$$

which take their minimal value in $\Gamma _{+}(g\cdot f) \cap \Delta _3$ exactly on $\gamma _{1}$ and $\gamma _2$, respectively, are $u_{1}^{\Delta _3}=(2,1)$ and $u_{2}^{\Delta _3}=(4,-1)$. Let us observe that

$$\begin{aligned} \begin{array}{lllll} \gamma (g)_{1}^{\Delta _3} &{} := &{} \Gamma (g|_{\Delta _3};u_{1}^{\Delta _3}) &{} = &{} \left\{ (1,0) \right\} \\ \gamma (g)_{2}^{\Delta _3} &{} := &{} \Gamma (g|_{\Delta _3};u_{2}^{\Delta _3}) &{} = &{} \alpha _1 \\ d_{1}^{\Delta _3} &{} := &{} d_{2}^{\Delta _3} &{} := &{} 6 \\ K_1^{\Delta _3} &{} = &{} K_2^{\Delta _3} &{} = &{} 1 \end{array}, \end{aligned}$$

where $\alpha _1$ is the 1-dimensional compact face of $\Gamma _{+}(g)$. Applying Theorem 3.7, we have $\mathrm{B}_{f,X_{\sigma }^{g}}(0)= 12$. Therefore, we obtain the following equality

$$\begin{aligned} \mathrm{B}_{f,X_{\sigma }}(0) - \mathrm{B}_{f,X_{\sigma }^{g}}(0) = -3 - 12 =-15, \end{aligned}$$

which means that the number of stratified Morse critical points on the top stratum $T_{\Delta _3} \cap f^{-1}(\delta )\cap B_{\varepsilon }(0)$ appearing in a morsefication of $g : X_{\sigma } \cap f^{-1}(\delta ) \cap B_{\varepsilon }(0) \rightarrow \mathbb {C}$ is 15. Moreover, if we consider $h, l: X_{\sigma } \rightarrow \mathbb {C}$ the polynomial functions given by

$$\begin{aligned} h(z_1,z_2,z_3) = -z_1^2 z_3^2, \qquad l(z_1,z_2,z_3) = z_3^3, \end{aligned}$$

and observe that

$$\begin{aligned} \Gamma _+(h) \subsetneqq \Gamma _+(f), \qquad \Gamma _+(l) \subsetneqq \Gamma _+(g), \end{aligned}$$

by Corollary 3.6 we have

$$\begin{aligned} \mathrm{B}_{f_t,X_{\sigma }}(0) = \mathrm{B}_{f,X_{\sigma }}(0) = -3, \qquad \mathrm{B}_{f_t,X_{\sigma }^{g_s}}(0) = \mathrm{B}_{f,X_{\sigma }^{g}}(0) = 12, \end{aligned}$$

where $f_t(x)=f(x)+t \cdot h(x)$ is a deformation of the cusp $f_0(z_1,z_2,z_3) = z_2^2 - z_1^3$ (see Fig. 1) and $g_s(x)=g(x)+ s \cdot l(x)$. Consequently,

$$\begin{aligned} \mathrm{B}_{f_t,X_{\sigma }}(0) - \mathrm{B}_{f_t,X_{\sigma }^{g_s}}(0) = -3 - 12 =-15, \end{aligned}$$

for all $t, s \in \mathbb {C}$.

6 Indices of vector fields

A toric surface $X_{\sigma }$, which is a cyclic quotient singularity, always possesses a smoothing [37, Satz 10]. Therefore, when we consider a radial continuous vector field v on $X_{\sigma }$ with an isolated singularity at 0, we can relate the Euler characteristic of a fiber of this smoothing with the $\mathrm {GSV}$ index of v in $X_{\sigma }$. The definition of this index for smoothable isolated singularity can be found in [8, Section 3].

In particular, for the case of toric surfaces which are also isolated determinantal singularities, we have the following result concerning $\mathrm {GSV}$ index.

Let $X_{\sigma } \subset \mathbb {C}^n$ be a toric surface that is also an isolated determinantal singularity, i.e., $\sigma$ is generated by the vectors $v_1 = p e_{1} - q e_{2}$ and $v_{2} = e_{2}$, where $0< q < p$, p, q are coprime, and whose Hirzebruch–Jung continued fraction is

$$\begin{aligned} \frac{p}{p-q} = [[a_2, 2, 2, \ldots , 2, a_{n-1}]]. \end{aligned}$$

Consider $f_t(x) = f(x)+\sum _{j=1}^{r} \theta _{j}(t)\cdot h_j(x)$ a family of non-degenerate polynomial functions on $X_{\sigma }$, which satisfies the conditions

$$\begin{aligned} \Gamma _{+}(h_j) \subsetneqq \Gamma _{+}(f), \ \ \text {for all} \ \ j=0,\ldots ,r. \end{aligned}$$

If this family has an isolated singularity at the origin, then the following result holds.

Proposition 6.1

Let $v_t$ be the vector field given by the gradient of the function $f_t$. Then, the following statements are equivalent:

• (a) $\mathrm{Eu}_{f_t,X_{\sigma }}(0)$ is constant for the family;

• (b) $\mathrm{Ind}_{GSV}(v_t,X_{\sigma },F)$ is constant for the family, where F is the flat map associated to the smoothing of $X_{\sigma }$.

Proof

By [29] the determinantal Milnor number of the function f on the Isolated Determinantal Singularity $X_{\sigma }$ is

$$\begin{aligned} \mu (f|_{X_{\sigma }}) = \# \Sigma (\widetilde{f}|_{{X_{\sigma }}_s}), \end{aligned}$$

where ${X_{\sigma }}_s$ is a fiber of a smoothing of $X_{\sigma }$, $\widetilde{f}|_{{X_{\sigma }}_s}$ is a morsefication of f and $\# \Sigma (\widetilde{f}|_{{X_{\sigma }}_s})$ denote the number of Morse points of $\widetilde{f}$ on ${X_{\sigma }}_s$. From the definition of the GSV index in the case of smoothable varieties (see [8]) we have

$$\begin{aligned} \mu (f|_{X_{\sigma }}) = \mathrm{Ind}_{GSV}(v,X_{\sigma },F). \end{aligned}$$

Then the proof follows by [1], where it is proved that $\mathrm{Eu}_{f_t,X_{\sigma }}(0)$ is constant for the family if and only if $\mu (f_t|_{X_{\sigma }})$ is constant for the family. $\square$

In [10, Definition 2.5], the authors extended the concept of $\mathrm {GSV}$ index and proved a Lê-Greuel formula (see [10, Theorem 3.1]) which holds with the hypotheses of Theorem 2.5. However, in [10] the authors worked with the constructible function given by the characteristic function, while in [12] is considered the local Euler obstruction. Hence the $\mathrm {GSV}$ index and the Brasselet number are not related in general.

Assuming that $f_t$ is generically a submersion, for non-degenerate complete intersections, we have the following result.

Proposition 6.2

Let $S_{\sigma } = \mathbb {Z}_{+}^n$ and $X_{\sigma } = \mathbb {C}^n$ be the smooth n-dimensional toric variety. Let $(g,f): (X_{\sigma },0) \rightarrow (\mathbb {C}^2,0)$ be a non-degenerate complete intersection, such that $\mathcal {T}_g$ is a Whitney stratification of $X_{\sigma }^{g}$. If

$$\begin{aligned} \Bigl (g_s(x),f_t(x) \Bigr )= \Bigl (g(x) + \sum _{i=1}^{m}\xi _{i}(s)\cdot l_i(x), f(x)+\sum _{j=1}^{r} \theta _{j}(t)\cdot h_j(x) \Bigr )\end{aligned}$$

is a family of non-degenerate complete intersections with $h_j$ and $l_i$ satisfying the condition (3.6) for all $i=1,\ldots ,m$ and $j=1,\ldots ,r$, such that $\mathcal {T}_{g_s}$ is a Whitney stratification of $X_{\sigma }^{g_{s}}$ and $g_s$ is prepolar with respect to $\mathcal {T}^{f_t}$ at the origin. Then, $\mathrm{Ind}_{GSV}(g_s, 0; f_t )$ is invariant to the family.

Proof

In [10, Section 5.2], the authors used [12, Theorem 4.2] (considering the Euler characteristic as constructible function) to provide the following interpretation to the $\mathrm {GSV}$ index,

$$\begin{aligned}&\sum _{\Delta \prec \check{\sigma }} \big ( \chi \big (T_{\Delta } \cap X_{\sigma } \cap B_{\varepsilon }(0) \cap f^{-1}(\delta ) \big ) - \chi \big (T_{\Delta } \cap X_{\sigma }^{g} \cap B_{\varepsilon }(0) \cap f^{-1}(\delta ) \big ) \big )\\&\quad = \mathrm{Ind}_{GSV}(g, 0; f ), \end{aligned}$$

where $\mathrm{Ind}_{GSV}(g, 0; f )$ is the GSV-index of g on $X^{f}$ relative to the function f (see [10, Definition 2.5]). Moreover, $f_t$ is a family of non-degenerate polynomial functions, since $(g_s,f_t)$ is non-degenerate complete intersections, for all $s,t \in \mathbb {C}$. Then, to compute $\mathrm{Ind}_{GSV}(g, 0; f )$ above we apply [27, Corollary 3.5] to the first term of the equality above and to the second term of the equality above we used Eqs. (3.2), (3.3). Therefore, the result follows from the fact that $h_j$ and $l_i$ satisfy the condition (3.6) for all $i=1,\ldots ,m$ and $j=1,\ldots ,r$. $\square$

Example 6.3

Consider the toric surface $X_{\sigma } = V(I_{\sigma }) \subset \mathbb {C}^3$, with $I_{\sigma }$ the ideal generated by $z_1z_3 - z_2^{2}$. Let $f_t$ and $g_s$ be the families of functions of Example 5.7, then

$$\begin{aligned} \mathrm{Ind}_{GSV}(g_s, 0; f_t ) = -15 \end{aligned}$$

for all $t, s \in \mathbb {C}$.