Fixed-Parameter Algorithms for Unsplittable Flow Cover

Abstract

The Unsplittable Flow Cover problem (UFP-cover) models the well-studied general caching problem and various natural resource allocation settings. We are given a path with a demand on each edge and a set of tasks, each task being defined by a subpath and a size. The goal is to select a subset of the tasks of minimum cardinality such that on each edge e the total size of the selected tasks using e is at least the demand of e. There is a polynomial time 4-approximation for the problem (Bar-Noy et al. STOC 2001) and also a QPTAS (Höhn et al. ICALP 2018). In this paper we study fixed-parameter algorithms for the problem. We show that it is W[1]-hard but it becomes FPT if we can slighly violate the edge demands (resource augmentation) and also if there are at most k different task sizes. Then we present a parameterized approximation scheme (PAS), i.e., an algorithm with a running time of $f(k)\cdot n^{O_{\epsilon }(1)}$ that outputs a solution with at most (1 + 𝜖)k tasks or asserts that there is no solution with at most k tasks. In this algorithm we use a new trick that intuitively allows us to pretend that we can select tasks from OPT multiple times. We show that the other two algorithms extend also to the weighted case of the problem, at the expense of losing a factor of 1 + 𝜖 in the cost of the selected tasks.

1 Introduction

In the Unsplittable Flow Cover problem (UFP-cover) we are given a path G = (V,E) where each edge e has a demand $u_{e}\in \mathbb {N}$, and a set of tasks T where each task i ∈ T has a start vertex s_i ∈ V and an end vertex t_i ∈ V, defining a path P(i), and a size $p_{i}\in \mathbb {N}$, and a cost $c_{i}\in \mathbb {N}$. The goal is to select a subset of the tasks $T^{\prime }\subseteq T$ of minimum cost $c(T^{\prime }):={\sum }_{i\in T^{\prime }}c_{i}$ that covers the demand of each edge, i.e., such that ${p(T^{\prime }\cap T_{e}):=}{\sum }_{i\in T^{\prime }\cap T_{e}}p_{i}\ge u_{e}$ for each edge e where T_e denotes the set of tasks i ∈ T for which e lies on P(i). It is the natural covering version of the well-studied Unsplittable Flow on a Path problem (UFP), see e.g., [9, 22, 23] and references therein. In this paper we mainly focus on the unweighted case, i.e., when c_i = 1 for all i ∈ T, and we refer to the weighted case only if this stated explicitly. UFP-cover is a generalization of the (unweighted) knapsack cover problem [11], and it can model general caching in the fault model where we have a cache of fixed size and receive requests for non-uniform size pages, the goal being to minimize the total number of cache misses (see [1, 5, 16] and Appendix A). Caching and generalizations of it have been studied for several decades in computer science, see e.g., [1, 8, 21, 25]. Also, UFP-cover is motivated by many resource allocation settings in which for instance the path specifies a time interval and the edge demands represent minimum requirements for some resource like energy, bandwidth, or number of available machines at each point in time.

UFP-cover is strongly NP-hard, since it generalizes general caching in the fault model [16], and the best known polynomial time approximation algorithm for it is a 4-approximation [5] with no improvement in almost 20 years. However, the problem admits a QPTAS for the case of quasi-polynomial input data [24] which suggests that better polynomial time approximation ratios are possible.

In this paper, we study the problem for the first time under the angle of fixed parameter tractability (FPT). We define our parameter k to be the number of tasks in the desired solution and seek algorithms with a running time of f(k)n^O(1) for some function f, that either find a solution of size at most k or state that there is no such solution.¹ We show that by allowing such a running time we can compute solutions that are almost optimal.

1.1 Our Contribution

We prove that UFP-cover is W[1]-hard, which makes it unlikely to admit an FPT-algorithm (see Section 6). In particular, this motivates studying FPT-approximation algorithms or other relaxations of the problem. As a warm-up, we first show in Section 2 that the problem becomes FPT when we assume that the number of different task sizes in the input is additionally bounded by a parameter. This algorithm intuitively works as follows. We recursively guess the size of a task of the optimal solution that contains the leftmost edge and add to the solution one such task with rightmost endpoint.

Theorem 1

There is an algorithm that solves UFP-cover in time π^O(k) ⋅ O(n), assuming that |{p_i : i ∈ T}|≤π.

Then, in Section 3, we show that under slight resource augmentation the problem becomes FPT. We define an additional parameter δ > 0 controlling the amount of resource augmentation and we compute either a solution that is feasible if we decrease the demand of each edge e to u_e/(1 + δ), or we assert that there is no solution of size k for the original edge demands. Key to our result is to prove that due to the resource augmentation we can assume that each edge e is completely covered by tasks whose size is comparable to u_e or it is covered by at least one task whose size is much larger than u_e. Based on this we design an algorithm that intuitively sweeps the path from left to right and on each uncovered edge e we guess which of the two cases applies. In the former case, we show that due to the resource augmentation we can restrict ourselves to only f(k,δ) many guesses for the missing tasks using e. In the latter case e belongs to a subpath in which each edge is covered by a task that is much larger than the demand of e. We guess the number of tasks in this subpath and select tasks to maximize the length of the latter. This yields a subproblem that we solve recursively and we embed the recursion into a dynamic program.

Theorem 2

There is an algorithm for UFP-cover with running time $k^{O\left (\frac {k}{\delta }\log k\right )}\cdot n^{O(1)}$ that either outputs a solution of size at most k that is feasible if the edge capacities are decreased by a factor 1 + δ or asserts that there is no solution of size k for the original edge capacities.

We use the above algorithm to obtain in Section 4 a simple FPT-2-approximation algorithm without resource augmentation.

Then, in Section 5, we present a parameterized approximation scheme (PAS) for UFP-cover, i.e., an algorithm with a running time of $f(k)\cdot n^{O_{\epsilon }(1)}$ that outputs a solution with at most (1 + 𝜖)k tasks or assert that there is no solution with at most k tasks. Notice that since the problem is W[1]-hard and is parameterized by the size of the solution, we cannot avoid the dependency on 𝜖 of the exponent of n in the running time (see Corollary 1). Our algorithm is based on a lemma developed for UFP in which we have the same input as in UFP-cover but we want to maximize the weight of the selected tasks $T^{\prime }$ and require that their total size is upper-bounded by u_e on each edge e, i.e., ${\sum }_{i\in T^{\prime }\cap T_{e}}p_{i}\le u_{e}$. Informally, the mentioned lemma states that we can remove a set OPT_SL from OPT of negligible cardinality such that on each edge e we remove one of the largest tasks of OPT using e. This yields some slack that we can use in order to afford inaccuracies in the computation. Translated to UFP-cover, the natural correspondence would be a solution in which the tasks in OPT_SL are not removed but selected twice. This is not allowed in UFP-cover. However, we guess a set of tasks $T^{\prime }$ that intuitively yields as much slack as OPT_SL and whose size is also negligible. If $OPT\cap T^{\prime } \ne \emptyset$ then we cannot add the tasks in $T^{\prime }$ to OPT to gain slack since some of them are already included in OPT. Therefore, we use the following simple but useful trick: we guess $T^{\prime }\cap OPT$ for which there are $2^{|T^{\prime }|} \le 2^{O(\epsilon k)}$ options, select the tasks in $T^{\prime }\cap OPT$, and recurse on the remaining instance. Since the cardinality of OPT is bounded by k, the whole recursion tree has a complexity of $k^{O(k^{3})}$ which depends only on our parameter k.

If $OPT\cap T^{\prime } =\emptyset$ then $T^{\prime }\cup OPT$ is a (1 + 𝜖)-approximate solution with some slack and we can use the slack in our computation. We compute a partition of E into O(k) intervals. Some of these intervals are dense, meaning that there are many tasks from OPT that start or end in them. We ensure that for each dense interval there is a task in $T^{\prime }$ that covers the whole interval and whose size is at least a Ω(1/k)-fraction of the demand of each edge in the interval. Intuitively this is equivalent to decreasing the demand on each edge by a factor of 1 + Ω(1/k). If we had only dense intervals we could apply the FPT-algorithm for resource augmentation from above for the remaining problem. On the other hand, if only few tasks start or end in an interval we say that it is sparse. If all intervals are sparse, we devise a dynamic program that processes them in the order of their amount of slack and guesses their tasks step by step. We use the slack in order to be able to “forget” some of the previously guessed tasks which yields a DP with only polynomially many cells. These guessing steps are the main responsible for the $n^{O_{\epsilon }(1)}$ part of the running time, since at each iteration we guess subsets of O_𝜖(1) many tasks.

Unfortunately, in an instance there can be dense and sparse intervals and our algorithms above for the two special cases are completely incompatible. Therefore, we identify a type of tasks in OPT such that we can guess tasks that cover as much as those in OPT, while losing only a factor of 1 + 𝜖. Using some charging arguments, we show that then we can split the remaining problem into two independent subinstances, one with only dense intervals and one with only sparse intervals which we then solve with the algorithms mentioned above.

Theorem 3

There is a parameterized approximation scheme for UFP-cover.

Our algorithm under resource augmentation, the FPT-2-approximation and the parameterized approximation scheme are presented in the unweighted case. We explain in Section 3.2 how to extend the first two results to the weighted case, at the expense of a factor of 1 + 𝜖 in the approximation ratio.

1.2 Other Related Work

The study of parameterized approximation algorithms was initiated independently by Cai and Huang [10], Chen, Grohe, and Grüber [14], and Downey, Fellows, and McCartin [18]. Good surveys on the topic were given by Marx [27], and more recently by Feldmann, Karthik C. S., Lee and Manurangsi [19]. Recently, the notion of approximate kernels was introduced [26]. Independently, Bazgan [7] and Cesati and Trevisan [12] established an interesting connection between approximation algorithms and parameterized complexity by showing that EPTASs, i.e., (1 + 𝜖)-approximation algorithms with running time f(𝜖)n^O(1), imply FPT algorithms for the decision version. Hence a W[1]-hardness result for a problem makes the existence of an EPTAS for it unlikely.

For the unweighted case of UFP (packing) a PAS is known [29]. Note that in the FPT setting UFP is easier than UFP-cover since we can easily make the following simplifying assumptions that we cannot make in UFP-cover. First, we can assume that the input tasks are not too small: if there are k input tasks whose size is smaller than 1/k times the capacity of any of the edges they use, then we can simply output those tasks and we are done; if there are less than k of such tasks, we can assume we know exactly which of them OPT selects by enumerating the 2^k possible options, and only large tasks remain. Second, the tasks are not too big since the size of a task can be assumed to be at most the minimum capacity of an edge in its path. Third, we can easily find a set of at most k edges that together intersect the path of each input task (i.e., a hitting set for the input task’s paths) unless a simple greedy algorithm finds a solution of size k [29]. The best known polynomial time approximation algorithm for UFP has a ratio of 5/3 + 𝜖 [23] and the problem admits a QPTAS [3, 6].

Recently, polynomial time approximation algorithms for special cases of UFP-cover under resource augmentation were found: an algorithm computing a solution of optimal cost if p_i = c_i for each task i and a (1 + 𝜖)-approximation if the cost of each task equals its “area”, i.e., the product of p_i and the length of P(i) [17]. UFP-cover is a special case of the general scheduling problem (GSP) on one machine in the absence of release dates. The best known polynomial time result for GSP is a (4 + 𝜖)-approximation [15] and a QPTAS for quasi-polynomial bounded input data [2]. Also, UFP-cover is a special case of the capacitated set cover problem, e.g., [4, 13].

2 Few Different Task Sizes

In this section, we show that UFP-cover is FPT when it is parameterized by k + π where π is the number of different task sizes in the input. We are given two parameters k and π and assume |{(p_i : i ∈ T}|≤π. We seek to compute a solution $T^{\prime }\subseteq T$ with $|T^{\prime }|\le k$ such that for each edge e it holds that $p(T^{\prime }\cap T_{e}) \ge u_{e}$ or assert that there is no such solution. Partition the set T into at most π sets of tasks of equal size denoted by T^(ℓ) = {i ∈ T∣p_i = ℓ}.

Assume that there exists a solution OPT with at most k tasks that cover all demands. Our algorithm sweeps the path from left to right and guesses the tasks in OPT step by step (in contrast to similar such algorithms it is not a dynamic program). We maintain a set $T^{\prime }$ of previously selected tasks and a pointer indicating an edge e. We initialize the algorithm with e being the leftmost edge of E and $T^{\prime }:=\emptyset$. For the sake of the analysis we also maintain a set $OPT^{\prime }$ that we initialize equal to OPT. Suppose that the pointer is at some edge e. If the tasks in $T^{\prime }$ already cover the demand of e, i.e., $p(T_{e}\cap T^{\prime })\ge u_{e}$, then we move the pointer to the edge on the right of e. Otherwise, $OPT^{\prime }\cap T_{e}$ contains at least one task i. We guess its size ℓ and add to $T^{\prime }$ the task in $(T_{e}\cap T^{(\ell )})\setminus T^{\prime }$ with rightmost endvertex. Then update $OPT^{\prime }:= OPT^{\prime }\setminus \{i\}$. Formally, when we say that we guess ℓ (or other quantities in this and the other algorithms in this paper) we mean that we enumerate all possibilities for the respective quantity and continue the algorithm for each possible value, maybe guessing other quantities later. At the very end, this yields one solution for each (combined) possible outcome for all guesses of the algorithm. We reject a solution if it is not feasible (i.e., does not cover the demand of all edges). Also, we stop the algorithm if the quantities guessed so far imply that too many tasks will be selected at the end, and we reject the so far computed solution immediately. At least one solution must remain at the end since one set of guesses is always correct, and we output one of the remaining solutions. In particular, we stop if $|T^{\prime }|> k$ since we want to select more than k tasks. Hence, the total number of possible guesses overall is bounded by π^O(k). Each of them yields a set $T^{\prime }$. In case that the resulting set $T^{\prime }$ is not a feasible solution we reject the guesses that lead to $T^{\prime }$.

Otherwise, assume that at some point during the execution, all the previous guesses were correct. Since we move the pointer when the current edge is covered by $T^{\prime }$ all edges on the left of the pointer must be covered by the solution. Then the choice of the task with the rightmost endpoint vertex ensures that for any edge $e^{\prime }$ that is on the right of the current pointer e (including e), we have $p(T^{\prime }\cap T_{e^{\prime }})\ge p((OPT\setminus OPT^{\prime })\cap T_{e^{\prime }})$. Indeed, for any task i in $OPT\setminus OPT^{\prime }$ whose path P(i) contains e, there exists a task in $T^{\prime }$ of the same size, that contains e and with the rightmost endpoint, so its path contains all edges on the right of e covered by i.

The total number of guesses is bounded by π^O(k) and for each guess we can compute the right task to add to the solution in time O(n). Hence, we obtain:

Theorem 4

There is an algorithm that solves UFP-cover in time π^O(k) ⋅ O(n), assuming that |{p_i : i ∈ T}|≤π.

Extension to the Weighted Case

Recall that in the weighted case each task i ∈ T has a cost c_i (besides its path P(i) and its size p_i), and our objective is to minimize the total cost of the solution $c(T^{\prime })={\sum }_{i\in T^{\prime }} c_{i}$.

We can easily adapt the previous algorithm to the case where the number of combinations of the size and the cost of a task in the input is bounded, and obtain the following result:

Theorem 5

There is an algorithm that solves UFP-cover in time π^O(k) ⋅ O(n), assuming that |{(p_i,c_i) : i ∈ T}|≤π.

Here the only difference is that we now partition the set T into at most π sets of tasks of equal size and equal cost, and at each iteration of the algorithm we guess the size and the cost of the next task from OPT not yet considered.

In Section 3.2, we explain how to obtain a FPT-(1 + 𝜖)-approximation when the number of sizes in the input is bounded by a parameter, but the number of costs is arbitrary.

3 Resource Augmentation

In this section, we turn to the case where we have resource augmentation but the number of different task sizes is arbitrary. As a consequence of Theorem 1, we first show that UFP-cover with (1 + δ) resource augmentation, can be solved in time f(k,δ) ⋅ n^O(1) if the edge demands come in a polynomial range, i.e., when the maximum demand $\max \limits _{e} u_{e}$ over all edges is n^O(1). In Section 3.1 we generalize this algorithm to arbitrary edge demands.

Given parameters $k\in \mathbb {N}$ and δ > 0, we seek to compute a solution $T^{\prime }\subseteq T$ with $|T^{\prime }|\le k$ such that for each edge e it holds that $p(T^{\prime }\cap T_{e}) \ge \tilde {u}_{e}= u_{e}/(1+\delta )$ or assert that there is no solution $T^{\prime }\subseteq T$ with $|T^{\prime }|\le k$ such that for each edge e it holds that $p(T^{\prime }\cap T_{e})\ge u_{e}$.

The idea is to round the task sizes and then use our algorithm for bounded number of task sizes. Let OPT denote a solution with at most k tasks. We partition the tasks into groups such that sizes of the tasks from the same group differ by at most a factor of 1 + δ. For each $\ell \in \mathbb {N}$ we define the group T^(ℓ) := {i ∈ T|p_i ∈ [(1 + δ)^ℓ,(1 + δ)^ℓ+ 1)}. For each ℓ we round the sizes of the tasks in T^(ℓ) to (1 + δ)^ℓ, i.e., for each i ∈ T^(ℓ) we define its rounded size to be $\tilde {p}_{i}:=(1+\delta )^{\ell }$ (for convenience, we allow rounded task sizes and edge demands to be fractional). As we show in the next lemma, this rounding step is justified due to our resource augmentation. For a set of tasks $T^{\prime }$, we define $\tilde {p}(T^{\prime }):={\sum }_{i\in T^{\prime }}\tilde {p}_{i}$.

Lemma 1

By decreasing the demand of each edge e to $\tilde {u}_{e}:=u_{e}/(1+\delta )$ we can assume for each $\ell \in \mathbb {N}$ that each task i ∈ T^(ℓ) has a size of $\tilde {p}_{i}=(1+\delta )^{\ell }$, i.e., for each edge e it holds that $\tilde {p}(OPT\cap T_{e})\ge \tilde {u}_{e}$.

Proof

By the definition of $\tilde {p}_{i}$, $p_{i}\leq (1+\delta )\tilde {p}_{i}$ for all tasks i ∈ T, so we get that for any edge e ∈ E, $\tilde {p}(OPT\cap T_{e})\geq \frac {1}{1+\delta }p(OPT\cap T_{e})\geq \frac {1}{1+\delta }u_{e}$. □

Note that w.l.o.g. we can assume that $p_{i}\le \max \limits _{e}u_{e}$ for each task i. (Otherwise one could define a new instance where all tasks such that $p_{i}>\max \limits _{e}u_{e}$ have now size $\max \limits _{e}u_{e}$; then, a set of tasks is feasible for the new sizes if and only if it is feasible for the initial sizes). Assume now that the edge demands are in a polynomial range. Hence, there are only $O(\log _{1+\delta }n)$ groups T^(ℓ) with T^(ℓ)≠∅. The optimal solution contains tasks from at most k of these groups. We guess the groups T^(ℓ) that satisfy that OPT ∩ T^(ℓ)≠∅ in time $\left (\begin {array}{cc}O(\log _{1+\delta }n) \\ k \end {array}\right )=\left (\frac {1}{\delta }\log n\right )^{O(k)}$. Note that the latter quantity is of the form f(k,δ) ⋅ n^O(1), since $(\log n)^{O(k)}\leq n+k^{O(k^{2})}$ [28]. We delete the tasks from all other groups. This yields an instance with at most k different (rounded) task sizes, and then we can apply Theorem 1 with π = k. Hence, there is an algorithm with running time $(\frac {1}{\delta }\log n)^{O(k)}\cdot k^{O(k^{2})}\cdot n^{O(1)}=f(k,\delta )\cdot n^{O(1)}$ if the edge demands are in a polynomial range.

3.1 Arbitrary Demands

We extend the above algorithm now to the case of arbitrary demands. We define the rounded edge demands $\{\tilde {u}_{e}\}_{e\in E}$ and task sizes $\{\tilde {p}_{i}\}_{i\in T}$ exactly as above. We apply a shifting step that intuitively partitions the groups above into supergroups such that the sizes of two tasks in different supergroups differ by at least a factor of 2k/δ. In particular, one task from one supergroup will be larger than any k tasks from supergroups with smaller tasks together. We define K to be the smallest integer such that k(1 + δ)^−K− 1 < δ/2, i.e., $K=O(\frac {1}{\delta }\log k)$. Let α ∈{0,...,k} be an offset to be defined later. Intuitively, we remove an $\frac {1}{k+1}$-fraction of all groups T^(ℓ) and combine the remaining groups into supergroups. With a shifting argument we ensure that no task from OPT is contained in a deleted group. Formally, we define a supergroup ${\mathcal {T}}^{(s)}:=\bigcup _{\ell =K(\alpha +s(k+1))}^{K(\alpha +(s+1)(k+1)-1)-1}T^{(\ell )}$ for each integer s. In particular, each supergroup contains K ⋅ k groups.

Lemma 2

There exists an offset α ∈{0,...,k} such that for each task i ∈ OPT there is a supergroup $\mathcal {T}^{(s)}$ such that $i\in {\mathcal {T}}^{(s)}$.

Proof

For each of the tasks i ∈ OPT there is exactly one value for α such that i is not contained in any supergroup ${\mathcal {T}}^{(s)}$. Indeed, given α, supergroups miss all the tasks from groups T^(ℓ) such that $\ell \pmod {K(k+1)} \in I_{\alpha } := K(\alpha -1), \dots , K\alpha -1$ and the family $(I_{\alpha })_{\alpha =0}^{k}$ forms a partition of all possible remainders in the Euclidean division by K(k + 1). Then, since there are k + 1 options for α by the pigeon hole principle there is one value for α such that each task i ∈ OPT is contained in some supergroup ${\mathcal {T}}^{(s)}$. □

The first step in our algorithm is to guess the value α due to Lemma 2, for which there are k + 1 options. Note that if the edge demands are not polynomially bounded there can be up to Ω(n) groups, so we can no longer guess which groups contain tasks from OPT. Instead, for each edge e we define a level s_e to be the largest value s such that $(1+\delta )^{K(\alpha +s(k+1))}\le \hat {u}_{e}:=\tilde {u}_{e}/(1+\delta )$. Note that (1 + δ)^{K(α+s(k+ 1))} is a lower bound on the size of each task in ${\mathcal {T}}^{(s)}$. In the next lemma, using resource augmentation we prove that for each edge e it holds that the tasks in ${\mathcal {T}}^{(s_{e})}\cap OPT$ are sufficient to cover the demand of e or that in OPT the edge e is completely covered by one task in a supergroup ${\mathcal {T}}^{(s^{\prime })}$ with $s^{\prime }>s_{e}$.

Lemma 3

For each edge e it holds that $p(OPT\cap \mathcal {T}^{(s_{e})}\cap T_{e})\ge \hat {u}_{e}$ or that there is a task $i\in OPT\cap \bigcup _{s=s_{e}+1}^{\infty }{\mathcal {T}}^{(s)}\cap T_{e}$. In the latter case it holds that $p_{i}\ge \tilde {p}_{i}\ge \hat {u}_{e}$.

Proof

Consider an edge e and suppose that $p(OPT\cap \mathcal {T}^{(s_{e})}\cap T_{e})<\hat {u}_{e}$. We claim that then $p(OPT\cap \bigcup _{\ell :\ell \le s_{e}}{\mathcal {T}}^{(\ell )}\cap T_{e})<\tilde {u}_{e}$. This holds since any k tasks in $\bigcup _{\ell \le s_{e}-1}{\mathcal {T}}^{(s_{e})}$ have a total demand of at most $k\cdot (1+\delta )^{K(\alpha +s_{e}(k+1)-1)+1}\le k\cdot (1+\delta )^{K(\alpha +s_{e}(k+1))}\cdot (1+\delta )^{-K-1}\le k(1+\delta )^{-K-1}\cdot \hat {u}_{e}<\delta \hat {u}_{e}$. This implies that $p(OPT\cap \bigcup _{\ell :\ell \le s_{e}}{\mathcal {T}}^{(\ell )}\cap T_{e})<\delta \hat {u}_{e}+\hat {u}_{e}=\tilde {u}_{e}$. Since $p(OPT\cap T_{e})\ge u_{e}>\tilde {u}_{e}$ there must be a task $i\in OPT\cap \bigcup _{s=s_{e}+1}^{\infty }\mathcal {T}^{(s)}\cap T_{e}$. Now suppose there is a task $i\in \mathcal {T}^{(s^{\prime })}$ for some $s^{\prime }\geq s_{e}+1$. This means that $\tilde {p}_{i}\geq (1+\delta )^{K(\alpha +s^{\prime }(k+1))}$ and by the definition of s_e, we have that $(1+\delta )^{K(\alpha +s^{\prime }(k+1))}>\hat {u}_{e}$. □

In order to solve our problem, we define a set of subproblems that we solve via dynamic programming. Let us denote $\mathcal {T}^{(\ge s)}:=\bigcup _{s^{\prime }\ge s}\mathcal {T}^{(s^{\prime })}$. Each subproblem is characterized by a subpath $\tilde {E}\!\subseteq \! E$, and integers $\tilde {k},\tilde {s}$ with $0\!\le \!\tilde {k}\!\le \! k$ and $\tilde {s}\in \{-1,...,$ $O(\log \max \limits _{e}u_{e})\}$. A tuple $(\tilde {E},\tilde {k},\tilde {s})$ represents the following subproblem: select a set of tasks $T^{\prime }\subseteq {\mathcal {T}^{(\ge \tilde {s})}}$ with $|T^{\prime }|\le \tilde {k}$ such that for each edge $e\in \tilde {E}$ it holds that ${\sum }_{i\in T^{\prime }\cap T_{e}}\tilde {p}_{i}\ge \hat {u}_{e}$. Note that the subproblem (E,k,− 1) corresponds to the original problem that we want to solve. Moreover, since we are only interested in values $\tilde {s}$ for which $\mathcal {T}^{(\tilde {s})}$ is non-empty, the number of DP-cells is polynomial in the input length.

Suppose we are given a subproblem $(\tilde {E},\tilde {k},\tilde {s})$ and assume that we already solved each subproblem of the form $(\tilde {E}^{\prime },\tilde {k}^{\prime },\tilde {s}^{\prime })$ where $\tilde {E}^{\prime }\subseteq \tilde {E}$, $\tilde {k}^{\prime }\le \tilde {k}$, and $\tilde {s}^{\prime }>\tilde {s}$. Denote by $\widetilde {OPT}$ a feasible solution to the subproblem $(\tilde {E},\tilde {k},\tilde {s})$. Our algorithm sweeps the path $\tilde {E}$ from left to right and guesses the tasks in $\widetilde {OPT}$ step by step. We maintain a pointer at some edge e and a set $T^{\prime }$ of previously selected tasks. We initialize the algorithm with e being the leftmost edge of $\tilde {E}$ and $T^{\prime }:=\emptyset$. Suppose that the pointer is at some edge e. If the tasks in $T^{\prime }$ already cover the reduced demand of e, i.e., $\tilde {p}(T^{\prime }\cap T_{e})\ge \hat {u}_{e}$, then we move the pointer to the edge on the right of e. Otherwise, in $\widetilde {OPT}$ the edge e must be covered by a task that is not in $T^{\prime }$. We guess whether $p(\widetilde {OPT}\cap {\mathcal {T}}^{(\ge \tilde {s}+1)}\cap T_{e})\ge \hat {u}_{e}$ or $p(\widetilde {OPT}\cap {\mathcal {T}}^{(\tilde {s})}\cap T_{e})\ge \hat {u}_{e}$. Since we assumed that e is covered by a task in $\mathcal {T}^{(\ge \tilde {s})}$, Lemma 3 implies that one of these two cases applies.

Suppose we guessed that $p(OPT\cap \mathcal {T}^{(\ge \tilde {s}+1)}\cap T_{e})\ge \hat {u}_{e}$. For any two edges e₁,e₂ denote by $P_{e_{1},e_{2}}$ the subpath of E starting with e₁ and ending with e₂ (including e₁ and e₂). Let $e^{\prime }$ be the rightmost edge on the right of e such that for each edge $e^{\prime \prime }\in P_{e,e^{\prime }}$ the set $OPT\cap T_{e^{\prime \prime }}$ contains at least one task in ${\mathcal {T}}^{(\ge \tilde {s}+1)}$. Let $\tilde {k}^{\prime }$ denote the number of tasks in $OPT\cap {{\mathcal {T}}^{(\ge \tilde {s}+1)}}$ whose path intersects $P_{e,e^{\prime }}$. We guess $\tilde {k}^{\prime }$. Then we determine the rightmost edge $e^{\prime \prime }$ such that $(P_{e,e^{\prime \prime }},\tilde {k}^{\prime },\tilde {s}^{\prime })$ is a yes-instance, where $\tilde {s}^{\prime }\ge \tilde {s}+1$ is the smallest integer such that ${\mathcal {T}}^{(\tilde {s}^{\prime })}{\ne \emptyset }$. We add to $T^{\prime }$ the tasks in the solution of $(P_{e,e^{\prime \prime }},\tilde {k}^{\prime },\tilde {s}^{\prime })$ and move the pointer to the edge on the right of $e^{\prime \prime }$.

Assume now that we guessed that $p(OPT\cap \mathcal {T}^{(\tilde {s})}\cap T_{e})\ge \hat {u}_{e}$. Recall that $\mathcal {T}^{(\tilde {s})}$ consists of only Kk non-empty groups T^(ℓ). For each of these groups T^(ℓ) we guess $k_{\ell }:=|OPT\cap T_{e}\cap T^{(\ell )}|-|T^{\prime }\cap T_{e}\cap T^{(\ell )}|$. Note that there are only (k + 1)^Kk possible guesses. For each group T^(ℓ) we add to $T^{\prime }$ the k_ℓ tasks in $(T_{e}\cap T^{(\ell )})\setminus T^{\prime }$ with rightmost endvertex. Then we move the pointer to the edge on the right of e.

Like before, at each guessing step, we enumerate only guesses that ensure that we do not select more than $\tilde {k}$ tasks altogether. Hence, the total number of possible guesses overall is bounded by $2^{\tilde {k}}(\tilde {k}+1)^{O(K\tilde {k})}=k^{O(\frac {k}{\delta }\log k)}$. We store in the cell $(\tilde {E},\tilde {k},\tilde {s})$ the set $T^{\prime }$ of minimum size that was found in the $k^{O(\frac {k}{\delta }\log k)}$ guesses, assuming that one of them has size at most $\tilde {k}$. Therefore, for each cell $(\tilde {E},\tilde {k},\tilde {s})$, in time $n^{O(1)}\cdot k^{O(\frac {k}{\delta }\log k)}$ we can compute a corresponding solution of size at most $\tilde {k}$, if one such solution exists. Finally, we output the solution in the cell (E,k,− 1) if it contains a feasible solution. If it does not contain a feasible solution we output that there is no solution of size k for the original edge capacities u.

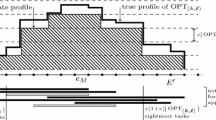
In summary, our algorithm first guesses the value α according to Lemma 2. Then, it creates the dynamic programming table with one DP-cell for each tuple $(\tilde {E},\tilde {k},\tilde {s})$ where $\tilde {E}\subseteq E$ and the values $\tilde {k}$ and $\tilde {s}$ are integers with $0\le \tilde {k}\le k$ and $-1\le \tilde {s}\le O(\log \max \limits _{e}u_{e})$. It sorts the DP-cells such that the cell of a tuple $(\tilde {E}^{\prime },\tilde {k}^{\prime },\tilde {s}^{\prime })$ appears before the cell of a tuple $(\tilde {E},\tilde {k},\tilde {s})$ if $\tilde {E}^{\prime }\subseteq \tilde {E}$, $\tilde {k}^{\prime }\le \tilde {k}$, and $\tilde {s}^{\prime }>\tilde {s}$. It considers the cells in this order and for each cell $(\tilde {E},\tilde {k},\tilde {s})$ it computes a solution for each of the $k^{O(\frac {k}{\delta }\log k)}$ possible guesses described above, and stores in $(\tilde {E},\tilde {k},\tilde {s})$ the found solution of minimum size, assuming that this solution has size at most $\tilde {k}$. See Fig. 1 for an illustration of the algorithm. Theorem 2 follows by proving that this algorithm is correct and has the claimed running time.

Fig. 1

Sketch of the execution of the dynamic program for arbitrary demands under resource augmentation. Here the algorithm is calculating the solution for the subproblem $(\tilde {E},\tilde {k},\tilde {s})$. Before reaching edge e it has selected only tasks from ${\mathcal {T}}^{(\tilde {s})}$. At edge e it guesses that all edges in $P_{e,e^{\prime \prime }}$ are completely covered by tasks in ${\mathcal {T}}^{(\geq \tilde {s}+1)}$ (which are much larger), so it recurses in $P_{e,e^{\prime \prime }}$, guessing appropriate values for $\tilde {k}^{\prime }\leq \tilde {k}$ and $\tilde {s}^{\prime }\geq \tilde {s}+1$. Then it continues to the right of $e^{\prime \prime }$

Proof Proof of Theorem 2

We prove by induction that, given a cell $(\tilde {E},\tilde {k},\tilde {s})$, if in OPT each edge $e\in \tilde {E}$ is used by at least one task in $\mathcal {T}^{(\ge \tilde {s})}$ and if the set of tasks $\widetilde {OPT} = \{ i \in OPT\cap \mathcal {T}^{(\geq \tilde {s})}: P(i)\cap \tilde {E}\neq \emptyset \}$ satisfies that $|\widetilde {OPT}|\le \tilde {k}$, and satisfies the reduced demands in $\tilde {E}$, then the solution $T^{\prime }$ computed in the cell $(\tilde {E},\tilde {k},\tilde {s})$ satisfies all reduced demands in $\tilde {E}$ and has size at most $|\widetilde {OPT}|\leq \tilde {k}$.

Given a cell $(\tilde {E},\tilde {k},\tilde {s})$, we assume that this is true for any cell $(\tilde {E}^{\prime },\tilde {k}^{\prime },\tilde {s}^{\prime })$ where $\tilde {E^{\prime }}\subseteq \tilde {E}$, $\tilde {k^{\prime }}\le \tilde {k}$ and $\tilde {s}^{\prime }>\tilde {s}$. Let $\widetilde {OPT}$ be a solution as described above. Notice that if $\widetilde {OPT}$ does not satisfy the conditions above then there is nothing to prove. Let $T^{\prime }$ be the computed solution for the cell $(\tilde {E},\tilde {k},\tilde {s})$.

We partition $\tilde {E}$ into consecutive sub-intervals $\tilde {E}=\tilde {E}_{1} \dot {\cup } \tilde {E}^{\prime }_{1} \dot {\cup } {\dots } \dot {\cup } \tilde {E}_{r}\dot {\cup } \tilde {E}^{\prime }_{r} \dot {\cup } \tilde {E}_{r+1}$ such that each $\tilde {E}^{\prime }_{i}$ is a maximal sub-interval containing edges e where $p(\widetilde {OPT}\cap T_{e} \cap \mathcal {T}^{(\ge \tilde {s}+1)})\ge \hat {u}_{e}$. Let the intervals $\tilde {E}_{i}$ be the maximal sub-intervals containing all other edges in $\tilde {E}$. Notice that according to Lemma 3, for all edges e in $\tilde {E}_{i}$, the reduced demand is entirely covered by tasks in $\mathcal {T}^{(\tilde {s})}$, i.e. $p(\widetilde {OPT}\cap \mathcal {T}^{(\tilde {s})}\cap T_{e})\ge \hat {u}_{e}$. Suppose that the algorithm made guesses correctly according to this partition: if the demand of the current edge e is not covered, then if $e \in \tilde {E}^{\prime }_{i}$ for some i then it guesses that $p(OPT\cap {\mathcal {T}}^{(\ge \tilde {s}+1)}\cap T_{e})\ge \hat {u}_{e}$ and it guesses $|\widetilde {OPT}\cap \left (\bigcup _{e\in \tilde {E}^{\prime }_{i}}T_{e}\right ) \cap \mathcal {T}^{(\ge \tilde {s}+1)}|$ for $\tilde {k}^{\prime }$, otherwise it guesses that $p(OPT\cap {\mathcal {T}}^{(\tilde {s})}\cap T_{e})\ge \hat {u}_{e}$.

Then, for each sub-interval $\tilde {E}^{\prime }_{i}$ we added to $T^{\prime }$ the solution of a cell $({\hat {E}}^{\prime }_{i},\tilde {k}_{i}^{\prime },\tilde {s}^{\prime })$, where $\tilde {k}_{i}^{\prime }=|\widetilde {OPT}\cap \left (\bigcup _{e\in \tilde {E}^{\prime }_{i}}T_{e}\right ) \cap \mathcal {T}^{(\ge \tilde {s}+1)}|$, the left endpoint of ${\hat {E}}^{\prime }_{i}$ is on the right of or identical to the left endpoint of $\tilde {E}^{\prime }_{i}$ and the right endpoint of ${\hat {E}}^{\prime }_{i}$ is on the right of or identical to the right endpoint of $\tilde {E}^{\prime }_{i}$. Since $\tilde {E}^{\prime }_{i}$ is chosen maximally, no edge in $\tilde {E}_{i}$ is covered by any task in $\widetilde {OPT}\cap \mathcal {T}^{(\ge \tilde {s}{+1})}$. This implies that all tasks in $\widetilde {OPT}\cap \mathcal {T}^{(\ge \tilde {s} {+1)}}$ intersect only one sub-interval $\tilde {E}^{\prime }_{i}$. It follows, using the induction hypothesis for each $({\hat {E}}^{\prime }_{i},\tilde {k}^{\prime }_{i},\tilde {s}^{\prime })$ that the solution $T^{\prime }$ satisfies the reduced demand in each sub-interval $\tilde {E}^{\prime }_{i}$ and

$$ \begin{array}{@{}rcl@{}} |T^{\prime}\cap \left( \bigcup\limits_{i}\bigcup\limits_{e\in \tilde{E}^{\prime}_{i}} T_{e} \right)\cap \mathcal{T}^{(\ge \tilde{s}+1)}|& \le& \sum\limits_{i} \left|\widetilde{OPT}\cap \left( \bigcup\limits_{e\in \tilde{E}^{\prime}_{i}} T_{e} \right)\cap \mathcal{T}^{(\ge \tilde{s}+1)}\right|\\ &=& \left|\widetilde{OPT}\cap \left( \bigcup\limits_{i}\bigcup\limits_{e\in \tilde{E}^{\prime}_{i}} T_{e} \right)\cap \mathcal{T}^{(\ge \tilde{s}+1)}\right| . \end{array} $$

For all sub-intervals $\tilde {E}_{i}$, it is possible that the same task is used to cover demands in distinct sub-intervals. However, since the tasks are added from left to right and chosen to maximize their rightmost endvertex, when the guesses are correct, it holds for each edge e in some $\tilde {E}_{i}$ that e is contained in some set $\hat {E}^{\prime }_{i}$ (in which case its demand is covered by tasks in $T^{\prime }\cap \mathcal {T}^{(\ge \tilde {s}+1)}$) or that $p(T^{\prime }\cap T_{e})\ge {\sum }_{j\in OPT\cap T_{e}} \tilde {p}_{j}\ge \hat {u}_{e}$. Moreover,

$$ \left|T^{\prime}\cap \left( \bigcup\limits_{i}\bigcup\limits_{e\in \tilde{E}_{i}} T_{e} \right)\cap \mathcal{T}^{(\tilde{s})}\right|\le \left|\widetilde{OPT}\cap \left( \bigcup\limits_{i}\bigcup\limits_{e\in \tilde{E}_{i}} T_{e} \right)\right| . $$

When we combine both equations we get what we wanted to establish the induction, i.e., that $|T^{\prime }|{\le } |\widetilde {OPT}|$. □

3.2 Extension to the Weighted Case

We can convert the previous algorithm into a parameterized approximation scheme (PAS) for the resource augmentation setting. Hence, for given k and 𝜖 > 0, our algorithm finds in time $f(k,\epsilon )\cdot n^{O_{\epsilon }(1)}$ a solution $T^{\prime }$ with at most (1 + 𝜖)k tasks and a cost $c(T^{\prime })\leq (1+\epsilon )c(OPT(k))$ (recall that OPT(k) denotes the optimal solution with at most k tasks) such that $p(T^{\prime }\cap T_{e})\geq u_{e}/(1+\delta )$ for all e ∈ E, or asserts that there is no solution such that $p(T^{\prime }\cap T_{e})\geq u_{e}$ for all e ∈ E and $|T^{\prime }|\leq k$.

The key change in the algorithm for resource augmentation is to round the costs to powers of 1 + 𝜖 (which loses a factor of 1 + 𝜖 in the approximation ratio) and then partition the tasks into groups $T^{(\ell ,\ell ^{\prime })}$ according to their size and their cost, rather than only based on their size.

For this we guess the most expensive task in OPT(k). Let i^∗ be this task. We discard all tasks i with $c_{i}>c_{i^{*}}$. Then we round the cost c_i of each task i ∈ T to the next smaller power of 1 + 𝜖 or even to zero if c_i is very small compared to $c_{i^{*}}$. Formally, we define $\tilde {c}_{i}:=(1+\epsilon )^{\left \lfloor \log _{1+\epsilon }c_{i}\right \rfloor }$ if $c_{i}\ge \epsilon c_{i^{*}}/k$ and $\tilde {c}_{i}:=0$ if $c_{i}<\epsilon c_{i^{*}}/k$. Let ${\Gamma }\le O(\log _{1+\epsilon }k/\epsilon )$ denote the number of different task costs. The next lemma implies that our rounding loses at most a factor of 1 + 𝜖.

Lemma 4

For any solution $T^{\prime }$ with $|T^{\prime }|\le O(k)$, and such that $c_{i}\leq c_{i^{*}}$ for all $i\in T^{\prime }$, it holds that ${\sum }_{i\in T^{\prime }}c_{i}\le (1+O(\epsilon )){\sum }_{i\in T^{\prime }}\tilde {c}_{i}$.

Proof

Partition $T^{\prime }$ into $A=\{i\in T^{\prime }:c_{i}<\epsilon c_{i^{*}}/k\}$ and $B=T^{\prime }\setminus A$. Since |A|≤ O(k), we know that ${\sum }_{i\in A}c_{i}\leq O(\epsilon ) c_{i^{*}}\leq O(\epsilon ) {\sum }_{i\in T^{\prime }}c_{i}$, since $c_{i^{*}}$ is a lower bound for OPT(k). By the definition of $\tilde {c}_{i}$, $c_{i}\leq (1+\epsilon )\tilde {c}_{i}$ for all i ∈ B, so ${\sum }_{i\in B}c_{i}\leq (1+\epsilon ){\sum }_{i\in B}\tilde {c}_{i}$. Finally, ${\sum }_{i\in T^{\prime }}c_{i}={\sum }_{i\in A}c_{i}+{\sum }_{i\in B}c_{i}\leq O(\epsilon ){\sum }_{i\in T^{\prime }}c_{i}+(1+\epsilon ){\sum }_{i\in T^{\prime }}\tilde {c}_{i}$, and we conclude noting that $\frac {1+\epsilon }{1-O(\epsilon )}\leq (1+O(\epsilon ))$. □

We define for each $\ell \in \mathbb {N}$ a group $T^{(\ell ,0)}:=\{i\in T|p_{i}\in [(1+\delta )^{\ell },(1+\delta )^{\ell +1})\wedge \tilde {c}_{i}=0\}$ and additionally for each $\ell ^{\prime }>0$ we define $T^{(\ell ,\ell ^{\prime })}:=\{i\in T|p_{i}\in [(1+\delta )^{\ell },(1+\delta )^{\ell +1})\wedge \tilde {c}_{i}=(1+\epsilon )^{\ell ^{\prime }}\}$. For each $(\ell ,\ell ^{\prime })$ we round the sizes of the tasks in $T^{(\ell ,\ell ^{\prime })}$ to (1 + δ)^ℓ, i.e., for each $i\in T^{(\ell ,\ell ^{\prime })}$ we define its rounded size to be $\tilde {p}_{i}:=(1+\delta )^{\ell }$. Then, we define a supergroup ${\mathcal {T}}^{(s,\ell ^{\prime })}:=\bigcup _{\ell =K(\alpha +s(k+1))}^{K(\alpha +(s+1)(k+1)-1)-1}T^{(\ell ,\ell ^{\prime })}$ for each integer s and each $\ell ^{\prime }$, and redefine the notation $\mathcal {T}^{(\ge s)}:=\bigcup _{\ell ^{\prime }}\bigcup _{s^{\prime }\ge s} \mathcal {T}^{(s^{\prime },\ell ^{\prime })}$.

Our PAS is analogous to the algorithm described in the previous subsection. We run a dynamic program whose cells are defined by a tuple $(\tilde {E},\tilde {k},\tilde {s})$. This represents the subproblem of selecting a set of tasks $T^{\prime }\subseteq \mathcal {T}^{(\ge \tilde {s})}$ that minimizes $\tilde {c}(T^{\prime })$ such that $|T^{\prime }|\leq \tilde {k}$ and $\tilde {p}(T^{\prime }\cap T_{e})\geq \hat {u}_{e}$ for each edge $e\in \tilde {E}$. The recursion to fill the DP table is almost identical. The only differences are that we select solutions that minimize the (rounded) cost instead of simply finding a yes-instance, and that ${\mathcal {T}}^{(\geq \tilde {s})}\setminus {\mathcal {T}}^{(\tilde {s}+1)}$ contains up to ΓKk non-empty groups instead of just Kk as before.

Remark 1

Using the exact same rounding technique, we can convert the algorithm of Section 2 into a PAS in the weighted setting for the case where the number of different task sizes is bounded by π (rather than the number of different combinations of task size and cost), i.e., where |{p_i : i ∈ T}|≤π.

4 FPT-2-Approximation Algorithm

We present an FPT-2-approximation algorithm without resource augmentation (for arbitrary edge demands), i.e., an algorithm that runs in time f(k)n^O(1) and finds a solution of size at most 2k or asserts that there is no solution of size at most k. Suppose we are given an instance (I,k). First, we call the algorithm for resource augmentation from Section 3 with δ = 1. If this algorithm asserts that there is no solution of size at most k then we stop. Otherwise, let ALG denote the found solution. We guess ALG ∩ OPT. Note that there are only 2^k possibilities for ALG ∩ OPT. If ALG ∩ OPT = ∅ then the solution OPT ∪ ALG covers each edge e to an extent of at least 3/2 ⋅ u_e, i.e., p((OPT ∪ ALG) ∩ T_e) ≥ 3/2 ⋅ u_e. Therefore, we create a new UFP-cover instance $I^{\prime }$ whose input tasks are identical with the tasks in I and in which the demand of each edge e is changed to $u^{\prime }_{e}:=3/2\cdot u_{e}$. We invoke our algorithm for the resource augmentation setting from Section 3 to $I^{\prime }$ where we look for a solution of size at most |ALG| + k ≤ 2k and we set δ := 1/2. Let $ALG^{\prime }$ be the returned solution. It holds that $|ALG^{\prime }|\le |ALG|+k\le 2k$ and $ALG^{\prime }$ covers each edge e to an extent of at least 3/2 ⋅ u_e/(1 + 1/2) = u_e. We output $ALG^{\prime }$.

If ALG ∩ OPT≠∅ then we generate a new instance $I^{\prime \prime }$ in which the tasks in ALG ∩ OPT are already taken, i.e., the demand of each edge e is reduced to $u^{\prime \prime }_{e}:=u_{e}-p(ALG\cap OPT\cap T_{e})$ and the set of input tasks consists of T ∖ (ALG ∩ OPT). We recurse on $I^{\prime \prime }$ where the parameter k is set to k −|ALG ∩ OPT|. Observe that $OPT^{\prime \prime }:=OPT\setminus ALG$ is a solution to $I^{\prime \prime }$ and if |OPT|≤ k then $|OPT^{\prime \prime }|\le k-|ALG\cap OPT|$. The resulting recursion tree has depth at most k with at most 2^k children per node and hence it has at most $2^{O(k^{2})}$ nodes in total. This yields the following theorem.

Theorem 6

There is an algorithm for UFP-cover with a running time of $2^{O(k^{2})}\cdot n^{O(1)}$ that either finds a solution of size at most 2k or asserts that there is no solution of size k.

Proof

Assume that the recursive call yields a solution $ALG^{\prime \prime }$ to $I^{\prime \prime }$. Then we return $ALG^{\prime \prime }\cup (ALG\cap OPT)$. This leads to a 2-approximation: assume inductively that $|ALG^{\prime \prime }|\le 2(k-|ALG\cap OPT|)$. Then $|ALG^{\prime \prime }\cup (ALG\cap OPT)|\le 2k-|ALG\cap OPT|\le 2k$.

Each node in the recursion tree requires a running time of f(k,𝜖) ⋅ n^O(1) due to Theorem 2. It remains to bound the size of the recursion tree given by the guesses of ALG ∩ OPT. After every new guess, either ALG ∩ OPT = ∅, which terminates the recursion, or the parameter k is reduced in one unit. Then the depth of the recursion tree is at most k and on each new recursion there are only 2^k possibilities, which in total gives at most $2^{k^{2}}$ nodes. The running time is then $2^{k^{2} + O(\frac {k}{\delta }\log k)}\cdot n^{O(1)}$, which is $2^{O(k^{2})}\cdot n^{O(1)}$ because δ = 1/2. □

Remark 2

It is easy to verify that we can get an FPT-(2 + 𝜖)-approximation algorithm for the weighted case, if we use our PAS for the weighted case under resource augmentation instead.

5 Parameterized Approximation Scheme

In this section, we present a PAS for UFP-cover. Given a parameter k, we seek to compute a solution of size at most (1 + 𝜖)k or assert that there is no solution of size at most k. The running time of our algorithm is $k^{O(k^{2}\log k)}n^{(1/\epsilon )^{O(1/\epsilon )}}$. Let OPT denote a solution with at most k tasks and let 𝜖 > 0 such that $1/\epsilon \in \mathbb {N}$.

First, we run the 4-approximation algorithm from [5] to obtain a solution S. If |S| > 4k then OPT > k and we stop. Intuitively, we will use S later to guide our computations. Similarly as before, we partition the tasks into groups such that tasks from the same group have the same size, up to a factor 1 + 𝜖. Formally, for each integer ℓ we define T^ℓ := {i ∈ T,p_i ∈ [(1 + 𝜖)^ℓ,(1 + 𝜖)^ℓ+ 1)} and we say that a task i is of level ℓ if i ∈ T^ℓ.

For each edge e let $OPT_{e}^{1/\epsilon }$ denote the 1/𝜖 largest tasks in OPT ∩ T_e (breaking ties in an arbitrary fixed way). Intuitively, we would like to select the tasks OPT_SL due to the following lemma from [6, Lemma 3.1]. On a high level, OPT_SL is a set of size O(k𝜖) that contains for every edge one of the 1/𝜖 largest tasks that cover it in OPT.

Lemma 5

[6] For any 𝜖 > 0, there is a set $OPT_{SL}\subseteq OPT$ with |OPT_SL|≤ γ𝜖|OPT| such that for each edge e with |OPT ∩ T_e|≥ 1/𝜖 it holds that $OPT_{SL}\cap OPT_{e}^{1/\epsilon }\neq \emptyset$, where γ is a universal constant that is independent of the given instance.

The intuition is that if in OPT we selected each task in OPT_SL twice, then we would cover each edge e to a larger extent than necessary, while increasing the number of selected tasks only by a factor 1 + O(𝜖). This would yield some slack which we would like to use in our computation.

Of course, we cannot select the tasks in OPT_SL twice. Instead, we run the following algorithm that computes a set $T_{S}=T_{S}^{(1)}\cup T_{S}^{(2)}\cup T_{S}^{(3)}$ with at most O(|OPT_SL|) tasks that gives us similar slack as OPT_SL on each edge. The reader may imagine that $T_{S}^{(1)}\cup T_{S}^{(2)}=OPT_{SL}$ and that $T_{S}^{(3)}$ are additional tasks that we select.

We initialize $T_{S}^{(1)}=\emptyset$. Let $\tilde {V}$ be the set of start and end vertices of the tasks in S. We partition E according to the vertices in $\tilde {V}$. Formally, we consider the partition $E=\tilde {I}_{1}\dot {\cup }\cdots \dot {\cup }\tilde {I}_{\tilde {r}}$ of E such that for each $\tilde {I}_{j}=\{v_{j}^{(1)},...,v_{j}^{(s)}\}$ we have that $v_{j}^{(1)}\in \tilde {V}$ and $v_{j}^{(s)}\in \tilde {V}$ and for each $s^{\prime }\in \{2,...,s-1\}$ we have that $v_{j}^{(s^{\prime })}\not \in \tilde {V}$. We say that a task i starts in an interval $\tilde {I}_{j}$ if $\tilde {I}_{j}$ is the leftmost interval that contains an edge of P(i) and a task i ends in an interval $\tilde {I}_{j}$ if $\tilde {I}_{j}$ is the rightmost interval that contains an edge of P(i). For each pair of intervals $\tilde {I}_{j},\tilde {I}_{j^{\prime }}$ we guess whether there is a task from OPT_SL that starts in $\tilde {I}_{j}$ and ends in $\tilde {I}_{j^{\prime }}$. If yes, we add to $T_{S}^{(1)}$ the largest input task that starts in $\tilde {I}_{j}$ and ends in $\tilde {I}_{j^{\prime }}$. Additionally, for each interval $\tilde {I}_{j}$ in which at least one task from OPT_SL starts or ends we add to $T_{S}^{(1)}$ the largest task i^∗∈ T such that $\tilde {I}_{j}\subseteq P(i^{*})$ and define $\bar {b}_{j}:=p_{i^{*}}$. Such a task i^∗ exists since S contains one such task. Notice that, unlike the corresponding task in OPT_SL, the task i^∗ added to $T_{S}^{(1)}$ may not necessarily start (or end) in $\tilde {I}_{j}$. For each other intervals $\tilde {I}_{j}$ we define $\bar {b}_{j}:=0$. See Fig. 2 for an illustration of the construction of $T_{S}^{(1)}$. Let L denote the set of values ℓ such that there is an interval $\tilde {I}_{j}$ and a task i ∈ T^ℓ with $p_{i}\in [\frac {1}{2k}\bar {b}_{j},4k\bar {b}_{j}]$ (intuitively, we will show later that we will not need tasks from sets $T^{\ell ^{\prime }}$ with $\ell ^{\prime }\notin L$).

Fig. 2

Construction of the set $T_{S}^{(1)}$. From bottom to top, the first rectangle represents a task from OPT_SL that starts in an interval $\tilde I_{j}$ and ends in $\tilde I_{j}$. The second task is the largest input task that starts in $\tilde I_{j}$ and ends in $\tilde I_{j}$. The third and fourth are the largest input tasks that respectively cover $\tilde I_{j^{\prime }}$ and $\tilde I_{j}$

Next, we define a set $T_{S}^{(2)}$ of additional slack tasks. We maintain a queue $Q\subseteq V$ of vertices that we call interesting and a set of tasks $T_{S}^{(2)}$. At the beginning, we initialize $T_{S}^{(2)}:=\emptyset$ and $Q:=\tilde {V}$. In each iteration we extract an arbitrary vertex v from Q. Let $Q^{\prime }$ be the set of vertices that were removed from the queue Q in an earlier iteration. It is initialized $Q^{\prime }=\emptyset$. For each vertex v let T_v denote the set of input tasks i whose path P(i) uses v, i.e., such that P(i) contains an edge e incident to v. For each group T^ℓ with ℓ ∈ L we guess whether there is a task in OPT_SL that uses v but that does not use any vertex in $Q^{\prime }$, i.e., we guess whether there is a task in $OPT_{SL}\cap T^{\ell }\cap T_{v}\setminus \bigcup _{v^{\prime }\in Q^{\prime }}T_{v^{\prime }}$. If we guess such a task does not exist, we remove v from Q, add it to $Q^{\prime }$, and we move to the next vertex in Q. If we guess such a task exists, we add to $T_{S}^{(2)}$ the task with leftmost startvertex and the task with rightmost endvertex from $T^{\ell }\cap T_{v}\setminus \bigcup _{v^{\prime }\in Q^{\prime }}T_{v^{\prime }}$. For each added task, we add its start- and its endvertex to Q if it has not been in Q before. Then we remove v from Q and add it to $Q^{\prime }$. The algorithm terminates once Q is empty. Let $T_{S}^{(2)}$ be the resulting set. Figure 3 illustrates one iteration of the construction of $T_{S}^{(2)}$.

Fig. 3

One iteration of the construction of $T_{S}^{(2)}$. Vertices in Q are represented by black dots, and vertices already in $Q^{\prime }$ are represented by big crosses. In the current iteration, we consider vertex v ∈ Q. Here, there is a task (dashed rectangle) from OPT_SL ∩ T^ℓ that covers v but no vertices in $Q^{\prime }$. Other rectangles are the other input rectangles of the same rounded size that cover v but no vertices in $Q^{\prime }$. We add to $T_{S}^{(2)}$ the two rectangles with farthest endpoints (in gray)

We prove some basic properties of the tasks in $T_{S}^{(1)}\cup T_{S}^{(2)}$.

Lemma 6

If the guesses are correct, the tasks in $T_{S}^{(1)}\cup T_{S}^{(2)}$ fulfill the following properties:

• 1. $|T_{S}^{(1)}\cup T_{S}^{(2)}|\le O(\epsilon k)$,

• 2. for each interval $\tilde {I}_{j}$ in which at least one task from OPT_SL starts or ends, the maximum demand of an edge $e\in \tilde {I}_{j}$ is upper-bounded by $4k\bar {b}_{j}$,

• 3. $|L|\le O_{\epsilon }(k\log k)$.

Proof

• 1. At the end of the construction of $T_{S}^{(1)}$, we have added, for each task in OPT_SL that starts in $\tilde {I}_{j}$ and ends in $\tilde {I}_{j^{\prime }}$: at most one task that starts in $\tilde {I}_{j}$ and ends in $\tilde {I}_{j^{\prime }}$; at most one task that covers $\tilde {I}_{j}$; and at most one task that covers $\tilde {I}_{j^{\prime }}$. Then, $|T_{S}^{(1)}|\le 3|OPT_{SL}|$. By the construction of $T_{S}^{(2)}$, each task of OPT_SL is guessed at most once (otherwise the second time this task would cover a vertex in $Q^{\prime }$). Since at most two tasks are added in $T_{S}^{(2)}$ after each correct guess, we have that $|T_{S}^{(2)}|\le 2|OPT_{SL}|$. We conclude using Lemma 5 that $|T_{S}^{(1)}\cup T_{S}^{(2)}|\le O(\epsilon |OPT|)=O(\epsilon k)$.

• 2. Property 2 follows since the size of the task i^∗ selected for $\tilde {I}_{j}$ is at least as large as the size of the largest task i ∈ S with $\tilde {I}_{j}\subseteq P(i)$ and each task i ∈ S starts or ends at a vertex in $\tilde {V}$.

• 3. Since |S|≤ 4k, we have $|\tilde V|\le 8k$ and then the number of intervals $\tilde I_{j}$ is 8k. For each interval $\tilde I_{j}$, the tasks with size between $\frac {1}{2k}\bar b_{j}$ and $4k \bar b_{j}$ are contained in at most $\log _{1+\epsilon } 8k^{2}$ groups T_ℓ. Thus, $|L|\le 8k\log _{1+\epsilon } 8k^{2} = O_{\epsilon }(k\log k)$.

□

Let now $V^{\prime }$ be the set of start- and endvertices of tasks in $S\cup T_{S}^{(1)}\cup T_{S}^{(2)}$ and let I₀ ∪ I₁ ∪⋯ ∪ I_r = E be the partition into subpaths defined by the vertices in $V^{\prime }$. In the following, we partition intervals into three groups according to the number of tasks from OPT that start or end in them. Given an interval I, let d be the number of tasks that start or end in I. Let $\alpha \in \{5,\dots ,5/{\epsilon }\}$ be a constant defined due to the following lemma. We say that I is sparse if d ≤ 1/𝜖^α, medium if 1/𝜖^α < d ≤ 1/𝜖^α+ 5 and dense if d > 1/𝜖^α+ 5. We will later make use of the fact that the number of tasks that start or end in sparse and dense intervals are a factor 1/𝜖⁵ apart.

Lemma 7

There exists an integer $\alpha \in \{5,\dots ,5/\epsilon \}$ such that the number of tasks in OPT that start or end in a medium interval is at most 2𝜖k.

Proof

Let m_α be the number of tasks from OPT that start or end in a medium interval, for a given α in {5,⋯ ,5/𝜖}. Remark that for any two distinct $\alpha ,\alpha ^{\prime }$ in $\{5t|t\in \{1,\dots ,1/\epsilon \}\}$, the corresponding sets of medium intervals are disjoints, so that each task starts or ends in a medium interval for at most two values in this set. Therefore, ${\sum }_{{t=1}}^{1/\epsilon }m_{5t}\le 2\vert OPT\vert \le 2k$, and in particular there exists an integer α in $\{5,\dots ,5/\epsilon \}$ such that m_α ≤ 2𝜖k. □

Algorithmically, we guess α and for each interval I_j we guess whether it is sparse, medium, or dense. Note that there are in total $\frac {5}{\epsilon }3^{O(k)}$ many guesses. We define now some more tasks (in addition to $T_{S}^{(1)}\cup T_{S}^{(2)}$) that will provide us with additional slack. For each medium or dense interval I_j we select the largest task i ∈ T such that $I_{j}\subseteq P(i)$. Also, for each maximal set of contiguous sparse intervals $I_{j}\cup I_{j+1}\cup \cdots \cup I_{j^{\prime }}=:\mathcal {I}$ we select the largest task i ∈ T such that $\mathcal {I}\subseteq P(i)$, if such a task exists. Let $T_{S}^{(3)}$ denote the resulting set of tasks. We call $T_{S}:=T_{S}^{(1)}\cup T_{S}^{(2)}\cup T_{S}^{(3)}$ the slack tasks. For each interval I_j we denote by $\hat {b}_{j}$ the slack in the interval given by T_S, i.e., $\hat {b}_{j}=\min \limits _{e\in I_{j}}p\left (T_{e}\cap T_{S}\right )$. To summarize, we obtained the following properties of our intervals and T_S.

Lemma 8

The tasks T_S and the intervals I₀,I₁,...,I_r have the following properties:

• $I_{0}\dot {\cup }I_{1}\dot {\cup }\cdots \dot {\cup }I_{r}$ is a partition of E into r + 1 = O(k) intervals

• |T_S|≤ O(𝜖k),

• for each edge e that is the leftmost or the rightmost edge of an interval I_j we have that there are at most 1/𝜖 tasks $i^{\prime }\in OPT\cap T_{e}$ such that $\hat {b}_{j}(1+\epsilon )<p_{i^{\prime }}<4k\hat {b}_{j}$,

• for each dense interval I_j we have that $\hat {b}_{j}\ge \frac {1}{4k}\max \limits _{e\in I_{j}}u_{e}$,

• for each maximal set of contiguous sparse intervals $I_{j}\cup I_{j+1}\cup \cdots \cup I_{j^{\prime }}=:\mathcal {I}$ we have that $\min \limits _{j^{\prime \prime }:j\le j^{\prime \prime }\le j^{\prime }}\hat {b}_{j^{\prime \prime }}$ is at least the size of the largest task i ∈ OPT with $\mathcal {I}\subseteq P(i)$, assuming that OPT contains such a task i.

Proof

We first show that |T_S|≤ O(𝜖k). In fact, note first that in $T_{S}^{(1)}$, if we guess correctly, we do not add more tasks than 3|OPT_SL|. Second, in $T_{S}^{(2)}$, if we guess correctly, we add at most |OPT_SL| new tasks until the queue Q empties. Third, in $T_{S}^{(3)}$ we add at most two tasks for each dense or medium interval, and the number of such intervals is at most 2|OPT|/𝜖^α. So in total we have at most O(𝜖k) tasks.

Now, consider an interval I_j. If no tasks from OPT_SL start or end in I_j, then we must have added to $T_{S}^{(1)}$ tasks that completely cover I_j as large as tasks in OPT_SL that completely cover I_j, if they exist. Thus, by Lemma 5, there are at most 1/𝜖 tasks in OPT ∩ T_e, for all e ∈ I_j that are larger than $\hat {b}_{j}$. If some task from OPT_SL starts or ends in I_j then we added a task i in $T_{S}^{(1)}$ that completely covers I_j, and thus u_e ≤ 4kp_i for all edges e ∈ I_j. And then in $T_{S}^{(2)}$ we added a task that completely covers I_j of level equal or higher as each task in OPT_SL that covers the outermost edges of I_j, because the outermost vertices of I_j must have been in Q in some iteration. Thus, by Lemma 5, there are no more than 1/𝜖 tasks in OPT of size larger than $\hat {b}_{j}(1+{\epsilon })$ using the leftmost or the rightmost edges of I_j.

By the definition of $T_{S}^{(3)}$, it contains for each dense or medium interval I_j, a task i such that $I_{j}\subseteq P(i)$ and of size as large as the task of maximum size of S that uses any edge of I_j. Thus $\hat {b}_{j}\geq p_{i}\geq \frac {1}{4k}\max \limits _{e\in I_{j}}u_{e}$. We also added for each maximal set of contiguous sparse intervals $\mathcal {I}$ the largest task i such that $\mathcal {I}\subseteq P(i)$, and thus $\max \limits _{i^{\prime }:\mathcal {I}\subseteq P(i^{\prime })}p_{i^{\prime }}\leq \min \limits _{I_{j}\subseteq \mathcal {I}}\hat {b}_{j}$. □

If T_S ∩ OPT = ∅ then OPT ∪ T_S is a solution of size (1 + O(𝜖))k in which each edge has some slack and hence we can use this slack algorithmically. We guess whether T_S ∩ OPT = ∅. If not, we guess OPT ∩ T_S and recurse on a new instance in which we assume that OPT ∩ T_S is already selected. Formally, this instance has input task $\bar {T}:=T\setminus (OPT\cap T_{S})$, each edge e ∈ E has demand $\bar {u}_{e}:=u_{e}-{\sum }_{i\in T_{e}\cap (OPT\cap T_{S})}p_{i}$, and the parameter is $\bar {k}:=k-|OPT\cap T_{S}|$. We will show later that the resulting recursion tree has size $k^{O(k^{2})}$. In the sequel, we will assume that OPT ∩ T_S = ∅ and solve the remaining problem without any further recursion in time f(k)n^O(1) for some function f.

5.1 Medium Intervals

We describe a routine that essentially allows us to reduce the problem to the case where there are no medium intervals. From Lemma 7 we know that there are at most 2𝜖k tasks in OPT that start or end in a medium interval. Therefore, for those tasks we can afford to make mistakes that cost us a constant factor, i.e., we can select O(𝜖k) instead of 2𝜖k of those tasks.

Let $T_{\text {med}}\subseteq T$ be the set of tasks that start or end in a medium interval. Let I_j be a medium interval. In OPT, the demand of the edges in I_j is partially covered by tasks i ∈ OPT ∖ T_med that completely cross I_j, i.e., such that $I_{j}\subseteq P(i)$. We guess an estimate for the total size of such tasks, i.e., an estimate for $\hat {p}_{j}=p\left (\left \{ i\in OPT\setminus {T_{\text {med}}}:I_{j}\subseteq P(i)\right \} \right )$. Formally, we guess $\hat {u}_{j}:=\lfloor \hat {p}_{j}/(\hat {b}_{j}/3)\rfloor$. The corresponding estimate of $\hat {p}_{j}$ is given by $\hat {u}_{j}\hat {b}_{j}/3$.

Lemma 9

We have that $\hat {u}_{j}\in \{0,...,3k\}$ and for each edge e ∈ I_j it holds that $p(T_{e}\cap OPT\cap {T_{\text {med}}})+\hat {u}_{j}\hat {b}_{j}/3+p(T_{e}\cap T_{S})\ge u_{e}$.

Proof

We first show that $\hat {u}_{j}\le 3k$. Since OPT has size k and T_S contains the largest input task that crosses I_j, no task in OPT ∖ T_med that crosses I_j can be larger than $\hat {b}_{j}$. Thus we have $\hat {p}_{j}/\hat {u}_{j}\le k$, which implies the claimed bound. Next, for each edge e ∈ I_j, we have

$$ \begin{array}{@{}rcl@{}} &&p(T_{e} \cap OPT\cap T_{\text{med}})+\hat{u}_{j}\hat{b}_{j}/3+p(T_{e}\cap T_{S})\\ & \ge& p(T_{e}\cap OPT\cap T_{\text{med}})+(p(T_{e}\cap OPT\setminus T_{\text{med}})-\hat{b}_{j}/3)+p(T_{e}\cap T_{S})\\ & \ge& p(T_{e}\cap OPT)\ge u_{e} . \end{array} $$

This gives the bound of the lemma. □

Since there are only O(k) intervals, there are only k^O(k) many guesses in total. We construct an auxiliary instance on the same graph G = (V,E) with input tasks T_med and demand $u_{e}^{\text {med}}=\max \limits \{u_{e}-p(T_{e}\cap (T_{S}))-\hat {u}_{\ell }\hat {b}_{\ell }/3,0\}$ for each e ∈ E in a medium interval, and $u_{e}^{\text {med}}=0$ for each edge e ∈ E in a sparse or dense interval. We run the 4-approximation algorithm [5] on this instance, obtaining a set of tasks $T_{\text {med}}^{\prime }\subseteq T_{\text {med}}$.

Lemma 10

In time n^O(1) we can compute a set $T_{\text {med}}^{\prime }\subseteq T_{\text {med}}$ with $|T_{\text {med}}^{\prime }|\le 4|OPT\cap T_{\text {med}}|\le O(\epsilon k)$ such that $p(T_{\text {med}}^{\prime }\cap T_{e})\ge u_{e}^{\text {med}}$ for each edge e ∈ E.

For our remaining computation for each medium interval I_j we define the demand u_e of each edge e ∈ I_j to be $u_{e}:=\hat {u}_{j}\hat {b}_{j}/3$. Lemma 9 implies that any solution $T^{\prime }$ for this changed instance yields a solution $T^{\prime }\cup T_{\text {med}}^{\prime }\cup T_{S}$ with at most $|T^{\prime }|+O(\epsilon k)$ tasks for the original instance. In the sequel, denote by $OPT^{\prime }$ the optimal solution to the new instance.

5.2 Heavy Vertices

Our strategy is to decouple the sparse and dense intervals. A key problem is that there are tasks $i\in OPT^{\prime }$ such that P(i) contains edges in sparse and in dense intervals. Intuitively, our first step is therefore to guess some of them in an approximate way.

There are vertices $v\in V^{\prime }$ that are used by many tasks in $OPT^{\prime }\cap T^{\ell }$ for some level ℓ. Formally, we say that for a set of tasks $T^{\prime }\subseteq T$ a vertex $v\in V^{\prime }$ is $(\ell ,T^{\prime })$-heavy if there are more than 1/𝜖^α+ 1 tasks $i\in T^{\prime }\cap T^{\ell }\cap T_{v}$ such that i starts or ends in a sparse or a medium interval. We are interested in vertices $v\in V^{\prime }$ that are $(\ell ,OPT^{\prime })$-heavy for some ℓ. It turns out that we can compute a small number of levels ℓ for which this can happen based on the slacks $\hat {b}_{j}$ of the intervals I_j.

Lemma 11

By losing half of the slack in each interval, we can assume that if $v\in V^{\prime }$ is $(\ell ,OPT^{\prime })$-heavy for some $\ell \in \mathbb {N}_{0}$, then $(1+\varepsilon )^{\ell }\in [\frac {1}{2k}\hat {b}_{j},4k\cdot \hat {b}_{j}]$ for some interval I_j.

Proof

Let $OPT^{\prime }_{small}:=\left \{ i\in OPT^{\prime }\mid p_{i}\le \frac {1}{2k}\min \limits _{j}\hat {b}_{j} \right \}$. This set covers in total a very small demand that can be compensated by the slack. Precisely, we have that for each edge e, and for each interval I_j, $p(T_{e}\cap OPT^{\prime }_{small})\le \frac {k}{2k}\hat {b}_{j}=\hat {b}_{j}/2$. Then, we can simply “forget” these tasks, by covering the corresponding demand by half of the slack, and then use the other half for the remaining computation. Any task from the remaining instance has now size at least $\frac {1}{2k}\hat {b}_{j}$ for at least one interval I_j. To prove that for some j it also holds that $(1+\epsilon )^{\ell }\leq 4k\hat {b}_{j}$, we take I_j as the interval closest to v to the right or to the left such that $(1+\epsilon )^{\ell }\geq \frac {1}{2k}\hat {b}_{j}$ and at least (1/𝜖^α+ 1)/2 tasks from $OPT^{\prime }\cap T^{\ell } \cap T_{v}$ use an edge of I_j. W.l.o.g. assume I_j is to the right of v. Then, the leftmost edge of I_j is used by more than 1/𝜖 tasks and then OPT_SL contains a task of size at least (1 + 𝜖)^ℓ that covers that edge. When constructing $T_{S}^{(2)}$ the start-vetex of I_j must have been an interesting vertex, so $T_{S}^{(2)}$ contains a task that covers I_j of size at least (1 + 𝜖)^ℓ, so $(1+\epsilon )^{\ell } \leq \hat {b}_{j}$. □

Therefore, let L denote the set of levels ℓ such that a vertex $v\in V^{\prime }$ can be $(\ell ,OPT^{\prime })$-heavy according to Lemma 11, i.e., $L:=\{\ell |\exists j:(1+\varepsilon )^{\ell }\in [\frac {1}{2k}\hat {b}_{j},4k\cdot \hat {b}_{j}]\}$. Intuitively, for each level ℓ ∈ L and each $(\ell ,OPT^{\prime })$-heavy vertex $v\in V^{\prime }$ we want to select a set of tasks $\bar {T}_{\ell ,v}\subseteq T^{\ell }\cap T_{v}$ that together cover as much as the tasks in $OPT^{\prime }$ due to which v is $(\ell ,OPT^{\prime })$-heavy, i.e., the tasks in $OPT^{\prime }\cap T^{\ell }\cap T_{v}$.

To this end, we do the following operation for each level ℓ ∈ L. We perform several iterations. We describe now one iteration and assume that $v^{\prime }\in V^{\prime }$ is the vertex that we processed in the previous iteration (at the first iteration $v^{\prime }$ is undefined and let $T_{v^{\prime }}:=\emptyset$ in this case). See Fig. 4 for a sketch of the strategy. Recall that $V^{\prime }$ is the set of start- and endvertices of the tasks in $S\cup T_{S}^{(1)} \cup T_{S}^{(2)}$, so $|V^{\prime }|=O(k)$. We guess the leftmost vertex $v\in V^{\prime }$ on the right of $v^{\prime }$ that is $(\ell ,OPT^{\prime }\setminus T_{v^{\prime }})$-heavy. Let $OPT^{\prime }_{\ell ,v}:=OPT^{\prime }\cap T^{\ell }\cap T_{v}\setminus T_{v^{\prime }}$. We want to compute a set $\bar {T}_{\ell ,v}$ that is not much bigger than $OPT^{\prime }_{\ell ,v}$, i.e., $|\bar {T}_{\ell ,v}|\le (1+O(\epsilon ))|OPT^{\prime }_{\ell ,v}|$ and that covers at least as much on each edge e as $OPT^{\prime }_{\ell ,v}$, i.e., $p(T_{e}\cap \bar {T}_{\ell ,v})\ge p(T_{e}\cap OPT^{\prime }_{\ell ,v})$. We initialize $\bar {T}_{\ell ,v}:=\emptyset$. We consider each pair of intervals I_j and $I_{j^{\prime }}$ such that all edges of I_j are on the left of v (but might have v as an endpoint) and all edges of $I_{j^{\prime }}$ are on the right of v (but might have v as an endpoint) and such that I_j or $I_{j^{\prime }}$ is sparse or medium. We guess the number $k_{j,j^{\prime }}^{v,\ell }$ of tasks from $OPT^{\prime }\cap T^{\ell }\cap T_{v}\setminus T_{v^{\prime }}$ that start in I_j and end in $I_{j^{\prime }}$ (and hence are contained in T_v). If I_j is sparse or medium (and hence then $I_{j^{\prime }}$ can be anything), we add to $\bar {T}_{\ell ,v}$ the $k_{j,j^{\prime }}^{v,\ell }$ tasks from $T^{\ell }\setminus T_{v^{\prime }}$ with rightmost endvertex that start in I_j and end in $I_{j^{\prime }}$. If I_j is dense (and hence then $I_{j^{\prime }}$ is sparse or medium) we add to $\bar {T}_{\ell ,v}$ the $k_{j,j^{\prime }}^{v,\ell }$ tasks from $T^{\ell }\setminus T_{v^{\prime }}$ with leftmost startvertex that start in I_j and end in $I_{j^{\prime }}$. Note that ${\sum }_{j,j^{\prime }}k_{j,j^{\prime }}^{v,\ell }=|OPT^{\prime }_{\ell ,v}|$. Intuitively, the tasks in $\bar {T}_{\ell ,v}$ cover each edge of E to a similar extent as the tasks in $OPT^{\prime }_{\ell ,v}$. We will show that the difference is compensated by additionally adding the following tasks to $\bar {T}_{\ell ,v}$: we add to $\bar {T}_{\ell ,v}$ the $\lfloor 2/{\epsilon }^{\alpha }+2{\epsilon }|OPT^{\prime }_{\ell ,v}|\rfloor$ tasks from $T^{\ell }\cap T_{v}\setminus (\bar {T}_{\ell ,v}\cup T_{v^{\prime }})$ with leftmost start vertex. After this, we add to $\bar {T}_{v}^{\ell }$ the $\lfloor 2/{\epsilon }^{\alpha }+2{\epsilon }|OPT^{\prime }_{\ell ,v}|\rfloor$ tasks from $T^{\ell }\cap T_{v}\setminus (\bar {T}_{\ell ,v}\cup T_{v^{\prime }})$ with rightmost end vertex. Let $\bar {T}_{\ell ,v}$ denote the resulting set. We prove that it covers as much as $OPT^{\prime }_{\ell ,v}$ and that it is not much bigger than $|OPT^{\prime }_{\ell ,v}|$.

Fig. 4

Sketch of the strategy to select tasks of level ℓ that cross a heavy vertex v but not $v^{\prime }$. For each pair of intervals $I_{j},I_{j^{\prime }}$ we guess $k_{j,j^{\prime }}^{v,\ell }$ the number of tasks from $OPT^{\prime }_{\ell ,v}$ that start in I_j and end in $I_{j^{\prime }}$, and select tasks accordingly. Then, from the unselected tasks of T_v, we add the $\lfloor 2/\epsilon ^{\alpha }+2\epsilon |OPT^{\prime }_{\ell ,v}|\rfloor$ longest to the left and the $\lfloor 2/\epsilon ^{\alpha }+2\epsilon |OPT^{\prime }_{\ell ,v}|\rfloor$ longest to the right to compensate the different sizes within T^ℓ and the errors we made within each interval. Adding these extra tasks is not too costly because at least 1/𝜖^α+ 1 tasks cross v, and therefore, they are at most $O(\epsilon )\cdot |OPT^{\prime }_{\ell ,v}|$

Lemma 12

For each edge e ∈ E in a dense or a sparse interval, we have that $p(T_{e}\cap \bar {T}_{\ell ,v})\ge p(T_{e}\cap OPT^{\prime }_{\ell ,v})$. For each edge e in a medium interval, we have that $p(T_{e}\cap \bar {T}_{\ell ,v}\setminus {T_{\text {med}}})\ge p(T_{e}\cap OPT^{\prime }_{\ell ,v}\setminus {T_{\text {med}}})$. Also, it holds that $|\bar {T}_{\ell ,v}|\le (1+O(\epsilon ))|OPT^{\prime }_{\ell ,v}|$.

Proof

Let $\bar {T}^{\prime }_{\ell ,v}$ denote the set $\bar {T}_{\ell ,v}$ after the first phase of the procedure, that is before adding the $\lfloor 2/{\epsilon }^{\alpha }+2{\epsilon }|OPT^{\prime }\cap T^{\ell }\setminus T_{v^{\prime }}|\rfloor$ tasks with leftmost startvertex. We assume that our guesses are correct and then in particular $\vert \bar {T}^{\prime }_{\ell ,v}\vert =\vert OPT^{\prime }_{\ell ,v}\vert$.

Let e ∈ E be an edge on the left-hand (resp. right-hand) side of v that lies in an dense or sparse interval I_j. The number of task from $\bar {T}^{\prime }_{\ell ,v}$ and $OPT^{\prime }_{\ell ,v}$ that start in some interval $I_{j^{\prime }}$ on the left-hand (resp. right-hand) side of I_j, i.e. with $j^{\prime }<j$ (resp. $j^{\prime }>j$), is equal if we have guessed correctly. When I_j is dense, since we added some tasks with leftmost startvertex (resp. rightmost endvertex), the number of tasks that start (resp. end) in I_j and intersect e is greater in $\bar {T}^{\prime }_{\ell ,v}$ than in $OPT^{\prime }_{\ell ,v}$. It follows that $\vert \bar {T}^{\prime }_{\ell ,v}\cap T_{e}\vert \ge \vert OPT^{\prime }_{\ell ,v}\cap T_{e}\vert$. However, this might not be true when I_j is sparse. Fortunately, the number of such tasks from $OPT^{\prime }_{\ell ,v}$ is bounded by 1/𝜖^α so that $\vert \bar {T}^{\prime }_{\ell ,v}\cap T_{e}\vert \ge \vert OPT^{\prime }_{\ell ,v}\cap T_{e}\vert -1/\epsilon ^{\alpha }$.

In all cases, the remaining uncovered demand $p(OPT^{\prime }_{\ell ,v}\cap T_{e})-p(\bar {T}^{\prime }_{\ell ,v}\cap T_{e})$ due to rounded sizes is at most $(1+\epsilon )^{\ell }\cdot (\epsilon \vert OPT^{\prime }_{\ell ,v}\cap T_{e}\vert +1/\epsilon ^{\alpha })$. This difference is compensated by the $\lfloor 2/\epsilon ^{\alpha }+2\epsilon |OPT^{\prime }_{\ell ,v}|\rfloor$ additional tasks with leftmost startvertex (resp. rightmost endvertex) added in $\bar {T}_{\ell ,v}$ at the end of the procedure. Indeed, assume first that all these tasks cover e. The additional demand covered is then at least $(1+\epsilon )^{\ell }\cdot \lfloor 2/{\epsilon }^{\alpha }+2{\epsilon }|OPT^{\prime }_{\ell ,v}|\rfloor \ge (1+\epsilon )^{\ell }\cdot (1/{\epsilon }^{\alpha }+{\epsilon }|OPT^{\prime }_{\ell ,v}|)$. On the other hand, if not all of them contain e then it means that $\bar {T}_{\ell ,v}$ contains all the tasks in T^ℓ ∩ T_e ∩ T_v that start or end in a sparse interval, and in particular $OPT^{\prime }_{\ell ,v}\cap T_{e}\subseteq \bar {T}_{\ell ,v}$ so that $p(\bar {T}_{\ell ,v}\cap T_{e})\ge p(OPT^{\prime }_{\ell ,v}\cap T_{e})$. When e is in a medium interval the proof works similarly, using additionally the estimation due to Lemma 9. Notice that thanks to this lemma we do not need to cover e using tasks from T_med and all other tasks intersecting e cross completely the medium interval. Finally, $\bar {T}_{\ell ,v}$ is not much bigger than $OPT^{\prime }_{\ell ,v}$. Indeed,

$$ \begin{array}{@{}rcl@{}} \vert\bar{T}_{\ell,v}\vert&\le&\vert\bar{T}^{\prime}_{\ell,v}\vert+\lfloor2/\epsilon^{\alpha}+2\epsilon|OPT^{\prime}_{\ell,v}|\rfloor\le\vert OPT^{\prime}_{\ell,v}\vert+2/{\epsilon}^{\alpha}+2{\epsilon}|OPT^{\prime}_{\ell,v}|\\&\le&(1+4\epsilon)\vert OPT^{\prime}_{\ell,v}\vert . \end{array} $$

The last inequality uses the fact that v is heavy, so that $1/\epsilon ^{\alpha }\le \epsilon |OPT^{\prime }_{\ell ,v}|$. That concludes the proof. □

We continue with the next iteration where now $v^{\prime }$ is defined to be the vertex v from above. We continue until in some iteration there is no vertex $v\in V^{\prime }$ on the right of $v^{\prime }$ that is $(\ell ,OPT^{\prime }\setminus T_{v^{\prime }})$-heavy. Let $V^{\prime }_{\ell }\subseteq V^{\prime }$ denote all vertices that at some point were guessed as being the $(\ell ,OPT^{\prime }\setminus T_{v^{\prime }})$-heavy vertex v above. Let $T_{H}:=\bigcup _{\ell \in L}\bigcup _{v\in V_{\ell }^{\prime }}\bar {T}_{\ell ,v}$ denote the set of computed tasks and define $OPT^{\prime }_{H}:=\bigcup _{\ell \in L}\bigcup _{v\in V_{\ell }^{\prime }}OPT^{\prime }_{\ell ,v}$.

Lemma 13

We have that $p(T_{e}\cap T_{H})\ge p(T_{e}\cap OPT^{\prime }_{H})$ for each edge e in a dense and a sparse interval, and $p(T_{e}\cap T_{H}\setminus {T_{\text {med}}})\ge p(T_{e}\cap OPT^{\prime }_{H}\setminus {T_{\text {med}}})$ for each edge e in a medium interval. Also, it holds that $|T_{H}|\le (1+O(\epsilon ))|OPT^{\prime }_{H}|$.

Proof

This follows directly from Lemma 12 applied to all $(\bar {T}_{\ell ,v})_{\ell ,v}$ and $(OPT^{\prime }_{\ell ,v})_{\ell ,v}$ that are pairwise disjoint. □

Lemma 14

For computing the set T_H there are at most k^O(k) possibilities for all guesses overall. Given the correct guess we can compute the resulting set T_H in time n^O(1).

Proof

Denote an operation of guessing $k^{v,\ell }_{j,j^{\prime }}$ tasks for the pair of intervals $I_{j},I_{j^{\prime }}$, for vertex v and level ℓ by the tuple $(\ell ,v,I_{j},I_{j^{\prime }},k^{v,\ell }_{j,j^{\prime }})$. Note that there are $|L|\cdot |V^{\prime }|\cdot O(k^{2})\cdot k = k^{O(1)}$ possible operations, and that we can make at most k operations where $k^{v,\ell }_{j,j^{\prime }}>0$ (otherwise we are adding too many tasks). Therefore, we have at most $\binom {k^{O(1)}}{k} = k^{O(k)}$ possibilities for all guesses. For each guess we can compute the resulting set T_H easily in time n^O(1) by simply selecting the corresponding tasks. □

It remains to compute a set of tasks $T^{\prime }$ such that $T^{\prime }\cup T_{H}\cup T_{S}$ is feasible. Intuitively, $T^{\prime }$ should cover as much as $OPT^{\prime }\setminus OPT^{\prime }_{H}$ on each edge. To this end, we decouple the problem into one for the dense intervals and one for the sparse intervals.

5.3 Dense Intervals

Recall that for each dense interval I_j we have that $\hat {b}_{j}\ge \frac {1}{4k}\max \limits _{e\in I_{j}}u_{e}$ (see Lemma 8). Hence, intuitively it suffices to compute a solution for I_j that is feasible under $(1+\frac {1}{4k})$-resource augmentation. So in order to compute a set of tasks $T^{\prime }$ that cover the remaining demand in all dense intervals I_j (after selecting T_H) we could apply the algorithm for resource augmentation from Section 3 directly as a black box. However, there are also the sparse intervals and it might be that there are tasks $i\in OPT^{\prime }\setminus OPT^{\prime }_{H}$ that are needed for a dense interval and for a sparse interval. We want to split the remaining problem into two disjoint subproblems. To this end, let $T_{D}\subseteq T$ denote the set of all tasks that start and end in a dense interval. We guess an estimate for the demand that such tasks cover in the sparse intervals. Therefore, for each sparse interval $I_{j^{\prime }}$ we guess a value $\hat {u}_{j^{\prime }}$ such that $\hat {u}_{j^{\prime }}=\left \lfloor \frac {p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})}{\hat {b}_{j}/4}\right \rfloor \cdot \hat {b}_{j}/4$ for each edge $e\in I_{j^{\prime }}$ (note that $p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})$ is identical for each edge $e\in I_{j^{\prime }}$). Then $p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})$ essentially equals $\hat {u}_{j^{\prime }}$ and we show that the difference is compensated by our slack, even if we cover a bit less than $\hat {u}_{j^{\prime }}$ units on each edge $e\in I_{j^{\prime }}$.

Lemma 15

Let $I_{j^{\prime }}$ be a sparse interval. Then $\hat {u}_{j^{\prime }}\in \left \{0,\frac {\hat {b}_{j}}{4},2\cdot \frac {\hat {b}_{j}}{4},\dots ,4k\cdot \frac {\hat {b}_{j}}{4}\right \}$ and $\hat {u}_{j^{\prime }}\le p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})\le \frac {1}{(1+\frac {1}{4k})}\hat {u}_{j^{\prime }}+p(T_{e}\cap T_{S})/2$ for each $e\in I_{j^{\prime }}$.

Proof

The inequality $\hat {u}_{j^{\prime }}\le p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})$ follows directly from the definition of $\hat {u}_{j^{\prime }}$. Moreover, either $p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})=0$ and the statement is true, or $\hat {b}_{j}$ is at least the size of the largest task that crosses $I_{j^{\prime }}$. It implies that $p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})\le k\cdot \hat {b}_{j}$. Finally, it follows from the inequality $1-\frac {1}{1+x}\le x$ that

$$ \begin{array}{@{}rcl@{}} &&p(T_{e}\cap T_{D}\cap OPT^{\prime}\setminus OPT^{\prime}_{H})-\frac{1}{(1+\frac{1}{4k})}\hat{u}_{j^{\prime}}\\&=& {\left( p(T_{e}\cap T_{D}\cap OPT^{\prime}\setminus OPT^{\prime}_{H})-\hat{u}_{j^{\prime}}\right)+\left( \hat{u}_{j^{\prime}}-\frac{1}{(1+\frac{1}{4k})}\hat{u}_{j^{\prime}}\right) }\\ &\le& { \frac{\hat{b}_{j}}{4}+ \frac{1}{4k}\hat{u}_{j^{\prime}} \le\frac{\hat{b}_{j}}{4}+\frac{1}{4k}\cdot k\cdot \hat{b}_{j} } = \frac{\hat{b}_{j}}{2}\le p(T_{e}\cap T_{S})/2 . \end{array} $$

□

We generate now an auxiliary instance where in each sparse interval $I_{j^{\prime }}$ we reduce the demand u_e of each edge $e\in I_{j^{\prime }}$ to $\hat {u}_{j^{\prime }}$ (but do not change the demand on any edge in a dense interval) and remove all input tasks i such that P(i) does not contain an edge of a dense interval. Also, for each remaining task i we shorten its path P(i) to a path $P^{\prime }(i)$ such that $P^{\prime }(i)$ is the longest path contained in P(i) that starts and ends on a vertex in a dense interval. We apply the algorithm from Section 3 with (1 + δ)-resource augmentation to this instance with δ := 1/4k. We obtain a solution T⁽¹⁾ such that for each edge e in an interval I_j, the solution T⁽¹⁾ covers at least $u_{e}-\hat {b}_{j}/2$ when I_j is dense and $\hat {u}_{j}-\hat {b}_{j}/2$ when I_j is sparse. Notice that according to Lemma 8, we have $\hat {b}_{j}\ge u_{e}/(4k)$ for each edge e in a dense interval I_j and for each edge e lying in a maximal set of contiguous sparse intervals that is completely crossed by at least one input task.

Lemma 16

In time $k^{O(k^{2}\log k)}\cdot n^{O(1)}$ we can compute a set T⁽¹⁾ such that

• for each edge e in a dense interval we have that p(T_e ∩ (T⁽¹⁾ ∪ T_H ∪ T_S)) ≥ u_e,

• for each edge e in a sparse interval $I_{j^{\prime }}$ we have that $p(T_{e}\cap T^{(1)}\cap T_{D})+p(T_{e}\cap T_{S})/2\ge p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})$.

Proof

For each edge e in a dense interval, either T⁽¹⁾ cover all the demand u_e or the uncovered demand is at most $\frac {1}{4k}p(T_{e}\cap (OPT^{\prime }\setminus OPT^{\prime }_{H}))\le \frac {1}{4k}u_{e}$. Then, using the fact that the slack is large enough, i.e. $\hat {b}_{j}\ge \frac {1}{4k}u_{e}$ (Lemma 8) and the fact that T_H covers at least as much as $OPT^{\prime }_{H}$ (Lemma 13), we have

$$ \begin{array}{@{}rcl@{}} &&p \left( T_{e}\cap\left( T^{(1)}\cup T_{H}\cup T_{S}^{(2)}\right)\right)=p\left( T_{e}\cap T^{(1)}\right)+p\left( T_{e}\cap T_{H}\right)+p(T_{e}\cap T_{S})\\ & \ge&\frac{1}{1+\frac{1}{4k}}p\left( T_{e}\cap(OPT^{\prime}\setminus OPT^{\prime}_{H})\right)+p\left( T_{e}\cap OPT^{\prime}_{H}\right)+\hat{b}_{j}\\ & \ge&\left( 1-\frac{1}{4k}\right)p\left( T_{e}\cap(OPT^{\prime}\setminus OPT^{\prime}_{H})\right)+p\left( T_{e}\cap OPT^{\prime}_{H}\right)+\frac{1}{4k}u_{e}\\&\ge& p\left( T_{e}\cap OPT^{\prime}\right)\ge u_{e} . \end{array} $$

For each edge e in a sparse interval $I_{j^{\prime }}$, we apply Lemma 15 observing that the solution T⁽¹⁾ ∩ T_D covers at least $\frac {1}{1+\frac {1}{4k}}\hat {u}_{j^{\prime }}$. □

Due to Lemma 16 the set T⁽¹⁾ ∪ T_H ∪ T_S covers the complete demand in each dense interval and some portion of the demand in each sparse interval. Therefore, for the remaining problem for each edge e in a sparse interval $I_{j^{\prime }}$ we change its demand to $\bar {u}_{e}:=u_{e}-\hat {u}_{j^{\prime }}$. Also, we remove all tasks in T_D from the input, i.e., we work with the input tasks $\bar {T}:=T\setminus T_{D}$. We claim that $\overline {OPT}:=OPT^{\prime }\setminus \left (OPT^{\prime }_{H}\cup T_{D}\right )$ is a solution to the residual instance.

Lemma 17

For each edge e in a sparse interval we have that $p(T_{e}\cap \overline {OPT})\ge \bar {u}_{e}$.

Proof

Follows from the fact that $\hat {u}_{j^{\prime }}$ is a lower bound on $p(T_{e}\cap T_{D}\cap OPT^{\prime }\setminus OPT^{\prime }_{H})$, for each edge e in a sparse interval. □

5.4 Sparse Intervals

Recall that in each sparse interval $I_{j^{\prime }}$ there are at most 1/𝜖^α tasks from OPT that start or end in $I_{j^{\prime }}$ (and hence the same is true for $\overline {OPT}\subseteq OPT$). Therefore, for each sparse interval we can guess these tasks in time $n^{O(1/\epsilon ^{\alpha })}$. Unfortunately, there can be up to Ω(k) sparse intervals, and therefore we cannot guess all these tasks directly. However, note that each vertex $v\in V^{\prime }$ is used by at most 1/𝜖^α+ 1 tasks in $\overline {OPT}\cap T^{\ell }$ for each group T^ℓ. Using this, we devise a dynamic program (DP) that processes the intervals in the order of their slacks $\hat {b}_{j}$ and guesses step by step the at most 1/𝜖^α tasks that start or end in each of them. In order to restrict the number of DP-cells (and thus the running time) to a polynomial, we use the tasks in T_S in order to “forget” some previously guessed tasks, i.e., we argue that the forgotten tasks have a total size that is at most the size of the slack due to T_S. Let us define a constant $\beta :=1+\log _{1+\epsilon }\left (\frac {6}{\epsilon ^{\alpha +2}}\right )$ and a constant Γ := 1/𝜖^α + 1/𝜖 + (β + 2)/𝜖^α+ 1. Formally, each DP-cell is described by

• two intervals $I_{j},I_{j^{\prime }}$ such that for each interval $I_{j^{\prime \prime }}$ between I_j and $I_{j^{\prime }}$ it holds that $\hat {b}_{j^{\prime \prime }}\ge \max \limits \{\hat {b}_{j},\hat {b}_{j^{\prime }}\}$,

• two sets of tasks $T^{\prime }_{j}$ and $T^{\prime }_{j^{\prime }}$ of size at most Γ such that for each $i\in T^{\prime }_{j}$ (resp. $i\in T^{\prime }_{j^{\prime }}$) it holds that P(i) ∩ I_j≠∅ (resp. $P(i)\cap I_{j^{\prime }}\ne \emptyset$) and $p(T_{e}\cap T^{\prime }_{j})+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$ (resp.$p(T_{e}\cap T^{\prime }_{j^{\prime }})+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$) for each edge e ∈ I_j (resp. $e\in I_{j^{\prime }}$), i.e., the tasks in $T^{\prime }_{j}$ (resp. $T^{\prime }_{j^{\prime }}$) essentially cover the demand of I_j (resp. $I_{j^{\prime }}$).

Such a cell $(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ represents the subproblem of selecting a set of tasks $\hat {T}$ such that the path of each task $i\in \hat {T}$ lies between I_j and $I_{j^{\prime }}$ and does not use any edge of $I_{j}\cup I_{j^{\prime }}$ and such that $T^{\prime }_{j}\cup T^{\prime }_{j^{\prime }}\cup \hat {T}$ cover the demand $\bar {u}_{e}$ for each edge between I_j and $I_{j^{\prime }}$ together with half of the slack, i.e., $p(T_{e}\cap (T^{\prime }_{j}\cup T^{\prime }_{j^{\prime }}\cup \hat {T}))+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$.

Suppose we are given a cell $(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ and we want to compute a solution $DP(I_{j},I_{j^{\prime }}, T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ for it. Let $I_{j^{\prime \prime }}$ denote the interval between I_j and $I_{j^{\prime }}$ with smallest slack $\hat {b}_{j^{\prime \prime }}$ (breaking ties arbitrarily). Let $\ell ^{\prime \prime }$ be the greatest integer such that $(1+\epsilon )^{\ell ^{\prime \prime }}\le \hat {b}_{j^{\prime \prime }}$. Let $T^{\ge \ell ^{\prime \prime }-\beta }:=\bigcup _{\ell \ge \ell ^{\prime \prime }-\beta }T^{\ell }$. The intuition is that we guess the tasks in $\overline {OPT}$ that use $I_{j^{\prime \prime }}$ and when we recurse we forget all tasks that are not in $T^{\ge \ell ^{\prime \prime }-\beta }$. We will show that our slack compensates the forgotten tasks. Therefore, we can ensure that if we always guess all tasks from $\overline {OPT}$ correctly then we will have only subproblems $(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ where $|T^{\prime }_{j}|\le {\Gamma }$ and $|T^{\prime }_{j^{\prime }}|\le {\Gamma }$. Formally, we enumerate all sets of tasks $T^{\prime }_{j^{\prime \prime }}\subseteq T^{\ge \ell ^{\prime \prime }-\beta }$ such that there are at most Γ tasks in $T^{\prime }_{j^{\prime \prime }}$, $P(i)\cap I_{j^{\prime \prime }}\ne \emptyset$ for each $i\in T^{\prime }_{j^{\prime \prime }}$, and the tasks in $T^{\prime }_{j^{\prime \prime }}$ cover the demand of $I_{j^{\prime \prime }}$ together with half of the slack in T_S, i.e., $p(T_{e}\cap T^{\prime }_{j^{\prime \prime }})+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$ for each edge $e\in I_{j^{\prime \prime }}$. For a fixed guess of $T^{\prime }_{j^{\prime \prime }}$ we associate the solution $T^{\prime }_{j}\cup T^{\prime }_{j^{\prime }}\cup T^{\prime }_{j^{\prime \prime }}\cup DP(I_{j},I_{j^{\prime \prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime \prime }})\cup DP(I_{j^{\prime \prime }},I_{j^{\prime }},T^{\prime }_{j^{\prime \prime }},T^{\prime }_{j^{\prime }})$. We define $DP(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ to be the solution of minimum size associated to one of the enumerated sets $T^{\prime }_{j^{\prime \prime }}$. For DP-cells $(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$ such that there is no interval between I_j and $I_{j^{\prime }}$ we define $DP(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }}):=\emptyset$. See Fig. 5 for a sketch of the recursion. For convenience, assume that we append two dummy intervals I_− 1 and I_r+ 1 on the left and on the right of E that are not used by any task and that have zero demand on each of their edges. Also, we define them to have zero slack, i.e., $\hat {b}_{-1}=\hat {b}_{r+1}=0$. We output the solution DP(I_− 1,I_r+ 1,∅,∅).

Fig. 5

Sketch of a recursive call of the DP to cover sparse intervals. The subproblem is defined by intervals I_j and $I_{j^{\prime }}$, and sets of at most Γ tasks $T^{\prime }_{j}$ and $T^{\prime }_{j^{\prime }}$ that cover them, and such that all intervals in between have more slack than $\max \limits \{\hat {b}_{j},\hat {b}_{j^{\prime }}\}$. We find $I_{j^{\prime \prime }}$, an interval of smallest slack between I_j and $I_{j^{\prime }}$, guess the at most Γ tasks in $T^{\protect \geq \ell ^{\prime \prime }-\beta }$ needed to cover its demand, and recurse between I_j and $I_{j^{\prime \prime }}$ and between $I_{j^{\prime \prime }}$ and $I_{j^{\prime }}$. Tasks that are too small (that are not in $T^{\protect \geq \ell ^{\prime \prime }-\beta }$) can be forgotten because they are compensated by the slack

In order to show that the above DP is correct, one key step is to argue that it is unproblematic to neglect the tasks that are not in $T^{\ge \ell ^{\prime \prime }-\beta }$ in each respective step. This is shown in the following lemma.

Lemma 18

Let $I_{j},I_{j^{\prime }}$ be two intervals such that for each interval $I_{j^{\prime \prime }}$ between I_j and $I_{j^{\prime }}$ it holds that $\hat {b}_{j^{\prime \prime }}\ge \max \limits \{\hat {b}_{j},\hat {b}_{j^{\prime }}\}$. Let $\ell ^{\prime \prime }$ be the greatest integer such that $(1+\epsilon )^{\ell ^{\prime \prime }}\le \hat {b}_{j^{\prime \prime }}$ for all intervals $I_{j^{\prime \prime }}$ between I_j and $I_{j^{\prime }}$. Then for each edge e between I_j and $I_{j^{\prime }}$ it holds that ${p}\left (T_{e}\cap \overline {OPT}\cap T^{\ge \ell ^{\prime \prime }-\beta }\right )+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$.

Proof

For each level ℓ , we have $\vert T^{\ell }\cap T_{e}\cap \overline {OPT}\vert \le 3/\epsilon ^{\alpha +1}$. This is because edge e must belong to a sparse interval $I_{j^{\prime \prime }}$, and all tasks in $T_{e}\cap \overline {OPT}$ either use the leftmost or the rightmost edge of $I_{j^{\prime \prime }}$, or start or end in $I_{j^{\prime \prime }}$. At most 2/𝜖^α+ 1 tasks in $T^{\ell }\cap T_{e}\cap \overline {OPT}$ use the leftmost or rightmost edge of $I_{j^{\prime \prime }}$ because there are no heavy vertices, and only 1/𝜖^α tasks start or end in $I_{j^{\prime \prime }}$. Then,

$$ \begin{array}{@{}rcl@{}} {p} \left( T_{e}\cap\overline{OPT}\setminus T^{\ge\ell^{\prime\prime}-\beta}\right)\!&\le&\!\sum\limits_{\ell<\ell^{\prime\prime}-\beta}\frac{3}{\epsilon^{\alpha+1}}\cdot(1+\epsilon)^{\ell+1}\le\frac{3}{\epsilon^{\alpha+1}}\cdot\frac{(1+\epsilon)^{\ell^{\prime\prime}-\beta+1}}{\epsilon}\\ \!& \le&\!\frac{3(1 + \epsilon)^{\ell^{\prime\prime}-\beta+1}}{(1 + \epsilon)^{\log_{1+\epsilon}\epsilon^{\alpha+2}}}\!\le\!(1 + \epsilon)^{\ell^{\prime\prime}}/2\!\le\!\hat{b}_{j^{\prime\prime}}/2\!\le\! p(T_{e}\cap T_{S})/2. \end{array} $$

This inequality together with Lemma 17 imply the inequality claimed. □

Also, we need to show that when we enumerate the sets $T^{\prime }_{j^{\prime \prime }}$ above, one candidate set consists of the tasks in $\overline {OPT}$ that use $I_{j^{\prime \prime }}$ but neither I_j nor $I_{j^{\prime }}$ and that in particular the latter set contains at most Γ tasks.

Lemma 19

Let $I_{j^{\prime \prime }}$ be a sparse interval and let $\ell ^{\prime \prime }$ be the greatest integer such that $(1+\epsilon )^{\ell ^{\prime \prime }}\le \hat {b}_{j^{\prime \prime }}$. Then there are at most Γ tasks in $\overline {OPT}\cap T^{\ge \ell ^{\prime \prime }-\beta }$ that use an edge of $I_{j^{\prime \prime }}$.

Proof

First, since $I_{j^{\prime \prime }}$ is sparse, there are at most 1/𝜖^α tasks $i\in \overline {OPT}$ that start or end in $I_{j^{\prime \prime }}$, but such that $I_{j^{\prime \prime }}\not \subseteq P(i)$. Then, from Lemma 8 there are at most 1/𝜖 tasks $i\in \overline {OPT}$ that cross $I_{j^{\prime \prime }}$, i.e. such that $I_{j^{\prime \prime }}\subseteq P(i)$, that have size $p_{i}>\hat {b}_{j^{\prime \prime }}$. Therefore, the remaining tasks $i\in \overline {OPT}\cap T^{\ge \ell ^{\prime \prime }-\beta }$ have a level between $\ell ^{\prime \prime }-\beta$ and $\ell ^{\prime \prime }+1$, and are such that $I_{j^{\prime \prime }}\subseteq P(i)$. Thus, they use both the leftmost edge and the rightmost edge of $I_{j^{\prime \prime }}$, and then there are at most 1/𝜖^α+ 1 tasks from each of these levels. We conclude that $\vert \overline {OPT}\cap T^{\ge \ell ^{\prime \prime }-\beta }\vert \le 1/\epsilon ^{\alpha }+1/\epsilon +(\beta +2)/\epsilon ^{\alpha +1}$. □

Equipped with Lemmas 18 and 19 we can prove that the above DP is correct by arguing that it will produce $\overline {OPT}$ if it makes the corresponding guesses for each DP-cell. Also, by construction the returned solution is feasible. This yields the following lemma.

Lemma 20

There is an algorithm with a running time of $n^{O(1/\epsilon ^{\alpha +4})}$ that computes a set $T^{(2)}\subseteq \bar {T}$ with $|T^{(2)}|\le |\overline {OPT}|$ and $p(T_{e}\cap T^{(2)})+p(T_{e}\cap T_{S})/2\ge \bar {u}_{e}$ for each edge e.

Proof

Note first that if the algorithm returns a solution, it must be feasible by construction. We argue inductively that it is feasible to guess the tasks in $\overline {OPT}$ so the solution must be such that $|T^{(2)}|\leq |\overline {OPT}|$. Consider a cell $(I_{j},I_{j^{\prime }},T^{\prime }_{j},T^{\prime }_{j^{\prime }})$, and let ℓ and $\ell ^{\prime }$ be the largest integers such that $(1+{\epsilon })^{\ell }\leq \hat {b}_{j}$ and $(1+{\epsilon })^{\ell ^{\prime }}\leq \hat {b}_{j^{\prime }}$. Assume that $T^{\prime }_{j}=\overline {OPT}\cap T^{\geq \ell -\beta }\cap \left \{ i\in T:P(i)\cap I_{j}\neq \emptyset \right \}$ and that $T^{\prime }_{j^{\prime }}=\overline {OPT}\cap T^{\geq \ell ^{\prime }-\beta }\cap \left \{ i\in T:P(i)\cap I_{j^{\prime }}\neq \emptyset \right \}$. Let $I_{j^{\prime \prime }}$ be the interval between I_j and $I_{j^{\prime }}$ with smallest $\hat {b}_{j^{\prime \prime }}$, and let $\ell ^{\prime \prime }$ be the largest integer such that $(1+{\epsilon })^{\ell ^{\prime \prime }}\leq \hat {b}_{j^{\prime \prime }}$. From Lemma 19 we know that the set $\overline {OPT}\cap T^{\geq \ell ^{\prime \prime }-\beta }\cap \left \{ i\in T:P(i)\cap I_{j^{\prime \prime }}\neq \emptyset \right \}$ contains at most Γ tasks, and from Lemma 18 that, together with half the size of the slack tasks, they cover the demand in the interval $I_{j^{\prime \prime }}$. So it is a feasible guess for the algorithm to take $T^{\prime \prime }=\overline {OPT}\cap T^{\geq \ell ^{\prime \prime }-\beta }\cap \left \{ i\in T:P(i)\cap I_{j^{\prime \prime }}\neq \emptyset \right \} \cap \left \{ i\in T:P(i)\cap I_{j}=P(i)\cap I_{j^{\prime }}=\emptyset \right \}$. Since by the definition of the cells $\hat {b}_{j^{\prime \prime }}\geq \max \limits \left \{ \hat {b}_{j},\hat {b}_{j^{\prime }}\right \}$, we have that $\ell ^{\prime \prime }\geq \max \limits \left \{ \ell ,\ell ^{\prime }\right \}$. Thus, we recover that $T^{\prime }_{j^{\prime \prime }}:=(T^{\prime \prime }\cup T^{\prime }_{j}\cup T^{\prime }_{j^{\prime }})\cap T^{\geq \ell ^{\prime \prime }-\beta }=\overline {OPT}\cap T^{\geq \ell ^{\prime \prime }-\beta }\cap \left \{ i\in T:P(i)\cap I_{j^{\prime \prime }}\neq \emptyset \right \}$. The base case is trivial, as no task intersects our dummy intervals.

We have O(k) many intervals, and O(n^Γ) many different subsets of T of size at most Γ. Thus, there are only O(k ⋅ n^Γ) many DP cells. For solving each cell we guess at most Γ tasks, so we solve each cell in time O(n^Γ). Thus, the algorithm terminates in time O(k ⋅ n^2Γ). Since ${\Gamma }\leq O(\beta /{\epsilon }^{\alpha +1})\leq O(\alpha \cdot \log _{1+{\epsilon }}(1/{\epsilon })/{\epsilon }^{\alpha +1})\leq O(1/{\epsilon }^{\alpha +4})$, the algorithm takes time $kn^{O(1/{\epsilon }^{\alpha +4})}$. □

It remains to argue that our computed sets $T_{\text {med}}^{\prime },T^{(1)},T^{(2)},T_{H},T_{S}$ together form a feasible solution and do not contain too many tasks.

Lemma 21

We have that $T_{\text {med}}^{\prime }\cup T^{(1)}\cup T^{(2)}\cup T_{H}\cup T_{S}$ is a feasible solution to the original input instance (T,E) and $|T_{\text {med}}^{\prime }\cup T^{(1)}\cup T^{(2)}\cup T_{H}\cup T_{S}|\le (1+O(\epsilon ))k$.

Proof

The feasibility follows directly from Lemmas 9, 13, 16, 17 and 20. First Lemmas 7 and 8 give us that $|T_{\text {med}}^{\prime }\cup T_{S}|=O(\epsilon k)$. From Lemma 13 we know that $|T_{H}|\leq (1+O(\epsilon ))|OPT^{\prime }_{H}|$. From Lemma 20 we know that $|T^{(2)}|\leq |\overline {OPT}|=|(OPT^{\prime }\setminus OPT^{\prime }_{H})\setminus T_{D})|$. Then, it is enough to prove that $|T^{(1)}|\leq |(OPT^{\prime }\setminus OPT^{\prime }_{H})\cap T_{D}|+{\epsilon } k$.

Recall that T⁽¹⁾ is obtained with our algorithm for instances with resource augmentation, that outputs an optimal solution. So it is enough to show that there is a solution for the problem in the dense intervals of size $|(OPT^{\prime }\setminus OPT^{\prime }_{H})\cap T_{D}|+{\epsilon } k$.

Let $\overline {OPT}_{DS}$ denote the subset of tasks of $\overline {OPT}$ that intersect some dense interval. Since each such task starts or ends in a sparse interval, the number of tasks in OPT_DS intersecting some vertex in $V^{\prime }$ is at most 1/𝜖^α+ 1 from each group T^ℓ. Then, for each dense interval I_j, let $\ell ^{\prime \prime }_{j}$ be the greatest integer such that $(1+\epsilon )^{\ell ^{\prime \prime }_{j}}\le \hat {b}_{j}$.

We consider now the subset of $\overline {OPT}_{DS}$ that contains all tasks for which there is at least one dense interval I_j such that its level is at least $\ell ^{\prime \prime }_{j}-\beta$, where $\beta =1+\log _{1+\epsilon }\frac {6}{\epsilon ^{\alpha +1}}$. Formally,

$$ \overline{OPT}^{\prime}_{DS}\!:=\!\left\{ i\in\overline{\mathit{OPT}}_{DS}\mid\exists I_{j}\text{ dense, such that }I_{j}\cap P(i)\neq\emptyset,\text{ and }p_{i}\in T^{\ge\ell^{\prime\prime}_{j}-\beta}\right\} . $$

We show that $\vert \overline {OPT}^{\prime }_{DS}\vert =O(\epsilon k)$. Consider a dense interval I_j with minimum slack $\hat {b}_{j}$ among all dense intervals and denote respectively e and $e^{\prime }$ the leftmost and the rightmost edge in I_j. Consider now the subset $\overline {OPT}_{DS}^{j}:=\overline {OPT}^{\prime }_{DS}\cap (T_{e}\cup T_{e^{\prime }})$ of tasks that intersect e or $e^{\prime }$. We know from Lemma 8 that the slask is such that there are at most 2/𝜖 tasks $i^{\prime }\in \overline {OPT}_{DS}^{j}$ such that $\hat {b}_{j}(1+\epsilon )<p_{i^{\prime }}<4k\hat {b}_{j}$, and recall that from each group there are at most 2/𝜖^α+ 1 tasks in $\overline {OPT}_{DS}^{j}$. Therefore we have

$$ \begin{array}{@{}rcl@{}} \vert\overline{OPT}_{DS}^{j}\vert & \le2/\epsilon+(\beta+1)\frac{2}{\epsilon^{\alpha+1}}\le2/\epsilon+\left( 2+(\alpha+2)\log_{1+\epsilon}\frac{1}{\epsilon}\right)\frac{2}{\epsilon^{\alpha+1}} . \end{array} $$

We know that α ≤ 5/𝜖 + 1, and $\log _{1+\epsilon }(1/\epsilon )\le 2/\epsilon ^{2}$ for small values of 𝜖. It follows that $\vert \overline {OPT}_{DS}^{j}\vert \le 21/\epsilon ^{\alpha +4}$. We recursively apply the same analysis to the set $\overline {OPT}^{\prime }_{DS}\setminus \overline {OPT}_{DS}^{j}$ going to the next dense interval of minimum slack.

At the end this proved that $\vert \overline {OPT}^{\prime }_{DS}\vert \le 21/\epsilon ^{\alpha +4}\cdot n_{D}$ where n_D is the number of dense intervals. Moreover, n_D is at most 2𝜖^α+ 5|OPT| since at least 1/𝜖^α+ 5 tasks from OPT start or end in each dense interval. This finally implies that $\vert \overline {OPT}^{\prime }_{DS}\vert \le 42\epsilon \vert OPT\vert =O(\epsilon k)$.

Then, the set of remaining tasks $\overline {OPT}_{DS}\setminus \overline {OPT}^{\prime }_{DS}$ only covers a tiny fraction of each edge e in a dense interval I_j. Indeed, we have that all tasks in $\overline {OPT}_{DS}\setminus \overline {OPT}^{\prime }_{DS}$ have a level at most $\ell ^{\prime \prime }_{j}-\beta$ where $\ell ^{\prime \prime }_{j}$ is such that $(1+\epsilon )^{\ell ^{\prime \prime }_{j}}\le \hat {b}_{j}$. Moreover, at most 1/𝜖^α+ 1 tasks from each group intersect e. Then, using the very same argument as in Lemma 18 we have that the demand covered is at most half of the slack for each edge: $p(T_{e}\cap (\overline {OPT}_{DS}\setminus \overline {OPT}^{\prime }_{DS}))\le \hat {b}_{j}/2$. There, $OPT^{\prime }\setminus (OPT^{\prime }_{H}\cup (\overline {OPT}_{DS}\setminus \overline {OPT}^{\prime }_{DS}))$ is a feasible solution for the auxiliary problem for dense intervals that we solve using Theorem 2. It follows that the solution T⁽¹⁾ returned by the resource augmentation algorithm has size at most $\vert OPT^{\prime }\setminus (OPT^{\prime }_{H}\cup (\overline {OPT}_{DS}\setminus \overline {OPT}^{\prime }_{DS}))\vert$ so that

$$ \begin{array}{@{}rcl@{}} && \vert T^{(1)}\cup T^{(2)}\cup T_{H}\cup T_{S}\cup T_{\text{med}}^{\prime}\vert\le\vert T^{(1)}\vert+\vert T^{(2)}\vert+\vert T_{H}\vert+\vert T_{S}\cup{T_{\text{med}}}^{\prime}\vert\\ & \le&\vert OPT^{\prime}\setminus(OPT^{\prime}_{H}\cup(\overline{OPT}_{DS}\setminus\overline{OPT}^{\prime}_{DS}))\vert+\vert OPT^{\prime}\setminus(OPT^{\prime}_{H}\cup T_{D})\vert\\ && +(1+O(\epsilon))\vert OPT^{\prime}_{H}\vert+O(\epsilon k)\\ & \le&\vert OPT^{\prime}\setminus OPT^{\prime}_{H}\vert+\vert\overline{OPT}^{\prime}_{DS}\vert\le\vert OPT^{\prime}\setminus OPT^{\prime}_{H}\vert+\vert OPT^{\prime}_{H}\vert+O(\epsilon k)\\ & \le&\vert OPT^{\prime}\vert+O(\epsilon k)\le(1+O(\epsilon)k) . \end{array} $$

This concludes the proof. □

We complete the proof of Theorem 3 by bounding our overall running time.

Lemma 22

We can compute the sets $T_{\text {med}}^{\prime },T^{(1)},T^{(2)},T_{H},T_{S}$ in time $k^{O(k^{2}\log k)}$ $n^{(1/\epsilon )^{O(1/\epsilon )}}$.

Proof

First, to obtain the set of slack tasks T_S we make k^O(k) guesses, because we select at most O(k) tasks from k^O(1) options. Then we guess which tasks are in OPT ∩ T_S and recurse until the intersection is empty. The recursion tree has depth at most k because OPT has size at most k, so if we extract an element from OPT at each recursive call, OPT is empty after k calls. Each node has at most k^O(k) ⋅ 2^k childs, this is, k^O(k) for the guessing of T_S and 2^k for the subsets of T_S. Therefore, to obtain the definitive T_S, we make in total at most $k^{O(k^{2})}$ guesses. Selecting the corresponding tasks takes time n^O(1). Then, assuming that the guesses are correct,

• 1. we make k^O(k) new guesses and compute for each guess, a candidate set $T_{\text {med}}^{\prime }$ in time n^O(1) (Lemma 10),

• 2. we make at most k^O(k) guesses and compute for each guess a candidate set T_H in time n^O(1) (Lemma 14).

• 3. we compute a set T⁽¹⁾ in time $k^{O(k^{2}\log k)}\cdot n^{O(1)}$ (Lemma 16).

• 4. we compute a set T⁽²⁾ in time $n^{(1/\epsilon )^{\alpha +4}}= n^{(1/\epsilon )^{O(1/\epsilon )}}$ (Lemma 20).

Thus, the overall running time of our algorithm is $k^{O(k^{2}\log k)}n^{(1/\epsilon )^{O(1/\epsilon )}}$. □

6 W[1]-Hardness

In this section we prove that UFP-cover is W[1]-hard if the parameter k represents the number of tasks in the optimal solution. Our proof goes along the lines of the proof that UFP (packing) is W[1]-hard for the same parameter as in [29].

Theorem 7

UFP-cover problem is W[1]-hard when parameterized by the number of tasks in the optimal solution.

An immediate consequence of this theorem is that the problem is unlikely to admit parameterized approximation scheme (EPAS), i.e., an algorithm with runtime f(k,𝜖)n^O(1) that computes a (1 + 𝜖)-approximation. This is because in the unweighted case, by setting 𝜖 = 1/(2k), we could obtain an optimal solution with such an algorithm.

Corollary 1

There is no EPAS for the UFP-cover problem, unless $W[1]\subseteq FPT$.

To prove the theorem we give a reduction from the k-subset sum problem which is W[1]-hard [20]. Given a set of n values A = {a₁,...,a_n}, a target value B and an integer k, the goal is to choose exactly k values from A that sum up to exactly B.

Suppose we are given an instance of k-subset sum. First, we claim that we can assume w.l.o.g. some properties of it.

Lemma 23

W.l.o.g. we can assume that there are values 𝜖₁,...,𝜖_n, not necessarily positive, such that a_i = B/k + 𝜖_i for each i ∈ [n] and that ${\sum }_{i=1}^{n}|\epsilon _{i}|<B/(2k)$.

Proof

Given an arbitrary instance specified by A = {a₁,...,a_n}, B and k, we define a new equivalent instance defined via values $A^{\prime }=\{a^{\prime }_{1},...,a^{\prime }_{n}\}$, $B^{\prime }$, and k. Let $M:=nB/k+{\sum }_{i=1}^{n}a_{i}$. Then for each i ∈ [n] we define $a^{\prime }_{i}:=2M+a_{i}$ and we set $B^{\prime }:=2kM+B$. Then $B^{\prime }/k=2M+B/k$ and $a^{\prime }_{i}=(2M+B/k)+(a_{i}-B/k)=B^{\prime }/k+(a_{i}-B/k)$ for each i ∈ [n]. We define 𝜖_i := a_i − B/k for each i ∈ [n] and then $a^{\prime }_{i}=B^{\prime }/k+{\epsilon }_{i}$ for each i ∈ [n]. Then it holds that ${\sum }_{i=1}^{n}|{\epsilon }_{i}|\le {\sum }_{i=1}^{n}a_{i}+nB/k=M<B^{\prime }/(2k)$. For any k indices i₁,...,i_k it holds that ${\sum }_{\ell =1}^{k}a_{i_{\ell }}=B$ if and only if ${\sum }_{\ell =1}^{k}a^{\prime }_{i_{\ell }}={\sum }_{\ell =1}^{k}(2M+a_{i_{\ell }})=2kM+B=B^{\prime }$. □

We construct an instance of UFP-cover that admits a solution with 2k tasks if and only if the given k-subset sum is a yes-instance. Our UFP-cover instance has a path with n + 2 vertices v₀,v₁,...,v_n+ 1. Denote the leftmost and the rightmost edge of the path by e_L and e_R, respectively. We define u(e_L) = u(e_R) = B. For all other edges e we define u(e) := B − B/(2k). Assume that the values in S are ordered such that a₁ ≥ a₂ ≥ ... ≥ a_n. Let j ∈ [n]. We introduce two tasks $i(j),i^{\prime }(j)$ with s(i(j)) := v₀, t(i(j)) := v_j, p(i(j)) := a_j $s(i^{\prime }(j)):=v_{j}$, $t(i^{\prime }(j))=v_{n+1}$, and $p(i^{\prime }(j)):=2B/k-a_{j}$. See Fig. 6 for a sketch.

Fig. 6

Sketch of the reduction used in order to prove Theorem 6. The sketch shows the tasks i(j) and $i^{\prime }(j)$ for only one index j. The figure is essentially identical to a figure in [29], taken with consent of the author

In order to get some intuition about the constructed instance, we prove the following lemma.

Lemma 24

Any feasible solution contains at least 2k tasks. Among them are k tasks covering e_L and k tasks covering e_R. If a task covers e_L then it does not cover e_R and vice versa.

Proof

We have that u(e_L) = B and each task covering e_L has a size a_i for some $i\in \{1,{\dots } n\}$. Hence, any set of at most k − 1 tasks covering e_L has a total size of at most $(k-1)B/k+{\sum }_{i=1}^{n}|{\epsilon }_{i}|<B(k-1)/k+B/(2k)<B=u(e_{L})$. Therefore, e_L must be covered by at least k tasks. Similarly, any set of at most k − 1 tasks covering e_R, corresponding to indices $J^{\prime }$ of the input values, has a total size of at most ${\sum }_{j\in J^{\prime }}(2B/k-a_{j})={\sum }_{j\in J^{\prime }}(2B/k-B/k-\epsilon _{j})\le (k-1)B/k+(k-1)\min \limits _{j}\epsilon _{j}\le (k-1)B/k+{\sum }_{i=1}^{n}|{\epsilon }_{i}|<B=u(e_{R})$ and thus also e_R must be covered by at least k tasks. The last statement follows from construction. Together this implies that any feasible solution contains at least 2k tasks. □

In the next lemma we show how to construct a solution with 2k tasks if the given k-subset sum instance is a yes-instance.

Lemma 25

If the given k-subset sum instance is a yes-instance, then the constructed UFP-cover instance has a solution with 2k tasks.

Proof

Let $J\subseteq [n]$ be k indices such that ${\sum }_{j\in J}a_{j}=B$. Then for each j ∈ J we select the tasks i(j) and $i^{\prime }(j)$. Let $T^{\prime }$ denote the resulting set of tasks. We verify that this yields a feasible solution. For the edge e_L we have that the total demand of tasks using it is

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i\in T^{\prime}\cap T_{e_{L}}}p_{i} & = & \sum\limits_{j\in J}p_{i(j)}\\ & = & \sum\limits_{j\in J}a_{j}\\ & = & B. \end{array} $$

For the edge e_R the total demand of the tasks using it is a_i = B/k + 𝜖_i

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i\in T^{\prime}\cap T_{e_{R}}}p_{i} & = & \sum\limits_{j\in J}p_{i^{\prime}(j)}\\ & = & \sum\limits_{j\in J}2B/k-a_{j}\\ & = & 2B-\sum\limits_{j\in J}a_{j}\\ & = & B. \end{array} $$

Consider an edge e with e_L≠e≠e_R. For each index j ∈ J we have that i(j) or $i^{\prime }(j)$ covers e. Hence, e is covered by at least k tasks in $T^{\prime }$. Thus, their total size is at least

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i\in T^{\prime}\cap T_{e}}p(i) & \ge & \sum\limits_{j\in J}\min\{a_{j},2B/k-a_{j}\}\\ & \ge & \sum\limits_{j\in J}\min\{B/k+\epsilon_{j},B/k-\epsilon_{j}\}\\ & \ge & B-\sum\limits_{i=1}^{n}|\epsilon_{i}|\\ & \ge & B-B/(2k)\\ & = & u(e). \end{array} $$

□

Conversely, we show that if the UFP-cover instance has a solution with at most 2k tasks then the k-subset sum instance is a yes-instance. Suppose we are given such a solution for the UFP-cover instance. First, we establish that for each j ∈ [n] the solution selects either both i(j) and $i^{\prime }(j)$ or none of these two tasks.

Lemma 26

Given a solution $T^{\prime }$ to the UFP-cover instance with 2k tasks. Then there is a solution $T^{\prime \prime }$ with 2k tasks such that for each j ∈ [n] we have that either $\{i(j),i^{\prime }(j)\}\subseteq T^{\prime \prime }$ or $\{i(j),i^{\prime }(j)\}\cap T^{\prime \prime }=\emptyset$.

Proof

First we observe that for each j ∈{1,...,n − 1} the edge {v_j,v_j+ 1} needs to be covered by at least k tasks in $T^{\prime }$, since the total size of any set of k − 1 tasks $\tilde {T}\subseteq T$ is at most ${\sum }_{i^{\prime }\in \tilde {T}} \max \limits _{i\in [n]}\{B/k+\epsilon _{i},B/k-\epsilon _{i}\}\le (k-1)B/k+{\sum }_{i\in [n]}|\epsilon _{i}|<B-B/(2k)$. On the other hand, any set of k tasks is sufficient to cover {v_j,v_j+ 1} since the size of any set of k tasks $\tilde {T}\subseteq T$ is at least ${\sum }_{i^{\prime }\in \tilde {T}} min_{i\in [n]}\{B/k+\epsilon _{i},B/k-\epsilon _{i}\}\ge B-{\sum }_{i\in [n]}|\epsilon _{i}|\ge B-B/(2k)$ which equals the demand of {v_j,v_j+ 1}. We transform $T^{\prime }$ to a solution $T^{\prime \prime }$ for which the claim of the lemma holds. First suppose that there is a j ∈{1,...,n − 1} such that the edge {v_j,v_j+ 1} is used by at least k + 1 tasks in $T^{\prime }$. Let j be the smallest value in {1,...,n − 1} with this property. Then there must be a task $i\in T^{\prime }$ that starts on v_j. The only such task is $i^{\prime }(j)$ and hence $i=i^{\prime }(j)$. However, k tasks would suffice to cover {v_j,v_j+ 1}. We observe that $p(i^{\prime }(j))=2B/k-a_{j}\le 2B/k-a_{j+1}=p(i^{\prime }(j+1))$. Therefore, we replace $i^{\prime }(j)$ by $i^{\prime }(j+1)$ in $T^{\prime }$ and note that also after this change $T^{\prime }$ is a feasible solution. We do this operation until for each j ∈ [n] the edge {v_j,v_j+ 1} is covered by exactly k tasks in $T^{\prime }$. Let $T^{\prime \prime }$ denote the resulting set.

Lemma 24 states that there are k tasks in $T^{\prime \prime }$ covering e_L and k tasks in $T^{\prime \prime }$ covering e_R. The lemma also states that a task covering e_L does not cover e_R and vice versa. Hence, there are exactly k tasks in $T^{\prime \prime }$ covering e_L and exactly k tasks in $T^{\prime \prime }$ covering e_R. Therefore, if $T^{\prime \prime }$ does not satisfy the claim of the lemma, then there must be an index j such that $i(j)\in T^{\prime }$ but $i^{\prime }(j)\notin T^{\prime }$. By construction, t(i(j)) = v_j and the edge {v_j− 1,v_j} is used by exactly k tasks in $T^{\prime \prime }$. However, the task $i^{\prime }(j)$ is the only input task whose start vertex is v_j and $i^{\prime }(j)\notin T^{\prime \prime }$. Therefore, the edge {v_j,v_j+ 1} is used by at most k − 1 tasks in $T^{\prime }$. However, as argued above, the total size of any set of k − 1 tasks is less than B − B/(2k) which equals the demand of {v_j,v_j+ 1}. Hence, the demand of {v_j,v_j+ 1} is not completely covered, which implies that $T^{\prime \prime }$ is infeasible, which yields a contradiction. □

Suppose we are given a solution $T^{\prime \prime }$ to the UFP instance with 2k tasks which satisfies the condition of Lemma 26. Let $J^{\prime \prime }$ be the set of indices j such that $i(j)\in T^{\prime \prime }$. Note that Lemma 26 implies that $|J^{\prime \prime }|=k$.

Lemma 27

We have that ${\sum }_{j\in J^{\prime \prime }}a_{j}=B$.

Proof

Let $T^{\prime \prime }_{L}\subseteq T^{\prime \prime }$ and $T^{\prime \prime }_{R}\subseteq T^{\prime \prime }$ denote the set of tasks in $T^{\prime \prime }$ using e_L and e_R, respectively. Then $B=u(e_{L})\le {\sum }_{i\in T^{\prime \prime }_{L}}p(i)={\sum }_{j\in J^{\prime \prime }}a_{j}$. On the other hand, due to Lemma 26 we have that $B=u(e_{R})\ge {\sum }_{i\in T^{\prime \prime }_{R}}p(i)={\sum }_{j\in J^{\prime \prime }}2B/k-a_{j}$ and hence ${\sum }_{j\in J^{\prime \prime }}a_{j}\ge ({\sum }_{j\in J^{\prime \prime }}2B/k)-B=B$. Therefore ${\sum }_{j\in J^{\prime \prime }}a_{j}=B$. □

Hence, we proved that the constructed UFP-cover instance has a solution with 2k tasks if and only if the k-subset sum instance is a yes-instance. This implies that UFP-cover is W[1]-hard when parameterized by the number of tasks in the optimal solution. This completes the proof of Theorem 6.

7 Conclusion and Open Questions

In this paper we presented a PAS for UFP-cover and showed that the problem is FPT under resource augmentation or if additionally the number of different task sizes are bounded by a parameter. It remains open whether the problem is FPT if only the number of task sizes is bounded by a parameter, but not the number of tasks in the optimal solution. Also, we showed that UFP-cover is W[1]-hard. Our W[1]-hardness proof is based on a reduction from the k-subset sum problem, which can be solved in pseudopolynomial time O(nB). Hence, it is open whether UFP-cover is FPT if the input data are polynomially bounded. Our PAS can be simplified in this setting, however, it crucially relies on the slack obtained by selecting 𝜖k additional tasks and thus does not solve the problem optimally in this case.

Appendix : A: Reduction from Generalized Caching in the Fault Model

A reduction from generalized caching in the fault model to UFP-cover was given in [1, 5]. For completeness we present the reduction here using our notation. In the fault model of general caching we are given a value $M\in {\mathbb {N}}$ that denotes the size of the cache and we are given a set of pages $\mathcal {P}$. Each page $q\in \mathcal {P}$ has a (not necessarily unit) size $s(q)\in {\mathbb {N}}$. Also we are given a set of requests $\mathcal {R}$ where each request $j\in \mathcal {R}$ is characterized by a time t_j ≥ 0 and a page $q_{j} \in \mathcal {P}$ meaning that at time t_j the page q_j has to be present in the cache. The goal is to decide at what times we bring each page into the cache in order to minimize the total number of these transfers, assuming that initially the cache is empty. We show here how to reduce this problem to UFP-cover with unit weights.

Lemma 28

Given an instance $(\mathcal {P},\mathcal {R},M)$ of general caching in the fault model, in polynomial time we can compute an instance (V,E,T,u) of UFP-cover such that for any solution to $(\mathcal {P},\mathcal {R},M)$ with cost C, there is a solution $T^{\prime }\subseteq T$ to (V,E,T,u) with $|T^{\prime }|=C$, and vice versa.

Proof

W.l.o.g. we can restrict ourselves to solutions of $(\mathcal {P},\mathcal {R},M)$ where each page enters the cache only when it is requested and leaves the cache only right after it is requested, and to instances where each page is requested at least once and $M< {\sum }_{q\in \mathcal {P}} s(q)$. Thus, a solution is completely defined by deciding at each point in time whether we evict the page that was just requested or whether we keep it in the cache until it is requested again. We construct the path (V,E) by defining one edge e(t) for each time t such that there is a request $j\in \mathcal {R}$ with t_j = t, and ordering the edges on the path by increasing values of t. For defining the tasks T, we initialize T := ∅. Then, for every page $q\in \mathcal {P}$ and every pair j₁,j₂ ∈ R of consecutive requests of page q, we add a task i(j₁,j₂) to T with size $p_{i(j_{1},j_{2})} = s(q)$. The subpath $P_{i(j_{1},j_{2})}$ is the one that starts in the right vertex of $e(t_{j_{1}})$ and ends in the left vertex of $e(t_{j_{2}})$. We define the demand of the edge e(t) to be $u_{e(t)}= p(T_{e(t)}) - M + {\sum }_{j\in R: t_{j}=t} s(q_{j})$ for every time t. We also add an extra edge e₀ at the left of E with capacity $u_{e_{0}}={\sum }_{q\in \mathcal {P}} s(q)$ and we add a task $i^{*}_{q}$ with $P_{i^{*}_{q}}= \{e_{0}\}$ and $p_{i^{*}_{q}}= s(q)$ for each page $q\in \mathcal {P}$. The cost of these tasks is exactly the total cost of loading each page into the cache once, i.e., the first time that the respective page is requested.

Given a solution to $(\mathcal {P},\mathcal {R},M)$, we construct a solution $T^{\prime }$ for (V,E,T,u) in the following way. For every page q and every pair of consecutive requests j₁,j₂ of page q, we add i(j₁,j₂) to $T^{\prime }$ if and only if page q is evicted from (and therefore re-loaded into) the cache between $t_{j_{1}}$ and $t_{j_{2}}$. We also add $i^{*}_{q}$ to $T^{\prime }$ for all $q\in \mathcal {P}$. It is clear that $|T^{\prime }|$ is exactly the number of times a page is brought into the cache in the original solution. We now check that $T^{\prime }$ is a feasible solution. Consider an edge e(t) ∈ E. Then $p(T_{e(t)}\setminus T^{\prime })$ is the sum of sizes of the pages that are in the cache at time t that are not requested exactly at time t. The total size of all pages in the cache is at most M, so $p(T_{e(t)}\setminus T^{\prime })+ {\sum }_{j\in R: t_{j}=t} s(q_{j})\leq M$. Then, as $p(T_{e(t)}) = p(T_{e(t)}\cap T^{\prime }) + p(T_{e(t)}\setminus T^{\prime })$ and $u_{e(t)} = p(T_{e(t)}) - M + {\sum }_{j\in R: t_{j}=t} s(q_{j})$ we conclude that $p(T^{\prime }\cap T_{e(t)})\geq u_{e(t)}$. Also it holds by construction that $p(T^{\prime }\cap T_{e_{0}})=u_{e_{0}}$.

Let now $T^{\prime }$ be a feasible solution to (V,E,T,u). Of course $i^{*}_{q}\in T^{\prime }$ for all $q\in \mathcal {P}$. This accounts for the first time each page is brought into the cache. We construct a solution $S^{\prime }$ to $(\mathcal {P},\mathcal {R},M)$ as follows. For every page q and every pair of consecutive requests j₁,j₂ of page q we keep page q in the cache between $t_{j_{1}}$ and $t_{j_{2}}$ if and only if $i(j_{1},j_{2})\not \in T^{\prime }$. Thus, for each element in $T^{\prime }$ we have to bring a page into the cache once, and then the cost of the solution is exactly $|T^{\prime }|$. We have to check that the size of the pages in the cache never exceeds M in $S^{\prime }$. In fact, note that the total size of the pages in the cache at time t is $p(T_{e(t)}\setminus T^{\prime }) +{\sum }_{j\in R: t_{j}=t} s(q_{j})$. But $p(T_{e(t)}\cap T^{\prime })\geq u_{e(t)}$, and therefore,

$$ \begin{array}{@{}rcl@{}} p(T_{e(t)}\cap T^{\prime}) &\geq& p(T_{e(t)}) - M + \sum\limits_{j\in R: t_{j}=t} s(q_{j}) \\ \Leftrightarrow\qquad \qquad \qquad M &\geq & p(T_{e(t)}) +p(T_{e(t)}\cap T^{\prime})+ \sum\limits_{j\in R: t_{j}=t} s(q_{j})\\ \Leftrightarrow\qquad\qquad\qquad M &\geq& p(T_{e(t)}\setminus T^{\prime}) +\sum\limits_{j\in R: t_{j}=t} s(q_{j}) . \end{array} $$

□