Abstract
Strategy Logic (SL) is a very expressive temporal logic for specifying and verifying properties of multi-agent systems: in SL, one can quantify over strategies, assign them to agents, and express LTL properties of the resulting plays. Such a powerful framework has two drawbacks: first, model checking SL has non-elementary complexity; second, the exact semantics of SL is rather intricate, and may not correspond to what is expected. In this paper, we focus on strategy dependences in SL, by tracking how existentially-quantified strategies in a formula may (or may not) depend on other strategies selected in the formula, revisiting the approach of [Mogavero et al., Reasoning about strategies: On the model-checking problem, 2014]. We explain why elementary dependences, as defined by Mogavero et al., do not exactly capture the intended concept of behavioral strategies. We address this discrepancy by introducing timeline dependences, and exhibit a large fragment of SL for which model checking can be performed in 2-EXPTIME under this new semantics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Temporal logics Since Pnueli’s seminal paper [36] in 1977, temporal logics have been widely used in theoretical computer science, especially by the formal-verification community. Temporal logics provide powerful languages for expressing properties of reactive systems, and enjoy efficient algorithms for satisfiability and model checking [13]. Since the early 2000s, new temporal logics have appeared to address open and multi-agent systems. While classical temporal logics (e.g. CTL [12, 37] and LTL [36]) could only deal with one or all the behaviours of the whole system, ATL [2] expresses properties of (executions generated by) behaviours of individual components of the system. This can be used to specify that a controller can enforce safety of a whole system, whatever the other components do. This is usually seen as a game where the controller plays against the other components, with the aim of maintaining safety of the global system; ATL can then express the existence of a winning strategy in such a game. ATL has been extensively studied since its introduction, both about its expressiveness and about its verification algorithms [2, 20, 28].
Adding strategic interactions in temporal logics Strategies in ATL are handled in a very limited way, and there are no real strategic interactions in that logic (which, in return, enjoys a polynomial-time model-checking algorithm). Indeed, ATL expresses properties such as “Player A has a strategy to enforce φ” (denoted 〈 〈A〉 〉φ), where φ is a property to be fulfilled along any execution resulting from the selected strategy; in other terms, this existential quantification over strategies of A always implicitly contains a universal quantification over all the strategies of all the other players. This only allows to express zero-sum objectives.
Over the last 10 years, various extensions have been defined and studied in order to allow for more strategy interactions [1, 8, 11, 30, 39]. Strategy Logic (SL for short) [11, 30] is such a powerful approach, in which strategies are first-class objects; formulas can quantify (universally and existentially) over strategies, store those strategies in variables, assign them to players, and express properties of the resulting plays. As a simple example, the existence of a winning strategy for Player A (with objective φA) against any strategy of Player B would be written as ∃σA. ∀σB. assign(A↦σA;B↦σB). φA. This precisely corresponds to formula 〈 〈A〉 〉φA of ATL (if the game only has two players).
SL can express much more: for example, it can express the existence of a strategy for Player A which allows Player B to satisfy one of two goals φB or \(\varphi ^{\prime }_{B}\): we would write
This expresses collaborative properties which are out of reach of ATL: formula \(\langle \!\langle {A}\rangle \!\rangle (\langle \!\langle {B}\rangle \!\rangle \varphi _{B} \wedge \langle \!\langle {B}\rangle \!\rangle \varphi ^{\prime }_{B})\) in ATL is equivalent to \((\langle \!\langle {B}\rangle \!\rangle \varphi _{B}\wedge \langle \!\langle {B}\rangle \!\rangle \varphi ^{\prime }_{B}\), since 〈 〈B〉 〉φB is understood as the existence of a winning strategy against any strategy of the other player(s).
As a last example, SL can express classical concepts in game theory, such as Nash equilibria with Boolean objectives. This provides an easy way of showing decidability of rational synthesis [14, 18, 26] or assume-admissible synthesis [7]): for instance, the existence of an admissible strategy for objective φ of Player A (i.e., a strategy that is strictly dominated by no other strategies [7]) is expressed as
Such a formula shows that complex strategy interactions may be useful for expressing classical properties of multi-player games.
This series of examples illustrates how SL is both expressive and convenient, at the expense of a very high complexity: SL model checking has non-elementary complexity (and satisfiability is undecidable, unless the problem is restricted to turn-based game structures) [27, 30].
The high expressiveness of this logic, together with the decidability of its model-checking problem, has led to numerous studies around SL, either considering fragments of the logic with more efficient algorithms, or more expressive variants of the logic (e.g. with quantitative aspects), or variations on the notion of strategies (e.g. with limited observation of the game).
On the one hand, limitations have been imposed to strategic interactions in order to get more efficient algorithms [29, 32]. A goal is an LTL condition imposed to a strategy profile (built from quantified strategies). The fragment SL[1G] then contains formulas in prenex form with a single goal (and nested combinations thereof); this fragment is very close to ATL⋆ [2] in terms of expressiveness, and its model-checking problem is 2-EXPTIME-complete. A BDD-based implementation of the model-checking algorithm for SL[1G], using a translation to parity games, is implemented in the tool MCMAS [10]. Several other fragments have been considered, e.g. allowing conjunctions (SL[CG]), disjunctions (SL[DG]), or general boolean combinations of goals (SL[BG]); model checking still is in 2-EXPTIME for the first two fragments [32], but it is non-elementary for SL[BG] [5].
On the other hand, various extensions have also been considered, in order to see how far the logic can be extended while preserving decidable model checking. In Graded SL, (existential) strategy quantifiers are decorated with quantitative constraints on the cardinality of the set of strategies satisfying a formula; this can be used e.g. to express uniqueness on Nash equilibria. Model checking is decidable (with non-elementary complexity) for Graded SL [3]. On a different note, Prompt SL extends SL with a parameterized modality F≤nφ, which bounds the number of steps within which φ has to hold. Similarly, Bounded-Outcome SL adds a bound on the number of outcomes that must satisfy a given path formula. Again, model checking is decidable for those extensions [17].
Finally, SL has also been studied with different notions of strategies. When limiting strategy quantification to memoryless strategies, model checking is PSPACE-complete (as there are exponentially many strategies), but satisfiability is undecidable even for turn-based game structures [27]. Different types of strategies, based on sequences of actions, states or atomic propositions, are also considered in [22], with a focus on bisimulation invariance. When considering partial-observation strategies, model checking is undecidable (as is already the case for ATL [15]); a decidable fragment of SL is identified in [4], with a hierarchical restriction on nested strategy quantifiers. This study of imperfect-information games has been extended with epistemic variants of SL, which allows to reason about the knowledge of agents. Model checking is undecidable in the general case, but several papers identify specific settings where model checking is decidable [9, 21, 25].
UnderstandingSL It has been noticed in recent works that the nice expressiveness of SL comes with unexpected phenomena. One such phenomenon is induced by the separation of strategy quantification and strategy assignment: when selecting a strategy to be played later, are the intermediary events part of the memory of that strategy? While both options may make sense depending on the applications, only one of them makes model checking decidable [6].
A second phenomenon—which is the main focus of the present paper—concerns strategy dependences [30]: in a formula such as ∀σA. ∃σB. φ, the existentially-quantified strategy σB may depend on the whole strategy σA; in other terms, the action returned by strategy σB after some finite history ρ may depend on what strategy σA would play on any other history \(\rho ^{\prime }\). Again, in some contexts, it may be desirable that the value of strategy σB after history ρ can be computed based solely on what has been observed along ρ (see Fig. 2 for an illustration). This approach was initiated in [30, 33], conjecturing that large fragments of SL (subsuming ATL*) would have 2-EXPTIME model-checking algorithms with such limited dependences.
Our contributions We follow this line of work by performing a more thorough exploration of strategy dependences in (a fragment of) SL. We mainly follow the framework of [33], based on a kind of Skolemization of the formula: for instance, a formula of the form (∀xi∃yi)i. φ is satisfied if there exists a dependence map𝜃 defining each existentially-quantified strategy yj based on the universally-quantified strategies (xi)i. In order to recover the classical semantics of SL, it is only required that the strategy 𝜃((xi)i)(yj) (i.e. the strategy assigned to the existentially-quantified variable yj by 𝜃((xi)i)) only depends on (xi)i<j.
Based on this definition, other constraints can be imposed on dependence maps, in order to refine the dependences of existentially-quantified strategies on universally-quantified ones. Elementary dependences [33] only allows existentially-quantified strategy yj to depend on the values of (xi)i<j along the current history. This gives rise to two different semantics in general, but on several fragments of SL (namely SL[1G], SL[CG] and SL[DG]), the classic and elementary semantics would coincide [29, 32].
The coincidence actually only holds for SL[1G]. As we explain in this paper, elementary dependences as defined and used in [29, 32] do not exactly capture the intuition that strategies should depend on the “behavior [of universal strategies] on the history of interest only” [32]: indeed, they only allow dependences on universally-quantified strategies that appear earlier in the formula, while we claim that the behaviour of all universally-quantified strategies should be considered. We address this discrepancy by introducing another kind of dependences, which we call timeline dependences, and which extend elementary dependences by allowing existentially-quantified strategies to additionally depend on all universally-quantified strategies along strict prefixes of the current history (as illustrated on Fig. 5).
We study and compare those three dependences (classic, elementary and timeline), showing that they correspond to three distinct semantics. Because the semantics based on dependence maps is defined in terms of the existence of a witness map, we show that the syntactic negation of a formula may not correspond to its semantic negation: there are cases where both a formula φ and its syntactic negation ¬φ fail to hold (i.e., none of them has a witness map). This phenomenon is already present, but had not been formally identified, in [30, 33]. The main contribution of the present paper is the definition of a large (and, in a sense, maximal) fragment of SL for which syntactic and semantic negations coincide under the timeline semantics. As an (important) side result, we show that model checking this fragment under the timeline semantics is 2-EXPTIME-complete.
Related works To the best of our knowledge, strategy dependences have only been considered in a series of recent works by Mogavero et al. [29, 30, 32, 33], both as a way of making the semantics of SL more realistic in certain situations, and as a way of lowering the algorithmic complexity of verification of certain fragments of SL.
The question of the dependence of quantifiers in first-order logic is an old topic: in [23], branching quantifiers are introduced to define how quantified variables may depend on each other. Similarly, Dependence Logic [38] and Independence-Friendly Logic [24] also add such restrictions on dependences of quantified variables on top of first-order logic. While the settings are quite different to ours, the underlying ideas are similar, and in particular share an interpretation in terms of games of imperfect information.
2 Definitions
2.1 Concurrent Game Structures
Let AP be a set of atomic propositions, \(\mathcal {V}\) be a set of variables, and Agt be a set of agents. A concurrent game structure is a tuple \(\mathcal {G} = (\textsf {Act},\textsf {Q},{\Delta },\textsf {lab})\) where Act is a finite set of actions, Q is a finite set of states, Δ: Q ×ActAgt →Q is the transition function, and lab: Q → 2AP is a labelling function. An element of ActAgt will be called a move vector. For any q ∈Q, we let succ(q) be the set \(\{q^{\prime }\in Q\mid \exists m\in \textsf {Act}^{\textsf {Agt}}.\ q^{\prime }={\Delta }(q,m)\}\). For the sake of simplicity, we assume in the sequel that \(\textsf {succ}(q)\not =\varnothing \) for any q ∈ Q. A game \(\mathcal {G}\) is said turn-based whenever for every state q ∈Q, there is a player own(q) ∈Agt (named the owner of q) such that for any two move vectors m1 and m2 with m1(own(q)) = m2(own(q)), it holds Δ(q,m1) = Δ(q,m2). Figure 1 displays an example of a (turn-based) game.
Fix a state q ∈Q. A play in \(\mathcal {G}\) from q is an infinite sequence  of states in Q such that q0 = q and qi ∈succ(qi− 1) for all i > 0. We write \(\textsf {Play}_{\mathcal {G}}(q)\) for the set of plays in \(\mathcal {G}\) from q. In this and all similar notations, we might omit to mention \(\mathcal {G}\) when it is clear from the context, and q when we consider the union over all q ∈ Q. A (strict) prefix of a play π is a finite sequence ρ = (qi)0≤i≤L, for some
of states in Q such that q0 = q and qi ∈succ(qi− 1) for all i > 0. We write \(\textsf {Play}_{\mathcal {G}}(q)\) for the set of plays in \(\mathcal {G}\) from q. In this and all similar notations, we might omit to mention \(\mathcal {G}\) when it is clear from the context, and q when we consider the union over all q ∈ Q. A (strict) prefix of a play π is a finite sequence ρ = (qi)0≤i≤L, for some  . We write Pref(π) for the set of strict prefixes of play π. Such finite prefixes are called histories, and we let \(\textsf {Hist}_{\mathcal {G}}(q)=\textsf {Pref}(\textsf {Play}_{\mathcal {G}}(q))\). We extend the notion of strict prefixes and the notation Pref to histories in the natural way, requiring in particular that ρ∉Pref(ρ). A (finite) extension of a history ρ is any history \(\rho ^{\prime }\) such that \(\rho \in \textsf {Pref}(\rho ^{\prime })\). Let ρ = (qi)i≤L be a history. We define first(ρ) = q0 and last(ρ) = qL. Let \(\rho ^{\prime }=(q^{\prime }_{j})_{j\leq L'}\) be a history from lastρ. The concatenation of ρ and \(\rho ^{\prime }\) is then defined as the path \(\rho \cdot \rho ^{\prime }=(q^{\prime \prime }_{k})_{k\leq L+L'}\) such that \(q^{\prime \prime }_{k}=q_{k}\) when k ≤ L and \(q^{\prime \prime }_{k}=q^{\prime }_{k-L}\) when L ≥ k (notice that we required \(q^{\prime }_{0}=q_{L}\)).
. We write Pref(π) for the set of strict prefixes of play π. Such finite prefixes are called histories, and we let \(\textsf {Hist}_{\mathcal {G}}(q)=\textsf {Pref}(\textsf {Play}_{\mathcal {G}}(q))\). We extend the notion of strict prefixes and the notation Pref to histories in the natural way, requiring in particular that ρ∉Pref(ρ). A (finite) extension of a history ρ is any history \(\rho ^{\prime }\) such that \(\rho \in \textsf {Pref}(\rho ^{\prime })\). Let ρ = (qi)i≤L be a history. We define first(ρ) = q0 and last(ρ) = qL. Let \(\rho ^{\prime }=(q^{\prime }_{j})_{j\leq L'}\) be a history from lastρ. The concatenation of ρ and \(\rho ^{\prime }\) is then defined as the path \(\rho \cdot \rho ^{\prime }=(q^{\prime \prime }_{k})_{k\leq L+L'}\) such that \(q^{\prime \prime }_{k}=q_{k}\) when k ≤ L and \(q^{\prime \prime }_{k}=q^{\prime }_{k-L}\) when L ≥ k (notice that we required \(q^{\prime }_{0}=q_{L}\)).
A strategy from q is a mapping \(\delta \colon \textsf {Hist}_{\mathcal {G}}(q) \to \textsf {Act}\). We write \(\textsf {Strat}_{\mathcal {G}}(q)\) for the set of strategies in \(\mathcal {G}\) from q. Given a strategy δ ∈Strat(q) and a history ρ from q, the translation\(\delta _{\overrightarrow \rho }\) of δ by ρ is the strategy \(\delta _{\overrightarrow \rho }\) from lastρ defined by \(\delta _{\overrightarrow \rho }(\rho ^{\prime })=\delta (\rho \cdot \rho ^{\prime })\) for any \(\rho ^{\prime }\in \textsf {Hist}(\textsf {last}(\rho ))\). A context (sometimes also called valuation) from q is a partial function \(\chi \colon \mathcal {V} \cup \textsf {Agt}\rightharpoonup \textsf {Strat}(q)\). As usual, for any partial function f, we write dom(f) for the domain of f.
Let q ∈ Q and χ be a context from q. If \(\textsf {Agt}\subseteq \textsf {dom}(\chi )\), then χ induces a unique play from q, called its outcome, and defined as  such that q0 = q and for every
such that q0 = q and for every  , we have qi+ 1 = Δ(qi,mi) with mi(A) = χ(A)((qj)j≤i) for every A ∈Agt.
, we have qi+ 1 = Δ(qi,mi) with mi(A) = χ(A)((qj)j≤i) for every A ∈Agt.
2.2 Strategy Logic with Boolean Goals
Strategy Logic (SL for short) was introduced in [11], and further extended and studied in [30, 34], as a rich logical formalism for expressing properties of games. SL manipulates strategies as first-order elements, assigns them to players, and expresses LTL properties on the outcomes of the resulting strategic interactions. This results in a very expressive temporal logic, for which satisfiability is undecidable [31, 34] and model checking is TOWER-complete [5, 30]. In this paper, we focus on a restricted fragment of SL, called SL[BG]♭ (where BG stands for boolean goals [30], and the symbol ♭ indicates that we do not allow nesting of (closed) subformulas; we discuss this latter restriction below).
Syntax Formulas in SL[BG]♭ are built along the following grammar
where x ranges over \(\mathcal {V}\), σ ranges over the set \(\mathcal {V}^{\textsf {Agt}}\) of full assignments, and p ranges over AP. A goal is a formula of the form ω in the grammar above; it expresses an LTL property ψ on the outcome of the mapping σ. Formulas in SL[BG]♭ are thus made of an initial block of first-order quantifiers (selecting strategies for variables in \(\mathcal {V}\)), followed by a boolean combination of such goals.
Free variables With any subformula ζ of some formula φ ∈SL[BG]♭, we associate its set of free agents and variables, which we write free(ζ). It contains the agents and variables that have to be associated with a strategy in order to unequivocally evaluate ζ (as will be seen from the definition of the semantics of SL[BG]♭ below). The set freeζ is defined inductively:
Subformula ζ is said to be closed whenever \(\textsf {free}(\zeta )=\varnothing \). We can now comment on our choice of considering the flat fragment of SL[BG]: the full fragment, as defined in [30], allows for nesting closedSL[BG] formulas in place of atomic propositions. The meaning of such nesting in our setting is ambiguous, because our semantics (in Sections 3–5) are defined in terms of the existence of a witness, which does not easily propagate in formulas. In particular, as we explain later in the paper, the semantics of the negation of a formula (there is a witness for ¬φ) does not coincide with the negation of the semantics (there is no witness for φ); thus substituting a subformula and substituting its negation may return different results.
Semantics Fix a state q ∈ Q, and a context \(\chi \colon \mathcal {V}\cup \textsf {Agt}\rightharpoonup \textsf {Strat}(q)\). We inductively define the semantics of a subformula α of a formula of SL[BG]♭ at q under context χ, requiring \(\textsf {free}(\alpha )\subseteq \textsf {dom}(\chi )\). We omit the easy cases of boolean combinations and atomic propositions.
Given a mapping \(\sigma \colon \textsf {Agt}\to \mathcal {V}\), the semantics of strategy assignments is defined as follows:

Notice that, writing \(\chi ^{\prime }=\chi [A\in \textsf {Agt}\mapsto \chi (\sigma (A))]\), we have \(\textsf {free}(\psi )\subseteq \textsf {dom}(\chi ^{\prime })\) if \(\textsf {free}(\alpha )\subseteq \textsf {dom}(\chi )\), so that our inductive definition is sound.
We now consider path formulas ψ = Xψ1 and ψ = ψ1Uψ2. Since \(\textsf {Agt}\subseteq \textsf {free}(\psi )\subseteq \textsf {dom}(\chi )\), the context χ induces a unique outcome  from q. For
from q. For  , we write outn(q,χ) = (qi)i≤n, and define \(\chi _{\overrightarrow n}\) as the context obtained by shifting all the strategies in the image of χ by outn(q,χ). Under the same conditions, we also define \(q_{\overrightarrow n}=\textsf {last}({\textsf {out}_{n} (q,\chi ))}\). We then set
, we write outn(q,χ) = (qi)i≤n, and define \(\chi _{\overrightarrow n}\) as the context obtained by shifting all the strategies in the image of χ by outn(q,χ). Under the same conditions, we also define \(q_{\overrightarrow n}=\textsf {last}({\textsf {out}_{n} (q,\chi ))}\). We then set

In the sequel, we use classical shorthands, such as ⊤ for p ∨¬p (for any p ∈AP), Fψ for ⊤Uψ (eventuallyψ), and Gψ for ¬F¬ψ (alwaysψ). It remains to define the semantics of the strategy quantifiers. This is actually what this paper is all about. We provide here the original semantics, and discuss alternatives in the following sections:

Example 1
We consider the (turn-based) game \(\mathcal {G}\) is depicted on Fig. 1. We name the players after the shape of the state they control. The SL[BG] formula φ to the right of Fig. 1 has four quantified variables and two goals. We show that this formula evaluates to true at q0: fix a strategy δy (to be played by player  ); because \(\mathcal {G}\) is turn-based, we identify the actions of the owner of a state with the resulting target state, so that δy(q0q1) will be either p1 or p2. We then define strategy δz (to be played by
); because \(\mathcal {G}\) is turn-based, we identify the actions of the owner of a state with the resulting target state, so that δy(q0q1) will be either p1 or p2. We then define strategy δz (to be played by  ) as δz(q0q2) = δy(q0q1). Then clearly, for any strategy assigned to player
) as δz(q0q2) = δy(q0q1). Then clearly, for any strategy assigned to player  , one of the goals of formula φ holds true, so that φ itself evaluates to true.
, one of the goals of formula φ holds true, so that φ itself evaluates to true.
Subclasses ofSL[BG] Because of the high complexity and subtlety of reasoning with SL and SL[BG], several restrictions of SL[BG] have been considered in the literature [29, 32, 33], by adding further restrictions to boolean combinations in the grammar defining the syntax:
SL[1G] restricts SL[BG] to a unique goal. SL[1G]♭ is then defined from the grammar of SL[BG]♭ by setting ξ ::= ω in the grammar;
the larger fragment SL[CG] allows for conjunctions of goals. SL[CG]♭ corresponds to formulas defined with ξ ::= ξ ∧ ξ∣ω;
similarly, SL[DG] only allows disjunctions of goals, i.e. ξ ::= ξ ∨ ξ∣ω;
finally, SL[AG] mixes conjunctions and disjunctions in a restricted way. Goals in SL[AG]♭ can be combined using the following grammar: ξ ::= ω ∧ ξ∣ω ∨ ξ∣ω.
In the sequel, we write a generic SL[BG]♭ formula φ as (Qixi)1≤i≤l. ξ(βj. ψj)j≤n where:
(Qixi)i≤l is a block of quantifications, with \(\{x_{i} \mid 1 \le i \le l\}\subseteq \mathcal {V}\) and Qi ∈{∃,∀}, for every 1 ≤ i ≤ l;
ξ(g1,...,gn) is a boolean combination of its arguments;
for all 1 ≤ j ≤ n, βj. ψj is a goal: βj is a full assignment and ψj is an LTL formula.
3 Strategy Dependences
We now follow the framework of [30, 33] and define the semantics of SL[BG]♭ in terms of dependence maps. This approach provides a fine way of controlling how existentially-quantified strategies depend on other strategies (in a quantifier block). Using dependence maps, we can limit such dependences.
Dependence maps Consider an SL[BG]♭ formula φ = (Qixi)1≤i≤l. ξ(βj. φj)j≤n, assuming w.l.o.g. that \(\{ x_{i} \mid 1\leq i\leq l\}=\mathcal {V}\). We let \(\mathcal {V}^{\forall } =\{ x_{i} \mid Q_{i}=\mathord \forall \}\subseteq \mathcal {V}\) be the set of universally-quantified variables of φ. A function \(\theta \colon \textsf {Strat}^{\mathcal {V}^{\forall }} \to \textsf {Strat}^{\mathcal {V}}\) is a φ-map (or map when φ is clear from the context) if 𝜃(w)(xi)(ρ) = w(xi)(ρ) for any \(w \in \textsf {Strat}^{\mathcal {V}^{\forall }}\), any \(x_{i}\in \mathcal {V}^{\forall }\), and any history ρ. In other words, 𝜃(w) extends w to \(\mathcal {V}\). This general notion allows any existentially-quantified variable to depend on all universally-quantified ones (dependence on existentially-quantified variables is implicit: all existentially-quantified variables are assigned through a single map, hence they all depend on the others); we add further restrictions later on. Using maps, we may then define new semantics for SL[BG]♭: generally speaking, formula φ = (Qixi)1≤i≤l. ξ(βj. φj)j≤n holds true if there exists a φ-map 𝜃 such that, for any \(w\colon \mathcal {V}^{\forall } \to \textsf {Strat}\), the valuation 𝜃(w) makes ξ(βj. φj)j≤n hold true.
Classic maps are dependence maps in which the order of quantification is respected:
In words, if w1 and w2 coincide on \(\mathcal {V}^{\forall }\cap \{x_{j}\mid j<i\}\), then 𝜃(w1) and 𝜃(w2) coincide on xi.
Elementary maps [29, 30] have to satisfy a more restrictive condition: for those maps, the value of an existentially-quantified strategy at any history ρ may only depend on the value of earlier universally-quantified strategies along ρ. This may be written as:
In this case, for any history ρ, if two valuations w1 and w2 of the universally-quantified variables coincide on the variables quantified before xi all along ρ, then 𝜃(w1)(xi) and 𝜃(w2)(xi) have to coincide at ρ.
The difference between both kinds of dependences is illustrated on Fig. 2: for classic maps, the existentially-quantified strategy x2 may depend on the whole strategy x1, while it may only depend on the value of x1 along the current history for elementary maps. Notice that a map satisfying (E) also satisfies (C).
Indeed, consider a map 𝜃 satisfying (E), and pick two strategy valuations w1 and w2 and an existential variable xi such that
In particular, for those xj, we have w1(xj)(ρ) = w2(xj)(ρ) for any history ρ (hence also for any of its prefixes). By (E), it follows 𝜃(w1)(xi)(ρ) = 𝜃(w2)(xi)(ρ). Since this holds for any history, we have shown 𝜃(w1)(xi) = 𝜃(w2)(xi).
Satisfaction relations Pick a formula \(\varphi =(Q_{i} x_{i})_{1\leq i\leq l} .\ \xi \left ( \beta _{j} .\ \varphi _{j} \right )_{j\leq n}\) in SL[BG]♭. We define:

As explained above, this actually corresponds to the usual semantics of SL[BG]♭ as given in Section 2 [30, Theorem 4.6]. When  , a map 𝜃 satisfying the conditions above is called a C-witness of φ for \(\mathcal {G}\) and q. Similarly, we define the elementary semantics [30] as:
, a map 𝜃 satisfying the conditions above is called a C-witness of φ for \(\mathcal {G}\) and q. Similarly, we define the elementary semantics [30] as:

Again, when such a map exists, it is called an E-witness. Notice that since Property (E) implies Property (C), we have  for any φ ∈SL[BG]♭. This corresponds to the intuition that it is harder to satisfy a SL[BG]♭ formula when dependences are more restricted. The contrapositive statement then raises questions about the negation of formulas.
for any φ ∈SL[BG]♭. This corresponds to the intuition that it is harder to satisfy a SL[BG]♭ formula when dependences are more restricted. The contrapositive statement then raises questions about the negation of formulas.
The syntactic vs. semantic negations If φ = (Qixi)1≤i≤lξ(βj. φj)j≤n is an SL[BG]♭ formula, its syntactic negation ¬φ is the formula \((\overline {Q}_{i} x_{i})_{i \le l} (\neg \xi )(\beta _{j}.\ \varphi _{j})_{j \le n}\), where \(\overline {Q}_{i} =\exists \) if Qi = ∀ and \(\overline {Q}_{i} = \forall \) if Qi = ∃. Looking at the definitions of  and
and  , it could be the case that e.g.
, it could be the case that e.g.  and
and  this only requires the existence of two adequate maps. However, since
this only requires the existence of two adequate maps. However, since  and
and  coincide, and since
coincide, and since  in the classical semantics of SI, we get
in the classical semantics of SI, we get  . Also, since
. Also, since  , we also get
, we also get  . As we now show, the converse implication holds for SL[1G]♭, but may fail to hold for SL[BG]♭.
. As we now show, the converse implication holds for SL[1G]♭, but may fail to hold for SL[BG]♭.
Proposition 1
There exist a game \(\mathcal {G}\) with initial state q0 and a formula φ ∈SL[BG]♭ such that  and
and  .
.
Proof
Consider the formula and the one-player game of Fig. 3. We start by proving that  . For a contradiction, assume that a witness map 𝜃 satisfying (E) exists, and pick any valuation w for the universal variable x. First, for the first goal in the conjunction to be fulfilled, the strategy assigned to y must play to q1 from q0.
. For a contradiction, assume that a witness map 𝜃 satisfying (E) exists, and pick any valuation w for the universal variable x. First, for the first goal in the conjunction to be fulfilled, the strategy assigned to y must play to q1 from q0.
We abbreviate this as 𝜃(w)(y)(q0) = q1 in the sequel. Now, consider two valuations w1 and w2 such that w1(x)(q0) = w2(x)(q0) = q2 and w1(x)(q0 ⋅ q1) = w2(x)(q0 ⋅ q1), but such that w1(x)(q0 ⋅ q2) = p1 and w2(x)(q0 ⋅ q2) = p2. In order to fulfill the second goal under both valuations w1 and w2, we must have 𝜃(w1)(y)(q0 ⋅ q1) = p1 and 𝜃(w2)(y)(q0 ⋅ q1) = p2. But this violates Property (E): since w1(x) and w2(x) coincide on q0 and on q0 ⋅ q1, we must have 𝜃(w1)(y)(q0 ⋅ q1) = 𝜃(w2)(y)(q0 ⋅ q1).
We now prove that  . Indeed, following the previous discussion, we easily get that
. Indeed, following the previous discussion, we easily get that  , by letting 𝜃(w)(y)(q0) = q1 and 𝜃(w)(y)(q0 ⋅ q1) = w(x)(q0 ⋅ q2) if w(x)(q0) = q2, and 𝜃(w)(y)(q0 ⋅ q1) = w(x)(q0 ⋅ q1) if w(x)(q0) = q1. As explained above, this entails
, by letting 𝜃(w)(y)(q0) = q1 and 𝜃(w)(y)(q0 ⋅ q1) = w(x)(q0 ⋅ q2) if w(x)(q0) = q2, and 𝜃(w)(y)(q0 ⋅ q1) = w(x)(q0 ⋅ q1) if w(x)(q0) = q1. As explained above, this entails  , and
, and  .
.
The proof above uses only one player and two quantifiers, but a complex combination of goals. The game and formula of Fig. 1 provide an alternative proof, with three players and four quantifiers, but a formula in SL[DG]♭ (which also entails the result for SL[CG]♭).
Indeed, we already proved (see Example 1) that  , by making strategy z play in q2 in the same direction as what strategy y plays in q1. Then it cannot be
, by making strategy z play in q2 in the same direction as what strategy y plays in q1. Then it cannot be  , since this would imply
, since this would imply  , and both φ and ¬φ would hold, which is impossible in the classical semantics. Thus
, and both φ and ¬φ would hold, which is impossible in the classical semantics. Thus  .
.
Now, in the elementary semantics, we require the existence of a dependence map 𝜃, defining in particular 𝜃(w)(z)(q0 ⋅ q2), and such that \(\theta (w)(z)(q_{0}\cdot q_{2})=\theta (w^{\prime })(z)(q_{0}\cdot q_{2})\) whenever \(w(y)(q_{0})=w^{\prime }(y)(q_{0})\). Consider the following two valuations w and \(w^{\prime }\):
Since \(w(y)(q_{0}) = w^{\prime }(y)(q_{0})\), we must have \(\theta (w)(z)(q_{0}\cdot q_{2})\!=\theta (w^{\prime })(z)(q_{0}\cdot q_{2})\). Then
if 𝜃(w)(z)(q0 ⋅ q2) = p2, then under the strategies prescribed by 𝜃(w), both disjuncts in φ are false.
otherwise, 𝜃(w)(z)(q0 ⋅ q2) = p1, and under the strategies prescribed by \(\theta (w^{\prime })\), again both disjuncts are false.
It follows that  . □
. □
We now prove hat this phenomenon does not occur in SL[1G]:
Proposition 2
For any game \(\mathcal {G}\) with initial state q0, and any formula φ ∈SL[1G]♭, it holds  .
.
Notice that this result follows from [30, Corollary 4.21], which states that  and
and  coincide on SL[1G]. However, since it is central to our approach, we develop a (new) full proof of this result.
coincide on SL[1G]. However, since it is central to our approach, we develop a (new) full proof of this result.
Proof
We begin with intuitive explanations before giving full details. We encode the satisfaction relation  into a two-player turn-based parity game: the first player of the parity game will be in charge of selecting the existentially-quantified strategies, and her opponent will select the universally-quantified ones. This will be encoded by replacing each state of \(\mathcal {G}\) with a tree-shaped module as depicted on Fig. 4. Following the strategy assignment of the SL[1G] formula φ, the strategies selected by those players will define a unique play, along which the LTL objective has to be fulfilled; this verification is encoded into a (doubly-exponential) parity automaton.
into a two-player turn-based parity game: the first player of the parity game will be in charge of selecting the existentially-quantified strategies, and her opponent will select the universally-quantified ones. This will be encoded by replacing each state of \(\mathcal {G}\) with a tree-shaped module as depicted on Fig. 4. Following the strategy assignment of the SL[1G] formula φ, the strategies selected by those players will define a unique play, along which the LTL objective has to be fulfilled; this verification is encoded into a (doubly-exponential) parity automaton.
We prove that  if, and only if, the first player wins; conversely,
if, and only if, the first player wins; conversely,  if the second player wins. Both claims crucially rely on the existence of memoryless optimal strategies for two-player parity games. Finally, by determinacy of those games, we get the expected result.
if the second player wins. Both claims crucially rely on the existence of memoryless optimal strategies for two-player parity games. Finally, by determinacy of those games, we get the expected result.
Notice that in this construction, Player P∃ has full observation, hence her moves may depend on all moves of Player P∀ along the current history. As a result, in our encoding, existentally-quantified strategies may depend on the value of all universally-quantified strategies along the current history; in the example of Fig. 4, this means that the moves selected by Player P∃ for x1 may depend on the moves selected by Player P∀ for x2 earlier in the game.
However, memoryless strategies are sufficient for both players to win parity games; a memoryles strategy for Player P∃ then precisely corresponds to an elementary dependence map, which proves our result.
We now give a full proof following this intuition.
Building a turn-based parity game\({\mathcal{H}}\) from \(\mathcal {G}\) and φ For the rest of the proof, we fix a game \(\mathcal {G}\) and a SL[1G] formula φ = (Qixi)i≤lβ. φ. Each state of \(\mathcal {G}\) is replaced with a copy of the tree-shaped quantification game depicted on Fig. 4. A quantification game \(\mathcal {Q}_{\varphi }\) is formally defined as follows:
it involves two players, P∃ and P∀;
the set of states is \(S_{\varphi }=\{ \mathfrak {m}\in \textsf {Act}^{*} \mid 0\leq {|\mathfrak {m}|} \leq l\}\), thereby defining a tree of depth l + 1 with directions Act. A state \(\mathfrak {m}\) in Sφ with \(0\leq {|\mathfrak {m}|}<l\) belongs to Player P∃ if, and only if, \(Q_{{|\mathfrak {m}|}+1}=\exists \).
from each \(\mathfrak {m}\) with \(0\leq {|\mathfrak {m}|}<l\), for all a ∈Act, there is a transition to \(\mathfrak {m}\cdot a\). The empty word 𝜖 ∈ Sφ is the starting node of the quantification game, and currently has no incoming transitions; states with \(|\mathfrak {m}|=l\) also currently have no outgoing transitions.
A leaf (i.e., a state \(\mathfrak {m}\) with \({|\mathfrak {m}|}=l\)) in a quantification game represents a move vector of domain \(\mathcal {V}=\{x_{i}\mid 1\leq i\leq l\}\): we identify each leaf \(\mathfrak {m}\) with the move vector \(\mathfrak {m}\), hence writing \(\mathfrak {m}(x_{i})\) for \(\mathfrak {m}(i)\).
We let D be a deterministic parity automaton over 2AP associated with φ. We write d0 for the initial state of D. Using quantification games, we can now define the turn-based parity game \({\mathcal{H}}\):
it involves players P∃ and P∀;
for each state q of \(\mathcal {G}\) and each state d of D, \({\mathcal{H}}\) contains a copy of the quantification game \(\mathcal {Q}_{\varphi }\), which we call the (q,d)-copy. Hence the set of states of \({\mathcal{H}}\) is the product of the state spaces of \(\mathcal {G}\), D and \(\mathcal {Q}_{\varphi }\).
the transitions in \({\mathcal{H}}\) are of two types:
internal transitions in each copy of the quantification game are preserved;
consider a state \((q,d,\mathfrak {m})\) where \({|\mathfrak {m}|}=l\); this is a leaf in the quantification game. Let \(q^{\prime }={\Delta }(q,m_{\beta })\), where mβ: Agt →Act is the move vector over Agt defined by \(m_{\beta }(A)=\mathfrak {m}(i-1)\) where xi = β(A) (i.e., assigning to each player A ∈Agt the action \(\mathfrak {m}(\beta (A))\)); then we add a transition from \((q,d,\mathfrak {m})\) to \((q^{\prime },d^{\prime },\epsilon )\) where \(d^{\prime }\) is the state of D reached from d when reading \(\textsf {lab}(q^{\prime })\). Notice that \((q,d,\mathfrak {m})\) then has at most one outgoing transition.
the priorities are inherited from those in D: state \((q,d,\mathfrak {m})\) has the same priority as d.
Correspondence between\(\mathcal {G}\) and \({\mathcal{H}}\) We begin with building a correspondence between the runs and strategies in \(\mathcal {G}\) and those in \({\mathcal{H}}\). In a sense, each step of a history in \(\mathcal {G}\) is split into several steps in \({\mathcal{H}}\); we thus refine the notion of history in \(\mathcal {G}\) in order to establish our correspondence. □
Definition 1
A lane in \(\mathcal {G}\) is a tuple (ρ,u,b,t) made of
a history ρ = (qj)0≤j≤a (for some integer a);
a function \(u\colon \mathcal {V} \times \textsf {Pref}(\rho ) \to \textsf {Act}\);
an integer b ∈ [0;l];
a function t: {x1,...,xb}→Act (t is the empty function if b = 0);
and such that
We can then build a one-to-one application \(\mathfrak {G}_{p}\) between histories in \({\mathcal{H}}\) and lanes in \(\mathcal {G}\). With a history π in \({\mathcal{H}}\), written
having length a ⋅ (l + 1) + b + 1 with 0 ≤ b < l, we associate a lane \(\mathfrak {G}_{p}(\pi )=((q_{j})_{j\leq a}, u, b, t)\) with
The resulting function \(\mathfrak {G}_{p}\) is clearly injective (different histories will correspond to different lanes), but also surjective. To prove the latter statement, we build the inverse function \(\mathfrak {H}_{p}\): for a lane ((qj)j≤a,u,b,t), we set \(\mathfrak {H}_{p}((q_{j})_{j\leq a}, u, b, t) =\pi \) where π is the history in \({\mathcal{H}}\) of length a ⋅ (l + 1) + b + 1 defined as
where dj is the state of D reached on input (qk)0≤k≤j− 1.
Because of the coherence condition (1), \(\mathfrak {H}_{p}((q_{j})_{j\leq a}, u, i, t)\) is indeed a history in \({\mathcal{H}}\). From the definitions, one can easily check that
and deduce that \(\mathfrak {H}_{p}\) is the inverse function of \(\mathfrak {G}_{p}\); therefore
Lemma 1
The application \(\mathfrak {G}_{p}\) is a bijection between lanes of \(\mathcal {G}\) and histories in \({\mathcal{H}}\), and \(\mathfrak {H}_{p}\) is its inverse function.
Extending the correspondence We can use \(\mathfrak {G}_{p}\) to describe another correspondence \(\mathfrak {G}\) between strategies for P∃ in \({\mathcal{H}}\) and maps in \(\mathcal {G}\). Remember that a map in \(\mathcal {G}\) is a function \(\theta \colon (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})^{\mathcal {V}^{\forall }} \to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})^{\mathcal {V}}\). Remember also that if Qj = ∀, then 𝜃(w)(xi)(ρ) = w(xi)(ρ), so that we only have to define the map for existentially-quantified variables.
Formally, the application \(\mathfrak {G}\) takes as input a strategy δ for player P∃ in \({\mathcal{H}}\), and returns a map in \(\mathcal {G}\). It will enjoy the following properties:
for any finite outcome π of δ in \({\mathcal{H}}\) ending at the root of a quantification game, there exists a function w such that \(\mathfrak {G}_{p}(\pi )=(\rho ,u,0,t_{\varnothing })\) where ρ is the outcome of \(\mathfrak {G}(\delta )(w)\) in \(\mathcal {G}\) under the assignment defined by β;
conversely, for any path ρ in \(\mathcal {G}\) that is an outcome of \(\mathfrak {G}(\delta )(w)\) for some w and under the assignment defined by β, then letting \(u(x,\rho ^{\prime })=\mathfrak {G}(\delta )(w)(x)(\rho ^{\prime })\), we have that (ρ,u,0,t∅) is a lane in \(\mathcal {G}\) and \(\mathfrak {H}_{p}(\rho ,u,0,t_{\emptyset })\) is an outcome of δ in \({\mathcal{H}}\) ending in the root of a quantification game.
We fix δ, and for all w, ρ and xi, we define \(\mathfrak {G}(\delta )(w)(x_{i})(\rho )\) by a double induction, first on the length of the history ρ in \(\mathcal {G}\), and second on the sequence of variables xi. We prove the properties above alongside the definition.
Initial step: we begin with the case where ρ is the single state q0.
We proceed by induction on existentially-quantified variables, merging the initialization step with the induction step as they are similar. Consider an existentially-quantified variable xi in \(\mathcal {V}\). Given \(w\colon \mathcal {V}^{\forall } \times \textsf {Pref}(\rho ) \cup \{\rho \} \to \textsf {Act}\), we define a function ti,w: [x1;xi− 1] →Act such that ti,w(x) = w(x,q0) for \(x\in \mathcal {V}^{\forall }\cap [x_{1};x_{i-1}]\), and \(t_{i,w}(x)=\mathfrak {G}(\delta )(w)(x)(q_{0})\) for \(x\in \mathcal {V}^{\exists }\cap [x_{1};x_{i-1}]\), assuming that they have been defined in the previous induction steps on variables. We can then create the lane lanei,w = (𝜖,u∅,i − 1,t) and define
$$ \mathfrak{G}(\delta)(w)(x_{i})(q_{0})=\delta(\mathfrak{H}_{p}(\textit{lane}_{i,w})) $$Pick an outcome π of δ in \({\mathcal{H}}\) of length l + 2, and write \(\mathfrak {m}\) for its l + 1-st state: it defines a valuation for the variables in \(\mathcal {V}\), hence defining a move vector mβ under the assignment β in Act. By construction of \({\mathcal{H}}\), this outcome ends in the state (q1,d1,𝜖) where q1 = Δ(q0,mβ) and d1 is the successor of the initial state d0 of D when reading lab(q1). We now prove that q0 ⋅ q1 is the outcome of \(\mathfrak {G}(\delta )(w)\) for some w. For this, we let \(w(x_{i})=\mathfrak {m}_{i}\) for all \(x_{i}\in \mathcal {V}^{\forall }\). By construction, \(\mathfrak {G}(\delta )(w)(x_{j})(q_{0})\) precisely corresponds to \(\mathfrak {m}(j)\), for all \(x_{j}\in \mathcal {V}^{\exists }\). In the end, under assignment β, \(\mathfrak {G}(\delta )(w)\) precisely returns the move vector mβ, hence proving our result.
The proof of the converse statement follows similar arguments: consider an outcome ρ = q0 ⋅ q1 of \(\mathfrak {G}(\delta )(w)\) for some w. The lane (ρ,u,0,t∅) defined with \(u(x,q_{0})=\mathfrak {G}(\delta )(w)(x)(q_{0})\) then corresponds through \(\mathfrak {H}_{p}\) to a play ending in (q1,d1,𝜖), and visiting the leaf \(\mathfrak {m}\) defined as \(\mathfrak {m}_{i}=u(x_{i},q_{0})\). By construction, this is an outcome of δ in \({\mathcal{H}}\).
induction step: we consider a history ρ in \(\mathcal {G}\), assuming we have already defined \(\mathfrak {G}(\delta )(w)(x_{i})(\rho ^{\prime })\) for all prefix \(\rho ^{\prime }\) of ρ, and for all w and all variable xi. We now define \(\mathfrak {G}(\delta )(w)(x_{i})(\rho )\), by induction on the list of variables. Again, the initialization step is merged with the induction step as they rely on the same arguments.
Consider an existentially-quantified variable xi, and \(w\colon \mathcal {V}^{\forall } \times \textsf {Pref}(\rho ) \cup \{\rho \} \to \textsf {Act}\). We define a function ti,w: [x1;xi− 1] →Act where ti,w associate with \(x\in \mathcal {V}^{\forall }\cap [x_{1};x_{i-1}]\) the action w(x)(π), and with \(x\in \mathcal {V}^{\exists }\cap [x_{1};x_{i-1}]\) the action \(\mathfrak {G}(\delta )(w)(x)(\rho )\). We also define \(u_{w}\colon \mathcal {V}\times \textsf {Pref}(\rho ) \to \textsf {Act}\) as \(u_{w}(x,\rho ^{\prime })=\mathfrak {G}(\delta )(w)(x)(\rho ^{\prime })\), for all prefixes \(\rho ^{\prime }\) of ρ. We can then create the lane lanei,w = (π,uw,i − 1,ti,w) and finally define
$$ \mathfrak{G}(\delta)(w)(x_{i})(\rho)=\delta(\mathfrak{H}_{p}(\textit{lane}_{i,w})). $$Using the same arguments as in the initial step, we prove our correspondence between the outcomes of δ in \({\mathcal{H}}\) and the outcomes of \(\mathfrak {G}(\delta )\) in \(\mathcal {G}\).
Notice that in the construction above, \(\mathfrak {G}(\delta )(w)(x_{i})(\rho )\) may depend on the value of \(w(x_{j},\rho ^{\prime })\) for j > i and \(\rho ^{\prime }\in \textsf {Pref}(\rho )\): indeed, in the inductive definition, we define \(\mathfrak {G}(\delta )(w)(x_{j})(\rho ^{\prime })\) before defining \(\mathfrak {G}(\delta )(w)(x_{i})(\rho )\). Hence in general \(\mathfrak {G}(\delta )\) is not an elementary map.
However, in case δ is memoryless, we notice that \(\mathfrak {G}(\delta )(w)(x_{i})(\rho )\) only depends on value of δ in the last state of the lane lanei,w, hence in particular not on uw. This removes the above dependence, and makes \(\mathfrak {G}(\delta )\) elementary.
Finally, notice that we can define a dual correspondence \(\overline {\mathfrak {G}}\) relating strategies of Player P∀ and elementary maps in \(\mathcal {G}\) where existential and universal variables are swapped.
Concluding the proof Using \(\mathfrak {G}\), we prove our final correspondence between \({\mathcal{H}}\) and \(\mathcal {G}\):
Lemma 2
Assume that P∃ is winning in \({\mathcal{H}}\) and let δ be a positional winning strategy. Then the elementary map \(\mathfrak {G}(\delta )\) is a witness that  .
.
Similarly, assume that P∀ is winning in \({\mathcal{H}}\) and let \(\overline {\delta }\) be a positional winning strategy. Then the elementary map \(\overline {\mathfrak {G}}(\overline {\delta })\) is a witness that  .
.
Proof
We prove the first point, the second one following similar arguments. Assume that P∃ is winning in \({\mathcal{H}}\), and pick a memoryless winning strategy δ. Toward a contradiction, assume further that \(\mathfrak {G}(\delta )\) is not a witness of  . Then there exists \(w_{0}\colon \mathcal {V}^{\forall } \to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})\) s.t.
. Then there exists \(w_{0}\colon \mathcal {V}^{\forall } \to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})\) s.t.  . We use w0 to build a strategy \(\overline {\delta }\) for Player P∀ in \({\mathcal{H}}\). Given a history
. We use w0 to build a strategy \(\overline {\delta }\) for Player P∀ in \({\mathcal{H}}\). Given a history
in \({\mathcal{H}}\), we define \(\rho ={\prod }_{0\leq j\leq a} q_{j}\) and set \( \overline {\delta }(\pi ) = \mathfrak {G}(\delta )(w)(x_{b})(\eta ) \) where
\(w\colon \textsf {Pref}(\rho ) \cup \{\rho \} \times (\mathcal {V}^{\forall } \cap [x_{1};x_{b}]) \to \textsf {Act}\) is such that \(w(\rho ^{\prime },x_{i})\) is the action to be played for going from \(\pi _{\leq {|\rho ^{\prime }|}\cdot (l+1)+i-1}\) to \(\pi _{\leq {|\rho ^{\prime }|}\cdot (l+1)+i}\) in \({\mathcal{H}}\);
\(\eta = {\prod }_{0\leq j< a}\ {\prod }_{0\leq i\leq l} (q_{j},d_{j},\mathfrak {m}_{j,i}))\).
Write  for the outcome of 𝜃(w0) under strategy assignment β in \(\mathcal {G}\). Then, by construction of \(\overline {\delta }\), the outcome of δ and \(\overline {\delta }\) in \({\mathcal{H}}\) will visit the
for the outcome of 𝜃(w0) under strategy assignment β in \(\mathcal {G}\). Then, by construction of \(\overline {\delta }\), the outcome of δ and \(\overline {\delta }\) in \({\mathcal{H}}\) will visit the  -copies of the quantification game, where dj is the state reached by reading \((q_{\phantom {\dot {i}\!}j^{\prime }})_{\phantom {\dot {i}\!}j^{\prime }\leq j}\) in the deterministic automaton D. Now, since
-copies of the quantification game, where dj is the state reached by reading \((q_{\phantom {\dot {i}\!}j^{\prime }})_{\phantom {\dot {i}\!}j^{\prime }\leq j}\) in the deterministic automaton D. Now, since  , we get that ν does not satisfy φ and therefore the outcome of δ and \(\overline {\delta }\) in \({\mathcal{H}}\) does not satisfy the parity condition. This is in contradiction with δ being the winning strategy of P∃, and proves that \(\mathfrak {G}(\delta )\) must be a witness that
, we get that ν does not satisfy φ and therefore the outcome of δ and \(\overline {\delta }\) in \({\mathcal{H}}\) does not satisfy the parity condition. This is in contradiction with δ being the winning strategy of P∃, and proves that \(\mathfrak {G}(\delta )\) must be a witness that  .
.
Proposition 2, together with the determinacy of parity games [16, 35] immediately imply that at least one of φ and ¬φ must hold in \(\mathcal {G}\) for  . This concludes our proof. □
. This concludes our proof. □
The following two results, already mentioned in [30], immediately follow: the first result uses the fact that  implies
implies  ; the second one uses the two-player game built in the proof.
; the second one uses the two-player game built in the proof.
Corollary 1
The relations  and
and  coincide over SL[1G].
coincide over SL[1G].
Corollary 2
Model checking SL[1G] is 2-EXPTIME-complete (for both semantics).
Remark 1
As an immediate corollary of (the proof of) Prop. 1, we have that the relations  and
and  differ on SL[CG]♭ (as well as on SL[DG]♭). This contradicts the claim in [32] that
differ on SL[CG]♭ (as well as on SL[DG]♭). This contradicts the claim in [32] that  and
and  would coincide on SL[CG] (and SL[DG]).
would coincide on SL[CG] (and SL[DG]).
Indeed, in [32], the satisfaction relation for SL[DG] and SL[CG] is encoded into a two-player game in pretty much the same way as we did in the proof of Proposition 2 for SL[1G]. While this indeed rules out dependences outside the current history, it also gives information to Player P∃ about the values (over prefixes of the current history) of strategies that are universally-quantified later in the quantification block. This proof technique works with SL[1G]♭ because the single goal can be encoded as a parity objective, for which memoryless strategies exist, so that the extra information is not crucial. In the next section, we investigate the role of this extra information for larger fragments of SL[BG]♭.
4 Timeline Dependences
Following the discussion above, we introduce a new type of dependences between strategies (which we call timeline dependences). They allow strategies to also observe (and depend on) all other universally-quantified strategies on the strict prefix of the current history. For instance, for a block of quantifiers ∀x1. ∃x2. ∀x3, the value of x2 after history ρ may depend on the value of x1 on ρ and its prefixes (as for elementary maps), but also on the value of x3 on the (strict) prefixes of ρ. Such dependences are depicted on Fig. 5. We believe that such dependences are relevant in many situations, especially for reactive synthesis, since in this framework strategies really base their decisions on what they could observe along the current history.
Formally, a map 𝜃 is a timeline map if it satisfies the following condition:
Using those maps, we introduce the timeline semantics of SL[BG]♭:

Such a map, if any, is called a T-witness of φ for \(\mathcal {G}\) and q. As in the previous section, it is easily seen that Property (E) implies Property (T), so that an E-witness is also a T-witness, and  for any formula φ ∈SL[BG]♭.
for any formula φ ∈SL[BG]♭.
Example 2
Consider again the game of Fig. 1 in Section 2. We have seen that  in Example 1, and that
in Example 1, and that  in the proof of Prop. 1. With timeline dependences, we have
in the proof of Prop. 1. With timeline dependences, we have  . Indeed, now 𝜃(w)(z)(q0 ⋅ q2) may depend on w(xA)(q0) and w(xB)(q0): we could then have e.g. 𝜃(w)(z)(q0 ⋅ q2) = p1 when w(xA)(q0) = q2, and 𝜃(w)(z)(q0 ⋅ q2) = p2 when w(xA)(q0) = q1. It is easily checked that this map is a T-witness of φ for q0.
. Indeed, now 𝜃(w)(z)(q0 ⋅ q2) may depend on w(xA)(q0) and w(xB)(q0): we could then have e.g. 𝜃(w)(z)(q0 ⋅ q2) = p1 when w(xA)(q0) = q2, and 𝜃(w)(z)(q0 ⋅ q2) = p2 when w(xA)(q0) = q1. It is easily checked that this map is a T-witness of φ for q0.
Comparison of and
and  As explained at the end of Section 3, the proof of Prop. 2 actually shows the following result:
As explained at the end of Section 3, the proof of Prop. 2 actually shows the following result:
Proposition 3
For any game \(\mathcal {G}\) with initial state q0, and any formula φ ∈SL[1G]♭, it holds 
We now prove that this does not extend to SL[CG]♭ and SL[DG]♭:
Proposition 4
The relations  and
and  differ on SL[CG]♭, as well as on SL[DG]♭.
differ on SL[CG]♭, as well as on SL[DG]♭.
Proof
The result for SL[DG]♭ is witnessed by Example 2. For SL[CG]♭, we consider the game structure and formula of Fig. 6. We first notice that  : indeed, in order to satisfy the first goal under any choice of xA, the strategy for y has to point to p1 from both q1 and q2. But then no choice of xB will make the second goal true.
: indeed, in order to satisfy the first goal under any choice of xA, the strategy for y has to point to p1 from both q1 and q2. But then no choice of xB will make the second goal true.
On the other hand, considering the timeline semantics, strategy y after q0 ⋅ q1 and q0 ⋅ q2 may depend on the choice of xA in q0. When w(xA)(q0) = q1, we let 𝜃(w)(y)(q0 ⋅ q1) = p1 and 𝜃(w)(y)(q0 ⋅ q2) = p2 and 𝜃(w)(xB)(q0) = q2, which makes both goals hold true. Conversely, if w(xA)(q0) = q2, then we let 𝜃(w)(y)(q0 ⋅ q2) = p1 and 𝜃(w)(y)(q0 ⋅ q1) = p2 and 𝜃(w)(xB)(q0) = q1, which also defines a timeline map witnessing  . □
. □
The syntactic vs. semantic negations While both semantics differ, we now prove that the situation w.r.t. the syntactic vs. semantic negations is similar. First, following Prop. 3 and 2, the two negations coincide on SL[1G]♭ under the timeline semantics. Moreover:
Proposition 5
For any formula φ in SL[BG]♭, for any game \( \mathcal {G} \) and any state q0, we have  .
.
Remember that the same result for  was proven easily from the implication
was proven easily from the implication  , and because the two negations coincide for
, and because the two negations coincide for  . The proof for
. The proof for  is more involved.
is more involved.
Proof
For a contradiction, assume that there exist two maps 𝜃 and \(\overline \theta \) witnessing  and
and  resp. Then
resp. Then


From 𝜃 and \(\overline {\theta }\), we build a strategy valuation χ on \(\mathcal {V}\) such that \(\theta {\kern -.5pt}(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }}) {\kern -.5pt}={\kern -.5pt} \overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})=\chi \). By (2) and (3), we get that  and
and  . It follows that there must exist a goal βj. φj for which
. It follows that there must exist a goal βj. φj for which  and
and  ; then the outcome corresponding to βj would satisfy both φj and ¬φj, which for LTL formulas is impossible.
; then the outcome corresponding to βj would satisfy both φj and ¬φj, which for LTL formulas is impossible.
We define χ(x)(ρ) inductively on histories and on the list of quantified variables. When ρ is the empty history q0, we consider two cases:
if \(x_{1}\in \mathcal {V}^{\forall }\), then \(\overline \theta (\overline {w})(x_{1})(q_{0})\) does not depend on \(\overline {w}\) at all, since \(\overline {\theta }\) is a timeline-map. Hence we let \(\chi (x_{1})(q_{0})=\overline {\theta }(\overline {w})(x_{1})(q_{0})\), for any \(\overline {w}\).
similarly, if \(x_{1}\in \mathcal {V}^{\exists }\), we let χ(x1)(q0) = 𝜃(w)(x1)(q0), which again does not depend on w.
Similarly, when χ(x)(q0) has been defined for all x ∈{x1,...,xi− 1}, we again consider two cases:
if \(x_{i}\in \mathcal {V}^{\forall }\), we define \(\overline {w}(x_{j})(q_{0})=\chi (x_{j})(q_{0})\) for all \(x_{j}\in \mathcal {V}^{\exists }\cap \{x_{1},...,x_{i-1}\}\), and let \(\chi (x_{i})(q_{0})=\overline {\theta }(\overline {w})(x_{i})(q_{0})\), which again does not depend on the value of \(\overline {w}\) besides those defined above;
symmetrically, if \(x_{i}\in \mathcal {V}^{\exists }\), we define w(xj)(q0) = χ(xj)(q0) for all \(x_{j}\in \mathcal {V}^{\forall }\cap \{x_{1},...,x_{i-1}\}\), and let χ(xi)(q0) = 𝜃(w)(xi)(q0).
Notice that this indeed enforces that \(\theta (\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }})(x_{i})(q_{0})=\chi (x_{i})(q_{0})\) when \(x_{i}\in \mathcal {V}^{\exists }\), and \(\overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})(x_{i})(q_{0})=\chi (x_{i})(q_{0})\) when \(x_{i}\in \mathcal {V}^{\forall }\).
The induction step is proven similarly: consider a history ρ and a variable xi, assuming that χ has been defined for all variables on all prefixes of ρ, and for variables in {x1,...,xi− 1} on ρ itself. Then:
if \(x_{i}\in \mathcal {V}^{\forall }\), we define \(\overline {w}(x_{j})(\rho ^{\prime })=\chi (x_{j})(\rho ^{\prime })\) for all \(x_{j}\in \mathcal {V}\) and all \(\rho ^{\prime }\in \textsf {Pref}(\rho )\), and \(\overline {w}(x_{j})(\rho )=\chi (x_{j})(\rho )\) for all \(x_{j}\in \mathcal {V}^{\exists }\cap \{x_{1},...,x_{i-1}\}\). We then let \(\chi (x_{i})(\rho )=\overline {\theta }(\overline {w})(x_{i})(q_{0})\), which does not depend on the value of \(\overline {w}\) besides those defined above;
the construction for the case when \(x_{i}\in \mathcal {V}^{\exists }\) is similar.
As in the initial step, it is easy to check that this construction enforces \(\theta (\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }}) = \overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})=\chi \), as required. □
Proposition 6
There exists a formula φ ∈SL[BG]♭, a (turn-based) game \(\mathcal {G}\) and a state q0 such that  and
and  .
.
Proof
For this proof, we reuse the game and formula of Fig. 3. Since the quantifier part is ∀x. ∃y, the timeline- and elementary semantics coincide for this formula. Since  , also
, also  .
.
The negation of φ is

Assume that there exists a timeline map \(\overline {\theta }\) witnessing  . Consider the valuations w1(y)(q0) = w2(y)(q0) = q2, and w1(y)(q0 ⋅ q2) = p1 and w2(y)(q0 ⋅ q2) = p2. Notice that the first disjunct is not satisfied under those valuations. We consider two (symmetric) possiblities:
. Consider the valuations w1(y)(q0) = w2(y)(q0) = q2, and w1(y)(q0 ⋅ q2) = p1 and w2(y)(q0 ⋅ q2) = p2. Notice that the first disjunct is not satisfied under those valuations. We consider two (symmetric) possiblities:
we may have both 𝜃(w1)(x)(q0) and 𝜃(w2)(x)(q0) to q1: then 𝜃(w1)(x)(q0 ⋅ q1) and 𝜃(w2)(x)(q0 ⋅ q1) must return the same move, since w1(y)(q0) = w2(y)(q0). If they play to p1, then none of the disjunct would be fulfilled under strategy valuation w1; if they play to p2, then all three disjunct are false under w2.
the argument is symmetric if 𝜃(w1)(x)(q0) = 𝜃(w2)(x)(q0) = q2.
Hence  □
□
5 The Fragment SL[EG]♭
In this section, we focus on the timeline semantics  . We exhibit a fragmentFootnote 1SL[EG]♭ of SL[BG]♭, containing SL[CG]♭ and SL[DG]♭, for which the syntactic and semantic negations coincide:
. We exhibit a fragmentFootnote 1SL[EG]♭ of SL[BG]♭, containing SL[CG]♭ and SL[DG]♭, for which the syntactic and semantic negations coincide:
Theorem 1
For any game \(\mathcal {G}\) with initial state q0, and any formula φ ∈SL[EG]♭, it holds  .
.
We prove this result in the sequel of this section. We first introduce semi-stable sets, which are the basis of the definition of SL[EG]♭; we then prove useful properties of those sets, and finally proceed to the proof of Theorem 1.
5.1 Semi-stable Sets
For  , we let {0,1}n be the set of mappings from [1,n] to {0,1}. We write 0n (or 0 if the size n is clear) for the function that maps all integers in [1,n] to 0, and 1n (or 1) for the function that maps [1,n] to 1. For f,g ∈{0,1}n, we define:
, we let {0,1}n be the set of mappings from [1,n] to {0,1}. We write 0n (or 0 if the size n is clear) for the function that maps all integers in [1,n] to 0, and 1n (or 1) for the function that maps [1,n] to 1. For f,g ∈{0,1}n, we define:
The set {0,1}n can be seen as the lattice of subsets of [1;n], with the above three operations corresponding to complement, intersection and union, respectively.
We then introduce the notion of semi-stable sets, on which the definition of SL[EG]♭ relies: a set \(F^{n}\subseteq \{0,1\}^{n}\) is semi-stable if for any f and g in Fn, it holds that
Example 3
Obviously, the set {0,1}n is semi-stable, as well as the empty set. It is easily seen that any singleton set also is semi-stable. For n = 2, the set {(0,1),(1,0)} is easily seen not to be semi-stable: taking f = (0,1) and g = (1,0) with s = (1,0), we get \((f\curlywedge s)\curlyvee (g\curlywedge \overline {s})=(0,0)\) and \((g\curlywedge s)\curlyvee (f\curlywedge \overline {s})=(1,1)\). Similarly, {(0,0),(1,1)} is not semi-stable. Any other subset of {0,1}2 is semi-stable.
We can now define SL[EG]♭ as follows:
where Fn ranges over semi-stable subsets of {0,1}n, for all  . The semantics of the operator Fn is defined as
. The semantics of the operator Fn is defined as

Equivalently:

so that SL[EG]♭ is indeed a fragment of SL[BG]♭. Notice that SL[CG]♭ corresponds to the case where Fn = {1n}, which is semi-stable, so that SL[EG]♭ encompasses SL[CG]♭. As we prove later, {0,1}n ∖{0n} also is semi-stable, which entails that SL[EG]♭ also subsumes SL[DG]♭.
Example 4
Consider the following formula, expressing the existence of a Nash equilibrium for two players with respective LTL objectives ψ1 and ψ2:
This formula has four goals, and it corresponds to the set
Taking f = (1,1,0,0) and g = (0,0,1,1), with s = (1,0,1,0) we have \((f\curlywedge s)\curlyvee (g\curlywedge \overline {s}) = (1,0,0,1)\) and \((g\curlywedge s)\curlyvee (f\curlywedge \overline {s}) = (0,1,1,0)\), none of which is in F4. Hence our formula is not (syntactically) in SL[EG]♭ (notice however that the existence of a Nash equilibrium can also be written as the disjunction (over all possible payoffs for the agents) of formulas in SL[CG]♭).
The definition of SL[EG] may look artificial. The main reason why we work with SL[EG] is that it is maximal for the first claim of Theorem 1 (see Prop. 9). But as the next result shows, it is actually a large fragment encompassing SL[AG] (hence also SL[CG] and SL[DG]):
Proposition 7
SL[EG]♭ contains SL[AG]♭. The inclusion is strict (syntactically).
Proof
Remember that boolean combinations in SL[AG]♭ follow the grammar ξ ::= ξ ∨ ω∣ξ ∧ ω∣ω. In terms of subsets of {0,1}n, it corresponds to considering sets defined in one of the following two forms:
depending whether \(\xi (p_{j})_{j}=\xi ^{\prime }(p_{j})_{j}\vee p_{n}\) or \(\xi (p_{j})_{j}=\xi ^{\prime }(p_{j})_{j}\wedge p_{n}\). Assuming (by induction) that \(F^{n-1}_{\xi ^{\prime }}\) is semi-stable, then we can prove that \(F^{n}_{\xi }\) also is. We detail the proof for the second case, the first case being similar.
Consider the case where \(F^{n}_{\xi }=\{f\in \{0,1\}^{n} \mid f(n)=1 \text { and} f_{|[1;n-1]}\in F^{n-1}_{\xi ^{\prime }}\}\). Pick any two elements f and g in \(F^{n}_{\xi }\), and s ∈{0,1}n. Since f(n) = g(n) = 1, we have \([(f\curlywedge s)\curlyvee (g\curlywedge \overline {s})](n)= [(f\curlywedge \overline {s})\curlyvee (g\curlywedge s)](n)=1\). Moreover, the restriction of \([(f\curlywedge s)\curlyvee (g\curlywedge \overline {s})]\) and of \([(f\curlywedge \overline {s})\curlyvee (g\curlywedge s)]\) to their first n − 1 bits is computed from the restriction of f, g and s to their first n − 1 bits. Since \(F^{n-1}_{\xi ^{\prime }}\) is semi-stable, one of \([(f\curlywedge s)\curlyvee (g\curlywedge \overline {s})]_{[1;n-1]}\) and \([(f\curlywedge \overline {s})\curlyvee (g\curlywedge s)]_{[1;n-1]}\) belongs to \(F^{n-1}_{\xi ^{\prime }}\), so that one of \([(f\curlywedge s)\curlyvee (g\curlywedge \overline {s})]\) and \([(f\curlywedge \overline {s})\curlyvee (g\curlywedge s)]\) is in \(F^{n}_{\xi }\).
That the inclusion is strict is proven by considering the semi-stable set H3 = {(1,1,1),(1,1,0),(1,0,1),)(0,1,1)}. Assume that it corresponds to a formula in SL[AG]♭: then the boolean combination ξ(x1,x2,x3) of that formula must be in one of the following forms:
It remains to prove that none of these cases corresponds to H3: the first case does not allow (1,1,0); the second case allows (0,0,1); the third case does not allow (1,0,1); the last case allows (0,0,0). □
5.2 Properties of semi-stable Sets
Before proving our main theorem, we show that semi-stable sets enjoy several nice structural properties. Our first lemma entails that SL[EG]♭ is closed under (syntactic) negation.
Lemma 3
Fn is semi-stable if, and only if, its complement is.
Proof
Assume Fn is not semi-stable, and pick f and g in Fn and s ∈{0,1}n such that none of \(\alpha =(f\curlywedge s)\curlyvee (g\curlywedge \overline {s})\) and \(\gamma =(g\curlywedge s)\curlyvee (f\curlywedge \overline {s})\) are in Fn. It cannot be the case that g = f, as this would imply α = f ∈ Fn. Hence α≠γ. We claim that α and γ are our witnesses for showing that the complement of Fn is not semi-stable: both of them belong to the complement of Fn, and \((\alpha \curlywedge s)\curlyvee (\gamma \curlywedge \overline {s})\) can be seen to equal f, hence it is not in the complement of Fn. Similarly for \((\gamma \curlywedge s)\curlyvee (\alpha \curlywedge \overline {s})=g\). □
Lemma 4
If \(F^{n}\subseteq \{0,1\}^{n}\) is semi-stable, then for any s ∈{0,1}n and any non-empty subset Hn of Fn, it holds that
Proof
For a contradiction, assume that there exist s ∈{0,1}n and \(H^{n} \subseteq F^{n}\) such that, for any f ∈ Hn, there is an element g ∈ Hn for which \({(f\curlywedge s) \curlyvee (g\curlywedge \overline {s}) \notin F^{n}}\). Then there must exist a minimal integer 2 ≤ λ ≤|Hn| and λ elements {fi∣1 ≤ i ≤ λ} of Hn such that
By Lemma 3, the complement of Fn is semi-stable. Hence, considering \((f_{\lambda -1}\curlywedge s)\curlyvee (f_{\lambda }\curlywedge \overline {s})\) and \((f_{\lambda }\curlywedge s)\curlyvee (f_{1}\curlywedge \overline {s})\), one of the following two vectors is not in Fn:
The second expression equals fλ, which is in Fn. Hence we get that \((f_{\lambda -1}\curlywedge s) \curlyvee (f_{1}\curlywedge \overline {s})\) is not in Fn, contradicting minimality of λ. □
For two elements f and g of {0,1}n, we write f ≤ g whenever f(i) = 1 implies g(i) = 1 for all i ∈ [1,n] (this corresponds to set inclusion when seeing {0,1}n as the lattice of subsets of [1;n]). Given \(B^{n}\subseteq \{0,1\}^{n}\), we write ↑Bn = {g ∈{0,1}n∣∃f ∈ Bn, f ≤ g}. A set \(F^{n}\subseteq \{0,1\}^{n}\) is upward-closed if Fn = ↑Fn. Notice that being upward-closed and being semi-stable are uncomparable (for instance, the set ↑{(0,0,1,1);(1,1,0,0)} is not semi-stable). We now explain how to transform a semi-stable set into an upward-closed one by flipping some of its bits. This will simplify the presentation of the proof of our main theorem.
Fix a vector b ∈{0,1}n. We define the operation \(\textsf {flip}_{b}\colon \{0,1\}^{n} \to \{0,1\}^{n}\) that maps any vector f to \((f\curlywedge b)\curlyvee (\overline {f} \curlywedge \overline {b})\). In other terms, flipb flips the i-th bit of its argument if bi = 0, and keeps this bit unchanged if bi = 1. In SL[EG]♭, flipping bits amounts to negating the corresponding goals. The first part of the following lemma thus indicates that our definition for SL[EG]♭ is sound.
Lemma 5
For any b ∈{0,1}n, if \(F^{n}\subseteq \{0,1\}^{n}\) is semi-stable, then so is flipb(Fn). Moreover, for any semi-stable set Fn, there exists b ∈{0,1}n such that flipb(Fn) is upward-closed.
Example 5
Take F2 = {(0,0),(1,0),(1,1)}. This set is semi-stable, but it is not upward-closed. Letting b = (1,0), we have flipb(F2) = {(0,1),(1,1),(1,0)}, which is upward-closed (and still semi-stable).
Proof
We begin with the first statement. Assume that Fn is semi-stable, and take \(f^{\prime }=\textsf {flip}_{b}(f)\) and \(g^{\prime }=\textsf {flip}_{b}(g)\) in flipb(Fn), and s ∈{0,1}n. By distributivity, we get
Write \(\alpha =(f\curlywedge s) \curlyvee (g \curlywedge \overline {s})\) and \(\beta = (\overline {f}\curlywedge s) \curlyvee (\overline {g}\curlywedge \overline {s})\). One can easily check that \(\beta =\overline {\alpha }\). We then have
This computation being valid for any f and g, we also have
with \(\gamma =(g\curlywedge s) \curlyvee (f \curlywedge \overline {s})\). By hypothesis, at least one of α and γ belongs to Fn, so that also at least one of \((f^{\prime }\curlywedge s) \curlyvee (g^{\prime }\curlywedge \overline {s})\) and \((g^{\prime }\curlywedge s) \curlyvee (f^{\prime }\curlywedge \overline {s})\) belongs to flipb(Fn).
The second statement of Lemma 5 trivially holds for Fn = ∅; thus in the following, we assume Fn to be non-empty. For 1 ≤ i ≤ n, let \(s_{i}\in \{0,1\}^{n}\) be the vector such that si(j) = 1 if, and only if, j = i. Applying Lemma 4, we get that for any i, there exists some fi ∈ Fn such that for any f ∈ Fn, it holds
We fix such a family (fi)i≤n then define g ∈{0,1}n as  , i.e. g(i) = fi(i) for all 1 ≤ i ≤ n. Starting from any element of Fn and applying (6) iteratively for each i, we get that g ∈ Fn. Since \(g\curlywedge s_{i}=f_{i}\curlywedge s_{i}\), we also have
, i.e. g(i) = fi(i) for all 1 ≤ i ≤ n. Starting from any element of Fn and applying (6) iteratively for each i, we get that g ∈ Fn. Since \(g\curlywedge s_{i}=f_{i}\curlywedge s_{i}\), we also have
By (5), since flipg(g) = 1, we get
Now, assume that flipg(Fn) is not upward closed: then there exist elements f ∈ Fn and h∉Fn such that flipg(f)(i) = 1 ⇒flipg(h)(i) = 1 for all i. Starting from f and iteratively applying (7) for those i for which flipg(h)(i) = 1 and flipg(f)(i) = 0, we get that flipg(h) ∈flipg(Fn) and h ∈ Fn. Hence flipg(Fn) must be upward closed. □
5.3 Defining Quasi-orders from semi-stable Sets
For \(F^{n}\subseteq \{0,1\}^{n}\), we write \(\overline {F^{n}}\) for the complement of Fn. Fix such a set Fn, and pick s ∈{0,1}n. For any h ∈{0,1}n, we define
Trivially \(\mathbb {F}^{n}(h,s) \cap \overline {\mathbb {F}^{n}}(h,s)=\emptyset \) and \(\mathbb {F}^{n}(h,s) \cup \overline {\mathbb {F}^{n}}(h,s)=\{0,1\}^{n}\). If we assume Fn to be semi-stable, then the family \((\mathbb {F}^{n}(h,s))_{h\in \{0,1\}^{n}}\) enjoys the following property:
Lemma 6
Fix a semi-stable set Fn and s ∈{0,1}n. For any \(h_{1}, h_{2}\in \{0,1\}^{n}\), either \(\mathbb {F}^{n}(h_{1},s) \subseteq \mathbb {F}^{n}(h_{2},s)\) or \(\mathbb {F}^{n}(h_{2},s)\subseteq \mathbb {F}^{n}(h_{1},s)\).
Proof
Assuming otherwise, there would exist \(h^{\prime }_{1}\in \mathbb {F}^{n}(h_{1},s)\backslash \mathbb {F}^{n}(h_{2},s)\) and \(h^{\prime }_{2}\in \mathbb {F}^{n}(h_{2},s)\backslash \mathbb {F}^{n}(h_{1},s)\). We then have:
Now consider \((h_{1}\curlywedge s)\curlyvee (h_{1}^{\prime }\curlywedge \overline {s})\), \((h_{2}\curlywedge s)\curlyvee (h_{2}^{\prime }\curlywedge \overline {s})\) and s. As Fn is semi-stable, one of the two following vector is in Fn:
The first vector is equal to \((h_{1}\curlywedge s)\curlyvee (h_{2}^{\prime }\curlywedge \overline {s})\) and the second to \((h_{2}\curlywedge s)\curlyvee (h_{1}^{\prime }\curlywedge \overline {s})\) and both are supposed to be in \(\overline {F^{n}}\), we get a contradiction. □
Given a semi-stable set Fn and s ∈{0,1}n, we can use the inclusion relation of Lemma 6 to define a relation \(\preceq _{s}^{F^{n}}\) (written ≼s when Fn is clear) over the elements of {0,1}n. It is defined as follows: h1 ≼sh2 if, and only if, \(\mathbb {F}^{n}(h_{1},s)\subseteq \mathbb {F}^{n}(h_{2},s)\).
This relation is a quasi-order: its reflexiveness and transitivity both follow from the reflexiveness and transitivity of the inclusion relation \(\subseteq \). By Lemma 6, this quasi-order is total. Intuitively, ≼s orders the elements of {0,1}n based on how “easy” it is to complete their restriction to s so that the completion belongs to Fn. In particular, only the indices on which s take value 1 are used to check whether h1 ≼sh2: given \(h_{1},h_{2}\in \{0,1\}^{n}\) such that \((h_{1}\curlywedge s)=(h_{2}\curlywedge s)\), we have \(\mathbb {F}(h_{1},s)=\mathbb {F}(h_{2},s)\), and h1 ≡sh2.
Example 6
Consider the set F3 = {(1,0,0),(1,1,0),(1,0,1),(0,1,1),(1,1,1)} represented on Fig. 7, which can be shown to be semi-stable.
Fix s = (1,1,0). Then \(\mathbb F^{3}((0,1,\star ),s)= \{0,1\}^{2}\times \{1\}\): the only way to complete (0,1,⋆) to an element in F3 is by replacing ⋆ with 1. Similarly, \(\mathbb F^{3}((1,1,\star ),s)=\mathbb F^{3}((1,0,\star ),s)=\{0,1\}^{3}\), and \(\mathbb F^{3}((0,0,\star ),s)=\varnothing \). It follows that (0,0,⋆) ≼s(0,1,⋆) ≼s(1,0,⋆) ≡s(1,1,⋆).
For \(s^{\prime }=(0,0,1)\), we can proceed similarly and get that \((\star ,\star ,0) \preceq _{s^{\prime }} (\star ,\star ,1)\).
We now prove a technical result over such orders, which will be useful for the proof of Lemma 11.
Lemma 7
Given a semi-stable set Fn, \(s_{1},s_{2}\in \{0,1\}^{n}\) such that \(s_{1} \curlywedge s_{2} =\textbf {0}\) and f,g ∈{0,1}n such that \(f\preceq _{\phantom {\dot {i}\!}s_{1}} g\) and \(f\preceq _{\phantom {\dot {i}\!}s_{2}} g\), it holds \(f\preceq _{\phantom {\dot {i}\!}s_{1}\curlyvee s_{2}} g\).
Example 7
Consider again the semi-stable set F3 of Example 6. Observe that for s1 = (1,0,0), it holds \((0,\star ,\star ) \preceq _{\phantom {\dot {i}\!}s_{1}} (1,\star ,\star )\), because for any x,y ∈{0,1}, if (0,x,y) ∈ F3, then also (1,x,y) ∈ F3; similarly, for s2 = (0,1,0), we have \((\star ,0,\star ) \preceq _{\phantom {\dot {i}\!}s_{2}} (\star ,1,\star )\). Lemma 7 entails that (0,0,⋆) ≼s(1,1,⋆), with s = (1,1,0).
Proof
Because \(f\preceq _{\phantom {\dot {i}\!}s_{1}} g\) and \(f\preceq _{\phantom {\dot {i}\!}s_{2}} g\), we have
Consider \(h^{\prime }\in \{0,1\}^{n}\) such that \(\alpha =(f\curlywedge (s_{1}\curlyvee s_{2})) \curlyvee (h^{\prime } \curlywedge \overline {(s_{1}\curlyvee s_{2})})\) is in Fn. Define the element \(h= \alpha \curlywedge \overline {s_{2}}\), then \( (f\curlywedge s_{2}) \curlyvee (h \curlywedge \overline {s_{2}}) = (f\curlywedge (s_{1}\curlyvee s_{2})) \curlyvee (h^{\prime } \curlywedge \overline {(s_{1}\curlyvee s_{2})}) \in F^{n} \). Using (8) with s2 and h, we get \( \beta = (g\curlywedge s_{2}) \curlyvee (h \curlywedge \overline {s_{2}}) \). As \(s_{1} \curlywedge s_{2} =\textbf {0}\), we can write \(\beta = (f\curlywedge s_{1}) \curlyvee (g\curlywedge s_{2}) \curlyvee (h^{\prime } \curlywedge \overline {(s_{1}\curlyvee s_{2})}) \in F^{n} \).
Now consider \(h= \beta \curlywedge \overline {s_{1}}\), we have \((f\curlywedge s_{1})\curlyvee (h\curlywedge \overline {s_{1}})=\beta \in F^{n}\). Using (8) with s1 and h, we get \((g \curlywedge (s_{1} \curlyvee s_{2})) \curlyvee (h^{\prime } \curlywedge \overline {(s_{1}\curlyvee s_{2})}) \in F^{n}\). Therefore \(\mathbb {F}^{n}(f,s_{1}\curlyvee s_{2})\subseteq \mathbb {F}^{n}(g,s_{1} \curlyvee s_{2})\) and \(f\preceq _{\phantom {\dot {i}\!}s_{1}\curlyvee s_{2}} g\). □
The following lemma is straightforward:
Lemma 8
Assuming Fn is upward-closed, for any f, g and s in {0,1}n, if f ≤ g (i.e. for all i, f(i) = 1 ⇒ g(i) = 1), then f ≼sg. In particular, 0 is a minimal element for ≼s, for any s.
Proof
Since f ≤ g, then also \((f\curlywedge s)\curlyvee (h\curlywedge \overline {s}) \leq (g\curlywedge s)\curlyvee (h\curlywedge \overline {s})\), for any h ∈{0,1}n. Since Fn is upward-closed, if \((f\curlywedge s)\curlyvee (h\curlywedge \overline {s})\) is in Fn, then so is \((g\curlywedge s)\curlyvee (h\curlywedge \overline {s})\). □
5.4 Sketch of Proof of Theorem 1
The proof of Theorem 1 is long and technical. Before giving the full details, we begin with some intuition how semi-stable sets, and the quasi-orders defined above, are used to prove the result. We first notice that the approach we used in Prop. 2 does not extend in general to formulas with several goals. Consider for instance formula (Qixi)i≤l(β1. φ1 ⇔ β2. φ2): if at some points the two goals give rise to two different outcomes, thus to two different subgames, the winning objectives in one subgame depends on what is achieved in the other subgame.
SL[EG]♭ has been designed to simplify such dependences between different subgames: when two (or more) outcomes are available at a given position, each subgame can be assigned an independent winning objective. This objective can be obtained from the quasi-orders ≼s associated with the SL[EG]♭ formula being checked. Consider again Example 6: associating the set F3 with three goals ω1, ω2 and ω3 (and adequate strategy quantifiers), we get a formula in SL[EG]♭. Assume that the moves selected by the players give rise to the same transition for ω1 and ω2, and to a different transition for ω3; this gives rise to two subgames. In the subgame reached when following the transition of ω1 and ω2 (hence with s = (1,1,0)), the optimal way of playing is given by (0,0,⋆) ≼s(0,1,⋆) ≼s(1,0,⋆) ≡s(1,1,⋆), independently of what may happen in the subgame reached by following the transition given by ω3; for instance, it is better to fulfill only ω1 than to fulfill only ω2 (i.e. (0,1,⋆) ≼s(1,0,⋆)), which can be observed on Fig. 7 by the fact that fulfilling ω1 is enough to make the whole formula hold true. In the subgame corresponding to ω3, the optimal way of playing is given by \((\star ,\star ,0) \preceq _{s^{\prime }} (\star ,\star ,1)\): it is always better to fulfill ω3, whatever happens on the other subgame.
Our proof follows the schema depicted on Fig. 8. Building on the idea depicted on Fig. 4, we would like to construct a turn-based parity game encoding the SL[EG]♭ model-checking instance at hand. Strategy quantifiers are encoded with tree-shaped quantification games as in Fig. 4, but now, the leaves of quantification games may give rise to different outcomes, depending on the goal being considered: Fig. 8 depicts the case of a leaf from which the first two goals would go in one direction (to q1 here) while the third goal follows a different direction (to q2). Notice that from the other leaves, the goals may have been grouped differently (and in particular, they may have all given rise to the same transition).
In a formula based on the semi-stable sets of Fig. 7, upon separation of the goals, the game splits into independent subgames
Now, consider the outcome generated by the first two goals: it goes to a subgame starting in state q1, and only the first two goals have to be tracked. From our observations above, we can compute an order defining the best way of satisfying the remaining two goals; this does not depend on what happens along the other outcome, generated by the third goal. We can thus consider this subgame alone, and apply the same construction with the remaining goals (using parity automata to keep track of the satisfaction of the LTL formulas in the goals). Since there are finitely many goals, we eventually end up in a situation where there is a single goal, or where the goals always give rise to the same outcomes; then the computation remains in the same subgame, and the situation corresponds to the case of Fig. 4.
We implement these ideas as follows: first, in order to keep track of the truth values of the LTL formulas ψi of each goal, we define a family of parity automata, one for each subset of goals of the formula under scrutiny. A subgame, as considered above, is characterized by a state q of the original concurrent game, a state dp of each of the parity automata, and a vector s ∈{0,1}n defining which goals are still active in that subgame. For each subgame, we can compute, by induction on s, the optimal set of goals that can be fulfilled from that configuration. The optimal strategies of both players in each subgame can be used to define (partial) optimal timeline dependence maps. We can then combine these partial maps together to get optimal dependence maps 𝜃 and \(\overline \theta \); using similar arguments as for the proof of Prop. 5, we get a valuation χ such that \(\theta (\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }})=\chi =\overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})\), from which we deduce that exactly one of φ and ¬φ holds.
5.5 Proof of Theorem 1
We can now prove our main theorem, which we first restate:
Theorem 1
For any game \(\mathcal {G}\) with initial state q0, and any formula φ ∈, SL[EG]♭ it holds 
Proof
Following Lemma 5, we assume for the rest of the proof that the set Fn of the SL[EG]♭ formula φ is upward-closed (even if it means negating some of the LTL objectives). We also assume it is non-empty, since the result is trivial otherwise.
The proof of Theorem 1 is in three steps:
we build a family of parity automata expressing the objectives that may have to be fulfilled along outcomes. A configuration of a subgame is then described by a state q of the game, a vector d of states of those parity automata, and a set s of goals that are still active in the current subgame;
we characterize the two ways of fulfilling a set of goals: either by fulfilling all goals along the same outcome, or by partitioning them among different branches;
we encode these two possibilities into 2-player parity games, and inductively compute optimal sets of goals (represented as vectors \(b_{q,d,s}\in \{0,1\}^{n}\)) that can be achieved from any given configuration. By determinacy of parity games, we derive timeline maps witnessing the fact that bq,d,s can be achieved, and the fact that it is optimal. If \(b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}} \in F^{n}\), we get a witness map for
 ; otherwise, we get one for
; otherwise, we get one for  .
.
□
5.5.1 Automata for Conjunctions of Goals
We use deterministic parity word automata to keep track of the goals to be satisfied. Since we initially have no clue about which goal(s) will have to be fulfilled along an outcome, we use a (large) set of automata, all running in parallel.
For s ∈{0,1}n and h ∈{0,1}n, we let Ds,h be a deterministic parity automaton accepting exactly the words over 2AP along which the following formula Φs,h holds:
where a conjunction over an empty set (i.e., if \((k\curlywedge s)(j)=0\) for all j) is true.
Notice that in Φs,h, we should also have imposed ¬φj for those indices j for which \((k\curlywedge s)(j)=0\). However, using Lemma 8, if h ≼sk and k ≤ k′, then also h ≼sk′, so that any conjunction containing more φj’s would also appear in Φs,h.
Notice that when s = 0, we have h ≼sk for any h and k, so that Φ0,h is true for any h ∈{0,1}n). From now on, we only consider vectors s ∈{0,1}n such that \(|s| = {\sum }_{1\leq i\leq n} s_{i}\geq 1\).
As an example, take s ∈{0,1}n with |s = 1|, writing j for the index where s(j) = 1; for any h ∈{0,1}n, if there is k ≽sh with k(j) = 0 (which in particular is the case when h(j) = 0), then the automaton Ds,h is universal; otherwise Ds,h accepts the set of words over 2AP along which φj holds.
We write \(\mathcal {D}= \{D_{s,h} \mid s\in \{0,1\}^{n},\ h\in \{0,1\}^{n}\}\) for the set of automata defined above. A vector of states of \(\mathcal {D}\) is a function associating with each automaton \(D\in \mathcal {D}\) one of its states. We write VS for the set of all vectors of states of \(\mathcal {D}\). For any vector d ∈VS and any state q of \(\mathcal {G}\), we let succ(d,q) to be the vector of states associating with each \(D\in \mathcal {D}\) the successor of state d(D) after reading lab(q); we extend succ to finite paths (qi)0≤i≤n in \(\mathcal {G}\) inductively, letting succ(d,(qi)0≤i≤n) = succ(succ(d,(qi)0≤i≤n− 1),qn).
An infinite path  in \( \mathcal {G} \) is accepted by an automaton D of \(\mathcal {D}\) whenever the word
in \( \mathcal {G} \) is accepted by an automaton D of \(\mathcal {D}\) whenever the word  is accepted by D. We write \({\mathcal{L}}(D)\) for the set of paths of \(\mathcal {G}\) accepted by D. Finally, for d ∈VS, we write \({\mathcal{L}} (D^{d}_{s,h})\) for the set of words that are accepted by Ds,h starting from the state d(Ds,h) of Ds,h.
is accepted by D. We write \({\mathcal{L}}(D)\) for the set of paths of \(\mathcal {G}\) accepted by D. Finally, for d ∈VS, we write \({\mathcal{L}} (D^{d}_{s,h})\) for the set of words that are accepted by Ds,h starting from the state d(Ds,h) of Ds,h.
Proposition 8
The following holds for any s ∈{0,1}n:
- 1.
Φs,0 ≡⊤ (i.e., Ds,0 is universal);
- 2.
for any \(h_{1},h_{2}\in \{0,1\}^{n}\), if h1 ≼sh2, we have \({\Phi }_{s,h_{2}} \Rightarrow {\Phi }_{s,h_{1}}\) (i.e., \({\mathcal{L}} (D_{s,h_{2}}) \subseteq {\mathcal{L}}(D_{s,h_{1}})\));
- 3.
for any h ∈ Fn, \({\Phi }_{\textbf {1},h}\equiv \bigvee _{k\in F^{n}}\bigwedge _{j\text { s.t.\ } k(j)=1}\ \varphi _{j}\).
Proof
Φs,0 contains the empty conjunction (k = 0) as a disjunct. Hence it is equivalent to true. When h1 ≼sh2, formula \({\Phi }_{s,h_{1}}\) contains more disjuncts than \({\Phi }_{s,h_{2}}\), hence the second result. Finally,  if f ∈ Fn, and is empty otherwise. Hence if h ∈ Fn, we have h ≼1k if, and only if, k ∈ Fn, which entails the result. □
if f ∈ Fn, and is empty otherwise. Hence if h ∈ Fn, we have h ≼1k if, and only if, k ∈ Fn, which entails the result. □
5.5.2 Two Ways of Achieving Goals
After a given history, a set of goals may be achieved either along a single outcome, in case the assignment of strategies to players gives rise to the same outcomes, or they may be split among different outcomes. We express those two ways of satisfying goals, by means of two operators parameterized by the current configuration.
The first operator covers the case where the goals currently enabled by s (those goals βi. φi for which s(i) = 1) are all fulfilled along the same outcome. For any d ∈VS and any two s and h in {0,1}n, the operator \({\Gamma }^{\textsf {stick}}_{d,s,h}\) is defined as follows: given a context χ with \(\mathcal {V} \subseteq \textsf {dom}(\chi )\) and a state q of \(\mathcal {G}\),

Intuitively, all the goals enabled by s must give rise to the same outcome, which is accepted by \(D_{s,h}^{d}\). In the formula above, χ ∘ βj corresponds to the strategy profile to be used for goal βj ⋅ φj.
We now consider the case where the active goals are partitioned among different outcomes.
Definition 2
A partition of an element s ∈{0,1}n is a sequence (sκ)1≤κ≤λ, with λ ≥ 2, of elements of {0,1}n with \(s_{1}\curlyvee {\dots } \curlyvee s_{\lambda } = s\) and where for any two \(\kappa \neq \kappa ^{\prime } \), \(s_{\kappa } \curlywedge s_{\kappa ^{\prime }}=\textbf {0}\).
An extended partition of s is a sequence τ = (sκ,qκ,dκ)1≤κ≤λ of elements of {0,1}n ×Q ×VS where (sκ)1≤κ≤λ is a partition of s, qκ are states of \(\mathcal {G}\), and dκ are vectors of states of the automata in \(\mathcal {D}\).
We write Part(s) for the set of all extended partitions of s. Notice that we only consider non-trivial partitions; in particular, if |s|≤ 1, then Part(s) = ∅. For any d ∈VS, any s in {0,1}n and any set of partitions Υs of s, the operator \({\Gamma }^{\textsf {sep}}_{d,s,{\Upsilon }_{s}}\) states that the goals currently enabled by s all follow a common history ρ for a finite number of steps, and then partition themselves according to some partition in Υs. The operator \({\Gamma }^{\textsf {sep}}_{d,s,{\Upsilon }_{s}}\) is defined as follows:

Notice that h does not appear explicitly in this definition, but \({\Gamma }^{\textsf {sep}}_{d,s,{\Upsilon }_{s}}\) will depend on h through the choice of Υs. The operators Γstick and Γsep are illustrated on Fig. 9.
5.5.3 Fulfilling Optimal Sets of Goals
We now inductively (on |s|) define new operators Γd,s,h combining the above two operators Γstick and Γsep, and selecting optimal ways of partitioning the goals among the outcomes.
Base case: |s| = 1 When only one goal is enabled, we only have to consider a single outcome, so that we let \({\Gamma }_{d,s,h}={\Gamma }^{\textsf {stick}}_{d,s,h}\), for any d ∈VS and h ∈{0,1}n. By Prop. 8, for any context χ such that \(\textsf {Agt}\subseteq \textsf {dom}(\chi )\), it holds  , hence also
, hence also  . Hence there must exist a maximal value b in the lattice {0,1}n such that
. Hence there must exist a maximal value b in the lattice {0,1}n such that  We write bq,d,s for one such value (notice that it need not be unique). By maximality, for any h such that bq,d,s ≺sh, we have
We write bq,d,s for one such value (notice that it need not be unique). By maximality, for any h such that bq,d,s ≺sh, we have  .
.
Induction step We assume that for any d ∈VS, any h ∈{0,1}n and any s ∈{0,1}n with |s ≤ k|, we have defined an operator Γd,s,h, and that for any q ∈Q, we have fixed an element \(b_{q,d,s}\in \{0,1\}^{n}\) for which  and such that for any h such that bq,d,s ≺sh, it holds
and such that for any h such that bq,d,s ≺sh, it holds  .
.
Pick s ∈{0,1}n with |s = k + 1|, together with an extended partition τ = (sκ,qκ,dκ)1≤κ≤λ. Then we must have |sκ| < k + 1 for all 1 ≤ κ ≤ λ, so that \({\Gamma }_{d_{\kappa },s_{\kappa },h}\) and \(b_{\phantom {\dot {i}\!}q_{\kappa },d_{\kappa },s_{\kappa }}\) have been defined at previous steps. We let

We then define
As previously, we claim that  for any χ such that \(\textsf {Agt}\subseteq \textsf {dom}(\chi )\). Indeed, for a given χ, if all the outcomes of the goals enabled by s follow the same infinite path, then this path is accepted by Ds,0 and
for any χ such that \(\textsf {Agt}\subseteq \textsf {dom}(\chi )\). Indeed, for a given χ, if all the outcomes of the goals enabled by s follow the same infinite path, then this path is accepted by Ds,0 and  ; otherwise, after some common history ρ, the outcomes are partitioned following some extended partition τ0, which obviously satisfies \(\textbf {0} \preceq _{s} c_{\phantom {\dot {i}\!}s,\tau _{0}}\) since 0 is a minimal element of ≼s. Hence in that case
; otherwise, after some common history ρ, the outcomes are partitioned following some extended partition τ0, which obviously satisfies \(\textbf {0} \preceq _{s} c_{\phantom {\dot {i}\!}s,\tau _{0}}\) since 0 is a minimal element of ≼s. Hence in that case  .
.
In particular, it follows that  , and we can fix a maximal element bq,d,s for which
, and we can fix a maximal element bq,d,s for which  and
and  for any h ≻sbq,d,s.
for any h ≻sbq,d,s.
This concludes the inductive definition of \({\Gamma }_{d,s,b_{q,d,s}}\). We now prove that it satisfies the following lemma:
Lemma 9
For any q ∈Q, any d ∈VS and any s ∈{0,1}n, it holds


Proof
The first result is a direct consequence of the construction: the values for bq,d,s have been selected so that  .
.
To prove the second part, we again turn the satisfaction of Γd,s,h, for h ≻sbq,d,s, into a parity game, as for the proof of Prop. 2. We only sketch the proof here, as it involves the same ingredients.
The parity game is obtained from \(\mathcal {G}\) by replacing each state by a quantification game. We also introduce two sink states, qeven and qodd, which are winning for Player P∃ and for Player P∀ respectively. When arriving at a leaf \((q,d,\mathfrak {m})\) of the (q,d)-copy of the quantification game, there may be one of the following three transitions available:
if there is a state \(q^{\prime }\) such that for all j with s(j) = 1, it holds \(q^{\prime }={\Delta }(q, m_{\beta _{j}})\) (in other terms, the moves selected in the current quantification game generate the same transition for all the goals enabled by s), then there is a single transition to \((q^{\prime },d^{\prime },\epsilon )\), where \(d^{\prime }=\textsf {succ}(d,q^{\prime })\).
otherwise, if there is an extended partition τ = (sκ,qκ,dκ)1≤κ≤λ of s such that cs,τ ≽sh and, for all \(1{}\leq {}\kappa {}\leq {}\lambda \), for all j such that \(s_{\kappa }(j){}={}1\), we have \({\Delta }(q,m_{\beta _{j}}){}={}q_{\kappa }\) and succ(d,qκ) = dκ, then there is a transition from \((q,d,\mathfrak {m})\) to qeven.
otherwise, there is a transition from \((q,d,\mathfrak {m})\) to qodd.
The priorities defining the parity condition are inherited from those in Ds,h.
Since  , Player P∃ does not have a winning strategy in this game, and by determinacy Player P∀ has one. From the winning strategy of Player P∀, we obtain a timeline map \(\overline \vartheta _{q,d,s,h}\) for \((\overline {Q}_{i} x_{i})_{1\leq i\leq l}\) witnessing the fact that
, Player P∃ does not have a winning strategy in this game, and by determinacy Player P∀ has one. From the winning strategy of Player P∀, we obtain a timeline map \(\overline \vartheta _{q,d,s,h}\) for \((\overline {Q}_{i} x_{i})_{1\leq i\leq l}\) witnessing the fact that  . □
. □
Remark 2
While the definition of \({\Gamma }_{d,s,b_{q,d,s}}\) (and in particular of bq,d,s) is not effective, the parity games defined in the proof above can be used to compute each bq,d,s and \({\Gamma }_{d,s,b_{q,d,s}}\). Indeed, such parity games can be used to decide whether  for all h, and selecting a maximal value for which the result holds. Then \(b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\in F^{n}\) implies
for all h, and selecting a maximal value for which the result holds. Then \(b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\in F^{n}\) implies  .
.
Each parity game has size doubly-exponential, with exponentially-many priorities; hence they can be solved in 2-EXPTIME. The number of games to solve is also doubly-exponential, so that the whole algorithm runs in 2-EXPTIME.
Applying Lemma 9, we fix a timeline map 𝜗q,d,s for (Qixi)1≤i≤l witnessing (9), and for each h ≻sbq,d,s, a timeline map \(\overline {\vartheta }_{q,d,s,h}\) for \((\overline {Q}_{i} x_{i})_{1\leq i\leq l}\) witnessing (9).
We now focus on the operator obtained at the end of the induction, when s = 1. Following Prop. 8, \({\mathcal{L}}(D_{\textbf {1},f})\) does not depend on the exact value of f, as soon as it is in Fn. We then let
where f is any element of Fn (remember Fn is assumed to be non-empty), d0 is the vector of initial states of the automata in \(\mathcal {D}\), and \({\Upsilon }_{\phantom {\dot {i}\!}F^{n}}=\{\textsf {Part}(\textbf {1}) \mid c_{\textbf {1},\tau } \in F^{n}\}\).
We write 𝜗1 and \(\overline \vartheta _{\textbf {1}}\) for the maps \(\vartheta _{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\) and \(\overline \vartheta _{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1},h}\) for some h ∈ Fn, as given by Lemma 9. From the discussion above, \(\overline \vartheta _{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1},h}\) does not depend on the choice of h in Fn, and we simply write it \(\overline \vartheta _{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\).
Then:
Lemma 10
If  , then 𝜗1 witnesses the fact that
, then 𝜗1 witnesses the fact that  Conversely, if
Conversely, if  , then \(\overline \vartheta _{\textbf {1}}\) witness the fact that
, then \(\overline \vartheta _{\textbf {1}}\) witness the fact that  .
.
Proof
The first part directly follows from the previous lemma. For the second part,  means that \(b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\notin F^{n}\). Hence for any f ∈ Fn, we have \(f\succ _{s} b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\), so that \(\overline \vartheta _{\phantom {\dot {i}\!}q_{0},d_{0}\textbf {1}}\) is a witness that
means that \(b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\notin F^{n}\). Hence for any f ∈ Fn, we have \(f\succ _{s} b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\), so that \(\overline \vartheta _{\phantom {\dot {i}\!}q_{0},d_{0}\textbf {1}}\) is a witness that  . □
. □
5.5.4 Compiling optimal maps
From Lemma 9, we have timeline maps for each q, d and s. We now compile them into two map 𝜃 and \(\overline {\theta }\). The construction is inductive, along histories.
Pick a history ρ starting from q0 and strategies for universally-quantified variables \(w\colon \mathcal {V}^{\forall } \to (\textsf {Hist} \to \textsf {Act})\). Assuming 𝜃 has been defined along all strict prefixes of ρ, a goal βj. φj is said active after ρ w.r.t. 𝜃(w) if the following condition holds:
In other terms, βj. φj is active after ρ w.r.t. 𝜃(w) if ρ is the outcome of strategies prescribed by 𝜃(w) under assignment βj. We let sρ,𝜃(w) be the element of {0,1}n such that sρ,𝜃(w)(j) = 1 if, and only if, βj. φj is active after ρ w.r.t. 𝜃(w).
We now define 𝜃(w)(xi)(ρ) for all \(x_{i}\in \mathcal {V}\):
if \(x_{i}\in \mathcal {V}^{\forall }\), we let 𝜃(w)(xi)(ρ) = w(xi)(ρ);
if \(x_{i}\in \mathcal {V}^{\exists }\), we consider two cases:
if sρ,𝜃(w) = 1, then all goals are still active, and 𝜃 follows the map 𝜗1: 𝜃(w)(xi)(ρ) = 𝜗1(w)(xi)(ρ).
otherwise, we let ρ1 be the maximal prefix of ρ for which \(s_{\rho _{1},\theta (w)} \not = s_{\rho ,\theta (w)}\). We may then write ρ = ρ1 ⋅ ρ2, and let q1 = last(ρ1) and d1 = succ(d0,ρ1). We then let \(\theta (w)(x_{i})(\rho )=\vartheta _{\phantom {\dot {i}\!}q_{1},d_{1},s_{\rho ,\theta (w)}} (w_{\overrightarrow {\rho _{1}}})(x_{i})(\rho _{2})\).
The dual map \(\overline {\theta }\) is defined in the same way, using maps \(\overline {\vartheta }\) in place of 𝜗.
The following result will conclude our proof of Theorem 1.
Lemma 11
There exists a context χ with domain \(\mathcal {V}\) such that \(\theta (\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }})=\chi \) and \(\overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})=\chi \). It satisfies

Proof We use the same technique as in the proof of Prop. 5: from 𝜃 and \(\overline {\theta }\), we build a strategy context χ on \(\mathcal {V}\) such that \(\theta (\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\forall }})=\chi \) and \(\overline {\theta }(\chi _{\phantom {\dot {i}\!}|\mathcal {V}^{\exists }})=\chi \).
We introduce some more notations. For \(w\colon \mathcal {V}^{\forall }\to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})\), we let
\({\pi ^{w}_{j}}\) be the outcome out(q0,(𝜃(w)((βj(A))A∈Agt)) for all 1 ≤ j ≤ n;
fw be the element of {0,1}n such that fw(j) = 1 if, and only if,
 ;
;\(R^{w} \subseteq \{0,1\}^{n}\times \textsf {Hist}_{\mathcal {G}}\) be the relation such that (s,ρ) ∈ Rw if, and only if, s = sρ,𝜃(w) and ρ is minimal (meaning for any strict prefix \(\rho ^{\prime }\) of ρ, it holds \((s,\rho ^{\prime })\notin R^{w}\)).
Lemma 12
For any \(w\colon \mathcal {V}^{\forall } \to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})\) and any ρ ∈Hist, letting dρ = succ(d0,ρ), it holds
Proof
Fix some \(w\in (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})^{\mathcal {V}^{\forall }}\). The proof proceeds by induction on |s|.
Base case: |s| = 1 Assume (s,ρ) ∈ Rw. As |s| = 1, there is a unique goal, say \(\beta _{j_{0}}.\ \varphi _{j_{0}}\), active along ρ w.r.t. 𝜃(w). By definition of 𝜃, \(\pi _{j_{0}}= \rho \cdot \eta \) where η is the outcome of \(\vartheta _{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}(w_{\overrightarrow \rho })((\beta _{j}(A))_{A\in \textsf {Agt}})\) from last(ρ).
Because |s| = 1, we have \({\Gamma }_{d_{\rho },s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}} = {\Gamma }^{\textsf {stick}}_{d_{\rho },s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}}\). The map \(\vartheta _{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}\) is a witness that  ; therefore it also witnesses that
; therefore it also witnesses that  . By definition of the Γstick operators, this implies that for any w, the outcome of \(\vartheta _{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}(w_{\overrightarrow \rho })\) from last(ρ) is accepted by the automaton \(D^{d_{\rho }}_{\phantom {\dot {i}\!}s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}}\); in particular, η is accepted by \(D^{d_{\rho }}_{\phantom {\dot {i}\!}s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}}\).
. By definition of the Γstick operators, this implies that for any w, the outcome of \(\vartheta _{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho }, s}(w_{\overrightarrow \rho })\) from last(ρ) is accepted by the automaton \(D^{d_{\rho }}_{\phantom {\dot {i}\!}s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}}\); in particular, η is accepted by \(D^{d_{\rho }}_{\phantom {\dot {i}\!}s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}}\).
The automaton \(D^{d_{\rho }}_{\phantom {\dot {i}\!}s,b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}}\) accepts paths which give better results (w.r.t. ≼s) for the objectives (βj. φj)j∣s(j)= 1 than \(b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}\). In other terms, we have \(b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s} \preceq _{s} f^{w}\).
Induction step We assume that the Proposition 12 holds for any elements s ∈{0,1}n of size |s| < α. We now consider for the induction step an element s ∈{0,1}n such that |s| = α and (s,ρ) ∈ Rw.
if the enabled goals all follow the same outcome, i.e., if there exists an infinite path η such that πj = ρ ⋅ η for all j having s(j) = 1, then with arguments similar to those of the base case, we get \(b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s} \preceq _{s} f^{w}\).
otherwise, the goals enabled by s split following an extended partition τ = (sκ,qκ,dκ)κ≤λ. We let η be the history from the last state of ρ to the point where the goals split.
The map \(\vartheta _{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}\) witnesses that
 ; therefore η may only reach a partition τ such that
$$ b_{\phantom{\dot{i}\!}\textsf{last}(\rho),d_{\rho},s} \preceq_{s} c_{s,\tau} $$(11)
; therefore η may only reach a partition τ such that
$$ b_{\phantom{\dot{i}\!}\textsf{last}(\rho),d_{\rho},s} \preceq_{s} c_{s,\tau} $$(11)This partition τ is such that for any 1 ≤ κ ≤ λ, it holds (sκ,ρ ⋅ η ⋅ qκ) ∈ Rw; using the induction hypothesis, we get
$$ s_{\kappa}\curlywedge b_{\phantom{\dot{i}\!}q_{\kappa},d_{\kappa},s_{\kappa}} \preceq_{\phantom{\dot{i}\!}s_{\kappa}} f^{w} $$(12)Then, using Lemma 7 repeatedly on the (sκ)1≤κ≤λ, and (12), we obtain
$$ \begin{array}{@{}rcl@{}} s_{1}\curlywedge b_{\phantom{\dot{i}\!}q_{1},d_{1},s_{1}} \preceq_{\phantom{\dot{i}\!}s_{1}} f^{w} &\Rightarrow& (s_{1} \curlywedge b_{\phantom{\dot{i}\!}q_{1},d_{1},s_{1}}) \curlyvee (s_{2} \curlywedge b_{\phantom{\dot{i}\!}q_{2},d_{2},s_{2}}) \preceq_{\phantom{\dot{i}\!}s_{1} \curlyvee s_{2}} f^{w} \\ & \Rightarrow& \dots \\ &\Rightarrow& (s_{1} \curlywedge b_{\phantom{\dot{i}\!}q_{1},d_{1},s_{1}}) \curlyvee {\dots} \curlyvee (s_{\lambda} \curlywedge b_{\phantom{\dot{i}\!}q_{\lambda},d_{\lambda},s_{\lambda}}) \preceq_{\phantom{\dot{i}\!}s_{1} \curlyvee {\dots} \curlyvee s_{\lambda}} f^{w} \\ &\Rightarrow& c_{s,\tau} \preceq_{s} f^{w}. \end{array} $$Combined with (11), we get \(b_{\phantom {\dot {i}\!}\textsf {last}(\rho ),d_{\rho },s}\preceq _{s} c_{s,\tau } \preceq _{s} f^{w}\).
□
Lemma 13
 if, and only if, \(b_{\phantom {\dot {i}\!}q_{0},d_{0} , \textbf {1}} \in F^{n}\).
if, and only if, \(b_{\phantom {\dot {i}\!}q_{0},d_{0} , \textbf {1}} \in F^{n}\).
Proof
Assume that \(b_{\phantom {\dot {i}\!}q_{0},d_{0} , \textbf {1}} \in \overline {F^{n}}\). Then  . Applying Lemma 10, the map \(\overline {\vartheta _{\textbf {1}}}\) (and therefore \(\overline {\theta }\), which act as \(\overline {\vartheta _{\textbf {1}}}\) before goals branch along different paths) witnesses
. Applying Lemma 10, the map \(\overline {\vartheta _{\textbf {1}}}\) (and therefore \(\overline {\theta }\), which act as \(\overline {\vartheta _{\textbf {1}}}\) before goals branch along different paths) witnesses  . This implies that
. This implies that  , which contradicts the hypothesis.□
, which contradicts the hypothesis.□
Conversely, if \(b_{\phantom {\dot {i}\!}q_{0},d_{0} , \textbf {1}} \in F^{n}\), then  , which is witnessed by map 𝜗1. Thus
, which is witnessed by map 𝜗1. Thus 
We are now ready to prove the first part of Lemma 11: consider a function \(w\colon \mathcal {V}^{\forall } \to (\textsf {Hist}_{\mathcal {G}} \to \textsf {Act})\). By Lemma 12 applied to w, s = 1, and ρ = q0, we get that \( b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}} \preceq _{\textbf {1}} f^{w}\). Now, by Lemma 13, \(b_{\phantom {\dot {i}\!}q_{0},d_{0} , \textbf {1}} \in F^{n}\), therefore the element fw, being greater than \( b_{\phantom {\dot {i}\!}q_{0},d_{0},\textbf {1}}\) for ≼1, must also be in Fn, which means that  .
.
The second implication of the lemma is proven using similar arguments.
Lemma 11 allows us to conclude that at least one of φ and ¬φ must hold on \( \mathcal {G} \) for  . Lemma 5 implies that at most one can hold. Combining both we get that exactly one holds.
. Lemma 5 implies that at most one can hold. Combining both we get that exactly one holds.
From this proof, we get:
Corollary 3
Model checking SL[EG] for  is 2-EXPTIME-complete.
is 2-EXPTIME-complete.
Remark 3
Notice that we do not get the twin of Corollary 1 here, and actually  and
and  differ over SL[EG]♭. Indeed, the proof of Prop. 4 provides a counterexample:
differ over SL[EG]♭. Indeed, the proof of Prop. 4 provides a counterexample:
as shown in the proof of Prop. 4, the game \(\mathcal {G}\) and formula φ ∈SL[CG]♭ of Fig. 6 are such that

considering the classical semantics, because of the conjunction of goals, any strategy for y for which the rest of the formula is fulfilled must play differently in states q1 and q2. On the other hand, in order to fulfill the first conjunct for any strategy xA, then the strategy y must play to p1 from both q1 and q2. Hence no such strategy exist.
5.6 Maximality of SL[EG]♭
Finally, we prove that SL[EG]♭ is, in a sense, maximal for the first property of Theorem 1:
Proposition 9
For any non-semi-stable boolean set \(F^{n} \subseteq \{0,1\}^{n}\), there exists a SL[BG]♭ formula φ built on Fn, a game \(\mathcal {G}\) and a state q0 such that  and
and  .
.
Proof We consider again the game \(\mathcal {G}\) depicted on Fig. 6, with two agents  and
and  . Let Fn be a non-semi-stable set over {0,1}n. Then there must exist f1,f2 ∈ Fn, and s ∈{0,1}n, such that \({(f_{1} \curlywedge s) \curlyvee (f_{2} \curlywedge \overline {s}) \notin F^{n}}\) and \((f_{2} \curlywedge s) \curlyvee (f_{1} \curlywedge \overline {s}) \notin F^{n}\). We then let
. Let Fn be a non-semi-stable set over {0,1}n. Then there must exist f1,f2 ∈ Fn, and s ∈{0,1}n, such that \({(f_{1} \curlywedge s) \curlyvee (f_{2} \curlywedge \overline {s}) \notin F^{n}}\) and \((f_{2} \curlywedge s) \curlyvee (f_{1} \curlywedge \overline {s}) \notin F^{n}\). We then let
where

and
Formulas φi have been built to satisfy the following property:
Lemma 14
Let ρ be a maximal run of \(\mathcal {G}\) from q0. Let k ∈{1,2} be such that ρ visits a state labelled with pk. Then for any 1 ≤ i ≤ n, we have  if, and only if, fk(i) = 1.
if, and only if, fk(i) = 1.
The following two lemmas conclude the proof:
Lemma 15
 .
.
Proof
Towards a contradiction, assume that  . Let 𝜃 be a timeline map witnessing this fact. We let σ1 (resp. σ2) be the strategy that maps history q0 to q1 (resp. q2). We let τ1 be such that τ1(q0 ⋅ q1) = p1. This defines a valuation w, respectively mapping y1, y2 and x1 to σ1, σ2 and τ1. Then the strategy τ2 = 𝜃(w)(x2) is such that
. Let 𝜃 be a timeline map witnessing this fact. We let σ1 (resp. σ2) be the strategy that maps history q0 to q1 (resp. q2). We let τ1 be such that τ1(q0 ⋅ q1) = p1. This defines a valuation w, respectively mapping y1, y2 and x1 to σ1, σ2 and τ1. Then the strategy τ2 = 𝜃(w)(x2) is such that

Now, consider the valuation \(w^{\prime }\) obtained from w by changing the strategy for x1 to \(\tau ^{\prime }_{1}\), where \(\tau ^{\prime }_{1}(q_{0}\cdot q_{1})=p_{2}\). Then \(\theta (w^{\prime })(x_{2})=\theta (w)(x_{2})=\tau _{2}\), since 𝜃 is a timeline map. Since 𝜃 witnesses the satisfaction of φ, we also have

Let v and \(v^{\prime }\) be the vectors in {0,1}n representing the values of the goals \((\beta _{1}.\ \varphi _{1},\dots ,\beta _{n}.\ \varphi _{n})\) under 𝜃(w) and \(\theta (w^{\prime })\), respectively. Then v and v′ are in Fn. However:
if τ2(q0 ⋅ q2) = p1, then under \(\theta (w^{\prime })\), for any 1 ≤ i ≤ n:
if si = 1, strategies σ1 and \(\tau ^{\prime }_{1}\) are applied, so that the game ends in p2; then \(v^{\prime }_{i}=1\) if, and only if, f2(i) = 1;
if si = 0, strategies σ2 and τ2 are used, and the game goes to p1; then \(v^{\prime }_{i}=1\) if, and only if, f1(i) = 1.
In the end, we have \(v^{\prime }=(f_{1}\curlywedge \overline {s}) \curlyvee (f_{2}\curlywedge s)\), which is not in Fn.
if τ2(q0 ⋅ q2) = p2, then under 𝜃(w), for any 1 ≤ i ≤ n:
if si = 1, strategies σ1 and τ1 are applied, so that the game ends in p1; then vi = 1 if, and only if, f1(i) = 1;
if si = 0, strategies σ2 and τ2 are used, and the game goes to p2; then vi = 1 if, and only if, f2(i) = 1.
In the end, we have \(v=(f_{1}\curlywedge s) \curlyvee (f_{2}\curlywedge \overline {s})\), which also is not in Fn.
Both cases lead to a contradiction, so that our hypothesis that  can only be wrong. □
can only be wrong. □
Lemma 16
 .
.
Proof
We use similar arguments as above: we assume  , and fix a witnessing timeline map \(\overline {\theta }\) for ¬φ.
, and fix a witnessing timeline map \(\overline {\theta }\) for ¬φ.
We consider four valuations w11, w12, w21 and w22 for x2, such that \(w^{jk}(x_{2})(\rho )=w^{j^{\prime }k^{\prime }}(x_{2})(q_{0})\) (the exact value is not important) and wjk(x2)(q0 ⋅ q1) = pi and wjk(x2)(q0 ⋅ q2) = pj. We let \(\sigma _{1}=\overline {\theta }(w^{jk})(y_{1})\), \(\sigma _{2}=\overline {\theta }(w^{jk})(y_{2})\) and \(\tau _{1}=\overline {\theta }(w^{jk})(x_{1})\). Notice that those strategies do not depend on i and j, since \(\overline {\theta }\) is a timeline map for ¬φ. We write \(v^{jk}_{i}\) for the vector representing the truth value of goal βi. φi under valuation \(\overline {\theta }(w^{jk})\).
Assume that σ2(q0) = q1, and that τ1(q0 ⋅ σ1(q0)) = p1. Then under w11 (i.e., when τ2(q0 ⋅ q1) = p1), for any 1 ≤ i ≤ n, the outcome of strategy assignment βi from q0 goes to p1. Hence v11 = f1, which is in Fn, contradicting the fact that \(\overline {\theta }\) witnesses  . Similar arguments apply if τ1(q0 ⋅ σ1(q0)) = p2, and when σ2(q0) = q2. Thus our assumption that
. Similar arguments apply if τ1(q0 ⋅ σ1(q0)) = p2, and when σ2(q0) = q2. Thus our assumption that  cannot be correct. □
cannot be correct. □
6 Conclusions and Future Works
In this paper, we have studied various semantics of SL, depending on how the successive strategy quantifiers in an SL formula may depend on each other. Following [30], we defined a natural translation of the elementary semantics of SL[1G] into a two-player turn-based parity game, and introduced a new timeline semantics for SL[BG] that better corresponds to this translation. For this new semantics, we defined a fragment SL[EG] for which the timeline semantics can be model-checked in 2-EXPTIME. Figure 10 represents the relations between those semantics (with implications in grey only valid for SL[1G]), as well as the maximal fragments of SL[BG] for which the semantical and syntactical negations coincide.
While our work clarifies the setting of strategy dependences in SL, those various semantics of SL remains to be fully understood, in particular as to which situations are better suited for which semantics. Of course, studying the decidability and complexity of model checking for the different semantics and fragments of SL[BG] is a natural continuation of this work. Studying quantitative or epistemic extensions of SL[EG] under the timeline semantics is also a natural direction to follow. Finally, since our approach relies on translations to two-player parity games, our model-checking algorithm would be a good candidate for being implemented e.g. in the tool MCMAS.
References
Ågotnes, T., Goranko, V., Jamroga, W.: Alternating-time temporal logics with irrevocable strategies. In: Samet, D. (ed.) Proceedings of the 11th Conference on Theoretical Aspects of Rationality and Knowledge (TARK’07), pp. 15–24 (2007)
Alur, R., Henzinger, T.A., Kupferman, O.: Alternating-time temporal logic. J. ACM 49(5), 672–713 (2002). https://doi.org/10.1145/585265.585270
Aminof, B., Malvone, V., Murano, A., Rubin, S.: Graded modalities in strategy logic. Inf. Comput. 261(4), 634–649 (2018). https://doi.org/10.1016/j.ic.2018.02.021
Berthon, R., Maubert, B., Murano, A., Rubin, S., Vardi, M.Y.: Strategy logic with imperfect information. In: Proceedings of the 32th Annual Symposium on Logic in Computer Science (LICS’17), pp. 1–12. IEEE Comp. Soc. Press. https://doi.org/10.1109/LICS.2017.8005136 (2017)
Bouyer, P., Gardy, P., Markey, N.: Weighted strategy logic with boolean goals over one-counter games. In: Harsha, P., Ramalingam, G. (eds.) Proceedings of the 35th Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS’15), volume 45 of Leibniz International Proceedings in Informatics, Leibniz-Zentrum für Informatik . https://doi.org/10.4230/LIPIcs.FSTTCS.2015.69, pp 69–83 (2015)
Bouyer, P., Gardy, P., Markey, N.: On the semantics of strategy logic. Inf. Process. Lett. 116(2), 75–79 (2016). https://doi.org/10.1016/j.ipl.2015.10.004
Brenguier, R., Raskin, J.-F., Sankur, O.: Assume-admissible synthesis. Acta Inform. 54(1), 41–83 (2017). https://doi.org/10.1007/s00236-016-0273-2
Brihaye, T., Da Costa, A., Laroussinie, F., Markey, N.: ATL with strategy contexts and bounded memory. In: Artemov, S.N., Nerode, A. (eds.) Proceedings of the International Symposium Logical Foundations of Computer Science (LFCS’09), volume 5407 of Lecture Notes in Computer Science, pp 92–106. Springer (2009). https://doi.org/10.1007/978-3-540-92687-0_7
Čermák, P., Lomuscio, A., Mogavero, F., Murano, A.: MCMAS-SLK: A model checker for the verification of strategy logic specifications. In: Biere, A., Bloem, R. (eds.) Proceedings of the 26th International Conference on Computer Aided Verification (CAV’14), volume 8559 of Lecture Notes in Computer Science, pp 525–532. Springer (2014). https://doi.org/10.1007/978-3-319-08867-9_34
Čermák, P., Lomuscio, A., Murano, A.: Verifying and synthesising multi-agent systems against one-goal strategy logic specifications. In: Bonet, B., Koenig, S. (eds.) Proceedings of the 29th AAAI Conference on Artificial Intelligence (AAAI’15), pp 2038–2044. AAAI Press (2015)
Chatterjee, K., Henzinger, T.A., Piterman, N.: Strategy logic. In: Caires, L., Vasconcelos, V.T. (eds.) Proceedings of the 18th International Conference on Concurrency Theory (CONCUR’07), volume 4703 of Lecture Notes in Computer Science, pp 59–73. Springer (2007). https://doi.org/10.1007/978-3-540-74407-8_5
Clarke, E.M., Emerson, E.A.: Design and synthesis of synchronization skeletons using branching-time temporal logic. In: Kozen, D.C. (ed.) Proceedings of the 3rd Workshop on Logics of Programs (LOP’81), volume 131 of Lecture Notes in Computer Science, pp 52–71. Springer (1982). https://doi.org/10.1007/BFb0025774
Clarke, E.M., Grumberg, O., Peled, D.A.: Model checking. MIT Press, New York (2000)
Condurache, R., Filiot, E., Gentilini, R., Raskin, J.-F., Sangiorgi, D.: The complexity of rational synthesis. In: Chatzigiannakis, I., Mitzenmacher, M., Rabani, Y. (eds.) Proceedings of the 43rd International Colloquium on Automata, Languages and Programming (ICALP’16) – Part II, volume 55 of Leibniz International Proceedings in Informatics, pp 121:1–121:15. Leibniz-Zentrum Für Informatik (2016). https://doi.org/10.4230/LIPIcs.ICALP.2016.121
Dima, C., Ţiplea, F.L.: Model-checking ATL under imperfect information and perfect recall semantics is undecidable. Research Report arXiv:http://arXiv.org/abs/1102.4225 (2011)
Emerson, E.A., Jutla, C.S.: Tree automata, mu-calculus and determinacy. In: Proceedings of the 32nd Annual Symposium on Foundations of Computer Science (FOCS’91), pp. 368–377. IEEE Comp. Soc. Press. https://doi.org/10.1109/SFCS.1991.185392 (1991)
Fijalkow, N., Maubert, B., Murano, A., Rubin, S.: Quantifying bounds in strategy logic. In: Ghica, D.R., Jung, A. (eds.) Proceedings of the 27th EACSL Annual Conference on Computer Science Logic (CSL’18), volume 119 of Leibniz International Proceedings in Informatics, pp 23:1–23:23. Leibniz-Zentrum Für Informatik (2018). https://doi.org/10.4230/LIPIcs.CSL.2018.23
Fisman, D., Kupferman, O., Lustig, Y.: Rational synthesis. In: Esparza, J., Majumdar, R. (eds.) Proceedings of the 16th International Conference on Tools and Algorithms for Construction and Analysis of Systems (TACAS’10), volume 6015 of Lecture Notes in Computer Science, pp 190–204. Springer (2010). https://doi.org/10.1007/978-3-642-12002-2_16
Gardy, P., Bouyer, P., Markey, N.: Dependences in strategy logic. In: Proceedings of the 35th Annual Symposium on Theoretical Aspects of Computer Science (STACS’18), volume 96 of Leibniz International Proceedings in Informatics, pp. 34:1–34:15. Leibniz-Zentrum Für Informatik (2018). https://doi.org/10.4230/LIPIcs.STACS.2018.34
Goranko, V., van Drimmelen, G.: Complete axiomatization and decidability of alternating-time temporal logic. Theor. Comput. Sci. 353(1-3), 93–117 (2006)
Guelev, D.P., Dima, C.: Epistemic ATL with perfect recall, past and strategy contexts. In: Fisher, M., van der Torre, L.W.N., Dastani, M., Governatori, G. (eds.) Proceedings of the 13th International Workshop on Computational Logic in Multi-Agent Systems (CLIMA’12), volume 7486 of Lecture Notes in Artificial Intelligence, pp 77–93. Springer (2012). https://doi.org/10.1007/978-3-642-32897-8_7
Gutierrez, J., Harrenstein, P., Perelli, G., Wooldridge, M.: Nash equilibrium and bisimulation invariance. In: Meyer, R., Nestmann, U. (eds.) Proceedings of the 28th International Conference on Concurrency Theory (CONCUR’17), volume 85 of Leibniz International Proceedings in Informatics, pp 17:1–17:16. Leibniz-Zentrum Für Informatik (2017). https://doi.org/10.4230/LIPIcs.CONCUR.2017.17
Henkin, L.: Some remarks on infinitely long formulas. In: Infinitistic Methods – Proceedings of the Symposium on Foundations of Mathematics, pp. 167–183. Pergamon Press (1961)
Hintikka, J., Sandu, G.: Informational independence as a semantical phenomenon. In: Fenstad, J.E., Frolov, I.T., Hilppinen, R. (eds.) Proceedings of the 8th International Congress of Logic, Methodology and Philosophy of Science, volume 70 of Studies in Logic and the Foundations of Mathematics, pp 571–589, North-Holland (1989). https://doi.org/10.1016/S0049-237X(08)70066-1
Huang, X., van der Meyden, R.: An epistemic strategy logic. ACM Trans. Comput. Log. 19(4), 26:1–26:45 (2018). https://doi.org/10.1145/3233769
Kupferman, O., Perelli, G., Vardi, M.Y.: Synthesis with rational environments. Ann. Math. Artif. Intell. 78(1), 3–20 (2016). https://doi.org/10.1007/s10472-016-9508-8
Laroussinie, F., Markey, N.: Augmenting ATL with strategy contexts. Inf. Comput. 245, 98–123 (2015). https://doi.org/10.1016/j.ic.2014.12.020
Laroussinie, F., Markey, N., Oreiby, G.: On the expressiveness and complexity of ATL. Logical Methods in Computer Science 4(2:7), 1–25 (2008). https://doi.org/10.2168/LMCS-4(2:7)2008
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: What makes ATL∗ decidable? A decidable fragment of strategy logic. In: Koutny, M., Ulidowski, I. (eds.) Proceedings of the 23rd International Conference on Concurrency Theory (CONCUR’12), volume 7454 of Lecture Notes in Computer Science, pp 193–208. Springer (2012)
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: Reasoning about strategies: On the model-checking problem. ACM Trans. Comput. Log. 15(4), 34:1–34:47 (2014). https://doi.org/10.1145/2631917
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: Reasoning about strategies: On the satisfiability problem. Logical Methods in Computer Science 13 (1:9), 1–37 (2017). https://doi.org/10.23638/LMCS-13(1:9)2017
Mogavero, F., Murano, A., Sauro, L.: On the boundary of behavioral strategies. In: Proceedings of the 28th Annual Symposium on Logic in Computer Science (LICS’13), pages 263–272. IEEE Comp. Soc. Press (2013)
Mogavero, F., Murano, A., Sauro, L.: A behavioral hierarchy of strategy logic. In: Bulling, N., van der Torre, L.W.N., Villata, S., Jamroga, W., Vasconcelos, W.W. (eds.) Proceedings of the 15th International Workshop on Computational Logic in Multi-Agent Systems (CLIMA’14), volume 8624 of Lecture Notes in Artificial Intelligence, pp 148–165. Springer (2014). https://doi.org/10.1007/978-3-319-09764-0_10
Mogavero, F., Murano, A., Vardi, M.Y.: Reasoning about strategies. In: Lodaya, K., Mahajan, M. (eds.) Proceedings of the 30th Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS’10), volume 8 of Leibniz International Proceedings in Informatics, pp 133–144. Leibniz-Zentrum Für Informatik (2010). https://doi.org/10.4230/LIPIcs.FSTTCS.2010.133
Mostowski, A.: Games with forbidden positions. Research report 78 university of Danzig (1991)
Pnueli, A.: The temporal logic of programs. In: Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS’77), pp. 46–57. IEEE Comp. Soc. Press. https://doi.org/10.1109/SFCS.1977.32 (1977)
Queille, J.-P., Sifakis, J.: Specification and verification of concurrent systems in CESAR. In: Dezani-Ciancaglini, M., Montanari, U. (eds.) Proceedings of the 5th International Symposium on Programming (SOP’82), volume 137 of Lecture Notes in Computer Science, pp 337–351. Springer (1982). https://doi.org/10.1007/3-540-11494-7_22
Väänänen, J.: Dependence Logic: A New Approach to Independence-Friendly Logic, volume 70 of London Mathematical Society Student Texts. Cambridge University Press, Cambridge (2007). https://doi.org/10.1017/CBO9780511611193
Wang, F., Huang, C.-H., Yu, F.: A temporal logic for the interaction of strategies. In: Katoen, J.-P., König, B. (eds.) Proceedings of the 22nd International Conference on Concurrency Theory (CONCUR’11), volume 6901 of Lecture Notes in Computer Science, pp 466–481. Springer (2011)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the Topical Collection on Special Issue on Theoretical Aspects of Computer Science (2018)
This work was supported by ERC project EQualIS (StG-308087). A preliminary version of this paper appeared in the proceedings of STACS’18 [19].
Rights and permissions
About this article
Cite this article
Gardy, P., Bouyer, P. & Markey, N. Dependences in Strategy Logic. Theory Comput Syst 64, 467–507 (2020). https://doi.org/10.1007/s00224-019-09926-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-019-09926-y




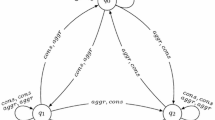





 as a two-player turn-based parity game
as a two-player turn-based parity game

 and
and  differ on
differ on 

 ; otherwise, we get one for
; otherwise, we get one for  .
.
 ;
; ; therefore η may only reach a partition τ such that
; therefore η may only reach a partition τ such that

