The Outer-connected Domination Number of Sierpiński-like Graphs

Abstract

An outer-connected dominating set in a graph G = (V, E) is a set of vertices D ⊆ V satisfying the condition that, for each vertex v ∉ D, vertex v is adjacent to some vertex in D and the subgraph induced by V∖D is connected. The outer-connected dominating set problem is to find an outer-connected dominating set with the minimum number of vertices which is denoted by $\tilde {\gamma }_{c}(G)$. In this paper, we determine $\tilde {\gamma }_{c}(S(n,k))$, $\tilde {\gamma }_{c}(S^{+}(n,k))$, $\tilde {\gamma }_{c}(S^{++}(n,k))$, and $\tilde {\gamma }_{c}(S_{n})$, where S(n, k), S ⁺(n, k), S ⁺⁺(n, k), and S _n are Sierpi$\acute {\mathrm {n}}$ski-like graphs.

1 Introduction

Let G = (V, E) be an undirected graph, where V(G) and E(G) are vertex and edge sets of G respectively. For simplicity, we also use V and E to represent V(G) and E(G), respectively, when only one graph is mentioned. All graphs considered in this paper are simple, i.e., with no loops and multiple edges. For any vertex v ∈ V and a set S ⊆ V, the open neighborhood of v in S is the set N _S (v) = {u ∈ S|u v ∈ E}. The closed neighborhood of v in S is N _S [v] = N _S (v) ∪ {v}. If S = V, then we simply write N(v) and N[v] rather than N _V (v) and N _V [v], respectively.

Definition 1.1

For a graph G, a set D ⊆ V is a dominating set if N[D] = V. The minimum size of a dominating set is the domination number, denoted by γ(G). The domination problem is to determine a minimum dominating set of a graph G.

Definition 1.2

For a graph G, a dominating set D is an outer-connected dominating set, abbreviated as OCD-set, if the subgraph induced by V∖D is connected. The outer-connected domination number, denoted by $\tilde {\gamma }_{c}(G)$, is the cardinality of a minimum OCD-set. The outer-connected domination problem is to determine a minimum OCD-set of a graph G.

It is clear that $\gamma (G)\leqslant \tilde {\gamma }_{c}(G)$. The concept of outer-connected domination problem in graphs was introduced in [3] and subsequently studied in [1, 11, 20]. The outer-connected domination problem has been shown to be NP-complete for bipartite graphs [3], doubly chordal graphs and undirected path graphs [20], where a graph G is called an undirected path graph if G is the intersection graph of a family of paths of a tree. In [20], MarkKeil and Pradhan proposed a linear time algorithm for computing a minimum OCD-set in proper interval graphs.

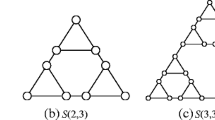
The Sierpiński graph S(n, k) consists of k copies of S(n − 1, k) for n > 1, where S(1, k) is a complete graph of k vertices [13]. Graphs very similar to Sierpiński graphs were named WK-recursive networks in [25].

For example, S(1, 3), S(2, 3), and S(3, 3) are shown in Fig. 1a, b, and c, respectively. In general, Sierpiński-like graphs include Sierpiński graphs, extended Sierpiński graphs, and Sierpiński gasket graphs. All those Sierpiński-like graphs will be introduced in Section 2.

Fig. 1

Sierpiński graphs

The results of this paper are as follows:

• (1) $\tilde {\gamma }_{c}(S(n,k)) = k^{n-1}$, for n ⩾ 1 and k ⩾ 3,

• (2) $\tilde {\gamma }_{c}(S^{+}(n,k)) = k^{n-1}$, for n ⩾ 1 and k ⩾ 3,

• (3) $\tilde {\gamma }_{c}(S^{++}(n,k)) = k^{n-1}+k^{n-2}$, for n ⩾ 1 and k ⩾ 3, and

• (4) $\tilde {\gamma }_{c}(S_{n}) = 3^{n-2}$ if n ⩾ 3; otherwise, $\tilde {\gamma }_{c}(S_{n}) = n$,

where S(n, k) denotes a Sierpiński graph, S ⁺(n, k) and S ⁺⁺(n, k) denote two different extended Sierpiński graphs, and S _n denotes a Sierpiński gasket graph.

The organization of this paper is as follows. In Section 2, we introduce Sierpiński-like graphs in detail. The outer-connected domination number of Sierpiński graphs and extended Sierpiński graphs are investigated in Sections 3 and 4, respectively. In Section 5, we investigate the outer-connected domination number of Sierpiński gasket graphs.

2 Sierpiński-like Graphs

The definitions of Sierpiński-like graphs are described as follows. The reader is referred to [2, 4, 7, 13, 22, 25] for the details. The vertex set of S(n, k) consists of all n-tuples of integers 1, 2, … , k, for integers n ⩾ 1 and k ⩾ 3, namely V(S(n, k)) = {1, 2, … , k}ⁿ. Accordingly, the label of vertex v, denoted by ℓ(v), is v ₁ v ₂⋯v _n in regular expression form. By using a convention on representing regular expressions, we always use w, x, y, and z to denote a substring of v ₁ v ₂⋯v _n and a, b, c, and d to denote a number in v ₁ v ₂⋯v _n , i.e., a, b, c, d ∈ {1, 2, … , k}. The length of a substring w is denoted by |w|. For example, ℓ(v) = w a b ^{n − h}, for 1 ⩽ h ⩽ n, means that the label of v begins with prefix w, then concatenates with number a, and finally ends with n − h b′s, where b ^h is the Kleene closure in regular expression. Thus |w| = h − 1. For convenience, we also say that v ₁ v ₂⋯v _n is a vertex if ℓ(v) = v ₁ v ₂⋯v _n .

Two different vertices u and v are adjacent in S(n, k) if and only if ℓ(u) = w a b ^{n − h} and ℓ(v) = w b a ^{n − h} with a ≠ b for some 1 ⩽ h ⩽ n. Note that if h = 1, then w = 𝜖 which is a null string. Furthermore, if h = n, then both b ^{n − h} and a ^{n − h} are empty. By the definition above, the subgraph of S(n, k) induced by the set of vertices whose labels begin with a is a Sierpiński subgraph S(n − 1, k) and is denoted by S _a (n − 1, k). Similarly, we also use S _w (n − |w|, k) to denote the subgraph induced by the vertices with prefix w in their labels. When n − |w|=1, it is obvious that S _w (1, k) is a complete graph and we call it a terminal clique. A vertex v is an extreme vertex of S _w (n − |w|, k) for 0 ⩽ |w| ⩽ n − 1 if v is of the form w a ^{n − |w|} for 1 ⩽ a ⩽ k. Therefore, there are exactly k extreme vertices in every S _w (n − |w|, k). Since the label of an extreme vertex v is a ⁿ in S(n, k), by definition, v has exactly k − 1 neighbors whose labels are of the form a ^{n − 1} b with b ≠ a. Every non-extreme vertex ℓ(v) = w a b ^{n − h} with a ≠ b in S(n, k) has exactly k neighbors whose labels are of the form w b a ^{n − h} and w a b ^{n − h − 1} c with 1 ⩽ c ⩽ k and c ≠ b. Thus the degree of every extreme vertex in S(n, k) is k − 1 while all other vertices have degree k. Figure 2 depicts S(3, 3) and S(3, 4). An interesting connection is that S(n, 3) for n ⩾ 1 is isomorphic to the graphs of the Tower of Hanoi puzzle with n disks [6, 13] and has been extensively studied (see [7, 9] for an overview and the references therein for the details). Lately, Hinz and Parisse determined the average eccentricity of Sierpiński graphs [8]. In [14], S. Klavžar, U. Milutinović and Ciril Petr investigate 1-perfect codes in S(n, k). Parisse studied metric properties of S(n, k)[21].

Fig. 2

Labeled Sierpiński graphs

The extended Sierpiński graphs S ⁺(n, k) and S ⁺⁺(n, k) were introduced by Klavžar and Mohar [15]. The graph S ⁺(n, k) is obtained from S(n, k) by adding a special vertex, say s, and edges joining s to all extreme vertices of S(n, k) (see Fig. 3a). The graph S ⁺⁺(n, k) is obtained from S(n, k) by adding a new copy of S(n − 1, k) which is denoted by S _{k + 1}(n − 1, k), and joining an extreme vertex a ⁿ in S(n, k) to the vertex b a ^{n − 1} in the added S _{k + 1}(n − 1, k) for 1 ⩽ a ⩽ k, where b = k + 1 (see Fig. 3b).

Fig. 3

Extended Sierpiński graphs: S ⁺(3,3) and S ⁺⁺(3,3)

The Sierpiński gasket graph S _n is a variant of the Sierpiński graph S(n, 3). The graph S _n can be obtained from S(n, 3) by contracting every edge of S(n, 3) that lies in no triangle. For example, compare Figs. 2a and 4. Vertices with labels 112 and 121 in S(3,3) are contracted to the vertex 1(12|21) in S ₃, where “|” is the union operation in regular expression. According to the definition of extreme vertices in S(n, k), the vertices with labels 1ⁿ, 2ⁿ, and 3ⁿ in S _n are also called extreme vertices. The labels of other vertices are of the form w(a b ^h|b a ^h) where 1 ⩽ h ⩽ n − 1, w ∈ {1, 2, … , k}^{n − h − 1}, and a and b are one of the pairs: 1 and 2, 1 and 3, or 2 and 3. For convenience, we also use w a b ^h or w b a ^h to represent the contracted vertex w(a b ^h|b a ^h). The vertices with labels 12^{n − 1}|21^{n − 1}, 13^{n − 1}|31^{n − 1}, and 23^{n − 1}|32^{n − 1} are called the waist vertices of S _n . The neighbors of the extreme vertex a ⁿ are of the form a ^{n − 2}(a b|b a) with a ≠ b. The neighbors of vertex v with label w(a b ^h|b a ^h) are of the form: w a b ^{h − 2}(b c|c b) and w b a ^{h − 2}(a d|d a) for c ≠ b and d ≠ a. The Sierpiński gasket graph S _n also contains 3^x copies of S _{n − x} which are denoted by S _{n − x, a} , for a ∈ {1, 2, 3}^x, where S _{n − x, a} contains all vertices whose labels begin with a.

Fig. 4

Sierpiński gasket graph S ₃

Many properties of Sierpiński-like graphs have been studied such as the hamiltonicity in S _n [16, 24] and in S(n, k) [13], the pancyclicity in S _n [24], the efficient domination number in S(n, k) [14], and the coloring number in S _n [16] and in S(n, k) [21]. The vertex-, edge-, and total-colorings on Sierpiński-like graphs have been studied by Jakovac and Klavžar [10]. Lin, Liu, and Wang determined the hub numbers in [18] and global strong defensive alliances in [19] of Sierpiński-like graphs. Moreover, Sierpiński gasket graphs play an important role in dynamic systems and probability [5, 12] as well as in psychology [17, 23].

3 Computing $\tilde {\gamma }_{c}(S(n,k))$

For a vertex v in S _w (n − |w|, k), a vertex u ∈ N(v) is an outer-neighbor of v if u is not in V(S _w (n − |w|, k)). Note that every extreme vertex v ∈ S _w (n − |w|, k) with |w| ≠ 0 has exactly one outer-neighbor while a non-extreme vertex has no outer-neighbor. Furthermore, if u is the outer-neighbor of v with respect to S _w (n − |w|, k), then v is also the outer-neighbor of u with respect to $S_{w^{\prime }}(n-|w^{\prime }|,k)$, where w′ is a prefix of u and |w′ | = |w|.

Lemma 3.1

For n ⩾ 1 and $k\geqslant 3, \tilde {\gamma }_{c}(S(n,k))\geqslant k^{n-1}$.

Proof

First, we claim that if D is an OCD-set of S(n, k) and the graph induced by V(S(n, k))∖D is not a terminal clique, then D ∩ V(S _w (1, k)) ≠ ∅ for any w with |w| = n − 1. Suppose to the contrary that there exists a terminal clique S _w (1, k) for some w such that D ∩ V(S _w (1, k)) = ∅. This implies that all outer-neighbors of the vertices in S _w (1, k) are in D. Let H be the graph induced by V(S(n, k))∖D. Since H is not a terminal clique, it contains at least two components and one of them is S _w (1, k). This contradicts that D is an OCD-set of S(n, k) and the claim holds.

Note that there are k ^{n − 1} terminal cliques in S(n, k). By the claim above, it follows that $\tilde {\gamma }_{c}(S(n,k))\geqslant k^{n-1}$. □

By Lemma 3.1, to prove that $\tilde {\gamma }_{c}(S(n,k)) = k^{n-1}$, it suffices to show that there exists an OCD-set whose cardinality is equal to k ^{n − 1}. In the following, we describe how to construct such an OCD-set. Hereafter, the plus operation on computing the label of a vertex is always taken modulo k. However, if the resulting value is 0, then we always use k to replace it.

Definition 3.2

Let v = v ₁ ⋯ v _n be a vertex in Sierpiński-like graphs S(n, k), S ⁺(n, k), S ⁺⁺(n, k) or S _n . Define f(v) = u ₁ ⋯ u _{n − 1} with u _i ≡ v _{i + 1}+v ₁−1 (mod k) for 1 ⩽ i ⩽ n − 1 as a folding operation on v. For brevity, let f ¹(v) = f(v), f ²(v) = f(f(v)), f ³(v) = f(f ²(v)), and so on.

Definition 3.3

For k odd, let F _{o, i} (n, k)(or simply F _i (n, k)) for 1 ⩽ i ⩽ k be the set of vertices v with f ^{n − 1}(v) = i, namely F _i (n, k) = {v : f ^{n − 1}(v) = i} for 1 ⩽ i ⩽ k. When k is even, define $F_{\mathrm {e}}(n,k) = \{v: v_{n}=v_{n-1}+\frac {k}{2}\}$.

For example, in S(3, 3), we have f(233) = 11 and f ²(233) = f(f(233)) = f(11) = 1. The set F ₁(3, 3) contains vertices 111, 123, 132, 212, 221, 233, 313, 322, and 331 in S(3,3) (see the black vertices in Fig. 2a). For S(3, 4), we have F _e(3, 4) = {x y : x ∈ {1, 2, 3, 4}, y ∈ {13, 24, 31, 42}} (see the black vertices in Fig. 2b). In Lemmas 3.4-3.7, we show that F _i (n, k), 1 ⩽ i ⩽ k, is an OCD-set of S(n, k) with k odd, and, in Lemmas 3.8-3.9, we show that F _e(n, k), 1 ⩽ i ⩽ k, is an OCD-set of S(n, k) with k even.

Lemma 3.4

Let v = v ₁ ⋯ v _n be a vertex in S(n, k), for n ⩾ 1 and k ⩾ 3 . Then

$$f^{n-1}(v)\equiv v_{n}+ \sum\limits_{i=1}^{n-1} 2^{n-i-1}\cdot (v_{i}-1) \pmod k.$$

Proof

Let v ^j = f ^j(v) for 1 ⩽ j ⩽ n − 1 and $v^{j}={v^{j}_{1}}{\cdots } v^{j}_{n-j}$. By definition, it is easy to derive that

$$\begin{array}{@{}rcl@{}} {v^{j}_{1}}\equiv v_{j+1}+2^{j-1}(v_{1}-1)+2^{j-2}(v_{2}-1)+\cdots+2^{0}(v_{j}-1)\pmod k. \end{array} $$

(1)

Since f ^{n − 1}(v) = v ^{n − 1} and there is exactly one number in v ^{n − 1}, it follows that $f^{n-1}(v) = v^{n-1}=v^{n-1}_{1}$. By (1), we have $f^{n-1}(v)\equiv v_{n}+ {\sum }_{i=1}^{n-1} 2^{n-i-1}\cdot (v_{i}-1) \pmod k$. This completes the proof. □

Lemma 3.5

For every terminal clique S _w (1, k) in S(n, k), we have |V(S _w (1, k)) ∩ F _i (n, k)| = 1, for 1 ⩽ i ⩽ k, n ⩾ 1, k ⩾ 3.

Proof

Suppose to the contrary that there are two distinct vertices u and v which are in V(S _w (1, k)) ∩ F _i (n, k) for some i with 1 ⩽ i ⩽ k. Let u = w u _n and v = w v _n . By Lemma 3.4, $f^{n-1}(wu_{n})\equiv u_{n}+ {\sum }_{i=1}^{n-1} 2^{n-i-1}\cdot (u_{i}-1) \pmod k$ and $f^{n-1}(wv_{n})\equiv v_{n}+ {\sum }_{i=1}^{n-1} 2^{n-i-1}\cdot (v_{i}-1) \pmod k$. By the definition of u and v, it follows that u _i = v _i for 1 ⩽ i ⩽ n − 1. Thus ${\sum }_{i=1}^{n-1} 2^{n-i-1}\cdot (u_{i}-1) = {\sum }_{i=1}^{n-1} 2^{n-i-1}\cdot (v_{i}-1)$. Since both u and v are in F _i (n, k) for some i with 1 ⩽ i ⩽ k, it follows that f ^{n − 1}(w u _n ) = f ^{n − 1}(w v _n ) = i. Thus u _n ≡ v _n (mod k). Since both u _n and v _n are smaller than or equal to k, this yields u = v, a contradiction. Thus |V(S _w (1, k)) ∩ F _i (n, k)| ⩽ 1. Since 0 ⩽ f ^{n − 1}(v) ⩽ k − 1 and there are no two distinct vertices u and v in V(S _w (1, k)) such that f ^{n − 1}(u) = f ^{n − 1}(v), by the pigeonhole principle, we have |V(S _w (1, k)) ∩ F _i (n, k)| = 1 for 1 ⩽ i ⩽ k. This completes the proof. □

Lemma 3.6

Let D be the set {wa ^n−|w| : 1 ⩽ a ⩽ k} of vertices in S(n, k) for 0 ⩽ |w| ⩽ n − 1. If k is odd, then |D ∩ F _i (n, k)| = 1 for 1 ⩽ i ⩽ k, n ⩾ 1, k ⩾ 3.

Proof

Let u and v be any two distinct vertices in D with u = w a ^{n − |w|} and v = w b ^{n − |w|}. Assume without loss of generality that a > b and w = w ₁ w ₂⋯w _|w|. To prove that |D ∩ F _i (n, k)| = 1 for 1 ⩽ i ⩽ k when k is odd, it suffices to show that f ^{n − 1}(u) ≠ f ^{n − 1}(v). By Lemma 3.4,

$$ f^{n-1}(u)\equiv a+ \sum\limits_{i=1}^{|w|} 2^{n-i-1}\cdot (w_{i}-1)+ \sum\limits_{i=|w|+1}^{n-1} 2^{n-i-1}\cdot (a-1) \pmod k $$

and

$$ f^{n-1}(v)\equiv b+ \sum\limits_{i=1}^{|w|} 2^{n-i-1}\cdot (w_{i}-1)+ \sum\limits_{i=|w|+1}^{n-1} 2^{n-i-1}\cdot (b-1) \pmod k. $$

Subtracting f ^{n − 1}(v) from f ^{n − 1}(u), we can obtain that $f^{n-1}(u)-f^{n-1}(v)\equiv a-b+{\sum }_{i=|w|+1}^{n-1} 2^{n-i-1}\cdot (a-b) \pmod k$. After simplifying, f ^{n − 1}(u) − f ^{n − 1}(v)≡2^{n − |w|−1}⋅(a − b) (mod k). Since $\gcd (2^{n-|w|-1},k) = 1$ and a − b < k, this yields 2^{n − |w|−1}⋅(a − b) ≢ 0 (mod k). This implies that f ^{n − 1}(u) ≠ f ^{n − 1}(v) and the lemma follows. □

Lemma 3.7

If k is odd, then F _i (n, k) is an OCD-set of S(n, k) for every 1 ⩽ i ⩽ k, n ⩾ 1, k ⩾ 3.

Proof

By Lemma 3.5, we know that F _i (n, k) is a dominating set of S(n, k) for every 1 ⩽ i ⩽ k. It remains to prove that the subgraph induced by V(S(n, k))∖F _i (n, k) for each 1 ⩽ i ⩽ k is connected. We prove it by induction on n.

First, consider the basis step, i.e., n = 1. Clearly, S(1, k) is a complete graph and F _i (1, k) for each 1 ⩽ i ⩽ k contains exactly one vertex. Thus the basis holds immediately.

Now we consider the induction step for n > 1. Since S(n, k) consists of k copies of S(n − 1, k), by the inductive hypothesis, the subgraph induced by V(S _a (n − 1, k))∖F _i (n, k) for each 1 ⩽ a ⩽ k is connected. It remains to prove that those induced subgraphs are connected. Assume that 1a ^{n − 1} ∈ F _i (n, k) for some 1 ⩽ i ⩽ k. By Lemma 3.6, all other extreme vertices, say 1b ^{n − 1}, of S ₁(n − 1, k) with b ≠ a are not in F _i (n, k). We claim that the outer-neighbor of 1b ^{n − 1}, i.e., b1^{n − 1} if exists, is not in F _i (n, k). Suppose to the contrary that b1^{n − 1} ∈ F _i (n, k). By Lemma 3.4,

$$\begin{array}{@{}rcl@{}} f^{n-1}\left(b1^{n-1}\right)&=& 1+2^{n-2}\cdot (b-1)+ \sum\limits_{i=2}^{n-1} 2^{n-i-1}\cdot (1-1)\pmod k\\ &=& 1+ 2^{n-2}\cdot (b-1)\pmod k\\ &=& i \pmod k \end{array} $$

and

$$\begin{array}{@{}rcl@{}} f^{n-1}\left(1a^{n-1}\right)&=& a+2^{n-2}\cdot (1-1)+\sum\limits_{i=2}^{n-1} 2^{n-i-1}\cdot (a-1)\pmod k\\ &=& a+\sum\limits_{i=2}^{n-1} 2^{n-i-1}\cdot (a-1)\pmod k\\ &=& 1+2^{n-2}\cdot(a-1)\pmod k\\ &=& i \pmod k. \end{array} $$

By the derivation above, we have 1+2^{n − 2}⋅(a − 1)≡1+2^{n − 2}⋅(b − 1) (mod k). Since k is odd and $\gcd (2^{n-2}, k) = 1$, this results in a = b, a contradiction. Thus the claim holds. Therefore, V(S(n, k))∖F _i (n, k) induces a connected subgraph. This establishes the proof of the lemma. □

Now we consider the case where k is even in S(n, k).

Lemma 3.8

If k is even and k > 0, then wa ² ∉ F _e (n,k).

Proof

Clearly, the equality $a=a+\frac {k}{2}$ does not hold unless k = 0. Thus the lemma follows immediately. □

Lemma 3.9

If k is even, then F _e (n, k) is an OCD-set of S(n, k), n ⩾ 1,k ⩾ 3.

Proof

It is obvious that F _e(n, k) is a dominating set of S(n, k) since every terminal clique has a unique vertex in F _e(n, k). All we have to prove is that the subgraph induced by V(S(n, k))∖F _e(n, k) is connected. We consider the following three cases.

Case 1

n = 1. Clearly, the subgraph induced by V(S(n, k))∖F _e(n, k) is connected when n = 1.

Case 2

n = 2.

Note that, by the definition of S(n, k), it follows that k ⩾ 4 when k is even. Accordingly, any vertex in the set {v : v ₂ = v ₁+1 or v ₂ = v ₁−1} is not in F _e(2, k). Thus, for induced subgraphs S _a (1, k)∖F _e(2, k) and S _{a + 1}(1, k)∖F _e(2, k) for 1 ⩽ a ⩽ k − 1, there exists an edge between vertices a(a + 1) and (a + 1)a. Note that a(a + 1) ∈ S _a (1, k) and (a + 1)a ∈ S _{a + 1}(1, k). Therefore, the subgraph induced by V(S _w (2, k))∖F _e(2, k) is connected.

Case 3

n ⩾ 3.

By using a similar argument as is Case 2, every subgraph induced by V(S _w (2, k))∖F _e(n, k) is connected, where |w| = n − 2. For 1 ⩽ |w| ⩽ n − 3, by Lemma 3.8, every extreme vertex in S _w (n − |w|, k) is not in F _e(n, k). Note that the extreme vertices in S _w (n − |w|, k) for 1 ⩽ |w| ⩽ n − 3 are of the form w′b a ^{n − |w|} for 1 ⩽ a ⩽ k, where w = w′b. By definition, vertex w′b a ^{n − |w|} is adjacent to w′a b ^{n − |w|} which is an extreme vertex of S _w (n − |w|, k) with w = w′a. Therefore, this implies that the subgraph induced by V(S _w (n, k))∖F _e(n, k) is connected.

Theorem 3.10

$\tilde {\gamma }_{c}(S(n,k)) = k^{n-1}$, n ⩾ 1, k ⩾ 3.

Proof

For the case where k is odd, by Lemma 3.5 and the number of terminal cliques in S(n, k), it follows that |F _i (n, k)| = k ^{n − 1} for 1 ⩽ i ⩽ k. When k is even, by the definition of F _e(n, k), we have |V(S _w (1, k)) ∩ F _e(n, k)|=1 and |F _e(n, k)| = k ^{n − 1}. By Lemmas 3.1, 3.7, and 3.9, the theorem follows. □

4 Computing $\tilde {\gamma }_{c}(S^{+}(n,k))$ and $\tilde {\gamma }_{c}(S^{++}(n,k))$

Recall that the graph S ⁺(n, k) is obtained from S(n, k) by adding a special vertex, say s, and edges joining s to all extreme vertices of S(n, k) (see Fig. 3a) and the graph S ⁺⁺(n, k) is obtained from S(n, k) by adding a new copy of S(n − 1, k) which is denoted by S _{k + 1}(n − 1, k), and joining an extreme vertex a ⁿ in S(n, k) to the vertex b a ^{n − 1} in the added S _{k + 1}(n − 1, k) for 1≤a≤k, where b = k + 1 (see Fig. 3b).

Lemma 4.1

For n ⩾ 1 and k ⩾ 3, $\tilde {\gamma }_{c}(S^{+}(n,k))\geqslant k^{n-1}$ and $\tilde {\gamma }_{c}(S^{++}(n,k))\geqslant k^{n-1}+k^{n-2}$.

Proof

By using a similar argument as in Lemma 3.1, we can show that if D is an OCD-set of S ⁺(n, k) (respectively, S ⁺⁺(n, k)) and the graph induced by V(S ⁺(n, k))∖D (respectively, V(S ⁺⁺(n, k))∖D) is not a terminal clique, then every terminal clique has at least one vertex in D. By definition, S ⁺(n, k) contains S(n, k) as a subgraph and S ⁺⁺(n, k) contains two disjoint subgraphs S(n, k) and S _{k + 1}(n − 1, k). Thus $\tilde {\gamma }_{c}(S^{+}(n,k))\geqslant k^{n-1}$ and $\tilde {\gamma }_{c}(S^{++}(n,k))\geqslant k^{n-1}+k^{n-2}$. This completes the proof. □

In the following, we show that there exists an OCD-set whose cardinality is exactly equal to the lower bound described in Lemma 4.1 for S ⁺(n, k) and S ⁺⁺(n, k).

Definition 4.2

Define

$$\begin{array}{@{}rcl@{}}F^{+}(n,k) = \left\{\begin{array}{ll} F_{\mathrm{o}, 1}(n,k) & \quad\text{if \textit{k} is odd,}\\ F_{\mathrm{e}}(n,k)\cup \{1^{n}\}\setminus \left\{1^{n-1}\left(1+\frac{k}{2}\right)\right\} & \quad\text{if \textit{k} is even,} \end{array}\right.\end{array} $$

and

$$F^{++}(n,k) = \left\{\begin{array}{lll} F_{\mathrm{o}, 1}(n,k)\cup F_{\mathrm{o}, 1}(n-1,k) & \quad\text{if \textit{k} is odd,}\\ F_{\mathrm{e}}(n,k)\cup F_{\mathrm{e}}(n-1,k) & \quad\text{if \textit{k} is even,} \end{array}\right.$$

where F _o,1(n, k) and F _e(n, k) are the OCD-sets of the subgraph S(n, k) of S ⁺(n, k)(or S ⁺⁺(n, k)) when k is odd and even, respectively, and F _o,1(n − 1, k) and F _e(n − 1, k) are the OCD-sets of the subgraph S _{k + 1}(n − 1, k) of S ⁺⁺(n, k).

Proposition 4.3

For n ⩾ 1 and k ⩾ 3, $\tilde {\gamma }_{c}(S^{+}(n,k)) = k^{n-1}$.

Proof

By Lemma 4.1, it suffices to show that F ⁺(n, k) is an OCD-set of S ⁺(n, k). By Lemmas 3.7 and 3.9, we know that F ⁺(n, k) is an OCD-set of S(n, k). When k is odd, vertex 1ⁿ is in F ⁺(n, k), namely F _o,1(n, k). Since s is adjacent to a ⁿ in S ⁺(n, k), vertex s of S ⁺(n, k) is dominated by vertex 1ⁿ. Note that all vertices a ⁿ for 1 ⩽ a ⩽ k are not in F ⁺(n, k) except a = 1. This implies that the subgraph induced by V(S ⁺(n, k))∖F ⁺(n, k) is connected. Thus F ⁺(n, k) is an OCD-set of S ⁺(n, k) when k is odd.

For the case where k is even, the set F ⁺(n, k) is equal to $F_{\mathrm {e}}(n,k)\cup \{1^{n}\}\setminus \left \{1^{n-1}\left (1+\frac {k}{2}\right )\right \}$. Clearly, the neighbors of $1^{n-1}(1+\frac {k}{2})$ in the terminal clique containing $1^{n-1}\left (1+\frac {k}{2}\right )$ are dominated by vertex 1ⁿ. Moreover, vertex s is also dominated by 1ⁿ. It is easy to verify that the subgraph induced by V(S ⁺(n, k))∖F ⁺(n, k) is connected. Thus F ⁺(n, k) is an OCD-set of S ⁺(n, k) when k is even. Note that |F ⁺(n, k)| = k ^{n − 1}. This completes the proof. □

Proposition 4.4

For n ⩾ 1 and k ⩾ 3, $\tilde {\gamma }_{c}(S^{++}(n,k)) = k^{n-1}+k^{n-2}$.

Proof

First we consider the case where k is odd. By Theorem 3.10, we know that F _o,1(n, k) and F _o,1(n − 1, k) in F ⁺⁺(n, k) are OCD-sets of subgraphs S(n, k) and S _{k + 1}(n − 1, k) of S ⁺⁺(n, k). Thus F ⁺⁺(n, k) is a dominating set of S ⁺⁺(n, k). Note that vertex 2ⁿ is in V(S(n, k))∖F _o,1(n, k) and (k + 1)2^{n − 1} is in V(S _{k + 1}(n − 1, k))∖F _o,1(n − 1, k). By definition, vertex 2ⁿ is adjacent to vertex (k + 1)2^{n − 1}. This implies that the subgraph induced by V(S ⁺⁺(n, k))∖F ⁺⁺(n, k) is connected. Thus this case holds.

Now we consider the case where k is even. Clearly, the set F ⁺⁺(n, k) which is equal to F _e(n, k) ∪ F _e(n − 1, k) is a dominating set of S ⁺⁺(n, k). Note that |F ⁺⁺(n, k)| = k ^{n − 1}+k ^{n − 2}. Since 1ⁿ and (k + 1)1^{n − 1} are adjacent and both of them are in the subgraph induced by V(S ⁺⁺(n, k))∖F ⁺⁺(n, k), it follows that F ⁺⁺(n, k) is an OCD-set of S ⁺⁺(n, k). This completes the proof. □

5 Computing $\tilde {\gamma }_{c}(S_{n})$

Recall that every non-extreme vertex in Sierpiński gasket graphs S _n is contracted from two adjacent vertices whose edge lies in no triangle in S(n, 3). The label of every contracted vertex can be expressed as w(a b ^h|b a ^h) for some 1 ⩽ h ⩽ n − 1 where the possible pairs of a and b are: 1 and 2, 1 and 3, or 2 and 3. It is easy to verify that $\tilde {\gamma }_{c}(S_{1}) = 1$, $\tilde {\gamma }_{c}(S_{2}) = 2$ and $\tilde {\gamma }_{c}(S_{3}) = 3$. Thus we assume that n ⩾ 3 in the rest of this section unless stated otherwise.

Theorem 5.1

(Theorem 7 in [24]) For n ⩾ 3, we have γ(S _n ) = 3ⁿ⁻².

Since $\tilde {\gamma }_{c}(S_{n})\geqslant \gamma (S_{n})$, we have the following corollary.

Corollary 5.2

For S _n with n ⩾ 3, we have $\tilde {\gamma }_{c}(S_{n})\geqslant 3^{n-2}$.

In the following, we introduce how to find an outer-connected dominating set D _n with cardinality 3^{n − 2} for n ⩾ 3. Define D _n = {v : v _{n − 2} v _{n − 1} v _n ∈ {1(12|21), 2(23|32), 3(13|31)}}. For example, D ₄ is depicted in Fig. 5.

Fig. 5

All black vertices are in D ₄

Lemma 5.3

For S _n with n ⩾ 4, the set D _n is an OCD-set in S _n with |D _n | = 3ⁿ⁻².

Proof

It is easy to verify that D ₄ is an OCD-set in S ₄. For S _n with n > 4, it is clear that every D ₄ of S _{4, a} for a ∈ {1, 2, 3}^{n − 4} is also an OCD-set of that S _{4, a} , and all extreme vertices of S _{4, a} are not in its corresponding D ₄. Thus D _n is the union of all those D ₄’s which form an OCD-set of S _n . Accordingly, |D _n | = 3^{n − 4}⋅3² = 3^{n − 2}. This completes the proof. □

Hence, we have our final result as follows:

Theorem 5.4

For S _n with n ⩾ 1,

$$\tilde{\gamma}_{c}(S_{n}) = \left\{\begin{array}{ll} n & \quad~~if~~n=1,2,\\ 3^{n-2} & \quad~if~~n\geqslant 3. \end{array}\right. $$