Localization crossover for the continuous Anderson Hamiltonian in 1-d

Abstract

We investigate the behavior of the spectrum of the continuous Anderson Hamiltonian $\mathcal{H}_{L}$, with white noise potential, on a segment whose size $L$ is sent to infinity. We zoom around energy levels $E$ either of order 1 (Bulk regime) or of order $1\ll E \ll L$ (Crossover regime). We show that the point process of (appropriately rescaled) eigenvalues and centers of mass converge to a Poisson point process. We also prove exponential localization of the eigenfunctions at an explicit rate. In addition, we show that the eigenfunctions converge to well-identified limits: in the Crossover regime, these limits are universal. Combined with the results of our companion paper (Dumaz and Labbé in Ann. Probab. 51(3):805–839, 2023), this identifies completely the transition between the localized and delocalized phases of the spectrum of $\mathcal{H}_{L}$. The two main technical challenges are the proof of a two-points or Minami estimate, as well as an estimate on the convergence to equilibrium of a hypoelliptic diffusion, the proof of which relies on Malliavin calculus and the theory of hypocoercivity.

1 Introduction

In a celebrated article [4], Anderson proposed the Hamiltonian $-\Delta + V$ on the lattice ${{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}^{d}$ as a simplified model for electron conduction in a crystal. The so-called disorder $V$ is a random potential that models the defects of the crystal. The question was whether those defects can trap the electron i.e. localize the electronic wave function. He argued that for a large enough disorder $V$, the spectrum is pure point and the eigenfunctions exponentially localized – a phenomenon now referred to as Anderson localization. Mathematically, one can see this model as the interpolation between the discrete Laplacian $-\Delta$ on the grid ${{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}^{d}$, which has delocalized eigenfunctions and the multiplication by a potential $V$ on each site, whose eigenfunctions are the coordinate vectors.

One of the first rigorous results of Anderson localization was obtained by Goldsheid, Molchanov and Pastur [15]: it concerned the continuum analogue of the above model in dimension $d=1$, namely the operator $-\partial _{x}^{2} +V$ on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$, for some specific random potential $V$. This was followed by a series of major articles [3, 10, 13, 23] to name but a few, in the discrete or the continuum setting, and for general dimension $d\ge 1$. One can summarize the main results as follows: (1) In dimension $d=1$, Anderson localization holds in the whole spectrum; (2) In dimension $d \geq 2$, for a large enough disorder or at a low enough energy, Anderson localization holds. In dimension $d \geq 3$, it is expected (but not proved) that there is a delocalized phase for $V$ weak enough while in dimension $d=2$, the question remains open. We refer to [6, 20] for more details.

In the present article, we consider the case where the potential is a white noise $\xi$ in dimension $d=1$. This is a random Gaussian distribution with covariance given by the Dirac delta: it models physical situations where the disorder is totally uncorrelated. Due to its universality property (white noise arises as scaling limit of appropriately rescaled noises with finite variance), this is a natural choice of potential in the continuum. However, white noise is a highly irregular potential as it is only distribution valued, and therefore falls out of scope of virtually all general results of the literature.

It is standard to tackle Anderson localization by considering first the Hamiltonian truncated to a finite box, before passing to the infinite volume limit. In this article we focus on the truncated Hamiltonian $\mathcal{H}_{L} = -\partial ^{2}_{x} + \xi$ on $(-L/2,L/2)$ with Dirichlet b.c., and investigate its entire spectrum in the limit $L\to \infty$. More precisely, we study the local statistics of the operator recentered around energy levels $E$ that are either finite or diverge with $L$: note that the infinite volume limit only captures energy levels that do not depend on $L$. The results of this article, complemented by those presented in our companion papers [7, 9], reveal a rich variety of behaviors for the eigenvalues/eigenfunctions of $\mathcal{H}_{L}$ according to the energy regime considered: in particular, delocalized eigenfunctions arise at large enough energies. This is to be compared with the aforementioned general results of Anderson localization in dimension $d=1$ that assert localization in the full spectrum. A proof of Anderson localization for the infinite volume Hamiltonian with white noise potential was given by Minami [25], see also [8] for an alternative proof.

Let us now present the main results of the present article, and their connections with the results already obtained in [7, 9]. We recenter $\mathcal{H}_{L}$ around some energy level $E=E(L)$ and distinguish five regimes:

• (1) Bottom: $E \sim -(\frac{3}{8} \ln L)^{2/3}$,

• (2) Bulk: $E$ is fixed with respect to $L$,

• (3) Crossover: $1 \ll E \ll L$,

• (4) Critical: $E \asymp L$,

• (5) Top: $E\gg L$.

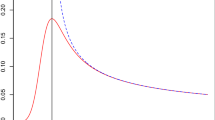
For each regime, we investigate the local statistics of the eigenvalues $\lambda _{i}$ near $E$, and the behavior of the corresponding normalized eigenfunctions $\varphi _{i}$. In [7, 9], we covered the Bottom, Critical and Top regimes, while in the present article we derive the Bulk and Crossover regimes. The main results are summarized on Fig. 1.

Fig. 1

The five regimes of $\mathcal{H}_{L}$

The transition between Poisson statistics and Picket Fence occurs in the Critical regime where $E\asymp L$. In [9], we prove that, in that regime, the eigenvalue statistics are given by the Sch point process introduced by Kritchevski, Valkó and Virág [24]. Actually, we obtain a convergence at the operator level, and show not only that the eigenvalues converge towards Sch but also that the eigenfunctions converge to a universal limit given by the exponential of a two-sided Brownian motion plus a negative linear drift. Note that this limit lives on a finite interval thus making the eigenfunctions delocalized. Our denomination universal is justified by the fact that this shape already appeared in the work of Rifkind and Virág [33] who conjectured that it should arise in various critical models.

In the present article, we show that in the Bulk and Crossover regimes, the local statistics of the eigenvalues (jointly with the centers of mass of the eigenfunctions) converge to a Poisson point process. Moreover, we establish exponential decay of the eigenfunctions (from their centers of mass) at an explicit rate, which is of order 1 in the Bulk regime and of order $E$ in the Crossover regime.

Actually we provide much more information about the eigenfunctions. We show that the eigenfunctions (recentered at their centers of mass and rescaled in space by 1 in the Bulk and by $E$ in the Crossover) converge to explicit limits. In the Bulk regime, the limits are some well-identified diffusions $Y_{E}$, whose law depend of $E$. In the Crossover regime, the limits are given by the same universal shape as in the Critical regime: namely, the exponential of a two-sided Brownian motion plus a negative linear drift. However since the space scale is $E \ll L$, the eigenfunctions are still localized and the limiting shape lives on an infinite interval, in contrast with the Critical regime. As $E\uparrow L$, one formally recovers delocalized states and this justifies a posteriori the denomination Crossover: this regime of energy interpolates between the (localized) Bulk regime and the (delocalized) Critical regime and shares features with both (Poisson statistics with the former and universal shape with the latter).

Finally, in the Bottom regime, investigated in [7], we also obtained Poisson statistics for the eigenvalues (and centers of mass). Furthermore we showed that the eigenfunctions are strongly localized: at space scale $1/(\log L)^{1/3}$ and recentered at their centers of mass, they converge to the deterministic limit $1/\cosh$.

Let us comment on the regime of energies $-(\frac{3}{8} \ln L)^{2/3} \ll E \ll -1$. In this case, the eigenvalues (and centers of mass) should still converge to a Poisson point process, while the eigenfunctions, at space scale $1/\sqrt{\vert E\vert }$ and recentered at their centers of mass, should still converge to the deterministic limit $1/\cosh$. A modification of the proof presented in [7] should suffice to prove these claims for energies $E$ that go to $-\infty$ fast enough.

Overall, our results provide a transition from strongly localized states to totally delocalized states and identify explicitly the local statistics of the eigenvalues together with the asymptotic shapes of the eigenfunctions.

Let us now comment on the technical challenges that these results represent. Since white noise is out of scope of usual standing assumptions, we do not rely on general results from Anderson localization literature, so that our article is self-contained. Let us point out two major difficulties that we encounter. First, the derivation of the two-points estimate, often called Minami estimate [26], is delicate in the context of the irregular potential given by the white noise, whereas some general 1-d results [21] are available for some related models with smoother potential. To prove this estimate, we rely on a thorough study of a joint diffusion, see Sect. 8. Second, in the Crossover regime the phase function rotates at an unbounded speed on the unit circle and this yields many technical challenges. In particular, to obtain quantitative (with respect to the unbounded parameter $E$) estimates on the convergence to equilibrium of this phase, we cannot simply apply Hörmander’s Theory of hypoellipticity in contrast with the situation in [5, 28]: we obtain these estimates using Malliavin Calculus and the theory of hypocoercivity, and this constitutes one of the main technical achievements of the present article, see Sect. 5.

Let us relate our results to other studies in the literature. The discrete counterpart¹ of our model is given by the $N\times N$ random tridiagonal matrix $-\Delta _{N} + \sigma _{N} \,V_{N}$ where $\Delta _{N}$ is the discrete Laplacian on $\{1,\ldots ,N\}$, $V_{N}$ is a diagonal matrix with i.i.d. entries of mean 0 and variance 1 and $\sigma _{N}$ a positive parameter, possibly depending on $N$. If $\sigma _{N}$ does not depend on the size $N$ of the matrix, then the limit $N\to \infty$ of the model falls into the scope of general 1-d Anderson localization results, and the spectrum is localized. On the other hand, one recovers delocalized states when $\sigma _{N} = O(N^{-1/2})$, see [11]. Actually for $\sigma _{N} = \sigma N^{-1/2}$ with $\sigma > 0$ the point process of eigenvalues of the matrix in the bulk converges to the Sch random point process [24] and the eigenfunctions are delocalized [33].

The aforementioned Russian model of Goldsheid, Molchanov and Pastur [15] deals with a potential $V(x) = F(B_{x})$ where $F$ is a smooth bounded function and $(B_{x},x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$ is a stationary Brownian motion taking values in a compact manifold. Molchanov [27, 28] established for this model Poisson statistics for the appropriately rescaled eigenvalues in the large volume limit and for energies that correspond to our Bulk regime; he mentioned that his results should remain true in the white noise case. The present article confirms this statement. Let us point out that the boundedness of $V$ provides many a priori estimates on the eigenvalues and eigenfunctions which are not available anymore in the white noise case.

Let us mention that Minami [26] showed that for Anderson operators in arbitrary dimension, the local statistics of the eigenvalues converge to Poisson point processes provided some control on the density of states and the exponential decay of the fractional moments of the Green’s function.

There are also connections with recent investigations in [22, 30, 31] of the aforementioned Russian model of Goldsheid, Molchanov and Pastur [15], in which, as in the random matrix model, a parameter depending on the size of the system is added in front of the potential to reduce its influence.

Our description of the local statistics of the eigenvalues/centers of mass is in the vein of results obtained by Nakano [29], on the local statistics of eigenvalues/eigenfunctions for discrete Anderson operators, and more recently by Germinet and Klopp [14], who proved precise results on the local and global eigenvalue statistics for a large class of Schrödinger operators. On the other hand, we provide a complete and explicit description of the asymptotic shape taken by the eigenfunctions: to the best of our knowledge, such results are very rare in the literature on Anderson localization.

2 Main results

Let $\xi$ be a Gaussian white noise on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$, that is, the derivative of a Brownian motion $B$. We consider the truncated Anderson Hamiltonian (sometimes also called Hill’s operator)

$$ \mathcal{H}_{L} = -\partial ^{2}_{x} + \xi \;,\quad x\in (-L/2,L/2)\;, $$

(1)

endowed with homogeneous Dirichlet boundary conditions. It was shown in [12] that this operator is self-adjoint on $L^{2}(-L/2,L/2)$ with pure point spectrum of multiplicity one bounded from below $\lambda _{1} < \lambda _{2} < \cdots$ We let $(\varphi _{k})_{k}$ be the corresponding eigenfunctions normalized in $L^{2}$ and satisfying²$\varphi _{k}'(-L/2) > 0$. These r.v. depend on $L$, but for notational simplicity we omit writing this dependence.

This operator has a deterministic density of states $n(E)$, see [12, 18]. This is defined as $n(E) := dN(E)/dE$ where

$$ N(E) := \lim _{L\to \infty} \frac{1}{L} \#\{\lambda _{i}: \lambda _{i} \le E\}\;,\quad E\in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\;. $$

(2)

Here the convergence is almost sure and the limit is deterministic. Roughly speaking, $1/(L n(E))$ measures the typical spacing between two consecutive eigenvalues lying near $E$ for the operator $\mathcal{H}_{L}$. From the explicit integral expression of $n(E)$, see [12], one deduces that $E\mapsto n(E)$ is smooth and that

$$\begin{aligned} n(E) \sim \frac{1}{2\pi \sqrt {E}}\;,\quad E\to +\infty \;. \end{aligned}$$

In the present article, we focus on two regimes of energy:

• (1) Bulk regime: the energy $E$ is fixed with respect to $L$,

• (2) Crossover regime: the energy $E = E(L)$ satisfies $1 \ll E \ll L$,

and investigate the asymptotic behavior as $L\to \infty$ of the eigenvalues $\lambda _{i}$ and of the eigenfunctions, seen as probability measures by considering $\varphi ^{2}_{i}(t) dt$. For every eigenfunction $\varphi _{i}$, a relevant statistics to its localization center is³ the center of mass $U_{i}$ defined through

$$ U_{i} := \int _{[-L/2,L/2]} t \varphi ^{2}_{i}(t) dt\;. $$

Our first result shows convergence, in both regimes, of the point process of rescaled eigenvalues and centers of mass.

Theorem 1

Poisson statistics

In the Bulk and the Crossover regimes, the following random measure on ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times [-1/2,1/2]$

$$ \sum _{i\ge 1} \delta _{(L\, n(E)(\lambda _{i} - E), U_{i}/L)} $$

converges in law as $L\to \infty$ to a Poisson random measure on ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times [-1/2,1/2]$ of intensity $d\lambda \otimes du$.

In this statement, the convergence holds for the vague topology on the set of Radon measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]$, that is, the smallest topology that makes continuous the maps $m\mapsto \langle m,f\rangle$ with $f:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\to {{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ bounded continuous and compactly supported in its first variable.

Our second result establishes exponential localization of the eigenfunctions from their centers of mass. In the Bulk regime, the exponential rate is given by $(1/2)\nu _{E}$ where

$$ \nu _{E} = \frac{ \int _{0}^{+\infty} \sqrt{u} \exp (-2 E u - \frac{u^{3}}{6} ) du}{\int _{0}^{\infty} \frac{1}{\sqrt{u}} \exp (-2 E u - \frac{u^{3}}{6}) du} \,, $$

(3)

while in the Crossover regime it is given by $1/(2E)$. This rate is of course related to the Lyapunov exponent of the underlying diffusions.

Theorem 2

Exponential localization

Fix $h >0$ and set $\Delta := [E-h/(Ln(E)),E+h/(Ln(E))]$. For every $\varepsilon > 0$ small enough, there exist some r.v. $c_{i}>0$ such that:

• (1) for every eigenvalue $\lambda _{i} \in \Delta$ we have in the Bulk regime

  $$ \big(\varphi _{i}(t)^{2} + \varphi '_{i}(t)^{2}\big)^{1/2} \le c_{i} \exp \Big(-\frac{(\nu _{E} - \varepsilon )}{2}\,|t-U_{i}|\Big)\;, \quad \forall t\in [-L/2,L/2]\;, $$

  and in the Crossover regime

  $$ \Big(\varphi _{i}(t)^{2} + \frac{\varphi '_{i}(t)^{2}}{E}\Big)^{1/2} \le \frac{c_{i}}{\sqrt {E}} \exp \Big(-\frac{(1-\varepsilon )}{2} \frac{|t-U_{i}|}{E}\Big)\;,\quad \forall t\in [-L/2,L/2]\;, $$

• (2) in both regimes, there exists $q=q(\varepsilon ) > 0$ such that

  $$ \limsup _{L\to \infty} \mathbb{E}\Big[\sum _{\lambda _{i} \in \Delta} c_{i}^{q} \Big] < \infty \;. $$

Our third result shows that the eigenfunctions (rescaled into probability measures) converge to a Poisson point process with an explicit intensity. Actually the convergence will be taken jointly with the eigenvalues and the centers of mass, so the result is a strengthening of Theorem 1.

Let us start with the definition of the probability measures associated with the eigenfunctions. Given the rate of exponential localization appearing in the previous result, one needs to recenter the eigenfunctions appropriately to get convergence, so we define for every eigenvalue $\lambda _{i}$

$$ w_{i}(dt) := \textstyle\begin{cases} \varphi _{i}(U_{i}+t)^{2} dt\quad &\text{ in the Bulk regime,} \\ E \varphi _{i}(U_{i}+tE)^{2} dt\quad & \text{ in the Crossover regime,} \end{cases} $$

which is an element of the set $\mathcal{M}= \mathcal{M}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$ of all probability measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ endowed with the topology of weak convergence.

In the statement below, we rely on a probability measure on ℳ that describes the law of the limits. In the Crossover regime, this probability measure $\sigma _{\infty}$ admits a simple definition: it is the law of the random probability measure

$$\begin{aligned} &\frac{Y_{\infty}(t+U_{\infty})^{2} dt}{\int Y_{\infty}(t+U_{\infty})^{2} dt} \;, \\ &\quad \text{with}\quad Y_{\infty}(t) := {\frac{1}{\sqrt {2}}} \exp \Big(- \frac{|t|}{8} + \frac{\mathcal{B}(t)}{2\sqrt {2}}\Big)\;,\quad U_{\infty }:= \frac{\int t Y_{\infty}(t)^{2} dt}{\int Y_{\infty}(t)^{2} dt}\;, \end{aligned}$$

(4)

where ℬ is a two-sided Brownian motion on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$.

In the Bulk regime, this probability measure $\sigma _{E}$ is the law of the random probability measure

$$\begin{aligned} \frac{Y_{E}(t+U_{E})^{2} dt}{\int Y_{E}(t+U_{E})^{2} dt}\;,\quad U_{E} := \frac{\int t Y_{E}(t)^{2} dt}{\int Y_{E}(t)^{2} dt}\;, \end{aligned}$$

(5)

where $Y_{E}$ is the concatenation at $t=0$ of two processes $(Y_{E}(t),t\ge 0)$ and $(Y_{E}(-t),t\ge 0)$ with explicit laws. The precise definition of $Y_{E}$ requires some notations and is given in Sect. 9.1.

Theorem 3

Shape

In the Bulk and the Crossover regimes, the random measure

$$ \mathcal{N}_{L} := \sum _{i\ge 1} \delta _{(L\, n(E)(\lambda _{i} - E), U_{i}/L, w_{i})}\;, $$

converges in law as $L\to \infty$ to a Poisson random measure on ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times [-1/2,1/2] \times \mathcal{M}$ of intensity $d\lambda \otimes du \otimes \sigma _{E}$ in the Bulk regime and of intensity $d\lambda \otimes du \otimes \sigma _{\infty}$ in the Crossover regime.

Here $\mathcal{N}_{L}$ is seen as a random element of the set of measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2] \times \mathcal{M}$ that give finite mass to $K\times [-1/2,1/2] \times \mathcal{M}$, for any given compact set $K\subset {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$. The topology considered in the convergence above is then the smallest topology on this set of measures that makes continuous the maps $m\mapsto \langle f,m\rangle$, for every bounded and continuous function $f:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2] \times \mathcal{M}\to {{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ that is compactly supported in its first coordinate.

Let us make some comments on the limits of these eigenfunctions. First of all, the localization length is of order 1 in the Bulk regime and $E$ in the Crossover regime: this is in line with the exponential decay of Theorem 2. Moreover, this localisation length increases with the level of energy, and this is coherent with the general fact that: the lower we look into the spectrum, the more localized the eigenfunctions are. Second, it suggests that for $E$ of order $L$ the eigenfunctions are no longer localized: this is rigorously proved in our companion paper [9].

Remark 2.1

Informally, our result shows that in the Crossover regime the eigenfunction $\varphi _{\lambda }$, properly rescaled, converges as a probability measure towards $Y_{\infty }$ (rescaled by its $L^{2}$ mass). It is possible to go further. Introduce the distorted polar coordinates $\frac{\varphi '_{\lambda }}{E} + i \varphi _{\lambda }= r_{\lambda }e^{i \theta _{\lambda }}$ and note that the phase $\theta _{\lambda }$ oscillates very fast (as soon as $E\to \infty$). After removing deterministic oscillations from the phase $\theta _{\lambda }$, the arguments presented in this article can be adapted to show that it converges towards a non-trivial limiting phase. Moreover, the modulus $r_{\lambda }$, after a proper rescaling, converges to $\sqrt{2} Y_{\infty }$.

We now outline the remaining of this article. We introduce in Sect. 3 the diffusions associated to our eigenvalue equation as they play a central role in this article. Then we detail in Sect. 4 our strategy of proof: this section presents the main intermediate results of this paper and contains the proofs of Theorems 1, 2 and 3. The subsequent sections are then devoted to proving these intermediate results, more details on their contents and relationships will be given at the end of Sect. 4.

3 The diffusions

The eigenvalue problem associated to the operator $\mathcal{H}_{L}$ gives rise to a family $y_{\lambda }$, $\lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ of ODEs, corresponding to the solution of the eigenvalue equation:

$$\begin{aligned} -y_{\lambda }''(t) + \xi (dt) y_{\lambda }(t) = \lambda y_{\lambda }(t) \;,\quad t\in (-L/2,L/2)\;. \end{aligned}$$

(6)

Up to fixing two degrees of freedom there is a unique solution to this equation for every parameter $\lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$. If we fix the starting conditions $y_{\lambda }(-L/2) = 0$ and $y_{\lambda }'(-L/2)$ to an arbitrary value different from 0, then the map $\lambda \mapsto y_{\lambda }(L/2)$ is continuous. The zeros of this map are the eigenvalues of $\mathcal{H}_{L}$, and the corresponding solutions $y_{\lambda }$ are the eigenfunctions of $\mathcal{H}_{L}$ (which are defined up to a multiplicative factor corresponding to $y_{\lambda }'(-L/2)$ of course).

It is crucial in our analysis to consider the evolution of both $y_{\lambda }$ and $y'_{\lambda }$, and this is naturally described by the complex function $y_{\lambda}' + i y_{\lambda}$. It will actually be convenient to work in polar coordinates (also called Prüfer variables): we consider $(r_{\lambda},\theta _{\lambda})$ where

$$ y_{\lambda}' + i y_{\lambda }= r_{\lambda }e^{i \theta _{\lambda }} \;. $$

The process $\theta _{\lambda }$ is called the phase of the above ODE. It is instrumental for the study of the spectrum of $\mathcal{H}_{L}$ as we will see later on. It is also convenient to define

$$ \rho _{\lambda }(t) := \ln r_{\lambda }^{2}(t)\;. $$

In these new coordinates, we have the following coupled stochastic differential equations:

$$\begin{aligned} d\theta _{\lambda }(t) &= \big(1 + (\lambda -1) \sin ^{2} \theta _{ \lambda }+ \sin ^{3}\theta _{\lambda }\cos \theta _{\lambda }\big) dt - \sin ^{2} \theta _{\lambda }dB(t)\;, \end{aligned}$$

(7)

$$\begin{aligned} d\rho _{\lambda }(t) &= \big(-(\lambda -1) \sin 2\theta _{\lambda }- \frac{1}{2} \sin ^{2} 2\theta _{\lambda }+ \sin ^{2} \theta _{ \lambda }\big)dt+ \sin 2\theta _{\lambda }dB(t)\;. \end{aligned}$$

(8)

where $dB(t) = \xi (dt)$.

The two degrees of freedom given by the initial conditions $y_{\lambda }(-L/2)$ and $y_{\lambda }'(-L/2)$ are transferred to $\theta _{\lambda }(-L/2)$ and $r_{\lambda }(-L/2)$ (or equivalently $\rho _{\lambda }(-L/2)$). Note that

$$ \begin{aligned}&y_{\lambda }(-L/2) = 0 \;\;\&\;\; y_{\lambda }'(-L/2) > 0 \\ &\quad \Longleftrightarrow \quad \theta _{\lambda }(-L/2) \equiv 0 [2\pi ] \;\;\&\;\; r_{\lambda }(-L/2) = y_{\lambda }'(-L/2)\;, \end{aligned}$$

while

$$ \begin{aligned}&y_{\lambda }(-L/2) = 0 \;\;\&\;\; y_{\lambda }'(-L/2) < 0 \\ &\quad \Longleftrightarrow \quad \theta _{\lambda }(-L/2) \equiv \pi [2\pi ] \;\;\&\;\; r_{\lambda }(-L/2) = -y_{\lambda }'(-L/2)\;. \end{aligned}$$

For any angle $\theta \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$, we define

$$ {\lfloor \theta \rfloor _{\pi }:= \lfloor \theta /\pi \rfloor \in{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}}\;,\quad \text{ and } \quad \{\theta \}_{ \pi }:= \theta - \lfloor \theta \rfloor _{\pi }{\pi } \in [0,\pi )\;. $$

Let us point out an important property of the process $\theta _{\lambda }$: at the times $t$ such that $\{\theta _{\lambda }(t)\}_{\pi }= 0$, the drift term is strictly positive while the diffusion coefficient vanishes. Consequently $\{\theta _{\lambda }\}_{\pi}$ cannot hit 0 from above: this readily implies that $t \mapsto \lfloor \theta _{\lambda }(t) \rfloor _{\pi}$ is non-decreasing. Moreover, the evolution of $\theta _{\lambda }$ depends only on $\{\theta _{\lambda }\}_{\pi}$ so that the latter is a Markov process. We let $p_{\lambda ,t}(\theta _{0}, \theta )$ be the density of its transition probability at time $t$ when it starts from $\theta _{0}$ at time 0. When this process starts from 0 at time 0, we drop the first variable and simply write $p_{\lambda ,t}(\theta )$.

At some occasions, we will write $\mathbb{P}_{(t_{0},\theta _{0})}$ for the law of the process $\theta _{\lambda }$ starting from $\theta _{0}$ at time $t_{0}$, and we will write $\mathbb{P}_{(t_{0},\theta _{0})\to (t_{1},\theta _{1})}$ to denote the law of the bridge of diffusion that starts from $\theta _{0}$ at time $t_{0}$ and is conditioned to reach $\theta _{1}+\pi{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}$ at time $t_{1}$.

Most of the time, we will take $\theta _{\lambda }(-L/2) = 0$ and $r_{\lambda }(-L/2) > 0$. In this setting, $\lambda$ is an eigenvalue of $\mathcal{H}_{L}$ iff $\{\theta _{\lambda }(L/2)\}_{\pi }= 0$ and then, the function $y_{\lambda}$ is the associated eigenfunction. Since $\lambda \mapsto \lfloor \theta _{\lambda }(L/2) \rfloor _{\pi}$ is non-decreasing, we deduce the so-called Sturm-Liouville property: almost surely,

$$\begin{aligned} \#\{\lambda _{i} \;:\; \lambda _{i} \leq \lambda \} = \lfloor \theta _{ \lambda }(L/2) \rfloor _{\pi}\;, \quad \text{ for all $\lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$\,,} \end{aligned}$$

(9)

This phase function $\theta _{\lambda }(\cdot )$ is a powerful tool to investigate the spectrum of $\mathcal{H}_{L}$. It has been used in numerous articles on 1d-Schrödinger operators, sometimes under the form of the so-called Riccati transform $y'_{\lambda }/y_{\lambda }$ which is nothing but $\text{cotan}\,\theta _{\lambda }$.

3.1 The distorted coordinates

For large energies, that is, whenever $\lambda$ is of order $E$ for some $E=E(L) \to \infty$, the phase $\theta _{\lambda }$ takes a time of order $1/\sqrt {E}$ to make one rotation so that the solutions $y_{\lambda }$, $y_{\lambda }'$ oscillate very fast. It is then more convenient to use distorted and sped up coordinates. We set

$$ \frac{y_{\lambda }'(tE)}{\sqrt{E}} + i y_{\lambda }(tE) =: r_{ \lambda }^{(E)}(t) e^{i \theta _{\lambda }^{(E)}(t)}\;,\quad t\in [-L/(2E),L/(2E)] \;, $$

and

$$ \begin{aligned}y_{\lambda }^{(E)}(t) &:= r_{\lambda }^{(E)}(t) \sin \theta _{\lambda }^{(E)}(t) \;, \\ (y_{\lambda }^{(E)})'(t) &= E^{3/2} r_{\lambda }^{(E)}(t) \cos \theta _{\lambda }^{(E)}(t)\;,\quad t\in [-L/(2E),L/(2E)]\;. \end{aligned}$$

Defining the Brownian motion $B^{(E)}(t) = E^{-1/2} B(tE)$ and setting $\rho _{\lambda }^{(E)} := \ln (r_{\lambda }^{(E)})^{2}$, the evolution equations take the form

$$\begin{aligned} d\theta _{\lambda }^{(E)} ={}& \Big(E^{3/2} + \sqrt{E} (\lambda -E) \sin ^{2} \theta _{\lambda }^{(E)} + \sin ^{3} \theta _{\lambda }^{(E)} \cos \theta _{\lambda }^{(E)}\Big) dt \\ &{}- \sin ^{2} \theta _{\lambda }^{(E)} dB^{(E)}(t)\;, \\ d\rho _{\lambda }^{(E)} ={}& \big(-\sqrt{E} (\lambda -E) \sin 2\theta _{ \lambda }^{(E)} - \frac{1}{2} \sin ^{2} 2 \theta _{\lambda }^{(E)} + \sin ^{2} \theta _{\lambda }^{(E)} \big) dt \\ &{} + \sin 2\theta _{\lambda }^{(E)} dB^{(E)}(t)\;. \end{aligned}$$

Let $p_{\lambda ,t}^{(E)}(\theta _{0}, \theta )$ be the density of the transition probability at time $t$ of the processes $\{\theta _{\lambda }^{(E)}\}_{\pi}$ starting from $\theta _{0}$ at time $t=0$. When this process starts from 0 at time 0, we drop the first variable and simply write $p_{\lambda ,t}^{(E)}(\theta )$. The change of variable formula shows that

$$ p_{\lambda ,t}^{(E)}(\theta ) = p_{\lambda ,{tE}}( \text{arccotan\,}(\sqrt {E} \text{cotan}\,\theta )) \frac{\sqrt {E}}{\sin ^{2} \theta + E \cos ^{2} \theta}\;. $$

(10)

Again, we use the notation $\mathbb{P}_{(t_{0},\theta _{0})}$, resp. $\mathbb{P}_{(t_{0},\theta _{0})\to (t_{1},\theta _{1})}$, to denote the law of the diffusion, resp. bridge of diffusion.

3.2 Condensed notation

The distorted coordinates will be used in the Crossover regime, while we will rely on the original coordinates in the Bulk regime. However most of our arguments apply indifferently to both cases. Consequently, we will adopt condensed notations as much as possible. First we introduce

$$ \mathbf{E}:= \textstyle\begin{cases} 1 & \text{ original coordinates}\;, \\ E&\text{ distorted coordinates}\;.\end{cases} $$

Moreover, when the arguments apply to both sets of coordinates, we will use the generic notation $\theta _{\lambda }^{(\mathbf{E})}$, $\rho _{\lambda }^{(\mathbf{E})}$ to denote $\theta _{\lambda }$, $\rho _{\lambda }$ in the original coordinates, and $\theta _{\lambda }^{(E)}$, $\rho _{\lambda }^{(E)}$ in the distorted coordinates. We will sometimes introduce quantities of interest such as processes, measures, etc. using the generic notation at once. For instance, we could have introduced the SDE satisfied by $\theta _{\lambda }$, $\rho _{\lambda }$ and $\theta _{\lambda }^{(E)}$, $\rho _{\lambda }^{(E)}$ by simply writing

$$\begin{aligned} &d\theta _{\lambda }^{(\mathbf{E})} = \Big(\mathbf{E}^{3/2} + \sqrt{ \mathbf{E}} (\lambda -\mathbf{E}) \sin ^{2} \theta _{\lambda }^{( \mathbf{E})} + \sin ^{3} \theta _{\lambda }^{(\mathbf{E})} \cos \theta _{\lambda }^{(\mathbf{E})}\Big) dt - \sin ^{2} \theta _{ \lambda }^{(\mathbf{E})} dB^{(\mathbf{E})}(t)\;, \end{aligned}$$

(11)

$$\begin{aligned} &d\rho _{\lambda }^{(\mathbf{E})} = \big(-\sqrt{\mathbf{E}} (\lambda - \mathbf{E}) \sin 2\theta _{\lambda }^{(\mathbf{E})} - \frac{1}{2} \sin ^{2} 2 \theta _{\lambda }^{(\mathbf{E})} + \sin ^{2} \theta _{ \lambda }^{(\mathbf{E})} \big) dt + \sin 2\theta _{\lambda }^{( \mathbf{E})} dB^{(\mathbf{E})}(t)\;. \end{aligned}$$

(12)

3.3 Invariant measure

The Markov process $\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi}$ admits a unique invariant probability measure whose density $\mu _{\lambda }^{(\mathbf{E})}$ has a simple integral expression, see Sect. A.4 of the Appendix for more details. Straightforward computations relying on this expression show the following estimates:

Lemma 3.1

Bounds on the invariant measure

Original coordinates. For any compact interval $\Delta \subset {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$, there are two constants $0 < c < C$ such that for all $\theta \in [0,\pi )$ and all $\lambda \in \Delta$ we have

$$ c \le \mu _{\lambda }(\theta ) < C\;,\qquad |\partial _{\theta }\mu _{ \lambda }(\theta )| < C\;. $$

Distorted coordinates. For any $h>0$ there are two constants $c,C > 0$ such that for all $E>1$, all $\theta \in [0,\pi )$ and all $\lambda \in \Delta := [E-\frac{h}{En(E)},E+\frac{h}{En(E)}]$

$$ c \le \mu _{\lambda }^{(E)}(\theta ) < C\;,\qquad |\partial _{\theta } \mu _{\lambda }^{(E)}(\theta )| < C\;. $$

Finally, we have as $E \to \infty$

$$ \sup _{\lambda \in \Delta } \sup _{\theta \in [0,\pi )} |\partial _{ \theta }\mu _{\lambda }^{(E)}(\theta )| \to 0\;,\quad \sup _{\lambda \in \Delta } \sup _{\theta \in [0,\pi )} \big|\mu _{\lambda }^{(E)}( \theta ) - \frac{1}{\pi }\big| \to 0\;. $$

The last convergence shows that our distorted coordinates are the “right ones” in the Crossover regime: as $E\to \infty$ the corresponding invariant measure converges to a non-degenerate limit given by the uniform measure on the circle.

Remark 3.2

The length of $\Delta$ is of order 1 for the original coordinates and of order $E^{-1/2}$ in the distorted coordinates. The parameter $L$ does not play any role in this setting. This should not be confused with the setting of Theorem 2 (and of many other estimates/statements of the article) where we consider an interval $\Delta$ on length $1/L \ll 1$ in the Bulk regime and of order $E^{1/2}/L \ll E^{-1/2}$ in the Crossover regime.

3.4 Rotation time and density of states

Let us introduce the first rotation time of the diffusion $\theta _{\lambda }^{(\mathbf{E})}$

$$ \zeta _{\lambda }^{(\mathbf{E})} := \inf \{t\ge 0: \theta _{\lambda }^{( \mathbf{E})}(t) = \theta _{\lambda }^{(\mathbf{E})}(0) + \pi \}\;. $$

Lemma 3.3

The law of $\zeta _{\lambda }^{(\mathbf{E})}$ is independent of the initial condition $\theta _{\lambda }^{(\mathbf{E})}(0)$.

Proof

Write $\theta _{\lambda }^{(\mathbf{E})}(0) = n\pi + \theta$ with $\theta \in [0,\pi [$ and $n\in{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$. Introduce $H_{\pi }:= \inf \{t\ge 0: \theta _{\lambda }^{(\mathbf{E})}(t) =(n+1) \pi \}$ and $H_{\theta }' := \inf \{t\ge 0 : \theta _{\lambda }^{(\mathbf{E})}(t+H_{ \pi }) =\theta _{\lambda }^{(\mathbf{E})}(0) + \pi \}$. By the strong Markov property, $H_{\theta }'$ is independent of $H_{\pi }$. Furthermore, $H'_{\theta }$ has the same law as $T_{0,\theta }$, and $H_{\pi }$ has the same law as $T_{\theta ,\pi }$ where $T_{\theta _{0},\theta _{1}}$ is the first hitting time of $\theta _{1}$ for the diffusion starting from $\theta _{0}$.

We thus showed that $\zeta _{\lambda }^{(\mathbf{E})} = H_{\pi }+ H'_{\theta }$ has the same law as $T_{0,\theta } + T_{\theta ,\pi }$ where $T_{\theta ,\pi }$ is independent of $T_{0,\theta }$. But the strong Markov property implies that $T_{0,\theta } + T_{\theta ,\pi }$ has the law of $\zeta _{\lambda }^{(\mathbf{E})}$ when $\theta _{\lambda }^{(\mathbf{E})}(0) = 0$, thus concluding the proof. □

As a consequence the expectation of $\zeta _{\lambda }^{(\mathbf{E})}$ does not depend on the initial condition and we thus set

$$ m_{\lambda }^{(\mathbf{E})} := \mathbb{E}[\zeta _{\lambda }^{( \mathbf{E})}]\;. $$

This expectation of the rotation time admits the following integral expression

$$\begin{aligned} m_{\lambda }^{(\mathbf{E})}= \frac{\sqrt{2 \pi }}{\mathbf{E}} \int _{0}^{ \infty } \frac{1}{\sqrt{u}} \exp (-2 \lambda u - \frac{u^{3}}{6}) du \; . \end{aligned}$$

(13)

In the original coordinates, this expression is established in [2]. On the other hand, the mere definition of our distorted coordinates implies that $\zeta _{\lambda }^{(E)}$ is equal in law to $\zeta _{\lambda }/ E$, so that $m_{\lambda }^{(E)} = m_{\lambda }/ E$ and the integral expression follows in this case as well.

Note that $m_{\lambda }$ is nothing but $1/N(\lambda )$, that is, the inverse of the integrated density of states introduced in (2). Indeed, by the law of large numbers, the number of rotations of $\theta _{\lambda }$ on the interval $[-L/2,L/2]$ is of order $L/m_{\lambda }$, so that the Sturm-Liouville property recalled above implies that the number of eigenvalues of $\mathcal{H}_{L}$ that lie below $\lambda$ is of the same order.

From the integral expression, one can check that

$$ m_{\lambda }\sim \frac{\pi }{\sqrt {\lambda}}\;,\quad \lambda \to \infty \;.$$

(14)

and this allows to recover the asymptotic of $N(\lambda )$ stated in the introduction. Let us finally mention that some moment estimates on $\zeta _{\lambda }^{(\mathbf{E})}$ are presented in Appendix A.3.

3.5 Forward and backward diffusions

We introduce in this paragraph the so-called forward and backward diffusions as their concatenation will be instrumental in our study. Let us consider the original coordinates first.

The eigenproblem is symmetric in law under the map $t\mapsto -t$ since $B'(\cdot )$ and $B'(-\cdot )$ have the same law. To take advantage of this symmetry, we consider the solutions $(r_{\lambda }^{\pm }=e^{\frac{1}{2} \rho _{\lambda }^{\pm}},\theta _{ \lambda }^{\pm})$ of

$$\begin{aligned} d\theta _{\lambda }^{\pm}(t) &= \Big(1 + (\lambda -1) \sin ^{2} \theta _{\lambda }^{\pm }+ \sin ^{3}\theta _{\lambda }^{\pm }\cos \theta _{\lambda }^{\pm}\Big) dt - \sin ^{2} \theta _{\lambda }^{\pm }dB^{ \pm}(t)\;, \end{aligned}$$

(15)

$$\begin{aligned} d\rho _{\lambda }^{\pm}(t) &=\big(-(\lambda -1) \sin 2\theta _{ \lambda }^{\pm }- \frac{1}{2} \sin ^{2} 2\theta _{\lambda }^{\pm }+ \sin ^{2} \theta _{\lambda }^{\pm }\big)dt+ \sin 2\theta _{\lambda }^{ \pm }dB^{\pm}(t)\;, \end{aligned}$$

(16)

for $t\in [-L/2,L/2]$ where

$$ B^{+}(t) := B(t)\;,\quad B^{-}(t) := B(L/2)-B(-t)\;. $$

The processes $(r_{\lambda }^{+},\theta _{\lambda }^{+})$ will be called the forward diffusions, while $(r_{\lambda }^{-},\theta _{\lambda }^{-})$ will be called the backward diffusions. We also introduce $(y^{\pm}_{\lambda })' + i y^{\pm}_{\lambda }:= r_{\lambda }^{\pm} \exp (i \theta ^{\pm}_{\lambda })$. Of course the forward diffusions coincide with the original diffusions $(r_{\lambda },\theta _{\lambda })$.

Take $\theta _{\lambda }^{+}(-L/2) = \theta _{\lambda }^{-}(-L/2) = 0$. We have already seen that $\lambda$ is an eigenvalue of $\mathcal{H}_{L}$ if and only if $\{\theta _{\lambda }^{+}(L/2)\}_{\pi }= 0$. From the symmetry of the eigenvalue problem, we can also read off the set of eigenvalues out of the backward diffusions: namely, $\lambda$ is an eigenvalue if and only if $\{\theta _{\lambda }^{-}(L/2)\}_{\pi }= 0$.

It will actually be convenient to combine these two criteria in the following way: one follows the forward diffusion up to some given time $u \in [-L/2,L/2]$, and the backward diffusion up to time $-u$. The set of eigenvalues can then be read off using the following fact (whose proof is postponed below):

Lemma 3.4

Take $\theta _{\lambda }^{\pm}(-L/2) = 0$. It holds:

$$\begin{aligned} \lambda \textit{ is an eigenvalue of }\mathcal{H}_{L}\; \textit{ if and only if }\; \{\theta _{\lambda }^{+}(u) + \theta _{ \lambda }^{-}(-u)\}_{\pi }= 0\,. \end{aligned}$$

It is therefore natural to consider concatenations of the forward and backward diffusions. For any time $u\in [-L/2,L/2]$, we set:

$$\begin{aligned} r_{\lambda }^{+}(u) = r_{\lambda }^{-}(-u) = 1\;, \end{aligned}$$

(17)

and we define⁴

$$ (\hat{r}_{\lambda }(t),\hat{\theta }_{\lambda }(t)) := \textstyle\begin{cases} (r_{\lambda }^{+}(t),\theta _{\lambda }^{+}(t)),\quad &t\in [-L/2,u] \;, \\ (r_{\lambda }^{-}(-t),k\pi - \theta _{\lambda }^{-}(-t)),\quad &t\in (u,L/2] \;, \end{cases} $$

(18)

where $k := \lfloor \theta _{\lambda }^{+}(u)+\theta _{ \lambda }^{-}(-u) \rfloor _{\pi }$. Note that $\hat{r}_{\lambda }$, $\hat{\theta }_{\lambda }$ depend on $u$, but for notational convenience we omit writing explicitly this dependence.

We also define the process $\hat{y}_{\lambda }$ by setting

$$\begin{aligned} \hat{y}_{\lambda }(t) := \hat{r}_{\lambda }(t) \sin \hat{\theta }_{ \lambda }(t)\;. \end{aligned}$$

(19)

Using the identity $(r_{\lambda }^{\pm }(t) \sin \theta _{\lambda }^{\pm }(t))' = r_{ \lambda }^{\pm }(t) \cos \theta _{\lambda }^{\pm }(t)$, we deduce that for all $t\in [-L/2,L/2] \backslash \{u\}$

$$ (\hat{y}_{\lambda })'(t) = \hat{r}_{\lambda }(t) \cos \hat{\theta }_{ \lambda }(t)\;, $$

and that this identity remains true at $u_{+}$ and $u_{-}$, with possibly a discontinuity there. When $\lambda _{i}$ is an eigenvalue, denoting $\|\cdot \|_{2}$ the $L^{2}$-norm, we have the identity (valid for all $u \in [-L/2,L/2]$):

$$\begin{aligned} \varphi _{i}(t) = \frac{\hat{y}_{\lambda _{i}}(t)}{\| \hat{y}_{\lambda _{i}} \|_{2}}, \qquad t \in [-L/2,L/2]\,. \end{aligned}$$

Proof of Lemma 3.4

If $\lambda$ is an eigenvalue of $\mathcal{H}_{L}$, and provided $\{\theta _{\lambda }^{\pm}(-L/2)\}_{\pi }= 0$, the functions $y^{+}_{\lambda }$ and $y^{-}_{\lambda }(-\cdot )$ coincide up to a multiplicative factor (which is related to the values $r_{\lambda }^{\pm}(-L/2)$). Consequently if $\lambda$ is an eigenvalue then we must have the following equality in $\{-\infty \}\cup {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$

$$ \lim _{\epsilon \downarrow 0} \frac{(y^{+}_{\lambda })'(u-\epsilon )}{y^{+}_{\lambda }(u - \epsilon )} = -\lim _{\epsilon \downarrow 0} \frac{(y^{-}_{\lambda })'(-u+\epsilon )}{y^{-}_{\lambda }(-u+\epsilon )} \;. $$

This is equivalent to $\text{cotan}\,( \theta ^{+}_{\lambda }(u_{-})) = \text{cotan}\,(\pi - \theta ^{-}_{\lambda }((-u)_{+}))$, which is itself equivalent to $\{\theta _{\lambda }^{+}(u_{-})\}_{\pi }= \{\pi -\theta _{\lambda }^{-}((-u)_{+}) \}_{\pi}$. Note that $\{\theta _{\lambda }^{+}(u_{-})\}_{\pi }= \{\theta _{\lambda }^{+}(u) \}_{\pi}$, and similarly $\{\pi -\theta _{\lambda }^{-}((-u)_{+})\}_{\pi }= \{\pi -\theta _{ \lambda }^{-}(-u)\}_{\pi}$. We end up with $\{\theta _{\lambda }^{+}(u)\}_{\pi }= \{\pi -\theta _{\lambda }^{-}((-u)) \}_{\pi}$ which is equivalent to $\{\theta _{\lambda }^{+}(u) + \theta _{\lambda }^{-}(-u)\}_{\pi }=0$.

On the other hand, if $\{\theta _{\lambda }^{+}(u) + \theta _{\lambda }^{-}(-u)\}_{\pi }= 0$ then the concatenation $\hat{y}_{\lambda }$ is continuously differentiable at $u$ (recall that $r_{\lambda }^{\pm}(\pm u)=1$), satisfies (6) at all points $t\in [-L/2,L/2]$ and satisfies the Dirichlet b.c., consequently $\lambda$ is an eigenvalue. □

With distorted coordinates, all the above quantities find naturally their counterparts. For $u\in [-L/(2E),L/(2E)]$, we denote by $\hat{y}^{(E)}_{\lambda }$, $\hat{r}^{(E)}_{\lambda }$, $\hat{\theta }^{(E)}_{\lambda }$ the concatenation of the respective backward $\theta ^{-,(E)}_{\lambda }$ and forward diffusions $\theta ^{+,(E)}_{\lambda }$ on $[-L/(2E),L/(2E)]$. In particular, $\hat{y}_{\lambda }^{(E)} = \hat{r}_{\lambda }^{(E)} \sin \hat{\theta }^{(E)}_{\lambda }$, $(\hat{y}_{\lambda }^{(E)})'/E^{3/2} = \hat{r}_{\lambda }^{(E)} \cos \hat{\theta }^{(E)}_{\lambda }$ and when $\{\theta _{\lambda }^{\pm }(-L/2)\}_{\pi }= 0$, the link between $\hat{y}^{(E)}_{\lambda _{i}}$ and $\varphi _{i}$ becomes:

$$\begin{aligned} \varphi _{i}(t) = \frac{\hat{y}^{(E)}_{\lambda _{i}}(t/E)}{\sqrt{E} \| \hat{y}^{(E)}_{\lambda _{i}}\|_{2}}, \qquad t \in [-L/2,L/2]\,. \end{aligned}$$

For both sets of coordinates and for any $u\in [-L/(2\mathbf{E}),L/(2\mathbf{E})]$ we will denote by $\mathbb{P}^{(u)}_{\theta ,\theta '}$ the product law $\mathbb{P}^{+}_{(-L/(2\mathbf{E}),0)\rightarrow (u,\theta )} \otimes \mathbb{P}^{-}_{(-L/(2\mathbf{E}),0)\rightarrow (-u,\theta ')}$ under which $\theta ^{\pm ,(\mathbf{E})}_{\lambda }$ are two independent bridges of diffusion between $(-L/(2\mathbf{E}),0)$ and $(u,{\theta +\pi{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{ \text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}})$ for $\theta _{\lambda }^{+,(\mathbf{E})}$, and between $(-L/(2\mathbf{E}),0)$ and $(-u,{\theta '+\pi{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{ \text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}})$ for $\theta _{\lambda }^{-,(\mathbf{E})}$. Then, the processes $\hat{r}_{\lambda }^{(\mathbf{E})}$, $\hat{\theta }_{\lambda }^{(\mathbf{E})}$ and $\hat{y}_{\lambda }^{(\mathbf{E})}$ are defined under $\mathbb{P}^{(u)}_{\theta ,\theta '}$ according to (18) and (19) with the original coordinates, and according to similar equations with distorted coordinates.

4 Strategy of proof

4.1 Convergence to equilibrium of the phase

Our proofs rely on the following exponential convergence of the transition probability of the phase $\theta _{\lambda }^{(\mathbf{E})}$ toward its equilibrium measure $\mu _{\lambda }^{(\mathbf{E})}$.

Theorem 4

Exponential convergence to the invariant measure

In the original coordinates, fix a compact set of energies $\Delta$. Then there exist $c,C>0$ such that for all $t\ge 1$

$$ \sup _{\lambda \in \Delta}\sup _{\theta _{0},\theta \in [0,\pi ]} |p_{ \lambda ,t}(\theta _{0},\theta ) - \mu _{\lambda }(\theta )| \le ce^{-C \, t}\;. $$

In the distorted coordinates, fix $h>0$ and set $\Delta = [E-\frac{h}{n(E)E},E+\frac{h}{n(E)E}]$. There exist $c,C > 0$ such that uniformly over all $E>1$ and for all $t\ge 1$

$$ \sup _{\lambda \in \Delta}\sup _{\theta _{0},\theta \in [0,\pi ]} |p_{ \lambda ,t}^{(E)}(\theta _{0},\theta ) - \mu _{\lambda }^{(E)}( \theta )| \le ce^{-C \, t}\;. $$

The proof of this estimate is delicate, especially in the distorted coordinates since the bound is uniform over all $E\in [1,\infty )$. The proof relies on tools from Malliavin calculus and the theory of hypocoercivity, it is an important technical step in our article. This result will be crucial for deriving the exponential decay of the eigenfunctions and evaluating the expectation of the number of eigenvalues in small intervals.

4.2 Goldscheid-Molchanov-Pastur (GMP) formula

We have seen that the Sturm-Liouville property allows to extract a lot of spectral information from the phase function. A major observation on which this article relies is that we can extract even more information through a beautiful formula, originally obtained by Goldscheid, Molchanov and Pastur [15] in a similar but smoother context, and that we name GMP formula from now on. This formula expresses the intensity of the point process

$$ \sum _{i\ge 1} \delta _{(\lambda _{i}, \varphi _{i}, \varphi '_{i})} $$

in terms of concatenations of the forward and backward diffusions introduced earlier. Roughly speaking, it shows that in average the eigenfunctions are concatenations of the forward and backward diffusions at uniform points $u \in (-L/2,L/2)$. Below $\|\cdot \|_{2}$ denotes the $L^{2}$-norm.

Proposition 4.1

GMP formula

Let $\mathcal{D}$ be the Skorohod space of càdlàg functions on $[-L/2, L/2]$. For any measurable map $G$ from ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times \mathcal{D}\times \mathcal{D}$ into ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}_{+}$, with the original coordinates we have

$$\begin{aligned} \mathbb{E}\big[\sum _{i\ge 1} G(\lambda _{i},\varphi _{i}, \varphi '_{i}) \big] &= \int _{u=-\frac{L}{2}}^{\frac{L}{2}} \int _{\lambda \in {{ \mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}} \int _{\theta =0}^{\pi }p_{\lambda ,\frac{L}{2}+u}(\theta ) p_{\lambda ,\frac{L}{2}-u}(\pi -\theta )\sin ^{2} \theta \\ &\qquad \qquad \qquad \times \mathbb{E}^{(u)}_{\theta ,\pi -\theta} \Big[G\Big(\lambda , \frac{\hat{y}_{\lambda }}{\|\hat{y}_{\lambda }\|_{2}}, \frac{(\hat{y}_{\lambda })'}{\|\hat{y}_{\lambda }\|_{2}}\Big)\Big] \, d \theta \, d\lambda \, du\,, \end{aligned}$$

and with the distorted coordinates this becomes

$$\begin{aligned} \mathbb{E}\big[\sum _{i\ge 1} G\big(\lambda _{i}, \varphi _{i} , \varphi '_{i} \big)\big] ={}& \sqrt {E} \int _{u=-\frac{L}{2E}}^{ \frac{L}{2E}} \int _{\lambda \in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{ \textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}} \int _{\theta =0}^{ \pi }p_{\lambda ,\frac{L}{2E}+u}^{(E)}(\theta ) p_{\lambda , \frac{L}{2E}-u}^{(E)}(\pi -\theta )\sin ^{2} \theta \\ &{} \times \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[G \Big(\lambda , \frac{\hat{y}^{(E)}_{\lambda }(\cdot /E)}{\sqrt{E}\|\hat{y}_{\lambda }^{(E)}\|_{2}}, \frac{(\hat{y}^{(E)}_{\lambda })'(\cdot /E)}{E^{3/2}\|\hat{y}_{\lambda }^{(E)}\|_{2} } \Big)\Big] \, d\theta \, d\lambda \, du\;. \end{aligned}$$

To exploit this formula, one needs to analyze both the transition probabilities of the phase and the concatenation $\hat{y}^{(\mathbf{E})}_{\lambda }$ for $\lambda$ in the regime of energies under consideration. Regarding the transition probabilities, Theorem 4 allows to replace them, up to an error that vanishes as $L\to \infty$, by the equilibrium measure whose expression is explicit. On the other hand, the concatenation of the diffusions can be thoroughly studied since the SDEs at stake are tractable.

Taking $G = 1_{\Delta}(\lambda )$, we will derive a Wegner estimate, that is an estimate on the number of eigenvalues in small (microscopic) intervals: this will be an important ingredient for the convergence to a Poisson point process, see Sect. 4.4. Studying carefully the concatenation $\hat{y}^{(\mathbf{E})}_{\lambda }$, we will prove the exponential decay of the eigenfunctions and we will derive their asymptotic behavior, see the next paragraph.

4.3 Exponential decay

Until the end of Sect. 4, we are given a function $E=E(L)$ of $L$ that satisfies either

• 1. Bulk regime: $E$ is fixed with respect to $L$,

• 2. Crossover regime: $E = E(L)$ satisfies $1 \ll E \ll L$,

and all the forthcoming estimates lie in that setting.

Let us fix again $h >0$ and let $\Delta := [E-\frac{h}{Ln(E)},E+\frac{h}{Ln(E)}]$. Introduce

$$\begin{aligned} \boldsymbol{\nu _{E}} := \textstyle\begin{cases} \nu _{E} & \text{ Bulk regime}\;, \\ 1&\text{ Crossover regime}\;, \end{cases}\displaystyle \end{aligned}$$

(20)

where $\nu _{E}$ was defined in (3). As we will see in Sect. 7.2, this quantity is related to the Lyapunov exponent of our diffusions, that is, the rate of linear growth in time of $\ln r_{\lambda }^{(\mathbf{E})}(t)$.

The main technical step towards the exponential decay is the following result:

Proposition 4.2

Exponential decay of the eigenfunctions

In the Bulk and Crossover regimes, for any $\varepsilon > 0$ small enough, there exists $q_{0}(\varepsilon ) > 0$ such that for all $q\in [0,q_{0}(\varepsilon )]$

$$ {\limsup _{L\to \infty } } \mathbb{E}\bigg[\sum _{ \lambda _{i} \in \Delta} \Big(\inf _{u\in [-L/2,L/2]} G_{u}(\lambda _{i}, \varphi _{i},\varphi _{i}') \Big)^{q} \bigg] < \infty \;, $$

where

$$ G_{u}(\lambda ,\varphi ,\psi ) := \sup _{t\in [-\frac{L}{2}, \frac{L}{2}]} \Big(\varphi ^{2}(t) + \frac{\psi ^{2}(t)}{\mathbf{E}} \Big)^{1/2} \sqrt {\mathbf{E}}\, e^{\frac{1}{2}(\boldsymbol{\nu _{E}} - \varepsilon ) \frac{|t-u|}{\mathbf{E}}}\;. $$

With this result at hand, we can present the proof of the exponential decay of the eigenfunctions.

Proof of Theorem 2

Fix $\varepsilon >0$ small enough. From the last proposition, we deduce that for every eigenvalue $\lambda _{i} \in \Delta$ there exists $\tilde{U}_{i}$ (depending on $\varepsilon$) such that

$$ \Big(\varphi _{i}(t)^{2} + \frac{\varphi '_{i}(t)^{2}}{\mathbf{E}} \Big)^{1/2} \le \frac{\tilde{c_{i}}}{\sqrt {\mathbf{E}}} \exp \Big(- \frac{(\boldsymbol{\nu _{E}}-\varepsilon )}{2} \frac{|t-\tilde{U}_{i}|}{\mathbf{E}}\Big)\;,\quad \forall t\in [-L/2,L/2] \;, $$

where $\tilde{c}_{i} := \inf _{u\in [-L/2,L/2]} G_{u}(\lambda _{i},\varphi _{ \lambda _{i}},\varphi _{\lambda _{i}}')$. Recentering the exponential term at $U_{i}$, we obtain

$$ \Big(\varphi _{i}(t)^{2} + \frac{\varphi '_{i}(t)^{2}}{\mathbf{E}} \Big)^{1/2} \le \frac{{c_{i}}}{\sqrt {\mathbf{E}}} \exp \Big(- \frac{(\boldsymbol{\nu _{E}}-\varepsilon )}{2} \frac{|t- U_{i}|}{\mathbf{E}}\Big)\;,\quad \forall t\in [-L/2,L/2]\;, $$

with $c_{i} = \tilde{c}_{i} \exp \Big( \frac{(\boldsymbol{\nu _{E}}-\varepsilon )}{2} \frac{|\tilde{U}_{i}- U_{i}|}{\mathbf{E}}\Big)$. We need some control on the distance $\tilde{U}_{i} - U_{i}$ to conclude the proof. From the definition of $U_{i}$ and since $\varphi _{i}^{2}(t) dt$ is a probability measure, we have

$$ \tilde{U}_{i} - U_{i} = \int (\tilde{U}_{i} -t) \varphi _{i}^{2}(t) dt \;. $$

By Jensen’s inequality, we thus have for any $a \in (0, \boldsymbol{\nu _{E}}-\varepsilon )$

$$\begin{aligned} \exp \Big( a \frac{|\tilde{U}_{i} - U_{i}|}{\mathbf{E}} \Big) &\le \int \exp \Big(a \frac{|\tilde{U}_{i} -t|}{\mathbf{E}}\Big) \varphi _{i}^{2}(t) dt \\ &\le \frac{\tilde{c_{i}}^{2}}{\mathbf{E}} \int \exp \Big((a-( \boldsymbol{\nu _{E}}-\varepsilon )) \frac{|\tilde{U}_{i} -t|}{\mathbf{E}} \Big) dt \\ &\le 2\frac{\tilde{c_{i}}^{2}}{\boldsymbol{\nu _{E}}-\varepsilon -a} \;. \end{aligned}$$

From the bound of the proposition, we already know that

$$ {\limsup _{L\to \infty } } \mathbb{E}\Big[ \sum _{ \lambda _{i} \in \Delta} \tilde{c}_{i}^{q} \Big] < \infty \;. $$

Using the previous bound, this remains true with $c_{i}$ instead of $\tilde{c}_{i}$, up to decreasing $q$. □

The main ideas of the proof of Proposition 4.2 are simple. First of all, we apply the GMP formula to rephrase our statement on the eigenfunctions in terms of the concatenation of the forward/backward processes. Second, we establish precise moment bounds on the exponential growth of $r^{(\mathbf{E})}_{\lambda }$. Third, we transfer these estimates to the concatenation $\hat{y}^{(\mathbf{E})}_{\lambda }$. We refer to Sect. 7 for the details.

4.4 Poisson statistics

Obviously, Theorem 3 implies Theorem 1 so we concentrate on the former statement. The argument is twofold. First, we introduce an approximation $\bar{\mathcal{N}}_{L}$ of the random measure $\mathcal{N}_{L}$ that possesses more independence, and we prove that it converges to the Poisson random measure of the statement. Second we show that $\mathcal{N}_{L}-\bar{\mathcal{N}}_{L}$ goes to 0.

There are some topological difficulties arising in the spaces at stake, which will be explained in more details in the proof of Theorem 3, see below. For the time being, we view the r.v. $\mathcal{N}_{L}$ and $\bar{\mathcal{N}}_{L}$ as random Radon measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$, where $\bar{\mathcal{M}}:= \mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$, the set of probability measures on $\bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$ endowed with the topology of weak convergence, and where $\bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$ is the compactification of ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$.

Let us present the approximation scheme that leads to the definition of $\bar{\mathcal{N}}_{L}$. We subdivide the interval $(-L/2,L/2)$ into $k$ (microscopic) disjoint boxes $(t_{j-1},t_{j})$ where $t_{j} = -L/2+ j L/k$ and where $k=k(L)$ is a quantity that goes to $+\infty$ at a sufficiently small speed.⁵ We consider the Anderson Hamiltonian $\mathcal{H}^{(j)}_{L} = -\partial ^{2}_{x} + \xi$ restricted to $(t_{j-1},t_{j})$ with Dirichlet b.c., and we denote by $\lambda ^{(j)}_{i}$ its eigenvalues, $\varphi ^{(j)}_{i}$ its eigenfunctions, ${U_{i}}^{(j)}$ its centers of mass and $w_{i}^{(j)}(dt) = \mathbf{E}\varphi ^{(j)}_{i}({U_{i}}^{(j)} + \mathbf{E}\,t)^{2} dt$ the associated probability measure (after recentering at $U_{i}^{(j)}$). We then define

$$ {\mathcal{N}}_{L}^{(j)} := \sum _{i} \delta _{(L\, n(E)(\lambda _{i}^{(j)} - E), U_{i}^{(j)}/L, w_{i}^{(j)})}\;, $$

as well as

$$ \bar{\mathcal{N}}_{L} := \sum _{j=1}^{k} {\mathcal{N}}_{L}^{(j)}\;. $$

(21)

Proposition 4.3

In the Bulk and Crossover regimes, provided $k\to \infty$ slowly enough, the random measure $\mathcal{N}_{L} - \bar{\mathcal{N}}_{L}$ converges in law to the null measure as $L\to \infty$.

The proof of this proposition is presented in Sect. 9.3 and relies on two inputs: (1) the eigenfunctions of $\mathcal{H}_{L}$ and $\mathcal{H}^{(j)}_{L}$ are exponentially localized, (2) $\bar{\mathcal{N}}_{L}$ converges to a Poisson random measure. Point (1) is the content of the previous proposition (the exponential localization of the eigenfunctions of $\mathcal{H}^{(j)}_{L}$ holds for exactly the same reasons). Point (2) is proven below. Given these two inputs, the proof of Proposition 4.3 consists in building a one-to-one correspondence between the atoms of $\mathcal{N}_{L}$ and $\bar{\mathcal{N}}_{L}$, when these measures are restricted to some arbitrary set $[-h,h]\times [-1/2,1/2]\times \bar{\mathcal{M}}$, and to show that the corresponding pairs of atoms are close in the topology at stake.

Let us now explain the main steps towards the convergence of $\bar{\mathcal{N}}_{L}$ to a Poisson random measure. We fix a constant $h >0$ (independent of $L$) and define the interval of energies

$$\begin{aligned} \Delta := \Big[E-\frac{h}{Ln(E)}, E+ \frac{h}{Ln(E)}\Big]\;. \end{aligned}$$

(22)

For convenience, we set

$$ N_{L}(\Delta ) := \#\{\lambda _{i} \in \Delta \} = \int \mathbf{1}_{[-h,h]}( \lambda ) \mathcal{N}_{L}(d\lambda ,dx,dw)\;,$$

(23)

as well as

$$ N_{L}^{(j)}(\Delta ) := \#\{\lambda _{i}^{(j)} \in \Delta \} = \int \mathbf{1}_{[-h,h]}(\lambda ) \mathcal{N}_{L}^{(j)}(d\lambda ,dx,dw) \;.$$

(24)

First, we control the second moments of $N_{L}^{(j)}(\Delta )$. Note that the $N_{L}^{(j)}(\Delta )$ are i.i.d., so it suffices to consider $j=1$. (We also state a similar estimate on $N_{L}(\Delta )$ for later convenience).

Proposition 4.4

In the Bulk and Crossover regimes, provided $k\to \infty$ slowly enough, we have

$$ \limsup _{L \to \infty } \mathbb{E}[N_{L}(\Delta )^{2}] < \infty \;, \quad \limsup _{L \to \infty } k\; \mathbb{E}[N^{(1)}_{L}(\Delta )^{2}] < \infty \;. $$

Second, we show that, with large probability, every box $(t_{j-1},t_{j})$ contains at most one eigenvalue that lies in the interval of energy $\Delta$.

Proposition 4.5

Minami estimate

In the Bulk and Crossover regimes, provided $k\to \infty$ slowly enough,

$$ \lim _{L\to \infty} k\mathbb{P}(N_{L}^{(1)}(\Delta ) \ge 2) = 0\;. $$

Our proof of this two points estimate, which is usually named after Minami [26], is technically involved and appears as one of the main achievements of this paper. As mentioned in the introduction, it relies on probabilistic tools, and can be viewed as an alternative approach to the strategy of proof of Molchanov [28] (in a smoother context). The proofs of Propositions 4.4 and 4.5 are given in Sect. 8.

Remark 4.6

The arguments presented in the proof are sufficient to prove the stronger statement: there exists $C>0$ such that for all $L$ large enough

$$ \mathbb{E}\Big[N_{L}^{(1)}(\Delta ) \big( N_{L}^{(1)}(\Delta ) - 1 \big) \Big] \le C n(E)^{2} \Big(\frac{L}{k} \Big)^{2} \vert \Delta \vert ^{2}\;. $$

This is another form of the so-called Minami estimate.

Third, we identify the limit of the intensity measure of $\bar{\mathcal{N}}_{L}$. Let $\boldsymbol{\sigma _{E}}$ be the measure $\sigma _{E}$ (introduced in (5)) in the Bulk regime, and $\sigma _{\infty}$ (defined in (4)) in the Crossover regime. Note that the definition in the Bulk regime will be given in Sect. 9, while the definition in the Crossover regime was presented above Theorem 3.

Proposition 4.7

Intensity of $\bar{\mathcal{N}}_{L}$

In the Bulk and Crossover regimes, provided $k\to \infty$ slowly enough, for any compactly supported, continuous function $f:{{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \bar {\mathcal{M}}\to{{ \mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$, we have

$$\begin{aligned} \lim _{L\to \infty } \mathbb{E}\Big[ \int f d\bar{\mathcal{N}}_{L} \Big] &= \int _{{{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}\times [-\frac{1}{2},\frac{1}{2}] \times \bar {\mathcal{M}}} f\; d\lambda \otimes dx \otimes \boldsymbol{\sigma _{E}}\;. \end{aligned}$$

The proof of this proposition is presented in Sect. 9.1: it combines many different arguments and definitions introduced earlier in the article.

Proofs of Theorems 1 and 3

As already explained, it suffices to concentrate on the stronger statement given by Theorem 3. Let us now explain the topological difficulties at stake. The space $\mathcal{M}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$ is not locally compact so that the tightness of $(\mathcal{N}_{L})_{L\ge 1}$ or $(\bar{\mathcal{N}}_{L})_{L\ge 1}$ is not elementary in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \mathcal{M}({{\mathchoice{ \text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$. One option would have been to prove directly this tightness (using the exponential decay of the eigenfunctions), but we prefer a simpler point of view. Namely, we deal with $\bar{\mathcal{M}}:= \mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$, the set of probability measures on $\bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$ endowed with the topology of weak convergence, where $\bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$ is the compactification of ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$. Note that $\mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$ is compact. We then view the r.v. $\mathcal{N}_{L}$ and $\bar{\mathcal{N}}_{L}$ as random Radon measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$, so that we are in a more common setting to prove convergences. It can be checked that if the convergence of Theorem 3 holds in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$, then it also holds in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \mathcal{M}({{\mathchoice{ \text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$.

Given Proposition 4.3, we only need to show that $\bar{\mathcal{N}}_{L}$ converges to a Poisson random measure of intensity $d\lambda \otimes dx \otimes \boldsymbol{\sigma _{E}}$. By standard criteria, see for instance [19, Th 16.16], the convergence follows if we can show that for any given compactly supported, continuous function $f:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [-1/2,1/2]\times \bar{\mathcal{M}}\to {{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ we have

$$ \mathbb{E}\Big[\exp \Big(i \int f d\bar{\mathcal{N}}_{L}\Big)\Big] \to \exp \Big(\int _{{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\times [-\frac{1}{2}, \frac{1}{2}] \times \bar {\mathcal{M}}}} (e^{if} -1) d\lambda \otimes dx \otimes \boldsymbol{\sigma _{E}}\Big)\;. $$

We fix such a function and concentrate on the proof of this convergence. From the independence of the $\mathcal{N}_{L}^{(j)}$ we have

$$ \mathbb{E}\Big[\exp \Big(i \int f d\bar{\mathcal{N}}_{L}\Big)\Big] = \prod _{j=1}^{k} \mathbb{E}\Big[\exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)} \Big)\Big]\;.$$

(25)

Choose $h>0$ large enough such that $f(\lambda ,\cdot ,\cdot )= 0$ whenever $\lambda \notin [-h,h]$, and set $\Delta$ as in (22). The main observation is that on the event $\{N_{L}^{(j)}(\Delta )=1\}$, the random measure ${\mathcal{N}}_{L}^{(j)}$ has at most one atom on the support of $f$ and therefore on this event

$$ \exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)}\Big) - 1 = \int (e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\;. $$

We can therefore write

$$\begin{aligned} \exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)}\Big) ={}& \mathbf{1}_{\{N_{L}^{(j)}( \Delta ) =0\}} + \mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 1\}} \exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)}\Big) \\ ={}& 1 + \mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 1\}} \Big( \exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)}\Big) -1\Big) \\ ={}& 1 + \mathbf{1}_{\{N_{L}^{(j)}(\Delta ) = 1\}} \int (e^{i f}-1) d{ \mathcal{N}}_{L}^{(j)} \\ &{}+ \mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 2\}} \Big(\exp \Big(i \int f d{\mathcal{N}}_{L}^{(j)}\Big)-1\Big)\;. \end{aligned}$$

The third term on the r.h.s. is bounded by a constant (independent of $j$ and $L$) times $\mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 2\}}$, so that by Proposition 4.5 its expectation is negligible compared to $1/k$. We write the expectation of the second term

$$\begin{aligned} \mathbb{E}\Big[\mathbf{1}_{\{N_{L}^{(j)}(\Delta ) = 1\}} \int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\Big] ={}&\mathbb{E}\Big[\int ( e^{i f}-1) d{ \mathcal{N}}_{L}^{(j)}\Big] \\ &{}- \mathbb{E}\Big[\mathbf{1}_{\{N_{L}^{(j)}( \Delta ) \ge 2\}} \int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\Big]\;. \end{aligned}$$

Set $C:=\|e^{i f}-1\|_{\infty }< \infty$. Using Proposition 4.4 there exists $C'>0$ such that for all $L$ large enough

$$ \mathbb{E}\Big[\int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\Big] \le C \mathbb{E}\big[N_{L}^{(j)}(\Delta )\big] \le C \mathbb{E}\big[N_{L}^{(j)}( \Delta )^{2}\big] \le \frac{C'}{k}\;. $$

Moreover

$$\begin{aligned} \Big| \mathbb{E}\Big[\mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 2\}} \int (e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\Big] \Big| &\le C \, \mathbb{E}[\mathbf{1}_{\{N_{L}^{(j)}(\Delta ) \ge 2\}} N_{L}^{(j)}( \Delta )] \\ &\le C\, \mathbb{P}(N_{L}^{(j)}(\Delta ) \ge 2)^{1/2}\, \mathbb{E}[N_{L}^{(j)}( \Delta )^{2}]^{1/2}\;. \end{aligned}$$

By Propositions 4.4 and 4.5, this last term is negligible compared to $1/k$, uniformly over all $j$ and $L$ large enough. Putting everything together, we obtain

$$\begin{aligned} \ln \mathbb{E}\Big[\exp (i \int f d{\mathcal{N}}_{L}^{(j)})\Big] &= \ln \Big(1 + \mathbb{E}\Big[\int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)} \Big] +o(1/k)\Big) \\ &= \mathbb{E}\Big[\int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)}\Big] +o(1/k) \end{aligned}$$

uniformly over all $j$ and all $L$ large enough. Plugging this identity into (25), we get

$$ \begin{aligned}\ln \mathbb{E}\Big[\exp \Big(i \int f d\bar{\mathcal{N}}_{L}\Big) \Big] &= \sum _{j} \mathbb{E}\Big[\int ( e^{i f}-1) d{\mathcal{N}}_{L}^{(j)} \Big] + o(1) \\ &= \mathbb{E}\Big[\int ( e^{i f}-1) d\bar{\mathcal{N}}_{L} \Big] + o(1)\;, \end{aligned}$$

which converges to the desired limit by Proposition 4.7 (note that $e^{i f}-1$ is compactly supported, since $f(\lambda ,\cdot ,\cdot )=0$ whenever $\lambda \notin [-h,h]$). □

The remaining sections are organized as follows. In Sect. 5, we prove the convergence to equilibrium stated in Theorem 4. In Sect. 6, we establish the GMP formula of Proposition 4.1 and collect some corollaries. In Sect. 7 we prove Proposition 4.2 on the exponential decay of the eigenfunctions. In Sect. 8 we establish the estimates on $N_{L}^{(j)}(\Delta )$ stated in Propositions 4.4 and 4.5. These four sections can be read independently of each other.

On the other hand, Sect. 9, where the proofs of Proposition 4.3 and 4.7 are presented, relies extensively on definitions and intermediate results collected in Sect. 7.

In order not to interrupt the flow of arguments, we have postponed to Appendix A some technical (but elementary) results used along the article.

5 Convergence to equilibrium

The goal of this section is to prove Theorem 4. This result is delicate for three reasons. First we stated $L^{\infty}$ bounds on the density thus requiring much finer control than the more usual total-variation bounds. Second, the (generator of the) diffusion that we are considering is not uniformly elliptic, but simply hypoelliptic, thus making both regularization and convergence estimates delicate. Third for $E\to \infty$, the drift term of the diffusion $\theta _{\lambda }^{(E)}$ is unbounded and makes the process rotate very fast on the circle: it is then a priori unclear whether one can obtain bounds on the density that are uniform over $E>1$.

The proof consists of two distinct steps. First, we show quantitative regularization estimates on the density of the diffusion. The existence and the smoothness of the density at any time $t>0$ is due to the hypoellipticity of the associated generator and follows from Hörmander’s Theorem [16]. However this result does not provide any quantitative estimate on this density: this is problematic in particular in the case where $E\to \infty$. We establish a quantitative estimate using Malliavin calculus (which was originally introduced to give a probabilistic proof of Hörmander’s Theorem).

Second, we show exponential convergence to equilibrium in $H^{1}$: by Sobolev embedding, this readily implies exponential convergence in $L^{\infty}$. From the first step, we know that at a time of order 1, the $H^{1}$-norm of the density is itself of order 1. To establish an exponential convergence to equilibrium, one would use coercivity in $H^{1}$ of the (adjoint in $L^{2}(\mu _{\lambda }^{(\mathbf{E})})$ of the) generator of the diffusion: however the lack of ellipticity prevents one from getting this coercivity. We thus rely on hypocoercivity techniques following Villani’s monograph [35]: we identify a “twisted” $H^{1}$-norm, equivalent to the original one, in which the (adjoint in $L^{2}(\mu _{\lambda }^{(\mathbf{E})})$ of the) generator of the diffusion is coercive. In particular, when working with distorted coordinates, we obtain a control on the coercivity constant which is uniform over $E > 1$.

From now on, all the functions are defined on the circle ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}/\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{ \text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}$ and take values in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$. We will denote by $\mathcal{C}^{k}$ the space of $k$-times continuously differentiable functions on the circle. Furthermore “uniformly over all parameters” will mean uniformly over all $\lambda \in \Delta$ when working with the original coordinates and uniformly over all $E >1$ and $\lambda \in \Delta$ with the distorted coordinates.

Remark 5.1

Let us mention that the result of Theorem 4 controls the exponential decay in $L^{\infty}$ while a control in $L^{2}$ would have sufficed for our purpose, however the proof would have been only marginally simpler if we had worked in $L^{2}$ instead of $L^{\infty}$.

5.1 Hypoellipticity - regularization step

We apply Malliavin calculus to the diffusion $\theta _{\lambda }^{(\mathbf{E})}$ following Norris [32] and Hairer [17]. We drop the superscript $(\mathbf{E})$ but we argue simultaneously in both sets of coordinates. We also drop the subscript $\lambda$. We let $\mathbb{P}_{\theta _{0}}$ denote the law of the diffusion starting from $\theta _{0}$ at time 0 and $p_{t}(\theta _{0},\cdot )$ the density of this diffusion. The goal of this step is to show the following estimate: for any $k\ge 1$, there exists $C_{k}>0$ such that uniformly over all parameters

$$ \sup _{\theta _{0}}\|p_{1}(\theta _{0},\cdot )\|_{\mathcal{C}^{k}} < C_{k} \;. $$

(26)

We write

$$ d\theta (t) = V_{0}(\theta (t)) dt + V_{1}(\theta (t))dB(t)\;, $$

with

$$ V_{0}(x) = \mathbf{E}^{3/2} + \sqrt{\mathbf{E}} (\lambda -\mathbf{E}) \sin ^{2} x + \sin ^{3} x \cos x\;,\quad V_{1}(x) = -\sin ^{2} x\;. $$

Remark 5.2

The diffusion is not elliptic since $V_{1}$ vanishes at $x=0$. However, it satisfies the so-called Hörmander’s Bracket Condition which can be stated as follows. Let us associate to any function $F$ an operator defined through $Ff(x) := F(x) f'(x)$. Introduce the Lie bracket $[A,B] := AB - BA$ for any two operators $A$, $B$. The condition then reads: there exists $k\ge 0$ (here $k=2$ works) such that

$$ \inf _{x\in [0,\pi )} \max _{F\in \mathscr{V}_{k}} |F|(x) > 0\;, $$

where $\mathscr{V}_{0} := \{V_{1}\}$ and $\mathscr{V}_{n+1} := \{[F,\tilde{V}_{0}], [F,V_{1}]: F\in \mathscr{V}_{n}\} \cup {\mathscr{V}_{n}}$ where $\tilde{V}_{0} = V_{0} + (1/2) V'_{1} V_{1}$.

We rely on the process $J_{0,t}$ which is the derivative of the flow associated to the SDE satisfied by $\theta$:

$$ dJ_{0,t} = \partial _{x} V_{0}(\theta (t)) J_{0,t} dt + \partial _{x} V_{1}( \theta (t)) J_{0,t} dB(t)\;,\quad J_{0,0} = 1\;. $$

We will also need the inverse $J_{0,t}^{-1}$ that satisfies

$$ dJ_{0,t}^{-1} = -\Big( \partial _{x} V_{0}(\theta (t)) - (\partial _{x} V_{1}(\theta (t))^{2} \Big)J_{0,t}^{-1} dt - \partial _{x} V_{1}( \theta (t)) J_{0,t}^{-1} dB(t)\;,\quad J_{0,0}^{-1} = 1\;. $$

We also set $J_{s,t} := J_{0,t} J_{0,s}^{-1}$.

Lemma 5.3

Fix $t > 0$. For every $p\ge 1$, there exists $c_{p} > 0$ such that uniformly over all parameters

$$ \sup _{\theta _{0}}\mathbb{E}_{\theta _{0}}\Big[\sup _{s\in [0,{ t}]} |J_{0,s}|^{p}\vee |J_{0,s}|^{-p}\Big]^{1/p} < c_{p} \;. $$

Proof

The proof is virtually the same for $J$ and $J^{-1}$. If we let $U$ be the logarithm of either of these processes, then it solves

$$ dU(t) = \alpha (t) dt + \beta (t) dB(t)\;, $$

where $\alpha$ and $\beta$ are adapted processes. The crucial observation is that $|\alpha (t)|$ and $|\beta (t)|$ are bounded by some deterministic constant $C>0$ uniformly over all parameters: indeed, the unbounded term $E^{3/2}$ that appears in $V_{0}$ (when working with the distorted coordinates) is “killed” upon differentiation. Lemma A.2 then suffices to conclude. □

Define the so-called Malliavin covariance matrix (which is a scalar here since our diffusion is one-dimensional):

$$ \mathscr{C}_{t} := \int _{0}^{t} J_{0,s}^{-2} V_{1}^{2}(\theta (s)) ds \;,\quad t\ge 0\;. $$

The following is a standard result of Malliavin calculus: the only specificity is that our estimates are uniform over all parameters (in particular, w.r.t. $E>1$ in the distorted coordinates) and this requires some extra care in the proof.

Proposition 5.4

Fix $t>0$. Assume that for every $p\ge 1$ there exists $K_{p}>0$ such that $\sup _{\theta _{0}}\mathbb{E}_{\theta _{0}}[\mathscr{C}_{t}^{-p}] < K_{p}$. Then for every $k\ge 1$ there exists $c_{k} > 0$ such that uniformly over all parameters

$$ \sup _{\theta _{0}}\|p_{t}(\theta _{0},\cdot )\|_{\mathcal{C}^{k}} < c_{k} \;. $$

Proof

Assume that for every $k\ge 1$ there exists $C_{k} > 0$ such that for all $\mathcal{C}^{\infty }$ function $G$ there exists a r.v. $Z_{k}$ such that

$$ \mathbb{E}_{\theta _{0}}[\partial ^{k} G(\theta (t))] = \mathbb{E}_{ \theta _{0}}[G(\theta (t)) Z_{k}]\;, $$

(27)

and such that uniformly over all parameters

$$ \sup _{\theta _{0}}\mathbb{E}_{\theta _{0}}[|Z_{k}|] \le C_{k} \;. $$

(28)

Then, we deduce that for all $\mathcal{C}^{\infty }$ function $G$ uniformly over all parameters

$$ \sup _{\theta _{0}}\mathbb{E}_{\theta _{0}}[\partial ^{k} G(\theta (t))] \le C_{k} \|G\|_{\infty }\;, $$

so that standard functional analysis arguments, see for instance [32, Th. 0.1], ensure that the bound of the statement holds.

To establish (27) and (28) we rely on the notion of Malliavin derivative that we do not recall, see for instance [17, Sect. 3 and 5]. Let $Y$ be a Malliavin differentiable r.v. and denote by $\mathscr{D}_{s} Y$ the Malliavin derivative at time $s$ of $Y$. We recall the following properties of the Malliavin derivative [17, Sect. 3]:

$$ \mathscr{D}_{s} f(X) = f'(X) \mathscr{D}_{s} X\;,\quad \mathscr{D}_{s} (XY) = X \mathscr{D}_{s} Y + Y \mathscr{D}_{s} X\;. $$

(29)

The key tool in Malliavin Calculus is the so-called integration by parts formula which writes

$$ \mathbb{E}_{\theta _{0}}\big[\langle \mathscr{D}_{\cdot }Q, u(\cdot ) \rangle _{L^{2}([0,t])}\big] = \mathbb{E}_{\theta _{0}}\Big[Q \int _{0}^{t} u(s) dB(s)\Big]\;, $$

for any (regular enough) adapted process $u$. In the sequel all derivatives will be taken in direction $u$ where $u(s) := J_{0,s}^{-1} V_{1}(\theta (s))$, $s\in [0,t]$. For convenience, we use the notation $\mathscr{D}_{u} Q := \langle \mathscr{D}_{\cdot }Q , u(\cdot ) \rangle _{L^{2}([0,t])}$. We also introduce the successive derivatives in direction $u$ by setting recursively $\mathscr{D}^{(k)}_{u} Q := \mathscr{D}_{u} (\mathscr{D}^{(k-1)}_{u} Q)$.

Let us state a general result on the Malliavin derivative of the solution of an SDE. Assume that $X = (X_{j})_{1\le j \le d} \in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}^{d}$ solves the autonomous SDE

$$ dX(s) = A(X(s)) dt + C(X(s)) dB(s)\;, $$

(30)

where $A$ and $C$ are smooth maps from ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}^{d}$ to ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}^{d}$. Then the $d$-dimensional process $Y =(Y_{j})_{1\le j \le d}$ whose $j$-th coordinate is $Y_{j}(s) := \langle \mathscr{D}_{\cdot }X_{j}(s), u(\cdot ) \rangle _{L^{2}([0,s])}$ solves

$$ d Y(s) = \nabla A(X(s)) Y(s) ds + \nabla C(X(s)) Y(s) dB(s) + C(X(s))u(s) ds\;,\quad Y(0) = 0\;. $$

In this last equation, $\nabla A(x)$ is the $d\times d$ matrix whose $(i,j)$-entry equals $\partial _{x_{j}} A_{i}(x)$, and similarly for $\nabla C(x)$. This result can be established as follows. First of all if $J^{X}(r,s)$ stands for the $d\times d$ Jacobian matrix associated to the SDE $X$ then for any $0\le r \le s$

$$ dJ^{X}(r,s) = \nabla A(X(s)) J^{X}(r,s) ds + \nabla C(X(s)) J^{X}(r,s) dB(s) \;,\quad J^{X}(r,r) = I\;, $$

see for instance [17, Eq. (5.2)]. By [17, Eq. (5.6)], $\mathscr{D}_{r} X_{j}(s) = \Big (J^{X}(r,s) C(X(r)) \Big )_{j}$ and consequently the following identity holds in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}^{d}$

$$ Y(s) = \int _{0}^{s} J^{X}(r,s) C(X(r)) u(r) dr\;, $$

from which we derive the above SDE.

In the particular case where $X=\theta$, we find

$$ \mathscr{D}_{s} \theta (t) = J_{s,t} V_{1}(\theta (s)) = J_{0,t} u(s) \;. $$

We observe that

$$ \mathscr{D}_{u} \theta (t) = \langle \mathscr{D}_{\cdot }\theta (t), u( \cdot )\rangle _{L^{2}([0,t])} = J_{0,t} \langle u, u\rangle _{L^{2}([0,t])} = J_{0,t} \mathscr{C}_{t} =:\mathscr{N}_{t}\;. $$

Combined with the chain rule (29), we deduce that for any integer $k\ge 1$,

$$ \mathscr{D}_{u} \mathscr{N}_{t}^{-k} = -k \mathscr{N}_{t}^{-(k+1)} \mathscr{D}_{u} \mathscr{N}_{t} = -k \mathscr{N}_{t}^{-(k+1)} \mathscr{D}_{u}^{(2)} \theta (t)\;. $$

Let us set $R(t) := \int _{0}^{t} u(s) dB(s)$. For every smooth function $G$ and any Malliavin differentiable r.v. $Z$, we apply the integration by parts formula to $Q=G(\theta (t)) \mathscr{N}_{t}^{-1} Z$ and get

$$ \mathbb{E}_{\theta _{0}}[G'(\theta (t)) Z] = \mathbb{E}_{\theta _{0}}[G( \theta (t)) \tilde{Z}]\;, $$

where $\tilde{Z}$ is given by

$$ \tilde{Z} := \mathscr{N}_{t}^{-1} \Big(Z R(t) - \mathscr{D}_{u} Z \Big) + Z \mathscr{N}_{t}^{-2} \mathscr{D}_{u}^{(2)} \theta (t)\;. $$

Starting with $Z_{0} = 1$ and applying iteratively this identity we obtain for some r.v. $Z_{k}$

$$ \mathbb{E}_{\theta _{0}}[\partial ^{k} G(\theta (t))] = \mathbb{E}_{ \theta _{0}}[G(\theta (t)) Z_{k}]\;, $$

thus proving (27). It remains to establish the bound (28).

First, observe that $Z_{k}$ is a polynomial in $\mathscr{N}_{t}^{-1}$, in $\mathscr{D}_{u} \theta (t)$, $\mathscr{D}_{u}^{(2)} \theta (t)$, … and in $R(t)$, $\mathscr{D}_{u} R(t)$, $\mathscr{D}_{u}^{(2)} R(t)$, …. Indeed, the class of all such polynomials contains $Z_{0}$, is stable under the action of $\mathscr{D}_{u}$, and thus, remains stable under the map that leads from $Z$ to $\tilde{Z}$.

The assumption of the statement together with Lemma 5.3 allow to bound the moments of $\mathscr{N}_{t}^{-1}$ uniformly over all parameters. In addition, the Burkholder-Davis-Gundy inequality combined with Lemma 5.3 allows to bound the moments of $R(t)$ uniformly over all parameters. We are left with bounding the moments of $\mathscr{D}_{u} \theta (t)$, $\mathscr{D}_{u}^{(2)} \theta (t)$, … and $\mathscr{D}_{u} R(t)$, $\mathscr{D}_{u}^{(2)} R(t)$, ….

Consider the triplet $X^{(0)}(s) = (\theta (s), J_{0,s}^{-1}, R(s)) \in{{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}^{3}$. This is the solution of an autonomous SDE of the form (30) with⁶

$$ \begin{aligned}A^{(0)}(x) &= (V_{0}(x_{1}),x_{2} (V_{1}'(x_{1})^{2} - V_{0}'(x_{1})),0) \;,\\ C^{(0)}(x) &= (V_{1}(x_{1}),-x_{2}V_{1}'(x_{1}),x_{2}V_{1}(x_{1})) \;. \end{aligned}$$

We can thus apply the general result stated above and let $Y^{(0)} \in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}^{3}$ be the process of the Malliavin derivative of $X^{(0)}$ in direction $u$. Note that the only problematic term is the first component of $A^{(0)}$ which contains the factor $\mathbf{E}^{3/2}$. However, the function $C^{(0)}$, together with the functions $\nabla A^{(0)}(x)$ and $\nabla C^{(0)}(x)$ that appear in the evolution equation of $Y^{(0)}$, are bounded uniformly over all parameters. This remains true for any higher order derivatives of these functions and this will suffice for our purpose.

We then consider the process $X^{(1)} := (X^{(0)}, Y^{(0)}) \in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}^{6}$. It is straightforward that $X^{(1)}$ solves an autonomous SDE of the form (30). We can thus iterate the arguments and build recursively some processes $X^{(n)}$ and $Y^{(n)}$. The functions $\nabla A^{(n)}(x)$ and $\nabla C^{(n)}(x)$ that appear in the evolution equation of $Y^{(n)}$ are bounded uniformly over all parameters.

Since the r.v. $\mathscr{D}_{u} \theta (t)$, $\mathscr{D}_{u}^{(2)} \theta (t)$, … and $\mathscr{D}_{u} R(t)$, $\mathscr{D}_{u}^{(2)} R(t)$, … eventually appear in the entries of the sequence $Y^{(n)}$, $n\ge 0$, it suffices to bound the moments of $\vert Y^{(n)}(t)\vert$ for any given $n\ge 0$.

We write $Y$ for a generic element among the sequence $Y^{(n)}$, $n\ge 0$. Recall that it solves

$$ d Y(s) = \nabla A(X(s)) Y(s) ds + \nabla C(X(s)) Y(s) dB(s) + C(X(s)) u(s) ds\;, $$

where $C(x)$, $\nabla A(x)$, $\nabla C(x)$ are bounded uniformly over all parameters. Applying Itô’s formula, one can check that the process $U(s) := \ln (1+\vert Y(s)\vert ^{2})$ satisfies

$$ U(t) = \int _{0}^{t} \sum _{j=1}^{d} \frac{2 Y_{j}(s) C_{j}(X(s))}{1+\vert Y(s)\vert ^{2}} u(s) ds + \int _{0}^{t} \alpha (s) ds + \int _{0}^{t}\beta (s) dB(s)\;, $$

where $\vert \alpha (s)\vert$ and $\vert \beta (s)\vert$ are adapted processes that are bounded by some deterministic constant $K>0$ uniformly over all parameters and all $s\ge 0$. Lemma A.2 allows to obtain bounds on the $p$-th moments of $\int _{0}^{t} \alpha (s) ds + \int _{0}^{t}\beta (s) dB(s)$. In addition, the moments of the first term on the r.h.s. can be bounded since there exists some deterministic constant $K'>0$ such that

$$ \vert \sum _{j=1}^{d} \frac{2 Y_{j}(s) C_{j}(X(s))}{1+\vert Y(s)\vert ^{2}} u(s) \vert \le K' \vert J_{0,s}^{-1} V_{1}(\theta (s))\vert \;. $$

 □

It remains to check the assumption of Proposition 5.4 at time $t=1$ (this is arbitrary). In the classical proof of Hörmander’s Theorem with Malliavin Calculus, this is where one uses the so-called Hörmander’s Bracket Condition (see Remark 5.2) via repeated applications of Itô’s formula involving the process $\mathscr{C}_{t}$, see for instance [17, Proof of Theorem 6.3]. This would work with the original coordinates, but with the distorted coordinates this does not seem to work out (easily). We proceed differently and write

$$\begin{aligned} \mathbb{E}_{\theta _{0}}[\mathscr{C}_{1}^{-p}] &= \mathbb{E}_{\theta _{0}} \Big[\Big(\int _{0}^{1} J_{0,s}^{-2} V_{1}(\theta (s))^{2} ds\Big)^{-p} \Big] \\ &\le \mathbb{E}_{\theta _{0}}\Big[\Big(\int _{0}^{1} V_{1}(\theta (s))^{2} ds\Big)^{-2p}\Big]^{1/2}\mathbb{E}_{\theta _{0}}\Big[\sup _{t\in [0,1]} J_{0,t}^{4p}\Big]^{1/2}\,. \end{aligned}$$

Lemma 5.3 allows to bound the second term. To bound the first term, we need some control on the time spent near $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ by the diffusion $\theta$: this is provided by Lemma A.6, that relies on a comparison of $\theta$ with the solution of the deterministic part of its SDE. This completes the proof of (26).

5.2 Hypocoercivity - convergence step

In this subsection, we argue simultaneously in the two sets of coordinates. We abbreviate $\mu _{\lambda }$ and $\mu _{\lambda }^{(E)}$ to $\mu$. All the $L^{p}$ spaces will be taken w.r.t. the measure $\mu$ (and not the Lebesgue measure). We write $\|\cdot \|$ and $\langle \cdot ,\cdot \rangle$ for the $L^{2}$ norm and inner product w.r.t. $\mu$.

By Lemma 3.1, uniformly over all parameters the measure $\mu$ is equivalent to Lebesgue measure. This implies that the corresponding $L^{p}$ norms are equivalent. In addition, we have the following Poincaré inequality

$$ \Big\| f - \int f d\mu \Big\| ^{2} \lesssim \|f'\|^{2}\;,$$

(31)

uniformly over all parameters. Indeed,

$$\begin{aligned} \Big\| f - \int f d\mu \Big\| ^{2} = \frac{1}{2} \iint (f(x)-f(y))^{2} \mu (dx) \mu (dy)\;, \end{aligned}$$

and

$$\begin{aligned} (f(x)-f(y))^{2} &= \Big(\int _{[x,y]} f'(u) du \Big)^{2} \\ &\le \int _{[x,y]} (|x-y| f'(u))^{2} \frac{du}{|x-y|} \le |x-y| \int _{0}^{\pi } \big\vert f'(u) \big\vert ^{2} du\;, \end{aligned}$$

so that

$$ \Big\| f - \int f d\mu \Big\| ^{2} \le \frac{1}{2} \iiint _{0}^{\pi }|x-y| \mu (dx) \mu (dy) \, \big\vert f'(u) \big\vert ^{2} du \le \frac{\pi }{2} \|f'\|^{2} \;. $$

For some constant $c>0$ (to be adjusted later on) we define the following $H^{1}$ norm (w.r.t. $\mu$)

$$ \| f\|_{H^{1}}^{2} := \|f\|^{2} + c \|f'\|^{2}\;. $$

Let ℒ be the generator of our diffusion

$$ \mathcal{L}f = \sigma ^{2} f'' + b f'\;, $$

where

$$ \begin{aligned}\sigma &= \frac{\sin ^{2} x}{\sqrt {2}}\;, \\ b &= \mathbf{E}^{3/2} + \sqrt {\mathbf{E}}(\lambda -\mathbf{E}) \sin ^{2} x + \sin ^{3} x \cos x {= \mathbf{E}^{3/2} + \sqrt{2} \sqrt {\mathbf{E}}( \lambda -\mathbf{E}) \sigma + \sigma \sigma '}\;. \end{aligned}$$

Let $\mathcal{L}^{*}$ be its adjoint in $L^{2}$. The unique decomposition of $-\mathcal{L}^{*}$ into a symmetric (actually self-adjoint) and an anti-symmetric part is given by $-\mathcal{L}^{*}= A^{*}A + B$ where

$$ A f = \sigma f'\;,\quad Bf = {\tilde{b} f'\;,\quad \tilde{b} := b - 2\sigma \sigma ' - \sigma ^{2} \frac{\mu '}{\mu }}\;, $$

and $A^{*}$ is the adjoint in $L^{2}$ of $A$

$$ A^{*} f = - \frac{(\sigma \mu f)'}{\mu}\;. $$

It is a standard fact that the centered density $q_{t} = (p_{t} / \mu - 1)$ w.r.t. the invariant measure of a diffusion satisfies the PDE

$$ \partial _{t} q_{t} = \mathcal{L}^{*}q_{t}\;. $$

In the previous section we dealt with regularity issues and showed that $p_{1}$ (and therefore $q_{1}$ since $\mu$ is bounded from above and below) is smooth: more precisely, its $\mathcal{C}^{1}$-norm is bounded uniformly over all parameters. Our goal is to prove an exponential decay of the $L^{\infty}$ norm of $p_{t}$. By Sobolev embedding it suffices to prove an exponential decay in $H^{1}$.

The natural route to such an estimate is to prove some coercivity: unfortunately this fails. Indeed, we have

$$ \langle f, \mathcal{L}^{*}f\rangle = - \| A f\|^{2}\;, $$

and since $\sigma$ vanishes at 0, $\| Af\|$ is not equivalent to $\| f'\|$ and so we cannot use Poincaré inequality to get a bound in terms of $\|f\|$. Actually it is possible to check that the operator $A^{*}A$ does not have spectral gap so that one cannot get exponential decay of the $L^{2}$-norm of $q_{t}$ from the previous computation. In $H^{1}$ the situation is similar. Generally speaking, if we work with “standard” norms then we do not have enough control on the derivative(s) of the function at stake near 0.

These computations do not take advantage of the anti-symmetric part $B$ of $\mathcal{L}^{*}$. The general idea of hypocoercivity [35] consists in exploiting the successive Lie brackets between $A$ and $B$ to recover some coercivity. One can check that $[A,B] f := AB f-BA f$ contains the term $-\mathbf{E}^{3/2} \sigma ' f'$ and $[[A,B],B] f$ contains the term $\mathbf{E}^{3} \sigma '' f'$: since $\sigma ''$ does not vanish anymore at $x=0$, these terms should offer the required control on the derivative at 0. To implement this idea, one constructs a twisted $H^{1}$-norm, denoted $\mathfrak{H}^{1}$, that contains some successive Lie brackets of $A$ and $B$, see below for the precise expression, and that satisfies the following properties.

Proposition 5.5

There exists a norm $\|\cdot \|_{\mathfrak{H}^{1}}$, derived from an inner product $\langle \cdot ,\cdot \rangle _{\mathfrak{H}^{1}}$ such that:

• (1) There exists $\kappa >0$ such that uniformly over all parameters we have

  $$ \|f\|_{H^{1}} \le \| f \|_{\mathfrak{H}^{1}} \le (1+\kappa ) \|f\|_{H^{1}} \;. $$

• (2) There exists $K>0$ such that uniformly over all parameters we have

  $$ \langle f, \mathcal{L}^{*}f\rangle _{\mathfrak{H}^{1}} \le -K \|f'\|^{2} \;. $$

With this proposition at hand, we can easily conclude the proof of the main result of this section.

Proof of Theorem 4

In the previous subsection, we showed that there exists $C_{1} > 0$ such that uniformly over all parameters

$$ \sup _{\theta _{0}}\|p_{1}(\theta _{0},\cdot )\|_{\mathcal{C}^{1}} < C_{1} \;. $$

(32)

Set $q_{t} := \frac{p_{t}}{\mu} - 1$ and recall that $\partial _{t} q_{t} = \mathcal{L}^{*}q_{t}$. The second property of the proposition then yields

$$ \partial _{t} \|q_{t}\|_{\mathfrak{H}^{1}}^{2} \le - 2K \|q_{t}'\|^{2} \;. $$

Since $\int q_{t} d\mu = 0$, Poincaré inequality (31) together with the first property of the proposition show that for some constant $K'>0$

$$ \partial _{t} \|q_{t}\|_{\mathfrak{H}^{1}}^{2} \le - K' \|q_{t}\|^{2}_{ \mathfrak{H}^{1}}\;. $$

Applying the first property again, we deduce that uniformly over all the parameters, for all $t \geq 1$,

$$ \|q_{t}\|_{H^{1}} \le c'\|q_{1}\|_{H^{1}} e^{-C'(t-1)}\;, $$

for some constants $c',C'>0$. Combining this bound with (32), applying the Sobolev embedding $H^{1}(dx) \subset L^{\infty}(dx)$ and the fact that $\mu$ is equivalent to the Lebesgue measure, we obtain the desired result. □

The rest of this subsection is devoted to the proof of Proposition 5.5. We start by introducing successive Lie brackets: actually we identify within the successive Lie brackets between $A$ and $B$ the terms $\mathbf{E}^{3/2} C_{k}$ that will allow us to gain coercivity and we denote the remainder $R_{k}$. Introduce $C_{0} f := A f$, and recursively for $k=1,2$

$$ C_{k} f := (-1)^{k} \sigma ^{(k)} f'\;,\quad R_{k} f:= [C_{k-1}, B] f - \mathbf{E}^{3/2} C_{k} f\;, $$

and finally

$$ C_{3} f := 0\;,\quad R_{3} f := [C_{2},B] f\;. $$

We now introduce a family of coefficients indexed by $\delta \in (0,1/4)$. Set $b_{-1} := \delta$ and for every $k\ge 0$

$$ a_{k} := \delta ^{6-2k} b_{k-1}\;,\quad b_{k} := \delta ^{5-2k}a_{k} \;. $$

One can check that for all $0\le k \le 2$

$$ b_{k} \le \delta a_{k}\;,\quad a_{k} \le \delta b_{k-1}\;,\quad a_{k}^{2} = {\delta b_{k-1} b_{k}}\;,\quad b_{k}^{2} = {\delta a_{k} a_{k+1}}\;. $$

(33)

We then introduce

$$ \| f \|_{\mathfrak{H}^{1}}^{2} :=\|f\|_{H^{1}}^{2} + \frac{1}{\mathbf{E}^{3/2}}\sum _{k=0}^{2} \Big( a_{k}\|C_{k} f\|^{2} + 2b_{k} \langle C_{k} f, C_{k+1} f\rangle \Big)\;, $$

as well as $\langle f,g \rangle _{\mathfrak{H}^{1}} = \langle f,g \rangle _{{H}^{1}} + \left [\mkern - 3 mu\left [f,g\right ]\mkern - 3 mu\right ]$ where

$$ \left [\mkern - 3 mu\left [f,g\right ]\mkern - 3 mu\right ] := \frac{1}{\mathbf{E}^{3/2}}\sum _{k=0}^{2} \Big( a_{k} \langle C_{k} f, C_{k} g\rangle + b_{k} (\langle C_{k} f, C_{k+1} g\rangle + \langle C_{k} g, C_{k+1} f \rangle ) \Big)\;. $$

This norm depends on two parameters, $c$ and $\delta$, that will be adjusted later on.

As $b_{k}^{2} = \delta a_{k} a_{k+1}$, we have

$$ \Big|2b_{k} \langle C_{k} f, C_{k+1} f\rangle \Big| \le { \sqrt{\delta }} a_{k} \|C_{k} f\|^{2} + {\sqrt{\delta }} a_{k+1} \|C_{k+1} f\|^{2}\;. $$

Note that for every $k\in \{0,1,2,3\}$, we have $\|C_{k} f\| \le 2\|f'\|$. Since $\mathbf{E}\ge 1$, we easily deduce that $0 \le \left [\mkern - 3 mu\left [f,f\right ]\mkern - 3 mu\right ] \le \kappa \|f'\|$ for some constant $\kappa >0$ independent of all parameters, and the first property of Proposition 5.5 follows.

The proof of the second property is carried out in two steps. First, we show that there exists a constant $C>0$ such that uniformly over all parameters,

$$ \langle f',(\mathcal{L}^{*}f)'\rangle \le C \| f'\|^{2}\;. $$

(34)

Second we show that there exists $\delta \in (0,1/4)$ and $K'>0$ such that uniformly over all parameters

$$ \langle f,\mathcal{L}^{*}f\rangle + \left [\mkern - 3 mu\left [f, \mathcal{L}^{*}f\right ]\mkern - 3 mu\right ] \le -K' \| f'\|^{2}\;. $$

(35)

With these two bounds at hand, we get

$$ \langle f, \mathcal{L}^{*}f\rangle _{\mathfrak{H}^{1}} {= \langle f,\mathcal{L}^{*}f\rangle + c \langle f',(\mathcal{L}^{*}f)' \rangle + \left [\mkern - 3 mu\left [f,\mathcal{L}^{*}f\right ] \mkern - 3 mu\right ]}\le (c\,C - K') \|f'\|^{2} \;. $$

It suffices to set $c:= K' (2C)^{-1}$ and $K=K'/2$ in order to deduce the second property of the proposition.

Remark 5.6

Our proof is close to [35, Proof of Theorem 24] and would be essentially the same if we had taken $c=0$, that is, if we had taken $\|f\|_{2}^{2}$ instead of $\|f\|_{H^{1}}^{2}$ in the definition of the $\mathfrak{H}_{1}$ norm. Actually, with the original coordinates, the proof would carry through with $c=0$. With the distorted coordinates however, the first property of Proposition 5.5 would fail with $c=0$.

We proceed with the proof of (34). For convenience, we define the operator $Df=f'$. We then have

$$ \langle f',(\mathcal{L}^{*}f)'\rangle = -\langle Df, DA^{*}A f \rangle - \langle Df, DBf\rangle \;. $$

Since $B$ is anti-symmetric we find $\langle Df, DBf\rangle = \langle Df, [D,B] f\rangle$. Note that $[D,B] f = (b - 2\sigma \sigma ' - \sigma ^{2} \frac{\mu '}{\mu})' f'$. The key point here is that the only unbounded factor ($\mathbf{E}^{3/2}$ which appears in $b$) is killed upon differentiation. A simple computation shows that there exists $C_{1}$ such that

$$ \big|\langle Df, [D,B] f\rangle \big| \le C_{1} \| {Df} \|^{2}\;. $$

(36)

On the other hand, we have

$$\begin{aligned} \langle Df, DA^{*}A f \rangle &= -\langle D^{2} f, A^{*}A f \rangle - \langle Df, \frac{\mu '}{\mu} A^{*}A f\rangle \\ &= \langle \sigma D^{2} f, \sigma D^{2} f\rangle + \langle D^{2} f, \frac{(\sigma ^{2} \mu )'}{\mu} Df\rangle - \langle Df, \frac{\mu '}{\mu} A^{*}A f\rangle \;. \end{aligned}$$

Recall the bounds on $\mu$ stated in Lemma 3.1. Recall that Young’s inequality yields $XY \le \varepsilon X^{2} + \frac{1}{4 \varepsilon } Y^{2}$ for all $\varepsilon >0$. There exists $C_{2}>0$ such that

$$ \big|\langle D^{2} f, \frac{(\sigma ^{2} \mu )'}{\mu} Df\rangle \big| \le C_{2} \| \sigma D^{2} f\| \| Df\| {\le C_{2} \Big( \frac{1}{4C_{2}}\| \sigma D^{2} f\|^{2} + C_{2}\| Df\|^{2} \Big)}\;, $$

and

$$\begin{aligned} \big|\langle Df, \frac{\mu '}{\mu} A^{*}A f\rangle \big| &\le C_{2} ( \|\sigma Df \| \|\sigma D^{2}f\| + \| Df\|^{2}) \\ &\le C_{2} \Big( \frac{1}{4C_{2}} \| \sigma D^{2} f\|^{2} + (C_{2}+1)\| Df\|^{2} \Big) . \end{aligned}$$

We deduce that there exists $C_{3} > 0$ such that

$$\begin{aligned} \langle Df, DA^{*}A f \rangle &\ge \| \sigma D^{2} f\|^{2} -C_{2}\Big(\frac{1}{2 C_{2}}\| \sigma D^{2} f\|^{2} + (2 C_{2}+1) \| Df \|^{2} \Big) \\ &\ge \frac{1}{2} \| \sigma D^{2} f\|^{2} - C_{3} \| Df \|^{2}\;. \end{aligned}$$

(37)

Combining (36) and (37) we obtain (34).

We turn to the proof of (35), which is very close to [35, Proof of Theorem 24]. The main difference lies in the unboundedness of the coefficients of the operator at stake, namely the term $E^{3/2}$ in $B$ in the distorted coordinates, that requires some additional care.

First of all, we say that an operator $Q$ is bounded relatively to some operators $\{E_{j}\}_{j}$ if

$$ \| Q f\|^{2} \lesssim \sum _{j} \| E_{j} f\|^{2}\;, $$

uniformly over all parameters.

Lemma 5.7

• (i) For every $0\le k \le 2$, $[A,C_{k}]$ is bounded relatively to $\{C_{j}\}_{0\le j \le k}$,

• (ii) For every $0\le k \le 2$, $[C_{k},A^{*}]$ is bounded relatively to $\{I\} \cup \{C_{j}\}_{0\le j \le k}$,

• (iii) For every $1\le k \le 2$, $R_{k}$ is bounded relatively to $\{C_{j}\}_{0\le j \le k-1}$,

• (iv) $R_{3}$ is bounded relatively to $\{\mathbf{E}^{3/2} C_{1}\} \cup \{\mathbf{E}^{3/2} C_{2}\}$.

Proof

Let us first point out that, apart from $\mathbf{E}^{3/2}$, all the terms appearing in $\sigma$, $b$ and $\tilde{b}$ are bounded uniformly over all parameters. In particular, as already noticed, $\sqrt{E} (\lambda -E)$ remains of order 1.

A computation shows that $[A,C_{k}]f = (-1)^{k}\big ( \sigma \sigma ^{(k+1)} - \sigma ' \sigma ^{(k)}\big ) f'$. For $k=0$, this vanishes. For $k=1,2$, we observe that $\|[A,C_{k}]f\|^{2} \lesssim \| \sigma f'\|^{2} + \| \sigma ' f'\|^{2} = \|C_{0} f\|^{2} + \|C_{1} f\|^{2}$. This proves (i). Regarding (ii), a computation yields $[C_{k},A^{*}] = (-1)^{k+1} \sigma ^{(k)} \Big ( \frac{(\sigma \mu )'}{\mu }\Big )' f + [A,C_{k}]f$. Using the bounds stated in Lemma 3.1, we deduce that the first term can be controlled by $\|f\|$, while the second term was already controlled at point (i). We turn to (iii). For $k\in \{1,2\}$, we compute $R_{k} f = (-1)^{k-1} \big (\sigma ^{(k-1)} \tilde{b}' - \sigma ^{(k)}( \tilde{b} - E^{3/2}) \big )f'$. For $k=1$, we find

$$ \sigma \tilde{b}' - \sigma '(\tilde{b} - E^{3/2}) = \sigma \tilde{b}' + \sigma \sigma ' \big( \sigma '+ \sigma \frac{\mu '}{\mu } - \sqrt{2} \sqrt{E}(\lambda -E)\big)\;, $$

so that the $L^{2}$-norm of $R_{1} f$ can be controlled by the $L^{2}$ norm of $C_{0} f$. For $k=2$, we find

$$ \sigma ' \tilde{b}' - \sigma ''(\tilde{b} - E^{3/2}) = \sigma ' \tilde{b}' + \sigma \sigma ''(\sigma ' + \sigma \frac{\mu '}{\mu } - \sqrt{2} \sqrt{E}(\lambda -E))\;. $$

Consequently

$$\begin{aligned} \| R_{2} f\|^{2} &\le 2 \| \sigma ' \tilde{b}' f'\|^{2} + 2\| \sigma \sigma ''(\sigma ' + \sigma \frac{\mu '}{\mu } - \sqrt{2} \sqrt{E}( \lambda -E))f'\|^{2} \\ &\lesssim \|\sigma f'\|^{2} + \| \sigma ' f' \|^{2} = \|C_{0} f\|^{2} + \|C_{1} f\|^{2}\;. \end{aligned}$$

Finally

$$ \| R_{3} f \|^{2} = \| \big(\sigma '' \tilde{b}' - \sigma ^{(3)} \tilde{b} \big)f' \|^{2} \lesssim \mathbf{E}^{3} \|f'\|^{2} $$

and this last expression is bounded from above, up to a multiplicative constant, by $\| \mathbf{E}^{3/2} C_{1} f\|^{2} + \| \mathbf{E}^{3/2} C_{2} f\|^{2}$. □

Recall that $-\mathcal{L}^{*}=A^{*}A + B$. We have

$$ \left [\mkern - 3 mu\left [f,-\mathcal{L}^{*}f\right ]\mkern - 3 mu \right ] = \frac{1}{\mathbf{E}^{3/2}} \sum _{k=0}^{2} \Big(a_{k} \big[(\mathrm{I})^{k}_{A} + (\mathrm{I})^{k}_{B}] + b_{k}[( \mathrm{II})^{k}_{A} + (\mathrm{II})^{k}_{B}\big]\Big)\;, $$

(38)

where

$$ (\mathrm{I})_{A}^{k} = \langle C_{k} f, C_{k} A^{*}A f\rangle \;, \quad (\mathrm{I})_{B}^{k} = \langle C_{k} f, C_{k} B f\rangle \;, $$

and

$$ \begin{aligned}(\mathrm{II})_{A}^{k} &= \langle C_{k} f, C_{k+1} A^{*}A f\rangle + \langle C_{k} A^{*}A f, C_{k+1} f\rangle \;, \\ (\mathrm{II})_{B}^{k} &= \langle C_{k} f, C_{k+1} B f\rangle + \langle C_{k} B f, C_{k+1} f \rangle ;. \end{aligned}$$

Linear algebra manipulations and the Cauchy-Schwarz inequality yield (see [35, Proof of Theorem 24, pp.25-26] for details, one simply needs to take $\lambda _{k}=\Lambda _{k}=\mathbf{E}^{3/2}$ therein):

$$\begin{aligned} (\mathrm{I})^{k}_{A} \ge \,& \|C_{k} A f\|^{2} - \|C_{k}Af\| \|[A,C_{k}]f \| - \|C_{k}f\|\|[C_{k},A^{*}]Af\|\;, \\ (\mathrm{I})^{k}_{B} \ge \,& -\mathbf{E}^{3/2}\|C_{k}f\|\|C_{k+1}f\| - \|C_{k} f\| \|R_{k+1} f\|\;, \\ (\mathrm{II})^{k}_{A} \ge \,& - \|C_{k}f\| \|[C_{k+1},A^{*}]Af\| - \|C_{k}Af \| \|C_{k+1} Af\| - \|C_{k+1} Af\| \|[A,C_{k}] f\| \\ & - \|C_{k} Af\| \|C_{k+1} Af\| - \|C_{k} Af\|\|[A,C_{k+1}] f\| - \|C_{k+1} f\| \|[C_{k},A^{*}]Af\|\;, \\ (\mathrm{II})^{k}_{B} \ge \,& \mathbf{E}^{3/2} \|C_{k+1} f\|^{2} - \|C_{k+1} f\| \|R_{k+1} f\| - \mathbf{E}^{3/2} \|C_{k} f\| \| C_{k+2} f\| \\ &{} - \|C_{k} f\| \|R_{k+2} f\|\;. \end{aligned}$$

At this point, the proof differs from [35, Proof of Theorem 24, pp.26]: indeed therein the parameters $\lambda _{k}$, $\Lambda _{k}$ are of order 1, while in our case they are taken equal to $\mathbf{E}^{3/2}$ and therefore need extra care.

Take $\epsilon =\sqrt {\delta}$. By Young’s inequality we have $XY \le \epsilon X^{2} + (4\epsilon )^{-1} Y^{2}$. We thus get⁷ for any $k\in \{0,1,2\}$

$$\begin{aligned} &a_{k} \big[(\mathrm{I})^{k}_{A} + (\mathrm{I})^{k}_{B}] + b_{k}[( \mathrm{II})^{k}_{A} + (\mathrm{II})^{k}_{B}\big] \\ &\quad \ge a_{k} \| C_{k} A f\|^{2} + b_{k} \mathbf{E}^{3/2} \|C_{k+1} f\|^{2} \end{aligned}$$

(39)

$$\begin{aligned} &\qquad {}-\epsilon \mathbf{E}^{3/2} b_{k-1} \|C_{k} f\|^{2} - \mathbf{E}^{3/2} \frac{a_{k}^{2}}{4\epsilon b_{k-1}} \|C_{k+1} f\|^{2} \end{aligned}$$

(40)

$$\begin{aligned} &\qquad {}-\epsilon b_{k-1} \|C_{k} f\|^{2} - \frac{a_{k}^{2}}{4\epsilon b_{k-1}} \|R_{k+1} f\|^{2} \end{aligned}$$

(41)

$$\begin{aligned} &\qquad {}-\epsilon a_{k} \|C_{k} A f\|^{2} - \frac{a_{k}}{4\epsilon} \|[A,C_{k}] f\|^{2} \end{aligned}$$

(42)

$$\begin{aligned} &\qquad {}-\epsilon b_{k-1} \|C_{k} f\|^{2} - \frac{a_{k}^{2}}{4\epsilon b_{k-1}} \|[C_{k},A^{*}]A f\|^{2} \end{aligned}$$

(43)

$$\begin{aligned} &\qquad {}-\epsilon b_{k} \|C_{k+1} f\|^{2} - \frac{b_{k}}{4\epsilon} \|R_{k+1} f\|^{2} \end{aligned}$$

(44)

$$\begin{aligned} &\qquad {}-\epsilon \mathbf{E}^{3/2} b_{k-1} \|C_{k} f\|^{2} - \mathbf{E}^{3/2} \frac{b_{k}^{2}}{4\epsilon b_{k-1}} \|C_{k+2} f\|^{2} \end{aligned}$$

(45)

$$\begin{aligned} &\qquad {}-\epsilon b_{k-1} \|C_{k} f\|^{2} - \frac{b_{k}^{2}}{4\epsilon b_{k-1}} \|R_{k+2} f\|^{2} \end{aligned}$$

(46)

$$\begin{aligned} &\qquad {}-\epsilon b_{k-1} \|C_{k} f\|^{2} - \frac{b_{k}^{2}}{4\epsilon b_{k-1}} \|[C_{k+1},A^{*}]A f\|^{2} \end{aligned}$$

(47)

$$\begin{aligned} &\qquad {}-\epsilon a_{k} \|C_{k} A f\|^{2} - \frac{b_{k}^{2}}{4\epsilon a_{k}} \|C_{k+1}A f\|^{2} \end{aligned}$$

(48)

$$\begin{aligned} &\qquad {}-\epsilon a_{k+1} \|C_{k+1} A f\|^{2} - \frac{b_{k}^{2}}{4\epsilon a_{k+1}} \|[A,C_{k}] f\|^{2} \end{aligned}$$

(49)

$$\begin{aligned} &\qquad {}-\epsilon a_{k} \|C_{k} A f\|^{2} - \frac{b_{k}^{2}}{4\epsilon a_{k}} \|C_{k+1}A f\|^{2} \end{aligned}$$

(50)

$$\begin{aligned} &\qquad {}-\epsilon a_{k} \|C_{k} A f\|^{2} - \frac{b_{k}^{2}}{4\epsilon a_{k}} \|[A,C_{k+1}] f\|^{2} \end{aligned}$$

(51)

$$\begin{aligned} &\qquad {}-\epsilon b_{k} \|C_{k+1} f\|^{2} - {\frac{b_{k}}{4\epsilon }} \|[C_{k},A^{*}]A f\|^{2}\;, \end{aligned}$$

(52)

with the further condition that (44) to (52), as well as (40), are not present for $k=2$.

The inequalities (33) combined with Lemma 5.7 ensure that for $\delta$ small enough (uniformly over all parameters) the sum over $k$ of all the terms from (40) to (52), except the first terms of (40) and (45) for $k=0$, is larger than

$$ -\frac{1}{4} \|A f\|^{2} - \frac{1}{2} \sum _{k=0}^{2} \Big(a_{k} \| C_{k} A f\|^{2} + b_{k} \mathbf{E}^{3/2} \|C_{k+1} f\|^{2}\Big)\;. $$

For more details see [35, Proof of Theorem 24, pp.27]. We now control the contribution to (38) of the first terms of (40) and (45) for $k=0$. This contribution is given by (recall that $\delta < 1/4$):

$$ -2\epsilon b_{-1} \mathbf{E}^{3/2} \|A f\|^{2} = -2\delta ^{3/2} \mathbf{E}^{3/2} \|Af\|^{2} \ge -\frac{1}{4} \mathbf{E}^{3/2}\|Af\|^{2} \;. $$

Consequently

$$ \begin{aligned}\left [\mkern - 3 mu\left [f,-\mathcal{L}^{*}f\right ]\mkern - 3 mu \right ] \ge{}& -\frac{1}{4}(1+\frac{1}{\mathbf{E}^{3/2}}) \|Af\|^{2} \\ &{} + \frac{1}{2\mathbf{E}^{3/2}} \sum _{k=0}^{2} \Big(a_{k} \| C_{k} A f\|^{2} + b_{k} \mathbf{E}^{3/2} \|C_{k+1} f\|^{2}\Big)\;. \end{aligned}$$

On the other hand, $\langle f, -\mathcal{L}^{*}f\rangle = \|Af\|^{2}$. Putting everything together, we thus showed that

$$\begin{aligned} &\langle f, -\mathcal{L}^{*}f\rangle + \left [\mkern - 3 mu\left [f,- \mathcal{L}^{*}f\right ]\mkern - 3 mu\right ] \\ &\quad \ge \frac{1}{2} \| Af \|^{2} + \frac{1}{2\mathbf{E}^{3/2}} \sum _{k=0}^{2} \Big(a_{k} \| C_{k} A f \|^{2} + b_{k} \mathbf{E}^{3/2} \|C_{k+1} f\|^{2}\Big) \\ &\quad \ge \frac{1}{2} \| Af \|^{2} + \frac{1}{2} \sum _{k=0}^{1} b_{k} \|C_{k+1} f\|^{2} \\ &\quad \ge \frac{1}{4} \int _{[0,\pi )} \big(\sin ^{4} x + b_{0} \sin ^{2} (2x) + 4 b_{1} \cos ^{2} (2x)\big) f'(x)^{2} \mu (x)dx \\ &\quad \ge K \|f'\|^{2}\;, \end{aligned}$$

for some $K$ only depending on $\delta$. This completes the proof.

6 GMP formula

In this section, we prove the GMP formula stated in Proposition 4.1 and we deduce some simple facts from it. Actually, we will prove a slightly stronger statement for later convenience:

Proposition 6.1

Fix $u \in (-L/(2 \mathbf{E}),L/(2 \mathbf{E}))$ and $a,b\in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}$. For any bounded and measurable map $G$ from ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\times \mathcal{D}\times \mathcal{D}$ into ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}_{+}$, we have

$$\begin{aligned} &\mathbb{E}\bigg[\sum _{i\ge 1} \big(a \varphi _{i}( \mathbf{E}u)^{2} + b\; \varphi _{i}'(\mathbf{E}u)^{2}\big)\;G(\lambda _{i},\;\varphi _{i}, \varphi _{i}')\bigg] \\ &= \frac{1}{\sqrt {\mathbf{E}}}\int _{\lambda \in {{\mathchoice{\textit{\textbf{R}}}{ \textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}} \int _{ \theta =0}^{\pi }p^{(\mathbf{E})}_{\lambda ,\frac{L}{2 \mathbf{E}}+u}( \theta ) p^{(\mathbf{E})}_{\lambda ,\frac{L}{2 \mathbf{E}}-u}(\pi - \theta ) (a\sin ^{2}\theta + b\,\mathbf{E}\cos ^{2} \theta ) \\ &\qquad \qquad \qquad \qquad \times \mathbb{E}^{(u)}_{\theta ,\pi - \theta}\bigg[G\Big(\lambda , \frac{\hat{y}^{(\mathbf{E})}_{\lambda }(\cdot /\mathbf{E})}{\sqrt{\mathbf{E}}\|\hat{y}^{(\mathbf{E})}_{\lambda }\|}, \frac{(\hat{y}^{(\mathbf{E})}_{\lambda })'(\cdot /\mathbf{E})}{\mathbf{E}^{3/2} \|\hat{y}^{(\mathbf{E})}_{\lambda }\|} \Big)\bigg] \, d\theta d\lambda \end{aligned}$$

Given this proposition, the proof of the GMP formula is simple.

Proof of Proposition 4.1

Recall that the eigenfunctions $\varphi _{i}$ are normalized in $L^{2}$. It suffices to take $a=1$, $b=0$ in the previous proposition, to integrate w.r.t. $u$ and to apply Fubini’s Theorem. □

Before we proceed to the proof of Proposition 6.1, note that $\lambda \mapsto \theta _{\lambda }^{(\mathbf{E})}$ is differentiable and let us introduce $z_{\lambda }^{(\mathbf{E})} = \partial _{\lambda }\theta _{\lambda }^{( \mathbf{E})}$, the derivative with respect to $\lambda$ of the angle $\theta _{\lambda }^{(\mathbf{E})}$. It satisfies the SDE

$$\begin{aligned} d z_{\lambda }^{(\mathbf{E})}(t) &= \sqrt {\mathbf{E}}\sin ^{2} \theta _{ \lambda }^{(\mathbf{E})} dt - z_{\lambda }^{(\mathbf{E})} \Big[ d \rho _{\lambda }^{(\mathbf{E})}(t) - \frac{1}{2} d \langle \rho _{ \lambda }^{(\mathbf{E})} \rangle _{t} \Big]\;. \end{aligned}$$

We thus obtain the following integral expression for $z^{(\mathbf{E})}_{\lambda }$:

$$\begin{aligned} z_{\lambda }^{(\mathbf{E})}(t) = \frac{1}{(r_{\lambda }^{(\mathbf{E})}(t))^{2}}\int _{- \frac{L}{2 \mathbf{E}}}^{t} \sqrt {\mathbf{E}}\,\sin ^{2} \theta _{ \lambda }^{(\mathbf{E})} (s) (r_{\lambda }^{(\mathbf{E})}(s))^{2} ds \;. \end{aligned}$$

(53)

Proof of Proposition 6.1

It suffices to prove the statement with the original coordinates, since the statement with the distorted coordinates follows from (10) and the change of variable $\theta \mapsto \text{arccotan\,}(\frac{1}{\sqrt {E}} \text{cotan}\, \theta )$ whose Jacobian is given by $(\sqrt {E} (\sin ^{2} \theta + \frac{1}{E} \cos ^{2} \theta ))^{-1}$.

By the monotone convergence theorem, we can assume that $G$ is a continuous map from ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times \mathcal{D}\times \mathcal{D}$ into ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}_{+}$ such that $G(\lambda ,\varphi ,\psi ) = 0$ whenever $\lambda \notin [-A,A]$ or $\|\varphi \|_{L^{\infty}} > A$ or $\|\psi \|_{L^{\infty}} > A$, for some given $A>0$. Fix $u \in (-L/2,L/2)$. Recall from Lemma 3.4 that the set of eigenvalues $(\lambda _{i})_{i\ge 1}$ coincides with the set of $\lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ such that

$$ \big\{ \theta _{\lambda }^{+}(u)+\theta _{\lambda }^{-}(-u) \big\} _{ \pi }= 0\;, $$

and the eigenfunction $\varphi _{\lambda }$ associated to the eigenvalue $\lambda$ coincides with $\hat{y}_{\lambda }/\|\hat{y}_{\lambda }\|$. Therefore,

$$\begin{aligned} &\sum _{i\ge 1} G(\lambda _{i},\varphi _{i}, \varphi '_{i}) \big(a \; \varphi _{i}(u)^{2} + b\; \varphi _{i}'(u)^{2}\big) \\ &= \sum _{\lambda \;:\;\big\{ \theta _{\lambda }^{+}(u)+\theta _{ \lambda }^{-}(-u) \big\} _{\pi }= 0} G\Big(\lambda , \frac{\hat{y}_{\lambda }}{\|\hat{y}_{\lambda }\|}, \frac{(\hat{y}_{\lambda })'}{\|\hat{y}_{\lambda }\|}\Big)\; \frac{a (\hat{y}_{\lambda }(u))^{2} + b ({{\hat{y}_{\lambda }}'(u)})^{2}}{\|\hat{y}_{\lambda }\|^{2}} \,. \end{aligned}$$

From the positivity of $z_{\lambda }^{\pm }$, we deduce that almost surely the map $\lambda \mapsto \theta ^{+}_{\lambda }(u) + \theta ^{-}_{\lambda }(-u)$ is a diffeomorphism from ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ to ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$. We denote its inverse by $\theta \mapsto \lambda (\theta )$. We can rewrite the last sum as:

$$\begin{aligned} \sum _{\theta \in \pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}} G\Big(\lambda (\theta ), \frac{\hat{y}_{\lambda (\theta )}}{\|\hat{y}_{\lambda (\theta )}\|}, \frac{(\hat{y}_{\lambda (\theta )})'}{\|\hat{y}_{\lambda (\theta )}\|} \Big)\; \frac{a( \hat{y}_{\lambda (\theta )}(u))^{2} + b ({{\hat{y}_{\lambda (\theta )}}'(u)})^{2}}{\|\hat{y}_{\lambda (\theta )}\|^{2} } \,. \end{aligned}$$

Set for any $\varepsilon \in (0,\pi )$

$$\begin{aligned} {G}_{\varepsilon }(u) :={}& \frac{1}{2\varepsilon } \int _{\theta \in \pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}+ [-\varepsilon ,\varepsilon ]} G\Big(\lambda ( \theta ), \frac{\hat{y}_{\lambda (\theta )}}{\|\hat{y}_{\lambda (\theta )}\|}, \frac{(\hat{y}_{\lambda (\theta )})'}{\|\hat{y}_{\lambda (\theta )}\|} \Big) \\ &{}\times \frac{a( \hat{y}_{\lambda (\theta )}(u))^{2} + b ({{\hat{y}_{\lambda (\theta )}}'(u)})^{2}}{\|\hat{y}_{\lambda (\theta )}\|^{2}} \;d\theta \;. \end{aligned}$$

(54)

Almost surely ${G}_{\varepsilon }(u)$ is bounded by $\|G\|_{\infty}(|a|+|b|) A^{2} \big(\#\{\lambda _{i} \in [-A,A]\} +2 \big)$. From Lemma A.4 in the Appendix, this r.v. has a finite expectation. Furthermore, by continuity ${G}_{\varepsilon }(u)$ converges a.s. as $\varepsilon \downarrow 0$ to

$$ \sum _{i\ge 1} G(\lambda _{i},\varphi _{i}, \varphi '_{i})\, \big(a \varphi _{i}(u)^{2} + b ({\varphi _{i}'(u)})^{2}\big)\;. $$

By the Dominated Convergence Theorem, we deduce that,

$$\begin{aligned} \mathbb{E}\Big[\sum _{i\ge 1} G(\lambda _{i},\varphi _{i}, \varphi '_{i}) \, \big(a\varphi _{i}(u)^{2} + b ({\varphi _{i}'(u)})^{2}\big) \Big]= \lim _{\varepsilon \downarrow 0} \mathbb{E}\big[{G}_{\varepsilon }(u) \big]\;. \end{aligned}$$

We now compute the expectation of ${G}_{\varepsilon }(u)$. Note that $\partial _{\lambda }(\theta _{\lambda }^{+}(u)+\theta _{\lambda }^{-}(-u)) = z_{\lambda }^{+}(u) + z_{\lambda }^{-}(-u)$. Using (53) and given the boundary condition imposed on $r_{\lambda }^{\pm}$, this equals $\|\hat{y}_{\lambda }\|^{2}$. We then apply the change of variable $\theta \mapsto \lambda (\theta )$ and obtain

$$\begin{aligned} {G}_{\varepsilon }(u)= \frac{1}{2\varepsilon }&\int _{\lambda \in {{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}} \mathbf{1}_{\{\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{ \text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}+ [-\varepsilon , \varepsilon ]\}}({\theta _{\lambda }^{+}(u)+\theta _{ \lambda }^{-}(-u)}) G\Big(\lambda , \frac{\hat{y}_{\lambda }}{\|\hat{y}_{\lambda }\|}, \frac{(\hat{y}_{\lambda })'}{\|\hat{y}_{\lambda }\|}\Big) \\ &\qquad \qquad \times \big( a \sin ^{2} \theta _{\lambda }^{+}(u) + b \cos ^{2} \theta _{\lambda }^{+}(u)\big)d\lambda \;. \end{aligned}$$

We then take expectation, use Fubini’s Theorem, and integrate with respect to the value of the forward diffusion at time $u$:

$$\begin{aligned} \mathbb{E}[{G}_{\varepsilon }(u)] &=\frac{1}{2\varepsilon }\int _{ \lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}} \int _{\theta =0}^{\pi} \int _{\theta ' = -\varepsilon }^{\varepsilon } p_{\lambda ,u}(\theta ) p_{\lambda ,L-u}( \pi -\theta + \theta ') (a\sin ^{2} \theta + b\cos ^{2}\theta ) \\ &\times \mathbb{E}^{(u)}_{\theta ,\pi - \theta - \theta '}\Big[G\Big( \lambda ,\frac{\hat{y}_{\lambda }}{\|\hat{y}_{\lambda }\|}, \frac{(\hat{y}_{\lambda })'}{\|\hat{y}_{\lambda }\|}\Big) \Big]d \theta ' d\theta d\lambda \;. \end{aligned}$$

By the Dominated Convergence Theorem, the boundedness of the transition probabilities and the continuity w.r.t. $\theta '$, we can permute the integrals with respect to $\lambda$, $\theta$ and the limit as $\varepsilon \downarrow 0$ to find

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \mathbb{E}[{G}_{\varepsilon }(u)] =& \int _{\lambda \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}} \int _{\theta =0}^{\pi }p_{\lambda ,u}( \theta ) p_{\lambda ,L-u}(\pi -\theta ) (a\sin ^{2}\theta + b\cos ^{2} \theta ) \\ &\qquad \times \mathbb{E}^{(u)}_{\theta ,\pi - \theta}\Big[G\Big( \lambda ,\frac{\hat{y}_{\lambda }}{\|\hat{y}_{\lambda }\|}, \frac{(\hat{y}_{\lambda })'}{\|\hat{y}_{\lambda }\|}\Big) \Big] \, d \theta d\lambda \;, \end{aligned}$$

thus concluding the proof. □

As a first application of the GMP formula, one can derive an expression of the density of states in terms of the stationary measure of the process $\{\theta _{\lambda }\}_{\pi}$. There is another (actually simpler) formula for this density of states given by $n(\lambda ) = \partial _{\lambda }(1/m_{\lambda })$ where $m_{\lambda }$ is introduced in Sect. A.3, see [12].

Corollary 6.2

The density of states satisfies

$$ n(\lambda ) = \int _{0}^{\pi }\mu _{\lambda }(\theta ) \mu _{\lambda }( \pi -\theta )\sin ^{2} \theta d\theta \;,\quad \lambda \in {{ \mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}\;. $$

We also have for any $E\ge 1$

$$ n(\lambda ) = \frac{1}{\sqrt {E}} \int _{0}^{\pi }\mu _{\lambda }^{(E)}( \theta ) \mu _{\lambda }^{(E)}(\pi -\theta )\sin ^{2} \theta d\theta \;,\quad \lambda \in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}\;. $$

Proof

Fix some interval $\Delta \subset {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ and set $N_{L}(\Delta ):= \#\{\lambda _{i}: \lambda _{i} \in \Delta \}$. By the uniform integrability stated in Lemma A.4, $\int _{\Delta }n(\lambda ) d\lambda$ is not only the a.s. limit of $N_{L}(\Delta )/L$ but also its limit in $L^{1}$. The GMP formula allows to compute $\mathbb{E}[N_{L}(\Delta )]$ by simply choosing $G(\lambda )=\mathbf{1}_{\Delta}(\lambda )$. By Theorem 4 one can then replace the product of the densities of the forward/backward diffusions $p_{\lambda ,\frac{L}{2}+u}(\theta ) p_{\lambda ,\frac{L}{2}-u}(\pi - \theta )$ by the product of the densities of the invariant measure $\mu _{\lambda }(\theta ) \mu _{\lambda }(\pi -\theta )$, and derive the first expression of the statement. The formula involving distorted coordinates follows from a change of variables. □

Recall the r.v. defined in (23) and (24).

Proposition 6.3

Wegner estimates

Fix $h>0$ and set $\Delta := [E- h/(L n(E)),E+h/(Ln(E))]$. In the Bulk and the Crossover regimes, we have as $L\to \infty$:

• (1) $\mathbb{E}[N_{L}(\Delta )] = 2h (1+o(1))$,

• (2) $\mathbb{E}[N_{L}^{(1)}(\Delta )] = \frac{2h}{k}(1+o(1))$.

Proof

By Proposition 4.1, we have:

$$\begin{aligned} \mathbb{E}\big[N_{L}(\Delta )\big]&= \sqrt {\mathbf{E}}\int _{- \frac{L}{2\mathbf{E}}}^{\frac{L}{2\mathbf{E}}} \int _{\lambda \in \Delta} \int _{\theta =0}^{\pi }p_{\lambda ,\frac{L}{2\mathbf{E}}+u}^{( \mathbf{E})}(\theta ) p_{\lambda ,\frac{L}{2\mathbf{E}}-u}^{( \mathbf{E})}(\pi -\theta )\sin ^{2} \theta d\theta d\lambda du \end{aligned}$$

If one replaces the transition probabilities by the equilibrium densities, then one gets

$$ \frac{L}{\sqrt {\mathbf{E}}} \int _{\lambda \in \Delta} \int _{\theta =0}^{ \pi }\mu _{\lambda }^{(\mathbf{E})}(\theta ) \mu _{\lambda }^{( \mathbf{E})}(\pi - \theta ) \sin ^{2} \theta d\theta d\lambda \;, $$

which goes to $2h$ by Corollary 6.2. The error made upon this replacement is of order $\mathbf{E}/L$ by Theorem 4 and Lemma 3.1 and therefore vanishes in the limit $L\to \infty$. Consequently we get the first estimate.

The second estimate is derived from the same argument, one simply replaces the interval $[-L/\mathbf{E},L/\mathbf{E}]$ by an interval of length $L/(\mathbf{E}k)$ and uses that $L/(\mathbf{E}k) \gg 1$. □

7 Exponential decay

The goal of this section is to prove the exponential decay of the eigenfunctions stated in Proposition 4.2. We first introduce in Sect. 7.1 the adjoint diffusions as they will naturally arise in the proof of the estimate of the exponential decay, then we compute the Lyapunov exponent associated to the diffusions in Sect. 7.2. Finally in Sect. 7.3 we present the proof of Proposition 4.2. Until the middle of Sect. 7.2, we investigate some properties of the diffusions for any parameter $\lambda$, that is, we do not work in the specific Bulk and Crossover regimes. From the middle of Sect. 7.2, we restrict ourselves to the Bulk and Crossover regimes, and we establish asymptotic estimates in $L$.

7.1 Adjoint diffusions

We introduce the process $\bar{\theta}_{\lambda }^{(\mathbf{E})}$ as the solution of the following SDE driven by a Brownian motion $\bar{B}^{(\mathbf{E})}$

$$ \begin{aligned} d\bar{\theta }_{\lambda }^{(\mathbf{E})}(t) &= \big(- \mathbf{E}^{3/2} - \sqrt {\mathbf{E}}(\lambda -\mathbf{E}) \sin ^{2} \bar{\theta }_{\lambda }^{(\mathbf{E})} + 3 \sin ^{3}(\bar{\theta }_{ \lambda }^{(\mathbf{E})})\cos (\bar{\theta }_{\lambda }^{(\mathbf{E})}) \\ &\quad +\sin ^{4} \bar{\theta }_{\lambda }^{(\mathbf{E})} \frac{\partial _{\theta }\mu _{\lambda }^{(\mathbf{E})}(\bar{\theta }_{\lambda }^{(\mathbf{E})})}{\mu _{\lambda }^{(\mathbf{E})}(\bar{\theta }_{\lambda }^{(\mathbf{E})})} \big)dt \\ &\quad - \sin ^{2} \bar{\theta }_{\lambda }^{(\mathbf{E})} d\bar{B}^{( \mathbf{E})}(t)\;. \end{aligned} $$

(55)

By coherence with previous notations, we denote by $\bar{\mathbb{P}}_{(s,\theta _{0})}$ the law of the process $\bar{\theta}_{\lambda }^{(\mathbf{E})}$ starting from $\theta _{0}$ at time $s$, and by $\bar{\mathbb{P}}_{(s,\theta _{0})\to (t,\theta _{1})}$ the law of the bridge from $(s,\theta _{0})$ to $(t,\theta _{1})$.

The process $\bar{\theta}_{\lambda }^{(\mathbf{E})}$ is the adjoint diffusion of $\theta _{\lambda }^{(\mathbf{E})}$ with respect to the invariant measure $\mu _{\lambda }^{(\mathbf{E})}$. In other words, its generator is the operator $\mathcal{L}^{*}$ which is the adjoint in $L^{2}(\mu _{\lambda }^{(\mathbf{E})})$ of the generator ℒ of $\theta _{\lambda }^{(\mathbf{E})}$, see the beginning of Sect. 5.2 for more details on the generators involved. Let us recall that this adjunction implies that the law of the process $\theta _{\lambda }^{(\mathbf{E})}$ starting from the invariant measure is the same as the law of the process $\bar{\theta }_{\lambda }^{(\mathbf{E})}$, read backward-in-time, and starting from the invariant measure. In mathematical terms: for any measurable set $A\subset \mathcal{C}([0,t],{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$, we have

$$ \int _{\theta _{0}=0}^{\pi }\mu _{\lambda }^{(\mathbf{E})}(\theta _{0}) \mathbb{P}_{(0,\theta _{0})}(A)d\theta _{0} = \int _{\theta _{1}=0}^{ \pi }\mu _{\lambda }^{(\mathbf{E})}(\theta _{1})\bar{\mathbb{P}}_{(0, \theta _{1})}(\bar{A})d\theta _{1}\;, $$

where $\bar{A} := \{f: f(t-\cdot ) \in A\}$ is the image of $A$ upon reversing time. Disintegrating this last expression, we further get

$$ \mu _{\lambda }^{(\mathbf{E})}(\theta _{0}) p_{\lambda ,t}^{( \mathbf{E})}(\theta _{0},\theta _{1}) \mathbb{P}_{(0,\theta _{0}) \to (t,\theta _{1})}(A) = \mu _{\lambda }^{(\mathbf{E})}(\theta _{1}) \bar{p}_{\lambda ,t}^{(\mathbf{E})}(\theta _{1},\theta _{0}) \bar {\mathbb{P}}_{(0,\theta _{1})\to (t,\theta _{0})}(\bar{A})\;, $$

(56)

We would like to introduce the counterpart of the process $\rho _{\lambda }^{(\mathbf{E})}$ at the level of the adjoint diffusion. We introduce the process $\bar{\rho}_{\lambda }^{(\mathbf{E})}$ as the solution of

$$ \begin{aligned} d\bar{\rho}_{\lambda }^{(\mathbf{E})} &= \Big(\sqrt {\mathbf{E}}(\lambda -\mathbf{E})\sin 2\bar{\theta }_{\lambda }^{( \mathbf{E})} + \frac{1}{2} \sin ^{2} 2\bar{\theta }_{\lambda }^{( \mathbf{E})} + \sin ^{2} \bar{\theta }_{\lambda }^{(\mathbf{E})} \\ &\quad - 8 \sin ^{2} \bar{\theta}^{(\mathbf{E})}_{\lambda }\cos ^{2} \bar{\theta}^{(\mathbf{E})}_{\lambda }- 2 \sin ^{3} \bar{\theta}^{( \mathbf{E})}_{\lambda }\cos \bar{\theta}^{(\mathbf{E})}_{\lambda } \frac{\partial _{\theta }\mu _{\lambda }^{(\mathbf{E})}(\bar{\theta }_{\lambda }^{(\mathbf{E})})}{\mu _{\lambda }^{(\mathbf{E})}(\bar{\theta }_{\lambda }^{(\mathbf{E})})} \Big)dt \\ &\quad + \sin 2\bar{\theta }_{\lambda }^{(\mathbf{E})} d\bar{B}^{( \mathbf{E})}(t)\;. \end{aligned} $$

(57)

Our next result shows that this is the “right” object.

Lemma 7.1

Under $\mathbb{P}_{\mu ^{(\mathbf{E})}_{\lambda }}$, the process $(\rho _{\lambda }^{(\mathbf{E})}(s)-\rho _{\lambda }^{(\mathbf{E})}(0), s\in [0,t])$ has the same law as the process $(\bar{\rho }_{\lambda }^{(\mathbf{E})}(t-s) - \bar{\rho }_{\lambda }^{( \mathbf{E})}(t), s\in [0,t])$ under $\bar{\mathbb{P}}_{\mu ^{(\mathbf{E})}_{\lambda }}$.

Proof

We give a sketch of proof. First of all, we show that the process $\rho _{\lambda }^{(\mathbf{E})}$, resp. $\bar{\rho}_{\lambda }^{( \mathbf{E})}$, is measurable w.r.t. the process $\theta _{\lambda }^{(\mathbf{E})}$, resp. $\bar{\theta }_{\lambda }^{( \mathbf{E})}$. Indeed, the drift term of the evolution equation only depends on $\theta _{\lambda }^{(\mathbf{E})}$, resp. $\bar{\theta}_{\lambda }^{( \mathbf{E})}$, while the martingale term can be expressed formally⁸ using Itô’s formula applied to $\ln \sin \theta _{\lambda }^{(\mathbf{E})}(t)$, resp. $\ln \sin \bar{\theta}_{\lambda }^{(\mathbf{E})}(t)$

$$ \int _{0}^{t} \sin 2\theta _{\lambda }^{(\mathbf{E})}(s) dB^{( \mathbf{E})}(s) = 2\Big(\ln \sin \theta _{\lambda }^{(\mathbf{E})}(0) - \ln \sin \theta _{\lambda }^{(\mathbf{E})}(t)\Big) + \int _{0}^{t} F( \theta _{\lambda }^{(\mathbf{E})}(s))ds\;, $$

with

$$ F(\theta ) = 2\text{cotan}\,\theta \big( \mathbf{E}^{3/2} + \sqrt{ \mathbf{E}}(\lambda - \mathbf{E}) \sin ^{2} \theta + \sin ^{3} \theta \cos \theta \big) - \sin ^{2} \theta \;, $$

respectively

$$ \int _{0}^{t} \sin 2\bar{\theta}_{\lambda }^{(\mathbf{E})}(s) d \bar{B}^{(\mathbf{E})}(s) = 2\Big(\ln \sin \bar{\theta}_{\lambda }^{( \mathbf{E})}(0) - \ln \sin \bar{\theta}_{\lambda }^{(\mathbf{E})}(t) \Big) + \int _{0}^{t} \bar{F}(\bar{\theta}_{\lambda }^{(\mathbf{E})}(s))ds \;, $$

with

$$ \begin{aligned}\bar{F}(\theta ) ={}& 2\text{cotan}\,\theta \big( -\mathbf{E}^{3/2} - \sqrt{\mathbf{E}}(\lambda - \mathbf{E}) \sin ^{2} \theta + 3 \sin ^{3} \theta \cos \theta + \sin ^{4} \theta \frac{\partial _{\theta }\mu _{\lambda }^{(\mathbf{E})}(\theta )}{\mu _{\lambda }^{(\mathbf{E})}(\theta )} \big) \\ &{} - \sin ^{2} \theta \;. \end{aligned}$$

As a consequence,

$$ \begin{aligned}\rho _{\lambda }^{(\mathbf{E})}(t) - \rho _{\lambda }^{(\mathbf{E})}(0) ={}& 2\Big(\ln \sin \theta _{\lambda }^{(\mathbf{E})}(0) - \ln \sin \theta _{\lambda }^{(\mathbf{E})}(t)\Big) + \int _{0}^{t} F(\theta _{ \lambda }^{(\mathbf{E})}(s))ds \\ &{}+ \int _{0}^{t} D(\theta _{\lambda }^{( \mathbf{E})}(s))ds\;, \end{aligned}$$

with

$$ D(\theta ) = -\sqrt{\mathbf{E}}(\lambda -\mathbf{E}) \sin 2\theta - \frac{1}{2} \sin ^{2} 2\theta + \sin ^{2} \theta \;. $$

The adjunction relation ensures that the law of $\rho _{\lambda }^{(\mathbf{E})}(t) - \rho _{\lambda }^{(\mathbf{E})}(0)$ under $\mathbb{P}_{\mu ^{(\mathbf{E})}_{\lambda }}$, coincides with the law of

$$ 2\Big(\ln \sin \bar{\theta}_{\lambda }^{(\mathbf{E})}(t) - \ln \sin \bar{\theta}_{\lambda }^{(\mathbf{E})}(0)\Big) + \int _{0}^{t} F( \bar{\theta}_{\lambda }^{(\mathbf{E})}(t-s))ds + \int _{0}^{t} D( \bar{\theta}_{\lambda }^{(\mathbf{E})}(t-s))ds\;, $$

under $\bar{\mathbb{P}}_{\mu ^{(\mathbf{E})}_{\lambda }}$. A simple computation then shows that this last quantity coincides with

$$ \bar{\rho }_{\lambda }^{(\mathbf{E})}(0) - \bar{\rho }_{\lambda }^{( \mathbf{E})}(t)\;. $$

This can be generalized to any finite dimensional marginals of the process. □

Finally, let us introduce the first rotation time $\bar{\zeta }_{\lambda }^{(\mathbf{E})}$ of the diffusion $\bar{\theta}_{\lambda }^{(\mathbf{E})}$

$$ \bar{\zeta}_{\lambda }^{(\mathbf{E})} := \inf \{t\ge 0: \bar{\theta}_{ \lambda }^{(\mathbf{E})}(t) = \bar{\theta}_{\lambda }^{(\mathbf{E})}(0) + \pi \}\;. $$

By the same argument as in Sect. 3.4, the law of this r.v. is independent of $\bar{\theta}_{\lambda }^{(\mathbf{E})}(0)$. Consequently, its law can be computed when starting from the invariant measure. Using the adjunction relation above, we thus deduce that $\bar{\zeta}_{\lambda }^{(\mathbf{E})}$ and $\zeta _{\lambda }^{(\mathbf{E})}$ have the same law, and therefore

$$ \bar {\mathbb{E}}[\bar{\zeta}_{\lambda }^{(\mathbf{E})}] = \mathbb{E}[ \zeta _{\lambda }^{(\mathbf{E})}] = m_{\lambda }^{(\mathbf{E})}\;. $$

7.2 Lyapunov exponent and the main growth estimate

Recall the definition of the SDEs (11) and (12). Take $\rho _{\lambda }^{(\mathbf{E})}(0) := 0$. The Lyapunov exponent is usually defined as the almost sure limit of

$$ \frac{\ln r_{\lambda }^{(\mathbf{E})}(t)}{t}\;,\quad t\to \infty \;. $$

This deterministic quantity is intimately related to the rate of exponential decay of the eigenfunctions. For technical convenience, we manipulate the almost sure limit of

$$ 2\frac{\ln r_{\lambda }^{(\mathbf{E})}(t)}{t} = \frac{\rho _{\lambda }^{(\mathbf{E})}(t)}{t} \;,\quad t\to \infty \;, $$

that we denote by $\nu _{\lambda }^{(\mathbf{E})}$. In other words, $\nu _{\lambda }^{(\mathbf{E})}$ is twice the Lyapunov exponent.

Our next proposition gives an explicit expression of this exponent. It also shows that the Lyapunov exponent associated with $\bar{\rho}_{\lambda }^{(\mathbf{E})}$ is the opposite of $\nu _{\lambda }^{(\mathbf{E})}$.

Proposition 7.2

Lyapunov exponent

The random variables $\zeta _{\lambda }^{(\mathbf{E})}$, ${\bar{\zeta}_{ \lambda }^{(\mathbf{E})}}$ and $\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{(\mathbf{E})})$, ${ \bar{\rho}_{\lambda }^{(\mathbf{E})}(\bar{\zeta}_{ \lambda }^{(\mathbf{E})})}$ are integrable, and we have

$$\begin{aligned} \nu _{\lambda }^{(\mathbf{E})} = \frac{\mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{(\mathbf{E})})]}{\mathbb{E}[\zeta _{\lambda }^{(\mathbf{E})}]} {= - \frac{\mathbb{E}[\bar{\rho}_{\lambda }^{(\mathbf{E})}(\bar{\zeta}_{\lambda }^{(\mathbf{E})})]}{\mathbb{E}[\bar{\zeta}_{\lambda }^{(\mathbf{E})}]}} \;. \end{aligned}$$

Moreover for any $\lambda \in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$

$$ \nu _{\lambda }^{(\mathbf{E})} = \mathbf{E}\; \frac{ \int _{0}^{+\infty} \sqrt{u} \exp (-2 \lambda u - \frac{u^{3}}{6} ) du}{\int _{0}^{\infty} \frac{1}{\sqrt{u}} \exp (-2 \lambda u - \frac{u^{3}}{6}) du} > 0\;.$$

(58)

We have a remarkably simple expression for the quantity $\nu _{\lambda }^{(\mathbf{E})}$, from which we can deduce important properties. In particular, a crucial point for our proof is that this expression is positive for all $\lambda$ and $E$. The proof of this proposition follows from elementary (but not straightforward) computations on the SDEs, and is deferred to the Appendix A.4.2.

Fix $h >0$ and set $\Delta := [E - \frac{h}{n(E) L},E + \frac{h}{n(E) L}]$ until the end of the section. Recall that in the Bulk regime, $E\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ is fixed while in the Crossover regime $E=E(L) \to \infty$ as $L\to \infty$.

It is easy to check that in both regimes, uniformly over all $\lambda \in \Delta$ we have as $L\to \infty$

$$ \nu _{\lambda }^{(\mathbf{E})}/\nu _{E}^{(\mathbf{E})} \to 1\;. $$

Moreover in the Crossover regime we have

$$ \nu _{E}^{(E)} \to 1, \quad \text{as }E \to \infty \;. $$

As a consequence, we can safely approximate $\nu _{\lambda }$ by $\nu _{E}$ in the Bulk regime, and $\nu _{\lambda }^{(E)}$ by 1 in the Crossover regime. A posteriori, this explains the definition of $\boldsymbol{\nu _{E}}$ in (20).

Finally, let us mention that uniformly over all $\lambda \in \Delta$ and all $L>1$

$$ m_{\lambda }^{(\mathbf{E})} \asymp \textstyle\begin{cases} 1&\text{ in the Bulk regime}\;, \\ {E^{-3/2}}&\text{ in the Crossover regime}\;. \end{cases} $$

(59)

The main estimate needed for the proof of Proposition 4.2 is presented in the following lemma. From now on, we work simultaneously in the Bulk and the Crossover regimes.

Lemma 7.3

Linear growth/decay of the diffusions $\rho _{\lambda }^{(\mathbf{E})}$ and $\overline{\rho}_{\lambda }^{(\mathbf{E})}$

Set $Z_{\lambda }^{(\mathbf{E})}(t) := \rho _{\lambda }^{(\mathbf{E})}(t) - \nu _{\lambda }^{(\mathbf{E})} t$ and $\bar{Z}_{\lambda }^{(\mathbf{E})}(t) := \bar{\rho}_{\lambda }^{( \mathbf{E})}(t) + \nu _{\lambda }^{(\mathbf{E})} t$. For any $\varepsilon > 0$, there exists $q>0$ such that

$$ {\limsup _{L\to \infty }} \sup _{\lambda \in \Delta} \sup _{\theta \in [0,\pi )} \mathbb{E}_{(0,\theta )}\Big[ \sup _{t \ge 0} e^{q |Z_{\lambda }^{(\mathbf{E})}(t)|} e^{-qt\varepsilon } \Big] < \infty \;, $$

and

$$ {\limsup _{L\to \infty }} \sup _{\lambda \in \Delta} \sup _{\theta \in [0,\pi )} \bar{\mathbb{E}}_{(0,\theta )}\Big[ \sup _{t \ge 0} e^{q |\bar{Z}_{\lambda }^{(\mathbf{E})}(t)|} e^{-qt \varepsilon }\Big] < \infty \;. $$

Proof

We present the proof in details for $Z_{\lambda }^{(\mathbf{E})}$, then we make a comment on how to treat $\bar{Z}_{\lambda }^{(\mathbf{E})}$. Let $n := \lfloor \mathbf{E}^{3/2} \rfloor$. Let $0 =:T_{0} < T_{1} <\cdots$ be the stopping times defined by

$$ T_{k} := \inf \{t>T_{k-1}: \theta _{\lambda }^{(\mathbf{E})}(t) = \theta _{\lambda }^{(\mathbf{E})}(T_{k-1})+n\pi \}\;. $$

The r.v. $T_{k}$ is equal in law to the sum of $kn$ i.i.d. r.v. distributed as $\zeta _{\lambda }^{(\mathbf{E})}$. We then define the i.i.d. r.v.

$$ G_{k} : = Z_{\lambda }^{(\mathbf{E})}(T_{k}) - Z_{\lambda }^{( \mathbf{E})}(T_{k-1})\;,\quad k\ge 1\;. $$

Decomposing $Z_{\lambda }^{(\mathbf{E})}(T_{k}) - Z_{\lambda }^{(\mathbf{E})}(T_{k-1})$ into the sum of the increments of $Z_{\lambda }^{(\mathbf{E})}$ in between the successive hitting times of $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ by the phase $\theta _{\lambda }^{(\mathbf{E})}$, we see that $\mathbb{E}[G_{k}] = 0$ by Proposition 7.2. Introduce also

$$ Y_{k} := \sup _{t\in [T_{k-1},T_{k}]} |Z_{\lambda }^{(\mathbf{E})}(t)-Z_{ \lambda }^{(\mathbf{E})}(T_{k-1})|\;,\quad k\ge 1\;. $$

We have for any $q\ge 0$

$$\begin{aligned} \sup _{t\ge 0} e^{q {Z}_{\lambda }^{(\mathbf{E})}(t)} e^{-qt \varepsilon } &\le \sum _{k\ge 0} e^{q(G_{1}+\cdots +G_{k})} e^{q Y_{k+1}} e^{-q T_{k} \varepsilon } \\ \sup _{t\ge 0} e^{-q {Z}_{\lambda }^{(\mathbf{E})}(t)} e^{-qt \varepsilon } &\le \sum _{k\ge 0} e^{-q(G_{1}+\cdots +G_{k})} e^{q Y_{k+1}} e^{-q T_{k} \varepsilon }\;. \end{aligned}$$

We aim at bounding the expectations of the two r.v. on the left hand side. By symmetry of the arguments, we only present the details on the bound of the first term. Using the Cauchy-Schwarz inequality twice and the fact that the $Y_{k}$’s, the $G_{k}$’s and the $(T_{k}-T_{k-1})$’s are i.i.d., we have for every $k\ge 0$

$$ \mathbb{E}[e^{q(G_{1}+\cdots +G_{k})} e^{q Y_{k+1}} e^{-q T_{k} \varepsilon }] \le \mathbb{E}[e^{4qG_{1}}]^{k/4} \mathbb{E}[e^{-4q T_{1} \varepsilon }]^{k/4} \mathbb{E}[e^{2q Y_{1}}]^{1/2}\;.$$

(60)

Assume that there exist $C_{0} > 0$ and $q_{0} > 0$ such that for all $L>1$, all $\lambda \in \Delta$ and all $q \in [-q_{0},q_{0}]$ we have

$$ \mathbb{E}[e^{q Y_{1}}] < C_{0}\;,\quad \mathbb{E}[e^{q T_{1}}] < C_{0} \;. $$

Note that $|G_{1}| \le Y_{1}$ almost surely. Note also that $\mathbb{E}[T_{1}]=n m_{\lambda }^{(\mathbf{E})}$ and recall $\mathbb{E}[G_{1}] = 0$. By Lemma A.1 we deduce that there exist $C_{1},q_{1} > 0$ such that the r.h.s. of (60) is bounded by

$$ (1+ 16C_{1} q^{2})^{k/4} (1-4q\varepsilon n m_{\lambda }^{(\mathbf{E})} + 16C_{1} q^{2} \varepsilon ^{2})^{k/4} {C_{0}^{1/2}}\;, $$

for all $q \in (0,q_{1})$. Recall from (59) that $m_{\lambda }^{(\mathbf{E})} \asymp \mathbf{E}^{-3/2}$ so that $nm_{\lambda }^{(\mathbf{E})}$ is bounded from below by a positive constant uniformly over all parameters. Recall also that $\varepsilon$ is fixed. We deduce that by choosing $q$ small enough, the last term is bounded by $C \eta ^{k}$ for some constants $C>0$ and $\eta \in (0,1)$. Summing this term over $k\ge 0$, we get the desired upper bound.

It remains to prove the exponential bounds on the non-negative r.v. $Y_{1}$ and $T_{1}$. Regarding $T_{1}$, we use Lemma A.3 to deduce that for $q > 0$ small enough we have

$$ \mathbb{E}[e^{q T_{1}}] = \mathbb{E}[e^{q \zeta _{\lambda}^{( \mathbf{E})}}]^{n} \le \Big(\frac{1}{1-qm_{\lambda }^{(\mathbf{E})}} \Big)^{n}=e^{-n\log (1-qm_{\lambda }^{(\mathbf{E})})}\;. $$

Since $nm_{\lambda }^{(\mathbf{E})}$ is of order 1, this suffices to conclude. We turn to $Y_{1}$. For any $x,T>0$ we have

$$ \mathbb{P}(Y_{1} > x) \le \mathbb{P}(T_{1} > T) + \mathbb{P}(\sup _{t \in [0,T]} |Z_{\lambda }^{(\mathbf{E})}(t)| > x)\;. $$

The first term on the r.h.s decays exponentially in $T$ by the exponential bound already obtained. The second term decays exponentially in $x^{2}/T$ by Lemma A.2 as soon as $x$ is large enough. Adjusting $T$ and $x$, we easily obtain an exponential decay in $x$ uniformly over all parameters, thus concluding the proof.

These arguments apply verbatim to $\bar{Z}_{\lambda }^{(\mathbf{E})}$. The only specific points are the last bounds on the exponential moments. Regarding $T_{1}$ the argument is exactly the same since $\bar{\zeta}_{\lambda }^{(\mathbf{E})}$ has the same law as $\zeta _{\lambda }^{(\mathbf{E})}$. Regarding $Y_{1}$, the only ingredient used for the exponential bound is the uniform boundedness of the coefficients of the SDE solved by $Z_{\lambda }^{(\mathbf{E})}$, and this remains true for $\bar{Z}_{\lambda }^{(\mathbf{E})}$. □

7.3 Proof of Proposition 4.2

By analogy with $G_{u}$, let us introduce the observable:

$$ H_{u}(\lambda ,\varphi ,\psi ) := \frac{1}{(\int \varphi ^{2}(s) ds)^{1/2}}\sup _{t\in [- \frac{L}{2\mathbf{E}},\frac{L}{2\mathbf{E}}]} \Big(\varphi ^{2}(t) + \frac{\psi ^{2}(t)}{\mathbf{E}^{3}}\Big)^{1/2} e^{\frac{1}{2}(\nu _{ \lambda }^{(\mathbf{E})} - \varepsilon ) |t-u|}\;. $$

Set $H = \inf _{u\in [-\frac{L}{2\mathbf{E}},\frac{L}{2\mathbf{E}}]} H_{u}$. By the GMP formula given in Proposition 4.1, it suffices to bound

$$\begin{aligned} &\sqrt {\mathbf{E}}\int _{u=-\frac{L}{2\mathbf{E}}}^{ \frac{L}{2\mathbf{E}}} \int _{\lambda \in \Delta} \int _{\theta =0}^{ \pi }p_{\lambda ,u+\frac{L}{2\mathbf{E}}}^{(\mathbf{E})}(\theta ) p_{ \lambda ,\frac{L}{2\mathbf{E}}-u}^{(\mathbf{E})}(\pi -\theta )\sin ^{2} \theta \\ &\qquad {}\times \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\Big(H\big( \lambda ,\hat{y}_{\lambda }^{(\mathbf{E})}, (\hat{y}_{\lambda }^{( \mathbf{E})})'\big)\Big)^{q}\Big] \, d\theta d\lambda du \\ &\quad \le\sqrt {\mathbf{E}}\int _{u=-\frac{L}{2\mathbf{E}}}^{ \frac{L}{2\mathbf{E}}} \int _{\lambda \in \Delta} \int _{\theta =0}^{ \pi }p_{\lambda ,u+\frac{L}{2\mathbf{E}}}^{(\mathbf{E})}(\theta ) p_{ \lambda ,\frac{L}{2\mathbf{E}}-u}^{(\mathbf{E})}(\pi -\theta )\sin ^{2} \theta \\ &\qquad {}\times \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\Big(H_{u}\big( \lambda ,\hat{y}_{\lambda }^{(\mathbf{E})}, (\hat{y}_{\lambda }^{( \mathbf{E})})'\big)\Big)^{q}\Big] \, d\theta d\lambda du\;. \end{aligned}$$

Note that at the second line, we have bounded $H$ by $H_{u}$ where $u$ is the concatenation time.

Under $\mathbb{P}^{(u)}_{\theta ,\pi -\theta}$ we have

$$\begin{aligned} H_{u}(\lambda ,\hat{y}_{\lambda }^{(\mathbf{E})}, (\hat{y}_{\lambda }^{( \mathbf{E})})') = \|\hat{y}_{\lambda }^{(\mathbf{E})}\|_{2}^{-1} \sup _{t\in [-\frac{L}{2\mathbf{E}},\frac{L}{2\mathbf{E}}]} \hat{r}_{ \lambda }^{(\mathbf{E})}(t) e^{\frac{1}{2}(\nu _{\lambda }^{( \mathbf{E})} - \varepsilon ) |t-u|}\;. \end{aligned}$$

(61)

The Lebesgue measure of $\Delta$ is $2h/(n(E)L) \asymp \sqrt {\mathbf{E}}/L$. Consequently, it suffices to show that

$$\begin{aligned} \int _{\theta =0}^{\pi }p_{\lambda ,u+\frac{L}{2\mathbf{E}}}^{( \mathbf{E})}(\theta ) p_{\lambda ,\frac{L}{2\mathbf{E}}-u}^{( \mathbf{E})}(\pi -\theta )\sin ^{2} \theta \;\mathbb{E}^{(u)}_{ \theta ,\pi -\theta}\Big[\Big(H_{u}\big(\lambda ,\hat{y}_{\lambda }^{( \mathbf{E})}, (\hat{y}_{\lambda }^{(\mathbf{E})})'\big)\Big)^{q}\Big] \, d\theta \end{aligned}$$

(62)

is bounded by some constant uniformly over all $u\in [-L/(2\mathbf{E}),L/2\mathbf{E}]$ and all $\lambda \in \Delta$.

By the Cauchy-Schwarz inequality and the bound $\sqrt{x} \le 1+x$ for any $x\ge 0$, we have

$$\begin{aligned} &\mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\Big(H_{u}\big(\lambda , \hat{y}_{\lambda }^{(\mathbf{E})}, (\hat{y}_{\lambda }^{(\mathbf{E})})' \big)\Big)^{q}\Big] \\ &\quad \le \Big(1+\mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\sup _{t\in [- \frac{L}{2\mathbf{E}},\frac{L}{2\mathbf{E}}]} \hat{r}_{\lambda }^{( \mathbf{E})}(t)^{2q} \exp \big(q(\nu _{\lambda }^{(\mathbf{E})} - \varepsilon ) |t-u|\big)\Big]\Big) \\ &\qquad {}\mathbb{E}^{(u)}_{\theta ,\pi - \theta}\Big[\|\hat{y}_{\lambda }^{(\mathbf{E})}\|_{2}^{-2q}\Big]^{1/2} \;. \end{aligned}$$

By Theorem 4, for all $L$ large enough the term

$$ \int _{\theta =0}^{\pi }p_{\lambda ,u+\frac{L}{2\mathbf{E}}}^{( \mathbf{E})}(\theta ) p_{\lambda ,\frac{L}{2\mathbf{E}}-u}^{( \mathbf{E})}(\pi -\theta )\sin ^{2} \theta d\theta \;, $$

is bounded by some constant uniformly over all parameters. To conclude, it therefore suffices to prove that for all $L$ large enough (for a different choice of $q$)

$$\begin{aligned} &\int _{0}^{\pi }p_{\lambda ,u+\frac{L}{2\mathbf{E}}}^{(\mathbf{E})}( \theta ) p_{\lambda ,\frac{L}{2\mathbf{E}}-u}^{(\mathbf{E})}(\pi - \theta )\sin ^{2} \theta \\ &\quad {}\times \mathbb{E}^{(u)}_{\theta ,\pi -\theta} \Big[\sup _{t\in [-\frac{L}{2\mathbf{E}},\frac{L}{2\mathbf{E}}]} \hat{r}_{\lambda }^{(\mathbf{E})}(t)^{q} \exp \big(\frac{q}{2}(\nu _{ \lambda }^{(\mathbf{E})} - \varepsilon ) |t-u|\big)\Big] \, d\theta \,, \end{aligned}$$

(63)

and

$$\begin{aligned} \sup _{\theta} \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\|\hat{y}_{ \lambda }^{(\mathbf{E})}\|_{2}^{-q}\Big]\;, \end{aligned}$$

(64)

are bounded by some constant uniformly over all $u$ and $\lambda$.

We aim at applying the estimates of Lemma 7.3. The difficulty is twofold. First, the estimates in the lemma concern unconditioned processes while in (63) we have (a concatenation of) conditioned processes. Second, in (63) the process $\hat{r}^{(\mathbf{E})}_{\lambda }$ is set to 1 at $u$ so we have to be careful with this normalisation in the bounds.

To deal with conditioned processes, we use our estimates on the convergence to equilibrium of the diffusions to prove the following.

Lemma 7.4

Absolute continuity of the bridges

There exists $t_{0}\ge 1$, a constant $C>0$ and $L_{0}\ge 1$ such that for all $L\ge L_{0}$, for all $\lambda \in \Delta$, $t>0$, $\theta \in [0,\pi )$ and for all events $A$ that depend on $\theta ^{(\mathbf{E})}_{\lambda }(s), s\in [0,t]$ we have

$$ \sup _{\theta '}\mathbb{P}_{(0,\theta ) \to (t+t_{0},\theta ')}(A) \le C\,\mathbb{P}_{(0,\theta )}(A)\;, $$

and

$$ \sup _{\theta '}\bar{\mathbb{P}}_{(0,\theta ) \to (t+t_{0},\theta ')}(A) \le C\,\bar{\mathbb{P}}_{(0,\theta )}(A)\;. $$

In addition, as $t_{0}\to \infty$ we have

$$ \begin{aligned}\mathbb{P}_{(0,\theta ) \to (t+t_{0},\theta ')}(A) &= (1+o(1)) \mathbb{P}_{(0,\theta )}(A)\;, \\ \bar{\mathbb{P}}_{(0,\theta ) \to (t+t_{0},\theta ')}(A) &= (1+o(1)) \bar{\mathbb{P}}_{(0,\theta )}(A) \;, \end{aligned}$$

uniformly over all $\theta ,\theta ' \in [0,\pi ]$, all $\lambda \in \Delta$ and all events $A$ as above.

Proof

The proof is identical for $\theta _{\lambda }^{(\mathbf{E})}$ and $\bar{\theta}_{\lambda }^{(\mathbf{E})}$ so we restrict to the former. For any given $t>0$ and for any event $A$ that only depends on the trajectory of $\theta _{\lambda }^{(\mathbf{E})}(s)$ for $s\in [0,t]$, by the Markov property we have

$$\begin{aligned} \mathbb{P}_{(0,\theta ) \to (t+t_{0},\theta ')}(A) &= \lim _{\delta \downarrow 0} \frac{\mathbb{E}_{(0,\theta )}\big[\mathbf{1}_{A} \mathbb{P}_{(0,\theta _{\lambda }^{(\mathbf{E})}(t))}(\theta _{\lambda }^{(\mathbf{E})}(t_{0}) \in [\theta '-\delta ,\theta '+\delta ])\big]}{\mathbb{P}_{(0,\theta )}(\theta _{\lambda }^{(\mathbf{E})}(t+t_{0}) \in [\theta '-\delta ,\theta '+\delta ])} \\ &= \lim _{\delta \downarrow 0} \frac{ \mathbb{E}_{(0,\theta )}\big[\mathbf{1}_{A} \Big( 1 + \frac{\mathbb{P}_{(0,\theta _{\lambda }^{(\mathbf{E})}(t))}(\theta _{\lambda }^{(\mathbf{E})}(t_{0}) \in [\theta '-\delta ,\theta '+\delta ])-\mu _{\lambda }^{(\mathbf{E})}(\theta ')}{\mu _{\lambda }^{(\mathbf{E})}(\theta ')}\Big)\big]}{\Big( 1 + \frac{\mathbb{P}_{(0,\theta )}(\theta _{\lambda }^{(\mathbf{E})}(t+t_{0}) \in [\theta '-\delta ,\theta '+\delta ])-\mu _{\lambda }^{(\mathbf{E})}(\theta ')}{\mu _{\lambda }^{(\mathbf{E})}(\theta ')}\Big)} \;. \end{aligned}$$

By Theorem 4 and Lemma 3.1 the quantity

$$ \sup _{\lambda \in \Delta }\sup _{\theta _{0},\theta \in [0,\pi ]} \frac{|p_{\lambda ,t}^{(\mathbf{E})}(\theta _{0},\theta ) - \mu _{\lambda }^{(\mathbf{E})}(\theta )|}{\mu _{\lambda }^{(\mathbf{E})}(\theta )} \;,$$

(65)

is finite for all $t_{0}\ge 1$ and converges to 0 as $t_{0}\to \infty$. This suffices to conclude. □

Let us now bound (64). By symmetry, we restrict to $u\in [-\frac{L}{2\mathbf{E}},0]$. For all $L$ large enough, we have $u+1 < L/(2\mathbf{E})$ and thus

$$\begin{aligned} \mathbb{E}^{(u)}_{\theta ,\pi -\theta}[\|\hat{y}_{\lambda }^{( \mathbf{E})}\|_{2}^{-q}] &\le \mathbb{E}^{(u)}_{\theta ,\pi -\theta} \Big[\Big(\int _{u}^{u+1} (\hat{y}_{\lambda }^{(\mathbf{E})}(t))^{2} dt \Big)^{-q/2}\Big]\;. \end{aligned}$$

This expression only involves the backward diffusion. Using (56) this last term equals

$$ \frac{\mu _{\lambda }^{(\mathbf{E})}(\pi -\theta )\bar{p}_{\lambda ,\frac{L}{2\mathbf{E}} -u}^{(\mathbf{E})}(\pi -\theta ,0)}{\mu _{\lambda }^{(\mathbf{E})}(0){p}_{\lambda ,\frac{L}{2\mathbf{E}} -u}^{(\mathbf{E})}(0,\pi -\theta )} \; \bar{\mathbb{E}}_{(0,\pi -\theta )\to (\frac{L}{2\mathbf{E}} -u,0)} \Big[\Big(\int _{0}^{1} (\bar{y}_{\lambda }^{(\mathbf{E})}(t))^{2} dt \Big)^{-q/2}\Big]\;, $$

with $\bar{r}_{\lambda }^{(\mathbf{E})}(0)=1$ (recall that $\hat{r}_{\lambda }^{(\mathbf{E})}(u)=1$). By Theorem 4 and Lemma 3.1, the prefactor is bounded by a constant uniformly over all parameters. By Lemma 7.4 the expectation can be bounded by a constant times

$$\begin{aligned} \bar{\mathbb{E}}_{\pi -\theta}\Big[\Big(\inf _{t\in [0,1]} \bar{r}_{ \lambda }^{(\mathbf{E})}(t)\Big)^{-2q}\Big]^{1/2}\; \bar{\mathbb{E}}_{ \pi -\theta}\Big[\Big(\int _{0}^{1} \sin ^{2} \bar{\theta}_{\lambda }^{( \mathbf{E})}(t) dt\Big)^{-q}\Big]^{1/2}\;. \end{aligned}$$

To bound the first term we apply Lemma 7.3. To bound the second term we use Lemma A.6.

We turn to (63), which is more involved. Let us denote by $\tilde{u} := u+L/(2\mathbf{E})$ the distance of $u$ to the left boundary of the interval and $\tilde{v} := -u + L/(2\mathbf{E})$ the distance to the right boundary. By symmetry, it suffices to bound

$$\begin{aligned} &\int _{0}^{\pi }p_{\lambda ,\tilde{u}}^{(\mathbf{E})}(\theta ) p_{ \lambda ,\tilde{v}}^{(\mathbf{E})}(\pi -\theta )\sin ^{2} \theta \\ &\quad {} \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[\sup _{t\in [- \frac{L}{2\mathbf{E}},u]} \hat{r}_{\lambda }^{(\mathbf{E})}(t)^{q} \exp \big(\frac{q}{2}(\nu _{\lambda }^{(\mathbf{E})} - \varepsilon ) |t-u| \big)\Big] \, d\theta \;. \end{aligned}$$

This expression only involves the forward diffusion. By shifting time appropriately, it rewrites

$$\begin{aligned} &\int _{0}^{\pi }p_{\lambda ,\tilde{u}}^{(\mathbf{E})}(\theta ) p_{ \lambda ,\tilde{v}}^{(\mathbf{E})}(\pi -\theta )\sin ^{2} \theta \\ &\quad {}\times \mathbb{E}_{(0,0)\to (\tilde{u},\theta )}\Big[\sup _{t\in [0, \tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})} \Big)^{q} \exp \big(\frac{q}{2}(\nu _{\lambda }^{(\mathbf{E})} - \varepsilon ) |t-\tilde{u}|\big)\Big] \, d\theta \;, \end{aligned}$$

with $r_{\lambda }^{(\mathbf{E})}(0)=1$. Let us take $t_{0}$ from Lemma 7.4. We distinguish two cases according to the relative values of $\tilde{u}$ and $3t_{0}$.

Assume $\tilde{u} \leq 3t_{0}$. Theorem 4 and Lemma 3.1 allow to bound $p_{\lambda ,\tilde{v}}^{(\mathbf{E})}(\pi -\theta )$ by a constant. Bounding $\sin ^{2}\theta$ by one, and integrating in $\theta$, we see that it suffices to bound:

$$\begin{aligned} \mathbb{E}_{(0,0)}\Big[\sup _{t\in [0,\tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})} \Big)^{q} \exp \big(\frac{q}{2}(\nu _{\lambda }^{(\mathbf{E})} - \varepsilon ) |t-\tilde{u}|\big)\Big]\,, \end{aligned}$$

which is itself bounded thanks to Lemma 7.3.

Assume $\tilde{u} > 3t_{0}$. It suffices to bound (uniformly over all the parameters):

$$\begin{aligned} \mathbb{E}_{(0,0) \to (\tilde{u},\theta )}\Big[\sup _{t\in [0,\tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2}(\nu _{\lambda }^{(\mathbf{E})}-\varepsilon )|t-\tilde{u}|} \Big)^{q}\Big]\,. \end{aligned}$$

(66)

Indeed, either $\tilde{v} > 3t_{0}$ and then we bound $p_{\lambda ,\tilde{u}}^{(\mathbf{E})}(\theta ) p_{\lambda ,\tilde{v}}^{( \mathbf{E})}(\pi -\theta )$ using Theorem 4 and Lemma 3.1; or $\tilde{v} \leq 3 t_{0}$ and then we apply the same arguments to bound $p_{\lambda ,\tilde{u}}(\theta )$ while we integrate over $\theta$ the term $p_{\lambda ,\tilde{v}}(\pi - \theta )$. To bound (66), we split the supremum into two parts:

• For the supremum over $t\in [2t_{0}, \tilde{u}]$, we use the adjoint diffusion and the identity (56) so that it suffices to bound

  $$ \bar{\mathbb{E}}_{(0,\theta ) \to (\tilde{u},0)}\Big[\sup _{t\in [0, \tilde{u}-2t_{0}]} \Big(\bar{r}_{\lambda }^{(\mathbf{E})}(t) e^{ \frac{1}{2}(\nu _{\lambda }^{(\mathbf{E})}-\varepsilon )t}\Big)^{q} \Big]\;, $$

  with $\bar{r}_{\lambda }^{(\mathbf{E})}(0)=1$. Using Lemma 7.4, the latter is bounded from above by a constant times

  $$ \bar{\mathbb{E}}_{(0,\theta )}\Big[\sup _{t\in [0,\tilde{u}-2t_{0}]} \Big(\bar{r}_{\lambda }^{(\mathbf{E})}(t) e^{\frac{1}{2}(\nu _{ \lambda }^{(\mathbf{E})}-\varepsilon )t}\Big)^{q}\Big]\;, $$

  and we can then apply Lemma 7.3.

• For the supremum over $t\in [0,2t_{0}]$, we write

  $$\begin{aligned} \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2}(\nu _{\lambda }^{(\mathbf{E})}-\varepsilon )(\tilde{u}-t)} = e^{\frac{1}{2}(Z_{\lambda }^{(\mathbf{E})}(t) - Z_{\lambda }^{( \mathbf{E})}(2t_{0}) -\varepsilon (2t_{0}-t))} e^{\frac{1}{2}(Z_{ \lambda }^{(\mathbf{E})}(2t_{0}) - Z_{\lambda }^{(\mathbf{E})}( \tilde{u}) -\varepsilon (\tilde{u}-2t_{0}))}\;. \end{aligned}$$

  Using the Cauchy-Schwarz inequality we thus find

  $$\begin{aligned} &\mathbb{E}_{(0,0) \to (\tilde{u},\theta )}\bigg[\sup _{t\in [0,2t_{0}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2}(\nu _{\lambda }^{(\mathbf{E})}-\varepsilon )|t-\tilde{u}|} \Big)^{q}\bigg] \\ \le \;& \mathbb{E}_{(0,0) \to (\tilde{u},\theta )}\Big[\sup _{t\in [0,2t_{0}]} e^{q(Z_{\lambda }^{(\mathbf{E})}(t) - Z_{\lambda }^{(\mathbf{E})}(2t_{0}) -\varepsilon (2t_{0}-t))}\Big]^{1/2} \\ &\qquad \times \mathbb{E}_{(0,0) \to (\tilde{u},\theta )}\Big[e^{q(Z_{ \lambda }^{(\mathbf{E})}(2t_{0}) - Z_{\lambda }^{(\mathbf{E})}( \tilde{u}) -\varepsilon (\tilde{u}-2t_{0}))}\Big]^{1/2}\;. \end{aligned}$$

  The second expectation on the r.h.s. can be bounded using the adjoint diffusion as above. By Lemma 7.4, the first expectation is bounded by a constant times

  $$ \mathbb{E}_{(0,0)}\Big[\sup _{t\in [0,2t_{0}]}e^{q(Z_{\lambda }^{( \mathbf{E})}(t) - Z_{\lambda }^{(\mathbf{E})}(2t_{0}) -\varepsilon (2t_{0}-t))} \Big]\;, $$

  which is itself bounded by a constant by Lemma 7.3.

This concludes the proof of Proposition 4.2.

8 Fine estimates on the diffusion

Set $\Delta := [E- h/(Ln(E)),E+h/(Ln(E))]$. In this section, we concentrate on the r.v. $N_{L}(\Delta )$ and $N_{L}^{(j)}(\Delta )$ and establish Propositions 4.4 and 4.5. To simplify the notation, we work on the interval $[0,L/\mathbf{E}]$ instead of $[-L/(2 \mathbf{E}),L/(2\mathbf{E})]$ since our arguments will only rely on diffusions going forward in time. As a consequence, in this whole section, the diffusion $\theta _{\lambda }^{(\mathbf{E})}$ starts from 0 or sometimes some value $\theta _{0}$ at time 0 and live on the interval of time $[0,L/\mathbf{E}]$.

Recall that $k=k(L)$ is the number of disjoint boxes $(t_{j-1},t_{j})$ into which the interval $(-L/2,L/2)$ is subdivided. All the results of this section hold true provided $k\to \infty$ slowly enough: within the proofs, various constraints will arise on this speed.

8.1 A thorough study of a joint diffusion

The whole discussion revolves around a thorough study of the joint diffusion $(\theta _{\lambda }^{(\mathbf{E})},\theta _{\mu}^{(\mathbf{E})})$ where $[\lambda ,\mu ] := \Delta$. Actually, it is more convenient to deal with $(\theta _{\lambda }^{(\mathbf{E})},\alpha )$ where

$$ \alpha (t) := \theta _{\mu}^{(\mathbf{E})}(t)-\theta _{\lambda }^{( \mathbf{E})}(t)\;,\quad t\ge 0\;. $$

Let us collect a few facts about this pair of processes.

Lemma 8.1

$(\{\alpha \}_{\pi }, \{\theta _{\lambda }\}_{\pi })$ is a Markov process. In addition, the process $t\mapsto \lfloor \alpha (t) \rfloor _{\pi }$ is non-decreasing.

Proof

Recall that $(\{\theta _{\mu }^{(\mathbf{E})}\}_{\pi },\{\theta _{\lambda }^{( \mathbf{E})}\}_{\pi })$ is a Markov process. Since $(\{\alpha \}_{\pi }, \{\theta _{\lambda }\}_{\pi })$ is the image of the latter through a bijection, we deduce the first property. For the second property, suppose that $\alpha (t) = k\pi$. Then $\theta ^{(\mathbf{E})}_{\mu }(t) = \theta ^{(\mathbf{E})}_{\lambda }(t) + k\pi$ and from the SDEs (11) we deduce that $d\alpha (t) = d(\theta ^{(\mathbf{E})}_{\mu }- \theta ^{(\mathbf{E})}_{ \lambda })(t) \geq 0$. □

Let us take $\theta _{\lambda }^{(\mathbf{E})}(0) = \theta _{\mu }^{(\mathbf{E})}(0) = 0$. Since we shifted the interval $[-L/(2\mathbf{E}), L/(2\mathbf{E})]$ to $[0,L/\mathbf{E}]$, the number of eigenvalues of $\mathcal{H}_{L}$ in the interval $[\lambda ,\mu ]$ is given by $N_{L}(\Delta ) = \lfloor \theta _{\mu}^{(\mathbf{E})}(L/\mathbf{E}) \rfloor _{\pi }- \lfloor \theta _{\lambda }^{(\mathbf{E})}(L/ \mathbf{E})\rfloor _{\pi}$. As this quantity is not very tractable, we instead look at $\lfloor \alpha (L/\mathbf{E})\rfloor _{\pi}$ but we need to argue that it is a faithful approximation of the former.

Since $x = \lfloor x \rfloor _{\pi }\pi +\{x\}_{\pi}$, we have the identity

$$ \alpha (L/\mathbf{E}) = N_{L}(\Delta )\pi + \{\theta _{\mu}^{( \mathbf{E})}(L/\mathbf{E})\}_{\pi }- \{\theta _{\lambda }^{( \mathbf{E})}(L/\mathbf{E})\}_{\pi}\;, $$

(67)

from which one deduces the following simple inequalities

$$ N_{L}(\Delta ) - 1 \le \lfloor {\alpha (L/\mathbf{E})} \rfloor _{\pi } \le N_{L}(\Delta )\;. $$

(68)

We define the length of the successive excursions of $\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi }$ as

$$ \zeta ^{(0)} := 0,\quad \zeta ^{(i)} := \inf \{t\ge 0: \theta _{ \lambda }^{(\mathbf{E})}(\zeta ^{(1)} + \cdots + \zeta ^{(i-1)}+t) = i \pi \} \text{ for }i \geq 1\;.$$

(69)

We introduce the analogous stopping times for $\alpha$, namely

$$ \tau ^{(0)} := 0,\quad \tau ^{(i)} := \inf \{t\ge 0: \alpha (\tau ^{(1)} + \cdots + \tau ^{(i-1)}+t) = i\pi \} \text{ for }i \geq 1\;. $$

At this point, let us observe that the $\zeta ^{(i)}$ are typically of order $\mathbf{E}^{-3/2}$ since their expectation equals $m_{\lambda }^{(\mathbf{E})}$. On the other hand, the $\tau ^{(i)}$ should typically be of order $L/\mathbf{E}$ since the number of eigenvalues in $\Delta$ is of order 1. This illustrates that the two processes $\theta _{\lambda }^{(\mathbf{E})}$ and $\alpha$ do not evolve at all on the same time-scale. It is also important to note that the $\tau ^{(i)}$’s are not i.i.d. since they are coupled by the values of the diffusion $\theta _{\lambda }^{(\mathbf{E})}$ at the times $\sum _{j=1}^{i-1} \tau ^{(j)}$’s.

To circumvent this difficulty, we show that the $\tau ^{(i)}$’s are stochastically larger than a sequence of i.i.d. r.v. whose law is almost the law of $\tau ^{(1)}$: this is the content of the next lemma, on which the rest of our arguments rely.

Lemma 8.2

Stochastic lower bound of the hitting times $\tau ^{(i)}$

Let $(\tilde{\tau}^{(i)},\tilde{\zeta}^{(i)})_{i\ge 1}$ be a sequence of i.i.d. r.v. such that each $(\tilde{\tau}^{(i)},\tilde{\zeta}^{(i)})$ has the law of $(\tau ^{(1)},\zeta ^{(1)})$. Then the sequence $(\tau ^{(i)})_{i\ge 1}$ is stochastically larger than the sequence $((\tilde{\tau}^{(i)} - \tilde{\zeta}^{(i)})_{+})_{i\ge 1}$, that is, for any $n\ge 1$ and any bounded and non-decreasing function $f:{{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}^{n}\to {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{ \textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$, we have

$$ \mathbb{E}[f(\tau ^{(1)},\ldots ,\tau ^{(n)})] \ge \mathbb{E}[f(( \tilde{\tau}^{(1)} - \tilde{\zeta}^{(1)})_{+},\ldots ,(\tilde{\tau}^{(n)} - \tilde{\zeta}^{(n)})_{+})]\;. $$

Proof

Define $X_{0} = 0$ and for every $i\ge 1$

$$ X_{i}:= \{\theta _{\lambda }^{(\mathbf{E})}(\tau ^{(1)}+\cdots +\tau ^{(i)}) \}_{\pi}\;. $$

The strong Markov property implies that the conditional law of $\tau ^{(i)}$ given $\mathcal{F}_{\tau ^{(1)} + \cdots +\tau ^{(i-1)}}$ is $\nu _{X_{i-1}}$, where $\nu _{x}$ is the law of $\tau ^{(1)}$ given $(\theta _{\lambda }^{(\mathbf{E})}(0),\alpha (0)) = (x,0)$. For any bounded and non-decreasing function $f:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}^{n}\to {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ we thus have

$$ \mathbb{E}\big[f(\tau ^{(1)},\ldots ,\tau ^{(n)}) \,|\, \mathcal{F}_{ \tau ^{(1)} + \cdots +\tau ^{(n-1)}}\big] = F(\tau ^{(1)},\ldots , \tau ^{(n-1)}, X_{n-1})\;, $$

where

$$ F(v_{1},\ldots ,v_{n-1},x_{n-1}) = \int _{y} f(v_{1},\ldots ,v_{n-1},y) \nu _{x_{n-1}}(dy)\;. $$

Let $\tilde{\nu}$ be the law of $(\tilde{\tau}^{(1)} - \tilde{\zeta}^{(1)})_{+}$. We claim that for every $x\in [0,\pi )$, $\nu _{x}$ is larger⁹ than $\tilde{\nu}$. We deduce that

$$ F(v_{1},\ldots ,v_{n-1},x_{n-1}) \ge G(v_{1},\ldots ,v_{n-1}) := \int _{y} f(v_{1},\ldots ,v_{n-1},y) \tilde{\nu}(dy)\;. $$

Note that $G$ is bounded and non-decreasing so that a simple recursion yields

$$ \begin{aligned}\mathbb{E}\big[f(\tau ^{(1)},\ldots ,\tau ^{(n)})] &\ge \int f(y_{1}, \ldots ,y_{n}) \tilde{\nu}(dy_{1})\ldots \tilde{\nu}(dy_{n}) \\ &=\mathbb{E}[f((\tilde{\tau }^{(1)} - \tilde{\zeta }^{(1)})_{+}, \ldots ,(\tilde{\tau }^{(n)} - \tilde{\zeta }^{(n)})_{+})]\;. \end{aligned}$$

To prove the claim, we fix $x\in [0,\pi )$ and we consider the process $(\theta _{\lambda }^{(\mathbf{E})},\alpha )$ starting from $(x,0)$ and driven by the Brownian motion $B$: the law of the associated r.v. $\tau ^{(1)}$ is therefore $\nu _{x}$. We consider an independent Brownian motion $\tilde{B}$ and we build a diffusion $(\tilde{\theta}_{\lambda },\tilde{\alpha})$ starting from $(0,0)$ as follows: up to the stopping time $S_{x}:= \inf \{t\ge 0: \tilde{\theta}_{\lambda }(t) = x\}$, the diffusion $(\tilde{\theta}_{\lambda },\tilde{\alpha})$ is driven by $\tilde{B}$; at any time $t\ge S_{x}$, the diffusion is driven by $B(t-S_{x})$. Consequently $\tilde{\theta}_{\lambda }(S_{x}+t) = \theta ^{(\mathbf{E})}_{ \lambda }(t)$ for all $t\ge 0$. We claim that for all $t \geq 0$, $\tilde{\alpha}(t+S_{x}) \geq \alpha (t)$. Indeed $\tilde{\alpha}(t+S_{x})+\theta _{\lambda }^{(\mathbf{E})}(t)$ and $\alpha (t) + \theta _{\lambda }^{(\mathbf{E})}(t)$ follow the same SDE (namely: the SDE satisfied by $\theta _{\mu }^{(\mathbf{E})}$) but start from ordered initial conditions and therefore remain ordered.

Thus we have almost surely

$$ (\tilde{\tau}^{(1)} - S_{\pi})_{+} \le (\tilde{\tau}^{(1)} - S_{x})_{+} \le {\tau}^{(1)}\;. $$

Since $S_{\pi}=\tilde{\zeta}^{(1)}$, we deduce that $(\tilde{\tau}^{(1)} - \tilde{\zeta}^{(1)})_{+}$ is stochastically lower than $\tau ^{(1)}$ (see Fig. 2 for an illustration of this coupling). This concludes the proof.

Fig. 2

Coupling of $(\theta _{\lambda },\alpha )$ and $(\tilde{\theta}_{\lambda },\tilde{\alpha})$

 □

We can now provide the proof of Proposition 4.4.

Proof of Proposition 4.4

We start with the bound of $N_{L}(\Delta )^{2}$. Without loss of generality, we can assume that $h$ is small. Indeed, since $N_{L}(\Delta \cup \Delta ') = N_{L}(\Delta ) + N_{L}(\Delta ')$ for any two disjoint intervals $\Delta$ and $\Delta '$, the bound of the second moment for a small interval propagates to larger intervals.

By (68), it suffices to prove that

$$ {\limsup _{L \to \infty } \mathbb{E}\big[ \lfloor \alpha (L/\mathbf{E}) \rfloor _{\pi }^{2}\big] < \infty \;.} $$

By Lemma 8.2, we have

$$\begin{aligned} \mathbb{P}({\tau ^{(1)}+\cdots +\tau ^{(n)}} \le L/ \mathbf{E}) &\le \mathbb{P}\big(\sum _{i=1}^{n} (\tilde{\tau}^{(i)} - \tilde{\zeta}^{(i)})_{+} \le L/\mathbf{E}\big) \\ &\le \mathbb{P}\big(( \tilde{\tau}^{(1)} - \tilde{\zeta}^{(1)})_{+} \le L/\mathbf{E}\big)^{n} \\ &\le \big(\mathbb{P}(\tilde{\tau}^{(1)} \le 2L/\mathbf{E}) + \mathbb{P}(\tilde{\zeta}^{(1)} > L/\mathbf{E})\big)^{n}\;. \end{aligned}$$

Observe that

$$ \mathbb{P}(\tilde{\tau}^{(1)} \le 2L/\mathbf{E}) = \mathbb{P}( \lfloor {\alpha (2L/\mathbf{E})} \rfloor _{\pi }\ge 1) \le \mathbb{P}(N_{2L}( \Delta ) \ge 1) \le \mathbb{E}[N_{2L}(\Delta )]\;, $$

which, by Proposition 6.3 and provided that $h$ is small enough, is smaller than $1/4$ for all $L$ large enough. Furthermore, recall that $m_{\lambda }^{(\mathbf{E})} \asymp \mathbf{E}^{-3/2}$, and by Markov’s inequality

$$ \mathbb{P}( \tilde{\zeta}^{(1)} > L/\mathbf{E}) \le m_{\lambda }^{( \mathbf{E})} \frac{\mathbf{E}}{L}\;, $$

which is also smaller than $1/4$ for all $L$ large enough. As a consequence

$$ \mathbb{E}\big[ \lfloor {\alpha (L/\mathbf{E})}\rfloor _{\pi}^{2} \big] = \sum _{n\ge 1} (2n-1)\mathbb{P}(\tau _{1}+\cdots +\tau _{n} \le L/\mathbf{E})\;, $$

is bounded uniformly over all $L$ large enough.

Regarding the bound of $N_{L}^{{(1)}}(\Delta )^{2}$, let us set $L'=L/(k\mathbf{E})$. One needs to show that

$$ \sup _{L > 1} k\mathbb{E}\big[ \lfloor \alpha (L') \rfloor _{\pi}^{2} \big] < \infty \;. $$

Repeating the same steps, we see that

$$ \mathbb{P}(\tilde{\tau}^{(1)} \le 2L') \le \mathbb{E}[N_{2L}^{{ (1)}}(\Delta )]\;, $$

which, by Proposition 6.3 and provided that $h$ is small enough, is bounded by $1/(4k)$ for all $L$ large enough. Moreover

$$ \mathbb{P}( \tilde{\zeta}^{(1)} > L') \le m_{\lambda }^{(\mathbf{E})} / L'\;, $$

which is smaller than $1/(4k)$ provided¹⁰$k^{2} \ll L\sqrt {\mathbf{E}}$. This suffices to conclude. □

Before we present the proof of Proposition 4.5, we need a last estimate whose proof is involved and therefore postponed to the next subsection.

Lemma 8.3

Key bound on $\alpha$ and $\theta$

Set $L' = L/(k\mathbf{E})$. Provided $k\to \infty$ slowly enough, we have $k \mathbb{P}(\{\alpha (L')\}_{\pi }+ \{\theta _{\lambda }(L')\}_{ \pi }\ge \pi ) \to 0$ as $L\to \infty$.

Proof of Proposition 4.5

Identities (67) and (68) remain true upon replacing $N_{L}(\Delta )$ by $N_{L}^{(1)}(\Delta )$ and the time $L/\mathbf{E}$, at which the processes are evaluated, by $L' := L/(k \mathbf{E})$.

Inequalities (68) imply that $N^{(1)}_{L}(\Delta ) = \lfloor {\alpha (L')} \rfloor _{\pi}$ or $N^{(1)}_{L}(\Delta ) = \lfloor {\alpha (L')} \rfloor _{\pi }+ 1$. Therefore, if $N^{(1)}_{L}(\Delta ) \ge 2$, then necessarily one of the two events $\{\lfloor {\alpha (L')} \rfloor _{\pi }\ge 2\}$ or $\{N^{(1)}_{L}(\Delta ) \neq \lfloor {\alpha (L')} \rfloor _{\pi}\}$ must be satisfied. We will control the probabilities of the two events. For the last event, note that (67) implies:

$$ N_{L}^{(1)}(\Delta ) = \lfloor {\alpha (L')}\rfloor _{\pi } \Leftrightarrow \{\theta ^{(\mathbf{E})}_{\mu}(L')\}_{\pi }- \{ \theta ^{\mathbf{E}}_{\lambda }(L')\}_{\pi }\ge 0\;. $$

Since we have

$$ \{\alpha (L')\}_{\pi }= \textstyle\begin{cases} \{\theta _{\mu}^{(\mathbf{E})}(L')\}_{\pi }- \{\theta _{\lambda }^{( \mathbf{E})}(L')\}_{\pi}\quad &\text{ if }\{\theta _{\mu}^{(\mathbf{E})}(L') \}_{\pi }- \{\theta _{\lambda }^{(\mathbf{E})}(L')\}_{\pi }\ge 0\;, \\ \pi + \{\theta _{\mu}^{(\mathbf{E})}(L')\}_{\pi }- \{\theta _{ \lambda }^{(\mathbf{E})}(L')\}_{\pi }\quad &\text{ if } \{\theta _{\mu}^{( \mathbf{E})}(L')\}_{\pi }- \{\theta _{\lambda }^{(\mathbf{E})}(L')\}_{ \pi }< 0\;. \end{cases} $$

we deduce that

$$ N_{L}^{(1)}(\Delta ) = \lfloor {\alpha (L')} \rfloor _{\pi } \Leftrightarrow \{\alpha (L')\}_{\pi }+ \{\theta _{\lambda }^{( \mathbf{E})}(L')\}_{\pi }< \pi \;. $$

Consequently

$$\begin{aligned} k\mathbb{P}(N_{L}^{(1)}(\Delta ) \ge 2) &\le k\mathbb{P}(\lfloor { \alpha (L')} \rfloor _{\pi }\ge 2) + k\mathbb{P}(\{\alpha (L')\}_{ \pi }+ \{\theta _{\lambda }^{(\mathbf{E})}(L')\}_{\pi }\ge \pi )\;. \end{aligned}$$

By Lemma 8.3 the second term on the r.h.s. goes to 0 as $L\to \infty$. Regarding the first term, by Lemma 8.2 we have

$$\begin{aligned} \mathbb{P}\big(\lfloor {\alpha (L')} \rfloor _{\pi }\ge 2\big) &= \mathbb{P}(\tau ^{(1)}+\tau ^{(2)} \le L') \le \mathbb{P}(( \tilde{\tau}^{(1)}-\tilde{\zeta}^{(1)})_{+} +(\tilde{\tau}^{(2)}- \tilde{\zeta}^{(2)})_{+} \le L') \\ &\le (\mathbb{P}((\tilde{\tau}^{(1)}-\tilde{\zeta}^{(1)})_{+} \le L'))^{2} \\ &\le (\mathbb{P}(\tilde{\tau}^{(1)} \le 2L')) + \mathbb{P}( \tilde{\zeta}^{(1)} \ge L'))^{2}\;. \end{aligned}$$

Applying the same arguments as in the previous proof, we get

$$ k\mathbb{P}\big(\lfloor {\alpha (L')} \rfloor _{\pi }\ge 2\big) \le k \Big(\frac{m_{\lambda }^{(\mathbf{E})}}{L'} + \frac{5h}{k}\Big)^{2}\;, $$

which goes to 0 since $m_{\lambda }\asymp \mathbf{E}^{-3/2}$ and provided¹¹$k^{3} \ll L^{2} \mathbf{E}$. □

8.2 Proof of Lemma 8.3

Recall that $L' := L/(k\mathbf{E})$. The proof relies on a small parameter (whose precise value is relatively arbitrary):

$$\begin{aligned} \varepsilon _{L} := \textstyle\begin{cases} \frac{1}{\ln \ln \ln L'} & \text{in the Bulk regime}\;, \\ \frac{1}{\ln \ln \ln L' \wedge \ln E}&\text{in the Crossover regime}\;. \end{cases}\displaystyle \end{aligned}$$

We also define $u_{L} := \ln \varepsilon _{L}^{-1}$.

From the estimates on the invariant measure stated in Lemma 3.1 and the convergence of the densities of Theorem 4, there exist two constant $c,C>0$ such that

$$ \mathbb{P}(\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi}(L') > \pi -3 \epsilon _{L}) \le c(\epsilon _{L} + e^{-CL'})\;, $$

for all $L$ large enough and therefore $k\mathbb{P}(\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi}(L') > \pi -3 \epsilon _{L})$ goes to 0 as $L\to \infty$, provided $k$ goes to $\infty$ slowly enough. To establish the lemma it suffices to show that

$$ \lim _{L\to \infty} k\mathbb{P}(\{\alpha (L')\}_{\pi }> \frac{5}{2} \epsilon _{L}) = 0\;. $$

(70)

Recall that $(\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi},\{\alpha \}_{\pi})$ is markovian. If we can show that for some $C>0$

$$ \lim _{L\to \infty} k \sup _{\theta _{0}, \alpha _{0} \in [0,\pi )} \mathbb{P}(\{\alpha (C \ln L')\}_{\pi }> \frac{5}{2} \epsilon _{L} \,| \, \theta _{\lambda }(0) = \theta _{0}, \alpha (0) = \alpha _{0}) = 0 \;,$$

(71)

then the Markov property applied at time $L'-C\ln L'$ yields (70). The order of magnitude $\ln L'$ will be justified by the discussion below.

The proof of this convergence relies on a thorough study of the process

$$ R := \log \tan (\{\alpha \}_{\pi}/2) \in [-\infty ,\infty )\;, $$

which happens to behave very much like a diffusion in ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ within a potential represented on Fig. 3 (note that this potential is similar to the one studied in [1] for the small $\beta$ limit of the Sine_β process). The main features of this potential are: $-\infty$ is an entrance point while $+\infty$ is an exit point; the potential admits a well centered at $-\ln L'$ and an unstable equilibrium point near 0; the drift generated by this potential is (roughly) a negative constant, resp. a positive constant, on $(-\ln L', 0)$, resp. on $(0,\ln L')$.

Fig. 3

Effective potential in which $R$ evolves

Actually, the process $\{\alpha \}_{\pi}$ (and therefore the process $R$) is not markovian as its evolution depends on the Markov process $\theta _{\lambda }$: however, $\theta _{\lambda }$ evolves at a smaller time-scale than $R$ so that after “averaging” over the evolution of $\theta _{\lambda }$, the process $R$ can be seen as a diffusion. One difficulty in our proofs will then consist in controlling the error made upon this replacement.

To alleviate the notation, we write $\mathbb{P}_{\theta _{0},R_{0}}$ for the law of $(\theta _{\lambda },R)$ starting from $(\theta _{0},R_{0})$ at time 0. The convergence (71) is implied by

$$ \lim _{L\to \infty} k \sup _{\theta _{0} \in [0,\pi ), R_{0} \in [- \infty ,\infty )} \mathbb{P}_{\theta _{0},R_{0}}(R(C \ln L') > -\ln \epsilon _{L}^{-1} ) = 0\;.$$

(72)

Recall $u_{L} := \ln \epsilon _{L}^{-1}$. We divide the proof of (72) according to the initial position of $R$. The first lemma shows that if $R$ starts in the interval $[-\infty ,-2 u_{L}]$, that is, within the well of the potential of Fig. 3, then it typically remains in $[-\infty ,-u_{L})$ up to time $C \ln L'$.

Lemma 8.4

Small initial values

For any constant $C>0$, provided $k\to \infty$ slowly enough, we have

$$ \lim _{L\to \infty} k \sup _{\theta _{0} \in [0,\pi ), R_{0} \in [- \infty ,-2 u_{L}]} \mathbb{P}_{\theta _{0},R_{0}}(\sup _{[0,C\ln L']} R > -u_{L}) = 0\;. $$

The second lemma shows that if $R$ starts in the interval $[-2 u_{L},2 u_{L}]$, that is, near the unstable equilibrium point of the potential of Fig. 3, then it typically escapes this interval by time $2\ln L'$.

Lemma 8.5

Intermediate initial values

Provided $k\to \infty$ slowly enough, we have

$$ \lim _{L\to \infty} k \sup _{\theta _{0} \in [0,\pi ), R_{0} \in [-2 u_{L},2 u_{L}]} \mathbb{P}_{\theta _{0},R_{0}}(|R| \textit{ does not hit } 2 u_{L} \textit{ by time } 2\ln L' ) = 0\;. $$

Finally we show that if $R$ starts in the interval $[2 u_{L},\infty )$, that is, near the exit point $+\infty$ of the potential of Fig. 3, then it typically explodes to $+\infty$ within a time of order $\ln L'$. As $R$ restarts from $-\infty$ when it hits $+\infty$, we are then back to the regime of the first lemma.

Lemma 8.6

Large initial values

Provided $k\to \infty$ slowly enough, there exists a constant $C>0$ such that

$$ \lim _{L\to \infty} k \sup _{\theta _{0} \in [0,\pi ), R_{0} \in [2 u_{L}, \infty )} \mathbb{P}_{\theta _{0},R_{0}}(R \textit{ does not hit } + \infty \textit{ by time }C\ln L' ) = 0\;. $$

It is straightforward to deduce (72) from the three lemmas and the Markov property.

Before we proceed with the proofs of these three lemmas, let us compute the SDE solved by $R$.

Lemma 8.7

$$\begin{aligned} dR &= \Big(\sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}(\alpha +\theta _{ \lambda }^{(\mathbf{E})}) \cosh R \;+\;\sqrt {\mathbf{E}}(\lambda - \mathbf{E}) \sin (\alpha +2\theta _{\lambda }^{(\mathbf{E})}) \\ &\quad \;+\; \frac{1}{2} \cos (\alpha +2\theta _{\lambda }^{(\mathbf{E})}) \\ &\quad \;+\; \frac{\tanh R}{4}(1+\cos (2 \alpha +4\theta _{\lambda }^{( \mathbf{E})}))\Big) dt - \sin (\alpha +2\theta _{\lambda }^{( \mathbf{E})}) dB^{(\mathbf{E})}(t)\;. \end{aligned}$$

Note that we intentionally left some occurrences of the process $\alpha$ in this expression. Depending on the range of values $\alpha$ (or equivalently, $R$) at which our analysis focuses, we will neglect some terms of this SDE.

Proof

Trigonometric identities yield

$$\begin{aligned} \sin ^{2} \theta _{\mu }^{(\mathbf{E})}-\sin ^{2} \theta _{\lambda }^{( \mathbf{E})} ={}& \sin \alpha \sin (\alpha + 2\theta _{\lambda }^{( \mathbf{E})})\;, \\ \sin ^{3} \theta _{\mu }^{(\mathbf{E})} \cos \theta _{\mu }^{( \mathbf{E})} - \sin ^{3} \theta _{\lambda }^{(\mathbf{E})} \cos \theta _{\lambda }^{(\mathbf{E})} ={}& \frac{1}{2}\sin \alpha \cos ( \alpha +2\theta _{\lambda }^{(\mathbf{E})}) \\ &{} - \frac{1}{2} \sin \alpha \cos \alpha \cos (2\alpha +4\theta _{\lambda }^{(\mathbf{E})}) \;. \end{aligned}$$

Starting from (11) and applying these identities, we can write the SDE solved by $\alpha$

$$\begin{aligned} d\alpha ={}& \Big(\sqrt{\mathbf{E}} (\mu -\lambda ) \sin ^{2} (\alpha + \theta _{\lambda }^{(\mathbf{E})}) + \sqrt{\mathbf{E}} (\lambda - \mathbf{E})\sin \alpha \sin (\alpha + 2\theta _{\lambda }^{( \mathbf{E})}) \\ &{}+ \frac{1}{2}\sin \alpha \cos (\alpha +2\theta _{ \lambda }^{(\mathbf{E})}) \\ &{}- \frac{1}{2} \sin \alpha \cos \alpha \cos (2\alpha +4 \theta _{\lambda }^{(\mathbf{E})})\Big)dt - \sin \alpha \sin ( \alpha + 2\theta _{\lambda }^{(\mathbf{E})}) dB^{(\mathbf{E})}(t)\;. \end{aligned}$$

If $f(x) = \log \tan (x/2)$, then $f'(x) = 1/\sin x$ and $f''(x) = -\cos (x)/\sin ^{2}(x)$. Let us assume that $\alpha (0) \in [0,\pi )$. Then $\alpha$ remains non-negative, and until its first hitting time of $\pi$ we obtain by Itô’s formula

$$ dR = \frac{1}{\sin \alpha } d\alpha - \frac{\cos \alpha }{2} \sin ^{2}( \alpha + 2\theta _{\lambda }^{(\mathbf{E})}) dt\;. $$

Using the identities $\sin \alpha = 1 / \cosh R$ and $\cos \alpha = - \tanh R$, the asserted expression for the SDE follows, at least until the first hitting time of $\pi$ by $\alpha$. Now if $\alpha \in [n\pi ,(n+1)\pi )$, then it is not difficult to check that $\{\alpha \}_{\pi }$, until its next hitting time of $\pi$, satisfies the same SDE as $\alpha$. Consequently, we can again apply Itô’s formula and derive the desired SDE for $R$. Patching together the successive excursions of $\alpha$, we derive the lemma. □

Proof of Lemma 8.4

By monotonicity, it suffices to consider the case $R_{0} = -2u_{L}$. Let $S := \inf \{t\ge 0: R(t) \in \{-(3/4) \ln L',-u_{L}\}\}$. We are going to prove that there exist $c,c'>0$ such that for all $L$ large enough

$$ \inf _{\theta _{0}\in [0,\pi )} \mathbb{P}_{\theta _{0},R_{0}}(R(S) = -(3/4) \ln L' ; S > c' \ln L') > 1 - \epsilon _{L}^{c}\;. $$

(73)

From this estimate and the Markov property, one deduces the statement of the lemma provided¹²$k \ll \epsilon _{L}^{-c}$.

Let us write $dR(t) = A(t) dt + dM(t)$ where $M(t) := \int _{0}^{t} - \sin (\alpha +2\theta _{\lambda }^{( \mathbf{E})}) dB^{(\mathbf{E})}(t)$ is the martingale part of the SDE. One can check that for all $t \le S$, the drift term satisfies

$$\begin{aligned} A(t) = C(t) + \mathcal{O}(\epsilon _{L} + (L')^{-1/4})\,, \end{aligned}$$

where

$$ C(t) = \sqrt {\mathbf{E}}(\lambda -\mathbf{E}) \sin (2\theta _{\lambda }^{( \mathbf{E})}) + \frac{1}{2} \cos (2\theta _{\lambda }^{(\mathbf{E})}) - \frac{1}{4}(1+\cos (4\theta _{\lambda }^{(\mathbf{E})}))\;. $$

Note that the first term in $C(t)$ is of order $O(\mathbf{E}/L)$ while the two others are of order $O(1)$ but it is more convenient to keep this term. By (92) we have $\mathbb{E}[\int _{0}^{\zeta _{\lambda }^{(\mathbf{E})}} C(s) ds] = - \nu _{\lambda }^{(\mathbf{E})} m_{\lambda }^{(\mathbf{E})}$. Recall that the expectation of $\zeta _{\lambda }^{(\mathbf{E})}$ is $m_{\lambda }^{(\mathbf{E})}$. Therefore for $t$ large enough and as long as $t < S$, the process $R(t)-R_{0}$ roughly behaves like $-\nu _{\lambda }^{(\mathbf{E})} t + M(t)$, where $\nu _{\lambda }^{(\mathbf{E})}$ is of order $O(1)$, so that it has a negligible probability to reach large values. Note that $-\nu _{\lambda }^{(\mathbf{E})}$, the value of the approximate drift, is consistent with the effective potential of Fig. 3.

To put that on firm ground, introduce $d\tilde{R}(t) := C(t) dt + dM(t)$ with $\tilde{R}(0) := R_{0}$. For any $\epsilon > 0$ there exists $q>0$ such that

$$ {\limsup _{L\to \infty }}\sup _{\theta _{0}}\mathbb{E}_{ \theta _{0},R_{0}}[\sup _{t\ge 0} e^{q |\tilde{R}(t) - R_{0} + \nu _{ \lambda }^{(\mathbf{E})} t|} e^{-q\epsilon t}] < \infty \;. $$

Indeed for the integral $\int _{0}^{t} C(s)ds$, it follows from the very same arguments as in Lemma 7.3 and we can deal with the martingale part using Lemma A.2.

Using $\sup _{s \leq t }|R(s) - \tilde{R}(s)| \leq \mathcal{O}(\epsilon _{L} + (L')^{-1/4}) \times t$ for all $t \leq S$, we therefore deduce that there exists $L_{0} >1$ such that

$$ \sup _{L>L_{0}}\sup _{\theta _{0}}\mathbb{E}_{\theta _{0},R_{0}}[ \sup _{t\in [0,S]} e^{q |R(t) - R_{0} + \nu _{\lambda }^{(\mathbf{E})} t|} e^{-2q\epsilon t}] < \infty \;. $$

Call $K$ the expression on the l.h.s. Provided $2\epsilon < \nu _{\lambda }^{(\mathbf{E})}$ we deduce that for all $L$ large enough

$$ \sup _{\theta _{0}}\mathbb{P}_{\theta _{0},R_{0}}(R(S) = -u_{L}) \le K e^{-q u_{L}}\;. $$

In addition, taking $c'>0$ small enough we observe that there exists $C'>0$ such that for all $L$ large enough

$$ R(S) = -(3/4) \ln L' \;;\;S \le c' \ln L' \Rightarrow \sup _{t\in [0,S]} |R(t) - R_{0} + \nu _{\lambda }^{(\mathbf{E})} t|-2\epsilon t \ge C' \ln L'\;, $$

and consequently for all $L$ large enough

$$ \sup _{\theta _{0}}\mathbb{P}_{\theta _{0},R_{0}}\big(R(S) = -(3/4) \ln L' \;;\;S \le c' \ln L'\big) \le K e^{-q C' \ln L'}\;. $$

This concludes the proof of (73). □

For our next proof, recall the definitions of the hitting times (69) and set $T_{k} = \zeta ^{(1)} +\cdots + \zeta ^{(k)}$. We set $n := \lfloor \mathbf{E}^{3/2} \rfloor$, $\tau _{k} := T_{nk}$ for every $k\ge 1$ and $\tau _{0}=0$. The sequence $\tau _{k}$ should not be confused with the sequence $\tau ^{(k)}$ introduced in Sect. 8.1.

Proof of Lemma 8.5

It suffices to prove the statement of the lemma with $\theta _{0} = 0$ and with $2\ln L'$ replaced by $\ln L'$. Indeed, if $\theta _{0} \ne 0$, then by Lemma A.3 there exists $c>0$ such that with probability at least $1-e^{-c \ln L' \mathbf{E}^{3/2}}$ the process $\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi}$ hits 0 by time $\ln L'$. Therefore, we now assume that $\theta _{0} = 0$.

Introduce the stopping time

$$ S := \inf \{t\ge 0: R(t) \notin [-2 u_{L},2 u_{L}]\}\;. $$

We claim that on any excursion of the diffusion $\theta _{\lambda }^{(\mathbf{E})}$ from $n{j}\pi$ to $n({j}+1)\pi$, $R$ has a small chance to escape from $[-2u_{L},2u_{L}]$ i.e.

$$ \inf _{R_{0} \in [-2 u_{L},2 u_{L}]} \mathbb{P}_{\theta _{0} = 0,R_{0}}(S < \tau _{1}) \ge \delta _{L}\;,\quad \delta _{L} := \exp (-\epsilon _{L}^{-33}) \;. $$

(74)

We postpone the proof of the claim and proceed with the proof of the lemma. By the strong Markov property, we have for all $R_{0} \in [-2u_{L},2u_{L}]$ and $N \geq 1$,

$$\begin{aligned} \mathbb{P}_{\theta _{0} = 0, R_{0}}(S \geq \tau _{N})&= \mathbb{P}_{ \theta _{0} = 0, R_{0}}(S \geq \tau _{N} | S \geq \tau _{N-1}) \; \mathbb{P}_{\theta _{0} = 0, R_{0}}(S \geq \tau _{N-1}) \\ &\leq \sup _{R'_{0} \in [-2u_{L},2u_{L}]} \mathbb{P}_{\theta _{0} = 0, R'_{0}}(S \geq \tau _{N}) \; \mathbb{P}_{ \theta _{0} = 0, R_{0}}(S \geq \tau _{N-1})\,, \end{aligned}$$

which gives with (74):

$$\begin{aligned} \mathbb{P}_{\theta _{0} = 0, R_{0}}(S \geq \tau _{N}) \leq (1-\delta _{L})^{N} \,. \end{aligned}$$

Set $N := {\kappa } \ln L'$ and define the event $\mathcal{B}:= \{\tau _{N} < \ln L'\}$. If ${\kappa } > 0$ is small enough then by Lemma A.3 there exists $c>0$ such that for all $L$ large enough we have

$$ \mathbb{P}(\mathcal{B}^{\complement }) < e^{-c \mathbf{E}^{3/2} \ln L'} \;. $$

Therefore uniformly over all $R_{0}\in [-2u_{L},2u_{L}]$

$$\begin{aligned} \mathbb{P}_{\theta _{0}=0,R_{0}}(S \le \ln L') &\ge \mathbb{P}_{ \theta _{0}=0,R_{0}}(\mathcal{B}\cap \{S \le \tau _{N}\}) \ge \mathbb{P}_{\theta _{0}=0,R_{0}}(S \le \tau _{N}) - \mathbb{P}( \mathcal{B}^{\complement }) \\ &\ge 1 - (1-\delta _{L})^{N} - e^{-c \mathbf{E}^{3/2} \ln L'} \end{aligned}$$

so that

$$ k \mathbb{P}_{\theta _{0}=0,R_{0}}(S > \ln L') < k e^{-\kappa \ln L' \delta _{L}} + k e^{-c \mathbf{E}^{3/2} \ln L'}\;. $$

Since $\epsilon _{L}^{-1} \le \ln \ln \ln L'$, we have $\ln L' \delta _{L} \to +\infty$. Provided $k$ does not go too fast to $+\infty$ (for instance provided $k \ll \ln L'$), we deduce that $k \mathbb{P}_{\theta _{0}=0,R_{0}}(S > \ln L')$ goes to 0 uniformly over all $R_{0}\in [-2u_{L},2u_{L}]$.

We now prove (74). Let us write $dR(t) = A(t) dt + dM(t)$ where

$$ M(t) = \int _{0}^{t} - \sin (\alpha +2\theta _{\lambda }^{(\mathbf{E})}) dB^{(\mathbf{E})}(s)\;. $$

Set $S' := \inf \{t\ge 0: R(t) \notin [-10 u_{L},10 u_{L}]\}$. Set $\alpha _{\pm }:= 2\arctan e^{\pm 10 u_{L}}$ and introduce the martingale

$$ N(t) := - \int _{0}^{t} \sin (\alpha _{-} \vee \alpha \wedge \alpha _{+} +2\theta _{\lambda }^{(\mathbf{E})}) dB^{(\mathbf{E})}(s)\;, $$

which coincides with $M(t)$ for all time $t \leq S'$. There exists $C>0$ such that whenever $t\le S'$, the drift satisfies $|A(t)| < C$ almost surely, and therefore

$$\begin{aligned} -Ct + N_{t} \leq R(t)-R(0) \leq Ct + N_{t}\;. \end{aligned}$$

(75)

Recall that $n= \lfloor \mathbf{E}^{3/2} \rfloor$ so that $nm_{\lambda }^{(\mathbf{E})}$ is of order 1. We then note that

$$\begin{aligned} \mathbb{P}(S < \tau _{1}) &\ge \mathbb{P}(\exists t < \tau _{1} \wedge S': N_{t} \ge Ct + 4 u_{L}) \\ &\ge \mathbb{P}(\exists t < (2nm_{\lambda }^{(\mathbf{E})})\wedge \tau _{1} \wedge S': N_{t} \ge 5 u_{L}) \\ &\ge \mathbb{P}(\exists t < (2nm_{\lambda }^{(\mathbf{E})})\wedge \tau _{1} \wedge S': \sup _{[0,t]} N = 5 u_{L} \;, \inf _{[0,t]} N \ge - u_{L})\;. \end{aligned}$$

Note that, if at some time $t < (2nm_{\lambda }^{(\mathbf{E})})\wedge \tau _{1}$ we have $\sup _{[0,t]} N = 5 u_{L}$ and $\inf _{[0,t]} N \ge - u_{L}$ then by the inequalities (75) we have $t < S'$. Consequently

$$\begin{aligned} \mathbb{P}(S < \tau _{1}) &\ge \mathbb{P}(\exists t < (2nm_{\lambda }^{( \mathbf{E})})\wedge \tau _{1}: \sup _{[0,t]} N = 5 u_{L} \;, \inf _{[0,t]} N \ge - u_{L})\;. \end{aligned}$$

Let $q_{r} := \inf \{s\ge 0: \langle N \rangle _{s} \ge r\}$, and define $\beta _{r} := N_{q_{r}}$. By Dubins-Schwarz’s Theorem, $\beta$ is a Brownian motion. We thus get for any $r>0$

$$ \begin{aligned} \mathbb{P}(S < \tau _{1}) &\ge \mathbb{P}(\beta _{r} \ge 5 u_{L} ; \inf _{[0,r]} \beta \ge - u_{L} ; q_{r} < (2nm_{ \lambda }^{(\mathbf{E})}) \wedge \tau _{1}) \\ &\ge \mathbb{P}(\beta _{r} \ge 5 u_{L} ; \inf _{[0,r]} \beta \ge - u_{L}) - \mathbb{P}(q_{r} \ge (2nm_{\lambda }^{(\mathbf{E})}) \wedge \tau _{1}) \;. \end{aligned} $$

(76)

We now set $r := \epsilon _{L}^{32}$. By symmetry

$$\begin{aligned} \mathbb{P}(\beta _{r} > 5 u_{L} ; \inf _{[0,r]} \beta \ge - u_{L}) &= \mathbb{P}(\sup _{[0,r]} \beta \le u_{L} ; \beta _{r} < -5u_{L}) \\ &= \mathbb{P}(\beta _{r} < -5u_{L}) - \mathbb{P}(\sup _{[0,r]} \beta > u_{L} ; \beta _{r} < -5u_{L})\;. \end{aligned}$$

By the Reflection Principle [34, Exercise III.3.14], this last term coincides with $\mathbb{P}(\beta _{r} < -7u_{L})$. Therefore, by symmetry again

$$\begin{aligned} \mathbb{P}(\beta _{r} > 5 u_{L} ; \inf _{[0,r]} \beta \ge - u_{L}) &= \mathbb{P}(\beta _{r} < -5u_{L}) - \mathbb{P}(\beta _{r} < -7u_{L}) \\ &= \mathbb{P}(-7 u_{L} < \beta _{r} < -5 u_{L}) \\ &=\mathbb{P}(5 u_{L} < \beta _{r} < 7 u_{L})\;. \end{aligned}$$

Since $u_{L}^{2}/r \to \infty$ as $L\to \infty$, there exists $c>0$ such that for all $L$ large enough

$$ \mathbb{P}(5 u_{L} < \beta _{r} < 7 u_{L}) = \frac{1}{\sqrt{2\pi r}} \int _{5u_{L}}^{7u_{L}} e^{-\frac{x^{2}}{2r}} dx \ge \frac{2u_{L}}{\sqrt{2\pi r}} e^{-\frac{49 u_{L}^{2}}{2r}} \ge e^{-c \frac{u_{L}^{2}}{r}}\;.$$

(77)

To bound from above $\mathbb{P}(q_{r} \ge (2nm_{\lambda }^{(\mathbf{E})}) \wedge \tau _{1})$, we distinguish the Bulk and the Crossover regimes.

We start with the Crossover regime. We have

$$\begin{aligned} \mathbb{P}(q_{r} \ge (2nm_{\lambda }^{(E)}) \wedge \tau _{1}) &= \mathbb{P}(\langle N\rangle _{(2n m_{\lambda }^{(E)}) \wedge \tau _{1}} \le r)\le \mathbb{P}(\tau _{1} > 2n m_{\lambda }^{(E)}) + \mathbb{P}( \langle N\rangle _{\tau _{1}} \le r)\;. \end{aligned}$$

From Lemma A.3, for all $\alpha \in [0,1)$

$$ \mathbb{P}(\tau _{1} > 2n m_{\lambda }^{(E)}) \le \mathbb{E}[e^{ \alpha \zeta _{\lambda }^{(E)} / m_{\lambda }^{(E)}}]^{n} e^{-2n \alpha } = e^{n \big( \ln \frac{1}{1-\alpha } - 2\alpha \big)}\;. $$

Consequently there exists $c'>0$ such that

$$ \mathbb{P}(\tau _{1} > 2n m_{\lambda }^{(E)}) \le e^{-c' E^{3/2}}\;. $$

Regarding the second term, we claim that

$$ \langle N\rangle _{\tau _{1}} = \int _{0}^{\tau _{1}} \sin ^{2}( \alpha _{-}\vee \alpha \wedge \alpha _{+} + 2\theta _{\lambda }^{(E)}) ds \ge \frac{1}{2} \epsilon _{L}^{20} \int _{0}^{\tau _{1}} \mathbf{1}_{\{\{\theta _{\lambda }^{(E)}(s)\}_{\pi }\le \epsilon _{L}^{11} \}} ds\;. $$

To prove the claim, note that $\arctan x \sim x$ as $x\to 0$ and $\arctan x \sim \frac{\pi }{2} - \frac{1}{x}$ as $x\to + \infty$. Consequently for all $L$ large enough

$$ \epsilon _{L}^{10} \le \alpha _{-}\vee \alpha \wedge \alpha _{+} \le \pi - \epsilon _{L}^{10}\;. $$

Fix $\kappa \in (0,1)$. If $\{\theta _{\lambda }^{(E)}(s)\}_{\pi }\le \epsilon _{L}^{11}$, then provided $L$ is large enough we find

$$ (1-\kappa ) \epsilon _{L}^{10} \le \{ \alpha _{-}\vee \alpha (s) \wedge \alpha _{+} + 2\theta _{\lambda }^{(E)}(s) \}_{\pi }\le \pi - (1- \kappa ) \epsilon _{L}^{10}\;, $$

and therefore, picking an appropriate value $\kappa$, we find $\sin ^{2}(\alpha _{-}\vee \alpha (s) \wedge \alpha _{+} + 2\theta _{ \lambda }^{(E)}(s)) \ge \frac{1}{2}\epsilon _{L}^{20}$.

We now bound from above $\mathbb{P}( \frac{1}{2} \epsilon _{L}^{20} \int _{0}^{\tau _{1}} \mathbf{1}_{\{\{\theta _{\lambda }^{(E)}(s)\}_{\pi }\le \epsilon _{L}^{11} \}} ds \le r)$. Note that the integral that appears in this r.v. is a sum of $n$ i.i.d. r.v. $X_{k}$ with

$$ X_{1} = \int _{0}^{\zeta _{\lambda }^{(E)}} \mathbf{1}_{\{|\theta _{ \lambda }^{(E)}(s)| \le \epsilon _{L}^{11}\}} ds\;. $$

Introduce $\sigma := \inf \{t\ge 0: \theta _{\lambda }^{(E)}(t) = \epsilon _{L}^{11} \}$. Note that $X_{1} \ge \sigma$. Consider the process $\theta _{\lambda }^{(E)}(\cdot \wedge \sigma )$. Since $n$ is of order $E^{3/2}$, its drift term is bounded by $n C'_{\alpha }$, where $C'_{\alpha }$ is a given constant independent of $L$, and the square of its diffusion coefficient is bounded by $C_{\beta }= \epsilon _{L}^{44}$. By Lemma A.2 there exists $\delta > 0$ such that for all $L$ large enough

$$ \mathbb{P}(X_{1} > \frac{\delta \epsilon _{L}^{11}}{n}) \ge \mathbb{P}(\sigma > \frac{\delta \epsilon _{L}^{11}}{n}) = \mathbb{P}( \sup _{s\in [0,\frac{\delta \epsilon _{L}^{11}}{n}]} \theta _{ \lambda }^{(E)}(s\wedge \sigma ) < \epsilon _{L}^{11}) \ge \frac{1}{2}\;. $$

Putting the previous arguments together, the computation boils down to an estimate on the Binomial distribution:

$$\begin{aligned} \mathbb{P}(\langle N\rangle _{\tau _{1}} \le r) \le \mathbb{P}\big( \sum _{k=1}^{n} \frac{\delta }{2n} \epsilon _{L}^{31} \mathbf{1}_{\{X_{k}> \frac{\delta \epsilon _{L}^{11}}{n}\}} \le r\big) &\le \mathbb{P}( \text{Bin}(n,1/2)\le \frac{2n \epsilon _{L}}{\delta }) \;. \end{aligned}$$

Let us point out that $\delta$ is independent of $L$, so that $\epsilon _{L}/\delta$ goes to 0 as $L\to \infty$ and therefore $\frac{2n \epsilon _{L}}{\delta }$ is much smaller than the mean of the Binomial distribution at stake. A multiplicative Chernoff bound gives for some constant $c'' >0$:

$$ \mathbb{P}(\text{Bin}(n,1/2) \le \frac{2n \epsilon _{L}}{\delta })\le e^{- \frac{n}{2}((1- 4\epsilon _{L}/\delta ) + (4 \epsilon _{L}/\delta ) \ln (4\epsilon _{L}/\delta ))} \le e^{-c'' E^{3/2}}\;. $$

We henceforth obtain (recalling that $u_{L} = \ln \epsilon _{L}^{-1}$)

$$ \mathbb{P}(S < \tau _{1}) \ge e^{-c \frac{\ln ^{2} \epsilon _{L}^{-1}}{\epsilon _{L}^{32}}} - e^{-c' E^{3/2}} - e^{-c'' E^{3/2}}\;. $$

Since $\epsilon _{L}^{-1} \le \ln E$, we obtain (74).

Let us now consider the Bulk regime, for which $n=1$ and $\tau _{1} = \zeta _{\lambda }$. We have

$$\begin{aligned} \mathbb{P}(q_{r} \ge (2nm_{\lambda }) \wedge \tau _{1}) &= \mathbb{P}( \langle N\rangle _{(2 m_{\lambda }) \wedge \zeta _{\lambda }} \le r) \;. \end{aligned}$$

Then we introduce $\sigma := \inf \{t\ge 0: \theta _{\lambda }(t) = \epsilon _{L}^{11} \}$, which is smaller than $\zeta _{\lambda }$, and we write

$$\begin{aligned} \langle N\rangle _{(2 m_{\lambda }) \wedge \zeta _{\lambda }} = \int _{0}^{(2 m_{\lambda }) \wedge \zeta _{\lambda }} \sin ^{2}(\alpha _{-}\vee \alpha \wedge \alpha _{+} + 2\theta _{\lambda }) ds \ge \frac{1}{2} \epsilon _{L}^{20}\big( \sigma \wedge (2 m_{\lambda })\big)\;. \end{aligned}$$

Since $m_{\lambda }$ is of order 1, we thus have

$$ \mathbb{P}(\langle N\rangle _{(2 m_{\lambda }) \wedge \zeta _{ \lambda }} \le r) \le \mathbb{P}( \sigma \wedge (2 m_{\lambda }) \le 2 \epsilon _{L}^{12}) = \mathbb{P}(\sigma \le 2 \epsilon _{L}^{12})\;. $$

To bound this last term, we consider the process $\theta _{\lambda }(\cdot \wedge \sigma )$. Its drift term is bounded by some constant $C_{\alpha }> 0$ (which is of order 1) and the quadratic variation of its martingale term is bounded by $C_{\beta }= \epsilon _{L}^{44}$. By Lemma A.2, we thus get

$$ \mathbb{P}(\sigma \le 2 \epsilon _{L}^{12}) \le \mathbb{P}(\sup _{s \in [0,2 \epsilon _{L}^{12}]} \theta _{\lambda }(s\wedge \sigma ) \ge \frac{1}{2} \epsilon _{L}^{11}) \le 2e^{- \frac{\epsilon _{L}^{-34}}{64}}\;. $$

Consequently

$$ \mathbb{P}(S < \tau _{1}) \ge e^{-c \frac{\ln ^{2} \epsilon _{L}^{-1}}{\epsilon _{L}^{32}}} - 2e^{- \frac{\epsilon _{L}^{-34}}{64}} \ge \delta _{L}\;. $$

 □

We turn to the case where the initial value is “large”.

Proof of Lemma 8.6

By monotonicity, it suffices to consider the case $R_{0} = 2 u_{L}$. Whenever $R(t) \in [u_{L},\infty )$,

$$\begin{aligned} dR(t) &= -\Big(\sqrt {\mathbf{E}}(\lambda -\mathbf{E}) \sin (2\theta _{ \lambda }^{(\mathbf{E})}) + \frac{1}{2} \cos (2\theta _{\lambda }^{( \mathbf{E})}) - \frac{1}{4}(1+\cos (4\theta _{\lambda }^{(\mathbf{E})})) \Big) dt \\ &\quad + \sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}\theta _{\lambda }^{( \mathbf{E})} \frac{\sinh ^{2} R}{\cosh R} dt- \sin (\alpha +2\theta _{ \lambda }^{(\mathbf{E})}) dB(t) \\ &\quad {} + \mathcal{O}(\epsilon _{L} + { (L')}^{-1}) dt\;. \end{aligned}$$

The proof consists of two steps. First, we apply essentially the same arguments as in the proof of Lemma 8.4 to show that with large probability $R$ hits $10\ln L'$ before $u_{L}$ within a time $C'\ln L'$. Second, we consider the process $R$ starting from $10 \ln L'$ and we show that with large probability, $R$ is bounded from below by the solution of an ODE which explodes within a time smaller than $\ln L'$.

We start with the first step. Recall that $R_{0} = 2u_{L}$. Let $S:= \inf \{t\ge 0: R(t) \in \{u_{L},10 \ln L'\}\}$. We claim that there exist $c,C'>0$ such that for all $L$ large enough

$$ \inf _{\theta _{0}\in [0,\pi )} \mathbb{P}_{\theta _{0},R_{0}}(R(S) = 10 \ln L' ; S < C' \ln L') > 1 - \epsilon _{L}^{c}\;. $$

(78)

Since $\sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}\theta _{\lambda }^{( \mathbf{E})} \frac{\sinh ^{2} R}{\cosh R} \ge 0$ up to time $S$, it suffices to show the desired estimate but for the process

$$ \tilde{R}(t) = R(t) - \int _{0}^{t} \sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}\theta _{\lambda }\frac{\sinh ^{2} R}{\cosh R} ds\;, $$

and the stopping time $\tilde{S} := \inf \{t\ge 0: \tilde{R}(t) \in \{u_{L},10 \ln L'\}\}$. Fix $\epsilon > 0$. The same arguments as in the proof of Lemma 8.4 show that there exist $q>0$ and $L_{0} >1$ such that

$$ \sup _{L>L_{0}}\sup _{\theta _{0}}\mathbb{E}_{\theta _{0},R_{0}} \big[\sup _{t\in [0,\tilde{S}]} e^{q |\tilde{R}(t) - R_{0} - \nu _{ \lambda }^{(\mathbf{E})} t|} e^{-2q\epsilon t}\big] < \infty \;. $$

Call $K$ the expression on the l.h.s. Provided $2\epsilon < \nu _{\lambda }^{(\mathbf{E})}$ we deduce that for all $L$ large enough

$$ \sup _{\theta _{0}}\mathbb{P}_{\theta _{0},R_{0}}\big(\tilde{R}( \tilde{S}) = u_{L}\big) \le \sup _{\theta _{0}}\mathbb{P}_{\theta _{0},R_{0}} \big(e^{q |\tilde{R}(\tilde{S}) - R_{0} - \nu _{\lambda }^{( \mathbf{E})} \tilde{S}|} e^{-2q\epsilon \tilde{S}} \ge e^{qu_{L}} \big) \le K e^{-q u_{L}}\;. $$

In addition, taking $c'>0$ large enough we observe that there exists $C'>0$ such that for all $L$ large enough

$$ \tilde{R}(\tilde{S}) = 10 \ln L' \; \&\; \tilde{S} > c' \ln L' \Rightarrow \sup _{t\in [0,\tilde{S}]} |\tilde{R}(t) - R_{0} - \nu ^{( \mathbf{E})}_{\lambda }t|-2\epsilon t \ge C' \ln L'\;, $$

and consequently for all $L$ large enough

$$ \sup _{\theta _{0}}\mathbb{P}_{\theta _{0},R_{0}}\big(\tilde{R}( \tilde{S}) = 10 \ln L' \;;\; \tilde{S} > c' \ln L'\big) \le K e^{-q C' \ln L'}\;. $$

This proves (78) for $\tilde{R}$, and by monotononicity, for $R$ as well.

We turn to the second step. We now take $R_{0} = 10 \ln L'$ and we set $S' := \inf \{t\ge 0: R(t) \in \{2\ln L', +\infty \}\}$. Take $\epsilon >0$ such that $2\epsilon < \nu _{\lambda }^{(\mathbf{E})}$. The same arguments as in the first step show that there exist $q>0$ and $L_{0} >1$ such that

$$ \sup _{L>L_{0}}\sup _{\theta _{0}}\mathbb{E}_{\theta _{0},R_{0}}[ \sup _{t\in [0,\tilde{S}']} e^{q |\tilde{R}(t) - R_{0} - \nu ^{( \mathbf{E})}_{\lambda }t|} e^{-2q\epsilon t}] < \infty \;, $$

where $\tilde{S}' := \inf \{t\ge 0: \tilde{R}(t) \in \{2\ln L', +\infty \} \}$. Call $K$ the expression on the l.h.s. Note that for any $t \ge 0$

$$ \tilde{R}(t) < 5 \ln L' \Rightarrow |\tilde{R}(t) - R_{0} - \nu ^{( \mathbf{E})}_{\lambda }t|-2\epsilon t > 5 \ln L'\;. $$

We deduce that with a probability at least $1-Ke^{-q 5 \ln L'}$, we have for all $t\in [0,\tilde{S}']$

$$ \tilde{R}(t) \ge 5 \ln L'\;. $$

Call $G$ this event. On $G$, if $\tilde{S}' < \infty$ then necessarily $\tilde{R}(\tilde{S}') = +\infty$ and then, $S' \le \tilde{S}'$ and $R(S') = +\infty$.

Note that there exists a constant $c>0$ such that for all $t\in [0,S']$

$$ \sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}\theta _{\lambda }^{( \mathbf{E})}(t) \frac{\sinh ^{2} R(t)}{\cosh R(t)} \ge \frac{c \mathbf{E}}{L} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(t) e^{R(t)} \;. $$

On the event $G$, for all $t\in [0,S']$ we thus have

$$\begin{aligned} R(t) &= \tilde{R}(t) + \int _{0}^{t} \sqrt {\mathbf{E}}(\mu -\lambda ) \sin ^{2}\theta _{\lambda }\frac{\sinh ^{2} R}{\cosh R} ds \\ &\ge 5 \ln L' + \frac{c \mathbf{E}}{L} \int _{0}^{t} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) e^{R(s)} ds\;. \end{aligned}$$

Set for any $r\ge 0$, $q_{r} := \inf \{t\ge 0: \int _{0}^{t} \sin ^{2} \theta _{\lambda }^{( \mathbf{E})}(s) ds \ge r\}$. Whenever $q_{r} \le S'$, a change-of-variable yields

$$ R(q_{r}) \ge 5 \ln L' + \frac{c \mathbf{E}}{L} \int _{0}^{r} e^{R(q_{v})} dv\;. $$

Now the solution to the differential equation

$$ f'(r) = \frac{c \mathbf{E}}{L} e^{f(r)}\;,\quad f(0) = 5\ln L'\;, $$

is explicitly given by $f(r) = -\ln (e^{-f(0)} - \frac{c \mathbf{E}}{L} r)$ which explodes at time

$$ r_{0} :=\frac{L}{c \mathbf{E}e^{f(0)}} = \frac{k}{c L^{\prime \,4}} \;. $$

Let us require $k\le c L^{\prime \,4}$. Then $f$ explodes by time 1. By comparison, on the event $G$ we also deduce that $r\mapsto R(q_{r})$ explodes before time 1. To conclude, we also need to estimate

$$ \sup _{\theta _{0}} \mathbb{P}_{\theta _{0}}(q_{1} > \ln L') = \sup _{ \theta _{0}} \mathbb{P}_{\theta _{0}}\Big(\int _{0}^{\ln L'} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds < 1\Big)\;. $$

Given $\theta _{0}$, recall $T_{k} = \inf \{t\ge 0:\theta _{\lambda }^{(\mathbf{E})}(t) = \theta _{0} + k\pi \}$ for any $k\ge 1$. Set $p:= \Big \lfloor \frac{\ln L'}{2 m_{\lambda }^{(\mathbf{E})}} \Big \rfloor$. We have

$$ \begin{aligned}\sup _{\theta _{0}} \mathbb{P}_{\theta _{0}}\Big(\int _{0}^{\ln L'} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds < 1\Big) \le{}& \sup _{ \theta _{0}} \mathbb{P}_{\theta _{0}}(T_{p} > \ln L') \\ &{}+ \sup _{ \theta _{0}} \mathbb{P}_{\theta _{0}}\Big(\int _{0}^{T_{p}} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds < 1\Big)\;. \end{aligned}$$

From Lemma A.3, there exists $c_{1}>0$ such that

$$ \sup _{\theta _{0}} \mathbb{P}(T_{p} > \ln L') \le e^{-c_{1} \ln L' \mathbf{E}^{3/2}}\;. $$

Now observe that $\int _{0}^{T_{p}} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds$ has the same law as a sum of $p$ i.i.d. r.v. $X_{j}$ with

$$ X_{1} := \int _{0}^{\zeta _{\lambda }^{(\mathbf{E})}} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds\;. $$

From Lemma A.2 (and similarly as we did in the previous proof), there exists $\delta > 0$ such that

$$ \mathbb{P}(X_{1} > \frac{\delta }{\mathbf{E}^{3/2}}) > \frac{1}{2}\;. $$

Therefore

$$ \sup _{\theta _{0}} \mathbb{P}_{\theta _{0}}\Big(\int _{0}^{T_{p}} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})}(s) ds < 1\Big) \le \mathbb{P}(\text{Bin}(p,1/2) < \frac{\mathbf{E}^{3/2}}{\delta })\;. $$

Note that there exists $c>0$ such that $p = \lfloor \frac{\ln L'}{2 m_{\lambda }^{(\mathbf{E})}}\rfloor \ge c \mathbf{E}^{3/2}\ln L'$. Using again a multiplicative Chernov bound, we get for some $c_{2} >0$,

$$ \mathbb{P}(\text{Bin}(p,1/2)< \frac{\mathbf{E}^{3/2}}{\delta }) \le e^{-c_{2} \ln L' \mathbf{E}^{3/2}}\;. $$

Putting everything together, in this second step we have shown that for $R_{0} = 10 \ln L'$

$$ \begin{aligned}\inf _{\theta _{0}} \mathbb{P}_{\theta _{0},R_{0}}(R \text{ does not hit } +\infty \text{ by time }\ln L' ) \le{}& Ke^{-q5\ln L'} + e^{-c_{1} \ln L' \mathbf{E}^{3/2}} \\ &{}+ e^{-c_{2} \ln L' \mathbf{E}^{3/2}} \;. \end{aligned}$$

Combining the two steps, we conclude provided $k\to \infty$ slowly enough. □

9 Poisson statistics

The goal of this section is to prove Propositions 4.7 and 4.3. The former provides the intensity of the random measure $\bar{\mathcal{N}}_{L}$, which was defined in (21): this result, combined with the arguments presented in Sect. 4.4, establishes the convergence of $\bar{\mathcal{N}}_{L}$ towards a Poisson random measure. Subsequently, Proposition 4.3 shows that $\mathcal{N}_{L} - \bar{\mathcal{N}}_{L}$ goes to 0 as $L\to \infty$, and therefore concludes the proof of the main theorems.

The proof of Proposition 4.7 is presented in Sects. 9.1 and 9.2, while Sect. 9.3 is devoted to the proof of Proposition 4.3.

9.1 The limiting intensity

Let us start by defining the two random processes $Y_{E}$ and $Y_{\infty}$ introduced before the statement of Theorem 3.

In the Crossover regime, we have defined for some two-sided Brownian motion ℬ,

$$ Y_{\infty}(t) := {\frac{1}{\sqrt {2}}} \exp \Big(- \frac{|t|}{8} + \frac{\mathcal{B}(t)}{2\sqrt {2}}\Big)\;,\quad t\in {{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\;. $$

In the Bulk regime, the definition of $Y_{E}$ requires more notations. Consider two independent adjoint diffusions $(\bar{\theta}^{+}_{E}(t), \bar{\rho}^{+}_{E}(t); t\ge 0)$ and $(\bar{\theta}^{-}_{E}(t), \bar{\rho}^{-}_{E}(t); t\ge 0)$, satisfying the SDEs (55) and (57), and starting from

$$ \bar{\theta}^{+}_{E}(0) = \theta \;,\quad \bar{\theta}^{-}_{E}(0) = \pi -\theta \;,\quad \bar{\rho}^{+}_{E}(0) = \bar{\rho}^{-}_{E}(0) = 0 \;. $$

In other words, we work under the product measure $\bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0, \pi -\theta )}$ with the additional convention that $\bar{r}^{\pm}_{E}(0)=1$. We let $\bar{y}_{E}^{\pm}(t) := e^{\frac{1}{2} \bar{\rho}_{E}^{\pm}(t)} \sin \bar{\theta}_{E}^{\pm}(t)$. We define their concatenation¹³

$$ \hat{\bar{y}}_{E}(t) := \textstyle\begin{cases} \bar{y}_{E}^{-}(t) &\text{ if } t\ge 0\;, \\ \bar{y}_{E}^{+}({-}t) &\text{ if } t\le 0\;. \end{cases} $$

We then consider a mixture of these concatenations over different values of $\theta$: under the probability measure

$$ \frac{\mu _{E}(\theta ) \mu _{E}(\pi -\theta ) \sin ^{2} \theta}{n(E)} \bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0, \pi -\theta )}(\cdot ) d\theta \;, $$

we define the process

$$\begin{aligned} Y_{E}(t) := \hat{\bar{y}}_{E}(t)\;,\quad t\in {{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\;. \end{aligned}$$

One can now provide the definition of the limiting probability measure $\boldsymbol{\sigma _{E}}$, which is a unified notation for the probability measures $\sigma _{E}$ in the Bulk regime and $\sigma _{\infty}$ in the Crossover regime that appear in the statement of Theorem 3. Let us denote by $\boldsymbol{Y_{E}}$ the process $Y_{E}$ in the Bulk regime, and the process $Y_{\infty}$ in the Crossover regime. In both regimes, $\boldsymbol{\sigma _{E}}$ is the law of the random element in $\bar{\mathcal{M}}$ defined as

$$ \boldsymbol{w_{E}}(dt) = \frac{\boldsymbol{Y_{E}}(t+\boldsymbol{U_{E}})^{2} dt}{\int \boldsymbol{Y_{E}}(t)^{2} dt} \;, $$

where $\boldsymbol{U_{E}}$ is the associated center of mass

$$ \boldsymbol{U_{E}} := \frac{\int t \boldsymbol{Y_{E}}(t)^{2} dt}{\int \boldsymbol{Y_{E}}(t)^{2} dt} \;. $$

The rest of this subsection is devoted to the proof of Proposition 4.7. From now on, let us fix some function $f$ as in Proposition 4.7, and we let $h>0$ be such that $f(\lambda ,\cdot ,\cdot ) = 0$ whenever $\lambda \notin [-h,h]$. We also set $\Delta := [E- h/(Ln(E)) , E + h/(Ln(E))]$.

Recall the notations for the concatenation of the diffusions from Sect. 3.5. For $u \in [-\frac{L}{2k\mathbf{E}},\frac{L}{2k\mathbf{E}}]$, let us consider the product law $\mathbb{P}^{+}_{(-L/(2k\mathbf{E}), 0) \to (u,\theta )} \otimes \mathbb{P}^{-}_{(-L/(2k\mathbf{E}), 0) \to (-u,\pi -\theta )}$. With a slight abuse of notation, we still denote this product law by $\mathbb{P}^{(u)}_{\theta ,\pi -\theta}$ (originally, this notation was for the time interval $[-L/(2\mathbf{E}), L/(2\mathbf{E})]$). Then, we define under this product law the probability measure on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ built from the concatenation process $\hat{y}_{\lambda }^{(\mathbf{E})}$:

$$ \frac{\hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2} dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2} dt} \;. $$

The support of this measure is $[-\frac{L}{2k\mathbf{E}},\frac{L}{2k\mathbf{E}}]$. We let $\hat{U}_{\lambda }/\mathbf{E}$ be the center of mass of this measure

$$ \frac{\hat{U}_{\lambda }}{\mathbf{E}} := \frac{\int t \,\hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2} dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2} dt} \;.$$

(79)

We then recenter the probability measure by defining:

$$ \hat{w}_{\lambda }^{(\mathbf{E})}(dt) := \frac{\hat{y}_{\lambda }^{(\mathbf{E})}(\hat{U}_{\lambda }/\mathbf{E}+ t)^{2} dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(\hat{U}_{\lambda }/\mathbf{E}+ t)^{2} dt} \;. $$

We introduce the measure

$$ \mathbb{Q}^{(u)}_{\lambda }(\cdot ):= \frac{1}{\sqrt {\mathbf{E}}\,n(\lambda )}\int _{\theta =0}^{\pi} \mu ^{( \mathbf{E})}_{\lambda }(\theta ) \mu ^{(\mathbf{E})}_{\lambda }(\pi - \theta ) \sin ^{2} \theta \;\mathbb{P}^{(u)}_{\theta ,\pi -\theta}( \cdot ) d\theta \;. $$

By Corollary 6.2, this is a probability measure. We now proceed with the proof of Proposition 4.7.

Proof of Proposition 4.7

Step 1. For any $j\in \{1,\ldots ,k\}$ we have

$$ \int f d\mathcal{N}^{(j)}_{L} = \sum _{i\ge 1} f\big(Ln(E)(\lambda _{i}^{(j)}-E),U_{i}^{(j)}/L,w_{i}^{(j)} \big)\;. $$

Note that the operator at stake here is $\mathcal{H}_{L}^{(j)}$ on $(t_{j-1},t_{j})$. Let $a_{j}$ be the midpoint of $(t_{j-1},t_{j})$. By the GMP formula of Proposition 4.1, using forward/backward processes on the interval $[-L/(2k\mathbf{E}),L/(2k\mathbf{E})]$ and then shifting the evaluations by $a_{j}$, we find (recall that $\Delta := [E- h/(Ln(E)) , E + h/(Ln(E))]$ and that $f(\mu ,\cdot ,\cdot ) = 0$ whenever $\mu \notin [-h,h]$)

$$ \begin{aligned} {I_{j}} &:= \mathbb{E}\Big[\sum _{i\ge 1} f \big(Ln(E)(\lambda _{i}^{(j)}-E),U_{i}^{(j)}/L ,w_{i}^{(j)}\big)\Big] \\ &= \sqrt {\mathbf{E}}\int _{u=-\frac{L}{2 k\mathbf{E}}}^{ \frac{L}{2k\mathbf{E}}} \int _{\lambda \in {\Delta }} \int _{\theta =0}^{\pi }p_{\lambda ,\frac{L}{2k\mathbf{E}}+u}^{( \mathbf{E})}(\theta ) p_{\lambda ,\frac{L}{2k\mathbf{E}}-u}^{( \mathbf{E})}(\pi -\theta )\sin ^{2} \theta \\ &\qquad \qquad \times \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[f \big(Ln(E)(\lambda -E) , (\hat{U}_{\lambda }+a_{j}) / L , \hat{w}_{ \lambda }^{(\mathbf{E})}\big)\Big]\, d\theta \, d\lambda \, du\;. \end{aligned} $$

(80)

Step 2. We now show that

$$ \begin{aligned}I_{j} ={}& \mathbf{E}\int _{u=-\frac{L}{2 k\mathbf{E}}+t_{L}}^{ \frac{L}{2k\mathbf{E}}-t_{L}} \int _{\lambda \in \Delta } n(\lambda ) \mathbb{Q}^{(u)}_{\lambda }\Big[f(Ln(E)(\lambda -E) ,(a_{j}+u \mathbf{E})/L, \hat{w}_{\lambda }^{(\mathbf{E})})\Big]\, \,d\lambda \,du \\ &{}+ o(1/k)\;, \end{aligned}$$

where $o(1/k)$ is a negligible term compared to $1/k$ uniformly over all $j$.

To that end, let us first observe that there exists a constant $C>0$ such that for all $L$ large enough, for all $u\in [-\frac{L}{2 k\mathbf{E}},\frac{L}{2k\mathbf{E}}]$ and $\lambda \in \Delta$

$$ \int _{\theta =0}^{\pi }p_{\lambda ,\frac{L}{2k\mathbf{E}}+u}^{( \mathbf{E})}(\theta ) p_{\lambda ,\frac{L}{2k\mathbf{E}}-u}^{( \mathbf{E})}(\pi -\theta ) d\theta \le C\;. $$

(81)

Indeed, at least one of the two densities that appear in this expression satisfies the conditions of Theorem 4, while the other can be integrated over $\theta$: consequently, the integral over $\theta$ of the product of the densities can be bounded by some constant independent of all $L$ large enough.

Note that $|\hat{U}_{\lambda }/L| \le 1/(2k)$ and $|u\mathbf{E}/L| \le 1/(2k)$ so that they vanish as $L\to \infty$. Since $f$ is uniformly continuous, we can replace the expectation term in (80) by

$$ \mathbb{E}^{(u)}_{\theta ,\pi -\theta}\Big[f(Ln(E)(\lambda -E) ,(a_{j}+u \mathbf{E})/L, \hat{w}_{\lambda }^{(\mathbf{E})})\Big]\;. $$

Indeed, denoting by $\kappa _{f}(\cdot )$ the modulus of continuity of $f$ and using (81), the error made upon this replacement is bounded by

$$\begin{aligned} &\sqrt {\mathbf{E}}\int _{u=-\frac{L}{2 k\mathbf{E}}}^{ \frac{L}{2k\mathbf{E}}} \int _{\lambda \in \Delta } \int _{\theta =0}^{ \pi }p_{\lambda ,\frac{L}{2k\mathbf{E}}+u}^{(\mathbf{E})}(\theta ) p_{ \lambda ,\frac{L}{2k\mathbf{E}}-u}^{(\mathbf{E})}(\pi -\theta )\sin ^{2} \theta \, \kappa _{f}(1/k) d\theta \, d\lambda \, du \\ &\le C\sqrt{\mathbf{E}} \frac{L}{k\mathbf{E}}\frac{2h}{Ln(E)}\kappa _{f}(1/k) \\ &= \frac{C \, 2h}{k} \frac{\kappa _{f}(1/k)}{\sqrt{\mathbf{E}} n(E)}\;. \end{aligned}$$

Since the modulus of continuity vanishes at 0, this term is negligible compared to $1/k$.

Let $t_{L}$ be such that $\ln (L/\mathbf{E}) \ll t_{L} \ll L/(k\mathbf{E})$. In (80), the integral over $u \in J:= [-\frac{L}{2 k\mathbf{E}}, -\frac{L}{2 k\mathbf{E}}+t_{L}] \cup [\frac{L}{2 k\mathbf{E}}-t_{L},\frac{L}{2 k\mathbf{E}}]$ can be bounded by

$$ \sqrt {\mathbf{E}}\int _{u\in J} \int _{\lambda \in \Delta } \int _{ \theta =0}^{\pi }p_{\lambda ,\frac{L}{2k\mathbf{E}}+u}^{(\mathbf{E})}( \theta ) p_{\lambda ,\frac{L}{2k\mathbf{E}}-u}^{(\mathbf{E})}(\pi - \theta ) d\theta \, d\lambda \, du\; \times \|f\|_{\infty }\;. $$

(82)

Using (81), this last quantity is bounded by a term of order

$$ \sqrt{\mathbf{E}} t_{L} \frac{1}{Ln(E)} \lesssim \frac{1}{k} \frac{k \mathbf{E}}{L} t_{L}\;, $$

which is negligible compared to $1/k$ as required.

In the remaining integral, Theorem 4 allows to replace both of the densities by the invariant measure, up to some negligible term $o(1/k)$. We are left with

$$\begin{aligned} &\sqrt {\mathbf{E}}\int _{u=-\frac{L}{2 k\mathbf{E}}+t_{L}}^{ \frac{L}{2k\mathbf{E}}-t_{L}} \int _{\lambda \in \Delta} \int _{ \theta =0}^{\pi }\mu _{\lambda }^{(\mathbf{E})}(\theta ) \mu _{ \lambda }^{(\mathbf{E})}(\pi -\theta ) \sin ^{2} \theta \\ &\qquad \qquad \qquad \times \mathbb{E}^{(u)}_{\theta ,\pi -\theta} \Big[f(Ln(E)(\lambda -E) ,(a_{j}+u\mathbf{E})/L, \hat{w}_{\lambda }^{( \mathbf{E})})\Big]\, d\theta \,d\lambda \, du \\ &= \mathbf{E}\int _{u=-\frac{L}{2 k\mathbf{E}}+t_{L}}^{ \frac{L}{2k\mathbf{E}}-t_{L}} \int _{\lambda \in \Delta} n(\lambda ) \mathbb{Q}^{(u)}_{\lambda }\Big[f(Ln(E)(\lambda -E) ,(a_{j}+u \mathbf{E})/L, \hat{w}_{\lambda }^{(\mathbf{E})})\Big]\, \,d\lambda \,du\;, \end{aligned}$$

where we used Corollary 6.2 at the second line. This completes Step 2.

Step 3. Summing over $j$ the quantities above, we have shown that

$$\begin{aligned} \mathbb{E}[\int f d\bar{\mathcal{N}}_{L}] ={}& \mathbf{E}\sum _{j} \int _{u=- \frac{L}{2 k\mathbf{E}}+t_{L}}^{\frac{L}{2k\mathbf{E}}-t_{L}} \int _{ \lambda \in \Delta } n(\lambda ) \\ &{}\times \mathbb{Q}^{(u)}_{\lambda }\Big[f(Ln(E)( \lambda -E) ,(a_{j}+u\mathbf{E})/L, \hat{w}_{\lambda }^{(\mathbf{E})}) \Big]\, \,d\lambda \,du + o(1)\;. \end{aligned}$$

Set $D_{L}:= \cup _{j} \Big ([\frac{t_{j}}{L} - t_{L}\frac{\mathbf{E}}{L}, \frac{t_{j}}{L} + t_{L}\frac{\mathbf{E}}{L}] \cap [-1/2,1/2]\Big )$.

Applying the change of variables $\mu = Ln(E)(\lambda -E)$ and $v = (a_{j}+u\mathbf{E})/L$, this rewrites

$$\begin{aligned} \mathbb{E}[\int f d\bar{\mathcal{N}}_{L}] ={}& \int _{v\in [-1/2,1/2]} \int _{\mu \in [-h,h]} \frac{n(\lambda (\mu ))}{n(E)} \mathbf{1}_{v \notin D_{L}} \\ &{}\times \mathbb{Q}^{(u(v))}_{\lambda (\mu )}\Big[f(\mu ,v, \hat{w}_{\lambda (\mu )}^{(\mathbf{E})})\Big]\, \,d\mu \,dv + o(1)\;, \end{aligned}$$

where $\lambda (\mu )$ and $u(v)$ are the reciprocals of the change of variables. Note that $n(\lambda ) / n(E) \to 1$ uniformly over all $\lambda \in \Delta$. Consequently we only have to show that as $L\to \infty$

$$ \int _{v\in [-1/2,1/2]} \int _{\mu \in [-h,h]} \mathbf{1}_{v\notin D_{L}} \mathbb{Q}^{(u(v))}_{\lambda (\mu )}\Big[f(\mu ,v, \hat{w}_{\lambda ( \mu )}^{(\mathbf{E})})\Big]\, \,d\mu \,dv\;, $$

converges to

$$ \int _{v\in [-1/2,1/2]}\int _{\mu \in [-h,h]} \int _{w\in \bar {\mathcal{M}}} f(\mu ,v,w) \; d\mu \,dv\, \boldsymbol{\sigma _{E}}(dw)\;. $$

To that end, it suffices to show that for any sequence $L_{k}\to \infty$, there exists a subsequence along which the convergence holds. Fix some sequence $L_{k}\to \infty$, and extract a subsequence $L_{k_{i}}$ in such a way that the Lebesgue measure of

$$ D:= \limsup _{i\to \infty } D_{L_{k_{i}}}\;, $$

vanishes. As $w\mapsto f(\mu ,v,w)$ is a bounded continuous function, using the Dominated Convergence Theorem, it suffices to show that along the subsequence $L_{k_{i}}$ and for any $v\notin D$

$$ \mathbb{Q}^{(u(v))}_{\lambda (\mu )}\Big[f(\mu ,v, \hat{w}_{\lambda ( \mu )}^{(\mathbf{E})})\Big] \to \int _{\bar{\mathcal{M}}} f(\mu ,v,w) \; \boldsymbol{\sigma _{E}}(dw)\;. $$

It is the object of Lemma 9.1 stated below. □

Lemma 9.1

We use the notations of the previous proof. For every $v\in [-1/2,1/2]\backslash D$ and for every $\mu \in [-h,h]$, the law of $\hat{w}_{\lambda (\mu )}^{(\mathbf{E})}$ under $\mathbb{Q}^{(u(v))}_{\lambda (\mu )}$ converges weakly, along the subsequence $L_{k_{i}}$, to $\boldsymbol{\sigma _{E}}$ on $\bar{\mathcal{M}}$.

9.2 Proof of Lemma 9.1

We fix some $v\in [-1/2,1/2]\backslash D$ and some $\mu \in [-h,h]$. For notational convenience, we write $L$ instead of $L_{k_{i}}$. We also set $\lambda = \lambda (\mu ) = E + \mu /(Ln(E))$ and $u = u(v) = (Lv - a_{j})/\mathbf{E}$ where $a_{j}$ is the midpoint of the interval $(t_{j-1},t_{j})$ in which $Lv$ falls. Since $v \notin D$, for all $L$ large enough $u\in [-\frac{L}{2k\mathbf{E}}+t_{L}, \frac{L}{2k\mathbf{E}}-t_{L}]$. Assume that we can show:

• (1) For every compactly supported, continuous function $g : {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\to{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ the r.v.

  $$ \int g(t) \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt\;, $$

  under $\mathbb{Q}^{(u)}_{\lambda }$ converges in law as $L\to \infty$ to

  $$ \int g(t) \boldsymbol{Y_{E}}(t)^{2} dt\;. $$

• (2) Control of the mass at infinity. There exists $q>0$ such that

  $$ \limsup _{x\to \infty }\limsup _{L\to \infty } \mathbb{Q}^{(u)}_{ \lambda }\Big(\int e^{q|t-u|} \hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2}dt > x \Big) = 0\;. $$

Given these two assumptions, we can proceed with the proof of the lemma.

Proof of Lemma 9.1

The control of the mass at infinity (2) allows to lift the convergence in law stated in (1): for every continuous function $g:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\to{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ with at most polynomial growth at infinity, the r.v.

$$ \int g(t) \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt\;, $$

under $\mathbb{Q}^{(u)}_{\lambda }$ converges in law to $\int g(t) \boldsymbol{Y_{E}}(t)^{2} dt$. This convergence remains true for $n$-dimensional vectors associated to continuous functions $g_{1},\ldots ,g_{n}$ with at most polynomial growth, for any $n\ge 1$. In particular

$$ \int \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt \Rightarrow \int \boldsymbol{Y_{E}}(t)^{2} dt\;, $$

and

$$ \frac{\hat{U}_{\lambda }}{\mathbf{E}}-u = \frac{\int t \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt} \Rightarrow \frac{\int t \boldsymbol{Y_{E}}(t)^{2} dt}{\int \boldsymbol{Y_{E}}(t)^{2} dt} = \boldsymbol{U_{E}}\;. $$

In addition, this implies [19, Th 16.16] that the following probability measures converge in law in $\bar {\mathcal{M}}$

$$ \frac{\hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2} dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(t+u)^{2}dt} \Rightarrow \frac{\boldsymbol{Y_{E}}(t)^{2} dt}{\int \boldsymbol{Y_{E}}(t)^{2} dt} \;. $$

(83)

Using Skorohod’s Representation Theorem, the previous convergences imply that the following convergence in law in $\bar {\mathcal{M}}$ holds

$$ \frac{\hat{y}_{\lambda }^{(\mathbf{E})}(t+\hat{U}_{\lambda }/\mathbf{E})^{2} dt}{\int \hat{y}_{\lambda }^{(\mathbf{E})}(t+\hat{U}_{\lambda }/\mathbf{E})^{2}dt} \Rightarrow \frac{\boldsymbol{Y_{E}}(t+\boldsymbol{U_{E}})^{2} dt}{\int \boldsymbol{Y_{E}}(t+\boldsymbol{U_{E}})^{2} dt} \;, $$

as required. □

Let us now prove the two assumptions above.

Proof of Assumption (2)

It suffices to show

$$ \limsup _{x\to \infty}\limsup _{L\to \infty} \sup _{{\theta }} {\mathbb{P}}^{(u)}_{\theta ,\pi -\theta}\Big(\int e^{q|t-u|} \hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2}dt > x \Big)= 0\;. $$

Recall that ${\mathbb{P}}^{(u)}_{\theta ,\pi -\theta }$ stands for $\mathbb{P}^{+}_{(-L/(2k\mathbf{E}), 0) \to (u,\theta )} \otimes \mathbb{P}^{-}_{(-L/(2k\mathbf{E}), 0) \to (-u,\pi -\theta )}$, consequently

$$\begin{aligned} &{\mathbb{P}}^{(u)}_{\theta ,\pi -\theta }\Big(\int e^{q|t-u|} \hat{y}_{\lambda }^{(\mathbf{E})}(t)^{2}dt > x \Big) \\ &\quad \le \mathbb{P}^{+}_{(-L/(2k \mathbf{E}), 0) \to (u,\theta )}\Big(\int _{t\le u} e^{q|t-u|} y_{ \lambda }^{(\mathbf{E}),+}(t)^{2}dt > x/2 \Big) \\ &\qquad {}+ \mathbb{P}^{-}_{(-L/(2k\mathbf{E}), 0) \to (-u,\pi -\theta )} \Big(\int _{t\ge u} e^{q|t-u|} y_{\lambda }^{(\mathbf{E}),-}(t)^{2}dt > x/2 \Big)\;. \end{aligned}$$

We concentrate on bounding the probability that concerns the forward diffusion, but the exact same arguments apply to the backward diffusion. Shifting the time parameter by $L/(2k\mathbf{E})$, writing $\tilde{u} = u + L/(2k \mathbf{E})$ and bounding $\sin ^{2} \theta _{\lambda }^{(\mathbf{E})}$ by 1, it suffices to show

$$ \limsup _{x\to \infty }\limsup _{L\to \infty } \sup _{\theta } { \mathbb{P}}_{(0,0) \to (\tilde{u}, \theta )}\Big(\int _{0}^{ \tilde{u}} e^{q|t-\tilde{u}|} \frac{r_{\lambda }^{(\mathbf{E})}(t)^{2}}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})^{2}} dt > x \Big) = 0\;, $$

with $r_{\lambda }^{(\mathbf{E})}(0)=1$. Take $q < \nu _{\lambda }^{(\mathbf{E})} - \varepsilon$. We find

$$\begin{aligned} \int _{0}^{\tilde{u}} e^{q|t-\tilde{u}|} \frac{r_{\lambda }^{(\mathbf{E})}(t)^{2}}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})^{2}} dt &\le \int _{0}^{\tilde{u}} e^{(q-\nu _{\lambda }^{(\mathbf{E})} + \varepsilon )|t-\tilde{u}|} dt \sup _{t\in [0,\tilde{u}]}\Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2} (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon )|t- \tilde{u}|}\Big)^{2} \\ &\le \frac{1}{\nu _{\lambda }^{(\mathbf{E})} - \varepsilon - q} \sup _{t \in [0,\tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2} (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon )|t- \tilde{u}|}\Big)^{2}\;. \end{aligned}$$

For any $q'>0$, set $x' = \big (x (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon - q) \big )^{q'/2}$ and observe that

$$\begin{aligned} &{\mathbb{P}}_{(0,0) \to (\tilde{u}, \theta )}\Big(\int _{0}^{ \tilde{u}} e^{q|t-\tilde{u}|} \frac{r_{\lambda }^{(\mathbf{E})}(t)^{2}}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})^{2}} dt > x \Big) \\ &\le{\mathbb{P}}_{(0,0) \to (\tilde{u}, \theta )}\Big( \frac{1}{\nu _{\lambda }^{(\mathbf{E})} - \varepsilon - q} \sup _{t \in [0,\tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2} (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon )|t- \tilde{u}|}\Big)^{2} > x \Big) \\ &\le{\mathbb{P}}_{(0,0) \to (\tilde{u}, \theta )}\Big(\sup _{t\in [0, \tilde{u}]}\Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2} (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon )|t- \tilde{u}|}\Big)^{q'} > x' \Big) \\ &\le \frac{1}{x'} {\mathbb{E}}_{(0,0) \to (\tilde{u}, \theta )}\Big[ \sup _{t\in [0,\tilde{u}]} \Big( \frac{r_{\lambda }^{(\mathbf{E})}(t)}{r_{\lambda }^{(\mathbf{E})}(\tilde{u})}e^{ \frac{1}{2} (\nu _{\lambda }^{(\mathbf{E})} - \varepsilon )|t- \tilde{u}|}\Big)^{q'}\Big]\;. \end{aligned}$$

The expectation coincides with (66), which we already proved is bounded uniformly over all parameters provided $q'>0$ is small enough (recall that $\tilde{u} \geq t_{L}$ and that $t_{L} \to \infty$ as $L\to \infty$ so that $t_{L} \geq t_{0}$). Since $x'\to \infty$ as $x\to \infty$, this suffices to conclude. □

Proof of Assumption (1)

The adjunction relation (56) shows that the process $\hat{y}_{\lambda }^{(\mathbf{E})}(t+u)$, $t\in [-u-L/(2k\mathbf{E}),-u+L/(2k\mathbf{E})]$ under $\mathbb{Q}^{(u)}_{\lambda }$ has the same law as the process

$$ \hat{\bar{y}}_{\lambda }^{(\mathbf{E})}(t+u) := \bar{y}_{\lambda }^{-}(t) \mathbf{1}_{t\ge 0} + \bar{y}_{\lambda }^{+}(-t) \mathbf{1}_{t< 0}\;, \quad t \in [-u-L/(2k\mathbf{E}),-u+L/(2k\mathbf{E})]\;, $$

under the probability measure

$$ \begin{aligned}&\int _{\theta }\frac{1}{\sqrt {\mathbf{E}}n(\lambda )} \mu ^{( \mathbf{E})}_{\lambda }(\theta ) \mu ^{(\mathbf{E})}_{\lambda }(\pi - \theta ) \sin ^{2} \theta (1+\kappa _{L}(u,\theta )) \\ &\quad {}\times \bar{\mathbb{P}}^{+}_{(0,\theta )\to (u+\frac{L}{2k\mathbf{E}}, 0)} \otimes \bar{\mathbb{P}}^{-}_{(0,\pi -\theta )\to ( \frac{L}{2k\mathbf{E}}-u, 0)}(\cdot ) d\theta \;, \end{aligned}$$

where

$$ \begin{aligned}\kappa _{L}(u,\theta ) ={}& \frac{\mu _{\lambda }^{(\mathbf{E})}(\theta )}{p_{\lambda ,\frac{L}{2k\mathbf{E}}+u}(0,\theta )} \frac{\bar{p}_{\lambda ,\frac{L}{2k\mathbf{E}}+u}(\theta ,0)}{\mu _{\lambda }^{(\mathbf{E})}(0)} \frac{\mu _{\lambda }^{(\mathbf{E})}(\pi -\theta )}{p_{\lambda ,\frac{L}{2k\mathbf{E}}-u}(0,\pi -\theta )} \\ &{}\times \frac{\bar{p}_{\lambda ,\frac{L}{2k\mathbf{E}}-u}(\pi -\theta ,0)}{\mu _{\lambda }^{(\mathbf{E})}(0)} - 1\;. \end{aligned}$$

This last probability measure can be written as the sum of two measures: one which is associated with $\kappa _{L}(u,\theta )$, and another with 1. The total-variation of the former can be bounded by

$$ \frac{1}{\sqrt{\mathbf{E}}n(\lambda )} \int _{0}^{\pi }\vert \kappa _{L}(u, \theta )\vert d\theta \;. $$

Since $u$ is $t_{L}$-away from $\pm L/(2k\mathbf{E})$, by Theorem 4 and Lemma 3.1 there exists a constant $c'>0$ such that $\vert \kappa _{L}(u,\theta )\vert \le c' e^{-Ct_{L}}$ and this quantity goes to 0 uniformly over all $\theta$, as $L\to \infty$.

We can therefore deal with the law of $\hat{\bar{y}}_{\lambda }^{(\mathbf{E})}(u+t)$, $t\in [-u-L/(2k\mathbf{E}),-u+L/(2k\mathbf{E})]$ under the probability measure

$$ \int _{\theta }\frac{1}{\sqrt {\mathbf{E}}n(\lambda )} \mu ^{( \mathbf{E})}_{\lambda }(\theta ) \mu ^{(\mathbf{E})}_{\lambda }(\pi - \theta ) \sin ^{2} \theta \; \bar{\mathbb{P}}^{+}_{(0,\theta )\to (u+ \frac{L}{2k\mathbf{E}}, 0)} \otimes \bar{\mathbb{P}}^{-}_{(0,\pi - \theta )\to (\frac{L}{2k\mathbf{E}}-u, 0)}(\cdot ) d\theta \;. $$

Fix a compactly supported, continuous function $g$. We can restrict ourselves to the law of $\hat{y}_{\lambda }^{(\mathbf{E})}(u+t)$, $t\in I$ where $I$ is a given bounded interval that contains the support of $g$. Thus, the last part of Lemma 7.4 ensures that we can disregard the conditioning of the diffusions and work under

$$ \tilde{\mathbb{Q}}_{\lambda }(\cdot ) := \frac{1}{\sqrt {\mathbf{E}}n(\lambda )} \int _{\theta }\mu ^{( \mathbf{E})}_{\lambda }(\theta ) \mu ^{(\mathbf{E})}_{\lambda }(\pi - \theta ) \sin ^{2} \theta \; \bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0,\pi -\theta )}(\cdot ) d\theta \;. $$

The rest of the proof is presented separately for the Bulk and the Crossover regimes. In the Bulk regime, we aim at showing that the random variable

$$ \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}}g(t) \big( \bar{y}_{\lambda }^{-}(t)^{2} \mathbf{1}_{t\ge 0} + \bar{y}_{\lambda }^{+}(-t)^{2} \mathbf{1}_{t< 0} \big) dt\;, $$

under the probability measure $\tilde{\mathbb{Q}}_{\lambda }(\cdot )$ converges as $L\to \infty$ to the random variable

$$ \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}}g(t) \big( \bar{y}_{E}^{-}(t)^{2} \mathbf{1}_{t \ge 0} + \bar{y}_{E}^{+}(-t)^{2} \mathbf{1}_{t< 0}\big) dt\;, $$

under $\tilde{\mathbb{Q}}_{E} (\cdot )$. Lemma A.5 shows that, as $L\to \infty$ and uniformly over all $\theta \in [0,\pi ]$

$$ \frac{1}{n(\lambda )} \mu _{\lambda }(\theta ) \mu _{\lambda }(\pi - \theta ) \to \frac{1}{n(E)} \mu _{E}(\theta ) \mu _{E}(\pi -\theta ) \;. $$

To conclude, it suffices to show that $\bar{y}_{\lambda }^{-}(t)^{2} \mathbf{1}_{t\ge 0} + \bar{y}_{ \lambda }^{+}(-t)^{2} \mathbf{1}_{t< 0}$ under $\bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0, \pi -\theta )}(\cdot )$ converges in law as $L\to \infty$ for the local uniform topology towards $\bar{y}_{E}^{-}(t)^{2} \mathbf{1}_{t\ge 0} + \bar{y}_{E}^{+}(-t)^{2} \mathbf{1}_{t< 0}$ under $\bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0, \pi -\theta )}(\cdot )$, and that this convergence is uniform over all $\theta \in [0,\pi ]$. This can be achieved through a coupling under which almost surely the process

$$ {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\times [0,\pi ]\times{{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\ni ( \lambda ,\theta ,t) \mapsto \bar{y}_{\lambda }^{-}(t)^{2} \mathbf{1}_{t \ge 0} + \bar{y}_{\lambda }^{+}(-t)^{2} \mathbf{1}_{t< 0}\;, $$

is continuous, and therefore uniformly continuous on $\Delta \times [0,\pi ]\times I$, where $I$ is the compact set defined above that contains the support of $g$.

We turn to the Crossover regime. Contrary to the Bulk regime, that the law of the process $Y_{\infty }$ is not a mixture over some parameter $\theta \in [0,\pi ]$. It suffices to show that uniformly over $\theta$ the r.v.

$$ \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}}g(t) \big( \bar{y}_{\lambda }^{-,(E)}(t)^{2} \mathbf{1}_{t\ge 0} + \bar{y}_{\lambda }^{+,(E)}(-t)^{2} \mathbf{1}_{t< 0}\big) dt\;, $$

under $\bar{\mathbb{P}}^{+}_{(0,\theta )} \otimes \bar{\mathbb{P}}^{-}_{(0, \pi -\theta )}(\cdot )$ converge in law as $L\to \infty$ to

$$ \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}}g(t) Y_{\infty }(t)^{2} dt\;. $$

Note that $(Y_{\infty }(t), t\ge 0)$ and $(Y_{\infty }(-t), t\ge 0)$ are i.i.d. Furthermore, $(\bar{y}_{\lambda }^{-,(E)}(t),t\ge 0)$ and $(\bar{y}_{\lambda }^{+,(E)}(t),t\ge 0)$ are independent and distributed according to $\bar{\mathbb{P}}_{(0,\theta )}$ and $\bar{\mathbb{P}}_{(0,\pi -\theta )}$. To prove the convergence, it is thus sufficient to show that for any compactly supported and continuous function $h:[0,\infty )\to{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$, uniformly over $\theta$ the r.v.

$$ \int _{[0,\infty )} h(t) {\bar{y}}_{\lambda }^{(E)}(t)^{2} dt\;, $$

under $\bar{\mathbb{P}}_{(0,\theta )}$ converges in law as $L\to \infty$ towards

$$ \int _{[0,\infty )} h(t) Y_{\infty }(t)^{2} dt\;. $$

This is the content of Lemma 9.2 which is stated right below, and whose proof is based on very similar arguments to those presented in [9, Prop. 3]. □

Lemma 9.2

Fix $h>0$ and set $\lambda = E + h/(Ln(E))$. In the Crossover regime, uniformly over all $\theta \in [0,\pi )$ the process

$$ (\bar{\theta}^{(E)}_{\lambda }(t)+E^{3/2}t, \bar{\rho}^{(E)}_{ \lambda }(t);t\ge 0)\;,\textit{ with }\bar{\theta}^{(E)}_{\lambda }(0) = \theta \;,\quad \bar{\rho}^{(E)}_{\lambda }(0) = 0\;; $$

converges in law to $(\bar{\Theta}(t),\bar{R}(t);t\ge 0)$ which solves the following SDEs:

$$\begin{aligned} d\bar{\Theta}(t) &= -\frac{1}{2} d\mathcal{B}(t) + \frac{1}{2\sqrt {2}} \Re ( e^{2i \bar{\Theta}(t)} d\mathcal{W}(t))\;,\quad t\ge 0 \\ d\bar{R}(t) &= - \frac{1}{4}dt + \frac{1}{\sqrt {2}}\Im (e^{2i \bar{\Theta}(t)} d\mathcal{W}(t))\;,\quad t\ge 0\;, \end{aligned}$$

starting from $\bar{\Theta}(0) = \theta$, $\bar{R}(0) = 0$, where $\mathcal{W}$ is a complex Brownian motion¹⁴and ℬ is an independent real Brownian motion.

As a consequence, for any compactly supported, continuous function $h:[0,\infty )\to{{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$, the following convergence in law as $L\to \infty$ holds uniformly over all $\theta \in [0,\pi )$

$$ \int h(t) {\bar{y}}_{\lambda }^{(E)}(t)^{2} dt \Rightarrow \int h(t) Y_{ \infty }(t)^{2} dt\;. $$

Proof of Lemma 9.2

The proof of the first part is essentially the same as the proof of [9, Prop. 3] (the proof therein concerns the convergence of the process $(\theta _{\lambda }^{(E)}, \varrho _{\lambda }^{(E)})$ in the regime of energy $L/E \to \tau \in (0,\infty )$) so we only present the main steps. Set $v_{\lambda }(t) = \bar{\theta}^{(E)}_{\lambda }(t)+E^{3/2}t$. Introduce the martingale

$$ d\bar{W}^{(E)}(t) = \sqrt{2} \cos (-2E^{3/2}t) d\bar{B}^{(E)}(t) + i \sqrt{2} \sin (-2E^{3/2}t) d\bar{B}^{(E)}(t)\;. $$

One can write the SDEs (55) and (57) solved by these two processes as follows

$$\begin{aligned} d v_{\lambda }(t) &= -\frac{1}{2} d\bar{B}^{(E)}(t) + \frac{1}{2\sqrt {2}}\Re ( e^{2i v_{\lambda }(t)} d\bar{W}^{(E)}(t)) + \mathcal{E}(v_{\lambda })(t) dt \\ d \bar{\rho}_{\lambda }^{(E)}(t) &= -\frac{1}{4} dt + \frac{1}{\sqrt {2}}\Im (e^{2i v_{\lambda }(t)} d\bar{W}^{(E)}(t)) + \mathcal{E}(\bar{\rho}_{\lambda }^{(E)})(t)dt\;, \end{aligned}$$

where $\mathcal{E}(v_{\lambda })(t)$ and $\mathcal{E}(\bar{\rho}_{\lambda }^{(E)})(t)$ should be seen as negligible terms

$$\begin{aligned} \mathcal{E}(v_{\lambda })(t) &= - \sqrt {E} (\lambda -E) \sin ^{2} \overline{\theta}_{\lambda }^{(E)} +\sin ^{4} \overline{\theta}_{ \lambda }^{(E)} \frac{\partial _{\theta }\mu _{\lambda }^{(E)}(\overline{\theta}_{\lambda }^{(E)})}{\mu _{\lambda }^{(E)}(\overline{\theta}_{\lambda }^{(E)})} \\ &\quad + 3\sin ^{3}(\overline{\theta}_{\lambda }^{(E)})\cos ( \overline{\theta}_{\lambda }^{(E)})\;, \\ \mathcal{E}(\bar{\rho}_{\lambda }^{(E)})(t) &= \sqrt {E} (\lambda -E) \sin 2\overline{\theta}_{\lambda }^{(E)} +\frac{3}{4} \cos 4 \bar{\theta}_{\lambda }^{(E)}(t) - \frac{1}{2} \cos 2\bar{\theta}_{ \lambda }^{(E)}(t) \\ &\quad - 2 \sin ^{3} \bar{\theta}^{(E)}_{\lambda }\cos \bar{\theta}^{(E)}_{ \lambda } \frac{\partial _{\theta }\mu _{\lambda }^{(E)}(\bar{\theta}_{\lambda }^{(E)})}{\mu _{\lambda }^{(E)}(\bar{\theta}_{\lambda }^{(E)})} \;. \end{aligned}$$

Note that the pair $\bar{\theta }^{(E)}_{\lambda }(t)+E^{3/2}t$, $\bar{\rho }^{(E)}_{ \lambda }(t)$ is indexed by $t\ge 0$ and $\theta \in [0,\pi ]$. Note also that the putative limit $\bar{\Theta }(t)$, $\bar{R}(t)$ is indexed by the same pair.

The proof consists of three steps. First, the tightness of these processes can be derived by estimating the moments of their increments, with the help of the Burkholder-Davis-Gundy inequality. Second, one shows that the integrals in time of the terms $\mathcal{E}(\cdot )$ are negligible: the main argument is a quantitative Riemann-Lebesgue Lemma, see [9, Lemma 4.1], that takes advantage of the rapid oscillations of $\bar{\theta}_{\lambda }^{(E)}(t) = v_{\lambda }(t) - E^{3/2}t$. Finally, one identifies the limit of any converging subsequence by a martingale problem. We refer to [9, Prop 4.2] for more details.

We turn to the last part of the statement. First of all, note that if we set $\beta (t) := \int _{0}^{t} \Im (e^{2i \bar{\Theta }(s)} d\mathcal{W}(s))$ then $\beta$ is a standard Brownian motion. Consequently the process

$$ \frac{1}{2}e^{\bar{R}(t)} = \frac{1}{2} e^{-\frac{t}{4} + \frac{\beta (t)}{\sqrt{2}}}\;,\quad t\ge 0\;, $$

has the same law as $Y^{2}_{\infty }(t), t\ge 0$. Fix ${h} : [0,\infty ) \to {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$ a compactly supported continuous function. By Skorohod’s Representation Theorem, we can assume that the process

$$ (\bar{\theta }^{(E)}_{\lambda }(t)+E^{3/2}t, \bar{\rho }^{(E)}_{ \lambda }(t);t\ge 0; \theta \in [0,\pi ])\;, $$

converges almost surely towards

$$ (\bar{\Theta }(t),\bar{R}(t);t\ge 0; \theta \in [0,\pi ])\;. $$

Then, using that the function $\sin ^{2}$ is Lipschitz, the term

$$ \int h(t) {\bar{y}}_{\lambda }^{(E)}(t)^{2} dt = \int h(t) e^{ \bar{\rho}^{(E)}_{\lambda }(t)} \sin ^{2} \bar{\theta}_{\lambda }^{(E)}(t) dt\;, $$

is asymptotically as close as desired to

$$ \begin{aligned}\int g(t) e^{\bar{R}(t)} \sin ^{2} \big(\bar{\Theta}(t) - E^{3/2}t \big) dt ={}& \frac{1}{2} \int g(t) e^{\bar{R}(t)} dt \\ &{} - \frac{1}{2} \int g(t) e^{\bar{R}(t)} \cos \big(2(\bar{\Theta}(t) - E^{3/2}t)\big) dt \;. \end{aligned}$$

The second term on the r.h.s. rewrites

$$ \frac{1}{2} \int g(t) e^{\bar{R}(t)}\Big( \cos \big(2\bar{\Theta}(t) \big)\cos (2E^{3/2}t) + \sin \big(2\bar{\Theta}(t)\big)\sin (2E^{3/2}t) \Big) dt\;, $$

and this goes to 0 as $L\to \infty$ by a quantitative Riemann-Lebesgue Lemma. □

9.3 Controlling the approximation

We fix $h>0$ and set $\Delta = [E-h/(Ln(E)),E+h/(Ln(E))]$.

Recall the definition of the points $(t_{j})_{j}$ at the beginning of Sect. 4.4. Let us introduce for $n\ge 1$ and $j\in \{0,\ldots ,k\}$, the following neighborhood of $t_{j}$:

$$ \mathcal{D}_{j}(n) := [t_{j}-nt_{L} \mathbf{E}, t_{j} + nt_{L} \mathbf{E}] \cap [-L/2,L/2]\;, $$

where $t_{L}$ is such that¹⁵$\ln ( L/\mathbf{E}) \ll t_{L} \ll L/(k\mathbf{E})$. We also set $\mathcal{D}(n) := \cup _{j} \mathcal{D}_{j}(n)$.

Recall that we have already proven Theorem 2. Fix $\varepsilon > 0$ small enough. We introduce the event $\mathcal{B}_{L}$ on which:

• (i) for every $\lambda _{i}\in \Delta$, we have

  $$ \Big(\varphi _{i}(t)^{2} + \frac{\varphi _{i}'(t)^{2}}{\mathbf{E}} \Big)^{1/2} \le \frac{t_{L}}{\sqrt {\mathbf{E}}} e^{-\frac{1}{2}( \boldsymbol{\nu _{E}}-\varepsilon )\frac{|t-U_{i}|}{\mathbf{E}}}\;, \quad \forall t\in [-L/2,L/2]\;, $$

• (ii) for every $\lambda _{i} \in \Delta$, we have $U_{i} \notin \mathcal{D}(3)$,

• (iii) we have $\int _{\mathcal{D}(2)} \Big(\sum _{\lambda _{i} \in \Delta} | \varphi _{i}| + \frac{|\varphi _{i}'|}{\sqrt {\mathbf{E}}}\Big)^{2} ds < e^{-(\boldsymbol{\nu _{E}}-2\varepsilon ) t_{L}}$,

Lemma 9.3

We have $\mathbb{P}(\mathcal{B}_{L}) \to 1$ as $L\to \infty$.

Proof

The proof requires the following preliminary estimate: there exists $c> 0$ such that uniformly over all $L$ large enough we have

$$ \mathbb{E}\Big[\int _{\mathcal{D}(4)} \sum _{\lambda _{i} \in \Delta} \Big(\varphi _{i}(v)^{2} + \frac{\varphi _{i}'(v)^{2}}{\mathbf{E}} \Big) dv\Big] \le c \frac{kt_{L} \mathbf{E}}{L}\;. $$

(84)

This bound easily follows from Proposition 6.1 (with $a=1$, $b=\mathbf{E}^{-1}$ and $G\equiv 1_{\Delta}$), Theorem 4 and Lemma 3.1.

Applying Markov’s inequality in the estimates of Theorem 2, we see that (i) holds true with a probability that goes to 1 as $L\to \infty$. We now work on this event.

Assume that there exists $\lambda _{i} \in \Delta$ such that $U_{i} \in \mathcal{D}(3)$. We find

$$ \int _{|s-U_{i}| \le t_{L} \mathbf{E}} \varphi _{i}^{2}(s)ds = 1 - \int _{|s-U_{i}| > t_{L} \mathbf{E}} \varphi _{i}^{2}(s)ds \ge 1 - \frac{2t_{L}^{2}}{\boldsymbol{\nu _{E}}-\varepsilon } e^{-( \boldsymbol{\nu _{E}}-\varepsilon )t_{L}}\;. $$

By assumption $\{s\in [0,L]: |s-U_{i}| \le t_{L} \mathbf{E}\} \subset \mathcal{D}(4)$. Markov’s inequality applied to (84) and our assumption $t_{L} \ll L/(k\mathbf{E})$ therefore show that the probability of (ii) goes to 1.

We now prove (iii). By Cauchy-Schwarz’s inequality we have

$$\begin{aligned} \Big(\sum _{\lambda _{i} \in \Delta} |\varphi _{i}| + \frac{|\varphi _{i}'|}{\sqrt {\mathbf{E}}} \Big)^{2} &\le N_{L}(\Delta ) \sum _{\lambda _{i} \in \Delta} \Big(|\varphi _{i}| + \frac{|\varphi _{i}'|}{\sqrt {\mathbf{E}}}\Big)^{2} \\ &\le 2 N_{L}(\Delta ) \sum _{\lambda _{i} \in \Delta} \varphi _{i}^{2} + \big(\frac{\varphi _{i}'}{\sqrt {\mathbf{E}}}\big)^{2}\;. \end{aligned}$$

We deduce that on the event where (i) and (ii) hold we have

$$\begin{aligned} \int _{\mathcal{D}(2)} \Big(\sum _{\lambda _{i} \in \Delta } | \varphi _{i}| + \frac{|\varphi _{i}'|}{\sqrt {\mathbf{E}}} \Big)^{2} ds &\le 2N_{L}(\Delta ) \sum _{\lambda _{i} \in \Delta } \int _{ \mathcal{D}(2)} \varphi _{i}^{2} + \big( \frac{\varphi _{i}'}{\sqrt {\mathbf{E}}}\big)^{2} ds \\ &\le 2N_{L}(\Delta )^{2} \int _{s\in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}:|s|\ge t_{L} \mathbf{E}} \frac{t_{L}^{2}}{\mathbf{E}} e^{-(\boldsymbol{\nu _{E}}-\varepsilon ) \frac{s}{\mathbf{E}}}ds \\ &\le 4 N_{L}(\Delta )^{2} \frac{t_{L}^{2}}{\boldsymbol{\nu _{E}}-\varepsilon }e^{-( \boldsymbol{\nu _{E}}-\varepsilon )t_{L}}\;. \end{aligned}$$

Markov’s inequality combined with Proposition 4.4 shows that $\mathbb{P}(N_{L}(\Delta )^{2} < t_{L}) \to 1$. We thus deduce (iii) (we use a factor $\varepsilon t_{L}$ in the exponential term to “kill” the prefactors). □

We also need estimates on the exponential decay of the $\varphi _{i}^{(j)}$. We let $\bar{\mathcal{B}}_{L}$ be the event on which for every $j\in \{1,\ldots ,k\}$ and for every $\lambda _{i}^{(j)}\in \Delta$, we have

$$ \Big(\varphi _{i}^{(j)}(t)^{2} + \frac{(\varphi _{i}^{(j)})'(t)^{2}}{\mathbf{E}}\Big)^{1/2} \le \frac{t_{L}}{\sqrt {\mathbf{E}}} e^{-\frac{1}{2}(\boldsymbol{\nu _{E}}- \varepsilon )\frac{|t-U_{i}^{(j)}|}{\mathbf{E}}}\;,\quad \forall t \in (t_{j-1},t_{j})\;. $$

Lemma 9.4

We have $\mathbb{P}(\bar{\mathcal{B}}_{L}) \to 1$ as $L\to \infty$.

Proof

A adaptation of the proof of Proposition 4.2 allows to show the counterpart of Theorem 2 for the operators $\mathcal{H}_{L}^{(j)}$. Namely, there exist some r.v. $c_{i}^{(j)}$ such that for every $\lambda _{i}^{(j)}\in \Delta$

$$ \Big(\varphi _{i}^{(j)}(t)^{2} + \frac{(\varphi _{i}^{(j)})'(t)^{2}}{\mathbf{E}}\Big)^{1/2} \le \frac{c_{i}^{(j)}}{\sqrt {\mathbf{E}}} e^{-\frac{1}{2}( \boldsymbol{\nu _{E}}-\varepsilon )\frac{|t-U_{i}^{(j)}|}{\mathbf{E}}} \;,$$

(85)

and for some $q>0$ we have

$$ \limsup _{L\to \infty} \mathbb{E}\Big[\sum _{j=1}^{k}\sum _{\lambda _{i}^{(j)} \in \Delta} (c_{i}^{(j)})^{q}\Big] < \infty \;. $$

This being given, the proof of the lemma follows from Markov’s inequality. □

Finally, we need some control on the gaps between the eigenvalues of $\mathcal{H}^{(j)}_{L}$ and on the distance of these eigenvalues to the boundary of $\Delta$. Take some $\delta _{L} \to 0$ as $L\to \infty$. Let $\mathcal{G}_{L}$ be the event on which for any $(i,j) \ne (i',j')$ we have

$${\lambda }_i^{(j)},{\lambda }_{i^{\prime }}^{(j^{\prime })}\in \mathrm{\Delta }⟹|Ln(E)({\lambda }_i^{(j)}-{\lambda }_{i^{\prime }}^{(j^{\prime })})|>{\delta }_L,$$

(86)

and

$$ \forall i,j\;,\quad \text{dist}(Ln(E)(\lambda _{i}^{(j)} - E), { \{-h,h\}}) > \delta _{L}\;. $$

Since we already know from the arguments in Sect. 4.4 that $\bar{\mathcal{N}}_{L}$ converges to a Poisson point process, we deduce that

$$ \mathbb{P}(\mathcal{G}_{L}) \to 1\;,\quad L\to \infty \;. $$

Note that this convergence holds for any given sequence $\delta _{L}$ that converges to 0. In the proof below, we will need to impose some restriction on the speed at which $\delta _{L}$ goes to 0.

Let us also state a simple fact of the theory of generalized Sturm-Liouville operators, see for instance [8, Sect. 3], which is based upon the work of Weidmann [36]. The domain of $\mathcal{H}_{L}$ is given by

$$\begin{aligned} \Big\{ f \in L^{2}([0,L]):& \;f(0) = f(L) = 0,\; f \text{ A.C.}, \; f'- Bf \text{ A.C.}, \\ &\text{and } -(f'-Bf)' - Bf' \in L^{2}([0,L])\Big\} \,. \end{aligned}$$

As a consequence, if one multiplies an element of the domain by some smooth function, compactly supported in $(t_{j-1},t_{j})$, then one gets an element of the domain of $\mathcal{H}_{L}^{(j)}$. We will use this fact in the next proof.

Finally, let us recall the Lévy-Prokhorov distance on $\mathcal{M}=\mathcal{M}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{ \text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$ that metrizes the weak convergence topology:

$$\begin{aligned} d_{\mathcal{M}}(w,w') :={}& \inf \big\{ \epsilon > 0: \forall B\in \mathcal{B}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}),\; w(B) \le w'(B^{\epsilon}) + \epsilon \text{ and } \\ &{} w'(B) \le w(B^{\epsilon}) + \epsilon \big\} \;, \end{aligned}$$

(87)

where $B^{\epsilon}$ is the $\epsilon$-neighborhood of $B$.

Recall also that we actually work on $\bar{\mathcal{M}}=\mathcal{M}( \bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}})$ and that one can define $d_{\bar{\mathcal{M}}}$ similarly as above: the only difference is that the $\epsilon$-neighborhoods need to be taken w.r.t. a distance that metrizes $\bar{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$. If one chooses this distance in such a way that the $\epsilon$-neighborhoods on $\bar {{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}$ always contain the $\epsilon$-neighborhoods on ${{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$, then one can check that for any measures $w,w' \in \mathcal{M}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}})$ we have

$$ d_{\bar{\mathcal{M}}}(w,w') \le d_{\mathcal{M}}(w,w')\;. $$

Consequently, since all the measures that we manipulate are actually elements of ℳ, in the sequel we will only deal with $d_{\mathcal{M}}$.

Proof of Proposition 4.3

Fix $\Delta := [E-h/(Ln(E)),E+h/(Ln(E))]$. We will show that, if we restrict ourselves to $[-h,h] \times [-1/2,1/2]\times \bar{\mathcal{M}}$, then with large probability there is a one-to-one correspondence between the atoms of $\mathcal{N}_{L}$ and of $\bar{\mathcal{N}}_{L}$, and that the distance between the corresponding pairs of atoms goes to 0 as $L\to \infty$. The proof consists of two steps.

Step 1. We argue deterministically on the event $\mathcal{B}_{L}\cap \bar{\mathcal{B}}_{L} \cap \mathcal{G}_{L}$ introduced above and for large enough $L$. Let $(\lambda ,\varphi )$ be an eigenvalue/eigenfunction of $\mathcal{H}_{L}$ such that $\lambda \in \Delta$. Let $U$ be its center of mass. From the conditions stated in the event $\mathcal{B}_{L}$, we know that there exists $j\in \{1,\ldots ,k\}$ such that

$$ U \in (t_{j-1}+3 t_{L} \mathbf{E},t_{j} - 3 t_{L} \mathbf{E})\;. $$

We consider a smooth function $\chi _{j} : [-L/2,L/2] \to [0,1]$ that equals 1 on $[t_{j-1}+2t_{L} \mathbf{E},t_{j}-2t_{L} \mathbf{E}]$ and 0 on $(t_{j-1} + t_{L} \mathbf{E},t_{j}-t_{L} \mathbf{E})^{\complement }$, and such that

$$ \sup _{t} |\chi _{j}'(t)|\vee |\chi _{j}''(t)| \le \frac{2}{t_{L}\mathbf{E}}\;. $$

We then set

$$ \psi := \frac{\varphi \chi _{j}}{\|\varphi \chi _{j}\|_{2}}\;. $$

Note that $\psi$ is a compactly supported function in $(t_{j-1}, t_{j})$ whose $L^{2}$ norm equals one. Furthermore, by (iii) of $\mathcal{B}_{L}$

$$\begin{aligned} \| \psi - \varphi \|_{2}^{2} \leq e^{-Kt_{L}}\;, \end{aligned}$$

(88)

for some constant $K>0$. From now on, the constant $K$ will never depend on $L$ and $j$, but may change from line to line.

By construction, $\psi$ belongs to the domain of $\mathcal{H}_{L}^{(j)}$ and we have

$$ \begin{aligned}&(\mathcal{H}_{L}^{(j)} - \lambda ) \psi \\ &\quad = \textstyle\begin{cases} 0 &\text{ on } (t_{j-1}+2t_{L} \mathbf{E}, t_{j} - 2t_{L} \mathbf{E}) \\ \|\varphi \chi _{j} \|^{-1}_{2} \; \big(- \varphi \chi _{j}'' - 2 \varphi ' \chi _{j}'\big) &\text{ on } (t_{j-1}, t_{j-1}+2t_{L} \mathbf{E}]\cup [t_{j} - 2t_{L} \mathbf{E},t_{j})\;. \end{cases}\displaystyle \end{aligned}$$

Henceforth by (iii) of $\mathcal{B}_{L}$

$$ \|(\mathcal{H}_{L}^{(j)} - \lambda ) \psi \|_{L^{2}(t_{j-1},t_{j})}^{2} \le \frac{1}{\mathbf{E}} e^{-K t_{L}}\;.$$

(89)

On the other hand, we can expand $\psi$ on the $L^{2}(t_{j-1},t_{j})$-basis made of the eigenfunctions of $\mathcal{H}_{L}^{(j)}$:

$$ \|(\mathcal{H}_{L}^{(j)} - \lambda ) \psi \|_{L^{2}(t_{j-1},t_{j})}^{2} = \sum _{i} |\lambda _{i}^{(j)} - \lambda |^{2} \langle \psi , \varphi _{i}^{(j)}\rangle ^{2}\;. $$

The r.h.s. is a convex combination of the $|\lambda _{i}^{(j)} - \lambda |^{2}$. Given the bound (89), there must exist some $\ell \ge 1$ such that

$$ |\lambda _{\ell}^{(j)} - \lambda |^{2} \le \frac{1}{\mathbf{E}} e^{-K t_{L}} \;. $$

Recall that $t_{L} \gg \ln (L/\mathbf{E})$ so that $L^{2} n(E)^{2} / \mathbf{E}\ll e^{Kt_{L}/4}$. We thus impose (recall that the speed at which $\delta _{L}$ goes to 0 can be taken as small as desired):

$$ \frac{L^{2} n(E)^{2}}{\mathbf{E}} e^{-\frac{K}{4} t_{L}} \ll \delta _{L}^{2} \;, $$

and we deduce that $Ln(E)|\lambda _{\ell }^{(j)} - \lambda | \le \frac{L n(E)}{\sqrt{\mathbf{E}}} e^{-\frac{K}{2} t_{L}} \ll \delta _{L}$. Given the definition of the event $\mathcal{G}_{L}$ we deduce that the integer $\ell$ above is unique, that $\lambda _{\ell }^{(j)} \in \Delta$, and that for all $i\ne \ell$

$$ Ln(E) |\lambda _{i}^{(j)} - \lambda | > \delta _{L} / 2\;. $$

We thus deduce that

$$\begin{aligned} \sum _{i: i\ne \ell } \langle \psi ,\varphi _{i}^{(j)}\rangle ^{2} & \le \sum _{i: i\ne \ell } |\lambda _{i}^{(j)} - \lambda |^{2} \langle \psi ,\varphi _{i}^{(j)}\rangle ^{2} \frac{(2Ln(E))^{2}}{\delta _{L}^{2}} \\ &\le \sum _{i} |\lambda _{i}^{(j)} - \lambda |^{2} \langle \psi , \varphi _{i}^{(j)}\rangle ^{2} \frac{(2Ln(E))^{2}}{\delta _{L}^{2}} \\ &\le \frac{(2Ln(E))^{2}}{\delta _{L}^{2} \mathbf{E}} e^{-Kt_{L}} \le e^{-K't_{L}} \;, \end{aligned}$$

for some constant $K'>0$. Therefore $\langle \psi ,\varphi _{\ell }^{(j)}\rangle ^{2} \ge 1-e^{-K' t_{L}}$, and thus

$$ \| \psi - \varphi _{\ell }^{(j)} \|_{2}^{2} \le 2e^{-K' t_{L}}\;. $$

Together with (88), we find (possibly for a smaller constant $K$)

$$ \| \varphi - \varphi _{\ell}^{(j)}\|^{2}_{2} \le e^{-K t_{L}}\;. $$

Let $w(dt) = \mathbf{E}\varphi (U+t\mathbf{E})^{2} dt$ be the probability measure built from $\varphi$ and recentered at its center of mass denoted by $U$. Recall that $w_{\ell}^{(j)}$ (introduced in Sect. 4.4) is the corresponding object for $\varphi _{\ell}^{(j)}$. By $\mathcal{B}_{L}$ and $\bar{\mathcal{B}}_{L}$, we have some exponential decay of $\varphi$ and $\varphi _{\ell}^{(j)}$ from their centers of mass. We thus apply Lemma A.7 (note that the constant $c$ in this lemma depends polynomially on $t_{L}$ and is killed by the exponential decay) and deduce that

$$ \frac{|U-U_{\ell}^{(j)}|}{\mathbf{E}} \le e^{- K t_{L}}\;,\quad d_{ \mathcal{M}}(w,w_{\ell}^{(j)}) \le e^{- K t_{L}}\;. $$

These quantities vanish when $L\to \infty$.

We have built a map that associates to any eigenvalue $\lambda \in \Delta$ of the operator $\mathcal{H}_{L}$ an eigenvalue $\lambda _{\ell}^{(j)} \in \Delta$ in such a way that

$$ |\lambda _{\ell}^{(j)} - \lambda |^{2} \le \frac{1}{\mathbf{E}} e^{-K t_{L}} \;,\quad \frac{|U-U_{\ell}^{(j)}|}{\mathbf{E}} \le e^{- K t_{L}}\;, \quad d_{\mathcal{M}}(w,w_{\ell}^{(j)}) \le e^{- K t_{L}}\;, $$

as well as $\| \varphi - \varphi _{\ell}^{(j)}\|^{2}_{2} \le e^{-Kt_{L}}$. This map is necessarily injective: indeed, we cannot find two orthonormal functions $\varphi$ and $\tilde{\varphi}$ satisfying

$$ \| \varphi - \varphi _{\ell}^{(j)}\|^{2}_{2} \le e^{-Kt_{L}}\;,\quad \| \tilde{\varphi}- \varphi _{\ell}^{(j)}\|^{2}_{2} \le e^{-Kt_{L}}\;. $$

To conclude the proof, it remains to show that this map is actually bijective, this is the purpose of the second step.

Step 2. Let $F_{L}$ be the event $\{\sum _{j=1}^{k} N_{L}^{(j)}(\Delta ) \ge N_{L}(\Delta )\}$. By the first step, $\mathbb{P}(F_{L}) \to 1$ as $L\to \infty$. Proposition 4.4 ensures uniform integrability of the collection of r.v. $N_{L}( \Delta )$, $L>L_{0}$ (for some $L_{0}>1$) so that

$$ \lim _{L\to \infty}\mathbb{E}[N_{L}(\Delta ) \mathbf{1}_{F_{L}^{ \complement }}] = 0\;. $$

Since

$$ 0 \le \mathbb{E}\Big[\big(N_{L}(\Delta )-\sum _{j} N^{(j)}_{L}( \Delta )\big)\mathbf{1}_{F_{L}^{\complement }}\Big] \le \mathbb{E} \Big[N_{L}(\Delta )\mathbf{1}_{F_{L}^{\complement }}\Big]\;, $$

we deduce that the term in the middle vanishes as $L\to \infty$. Combining this convergence with (1) and (2) of Proposition 6.3, we deduce that

$$ \lim _{L\to \infty} \mathbb{E}\Big[\big(\sum _{j} N^{(j)}_{L}(\Delta ) - N_{L}(\Delta )\big)\mathbf{1}_{F_{L}}\Big] = \lim _{L\to \infty} \mathbb{E}\Big[\sum _{j} N^{(j)}_{L}(\Delta ) - N_{L}(\Delta )\Big]= 0 \;. $$

Since $(\sum _{j} N^{(j)}_{L}(\Delta ) - N_{L}(\Delta ))\mathbf{1}_{F_{L}}$ is a non-negative r.v. taking values in ${{\mathchoice{\text{\textbf{N}}}{\text{\textbf{N}}}{\text{\scriptsize \textbf{N}}}{ \text{\tiny \textbf{N}}}}}$, we deduce that

$$ \lim _{L\to \infty}\mathbb{P}\Big(\sum _{j=1}^{k} N_{L}^{(j)}(\Delta ) = N_{L}(\Delta )\Big) = 1\;. $$

Consequently, the injective map constructed in Step 1 on $\mathcal{B}_{L}\cap \bar{\mathcal{B}}_{L}\cap \mathcal{G}_{L}$ is actually bijective, possibly on a smaller event, but whose probability still goes to one. □

Appendix A: Technical results

1.1 A.1 Simple estimate on the Laplace transform

The following elementary lemma provides a quantitative estimate on the difference between the Laplace transform of a r.v. and its Taylor expansion at 0 (here we only push the Taylor expansion to the second order).

Lemma A.1

Let $X$ be a real-valued r.v. Assume that there exist $C_{0}>0$ and $q_{0}>0$ such that $\mathbb{E}[e^{q|X|}] < C_{0}$ for all $q \le q_{0}$. Then, for any $q_{1} < q_{0}$ there exist a constant $C_{1} > 0$, that only depends on $C_{0}$, $q_{0}$ and $q_{1}$, which is such that for all $q\in [-q_{1},q_{1}]$

$$ \big| \mathbb{E}[e^{qX}] - 1 - q\mathbb{E}[X]\big| \le C_{1} q^{2}\;. $$

Proof

The map $q\mapsto \mathbb{E}[e^{qX}]$ is real-analytic on $(-q_{0},q_{0})$ and therefore for any such $q$ we have

$$ \mathbb{E}[e^{qX}] - 1 - q\mathbb{E}[X] = \sum _{k\ge 2} q^{k} \frac{\mathbb{E}[X^{k}]}{k!}\;. $$

By assumption $\sup _{k\ge 2} q_{0}^{k}\frac{|\mathbb{E}[X^{k}]|}{k!} \le C_{0}$ so that for any $|q| < q_{0}$ we have

$$ \big|\mathbb{E}[e^{qX}] - 1 - q\mathbb{E}[X]\big| \le C_{0} \frac{(q/q_{0})^{2}}{1-q/q_{0}}\;, $$

and the bound of the statement follows. □

1.2 A.2 Elementary deviation estimate for general SDEs

Lemma A.2

Let $X$ be the solution of $dX(t) = \alpha (t) dt + \beta (t) dB(t)$ with $X(0) = 0$. Assume that $\alpha$, $\beta$ are adapted processes and that there exist $C_{1},C_{2}>0$ such that almost surely for all $t\ge 0$

$$ |\alpha (t)| \le C_{1}\;,\quad |\beta (t)|^{2} \le C_{2}\;. $$

Then for all $x> 2C_{1} t$ we have

$$ \mathbb{P}(\sup _{s\in [0,t]} |X(s)| > x) \le 2\exp (- \frac{x^{2}}{8 C_{2} t})\;. $$

Proof

Let $M(t) := \int _{0}^{t} \beta (s) dB(s)$. Given the bound on the drift, it suffices to show that for all $y>C_{1} t$

$$ \mathbb{P}(\sup _{s\in [0,t]} |M(s)| > y) \le 2\exp (- \frac{y^{2}}{2 C_{2} t})\;. $$

This is precisely the exponential martingale inequality of [34, p.153-154]. □

1.3 A.3 Moments estimates

Lemma A.3

For every $\alpha \in [0,1)$

$$ \sup _{\lambda \in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}} \,\mathbb{E}\Big[\exp \Big( \frac{\alpha}{m_{\lambda }^{(\mathbf{E})}} \zeta _{\lambda }^{( \mathbf{E})}\Big)\Big] \le \frac{1}{1-\alpha}\;. $$

Proof

Since $\zeta _{\lambda }^{(E)}/m_{\lambda }^{(E)}$ is equal in law to $\zeta _{\lambda }/m_{\lambda }$, it suffices to work with the original coordinates. It is shown in [2, Appendix A] that for all $\alpha < 0$ we have

$$ \mathbb{E}[e^{\frac{\alpha}{m_{\lambda }} \zeta _{\lambda }}] = 1 + \alpha + \sum _{n\ge 2} \Big(\frac{\alpha}{m_{\lambda }}\Big)^{n} v(n, \lambda )\;, $$

for some $0 \le v(n,\lambda ) \le m_{\lambda }^{n}$. The function on the r.h.s. is analytic in $\alpha$ on $\{z\in {{\mathchoice{\text{\textbf{C}}}{\text{\textbf{C}}}{\text{\scriptsize \textbf{C}}}{ \text{\tiny \textbf{C}}}}}: |z| < 1\}$ so that a standard analytic continuation argument allows to deduce that the identity actually holds for all $\alpha \in (-\infty ,1)$. The bound of the statement then follows easily. □

Next, we obtain a bound on the exponential moment of the number of eigenvalues of $\mathcal{H}_{L}$ below some energy $E$. Therein, we work in the original coordinates exclusively.

Lemma A.4

Uniform bound of Laplace transform of the number of eigenvalues

There exists $q >0$, such that for every $E\in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}$

$$\begin{aligned} \sup _{{L \geq 1}} \,\mathbb{E}\Big[\exp \Big({ q\Big(\frac{m_{E}}{L}\wedge \frac{1}{2} \Big)} \#\{ \lambda _{i}: \lambda _{i} \le E\}\Big)\Big] < \infty \;. \end{aligned}$$

In particular, for any given $E\in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}$ the collection of r.v. $(\#\{\lambda _{i}: \lambda _{i} \le E\}/L)_{L \geq 1}$ is uniformly integrable.

Proof

Set $X := \#\{\lambda _{i}: \lambda _{i} \le E\}$. We need exponential tails on the probability that $X\ge k$. Let $\theta _{E}$ start from $\theta _{E}(0)=0$ and denote by $\zeta ^{(k)}_{E}, k\ge 1$ the i.i.d. r.v. which are such that $\sum _{i=1}^{k} \zeta ^{({i})}_{E}$ is the hitting time of $k\pi$ by $\theta _{E}$. By the Sturm-Liouville and the strong Markov properties, we have for all $q >0$,

$$\begin{aligned} \mathbb{P}( X \geq k) &= \mathbb{P}\Big(\sum _{i=1}^{k} \zeta _{E}^{(i)} \leq L\Big) =\mathbb{P}\Big(q \sum _{i=1}^{k} (1 - \zeta _{E}^{(i)}/m_{E}) \geq q k - q L/m_{E}\Big) \\ &\leq \mathbb{E}[\exp (q (1 - \zeta _{E}/m_{E}))]^{k} \exp (-q k + q L/m_{E}) \,. \end{aligned}$$

By Lemma A.1 and A.3, there exists a constant $C_{1}$ (independent of $E$) such that for all $q >0$ small enough,

$$\begin{aligned} \mathbb{P}( X \geq k)&\leq (1+ C_{1} q^{2})^{k} \exp (-q k + q L/m_{E}) \,. \end{aligned}$$

Taking $q_{0} >0$ small enough, we deduce that there exists $C>0$ such that for all for all $q \in [0,q_{0}]$ and all $u\ge 0$

$$\begin{aligned} \mathbb{P}( X \geq u) \leq 1 \wedge C\exp (- q \frac{2}{3} u + q \frac{L}{m_{E}})\;. \end{aligned}$$

Note that

$$ \mathbb{E}\Big[\exp \Big(q \Big(\frac{m_{E}}{L} \wedge \frac{1}{2} \Big) X \Big)\Big] = 1 + \int _{u\ge 0} q \Big(\frac{m_{E}}{L} \wedge \frac{1}{2} \Big) e^{q \Big(\frac{m_{E}}{L} \wedge \frac{1}{2} \Big) u} \mathbb{P}(X\ge u) du\;. $$

Using the estimate on the tail of $X$, one can bound separately the contributions to the integral coming from $u\le \frac{3}{2} \frac{L}{m_{E}}$ and $u > \frac{3}{2} \frac{L}{m_{E}}$, and conclude. □

1.4 A.4 Integral formulas

In this paragraph, we gather useful integral formulas about the invariant measure of the phase function.

1.4.1 A.4.1 Invariant measure

The phase function $\{\theta ^{(\mathbf{E})}_{\lambda }\}_{\pi}$ can be mapped to a simple additive SDE via the function $\text{cotan}$, namely $X^{(\mathbf{E})}_{\lambda }:= \text{cotan}\,\{\theta ^{(\mathbf{E})}_{ \lambda }\}_{\pi}$ satisfies the SDE:

$$\begin{aligned} dX^{(\mathbf{E})}_{\lambda }= - (V_{\lambda }^{(\mathbf{E})})'(X^{( \mathbf{E})}_{\lambda })dt + dB^{(\mathbf{E})}(t),\quad \text{with } V_{ \lambda }^{(\mathbf{E})}(x) := \lambda \sqrt{\mathbf{E}} x + \mathbf{E}^{3/2} \frac{x^{3}}{3}\,, \end{aligned}$$

and where $X^{(\mathbf{E})}_{\lambda }$ immediately restarts from $+\infty$ when it blows up to $-\infty$. The diffusion $X_{\lambda }^{(\mathbf{E})}$ admits a unique invariant measure whose density writes $f_{\lambda }^{(\mathbf{E})}(x)/m_{\lambda }^{(\mathbf{E})}$ where:

$$\begin{aligned} &f_{\lambda }^{(\mathbf{E})}(x) := 2 e^{-2V_{\lambda }^{(\mathbf{E})}(x)} \int _{-\infty}^{x} e^{2V_{\lambda }^{(\mathbf{E})}(y)} dy\;,\quad x \in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\;, \end{aligned}$$

(see [2, 7] for more details). Note that $\int _{-\infty}^{\infty} f_{\lambda }^{(\mathbf{E})}(x) dx$ coincides with $m_{\lambda }^{(\mathbf{E})}$, which is defined as the expectation of $\zeta _{\lambda }^{(\mathbf{E})}$.

Therefore, the unique invariant measure $\mu _{\lambda }^{(\mathbf{E})}$ of the Markov process $\{\theta _{\lambda }^{(\mathbf{E})}\}_{\pi}$ is the image of $f_{\lambda }^{(\mathbf{E})}(x) dx/m_{\lambda }^{(\mathbf{E})}$ through the map $x\mapsto \text{arccotan\,}x$. Its density writes

$$ \mu _{\lambda }^{(\mathbf{E})}(\theta ) = \frac{f_{\lambda }^{(\mathbf{E})}(\text{cotan}\,\theta )}{\sin ^{2} \theta \;m_{\lambda }^{(\mathbf{E})}} =g^{(\mathbf{E})}_{\lambda }(\text{cotan}\,\theta ) \;,\quad \theta \in [0,\pi )\;, $$

where $g^{(\mathbf{E})}_{\lambda }(x) = (1+x^{2}) f_{\lambda }^{(\mathbf{E})}(x) /m_{\lambda }^{(\mathbf{E})}$.

Proof of Lemma 3.1

We concentrate on the distorted coordinates: indeed, since the bounds need to be taken uniformly over the unbounded parameter $E>1$, this is the most involved setting. For simplicity, we make the further assumption that $E$ is large: that is, for fixed $h>0$ we will assume that $E>E_{0}(h)$ for some quantity $E_{0}(h)\ge 1$ to be defined below. The complementary case follows by adapting the arguments (and is actually simpler).

Let us abbreviate $V_{\lambda }^{(E)}$ by $V_{\lambda }$ to ease the notations. Pick $E_{0}(h)\ge 1$ such that for some constant $K>1$ and for all $E\ge E_{0}(h)$ and all $\lambda \in \Delta$

$$ \frac{h}{En(E)} \le \frac{E}{2}\;,\quad K^{-1} < n(E)\sqrt{E} \le K\;, \quad K^{-1} < E^{3/2}m_{\lambda }^{(E)} < K\;. $$

(90)

Since $V_{\lambda }'(x) = \lambda \sqrt {E} + E^{3/2} x^{2}$, the first bound implies that for all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$, $V'_{\lambda }(x) > 0$.

We claim that there exists $C>0$ such that for all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $\theta \in [0,\pi ]$

$$ \vert \partial _{\theta }\mu _{\lambda }^{(E)}(\theta ) \vert \le \frac{C}{E^{3/2}}\;. $$

Assume that the claim holds. Up to increasing $E_{0}(h)$, we can assume that for all $E\ge E_{0}(h)$, $\frac{1}{\pi } - \frac{C\pi }{E^{3/2}} >0$. Since $\mu _{\lambda }^{(E)}$ integrates to 1 on $[0,\pi ]$, this is enough to deduce that there exist $0 < c' < C'$ such that for all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $\theta \in [0,\pi ]$

$$ c' \le \mu _{\lambda }^{(E)}(\theta ) < C'\;,\qquad |\partial _{ \theta }\mu _{\lambda }^{(E)}(\theta )| < C'\;, $$

and that $\sup _{\lambda \in \Delta } \sup _{\theta \in [0,\pi )} |\mu _{ \lambda }^{(E)}(\theta ) - \frac{1}{\pi }| \to 0$ as $E \to \infty$. We are left with proving the claim.

Observe that $(f_{\lambda }^{(E)})' = 2 - 2 f_{\lambda }^{(E)} V'_{\lambda }$. Consequently $\partial _{\theta }\mu _{\lambda }^{(E)}(\theta ) = q_{\lambda }^{(E)}( \text{cotan}\,\theta )$ where

$$\begin{aligned} q_{\lambda }^{(E)}(x) = \frac{(1+x^{2})^{2}}{m_{\lambda }^{(E)}} \Big(-2 + 2 f_{\lambda }^{(E)}(x) V_{\lambda }'(x) - \frac{2x}{1+x^{2}} f_{\lambda }^{(E)}(x)\Big)\;. \end{aligned}$$

To prove the claim, it suffices to show that for all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$

$$ \vert q_{\lambda }^{(E)}(x) \vert \le \frac{C}{E^{3/2}}\;. $$

Applying successive integrations by parts we obtain

$$ \begin{aligned}f_{\lambda }^{(E)}(x) ={}&\frac{1}{V_{\lambda }'(x)} + \frac{V_{\lambda }''(x)}{2(V_{\lambda }'(x))^{3}} \\ &{} + e^{-2 V_{\lambda }(x)} \int _{-\infty }^{x} e^{2 V_{\lambda }(y)}\Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{2 (V_{\lambda }'(y))^{4}} \Big)dy\;. \end{aligned}$$

A computation yields

$$ \Big(-2 + 2 f_{\lambda }^{(E)}(x) V_{\lambda }'(x) - \frac{2x}{1+x^{2}} f_{\lambda }^{(E)}(x)\Big) = I_{1}(x) + I_{2}(x) \;, $$

with

$$ I_{1}(x) = \frac{V_{\lambda }''(x) - \frac{2x}{1+x^{2}}V_{\lambda }'(x) - \frac{x}{1+x^{2}} \frac{V_{\lambda }''(x)}{V_{\lambda }'(x)}}{V'_{\lambda }(x)^{2}} \;, $$

and

$$ I_{2}(x) = \Big(2V'_{\lambda }(x) - \frac{2x}{1+x^{2}} \Big) e^{-2V_{ \lambda }(x)} \int _{-\infty }^{x} e^{2 V_{\lambda }(y)}\Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{2 (V_{\lambda }'(y))^{4}} \Big)dy\;. $$

Recall from (90) that $m_{\lambda }^{(E)}$ is of order $E^{-3/2}$. To prove the claim, it suffices to check that $\vert I_{1}(x)\vert$ and $\vert I_{2}(x)\vert$ are bounded from above by a term of order $\frac{1}{E^{3} (1+x^{2})^{2}}$ uniformly over all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$. Regarding the first term, using (90), note that $\vert E^{3/2} - \lambda \sqrt{E} \vert \le K$ so that there exists a constant $C_{1}>0$ such that

$$\begin{aligned} E^{3/2} (1+x^{2})^{2} \vert I_{1}(x)\vert &= \frac{E^{3/2}(1+x^{2})}{\big(\lambda \sqrt {E} + E^{3/2} x^{2}\big)^{2}} \Big\vert 2x(E^{3/2} - \lambda \sqrt{E}) - \frac{2E^{3/2} x^{2}}{\lambda \sqrt{E} + E^{3/2} x^{2}}\Big\vert \\ &\le C_{1} \frac{E^{3/2}(1+x^{2})}{E^{3} \big(1 +x^{2}\big)^{2}} \big( \vert x \vert + 1\big) \end{aligned}$$

so that the desired bound follows. Regarding $I_{2}(x)$, assume that there exists $C>0$ such that for all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$

$$ \Big\vert e^{-2V_{\lambda }(x)} \int _{-\infty }^{x} e^{2 V_{ \lambda }(y)}\Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{2 (V_{\lambda }'(y))^{4}} \Big)dy \Big\vert \le C \frac{1}{E^{9/2}(1+x^{2})^{3}}\;. $$

(91)

Since there exists $C'>0$ such that uniformly over the same set of parameters we have $\vert 2V'_{\lambda }(x) - \frac{2x}{1+x^{2}} \vert \le C' E^{3/2} (1+x^{2})$, we deduce the desired bound. Let us now prove (91). First of all there exists $c>0$ such that uniformly over all $E\ge E_{0}(h)$, all $\lambda \in \Delta$ and all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$

$$ \Big\vert \frac{3 (V_{\lambda }''(x))^{2} - V_{\lambda }'''(x) V_{\lambda }'(x)}{2 (V_{\lambda }'(x))^{4}} \Big\vert = \Big\vert \frac{5 E^{3} x^{2} - E^{2} \lambda }{(\lambda \sqrt{E} + E^{3/2} x^{2})^{4}} \Big\vert \le \frac{c}{E^{3}(1+x^{2})^{3}}\;, $$

and such that the following rough bound holds

$$ \Big\vert \frac{3 (V_{\lambda }''(x))^{2} - V_{\lambda }'''(x) V_{\lambda }'(x)}{4 (V_{\lambda }'(x))^{5}} \Big\vert \le c\;. $$

Consequently there exists $C''>0$ such that

$$\begin{aligned} &\Big\vert e^{-2V_{\lambda }(x)} \int _{x-1}^{x} e^{2 V_{\lambda }(y)} \Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{2 (V_{\lambda }'(y))^{4}} \Big)dy \Big\vert \\ &\le e^{-2V_{\lambda }(x)} \int _{x-1}^{x} \frac{2V'_{\lambda }(y)}{2V'_{\lambda }(y)} e^{2 V_{\lambda }(y)} dy \sup _{y\in [x-1,x]} \frac{c}{E^{3}(1+y^{2})^{3}} \\ &\le e^{-2V_{\lambda }(x)} \Big(e^{2V_{\lambda }(x)} - e^{2V_{ \lambda }(x-1)}\Big) \sup _{y\in [x-1,x]} \frac{1}{2V'_{\lambda }(y)} \sup _{y\in [x-1,x]} \frac{c}{E^{3}(1+y^{2})^{3}} \\ &\le C'' \frac{1}{E^{9/2}(1+x^{2})^{4}}\;. \end{aligned}$$

In addition

$$\begin{aligned} &\Big\vert e^{-2V_{\lambda }(x)} \int _{-\infty }^{x-1} e^{2 V_{ \lambda }(y)}\Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{2 (V_{\lambda }'(y))^{4}} \Big)dy \Big\vert \\ &= \Big\vert e^{-2V_{\lambda }(x)} \int _{-\infty }^{x-1} 2V'_{ \lambda }(y) e^{2 V_{\lambda }(y)}\Big( \frac{3 (V_{\lambda }''(y))^{2} - V_{\lambda }'''(y) V_{\lambda }'(y)}{4 (V_{\lambda }'(y))^{5}} \Big)dy \Big\vert \\ &\le c e^{-2V_{\lambda }(x)} \int _{-\infty }^{x-1} 2V'_{\lambda }(y) e^{2 V_{\lambda }(y)}dy \\ &\le c e^{-2V_{\lambda }(x) + 2V_{\lambda }(x-1)} = c e^{-2\lambda \sqrt{E} - 2E^{3/2}((x-\frac{1}{2})^{2}+\frac{1}{12})}\;, \end{aligned}$$

and this suffices to conclude. □

Let us state an additional regularity result on the invariant measure and the density of states, which is used in Sect. 9.

Lemma A.5

The map $\lambda \mapsto (\mu _{\lambda }(\theta ),\theta \in [0,\pi ])$ is continuous from ${{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}$ into the set of continuous functions on $[0,\pi ]$. As a consequence, $\lambda \mapsto n(\lambda )$ is continuous.

Proof

The second part of the lemma is a consequence of the first part and of the integral formula for the density of states stated in Corollary 6.2. To prove the first part of the lemma, it suffices to check that $\lambda \mapsto \sup _{\theta }\vert \partial _{\lambda }\mu _{ \lambda }(\theta )\vert$ is locally bounded. Recall that $\mu _{\lambda }(\theta ) = g_{\lambda }(\text{cotan}\,\theta )$ where $g_{\lambda }(x) = (1+x^{2}) f_{\lambda }(x) / m_{\lambda }$ for all $x\in{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$. The desired property can then be deduced from direct computations on the integral formula for $f_{\lambda }(x)$ and $m_{\lambda }$. □

1.4.2 A.4.2 Expression of the Lyapunov exponent

Proof of Proposition 7.2

We already saw that $\zeta _{\lambda }^{(\mathbf{E})}$ is integrable. Assume that $\sup _{t\in [0,\zeta _{\lambda }^{(\mathbf{E})}]} \vert \rho _{ \lambda }^{(\mathbf{E})}(t)\vert$ is integrable. Decomposing the trajectory of $\rho _{\lambda }^{(\mathbf{E})}$ into i.i.d. excursions in between the successive hitting times of $\pi{{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ by $\theta _{\lambda }^{(\mathbf{E})}$, one deduces from the law of large numbers that almost surely

$$ \frac{\rho _{\lambda }^{(\mathbf{E})}(t)}{t} \to \frac{\mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{(\mathbf{E})})]}{\mathbb{E}[\zeta _{\lambda }^{(\mathbf{E})}]} \;,\quad t\to \infty \;. $$

This deterministic limit is denoted $\nu _{\lambda }^{(\mathbf{E})}$.

Before we check the integrability assumption and compute $\nu _{\lambda }^{(\mathbf{E})}$, let us deal with the adjoint diffusion. Arguments based on the strong Markov property show that the ratio of expectations that we obtained in the previous limit remains unchanged if we start the diffusion from its invariant measure, and the same holds with the adjoint diffusions. Applying the adjunction relations of Sect. 7.1, we deduce that

$$ \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] = -\bar {\mathbb{E}}[\bar{\rho}_{\lambda }^{( \mathbf{E})}(\bar{\zeta}_{\lambda }^{(\mathbf{E})})]\;,\quad \mathbb{E}[\zeta _{\lambda }^{(\mathbf{E})}] = \bar {\mathbb{E}}[ \bar{\zeta}_{\lambda }^{(\mathbf{E})}]\;, $$

so that the Lyapunov exponent of the adjoint diffusion is the opposite of $\nu _{\lambda }^{(\mathbf{E})}$.

Let us check the integrability assumption. The drift and diffusions coefficients of the (additive) SDE satisfied by $\rho _{\lambda }^{(\mathbf{E})}$ are bounded. Standard stochastic calculus arguments suffice to conclude and allow to show that

$$\begin{aligned} \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] = \mathbb{E}\Big[ \int _{0}^{\zeta _{\lambda }^{( \mathbf{E})}} \Big( -\sqrt {\mathbf{E}}(\lambda - \mathbf{E})\sin 2 \theta _{\lambda }^{(\mathbf{E})} -\frac{1}{2} \sin ^{2} 2\theta _{ \lambda }^{(\mathbf{E})} + \sin ^{2} \theta _{\lambda }^{(\mathbf{E})} \Big) dt \Big]\;. \end{aligned}$$

(92)

We now compute $\nu _{\lambda }^{(\mathbf{E})}$. Recall that $m_{\lambda }^{(\mathbf{E})} = \mathbb{E}[\zeta _{\lambda }^{( \mathbf{E})}]$ admits the explicit integral expression (13). To complete the proof, it suffices to show that

$$ \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] = \sqrt{2 \pi} \int _{0}^{+\infty} \sqrt{u} \exp (-2 \lambda u - \frac{u^{3}}{6} ) du\;. $$

By the standard characterization of the invariant probability measure of positive recurrent Markov processes, we have

$$\begin{aligned} \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] &= \int _{0}^{\pi }\Big( -\sqrt {\mathbf{E}}(\lambda - \mathbf{E})\sin 2\theta -\frac{1}{2} \sin ^{2} 2\theta + \sin ^{2} \theta \Big)\mu _{\lambda }^{(\mathbf{E})}(\theta ) m_{\lambda }^{( \mathbf{E})}d\theta \;. \end{aligned}$$

Applying the change of variable $x = \text{cotan}\,\theta$, we get

$$ \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] = \int \Big( \frac{2x \sqrt {\mathbf{E}}(\mathbf{E}-\lambda )}{1+x^{2}} + \frac{1-x^{2}}{(1+x^{2})^{2}}\Big) f_{\lambda}^{(\mathbf{E})}(x)dx\;. $$

(93)

We compute the r.h.s. of (93). By the Dominated Convergence Theorem, we have

$$ \mathbb{E}[\rho _{\lambda }^{(\mathbf{E})}(\zeta _{\lambda }^{( \mathbf{E})})] = \lim _{A\to \infty} \int _{-A}^{A} \Big(\sqrt {\mathbf{E}}(\mathbf{E}-\lambda )\frac{2x}{1+x^{2}} + \frac{1-x^{2}}{(1+x^{2})^{2}}\Big) f_{\lambda}^{(\mathbf{E})}(x)dx\;. $$

Fix $A>0$. We have (from now on, we abbreviate $f_{\lambda }^{(\mathbf{E})}$, $V_{\lambda }^{(\mathbf{E})}$ in $f_{\lambda }$, $V_{\lambda }$)

$$ \sqrt {\mathbf{E}}(\mathbf{E}-\lambda )\frac{2x}{1+x^{2}} = 2x \mathbf{E}^{3/2} - \frac{2x}{1+x^{2}} V'_{\lambda }(x)\;. $$

Using the identity $f_{\lambda }'(x) = -2V'_{\lambda }(x) f_{\lambda }(x) + 2$, an integration by parts yields

$$\begin{aligned} \int _{-A}^{A} - \frac{2x}{1+x^{2}} V'_{\lambda }(x) f_{\lambda }(x) dx &= \int _{-A}^{A} \frac{x}{1+x^{2}} (f'_{\lambda }(x)-2) dx \\ &= \Big[\frac{x}{1+x^{2}} f_{\lambda }(x)\Big]_{-A}^{A} - \int _{-A}^{A} \frac{1-x^{2}}{(1+x^{2})^{2}} f_{\lambda }(x) dx \\ &\quad - \int _{-A}^{A} \frac{2x}{1+x^{2}}\;. \end{aligned}$$

The last term vanishes by symmetry. We deduce from the previous computation that

$$ \begin{aligned}\int _{-A}^{A} \Big(\sqrt {\mathbf{E}}(\mathbf{E}-\lambda ) \frac{2x}{1+x^{2}} + \frac{1-x^{2}}{(1+x^{2})^{2}}\Big) f_{\lambda}(x)dx ={}& \int _{-A}^{A} 2x \mathbf{E}^{3/2} f_{\lambda }(x) dx \\ &{} + \Big[ \frac{x}{1+x^{2}} f_{\lambda }(x)\Big]_{-A}^{A}\;. \end{aligned}$$

The second term vanishes as $A\to \infty$. Indeed Lemma 3.1 ensures that $f_{\lambda }(x) \le C m_{\lambda }^{(\mathbf{E})} / (1+x^{2})$. Regarding the first term, we have

$$\begin{aligned} \int _{-A}^{A} 2x f_{\lambda }(x) dx &= \int _{-A}^{A} 4x e^{-2V_{ \lambda }(x)} \int _{-\infty}^{x} e^{2V_{\lambda }(y)} dy dx\;. \end{aligned}$$

We then apply the change of variables $(u,v) := (x-y,x+y)$ and get

$$\begin{aligned} \int _{-A}^{A} 2x f_{\lambda }(x) dx &= \int _{u \in (0,\infty )} \int _{v\in {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}} \mathbf{1}_{\{u+v \in [-2A,2A]\}} u e^{-2 \lambda \sqrt {\mathbf{E}}u - \frac{\mathbf{E}^{3/2}}{6}u^{3}} e^{- \frac{\mathbf{E}^{3/2}}{2} u v^{2}} dv du \\ &+ \int _{u \in (0,\infty )} \int _{v\in {{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}} \mathbf{1}_{\{u+v \in [-2A,2A]\}} v e^{-2 \lambda \sqrt {\mathbf{E}}u - \frac{\mathbf{E}^{3/2}}{6}u^{3}} e^{- \frac{\mathbf{E}^{3/2}}{2} u v^{2}} dv du\;. \end{aligned}$$

It is straightforward to check that the second term on the r.h.s. goes to 0 as $A\to \infty$. By the Dominated Convergence Theorem, the first term converges as $A\to \infty$ to

$$ \int _{0}^{+\infty} u e^{-2 \lambda \sqrt {\mathbf{E}}u - \frac{\mathbf{E}^{3/2}}{6} u^{3}} (\int _{-\infty}^{+\infty}e^{- \frac{\mathbf{E}^{3/2}}{2} u v^{2}} dv) du = \frac{\sqrt{2 \pi}}{ \mathbf{E}^{3/2}} \int _{0}^{+\infty} \sqrt{u} e^{-2 \lambda u - \frac{u^{3}}{6}} du \;, $$

as required. □

1.5 A.5 Control of the time spent near $\pi \mathbf{Z}$

In the previous sections, we needed a moment bound on the r.v.

$$ \Big(\int _{0}^{1} F(\theta _{\lambda }^{(\mathbf{E})}(t))dt\Big)^{-1} \quad \text{and}\quad \Big(\int _{0}^{1} F(\bar{\theta}_{\lambda }^{( \mathbf{E})}(t))dt\Big)^{-1}\;, $$

where $F$ is either $F(x) =\sin ^{2}(x)$ or $F(x) = \sin ^{4}(x)$. To prove such a bound, one needs to show that $\theta _{\lambda }^{(\mathbf{E})}$ does not spend too much time near $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ (since the function $F$ vanishes there).

In both cases, $F:{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}\to {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}_{+}$ is a $\pi$-periodic smooth function that satisfies, for some $k\ge 1$ and some $c>0$

$$ F(x) \ge c\, d(x,\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}})^{k}\;,\quad x\in {{\mathchoice{\text{\textbf{R}}}{ \text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\;,$$

(94)

where $d$ is the Euclidean distance. Our proof will only rely on this property, and therefore applies to a large class of functions $F$.

Lemma A.6

Control of the time spent near $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}$ by the phase function

Original coordinates. For any compact interval $\Delta \subset {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{\textit{\tiny \textbf{R}}}}}$, there exists a constant $q>0$ such that

$$ \sup _{\lambda \in \Delta} \sup _{\theta \in [0,\pi )} \mathbb{E}_{(0, \theta )}\Big[\exp \Big(q \big(\int _{0}^{1} F(\theta _{\lambda }(t)) dt \big)^{-\frac{1}{k+1}} \Big)\Big] < \infty \;. $$

Distorted coordinates. Fix $h>0$ and set $\Delta := [E-h/(n(E) E) , E + h/(n(E)E)]$. There exists a constant $q>0$ such that

$$ \sup _{E>1} \sup _{\lambda \in \Delta} \sup _{\theta \in [0,\pi )} \mathbb{E}_{(0,\theta )}\Big[\exp \Big(q \big(\int _{0}^{1} F(\theta _{ \lambda }^{(E)}(t)) dt\big)^{-\frac{1}{k+1}} \Big)\Big] < \infty \;. $$

The same holds with $\theta _{\lambda }$, $\theta _{\lambda }^{(E)}$ replaced by $\bar{\theta}_{\lambda }$, $\bar{\theta}_{\lambda }^{(E)}$, the adjoint diffusions defined in (55).

Proof

From now on, “all the parameters” will refer to $\lambda$ and $\theta$ when working with the original coordinates, and $E$, $\lambda$, $\theta$ when working with the distorted coordinates.

We only need to prove that there exists a constant $c' >0$ such that for all $\varepsilon >0$ small enough, and for all the parameters

$$\begin{aligned} \mathbb{P}_{(0,\theta )}\Big(\int _{0}^{1} F(\theta ^{(\mathbf{E})}_{ \lambda }(t))dt < \epsilon \Big) \leq \exp \big(- c' \;\varepsilon ^{- \frac{1}{k+1}}\big)\;. \end{aligned}$$

(95)

The idea of the proof is to consider the solution $\gamma _{\lambda }$ of the ODE corresponding to the deterministic part of our diffusion, to estimate the integral of $F(\gamma _{\lambda })$ on some interval $[0,T]$, with $T<1$, and to control the probability that $\gamma _{\lambda }$ and $\theta _{\lambda }^{(\mathbf{E})}$ differ on $[0,T]$.

Let $\gamma _{\lambda }$ be the solution of

$$ d\gamma _{\lambda }(t) = \Big(\mathbf{E}^{3/2} + \sqrt{\mathbf{E}} ( \lambda -\mathbf{E}) \sin ^{2} \gamma _{\lambda }+ \sin ^{3} \gamma _{ \lambda }\cos \gamma _{\lambda }\Big) dt\;, $$

starting from $\gamma _{\lambda }(0)=\theta _{\lambda }^{(\mathbf{E})}(0) = \theta$. We would like to bound from below the time spent by $\gamma _{\lambda }$ near $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ on the time interval $[0,T]$.

Let us introduce $a := \sup _{t\in [0,T]} d(\gamma _{\lambda }(t),\pi {{\mathchoice{ \text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}})$. We claim that:

• The distance $a$ is not too small i.e. there exists a constant $c_{0}\in (0,1)$ independent of all the parameters and of $T$ such that

  $$ a \ge c_{0} \min (T\mathbf{E}^{3/2},1) \ge c_{0} T\;.$$

  (96)

• The function $\gamma _{\lambda }$ spends some time above $a/2$: There exists a constant $c_{1}>0$ independent of all the parameters and of $T$ such that

  $$ \int _{0}^{T} \mathbf{1}_{\{d(\gamma _{\lambda }(t),\pi {{\mathchoice{ \text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}) > a/2\}} dt \ge c_{1} T\;.$$

  (97)

Given these two claims, we now control the difference between $\theta _{\lambda }^{(\mathbf{E})}$ and $\gamma _{\lambda }$. By Grönwall’s Lemma there exists a constant $C>0$ such that for all $T\in [0,1]$,

$$ \sup _{t\in [0,T]} |\theta _{\lambda }^{(\mathbf{E})}(t) - \gamma _{ \lambda }(t)| \le C \sup _{t\in [0,T]} |M(t)|\;, $$

where $M(t) := - \int _{0}^{t} \sin ^{2} \theta _{\lambda }^{(\mathbf{E})} dB(s)$. Let $\tau := \inf \{t\ge 0: |\theta _{\lambda }^{(\mathbf{E})}(t)-\gamma _{ \lambda }(t)| \ge a/4\}$. We deduce that

$$\begin{aligned} \mathbb{P}(\tau \le T) \leq \mathbb{P}\Big( \sup _{t\in [0,T\wedge \tau ]} |M(t)| \ge \frac{a}{4C}\Big)\;. \end{aligned}$$

Recall that $a = \sup _{t\in [0,T]} d(\gamma _{\lambda }(t),\pi {{\mathchoice{ \text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}})$. There exists a constant $C'>0$ such that for all $t \leq T\wedge \tau$, $\partial _{t}\langle M \rangle _{t} \le C' a^{4}$. Consequently Lemma A.2 yields the existence of $C_{0}>0$ such that

$$ \mathbb{P}(\tau \le T) \le 2e^{-\frac{C_{0}}{T}}\;. $$

Combining (94), (96) and (97), we deduce that on the event $\{\tau > T\}$ we have

$$ \int _{0}^{T} F(\theta _{\lambda }^{(\mathbf{E})}(t))dt = \int _{0}^{T} F(\gamma _{\lambda }(t) + \theta _{\lambda }^{(\mathbf{E})}(t)- \gamma _{\lambda }(t)) dt \ge c_{1} c \; T (a/4)^{k} \ge c_{2} T^{k+1} \;, $$

for some constant $c_{2}>0$ independent of all parameters and of $T$. For any $\varepsilon \in (0,c_{2}]$, one can choose $T\in [0,1]$ such that $\varepsilon = c_{2} T^{k+1}$. Then we have

$$ \mathbb{P}\Big(\int _{0}^{T} F(\theta _{\lambda }^{(\mathbf{E})}(t))dt < \varepsilon \Big) \le \mathbb{P}(\tau \le T) < 2\exp \Big(- C_{0} \Big(\frac{c_{2}}{\varepsilon }\Big)^{\frac{1}{k+1}}\Big)\;, $$

as required. It remains to prove the two claims stated above.

For the first point, there exists a constant $c'>0$ such that uniformly over the parameters the derivative of $\gamma _{\lambda }$ is larger than $c'\mathbf{E}^{3/2}$ whenever $\gamma _{\lambda }$ lies in some fixed neighborhood of $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$, say $[-\delta ,\delta ] + \pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{ \text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}$ with $\delta \leq {\pi /2}$. Set $c_{0} := \min (c'/4,\delta )$. We now distinguish two cases. If $d(\theta ,\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}})$ is larger than $\min ( (c'/4)T\mathbf{E}^{3/2} , \delta )$ then

$$ a \ge d(\theta ,\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}}) \ge \min ( (c'/4)T\mathbf{E}^{3/2} , \delta ) \ge c_{0} \min (T\mathbf{E}^{3/2},1)\;. $$

If $d(\theta ,\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{\text{\tiny \textbf{Z}}}}})$ is smaller than $\min ( (c'/4)T\mathbf{E}^{3/2} , \delta )$, then until $\gamma _{\lambda }$ reaches $\delta$ mod $[\pi ]$, its derivative is larger than $c'\mathbf{E}^{3/2}$. Therefore by time $T$, the distance of $\gamma _{\lambda }$ to $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ passes above $\min ((c'/2)T\mathbf{E}^{3/2},\delta )$, and this yields $a \ge c_{0} \min (T\mathbf{E}^{3/2},1)$. Finally, since $T\in [0,1]$ and $\mathbf{E}\ge 1$, the bound $c_{0} \min (T\mathbf{E}^{3/2},1) \ge c_{0} T$ is immediate.

For the second point, the absolute value of the derivative of $\gamma _{\lambda }$ is bounded from above by $K \mathbf{E}^{3/2}$ for some $K>0$. Consequently (the distance to $\pi {{\mathchoice{\text{\textbf{Z}}}{\text{\textbf{Z}}}{\text{\scriptsize \textbf{Z}}}{ \text{\tiny \textbf{Z}}}}}$ of) $\gamma _{\lambda }$ takes a time at least $a/(2K \mathbf{E}^{3/2})$ to go from $a/2$ to $a$ (or from $a$ to $a/2$). With the original coordinates, using (96) we thus get $a/(2K) \ge c_{0} T/(2K)$ as required.

Let us now consider the distorted coordinates: for convenience, we work under the further assumption that $E>E_{0}(h)$ where $E_{0}(h)\ge 1$ is a constant that depends only on $h$; the complementary case follows from an easy adaptation. Then the derivative of $\gamma _{\lambda }$ is larger than $E^{3/2}/2$ everywhere. First assume that $TE^{3/2} < 4\pi$. Then by (96) we have $a \ge c_{0} T E^{3/2}/(4\pi )$ and thus we find $a/(2K E^{3/2}) \ge c_{0} T /(8 \pi K)$ as required. We now assume that $TE^{3/2}\ge 4\pi$. The function $\gamma _{\lambda }$ makes a number of rotations over the circle which is at least ${\lfloor TE^{3/2}/(2\pi ) \rfloor } \ge 2$. Necessarily $a=\pi /2$. On each rotation, it spends a time at least $a/(2KE^{3/2})$ in the favorable region. We easily conclude to the second point of our claim. □

1.6 A.6 A bound on the centers of mass

Let $f$, $g$ be two functions with $L^{2}({{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}})$-norm equal to one such that $\int |t| f^{2}(t) dt < \infty$ and $\int |t| g^{2}(t) dt < \infty$. Let $V_{f}$, $V_{g}$ be their centers of mass, that is, $V_{f} := \int t f^{2}(t) dt$ and $V_{g}:=\int t g^{2}(t)dt$, and let $w_{f}$, $w_{g}$ be the associated probability measures on ${{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{ \text{\tiny \textbf{R}}}}}$ recentered at $V_{f}$, $V_{g}$, that is, $w_{f}(dt) = f^{2}(V_{f} +t)dt$ and $w_{g}(dt) = g^{2}(V_{g}+t)dt$.

Lemma A.7

Assume that there exist some constants $q,c>0$ and some $\delta \in (0,1/10)$ such that

$$ \begin{aligned}&\int |f(t)-g(t)|^{2} dt \le \delta ^{2}\;, \\ &\quad \textit{ and for all }t \in {{\mathchoice{\textit{\textbf{R}}}{\textit{\textbf{R}}}{\textit{\scriptsize \textbf{R}}}{ \textit{\tiny \textbf{R}}}}}\;,\quad |f(t)| \le c\, e^{-q|t-V_{f}|}\;,\quad |g(t)| \le c\, e^{-q|t-V_{g}|}\;. \end{aligned}$$

Then, there exists a function $C := C(q,c)>0$ depending only on $q$ and $c$, and which grows at most polynomially in $c$, such that $|V_{f} - V_{g}| \le C \delta ^{1/2}$ and $d_{\mathcal{M}}(w_{f},w_{g}) \le C\delta ^{1/2}$, where $d_{\mathcal{M}}$ is the Lévy-Prokhorov distance introduced in (87).

Proof

Let $X$, $Y$ be two r.v. with densities $f^{2}$ and $g^{2}$ respectively. Note that $V_{f} = \mathbb{E}[X]$ and $V_{g} = \mathbb{E}[Y]$. By assumption, we have for any $A>0$

$$ \mathbb{P}(|X-\mathbb{E}[X]| > A) < \frac{c^{2}}{q} e^{-{ 2}qA}\;,\quad \mathbb{P}(|Y-\mathbb{E}[Y]| > A) < \frac{c^{2}}{q} e^{-{2}qA}\;. $$

Furthermore

$$\begin{aligned} &\big| \mathbb{P}(|X-\mathbb{E}[Y]| \le A) - \mathbb{P}(|Y-\mathbb{E}[Y]| \le A) \big| \\ &\quad = \Big|\int _{[\mathbb{E}[Y]-A,\mathbb{E}[Y]+A]} (f^{2}(t) - g^{2}(t))dt\Big| \\ &\quad \le \big(\int |f(t) - g(t)|^{2}dt\big)^{1/2} \big(\int |f(t) + g(t)|^{2}dt \big)^{1/2} \\ &\quad \le 2{\delta}\;. \end{aligned}$$

Choose $A>0$ such that (it can be chosen in such a way that it grows logarithmically in $c$)

$$ 2\frac{c^{2}}{q} e^{-{2}qA} + 2{\delta} < 2 \frac{c^{2}}{q} e^{-{2}qA} + 2\frac{1}{10}< 1\;. $$

Assume that $|\mathbb{E}[X]-\mathbb{E}[Y]|>2A$. Then

$$ \mathbb{P}(|X-\mathbb{E}[Y]| \le A) \le \mathbb{P}(|X-\mathbb{E}[X]| > A) < \frac{c^{2}}{q} e^{-{2}qA}\;, $$

while

$$ \mathbb{P}(|Y-\mathbb{E}[Y]| \le A) \ge 1-\frac{c^{2}}{q} e^{-qA}\;, $$

so that

$$ \big| \mathbb{P}(|X-\mathbb{E}[Y]| \le A)-\mathbb{P}(|Y-\mathbb{E}[Y]| \le A)\big| > 1 - 2\frac{c^{2}}{q} e^{-qA} > 2{\delta}\;, $$

thus raising a contradiction. Consequently, $|\mathbb{E}[X]-\mathbb{E}[Y]|\le 2A$.

This being given, take $A' >0$ and define the interval $I := [\min (\mathbb{E}[X],\mathbb{E}[Y]) -A', \max (\mathbb{E}[X], \mathbb{E}[Y]) +A']$, and let $m$ be its midpoint. We have

$$\begin{aligned} \mathbb{E}[X] - m = \int _{I} (t-m) f^{2}(t) dt + \int _{{{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\backslash I} (t-m) f^{2}(t) dt\;, \\ \mathbb{E}[Y] - m = \int _{I} (t-m) g^{2}(t) dt + \int _{{{ \mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\backslash I} (t-m) g^{2}(t) dt\;. \end{aligned}$$

Since the length of $I$ is smaller than $2(A+A')$, we deduce that

$$ \begin{aligned}\Big| \int _{I} (t-m) f^{2}(t) dt - \int _{I} (t-m) g^{2}(t) dt\Big| &\le (A+A') \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}}|f^{2}(t)-g^{2}(t)| dt \\ &\le 2(A+A') \delta \;. \end{aligned}$$

Moreover,

$$\begin{aligned} \Big|\int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\backslash I} (t-m) f^{2}(t) dt \Big| & \le \int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\backslash [\mathbb{E}[X]-A',\mathbb{E}[X]+A'])}(|t- \mathbb{E}[X]| + A) c^{2} e^{-2q|t-\mathbb{E}[X]|} \\ &\le \Big(\frac{A'}{q} + \frac{1}{2q^{2}} + \frac{A}{q}\Big)c^{2}e^{-2qA'} \;. \end{aligned}$$

The same bound holds for $\big|\int _{{{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}\backslash I} (t-m) g^{2}(t) dt\big|$. This ensures that

$$ \big| \mathbb{E}[X]-\mathbb{E}[Y]\big| \le 2(A+A') \delta + 2\Big( \frac{A'}{q} + \frac{1}{2q^{2}} + \frac{A}{q}\Big)c^{2}e^{-2qA'}\;. $$

Choosing $A'=\delta ^{-1/2}$, we get the desired bound on $|V_{f}-V_{g}|$. Let $w'_{f}$ be the probability measure associated with $f^{2}$ recentered at $V_{g}$, that is, $w'_{f}(dt) = f^{2}(V_{g}+t)dt$. Then, it is easy to check that

$$ d_{\mathcal{M}}(w_{g},w'_{f}) \le \int |f^{2}-g^{2}|(t) dt \le 2 ( \int |f-g|^{2}dt)^{1/2} \le 2 \delta \;. $$

Furthermore for any Borel set $B\subset {{\mathchoice{\text{\textbf{R}}}{\text{\textbf{R}}}{\text{\scriptsize \textbf{R}}}{\text{\tiny \textbf{R}}}}}$, note that for any $\epsilon > |V_{f}-V_{g}|$ we have $V_{f} + B \subset V_{g} + B^{\epsilon}$ and $V_{g} + B \subset V_{f} + B^{\epsilon}$ so that

$$\begin{aligned} w_{f}(B) = \int _{V_{f}+B} f^{2}(t) dt \le \int _{V_{g}+B^{\epsilon}} f^{2}(t) dt = w_{f}'(B^{\epsilon})\;, \\ w_{f}'(B) = \int _{V_{g}+B} f^{2}(t) dt \le \int _{V_{f}+B^{\epsilon}} f^{2}(t) dt = w_{f}(B^{\epsilon})\;, \end{aligned}$$

so that $d_{\mathcal{M}}(w_{f},w'_{f}) \le |V_{f}-V_{g}|$, thus concluding the proof. □