Abstract
Let \(\mathrm {G}\) be the group \( (\mathrm {GL}_{2}\times \mathrm{GU}(1))/\mathrm {GL}_{1}\) over a totally real field F, and let \(\mathscr {X}\) be a Hida family for \(\mathrm {G}\). Revisiting a construction of Howard and Fouquet, we construct an explicit section \(\mathscr {P}\) of a sheaf of Selmer groups over \(\mathscr {X}\). We show, answering a question of Howard, that \(\mathscr {P}\) is a universal Heegner class, in the sense that it interpolates geometrically defined Heegner classes at all the relevant classical points of \(\mathscr {X}\). We also propose a ‘Bertolini–Darmon’ conjecture for the leading term of \(\mathscr {P}\) at classical points. We then prove that the p-adic height of \(\mathscr {P}\) is given by the cyclotomic derivative of a p-adic L-function. This formula over \(\mathscr {X}\) (which is an identity of functionals on some universal ordinary automorphic representations) specialises at classical points to all the Gross–Zagier formulas for \(\mathrm {G}\) that may be expected from representation-theoretic considerations. Combined with a result of Fouquet, the formula implies the p-adic analogue of the Beilinson–Bloch–Kato conjecture in analytic rank one, for the selfdual motives attached to Hilbert modular forms and their twists by CM Hecke characters. It also implies one half of the first example of a non-abelian Iwasawa main conjecture for derivatives, in \(2[F:\mathbf {Q}]\) variables. Other applications include two different generic non-vanishing results for Heegner classes and p-adic heights.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and statements of the main results
A beautiful construction of Heegner and Birch, based on the modularity of elliptic curves and the theory of complex multiplication, attaches to an elliptic curve \(A/\mathbf {Q}\) and an imaginary quadratic field E a point \(P\in A(E)\). The work of Gross–Zagier [45] related the height of P to the derivative of the L-function \(L'(A_{E}, 1)\), with striking applications to the Birch and Swinnerton-Dyer conjecture. An analogous result in p-adic coefficients was proved by Perrin-Riou [84] soon thereafter, if A has good ordinary reduction at the prime p.
The decade following those works saw a pair of similar results, by Nekovář [78] and Zhang [109], relating Heegner cycles on Kuga–Sato varieties to (p-adic) L-functions of higher-weight modular forms. We may single out two major innovations in the approach to Heegner points and Gross–Zagier formulas since then,Footnote 1 both answering the question of what ‘other’ Heegner points there are and how they fit together.
The first one starts from the observation by Mazur [73] and Perrin-Riou [85] that Heegner points should vary p-adically in anticyclotomic families, in the same way that the L-function of the elliptic curve \(A_{E}\) does; this observation inspired Howard [57] to prove a generalisation to such families of Perrin-Riou’s formula. Howard later significantly expanded the scope of Mazur and Perrin-Riou’s idea by proving that the Kummer classes of Heegner points also vary in Hida families of modular forms [58]; the question of the relation of the resulting ‘big’ classes to Heegner cycles was left open.
The second innovation was the observation by Gross [46] that Heegner points can be viewed as elements of spaces of \(\mathrm {H}'\)-invariant linear functionals on an automorphic representation of \((\mathrm {G}\times \mathrm {H})'\) (these reductive groups will be defined below),Footnote 2 so that the tools of representation theory may be brought in to conceive and prove more general formulas: a programme whose main achievement, in complex coefficients, is the work of Yuan–Zhang–Zhang [107] on Heegner points on Shimura curves.
In this work, we combine those two approaches. We construct Heegner classes for the Galois representation over a Hida family for \((\mathrm {G}\times \mathrm {H})'\), show that they specialise to (cohomological) Heegner cycles at all classical points, and prove a formula for their p-adic heights that is universal in the sense that it specialises to all the p-adic formulas suggested by the framework of Gross. (The analogous complex Gross–Zagier formulas are not currently knownFootnote 3 for motives of higher weight.) We obtain various applications to the arithmetic of motives attached to Hilbert modular forms.
In the rest of this first section we state our main theorems, and complete the discussion of their history.
We begin in Sect. 1.1 by presenting the results concerning the p-adic Beĭlinson–Bloch–Kato conjecture (Theorem A); they are applications of the general p-adic Gross–Zagier formula for a fixed representation, stated as Theorem B in Sect. 1.2.
In Sect. 1.3 we outline the construction and properties of the universal family of Heegner classes (Theorem C), referring to the “Bertolini–Darmon” conjecture of Sect. 7.3 for a further study of its classical specialisations. In Sect. 1.4 we state the universal formula of the title (Theorem D); a complementary ‘Waldspurger’ analogue will be proved in Sect. 7.2 (Theorem H).
Finally, in Sect. 1.5 we discuss some further applications: the first non-abelian example of an Iwasawa main conjecture for derivatives of p-adic L-functions (Theorem E); and two results on the generic non-vanishing of p-adic heights and Heegner cycles: one for CM motives (Theorem F), the other for Hida families containing a rank-0 elliptic curve with split multiplicative reduction (Theorem G). A further application, to a criterion for certain Bloch–Kato Selmer groups to be of rank zero, will appear separately.
1.1 The p-adic Beĭlinson–Bloch–Kato conjecture in analytic rank 1
The primary motivation for our work comes from the generalisations of the Birch and Swinnerton-Dyer (BSD) conjecture and its p-adic analogue, as proposed by Beĭlinson, Bloch–Kato, and Perrin-Riou [3, 11, 86]. Recall that if \(A/\mathbf {Q}\) is an elliptic curve, (BSD) is equivalent to the following statements. Denote by \(r_\mathrm{an}\) and \(L^{*}(A, 1)\) the order of vanishing and leading term of L(A, s) at \(s=1\). Then \(L^{*}(A,1) >0\) and for every prime p,
-
(a)
the Selmer group \(\mathrm{Sel}(V_{p}A):=(\varprojlim _{n} \mathrm{Sel}_{p^{n}}(A)) \otimes _{\mathbf {Z}_{p}} \mathbf {Q}_{p}\) has dimension equal to \(r_\mathrm{an}\);
-
(b)
the divisible part of
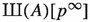 vanishes;
vanishes; -
(c)
the p-adic valuations of \(L^{*}(A, 1)/\Omega _{A} R_{A}\) and
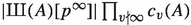 are equal.
are equal.
1.1.1 Selmer groups according to Bloch–Kato and Nekovář
If E is a number field and V is a geometric p-adic representation of its Galois group \(G_{E}\), Bloch and Kato [11] have proposed an analogue
of the Selmer group of A; it is an L-vector-subspace (where L is the field of scalars for V) of the first Galois cohomology group of V, consisting of those classes satisfying certain local conditions. According to the resulting variant of the conjecture of Beĭlinson [3], the dimension \(\dim _{L} H^{1}_{f}(E, V)\) should equal the order of vanishing of the L-function \(L(V^{*}(1), s)\) at \(s=0\).Footnote 4
Another definition of Selmer groups was proposed by Greenberg when V satisfies an ordinariness condition at the places above a prime p; specialised to the cases of interest to us, it recovers the Bloch–Kato Selmer groups. Nekovář observed that a variation of Greenberg’s definition works well in p-adic families, and developed this observation into the theory of Selmer complexes [81], that provides the foundation for the present work (Sect. 5). For nice p-adic families of \(G_{E}\)-representations, the theory allows to define groups
for all i.
1.1.2 The p-adic Beĭlinson–Bloch–Kato conjecture for Hilbert modular forms
Our main arithmetic results concern the p-adic analogue of the Beĭlinson–Bloch–Kato conjecture for the Galois representations attached to Hilbert modular forms and their twists by Hecke characters of CM fields.
Fix throughout the rest of this paper a rational prime p. Let F be a totally real field, let E be a CM quadratic extension of F, and let
Let L be a finite extension of \(\mathbf {Q}_{p}\) splitting F. A pair of cohomological weights for \(\mathrm {G}_{0}\) and \(\mathrm {H}\) is a pair of tuples \(\underline{w}:=(w; (w_{\sigma })_{\sigma :F\hookrightarrow L})\), \(\underline{l}=(l;(l_{\sigma })_{\sigma :F\hookrightarrow L} )\), each consisting of \([F:\mathbf {Q}]+1\) integers of the same parity, such that \(w_{\sigma }\ge 2\) for all \(\sigma :F\hookrightarrow L\). In this paper we will only consider cohomological weights and therefore omit the adjective ‘cohomological’. By a “Hilbert modular form over L of weight \(\underline{w}\)” (respectively a “Hecke character of E over L of weight \(\underline{l}\)”) we mean a cuspidal automorphic representation of \(\mathrm {G}_{0}(\mathbf {A})\) (respectively \(\mathrm {H}(\mathbf {A})\)) over L of weight \(\underline{w}\) (respectively weight \(\underline{l}\)) as defined in Definition 2.4.1 below.
If \(\pi _{0}\) is a Hilbert modular form and \(\chi \) a Hecke character over L, we denote by \(\Pi _{0}=\pi _{0}\otimes \chi \) the associated representation of \(\mathrm {G}_{0}\times \mathrm {H}\). We denote by \(V_{\pi _{0}}\) and \(V_{\chi }\) the corresponding 2- (respectively 1-) dimensional representations of \(G_{F}\) (respectively \(G_{E}\)), normalised so that \(L(V_{\pi _{0}}, s)= L(s+1/2, {\pi _{0}})\), and we let
Let \(\omega _{\pi _{0}}\) be the central character of \(\pi _{0}\) and let \(\omega _{\chi }:=\chi |_{F_{\mathbf {A}^{\infty }}^{\times }}\). If \(\omega _{\pi _{0}}\omega _{\chi }=1\), then V is conjugate-self-dual and pure of weight \(-1\), and the epsilon factor \(\varepsilon (V)\in \{\pm 1\}\).
Let \(\Gamma _{F}:= F_{\mathbf {A}^{\infty }}^{\times }/F^{\times }\hat{\mathscr {O}}^{p, \times }_{F}\) (identified with the Galois group of the maximal abelian extension of F unramified outside p by class field theory), and let
(We will also simply write \(\mathscr {E}_\mathrm{Z}\) for \(\mathscr {E}_\mathrm{Z/\mathbf {Q}_{p}}\).) Suppose that \( \pi _{0}\) is ordinary in the sense of Definition 2.4.3; equivalently, for all \(v\vert p\) the associated \(G_{F_{v}}\)-representation \(V_{\pi _{0}, v}\) reduces nontrivially as
and \(G_{F_{v}}\) acts on \(V_{\pi _{0},v}^{+}\) by the product of the cyclotomic character \(\chi _\mathrm{cyc}\) and a character \(\alpha _{v}^{\circ }\) valued in p-adic units. We may attach to V a meromorphic p-adic L-function
where the variable \(s\in \mathscr {E}_{\mathrm{Z}/L}\) may be thought of as a p-adic character of \(\Gamma _{F}\); we use the synonym \(\chi _{F, s}\) when we want to emphasise such nature of s, and we denote by “\(s=0\)” the trivial character \(\chi _{F, 0}=\mathbf {1}\).Footnote 5 More precisely, working in terms of the multivariable function \(\mathscr {L}_{p}(\mathscr {V}^{\sharp })\) of Theorem 1.4.1 below, we may define \(\mathscr {L}_{p}(V_{(\pi , \chi )})\) as the restriction
where \(z_{s}\) corresponds to the family of representations \(V_{\pi |G_{E}}\otimes \chi \chi _{F, s|G_{E}}\).
If \(\varepsilon (V)=-1\), then \(\mathscr {L}_{p}(V_{(\pi _{0}, \chi )}, 0)=0 \) and we denote by \(\mathscr {L}_{p}'(V_{(\pi _{0}, \chi )}, 0)=\mathrm{d}\mathscr {L}_{p}((V_{(\pi _{0}, \chi )})(0) \in T_{0}\mathscr {E}_{\mathrm{Z}/L}= \Gamma _{F}\hat{\otimes }L\) its first derivative.
Theorem A
Let \(\pi _{0}\) be a Hilbert modular form over L of weight \(\underline{w}\), and let \(\chi \) be a Hecke character of E over L of weight \(\underline{l}\). Let \(V:=V_{\pi _{0}|G_{E}}\otimes V_{\chi }\) . Suppose that:
- \((wt )\):
-
\( | l_{\sigma }|<w_{\sigma }\) for all \(\sigma :F\hookrightarrow L\);
- \((sd )\):
-
\(\omega _{\pi _{0}}\omega _{\chi }=1\) (which implies \(w+l=0\));
- \((\varepsilon )\):
-
\(\varepsilon (V)=-1\);
- \((ord )\):
-
\(\pi _{0}\) is ordinary;
- \((n-exc )\):
-
V is not exceptional: for no place \(w\vert v\vert p\) of E is \(V_{w}^{-}:=V^{-}_{\pi _{0}, v|G_{E_{w}}}\otimes \chi _{w}\) the trivial representation.
-
1.
We have
$$\begin{aligned} \mathscr {L}_{p}'(V_{(\pi , \chi )}, 0)\ne 0 \Longrightarrow \dim _{L} \widetilde{H}^{1}_{f}(E, V)\ge 1, \end{aligned}$$and we can exhibit an explicit nonzero element of \(\widetilde{H}^{1}_{f}(E, V) = {H}^{1}_{f}(E, V)\), whose p-adic height (cf. Proposition 5.3.3) is also non-zero.
-
2.
Let \(T\subset V\) be a stable lattice. If \(\mathscr {L}_{p}'(V_{(\pi , \chi )}, 0)\ne 0\) and moreover the conditions of [41, Theorem B.(i)] are satisfied, then:
-
(a)
we have
$$\begin{aligned} \dim _{L} \widetilde{H}^{1}_{f}(E, V)=1; \end{aligned}$$ -
(b)
let \(R_{T} \in \mathscr {O}_{L}\hat{\otimes }_{\mathbf {Z}_{p}}\Gamma _{F} \) be the regulator of the height pairing (1.2.12) on \(\widetilde{H}^{1}_{f}(E, T)\times \widetilde{H}^{1}_{f}(E, T^{*}(1))\). Then
$$\begin{aligned} \mathscr {L}_{p}'(V_{(\pi , \chi )}, 0) \succeq _{\mathbf {Z}_{p}} R_{T}\cdot | \widetilde{H}^{2}_{f}(E, T)_\mathrm{tors}| \end{aligned}$$in \(L\hat{\otimes }\Gamma _{F} \).
-
(a)
In the last formula we have used the following suggestive notation.
Notation
For a domain A with fraction field K and two A-submodules \(m_{1}, m_{2}\) of a K-vector space M we write \(m_{1}\succeq _{A} m_{2}\) if \(m_{1}\subseteq m_{2}\); the notation is extended to the case where some \(m_{i}\) is an element of M, in which case we interpret it as \(Am_{i}\).
Part 1 will be an immediate consequence of Theorem B, the Jacquet–Langlands correspondence, and the observation following (1.2.5) below. For a list of previous results in the direction of part 1 we refer to the discussion following Theorem B. Let us note, for now, that an analogue of this result in complex coefficients is not known.
Part 2 follows from invoking the results of Fouquet in [41], that generalise the bounds on Tate–Shafarevich groups of elliptic curves obtained by Kolyvagin using the methods of Euler systems.
Remark 1.1.1
Condition \((n-exc )\) guarantees that \(\mathscr {L}_{p}(V_{(\pi , \chi )}, s)\) has no exceptional zeros at \(s=0\), and it is equivalent to the identity \(\widetilde{H}^{1}_{f}(E, V)= {H}^{1}_{f}(E, V)\). We will also equivalently say that \(\Pi \) is not exceptional. For a characterisation of this condition, see Lemma 6.4.6.
Remark 1.1.2
In the simplest case where \(F=\mathbf {Q}\), \(\pi _{0}\) is a modular form with rational Fourier coefficients of weight \(w_{\sigma }=2\), and \(\chi =\mathbf {1}\), the representation \(V_{\pi _{0}}=V_{\mathfrak {p}}A\) is the rational p-adic Tate module of an elliptic curve \(A/\mathbf {Q}\). In this case \({H}^{1}_{f}(E, V)={\mathrm{Sel}}(V_{p}A_{E})\), and letting \(T=T_{p}A_{E}\), the group \(\widetilde{H}^{2}_{f}(E, T)_{\mathrm{tors}}\) equals [12, (1.36)] the quotient of  by its divisible submodule
by its divisible submodule  .
.
The group  , conjecturally 0, measures the failure of \(\mathrm{Sel}(V_{p}A_{E})\) to be generated by the classes of points in A(E). We do not address in this paper the analogous conjecture from [11] that \({H}^{1}_{f}(E, V)\) should be generated by the classes of algebraic cycles. Nevertheless our construction of a generator is sufficiently geometric to provide a good starting point to establish this conjecture, cf. Remark 6.2.2.
, conjecturally 0, measures the failure of \(\mathrm{Sel}(V_{p}A_{E})\) to be generated by the classes of points in A(E). We do not address in this paper the analogous conjecture from [11] that \({H}^{1}_{f}(E, V)\) should be generated by the classes of algebraic cycles. Nevertheless our construction of a generator is sufficiently geometric to provide a good starting point to establish this conjecture, cf. Remark 6.2.2.
1.1.3 A variant for selfdual Hilbert modular forms
Suppose that \(\pi _{0}\) is an ordinary Hilbert modular form, \(\omega _{\pi _{0}}=1\) (so that \(w=0\)), and \(\varepsilon (V_{\pi _{0}})=-1\). Assume that either \([F:\mathbf {Q}]\) is odd or there is a place \(v\not \mid p\infty \) of F such that \(\pi _{0,v}\) is not a principal series. Suppose that for no \(v\vert p\) is \(\pi _{0,v}\) the Steinberg representation. Let \(L_{p}(V_{\pi _{0}}, s)\) be the p-adic L-function of \(V_{\pi _{0}}\) constructed in [30]. If \(L'_{p}(V_{\pi _{0}},0)\ne 0\), then the conclusions (1) and (2a) of the previous theorem hold with (E, V) replaced by \((F, V_{\pi _{0}})\). (This is proved by a standard argument based on the choice of a suitable auxiliary E to reduce to the previous theorem.) A similar remark (at least for part (1)) applies when \(\pi _{0}\) has CM by E, cf. the proof of Theorem F in Sect. 7.1.4
1.1.4 Addendum to the historical overview: higher-rank cases
The general overview sketched in our opening page ignored a third important theme: Gross’s framework has been generalised in [42] to study special cycles attached to other pairs of groups \((\mathrm {G}, \mathrm {H})\). Several works have explored the consequences towards the Beĭlinson–Bloch–Kato conjecture of the possible non-vanishing of those cycles, most notably [69]. On the other hand, non-vanishing criteria in terms of L-functions have been obtained in a considerably more limited set of cases, mostly related to triple-product L-functions [9, 10, 28, 106, 108].Footnote 6 The relation with cyclotomic p-adic L-functions has not been studied beyond Heegner cycles.
1.2 The p-adic Gross–Zagier formula for arbitrary weight
Theorem A, like analogous previous results [31, 32, 35, 78, 84, 96], is an application of an explicit formula for the p-adic heights of a certain Selmer class (here rather a collection of classes). When the weights are trivial, that is \(\underline{w}=(0; (2,\ldots , 2))\) and \(\underline{l}=(0; (0, \ldots , 0))\), this is the class of a Heegner 0-cycle coming from CM points on quaternionic Shimura curves; this is the case studied in [32, 35], and earlier in complex coefficients by Yuan–Zhang–Zhang [107]. In general, it is the class of a 0-cycle supported at CM points, with coefficients in a local system corresponding to the weight of the representation. The specific choice of the (tower of) Shimura curves is dictated by the local root numbers of V, see the discussion preceding Definition 1.2.1.
1.2.1 Algebraic groups and Shimura varieties
Let \(\mathbf {B}\) be a quaternion algebra over \(F_{\mathbf {A}}\) (where \(\mathbf {A}\) denotes the adèles of \(\mathbf {Q}\)) with ramification set \(\Sigma \sqcup \{v\vert \infty \} \) satisfying \(|\Sigma | \equiv [F:\mathbf {Q}] -1\pmod {2}\). Then \(\mathrm {G}(\mathbf {A}):= \mathbf {B}^{\times }\) is not the points of an algebraic group ‘\(\mathrm {G}\)’ over \(\mathbf {Q}\), but we will still find convenient to use this suggestive notation and refer to \(\mathrm {G}\) as an incoherent algebraic group over \(\mathbf {Q}\) (see Sect. 2.1.1 for a more formal treatment). Let \(\mathrm {H}=\mathrm {Res}_{E/\mathbf {Q}}{} \mathbf{G}_{m}\) as above, and let \(\mathrm{Z}:= \mathrm {Res}_{F/\mathbf {Q}}{} \mathbf{G}_{m}\), that admits natural central embeddings in \(\mathrm {G}\) and \(\mathrm {H}\).
The list of (coherent or incoherent) groups of interest in this paper, often denoted collectively by \(\mathrm {G}_{*}\), is
where \(\mathrm{Z}\) is embedded diagonally in the product group.Footnote 7 We suppose that for every \(v\in \Sigma \), \(E_{v}/F_{v}\) is nonsplit. Then there is unique \(\mathbf {B}^{\times }\)-conjugacy class of \(F_{\mathbf {A}}\)-embeddings \(E_{\mathbf {A}}\hookrightarrow \mathbf {B}\), of which we fix one. It induces an embedding \(\mathrm{e}:\mathrm {H}\hookrightarrow \mathrm {G}\).
To the above groups and suitable Shimura data (Sect. 2.3.1), we associate corresponding towers of compactified Shimura varieties \(X_{*}\), respectively denoted
They are curves except for Y, \(Y'\) that have dimension 0. The embedding \(\mathrm{e}\) induces a diagonal embedding \(\mathrm {H}'\hookrightarrow (\mathrm {G}\times \mathrm {H})'\), hence a morphism of Shimura varieties
1.2.2 p-Adic automorphic representations
It is more natural to parametrise “cohomological automorphic representations over a p-adic field L” of a group \(\mathrm {G}_{*}\) by irreducible algebraic representations W of \(\mathrm {G}_{*}\).Footnote 8
Let \(G_{*, \infty }\) be \(\mathrm {G}_{*}(\mathbf {Q}_{p})\) with the Zariski topology (and for later purposes let \(G_{*, p}:=\mathrm {G}_{*}(\mathbf {Q}_{p})\) with the p-adic topology, \(G_{*}:=G_{* , p} \times G_{*,\infty }\)). We redefine throughout this work
Let W be an (algebraic) representation of \(G_{*, \infty }\) over L, and let \(\mathscr {W}\) be the corresponding étale local system on the tower \(X_{*}\). Then we define a (cuspidal, cohomological) automorphic representation of \(\mathrm {G}_{*}(\mathbf {A})\) over L of weight W to be a representation
of \(\mathrm {G}_{*}(\mathbf {A})\) occurring in \(H^{\bullet }(X_{*, \overline{E}}, \mathscr {W}^{\vee })\otimes W\).Footnote 9 (Here and in the rest of the paper, groups and Hecke algebras act on Shimura varieties and their homology on the right, on cohomology and on automorphic forms on the left. Left and right algebraic representations W are identified via \(w.g:=g^{-1}.w\).)
1.2.3 Automorphic and Galois representations
Let \(\Pi =\pi \otimes \chi \) be a cuspidal automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{})\) over L of weight \(W=W_{\mathrm {G}}\otimes W_{\mathrm {H}}\). Let \(V=V_{\Pi }=V_{\pi |G_{E}}\otimes V_{\chi }\) be the associated \(G_{E}\)-representation.
For a smooth proper variety \(Z'\) of dimension d over a characteristic-zero field \(F'\) and a p-adic local system \(\mathscr {W}'\), define
for all \(0\le i\le 2d\). For each level \(K\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{\infty }) \), let \(\overline{Z}_{K}:=Z_{K}\times _{\mathrm {Spec}\,E}\mathrm {Spec}\,{\overline{E}}\). We use the notation
and similarly for the other Shimura varieties over F, E, \(\overline{E}\) under consideration. Thanks to work of Carayol we can construct an injection (an isomorphism unless V is decomposable) of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{})\)-representations
1.2.4 Heegner cycles
Suppose that W satisfies (wt), then \(W^{H'_{\infty }}\cong W_{H'_{\infty }}\) is 1-dimensional, and \(\mathrm{e'}\) induces a canonical system of maps
for all \(V'\subset \mathrm {H}'(\mathbf {A}^{\infty })\cap K\). The image \(\Delta ^{\circ }_{W, f_{\infty }}\in \mathrm {H}_{0}(Z_{K}, \mathscr {W})\) of the normalised fundamental class
is well-defined and (after a modification if W is trivial) belongs to the kernel \(\mathrm {H}_{0}(Z_{K}, \mathscr {W})_{0}\) of \( \mathrm {H}_{0}(Z_{K}, \mathscr {W})\rightarrow \mathrm {H}_{0}(\overline{Z}_{K}, \mathscr {W})\). The images of \(\Delta ^{\circ }_{W, f_{\infty }}\) under the Abel–Jacobi maps \(\mathrm{AJ}:\mathrm {H}_{0}(Z_{K}, \mathscr {W})_{0} \rightarrow H^{1}(E, \mathrm {H}_{1}( \overline{Z}_{K}, \mathscr {W})) \) are compatible under pushforward along the tower \(Z_{K}\) and invariant under the \(\mathrm {H}'(\mathbf {A}^{})\)-action, hence they define an element
Via (1.2.3), \(P_{W}\) defines an \(\mathrm {H}'(\mathbf {A})\)-invariant functional
whose image should lie in \(H^{1}_{f}(E, V_{\Pi })\subset H^{1}(E, V_{\Pi })\) (see Remark 6.2.2 for a stronger conjecture). We show in Proposition 6.4.7 that this is the case if \(\mathbf {B}_{p}\) is split and \(\Pi \) is ordinary and not exceptional, which we define to mean that \(\mathbf {B}_{p}\) is split and the Jacquet–Langlands transfer \(\Pi _{0}\) of \(\Pi \) to \(\mathrm {G}_{0}\times \mathrm {H}\) (which is thus the ‘identity’ at p) satisfies those properties.
Our formula will give a criterion for the nonvanishing of \(P_{\Pi }\).
1.2.5 Multiplicity one
Representation theory provides a necessary condition. The space
is known, by a theorem of Waldspurger, Tunnell, and Saito [90, 102], to be nonzero if and only if the following condition is satisfied for all v:
- (\(\varepsilon _{v}\)):
-
Define \( \varepsilon (\mathbf {B}_{v}):=+1 \) (respectively \(-1\)) if \(\mathbf {B}_{v}\) is split (respectively nonsplit). Let \(\varepsilon (V_{v}):= \prod _{w\vert v}\varepsilon (V_{w})\), \(\chi _{v}(-1):=\prod _{w\vert v}\chi _{w}(-1)\); then
$$\begin{aligned} \varepsilon _{v}^{\mathrm {G}}(V):= \varepsilon (V_{v})\chi _{v}(-1)\eta _{v}(-1)\varepsilon (\mathbf {B}_{v}) =+1. \end{aligned}$$(1.2.5)
If this is the case, \((\Pi )^{*,\mathrm {H}'(\mathbf {A})}\) is 1-dimensional and moreover the global root number \(\varepsilon (V)=-1\). Conversely, if V is as in Theorem A and in particular satisfies \(\varepsilon (V)=-1\), there exists a unique incoherent totally definite quaternion algebra \(\mathbf {B}\) verifying \((\varepsilon _{v})\).
The conditions (\(\varepsilon _{v}\)) for a finite v generalise the classical “Heegner condition”. For \(v\vert p\), if \(\pi \) is ordinary the condition \((\varepsilon _{v})\) is satisfied unless v is nonsplit in E and \(\pi \) is exceptional at v (Lemma 6.4.6). The condition (\(\varepsilon _{\infty }\)) is equivalent to (wt).
Definition 1.2.1
We say that \(\Pi \) is locally distinguished by \(\mathrm {H}'\), or simply locally distinguished, if it satisfies conditions \((\varepsilon _{v}) \) for all v.
1.2.6 Local toric periods
Assume that \(\Pi \) is locally distinguished, and let \(\Pi ^{\vee }\) denote the contragredient representation of \(\Pi \). Then we know an explicit a generator of
as a product of local pairings, which we now define. The pair \(P_{\Pi }\otimes P_{\Pi ^{\vee }}\) will be measured against this generator.
For v a finite place of F, let \(\Pi _{v}\) be the local component of \(\Pi \), a representation of \((\mathbf {B}_{v}^{\times }\times E^{\times }_{v})/F_{v}^{\times }\supset H'_{v}:= E_{v}^{\times }/F_{v}^{\times }\); let \(dt_{v}\) be a Haar measure on \(H_{v}'\). For \(v=\infty \), let \(\Pi _{\infty }=W\) and let \(dt_{\infty }\) be a formal symbol synonymous with a constant \(\mathrm {vol}(H'_{\infty }, dt_{\infty })\in L\). In all cases, let \(\Pi _{v}^{*, H'_{v}}:=\mathrm {Hom}\,_{H_{v}'}(\Pi _{v}, L)\) and let \((\ , \ )_{v}\) be an invariant pairing on \(\Pi _{v}\otimes \Pi _{v}^{\vee }\).
Let \(V_{v}\) (respectively \(V_{\pi , v}\)) be the restriction to \(G_{E_{v}}:=\prod _{w\vert v}G_{E,w}\) (respectively \(G_{F_{v}}\)) of the Galois representation associated with \(\Pi \) (respectively \(\pi \)) if v is finite, and the Hodge structure associated with W (reps. \(W_{\mathrm {G}}\)) if \(v=\infty \). Let us also introduce the convenient notation
(to be thought of as referring to a ‘virtual motive’).
Let \(\eta :F^{\times }_{\mathbf {A}}/F^{\times }\rightarrow \{\pm 1\}\) be the character associated with E/F, and let
Then
is an explicit generator of \(\Pi _{v}^{*, H'_{v}}\otimes _{L} (\Pi _{v}^{\vee })^{*, H'_{v}}\). Here for \(v\not \mid \infty \) the integral is absolutely convergent (after making any choice of \(L\hookrightarrow \mathbf {C}\)), and for \(v =\infty \) we understand
where \(\mathrm{p}_{H'_{\infty }}\) is the natural projection.
Given \(f_{3,v}, f_{4,v}\in \Pi _{v}\otimes \Pi _{v}^{\vee }\) such that \((f_{3,v}, f_{4,v})_{v}\ne 0\), the quantity
is independent of the choice of \((\ , \ )_{v}\); it equals \(\mathrm {vol}(\mathscr {O}_{E,v}^{\times }/\mathscr {O}_{F, v}^{\times }, dt_{v})\) if all the data are unramified.
Fix a choice of measures \(dt_{v}\) such that for \(dt=\prod _{v }dt_{v}\),
Then we define for \(f_{1}\in \Pi _{H'_{}}\), \(f_{2}\in \Pi ^{\vee }_{H'_{}}\), \(f_{3}\in \Pi \), \( f_{4}\in \Pi ^{\vee }\) such that \(\prod _{v}(f_{3,v}, f_{4,v})_{v}\ne 0\):
1.2.7 Global pairings and p-adic heights
Let \(V^{\iota }:=V_{\Pi ^{\vee }}\). Fix a Galois-equivariant pairing
Poincaré duality provides a canonical Galois- and Hecke- equivariant pairing \( \mathrm {H}_{1}(\overline{Z}_{K},\mathscr {W}) \otimes \mathrm {H}_{1}(\overline{Z}_{K}, {\mathscr {W}}^{\vee })\rightarrow L(1)\). Via (1.2.3) and (1.2.10), it induces dual pairings \((\ , \ )_{\Pi }^{K}:\Pi ^{K} \otimes \Pi ^{\vee , K} \rightarrow L \) for all K. Letting \(L_{K}\) be the Hodge bundle on \(Z_{K}\), the following pairing ((4.1.7) in the text) is well defined:
On the other hand, if \(\pi \) is ordinary the restriction \(V_{w}\) of V to \(G_{E_{w}}\), \(w\vert p\), is reducible
and there is an analogous reduction for \(V^{\iota }\) such that \(V^{+}_{w}\) and \(V^{\iota , +}_{w}\) are exact orthogonal of each other under (1.2.10). These data allow to define a height pairing
on Nekovář’s Selmer groups as in Proposition 5.3.3. When W is trivial, the representation \(V=V_{\mathfrak {p}}A_{E}\otimes \chi \) is a factor of the Tate module of an abelian variety, and (under (n-exc)) the pairing \(h_{V}\) coincides with all other p-adic height pairings on abelian varieties defined in the literature: see [32] for a review.
1.2.8 The formula
We can now state the p-adic Gross–Zagier formula for V.
Theorem B
Let \(\Pi =\pi \otimes \chi \) be an ordinary, locally distinguished, non-exceptional automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{})\) over L. Let \(V=V_{\Pi }\).
The image of \(P_{\Pi }\) lies in \(H^{1}_{f}(E, V)\), and for all \(f_{1}\in \Pi _{H'_{\infty }}\), \(f_{2}\in \Pi ^{\vee }_{H'_{{\infty }}}\), \(f_{3}\in \Pi \), \(f_{4}\in \Pi ^{\vee }\) such that \((f_{3}, f_{4})_{\Pi }\ne 0\), we have
where \(e_{p\infty }(V_{(\pi , \chi )}) \in L^{\times }\) is the p-interpolation factor for \(\mathscr {L}_{p}(V_{(\pi ,\chi )}, s)\) defined in (1.4.6) below.
When \(\mathrm {G}=\mathrm {GL}_{2/\mathbf {Q}}\), V is crystalline at p, p splits in E, \(\chi \) is unramified and the \(f_{i}\) are newforms, a version of this result was proved by Perrin-Riou [84] when W is trivial, and by Nekovář [78] and Shnidman [96] when W has even weights. The general case with trivial W was proved in [32, 35].
Remark 1.2.2
Establishing Gross–Zagier formulas in this generality has proven useful for arithmetic applications, such as those in [14, 15, 100] and Theorem F below.
Explicit versions of the formula can be obtained by evaluating the functional Q at well-chosen \(f_{i}\). This is a local problem, solved in [18].
Remark 1.2.3
For a variant of Theorem B that is valid in the exceptional case as well, see Theorem \(\text {B}^{\, \mathrm {ord}}\). That variant is often trivially \(0=0\) in the exceptional case, but not always, and indeed Remark 7.3.4 sketches a new proof of the Greenberg–Stevens theorem [43] based on it. For a further discussion going beyond any trivial or non-trivial vanishing, see Remark 1.3.3 and Sect. 7.3.
1.3 The universal Heegner classes
We explain the interpolation of the Heegner cycles \(P_{\Pi }\) as \(\Pi \) varies over a Hida family for \((\mathrm {G}\times \mathrm {H})'\).
Suppose from now on that \(\mathbf {B}_{p}\) is split and fix an isomorphism \(\mathrm {G}_{\mathbf {Q}_{p}}\cong \mathrm {Res}_{F_{p}/\mathbf {Q}_{p}}\mathrm {GL}_{2}\), giving a model of \(\mathrm {G}\) (hence \((\mathrm {G}\times \mathrm {H})'\)) over \(\mathbf {Z}_{(p)}\). We let \(N_{\mathrm {G}, 0}:=\left( {\begin{matrix}1&{}\mathscr {O}_{F, p}\\ &{}1\end{matrix}}\right) \subset \mathrm {G}(\mathbf {Q}_{p})\) and \(N_{0}\) be the image of \(N_{\mathrm {G}, 0}\) in \((G\times H)'_{p}\). Finally we denote by \(\mathrm {U}_{p}\) the usual operator in the Iwahori–Hecke algebra of \((G\times H)'_{p}\), and by \(\mathrm {U}_{p\infty }\) its product with \( (\left( {\begin{matrix}p&{}\\ &{}1\end{matrix}}\right) , 1)\in (G\times H)'_{\infty }\).
For a localisation \(\mathrm{M}\) of a finite \(\mathbf {Z}_{p}\)-module \(\mathrm{M}^{\circ }\) on which the operator \(\mathrm {U}_{p\infty }\) acts (on the left or the right), we denote by \(\mathrm{M}^{\mathrm {ord}}\) the image of \(\mathrm{M}\) under Hida’s ordinary projector
1.3.1 Hida families for \((\mathrm {G}\times \mathrm {H})'\)
Pick an arbitrary \((\mathrm {G}\times \mathrm {H})'(\mathbf {Z}_{p})\)-stable lattice \(W^{\circ }\subset W\), yieding a sub-local system \(\mathscr {W}^{\circ }\subset \mathscr {W}\). Then we define, for any \(K=K^{p}K_{p}\) with \(K_{p}\supset N_{0}\),
Let \(K^{p}\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\) be an open compact subgroup. Consider the ordinary completed homology of \(\overline{Z}_{K^{p}}\)
where \( M_{K}^{\circ }=\) (1.3.1) with W the trivial representation, and the limit is over K such that \(K_{p}\supset N_{0}\) (“level \(\Gamma _{1}^{1}(p^{\infty })\)”). By the work of Hida, \(M_{K^{p}}\) is a finite flat module over a certain weight algebra \(\Lambda =\Lambda _{K^{p}} \simeq \mathbf {Q}_{p}[\Delta ]\otimes _{\mathbf {Z}_{p}} \mathbf {Z}_{p}\llbracket T_{1}, \ldots , T_{2[F:\mathbf {Q}]+1+\delta _{F ,p}}\rrbracket \) where \(\Delta \) is a finite group and \(\delta _{F, p}\) is the Leopoldt defect of F.
Let \(\mathbf{T}^\mathrm{sph, \mathrm {ord}}_{K^{p}, \mathbf {Q}_{p}}\subset \mathrm {End}\,_{\Lambda }(M_{K^{p}})\) be the image of the algebra generated by the spherical Hecke operators and the operators \(\mathrm {U}_{v}\), \(v\vert p\). The ‘ordinary eigenvariety’
contains a dense subset \(\mathscr {E}^{\mathrm {ord}, \mathrm {cl}}\) (more precisely a reduced 0-dimensional ind-subscheme) of regular points, in bijection with the set of \(G_{\mathbf {Q}_{p}}\)-orbits of those ordinary automorphic representations \(\Pi \) of \((\mathrm {G}\times \mathrm {H})'\) over \(\mathbf {Q}_{p}\) such that \(\Pi ^{K^{p}}\ne 0\).
Let us fix an irreducible component
that is a Hida family for \((\mathrm {G}\times \mathrm {H})'\). We let \(\mathscr {X}^{\mathrm {cl}}:=\mathscr {X}\cap \mathscr {E}^{\mathrm {ord}, \mathrm {cl}} \).
Definition 1.3.1
A Hida family \(\mathscr {X}\) for \((\mathrm {G}\times \mathrm {H})'\) is said to be locally distinguished (by \(\mathrm {H}'\)) if it satisfies the conditions
- \((\varepsilon _{v})'\):
-
for every (equivalently,Footnote 10 one) classical point \(z\in \mathscr {X}\) (of weight satisfying (wt)), the Galois representation \(\mathscr {V}_{z}\) attached to the representation \(\Pi _{z}\) satisfies (\(\varepsilon _{v}\))
for all \(v\not \mid p\infty \).
1.3.2 Sheaves on \(\mathscr {X}\)
The Hida family \(\mathscr {X}\) comes with a coherent sheaf \(\mathscr {M}_{K^{p}}\) corresponding to \(M_{K^{p}}\); moreover in fact for each \(K^{p}{}'\subset K^{p}\) the module \(M_{K^{p}{}'}\) gives rise to a coherent \(\mathscr {O}_{\mathscr {X}}\)-module
with \(\mathscr {O}_{\mathscr {X}}\)-linear Hecke- and Galois actions. Fix an arbitrary \(K^{p}{}'\subset K^{p}\), ‘sufficiently large’ at the places in \(\Sigma \).Footnote 11 Let S be a finite set of primes, not containing those above p, such that all data \(\mathrm {G}, \mathrm {H},K^{p}{}'\) are unramified outside Sp. Let \(G_{E, Sp}\) be the Galois group of the maximal extension of E unramified outside Sp. We prove in the text that the following statements are true up to replacing \(\mathscr {X}\) by an open subset containing \(\mathscr {X}^{\mathrm {cl}}\):
-
there exists a locally free sheaf \(\mathscr {V}\) of rank 2 with a \(G_{E, Sp}\)-action, such that for all \(z\in \mathscr {X}^{\mathrm {cl}}\), the representation \(\mathscr {V}_{|z}\) is associated with \(\Pi _{z}\) via the Langlands correspondence;
-
for each \(w\vert p\) there is an exact sequence of \(\mathscr {O}_{\mathscr {X}}[G_{E,w}]\)-modules
$$\begin{aligned} 0\rightarrow \mathscr {V}_{w}^{+}\rightarrow \mathscr {V}_{w}\rightarrow \mathscr {V}^{-}_{w}\rightarrow 0, \end{aligned}$$(1.3.2)where the \(\mathscr {V}_{w}^{\pm } \) are line bundles over \(\mathscr {X}\), specialising to (1.2.11) at all \(z\in \mathscr {X}^{\mathrm {cl}}\);
-
assume from now on that \(\mathscr {X}\) is locally distinguished. There is a locally free \(\mathscr {O}_{\mathscr {X}}\)-module
$$\begin{aligned} \Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }} \end{aligned}$$interpolating the spaces of \((E_{\Sigma }^{\times }/F_{\Sigma }^{\times })\)-coinvariants, \(K^{p}{}'\)-invariants of \(\Pi _{z}^{\mathrm {ord}}\) for \(z\in \mathscr {X}^{\mathrm {cl}}\);
-
we have a map of Hecke modules over \(\mathscr {O}_{\mathscr {X}}\)
$$\begin{aligned} \Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }}\rightarrow \mathrm {Hom}\,_{\mathscr {O}_{\mathscr {X}}[G_{E, Sp}]}(\mathscr {M}_{K^{p}{}'}^{H_{\Sigma }'}, \mathscr {V}) \end{aligned}$$(1.3.3)whose specialisations over \(\mathscr {X}^{\mathrm {cl}}\) are deduced by (1.2.3).
1.3.3 The universal Heegner class
We construct in the appendix (Proposition A.2.4) an operator \(\gamma _{H'}^{\mathrm {ord}}\), that is the key to the interpolation of Heegner cycles. It is a limit of of Hecke operators at \(p\infty \), intertwining toric and ordinary parts:
Consider the class
It is invariant under \(\mathrm {H}'(\mathbf {A}^{p\infty })\), hence:
-
as \(K^{p}{}'\) varies, it defines an \(\mathrm {H}'(\mathbf {A}^{p\infty })\)-invariant functional
$$\begin{aligned} P_{\Pi }^{\mathrm {ord}}= P_{W}\circ \gamma _{H'}^{\mathrm {ord}} :\Pi ^{\mathrm {ord}}\rightarrow H^{1}(E, V_{\Pi }) \end{aligned}$$(1.3.4)and in fact, as we shall prove, valued in \(H^{1}_{f}(E, V_{\Pi })\).
-
restricting (without loss of generality as we will see in a moment) to the case where W is trivial, its localisation over \(\mathscr {X}\) defines a global section \(\mathscr {P}_{K^{p}{}'}\) of \( H^{1}(G_{E, Sp},\mathscr {M}_{K^{p}{}'}^{H_{\Sigma }'})\).
Using Nekovář’s theory of Selmer complexes we show that the universal class \(\mathscr {P}_{K^{p}{}'}\) is a section of a sheaf of Selmer groups \(\widetilde{H}^{1}_{f}({E},\mathscr {M}_{K^{p}{}'}^{H_{\Sigma }'})\), where the subscript f signifies a local condition at p coming from (1.3.2), and for Selmer groups we use E in place of \(G_{E, Sp}\) for short. Then by (1.3.3) the class \(\mathscr {P}_{K^{p}{}'}\) defines a map of \(\mathscr {O}_{\mathscr {X}}\)-modules
When \(\mathrm {G}=\mathrm {GL}_{2/\mathbf {Q}}\), the value of \(\mathscr {P}_{K^{p}{}'}\) on a family of newforms is the class originally defined by Howard in [58]. (The statement that the fibre of \(\mathscr {P}_{K^{p}{}'}\) at all classical points lands in the Selmer group is in new even in the context of [58].) There, Howard asked whether his class interpolates Heegner cycles at all classical points of \(\mathscr {X}\). The first part of the following theorem summarises the results described above. The second part, whose proof is simple and direct, provides an affirmative answer to the generalisation of Howard’s question.Footnote 12
Theorem C
Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\). There exist an open subset \(\mathscr {X}'\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\) and a map
of sheaves over \(\mathscr {X}'\), satisfying the following properties:
-
1.
\(\mathscr {P}_{K^{p}{}'}\) is invariant under the action of the away-from-\(p\Sigma \)-Hecke algebra of \(\mathrm {H}'\);
-
2.
for all \(z\in \mathscr {X}^{\mathrm {cl}}\) corresponding to a representation \(\Pi _{z}\) satisfying \((wt )\), denote by \(P^{\mathrm {ord}}_{\Pi _{z}, K^{p}{}'}\) the restriction of (1.3.4) to \((\Pi _{z})_{H'_{\Sigma }}^{K_{p}', \mathrm {ord}}\); then
$$\begin{aligned} \mathscr {P}_{K^{p}{}'|z} = P^{\mathrm {ord}}_{\Pi _{z},K^{p}{}'} \end{aligned}$$under the natural map \({H}^{1}(G_{E, Sp}, \mathscr {V})_{|z}\rightarrow {H}^{1}_{}(G_{E, Sp}, V_{\Pi _{z}})\).
An answer to Howard’s question in its original context was earlier given by Castella [22, 23] by an indirect method, under the assumption that p splits in E.
Remark 1.3.2
It follows from the results of [26] that, under mild conditions, the class \(\mathscr {P}\) is non-torsion over \(\mathscr {X}\), cf. the discussion after [41, Theorem B].
Remark 1.3.3
Theorem C is far from being the last word on \(\mathscr {P}\): first, the class \(\mathscr {P}\) may vanish at some classical points; second, we can consider its specialisation in Nekovář’s Selmer group \(\widetilde{H}^{1}_{f}(E, V_{\Pi _{z}})\), which equals \(H^{1}_{f}(E, V_{\Pi _{z}}) \) when z is not exceptional but is larger otherwise. In Sect. 7.3, we address both problems by proposing a conjecture for the order of vanishing and leading term of \(\mathscr {P}\) at any classical point, generalising conjectures by Bertolini–Darmon. The same Conjecture Pf will also give a prediction for the leading terms of universal toric periods on distinguished Hida families for coherent quaternionic groups, discussed in Sect. 7.2, and in that case we will describe some new evidence in higher rank coming from the ‘plectic’ world via [39].
1.4 The universal formula
We first recall the p-adic L-function constructed in [36], then state our formula for the p-adic height of \(\mathscr {P}_{K^{p}{}' }\).
At times we refer to the main body of the paper for the precise definition of some of the objects.
1.4.1 Dualities over Hida families
The space \(\mathscr {E}^{\mathrm {ord}}\) is endowed with an involution \(\iota \) corresponding to \(\Pi _{z}\mapsto \Pi _{z}^{\vee }\). Fix a locally distinguished Hida family \(\mathscr {X}\); then the constructions of Sect. 1.3 can be performed over \(\mathscr {X}\). Denoting by \((-)^{\iota }\) the pullback under \(\iota \) of an object over \(\mathscr {X}\), we have dualities
interpolating (1.2.10). These data, together with their deformation to a Hida family \(\mathscr {X}^{\sharp }\) for \(\mathrm {G}\times \mathrm {H}\), allow to define a height pairing as in Proposition 5.3.4,
As usual after possibly restricting to an open subset containing \(\mathscr {X}^{\mathrm {cl}}\), we construct:
-
pairings
$$\begin{aligned} ((\ , \ )) :\Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }} \otimes _{\mathscr {O}_{\mathscr {X}}} (\Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }})^{\iota }\rightarrow \mathscr {O}_{\mathscr {X}} \end{aligned}$$interpolating the \(p\infty \)-modification \((\ ,\ )^{\mathrm {ord}}_{\Pi }:=\) (4.1.8) of \((,)_{\Pi }\);
-
\(\mathscr {O}_{\mathscr {X}}^{\times }\)-module maps
$$\mathscr {Q}:( \Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }} \otimes _{\mathscr {O}_{\mathscr {X}}^{\times }} \Pi ^{K^{p}{}', \mathrm {ord}, \iota }_{H'_{\Sigma }}) \otimes _{\mathscr {O}_{\mathscr {X}}^{\times }} ( \Pi ^{K^{p}{}', \mathrm {ord}}_{H'_{\Sigma }} \otimes _{\mathscr {O}_{\mathscr {X}}^{\times }} \Pi ^{K^{p}{}', \mathrm {ord}, \iota }_{H'_{\Sigma }})^{\times , -1}\rightarrow \mathscr {K}_{\mathscr {X}}$$interpolating the \(p\infty \)-modification \(Q^{\mathrm {ord}}=\) (4.3.3) of Q. Here, \(\mathscr {K}_{\mathscr {X}}\) is the sheaf of fractions of \(\mathscr {O}_{\mathscr {X}}\) and the superscript ‘\(\times , -1\)’ denotes the subgroup of those \(f_{3}\otimes f_{4} \) satisfying \(((f_{3}, f_{4}))\ne 0\) and suggests the ‘denominator’ invariance of the pairing in the last two variables.
1.4.2 The p-adic L-function
Let \(\mathscr {E}_{0}^{\sharp , \mathrm {ord}}:= \mathscr {E}_{\mathrm {G}_{0}\times \mathrm {H}}^{\mathrm {ord}} \) be the ordinary eigenvariety for \(\mathrm {G}_{0}\times \mathrm {H}\) (see [50, 51]); for appropriate choices of tame levels, there is a map \(\iota _\mathrm{JL}:\mathscr {E}^{\mathrm {ord}}_{\mathrm {G}\times \mathrm {H}} \rightarrow \mathscr {E}_{\mathrm {G}_{0}\times \mathrm {H}}^{\mathrm {ord}}\), which is a closed immersion onto a union of irreducible components. Let \(\mathscr {X}_{0}^{\sharp }:=\iota _\mathrm{JL}(\mathscr {X}^{\sharp })\subset \mathscr {E}^{\sharp , \mathrm {ord}}\). We recall the p-adic L-function on \(\mathscr {X}^{\sharp }\) constructed in [36].
Let \(\mathscr {X}_{0}^{\sharp , \mathrm {cl}} = \iota _\mathrm{JL}(\mathscr {X}_{}^{\sharp , \mathrm {cl}}) \subset \mathscr {X}_{0}^{\sharp }\) be the ind-scheme of classical points. If \((x,y)\in \mathscr {X}_{0}^{\sharp , \mathrm {cl}}(\mathbf {C})\) is a geometric point corresponding to a closed point \((x_{0}, y_{0})\in \mathscr {X}_{0}^{\sharp ,\mathrm {cl}}\) together with an embedding \(\iota :\mathbf {Q}_{p}(x_{0}, y_{0}) \hookrightarrow \mathbf {C}\), we denote \(\pi _{x} =\pi _{x_{0}}^{\iota }, \chi _{y}=\chi _{y_{0}}^{\iota }\), which are complex automorphic representations of \(\mathrm {G}_{0}(\mathbf {A})\) and \(\mathrm {H}(\mathbf {A})\) respectively. We then denote \(V_{(x_{0},y_{0})}^{\sharp }:= V_{(\pi _{x_{0}}, \chi _{y_{0}})}\) and let
be the product (defined by analytic continuation) of all of the factors (1.2.7).
Recall that if W is a complex Weil–Deligne representation of the Weil group of a local field \(F_{v}\) and \(\psi _{v}:F_{v}\rightarrow \mathbf {C}^{\times }\) is a nontrivial character, the inverse Deligne–Langlands \(\gamma \)-factor isFootnote 13
and \(\psi _{E, w}=\psi _{v}\circ \mathrm {Tr}_{E_{w}/F_{v}}\).
If \(\pi =\pi _{x_{0}}\), \(\chi =\chi _{y_{0}}\) are as just above (with weights \(\underline{w}=\underline{w}_{x_{0}}\), \(\underline{l}=\underline{l}_{y_{0}}\)), let \(\mathrm {ad}(V_{\pi ,v})(1)^{++}:= \mathrm {Hom}\,(V_{\pi ,v}^{-}, V_{\pi , v}^{+})\). Let \(\psi =\prod _{v}\psi _{v}:F\backslash \mathbf {A}_{F}\rightarrow \mathbf {C}^{\times }\) be the standard additive character such that \(\psi _{\infty }(\cdot ) = e^{2\pi i \mathrm {Tr}_{F_{\infty }/\mathbf {R}}(\cdot )}\); let \(\psi _{E}=\prod _{w}\psi _{E, w}=\psi \circ \mathrm {Tr}_{\mathbf {A}_{E}/\mathbf {A}_{F}}\). For a place \(v\vert p \) of F, let \(d_{v}\) be a generator of the different ideal of \(F_{v}\), and define
where \(\iota \mathrm{WD}\) is the functor from potentially semistable Galois representations to complex Weil–Deligne representations of [38]. Finally, we define
At least if \(w+l=0\), these belong to \(\iota \mathbf {Q}_{p}(x_{0}, y_{0})\), and we may define
The following is the main theorem of [36].
Theorem 1.4.1
There exists a meromorphic function
whose polar locus \(\mathscr {D}\) does not intersect \(\mathscr {X}_{0}^{\mathrm {cl}}\), uniquely characterised by the following property.
For each \(z=(x, y)\in \mathscr {X}_{0}^{\sharp , \mathrm {cl}}(\mathbf {C})- \mathscr {D}(\mathbf {C})\) corresponding to an automorphic representation \(\pi _{x}\otimes \chi _{y}\) of \(\mathrm {G}_{0}(\mathbf {A})\times \mathrm {H}(\mathbf {A})\) of weight \((\underline{w}_{x}, \underline{l}_{y})\) satisfying the conditions
we have
1.4.3 Main theorem
Under the condition of local distinction of \(\mathscr {X}\), the function \(\mathscr {L}_{p}(\mathscr {V}^{\sharp })\) vanishes identically on \(\mathscr {X}_{0}\). Let \(\mathscr {N}^{*}_{\mathscr {X}_{0}/\mathscr {X}_{0}^{\sharp }} =\mathscr {I}_{\mathscr {X}_{0}}/\mathscr {I}_{\mathscr {X}_{0}}^{2}\otimes _{\mathscr {O}_{\mathscr {X}_{0}^{\sharp }}}\mathscr {O}_{\mathscr {X}_{0}} \cong \mathscr {O}_{\mathscr {X}_{0}}\hat{\otimes }\Gamma _{F}\) be the conormal sheaf and let
be the image of \(\mathscr {L}_{p}(\mathscr {V}^{\sharp })\).
Theorem D
Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\). Abbreviate \(\Pi ^{(\iota )}:= \Pi ^{K^{p}{}', \mathrm {ord}, (\iota )}_{H'_{\Sigma }}\), \(\mathscr {O}:=\mathscr {O}_{\mathscr {X}}\), \(\mathscr {K}:=\mathscr {K}_{\mathscr {X}}\).
Then there is an open subset \(\mathscr {X}'\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\) such that all of the above constructions can be made over \(\mathscr {X}'\), and
an equality of \(\mathscr {K}\hat{\otimes }_{\mathbf {Z}_{p}}\Gamma _{F}\)-valued \(\mathscr {O}\)-linear functionals on \((\Pi \otimes _{\mathscr {O}} \Pi ^{\iota })\otimes _{\mathscr {O}^{\times }} (\Pi \otimes _{\mathscr {O}} \Pi ^{\iota })^{\times , -1}\).
The formula of the theorem in fact also holds at exceptional points \(z\in \mathscr {X}^{\mathrm {cl}}\), see Theorem \(\text {B}^{\, \mathrm {ord}}\).
1.5 Applications
We turn to some arithmetic applications of the main theorems (in addition to Theorem A).
1.5.1 On the Iwasawa Main Conjecture for derivatives
We use the notation introduced after Theorem A.
Theorem E
Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\), satisfying the further conditions of [41, Theorem B.(iii)]. Let \(\mathscr {X}'\subset \mathscr {X}\) be the open subset of Theorem D; up to shrinking \(\mathscr {X}'\) we may assume it is a regular scheme. Let \(\mathscr {R}\subset \mathscr {O}_{\mathscr {X}'}\hat{\otimes } \Gamma _{F}\) be the regulator of the height pairing (1.4.2) over \(\mathscr {X}'\). Then
The proof, based on Theorem D and [41, Theorem B.(iii)], is virtually identical to that of [32, Theorem D], based on Theorem C.4 ibid. and [41, Theorem B.(ii)].
1.5.2 Generic non-vanishing of p-adic heights for self-dual CM motives
It is conjectured that cyclotomic p-adic height pairings are non-vanishing (and even non-degenerate). Results in this direction have been quite rare. The next theorem generalises a variant of the main theorem of [14], to which we refer for a discussion of the background.
Consider the set of locally algebraic Hecke characters
satisfying the special self-duality condition
This is precisely the set of classical points of the closed subspace
cut out by the condition (1.5.1) on continuous characters. The space \(\mathscr {E}^{\mathrm {ord}, \mathrm{sd}}_{\mathrm {H}}\) is a torsor for \(\mathscr {E}^{\mathrm {ord}}_{\mathrm {H}'}\); in particular it is smooth of dimension \([F:\mathbf {Q}]\). Let \(\mathscr {Y}\subset \mathscr {E}^{\mathrm {ord}, \mathrm{sd}}_{\mathrm {H}}\) be an irreducible component; then there is a sign \(\epsilon \in \{\pm 1\}\) such that for all \(x\in \mathscr {Y}_{}^\mathrm{cl}\), \(\varepsilon (1,\chi ) =\epsilon \); we then say that \(\mathscr {Y}^{\mathrm {cl}} \) has type \(\epsilon \).
Denote by \(h_E^-=h_E/h_F\) the relative class number of E/F and by \(D_{F}\) the absolute discriminant of F.
Theorem F
Let \(\mathscr {Y}\subset \mathscr {E}^{\mathrm {ord}, \mathrm{sd}}_{\mathrm {H}}\) be an irreducible component of type \(-1\). Suppose that all primes \(v\vert p\) of F split in E, the extension E/F is ramified, and \(p \not \mid 2 D_{F} h_E^-\).
Then, there exists a non-empty open subset \(\mathscr {Y}'\subset \mathscr {Y}\) such that for all \(y\in \mathscr {Y}^{\mathrm {cl}}\cap \mathscr {Y}'\), the Selmer group \(H^{1}_{f}({E}, \chi _{y})\) is nonzero and the p-adic height pairing
is non-vanishing.
1.5.3 Non-vanishing of universal Heegner classes along some classical Hida families
Part 3 of the following theorem is also a contribution to the non-vanishing conjecture for p-adic heights. Parts 1 and 2 provide, to the best of the author’s knowledge, the first piece of theoretical evidence towards conjectures of Greenberg [44] and Howard [58].
Theorem G
Let \(\mathscr {X}_{0}\) be a Hida family for \(\mathrm{PGL}_{2/\mathbf {Q}}\), and let \(\mathscr {X}_{0}^{\sharp }\) be the Hida family for \(\mathrm {GL}_{2/\mathbf {Q}}\) containing \(\mathscr {X}_{0}\). Denote by \(\mathscr {V}_{0}\), \(\mathscr {V}_{0}^{\sharp }\) the associated rank-2 representations of \(G_{\mathbf {Q}}\).
Suppose that \(\mathscr {X}_{0}\) contains a point corresponding to an elliptic curve A with split multiplicative reduction at p, satisfying \(L(A, 1)\ne 0\). Then:
-
1.
a universal Heegner class \(\mathscr {P}_{0}\) is nonvanishing along \(\mathscr {X}_{0}\);
-
2.
the Selmer group \(\widetilde{H}^{1}_{f}(\mathbf {Q}, \mathscr {V}_{0})\) has generic rank 1, generated by \(\mathscr {P}_{0}\);
-
3.
the p-adic height pairing \(h_{\mathscr {V}_{0}/\mathscr {V}_{0}^{\sharp }} \) is non-vanishing.
1.6 Outline of the proofs
The basic strategy to prove the main results is very simple. When W is trivial, Theorem B was proved in [32, 35] under some technical assumptions. As the set of points of trivial weight in \(\mathscr {X}^{\mathrm {cl}}\) satisfying those assumptions is still dense in \(\mathscr {X}\), this suffices to deduce Theorem D once its terms are defined; by a multiplicity-one argument and an explicit local computation, this in turn implies Theorem B for all W. Much of this work is therefore an exercise in p-adic interpolation to construct the objects of Sects. 1.3–1.4; the table of contents, and the internal references given so far, should suffice to guide the reader through the paper.
An illustration of the proof of Theorems B and D. Each of the (infinitely many) floors corresponds to a representation \(\Pi \) as in Theorem B, each apartment to a quadruple \(\mathbf{f}=(f_{1}, f_{2}, f_{3}, f_{4})\), and the building to a Hida family. A light being on indicates that the corresponding Gross–Zagier formula is proven. On ‘most’ floors corresponding to a \(\Pi \) of trivial weight, all lights are on by [32, 35]. In this paper, we construct the lift corresponding to the formula of Theorem D, with doors (interpolation statements) onto special apartments in each floor (the formulas of Theorem \(\text {B}^{\, \mathrm {ord}}\) in Sect. 7.1.1, equivalent to Theorem B for certain special quadruples \(\mathbf{f}\)). As soon as the lights in a dense set of floors in the building are on, the light in the lift is on; this allows to turn on the light in all the special apartments. Finally, the multiplicity-one principle allows to propagate the electricity among different apartments on the same floor
The proof of Theorem C is completed in Sect. 6.4.3 and the proof of Theorems B, D is completed in Sect. 7.1, where we also prove Theorem F. Theorem G is proved at the end of Sect. 7.3 using a known case of the conjecture made there. Constructions and calculations of a local nature are gathered in “Appendix A”.
We highlight some of the key tools we use (many have already been mentioned):
-
Nekovář’s theory of Selmer complexes and p-adic heights ([81], see also [103, Appendix C]), applied to Hida theory;
-
the local Langlands correspondence in families as described in [34], that is necessary for the interpolation of the terms \(Q_{v}\);
-
Emerton’s point of view [37] on p-adic cohomological automorphic representations as having a component at ‘infinity’ that is an algebraic representation of the relevant group; in our context, this further allows to properly consider ‘incoherent’ reductive groups;
-
the multiplicity-one result for \(\mathrm {H}'(\mathbf {A})\)-invariant functionals;
-
the definition and study of semi-local operators at \(p\infty \), as the key to transitioning between ordinary and anti-ordinary or toric parts of a module;
-
the explicit evaluation of certain local toric periods in terms of gamma factors.
We view the framework introduced in the appendix as the main technical novelty contributed by the present work, and we hope that the underlying approach will prove useful in many other contexts.Footnote 14
1.6.1 Further directions
We have not paid attention to the integral aspects; doing so may also remove the need to restrict to open subsets of \(\mathscr {X}\) at various points, e.g. by restricting to newforms or using the local Langlands correspondence in integral families of Emerton, Helm, and Moss (see references in [34]). (However, this would require imposing some residual irreducibility assumptions for the representation \(\mathscr {V}_{v}\).) This may lead to non-vanishing results for higher-weight Heegner cycles, automorphic toric periods, and L-values: an example we have in mind is the anticyclotomic non-vanishing result of [25], based on a construction not unlike that of Theorem H.
In a different direction, all of the constructions of this paper could be generalised, with work, to the context of eigenvarieties; the Gross–Zagier formulas should also extend to that context.
1.7 Related contemporary work
After a first version of this paper was made publicly available, the following partly related works have appeared.
-
In [63], the authors construct universal Heegner classes for Coleman families of elliptic modular forms (with classical restrictions); then they prove that these classes interpolate the images of Heegner cycles, by a method not dissimilar to that of the present work. Similar results are also independently proved in [83] in the ordinary case, and (by a different method) in [16] in the case where p splits in the field of complex multiplications.
-
In [17], the authors use [16, 63] and a strategy similar to the one of the present paper to prove the p-adic Gross–Zagier formula for critical-slope refinements of elliptic modular forms, conditionally on work in preparation of Kobayashi on such formula for small-slope refinements. Their idea is to deduce, from the latter, a p-adic Gross–Zagier formula in a Coleman family, within which the objects considered by Kobayashi form a dense subset; then specialise the formula to other classical points.
-
In [67], Loeffler gives a method to construct p-adic families of cohomology classes attached to inclusions of reductive groups \(\mathrm {H}_{1}\subset \mathrm {H}_{2}\) such that \(\mathrm {H}_{2}/\mathrm {H}_{1}\) is a spherical variety. His local-at-p construction vastly generalises the one of Proposition A.2.4. A difference is that in [67], the weight variation is not addressed (accordingly, that construction does not use the ‘infinite’ place).
1.8 Notation
Throughout the paper we use the following notation unless otherwise noted.
-
\(\mathbf {A}\) is the ring of adèles of \(\mathbf {Q}\);
-
the fields F and E are as in the introduction, \(\eta =\eta _{E/F}:F_{\mathbf {A}}^{\times }/F^{\times }\rightarrow \{\pm 1\}\) is the associated quadratic character, and we denote by \(\overline{E}\) a fixed algebraic closure of E;
-
we denote by \(G_{E}\) the absolute Galois group of a field E; if E is a number field and S is a finite set of places, we denote by \(G_{E, S}\) the Galois group of the maximal extension of E unramified outside \(S\infty \);
-
for a place w of a number field E, we denote by \(\varpi _{w}\) a fixed uniformiser at w, and by \(q_{w} \) the cardinality of the residue field;
-
the class field theory isomorphism is normalised by sending uniformisers to geometric Frobenii; for E a number field (respectively a local field), we will then identify characters of \(G_{E}\) with characters of \(E_{\mathbf {A}}^{\times }/E^{\times }\) (respectively \(E^{\times })\) without further comment;
-
let \(\mu \subset \mathbf {Q}_{p}^{\times }\) be the subgroup of roots of unity, and let \(\langle \cdot \rangle _{p}:\mathbf {Q}_{p}^{\times }\rightarrow 1+2p\mathbf {Z}_{p}\subset \mathbf {Q}_{p}^{\times } \) be the unique continuous character such that \(x_{p}\langle x\rangle _{p}^{-1}\) has values in \(\mu \). The p-adic cyclotomic character of \(\mathbf {Q}\) is
$$\begin{aligned} \chi _{\mathrm{cyc}, \mathbf {Q}}(x):=|x|_{\mathbf {A}^{\infty }}\langle x_{p}\rangle _{p} , \end{aligned}$$a character on \(\mathbf {A}^{\infty ,\times }/\mathbf {Q}^{\times }\). If E is a number field, the p-adic cyclotomic character of E is the character
$$\begin{aligned} \begin{aligned} \chi _{\mathrm{cyc}, E}=\chi _{\mathrm{cyc}, \mathbf {Q}} \circ N_{E/\mathbf {Q}}:E_{\mathbf {A}^{\infty }}^{\times }/E^{\times }\rightarrow \mathbf {Q}_{p}^{\times }.\end{aligned}\end{aligned}$$(1.8.1)
2 Automorphic and Galois representations
In this section we define the basic set up regarding ordinary automorphic representations for our groups, and the associated Galois representations.
2.1 Groups
We introduce our notation on groups and related objects.
2.1.1 Incoherent reductive groups
Let F be a global field. For the purposes of this discussion, a ‘coherent’ reductive group over F is just a reductive algebraic group in the usual sense. The following notion is probably appropriate only in the context of orthogonal or unitary groups, cf. [47]; we do not explicitly restrict to that case just for the sake of brevity.
An F-incoherent reductive group \(\mathrm {G}\) over F is a collection of reductive groups \(\mathrm {G}_{v}/F_{v}\), for v a place of F, such that for each place w of F there is a coherent reductive group \(\mathrm {G}(w)/F\) that is w-nearby to \(\mathrm {G}\) in the following sense: for each place \(v\ne w\), \(\mathrm {G}(w)\times _{F}F_{v}\cong \mathrm {G}_{v}\), and the groups \(\mathrm {G}(w_{})\times _{F}F_{w}\) and \(\mathrm {G}_{w} \) are non-isomorphic inner forms of each other.
Let \(F/F_{0}\) be a finite extension of global fields. An F-incoherent reductive group \(\mathrm {G}\) over \(F_{0}\) is a collection of reductive groups \(\mathrm {G}_{v_{0}}/F_{0, v_{0}}\), indexed by the places \(v_{0}\) of \(F_{0}\), satisfying the following. For each \(v_{0}\), we may write \(\mathrm {G}_{v_{0}}=\mathrm {Res}_{F_{v_{0}}/F_{0,v_{0}}}\mathrm {G}_{F, v_{0}}:=\prod _{v\vert v_{0}}\mathrm {Res}_{F_{v}/F_{0, v_{0}}} G_{F, v}\) for a collection of reductive groups \(G_{F, v}/F_{v}\) that forms an F-incoherent algebraic group \(\mathrm {G}_{F}\) over F. In this situation, we write \(\mathrm {G}=\mathrm {Res}_{F/{F_{0}}} \mathrm {G}_{F}\). We write just ‘incoherent’ when F is unimportant or understood from context. We also write \(\mathrm {G}(F_{v_{0}}):= \mathrm {G}_{v_{0}}(F_{v_{0}})\) for short.
By definition, for all but finitely many \(v_{0}\), the group \(\mathrm {G}_{v_{0}}\) is unramified. In particular, if S is a finite set of places of \(F_{0}\), it makes sense to consider the restricted tensor product \(\mathrm {G}(\mathbf {A}^{S}):= \prod '_{v_{0}\notin S}\mathrm {G}(F_{v_{0}})\).
It will be convenient to consider a p-adic variant in the case where \(F=\mathbf {Q}\) and \(\mathrm {G}_{F, \infty }\) is anisotropic modulo its centre (so that all its admissible representations are finite-dimensional). In this case we redefine, for any finite set of finite places S,
where \( \mathrm {G}_{\infty }:=\mathrm {G}_{p}(\mathbf {Q}_{p}) \) with the Zariski topology.
The main example of interest to us is the following: F is our totally real number field, \(F_{0}=\mathbf {Q}\), and \(\mathrm {G}_{F_{v}}=\mathbf {B}_{v}^{\times }\). The conditions are satisfied since, for each place w, there is a quaternion algebra B(w) over F such that \(\mathbf {B}_{v}\cong B(w)_{v}\) if and only if \(w\ne v\). Other examples are obtained as follows: if \(\mathrm {G}\) is an incoherent group and \(\mathrm {H}\) is a coherent group, the product \(\mathrm {G}\times \mathrm {H}\) (whose precise definition is left to the reader) is an incoherent group.
2.1.2 Hecke algebras
Let \({\mathrm {G}}\) be a coherent or incoherent reductive group over \(\mathbf {Q}\), A a ring.
If S is a finite set of primes of \(\mathbf {Q}\) different from p, let
be the Hecke algebras. If \(U\subset \mathrm {G}(\mathbf {A}^{\infty })\) is a compact open subgroup we let \(\mathscr {H}_{\mathrm {G},U,A}\) and \(\mathscr {H}_{G, U, A}^{S}\) be the respective subalgebras of functions that are bi-U-invariant. If S is U-spherical in the sense that \(U_{v}\) is maximal for all \(v\notin S\), we say that \( \mathscr {H}_{\mathrm {G},U}^{S}\) is a spherical Hecke algebra.
If M is an A-module with a smooth A-module action by \({{\mathscr {H}}}= \mathscr {H}_{{\mathrm {G}}}\), \(\mathscr {H}_{{\mathrm {G}}}^{S}\), \(\mathscr {H}_{{\mathrm {G}},U}\), or \(\mathscr {H}_{{\mathrm {G}},U}^{S}\), we let \(\mathscr {H}({M})\subset \mathrm {End}\,_{A}(M)\) by the image of \(\mathscr {H}\). We define the spherical Hecke algebra acting on M to be
if the limit, taken over pairs (S, U) such that S is U-spherical, stabilises. It is equipped with an involution \(\iota \) coming from the involution on \(\mathrm {G}_{*}(\mathbf {A})\).
2.1.3 Subgroups of \(\mathrm {G}_{*}\)
We restrict, for the rest of this subsection, to the groups in (1.2.1), denoted collectively by \(\mathrm {G}_{*}\). Assuming that \(\mathbf {B}_{p}\) is split, we fix an identification \(G:=\mathrm {G}(\mathbf {Q}_{p})\cong \mathrm {GL}_{2}(F_{p})\) for the rest of the paper, by which we obtain \(\mathbf {Z}_{p}\)-models \(\mathrm {G}_{*/\mathbf {Z}_{p}}\) for all of the groups \(\mathrm {G}_{*/\mathbf {Q}_{p}}\).
Let \(N_{\mathrm {G}}\subset \mathrm {G}(\mathbf {Q}_{p})\cong \mathrm {GL}_{2}(F_{p})\) be the subgroup of unipotent matrices. Let \(N_{\mathrm {H}}=\{ 1\}\subset \mathrm {H}(\mathbf {Q}_{p})\), and for \(?=\emptyset \) (respectively \(?= {}'\)), let \(N_{(\mathrm {G}\times \mathrm {H})^{?}}:=N_{\mathrm {G}}\times \{1\}\) (respectively its image in \((\mathrm {G}\times \mathrm {H})'(\mathbf {Q}_{p})\)). Finally, let \(N_{\mathrm {G}_{*},0}:= N_{\mathrm {G}_{*}}\cap \mathrm {G}_{*/\mathbf {Z}_{p}}(\mathbf {Z}_{p})\).
Let \(T_{\mathrm {G}_{*}}\subset \mathrm {G}_{*}(\mathbf {Q}_{p})\) be the maximal torus consisting of diagonal matrices when \(\mathrm {G}_{*}=\mathrm {G}\) and compatible with this choice when \(\mathrm {G}_{*}\) is any other group. Let \(T_{\mathrm {G},0}:= T_{\mathrm {G}_{*}}\cap \mathrm {G}_{*}(\mathbf {Z}_{p})\) the integral subgroup. Let \(T_{\mathrm {G}_{*}}^{+}\subset T_{\mathrm {G}_{*}}\) be the normaliser of \(N_{\mathrm {G}_{*}, 0}\) in \(T_{\mathrm {G}_{*}}\), so that \(T_{\mathrm {G}}^{+}:=\prod _{v\vert p}T_{\mathrm {G}, v}^{+}\) with
2.1.4 Involutions
We denote by \(\iota \) the involutions on \(\mathscr {H}^\mathrm{sph}_{\mathrm {G}}\) induced by \(g\mapsto g^\mathrm{T,-1}\), and on \(\mathrm {H}\) induced by \(h\mapsto h^{-1}\).
We also denote by \(\iota \) the involution of \(T_{\mathrm {G}_{*}}\) deduced by the involutions
where \(\nu \) denotes the reduced norm if \(\mathrm {G}_{*}=\mathrm {G}\), the norm \(N_{E/F}\) if \(\mathrm {G}=\mathrm {H}\). It preserves the sub-semigroups \(T_{\mathrm {G}_{*}}^{+}\).
2.1.5 Congruence subgroups
Let \(G=\mathrm {GL}_{2}(F_{p})\), \(H=E_{p}^{\times }\), \(H'=E_{p}^{\times }/F_{p}^{\times }\), \((G\times H)':=(G\times H)/F_{p}^{\times }\) where \(F_{p}^{\times }\) is identified with the centre of \(G\times H\).
For \(r\in \mathbf {N}\), define the compact subgroups \(U(\varpi _{v}^{r})\subset U^{1}_{1}(\varpi _{v}^{r})\subset \mathrm {GL}_{2}(F_{v})\) by
For each place \(v\vert p\) of F, we fix \(\epsilon _{v}\in F_{v}^{\times }\) such that \(E_{v}=F_{v}(\sqrt{\epsilon _{v}})\); for technical reasons it will be convenient to assume that \(v(\epsilon _{v})\ge 1\).
For \(\underline{r}=(r_{v})\in \mathbf {N}^{\{v\vert p\}}\), we define the compact open subgroups \(V_{F,v, r_{v}}:=1+\varpi ^{r_{v}}_{v}\mathscr {O}_{F,v}\subset F_{v}^{\times }\) and
as follows:
We also define \(V_{p, \underline{r}}':= V_{p, \underline{r}}F_{p}^{\times }/F_{p}^{\times }\subset H'\), and
to be the images of \(U_{p, \underline{r}}\times V_{p, \underline{r}}\), \(U_{p}(p^{\underline{r}})\times V_{p, \underline{r}}\) respectively.
We also denote
If \(p\mathscr {O}_{F,p}=\prod _{v}\varpi _{v}^{e_{v}}\mathscr {O}_{F,v}\), we associate to an integer r the tuple \(\underline{r}:= (e_{v}r)_{v\vert p}\). Denoting by \(U_{*}\) any of the symbols U, V, K, we then let \(U_{*,p,r}:=U_{*,p,\underline{r}}\), \(U_{*, p}(p^{r}):=U_{*,p}(p^{\underline{r}})\).
2.2 Algebraic representations
We set up some notation for algebraic representations of a (coherent or incoherent) reductive group \(\mathrm {G}\) over \(\mathbf {Q}\), then discuss in some more detail the situation for the groups of interest to us. Let L be an extension of \(\mathbf {Q}_{p}\), W a finite-dimensional irreducible algebraic (left) representation of \(\mathrm {G}\) over L. Throughout the paper, we tacitly identify left and right algebraic representations of \(\mathrm {G}\) via \(g.w=w. g^{-1}\).
2.2.1 Highest-weight character
We suppose that \(\mathrm {G}=\mathrm {G}_{*}\) is one of the groups of Sect. 2.1. Let \(T_{\mathrm {G}_{*}}\subset G_{*}\) be the fixed torus and let \(N_{\mathrm {G}_{*}}\subset G_{*}\) be the fixed unipotent subgroup. If W is an irreducible left (respectively right) representation of \(\mathrm {G}_{*}\), we denote by \(\sigma _{W}\) the character by which \(T_{\mathrm {G}_{*}}\) acts on the line of highest-weight vectors \(W^{N_{\mathrm {G}_{*}}}\) (respectively highest-weight covectors \(W_{N_{\mathrm {G}_{*}}}\)).
The highest-weight character of W is related to that of its dual by
where \({\iota }\) is the involution (2.1.1).
2.2.2 Quaternionic special case
Suppose that \(\mathrm {G}(\mathbf {A}^{\infty })\) is the group of units of a quaternion algebra \(\mathbf {B}^{\infty }\) over \(\mathbf {A}^{\infty }\). Let L be an extension of \(\mathbf {Q}_{p}\) splitting F and \(B_{p}\). A (cohomological) weight for \(\mathrm {G}\) over L is a list \(\underline{w}=(w; (w_{\sigma })_{\tau :F\hookrightarrow L})\) of \([F:\mathbf {Q}]+1\) integers of the same parity such that \(w_{\sigma }\ge 2\) for all \(\sigma :F\hookrightarrow L\). Denote by \(\mathrm{Std}_{\sigma }\cong (L^{\oplus 2})^{*}\) (respectively, \(\mathrm{Nm}_{\sigma }\cong L\)) the standard (respectively, reduced norm) representation of \({\mathrm {G}}(\mathbf {Q}_{p})=B_{p}^{\times }\) factoring through \((B_{p}\otimes _{F_{p}, \sigma } L)^{\times }\cong \mathrm {GL}_{2}(F_{p}\otimes _{\sigma } L)\). We associate to the weight \(\underline{w}\) the algebraic representation
of \(\mathrm {G}_{/\mathbf {Q}_{p}}\), whose dual is \(W_{\mathrm {G}, \underline{w}^{\vee }}\) with \(\underline{w}^{\vee }=(-w; (w_{\sigma }))\).
Suppose for a moment that \(L/\mathbf {Q}_{p}\) is Galois, then \(\mathrm {Gal}(L/\mathbf {Q}_{p})\) acts on the set of all weights \(\underline{w}\) and, letting \(L(\underline{w})\subset L\) be the fixed field of the stabiliser of \(\underline{w}\), the representation \(W_{\mathrm {G}, \underline{w}}\) descends to a representation over \(L(\underline{w})\). It is then convenient to use the following terminology: if W is an algebraic representation of \(\mathrm {G}\) over L and \(\underline{w}\) is a cohomological weight over a finite extension \(L'/L\), we say that W is of weight \(\underline{w}\) (with respect to \(L\hookrightarrow L'\)) if \(W\otimes _{L}L' \cong W_{\mathrm {G},\underline{w}}\).
Explicitly, \(W_{\mathrm {G},\underline{w}}\) may be described as the space of tuples \(p=(p_{\sigma })_{\sigma :F\hookrightarrow L}\) such that \(p_{\sigma }\in L[x_{\sigma }, y_{\sigma }]\) is a homogeneous polynomial of degree \(w_{\sigma }-2\), with action on each \(\sigma \)-component by
The representation \(W_{\mathrm {G}, \underline{w}}\) admits a natural \(\mathscr {O}_{L}\)-lattice, stable under the action of a maximal order in \(\mathrm {G}(\mathbf {Q}_{p})\),
consisting of tuples of polynomials with coefficients in \(\mathscr {O}_{L}\).
If \(W=W_{\mathrm {G}, \underline{w}}\), we have \(\sigma _{W}:=\otimes _{v}\sigma _{W,v}:T_{v}\rightarrow L^{\times }\) with
By abuse of notation we still denote by \(\sigma _{W}=\otimes \sigma _{W,v}\) the algebraic character of \(F_{p}^{\times }\) defined by
2.2.3 Toric special case
Let L be a finite extension of \(\mathbf {Q}_{p}\) splitting E. A cohomological weight for \(\mathrm {H}\) is a list \(\underline{l}:= (l, (l_{\sigma })_{\sigma :F\hookrightarrow L})\) of \([F:\mathbf {Q}]+1\) integers of the same parity. For each \(\sigma :F\hookrightarrow L\), fix an arbitrary extension \(\sigma '\) of \(\sigma \) to E (this choice will only intervene in the numerical labelling of representations of \(\mathrm {H}\)). We let
as a 1-dimensional vector space over L with action by \(\mathrm {H}(\mathbf {Q}_{p})=E_{p}^{\times }\). After choosing an identification of this space with L, it admits a lattice \(W_{\mathrm {H},\underline{l}}^{\circ }\), stable under the action of \(\mathscr {O}_{E, p}^{\times }\). IfW is an algebraic representation of \(\mathrm {H}\) over L and \(\underline{l}\) is a cohomological weight over a finite extension \(L'/L\), we say that W is of weight \(\underline{l}\) (with respect to \(L\hookrightarrow L'\)) if \(W\otimes _{L}L'\cong W_{\mathrm {H},\underline{l}}\).
2.3 Shimura varieties and local systems
We again write \(\mathrm {G}_{*}\) to denote any of the groups (1.2.1).
2.3.1 Shimura varieties
For \(\tau \) an infinite place of F, let \(\mathrm {G}_{\tau }=\mathrm {Res}_{F/\mathbf {Q}}\mathrm {G}_{F}(\tau )\) be the \(\tau \)-nearby group as in Sect. 2.1.1. Consider the Shimura datum \((\mathrm {G}_{\tau }, \{h_{\mathrm {G}, \tau }\})\), where \(h_{\mathrm {G}, \tau }:\mathrm{S}:=\mathrm {Res}_{\mathbf {C}/\mathbf {R}}{} \mathbf{G}_{m}\rightarrow \mathrm {G}_{\mathbf {R}}\) the Hodge cocharacter of [19, §0.1]. Let \(h_{\mathrm {H}}:\mathrm{S} \rightarrow \mathrm {H}_{\mathbf {R}}\) be the unique cocharacter such that \(\mathrm{e}_{\mathbf {R}}\circ h_{\mathrm {H}}=h_{\mathrm {G}}\). By products and projections we deduce Hodge cocharacters \(h_{\mathrm {G}_{*}, \tau }\), hence Shimura data \((\mathrm {G}_{*, \tau }, h_{\mathrm {G}_{*, \tau }})\), for any of the groups (1.2.1); from \(h_{\mathrm {H}, \tau }\) we also obtain an extension of \(\tau \) to an embedding \(\tau :E\hookrightarrow \mathbf {C}\). Then we obtain towers of Shimura varieties \(X_{*, \tau }/\tau E_{*}\), where the reflex field \(E_{*}:=E\) unless \(\mathrm {G}_{*}=\mathrm {G}\), in which case \(E_{*}=F\). These data descend to \(E_{*}\): there are towers
such that \(X_{*}\times _{\mathrm {Spec}\,E_{*}} \mathrm {Spec}\,\tau E_{*}=X_{*,\tau }\), see [107, § 3.1]. Throughout this paper, we will also use the notation \(\overline{X}_{*}:=X\times _{\mathrm {Spec}\,E_{*}}\mathrm {Spec}\,{\overline{E}_{*}}\).
We will use also the specific names (1.2.2) for those varieties; an explicit description of some of them is as follows:
if \(K\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{\infty })\) is the image of \(U\times V\).
2.3.2 Automorphic local systems
Let W be an irreducible cohomological right algebraic representation of \(\mathrm {G}_{*}\) over L, let \(U_{*}\subset \mathrm {G}_{*}(\mathbf {A}^{\infty })\) be a sufficiently small (in the sense of Lemma 2.3.1 below) compact open subgroup, let \(W^{\circ }\subset W \) be a \(U_{*,p}\)-stable \(\mathscr {O}_{L}\)-lattice, and let \(U_{*,p, n}\subset U_{*,p}\) be a subgroup acting trivially on \(W^{\circ }/p^{n}W^{\circ }\).
Lemma 2.3.1
If \(U^p_*\) is sufficiently small (a condition independent of n), then:
-
1.
The quotient \(\overline{\mathrm {G}}_n:=U_{*,p}/U_{*,p, n}(\mathrm{Z}_{\mathrm {G}_*}(\mathbf {Q}) \cap U_*)_p\) acts freely on \(X_{U_*^pU_{*,p,n}}\), hence \(X_{*,U_*^pU_{*,p,n}}\rightarrow X_{*, U_*}\) is an étale cover with Galois group \(\overline{\mathrm {G}}_{*,n}\).
-
2.
The group \(\mathrm{Z}_{\mathrm {G}_*}(\mathbf {Q}) \cap U_*\) acts trivially on \(W^{\circ }\).
Proof
The first assertion is [19, Lemme 1.4.1.1] when \(\mathrm {G}_*=\mathrm {G}\) (other cases are similar or easier). For the second assertion, we may reduce to the case \(\mathrm {G}_*=\mathrm {G}\) or \(\mathrm {G}_*=\mathrm {H}\), with centre \(\mathrm{Z}_{\mathrm {G}_*}=\mathrm{Res}_{E_*/\mathbf {Q}}\mathrm {G}_m\). For any \(U_*\), the group \(\mathrm{Z}_{\mathrm {G}_*}(\mathbf {Q}) \cap U_*\) has has finite index in \(\mathscr {O}_{E_*}^\times \), therefore for sufficiently small \(U_*^p\) it is contained in the finite-index subgroup \(\mathscr {O}_{F}^{\times , 1}:=\{z\in \mathscr {O}_F^\times \, :\, N_{F/\mathbf {Q}}(z)=1\}\subset \mathscr {O}_{E_*}^\times \). But since W is of cohomological weight, the group \(\mathscr {O}_{F}^{\times , 1}\) acts trivially. \(\square \)
Assume first that \(X_{*}\) is compact. Then, by the lemma,
defines a locally constant étale \(\mathscr {O}_{L}/p^{n}\mathscr {O}_{L}\)-module \(\mathscr {W}^{n}\)over \(X_{*,U_{*}}\). We let
an \(\mathscr {O}_{L}\)-local system on \(X_{*, U_{*}}\), and consider
The L-local system \(\mathscr {W}\) is compatible with pullback in the tower \(\{X_{*, U_{*}}\}\) and, up to isomorphism, independent of the choice of lattice \(W^{\circ }\). When \(X_{*}\) is the compactification of a noncompact Shimura variety \(X_{*}'\) (essentially only when \(\mathrm {G}=\mathrm {GL}_{2/\mathbf {Q}}\)), we perform the above construction on \(X'_{*}\) and then push the resulting sheaf forward to \(X_{*}\).
2.4 Ordinary automorphic representations
Keep the assumption that \(\mathrm {G}_{*}\) is one of the groups in (1.2.1).
2.4.1 p-adic automorphic representations
Let L be an extension of \(\mathbf {Q}_{p}\), W a finite-dimensional irreducible algebraic left representation of \(G_{*,\infty }=\mathrm {G}_{*}(\mathbf {Q}_{p})\) over L.
Definition 2.4.1
A (regular algebraic cuspidal) automorphic representation of \(\mathrm {G}_{*}(\mathbf {A}^{})\) over L of weight W is an irreducible admissible locally algebraic representation \(\pi \) of
that can be factored as
such that \(\mathrm {G}_{*}(\mathbf {A}^{\infty })\) acts smoothly on \(\pi ^{\infty }\), \(\mathrm {G}_{*, \infty }\) acts algebraically, and \(\pi \) occurs as a subrepresentation of
where \(X_{*}\) is the compactified Shimura variety attached to \(\mathrm {G}_{*}\), and \(\mathscr {W}^{\vee }\) is the local system on X attached to \(W^{\vee }\).
In the quaternionic or toric case, we say that \(\pi \) is of weight \(\underline{w}\) (a cohomological weight for \(\mathrm {G}\) over some finite extension \(L'/L\)) if W is of weight \(\underline{w}\) as defined after (2.2.2) (respectively (2.2.6)).Footnote 15
We will use subscripts p, respectively \(\infty \), respectively \(p\infty \), to denote an element of \(\mathrm {G}(\mathbf {A})\) in the copy of \(\mathrm {G}(\mathbf {Q}_{p})\) contained in \(\mathrm {G}(\mathbf {A}^{\infty })\), respectively in the ‘algebraic copy’ \(G_{\infty }\), respectively the diagonal copy in the product of the previous two.
Remark 2.4.2
The previous definition follows the work of Emerton [37]. It slightly departs from it in that in [37], one restricts to considering the action of the product of \(\mathrm {G}(\mathbf {A}^{p\infty })\) and the diagonal copy of \(\mathrm {G}(\mathbf {Q}_{p})\). While this is indeed the part that acts integrally, we do have use for the non-integral action of each individual copy (cf. Sect. A.2). The corresponding local notions are introduced in Definition A.1.1.
2.4.2 Quaternionic special case and ordinarity
Suppose that \(\mathrm {G}_{*} =\mathrm {G}\) and \(\mathbf {B}_{p}\) is split, or that \(\mathrm {G}_{*}=\mathrm {G}_{0}=\mathrm {Res}_{F/\mathbf {Q}}\mathrm {GL}_{2}\) for a totally real field F. An automorphic representation \(\pi \) over L of weight \(W_{\mathrm {G}_{*}, \underline{w}}\) is also said to be of weight \(\underline{w}\).
Definition 2.4.3
We say that an automorphic representation \(\pi \) of \(\mathrm {G}_{*}(\mathbf {A}^{})\) over L of classical weight \(W=W_{\mathrm {G}_{*}, \underline{w}}\) is ordinary at v with unit character \(\alpha _{v}^{\circ }\) if there exists a smooth character \(\alpha _{v}\) of \(T_{v}\) such that \(\pi _{v}\) is the unique irreducible subrepresentation of \(\mathrm{Ind}(\alpha _{v}\cdot ( |\ |_{v} , |\ |_{v}^{-1}))\) and the locally algebraic character
takes values in \( \mathscr {O}_{L}^{\times }\).Footnote 16
(It follows from the parity conditions on the weights that the indicated subrepresentation is always infinite-dimensional; moreover if \(\pi _{v}\) is ordinary then the character \(\alpha _{v}\) of \(T_{v}\) is uniquely determined by \(\pi _{v}\).) We say that \(\pi \) is ordinary if it is ordinary at all \(v\vert p\).
Let \(v\vert p \) be a prime of F and \(\varpi _{v}\) a uniformiser. For \(t\in T_{v}^{+}\) or \(x\in F_{v}^{\times }\) with \(v(x)\ge 0\), define the double coset operators
which act on the \(N_{0}\)-fixed vectors of any locally algebraic representation of \(\mathrm {GL}_{2}(F_{v})\) (see also Sect. A.1 for further details). Then \(\pi \) is ordinary at v with unit character \(\alpha _{v}^{\circ }\) if and only if, for sufficiently large r, the space of \(U_{1}^{1}(\varpi _{v}^{r})\)-fixed vectors in the locally algebraic representation
of \(\mathrm {GL}_{2}(F_{v})\) contains a (necessarily unique) line of eigenvectors for the diagonal action of the operators \(\mathrm {U}_{x}\), \(x\in F_{v}^{\times }\), with eigenvalue \(\alpha ^{\circ }(x)\). Specifically, if \(w_{v}\in \pi _{v}\) is a \(\mathrm {U}_{x}\)-eigenvector of eigenvalue \(\alpha _{v}(\varpi _{v})\), then such line is
where \(W^{N_{v}}\) is the line of highest-weight vectors of W.
If \(\pi \) is an automorphic representation that is ordinary at all \(v\vert p\), extend \(\alpha _{v}^{\circ }\) to a character of \(T_{v}^{+}\) by the formula (2.4.1), and let \(\alpha ^{\circ }=\prod _{v\vert p}\alpha _{v}^{\circ }:T^{+}=\prod T_{v}^{+}\rightarrow L^{\times }\); then we define
as a smooth representation of \(\mathrm {G}(\mathbf {A}^{p\infty })\) and a locally algebraic representation of \(T^{+}\) on which \( T^{+}\) acts by \(\mathrm {U}_{t}\mapsto \alpha _{v}^{\circ }(t)\).
2.4.3 Toric special case
Suppose now that E is a CM field and that \(\mathrm {G}_{*}=\mathrm {H}:=\mathrm{Res}_{E/\mathbf {Q}}\mathrm {G}_{m}\). Then a p-adic automorphic representation of \(\mathrm {H}\) of weight \(W_{\mathrm {H}, \underline{l}}\) is simply the space of scalar multiples of a locally algebraic character \(\chi :E^{\times }\backslash E_{\mathbf {A}^{\infty }}^{\times }\rightarrow L^{\times }\) whose restriction to a sufficiently small open subgroup of \(E_{p}^{\times }\) coincides with the character of \(W_{\mathrm {H}, \underline{l}}\).
2.4.4 Convention
We use the convention that all automorphic representations of \(\mathrm {H}(\mathbf {A}^{\infty })\) are ordinary, and that a representation \(\pi \otimes \chi \) of \(\mathrm {G}\times \mathrm {H}\) of cohomological weight is cuspidal and ordinary if \(\pi \) and \(\chi \) are.
2.5 Galois representations
Let \(\mathrm {G}\) be as in Sect. 2.4.2.
2.5.1 Galois representations attached to automorphic representations of \(\mathrm {G}(\mathbf {A}^{})\)
The following notation is used throughout the paper: if V is a representation of \(G_{F}\) and v is a prime of F, we denote by \(V_{v}\) the restriction of V to a decomposition group at v.
Theorem 2.5.1
(Ohta, Carayol, Saito). Let L be a finite extension of \(\mathbf {Q}_{p}\), let W be an irreducible algebraic representation of \(\mathrm {G}\) over L, and let \(\pi \) be an automorphic representation of \(\mathrm {G}(\mathbf {A}^{\infty })\) of weight W over L. Let S be a finite set of non-archimedean places of F containing all the places at which \(\pi \) is ramified and the places above p. There exists a 2-dimensional L-vector space \(V_{\pi }\) and an absolutely irreducible Galois representation
uniquely determined by the property that for every finite place \(v\notin S\) of F,
where \(\mathrm{Fr}_{v}\) is a geometric Frobenius, \(T_{v}\in \mathscr {H}^\mathrm{sph}_{\mathrm {GL}_{2}(F_{v})}\) is the element corresponding to the double class \(K_{0}(1)\left( {\begin{matrix}\varpi _{v}&{}\\ &{}1\end{matrix}}\right) K_{0}(1)\), and \(\lambda _{\pi _{v}}:\mathscr {H}_{\mathrm {GL}_{2}(F_{v})}^\mathrm{sph}\rightarrow L\) is the character giving the action on \(\pi _{v}^{K_{0}(1)}\).
For a prime v of F, let \(\rho _{v}\) be the restriction of \(\rho \) to a decomposition group at v.
-
1.
The representation \(\rho _{v}\) is unramified for almost all v and potentially semistable for \(v\vert p\). For every finite place v, the Weil–Deligne representation \(r_{v}\) attached to \(\rho _{v}\) is associated with \(\pi _{v}\) via the local Langlands correspondence normalised “à la Hecke” [29, § 3.2]:
$$\begin{aligned} L(s, r_{{v}})=L(s+1/2, \pi _{v}). \end{aligned}$$ -
2.
For every finite place v, \(r_{v}\) satisfies the weight-monodromy conjecture: its monodromy filtration is pure of weight \(w-1\). The monodromy filtration is trivial if and only if \(\pi _{v}\) is not a special representation.
-
3.
For any archimedean place v, the representation \(\rho _{v}\) is odd, that is if \(c_{v}\in G_{F_{v}}\) is the complex conjugation, \(\det \rho _{v}(c_{v})=-1\).
-
4.
If \(W=W_{\mathrm {G}, \underline{w}}\) with \(\underline{w}=(w; (w_{\sigma })_{\sigma :F\hookrightarrow \overline{L}})\), then for each \(v\vert p\) and \(\sigma :F_{v}\hookrightarrow \overline{L}\),
-
the \(\sigma \)-Hodge–Tate weightsFootnote 17 of \(\rho _{v}\otimes _{L }\overline{L}\) are
$$\begin{aligned} -1-{w+w_{\sigma }-2\over 2}, \quad -{w-w_{\sigma }+2\over 2}. \end{aligned}$$ -
if \(\pi \) is ordinary at v in the sense of Definition 2.4.3, then there is a unique exact sequence in the category of \(G_{F,v}\)-representations
$$\begin{aligned} 0\rightarrow V^{+}_{\pi , v} \rightarrow V_{\pi , v} \rightarrow V_{\pi ,v}^{-} \rightarrow 0, \end{aligned}$$(2.5.2)such that \(V^{\pm }_{\pi , v}\) is 1-dimensional. The Galois group \(G_{F, v}\) acts on \(V^{+}_{\pi ,v}\) by the character
$$\begin{aligned} \alpha _{\pi ,v}^{\circ }\chi _{\mathrm{cyc},v}:F_{v}^{\times }\rightarrow L^{\times }, \end{aligned}$$where \(\alpha _{\pi ,v}^{\circ }\) is (2.4.1).
-
Proof
The construction and statements 1 and 2 for \(v\vert p\) are the main results of Carayol in [19]. Statements 1 and 2 for \(v\vert p \) were proved by Saito [91, Theorems 2.2, 2.4]. For the last two statements, we refer to [101, Proposition 6.7] and references therein; note that in comparison with the notation of [101], our \(\rho \) equals their \(\rho _{f}(1)\), and our \((w; \underline{w})\) is their \((w-2, {{\underline{k}}})\). \(\square \)
2.5.2 Realisation in the homology of Shimura varieties
Let \(\mathrm {G}_{*}\) be again one of the groups of (1.2.1). We introduce a new piece of notation. Let
and similarly for a finite set of places S, \(G_{F, E, S}:=G_{F, S}\times G_{E,S}\). If \(\mathrm {G}_{*}=\mathrm {G}\times \mathrm {H}\) or \((\mathrm {G}\times \mathrm {H})'\), we redefine
(This is an abuse of notation, as we have not redefined \(E_{*}\).) This product of Galois groups acts on the homology \(\overline{X}_{*}\): this is clear by the Künneth formula in the case of \(\mathrm {G}\times \mathrm {H}\), and follows from that case and the Galois-invariance of the quotient map for \((\mathrm {G}\times \mathrm {H})'\).
The following is the main result of [20] in the special case \(\mathrm {G}_{*}=\mathrm {G}\); the general case may be deduced from the special case together with the case \(\mathrm {G}_{*}=\mathrm {H}\) (that is class field theory).
Proposition 2.5.2
(Carayol). Let \(U_{*}\subset \mathrm {G}_{*}(\mathbf {A}^{\infty })\) be a compact open subgroup, W be an irreducible right algebraic representation of \( \mathrm {G}_{*}\) over L, \(\mathscr {W}\) the local system on \(X_{*, U_{*}}\) associated with W. Let \(L'\) be a sufficiently large finite Galois extension of L.
Then there is an isomorphism of \(\mathscr {H}_{\mathrm {G}_{*}, U_{*}, L}[G_{E_{*},S}]\)-modules
equivariant for the action of \(\mathrm {Gal}(L'/L)\), where \(\pi \) runs through all equivalence classes of automorphic representations of \(\mathrm {G}_{*}(\mathbf {A})\) of weight W over \(L'\).
3 Sheaves on Hida families
We construct the universal Hecke- and Galois- modules over Hida families for \((\mathrm {G}\times \mathrm {H})'\) and prove a local-global compatibility result. We claim no originality for the results of Sects. 3.1–3.2.1.
3.1 Hida theory
We let \(\mathrm {G}_{*}\) denote any of the groups \(\mathrm {G}\), \(\mathrm {H}\), \((\mathrm {G}\times \mathrm {H})\), \((\mathrm {G}\times \mathrm {H})'\), and let \(r\in \mathbf {N}^{\{v\vert p\}}\). We will use the notation from Sect. 2.1. For \(U_{*}^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })\) we let \(X_{*, U_{*}^{p},r}:=X_{*, U_{*}^{p}U_{*,r}}\) be the corresponding Shimura variety.
When M is a \(\mathbf {Z}_{p}\)-module with action by \(T_{\mathrm {G}_{*}}^{+}\), arising as limit of ordinary parts of p-adic coadmissible \(\mathrm {G}_{*}(\mathbf {Q}_{p})\times G_{*, \infty }\)-modules (see Definition A.1.2 and Sect. A.1.3), we denote this action by
and adopt the notation of (2.4.2).
3.1.1 Weight spaces
Let \(U_{*}^{p}\subset \mathrm {G}_{*}(\mathbf {A}^{p\infty })\) be a compact open subgroup, and define \(Z_{\mathrm {G}_{*}, U^{p}_{*}} \subset \mathrm{Z}_{\mathrm {G}}(\mathbf {Q})\) by
In all cases, let \(\overline{T}_{\mathrm {G}_{*},U_{*}^{p},0}:=T_{\mathrm {G},0}/\overline{Z_{\mathrm {G}_{*}, U_{*}}}\), where \(\overline{\Box }\) denotes the closure for the p-adic topology, and let \( \overline{T}_{\mathrm {G}_{*}, U^{p}_{*}, r}\subset \overline{T}_{\mathrm {G}, U^{p}_{*},0}\) be the image of \(T_{\mathrm {G}_{*},U^{p}_{*},r}\). Let
and for an irreducible algebraic representation W of \(\mathrm {G}_{*}\) consider the ideals
For each fixed W and varying r, the ideals \(I_{\mathrm {G}_{*},U^{p}_{*}, W, r}\) form a fundamental system of neighbourhoods of zero in \(\Lambda ^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\otimes \mathscr {O}_{L}\), so that
with
where the isomorphism is given by \([t]\mapsto \sigma _{W}^{-1}(t)[\overline{t}]\). When \(W=\mathbf {Q}_{p}\), we omit W from the notation. We also omit the subscript \(U^{p}_{*}\) when it is unimportant or understood from context.
Writing \(\overline{T}_{\mathrm {G}_{*},U^{p}_{*},0}\cong \Delta \times \mathbf {Z}_{p}^{\mathrm{d}(\mathrm {G}_{*})}\) for a finite torsion group \(\Delta \), we have an isomorphism \(\Lambda _{\mathrm {G}_{*}, U^{p}_{*}}\cong \mathbf {Z}_{p}[\Delta ]\otimes \mathbf {Z}_{p}\llbracket X_{1}, \ldots X_{\mathrm{d}(\mathrm {G}_{*})}\rrbracket \) for an integer \({\mathrm{d}(\mathrm {G}_{*})}\) given byFootnote 18
where \(\delta =\delta _{F, p}\) is the Leopoldt defect of F at p; see [41, § 2.2.3.3] for \(\mathrm{d}(\mathrm {G})\).
Definition 3.1.1
The weight space is
Let W be an irreducible cohomological algebraic representation of \(\mathrm {G}_{*}\). The zero-dimensional subscheme of classical points of weight W and level r is
The ind-subschemes of all classical points of weight W and of of all classical points are respectively
where as usual the union runs through the algebraic representations of cohomological weight.
3.1.2 Ordinary completed homology
Let W be an irreducible right algebraic representation of \(\mathrm {G}_{*}(\mathbf {Q}_{p})\) over L, and fix a \(\mathrm {G}(\mathbf {Z}_{p})\)-stable \(\mathscr {O}_{L}\)-lattice \(W^{\circ }\subset W\). Let \(\mathscr {W}\) be the local system attached to W, and for \(U_{*}^{p}\subset \mathrm {G}_{*}(\mathbf {A}^{p\infty })\), \(r\ge 0\) consider the ordinary parts
with respect to the action of \(T_{\mathrm {G}_{*}}^{+}\) by \(\mathrm {U}_{t}\otimes t\), as defined in Sect. A.1.3. The ordinary completed homology of \(X_{\mathrm {G}_{*}, U^{p}_{*}}\) is
an \(\mathscr {O}_{L}\)-module. It depends on the choice of lattice \(W^{\circ }\subset W\), whereas the L-vector space
does not. When \(\mathscr {W}={\mathbf {Q}_{p}}\) is the trivial local system, we omit it from the notation, thus
3.1.3 Independence of weight and Control Theorem
For a \(\mathbf {Z}_{p}\)-algebra A, let \(\mathscr {H}_{\mathrm {G}_{*}, U^{p}_{*}, p, A}^{\mathrm {ord}}:= A[T_{\mathrm {G}_{*}}]\otimes _{\mathbf {Z}_{p}[T^{+}_{\mathrm {G}_{*},0}]}\Lambda ^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\). For \(?= S,\emptyset , \mathrm{sph}\), consider the \(\Lambda _{\mathrm {G}_{*}, U^{p}_{*},A}\)-algebra
For every irreducible algebraic representation W over L and \(\mathscr {O}_{L}\)-algebra A, the space \(M^{\circ }_{\mathrm {G}_{*}, U_{*}^{p}, W}\otimes A\) is a module over \(\mathscr {H}^{\mathrm {ord}}_{\mathrm {G}_{*}, U^{p}_{*},A}\), where \([t]\in A[T_{\mathrm {G}_{*}}^{+}]\) acts by the double coset operator \(\mathrm {U}_{t}\).
The base ring A will be omitted from the notation when it can be understood from the context.
Let \(U_{*, r}=U^{p}_{*}U_{*, r, p}\) be as in Sect. 2.1 and let \(X_{*, r}:=X_{*, U_{*,r}}\).
Proposition 3.1.2
Let W be an irreducible right algebraic representation of \(\mathrm {G}_{*/\mathbf {Q}_{p}}\) over L, \(\mathscr {W}\) the corresponding local system. Then:
-
1.
If \(\mathrm {G}_{*}=\mathrm {G}\), \(\mathrm {H}\), then \(M_{\mathrm {G}_{*}, U_{*}^{p},W}^{\circ }\) is a projective \(\Lambda ^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\otimes \mathscr {O}_{L}\)-module of finite type. For all of the groups \(\mathrm {G}_{*}\), the \(\Lambda ^{\circ }_{(\mathrm {G}\times \mathrm {H})'}\otimes \mathscr {O}_{L}\)-module \(M_{(\mathrm {G}\times \mathrm {H})',K^{p}, W}^{\circ }\) is of finite type, and \(M_{(\mathrm {G}\times \mathrm {H})',K^{p},W}\) is a projective \(\Lambda _{(\mathrm {G}\times \mathrm {H})'}\otimes L\)-module of finite type.
-
2.
We have natural \(\mathscr {H}_{\mathrm {G}_{*}, U^{p}_{*}}^{\mathrm {ord}}\)-equivariant isomorphisms
$$\begin{aligned} j_{W}:M_{\mathrm {G}_{*}, U_{*}^{p}}\otimes \mathscr {O}_{L}\cong M_{\mathrm {G}_{*}, U_{*}^{p},W}. \end{aligned}$$(3.1.5) -
3.
Consider
$$\begin{aligned} M_{\mathrm {G}_{*}, U^{p}_{*}, W,r}:= M_{\mathrm {G}_{*}, U^{p}_{*}}\otimes _{\Lambda _{\mathrm {G}_{*}, U^{p}_{*}}}\Lambda _{\mathrm {G}_{*}, U^{p}_{*}, W, r}. \end{aligned}$$(3.1.6)There is a natural \(\mathscr {H}_{\mathrm {G}_{*}, U^{p}_{*}}^{\mathrm {ord}}\)-equivariant isomorphism
$$\begin{aligned} M_{\mathrm {G}_{*}, U_{*}, W, r} \cong \mathrm {H}_{d}(\overline{X}_{*, r}, \mathscr {W})^{\mathrm {ord}}. \end{aligned}$$
Proof
We first treat part 1 when \(W=\mathbf {Q}_{p}\). Then we will deal with part 2, which implies that part 1 holds for any W.
If \(\mathrm {G}_{*}=\mathrm {G}\), the result is proved in [55, Thoerem 1.2, cf. also Remark 1.1]. If \(\mathrm {G}_{*}=\mathrm {H}\), \(U^{p}_{*}=V^{p}\), then the module under consideration is isomorphic to \(\mathbf {Z}_{p} \llbracket E^{\times }\backslash E_{\mathbf {A}^{\infty }}^{\times }/V^{p}\rrbracket \), which is finite free over \(\Lambda ^{\circ }_{\mathrm {H},V^{p}}=\mathbf {Z}_{p}\llbracket \overline{\mathscr {O}_{E}^{\times }\cap V^{p}}\backslash \mathscr {O}_{E, p}^{\times } \rrbracket \) as \( \overline{\mathscr {O}_{E}^{\times }\cap V^{p}}\backslash \mathscr {O}_{E, p}^{\times }\subset E^{\times }\backslash E_{\mathbf {A}^{\infty }}^{\times }/V^{p}\) is a subgroup of finite index.
If \(\mathrm {G}_{*}=\mathrm {G}\times \mathrm {H}\), by the Künneth formula we have \(M^{\circ }_{\mathrm {G}\times \mathrm {H}, U^{p}\times V^{p}}= M^{\circ }_{\mathrm {G}, U^{p}}\hat{\otimes } M^{\circ }_{\mathrm {H}, V^{p}}\), which by the previous results is a finite type projective module over \(\Lambda ^{\circ }_{\mathrm {G}\times \mathrm {H}} = \Lambda ^{\circ }_{\mathrm {G}}\hat{\otimes } \Lambda ^{\circ }_{\mathrm {H}}\). Finally, if \(\mathrm {G}_{*}=(\mathrm {G}\times \mathrm {H})'\) and \(K^{p}\) is the image of \(U^{p}\times V^{p}\), by the description of \(Z_{K}\) in (2.3.1) we have
As \(M^{\circ }_{\mathrm {G}\times \mathrm {H}, U^{p}\times V^{p}}\) is a projective \(\Lambda ^{\circ }_{\mathrm {G}\times \mathrm {H}, U^{p}\times V^{p}}\)-module of finite type, the quotient \(M^{\circ }_{\mathrm {G}, \times \mathrm {H}, U^{p}\times V^{p}}/{F, p}^{\times } = M_{\mathrm {G}, \times \mathrm {H}, U^{p}N_{\mathrm {G},{0}}\times V^{p}} \otimes _{\Lambda ^{\circ }_{\mathrm {G}\times \mathrm {H}}}\Lambda ^{\circ }_{(\mathrm {G}\times \mathrm {H})'}\) is a projective \(\Lambda ^{\circ }_{(\mathrm {G}\times \mathrm {H})', K^{p}}\)-module of finite type, and \(M^{\circ }_{(\mathrm {G}\times \mathrm {H})',K^{p}}\) is its quotient by the free action of the finite group \(F_{\mathbf {A}^{\infty }}^{\times }/ F^{\times }\cdot F_{p}^{\times }((U^{p}\cap F_{\mathbf {A}^{p\infty }}^{\times }) \cap (V^{p}\cap F_{\mathbf {A}^{p\infty }}^{\times }))).\) After inverting p, the quotient map admits a section, hence \(M_{(\mathrm {G}\times \mathrm {H})',K^{p}}\) is projective over \(\Lambda _{(\mathrm {G}\times \mathrm {H})'}\).
We now turn to part 2. As above it suffices to prove the result when \(\mathrm {G}_{*}=\mathrm {G}, \mathrm {H}\). Let \(\mathrm {G}_{*}=\mathrm {G}\), and suppose that \(W=W_{\mathrm {G}, \underline{w}}^{*}\). Let \(W^{\circ }\subset W\) be the lattice of (2.2.4), \(r\ge 1\). We have a \(\Lambda _{r}\)-linear map
induced by cap productFootnote 19 via the isomorphism of \(\Lambda _{r}\)-modules \(H^{0}(\overline{X}_{r}, \mathscr {W}^{\circ }/ p^{r} \mathscr {W}^{\circ })\cong W^{\circ ,N_{0}}/p^{r}\).
The maps (3.1.8) are compatible with variation in r, and taking limits we obtain the map (3.1.5), which Hida [49, § 8], [55, Theorem 2.4] proved to be an isomorphism; the asserted equivariance properties are clear from the construction.
When \(\mathrm {G}_{*}=\mathrm {H}\) the construction is similar but easier, as each W is 1-dimensional and each of the analogous maps \(j_{W,r}\) is an isomorphism.
Finally, we address part 3. As above we may reduce to the case \(W=\mathbf {Q}_{p}\) and \(\mathrm {G}_{*}=\mathrm {H}\) or \(\mathrm {G}_{*}=\mathrm {G}\). The former is clear, and the latter is, in view of part 2, equivalent to the statement
which is the control theorem of [55, Theorem 1.2 (3)]. \(\square \)
3.1.4 Ordinary eigenvarieties
The space \(M^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\) has the structure of an \(\mathscr {H}_{\mathrm {G}_{*}, U^{p}_{*}}^{ \mathrm {ord}}\)-module (in particular of \(\Lambda ^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\)-module), and for \(?=\emptyset , \mathrm{sph}\) and A a \(\mathbf {Z}_{p}\)-algebra, we let
be the image of \(\mathscr {H}_{\mathrm {G}_{*}, U^{p}_{*}, A}^{\mathrm{?}, \mathrm {ord}}\) in \(\mathrm {End}\,_{A}(M^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\otimes A)\), that is independent of the particular spherical Hecke algebra chosen when \(?=\mathrm{sph}\). When \(A=\mathbf {Z}_{p}\) we omit it from the notation.
We may now define
When \(\mathrm {G}_{*}=\mathrm {H}\), we will omit the superscript ‘\({\mathrm {ord}}\)’.
Let
Referring to Definition 3.1.1, the zero-dimensional (ind)-subscheme of classical points (respectively classical points of weight W, for an algebraic representation W of \(\mathrm {G}_{*}\), respectively classical points of weight W and level r) is
We denote by
the sheaf on \( \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}_{*}, U_{*}^{p}}\) corresponding to \(M_{\mathrm {G}_{*}, U^{p}_{*}}\).
Notation
When \(\mathrm {G}_{*}= (\mathrm {G}\times \mathrm {H})'\), we omit the subscripts, thus e.g. for \(K^{p}\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\) we write
By (3.1.7), \(\mathbf{T}_{K^{p}}^{\mathrm{sph}, \mathrm {ord}}\) is a quotient of \(\mathbf{T}_{\mathrm {G}\times \mathrm {H}, U^{p}\times V^{p}}^{\mathrm{sph}, \mathrm {ord}}\) and correspondingly we have a closed immersion
Proposition 3.1.3
The ring \( \mathbf{T}_{\mathrm {G}_{*}, U^{p}_{*} }^{\mathrm{sph}, \mathrm {ord}}\) is finite flat over \(\Lambda ^{\circ }_{\mathrm {G}_{*}, U^{p}_{*}}\), hence semi-local. The maximal ideals of \( \mathbf{T}_{\mathrm {G}_{*}, U^{p}}^{\mathrm{sph}, \mathrm {ord}} \) are in bijection with \(G_{\mathbf{F}_{p}}\)-orbits of characters \(\overline{\lambda }:\mathbf{T}_{\mathrm {G}_{*}, U^{p}_{*}}^{\mathrm{sph}, \mathrm {ord}}\rightarrow \overline{\mathbf{F}}_{p}\).
Proof
The first statement is easy for the group \(\mathrm {H}\) and it is proved in [55] for the group \(\mathrm {G}\). Together they imply the statement for \(\mathrm {G}\times \mathrm {H}\) and hence \((\mathrm {G}\times \mathrm {H})'\). As \( \mathbf{T}_{\mathrm {G}_{*}, U^{p}}^{\mathrm{sph}, \mathrm {ord}} \) is topologically finitely generated over \(\mathbf {Z}_{p}\), the residue fields of its maximal ideals are finite extensions of \(\mathbf{F}_{p}\); this implies the second statement. \(\square \)
Lemma 3.1.4
Let W be an irreducible algebraic representation of \(\mathrm {G}_{*}\). The set \(\mathscr {E}^{\mathrm {ord}, \mathrm {cl}, W}_{\mathrm {G}*, U_{*}}\) of classical points of weight W is Zariski-dense in \(\mathscr {E}^{\mathrm {ord}}_{G_{*}, U_{*}^{p}}\).
Proof
By the previous proposition, the map \(\kappa _{\mathrm {G}_{*}}\) is finite hence closed. Then the Zariski-density of \(\mathscr {E}^{\mathrm {ord}, \mathrm {cl}, W}_{\mathrm {G}*, U_{*}}=\kappa _{\mathrm {G}_{*}}^{-1} ( \mathfrak {W}_{\mathrm {G}_{*}, U^{p}_{*}}^{W})\) reduces to the Zariski-density of \(\mathfrak {W}_{\mathrm {G}_{*}, U^{p}_{*}}^{W} \subset \mathfrak {W}_{\mathrm {G}_{*}, U^{p}_{*}}\), which follows from (3.1.2); cf. aso [97, Lemma 3.8]. \(\square \)
3.1.5 Abelian case
The structure of the eigenvariety for the abelian groups \(\mathrm {H}:=\mathrm{Res}_{E/\mathbf {Q}}\mathrm {G}_{m}\) and \(\mathrm{Z}=\mathrm{Res}_{F/\mathbf {Q}}\mathrm {G}_{m}\) is very simple, and we make it explicit for the group \(\mathrm {H}\): we have
the set \( Y_{V^{p}}(\overline{E})\) is a principal homogeneous space for \( \Gamma _{E,V^{p}}:=\mathrm {H}(\mathbf {Q})\backslash \mathrm {H}(\mathbf {A}^{\infty })/ V^{p}= E^{\times }\backslash E_{\mathbf {A}^{\infty }}^{\times }/V^{p}\), and
(We omit the superscript ‘\(\mathrm {ord}\)’ which is meaningless here.) The classical points \(\mathscr {E}_{\mathrm {H}, V^{p}}^{\mathrm {cl}}\subset \mathscr {E}_{\mathrm {H}, V^{p}}(\overline{\mathbf {Q}}_{p})\) parametrise locally algebraic characters of \(\Gamma _{E, V^{p}}\). Finally, the sheaf \(\mathscr {M}_{\mathrm {H}, V^{p}}\) is a trivial line bundle, with actions by \(G_{E}\) given by the universal character
and by \(\mathrm {H}(\mathbf {A}^{\infty })\) given by the inverse \(\chi _{\mathrm {H}, \mathrm univ}^{-1}\) of the corresponding automorphic character. We may formally write
as a tensor product of two trivial sheaves, the first one endowed with the \(\mathrm {H}(\mathbf {A}^{})\)-action only, and the second one with the Galois action by \( \chi _\mathrm{univ}\) only.
3.1.6 Fibres of the sheaves \(\mathscr {M}\)
Let
be the tautological character, and define
Proposition 3.1.5
Let \(x\in \mathscr {E}^{\mathrm {ord}, \mathrm {cl},W}_{\mathrm {G}, U^{p}}\) be a classical point of weight W and level r.
Then:
-
1.
Let \(U:=U^{p}U_{p,r}\), and let \(\mathscr {W}\) be the local system on X associated with W. We have an isomorphism of \(\mathscr {H}^{\mathrm {ord}}_{\mathrm {G}, U^{p}, \mathbf {Q}_{p}(x)}\)-modules
$$\begin{aligned} (\mathscr {M}_{\mathrm {G}, U^{p}})_{x}\cong \mathrm {H}_{1}(X_{U, \overline{F}}, \mathscr {W}_{\mathrm {G}, \underline{w}})^{\mathrm {ord}}\otimes _{\mathscr {H}^\mathrm{sph}_{\mathrm {G}, U^{p}}, \lambda _{x}} \mathbf {Q}_{p}(x). \end{aligned}$$ -
2.
There exists a unique automorphic representation \({\pi }_{x}\) of \(\mathrm {G}(\mathbf {A}^{})\) over \({\mathbf {Q}}_{p}(x)\) of spherical character \(\lambda _{x}^{p}\), weight W, and unit character \(\alpha _{x}^{\circ }\). It satisfies the property
$$\begin{aligned} \pi _{x}^{ {\mathrm {ord},U^{p}}} \cong \mathrm {Hom}\,_{\mathbf {Q}_{p}(x)[G_{F, S}]}((\mathscr {M}_{\mathrm {G}, U^{p}})_{x} , \rho _{x}) \end{aligned}$$(3.1.13)as left \(\mathscr {H}^{\mathrm {ord}}_{\mathrm {G}, U}\otimes \mathbf {Q}_{p}(x)\)-modules.
Proof
Part 1 follows from Proposition 3.1.2.3.
For part 2, fix an embedding \(\mathbf {Q}_{p}(x)\hookrightarrow \overline{\mathbf {Q}}_{p}\). By strong multiplicity-one, a representation \(\overline{\pi }\) over \(\overline{\mathbf {Q}}_{p}\) with character \(\lambda _{x}^{p}\) is unique if it exists. By comparing part 1 with (2.5.3), we find that \(\overline{\pi }\) exists and that for such \(\overline{\pi }\) property (3.1.13) holds after base-change to \(\overline{\mathbf {Q}}_{p}\). Let \(V_{\overline{\pi }}\) be the Galois representation associated with \(\pi \) by Theorem 2.5.1, then by looking at Frobenius traces, we see that \(V_{\overline{\pi }}\) has a model \(V_{\pi }\) over \(\mathbf {Q}_{p}(x)\). It follows again from (2.5.3) that \(\pi :=\lim _{U'}\mathrm {Hom}\,(H_{1}(\overline{X}_{U}, \mathscr {W}), V_{\pi }) \) is a model of \(\overline{\pi }\) that satisfies (3.1.13). \(\square \)
In the rest of the paper, we will use without further comment the notation \(\pi _{x}^{}\) for the representation of \(\mathrm {G}(\mathbf {A}^{})\) defined above, for \(x\in \mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {ord},\mathrm {cl}}\).
Corollary 3.1.6
Let \(z\in \mathscr {E}_{K^{p}}^{\mathrm {ord}, \mathrm {cl}}\) be a classical point, and write \(z=(x,y)\) via (3.1.9) and \(L:=\mathbf {Q}_{p}(z)\). Let \(\omega _{x}\) be the central character of \(\pi _{x}\), let \(\chi _{\mathrm {H},y}\) be the character of \(\mathrm {H}(\mathbf {A}^{\infty })\) obtained by specialising \(\chi _{\mathrm {H}, \mathrm univ}\), and let \(\chi _{y}\) be the corresponding locally algebraic character of \(G_{E,S}\). Write \(L:=\mathbf {Q}_{p}(z)\). Then \(\omega _{z}:=\chi _{y|F_{\mathbf {A}^{\infty , \times }}}\omega _{x} = \mathbf {1}\), and
as \(\mathscr {H}^{K_{S}}_{S, L}\otimes _{L} L[G_{E,S}]\)-modules. Here, \(G_{E, S}\) acts trivially on the first two tensor factors, and the natural action of \(\mathscr {H}_{\mathrm {G}\times \mathrm {H}}^{U_{S}\times V_{S}}\) on the first two factors is extended trivially to the whole tensor product, and it factors to an action of \(\mathscr {H}^{K_{S}}_{S}\).
Proof
Let \(\lambda _{x, F}^{p}\) and \(\lambda _{y, F}^{p}\) be the restrictions of the characters \(\lambda _{x}\), \(\lambda _{y}\) to \(\mathbf {Z}[F^{\times }_{\mathbf {A}^{Sp\infty , \times }}/K_{F}^{Sp}]\), and let \(\lambda _{F}\) be the restriction of \(\lambda _{F,x}\lambda _{F,y}\) to \(\Delta '=F^{\times }_{\mathbf {A}^{Sp\infty , \times }}/K_{F}^{Sp}\). As this groups acts trivially on \(M_{K^{p}}\) by (3.1.7), we have \(\lambda _{F}=\mathbf {1}\). On the other hand \(\lambda _{F}\) equals the restriction of \(\omega _{z}\) to \(\Delta '\). We deduce that \(\omega _{z}\) factors through \(C=F^{\times }_{\mathbf {A}^{\infty }}/F^{\times }F_{\mathbf {A}^{Sp\infty }}K_{F, S}K_{F,p}\) for some open compact \(K_{F,p}\subset F_{p}^{\times }\). By weak approximation, \(C=\{1\}\), therefore \(\omega _{z}=\mathbf {1}\).
By Proposition 3.1.5, (3.1.11), and (3.1.7), the asserted result holds provided we quotient the right-hand side by the action of \(F_{\mathbf {A}^{\infty }}^{\times }\), however this group acts by \(\omega _{z}\), hence trivially. \(\square \)
Proposition 3.1.7
The natural map \(\kappa :\mathscr {E}^{\mathrm {ord}}_{K^{p}} \rightarrow \mathfrak {W}_{K^{p}}\) is étale over a neighbourhood of the classical points in \(\mathfrak {W}^{\mathrm {cl}}_{K^{p}}\). In particular, the space \(\mathscr {E}^{\mathrm {ord}}_{K^{p}}\) is regular at all \(z\in \mathscr {E}^{\mathrm {ord}, \mathrm {cl}}_{K^{p}}\).
Proof
As \(\kappa \) is finite flat by Proposition 3.1.3, it suffices to check that the fibre of \(\kappa \) over any \(x\in \mathfrak {W}^{\mathrm {cl}}_{K^{p}}(\overline{\mathbf {Q}}_{p})\) is isomorphic to \(\overline{\mathbf {Q}}_{p}^{m}\) for some m. By 3.1.2, 3.1.6 and (2.5.3), this fibre is the spectrum of the image \(A_{x}\) of \(\mathscr {H}_{K^{p}}^{\mathrm{sph}, \mathrm {ord}}\) in \(\bigoplus _{z\in \kappa ^{-1}(x)} (\Pi _{z}^{K^{p}, \mathrm {ord}})^{\oplus 2}\), where the \(\Pi _{z}\) form a list of distinct irreducible representations of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\) over \(\overline{\mathbf {Q}}_{p}\). By strong multiplicity-one, we have \(A_{x}\cong \oplus _{z}\overline{\mathbf {Q}}_{p}\). This proves étaleness. As \(\mathfrak {W}_{K^{p}}\) is regular, we deuce that so is \(\mathscr {E}_{K^{p}}^{\mathrm {ord}}\) in a neighbourhood of classical points. \(\square \)
3.2 Galois representations in families
We recall the existence of a universal family of Galois representations over \(\mathscr {X}\).
3.2.1 Representations associated with irreducible pseudocharacters
Recall that an n-dimensional pseudocharacterof G over a scheme \(\mathscr {X}\) is a function \(T:G\rightarrow \mathscr {O}(\mathscr {X})\) that ‘looks like’ the trace of an n-dimensional representation of G over \(\mathscr {O}(\mathscr {X})\), see [88] for the precise definition. A pseudocharacter T is said to be (absolutely) irreducible at a point \(x\in \mathscr {X}\) if, for any (equivalently, all) geometric point \(\overline{x}\) of \(\mathscr {X}\) with image x, the pullback \(\overline{x}^{*}T\) is not the sum of two pseudocharacters of dimensions k, \(n-k\) with \(0< k<n\). The irreducibility locus of T is the set of points of \(\mathscr {X}\) at which T is irreducible; it is open [24, § 7.2.3].
We start by proving that, if T is irreducible, a representation with trace T is essentially unique when it exists.
Lemma 3.2.1
Let \(\mathscr {X}\) be an integral scheme and let \(\mathscr {V}_{1}\), \(\mathscr {V}_{2}\) be vector bundles of rank \(n>0\) over \(\mathscr {X}\). Suppose that there is an isomorphism \(F:\mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}}(\mathscr {V}_{1})\rightarrow \mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}}(\mathscr {V}_{2})\). Then there is an invertible \(\mathscr {O}_{\mathscr {X}}\)-module \(\mathscr {L}\) and an isomorphism
inducing F in the sense that \(F(T)\otimes \mathrm{id}_{\mathscr {L}} =g Tg^{-1}\) for all sections T of \(\mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}}(\mathscr {V}_{1})\).
Proof
By [65, Ch. IV], any automorphism of an Azumaya algebra (such as \( \mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}}(\mathscr {V}_{i})\)) is Zariski-locally inner. Therefore there exists an open cover \(\{U_{i}\}\) of \(\mathscr {X}\) and isomorphisms \(g_{i}:\Gamma (U_{i}, \mathscr {V}_{1})\rightarrow \Gamma (U_{i}, \mathscr {V}_{2})\) such that
for all \(T \in \mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}(U_{i})}(V_{1})\). Let \(U_{ij}:=U_{i}\cap U_{j}\) and
an automorphism of \(\mathscr {V}_{1}\) over \(U_{ij}\). By (3.2.1), \(c_{ij} \) commutes with every \(T \in \mathrm {End}\,_{\mathscr {O}_{\mathscr {X}}(U_{ij})}(\mathscr {V}_{1})\), hence it is a scalar in \(\mathscr {O}_{\mathscr {X}}(U_{ij})^{\times }\). One verifies easily that the \(c_{ij}\) form a cocycle in \(H^{1}(\mathscr {X},\mathscr {O}_{\mathscr {X}}^{\times })\). Let \(\mathscr {L}\) denote the associated invertible sheaf, which is trivialised by the cover \(\{U_{i}\}\). Then we may view \(g_{i}:\Gamma (U_{i}, \mathscr {V}_{1})\rightarrow \Gamma (U_{i}, \mathscr {V}_{2}\otimes \mathscr {L})\). By (3.2.2), the \(g_{i}\) glue to the desired isomorphism \(g:\mathscr {V}_{1}\cong \mathscr {V}_{2}\otimes \mathscr {L}\). \(\square \)
Lemma 3.2.2
Let \(\mathscr {X}\) be an integral scheme and \(\mathscr {T}:G_{F, S}\rightarrow \mathscr {O}(\mathscr {X})\) an irreducible pseudocharacter of dimension n. Let \(\mathscr {V}_{1}\), \(\mathscr {V}_{2}\) be representations of \(G_{F,S} \) with trace \(\mathscr {T}\). Then there exist a line bundle \(\mathscr {L}\) with trivial Galois action and a \(G_{F, S}\)-equivariant isomorphism
Proof
Write \(G=G_{F,S}\) and let \(\mathscr {A}:=\mathscr {O}_{\mathscr {X}}[G]/\mathrm {Ker}\,(\mathscr {T})\). By [88, Theorem 5.1], \(\mathscr {A}\) is an Azumaya algebra of rank 4. By [92, Corollary 2.9], the two natural injective maps \(\alpha _{i}:\mathscr {A}\rightarrow {\mathrm {End}\,}_{\mathscr {O}_{\mathscr {X}}}(\mathscr {V}_{i})\) are isomorphisms. Then we conclude by the previous lemma. \(\square \)
3.2.2 Galois representations in ordinary families
We prove the analogue in Hida families of Theorem 2.5.1.
Lemma 3.2.3
Let \(\overline{\lambda }:\mathbf{T}_{\mathrm {G}, U^{p}}^\mathrm{sph,ord} \rightarrow \overline{\mathbf{F}}_{p}\) be a character. Then there is a unique semisimple representation \(\overline{\rho }:G_{F,S}\rightarrow \mathrm {GL}_{2}(\overline{\mathbf{F}}_{p})\) such that \(\mathrm {Tr}(\overline{\rho }(\mathrm{Fr}_{v}))=q_{v}^{-1}\overline{\lambda }(T_{v})\) for all \(v\notin S\).
Proof
The existence follows by lifting \(\overline{\lambda }\) to the character \(\lambda _{x}\) associated with a classical point x (that is possible thanks to Lemma 3.1.4), then taking the semisimplification of the reduction modulo p of a lattice in the representation \(\rho _{x}:=\rho _{\pi _{x}}\) of Theorem 2.5.1; the uniqueness is a consequence of the Brauer–Nesbitt theorem. \(\square \)
By Proposition 3.1.3 we may decompose \(\mathbf{T}_{\mathrm {G}, U^{p}}^{\mathrm{sph}, \mathrm {ord}}\cong \prod _{\mathfrak {m}} \mathbf{T}_{\mathrm {G}, U^{p}, \mathfrak {m}}^{\mathrm{sph} \mathrm {ord}}\) and consequently the generic fibre of the associated schemes also decomposes as
We will say that a connected subset \(\mathscr {X}\subset \mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {ord}}\) has residual representation \(\overline{\rho }:G_{F}\rightarrow \mathrm {GL}_{2}(\overline{\mathbf{F}}_{p})\) if \(\mathscr {X}\) is contained in some \(\mathscr {E}_{\mathrm {G}, U^{p}, \mathfrak {m}}^{\mathrm {ord}}\) such that the character \(\lambda _{\mathfrak {m}}\otimes _{\mathbf{F}_{p}(\mathfrak {m})}\overline{\mathbf{F}}_{p} \) associated with \(\mathfrak {m}\) is the character of \(\overline{\rho }\).
Proposition 3.2.4
Let \(\mathscr {X}_{\mathrm {G}}\) be an irreducible component of \(\mathscr {E}_{\mathrm {G}}\) (that is, a Hida family). Then there exist:
-
an open subset \(\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}\) containing \(\mathscr {X}_{\mathrm {G}}^\mathrm{cl}:=\mathscr {X}_{\mathrm {G}}\cap \mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {cl}}\);
-
a locally free \(\mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}\)-module \(\mathscr {V}_{\mathrm {G}}\) of rank two over \(\mathscr {X}'_{\mathrm {G}}\), such that
$$\begin{aligned} \mathscr {V}_{\mathrm {G}, x}\cong V_{\pi _{x}} \end{aligned}$$for all \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\);
-
a filtration
$$\begin{aligned} 0\rightarrow \mathscr {V}_{\mathrm {G}, v}^{+}\rightarrow \mathscr {V}_{\mathrm {G}, v}\rightarrow \mathscr {V}_{\mathrm {G},v}^{-}\rightarrow 0, \end{aligned}$$(3.2.4)where the \(\mathscr {V}_{\mathrm {G},v}^{\pm }\) are locally free \(\mathscr {O}_{\mathscr {X}'_{\mathrm {G}}}\)-modules of rank 1, and \(G_{F_{v}}\) acts on \(\mathscr {V}_{\mathrm {G}, v}^{+}\) by the character associated, via local class field theory, with the character
$$\begin{aligned} \alpha _{|F_{v}^{\times }}^{\circ } \langle \ \rangle _{F_{v}} \end{aligned}$$(3.2.5)deduced from (3.1.12).
The representation \(\mathscr {V}_{\mathrm {G}}\) is uniquely determined up to automorphisms and twisting by line bundles with trivial Galois action.
The result is due to Hida and Wiles ([41, § 3.2.3] and references therein), except for the existence of (3.2.4) when the residual Galois representation of \(\mathscr {X}_{\mathrm {G}}\) is reducible.
Proof
Let \(\mathscr {T}:G_{F, S}\rightarrow \mathscr {O}(\mathscr {X}_{\mathrm {G}})\) be the pseudocharacter defined by \(\mathscr {T}(\mathrm{Fr}_{v})=q_{v}^{-1}\lambda (T_{v})\), where \(\lambda :\mathbf{T}_{\mathrm {G}, U^{p}}^\mathrm{sph}\rightarrow \mathscr {O}(\mathscr {X}_{\mathrm {G}})\) is the tautological character. Let \(\mathscr {X}_{\mathrm {G}} ^\mathrm{irr}\subset \mathscr {X}_{\mathrm {G}}\) be the (open) irreducibility locus. By Theorem 2.5.1, \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\subset \mathscr {X}_{\mathrm {G}}^\mathrm{irr}\). By Lemma 3.2.2, a representation \(\mathscr {V}_{\mathrm {G}}\) is unique up to Galois-trivial twists if it exists. We show existence.
By [88, Theorem 5.1], \(\mathscr {A}:=\mathscr {O}_{\mathscr {X}_{\mathrm {G}}^\mathrm{irr}}[G_{F, S}]/ \mathrm {Ker}\,(\mathscr {T})\) is an Azumaya algebra of rank 4 over \(\mathscr {E}_{\mathrm {G}'}\) and the natural map
satisfies \(\mathrm{Tr}\circ \rho = \mathscr {T}\) (where \(\mathrm {Tr}\) is the reduced trace of \({\mathscr {A}}\)). Let \(c\in G_{F, S}\) be a complex conjugation; we have an isomorphism \({\mathscr {A}}={{\mathscr {A}}} (\rho (c)-1)\oplus {{\mathscr {A}}}(\rho (c)+1)=:\mathscr {V}_{+1}\oplus \mathscr {V}_{-1}\). Each of the c-eigen-summands \(\mathscr {V}_{\pm 1}\) is a locally free \(\mathscr {O}_{\mathscr {X}_{\mathrm {G}}^\mathrm{irr}}\)-module (since so is \({\mathscr {A}}\)), whose rank is 2: indeed at any classical geometric point \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C}_{p})\), the specialisation \(\rho _{x}\) is odd, hence we can pick an isomorphism \({{\mathscr {A}}}_{x}\cong M_{2}(\mathbf {C}_{p})\) sending \(\rho _{x}(c)\) to \(\left( {\begin{matrix}1&{}\\ &{}-1\end{matrix}}\right) \) from which it is immediate that \(\mathscr {V}_{\pm 1, x}\) has rank 2; since classical points are dense, we conclude that \(\mathscr {V}_{\pm 1}\) also has rank 2.
Let \(\mathscr {V}_{\mathrm {G}}\) be either of \(\mathscr {V}_\mathrm{1, \pm }\). By [92, Corollary 2.9 (a)], the natural map
is an isomorphism; we view it as an identification to obtain a representation \(\rho '\) with trace \(\mathscr {T}\). As an irreducible 2-dimensional Galois representation over a field is uniquely determined by its trace, the representation \(\mathscr {V}_{\mathrm {G}, x}\) is isomorphic to \(V_{\pi _{x}}\).
We now show the existence of the filtration up to further restricting the base. Fix a place \(v\vert p\) of F, and let \(\det _{v}:G_{F_{v}}\rightarrow \mathscr {O}(\mathscr {X}_{\mathrm {G}}^\mathrm{irr})^{\times }\) be the character giving the action on \(\det \mathscr {V}_{\mathrm {G},v}\). Let \(\mathscr {V}_{0,v}^{+}\) be the trivial sheaf \(\mathscr {O}_{\mathscr {X}^\mathrm{irr}_{\mathrm {G}}}\) with \(G_{F_{v}}\)-action by the character (3.2.5), \(\mathscr {V}_{0,v}:=\mathscr {V}_{\mathrm {G},v}\), \(\mathscr {V}_{0,v}^{-}:=(\mathscr {V}_{0,v}^{+})^{-1}(\det _{v})\). Finally, for \(?=+, -. \emptyset \), let
Then for all \(x\in \mathscr {X}_{\mathrm {G}}^\mathrm{cl}\), by Theorem 2.5.1 we have exact sequences
which we wish to extend to a neighbourhood of \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\). From a consideration of weights based on Theorem 2.5.1, we see that for all \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\), \(H^{0}({F_{v}}, \mathscr {W}_{v,x}^{-})= H^{2}(F_{v}, \mathscr {W}_{v,x}^{-})=0\). Then from (3.2.6) we deduce
for all \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\), and from the Euler–Poincaré formula and (3.2.6) we deduce that
for all \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}.\)
By Proposition 5.2.3.3 below, (3.2.7) and (3.2.8) imply that the natural map
is an isomorphism for all \(x\in \mathscr {X}_{\mathrm {G}}^\mathrm{cl}\). Hence the sheaf \(\mathscr {L}:= H^{0}(F_{v}, \mathscr {W}_{v})\) is locally free of rank one in a neighborhood \(\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}^\mathrm{irr}\) of \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\). Defining
the natural map \(\mathscr {V}_{\mathrm {G}, v}^{+}\rightarrow \mathscr {V}_{\mathrm {G},v|\mathscr {X}_{\mathrm {G}}'}\) is injective, and its cokernel \(\mathscr {V}_{\mathrm {G},v}^{-}\) has rank one at each \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\). Up to further restricting \(\mathscr {X}_{\mathrm {G}}'\), \(\mathscr {V}_{\mathrm {G},v}^{-}\) is also locally free of rank one. It follows immediately from the construction that the exact sequence
has the asserted properties. \(\square \)
Proposition 3.2.5
In the situation of Proposition 3.2.4, the natural injective map
is an isomorphism over an open subset \(\mathscr {X}_{\mathrm {G}}''\subset \mathscr {X}_{\mathrm {G}}\) containing \(\mathscr {X}^{\mathrm {cl}}\).
Proof
By Theorem 2.5.1, \(\rho _{x}\) is absolutely irreducible for all \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\).
We deduce that for each \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\), the map \(i_{x}\) is an isomorphism. Then we may take for \(\mathscr {X}''_{\mathrm {G}}\) the open complement of the support of \(\mathrm{Coker}(i)\). \(\square \)
3.3 Universal ordinary representation and local-global compatibility
The idealised description of what is achieved in this subsection would be to define a universal ordinary automorphic representation of \(\mathrm {G}(\mathbf {A}^{\infty })\) over an irreducible component \(\mathscr {X}\) of \(\mathscr {E}_{\mathrm {G}}^{\mathrm {ord}}\); then show that it decomposes as the product of the representations of the local groups \(\mathbf {B}_{v}^{\times }\), for \(v\not \mid p\),Footnote 20 associated to \(\mathscr {V}|_{G_{F,v}}\) by a local Langlands correspondence in families. The definition should be an elaboration of
For technical reasons, a few modifications are necessary:
-
the local Langlands correspondence in families is not defined for the unit groups of division algebras;Footnote 21 therefore we “remove” the components at the ramification primes \(\Sigma \) of \(\mathbf {B}\), in the following way: we consider a component of \(\mathscr {E}\) rather than \(\mathscr {E}_{\mathrm {G}}\), and we take \({H_{\Sigma }'}\)-coinvariants in an analogue \(\Pi \) of (3.3.1). For sufficiently large levels, this isolates a local factor of \(\Pi \) that is generically free of rank one along locally distinguished Hida families;
-
in the limit in (3.3.1), we fix an arbitrarily large finite set of primes \(\Sigma '\), disjoint from \(\Sigma \) and from \(S_{p}\), and we let only the \(\Sigma '\)-component of \(U^{p}{}'\) shrink, so as to get a representation of \(\mathbf {B}_{\Sigma '}^{\times }\);
-
we replace the abstractly constructed \(\mathscr {V}=\mathscr {V}_{\mathrm {G}}\otimes \mathscr {V}_{\mathrm {H}}\) (where \(\mathscr {V}_{\mathrm {H}}=\chi _\mathrm{univ}\)) by a more geometric incarnation using the sheaf \(\mathscr {M}\) in ‘new’ level (with respect to the chosen irreducible component).
We use the correspondence studied in [34], with the caveat that strictly speaking the normalisation chosen there differs by the one fixed here in Theorem 2.5.1.1 by a Tate twist. This is only a matter of book-keeping, and in order to avoid excessive notational burden, we do not signal such Tate twists when referring to the results of [34] in the rest of this paper.
3.3.1 Irreducible components
Let \(\mathscr {X}_{\mathrm {G}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\) be an irreducible component. Fix a place v of F not in \(\Sigma \cup S_{p}\). Recall that the v-level of a representation \(\pi _{v}\) of \(\mathrm {GL}_{2}(F_{v})\) is the smallest m such that \(\pi _{v}^{U_{1}(\varpi _{v}^{m})}\ne 0\), where \(U_{1}(\varpi _{v}^{m})= \{\left( {\begin{matrix}a&{}b\\ c&{}d\end{matrix}}\right) \in \mathrm {GL}_{2}(\mathscr {O}_{F,v})\, :\, c\equiv d-1\equiv 0 \pmod {\varpi _{v}^{m}\mathscr {O}_{F,v}}\}\). Let \(m_{x,v}\) be the v-level of \(x\in \mathscr {X}^{\mathrm {cl}}\).
Lemma 3.3.1
The function \(x\mapsto m_{x,v}\) is constant on \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\).
Proof
By [20], \(m_{x,v}\) equals the conductor of the \(G_{F_{v}}\)-representation \(\mathscr {V}_{x}\); as all those Galois representations are pure, we may conclude by [89, Theorem 3.4]. \(\square \)
We may then define the v-level \(m_{v}\) of \(\mathscr {X}_{\mathrm {G}}\) to be the common value of the \(m_{x,v}\) for \(x\in \mathscr {X}^{\mathrm {cl}}\). By the following lemma, it is not restrictive to make the following assumption: for all \(v\notin \Sigma \cup S_{p}\), we have \(U_{v}=U_{1}{(\varpi }_{v}^{m_{v}(\mathscr {X}_{\mathrm {G}})})\). (We say that \(\mathscr {X}_{\mathrm {G}}\) is a v-new component of \(\mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {ord}}\).)
Lemma 3.3.2
Let \({}'\mathscr {X}_{\mathrm {G}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}{}'}\) be an irreducible component, and suppose that \(U^{p}{}'=\prod _{v\not \mid p} U_{v}'\). Let \(m_{v}\) be the level of \(\mathscr {X}_{\mathrm {G}}\) and let \(U^{p}=\prod _{v\not \mid p} U_{v}\), with \(U_{v}=U_{1}(\varpi _{v}^{m_{v}})\supset U_{v}'\) for all \(v\notin \Sigma \cup S_{p}\), and \(U_{v}=U_{v}'\). There exists a unique irreducible component \(\mathscr {X}_{\mathrm {G}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\) whose image under the natural embedding \(\mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}{}'}\) is \({}'\mathscr {X}_{\mathrm {G}}\).
Proof
Let \(x'\in {}'\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\) be any classical point. By [19], its level (that is, the level of \(\pi _{x,v}\)) is \(m_{v}\) if and only if \(\pi _{x,v}\) already occurs in the cohomology of \(X_{\overline{F}}\) at v-level \(m_{v}\), equivalently if and only if (the system of Hecke- and \(\mathrm {U}_{v}\)-eigenvalues associated with) \(\pi _{x,v}\) occurs in a quotient of \(\mathscr {M}_{U^{p}}\); that is, if \(x'\) comes from a point x of \(\mathscr {E}_{\mathrm {G}, U^{p}}\). Let \(\mathscr {X}_{\mathrm {G}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\) be the irreducible component containing x, which is unique by Proposition 3.1.7. As \(\mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}{}'}\) are equidimensional of the same dimension, the image of \(\mathscr {X}_{\mathrm {G}}\) in \(\mathscr {E}_{\mathrm {G}, U^{p}{}'}\) is an irreducible component, necessarily \({}'\mathscr {X}_{\mathrm {G}}\). \(\square \)
We now deal with the level at \(\Sigma \).
Lemma 3.3.3
Let \(v\in \Sigma \). There exists a compact open \(U_{v}'\subset U_{v}\) such that for every classical point \(x'\in \mathscr {X}_{\mathrm {G}}\), we have \(\pi _{x',v}^{U'_{v}}=\pi _{x',v}\), where \(\pi _{x,v}\) is the local component at v of \(\pi _{x}\otimes \overline{\mathbf {Q}}_{p}\).
Proof
Fix a classical point \(x\in \mathscr {X}_{\mathrm {G}} \subset \mathscr {E}^{\mathrm {ord}}_{\mathrm {G}, U^{p}}\), and let \(U_{v}'\subset U_{v}\) be such that \(\pi _{x,v}^{U'_{v}}=\pi _{x,v}\). (This will hold for sufficiently small \(U_{v}'\) as \(\pi _{x,v}\) is finite-dimensional.) We show that \(U_{v}'\) satisfies the desired property at all classical \(x'\in \mathscr {X}_{\mathrm {G}}\). Let \(\mathfrak {X}_{v/\mathbf {Q}_{p}}\) be the Bernstein variety of \(\mathrm {GL}_{2}(F_{v})\), a scheme over \(\mathbf {Q}_{p}\) (see [34], to which we refer for more background). By [34, Theorem 3.2.1], the representation \(\mathscr {V}_{\mathrm {G}}\) of \(G_{F_{v}}\) gives a map \(f:\mathscr {X}_{\mathrm {G}}\rightarrow \mathfrak {X}_{v/\mathbf {Q}_{p}}\), compatibly with the local Langlands correspondence in the sense that for all \(x\in \mathscr {X}_{\mathrm {G}}\), f(x) is the point corresponding to the supercuspidal support of the representation \(\pi _{x,v}'\) of \(\mathrm {GL}_{2}(F_{v})\) over \(\mathbf {Q}_{p}(x)\) attached to the representation \(\mathscr {V}_{\mathrm {G}, x}\). Note that for classical points x, \(\pi _{x,v}=\mathrm{JL}_{v}(\pi '_{x,v} \otimes _{\mathbf {Q}_{p}(x)}\overline{\mathbf {Q}_{p}})\), where \(\mathrm{JL}_{v}\) is the Jacquet–Langlands correspondence.
After base-change to \(\overline{\mathbf {Q}}_{p}\), we may consider the finitely many maps \(f_{i}:\mathscr {X}_{i}\rightarrow \mathfrak {X}_{v/\overline{\mathbf {Q}}_{p}}\), where the \(\mathscr {X}_{i}\) are the connected components of \(\mathscr {X}_{\mathrm {G},\overline{\mathbf {Q}}_{p}}\). The image of \(f_{i}\) is contained in a connected component \(\mathfrak {X}_{i}\) of \(\mathfrak {X}_{v/\overline{\mathbf {Q}}_{p}}\). These components are in bijection with inertial classes of supercuspidal supports for \(\mathrm {GL}_{2}(F_{v})\), and for the class \(\sigma =\sigma _i \) of \(\mathfrak {X}_i\) there are three possibilities:
-
\(\sigma \) corresponds to the class of a supercuspidal representation \(\sigma _0\) of \(\mathrm {GL}_{2}(F_{v})\) over \(\overline{\mathbf {Q}}_{p}\). In this case, there is an unramified character \(\omega :F_{v}^{\times }\rightarrow \mathscr {O}(\mathfrak {X}_i)^{\times }\) such that every \(y'\in \mathfrak {X}_{i}\) corresponds to \(\sigma _0\otimes \omega _{y'}\). Hence for every classical \(x'\in \mathscr {X}_{i}\), we have
$$\begin{aligned} \pi _{x',v}\cong \mathrm{JL}_{v}( \sigma _0\otimes \omega _{f_{i}(x')})=\mathrm{JL}_{v}( \sigma _0)\otimes \omega _{f_{i}(x')}\cong \pi _{x,v}\otimes \omega _{f_{i}(x')}. \end{aligned}$$As \(\omega _{f(x')}\) is unramified, it follows that \(\pi _{x',v}^{U_{v}}=\pi _{x',v}\).
-
\(\sigma \) corresponds to the class of the supercuspidal support of \(\mathrm{St}\otimes \omega _{0}\), where \(\mathrm{St}\) is the Steinberg representation and \(\omega _{0}:F_{v}^{\times }\rightarrow \overline{\mathbf {Q}}_{p}^{\times }\) is a character. Then there exist a closed subset \(\mathfrak {X}_{i}'\subset \mathfrak {X}_{i}\) and an unramified character \(\omega :F_{v}^{\times }\rightarrow \mathscr {O}(\mathfrak {X}_{i})^{\times }\) such that every \(y'\in \mathfrak {X}_{i}'\) corresponds to the supercuspidal support of \(\mathrm{St} \otimes \omega _{0}\omega _{y'}\), and such that every \(y'\in \mathfrak {X}_{i}-\mathfrak {X}_{i}'\) corresponds to the support of an irreducible principal series representation. It follows that for every classical \(x'\in \mathscr {X}_{i}\), the image \(f_{i}(x')\in \mathfrak {X}_{i}'\) (since \(\pi _{x,v}'\otimes \overline{\mathbf {Q}}_{p}\) is in the domain of \(\mathrm{JL}_{v}\)), and that \(\pi _{x',v} =\mathrm{JL}_{v}(\mathrm{St}\otimes \omega _{0}\omega _{f_{i}(x')})=\omega _{0}\omega _{f_{i}(x')}\circ \mathrm{Nm}\). We conclude as above.
-
no element of the inertial class \(\sigma \) is the supercuspidal support of a special or supercuspidal representation. This case is excluded as only those representations are in the image of the Jacquet–Langlands correspondence. \(\square \)
3.3.2 Galois representation from geometry
Let \(U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })\), \(V^{p}\subset \mathrm {H}(\mathbf {A}^{p\infty })\) be compact open subgroups. We will consider various compact open subgroups \(U^{p}\subset U^{p}_{*} \subset \mathrm {G}(\mathbf {A}^{p\infty })\), and will correspondingly denote by \(K^{p}_{*}\) be the image of \(U^{p}_{*}\times V^{p}\) in \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\). Let \(\mathscr {X}\) be an irreducible component of \(\mathscr {E}_{K_{}^{p}}^{\mathrm {ord}}\subset \mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {ord}}\times \mathscr {E}_{\mathrm {H}, V^{p}}\), and let \(\mathscr {X}_{\mathrm {G}}\subset \mathscr {E}_{\mathrm {G}, U^{p}}^{\mathrm {ord}}\) be the irreducible component such that \(\mathscr {X}\subset \mathscr {X}_{\mathrm {G}\times \mathrm {H}}:=\mathscr {X}_{\mathrm {G}}\times \mathscr {E}_{\mathrm {H}, V^{p}}\).
Suppose from now on that \(\mathscr {X}\) is locally distinguished by \(\mathrm {H}'\) (Definition 1.3.1). Let \(\mathscr {V}_{\mathrm {G}}\) be the \(\mathscr {O}_{\mathscr {X}_{\mathrm {G}}''}[G_{F, S}]\)-module constructed in Proposition 3.2.4 and Proposition 3.2.5, and let \(\mathscr {V}_{\mathrm {H}}\) be the universal character \(\chi _\mathrm{univ}\) of \(G_{E, S}\) from (3.1.10). Let
an open subset, and consider the \(G_{F, E, S}\)-representation
We define another sheaf \(\mathscr {V}\) with \(G_{F, E, S}\)-action, that will provide a more convenient and concrete substitute for \(\mathscr {V}'\) on (an open subset of) \(\mathscr {X}^{(0)}\).
Let
with \(U_{v}'\) as in Lemma 3.3.3. Let \(K_{0}^{p}{}'=(U_{0}^{p}{}'\times V^{p})F_{\mathbf {A}^{p\infty }}^{\times }/F_{\mathbf {A}^{p\infty }}^{\times }\), and let
viewed a sheaf over \(\mathscr {X}\).
Lemma 3.3.4
The sheaf \(\mathscr {V}\) is a direct summand of \(\mathscr {M}_{K_{0}^{p}{}'}\).
Proof
The group \({H_{\Sigma }'}=\prod _{v\in \Sigma } E_{v}^{\times }/F_{v}^{\times }\) acts on the locally free sheaf \(\mathscr {M}_{K^{p}_{0}{}'}\) through a quotient by an open subgroup. Since \(H_{\Sigma }'\) is compact, such a quotient is finite; therefore the inclusion \(\mathscr {V}\subset \mathscr {M}_{K_{0}^{p}{}'}\) splits. \(\square \)
Proposition 3.3.5
There is an open subset \(\mathscr {X}^{(1)}\subset \mathscr {X}\) containing all classical points such that \(\mathscr {V}\) is locally free of rank 2 along \(\mathscr {X}^{(1)}\). For every \(z=(x,y)\in \mathscr {X}^{ \mathrm {cl}}\) we have
as a \(G_{F, E, S}\)-representation.
Proof
By Corollary 3.1.6, for \(z=(x,y)\in \mathscr {X}^{\mathrm {cl}}\) we have
(where the first pair of factors is a representations of \(\mathrm {G}\times \mathrm {H}(\mathbf {A}^{p\infty })\) and the second one is a a representation of \(G_{E}\)). By Lemma 3.3.4, taking \({H_{\Sigma }'}\)-invariants commutes with specialisation, and we find that
The first factor is 1-dimensional by the theory of local newforms, and the second factor is 1-dimensional by assumption \((\varepsilon _{v})'\).
Since the fibre-rank of \(\mathscr {V}\) is 2 in the dense set \(\mathscr {X}^{\mathrm {cl}}\), there is an open neighbourhood of this set over which \(\mathscr {V}\) is locally free of rank 2. \(\square \)
Corollary 3.3.6
There exist: an open subset \(\mathscr {X}^{(2)}\subset \mathscr {X}^{(0)}\cap \mathscr {X}^{(1)}\) containing \(\mathscr {X}^{\mathrm {cl}}\) such that
an invertible sheaf \(\mathscr {L}\) over \(\mathscr {X}^{(2)}\) with trivial Galois action, and a \(G_{F, E, S}\)-equivariant isomorphism of sheaves on \(\mathscr {X}^{(2)}\)
Proof
By Proposition 3.3.5 and the construction of \(\mathscr {V}'\), the representations \(\mathscr {V}\), \(\mathscr {V}'\) have a common trace \(\mathscr {T}:G_{F, E, S}\rightarrow \mathscr {O}(\mathscr {X}^{(1)}) \). Since this is an irreducible pseudocharacter, the assertions follow from Lemma 3.2.2 and (the argument of) Proposition 3.2.5. \(\square \)
3.3.3 The universal ordinary representation
In what follows, all sheaves \(\mathscr {M}_{K^{p}_{*}}\) will be considered as sheaves over \(\mathscr {X}\) (or open subsets of \(\mathscr {X}\)). Note that, as the action of \(H'_{\Sigma }\) on \(\mathscr {M}_{\mathrm {G}}\), \( \mathscr {M}_{\mathrm {H}}\) commutes with the Galois action, the sheaves \(\mathscr {M}_{K^{p}_{*}}\) retain an action of \(G_{F, E, S}\).
We will use the following well-known fact.
Lemma 3.3.7
Let R be a ring and let \(T:M\rightarrow N\) be a map of free R-modules of the same rank. The set of those \(x\in \mathrm {Spec}\,R\) such that \(T\otimes R/\mathfrak {p}_{x}\) is an isomorphism is open in \(\mathrm {Spec}\,R\).
Proof
The locus is the complement of \(V(\det T)\). \(\square \)
In what follows, similarly to Sect. 2.1.5, if ‘?’ is any decoration, \(U_{?}^{p}\) is a subgroup of \(\mathrm {G}(\mathbf {A}^{p\infty })\), and \(V^{p}\subset \mathrm {H}(\mathbf {A}^{p\infty })\) is a fixed subgroup, we denote by \(K_{?}^{p}\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\) the image of \(U_{?}^{p}\times V^{p}\).
Proposition 3.3.8
Fix a finite set of primes \(\Sigma '\) disjoint from \(\Sigma \cup S_{p}\), such that \(U_{v}\) is maximal for all \(v\notin {\Sigma '}\cup \Sigma \cup S_{p}\), and consider the set \(\mathscr {U}\) of subgroups \(U^{p}{}'=\prod _{v\not \mid p}U_{v}'\subset U^{p}\) with \(U'_v\) as in Lemma 3.3.3 for all \(v\in \Sigma \), and \(U_{v}'=U_{v}\) for all \(v\notin {\Sigma '}\cup \Sigma \cup S_{p}\). (In particular \(U_{0}'\in \mathscr {U}\).)
-
1.
There exists a cofinal sequence \((U^{p}_{i}{}')_{i\ge 0}\subset \mathscr {U} \), and open subsets \(\mathscr {X}_{i}\subset \mathscr {X}^{(2)}\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\) such that \(\mathscr {X}_{j}\subset \mathscr {X}_{i}\) for \(i\le j\), satisfying the following: there are integers \(r_{i}\) and \(G_{F ,E}\)-equivariant maps
$$\begin{aligned} T_{i}:\mathscr {V}^{\oplus r_{i}}= (\mathscr {M}_{ K^{p}_{0}{}'}^{{H_{\Sigma }'}} )^{\oplus r_{i}} \rightarrow \mathscr {M}_{K^{p}_{i}{}'}^{{H_{\Sigma }'}} \end{aligned}$$that are isomorphisms over \(\mathscr {X}_{i}\).
-
2.
For each \(U^{p}{}'\in \mathscr {U}\), there is an open subset \(\mathscr {X}_{U^{p}{}'}\subset \mathscr {X}^{(2)}\) containing \(\mathscr {X}^{\mathrm {cl}}\) such that the restriction to \(\mathscr {X}_{U^{p}{}'}\) of
$$\begin{aligned} \Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}}:=\underline{\mathrm {Hom}\,}_{\mathscr {O}_{\mathscr {X}}[G_{F, E, S}]}(\mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}},\mathscr {V}) \end{aligned}$$(3.3.3)is a locally free \(\mathscr {O}_{\mathscr {X}_{U^{p}{}'}}\)-module, and we have an isomorphism of locally free sheaves with Hecke- and Galois- actions
$$\begin{aligned} \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}} \cong ( \Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}} )^{\vee } \otimes \mathscr {V}. \end{aligned}$$Moreover \(\Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}}\subset \Pi ^{K^{p}{}'', \mathrm {ord}}_{{H_{\Sigma }'}} \) for \(U^{p}{}''\subset U^{p}{}'\) via the natural projections \(\mathscr {M}_{ K^{p}{}''}^{{H_{\Sigma }'}}\rightarrow \mathscr {M}_{ K^{p}{}'}^{{H_{\Sigma }'}} \).
-
3.
The \( \mathscr {H}_{\mathrm {G}\times \mathrm {H}, {\Sigma '}}^{K^{p}{}'}\)-module \(\Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}}\) is generated by \(\Pi ^{K_{0}^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}} \) over \(\mathscr {X}_{U^{p}{}'}\).
-
4.
For each \(z=(x,y)\in \mathscr {X}^{\mathrm {cl}}\), we have
$$\begin{aligned} (\Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}})_{z}\cong (\pi _{x}^{U^{p}{}', \mathrm {ord}})_{{H_{\Sigma }'}}\otimes \chi _{y}, \end{aligned}$$with the notation of (2.4.3).
Proof
It suffices to prove part 1 for a sequence of subgroups \(U_{i}^{p}{}'=\prod _{v\not \mid p}U_{i,v}'\) that are \(\mathbf {B}_{S}^{\times }\)-conjugate to a cofinal sequence (if \(U_{i}^{p}{}''=g_{i}U_{i}^{p}{}'g_{i}^{-1}\) is cofinal and \((U_{i}^{p}{}', T_{i})\) satisfies the desired condition, then \((U_{i}^{p}{}'', g_{i}^{-1}\circ T_{i} )\) also satisfies the desired condition). We thus take any sequence with \(U_{i,v}'=U_{1}(\varpi ^{m_{i,v}})\) for \(v\notin {\Sigma '}\cup \Sigma \cup S_{p}\), with \(m_{i,v} \ge m_{v}\) and such that \(\min _{v\in {\Sigma '}}m_{i,v}\rightarrow \infty \).
Let \(r_{i}=\prod _{v}(1+m_{i,v}-m_{v})\). By the local theory of oldforms of [21] and the isomorphisms (3.3.2) and
there are Hecke operators
such that the map \(T_{i}:=\prod _{v\in S} \oplus _{j_{v}} T_{i, v, j_{v}} \) is an isomorphism after specialisation at any z in the dense set \( \mathscr {X}^\mathrm{cl}\). Hence \(T_{i}\) is an isomorphism in an open neighbourhood \(\mathscr {X}_{i}\) of \( \mathscr {X}^{\mathrm {cl}}\) (which we possibly shrink to make sure it is contained in \(\mathscr {X}^{(2)}\)). Together with Lemma 3.3.7, this concludes the proof of part 1. Part 2 is a consequence of part 1 and the absolute irreducibility of \(\mathscr {V}\), in the special case \(U^{p}{}'=U^{p}_{i}{}'\), with \(\mathscr {X}_{U^{p}{}'}=\mathscr {X}_{i}\). The general case is deduced from the special case: if \(U^{p}{}'\subset U_{i}^{p}{}'\), let \(\mathscr {X}_{U^{p}{}'}:=\mathscr {X}_{i}\) and take on both sides the locally free summands consisting of \(U^{p}{}'\)-invariants (for the first assertion) or coinvariants (for the second assertion). For part 3, we may again reduce to the special case \(U^{p}{}'=U^{p}_{i}{}'\); then the space \(\Pi ^{U_{i}^{p}{}'}\) is generated by the images of the transposes of various “oldforms” degeneracy maps \(T_{i}\) from part 1, that are elements of the Hecke algebra \(\mathscr {H}_{\mathrm {G}, S}^{U^{p}{}'}\). Finally, part 4 follows from (3.3.4). \(\square \)
Definition 3.3.9
(Universal ordinary representation). Let \(\mathscr {U}\) be as in Proposition 3.3.8, and fix an arbitrary \( U' \in \mathscr {U}\). Let
be as in Proposition 3.3.8, and let
as in (3.3.3). The universal ordinary representation
is the \(\mathscr {O}_{\mathscr {X}^{(3)}}[(\mathbf {B}_{{\Sigma '}}^{\times }\times E_{{\Sigma '}}^{\times })/F_{{\Sigma '}}^{\times }]\)-submodule generated by \(\Pi _{{H_{\Sigma }'}}^{K^{p}{}', \mathrm {ord}}\).
3.3.4 Local-global compatibility
The next theorem describes \(\Pi ^{K^{{S}p}{}', \mathrm {ord}}_{{{H_{\Sigma }'}}}\), as a sheaf with an action by \(\mathbf {B}_{{\Sigma '}}^{\times }\times E^{\Sigma \infty ,\times }\), in terms of the local Langlands correspondence in families of [34], denoted by
This correspondence attaches, to any family \(\mathscr {V}_{\mathrm {G}}\) of representations of \(\prod _{v\in {\Sigma '} } G_{F_{v}}\) on a rank-2 locally free sheaf over a Noetherian scheme \(\mathscr {Y}/\mathbf {Q}\), a family of representations of \(\mathrm {GL}_{2}(F_{{\Sigma '}})\) on a torsion-free sheaf over \(\mathscr {Y}\). The latter representation is co-Whittaker in the sense of [34, Definition 4.2.2]; in particular it admits a unique Whittaker model.
Theorem 3.3.10
(Local-global compatibility). Let
be the representation of \(\mathrm {GL}_{2}(F_{\Sigma '})\) over \(\mathscr {X}^{(3)}\) associated with \(\mathscr {V}_{\mathrm {G}}\) by the local Langlands correspondence in families for \(\mathrm {GL}_{2}(F_{{\Sigma '}})\) of [34]; let \(\chi _{\mathrm {H}, \mathrm{univ}, {\Sigma '}}\) be the pullback to \(\mathscr {X}^{(3)}\) of the sheaf \(\chi _{\mathrm {H}, \mathrm univ}\) of (3.1.11), with the \(\mathrm {H}(\mathbf {A}^{\infty })\)-action restricted to \(E_{{\Sigma '}}^{\times }\).
Then there exist an open subset \(\mathscr {X}^{(4)}\subset \mathscr {X}^{ (3)}\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\), a line bundle \( \Pi ^{K^{Sp}{}',S, \mathrm {ord}}_{{H_{\Sigma }'}}\) over \(\mathscr {X}^{ (4)}\), and an isomorphism of \(\mathscr {O}_{\mathscr {X}^{(4)}}[\mathrm {GL}_{2}(F_{{\Sigma '}})\times E_{{\Sigma '}}^{\times }]\)-modules
Proof
For \(*=\emptyset , '\), consider
a torsion-free sheaf over \(\mathscr {X}^{(3)}\) with action by \(\mathbf {B}_{{\Sigma '}}^{\times }=\mathrm {GL}_{2}(F_{{\Sigma '}})\). There is an obvious isomorphism
By Proposition 3.3.8.4 and the local freeness of each \({}'\Pi ^{K^{p}{}''}_{{H_{\Sigma }'}}\) near \(\mathscr {X}^{\mathrm {cl}}\), the fibre of \(({}'\pi _{\mathrm {G}, S}')^{U_{S}'}\) at any \(z=(x,y)\in \mathscr {X}^{\mathrm {cl}}\) equals \(\pi _{\mathrm {G},S}(\mathscr {V}_{\mathrm {G},x})^{U_{S}''}\); by Proposition 3.3.8.3 the same is true if one replaces \(({}^{}\pi '_{\mathrm {G}, {\Sigma '}})^{U_{{\Sigma '}}''}\) by the submodule \((\pi '_{\mathrm {G}, {\Sigma '}})^{U_{S}''}\). In conclusion, taking the limit over \(U^{p}{}''\in \mathscr {U} \) we find that the smooth, finitely generated, admissible \(\mathscr {O}_{\mathscr {X}^{(3)}}[\mathrm {GL}_{2}(F_{{\Sigma '}})]\)-module \(\pi '_{\mathrm {G},{\Sigma '}}\) satisfies
for all \((x, y)\in \mathscr {X}^{\mathrm {cl}}\). Then by [34, Theorem 4.4.3], there exist an open subset \(\mathscr {X}^{(4)}\subset \mathscr {X}^{(3)}\) containing \(\mathscr {X}^{\mathrm {cl}} \) and a line bundle that we denote by \( \Pi ^{K^{Sp},S, \mathrm {ord}}_{{H_{\Sigma }'}}\), such that
Substituting in (3.3.5) gives the desired result. \(\square \)
4 Pairings
4.1 Global dualities
We construct Hecke- and/or Galois-equivariant duality pairings on the sheaves constructed in the previous section. The results of this somewhat technical subsection are summarised in Propositions 4.1.7, 4.1.8.
4.1.1 Pairings, symmetries and involutions
If \(\epsilon \in \{\pm 1\}\), R is a ring or sheaf of rings, and M, J are R-modules, an R-bilinear pairing \((\ , \ ):M\otimes M\rightarrow J\) is said to be \(\epsilon \)-symmetric if it satisfies \((m, m')=\epsilon \cdot (m', m)\). If R is equipped with an involution \(\iota \), denote by \((\cdot )^{\iota }\) both the functor \(\otimes _{R, \iota }R\) and the maps \(m\mapsto m\otimes 1\); an \((R, \iota )\)-sesquilinear pairing \((\ , \ ):M\otimes M^{\iota }\rightarrow J\) is said to be \(\epsilon \)-hermitian if it satisfies \( (m, n)= \epsilon \cdot \iota ((n^{\iota }, m^{\iota })^{\iota })\). We will also use the prefix ‘skew-’ (respectively no prefix) if \(\epsilon =-1\) (respectively \(+1\)).
4.1.2 Involutions
We denote by the same name \(\iota \) the involutions on \(\mathscr {H}_{\mathrm {G}_{*}}^\mathrm{sph}\), \(\mathscr {H}_{\mathrm {G}_{*}}^\mathrm{sph, \mathrm {ord}}\) \(\Lambda _{\mathrm {G}_{*}, U^{p}_{*}} \), \(\mathscr {E}_{\mathrm {G}_{*}}^{\mathrm {ord}}\) deduced from those of Sect. 2.1.4. If M is a module over any of the above rings (or sheaf of modules over any of the above spaces), we let \(M^{\iota }= \iota ^{*} M\).
Lemma 4.1.1
Let W be an irreducible algebraic representation of \(\mathrm {G}_{*}\) over L.
-
1.
We have \(\sigma _{W^{\vee }}(t)=\sigma _{W}(t^{\iota })\) for all \(t\in T_{\mathrm {G}_{*}}\).
-
2.
If \(\pi ^{\mathrm {ord}}\) is the ordinary part of an automorphic representation of \(\mathrm {G}_{*}(\mathbf {A}^{\infty })\) over L of weight W, unramified of level \(U_{*}^{S}\) outside of a finite set of primes S, then there is an isomorphism of \(\mathscr {H}_{\mathrm {G}_{*}, U^{S}}^{\mathrm{sph}, \mathrm {ord}}\)-modules \(\pi ^{\vee ,U_{*}^{S}, \mathrm {ord}}\cong (\pi ^{U_{*}^{S},\mathrm {ord}})^{\iota }\).
-
3.
There is an identification
$$\begin{aligned} (\mathscr {E}_{G_{*}}^{\mathrm {cl}, W})^{\iota }=\mathscr {E}_{\mathrm {G}_{*}}^{\mathrm {cl}, W^{\vee }} \end{aligned}$$such that \(\pi ^{\mathrm {ord}}_{\iota (x)}=(\pi _{x})^{\vee , \mathrm {ord}}\).
Proof
All results can be reduced to the case \(\mathrm {G}_{*}=\mathrm {H}\), which is trivial, or \(\mathrm {G}_{*}=\mathrm {G}\), that we address. Part 1 follows from the explicit description of \(\sigma _{W}\) in (2.2.5) and \(W_{\mathrm {G}, (w; (w_{\sigma }))}^{\vee }\cong W_{\mathrm {G},(-w; (w_{\sigma }))}\) (see (A.4.2) below for an explicit duality).
For part 2, we use \(\pi ^{\vee }=\pi \otimes \omega ^{-1}\) where \(\omega \) is the central character of \(\pi \), and verify the statement separately for the spherical Hecke algebra and for the operators \(\mathrm {U}_{t}\). For the former, it is well known that the spherical Hecke algebra is generated by operators T(z) and \(T(\left( {\begin{matrix}x&{}\\ &{}1\end{matrix}}\right) )=T(\left( {\begin{matrix}1&{}\\ &{}x\end{matrix}}\right) )\) for \(z,x\in F_{S}^{\times }\); denoting by \(\lambda _{\pi ^{?}}(\cdot ) \) the eigenvalue of \(T(\cdot ) \) on \((\pi ^{?})^{U^{S}}\), we then have \(\lambda _{\pi }(z^{\iota })=\lambda _{\pi }(z^{-1})=\omega (z)^{-1}=\lambda _{\pi ^{\vee }}(z)\), and
as desired.
For the operators \(\mathrm {U}_{t}\), we verify that if \(\pi \) is ordinary at v with unit character \(\alpha _{v}^{\circ }=\alpha _{v}\sigma _{W}^{-1}\) (as a character of \(T_{\mathrm {G}, v}^{+}\)), then \(\pi ^{\vee }\) is ordinary at v with unit character
This follows from observing
Finally, part 3 follows from parts 1 and 2. \(\square \)
4.1.3 Homological and cohomological dualities
We shall define various pairings \(\langle \ , \ \rangle _{?}\) in the (ordinary, completed) homology of Shimura varieties, starting from the Poincaré duality pairings. Then we will use them to construct corresponding pairings \((\, \ )_{?}\) on spaces of representations, as follows.
Construction 4.1.2
Let A be a ring, G a group, and let \(M_{1}, M_{2}, V_{1}, V_{2}, A(d)\) be A[G]-modules, projective and of finite type over A; denote
Let \(f_{i}\in \pi _{i}:=\mathrm {Hom}\,( M_{i}, V_{i})\) be A[G]-maps, suppose we have fixed an identification \(V_{2}^{D}\cong V_{1}\); let \(\langle \ , \ \rangle \) be a perfect pairing \(M_{1}\times M_{2} \rightarrow A(d)\), inducing \(u_{\langle ,\rangle } :M_{2}^{D}\rightarrow M_{1}\). Let \(f_{2}^{D}:V_{2}^{D}\cong V_{1}\rightarrow M_{2}^{D}\) be the dual map, then we define a pairing on \(\pi _{1}\times \pi _{2}\) by
4.1.4 Homological dualities/1
Fix lattices \(W^{\circ }\) and \(W^{\vee , \circ }\) on any right algebraic representation of \(\mathrm {G}_{*}\) over L, and denoted by \(\langle \ , \ \rangle ^{W}:W\otimes W^{\vee }\rightarrow L\) the natural invariant pairing. This may not preserve the lattices but it does so up to a bounded denominator which we denote by \(p^{-|W|}\).Footnote 22
We may then consider the Poincaré duality pairings
where the second map is induced by \(\langle , \rangle ^{W}\) and summation over the connected components of \(\overline{X}_{*, U_{*}}\). These pairings are integral up to a bounded denominator \(p^{-|W|}\) and satisfy
for any T in \(\mathscr {H}_{\mathrm {G}_{*}, U_{*}}^{p}\), as well as the projection formula
for all pairs of levels \(U_{*}'\subset U_{*}\); here \(\mathrm{p}_{U'_{*}/U_{*}}:X_{U'_{*}}\rightarrow X_{U_{*}}\) is the projection.
4.1.5 Homological dualities/2
We start to promote and modify the Poincaré duality pairings. The following lemma is clear.
Lemma 4.1.3
Let R be a ring, S a finite R-algebra, M a finite S-module.
-
1.
Suppose that S is étale over R. Then there is a natural isomorphism
$$\begin{aligned} \alpha :\mathrm {Hom}\,_{R}(M, R)\rightarrow \mathrm {Hom}\,_{S}(M, \mathrm {Hom}\,_{R}(S, R)) \rightarrow \mathrm {Hom}\,_{S}(M, S) \end{aligned}$$where the first map is \(\lambda \mapsto (m\mapsto (s\mapsto \lambda (s m)).\) and the second one comes from the isomorphism \(S\cong \mathrm {Hom}\,_{R}(S, R)\) induced by the relative trace map.
-
2.
Suppose that \(S=R[T]\) for a finite abelian group T, then there is an isomorphism \(\beta :\mathrm {Hom}\,_{R}(M, R)\rightarrow \mathrm {Hom}\,_{R[T]}(M, R[T])\) given by \(\lambda \mapsto (m\mapsto \sum _{t}\lambda (tm) [t^{-1}])\).
If \(S=R[T]\) is étale over R then we have \(\alpha (\lambda )=|T|^{-1}\beta (\lambda )\).
If \(S=R[T]\) for a finite abelian group T, one verifies that the isomorphism of the lemma is given by
We may apply case 2 of the lemma to
(with the isomorphism of (3.1.3)). We obtain, from the pairings \(\langle \ , \rangle _{V_{r}, W}\), pairings
and thanks to an easily verified compatibility, a well-defined pairing
4.1.6 Automorphic inner products
Let
where ‘\(\mathrm {vol}\)’ denotes the volume with respect to the metric deduced from the hyperbolic metric \(dxdy/2\pi y^{2}\) (using the complex uniformisation (2.3.1)), when \(\mathrm {G}_{*}=\mathrm {G}\), and the counting metric, when \(\mathrm {G}_{*}=\mathrm {H}\). By [107, Lemma 3.1], \(\mathrm{v}(U_{*})\in \mathbf {Q}^{\times }\) and, when \(d=\dim X_{*}=1\), it equals the degree of the Hodge bundle \(L_{U_{*}}\) defined as in loc.cit. We have
where the last equality can be easily seen e.g. from the complex uniformisation (2.3.1). We set for any \(r\ge 1\)
where \(U_{*,0}(p^{r})_{p}\subset \mathrm {G}_{*}(\mathbf {Q}_{p})\) is a maximal compact subgroup if \(\mathrm {G}_{*}=\mathrm {H}, \mathrm {H}'\), it is the group of those matrices that are upper triangular modulo \(p^{r}\) if \(\mathrm {G}_{*}=\mathrm {G}\), and it is deduced from those by product and quotient if \(\mathrm {G}_{*}=\mathrm {G}\times \mathrm {H}, (\mathrm {G}\times \mathrm {H})'\). The right hand side of (4.1.6) is independent of \(r\ge 1\).
Let \(\pi \) be an automorphic representation of \(\mathrm {G}_{*}(\mathbf {A}^{\infty })\) of weight \(W^{*}\) over L, \(V_{\pi }\) the corresponding \(G_{E_{*}}\)-representation. Then we have an isomorphism \(V_{\pi ^{\vee }}\cong V_{\pi }^{*}(1)\), hence we may use Construction 4.1.2 with \(A=L\), \(G=G_{E_{*}}\), \(M_{1}= \mathrm {H}_{d}(\overline{X}_{*,U_{*}}, \mathscr {W})\), \(M_{2}= \mathrm {H}_{d}(\overline{X}_{*,U_{*}}, \mathscr {W}^{\vee })\), \(V_{1}=V_{\pi }\), \(V_{2}=V_{\pi ^{\vee }}\) and the pairings (4.1.2). Using (2.5.3), we obtain
One verifies thanks to (4.1.3) and (4.1.5) that the pairing
is well-defined.
When \(\mathrm {G}_{*}=\mathrm {H}\), denoting \(\pi =\chi _{\mathrm {H}}\), we may alternatively apply Construction 4.1.2 to \(A, M_{1}, M_{2}, V_{1}, V_{2}\) as above and the image of the pairings \(\langle \langle \ , \rangle \rangle _{V^{p},r W} \) under the map \(\Lambda _{\mathrm {H}, r, W}\rightarrow L\) given by \([t]\mapsto \chi _{\mathrm {H}}(t)\), and denote the resulting pairings on \(\chi _{\mathrm {H}}\times \chi _{\mathrm {H}}^{-1}\) by \((\ , \ )_{\langle \langle , \rangle \rangle _{\chi _{\mathrm {H}},V^{p},r}}\). As \(|\overline{T}_{\mathrm {H}, 0}/\overline{T}_{\mathrm {H}, r}|\cdot \mathrm{v}(V^{p})=\mathrm{v}(V^{p}V_{p,r})\) by (4.1.5), we have
and in particular the right-hand side is independent of \(V^{p}\).
Assume for the rest of this subsection that \(\mathrm {G}_{*}=\mathrm {G},\mathrm {G}\times \mathrm {H}, (\mathrm {G}\times \mathrm {H})'\). Then we need a twist in order to isolate the toric action and to obtain the \(\iota \)-equivariance of the pairings under the action of the \(\mathrm {U}_{p\infty }\)-operators.
Let \(\pi =\pi ^{\infty }\otimes W\) be an ordinary representation of \(\mathrm {G}_{*}(\mathbf {A})\). Using the transformation \(w_\mathrm{a}^{\mathrm {ord}}\) defined in Proposition A.2.1, we define a pairing
See Lemma A.2.2 for its nondegeneracy.
4.1.7 Homological dualities/3
Analogously to the previous paragraph, we define a twisted Poincaré pairing
of which we will especially consider the restriction to the ordinary parts of homology.
Lemma 4.1.4
Let \(\pi \) be an ordinary representation of \(\mathrm {G}_{*}(\mathbf {A})\), and identify
for sufficiently large r similarly to Proposition 3.1.5. Then Construction 4.1.2 provides a pairing \((,)_{\langle , \rangle _{W, r}^{\mathrm {ord}}}\) on \(\pi ^{\mathrm {ord}}\times \pi ^{\vee ,\mathrm {ord}}\); it is related to (4.1.8) by
Proof
This follows by chasing the definitions.\(\square \)
By applying case 2 of Lemma 4.1.3 as in (4.1.4), corrected by a factor \(p^{r[F:\mathbf {Q}]}\),Footnote 23 we obtain from (4.1.9) pairings
Lemma 4.1.5
The parings (4.1.11) satisfy \(\langle \langle x_{r}T, y_{r}\rangle \rangle _{W, r}=\langle \langle x_{r}, y_{r}T^{\iota }\rangle \rangle _{U^{p}_{*},W, r}\) for all \(T\in \mathscr {H}_{\mathrm {G}, r}^{\mathrm {ord}}\) and all \(x_{r}\in H_{d}(\overline{X}_{*,U_{*}^{p},r}, \mathscr {W})\), \( y_{r}\in H_{d}(\overline{X}_{*,U_{*}^{p},r}, \mathscr {W}^{\vee })\).
For \(z\in M_{\mathrm {G}_{*}, \mathscr {W}}\), denote by \(z_{r}\) its image in \(M_{\mathrm {G}_{*}, \mathscr {W}, r}:=H_{d}(\overline{X}_{*,U_{*}^{p},r}, \mathscr {W})^{\mathrm {ord}}\). The pairing
is well-defined.
The above construction is a minor variation on the one of [41, § 2.2.4], to which we refer for the proof of the lemma. As usual, when \(W=\mathbf {Q}_{p}\) we shall omit it from the notation.
Lemma 4.1.6
The diagram

where the left vertical map comes from Proposition 3.1.2.2 and the right vertical map is \([t]\mapsto \sigma _{W}^{-1}(t)[t]\), is commutative.
Proof
For simplicity we write down the proof for the group \(\mathrm {G}_{*}=\mathrm {G}\) and we drop the subscripts \(U^{p}\). Poincaré duality and the pairings \( \langle \ , \ \rangle ^{W} \) preserve integral structures up to \(p^{-|W|}\). Then by construction it suffices to show the identity
for all \(r\ge 1\) and x, y in \( H_{d}(\overline{X}_{ r},\mathbf {Z}_{p})\).
By definition in (3.1.8), we have
where \(\zeta _{r}\in W^{\circ , N_{0}}/p^{r}\) and \(\zeta _{r}^{*}\in W^{\circ }_{N_{0}}/p^{r}\) are elements pairing to 1; we denote by \(\zeta _{r}^{\vee }\), \(\zeta _{r}^{\vee , *}\) the analogous elements for \(j_{W^{\vee }, r}\). Then we need to show that
By the definition of \(w_\mathrm{a}^{\mathrm {ord}}\) in Proposition A.2.1, this reduces to the identity
which can be immediately verified using an explicit model for the pairing such as given in (A.4.2). \(\square \)
4.1.8 Dualities over Hida families
Let \(\mathscr {X}\) be an irreducible component of \(\mathscr {E}_{K^{p}}^{\mathrm {ord}}\). By Proposition 3.1.7, the map \(\mathscr {E}^{\mathrm {ord}}_{K^{p}}\rightarrow \mathrm {Spec}\,\Lambda _{\mathbf {Q}_{p}}\) is étale in a neighbourhood \(\mathscr {X}'\) of \(\mathscr {X}^{\mathrm {cl}}\), hence we may apply case 1 of Lemma 4.1.3 to deduce from (4.1.12) a pairing
We summarise the situation.
Proposition 4.1.7
(Duality). Let \(\mathscr {X}^{(5)}\supset \mathscr {X}^{\mathrm {cl}}\) be the intersection of the subset \(\mathscr {X}^{(4)} \) of Theorem 3.3.10 with the locus where the map \(\mathscr {X}\rightarrow \mathrm {Spec}\,\Lambda _{\mathbf {Q}_{p}} \) is étale. There exist
-
a perfect, \(G_{E}\)-equivariant, skew-hermtian pairing
$$\begin{aligned} \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}}\otimes _{\mathscr {O}_{\mathscr {X}^{(5)}}} \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'},\iota }\rightarrow \mathscr {O}_{\mathscr {X}^{(5)}}(1). \end{aligned}$$(4.1.14)induced from (4.1.13);
-
a perfect, \(G_{E}\)-equivariant, skew-hermtian pairing
$$\begin{aligned} \mathscr {V}\otimes _{\mathscr {X}^{(5)}} \mathscr {V}^{\iota } \rightarrow \mathscr {O}_{\mathscr {X}^{(5)}}(1).. \end{aligned}$$(4.1.15) -
a perfect pairing
$$\begin{aligned} ((\ , \ )):= \mathrm{v}(K^{p}{}')^{-1}\cdot ( \ , \ )_{\langle \langle , \rangle \rangle _{K^{p}{}'}} :\Pi _{{H_{\Sigma }'}}^{K^{p}{}'}\otimes _{\mathscr {O}_{\mathscr {X}^{(5)}}} (\Pi _{{H_{\Sigma }'}}^{K^{p}{}'})^{\iota } \rightarrow \mathscr {O}_{\mathscr {X}^{(5)}}, \end{aligned}$$(4.1.16)where \((\ , )_{\langle \langle , \rangle \rangle _{K^{p}{}'}}\) is deduced from (4.1.14), (4.1.15) and the isomorphism of Proposition 3.3.8.2 via Construction 4.1.2.
Proof
Observe that the natural map
(where \({}^{*}\) denotes \(\mathscr {O}_{\mathscr {X}^{(5)}}\)-dual) is an isomorphism; as (4.1.13) is equivariant for the action of the full Hecke algebra, this implies that its restriction (4.1.14) is perfect. It is skew-hermitian by Lemma 4.1.5 and the fact that the Poincaré pairing (4.1.2), when W is trivial, is skew-symmetric.
We find the pairing (4.1.15) by specialising (4.1.14) to \(K^{p}{}'=K^{p}\), and the pairing (4.1.16) as described. \(\square \)
4.1.9 Specialisations
We describe the specialisation of the pairing ((, )) just constructed.
For each algebraic representation W of \((\mathrm {G}\times \mathrm {H})\), denote by
the set of classical points of weight W (omitted from the notation when \(W=\mathbf {Q}_{p}\)) and level r. Denote by a subscript ‘W, r’ the pullbacks of sheaves or global sections from \(\mathscr {X}^{(5)}\) to \(\mathscr {X}_{r}^{\mathrm {cl}, W}\) (which is a finite étale scheme over \(\mathbf {Q}_{p}\)). We let
where the last equality is by Proposition 3.1.2.3. We denote
Proposition 4.1.8
Let \(f_{1}\), respectively \(f_{2}\) be globalFootnote 24 sections of \(\Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}}=\underline{\mathrm {Hom}\,}_{\mathscr {O}_{\mathscr {X}^{(5)}}[G_{F, E}]}(\mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}},\mathscr {V}) \), respectively \((\Pi ^{K^{p}{}', \mathrm {ord}}_{{H_{\Sigma }'}})^{\iota }\). Let
be \(\mathscr {O}_{\mathscr {X}^{\mathrm {cl}, W}_{r}}[G_{F, E}]\)-linear maps.
Let \(x\in \mathscr {X}^{\mathrm {cl}, W}_{r}\), \(\pi := \pi (x) \) and let
be \(\mathbf {Q}_{p}(x)[G_{F, E}]\)-linear maps.
The following hold.
-
1.
Suppose that for \(i=1,2\), the map \(f_{i, W, r}\) arises as the specialisation of \(f_{i}\). Then
$$\begin{aligned} {((f_{1}, f_{2}))}|_{\mathscr {X}_{r}^{\mathrm {cl}, W}}= ((f_{1, W, r}, f_{2, W, r}))_{{W,r}}\quad \text {in } \mathscr {O}(\mathscr {X}_{r}^{\mathrm {cl}, W}). \end{aligned}$$ -
2.
Suppose that for \(i=1, 2\), the map \(f_{i, x}\) factors through the projection
$$\begin{aligned} \mathrm{p}^{?}:\mathrm {H}_{1}(\overline{Z}_{K^{p}{}',r} , \mathscr {W}^{?})\rightarrow \mathrm {H}_{1}(\overline{Z}_{K^{p}{}',r} , \mathscr {W}^{?})^{\mathrm {ord}}_{{H_{\Sigma }'}}&\cong H_{1}(\overline{Z}_{K^{p}{}',r} , \mathscr {W})^{\mathrm {ord},{H_{\Sigma }'}} \\&= M_{K^{p}{}', W, r}^{{H_{\Sigma }'}}, \end{aligned}$$where \(?=\emptyset \) if \(i=1\), \(?=\vee \) if \(i=2\); and that \(f_{i,x}\) coincides with the specialisation of \(f_{i, W, r}\) at x. Then
$$\begin{aligned} ((f_{1}, f_{2}))_{W, r }(x) = (f_{1,x}, f_{2,x})^{\mathrm {ord}}_{\pi } =\dim W\cdot (w_\mathrm{a}^{\mathrm {ord}} f_{1}, f_{2})_{\pi } \quad \text {in } \mathbf {Q}_{p}(x). \end{aligned}$$(4.1.17)
Proof
We simplify the notation by omitting the superscripts \( {{H_{\Sigma }'}}\) and subscripts \(K^{p}{}'\); moreover we ignore the normalisations \(\mathrm{v}(K^{p}{}')^{-1}\) that are present in all of the pairings to be compared.
Part 1 follows from the definition (4.1.12) if \(W=\mathbf {Q}_{p}\), and similarly we can also identify \(((\ , \ ))_{W,r}\) with the restriction to \(\mathscr {X}_{r}^{\mathrm {cl}, W}\) of the pairing on functions on \(M_{W}\) deduced from \(\langle \langle \ , \ \rangle \rangle _{W}\) via Construction 4.1.2. By Lemma 4.1.6 this implies that the desired statement holds for all W.
For Part 2, let \(H_{W,r}:=\mathscr {O}(\mathscr {X}_{r}^{\mathrm {cl}, W})\). First notice that, by the construction of case 1 of Lemma 4.1.3, the diagram of \(H_{W, r}\)-modules

is commutative.
On the other hand, let \(x\in \mathscr {X}_{\mathrm {cl}}^{W, r}\) and let \(\alpha _{x}\) be the associated character of \(T^{+}\). By definition in (4.1.11), the pairing \(\langle \langle , \rangle \rangle _{\Lambda , W}\) specialises, on \(M_{W,r|x}\otimes M_{W, r|x}^{\iota }\), to
It follows that \(u_{\langle \langle , \rangle \rangle _{W, r}}\) specialises at x to \(p^{-r[F:\mathbf {Q}]}|\overline{T}_{0}/\overline{T}_{r}|^{-1}u_{\langle , \rangle '_{W,r}}\), hence that the specialisation of \(((, ))(x)=\mathrm{v}({K^{p}{}'})^{-1}(,)_{\langle \langle ,\rangle \rangle _{W,r}}(x)\) is
where we have used \(|\overline{T}_{0}/\overline{T}_{r}|= \mathrm{v}(K^{p}{}' K_{0}(p^{r})_{p }) / \mathrm{v}(K^{p}{}' K_{1}^{1}(p)^{r}_{p } )\) (by (4.1.5)) and (4.1.10).
This establishes the first equality of (4.1.17); the second one is just a reminder of (4.1.8). \(\square \)
4.2 Local toric pairings
Let F be a non-archimedean local field, E a quadratic étale algebra over F with associated character \(\eta :F^{\times }\rightarrow \{\pm 1\}\), B a quaternion algebra over F, \(G=B^{\times }\), \(H=E^{\times }\), \(H'=H/F^{\times }\), and suppose given an embedding \( H\hookrightarrow G\)
4.2.1 Definition of the pairing
Let \(\pi \) be a smooth irreducible representation of G over a finite extension L of \(\mathbf {Q}_{p}\), with a central character \(\omega :F^{\times }\rightarrow L^{\times }\). Let \(\chi :E^{\times }\rightarrow L^{\times }\) a character such that \(\chi |_{F^{\times }}\cdot \omega =\mathbf {1}\). We identify \(\chi \) with a representation \(L\chi \) of \(E^{\times } \) on L, and when more precision is needed we denote by \(e_{\chi }\) the basis element corresponding to the character \(\chi \) in \(L\chi \). Let \(\Pi :=\pi \otimes \chi \), a representation of \((G\times H)'=(G\times H)/F^{\times }\) over L. We assume that \(\pi \) is essentially unitarisable, that is that for any embedding \(\iota :L\hookrightarrow \mathbf {C}\), a twist of \(\iota \pi \) is isomorphic to the space of smooth vectors of a unitary representations. (This holds automatically if \(\pi \) arises as the local component of a cuspidal automorphic representation over L.) Let \(\pi ^{\vee }\) be the smooth dual, \(\Pi ^{\vee }:=\pi ^{\vee }\otimes \chi ^{-1}\)
Assume from now on that the modified local sign \(\varepsilon (\Pi )=\) (1.2.5) equals \(+1\). Then, by the result of Tunnell and Saito mentioned in the introduction, the space
has dimension 1 over L. Moreover the choices of an invariant pairing \((\ , \ )\) on \(\Pi \otimes \Pi ^{\vee }\) and a Haar measure dt on \(\mathrm {H}'\) give a generator
defined by the absolutely convergent integral
for any \(\iota :L\hookrightarrow \mathbf {C}\); here \(\mathscr {L}(V_{v}, 0)=\) (1.2.7).
Recall also from the introduction (1.2.8) that
is independent of \((\ ,\ )\) whenever it is defined.
We study the pairing, or some of its variations, in a few different contexts.
4.2.2 Interpretation in the case \(E=F \oplus F\)
In this case \(G=\mathrm {GL}_{2}(F)\), and the integral (4.2.1) has an interpretation as product of zeta integrals. Let \(\mathscr {K}(\pi )\) and \(\mathscr {K}(\pi ^{\vee })\) be Kirillov models over L as in [32, § 2.3]. By [32, Lemma 2.3.2], the L-line of invariant pairings on \(\mathscr {K}(\pi )\times \mathscr {K}(\pi ^{\vee })\) is generated by an element \((\ , \ )\) such that, for each \(\iota :L\hookrightarrow \mathbf {C}\), we have
where the integral is absolutely convergent (as \(\iota \pi \) is essentially unitarisable) and \(d^{\times }y\) is any L-valued Haar measure. Identify \(E^{\times }\) with the diagonal torus in \(\mathrm {GL}_{2}(F)\) and write \(\chi =(\chi _{1}, \chi _{2})\) according to the decomposition \(E=F\oplus F\); noting that \(\chi _{2}=\omega ^{-1}\chi _{1}\) and \(\pi =\pi ^{\vee }\otimes \omega ^{-1}\), we indentify \(Q_{(, ), dt}\) with
where \(I(\cdot , \cdot , 1/2)\) is the zeta integral of [34, § 5.2] for \(\mathrm {GL}_{2}(F)\times \mathrm {GL}_{1}(F)\), and \(\doteq \) denotes an equality up to constants in \(L^{\times }\) depending on the choices of measures.
4.2.3 Special line in the unramified case
We study the first one in a short list of special cases in which there are ‘canonical’ lines in \(\Pi \), \(\Pi ^{\vee }\), on which the value of the pairings Q can be explicitly computed.
Lemma 4.2.1
[105, Lemme 14]. Suppose that B is split, E/F is unramified, and both \(\pi \) and \(\chi \) are unramified. Let \(K\subset (G\times E^{\times })/F^{\times }\) be a maximal compact subgroup. Then
for all v, respectively w, in the lines \(\Pi ^{K}\), respectively \((\Pi ^{\vee })^{K}\).
4.2.4 Special line when B is nonsplit
Suppose now that B is nonsplit and that \(\Pi \) is an irreducible representation of \((G\times E^{\times })/F^{\times }\) as above. Note that \(\Pi \) is finite-dimensional and \(H'\) is compact, so that \(\Pi ^{\vee }=\Pi ^{*}\) and the natural maps \(\Pi ^{H'}\rightarrow \Pi _{H'}\) (\(=H'\)-coinvariants) and \(\Pi ^{*,H'} \rightarrow (\Pi ^{H'})^{*}\) are isomorphisms. Moreover the non-degenerate pairing \((\ , \ )\) restricts to a non-degenerate pairing on \(\Pi _{H'}\otimes \Pi ^{\vee }_{H'}\). Then we may compare the restrictions of the pairings \(Q_{(\ , \ )}\) of \((\ , \ )\) to the line \(\Pi ^{H'}\otimes \Pi ^{\vee ,H'}\).
Lemma 4.2.2
In the situation of the previous paragraph, we have
as elements of \((\Pi ^{H'})^{*}\otimes (\Pi ^{\vee ,H'})^{*}\).
Proof
This follows from the definition in (4.2.1), since in this case the integration over the compact set \(E^{\times }/F^{\times }\) converges. \(\square \)
4.3 Ordinary toric pairings
We define a variant for ordinary forms of the pairing Q.
4.3.1 Definition of the ordinary paring
Let \(\Pi =\pi \otimes \chi \) be an ordinary automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{})\) over L. When referring to local objects considered in the previous paragraphs or products thereof, we append subscripts as appropriate.
For each \(v\vert p\), let
be the character by which \(E_{v}^{\times }\) (or equivalently \(\prod _{w\vert v} G_{E_{w}}^\mathrm{ab}\)) acts on \(V_{\pi ,v}^{+} \otimes \chi _{v}\), and let \(\mathrm{j}_{v}\in E_{v}\) be the purely imaginary element fixed in (A.1.2). Define
For measures \(dt_{v}=dt_{v, p}\) on \(H'_{v}\), \(dt_{v,\infty }\) on \(H'_{v, \infty }\) (the latter a merely formal notion as in the introduction), define
The denominators in the right-hand sides are the volumes of \(\mathrm {vol}(\mathscr {O}_{E, v}^{\times }/\mathscr {O}_{F, v}^{\times })\), respectively \(\mathbf {C}^{\times }/\mathbf {R}^{\times }\), for the ratio of (rational normalisations of) selfdual measures, cf. [107, § 1.6.2] and the proof of Proposition A.3.4.
Definition 4.3.1
Let \(dt=dt^{p\infty }dt_{p\infty }\) be a decomposition of the adèlic measure dt specified in (1.2.9). Then we define:
-
for each \(f_{1, p \infty }, f_{3,p \infty }\in \Pi _{p \infty }^{\mathrm {ord}}\), \(f_{2, p \infty }, f_{4,p \infty }\in \Pi _{p \infty }^{\vee , \mathrm {ord}}\) with \(f_{3,p \infty }\otimes f_{4,p \infty }^{\mathrm {ord}}\ne 0\),
$$\begin{aligned} Q^{\mathrm {ord}}_{dt_{p\infty }}\left( {f_{1,p\infty }\otimes f_{2,p\infty }\over f_{3,p\infty }\otimes f_{4,p\infty }}\right) :=\mu ^{+}(\mathrm{j})^{} {\mathrm {vol}^{\circ }(H'_{p\infty }, dt_{p\infty })} \cdot {f_{1, p\infty }\otimes f_{2, p\infty }\over f_{3, p\infty }\otimes f_{4, p\infty }}. \end{aligned}$$(4.3.2) -
for each \(f_{1}, f_{3}\in \Pi ^{\mathrm {ord}}\), \(f_{2}, f_{4}\in \Pi ^{\vee , \mathrm {ord}}\) with \((f_{3}, f_{4})^{\mathrm {ord}}\ne 0\),
$$\begin{aligned} Q^{\mathrm {ord}} \left( {f_{1}\otimes f_{2}\over f_{3}\otimes f_{4}}\right) :=Q^{p\infty }_{dt^{p\infty }}\left( {f_{1}^{p\infty }\otimes f_{2}^{p\infty }\over f_{3}^{p\infty }\otimes f_{4}^{p\infty }}\right) \cdot Q^{\mathrm {ord}}_{dt_{p\infty }}\left( {f_{1,p\infty }\otimes f_{2,p\infty }\over f_{3,p\infty }\otimes f_{4,p\infty }}\right) . \end{aligned}$$(4.3.3)
The normalisation at \(p\infty \) is justified by the clean formula of Proposition 4.3.4 below.
Remark 4.3.2
Suppose that \(\Pi \) is locally distinguished, so that as explained in the introduction the functional \(Q_{dt}\) is nonzero. Then the functional \(Q^{\mathrm {ord}}_{dt}\) is also nonzero.
4.3.2 Decomposition
Fix a decomposition \(dt= \prod _{v\not \mid p \infty } dt_{v} dt_{p\infty }\) such that for all but finitely many v, \(\mathrm {vol}(\mathscr {O}_{E,v}^{\times }/\mathscr {O}_{F, v}^{\times })=1\). Let \(\Sigma '\) be a finite set of finite places of F disjoint from \(\Sigma \) and \(S_{p}\) and containing the other places of ramification of \(\Pi \), and those such that \(\mathrm {vol}(\mathscr {O}_{E,v}^{\times }/\mathscr {O}_{F, v}^{\times })\ne 1\). Let \(K^{p}\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty })\) be an open compact subgroup that is maximal away from \(S:=\Sigma \cup \Sigma '\) and such that \(\Pi _{v}^{K_{v}}=\Pi _{v}\) for \(v\in \Sigma \).
Lemma 4.3.3
For all \(f_{1}, f_{3} \in \Pi ^{K^{p}, \mathrm {ord}}_{H_{\Sigma }'}\), \(f_{2}, f_{4} \in \Pi ^{\vee , K^{p}, \mathrm {ord}}_{H_{\Sigma }'}\) with \((f_{3}, f_{4})^{\mathrm {ord}}\ne 0\), we have
Proof
This follows from the definitions and the results of Sect. 4.2. \(\square \)
4.3.3 Relation to between the toric pairing and its ordinary variant
We gather the conclusion of the computations from the appendix.
Proposition 4.3.4
Let \(\Pi =\pi \otimes \chi = \Pi ^{\infty } \otimes W\) be an ordinary representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A})\). Let \(w_\mathrm{a}^{\mathrm {ord}}\) and \(\gamma _{H'}^{\mathrm {ord}} \) be the operators defined in Propositions A.2.1 and A.2.4. Let \(e_{p}(V_{(\pi , \chi )})= \) (1.4.6) be the interpolation factor of the p-adic L-function. For all \(f_{1}\), \(f_{3}\in \Pi ^{\mathrm {ord}}\), \(f_{2}\), \(f_{4}\in \Pi ^{\mathrm {ord}}\) with \((f_{3}, f_{4})^{\mathrm {ord}}\ne 0\), we have
Proof
There is a decomposition \(Q_{p\infty , dt_{p\infty }}^{\mathrm {ord}} = \prod _{v\vert p}Q_{v,dt_{v}}^{\mathrm {ord}}\cdot \prod _{v\vert p}Q_{v, \infty , dt_{v, \infty }}^{\mathrm {ord}}\), whose terms are defined in Sects. A.3–A.4. The only point worth stressing is that if \(\mu _{v}^{+}\), respectively \(\mu _{v, \infty }^{+}\) is the character defined in Sect. A.3.3,Footnote 25 respectively Sect. A.4.3, then the decomposition \(\mu ^{+}=\mu ^{+, \mathrm{sm}}\mu ^{+, \mathrm{alg}}\) of \(\mu ^{+}\) into a product of a smooth and an algebraic character is given by \(\mu ^{+, \mathrm{sm}}=\prod _{v\vert p }\mu _{v}^{+}\), \(\mu ^{+, \mathrm{alg}}= \prod _{v\vert p}\mu _{v, \infty }^{+}\).
Then the result follows from Propositions A.3.4 and A.4.3. \(\square \)
4.4 Interpolation of the toric pairings
We interpolate the pairings \(Q^{\mathrm {ord}}_{dt}\) along Hida families
4.4.1 Interpolation of the local pairings
We use the same notation F, E of Sect. 4.2.
Lemma 4.4.1
Let \(\mathscr {X}\) be a scheme over \(\mathbf {Q}\) and let \(r'=(r, N)\) be a Weil–Deligne representation of \(W_{F}\) on a rank-2 locally free sheaf over \(\mathscr {X}\). Suppose that \(\mathscr {X}\) contains a dense subset \(\mathscr {X}^{\mathrm {cl}}\) such that \(r'_{x}\) is pure for all \(x\in \mathscr {X}^{\mathrm {cl}}\). Let \(\mathrm {ad}(r')\) be the rank-3 adjoint representation. Then there exist an open subset \(\mathscr {X}''\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\) and functions
such that for every \(x\in \mathscr {X}'\) we have \(L(0, r')^{-1}(x)=L(0, r'_{x})^{-1}\) and \(L(1, r', \mathrm {ad})(x)=L(1, \mathrm {ad}(r'_{x}))\).
Proof
By [34, § 5.1], there exist an open set \(\mathscr {X}'''\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\) and functions \(L(0, r')^{-1}\), respectively \(L(1, r', \mathrm {ad})^{-1}\), in \(\mathscr {O}(\mathscr {X}''')\) interpolating \(L(0, r'_{x})^{-1}\), respectively \(L(1, \mathrm {ad}(r'_{x}))^{-1}\), for all \(x\in \mathscr {X}'\). By purity, \(L(1,r, \mathrm {ad})^{-1}\) does not vanish on \(\mathscr {X}^{\mathrm {cl}}\), hence it is invertible in an open neighbourhood \(\mathscr {X}''\) of \(\mathscr {X}^{\mathrm {cl}}\) in \(\mathscr {X}'''\). \(\square \)
Let \(\mathscr {X}\) be an integral scheme, \(\mathscr {F}^{\times }\) be a \(\mathscr {K}_{\mathscr {X}}^{\times }\)-module, then we define \(\mathscr {F}^{\times ,-1}\) to be the \(\mathscr {K}_{\mathscr {X}}\)-module such that for each open \(\mathscr {U}\subset \mathscr {X}\),
with \(\mathscr {K}_{\mathscr {X}}^{\times }\)-action given by \(a\cdot f^{-1}=(a^{-1}f)^{-1}\).
Proposition 4.4.2
Consider the situation of Lemma 4.4.1. Let
be the \(\mathscr {O}_{\mathscr {X}}[\mathrm {GL}_{2}(F)]\)-module attached to \(r'\) by the local Langlands correspondence in families of [34], let \(\omega :F^{\times }\rightarrow \mathscr {O}(\mathscr {X})^{\times }\) be its central character, and let \(\chi :E^{\times }\rightarrow \mathscr {O}(\mathscr {X})^{\times }\) be a character such that \(\omega \cdot \chi |_{F^{\times }}=\mathbf {1}\). Let \(\pi ^{\vee }:=\pi (\rho ^{*}(1))\) and let \(\Pi =\pi \otimes \chi \), \(\Pi ^{\vee }=\pi ^{\vee }\otimes \chi ^{-1}\). Let \((\Pi \otimes _{\mathscr {O}_{\mathscr {X}}^{\times }}\Pi ^{\vee })^{\times }\) be the \(\mathscr {O}_{\mathscr {X}}^{\times }\)-submodule of those \(f_{3}\otimes f_{4}\) such that \((f_{3}, f_{4})\ne 0\).
Then there exist: an open subset \(\mathscr {X}'\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\); letting \(\mathscr {O}:=\mathscr {O}_{\mathscr {X}'}\), \(\mathscr {K}:=\mathscr {K}_{\mathscr {X}'} \), an \(\mathscr {O}^{\times }\)-submodule \((\Pi \otimes _{\mathscr {O}_{\mathscr {X}}^{\times }}\Pi ^{\vee })^{\times }\) specialising at all \(z\in \mathscr {X}^{cl}\) to the space of \(f_{3,z}\otimes f_{4,z}\) such that \((f_{3, z}, f_{4, z})_{z}\ne 0\); and a map of \(\mathscr {O}\)-modules
satisfying the following properties:
-
1.
For all \(t_{1}, t_{2}\in E^{\times }/F^{\times }\), \(g\in (\mathrm {GL}_{2}(F)\times E^{\times })/F^{}\),
$$\begin{aligned} \mathscr {Q}_{dt}\left( { \Pi (t_{1})f_{1}\otimes \Pi ^{\vee }(t_{2})f_{2})\over \Pi ( g)f_{3}\otimes f_{4}}\right) = \mathscr {Q}_{dt}\left( {f_{1}\otimes f_{2}\over f_{3}\otimes \Pi ^{\vee }(g^{-1})f_{4}}\right) ; \end{aligned}$$ -
2.
For all \(x\in \mathscr {X}^{\mathrm {cl}}\),
$$\begin{aligned} \mathscr {Q}^{}_{dt | x} =Q_{dt}, \end{aligned}$$where \(Q_{dt}\) is the paring on \(\Pi _{x}\otimes \Pi _{x}^{\vee }\) of (4.2.2).
Proof
For each \(x\in \mathscr {X}^\mathrm{cl}\), \(\pi _{x}\) corresponds to a pure Weil–Deligne representation under local Langlands, hence it is essentially unitarisable (and in fact tempered, see [99, Lemma 1.4 (3)]). Then by [34, Lemma 5.2.5] there is an open neighbourhood \(\mathscr {X}'\) of \(\mathscr {X}^{\mathrm {cl}}\) in \(\mathscr {X}\) and an invariant pairing over \(\mathscr {X}'\)
specialising to the pairing \((\ , \ )_{x}\) defined by (4.2.3) at all \(x\in \mathscr {X}^{\mathrm {cl}}\). It induces an invariant pairing \( \Pi \otimes \Pi ^{\vee }\rightarrow \mathscr {O}_{\mathscr {X}'}\) still denoted by \((\ , \, )\).
By Lemma 4.4.1, up to possibly shrinking \(\mathscr {X}'\), we have regular functions on \(\mathscr {X}'\) interpolating \(z\mapsto L(1/2, \pi _{z,E}\otimes \chi _{z})^{-1}=L(0, r_{z}|_{W_{E}'} \otimes \chi _{z})^{-1}\) and \(x\mapsto L(1, \pi _{x}, \mathrm {ad})=L(1, r_{x}', \mathrm {ad})\).
If E/F is split, [34, Proposition 5.2.4] applied to (4.2.4) gives an element \(\mathscr {Q}_{(, ),dt}:\Pi _{E^{\times }}\otimes \Pi _{E^{\times }}^{\vee }\rightarrow \mathscr {O}_{\mathscr {X}' }\) interpolating \(Q_{(, )_{x}}\) for \(x\in \mathscr {X}^{\mathrm {cl}}\), and we define
If E/F is nonsplit, by the previous discussion we can interpolate all terms occurring in the definition (4.2.1) (note that the integral there is just a finite sum), to obtain a pairing \(\mathscr {Q}_{(,)}\) over \(\mathscr {X}'\) interpolating \(\mathscr {Q}_{(,)_{x}}\) for \(x\in \mathscr {X}^{\mathrm {cl}}\). Then we again define \(\mathscr {Q}^{}\) by (4.4.2). \(\square \)
4.4.2 Product of local pairings
We consider the global situation, resuming with the setup of Sects. 3.3–4.1.
Let \(\Pi :=\Pi ^{K^{p}{}', \mathrm {ord}}_{{{H_{\Sigma }'}}}\) over \(\mathscr {X}^{(5)}\). Recall that we have a decomposition
from Theorem 3.3.10.
Let \( (\Pi \otimes _{\mathscr {K}^{\times }_{\mathscr {X}^{(5)}}}\Pi ^{\iota })^{\times } \subset \Pi \otimes _{\mathscr {K}^{\times }_{\mathscr {X}^{(5)}}}\Pi ^{\iota }\) be the \(\mathscr {O}_{\mathscr {X}^{(5)}}^{\times }\)-submodule of sections \(f_{3}\otimes _{\mathscr {O}_{\mathscr {X}^{(5)}}^{\times }} f_{4}\) such that \(f_{3}\otimes f_{4}\ne 0\) and \((f_{3,v},f_{4,v})_{v}\ne 0\) for each the pairings \((, )_{v}=\) (4.4.1), \(v\in \Sigma '\).
Theorem 4.4.3
Let \(\Pi :=\Pi _{{H_{\Sigma }'}}^{K^{p}{}', \mathrm {ord}}\) and \(\mathscr {X}^{(5)}\) be as in Proposition 4.1.7, and let \( (\Pi \otimes _{\mathscr {K}_{\mathscr {X}^{(5)}}}\Pi ^{\iota })^{\times } \subset \Pi \otimes _{\mathscr {K}_{\mathscr {X}^{(5)}}}\Pi ^{\iota }\) be the submodule defined above. Then there exist an open subset \(\mathscr {X}^{(6)}\subset \mathscr {X}^{(5)}\) containing \(\mathscr {X}^{\mathrm {cl}}\) and, letting \(\mathscr {O}=\mathscr {O}_{\mathscr {X}^{(6)}}\), \(\mathscr {K}:=\mathscr {K}_{\mathscr {X}^{(6)}}\), a map of \(\mathscr {O}^{\times }\)-modules
satisfying:
-
1.
For any \(t_{1}, t_{2}\in E_{\Sigma '}^{\times }/F_{\Sigma '}^{\times }\subset (\mathrm {GL}_{2}(F_{\Sigma '})\times E_{\Sigma '}^{\times })/F_{\Sigma '}^{\times }\), any \(h\in \mathscr {H}_{S, K_{\Sigma '}}\) and any section
$$\begin{aligned} (f_{1}\otimes f_{2}) \otimes (f_{3}\otimes f_{4})^{-1} \quad \text { of } \quad ( \Pi \otimes _{\mathscr {K}} \Pi ^{\iota })\otimes _{\mathscr {K}^{\times }} ({\Pi } \otimes _{\mathscr {K}^{\times }} {\Pi }^{\iota })^{\times , -1}, \end{aligned}$$we have
$$\begin{aligned} \mathscr {Q}^{}\left( {\Pi _{\Sigma '}(t_{1})f_{1} \otimes \Pi _{\Sigma '}^{\iota }(t_{2})f_{2} \over \Pi ( h)f_{3} \otimes f_{4}}\right) = \mathscr {Q}^{}\left( { f_{1}\otimes f_{2} \over f_{3} \otimes \Pi ^{\iota }(h)f_{4}}\right) ; \end{aligned}$$in the left-hand side, \(\Pi _{\Sigma '}\), respectively \(\Pi _{\Sigma '}^{\iota }\) denote the actions of the Hecke algebras at S on \(\Pi \), respectively \( \Pi ^{\iota }\).
-
2.
For all \(x\in \mathscr {X}^{\mathrm {cl}}\),
$$\begin{aligned} \mathscr {Q}^{}_{dt |x}=Q^{\mathrm {ord}}, \end{aligned}$$where \(Q_{}^{\mathrm {ord}}\) is the restriction of the pairing on \(\Pi _{x}^{\vee , \mathrm {ord}}\otimes \Pi _{x}^{\vee ,\mathrm {ord}}\) of Definition 4.3.1.
Proof
By (4.3.2), (4.3.3), (4.3.4), and (4.4.3), we need to interpolate:
-
the terms \(\mathscr {L}(V_{(\pi , \chi ), v}\) for \(v\in \Sigma \): this is Lemma 4.4.1;
-
the characters \(\mu _{v}^{+}\) for \(v\vert p\): this follows form the existence of the filtration (3.2.4) over an open subset of \(\mathscr {X}\).
-
the term \(Q_{dt, \Sigma '}:=\prod _{v\in \Sigma '}Q_{dt, v}\), According to the proof of [34, Theorem 4.4.1], the representation \(\pi _{\mathrm {G}, {\Sigma '}}(\mathscr {V}_{\mathrm {G}})\) is the maximal torsion-free quotient of \(\otimes _{v\in {\Sigma '}}\pi _{\mathrm {G},v}(\mathscr {V}_{\mathrm {G}})\). For sections \(f_{i,{\Sigma '}}\) that are images of \(\otimes _{v\in {\Sigma '}}f_{i,v}\), with \(f_{i,v}\) sections of \( \pi _{\mathrm {G},v}(\mathscr {V}_{\mathrm {G}})\otimes \chi _{\mathrm {H}, \mathrm{univ},v}\) if \(i=1,3\), or of \( \pi _{\mathrm {G},v}(\mathscr {V}_{\mathrm {G}}^{\iota })\otimes \chi ^{-1}_{\mathrm {H}, \mathrm{univ},v}\) if \(i=2,4\), let
$$\begin{aligned} \mathscr {Q}^{}_{{\Sigma '}}\left( { f_{1, {\Sigma '}}\otimes f_{2, {\Sigma '}}\over f_{3, {\Sigma '}}\otimes f_{4, {\Sigma '}}}\right) := \prod _{v\in {\Sigma '}} \mathscr {Q}_{v}\left( {f_{1,v}\otimes f_{2,v}\over f_{3,v}\otimes f_{4,v}}\right) , \end{aligned}$$where the factors in the right-hand side are provided by Proposition 4.4.2. This is well-defined independently of the choices of \(f_{i,v}\) as \(\mathscr {K}\) is torsion-free.
This completes the interpolation of (4.3.3) into a function \(\mathscr {Q}\), that satisfies properties 1 and 2 by construction and the corresponding properties from Proposition 4.4.2. \(\square \)
5 Selmer sheaves and p-adic heights
In this section we present the theory of Selmer complexes and p-adic heights needed in the rest of the paper. The foundational material is taken from the book of Nekovář [81].
5.1 Continuous cohomology
Let \((R^{\circ }, \mathfrak {m})\) be a complete Noetherian local ring, let G be a topological group.
5.1.1 Continuous cochains for (ind-) admissible R[G]-modules
Let M be an \(R^{\circ }[G]\)-module. We say that M is admissible of finite type if it is of finite type as an \(R^{\circ }\)-module and the action \(G\times M\rightarrow M\) is continuous (when M is given the \(\mathfrak {m}\)-adic topology). We say that M is ind-admissible if \(M=\bigcup _{\alpha }M_{\alpha }\) where \(\{M_{\alpha }\}\) is the set of finite-type admissible \(R^{\circ }[G]\)-submodules of M.
The complex of continuous cochains of M is denoted by \(C^{\bullet }_\mathrm{cont}(G, M)\); it is defined in the usual way [81, (3.4.1)] when M is admissible of finite type, and by \(C^{i}_\mathrm{cont}(G, M):= \varinjlim _{\alpha } C^{i}_\mathrm{cont}(G, M_{\alpha })\) when we have a presentation \(M=\bigcup _{\alpha }M_{\alpha }\) as above. The image of \(C^{\bullet }_\mathrm{cont}(G, M)\) in the derived category of \(D({}_{R}\mathrm{Mod})\) of \(R^{\circ }\)-modules is denoted by
and its cohomology groups by
(we omit the subscript ‘cont’ as we will only be working with continuous cohomology).
5.1.2 Localisation
Let
for some multiplicative subset \(\mathcal {S}\subset R^{\circ }\), and let M be an R[G]-module. We say that M is ind-admissible if it is ind-admissible as an \(R^{\circ }[G]\)-module, and that it is of finite type if it is of finite type as an R-module. Suppose that \(M:=M^{\circ }\otimes _{R^{\circ }} R\) for an ind-admissible \(R^{\circ }[G]\)-module \(M^{\circ }\). Then M is ind-admissible as an \(R^{\circ }[G]\)-module and there is a canonical isomorphism
([81, (3.7.4)]).
Remark 5.1.1
Let
be the category of schemes isomorphic to open subschemes of \(\mathrm {Spec}\,R^{\circ }\), with maps being open immersions. It follows from the previous paragraph that, for any object X of \(\mathscr {C}\), the condition of ind-admissibility is defined for all quasicoherent \(\mathscr {O}_{X}[G]\)-modules, and the functors \(\mathrm{R}\Gamma (G,- )\) are well-defined on ind-admissible \(\mathscr {O}_{X}[G]\)-modules. Moreover, both the ind-admissibility condition and the functors \(\mathrm{R}\Gamma (G, - )\) are compatible with restriction along open immersions in \(\mathscr {C}\).
In the following, we will not further comment on the generalisation indicated in the previous remark when referring to sources only considering \(R^{\circ }[G]\)-modules.
5.1.3 Completed product
For \(i=1,2\), let \(R_{i}^{\circ }\) be complete noetherian local rings, and let \(R^{\circ }:= R_{1}^{\circ }\hat{\otimes } R_{2}^{\circ }\). We have a functor
defined on objects by \(\mathrm {Spec}\,R_{1}^{\circ }[1/f_{1}] \hat{\times } \mathrm {Spec}\,R_{1}^{\circ }[1/f_{2}]:= \mathrm {Spec}\,R_{1}^{\circ }\hat{\otimes }R_{2}^{\circ }[1/f_{1}\otimes 1, 1/1\otimes f_{2}]\) and glueing.
5.1.4 Notation
Throughout the rest of this section, X will denote an object of \(\mathscr {C}_{R^{\circ }}\). If \(\mathscr {A}=\mathscr {O}_{X}, \mathscr {O}_{X}[G]\), we denote by \(D({}_{\mathscr {A}}\mathrm{Mod})\) the derived category of \(\mathscr {A}\)-moduels. We use sub- or superscripts
to denote the full subcategory of objects quasi-isomorphic to complexes of \(\mathscr {A}\)-modules that are respectively termwise of finite type, termwise ind-admissible, bounded below, bounded above, bounded, concentrated in degrees [a, b], bounded, perfect (= bounded and termwise projective and of finite type).
Proposition 5.1.2
[81, (3.5.6)]. The functor \(\mathrm{R}\Gamma (G, -)\) can be extended to a functor on the category of bounded-below complexes of ind-admissible \(\mathscr {O}_{X}[G]\)-modules, with values in bounded-below complexes of \(\mathscr {O}_{X}\)-modules [81, (3.4.1.3), (3.5.1.1)]. It descends to an exact functor
5.1.5 Base-change
Suppose that \(R\twoheadrightarrow R'=R/I\) is a surjective map of rings. Let \(j:R^{\circ } \rightarrow R= R^{\circ }[\mathscr {S}^{-1}]\) be the natural map and let \(I^{\circ }:= j^{-1}(I)\). Then \(R^{\circ }{}':= R^{\circ }/I^{\circ }\) is also complete local Noetherian, and we may write \(R'= R^{\circ }{}'[\mathscr {S}']^{-1}\) where \(\mathscr {S}'\) is the image of \(\mathscr {S}\) in \(R^{\circ }{}'\). Let \(M'\) be an ind-admissible \(R'\)-module, then \(C^{\bullet }_\mathrm{cont}(G, M')\) is the same whether we consider \(M'\) as an \(R'\)-module or as an R-module: in the special case \(R=R^{\circ }\) this follows from the fact that the maximal ideal of \(R^{\circ }{}'\) is the image of the maximal ideal of \(R^{\circ }\), so that the \(\mathfrak {m}\)-adic and \(\mathfrak {m}'\)-adic topologies on finitely generated \(R^{\circ }{}'\)-modules coincide; the general case follows from the special case by localisation (5.1.1).
More generally, if \(Y\subset X \) is a closed subset, the functor \(\mathrm{R}\Gamma (G, -)\) on \(\mathscr {O}_{Y}[G]\)-modules coincides with the restriction of the functor on \(\mathscr {O}_{X}[G]\)-modules of the same name.
Proposition 5.1.3
Let M be an ind-admissible \(\mathscr {O}_{X}[G]\)-module and let N be an \(\mathscr {O}_{X}\)-module of finite projective dimension. Then there is a natural isomorphism in \(D^\mathrm{b}({}_{\mathscr {O}_{X}}\mathrm{Mod})\)
Proof
Let \(P^{\bullet }\) be a finite projective resolution of N. The natural map of complexes of \(\mathscr {O}_{X}\)-modules
is an isomorphism by [81, (3.4.4)].Footnote 26 The desired result follows from the definition of derived tensor product. \(\square \)
The proposition applies when \(N=\mathscr {O}_{Y}\) with \(Y\subset X\) a local complete intersection, or when X is regular and N is any coherent \(\mathscr {O}_{X}\)-module. We highlight the following case.
Corollary 5.1.4
Let M be an ind-admissible \(\mathscr {O}_{X}[G]\)-module that is flat as an \(\mathscr {O}_{X}\)-module, and let \(x\in X\) be a nonsingular point. Then there is an isomorphism in \(D^\mathrm{b}({}_{\kappa (x)}\mathrm{Mod})\)
hence a second-quadrant spectral sequence
Proof
After possibly localising at x, we may assume that \(X=\mathrm {Spec}\,R\) is the spectrum of a local ring, which by assumption will be regular. Then \(\kappa (x)\) has finite projective dimension over R, and the result follows from the previous proposition. \(\square \)
5.1.6 Continuous cohomology as derived functor
For \(i=0, 1\), the functors \(M\mapsto H^{i}(G,M)\) on the category of ind-admissible R-modules coincide with the ith derived functors of \(M\mapsto M^{G}\) [81, (3.6.2)(v)].
5.2 Specialisations
From here on we further assume that \(R^{\circ }\) has finite residue field of characteristic p.
5.2.1 Finiteness conditions
Let G be a profinite group. We consider the condition
and define the p-cohomological dimension of G to be
Lemma 5.2.1
If G satisfies (F) then the cohomology groups of ind-admissible \(\mathscr {O}_{X}[G]\)-modules of finite type are \(\mathscr {O}_{X}\)-modules of finite type [81, (4.2.5), (4.2.10)]. The cohomology of any ind-admissible \(\mathscr {O}_{X}[G]\)-module vanishes in degrees \(>\mathrm{cd}_{p}(G)\) [81, (4.26)].
When E is a number field, S is a finite set of places of E and \(G=G_{E, S}\), condition (F) is satisfied and \(\mathrm{cd}_{p}(G)= 3\). When \(E_{w}\) is a local field and \(G=G_{E_{w}}\), condition (F) is satisfied and \(\mathrm{cd}_{p}(G)= 2 \). In the latter case we use the notation \(H^{i}(E_{w}, M) \) for \(H^{i}(G, M)\).
5.2.2 Projective limits, specialisations
We give two results on the compatibility of G-cohomology with other functors.
Lemma 5.2.2
Let G be a profinite group satisfying (F) and let \(M=\varprojlim _{n} M_{n}\) be the limit of a countable projective system of admissible \(R^{\circ }\)-modules of finite type. Then for all i the natural map
is an isomorphism.
Proof
In the special case \(M_{n}=M/\mathfrak {m}^{n}M\), it is shown in [81, Corollary 4.1.3] that the map under consideration is surjective with kernel \(\lim ^{(1)}_{n} H^{i-1}(G, M_{n})\); this vanishes since by (F) those cohomology groups are finite, hence the projective system they form satisfies the Mittag-Leffler condition. The general case follows from applying the special case to M and the \(M_{n}=\varprojlim _{r}M_{n}/\mathfrak {m}^{r}M_{n}\). \(\square \)
Proposition 5.2.3
Let G be a profinite group satisfying (F) and \(\mathrm{cd}_{p}(G)=e<\infty \). Let M be an ind-admissible \(\mathscr {O}_{X}[G]\)-module of finite type. Let \(x\in X\) be a nonsingular point, let \(i_{0}\ge 0\) and suppose that
for all \(i\ge i_{0}+1\).
-
1.
For all \(i\ge i_{0}+1\), the support of the finitely generated R-module \(H^{i}(G, M)\) is a proper closed subset not containing x.
-
2.
The natural map
$$\begin{aligned} H^{i_{0}}(G, M)\otimes _{\mathscr {O}_{X}}\kappa (x)\rightarrow H^{i_{0}}(G, M\otimes _{R} \kappa (x)) \end{aligned}$$is an isomorphism.
-
3.
Suppose further that \(i_{0}=1\), and that for y in some dense open subset of X, \(\dim _{\kappa (y)} H^{1}(G, M\otimes \kappa (y))= \dim _{\kappa (x)} H^{1}(G, M\otimes \kappa (x))\). Then the natural map
$$\begin{aligned} H^{{0}}(G, M)\otimes _{R}\kappa (x)\rightarrow H^{{0}}(G, M\otimes _{\mathscr {O}_{X}} \kappa (x)) \end{aligned}$$is an isomorphism.
Proof
By Nakayama’s lemma and the vanishing assumption, the first statement is equivalent to
Therefore, for the proof of the first and second statements it is enough to prove (5.2.1) for all \(i\ge i_{0}\), which we do by decreasing induction on i.
For \(i\ge e+1\) the result is automatic. In general, Corollary 5.1.4 gives a second-quadrant spectral sequence
By induction hypothesis, all terms on the diagonal \(q-p=i\) vanish except possibly the one with \(p=0\), and the differentials with source and target such term are 0. It follows that \(H^{i}(G, M\otimes _{\mathscr {O}_{X} }\kappa (x))=E_{\infty }^{0, i}=E_{2}^{0, i}=H^{i}(G, M)\otimes _{\mathscr {O}_{X}}\kappa (x) \).
Finally, under the assumptions of part 3, the finitely generated R-module \(H^{1}(G, M)\) is locally free of constant rank in a neighbourhood of x. Hence in the exact sequence
deduced from (5.2.2), the last term vanishes. \(\square \)
5.3 Selmer complexes and height pairings
As in the preceding subsection, let \(R^{\circ }\) be a Noetherian local ring with finite residue field of characteristic p, X an object of \(\mathscr {C}_{R}\).
When \(E_{w}\) is a local field, we write \(\mathrm{R}\Gamma (E_{w}, -):= \mathrm{R}\Gamma (G_{E_{w}}, -)\) and similarly for its cohomology groups. For number fields, we will only use the analogous shortened notation for Selmer groups.
5.3.1 Greenberg data
Let E be a number field, Sp a finite set of finite places of E containing those above p. Fix for every \(w\vert p\) an embedding \(\overline{E}\hookrightarrow \overline{ E}_{{w}}\) inducing an embedding \(G_{w}:=G_{E_{w}}\hookrightarrow G_{E, Sp}\). If M is an \(\mathscr {O}_{X}[G_{E, Sp}]\)-module, we denote by \(M_{w}\) the module M considered as an \(\mathscr {O}_{X}[G_{w}]\)-module.
Definition 5.3.1
A Greenberg datum \( ( M, (M_{w}^{+})_{w\in Sp})\) (often abusively abbreviated by M in what follows) over X consists of
-
an ind-admissible \(\mathscr {O}_{X}[G_{E, Sp}]\)-module M, finite and locally free as an \(\mathscr {O}_{X}\)-module;
-
for every \(w\in Sp\) a Greenberg local condition, that is a short exact sequence
$$\begin{aligned} 0 \rightarrow M_{w}^{+}{\mathop {\rightarrow }\limits ^{i_{w}^{+}}} M_{w}\rightarrow M_{w}^{-}\rightarrow 0 \end{aligned}$$of ind-admissible \(\mathscr {O}_{X}[G_{w}]\)-modules, finite and locally free as \(\mathscr {O}_{X}\)-modules.
In this paper, at places \(w \not \mid p\) we will only consider the strict Greenberg conditions \(M_{w}^{+}=0\).
5.3.2 Selmer complexes
Given a Greenberg datum \(M= (M, (M_{w}^{+})_{w\in Sp})\), the Selmer complex
is the image of the complex
in \(D({}_{\mathscr {O}_{X}}^\mathrm{ft}\mathrm{Mod})\). Its cohomology groups are denoted by \(\widetilde{H}^{i}_{f}(E, M)\). We have an exact triangle
Proposition 5.3.2
The Selmer complex \(\widetilde{\mathrm{R}{\Gamma }}_{f}(E, M)\) and all terms of (5.3.1) belong to \(D_\mathrm{perf}^{[0,3]}({}_{\mathscr {O}_{X}}\mathrm{Mod})\).
Proof
As in [81, Proposition 9.7.2 (ii)]. \(\square \)
From the triangle (5.3.1) we extract an exact sequence
where the last term is the (Greenberg) Selmer group
5.3.3 Height pairings
For \(?=\emptyset ,\iota \), let \(M^{?}=(M^{?}, (M_{w}^{?,+}))\) be a strict Greenberg datum for \(G_{E, Sp} \) over X. Suppose given a perfect pairing of \(\mathscr {O}_{X}[G_{E, Sp}]\)-modules
such that \(M^{+}_{w}\) and \(M^{+, \iota }_{w}\) are exact orthogonal of each other. Let \(\Gamma _{F}\) be a profinite abelian group.
For every pair of Greenberg data M, \(M^{\iota }\) as above, there is a height pairing
constructed in [81, §11.1]. The following is a special case of [103, Appendix C, Lemma 0.16].
Proposition 5.3.3
For each regular point \(x\in X\) and \(P_{1}\otimes P_{2}\in \widetilde{H}^{1}_{f}(E, M)\otimes _{\mathscr {O}_{X}} \widetilde{H}^{1}_{f}(E, M^{\iota })\), we have
Venerucci has defined height pairings in an even more general context. Let \(M_{X}\) be a strict Greenberg datum over X as above, let \(Y\subset X\) be a local complete intersection, and let \(M_{Y}^{?}\) be the restriction of \(M_{X}^{?}\). Let \(\mathscr {N}_{Y/X}^{*}\) be the conormal sheaf of \(Y\rightarrow X\). Then there is a height pairing
constructed in [103, Appendix C, § 0.21].
We note its relation to (5.3.5) in a special case, and its symmetry properties in a conjugate-self-dual case.
Proposition 5.3.4
The pairing (5.3.6) satisfies the following properties.
-
1.
Let \(\Gamma _{F}\) be a profinite abelian quotient of \(G_{E, Sp}\), let \(X=Y\hat{\times }_{\mathrm {Spec}\,\mathbf {Q}_{p}}\mathrm {Spec}\,\mathbf {Z}_{p}\llbracket \Gamma _{F}\rrbracket _{\mathbf {Q}_{p}}\) (where \(\hat{\times }=\) (5.1.2)), and assume that \(M_{X}^{?}=M_{Y}^{?}\otimes _{\mathbf {Z}_{p}} \mathbf {Z}_{p}\llbracket \Gamma _{F} \rrbracket \) for \(?=\emptyset , \iota \), where if \(?=\emptyset \) (respectively \(?=\iota \)) then \(G_{E, Sp}\) acts on \(\Gamma _{F}\) through the tautological character (respectively its inverse). Then
$$\begin{aligned} h_{M_{Y}/M_{X}} = h_{M_{Y}}=(5.3.5). \end{aligned}$$ -
2.
Suppose that there is an involution \(\iota :X\rightarrow X\) stabilising Y and such that \(M_{X}^{\iota }= M_{X}\otimes _{\mathscr {O}_{X}, \iota }\mathscr {O}_{X}\), \(M_{X,w}^{+,\iota }= M_{X, w}^{+}\otimes _{\mathscr {O}_{X}, \iota }\mathscr {O}_{X}\). Let \(\epsilon , \epsilon '\in \{\pm 1\}\). Assume that the pairing (5.3.4) is \(\epsilon \)-hermitian (Sect. 4.1.1), that \(\mathrm{d}_{Y/X}\iota = \epsilon '\mathrm {id}\) on \(\mathscr {N}_{Y/X}^{*}\), and that there is an \(\mathscr {O}_{Y}\)-linear isomorphism
$$\begin{aligned} \mathrm{c}:\widetilde{H}^{1}_{f}(E, M_{Y}^{\iota }) = \widetilde{H}^{1}_{f}(E, M_{Y})^{\iota } \rightarrow \widetilde{H}^{1}_{f}(E, M_{Y}) . \end{aligned}$$Then the pairing
$$\begin{aligned} \begin{aligned} h_{M_{Y}/M_{X}}^{\Box } :\widetilde{H}^{1}_{f}(E, M_{Y})\otimes _{\mathscr {O}_{Y}} \widetilde{H}^{1}_{f}(E, M_{Y})&\rightarrow \mathscr {N}_{Y/X}^{*}\\ (z, z')&\mapsto h_{M_{Y}/M_{X}}(z, \mathrm{c} z') \end{aligned} \end{aligned}$$(5.3.7)is \(\epsilon \epsilon '\)-symmetric.
In our main application in Theorem D, we have \(Y=\mathscr {X}\) (or an open subset), the Hida family for \((\mathrm {G}\times \mathrm {H})'\); \(X=\mathscr {X}^{\sharp }\), the Hida family for \(\mathrm {G}\times \mathrm {H}\) containing X; and \(M_{Y}=\mathscr {V}\), \(M_{X}=\mathscr {V}^{\sharp }\), the corresponding universal \(G_{E}\)-representations. In that case, the height pairing \(h_{\mathscr {V}/\mathscr {V}^{\sharp }}\) is simply 1/2 of the pairing \(h_{\mathscr {V}}\) of Proposition 5.3.3.
Proof
Part 1 follows from the construction. (We omit further details since, by the remark preceding the present proof, we do not actually need it in this paper). We prove the symmetry properties. Let I be the ideal sheaf of Y; up to restricting to some open subset of X we may assume that I is generated by a regular sequence \(x=(x_{1}, \ldots , x_{r})\). Then \(\mathscr {N}_{Y/X}^* = I/I^2\) is finite locally free generated by \(([x_1], \ldots , [x_r])\). Let \(\partial _i \in N = (I/I^2)^\vee \) be the map \(\partial _i([x_j])=\delta _{ij}\). It suffices to show that \(h_i:=\partial _i \circ h\) is \(\epsilon \epsilon '\)-hermitian for all i. By [103, Appendix C, Proposition 0.5], \(h_i\) is identified with \( h_{M_{Y}/M_{X_{i}}}\), where \(X_i=V_{X}((x_j)_{j\ne I})\) so that \(Y=V_{X_{i}}(x_{i})\). Hence it suffices to prove the claim for \(r=1\).
We argue similarly to [103, Proof of Corollary 10.10]. Assume thus \(r=1\), write x in place of \(x_{1}\), and let K be the fraction field of X. By [81] and [103, Appendix A, § 0.7] we have an \(\epsilon \)-hermitian Cassels–Tate pairing
and by [103, Appendix C, Proposition 0.17], we have a map
such that \(h_{M_{Y}/M_{X}}\) coincides with
Since all the above maps are \(\iota \)-equivariant, we find that \(h_{M_{Y}/M_{X}}\) is \(\epsilon \)-hermitian as well. The desired assertion follows from this and the fact that \(\iota \) acts by \(\varepsilon '\) on \(\mathscr {N}^{*}_{Y/X}\). \(\square \)
6 Universal Heegner class
6.1 Tate cycles and Abel–Jacobi maps
Let X/E be an algebraic variety over a number field, and let R be a finite extension of \(\mathbf {Q}_{p}\), or its ring of integers, or a finite quotient of its ring of integers.
6.1.1 Tate cycles
If \(\mathscr {W}\) is an étale local system of \(R[G_{E}]\)-modules on X, the R-module of Tate (0)-cycles is the space
where the sum runs over the closed points of X and, if \(x\in X\) and \(\overline{x}:= x\times _{\mathrm {Spec}\,E}\mathrm {Spec}\,\overline{E}\), we define \(H^{0}(x, \mathscr {W}):= H^{0}(\overline{x}, \mathscr {W})^{G_{E}}\). Elements of the latter space are written \(\sum _{\overline{x}'} [\overline{x}' ]\otimes \xi _{\overline{x}'}\), where \(\overline{x}'\) runs through the points of \(\overline{x}\). When \(\mathscr {W}=R\), the module \(\mathscr {Z}_{0}(X, R)\) is simply the usual R-module of 0-cycles with coefficients in R. Its quotient by the relation of rational equivalence is denoted \(\mathrm{CH}_{0}(X, R)\).
When X has dimension 0, its fundamental class is the Tate cycle with trivial coefficients
If \(a=\sum _{\overline{x}'}[\overline{x}'] \otimes \xi _{\overline{x}'}\in \mathscr {Z}_{0}(X, \mathscr {W})\) its support \(|a|\subset \overline{X}\) is the support of the divisor \(\sum [\overline{x}']\), where the sum extends to those \(\overline{x}' \) such that \(\xi _{\overline{x}'}\ne 0\).
6.1.2 Abel–Jacobi map
A Tate cycle \(a\in \mathscr {Z}_{0}(X, \mathscr {W})\) yields a map \(R\rightarrow H^{0}(|a|, \mathscr {W})^{G_{E}}\) and, if X has dimension 1, the latter cohomology group maps to \(H^{2}_{|a|}(\overline{X}, \mathscr {W}(1)) \). The image of \(1\in R\) under the compostion
is denoted by \(\overline{\mathrm{cl}}(a)\). Consider the exact sequence
Let e be a Galois-equivariant idempotent acting on the right on \(H^{*}(\overline{X}, \mathscr {W}(1) )\), such that \(\overline{\mathrm{cl}}(a)e=0\). Then we may apply the idempotent e to (6.1.1) and pull back the resulting exact sequence via the map \(R\rightarrow H^{2}_{|a|}(\overline{X}, \mathscr {W}(1))\) given by a, obtaining an extension
in the category of \(G_{E}\)-representations over R. The map sending a to the class \(\mathrm{AJ}(a)e\) of this extension is called the e-Abel–Jacobi map,
where the last equality is just a reminder of our notational conventions. When \(e=\mathrm{id}\), it is omitted from the notation. When \(\mathscr {W}=R\) and e acts via correspondences, the map \(\mathrm{AJ}e\) factors through \(\mathrm{CH}_{0}(X, R)e\).
6.2 Heegner cycles
We use the notation from Sect. 2.1 for compact subgroups \(U_{*,p, \underline{r}}\subset U_{*,p}(p^{\underline{r}})\subset \mathrm {G}_{*}(\mathbf {Q}_{p})\) and let \(X_{*, U^{p}_{*}{}',\underline{r}}\rightarrow X_{*, U^{p}{}'}(p^{\underline{r}})\) be the associated Shimura varieties; the level \(U_{*}^{p}{}'\) will be fixed and often omitted from the notation. If \(p\mathscr {O}_{F,p}=\prod _{v\vert p }\varpi _{v}^{e_{v}}\mathscr {O}_{F, v}\) we use r as a shorthand for \(\underline{r}=(e_{v}r)_{v\vert p}\).
6.2.1 Embeddings of Shimura varieties
For any pair of subgroups \(V'\subset \mathrm {H}'(\mathbf {A}^{\infty })\), \(K\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{\infty })\) such that \(K \cap \mathrm {H}'(\mathbf {A}^{\infty }) \supset V\), we define the diagonal embedding
if \(\tilde{y}\) is any lift of y to \(Y_{V}\) for some \(V\subset \mathrm {H}(\mathbf {A}^{\infty })\) such that \(VF_{\mathbf {A}^{\infty }}^{\times }\subset V'\).
Let \(W=W_{\mathrm {G}}\otimes W_{\mathrm {H}}\) be an irreducible right algebraic representation of \((\mathrm {G}\times \mathrm {H})'\) over \(L\supset \mathbf {Q}_{p}\). If W satisfies (wt), the space \( W^{H'}\) is 1-dimensional over L. Let \(\mathscr {W}\) be the étale sheaf on the Shimura tower Z associated with W; any \(\xi \in W^{H'}\) induces a map \( \mathbf {Q}_{p}\rightarrow \mathrm{e}'^{*}\mathscr {W}\) of étale sheaves on the tower \(Y'\); by adjunction we obtain a canonical map \( \mathbf {Q}_{p}\rightarrow \mathrm{e}'^{*}\mathscr {W}\otimes W^{\vee }_{H'}\) where the second factor is simply an L-line.
We let
be the compositions of the maps described above and, respectively, \(\mathrm{e}'_{W, *}\) or \(\mathrm{e}'_{\underline{r}, *}\).
6.2.2 CM cycles
Let \([Y_{V'}']\in \mathscr {Z}_{0}(Y'_{V'}, \mathbf {Z}_{p})\) be the fundamental class. For any pair of levels K, V such that \(\mathrm{e}_{W,(K, V')} \) is defined, let
When \( W\ne \mathbf {Q}_{p}\), we consider the elements
When \(W=\mathbf {Q}_{p}\), we consider the modification
where \(\xi _{\text {Hodge}} \) is the Hodge class of [107, §3.1.3], whose introduction is motivated by the following lemma.
Lemma 6.2.1
The image under pushforward of \(\Delta ^{\circ }_{W,(K'', V'')} \) in \( \mathscr {Z}_{0}(Z_{K}, \mathscr {W})\) (if \(W\ne \mathbf {Q}_{p}\)) or \(\mathrm{CH}_{0}(Z_{K})_{\mathbf {Q}_{p}}\) (if \(W=\mathbf {Q}_{p})\) is independent of \(V'', K''\) such that \(V''\subset K''\cap \mathrm {H}'(\mathbf {A}^{\infty }) \) and \(K'\subset K\). We have
Proof
If \(W\ne \mathbf {Q}_{p}\), the first assertion is clear; the second one is automatic as \(H^{2}(\overline{Z}_{K}, \mathscr {W}(1))=0\) (see the argument in [91, bottom of p. 1089]). If \(W=\mathbf {Q}_{p}\), the assertions amount, respectively, to the compatibility of the Hodge classes under pushforward and the fact that, by construction, the 0-cycle \(\Delta _{K, V}^{\circ }\) has degree zero; both facts are explained in [107, §3.1.3]. \(\square \)
6.2.3 Cycles, Selmer classes, and functionals
Let
The classes \(P_{W,( K, V')}\) are also compatible under pushforward and yields elements
The space in the right-hand side has a right action by \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{\infty })\), and \(P_{W}\) is invariant under \(\mathrm {H}'(\mathbf {A}^{\infty })\). Via (2.5.3) and the biduality \(W^{\vee \vee }=W\), \(P_{W}\) yields, for each ordinary representation \(\Pi \) of weight W, a map
Using the map \(\gamma _{H'}^{\mathrm {ord}}:\Pi ^{\mathrm {ord}}\rightarrow \Pi _{H'} \) from Proposition A.2.4, we also obtain a map
Remark 6.2.2
We conjecture that (i) there exist an algebraic variety \(N_{W,(K, V')}/E\) of odd dimension \(2d_{W}+1\), a homologically trivial cycle \(\mathfrak {Z}_{W, (K, V')}\in \mathrm{CH}_{d_{W}}(N_{W, (K, V')})_{0}\), and a map
such that \(P_{W, (K, V')} =\lambda (\mathrm{AJ}(\mathfrak {Z}_{W, (, V')}))\); (ii) the elements \(P_{W, (K, V')}\) belong to \( H^{1}_{f}(E, H_{1}(\overline{Z}_{K}, \mathscr {W}))\), so that the maps \(P_{\Pi }\) take values in \(H^{1}_{f}(E, V_{\Pi })\).
When \(\mathrm {G}=\mathrm {GL}_{2/\mathbf {Q}}\), one can prove (i) with \(N_{W, (K, V')}\) a Kuga–Sato variety for \(Z_{K}\), generalising [78, Proposition II.2.4]. The (probably not insurmountable) difficulty in the general case is that, if \(F\ne \mathbf {Q}\), the Shimura variety Z is not of PEL-type. Part (ii) should essentially be a consequence of either (a) part (i), via [79, 82], or (b) granted a generalisation of the theory of locc. citt. to nontrivial coefficients system, of the weaker assertion that, for a finite place w of E, the image of \(\Delta _{W, (K, V')}\) in \(H_{0}({Z}_{K, E_{w}},\mathscr {W})\) comes from a corresponding class in the syntomic cohomology of \(Z_{K, E_{w}}\) with coefficients in \(\mathscr {W}\).
6.3 Universal Heegner class
We use the local construction described in Sect. A.2.2 to turn the \(\mathrm {H}'(\mathbf {A})\)-invariant class \(P_{W}\) into an \(\mathrm {H}'(\mathbf {A}^{p\infty })\)-invariant class \(\mathscr {P}_{W}\) with values in the ordinary completed homology. Then we show that \(\mathscr {P}_{W}\) is independent of W and it interpolates \(P^{\circ }_{\Pi }\) at all representations \(\Pi \) satisfying (ord), (n-exc).
6.3.1 Construction
Let \(d_{\underline{r}}:=|Y'_{\underline{r}}(\overline{E})|\) and let \( d^{\circ } = d_{\underline{r}}\prod _{v\vert p}q_{v}^{-r_{v}} \in \mathbf {Z}_{\ge 1}\), which is the limit of an eventually constant sequence. Recall that for the tame level \(K^{p}{}'\subset ( \mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p\infty }), \) we denote \(M^{\circ }_{K^{p}{}', W}:= \varprojlim _{r}\mathrm {H}_{1} (\overline{Z}_{W,r}, \mathscr {W}^{\circ })^{\mathrm {ord}}\).
Definition 6.3.1
The universal Heegner point of weight W is the element
where we still denote by \(\gamma _{H'}^{\mathrm {ord}}\) the map induced by the map
of Proposition A.2.4. As usual, we simply write \(\mathscr {P}:= \mathscr {P}_{\mathbf {Q}_{p}}\). When we want to emphasise the choice of \(K^{p}{}'\) we write \(\mathscr {P}_{K^{p}{}', W}\) instead of \(\mathscr {P}_W\).
6.3.2 Independence of weight
The class \(\mathscr {P}_{W}\) does not depend on W.
Proposition 6.3.2
Under the identification
induced from the isomorphism \(j_{W}\) of Proposition 3.1.2.2, we have
Proof
We show that the difference \(j_{W, *}(\mathscr {P})- \mathscr {P}_{W}\) is p-divisible. Since \(H^{1}(G_{E, Sp}, M^{\circ }_{K^{p}{}',W}) \) is a finitely generated module over the ring \(\Lambda ^{\circ }_{K^{p}{}'}\) by Lemma 5.2.1, any p-divisible element is zero. We will use some of the notation and results of the Appendix, in particular the matrices \(\gamma \) defined in Sect. A.1, the involution \(\iota =(-)^\mathrm{T, -1}\) on \(\mathrm {GL}_{2}\), and the operator \(\gamma _{H'}^{\mathrm {ord}} \) of Proposition A.2.4.
We tacitly multiply both sides by \(d^{\circ }\), so that they belong to the lattices (6.3.2). By the definitions of \(\mathscr {P}_{W}\) and \(j_{W}\), we need to show the following. Denote by \([ -]_{r}\) the reduction modulo \(p^{r}\), and by c(W) the constant (A.2.3); then we should have
under the map
where \(\zeta _{r}\otimes \zeta _{r}^{\vee }\) is the unique element pairing to 1.
As the local system \(\mathscr {W}^{\circ }/p^{r}\mathscr {W}^{\circ }\) is trivial on \(\overline{Z}_{K^{p}K_{p}(p^{r})}\), we have
in
where \(\xi \otimes \xi ^{\vee }\) is the unique element pairing to 1. Note first that the image of \( [p^{r[F:\mathbf {Q}]}\Delta _{W, \underline{r}}]_{r}\) under \(\gamma _{r, p}\mathrm {U}_{p}^{-r}\gamma _{0, \infty }^{\iota }\) belongs to the right-hand side of (6.3.3): indeed it suffices to show that for any \(\xi \in W^{\circ }\), the class \([\xi \gamma _{r}]_{r}\) is fixed by \(N_{0, r}\), which follows from the congruence
valid for any \(n\in N_{0, r}\).
It remains to see that if \(\xi \otimes \xi ^{\vee }\) pairs to 1, then so does \(c(W)^{-1}\cdot \xi \gamma _{r, p}\otimes \xi ^{\vee }\gamma _{0, \infty }^{\iota }\) in the limit \(r\rightarrow \infty \). This is proved in Lemma A.4.2. \(\square \)
6.4 Local properties of the universal Heegner class
Recall that \(\mathscr {X}\) is an irreducible component of \(\mathscr {E}_{K^{p}}\) hence of the form \(\mathrm {Spec}\,R\) with \(R=R^{\circ }[1/p ]\) and \(R^{\circ }= \mathbf{T}_{(\mathrm {G}\times \mathrm {H})', K^{p}, \mathfrak {m}}^{\mathrm{sph}, \mathrm {ord}}/\mathfrak {a}\) for some maximal and minimal ideals \(\mathfrak {m}\subset \mathfrak {a}\subset \mathbf{T}_{(\mathrm {G}\times \mathrm {H})', K^{p}}\). The ring \(R^{\circ }\) satisfies the assumptions of Sect. 5.3, hence Greenberg data over open subsets of \(\mathscr {X}\) give rise to sheaves of Selmer complexes.
Let \(\mathscr {X}^{(i)}\subset \mathscr {X}\subset \mathscr {E}_{K^{p}{}'}\) be the open sets defined in Sect. 3. Proposition 3.2.4 provides a strict Greenberg datum \((\mathscr {V}, (\mathscr {V}_{w}^{+})_{w\vert p}, (0)_{w\in S})\) over \(\mathscr {X}\). Via Proposition 3.3.8.2 we obtain a strict Greenberg datum \((\mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}}, (\mathscr {M}_{K^{p}{}', w}^{{H_{\Sigma }'}, +})_{w\vert p}, (0)_{w\in S}) \) over \(\mathscr {X}^{(3)}\) with
We begin the study of the Selmer complexes attached to the above Greenberg data, with the goal to promote \(\mathscr {P}\) to a section of \(\widetilde{H}^{1}_{f}({E}, \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}})\) over a suitable open subset of \(\mathscr {X}\).
6.4.1 Comparison of Bloch–Kato and Greenberg Selmer groups
Let \(z\in \mathscr {X}^{\mathrm {cl}}\) and let \(V=\mathscr {V}_{|z}\). We compare two notions of Selmer groups for V.
Lemma 6.4.1
Let \(w\not \mid p\) be a place of E. Then, for all i,
Proof
As observed in [80, Proposition 2.5], this is implied by the prediction from the weight-monodromy conjecture that the monodromy filtration on \(\mathscr {V}_{z}\) is pure of weight \(-1\). Writing \(z=(x, y)\in \mathscr {E}^{\mathrm {ord}, \mathrm {cl}}\subset \mathscr {E}_{\mathrm {G}}^{\mathrm {ord},\mathrm {cl}}\times \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm {cl}}\), the weight-mondromy conjecture for \(\mathscr {V}_{z}\) follows from the corresponding statement for \(\mathscr {V}_{\mathrm {G},x}\), that is Theorem 2.5.1.2. \(\square \)
Let \(H^{1}_{f, \mathrm{Gr}}({E}, V)\) be the Greenberg Selmer group. Bloch and Kato [11] have defined subspaces \(H^{1}_{f}(E_{w}, V)\subset H^{1}(E_{w}, V)\) and a Selmer group
Lemma 6.4.2
Suppose that \(\Pi _{z}\) satisfies \((wt )\). We have
where the right-hand side is the Greenberg Selmer group as in (5.3.3).
Proof
We need to show that for all \(w\in Sp\), \( H^{1}_{f}(E_{w}, V)= \mathrm {Ker}\,\left( H^{1}(E_{w}, V)\right. \left. \rightarrow H^{1}_{f}(E_{w}, V_{w}^{-})\right) \). This is automatic for \(w\not \mid p\) by Lemma 6.4.1. For \(w\vert p\) this is [81, (12.5.8)]: the context of loc. cit is more restricted but the proof still applies, the key point being that (12.5.7)(1)(i) ibid. still holds for all w under the weight condition (wt). \(\square \)
Lemma 6.4.3
Let \(w\not \mid p\) be a finite place of E. Then \(H^{1}(E_{w},\mathscr {V})\) and \(H^{1}(E_{w}, \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}}) \) are supported in a closed subset of \(\mathscr {X}\) (respectively \(\mathscr {X}^{(3)}\)) disjoint from \(\mathscr {X}^{ \mathrm {cl}}\).
Proof
This follows from Proposition 5.2.3 and Lemma 6.4.1. \(\square \)
6.4.2 Local Selmer properties of \(\mathscr {P}\)
Let \(w\not \mid p\) be a place of E as above. As
over \(\mathscr {X}^{(3)}\), the support of \(H^{1}(E_{w}, \mathscr {M}_{K^{p}{}'}^{{H_{\Sigma }'}}) \) is in fact the intersection of \(\mathscr {X}^{(3)}\) and of the support of \(H^{1}(E_{w},\mathscr {V})\). We denote by
the open complement in \(\mathscr {X}^{(3)}\) of the support of \(H^{1}(E_{w},\mathscr {V})\) .
Lemma 6.4.4
Let \(w\vert p\) be a place of E, with underlying place v of F. The image \(\mathrm{loc}_{w}^{-}(\mathscr {P})\) of \(\mathscr {P}\) in
vanishes over \(\mathscr {X}^{(3)}\).
Proof
We lighten the notation by dropping form the notation the superscript ‘(3)’ and all decorations from \(\mathscr {M}\), \(\mathscr {M}_{w}^{-}\). Let \(\tilde{\mathscr {X}} := \mathrm {Spec}\,_{\mathscr {X}} \mathscr {O}_{\mathscr {X}} [([\sqrt{z}])_{z\in A}]\), where A is a (finite) set of topological generators for \(F^{\times }\backslash \mathbf {A}_{F}^{\infty \times }/(K^{p}{}'\cap \mathrm{Z}(\mathbf {A}_{F}^{p\infty \times }))\). As \(\tilde{\mathscr {X}}\rightarrow \mathscr {X}\) is faithfully flat, we may prove the statement after a base-change to \(\tilde{\mathscr {X}}\); we denote base-changed sheaves and sections thereof with a tilde \(\tilde{\Box }\).
Let \(\chi :E^{\times } \backslash \mathbf {A}_{E}^{\infty \times }\rightarrow G_{E}^\mathrm{ab}\rightarrow \mathscr {O}(\mathscr {X})^{\times }\) be the universal character, and let \(\omega =\chi _{|F^{\times }\backslash \mathbf {A}_{F}^{\infty \times }}\), so that \(\det \mathscr {V}_{\mathrm {G}|\mathscr {X}} (-1)=\omega \). Let \(\omega ^{1/2} :F^{\times }\backslash \mathbf {A}_{F}^{\infty \times } \rightarrow \mathscr {O}(\tilde{\mathscr {X}})^{\times }\) be a square root of \(\omega \). We may write
where now \(\tilde{\chi }':G_{E} \rightarrow \mathrm {Gal}(E_{\infty }/E)\) is the projection for the abelian extension \(E_{\infty }/E\) such that \(\mathrm {Gal}(E_{\infty }/E) \) is the maximal pro-p quotient of \(E^{\times }\mathbf {A}_{F}^{\infty \times } \backslash \mathbf {A}_{E}^{\infty \times } /V^{p}{}'\).
Write \(E_{\infty }=\bigcup _{n\ge 0} E_{n}\) as an increasing union of finite extensions, where \(E_{0}=E\) and eventually \(E_{n+1}/E_{n}\) is totally ramified at each prime above p, and let \(\tilde{\chi }'_{n}:G_{E}\rightarrow \mathrm {Gal}(E_{n}/E)\) be the natural projection. Let \(\alpha ^{\circ }_{v}\) be the character giving the \(G_{F_{v}}\)-action on \(\mathscr {V}_{\mathrm {G}}^{+}(-1)\), so that
where for a character \(\omega '_{v}\) of \(G_{F_{v}}\), we denote \(\omega '_{w}:=\omega '_{v|\mathrm {G}_{E_{w}}}\). Let
Then the same argument as in [58, proof of Proposition 2.4.5, primes \(v\vert p\)] shows that the image \(\mathrm{loc}_{w}^{-}(\tilde{\mathscr {P}})\) vanishes in \(H^{1}(E_{w},\mathscr {M}^{-}_{n,w})= \prod _{w'\vert w} H^{1}(E_{n},\tilde{\mathscr {M}}^{-}_{0,w})\) for each n; here \(w'\) runs through the (eventually constant) set of primes of \(E_{n}\) above w. Since \(H^{1}(E_{w},\tilde{\mathscr {M}}^{-}_{w}) =\varprojlim _{n} H^{1}(E_{w}, {\tilde{\mathscr {M}}}^{-}_{n, w})\) by Proposition 5.2.2, the lemma is proved. \(\square \)
Corollary 6.4.5
Let \(\mathscr {X}^{(3, f)}:=\bigcap _{w\in S} \mathscr {X}^{(3,w)}\supset \mathscr {X}^{\mathrm {cl}}\), where the sets \(\mathscr {X}^{(3, w)}\) are as defined in (6.4.1). Then \(\mathscr {P}\) defines a section
Proof
This follows from Lemmas 6.4.3 and 6.4.4. The displayed equality is a consequence of (5.3.2). \(\square \)
6.4.3 Proof of Theorem C
Via Proposition 3.3.8.2, we may view the class \(\mathscr {P}=\mathscr {P}_{K^{p}}=\mathscr {P}_{K^{p}, \mathbf {Q}_{p}}\) (Definition 6.3.1) as an \(\mathscr {H}_{K}^{p\Sigma }\)-equivariant functional
By the results of Sect. 6.4.2, \(\mathscr {P}\) takes values in the Selmer group \(\widetilde{H}^{1}_{f}(E, \mathscr {V})(\mathscr {X}^{(3,f)})\). It satisfies the asserted interpolation properties by the definitions of the classes \(\mathscr {P}_{W}\) in Sect. 6.3 and Proposition 6.3.2.
6.4.4 Exceptional locus of \(\mathscr {X}\)
Let w|v be places of E and F above p, and let \(\mu _{w}^{\pm }:E_{w}^{\times }\rightarrow \mathscr {O}(\mathscr {X})^{\times }\) be the characters giving the Galois action on \(\mathscr {V}^{\pm }\). Let \(\mathscr {X}^{\mathrm{exc},v }\subset \mathscr {X}\) be the closed subset defined by \(\mu _{w}^{-}=1\) for some (hence automatically all) places \(w\vert v\) of E. We let
We say that an ordinary automorphic representation of \(\Pi =\Pi _{|z}\) over a p-adic field is exceptional at the place \(v\vert p\) if \(z\in \mathscr {X}^{\mathrm {exc}, v}\).
We may characterise the exceptional representations, and seize the opportunity to collect some useful results; see also Lemma A.2.5.
Lemma 6.4.6
Let \(\Pi =\pi \otimes \chi \) be an ordinary automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A})\) over a p-adic field L, of numerical weights \(\underline{w}\), \(\underline{l}\).
-
1.
Let \(v\vert p\) be a place of F. The following are equivalent:
-
(a)
the representation \(\Pi \) is exceptional at v;
-
(b)
\(e_{v}(V_{(\pi , \chi )})=\) (1.4.4) \(=0\);
-
(c)
the following conditions hold:
-
the smooth representation \(\pi _{v}\) of \(G_{v}\) is special of the form \(\mathrm{St}\otimes \alpha _{v}\);
-
for some (equivalently all) places \(w\vert v \) of E, we have \(\chi _{w} \cdot \alpha _{v}\circ N_{E_{w}/F_{v}}=\mathbf {1}\).
-
\(w_{\sigma }=2\) and \(l_{\sigma }=0\) for all \(\sigma :F\hookrightarrow \overline{L}\) inducing the place v.
-
-
(a)
-
2.
Let \(S_{p}^\mathrm{exc}= S_{p}^\mathrm{exc,\, s} \cup S_{p}^\mathrm{exc, \, ns}\) be the set of places \(v\vert p\) (respectively those that moreover are split, nonsplit in E) where \(\Pi \) is exceptional.
-
(a)
The kernel of the natural surjective map
$$\begin{aligned} \widetilde{H}^{1}_{f}(E, V_{\Pi }) \rightarrow {H}^{1}_{f}(E, V_{\Pi }) \end{aligned}$$has dimension \(2 |S_{p}^\mathrm{exc, \, s}| + |S_{p}^\mathrm{exc, \, ns}|\).
-
(b)
Assume that \(\mathrm {G}\) is associated with a quaternion algebra \(\mathbf {B}\) that is split at all places \(v\vert p\). Then
$$\begin{aligned} \varepsilon _{v}^{\mathrm {G}}(V_{\Pi }) = -1\quad \Longleftrightarrow \quad v\in S_{p}^\mathrm{exc, \, ns}. \end{aligned}$$
-
(a)
Proof
Consider part 1. We first prove the equivalence of the first two conditions. The adjoint gamma factor in the denominator of each \(e_{v}(V_{(\pi , \chi )})\) is always defined and nonzero, whereas the gamma factor in the numerator is never zero and it has a pole if and only if, for some \(w\vert v\), \(V_{w}^{+}\) is the cyclotomic character of \(E_{w}^{\times }\). This happens precisely when, for some \(w\vert v\), \(V_{w}^{-}\) is the trivial character – that is, when \(\Pi \) is exceptional at v.
Now let us prove the equivalence to (c). Let \(V=V_{\Pi }=V_{\pi |G_{E}}\otimes V_{\chi }\). By the weight-monodromy conjecture (Theorem 2.5.1.2), the 1-dimensional representations \(V^{\pm }_{\pi ,v}\) are both of motivic weight \(-1\), thus have no \(G_{E_{w}}\)-invariants for any \(w\vert v\), unless \(\pi _{ v}\) is a special representation. In the latter case \(V^{+}_{w|z}\) (respectively \(V_{w}^{-})\) is of weight \(-2\) (respectively 0). This is compatible with the ordinariness requirement only when the weight \(\underline{w}\) is 2 at v as in the statement of the lemma. The second condition in (c) is immediate from the definition of (a).
Consider now part 2. The first statement follows directly from (5.3.2). Let us prove the second one. By the results recalled in Sect. 1.2.5 and [105, Lemme 10], the condition \( \varepsilon _{v}^{\mathrm {G}}(V_{\Pi }) = -1\) is equivalent to the vanishing of the functional \(Q=Q_{\Pi _{v}}=\) (4.2.1) and of the space \(\Pi _{v}^{*, H'_{v}}\). These conditions are never met if v splits in E or \(\pi _{v}\) is a principal series, and otherwise they are equivalent to the nonvanishing of \((\Pi _{v}')^{*, H_{v}'}\), where \(\Pi '_{v}=\pi _{v}'\otimes \chi _{v}\) and \(\pi _{v}'\) denotes the Jacquet–Langlands transfer of \(\pi _{v}\) to the nonsplit quaternion algebra \(B_{v}'^{\times }\) over \(F_{v}\).
Assume that v is nonsplit in E. If \(\pi _{v}\) is exceptional, then by part 1 we have \(\pi _{v}' = \chi _{v}\circ \mathrm{Nm}\), where \(\mathrm{Nm} \) is the reduced norm of \(B_{v}'\), so that obviously \((\Pi _{v}')^{*, H_{v}'}\ne 0\). If \(\pi _{v}\) is not exceptional, then by the explicit computation of Proposition A.3.4 we have \(Q_{\Pi _{v}'}\ne 0\) (see also [35, Corollary A.2.3] for a variant of the last argument). \(\square \)
6.4.5 Heegner classes belong to the Bloch–Kato Selmer group
We can now prove the first assertion of Theorem B.
Proposition 6.4.7
If \(\Pi \) is not exceptional or has trivial weight, the map \(P_{\Pi }\) of (1.2.4) takes values in \(H^{1}_{f}(E, V_{\Pi })\subset H^{1}(G_{E, Sp},V_{\Pi })\).
Proof
If \(\Pi \) has trivial weight this is clear. Assume that \(\Pi \) is not exceptional. Let \(\partial :H^{1}(E, V)/H^{1}_{f}(E , V)\rightarrow L\) be any linear map. Then we need to show that the \(\mathrm {H}'(\mathbf {A})\)-invariant map \(\partial P_{\Pi }:\Pi \rightarrow L\) is zero. By Corollary 6.4.5 and Theorem C, whose proof we have just completed, the map \(P_{\Pi }^{\mathrm {ord}}\) takes values in \(H^{1}_{f}(E, V)\); equivalently, \(\partial P_{\Pi }\gamma _{H'}^{\mathrm {ord}} =0\). Since \(\Pi \) is not exceptional, by Lemma A.2.5 this means that \(\partial P_{\Pi }=0\). \(\square \)
6.4.6 Enhanced ordinary Heegner classes for exceptional representations
For any \(z=(x, y)\in \mathscr {X}^{\mathrm {cl}}\) corresponding to a representation \(\Pi \), define the enhanced Heegner class
By the results established so far, \( \widetilde{P}_{\Pi }^{\mathrm {ord}}\) has image \(P_{\Pi }^{\mathrm {ord}}\) under the natural map \( \widetilde{H}^{1}_{f}(E, V_{\Pi })\rightarrow {H}^{1}_{f}(E, V_{\Pi })\); as noted in Lemma 6.4.6, this map fails to be an isomorphism precisely when \(\Pi \) is exceptional.
7 The main theorems, and a conjecture
In this section, we prove our main theorems (Sect. 7.1, or Sect. 7.3.6 for Theorem G), as well as a universal Waldspurger formula for families of ‘sign \(+1\)’ (Sect. 7.2). Then, we discuss a conjecture on the leading terms of universal Heegner points (and toric periods) at classical points (Sect. 7.3).
7.1 Proofs of the main theorems
Both of our central theorems (Theorems B and D) ultimately follow from [32, 35], where Theorem B is established when W is trivial, by an argument combining interpolation and multiplicity-one principles.
7.1.1 p-adic Gross–Zagier formula for ordinary forms
We start by stating a variant of Theorem B, valid under the same assumptions.
Theorem
\(\text {B}^{\, \mathrm {ord}}\). Let \(\Pi =\pi \otimes \chi \) be an ordinary, locally distinguished automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A})\) over L. Let \(V=V_{\Pi }\), and let \(\widetilde{P}_{\Pi }^{\mathrm {ord}} \in \widetilde{H}^{1}_{f}(E, V_{\Pi })\) be the enhanced Heegner class defined in (6.4.4).
Then for all \(f_{1}^{}\in \Pi _{H'_{\infty }}^{\mathrm {ord}}\), \(f_{2}^{}\in \Pi ^{\vee , \mathrm {ord}}_{H'_{{\infty }}}\), \(f_{3}^{}\in \Pi ^{\mathrm {ord}}\), \(f_{4}^{}\in \Pi ^{\vee , \mathrm {ord}}\) with \((f_{3}, f_{4})^{\mathrm {ord}}\ne 0\), we have
Remark 7.1.1
In contrast to Theorem B:
-
Theorem \(\text {B}^{\, \mathrm {ord}}\) also holds for exceptional \(\Pi \);
-
we have only included the Gross–Zagier formula and omitted an analogue to the first statement of Theorem B, that is that \(\widetilde{P}_{\Pi }^{\mathrm {ord}}\) takes values in \(\widetilde{H}^{1}_{f}(E, V)\), as that has already been established.
Lemma 7.1.2
Suppose that \(\Pi \) is not exceptional. Theorem \(\text {B}^{\, \mathrm {ord}}\) is equivalent to Theorem B.
Proof
Using freely the notation and results of “Appendix A”, we first show that Theorem \(\text {B}^{\, \mathrm {ord}}\) for \(f_{1}\), \(f_{2}\), \(f_{3}\), \(f_{4}\) is equivalent to Theorem B for
let us call such \((f_{1}', f_{2}', f_{3}', f_{4}' )\) a ‘special quadruple’.
Indeed, by the definitions (6.2.3), (4.1.8), the left hand side of (7.1.1) equals
whereas by Proposition 4.3.4,
By the multiplicity-one principle, Theorem B for special quadruples implies Theorem B in general, since under our assumptions the functional Q is non-vanishing on special quadruples: this again follows from Proposition 4.3.4 and Lemma 6.4.6.1.(a)–(b). \(\square \)
7.1.2 Comparison of p-adic L-functions
We describe how, upon restricting \( \mathscr {L}_{p}(\mathscr {V}^{\sharp })\) to the cyclotomic line through a point of trivial weight, we recover the p-adic L-function of [32, 35].
Lemma 7.1.3
Let \(z=(x, y)\in \mathscr {E}_{\mathrm {G}_{0}}^{\mathrm {ord}, \mathrm cl}\times \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm {cl}}\) be a point corresponding to a representation \(\pi _{0 ,x}\otimes \chi _{y}\) of weights \((0; (2, \ldots , 2))\), \((0;0, \ldots , 0)\). Let A denote the modular abelian variety attached to \(\pi _{0,x}\), and let
be the p-adic L-function of [35, Theorem A]. Consider the map
Then
Proof
This is immediate from the respective interpolation properties. (Note that the first equality in (7.1.2) is just a reminder of (1.1.1).) \(\square \)
7.1.3 Interpolation argument and proof of the main theorems
Let \(\mathscr {X}\subset \mathscr {E}^{\mathrm {ord}}_{K^{p}}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\), as in Definition 1.3.1. Fix a level \(K^{p}{}'\subset K^{p}\). Let
be the intersection of the open subsets of \(\mathscr {X}\) of Theorem 4.4.3 and Corollary 6.4.5.
Recall that we denote by \(\mathscr {X}^{\mathrm {cl}, W}\) the set of classical points of weight W, and by \(\mathscr {X}^{\mathrm {cl}, n-exc }\) the set of non-exceptional classical points. When \(W=\mathbf {Q}_{p}\) is the trivial weight, we also define
by the following conditions on the classical point \(z=(x, y)\) (equivalently, on the representation \(\Pi _{z}\)):
-
(p-crys)
for all \(v\vert p\), the representation \(V_{x|G_{F_{v}}}\) is potentially crystalline (equivalently, \(\pi _{x,v}\) is a principal series; the second inclusion above follows from Lemma 6.4.6);
-
(ram)
\(\chi _{y,p}\) is sufficiently ramified in the following sense: let \(r_{v}\ge 1\) be minimal such that \(1+\varpi _{v}^{r_{v}} \mathscr {O}_{F_{v}}\) is contained in the kernel of \(\omega _{x,v}\), and let \(U_{F,p}^{\circ }=\prod _{v\vert p} (1+\varpi _{v}^{r_{v}} \mathscr {O}_{F_{v}})\); then \(\chi _{y, p}\) is is nontrivial on \(N_{E_{p}/F_{p}}^{-1}(U_{F,p}^{\circ })\cap \mathscr {O}_{E_{p}}^{\times }\).
Lemma 7.1.4
The subset \(\mathscr {X}^{\mathrm {cl},\ p-crys , \ \mathbf {Q}_{p}, ram } \subset \mathscr {X}'\) is dense.
Proof
Denote by \(\mathrm{p}_{\mathrm {G}} :\mathscr {X}' \rightarrow \mathscr {E}_{\mathrm {G}}\) the natural projection. If ‘?’ is any relevant decoration, let \(\mathscr {X}_{\mathrm {G}}^{?}:= \mathrm{p}_{\mathrm {G}}(\mathscr {X}^{?})\); for \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}\), let \(\mathscr {X}_{x, \mathrm {H}}^{?}:= \mathrm{p}_{\mathrm {G}}^{-1}(x)\cap \mathscr {X}^{?}\).
For each \(x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}, p-crys, \mathbf {Q}_{p}}\), the set \( \mathscr {X}_{x,\mathrm {H}}^{\mathrm {cl}, \ \mathbf {Q}_{p}, ram }\) contains contains all but finitely many points in \( \mathscr {X}_{x, \mathrm {H}}^{\mathrm {cl}, \, \mathbf {Q}_{p}}\), which is dense in \(\mathscr {X}_{x, \mathrm {H}}\). Thus the closure of \(\mathscr {X}^{\mathrm {cl},\ \text {p-crys}, \ \mathbf {Q}_{p}, \text { ram}}\) contains all of \(\mathscr {X}^{\mathrm {cl},\ \text {p-crys},\ \mathbf {Q}_{p}}\).
Now we observe that \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}, \ \text {p-crys},\ \mathbf {Q}_{p}} = \mathscr {Y}_{\mathrm {G}}\cap \mathscr {X}_{\mathrm {G}}^{\mathrm {cl},\ \mathbf {Q}_{p}}\) for the open subset
which is non-empty as it contains \(\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}, W_{\mathrm {G}}}\) for any representation \(W_{\mathrm {G}}\) whose partial weights are all \(\ge 3\) (cf. the proof of Lemma 6.4.6.1 (c)). Therefore \(\mathscr {X}^{\mathrm {cl},\ \text {p-crys},\ \mathbf {Q}_{p}}\) is the intersection of the non-empty open \(\mathrm{p}_{\mathrm {G}}^{-1}(\mathscr {Y}_{\mathrm {G}})\) with \(\mathscr {X}^{\mathrm {cl}, \, \mathbf {Q}_{p}}\), which is dense in \(\mathscr {X}'\) by Lemma 3.1.4. We conclude that \(\mathscr {X}^{\mathrm {cl},\ \text {p-crys},\ \mathbf {Q}_{p}}\) and \(\mathscr {X}^{\mathrm {cl},\ \text {p-crys}, \ \mathbf {Q}_{p}, \text { ram}}\) are dense in \(\mathscr {X}'\). \(\square \)
Proposition 7.1.5
The following are equivalent.
-
1.
Theorem D holds over \(\mathscr {X}'_{K^{p}{}'}\) for all \(K^{p}{}'\subset K^{p}\).
-
2a.
Theorem \(\text {B}^{\, \mathrm {ord}}\) holds for all representations \(\Pi \) corresponding to points of \(\mathscr {X}^{\mathrm {cl}}\) satisfying \((wt) \).
-
2b.
Theorem \(\text {B}^{\, \mathrm {ord}}\) holds for all representations \(\Pi \) corresponding to points of \(\mathscr {X}^{\mathrm {cl}, p-crys , \ \mathbf {Q}_{p}, ram }\).
-
3a.
Theorem B holds for all representations \(\Pi \) corresponding to points of \(\mathscr {X}^{\mathrm {cl}, n-exc }\) satisfying \((wt) \).
-
3b.
Theorem B holds for all representations \(\Pi \) corresponding to points of \(\mathscr {X}^{\mathrm {cl}, p-crys , \ \mathbf {Q}_{p}, ram }\).
Proof
For any point \(z\in \mathscr {X}^{\mathrm {cl}, n-exc }\) satisfying \((wt) \), denote by \(\Pi _{z}\) the associated automorphic representation, by \(V_{z}\) the associated Galois representation . We have proved the following specialisation-at-z properties of objects defined over (open subsets of) \(\mathscr {X}\):
-
the \(\mathscr {O}_{\mathscr {X}'}\)-module \(\Pi _{H'_{\Sigma }}^{K^{p}{}', \mathrm {ord}}\) (respectively \((\Pi _{H'_{\Sigma }}^{K^{p}{}', \mathrm {ord}})^{\iota }\) specialises to \(\Pi _{z,H'_{\Sigma }}^{K^{p}{}', \mathrm {ord}}\) (respectively \(\Pi _{z,H'_{\Sigma }}^{\vee , K^{p}{}', \mathrm {ord}}\)), by Proposition 3.3.8.4 (and the definition of the involution \(\iota \));
-
the Galois representation \(\mathscr {V}\) (respectively \(\mathscr {V}^{\iota }\)) and its ordinary filtrations specialise to \(V=V_{\Pi }\) (respectively \(V_{\Pi ^{\vee }}\)) with its ordinary filtrations, by construction (Proposition 3.2.4);
-
there is a natural map \(\widetilde{H}^{1}_{f}(E, \mathscr {V})_{|z}\rightarrow \widetilde{H}^{1}_{f}(E, V)\);
-
the class \(\mathscr {P}_{K^{p}{}'}\) specialises to the restriction of \(P^{\mathrm {ord}}_{\Pi _{z}}\) to \(\Pi _{z,H'_{\Sigma }}^{K^{p}{}', \mathrm {ord}}\) under the above map, by Theorem C whose proof is completed in Sect. 6.4.3;
-
the product of local terms \(\mathscr {Q}\) specialises to the restriction of \(Q^{\mathrm {ord}} \) to the spaces of \(H'_{\Sigma }\)-coinvariants, \(K^{p}{}'\)-invariants in \(\Pi _{z}^{\mathrm {ord}}\), \(\Pi _{z}^{\vee ,\mathrm {ord}}\), by Theorem 4.4.3.
Let us complete the proof that either side of Theorem D specialises to 1/2 times the corresponding side of Theorem \(\text {B}^{\, \mathrm {ord}}\). Consider the diagram \(\mathscr {X}_{0}\rightarrow \mathscr {X}_{0}^{\sharp }\rightarrow \mathscr {E}_\mathrm{Z}\). It is not a product, even Zariski-locally; however the conormal sheaf is trivial. (This is dual to the fact that \(\mathrm {G}\times \mathrm {H}\rightarrow (\mathrm {G}\times \mathrm {H})'\) is a \(\mathrm{Z}\)-torsor for the étale topology but not for the Zariski topology.) The immersion \(\mathscr {X}\hat{\times } \mathscr {E}_\mathrm{Z}\rightarrow \mathscr {X}^{\sharp }\) given by ‘\((\Pi , \chi _{F})\mapsto \Pi \otimes \chi _{F}\)’ induces the map on conormal sheaves
that is multiplication by 1/2 under the canonical identifications. Hence:
-
the p-adic height pairing \({h}_{\mathscr {V}}=h_{\mathscr {V}^{\sharp }|\mathscr {X}}\) specialises to \({1\over 2} h_{V}={1\over 2} h_{V\otimes \chi _{F, \mathrm{univ}|G_{E} }| z}\), by Sect. 5.3.3;
-
the derivative \(\mathrm{d}^{\sharp } \mathscr {L}_{p}(\mathscr {V})\) specialises to \({1\over 2} \mathscr {L}_{p}'(V, 0)\) in \(\mathbf {Q}_{p}(z)\hat{\otimes } \Gamma _{F}\), by the definition in (1.1.1).
We may now complete the proof. By the specialisation properties summarised above, we have \(1.\Rightarrow 2.a\) (\(\Rightarrow 2.b\)). By Lemma 7.1.2, we have \(2.a \Rightarrow 3.a\), \(2.b \Leftrightarrow 3.b\). By Lemma 7.1.4 and the specialisation properties, \(2.b\Rightarrow 1.\) \(\square \)
Proof of Theorems B, D, and \(\text {B}^{\, \mathrm {ord}}\) The first assertion of Theorem B was proved in Proposition 6.4.7. For a representation \(\Pi \) of trivial weight satisfying the conditions (p-crys), (ram), the formula of Theorem B is [35, Theorem B] (cf. Lemma 7.1.3). By Proposition 7.1.5, this implies Theorem D and the general case of Theorems B, \(\text {B}^{\, \mathrm {ord}}\). \(\square \)
7.1.4 Applications to non-vanishing/1: self-dual CM families
We prove the generic non-vanishing result of Theorem F. Recall that \(\mathscr {Y}\) is a component of the subvariety \(\mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm sd}\subset \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}}\) cut out by the condition \(\chi _{F_{\mathbf {A}}^{\times }}=\eta \chi _{\mathrm{cyc}, F}\), and such that \(\varepsilon (\chi _{y}, 1)=-1\) generically along \(\mathscr {Y}\).
Proof of Theorem F
Recall that a p-adic CM type of E over \(\overline{\mathbf {Q}}_{p}\) is a choice \(\Sigma \) of a place \(w\vert v\) of E for each place \(v\vert p\) of F (we identify primes above p with embeddings into \(\overline{\mathbf {Q}}_{p}\)). For each of the p-adic CM types \(\Sigma \) of E and each connected component \(\mathscr {Y}^{\sharp }\) of \(\mathscr {E}^{\mathrm {ord}}_{\mathrm {H}}\), there is a Katz p-adic L-function
It is characterised (see [52, 64]) by its values at the subset \(\mathscr {Y}^{\sharp , \mathrm {cl}.\Sigma }\subset \mathscr {Y}^{\sharp , \mathrm {cl}}\) of those y such that the algebraic part of \(\chi _{y}\) is \(t\mapsto \prod _{\sigma \in \Sigma } \sigma (t)^{w} \sigma (t/t^{c})^{k_{\sigma }}\) for integers \(w, k_{\sigma }\) such that either \(w\ge 1\), or \(w<1\) and \(w+k_{\sigma }>0\) for all \(\sigma \in \Sigma \). The interpolation property relates \(L_{\Sigma }(y)\) to \(L(1, \chi _{y})\). It is easy to see that for a given \(y\in \mathscr {E}^{\mathrm {ord}, \mathrm sd}_{\mathrm {H}}\), there is a unique CM type \(\Sigma \) such that y belongs to the interpolation subset of \(L_{\Sigma }\). For such y and \(\Sigma \), we denote by \(L_{p}(\chi _{y}, s)\in \mathscr {O}(\mathscr {E}_{\mathrm{Z}/\mathbf {Q}_{p}(y)})\) the function \(s \mapsto L_{\Sigma }(y(s))\) where \(\chi _{y(s)}=\chi \cdot \chi _{F,s}\circ N_{E/F})\).
Consider now the setup of the theorem, and let \(\mathscr {Y}^{\sharp }\subset \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}}\) be the component containing \(\mathscr {Y}\). By [13], under our assumptions the normal derivative \(d^{\sharp } L_{\Sigma }\in \mathscr {N}^{*}_{\mathscr {Y}/\mathscr {Y}^{\sharp }}\) is non-vanishing. Let \(\mathscr {Y}'_{\Sigma }\) be the complement of its zero locus, and let
Let \(y\in \mathscr {Y}^{\mathrm {cl}}\cap \mathscr {Y}'\), and let \(\chi :=\chi _{y}\). It is easy to see that there is a unique \(\Sigma \) such that \(y\in \mathscr {Y}^{\sharp , \mathrm {cl}, \Sigma }\).
We claim that there exists a a finite-order character \(\chi _{0}\in \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm {cl}}\), such that the character
(that has the same algebraic part as \(\chi ^{c}:=\chi \circ c\), and defines a point \(y'\in \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm{sd}, \mathrm {cl}}\)) satisfies the following properties:
-
\(L(1, \chi ')\doteq L_{p}(\chi ', 0)\ne 0\), where \(\doteq \) denotes equality up to a nonzero constant;
-
\(H^{1}_{f}(E, \chi ')=0\).
Granted the claim, we have a decomposition of \(G_{E}\)-representations
and a corresponding factorisation
where \(\pi _{0}=\theta (\chi \chi _{0})\) (the theta lift), and \(\pi _{0}\otimes \chi _{0}^{-1}\) descends to a representation of \((\mathrm {G}_{0}\times \mathrm {H})'(\mathbf {A})\). It follows that \(\mathscr {L}_{p}'(V_{(\pi _{0}, \chi _{0}^{-1})},0)\ne 0\). By Theorem A, we have a class
whose p-adic height is non-vanishing. Since \(H^{1}_{f}({E},\chi ')=H^{1}_{f}({E},\chi '^{c})) =0\), the class Z is as desired.
It remains to prove the claim. Let \(\mathscr {Y}_{1}\subset \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm{sd}}\) be a component over which the anticyclotomic Main Conjecture is known—that is, one containing a finite-order character satisfying the properties of [56]). By applying [14, Lemma 2.5] to any character corresponding to a point of \(\mathscr {Y}_{1}^{\mathrm {cl}}\), we find another component \(\mathscr {Y}_{2}\subset \mathscr {E}_{\mathrm {H}}^{\mathrm {ord}, \mathrm{sd}}\), whose classical points correspond to characters \(\chi _{2}\) with
moreover from the proof in loc. cit. one sees that \(\mathscr {Y}_{2}\) may be taken to still satisfy the assumptions of [56]. Then the function \(L_{\Sigma c|\mathscr {Y}_{2}}\) is non-vanishing by [59]; hence, by the density of classical points with a given weight, we may find \(y'\in \mathscr {Y}_{2}^{\mathrm {cl}}\) corresponding to a character \(\chi '\) satisfying the first among the required conditions. By the anticylcotomic Main Conjecture for \(\mathscr {Y}_{2}\) proved in [54, 56], that is equivalent to the second condition. Finally, the ratio \(\chi '/\chi ^{c} \) is an anticyclotomic character (that is, trivial on \(F_{\mathbf {A}}^{\times }\)), hence [53, Lemma 5.3.1] of the form \(\chi _{0}^{c}\chi _{0}^{-1}\) for some finite-order character \(\chi _{0}\). \(\square \)
7.2 A universal Waldspurger formula
We describe the complementary picture over locally distinguished families attached to coherent quaternion algebras over F. Unexplained notions and notation will be entirely parallel to what defined in the introduction.
Let B be a totally definite quaternion algebra over F, let \(\Sigma \) be the set of finite places where B is ramified, and let \(\mathrm {G}_{/\mathbf {Q}}\) be the algebraic group with \(\mathrm {G}(R)=(B\otimes R)^{\times }\) for any \(\mathbf {Q}\)-algebra R. Let E be a CM quadratic extension of F, admitting an F-algebra embedding \(\mathrm{e}:E\hookrightarrow B\) which we fix. We use the same symbols as in the introduction for the towers of Shimura varieties associated to the groups as in (1.2.1). Here, all those Shimura varieties are 0-dimensional.
Let L be a p-adic field and let \(\Pi \) be an automorphic representation of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A}):=(\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{\infty })\times (\mathrm {G}\times \mathrm {H}')_{/\mathbf {Q}_{p}}\) over L of weight W, by which we mean one occurring in \(\mathrm {H}^{0}(\overline{Z}, \mathscr {W}^{\vee })\otimes W\). The normalised fundamental class of Y gives rise to an element \(P\in \mathrm {H}_{0}(Z, \mathscr {W})^{\mathrm {H}'(\mathbf {A})}\) and to an \(\mathrm {H}'(\mathbf {A})\)-invariant functional
which may be nonzero only if \(\Pi \) is locally distinguished by \(\mathrm {H}'\). If \(\Pi \) is ordinary, we again define \(P^{\mathrm {ord}}:= P\gamma _{H'}^{\mathrm {ord}} \).
Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\), which via a Jacquet–Langlands map is isomorphic to a Hida family \(\mathscr {X}_{0}\) for \((\mathrm {G}_{0}\times \mathrm {H})'\). For each compact open subgroup \(K^{p}\subset (\mathrm {G}\times \mathrm {H})'(\mathbf {A}^{p})\), there is a ‘universal ordinary representation’ \(\Pi ^{K^{p},\mathrm {ord}}_{H'_{\Sigma }}\) of \((\mathrm {G}\times \mathrm {H})'(\mathbf {A})\) over \(\mathscr {X}\). As in Theorem C, there exists an \(\mathrm {H}'(\mathbf {A}^{p\infty })\)-invariant, \(\mathscr {O}_{\mathscr {X}}\)-linear functional
interpolating (the restrictions of) \(P_{\Pi _{z}}^{\mathrm {ord}}\) at all \(z\in \mathscr {X}^{\mathrm {cl}}\) satisfying (wt).
Starting from the natural pairings \(\mathrm {H}_{0} (\overline{Z}_{K} , \mathscr {W})\otimes \mathrm {H}_{0} (\overline{Z}_{K} ,\mathscr {W}^{\vee })\rightarrow L\), we may define pairings \((\ , \ )_{\Pi }\) on each representation \(\Pi \) over a field by the formula (4.1.7) (using the counting measure for \(\mathrm{v}(K)\)); then we obtain modified pairings \((\ , \ )^{\mathrm {ord}}_{\Pi }\) on each \(\Pi ^{\mathrm {ord}}\otimes \Pi ^{\vee , \mathrm {ord}}\), and a pairing \(((\ , \ ))\) on the universal representations over \(\mathscr {X}\), interpolating modified pairings \((\ , \ )^{\mathrm {ord}}_{\Pi _{z}}\).
Finally, the functional \(\mathscr {Q}\), over an open \(\mathscr {X}'\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\), is also constructed as in Sect. 4.4; in the argument using the local Langlands correspondence, we use the rank-2 family of Galois representations pulled back from \(\mathscr {X}_{0}\).
Theorem H
Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\). Abbreviate \(\Pi ^{(\iota )}:= \Pi ^{K^{p}{}', \mathrm {ord}, (\iota )}_{H'_{\Sigma }}\), \(\mathscr {O}:=\mathscr {O}_{\mathscr {X}}\), \(\mathscr {K}:=\mathscr {K}_{\mathscr {X}}\).
There is an open subset \(\mathscr {X}'\subset \mathscr {X}\) containing \(\mathscr {X}^{\mathrm {cl}}\), such that
an equality of \(\mathscr {K}\)-valued \(\mathscr {O}\)-linear functionals on \((\Pi \otimes _{\mathscr {O}} \Pi ^{\iota })\otimes _{\mathscr {O}^{\times }} (\Pi \otimes _{\mathscr {O}} \Pi ^{\iota })^{\times , -1}\).
Similarly to Sect. 7.1, this universal formula follows from its specialisations at all classical points satisfying (wt); those are known by modifying the main result of [105] as in Theorem \(\text {B}^{\, \mathrm {ord}}\).
The formula essentially reduces the study of \(\mathscr {L}_{p}(\mathscr {V}^{\sharp })_{|\mathscr {X}}\) to the study of the universal Waldspurger periods \(\mathscr {P}\). This is particularly interesting in the case of exceptional zeros, as we discuss next.
7.3 Bertolini–Darmon conjectures and exceptional zeros
We first formulate a conjecture on the behaviour of \(\mathscr {P}\) at a point \(z\in \mathscr {X}^{\mathrm {cl}}\) and gather some old and new evidence in its favour. In view of Sect. 6.4.6, the conjecture is often particularly interesting when z is exceptional. Then we deduce from our constructions and a known exceptional case of the conjecture a proof of Theorem G.
The conjecture requires some algebraic preliminaries.
7.3.1 Pfaffian regulators
Let L be a field of characteristic 0, and let M, T be a finite-dimensional L-vector spaces. Let \(h:M\otimes M\rightarrow T\) be a skew-symmetric pairing, and let \(r=\dim _{L}M\).
If r is even, we define the Pfaffian regulator
to be the Pfaffian of the skew-symmetric matrix \(h(x_{i}, x_{j})_{ij}\) for any L-basis \(x_{i}\) of M. It is well-defined modulo \(L^{\times }\).
If r is odd, we define an enhanced Pfaffian regulator
as follows. It suffices to define \(\partial ^{e}\mathrm{Pf}^{-}(h) \) for any basis \(\partial _{1}, \ldots , \partial _{d}\) of \(T^{\vee }\) and all tuples \(e=(e_{i})_{i=1}^{d}\) with \(\sum _{i=1}^{d}e_{i}= (r-1)/2\); here \(\partial ^{e}:= \prod _{i=1}^{d} \partial _{i}^{e_{i}} \). Let \(I\subset \{1, \ldots , d\}\) be the support of the tuple e. Let \(M_{I} \subset M\) be the sum, over \(i \in I\), of the radicals of the pairings \(\partial _{i} h\). If \(\dim M_{I}\ge 2\), we define \( \partial ^{e} \mathrm{Pf}^{-}(h) :=0\). If \(\dim M_{I}=1\) and \(x\in M_{i}\) is a generator, denote by \(\overline{h}\) the induced pairing on \(\overline{M}:= M/M_{I}\); we define
Remark 7.3.1
In the even case, we have of course \(\mathrm{Pf}^{+}(M, h) ^{2} = R(M, h)\in ( \mathrm{Sym}^{r}T )/ L^{\times ,2}\), where R(M, h) is the discriminant of the pairing h. In the odd case, assume further given a symmetric bilinear pairing \(h^{\sharp }:M\otimes M\rightarrow T^{\sharp }\). Let \(h'=h\oplus h^{\sharp }:M\otimes M\rightarrow T':-T\oplus T^{\sharp }\), and let \(R(M, h')\in \mathrm{Sym}^{r}( T')/L^{\times , 2}\) be its discriminant. Then it is easy to verify that
is the image of \(R(M, h')\) under the natural projection.
Remark 7.3.2
If L is the fraction field of a domain \(\mathscr {O}\) and M is endowed with an \(\mathscr {O}\)-lattice, it is possible to lift the ambiguity in the definitions to an element of \(\mathscr {O}^{\times }\).
7.3.2 A conjecture à la Bertolini–Darmon
Let \(\mathrm {G}\) be either as in the introduction or as in Sect. 7.2. We define a sign \(\epsilon := -1\) in the former case and \(\epsilon := +1\) in the latter case. Let \(\mathscr {X}\) be a locally distinguished Hida family for \((\mathrm {G}\times \mathrm {H})'\), and let
be a classical point. We denote by \(\mathscr {P}\) the universal Heegner class (if \(\epsilon =-1\)) or toric period (if \(\epsilon =+1\)), viewed as a family of functionals as in (6.4.2), (7.2.1), parametrised by a subset \(\mathscr {X}'\subset \mathscr {X}\). Assume that \(\mathscr {X}'\) can be taken to be a neighbourhood of \(z\in \mathscr {X}\).
Let \(T_{z}^{*}\mathscr {X}={\mathfrak {m}}_{z}/\mathfrak {m}_{z}^{2}\) be the cotangent space to \(\mathscr {X}\) at z (where \(\mathfrak {m}_{z}\subset \mathscr {O}_{\mathscr {X}, z}\) is the maximal ideal), and for any \(r\in \mathbf {N}\) let
be the natural projection. It is easy to see that the involution \(\iota \) of Sect. 2.1.4 satisfies \(\mathrm{d}_{z}^{\parallel }\iota =\mathrm {id}\) (whereas \(\mathrm{d}_{z}^{\sharp } \iota =-\mathrm {id}\)).
Let \(V=\mathscr {V}_{|z}\), and let \(\mathrm{c} :\widetilde{H}^{1}_{f}(E, V^{\iota }) \rightarrow \widetilde{H}^{1}_{f}(E, V)\) be the isomorphism induced by the adjoint action, on \(G_{E, S}\), of a lift of the complex conjugation in \(\mathrm {Gal}(E/F)\). Let
be the Nekovář–Venerucci height pairing as in (5.3.7). Since the pairing of Proposition 4.1.7 is skew-hermitian, by Proposition 5.3.4 the pairing \(h^{\parallel }\) is skew-symmetric. Define
Conjecture Pf
Let \(\widetilde{r}:= \dim _{L}\widetilde{H}^{1}_{f}(E, V)\). We have \((-1)^{\widetilde{r}}=\epsilon \), the universal element \(\mathscr {P}\) vanishes to order at least \(\lfloor {\widetilde{r}/2}\rfloor \) at z, and for any generator \(\wp \in (\Pi ^{\mathrm {ord}})^{*, \mathrm {H}'(\mathbf {A}^{p\infty )}}\) and all \(f\in \Pi ^{\mathrm {ord}}\), we have
in \([\widetilde{H}^{1}_{f}(E, V)^{(1+\epsilon )/2}\otimes _{\mathbf {Q}_{p}(z)} \mathrm{Sym}_{\mathbf {Q}_{p}(z)}^{{\lfloor {\widetilde{r}/2}\rfloor }}T_{z}^{*}\mathscr {X}]\, / \mathbf {Q}_{p}(z)^{\times }\).
7.3.3 Relation to the original conjectures of Bertolini–Darmon
Define \(\mathscr {X}^\mathrm{a}:= \mathscr {X}\cap ( \{x\}\times \mathscr {E}_{\mathrm {H}'})\) (the anticyclotomic family), \(\mathscr {X}^\mathrm{wt} := \mathscr {X}\cap (\mathscr {E}_{\mathrm {G}}\times \{y\})\) (the weight family). In the classical case when E is imaginary quadratic, \(\pi \) is associated with an elliptic curve over \(\mathbf {Q}\), \(\chi =\mathbf {1}\), and we restrict to the anticyclotomic variable \(\mathscr {X}^\mathrm{a}\), Conjecture Pf is a variant of conjectures of Bertolini–Darmon, surveyed in [6] and (in a form slightly closer to the one of the present work) in [33, § 4]. The Bertolini–Darmon conjectures were partly generalised to higher-weight modular forms in [71].
Remark 7.3.3
By using natural \(G_{E, S}\)-stable lattices in V, or better lattices in \(\widetilde{H}^{1}_{f}(E, V)\) spanned by motivic elements, it is possible to define the Pfaffian regulators up to an ambiguity that is a unit in the ring of integers of a local field or of a number field (recall Remark 7.3.2). It should then possible to refine the conjecture up to such ambiguity (by including the appropriate constants), as in the original works of Bertolini–Darmon (see [33, Conjecture 4.2.1]).
In view of Remark 7.3.1, inserting Conjecture Pf into Theorem D would yield a multivariable formula relating higher partial derivatives of p-adic L-functions with suitable height regulators, in the spirit of the Birch and Swinnerton-Dyer conjecture; the argument is the same as that of [33, Proposition 5.1.1]. We plan to return to formulate such conjectural formulas in the appropriate generality in future work.
7.3.4 Evidence for Conjecture Pf in low rank
The preliminary parity conjecture
is known in many cases as a consequence of the work of Nekovář (see [81, Theorem 12.2.3]. Indeed, the statement proved in loc. cit., in view of the functional equation of \(\mathscr {L}(V_{(\pi , \chi )},s)\), is that
where \(r=\dim H^{1}_{f}(E, V)\) and \(\varepsilon =\varepsilon (V)\). Now if \(r^\mathrm{exc}= r^\mathrm{exc, \, s}+ {r}^\mathrm{exc,\, ns}\) denotes the number of exceptional primes of F above p (respectively, the number of those that moreover are split or nonsplit in E), by Lemma 6.4.6.2 we have \(\epsilon =\varepsilon \cdot (-1)^{r^\mathrm{exc,\, ns}}\), and \(\widetilde{r}= r+2r^\mathrm{exc,\, s}+ r^\mathrm{exc, \, ns}\). Thus (7.3.4) is equivalent to (7.3.3).
Let us now review the conjectural vanishing and leading-term formula. Most of the available evidence is concentrated in the case where V arises from the classical context of Sect. 7.3.3, to which we restrict unless otherwise noted for the rest of this discussion. (All the results mentioned below hold under various additional assumptions, which we will not recall.)
If \(\mathscr {X}\) is replaced with \(\mathscr {X}^\mathrm{a}\) (the original Bertolini–Darmon case), the conjecture is known if \(\mathscr {L}(V_{(\pi , \chi )},s)\) vanishes to order 0 or 1 at \(s=0\), see [33, Theorem 4.2.5] and references therein, as well as [70]. Some of those results have been generalised to higher weight [62, 72] or to totally real fields [4, 61, 75].
When \(\mathscr {X}\) is replaced by \(\mathscr {X}^\mathrm{wt}\), p is inert in E, V is exceptional, and \(\epsilon =+1\), Bertolini–Darmon [7] proved a formula for \(\mathrm{d}_{z}^{\parallel } \mathscr {P}_{|\mathscr {X}^\mathrm{wt}}\), which implies the projection of (7.3.2) to \(T_{z}^{*}\mathscr {X}^\mathrm{wt}\) when \(\mathrm{ord}_{s=0}\mathscr {L}(V_{(\pi , \chi )}, s)=1\). The interpretation of the formula of Bertolini–Darmon in terms of height pairings was observed by Venerucci (see [104, Theorem 2.1 and Theorem 4.2.2]), whose work was a second important influence in the formulation of Conjecture Pf. The Bertolini–Darmon formula was generalised to higher-weight modular forms by Seveso [95] and to elliptic curves over totally real fields by Mok [74].
7.3.5 Evidence for Conjecture Pf in higher rank
Lower bounds for the order of vanishing of \(\mathscr {P}_{|\mathscr {X}^\mathrm{a}}\) have been obtained in two recent works for \(\epsilon =1\). In the context of elliptic curves over totally real fields, [4, Theorem 5.5] gives a bound (that is coarser than predicted by Conjecture Pf) in terms of the number of exceptional primes. In a classical context (and if if p splits in E), Agboola–Castella [1, Corollary 6.5] prove a bound that is finer than that of Conjecture Pf. (That refined bound is predicted by Bertolini–Darmon; it is related to some trivial degeneracies of the anticyclotomic height pairing, as touched upon also in the paragraphs preceding (7.3.7) below.)
Regarding the formula of Conjecture Pf, an interesting anticyclotomic case can be deduced from the recent work [39], as we now explain.
The work of Fornea–Gehrmann
Suppose that A is a modular elliptic curve over the totally real field F, such that the set \(S_{p}^\mathrm{exc}\) of places v|p where A has multiplicative reduction consists of exactly r primes \(v_{1}, \ldots , v_{r}\) inert in E. Let \(\phi :\bigotimes _{i=}^{r} E_{v_{i}}^{\times }\rightarrow \bigotimes _{i=1}^{r} {A}(E_{v_{i}})\) be the product of Tate unifomisations, and let \(\hat{\phi }\) be the induced map on p-adic completions.
One of the main constructions of [39] produces an explicit element \(Q_{A}\in \bigotimes _{i=1}^{r} E_{v_{i}}^{\times }\hat{\otimes } \mathbf {Q}_{p}\), which carries a precise conjectural relation to the arithmetic of A. Partition \(S_{p}^{\mathrm {exc}}= S_{p}^{\mathrm {exc}, +}\sqcup S_{p}^{\mathrm {exc}, -}\) according to whether the multiplicative reduction is, respectively, split or nonsplit, and let \(r^{+}:= |S_{p}^{\mathrm {exc}, +}|\). Denote \( \hat{A}(E_{v})=A(E_{v})\hat{\otimes }\mathbf {Q}_{p}\) and let \(\hat{A}(E_{v})^{\pm }\) be its ±-eigenspaces for the conjugation \(c_{v}\in \mathrm {Gal}(E_{v}/F_{v})\).
Assume that \(A_{E}\) has rank \(r_{A}\ge r\) and let \(r_{A}^{+}\) be the rank of A. According to [40, Conjectures 1.3, 1.5], we haveFootnote 27
where \((x_{1}, \ldots , x_{r})\) is a basis of \(A(E)_{\mathbf {Q}}\), and for \(v\in S_{p}^{\mathrm {exc}, \pm } \) we denote by \(\hat{x}_{v}^\mathrm{a}\) the eigen-projection of \(x\in A(E)\) to \( \hat{A}(E_{v})^{\mp }\). The symbol \(\doteq \) denotes equality up to a constant in \(\mathbf {Q}^{\times }\).
For \(V=V_{p}A_{E}\), assuming the finiteness of  we have \(\widetilde{r}:=\dim \widetilde{H}^{1}_{f}(E, V) =r+r_{A}\) (see Lemma 6.4.6.1(a) or (7.3.7) below), and the parity conjecture is known. Hence if \(r_{A}\equiv r\pmod 2\), which we henceforth assume, V corresponds to a point z of a locally distinguished Hida family \(\mathscr {X}\) of sign \(\epsilon =+1\) (for a unique choice of the coherent quaternionic group \(\mathrm {G}\)). Let
we have \(\widetilde{r}:=\dim \widetilde{H}^{1}_{f}(E, V) =r+r_{A}\) (see Lemma 6.4.6.1(a) or (7.3.7) below), and the parity conjecture is known. Hence if \(r_{A}\equiv r\pmod 2\), which we henceforth assume, V corresponds to a point z of a locally distinguished Hida family \(\mathscr {X}\) of sign \(\epsilon =+1\) (for a unique choice of the coherent quaternionic group \(\mathrm {G}\)). Let
be the natural projection, and let \(\ell _\mathrm{exc, \otimes }^\mathrm{a}:=\bigotimes _{i=1}^{r}\ell ^\mathrm{a}_{v_{i}}:\bigotimes _{i=1}^{r} E_{v_{i}}^{\times }\hat{\otimes }\mathbf {Q}_{p} \rightarrow \mathrm{Sym}^{r}\Gamma ^\mathrm{a}\). Denoting by \(\mathrm{d}_{z}^\mathrm{a}\) the component of \(\mathrm{d}_{z}^{\parallel }\) along \(\mathscr {X}^\mathrm{a}\), Theorem A of [39] (which relies on the aforementioned lower bound from [4]) proves
for a suitable test vector \(f^{\circ }\in \Pi ^{\mathrm {ord}}\).
Comparison with Conjecture Pf
We show that granted (7.3.5) and the finiteness of  , the formula (7.3.6) is equivalent to the conjectured (7.3.2).
, the formula (7.3.6) is equivalent to the conjectured (7.3.2).
Let \(h^\mathrm{a}:\widetilde{H}^{1}_{f}(E, V) \otimes \widetilde{H}^{1}_{f}(E, V) \rightarrow T_{z}^{*}\mathscr {X}^\mathrm{a}=\Gamma ^\mathrm{a}\) be the projection of \(h^{\parallel }\), and let
Let \(\widetilde{H}^{1}_{f}(E, V)^{\pm }\) be the eigenspaces for the complex conjugation \(c\in \mathrm {Gal}(E/F)\). Since \(h_{z/\mathscr {X}^\mathrm{a}}\) enjoys the c-equivariance property \(h_{z/\mathscr {X}^\mathrm{a}}(cx, cx')=c. h_{z/\mathscr {X}^\mathrm{a}}(x, x')\) and c acts by \(-1\) on \(\Gamma ^\mathrm{a}\), by construction the pairing \(h^\mathrm{a}\) satisfies \(h(cx, cx')= -h(x, x')\), so that each of \(\widetilde{H}^{1}_{f}(E, V)^{\pm }\) is \(h^\mathrm{a}\)-isotropic. In particular, Conjecture Pf agrees with (7.3.6) and (7.3.5) that, in the first case of the latter, we have \((\mathrm{d}_{z}^\mathrm{a})^{r}\mathscr {P}=0\).
Assume now we are in the second case of (7.3.5), so that each of \(\widetilde{H}^{1}_{f}(E, V)^{\pm }\) has dimension r and \(h^\mathrm{a}\) need not be degenerate. For \(1\le i\le r\), let \(q_{i}=q_{v_{i}}\in E_{v_{i}}^{\times }\) be a Tate parameter for \(A/E_{v}\). By [77, § 7.14] we explicitly have
where \(\log _{A, v}^\mathrm{a}:\hat{A}(E_{v})\otimes \mathbf {Q}_{p} \cong E_{v}^{\times }/q_{v}^{\mathbf {Z}}\hat{\otimes }\mathbf {Q}_{p} \cong \mathscr {O}_{E_{v}}^{\times }\hat{\otimes }\mathbf {Q}_{p} {\mathop {\longrightarrow }\limits ^{\ell _{v}^\mathrm{a}}} \Gamma ^\mathrm{a}\). Note that \(\log _{A, v}^\mathrm{a}\) factors through \(x\mapsto \hat{x}_{v}^\mathrm{a}\).
Up to changing the basis \(x_{i}\) of \(A(E)_{\mathbf {Q}}\) and reordering the \(v_{i}\), we may assume that the basis
of \(\widetilde{H}^{1}_{f}(E, V)\) is the concatenation of a basis of \(\widetilde{H}^{1}_{f}(E, V)^{+}\) and a basis of \(\widetilde{H}^{1}_{f}(E, V)^{-}\), respectively. Using this basis, (7.3.7), and the identity \(\mathrm{pf} \left( {\begin{matrix}&{}M\\ -M^\mathrm{t}&{}\end{matrix}}\right) =\pm \det M\), we haveFootnote 28
where the \(r\times r\) matrix M is block-left-upper-triangular with anti-diagonal blocks \(M_{k} = (\log _{A,v_{j}}^\mathrm{a}(x_{i}))_{i, j \in I_{k}}\) for \(I_{1}=\{ r^{+}+1,\ldots , r\}\), \(I_{2}=\{ 1, \ldots , r^{+}\}\).
On the other hand, we note that under (7.3.5), we have \(\ell _\mathrm{exc, \otimes }^\mathrm{a}(Q_{A}) = \det N\) where the \(r\times r\) matrix \(N_{ij}= \log ^\mathrm{a}_{A,v_{j}}(\hat{x}_{i, v}) = h^\mathrm{a}(x_{i}, q_{j})\) is block-diagonal with blocks \(N_{1}=M_{2}\), \(N_{2}=M_{1}\). Thus \(\ell _\mathrm{exc, \otimes }^\mathrm{a}(Q_{A}) = \mathrm{Pf}^{\, \mathrm a, +}(V)\), and (7.3.6) is equivalent to (7.3.2).
7.3.6 Applications to non-vanishing/2: exceptional families
We prove Theorem G.Footnote 29 Recall that \(\mathscr {X}_{0}\) is a Hida family for \(\mathrm{PGL}_{2/\mathbf {Q}}\), that contains a classical point \(x_{0}\in \mathscr {X}(\mathbf {Q}_{p})\) corresponding to an elliptic curve A with split multiplicative reduction at p satisfying \(L(A, 1)=L(V_{p}A, 0)\ne 0\).
Proof of Theorem G
Let E be an imaginary quadratic field, with associated quadratic character \(\eta \), satisfying the following: p is inert in A, all other primes dividing the conductor of A split in E, and the twisted L-value \(L(A, \eta , 1)\ne 0\). Then A has split multiplicative reduction over E with Tate parameter
Let \(\Omega _{A_{E}}\in \mathbf {C}^{\times }\) be the Néron period, and let let \(\mathrm {H}:=\mathrm{Res}_{E/\mathbf {Q}}{} \mathbf{G}_{m}\).
By construction, \(\varepsilon _{v}(V_{p}A_{E})=1\) for all finite \(v\not \mid p\), hence the Hida family \(\mathscr {X}\subset \mathscr {E}_{(\mathrm {GL}_{2}\times \mathrm {H})'}^{\mathrm {ord}}\) containing the image of \(\mathscr {X}_{0}\times \{\mathbf {1}\}\) is locally distinguished. Let \(\mathscr {X}^{\sharp }\subset \mathscr {E}_{(\mathrm {GL}_{2}\times \mathrm {H})}^{\mathrm {ord}}\) be the Hida family containing \(\mathscr {X}\). Let \(\Pi \) be the universal ordinary representation over \(\mathscr {X}\) and let \(f\in \Pi \) be such that \(f_{|x_{0}}\) is a test vector (that is, a vector not annihilated by any \(\mathrm {H}'(\mathbf {A}^{p})\)-invariant functional \(\lambda :\Pi _{|x_{0}}\rightarrow \mathbf {Q}_{p}\)). Let \(\mathscr {P}_{0, E}\) be the pullback of \(\mathscr {P}(f)\) to \(\mathscr {X}_{0}\), and let \(\mathscr {P}_{0}:={1\over 2}\mathrm {Tr}_{E/\mathbf {Q}}\mathscr {P}_{0, E}\). By Corollary 6.4.5,
By the main result of [5] (as reformulated in [6, Theorem 5.4, § 5.2]),Footnote 30 there is a constant \(c\in \mathbf {Q}_{p}^{\times }\) such that
using the description \( \widetilde{H}^{1}_{f}({\mathbf {Q}}, V_{p}A_{E})= \mathbf {Q}_{p}\cdot [q] \oplus H^{1}_{f}({\mathbf {Q}}, V_{p}A_{E})\) as in (7.3.7).
In particular, \(\mathscr {P}_{0, E}(x_{0})= \mathscr {P}_{0}(x_{0})\) is a nonzero multiple of [q], which is \(\mathrm {Gal}(E/\mathbf {Q})\)-invariant. Hence \(\mathscr {P}_{0, E}\) and \(\mathscr {P}_{0}\) are non-vanishing. Then by [76], \(\widetilde{H}^{1}_{f}({\mathbf {Q}}, \mathscr {V}_{0})\) has generic rank 1.
Moreover,
where \(\ell :\mathbf {Q}_{p}^{\times }\rightarrow \Gamma _{\mathbf {Q}}\) is the universal logarithm (see again [77, § 7.14] for the second equality). By [2], the right-hand side is nonzero, hence \(h_{\mathscr {V}_{0}/\mathscr {V}_{0}^{\sharp }}(\mathscr {P}_{0}, \mathscr {P}_{0}^{\iota })\ne 0\). \(\square \)
Remark 7.3.4
As noted in [33, 35], the combination of Theorem D (or rather Theorem \(\text {B}^{\, \mathrm {ord}}\)) and a precise form of (7.3.8) gives a new proof ot the following theorem of Greenberg–Stevens [43]: for \(A_{/\mathbf {Q}_{p}}\) an elliptic curve of split multiplicative reduction at p and \(L_{p}(V_{p}A)\in \mathbf {Z}_{p}\llbracket \Gamma _{\mathbf {Q}}\rrbracket _{\mathbf {Q}_{p}}\) its p-adic L-function,
Notes
Two other recent ideas that our work does not touch upon are nevertheless too important to be ignored: the conjecture of Darmon and Guitart–Madseu–Şengün that there should exist Heegner points attached to any quadratic extension of number fields (see [27, 48]), and the formulas for the p-adic logarithms of Heegner points of [8, 68].
N.B.: the notation \(\mathrm {G}\) used in the informal abstract differs from the notation of the paper.
See however the very recent [87]. (Note added during revision.)
Provided V contains no copies of the trivial representation. Of course in general the meromorphic continuation of L(V, s) is itself conjectural. Note that when V is self-dual, or E is a CM field and V is conjugate-self-dual, we have \(L(V,s)=L(V^{*}(1), s)\).
Other authors consider p-adic L-functions of a variable \(s'\in \mathbf {Z}_{p}\). In our language this corresponds to restricting \(\mathscr {L}_{p}(V, s)\) along the embedding \(\mathbf {Z}_{p}=\mathrm {Spec}\,\mathbf {Z}_{p}\llbracket \mathbf {Z}_{p}\rrbracket _{\mathbf {Q}_{p}}(\mathbf {Q}_{p})\rightarrow \mathscr {E}_{\mathrm{Z}/L}(\mathbf {Q}_{p})\), \(s'\mapsto \chi _{\mathrm{cyc}, F}^{s'}\) where \(\chi _{\mathrm{cyc}, F}=\) (1.8.1) is the cyclotomic character of F.
In a related context, see also the very recent breakthrough of Li–Liu [66]. (Note added during revision.)
In fact, the (incoherent) group that truly underlies our constructions is \((\mathrm {G}\times _\mathrm{Z}\mathrm {H})' = \{(g, h)\, | \, \nu _{\mathrm {G}}(g)=\nu _{\mathrm {H}}(h)\}\) (where \(\nu _{?}:?\rightarrow \mathrm{Z}\) arises from the reduced norm map of \(\mathbf {B}\) (for \(?=\mathrm {G}\)) or from the norm of E/F (for \(?=\mathrm {H}\)). That is, the universal Heegner class and the other associated objects described below descend to the ordinary eigenvariety for \((\mathrm {G}\times _\mathrm{Z}\mathrm {H})'\) (a quotient of the one for \((\mathrm {G}\times \mathrm {H})'\)). Nevertheless, for the sake of simplicity we will content ourselves with working with \((\mathrm {G}\times \mathrm {H})'\).
See Definition 2.4.1: the W/L of interest to us are in bijection with (finite) \(G_{L}\)-orbits of cohomological ‘numerical’ weights as defined above. From now on all numerical or representation-theoretic weights will be tacitly understood to be cohomological.
This approach is inspired by the work of Emerton [37].
By [34, Corollary 5.3.3].
In the sense that for each \(z\in \mathscr {X}^{\mathrm {cl}}\), \(v\in \Sigma \), the finite-dimensional constituent \(\Pi _{z,v}\) of \(\Pi _{z}\) is fixed by \(K_{v}\).
The normalisations of L- and \(\varepsilon \)-factors are as in [98].
These notions depend of course on \(L\hookrightarrow L'\); nevertheless they will only be used to impose conditions on the weights that are invariant under the Galois group of L.
This notion agrees with the notion of \(\pi \) being nearly ordinary as defined in the work of Hida (e.g. [50]).
If V is a Hodge–Tate representation of \(G_{F_{v}}\) over \(\overline{L}\) and \(\sigma :F_{v}\hookrightarrow \overline{L}\), the \(\sigma \)-Hodge–Tate weights of V are the degrees in which the graded module
$$\begin{aligned} ( \oplus _{n} \mathbf {C}_{v}(n)\otimes _{\overline{F}_{v},\sigma } V)^{G_{F_{v}}} \end{aligned}$$is nonzero; here \(\mathbf {C}_{v}\) is a completion of \(\overline{F}_{v}\) and, in the tensor product, \(\sigma \) is extended to an isomorphism \(\overline{F}_{v}\rightarrow \overline{L}\). In particular our convention is that the Hodge–Tate weight of the cyclotomic character of \(\mathbf {Q}_{p}\) is \(-1\).
I am grateful to David Loeffler and Sarah Zerbes for explaining to me this point of view on the Control Theorem.
The action of \(\mathbf {B}_{p}^{\times }\) has already been traded for an action of the torus, subsumed into the \(\mathscr {E}_{\mathrm {G}}\)-module structure.
There is an essential reason for this, namely the possible presence of Schur indices in representations of those groups.
This factor accounts for the ‘\(K_{0}(p^{r})\)’-part of the level.
The same statements hold with some extra notational burden if \(f_{1}, f_{2}\) are only defined over an open subset of \(\mathscr {X}^{(5)}\).
Note that despite the similar notation, the character \(\mu _{v}\) is defined using the Weil–Deligne representations rather than the continuous Galois representations.
In loc. cit., the ring denoted by R is our \(R^{\circ }\), but as our X is open in \(\mathrm {Spec}\,R^{\circ }\), the \(\mathscr {O}_{X}\)-modules \(P^{n}\) are also flat as \(R^{\circ }\)-modules and the cited result applies.
In locc. citt., some restrictive assumptions are made (in particular that E is not CM), but the conjectures make sense even without those and indeed closely related conjectures appear in [39] without those assumptions. Moreover, our statement slightly differs from the ones of [39], which instead of postulating that \((x_{1}, \ldots , x_{r})\) is a basis, postulates that \(\hat{\phi }(Q_{A})\ne 0 \) under the extra assumption that \(\mathrm {Res}_{F/\mathbf {Q}}A\) is simple (equivalently L(A, s) is primitive). Our slight reformulation appears more uniform and still addresses [39, Remark 1.1] (cf. the comment following [39, Conjecture 1.5]).
All the equalities to follow ignore signs and in fact, by our coarse definitions, only make sense at best up to \(\mathbf {Q}^{\times }\).
A less interesting variant of it was sketched in [35].
In the works of Bertolini–Darmon, an explicit test vector f is chosen; cf. [33] for more details on bridging the setups.
Note that \(\pi \) admits a refinement if and only if it is neither supercuspidal nor 1-dimensional.
To compare with (1.2.7), we have \(\zeta _{\mathbf {R}}(2)/L(1, \eta _{\mathbf {C}/\mathbf {R}})=1.\)
References
Agboola, A., Castella, F.: On anticyclotomic variants of the \(p\)-adic Birch and Swinnerton-Dyer conjecture. J. Théor. Nombres Bordeaux 33(3), 629–658 (2021). (English, with English and French summaries)
Barré-Sirieix, K., Diaz, G., Gramain, F., Philibert, G.: Une preuve de la conjecture de Mahler-Manin. Invent. Math. 124(1–3), 1–9 (1996). https://doi.org/10.1007/s002220050044. (French)
Beĭlinson, A.A.: Higher Regulators and Values of \(L\)-Functions. Current problems in mathematics, vol. 24. Itogi Nauki i Tekhniki, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, pp. 181–238 (1984). (Russian)
Bergunde, F., Gehrmann, L.: Leading terms of anticyclotomic Stickelberger elements and \(p\)-adic periods. Trans. Am. Math. Soc. 370(9), 6297–6329 (2018). https://doi.org/10.1090/tran/7120
Bertolini, M., Darmon, H.: A rigid analytic Gross-Zagier formula and arithmetic applications. Ann. Math. (2) 146(1), 111–147 (1997). https://doi.org/10.2307/2951833. (With an appendix by Bas Edixhoven)
Bertolini, M., Darmon, H.: The \(p\)-adic \(L\)-Functions of Modular Elliptic Curves. Mathematics Unlimited—2001 and Beyond, pp. 109–170. Springer, Berlin (2001)
Bertolini, M., Darmon, H.: Hida families and rational points on elliptic curves. Invent. Math. 168(2), 371–431 (2007). https://doi.org/10.1007/s00222-007-0035-4
Bertolini, M., Darmon, H., Prasanna, K.: Generalized Heegner cycles and \(p\)-adic Rankin \(L\)-series. Duke Math. J. 162(6), 1033–1148 (2013). https://doi.org/10.1215/00127094-2142056. (With an appendix by Brian Conrad)
Bertolini, M., Seveso, M.A., Venerucci, R.: Reciprocity laws for balanced diagonal classes. Astérisque (To appear)
Blanco-Chacón, I., Fornea, M.: Twisted triple product \(p\)-adic \(L\)-functions and Hirzebruch–Zagier cycles. J. Inst. Math. Jussieu 19(6), 1947–1992 (2020). https://doi.org/10.1017/s1474748019000021
Bloch, S., Kato, K.: \(L\)-functions and Tamagawa Numbers of Motives. The Grothendieck Festschrift, Vol. I, Progr. Math., vol. 86, pp. 333–400. Birkhäuser Boston, Boston (1990)
Burns, D., Flach, M.: Motivic \(L\)-functions and Galois module structures. Math. Ann. 305(1), 65–102 (1996). https://doi.org/10.1007/BF01444212
Burungale, A.A.: On the \(\mu \)-invariant of the cyclotomic derivative of a Katz \(p\)-adic \(L\)-function. J. Inst. Math. Jussieu 14(1), 131–148 (2015). https://doi.org/10.1017/S1474748013000388
Burungale, A.A., Disegni, D.: On the non-vanishing of \(p\)-adic heights on CM abelian varieties, and the arithmetic of Katz \(p\)-adic \(L\)-functions. Ann. Inst. Fourier (Grenoble) 70(5), 2077–2101 (2020)
Burungale, A.A., Tian, Y.: \(p\)-converse to a theorem of Gross–Zagier, Kolyvagin and Rubin. Invent. Math. 220(1), 211–253 (2020). https://doi.org/10.1007/s00222-019-00929-7
Büyükboduk, K., Lei, A.: Interpolation of generalized Heegner cycles in Coleman families. J. Lond. Math. Soc. (2) 104(4), 1682–1716 (2021). https://doi.org/10.1112/jlms.12471
Büyükboduk, K., Pollack, R., Sasaki, S.: \(p\)-adic Gross–Zagier formula at critical slope and a conjecture of Perrin-Riou (Preprint)
Cai, L., Shu, J., Tian, Y.: Explicit Gross–Zagier and Waldspurger formulae. Algebra Number Theory 8(10), 2523–2572 (2014). https://doi.org/10.2140/ant.2014.8.2523
Carayol, H.: Sur la mauvaise réduction des courbes de Shimura. Compositio Math. 59(2), 151–230 (1986). (French)
Carayol, H.: Sur les représentations \(l\)-adiques associées aux formes modulaires de Hilbert. Ann. Sci. École Norm. Sup. (4) 19(3), 409–468 (1986). (French)
Casselman, W.: On some results of Atkin and Lehner. Math. Ann. 201, 301–314 (1973)
Castella, F.: Heegner cycles and higher weight specializations of big Heegner points. Math. Ann. 356(4), 1247–1282 (2013)
Castella, F.: On the \(p\)-adic variation of Heegner points. J. Inst. Math. Jussieu 19(6), 2127–2164 (2020). https://doi.org/10.1017/s1474748019000094
Chenevier, G.: Familles \(p\)-adiques de formes automorphes pour \({\rm GL}_n\). J. Reine Angew. Math. 570, 143–217 (2004). https://doi.org/10.1515/crll.2004.031. (French, with English summary)
Chida, M., Hsieh, M.-L.: Special values of anticyclotomic \(L\)-functions for modular forms. J. Reine Angew. Math. 741, 87–131 (2018). https://doi.org/10.1515/crelle-2015-0072
Cornut, C., Vatsal, V.: CM points and quaternion algebras. Doc. Math. 10, 263–309 (2005)
Darmon, H.: Integration on \(\cal{H} _p\times \cal{H}\) and arithmetic applications. Ann. of Math. (2) 154(3), 589–639 (2001)
Darmon, H., Rotger, V.: Diagonal cycles and Euler systems I: A \(p\)-adic Gross–Zagier formula. Ann. Sci. Éc. Norm. Supér. (4) 47(4), 779–832 (2014). https://doi.org/10.24033/asens.2227. (English, with English and French summaries)
Deligne, P.: Formes modulaires et représentations de \({\rm GL}(2)\), Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Springer, Berlin, 1973, pp. 55-105. Lecture Notes in Math., Vol. 349 (French)
Dimitrov, M.: Automorphic symbols, \(p\)-adic \(L\)-functions and ordinary cohomology of Hilbert modular varieties. Am. J. Math. 135(4), 1117–1155 (2013). https://doi.org/10.1353/ajm.2013.0035
Disegni, D.: \(p\)-adic heights of Heegner points on Shimura curves. Algebra Number Theory 9(7), 1571–1646 (2015). https://doi.org/10.2140/ant.2015.9.1571
Disegni, D.: The \(p\)-adic Gross–Zagier formula on Shimura curves. Compos. Math. 153(10), 1987–2074 (2017)
Disegni, D.: On the \(p\)-adic Birch and Swinnerton-Dyer conjecture for elliptic curves over number fields. Kyoto J. Math. 60(2), 473–510 (2020). https://doi.org/10.1215/21562261-2018-0012
Disegni, D.: Local Langlands correspondence, local factors, and zeta integrals in analytic families. J. Lond. Math. Soc. (2) 101(2), 735–764 (2020). https://doi.org/10.1112/jlms.12285
Disegni, D.: The \(p\)-adic Gross–Zagier formula on Shimura curves, II: nonsplit primes. J. Inst. Math. Jussieu (To appear). https://doi.org/10.1017/S1474748021000608
Disegni, D.: \(p\)-adic \(L\)-functions via local-global interpolation: the case of GL\(_2\times \)GU(1). Can. J. Math. (to appear). https://doi.org/10.4153/S0008414X22000256
Emerton, M.: On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms. Invent. Math. 164(1), 1–84 (2006). https://doi.org/10.1007/s00222-005-0448-x
Fontaine, J.-M.: Représentations \(l\)-adiques potentiellement semi-stables. Astérisque 223, 321–347 (1994). (French). Périodes \(p\)-adiques (Bures-sur-Yvette, 1988)
Fornea, M., Gehrmann, L.: Plectic Stark–Heegner points. arXiv:2104.12575v1
Fornea, M., Guiitart, X., Masdeu, M.: Plectic p-adic invariants. arXiv:2104.12566v1
Fouquet, O.: Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms. Compos. Math. 149(3), 356–416 (2013). https://doi.org/10.1112/S0010437X12000619
Gan, W.T., Gross, B.H., Prasad, D.: Symplectic local root numbers, central critical \(L\) values, and restriction problems in the representation theory of classical groups. Astérisque 346, 1–109 (2012). (English, with English and French summaries). Sur les conjectures de Gross et Prasad. I
Greenberg, R., Stevens, G.: \(p\)-adic \(L\)-functions and \(p\)-adic periods of modular forms. Invent. Math. 111(2), 407–447 (1993). https://doi.org/10.1007/BF01231294
Greenberg, R.: Elliptic curves and \(p\)-adic deformations. In: Elliptic Curves and Related Topics, CRM Proc. Lecture Notes, vol. 4, pp. 101–110. Amer. Math. Soc., Providence (1994)
Gross, B.H., Zagier, D.B.: Heegner points and derivatives of \(L\)-series. Invent. Math. 84(2), 225–320 (1986). https://doi.org/10.1007/BF01388809
Gross, B.H.: Heegner points and representation theory. Heegner Points and Rankin \(L\)-Series, Math. Sci. Res. Inst. Publ., vol. 49, pp. 37–65. Cambridge Univ. Press, Cambridge (2004). https://doi.org/10.1017/CBO9780511756375.005
Gross, B.H.: Incoherent definite spaces and Shimura varieties (Preprint)
Guitart, X., Masdeu, M., Şengün, M.H.: Darmon points on elliptic curves over number fields of arbitrary signature. Proc. Lond. Math. Soc. (3) 111(2), 484–518 (2015)
Hida, H.: On \(p\)-adic Hecke algebras for \({\rm GL}_2\) over totally real fields. Ann. Math. (2) 128(2), 295–384 (1988). https://doi.org/10.2307/1971444
Hida, H.: On nearly ordinary Hecke algebras for \({\rm GL}(2)\) over totally real fields. Algebraic Number Theory, Adv. Stud. Pure Math., vol. 17, pp. 139–169, Academic Press, Boston (1989)
Hida, H.: On \(p\)-adic \(L\)-functions of \({\rm GL}(2)\times {\rm GL}(2)\) over totally real fields. Ann. Inst. Fourier (Grenoble) 41(2), 311–391 (1991). (English, with French summary)
Hida, H., Tilouine, J.: Anti-cyclotomic Katz \(p\)-adic \(L\)-functions and congruence modules. Ann. Sci. École Norm. Sup. (4) 26(2), 189–259 (1993)
Hida, H.: Hilbert Modular Forms and Iwasawa Theory, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford (2006)
Hida, H.: Anticyclotomic main conjectures. Doc. Math. Extra Vol., 465–532 (2006)
Hida, H.: Control of nearly ordinary Hecke algebras (2009). (Preprint)
Hida, H.: Quadratic exercises in Iwasawa theory. Int. Math. Res. Not. IMRN 5, 912–952 (2009). https://doi.org/10.1093/imrn/rnn151
Howard, B.: The Iwasawa theoretic Gross–Zagier theorem. Compos. Math. 141(4), 811–846 (2005). https://doi.org/10.1112/S0010437X0500134X
Howard, B.: Variation of Heegner points in Hida families. Invent. Math. 167(1), 91–128 (2007). https://doi.org/10.1007/s00222-006-0007-0
Hsieh, M.-L.: On the \(\mu \)-invariant of anticyclotomic \(p\)-adic \(L\)-functions for CM fields. J. Reine Angew. Math. 688, 67–100 (2014). https://doi.org/10.1515/crelle-2012-0056
Hsieh, M.-L.: Hida families and \(p\)-adic triple product \(L\)-functions. Am. J. Math. 143(2), 411–532 (2021)
Hung, P.-C.: On the derivative of anticyclotomic \(p\)-adic \(L\)-functions for Hilbert modular forms. Int. J. Number Theory 14(3), 615–630 (2018). https://doi.org/10.1142/S1793042118500379
Iovita, A., Spieß, M.: Derivatives of \(p\)-adic \(L\)-functions, Heegner cycles and monodromy modules attached to modular forms. Invent. Math. 154(2), 333–384 (2003). https://doi.org/10.1007/s00222-003-0306-7
Jetchev, D., Loeffler, D., Zerbes, S.L.: Heegner points in Coleman families. Proc. Lond. Math. Soc. (3) 122(1), 124–152 (2021). https://doi.org/10.1112/plms.12363
Katz, N.M.: \(p\)-adic \(L\)-functions for CM fields. Invent. Math. 49(3), 199–297 (1978). https://doi.org/10.1007/BF01390187
Knus, M.-A., Ojanguren, M.: Théorie de la descente et algèbres d’Azumaya, Lecture Notes in Mathematics, vol. 389. Springer, Berlin (1974). (French)
Li, C., Liu, Y.: Chow groups and \(L\)-derivatives of automorphic motives for unitary groups. Ann. Math. (2) 194(3), 817–901 (2021). https://doi.org/10.4007/annals.2021.194.3.6
Loeffler, D.: Spherical varieties and norm relations in Iwasawa theory. J. Théor. Nombres Bordeaux 33(3), 1021–1043 (2021). https://doi.org/10.1007/s10884-020-09844-5. (English, with English and French summaries)
Liu, Y., Zhang, S., Zhang, W.: A \(p\)-adic Waldspurger formula. Duke Math. J. 167(4), 743–833 (2018). https://doi.org/10.1215/00127094-2017-0045
Liu, Y., Tian, Y., Xiao, L., Zhang, W., Zhu, X.: On the Beilinson–Bloch–Kato conjecture for Rankin– Selberg motives. Invent. Math. (To appear)
Longo, M., Pati, M.R.: Exceptional zero formulae for anticyclotomic \(p\)-adic \(L\)- functions of elliptic curves in the ramified case. J. Number Theory 190, 187–211 (2018). https://doi.org/10.1016/j.jnt.2018.02.010
Longo, M., Vigni, S.: A refined Beilinson–Bloch conjecture for motives of modular forms. Trans. Am. Math. Soc. 369(10), 7301–7342 (2017). https://doi.org/10.1090/tran/6947
Masdeu, M.: CM cycles on Shimura curves, and \(p\)-adic \(L\)-functions. Compos. Math. 148(4), 1003–1032 (2012). https://doi.org/10.1112/S0010437X12000206
Mazur, B.: Modular curves and arithmetic. In: Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983). PWN, Warsaw, pp. 185–211 (1984)
Mok, C.P.: Heegner points and \(p\)-adic \(L\)-functions for elliptic curves over certain totally real fields. Comment. Math. Helv. 86(4), 867–945 (2011). https://doi.org/10.4171/CMH/243
Molina, S.: Anticyclotomic \(p\)-adic \(L\)-functions and the exceptional zero phenomenon. Trans. Am. Math. Soc. 372(4), 2659–2714 (2019). https://doi.org/10.1090/tran/7646
Nekovář, J.: Kolyvagin’s method for Chow groups of Kuga-Sato varieties. Invent. Math. 107(1), 99–125 (1992). https://doi.org/10.1007/BF01231883
Nekovář, J.: On \(p\)-adic height pairings. Séminaire de Théorie des Nombres, Paris, 1990.91, Progr. Math., vol. 108, pp. 127–202. Birkhäuser Boston, Boston (1993)
Nekovář, J.: On the \(p\)-adic height of Heegner cycles. Math. Ann. 302(4), 609–686 (1995). https://doi.org/10.1007/BF01444511
Nekovář, J.: Syntomic cohomology and \(p\)-adic regulators (1998)
Nekovář, J.: \(p\)-adic Abel–Jacobi maps and \(p\)-adic heights. The Arithmetic and Geometry of Algebraic Cycles (Banff, AB, 1998), CRM Proc. Lecture Notes, vol. 24, pp. 367–79. Amer. Math. Soc., Providence (2000)
Nekovář, J.: Selmer complexes. Astérisque 310, viii+559 (2006) (English, with English and French summaries)
Nekovář, J., Nizioł, W.: Syntomic cohomology and \(p\)-adic regulators for varieties over \(p\)-adic fields. Algebra Number Theory 10(8), 1695–1790 (2016). (With appendices by Laurent Berger and Frédéric Déglise)
Ota, K.: Big Heegner points and generalized Heegner cycles. J. Number Theory 208, 305–334 (2020). https://doi.org/10.1016/j.jnt.2019.08.005
Perrin-Riou, B.: Points de Heegner et dérivées de fonctions \(L\)\(p\)-adiques. Invent. Math. 89(3), 455–510 (1987). https://doi.org/10.1007/BF01388982. (French)
Perrin-Riou, B.: Fonctions \(L\)\(p\)-adiques, théorie d’Iwasawa et points de Heegner. Bull. Soc. Math. France 115(4), 399–456 (1987). (French, with English summary)
Perrin-Riou, B.: Fonctions \(L\)\(p\)-adiques des représentations \(p\)-adiques (1995). (French, with English and French summaries)
Qiu, C.: Modularity and Heights of CM cycles on Kuga-Sato varieties (Preprint)
Rouquier, R.: Caractérisation des caractères et pseudo-caractères. J. Algebra 180(2), 571–586 (1996). https://doi.org/10.1006/jabr.1996.0083. (French)
Saha, J.P.: Conductors in p-adic families. Ramanujan J. 44(2), 359–366 (2017)
Saito, H.: On Tunnell’s formula for characters of \({\rm GL}(2)\). Compositio Math. 85(1), 99–108 (1993)
Saito, T.: Hilbert modular forms and \(p\)-adic Hodge theory. Compos. Math. 145(5), 1081–1113 (2009). https://doi.org/10.1112/S0010437X09004175
Saltman, D.J.: Lectures on division algebras. In: CBMS Regional Conference Series in Mathematics, vol. 94, Published by American Mathematical Society, Providence, RI; on behalf of Conference Board of the Mathematical Sciences, Washington, DC (1999)
Schneider, P., Teitelbaum, J.: Algebras of \(p\)-adic distributions and admissible representations. Invent. Math. 153(1), 145–196 (2003). https://doi.org/10.1007/s00222-002-0284-1
Schneider, P., Teitelbaum, J.: Duality for admissible locally analytic representations. Represent. Theory 9, 297–326 (2005). https://doi.org/10.1090/S1088-4165-05-00277-3
Seveso, M.A.: Heegner cycles and derivatives of \(p\)-adic \(L\)-functions. J. Reine Angew. Math. 686, 111–148 (2014). https://doi.org/10.1515/crelle-2012-0027
Shnidman, A.: \(p\)-adic heights of generalized Heegner cycles. Ann. Inst. Fourier (Grenoble) 66(3), 1117–1174 (2016). (English, with English and French summaries)
Skinner, C.M., Wiles, A.J.: Residually reducible representations and modular forms. Inst. Hautes Etudes Sci. Publ. Math. 89(1999), 5–126 (2000)
Tate, J.: Number theoretic background. In: Automorphic Forms, Representations and \(L\)-functions (Corvallis, Ore., 1977), Proc. Sympos. Pure Math., vol. XXXIII, pp. 3–26. Amer. Math. Soc., Providence (1979)
Taylor, R., Yoshida, T.: Compatibility of local and global Langlands correspondences. J. Am. Math. Soc. 20(2), 467–493 (2007)
Tian, Y.: Congruent numbers and Heegner points. Camb. J. Math. 2(1), 117–161 (2014). https://doi.org/10.4310/CJM.2014.v2.n1.a4
Tian, Y., Xiao, L.: \(p\)-adic cohomology and classicality of overconvergent Hilbert modular forms. Astérisque 382, 73–162 (2016). (English, with English and French summaries)
Tunnell, J.B.: Local \(\epsilon \)-factors and characters of \({\rm GL}(2)\). Am. J. Math. 105(6), 1277–1307 (1983). https://doi.org/10.2307/2374441
Venerucci, R.: \(p\)-adic regulators and \(p\)-adic families of modular forms. Thesis, Università di Milano (2012). https://air.unimi.it/retrieve/handle/2434/219975/275017/phd_unimi_R08514.pdf
Venerucci, R.: Exceptional zero formulae and a conjecture of Perrin-Riou. Invent. Math. 203(3), 923–972 (2016). https://doi.org/10.1007/s00222-015-0606-8
Waldspurger, J.-L.: Sur les valeurs de certaines fonctions \(L\) automorphes en leur centre de symétrie. Compositio Math. 54(2), 173–242 (1985). (French)
Xue, H.: Arithmetic theta lifts and the arithmetic Gan–Gross–Prasad conjecture for unitary groups. Duke Math. J. 168(1), 127–185 (2019). https://doi.org/10.1215/00127094-2018-0039
Yuan, X., Zhang, S.-W., Zhang, W.: The Gross–Zagier Formula on Shimura Curves, Annals of Mathematics Studies, vol. 184. Princeton University Press, Princeton (2012)
Yuan, X., Zhang, S.-W., Zhang, W.: Triple product L-series and Gross–Kudla–Schoen cycles (Preprint)
Zhang, S.: Heights of Heegner cycles and derivatives of \(L\)-series. Invent. Math. 130(1), 99–152 (1997). https://doi.org/10.1007/s002220050179
Acknowledgements
I would like to thank Joël Bellaiche, Ashay Burungale, Gaëtan Chenevier, Olivier Fouquet, Ming-Lun Hsieh, David Loeffler, Michele Fornea, Jonathan Pottharst, Ye Tian, Rodolfo Venerucci, and Sarah Zerbes for useful conversations or correspondence or mathoverflow answers. I am also grateful to the referee for coaxing me to write Sect. 7.3, and to Simone Dell’Ariccia for Fig. 1. Finally, I would like to thank Shouwu Zhang for a vague question he asked me in 2010; this paper may be a partial answer.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by ISF grant 1963/20 and BSF grant 2018250. During the preparation of a first draft of this paper, the author was supported by a public grant of the Fondation Mathématique Jacques Hadamard.
Appendix A. p-adic semilocal constructions
Appendix A. p-adic semilocal constructions
1.1 Preliminaries
Throughout this appendix, unless otherwise noted L denotes a field of characteristic zero (admitting embeddings into \(\mathbf {C}\)).
1.1.1 Admissible and coadmissible representations
Let \(\mathrm {G}\) be a reductive group over \(\mathbf {Q}_{p}\). We denote
where \(G_{p}\) and \(G_{\Delta }\) have the p-adic topology, \(G_{\infty }\) has the Zariski topology, and \(\Delta \) is the (continuous) diagonal embedding. The difference between \(G_{p}\), \(G_{\infty }\), \(G_{\Delta }\) will be in the category of modules we choose to consider. Namely, we consider the categories of smooth admissible representations of \(G_{p}\) over L, of algebraic representations of \(G_{\infty }\) over L, and the products of such for G; we call the latter locally algebraic representations of G over L.
Definition A.1.1
Suppose that L is a finite extension of \(\mathbf {Q}_{p}\). A p-adic locally algebraic admissible representation \(\Pi \) of G over L is one such that for each compact open subgroup \(K\subset G_{\Delta }\), there exists a family of \(\mathscr {O}_{L}\)-lattices \(\Pi ^{K, \circ }\subset \Pi ^{K}\), for \(K\subset G_{\Delta }\), with the property that \(\Pi ^{K', \circ }\cap \Pi ^{K}= \Pi ^{K, \circ }\) for all \(K'\subset K\).
The typical example of a p-adic locally algebraic admissible representation is \(\varinjlim _{K_{p}\subset G_{p}} H^{i}(Y_{K^{p}K_{p}}, \mathscr {W})\otimes W^{\vee }\), where \(Y_{K}\) is the system of locally symmetric spaces attached to a model \(\mathrm {G}_{\mathbf {Q}}\) of \(\mathrm {G}\) over \(\mathbf {Q}\), and \(\mathscr {W}\) is the automorphic local system attached to the algebraic representation W of \(G_{\infty }\).
There is a dual notion, introduced in [93, p. 152], see also [94]. Assume that L is endowed with a discrete valuation (possibly trivial), giving it a norm \(|\cdot |\). Let \(G'\) be one of the groups (A.1.1) or an open subgroup. For \(K\subset G'\) a compact open subgroup, let \(\mathscr {D}_{G',K}=\mathscr {H}_{G', K}:=C^{\infty }_{c}(K\backslash G'/K,L)\) and \(\mathscr {D}_{G'}=\varprojlim \mathscr {D}_{G',K}\) be the Hecke algebras of distributions; they are endowed with a natural topology as L-vector space, respectively as the inverse limit. A coadmissible \(G'\)-representation M over \((L, |\cdot |)\) is a topological right \(\mathscr {D}_{G'}\)-module such that, for any compact subgroup \(G^{\circ }\subset G'\), the \(\mathscr {D}_{G^{\circ }}\)-module M admits a presentation of the following form: there exists a system of topological \(\mathscr {D}_{G^{\circ }, K}\)-modules \(M_{K}\) and isomorphisms \(M_{K}\cong M_{K'}\otimes _{\mathscr {D}_{G^{\circ }, K'}} \mathscr {D}_{G^{\circ }, K}\) for \(K'\subset K\subset G^{\circ }\), such that \(M\cong \varprojlim _{K} M_{K}\).
Considering first a field L as endowed with a trivial valuation, we shall consider coadmissible representations M of \(G_{p}\) over L that are smooth in the sense the Lie algebra \(\mathfrak {g}\) of \(G_{p}\) acts trivially; coadmissible representations W of \(G_{\infty }\) that are algebraic (those are just algebraic representations); and the products of such as representations of G, which we call locally algebraic coadmissible representations of G.
Definition A.1.2
Suppose that L is a finite extension of \(\mathbf {Q}_{p}\); denote by \(|\cdot |\) the p-adic norm and by \(|\cdot |_\mathrm{triv}\) the trivial norm on L. A p-adic locally algebraic coadmissible representation M of G over L is one as above for \((L, |\cdot |_\mathrm{triv})\), whose restriction to \(G_{\Delta }\) is coadmissible for \((L, |\cdot |)\).
The typical example of a p-adic locally algebraic coadmissible representation is \(\varprojlim _{K_{p}} H_{i}(Y_{K^{p}K_{p}}, \mathscr {W})\otimes W^{\vee }\), where the notation is as after Definition A.1.1.
1.1.2 Notation
Consider the groups (1.2.1). For a place \(v\vert p\) of F, we let
as topological groups. We use the parallel notation \(G_{*, v, \infty }\) for \(G_{*,v}\) viewed as the group of points of an algebraic group over \(F_{v}\).
We assume from now on that \(\mathbf {B}_{p}\) is split and fix an isomorphism \(\mathrm {G}_{\mathbf {Q}_{p}}\cong \mathrm {Res}_{F_{p}/\mathbf {Q}_{p}}\mathrm {GL}_{2}\), giving a model of \(\mathrm {G}_{*}\) over \(\mathbf {Z}_{p}\). We define involutions
that induce involutions \(\iota \) on all our groups. The embedding \(\mathrm {H}'\hookrightarrow (\mathrm {G}\times \mathrm {H})'\) is compatible with the involutions.
For \(t\in T_{\mathrm {G}_{*}, p}\), let \(\mathrm {U}_{t}:= K_{p, r} t K_{p,r}\in \mathscr {H}^{K_{p,r}}_{G_{*, p}}\) for any \(r\ge 1\), and
When \(x\in F_{p}^{\times }\), we abuse notation by writing \(\mathrm {U}_{x}= \mathrm {U}_{\left( {\begin{matrix}x&{}\\ &{}1\end{matrix}}\right) }\); we also write
for short.
1.1.3 Ordinary parts of admissible or coadmissible \(G_{*}\)-modules
Let L be a finite extension of \(\mathbf {Q}_{p}\). Let \(\Pi =\Pi _{p}\otimes W\) be a p-adic locally algebraic admissible representation of \(G_{*}\) Let us write
where \(N_{0, r}:=K_{p, r}\). Choose \(\mathscr {O}_{L}\)-lattices \(W^{\circ }\subset W\), \(\Pi _{p}^{\circ , K}\subset \Pi _{p}^{K}\), stable under the Hecke action, and compatibly with the transition maps associated with \(K'\subset K\). Then \(\Pi ^{\circ , N_{0}}:=\Pi _{p}^{\circ , N_{0}} \otimes W^{\circ , N}= \varinjlim _{r} \Pi _{p}^{\circ , K_{p,r}} \otimes W^{\circ , N}\) is stable under the action of \(\mathrm {U}_{p\infty }\). As shown by Hida, the idempotent
is then well-defined and its image is denoted by \(\Pi ^{\circ , \mathrm {ord}}\). The space \(\Pi ^{\circ , \mathrm {ord}}\) is the maximal split \(\mathscr {O}_{L}\)-submodule of \(\Pi ^{\circ , N_{0}}\) over which \(\mathrm {U}_{p\infty }\) acts invertibly. We also write \(e^{\mathrm {ord}}\) for \(e^{\mathrm {ord}}\otimes 1:\Pi ^{N_{0}}=\Pi ^{\circ , N_{0}}\otimes L\rightarrow \Pi ^{N_{0}}\), and we let \(\Pi ^{\mathrm {ord}}=e^{\mathrm {ord}}\Pi ^{N_{0}}\) be its image. If \(\Pi _{p}\) and W are irreducible, then \(\Pi ^{\mathrm {ord}}\) has dimension either 0 or 1; in the latter case we say that \(\Pi \) is ordinary. (This notion is independent of the choice of lattices.)
Let \(\mathrm{M}=\mathrm{M}_{p}\otimes W^{\vee }\) be a p-adic locally algebraic coadmissible right module for \(G_{*}\) over L. By definition of coadmissibility, the system \((\mathrm{M}_{p,K})_{K\subset G_{*,p}}\) is endowed with a compatible system \(\mathscr {H}_{\mathrm {G}_{*}(\mathbf {Z}_{p}), K}\)-stable lattices \(\mathrm{M}_{p,K}^{\circ }\), so that for some \(\mathrm {G}_{*}(\mathbf {Z}_{p})\)-stable lattice \(W^{\vee , \circ }\), \(\mathrm{M}^{\circ }_{N_{0}}:= \varprojlim \mathrm{M}^{\circ }_{p, K_{p, r}}\otimes W^{\vee , \circ }_{N_{0}}\) is stable under \(\mathrm {U}_{p\infty }\). Then we can again define \(e^{\mathrm {ord}}:\mathrm{M}^{(\circ )}_{N_{0}} \rightarrow \mathrm{M}^{(\circ )}_{N_{0}}\). Its image
is called the ordinary part of \(\mathrm{M}^{(\circ )}_{N_{0}} \).
The ordinary parts \(\Pi ^{\mathrm {ord}}\), \(\mathrm{M}^{\mathrm {ord}}\) retain an action of the operators \(\mathrm {U}_{t, p\infty }\).
1.1.4 Special group elements, and further notation
The following notation will be in use throughout this appendix. Let \(v\vert p\) be a place of F. We denote by \(e_{v}\) be the ramification degree of \(E_{v}/F_{v}\), and fix a uniformiser \(\varpi _{v}\in F_{v}\) chosen so that \(\prod _{v\vert p}\varpi _{v}^{e_{v}}=p\). Let \(\mathrm{Tr}_{v}=\mathrm {Tr}_{E_{v}/F_{v}}\) and \(\mathrm{Nm}_{v}:=\mathrm{Nm}_{E_{v}/F_{v}}\) be the trace and norm. Fix an isomorphism \(\mathscr {O}_{E, v}=\mathscr {O}_{F, v}\times \mathscr {O}_{F, v}\) if v is split. If v is nonsplit, let c be the Galois conjugation of \(E_{v}/F_{v}\), and fix an element \(\theta _{v}\in \mathscr {O}_{E,v}\) such that \(\mathscr {O}_{E, v}=\mathscr {O}_{F,v}[\theta _{v}]\) (thus \(\theta _{v}\) is a unit if v is inert and a uniformiser if v is ramified). We define a purely imaginary \(\mathrm{j}_{v}\in E_{v}^{\times }\) to be
We assume that \(E_{v}\) embeds in \(\mathbf {B}_{v}\) and fix the embedding \(E_{v}\rightarrow \mathbf {B}_{v}\) to be
For \(r\ge 0\), let
and
1.2 Toric, ordinary, and anti-ordinary parts
Let L be a finite extension of \(\mathbf {Q}_{p}\). We perform some twists.
1.2.1 Ordinary and anti-ordinary parts
Let \(w:=\left( {\begin{matrix}&{}1\\ -1&{}\end{matrix}}\right) \in G_{*,\Delta }\) and let \(\pi ^{w}\) be the representation on the same space as \(\pi \) but with G-action given by \(\pi ^{w}(g)v:=\pi (w^{-1}gw)v\). Let \(N^{-}:= w^{-1}Nw\), and \(U_{p\infty }^{-}:= U_{w^{-1}\left( {\begin{matrix}p&{}\\ &{}1\end{matrix}}\right) w, p\infty }\).
Let \(\pi =\pi _{p}\otimes W\) be a p-adic admissible locally algebraic representation of G over L. The anti-ordinary part of \(\pi \) is the space
of ‘ordinary’ elements with respect to \(N^{-}\) and \(U_{p\infty }^{-}\). Because \(\pi ^{w}\) is isomorphic to \(\pi \), the spaces \(\pi ^\mathrm{a}\) and \(\pi ^{\mathrm {ord}}\) have the same dimension.
Let \(M=M_{p}\otimes W\) be a p-adic coadmissible locally algebraic representation of G over L. The anti-ordinary part of M is the quotient
of M that is its ‘ordinary’ part with respect to \(N_{0}^{-}\) and and \(U_{p\infty }^{-}\).
Proposition A.2.1
Let W be an algebraic representation of \(G_{\infty }\).
-
1.
Let \(\pi \) be a p-adic locally algebraic admissible representation of G. There is an isomorphism
$$\begin{aligned} w^{\mathrm {ord}}_\mathrm{a}:\pi ^{\mathrm {ord}}&\rightarrow \pi ^\mathrm{a}\\ f&\mapsto \lim _{r\rightarrow \infty } p^{r[F:\mathbf {Q}]} w_{r,p}w_{0, \infty }^{\iota }\mathrm {U}_{p}^{-r}f, \end{aligned}$$where the sequence stabilises as soon as \(r\ge 1 \) is such that \(f_{p}\in \pi _{p}^{U_{1}^{1}(p^{r})}\).
-
2.
Let M be a p-adic locally algebraic coadmissible representation of G. There is a map
$$\begin{aligned} w^{\mathrm {ord}}_\mathrm{a}:M^{\mathrm {ord}}&\rightarrow M^\mathrm{a}\\ m=m_{p}\otimes m_{\infty }&\mapsto \lim _{r\rightarrow \infty } p^{r[F:\mathbf {Q}]} [m (U_{p}^{})^{-r} w_{r,p}]_{N_{0}^{-}} \otimes [m_{\infty }w_{0, \infty }^{\iota }]_{N^{-}}, \end{aligned}$$where before applying \(w_{*}\), we take arbitrary lifts from \(N_{0}^{}\)-coinvariants to the module M.
Proof
That the maps are well-defined is a standard result left to the reader. At least for admissible representations, the map is an isomorphism (equivalently, nonzero) because of Lemma A.3.3 below. \(\square \)
Let \(\pi _{v}^{\mathrm {ord}}\) (respectively \(\pi _{v}^\mathrm{a}\)) denote the preimage of \(\pi ^{\mathrm {ord}}\) (respectively \(\pi ^\mathrm{a}\)) in \(\pi _{v}\), and let \(W_{v}\) be the \(G_{v, \infty }\)-component of W. The following local components of the above map are similarly well-defined:
Lemma A.2.2
Let \(\pi \) be an ordinary representation of G. If \((\ , \ ):\pi \otimes \pi ^{\vee }\rightarrow L\) is a nondegenerate G-invariant pairing, then the pairing
is a nondegenerate pairing.
Proof
It suffices to see this for a specific pairing \((\ , \ )\): we may take the product of the pairings (A.3.2) below, that are known to be nondegenerate, and any nondegenerate pairing on \(W\otimes W^{\vee }\). Then the result follows from Lemmas A.3.3 and A.4.1 below. \(\square \)
1.2.2 Ordinary and toric parts
We construct a map from the ordinary part of a representation of \((G\times H)'\) to its toric coinvariants, as well as a dual map in the opposite direction for coadmissibe modules. These map are the key to the interpolation of toric periods.
Suppose that \(W_{(v)}\) (respectively \(W=\bigotimes _{v\vert p}W_{v}\) is an algebraic representation of \((G\times H)_{(v) , \infty }\) (respectively \((G\times H)'_{\infty }\)) over L such that, for a field extension \(L'/L\) splitting E, \(W_{(v), \infty }\otimes _{L} L'=\bigotimes _{\sigma :F_{(v)}\hookrightarrow L} W_{\sigma }\) with
for some integers \(k_{\sigma }\ge 2, |l_{\sigma }|<k_{\sigma }, w\) of the same parity. (Here we have chosen, for each \(\sigma :F\hookrightarrow L\), an extension \(\sigma :E\hookrightarrow L\).) Then we define a constant
(Note that \(\mathrm{j}_{v}^{-w-k_{\sigma }+2 }=1\) if v splits in E, as \(w+k_{\sigma }-2\) is even.)
Lemma A.2.3
Recall the congruence subgroups \(V_{v,r}'\), \(K_{v,r}\) defined in Sect. 2.1.5. For all \(r\ge 1\), we have the identity of Hecke operators in the Hecke algebra for \((G\times H)'_{v}\):
Proof
This is a consequence of the following matrix identity.
Let \(v\vert p\) be a prime of F. For \(r\in \mathbf {Z}_{\ge 1}\), \(j\in \mathscr {O}_{F,v}\) let \(b_{j,v}:= \left( \begin{array}{cc}\varpi &{}j\\ &{}1\end{array}\right) \). In the split case, let
In the nonsplit case, let
Then
in \(\mathrm {GL}_{2}(F_{v})\). \(\square \)
Proposition A.2.4
Let W be an algebraic representation of \((G\times H)'_{\infty }\).
-
1.
Let \(\Pi =\Pi _{p}\otimes W\) be a p-adic locally algebraic admissible representation of \((G\times H)'\). There is a map
$$\begin{aligned} \gamma _{H'}^{\mathrm {ord}} :\Pi ^{\mathrm {ord}}&{\rightarrow } \Pi _{H'}\nonumber \\ f&\mapsto \lim _{r} \ {H'_{}}[ p^{r[F:\mathbf {Q}]} \cdot c(W)^{-1}\cdot \gamma _{r, p\infty } \mathrm {U}_{p\infty }^{-r} f], \end{aligned}$$(A.2.4)where \({H'_{}}[-]:\Pi \rightarrow \Pi _{H'}\) is the natural projection. The sequence in the right hand side of (A.2.4) stabilises as soon as \(f_{p}\in \Pi ^{K_{p, r}}\), where \(K_{p, r}\subset (G\times H)_{p}'\) is defined at the end of Sect. 2.1.
-
2.
Let \(\mathrm{M}:= \mathrm{M}_{p}\otimes W^{\vee }\) be a p-adic locally algebraic coadmissible representation of \((G\times H)'\). There is a map
$$\begin{aligned} \gamma _{H'}^{\mathrm {ord}} :\mathrm{M}^{H'}&\rightarrow \mathrm{M}^{\mathrm {ord}}\\ m&\mapsto \lim _{r}\ [ p^{r[F:\mathbf {Q}]} \cdot c(W)^{-1}\cdot m \gamma _{r,p\infty }] {N_{0,r}} e^{\mathrm {ord}} \mathrm {U}_{p\infty }^{-r}, \end{aligned}$$where \([ -]{N_{0,r}}:\mathrm{M} \rightarrow \mathrm{M}_{N_{0}}\) is the natural projection.
The constant c(W) is justified by Lemma A.4.2 below.
Proof
For part 1, let \(f\in \Pi _{p}^{K_{p, r}}\). Then it follows from Lemma A.2.3 that, denoting by \([f_{r}]_{H'}\) the sequence in the right hand side of (A.2.4), we have
hence \([f_{r+1}-f_{r}]_{H'}=0 \) and the sequence stabilises.
For part 2, Lemma A.2.3 similarly implies (the boundedness and) the convergence of the sequence in \(\varprojlim _{r} \mathrm{M}_{N_{0, r}}^{\mathrm {ord}}\). \(\square \)
Let \(\Pi _{v}^{\mathrm {ord}}\) denote the preimage of \(\Pi ^{\mathrm {ord}}\) in \(\Pi _{v}\), and let \(W_{v}\) be the \((G\times H)'_{v, \infty }\)-component of W. The following local components of the above maps are similarly well-defined:
1.2.3 Exceptional representations and vanishing of \(P^{\mathrm {ord}}\)
We show that \(\gamma _{H'}^{\mathrm {ord}} \) acts by zero precisely on those representations that are exceptional.
Lemma A.2.5
Let \(\Pi =\pi \otimes \chi \) be an ordinary, distinguished, irreducible representation of \((G\times H)'\). The following are equivalent:
-
1.
\(\Pi \) is exceptional;
-
2.
\(e_{v}(V_{(\pi , \chi )}) = 0\);
-
3.
there exists \(P\in \Pi ^{*, H'} -\{ 0\}\) such that \(P^{\mathrm {ord}}:=P \gamma _{H'}^{\mathrm {ord}} =0\);
-
4.
for all \(P\in \Pi ^{*, H'}\), we have \(P^{\mathrm {ord}}=0\);
Proof
The equivalence of 1. and 2. is a reminder from Lemma 6.4.6. The equivalence of 3. and 4. is a consequence of multiplicity-one. Consider 3. Let \(P\in \Pi ^{*, H'}\). Identify \(\Pi ^{\vee }=\Pi ^{\iota }\) (the representation on the same space as \(\Pi \), with group action twisted by the involution \(\iota \)). Then the identity map on spaces yields isomorphisms \(\Pi ^{*, H'}\cong \Pi ^{\vee , *, H'}\) and \(\Pi ^{\mathrm {ord}, *}\cong \Pi ^{\vee , \mathrm {ord}, *}\), and it follows from the explicit description of \(\gamma _{H'}^{\mathrm {ord}} \) that if \(P^{\vee }\) denotes the image of P, then the image of \(P^{\vee }\) is \(P^{\vee ,\mathrm {ord}}\). Hence, \(P^{\mathrm {ord}}\) is zero if and only if so is \(P^{\vee , \mathrm {ord}}\), if and only if so is \(P\otimes P^{\vee }\circ \gamma _{H'}^{\mathrm {ord}} \otimes \gamma _{H'}^{\mathrm {ord}} \). Now by the theory recalled in Sect. 1.2.6 , \(P \otimes P^{\vee }\) is necessarily a multiple of the explicit functional \(Q_{dt, (, )}\) defined there. Therefore it suffices to show that \(Q_{dt, (, )}\) vanishes on the line \(\gamma _{H'}^{\mathrm {ord}} \Pi ^{\mathrm {ord}}\otimes \gamma _{H'}^{\mathrm {ord}} \Pi ^{\vee , \mathrm {ord}}\) if and only if \(e_{v}(V_{(\pi , \chi )}) = 0\). This follows from the explicit computations of Propositions A.3.4 and A.4.3 below, cf. also Proposition 4.3.4. \(\square \)
1.3 Pairings at p
The goal of this subsection is to relate the p-components of the toric terms Q and their ordinary variants \(Q^{\mathrm {ord}}\), as defined in Sects. 4.2–4.3.
Let \(v \vert p\) be a place of F.
1.3.1 Integrals and gamma factors
If \(\pi \) (respectively \(\chi \)) is an irreducible representation of \(G_{v}\) over L, we denote by \(V_{\pi }\) (respectively \(V_{\chi })\) the associated 2- (respectively 1-) dimensional Frobenius-semisimple representation of \(\mathrm{WD}_{F_{v}}\) (respectively of \(\mathrm{WD}_{E_{v}}:=\prod _{w\vert v}\mathrm{WD}_{E_{w}}\); we choose the “Hecke” normalisation, so that \(\det V_{\pi }\) is the cyclotomic character if \(\pi \) is self-dual. If \(\Pi =\pi \otimes \chi \) is an irreducible representation of \((G\times H)'_{v}\), we denote by \(V_{\Pi }= V_{\pi |\mathrm{WD}_{E_{v}}}\otimes V_{\chi }\) the associated 2-dimensional representation of \(\mathrm{WD}_{E_{v}}\). If \(E_{*} \) is F or E, \(w\vert p\) is a prime of \(E_{*}\) and V is any representation of \(\mathrm{WD}_{E_{*,v}}\) as above, we let \(V_{w}:= V_{|\mathrm{WD}_{E_{*, w}}}\).
If \(\psi :F_{v}\rightarrow \mathbf {C}^{\times }\) is a nontrivial character, we denote by \(d_{\psi } y\) the selfdual Haar measure on \(F_{v}\) and \(d^{\times }_{\psi }y:= d_{\psi }y/|y|\). The level of \(\psi \) is the largest n such that \(\psi _{|\varpi ^{-n}\mathscr {O}_{F, v}}=1\). We recall that if \(\psi \) has level 0, then \(\mathrm {vol}(\mathscr {O}_{F, v},d_{\psi }y)=1\).
Recall the Deligne–Langlands \(\gamma \)-factor of (1.4.3).
Lemma A.3.1
[35, Lemma A.1.1]. Let \(\mu :F_{v}^{\times }\rightarrow \mathbf {C}^{\times }\) and \(\psi :F_{v}\rightarrow \mathbf {C}^{\times }\) be characters, with \(\psi _{v}\ne 1\). Let \(d^{\times }y\) be a Haar measure on \(F_{v}^{\times }\). Then
1.3.2 Local pairing
The following isolates those representations that can be components of an ordinary representation.
Definition A.3.2
A refined representation \((\pi , \alpha )\) of \(G_{v}\) over a field L consists of a smooth irreducible infinite-dimensional representation \(\pi \) and a character \(\alpha :F_{v}\rightarrow L^{\times }\), such that \(\pi \) embeds into the un-normalised induction \(\mathrm{Ind}( |\ |\alpha , |\ |^{-1}\omega \alpha ^{-1}))\) for some other character \(\omega :F_{v}^{\times }\rightarrow L^{\times }\).Footnote 31 Sometimes we abusively simply write \(\pi \) instead of \((\pi , \alpha )\). A refined representation \(\Pi =\pi \otimes \chi \) \((G\times H)'_{v}\) is the product of a refined representation \(\pi =(\pi , \alpha )\) of G and a character \(\chi \) of H, such that \(\omega \chi _{|F_{v}^{\times }}=\mathbf {1}\).
If \((\pi , \alpha )\) is a refined representation of \(G_{v}\), we let \(\pi ^{\mathrm {ord}}\subset \pi ^{N_{0}}\) be the unique line on which the operator \(\mathrm {U}_{t}\) acts by \(\alpha (t)\). If \(\Pi =\pi \otimes \chi \) is a refined representation of \((G\times H)'_{v}\), we let \(\Pi ^{\mathrm {ord}}:=\pi ^{\mathrm {ord}}\otimes \chi \). The associated Weil–Deligne representation \(V_{\pi }\) is reducible, and we have a unique filtration
such that \(\mathrm{WD}_{F_{v}}\) acts on \(V_{\pi }^{+}\) through the character \(\alpha |\cdot |\).
Let \(\pi \) be a refined representation of \(G_{v}\) over L, and let \((\ , \ )_{\pi }:\pi \otimes \pi ^{\vee }\rightarrow L\) be a G-invariant pairing. Then we define
where \(w^{\mathrm {ord}}_\mathrm{a} \) is the operator denoted \(w_{\mathrm{a}, v}^{\mathrm {ord}}\) in (A.2.1). If \(\Pi \) is a refined representation of \((G\times H)_{v}'\) over L and \((\ , \ ) =(\ , \ )_{\pi }(\ ,\ )_{\chi }:\Pi \otimes \Pi ^{\vee } \rightarrow L\) is a pairing, we define \((\ , \ )^{\mathrm {ord}}:= (\ , \ )_{\pi }^{\mathrm {ord}} (\ ,\ )_{\chi }\), a pairing on \(\Pi ^{\mathrm {ord}}\otimes \Pi ^{\vee , \mathrm {ord}}\).
Lemma A.3.3
Let \((\pi , \alpha )\) be a refined representation of \(G_{p}\) over \(\mathbf {C}\), with central character \(\omega \) as in Definition A.3.2. Let \(\alpha ^{\vee }=\alpha \omega ^{-1}\). Let
Fix a character \(\psi :F_{v}\rightarrow \mathbf {C}^{\times }\) of level 0, and Kirillov models of \(\iota \pi _{v}\), \(\pi _{v}^{\vee }\) with respect to \(\psi _{v}\), \(-\psi _{v}\). Let
Suppose that \(( \ , \ )_{\pi ,{v}}\) is, in the Kirillov models, the pairing
Then
Proof
We omit all remaining subscripts v and argue similarly to [60, Lemma 2.8]. The inner product \((f, f^{\vee })^{\mathrm {ord}}_{\pi }\) is the value at \(s=0\) of
By the functional equation for \(\mathrm {GL}_{2}\), this equals
using the fact that the domain of integration can be replaced with \(F^{\times }\), the additivity of gamma factors, and the relation \(\alpha ^{\vee }=\alpha \omega ^{-1}\). Evaluating at \(s=0\) we find \(\gamma (\mathrm {ad}(V_{\pi })^{++}(1), \psi )^{-1}\) as desired. \(\square \)
1.3.3 Local toric period
We compute the value of the local toric periods on the lines of interest to us. Let \(\Pi =\pi \otimes \chi \) be a refined representation of \((G\times H)'_{v}\). Let dt be a measure on \(H'_{v}\), and set as in (4.3.1)
Then for all \(f_{1}, f_{3}\in \Pi ^{\mathrm {ord}}\), \(f_{2},f_{4}\in \Pi ^{\vee , \mathrm {ord}}\) with \(f_{3}, f_{4}\ne 0\), we define
where \(\mathrm{j}_{v}=\) (A.1.2) and \(\mu ^{+}=\chi _{v}\cdot \alpha |\cdot |\circ N_{E_{v}/F_{v}}\) is the character giving the action of \(E_{v}^{\times }\) on \(V^{+}:=V_{\pi }^{+}\otimes \chi \).
Proposition A.3.4
Let \(\Pi =\pi \otimes \chi \) be a refined representation of \((G\times H)'_{v}\) over L, with associated Weil–Deligne representation \(V=V_{\pi |\mathrm{WD}_{E_{v}}}\otimes \chi \). Let \({\gamma _{H'}^{\mathrm {ord}} }={\gamma _{H'}^{\mathrm {ord}} }_{,v}\) be as defined in (A.2.5). Then
Here
is defined independently of any choice of an embedding \(\iota :L\hookrightarrow \mathbf {C}\) and nontrivial character \(\psi :F_{v}\rightarrow \mathbf {C}^{\times }\).
Proof
Identify \(\chi ^{\pm 1}\) with L and assume that \(f_{i}=f_{i, \pi }f_{i, \chi }\) with \(f_{i, \chi }\) identified with 1. Fix \(\iota :L\hookrightarrow \mathbf {C}\) (omitted from the notation) and \(\mathbf {1}\ne \psi :F_{v}\rightarrow \mathbf {C}^{\times }\). Identify \(\pi \), \(\pi ^{\vee }\) with Kirillov models with respect to \(\psi \), \(-\psi \). Let \((\ , \ )=(\ , \ )_{\pi }\cdot (\, \ )_{\chi }\) be the invariant pairing on \(\Pi \otimes \Pi ^{\vee }\) such that \(( \ , \ )_{\pi } =\) (4.2.3) and \((1 \ ,1 \ )_{\chi }=1\). Assume, after a harmless extension of scalars, that \(dt=|D_{v}|^{-1/2} d^{\times }_{\psi _{E}}z/d^{\times }_{\psi }y\), which gives \(\mathrm {vol}^{\circ }(H', dt)=1\). Let \(f_{1}=f_{3}=f_{\pi }\), \(f_{2}=f_{4}=f_{\pi }^{\vee }\) with \(f_{\pi }^{(\vee )}\) as in (A.3.1).
In view of the definitions (4.2.2), (A.3.3) and of Lemma A.3.3, it suffices to show that
We denote by \(\alpha \) the refinement of \(\pi \), and we fix \(r\ge 1\) to be larger than the valuations of the conductors of \(\pi \) and of the norm of the conductor of \(\chi \).
Split case. Suppose first that \(E_{v}/F_{v}\) is split and identify \(E_{v}^{\times }=F_{v}^{\times }\times F_{v}^{\times }\) as usual. Then as in [32, Lemma 10.12] we find
where we have used Lemma A.3.1.
Nonsplit case. Now suppose that \(E_{v}=E_{w}\) is a field and drop all subscripts v, w. We abbreviate \(\mathrm{T}:=\mathrm {Tr}(\theta )\), \(\mathrm {N}:=\mathrm{Nm}(\theta )\).
We have
There is a decomposition
that is an isometry when \(H'_{1}\), \(H_{2}'\) are endowed with the measures \(d_{\psi }b\), \(d_{\psi }a\).
Let \(r':= r+e-1\) and let us redefine, for the purposes of this proof, \(w_{r'}:= \left( {\begin{matrix}&{}1\\ -\mathrm {N}^{-1}\varpi ^{-r}&{}\end{matrix}}\right) \). Let \(\sim _{r'} \) denote the relation in \(\mathrm {GL}(2, F)\) of equality up to right multiplication by an element of \(U_{1}^{1}(\varpi ^{r'})\), and let \(t^{(r)}:= \gamma _{r}^{-1}t\gamma _{r}\).
Contribution from \(H_{1}'\). For \(t=1+b\theta \in H_{1}'\), we have
Hence the integral over \(H_{1}'\) equals
We show that the domain of integration in y can be harmlessly extended to \(F^{\times }\), i.e. that
vanishes. Consider first the contribution from \(v(b)\ge r\). On this domain, \(\mu ^{+}(1+b\theta )=1\) and integration in db yields \(\int _{\varpi ^{r}\mathscr {O}_{F}}\psi (by)\, db= \mathbf {1}_{\varpi ^{-r}\mathscr {O}_{F}}(y)\), that vanishes on \(v(y)\le -r-1\). Consider now the contribution from \(v(b)\le r-1\)
Let n be the conductor of \(\mu ^{+}_{|F^{\times }}\). Then (A.3.5) vanishes if \(n=0\); otherwise only the annulus \(v(y)=-n-1\) contributes, and after a change of variable \(y'=by\) we obtain
On our domain \(\mu ^{+}(1+b\theta )=1\), and \(\int \mu ^{+}(b)^{-1}=0\) as \(\mu ^{+}_{|F^{\times }} \) is ramified.
We conclude that the contribution from \(H_{1}'\) is
Contribution from \(H_{2}'\). For \(t=a\mathrm{N}+\theta \in H_{2}'\), we have
Then the integral over \(H_{2}'\) is

where we have observed that \(w_{r'}f^{\vee }\) vanishes outside \(\mathscr {O}_{F}\), and that \(\psi (-ay)=1\) for \(y\in \mathscr {O}_{F}\). Applying first the same argument as in the proof of Lemma A.3.3, then Lemma A.3.1, this equals
Conclusion. Summing up the two contributions to (A.3.4) yields
as desired. \(\square \)
1.4 Pairings at infinity
Fix a place \(v\vert p\) of F.
1.4.1 Models for algebraic representations and pairings
Suppose that W is the representation (A.2.2) of \((G\times H)_{v, \infty }'\) over \(L{\mathop {\hookleftarrow }\limits ^{\sigma }} E\). We identify W with the space of homogeneous polynomials p(x, y) of degree \(k-2\) in L[x, y], where x and y are considered as the components of a column (respectively row) vector if W is viewed as a right (respectively left) representation. In those two cases, the action is respectively:
In either case, we fix the invariant pairing
Lemma A.4.1
Let \(W=\) (A.2.2), viewed as a left representation of \(G_{v, \infty }\) only. Let \(w_\mathrm{a}^{\mathrm {ord}}:W^{N}\rightarrow W_{N}\) be the map denoted by \(w_{\mathrm{a}, v, \infty }^{\mathrm {ord}}\) of (A.2.1). Fix the models and pairing described above. Then \(W^{N}\) is spanned by \(x^{k-2}\) and \(W_{N}\) is spanned by the image of \(y^{k-2}\), and
1.4.2 The map \(\gamma _{H'}^{\mathrm {ord}} \) is unitary on algebraic representations
We start with a lemma completing the proof of Proposition 6.3.2.
Suppose that \(M_{p}=M_{p, 0}\otimes W_{p}\) is a decomposition of a locally algebraic coadmissible right \((G\times H)'_{p}\)-representation over L, into the product of a smooth and an irreducible algebraic representation, respectively. Let \(W^{\vee }_{\infty }\) be the dual representation to \(W_{p}\), viewed as a right representation of \((G\times H)'_{\infty }\). Assume that L is a p-adic field and that the \((G\times H)'\)-module \(M_{p}\otimes W^{\vee }_{\infty }\) is p-adic coadmissible. Then the operator \(\gamma _{H'}^{\mathrm {ord}} \) on it (whose definition of Proposition A.2.4 extends verbatim to the case where \(M_{p}\) is only locally algebraic) decomposes as
according to the decomposition \(M_{p}\otimes W^{\vee }_{\infty }=M_{p, 0}\otimes W_{p}\otimes W^{\vee }_{\infty }\)
Lemma A.4.2
In relation to the situation just described, the operator
is unitary. That is, for any invariant pairing \((\ , \ )\) on \(W\otimes W^{\vee }\) and \(\xi \in W^{H'}\), \(\xi ^{\vee }\in W^{\vee , H'}\), the images of \(\xi \otimes \xi ^{\vee }\) and \({}^\mathrm{alg}\gamma _{H'}^{\mathrm {ord}} (\xi \otimes \xi ^{\vee })\) under the pairings induced by \((\ , \ )\) coincide.
Proof
We may fix a place \(v\vert p\), and consider the factor representations \(W_{v}\otimes W_{v,\infty }^{\vee }\) of \((G\times H)'_{v} \times (G\times H)'_{v, \infty }\). After extension of scalars, we may decompose \(W_{v}=\bigotimes _{\sigma :F\rightarrow \overline{Q}_{p}}W_{v}^{\sigma }\) where each \(W_{v}^{\sigma }\) is one of the representations (A.2.2) for suitable integers w, k, l. Thus we are reduced to proving the unitarity of the relevant component of \({}^\mathrm{alg}\gamma _{H'}^{\mathrm {ord}} \) on the representation \(W_{v}^{\sigma }\otimes W_{v, \infty }^{\vee , \sigma }\). We omit all subscripts.
Split case. Suppose first that v splits in E. Then \(W^{H'}= Lx^{(k-2-l)/2} y^{(k-2+l)/2}\), and if
then
satisfies \(( \xi , \xi ^{\vee })=1\). We have
and
projects into \(W^{\vee }_{N} {\mathop {\leftarrow }\limits ^{\cong }} Lx^{k-2}\) to
Hence
Nonsplit case. Suppose now that v does not split in E. Let \(z:= x+\theta ^{c} y\), \(\overline{z}:=x+\theta y\). Then \(W^{H'} = L z^{(k-2-l)/2}\overline{z}^{ (k-2+l)/2}\), and if
then
satisfies \(( \xi , \xi ^{\vee })=1\). We have
and
projects into \(W^{\vee }_{N} {\mathop {\leftarrow }\limits ^{\cong }} Lx^{k-2}\) to
Then
\(\square \)
1.4.3 Algebraic toric period
Let \(W =W_{G} \otimes W_{H}\) be an algebraic representation of \((G\times H)'_{v,\infty }\) over L. For any \(\iota :L\hookrightarrow \mathbf {C}\), let \(\iota V_{ }\) (respectively \(\iota V_{G}\)) be the Hodge structure associated with W (respectively \(W_{G}\)), and letFootnote 32
Let dt be a ‘measure’ on \(H'_{v, \infty }\), by which we simply mean a value \(\mathrm {vol}(H'_{v, \infty }, dt)\) similarly to Sect. 1.2.6, and set as in (4.3.1)
Let \((\ , \ )=(\ , \ )_{W_{G}}\cdot (\, \ )_{W_{H}}\) be a nondegenerate invariant pairing on \(W. \otimes W^{\vee }\).
Then for all \(f_{1}, f_{3}\in W\), \(f_{2},f_{4}\in W^{\vee }\) with \((f_{3}, f_{4})\ne 0\), we define
where \(\mathrm{p}_{H'}\) denotes the idempotent projector onto \(H'_{v, \infty }\)-invariants.
Let \(\sigma _{W_{G}}:F_{v}^{\times }\rightarrow L^{\times }\) be the character giving the action of \(\left( \begin{array}{cc}F_{v}^{\times }&{}\\ &{}1\end{array}\right) \) on \(W_{G}^{N}\), let \(\chi :E_{v}^{\times }\rightarrow L^{\times } \) be the algebraic character attached to \(W_{H}\), and let
Let \(\mathrm{j}_{v}=\) (A.1.2). Then for all \(f_{1}, f_{3}\in W^{N}:=W_{G}^{N}\otimes W_{H}\), \(f_{2}, f_{4}\in W^{\vee , N}\) with \(f_{3}, f_{4}\ne 0\), we define
Proposition A.4.3
Let W be a representation of \((G\times H)'_{v, \infty }\) over L. Let \({\gamma _{H'}^{\mathrm {ord}} }={\gamma _{H'}^{\mathrm {ord}} }_{,v, \infty }\) be as defined in (A.2.5), and let \(w_\mathrm{a}^{\mathrm {ord}}=w_{\mathrm{a}, v, \infty }^{\mathrm {ord}}\) be as defined in (A.2.1). Then for all \(f_{1}, f_{3}\in W^{N}\), \(f_{2}, f_{4}\in W^{\vee , N}\) with \(f_{3}, f_{4}\ne 0\),
Proof
After possibly extending scalars we may assume that L splits E and pick an extensions of each \(\sigma :F\hookrightarrow L\) to a \(\sigma :E\hookrightarrow L\). We then have \(W=\bigotimes _{\sigma :F\hookrightarrow L}W_{\sigma } \) with \(W_{\sigma }=\) (A.2.2) for suitable integers \(w, k_{\sigma },l_{\sigma }\), and analogously \(\mu ^{+}(t)= \prod _{\sigma :F\hookrightarrow L}\mu _{\sigma }^{+}\) with
If v splits in E, this simplifies to \(\mu _{\sigma }^{+}(\mathrm{j}) = (-1)^{(k_{\sigma }-2+l_{\sigma })/2}\).
Moreover, \(\mathscr {L}(V, 0)= \prod _{\sigma }\mathscr {L}(V_{\sigma }, 0)\) with
Fix a \(\sigma :F\hookrightarrow L\) for the rest of this proof, work with \(W_{\sigma } \) only, and we drop \(\sigma \) from the notation. We may assume that \(f:=f_{1}\), \(f^{\vee }:= f_{2}\) both equal \(x^{k-2}\) in the models (A.4.1), and that \(\mathrm {vol}(H', dt)=1\). By the definitions above and Lemma A.4.1, we then need to prove that
Recall in what follows that \(\gamma _{H'}^{\mathrm {ord}} \) contains the factor \(c(W) =\) (A.2.3).
Split case. Suppose first that v splits in E. Then \(W^{H'} = L x^{(k-2-l)/ 2}y^{(k-2+l)/ 2 }\), and \(c(W)^{-1}\gamma _{0}^{\iota } f= c(W)^{-1} (x-y)^{k-2}\) projects to
It follows that
Nonsplit case. Suppose now that v is nonsplit in E. Let \(z:= x-\theta ^{c,-1} y\), \(\overline{z}:=x-\theta ^{ -1}y\), then \(W^{H'}=L z^{(k-2-l)/ 2}\overline{z}^{(k-2+l)/ 2 }\) and
projects to
By the invariance of the pairing,
so that again
\(\square \)
Rights and permissions
About this article
Cite this article
Disegni, D. The universal p-adic Gross–Zagier formula. Invent. math. 230, 509–649 (2022). https://doi.org/10.1007/s00222-022-01133-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-022-01133-w




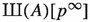 vanishes;
vanishes;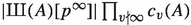 are equal.
are equal.