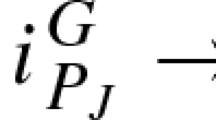Cohomology of p-adic Stein spaces

Abstract

We compute p-adic étale and pro-étale cohomologies of Drinfeld half-spaces. In the pro-étale case, the main input is a comparison theorem for p-adic Stein spaces; the cohomology groups involved here are much bigger than in the case of étale cohomology of algebraic varieties or proper analytic spaces considered in all previous works. In the étale case, the classical p-adic comparison theorems allow us to pass to a computation of integral differential forms cohomologies which can be done because the standard formal models of Drinfeld half-spaces are pro-ordinary and their differential forms are acyclic.

1 Introduction

Let p be a prime. Let ${{\mathscr {O}}}_K$ be a complete discrete valuation ring of mixed characteristic (0, p) with perfect residue field k and fraction field K. Let F be the fraction field of the ring of Witt vectors ${{\mathscr {O}}}_F=W(k)$ of k. Let $\overline{K}$ be an algebraic closure of K, $C=\widehat{\overline{K} }$ its p-adic completion and ${{\mathscr {G}}}_K=\mathrm {Gal} (\overline{K} /K)$.

1.1 The p-adic étale cohomology of Drinfeld half-spaces

This paper reports on some results of our research project that aims at understanding the p-adic (pro-)étale cohomology of p-adic symmetric spaces. The main question of interest being: does this cohomology realize the hoped for p-adic local Langlands correspondence in analogy with the $\ell$-adic situation? When we started this project we did not know what to expect and local computations were rather discouraging: geometric p-adic étale cohomology groups of affinoids and their interiors are huge and not invariant by base change to a bigger complete algebraically closed field. However there was one computation done long ago by Drinfeld [23] that stood out. Let us recall it.

Assume that $[K: {{\mathbf {Q}}}_p]<\infty$ and let ${{\mathbb {H}}}_K={{\mathbb {P}}}^1_K{{\setminus }}{{\mathbb {P}}}^1(K)$ be the Drinfeld half-plane, thought of as a rigid analytic space. It admits a natural action of $G:=\mathrm{GL}_2(K)$. We set ${{\mathbb {H}}}_C:={{\mathbb {H}}}_{K,C}$.

Fact 1.1

(Drinfeld) If $\ell$ is a prime number (including $\ell =p$ !), there exists a natural isomorphism of $G\times {{\mathscr {G}}}_K$-representations

$$\begin{aligned} H^1_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}_C, {{\mathbf {Q}}}_\ell (1))\simeq \mathrm{Sp}^{\mathrm {cont} }({ {{\mathbf {Q}}}_\ell })^*, \end{aligned}$$

where $\mathrm{Sp}^{\mathrm {cont} }({ {{\mathbf {Q}}}_\ell }):={{\mathscr {C}}}({{\mathbb {P}}}^1(K), {{\mathbf {Q}}}_\ell )/ {{\mathbf {Q}}}_\ell$ is the continuous Steinberg representation of G with coefficients in ${{\mathbf {Q}}}_\ell$ equipped with a trivial action of ${{\mathscr {G}}}_K$ and $(-)^*$ denotes the weak topological dual.

The proof is very simple: it uses Kummer theory and vanishing of the Picard groups (of the standard Stein covering of ${{\mathbb {H}}}_K$) [27, 17, § 1.4]. This result was encouraging because it showed that the p-adic étale cohomology was maybe not as pathological as one could fear.

Drinfeld’s result was generalized by Schneider–Stuhler [71], for $\ell \ne p$, to higher dimensions. Let $d\ge 1$ and let ${{\mathbb {H}}}^d_K$ be the Drinfeld half-space [24] of dimension d, i.e.,

$$\begin{aligned} {{\mathbb {H}}}^d_K:={{\mathbb {P}}}^d_K{\setminus } \bigcup _{H\in {{\mathscr {H}}}}H, \end{aligned}$$

where ${{\mathscr {H}}}$ denotes the set of K-rational hyperplanes. We set $G:=\mathrm{GL}_{d+1}(K)$. If $1\le r\le d$, and if $\ell$ is a prime number, denote by $\mathrm{Sp}_r( {{\mathbf {Q}}}_\ell )$ and $\mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_\ell )$ the generalized locally constant and continuous Steinberg ${{\mathbf {Q}}}_\ell$-representations of G (see Sect. 5.2.1), respectively, equipped with a trivial action of ${{\mathscr {G}}}_K$.

Theorem 1.2

(Schneider–Stuhler) Let $r\ge 0$ and let $\ell \ne p$. There are natural $G\times {{\mathscr {G}}}_K$-equivariant isomorphisms

$$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_{\ell })^*,\quad H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))\simeq \mathrm{Sp}_r( {{\mathbf {Q}}}_{\ell })^*. \end{aligned}$$

The computations of Schneider–Stuhler work for any cohomology theory that satisfies certain axioms, the most important being the homotopy property with respect to the open unit ball, which fails rather dramatically for the p-adic (pro-)étale cohomology since the p-adic étale cohomology of the unit ball is huge. Nevertheless, we prove the following result.

Theorem 1.3

Let $r\ge 0$.

• 1. There is a natural isomorphism of $G\times {{\mathscr {G}}}_K$-locally convex topological vector spaces (over ${{\mathbf {Q}}}_p$).

  $$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_p(r))\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^*. \end{aligned}$$

  These spaces are weak duals of Banach spaces.

• 2. There is a strictly exact sequence of $G\times {{\mathscr {G}}}_K$-Fréchet spaces

  

• 3. The natural map $H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_p(r))\rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_p(r))$ identifies étale cohomology with the space of G-bounded vectors¹ in the pro-étale cohomology.

Hence, the p-adic étale cohomology is given by the same dual of a Steinberg representation as its $\ell$-adic counterpart. However, the p-adic pro-étale cohomology is a nontrivial extension of the same dual of a Steinberg representation that describes its $\ell$-adic counterpart by a huge space.

Remark 1.4

• (i) In [17] we have generalized the above computation of Drinfeld in a different direction, namely, to the Drinfeld tower [24] in dimension 1. We have shown that, if $K= {{\mathbf {Q}}}_p$, the p-adic local Langlands correspondence (see [16, 19]) for de Rham Galois representations of dimension 2 (of Hodge–Tate weights 0 and 1 and not trianguline) can be realized inside the p-adic étale cohomology of the Drinfeld tower (see [17, Th. 0.2] for a precise statement). The two important cohomological inputs were:

  • 1. a p-adic comparison theorem that allows us to recover the p-adic pro-étale cohomology from the de Rham complex and the Hyodo–Kato cohomology; the latter being compared to the $\ell$-adic étale cohomology computed, in turn, by non-abelian Lubin–Tate theory,

  • 2. the fact that the p-adic étale cohomology is equal to the space of G-bounded vectors in the p-adic pro-étale cohomology.

  In contrast, here we obtain the third part of Theorem 1.3 only after proving the two previous parts. In fact, for a general rigid analytic variety, we do know that the natural map from p-adic étale cohomology to p-adic pro-étale cohomology does not have to be injective: this is the case, for example, for a unit open ball over a field that is not spherically complete.

• (ii) There are now two other proofs [11, 64] of point 2 of the Theorem.

Remark 1.5

The proof of Theorem 1.3 establishes a number of other isomorphisms (see Theorem 6.28) refining results of [22, 44, 71].

Remark 1.6

• (i) For $r \ge d+1$, all spaces in Theorem 1.3 are 0.

• (ii) For $1\le r\le d$, the spaces on the left and on the right in the exact sequence in Theorem 1.3 describing the pro-étale cohomology of ${{\mathbb {H}}}^d_C$, despite being huge spaces, have some finiteness properties: they are both duals of admissible locally analytic representations of G (over C on the left and ${{\mathbf {Q}}}_p$ on the right), of finite length [on the left, this is due to Orlik and Strauch ( [62] combined with [66])].

Remark 1.7

For small Tate twists ($r\le p-1)$, the Fontaine–Messing period map, which is an essential input in the proof of Theorem 1.3, is an isomorphism “on the nose”. It is possible then that our proof of Theorem 1.3, with a better control of the constants, could give the integral p-adic étale cohomology of the Drinfeld half-space for small Tate twists, that is, a topological isomorphism

$$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C,{{\mathbf {F}}}_p(r))\simeq \mathrm{Sp}_r({{\mathbf {F}}}_p)^*. \end{aligned}$$

By combining the results of Chapter 6 of this paper with the integral p-adic Hodge Theory of Bhatt–Morrow–Scholze [5, 6] and Česnavičius–Koshikawa [12] one can actually prove such a result for all twists [18].

1.2 A comparison theorem for p-adic pro-étale cohomology

The proof of Theorem 1.3 uses the result below, which is the main theorem of this paper and generalizes the above mentioned comparison theorem to rigid analytic Stein spaces² over K with a semistable reduction. Let the field K be as stated at the beginning of the introduction.

Theorem 1.8

Let $r\ge 0$. Let X be a semistable Stein weak formal scheme³ over ${{\mathscr {O}}}_K$. There exists a commutative ${{\mathscr {G}}}_K$-equivariant diagram of Fréchet spaces

The rows are strictly exact and the maps $\widetilde{\beta }$ and $\iota _{\mathrm {HK} }\otimes \theta$ are strict (and have closed images). Moreover,

$$\begin{aligned} \ker (\widetilde{\beta })\simeq \ker (\iota _{\mathrm {HK} }\otimes \theta )\simeq (H^r_{\mathrm {HK} }(X_{{k}})\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}. \end{aligned}$$

Here $H^r_{\mathrm {HK} }(X_{{k}})$ is the overconvergent Hyodo–Kato cohomology of Grosse-Klönne [32],

$$\begin{aligned} \iota _{\mathrm {HK} }:H^r_{\mathrm {HK} }(X_{{k}})\otimes _FK{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {dR} }(X_C) \end{aligned}$$

is the Hyodo–Kato isomorphism, $\mathbf{B}^+_{\mathrm {st} }$ is the semistable ring of periods defined by Fontaine, and $\theta : \mathbf{B}^+_{\mathrm {st} }\rightarrow C$ is Fontaine’s projection.

Example 1.9

In the case the Hyodo–Kato cohomology vanishes we obtain a particularly simple formula. Take, for example, the rigid affine space ${{\mathbb {A}}}^d_K$. For $r\ge 1$, we have $H^r_{\mathrm {dR} }({{\mathbb {A}}}^d_K)=0$ and, by the Hyodo–Kato isomorphism, also $H^r_{\mathrm {HK} }({{\mathbb {A}}}^d_K)=0$. Hence the above theorem yields an isomorphism

$$\begin{aligned} H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {A}}}^d_C, {{\mathbf {Q}}}_p(r)) \overset{\sim }{\leftarrow } \Omega ^{r-1}({{{\mathbb {A}}}^d_C})/\ker d. \end{aligned}$$

This was our first proof of this fact but there is a more direct argument in [21]. Another approach, using relative fundamental exact sequences in pro-étale topology and their pushforwards to étale topology, can be found in [51].

Remark 1.10

• (i) We think of the above theorem as a one-way comparison theorem, i.e., the pro-étale cohomology $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))$ is the pullback of the diagram

  

  built from the Hyodo–Kato cohomology and a piece of the de Rham complex.

• (ii) When we started doing computations of pro-étale cohomology groups (for the affine line), we could not understand why the p-adic pro-étale cohomology seemed to be so big while the Hyodo–Kato cohomology was so small (actually 0 in that case): this was against what the proper case was teaching us. If X is proper, $\Omega ^{r-1}({X_K})/\ker d=0$ (since the Hodge–de Rham spectral sequence degenerates) and the upper line of the above diagram becomes

  $$\begin{aligned}&0\rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_C, {{\mathbf {Q}}}_p(r)) \rightarrow (H^r_{\mathrm {HK} }(X_k)\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^r}\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \rightarrow (H^r_{\mathrm {dR} }(X_K)\widehat{\otimes }_K \mathbf{B}_{\mathrm {dR} }^+)/\mathrm{Fil}^r \rightarrow 0. \end{aligned}$$

  Hence the huge term on the left disappears, and an extra term on the right shows up. This seemed to indicate that there was no real hope of computing p-adic étale and pro-étale cohomologies of big spaces. It was learning about Drinfeld’s result that convinced us to look further.⁴

1.3 Proof of Theorem 1.8

The starting point of computations of pro-étale and étale cohomologies in these theorems is the same: the classical comparison theorem between p-adic nearby cycles and syntomic sheaves [20, 79]. When applied to the Stein spaces we consider here it yields:

Proposition 1.11

Let X be a semistable Stein formal scheme⁵ over ${{\mathscr {O}}}_K$. Then the Fontaine–Messing period morphisms

$$\begin{aligned}&\alpha ^{\mathrm{FM}}: \mathrm {R} \Gamma _{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_C}, {{\mathbf {Q}}}_p(r))\rightarrow \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_C, {{\mathbf {Q}}}_p(r)),\\&\alpha ^{\mathrm{FM}}: \mathrm {R} \Gamma _{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_C}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}\rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_C, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

are strict quasi-isomorphisms after truncation $\tau _{\le r}$.

Here the crystalline geometric syntomic cohomology is that defined by Fontaine–Messing (see Sect. 3.3.1 for the details)

$$\begin{aligned} \mathrm {R} \Gamma _{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_C}, {{\mathbf {Z}}} _p(r)):=&\ {[}\mathrm {R} \Gamma _{\mathrm {cr} }({X}_{{{\mathscr {O}}}_C})^{\varphi =p^r}\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }({X}_{{{\mathscr {O}}}_C})/F^r],\\ F^r\mathrm {R} \Gamma _{\mathrm {cr} }({X}_{{{\mathscr {O}}}_C}):=&\ \mathrm {R} \Gamma _{\mathrm {cr} }({X}_{{{\mathscr {O}}}_C},{{\mathscr {J}}}^{[r]}), \end{aligned}$$

where the crystalline cohomology is absolute, i.e., over W(k), and $[A\rightarrow B]$ denotes the mapping fiber. The syntomic cohomology $\mathrm {R} \Gamma _{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_C}, {{\mathbf {Q}}}_p(r))$ is defined by taking $\mathrm {R} \Gamma _{ \mathrm {syn} }(-, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}$ on quasi-compact pieces and then gluing.

The next step is to transform the Fontaine–Messing type syntomic cohomology (that works very well for defining period maps from syntomic cohomology to étale cohomology but is not terribly useful for computations) into Bloch–Kato type syntomic cohomology (whose definition is motivated by the Bloch–Kato’s definition of Selmer groups; it involves much more concrete objects). This can be done in the case of the pro-étale topology⁶ but only partially in the case of the étale topology.

1.3.1 Pro-étale cohomology

For the pro-étale topology, we define a Bloch–Kato syntomic cohomology (denoted by $\mathrm {R} \Gamma ^{\mathrm{BK}}_{ \mathrm {syn} }({X}_{C}, {{\mathbf {Q}}}_p(r))$) using overconvergent differential forms which, due to imposed overconvergence, behaves reasonably well locally. Then we construct a map from Fontaine–Messing to Bloch–Kato syntomic cohomology as shown in the top part of the following commutative diagram, where the rows are distinguished triangles

Here $\mathrm {R} \Gamma _{\mathrm {cr} }({{X}}_{{{\mathscr {O}}}_C},F)$ and its filtration are defined by the same procedure as $\mathrm {R} \Gamma _{ \mathrm {syn} }({{X}}_{{{\mathscr {O}}}_C}, {{\mathbf {Q}}}_p(r))$ (starting from rational absolute crystalline cohomology). The horizontal triangles are distinguished (the top two by definition). The construction of the top vertical maps and the proof that they are isomorphisms is nontrivial and constitutes the technical heart of this paper. These maps are basically Künneth maps, that use the interpretation of period rings as crystalline cohomology of certain “base” rings (for example, $\mathbf{A}_{\mathrm {cr} }\simeq \mathrm {R} \Gamma _{\mathrm {cr} }({{\mathscr {O}}}_{C})$), coupled with a rigidity of $\varphi$-eigenspaces of crystalline chomology, and followed by a change of topology (from crystalline to overconvergent) that can be done because $X_K$ is Stein (hence $X_k$ has proper and smooth irreducible components). To control the topology we work in the derived category of locally convex topological vector spaces over ${{\mathbf {Q}}}_p$ which, since ${{\mathbf {Q}}}_p$ is spherically complete, is reasonably well-behaved.

The bottom vertical maps are induced by the projection $\theta : \mathbf{B}^+_{\mathrm {dR} }\rightarrow C$ and use the fact that, since $X_K$ is Stein, we have $\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\simeq \Omega ^{\scriptscriptstyle \bullet }({X_K})$. The diagram in Theorem 1.8 follows by applying $H^r$ to the above diagram.

1.4 Proof of Theorem 1.3

To prove the pro-étale part of Theorem 1.3, by Theorem 1.8, it suffices to show that

$$\begin{aligned} (H^r_{\mathrm {HK} }(X_k)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^r}\simeq \mathrm{Sp}_r( {{\mathbf {Q}}}_p)^*. \end{aligned}$$

(1.12)

But we know from Schneider–Stuhler [71] that there is a natural isomorphism $H^r_{\mathrm {dR} }(X_K)\simeq \mathrm{Sp}_r(K)^*$ of G-representations. Moreover, we know that both sides are generated by standard symbols, i.e., cup products of symbols of K-rational hyperplanes thought of as invertible functions on $X_K$ (this is because $\mathrm{Sp}_r(K)^*$ is so by definition, and Iovita–Spiess prove that so is $H^r_{\mathrm {dR} }(X_K)$) and that this isomorphism is compatible with symbols [44, Th. 4.5]. Coupled with the Hyodo–Kato isomorphism and the irreducibility of the representation $\mathrm{Sp}_r(K)^*$ this yields a natural isomorphism $H^r_{\mathrm {HK} }(X_k)\simeq \mathrm{Sp}_r(F)^*$. This isomorphism is unique once we impose that it should be compatible with the standard symbols. It follows that we have a natural isomorphism $H^r_{\mathrm {HK} }(X_k)^{\varphi =p^r}\simeq \mathrm{Sp}_r( {{\mathbf {Q}}}_p)^*$, which implies $H^r_{\mathrm {HK} }(X_k)\cong F\otimes _{ {{\mathbf {Q}}}_p}H^r_{\mathrm {HK} }(X_k)^{\varphi =p^r}$ and (1.12).

1.4.1 Étale cohomology

The situation is more complicated for étale cohomology. Let X be a semistable Stein formal scheme over ${{\mathscr {O}}}_K$. An analogous computation to the one above yields the following strict quasi-isomorphism of distinguished triangles (see Sect. 6.4)

where ${{\mathscr {O}}}_F^0$ denotes ${{\mathscr {O}}}_F$ equipped with the log-structure induced by $1\mapsto 0$ and $\mathbf{A}_{\mathrm {st} }$, $\mathbf{A}_{\mathrm {cr} ,K}$ are certain period rings. But, in general, the map $\gamma _{\mathrm {HK} }$ is difficult to identify. In the case of the Drinfeld half-space though its domain and target simplify significantly by the acyclicity of the sheaves of differentials proved by Grosse-Klönne [33, 35]. This makes it possible to describe it and, as a result, to compute the étale syntomic cohomology.

Let X be the standard formal model of ${{\mathbb {H}}}^d_K$ [32, 6.1]. Set

$$\begin{aligned} \mathrm{HK}_r:=(\mathrm {R} \Gamma _{\mathrm {cr} }(X_k/{{\mathscr {O}}}_F^0)\widehat{\otimes }_{{{\mathscr {O}}}_F}\mathbf{A}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}^{N=0,\varphi =p^r}. \end{aligned}$$

We show that there are natural $G\times {{\mathscr {G}}}_K$-equivariant strict (quasi-)isomorphisms (see Lemma 6.37, Proposition 6.23)

$$\begin{aligned}&H^r\mathrm{HK}_r \simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_{\overline{k}},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p},\ H^{r-1}\mathrm{HK}_r \simeq (H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_{\overline{k}},W\Omega ^{r-1}_{\log })\widehat{\otimes }_{{{\mathscr {O}}}_F}\mathbf{A}^{\varphi =p}_{\mathrm {cr} })_{ {{\mathbf {Q}}}_p},\nonumber \\&(\mathrm {R} \Gamma _{\mathrm {dR} }(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}\mathbf{A}_{\mathrm {cr} ,K})/F^r \simeq \oplus _{r-1\ge i\ge 0}(H^0(X,\Omega ^i)\widehat{\otimes }_{{{\mathscr {O}}}_K}\mathbf{A}_{\mathrm {cr} ,K})/F^{r-i}[-i], \end{aligned}$$

(1.13)

where $W\Omega ^r_{\log }$ is the sheaf of logarithmic de Rham–Witt differentials. They follow from the isomorphisms (see Proposition 6.23)

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_{\overline{k}},W\Omega ^r_{\log })\widehat{\otimes }_{ {{\mathbf {Z}}} _p}W(\overline{k})&{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {cr} }(X_{\overline{k}}/W(\overline{k})^0),\nonumber \\ \iota _{\mathrm {HK} }: H^r_{\mathrm {cr} }(X_k/{{\mathscr {O}}}_F^0)\otimes _{{{\mathscr {O}}}_F}K&\simeq H^r_{\mathrm {dR} }(X)\otimes _{{{\mathscr {O}}}_K}K. \end{aligned}$$

(1.14)

The second one is just the original Hyodo–Kato isomorphism from [38]. The first one follows from the acyclicity of the sheaves $\Omega ^j_X$ (see Lemma 6.20) and the fact that $X_k$ is pro-ordinary (see Corollary 6.18), which, in turn and morally speaking, follows from the fact that $X_k$ is a normal crossing scheme whose closed strata are classically ordinary (being products of blow-ups of projective spaces). Now, the acyclicity of the sheaves $\Omega ^j_X$ again and the fact that the differential is trivial on their global sections (both facts proved by Grosse-Klönne [33, 35]) imply (1.13).

Hence, we obtain the long exact sequence

We check that the map $\gamma ^{\prime }_{\mathrm {HK} }$ is surjective (see Corollary 6.42): (a bit surprisingly) the Hyodo–Kato isomorphism $\iota _{\mathrm {HK} }$ above holds already integrally and $\gamma _{\mathrm {HK} }^{\prime }=\iota _{\mathrm {HK} }\otimes \theta$, where $\theta : \mathbf{A}_{\mathrm {cr} }^{\varphi =p}\rightarrow {{\mathscr {O}}}_C$ is the canonical projection. This yields the isomorphism

$$\begin{aligned} H^r_{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_C}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}{\mathop {\rightarrow }\limits ^{\sim }} H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_{\overline{k}},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p}. \end{aligned}$$

A careful study of the topology allows to conclude that this isomorphism is topological. Hence it remains to show that there exists a natural topological isomorphism

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_{\overline{k}},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p}\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^*. \end{aligned}$$

(1.15)

We do that (see Theorem 6.45) by showing that we can replace $\overline{k}$ by k and using the maps

$$\begin{aligned}&H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_k,W\Omega ^r_{\log })\otimes _{ {{\mathbf {Z}}} _p}K {\mathop {\rightarrow }\limits ^{f}} H^r_{\mathrm {dR} }(X_K)^{{G-\mathrm{bd}}}\\&\simeq (\mathrm{Sp}_r(K)^*)^{{G-\mathrm{bd}}} {\mathop {\leftarrow }\limits ^{\sim }} \mathrm{Sp}_r^{\mathrm {cont} }( {{\mathbf {Q}}}_p)^*\otimes _{ {{\mathbf {Q}}}_p} K. \end{aligned}$$

Here, the second isomorphism is that of Schneider–Stuhler [71]. The map f (a composition of natural maps with the Hyodo–Kato isomorphism) is injective by pro-ordinarity of Y. It is surjective because $H^0_{\acute{\mathrm{e}}\mathrm {t}}(X_k,W\Omega ^r_{\log })$ is compact and nontrivial and $\mathrm{Sp}^{\mathrm{cont}}_r( {{\mathbf {Z}}} _p)/p\simeq \mathrm{Sp}_r({{\mathbf {F}}}_p)$ is irreducible—a nontrivial fact proved by Grosse-Klönne [36, Cor. 4.3]. This yields an isomorphism (1.15).

Part (3) of Theorem 1.3 follows now easily from the two previous (compatible) parts and the fact that

$$\begin{aligned} (\mathrm{Sp}_r(K)^*)^{{G-\mathrm{bd}}} \simeq \mathrm{Sp}_r^{\mathrm {cont} }( {{\mathbf {Q}}}_p)^*\otimes _{ {{\mathbf {Q}}}_p} K, \quad H^r_{\mathrm {dR} }(X_K)^{{G-\mathrm{bd}}} \simeq H^r_{\mathrm {dR} }(X)\otimes _{{{\mathscr {O}}}_K}K \end{aligned}$$

(the latter isomorphism uses the fact that X can be covered by G-translates of an open subscheme U such that $U_K$ is an affinoid).

1.4.2 Notation and conventions

Let ${{\mathscr {O}}}_K$ be a complete discrete valuation ring with fraction field K of characteristic 0 and with perfect residue field k of characteristic p. Let $\varpi$ be a uniformizer of ${{\mathscr {O}}}_K$ that we fix in this paper. Let $\overline{K}$ be an algebraic closure of K and let ${{\mathscr {O}}}_{\overline{K} }$ denote the integral closure of ${{\mathscr {O}}}_K$ in $\overline{K}$. Let W(k) be the ring of Witt vectors of k with fraction field F (i.e, $W(k)={{\mathscr {O}}}_F$); let e be the ramification index of K over F. Set ${{\mathscr {G}}}_K=\mathrm {Gal} (\overline{K}/K)$, and let $\sigma$ be the absolute Frobenius on $W(\overline{k})$.

We will denote by ${{\mathscr {O}}}_K$, ${{\mathscr {O}}}_K^{\times }$, and ${{\mathscr {O}}}_K^0$, depending on the context, the scheme $\mathrm {Spec} ({{{\mathscr {O}}}_K})$ or the formal scheme $\mathrm {Spf} ({{\mathscr {O}}}_K)$ with the trivial, the canonical (i.e., associated to the closed point), and the induced by ${{\mathbf {N}}}\rightarrow {{\mathscr {O}}}_K, 1\mapsto 0$, log-structure, respectively.

Unless otherwise stated all formal schemes are p-adic, locally of finite type, and equidimensional. For a (p-adic formal) scheme X over ${{\mathscr {O}}}_K$, let $X_0$ denote the special fiber of X; let $X_n$ denote its reduction modulo $p^n$, if $n\ge 1$.

We will denote by $\mathbf{A}_{\mathrm {cr} }, \mathbf{B}^+_{\mathrm {cr} }, \mathbf{B}^+_{\mathrm {st} },\mathbf{B}^+_{\mathrm {dR} }$ the crystalline, semistable, and de Rham period rings of Fontaine. We have $\mathbf{B}^+_{\mathrm {st} }=\mathbf{B}^+_{\mathrm {cr} }[u]$ and $\varphi (u)=pu, N(u)=-1$. The embedding $\iota =\iota _{\varpi }: \mathbf{B}^+_{\mathrm {st} }\rightarrow \mathbf{B}^+_{\mathrm {dR} }$ is defined by $u\mapsto u_{\varpi }=\log ([\varpi ^{\flat }]/\varpi )$ and the Galois action on $\mathbf{B}^+_{\mathrm {st} }$ is induced from the one on $\mathbf{B}^+_{\mathrm {dR} }$ via this embedding.

Unless otherwise stated, we work in the derived (stable) $\infty$-category ${{\mathscr {D}}}(A)$ of left-bounded complexes of a quasi-abelian category A (the latter will be clear from the context). Many of our constructions will involve (pre)sheaves of objects from ${{\mathscr {D}}}(A)$. The reader may consult the notes of Illusie [43] and Zheng [85] for a brief introduction to how to work with such (pre)sheaves and [53, 54] for a thorough treatment.

We will use a shorthand for certain homotopy limits: if $f:C\rightarrow C'$ is a map in the derived $\infty$-category of a quasi-abelian category, we set

2 Review of p-adic functional analysis

We gather here some basic facts from p-adic functional analysis that we use in the paper. The reader is advised, on the first reading, to ignore this chapter and topological issues in ensuing computations.

2.1 The category of locally convex K-vector spaces

We start with the rational case, where we work in the category of locally convex K-vector spaces. Our main references are [25, 68, 72].

2.1.1 Derived category of locally convex Kvector spaces

A topological K-vector space⁷ is called locally convex (convex for short) if there exists a neighbourhood basis of the origin consisting of ${{\mathscr {O}}}_K$-modules. Since K is spherically complete, the theory of such spaces resembles the theory of locally convex topological vector spaces over ${{\mathbf {R}}}$ or ${{\mathbf {C}}}$ (with some simplifications).

We denote by $C_K$ the category of convex K-vector spaces. It is a quasi-abelian category⁸ [68, 2.1.11]. Kernels, cokernels, images, and coimages are taken in the category of vector spaces and equipped with the induced topology [68, 2.1.8]. A morphism $f:E\rightarrow F$ is strict if and only if it is relatively open, i.e., for any neighbourhood V of 0 in E there is a neighbourhood $V^{\prime }$ of 0 in F such that $f(V)\supset V^{\prime }\cap f(E)$ [68, 2.1.9].

Our convex K vector spaces are not assumed to be separated. We often use the following simple observation: if Fis separated and we have an injective morphism$f:E\rightarrow F$thenEis separated as well; if, moreover,Fis finite dimensional andfis bijective thenfis an isomorphism in$C_K$.

The category $C_K$ has a natural exact category structure: the admissible monomorphisms are embeddings, the admissible epimorphisms are open surjections. A complex $E\in C(C_K)$ is called strict if its differentials are strict. There are truncation functors on $C(C_K)$:

$$\begin{aligned} \tau _{\le n}E&:=\cdots \rightarrow E^{n-2}\rightarrow E^{n-1}\rightarrow \ker (d_n)\rightarrow 0\rightarrow \cdots \\ \tau _{\ge n} E&:=\cdots \rightarrow 0\cdots \rightarrow \mathrm {coim}\, (d_{n-1}) \rightarrow E^n\rightarrow E^{n+1}\rightarrow \cdots \end{aligned}$$

with cohomology objects

$$\begin{aligned} \widetilde{H}^n(E):= \tau _{\le n}\tau _{\ge n}(E)=(\mathrm {coim}\, (d_{n-1})\rightarrow \ker (d_n)). \end{aligned}$$

We note that here $\mathrm {coim}\, (d_{n-1})$ and $\ker (d_n)$ are equipped naturally with the quotient and subspace topology, respectively. The cohomology $H^*(E)$ taken in the category of K-vector spaces we will call algebraic and, if necessary, we will always equip it with the sub-quotient topology.

We will denote the left-bounded derived $\infty$-category of $C_K$ by ${{\mathscr {D}}}(C_K)$. A morphism of complexes that is a quasi-isomorphism in ${{\mathscr {D}}}(C_K)$, i.e., its cone is strictly exact, will be called a strict quasi-isomorphism. We will denote by $D(C_K)$ the homotopy category of ${{\mathscr {D}}}(C_K)$ [68, 1.1.5].

For $n\in {{\mathbf {Z}}}$, let $D_{\le n}(C_K)$ (resp. $D_{\ge n}(C_K)$) denote the full subcategory of $D(C_K)$ of complexes that are strictly exact in degrees $k >n$ (resp. $k<n$).⁹ The above truncation maps extend to truncations functors $\tau _{\le n}: D(C_K)\rightarrow D_{\le n}(C_K)$ and $\tau _{\ge n}: D(C_K)\rightarrow D_{\ge n}(C_K)$. The pair $(D_{\le n}(C_K),D_{\ge n}(C_K)$) defines a t-structure on $D(C_K)$ by [73]. The (left) heart $D(C_K)^{\heartsuit }$ is an abelian category $LH(C_K)$: every object of $LH(C_K)$ is represented (up to equivalence) by a monomorphism $f:E\rightarrow F$, where F is in degree 0; if f is strict this object is also represented by the cokernel of f (the whole point of this construction is to keep track of the two possibly different topologies on E: the given one and the one inherited by the inclusion into F).

We have an embedding $I: C_K\hookrightarrow LH(C_K)$, $E\mapsto (0\rightarrow E)$, that induces an equivalence $D(C_K){\mathop {\rightarrow }\limits ^{\sim }} D(LH(C_K))$ which is compatible with the t-structures. These t-structures pull back to t-structures on the derived dg categories ${{\mathscr {D}}}(C_K), {{\mathscr {D}}}(LH(C_K))$ and so does the above equivalence. There is a functor (the classical part) $C: LH(C_K)\rightarrow C_K$ that sends the monomorphism $f: E\rightarrow F$ to $\mathrm {coker}\, f$. We have $CI\simeq \mathrm {Id} _{C_K}$ and a natural epimorphism $e: \mathrm {Id} _{LH(C_K)}\rightarrow IC$.

We will denote by $\widetilde{H}^n: {{\mathscr {D}}}(C_K)\rightarrow {{\mathscr {D}}}(LH(C_K))$ the associated cohomological functors. Note that $C\widetilde{H}^n=H^n$ and we have a natural epimorphism $\widetilde{H}^n\rightarrow IH^n$. If, evaluated on E, this epimorphism is an isomorphism we will say that the cohomology $\widetilde{H}^n(E)$ is classical.

We will often use the following simple facts ([73, Prop. 1.2.28, Cor. 1.2.27]):

• 1. If, in the following short exact sequence in $LH(C_K)$, both $A_1$ and $A_2$ are in the essential image of I then so is A:

  $$\begin{aligned} 0\rightarrow A_1\rightarrow A\rightarrow A_2\rightarrow 0. \end{aligned}$$

• 2. A complex $E\in C(C_K)$ is strictly exact in a specific degree if and only if ${{\mathscr {D}}}(I)(E)$ is exact in the same degree.

All the above has a dual version: we have a notion of a costrict morphism, a right abelian envelope $I: C_K\rightarrow RH(C_K)$, and the cohomology objects $\widetilde{H}^n: {{\mathscr {D}}}(C_K)\rightarrow {{\mathscr {D}}}(RH(C_K)),$$\widetilde{H}^n:= (\mathrm {coker}\, (d_{n-1})\rightarrow \mathrm {im}\, (d_n))$ in degrees 0 and 1 (which we will, if necessary, write as $RH^n$). We have $C\widetilde{H}^n=H^n$, where $C: RH(C_K)\rightarrow C_K$ sends the epimorphism $f: E\rightarrow F$ to $\ker f$. There is a natural monomorphism $IH^n\rightarrow \widetilde{H}^n$; if, evaluated on E, this monomorphism is an isomorphism we will say that the cohomology $\widetilde{H}^n(E)$ is classical.

2.1.2 Open mapping theorem

Let $f:X\rightarrow Y$ be a continuous surjective map of locally convex K-vector spaces. We will need a well-known version of the Open Mapping Theorem that says that f is open if both X and Y are LF-spaces, i.e., countable inductive limits of Fréchet spaces.¹⁰

If E, F are Fréchet, $f:E\rightarrow F$ is strict if and only if f(E) is closed in F (the “if” part follows from the Open Mapping Theorem, the “only if” part from the fact that a Fréchet space is a metric space and a complete subspace of a metric space is closed). The following lemma is a simple consequence of this observation but we spell it out because we will use all the time.

Lemma 2.1

• 1. Let E be a complex of Banach or Fréchet spaces. If E has trivial algebraic cohomology then it is strictly acyclic.

• 2. A morphism $E_1\rightarrow E_2$ of complexes of Banach or Fréchet spaces that is an (algebraic) quasi-isomorphism is a strict quasi-isomorphism.

Proof

The second point follows from the first one by applying the latter to the cone of the morphism. For the first point, note that the kernel of a differential is a closed subspace of a Fréchet space hence a Fréchet space and we can evoke the observation above the lemma. $\square$

2.1.3 Tensor products

Let V, W be two convex K-vector spaces. The abstract tensor product $V\otimes _K W$ can be equipped with several natural topologies among them the projective and injective tensor product topologies: $V\otimes _{K,\pi }W$ and $V\otimes _{K, \varepsilon }W$. Recall that the projective tensor product topology is universal for jointly continuous bilinear maps $V \times W \rightarrow U$; the injective tensor product topology, on the other hand, is defined by cross seminorms that satisfy a product formula and is the “weakest” topology with such property. There is a natural map $V\otimes _{K,\pi }W\rightarrow V\otimes _{K, \varepsilon }W$. We denote by $V\widehat{\otimes }_{K,\alpha }W$, $\alpha =\pi , \varepsilon$, the Hausdorff completion of $V\otimes _{K,\alpha } W$ with respect to the topology $\alpha$.

Recall the following facts.

• 1. The projective tensor product functor $(-)\otimes _{K,\pi }W$ preserves strict epimorphisms; the injective tensor product functor $(-)\otimes _{K, \varepsilon }W$ preserves strict monomorphisms.

• 2. The natural map $V\otimes _{K,\pi }W\rightarrow V\otimes _{K, \varepsilon }W$ is an isomorphism¹¹ [67, Th. 10.2.7]. In what follows we will often just write $V\otimes _KW$ for both products.

• 3. From (1), (2), and the exactness properties of Hausdorff completion [80, Cor. 1.4], it follows that the tensor product functor $(-)\widehat{\otimes }_KW: C_K\rightarrow C_K$ is left exact, i.e., it carries strictly exact sequences

  $$\begin{aligned} 0\rightarrow V_1\rightarrow V_2\rightarrow V_3\rightarrow 0 \end{aligned}$$

  to strictly exact sequences

  $$\begin{aligned} 0\rightarrow V_1\widehat{\otimes }_KW\rightarrow V_2\widehat{\otimes }_K W\rightarrow V_3\widehat{\otimes }_K W. \end{aligned}$$

  Moreover, the image of the last map above is dense [80, p. 45]. It follows that this map is surjective if its image is complete as happens, for example, in the case when the spaces $V_*, W$ are Fréchet [80, Cor. 1.7].

• 4. For $V=\varprojlim _nV_n$, where each $V_n$ is a Fréchet space, and for a Fréchet space W, there is a natural isomorphism

  $$\begin{aligned} V\widehat{\otimes }_{K,\pi } W=(\varprojlim _nV_n)\widehat{\otimes }_{K,\pi }W {\mathop {\rightarrow }\limits ^{\sim }} \varprojlim _n(V_n\widehat{\otimes }_{K,\pi }W). \end{aligned}$$

  For products this is proved in [70, Prop. 9, p. 192] and the general case follows from the fact that tensor product is exact on sequences of Fréchet spaces.

• 5. Let $\{V_n\}$, $n\in {{\mathbf {N}}}$, be a regular¹² inductive system of Fréchet spaces with injective nuclear¹³ transition maps. Then, for any Banach space W, we have an isomorphism [55, Th. 1.3]

  $$\begin{aligned} (\varinjlim _nV_n)\widehat{\otimes }_K W{\mathop {\leftarrow }\limits ^{\sim }} \varinjlim _n (V_n\widehat{\otimes }_K W). \end{aligned}$$

2.1.4 Acyclic inductive systems

If $\{V_n\}_n, {n\in {{\mathbf {N}}}}$ is an inductive system of locally convex K-vector spaces then it is called acyclic if $\mathrm {L} ^1\mathrm {hocolim}\, _nV_n=0$. We will find useful the following criterium of acyclicity [83, Th. 1.1].

Proposition 2.2

An inductive system $\{V_n\}_n, n\in {{\mathbf {N}}}$, of Fréchet spaces with injective transition maps is acyclic if and only if in every space $V_n$ there is a convex neighbourhood $U_n$ of 0 such that

• 1. $U_n\subset U_{n+1}, n\in {{\mathbf {N}}}$, and

• 2. For every $n\in {{\mathbf {N}}}$ there is $m >n$ such that all topologies of the spaces $V_k$, $k>m$, coincide on $U_n$.

2.1.5 Derived tensor products

The category $C_K$ has enough injectives hence we have the right derived functor $V\widehat{\otimes }_K^R W$ of the tensor functor $V\widehat{\otimes }_K W$. We will need to know the conditions under which it is strictly quasi-isomorphic to the tensor functor.

Lemma 2.3

The natural map

$$\begin{aligned} V\widehat{\otimes }_KW\rightarrow V\widehat{\otimes }^R_KW \end{aligned}$$

is a quasi-isomorphism when

• 1. both V and W are Fréchet spaces,

• 2. $V=\varinjlim _n V_n$, for an acyclic inductive system $\{V_n\}, n\in {{\mathbf {N}}}$, of Banach spaces, and W is a Banach space.

Proof

In the first case, take an injective resolution $W\rightarrow I^{\scriptscriptstyle \bullet }$ of W by Fréchet spaces $I^i$, $i\ge 0$. This means that the map $W\rightarrow I^{\scriptscriptstyle \bullet }$ is a strict quasi-isomorphism. Such a resolution exists by [68, Prop. 2.1.12]. Tensoring this resolution with V we get a sequence

$$\begin{aligned} 0\rightarrow V\widehat{\otimes }W\rightarrow V\widehat{\otimes }I^0\rightarrow V\widehat{\otimes }I^1\rightarrow \cdots \end{aligned}$$

(2.4)

By Sect. 2.1.3, this sequence is strictly exact, as wanted.

In the second case, we take an injective resolution $W\rightarrow I^{\scriptscriptstyle \bullet }$ of W by Banach spaces $I^i$, $i\ge 0$. Such a resolution exists by loc. cit. Tensoring this resolution with V we get a sequence (2.4) as above. Since $V=\varinjlim _nV_n$, by Sect. 2.1.3, this sequence is an inductive limit of sequences

$$\begin{aligned} 0\rightarrow V_n\widehat{\otimes }W\rightarrow V_n\widehat{\otimes }I^0\rightarrow V_n\widehat{\otimes }I^1\rightarrow \cdots \end{aligned}$$

which are strictly exact by Sect. 2.1.3. Hence, by Sect. 2.1.4, the sequence (2.4) is strictly exact, as wanted. $\square$

2.2 The category of pro-discrete ${{\mathscr {O}}}_K$-modules

For integral topological questions we have found it convenient to work in the category $PD_K$ of pro-discrete ${{\mathscr {O}}}_K$-modules. For details see [9, § 2], [84, § 1], [45, 46].

2.2.1 The category of pro-discrete ${{\mathscr {O}}}_K$modules and its ind-completion

Objects in the category $PD_K$ are topological ${{\mathscr {O}}}_K$-modules that are countable inverse limits, as topological ${{\mathscr {O}}}_K$-modules, of discrete ${{\mathscr {O}}}_K$-modules $M^i$, $i{\,\in \,}{{\mathbf {N}}}$. It is a quasi-abelian category. It has countable filtered projective limits. Countable product is exact.

Objects in $PD_K$ are not necessarily separated for the p-adic topology: for example Banach spaces are objects of $PD_K$ (if B is a Banach with unit ball $B_0$, then $B=\varprojlim B/p^nB_0$), hence also countable products or projective limits of Banach spaces (i.e. Fréchet spaces) are objects of $PD_K$.

Inside $PD_K$ we distinguish the category $PC_K$ of pseudocompact ${{\mathscr {O}}}_K$-modules, i.e., pro-discrete modules such that each $M_i$ is of finite length (we note that if K is a finite extension of ${{\mathbf {Q}}}_p$ this is equivalent to M being profinite). It is an abelian category. It has countable exact products as well as exact countable filtered projective limits.

Let $\mathrm {Ind}(PD_K)$ be the ind-completion of $PD_K$. That is, $PD_K$ is a full subcategory of $\mathrm {Ind}(PD_K)$ and $\mathrm {Ind}(PD_K)$ has the universal property that any functor $F: PD_K\rightarrow C$ into a category with filtered inductive limits extends uniquely to a functor $\widetilde{F}: \mathrm {Ind}(PD_K)\rightarrow C$ which preserves filtered inductive limits. In particular, any functor $F: PD_K\rightarrow C$ induces a compatible functor $\widetilde{F}: \mathrm {Ind}(PD_K)\rightarrow \mathrm {Ind}(C)$ and if C has filtered inductive limits then the inclusion $C\rightarrow \mathrm {Ind}(C)$ has a canonical left inverse $\mathrm {Ind}(C)\rightarrow C$.

The category $\mathrm {Ind}(PD_K)$ is also quasi-abelian [45, Th. 1.3.1]. The natural functor $PD_K\rightarrow \mathrm {Ind}(PD_K)$ is exact. The category $\mathrm {Ind}(PD_K)$ admits filtered inductive limits and projective limits. The $\varprojlim$ functor is left exact. For any functor $F:PD_K\rightarrow C$ to a quasi-abelian category, the functor F is left, resp. right, exact if and only if so is the functor $\widetilde{F}$.

2.2.2 Tensor product

For $M,N\in PD$ we define the completed tensor product

$$\begin{aligned} M\widehat{\otimes }_{{{\mathscr {O}}}_K}N:=\varprojlim _{U\in {{\mathscr {U}}}_M, V\in {{\mathscr {U}}}_N}M/U\otimes _{{{\mathscr {O}}}_K}N/V, \end{aligned}$$

where ${{\mathscr {U}}}_M, {{\mathscr {U}}}_N$ denote the inductive system of open submodules of M, N and $M/U\otimes _{{{\mathscr {O}}}_K}N/V$ is given the discrete topology. It is a pro-discrete ${{\mathscr {O}}}_K$-module. It satisfies the usual universal property with respect to pro-discrete ${{\mathscr {O}}}_K$-modules [84, Prop. 6.1]. In general, the completed tensor product is neither right nor left exact. It is however right exact when restricted to $PC_K$ [84, Prop. 1.10]. It commutes also with filtered limits $\{N_i\}_i$ such that $N=\varprojlim _iN_i$ surjects onto $N_i$, $i\in I$ [84, Prop. 1.7]; in particular, it commutes with products of pro-discrete ${{\mathscr {O}}}_K$-modules and with filtered limits of pseudocompact ${{\mathscr {O}}}_K$-modules.

2.2.3 The functor to convex spaces

Since $K \simeq \varinjlim ({{\mathscr {O}}}_K\overset{\varpi }{\rightarrow } {{\mathscr {O}}}_K\overset{\varpi }{\rightarrow }{{\mathscr {O}}}_K\overset{\varpi }{\rightarrow } \cdots )$, the algebraic tensor product $M\otimes _{{{\mathscr {O}}}_K}K$ is an inductive limit:

$$\begin{aligned} M\otimes _{{{\mathscr {O}}}_K}K\simeq \varinjlim (M\overset{\varpi }{\rightarrow } M\overset{\varpi }{\rightarrow }M\overset{\varpi }{\rightarrow } \cdots ). \end{aligned}$$

We equip it with the induced inductive limit topology. This defines a tensor product functor

$$\begin{aligned} (-){\otimes }K: PD_K\rightarrow C_{K}, \quad M\mapsto M\otimes _{{{\mathscr {O}}}_K}K. \end{aligned}$$

Since $C_K$ admits filtered inductive limits, the functor $(-){\otimes }K$ extends to a functor $(-){\otimes }K: \mathrm {Ind}(PD_K)\rightarrow C_{K}$.

Remark 2.5

Recall that K belongs to $PD_K$: $K\simeq \varprojlim (K/{{\mathscr {O}}}_K{\mathop {\leftarrow }\limits ^{\varpi }}K/{{\mathscr {O}}}_K{\mathop {\leftarrow }\limits ^{\varpi }} \cdots )$. The above tensor functor should be distinguished from the functor $(-)\widehat{\otimes }K: PD_K\rightarrow PD_K$ discussed above which is always 0 and which we will never use.

The functor $(-){\otimes }K$ is right exact but not, in general, left exact.¹⁴ For example, the short strict exact sequence

$$\begin{aligned} 0\rightarrow \prod _{i\ge 0}p^i {{\mathbf {Z}}} _p{\mathop {\longrightarrow }\limits ^{ \mathrm {can} }}\prod _{i\ge 0} {{\mathbf {Z}}} _p\rightarrow \prod _{i\ge 0} {{\mathbf {Z}}} _p/p^i\rightarrow 0 \end{aligned}$$

tensored with ${{\mathbf {Q}}}_p$ is not costrict exact on the left (note that $(\prod _{i\ge 0} {{\mathbf {Z}}} _p/p^i){\otimes } {{\mathbf {Q}}}_p$ is not Hausdorff). We will consider its (compatible) left derived functors

$$\begin{aligned}&(-){\otimes }^LK: {{\mathscr {D}}}^{-}(PD_K)\rightarrow \mathrm {Pro} ({{\mathscr {D}}}^{-}(C_K)), \\&\quad (-){\otimes }^LK: {{\mathscr {D}}}^{-}(\mathrm {Ind}(PD_K))\rightarrow \mathrm {Pro} ({{\mathscr {D}}}^{-}(C_K)). \end{aligned}$$

The following fact is probably well-known but we could not find a reference (see however [9, Prop. 3.9, Cor. 3.13] for the case of profinite modules).

Proposition 2.6

If E is a complex of torsion free and p-adically complete (i.e., $E\simeq \varprojlim _n E/p^n$) modules from $PD_K$ then the natural map

$$\begin{aligned} E{\otimes }^LK\rightarrow E{\otimes }K \end{aligned}$$

is a strict quasi-isomorphism.

Proof

By [48, Lemma 14.1] our proposition is implied by the following lemma that shows that the terms of the complex E are F-acyclic for the functor $F=(-){\otimes }K$. $\square$

Lemma 2.7

If $0\rightarrow A\rightarrow B\overset{\pi }{\rightarrow } C\rightarrow 0$ is a strict exact sequence of pro-discrete ${{\mathscr {O}}}_K$-modules and C is torsion free and p-adically complete then $\pi :B\rightarrow C$ admits a ${{\mathscr {O}}}_K$-linear continuous section and $B\simeq A\oplus C$ as a topological ${{\mathscr {O}}}_K$-module.

Proof

The strict exact sequence $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ is a limit of exact sequences $0\rightarrow A^i\rightarrow B^i\rightarrow C^i\rightarrow 0$, where all the terms are discrete and $A^{i+1}\rightarrow A^i$ is surjective (idem for B and C) [9, Rem. 2.9]. Let $A_i$ be the kernel of $A\rightarrow A^i$ (idem for B and C). Now, if $X=A,B,C$, the $X_i$ form a decreasing filtration and a series $\sum x_n$, $x_n\in X$, converges in X if and only if, for all $i\in {{\mathbf {N}}}$, there exists n(i) such that $x_n\in X_i$ for all $n\ge n(i)$. Moreover, the sequence $0\rightarrow A_i\rightarrow B_i\rightarrow C_i\rightarrow 0$ is exact for all i (since $A^i\rightarrow B^i$ is injective).

Let ${\overline{C}}=C/\varpi$ and let ${\overline{C}}_i$ be the image of $C_i$ in ${\overline{C}}$. The ${\overline{C}}_i$, $i\in {{\mathbf {N}}}$, form a decreasing filtration of ${\overline{C}}$ and ${\overline{C}}_i/{\overline{C}}_{i+1}$ is a discrete k-module (it is a quotient of $C_i/C_{i+1}\subset C^{i+1}$). Choose a basis $({\overline{e}}_{i,j})_{j\in J_i}$ of ${\overline{C}}_i/{\overline{C}}_{i+1}$ over k, a lifting ${\tilde{e}}_{i,j}$ of ${\overline{e}}_{i,j}$ in ${\overline{C}}_i$, a lifting $e_{i,j}$ of ${\tilde{e}}_{i,j}$ in $C_i$, and a lifting ${\hat{e}}_{i,j}$ of $e_{i,j}$ in $B_i$ (it exists because $B_i\rightarrow C_i$ is surjective).

Let $Y=\prod _{i\in {{\mathbf {N}}}}\ell _\infty ^0(J_i,{{\mathscr {O}}}_K)$, where $\ell _\infty ^0(J_i,{{\mathscr {O}}}_K)$ is the space of sequences $(y_{i,j})_{j\in J_i}$ with values in ${{\mathscr {O}}}_K$, going to 0 at infinity. If $y=((y_{i,j})_{j\in J_i})_{i\in I}\in Y$, the double series $\sum _{i\in {{\mathbf {N}}}}(\sum _{j\in J_i}y_{i,j}e_{i,j})$ and $\sum _{i\in {{\mathbf {N}}}}(\sum _{j\in J_i}y_{i,j}{\hat{e}}_{i,j})$ converge in C and B respectively: the series corresponding to a fixed i converges because $y_{i,j}\rightarrow 0$ when $j\rightarrow \infty$ and its sum belongs to $C_i$ or $B_i$ and hence the series $\sum _i$ converges as well. We denote by $\iota _C(y)$ and $\iota _B(y)$ the sums of these series. The map $\iota _X:Y\rightarrow X$, $X=B,C$, is a continuous injection (to check injectivity, it suffices to argue modulo $\varpi$, where it is clear). Moreover, we have $\pi \circ \iota _B=\iota _C$.

To finish the proof of the lemma it suffices to show that $\iota _C$ is a topological isomorphism (because then $s=\iota _B\circ \iota _C^{-1}$ gives the desired continuous section and we have a topological isomorphism $A\oplus C{\mathop {\rightarrow }\limits ^{\sim }} B$ sending (a, c) to $a+s(c)$ with the inverse given by $b\mapsto (b-s(\pi (b)),\pi (b))$).

Let us proving it first modulo $\varpi$. For $c\in {\overline{C}}$, one constructs an element of ${\overline{Y}}$ using the following algorithm. Set $c_0=c$ and ${\overline{C}}_0={\overline{C}}$. The image of $c_0$ in ${\overline{C}}_0/{\overline{C}}_1$ can be written, uniquely, in the form $\sum _{j\in J_0}y_{0,j}e_{0,j}$ (and there is only a finite number of nonzero $y_{0,j}$’s). Hence $c_1=c-\sum _{j\in J_0}y_{0,j}{\tilde{e}}_{0,j}\in {\overline{C}}_1$. The image of $c_1$ in ${\overline{C}}_1/{\overline{C}}_2$ can be written, in a unique way, in the form $\sum _{j\in J_1}y_{1,j}e_{1,j}$ (and there is only a finite number of nonzero $y_{1,j}$’s). Hence $c_2=c_1-\sum _{j\in J_1}y_{1,j}{\tilde{e}}_{1,j}\in {\overline{C}}_2$. We continue in this way and get in the end an element $y_c=((y_{i,j})_{j\in J_i})_{i\in I}$ of ${\overline{Y}}$ whose image by $\iota _C$ is c and $c\mapsto y_c$ is a continuous inverse of $\iota _C$ (modulo $\varpi$): it is an inverse since we have uniqueness at every stage.

Let ${\overline{\alpha }}:{\overline{C}}\rightarrow {\overline{Y}}$ be the inverse of $\iota _C$ constructed above. Write $[\ ]:{\overline{Y}}\rightarrow Y$ for the map sending $((y_{i,j})_{j\in J_i})_{i\in I}$ to $(([y_{i,j}])_{j\in J_i})_{i\in I}$, where $[\ ]:k\rightarrow {{\mathscr {O}}}_K$ is the Teichmüller lift; it is a continuous map. The inverse $\alpha :C\rightarrow Y$ of $\iota _C$ is given by the following algorithm: for $c\in C$, set $c_0=c$, $c_1=\frac{1}{\varpi }(c_0-\iota _C([{\overline{\alpha }}({\overline{c}}_0)]))$ (we write ${\overline{c}}_0$ for the image of $c_0$ modulo $\varpi$ and we can divide by $\varpi$ since C has no torsion). Then set $c_2=\frac{1}{\varpi }(c_1-\iota _C([{\overline{\alpha }}({\overline{c}}_1)]))$, etc. Finally, set $\alpha (c)=\sum _{n\ge 0}\varpi ^n[{\overline{\alpha }}({\overline{c}}_n)]$. We have $\iota _C(\alpha (c))=\sum _{n\ge 0}\varpi ^n\iota _C([{\overline{\alpha }}({\overline{c}}_n)])= \sum _{n\ge 0}(\varpi ^nc_n-\varpi ^{n+1}c_{n+1})=c_0=c.$ Hence $\alpha =\iota _C^{-1},$ as wanted. $\square$

3 Syntomic cohomologies

The period map of Fontaine–Messing (see Sect. 3.3.2) gives a description of (pro-)étale cohomology in terms of the syntomic cohomology of Fontaine–Messing. This syntomic cohomology can be made more concrete (see Sect. 3.3.3) by mimicking the construction of Selmer groups by Bloch and Kato [8]: syntomic cohomology is described as derived filtered eigenspaces of Frobenius acting on the geometric Hyodo–Kato cohomology [38]. Now, the geometric Hyodo–Kato cohomology behaves very badly locally (as does the de Rham cohomology) and the standard way to fix this problem is to do everything in an overconvergent way. So we define (see Sect. 3.2.2) overconvergent syntomic cohomology a la Bloch–Kato, replacing the usual Hyodo–Kato cohomology by the overconvergent Hyodo–Kato cohomology of Grosse-Klönne [32] which we review in Sect. 3.1. In the next chapter, we will show (Theorem 4.1) that these two syntomic cohomologies coincide for Stein spaces. This definition a la Bloch–Kato makes it easy to show (Proposition 3.36) that the overconvergent syntomic cohomology sits in a “fundamental diagram” involving the de Rham complex and overconvergent Hydo–Kato cohomology. It follows that so does pro-étale cohomology and this “fundamental diagram” will become our main tool for computations of the latter later on in the paper.

3.1 Overconvergent Hyodo–Kato cohomology

We will review in this section the definition of the overconvergent Hyodo–Kato cohomology and the overconvergent Hyodo–Kato isomorphism due to Grosse-Klönne [32]. We will pay particular attention to topological issues.

3.1.1 Dagger spaces and weak formal schemes

We will review, very briefly, basic facts concerning dagger spaces and weak formal schemes. Our main references are [29, 56, 81], where the interested reader can find a detailed exposition.

Let, for a moment, K denote the usual K or C. We start with dagger spaces. For $\delta \in {\mathbb {R}}^+$, set

$$\begin{aligned} T_n(\delta )= & {} K\{\delta ^{-1}X_1,\ldots ,\delta ^{-1}X_n\}\\ {}:= & {} \{\sum _v a_vX^v\in K[[X_1,\ldots ,X_n]]\mid \lim _{ |v|\rightarrow \infty } |a_v|\delta ^{|v|}=0\}. \end{aligned}$$

Here $| v|=\sum _{i=1}^{n} v_i$, $v=(v_1,\ldots ,v_n)\in {{\mathbf {N}}}^n$. We have $T_n:=K\{X_1,\ldots ,X_n\}=T_n(1)$. If $\delta \in p^ {{\mathbf {Q}}}$, this is an affinoid K-algebra; the associated Banach norm $|{\scriptscriptstyle \bullet }|_{\delta }: T_n(\delta )\rightarrow {\mathbb {R}}$, $|\sum a_vX^v|_{\delta }= \max _v |a_v|\delta ^{|v|}$. We set

$$\begin{aligned} K[X_1,\ldots ,X_n]^{\dagger }:=\bigcup _{\delta>1,\delta \in p^ {{\mathbf {Q}}}}T_n(\delta )=\bigcup _{\delta >1}T_n(\delta ) \end{aligned}$$

It is a Hausdorff LF-space.

A dagger algebraA is a topological K-algebra isomorphic to a quotient of the overconvergent Tate algebra $K[X_1,\ldots ,X_d]^{\dagger }$. It is canonically a Hausdorff LF-algebra [1, Cor. 3.2.4]. It defines a sheaf of topological K-algebras ${{\mathscr {O}}}^{\dagger }$ on $\mathrm {Sp} \widehat{A}$, $\widehat{A}$ being the p-adic completion of A, which is called a dagger structure on $\mathrm {Sp} \widehat{A}$. The pair $\mathrm {Sp} (A):=(|\mathrm {Sp} \widehat{A}|,{{\mathscr {O}}}^{\dagger })$ is called a dagger affinoid.

A dagger space¹⁵X is a pair $(\widehat{X},{{\mathscr {O}}}^{\dagger })$ where $\widehat{X}$ is a rigid analytic space over K and ${{\mathscr {O}}}^{\dagger }$ is a sheaf of topological K-algebras on $\widehat{X}$ such that, for some affinoid open covering $\{\widehat{U}_i\rightarrow \widehat{X}\}$, there are dagger structures $U_i$ on $\widehat{U}_i$ such that ${{\mathscr {O}}}^{\dagger }|\widehat{U}_i\simeq {{\mathscr {O}}}^{\dagger }_{U_i}$. The set of global sections $\Gamma (X,{{\mathscr {O}}}^{\dagger })$ has a structure of a convex K-vector space given by the projective limit $\varprojlim _Y \Gamma (Y,{{\mathscr {O}}}^{\dagger }|Y)$, where Y runs over all affinoid subsets of X. In the case of dagger affinoids this agrees with the previous definition.

Let $X=\mathrm {Sp} (A)\rightarrow Y=\mathrm {Sp} (B)$ be a morphism of affinoid dagger spaces and let $U\subset X$ be an affinoid subdomain. We write $U\Subset _Y X$ if there exists a surjection $\tau :B[X_1,\ldots ,X_r ]^{\dagger } \rightarrow A$ and $\delta \in p^ {{\mathbf {Q}}},\delta >1,$ such that $U\subset \mathrm {Sp} (A[\delta ^{-1}\tau (X_1),\ldots ,\delta ^{-1}\tau (X_r)]^{\dagger })$. A morphism $f:X\rightarrow Y$ of dagger (or rigid) spaces is called partially proper if f is separated and if there exist admissible coverings $Y=\bigcup Y_i$ and $f^{-1}(Y_i)=\bigcup X_{ij}$, all i, such that for every $X_{ij}$ there exists an affinoid subset $\widetilde{X}_{ij}\subset f^{-1}(Y_i)$ with $X_{ij}\Subset _Y\widetilde{X}_{ij}$. A partially proper dagger space that is quasi-compact is called proper. This notion is compatible with the one for rigid spaces. In fact, the category of partially proper dagger spaces is equivalent to the category of partially proper rigid spaces [29, Th. 2.27]. In particular, the rigid analytification of a finite type scheme over K is partially proper.

A dagger (or rigid) space X is called Stein if it admits an admissible affinoid covering $X=\bigcup _{i\in {{\mathbf {N}}}}U_i$ such that $U_i\subset ^{\dagger }U_{i+1}$ for all i; we call the covering $U_i,i\in {{\mathbf {N}}}$, a Stein covering. Here the notation $U_i\subset ^{\dagger } U_{i+1}$ means that the map $\widehat{U}_i=\mathrm {Sp} (C)\subset \widehat{U}_{i+1}=\mathrm {Sp} (D)$ is an open immersion of affinoid rigid spaces induced by a map $D\simeq T_n(\delta )/I\rightarrow C\simeq T_n/IT_n$ for some I and $\delta >1$. Stein spaces are partially proper.

We pass now to weakly formal schemes; the relation between dagger spaces and weak formal schemes parallels [50] the one between rigid spaces and formal schemes due to Raynaud. A weakly complete${{\mathscr {O}}}_K$-algebra $A^{\dagger }$ (with respect to $(\varpi )$) is an ${{\mathscr {O}}}_K$-algebra which is $\varpi$-adically separated and which satisfies the following condition: for any power series $f\in {{\mathscr {O}}}_K\{X_1,\ldots ,X_n\}$, $f=\sum a_vX^v,$ such that there exists a constant c for which $c(v_p(a_v)+1)\ge |v|$, all v, and for any n-tuple $x_1,\ldots ,x_n\in A^{\dagger }$, the series $f(x_1,\ldots ,x_n)$ converges to an element of $A^{\dagger }$. The weak completion of an ${{\mathscr {O}}}_K$-algebra A is the smallest weakly complete subalgebra $A^{\dagger }$ of $\widehat{A}$ containing the image of A.

A weak formal scheme is a locally ringed space $(X,{{\mathscr {O}}})$ that is locally isomorphic to an affine weak formal scheme. An affine weak formal scheme is a locally ringed space $(X,{{\mathscr {O}}})$ such that $X=\mathrm {Spec} (A^{\dagger }/\varpi )$ for some weakly complete finitely generated ${{\mathscr {O}}}_K$-algebra $A^{\dagger }$ and the sheaf ${{\mathscr {O}}}$ is given on the standard basis of open sets by $\Gamma (X_{\overline{f}},{{\mathscr {O}}})=(A^{\dagger }_f)^{\dagger }$, $f\in A^{\dagger }$. We say that $X=\mathrm {Spwf} (A^{\dagger })$, the weak formal spectrum of $A^{\dagger }$. For a weak formal scheme X, flat over ${{\mathscr {O}}}_K$, the associated dagger space $X_K$ is partially proper if and only if all irreducible closed subsets Z of X are proper over ${{\mathscr {O}}}_K$ [39, Rem. 1.3.18].

We come back now to K being a discrete valuation field. A weak formal scheme over ${{\mathscr {O}}}_K$ is called semistable if, locally for the Zariski topology, it admits étale maps to the weak formal spectrum

$$\begin{aligned} \mathrm {Spwf} ({{\mathscr {O}}}_K[X_1,\ldots ,X_n]^{\dagger }/(X_1\cdots X_r-\varpi )), \quad 1\le r\le n. \end{aligned}$$

We equip it with the log-structure coming from the special fiber. We have a similar definition for formal schemes. A (weak) formal scheme X is called Stein if its generic fiber $X_K$ is Stein. It is called Stein with a semistable reduction if it has a semistable reduction over ${{\mathscr {O}}}_K$ (and then the irreducible components of $Y:=X_0$ are proper and smooth) and there exist closed (resp. open) subschemes $Y_s$, $s\in {{\mathbf {N}}},$ (resp. $U_s$, $s\in {{\mathbf {N}}}$) of Y such that

• 1. each $Y_s$ is a finite union of irreducible components,

• 2. $Y_s\subset U_s\subset Y_{s+1}$ and their union is Y,

• 3. the tubes $\{]U_{s}[_{X}\},s\in {{\mathbf {N}}},$ form a Stein covering of $X_K$.

We will call the covering $\{U_s\},s\in {{\mathbf {N}}},$ a Stein covering of Y. The schemes $U_s, Y_s$ inherit their log-structure from Y (which is canonically a log-scheme log-smooth over $k^{0}$). The log-schemes $Y_s$ are not log-smooth (over $k^0$) but they are ideally log-smooth, i.e., they have a canonical idealized log-scheme structure and are ideally log-smooth for this structure.¹⁶

3.1.2 Overconvergent Hyodo–Kato cohomology

Let X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. We would like to define the overconvergent Hyodo–Kato cohomology as the rational overconvergent rigid cohomology of $X_0$ over ${{\mathscr {O}}}_F^0$:

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {HK} }(X_0):=\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0). \end{aligned}$$

The foundations of log-rigid cohomology missing¹⁷ this has to be done by hand [32, § 1].

Let Y be a fine $k^0$-log-scheme. Choose an open covering $Y=\cup _{i\in I}Y_i$ and, for every $i\in I$, an exact closed immersion $Y_i\hookrightarrow Z_i$ into a log-smooth weak formal ${{\mathscr {O}}}_F^0$-log-scheme $Z_i$. For each nonempty finite subset $J\subset I$ choose (perhaps after refining the covering) an exactification¹⁸ [49, Prop. 4.10]

$$\begin{aligned} Y_J=\cap _{i\in J}Y_i{\mathop {\rightarrow }\limits ^{\iota }} Z_J{\mathop {\rightarrow }\limits ^{f}} \prod _{{{\mathscr {O}}}_F^0}(Z_i)_{i\in J} \end{aligned}$$

of the diagonal embedding $Y_J\rightarrow \prod _{{{\mathscr {O}}}_F^0}(Z_i)_{i\in J}$. Let $\Omega ^{\scriptscriptstyle \bullet }_{Z_J/{{\mathscr {O}}}^0_F}$ be the de Rham complex of the weak formal log-scheme $Z_J$ over ${{\mathscr {O}}}_F^0$. This is a complex of sheaves on $Z_J$; tensoring it with F we obtain a complex of sheaves $\Omega ^{\scriptscriptstyle \bullet }_{Z_{J,F}}$ on the F-dagger space $Z_{J,F}$. By [32, Lemma 1.2], the tube $]Y_J[_{Z_J}$ and the restriction $\Omega ^{\scriptscriptstyle \bullet }_{]Y_J[_{Z_J}}:=\Omega ^{\scriptscriptstyle \bullet }_{Z_{J,F}}|_{]Y_J[_{Z_J}}$ of $\Omega ^{\scriptscriptstyle \bullet }_{Z_{J,F}}$ to $]Y_J[_{Z_J}$ depend only on the embedding system $\{Y_i\hookrightarrow Z_i\}_i$ not on the chosen exactification $(\iota ,f)$. Equip the de Rham complex $\Gamma (]Y_J[_{Z_J},\Omega ^{\scriptscriptstyle \bullet })$ with the topology induced from the structure sheaf of the dagger space $]Y_J[_{Z_J}$.

For $J_1\subset J_2$, one has natural restriction maps $\delta _{J_1,J_2}:]Y_{J_2}[_{Z_{J_2}}\rightarrow ]Y_{J_1}[_{Z_{J_1}}$ and $\delta ^{-1}_{J_1,J_2}\Omega ^{\scriptscriptstyle \bullet }_{]Y_{J_1}[_{Z_{J_1}}}\rightarrow \Omega ^{\scriptscriptstyle \bullet }_{]Y_{J_2}[_{Z_{J_2}}}$. Well-ordering I, we get a simplicial dagger space $]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}}$ and a sheaf $\Omega ^{\scriptscriptstyle \bullet }_{]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}}}$ on $]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}}$. Consider the complex $\mathrm {R} \Gamma (]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}},\Omega ^{\scriptscriptstyle \bullet })$. We equip it with the topology induced from the product topology on every cosimplicial level. In the classical derived category of F-vector spaces this complex is independent of choices made but we will make everything independent of choices by simply taking limit over all the possible choices. We define a complex in ${{\mathscr {D}}}(C_F)$

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0) :=\mathrm {hocolim}\, \Gamma (]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}},\Omega ^{\scriptscriptstyle \bullet }), \end{aligned}$$

(3.1)

where the limit is over the category of hypercovers built from the data that we have described above.¹⁹ Note that the data corresponding to affine coverings form a cofinal system. We set

$$\begin{aligned} \widetilde{H}^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0):=\widetilde{H}^i \mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0),\quad {H}^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0):={H}^i \mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0). \end{aligned}$$

The complex $\mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ is equipped with a Frobenius endomorphism $\varphi$ defined by lifting Frobenius to the schemes $Z_i$ in the above construction. In the case Y is log-smooth over $k^0$ we also have a monodromy endomorphism²⁰$N=\mathrm {Res} (\bigtriangledown (\mathrm {dlog} 0))$ defined by the logarithmic connection satisfying $p\varphi N=N\varphi$.

Proposition 3.2

Let Y be a semistable scheme over k with the induced log-structure [32, 2.1].

• 1. If Y is quasi-compact then $H^*_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ is a finite dimensional F-vector space with its unique locally convex Hausdorff topology.

• 2. The endomorphism $\varphi$ on $H^*_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ is a homeomorphism.

• 3. If k is finite then $H^*_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ is a mixed F-isocrystal, i.e., the eigenvalues of the linearized Frobenius $\varphi ^f$, where $|k|=p^f$, are Weil numbers.

Proof

All algebraic statements concerning the cohomology are proved in [32, Th. 5.3]. They follow immediately from the following weight spectral sequence [32, 5.2, 5.3] that reduces the statements to the analogous ones for (classically) smooth schemes over k

$$\begin{aligned} E^{-k,i+k}_1&=\bigoplus _{j\ge 0, j\ge -k}\prod _{S\in \Theta _{2j+k+1}}H^{i-2j-k}_{\mathrm {rig} }(S/{{\mathscr {O}}}_F)\Rightarrow H^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0). \end{aligned}$$

(3.3)

Here $\Theta _j$ denotes the set of all intersections S of j different irreducible components of Y that are equipped with trivial log-structure. By assumptions, the intersections S are smooth over k.

Let us pass to topology. Recall the following fact (that we will repeatedly use in the paper)

Lemma 3.4

([29, Lemma 4.7], [30, Cor. 3.2]) Let X be a smooth Stein space or a smooth affinoid dagger space. All de Rham differentials $d_i:\Omega ^i(X)\rightarrow \Omega ^{i+1}(X)$ are strict and have closed images.

Remark 3.5

The above lemma holds also for log-smooth Stein spaces with the log-structure given by a normal crossing divisor. The proof in [30, Cor. 3.2] goes through using the fact that for such quasi-compact log-smooth spaces the rigid de Rham cohomology is isomorphic to the rigid de Rham cohomology of the open locus where the log-structure is trivial (hence it is finite dimensional and equipped with the canonical Hausdorff topology).

We claim that, in the notation used above, if $Y_J$ is affine, then the complex

$$\begin{aligned} \Gamma (]Y_J[_{Z_J},\Omega ^{\scriptscriptstyle \bullet }) =\mathrm {R} \Gamma (]Y_J[_{Z_J},\Omega ^{\scriptscriptstyle \bullet }) \end{aligned}$$

has finite dimensional algebraic cohomology $H^*$ whose topology is Hausdorff. Moreover, its cohomology $\widetilde{H}^*$ is classical. Indeed, note that, using the contracting homotopy of the Poincaré Lemma for an open ball, we may assume that the tube $]Y_{J}[_{Z_J}$ is the generic fiber of a weak formal scheme lifting $Y_{J}$ to ${{\mathscr {O}}}^0_F$. Now, write $H^i=\ker d_i/\mathrm {im}\, d_{i-1}$ with the induced quotient topology. By the above lemma, the natural map $\mathrm {coim}\, d_{i-1}\rightarrow \mathrm {im}\, d_{i-1}$ is an isomorphism and $\mathrm {im}\, d_{i-1}$ is closed in $\ker d_i$. Hence $\widetilde{H}^i$ is classical and $\widetilde{H}^i{\mathop {\rightarrow }\limits ^{\sim }} H^i$ is Hausdorff, as wanted.

Note that, by the above, a map between two de Rham complexes associated to two (different) embeddings of $Y_I$ is a strict quasi-isomorphism. This implies that, if Y is affine, all the arrows in the system (3.1) are strict quasi-isomorphisms and the cohomology of $\mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ is isomorphic to the cohomology of $\Gamma (]Y_{{\scriptscriptstyle \bullet }}[_{Z_{{\scriptscriptstyle \bullet }}},\Omega ^{\scriptscriptstyle \bullet })$ for any embedding data.

This proves claim (1) of our proposition for affine schemes; the case of a general quasi-compact scheme can be treated in the same way (choose a covering by a finite number of affine schemes). Claim (2) follows easily from claim (1). $\square$

Remark 3.6

In an analogous way to $\mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_F^0)$ we define complexes

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(Y/{{\mathscr {O}}}_K^{\times })\in {{\mathscr {D}}}(C_K). \end{aligned}$$

For a quasi-compact Y, their cohomology groups are classical; they are finite K-vector spaces with their canonical Hausdorff topology.

3.1.3 Overconvergent Hyodo–Kato isomorphism

Set $r^+:=k[T], r^{\dagger }:={{\mathscr {O}}}_F[T]^{\dagger }$ with the log-structure associated to T. Let X be a log-scheme over $r^+:= k[T]$ (in particular, we allow log-schemes over $k^0$). Assume that there exists an open covering $X=\cup _{i\in I}X_i$ and, for every i, an exact closed immersion $X_i\hookrightarrow \widetilde{X}_i$ into a log-scheme log-smooth over $\tilde{r}:= {{\mathscr {O}}}_F[T]$. For each nonempty finite subset $J\subset I$, choose an exactification (product is taken over $\tilde{r}$)

$$\begin{aligned} X_J:=\cap _{i\in J}X_i{\mathop {\hookrightarrow }\limits ^{\iota }}\widetilde{X}_J{\mathop {\rightarrow }\limits ^{f}}\prod _{i\in J}\widetilde{X}_i \end{aligned}$$

of the diagonal embedding as in Sect. 3.1.2.

Let ${{\mathscr {X}}}_J$ be the weak completion of $\widetilde{X}_J$. Define the de Rham complex $\Omega ^{\scriptscriptstyle \bullet }_{{{\mathscr {X}}}_J/r^{\dagger }}$ as the weak completion of the de Rham complex $\Omega ^{\scriptscriptstyle \bullet }_{\widetilde{X}_J/\tilde{r}}$. The tube $]X_J[_{{{\mathscr {X}}}_J}$ with the complex ($\Omega ^{\scriptscriptstyle \bullet }_{{{\mathscr {X}}}_J/r^{\dagger }}\otimes {{\mathbf {Q}}})|_{]X_J[_{{{\mathscr {X}}}_J}}$ is independent of the chosen factorization $(\iota , f)$. For varying J one has natural transition maps, hence a simplicial dagger space $]X_{{\scriptscriptstyle \bullet }}[_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}}$ and a complex

$$\begin{aligned} (\Omega ^{\scriptscriptstyle \bullet }_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}/r^{\dagger }}\otimes {{\mathbf {Q}}})|_{]X_{{\scriptscriptstyle \bullet }}[_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}}} \end{aligned}$$

(3.7)

One shows that, in the derived category of vector spaces over ${{\mathbf {Q}}}_p$,

$$\begin{aligned} \mathrm {R} \Gamma (]X_{{\scriptscriptstyle \bullet }}[_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}},\Omega ^{\scriptscriptstyle \bullet }_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}/r^{\dagger }}\otimes {{\mathbf {Q}}}|_{]X_{{\scriptscriptstyle \bullet }}[_ {{{\mathscr {V}}}_{{\scriptscriptstyle \bullet }}}}) \end{aligned}$$

is independent of choices. We make it though functorial as a complex by going to limit over all the choices and define a complex in ${{\mathscr {D}}}(C_F)$

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X/r^{\dagger }):=\mathrm {hocolim}\, \Gamma (]X_{{\scriptscriptstyle \bullet }}[_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}},(\Omega ^{\scriptscriptstyle \bullet }_{{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}/r^{\dagger }}\otimes {{\mathbf {Q}}})|_{]X_{{\scriptscriptstyle \bullet }}[_ {{{\mathscr {X}}}_{{\scriptscriptstyle \bullet }}}}), \end{aligned}$$

where the index set runs over the data described above.

Cohomology $\mathrm {R} \Gamma _{\mathrm {rig} }(X/r^{\dagger })$ is equipped with a Frobenius endomorphism $\varphi$ defined by lifting mod p Frobenius to the schemes $\widetilde{X}_i$ in the above construction in a manner compatible with the Frobenius on $r^{\dagger }$ induced by $T\mapsto T^p$. If X is log-smooth over $k^0$, we also have a monodromy endomorphism $N=\mathrm {Res} (\bigtriangledown (\mathrm {dlog} T))$ defined by the logarithmic connection satisfying $p\varphi N=N\varphi$. The map $p_0: \mathrm {R} \Gamma _{\mathrm {rig} }(X/r^{\dagger })\rightarrow \mathrm {R} \Gamma _{\mathrm {rig} }(X/{{\mathscr {O}}}_F^0)$ induced by $T\mapsto 0$ is compatible with Frobenius and monodromy.

For a general (simplicial) log-scheme with boundary $(\overline{X},X)$ over $r^+$ satisfying certain mild condition²¹ the definition of rigid cohomology $\mathrm {R} \Gamma _{\mathrm {rig} }((\overline{X},X)/r^{\dagger })$ is analogous. For details of the construction we refer the reader to [32, 1.10] and for the definition of log-schemes with boundary to [31].

Let $X_0$ be a semistable scheme over k with the induced log-structure [32, 2.1]. Let $\{X_i\}_{i\in I}$ be the irreducible components of $X_0$ with induced log-structure. Denote by $M_{{\scriptscriptstyle \bullet }}$ the nerve of the covering $\coprod _{i\in I}X_i\rightarrow X_0$. We define the complex $\mathrm {R} \Gamma _{\mathrm {rig} }(M_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}}^0_F)\in {{\mathscr {D}}}(C_K)$ in an analogous way to $\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}^0_F)$ using the embedding data described in [32, 1.5].

Lemma 3.8

Let ${{\mathscr {O}}}$ denote ${{\mathscr {O}}}_F^0$ or ${{\mathscr {O}}}_K^{\times }$. The natural map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}})\rightarrow \mathrm {R} \Gamma _{\mathrm {rig} }(M_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}}) \end{aligned}$$

is a strict quasi-isomorphism.

Proof

It suffices to argue locally, so we may assume that there exists an exact embedding of $X_0$ into a weak formal scheme X that is log-smooth over ${{\mathscr {O}}}$.

Let us first prove that the above map is a quasi-isomorphism. The complex $\mathrm {R} \Gamma _{\mathrm {rig} }(M_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}})$ can be computed by de Rham complexes on the tubes $]M_J[_X$, where, for a nonempty subset $J\subset I$, we set $M_J=\cap _{j\in J}X_j$ with the induced log-structure. To compute $\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}})$, recall that, for a weak formal scheme X and a closed subscheme Z of its special fiber, if $Z=\cup _{i\in I}Z_i$ is a finite covering by closed subschemes of Z, then the dagger space covering $]Z[_X=\cup _{i\in I}]Z_i[_X$ is admissible open [32, 3.3]. Hence $\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}})$ can be computed as the de Rham cohomology of the nerve of the covering $X_K=\cup _{i\in I}]M_i[_X$. Since the two above mentioned simplicial de Rham complexes are equal, we are done.

Now, strictness of the above quasi-isomorphism follows from the fact that the cohomology groups of the left complex are finite dimensional vector spaces (over F or K) with their canonical Hausdorff topology and so are the cohomology groups of the right complex (basically by the same argument using the quasi-isomorphism $\mathrm {R} \Gamma _{\mathrm {rig} }(M_J/{{\mathscr {O}}}){\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {rig} }(M_J^{ \mathrm {tr} }/{{\mathscr {O}}})$ [32, Lemma 4.4], where $M^{ \mathrm {tr} }_J$ denotes the open set of $M_J$, where the horizontal log-structure is trivial.) $\square$

Let $J\subset I$ and $M=M_J=\cap _{j\in J}X_j$. Grosse-Klönne [32, 2.2] attaches to M finitely many log-schemes with boundary $(P^{J^{\prime }}_M,V^{J^{\prime }}_M)$, $\emptyset \subsetneq J^{\prime }\subset J$. We think of $(P^{J^{\prime }}_M,V^{J^{\prime }}_M)$ as the vector bundle $V^{J^{\prime }}_M$ on M (built from the log-structure corresponding to $J^{\prime }$) that is compactified by  $P^{J^{\prime }}_M$—a direct sum of projective space bundles. It is a log-scheme with boundary over $r^+$ which, in particular, means that $V^{J^{\prime }}_M$ is a genuine log-scheme over $r^+$ (however this is not the case for $P^{J^{\prime }}_M$). This construction of Grosse-Klönne corresponds to defining the Hyodo–Kato isomorphism using not the deformation space $r^{\mathrm{PD}}_{\varpi }$ as in the classical constructions but its compactification (a projective space). The key advantage being that the cohomology of the structure sheaf of the new deformation space is now trivial.

The following proposition is the main result of [32].

Proposition 3.9

Let $\emptyset \ne J^{\prime }\subset J\subset I$ and let ${{\mathscr {O}}}_F(0)={{\mathscr {O}}}_F^0,{{\mathscr {O}}}_F(\varpi )={{\mathscr {O}}}_K^{\times }$. The map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }((P^{J^{\prime }}_M,V^{J^{\prime }}_M)/r^{\dagger })\otimes _FF(a)\rightarrow \mathrm {R} \Gamma _{\mathrm {rig} }(M/{{\mathscr {O}}}_F(a)),\quad a=0,\varpi , \end{aligned}$$

defined by restricting to the zero section $M=M_J\rightarrow P^{J^{\prime }}_M$ and sending $T\mapsto a$, is a strict quasi-isomorphism.

Proof

The algebraic quasi-isomorphism was proved in [32, Th. 3.1]. To show that this quasi-isomorphism is strict we can argue locally, for $X_0$ affine. Then the cohomology of the complex on the right is a finite rank vector space over F(a) with its natural locally convex and Hausdorff topology. Algebraic quasi-isomorphism and continuity of the restriction map imply that the cohomology of the complex on the left is Hausdorff as well. Since it is a locally convex space the map has to be an isomorphism in $C_{F(a)}$, as wanted. $\square$

Example 3.10

We have found that the best way to understand the above proposition is through an example supplied by Grosse-Klönne himself in [32]. Let $X_0$ be of dimension 1 and let M be the intersection of two irreducible components. Hence the underlying scheme of M is equal to $\mathrm {Spec} k$. Let U be the 2-dimensional open unit disk over K with coordinates $x_1,x_2$, viewed as a dagger space. Consider its two closed subspaces: $U^0$ defined by $x_1x_2=0$ and $U^{\varpi }$ defined by $x_1x_2=\varpi$.

Let $\widetilde{\Omega }_U^{\scriptscriptstyle \bullet }$ be the de Rham complex of U with log-poles along the divisor $U^0$; let $\Omega _U^{\scriptscriptstyle \bullet }$ be its quotient by its sub-${{\mathscr {O}}}_U$-algebra generated by $\mathrm {dlog} (x_1x_2)$. Denote by $\Omega ^{\scriptscriptstyle \bullet }_{U^0}$ and $\Omega ^{\scriptscriptstyle \bullet }_{U^{\varpi }}$ its restriction to $U^0$ and $U^{\varpi }$, respectively. We note that $U^{\varpi }$ is (classically) smooth and that $\Omega ^{\scriptscriptstyle \bullet }_{U^{\varpi }}$ is its (classical) de Rham complex. We view the $k^0$-log-scheme M as an exact closed log-subscheme of the formal log-scheme $\mathrm {Spf} ({{\mathscr {O}}}_F[[x_1,x_2]]/(x_1x_2))$ that is log-smooth over ${{\mathscr {O}}}_F^0$ or of the formal log-scheme $\mathrm {Spf} ({{\mathscr {O}}}_K[[x_1,x_2]]/(x_1x_2-\varpi ))$ that is log-smooth over ${{\mathscr {O}}}_K^{\times }$. The corresponding tubes are $U^0$ and $U^{\varpi }$. We have

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(M/{{\mathscr {O}}}_F^0)\otimes _FK=\mathrm {R} \Gamma (U^0,\Omega ^{\scriptscriptstyle \bullet }),\quad \mathrm {R} \Gamma _{\mathrm {rig} }(M/{{\mathscr {O}}}_K^{\times })=\mathrm {R} \Gamma (U^{\varpi },\Omega ^{\scriptscriptstyle \bullet }).\nonumber \\ \end{aligned}$$

(3.11)

We easily see that $H^*(U^0,\Omega ^{\scriptscriptstyle \bullet })\simeq H^*(U^{\varpi },\Omega ^{\scriptscriptstyle \bullet })$; in particular, $H^1(U^0,\Omega ^{\scriptscriptstyle \bullet }_{U^0})=H^1(U^{\varpi },\Omega ^{\scriptscriptstyle \bullet })$ is a one dimensional K-vector space generated by $\mathrm {dlog} x_1$.

The quasi-isomorphism between the cohomologies in (3.11) is constructed via the following deformation space (P, V):

$$\begin{aligned}&P:=({{\mathbb {P}}}^1_K\times {{\mathbb {P}}}^1_K)^{\mathrm {an} }=((\mathrm {Spec} (K[x_1])\cup \{\infty \})\times (\mathrm {Spec} (K[x_2])\cup \{\infty \}))^{\mathrm {an} },\\&V:=(\mathrm {Spec} (K[x_1,x_2]))^{\mathrm {an} }. \end{aligned}$$

Let $\widetilde{\Omega }^{\scriptscriptstyle \bullet }_P$ be the de Rham complex of P with log-poles along the divisor

$$\begin{aligned} (\{0\}\times {{\mathbb {P}}}^1_K)\cup ({{\mathbb {P}}}^1_K\times \{0\})\cup (\{\infty \}\times {{\mathbb {P}}}^1_K)\cup ({{\mathbb {P}}}^1_K\times \{\infty \}). \end{aligned}$$

The section $\mathrm {dlog} (x_1x_2)\in \widetilde{\Omega }^1_U(U)=\widetilde{\Omega }^1_P(U)$ extends canonically to a section $\mathrm {dlog} (x_1x_2)\in \widetilde{\Omega }^1_P(P)$. Let $\Omega ^{\scriptscriptstyle \bullet }_P$ be the quotient of $\widetilde{\Omega }^{\scriptscriptstyle \bullet }_P$ by its sub-${{\mathscr {O}}}_P$-algebra generated by $\mathrm {dlog} (x_1x_2)$. The natural restriction maps

are quasi-isomorphisms. This is because we have killed one differential of $\widetilde{\Omega }_P$ and the logarithmic differentials of ${{\mathbb {P}}}^1_ {{{\mathscr {O}}}_K}$ are isomorphic to the structure sheaf hence have cohomology which is 1-dimensional in degree 0 and trivial otherwise.

Varying the index set $J^{\prime }$ in a coherent way one glues the log-schemes $(P^{J^{\prime }}_M,V^{J^{\prime }}_M)$ into a simplicial $r^+$-log-scheme $(P_{{\scriptscriptstyle \bullet }},V_{{\scriptscriptstyle \bullet }})$ with boundary. Set

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(\overline{X}_0/r^{\dagger }):=\mathrm {R} \Gamma _{\mathrm {rig} }((P_{{\scriptscriptstyle \bullet }},V_{{\scriptscriptstyle \bullet }})/r^{\dagger }). \end{aligned}$$

We have the corresponding simplicial log-scheme $M^{\prime }_{{\scriptscriptstyle \bullet }}$ over $k^0$. There is a natural map $M_{{\scriptscriptstyle \bullet }}\rightarrow M^{\prime }_{{\scriptscriptstyle \bullet }}$ (that induces a strict quasi-isomorphism $\mathrm {R} \Gamma _{\mathrm {rig} }(M^{\prime }_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}}_F^0) {\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {rig} }(M_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}}_F^0)$) and a natural map $M^{\prime }_{{\scriptscriptstyle \bullet }} \rightarrow (P_{{\scriptscriptstyle \bullet }},V_{{\scriptscriptstyle \bullet }})$. The following proposition is an immediate corollary of Proposition 3.9 and Lemma 3.8.

Proposition 3.12

([32, Th. 3.4]) Let $a=0,\varpi$. The natural maps

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F(a))\rightarrow \mathrm {R} \Gamma _{\mathrm {rig} }(M^{\prime }_{{\scriptscriptstyle \bullet }}/{{\mathscr {O}}}_F(a)) \leftarrow \mathrm {R} \Gamma _{\mathrm {rig} }(\overline{X}_0/r^{\dagger })\otimes _FF(a) \end{aligned}$$

are strict quasi-isomorphisms.

Let X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. We define the overconvergent Hyodo–Kato cohomology of $X_0$ as $\mathrm {R} \Gamma _{\mathrm {HK} }(X_0):=\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)$. Recall that the Hyodo–Kato map

$$\begin{aligned} \iota _{\mathrm {HK} }: \mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(X_K) \end{aligned}$$

is defined as the zigzag (using the maps from the above proposition)

It yields the (overconvergent) Hyodo–Kato strict quasi-isomorphism

$$\begin{aligned} \iota _{\mathrm {HK} }: \mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\otimes _F K{\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {dR} }(X_K). \end{aligned}$$

Remark 3.13

The overconvergent Hyodo–Kato map, as its classical counterpart, depends on the choice of the uniformizer $\varpi$. This dependence takes the usual form [79, Prop. 4.4.17].

3.2 Overconvergent syntomic cohomology

In this section we will define syntomic cohomology (a la Bloch–Kato) using overconvergent Hyodo–Kato and de Rham cohomologies of Grosse-Klönne and discuss the fundamental diagram that it fits into. We call this definition “a la Bloch–Kato” because it is inspired by Bloch–Kato’s definition of local Selmer groups [8].

3.2.1 Period rings ${\widehat{\mathbf{B}}}^+_{\mathrm {st} }$, $\mathbf{A}_{\mathrm {cr} ,K}$

We will recall the definition of the rings of periods $\widehat{\mathbf{B}}^+_{\mathrm {st} }$ and $\mathbf{A}_{\mathrm {cr} ,K}$ that we will need. We denote by $r^+_\varpi$ the algebra ${{\mathscr {O}}}_F[[T]]$ with the log-structure associated to T. Sending T to $\varpi$ induces a surjective morphism $r_\varpi ^+\rightarrow {{\mathscr {O}}}_K^{\times }$. We denote by $r_\varpi ^{\mathrm{PD}}$ the p-adic divided power envelope of $r_\varpi ^+$ with respect to the kernel of this morphism. Frobenius is defined by $T\mapsto T^p$, monodromy by $T\mapsto T$.

We start with the definition of the ring of periods $\widehat{\mathbf{B}}^+_{\mathrm {st} }$ [79, p. 253]. Let

$$\begin{aligned} \widehat{\mathbf{A}}_{\mathrm {st} ,n}:=H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/r^{\mathrm{PD}}_{\varpi ,n}), \quad \widehat{\mathbf{A}}_{\mathrm {st} }:=\varprojlim _n\widehat{\mathbf{A}}_{\mathrm {st} ,n},\quad \widehat{\mathbf{B}}^+_{\mathrm {st} }:=\widehat{\mathbf{A}}_{\mathrm {st} }[1/p]. \end{aligned}$$

We note that $\widehat{\mathbf{B}}^+_{\mathrm {st} }$ is a Banach space over F (which makes it easier to handle topologically than $\mathbf{B}^+_{\mathrm {st} }$). The ring $\widehat{\mathbf{A}}_{\mathrm {st} ,n}$ has a natural action of ${{\mathscr {G}}}_K$, Frobenius $\varphi$, and a monodromy operator N. We have a morphism $\mathbf{A}_{\mathrm {cr} ,n}\rightarrow \widehat{\mathbf{A}}_{\mathrm {st} ,n}$ induced by the map $H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}/{{\mathscr {O}}}_{F,n})\rightarrow H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/r^{\mathrm{PD}}_{\varpi ,n})$. Both it and the natural map $r^{\mathrm{PD}}_{\varpi ,n}\rightarrow \widehat{\mathbf{A}}_{\mathrm {st} ,n}$ are compatible with all the structures (Frobenius, monodromy, and Galois action). Moreover, we have the exact sequence

$$\begin{aligned} 0\rightarrow \mathbf{A}_{\mathrm {cr} ,n}\rightarrow \widehat{\mathbf{A}}_{\mathrm {st} ,n}{\mathop {\rightarrow }\limits ^{N}} \widehat{\mathbf{A}}_{\mathrm {st} ,n}\rightarrow 0. \end{aligned}$$

(3.14)

We can view $\widehat{\mathbf{A}}_{\mathrm {st} ,n}$ as the ring of the PD-envelope of the closed immersion

$$\begin{aligned} \mathrm {Spec} {{\mathscr {O}}}_{C,n}^{\times }\hookrightarrow \mathrm {Spec} (\mathbf{A}^{\times }_{\mathrm {cr} ,n}\otimes _{{{\mathscr {O}}}_{F,n}}r^+_{\varpi ,n}) \end{aligned}$$

defined by the maps $\theta : \mathbf{A}_{\mathrm {cr} ,n}\rightarrow {{\mathscr {O}}}_{C,n}$ and $r^+_{\varpi ,n} \rightarrow {{\mathscr {O}}}_{K,n}$, $T\mapsto \varpi$. Here $\mathbf{A}^{\times }_{\mathrm {cr} ,n}$ is $\mathbf{A}_{\mathrm {cr} ,n}$ equipped with the unique log-structure extending the one on ${{\mathscr {O}}}^{\times }_{C,n}$. This makes $\mathrm {Spec} {{\mathscr {O}}}_{C,1}^{\times }\hookrightarrow \mathrm {Spec} \widehat{\mathbf{A}}_{\mathrm {st} ,n}$ into a PD-thickening in the crystalline site of ${{\mathscr {O}}}_{\overline{K},1}^{\times }$. It follows [47, § 3.9] that

$$\begin{aligned} {\widehat{\mathbf{A}}}_{\mathrm {st} ,n}\simeq \mathrm {R} \Gamma _{\mathrm {cr} }({{\mathscr {O}}}^{\times }_{C,n}/r^{\mathrm{PD}}_{\varpi ,n}). \end{aligned}$$

(3.15)

There is [47, Th. 3.7] a canonical $\mathbf{B}^+_{\mathrm {cr} }$-linear isomorphism $\mathbf{B}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\sim }}\widehat{\mathbf{B}}_{\mathrm {st} }^{+,N-\mathrm{nilp}}$ compatible with the action of ${{\mathscr {G}}}_K$, $\varphi$, and N.

We will now pass to the definition of the ring of periods $\mathbf{A}_{\mathrm {cr} ,K}$ [79, § 4.6]. Let

$$\begin{aligned} {\mathbf{A}}_{\mathrm {cr} ,K,n}:=H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/{{\mathscr {O}}}_{K,n}^{\times }), \quad {\mathbf{A}}_{\mathrm {cr} ,K}:=\varprojlim _n{\mathbf{A}}_{\mathrm {cr} ,K,n}.\end{aligned}$$

The ring ${\mathbf{A}}_{\mathrm {cr} ,K,n}$ is a flat ${{\mathbf {Z}}} /p^n$-module and ${\mathbf{A}}_{\mathrm {cr} ,K,n+1}\otimes {{\mathbf {Z}}} /p^n\simeq {\mathbf{A}}_{\mathrm {cr} ,K,n}$; moreover, it has a natural action of ${{\mathscr {G}}}_K$. These properties generalize, for $r\in {{\mathbf {Z}}}$, to $H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/{{\mathscr {O}}}_{K,n}^{\times },{{\mathscr {J}}}^{[r]})$, and we have $H^i_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/{{\mathscr {O}}}_{K,n}^{\times },{{\mathscr {J}}}^{[r]})=0$, $i\ge 1$, $r\in {{\mathbf {Z}}}$. Set

$$\begin{aligned} F^r{\mathbf{A}}_{\mathrm {cr} ,K,n}:=H^0_{\mathrm {cr} }({{\mathscr {O}}}_{C,n}^{\times }/{{\mathscr {O}}}_{K,n}^{\times },{{\mathscr {J}}}^{[r]}),\quad F^r{\mathbf{A}}_{\mathrm {cr} ,K}:=\varprojlim _nF^r{\mathbf{A}}_{\mathrm {cr} ,K,n}. \end{aligned}$$

We have

$$\begin{aligned} F^r{\mathbf{A}}_{\mathrm {cr} ,K,n}\simeq&\ \mathrm {R} \Gamma _{\mathrm {cr} }({{\mathscr {O}}}^{\times }_{C,n}/{{\mathscr {O}}}^{\times }_{K,n},{{\mathscr {J}}}^{[r]}),\\ F^r{\mathbf{A}}_{\mathrm {cr} ,K,n}/F^s\simeq&\ \mathrm {R} \Gamma _{\mathrm {cr} }({{\mathscr {O}}}^{\times }_{C,n}/{{\mathscr {O}}}^{\times }_{K,n},{{\mathscr {J}}}^{[r]}/{{\mathscr {J}}}^{[s]}), \quad r\le s. \end{aligned}$$

The natural map $\mathrm {gr} ^r_F\mathbf{A}_{\mathrm {cr} ,n}\rightarrow \mathrm {gr} ^r_F\mathbf{A}_{\mathrm {cr} ,K,n}$ is a $p^a$-quasi-isomorphism for a constant a depending on K, $a\sim v_p(d_{K/F})$, [79, Lemma 4.6.2]. We set

$$\begin{aligned} \mathbf{B}^+_{\mathrm {cr} ,K}:=\mathbf{A}_{\mathrm {cr} ,K}[1/p]. \end{aligned}$$

There is a natural ${{\mathscr {G}}}_K$-equivariant map $\iota :\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow \mathbf{B}_{\mathrm {dR} }^+$ induced by the maps

$$\begin{aligned} p_{\varpi }:{\widehat{\mathbf{B}}}^+_{\mathrm {st} } \rightarrow \mathbf{B}^+_{\mathrm {cr} ,K},\quad \mathbf{B}^+_{\mathrm {cr} }/F^r{\mathop {\rightarrow }\limits ^{\sim }}\mathbf{B}^+_{\mathrm {cr} ,K}/F^r{\mathop {\leftarrow }\limits ^{\sim }}\mathbf{B}^+_{\mathrm {cr} }/F^r, \end{aligned}$$

where $p_{\varpi }$ denotes the map induced by sending $T\mapsto \varpi$. The composition ${\mathbf{B}}^+_{\mathrm {st} }{\rightarrow } {\widehat{\mathbf{B}}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\iota }}{\widehat{\mathbf{B}}}^+_{\mathrm {dR} }$ is the map $\iota =\iota _{\varpi }$ from Sect. 1.4.2.

3.2.2 Overconvergent geometric syntomic cohomology

Let X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. Take $r\ge 0$. We define the overconvergent geometric syntomic cohomology of $X_K$ by the following mapping fiber (taken in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$)

This is an overconvergent analog of the algebraic geometric syntomic cohomology studied in [59]. Here, we wrote $[\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0,\varphi =p^r}$ for the homotopy limit of the commutative diagram²²

The filtration on $\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\widehat{\otimes }_K^R\mathbf{B}^+_{\mathrm {dR} }$ is defined by the formula

$$\begin{aligned} F^r(\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\widehat{\otimes }_K^R\mathbf{B}^+_{\mathrm {dR} }):=\mathrm {hocolim}\, _{i+j\ge r}F^i\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\widehat{\otimes }_K^RF^j\mathbf{B}^+_{\mathrm {dR} }. \end{aligned}$$

Set

$$\begin{aligned} \mathrm{HK}(X_{C},r):= & {} [\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0,\varphi =p^r},\\ \mathrm{DR}(X_{C},r):= & {} (\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\widehat{\otimes }_K^R\mathbf{B}^+_{\mathrm {dR} })/F^r. \end{aligned}$$

Hence

Example 3.16

Assume X to be quasi-compact. We claim that then the complex

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} } \end{aligned}$$

has classical cohomology isomorphic to $H^*_{\mathrm {HK} }(X_{0})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }$, a finite rank free module over $\widehat{\mathbf{B}}^+_{\mathrm {st} }$. To show this, consider the distinguished triangle

$$\begin{aligned} H^0_{\mathrm {HK} }(X_0)\rightarrow \mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\rightarrow \tau _{\ge 1}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}). \end{aligned}$$

Tensoring it with $\widehat{\mathbf{B}}^+_{\mathrm {st} }$ we obtain the distinguished triangle

$$\begin{aligned} H^0_{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow \mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow (\tau _{\ge 1}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}))\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }.\quad \qquad \end{aligned}$$

(3.17)

Note that, since $H^0_{\mathrm {HK} }(X_0)$ is a finite rank vector space over F, we have the natural strict quasi-isomorphism

$$\begin{aligned} H^0_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\sim }} H^0_{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }. \end{aligned}$$

(3.18)

Since $\widetilde{H}^0((\tau _{\ge 1}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}))\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} })=0$, this implies that

$$\begin{aligned}&H^0_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\sim }}\widetilde{H}^0(\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }),\\&\widetilde{H}^i(\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }){\mathop {\rightarrow }\limits ^{\sim }} \widetilde{H}^i((\tau _{\ge 1}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}))\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }),\quad i\ge 1. \end{aligned}$$

Repeating now, for $(\tau _{\ge 1}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}))\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }$, $(\tau _{\ge 2}\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0}))\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }$, etc, the above computation, we get that

$$\begin{aligned} \widetilde{H}^i(\mathrm {R} \Gamma _{\mathrm {HK} }(X_{0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} } )\simeq H^i_{\mathrm {HK} }(X_{0})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} },\quad i\ge 0\,, \end{aligned}$$

(3.19)

as wanted.

Lemma 3.20

Let X be quasi-compact. The above isomorphism induces a natural isomorphism

$$\begin{aligned} \widetilde{H}^i(\mathrm{HK}(X_C,r))\simeq ({H}^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0,\varphi =p^r}, \quad i\ge 0, \end{aligned}$$

of Banach spaces (so $\widetilde{H}^i(\mathrm{HK}(X_C,r))$ is classical).

Proof

The argument here is similar to the one given in [59, Cor. 3.26] for the Beilinson–Hyodo–Kato cohomology but requires a little bit more care. We note that ${H}^i_{\mathrm {HK} }(X_0)$ is a finite dimensional $(\varphi ,N)$-module (by Proposition 3.2). For a finite $(\varphi , N)$-module M, we have the following short exact sequences

$$\begin{aligned} 0\rightarrow&M\otimes _{F}\mathbf{B}^+_{\mathrm {cr} }{\mathop {\rightarrow }\limits ^{\beta }} M\otimes _{F}\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{N}} M\otimes _{F}\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow 0,\nonumber \\ 0\rightarrow&(M\otimes _{F}\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^r}\rightarrow M\otimes _{F}\mathbf{B}^+_{\mathrm {cr} }{\mathop {\longrightarrow }\limits ^{p^r-\varphi }} M\otimes _{F}\mathbf{B}^+_{\mathrm {cr} }\rightarrow 0. \end{aligned}$$

(3.21)

The first one follows, by induction on m such that $N^m=0$ on M, from the fundamental exact sequence, i.e., the same sequence for $M=F$. The map $\beta$ is the (Frobenius equivariant) trivialization map defined as follows

$$\begin{aligned} \beta : M\otimes \mathbf{B}^+_{\mathrm {cr} } {\mathop {\rightarrow }\limits ^{\sim }} (M\otimes \widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0},\quad m\otimes b&\mapsto \exp (Nu)m\otimes b. \end{aligned}$$

(3.22)

We note here that it is not Galois equivariant; however this will not be a problem in this proof. The second exact sequence follows from [20, Rem. 2.30].

We will first show that

$$\begin{aligned} \widetilde{H}^i([\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0})\simeq ({H}^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0}. \end{aligned}$$

(3.23)

Set ${\mathrm {HK} }:=\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }$. We have the long exact sequence

$$\begin{aligned} {\mathop {\rightarrow }\limits ^{N}}\widetilde{H}^{i-1}({\mathrm {HK} })\rightarrow \widetilde{H}^i([{\mathrm {HK} }]^{N=0})\rightarrow \widetilde{H}^i({\mathrm {HK} }^{}){\mathop {\rightarrow }\limits ^{N}} \widetilde{H}^i({\mathrm {HK} })\rightarrow \widetilde{H}^{i+1}([{\mathrm {HK} }]^{N=0})\rightarrow \end{aligned}$$

By the isomorphism (3.19) and the exact sequence (3.21), it splits into the short exact sequences

$$\begin{aligned} 0\rightarrow \widetilde{H}^i([{\mathrm {HK} }]^{N=0})\rightarrow H^i_{\mathrm {HK} }(X_0)\otimes _F\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{N}}H^i_{\mathrm {HK} }(X_0)\otimes _F\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow 0 \end{aligned}$$

The isomorphism (3.23) follows. By (3.21), we also have

$$\begin{aligned} \widetilde{H}^i([{\mathrm {HK} }]^{N=0})\simeq H^i_{\mathrm {HK} }(X_0)\otimes _F\mathbf{B}^+_{\mathrm {cr} }. \end{aligned}$$

Now, set $D:=[{\mathrm {HK} }]^{N=0}$. We have the long exact sequence

$$\begin{aligned} {\mathop {\longrightarrow }\limits ^{\varphi -p^r}} \widetilde{H}^{i-1}(D)\rightarrow \widetilde{H}^{i}([D]^{\varphi =p^r})\rightarrow \widetilde{H}^{i}(D){\mathop {\longrightarrow }\limits ^{\varphi -p^r}} \widetilde{H}^{i}(D)\rightarrow \widetilde{H}^{i+1}([D]^{\varphi =p^r})\rightarrow \end{aligned}$$

Since $\widetilde{H}^i(D)\simeq H^i_{\mathrm {HK} }(X_0)\otimes _F\mathbf{B}^+_{\mathrm {cr} }$, the sequence (3.21) implies that the above long exact sequence splits into the short exact sequences

$$\begin{aligned} 0\rightarrow \widetilde{H}^{i}([D]^{\varphi =p^r})\rightarrow H^i_{\mathrm {HK} }(X_0)\otimes _F\mathbf{B}^+_{\mathrm {cr} }{\mathop {\longrightarrow }\limits ^{\varphi -p^r}}H^i_{\mathrm {HK} }(X_0)\otimes _F\mathbf{B}^+_{\mathrm {cr} }\rightarrow 0 \end{aligned}$$

Our lemma follows from the sequence in (3.21). $\square$

Assume now that X is Stein and let $\{U_n\}, n\in {{\mathbf {N}}},$ be a Stein covering. We claim that we have a natural strict quasi-isomorphism

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\sim }} \mathrm {holim}\, _n(\mathrm {R} \Gamma _{\mathrm {HK} }(U_{n,0})\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }). \end{aligned}$$

(3.24)

To show this we will compute the cohomology of both sides. Since, by Lemma 2.3, the natural map

$$\begin{aligned} H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} },\quad i\ge 0, \end{aligned}$$

is a strict quasi-isomorphism, the argument in Example 3.16 goes through and we get that

$$\begin{aligned} \widetilde{H}^i(\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} })\simeq H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} },\quad i\ge 0. \end{aligned}$$

Similarly, applying $\mathrm {holim}\,$ to the analogs of the distinguished triangle (3.17), we get the distinguished triangles

We have

(3.25)

The vanishing in the second line can be seen by evoking the Mittag–Leffler criterium in the category of convex vector spaces [68, Cor. 2.2.12]: the projective system $\{H^0_{\mathrm {HK} }(U_{n,0})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }\}$ is Mittag–Leffler because so is the projective system $\{H^0_{\mathrm {HK} }(U_{n,0})\}$. Now, the argument in Example 3.16 can be repeated and it will yield that

The computations of cohomology of both sides of (3.24) being compatible, to prove that they are strictly quasi-isomorphic, it remains to show that the natural map

is an isomorphism. But this follows from the fact that each $H^i_{\mathrm {HK} }(U_{n,0})$ is a finite rank vector space (see Sect. 2.1.3).

To sum up the above discussion:

Lemma 3.26

The cohomology of $\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }$ is classical and we have

$$\begin{aligned} \widetilde{H}^i(\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} })\simeq {H}^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }\simeq \varprojlim _n({H}^i_{\mathrm {HK} }(U_{n,0})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} }).\nonumber \\ \end{aligned}$$

(3.27)

Lemma 3.28

The cohomology $\widetilde{H}^i([\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0,\varphi =p^r})$ is classical and we have natural isomorphisms

$$\begin{aligned} H^i([\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0,\varphi =p^r})\simeq (H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0,\varphi =p^r}. \end{aligned}$$

In particular, the space $H^i([\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0,\varphi =p^r})$ is Fréchet. Moreover,

$$\begin{aligned} \widetilde{H}^i([\mathrm {R} \Gamma _{\mathrm {HK} }(X_0)\widehat{\otimes }_F^R\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0})\simeq (H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0} \simeq H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {cr} }, \end{aligned}$$

where the last isomorphism is not, in general, Galois equivariant.

Proof

For the first claim, we argue as in the proof of Lemma 3.20 using analogs of the exact sequences (3.21) (for $M=H^i_{\mathrm {HK} }(X_0)$):

$$\begin{aligned} 0\rightarrow&H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {cr} }{\mathop {\rightarrow }\limits ^{\beta }} H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{N}} H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\widehat{\mathbf{B}}^+_{\mathrm {st} }\rightarrow 0,\nonumber \\ 0\rightarrow&(H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^r}\rightarrow H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {cr} }{\mathop {\longrightarrow }\limits ^{p^r-\varphi }} H^i_{\mathrm {HK} }(X_0)\widehat{\otimes }_{F}\mathbf{B}^+_{\mathrm {cr} }\rightarrow 0. \end{aligned}$$

(3.29)

These sequences are limits of sequences (3.21) applied to $H^i_{\mathrm {HK} }(U_{n,0})$, $n\in {{\mathbf {N}}}$. We wrote $\beta :=\varprojlim _n\beta _n$ and used the isomorphism (3.27) (and its analog for $\mathbf{B}^+_{\mathrm {cr} }$) as well as the vanishings

$$\begin{aligned} \widetilde{H}^j\mathrm {holim}\, _n(H^i_{\mathrm {HK} }(U_{n,0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {cr} })=0\,, \quad \widetilde{H}^j\mathrm {holim}\, _n((H^i_{\mathrm {HK} }(U_{n,0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^r})=0\,, \end{aligned}$$

for $j\ge 1$. The vanishing of the first cohomology follows from the fact that the projective system $\{H^i_{\mathrm {HK} }(U_{n,0})\}$ is Mittag–Leffler. The vanishing of the second cohomology is a little subtler. Note that the system of Banach spaces $\{(H^i(U_{n,0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^r}\}$ can be lifted to a system of finite dimensional BC spaces with Dimensions $(d_i,h_i)$, $d_i,h_i\ge 0$ [14, Prop. 10.6]. The images of the terms in the system in a fixed BC space form a chain with decreasing dimensions D (in lexicographical order). Since the height h of any BC subspace of these spaces is also $\ge 0$ [15, Lemma 2.6], they stabilize. Hence the original system satisfies the Mittag–Leffler criterium from [68, Cor. 2.2.12] and, hence, it is acyclic.

The last claim of the lemma was proved while proving the first claim. $\square$

Example 3.30

Assume that X is affine or Stein. In that case $\Omega ^i(X_K)$ is an LB-space or a Fréchet space, respectively. The de Rham cohomology $\widetilde{H}^i_{\mathrm {dR} }(X_K)$ is classical; it is a finite dimensional K-vector space with its natural Hausdorff topology or a Fréchet space, respectively.

$\bullet$Assume first thatXis Stein. We claim that (in ${{\mathscr {D}}}(C_K)$)

$$\begin{aligned} F^r(\mathrm {R} \Gamma _{\mathrm {dR} }(X_K) \widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} })&\simeq F^r(\Omega ^{\scriptscriptstyle \bullet }({X_K})\widehat{\otimes }_{K}\mathbf{B}^+_{\mathrm {dR} })\nonumber \\&=({{\mathscr {O}}}({X_K})\widehat{\otimes }_K F^r\mathbf{B}^+_{\mathrm {dR} }\rightarrow \Omega ^1({X_K})\widehat{\otimes }_K F^{r-1}\mathbf{B}^+_{\mathrm {dR} }\rightarrow \cdots )\nonumber \\ \mathrm{DR}(X_{C},r) = (\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)&\widehat{\otimes }^R_K \mathbf{B}^+_{\mathrm {dR} })/F^r \simeq (\Omega ^{\scriptscriptstyle \bullet }({X_K})\widehat{\otimes }_{K}\mathbf{B}^+_{\mathrm {dR} })/F^r\nonumber \\ = \big ({{\mathscr {O}}}({X_K})&\widehat{\otimes }_K \mathbf{B}_r\rightarrow \Omega ^1({X_K})\widehat{\otimes }_K\mathbf{B}_{r-1}\rightarrow \cdots \rightarrow \Omega ^{r-1}({X_K})\widehat{\otimes }_K\mathbf{B}_{1}\big )\,, \end{aligned}$$

(3.31)

where $\mathbf{B}_i=\mathbf{B}_{\mathrm {dR} }^+/F^i$.

In low degrees we have

$$\begin{aligned} \mathrm{DR}(X_{C},0)&=0,\quad \mathrm{DR}(X_{C},1)\simeq {{\mathscr {O}}}({X_K})\widehat{\otimes }_K C,\\ \mathrm{DR}(X_{C},2)&\simeq ({{\mathscr {O}}}({X_K})\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^2)\rightarrow \Omega ^1({X_K})\widehat{\otimes }_K C). \end{aligned}$$

To prove the first strict quasi-isomorphism in (3.31), it suffices to show that the natural map

$$\begin{aligned} \Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }_K\mathbf{B}^+_{\mathrm {dR} } \rightarrow \Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} } \end{aligned}$$

is a strict quasi-isomorphism. Or that so is the map

$$\begin{aligned} \Omega ^i(X_K)\widehat{\otimes }_K\mathbf{B}^+_{\mathrm {dR} } \rightarrow \Omega ^i(X_K)\widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} }, \quad i\ge 0. \end{aligned}$$

(3.32)

But this follows from Lemma 2.3 since both $\Omega ^i(X_K)$ and $\mathbf{B}^+_{\mathrm {dR} }$ are Fréchet spaces.

To prove the second strict quasi-isomorphism above, i.e., the natural strict quasi-isomorphism

$$\begin{aligned} F^r(\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }_K\mathbf{B}^+_{\mathrm {dR} } ){\mathop {\rightarrow }\limits ^{\sim }} \mathrm {hocolim}\, _{i+j\ge r}(F^i\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_KF^j\mathbf{B}^+_{\mathrm {dR} }), \end{aligned}$$

since the inductive limit is, in fact, finite, it suffices to show that the natural map

$$\begin{aligned} F^i\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }_KF^j\mathbf{B}^+_{\mathrm {dR} }\rightarrow F^i\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_KF^j\mathbf{B}^+_{\mathrm {dR} } \end{aligned}$$

is a strict quasi-isomorphism and this follows from the strict quasi-isomorphism (3.32).

Recall that the de Rham complex is built from Fréchet spaces and it has strict differentials. The complex $\mathrm{DR}(X_{C},r)$ is a complex of Fréchet spaces as well. Its differentials are also strict: write the i’th differential as a composition

(3.33)

Since $\Omega ^i(X_K)$ is a Fréchet space and $\mathbf{B}^+_{\mathrm {dR} }/F^{i}$ is a Banach space the first map is surjective and strict (we use here point (3) from Sect. 2.1.3)). The second map is induced from the differential $d_i: \Omega ^i(X_K) \rightarrow \Omega ^{i+1}(X_K)$, which is strict, hence it is strict since everything in sight is Fréchet. It follows that the cohomology $\widetilde{H}^i\mathrm{DR}(X_{C},r)$ is classical and Fréchet as well.

$\bullet$Assume now thatXis affine. Then the computation is a bit more complicated because $\Omega ^i(X_K)$ and $\mathbf{B}^+_{\mathrm {dR} }$ (an LB-space and a Fréchet space, respectively) do not interact well with tensor products. We claim that (in ${{\mathscr {D}}}(C_K)$)

$$\begin{aligned} F^r(\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)\widehat{\otimes }^R_K(\mathbf{B}^+_{\mathrm {dR} }/F^r))&\simeq F^r(\Omega ^{\scriptscriptstyle \bullet }({X_K})\widehat{\otimes }_{K}(\mathbf{B}^+_{\mathrm {dR} }/F^r)) \\&=\big ({{\mathscr {O}}}({X_K})\widehat{\otimes }_K F^r\mathbf{B}_r\rightarrow \Omega ^1({X_K})\widehat{\otimes }_K F^{r-1}\mathbf{B}_r\rightarrow \cdots \big )\\ \mathrm{DR}(X_{C},r) = (\mathrm {R} \Gamma _{\mathrm {dR} }(X_K)&\widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} })/F^r \simeq (\Omega ^{\scriptscriptstyle \bullet }({X_K})\widehat{\otimes }_{K}(\mathbf{B}^+_{\mathrm {dR} }/F^r))/F^r\,,\\ = \big ({{\mathscr {O}}}({X_K})&\widehat{\otimes }_K\mathbf{B}_r\rightarrow \Omega ^1({X_K})\widehat{\otimes }_K\mathbf{B}_{r-1})\rightarrow \cdots \rightarrow \Omega ^{r-1}({X_K})\widehat{\otimes }_K\mathbf{B}_{1}\big )\,, \end{aligned}$$

where $\mathbf{B}_i=\mathbf{B}_{\mathrm {dR} }/F^i$.

The first and the second strict quasi-isomorphisms we can prove just as in the Stein case. We can again invoke Lemma 2.3 here because $F^i\mathbf{B}^+_{\mathrm {dR} }/F^j\mathbf{B}^+_{\mathrm {dR} }$ is a Banach space and $\Omega ^i(X_K)$ can be represented by an inductive limit of an acyclic inductive system of Banach spaces. It remains to prove the third strict quasi-isomorphism, i.e., that the natural map

$$\begin{aligned} (\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} })/F^r \rightarrow (\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_K(\mathbf{B}^+_{\mathrm {dR} }/F^r))/F^r \end{aligned}$$

is a strict quasi-isomorphism. But this easily follows from the distinguished triangle

$$\begin{aligned} \Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_KF^r\mathbf{B}^+_{\mathrm {dR} } \rightarrow F^r(\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_K\mathbf{B}^+_{\mathrm {dR} }) \rightarrow F^r(\Omega ^{\scriptscriptstyle \bullet }(X_K)\widehat{\otimes }^R_K(\mathbf{B}^+_{\mathrm {dR} }/F^r)). \end{aligned}$$

Concerning cohomology, we claim that the cohomology $\widetilde{H}^i\mathrm{DR}(X_{C},r)$ is classical and that it is an LB-space; for $i\ge r$, $\widetilde{H}^i\mathrm{DR}(X_{C},r)=0$. Recall that the de Rham complex is built from LB-spaces and that it has strict differentials. The complex $\mathrm{DR}(X_{C},r)$ is a complex of LB-spaces as well (use Sect. 2.1.3, point (5)). Its differentials are also strict. Indeed, write the i’th differential as a composition (3.33). The first map in this composition is a strict surjection: the surjection $\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1}\rightarrow \mathbf{B}^+_{\mathrm {dR} }/F^{r-i}$ has a continuous K-linear section since both spaces are K-Banach. The second map factors as

$$\begin{aligned} \Omega ^i(X_K) \widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1}) {{\mathop {\longrightarrow }\limits ^{d_i\otimes \mathrm {Id} }}} \mathrm {im}\, d_i\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1})\hookrightarrow \Omega ^{i+1}(X_K) \widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1}). \end{aligned}$$

Here, the first map is strict. Since a composition of a strict map and a strict injection is strict the i’th differential in $\mathrm{DR}(X_{C},r)$ is strict. It follows that the cohomology $\widetilde{H}^i\mathrm{DR}(X_{C},r)$ is classical, as wanted. The claimed vanishing is now clear.

Moreover, we easily compute that we have a strict exact sequence

$$\begin{aligned} 0\rightarrow \Omega ^i(X_C)/\mathrm {im}\, d_{i-1}\rightarrow {H}^i\mathrm{DR}(X_{C},r)\rightarrow H^i_{\mathrm {dR} }(X_K)\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1})\rightarrow 0 \end{aligned}$$

Since $\Omega ^i(X_C)/\mathrm {im}\, d_{i-1}$ is Hausdorff so is ${H}^i\mathrm{DR}(X_{C},r)$. Since, by [25, Th. 1.1.17], a Hausdorff quotient of a Hausdorff LB-space is an LB-space, to show that ${H}^i\mathrm{DR}(X_{C},r)$ is an LB-space it suffices to show that so is $\ker \tilde{d}_i$, for

$$\begin{aligned} \tilde{d}_i: \Omega ^i({X_K})\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i}) \rightarrow \Omega ^{i+1}({X_K})\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1}). \end{aligned}$$

But we easily compute that there is a strict exact sequence

$$\begin{aligned} 0\rightarrow \Omega ^i({X_K})\widehat{\otimes }_K(\mathrm {gr} ^{r-i-1}_F\mathbf{B}^+_{\mathrm {dR} })\rightarrow \ker \tilde{d}_i\rightarrow \ker d_i\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1})\rightarrow 0 \end{aligned}$$

that is, in fact, split because the surjection $\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1}\rightarrow \mathbf{B}^+_{\mathrm {dR} }/F^{r-i}$ has a continuous K-linear section. It follows that, since $\ker d_i$ is a space of compact type (this follows from [25, Prop. 1.1.41] and the fact that $\Omega ^i({X_K})$ is a space of compact type) the space $\ker d_i\widehat{\otimes }_K(\mathbf{B}^+_{\mathrm {dR} }/F^{r-i-1})$ is LB (use Sect. 2.1.3, point (5)) and, finally, so is $\ker \tilde{d}_i$, as wanted.

Let X be affine or Stein. We can conclude from the above that our syntomic cohomology fits into the long exact sequence

where all the terms but the syntomic one were shown to be classical and LB or Fréchet, respectively. We will show later that the syntomic cohomology has these properties as well (see Proposition 3.36).

Example 3.34

Assume that X is affine or Stein and geometrically irreducible. For $r=0$, from the above computations, we obtain the isomorphism

$$\begin{aligned} \widetilde{H}^0_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p){\mathop {\rightarrow }\limits ^{\sim }} (H^0_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{\varphi =p,N=0}\simeq \mathbf{B}_{\mathrm {cr} }^{+,\varphi =1}= {{\mathbf {Q}}}_p. \end{aligned}$$

Hence $\widetilde{H}^0_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p)$ is classical.

For $r=1$, we obtain the following exact sequence

$$\begin{aligned}&H^0 \mathrm{HK}(X_{C},1){{\mathop {\longrightarrow }\limits ^{\iota _{\mathrm {HK} }\otimes \iota }}} {{\mathscr {O}}}(X_K) \widehat{\otimes } _K C \rightarrow \widetilde{H}^1_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(1))\rightarrow (H^1_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{\varphi =p,N=0} \, \rightarrow 0 \end{aligned}$$

Since $H^0_{\mathrm {HK} }(X_0)=F$, we have $H^0 \mathrm{HK}(X_{C},1)=\mathbf{B}^{+,\varphi =p}_{\mathrm {cr} }$ and the map $\iota _{\mathrm {HK} }\otimes \iota$ from $H^0 \mathrm{HK}(X_{C},1)$ to ${{\mathscr {O}}}(X_K) \widehat{\otimes } _K C$ is induced by $\mathbf{B}^+_{\mathrm {cr} }\rightarrow \mathbf{B}_{\mathrm {dR} }^+\rightarrow \mathbf{B}^+_{\mathrm {dR} }/F^1$. Since we have the fundamental sequence

$$\begin{aligned} 0\rightarrow {{\mathbf {Q}}}_p(1) \rightarrow \mathbf{B}^{+,\varphi =p}_{\mathrm {cr} }\rightarrow \mathbf{B}^+_{\mathrm {dR} }/F^1\rightarrow 0 \end{aligned}$$

we get the exact sequence

$$\begin{aligned}&0\rightarrow C\rightarrow {{\mathscr {O}}}(X_C) {\mathop {\longrightarrow }\limits ^{\partial }} \widetilde{H}^1_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(1))\rightarrow (H^1_{\mathrm {HK} }(X_0)\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{\varphi =p,N=0} \rightarrow 0 \end{aligned}$$

Hence $\widetilde{H}^1_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(1))$ is classical.

3.2.3 Fundamental diagram

We will construct the fundamental diagram that syntomic cohomology fits into. We start with an example.

Example 3.35

Fundamental diagram; the case of$r=1$.

Assume that X is affine or Stein and geometrically irreducible. We claim that we have the following commutative diagram with strictly exact rows.

The top row is the strictly exact sequence from the Example 3.2.2. The bottom row is induced by the natural exact sequence defining $H^1_{\mathrm {dR} }(X_K)$. By Sect. 2.1.3, it is isomorphic to the sequence

$$\begin{aligned} 0\rightarrow {{\mathscr {O}}}(X_C)/C {\mathop {\rightarrow }\limits ^{d}} \Omega ^1(X_C)^{d=0} \rightarrow H^1_{\mathrm {dR} }(X_C)\rightarrow 0. \end{aligned}$$

Hence it is strictly exact by Lemma 3.4. The map $\iota _{\mathrm {HK} }\otimes \theta$ is induced by the composition

The map $\beta$ is induced by the composition

(The fact that the first map lands in $F^1$ is immediate from the definition of $\mathrm {R} \Gamma _{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(1))$.) Clearly they make the right square in the above diagram commute. To see that the left square commutes as well it is best to consider the following diagram of maps of distinguished triangles

The map $\tilde{\beta }$ is the map on mapping fibers induced by the commutative bottom left square. We have $\beta =\theta \tilde{\beta }$. It remains to check that the induced map ${{\mathscr {O}}}(X_K)\widehat{\otimes }_K C\rightarrow \Omega ^1(X_K)\widehat{\otimes }_KC$ from the right column of the above diagram is equal to d, but this is easy.

And here is the general case.

Proposition 3.36

Let X be an affine or a Stein weak formal scheme. Let $r\ge 0$. There is a natural map of strictly exact sequences

Moreover, $\ker (\iota _{\mathrm {HK} }\otimes \theta )\simeq (H^r_{\mathrm {HK} }(X_{0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}$, $H^r_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r))$ is LB or Fréchet, respectively, and the maps $\beta$, $\iota _{\mathrm {HK} }\otimes \theta$ are strict and have closed images.

Proof

To deal easier with topological issues, we start with changing the period ring in the proposition from $\mathbf{B}^+_{\mathrm {st} }$ to $\widehat{\mathbf{B}}^+_{\mathrm {st} }$. That is, we will show that the natural map $\iota _{\mathrm {st} }: {\mathbf{B}}^+_{\mathrm {st} }\rightarrow \widehat{\mathbf{B}}^+_{\mathrm {st} }$ induces a commutative diagram (in $C_{ {{\mathbf {Q}}}_p}$)

(3.37)

The commutativity is clear since the composition $\mathbf{B}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\iota _{\mathrm {st} }}} \widehat{\mathbf{B}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\iota }} \mathbf{B}^+_{\mathrm {dR} }$ is just the original map $\iota : {\mathbf{B}}^+_{\mathrm {st} }\rightarrow \mathbf{B}^+_{\mathrm {dR} }$. To see that $1\otimes \iota _{\mathrm {st} }$ is a strict isomorphism it suffices to look at the diagram

where $\widehat{\beta }$ is the trivialization from (3.22). The map $\widehat{\beta }$ is well-defined because N is nilpotent on $H^r_{\mathrm {HK} }(X_0)$ and factorizes through the map $\iota _{\mathrm {st} }$ yielding the map $\beta$ and making the above diagram commute. The map $\widehat{\beta }$ is a strict isomorphism. It follows that both $\beta$ and $\iota _{\mathrm {st} }$ are algebraic isomorphisms and this easily implies that $\iota _{\mathrm {st} }$ is a strict isomorphism, as wanted.$\square$

We will now prove our proposition with $\mathbf{B}^+_{\mathrm {st} }$ replaced by $\widehat{\mathbf{B}}^+_{\mathrm {st} }$. The following map of exact sequences (where $\Omega ^i$, $H^i_{\mathrm{dR}}$ and $H^i_{\mathrm{HK}}$ stand for $\Omega ^i(X_C)$, $H^i_{\mathrm{dR}}(X_K)$ and $H^i_{\mathrm{HK}}(X_0)$, respectively) is constructed in an analogous way to the case of $r=1$ treated in the above example

(3.38)

To prove the first claim of the proposition it suffices to show that the map $\iota _{\mathrm {HK} }\otimes \theta$ in degree $r-1$ is surjective. For that we will need the following lemma.

Lemma 3.39

Let M be an effective²³ finite $(\varphi ,N)$-module over F. The sequence

$$\begin{aligned} 0\rightarrow (M\otimes _F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{\varphi =p^j,N=0}{\mathop {\rightarrow }\limits ^{t}}(M\otimes _F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{\varphi =p^{j+1},N=0}{\mathop {\longrightarrow }\limits ^{1\otimes \theta }}M\otimes _FC \end{aligned}$$

is exact. Moreover, the right arrow is a surjection if the slopes of Frobenius are $\le j$.

Proof

Using the trivialization (3.22) and the fact that $\theta (u)=0$, we get the following commutative diagram

Hence it suffices to prove the analog of our lemma for the bottom sequence.

First we will show that the following sequence

$$\begin{aligned} 0\rightarrow (M\otimes _F\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^j}{\mathop {\rightarrow }\limits ^{t}}(M\otimes _F\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^{j+1}}{\mathop {\longrightarrow }\limits ^{1\otimes \theta }}M\otimes _FC \end{aligned}$$

(3.40)

is exact. Multiplication by t is clearly injective. To show exactness in the middle it suffices to show that

$$\begin{aligned} (M\otimes _FF^1\mathbf{B}^+_{ \mathrm {cr} })^{\varphi =p^{j+1}}=(M\otimes _Ft\mathbf{B}^+_{ \mathrm {cr} })^{\varphi =p^{j+1}}, \end{aligned}$$

where $F^1\mathbf{B}^+_{ \mathrm {cr} }:=\mathbf{B}^+_{\mathrm {cr} }\cap F^1\mathbf{B}^+_{\mathrm {dR} }.$ Or that $(F^1\mathbf{B}^+_{ \mathrm {cr} })^{\varphi =p^{j+1-\alpha }}=(t\mathbf{B}^+_{ \mathrm {cr} })^{\varphi =p^{j+1-\alpha }}.$ But this follows from the fact that

$$\begin{aligned} (F^1\mathbf{B}^+_{ \mathrm {cr} })^{\varphi =p^{j+1-\alpha }}\subset \{x\in \mathbf{B}^+_{\mathrm {cr} }|\theta (\varphi ^k(x))=0, \forall k\ge 0\}=t\mathbf{B}^+_{\mathrm {cr} }. \end{aligned}$$

It remains to show that if the Frobenius slopes of M are $\le j$ then the last arrow in the sequence (3.40) is a surjection. To see this, we note that all the terms in the sequence are C-points of finite dimensional BC spaces²⁴ and the maps can be lifted to maps of such spaces. It follows that the cokernel of multiplication by t is a finite dimensional BC space. We compute its Dimension [20, 5.2.2]:

$$\begin{aligned} \mathrm {Dim} (M\otimes _F&\mathbf{B}^+_{\mathrm {cr} }) ^{\varphi =p^{j+1}}- \mathrm {Dim} (M\otimes _F\mathbf{B}^+_{\mathrm {cr} })^{\varphi =p^{j}}\\&=\sum _{r_i\le j+1}(j+1-r_i,1)-\sum _{r_i\le j}(j-r_i,1)\\&=\ ((j+1)\dim _F M-t_N(M),\dim _F M)\\ {}&\quad -\,(j\dim _F M-t_N(M),\dim _F M)\\&= \ (\dim _F M,0). \end{aligned}$$

Here $r_i$’s are the slopes of Frobenius repeated with multiplicity, $t_N(M)=v_p(\det \varphi )$, and the second equality follows from the fact that the slopes of Frobenius are $\le j$. Since this Dimension is the same as the Dimension of the BC space corresponding to $M\otimes _FC$, we get the surjection we wanted.

Let us come back to the proof of Proposition 3.36.

$\bullet$Assume first thatXis quasi-compact. By the above lemma, to prove that the map $\iota _{\mathrm {HK} }\otimes \theta$ is surjective in degree $r-1$ and that its kernel in degree r is isomorphic to $(H^r_{\mathrm {HK} }(X_{0})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{\varphi =p^{r-1},N=0}$ it suffices to show that the slopes of Frobenius on $H^i_{\mathrm{HK}}(X_0)$ are  $\le i$. For that we use the weight spectral sequence (3.3) to reduce to showing that, for a smooth scheme Y over k, the slopes of Frobenius on the (classical) rigid cohomology $H^j_{\mathrm {rig} }(Y/F)$ are $\le j$. But this is well-known [13, Th. 3.1.2].

We have shown that syntomic cohomology fits into an exact sequence

Hence, since it is an extension of two classical objects, it is classical. Since $H^r_{\mathrm {dR} }(X_K)$ is a finite dimensional vector space over K the surjective map $\pi$ in the diagram (3.38) has a section. Since the syntomic cohomology is the equalizer of the maps $\iota _{\mathrm {HK} }\otimes \theta$ and $\pi$ this section lifts to a section of the surjection $\pi _1$ above. Hence ${H}^r_{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r))$ is an LB-space. Since the map $\iota _{\mathrm {HK} }\otimes \theta$ lifts to a map of finite Dimensional BC spaces it is strict and has a closed image. It follows that so does the pullback map $\beta$.

$\bullet$Assume now thatXis Stein with a Stein covering$\{U_i\},i\in {{\mathbf {N}}}.$ Since the map $\iota _{\mathrm {HK} }\otimes \theta$ is the projective limit of the maps

$$\begin{aligned} (\iota _{\mathrm {HK} }\otimes \theta )_i: (H^{*}_{\mathrm {HK} }(U_{i})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0,\varphi =p^r}\rightarrow H^{*}_{\mathrm {dR} }(]U_i[_X)\widehat{\otimes }_KC \end{aligned}$$

the computation above yields the statement on the kernel in degree r. For the surjectivity in degree $r-1$, we use the vanishing, shown in the proof of Lemma 3.28, of $H^1\mathrm {holim}\, _i(H^r_{\mathrm {HK} }(U_{i})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}.$

Since the maps $(\iota _{\mathrm {HK} }\otimes \theta )_i$ are strict and have closed images and we have vanishing of $H^1\mathrm {holim}\, _i(H^r_{\mathrm {HK} }(U_{i})\widehat{\otimes }_F\widehat{\mathbf{B}}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}$, it follows that the projective limit map $\iota _{\mathrm {HK} }\otimes \theta$ inherits these properties and then so does the pullback map $\beta$. Finally, since the syntomic cohomology is the equalizer of the maps $\iota _{\mathrm {HK} }\otimes \theta$ and $\pi$ of Fréchet spaces it is Fréchet. $\square$

Remark 3.41

Assume that X is affine. The image of the map $\iota _{\mathrm {HK} }\otimes \theta$ in degree r in the fundamental diagram is the C-points of a finite dimensional BC space that is the cokernel of the map:

$$\begin{aligned} (H^r_{\mathrm {HK} }(X_{0})\otimes _F{{\mathbb {B}}}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}{\mathop {\rightarrow }\limits ^{t}} (H^r_{\mathrm {HK} }(X_{0})\otimes _F{{\mathbb {B}}}^+_{\mathrm {st} })^{N=0,\varphi =p^{r}}. \end{aligned}$$

Its Dimension is equal to

$$\begin{aligned} \sum _{r_i\le r}(r-r_i,1)-\sum _{r_i\le r-1}(r-1-r_i,1)=\sum _{r_i \le r-1}(1,0)+\sum _{r-1 < r_i \le r}(r-r_i,1). \end{aligned}$$

3.3 Crystalline syntomic cohomology

The classical crystalline syntomic cohomology of Fontaine–Messing and the related period map to étale cohomology generalize easily to formal schemes. We define them and then modify this syntomic cohomology in the spirit of Bloch–Kato to make it more computable.

3.3.1 Definition a la Fontaine–Messing

Let X be a semistable p-adic formal scheme over ${{\mathscr {O}}}_K$. This means that, locally for the Zariski topology, $X=\mathrm {Spf} (R)$, where R is the p-adic completion of an algebra étale over ${{\mathscr {O}}}_K\{T_1,\dots ,T_n\}/(T_{1}\cdots T_{m}-\varpi ).$ That is, we do not allow self-intersections. We equip X with the log-structure induced by the special fiber.

Set $\overline{X}:=X_{{{\mathscr {O}}}_C}$. For $r\ge 0$, we have the geometric syntomic cohomology of Fontaine–Messing [26]

$$\begin{aligned} \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} /p^n(r))&:= [F^r\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X}_{n}){\mathop {\longrightarrow }\limits ^{\varphi -p^r}}\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X}_n)]\,, \quad \\ F^r\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X}_n)&:=\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X}_n,{{\mathscr {J}}}^{[r]})\\ \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))&:=\mathrm {holim}\, _n\mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} /p^n(r)). \end{aligned}$$

Crystalline cohomology used here is the absolute one, i.e., over ${{\mathscr {O}}}_{F,n}$ and ${{\mathscr {J}}}^{[r]}$ is the r’th level of the crystalline Hodge filtration sheaf. We have

$$\begin{aligned} \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}&=[F^r\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}{\mathop {\longrightarrow }\limits ^{\varphi -p^r}} \mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}]\nonumber \\&=[\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}^{\varphi =p^r}\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}/F^r] \end{aligned}$$

(3.42)

and similarly with ${{\mathbf {Z}}} _p$ and ${{\mathbf {Z}}} /p^n$ coefficients.

The above geometric syntomic cohomology is related, via period morphisms, to the étale cohomology of the rigid space $X_C$ (see below) and hence allows to describe the latter using differential forms. To achieve the same for pro-étale cohomology, we need to modify the definition of syntomic cohomology a bit. Consider the complexes of sheaves on X associated to the presheaves (U is an affine Zariski open in X and $\overline{U}:=U_{{{\mathscr {O}}}_C}$)

$$\begin{aligned} {{\mathscr {A}}}_{\mathrm {cr} }&:= (U\mapsto (\mathrm {holim}\, _n\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{U}_n))_{ {{\mathbf {Q}}}_p}),\\ F^r{{\mathscr {A}}}_{\mathrm {cr} }&:=(U\mapsto (\mathrm {holim}\, _nF^rR\Gamma _{\mathrm {cr} }(\overline{U}_n))_{ {{\mathbf {Q}}}_p}),\\ {{\mathscr {S}}}(r)&:=(U\mapsto \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{U}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}). \end{aligned}$$

We have

$$\begin{aligned} {{\mathscr {S}}}(r)=[ F^r{{\mathscr {A}}}_{\mathrm {cr} }{\mathop {\longrightarrow }\limits ^{\varphi -p^r}} {{\mathscr {A}}}_{\mathrm {cr} }]=[ {{\mathscr {A}}}_{\mathrm {cr} }^{\varphi =p^r}\rightarrow {{\mathscr {A}}}_{\mathrm {cr} }/F^r]. \end{aligned}$$

We define

Hence

(3.43)

There is a natural map

$$\begin{aligned} \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}\rightarrow \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

(3.44)

It is a quasi-isomorphism in the case X is of finite type but not in general (since in the case of ${{\mathbf {Z}}} _p(r)$ we do all computations on U’s as above integrally and invert p at the very end and in the case of ${{\mathbf {Q}}}_p(r)$ we invert p already on each U).

By proceeding just as in the case of overconvergent syntomic cohomology (and using crystalline embedding systems instead of dagger ones) we can equip both complexes in (3.44) with a natural topology for which they become complexes of Banach spaces over ${{\mathbf {Q}}}_p$ in the case X is quasi-compact.²⁵ We used here the simple fact that an exact sequence of Fréchet spaces is strictly exact.

The defining mapping fibers (3.42) and (3.44) are taken in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$. Moreover, the change of topology map in (3.44) is continuous (and a strict quasi-isomorphism if X is of finite type).

3.3.2 Period map

We are interested in syntomic cohomology a la Fontaine–Messing because of the following comparison [20, 79].

Proposition 3.45

Let X be a semistable finite type formal scheme over ${{\mathscr {O}}}_K$. The Fontaine–Messing period map²⁶ [26]

$$\begin{aligned} \alpha _{\mathrm{FM}}: \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Q}}}_p(r))\rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

is a quasi-isomorphism after truncation $\tau _{\le r}$.

We equip the pro-étale and étale cohomologies $\mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))$, and $\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))$ with a natural topology by proceeding as in the case of overconvergent rigid cohomology by using as local data compatible complexes of free ${{\mathbf {Z}}} /p^n$-modules .²⁷ If X is quasi-compact, we obtain in this way complexes of Banach spaces over ${{\mathbf {Q}}}_p$.

Corollary 3.46

Let X be a semistable formal scheme over ${{\mathscr {O}}}_K$. There is a natural Fontaine–Messing period map

$$\begin{aligned} \alpha _{\mathrm{FM}}: \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Q}}}_p(r))\rightarrow \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

(3.47)

that is a strict quasi-isomorphism after truncation $\tau _{\le r}$.

Proof

Cover X with quasi-compact formal schemes and invoke Proposition 3.45; we obtain a quasi-isomorphism

$$\begin{aligned} \alpha _{\mathrm{FM}}:\tau _{\le r} \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Q}}}_p(r))\rightarrow \tau _{\le r}\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

To see that it is strict, it suffices to note that, locally, the period map is a zigzag between complexes of Banach spaces and invoke Lemma 2.1.

It remains to show that, for a quasi-compact X, the natural map

$$\begin{aligned} \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))\rightarrow \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

is a (strict) quasi-isomorphism. From [74, Cor. 3.17] we know that this is true with ${{\mathbf {Z}}} /p^n$-coefficients. This implies that we have a sequence of quasi-isomorphisms

$$\begin{aligned} \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} _p(r))&=\mathrm {holim}\, _n\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} /p^n(r)) \simeq \mathrm {holim}\, _n\mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} /p^n(r)) \\&\simeq \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C},\mathrm {holim}\, _n {{\mathbf {Z}}} /p^n(r))\\&\simeq \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C},\varprojlim _n {{\mathbf {Z}}} /p^n(r))=\mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} _p(r)), \end{aligned}$$

where the third quasi-isomorphism follows from the fact that $\mathrm {R} \Gamma$ and $\mathrm {holim}\,$ commute and the fourth one follows from [74, Prop. 8.2].

It remains to show that

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_C, {{\mathbf {Z}}} _p(r))\otimes {{\mathbf {Q}}}_p{\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_C, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

But, since $|X_C|$ is quasi-compact, the site $X_{C,\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}$ is coherent [74, Prop. 3.12]. Hence its cohomology commutes with colimits of abelian sheaves, yielding the above quasi-isomorphism. $\square$

3.3.3 Definition a la Bloch–Kato

Crystalline geometric syntomic cohomology a la Fontaine–Messing can be often described in a very simple way using filtered de Rham complexes and Hyodo–Kato cohomology (if the latter can be defined) and the period rings $\mathbf{B}^+_{\mathrm {st} },\mathbf{B}^+_{\mathrm {dR} }$.This was done for proper algebraic and analytic varieties in [20, 59]. In this section we adapt the arguments from loc. cit. to the case of some non-quasi-compact rigid varieties. The de Rham term is the same, the Hyodo–Kato term is more complicated, and the role of the period ring $\mathbf{B}^+_{\mathrm {st} }$ is played by $\widehat{\mathbf{B}}^+_{\mathrm {st} }$.

Let $r\ge 0$. For a semistable formal scheme X over ${{\mathscr {O}}}_K$, we define the crystalline geometric syntomic cohomology a la Bloch–Kato (as an object in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$)

Here $\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p)$ is defined in an analogous way to $\mathrm {R} \Gamma _{\mathrm {cr} }(X, {{\mathbf {Q}}}_p)$ (hence it is rational; the corresponding integral cohomology we will denote simply by $\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi })$). The completed tensor product $\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p) \widehat{\otimes }^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}\widehat{\mathbf{B}}^+_{\mathrm {st} }$ is defined in the following way (note that $r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}$ is not a field hence we can not use the tensor product in the category of convex vector spaces): if X is of finite type, we set

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p) \widehat{\otimes }^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}\widehat{\mathbf{B}}^+_{\mathrm {st} }:=(\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }) \widehat{\otimes }_{r^{\mathrm{PD}}_{\varpi }}\widehat{\mathbf{A}}^+_{\mathrm {st} }){\otimes }^L{ {{\mathbf {Q}}}_p}, \end{aligned}$$

where the integral objects are in the category $D(\mathrm {Ind}(PD_{ {{\mathbf {Q}}}_p}))$; for a general X, we lift the above definition from formal schemes of finite type via the étale cohomological descent.

Proposition 3.48

There exists a functorial quasi-isomorphism in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$

$$\begin{aligned} \iota _{\mathrm{BK}}:\mathrm {R} \Gamma ^{\mathrm{BK}}_{ \mathrm {syn} }({X}_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p(r)) {\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{ \mathrm {syn} }(X_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

Proof

The comparison map $\iota _{\mathrm{BK}}$ will be induced by a pair of maps $(\iota ^1_{\mathrm{BK}},\iota ^2_{\mathrm{BK}})$, basically Künneth cup product maps, that make the following diagram commute (in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$).

• (i) Construction of the map$\iota ^1_{\mathrm{BK}}$. We may argue locally and assume that X is quasi-compact. Consider the following maps in ${{\mathscr {D}}}(C_F)$

  $$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p){\widehat{\otimes }}^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{\cup }}\mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{C}}/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p)\leftarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p). \end{aligned}$$

  (3.49)

  We claim that the cup product map is a quasi-isomorphism: indeed, the proof of an analogous result in the case of schemes [79, Prop. 4.5.4] goes through in our setting. Recall the key points. By (3.15) and the fact that $\mathbf{A}_{\mathrm {st} ,n}$ is flat over $r^{\mathrm{PD}}_{\varpi ,n}$, it suffices to prove that the Künneth morphism

  $$\begin{aligned} \cup : \quad \mathrm {R} \Gamma _{\mathrm {cr} }(X_n/r^{\mathrm{PD}}_{\varpi ,n})\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}\mathrm {R} \Gamma _{\mathrm {cr} }({{\mathscr {O}}}^{\times }_{\overline{K} ,n}/r^{\mathrm{PD}}_{\varpi ,n}) \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{\overline{K} },n}/r^{\mathrm{PD}}_{\varpi ,n})\nonumber \\ \end{aligned}$$

  (3.50)

  is a quasi-isomorphism. By unwinding both sides one finds a Künneth morphism for certain de Rham complexes. It is a quasi-isomorphism because these complexes are “flat enough” which follows from the fact that the map $X_{{{\mathscr {O}}}_{\overline{K} ,n}}\rightarrow {{\mathscr {O}}}_{K,n}^{\times }$ is log-syntomic. This finishes the argument. Both maps in (3.49) are compatible with the monodromy operator N. Moreover, we have the distinguished triangle [47, Lemma 4.2]

  $$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{\overline{K} ,n}}/{{\mathscr {O}}}_{F,n})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{\overline{K} ,n}}/r^{\mathrm{PD}}_{\varpi ,n}){\mathop {\rightarrow }\limits ^{N}} \mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{\overline{K} ,n}}/r^{\mathrm{PD}}_{\varpi ,n}).\nonumber \\ \end{aligned}$$

  (3.51)

  It follows that the last map in (3.49) is a quasi-isomorphism after taking the (derived) $N=0$ part. Hence applying $N=0$ to the terms in (3.49) we obtain a functorial quasi-isomorphism in ${{\mathscr {D}}}(C_F)$ (for strictness, note that, rationally, we worked only with complexes of Banach spaces)

  $$\begin{aligned} \iota _{\mathrm{BK}}^1: [\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p) \widehat{\otimes }^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}\widehat{\mathbf{B}}^+_{\mathrm {st} }]^{N=0} {\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {cr} }(X_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p). \end{aligned}$$

  (3.52)

• (ii) Construction of the map$\iota ^2_{\mathrm{BK}}$. We may argue locally and assume that X is quasi-compact. Consider the maps

  

  (3.53)

  The cup product map is a Künneth map and it is a quasi-isomorphism for the same reason as the map (3.50). The second map—the change of base map from ${{\mathscr {O}}}_F$ to ${{\mathscr {O}}}_K^{\times }$—is a quasi-isomorphism (up to a universal constant) by [59, Cor. 2.4]. Rationally, the above maps induce a map

  $$\begin{aligned} \iota _{\mathrm{BK}}^2: (\mathrm {R} \Gamma _{\mathrm {dR} }({X}_K)\widehat{\otimes }^R_{K}{\mathbf{B}}^+_{\mathrm {dR} })/F^r {\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {cr} }({X}_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p)/F^r. \end{aligned}$$

  Since ${\mathbf{B}}^+_{\mathrm {dR} }$ is a Fréchet space, the natural map

  $$\begin{aligned} (\mathrm {R} \Gamma _{\mathrm {dR} }({X}_K)\widehat{\otimes }_{K}{\mathbf{B}}^+_{\mathrm {dR} })/F^r\rightarrow (\mathrm {R} \Gamma _{\mathrm {dR} }({X}_K)\widehat{\otimes }^R_{K}{\mathbf{B}}^+_{\mathrm {dR} })/F^r \end{aligned}$$

  is a strict quasi-isomorphism, hence so is the map $\iota _{\mathrm{BK}}^2$.

Compatibility of the maps $\iota _{\mathrm{BK}}^1,\iota _{\mathrm{BK}}^2$ can be inferred from the natural commutative diagram

$\square$

4 Comparison of syntomic cohomologies

We have defined two geometric syntomic cohomologies: the crystalline one and the overconvergent one. We will show now (Theorem 4.1) that they are naturally isomorphic for Stein spaces and that, as a result, the p-adic pro-étale cohomology fits into a fundamental diagram (Theorem 4.12). We use this result to describe the pro-étale cohomology of affine spaces, tori, and curves (see Sect. 4.3).

4.1 Comparison morphism

Let X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. Let $\widehat{X}$ be the associated formal scheme. The purpose of this section is to prove that the change of convergence map from overconvergent syntomic cohomology to crystalline syntomic cohomology is a strict quasi-isomorphism assuming that X is Stein.

Theorem 4.1

Let $r\ge 0$. There is a functorial map in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$

$$\begin{aligned} \iota _{\mathrm {rig} }: \mathrm {R} \Gamma _{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r))\rightarrow \mathrm {R} \Gamma ^{\mathrm{BK}}_{ \mathrm {syn} }(\widehat{X}_{{{\mathscr {O}}}_{C}}, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

It is a quasi-isomorphism if X is Stein.

Proof

We will induce the comparison map $\iota _{\mathrm {rig} }$ in our theorem by a pair of maps $(\iota ^1_{\mathrm {rig} },\iota ^2_{\mathrm {rig} })$ defined below that make the following diagram commute (in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$)

The map $\iota ^1_{\mathrm {rig} }$ is compatible with monodromy. Both maps $\iota ^1_{\mathrm {rig} },\iota ^2_{\mathrm {rig} }$ are quasi-isomorphisms if X is Stein.$\square$

(i) Definition of maps$\iota ^1_{\mathrm {rig} }$and$\iota _{\mathrm {rig} }^2$.

$(\star )$Map$\iota _{\mathrm {rig} }^2.$ The map $\iota _{\mathrm {rig} }^2$, the easier of the two maps, is just the map from de Rham cohomology of a weak formal scheme to de Rham cohomology of its completion; in the case X is Stein, it is an isomorphism induced by the canonical identification of coherent cohomology of a partially proper dagger space and its rigid analytic avatar [29, Th. 2.26].

$(\star )$Map$\iota _{\mathrm {rig} }^1.$ To define the map $\iota _{\mathrm {rig} }^1$, consider first the change of convergence map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0){\widehat{\otimes }}^R_{F}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F){\widehat{\otimes }}^R_{F}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }. \end{aligned}$$

(4.2)

It is compatible with Frobenius and monodromy. We claim that if X is Stein it is a strict quasi-isomorphism. It suffices to show this for the change of topology map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

(4.3)

But before we proceed to do that, a small digression about convergent cohomology that we will use.

Remark 4.4

(Review of convergent cohomology).

Contrary to the case of rigid cohomology, the theory of (relative) convergent cohomology is well developed [60, 75, 76]. Recall the key points. The set up is the following: the base ${{\mathscr {B}}}$ is a p-adic formal log-scheme over ${{\mathscr {O}}}_F$, $B:={{\mathscr {B}}}_1$; we look at convergent cohomology of X over ${{\mathscr {Y}}}$, where X is a log-scheme over B and ${{\mathscr {Y}}}$ is a p-adic formal log-scheme over ${{\mathscr {B}}}$.

• 1. There exist a convergent site defined in analogy with the crystalline site, where the role of PD-thickenings (analytically, objects akin to closed discs of a specific radius $<1$) is played by enlargements (p-adic formal schemes; analytically, closed discs of any radius $<1$). Convergent cohomology is defined as the cohomology of the rational structure sheaf on this site.

• 2. Invariance under infinitesimal thickenings. If $i:X\rightarrow X^{\prime }$ is a homeomorphic exact closed immersion then the pullback functor $i^*$ induces a quasi-isomorphism on convergent cohomology [60, 0.6.1], [76, Prop. 3.1].

• 3. Poincaré Lemma. It states that, locally, convergent cohomology can be computed by de Rham complexes of convergent tubes in p-adic formal log-schemes log-smooth over the base (playing the role of PD-envelopes) [76, Th. 2.29]. Analytically, this means that the fixed closed discs used in the crystalline theory are replaced by open discs.

• 4. There is a natural map from convergent cohomology to crystalline cohomology. It is a quasi-isomorphism for log-schemes log-smooth over ${{\mathscr {Y}}}_1$ [76, Th. 2.36]. In particular,²⁸ for a semistable scheme $X_0$ over $k^0$, there is a natural quasi-isomorphism

  $$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {conv} }(X_0/{{\mathscr {O}}}_F^0){\mathop {\rightarrow }\limits ^{\sim }} \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

Proposition 4.5

([32, Th. 5.3]) Let X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. Assume that all irreducible components of $X_0$ are proper. Then the natural morphism (induced by mapping weak formal log-schemes to their completions)

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {conv} }(X_0/{{\mathscr {O}}}_F^0) \end{aligned}$$

is a quasi-isomorphism.

Proof

Recall that we have two compatible weight spectral sequences [32, 5.2, 5.3]

$$\begin{aligned} E^{-k,i+k}_1&=\bigoplus _{j\ge 0, j\ge -k}\bigoplus _{S\in \Theta _{2j+k+1}}H^{i-2j-k}_{\mathrm {rig} }(S/{{\mathscr {O}}}_F)\Rightarrow H^i_{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0),\\ E^{-k,i+k}_1&=\bigoplus _{j\ge 0, j\ge -k}\bigoplus _{S\in \Theta _{2j+k+1}}H^{i-2j-k}_{\mathrm {conv} }(S/{{\mathscr {O}}}_F)\Rightarrow H^i_{\mathrm {conv} }(X_0/{{\mathscr {O}}}_F^0) \end{aligned}$$

Here $\Theta _j$ denotes the set of all intersections S of j different irreducible components of X that are equipped with trivial log-structures. By assumptions, they are smooth and proper over k. It suffices then to prove that the maps $H^*_{\mathrm {rig} }(S/{{\mathscr {O}}}_F)\rightarrow H^*_{\mathrm {conv} }(S/{{\mathscr {O}}}_F)$ are isomorphisms. Since S is proper this is classical [2, Prop. 1.9]. $\square$

Hence, $\mathrm {R} \Gamma _{\mathrm {conv} }(X_0/{{\mathscr {O}}}_F^0)$ is a convergent version of $\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)$, i.e., a version where we use p-adic formal schemes and rigid spaces instead of weak formal schemes and dagger spaces.

Now, coming back to the change of topology map (4.3), note that it factors as

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {conv} }(X_0/{{\mathscr {O}}}_F^0){\mathop {\rightarrow }\limits ^{\sim }} \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

(4.6)

We topologized the convergent cohomology in the same way we did rigid cohomology. The second map is quasi-isomorphism because $X_0$ is semistable (hence, locally, admitting liftings). By Proposition 4.5, the first map is a quasi-isomorphism as well. We claim that the composition (4.6) is a strict quasi-isomorphism. We will reduce checking this to $X_0$ proper where it will be clear. Take the subschemes $\{U_i\}, \{Y_i\}, i\in {{\mathbf {N}}},$ of $X_0$ as in Sect. 3.1.1. We have strict quasi-isomorphisms

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0){\mathop {\rightarrow }\limits ^{\sim }}\mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {rig} }(U_i/{{\mathscr {O}}}_F^0){\mathop {\rightarrow }\limits ^{\sim }} \mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {rig} }(Y_i/{{\mathscr {O}}}_F^0). \end{aligned}$$

The first one by Example 3.16, the second one trivially. We have similar strict quasi-isomorphisms for the crystalline cohomology

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F){\mathop {\rightarrow }\limits ^{\sim }}\mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {cr} }(U_i/{{\mathscr {O}}}_F^0,F){\mathop {\rightarrow }\limits ^{\sim }} \mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {cr} }(Y_i/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

The second one is again trivial. The first one follows from the fact that it is a quasi-isomorphism of complexes of Fréchet spaces. It remains to show that the natural map

$$\begin{aligned} \mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {rig} }(Y_i/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {holim}\, _i\mathrm {R} \Gamma _{\mathrm {cr} }(Y_i/{{\mathscr {O}}}_F^0) \end{aligned}$$

is a strict quasi-isomorphism. Or that, so is the natural map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(Y_i/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_i/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

We factor this map as

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {rig} }(Y_i/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {conv} }(Y_i/{{\mathscr {O}}}_F^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_i/{{\mathscr {O}}}_F^0,F). \end{aligned}$$

Since the idealized log-scheme $Y_i$ is ideally log-smooth over $k^0$ the second map is a quasi-isomorphism. Since $Y_i$ is also proper, so is the first map. This finishes the proof that the map (4.3) is a strict quasi-isomorphism.

We will define now the following functorial quasi-isomorphism in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$

$$\begin{aligned} h_{\mathrm {cr} }: [\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p) {\widehat{\otimes }}^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }]^{\varphi =p^r}{\rightarrow }[\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F){\widehat{\otimes }}^R_{F}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }]^{\varphi =p^r}. \end{aligned}$$

(4.7)

We may assume that X is quasi-compact. Let J be the kernel of the map $p_0: r^{\mathrm{PD}}_{\varpi }\rightarrow {{\mathscr {O}}}_F$, $T\mapsto 0$. The map $p_0$ is compatible with Frobenius and monodromy (“$\log T\mapsto \log 0$”). Consider the exact sequence

$$\begin{aligned} 0\rightarrow J_n\rightarrow r^{\mathrm{PD}}_{\varpi , n}{\mathop {\rightarrow }\limits ^{p_0}} {{\mathscr {O}}}_{F,n}\rightarrow 0. \end{aligned}$$

Tensoring it with $\widehat{\mathbf{A}}_{\mathrm {st} ,n}$, we get the following exact sequence

$$\begin{aligned} 0\rightarrow J_n\otimes _{r^{\mathrm{PD}}_{\varpi ,n}}\widehat{\mathbf{A}}_{\mathrm {st} ,n}\rightarrow \widehat{\mathbf{A}}_{\mathrm {st} , n}{\mathop {\rightarrow }\limits ^{p_0}} {{\mathscr {O}}}_{F,n}\otimes _{r^{\mathrm{PD}}_{\varpi ,n}}\widehat{\mathbf{A}}_{\mathrm {st} ,n}\rightarrow 0 \end{aligned}$$

We used here the fact that $\widehat{\mathbf{A}}_{\mathrm {st} ,n}$ is flat over $r^{\mathrm{PD}}_{\varpi ,n}$. Going to limit with n, we get the exact sequence

$$\begin{aligned} 0\rightarrow J\widehat{\otimes }_{r^{\mathrm{PD}}_{\varpi }}\widehat{\mathbf{A}}_{\mathrm {st} }\rightarrow \widehat{\mathbf{A}}_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{p_0}} {{\mathscr {O}}}_{F}\widehat{\otimes }_{r^{\mathrm{PD}}_{\varpi }}\widehat{\mathbf{A}}_{\mathrm {st} }\rightarrow 0 \end{aligned}$$

(4.8)

Set $E:=J\widehat{\otimes }_{r^{\mathrm{PD}}_{\varpi }}\widehat{\mathbf{A}}_{\mathrm {st} }$.

Tensoring the last sequence with $\mathrm {R} \Gamma _{\mathrm {cr} }(X_n/r^{\mathrm{PD}}_{\varpi ,n})$ and $\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_{F,n})$, respectively, we obtain the following distinguished triangles

The last terms in these triangles are quasi-isomorphic. Indeed, by direct local computations we see that the natural map

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(X_n/r^{\mathrm{PD}}_{\varpi ,n})\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}{{\mathscr {O}}}_{F,n}\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_{F,n}) \end{aligned}$$

is a quasi-isomorphism. Hence

$$\begin{aligned} {{\mathscr {O}}}_{F,n}{\otimes }_{r^{\mathrm{PD}}_{\varpi ,n}}\widehat{\mathbf{A}}_{\mathrm {st} ,n}\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}\mathrm {R} \Gamma _{\mathrm {cr} }(X_n/r^{\mathrm{PD}}_{\varpi ,n})&\simeq \widehat{\mathbf{A}}_{\mathrm {st} ,n}\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_{F,n})\\&\simeq \widehat{\mathbf{A}}_{\mathrm {st} ,n}\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}{{\mathscr {O}}}_{F,n}\otimes ^L_{{{\mathscr {O}}}_{F,n}}\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_{F,n}). \end{aligned}$$

The complexes

$$\begin{aligned} {[} E_{ {{\mathbf {Q}}}_p}\widehat{\otimes }^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p)]^{\varphi =p^r},\quad [E_{ {{\mathbf {Q}}}_p}\widehat{\otimes }^R_{{F}}\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_{F},F)]^{\varphi =p^r}\nonumber \\ \end{aligned}$$

(4.9)

are strictly acyclic:²⁹ this is an immediate consequence of the fact that Frobenius $\varphi$ is highly topologically nilpotent on J (hence $p^r-\varphi$ is rationally invertible). This implies that the following maps

(4.10)

are strict quasi-isomorphisms. We define the map $h_{\mathrm {cr} }$ to be equal to the above zigzag. It is compatible with the monodromy operator (for the first map in the zigzag use the fact that the monodromy operator is defined by compatible residue maps).

We define a map in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$

$$\begin{aligned} \iota _{\mathrm {rig} }^1: [\mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0) \widehat{\otimes }^R_{F}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }]^{\varphi =p^r}{\rightarrow } [\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p){\widehat{\otimes }}^R_{r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}}{\widehat{\mathbf{B}}}^+_{\mathrm {st} }]^{\varphi =p^r}\nonumber \\ \end{aligned}$$

(4.11)

as the composition of the maps in (4.2) and (4.7). Both maps being compatible with the monodromy operator so is $\iota ^1_{\mathrm {rig} }$.

ii) Compatibility of the maps$\iota ^1_{\mathrm {rig} },\iota ^2_{\mathrm {rig} }$. Let $r\ge 0$. The compatibility of the maps $\iota ^1_{\mathrm {rig} },\iota ^2_{\mathrm {rig} }$ can be shown by the commutative diagram

Here the map $f_2$ is the change of convergence map defined by the composition

$$\begin{aligned} f_2:\mathrm {R} \Gamma _{\mathrm {rig} }({X}_0/r^{\dagger })\rightarrow \mathrm {R} \Gamma _{\mathrm {conv} }({X}_0/\hat{r}){\mathop {\leftarrow }\limits ^{\sim }} \mathrm {R} \Gamma _{\mathrm {conv} }({X}_1/\hat{r})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathbf {Q}}}_p), \end{aligned}$$

where $\hat{r}:={{\mathscr {O}}}_F\{T\}$. The quasi-isomorphism is actually a natural isomorphism by the invariance under infinitesimal thickenings. The map $f_2$ is clearly compatible with the projection $p_{\varpi }$ and the map $\iota ^2_{\mathrm {rig} }$. The map $h_{\mathrm {rig} }$ is defined in the same way as the map $h_{\mathrm {cr} }$: we just replace ${\mathrm {cr} }$ by $\mathrm {rig}$ and $r^{\mathrm{PD}}_{\varpi }$ by $r^{\dagger }$. It is clear that the maps $h_*$ are compatible.

The map $f_1$ is induced by the composition

The fact that the last quasi-isomorphism is strict needs a justification. We may assume that $X_0$ is affine and take a log-smooth lifting Y of $X_0$ to $r^{\dagger }$. Since the sheaf of differentials of $Y_F$ is free we are reduced to showing strict acyclicity of the Čech complex of overconvergent functions for the covering corresponding to $\{M_{i}\},i\in I$. Using a dagger presentation of $Y_F$, this complex can be written as an inductive limit of Čech complexes for analogous coverings of rigid analytic affinoids. The latter complexes being strictly acyclic (because they are acyclic and we have the Open Mapping Theorem for Banach spaces) and the inductive system being acyclic, the former complex is acyclic as well. For the above diagram we need strictness of the last quasi-isomorphism with terms tensored with $\widehat{\mathbf{B}}^+_{\mathrm {st} }$ but this is automatic since we have taken derived tensor products. Finally, it is easy to check (do it first without the period ring $\widehat{\mathbf{B}}^+_{\mathrm {st} }$) that the map $f_1$ makes the two small adjacent triangles in the above diagram commute. $\square$

4.2 Fundamental diagram

Having the comparison theorem proved above, we can now deduce a fundamental diagram for pro-étale cohomology from the one for overconvergent syntomic cohomology.

Theorem 4.12

Let X be a Stein semistable weak formal scheme over ${{\mathscr {O}}}_K$. Let $r\ge 0$. There is a natural map of strictly exact sequences of Fréchet spaces

Moreover, $\ker \tilde{\beta }\simeq (H^r_{\mathrm {HK} }(X_{0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}$, and the vertical maps have closed images.

Proof

We define $\tilde{\beta }:=p^{-r}\beta \iota _{\mathrm {rig} }^{-1}\iota _{\mathrm{BK}}^{-1}\alpha _{\mathrm{FM}}^{-1}$, using Corollary 3.46, Proposition 3.48, and Theorem 4.1; the twist by $p^{-r}$ being added to make this map compatible with symbols. The theorem follows immediately from Proposition 3.36. $\square$

Remark 4.13

The above diagram can be thought of as a one-way comparison theorem, i.e., the pro-étale cohomology $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))$ is the pullback of the diagram

built from the Hyodo–Kato cohomology and a piece of the de Rham complex. For a striking comparison, recall that if X is a proper semistable formal scheme over ${{\mathscr {O}}}_K$ then the Semistable Comparison Theorem from [20] shows that we have the exact sequence

(4.14)

i.e., the pro-étale cohomology $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Q}}}_p(r))$ is the pullback of the diagram

Of course, in this case the étale and the pro-étale cohomologies agree. The sequence (4.14) is obtained in an analogous way to the top sequence in the fundamental diagram above. With the degeneration of the Hodge–de Rham spectral sequence and the theory of finite dimensional BC spaces forcing the injectivity on the left.

Remark 4.15

The following commutative diagram illustrates the relationship between syntomic cohomology of ${{\mathbf {Q}}}_p(r)$ and ${{\mathbf {Q}}}_p(r-1)$

Here we wrote $\mathrm{HK}^i_r,\mathrm{DR}^i_r,$ and $\mathrm{Syn}^i_r$ for the i’th cohomology of the complexes $\mathrm{HK}(X_{C},r),\mathrm{DR}(X_{C},r)$ and $\mathrm {R} \Gamma _{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r))$, and $H^i_{\mathrm {dR} }:=H^i_{\mathrm {dR} }(X_C)$.

We claim that the rows of the above diagram are strictly exact. Indeed, the two top rows arise from the definition of $\mathrm {R} \Gamma _{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r-1))$, $\mathrm {R} \Gamma _{ \mathrm {syn} }(X_{C}, {{\mathbf {Q}}}_p(r))$; the map between them is the multiplication by $t\in (\mathbf{B}_{\mathrm {cr} }^+)^{\varphi =p}\cap F^1\mathbf{B}_{\mathrm {dR} }$. These rows are clearly strictly exact. It suffices now to show that the columns form short strictly exact sequences (with zeros at the ends). Indeed, for $i\le r-1$, multiplication by t induces an isomorphism (using comparison with pro-étale cohomology)

$$\begin{aligned} \mathrm{Syn}^i_r\cong t\,\mathrm{Syn}^i_{r-1} \end{aligned}$$

as well as the following strictly exact sequences

$$\begin{aligned} 0\rightarrow&\mathrm{DR}^i_{r-1}{\mathop {\rightarrow }\limits ^{t}} \mathrm{DR}^i_r\rightarrow H^i_{\mathrm{dR}}(X_K)\widehat{\otimes }_K C\rightarrow 0,\quad r\ge i+2,\nonumber \\ 0\rightarrow&\mathrm{HK}^i_{r-1}{\mathop {\rightarrow }\limits ^{t}} \mathrm{HK}^i_r\rightarrow H^i_{\mathrm{dR}}(X_K)\widehat{\otimes }_K C\rightarrow 0. \end{aligned}$$

(4.16)

The second one from Lemma 3.39; the first strictly exact sequence follows from the strictly exact sequence

4.3 Examples

We will now illustrate Theorem 4.12 with some simple examples.

4.3.1 Affine space

Let $d\ge 1$. Let ${{\mathbb {A}}}^d_K$ be the d-dimensional rigid analytic affine space over K. Recall that $H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {A}}}_{C}^d, {{\mathbf {Q}}}_p)=0$ for $r \ge 1$ [2, Th. 7.3.2]. On the other hand, as the following proposition shows, the pro-étale cohomology of ${{\mathbb {A}}}_{C}^d$ is highly nontrivial in nonzero degrees.

Proposition 4.17

Let $r\ge 1$. There is a ${{\mathscr {G}}}_K$-equivariant isomorphism in $C_{ {{\mathbf {Q}}}_p}$ (of Fréchet spaces)

$$\begin{aligned} \Omega ^{r-1}({{\mathbb {A}}}^d_C)/\ker d{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {A}}}_{C}^d, {{\mathbf {Q}}}_p(r)). \end{aligned}$$

Remark 4.18

A simpler and more direct proof of this result (but still using syntomic cohomology) has been given in [21]. See [51] for another proof working directly with the fundamental exact sequence in the pro-étale topology.

Proof

Let ${{\mathscr {A}}}^d$ denote a semistable weak formal scheme over ${{\mathscr {O}}}_K$ such that ${{\mathscr {A}}}^d_K\simeq {{\mathbb {A}}}^d_K$. We will explain below how such a model ${{\mathscr {A}}}^d$ can be constructed. By Theorem 4.12, we have a ${{\mathscr {G}}}_K$-equivariant exact sequence (in $C_{ {{\mathbf {Q}}}_p}$)

Recall that $H^r_{\mathrm {dR} }({{\mathbb {A}}}^d_K)=0$. Since, by the Hyodo–Kato isomorphism $H^r_{\mathrm {HK} }({{\mathscr {A}}}^d_0)\otimes _FK\simeq H^r_{\mathrm {dR} }({{\mathbb {A}}}^d_K)$, we have $H^r_{\mathrm {HK} }({{\mathscr {A}}}^d_0)=0$. Our proposition follows from the above exact sequence.

It remains to show that we can construct a semistable weak formal scheme ${{\mathscr {A}}}^d$ over ${{\mathscr {O}}}_K$ whose generic fiber is ${{\mathbb {A}}}^d_K$. For $d=1$, we can define a model ${{\mathscr {A}}}^1$ using Theorem 4.9.1 of [27]. That theorem describes a construction of a formal semistable model for any analytic subspace ${{\mathbb {P}}}_K{\setminus }{{\mathscr {L}}}^*$, where ${{\mathscr {L}}}$ is an infinite compact subset of K-rational points of the projective line ${{\mathbb {P}}}_K$ and ${{\mathscr {L}}}^*$ is the set of its limit points. The proof of the theorem can be easily modified to yield a weak formal model. To define the model ${{\mathscr {A}}}^1$ we want we apply this theorem with ${{\mathscr {L}}}=\{\infty \}\cup \{\varpi ^n|n\in {{\mathbf {Z}}} , n\le 0\}$. We note that the special fiber of ${{\mathscr {A}}}^1$ is a half line of projective lines.

To construct a model ${{\mathscr {A}}}^d$ for $d>1$, first we consider the d-fold product Y of the logarithmic weak formal scheme associated to ${{\mathscr {A}}}^1$. Product is taken over ${{\mathscr {O}}}_K^{\times }$. It is not a semistable scheme but it is log-smooth over ${{\mathscr {O}}}_K^{\times }$. Hence its singularities can be resolved using combinatorics of monoids describing the log-structure. In fact, using Lemma 1.9 of [69], one can define a canonical ideal sheaf of Y that needs to be blown-up to obtain a semistable model ${{\mathscr {A}}}^d$ we want. $\square$

4.3.2 Torus

Let $d\ge 1$. Let ${{\mathbb {G}}}^d_{m,K}$ be the d-dimensional rigid analytic torus over K. Let ${{\mathscr {Y}}}^d$ denote a semistable weak formal scheme over ${{\mathscr {O}}}_K$ such that ${{\mathscr {Y}}}^d_K\simeq {{\mathbb {G}}}^d_{m,K}$. Such a model ${{\mathscr {Y}}}^d$ exists. For $d=1$, we can define a model ${{\mathscr {Y}}}^1$ using Theorem 4.9.1 of [27]; just as in the case of ${{\mathbb {A}}}^1_K$ above. More specifically, to define the model ${{\mathscr {Y}}}^1$ we want we apply this theorem with ${{\mathscr {L}}}=\{\infty , 0\}\cup \{\varpi ^n|n\in {{\mathbf {Z}}} \}$. We note that the special fiber of ${{\mathscr {Y}}}^1$ is a line of projective lines. To construct a model ${{\mathscr {Y}}}^d$ for $d>1$, we use products as above.

To compute the pro-étale cohomology, we will use Theorem 4.12. To make it explicit, we need to compute $(H^r_{\mathrm {HK} }({{\mathscr {Y}}}^d_{0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^r}$. For $d=1$, we have

$$\begin{aligned} H^r_{\mathrm {dR} }({{\mathbb {G}}}_{m,K})={\left\{ \begin{array}{ll} K &{} \text{ if } r=0,\\ c_1^{\mathrm {dR} }(z) K&{} \text{ if } r=1,\\ 0 &{} \text{ if } r>1. \end{array}\right. } \end{aligned}$$

Here z is a coordinate of the torus and $c_1^{\mathrm {dR} }(z)$ is its de Rham Chern class, i.e. dz / z (see Chapter 7). For $d>1$, we can use the Künneth formula to compute that $H^r_{\mathrm {dR} }({{\mathbb {G}}}^d_{m,K})$ is a K-vector space of dimension $\left( {\begin{array}{c}d\\ r\end{array}}\right)$ generated by the tuples $c_1^{\mathrm {dR} }(z_{i_1})\cdots c_1^{\mathrm {dR} }(z_{i_r})$. Similarly, $H^r_{\mathrm {HK} }({{\mathscr {Y}}}^d_{0})$ is an F-vector space of dimension $\left( {\begin{array}{c}d\\ r\end{array}}\right)$ generated by the tuples $c_1^{\mathrm {HK} }(z_{i_1})\cdots c_1^{\mathrm {HK} }(z_{i_r})$. By Lemma 7.8, the Hyodo–Kato and the de Rham symbols are compatible under the Hyodo–Kato map $\iota _{\mathrm {HK} }$.

Since $\varphi (c_1^{\mathrm {HK} }(z_{i_j}))=pc_1^{\mathrm {HK} }(z_{i_j})$ and $N(c_1^{\mathrm {HK} }(z_{i_j}))=0$, we get that

$$\begin{aligned} (H^r_{\mathrm {HK} }({{\mathscr {Y}}}^d_{0})\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^r}=H^r_{\mathrm {HK} }({{\mathscr {Y}}}^d_{0})^{\varphi =p^r}=\wedge ^r {{\mathbf {Q}}}_p^d \end{aligned}$$

and that it is a ${{\mathbf {Q}}}_p$-vector space of dimension $\left( {\begin{array}{c}d\\ r\end{array}}\right)$ generated by the tuples $c_1^{\mathrm {HK} }(z_{i_1})\cdots c_1^{\mathrm {HK} }(z_{i_r})$. Hence, Theorem 4.12 gives us a map of ${{\mathscr {G}}}_K$-equivariant exact sequences (in $C_{ {{\mathbf {Q}}}_p}$)

Recall, for comparison, that $H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {G}}}^d_{m,C}, {{\mathbf {Q}}}_p(r))\simeq \wedge ^r {{\mathbf {Q}}}_p^d$, a ${{\mathbf {Q}}}_p$-vector space generated by the tuples $c_1^{\acute{\mathrm{e}}\mathrm {t}}(z_{i_1})\cdots c_1^{\acute{\mathrm{e}}\mathrm {t}}(z_{i_r})$.

4.3.3 Curves

Let X be a Stein curve over K with a semistable model ${{\mathscr {X}}}$ over ${{\mathscr {O}}}_K$. The diagram from Theorem 4.12 takes the following form³⁰

5 Pro-étale cohomology of Drinfeld half-spaces

We will use the fundamental diagram of Theorem 4.12 to compute the p-adic pro-étale cohomology of Drinfeld half-spaces (Theorem 5.13). This boils down to understanding the Hyodo–Kato cohomology groups as $(\varphi ,N)$-modules and as representations of $\mathrm{GL}_{d+1}(K)$. The latter can be done by using the comparison with de Rham cohomology and results of Schneider–Stuhler (see Theorem 5.8); the computation of $\varphi$ and N uses an explicit description a la Iovita–Spiess (see Theorem 5.10 and Lemma 5.11) of Hyodo–Kato cohomology of Drinfeld half-spaces in terms of symbols of rational hyperplanes.

5.1 Drinfeld half-spaces and their standard formal models

Let K be a finite extension of ${{\mathbf {Q}}}_p$. Let ${{\mathbb {H}}}^d_K$, $d\ge 1$, be the d-dimensional Drinfeld half-space over K: the K-rigid space that is the complement in ${{\mathbb {P}}}^d_K$ of all K-rational hyperplanes. If ${\mathscr {H}}={\mathbb {P}}((K^{d+1})^*)={\mathbb {P}}^d(K)$ is the space of K-rational hyperplanes in $K^{d+1}$ (this is a profinite set), we have

$$\begin{aligned} {{\mathbb {H}}}^d_K={{\mathbb {P}}}^d_K{\setminus } \cup _{H\in {\mathscr {H}}} H. \end{aligned}$$

The group $G:=\mathrm{GL}_{d+1}(K)$ acts on it. We will drop the subscript K if there is no danger of confusion.

${{\mathbb {H}}}^d_K$ is a rigid analytic Stein space hence also a dagger analytic Stein space. It has a (standard) G-equivariant semistable weak formal model $\widetilde{{\mathbb {H}}}^d_K$ [32, 6.1] (that is Stein). Recall that the set of vertices of the Bruhat–Tits building $\mathrm{BT}$ of $\mathrm{PGL}_{d+1}(K)$ is the set of homothety classes of lattices in $K^{d+1}$. It corresponds to the set of irreducible components of $Y:=\widetilde{{\mathbb {H}}}^d_{K,0}$. For $s\ge 0$, let $\mathrm{BT}_s$ denote the Bruhat–Tits building truncated at s, i.e., the simplicial subcomplex of $\mathrm{BT}$ supported on the vertices v such that the combinatorial distance $d(v,v_0)\le s$, $v_0=[{{\mathscr {O}}}_K^{d+1}]$. Here, for a lattice L, [L] denotes the homothety class of L. Let $Y_s$ denote the union of the irreducible components corresponding to the vertices of $\mathrm{BT}_s$. It is a closed subscheme of Y that we equip with the induced log-structure. We will sometimes write $Y_{\infty }$ for the whole special fiber Y. We denote by $Y_s^{\circ }:=Y_s{\setminus } (Y_s\cap \overline{(Y{\setminus } Y_{s})})$, where the bar denotes closure. We have immersions $Y_{s-1}\subset Y_s^{\circ }\subset Y_s$, where the first one is closed and the second one is open.

5.2 Generalized Steinberg representations

We will briefly review the definitions and basic properties of the generalized Steinberg representations that we will need.

5.2.1 Locally constant special representations

Let B be the upper triangular Borel subgroup of G and $\Delta =\{1,2,\ldots ,d\}$. We identify the Weyl group W of G with the group of permutations of $\{1,2,\ldots ,d+1\}$ and with the subgroup of permutation matrices in G. Then W is generated by the elements $s_i=(i, i+1)$ for $i\in \Delta$.

For each subset J of $\Delta$ we let:

• $W_J$ be the subgroup of W generated by the $s_i$ with $i\in J$.

• $P_J=BW_JB$, the parabolic subgroup of G generated by B and $W_J$.

• $X_J=G/P_J$, a compact topological space.

If A is an abelian group and $J\subset \Delta$, let

$$\begin{aligned} \mathrm{Sp}_J(A)=\frac{\mathrm{LC}(X_J, A)}{\sum _{i\in \Delta {\setminus } J} \mathrm{LC}(X_{J\cup \{i\}}, A)}, \end{aligned}$$

where $\mathrm{LC}$ means locally constant functions with values in A (automatically with compact support since the $X_J$’s are compact). This is a smooth G-module over A and we have a natural isomorphism $\mathrm{Sp}_J(A)=\mathrm{Sp}_J({\mathbf {Z}})\otimes A$. For $J=\emptyset$ we obtain the usual Steinberg representation with coefficients in A, while for $J=\Delta$ we have $\mathrm{Sp}_J(A)=A$ (since $X_J$ is a point). For $r\in \{0,1,\ldots ,d\}$ we use the simpler notation

$$\begin{aligned} \mathrm{Sp}_r(A)=\mathrm{Sp}_{\{1,2,\ldots ,d-r\}}(A). \end{aligned}$$

For $r> d$, we set $\mathrm{Sp}_r(A)=0$.

Proposition 5.1

If A is a field of characteristic 0 or p then the $\mathrm{Sp}_J(A)$’s (for varying J) are the irreducible constituents of $\mathrm{LC}(G/B, A)$, each occurring with multiplicity 1.

Proof

This is due to Casselman in characteristic 0 (see [10, X, Th. 4.11]) and to Grosse-Klönne [36, Cor. 4.3] in characteristic p. $\square$

Remark 5.2

The proposition does not hold for A a field of characteristic $\ell \ne p$, see [82, III, Th. 2.8].

The rigidity in characteristic p given by the previous theorem has consequences in characteristic 0 that will be very useful to us later on.

Corollary 5.3

If J is a subset of $\Delta$, then $\mathrm{Sp}_J({{\mathscr {O}}}_K)$ is, up to a $K^*$-homothety, the unique G-stable ${{\mathscr {O}}}_K$-lattice in $\mathrm{Sp}_J(K)$.

Proof

This follows easily from Proposition 5.1 and the fact that $\mathrm{Sp}_J({{\mathscr {O}}}_K)$ is finitely generated over ${{\mathscr {O}}}_K[G]$, see [36, Cor. 4.5] for the details. $\square$

5.2.2 Topology

If $\Lambda$ is a topological ring, then $\mathrm{Sp}_J(\Lambda )$ has a natural topology: the space $X_J$ being profinite, we can write $X_J=\varprojlim _{n} X_{n,J}$ for finite sets $X_{n,J}$ and then $\mathrm{LC}(X_J, \Lambda )=\varinjlim _{n} \mathrm{LC}(X_{n,J}, \Lambda )$, each $\mathrm{LC}(X_{n,J}, \Lambda )$ being a finite free $\Lambda$-module endowed with the natural topology. In particular, if $\Lambda$ is a finite extension of ${{\mathbf {Q}}}_p$, this exhibits $\mathrm{Sp}_J(\Lambda )$ as an inductive limit of finite dimensional $\Lambda$-vector spaces, and the corresponding topology is the strongest locally convex topology on the $\Lambda$-vector space $\mathrm{Sp}_J(\Lambda )$, which is an LF-space.

If M is a topological $\Lambda$-module, let $M^*:=\mathrm{Hom}_{\mathrm{cont}}(M,\Lambda )$ equipped with the weak topology. Then $\mathrm{LC}(X_J,\Lambda )^*$ is naturally isomorphic to $\varprojlim _{n} \mathrm{LC}(X_{n,J}, \Lambda )^*$, i.e., a countable inverse limit of finite free $\Lambda$-modules. In particular, if L is a finite extension of ${{\mathbf {Q}}}_p$ then $\mathrm{Sp}_J(L)^*$ is a nuclear Fréchet space (in fact a countable product of Banach spaces) and $\mathrm{Sp}_J({{\mathscr {O}}}_L)^*$ is a compact ${{\mathscr {O}}}_L$-module, which is torsion free. Therefore $\mathrm{Sp}_J({{\mathscr {O}}}_L)^*\otimes L$ has a natural structure of a weak dual of an L-Banach space.

5.2.3 Continuous special representations

Consider now the corresponding continuous special representation

$$\begin{aligned} \mathrm{Sp}^{\mathrm{cont}}_J(\Lambda )=\frac{{\mathscr {C}}(X_J, \Lambda )}{\sum _{\alpha \in \Delta {\setminus } J} {\mathscr {C}}(X_{J\cup \{\alpha \}}, \Lambda )}. \end{aligned}$$

Arguing as above, we see that, for any finite extension L of ${{\mathbf {Q}}}_p$, the space $\mathrm{Sp}^{\mathrm{cont}}_J(L)$ has a natural structure of an L-Banach space, with the unit ball given by $\mathrm{Sp}^{\mathrm{cont}}_J({{\mathscr {O}}}_L)$. The action of G on all these spaces is continuous and we can recover $\mathrm{Sp}_J(L)$ from $\mathrm{Sp}^{\mathrm{cont}}_J(L)$ as the space of smooth vectors (for the action of G).

The rigidity in characteristic p given by Proposition 5.1 and Corollary 5.3 yields:

Corollary 5.4

Let J be a subset of $\Delta$ and L a finite extension of ${{\mathbf {Q}}}_p$.

• a) The universal unitary completion of $\mathrm{Sp}_J(L)$ is $\mathrm{Sp}^{\mathrm{cont}}_J(L)$.

• b) The space of G-bounded vectors in $\mathrm{Sp}_J(L)^*$ is $\mathrm{Sp}^{\mathrm{cont}}_J(L)^*$.

Proof

• a) Follows from Corollary 5.3 and the fact that $\mathrm{St}^{\mathrm{cont}}_J({{\mathscr {O}}}_L)$ is the p-adic completion of $\mathrm{Sp}_J({{\mathscr {O}}}_L)$ (which in turn uses that $\mathrm{Sp}_J(A)=\mathrm{Sp}_J({\mathbf {Z}})\otimes A$ for all A, and this is a free A-module).

• b) Follows by duality from a). $\square$

Remark 5.5

One can also define a locally analytic generalized Steinberg representation $\mathrm{Sp}_J^{\mathrm{an}}(L)$ for any finite extension L or ${{\mathbf {Q}}}_p$ (or any closed subfield of complex numbers). It is naturally a space of compact type, whose dual is a nuclear Fréchet space. It contains $\mathrm{Sp}_J(L)$ as a closed subspace (it is closed because it is the space of vectors killed by the Lie algebra of G). The dual of $\mathrm{Sp}_J^{\mathrm{an}}(L)$ surjects onto the dual of $\mathrm{Sp}_J(L)$ and contains the dual of $\mathrm{Sp}^{\mathrm{cont}}_J(L)$ as a dense subspace. The big difference is that $\mathrm{Sp}_J^{\mathrm{an}}(L)$ is topologically reducible as a G-module. Its Jordan–Hölder constituents are described in [65].

5.3 Results of Schneider–Stuhler

We recall the cohomological interpretation of the representations $\mathrm{Sp}_r({\mathbf {Z}})$, following [71]. Recall that ${\mathscr {H}}$ is the space of K-rational hyperplanes in $K^{d+1}$. For $r\in \{1,2,\ldots ,d\}$ we define simplicial profinite sets $Y_{{\scriptscriptstyle \bullet }}^{(r)}$, ${\mathscr {T}}^{(r)}_{{\scriptscriptstyle \bullet }}$ as follows:

$\bullet$$Y_s^{(r)}$ is the closed subset of ${\mathscr {H}}^{s+1}$ of tuples $(H_0,\ldots ,H_s)\in {\mathscr {H}}^{s+1}$ with

$$\begin{aligned} \dim _K(\sum _{i=0}^s K\ell _{H_i})\le r, \end{aligned}$$

where $\ell _{H_i}\in (K^{d+1})^*$ is any equation of $H_i$.

$\bullet$${\mathscr {T}}_{s}^{(r)}$ is the set of flags $W_0\subset \ldots \subset W_s$ in $(K^{d+1})^*$ for which $\dim _K W_i\in \{1,\ldots ,r\}$ for all i. This set has a natural profinite topology.

In both cases the face/degeneracy maps are the obvious ones, i.e. omit/double one hyperplane in a tuple, resp. a vector subspace in a flag. With the topology forgotten, ${\mathscr {T}}^{(d)}_{{\scriptscriptstyle \bullet }}$ is the Tits³¹ (not Bruhat-Tits!) building of G.

The following result is due to Schneider and Stuhler:

Proposition 5.6

For all $r\in \{1,2,\ldots ,d\}$ we have natural isomorphisms (where $\widetilde{H}$ denotes reduced cohomology)

$$\begin{aligned} \widetilde{H}^{r-1}(|{\mathscr {T}}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq \widetilde{H}^{r-1}(|Y^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq \mathrm{Sp}_r({\mathbf {Z}}). \end{aligned}$$

Proof

The isomorphism $\widetilde{H}^{r-1}(|{\mathscr {T}}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq \widetilde{H}^{r-1}(|Y^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})$ is proved in [71, Ch. 3, Prop. 5]. To identify these objects with $\mathrm{Sp}_r({\mathbf {Z}})$, assuming for simplicity $r>1$ from now on, consider the clopen subset $\mathscr {NT}_s^{(r)}\subset {\mathscr {T}}_{s}^{(r)}$ of ${\mathscr {T}}_{s}^{(r)}$ consisting of flags $W_0\subset \ldots \subset W_s$ for which all inclusions are strict. Using the obvious isomorphism $\widetilde{H}^{r-1}(|\mathscr {NT}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq \widetilde{H}^{r-1}(|{\mathscr {T}}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})$ the result follows from the exact sequence³²

$$\begin{aligned} \mathrm{LC}( \mathscr {NT}^{(r)}_{r-2}, {\mathbf {Z}})\rightarrow \mathrm{LC}(\mathscr {NT}^{(r)}_{r-1}, {{\mathbf {Z}}} )\rightarrow H^{r-1}(|\mathscr {NT}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\rightarrow 0 \end{aligned}$$

and the identifications

$$\begin{aligned} \mathscr {NT}^{(r)}_{r-1}\simeq X_{\{1,2,\ldots ,d-r\}}, \quad \mathscr {NT}^{(r)}_{r-2}\simeq \coprod _{i=d-r+1}^d X_{\{1,\ldots ,d-r, i\}} \end{aligned}$$

$\square$

Remark 5.7

For all $r\in \{1,2,\ldots ,d\}$ and all q there are natural isomorphisms

$$\begin{aligned} H^q(|\mathscr {NT}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq H^q(|{\mathscr {T}}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq H^q(|Y^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}}) \end{aligned}$$

and these spaces are nonzero only for $q=0, r-1$, with $H^0$ being given by ${\mathbf {Z}}$ for $r>1$ and by $\mathrm{LC}({\mathbf {P}}((K^{d+1})^*), {\mathbf {Z}})$ for $r=1$. See [71, Ch. 3, Prop. 6] for the details.

The following theorem is one of the main results of [71]. See also [63] for a different argument (at least for a) and the compactly supported analogue of b)).

Theorem 5.8

(Schneider–Stuhler) Let $r\ge 0$.

• a) For a prime $\ell \ne p$, there are natural isomorphisms of $G\times {{{\mathscr {G}}}}_K$-modules

  $$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))\simeq \mathrm{Sp}_r( {{\mathbf {Z}}} _\ell )^*\otimes {{\mathbf {Q}}}_{\ell },\quad H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))\simeq \mathrm{Sp}_r( {{\mathbf {Q}}}_{\ell })^*. \end{aligned}$$

• b) There is a natural isomorphism of G-modules

  $$\begin{aligned} H^r_{\mathrm{dR}}({{\mathbb {H}}}^d_K)\simeq \mathrm{Sp}_r(K)^*. \end{aligned}$$

Proof

Let $H^*$ be any of the cohomologies occuring in the theorem. It has the properties required by Schneider–Stuhler [71, Ch. 2]. The crucial among them is the homotopy invariance property: if D is the 1-dimensional open unit disk then, for any smooth affinoid X, the projection $X\times D\rightarrow X$ induces a natural isomorphism $H^*(X){\mathop {\rightarrow }\limits ^{\sim }}H^*(X\times D)$. For de Rham cohomology this is very simple (see the discussion preceding Prop. 3 in [71, Ch. 2]); for $\ell$-adic étale and pro-étale cohomologies this follows from the “homotopy property” of $\ell$-adic étale cohomology with respect to a closed disk [71, proof of Th. 6.0.2], and the fact that $\ell$-adic étale and pro-étale cohomologies are the same on affinoids.

We recall very briefly the key arguments, without going into the rather involved combinatorics. If $H\in {\mathscr {H}}$ and $n\ge 1$, let $U_n(H)$ be the open polydisk in the affine space ${{\mathbb {P}}}_K^d{\setminus } H$ given by³³$|\ell _H(z)|>|\pi |^n$. The open subsets $U_n=\cap _{H\in {\mathscr {H}}} U_n(H)$ form a Stein covering of ${{\mathbb {H}}}^d_K$ and $U_n=\cap _{H\in {\mathscr {H}}_n} U_n(H)$, for a finite subset ${\mathscr {H}}_n$ of ${\mathscr {H}}$, in bijection with ${{\mathbb {P}}}^d(({{\mathscr {O}}}_K^{d+1}/\pi ^n)^*)$. Writing $H^*(X,U)$ for the “cohomology with support in $X{\setminus } U$” (more precisely, the derived functors of the functor “sections vanishing on U”), a formal argument (see the discussion following [71, Ch. 3, Cor. 5]) gives a spectral sequence

$$\begin{aligned} E_1^{-j, i}(n)=\bigoplus _{H_{0},\ldots ,H_{j}\in {\mathscr {H}}_n} H^i({{\mathbb {P}}}_K^d, U_n(H_{0})\cup \ldots \cup U_n(H_{j}))\Rightarrow H^{i-j}({{\mathbb {P}}}^d_K, U_n). \end{aligned}$$

Now, $U_n(H_{0})\cup \ldots \cup U_n(H_{j})$ is a locally trivial fibration over a projective space, whose fibers are open polydisks [71, Ch. 1, Prop. 6]. Using the homotopy invariance of cohomology, one computes $H^i({{\mathbb {P}}}_K^d, U_n(H_{0})\cup \ldots \cup U_n(H_{j}))$, in particular this is always equal to $A=H^0(\mathrm{Sp}(K))$ or 0 (with a simple combinatorial recipe allowing to distinguish the two cases). The spectral sequence simplifies greatly and³⁴ letting $n\rightarrow \infty$ gives (using also Proposition 5.6 and Remark 5.7) a spectral sequence

$$\begin{aligned} E_2^{-j,i}\Rightarrow H^{i-j}({{\mathbb {P}}}^d_K, {{\mathbb {H}}}^d_K), \end{aligned}$$

where

$$\begin{aligned} E_2^{-j,i}=\mathrm{Hom}_{{\mathbf {Z}}} (H^j(|{\mathscr {T}}_{{\scriptscriptstyle \bullet }}^{(\frac{i}{2})}|, {\mathbf {Z}}), A) \end{aligned}$$

if $i\in [2, 2d]$ is even and $j\in \{0, \frac{i}{2}-1\}$, and 0 otherwise. The analysis of this spectral sequence combined with Proposition  5.6 yields the cohomology groups $H^i({{\mathbb {P}}}^d_K, {{\mathbb {H}}}^d_K)$. The result follows from the exact sequence

$$\begin{aligned} \cdots \rightarrow H^i({{\mathbb {P}}}^d_K)\rightarrow H^i({{\mathbb {H}}}^d_K)\rightarrow H^{i+1}({{\mathbb {P}}}^d_K, {{\mathbb {H}}}^d_K)\rightarrow H^{i+1}({{\mathbb {P}}}^d_K)\rightarrow \cdots \end{aligned}$$

$\square$

Combining Theorem 5.8 and Corollary 5.4 yields:

Corollary 5.9

The space of G-bounded vectors in $H^r_{\mathrm{dR}}({{\mathbb {H}}}^d_K)$ is isomorphic to $\mathrm{Sp}^{\mathrm{cont}}_r(K)^*$.

5.4 Generalization of Schneider–Stuhler

We will extend the results of Schneider–Stuhler to Hyodo–Kato cohomology. To do that we will use the description of the isomorphisms in Theorem 5.8 via symbols.

5.4.1 Results of Iovita–Spiess

All the isomorphisms in Theorem 5.8 are rather abstract, but following Iovita–Spiess [44] one can make them quite explicit as follows. Let $\mathrm{LC}^{c}({\mathscr {H}}^{r+1}, {\mathbf {Z}})$ be the space of locally constant functions $f: {\mathscr {H}}^{r+1}\rightarrow {\mathbf {Z}}$ such that, for all $H_0,\ldots ,H_{r+1}\in {\mathscr {H}}$,

$$\begin{aligned} f(H_1,\ldots ,H_{r+1})-f(H_0, H_2,\ldots , H_{r+1})+\cdots +(-1)^{r+1}f(H_0,\ldots ,H_{r})=0 \end{aligned}$$

and moreover, if $\ell _{H_i}$ are linearly dependent, then $f(H_0,\ldots ,H_r)=0$ (i.e., f vanishes on $Y_r^{(r)}$). Define analogously ${\mathscr {C}}^{c}({\mathscr {H}}^{r+1}, {\mathbf {Z}})$. It is not difficult to see that we have a natural isomorphism (see the proof of Proposition  5.6 for the notation used below)

$$\begin{aligned} \widetilde{H}^{r-1}(|\mathscr {NT}^{(r)}_{{\scriptscriptstyle \bullet }}|, {\mathbf {Z}})\simeq \mathrm{LC}^{c}({\mathscr {H}}^{r+1}, {\mathbf {Z}}) \end{aligned}$$

and, in particular, (using Proposition 5.6) a natural isomorphism

$$\begin{aligned}\mathrm{Sp}_r({\mathbf {Z}})\simeq \mathrm{LC}^{c}({\mathscr {H}}^{r+1}, {\mathbf {Z}}).\end{aligned}$$

If S is a profinite set and A an abelian group, let

$$\begin{aligned} D(S,A)=\mathrm{Hom}(\mathrm{LC}(S,{\mathbf {Z}}), A) \end{aligned}$$

be the space of A-valued locally constant distributions on S. If L is a discrete valuation nonarchimedean field let M(S, L) be the space of L-valued measures, i.e., bounded L-valued distributions. It has a natural topology that is finer than the subspace topology induced from D(S, L) [44, Ch. 4].

The inclusion $\mathrm{LC}^{c}({\mathscr {H}}^{r+1}, {\mathbf {Z}})\subset \mathrm{LC}({\mathscr {H}}^{r+1}, {\mathbf {Z}})$ gives rise to a continuous strict surjection

$$\begin{aligned} D({\mathscr {H}}^{r+1}, A)\rightarrow \mathrm{Hom}(\mathrm{Sp}_r({\mathbf {Z}}), A). \end{aligned}$$

Define the space $D({\mathscr {H}}^{r+1}, A)_{\mathrm{deg}}$ of degenerate distributions as the kernel of this map. Combining this with the previous theorem we obtain surjections:

$$\begin{aligned}&D({\mathscr {H}}^{r+1}, K)\rightarrow H^s_{\mathrm{dR}}({{\mathbb {H}}}^d_K), \quad M({\mathscr {H}}^{r+1}, {{\mathbf {Q}}}_{\ell })\rightarrow H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r)),\\&D({\mathscr {H}}^{r+1}, {{\mathbf {Q}}}_{\ell })\rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(s)). \end{aligned}$$

These surjections can be made explicit: for each $(H_0,\ldots \,,H_r)\in {\mathscr {H}}^{r+1}$, the invertible functions (on ${{\mathbb {H}}}^d_K$) $\frac{\ell _{H_1}}{\ell _{H_0}},\ldots \,, \frac{\ell _{H_r}}{\ell _{H_0}}$ give rise (either by taking $\mathrm{dlog}$ and wedge-product or by taking the corresponding symbols in étale cohomology and then cup-product) to a symbol $[H_0,\ldots ,H_r]$ living in $H^r_{\mathrm{dR}}({{\mathbb {H}}}^d_K)$, resp. in $H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))$, resp. $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))$. For example, for de Rham cohomology $[H_0,\ldots \,,H_r]$ is the class of the closed r-form

$$\begin{aligned}\mathrm{dlog}\frac{\ell _{H_1}}{\ell _{H_0}}\wedge \cdots \wedge \mathrm{dlog}\frac{\ell _{H_r}}{\ell _{H_0}}\end{aligned}$$

in $H^r_{\mathrm{dR}}({{\mathbb {H}}}^d_K)$.

One shows that the following regulator map is well-defined

$$\begin{aligned} r_{\mathrm {dR} }: D({\mathscr {H}}^{r+1}, K)\rightarrow H^r_{\mathrm {dR} }({{\mathbb {H}}}^d_K), \quad \mu \mapsto \int _{{\mathscr {H}}^{r+1}} [H_0,\ldots \,,H_r]\, \mu (H_0,\ldots \,,H_r). \end{aligned}$$

The problem here is that the map $(H_0,\ldots \,,H_r)\mapsto [H_0,\ldots \,,H_r]$ is not locally constant on ${{\mathbb {H}}}^d_K$; however it is so on $U_n$ (see the proof of Theorem 5.8 for the notation), for all n, which makes it possibe to give a meaning to the integral. The same integral works for $\ell$-adic étale and pro-étale cohomologies yielding the regulator maps

$$\begin{aligned}&r_{\acute{\mathrm{e}}\mathrm {t}}: M({\mathscr {H}}^{r+1}, {{\mathbf {Q}}}_{\ell })\rightarrow H^r_{\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r)),\quad r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}:\\&D({\mathscr {H}}^{r+1}, {{\mathbf {Q}}}_{\ell })\rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r)). \end{aligned}$$

This can be easily seen in the case of étale cohomology. For the pro-étale cohomology, the key point is that we can write

$$\begin{aligned} H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r))=\varprojlim _{n} H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(U_{n,C}, {{\mathbf {Q}}}_{\ell }(r)), \end{aligned}$$

where $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(U_{n,C}, {{\mathbf {Q}}}_{\ell }(r))$ is finite dimensional and the map

$$\begin{aligned}&{\mathscr {H}}^{r+1}\rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({{\mathbb {H}}}^d_C, {{\mathbf {Q}}}_{\ell }(r)) \rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}(U_{n,C}, {{\mathbf {Q}}}_{\ell }(r)),\\&\quad (H_0,\ldots \,,H_r)\mapsto [H_0,\ldots \,,H_r], \end{aligned}$$

is locally constant for all n, by arguing as in [44, Lemma 4.4]. All these regulators are continuous.

One can show that the above maps induce the isomorphisms in Theorem 5.8 by imitating the arguments in [44].

Theorem 5.10

(Iovita–Spiess, [44, Th. 4.5]) The following diagram of Fréchet G-spaces commutes

and the sequence is strictly exact. Similarly for $\ell$-adic étale and pro-étale cohomologies.

5.4.2 Generalization of the results of Iovita–Spiess

Set $X:=\widetilde{{{\mathbb {H}}}}^d_K$ and $Y:=\widetilde{{{\mathbb {H}}}}^d_{K,0}$. The above results of Iovita–Spiess can be generalized to Hyodo–Kato cohomology.

Lemma 5.11

Let $r\ge 0$. There are natural isomorphisms of Fréchet spaces

$$\begin{aligned} H^r_{\mathrm {HK} }(Y)\simeq \mathrm{Sp}_r(F)^*,\quad H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\simeq \mathrm{Sp}_r( {{\mathbf {Q}}}_p)^* \end{aligned}$$

that are compatible with the isomorphism $H^r_{\mathrm {dR} }(X_K)\simeq \mathrm{Sp}_r(K)^*$ from Theorem 5.8 and the natural maps $\mathrm{Sp}_r( {{\mathbf {Q}}}_p)^*\rightarrow \mathrm{Sp}_r(F)^*\rightarrow \mathrm{Sp}_r(K)^*$.

Proof

We start with $H^r_{\mathrm {HK} }(Y)$. Consider the following diagram

Here the regulator map $r_{\mathrm {HK} }$ is defined in an analogous way to the map $r_{\mathrm {dR} }$ but by using the overconvergent Hyodo–Kato Chern classes $c^{\mathrm {HK} }_1$ defined in Chapter 7. It is continuous. The outer diagram clearly commutes. The small triangle commutes by Theorem 5.10. The square commutes by Lemma 7.8. Chasing the diagram we construct the broken arrow $f:\mathrm{Sp}_r(F)^*\rightarrow H^r_{\mathrm {HK} }(Y)$, a continuous map that makes the left bottom triangle commute; it is easy to check that it makes the right bottom triangle commute as well. This implies that the map f is injective. Since $H^r_{\mathrm {HK} }(Y)$ is topologically irreducible as a G-module (use the Hyodo–Kato isomorphism), it is also surjective (use the fact that $\mathrm{Sp}_r(F)^*$ is closed in $\mathrm{Sp}_r(K)^*$).

The argument for $H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}$ is similar. But first we need to show that the natural map

$$\begin{aligned} H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\otimes _{ {{\mathbf {Q}}}_p}F\rightarrow H^r_{\mathrm {HK} }(Y) \end{aligned}$$

(5.12)

is an injection. We compute

$$\begin{aligned} H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\otimes _{ {{\mathbf {Q}}}_p}F&\simeq (\varprojlim _s H^r_{\mathrm {HK} }(Y_s))^{\varphi =p^r}\otimes _{ {{\mathbf {Q}}}_p}F\simeq (\varprojlim _s H^r_{\mathrm {HK} }(Y_s)^{\varphi =p^r})\otimes _{ {{\mathbf {Q}}}_p}F\\&\simeq \varprojlim _s (H^r_{\mathrm {HK} }(Y_s)^{\varphi =p^r}\otimes _{ {{\mathbf {Q}}}_p}F) \hookrightarrow \varprojlim _s H^r_{\mathrm {HK} }(Y_s)\simeq H^r_{\mathrm {HK} }(Y), \end{aligned}$$

as wanted. For the injection above we have used the fact that all $H^r_{\mathrm {HK} }(Y_s)$ are finite dimensional over F.

We look now at the commutative diagram

The key point is that, as shown in Sect. 7.2.1, the map $r_{\mathrm {HK} }$ restricted to $D({{\mathscr {H}}}^{r+1}, {{\mathbf {Q}}}_p)$ factors through $H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}$. Arguing as above we construct the continuous map $f^{\prime }$. It is clearly injective. It is surjective by (5.12). $\square$

5.5 Pro-étale cohomology

We are now ready to compute the p-adic pro-étale cohomology of ${{\mathbb {H}}}^d_C$. Let $r\ge 0$. Since the linearized Frobenius on $H^r_{\mathrm {HK} }(Y)$ is equal to the multiplication by $q^r$, where $q= |k|$. [32, Cor. 6.6] and $N\varphi =p\varphi N$ [32, Prop. 5.5], the monodromy operator is trivial on $H^r_{\mathrm {HK} }(Y)$. Hence the first isomorphism below is Galois equivariant.

$$\begin{aligned} (H^r_{\mathrm {HK} }(Y)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} }&)^{N=0,\varphi =p^r} \simeq (H^r_{\mathrm {HK} }(Y)\widehat{\otimes }_{F}\mathbf{B}^{+}_{\mathrm {cr} })^{\varphi =p^r} \simeq (H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\widehat{\otimes }_{ {{\mathbf {Q}}}_p}\mathbf{B}^{+}_{\mathrm {cr} })^{\varphi =p^r}\\&\simeq H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\widehat{\otimes }_{ {{\mathbf {Q}}}_p}\mathbf{B}^{+,\varphi =1}_{\mathrm {cr} }\simeq \mathrm{Sp_r( {{\mathbf {Q}}}_p})^*\widehat{\otimes }_{ {{\mathbf {Q}}}_p}\mathbf{B}_{\mathrm {cr} }^{+,\varphi =1}= \mathrm{Sp_r( {{\mathbf {Q}}}_p})^*. \end{aligned}$$

The second isomorphism follows from the proof of Lemma 5.11, the fourth one—from this lemma itself, and the third one is clear. Using the above isomorphisms and Lemma 5.11, the map $\iota _{\mathrm {HK} }\otimes \theta : (H^r_{\mathrm {HK} }(Y)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^r} \rightarrow H^r_{\mathrm {dR} }(X_K)\widehat{\otimes }_K C$ can be identified with the natural map $\mathrm{Sp}_r( {{\mathbf {Q}}}_p)^*\rightarrow \mathrm{Sp}_r(K)^*\widehat{\otimes }_KC$.

Similarly, we compute that

$$\begin{aligned} (H^r_{\mathrm {HK} }(Y)\widehat{\otimes }_F\mathbf{B}^+_{\mathrm {st} })^{N=0,\varphi =p^{r-1}}&\simeq H^r_{\mathrm {HK} }(Y)^{\varphi =p^r}\widehat{\otimes }_{ {{\mathbf {Q}}}_p}\mathbf{B}^{+,\varphi =p^{-1}}_{\mathrm {cr} }= 0. \end{aligned}$$

Combined with Theorem 4.12, these yield the following theorem.

Theorem 5.13

Let $r\ge 0$. There is a natural map of strictly exact sequences of $G\times {{\mathscr {G}}}_K$-Fréchet spaces (over ${{\mathbf {Q}}}_p$)

where the vertical maps are closed immersions.

6 Étale cohomology of Drinfeld half-spaces

The purpose of this is to compute the p-adic étale cohomology of the Drinfeld half-space (Theorem 6.45). Using a comparison theorem (see Proposition 6.1 below) this reduces to the computation of the Fontaine–Messing syntomic cohomology. The latter then is transformed into a syntomic cohomology built from the crystalline Hyodo–Kato cohomology and the integral de Rham cohomology (see Sect. 6.4). These differential cohomologies can be computed explicitly (Corollary 6.25 and Theorem 6.28) due to the fact that the standard formal model of the Drinfeld half-space is pro-ordinary and the sheaves of integral differentials are acyclic (a result of Grosse-Klönne).

Throughout this chapter we work in the category of pro-discrete modules (see Sect. 2.2 for a quick review and Remark 6.2 for how the topology is defined on the various cohomology complexes).

6.1 Period isomorphism

Proposition 6.1

Let X be a semistable formal scheme over ${{\mathscr {O}}}_K$. Let $r\ge 0$, $\overline{X}:=X_{{{\mathscr {O}}}_C}$. There is a natural Fontaine–Messing period map

$$\begin{aligned} \alpha _{\mathrm{FM}}: \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r)){\otimes }^L {{\mathbf {Q}}}_p\rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} _p(r)){\otimes }^L {{\mathbf {Q}}}_p \end{aligned}$$

that is a strict quasi-isomorphism (in ${{\mathscr {D}}}(C_{ {{\mathbf {Q}}}_p})$) after truncation $\tau _{\le r}$.

Proof

Let Y be a semistable finite type formal scheme over ${{\mathscr {O}}}_K$. Fontaine–Messing in [26, III.5] have defined an integral period map

$$\begin{aligned} \widetilde{\alpha }_{\mathrm{FM}}:\mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{Y}, {{\mathbf {Z}}} _p(r))\rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(Y_{C}, {{\mathbf {Z}}} _p(r)^{\prime }), \end{aligned}$$

where ${{\mathbf {Z}}} _p(r)^{\prime }:=(p^aa!)^{-1} {{\mathbf {Z}}} _p(r)$, for $r=(p-1)a+b, a,b\in {{\mathbf {Z}}} , 0\le b\le p-1$. The map $\tau _{\le r}\widetilde{\alpha }_{\mathrm{FM}}$ is a $p^N$-quasi-isomorphism for a universal constant $N=N(r)$. This means that its kernel and cokernel on cohomology groups in degrees $0\le i\le r$ are annihilated by $p^N$. It follows that the cone of $\widetilde{\alpha }_{\mathrm{FM}}$ has cohomology annihilated by $p^N$, $N=N(r)$, as well.

We define

$$\begin{aligned} \widetilde{\alpha }_{\mathrm{FM}}:\mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))\rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} _p(r)^{\prime }) \end{aligned}$$

by cohomological descent from the above $\widetilde{\alpha }_{\mathrm{FM}}$. The above local arguments imply that $(\tau _{\le r} \widetilde{\alpha }_{\mathrm{FM}}){\otimes }^L{ {{\mathbf {Q}}}_p}$ is a quasi-isomorphism. We set ${\alpha }_{\mathrm{FM}}:=p^{-r}(\widetilde{\alpha }_{\mathrm{FM}}{\otimes }^L{ {{\mathbf {Q}}}_p})$. This twist by $p^{-r}$ is necessary to make the period morphism compatible with Chern classes.

It remains to show that $(\tau _{\le r} \widetilde{\alpha }_{\mathrm{FM}}){\otimes }^L{ {{\mathbf {Q}}}_p}\simeq \tau _{\le r} (\widetilde{\alpha }_{\mathrm{FM}}{\otimes }^L {{\mathbf {Q}}}_p)$ and that this quasi-isomorphism is strict.

Remark 6.2

Before doing that, let us recall how topology is defined on the domain and target of $\widetilde{\alpha }_{\mathrm{FM}}$. Locally, for a quasi-compact étale open $U\rightarrow X$, we get complexes of (topologically free) ${{\mathbf {Z}}} _p$-modules with p-adic topology. For a quasi-compact étale hypercovering $U_{{\scriptscriptstyle \bullet }}$ of X, we take the total complex of the Čech complex of such complexes. Hence in every degree we have a product of ${{\mathbf {Z}}} _p$-modules with p-adic topology. The functor $(-){\otimes } {{\mathbf {Q}}}_p$ from Sect. 2.2, by Proposition 2.6, associates to these complexes of pro-discrete ${{\mathbf {Z}}} _p$-modules complexes of locally convex ${{\mathbf {Q}}}_p$-vector spaces by tensoring them degree-wise with ${{\mathbf {Q}}}_p$ and taking the induced topology. These new complexes represent the domain and target of $\widetilde{\alpha }_{\mathrm{FM}}{\otimes }^L {{\mathbf {Q}}}_p$. We note that we have a strict quasi-isomorphism $\tau _{\le r}(\widetilde{\alpha }_{\mathrm{FM}}{\otimes }^L {{\mathbf {Q}}}_p)\simeq (\tau _{\le r}\widetilde{\alpha }_{\mathrm{FM}}){\otimes }^L {{\mathbf {Q}}}_p$ (again use Proposition 2.6).

Now, note that the map $\widetilde{\alpha }_{\mathrm{FM}}$, being a $p^N$-isomorphism on cohomology, has a $p^N$-inverse in $D(\mathrm {Ind}(PD_{ {{\mathbf {Q}}}_p}))$, i.e., $\widetilde{\beta }:\tau _{\le r}\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{C}, {{\mathbf {Z}}} _p(r)^{\prime })\rightarrow \tau _{\le r} \mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))$ such that $\widetilde{\alpha }\widetilde{\beta }=p^N$ and $\widetilde{\beta }\widetilde{\alpha }=p^N$ (not the same $N=N(r)$, of course). It follows that $(\tau _{\le r} \widetilde{\alpha }_{\mathrm{FM}}){\otimes }^L{ {{\mathbf {Q}}}_p}$ has an inverse in $D(C_{ {{\mathbf {Q}}}_p})$, hence it is strict. $\square$

6.2 Cohomology of differentials

We gather in this section computations of various bounded differential cohomologies of the Drinfeld half-space. Let

$$\begin{aligned} \widetilde{X}:=\widetilde{{{\mathbb {H}}}}^d_K,\quad {X}:=(\widetilde{{{\mathbb {H}}}}^d_K)^{\wedge } \end{aligned}$$

be the standard weak formal model, resp. formal model, of the Drinfeld half-space ${{\mathbb {H}}}^d_K$. It is equipped with an action of $G=\mathrm{GL}_{d+1}(K)$ compatible with the natural action on the generic fiber. Let

$$\begin{aligned} Y:=X_0,\quad \overline{Y}:=Y_{\overline{k}}. \end{aligned}$$

Let $F^0$ be the set of irreducible components of the special fiber Y. They are isomorphic smooth projective schemes over k that we see as log-schemes with the log-structure induced from Y. Let T be the central irreducible component of Y, i.e., the irreducible component with stabilizer $K^*\mathrm{GL}_{d+1}({{\mathscr {O}}}_K)$. It is obtained from the projective space ${{\mathbb {P}}}^d_k$ by first blowing up all k-rational points, then blowing up the strict transforms of k-rational lines, etc. For $0\le j\le d-1,$ let ${{\mathscr {V}}}^j_0$ be the set of all k-rational linear subvarieties Z of ${{\mathbb {P}}}^d_k$ with $\dim (Z)=j$ and let ${{\mathscr {V}}}_0:=\bigcup _{j=0}^{d-1}{{\mathscr {V}}}^j_0$. The set ${{\mathscr {V}}}$ of all strict transforms in T of elements of ${{\mathscr {V}}}_0$ is a set of divisors of T; together with the canonical log-structure of the log-point $k^0$, it induces the log-structure on T.

Let $\widetilde{\theta }_0,\ldots ,\widetilde{\theta }_d$ be the standard projective coordinate functions on ${{\mathbb {P}}}^d_k$ and on T. For $i,j\in \{0,\ldots ,d\}$ and $g\in G$ we call $g\mathrm {dlog} (\widetilde{\theta }_i/\widetilde{\theta }_j)$ a standard logarithmic differential 1-form on T; exterior products of such forms we call standard logarithmic differential forms on T.

6.2.1 Cohomology of differentials on irreducible components

As proved by Grosse-Klönne the sheaves of differentials on T are acyclic and the standard logarithmic differential forms generate the k-vector space of global differentials.

Proposition 6.3

([33, Th. 2.3, Th. 2.8], [35, Prop. 1.1])

• 1. $H^i(T,\Omega ^j)=0$, $i>0,j\ge 0$.

• 2. The k-vector space $H^0(T,\Omega ^j)$, $j\ge 0$, is generated by standard logarithmic forms. In particular, it is killed by d.

• 3. $H^i_{\mathrm {cr} }(T/{{\mathscr {O}}}_F^0)$ is torsion free and

  $$\begin{aligned} H^i_{\mathrm {cr} }(T/{{\mathscr {O}}}_F^0)\otimes _{{{\mathscr {O}}}_F}k=H^i_{\mathrm {dR} }(T)=H^0(T,\Omega ^i_T). \end{aligned}$$

We note here that, the underlying scheme of T being smooth, the crystalline cohomology $H^i_{\mathrm {cr} }(T/{{\mathscr {O}}}_F^0)=H^i_{\mathrm {cr} }(T^{\prime }/{{\mathscr {O}}}_F)$, where $T^{\prime }$ is the underlying scheme of T equipped with the log-structure given by the elements of ${{\mathscr {V}}}$.

For $0\le j\le d$, let ${{\mathbb {L}}}^j_T$ be the k-vector subspace of $\Omega ^j_T(T^0)$, $T^0:=T{\setminus }\cup _{V\in {{\mathscr {V}}}}V$, generated by all j-forms $\eta$ of the type

$$\begin{aligned} \eta =y_1^{m_1}\cdots y_j^{m_j}\mathrm {dlog} y_1\wedge \cdots \wedge \mathrm {dlog} y_j \end{aligned}$$

with $m_i\in {{\mathbf {Z}}}$ and $y_i\in {{\mathscr {O}}}(T^0)^*$ such that $y_j=\widetilde{\theta }_j/\widetilde{\theta }_0$ for an isomorphism of k-varieties ${{\mathbb {P}}}^d_k\simeq \mathrm{Proj} (k[\widetilde{\theta }_0,\cdots ,\widetilde{\theta }_d])$. By Theorem 6.3, $H^0(T,\Omega ^j)$ is the k-vector subspace of ${{\mathbb {L}}}^j_T$ generated by all j-forms $\eta$ as above with $m_i=0$ for all $0\le i\le j$.

Let ${{\mathbb {L}}}^j_T$, resp. ${{\mathbb {L}}}^{j,0}_T$, be the constant sheaf on T with values ${{\mathbb {L}}}^j_T$, resp. $H^0(T,\Omega ^j_T)$. For a non-empty subset S of ${{\mathscr {V}}}$ such that $E=\cap _{V\in S}V$ is non-empty, define the subsheaf ${{\mathbb {L}}}^j_E$ of $\Omega ^j_T\otimes {{\mathscr {O}}}_E$ as the image of the composite

$$\begin{aligned} {{\mathbb {L}}}^j_T\rightarrow \Omega ^j_T\rightarrow \Omega ^j_T\otimes {{\mathscr {O}}}_E. \end{aligned}$$

Proposition 6.4

([35, Th. 1.2]) The canonical maps

$$\begin{aligned} {{\mathbb {L}}}^{j,0}_T\hookrightarrow {{\mathbb {L}}}^j_T\hookrightarrow \Omega ^j_T, \quad {{\mathbb {L}}}^j_E\hookrightarrow \Omega ^j_T\otimes {{\mathscr {O}}}_E \end{aligned}$$

induce isomorphisms on Zariski cohomology groups.

6.2.2 Cohomology of differentials on X and truncations of Y

We quote an important result of Grosse-Klönne proving acyclicity of the sheaves of differentials on X and vanishing of the differential on their global sections.

Proposition 6.5

([33, Th. 4.5], [35, Prop. 4.5]) Let $j\ge 0$.

• 1. We have topological isomorphisms³⁵

  $$\begin{aligned}&H^i(X,\Omega ^j_X)=0\quad \mathrm{and}\quad H^i(X,\Omega ^j_X\otimes _{{{\mathscr {O}}}_K}k)=0,\quad i >0,\\&H^0(X,\Omega ^j_X)\otimes _{{{\mathscr {O}}}_K}k\simeq H^0(X,\Omega ^j_X\otimes _{{{\mathscr {O}}}_K}k). \end{aligned}$$

• 2. $d=0$ on $H^0(X,\Omega ^j_X).$

Corollary 6.6

We have topological isomorphisms $H^j_{\mathrm {dR} }(X){\mathop {\leftarrow }\limits ^{\sim }} H^0(X,\Omega ^j_X)$, for all $j\ge 0$. In particular, these groups are torsion-free.

The above theorem can be generalized to the idealized log-schemes $Y_s, s\in {{\mathbf {N}}},$ defined in Sect. 5.1 in the following way.

Proposition 6.7

Let $j\ge 0$, $s\in {{\mathbf {N}}}$.

• 1. $H^i(Y_s,\Omega ^j)=0$ for $i>0$.

• 2. $d=0$ on $H^0(Y_s,\Omega ^j).$

Proof

For the first claim, the argument is analogous to the one of Grosse-Klönne for $s=\infty$. We will sketch it briefly. Take $s\ne \infty$. Since $\Omega ^j_{Y_s}$ is locally free over ${{\mathscr {O}}}_{Y_s}$, we have the Mayer–Vietoris exact sequence

$$\begin{aligned} 0\rightarrow \Omega ^j_{Y_s}\rightarrow \bigoplus _{Z\in F^0_s}\Omega ^j_{Y_s}\otimes {{\mathscr {O}}}_Z\rightarrow \bigoplus _{Z\in F^1_s}\Omega ^j_{Y_s}\otimes {{\mathscr {O}}}_Z\rightarrow \cdots \end{aligned}$$

where $F^r_s$ is the set of non-empty intersections of $(r+1)$ pairwise distinct irreducible components of $Y_s$ and is a finite set (which is also the set of r-simplices of $\mathrm{BT}_s$). By [33, Cor. 1.6], $H^i(Z,\Omega ^j_{Y_s}\otimes {{\mathscr {O}}}_Z)=0$, $i>0$, for every $Z\in F^r_s$. Hence to show that $H^i(Y_s,\Omega ^j_{Y_s})=0$, $i>0$, we need to prove that $H^i(\mathrm{BT}_s,{{\mathscr {F}}})=0$, for $i>0$, where ${{\mathscr {F}}}$ is the coefficient system on $\mathrm{BT}_s$ defined by ${{\mathscr {F}}}(Z)=H^0(Y,\Omega ^j_{Y_s}\otimes {{\mathscr {O}}}_Z)$, for $Z\in F^r_s$. We will use for that an analog of Grosse-Klönne’s acyclicity condition. For a lattice chain in $\mathrm{BT}_s$

$$\begin{aligned} \varpi L_r\subsetneq L_1\subsetneq \cdots \subsetneq L_r \end{aligned}$$

we call the ordered r-tuple $([L_1],\ldots ,[L_r])$, a pointed $(r-1)$-simplex (with underlying $(r-1)$-simplex the unordered set $\{[L_1],\ldots ,[L_r]\}$). Denote it by $\widehat{\eta }$ and consider the set

$$\begin{aligned} N_{\widehat{\eta }}=\{[L]\mid \varpi L_r\subsetneq L\subsetneq L_1\}. \end{aligned}$$

We note that $N_{\widehat{\eta }}$ is a subset of vertices of $\mathrm{BT}_s$. A subset $M_0$ of $N_{\widehat{\eta }}$ is called stable if, for all $L,L^{\prime }\in M_0$, the intersection $L\cap L^{\prime }$ also lies in $M_0$.$\square$

Lemma 6.8

Let ${{\mathscr {F}}}$ be a cohomological coefficient system on $\mathrm{BT}_s$. Let $1\le r \le d$. Suppose that for any pointed $(r-1)$-simplex $\widehat{\eta }\in \mathrm{BT}_s$ with underlying $(r-1)$-simplex $\eta$ and for any stable subset $M_0$ of $N_{\widehat{\eta }}$ the following subquotient complex of the cochain complex $C(\mathrm{BT}_s,{{\mathscr {F}}})$ with values in ${{\mathscr {F}}}$ is exact

$$\begin{aligned} {{\mathscr {F}}}(\eta )\rightarrow \prod _{z\in M_0}{{\mathscr {F}}}(\{z\}\cup \eta )\rightarrow \prod _{z,z^{\prime }\in M_0,\{z,z^{\prime }\}\in \mathrm {F} ^1_s}{{\mathscr {F}}}(\{z,z^{\prime }\}\cup \eta ). \end{aligned}$$

Then the r-th cohomology group $H^s(\mathrm{BT}_s,{{\mathscr {F}}})$ of $C(\mathrm{BT}_s,{{\mathscr {F}}})$ vanishes.

Proof

For $\mathrm{BT}$ this is the main theorem of [34]. The argument used in its proof [34, Th. 1.2] carries over to our case: when applied to a cocycle from $\mathrm{BT}_s$, the recursive procedure of producing a coboundary in the proof of Theorem 1.2 in loc. cit. “does not leave” $\mathrm{BT}_s$. $\square$

Hence it suffices to check that the above condition is satisfied for our ${{\mathscr {F}}}$. But this was checked in [33, Cor. 1.6].

The second claim of the proposition follows from Proposition 6.3 and the injection

6.2.3 Ordinary log-schemes

A quick review of basic facts concerning ordinary log-schemes.

Let $W_n\Omega _{Y}^{\scriptscriptstyle \bullet }$ denotes the de Rham–Witt complex of $Y/k^0$ [37]. Recall first [40, Prop. II.2.1] that if T is a log-smooth and proper log-scheme over $k^0$, for a perfect field k of positive characterstic p, then $H^i_{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^j)$ is of finite length and we have $\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^j) {\mathop {\rightarrow }\limits ^{\sim }} \mathrm {holim}\, _n\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^j)$ for $W\Omega ^j:=\varprojlim _n W_n\Omega ^j$. It follows that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^j) {\mathop {\rightarrow }\limits ^{\sim }} \varprojlim _nH^i_{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^j).$ The module $M_{i,j}$ of p-torsion of this group is annihilated by a power of p and $H^i_{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^j)/M_{i,j}$ is a free ${{\mathscr {O}}}_F$-module of finite type [40, Th. II.2.13]. However, $H^0_{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^j)$ is itself a free ${{\mathscr {O}}}_F$-module of finite type [40, Cor. II.2.17 ]. On the other hand, the complex $\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^{\scriptscriptstyle \bullet })$ is perfect and $\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W\Omega ^{\scriptscriptstyle \bullet })\otimes ^L_{{{\mathscr {O}}}_F}{{\mathscr {O}}}_{F,n}\simeq \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^{\scriptscriptstyle \bullet })$ [40, Th. II.2.7].

Let V be a fine (idealized) log-scheme over $k^0$ that is of Cartier type. We have the subsheaves of boundaries and cocycles of $\Omega ^j_V$ (thought of as sheaves on $V_{\acute{\mathrm{e}}\mathrm {t}}$)

$$\begin{aligned} B^j_V:=\mathrm {im}\, (d:\Omega ^{j-1}_V\rightarrow \Omega ^j_V),\quad Z^j_V:=\ker (d:\Omega ^j_V\rightarrow \Omega ^{j+1}_V). \end{aligned}$$

Assume now thatVis proper and log-smooth. Recall that it is called ordinary if for all $i,j\ge 0$, $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,B^j)=0$ (see [7, 41]).

We write $W_n\Omega ^r_{{-},\log }$ for the de Rham-Witt sheaf of logarithmic forms.

Proposition 6.9

([52, Th. 4.1]) The following conditions are equivalent (we write $\overline{V}$ for $V_{\overline{k}}$).

• 1. $V/k^0$ is ordinary.

• 2. For $i,j\ge 0$, the inclusion $\Omega ^j_{\overline{V},\log } \subset \Omega ^j_{\overline{V}}$ induces a canonical isomorphism of $\overline{k}$-vector spaces

  $$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V}, \Omega ^j_{\log })\otimes _{{{\mathbf {F}}}_p}\overline{k}{\mathop {\rightarrow }\limits ^{\sim }} H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V},\Omega ^j). \end{aligned}$$

• 3. For $i,j,n\ge 0$, the canonical maps

  $$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V},W_n\Omega ^j_{\log })\otimes _{ {{\mathbf {Z}}} /p^n}W_n(\overline{k})&\rightarrow H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V},W_n\Omega ^j),\\ H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V},W\Omega ^j_{\log })\otimes _{ {{\mathbf {Z}}} _p}W(\overline{k})&\rightarrow H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{V},W\Omega ^j), \end{aligned}$$

  where $W\Omega ^r_{\log }:=\varprojlim _nW_n\Omega ^r_{\log }$, are isomorphisms.

• 4. For $i,j\ge 0$, the de Rham–Witt Frobenius

  $$\begin{aligned} \mathrm{F}: H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,W\Omega ^j)\rightarrow H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,W\Omega ^j) \end{aligned}$$

  is an isomorphism.

Example 6.10

The above result implies that, by the Projective Space Theorem, projective spaces are ordinary, and, more generally, so are projectivizations of vector bundles [42, Prop. 1.4]. This implies, by the blow-up diagram, the following:

Proposition 6.11

([42, Prop. 1.6]) Let X be a proper smooth scheme over k. Let $Y\subset X$ be a smooth closed subscheme, $\widetilde{X}$ the blow-up of Y in X. Then X and Y are ordinary if and only if $\widetilde{X}$ is ordinary.

And this, in turn, by the weight spectral sequence, implies the following:

Proposition 6.12

([42, Prop. 1.10]) Assume that $k=\overline{k}$. Let Y be a semistable scheme over k. Assume that it is a union of irreducible components $Y_i$, $1 \le i \le r$ such that for all $I \subset \{1,\cdots ,r\}$, the intersection $Y_I$ is smooth and ordinary. Then Y, as a log-scheme over $k^0$, is ordinary.

Proof

As suggested by Illusie in [42, Rem. 2.8], this can be proved using the weight spectral sequence

$$\begin{aligned} E^{-k,i+k}_1&=\bigoplus _{j\ge 0, j\ge -k}H^{i-s-j}_{\acute{\mathrm{e}}\mathrm {t}}(Y_{2j+k+1},W\Omega ^{s-j-k})(-j-k)\Rightarrow H^{i-s}_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^s). \end{aligned}$$

Here $Y_{t}$ denotes the intersection of t different irreducible components of Y that are equipped with the trivial log-structure. Such spectral sequences were constructed in [57, 3.23], [58, 4.1.1]. They are Frobenius equivariant (the Tate twist $(-j-k)$ refers to the twist of Frobenius by $p^{j+k}$) [58, Th. 9.9]; hence, without the Twist twist, compatible with the de Rham–Witt Frobenius F.

Now, by assumptions, all the schemes $Y_t$ are smooth and ordinary. It follows, by Proposition 6.9, that the Frobenius F induces an isomorphism on $E^{-k,i+k}_1$. Hence also on the abutment $H^{i-s}_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^s_Y)$, as wanted. $\square$

We drop now the assumption thatVis proper. Recall that we have the Cartier isomorphism

$$\begin{aligned} C: Z^j/ B^j {\mathop {\rightarrow }\limits ^{\sim }}\Omega ^j,\quad x^p\mathrm {dlog} y_1\wedge \ldots \wedge \mathrm {dlog} y_j \mapsto x\mathrm {dlog} y_1\wedge \ldots \wedge \mathrm {dlog} y_j. \end{aligned}$$

Lemma 6.13

Assume that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)=0$ and that $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)$ for all $i\ge 1$ and $j\ge 0$. Then V is ordinary [52, § 4], i.e., for $i,j\ge 0$, we have $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V, B^j)=0.$

Proof

Consider the exact sequences

$$\begin{aligned} 0\rightarrow B^j\rightarrow Z^j{\mathop {\rightarrow }\limits ^{f}} \Omega ^j\rightarrow 0,\quad 0\rightarrow Z^j\rightarrow \Omega ^j\rightarrow B^{j+1}\rightarrow 0, \end{aligned}$$

(6.14)

where the map f is the composition $Z^j\rightarrow Z^j/B^j{\mathop {\rightarrow }\limits ^{\sim }} \Omega ^j$ of the natural projection and the Cartier isomorphism. Since $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)=0,i >0,$ the first exact sequence yields the isomorphisms

$$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(V, B^j){\mathop {\rightarrow }\limits ^{\sim }} H^i_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^j),\quad i\ge 2. \end{aligned}$$

(6.15)

It also yields the long exact sequence

$$\begin{aligned} 0\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, B^j) {\rightarrow } H^0_{\acute{\mathrm{e}}\mathrm {t}}( V,Z^j){\rightarrow } H^0_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j){\mathop {\rightarrow }\limits ^{\partial }} H^1_{\acute{\mathrm{e}}\mathrm {t}}(V, B^j){\rightarrow } H^1_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^j)\rightarrow 0. \end{aligned}$$

(6.16)

Since $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)$ and hence the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^j)\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)$ is an isomorphism, the second exact sequence from (6.14) yields the isomorphisms (since we assumed $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,\Omega ^j)=0$ for $i>0$)

$$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(V, B^{j+1}){\mathop {\rightarrow }\limits ^{\sim }} H^{i+1}_{\acute{\mathrm{e}}\mathrm {t}}( V,Z^j),\quad i\ge 0. \end{aligned}$$

(6.17)

To prove the lemma, we will argue by increasing induction on j; the case of $j=0$ being trivial since $B^0=0$. Assume thus that our lemma is true for j and all $i\ge 0$. We will show that this implies that it is true for $j+1$ and all $i\ge 0$. Since $H^1_{\acute{\mathrm{e}}\mathrm {t}}( V, B^j)=0$ by assumption, the exact sequence (6.16) implies that $H^1_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^j)=0$. And this implies, by (6.15), that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^r)=0,i\ge 1$. This, in turn, yields, by (6.17), that $H^i_{\acute{\mathrm{e}}\mathrm {t}}( V, B^{j+1})=0$, $i\ge 0$. This concludes the proof of the lemma. $\square$

6.2.4 ${{\mathbb {H}}}_K$ as a pro-ordinary log-scheme

It follows from Lemma 6.13 and Proposition 6.7 that:

Corollary 6.18

The idealized log-schemes $Y_s, s\in {{\mathbf {N}}}\cup \{\infty \}$, are ordinary.

Remark 6.19

Proposition 6.12 and Proposition 6.11 show that the underlying scheme of $Y_s,$ for $s<\infty ,$ is (classically) ordinary by using the weight spectral sequence. One should be able to prove Corollary 6.18 in an analogous way.

Lemma 6.20

For $i\ge 1, j\ge 0$, we have

• 1. $H^i_{\acute{\mathrm{e}}\mathrm {t}}(Z, W_n\Omega ^j)=0$, for $Z=Y,T$,

• 2. $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^j)$.

• 3. For $V=Y,\overline{Y}$, the following sequence is strictly exact³⁶

  $$\begin{aligned}0\rightarrow H^0(V, \Omega ^j){\mathop {\rightarrow }\limits ^{V^n}} H^0(V, W_{n+1}\Omega ^j)\rightarrow H^0(V, W_n\Omega ^j)\rightarrow 0, \end{aligned}$$

Proof

For claim (1), we start with $Z=Y$. We have subsheaves

$$\begin{aligned} 0=B_0^j\subset B^j_1\subset \ldots \subset Z^j_1\subset Z^j_0=\Omega ^j_Y \end{aligned}$$

such that $B_1^j=B^j_Y$, $Z_0^j=\Omega ^j_Y$, $Z_1^j=Z^j_Y$ and for all n we have inverse Cartier isomorphisms

$$\begin{aligned} C^{-1}:B_n^j{\mathop {\rightarrow }\limits ^{\sim }} B^j_{n+1}/B^j_1, \quad C^{-1}: Z^j_n{\mathop {\rightarrow }\limits ^{\sim }} Z^j_{n+1}/B^j_1. \end{aligned}$$

By Proposition 6.5 and Lemma 6.13, we have $H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,B^j_1)=H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,Z^j_1)=0$ for $i>0$, thus the same holds with $B^j_1$ and $Z^j_1$ replaced by $B^j_n$ and $Z^j_n$. On the other hand, define $R_n^j$ by the exact sequence

$$\begin{aligned} 0\rightarrow R_n^j\rightarrow B_{n+1}^j\oplus Z^{j-1}_n\rightarrow B^j_1\rightarrow 0, \end{aligned}$$

(6.21)

the last map being $(C^n, dC^{n-1})$. By the previous discussion, $H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,R_n^j)=0$ for $i>0$. Hyodo and Kato prove [38, Th. 4.4] that we have an exact sequence

$$\begin{aligned} 0\rightarrow \frac{\Omega ^j\oplus \Omega ^{j-1}}{R_n^j}\rightarrow W_{n+1}\Omega ^j\rightarrow W_n\Omega ^j\rightarrow 0. \end{aligned}$$

(6.22)

Note that $\frac{\Omega ^j\oplus \Omega ^{j-1}}{R_n^j}$ does not have higher cohomology since each of $\Omega ^j, \Omega ^{j-1}, R_n^j$ has this property (use Proposition 6.5). Using the previous exact sequence, the result follows by induction on n (using that $W_1\Omega ^j\simeq \Omega ^j$).

In the case of $Z=T$ we argue in a similar way using Proposition 6.3 instead of Proposition 6.5.

For claim (2), since $\Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T,W_n\Omega ^j)\hookrightarrow \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(T_{\overline{k}},W_n\Omega ^j)$, we can pass to $T_{\overline{k}}$. But then, by ordinarity of $T_{\overline{k}}$, we have (see Proposition 6.9)

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(T_{\overline{k}},W_n\Omega ^j)\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(T_{\overline{k}},W_n\Omega ^j_{\log })\otimes _{ {{\mathbf {Z}}} /p^n}W_n(\overline{k}) \end{aligned}$$

and the latter group clearly has a trivial differential.

To prove claim (3), we note first that Lemma 6.13 applies to both Y and $\overline{Y}$. For Y this follows from Proposition 6.5. For $\overline{Y}$, we use Corollary 6.18 to write down a sequence of quasi-isomorphisms

$$\begin{aligned} \mathrm {R} \Gamma (\overline{Y},\Omega ^j)&\simeq \mathrm {holim}\, _s\mathrm {R} \Gamma (\overline{Y}^{\circ }_s,\Omega ^j)\simeq \mathrm {holim}\, _s\mathrm {R} \Gamma (\overline{Y}_s,\Omega ^j)\\&\simeq \mathrm {holim}\, _sH^0(\overline{Y}_s,\Omega ^j)\simeq \varprojlim _sH^0(\overline{Y}_s,\Omega ^j). \end{aligned}$$

It follows that $H^i(\overline{Y},\Omega ^j)=0$ for $i>0$. To see that $d=0$ on $H^0(\overline{Y},\Omega ^j)$ we use the embedding $H^0(\overline{Y},\Omega ^j)\hookrightarrow \prod _{C\in F^0}H^0(\overline{C},\Omega ^j)$ and Proposition 6.3.

Now, set $V=Y,\overline{Y}$. By Lemma 6.13, we have $H^i_{\acute{\mathrm{e}}\mathrm {t}}(V,B^j)=0$$i,j\ge 0$. Note that, by (6.22), we have the exact sequence

It remains to show that the natural map from $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, \Omega ^j)$ to the leftmost term is an isomorphism, or that, the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, R_n^j)\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, \Omega ^{j-1})$ is an isomorphism. The exact sequence (6.21) yields that the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, R_n^j)\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, Z_n^{j-1})$ is an isomorphism. It remains thus to show that so is the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, Z_n^{j-1})\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, \Omega ^{j-1})$.

For that it suffices to show that the natural maps $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, Z_{n+1}^{j-1})\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, Z^{j-1}_n)$, $n\ge 0$, are isomorphisms. We will argue by induction on $n\ge 0$. Since $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(V, \Omega ^{j-1})$ this is clear for $n=0$. Assume now that this is true for $n-1$. We will show it for n itself. Consider the commutative diagram

The right vertical map is an isomorphism by the inductive assumption. The top and bottom isomorphisms follow from the isomorphisms $C^{-1}: Z^j_i{\mathop {\rightarrow }\limits ^{\sim }}Z^j_{i+1}/B^j_1$, for $i\ge 0$. We get that the left vertical map is an isomorphism, as wanted.

Finally, to see that the exact sequence in claim (3) is strictly exact note that for Y this follows from compactness of $H^0(Y,\Omega ^j)$ and $H^0(Y,W_{n+1}\Omega ^j)$ and for $\overline{Y}$ this follows from the case of Y by étale base change. $\square$

6.2.5 Cohomology of differentials II

We will need a generalization of the above results and a more careful discussion of topological issues.

Proposition 6.23

Let $j\ge 0$. Let S be a topological ${{\mathscr {O}}}_K$-module and let R be a topological W(k)- or $W(\overline{k})$-module. Assume that S and R are topologically orthonormalizable.

• 1. The following natural maps are strict quasi-isomorphisms (in ${{\mathscr {D}}}(\mathrm {Ind}(PD_?))$, with $?=K,F, {{\mathbf {Q}}}_p$)

  $$\begin{aligned} H^0(X,\Omega ^j_{X,n})\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n&{\mathop {\rightarrow }\limits ^{\sim }} \mathrm {R} \Gamma (X,\Omega ^j_{X,n})\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n,\\ H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}R_n&\overset{\sim }{\rightarrow }\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}R_n,\\ \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n&\overset{\sim }{\rightarrow }\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j) \widehat{\otimes }_{W_n(\overline{k})}R_n,\\ H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n&\overset{\sim }{\rightarrow } \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n. \end{aligned}$$

• 2. $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}({X},\Omega ^j_{{X},n})\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n$ and on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^j_{Y}) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n .$

• 3. The following natural map is a strict quasi-isomorphism

  $$\begin{aligned} \bigoplus _{j\ge r}H^0(X,\Omega ^j_{X,n})[-j]{\mathop {\rightarrow }\limits ^{\sim }}F^r\mathrm {R} \Gamma _{\mathrm {dR} }(X_n), \quad r\ge 0. \end{aligned}$$

Remark 6.24

The completed tensor products for the above complexes of pro-discrete modules can be made more explicit using a Stein covering $\{U_i\},\,i\in {{\mathbf {N}}}$ of Y. For example:

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F,n}^0) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}{\widehat{\mathbf{A}}}_{\mathrm {st} ,n}\simeq \mathrm {holim}\, _i (\mathrm {R} \Gamma _{\mathrm {cr} }(U_{i}/{{\mathscr {O}}}_{F,n}^0) {\otimes }_{{{\mathscr {O}}}_{F,n}}{\widehat{\mathbf{A}}}_{\mathrm {st} ,n}). \end{aligned}$$

Note that ${\widehat{\mathbf{A}}}_{\mathrm {st} ,n}$ has discrete topology.

Proof

Note that the last claim follows from the previous two claims.

In the rest of the proof, to lighten the notation, we will write simply $\mathrm {R} \Gamma (Z,\Omega ^{\scriptscriptstyle \bullet }_n):=\mathrm {R} \Gamma (Z,\Omega ^{\scriptscriptstyle \bullet }_{Z,n})$ for the de Rham cohomology of the log-scheme $Z_n$. We have the spectral sequence

$$\begin{aligned} E_2^{q,i}=\widetilde{H}^q\mathrm {holim}\, _s (\widetilde{H}^i_{}({Y}^{\circ }_s,\Omega ^j_n){\otimes }_{{{\mathscr {O}}}_{K,n}} S_n)\Rightarrow \widetilde{H}^{q+i}_{}(\mathrm {R} \Gamma (X,\Omega ^j_n)\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n). \end{aligned}$$

Since the pro-systems

$$\begin{aligned} \{\widetilde{H}^i_{}({Y}^{\circ }_s,\Omega ^j_{n}){\otimes }_{{{\mathscr {O}}}_{K,n}} S_n\},s\ge 0,\quad \{\widetilde{H}^i_{}({Y}_s,\Omega ^j_{n}){\otimes }_{{{\mathscr {O}}}_{K,n}} S_n\},s\ge 0, \end{aligned}$$

are equivalent (and $\widetilde{H}^i_{}({Y}_s,\Omega ^j_{n})$ is classical and of finite type since $Y_s$ is ideally log-smooth and proper over $k^0$), they both have trivial $\widetilde{H}^q\mathrm {holim}\, _s$, $q>0$. Hence the spectral sequence degenerates and we have

$$\begin{aligned} \widetilde{H}^i_{}(\mathrm {R} \Gamma (X,\Omega ^j_{n})\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n) \simeq \varprojlim _s(\widetilde{H}^i_{}({Y}^{\circ }_s,\Omega ^j_{n}){\otimes }_{{{\mathscr {O}}}_{K,n}} S_n)\simeq \varprojlim _s(H^i_{}({Y}_s,\Omega ^j_{n}){\otimes }_{{{\mathscr {O}}}_{K,n}} S_n). \end{aligned}$$

In particular, it is classical.

Moreover, using a basis $\{e_{\lambda }\}, \lambda \in I,$ of $S_n$ over ${{\mathscr {O}}}_{K,n}$, we get an embedding

$$\begin{aligned} \varprojlim _s(\widetilde{H}^{i}(Y^{\circ }_s,\Omega ^j_{n}){\otimes }_{{{\mathscr {O}}}_{K,n}}S_n) \hookrightarrow \prod _{\lambda \in I} H^{i}_{}(X,\Omega ^j_{n})e_{\lambda } \end{aligned}$$

Since the latter groups are trivial for $i>0$, by Proposition 6.5, the vanishing of $\widetilde{H}^i_{}(\mathrm {R} \Gamma (X,\Omega ^j_{n})\widehat{\otimes }_{{{\mathscr {O}}}_{K,n}} S_n)$ follows. This embedding also shows that $d=0$ on $H^0$ in part (2) of the proposition.

The proof for the second map in part (1) of the proposition is analogous with Lemma 6.20 replacing Proposition 6.5.

For the proof for the third map in part (1) of the proposition, consider now the sequence of strict quasi-isomorphisms

$$\begin{aligned} \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}&,W_n \Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n = \mathrm {holim}\, _s(\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}^{\circ }_s,W_n\Omega ^j_{\log }) {\otimes }_{ {{\mathbf {Z}}} /p^n}R_n)\\&\simeq \mathrm {holim}\, _s(\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s,W_n\Omega ^j_{\log }) {\otimes }_{ {{\mathbf {Z}}} /p^n}R_n) \overset{\sim }{\rightarrow } \mathrm {holim}\, _s(\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s,W_n\Omega ^j) {\otimes }_{W_n(\overline{k})}R_n)\\&\simeq \mathrm {holim}\, _s(\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}^{\circ }_s,W_n\Omega ^j_{}) {\otimes }_{W_n(\overline{k})}R_n) = \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j) \widehat{\otimes }_{W_n(\overline{k})}R_n. \end{aligned}$$

The second and the fourth strict quasi-isomorphisms are clear. The third strict quasi-isomorphism follows from the fact that, by Corollary 6.18, the log-scheme $\overline{Y}_s$ is ordinary and we have Proposition 6.9.

For the fourth strict quasi-isomorphism in part (1) of the proposition, use the second and the third one to reduce to showing that we have a natural topological isomorphism

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j) \widehat{\otimes }_{W_n(\overline{k})}R_n. \end{aligned}$$

But, by Proposition 6.9, we have topological isomorphisms

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}} (\overline{Y},W_n\Omega ^j_{\log })&\widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}R_n=\varprojlim _s (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}^{\circ }_s,W_n\Omega ^j_{\log }) {\otimes }_{ {{\mathbf {Z}}} /p^n}R_n)\\&\simeq \varprojlim _s (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s,W_n\Omega ^j_{\log }) {\otimes }_{ {{\mathbf {Z}}} /p^n}R_n) \simeq \varprojlim _s (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s,W_n\Omega ^j) {\otimes }_{W_n(\overline{k})}R_n)\\&\simeq \varprojlim _s (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}^{\circ }_s,W_n\Omega ^j) {\otimes }_{W_n(\overline{k})}R_n) = H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j) \widehat{\otimes }_{W_n(\overline{k})}R_n. \end{aligned}$$

It remains to show that $d=0$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}({Y},W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}R_n$. First assume R to be a $W(\overline{k})$-module. Arguing as above we obtain an embedding (notation as above)

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}R_n \overset{\sim }{\longrightarrow } H^0_{\acute{\mathrm{e}}\mathrm {t}}({\overline{Y}},W_n\Omega ^j_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}\mathrm {R} _n \hookrightarrow \prod _{\lambda \in I} H^0_{\acute{\mathrm{e}}\mathrm {t}}({\overline{Y}},W_n\Omega ^j_{\log }) e_{\lambda }. \end{aligned}$$

$d=0$ follows. If R is only a W(k)-module, we write

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}({Y},W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}R_n\hookrightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^j) \widehat{\otimes }_{{{\mathscr {O}}}_{F,n}}(W_n(\overline{k})\otimes _{{{\mathscr {O}}}_{F,n}} R_n) \end{aligned}$$

to obtain $d=0$ in this case as well. $\square$

Corollary 6.25

• 1. For $j\ge 0$, we have a canonical topological isomorphism³⁷

  $$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })\widehat{\otimes }_{{{\mathbf {F}}}_p}\overline{k}{\mathop {\rightarrow }\limits ^{\sim }} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},\Omega ^j). \end{aligned}$$

• 2. For $j,n\ge 0$, the canonical maps

  $$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log })\widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}W_n(\overline{k})&\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j),\\ H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^j_{\log })\widehat{\otimes }_{ {{\mathbf {Z}}} _p}W(\overline{k})&\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^j) \end{aligned}$$

  are topological isomorphisms.³⁸ In higher degrees all the above cohomology groups are trivial.

• 3. The cohomologies $\widetilde{H}^i(X, \Omega ^j_X)$ and $\widetilde{H}^j_{\mathrm {dR} }(X)$ are classical, ${H}^i(X, \Omega ^j_X)=0$ for $i>0$, and ${H}^j_{\mathrm {dR} }(X)\simeq {H}^0(X, \Omega ^j_X).$

Proof

The first two quasi-isomorphisms are actually included in the above proposition. For the third quasi-isomorphism, both sides are nontrivial only in degree zero: by Lemma 6.20 and the second isomorphism of this corollary, the projective systems $\{H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j_{\log })\widehat{\otimes }_{ {{\mathbf {Z}}} /p^n}W_n(\overline{k})\}_n$ and $\{H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^j)\}_n$ are Mittag–Leffler. In degree zero we pass, as usual, to the limit over the truncated subschemes of the special fiber and there, since these subschemes are ordinary, we have a term-wise isomorphism, as wanted.

For the cohomology $\widetilde{H}^i(X, \Omega ^j_X)$, the fact that it is classical follows from the fact that the cohomology $\widetilde{H}^i(X_n, \Omega ^j)$ is classical and nontrivial only for $i=0$, which was proved in Proposition 6.23, and the fact that the natural maps $H^0(X_{n+1},\Omega ^j)\rightarrow H^0(X_n,\Omega ^j)$ are surjective: a direct consequence, via Proposition 6.23, of Lemma 6.20.

For the cohomology $\widetilde{H}^j_{\mathrm {dR} }(X)$, we have $\widetilde{H}^j_{\mathrm {dR} }(X_n){\mathop {\leftarrow }\limits ^{\sim }} H^0(X_n,\Omega ^j)$ by Proposition 6.23. It follows, since the maps $H^0(X_{n+1},\Omega ^j)\rightarrow H^0(X_n,\Omega ^j)$ are surjective, taht $\widetilde{H}^j_{\mathrm {dR} }(X)$ is classical (by a Mittag–Leffler argument). $\square$

Remark 6.26

There is an alternative argument which proves Proposition 6.23 and which does not use ordinarity of the truncated log-scheme $Y_s$. It starts with proving the above corollary. We present it in the Appendix.

6.2.6 de Rham cohomologies of the model and the generic fiber

Proposition 6.27 below will be crucial in understanding the de Rham cohomology of the model and its variants. Define the map

$$\begin{aligned} \iota _Y: H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet }_Y)\simeq H^i_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F)\rightarrow H^i_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F,F){\mathop {\leftarrow }\limits ^{\sim }}H^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}^0_F){\mathop {\longrightarrow }\limits ^{\iota _{\mathrm {HK} }}}H^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}^{\times }_K). \end{aligned}$$

Proposition 6.27

• 1. The above map induces an injection

  $$\begin{aligned} \iota _Y: H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet }){\otimes }_{{{\mathscr {O}}}_F}K\hookrightarrow H^i_{\mathrm {rig} }(Y/{{\mathscr {O}}}^{\times }_K). \end{aligned}$$

• 2. The canonical map

  $$\begin{aligned} H^i_{\mathrm {dR} }(X){\otimes }_{{{\mathscr {O}}}_K}K\rightarrow H^i_{\mathrm {dR} }(X_K) \end{aligned}$$

  is injective.

Proof

For the first claim, it suffices to show that we have a commutative diagram

where ${C_j},j\in {{\mathbf {N}}}$, is the set of irreducible components of Y and the map $\iota _{C_j}$ is defined in an analogous way to the map $\iota _Y$ but by replacing the Hyodo–Kato map by the composition

$$\begin{aligned} H^i_{\mathrm {rig} }(C_j/{{\mathscr {O}}}^0_F){\mathop {\rightarrow }\limits ^{\sim }} H^i_{\mathrm {rig} }(C_j^0/{{\mathscr {O}}}^0_F){\mathop {\longrightarrow }\limits ^{\iota _{\mathrm {HK} }}} H^i_{\mathrm {rig} }(C_j^0/{{\mathscr {O}}}^{\times }_K){\mathop {\leftarrow }\limits ^{\sim }} H^i_{\mathrm {rig} }(C_j/{{\mathscr {O}}}^{\times }_K). \end{aligned}$$

Since the Hyodo–Kato map is compatible with Zariski localization the above diagram commutes.

We claim that we have natural isomorphisms

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^i){\mathop {\rightarrow }\limits ^{\sim }} H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet }),\quad H^0_{\acute{\mathrm{e}}\mathrm {t}}(C_j,W\Omega ^i){\mathop {\rightarrow }\limits ^{\sim }} H^i_{\acute{\mathrm{e}}\mathrm {t}}(C_j,W\Omega ^{\scriptscriptstyle \bullet }). \end{aligned}$$

Indeed, set $Z=Y,C_j$. We have $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Z,W\Omega ^i)=\varprojlim _nH^0_{\acute{\mathrm{e}}\mathrm {t}}(Z,W_n\Omega ^i)$. Since, by Proposition 6.23 and Lemma 6.20,

$$\begin{aligned}\mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(Z,W_n\Omega ^{\scriptscriptstyle \bullet })\simeq \oplus _jH^0_{\acute{\mathrm{e}}\mathrm {t}}(Z,W_n\Omega ^j)[-j], \end{aligned}$$

this implies that

$$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(Z,W\Omega ^{\scriptscriptstyle \bullet })\simeq \varprojlim _nH^i_{\acute{\mathrm{e}}\mathrm {t}}(Z,W_n\Omega ^{\scriptscriptstyle \bullet })\simeq \varprojlim _nH^0_{\acute{\mathrm{e}}\mathrm {t}}(Z,W_n\Omega ^i), \end{aligned}$$

as wanted. In particular, there is no torsion.

It follows that the maps $\iota _{C_j}$ in the above diagram are injections: they are isomorphisms after tensoring the domains with K and the domains are torsion-free. The map $\alpha$ is an injection because so is, by definition, the map $\alpha ^{\prime }$ in the commutative diagram

where $Y_{ \mathrm {tr} }$ denotes the nonsingular locus of Y.

We note that the above computation shows also that the natural map $H^i_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F){\otimes }_{{{\mathscr {O}}}_F}F\rightarrow H^i_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F,F)$ is an injection. This will be useful in proving the second claim of the proposition. Using the diagram (7.7) we can form a commutative diagram

Here the first map $\iota _{\mathrm {HK} }$ is the bounded Hyodo–Kato isomorphism described in Chapter 7. Since the first bottom map is an injection so is the top map, as wanted. $\square$

6.3 Relation to Steinberg representations

We proved in the previous section that, for all $i>0$, the spaces $H^i_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^r)$ and $H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log })$ vanish. The purpose of this section is to prove the following result describing the corresponding spaces for $i=0$ in terms of generalized Steinberg representations.

Theorem 6.28

Let $r\ge 0$.

• 1. We have natural isomorphisms of locally convex topological ${{\mathbf {Q}}}_p$-vector spaces (more precisely, weak duals of Banach spaces)

  • (a) $H^0(Y, W\Omega ^r){\otimes }_{{{\mathscr {O}}}_F}F\simeq H^r(Y, W\Omega ^{\scriptscriptstyle \bullet }){\otimes }_{{{\mathscr {O}}}_F}F\simeq \mathrm{Sp}^{\mathrm {cont} }_r(F)^*$,

  • (b) $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, W\Omega ^r_{\mathrm{log}}){\otimes } {{\mathbf {Q}}}_p\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^*$,

  • (c) $H^0(X,\Omega ^r){\otimes }_{{{\mathscr {O}}}_K}K\simeq H^r_{\mathrm {dR} }(X){\otimes }_{{{\mathscr {O}}}_K}K\simeq \mathrm{Sp}_r^{\mathrm {cont} }(K)^*$,

  • (d) $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\mathrm{log}}){\otimes } {{\mathbf {Q}}}_p\simeq \mathrm{Sp}_r^{\mathrm {cont} }( {{\mathbf {Q}}}_p)^*.$

  They are compatible with the canonical maps between Steinberg representations and with the isomorphisms

  $$\begin{aligned} H^r_{\mathrm {dR} }(X_K)\simeq \mathrm{Sp}_r(K)^*,\quad H^r_{\mathrm {HK} }(X)\simeq \mathrm{Sp}_r(F)^* \end{aligned}$$

  from Theorem 5.10 and Lemma 5.11.

• 2. We have natural isomorphisms of pro-discrete ${{\mathbf {Z}}} _p$-modules

  • (a) $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^r)\simeq H^r_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet })\simeq \mathrm{Sp}^{\mathrm {cont} }_r({{\mathscr {O}}}_F)^*$ and $H^0(Y, \Omega ^r)\simeq \mathrm{Sp}_r(k)^*$,

  • (b) $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^r_{\log })\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Z}}} _p)^*$ and $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r_{\mathrm{log}})\simeq \mathrm{Sp}_r({\mathbf {F}}_p)^*$,

  • (c) $H^0(X,\Omega ^r)\simeq H^r_{\mathrm {dR} }(X)\simeq \mathrm{Sp}^{\mathrm {cont} }_r({{\mathscr {O}}}_K)^*,$

  • (d) $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\mathrm{log}})\simeq \mathrm{Sp}_r^{\mathrm {cont} }({{\mathbf {Z}}}_p)^*$ and $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},\Omega ^r_{\mathrm{log}})\simeq \mathrm{Sp}_r({{\mathbf {F}}}_p)^*$.

  They are compatible with the canonical maps between Steinberg representations and with the above isomorphisms.

Proof

Consider the following diagram

(6.29)

The bottom square clearly commutes. The first (continuous) regulator $r_{\mathrm {HK} }$ is defined by integrating the crystalline Hyodo–Kato Chern classes $c_1^{\mathrm {HK} }$ defined in Chapter 7. By Sect. 7.2.1 it makes the top square commute. The right triangle commutes by Lemma 5.11. It follows that there exists a broken arrow (we will call it $r_{\mathrm {HK} }$ as well) that makes the left triangle commute. This map is continuous and also clearly makes the adjacent square commute. Hence it is an injection. We will prove that it is an isomorphism after inverting p.

The above combined with Proposition 6.27 and Theorem 5.11 gives the embeddings

$$\begin{aligned} \mathrm{Sp}_r^{\mathrm{cont}}({{\mathscr {O}}}_F)^*{\otimes }_{{{\mathscr {O}}}_F} F{\mathop {\hookrightarrow }\limits ^{r_{\mathrm {HK} }}} H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, W\Omega ^r){\otimes }_{{{\mathscr {O}}}_F} F{\mathop {\hookrightarrow }\limits ^{f}} H^r_{\mathrm{\mathrm {HK} }}(Y)\simeq \mathrm{Sp}_r(F)^*. \end{aligned}$$

Their composite is the canonical embedding. The image of the map f must be in the subspace of G-bounded vectors of $\mathrm{Sp}_r(K)^*$, since $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, W\Omega ^r)$ is compact (it is naturally an inverse limit of finite free ${{\mathscr {O}}}_F$-modules). That subspace is identified with $\mathrm{Sp}_r^{\mathrm{cont}}(F)^*\simeq \mathrm{Sp}_r^{\mathrm{cont}}({{\mathscr {O}}}_F)^*{\otimes }_{{{\mathscr {O}}}_F} F$ by Corollary 5.9. It follows that the map $r_{\mathrm {HK} }$ is an isomorphism.

In fact, the above map $r_{\mathrm {HK} }$ is already an integral isomorphism (as stated in part (2a)). To see this, consider the commutative diagram

$H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, W\Omega ^r)$ is a G-equivariant lattice in $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, W\Omega ^r)_{ {{\mathbf {Q}}}_p}\simeq \mathrm{Sp}_r^{\mathrm{cont}}(F)^*$ hence, by Corollary 5.3, it is homothetic to $\mathrm{Sp}_r^{\mathrm{cont}}({{\mathscr {O}}}_F)^*$. It follows that $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r)\simeq \mathrm{Sp}_r^{\mathrm{cont}}(k)^*$ is irreducible. Moreover, the bottom map $r_{\mathrm {HK} }$ is nonzero: by construction of the top map $r_{\mathrm {HK} }$, the symbol $\mathrm {dlog} z_1\wedge \cdots \wedge \mathrm {dlog} z_r$ for coordinates $z_1,\ldots , z_r$ of ${{\mathbb {P}}}^d_K$ is in the image. It follows that it is an isomorphism hence so is the top map $r_{\mathrm {HK} }$ as well. Moreover, the latter is a topological isomorphism since the domain is compact and the target is Hausdorff. It follows that its rational version is a topological isomorphism as well, which proves part (1a) of the theorem.

The proof of part (1b) is very similar to the proof of part (1a), so we will be rather brief. Consider the commutative diagram

(6.30)

Here the (continuous) regulator $r_{\log }$ is defined by integrating the crystalline logarithmic de Rham–Witt Chern classes $c_1^{\log }$ defined in Chapter 7. Arguing as above we can construct the broken arrow, which is again a continuous map, making the whole diagram commute. It easily follows that both maps f and $r_{\log }$ are isomorphisms. Now, to prove that they are topological isomorphisms we argue first integrally, as for part (2b), and then rationally as for part (2a).

For part (1c) one repeats the argument starting with the following commutative diagram

(6.31)

where the continuous (bounded) regulator $r_{\mathrm {dR} }$ is defined by integrating the integral de Rham Chern classes $c_1^{\mathrm {dR} }$ defined in Chapter 7, and using the fact that, by Proposition 6.27, we have

$$\begin{aligned} H^r_{\mathrm {dR} }(X){\otimes }_{{{\mathscr {O}}}_K}K\hookrightarrow H^r_{\mathrm {dR} }(X) \simeq \mathrm{Sp}_r(K)^* \end{aligned}$$

and, by Proposition 6.23, we have $H^r_{\mathrm {dR} }(X)\simeq H^0(X,\Omega ^r)$. The integral part (2c) follows as above.

Parts (1d) and (2d) follow from parts (1b) and (2b) and the following lemma. $\square$

Lemma 6.32

For $n\ge 1$, we have canonical topological isomorphisms

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W_n\Omega ^r_{\mathrm{log}}){\mathop {\rightarrow }\limits ^{\sim }}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_n\Omega ^r_{\mathrm{log}}),\quad H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^r_{\mathrm{log}}){\mathop {\rightarrow }\limits ^{\sim }}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\mathrm{log}}). \end{aligned}$$

Proof

It suffices to prove the first isomorphism and, since both sides satisfy p-adic devissage, it suffices to do it for $n=1$. We have $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^r_{\log }){\mathop {\rightarrow }\limits ^{\sim }}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^r)^{C=1}$. On the other hand, by étale base change, we have a topological isomorphism $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^r)\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r)\widehat{\otimes }_{k}\overline{k}$. And parts (2a) and (2b) of the theorem show that the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r_{\log })\widehat{\otimes }_{{\mathbf {F}}_p} k \rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r)$ is a topological isomorphism. Hence, since $C=1$ on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r_{\log })$, we obtain topological isomorphisms

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^r_{\log }) {\mathop {\leftarrow }\limits ^{\sim }}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^r)^{C=1}{\mathop {\leftarrow }\limits ^{\sim }}(H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r_{\log })\widehat{\otimes }_{{\mathbf {F}}_p} \overline{k})^{C=1}{\mathop {\leftarrow }\limits ^{\sim }}H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y, \Omega ^r_{\log }), \end{aligned}$$

as wanted. $\square$

Remark 6.33

Consider the commutative diagram

The dashed arrow is defined to make the diagram commute. It is continuous. It can be thought of as an integral Hyodo–Kato map. Compatibilities used in the proof of Theorem 6.28 ensure that it is compatible with the bounded and the overconvergent Hyodo–Kato maps. Because the natural map $\mathrm{Sp}^{\mathrm {cont} }_r({{\mathscr {O}}}_F)^*\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K{\mathop {\rightarrow }\limits ^{\sim }} \mathrm{Sp}^{\mathrm {cont} }_r({{\mathscr {O}}}_K)^*$ is an isomorphism, we get the integral Hyodo–Kato (topological) isomorphism

$$\begin{aligned} \iota _{\mathrm {HK} }: H^r_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet })\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {dR} }(X). \end{aligned}$$

6.4 Computation of syntomic cohomology

We will prove in this section that the geometric syntomic cohomology of X can be computed using the logarithmic de Rham–Witt cohomology. To simplify the notation we will write $(-)_{ {{\mathbf {Q}}}_p}$ for $(-){\otimes }^L {{\mathbf {Q}}}_p$.

6.4.1 Simplification of syntomic cohomology

Let X now be a semistable Stein formal scheme over ${{\mathscr {O}}}_K$.

Lemma 6.34

Let $r\ge 0$. There exist natural and compatible strict quasi-isomorphisms

$$\begin{aligned} \iota _{\mathrm {cr} }&: [\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}]^{\varphi =p^r}{\mathop {\rightarrow }\limits ^{\sim }}[(\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{N=0,\varphi =p^r},\\ \iota _{\mathrm {cr} }&: [\mathrm {R} \Gamma _{\mathrm {cr} }(X)_{ {{\mathbf {Q}}}_p}]^{\varphi =p^r}{\mathop {\rightarrow }\limits ^{\sim }}[\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0)_{ {{\mathbf {Q}}}_p}] ^{N=0,\varphi =p^r}. \end{aligned}$$

Proof

By (3.49), (3.50), we have a natural strict quasi-isomorphism

$$\begin{aligned} \iota _{\mathrm{BK}}^1:\ [\mathrm {R} \Gamma _{\mathrm {cr} }(X_n/r^{\mathrm{PD}}_{\varpi ,n}) \widehat{\otimes }_{r^{\mathrm{PD}}_{\varpi ,n}}\widehat{\mathbf{A}}_{\mathrm {st} ,n}]^{N=0} {\mathop {\rightarrow }\limits ^{\sim }} \mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X}_n). \end{aligned}$$

To check the strictness one can look locally and there everything is discrete. We can also adapt the proof of Theorem 4.1 (and proceed as in the proof of Proposition 6.1: note that both crystalline cohomology complexes are in the bounded derived category) to construct a natural strict quasi-isomorphism

$$\begin{aligned} h_{\mathrm {cr} }: \ [(\mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }){\widehat{\otimes }}_{r^{\mathrm{PD}}_{\varpi }}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{\varphi =p^r}{\mathop {\rightarrow }\limits ^{\sim }} [(\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{\varphi =p^r}. \end{aligned}$$

In fact, it suffices to note that the complexes (4.9) used in that proof have cohomology annihilated by $p^N$, for a constant $N=N(d,r)$, $d=\dim X_0$.

Define the first map in the lemma by $\iota _{\mathrm {cr} }:=h_{\mathrm {cr} }\iota _{\mathrm{BK}}^{-1}$. The definition of the second map $\iota _{\mathrm {cr} }$ is analogous (but easier: there is no need for the zigzag in the definition of $h_{\mathrm {cr} }$). $\square$

Let $r\ge 0$. From the maps in (3.53) we induce a natural strict quasi-isomorphism

$$\begin{aligned} \iota _{\mathrm{BK}}^2: (\mathrm {R} \Gamma _{\mathrm {dR} }(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}\mathbf{A}_{\mathrm {cr} ,K})_{ {{\mathbf {Q}}}_p}/F^r {\mathop {\rightarrow }\limits ^{\sim }}\mathrm {R} \Gamma _{\mathrm {cr} }(\overline{X})_{ {{\mathbf {Q}}}_p}/F^r. \end{aligned}$$

(6.35)

Set $\gamma _{\mathrm {HK} }:=(\iota _{\mathrm{BK}}^2)^{-1}\iota _{\mathrm {cr} }^{-1}$. The above discussion yields the following strict quasi-isomorphism

(6.36)

By construction, it is compatible with its pro-analog (3.43), i.e., we have a natural continuous map of distinguished triangles, where all the horizontal maps are the canonical maps

6.4.2 Computation of the Hyodo–Kato part

We come back now to the Drinfeld half-space.

Lemma 6.37

The cohomology of $[(\mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F}^0) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{N=0,\varphi =p^r}$ is classical and we have the natural topological isomorphisms

$$\begin{aligned} H^r([(\mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F}^0)&\widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{N=0,\varphi =p^r})\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log }){\otimes }{ {{\mathbf {Q}}}_p},\nonumber \\ H^{r-1}([(\mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F}^0)&\widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} })_{ {{\mathbf {Q}}}_p}]^{N=0,\varphi =p^r})\simeq (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p}_{\mathrm {cr} }){\otimes }{ {{\mathbf {Q}}}_p}. \end{aligned}$$

(6.38)

Proof

By Proposition 6.23, we have strict quasi-isomorphisms³⁹

$$\begin{aligned} \mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F}^0)&\widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} } \simeq \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet }) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} } \overset{\sim }{\leftarrow } H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^{\scriptscriptstyle \bullet }) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} }\\&\overset{\sim }{\leftarrow }\bigoplus _{i\ge 0}H^0_{\acute{\mathrm{e}}\mathrm {t}}(Y,W\Omega ^i) \widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} }[-i] \simeq \bigoplus _{i\ge 0}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i) \widehat{\otimes }_{W(\overline{k})}{\widehat{\mathbf{A}}}_{\mathrm {st} }[-i]. \end{aligned}$$

The first claim of the lemma follows.

Let M be a finite type free $(\varphi ,N)$-module over $W(\overline{k})$. Note that N is nilpotent. We claim that we have a short exact sequence

$$\begin{aligned} 0\rightarrow M\otimes _{W(\overline{k})} \mathbf{A}_{\mathrm {cr} }\rightarrow M\otimes _{W(\overline{k})}\widehat{\mathbf{A}}_{\mathrm {st} }{\mathop {\rightarrow }\limits ^{N}}M\otimes _{W(\overline{k})}\widehat{\mathbf{A}}_{\mathrm {st} }\rightarrow 0. \end{aligned}$$

Indeed, if $N=0$, this is clear from the short exact sequence (3.14). For a general M, we argue by induction on m such that $N^m=0$ using the short exact sequence

$$\begin{aligned} 0\rightarrow M_0\rightarrow M{\mathop {\rightarrow }\limits ^{N}}M_1\rightarrow 0, \end{aligned}$$

where $M_0=\ker N, M_1=\mathrm {im}\, N$. $M_0,M_1$ are finite type free $(\varphi ,N)$-modules such that $N^{m-1}=0$. It follows that we have strict quasi-isomorphisms (reduce to the truncated log-schemes $Y_s$ and pass to the limit)

$$\begin{aligned} {[}\mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}_{F}^0)&\widehat{\otimes }_{{{\mathscr {O}}}_{F}}{\widehat{\mathbf{A}}}_{\mathrm {st} }]^{N=0} \simeq \bigoplus _{i\ge 0}[H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i) \widehat{\otimes }_{W(\overline{k})}{\widehat{\mathbf{A}}}_{\mathrm {st} }]^{N=0}[-i]\\&\simeq \bigoplus _{i\ge 0}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i) \widehat{\otimes }_{W(\overline{k})}{\mathbf{A}}_{\mathrm {cr} }[-i] \simeq \bigoplus _{i\ge 0}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}_{\mathrm {cr} }[-i] \end{aligned}$$

We will show now that we have natural strict quasi-isomorphisms

$$\begin{aligned}{}[H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}_{\mathrm {cr} }]^{\varphi =p^r}_{ {{\mathbf {Q}}}_p}&\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p}\nonumber \\ [H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}_{\mathrm {cr} }]^{\varphi =p^r}_{ {{\mathbf {Q}}}_p}&\simeq (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p}_{\mathrm {cr} })_{ {{\mathbf {Q}}}_p}. \end{aligned}$$

(6.39)

For $i\ge 0$, set $C_i:= H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}_{\mathrm {cr} }.$ We claim that, for $j\ge i$, the classical eigenspace

$$\begin{aligned} C_i^{\varphi =p^j}= H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p^{j-i}}_{\mathrm {cr} }. \end{aligned}$$

(6.40)

To see that, write, using the notation from the proof of Proposition 6.23, $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i_{\mathrm{log}})\simeq \varprojlim _sH^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s,W\Omega ^i_{\mathrm{log}})$ or, to simplify the notation, $A^i:=A=\varprojlim _sA_s$. Note that $A_s$ is a finite type free ${{\mathbf {Z}}} _p$-module. Replace $A_s$ with $B_s:=\cap _{s^{\prime }>s}\mathrm {im}\, (A_{s^{\prime }}\rightarrow A_s)$. Then the maps $B_{s+1}\rightarrow B_s$ are surjective and $A=\varprojlim _s B_s$. Choose basis of $B_s$, $s\ge 1$, compatible with the projections, i.e., the chosen basis of $B_{s+1}$ includes a lift of the chosen basis of $B_s$. Using this basis we can write

$$\begin{aligned} A\simeq&{{\mathbf {Z}}} _p^{I_1}\times {{\mathbf {Z}}} _p^{I_2}\times {{\mathbf {Z}}} _p^{I_3}\times \cdots ,\quad A\widehat{\otimes }_{ {{\mathbf {Z}}} _p}\mathbf{A}_{\mathrm {cr} }\simeq \mathbf{A}_{\mathrm {cr} }^{I_1}\times \mathbf{A}_{\mathrm {cr} }^{I_2}\times \mathbf{A}_{\mathrm {cr} }^{I_3}\times \cdots . \end{aligned}$$

(6.41)

Since the Frobenius on $A^i=H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^i_{\log })$ is equal to the multiplication by $p^i$ we obtain the equality we wanted.

Consider now the following exact sequences

$$\begin{aligned} 0 \rightarrow C^{\varphi =p^r}_{r}\rightarrow C_r {\mathop {\longrightarrow }\limits ^{\varphi -p^r}} C_r,\quad \quad 0 \rightarrow C^{\varphi =p^r}_{r-1}\rightarrow C_{r-1}{\mathop {\longrightarrow }\limits ^{\varphi -p^r}}C_{r-1}. \end{aligned}$$

Since the map $\mathbf{A}_{\mathrm {cr} }{\mathop {\longrightarrow }\limits ^{p^i-\varphi }} \mathbf{A}_{\mathrm {cr} }$, $i\ge 0$, is $p^i$-surjective, the maps $\varphi -p^r$ above are rationally surjective (use the basis (6.41) and the fact that the Frobenius on $A^i$ is equal to the multiplication by $p^i$). Hence, rationally, the derived eigenspaces $[C_i]^{\varphi =p^r}$, $i=r,r-1$, are equal to the classical ones $C_i^{\varphi =p^r}$, $i=r,r-1.$ Since, by (6.40), we have $C_r^{\varphi =p^r}=H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log })$ and $C_{r-1}^{\varphi =p^r}=H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}\mathbf{A}_{\mathrm {cr} }^{\varphi =p}$, the strict quasi-isomorphisms in (6.39) follow.

It remains to show that the natural maps

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p}&\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log }){\otimes }{ {{\mathbf {Q}}}_p},\\ (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p}_{\mathrm {cr} })_{ {{\mathbf {Q}}}_p}&\rightarrow (H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p}_{\mathrm {cr} }){\otimes }{ {{\mathbf {Q}}}_p}. \end{aligned}$$

are strict quasi-isomorphisms but this follows from Proposition 2.6. $\square$

6.4.3 Computation of syntomic cohomology

Corollary 6.42

Let $r\ge 0$. The r-th cohomology of $\mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p}$ is classical and there exists a natural topological isomorphism

$$\begin{aligned} H^r(\mathrm {R} \Gamma _{ \mathrm {syn} }(\overline{X}, {{\mathbf {Z}}} _p(r))_{ {{\mathbf {Q}}}_p})\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log }){\otimes }{ {{\mathbf {Q}}}_p}. \end{aligned}$$

Proof

We note that, by Proposition 6.23, there exist natural strict quasi-isomorphisms

$$\begin{aligned} \oplus _{i\ge 0}H^0(X,\Omega ^i)\widehat{\otimes }_{{{\mathscr {O}}}_{K}}F^{r-i}\mathbf{A}_{\mathrm {cr} ,K}[-i]&{\mathop {\rightarrow }\limits ^{\sim }} F^r(\mathrm {R} \Gamma _{\mathrm {dR} }(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}\mathbf{A}_{\mathrm {cr} ,K}),\\ \oplus _{r-1\ge i\ge 0}H^0(X,\Omega ^i)\widehat{\otimes }_{{{\mathscr {O}}}_{K}}(\mathbf{A}_{\mathrm {cr} ,K}/F^{r-i})[-i]&{\mathop {\rightarrow }\limits ^{\sim }} (\mathrm {R} \Gamma _{\mathrm {dR} }(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}\mathbf{A}_{\mathrm {cr} ,K})/F^r. \end{aligned}$$

This, combined with the strict quasi-isomorphisms (6.38), changes the map $\gamma _{\mathrm {HK} }$ from (6.36) into

$$\begin{aligned} \gamma _{\mathrm {HK} }^{\prime }: \ (H^0_{\acute{\mathrm{e}}\mathrm {t}}({Y},W\Omega ^{r-1}_{\log }) \widehat{\otimes }_{ {{\mathbf {Z}}} _p}{\mathbf{A}}^{\varphi =p}_{\mathrm {cr} }){\otimes }{ {{\mathbf {Q}}}_p}\rightarrow (H^0(X,\Omega ^{r-1})\widehat{\otimes }_{{{\mathscr {O}}}_{K}}{{\mathscr {O}}}_C){\otimes }{ {{\mathbf {Q}}}_p}. \end{aligned}$$

Hence we obtain the long exact sequence

It suffices to show that $\gamma ^{\prime }_{\mathrm {HK} }$ is strictly surjective. For that we will need to trace carefully its definition. Consider thus the following commutative diagram

(6.43)

Here, the fact that the bottom square commutes follows from the proofs of Proposition 3.48 and Theorem 4.1. Taking $\widetilde{H}^{r-1}$ of the above diagram we obtain the outer diagram in the commutative diagram

Since $d=0$ on $(H^0(X,\Omega ^{r-1})\widehat{\otimes }_{{{\mathscr {O}}}_{K}}{{\mathscr {O}}}_C){\otimes }{ {{\mathbf {Q}}}_p}$, we get the shown factorization of the slanted map and the commutative square. This square is seen (by a careful chase of diagram (6.43)) to be compatible with the projections $\theta : \mathbf{A}^{\varphi =p}_{\mathrm {cr} }\rightarrow {{\mathscr {O}}}_C,$$\theta : \mathbf{B}^{+,\varphi =p}_{\mathrm {cr} }\rightarrow C$. Using them, we obtain the commutative diagram

and reduce our problem to showing that the induced map $\gamma _C$ is surjective.

We will, in fact, show that $\gamma _C$ is an isomorphism. Note that the right vertical map in the above diagram is injective: use the fact that the natural map $H^{r-1}_{\mathrm {dR} }({X})\rightarrow H^{r-1}_{\mathrm {dR} }({X}_K)$ is an injection (in particular the domain is torsion-fee). By Remark 6.33, the above diagram yields that $\gamma _C=(\iota _{\mathrm {HK} }\otimes 1){\otimes }{ {{\mathbf {Q}}}_p}$. Since the integral Hyodo–Kato map $\iota _{\mathrm {HK} }: H^0_{\acute{\mathrm{e}}\mathrm {t}}({Y},W\Omega ^{r-1}_{\log })\otimes _{ {{\mathbf {Z}}} _p}{{\mathscr {O}}}_K{\mathop {\rightarrow }\limits ^{\sim }} H^0(X,\Omega ^{r-1})$ is a topological isomorphism, so is $\gamma _C$, as wanted.

To check that the map $\gamma ^{\prime }_{\mathrm {HK} }$ is strict, consider the factorization

As mentioned above, the map $\gamma _{C}$ is a topological isomorphism. Hence it suffices to show that the vertical map is strict. But this is clear because the surjection $\theta : {\mathbf{A}}^{\varphi =p}_{\mathrm {cr} }\rightarrow {{\mathscr {O}}}_C$ has a ${{\mathbf {Z}}} _p$-linear continuous section. $\square$

6.5 Main theorem

Before proving the main theorem of this section let us state the following corollary. Recall that X, resp. $\widetilde{X}$, is the standard formal, resp. weak formal, model of the Drinfeld half-space ${{\mathbb {H}}}^d_K$, $Y=X_0$, $\overline{Y}=Y_{\overline{k}}$.

Corollary 6.44

Let $r\ge 0$. The cohomology $\widetilde{H}^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))$ is classical and there is a natural topological isomorphism

$$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p}. \end{aligned}$$

It is compatible with the étale and the logarithmic de Rham–Witt Chern classes.

Proof

The first claim follows from the comparison between étale and syntomic cohomologies in Proposition 6.1 and the computation of syntomic cohomology in Corollary 6.42.

The second claim follows from the compatibility of the étale, syntomic, crystalline, $c_1^{\mathrm {st} }$, crystalline Hyodo–Kato, and logarithmic de Rham–Witt Chern classes discussed in Chapter 7. $\square$

We are now ready to prove the following result.

Theorem 6.45

Let $r\ge 0$.

• 1. There is a natural topological isomorphism of $G\times {{\mathscr {G}}}_K$-modules

  $$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^*\simeq \mathrm{Sp}_r( {{\mathbf {Z}}} _p)^*{\otimes } {{\mathbf {Q}}}_p. \end{aligned}$$

• 2. There are natural topological isomorphisms of G-modules

  $$\begin{aligned}&H^r_{\mathrm {dR} }({X})_K\simeq \mathrm{Sp}^{\mathrm {cont} }_r(K)^*,\quad H^r_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F)_{ {{\mathbf {Q}}}_p}\simeq \mathrm{Sp}^{\mathrm {cont} }_r(F)^*,\\&H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\overline{Y},\log })_{ {{\mathbf {Q}}}_p}\simeq {\left\{ \begin{array}{ll} \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^* &{} \text{ if } i=0,\\ 0 &{} \text{ if } i>0. \end{array}\right. } \end{aligned}$$

• 3. The regulator maps

  $$\begin{aligned}&r_{\mathrm {dR} }: M({{\mathscr {H}}}^{d+1},K)\rightarrow H^r_{\mathrm {dR} }({X})_K,\quad r_{\mathrm {HK} }: M({{\mathscr {H}}}^{d+1},F)\rightarrow H^r_{\mathrm {cr} }(Y/{{\mathscr {O}}}^0_F)_{ {{\mathbf {Q}}}_p},\\&r_{\log }: M({{\mathscr {H}}}^{d+1}, {{\mathbf {Q}}}_p)\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W\Omega ^r_{\log })_{ {{\mathbf {Q}}}_p} \end{aligned}$$

  are strict surjective maps (of weak duals of Banach spaces), $G\times {{\mathscr {G}}}_K$-equivariant, compatible with the isomorphisms in (1) and (2), and their kernels are equal to the space of degenerate measures (defined as the intersection of the space of measures with the set of degenerate distributions).

• 4. The natural map

  $$\begin{aligned} H^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r)) \rightarrow H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

  is an injection and identifies $H^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))$ with the G-bounded vectors of $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))$.

Proof

Point (2) follows from Theorem 6.28 and Proposition 6.23. Point (1) follows from Corollary 6.44, Lemma 6.32, and the computation of the logarithmic de Rham–Witt cohomology in Theorem 6.28.

To prove point (4) consider the commutative diagram, where the bottom sequence is strictly exact:

Commutativity can be checked easily by looking at symbols. The change of topology map $\varepsilon$ has image in $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))^{{G-bd}}$ (since $\mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Z}}} _p)^*$ is compact). We need to show that this image is the whole of $H^r_{\mathrm {pro}\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r))^{{G-bd}}$. To prove that, since $(\mathrm{Sp}_r( {{\mathbf {Q}}}_p)^*)^{{G-bd}}\simeq \mathrm{Sp}^{\mathrm {cont} }_r( {{\mathbf {Q}}}_p)^*$, it is enough to show that $(d\Omega ^{r-1}(X_C))^{{G-bd}}= 0$ or, equivalently, that $(\Omega ^{r-1}(X_C)^{d=0})^{{G-bd}}\rightarrow H^{r-1}_{\mathrm {dR} }(X_C)$ is an injection. It is enough to show that $\Omega ^{r-1}(X_C)^{{G-bd}}\rightarrow H^{r-1}_{\mathrm {dR} }(X_C)$ is injective or that, by an analogous argument to the one we used in the proof of Proposition 6.23, so is the map $\Omega ^{r-1}(X_K)^{{G-bd}}\rightarrow H^{r-1}_{\mathrm {dR} }(X_K)$.

Now, since, the map $\Omega ^{r-1}(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}K\rightarrow \Omega ^{r-1}(X_K)^{{G-bd}}$ is an isomorphism (use the fact that X can be covered by G-translates of an open subscheme U such that $U_K$ is an affinoid), it suffices to show that $\Omega ^{r-1}(X)\widehat{\otimes }_{{{\mathscr {O}}}_K}K\rightarrow H^{r-1}_{\mathrm {dR} }(X_K)$ is an injection. But this we have done in Proposition 6.27.

Point (3) follows from the construction and Chapter 7. More precisely, the fact that the regulator maps $r_{\mathrm {dR} }, r_{\mathrm {HK} }, r_{\log }$ are compatible with the isomorphisms in points (1) and (2) follow from diagrams  6.31, 6.29, 6.30, respectively.

Finally, the fact that the regulators in point (3) are strict follows from the fact that so are the corresponding maps $M({{\mathscr {H}}}^{r+1}, {{\mathbf {Z}}} _p) \rightarrow \mathrm{Sp}_r( {{\mathbf {Z}}} _p)^*$, etc, as surjective continuous maps of profinite modules, and tensoring with ${{\mathbf {Q}}}_p$ is right exact. $\square$

Remark 6.46

We will show in [18] that there is a regulator map

$$\begin{aligned} r_{\acute{\mathrm{e}}\mathrm {t}}: M({{\mathscr {H}}}^{d+1}, {{\mathbf {Q}}}_p)\rightarrow H^r_{\acute{\mathrm{e}}\mathrm {t}}({X}_C, {{\mathbf {Q}}}_p(r)) \end{aligned}$$

compatible with the étale Chern class maps. Corollary 6.44 then implies that we have an analog of point (3) of Theorem 6.45 in this setting.

7 Symbols

We gather in this chapter a few basic facts concerning symbol maps and their compatibilities that we need in this paper. We use the notation from Chapter 6.

7.1 Hyodo–Kato isomorphisms

Let X be a semistable Stein weak formal scheme over ${{\mathscr {O}}}_K$. In the first part of this paper we have used the Hyodo–Kato isomorphism as defined by Grosse-Klönne in [32], $\iota _{\mathrm {HK} }: H^r_{\mathrm {HK} }(X_0)\otimes _FK{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {dR} }(X_K)$. But one can use the original Hyodo–Kato isomorphism defined for quasi-compact formal schemes in [38]. Doing that we obtain two Hyodo–Kato isomorphisms. One that, modulo canonical identifications, turns out to be the same as the one of Grosse-Klönne, the other identifies bounded Hyodo–Kato and de Rham cohomologies.

Proposition 7.1

We have compatible Hyodo–Kato (topological) isomorphisms

$$\begin{aligned} \quad&\iota _{\mathrm {HK} }: H^r_{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_F,F){\otimes }_FK{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {dR} }(\widehat{X}_K),\nonumber \\&\iota _{\mathrm {HK} }: (H^r_{\mathrm {cr} }(X_0/{{\mathscr {O}}}^0_F)\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K){\otimes }{K}{\mathop {\rightarrow }\limits ^{\sim }} H^r_{\mathrm {dR} }(\widehat{X}){\otimes }{K}. \end{aligned}$$

(7.2)

Proof

As mentioned above they are induced by the original Hyodo–Kato isomorphism [38]. We will describe them in more detail.

To start, assume that we have a quasi-compact semistable formal scheme Y over ${{\mathscr {O}}}_K$. We will work in the classical derived category. Recall that the Frobenius $\varphi$

$$\begin{aligned}&r^{\mathrm{PD}}_{\varpi ,n,\varphi }\otimes ^L_{r^{\mathrm{PD}}_{\varpi ,n}}\mathrm {R} \Gamma _{\mathrm {cr} }(Y_1/r^{\mathrm{PD}}_{\varpi ,n})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_1/r^{\mathrm{PD}}_{\varpi ,n}),\\&{{\mathscr {O}}}_{F,n,\varphi }\otimes ^L_{{{\mathscr {O}}}_{F,n}}\mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0) \end{aligned}$$

has a $p^N$-inverse $\psi$, for $N=N(d)$, $d=\dim Y_0$. This is proved in [38, 2.24].$\square$

Lemma 7.3

The projection $p_0: \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{\varpi ,n})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)$ has a functorial (for maps between formal schemes and a change of n) and Frobenius-equivariant $p^{N_{\iota }}$-section

$$\begin{aligned} \iota _{\varpi ,n}: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{\varpi ,n}), \end{aligned}$$

i.e., $p_0\iota _{\varpi ,n}=p^{N_{\iota }}$, $N_{\iota }=N(d,e)$. Moreover, the resulting map

$$\begin{aligned} \iota _{\varpi ,n}: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)\otimes ^L_{{{\mathscr {O}}}_{F,n}}r^{\mathrm{PD}}_{\varpi ,n} \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{\varpi ,n}) \end{aligned}$$

is a $p^N$-quasi-isomorphism, $N=N(d,e)$,

Proof

This follows easily from the proof of Proposition 4.13 in [38] which deals with the case $K=F$; the key point being that the Frobenius on $\mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)$ is close to a quasi-isomorphism and the Frobenius on the $\mathrm{PD}$-ideal of $r^{\mathrm{PD}}_{\varpi }$ is close to zero. Hence, we just need to pass from F to K.

By [38, Prop. 4.13], the projection $p_0: \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{p,n})\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)$ has a functorial (for maps between formal schemes and a change of n) and Frobenius-equivariant $p^{N_{\iota }}$-section

$$\begin{aligned}\iota _{p,n}: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{\varpi ,n}), \end{aligned}$$

i.e., $p_0\iota _{p,n}=p^{N_{\iota }}$, $N_{\iota }=N(d)$. To pass from F to K, consider the following commutative diagram:

Here the map g is defined by $T\mapsto T^{p^e}$ and $a\mapsto \varphi ^e(a), a\in W_n(k)$. The composites of the horizontal arrows are the $p^e$ iterations of the Frobenius. Set

$$\begin{aligned} \iota _{\varpi ,n}:= g^*\iota _{p,n}\psi ^e. \end{aligned}$$

We have

$$\begin{aligned} p_{0} \iota _{\varpi ,n}=p_0 g^*\iota _{p,n}\psi ^e=\varphi ^ep_0\iota _{p,n}\psi ^e=\varphi ^e\psi ^ep^{N_{\iota }}=p^{M}, \end{aligned}$$

for $M=M(d,e)$, as wanted.

It is easy to see that the resulting map

$$\begin{aligned} \iota _{\varpi ,n}: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)\otimes ^L_{{{\mathscr {O}}}_{F,n}}r^{\mathrm{PD}}_{\varpi ,n} \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/r^{\mathrm{PD}}_{\varpi ,n}) \end{aligned}$$

is a $p^N$-quasi-isomorphism, $N=N(d,e)$: we use the analogous result for F (see [38, Lemma 5.2]) and the fact that the right square in the above diagram is cartesian. $\square$

Lemma 7.3 implies that the composite

$$\begin{aligned} p_{\varpi } \iota _{\varpi ,n}: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F,n}^0)\otimes ^L_{{{\mathscr {O}}}_{F,n}}{{\mathscr {O}}}_{K,n} \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}^{\times }_{K,n}) \end{aligned}$$

is a $p^N$-quasi-isomorphism, $N=N(d,e)$. Taking $\mathrm {holim}\, _n$ of the last map we obtain a map

$$\begin{aligned} p_{\varpi } \iota _{\varpi }: \mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F}^0)\otimes ^L_{{{\mathscr {O}}}_{F}}{{\mathscr {O}}}_{K} \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(Y/{{\mathscr {O}}}^{\times }_{K}),\quad \iota _{\varpi }=\mathrm {holim}\, _n\iota _{\varpi ,n}, \end{aligned}$$

that is a $p^N$-quasi-isomorphism, $N=N(d,e)$. The twisted Hyodo–Kato map is defined as $\widetilde{\iota }_{\mathrm {HK} }=\rho ^{-1} p_{\varpi }\iota _{\varpi }$. We have the commutative diagram

We note that the map $\widetilde{\iota }_{\mathrm {HK} }:\mathrm {R} \Gamma _{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F}^0)\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K\rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(Y)$ is a $p^N$-quasi-isomorphism, $N=N(d,e)$. Modulo $p^N, N=N(d,e)$, it is independent of the choices made. The Hyodo–Kato map

$$\begin{aligned} {\iota }_{\mathrm {HK} }: H^i_{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F}^0){\otimes }F\rightarrow H^i_{\mathrm {dR} }(Y){\otimes }K \end{aligned}$$

is defined as ${\iota }_{\mathrm {HK} }:=p^{-N_{\iota }}\widetilde{\iota }_{\mathrm {HK} }$. We have obtained the Hyodo–Kato (topological) isomorphism

$$\begin{aligned} {\iota }_{\mathrm {HK} }: (H^i_{\mathrm {cr} }(Y_0/{{\mathscr {O}}}_{F}^0)\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K){\otimes }K{\mathop {\rightarrow }\limits ^{\sim }} H^i_{\mathrm {dR} }(Y){\otimes }K. \end{aligned}$$

For a Stein semistable weak formal scheme X, we choose a Stein covering $\{U_s\}$, $s\in {{\mathbf {N}}}$, and define the compatible Hyodo–Kato maps

$$\begin{aligned}&\iota _{\mathrm {HK} }:=\varprojlim _s\iota _{\mathrm {HK} ,U_s}: H^i_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0,F)\rightarrow H^i_{\mathrm {dR} }(\widehat{X}_K),\nonumber \\&\iota _{\mathrm {HK} }:=p^{-N_{\iota }}(\varprojlim _s\widetilde{\iota }_{\mathrm {HK} ,U_s}{\otimes }{ {{\mathbf {Q}}}_p}): H^i_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0){\otimes }{ {{\mathbf {Q}}}_p}\rightarrow H^i_{\mathrm {dR} }(\widehat{X}){\otimes }{ {{\mathbf {Q}}}_p}. \end{aligned}$$

(7.4)

We used here the fact that (topologically)

$$\begin{aligned}&H^i_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0,F)\simeq \varprojlim _sH^{i}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0,F)\,,\quad H^i_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0)\simeq \varprojlim _sH^{i}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0)\,, \nonumber \\&H^i_{\mathrm {dR} }(\widehat{X}_K)\simeq \varprojlim _sH^{i}_{\mathrm {dR} }(]U_s[_{\widehat{X}_K})\,, \quad H^i_{\mathrm {dR} }(\widehat{X})\otimes { {{\mathbf {Q}}}_p}\simeq (\varprojlim _sH^{i}_{\mathrm {dR} }(\widehat{X}|_{U_s}))\otimes { {{\mathbf {Q}}}_p}. \end{aligned}$$

(7.5)

The third isomorphism, since $X_K$ is Stein, is standard. The first two follow from the vanishing of the derived functors

$$\begin{aligned} H^1\mathrm {holim}\, _sH^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0,F),\quad H^1\mathrm {holim}\, _sH^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0), \end{aligned}$$

which, in turn, follow from the fact that the pro-systems ($s\in {{\mathbf {N}}}$)

$$\begin{aligned} \{H^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0,F)\}=\{H^{i-1}_{\mathrm {cr} }(Y_{s}/{{\mathscr {O}}}_{F}^0,F)\},\quad \{H^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0)\}=\{H^{i-1}_{\mathrm {cr} }(Y_{s}/{{\mathscr {O}}}_{F}^0)\} \end{aligned}$$

are Mittag-Leffler. To show the last isomorphism in (7.5), it suffices to show the vanishining of $(H^1\mathrm {holim}\, _sH^{i-1}_{\mathrm {dR} }(\widehat{X}|_{U_s}))\otimes { {{\mathbf {Q}}}_p}$. For that, we will use the fact that the twisted Hyodo–Kato map

$$\begin{aligned} \widetilde{\iota }_{\mathrm {HK} }: H^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^{0})\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K\rightarrow H^{i-1}_{\mathrm {dR} }(\widehat{X}|_{U_s}) \end{aligned}$$

is a $p^N$-isomorphism. Which implies that so is the induced map

$$\begin{aligned} H^1\mathrm {holim}\, _s(H^{i-1}_{\mathrm {cr} }(U_s/{{\mathscr {O}}}_F^0)\otimes _{{{\mathscr {O}}}_F}{{\mathscr {O}}}_K)\rightarrow H^1\mathrm {holim}\, _sH^{i-1}_{\mathrm {dR} }(\widehat{X}|_{U_s}). \end{aligned}$$

But, since the pro-system $\{H^{i-1}_{\mathrm {cr} }(U_{s}/{{\mathscr {O}}}_{F}^0)\}=\{H^{i-1}_{\mathrm {cr} }(Y_{s}/{{\mathscr {O}}}_{F}^0)\}$ is Mittag–Leffler, the first derived limit made rational is trivial, as wanted.

Now, by definition, the Hyodo–Kato maps from (7.4) are topological isomorphisms. $\square$

Corollary 7.6

The Hyodo–Kato isomorphisms from Proposition 7.1 are compatible with the Grosse-Klönne Hyodo–Kato isomorphism. That is, we have a commutative diagram

Proof

We may argue locally and assume that X is quasi-compact. Then, this can be checked by the diagram (we use the notation from Sect. 4.1).

(7.7)

Indeed, we easily reduce to checking that the dotted diagram commutes. Since all the maps are compatible with Frobenius and $H^i_{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)$ is finite dimensional, this is proved by a standard argument using the fact that Frobenius on T is highly nilpotent. $\square$

7.2 Definition of symbols

We define now various symbol maps and show that they are compatible.

Let X be a semistable formal scheme over ${{\mathscr {O}}}_K$. Let M be the sheaf of monoids on X defining the log-structure, $M^{\mathrm {gp} }$ its group completion. This log-structure is canonical, in the terminology of Berkovich [4, 2.3], i.e., $M(U)=\{x\in {{\mathscr {O}}}_X(U)| x_K\in {{\mathscr {O}}}^{*}_{X_K}(U_K)\}$. This is shown in [4, Th. 2.3.1], [3, Th. 5.3] and applies also to semistable formal schemes with self-intersections. It follows that $M^{\mathrm {gp} }(U)={{\mathscr {O}}}(U_K)^*$.

7.2.1 Differential symbols

We have the crystalline first Chern class maps of complexes of sheaves on $X_{\acute{\mathrm{e}}\mathrm {t}}$ [79, 2.2.3]

$$\begin{aligned} c_1^{\mathrm {st} }: M^{\mathrm {gp} }\rightarrow M^{\mathrm {gp} }_n\rightarrow R\varepsilon _*{{\mathscr {J}}}^{[1]}_{X_n/r^{\mathrm{PD}}_{\varpi ,n}}[1],\quad c_1^{\mathrm {HK} }: M^{\mathrm {gp} }\rightarrow M^{\mathrm {gp} }_0\rightarrow R\varepsilon _*{{\mathscr {J}}}^{[1]}_{X_0/{{\mathscr {O}}}_{F,n}^0}[1]. \end{aligned}$$

Here, the map $\varepsilon$ is the projection from the corresponding crystalline-étale site to the étale site. These maps are clearly compatible. We get the induced functorial maps

$$\begin{aligned}&c_1^{\mathrm {st} }:H^0(X_K,{{\mathscr {O}}}_{X_K}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi }, {{\mathscr {J}}}^{[1]})[1],\\&c_1^{\mathrm {HK} }:H^0(X_K,{{\mathscr {O}}}_{X_K}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0,{{\mathscr {J}}}^{[1]})[1]. \end{aligned}$$

The Hyodo–Kato classes above can be also defined using the de Rham-Witt complexes. That is, one can define (compatible) Hyodo–Kato Chern class maps [22, 2.1]

$$\begin{aligned}&c_1^{\log }:H^0(X_K,{{\mathscr {O}}}_{X_K}^*) \rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{0},W\Omega ^{\scriptscriptstyle \bullet }_{X_0,\log })[1],\\&c_1^{\mathrm {HK} }:H^0(X_K,{{\mathscr {O}}}_{X_K}^*) \rightarrow \mathrm {R} \Gamma _{\acute{\mathrm{e}}\mathrm {t}}(X_{0},W\Omega ^{\scriptscriptstyle \bullet }_{X_0})[1]. \end{aligned}$$

They are compatible with the classical crystalline Hyodo–Kato Chern class maps above (use [28, I.5] and replace ${{\mathscr {O}}}^*$ by $M^{\mathrm {gp} }$).

We also have the de Rham first Chern class map

$$\begin{aligned} c_1^{\mathrm {dR} }: M^{\mathrm {gp} }\rightarrow M^{\mathrm {gp} }_n{\mathop {\longrightarrow }\limits ^{\mathrm {dlog} }} \Omega ^{\scriptscriptstyle \bullet }_{X_n/{{\mathscr {O}}}^{\times }_{K,n}} [1]. \end{aligned}$$

It induces the functorial map

$$\begin{aligned} c_1^{\mathrm {dR} }:H^0(X_K,{{\mathscr {O}}}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(X )[1]. \end{aligned}$$

It is evident that, by the canonical map $\mathrm {R} \Gamma _{\mathrm {dR} }(X)\rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(X_K)$, this map is compatible with the rigid analytic class (defined using $\mathrm {dlog}$)

$$\begin{aligned} c_1^{\mathrm {dR} }:H^0(X_K,{{\mathscr {O}}}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(X_K )[1]. \end{aligned}$$

Let now X be a semistable weak formal scheme over ${{\mathscr {O}}}_K$. The overconvergent classes

$$\begin{aligned} c_1^{\mathrm {HK} }:H^0(X_K,{{\mathscr {O}}}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {rig} }(X_0/{{\mathscr {O}}}_{F}^0)[1],\quad c_1^{\mathrm {dR} }:H^0(X_K,{{\mathscr {O}}}^*) \rightarrow \mathrm {R} \Gamma _{\mathrm {dR} }(X _K)[1] \end{aligned}$$

are defined in an analogous way to the crystalline Hyodo–Kato classes and the rigid analytic de Rham classes (of $\widehat{X}_K$), respectively. Clearly they are compatible with those.

Lemma 7.8

Let X be a semistable Stein weak formal scheme over ${{\mathscr {O}}}_K$. The Hyodo–Kato maps

$$\begin{aligned}&\iota _{\mathrm {HK} }: H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0)\otimes { {{\mathbf {Q}}}_p}\rightarrow H^1_{\mathrm {dR} }(\widehat{X})\otimes { {{\mathbf {Q}}}_p},\quad \iota _{\mathrm {HK} }: H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0,F)\rightarrow H^1_{\mathrm {dR} }(\widehat{X}_K), \\&\iota _{\mathrm {HK} }: H^1_{\mathrm {rig} }(X_0/{{\mathscr {O}}}_F^0)\rightarrow H^1_{\mathrm {dR} }({X}_K) \end{aligned}$$

are compatible with the Chern class maps from $H^0(\widehat{X}_K,{{\mathscr {O}}}^*)$ and $H^0(X_K,{{\mathscr {O}}}^*)$.

Proof

For the first two maps, note that we can assume that X is quasi-compact. This is because in the second map the cohomologies are projective limits and in the first map this is true up to a universal constant (see the proof of Proposition 7.1). Now, the proof of an analogous lemma in the algebraic setting goes through with only small changes [59, Lemma 5.1]. We will present it for the second map (the proof for the first map is similar with a careful bookkeeping of the appearing constants).

Since $\iota _{\mathrm {HK} }=\rho ^{-1}p_{\varpi }\iota ^{\prime }_{\varpi }$, $\iota ^{\prime }_{\varpi }=p^{-N_{\iota }}\iota _{\varpi }$, and the map $p_{\varpi }$ is compatible with first Chern classes, it suffices to show the compatibility for the section $\iota ^{\prime }_{\varpi }$. Let $x\in H^0(\widehat{X}_K,{{\mathscr {O}}}^*_{\widehat{X}_K})$. Since the map $\iota ^{\prime }_{\varpi }$ is a section of the map $p_0$ and the map $p_0$ is compatible with first Chern classes, we have that the element $\zeta \in H^1_{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi })$ defined as $\zeta =\iota ^{\prime }_{\varpi }(c_1^{\mathrm {HK} }(x))-c_1^{\mathrm {st} }(x)\in \ker p_0$. We will show that $\zeta$ is zero.

Consider now the linearization of the map $\iota ^{\prime }_{\varpi }$

$$\begin{aligned} \beta :\quad (H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0)\otimes { {{\mathbf {Q}}}_p})\widehat{\otimes }_{F}r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}\rightarrow H^1_{\mathrm {cr} }(X/r^{\mathrm{PD}}_{\varpi })\otimes { {{\mathbf {Q}}}_p} \end{aligned}$$

(7.9)

It is an isomorphism: this is because we have the $p^N$-quasi-isomorphism, $N=N(d,e)$, (see Lemma 7.3)

$$\begin{aligned} \iota _{\varpi }: \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0)\widehat{\otimes }_{{{\mathscr {O}}}_{F}}r^{\mathrm{PD}}_{\varpi }\rightarrow \mathrm {R} \Gamma _{\mathrm {cr} }(X_0/r^{\mathrm{PD}}_{\varpi }) \end{aligned}$$

and $\mathrm {R} \Gamma _{\mathrm {cr} }(X_0/{{\mathscr {O}}}_{F}^0)\widehat{\otimes }_{{{\mathscr {O}}}_{F}}r^{\mathrm{PD}}_{\varpi }$ is p-adically derived complete and $r^{\mathrm{PD}}_{\varpi ,n}$ is free over ${{\mathscr {O}}}_{F,n}$. Hence, we can write $\zeta =\beta (\zeta ^{\prime })$, for $\zeta ^{\prime }\in H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0)_{ {{\mathbf {Q}}}_p}\widehat{\otimes }_{F}r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}$. Since $p_0\beta (\zeta ^{\prime })=0$, we have $\zeta ^{\prime }\in \ker ( \mathrm {Id} \otimes p_0)=(H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0)\otimes { {{\mathbf {Q}}}_p})\widehat{\otimes }_{F}I_{0, {{\mathbf {Q}}}_p}$, where we defined the ideals $I_n$ of $r^{\mathrm{PD}}_{\varpi }$ as

$$\begin{aligned} I_n:=\Big \{\sum _{i\ge p^n}\tfrac{a_i}{\lfloor i/e\rfloor !}T^i, \lim _{i\mapsto \infty }a_i=0\Big \}. \end{aligned}$$

Note that we have the exact sequence

$$\begin{aligned} 0\rightarrow I_{0, {{\mathbf {Q}}}_p}\rightarrow r^{\mathrm{PD}}_{\varpi , {{\mathbf {Q}}}_p}\rightarrow F\rightarrow 0. \end{aligned}$$

Since the map $\iota ^{\prime }_{\varpi }$ is compatible with Frobenius, $\varphi (c_1^{\mathrm {HK} }(x))=pc_1^{\mathrm {HK} }(x)$, $\varphi (c_1^{\mathrm {st} }(x))=pc_1^{\mathrm {st} }(x)$, and $\beta$ is an isomorphism, we have $\varphi ^n(\zeta ^{\prime })=p^n\zeta ^{\prime }$. Since $\varphi ^n(I_0)\subset I_n$, this implies that $\zeta ^{\prime }\in \bigcap _{n=1}^{\infty }(H^1_{\mathrm {cr} }(X_0/{{\mathscr {O}}}_F^0)\otimes {{{\mathbf {Q}}}_p})\widehat{\otimes }_{F}I_{n, {{\mathbf {Q}}}_p}$, which is not possible unless $\zeta ^{\prime }$ is zero. This implies that $\zeta =0$, as wanted.

For the last map in the lemma, we use the commutative diagram from Corollary 7.6

the compatibilities from Sect. 7.2.1, and the compatibility of the second map in this lemma with Chern classes that we have shown above. $\square$

Alternative proof of Corollary 6.25

We present in this appendix an alternative proof of Corollary 6.25 (hence also of Proposition 6.23 which easily follows from it) that does not use the ordinarity of the truncated log-schemes $Y_s$.

Let $X/k^0$ be a fine log-scheme of Cartier type. Recall that we have the subsheaves

$$\begin{aligned} Z_{\infty }^j=\cap _{n\ge 0} Z_n^j, \quad B_{\infty }^j=\cup _{n\ge 0} B_n^j \end{aligned}$$

of $\Omega ^j=\Omega ^j_{X/k^0}$ (in what follows we will omit the subscripts in differentials if understood). Via the maps $C: Z_{n+1}^j\rightarrow Z_n^j$ (with kernels $B_n^j$), $Z_{\infty }^j$ is the sheaf of forms $\omega$ such that $dC^n \omega =0$ for all n. This sheaf is acted upon by the Cartier operator C, and we recover

$$\begin{aligned} B_{\infty }^j=\cup _{n\ge 0} (Z_{\infty }^j)^{C^n=0}, \quad \Omega ^j_{\log }=(Z_{\infty }^j)^{C=1}. \end{aligned}$$

The following result is proved in [40, 2.5.3] for classically smooth schemes. It holds most likely in much greater generality than the one stated below, but this will be sufficient for our purposes.

Lemma A.1

Assume that $X/k^0$ is semi-stable (with the induced log structure) and that k is algebraically closed. Then the natural map of étale sheaves

$$\begin{aligned} B_{\infty }^j\oplus (\Omega ^j_{\log }\otimes _{{\mathbf {F}}_p} k)\rightarrow Z_{\infty }^j \end{aligned}$$

is an isomorphism.

Proof

It suffices to show that, for X as above and affine, $B_{\infty }^j(X)\oplus (\Omega ^j_{\log }(X)\otimes _{{\mathbf {F}}_p} k)\rightarrow Z_{\infty }^j(X)$ is an isomorphism. Take an open dense subset $j: U\hookrightarrow X$ which is smooth over k. Then $\Omega ^i_{X}$ is a subsheaf of $j_*\Omega ^i_U$ and so $Z^i_{\infty ,X}$ is a subsheaf of $j_*Z^i_{\infty , U}$, giving an inclusion $Z^i_{\infty , X}(X)\subset Z^i_{\infty , U}(U)$. By a result of Raynaud [40, Prop. 2.5.2], $Z^i_{\infty , U}(U)$ is a union of finite dimensional k-vector spaces stable under C. We deduce that $Z^i_{\infty , X}(X)$ is also such a union.

The result follows now from the following basic result of semi-linear algebra (this is where the hypothesis that k is algebraically closed is crucial): if E is a finite dimensional k-vector space stable under C, then $E=E_{\mathrm{nilp}}\oplus E_{\mathrm{inv}}$, where $E_{\mathrm{nilp}}=\cup _{n} E^{C^n=0}$, $E_{\mathrm{inv}}=\cap _{n} C^n(E)$, and the natural map $E^{C=1}\otimes _{{\mathbf {F}}_p} k\rightarrow E_{\mathrm{inv}}$ is an isomorphism. $\square$

Proof of Corollary 6.25

(1) We prove this in several steps. We start with the case $i=0$ (the most delicate). By Lemma A.1,

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, Z_{\infty }^j)\simeq H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, B_{\infty }^j)\oplus H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }\otimes _{{\mathbf {F}}_p} k). \end{aligned}$$

We need the following intermediate result:

Lemma A.2

We have $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, B_{\infty }^j)=0$.

Proof

We note that $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, B_n^j)=0$ for all n: because we have $B^j_n\simeq B^j_{n+1}/B^j_1$ this follows from Lemma 6.13. This however does not allow us to deduce formally our lemma because $B_{\infty }^j=\cup _{n} B_n^j$ and $\overline{Y}$ is not quasi-compact. Instead, we argue as follows: the formation of the sheaves $B_{\infty }^j$ being functorial, we have a natural map $\alpha : H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, B_{\infty }^j)\rightarrow \prod _{C\in F^0} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{C}, B_{\infty }^j)$. It suffices to prove that $\alpha$ is injective and that $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{T}, B_{\infty }^j)=0$. To prove the injectivity of $\alpha$, it suffices to embed both the domain and target of $\alpha$ in $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j)$ and $\prod _{C} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{C}, \Omega ^j)$, and to use the injectivity of the natural map $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j)\rightarrow \prod _{C} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{C}, \Omega ^j)$. Next, since $\overline{T}$ is quasi-compact,

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{T}, B_{\infty }^j)=\varinjlim _{n} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{T}, B_n^j)=0, \end{aligned}$$

the second equality being a consequence of Proposition 6.3 and Lemma 6.13 (as above, in the case of $\overline{Y}$). $\square$

Consider now the sequence of natural maps

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }){\widehat{\otimes }}_{{{\mathbf {F}}}_p}\overline{k}{\mathop {\rightarrow }\limits ^{\sim }} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }\otimes _{{\mathbf {F}}_p} \overline{k}){\mathop {\rightarrow }\limits ^{\sim }} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, Z_{\infty }^j) \rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j). \end{aligned}$$

The first map is clearly a topological isomorphism, the second one is a topological isomorphism by Lemma A.2. Hence it remains to show that the last map is a topological isomorphism as well. Or that all the natural maps $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},Z^j_{n})\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},\Omega ^j)$, $n\ge 1$, are topological isomorphisms. But this was done in the proof of Lemma 6.20. This gives the desired result for $i=0$.

We prove next the result for $i>0$, i.e., that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })\widehat{\otimes }_{{\mathbf {F}}_p}\overline{k}=0$ for $i\ge 1$. We start with showing that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })=0$. The exact sequence

yield the exact sequence

and $H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })=0$ for $i>1$. It suffices therefore to prove that $1-C^{-1}$ is surjective on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j)$. For this, write $A_s=H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, \Omega ^j_{\log })$. As we have already seen, we have an isomorphism

$$\begin{aligned} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j)\simeq \varprojlim _s (A_s\otimes _{{\mathbf {F}}_p} \overline{k})=H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }){\widehat{\otimes }}_{{{\mathbf {F}}}_p}\overline{k}. \end{aligned}$$

We have $C^{-1}=\varprojlim _{s}(1\otimes \varphi )$ ($\varphi$ being the absolute Frobenius on $\overline{k}$; note that $C-1=0$ on $A_s$). To conclude that $1-C^{-1}$ is surjective on $H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j)$, it suffices to pass to the limit in the exact sequences

$$\begin{aligned} 0\rightarrow A_s\rightarrow A_s\otimes _{{\mathbf {F}}_p} \overline{k}{\mathop {\longrightarrow }\limits ^{1-\varphi }} A_s\otimes _{{\mathbf {F}}_p} \overline{k}\rightarrow 0, \end{aligned}$$

whose exactness is ensured by the Artin-Schreier sequence for $\overline{k}$ and the fact that $(A_s)_{s}$ is Mittag-Leffler.

This shows that $H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })=0$ for $i>0$. Choosing a basis $(e_{\lambda })_{\lambda \in I}$ of $\overline{k}$ over ${\mathbf {F}}_p$ we obtain an embedding

$$\begin{aligned} H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }){\widehat{\otimes }}_{{{\mathbf {F}}}_p}\overline{k}\subset \prod _{\lambda \in I} H^i_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log })=0, \end{aligned}$$

which finishes the proof of (1).

(2) We prove the claim for $W_n$ by induction on n, the case $n=1$ being part (1). We pass from n to $n+1$ using the strictly exact sequences

$$\begin{aligned}&0\rightarrow H^0(\overline{Y}, \Omega ^j){\mathop {\rightarrow }\limits ^{V^n}} H^0(\overline{Y}, W_{n+1}\Omega ^j)\rightarrow H^0(\overline{Y}, W_n\Omega ^j)\rightarrow 0,\\&0\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }){\widehat{\otimes }}_{{{\mathbf {F}}}_p}\overline{k}{\mathop {\rightarrow }\limits ^{V^n}}H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_{n+1}\Omega ^j_{\log }){\widehat{\otimes }}_{ {{\mathbf {Z}}} /p^{n+1}}W_{n+1}(\overline{k})\\&\quad \quad \quad \rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y},W_{n}\Omega ^j_{\log }){\widehat{\otimes }}_{ {{\mathbf {Z}}} /p^n}W_n(\overline{k})\rightarrow 0, \end{aligned}$$

as well as the natural map between them. The first sequence is exact by Lemma 6.20. To show that the second sequence is exact, consider, as above, the exact sequences

$$\begin{aligned} 0\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, \Omega ^j_{\log }){\mathop {\rightarrow }\limits ^{V^n}} H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, W_{n+1}\Omega ^j_{\log })\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, W_n\Omega ^j_{\log })\rightarrow H^1_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, \Omega ^j_{\log }). \end{aligned}$$

Tensoring over ${\mathbf {Z}}$ by $W_{n+1}(\overline{k})$, we can rewrite them as

$$\begin{aligned} 0\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, \Omega ^j_{\log })\otimes _{{\mathbf {F}}_p} \overline{k}&\rightarrow H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, W_{n+1}\Omega ^j_{\log })\otimes _{{\mathbf {Z}}/p^{n+1}} W_{n+1}(\overline{k})\\ \rightarrow&H^0_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, W_n\Omega ^j_{\log })\otimes _{{\mathbf {Z}}/p^n} W_n(\overline{k}) \rightarrow H^1_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}_s^{\circ }, \Omega ^j_{\log })\otimes _{{\mathbf {F}}_p} \overline{k}. \end{aligned}$$

To lighten the notation, write them simply as $0\rightarrow A_s\rightarrow B_s\rightarrow C_s\rightarrow D_s$. Using that $(A_s)_s, (C_s)_s$ are finite $W_n(\overline{k})$-modules and that $\varprojlim _s D_s= H^1_{\acute{\mathrm{e}}\mathrm {t}}(\overline{Y}, \Omega ^j_{\log }){\widehat{\otimes }}_{{{\mathbf {F}}}_p}\overline{k}=0$ (as follows from (1)), we obtain the exact sequence

$$\begin{aligned} 0\rightarrow \varprojlim _s A_s\rightarrow \varprojlim _s B_s\rightarrow \varprojlim _s C_s\rightarrow 0, \end{aligned}$$

which finishes the proof of (2) for $W_n$, $n\ge 1$. Passing to the limit over n gives us the proof for W. $\square$