Integral models of Hilbert modular varieties in the ramified case, deformations of modular Galois representations, and weight one forms

Abstract

We prove the strong Artin conjecture for continuous, totally odd, two-dimensional representations of the absolute Galois group of a totally real field F.

1 Introduction

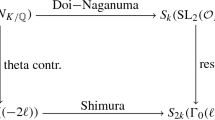
This work grew out of Buzzard and Taylor’s attempt to generalise, to the Hilbert case, Taylor’s programme ([53]) to prove new cases of the strong Artin conjecture for odd continuous two-dimensional Galois representations in the icosahedral case. We complete the programme in the Hilbert case in this paper by a method slightly different from what they probably had in mind.

In 1999, Buzzard and Taylor [7, 9] made substantial progress on the strong Artin conjecture for odd, continuous representations $\rho : {\mathrm {Gal}}(\overline{\mathbf {Q}}/\mathbf {Q})\rightarrow {\mathrm {GL}}_2(\mathbf {C})$ of the absolute Galois group ${\mathrm {Gal}}(\overline{\mathbf {Q}}/\mathbf {Q})$ of $\mathbf {Q}$, which culminated in [8] and subsequently in [54]. In proving the hitherto intractable ‘icosahedral’ case of the conjecture, Buzzard and Taylor built on the work of Katz in the 70s and Coleman in the 90s on the theory of p-adic modular forms, to prove a modular lifting theorem which constructs a weight one eigenform corresponding to an odd two-dimensional p-adic representation ${\mathrm {Gal}}(\overline{\mathbf {Q}}/\mathbf {Q})\rightarrow {\mathrm {GL}}_2(\overline{\mathbf {Q}}_p)$ (potentially) unramified at p. One of the key observations they made in [9] was the idea that one can use Hida theory of p-adic modular forms to draw results about weight one forms from results about weight two forms in the form of modular lifting theorems by Wiles, Taylor–Wiles and Diamond.

In generalising Taylor’s strategy to the Hilbert case, one has to work with sections of the determinant of the ‘universal’ cotangent sheaf over (admissible subsets of) Hilbert modular varieties. Rapoport [39] probably was the first to consider a $[F:\mathbf {Q}]$-dimensional moduli space Y of abelian varieties with real multiplication (HBAV) by a totally real field F satisfying some PEL conditions (in particular of ‘level prime to p’); and [39] shows that Y gives rise to a $\mathbf {Z}_p$-integral model for the (connected) Shimura variety corresponding, in particular, to the algebraic $\mathbf {Q}$-group G, defined by the pull-back of ${\mathrm {Res}}_{F/\mathbf {Q}} {\mathrm {GL}}_2\rightarrow {\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}$ along $\mathbb {G}\rightarrow {\mathrm {Res}}_{F/\mathbf {Q}} \mathbb {G}$ (where $\mathbb {G}$ denotes the multiplicative group scheme base-changed over to F). The determinant of the cotangent bundle of the universal HBAV defines an automorphic line bundle $\mathscr {A}_Y$ of parallel weight one and one may identify weight one holomorphic modular forms with integral coefficients with global sections of $\mathscr {A}_Y$ over the moduli space Y. With the assumption that p divides the discriminant of F, one is naturally led to work with the models Deligne–Pappas constructed in [13]. However, they no longer satisfy the ‘Rapoport condition’—the Lie algebras of HBAVs A over S have to be locally free $O_F\otimes _\mathbf {Z}O_S$-modules of rank one–and they are not smooth over the base as aresult; in particular, one can calculate local models to deduce that the special fibre at a prime p which ramifies in F is singular in codimension 2 and geometry of the corresponding rigid space is discouragingly complicated for arithmetic applications. To at least resolve the difficulties arising from geometry, it was suggested by Buzzard and Taylor to the author to ‘resolve’ the singularities of the Deligne–Pappas models using ideas from Pappas–Rapoport [35].

Fix an embedding $\overline{\mathbf {Q}}$ into $\overline{\mathbf {Q}}_p$. In this paper, we constructs an integral model $Y^{\mathrm {PR}}_U$ of G of level $U\subset G(\mathbb {A}^\infty )$ with $U\cap G(\mathbf {Q}_p)=G(\mathbf {Z}_p)$ over the ring of integers O of a finite extension L of $\mathbf {Q}_p$ containing the image of every embedding $F\rightarrow \overline{\mathbf {Q}}\rightarrow \overline{\mathbf {Q}}_p$, and prove that it is smooth over O. We also define a model $Y_{U{\mathrm {Iw}}}^{\mathrm {PR}}$ with Iwahori level at the primes of F above p, analogous to the construction given by Pappas [34] and Katz–Mazur [29]. Note that our models all have explicit descriptions as moduli problems. This is critical, for example, when one defines Hecke operators moduli-theoretically as in the work of Katz [28] and consider overconvergent eigenforms. We accordingly build a p-adic theory of Hilbert modular forms on the models $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$. For applications, we shall prove a modular lifting theorem which generalises a result of [9]. More precisely,

Theorem 1

Suppose $p>3$ and let L be a finite extension of $\mathbf {Q}_p$ with ring O of integers and maximal ideal $\lambda$. Let

$$\begin{aligned} \rho : {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(O) \end{aligned}$$

be a continuous representation such that

• $\rho$ is totally odd,

• $\rho$ is ramified at only finitely many primes of F,

• $\overline{\rho }=(\rho \ {\mathrm {mod}}\ \lambda )$ is absolutely irreducible when restricted to ${\mathrm {Gal}}(\overline{F}/F(\zeta _p))$,

• if $p=5$ and the projective image of $\overline{\rho }$ is isomorphic to ${\mathrm {PGL}}_2(\mathbf {F}_5)$, the kernel of the projective representation of $\overline{\rho }$ does not fix $F(\zeta _5)$,

• there exists a cuspidal automorphic representation $\varPi$ of ${\mathrm {GL}}_2/F$ which are ordinary at every place of F above p such that $\overline{\rho }_\varPi \simeq \overline{\rho }$,

• the image of inertia subgroup at every finite place of F above p is finite.

Then there exists a cuspidal Hilbert modular eigenform defined as a section of the automorphic bundle $\mathscr {A}_X(-{\mathrm {cusps}})$ over the p-adic generic fibre $X=X_{U{\mathrm {Iw}}}^{\mathrm {PR}}[1/\lambda ]$ of a compactification $X_{U{\mathrm {Iw}}}^{\mathrm {PR}}$ of $Y_{U{\mathrm {Iw}}}^{\mathrm {PR}}$ of parallel weight one, whose associated Galois representation, in the sense of Rogawski-Tunnell/Wiles, is isomorphic to $\rho$.

Assuming that p splits completely in F and that $\rho$, when restricted to every place of F above p, is the direct sum of two characters which are distinct mod $\lambda$, the theorem is proved in [43]. Assuming p is unramified in F and that the restriction of $\rho$ at every place of F above p is the direct sum of two characters whose ratio is non-trivial mod $\lambda$ and is unramified (resp. tamely ramified), the theorem is proved in [26] (resp. [27]). On the other hand, Pilloni [37] has a a result stronger than [26] allowing small ramification of p in F, while Pilloni and Stroh have a paper [38] announcing the same set of statements as the main theorem above (although our approach is completely different from theirs).

The theorem is established in two major steps. Given a residually automorphic p-adic representation $\rho$ as above (note that $\overline{\rho }$ is not assumed ‘p-distinguished’), we firstly prove an $R=T$ theorem for p-ordinary representations/forms such that $\rho$ defines a map from R to O, where R parameterises deformations of $\overline{\rho }$ which are reducible at every place of F above p (as in [19]) and where T is a Hida (nearly) ordinary Hecke algebra localised at $\overline{\rho }$. Our $R=T$ theorem holds without recourse to taking reduced quotients (we indeed prove that, not only T but R is also reduced); we do this by following Snowden’s insight in [49], non-trivially observing that the relevant local deformation rings (including those at places above p) are Cohen–Macaulay. The maps from T to O, corresponding to $\rho$ and eigenvalues of $\rho ({\mathrm {Frob}}_\mathfrak {p})$ for all places $\mathfrak {p}$ above p, define a family of p-adic overconvergent cuspidal Hilbert modular eigenforms of weight one which are ‘in companion’. The construction, however, is no longer as straightforward as the case $\rho$ is split with distinct eigenvalues at places above p (as in [7, 9], and [26]), and we follow Taylor’s idea in the case $F=\mathbf {Q}$, combined with the reducedness of R, to deal with the general case. We then follow Kassaei’s paper [26] morally to ‘glue’ these p-adic companion forms in order to construct a classical weight one form over X. The beautiful idea of Buzzard and Taylor [9] that, from their q-expansion coefficients (by the strong multiplicity one theorem), one can spot a set of linear equations satisfied by the p-adic companion eigenforms is sill very much in force in this paper.

It is absolutely crucial that we work with $Y^{\mathrm {PR}}_{U}$ and $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$. Suppose for brevity that p has only one prime $\mathfrak {p}$ in F. Let k be the residue field of $\mathfrak {p}$ and let $|k|=p^{f}$. Let A be a HBAV over an O-scheme of the type considered by Deligne–Pappas [13], equipped with a finite flat $O_F$-subgroup scheme C of $A[\mathfrak {p}]$ of order |k| which equals its orthogonal for the Weil paring on $A[\mathfrak {p}]$. In proving analytic continuation results, it is desirable to describe, for a fixed C, exactly the locus where

$$\begin{aligned} {\mathrm {deg}}(C)>{\mathrm {deg}}(A[\mathfrak {p}]/D) \end{aligned}$$

hold¹ for all $O_F$-subgroup schemes $D\subset A[\mathfrak {p}]$ that intersect trivially with C in $A[\mathfrak {p}]$.

If $F=\mathbf {Q}$, it is proved in [28] (and made more precise in [7]) that one can explicitly ‘solve equations’ in one-dimensional formal groups to compute and compare ${\mathrm {deg}}(C)$ and ${\mathrm {deg}}(D)$ explicitly. In the general unramifed Hilbert case, in dealing with this problem, Goren–Kassaei [20] finds a way to understand degrees near ordinary loci in terms of local geometry of Hilbert modular varieties, and instead solves ‘local equations’ of HMVs. When p ramified in F, $A[\mathfrak {p}]$ is no longer a truncated Barsotti–Tate of level 1 in general (indeed, $A[\mathfrak {p}]$ is truncated Barsotti–Tate of level 1 if and only if A satisfies the Rapoport condition), and it is not a straightforward task to compute the Dieudonne module of $A[\mathfrak {p}]$ in the standard sense, let alone deducing results about ${\mathrm {deg}}(C)$ and ${\mathrm {deg}}(D)$. Indeed, the gist of work of Andreatta–Goren [1] is to keep track of the relative Frobenius in characteristic p that is no longer ‘well-behaved’ in the presence of ramification. We propose a solution to these issues by working with the integral models $Y^{\mathrm {PR}}_{U}$ and $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ over O. More precisely, we

• define new invariants for HBAVs parameterised by the $\kappa$-fibre $\overline{Y}^{\mathrm {PR}}_U$ (where $\kappa$ is the residue field of O), by which we single out HBAVs in co-dimension $\le 1$ that are ‘not too supersingular’ and ‘well-behaved’ for analytic continuation (and analytic continuation results are established exclusively over this locus);

• define a finer degree which reads geometry of the $\kappa$-fibre $\overline{Y}^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ of $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ better;

• use these invariants to understand geometry of fibres of the forgetful functor/morphism from $\overline{Y}^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ to $\overline{Y}^{\mathrm {PR}}_{U}$;

• over the p-adic generic fibre of $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$, we make appeal to its comparatively simple set of local equations to prove a canonical subgroup theorem, and make use of ‘mod $\mathfrak {p}$ Dieudonne crystals’, in place of Breuil-Kisin modules in the unramfied case, to prove analytic continuation results we need in the general ramified case.

The condition that $\rho _\varPi$ is (nearly) ordinary at all place of F above p is essential in our approach; more precisely, essential in constructing overconvergent companion forms. On the other hand, it is quite likely that one can extend the main theorem to $p=2$ (See [44]). In return for assuming that $\overline{\rho }$ is indeed a direct sum of distinct characters at every place of F above p, Skinner–Wiles [48] allows us to ‘extend’ our main theorem ‘orthogonally’ to the case $\overline{\rho }$ is reducible. The general residually reducible case requires some more work, and is considered also in [44].

A conjecture of Fontaine–Mazur asserts that an n-dimensional continuous irreducible p-adic representation of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of a number field F, which are unramified outside a finite set of places and which are finite when restricted to the inertia subgroup at every place of F above p, has finite image. Since p-adic Galois representations associated to classical weight one forms have finite image, the Fontaine–Mazur conjecture for $\rho$ exactly as above follows immediately. Many more cases of the Fontaine–Mazur conjectures are proved in [44].

Finally, combined with a theorem about modularity of mod 5 representation $\overline{\rho }$, we shall prove the strong Artin conjecture:

Theorem 2

The strong Artin conjecture for two-dimensional, totally odd, continuous representations $\rho : {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(\mathbf {C})$ of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of a totally real field F, holds.

By work of Artin, Langlands, and Tunnell, the ‘soluble’ cases where the image of projective representation of $\rho$ is dihedral, octahedral, and tetrahedral are known; and the theorem proves the icosahedral case completely.

We remark that the p-adic integral models we construct also have applications to p-adic theory of Hilbert modular forms. As Johansson [25] demonstrates, one can prove an analogue of Coleman’s theorem, ‘overconvergent modular forms of small slope are classical’, using our models. His approach is a generalisation to quaternion Hilbert modular forms of Coleman’s original ‘cohomological approach’, while one can take Kassaei’s ‘gluing approach’ with our p-adic integral models to prove it. It is also likely that one can extend the ‘geometric’ construction of an eigenvariety for Hilbert modular forms by Andreatta–Iovita–Stevens and Pilloni to the general ramified case, and prove various Langlands functoriality in p-adic families.

The author would like to thank his Ph.D. supervisor Kevin Buzzard, Fred Diamond, Toby Gee, Payman Kassaei, Vytas Pa$\check{{\mathrm {s}}}$k$\bar{{\mathrm { u}}}$nas, Timo Richarz, and Teruyoshi Yoshida for helpful comments and conversations on numerous occasions. He would also like to thank Alain Genestier for a helpful comment.

Sections 3 and 5.1 were originally written as a chapter in author’s Ph.D. thesis at Imperial College London, and owes their existence to various ideas he discussed and numerous conversations he had with Kevin Buzzard, as well as to the financial support he received from EPSRC through him in the form of an EPSRC Project Grant (PI Kevin Buzzard). While this paper was prepared, the author was financially supported by EPSRC and DFG/SFB. And he would like to thank all these research councils for their support. Last but not least, he would like to thank Kevin Buzzard, Fred Diamond, Payman Kassaei, and Vytas Pa$\check{{\mathrm {s}}}$k$\bar{{\mathrm { u}}}$nas for moral support while this paper was being prepared.

The author acknowledges most gratefully that, if it were not for Kassaei’s paper [26], Taylor’s idea (to deal with the case $\rho ({\mathrm {Frob}}_\mathfrak {p})$ has equal eigenvalues for places $\mathfrak {p}$ of F above p) and countless conversations and discussions he had with Diamond, this paper could not have been completed. He is grateful to Taylor for having given him permission to use his argument (in $F=\mathbf {Q}$) to deal with the p-non-distinguished case.

2 Deformation rings and Hecke algebras (following Geraghty)

This section follows [11] and [19].

Let L be a finite extension of $\mathbf {Q}_p$ with ring of integers O, maximal ideal $\lambda$, and residue field k.

For every finite place ${\mathrm {Q}}$, let $F_{\mathrm {Q}}$ denote the completion of F at ${\mathrm {Q}}$ with ring of integers $O_{F_{\mathrm {Q}}}$, $D_{\mathrm {Q}}\simeq {\mathrm {Gal}}(\overline{F}_{\mathrm {Q}}/F_{\mathrm {Q}})$ denote the decomposition subgroup at ${\mathrm {Q}}$ and $I_{\mathrm {Q}}$ denote the inertia subgroup at ${\mathrm {Q}}$ of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of a totally real field F. Let ${\mathrm {Art}}_{\mathrm {Q}}$ denote the local Artin map, normalised to send a uniformiser $\pi _{\mathrm {Q}}$ of $O_{F_{\mathrm {Q}}}$ to a geometric Frobenius element ${\mathrm {Frob}}_{\mathrm {Q}}$.

Let

$$\begin{aligned} \overline{\rho }: {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_n(k) \end{aligned}$$

be a totally odd (i.e., the image of complex conjugation with respect to every embedding of F into $\mathbf {R}$ is non-trivial), continuous, irreducible representation of ${\mathrm {Gal}}(\overline{F}/F)$. For every prime ${\mathrm {Q}}$ of F, let $\overline{\rho }_{\mathrm {Q}}$ denote the restriction to the decomposition group $D_{\mathrm {Q}}$ at a place ${\mathrm {Q}}$ of F.

For every prime ${\mathrm {Q}}$ of F, let $R_{\mathrm {Q}}^\Box$ denote the universal ring for liftings of $\overline{\rho }_{\mathrm {Q}}$.

Let S be a finite set of places in F containing the set $S_{\mathrm {P}}$ of all places of F above p and the set $S_\infty$ of all infinite places of F, and let T be a subset of S. Suppose that T does not contain $S_\infty$.

Let $F_S$ denote the maximal extension unramified outside S, and let $G_S={\mathrm {Gal}}(F_S/F)$. Let

$$\begin{aligned} \varSigma =(S, T, (I_{\mathrm {Q}}^\Box )_{{\mathrm {Q}}\in S}) \end{aligned}$$

be a deformation data, where $I_{\mathrm {Q}}^\Box \subset R_{\mathrm {Q}}^\Box$ is an ideal defining a local deformation problem $\varSigma _{\mathrm {Q}}$ and a subspace $L_{\mathrm {Q}}\subset H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })$ (2.2.4, [11]), and we define $H^t_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ as follows: Firstly, let

$$\begin{aligned}C_\varSigma ^{0, {\mathrm {loc}}}(G_S, {\mathrm {ad}}\overline{\rho })=\bigoplus _{{\mathrm {Q}}\in S-T} (0)\oplus \bigoplus _{{\mathrm {Q}}\in T} C^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }),\end{aligned}$$

$$\begin{aligned} C_\varSigma ^{1, {\mathrm {loc}}}(G_S, {\mathrm {ad}}\overline{\rho })=\bigoplus _{{\mathrm {Q}}\in S-T}C^1(D_{\mathrm {Q}},{\mathrm {ad}}\overline{\rho })/M_{\mathrm {Q}}\oplus \bigoplus _{{\mathrm {Q}}\in T} C^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }), \end{aligned}$$

where $M_{\mathrm {Q}}$ denotes the pre-image in $C^1(D_{\mathrm {Q}},{\mathrm {ad}}\overline{\rho })$ of $L_{\mathrm {Q}}$, and let

$$\begin{aligned} C_\varSigma ^{t,{\mathrm {loc}}}(G_S, {\mathrm {ad}}\overline{\rho })=\bigoplus _{{\mathrm {Q}}\in S} C^{t}(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }) \end{aligned}$$

for $t\ge 2$; and let

$$\begin{aligned} C_\varSigma ^t(G_S, {\mathrm {ad}}\overline{\rho })=C^t(G_S, {\mathrm {ad}}\overline{\rho })\bigoplus C_\varSigma ^{t-1,{\mathrm {loc}}}(G_S, {\mathrm {ad}}\overline{\rho }) \end{aligned}$$

with the boundary map $C_\varSigma ^t(G_S, {\mathrm {ad}}\overline{\rho })\rightarrow C_\varSigma ^{t+1}(G_S, {\mathrm {ad}}\overline{\rho })$ sending $(\phi , (\phi ^{\mathrm {loc}}_{\mathrm {Q}}))$ to $(\partial \phi , ({\mathrm {res}}_{\mathrm {Q}} \phi -\partial \phi ^{\mathrm {loc}}_{\mathrm {Q}}))$. We then define $H^t_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ to be the cohomology group defined by the complex.

Let $\mathcal {C}=\mathcal {C}_O$ denote the category of O-algebras as defined in 2.2 of [11]; its objects are inverse limits of objects in the category $\mathcal {C}^f$ of Artinian local O-algebras R for which the structure map $O\rightarrow R$ induces an isomorphism on residue fields and its morphisms are homomorphisms of O-algebras which induce isomorphisms on residue fields. Let $R_\varSigma ^\Box$ denote the universal ring for T-framed deformation of type $(\varSigma _{\mathrm {Q}})_{{\mathrm {Q}}\in S}$ (when T is non-empty). If T is empty, write $R_\varSigma$. We let $R_\varSigma ^{ {\mathrm {loc}}}$ denote the completed tensor product of $R^\Box _{\mathrm {Q}}/I_{\mathrm {Q}}^\Box$ for ${\mathrm {Q}}$ in T, and let $R_T^\Box$ denote the formal power series ring in $n^2|T|-1$ variables with coefficients in O normalised such that

$$\begin{aligned} R^\Box _\varSigma \simeq R_\varSigma \otimes R^\Box _T. \end{aligned}$$

Proposition 1

$R^\Box _\varSigma$ is the quotient of a power series ring over $R_\varSigma ^{ {\mathrm {loc}}}$ in ${\mathrm {dim}}\, H^1_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ variables. If furthermore $H^2_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })=(0)$, then it is indeed a power series ring over $R_\varSigma ^{ {\mathrm {loc}}}$ in ${\mathrm {dim}}\, H^1_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ variables.

Proof

Corollary 2.2.12, [11]. $\square$

The local Tate duality

$$\begin{aligned} {\mathrm {ad}}\overline{\rho }\times {\mathrm {ad}}\overline{\rho }(1)\longrightarrow k(1) \end{aligned}$$

given by the ‘trace pairing’ gives rise to the perfect pairing

$$\begin{aligned} H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })\times H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }(1))\longrightarrow k. \end{aligned}$$

The orthogonal complement $L_{\mathrm {Q}}^\perp$ of $L_{\mathrm {Q}}\subset H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })$ will be taken with respect to the pairing.

Following 2.3 [11], given a deformation problem $\varSigma =(S, T, (L_{\mathrm {Q}})_{{\mathrm {Q}}\in S}, (I_{\mathrm {Q}}^\Box )_{{\mathrm {Q}}\in S})$, define

$$\begin{aligned} H^1_{\varSigma ^\perp }(G_S, {\mathrm {ad}}\overline{\rho }(1)) \end{aligned}$$

to be the kernel of the map

$$\begin{aligned} H^1(G_S, {\mathrm {ad}}\overline{\rho }(1))\longrightarrow \bigoplus _{S-T} H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }(1))/L_{\mathrm {Q}}^\perp . \end{aligned}$$

Proposition 2

Suppose $n=2$.

$$\begin{aligned}&{\mathrm {dim}}\, H^1_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })\\&={\mathrm {dim}}\, H^1_{\varSigma ^\perp }(G_S, {\mathrm {ad}}\overline{\rho }(1))+{\mathrm {dim}}\, H^0_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })-{\mathrm {dim}}\, H^0(G_S, {\mathrm {ad}}\overline{\rho }(1))\\&\quad +\sum _{{\mathrm {Q}}\in S-T}{\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }) \end{aligned}$$

Proof

It follows from the long exact sequence defining $H^t_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ that

$$\begin{aligned}&\sum _t (-1)^t {\mathrm {dim}}\, H_\varSigma ^t(G_S, {\mathrm {ad}}\overline{\rho })\\&\quad =\sum _t (-1)^t {\mathrm {dim}}\, H^t(G_S, {\mathrm {ad}}\overline{\rho })-\sum _{{\mathrm {Q}}\in S}\chi (D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })\\&\qquad -\sum _{{\mathrm {Q}}\in S-T}({\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })), \end{aligned}$$

hence, we deduce ${\mathrm {dim}}\, H^1_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ is

$$\begin{aligned}&{\mathrm {dim}}\, H_\varSigma ^0(G_S, {\mathrm {ad}}\overline{\rho })+{\mathrm {dim}}\, H_\varSigma ^2(G_S, {\mathrm {ad}}\overline{\rho })-{\mathrm {dim}}\, H_\varSigma ^3(G_S, {\mathrm {ad}}\overline{\rho })-\chi (G_S, {\mathrm {ad}}\overline{\rho })\\&\quad +\sum _{{\mathrm {Q}}\in S}\chi (D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })+\sum _{{\mathrm {Q}}\in S-T} ({\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })). \end{aligned}$$

By the Poitou–Tate global duality, we deduce ${\mathrm {dim}}\, H_\varSigma ^3(G_S, {\mathrm {ad}}\overline{\rho })={\mathrm {dim}}\, H^0(G_S, {\mathrm {ad}}\overline{\rho }(1))$, and ${\mathrm {dim}}\, H^2_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })={\mathrm {dim}}\, H^1_{\varSigma ^\perp }(G_S, {\mathrm {ad}}\overline{\rho }(1))$. By the global Euler characteristic formula ([33], Theorem 5.1), $\chi (G_S, {\mathrm {ad}}\overline{\rho })=-2[F:\mathbf {Q}]$. By the local Euler characteristic formulae (Theorem 2.13 in [33] and Theorem 5, Chapter II, 5.7 in [45]) $\sum _S\chi (D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })=-2[F:\mathbf {Q}]$. Combining these, we get the assertion. $\square$

Suppose that $S_{\mathrm {Q}}$ is a set of primes ${\mathrm {Q}}$ of F not in S such that

• $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod p;

• $\overline{\rho }_{\mathrm {Q}}$ is unramified, and is a direct sum of unramified characters $\overline{\rho }_{1}$ and $\overline{\rho }_2$, where $\overline{\rho }_1({\mathrm {Frob}}_{\mathrm {Q}})$ and $\overline{\rho }_2({\mathrm {Frob}}_{\mathrm {Q}})$ distinct.

Define $L_{\mathrm {Q}}\subset H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })$ to be the subspace of classes corresponding to conjugacy classes of liftings $\rho$ which are direct sum of characters $\rho _1$ and $\rho _2$ such that $\rho _t$ lifts $\overline{\rho }_t$ ($t=1, 2$) and $\rho _2$ is unramified; hence ${\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\ H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })=1$ (see 2.4.6 in [11]).

Fixing a deformation data $\varSigma$ as above, let

$$\begin{aligned} \varSigma _{\mathrm {Q}}=(S\cup S_{\mathrm {Q}}, T, (L_{\mathrm {Q}})_{{\mathrm {Q}}\in S\cup S_{\mathrm {Q}}}, (I_{\mathrm {Q}}^\Box )_{{\mathrm {Q}}\in S\cup S_{\mathrm {Q}}} ). \end{aligned}$$

The restriction to the inertia subgroup $I_{\mathrm {Q}}$ at ${\mathrm {Q}}$ in $S_{{\mathrm {Q}}}$ (as in the preceding section), of the determinant of a lifting $\rho$ of $\overline{\rho }$ of type $\varSigma _{{\mathrm {Q}}}$ as above factors through the composition of the local Artin map (restricted to $I_{\mathrm {Q}}$) followed by the surjection to the maximal pro-p quotient $\varDelta _{\mathrm {Q}}$ of $(O_F/{\mathrm {Q}})^\times$. As a result, we have a map $\varDelta _{\mathrm {Q}}\rightarrow R_{\varSigma _{\mathrm {Q}}}$; and $\prod _{\mathrm {Q}} \varDelta _{\mathrm {Q}}\rightarrow R_{\varSigma _{\mathrm {Q}}}$ where ${\mathrm {Q}}$ ranges over $S_{\mathrm {Q}}$.

We now apply the formula above to $\varSigma _{\mathrm {Q}}$ to compute ${\mathrm {dim}}\, H^1_{\varSigma _{\mathrm {Q}}}(G_{S\cup S_{\mathrm {Q}}}, {\mathrm {ad}}\overline{\rho })$.

Proposition 3

Suppose $n=2$, and suppose that $\overline{\rho }$ is absolutely irreducible when restricted to ${\mathrm {Gal}}(\overline{F}/F(\zeta _p))$. Suppose that T is non-empty. Suppose for a finite place ${\mathrm {Q}}$ in $S-T$ that ${\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })=0$ if ${\mathrm {Q}}$ is not in $S_{\mathrm {P}}$, while ${\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })=[F_{\mathrm {Q}}:\mathbf {Q}_p]$ if ${\mathrm {Q}}$ is in $S_{\mathrm {P}}$. Then

$$\begin{aligned}&{\mathrm {dim}}\, H^1_{\varSigma _{\mathrm {Q}}}(G_{S\cup S_{\mathrm {Q}}}, {\mathrm {ad}}\overline{\rho })\\&\quad ={\mathrm {dim}}\, H^1_{\varSigma _{\mathrm {Q}}^\perp }(G_{S\cup S_{\mathrm {Q}}}, {\mathrm {ad}}\overline{\rho }(1))+|S_{\mathrm {Q}}|-\sum _{{\mathrm {Q}} | \infty }1-\sum _{{\mathrm {Q}}\in T\cap S_{\mathrm {P}}} [F_{\mathrm {Q}}: \mathbf {Q}_p]. \end{aligned}$$

Proof

Since ${\mathrm {dim}}\, H^0_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })$ is 0 (resp. 1) when T is non-empty (resp. empty), ${\mathrm {dim}}\, H^0_\varSigma (G_S, {\mathrm {ad}}\overline{\rho })-{\mathrm {dim}}\, H^0(G_S, {\mathrm {ad}}\overline{\rho }(1))=0$, and it suffices to check

$$\begin{aligned} \sum _{{\mathrm {Q}}\in (S\cup S_{\mathrm {Q}})-T} {\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho }) \end{aligned}$$

equals

$$\begin{aligned} |S_{\mathrm {Q}}|-\sum _{{\mathrm {Q}} |\infty }1-\sum _{{\mathrm {Q}}\in (T\cap S_{\mathrm {P}})}[F_{\mathrm {Q}}:\mathbf {Q}_p]. \end{aligned}$$

By the definition of $S_{\mathrm {Q}}$, it is equivalent to check

$$\begin{aligned} \sum _{{\mathrm {Q}}\in (S-T)} {\mathrm {dim}}\, L_{\mathrm {Q}}-{\mathrm {dim}}\, H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })=-\sum _{{\mathrm {Q}} |\infty }1 -\sum _{{\mathrm {Q}}\in (T\cap S_{\mathrm {P}})}[F_{\mathrm {Q}}:\mathbf {Q}_p]. \end{aligned}$$

By the assumptions of the proposition, it is equivalent to the validity of

$$\begin{aligned} \sum _{{\mathrm {Q}}\in (S-T)\cap S_{\mathrm {P}}}[F_{\mathrm {Q}}:\mathbf {Q}_p]+\sum _{{\mathrm {Q}}\in (T\cap S_{\mathrm {P}})}[F_{\mathrm {Q}}:\mathbf {Q}_p]=-\left( \sum _{{\mathrm {Q}}|\infty }-2\right) - \sum _{{\mathrm {Q}}|\infty } 1 \end{aligned}$$

but this holds as both sides equal $[F:\mathbf {Q}]$. $\square$

2.1 Universal rings for local liftings

In this section, we define universal rings for liftings/deformations that we need.

As in the previous section, $S_{\mathrm {P}}$ denote the set of all primes above p and $S_\infty$ denote the set of infinite places of F. Let $S_{\mathrm {R}}, S_{\mathrm {L}}$ and $S_{{\mathrm {A}}}$ denote disjoint finite sets of finite primes of F not dividing p. Suppose furthermore that $S_{{\mathrm {A}}}$ is non-empty and any prime ${\mathrm {Q}}$ of $S_{\mathrm {R}}\cup S_{\mathrm {L}}$ satisfies $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod p.

Suppose that p is odd. Suppose now that

$$\begin{aligned} \overline{\rho }: {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(k) \end{aligned}$$

is a continuous representation of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of F such that

• $\overline{\rho }$ is totally odd,

• $\overline{\rho }$ is unramified outside $S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}$,

• $\overline{\rho }$, when restricted to any prime in $S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{{\mathrm {L}}}$, is trivial,

• the restriction to ${\mathrm {Gal}}(\overline{F}/F(\zeta _p))$ of $\overline{\rho }$ is absolutely irreducible.

• $\overline{\rho }$, when restricted to any prime ${\mathrm {Q}}$ in $S_{{\mathrm {A}}}$, is unramified and $H^0(D_{\mathrm {Q}}, {\mathrm {ad}}\, \overline{\rho }(1))=0$ (it is possible to find a such ${\mathrm {Q}}$, indeed satisfying $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\not \equiv 1$ mod p, follows for example from Proposition 4.11 in [12]),

• if $p=5$ and the projective image of $\overline{\rho }$ is ${\mathrm {PGL}}_2(\mathbf {F}_5)$, the kernel of the projective representation of $\overline{\rho }$ does not fix $F(\zeta _5)$,

We remark that S earlier will be $S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}\cup S_\infty$ and T will be $S-S_\infty$.

For every place $\mathfrak {p}$ of F above p, let $G_\mathfrak {p}$ denote the image of the inertia subgroup $I_\mathfrak {p}$ in the pro-p-completion of the maximal abelian quotient of the decomposition group $D_\mathfrak {p}$ at $\mathfrak {p}$, and let G denote the product of $G_\mathfrak {p}$ over all $\mathfrak {p}$ above p. The local Artin map ${\mathrm {Art}}_\mathfrak {p}$ identifies $G_\mathfrak {p}$ with $1+\pi O_\mathfrak {p}$ where $\pi =\pi _\mathfrak {p}$ is a uniformiser. Let $\varSigma _\mathfrak {p}$ denote the $\mathbf {Q}_p$-linear embeddings of $F_\mathfrak {p}$ into L.

Let $\mathbb {G}$ denote the multiplicative group over F and let ${\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}$ denote the Weil restriction. Let $T\simeq \mathbb {G}\times \mathbb {G}$ denote the algebraic group of diagonal torus over F in ${\mathrm {GL}}_{2/F}$ and let ${\mathrm {Res}}_{F/\mathbf {Q}}T$ denote its Weil restriction, which is isomorphic to ${\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}\times {\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}$. By slight abuse of notation, we continue to use the same symbols to mean the integral models of the aforementioned algebraic groups.

For every integer $r\ge 1$, let ${\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}_p)[p^r]\subset {\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}_p)$ denote the kernel

$$\begin{aligned} {\mathrm {ker}}({\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}_p)\rightarrow {\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}/p^r\mathbf {Z})) \end{aligned}$$

of the standard ‘reduction mod $p^r$’ morphism. Simialrly, define ${\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}(\mathbf {Z}_p)[p^r]$. Granted, we may identify ${\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}_p)[p]$ with $G\times G$ and ${\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}(\mathbf {Z}_p)[p]$ with G. When convenient and no confusion is expected, we may write $\varDelta =\varDelta _T$ (resp. $\varDelta _\mathbb {G}$) to mean ${\mathrm {Res}}_{F/\mathbf {Q}}T(\mathbf {Z}_p)[p]$ (resp. ${\mathrm {Res}}_{F/\mathbf {Q}}\mathbb {G}(\mathbf {Z}_p)[p]$).

We define the ‘local’ Iwasawa algebra $\varLambda _\mathfrak {p}$ to be the O-algebra $O[[G_\mathfrak {p}\times G_\mathfrak {p}]]$ of the pro-p-group $G_\mathfrak {p}\times G_\mathfrak {p}$, and let $\varLambda _p$ denote the Iwasawa algebra $\hat{\bigotimes }_\mathfrak {p} \varLambda _\mathfrak {p}$. The ‘global’ Iwasawa algebra $\varLambda _p$ is identified with $O[[G\times G]]$, and hence with $O[[ \varDelta ]]$.

The O-algebra $\varLambda _p$ parameterises the pairs of characters $\chi =(\chi _1, \chi _2)=\prod _\mathfrak {p}(\chi _{\mathfrak {p}, 1}, \chi _{\mathfrak {p}, 2})$ of G which take values in objects of $\mathcal {C}$ and which are liftings of the trivial character in $k^\times$; each algebraic character $\chi _{\mathfrak {p}, t}$ of $G_\mathfrak {p}$ is parametrised by a $|\varSigma _\mathfrak {p}|$-tuple $\lambda _{\mathfrak {p}, t}=(\lambda _{ \tau , t})_\tau$ of integers with $\tau$ ranging over $\varSigma _\mathfrak {p}$. By slight abuse of notation, by a tuple $\lambda =(\lambda _{\mathfrak {p},1}, \lambda _{\mathfrak {p}, 2})_\mathfrak {p}$ of integers as above, we shall also mean the pair of algebraic characters corresponding to $\lambda$.

Define $\varLambda$ to be the quotient $O[\varDelta /\overline{(O_{F, +}^\times \cap \varDelta ) }]]$ of $O[[\varDelta ]]$ parameterising all characters which satisfy the ‘parity condition’, i.e., factor through the p-adic closure $\overline{O_{F, +}^\times \cap \varDelta }$ of the diagonal image of the totally positive units $O^\times _{F, +}$ in $\varDelta =G\times G$. Note that $\varLambda$ is of relative dimension $1+[F:\mathbf {Q}]+\epsilon _{\mathrm {L}}$ over O, where $\epsilon _{\mathrm {L}}=0$ if the Leopoldt conjecture of the pair F and p holds.

If w is a fixed integer, the set of $2[F:\mathbf {Q}]$-tuples $\lambda$ (corresponding to a pair of algebraic characters by definition) such that $\lambda _{\tau , 1}\ge \lambda _{\tau , 2}$ and $\lambda _{\tau , 1}+\lambda _{\tau , 2}=w$ for every $\mathfrak {p}$ and $\tau$ in $\varSigma _\mathfrak {p}$ is in bijection with the set of $[F:\mathbf {Q}]$-tuples $k=(k_\tau )$ such that $k_\tau \ge 2$ and $k_\tau \equiv w$ mod 2 by decreeing that $\lambda =(\lambda _{\tau , 1}, \lambda _{\tau , 2})$ corresponds to $k=(\lambda _{1, \tau }-\lambda _{2, \tau }+2)$ and, conversely, $k=(k_\tau )$ corresponds to $\lambda =((w+k_\tau -2)/2, (w-k_\tau +2)/2)$.

2.2 Local liftings at places above p

Let L be a finite extension of $\mathbf {Q}_p$, and let O denote its ring of integers with maximal ideal $\lambda$ and residue field k . Let $V=O^2$. Let $\mathfrak {p}$ be a place of F above p that we fix, and let $\rho _\mathfrak {p}: D_\mathfrak {p}\rightarrow {\mathrm {GL}}_2(R_\mathfrak {p}^\Box )$ denote the universal lifting of the restriction $\overline{\rho }_\mathfrak {p}$ (assumed to be trivial) to the decomposition group $D_\mathfrak {p}$ at $\mathfrak {p}$ of $\overline{\rho }$ above.

Define a functor ${\mathrm {Gr}}^\Box _\mathfrak {p}$ which sends an O-algebra R to the set of data consisting of

• a filtration ${\mathrm {Fil}}\,(V\otimes _OR)=(0=(V\otimes _O R)(0)\subset (V\otimes _O R)(1)\subset (V\otimes _O R)(2)=V\otimes _O R)$ of $V\otimes _O R$,

• a map $R_\mathfrak {p}^\Box \rightarrow R$ whose composition $\rho _\mathfrak {p}\otimes _O R: D_\mathfrak {p}\rightarrow {\mathrm {GL}}_2(R)$ with the universal lifting $D_\mathfrak {p}\rightarrow {\mathrm {GL}}_2(R_\mathfrak {p}^\Box )$ preserves the filtration.

Define a functor ${\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}$ which sends an O-algebra R to the set of data consisting of an R-valued point of ${\mathrm {Gr}}^\Box _\mathfrak {p}$ as above, together with an O-algebra morphism $\tau$ from $\varLambda _\mathfrak {p}$ to R, satisfying the following condition: if $\chi =(\chi _1, \chi _2)$ is the universal pair of characters $G_\mathfrak {p}\rightarrow \varLambda _\mathfrak {p}$, the R-valued character, defined as the projection of $I_\mathfrak {p}$ to $G_\mathfrak {p}$ followed by $\chi _t\otimes _\tau R$, matches up with the action via $\rho _\mathfrak {p}\otimes _O R$ on $(V\otimes _O R)(t)/(V\otimes _O R)(t-1)$, when restricted to $I_\mathfrak {p}$.

Lemma 1

The functor ${\mathrm {Gr}}_\mathfrak {p}^\Box$ (resp. ${\mathrm {Gr}}_{\varLambda _\mathfrak {p}}^\Box$) is representable by a scheme $X_{{\mathrm {Gr}}^\Box _\mathfrak {p}}$ (resp. $X_{{\mathrm {Gr}}_{\varLambda _\mathfrak {p}}^\Box }$).

Proof

This is standard. $\square$

Forgetting filtrations for every S-point defines a morphism $X_{{{\mathrm {Gr}}^\Box _\mathfrak {p}}}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^\Box$, while, by definition, we have a closed immersion $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^\Box \hat{\otimes }_O\varLambda _\mathfrak {p}$ (Lemma 3.1.2 in [19]). We define $R_\mathfrak {p}^{\Box , {\mathrm {ord}}}=R_\mathfrak {p}^\Box /I_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ by letting ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ be the schematic closure of the image of $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}[1/p]\hookrightarrow X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^\Box \hat{\otimes }_O\varLambda _\mathfrak {p}$. By the projection, $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}$ is thought of as a $\varLambda _\mathfrak {p}$-scheme; and, similarly, $R_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ is a $\varLambda _\mathfrak {p}$-algebra. In particular, let $\kappa$ denote the morphism ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}\rightarrow {\mathrm {Spec}}\, \varLambda _\mathfrak {p}$.

Let $\xi$ denote a closed point of ${\mathrm {Spec}}\, L_\xi \rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}[1/p]$ for a finite extension $L_\xi$ of L and $\chi =(\chi _1, \chi _2)$ denote a pair of characters corresponding to the point $\kappa \circ \xi$ of ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}[1/p]$. Suppose that $\chi _1$ and $\chi _2$ are distinct and that $\epsilon \chi _2$ and $\chi _1$ are also distinct (where $\epsilon$ is the cyclotomic character). The pair of characters satisfying these conditions are evidently dense in ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}[1/p]$.

Lemma 2

The fibre ${\mathrm {Spec}}\, R_{\mathfrak {p}, \chi }^{\Box , {\mathrm {ord}}}$ of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ at $\chi$ along $\kappa$ is regular of dimension $[F_\mathfrak {p}:\mathbf {Q}_p]+4$; and the localisation ${\mathrm {Spec}}\, R_{\mathfrak {p}, \xi }^{\Box , {\mathrm {ord}}}$ of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ at $\xi$ is regular of dimension $3[F_\mathfrak {p}:\mathbf {Q}_p]+4$.

Proof

The assertions follow from Lemma 3.2.2 in [19]. $\square$

Proposition 4

Suppose that $[F_\mathfrak {p}:\mathbf {Q}_p]>2$. Let $\varGamma$ be a minimal ideal of $\varLambda _\mathfrak {p}$. Then ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}\otimes _{\varLambda _\mathfrak {p}} \varLambda _\mathfrak {p}/\varGamma$ is geometrically irreducible of relative dimension $3[F_\mathfrak {p}:\mathbf {Q}_p]+4$ over O.

Proof

This is proved essentially in Corollary 3.4.2 in [19] or Proposition 3.14 in [56]. The essence of the proof is to establish that every irreducible component of $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}[1/p]$ is of dimension $3[F_\mathfrak {p}: \mathbf {Q}_p]+4$, which one checks by computing (Lemma 3.2.3 in [19]) its completed local ring at a closed point whose projection to ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}$ corresponds to a pair of characters $\chi =(\chi _1, \chi _2)$ such that $\chi _1=\epsilon \chi _2$ does not hold. It follows that for every minimal ideal $\varGamma$ of $\varLambda _\mathfrak {p}$, ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}\otimes _{\varLambda _\mathfrak {p}}\varLambda _\mathfrak {p}/\varGamma$ is irreducible of dimension at most $1+3[F_\mathfrak {p}:\mathbf {Q}_p]+4$. However, it follows from the ‘moduli description’ of the morphism $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}[1/p]\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}[1/p]$ of ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}[1/p]$-schemes that the morphism is finite (more precisely, quasi-finite with its fibres singletons, but, combined with the projectivity of the morphism, the finiteness holds) if it is pull-back over to the open subscheme of ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}[1/p]$ corresponding to the pairs of distinct characters, and this suffices to establish the assertion as in the proof of Corollary 3.4.2 in [19]. $\square$

We need a variant of $R_\mathfrak {p}^{\Box , {\mathrm {ord}}}$ that further parameterises ‘eigenvalues of the characteristic polynomial of a Frobenius element of $D_\mathfrak {p}$’. Let $\phi =\phi _\mathfrak {p}$ be a Frobenius lift in $D_\mathfrak {p}$ that we fix. We proceed differently from Pilloni–Stroh’s construction in Section 4.1 of [38] in the ordinary case.

Let $R_\mathfrak {p}^{\Box , +}$ denote the universal ring for the liftings $\rho$ of (the trivial two-dimensional representation) $\overline{\rho }_\mathfrak {p}$, together with choices of roots of the quadratic polynomial $X^2-{\mathrm {tr}}\, \rho (\phi )X+{\mathrm {det}}\, \rho (\phi )=0$.

Define $R^{\Box , {\mathrm {ord}}, +}_\mathfrak {p}$ by the pull-back:

$$\begin{aligned} \begin{array}{ccc} {\mathrm {Spec}}\, R^{\Box , {\mathrm {ord}}, +}_\mathfrak {p}&{}\longrightarrow &{} {\mathrm {Spec}}\, R^{\Box , +}_\mathfrak {p}\hat{\otimes }\varLambda _\mathfrak {p}\\ \big \downarrow &{}&{}\big \downarrow \\ {\mathrm {Spec}}\, R^{\Box , {\mathrm {ord}}}_\mathfrak {p}&{}\longrightarrow &{} {\mathrm {Spec}}\, R^{\Box }_\mathfrak {p}\hat{\otimes }\varLambda _\mathfrak {p}\\ \end{array} \end{aligned}$$

where the horizontal morphisms are closed immersions. Similarly, define $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}^+$ to be the pull-back of $X_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}$ along ${\mathrm {Spec}}\, R^{\Box ,+}_\mathfrak {p}\hat{\otimes }\varLambda _\mathfrak {p}\rightarrow {\mathrm {Spec}}\, R^{\Box }_\mathfrak {p}\hat{\otimes }\varLambda _\mathfrak {p}$. As the formation of scheme-theoretic closure commutes with flat base change, ${\mathrm {Spec}}\, R^{\Box , {\mathrm {ord}}, +}_\mathfrak {p}$ is also the scheme-theoretic closure of the morphism $X^+_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}[1/p]\hookrightarrow X^+_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}} \rightarrow {\mathrm {Spec}}\, R^{\Box , +}_\mathfrak {p}\hat{\otimes }\varLambda _\mathfrak {p}$.

Proposition 5

Suppose that $[F_\mathfrak {p}:\mathbf {Q}_p]>2$. Let $\varGamma$ be a minimal ideal of $\varLambda _\mathfrak {p}$. Then ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}\otimes _{\varLambda _\mathfrak {p}} \varLambda _\mathfrak {p}/\varGamma$ is geometrically irreducible of relative dimension $3[F_\mathfrak {p}:\mathbf {Q}_p]+4$ over O. Furthermore, $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}\otimes _{\varLambda _\mathfrak {p}} \varLambda _\mathfrak {p}/\varGamma$ is flat over O, Cohen–Macaulay and reduced; and $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}\otimes _{\varLambda _\mathfrak {p}} \varLambda _\mathfrak {p}/(\varGamma , \lambda )$ is reduced.

Proof

For the first assertion, the proof of Proposition 4 works verbatim if the morphism $X^+_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}[1/p] \rightarrow {\mathrm {Spec}}\, R^{\Box , {\mathrm {ord}}, +}_\mathfrak {p}[1/p]$ is finite when restricted to the open subscheme of ${\mathrm {Spec}}\, \varLambda _\mathfrak {p}[1/p]$ corresponding to the pairs of distinct characters. But this is immediate.

To prove the second assertion, we define another $\varLambda _\mathfrak {p}$-algebra $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ which is universal for ‘explicit’ liftings of $\overline{\rho }_\mathfrak {p}$. This is more amenable to explicit calculations, and we shall write down a set of explicit equations to establish that it is Cohen–Macaulay, reduced and flat over O.

Let $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ denote the quotient of $R_\mathfrak {p}^{\Box , +}\hat{\otimes }\varLambda _\mathfrak {p}$ parametrising $(\rho , \alpha ( \phi ), \chi )$ where $\chi =(\chi _1, \chi _2)$ and where $\alpha (\phi )$ denote a root of the polynomial $X^2-{\mathrm {tr}}\, \rho (\phi )X+{\mathrm {det}}\, \rho (\phi )=0$ satisfying the following conditions:

• (I) ${\mathrm {tr}}\, \rho (z)=\chi _1(z)+\chi _2(z)$ for z in $I_\mathfrak {p}$,

• (II) ${\mathrm {tr}}\, \rho (\phi )=\alpha (\phi )+\beta (\phi )$ where $\beta (\phi )$ denotes ${\mathrm {det}}\, \rho (\phi )/\alpha (\phi )$,

• (III) ${\mathrm {det}}\, (\rho (\phi )-\beta (\phi ))=0$,

• (IV) $1+{\mathrm {det}}(\chi _2(z)^{-1}\rho (z))={\mathrm {tr}}\, (\chi _2(z)^{-1}\rho (z))$ for z in $G_\mathfrak {p}$,

• (V) $(\rho (z)-\chi _2(z))(\rho (z^+)-\chi _2(z^+))=(\chi _1(z)-\chi _2(z))(\rho (z^+)-\chi _2(z^+))$ for z and $z^+$ in $I_\mathfrak {p}$,

• (VI) $(\rho (\phi )-\alpha (\phi ))(\rho (z)-\chi _2(z))=(\beta (\phi )-\alpha (\phi ))(\rho (z)-\chi _2(z))$ for z in $I_\mathfrak {p}$, or equivalently,

  $$\begin{aligned} \rho (\phi z)=\beta (\phi )(\rho (z)-\chi _2(z))+\chi _2(z)\rho (\phi ). \end{aligned}$$

Let $\{z_\tau \}_\tau$, where $1\le \tau \le [F_\mathfrak {p}:\mathbf {Q}_p]$, be the generators of $I_\mathfrak {p}$. In writing

$$\begin{aligned} \rho (\phi )=\begin{pmatrix} \beta (\phi )&{}\quad 0\\ 0&{}\quad \beta (\phi )\end{pmatrix}+\begin{pmatrix}A_\phi &{}\quad B_\phi \\ C_\phi &{}\quad D_\phi \end{pmatrix} \end{aligned}$$

and, for every $1\le \tau \le [F_\mathfrak {p}:\mathbf {Q}_p]$,

$$\begin{aligned} \rho (z_\tau )=\begin{pmatrix} \chi _2(z_{\tau })&{}\quad 0\\ 0&{}\quad \chi _{2}(z_\tau )\end{pmatrix}+\begin{pmatrix}A_\tau &{}\quad B_\tau \\ C_\tau &{}\quad D_\tau \end{pmatrix}, \end{aligned}$$

it is possible to check that $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ is given by the formal power series ring with coefficients in O with $(4+1)[F_\mathfrak {p}:\mathbf {Q}_p]+(4+1)=5[F_\mathfrak {p}:\mathbf {Q}_p]+5$ variables

$$\begin{aligned} \{A_\tau , B_\tau , C_\tau , D_\tau , \chi _{2}(z_\tau )\}_\tau , A_\phi , B_\phi , C_\phi , D_\phi , \beta (\phi ) \end{aligned}$$

with their relations given by the 2 by 2 minors in

$$\begin{aligned} \begin{pmatrix} A_\phi &{}C_\phi &{}-C_1&{}-D_1&{}\cdots &{}-C_d&{}-D_d\\ B_\phi &{}D_\phi &{}A_1&{}B_1&{}\cdots &{}A_d&{}B_d \end{pmatrix} \end{aligned}$$

where $d=[F_\mathfrak {p}:\mathbf {Q}_p]$. Let $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ denote the quotient of the polynomial ring by the ideal given by the same set of variables with the same set of relations.

By definition, $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ is determinantal in the sense of Section 1-C in [6] or Section 7 in [5], while $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ is determinantal according to Section 18.5 in [15]. As the Cohen–Macaulay-ness and the flatness (over O) pass from $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ to $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$, we establish these properties for $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$.

Firstly, $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ is Cohen–Macaulay (see Theorem 18.18 in [15], or Corollary 2.8 in Section 2.B in [6]). It is also possible to explicitly spot a regular sequence in $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ and use that to prove $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ is Cohen–Macaulay directly, as in the proof of Proposition 2.7 in [47]. Eisenbud (see Section 18.5 with its reference to Exercises 10.9 and 10.10 in [15]) also claims, without a proof, that it is of relative dimension

$$\begin{aligned} 5[F_\mathfrak {p}:\mathbf {Q}_p]+5-(2[F_\mathfrak {p}: \mathbf {Q}_p]+1)=3[F_\mathfrak {p}:\mathbf {Q}_p]+4 \end{aligned}$$

over O; this will be checked directly in the forthcoming argument.

The reducedness of $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ indeed follows from the defining equations. To see this, we shall prove that the L-algebra $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }[1/\lambda ]$ and the k-algebra $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }/\lambda$ are both domains of the same dimension $3[F_\mathfrak {p}:\mathbf {Q}_p]+4$. Granted, it follows from Lemma 2.2.1 in [49] (also see Theorem 23.1 in [32]) that $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ is flat over O and follows, as result, that $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }\subset R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }[1/\lambda ]$ is reduced.

To see that the naturally graded L-algebra $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }[1/\lambda ]$ is a domain, one notes that ${\mathrm {Proj}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }[1/\lambda ]$ is covered by the open sets $\{X\ne 0\}$ where X ranges over the single-variable equations defined by those appearing in the relations defining $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$, i.e, X is any one of the $4+4[F_\mathfrak {p}:\mathbf {Q}_p]$ variables in the list

$$\begin{aligned} \{A_\phi , B_\phi , C_\phi , D_\phi ; \{A_\tau , B_\tau , C_\tau , D_\tau \}_\tau \}. \end{aligned}$$

Each covering $\{X\ne 0\}$ is isomorphic to the domain $(\mathbf {A}_L-\{0\})\times \mathbf {A}_L^{2([F_\mathfrak {p}:\mathbf {Q}_p]+1)+[F_\mathfrak {p}:\mathbf {Q}_p]+1}$ (where the right-most ‘$[F_\mathfrak {p}:\mathbf {Q}_p]+1$’ reads $\{\chi _{2}(z_\tau )\}_\tau$ and $\beta (\phi )$, for example), therefore $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }[1/\lambda ]$ is a domain. The same proof (with k in place of L) works in the case of $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger , \vee }$ (as the ‘coefficient’ k is, again, a field).

To transfer our calculations so far about $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ to $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$, we shall prove that they are isomorphic.

Firstly, one observes that there is a natural map,

$$\begin{aligned} X^+_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger } \end{aligned}$$

which, when followed by the closed immersion ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , +}\hat{\otimes }_O\varLambda _\mathfrak {p}$, factors through $X^+_{{\mathrm {Gr}}^\Box _{\varLambda _\mathfrak {p}}}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , +}\hat{\otimes }_O\varLambda _\mathfrak {p}$. It then follows from the universal property of the scheme-theoretic closure ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$ that there is a closed immerion

$$\begin{aligned} {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}\rightarrow {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger } \end{aligned}$$

giving rise to a surjection $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }\rightarrow R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$.

To prove that the surjection is indeed bijective, we follow the proof of Lemma 4.7.3 in [49] to show that ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }[1/\lambda ]\subset {\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}[1/\lambda ]$ (and as a result $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }[1/\lambda ]\simeq R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}[1/\lambda ]$) ‘moduli-theoretically’ using the Eqs. (I)–(VI) defining $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$.

Let $(\rho , \alpha (\phi ), \chi =(\chi _1, \chi _2))$ be a closed point of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ defined over a finite extension K of $L=O[1/\lambda ]$. For simplicity, we write $\alpha =\alpha (\phi )$ and $\beta ={\mathrm {det}}\, \rho (\phi )/\alpha (\phi )$. From (I) and (IV), we may deduce that the restriction of $\rho$ to $I_\mathfrak {p}$ is either an extension of $K(\chi _2)$ by $K(\chi _1)$ or an extension of $K(\chi _1)$ by $K(\chi _2)$.

Suppose that it is the latter. We may then choose a basis of $\rho$ to write the restriction of $\rho$ to $I_\mathfrak {p}$ to be of the form $\rho |_{I_\mathfrak {p}}=\begin{pmatrix}\chi _2&{}c\\ 0&{}\chi _1\end{pmatrix}$. But it follows from (V) that

$$\begin{aligned} c(z)(\chi _1(z^+)-\chi _2(z^+))=(\chi _1(z)-\chi _2(z))c(z^+), \end{aligned}$$

i.e.,

$$\begin{aligned} ((\chi _2/\chi _1)(z^+)-1)c(z)=((\chi _2/\chi _1)(z)-1)c(z^+). \end{aligned}$$

If $\chi _1$ and $\chi _2$ are distinct, $\chi _2/\chi _1$ is non-trivial and we may therefore see the equality as saying that the co-cycle c in $H^1(D_\mathfrak {p}, K(\chi _2/\chi _1))$ is coboundary, in other words, $\rho$ is split when restricted to $I_\mathfrak {p}$. Hence the restriction to $I_\mathfrak {p}$ of $\rho$ is of the form $\begin{pmatrix} \chi _1&{}*\\ 0&{}\chi _2\end{pmatrix}$, in other words, $(\rho , \chi )$ defines a K-point of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}}[1/\lambda ]$.

Suppose $\chi _1=\chi _2$. With respect to the basis chosen above, suppose that $\rho (\phi )=\begin{pmatrix} \beta ^\sim &{}*\\ 0&{}\alpha ^\sim \end{pmatrix}$. By (III), we may deduce that $(\beta ^\sim -\beta )(\alpha ^\sim -\beta )=0$. Hence either $(\alpha ^\sim , \beta ^\sim )=(\alpha , \beta )$ or $(\alpha ^\sim , \beta ^\sim )=(\beta , \alpha )$ holds. By (VI), one can check that the latter occurs only when the restriction of $\rho$ to $I_\mathfrak {p}$ is split. In any case, $(\rho , \alpha , \chi )$ defines a K-point of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}[1/\lambda ]$.

Suppose that $\chi _1$ and $\chi _2$ are distinct. It then follows from (VI) that $(\beta ^\sim -\alpha )(\chi _1-\chi _2)=(\beta -\alpha )(\chi _1-\chi _2)$. As $\chi _1$ and $\chi _2$ are distinct, $\beta ^\sim =\beta$, and $\alpha ^\sim =\alpha$ as a result. It therefore follows that $(\rho , \alpha , \chi )$ defines a K-point of ${\mathrm {Spec}}\, R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}[1/\lambda ]$ and thereby establishes that the surjection $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }[1/\lambda ]\rightarrow R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}[1/\lambda ]$ is indeed an isomorphism.

As $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$ is flat over O and $\lambda$ thus is not a zero-divisor in $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }$, the kernel of the surjection $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }\rightarrow R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$ is indeed trivial, i.e., $R_\mathfrak {p}^{\Box , {\mathrm {ord}}, \dagger }\simeq R_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$. This concludes our proof of the proposition. $\square$

2.3 Local liftings at places not dividing p

$S_{\mathrm {R}}$: Suppose that $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod p. Let O be as above. By enlarging O if necessary to assume that $\mu _{|k_{\mathrm {Q}}|-1}\subset (1+\lambda )$. Suppose that $\chi _{{\mathrm {Q}}, 1}, \chi _{{\mathrm {Q}}, 2}: D_{\mathrm {Q}}\rightarrow (1+\lambda )\subset O^\times$ are characters of finite order such that their reductions mod $\lambda$ are trivial. Write $\chi =\chi _{\mathrm {Q}}$ to mean the pair $(\chi _{{\mathrm {Q}},1}, \chi _{{\mathrm {Q}},2})$.

Lemma 3

There exists an ideal $I_{\mathrm {Q}}^{\Box , \chi }$ of $R_{\mathrm {Q}}^\Box$ which corresponds to the liftings $\rho$ of the trivial representation $\overline{\rho }_{\mathrm {Q}}$ such that

• the characteristic polynomial of the restriction of $\rho$ to the inertia subgroup $I_{\mathrm {Q}}$ at ${\mathrm {Q}}$ in X is of the form $(X-\chi _{{\mathrm {Q}}, 1}({\mathrm {Art}}_{\mathrm {Q}}(g))^{-1})(X-\chi _{{\mathrm {Q}}, 2}({\mathrm {Art}}_{\mathrm {Q}}(g))^{-1})$ for every g in $I_{\mathrm {Q}}$;

• $R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , \chi }$ is flat over O, reduced, Cohen–Macaulay and of equi-dimensional of relative dimension 4 over O;

• $R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , \chi }[1/p]$ is formally smooth over L;

• $R_{\mathrm {Q}}^\Box /(\lambda , I_{\mathrm {Q}}^{\Box , \chi })$ is reduced;

• the generic point of every irreducible component of $R_Q^\Box /I_Q^{\Box , \chi }$ has characteristic zero.

Furthermore,

• if $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are distinct, then $R^\Box _{\mathrm {Q}}/I_{\mathrm {Q}}^{\Box , \chi }$ is geometrically irreducible of relative dimension 4 over O;

• if $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are both trivial and if L is sufficiently large, every minimal prime of $R^\Box _{\mathrm {Q}}/(\lambda , I^{\Box , \chi }_{\mathrm {Q}})$ contains a unique minimal prime of $R^\Box _{\mathrm {Q}}/(\lambda , I^{\Box , \chi }_{\mathrm {Q}})$.

Proof

Following the notation of [47], when $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are distinct, let $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , \chi }$ be $R^\Box (\overline{\rho }_{\mathrm {Q}}, \tau )$ with the inertial type $\tau$ given by a representation of $I_{\mathrm {Q}}$ sending g in $I_{\mathrm {Q}}$ to $\begin{pmatrix}\chi _{{\mathrm {Q}}, 1}(g)&{}*\\ 0&{}\chi _{{\mathrm {Q}}, 2}(g)\end{pmatrix}$ and $N=0$. When $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are both trivial, let ${\mathrm {Spec}}\, R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , \chi }$ denote the union of ${\mathrm {Spec}}\, R^\Box (\overline{\rho }_{\mathrm {Q}}, \tau )$ where the inertial types $\tau$ range over those given by the trivial representation of I with open kernel (when $N=0$, it corresponds to the unramified liftings while non-trivial N corresponds to the ‘Steinberg’ liftings).

Firstly, observe that $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , \chi }$ is flat over O and reduced by definition. Proposition 5.8 in [47] proves that $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , \chi }$ is Cohen–Macaulay (equi-dimensional of relative dimension 4 over O) and, less explicitly, $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , \chi }[1/p]$ is formally smooth over L.

When $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are distinct, Proposition 5.8 in [47] also proves that $R_{\mathrm {Q}}^{\Box }/(\lambda , I_{\mathrm {Q}}^{\Box , \chi })$ is reduced. Furthermore, the proof of Proposition 3.1 in [52] proves that $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , \chi }$ is geometrically integral.

When $\chi _{{\mathrm {Q}}, 1}=\chi _{{\mathrm {Q}}, 2}=1$, as $\lambda$ is $R_{\mathrm {Q}}^{\Box }/I_{\mathrm {Q}}^{\Box , (1,1)}$-regular, $R_{\mathrm {Q}}^{\Box }/(\lambda , I_{\mathrm {Q}}^{\Box , (1,1)})$ is Cohen–Macaulay by Theorem 17.3 in [32]. On the other hand, the proof of Lemma 3.2 in [52], combined with the corollary of Theorem 23.9 in [32], establishes that $R_{\mathrm {Q}}^{\Box }/(\lambda , I_{\mathrm {Q}}^{\Box , (1,1)})$ is generically reduced. The reducedness of $R_{\mathrm {Q}}^{\Box }/(\lambda , I_{\mathrm {Q}}^{\Box , (1,1)})$ therefore follows. The last assertion is proved in Proposition 3.1 in [52]. $\square$

$S_{\mathrm {L}}$:

Lemma 4

Suppose ${\mathrm {Q}}$ satisfies $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod p. Then there exists an ideal $I_{\mathrm {Q}}^{\Box , {\mathrm {St}}}$ of $R_{\mathrm {Q}}^\Box$, containing $I_{\mathrm {Q}}^{\Box , (1,1)}$ above, which corresponds to the liftings of the trivial representation $\overline{\rho }_{\mathrm {Q}}: D_{\mathrm {Q}}\rightarrow {\mathrm {GL}}_2(k)$ such that

• the characteristic polynomial of $\rho$ when restricted to $I_{\mathrm {Q}}$ (resp. $\rho ({\mathrm {Frob}}_{\mathrm {Q}})$ where ${\mathrm {Frob}}_{\mathrm {Q}}$, by abuse of notation, is a lifting of the arithmetic Frobenius) is of the form $(X-1)^2$ (resp. $(X-|k_{\mathrm {Q}}|)(X-\alpha |k_{\mathrm {Q}}|)$ for some $\alpha$);

• $R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , {\mathrm {St}}}$ is flat over O, reduced, Cohen–Macaulay and equi-dimensional of relative dimension 4 over O;

• $(R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , {\mathrm {St}}})[1/p]$ is formally smooth;

• $R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , {\mathrm {St}}}$ is geometrically integral;

• the generic point of $R_{\mathrm {Q}}^\Box /I_{\mathrm {Q}}^{\Box , {\mathrm {St}}}$ has characteristic zero.

Proof

This is proved in Proposition 3.1 of [52], Proposition 3.17 in [56] and Proposition 5.8 in [47] as in the proof of Lemma 3. $\square$

$S_{\mathrm {A}}$: For every ${\mathrm {Q}}$ in $S_{{\mathrm {A}}}$, $R_{\mathrm {Q}}^\Box$ is formally smooth of relative dimension 4, and let $I_{\mathrm {Q}}=(0)$.

$S_{{\mathrm {Q}}, \nu }$:

Lemma 5

Let $\nu \ge 1$ be an integer. Suppose that ${\mathrm {Q}}$ satisfies $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod $p^\nu$. Suppose that $\overline{\rho }_{\mathrm {Q}}$ is unramified, and is the direct sum of (unramified) characters $\chi _{{\mathrm {Q}}, 1}, \chi _{{\mathrm {Q}}, 2}: D_{\mathrm {Q}}\rightarrow k^\times$. Then there exists an ideal $I_{\mathrm {Q}}^\Box$ of $R_{\mathrm {Q}}^\Box$ which corresponds to the liftings $\rho =\chi _{{\mathrm {Q}}, 1}\oplus \chi _{{\mathrm {Q}}, 2}$ of $\overline{\rho }_{\mathrm {Q}}$ such that $\chi _{{\mathrm {Q}}, t}$ lifts $\overline{\chi }_{{\mathrm {Q}}, t}$ for $t=1, 2$, and $\chi _{{\mathrm {Q}}, 2}$ is unramified.

Proof

See Section 2.4.6 in [11], or Definition 4.1 and Lemma 4.2 in [57]. $\square$

We shall suppose that $|S_{{\mathrm {Q}}, \nu }|=q$ is independent of $\nu$. Existence of a such set of ‘Taylor-Wiles primes’ will be stated with a reference in the following.

In the following, let $\varSigma _\chi$ denote the deformation data defined by

• $S=S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}\cup S_\infty$;

• $T=S-S_\infty$;

and the ideals of universal rings for local liftings at T, namely

• $I_\mathfrak {p}^{\Box , {\mathrm {ord}}, +}$ for every $\mathfrak {p}$ in ${S_{\mathrm {P}}}$ assuming $[F_\mathfrak {p}:\mathbf {Q}_p]>2$;

• a tuple $\chi =(\chi _{\mathrm {Q}}=(\chi _{{\mathrm {Q}},1}, \chi _{{\mathrm {Q}},2}))$ of characters where ${\mathrm {Q}}$ ranges over $S_{\mathrm {R}}$, and $I_{\mathrm {Q}}^{\Box , \chi _{\mathrm {Q}}}$ for every ${\mathrm {Q}}$ in $S_{\mathrm {R}}$;

• $I_{\mathrm {Q}}^{\Box , {\mathrm {St}}}$ for every ${\mathrm {Q}}$ in ${S_{\mathrm {L}}}$;

• $I_{\mathrm {Q}}^\Box =(0)$ for every ${\mathrm {Q}}$ in $S_{{\mathrm {A}}}$ (any lifting of $\overline{\rho }_{\mathrm {Q}}$ for ${\mathrm {Q}}$ in $S_{\mathrm {A}}$ is necessarily unramified);

The ideals $I_{\mathrm {Q}}^\Box$ of $R^\Box _{\mathrm {Q}}$ for every ${\mathrm {Q}}$ in S define a subspace $L_{\mathrm {Q}}\subset H^1(D_{\mathrm {Q}}, {\mathrm {ad}}\overline{\rho })$. When $\chi _{\mathrm {Q}}$ is trivial for all ${\mathrm {Q}}$ in $S_{\mathrm {R}}$, we write $\varSigma$ instead.

Let $\mathcal {C}$ denote the category as defined in 2.2, [11], with $\varLambda _p$ in place of O. The functor which sends an object R of $\mathcal {C}$ to the set of T-framed deformations of $\overline{\rho }$ of type $\varSigma _\chi$ is represented by a complete local noetherian $\varLambda _p$-algebra $R^\Box _{\varSigma _\chi }$. If T is empty, write it $R_{\varSigma _\chi }$.

Lemma 6

If $p=5$ and the projective image of $\overline{\rho }$ is isomorphic to ${\mathrm {PGL}}_2(\mathbf {F}_5)$, assume that the kernel of the projective representation of $\overline{\rho }$ does not fix $F(\zeta _5)$.

For every integer $\nu \ge 1$ there exists a finite set $S_{{\mathrm {Q}}, \nu }$ of ${\mathrm {Q}}$ such that

• $\mathbf {N}_{F/\mathbf {Q}}{\mathrm {Q}}\equiv 1$ mod $p^\nu$;

• $\overline{\rho }$ at ${\mathrm {Q}}$ is a direct sum of two distinct characters which are unramified;

• $|S_{{\mathrm {Q}}, \nu }|=q$,

and if we let $\varSigma _{\chi , {\mathrm {Q}}, \nu }$ denote the deformation data $(S\cup S_{{\mathrm {Q}}, \nu }, T, \dots )$ defined by the ideals of universal rings for local liftings at T exactly as in $\varSigma _\chi =(S, T, \dots )$, together with $I_{\mathrm {Q}}^\Box$ for ${\mathrm {Q}}$ in $S_{{\mathrm {Q}}, \nu }$ defined as above, then $R^\Box _{\varSigma _{\chi , {\mathrm {Q}}, \nu }}$ is topologically generated over $R^{{\mathrm {loc}}}_{\varSigma _\chi }$ by $r=q-2[F:\mathbf {Q}]$ elements.

Proof

The proof of Proposition 2.5.9, [11] works verbatim (with $n=2$) to constructs the sets $S_{{\mathrm {Q}}, \nu }$ as required. The last assertion follows from Proposition 3. $\square$

2.4 Hecke algebras

Let $\mathbb {A}_F$ denote the ring of adeles of F and let $\mathbb {A}_F^\infty$ denote its finite part. Let D be the quaternion algebra over F ramified exactly at $S_{\mathrm {L}}\cup S_\infty$ such that $|S_{\mathrm {L}}\cup S_\infty |$ is even. Let G denote the corresponding algebraic group over F such that $G(F)=D^\times$. Once for all, we fix a maximal order $O_D$ of D, and for every finite place ${\mathrm {Q}}$ not in $S_{\mathrm {L}}$, we fix an isomorphism $G(O_{F_{\mathrm {Q}}})\simeq {\mathrm {GL}}_2(O_{F_{\mathrm {Q}}})$. For a finite place ${\mathrm {Q}}$ of F, we shall let ${\mathrm {Iw}}(O_{F_{\mathrm {Q}}})$ denote the subgroup of matrices in ${\mathrm {GL}}_2(O_{F_{\mathrm {Q}}})$ which reduce mod ${\mathrm {Q}}$ to upper triangular matrices.

Let $\chi$ be a set of characters indexed by $S_{\mathrm {R}}$ such that $\chi _{\mathrm {Q}}=(\chi _{{\mathrm {Q}}, 1}, \chi _{{\mathrm {Q}}, 2})$ for every ${\mathrm {Q}}$ in $S_{\mathrm {R}}$ defines a character of ${\mathrm {Iw}}(O_{F_{\mathrm {Q}}})\subset {\mathrm {GL}}_2(O_{F_{\mathrm {Q}}})$, trivial on the subgroup of matrices in ${\mathrm {GL}}_2(O_{F_{\mathrm {Q}}})$ which reduce mod ${\mathrm {Q}}$ to the unipotent matrices.

For an algebraic character $\lambda =(\lambda _{\mathfrak {p}, 1}, \lambda _{\mathfrak {p}, 2})$ of $\varLambda _p$ such that $\lambda _{\tau , 1}\ge \lambda _{\tau , 2}$ for every $\tau$ in $S_\mathfrak {p}$, let $V_{\lambda , \chi }$ be the O-tensor module

$$\begin{aligned}V_{\mathrm {P}}\otimes V_{\mathrm {R}}\otimes V_{\mathrm {L}}\end{aligned}$$

where $V_{\mathrm {P}}$ is the $S_{\mathrm {P}}$-tensor product $\bigotimes V_\mathfrak {p}$ with $V_\mathfrak {p}=\bigotimes _{\tau } {\mathrm {Sym}}^{\lambda _\tau }{\mathrm {det}}^{\gamma _{\tau }}O^2$ where $\lambda _\tau =\lambda _{\tau , 1}-\lambda _{\tau , 2}$ and $\gamma _\tau =\lambda _{\tau , 2}$ for every $\tau$ in ${\mathrm {Hom}}_{\mathbf {Q}_p}(F_\mathfrak {p}, L)$; $V_{\mathrm {R}}=\bigotimes O(\chi _{\mathrm {Q}})$ and we let the $S_{\mathrm {R}}$-product $\prod {\mathrm {Iw}}(O_{F_{\mathrm {Q}}})$ act by $\chi$; $V_{\mathrm {L}}$ is the $S_{\mathrm {L}}$-tensor product of the one-dimensional trivial representation of $(D\otimes _F F_{\mathrm {Q}})^\times$ for ${\mathrm {Q}}$ in $S_{\mathrm {L}}$, which is given by the the determinant $(D\otimes _F F_{\mathrm {Q}})^\times \rightarrow F_{\mathrm {Q}}^\times$ (followed by the trivial character $F_{\mathrm {Q}}^\times \rightarrow F_{\mathrm {Q}}^\times$) and corresponds by the Jacquet–Langlands correspondence to the special representation ${\mathrm {Sp}}_2$ (Chapter I, Section 3 in [21]) of the trivial character, which in turn corresponds by the local Langlands correspondence to a two-dimensional reducible local Galois representation with the cyclotomic and the trivial characters on the diagonal.

For an O-algebra A, let $S_\lambda ^\chi (A)$ denote the space of functions

$$\begin{aligned} f: G(F)\backslash G(\mathbb {A}_F^f)\rightarrow V_{\lambda , \chi }\otimes _O A. \end{aligned}$$

Let $G(\mathbb {A}_F^{\infty \cup T} )\times \prod G(O_{F_{\mathrm {Q}}})\times \prod {\mathrm {Iw}}(O_{F_{\mathrm {Q}}})$, where $T=S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}$ and where in the first (resp. second) product ${\mathrm {Q}}$ ranges over $S_{\mathrm {P}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}$ (resp. $S_{\mathrm {R}}$), act on $S^\chi _\lambda (A)$ by

$$\begin{aligned} (\gamma f)(g)=(\gamma _{S_{\mathrm {P}}\cup S_{\mathrm {R}}}) f(g\gamma ) \end{aligned}$$

where $\gamma _{S_{\mathrm {P}}\cup S_{\mathrm {R}}}$ is the projection of $\gamma$ onto the $S_{\mathrm {P}}\cup S_{\mathrm {R}}$-components.

Let $U=U^D$ be an open compact subgroup of $G(\mathbb {A}_F^{\infty \cup T} )\times \prod G(O_{F_{\mathrm {Q}}})\times \prod {\mathrm {Iw}}(O_{F_{\mathrm {Q}}})$, where the first product ranges over $S_{\mathrm {P}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}$ and the second over $S_{\mathrm {R}}$, such that $U_{\mathrm {Q}}$ is a maximal compact subgroup of $G(F_{\mathrm {Q}})$ for every ${\mathrm {Q}}$ in $S_{\mathrm {L}}$ and such that $U_{\mathrm {Q}}$ for every ${\mathrm {Q}}$ in $S_{{\mathrm {R}}}$ is the subgroup of matrices which reduce mod the maximal ideal to the identity matrix. In this case, because of the primes in $S_{\mathrm {A}}$, U is sufficiently small in the sense that, for every t in $G(\mathbb {A}_F^\infty )$, the finite group $(U\cap t^{-1} G(F) t)/O_F^\times$ is $\{1\}$.

For integers $N\ge 1$ and $\nu \ge 1$, let $S_{{\mathrm {Q}}, \nu }$ as in the previous section, and define $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ to be a sufficiently small open compact subgroup of $G(\mathbb {A}_F^\infty )$ as above such that, at every $\mathfrak {p}$ above p, it reduces modulo the N-th power of $\mathfrak {p}$ to the upper triangular unipotent matrices while, at every ${\mathrm {Q}}$ in $S_{{\mathrm {Q}}, \nu }$, reduces mod ${\mathrm {Q}}$ to the upper triangular matrices. We also define $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}$ to be the subgroup of $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ that is identical to $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ away from the primes in $S_{{\mathrm {Q}}, \nu }$ but, for every ${\mathrm {Q}}$ in $S_{{\mathrm {Q}}, \nu }$, $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}\cap {\mathrm {GL}}_2(F_{\mathrm {Q}})$ consists of all matrices in $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}\cap {\mathrm {GL}}_2(F_{\mathrm {Q}})\subset {\mathrm {GL}}_2(O_{F_{\mathrm {Q}}})$ whose right-bottom entries reduce mod ${\mathrm {Q}}$ to the elements of $(O_F/{\mathrm {Q}})^\times$ that map trivially when passing to the maximal pro-p-quotient $\varDelta _{{\mathrm {Q}}}$ of $(O_F/{\mathrm {Q}})^\times$. In other words, $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}$ is defined such that $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}/U_{\varSigma _{{\mathrm {Q}}, \nu }, N}\simeq \prod _{\mathrm {Q}} \varDelta _{\mathrm {Q}}$ where ${\mathrm {Q}}$ ranges over $S_{{\mathrm {Q}}, \nu }$.

When $S_{{\mathrm {Q}}, \nu }$ is empty, we shall write $U_N$. By slight abuse of notation, the N-direct limit of $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}$ (resp. $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$) will be denoted by $U_{\varSigma _{{\mathrm {Q}}, \nu }}$ (resp. $U_{ {\mathrm {Iw}}_{{\mathrm {Q}}, \nu }}$).

Let $S_\lambda ^\chi (U, A)$ denote the set $f\in S_\lambda ^\chi (A)$ such that $\gamma f=f$ for every $\gamma \in U$.

Definition

When $\chi _{\mathrm {Q}}$ is trivial, i.e., $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are both trivial, for every ${\mathrm {Q}}$ in $S_{\mathrm {R}}$, in which case we will often say $\chi$ is trivial, we in particular write $S_\lambda (U, A)$. If, on the other hand, $\chi _{{\mathrm {Q}}, 1}$ and $\chi _{{\mathrm {Q}}, 2}$ are distinct for all ${\mathrm {Q}}$ in $S_{\mathrm {R}}$, we say that $\chi _{\mathrm {Q}}$ is distinct. We only need these two extreme cases.

For ${\mathrm {Q}}$ not in $S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_\infty$, $A[U_{\mathrm {Q}}\backslash GL_2(F_{\mathrm {Q}})/U_{\mathrm {Q}}]$ acts on $S_\lambda ^\chi (U, A)$: for g in $GL_2(F_{\mathrm {Q}})$, if $[U_{\mathrm {Q}} g U_{\mathrm {Q}}]=\coprod _\gamma \gamma U_{\mathrm {Q}}$, define the Hecke operator corresponding to g by $\sum _\gamma \gamma f$. Let $T_{\mathrm {Q}}$$\left( \hbox {resp.} S_{\mathrm {Q}}\right)$ denote the Hecke operator corresponding to $\begin{pmatrix}\pi _{\mathrm {Q}}&{}0\\ 0&{}1\end{pmatrix}$$\left( \hbox {resp.} \begin{pmatrix}\pi _{\mathrm {Q}}&{}0\\ 0&{}\pi _{\mathrm {Q}}\end{pmatrix}\right)$ where $\pi _{\mathrm {Q}}$ is a uniformiser of $O_{F_{\mathrm {Q}}}$.

For $U=U_N$ or $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}$, $S_\lambda ^{\chi }(U, A)$ comes equipped with the Hecke operator $U_\mathfrak {p}$$\left( \hbox {resp.} S_\mathfrak {p}\right)$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$, corresponding to the matrix $\begin{pmatrix}\pi _\mathfrak {p}&{}0\\ 0&{}1\end{pmatrix}$$\left( \hbox {resp.} \begin{pmatrix}\pi _\mathfrak {p}&{}0\\ 0&{}\pi _\mathfrak {p}\end{pmatrix}\right)$ but normalised by multiplying the product over $\tau$ in $\varSigma _\mathfrak {p}$ of $\tau (\pi _\mathfrak {p})^{-\lambda _{2, \tau }}$ (resp. $\tau (\pi _\mathfrak {p})^{-(\lambda _{1, \tau }+\lambda _{2, \tau })}$). The normalisation is in common with [22] for example. It also has action of $S_{\tau }$ (this is denoted by $\langle \tau \rangle$ in Definition 2.3.1 of[19], but we save $\langle \ \rangle$ for another operator) corresponding an element $\tau$ in the diagonal torus $T(O_\mathfrak {p})=\begin{pmatrix}O_\mathfrak {p}^\times &{}0\\ 0&{}O_\mathfrak {p}^\times \end{pmatrix}$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$. If $\tau$ is a tuple $(\tau _\mathfrak {p})_\mathfrak {p}$ of $\tau _\mathfrak {p}$ in $T(O_\mathfrak {p})$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$, let $S_\tau$ denote the product of $S_{\tau _\mathfrak {p}}$ over $\mathfrak {p}$.

When $U=U_N$ or $U_{\varSigma _{{\mathrm {Q}}, \nu }, N}$, we follow Geraghty Definition 2.6.2 in [19] to define

$$\begin{aligned} \langle \tau \rangle =\gamma ^{-1}_\tau S_\tau , \end{aligned}$$

where $\gamma _\tau =\prod _\mathfrak {p} \gamma _{\tau , \mathfrak {p}}$ and $\gamma _{\tau , \mathfrak {p}}=\tau _{\mathfrak {p}, 2}$ for $\tau _\mathfrak {p}=(\tau _{\mathfrak {p}, 1}, \tau _{\mathfrak {p}, 2})$ in $T(O_\mathfrak {p})$ for every $\mathfrak {p}$.

Let $T_{\lambda , \varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, A)$ denote the Hecke algebra generated by the images in ${\mathrm {End}}(S_\lambda ^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, A))$ of $T_{\mathrm {Q}}$ and $S_{\mathrm {Q}}$ for ${\mathrm {Q}}$ not in $S\cup S_{{\mathrm {Q}}, \nu }$, $U_\mathfrak {p}$ for $\mathfrak {p}$ in $S_{\mathrm {P}}$, and $S_\tau$ for $\tau \in T$. When $S_{{\mathrm {Q}}, \nu }$ is empty, we shall write $T_{\lambda , \varSigma _\chi }(U_N, A)$.

When $A=O$, we will not make references to A henceforth. When $\lambda _{ \tau , 1}=\lambda _{ \tau , 2}=0$ for every $\tau$ in $S_\mathfrak {p}$ and $\mathfrak {p}$ in $S_{\mathrm {P}}$, write 2 in place of $\lambda$.

Section 2.4 of [19] defines the ‘Hida’ idempotent e on $S_\lambda ^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N})$, $S_\lambda ^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, L/O)$, and $T_{\lambda , \varSigma _{{{\mathrm {Q}}, \nu }}}(U_{\varSigma _{{\mathrm {Q}}, \nu }, N})$, and define

$$\begin{aligned}&S^{\chi , {\mathrm {ord}}}(U_{\varSigma _{{\mathrm {Q}}, \nu }})\\&\quad (\hbox {resp. } S^{\chi , {\mathrm {ord}}}(U_{\varSigma _{{\mathrm {Q}}, \nu }}, L/O)) \end{aligned}$$

to be the N-direct limit of $e S_2^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N})$ (resp. $e S_2^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, L/O)$); and

$$\begin{aligned} T^{{\mathrm {ord}}}_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }}) \end{aligned}$$

to be the N-inverse limit of $e T_{2, \varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }, N})$. When $S_{{\mathrm {Q}}, \nu }$ is empty, we shall write $S^{\chi , {\mathrm {ord}}}(U), S^{\chi , {\mathrm {ord}}}(U, L/O)$ and $T^{ {\mathrm {ord}}}_{\varSigma _\chi }(U)$ respectively. Naturally, $T^{\chi , {\mathrm {ord}}}_{\varSigma _{\chi , {\mathrm {Q}},\nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$ and $S^{\chi , {\mathrm {ord}}}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$ are algebras over $\varLambda _p$, and hence over $\varLambda$, by $\langle \ \rangle$.

Lemma 7

• $T_{\varSigma _\chi }^{\mathrm {ord}}(U)$ is reduced.

• $T_{\varSigma _\chi }^{\mathrm {ord}}(U)$ is a finite faithful $\varLambda$-module, $S^{\chi , {\mathrm {ord}}}(U)$ is a faithful $T_{\varSigma _\chi }^{\mathrm {ord}}(U)$-module and is finite free over $\varLambda$.

Proof

The first assertion follows from Lemma 2.4.4 in [19]. The second assertion follows from Propositions 2.5.3 and 2.5.4 in [19]. $\square$

Let $\mathfrak {m}$ be a maximal ideal of $T^{ {\mathrm {ord}}}_{\varSigma _\chi }(U)$ when $\chi$ is trivial. Since $S^{\mathrm {ord}}(U)/\lambda =S^{\chi , {\mathrm {ord}}}(U)/\lambda$, it induces a maximal $\mathfrak {m}_\chi \subset T^{{\mathrm {ord}}}_{\varSigma _\chi }(U)$. Let $\mathfrak {m}_{{\chi , {\mathrm {Q}}, \nu }}\subset T^{ {\mathrm {ord}}}_{\varSigma _{\chi , {\mathrm {Q}}}}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$ be the maximal ideal defined by the surjection

$$\begin{aligned} T^{{\mathrm {ord}}}_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})\rightarrow T^{{\mathrm {ord}}}_{\varSigma _\chi }(U). \end{aligned}$$

Define $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$, also denoted by $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}$, by letting

$$\begin{aligned} (H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }})^\vee \subset S^{\chi , {\mathrm {ord}}}(U_{\varSigma _{{\mathrm {Q}}, \nu }}, L/O)_{\mathfrak {m}_{{\chi , {\mathrm {Q}}, \nu }}}^\vee \end{aligned}$$

(where by the dual $\vee$ we mean the ‘Pontrjagin dual’ ${\mathrm {Hom}}_{O} (-, L/O)$) as in Section 4.2 of [19], let $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }})$ denote the one defined similarly with $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }}$ in place of $U_{\varSigma _{{\mathrm {Q}}, \nu }}$and let

$$\begin{aligned}T_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}\subset {\mathrm {End}}(H_{\varSigma _{\chi , {\mathrm {Q}},\nu }})\end{aligned}$$

denote the image of $T^{{\mathrm {ord}}}_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})_{\mathfrak {m}_{{\chi , {\mathrm {Q}}, \nu }}}$ in ${\mathrm {End}}(H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }})$. When $S_{{\mathrm {Q}}, \nu }=\varnothing$, we simply write $T_{\varSigma _\chi }$ and $H_{\varSigma _\chi }$ for $T_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}$ and $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}$. Let $H^{\Box }_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}=H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}\otimes _{R_{\varSigma _{\chi , {\mathrm {Q}}, \nu }} }R_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}^{\Box }$; when $S_{{\mathrm {Q}}, \nu }=\varnothing$, we simply write it $H^{\Box }_{\varSigma _{\chi }}$.

Recall that $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }}/U_{\varSigma _{{\mathrm {Q}}, \nu }}$ is isomorphic to the $\prod _{\mathrm {Q}} \varDelta _{\mathrm {Q}}$ where ${\mathrm {Q}}$ ranges over $S_{{\mathrm {Q}}, \nu }$ and where $\varDelta _{\mathrm {Q}}$ is the maximal pro-p quotient of $(O_F/{\mathrm {Q}})^\times$ for every ${\mathrm {Q}}$. Let $\varDelta _{{\mathrm {Q}}, \nu }$ denote the quotient $(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }}\cap \mathbb {A}_F^{\infty \times })O_F^\times /(U_{\varSigma _{{\mathrm {Q}}, \nu }}\cap \mathbb {A}_F^{\infty \times })O_F^\times \simeq (\prod _{\mathrm {Q}}\varDelta _{\mathrm {Q}})/\overline{O}_F^\times$ by the image $\overline{O}_F^\times$ of the units $O_F^\times$.

Lemma 8

The co-invariants of $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$ by $O[\varDelta _{{\mathrm {Q}}, \nu }]$ is isomorphic to $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }})$ by the trace map corresponding to $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }}/U_{\varSigma _{{\mathrm {Q}}, \nu }}$, and $H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}=H_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}(U_{\varSigma _{{\mathrm {Q}}, \nu }})$ is a finite faithful and free module over $\varLambda [\varDelta _{{\mathrm {Q}}, \nu }]$.

Proof

For a sufficiently small open compact subgroup U of $G(\mathbb {A}_F^\infty )$,

$$\begin{aligned} G(\mathbb {A}_F^\infty )=\coprod _t G(F)t U \end{aligned}$$

holds, where t ranges over a finitely many representatives in $G(\mathbb {A}_F^\infty )$; and $(t^{-1} G(F)t\cap U)/O_F^\times$ is trivial. For an O-module A, it therefore follows that

$$\begin{aligned} S_2^\chi (U, A)\simeq \bigoplus _t (V_{2, \chi }\otimes _O A)^{t^{-1} G(F)t\cap U}. \end{aligned}$$

The first assertion follows if the co-invariants $S^\chi _2(U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, O)_{\varDelta _{{\mathrm {Q}}, \nu }}$ is isomorphic to $S^\chi _2(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}, O)$. This, in turn, follows (by the standard duality pairing and Pontryagin duality) if the invariants $S^\chi _2(U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, L/O)^{\varDelta _{{\mathrm {Q}}, \nu }}$ is isomorphic to $S^\chi _2(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}, L/O)$. As the order of $t^{-1}G(F)t\cap U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ and the order of $\varDelta _{{\mathrm {Q}}, \nu }=(\prod _{\mathrm {Q}}\varDelta _{\mathrm {Q}})/\overline{O}_F^\times$ are coprime, this holds.

To prove the second assertion, it is enough to prove $|S^\chi _2(U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, L)||\varDelta _{{\mathrm {Q}}, \nu }|=| S^\chi _2(U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}, L)|$ by Nakayama’s lemma. But this follows as one observes, as $U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ is sufficiently small,

$$\begin{aligned} S_2^\chi (U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}, L)\simeq \bigoplus _t V_{2, \chi }^{t^{-1} G(F)t\cap U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}} \end{aligned}$$

and therefore

$$\begin{aligned} S_2^\chi (U_{\varSigma _{{\mathrm {Q}}, \nu }, N}, L)\simeq \bigoplus _t \bigoplus _{\varDelta _{{\mathrm {Q}}, \nu }} V_{2, \chi }^{t^{-1} G(F)t\cap U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}} \end{aligned}$$

as the order of $\varDelta _{{\mathrm {Q}}, \nu }$ and $t^{-1} G(F)t\cap U_{{\mathrm {Iw}}_{{\mathrm {Q}}, \nu }, N}$ are coprime. $\square$

Let $\varLambda ^\Box =\varLambda \hat{\otimes } R_T^\Box$ where $T=S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}$ and let $\varDelta _{{\mathrm {Q}}, \infty }$ be the free $\mathbf {Z}_p$-module $(\prod _q \mathbf {Z}_p)/\overline{O}_F^\times$ of rank $q-{\mathrm {rk}}\overline{O}_F^\times \ge q-([F:\mathbf {Q}]-1)$ by Dirichlet’s unit theorem, which surjects onto $\varDelta _{{\mathrm {Q}}, \nu }=(\prod _{{\mathrm {Q}}} \varDelta _{\mathrm {Q}})/\overline{O}_F^\times$ for every $\nu$. Let J denote the kernel of the homomorphism $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]\rightarrow \varLambda$ which sends $\varDelta _{{\mathrm {Q}}, \infty }$ to 1 and all $4|T|-1$ variables in $R^{\Box }_T$ to 0. Let $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}=R_{\varSigma _\chi }^{{\mathrm {loc}}}[[X_1,\ldots , X_r]]$. Following Geragthy 4.3, [19], the $H^{\Box }_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}$ patch together to yield a $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}\hat{\otimes } \varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$-module $H^{\Box }_{\varSigma _\chi , \infty }$.

Lemma 9

Let $\triangle$ be a minimal ideal of $\varLambda$.

• If $\chi$ is distinct, ${\mathrm {Spf}}\, R_{\varSigma _\chi }^{\mathrm {loc}}\otimes \varLambda /\triangle$ is O-flat and geometrically irreducible of relative dimension $1+2[F:\mathbf {Q}]+\epsilon _{\mathrm {L}}+4|T|$.

• If $\chi$ is trivial and if L is sufficiently large, ${\mathrm {Spf}}\, R_\varSigma ^{\mathrm {loc}}\otimes \varLambda /\triangle$ is equi-dimensional of relative dimension $1+2[F:\mathbf {Q}]+\epsilon _{\mathrm {L}}+4|T|$; furthermore, every minimal prime of $R_\varSigma ^{\mathrm {loc}}\otimes \varLambda /(\triangle , \lambda )$ contains a unique minimal prime of $R_\varSigma ^{{\mathrm {loc}}}\otimes \varLambda /\triangle$. Furthermore, $R_\varSigma ^{\mathrm {loc}}$ is O-flat, Cohen–Macaulay and $R^{\mathrm {loc}}_\varSigma /\lambda$ is generically reduced.

Proof

See Lemma 4.12 in [19] and Lemma 3.3 [3]. When $\chi$ is trivial and K is sufficiently large, it follows from Lemma 3.3 in [3] that every prime, minimal amongst those containing $\lambda$, contains a unique minimal prime.

It follows from Propositions 5, 3 and 4 that $R_\varSigma ^{{\mathrm {loc}}}\otimes \varLambda$ is Cohen–Macaulay. Lemma 1.4 in [56] establishes that the fibres $R^{\mathrm {loc}}_\varSigma /\lambda$ is generically reduced.

$\square$

Remark

The Cohen–Macaulayness of $R_{\varSigma , \infty }^{\mathrm {loc}}$ is critical to our proof of $R_\varSigma \simeq T_\varSigma$ without recourse to taking the reduced quotients. This is based on Snowden’s insight in [49].

Lemma 10

As $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}/\lambda \simeq R_{\varSigma , \infty }^{{\mathrm {loc}}}/\lambda$-modules, $H^{\Box }_{\varSigma _\chi , \infty }/\lambda \simeq H^{\Box }_{\varSigma , \infty }/\lambda$ holds. Furthermore, $H^{\Box }_{\varSigma _\chi , \infty }$ (resp. $H^{\Box }_{\varSigma , \infty }$) is a finite free module over $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$ (resp. $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$) (and hence are finitely generated $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}$-modules); and $H^{\Box }_{\varSigma _\chi , \infty }/J \simeq H_{\varSigma _\chi }$ and $H^{\Box }_{\varSigma , \infty }/J \simeq H_{\varSigma }$ holds respectively.

Proof

See Proposition 2.5.3 and Corollary 2.5.4 in [19] $\square$

The following is a summary of Geraghty’s results [19] about Hida theory that we shall implicitly use; their proofs can be found in [19]. See Proposition 3.4.4 in [11], Lemma 2.6.4, Proposition 2.7.4, and Lemma 4.2.2 in [19] for example.

If $\lambda : \varLambda \rightarrow O^\times$ is an algebraic character defined by the set $\lambda =(\lambda _{\mathfrak {p}, 1}, \lambda _{\mathfrak {p}, 2})$ of integers, and if a character $\gamma : \varLambda \rightarrow O^\times$ is of finite order, we shall let $\varGamma _{\lambda , \gamma }$ denote the ideal ${\mathrm {ker}}(\gamma {(-\lambda _2, -\lambda _1-1)} )$ of $\varLambda$ where $(-\lambda _2, -\lambda _1-1)$ denote the character $\varLambda _p\rightarrow O^\times$ defined by the product of $(-\lambda _{\tau , 2}, -\lambda _{\tau , 1}-1)$ over $\tau$ in $S_\mathfrak {p}$ for all $\mathfrak {p}$ in $S_{\mathrm {P}}$.

If ${\mathrm {ker}}\, \gamma$ contains the product over $\mathfrak {p}$ of ${\mathrm {ker}}(T(O_\mathfrak {p})\twoheadrightarrow T(O_\mathfrak {p}/\mathfrak {p}^N))$ for an integer $N\ge 1$, the quotient $T^{\mathrm {ord}}_{\varSigma _\chi }\otimes _{\varLambda } \varLambda _{ \varGamma _{\lambda , \gamma }}/\varGamma _{\lambda , \gamma }$ surjects onto the maximal quotient of $T^{\mathrm {ord}}_{\lambda , \varSigma _\chi }(U_N)$ where $S_\tau$ operates as $\gamma _\tau$ for every $\tau$ in $T_G$; furthermore, the kernel of the surjection is nilpotent.

There exists a continuous representation

$$\begin{aligned} \overline{\rho }=\overline{\rho }_{\mathfrak {m}_{\chi , {\mathrm {Q}}, \nu }}:{\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(T_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}/\mathfrak {m}_{\chi ,{\mathrm {Q}}, \nu }) \end{aligned}$$

such that

• $\overline{\rho }$ is unramified outside S, and

  $$\begin{aligned}{\mathrm {tr}}\overline{\rho }({\mathrm {Frob}}_{\mathrm {Q}})=T_{\mathrm {Q}}\end{aligned}$$

  and

  $$\begin{aligned} {\mathrm {det}}\overline{\rho }({\mathrm {Frob}}_{\mathrm {Q}})=(\mathbf {N}_{F/\mathbf {Q}} {\mathrm {Q}})S_{\mathrm {Q}} \end{aligned}$$

  for every ${\mathrm {Q}}$ not in S,

• for every place ${\mathrm {Q}}$ in $S_{\mathrm {R}}$, the characteristic polynomial in X of the restriction of $\overline{\rho }(g)$ is of the form $(X-\chi _{{\mathrm {Q}}, 1}({\mathrm {Art}}_{\mathrm {Q}}(g))^{-1})(X-\chi _{{\mathrm {Q}}, 2}({\mathrm {Art}}_{\mathrm {Q}}(g))^{-1})$ for every g in $I_{\mathrm {Q}}$.

• for every place ${\mathrm {Q}}$ in $S_{\mathrm {L}}$, the characteristic polynomial of $\overline{\rho }({\mathrm {Frob}}_{\mathrm {Q}})$ (resp. $\overline{\rho }(g)$) is of the form $(X-|k_{\mathrm {Q}}|)(X-\alpha |k_{\mathrm {Q}}|)$ for some $\alpha$ (resp. $(X-1)^2$) for a Frobenius lifting ${\mathrm {Frob}}_{\mathrm {Q}}$ (resp. for every g in $I_{\mathrm {Q}}$),

• $\overline{\rho }$ is unramified at every place in $S_{{\mathrm {A}}}$.

• $\overline{\rho }$ is a direct sum of two distinct unramified characters when restricted to every place of $S_{{\mathrm {Q}}, \nu }$.

Suppose that $\mathfrak {m}_{\chi }$ is non-Eisenstein. There exists a continuous representation

$$\begin{aligned} \rho =\rho _{\mathfrak {m}_{\chi ,{\mathrm {Q}}, \nu }}: {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(T_{\varSigma _{\chi , {\mathrm {Q}}, \nu }}) \end{aligned}$$

for which the following hold:

• $\rho$ is a conjugate lifting of $\overline{\rho }$ of type $\varSigma _{\chi , {\mathrm {Q}}, \nu }$.

• Suppose $S_{{\mathrm {Q}}, \nu }=\varnothing$. The maximal ideal $\mathfrak {m}_\chi$ uniquely determines an irreducible component of ${\mathrm {Spec}}\, \varLambda _p$ over which it lies, and the component is characterised by a character of the torsion subgroup of $\varLambda$. Suppose that $\gamma$ equals $-(\lambda _{\mathfrak {p}, 2}, \lambda _{\mathfrak {p}, 1})_\mathfrak {p}$ when restricted to the torsion subgroup. If $\varGamma$ is a dimension one prime ideal of $T_{\varSigma _{\chi }}$ lying above $\varGamma _{\lambda , \gamma }$,

  $$\begin{aligned} \rho _{\mathfrak {m}_\chi , \varGamma }: {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(L_\varGamma ),\end{aligned}$$

  where $L_\varGamma$ denote the field of fractions of $T_{\varSigma _{\chi }}/\varGamma$, satisfies:

  • for every $\mathfrak {p}$ in $S_{\mathrm {P}}$, the restriction $\rho _{\mathfrak {m}_\chi , \varGamma , \mathfrak {p}}$ of $\rho _{\mathfrak {m}_\chi , \varGamma }$ to $D_\mathfrak {p}$ is de Rham/potentially semi-stable with Hodge–Tate weights $(\lambda _{\tau , 1}+1, \lambda _{\tau , 2})_\tau$;

  • $\rho _{\mathfrak {m}_\chi , \varGamma , \mathfrak {p}}$ is reducible of the form $\begin{pmatrix} \xi _{1,\mathfrak {p}}&{}\quad *\\ 0&{}\epsilon ^{-1}\xi _{2,\mathfrak {p}}\end{pmatrix}$ where $\xi _{1, \mathfrak {p}}\circ {\mathrm {Art}}_\mathfrak {p}$ (resp. $\xi _{2, \mathfrak {p}}\circ {\mathrm {Art}}_\mathfrak {p}$), as a character of $O_\mathfrak {p}^\times$, is given by $((-\lambda _{\tau , 2})\circ \tau )_\tau$ (resp. $((-\lambda _{ \tau , 1})\circ \tau )_\tau$ ); and $\xi _{1, \mathfrak {p}}\circ {\mathrm {Art}}_\mathfrak {p}(\pi _\mathfrak {p})=U_\mathfrak {p}$ mod $\varGamma$, and $\xi _{2, \mathfrak {p}}\circ {\mathrm {Art}}_\mathfrak {p}(\pi _\mathfrak {p})=S_\mathfrak {p}/U_\mathfrak {p}$ mod $\varGamma$.

In applications, we consider $\varGamma$ corresponding to $\lambda _{\tau , 1}-\lambda _{ \tau , 2}=-1$ for $\tau$ in $S_\mathfrak {p}$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$.

2.5 $R=T$

Suppose that $\overline{\rho }$ as in the previous section is modular, i.e., $\overline{\rho }\simeq \overline{\rho }_\mathfrak {m}$ for a non-Eisenstein maximal ideal $\mathfrak {m}\subset T^{\mathrm {ord}}_\varSigma (U)$.

Theorem 3

$H^{\Box }_{\varSigma , \infty }$ is a (Cohen–Macaulay) faithful $R_{\varSigma , \infty }^{{\mathrm {loc}}}$-module.

Proof

For every minimal prime $\triangle$ of $\varLambda$, the Krull-dimension of $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}/\triangle$, for a distinct $\chi$, is

$$\begin{aligned} \begin{array}{rl} &{}1+r+(1+2[F:\mathbf {Q}]+\epsilon _{\mathrm {L}})+4|{S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}} |\\ &{}\quad =1+(q-2[F:\mathbf {Q}])+(1+2[F:\mathbf {Q}]+\epsilon _{\mathrm {L}})+ 4|S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}|. \end{array} \end{aligned}$$

On the other hand, the $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}$-depth of $H^{\Box }_{\varSigma _\chi , \infty }/\triangle$ is at least the $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$-depth of $H^{\Box }_{\varSigma _\chi , \infty }/\triangle$. As $H^{\Box }_{\varSigma _\chi , \infty }/\triangle$ is free as a $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$-module, the latter depth equals the Krull-dimension of $\varLambda ^\Box [[\varDelta _{{\mathrm {Q}}, \infty }]]$ which is greater than or equal to

$$\begin{aligned} 1+(1+[F:\mathbf {Q}]+\epsilon _{\mathrm {L}})+4|S_{\mathrm {P}}\cup S_{\mathrm {R}}\cup S_{\mathrm {L}}\cup S_{{\mathrm {A}}}|-1 +q-([F:\mathbf {Q}]-1). \end{aligned}$$

Since ${\mathrm {Spec}}\, R^{{\mathrm {loc}}}_{\varSigma _\chi , \infty }/\triangle$ is irreducible, it then follows from Lemma 2.3 in [52] that $H^{\Box }_{\varSigma _\chi , \infty }/\triangle$ is a nearly faithful $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}/\triangle$-module. By Lemma 2.2, 1, [52], $H^{\Box }_{\varSigma _\chi , \infty }/(\triangle , \lambda )$ is a nearly faithful $R_{\varSigma _\chi , \infty }^{{\mathrm {loc}}}/(\triangle , \lambda )$-module, hence $H^{\Box }_{\varSigma , \infty }/\triangle$ is a nearly faithful $R_{\varSigma , \infty }^{{\mathrm {loc}}}/\triangle$-module. It then follows from Lemma 2.2, 2, [52], that $H^{\Box }_{\varSigma , \infty }/\triangle$ is a nearly faithful $R_{\varSigma , \infty }^{{\mathrm {loc}}}/\triangle$-module. As this holds for any minimal prime $\triangle$, one concludes that $H^{\Box }_{\varSigma , \infty }$ is a nearly faithful $R_{\varSigma , \infty }^{{\mathrm {loc}}}$-module.

On the other hand, one may observe that p and the generators of J define a system of parameters of $R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle$. Since $R_{\varSigma , \infty }^{{\mathrm {loc}}}/\triangle$ is Cohen–Macaulay, it follows from Theorem 17.4 in [32] that it indeed defines a regular sequence of the noetherian local ring. In particular, p is $R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle$-regular. It therefore follows from Lemma 9 that $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , \lambda )$ is Cohen–Macaulay and that $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , \lambda )$ is reduced. The regularity also establishes that $R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle$ is reduced and, by extension, $R_{\varSigma , \infty }^{\mathrm {loc}}$ is reduced. The faithfulness of $H_{\varSigma , \infty }^\Box$ as an $R_{\varSigma , \infty }^{\mathrm {loc}}$-module follows. $\square$

By the theorem above, $H^{\Box }_{\varSigma , \infty }/J\simeq H_\varSigma$ is a nearly faithful $R_{\varSigma , \infty }^{{\mathrm {loc}}}/J$-module. Hence the maximal reduced quotient of $R_\varSigma$ is isomorphic to $T_\varSigma$. To promote this isomorphism on the reduced quotients to the isomorphism $R_\varSigma \simeq T_\varSigma$, it suffices to prove that $R_\varSigma$ itself is also reduced. In achieving the reducedness, the key input is Snowden’s insight in [49] (Sect. 5 to be more precise), i.e. by establishing that $R_{\varSigma , \infty }^{\mathrm {loc}}\simeq R_{\varSigma , \infty }$ is Cohen–Macaulay and, by extension, $R_{\varSigma , \infty }^{\mathrm {loc}}/J$ is Cohen–Macaulay and O-flat.

As the preceding theorem proves that $R_{\varSigma , \infty }^{\mathrm {loc}}/J$ is isomorphic to $R_\varSigma$, it is enough to establish that $R_{\varSigma , \infty }^{\mathrm {loc}}/J$, or equivalently $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)$ is reduced for every minimal prime $\triangle$. To this end, we need a lemma which paraphrases Lemma 8.5 in [23]:

Lemma 11

Let R be a noetherian local ring and let M be a faithful, Cohen–Macaulay, finitely generated R-module. Let $r, r_1, \dots , r_N$ be a system of parameters of R, let J denote the ideal generated by $r_1, \dots , r_N$ and let $\overline{R}=R/J$ and $\overline{M}=M\otimes _R R/J$. Suppose that

• $\overline{M}[1/r]$ is a semi-simple $\overline{R}[1/r]$-module,

• for every prime ideal $\mathfrak {P}$ in R[1 / r] which is the pre-image of a maximal ideal $\mathfrak {m}$ that lies in ${\mathrm {Supp}}_{\overline{R}[1/r]}(\overline{M}[1/r])$, the localisation $R[1/r]_\mathfrak {P}$ is regular.

Then $\overline{R}[1/r]$ is reduced.

Proof of the lemma

Since M is a finitely generated Cohen–Macaulay module over R, for a prime $\mathfrak {P}$ as in the second assumption, $M[1/r]_\mathfrak {P}$ is a finitely generated Cohen–Macaulay module over $R[1/r]_\mathfrak {P}$. It then follows from Auslander–Buchsbaum that $M[1/r]_\mathfrak {P}$ is finite free over $R[1/r]_\mathfrak {P}$; in particular, $\overline{M}[1/r]_\mathfrak {m}$ is finite free over $\overline{R}[1/r]_\mathfrak {m}$. One may then deduce from the semi-simplicity assumption that the Jacobson radical of $\overline{R}[1/r]_\mathfrak {m}$ is zero, and therefore the nilradical of $\overline{R}[1/r]_\mathfrak {m}$ is zero.

On the other hand, M is assumed to be faithful over R, and therefore $\overline{M}[1/r]$ is nearly faithful over $\overline{R}[1/r]$, or equivalently, ${\mathrm {Supp}}_{\overline{R}[1/r]}(\overline{M}[1/r])={\mathrm {Spec}}\, \overline{R}[1/r]$. As $\overline{R}[1/r]$ is aritinian, ${\mathrm {Spec}}\, \overline{R}[1/r]$ equals the maximum spectrum ${\mathrm {Max}}\, \overline{R}[1/r]$ and an isomorphism

$$\begin{aligned} \overline{R}[1/r]\simeq \prod _\mathfrak {m}\overline{R}[1/r]_\mathfrak {m}, \end{aligned}$$

where $\mathfrak {m}$ ranges over ${\mathrm {Max}}\, \overline{R}[1/r]={\mathrm {Supp}}_{\overline{R}[1/r]}(\overline{M}[1/r])$, holds. As each $\overline{R}[1/r]_\mathfrak {m}$ is reduced, the assertion follows. $\square$

Corollary 1

$R_\varSigma \simeq T_\varSigma$

Proof

For a minimal ideal $\varGamma$ of $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J, p)$, we apply Lemma 11 to the localisation $(R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle )_\varGamma$ of $R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle$ at $\varGamma$ to establish that $(R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J))_\varGamma [1/p]$ is reduced. It therefore follows that $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)[1/p]$ is generically reduced. As it is Cohen–Macaulay by Lemma 9 (and Theorem 2.1.3 in [5]), it is indeed reduced. To promote the reducedness of $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)[1/p]$ to the reducedness of $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)$, it suffices to establish that $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)$ is p-torsion free so that $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)$ embeds into $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)[1/p]$. But since $R_{\varSigma , \infty }^{\mathrm {loc}}/\triangle$ is noetherian local, p is $R_{\varSigma , \infty }^{\mathrm {loc}}/(\triangle , J)$-regular and the p-torsion freeness follows. $\square$

3 Models of Hilbert modular varieties

3.1 Pappas–Rapoport integral models

Let F be a totally real field with $[F:\mathbf {Q}]=d$ and let $O_F$ denote the ring of integers. Let $D=D_{F/\mathbf {Q}}$ denote the different of F. Fix an embedding $\overline{\mathbf {Q}}\hookrightarrow \overline{\mathbf {Q}}_p$ once for all.

For every place $\mathfrak {p}$ of F above p, we shall denote the completion of F at $\mathfrak {p}$ by $F_\mathfrak {p}$, its ring of integers by $O_\mathfrak {p}$, and a uniformiser $\pi _\mathfrak {p}$ (or $\pi$ when the reference to $\mathfrak {p}$ is clear from the context); denote the ramification index by $e_\mathfrak {p}$ (or e when the reference to $\mathfrak {p}$ is clear from the context) and the residue degree by $f_\mathfrak {p}$. Let $\hat{F}_\mathfrak {p}$ denote the maximal unramified extension of $\mathbf {Q}_p$ in $F_\mathfrak {p}$; and let $E\in \hat{F}_\mathfrak {p}[u]$ denote the Eisenstein polynomial in u defining the totally ramified extension $F_\mathfrak {p}$ over $\hat{F}_\mathfrak {p}$ of degree $e_\mathfrak {p}$.

Let L be a finite extension of $\mathbf {Q}_p$ which contains the image of every embedding of $F\hookrightarrow \overline{\mathbf {Q}}\hookrightarrow \overline{\mathbf {Q}}_p$; and let O denote its ring of integers and let $\kappa$ denote the residue field.

For every place $\mathfrak {p}$ of F above p, we shall let $\varSigma _\mathfrak {p}$ denote ${\mathrm {Hom}}_{\mathbf {Q}_p}(F_\mathfrak {p}, L)$ and let $\hat{\varSigma }_{\mathfrak {p}}$ denote ${\mathrm {Hom}}_{\mathbf {Q}_p}( \hat{F}_{\mathfrak {p}}, L)$. For every $\tau \in \hat{\varSigma }_{\mathfrak {p}}$, let $\hat{\varSigma }_{\mathfrak {p}, \tau }$ denote the set of elements in $\varSigma _\mathfrak {p}$ whose restriction to $\hat{F}_\mathfrak {p}$ is $\tau$, and we fix, once for all, a bijection between $\varSigma _{\mathfrak {p}, \tau }$ and the set of integers between 1 and $e_\mathfrak {p}$; if we let $E_\tau \in L[u]$ denote the image of E by $\tau$ for $\tau \in \hat{\varSigma }_{\mathfrak {p}}$, it mean that we order (and fix) the roots of $E_\tau$ in L.

For every place $\mathfrak {p}$ of F above p and $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$, let $\gamma _\tau ^t$, for every $1\le t\le e_\mathfrak {p}$, be the image of $\pi _\mathfrak {p}$ by the element of $\varSigma _{\mathfrak {p}, \tau }$ corresponding to t; and let $E_\tau (t)$ be the polynomial $(u-\gamma ^t_\tau )(u-\gamma _\tau ^{t+1})\cdots (u-\gamma _\tau ^{e_\mathfrak {p}})$ in u with coefficients in O (and hence in $O_S$ for any O-scheme S).

Let $V=F^2$ and let $(\ , \ )$ denote the standard non-generate alternating bilinear pairing on V. Let $B=F$ thought of coming equipped with identity ‘involution’. Define the closed algebraic subgroup G over $\mathbf {Q}$ of $GL_B(V)={\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_2$ as in 6.1 in [40].

Let U be an open compact subgroup of $G(\mathbb {A}^{\infty })$ such that $U\cap G(\mathbf {Q}_p)=G(\mathbf {Z}_p)$. Indeed we suppose that U is the principal congruence subgroup mod n of $G(\mathbb {A}^\infty )$, and suppose that $n\ge 3$ and is prime to p.

Fix, once for all, a set of representatives $\ell \in \mathbb {A}_F^\times$ for the strict ideal class group $\mathbb {A}_F^\times /F^\times (O_F\otimes _\mathbf {Z}\mathbf {Z}^\wedge )^\times (F\otimes _\mathbf {Q}\mathbf {R})^\times _{+}$ of F; by abuse of notation, let $\ell$ also denote the corresponding fractional ideal of F.

By ‘${_+}$’ we shall always mean ‘the subgroup of its totally positive elements’.

For every (fixed) representative $\ell$, define $\mathcal {M}^{\mathrm {DP}}_{U, \ell }$ to be the functor which sends an O-scheme S to the set of isomorphism classes of data $(A, i, \lambda , \eta )$ consisting of

• an abelian scheme A / S of relative dimension $d=[F:\mathbf {Q}]$

• $i:O_F\rightarrow {\mathrm {End}}(A/S)$

• an $O_F$-linear morphism of étale sheaves $\lambda : (\ell , \ell _+)\rightarrow ({\mathrm {Sym}}(A/S), {\mathrm {Pol}}(A/S))$ which is indeed an isomorphism, and by which the natural morphism $A\otimes {\mathrm {Sym}}(A/S)\rightarrow A^\vee$ is also an isomorphism (note that these are equivalent to the condition Deligne–Pappas defines: a homomorphism $(\ell , \ell _+)\rightarrow ({\mathrm {Sym}}(A/S),{\mathrm {Pol}}(A/S))$ of $O_F$-modules such that the composite $A\otimes \ell \rightarrow A\otimes {\mathrm {Sym}}(A/S)\rightarrow A^\vee$ is an isomorphism);

• an $O_F$-linear isomorphism $A[n]\simeq O_F\otimes _\mathbf {Z}(\mathbf {Z}/n\mathbf {Z})$.

The functor is representable by a scheme over O which we shall denote by $Y^{\mathrm {DP}}_{U, \ell }$; it follows from local model theory that its fibre $\overline{Y}^{\mathrm {DP}}_{U, \ell }$ over ${\mathrm {Spec}}\, \kappa$ is smooth outside a codimension 2 closed subscheme. The main result of this section is to construct an integral model over O which is smooth over O (and hence its fibre over $\kappa$ is smooth).

For every $\ell$ as above, define $\mathcal {M}^{\mathrm {PR}}_{U, \ell }$ to be the functor which sends an O-scheme S to the set of isomorphism classes of data $(A, i, \lambda , \eta )$ where

• $(A, i, \lambda , \eta )$ define a S-valued point of $\mathcal {M}^{\mathrm {DP}}_{U, \ell }$

• For every place $\mathfrak {p}$ of F above p and every $\tau \in \hat{\varSigma }_\mathfrak {p}$, the $\tau$-component ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau$ of the $O_S$-dual ${\mathrm {Lie}}^\vee (A^\vee /S)$ of the sheaf ${\mathrm {Lie}}(A^\vee /S)$ of Lie algebras of the dual abelian variety A over S, comes equipped with a filtration

  $$\begin{aligned} 0= & {} {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (0)\subset {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (e_\mathfrak {p})\\= & {} {\mathrm {Lie}}^\vee (A^\vee /S)_\tau \subset H_{{\mathrm {dR}}}^{1}(A/S)^\vee _\tau \end{aligned}$$

  such that ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t)$ is, Zariski locally on S, a direct summand of ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau$ of rank t and is a sheaf of $O_\mathfrak {p}\otimes _{\tau }O_S$-submodule (where $\otimes$ is meant over $\hat{F}_\mathfrak {p}$) of ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau$, satisfying the condition

  $$\begin{aligned} (\pi _\mathfrak {p}\otimes 1-1\otimes \gamma ^t_\tau ){\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t)\subset {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t-1). \end{aligned}$$

For every $\tau \in \hat{\varSigma }_{\mathfrak {p}}$ and every $1\le t\le e_\mathfrak {p}$, let

$$\begin{aligned} {\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)={\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t)/{\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t-1), \end{aligned}$$

and let

$$\begin{aligned} {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)=H^1_{\mathrm {dR}}(A/S)_\tau ^\vee /{\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t-1); \end{aligned}$$

the former (resp. the latter) is a locally free sheaf of $O_S$-modules of rank 1 (resp. $2e_\mathfrak {p}-(t-1)$).

Let

$$\begin{aligned} {D}^\sim (A/S)_\tau (t)={\mathrm {ker}}(E_\tau (t)\, |\, {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)) \end{aligned}$$

and

$$\begin{aligned} D(A/S)_\tau (t)= & {} {\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^t\, |\, D^\sim (A/S)_\tau (t))\\= & {} {\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma ^t_\tau \, |\, {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)). \end{aligned}$$

We know the ranks of these $O_S$-modules:

Lemma 12

For every $\tau \in \hat{\varSigma }_{\mathfrak {p}}$ and for every $1\le t\le e_\mathfrak {p}$,

• ${D}^\sim (A/S)_\tau (t)$ is a locally free sheaf of $O_S[u]/E_\tau (t)$-modules of rank 2 and is also a locally free sheaf of $O_S$-modules of rank $2(e_\mathfrak {p}-t+1)$;

• $D(A/S)_\tau (t)$ is a locally free sheaf of $O_S$-modules of rank 2.

Proof

This is essentially Proposition 5.2(b) of [36] with $d=2$. $\square$

Lemma 13

For every $\tau \in \hat{\varSigma }_{\mathfrak {p}}$ and every $1\le t\le e_\mathfrak {p}$, ${\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)$ is locally a rank 1 direct summand of $D(A/S)_\tau (t)$ as an $O_S$-module.

Proof

Since this is not proved in [36], we shall give a complete proof. By definition, ${\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)$ is a subsheaf of $O_S$-modules of $D(A/S)_\tau (t)$. It suffices to prove that the quotient $D(A/S)_\tau (t)/{\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)$ is locally free of rank 1. Consider the exact sequence

$$\begin{aligned}&0\rightarrow D(A/S)_\tau (t)/{\mathrm {Gr}}^{ \vee }(A^\vee /S)_\tau (t)\rightarrow {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/{\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)\\&\quad \rightarrow {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/ D(A/S)_\tau (t)\rightarrow 0. \end{aligned}$$

Firstly observe that the middle term

$$\begin{aligned} {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/{\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t)\simeq {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t+1), \end{aligned}$$

and it is locally free of rank $2e_\mathfrak {p}-t$; hence it suffices to show that ${{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/D(A/S)_\tau (t)$ is locally free of rank $2e_\mathfrak {p}-(t+1)$. The preceding lemma asserts that $D(A/S)_\tau (t)$ is locally a direct summand of $D^\sim (A/S)_\tau (t)$ with the quotient $D^\sim (A/S)_\tau (t)/D(A/S)_\tau (t)$ locally free of rank $2(e_\mathfrak {p}-t+1)-2=2(e_\mathfrak {p}-t)$. It is proved in the proof of Proposition 5.2 in [36] that $D^\sim (A/S)_\tau (t)$ is locally a direct summand of ${{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)$ with the quotient ${{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/D^\sim (A/S)_\tau (t)$ locally free of rank $t-1$. Hence the quotient ${{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(A/S)_\tau (t)/D(A/S)_\tau (t)$ is locally free of rank $2(e_\mathfrak {p}-t)+(t-1)=2e_\mathfrak {p}-(t+1)$, as desired. $\square$

Proposition 6

The functor $\mathcal {M}_{U, \ell }^{\mathrm {PR}}$ is representable by a smooth scheme, which we shall henceforth denote by $Y_{U, \ell }^{\mathrm {PR}}$, over O. Furthermore, the forgetful morphism, $Y_{U, \ell }^{\mathrm {PR}}\rightarrow Y_{U, \ell }^{\mathrm {DP}}$ is proper.

Proof

Representability: Define $\mathcal {M}^{\mathrm {Gr}}_{U, \ell }$ to be the functor which sends an O-scheme S to the set of isomorphism classes of data as in $\mathcal {M}^{\mathrm {PR}}_{U, \ell }$, except that it ‘forgets’ the last condition about the prescribed action of $O_F$; then $\mathcal {M}^{\mathrm {Gr}}_{U,\ell }\rightarrow \mathcal {M}^{\mathrm {DP}}_{U, \ell }$, forgetting filtrations, is clearly relatively representable and proper, hence $\mathcal {M}^{\mathrm {Gr}}_{U, \ell }$ is representable. The relative representability of $\mathcal {M}^{\mathrm {PR}}_{U, \ell }\rightarrow \mathcal {M}^{\mathrm {Gr}}_{U, \ell }$ follows from Lemma 1.3.4 in [29], for example.

Smoothness$Y^{\mathrm {PR}}_{U, \ell }$ is locally of finite presentation, and it suffices to show its formal smoothness in the following sense. Choose a closed point of $Y^{\mathrm {PR}}_{U, \ell }$, and let $R^{\mathrm {PR}}_{U, \ell }$ denote the completed local ring of $Y^{\mathrm {PR}}_{U, \ell }$ at the closed point and $M^{\mathrm {PR}}_{U, \ell }$ its maxim ideal. Let $\mathcal {M}_{U, \ell }^{{\mathrm {PR}}, \wedge }$ denote the ‘local formal moduli’ functor ${\mathrm {Spf}}\, R^{\mathrm {PR}}_{U, \ell }$, and let R be a complete noetherian local ring with maximal ideal M such that $R/M\simeq R^{\mathrm {PR}}_{U, \ell }/M^{\mathrm {PR}}_{U, \ell }$. It suffices to prove that

$$\begin{aligned} \mathcal {M}_{U, \ell }^{{\mathrm {PR}}, \wedge }(S)\rightarrow \mathcal {M}_{U, \ell }^{{\mathrm {PR}}, \wedge }(\overline{S}), \end{aligned}$$

induced by $\overline{S}{\mathop {=}\limits ^{{\mathrm {def}}}}{\mathrm {Spec}}\, R/M^{l-1}\rightarrow S{\mathop {=}\limits ^{{\mathrm {def}}}}{\mathrm {Spec}}\, R/M^{l}$ for an integer $l\ge 2$ which we fix, is surjective. We shall show this by the Grothendieck-Messing crystalline Dieudonne theory.

Let $(\overline{A}/\overline{S}, i, \lambda , \eta , ({\mathrm {Lie}}^\vee (\overline{A}^\vee /\overline{S})_\tau (1)\subset \dots \subset {\mathrm {Lie}}^\vee (\overline{A}^\vee /\overline{S})_\tau ))$ be a point of $\mathcal {M}^{\mathrm {PR}}_{U, \ell }$ over $\overline{S}$. Then, for every $\tau$, ${\mathrm {Gr}}^\vee (\overline{A}^\vee /\overline{S})_\tau (t)$ is locally a $O_{\overline{S}}$-direct summand of the locally free sheaf $D(\overline{A}/\overline{S})_\tau (t)$ of $O_{\overline{S}}$-modules of rank 2 by the preceding lemma.

Let $\gamma _\tau ^t$ be a lifting in $O_S$ of $\overline{\gamma }_\tau ^t$ in $O_{\overline{S}}$. The $O_S$-dual $H^{1}_{\mathrm {cr}}(\overline{A}/S)^\vee$ of the crystalline cohomology sheaf of $O_S$-module is a locally free sheaf of $O_F\otimes O_S$-modules of rank 2, and ${\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^1\, |\, H^{1}_{\mathrm {cr}}(\overline{A}/S)^\vee _\tau )$ defines a locally free sheaf of $O_S$-modules of rank 2 which lifts $D(\overline{A}/\overline{S})_\tau (1)$. It then follows that there exists a locally free subsheaf ${\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (1)$ of ${\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^1\, |\, H^{1}_{\mathrm {cr}}(\overline{A}/S)_\tau ^\vee )$ of rank 1 which lifts ${\mathrm {Lie}}^\vee (\overline{A}^\vee /\overline{S})_\tau (1)$.

Suppose, for $1\le l\le t$, that every ${\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (l)$, locally free of rank l over S, lifts ${\mathrm {Lie}}^\vee (\overline{A}^\vee /\overline{S})_\tau (l)$ and which satisfy ${\mathrm {Gr}}^\vee (\overline{A}^\vee /S)_\tau (l)\subset {\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^l\, |\, H^{1}_{\mathrm {cr}}(\overline{A}/S)^\vee _\tau /{\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (l-1))$ for $1\le l\le t$.

One may and will define ${\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (t+1)$ to be a rank $t+1$ locally free $O_S$-submodule of $H^{1}_{\mathrm {cr}}(\overline{A}/S)^\vee$ satisfying the condition that its quotient ${\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (t+1)/{\mathrm {Lie}}^\vee (\overline{A}^\vee /S)_\tau (t)$ defines a rank 1 direct summand of ${\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^{t+1}\, |\, H^{1}_{\mathrm {cr}}(\overline{A}/S)^\vee _\tau /{\mathrm {Lie}}^\vee (\overline{A}/S)_\tau (t))$ which is an $O_S$-module of rank 2 lifting $D(\overline{A}/\overline{S})_\tau (t+1)$.

It then follows from the Grothendieck-Messing crystalline Dieudonné deformation theory that there exists a Hilbert–Blumenthal abelian variety A over S whose pull-back to $\overline{S}$ is $(\overline{A}/\overline{S}, i)$ and ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau \times _{S}{\overline{S}}\simeq {\mathrm {Lie}}^\vee (\overline{A}^\vee /\overline{S})_\tau$ for every $\tau$. Evidently, ${\mathrm {Lie}}(A/S)$ satisfies that the Kottwitz ‘determinant’ condition (Definition 2.4 in [58]), and it follows from Corollary 2.10 of Vollaard [58] that $\lambda$ lifts over to S. $\square$

Let $Y_U^{\mathrm {PR}}$ denote the disjoint union $Y_{U, \ell }^{\mathrm {PR}}$ over $\ell$.

Let $\mathfrak {P}$ denote the product of all prime ideals of $O_F$ above p. For a representative $\ell$, let $\ell _\mathfrak {P}$ denote the element (or its corresponding fractional ideal) in the fix set of representatives representing the fractional ideal $\ell \mathfrak {P}$.

Define $\mathcal {M}^{{\mathrm {DP}}}_{U{\mathrm {Iw}}, \ell }$ to be the functor which sends an O-scheme S to the set of isomorphism classes of $O_F$-linear isogenies

$$\begin{aligned} f: A/S\rightarrow B/S \end{aligned}$$

of degree $|O_F/\mathfrak {P}|$ such that ${\mathrm {ker}}\, f\subset A[\mathfrak {P}]$, where A and B come equipped with PEL structure defining S-points of $Y^{{\mathrm {DP}}}_{U, \ell }$ and $Y^{\mathrm {DP}}_{U, \ell _\mathfrak {P}}$ respectively such that $(f^\vee \circ {\mathrm {Sym}}(B/S)\circ f, f^\vee \circ {\mathrm {Pol}}(B/S)\circ f)$ equals $(\mathfrak {P}{\mathrm {Sym}}(A/S), \mathfrak {P}{\mathrm {Pol}}(A/S))$. One can check that the last condition is equivalent to demanding that $C={\mathrm {ker}}\, f$ is an isotropic subgroup of $A[\mathfrak {P}]$ in the sense that, for any $\lambda$ in ${\mathrm {Sym}}(A/S)$ (in fact, it suffices for any $\lambda$ of degree prime to p), $\lambda$ maps C to $(A[\mathfrak {P}]/C)^\vee$. The functor is representable by an O-scheme $Y^{\mathrm {DP}}_{U{\mathrm {Iw}}, \ell }$.

Similarly, we define $\mathcal {M}^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ to be the functor which sends an O-scheme S to the set of isomorphism classes of $O_F$-linear isogenies $f: A/S\rightarrow B/S$ of degree $|O_F/\mathfrak {P}|$ such that ${\mathrm {ker}}\, f\subset A[\mathfrak {P}]$ defining an S-point of $Y^{\mathrm {DP}}_{U{\mathrm {Iw}}, \ell }$, where A and B are respectively S-points of $Y^{{\mathrm {PR}}}_{U, \ell }$ and $Y^{\mathrm {PR}}_{U, \ell _\mathfrak {P}}$ such that the filtrations commutes the diagram of locally free $O_S$-sheaves:

$$\begin{aligned} \begin{array}{ccccc} H^{1\vee }_{\mathrm {dR}}(A/S)_\tau &{}\longrightarrow &{} H^{1\vee }_{\mathrm {dR}}(B/S)_\tau &{}\longrightarrow &{}H^{1\vee }_{\mathrm {dR}}(A/S)_\tau \\ \cup &{}&{}\cup &{}&{}\cup \\ {\mathrm {Lie}}^\vee (A^\vee /S)_\tau &{}\longrightarrow &{}{\mathrm {Lie}}^\vee (B^\vee /S)_\tau &{}\longrightarrow &{}{\mathrm {Lie}}^\vee (A^\vee /S)_\tau \\ ||&{}&{}||&{}&{}||\\ {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (e_\mathfrak {p})&{}\longrightarrow &{}{\mathrm {Lie}}^\vee (B^\vee /S)_{\tau }(e_\mathfrak {p})&{}\longrightarrow &{} {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (e_\mathfrak {p})\\ \cup &{}&{}\cup &{}&{}\cup \\ {\mathrm {Lie}}^\vee (A^\vee /S)_{\tau }(e_\mathfrak {p}-1)&{}\longrightarrow &{} {\mathrm {Lie}}^\vee (B^\vee /S)_{ \tau }(e_\mathfrak {p}-1)&{}\longrightarrow &{}{\mathrm {Lie}}^\vee (A^\vee /S)_\tau (e_\mathfrak {p}-1)\\ \cup &{}&{}\cup &{}&{}\cup \\ \vdots &{}&{}\vdots &{}&{}\vdots \\ \cup &{}&{}\cup &{}&{}\cup \\ {\mathrm {Lie}}^\vee (A^\vee /S)_\tau (1)&{}\longrightarrow &{} {\mathrm {Lie}}^\vee (B^\vee /S)_{\tau }(1)&{}\longrightarrow &{}{\mathrm {Lie}}^\vee (A^\vee /S)_\tau (1) \end{array} \end{aligned}$$

If we let $C=\prod _\mathfrak {p} C_\mathfrak {p}\subset A[\mathfrak {P}]=\prod _{\mathfrak {p}} A[\mathfrak {p}]$ denote the kernel of $\pi : A/S\rightarrow B/S$, one can see that ${\mathrm {Lie}}^\vee (C^\vee /S)$ comes equipped with a filtration

$$\begin{aligned} 0= & {} {\mathrm {Lie}}^\vee (C^\vee /S)_\tau (0)\subset {\mathrm {Lie}}^\vee (C^\vee /S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (C^\vee /S)_\tau (e_\mathfrak {p})\\= & {} {\mathrm {Lie}}^\vee (C^\vee /S)_\tau \end{aligned}$$

defined by ${\mathrm {coker}}({\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t)/{\mathrm {Lie}}^\vee (A^\vee /S)_\tau (t-1)\rightarrow {\mathrm {Lie}}^\vee (B^\vee /S)_\tau (t)/{\mathrm {Lie}}^\vee (B^\vee /S)_\tau (t-1))$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$, $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$, and $1\le t\le e_\mathfrak {p}$; and each ${\mathrm {Lie}}^\vee (C^\vee /S)_\tau (t)/ {\mathrm {Lie}}^\vee (C^\vee /S)_\tau (t-1)$ is killed by $\pi _\mathfrak {p}$.

Proposition 7

The functor $\mathcal {M}^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ is representable by an O-scheme.

Proof

It is clear that $\mathcal {M}^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ is relatively representable over $\mathcal {M}^{\mathrm {DP}}_{U{\mathrm {Iw}}, \ell }$. $\square$

Let $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ denote the O-scheme representing $\mathcal {M}^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ in the proposition and let $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ denote the disjoint union of $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$ over $\ell$ ranging over the fixed set of representatives as before.

As the definition of $Y^{\mathrm {PR}}_{U}$ and $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}}$ are based on the local model constructions of Pappas–Rapoport [36], it is clear what their local models should be.

3.2 Compactification

Fix a representative $\ell$; we shall compactify $Y_{U, \ell }^{\mathrm {PR}}$ and $Y_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}$ following Rapoport’s [39] and Stroh’s [50] observations. Fix the integer $n\ge 3$ defined in the previous section.

By a $\ell$-cusp degeneration data $\mathcal {C}$, we shall mean two fractional ideals M and N of F, an exact sequence

$$\begin{aligned} 0\rightarrow D^{-1}M^{-1}\rightarrow L\rightarrow N\rightarrow 0 \end{aligned}$$

of projective $O_F$-modules, and an isomorphism $MN^{-1}\simeq D$; suppose furthermore that it comes equipped with a choice of an isomorphism $L/n L\simeq (O_F/n O_F)^2$.

Given an $\ell$-cusp degeneration data $\mathcal {C}$ as above, let $M^+ =M N$, $M^+_n=n^{-1}M^+$, and $M^{+ \vee }={\mathrm {Hom}}_\mathbf {Z}(M^+, \mathbf {Z})$; let $M^{+ \vee }_{\mathbf {R}, +}$ denote the submodule of the positive elements in $M^{+ \vee }\otimes \mathbf {R}$ where its positivity is defined via the isomorphism $M^{+ \vee }\simeq \ell M^{-2} D^{-1}$ and the positivity of each of the fractional ideals on the RHS.

Let $\varSigma$ denote a rational polyhedral cone decomposition $\{\tau \}$ of $M^{+ \vee }_{\mathbf {R}, +}\cup \{0\}$; we may and will choose it so that it is level-n-admissible in the sense that it satisfies the conditions of 3.2 and 3.3 of [10] (see p. 299 of [39]). Let $S_\ell ={\mathrm {Spec}}\, R$ with $R=O[M_n^+]$, and let $S_\ell \hookrightarrow S_{\ell , \tau }={\mathrm {Spec}}\, R_\tau$ denote the affine torus embedding where $R_\tau =O[M_n^+\cap \tau ^\vee ]$.

As Stroh [50] puts it, we may think of $S_\ell$ as a moduli space (stack) of Deligne 1-motives corresponding to an $\ell$-cusp degeneration data $\mathcal {C}$: let $X={\mathrm {Spec}}\, A$ be a normal scheme, Y an open dense subscheme, and $Z=X-Y={\mathrm {Spec}}\, A/I$ for an ideal I of A. In our context, a Mumford 1-motive over $(Y\hookrightarrow X)$ in the sense of Stroh is a set of data: the semiabelian variety $\widetilde{\mathbb {G}}=\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1}$ thought of as it is defined over X (where $\mathbb {G}$ is the multiplicative group scheme base-changed over to F), a ‘lattice’ N over X (i.e. a locally constant étale sheaf of finite free abelian groups), and a complex $q: N\rightarrow \widetilde{\mathbb {G}}$ of fppf sheaves of abelian groups over Y defined by an $O_F$-linear homomorphism $N\rightarrow \widetilde{\mathbb {G}}(Y)$ whose induced homomorphism ${\mathrm {tr}}_{F/\mathbf {Q}}\circ q:M^+\rightarrow \mathbb {G}(Y)$ maps $M^+_+$ to I.

Let ${\mathrm {Spf}}\, \hat{R}_\tau$ denote the affine formal completion of $S_{\ell , \tau }$ along $S_{\ell , \tau }-S_\ell$. Let $X_{\ell , \tau }={\mathrm {Spec}}\, \hat{R}_\tau$, let $Y_{\ell , \tau }$ denote its open dense subscheme defined by the pull-back of $X_{\ell , \tau }$ over $S_{\ell }$ along $S_{\ell }\hookrightarrow S_{\ell , \tau }$, and let $Z_{\ell , \tau }$ denote the complement $X_{\ell , \tau }-Y_{\ell , \tau }$.

Rapoport’s application [39] of the Mumford construction (in the ‘split case’) gives rise to a semi-abelian scheme

$$\begin{aligned} (\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N} \end{aligned}$$

over $X_{\ell , \tau }$ such that

• the pull-back to $Y_{\ell , \tau }$ of $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$ is a HBAV [see (i) and (ii) of [39], p. 297] which is $\ell$-polarisable [see (v) and (vi) in [39], p. 298] which comes equipped with a level n-structure [see (iii) and (iv) in [39], pp. 297–298], and whose dual Lie algebra ‘sheaf’ M comes equipped with a canonical PR-filtration in the sense of Sect. 3.1 (and gives rise to a map from $Y_{\ell , \tau }$ to $Y_{U, \ell }^{\mathrm {PR}}$),

• if A denote the universal HBAV over $Y_{U, \ell }^{\mathrm {PR}}$, the p-torsion of $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$ over $Y_{\ell , \tau }$, i.e., the pull-back to $Y_{\ell , \tau }$ of $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$, is canonically isomorphic to the p-torsion of the fibre product of A and $Y_{\ell , \tau }$ over $Y_{U, \ell }^{\mathrm {PR}}$.

Definition

Suppose that $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N})$ over $Y_{\ell , \tau }$ comes equipped with a Raynaud submodule scheme $C_\mathfrak {p}$ of $((\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N})[\mathfrak {p}]$ of rank 1 for all $\mathfrak {p}$ in $S_{\mathrm {P}}$. Let $S_{{\mathrm {P}}, \times }$ and $S_{{\mathrm {P}}, {et}}$ be subsets of $S_{\mathrm {P}}$ defined such that $\mathfrak {p}$ lies in $S_{{\mathrm {P}}, \times }$ if $C_\mathfrak {p}$ is multiplicative while it lies in $S_{{\mathrm {P}},{et}}$ if it is étale; in which case $S_{{\mathrm {P}}, \times }$ and $S_{{\mathrm {P}}, {et}}$ are disjoint and their union is $S_{\mathrm {P}}$.

Definition

Let $S_{ {\mathrm {I}}, \ell }$ denote the disjoint union over all partitions $(S_{{\mathrm {P}}, \times }, S_{{\mathrm {P}}, {et}})$ of $S_{\mathrm {P}}$ of $S_\ell$; and define $X_{{\mathrm {I}}, \tau }$ and $Y_{{\mathrm {I}}, \tau }$ similarly.

Let ${\mathrm {Spec}}\, R_\tau ^+$ denote the henselisation of $(S_{\ell , \tau }, S_{\ell , \tau }-S_\ell )$. Then it follows exactly as in Proposition 2.3.3.1 in [50] that there exists semi-abelian scheme $((\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N})^+$ which is ‘as universal’ as $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$ is. It furthermore follows as in 2.4 in [50] that there exists an étale extension $R_\tau ^{et}$ over $R_\tau$ and a semi-abelian scheme $((\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N})^{et}$ which satisfies the same properties as $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$ with $((\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N})^{et}$ in place of $(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^{N}$.

Definition

Let $X_{ {\mathrm {I}}, \ell , \tau }^{et}$ denote the pull-back to $S_{{\mathrm {I}}, \ell , \tau }$ of $X_{\ell , \tau }^{ {et}}$ over $S_{\ell , \tau }$ along the natural forgetful map from $S_{ {\mathrm {I}}, \ell , \tau }$ to $S_{\ell , \tau }$. Similarly define $Y_{{\mathrm {I}}, \ell , \tau }^{et}$ to be the pull-back to $S_{{\mathrm {I}} ,\ell }$ of $Y_{\ell , \tau }^{ {et}}$ over $S_\ell$ along $S_{{\mathrm {I}}, \ell }\rightarrow S_\ell$.

Definition

Let $Y^{et}_{\ell , \varSigma }=\coprod _{\mathcal {C}}\coprod _\tau Y_{\ell , \tau }^{et}$ and $X^{et}_{\ell , \varSigma }=\coprod _{\mathcal {C}} \coprod _\tau X_{\ell , \tau }^{et}$ where $\mathcal {C}$ ranges over the set of isomorphism classes (i.e. homotheties of ideals) of $\ell$-cusp degeneration data and where $\tau$ ranges over $\varSigma$ with $\mathcal {C}$ given. Define $X^{et}_{{\mathrm {I}}, \ell , \varSigma }$ and $Y_{{\mathrm {I}}, \ell , \varSigma }^{et}$ similarly.

Lemma 14

The quotient algebraic stack of $Y^{et}_{\ell , \varSigma }$ by $\mathcal {R}=Y_{\ell , \varSigma }^{et}\times _{Y^{\mathrm {PR}}_{U, \ell }} Y^{et}_{\ell , \varSigma }$ is isomorphic to $Y^{\mathrm {PR}}_{U, \ell }$. Similarly, the quotient algebraic stack of $Y^{et}_{{\mathrm {I}}, \ell , \varSigma }$ by $\mathcal {R}_{\mathrm {I}}=Y_{{\mathrm {I}}, \ell , \varSigma }^{et}\times _{Y^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }} Y^{et}_{{\mathrm {I}}, \ell , \varSigma }$ is isomorphic to $Y^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$.

Recall that $Y_{U, \ell }^{\mathrm {PR}}$ is smooth over O, and $Y_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}$ is normal. The second assertion can be checked by its local model.

Definition

Let $X_{U, \ell }^{\mathrm {PR}}$ denote the quotient algebraic stack of $X_{\ell , \varSigma }^{et}$ by the normalisation of $X_\varSigma ^{et}\times X^{et}_{\ell , \varSigma }$ in $\mathcal {R}$.

Let $X_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}$ denote the quotient algebraic stack of $X_{{\mathrm {I}}, \ell , \varSigma }^{et}$ by the normalisation of $X_{{\mathrm {I}}, \ell , \varSigma }^{et}\times X^{et}_{{\mathrm {I}}, \ell , \varSigma }$ in $\mathcal {R}_{\mathrm {I}}$.

Proposition 8

$X_{U, \ell }^{\mathrm {PR}}$ and $X_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}$ are proper over O.

Proof

See Proposition 3.1.5.2 and Théorème 3.1.8.3 in [50]. $\square$

Recall that U is the full congruence subgroup of level n for an integer $n\ge 3$ prime to p.

Let $O_{F, +}^\times$ denote the totally positive units in F and $O_{F, +, n}^\times$ denote the subgroup of the squares of elements in $O_F^\times$, i.e., units, congruent to 1 mod n.

As explained more carefully in Section 2 in [14], observe that $O_{F, +}^\times$ acts (and $O_{F, +, n}^\times$ acts trivially) on $\ell$-polarisations, hence acts on $X^{\mathrm {PR}}_{U, \ell }$ and on $X^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$. Let $O_{F, +}^{\times , +}=O_{F, +}^\times /O_{F, +, n}^\times$. Furthermore, Section 2 in [14] explains that ${\mathrm {GL}}_2(O_F\otimes _\mathbf {Z}\hat{\mathbf {Z}})$ acts on $X^{\mathrm {PR}}_{U, \ell }$ and $X^{\mathrm {PR}}_{U{\mathrm {Iw}}, \ell }$.

Definition

Let K denote the preimage in ${\mathrm {GL}}_2(O_F\otimes _\mathbf {Z}\hat{\mathbf {Z}})=({\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_{2})(\hat{\mathbf {Z}})$ of $\begin{pmatrix} *&{}*\\ 0&{}1\end{pmatrix}\subset ({\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_{2})(\mathbf {Z}/n\mathbf {Z})$ by the reduction mod n map $({\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_{2})(\hat{\mathbf {Z}})\rightarrow ({\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_2)(\mathbf {Z}/n\mathbf {Z})$ and let $X_{K}^{\mathrm {PR}}$ (resp. $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$) denote the disjoint union over $\ell$ of $X_{K, \ell }^{\mathrm {PR}}=X_{U, \ell }^{\mathrm {PR}}/(O_{F, +}^{\times , +}\times K)$ (resp. $X_{K{\mathrm {Iw}}, \ell }^{\mathrm {PR}}=X_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}/(O_{F, +}^{\times , +}\times K)$). We similarly define $Y^{\mathrm {PR}}_{K}$ (resp. $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}}$) to be the disjoint union over $\ell$ of $Y^{\mathrm {PR}}_{K, \ell }=Y_{U, \ell }^{\mathrm {PR}}/(O_{F, +}^{\times , +}\times K)$ (resp. $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}, \ell }=Y_{U{\mathrm {Iw}}, \ell }^{\mathrm {PR}}/(O_{F, +}^{\times , +}\times K)$) . The set of geometrically connected components of $Y^{\mathrm {PR}}_K$ may be identified with the strict ideal class group $\mathbb {A}_F^{\infty , \times }/F_+^\times (O_F\otimes _\mathbf {Z}\hat{\mathbf {Z}})^\times$.

The formation of $O_{F, +}^{\times , +}$-invariants does not change p-adic and mod p geometry of $X_{U}^{\mathrm {PR}}$ and $X_{U{\mathrm {Iw}}}^{\mathrm {PR}}$ we are interested.

4 Hecke operators, odds and ends

4.1 Classical p-adic Hilbert modular eigenforms

Let V denote the open compact subgroup K or $K{\mathrm {Iw}}$ of $({\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_2)(\hat{\mathbf {Z}})$ as above. With that choice made, let $X_{V, \ell }^{\mathrm {PR}}$ denote its toroidal compactification over O defined as above. While the smooth O-scheme $X_{K, \ell }^{\mathrm {PR}}$ depend on a choice of an admissible polyhedral cone decomposition, we shall not refer to the choice. Furthermore, we may and will choose an admissible polyhedral cone decomposition for $V=K{\mathrm {Iw}}$ compatible with the choice we make for $X_{K, \ell }^{\mathrm {PR}}$.

Let $(A/S, i, \lambda , \eta , ({\mathrm {Lie}}^\vee ({A}^\vee /S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (A^\vee /S)_\tau ))$ be an S-point of $Y^{\mathrm {PR}}_{V, \ell }$ for an O-scheme S. Let $L_S$ denote the direct sum of two copies of O, ‘base-changed’ over O to $O_S$. The cotangent sheaf ${\mathrm {Lie}}^\vee (A/S)$ of A over S is a direct sum of locally free sheaves ${\mathrm {Lie}}^\vee (A/S)_\tau$ of $O_S$-modules of rank $e_\mathfrak {p}$ for $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}={\mathrm {Hom}}_{\mathbf {Q}_p}(\hat{F}_\mathfrak {p}, L)$ for every $\mathfrak {p}$ in $S_{\mathrm {P}}$. For every $\tau$, the polarisation $\lambda$ equips ${\mathrm {Lie}}^\vee (A/S)_\tau$ with a filtration

$$\begin{aligned} 0={\mathrm {Lie}}^\vee (A/S)_\tau (0)\subset {\mathrm {Lie}}^\vee (A/S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (A/S)_\tau (e_\mathfrak {p}) ={\mathrm {Lie}}^\vee (A/S)_\tau \subset H_{{\mathrm {dR}}}^{1}(A/S)_\tau \end{aligned}$$

defined on ${\mathrm {Lie}}^\vee (A^\vee /S)_\tau$. The locally free sheaf ${\mathrm {ker}}( \pi \otimes 1-1\otimes \gamma _\tau ^t\, |\, H^{1}_{\mathrm {dR}}(A/S)/{\mathrm {Lie}}^\vee (A/S)(t-1))$ of $O_S$-modules is of rank 2 for every $1\le t\le e_\mathfrak {p}$, and

$$\begin{aligned}&{\mathrm {Lie}}^\vee (A/S)_\tau (t)/{\mathrm {Lie}}^\vee (A/S)_\tau (t-1)\\&\quad \subset {\mathrm {ker}}( \pi \otimes 1-1\otimes \gamma _\tau ^t\, |\, H^{1}_{\mathrm {dR}}(A/S)/{\mathrm {Lie}}^\vee (A/S)(t-1)). \end{aligned}$$

The covering over S, defined as the Zariski sheaf over S of isomorphisms

$$\begin{aligned} {\mathrm {ker}}( \pi \otimes 1-1\otimes \gamma _\tau ^t\, |\, H^{1}_{\mathrm {dR}}(A/S)/{\mathrm {Lie}}^\vee (A/S)(t-1))\simeq L_S \end{aligned}$$

for all $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$, $1\le t\le e_\mathfrak {p}$, and $\mathfrak {p}$ in $S_{\mathrm {P}}$, which sends ${\mathrm {Gr}}^\vee (A/S)_\tau (t)={\mathrm {Lie}}^\vee (A/S)_\tau (t)/{\mathrm {Lie}}^\vee (A/S)_\tau (t-1)$ to a line in $L_S$ which equals its orthogonal for the standard alternating form on $L_S$, is a torsor with respect to the $\varSigma$-product of a Borel subgroup B of the base-change ${\mathrm {GL}}_{2/O}$ (by the standard embedding of $\mathbf {Q}$ into L), where $\varSigma ={\mathrm {Hom}}_\mathbf {Q}(F, L)$. In the unramified case, this sort of construction is standard (using the smooth model of Rapoport [39]); the Pappas–Rapoport filtration exactly makes it possible to see all isotypic components, which does not seem possible with the integral models defined in [13].

For a pair $\lambda =(k, w)$ consisting of a $[F:\mathbf {Q}]$-tuple of integers $k=\sum k_\iota \iota$ where $\iota$ ranges over $\varSigma$ and an integer w such that $k_\iota \equiv w$ mod 2, consider the following invertible sheaf of $O_S$-modules:

$$\begin{aligned} \bigotimes _{\iota } {\mathrm {Gr}}^\vee (A/S)_\tau (t)^{\otimes k_\iota -2}\otimes \varOmega _{{\mathrm {dR}}, \iota }^1\otimes {\mathrm {Std}}_\iota ^{\otimes (w-k_\iota )/2} \end{aligned}$$

where all tensor products are defined for $O_S$-modules, and the first tensor product ranges over $\varSigma$ where, for every $\iota$ in $\varSigma$, there exists a unique prime $\mathfrak {p}$ above p such that $\iota : F\otimes _\mathbf {Q}\mathbf {Q}_p\rightarrow L$ factors through $F_\mathfrak {p}$ and its restriction to the unramified extension $\hat{F}_\mathfrak {p}$ over $\mathbf {Q}_p$ is exactly $\tau$ and $\iota$, as an element of $\varSigma _{\mathfrak {p}, \tau }$ corresponds to $1\le t\le e_\mathfrak {p}$; and where $\varOmega _{{\mathrm {dR}}, \iota }^1$ is the $\iota$-isotypic component of the sheaf of relative differentials of S over O, and where ${\mathrm {Std}}_\iota$ is the invertible sheaf of $O_S$-module corresponding to the standard representation of the centre in B followed by the projection to S by $\iota$.

Let $\mathscr {A}_\lambda$ denote the invertible sheaf on $Y^{\mathrm {PR}}_V$ obtained when applying the construction to the universal HBAV A over $S=Y^{\mathrm {PR}}_V$. The invertible sheaf extends to $X^{\mathrm {PR}}_V$, which we shall again call $\mathscr {A}_\lambda$. It should be possible to use these sheaves to define an eigenvariety for Hilbert modular forms in the general ramified case.

Definition

We define a section of the induced invertible sheaf $\mathscr {A}_\lambda$ over $X^{\mathrm {PR}}_K$ (resp. $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$) for $\lambda =(k, w)$, to be a p-adic classical cusp Hilbert modular form (on ${\mathrm {Res}}_{F/\mathbf {Q}}{\mathrm {GL}}_2$) over O of level K (resp. $K\cap {\mathrm {Iw}}$) and of weight $\lambda$, or of weight k and central character of weight w.

Remark

We will only interested in the case of $\lambda =(k, w)$ where $k_\iota =1$ for every $\iota$ in $\varSigma$.

For every prime $\mathfrak {p}$ of F above p, let $w_\mathfrak {p}$ denote the automorphism of $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ defined on the non-cuspidal points by the automorphism sending (A, C) to $(A/C_\mathfrak {p}, A[\mathfrak {p}]/C_\mathfrak {p}\times C^\mathfrak {p})$ where by $C^\mathfrak {p}$, we mean the finite flat subgroup ‘C away from $\mathfrak {p}$’.

Let $\pi _1$, or $\pi$ when it is clear what it is meant (resp. $\pi _{2, \mathfrak {p}}$ or $\pi _\mathfrak {p}$), denote the morphism $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}\rightarrow X^{\mathrm {PR}}_{K}$ defined on the non-cuspidal points by the correspondence sending (A, C) to A (resp. to $A/C_\mathfrak {p}$).

We define Hecke operators on $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$. For a prime ${\mathrm {Q}}$ of F not dividing p (with a uniformiser $\pi _{\mathrm {Q}}$), let $X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathrm {Q}}}$ denote the toroidal compactification of the fine moduli O-space $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathrm {Q}}}$ of A, parameterised by $Y^{{\mathrm {PR}}}_{K{\mathrm {Iw}}}$, together with a finite flat subgroup scheme $D=D_{\mathrm {Q}}$ of the finite étale group scheme $A[\pi _{\mathrm {Q}}]$, étale locally isomorphic to $(O_F/\pi _{\mathrm {Q}})^2$, of order $\mathbf {N}_{F/\mathbf {Q}} {\mathrm {Q}}$ which locally f.p.p.f. admits a $O_F/\pi _{\mathrm {Q}}$-generator. It follows from the proof of Theorem 3.7.1 in [29] that the forgetful map $\pi _{1, {\mathrm {Q}}}: Y^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathrm {Q}}}\rightarrow Y^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ is a relatively representable morphism which is finite étale. Let $\pi _{2, {\mathrm {Q}}}$ denote the extension to $X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathrm {Q}}}\rightarrow X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ of the morphism defined by sending a non-cuspidal point (A, D) to A / D.

For $\mathfrak {p}$ above p, let $X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]$ denote the toroidal compactification of the fine moduli L-space $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]$ which is the finite étale covering over $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}}[1/p]$ parameterising (A, C) together with a finite flat subgroup scheme D of the étale group scheme $A[\mathfrak {p}]$ of order $\mathbf {N}_{F/\mathbf {Q}}\mathfrak {p}$ which has only trivial intersection with C. It again follows from the proof of Theorem 3.7.1 in [29] that the forgetful map $\pi _{1, \mathfrak {p}}: Y^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]\rightarrow Y^{\mathrm {PR}}_{K{\mathrm {Iw}}}[1/p]$ is a relatively representable morphism which is finite étale. Let $\pi _{2, \mathfrak {p}}$ denote the morphism $X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]\rightarrow X^{\mathrm {PR}}_{K{\mathrm {Iw}}}[1/p]$ defined on the non-cuspidal points by the representable morphism sending (A, C, D) to $(A/D, (C+D)/D)$.

Let $\pi _1, \pi _2$ denote either $\pi _{1, {\mathrm {Q}}}, \pi _{2, {\mathrm {Q}}}: X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathrm {Q}}}\rightarrow X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ or $\pi _{1, \mathfrak {p}}, \pi _{2, \mathfrak {p}}: X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]\rightarrow X^{\mathrm {PR}}_{K{\mathrm {Iw}}}[1/p]$.

Let $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ denote the Raynaud generic fibre associated to the formal completion of $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ along its fibre. By slight abuse of notation, we let $X^{{\mathrm {PR}}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]^{{\mathrm {R}}\text{- }{\mathrm {a}}}$ denote the Tate rigid analytic space associated to the generic fibre $X^{{\mathrm {PR}}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}[1/p]$. Let $\mathscr {A}_{\lambda , {\mathrm {R}}\text {-}{\mathrm {a}}}$ denote the Raynaud analytification of the invertible sheaf $\mathscr {A}_\lambda$ over $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}}$ and $X_{K}^{{\mathrm {PR}}}$.

By definition, we have $\pi _2^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}\rightarrow \pi _1^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$. If U and V are admissible open subsets of $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ in the case of ${\mathrm {Q}}$ and $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}[1/p]^{{\mathrm {R}}\text{- }{\mathrm {a}}}$ in the case of $\mathfrak {p}$ satisfying $\pi _1^{-1}(U)\subseteq \pi _2^{-1}(V)$, we have a homomorphism of sections

$$\begin{aligned} \begin{array}{rcccccccl} \mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(V)&{}\longrightarrow &{}(\pi _{2, *}\pi _2^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}})(V)&{}&{}(\pi _{1, *}\pi _2^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}})(U)&{}\longrightarrow &{}(\pi _{1, *}\pi _1^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}})(U)&{}\longrightarrow &{} \mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(U) \\ &{}&{}||&{}&{}||&{}&{}&{}&{}\\ &{}&{}\pi _2^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(\pi _2^{-1}V)&{}\longrightarrow &{}\pi _2^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(\pi _1^{-1}U)&{}&{}&{}&{} \end{array} \end{aligned}$$

where the rightmost map is the map of U-sections of the trace morphism; and we shall call it ${\mathrm {HeckeCor}}(\mathfrak {p})(U)$ or ${\mathrm {HeckeCor}}({\mathrm {Q}})(U)$ depending on the case with $\mathfrak {p}$ or ${\mathrm {Q}}$.

Let $U_\mathfrak {p}$ denote the morphism

$$\begin{aligned} (\mathbf {N}_{F/\mathbf {Q}} \mathfrak {p})^{-1}{\mathrm {HeckeCor}}(\mathfrak {p})(U): \mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(V){\longrightarrow } \mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}(U) \end{aligned}$$

We define $T_{\mathrm {Q}}$ ($U_{\mathrm {Q}}$ if ${\mathrm {Q}}$ divides the level of U) exactly the same with ${\mathrm {Q}}$ in place of $\mathfrak {p}$.

Finally we define an operator $w_\mathfrak {p}$ of sections of the invertible rigid analytic sheaf $\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$ over an admissible open subset U of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. For a section f of $\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$ over U, the pull-back $w_\mathfrak {p}^*f$ is a section over $w_\mathfrak {p} U$ of $w_\mathfrak {p}^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$; its pull-back $\pi _{2, \mathfrak {p}}^*w_\mathfrak {p}^*f$ is a section over $w_\mathfrak {p} U$ of $\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$, which we shall call $w_\mathfrak {p}(f)$.

4.2 Overconvergent p-adic Hilbert modular forms

We shall define an invariant ‘finer’ than the degree functions of Raynaud [41] and Fargues [18]. This is specific to HBAVs of Pappas–Rapoport type parameterised by $X_{K {\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, and is a key technical input that allows us to perform analogues of Kassaei’s calculations in the unramified case [26]. One significant advantage of our construction is that, as we shall see it in Lemma 27 for example, it reads p-adic geometry of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ qualitatively more than the standard degree function on the Raynaud generic fibre of $Y_{K{\mathrm {Iw}}}^{{\mathrm {DP}}}$.

Let K be a finite extension of L; and let $\mathscr {O}_K$ denote its ring of integers and let $\nu _K$ denote the valuation on K normalised such that $\nu _K(p)=1$. Let $S={\mathrm {Spec}}\, \mathscr {O}_K$.

Following Tate [51],

Definition

Let $\mathscr {O}$ be an associative ring with a unit. An $\mathscr {O}$-module scheme over a scheme S is a commutative group scheme G over S together with a unitary ring homomorphism $\mathscr {O}\rightarrow {\mathrm {End}}(G/S)$; this makes G(T) for every S-scheme T a free $\mathscr {O}$-module. If $\mathscr {O}$ is of characteristic p and the $\mathscr {O}$-rank of G(T) is independent of T and indeed 1, we call G a Raynaud $\mathscr {O}$-module scheme (or $\mathscr {O}$-vector space scheme if $\mathscr {O}$ is a field).

Let $f: A/S\rightarrow B/S$ denote a (closed) non-cuspidal S-point of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ corresponding to a K-point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$. For every $\mathfrak {p}$ in $S_{\mathrm {P}}$, $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$, and $1\le t\le e_\mathfrak {p}$, define ${\mathrm {deg}}((A, C)/S)_\tau (t)$ in [0, 1 / e] to be the $\nu _K$ of a generator in $\mathscr {O}_K$ of the annihilator of ${\mathrm {coker}}({\mathrm {Gr}}^\vee (A^\vee /S)_\tau (t) \rightarrow {\mathrm {Gr}}^\vee (B^\vee /S)_\tau (t))$.

The sum of all the ${\mathrm {deg}}((A, C)/S)_\tau (t)$ equals the degree function of Raynaud [41] and Fargues [18]. While it is defined pointwise, this definition works ‘in families’, i.e., one may take S to be an admissible covering of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ (and glue).

Note that our degree functions are defined solely as a result of filtrations defined on both ends of the isogeny f. Incorporating one’s ‘choices of uniformisers’ into the equation is what seems to be achieved by this definition.

Suppose that a cusp corresponding to a (class of) $\ell$-cusp degeneration data $\mathcal {C}$ as above correspond to a semi-abelian $A=(\mathbb {G}\otimes _\mathbf {Z} D^{-1}M^{-1})/q^N$ over $S=\coprod _\tau X_{\ell , \tau }$, whose pull-back to $\coprod _\tau Y_{\ell , \tau }$ is a HBAV and which comes equipped with an isotropic $O_F$-stable Raynaud submodule scheme $C=\prod _\mathfrak {p} C_\mathfrak {p}\subset \prod _\mathfrak {p} (\mathbb {G}\otimes D^{-1}M^{-1}/q^N)[\mathfrak {p}]$ as above, let ${\mathrm {deg}}(A)_\tau (t)$ be 0 (resp. 1) for every $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$ and $1\le t\le e_\mathfrak {p}$ whenever $\mathfrak {p}$ is in $S_{{\mathrm {P}}, \times }$ (resp. $S_{{\mathrm {P}},et}$). In fact, analytic functions on $Y_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$ defining degrees extend to $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$, allowing us to define admissible open subsets in terms of degrees.

Definition

For $\lambda =(k, w)$ as above, a p-adic overconvergent (cusp) Hilbert modular form over O of level $K\cap {\mathrm {Iw}}$ of weight k (and central character of weight w) is defined to be an element in the direct limit, over the positive rationals $\varepsilon$, of the sections of $\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$ over the admissible open subset of points $\xi$ in $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$ satisying ${\mathrm {deg}}(\xi )\le \varepsilon$.

5 Mod p geometry of modulil spaces of p-divisible groups

In this section, we study mod p geometry of $X_K^{\mathrm {PR}}$ and $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$, by phrasing the essential part of arguments in terms of stacks, or morally ‘local Shimura varieties’, of p-divisible groups. We define two new invariants for p-divisible groups of Pappas–Rapoport type, namely

• $\varSigma _{\mathrm {BT}}$ where ‘BT’ stands for Bruhat–Tits as we consider ‘combinatorial choices of lines in vectors spaces of a fixed dimension’ at Pappas–Rapoport filtrations; this invariant generalises the ‘Deligne–Pappas invariant’ in [13],

• and $\varSigma _{\mathrm {EO}}$, which is based on the observation of Reduzzi–Xiao [42].

$\varSigma _{\mathrm {EO}}$ will be used as an essential geometric input in proving an analytic continuation theorem (Proposition 22), which allows us to pass from one ‘canonical end’ of the valuation hypercube to near the far (opposite) end of the hypercube. In Section 5.4, the ‘Rapoport–Zink’ [40] stratification is introduced. Propositions 12 and 13 are the key observations in characteristic p that are to be used in studying the dynamics of $U_\mathfrak {p}$-operator in characteristic zero generic fibre. In fact they play the same role as Lemma 2.1 in [26].

Let p be a rational prime. Fix once for all an algebraic closure $\overline{\mathbf {Q}}_p$ of $\mathbf {Q}_p$. In this section, let $\pi$ a uniformiser in the ring $\mathscr {O}$ of integers of $F_\mathfrak {p}$, e the ramification index, and f the residue degree.

Let $L\subset \overline{\mathbf {Q}}_p$ be an extension of $\mathbf {Q}_p$ containing the image of every conjugate of F in $\overline{\mathbf {Q}}_p$, and let O denote its ring of integers; and let $\kappa$ denote its residue field, and $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ denote the set of all $\mathbf {Q}_p$-linear embeddings of the residue field $\mathbb {F}=\mathbb {F}_\mathfrak {p}$ of $F_\mathfrak {p}$ into $\kappa$. Let $\mathfrak {f}$ denote the element of $\hat{\varSigma }$ which is (the unique lifting of) the standard Frobenius automorphism.

The map sending $\pi \otimes 1$ to a variable u defines an isomorphism

$$\begin{aligned} \mathscr {O}\otimes \kappa \simeq \bigoplus \kappa [u]/u^{e} \end{aligned}$$

where $\bigoplus$ ranges over $\hat{\varSigma }$.

Let X be a Barsotti–Tate (Définition 1.5 in [24]) p-divisible group over a $\kappa$-scheme S of dimension ef ([24] Remarques 2.2.2, (b)) and of height 2ef, equipped with endomorphism $i: \mathscr {O}\rightarrow {\mathrm {End}}(X/S)$. Suppose that it is principally polarisable, i.e., there exists an $\mathscr {O}$-linear isomorphism $\lambda : X/S\rightarrow X^\vee /S$. It then follows that ${\mathrm {Lie}}(X/S)_\tau$ is a locally free sheaf of $O_S$-modules of rank ef, while the S-dual (5.3 in [4]) $D^\vee (X/S)$ of the Dieudonné crystal sheaf $\mathbf {D}(X/S)_S$ on the (small) site S is a locally free sheaf of $\mathscr {O}\otimes _{\mathbf {Z}_p} O_S$-modules of rank 2. The dual $D^\vee (X/S)$ comes equipped with Frobenius-semi-linear endomorphisms F and V defined by duality in terms of V and F on the Dieudonné crystal D(X / S) respectively; hence $D^\vee (X/S)$ is isomorphic to $D(X^\vee /S)$ as Dieudonné modules, and ${\mathrm {Lie}}^\vee (X^\vee /S)\simeq VD^\vee (X/S)$ for example.

Definition

For a closed immersion of S into the first-order thickening $S[\epsilon ]/\epsilon ^2$, let $D^\vee (X/S[\epsilon ]/\epsilon ^2)$ denote the S-dual of the Dieudonné crystal $\mathbf {D}(X/S)$ on the site $S[\epsilon ]/\epsilon ^2$. For a homomorphism $\varphi : L\rightarrow M$ of $O_S$-modules, we shall let $L[\varphi ]$ denote the kernel $\varphi$ in L.

5.1 Filtered Deligne–Pappas/Kottwitz–Rapoport

Definition

A principally polarisable Barsotti–Tate p-divisible group X / S as above is said to be filtered if, for every $\tau$ in $\hat{\varSigma }$, the $\tau$-component ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ of the dual of the Lie algebra sheaf ${\mathrm {Lie}}(X^\vee /S)$ of the dual p-divisible group $X^\vee$ over S, comes equipped with a filtration

$$\begin{aligned} 0={\mathrm {Lie}}^\vee (X^\vee /S)_\tau (0)\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e) ={\mathrm {Lie}}^\vee (X^\vee /S)_\tau \subset D^\vee (X/S)_\tau \end{aligned}$$

such that ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)$ is, Zariski locally on S, a direct summand of ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ of rank t and is a sheaf of $\mathscr {O}\otimes _{\tau }O_S$-submodule of ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$, satisfying, if we let u denote $\pi \otimes 1$,

$$\begin{aligned}u({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t))\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1). \end{aligned}$$

For brevity, we often write ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ to mean the quotient ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1)$.

Lemma 15

For every $\tau$ in $\hat{\varSigma }$,

$$\begin{aligned}&u({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (1))=0, u^2({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (2))=0, \dots ,\\&u^e({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e))=0 \end{aligned}$$

Proof

Since $u({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1))\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)$, it follows that $u^{t+1} ({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1))\subset u^{t}({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t))$; hence it suffices to show that $u({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (1))=0$ but this holds by definition. $\square$

Lemma 16

$u^{e-t}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau \subseteq {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)$ for every $1\le t\le e$.

Proof

This can be proved by induction. When $t=e$, the equality evidently holds. Suppose $u^{e-(t+1)}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau \subseteq {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1)$ holds for $t\le e-1$. Then

$$\begin{aligned} u^{e-t}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau =uu^{e-(t+1)}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau \subseteq u{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1) \subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t). \end{aligned}$$

Definition

Since X / S is principally polarisable, ${\mathrm {Lie}}(X/S)$ is also filtered if it is filtered. Indeed, by duality, ${\mathrm {Lie}}(X/S)$ comes equipped with surjections:

$$\begin{aligned}&{\mathrm {Lie}}(X/S)_\tau \simeq {\mathrm {Lie}}^\vee (X^\vee /S)^\vee ={\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e)^\vee \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-1)^\vee \\&\quad \rightarrow \cdots \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (1)^\vee \rightarrow 0 \end{aligned}$$

such that every kernel is a locally free sheaf of $O_S$-modules of rank 1 and is annihilated by u; indeed, ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)$ is isomorphic to the dual of ${\mathrm {ker}}({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t+1)^\vee \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)^\vee )$.

Define ${\mathrm {Lie}}(X/S)_\tau (t)$ to be the kernel of the composite of surjections:

$$\begin{aligned} {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e)^\vee \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-1)^\vee \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-t)^\vee . \end{aligned}$$

Then ${\mathrm {Lie}}(X/S)_\tau$ comes equipped with a filtration

$$\begin{aligned} 0={\mathrm {Lie}}(X/S)_\tau (0)\subset {\mathrm {Lie}}(X/S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}(X/S)_\tau (e)={\mathrm {Lie}}(X/S)_\tau \end{aligned}$$

which is analogous to the filtration on ${\mathrm {Lie}}^\vee (X^\vee /S)$; in particular, the assertions in the preceding lemmas hold for ${\mathrm {Lie}}(X/S)$ in place of ${\mathrm {Lie}}^\vee (X^\vee /S)$. Note that, by definition, ${\mathrm {Lie}}(X/S)_\tau (t+1)/{\mathrm {Lie}}(X/S)_\tau (t)$ is dual to ${\mathrm {ker}}( {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-t-1)\rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-t))={\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-t)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e-t-1)$.

Definition

Let $S^{{\mathrm {BT}}}$ denote the stack of principally polarisable filtered Barsotti–Tate p-divisible groups over ${\mathrm {Spec}}\, \kappa$. The stack $S^{\mathrm {BT}}$ parametrises that p-divisible groups arising from points of $Y_{K}^{\mathrm {PR}}$ as defined in Sect. 3.

Definition

For a principally polarisable filtered p-divisible group X over a $\kappa$-scheme S, let

$$\begin{aligned} \mathbf {D}(X/S)_\tau (t)={\mathrm {ker}}(u\, |\, D^\vee (X/S)_\tau /{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1)) \end{aligned}$$

for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$. It is a locally free sheaf of $O_S$-modules of rank 2 [see Proposition 5.2(b) of [36] with $d=2$].

5.2 Bruhat–Tits

For every $\tau$ in $\hat{\varSigma }$, define a set $\varSigma _{{\mathrm {BT}}, \tau }$ of e integers $\varSigma _{{\mathrm {BT}}, \tau }=\{\nu _{{\mathrm {BT}}, \tau }(1), \dots , \nu _{{\mathrm {BT}}, \tau }(e)\}$ satisfying:

• $\nu _{{\mathrm {BT}}, \tau }(1)=0;$

• for every $2\le t\le e$, exactly one of the conditions, (BT-1): $\nu _{{\mathrm {BT}}, \tau }(t-1)=\nu _{{\mathrm {BT}}, \tau }(t)$, or (BT-2): $\nu _{{\mathrm {BT}}, \tau }(t-1)+1=\nu _{{\mathrm {BT}}, \tau }(t)$ is satisfied;

• for every t,

  $$\begin{aligned} t-\nu _{{\mathrm {BT}}, \tau }(t)\ge \nu _{{\mathrm {BT}}, \tau }(t). \end{aligned}$$

When convenient, we let $\nu _{{\mathrm {BT}}, \tau }(0)=0$, and let $\nu _{{\mathrm {BT}}, \tau }$ denote $\nu _{{\mathrm {BT}}, \tau }(e)$.

Remark

The number of t’s satisfying (BT-2) equals $\nu _{{\mathrm {BT}}, \tau }$.

Definition

Let $\varSigma _{{\mathrm {BT}}, \tau , 1}$ (resp. $\varSigma _{{\mathrm {BT}}, \tau , 2}$) denote the subset of $\{1, \dots , e\}$ consisting of 1 and the set of $2\le t\le e$ satisfying (BT-1) (resp. consisting of $1\le t\le e$ satisfying (BT-2)). Evidently $\varSigma _{{\mathrm {BT}}, \tau , 1}$ and $\varSigma _{{\mathrm {BT}}, \tau , 2}$ defines a partition of $\{1, \dots , e\}$.

Definition

Given $\varSigma _{{\mathrm {BT}}, \tau }$, define a subset $\gamma _{{\mathrm {BT}}, \tau }$ of $\{1, \dots , e\}$ the following way. Firstly, for every $\tau$, we define a map $\zeta _{ \tau }$ (dependent of $\varSigma _{{\mathrm {BT}}, \tau }$) from $\{1, \dots , e\}$ to the set of length e (labeled) sequences of two elements $\{e_1, e_2\}$, by defining $\zeta _{ \tau }(t)=e_1$ if t lies in $\varSigma _{{\mathrm {BT}}, \tau , 1}$ and $\zeta _{ \tau }(t)=e_2$ if t lies in $\varSigma _{{\mathrm {BT}}, \tau , 2}$. We then turn the resulting sequence $\zeta _{ \tau }(1), \dots , \zeta _{ \tau }(e)$ of ‘words’ into its reduced expression by sequentially (as t increases) eliminating the adjacent pair $e_1e_2$; the corresponding pairs of indices in $\{1, \dots , e\}$, or an index that is in pair, so eliminated will be referred to as $\varSigma _{{\mathrm {BT}}, \tau }$-redundant. Finally define $\gamma _{{\mathrm {BT}}, \tau }$ to be the set of all $1\le t\le e$ that is not $\varSigma _{{\mathrm {BT}}, \tau }$-redundant. By definition, $|\gamma _{{\mathrm {BT}}, \tau }|=e-2\nu _{{\mathrm {BT}}, \tau }$, which is defined to be non-negative.

Definition

For every integer $1\le N\le e$, let $D^\vee (X^\vee /S)_\tau \langle N\rangle$ denote the image of $D^\vee (X^\vee /S)_\tau$ by $u^N$.

Definition

Given data $\varSigma$ consisting of $\varSigma _{\mathrm {BT}}=(\varSigma _{{\mathrm {BT}}, \tau })_\tau$, define $S_{\varSigma }^{{\mathrm {BT}}}$ to be the closed $\kappa$-substack of $S^{\mathrm {BT}}$ of principally polarisable filtered p-divisible groups X over $\kappa$-schemes S satisfying

$$\begin{aligned} D^\vee (X/S)_\tau \langle e-\nu _{{\mathrm {BT}}, \tau }(t)\rangle \subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)\subset D^\vee (X^\vee /S)_\tau \langle e-(t-\nu _{{\mathrm {BT}}, \tau }(t))\rangle . \end{aligned}$$

Observe that when $\varSigma _{\mathrm {BT}}$ is defined by demanding that $\nu _{{\mathrm {BT}}, \tau }(t)=0$ for every $\tau$ in $\hat{\varSigma }$ and t, the stack $S^{{\mathrm {BT}}}_\varSigma$ is nothing other than $S^{\mathrm {BT}}$.

For two sets of data $\varSigma =\{\nu _{{\mathrm {BT}}, \tau }(t)\}$ and $\varSigma ^+=\{l_{{\mathrm {BT}}, \tau }(t)\}$ as above, we may define a partial order $\varSigma ^+\le \varSigma$ if $l_{{\mathrm {BT}}, \tau }(t)\le \nu _{{\mathrm {BT}}, \tau }(t)$ holds for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$. If this is the case, $D^\vee (X/S)_\tau \langle e-l_{{\mathrm {BT}}, \tau }\rangle$ is contained in $D^\vee (X/S)_\tau \langle e-\nu _{{\mathrm {BT}}, \tau }\rangle$, while $D^\vee (X/S)_\tau \langle e-(t-\nu _{{\mathrm {BT}}, \tau })\rangle$ is contained in $D^\vee (X/S)_\tau \langle e-(t-l_{{\mathrm {BT}}, \tau })\rangle$, hence $S^{{\mathrm {BT}}}_{\varSigma ^+}$ defines a closed $\kappa$-substack of $S^{{\mathrm {BT}}}_\varSigma$.

Definition

If a principally polarisable filtered p-divisible group X over a $\kappa$-scheme X lies in the S-fibre of $S^{{\mathrm {BT}}}_\varSigma -\bigcup _{\varSigma ^+<\varSigma } S^{\mathrm {BT}}_{\varSigma ^+}$, we say that X is of type $\varSigma =\varSigma _{\mathrm {BT}}$ and let $\nu _{{\mathrm {BT}}}(X/S)_\tau (t)$ and $\gamma _{{\mathrm {BT}}, \tau }(X/S)$ respectively denote $\nu _{{\mathrm {BT}}, \tau }(t)$ and $\gamma _{{\mathrm {BT}}, \tau }$ corresponding to $\varSigma$.

Proposition 9

For $\varSigma =\varSigma _{\mathrm {BT}}$ as above, the closed immersion from $S_{ \varSigma }^{{\mathrm {BT}}}$ to $S^{\mathrm {BT}}$ is representable and formally smooth of relative dimension $\sum _\tau e-(e-2\nu _{{\mathrm {BT}}, \tau })=\sum _\tau 2\nu _{{\mathrm {BT}}, \tau }$.

In earlier versions of the paper, we gave a ‘linear algebra’ proof of this proposition by carefully inspecting the moduli problem. In the following, we opt for a proof that is admittedly rather highbrow, yet sheds more light on Pappas–Rapoport constructions ([35] and [36]), in particular, on their relevance to Deligne–Pappas constructions.

For simplicity and for ease of reference to [35] and [36], we assume $|\hat{\varSigma }|=1$. The transfer of a proof to the general case is straightforward, as the case $|\hat{\varSigma }|=1$ typifies what happens at every $\tau$ in $\hat{\varSigma }$ independently.

Let k be a field of characteristic p and let k[[u]] (resp. k((u))) be the power series (resp. Laurent series) ring k[[u]] with coefficients in k and a variable u.

Let $F_\mathscr {A}$ denote a free k((u))-module of rank 2 and fix a k((u))-basis. Let $\mathscr {A}\subset F_\mathscr {A}$ denote the free k[[u]]-module generated by the basis over k[[u]].

For a k-algebra R, by a $k[[u]]\otimes _k R$-lattice in $\mathscr {A}\otimes _k R\simeq R((u))^2$, we mean a submodule over R[[u]] of $F_\mathscr {A}\otimes _k R$ which is, locally on ${\mathrm {Spec}}\, R$, a free R module of rank 2 and, when u is inverted, it gives rise to $F_\mathscr {A}\otimes _k R$. We often say ‘...parameterises k[[u]]-lattices of $F_\mathscr {A}$’ to abbrivaite this functorial view.

Let G denote ${\mathrm {GL}}_2(k((u)))$ and K denote the subgroup scheme of ${\mathrm {GL}}_2(k((u)))$ whose k-valued points stabilise the lattice $\mathscr {A}$. We see G (resp. K) as the (resp. positive) loop group of ${\mathrm {GL}}_2$ and let G / K be the fpqc sheaf quotient, i.e., the affine Grassmannian of ${\mathrm {GL}}_2$. For brevity, let X denote the e copies of G / K, which is also an ind k-scheme.

For an element $\tau$ of dominant coweight ${\mathrm {GL}}_2$, let $G(\tau )$ denote the closure of $K \tau K$ in G.

Fix a positive integer $\ell$. Let

$$\begin{aligned} \phi =(\phi _1, \dots , \phi _\ell ) \end{aligned}$$

be an $\ell$-tuple of coweights of ${\mathrm {GL}}_2$ which are either trivial or (dominant) minuscule, in other words, by the standard identification of the coweights with $\mathbf {Z}^2$, $\phi$ is an $\ell$ tuple of vectors (0, 0) or (1, 0).

Let $G(\phi )$ denote the closed subscheme of the $\ell$ copies of G which parameterises $(\gamma _1, \dots , \gamma _\ell )\in G\times \cdots \times G$ such that $\gamma _{t-1}\gamma _{t}^{-1}$ lies in $G({\phi _t})$ (where we set $\gamma _{t}=1$ when $t=0$); it is evidently a closed subscheme of the $\ell$ copies of G. We define right action of $K^\ell$ by right translations component-by-component.

On the other hand, define an isomorphism

$$\begin{aligned} G({\phi _1})\times \cdots \times G({\phi _\ell })\rightarrow G({\phi }) \end{aligned}$$

by

$$\begin{aligned} (\gamma _1, \dots , \gamma _\ell )\mapsto (\gamma _1, \gamma _1\gamma _2, \ldots , \gamma _{1} \cdots \gamma _\ell ). \end{aligned}$$

By this isomorphism, the aforementioned right action of $K^\ell$ on $G(\phi )$ induces right action of $K^\ell$ on $G(\phi _1)\times \cdots \times G(\phi _\ell )$:

$$\begin{aligned} (\gamma _1, \dots , \gamma _\ell )(\beta _1, \dots , \beta _\ell )=(\gamma _1\beta _1, \beta _1^{-1}\gamma _2\beta _2, \dots , \beta _{\ell -1}^{-1}\gamma _\ell \beta _\ell ). \end{aligned}$$

The isomorphism $G(\phi _1)\times \cdots \times G(\phi _\ell )\rightarrow G(\phi )$ induces an isomorphism $D(\phi ):= (G(\phi _1)\times \cdots \times G(\phi _\ell ))/K^\ell \rightarrow G(\phi )/K^\ell$ of the right $K^\ell$-quotients (in the fpqc topology) and it is possible to interpret them slightly differently.

The quotient $G(\phi )/K^\ell \subset X$ parameterises, for a k-algebra R, the set of $k[[u]]\otimes _k R$-lattices

$$\begin{aligned} \mathscr {A}=\mathscr {A}(0)\supset \mathscr {A}(1)\supset \cdots \supset \mathscr {A}(\ell ) \end{aligned}$$

in $F_\mathscr {A}$ such that, for every $1\le t\le \ell$, the relative position $\rho (\mathscr {A}(t-1), \mathscr {A}(t))$ satisfies the inequality $\rho (\mathscr {A}(t-1), \mathscr {A}(t))\le \phi _t$ in terms of the standard partial order on the dominant coweights of ${\mathrm {GL}}_2$. The condition about the relative positions indeed implies that $u\mathscr {A}(t-1)\subset \mathscr {A}(t)\subset \mathscr {A}(t-1)$ for all t. Furthermore, if t is an index such that $\phi _t$ is trivial, $\mathscr {A}(t-1)=\mathscr {A}(t)$; hence there are only maximum $\ell -|\{1\le t\le \ell \, |\, \phi _t \text{ is } \text{ miniscule }\}|$ distinct lattices in each chain $\mathscr {A}(1)\supset \cdots \supset \mathscr {A}(\ell )$ contained in $\mathscr {A}$.

With this ‘moduli viewpoint’, the isomorphism from $G(\phi )/K^\ell$ to $D(\phi )$ is given by sending a chain of lattices $(\mathscr {A}(1)\supset \cdots \supset \mathscr {A}(\ell ))$ in $F_\mathscr {A}$ as above to $(\mathscr {A}/\mathscr {A}(1), \mathscr {A}(1)/\mathscr {A}(2), \dots , \mathscr {A}(e-1)/\mathscr {A}(\ell ))$.

On the other hand, $D(\phi )=(G(\phi _1)\times \cdots \times G(\phi _\ell ))/K^\ell$ is thought of as a left G-homogenous bundle that is given by iterated $\mathbb {P}^1$-fibrations in the following sense:

• Let K act on G, and hence on $G(\phi _\ell )$, from right by right translations and let $L(\phi _\ell )$ denote the quotient $G(\phi _\ell )/K\subset G/K$, which come equipped with natural left G action by left translations.

• Fixing $t\ge 0$, suppose $D(\phi _{\ell -t},\dots , \phi _\ell )$ is a left G-equivariant bundle over $G(\phi _{\ell -t})/K$. We then define

  $$\begin{aligned} D(\phi _{\ell -(t+1)}, \phi _{\ell -t}, \dots , \phi _\ell )=(G(\phi _{\ell -(t+1)})\times D(\phi _{\ell -t}, \dots , \phi _\ell ))/K \end{aligned}$$

  where we see $D(\phi _{\ell -t}, \dots , \phi _\ell )$ as a right K-module by left-inverse translations and K acts on $G(\phi _{\ell -(t+1)})$ by right translations. We let G acts on $D(\phi _{\ell -(t+1)}, \dots , \phi _\ell )$ from left by letting it act on the $G(\phi _{e-(t+1)})$-factor only by left translations; as a result, $D(\phi _{\ell -(t+1)}, \dots , \phi _\ell )$ is a G-equivariant bundle over over $G(\phi _{\ell -(t+1)})/K$.

If $\phi _t$ is minuscle, $G(\phi _t)/K$ is $\mathbb {P}^1$ over k which is smooth and consequently, $D(\phi )$ is smooth of dimension

$$\begin{aligned} |\{1\le t\le \ell \, |\, \phi _t \text{ is } \text{ miniscule }\}|=\langle \phi _1+\cdots \phi _\ell , (1, -1)\rangle \end{aligned}$$

where $\langle \ , \ \rangle$ is the standard scaler product on $\mathbb {R}^2$ and where we see the dominant weight $\phi _1+\cdots +\phi _\ell$ as a pair of integers. One normally thinks of $D(\phi )$ as a resolution² of $G(\phi _1+\dots +\phi _\ell )/K$ by iterated $\mathbb {P}^1$-fibrations. As [36] Section 6 establishes, $G(\phi _1)\times \cdots \times G(\phi _\ell )$ is naturally thought of as a $K^{\ell -1}$-torsor over $D(\phi )$.

Definition

Let $X^{\mathrm {PR}}$ be the closed ind-subscheme of X parametrising k[[u]]-lattice chains $\mathscr {A}\supset \mathscr {A}(1)\supset \cdots \supset \mathscr {A}(\ell )$ in $F_\mathscr {A}$ such that

$$\begin{aligned} \mathscr {A}\supset \mathscr {A}(1)\supset \cdots \supset \mathscr {A}(\ell )=\mathscr {E}(\ell )\supset \mathscr {E}(\ell -1)\supset \cdots \mathscr {E}(1)\supset u^\ell \mathscr {A} \end{aligned}$$

where, for every $1\le t\le \ell$, we denote

$$\begin{aligned} \mathscr {E}(t)=u^{\ell -t}\mathscr {A}(t). \end{aligned}$$

Definition

Let $X^{\mathrm {PR}}({\phi })$ denote $G(\phi )/K^\ell$.

By definition, $X^{\mathrm {PR}}({\phi })$ is a closed ind-subscheme of $X^{\mathrm {PR}}$. Also, since $D(\phi )$ is smooth over k, so is $X^{\mathrm {PR}}({\phi })$. Evidently, if $\phi$ is such that $\phi _t$ is miniscule for every $1\le t\le \ell$, then $X^{\mathrm {PR}}(\phi )=X^{\mathrm {PR}}$.

We now recall Pappas–Rapoport local models. Unless otherwise specified, $\ell$ is chosen to be e in the following.

Fix an isomorphism $\mathscr {O}\otimes _{\mathbb {Z}_p} k\simeq k[u]/u^e$ sending $\pi \otimes 1$ to u and A denote a free R-module $\mathscr {A}\otimes _{k[[u]]} k[[u]]/u^e$.

The Pappas–Rapoport local model $N^{\mathrm {PR}}$ parameterises, for a k-algbera R, the iset of of locally free R-modules

$$\begin{aligned} 0=A(0)\subset A(1)\subset \cdots A(e)\subset A\otimes R \end{aligned}$$

such that A(t) is, locally on ${\mathrm {Spec}}\, R$, a free R-module of rank t and such that $\pi \otimes 1\in (\mathscr {O}\otimes k)\otimes _k R$ annihilates $A(t)/A(t-1)$ for every $1\le t\le e$.

For a such chain of locally free R-modules $A(1)\subset \cdots \subset A(e)$, if $\mathscr {E}(1)\subset \cdots \subset \mathscr {E}(e)\subset \mathscr {A}\otimes _k R$ denote a chain of k[[u]]-lattices in $\mathscr {A}$ lifting $A(1)\subset \cdots \subset A(e)$ by $\mathscr {A}\otimes _k R\rightarrow A\otimes _k R$ then the map

$$\begin{aligned} f: (A(1)\subset \dots \subset A(e))\mapsto (\mathscr {E}(1)\subset \cdots \subset \mathscr {E}(e)\subset u^{-1}\mathscr {E}(e-1) \subset \cdots \subset u^{1-e}\mathscr {E}(1)) \end{aligned}$$

gives a bijection between $N^{\mathrm {PR}}$ and $X^{\mathrm {PR}}$ where the ‘converse’ $f^{-1}$ is given by sending $(\mathscr {A}(1)\supset \cdots \supset \mathscr {A}(e))$ to the image of $(u^{e-1}\mathscr {A}(1)\subset u^{e-2}\mathscr {A}(e-2)\subset \cdots \subset u^{e-t}\mathscr {A}(t)\subset \cdots \subset \mathscr {A}(1)\subset \mathscr {A}\otimes _k R)$ in $A\otimes _k R$ by reduction $\mathscr {A}\otimes _k R\rightarrow A\otimes _k R$ mod $u^e$.

For $\phi =(\phi _1, \dots , \phi _e)$, we define a closed stratum $N^{\mathrm {PR}}({\phi })$ of $N^{\mathrm {PR}}$ parameterising locally free modules $A(1)\subset \cdots \subset A(e)\subset A$ such that the relative position $\rho (A(t-1), A(t))$, naturally thought of as an element of ${\mathrm {GL}}_2(k[u]/u^e)\backslash {\mathrm {GL}}_2(k((u)))/{\mathrm {GL}}_2(k[u]/u^e)$ lies in the closure of ${\mathrm {GL}}_2(k[u]/u^e) \phi _t {\mathrm {GL}}_2(k[u]/u^e)$ in G for every $1\le t\le e$.

The map $f: N^{\mathrm {PR}}\rightarrow X^{\mathrm {PR}}$ gives rise to an isomorphism

$$\begin{aligned} N^{\mathrm {PR}}({\phi })\rightarrow X^{\mathrm {PR}}({\phi }). \end{aligned}$$

We finally prove the proposition. We define a closed subscheme $N^{\mathrm {PR}}_{\varSigma }$ of $N^{\mathrm {PR}}$ with $\varSigma =\varSigma _{\mathrm {BT}}=\{\nu _{\mathrm {BT}}(1), \dots , \nu _{\mathrm {BT}}(e)\}$: it parametrises the set of locally free modules $A(1)\subset \cdots A(e)\subset A$ such that A(t) is, locally on ${\mathrm {Spec}}\, R$, a free R-module of rank t and satisfies

$$\begin{aligned} A\langle e-\nu _{\mathrm {BT}}(t)\rangle \subset A(t)\subset A\langle e-(t-\nu _{{\mathrm {BT}}}(t))\rangle \end{aligned}$$

for every $1\le t\le e$. Note that the condition, evidently closed, is placed to specify the elementary divisors, i.e., a pair of integers defined as the u-valuations of a two generators of A(t) when written in terms of $k[u]/u^e$-basis of A. More precisely, the elementary divisors of A(t) is a pair $e-\nu _{\mathrm {BT}}(t)$ and $e-(t-\nu _{\mathrm {BT}}(t))$, which satisfy the inequality $e-\nu _{\mathrm {BT}}(t)\ge e-(t-\nu _{\mathrm {BT}}(t))$ by definition and which we might see as a dominant weight of ${\mathrm {GL}}_2$. If we let $\mathscr {E}(1)\subset \cdots \subset \mathscr {E}(e)\subset \mathscr {A}$ denote a chain of liftings in $\mathscr {A}$ of $A(1)\subset \cdots A(e)$, the elementary divisors of $\mathscr {E}(t)$ remain the pair $(e-\nu _{\mathrm {BT}}(t), e-(t-\nu _{\mathrm {BT}}(t)))$ but $\mathscr {E}(t)\langle -(e-t)\rangle$ has elementary divisors $(t-\nu _{\mathrm {BT}}(t), \nu _{\mathrm {BT}}(t))$ for every $1\le t\le e$.

The scheme $N^{\mathrm {PR}}_\varSigma$ is a local model for $S_\varSigma ^{{\mathrm {BT}}}$ and the proposition follows from the smoothness of $N^{\mathrm {PR}}_\varSigma$ which we prove in the following Lemma.

Lemma 17

Let $\varSigma =\varSigma _{\mathrm {BT}}=\{\nu _{\mathrm {BT}}(1), \dots , \nu _{\mathrm {BT}}(e)\}$. Define $\phi$ by $\phi _t$ is minuscle if t lies in $\gamma _{\mathrm {BT}}$; and $\phi _t$ is trivial if t is redundant, for every $1\le t\le e$. Then

$$\begin{aligned} N_\varSigma ^{\mathrm {PR}}\simeq N^{\mathrm {PR}}(\phi ). \end{aligned}$$

In particular, $N^{\mathrm {PR}}_\varSigma$ is smooth of dimension $|\gamma _{\mathrm {BT}}|=e-2\nu _{\mathrm {BT}}$ over k.

Proof

Since $X^{\mathrm {PR}}(\phi )$ is isomorphic to $N^{\mathrm {PR}}(\phi )$, we prove the assertion as an isomorphism of closed subschemes in $X^{\mathrm {PR}}$. For a k -algebra R, let $\mathscr {E}(1)\subset \cdots \subset \mathscr {E}(e)\subset \mathscr {A}$ denote a chain of lattices in $F_\mathscr {A}\otimes _k R$ that reduced to an R-point of $N^{\mathrm {PR}}_\varSigma$. For every $1\le t\le e$, let $\mathscr {A}(t)$ denote $\mathscr {E}(t)\langle -(e-t)\rangle$. Then one observes that the $\mathscr {A}(t)\langle -\nu _{\mathrm {BT}}(t)\rangle$ as t ranges over $\gamma _{\mathrm {BT}}$ define an R-valued point of $X^{\mathrm {PR}}(\varphi )$ where $\varphi$ is the $|\gamma _{\mathrm {BT}}|=(e-2\nu _{\mathrm {BT}})$-tuple of minuscule dominant coweight (1, 0). It is easy to check that this defines an isomorphism $N_\varSigma ^{\mathrm {PR}}\simeq X^{\mathrm {PR}}(\varphi )$. By the definition of $\phi$, $X^{\mathrm {PR}}(\phi )$ is evidently isomorphic to $X^{\mathrm {PR}}(\varphi )$. $\square$

Remark

We have $N^{\mathrm {PR}}_\varSigma \simeq N^{\mathrm {PR}}(\phi )\simeq X^{\mathrm {PR}}(\phi )\simeq D(\phi )$. In particular, $D(\phi )$ can be seen as a resolution of $G(\phi _1+\dots +\phi _e)/K$. The local model corresponding to $G(\phi _1+\cdots +\phi _e)/K$ therefore parameterises, for a k-algebra R, the set of locally free R-module $A(e)\subset A\otimes _k R$ of rank e satisfying the condition

$$\begin{aligned} A\langle e-\nu _{\mathrm {BT}}\rangle \subset A(e)\subset A\langle \nu _{\mathrm {BT}}\rangle . \end{aligned}$$

This is precisely the closed k-singular stratum of the Deligne–Pappas local model, 4.2 in [13]; and $N^{\mathrm {PR}}_\varSigma$ is thought of as a resolution of the stratum at the singularities.

Proof of Proposition 9

Since $N^{\mathrm {PR}}_\varSigma$ is a local model for $S_\varSigma ^{\mathrm {PR}}$ when $|\hat{\varSigma }|=1$, the proposition follows from the lemma above, combined with the observation that $N^{\mathrm {PR}}(\phi )\simeq D(\phi )$ is smooth over $k=\kappa$ of dimension $e-2\nu _{\mathrm {BT}}$ and $N^{\mathrm {PR}}\simeq X^{\mathrm {PR}}$ is smooth of dimension e. $\square$

5.3 Ekedahl–Oort

In this section, we shall consider an ‘Ekedahl-Oort stratification’ on $S^{\mathrm {BT}}$. To this end, we use a slight variant of the construction of ‘partial Hasse invariants’ by Reduzzi and Xiao in [42]; the ‘source’ of our maps are on $\mathbf {D}(X/S)_\tau (t)$ in comparison to [40] on ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$. We emphasise that the idea is essentially Reduzzi–Xiao’s.

Let S be a $\kappa$-scheme S and X be a filtered principally polarisable Barsotti–Tate p-divisible group over S. The Verschiebung $V_{X^\vee }: X^{\vee }\rightarrow X^{\vee (1/p)}$ defines, for every $\tau$ in $\hat{\varSigma }$, a $\varphi ^{-1}$-semi-linear homomorphism

$$\begin{aligned}&{\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}\circ \tau }\rightarrow ( {\mathrm {Lie}}^\vee (X^\vee /S)\times _{\varphi ^{-1}} S)_\tau \simeq {\mathrm {Lie}}^\vee (X^{\vee (1/p)}/S)_\tau \\&\quad {\mathop {\longrightarrow }\limits ^{V_{X^\vee }}}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau \end{aligned}$$

of $O_S$-modules that we shall denote simply by V, where $\varphi$ denote the (absolute) Frobenius morphism on S.

Lemma 18

V above sends ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ to ${\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(t)$.

Proof

Since $u^{t}{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)=0$, one sees that ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)\subset u^{e-t}D^\vee (X/S)_\tau$. As V is u-linear, $V({\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t))\subset u^{e-t}VD^\vee (X/S)_\tau =u^{e-t}{\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }$. It follows from Lemma 16 that $u^{e-t}{\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }\subset {\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(t)$. Combining these two, the assertion follows. $\square$

For $2\le t\le e$, we let

$$\begin{aligned} \varDelta _\tau ^t: \mathbf {D}(X/S)_\tau (t)\longrightarrow \mathbf {D}(X/S)_\tau (t-1) \end{aligned}$$

denote the multiplication-by-u-map, and, when $t=1$, we let

$$\begin{aligned} \varDelta _\tau ^1: \mathbf {D}(X/S)_\tau (1)\longrightarrow {\mathrm {Gr}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(e)\subset \mathbf {D}(X/S)_\tau (e) \end{aligned}$$

be the map ‘$V\circ u^{-e+1}$’ that sends an element $u^{e-1}\xi$ in $\mathbf {D}(X/S)_\tau (1)={\mathrm {ker}}(u\, |\, D^\vee (X/S)_\tau )$ with $\xi$ in $D^\vee (X/S)_\tau$ to the class $V(\xi )+{\mathrm {Lie}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(e-1)$ in ${\mathrm {Gr}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(e)$.

For $2\le t\le e$, $\mathbf {D}(X/S)_\tau (t)$ is nothing other than $u^{-1}{\mathrm {Lie}}^\vee (X/S)_\tau (t-1)/{\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1)$, and therefore the image of $\varDelta _\tau ^t$ is ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t-1)$. The rank of the kernel $\mathbf {D}(X/S)_\tau (t)[\varDelta _{\tau }^t]$ is 1 as a result. Similarly, the image of $\varDelta _\tau ^1$ is ${\mathrm {Gr}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(e)$. As pointed out in Lemma 3.8 in [42], the restriction to ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ of the composite $\varDelta _{\mathfrak {f}^{-1}\circ \tau }^{t+1}\circ \cdots \circ \varDelta _{\mathfrak {f}^{-1}\circ \tau }^e\circ \varDelta _\tau ^1\circ \cdots \circ \varDelta _\tau ^t$:

$$\begin{aligned}&\mathbf {D}(X/S)_\tau (t){\mathop {\longrightarrow }\limits ^{\varDelta _\tau ^t}} \cdots {\mathop {\longrightarrow }\limits ^{\varDelta _\tau ^2}} \mathbf {D}(X/S)_\tau (1) {\mathop {\longrightarrow }\limits ^{\varDelta _\tau ^{1}}} \mathbf {D}(X/S)_{\mathfrak {f}^{-1}\circ \tau }(e) {\mathop {\longrightarrow }\limits ^{\varDelta _{\mathfrak {f}^{-1}\circ \tau }^e}} \cdots \\&\quad {\mathop {\longrightarrow }\limits ^{\varDelta _{\mathfrak {f}^{-1}\circ \tau }^{t+1}}} \mathbf {D}(X/S)_{\mathfrak {f}^{-1}\circ \tau }(t) \end{aligned}$$

defines the Verschiebung map

$$\begin{aligned} V: {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)\longrightarrow {\mathrm {Gr}}^\vee (X^\vee /S)_{\mathfrak {f}^{-1}\circ \tau }(t) \end{aligned}$$

induced by Lemma 18. When $f=1$, we recover the standard Verschiebung.

For every $\tau$ in $\hat{\varSigma }$, let $\gamma _{{\mathrm {EO}}, \tau }$ denote a subset of $\{1, \dots , e\}$, and $\varSigma _{\mathrm {EO}}$ denote the $\hat{\varSigma }$-tuple $(\gamma _{{\mathrm {EO}}, \tau })_\tau$ as $\tau$ ranges over $\hat{\varSigma }$.

For $\varSigma =\varSigma _{\mathrm {EO}}$, we define $S^{{\mathrm {BT}}}_{\varSigma }$ to be the $\kappa$-substack of $S^{\mathrm {BT}}$ parameterising filtered principally polarisable p-divisible groups X over $\kappa$-schemes S such that, for every $\tau$ in $\hat{\varSigma }$, $\varDelta _\tau ^t$ is zero if t lies in $\gamma _{{\mathrm {EO}}, \tau }$.

Remark

In the light of the proof of Proposition 9, it is possible to relate $\varSigma _{\mathrm {BT}}$ and $\varSigma _{\mathrm {EO}}$.

For two sets of data $\varSigma =\varSigma _{\mathrm {EO}}=(\gamma _{{\mathrm {EO}}, \tau })_\tau$ and $\varSigma ^+=\varSigma ^+_{\mathrm {EO}}=(\gamma ^+_{{\mathrm {EO}}, \tau })_\tau$, we may define a partial order $\varSigma ^+\le \varSigma$ if $\gamma _{{\mathrm {EO}},\tau }\le \gamma ^+_{{\mathrm {EO}}, \tau }$ holds for every $\tau$ in $\hat{\varSigma }$. If $\varSigma ^+\le \varSigma$ but $\varSigma ^+$ is distinct from $\varSigma$, we write $\varSigma ^+<\varSigma$. If this is the case, $S^{{\mathrm {BT}}}_{\varSigma ^+}$ defines a closed $\kappa$-substack of $S^{{\mathrm {BT}}}_\varSigma$.

Definition

If a principally polarisable filtered p-divisible group X over a $\kappa$-scheme S lies in the S-fibre of $S_\varSigma ^{{\mathrm {BT}}}-\bigcup _{\varSigma ^+< \varSigma } S^{\mathrm {BT}}_{\varSigma ^+}$, we say that X of of type $\varSigma _{\mathrm {EO}}$, and let $\gamma _{{\mathrm {EO}}, \tau }(X/S)$ denote $\gamma _{{\mathrm {EO}}, \tau }$ corresponding to $\varSigma _{\mathrm {EO}}$.

Proposition 10

Let $\varSigma$ denote $\varSigma _{\mathrm {EO}}$. The closed immersion from $S^{\mathrm {BT}}_{\varSigma }$ to $S^{\mathrm {BT}}$ is representable and formally smooth of relative dimension $\sum _\tau |\varSigma _{ {\mathrm {EO}}, \tau }|$.

Proof

Let U be a $\kappa$-scheme. Let S be a U-scheme, and $S[\epsilon ]/\epsilon ^2$ its first-order thickening. Let X be a principally polarisable filtered Barsotti–Tate p-divisible group over S defining an S-point of the fibre $S^{\mathrm {BT}}_{\varSigma , U}$ over U. As $S^{\mathrm {BT}}_{\varSigma , U}$ is given by the vanishing sections over S of line bundles $\varDelta _\tau ^t$ for t in $\gamma _{{\mathrm {EO}}, \tau }$ for every $\tau$, the relative dimension of $S^{\mathrm {BT}}_{\varSigma , U}\hookrightarrow S^{\mathrm {BT}}_{U}$ is at most $\sum _\tau |\varSigma _{{\mathrm {EO}}, \tau }|$. It therefore suffices to establish that the tangent space of $S_{\varSigma , U}^{\mathrm {BT}}$ at X / S has codimension $\sum _\tau |\varSigma _{{\mathrm {EO}}, \tau }|$ in the tangent space of $S^{\mathrm {BT}}_{U}$. Fix $\tau$ and $1\le t\le e$, and suppose that ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1)$ lifts to $S[\epsilon ]/\epsilon ^2$. If t lies in $\gamma _{{\mathrm {EO}}, \tau }$, it follows, by definition, that ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau$ is contained in the rank 1 module $\mathbf {D}(X/S)_\tau (t)[\varDelta _\tau ^t]$, and therefore they are equal. As $\mathbf {D}(X/S)_\tau (t)[\varDelta _\tau ^t]$ lifts uniquely to $S[\epsilon ]/\epsilon ^2$, so does ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$. $\square$

5.4 Rapoport–Zink

Let $S^{\mathrm {BT}}_{\mathrm {I}}$ denote the $\kappa$-stack of principally polarisable filtered Barsotti–Tate p-divisible groups equipped with $\mathscr {O}$-linear isogenies to principally polarisable filtered Barsotti–Tate p-divisible groups. More precisely, the fibre of $S^{\mathrm {BT}}_{\mathrm {I}}$ over a $\kappa$-scheme of S parameterises (the set of isomorphism classes of) of $\mathscr {O}$-linear isogenies $f: X/S\rightarrow Y/S$ of principally polarisable Barsotti–Tate p-divisible groups X and Y over S such that

• $C={\mathrm {ker}}\, f$ is a finite flat $\mathscr {O}$-subgroup of $X[\pi ]$ of order $| \mathscr {O}/\pi |=|\mathbb {F}|$ such that any principal polarisation on X induces an isomorphism $X[\pi ]\simeq X[\pi ]^\vee$ which sends C to $(X[\pi ]/C)^\vee$ isomorphically,

• for every $\tau$ in $\hat{\varSigma }$, both

  $$\begin{aligned} {\mathrm {Lie}}^\vee (f^\vee ):{\mathrm {Lie}}^\vee (X^\vee /S)_\tau \rightarrow {\mathrm {Lie}}^\vee (Y^\vee /S)_\tau \end{aligned}$$

  and

  $$\begin{aligned}{\mathrm {Lie}}^\vee (f^\wedge )^{ \vee }: {\mathrm {Lie}}^\vee (Y^\vee /S)_\tau \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau , \end{aligned}$$

  given by $f:X\rightarrow Y$ and the ‘dual’ isogeny $Y/S\rightarrow X/S$ such that $f^\wedge \circ f=\pi$ on X and $f\circ f^\wedge =\pi$ on Y, will be denoted again by $f^\vee$ and $(f^\wedge )^\vee$ respectively by slight abuse of notation, commute with their respective filtrations, and let

  $$\begin{aligned} f^\vee :{\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t) \end{aligned}$$

  and

  $$\begin{aligned} (f^\wedge )^\vee :{\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t) \end{aligned}$$

  also denote the corresponding morphisms.

For pairs of $\mathscr {O}$-isogenies f and $f^\wedge$ as above, we define analogues of the invariants defined in [40] and [20].

Definition

For every $\tau$ in $\hat{\varSigma }$, define $\gamma _{{\mathrm {RZ}}, \tau }(f)$ (resp. $\nu _{{\mathrm {RZ}}, \tau }(f)$) to be the set of $1\le t\le e$ such that $f^\vee$ (resp. $(f^\wedge )^{\vee }$) is zero on ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ (resp. ${\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t)$).

Note that, as $\pi =0$, for every $1\le t \le e$, either t lies in $\gamma _{{\mathrm {RZ}}, \tau }$ or in $\nu _{{\mathrm {RZ}}, \tau }$, or indeed in both.

Definition

Let $\varSigma$ denote a tuple $(\nu _{{\mathrm {RZ}}, \tau }, \gamma _{{\mathrm {RZ}}, \tau })_\tau$, where $\tau$ ranges over $\hat{\varSigma }$, of subsets $\gamma _{{\mathrm {RZ}}, \tau }\subseteq \{1, \dots , e\}$ and $\nu _{{\mathrm {RZ}}, \tau }\subseteq \{1, \dots , e\}$, satisfying the following condition that every $1\le t\le e$ lies in at least one of $\gamma _{{\mathrm {RZ}}, \tau }$ or $\nu _{{\mathrm {RZ}}, \tau }$ for every $\tau$ in $\hat{\varSigma }$.

For a such $\varSigma$, define $S^{\mathrm {BT}}_{{\mathrm {I}}, \varSigma }$ to be the closed $\kappa$-substack of $\mathscr {O}$-isogenies $f: X/S\rightarrow Y/S$ of filtered principally polarisable Barsotti–Tate p-divisible groups over S such that

• $f^\vee : {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t)$ is zero for every t that lies in $\gamma _{{\mathrm {RZ}}, \tau }$, i.e., $\gamma _{{\mathrm {RZ}}, \tau }\subseteq \gamma _{{\mathrm {RZ}}, \tau }(f)$,

• $(f^\wedge )^\vee : {\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ is zero for every t that lies in $\nu _{{\mathrm {RZ}}, \tau }$, i.e., $\nu _{{\mathrm {RZ}}, \tau }\subseteq \nu _{{\mathrm {RZ}}, \tau }(f^\wedge )$.

Proposition 11

For $\varSigma$ as above, the closed immersion of $S^{\mathrm {BT}}_{{\mathrm {I}}, \varSigma }$ into $S^{\mathrm {BT}}_{\mathrm {I}}$ is representable of relative dimension $\sum _{t=1}^e ( f-(f-|\gamma _{{\mathrm {RZ}}, t}|+f-|\nu _{{\mathrm {RZ}}, t}|))=\sum _{t=1}^e (|\gamma _{{\mathrm {RZ}}, t}|+|\nu _{{\mathrm {RZ}}, t}|-f)$.

Proof

This can be proved as Theorem 2.5.2 in [20]. $\square$

If $\gamma _{{\mathrm {RZ}}, t}\cap \nu _{{\mathrm {RZ}}, t}=\varnothing$, $|\gamma _{{\mathrm {RZ}}, t}|+|\nu _{{\mathrm {RZ}}, t}|=f$, and if this is the case for every $1\le t\le e$, the relative dimension of the closed immersion is 0.

Lemma 19

Let $f: X/S\rightarrow Y/S$ and its dual isogeny $f^\wedge : Y/S\rightarrow X/S$ be as above. Then the equalities $\mathbf {D}(X/S)_\tau (t)[f^\vee ]=(f^\wedge )^\vee (\mathbf {D}(Y/S)_\tau (t))$ and $\mathbf {D}(X/S)_\tau (t)[(f^\wedge )^\vee ]=f^\vee (\mathbf {D}(Y/S)_\tau (t))$ hold, and they are all of rank 1.

Proof

One observes firstly that, as $(f^\wedge )^\vee (\mathbf {D}(Y/S)_\tau (t))$ is contained in $\mathbf {D}(X/S)_\tau (t)[f^\vee ]$, it suffices to check that they are both of rank 1 over S. However, it follows immediately from Proposition 5.2 in [36] that $\mathbf {D}(X/S)_\tau (t)[f^\vee ]$ is locally free of rank 1 over S. A similar argument shows that $\mathbf {D}(Y/S)_\tau (t)[(f^\wedge )^\vee ]$ is rank 1 over S and, as $\mathbf {D}(Y/S)_\tau (t)$ is rank 2 over S, $(f^\wedge )^\vee (\mathbf {D}(Y/S)_\tau (t))$ is rank 1 over S. An analogous argument proves the other equality. $\square$

Proposition 12

Let $f: X/S\rightarrow Y/S$ and $f^\wedge : Y/S\rightarrow X/S$ be as above. If $t\ge 2$ and $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$ while t lies in $\gamma _{{\mathrm {RZ}}, \tau }$, then t lies in $\gamma _{{\mathrm {EO}}, \tau }(X/S)$. If $t=1$ and e lies in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }$, then $t=1$ lies in $\gamma _{{\mathrm {EO}}, \tau }(X/S)$.

Proof

Firstly suppose $t\ge 2$. The assumption that $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$ implies that $(f^\wedge )^\vee$ vanishes on the image by $\varDelta =\varDelta _\tau ^t$ of $\mathbf {D}(Y/S)_\tau (t)$. As $\varDelta \mathbf {D}(Y/S)_\tau (t)\simeq \mathbf {D}(Y/S)_\tau (t)/\mathbf {D}(Y/S)_\tau (t)[\varDelta ]$ and similarly for X, it then follows that $(f^\wedge )^\vee (\mathbf {D}(Y/S)_\tau (t))\subset \mathbf {D}(X/S)_\tau (t)[\varDelta ]$. On the other hand, t is in $\gamma _{{\mathrm {RZ}}, \tau }(f)$ and therefore ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ is contained in $\mathbf {D}(X/S)_\tau (t)[f^\vee ]=(f^\wedge )^\vee (\mathbf {D}(Y/S)_\tau (t))$. Combining, one deduces that ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ is contained in $\mathbf {D}(X/S)_{ \tau }(t)[\varDelta ]$. As $\varDelta {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ is zero, t lies in $\gamma _{{\mathrm {EO}}, \tau }$.

The case $t=1$ is similar, except that one has to be careful that the image by $\varDelta _\tau ^1$ of $\mathbf {D}(Y/S)_\tau (1)$ is ${\mathrm {Gr}}^\vee (X/S)_{\mathfrak {f}^{-1}\circ \tau }(e)$. $\square$

Proposition 13

Let $f: X/S\rightarrow Y/S$ and $f^\wedge : Y/S\rightarrow X/S$ be as above. If $t\ge 2$ and if either

• $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$ while t does not lie in $\gamma _{{\mathrm {RZ}}, \tau }$,

• or $t-1$ does not lie in $\nu _{{\mathrm {RZ}}, \tau }$ while t lies in $\gamma _{{\mathrm {RZ}}, \tau }$,

holds, then t does not lie in $\gamma _{{\mathrm {EO}}, \tau }(X/S)$. If $t=1$, if either

• e lies in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ does not lie in $\gamma _{{\mathrm {RZ}}, \tau }$,

• or e does not lie in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }$,

holds, then $t=1$ does not lie in $\gamma _{{\mathrm {EO}}, \tau }(X/S)$.

Proof

Suppose that $t\ge 2$. The case $t=1$ is similar as in Proposition 12. Firstly, suppose that $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$ but t does not in $\gamma _{{\mathrm {RZ}}, \tau }$. It then follows exactly as in the proof of Proposition 12, using the assumption that $t-1$ lies in $\nu _{{\mathrm {RZ}},\tau }$, that $\mathbf {D}(X/S)_\tau (t)[f^\vee ]=(f^\wedge )^\vee \mathbf {D}(Y/S)_\tau (t)\subset \mathbf {D}(X/S)_\tau (t)[\varDelta ]$. Observing that they all are of rank 1, one sees that they are equal. Therefore, if ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ lay in $\mathbf {D}(X/S)_\tau (t)[\varDelta ]$, it would contradict the assumption that t does not lie in $\gamma _{{\mathrm {RZ}}, \tau }$. As ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ does not lie in $\mathbf {D}(X/S)_\tau (t)[\varDelta ]$, t does not lie in $\gamma _{{\mathrm {EO}}, \tau }$.

Secondly, suppose that t lies in $\gamma _{{\mathrm {RZ}}, \tau }$ but it does not in $\nu _{{\mathrm {RZ}}, \tau }$. One observes that ${\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)\subset \mathbf {D}(X/S)_\tau (t)[f^\vee ]= (f^\wedge )^\vee \mathbf {D}(Y/S)_\tau (t)$ are equal (of rank 1). One also observes that $\varDelta (\mathbf {D}(Y/S)_\tau (t))$ is ${\mathrm {Gr}}^\vee (Y^\vee /S)_{\tau }(t)$ and in particular it is of rank 1. It then follows that

$$\begin{aligned} \varDelta {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)= & {} \varDelta (f^\wedge )^\vee \mathbf {D}(Y/S)_\tau (t)=(f^\wedge )^\vee \varDelta \mathbf {D}(Y/S)_\tau (t)\\= & {} (f^\wedge )^\vee {\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t-1) \end{aligned}$$

but the assumption that t does not lie in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(f)$ implies that $\varDelta {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)$ is non-zero. Consequently t does not lie in $\gamma _{{\mathrm {EO}}, \tau }$. $\square$

Swapping f for $f^\wedge$ and $f^\wedge$ for f, it is possible to prove:

Proposition 14

If $t\ge 2$ and $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }$ while t lies in $\nu _{{\mathrm {RZ}}, \tau }$, then t lies in $\gamma _{{\mathrm {EO}}, \tau }(Y/S)$. If $t=1$ and e lies in $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$, then $t=1$ lies in $\gamma _{{\mathrm {EO}}, \tau }(Y/S)$.

On the other hand, if $t\ge 2$ and if either

• $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }$ while t does not lie in $\nu _{{\mathrm {RZ}}, \tau }$,

• or $t-1$ does not lie in $\gamma _{{\mathrm {RZ}}, \tau }$ while t lies in $\nu _{{\mathrm {RZ}}, \tau }$,

holds, then t does not lie in $\gamma _{{\mathrm {EO}}, \tau }(Y/S)$. If $t=1$, if either

• e lies in $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ does not lie in $\nu _{{\mathrm {RZ}}, \tau }$,

• or e does not lie in $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $t=1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$,

holds, then $t=1$ does not lie in $\gamma _{{\mathrm {EO}}, \tau }(Y/S)$.

Proof

See the proofs of Proposition 12 and Proposition 13. $\square$

5.5 Calculations with de Rham–Breuil modules

As in the previous sections, let $\pi$ be a uniformiser in the valuation ring $\mathscr {O}$ of $F_\mathfrak {p}$, e the ramification index, and f the residue degree. Let $\mathbb {F}=\mathscr {O}/\pi$ denote the residue field. Let $\mathscr {O}_L$ denote the valuation ring of a finite extension L of $F_\mathfrak {p}$ which contains the image of every embedding of $F_\mathfrak {p}$ into $\overline{\mathbf {Q}}_p$. Write the set $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and the Frobenius automorphism $\mathfrak {f}$ in $\hat{\varSigma }$ as in the previous section.

Let K denote a finite extension of L with ring $\mathscr {O}_K$ of integers, a uniformiser $\xi$, the ramification index $e_K$ and $k=\mathscr {O}_K/\xi \mathscr {O}_K$ the residue field. We normalise the valuation on K so that p has valuation 1. Unless otherwise specified, $S={\mathrm {Spec}}\, \mathscr {O}_K$ and $\overline{S}={\mathrm {Spec}}\, \overline{\mathscr {O}}_K$ where $\overline{\mathscr {O}}_K=\mathscr {O}_K/\pi \mathscr {O}_K$ in this section.

By a Barsotti–Tate p-divisible group (which comes equipped with an endomorphism $\mathscr {O}\rightarrow {\mathrm {End}}(X/S)$), we shall mean it in the sense of Définition 1.5 in [24] over S, and is of dimension fe and of height 2fe.

Definition

A principally polarisable Barsotti–Tate p-divisible group X over S is said to be filtered if, for every $\tau$ in $\hat{\varSigma }$, ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ comes equipped with a filtration

$$\begin{aligned} 0={\mathrm {Lie}}^\vee (X^\vee /S)_\tau (0)\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (1)\subset \cdots \subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (e) ={\mathrm {Lie}}^\vee (X^\vee /S)_\tau \subset D^\vee (X/S)_\tau \end{aligned}$$

such that ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)$ is, locally on S, a direct summand of ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ of rank t and is a sheaf of $\mathscr {O}\otimes _{\tau } \mathscr {O}_K$-submodule satisfying the condition

$$\begin{aligned} (\pi \otimes 1-1\otimes \gamma _\tau ^t){\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t)\subset {\mathrm {Lie}}^\vee (X^\vee /S)_\tau (t-1) \end{aligned}$$

where $\gamma _\tau ^1, \dots , \gamma _\tau ^e$ are the fixed roots of the Eisenstein polynomial $E_\tau$ over $\mathscr {O}\otimes _{\tau }\mathscr {O}_L$ which may also be thought of as over $\mathscr {O}\otimes _\tau \mathscr {O}_K$ as defined in Sect. 3.

Definition

If X is a principally polarisable Barsotti–Tate p-divisible group over S, and C is an $\mathbb {F}$-subgroup of $X[\pi ]$ of order $|\mathbb {F}|$ such that any principal polarisation $X\rightarrow X^\vee$ on X induces an isomorphism $X[\pi ]\simeq X[\pi ]^\vee$ which sends C to $(X[\pi ]/C)^\vee$, we say that C is a Raynaud $\mathbb {F}$-vector subspace scheme of X for brevity.

Furthermore, we say that C is filtered if it is the kernel of an $\mathscr {O}$-linear isogeny $f: X/S\rightarrow Y/S$ of filtered principally polarisable Barsotti–Tate p-divisible groups over S such that both ${\mathrm {Lie}}^\vee f^\vee : {\mathrm {Lie}}^\vee (X^\vee /S)_\tau \rightarrow {\mathrm {Lie}}^\vee (Y^\vee /S)_\tau$ and ${\mathrm {Lie}}^\vee (f^\wedge )^{ \vee }: {\mathrm {Lie}}^\vee (Y^\vee /S)_\tau \rightarrow {\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ commute with filtrations on ${\mathrm {Lie}}^\vee (X^\vee /S)_\tau$ and ${\mathrm {Lie}}^\vee (Y^\vee /S)_\tau$.

Lemma 20

A principal polarisation $\lambda : X\rightarrow X^\vee$ defines an isomorphism from C onto the Cartier dual $(X[\pi ]/C)^\vee$ of Raynaud submodule scheme.

Proof

By definition, the image by $\lambda$ of C is contained in $(X[\pi ]/C)^\vee$. Since both are Raynaud submodule scheme, $\lambda$ defines an isomorphism. $\square$

Fix a filtered principally polarisable Barsotti–Tate p-divisible group X over S equipped with a filtered Raynaud submodule scheme C which is the kernel of an $\mathscr {O}$-linear isogeny $f: X\rightarrow Y=X/C$; f gives rises to a map of $\mathscr {O}_K$-modules

$$\begin{aligned} {\mathrm {Lie}}^\vee f^\vee : {\mathrm {Gr}}^\vee (X^\vee /S)_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (Y^\vee /S)_\tau (t) \end{aligned}$$

for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$, and define ${\mathrm {deg}}((X, C)/S)_\tau (t)$ in [0, 1] to be the (normalised) valuation of a generator in $\mathscr {O}_K$ of the annihilator of its cokernel.

We remark that these invariants are qualitatively ‘finer’ than degrees defined by Fargues in [18], and are exactly the reason we succeed in better understanding p-adic geometry of Hilbert modular varieties of level at p.

Let

$$\begin{aligned} {\mathrm {deg}}((X, C)/S)=\sum _\tau \sum _{t} {\mathrm {deg}}((X, C)/S)_\tau (t) \end{aligned}$$

where t ranges over $1\le t\le e$ and $\tau$ ranges over $\hat{\varSigma }$. By definition, ${\mathrm {deg}}((X, C)/S)$ ranges over [0, ef].

We consider ‘Breuil modules’ of p-torsion subgroups of filtered principally polarisable Barsotti–Tate p-divisible groups over S. Because it seems difficult (if not impossible, perhaps) to ‘integrally’ incorporate Pappas–Rapoport filtrations (which are inherently ‘of de Rham’) into Breuil modules of p-torsion (or worse still, $\pi$-torsion) subgroups, we instead work directly with de Rham crystals over the ‘truncated’ valuation ring $\overline{S}$. To this end suppose $e>1$; when $e=1$, we simply make appeal to calculations with Breuil modules in Section 3 of [26] which is our model for the construction in the following. Parenthetically, Section 3 of [26] is based on Kisin’s proof in [31] of a conjecture of Breuil when $p>2$; the conjecture itself is also proved by Kisin [30] in the connected case when $p=2$ and by Kim, Lau, Liu in the general $p=2$ case, and the argument in [26] works verbatium when $p=2$.

Fix a filtered principally polarisable Barsotti–Tate p-divisible group X over S. For every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$, let

$$\begin{aligned} {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(X^\vee [p]/ S)_\tau (t)=\mathbf {D}(X^\vee [p]/S)_S/{\mathrm {Lie}}^\vee (X^\vee [p]/ S)_\tau (t-1) \end{aligned}$$

and let $D(X^\vee [p]/S)_\tau (t)$ denote the free rank 2 module over $\mathscr {O}_K$

$$\begin{aligned}&{\mathrm {ker}}(\pi \otimes 1-1\otimes \gamma _\tau ^t\, |\, {{\mathrm {G}}} {\mathrm {r}}^{\sim \vee }(X^\vee [p]/ S)_\tau (t))\\&\quad =(\xi \otimes 1-1\otimes \gamma _\tau ^t)^{-1} {\mathrm {Lie}}^\vee (X^\vee [p]/S)_\tau (t-1)/ {\mathrm {Lie}}^\vee (X^\vee [p]/ S)_\tau (t-1), \end{aligned}$$

which contains the rank 1 $\mathscr {O}_K$-module ${\mathrm {Gr}}^\vee (X^\vee [p]/ S)_\tau (t)$ by definition. Let $D(X^\vee [p]/\overline{S})_\tau (t)$ denote the pull-back of $D(X^\vee [p]/S)_\tau (t)$ to $\overline{S}$; it is a rank 2 module over $\overline{\mathscr {O}}_K$. Let $D(\overline{X}^\vee [p]/k)_\tau (t)$ denote the pull-back to the closed fibre ${\mathrm {Spec}}\, k$; it is a rank 2 module over k.

Let

$$\begin{aligned} \varDelta _{\tau }^t: D(X^\vee [p]/\overline{S})_\tau (t)\longrightarrow D(X^\vee [p]/\overline{S})_\tau (t-1) \end{aligned}$$

denote the map defined by multiplication by u if $t> 1$ and

$$\begin{aligned} \varDelta _{\tau }^1: D(X^\vee [p]/\overline{S})_\tau (1)\longrightarrow D(X^\vee [p]/\overline{S})_{\mathfrak {f}^{-1}\circ \tau }(e) \end{aligned}$$

denote $V\circ (u^{e-1})^{-1}$ if $t=1$. By definition, the image of $\varDelta _\tau ^t$ is exactly ${\mathrm {Gr}}^\vee (X^\vee [p]/ \overline{S})_\tau (t-1)$ if $t>1$ and ${\mathrm {Gr}}^\vee (X^\vee [p]/\overline{S})_{\mathfrak {f}^{-1}\circ \tau }(e)$ if $t=1$.

Let C denote a filtered Raynaud submodule scheme of $X[\pi ]$ and let $Y=X/C$ be the filtered principally polarisable Barsotti–Tate p-divisible group over S. Let $D(C/S)_\tau (t)$ denote the kernel of $D(X^\vee [p]/S)\rightarrow D(Y^\vee [p]/S)_\tau (t)$. If G is one of the $X^\vee [p]$, $Y^\vee [p]$ or C, let $D(G/\overline{S})$ (resp. $D(\overline{G}/k)$) denote the pull-back of D(G / S) to $\overline{S}$ (resp. ${\mathrm {Spec}}\, k$).

The image of $D(X^\vee [p]/\overline{S})_\tau (t)$ in $D(Y^\vee [p]/\overline{S})_\tau (t)$ defines a rank 1 submodule over $\overline{\mathscr {O}}_K$ and consequently $D(C/\overline{S})_\tau (t)$ is free of rank 1 over $\overline{\mathscr {O}}_K$. This follows if it holds over S, which in turn follows by Nakayama if the image of $D(\overline{X}^\vee [p]/k)_\tau (t)$ defines a rank 1 subspace of $D(\overline{Y}^\vee [p]/k)_\tau (t)$. But this follows from Lemma 19.

Indeed, given $\overline{X}$ over k, the existence of a filtered Raynaud $\mathbb {F}$-vector subspace scheme of $\overline{X}$ over k is equivalent to the existence of a family of subspaces $\varXi _\tau ^t$ of $D(\overline{X}^\vee [p]/k)_\tau (t)$ of rank 1 for all $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ satisfying the conditions:

• $\varDelta _\tau ^t(\varXi _\tau ^t)\subset \varXi _\tau ^{t-1}$ if $t>1$ (in which case, $\varDelta _\tau ^t$ is multiplication by u);

• and $\varDelta _\tau ^1(\varXi _\tau ^1)\subset \varXi _{\mathfrak {f}^{-1}\circ \tau }^e$ if $t=1$ (in which case $\varDelta _\tau ^1=V\circ u^{1-e}$).

To see the claim, suppose firstly that one is given a family of vector subspaces $\varXi _\tau ^t$ as above. As one can immediately see, by definition (observing that both have the same rank over k), that $D(\overline{X}^\vee [p]/k)_\tau (1)=u^{e-1}D(\overline{X}^\vee [p]/k)_\tau$ where $D(\overline{X}^\vee [p]/k)_\tau$ denotes the $\tau$-isotypic part of the Dieudonne module $D(\overline{X}^\vee [p]/k)$ over k, define $\varXi _\tau$ to be the e-dimensional vector subspace $u^{1-e}\varXi _\tau ^1$ of $D(\overline{X}^\vee [p]/k)_\tau$ and $\varXi =\bigoplus _\tau \varXi _\tau \subset D(\overline{X}^\vee [p]/k)$. It is immediate to see that, for every $\tau$, $\varXi _\tau$ satisfies, for the Verschiebung V on $D(\overline{X}^\vee [p]/k)$,

$$\begin{aligned} V\varXi _\tau =V(u^{1-e}\varXi _\tau ^1)\subset \varXi _{\mathfrak {f}^{-1}\circ \tau }^e\subset u^{-1}\varXi _{\mathfrak {f}^{-1}\circ \tau }^{e-1} \subset \cdots \subset u^{-(e-1)}\varXi _{\mathfrak {f}^{-1}\circ \tau }^1=\varXi _{\mathfrak {f}^{-1}\circ \tau } \end{aligned}$$

and therefore $\varXi$ is a Dieudonne submodule of $D(\overline{X}^\vee [p]/k)$ with its quotient $D(\overline{X}^\vee [p]/k)/\varXi$ free of rank 1 over $\mathbb {F}\otimes k$. By Dieudonne theory, there exists a Raynaud $\mathbb {F}$-vector space scheme $\overline{C}$ of rank 1 in $\overline{X}[p]$ such that its corresponding Dieudonne module is exactly $\varXi$.

On the other hand, the converse of the claim is clear and will be left unattended.

Suppose that $\xi ^t_{\tau , 1}, \xi ^t_{\tau , 2}$ form a $\overline{\mathscr {O}}_K$-basis of $D(X^\vee [p]/ \overline{S})_\tau (t)$ such that $\xi _{\tau , 1}^t$ defines a $\overline{\mathscr {O}}_K$-basis of $D(C/ \overline{S})_\tau (t)$ in $D(X^\vee [p]/\overline{S})_\tau (t)$, and $\xi _{\tau , 2}^t$ maps onto a $\overline{\mathscr {O}}_K$-basis of the image of $D(X^\vee [p]/\overline{S})$ in $D(Y^\vee [p]/\overline{S})_\tau (t)$.

For every $\tau$, we may and will assume if $t>1$

$$\begin{aligned} \varDelta _\tau ^t(\xi ^t_{\tau , 1})=\xi ^{\rho _\tau ^{t-1}} R^{t-1}_\tau \xi ^{t-1}_{\tau , 1} \end{aligned}$$

and

$$\begin{aligned} \varDelta _\tau ^t(\xi ^t_{\tau , 2})=S_\tau ^{t-1} \xi ^{t-1}_{\tau , 1}+\xi ^{\chi ^{t-1}_\tau } T^{t-1}_\tau \xi ^{t-1}_{\tau , 2} \end{aligned}$$

where $R_\tau ^{t-1}, S^{t-1}_\tau , T^{t-1}_\tau$ are elements of $\overline{\mathscr {O}}_K$ and $R^{t-1}_\tau , T^{t-1}_\tau$ are in particular units in $\overline{\mathscr {O}}_K$; and similarly if $t=1$,

$$\begin{aligned} \varDelta _\tau ^1(\xi ^1_{\tau , 1})=\xi ^{\rho _{\mathfrak {f}^{-1}\circ \tau }^e} R^{e}_{\mathfrak {f}^{-1}\circ \tau } \xi ^{e}_{\mathfrak {f}^{-1}\circ \tau , 1} \end{aligned}$$

and

$$\begin{aligned} \varDelta _\tau ^1(\xi ^1_{\tau , 2})=S_{\mathfrak {f}^{-1}\circ \tau }^{e} \xi ^{e}_{\mathfrak {f}^{-1}\circ \tau , 1}+\xi ^{\chi ^e_{\mathfrak {f}^{-1}\circ \tau } }T^{e}_{\mathfrak {f}^{-1}\circ \tau }\xi ^{e}_{\mathfrak {f}^{-1}\circ \tau , 2}. \end{aligned}$$

By construction, if $t>1$, it is an easy exercise to check:

Lemma 21

Fix $\tau$ in $\hat{\varSigma }$ and $1< t\le e$. Then $\chi _\tau ^{t-1}$ equals $e_K{\mathrm {deg}}((X, C)/S)_\tau (t-1)$ while $\rho _\tau ^{t-1}$ satisfies the inequality $\rho _\tau ^{t-1}\ge e_K( 1/e-{\mathrm {deg}}((X, C)/ S)_\tau (t-1))=e_K{\mathrm {deg}}((X/C, X[\pi ]/C)/ S)_\tau (t-1)$.

Proof

To see the first assertion about $\chi _\tau ^{t-1}$, observe that $\chi _\tau ^t$ computes the truncated valuation of the annihilator in $\overline{\mathscr {O}}_K$ of ${\mathrm {Coker}}({\mathrm {Gr}}^\vee (X^\vee [p]/\overline{S})_\tau (t-1)\rightarrow {\mathrm {Gr}}^\vee (Y^\vee [p]/\overline{S})_\tau (t-1))$. Since the normalised truncated valuation of the uniformiser $\xi$ is $e_K/e$, the assertion follows.

The assertion about $\rho _\tau ^{t-1}$ follows as $\varDelta _\tau ^{t} D(C/\overline{S})_\tau (t)$ is contained in ${\mathrm {ker}}({\mathrm {Gr}}^\vee (X^\vee [p]/\overline{S})_\tau (t-1)\rightarrow {\mathrm {Gr}}^\vee (Y^\vee [p]/\overline{S})_\tau (t-1))$. $\square$

Similarly,

Lemma 22

Fix $\tau$ in $\hat{\varSigma }$. Then $\chi _{\mathfrak {f}^{-1}\circ \tau }^e$ equals $e_K{\mathrm {deg}}((X, C)/S)_{\mathfrak {f}^{-1}\circ \tau }(e)$ and $\rho _{\mathfrak {f}^{-1}\circ \tau }^e$ satisfies the inequality $\rho _{\mathfrak {f}^{-1}\circ \tau }^e\ge e_K(1/e-{\mathrm {deg}}((X, C)/S)_{\mathfrak {f}^{-1}\circ \tau }(e))=e_K{\mathrm {deg}}((X/C, X[\pi ]/C)/S)_{\mathfrak {f}^{-1}\circ \tau }(e)$.

Let D be another Raynaud submodule scheme of $X[\pi ]$ distinct from C. For every $\tau$ and $1\le t\le e$, we may suppose that the image of $D(D/\overline{S})_\tau (t)$ is generated by $\xi ^t_{\tau , 1}+\varepsilon ^t_\tau \xi ^t_{\tau , 2}$ for some element $\varepsilon _\tau ^t$ in $\overline{\mathscr {O}}_K$; and if $t>1$

$$\begin{aligned} \varDelta _\tau ^t(\xi ^t_{\tau , 1}+\varepsilon ^t_\tau \xi ^t_{\tau , 2})= \xi ^{\rho _\tau ^{t-1, \sim }} U^{t-1}_\tau (\xi ^{t-1}_{\tau , 1}+\varepsilon ^{t-1}_{\tau }\xi ^{t-1}_{\tau , 2}) \end{aligned}$$

and if $t=1$

$$\begin{aligned} \varDelta _\tau ^1(\xi ^1_{\tau , 1}+\varepsilon ^1_\tau \xi ^1_{\tau , 2})= \xi ^{\rho _{\mathfrak {f}^{-1}\circ \tau }^{e, \sim }} U^{e}_{\mathfrak {f}^{-1}\circ \tau }(\xi ^{e}_{\mathfrak {f}^{-1}\circ \tau , 1}+\varepsilon ^{e}_{\mathfrak {f}^{-1}\circ \tau }\xi ^{e}_{\mathfrak {f}^{-1}\circ \tau , 2}) \end{aligned}$$

for some unit $U^t_\tau$ in $\overline{\mathscr {O}}_K$, where $\rho _\tau ^{t, \sim }$, when $t>1$, similarly satisfies the inequality

$$\begin{aligned} \rho _\tau ^{t, \sim }\ge e_K/e-{\mathrm {deg}}((X, D)/S)_\tau (t)={\mathrm {deg}}(X/D, X[\pi ]/S)_\tau (t) \end{aligned}$$

as in the case for C (Lemma 21). One can readily observe that $\varepsilon _\tau ^t$ is non-zero in $\overline{\mathscr {O}}_K$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$; otherwise $\varepsilon _\tau ^t=0$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$, and C would equal D which contradicts the assumption that C and D are distinct.

In the light of Lemmas 21 and 22, let $\chi _\tau ^{t, \sim }$ denote ${\mathrm {deg}}((X, D)/S)_\tau (t)$ for brevity. The cokernel of the embedding of $D(D/\overline{S})_\tau (t)$ into $D(X^\vee [p]/\overline{S})_\tau (t)$ is generated by the image of $\xi _{\tau , 2}^t$, and as its image is

$$\begin{aligned} \varDelta _\tau ^t(\xi _{\tau , 2}^t)+ \overline{\mathscr {O}}_K(\xi _{\tau , 1}^{t-1}+\varepsilon _\tau ^{t-1}\xi _{\tau , 2}^{t-1})= & {} (\xi ^{\chi _\tau ^{t-1}}T_\tau ^{t-1}-S_\tau ^{t-1} \varepsilon _\tau ^{t-1})\xi _{\tau , 2}^{t-1}\\&+\,\overline{\mathscr {O}}_K(\xi _{\tau , 1}^{t-1}+\varepsilon _\tau ^{t-1}\xi _{\tau , 2}^{t-1}), \end{aligned}$$

$e_K/e$ minus the truncated valuation in $\overline{\mathscr {O}}_K$ of $\xi ^{\chi _\tau ^{t-1}}T_\tau ^{t-1}-S_\tau ^{t-1}\varepsilon _\tau ^{t-1}$ computes $\chi _\tau ^{t-1, \sim }$. Similar when $t=1$.

Equating the coefficients of $\xi ^{t-1}_{\tau , 1}$ and $\xi ^{t-1}_{\tau , 2}$ if $t>1$ and $\xi _{\mathfrak {f}^{-1}\circ \tau , 1}^e$ and $\xi _{\mathfrak {f}^{-1}\circ \tau , 2}^e$ if $t=1$, we have the following equations (which, for ease of reference in the following, we name and ): if $t>1$

and

and if $t=1$

and

where, by slight abuse of notation, $\varphi$ again denotes the absolute Frobenius on $\overline{\mathscr {O}}_K$. From ’s, we deduce the following Lemma 23 and Corollary 2 which are not strictly necessary for our proof of the main theorem but serve as a ‘sanity check’:

For every $t\ge 1$ and $\tau$ in $\hat{\varSigma }$, let $\mathfrak {s}^t_\tau [\chi ]$ denote

$$\begin{aligned} \chi _{\mathfrak {f}^{-1}\circ \tau }^e+\cdots +\chi _{\mathfrak {f}^{-1}\circ \tau }^t, \end{aligned}$$

and, for every $t>1$ and $\tau$ in $\hat{\varSigma }$, let $\mathfrak {s}_\tau ^{t, \lnot }[\chi ]$ denote

$$\begin{aligned} \chi _\tau ^{t-1}+\cdots +\chi _\tau ^1. \end{aligned}$$

Similarly define $\mathfrak {s}_\tau ^t[\overset{\sim }{\chi }]$ and $\mathfrak {s}_\tau ^{t, \lnot }[\overset{\sim }{\chi }]$ with $\overset{\sim }{\chi }$ in place of $\chi$; and $\mathfrak {s}_\tau ^t[\overset{\sim }{\rho }]$ and $\mathfrak {s}_\tau ^{t, \lnot }[\overset{\sim }{\rho }]$ with $\overset{\sim }{\rho }$.

For brevity, for every $t\ge 1$ and $\tau$ in $\hat{\varSigma }$, let

$$\begin{aligned} \mathfrak {s}_\tau ^t{\mathop {=}\limits ^{{\mathrm {def}}}}\mathfrak {s}_\tau ^t[\chi ]-\mathfrak {s}_\tau ^t[\overset{\sim }{\rho }] \end{aligned}$$

and, for every $t>1$ and $\tau$ in $\hat{\varSigma }$,

$$\begin{aligned} \mathfrak {s}_\tau ^{t, \lnot }{\mathop {=}\limits ^{{\mathrm {def}}}}\mathfrak {s}_\tau ^{t, \lnot }[\chi ]-\mathfrak {s}_\tau ^{t, \lnot }[\overset{\sim }{\rho }]. \end{aligned}$$

By Lemma 21,

$$\begin{aligned} \mathfrak {s}_\tau ^t\le \mathfrak {s}_\tau ^t[\chi ]+\mathfrak {s}_\tau ^t[\overset{\sim }{\chi }]-(e-(t-1))e_K/e \end{aligned}$$

and

$$\begin{aligned} \mathfrak {s}_\tau ^{t, \lnot }\le \mathfrak {s}_\tau ^{t, \lnot }[\chi ]+\mathfrak {s}_\tau ^{t, \lnot }[\overset{\sim }{\chi }]-(t-1)e_K/e \end{aligned}$$

hold.

Lemma 23

Fix $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$. The valuation of $\varepsilon _\tau ^t$ is calculated by

$$\begin{aligned} \left( \sum _{1\le N\le f} p^{f-N}\mathfrak {s}_{\mathfrak {f}^N\circ \tau }^{t, \lnot }+p^{f-(N-1)}\mathfrak {s}_{\mathfrak {f}^N\circ \tau }^t\right) /(p^f-1) \end{aligned}$$

if $t>1$ and by

$$\begin{aligned} \left( \sum _{1\le N\le f} p^{f-(N-1)} \mathfrak {s}_{\mathfrak {f}^N\circ \tau }^1\right) /(p^f-1) \end{aligned}$$

if $t=1$.

Remark

This is an analogue of Lemma 3.3 of [26].

Proof

Suppose $t>1$. Since $\varepsilon _{\mathfrak {f}\circ \tau }^t=(\xi ^{\rho _{\mathfrak {f}\circ \tau }^{t-1, \sim }}U_{\mathfrak {f}\circ \tau }^{t-1}/\xi ^{\chi _{\mathfrak {f}\circ \tau }^{t-1}} T_{\mathfrak {f}\circ \tau }^{t-1})\varepsilon _{\mathfrak {f}\circ \tau }^{t-1}$, and $\varDelta _{\tau }^{t+1}\circ \cdots \circ \varDelta _{\tau }^e\circ \varDelta _{\mathfrak {f}\circ \tau }^1\circ \cdots \circ \varDelta _{\mathfrak {f}\circ \tau }^t=u^{e-t}\circ V\circ (u^{e-t})^{-1}$ is the Verschiebung V on $D(X^\vee [p]/\overline{S})_{\mathfrak {f}\circ \tau }(t)$, one may deduce that the image of $\varepsilon _{\mathfrak {f}\circ \tau }^t$ by V is computed by

$$\begin{aligned}&\varphi ^{-1}(\xi ^{\rho _{\mathfrak {f}\circ \tau }^{t-1, \sim }}U_{\mathfrak {f}\circ \tau }^{t-1}/\xi ^{\chi _{\mathfrak {f}\circ \tau }^{t-1}}T_{\mathfrak {f}\circ \tau }^{t-1})\cdots \varphi ^{-1}(\xi ^{\rho _{\mathfrak {f}\circ \tau }^{1, \sim }}U_{\mathfrak {f}\circ \tau }^{1}/\xi ^{\chi _{\mathfrak {f}\circ \tau }^{1}}T_{\mathfrak {f}\circ \tau }^{1})(\xi ^{\rho _{\tau }^{ e, \sim }}U_{\tau }^{e}/\xi ^{\chi _{\tau }^{e}}T_{\tau }^{e})\\&\quad \cdots (\xi ^{\rho _{\tau }^{ t, \sim }}U_{\tau }^{t}/\xi ^{\chi _{\tau }^{t}}T_{\tau }^{t})\varepsilon _{\tau }^t. \end{aligned}$$

In other words, the p-th power of $\varepsilon _\tau ^t$ is $\varepsilon _{\mathfrak {f}\circ \tau }^t$ times

$$\begin{aligned}&\xi ^{\chi _{\mathfrak {f}\circ \tau }^{t-1}+\cdots +\chi _{\mathfrak {f}\circ \tau }^{1}+p(\chi _{\tau }^{e}+\cdots +\chi _{\tau }^{t})} T_{\mathfrak {f}\circ \tau }^{t-1}\\&\quad \cdots T_{\mathfrak {f}\circ \tau }^{1}(T_{\tau }^{e}\cdots T_\tau ^t)^p/\xi ^{\rho _{\mathfrak {f}\circ \tau }^{t-1, \sim }+\cdots +\rho _{\mathfrak {f}\circ \tau }^{1, \sim }+p(\rho _{\tau }^{e, \sim }+\cdots +\rho _{\tau }^{ t, \sim })} U_{\mathfrak {f}\circ \tau }^{t-1}\\&\quad \cdots U_{\mathfrak {f}\circ \tau }^{1}(U_{\tau }^{e}\cdots U_\tau ^t)^p. \end{aligned}$$

Similarly, the p-th power of $\varepsilon _\tau ^1$ is $\varepsilon _{\mathfrak {f}\circ \tau }^1$ times

$$\begin{aligned} \xi ^{p(\chi _{\tau }^{e}+\cdots +\chi _{\tau }^{1})} (T_{\tau }^{e}\cdots T_\tau ^1)^p/\xi ^{p(\rho _{\tau }^{e, \sim }+\cdots +\rho _{\tau }^{1, \sim })} (U_{\tau }^{e}\cdots U_\tau ^1)^p. \end{aligned}$$

Repeating the argument, we get the assertion. $\square$

Corollary 2

For every $1\le t\le e$ and $\tau$ in $\hat{\varSigma }$,

$$\begin{aligned}&\sum _{1\le N\le f} p^{f-N}\left( \chi _{\mathfrak {f}^N\circ \tau }^1+\cdots +\chi _{\mathfrak {f}^N\circ \tau }^{t-1}+p(\chi _{\mathfrak {f}^{N-1}\circ \tau }^t+\cdots +\chi _{\mathfrak {f}^{N-1}\circ \tau }^e)\right) \\&\quad =\sum _{1\le N\le f} p^{f-N}\left( \mathfrak {s}^{t, \lnot }_{\mathfrak {f}^N\circ \tau }[\chi ]+p\mathfrak {s}^t_{\mathfrak {f}^N\circ \tau }[\chi ]\right) \\&\quad \ge \sum _{1\le N\le f} p^{f-N}\left( (t-1)e_K/e+p(e-(t-1))e_K/e \right. \\&\qquad \left. -(\mathfrak {s}^{t, \lnot }_{\mathfrak {f}^N\circ \tau }[\overset{\sim }{\chi }] +p\mathfrak {s}^t_{\mathfrak {f}^N\circ \tau }[\overset{\sim }{\chi }]) \right) \\&\quad =\sum _{1\le N\le f} p^{f-N}\left( (e_K/e-\chi _{\mathfrak {f}^N\circ \tau }^{1, \sim })+\cdots +(e_K/e-\chi _{\mathfrak {f}^N\circ \tau }^{t-1, \sim })\right. \\&\quad \left. +p(e_K/e-\chi _{\mathfrak {f}^{N-1}\circ \tau }^{ t, \sim })+\cdots +p(e_K/e-\chi _{\mathfrak {f}^{N-1}\circ \tau }^{e, \sim })\right) \end{aligned}$$

if $t>1$ and

$$\begin{aligned}&\sum _{1\le N\le f}p^{f-N}\left( \chi _{\mathfrak {f}^N\circ \tau }^1+\cdots +\chi _{\mathfrak {f}^N\circ \tau }^e\right) \\&\quad =\sum _{1\le N\le f} p^{f-N}\mathfrak {s}^1_{\mathfrak {f}^N\circ \tau }[\chi ]\\&\quad \ge \sum _{1\le N\le f} p^{f-N}(e_K/e-\mathfrak {s}^1_{\mathfrak {f}^N\circ \tau }[\overset{\sim }{\chi }])\\&\quad =\sum _{1\le N\le f} p^{f-N}\left( (e_K/e-\chi _{\mathfrak {f}^{N-1}\circ \tau }^{1, \sim })+\cdots +(e_K/e-\chi _{\mathfrak {f}^{N-1}\circ \tau }^{e, \sim })\right) \end{aligned}$$

when $t=1$.

Proof

This follows from the preceding lemma, noting that the valuation of $\varepsilon _\tau ^{t}$ is non-negative and $\chi _\tau ^t-\rho _\tau ^{t, \sim }\le \chi _\tau ^t+\chi _{\tau }^{t, \sim }-e_K/e$. $\square$

Remark

Since $\chi _\tau ^t=e_K{\mathrm {deg}}((X, C)/S)_\tau (t)$ and $\chi _\tau ^{ t, \sim }=e_K{\mathrm {deg}}((X, D)/S)_\tau (t)$, the case when $t=e=1$ recovers Corollary 3.4 in [26].

The following three lemmas replace calculations with Breul modules in [26] and essential for our proof of the main theorem.

Lemma 24

Fix $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$. If $t>1$ and if $\chi _\tau ^{t-1}=0$, then $\chi _\tau ^{t-1, \sim }\ne 0$. Similarly if $\chi _\tau ^e=0$ then $\chi _\tau ^{ e, \sim }\ne 0$.

Proof

Suppose $t>1$ and $\chi _\tau ^{t-1}=0$. If $\chi _\tau ^{t-1, \sim }=0$, it would follow from Lemma 21 that $\rho ^{ t-1, \sim }=e_K/e$. However, it then follows from the equality that $\varepsilon _\tau ^{t}=(\xi ^{\rho ^{t-1, \sim }}U_\tau ^{t-1}/\xi ^{\chi _\tau ^{t-1}} T_\tau ^{t-1})\varepsilon _\tau ^{t-1}$, and therefore the truncated valuation of $\varepsilon _\tau ^t$ would be greater than and equal to $e_K/e$ and $\varepsilon _\tau ^t$ would be 0 in $\overline{\mathscr {O}}_K$, which is a contradiction. The case when $t=1$ is similar. $\square$

We know a great deal at the ‘far end of the valuation hypercube’:

Lemma 25

Suppose that there exists $\dagger$ in $\hat{\varSigma }$ and $1\le l\le e$ such that

• every $\chi ^t_\tau =e_K/e$ as $\tau$ ranges over $\hat{\varSigma }$ and $1\le t\le e$, except when $\tau =\dagger$, $t=l-1$, and $l>1$ (resp. $l=1$), at which $0<\chi _\dagger ^{l-1}<e_K/e$ (resp. $0<\chi _{\mathfrak {f}^{-1}\circ \dagger }^{l-1}<e_K/e$) holds,

• the induced map $\varDelta _\tau ^t$ on ${\mathrm {Gr}}^\vee (X^\vee /k)_\tau (t)$ does not vanish except when $\tau =\dagger$ and $t=l$ at which it does.

Then $\rho _\tau ^t=0$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ expect when $\tau =\dagger$ and $t=l-1$.

Proof

Suppose firstly that either $\tau$ is not $\dagger$ or if $\tau =\dagger$, t is neither l nor $l-1$. In this case, since the image of $\varDelta _\tau ^{t+1}$ is ${\mathrm {Gr}}^\vee (X^\vee /\overline{S})_\tau (t)$ and $\xi ^{\chi _\tau ^t}=0$ in $\overline{\mathscr {O}}_K$, ${\mathrm {Gr}}^\vee (X^\vee /\overline{S})_\tau (t)$ is generated by $\xi _{\tau , 1}^t$. It then follows from the second assumption that $\rho _\tau ^{t-1}=0$.

Suppose that $\tau =\dagger$ and $t=l-1$. In this case, ${\mathrm {Gr}}(X^\vee /\overline{S})_\tau (t)$ is generated by $\varDelta _\tau ^{t+1}(\xi _{\tau , 2}^{t+1})=\xi _{\tau , 1}^{t}+\xi ^{\chi _\tau ^{t}} \xi _{\tau , 2}^{t}$ (up to multiplying $\xi _{\tau , 1}^t$ and $\xi _{\tau , 2}^t$ by units in $\overline{\mathscr {O}}_K$ if necessary), since it follows from Lemma 21 that $\rho _\tau ^t\ge e_K/e-\chi _\tau ^t>0$ and $\chi _\tau ^t>0$ that $S^{t}_\tau$ has to be a unit in $\overline{\mathscr {O}}_K$.

Because $\chi _\tau ^{t-1}=e_K/e$,

$$\begin{aligned} \varDelta _\tau ^t{\mathrm {Gr}}(X^\vee /\overline{S})_\tau (t)=\varDelta _\tau ^{t}(\xi _{\tau , 1}^{t}+\xi ^{\chi _\tau ^{t}}\xi _{\tau , 2}^{t})=(\xi ^{\rho _\tau ^{t-1}}+\xi ^{\chi _\tau ^{t}} S_\tau ^{t-1})\xi _{\tau , 1}^{t-1} \end{aligned}$$

and it follows from the second assumption and $\chi _\tau ^{t}>0$ that $\rho _\tau ^{t-1}$ is zero. $\square$

Maintaining the notation and assumptions in Lemma 25, we have:

Lemma 26

• The valuation of $\varepsilon _\tau ^t$ is zero for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ except when $\tau =\dagger$ and $t=l$.

• $\rho ^{t, \sim }_\tau =e_K/e$ for every $\tau \in \hat{\varSigma }$ and $1\le t\le e$ except when $\tau =\dagger$ and $t=l-1$ or l.

• The valuation of $S_\tau ^t$ is zero for every $\tau \in \hat{\varSigma }$ and $1\le t\le e$ except when $\tau =\dagger$ and $t=l-1$.

Proof

Suppose firstly that the (truncated) valuation of $\varepsilon _\dagger ^{l+1}$ is positive. It then follows from the equation and $\rho _\dagger ^{l}=0$ by Lemma 25 that $\rho _\dagger ^{l, \sim }=0$. Combined with $\chi _\dagger ^{l}=e_K/e$ and the valuation of $\varepsilon _\dagger ^{l+1}$ being non-negative, it follows from that the valuation of $\varepsilon _\dagger ^{l+1}$ is non-positive, which is a contradiction. The valuation of $\varepsilon _\dagger ^{l+1}$ is therefore zero.

If t is an integer satisfying $l+1\le t<e$ and if we suppose that the truncated valuation of $\varepsilon _\dagger ^t$ is zero, the equation then forces $\rho _\dagger ^{t, \sim }=e_K/e$ and the truncated valuation of $\varepsilon _\dagger ^{t+1}$ to be zero, in order to attain the valuation of $\varepsilon ^{t+1}$ to be non-negative (because $\chi _\dagger ^t=e_K/e$). As the valuation of $\varepsilon _\dagger ^{t+1}$ is zero, $\rho _\dagger ^{t}=0$ and $\rho _\dagger ^{t, \sim }=e_K/e$, it follows from that the valuation of $S_\dagger ^t$ is zero. Continuing the argument (when ‘$t=e$’, we use for $\tau =\dagger , \mathfrak {f}\circ \dagger , \dots$ and so on), we get the assertion.

The case when $\tau =\dagger$ and $t=l-1$ is proved in the proof of Lemma 25.   $\square$

Still maintaining the assumptions of Lemma 25,

Corollary 3

$\chi _\tau ^{ t, \sim }=e_K/e$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ except when $\tau =\dagger$ and $t=l$.

Proof

Suppose that either $\tau$ is not $\dagger$ or if $\tau =\dagger$, t is not l. It follows from Lemma 26 that the valuations of $\varepsilon _\tau ^t$ and $S_\tau ^t$ are both zero. As $\chi _\tau ^{ t, \sim }$ is computed by $e_K/e$ minus the valuation of $\xi ^{\chi _\tau ^{t}}-S_\tau ^t \varepsilon _\tau ^t$ and $\chi _\tau ^t=e_K/e$ by assumption, the assertion follows. $\square$

6 Overconvergent companion forms are classical

Results in this section establish links between geometry of the fibre $\overline{X}_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ and p-adic geometry of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ defined in terms of degrees.

6.1 ‘Global’ mod p and p-adic geometry

A non-cuspidal point $\xi$ of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$ corresponds to a closed point of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ thence to an S-point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}}$, where $S={\mathrm {Spec}}\, \mathscr {O}_K$ for the ring $\mathscr {O}_K$ of integers of a finite extension K of L with residue field k. Let $\zeta$ denote its image in $X_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ by the forgetful morphism $\pi : X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}\rightarrow X_{K}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$. By $\overline{\xi }$, we shall mean the $\overline{S}$-point ($\overline{S}={\mathrm {Spec}}\, k$) of the $\kappa$-scheme $\overline{X}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}}$ defined by $\xi$ and let $\overline{\zeta }$ denote its image by $\overline{\pi }: \overline{X}_{K {\mathrm {Iw}}}^{{\mathrm {PR}}}\rightarrow \overline{X}_{K}^{{\mathrm {PR}}}$. We shall freely use the invariants defined in the previous section for the corresponding component of the Barsotti–Tate p-divisible group (which is filtered and principally polarisable), given respectively by $\overline{\zeta }$ and $\overline{\xi }$.

Remark/Definition. By slight abuse of notation, we often write $\gamma _{{\mathrm {EO}}, \tau }(\overline{\xi }/\overline{S})$ to mean the $\gamma _{{\mathrm {EO}}, \tau }$-invariant of the source of the isogeny corresponding to $\xi$.

Proposition 15

The formal completion $\hat{\overline{R}}_{K{\mathrm {Iw}}}$ of $\overline{Y}^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ at $\overline{\xi }$ is the tensor product over $\hat{\varSigma }_{\mathfrak {p}}$ for all $\mathfrak {p}$ in $S_{\mathrm {P}}$ of

$$\begin{aligned} \hat{\bigotimes } k[[\overline{{\mathrm {x}}}_{\tau }^t]]\hat{\otimes }\hat{\bigotimes } k[[\overline{{\mathrm {y}}}^{ t}_{\tau }, \overline{{\mathrm {z}}}_{\tau }^t]]/(\overline{{\mathrm {y}}}^{ t}_{\tau } \overline{{\mathrm {z}}}_{\tau }^t) \end{aligned}$$

where the left-most ranges over those $1\le t\le e_\mathfrak {p}$ which do not lie in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })\cap \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$, while the right-most tensor product is over the set of $1\le t\le e_\mathfrak {p}$ which lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })\cap \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$; the formal completion $\hat{\overline{R}}_K$ of $\overline{Y}^{\mathrm {PR}}_{K}$ is

$$\begin{aligned} \hat{\bigotimes } k[[\overline{u}_{\tau }^t]] \end{aligned}$$

where the tensor product ranges over all $\hat{\varSigma }_{\mathfrak {p}}\times \{1\le t\le e_\mathfrak {p}\}$ for $\mathfrak {p}$ in $S_{\mathrm {P}}$.

Proof

Follows from local model calculations. $\square$

On the Raynaud generic fibre ${\mathrm {sp}}^{-1}(\overline{\xi })\subset X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$, there are ‘local parameters’, i.e., analytic functions which specialise to $\overline{{\mathrm {x}}}_\tau ^t, \overline{{\mathrm {y}}}^{ t}_\tau , \overline{{\mathrm {z}}}_\tau ^t, \overline{u}_\tau ^t$; we shall denote them by ${\mathrm {x}}_\tau ^t, {\mathrm {y}}^{ t}_\tau , {\mathrm {z}}^t_\tau , u_\tau ^t$ satisfying ${\mathrm {y}}_\tau ^t {\mathrm {z}}_{\tau }^{t}=\pi _\mathfrak {p}$ for every $\tau$ in $\hat{\varSigma }_{\mathfrak {p}}$.

Proposition 16

The formal completion of $Y^{\mathrm {PR}}_{K{\mathrm {Iw}}}$ at $\overline{\xi }$ is the tensor product over $\hat{\varSigma }_{\mathfrak {p}}$ for all $\mathfrak {p}$ in $S_{\mathrm {P}}$ of

$$\begin{aligned} \hat{\bigotimes } \mathscr {O}_K[[{\mathrm {x}}_{\tau }^t]]\hat{\otimes } \hat{\bigotimes } \mathscr {O}_K [[{\mathrm {y}}^{ t}_{\tau }, {\mathrm {z}}_{\tau }^t]]/({\mathrm {y}}^{ t}_{\tau } {\mathrm {z}}_{\tau }^t-\pi _\mathfrak {p}) \end{aligned}$$

where the left-most ranges over those $1\le t\le e_\mathfrak {p}$ which do not lie in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })\cap \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$ while the right-most tensor product is over the set of $1\le t\le e_\mathfrak {p}$ which lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })\cap \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$; the formal completion of $X_{K}^{{\mathrm {PR}}}$ at $\overline{\zeta }$ is

$$\begin{aligned} \hat{\bigotimes } \mathscr {O}_K[[u_{\tau }^t]] \end{aligned}$$

where the tensor product ranges over all $\hat{\varSigma }_{\mathfrak {p}}\times \{1\le t\le e_\mathfrak {p}\}$ for $\mathfrak {p}$ in $S_{\mathrm {P}}$.

Proof

This follows from local model calculations. $\square$

Definition

Let $\xi$ be a point of $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$. When $\xi$ is not a cusp, it corresponds to an S-point (A, C) of $X^{\mathrm {PR}}_{K{\mathrm {Iw}}}$, where $S={\mathrm {Spec}}\, \mathscr {O}_K$ for the ring $\mathscr {O}_K$ of integers of a finite extension K of L (whose normalised valuation takes p to 1). For every $\mathfrak {p}$, $\tau$ in $\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e_\mathfrak {p}$ that we fix, we shall define a measure ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi )_\tau (t)$ of (over)convergence/supersingularity on $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ that may be thought of as a ‘local model’ of ${\mathrm {deg}}(\xi )_\tau (t)$ defined earlier and of seeing intrinsic geometry of $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ (hence our notation, but we apologise for our nomenclature).

Firstly if $\xi$ is indeed a cusp, let ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi )_\tau (t)={\mathrm {deg}}(\xi )_\tau (t)$. If $\xi$ is not a cusp, and

• if $t\not \in \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t\in \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, let ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi /S)_\tau (t)=1/e_\mathfrak {p}$;

• if $t\in \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t\in \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, define ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi /S)_\tau (t)$ to be the minimum of 1 and the valuation (on $\mathscr {O}_K$) of ${\mathrm {y}}_\tau ^t$ evaluated at the point $\xi$;

• if $t\in \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t\not \in \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, let ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi /S)_\tau (t)=0$.

If $\zeta$ is a point of $X_K^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}$, define ${\mathrm {deg}}_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\zeta )_\tau (t)$ for $\tau$ in $\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e_\mathfrak {p}$ as follows: if $\zeta$ is not a cusp and if $t\in \gamma _{{\mathrm {EO}},\tau }(\overline{\zeta }/\overline{S})$, define ${\mathrm {deg}}_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\zeta /S)_\tau (t)$ to be the minimum of 1 and the valuation of $u^t_\tau$ evaluated at the point $\zeta$; otherwise let ${\mathrm {deg}}_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\zeta )_\tau (t)=0$.

These ${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi )_\tau (t)$’s are the invariants first introduced by Coleman in the curve case; and are subsequently used in gluing overconvergent eigenforms in [7,8,9] in the modular curve case and [26] in the unramified Hilbert case, in order to to construct classical weight one forms.

Lemma 27

${\mathrm {deg}}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\xi )_\tau (t)={\mathrm {deg}}(\xi )_\tau (t)$.

Proof

It suffices to show the equality when $\xi$ is non-cuspidal. Suppose that it corresponds to an S-point (A, C) / S and let B denote the target of the corresponding isogeny A / C for brevity. If t does not lie in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })$ but lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$, the map ${\mathrm {Gr}}^\vee (\overline{A}^\vee /\overline{S})_\tau (t)\rightarrow {\mathrm {Gr}}^\vee (\overline{B}^\vee /\overline{S})_\tau (t)$ on the special fibres induced from the isogeny is zero, hence the normalised valuation of ${\mathrm {Gr}}^\vee ({A}^\vee /{S})_\tau (t)\rightarrow {\mathrm {Gr}}^\vee ({B}^\vee /{S})_\tau (t)$ is 1. Similarly for the case when t lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })$ but does not lie in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$. When $t\in \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi })\cap \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi })$, we note from Proposition 16 that the coordinates ${\mathrm {y}}_\tau ^t$ and ${\mathrm {z}}_\tau ^t$ are chosen such that, for example, the annihilator of ${\mathrm {coker}}({\mathrm {Gr}}^\vee ({A}^\vee /{S})_\tau (t)\rightarrow {\mathrm {Gr}}^\vee ({B}^\vee /{S})_\tau (t))$ is locally defined by ${\mathrm {y}}_\tau ^t$ evaluated at $\xi$. As ${\mathrm {deg}}(\xi /S)_\tau (t)$ is defined to be its valuation, the assertion follows. $\square$

Definition

In the light of the lemma, we shall let ${\mathrm {deg}}(\zeta /S)_\tau (t)$ denote ${\mathrm {deg}}_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}(\zeta /S)_\tau (t)$. In fact, it is also possible to define ${\mathrm {deg}}(\zeta /S)_\tau (t)$ ‘more directly’.

6.2 Canonical subgroups and analytic continuation in a tubular neighbourhood of the multiplicative ordinary locus

In this section, we prove a few results constructing canonical subgroups of Hilbert–Blumenthal abelian varieties A of Pappas–Rapoport type as ‘canonical’ Raynaud vector subspace schemes of $A[\mathfrak {p}]$ for every place $\mathfrak {p}$ of F above p. As it does not seem possible to ‘see’ Pappas–Rapoport filtrations on Breuil modules, linear algebra calculations ‘on points’ does not take us far; perhaps enlarging coefficients of Breuil modules (in the sense of Section 1.2 in [31]) to allow roots of Eisenstein polynomials and hoping for (faithfully flat) descent might be one possible approach. It may also be possible to follow Fargues ([17]) and construct a ‘canonical’ subgroup of the p-torsion subgroup A[p], and subsequently single out its F-stable part killed by all $\mathfrak {p}$.

We, on the other hand, take the Goren–Kassaei approach ([20]) of making essential use of geometry of relevant moduli spaces, in order to construct ‘canonical subgroups’. Note that it is important to construct canonical subgroups for HBAVs, whether $A[\mathfrak {p}]$ is BT level one or not for every $\mathfrak {p}$, for it is humbly used to establish that weight one specialisations of Hida (nearly ordianary) families define overconvergent eigenforms.

Proposition 17

Let $\overline{\xi }$ be a point over $\overline{S}$ of $\overline{X}_{K{\mathrm {Iw}}}^{\mathrm {PR}}$. Fix $\mathfrak {p}$, $\tau$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e=e_\mathfrak {p}$. Suppose that

• if $t\ge 2$, $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and that t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$;

• if $t=1$, e lies in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$ and that $t=1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$.

For $\pi ^*: \hat{\overline{R}}_{K}\rightarrow \hat{\overline{R}}_{K{\mathrm {Iw}}}$, the following equations in $\hat{\overline{R}}_{K{\mathrm {Iw}}}$ hold:

If $t\ge 2$, and

• (I) t lies $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there elements $\gamma _\tau ^t$ and $\rho _\tau ^{t-1}$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^t)=\gamma _\tau ^t {\mathrm {y}}_\tau ^t+\rho _{\tau }^{t-1} {\mathrm {z}}_{\tau }^{t-1 (p)} \end{aligned}$$

  where, by slight abuse of notation, $S_\tau ^{t-1 (p)}$ denotes the p-th power of $S_\tau ^{t-1}$;

• (II) t lies $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t-1$ does not lie in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there exists an element $\gamma _\tau ^t$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^t)=\gamma _\tau ^t {\mathrm {y}}_\tau ^t; \end{aligned}$$

• (III) t does not lie in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there exists an element $\rho _\tau ^{t-1}$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^t)=\rho _\tau ^{t-1} {\mathrm {z}}_\tau ^{t-1 (p)}; \end{aligned}$$

• (IV) neither t lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ nor $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$

  $$\begin{aligned} \pi ^*( u_\tau ^t)=0. \end{aligned}$$

If $t=1$, and

• (I) $t=1$ lies $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$ and e lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there elements $\gamma _\tau ^1$ and $\rho _\tau ^1$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^1)=\gamma _\tau ^1 {\mathrm {y}}_\tau ^1+\rho _{\tau }^{e} {\mathrm {z}}_{\mathfrak {f}^{-1}\circ \tau }^{e ( p)}; \end{aligned}$$

• (II) $t=1$ lies $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$ and e does not lie in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there exists an element $\gamma _\tau ^1$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^1)=\gamma _\tau ^1 {\mathrm {y}}_\tau ^1; \end{aligned}$$

• (III) $t=1$ does not lie in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$ and e lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, there exists an element $\rho _{\mathfrak {f}^{-1}\circ \tau }^e$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}^\times$ such that

  $$\begin{aligned} \pi ^*(u_\tau ^1)=\rho _{\mathfrak {f}^{-1}\circ \tau }^e {\mathrm {z}}_{\mathfrak {f}^{-1}\circ \tau }^{e (p)}; \end{aligned}$$

• (IV) neither $t=1$ lies in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$ nor e lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$

  $$\begin{aligned} \pi ^*( u_\tau ^1)=0. \end{aligned}$$

Remark

This is a generalisation of Lemma 2.8.1 in [20]. The case $t=e=1$ recovers their result.

Proof

We shall only sketch a proof, which is a generalisation of the proof of Lemma 2.8.1 in [20]. For brevity, for every $\tau$ in $\hat{\varSigma }$, let $\nu _{{\mathrm {RZ}}, \tau }$ (resp. $\gamma _{{\mathrm {RZ}}, \tau }$) denote $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ (resp. $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$). An irreducible components of $\overline{X}_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ passing through $\overline{\xi }$ is parameterised by a subset $J=\sum _\tau J_\tau$ of $J_{{\mathrm {RZ}}}=\sum _\tau J_{{\mathrm {RZ}}, \tau }$ where $J_{{\mathrm {RZ}}, \tau }=\nu _{{\mathrm {RZ}}, \tau }\cap \gamma _{{\mathrm {RZ}}, \tau }$ in the sense that, if $\hat{\overline{R}}_{K{\mathrm {Iw}}, J}$ denote the ideal of $\hat{\overline{R}}_{K{\mathrm {Iw}}}$ generated by $\overline{{\mathrm {y}}}_\tau ^t$ for all t lying in $J_{{\mathrm {RZ}}, \tau }-J_\tau$ and $\overline{{\mathrm {z}}}_\tau ^t$ for all t lying in $J_\tau$ as $\tau$ ranges over $\hat{\varSigma }$, the intersection ${\mathrm {Spf}}\, (\hat{\overline{R}}_{K{\mathrm {Iw}}}/\hat{\overline{I}}_{K{\mathrm {Iw}}, J})\cap {\mathrm {Spf}}\, \hat{\overline{R}}_{K{\mathrm {Iw}}}$ is the formal completion at $\overline{\xi }$ of the irreducible component $\overline{X}^+_{K{\mathrm {Iw}}, \varSigma _J}$ where $\varSigma _J=(\nu _{{\mathrm {RZ}}, J, \tau }, \gamma _{{\mathrm {RZ}}, J, \tau })$ defined by

• $\gamma _{{\mathrm {RZ}}, J, \tau }=\gamma _{{\mathrm {RZ}}, \dagger }-J_\tau$,

• $\nu _{{\mathrm {RZ}}, J, \tau }=\{1, \dots , e\}-\gamma _{{\mathrm {RZ}}, J, \tau }$.

We now fix $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ as in the assertion of the proposition. We deal with the case (I) and leave the rest as an exercise for the reader. There are four different ‘types’ of $J_\tau \subset J_{{\mathrm {RZ}}, \tau }$ to consider:

• (A) both $t-1$ and t lie in $J_\tau$;

• (B) both $t-1$ and t lie in $J_{{\mathrm {RZ}}, \tau }-J_\tau$;

• (C) $t-1$ lies in $J_\tau$ while t lies in $J_{{\mathrm {RZ}}, \tau }-J_\tau$;

• (D) $t-1$ lies in $J_{{\mathrm {RZ}}, \tau }-J_\tau$ while t lies in $J_\tau$.

(I-A) Since $t-1$ lies in $J_\tau$, $t-1$ does not lie in $\gamma _{{\mathrm {RZ}}, J, \tau }$, hence $t-1$ lies in $\nu _{{\mathrm {RZ}}, J, \tau }$. Also t lies in $\gamma _{{\mathrm {RZ}}, \tau }$ and in $J_\tau$, therefore t does not lie in $\gamma _{{\mathrm {RZ}}, J, \tau }$. As any point $\overline{\zeta }$ in $\overline{X}^+_{K{\mathrm {Iw}}, \varSigma _J}$ satisfies the conditions that $\nu _{{\mathrm {RZ}}, \tau }(\overline{\zeta })$ contains $\nu _{{\mathrm {RZ}}, J, \tau }$ (and $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\zeta })$ contains $\gamma _{{\mathrm {RZ}}, J, \tau }$), $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\zeta })$. It then follows from Proposition 12 that t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\zeta })$ if and only if t lies in $\gamma _{{\mathrm {EO}}, \tau }(\overline{\zeta })$.

(I-B) Since t lies in $\gamma _{{\mathrm {RZ}}, \tau }$ but does not lie in $J_\tau$, t lies in $\gamma _{{\mathrm {RZ}}, J \tau }$. Also $t-1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }$ but does not lie in $J_\tau$, hence $t-1$ lies in $\gamma _{{\mathrm {RZ}}, J, \tau }$ and consequently $t-1$ does not lie in $\nu _{{\mathrm {RZ}}, J, \tau }$. It then follows from Proposition 12 that, for any point $\overline{\zeta }$ in $\overline{X}^+_{K{\mathrm {Iw}}, \varSigma _J}$, $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }$ if and only if t lies in $\gamma _{{\mathrm {EO}}, \tau }(\overline{\zeta })$.

(I-C) As t lies in $\gamma _{{\mathrm {RZ}}, \tau }$ but does not lie in $J_\tau$, t lies in $\gamma _{{\mathrm {RZ}}, J, \tau }$. Also $t-1$ lies in $J_\tau$, hence $t-1$ does not lie in $\gamma _{{\mathrm {RZ}}, J, \tau }$, and $t-1$ lies in $\nu _{{\mathrm {RZ}}, J, \tau }$. It then follows from Proposition 12 that, for any point $\overline{\zeta }$ in $\overline{X}^+_{K{\mathrm {Iw}}, \varSigma _J}$, t always lie in $\gamma _{{\mathrm {EO}}, \tau }(\overline{\zeta })$.

Applying (I-A) to $J=J_{{\mathrm {RZ}}}$ and (I-B) to $J=\varnothing$, as well as a simple but tedious calculation that $\bigcap _{J} \hat{\overline{I}}_{K{\mathrm {Iw}}, J}$, where J ranges over the subsets J of $J_{\mathrm {RZ}}$ satisfying the conditions in (C), is generated by $\overline{{\mathrm {y}}}_\tau ^t$ and $\overline{{\mathrm {z}}}_\tau ^{t-1}$, we get the assertion in (I). The other cases may be similarly deduced.

Corollary 4

Let $\xi$ be a point over S of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ and $\zeta$ denote its image by $\pi$ in $X_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. Fix $\mathfrak {p}$, $\tau$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e=e_\mathfrak {p}$. Then

• the conditions $t\ge 2$, $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, and t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ holds, if and only if ${\mathrm {deg}}(\xi /S)_\tau (t-1)< 1/e$ and $0< {\mathrm {deg}}(\xi /S)_\tau (t)$;

• the conditions $t=1$, e lies in $\nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }(\overline{\xi }/\overline{S})$, and $t=1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ hold if and only if ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)< 1/e$ and $0<{\mathrm {deg}}(\xi /S)_\tau (1)$.

Suppose that the preceding (equivalent) assertions hold. Then, for $t\ge 2$,

• (I) ${\mathrm {deg}}(\zeta /S)_\tau (t)$ equals the normalised valuation on ${\mathrm {sp}}^{-1}(\overline{\xi })$ of $(\gamma _\tau ^t {\mathrm {y}}_\tau ^t+\rho _{\tau }^{t-1} {\mathrm {z}}_{\tau }^{t-1 (p)})(\xi )$ if $0<{\mathrm {deg}}(\xi /S)_\tau (t-1)$ and ${\mathrm {deg}}(\xi /S)_\tau (t)<1/e$;

• (II) ${\mathrm {deg}}(\zeta /S)_\tau (t)={\mathrm {deg}}(\xi /S)_\tau (t)$ if ${\mathrm {deg}}(\xi /S)_\tau (t-1)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)<1/e$;

• (III) ${\mathrm {deg}}(\zeta /S)_\tau (t)=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$ if $0<{\mathrm {deg}}(\xi /S)_\tau (t-1)$ and ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$;

• (IV) ${\mathrm {deg}}(\zeta /S)_\tau (t)=1/e$ if ${\mathrm {deg}}(\xi /S)_\tau (t-1)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$.

When $t=1$,

• (I) ${\mathrm {deg}}(\zeta /S)_\tau (1)$ equals the normalised valuation on ${\mathrm {sp}}^{-1}(\overline{\xi })$ of $(\gamma _\tau ^1 {\mathrm {y}}_\tau ^1+\rho _{\mathfrak {f}^{-1}\circ \tau }^{e} {\mathrm {z}}_{\mathfrak {f}^{-1}\circ \tau }^{e (p)})(\xi )$ if $0<{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)$ and ${\mathrm {deg}}(\xi /S)_\tau (1)<1/e$;

• (II) ${\mathrm {deg}}(\zeta /S)_\tau (1)={\mathrm {deg}}(\xi /S)_\tau (1)$ if ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (1)<1/e$;

• (III) ${\mathrm {deg}}(\zeta /S)_\tau (1)=p(1/e-{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e))$ if $0<{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)$ and ${\mathrm {deg}}(\xi /S)_\tau (1)=1/e$;

• (IV) ${\mathrm {deg}}(\zeta /S)_\tau (1)=1/e$ if ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (1)=1/e$.

Proof

This follows immediately from the definition of ${\mathrm {deg}}(\zeta /S)_\tau (t)$ and Lemma 27. $\square$

For every $\mathfrak {p}$, let $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}}$ (resp. $D^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}}$) denote the admissible open subset of points $\xi$ over S of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ such that

• for every $t\ge 2$ and $\tau$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)< & {} p/e\\ (\text{ resp. } {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)> & {} p/e) \end{aligned}$$

  holds;

• for $t=1$ and every $\tau$ in $\hat{\varSigma }$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)< & {} p/e\\ (\text{ resp. } {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)> & {} p/e) \end{aligned}$$

  holds.

Let $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}}$ denote the intersection, over all places $\mathfrak {p}$ above p, of $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}},$ while $D^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}}$ denote the union of $(\bigcap _{\mathfrak {p}\in \varSigma } D^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}}) \cap (\bigcap _{\mathfrak {p}\not \in \varSigma } C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}})$ as $\varSigma$ ranges over the set of non-empty subsets $\varSigma$ of the set of places above p. By definition, if a point of $X^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}}$ lies in $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}}\cup D^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}}$, then it lies in $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}}\cup D^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K{\mathrm {Iw}}, \mathfrak {p}}$ for every $\mathfrak {p}$.

Let $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K, \mathfrak {p}}$ denote the admissible open subset of points $\zeta$ over S of $X_K^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ such that

• for every $t\ge 2$ and $\tau$ in $\hat{\varSigma }$,

  $$\begin{aligned} {\mathrm {deg}}(\zeta /S)_\tau (t)+p{\mathrm {deg}}(\zeta /S)_\tau (t-1)<p/e_\mathfrak {p} \end{aligned}$$

  holds;

• for $t=1$ and every $\tau$ in $\hat{\varSigma }$

  $$\begin{aligned} {\mathrm {deg}}(\zeta /S)_\tau (1)+p{\mathrm {deg}}(\zeta /S)_{\mathfrak {f}^{-1}\circ \tau }(e)<p/e_\mathfrak {p} \end{aligned}$$

  holds.

Let $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K}$ denote the intersection, over all places $\mathfrak {p}$ above p, of $C^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}_{K, \mathfrak {p}}$.

Remark

These admissible open sets (the loci of ‘canonical subgroups’ and ‘anti-canonical subgroups’) generalise those defined in Section 5.3 in [20]. If $t=e=1$, we recover their results.

Proposition 18

Let $\xi$ be a point over S of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ and $\zeta$ denote its image by $\pi$ in $X_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. Fix $\mathfrak {p}$, $\tau$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e=e_\mathfrak {p}$.

Suppose that

• if $2\le t\le e-1$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t+1)+p{\mathrm {deg}}(\xi /S)_\tau (t)< & {} p/e,\\ {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)< & {} p/e; \end{aligned}$$

• if $t=e$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1)+p{\mathrm {deg}}(\xi /S)_\tau (e)< & {} p/e,\\ {\mathrm {deg}}(\xi /S)_\tau (e)+p{\mathrm {deg}}(\xi /S)_\tau (e-1)< & {} p/e; \end{aligned}$$

• if $t=1$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(2)+p{\mathrm {deg}}(\xi /S)_\tau (1)< & {} p/e,\\ {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)< & {} p/e. \end{aligned}$$

Then ${\mathrm {deg}}(\zeta /S)_\tau (t)={\mathrm {deg}}(\xi /S)_\tau (t)$ holds.

On the other hand, suppose that

• if $2\le t\le e$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)>p/e, \end{aligned}$$

• if $t=1$,

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1)+p{\mathrm {deg}}(\xi /S)_\tau (e)>p/e, \end{aligned}$$

Then

$$\begin{aligned} {\mathrm {deg}}(\zeta /S)_\tau (t)=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1)) \end{aligned}$$

holds if $2\le t\le e$, and

$$\begin{aligned} {\mathrm {deg}}(\zeta /S)_{\mathfrak {f}\circ \tau }(1) =p(1/e-{\mathrm {deg}}(\xi /S)_{\tau }(e)) \end{aligned}$$

holds if $t=1$.

Remark

This is a generalisation/refinement of Lemma 5.3.4 in [20].

Proof

Firstly, we sketch the first case when $2\le t<e-1$. From the first given inequality, one may deduce immediately that ${\mathrm {deg}}(\xi /S)_\tau (t)$ cannot be 0 and therefore either ${\mathrm {deg}}(\xi /S)_\tau (t)=0$ or $0<{\mathrm {deg}}(\xi /S)_\tau (t)<1/e$ holds.

Suppose ${\mathrm {deg}}(\xi /S)_\tau (t)=0$. In which case, t does not lie in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ by definition. On the other hand, by the second given inequality, ${\mathrm {deg}}(\xi /S)_\tau (t-1)$ can not be 1 / e, hence $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. It follows from Proposition 13 that t does not lie in $\gamma _{{\mathrm {EO}}, \tau }(\overline{\xi }/\overline{S})$, hence ${\mathrm {deg}}(\zeta /S)_\tau (t)=0$ by definition.

Suppose $0<{\mathrm {deg}}(\xi /S)_\tau (t)<1/e$ holds. As ${\mathrm {deg}}(\xi /S)_\tau (t-1)$ cannot be 1 / e, it follows that $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. On the other hand, ${\mathrm {deg}}(\xi /S)_\tau (t)$ cannot be 0, and t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. We there see that the assumptions of Proposition 4 are satisfied.

If ${\mathrm {deg}}(\xi /S)_\tau (t-1)=0$, then the case (II) applies, and ${\mathrm {deg}}(\zeta /S)_\tau (t)={\mathrm {deg}}(\xi /S)_\tau (t)$. If ${\mathrm {deg}}(\xi /S)_\tau (t-1)>0$, then the case (I) applies, and ${\mathrm {deg}}(\zeta /S)_\tau (t)$ is computed by the normalised valuation $\nu$ of $(\gamma _\tau ^t {\mathrm {y}}_\tau ^t+\rho _\tau ^t {\mathrm {z}}_\tau ^{t-1(p)})(\xi )$ for some units $\gamma _\tau ^t$ and $\rho _\tau ^{t-1}$ in $\hat{\overline{R}}_{K{\mathrm {Iw}}}$. However, as ${\mathrm {deg}}(\xi /S)_\tau <p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$, it follows that the normalised valuation of $\rho _\tau ^t {\mathrm {y}}_\tau ^t$ evaluated at $\xi$ is strictly less than $p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))=p(1/e-\nu ( {\mathrm {y}}_\tau ^{t-1}(\xi )))=p\nu ({\mathrm {z}}_\tau ^{t-1}(\xi ))=p\nu (\rho _\tau ^{t-1}{\mathrm {z}}_\tau ^{t-1}(\xi ))=\nu (\rho _\tau ^{t-1}{\mathrm {z}}_\tau ^{t-1(p)}(\xi ))$, and therefore ${\mathrm {deg}}(\zeta /S)_\tau (t)={\mathrm {deg}}(\xi /S)_\tau (t)$.

We shall prove the second assertion when $2\le t\le e$. By the given inequality, ${\mathrm {deg}}(\xi /S)_\tau (t-1)>0$ and therefore either ${\mathrm {deg}}(\xi /S)_\tau (t-1)=1/e$ or $0<{\mathrm {deg}}(\xi /S)_\tau (t-1)<1/e$ holds. On the other hand, it also follows that ${\mathrm {deg}}(\xi /S)_\tau (t)>0$ and t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$.

Suppose that ${\mathrm {deg}}(\xi /S)_\tau (t-1)=1/e$. In which case, $t-1$ does not lie in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. It therefore follows from Proposition 13 that t does not lie in $\gamma _{{\mathrm {EO}}, \tau }(\overline{\xi }/\overline{S})$, and ${\mathrm {deg}}(\zeta /S)_\tau (t)=0=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$ as desired.

Suppose that $0<{\mathrm {deg}}(\xi /S)_\tau (t-1)<1/e$. In which case, $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. If ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$, then it follows from Corollary 4 that ${\mathrm {deg}}(\zeta /S)_\tau (t)=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$. If $0<{\mathrm {deg}}(\xi /S)_\tau (t)<1/e$, it also follows from Corollary 4 that ${\mathrm {deg}}(\zeta /S)_\tau (t)$ is computed by the normalised valuation $\nu$ of $(\gamma _\tau ^t {\mathrm {y}}_\tau ^t+\rho _\tau ^{t-1} {\mathrm {z}}_\tau ^{t-1 (p)})(\xi )$ for some units in $\hat{\overline{R}}_{K{\mathrm {Iw}}}$. However, the given inequality implies that ${\mathrm {deg}}(\xi /S)_\tau (t)>p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$, hence $\nu (\gamma _\tau ^t{\mathrm {y}}_\tau ^t(\xi ))>\nu (\rho _\tau ^{t-1} {\mathrm {z}}_\tau ^{t-1(p)}(\xi ))$. It therefore follows that ${\mathrm {deg}}(\zeta /S)_\tau (t)=\nu (\rho _\tau ^{t-1}{\mathrm {z}}_\tau ^{t-1(p)}(\xi ))=p\nu ({\mathrm {z}}_\tau ^{t-1}(\xi ))=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t-1))$. The other cases follow similarly. $\square$

Lemma 28

Fix $\mathfrak {p}$ and $1\le t\le e=e_\mathfrak {p}$.

• If $2\le t\le e-1$, suppose that the following hold

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)\le p/e\end{aligned}$$

  and

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t+1)+p{\mathrm {deg}}(\xi /S)_\tau (t)\ge p/e; \end{aligned}$$

• if $t=e$, suppose

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (e)+p{\mathrm {deg}}(\xi /S)_\tau (e-1)\le p/e \end{aligned}$$

  and

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1)+p{\mathrm {deg}}(\xi /S)_\tau (e)\ge p/e; \end{aligned}$$

• if $t=1$, suppose

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)\le p/e \end{aligned}$$

  and

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (2)+p{\mathrm {deg}}(\xi /S)_\tau (1)\ge p/e. \end{aligned}$$

Then ${\mathrm {deg}}(\zeta /S)_\tau (t+1)+p{\mathrm {deg}}(\zeta /S)_\tau (t)\ge p/e$. In particular, $\zeta$ does not lie in $C_{K, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$.

Remark

This is a generalisation of Lemma 5.3.6 in [20].

Proof

We prove the case $2\le t\le e-1$. Since ${\mathrm {deg}}(\xi /S)_\tau (t-1)$ cannot be 1 / e, $t-1$ lies in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. Also since ${\mathrm {deg}}(\xi /S)_\tau (t)$ cannot be 0, t lies in $\gamma _{{\mathrm {RZ}}, \tau } (\overline{\xi }/\overline{S})$. There are four cases (corresponding exactly to the four cases in Proposition 4) to deal with:

• (I) ${\mathrm {deg}}(\xi /S)_\tau (t-1)>0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)<1/e$;

• (II) ${\mathrm {deg}}(\xi /S)_\tau (t-1)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)<1/e$;

• (III) ${\mathrm {deg}}(\xi /S)_\tau (t-1)>0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$;

• (IV) ${\mathrm {deg}}(\xi /S)_\tau (t-1)=0$ and ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$.

Suppose (I). In this case, ${\mathrm {deg}}(\zeta /S)_\tau (t)$ is computed by the normalised valuation of $(\gamma _\tau ^t {\mathrm {y}}_\tau ^t+\rho _\tau ^t {\mathrm {z}}_\tau ^{t-1(p)})(\xi )$. As it follows from the first inequality in the assumption $\nu ({\mathrm {y}}_\tau ^t(\xi ))\le \nu ({\mathrm {z}}_\tau ^{t-1(p)}(\xi ))$ that ${\mathrm {deg}}(\zeta /S)_\tau (t)\ge {\mathrm {deg}}(\xi /S)_\tau (t)$. On the other hand, ${\mathrm {deg}}(\xi /S)_\tau (t)$ is not 1 / e and it follows from the second inequality in the assumption that ${\mathrm {deg}}(\xi /S)_\tau (t+1)>0$, hence $t+1$ lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$.

If ${\mathrm {deg}}(\xi /S)_\tau (t+1)=1/e$, combined with ${\mathrm {deg}}(\xi /S)_\tau (t)>0$, Corollary 4, (III), applies and ${\mathrm {deg}}(\zeta /S)_\tau (t+1)=p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t))$. It then follows that

$$\begin{aligned} {\mathrm {deg}}(\zeta /S)_\tau (t+1)+p{\mathrm {deg}}(\zeta /S)_\tau (t)\ge & {} p(1/e-{\mathrm {deg}}(\xi /S)_\tau (t))\\&+p{\mathrm {deg}}(\xi /S)_\tau (t)=p/e. \end{aligned}$$

If, on the other hand, ${\mathrm {deg}}(\xi /S)_\tau (t+1)<1/e$, Corollary 4, (I), applies, and ${\mathrm {deg}}(\zeta /S)_\tau (t+1)$ is computed by the normalise valuation $\nu$ of $(\gamma _\tau ^{t+1} {\mathrm {y}}_\tau ^{t+1}+\rho _\tau ^t {\mathrm {z}}_\tau ^{t (p)})(\xi )$. The second inequality in the assumption implies that $\nu (\gamma _\tau ^{t+1}{\mathrm {y}}_\tau ^{t+1}(\xi ))\ge \nu (\rho _\tau ^t {\mathrm {z}}_\tau ^{t (p)}(\xi ))$, hence ${\mathrm {deg}}(\zeta /S)_\tau (t+1)\ge p\nu ({\mathrm {z}}_\tau ^t(\xi ))$. It then follows that

$$\begin{aligned} {\mathrm {deg}}(\zeta /S)_\tau (t+1)+p{\mathrm {deg}}(\zeta /S)_\tau (t)\ge & {} p\nu ({\mathrm {z}}_\tau ^t(\xi ))+p\nu ({\mathrm {y}}_\tau ^t(\xi ))\\= & {} p\nu ({\mathrm {y}}_\tau ^t(\xi )+{\mathrm {z}}_\tau ^t(\xi ))=p/e. \end{aligned}$$

The other cases can be proved similarly. $\square$

Proposition 19

$\pi ^{-1}(C_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}})=C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$.

Proof

This can be proved as in Section 5.3 of [20]. Firstly observe that the proof of Proposition 18 proves that $\pi ^{-1}(C_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}})\supseteq C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$.

Suppose that $\xi$ does not lie in $C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. Then there exists $\mathfrak {p}$ such that $\xi$ does not lie in $C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. Because $\xi$ does not lie in $D_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ in particular, there is a pair of $\dagger$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and $1\le l\le e=e_\mathfrak {p}$ such that the following hold:

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\dagger (l)+p{\mathrm {deg}}(\xi /S)_\dagger (l-1)\le p/e \end{aligned}$$

if $l>1$, or

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\dagger (1)+p{\mathrm {deg}} (\xi /S)_{\mathfrak {f}^{-1}\circ \dagger }(e)\le p/e \end{aligned}$$

when $l=1$. We ‘order’ the ef pairs $\hat{\varSigma }\times ([1, e]\cap \mathbf {Z})$ by

$$\begin{aligned}&(\dagger , l), (\dagger , l+1), \dots , (\dagger , e), (\mathfrak {f}\circ \dagger , 1), \dots , (\mathfrak {f}\circ \dagger , e), \\&\quad \dots , (\mathfrak {f}^{-1}\circ \dagger , 1), (\mathfrak {f}^{-1}\circ \dagger , e), (\dagger , 1), \dots , (\dagger , l-1) \end{aligned}$$

if $l>1$ and

$$\begin{aligned} (\dagger , 1), \dots , (\dagger , e), (\mathfrak {f}\circ \dagger , 1), \dots , (\mathfrak {f}\circ \dagger , e), \dots , (\mathfrak {f}^{-1}\circ \dagger , 1), \dots , (\mathfrak {f}^{-1}\circ \dagger , e) \end{aligned}$$

if $l=1$. Since $\xi$ does not lie in $C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, there exists a pair of $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ such that the following hold:

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t+1)+{\mathrm {deg}}(\xi /S)_\tau (t)\ge p/e \end{aligned}$$

if $t\le e-1$, or

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}} (\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)\ge p/e \end{aligned}$$

if $t=e$. We may choose the pair to be ‘minimum’ (i.e. ‘left-most’ in the arrangement above) amongst those satisfying the condition. By the ‘minimality’,

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_\tau (t-1)< p/e \end{aligned}$$

if $1<t\le e-1$,

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (1)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e)< p/e \end{aligned}$$

if $t=1$, or

$$\begin{aligned} {\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e) +p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e-1)< p/e \end{aligned}$$

if $t=e$, holds as otherwise ${\mathrm {deg}}(\xi /S)_\dagger (l)+p{\mathrm {deg}}(\xi /S)_\dagger (l-1)\le p/e$ if $l>1$, or ${\mathrm {deg}}(\xi /S)_\dagger (1)+p{\mathrm {deg}} (\xi /S)_{\mathfrak {f}^{-1}\circ \dagger }(e)\le p/e$ holds. In any case, the assumptions of the preceding lemma are satisfied, and $\xi$ would not lie in $C_{K, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. $\square$

Theorem 4

An overconvergent Hilbert modular form, which is an eigenform for $K_\mathfrak {p}$ with non-zero eigenvalue for all $\mathfrak {p}$ in $S_{\mathrm {P}}$, extends to $C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$.

Proof

Let $\xi$ is a point over S of $C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, and suppose that it corresponds to (A, C) over S. Fix a place $\mathfrak {p}$ above p. It suffices to establish that, for a Raynaud submodule scheme D of $A[\mathfrak {p}]$ distinct from C, $(A/D, (C+D)/D)$ lies in $C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ and ${\mathrm {deg}}((A/D, (C+D)/D)<{\mathrm {deg}}(A, C)$. As $\xi$ defines a point of $C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, it follows from the preceding proposition that, if $\zeta$ denotes the point corresponding to (A, D), $\zeta$ lies in either $C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ or $D_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$.

If $\zeta$ lay in $C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, it follows from Proposition 18 that ${\mathrm {deg}}(\xi /S)_\tau (t)={\mathrm {deg}}(\zeta /S)_\tau (t)$ for every $\tau$ and $1\le t\le e$ and C would equal D, which is a contradiction. Hence $\zeta$ lies in $D_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, as $\zeta$ lies in $\pi ^{-1}(C_{K}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}})= C_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\subset C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\cup D_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ . Granted, it follows from Proposition 18 that if $t\ge 2$, ${\mathrm {deg}}(\xi /S)_\tau (t)=p(1/e-{\mathrm {deg}}(\zeta /S)_\tau (t-1))$, and ${\mathrm {deg}}((A/D, (C+D)/D)/S)_\tau (t-1)={\mathrm {deg}}(\xi /S)_\tau (t)/p,$ while if $t=1$, ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1)=p(1/e-{\mathrm {deg}}(\zeta /S)_\tau (e))$, and therefore ${\mathrm {deg}}((A/D, (C+D)/D)/S)_\tau (e)={\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1)/p$. It is immediate to see that $(A/D, (C+D)/D)$ lies in $C_{K{\mathrm {Iw}}, \mathfrak {p}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ and ${\mathrm {deg}}((A/D, (C+D)/D)/S)={\mathrm {deg}}(\xi /S)/p< {\mathrm {deg}}(\xi /S)$ as desired. $\square$

Remark

The proof of the theorem indeed proves that $U_\mathfrak {p}$, for every $\mathfrak {p}$ above p, acts completely continuously on the space of overconvergent p-adic Hilbert modular eigenforms in our sense.

6.3 Throwing away loci of ‘large’ co-dimension

In this section, in preparation of proving strong analytic continuation theorems on the Raynayd generic fibre $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$, we define various admissible open subsets $X_{K{\mathrm {Iw}}}^+$ of ‘co-dimension $\le 1$’ (which contains the multiplicative ordinary locus), based on the observation in Proposition 10. It is an analogue of those defined in Section 5.2 in [26].

Let $\mathscr {O}_K$ denote the ring of integers of a finite extension K of L and k be its residue field. Let $S={\mathrm {Spec}}\, \mathscr {O}_K$ and $\overline{S}={\mathrm {Spec}}\, k$.

The (standard) Barsotti–Tate p-divisible group of A over S defining an S-point of $Y^{\mathrm {PR}}_K$ is a product of filtered principally polarisable Barsotti–Tate p-divisible groups $X_\mathfrak {p}$ (of dimension $e_\mathfrak {p} f_\mathfrak {p}$ and of height $2e_\mathfrak {p} f_\mathfrak {p}$) over S where $\mathfrak {p}$ ranges over $S_{\mathrm {P}}$; for each $\mathfrak {p}$, one can define invariants as in Section 5 for $\overline{X}_\mathfrak {p}$ over $\overline{S}$ according to which one can stratify moduli spaces of Barsotti–Tate p-divisible groups. To that end, let $\varSigma = \varSigma _{\mathrm {EO}}$ (resp. $\varSigma =\varSigma _{\mathrm {RZ}}$) be a tuple $(\varSigma _\mathfrak {p})_\mathfrak {p}$ where $\mathfrak {p}$ ranges over $S_{\mathrm {P}}$ with each $\varSigma _\mathfrak {p}$ defined as in Section 5; and we shall let $\overline{Y}_{K, \varSigma }^{\mathrm {PR}}$ (resp. $\overline{Y}_{K{\mathrm {Iw}}, \varSigma }^{\mathrm {PR}}$) denote the closed $\kappa$-subscheme of the special fibre $\overline{Y}_{K}^{\mathrm {PR}}$ (resp. $\overline{Y}_{K{\mathrm {Iw}}}^{\mathrm {PR}}$) defined by demanding that the corresponding principally polarisable filtered Barsotti–Tate p-divisible group $X=\overline{X}_\mathfrak {p}$ lies in the closed substack of $S^{{\mathrm {BT}}}$ (resp. $S^{\mathrm {BT}}_{{\mathrm {I}}}$) defined by $\varSigma _\mathfrak {p}$ as in Section 5 for every $\mathfrak {p}$ in $S_{\mathrm {P}}$.

Let $\overline{Y}^{{\mathrm {PR}}, ++}_K$ denote the union (over $\varSigma$) of subscheme $\overline{Y}^{\mathrm {PR}}_{K, \varSigma }$ of $\overline{Y}^{\mathrm {PR}}_{K}$ where $\varSigma = \varSigma _{\mathrm {EO}}$ is defined such that, there exists $\mathfrak {p}$ in $S_{\mathrm {P}}$ such that

$$\begin{aligned}{}[F_\mathfrak {p}:\mathbf {Q}_p]-2\ge \sum _{\tau } e- |\gamma _{{\mathrm {EO}}, \tau }|, \end{aligned}$$

where $\tau$ ranges over $\hat{\varSigma }_\mathfrak {p}$, holds. It follows from Propositions 10 and 9 respectively that every such $\overline{Y}^{\mathrm {PR}}_{K, \varSigma }$ is of co-dimension $\ge 2$ in $\overline{Y}_K^{\mathrm {PR}}$.

Let

$$\begin{aligned} \overline{Y}_K^{{\mathrm {PR}}, +}=\overline{Y}_K^{\mathrm {PR}}-\overline{Y}_K^{{\mathrm {PR}}, ++} \end{aligned}$$

and let

$$\begin{aligned} \overline{Y}^{{\mathrm {PR}}, +}_{K{\mathrm {Iw}}}=\pi ^{-1}\left( \overline{Y}^{{\mathrm {PR}}, +}_K\right) . \end{aligned}$$

As it is useful in defining ‘compactifications’ of the admissible open sets above, if $\varSigma =\varSigma _{\mathrm {RZ}}$, and if, for every $\mathfrak {p}$ in $S_{\mathrm {P}}$, one of the following:

• (St-1)$\nu _{{\mathrm {RZ}}, \tau }=\{1, \dots , e_\mathfrak {p}\}$ while $\gamma _{{\mathrm {RZ}}, \tau }=\varnothing$ for every $\tau$ in $\hat{\varSigma }_\mathfrak {p}$,

• (St-2)$\nu _{{\mathrm {RZ}}, \tau }=\varnothing$ while $\gamma _{{\mathrm {RZ}}, \tau }= \{1, \dots , e_\mathfrak {p}\}$ for every $\tau$ in $\hat{\varSigma }_\mathfrak {p}$,

holds, we say that $\varSigma$ is semi-stable.

If $\varSigma$ is semi-stable, let $S_{{\mathrm {P}}, \varSigma }$ denote the set of all $\mathfrak {p}$ in $S_{\mathrm {P}}$ such that $\varSigma _\mathfrak {p}$ satisfies (St-1). If $\varSigma$ is semi-stable, let $\overline{X}^{\mathrm {PR}}_{K{\mathrm {Iw}}, \varSigma }$ denote the Zariski closure of $\overline{Y}_{K{\mathrm {Iw}}, \varSigma }^{\mathrm {PR}}$ in $\overline{X}_{K{\mathrm {Iw}}}^{\mathrm {PR}}$. Let $\overline{Z}^{\mathrm {PR}}_{K{\mathrm {Iw}}, \varSigma }$ denote the complement in $\overline{X}^{\mathrm {PR}}_{K{\mathrm {Iw}}, \varSigma }$ of the union of $\overline{Y}^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\varSigma ^+}}$ as $\varSigma ^+$ ranges over all $\varSigma ^+=(\nu _{{\mathrm {RZ}}, \tau , +},{\gamma _{{\mathrm {RZ}}, \tau , +}})_\tau$ which are not equal to $\varSigma$ such that $\nu _{{\mathrm {RZ}}, \tau , +}$ contains $\nu _{{\mathrm {RZ}}, \tau }$ and $\gamma _{{\mathrm {RZ}}, \tau , +}$ contains $\gamma _{{\mathrm {RZ}}, \tau }$ simultaneously.

Definition

Let $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ denote the union of ${\mathrm {sp}}^{-1}(\overline{Y}^{{\mathrm {PR}}, +}_{K{\mathrm {Iw}}})$ and ${\mathrm {sp}}^{-1}(\overline{Z}^{\mathrm {PR}}_{K{\mathrm {Iw}}, \varSigma })$ for all semi-stable $\varSigma$. If we let $\overline{X}_{K}^{{\mathrm {PR}}, +}$ denote $\overline{X}_{K}^{\mathrm {PR}}-\overline{Y}_{K}^{{\mathrm {PR}}, ++}$ and $\overline{X}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ denote $\pi ^{-1}(\overline{X}_{K}^{{\mathrm {PR}}, +})$, it follows by definition that

$$\begin{aligned} X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}={\mathrm {sp}}^{-1}(\overline{X}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}). \end{aligned}$$

6.4 Overconvergent eigenforms of weight one

We shall use the notation used in Section 3.

Theorem 5

Suppose $p>3$ and let L be a finite extension of $\mathbf {Q}_p$ with ring O of integers and maximal ideal $\lambda$. Let

$$\begin{aligned} \rho : {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(O) \end{aligned}$$

be a continuous representation such that

• $\rho$ is totally odd,

• $\rho$ is ramified at only finitely many primes of F,

• $\overline{\rho }=(\rho \ {\mathrm {mod}}\ \lambda )$ is of the form as supposed in Section 2, and there exists a non-Eisenstein maximal ideal $\mathfrak {m}$ of $T^{\mathrm {ord}}_\varSigma (K)$ such that $\overline{\rho }\sim \overline{\rho }_\mathfrak {m}$,

• $\overline{\rho }$ is absolutely irreducible when restricted to ${\mathrm {Gal}}(\overline{F}/F(\zeta _p))$,

• if $p=5$ and the projective image of $\overline{\rho }$ is isomorphic to ${\mathrm {PGL}}_2(\mathbf {F}_5)$, the kernel of the projective representation of $\overline{\rho }$ does not fix $F(\zeta _5)$,

• $\overline{\rho }$ is trivial at every finite place of F above p,

• $\rho$ is unramified at every place $\mathfrak {p}$ of F above p, and $\rho ({\mathrm {Frob}}_\mathfrak {p})$, where ${\mathrm {Frob}}_\mathfrak {p}$ is the arithmetic Frobenius, is equivalent to $\begin{pmatrix} \alpha _\mathfrak {p}&{}*\\ 0&{}\beta _\mathfrak {p}\end{pmatrix}$.

Let $S_{{\mathrm {P}}, {\mathrm {e}}}$ (‘e’ for ‘equal’) denote the subset of all primes $\mathfrak {p}$ of F above p such that $\alpha _\mathfrak {p}=\beta _\mathfrak {p}$, and let $S_{{\mathrm {P}}, {\mathrm {d}}}$ (‘d’ for ‘distinct’) for denote the subset all primes $\mathfrak {p}$ of F above p such that $\alpha _\mathfrak {p}$ and $\beta _\mathfrak {p}$ are distinct; $S_{\mathrm {P}}$ is the disjoint union of $S_{{\mathrm {P}}, {\mathrm {e}}}$ and $S_{{\mathrm {P}}, {\mathrm {d}}}$.

Then there exists a family of overconvergent cuspidal Hilbert modular forms $F_\varSigma$ of parallel weight one and of level $K{\mathrm {Iw}}$ where $\varSigma =\varSigma _{\mathrm {d}}\times \varSigma _{\mathrm {e}}$ where $\varSigma _{\mathrm {d}}\subset S_{{\mathrm {P}}, {\mathrm {d}}}$ and $\varSigma _{\mathrm {e}}\subset S_{{\mathrm {P}}, {\mathrm {e}}}$ such that

$$\begin{aligned} U_\mathfrak {p} F_\varSigma= & {} \beta _\mathfrak {p} F_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F_\varSigma= & {} \alpha _\mathfrak {p} F_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } S_{{\mathrm {P}}, {\mathrm {d}}}-\varSigma _{\mathrm {d}},\\ U_\mathfrak {p}F_\varSigma= & {} \alpha _\mathfrak {p} F_\varSigma +F_{\varSigma -\{\mathfrak {p}\}}\quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {e}},\\ U_\mathfrak {p} F_\varSigma= & {} \alpha _\mathfrak {p} F_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } S_{{\mathrm {P}}, {\mathrm {e}}}-\varSigma _{\mathrm {e}},\\ U_{\mathrm {Q}} F_\varSigma= & {} 0 \quad \hbox { for every } {\mathrm {Q}} \hbox { in } T-S_{\mathrm {P}},\\ T_{\mathrm {Q}} F_\varSigma= & {} {\mathrm {tr}}\, \rho ({\mathrm {Frob}}_{\mathrm {Q}} ) F_\varSigma \quad \hbox { for every } {\mathrm {Q}} \hbox { not in } T, \end{aligned}$$

where $\alpha _\mathfrak {p}$ and $\beta _\mathfrak {p}$ denote, by slight abuse of notation, the roots of characteristic polynomial of $\rho ({\mathrm {Frob}}_\mathfrak {p})$ and where T denotes the (disjoint) union of $S_{\mathrm {P}}$, $S_{\mathrm {R}}$, $S_{\mathrm {L}}$, and $S_{\mathrm {A}}$, and such that its associated Galois representation is isomorphic to $\rho$.

Proof

Corollary 1 gives rise to a cuspidal p-adic Hilbert modular eigenform $F_\varSigma$ such that

• $T_{\mathrm {Q}} F_\varSigma ={\mathrm {tr}}\, \rho ({\mathrm {Frob}}_{\mathrm {Q}} )F_\varSigma$ for every ${\mathrm {Q}}$ not T;

• $U_\mathfrak {p} F_\varSigma =\alpha _\mathfrak {p}$ if $\mathfrak {p}$ lies in $S_{{\mathrm {P}}, {\mathrm {d}}}-\varSigma _{\mathrm {d}}$, while $U_\mathfrak {p} F_\varSigma =\beta _\mathfrak {p}$ if $\mathfrak {p}$ lies in $\varSigma _{\mathrm {d}}$;

• $U_\mathfrak {p} F_\varSigma =\alpha _\mathfrak {p}F_\varSigma +F_{\varSigma -\{\mathfrak {p}\}}$ if $\mathfrak {p}$ lies in $\varSigma _{ {\mathrm {e}}}$ while $U_\mathfrak {p}F_\varSigma =\alpha _\mathfrak {p}F_\varSigma$ if $\mathfrak {p}$ lies in $S_{{\mathrm {P}}, {\mathrm {e}}}-\varSigma _{\mathrm {e}}$.

Furthermore, Lemmas 1.6–1.8 in [55] prove that we may increase the level K at ${\mathrm {Q}}$ if necessary to assume that $F_\varSigma$ maps $U_{\mathrm {Q}}$ to 0 for every ${\mathrm {Q}}$ in $T-S_{\mathrm {P}}$.

The proof that $F_\varSigma$ defines overconvergent modular eigenforms is analogous to Lemma 1 in [9], with a characteristic zero lifting of a sufficiently large power of the Hasse invariant of parallel weight $p-1$ on $X^{\mathrm {PR}}_K[1/p]$ in place of the Eisenstein series E of weight $p-1$ in the proof. It is necessary to establish that the Hecke operator at every place of F above p, acts completely continuously on the space of overconvergent eigenforms (in our sense), but this has been proved already; see Remark at the end of preceding section. $\square$

In [44], this theorem is extended to the case where not only no assumption is made on p, but $\overline{\rho }$ is allowed to be reducible when restricted to ${\mathrm {Gal}}(\overline{F}/F(\zeta _p))$ (if it is not induced from a imaginary quadratic field in $F(\zeta _p)$ in which every prime of F above p splits completely).

6.5 Overconvergent eigenforms of weight one, in companion, are classical

We shall prove that those overconvergent eigenmforms of weight one constructed in the theorem immediately above are indeed classical, which is the last step of proving the main theorem of this paper. We firstly prove a result (Proposition 20) of paramount importance, which describes the degrees of a point in $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$. Indeed, it is to obtain a result of this kind that we study mod p/p-adic geometry of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ carefully.

The construction of a weight one form on $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ and ‘by extension’ over to $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ is achieved by induction, designed on the observation made in Proposition 20. Proposition 22 is an analogue of Proposition 5.7 in [26]. However, as in [26], in order to extend the eigenform to the vertex of the valuation hypercube (the $[F_\mathfrak {p}: \mathbf {Q}_p]$ copies of the interval [0, 1] for every $\mathfrak {p}$) at the ‘furthest end’, it is also necessary to glue its companion forms to it by q-expansion calculations (Lemma 30). We also establish an analogue, Proposition 23, of Lemma 5.9 in [26].

Proposition 20

Let $\xi$ be a non-cuspidal S-point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ and let $\zeta$ denote its image by the forgetful morphism. Suppose that $\gamma _{{\mathrm {EO}}, \tau }(\overline{\zeta })$, as $\tau$ ranges over $\hat{\varSigma }_\mathfrak {p}$ for every $\mathfrak {p}$, are not simultaneously empty. Then, for every $\mathfrak {p}$, there exist $\dagger$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {p}$ and an integer $1\le l\le e=e_\mathfrak {p}$ such that if we arrange the ${\mathrm {deg}}(\xi /S)_\tau (t)$ as

$$\begin{aligned} \ldots , {\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(e), {\mathrm {deg}}(\xi /S)_\tau (1), \ldots , {\mathrm {deg}}(\xi /S)_\tau (e), {\mathrm {deg}}(\xi /S)_{\mathfrak {f}\circ \tau }(1),\ldots , \end{aligned}$$

i.e. a sequence of $f=f_\mathfrak {p}$ blocks of cardinality e, ordered by $\hat{\varSigma }$, with each block, in itself, being ordered by the index $1\le t\le e$, the sequence starting with ${\mathrm {deg}}(\xi /S)_\dagger (l)$ takes values $1/e, \cdots , 1/e$, in [0, 1 / e), $0, \dots , 0$.

Fix $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ such that ${\mathrm {deg}}(\xi /S)_\tau (t)$ lies in [0, 1 / e) above. In which case, ${\mathrm {deg}}(\xi /S)_\tau (t)$ is indeed 0, i.e. ${\mathrm {deg}}(\xi /S)_\tau (t)$ is the first 0 immediately after 1 / e, if and only if $t-1\not \in \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and $t\not \in \gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ hold. On the other hand, ${\mathrm {deg}}(\xi /S)_\tau (t)$ lies in (0, 1 / e) if and only if t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})\cap \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$.

Proof

In this proof, we shall omit our reference to $\overline{\xi }$ and $\overline{\zeta }$ for the invariants defined in Sect. 5. We also fix $\mathfrak {p}$, and omit our reference where possible.

By assumption, if $[F_\mathfrak {p}:\mathbf {Q}_p]=\sum _{\tau } e- |\gamma _{{\mathrm {EO}}, \tau }|$, then $\gamma _{{\mathrm {EO}}, \tau }=\varnothing$ hold for every $\tau$, but this is excluded. Hence it follows that there exists $\dagger$ in $\hat{\varSigma }$ such that,

• for every $\tau$ in $\hat{\varSigma }$, distinct from $\dagger$, $\gamma _{{\mathrm {EO}}, \tau }=\varnothing$;

• for $\dagger$, $\gamma _{{\mathrm {EO}}, \dagger }=\{l\}$ for some $1\le l\le e$.

We then make appeal to Propositions 12 and 13: if t lies in $\gamma _{{\mathrm {EO}}, \tau }$, then

• $t\ge 2$ and either the case $t-1\in \nu _{{\mathrm {RZ}}, \tau }$ while $t\in \gamma _{{\mathrm {RZ}}, \tau }$, or the case $t-1\not \in \nu _{{\mathrm {RZ}}, \tau }$ while $t\not \in \gamma _{{\mathrm {RZ}}, \tau }$ holds.

• $t=1$ and either the case $e\in \nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $1\in \gamma _{{\mathrm {RZ}}, \tau }$, or the case $e\not \in \nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $1\not \in \gamma _{{\mathrm {RZ}}, \tau }$ holds,

while t does not lie in $\gamma _{{\mathrm {EO}}, \tau }$ if

• $t\ge 2$ and either the case $t-1\in \nu _{{\mathrm {RZ}}, \tau }$ while $t\not \in \gamma _{{\mathrm {RZ}}, \tau }$, or the case $t-1\not \in \nu _{{\mathrm {RZ}}, \tau }$ while $t\in \gamma _{{\mathrm {RZ}}, \tau }$ holds.

• $t=1$ and either the case $e\in \nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $1\not \in \gamma _{{\mathrm {RZ}}, \tau }$, or the case $e\not \in \nu _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \tau }$ while $1\in \gamma _{{\mathrm {RZ}}, \tau }$ holds,

and ascertain the tuples $\{\nu _{{\mathrm {RZ}}, \tau }, \gamma _{{\mathrm {RZ}}, \tau }\}$ for all $\tau$ in $\hat{\varSigma }$. $\square$

Proposition 21

Let $\xi$ be a non-cuspidal S-point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$. Suppose that ${\mathrm {deg}}(\xi /S)_\tau (t)$ is of the form in the preceding proposition, except we demand further that, for every $\mathfrak {p}$, ${\mathrm {deg}}(\xi /S)$ is not an integer multiple of $1/e_\mathfrak {p}$, or equivalently, if t lies in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})\cap \nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$, it is assumed that ${\mathrm {deg}}(\xi /S)_\tau (t)$ lies in (0, 1 / e). Then $\xi$ lies in $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$.

Proof

It suffices to establish $|\sum _\tau \gamma _{{\mathrm {EO}}, \tau }(\overline{\xi })|=1$ as $\tau$ ranges over $\hat{\varSigma }_\mathfrak {p}$, for every place $\mathfrak {p}$ of F above p. Fix $\mathfrak {p}$ and we shall omit the reference. By assumption, there is no $1\le t\le e$ such that $t-1$ not lying in $\nu _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$ and t not lying in $\gamma _{{\mathrm {RZ}}, \tau }(\overline{\xi }/\overline{S})$. The assertion therefore follows from Propositions 12 and 13. $\square$

Fix a proper subset $\varGamma$ of $S_{\mathrm {P}}$. Fix, furthermore, a prime $\mathfrak {P}$ above p (with a fixed uniformiser $\pi$) which is not in $\varGamma$. When convenient, we shall omit our reference to $\mathfrak {P}$ (and only for $\mathfrak {P}$) from notation.

Definition

For an interval $I\subseteq [0, f]$ be an interval, we shall let $X_{K{\mathrm {Iw}}}^{+, \varGamma }I$ denote the union of ${\mathrm {sp}}^{-1}(\overline{Z}^{\mathrm {PR}}_{K{\mathrm {Iw}}, \varSigma })$ for semi-stable $\varSigma$, such that $S_{{\mathrm {P}}, \varSigma }$ contains $S_{\mathrm {P}}-\varGamma$, and the set of non-cuspidal points $\xi$ over S in $Y_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ such that

• for $\mathfrak {p}$ in $\varGamma$,

  $$\begin{aligned} 0\le {\mathrm {deg}}(\xi /S)_\tau (t)\le 1/e_\mathfrak {p} \end{aligned}$$

  for every $\tau$ in $\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e_\mathfrak {p}$;

• for $\mathfrak {p}$ not in $\varGamma \cup \{\mathfrak {P}\}$, ${\mathrm {deg}}(\xi /S)_\tau (t)$ satisfies that

  $$\begin{aligned} {\mathrm {deg}}(\xi /S)_\tau (t)+p{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \tau }(t)<p/e_\mathfrak {p} \end{aligned}$$

  for every $\tau$ in $\hat{\varSigma }_\mathfrak {p}$ and $1\le t\le e_\mathfrak {p}$;

• for $\mathfrak {p}=\mathfrak {P}$, ${\mathrm {deg}}(\xi /S)$ lies in I.

It is an admissible open subset of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ by Maximum Modulus Principle.

For brevity, let

$$\begin{aligned} r=r_\mathfrak {P}=1/p+1/p^2+\cdots +1/p^{f-1}<1/(p-1)<1 \end{aligned}$$

if $e=1$.

Proposition 22

If $e=e_\mathfrak {P}>1$ and $f=f_\mathfrak {P}\ge 1$, a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0,1/e)$ which is a $U_\mathfrak {P}$-eigenform with non-zero eigenvalue, extends to $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$.

If $e=1$ and $f>1$ (resp. $f=1$), a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, 1)$ (resp. $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, p/(p+1))$) which is a $U_\mathfrak {P}$-eigenform with non-zero eigenvalue, extends to $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f-r)$ (resp. $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, 1)$).

Proof

When $e=1$, Proposition 20 recovers Lemma 5.3 in [26] and the assertion follows from a straightforward generalisation of the proof of Proposition 5.7 in [26]. Suppose therefore that $e>1$. For clarity, we break our proof into two steps.

Step 1 Extending a U-eigenform, with non-zero eigenvalue, from $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0,1/e)$ to $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0,f-1/e]$.

Suppose $\xi$ is a non-cuspidal point of $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f-1/e]$. Let (A, C) denote the corresponding HBAV over S together with a Raynaud vector subspace scheme C of A.

Suppose that there exists $\dagger$ in $\hat{\varSigma }$ such that $\gamma _{{\mathrm {EO}}, \dagger }(\overline{\xi }/\overline{S})=\{l\}$ for some $1\le l\le e$. It follows from Proposition 20 that ${\mathrm {deg}}(\xi /S)_\dagger (l-1)=0$ if $l>1$ or ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \dagger }(e)=0$ if $l=1$. For brevity, we assume $l>1$. It then follows from Lemma 24 that, if $\zeta$ denotes the point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ corresponding to (A, D) for a Raynaud vector space subscheme D such that $D[\pi ]$ is distinct from $C[\pi ]$, all ${\mathrm {deg}}(\zeta /S)_\dagger (l), {\mathrm {deg}}(\zeta /S)_\dagger (l+1),\dots$ are 1 / e except ${\mathrm {deg}}(\zeta /S)_\dagger (l-1)$ which satisfies $0<{\mathrm {deg}}(\zeta /S)_\dagger (l-1)<1/e$. Because of Proposition 20 and the observation that ${\mathrm {deg}}((A/D, A[\pi ])/S)_\tau (t)=1/e-{\mathrm {deg}}(\zeta /S)_\tau (t)$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$, the point corresponding to $(A/D, A[\pi ]/D)$ lies in $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ and $0<{\mathrm {deg}}((A/D, A[\pi ]/D)/S)<1/e$.

Step 2 Extending a U-eigenform, with non-zero eigenvalue, from $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f-1/e]$ to $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$.

Let $\xi$ be a point of $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)-X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f-1/e]$. As in Step 1, let (A, C) denote the corresponding HBAV over $S={\mathrm {Spec}}\, \mathscr {O}_K$ (where $\mathscr {O}_K$ is the ring of integers of a finite extension K of L) together with a Raynaud vector subspace scheme C of A, and suppose that $\gamma _{{\mathrm {EO}}, \dagger }(\overline{\xi }/\overline{S})=\{l\}$ for some $\dagger$ in $\hat{\varSigma }$ and $1\le l\le e$. By assumption, ${\mathrm {deg}}(\xi /S)_\dagger (l), {\mathrm {deg}}(\xi /S)_\dagger (l+1), \dots ,$ are all 1 / e except the last in the arrangement for which $0<{\mathrm {deg}}(\xi /S)_\dagger (l-1)<1/e$ if $l>1$, or $0<{\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \dagger }(e)<1/e$ if $l=1$, holds. For brevity, suppose $l>1$.

We use the set of notation introduced in Sect. 5.5. Let D be a Raynaud vector space subscheme which is distinct from C in $A[\pi ]$ and let $\zeta$ denote the point corresponding to (A, D) as in Step 1. It follows from Lemma 25 that $\rho _\tau ^t=0$ except when $\tau$ is $\dagger$ and t is $l-1$. It is enough to establish that $\chi ^{D, l-1}_\dagger >0$ as it then follows from Proposition 20 that all ${\mathrm {deg}}(\zeta /S)_\dagger (l), {\mathrm {deg}}(\zeta /S)_\dagger (l+1),\dots$ are 1 / e, except $0<{\mathrm {deg}}(\zeta /S)_\dagger (l-1)<1/e$, and the assertion of Step 2 follows as concluded in Step 1.

Suppose that ${\mathrm {deg}}(\zeta /S)_\dagger (l-1)=\chi _\dagger ^{D, l-1}=0$. In which case, $\rho _\dagger ^{D, l-1}=e_K/e$ by Lemma 21. It therefore follows from with $\pi ^{\rho _\dagger ^{D, l-1}} U_\dagger ^{l-1}=0$ in $\overline{R}$ that $\varepsilon _\dagger ^l \pi ^{\chi _\dagger ^{l-1}}=0$ in $\overline{\mathscr {O}}_K$. On the other hand, Corollary 3, combined with Proposition 20, establishes, in particular, that $\chi ^{D, l}_\dagger =e_K/e$ (we know $\chi _\dagger ^l=e_K/e$ and $\chi ^{D, l}_\dagger >0$ but it takes the knowledge of $\chi _\dagger ^{D, l+1}=e_K/e$ and Proposition 20 to conclude this claim). Since $e_K/e-\chi _\dagger ^{D, l}$ is computed (see the formula for $\chi _\dagger ^{D, l}$) by the valuation of $S_\dagger ^l \varepsilon _\dagger ^l$ in $\overline{R}$ (because $\chi _\dagger ^l=e_K/e$), it follows that the valuation of $\varepsilon _\dagger ^l$ (and of $S_\dagger ^l$) is zero. Combined with the claim earlier, this would imply that $\chi _\dagger ^{l-1}=e_K/e$ which contradicts the assumption that $\chi _\dagger ^{l-1}=e_K{\mathrm {deg}}(\xi /S)_\dagger (l-1)<e_K/e$. $\square$

Proposition 23

Let $\xi$ be a point of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ which corresponds to (A, C) defined over $S={\mathrm {Spec}}\, R$ for the ring R of integers of a finite extension of L. Fix a prime $\mathfrak {P}$ above p with a uniformiser $\pi$. Suppose that

• (I) if $e_\mathfrak {P}>1$ and $f_\mathfrak {P}\ge 1$, there exists $\dagger$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {P}$ and $1\le t\le e$ such that ${\mathrm {deg}}(\xi /S)_\tau (t)=1/e$ for every $\tau$ in $\hat{\varSigma }$ and $1\le t\le e$ except for $\tau =\dagger$ and $t=l-1$ at which $0<{\mathrm {deg}}(\xi /S)_\dagger (l-1)<1/e$ holds;

• (II) if $e=1$ and $f>1$, there exists $\dagger$ in $\hat{\varSigma }=\hat{\varSigma }_\mathfrak {P}$ such that ${\mathrm {deg}}(\xi /S)_\tau =1$ for every $\tau$ in $\hat{\varSigma }$ distinct from $\mathfrak {f}^{-1}\circ \dagger$ while ${\mathrm {deg}}(\xi /S)_{\mathfrak {f}^{-1}\circ \dagger }$ lies in the open interval $(f-1, f-r)$

• (III) if $e=1$ and $f=1$, ${\mathrm {deg}}(\xi /S)$ lies in (0, 1)

Then, for any Raynaud submodule scheme D of $A[\pi ]$ over S that is distinct from C in $A[\pi ]$, (A, D) / S defines a S-point $\zeta$ of $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ such that ${\mathrm {deg}}(\zeta /S)$ lying in $(f-1/e, f)$, (resp. $(f-1, f-r)$, resp. (0, 1)) if (I) (resp. (II), resp. (III)) holds.

Proof

The case (III) is proved in [43] while the case (II) is dealt with in [26]. The case (I) follows from the preceding proposition . $\square$

Remark

This is a generalisation of Kassaei’s ‘saturation’ (see Lemma 5.9 in [26]).

Definition

Let $\varSigma _{K{\mathrm {Iw}}}^{+}$ be the admissible open subset of points $\xi$ over S in $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ such that, for every $\mathfrak {p}$, ${\mathrm {deg}}(\xi /S)$ lies in $(f_\mathfrak {p}-1/e_\mathfrak {p}, f_\mathfrak {p})$ (resp. $(f_\mathfrak {p}-1, f_\mathfrak {p}-r_\mathfrak {p})$, resp. (0, 1)) when (I) (resp. (II), resp. (III)) of Proposition 23 holds.

Lemma 29

For every representative $\ell$, if $f>1$ (resp. $f=1$), the pull-back $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f)$ of $X_{K{\mathrm {Iw}}}^{+, \varGamma } [0, f)\hookrightarrow X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ (resp. the pull-back $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, 1)$ of $X_{K{\mathrm {Iw}}}^{+, \varGamma } [0, 1)\hookrightarrow X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$) along $X_{K{\mathrm {Iw}}, \ell }^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}\hookrightarrow X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, {\mathrm {R}}\text{- }{\mathrm {a}}}$ is connected.

Proof

This can be proved as in Lemma 6.3 in [26]. We sketch our proof for the case $f>1$. Firstly, we show $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1)/e]$ is connected.

The connectedness of$X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1)/e]$: In the special fibre $\overline{X}_{K{\mathrm {Iw}}, \ell }$, the irreducible components are parameterised as $\overline{X}^\varSigma$ where $\varSigma =\varSigma _{\mathrm {RZ}}=(\gamma _{{\mathrm {RZ}}, \tau }, \nu _{{\mathrm {RZ}}, \tau })$ (see Sect. 5.4) satisfies the conditions that hold for every $\mathfrak {p}$: every $1\le t\le e_\mathfrak {p}$ lies either $\gamma _{{\mathrm {RZ}}, \tau }$ or $\nu _{{\mathrm {RZ}}, \tau }$, but it does not lie simultaneously in $\gamma _{{\mathrm {RZ}}, \tau }$ and $\nu _{{\mathrm {RZ}}, \tau }$ for every $\tau$ in $\hat{\varSigma }_\mathfrak {p}$.

To attain some clarity in our exposition, we may and will henceforth suppose that $|S_{\mathrm {P}}|=1$, and we omit our reference to $\mathfrak {P}$ when convenient.

For $0\le N\le d-1$ which is of the form $N=e(\chi -1)+t$ for some $1\le \chi \le f$ and $0\le t\le e-1$, let $\varSigma _N$ denote $\varSigma _{{\mathrm {RZ}}, N}$ defined by

• $\gamma _{{\mathrm {RZ}}, \dagger }=\cdots =\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-(\chi +1)}\circ \dagger }=\varnothing$,

• $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-\chi }\circ \dagger }=\{e-(t-1), \dots , e-1, e\}$ (in particular, $|\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-\chi }\circ \dagger }|=t$),

• $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-(\chi -1)}\circ \dagger }=\cdots =\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \dagger }=\{1, \dots , e\}$

• $\nu _{{\mathrm {RZ}}, \tau }=\{1, \dots , e\}-\gamma _{{\mathrm {RZ}}, \tau }$ for every $\tau$ in $\hat{\varSigma }$.

For example, when $N=d-1$ in which case $\chi =f$ and $t=e-1$, then $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-1}\circ \dagger }=\{e\}$ while $\gamma _{{\mathrm {RZ}}, \tau }=\varnothing$ for every $\tau$ in $\hat{\varSigma }$ distinct from $\mathfrak {f}^{-1}\circ \dagger$. At the other end of the spectrum, if $N=0$ ($\chi =1$ and $t=0$), then $\gamma _{{\mathrm {RZ}}, \tau }=\{1, \dots , e\}$ for every $\tau$ in $\hat{\varSigma }$.

When $N=0$, let $\overline{X}_{\varSigma _N}$ denote $\overline{X}^\varSigma -( \overline{X}^\varSigma \cap \overline{X}^{\varSigma ^\varnothing })$ where $\varSigma =\varSigma _{\mathrm {RZ}}$ is defined by $\gamma _{{\mathrm {RZ}}, \tau }=\{1, \dots e\}$ for every $\tau$ in $\hat{\varSigma }$ and where $\varSigma ^\varnothing$ differes from $\varSigma$ by the corresponding $\gamma _{{\mathrm {RZ}}, \tau }^\varnothing =\varnothing$ for every $\tau$ in $\hat{\varSigma }$. For $N\ge 1$, let $\overline{X}_{\varSigma _N}$ denote the union of $\overline{X}^{\varSigma _J}$ as J ranges over $0\le J\le N-1$.

Let $\overline{X}^+_{\varSigma _N}$ denote $\overline{X}_{\varSigma _N}\cap \overline{X}_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$. As $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1)/e]={\mathrm {sp}}^{-1}(\overline{X}^+_{\varSigma _{d-1}})$, it suffices to prove that $\overline{X}^+_{\varSigma _{N}}$ is connected when $N=d-1$. We prove the connectedness by induction. One checks firstly that $\overline{X}^+_{\varSigma _N}$ is connected when $N=0$ by the density and the connectedness of the multiplicative ordinary locus of $\overline{X}^{\mathrm {PR}}_{K{\mathrm {Iw}}}$. Secondly, we assume the connectedness of $\overline{X}^+_{\varSigma _{N-1}}$ to prove the connectedness of $\overline{X}^+_{\varSigma _N}$. Let $\overline{\xi }$ be a point of $\overline{X}^+_{\varSigma _N}-\overline{X}^+_{\varSigma _{N-1}}$. Write $\varSigma$ for $\varSigma _{\mathrm {RZ}}(\overline{\xi })$, which is $\varSigma _{{\mathrm {RZ}}, N}$ as above.

Let $\varSigma ^+$ be exactly the same as $\varSigma$ except at $\mathfrak {f}^{-\chi }\circ \dagger$ at which we demand $\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-\chi }\circ \dagger }=\{e-t, \dots , e\}=\gamma _{{\mathrm {RZ}}, \mathfrak {f}^{-\chi }\circ \dagger }\cup \{e-t\}$. One observes that $\varSigma ^+$ is nothing other than $\varSigma _{{\mathrm {RZ}}, N-1}$, and $\overline{X}^{\varSigma ^+}$ is a member of the union $\overline{X}_{\varSigma _{N-1}}$. We then conclude our argument by showing, if X is an irreducible component of $\overline{X}^\varSigma$ passing through $\overline{\xi }$, that $X\cap \overline{X}^{+}_{K{\mathrm {Iw}}, \ell }$ is connected and $(X\cap \overline{X}^{+}_{K{\mathrm {Iw}}, \ell })\cap \overline{X}^{\varSigma ^+}\ne \varnothing$.

The connectedness of$X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f)$: It suffices to prove the connectedness of $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1+\gamma )/e]$ for some $\gamma \in (0, 1)\cap \mathbf {Q}$. Suppose that $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1+\gamma )/e]$ is not connected. Then there exists a connected component X of $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1+\gamma )/e]$ which does not intersect $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1)/e]$. By the quasi-compactness of X, there exists $\nu <\gamma /e$ such that $X_{K{\mathrm {Iw}}, \ell }^{+, \varGamma } [0, f-1+(e-1+\nu )/e]\cap X=\varnothing$.

Let $\xi$ be a point of X. In which case, $\nu (\xi )=f-1+(e-1)/e+\nu (\xi )_{\mathfrak {f}^{-1}\circ \dagger }(e)$, where $\nu (\xi )_{\mathfrak {f}^{-1}\circ \dagger }(e)$ denotes the valuation of ${\mathrm {y}}_{\mathfrak {f}^{-1}\circ \dagger }^e(\xi )$ as defined in Sect. 6.1, while it follows from the definition of $\nu$ that $\nu (\xi )>f-1+(e-1)/e+\nu$. Combining, one deduces that $\nu (\xi )_{\mathfrak {f}^{-1}\circ \dagger }(e)>\nu$. In fact, for any point $\zeta$ in $X\cap {\mathrm {sp}}^{-1}(\overline{\xi })$, the strict inequality $\nu (\zeta )_{\mathfrak {f}^{-1}\circ \dagger }(e)>\nu$ holds.

On the other hand, the admissible open subset ${\mathrm {sp}}^{-1}(\overline{\xi })[0, f-1+(e-1+\gamma )/e]$ of points $\zeta$ in ${\mathrm {sp}}^{-1}(\overline{\xi })$, such that $0\le {\mathrm {deg}}(\zeta )\le f-1+(e-1+\gamma )/e$ holds, is evidently connected and is contained in X. As for any point $\zeta$ in ${\mathrm {sp}}^{-1}(\overline{\xi })[0, f-1+(e-1+\gamma )/e]$, ${\mathrm {deg}}(\zeta )$ is given by $f-1+(e-1)/e+\nu (\zeta )_{\mathfrak {f}^{-1}\circ \dagger }(e)$, one may therefore deduce $\nu (\zeta )_{\mathfrak {f}^{-1}\circ \dagger }(e)\le \gamma /e$ holds. This is a contradiction. $\square$

Suppose that the level K of overconvergent modular forms is K as in Theorem 5. In particular, let T denote the disjoint union of $S_{\mathrm {P}}, S_{\mathrm {R}}, S_{{\mathrm {L}}}, S_{{\mathrm {A}}}$.

Proposition 24

Fix a subset $\varGamma$ of $S_{\mathrm {P}}$ such that $|\varGamma |\le |S_{\mathrm {P}}|-1$. Suppose that $S_{\mathrm {P}}$ is a disjoint union of two subsets $S_{{\mathrm {P}}, {\mathrm {e}}}$ and $S_{{\mathrm {P}}, {\mathrm {d}}}$. Let $\varGamma _{\mathrm {e}}$ (resp. $\varGamma _{\mathrm {d}}$) denote $\varGamma \cap S_{{\mathrm {P}}, {\mathrm {e}}}$ (resp. $\varGamma \cap S_{{\mathrm {P}}, {\mathrm {d}}}$).

For every $\varSigma =\varSigma _{\mathrm {d}}\times \varSigma _{\mathrm {e}}\subset S_{\mathrm {P}}-\varGamma =(S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}})\times (S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}})$, suppose that $F_\varSigma$ is a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f-r)$ if $f=f_\mathfrak {P}>1$ and $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, 1)$ if $f=1$ satisfying

$$\begin{aligned} U_\mathfrak {p} F^\varGamma _{\varSigma }= & {} \alpha _\mathfrak {p} F^\varGamma _\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } (S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}})-\varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F^\varGamma _\varSigma= & {} \beta _\mathfrak {p} F^\varGamma _\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F^\varGamma _\varSigma= & {} \alpha _\mathfrak {p} F^\varGamma _\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } (S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}})-\varSigma _{\mathrm {e}}\\ U_\mathfrak {p} F^\varGamma _\varSigma= & {} \alpha _\mathfrak {p} F_\varSigma ^\varGamma +F^\varGamma _{\varSigma -\{\mathfrak {p}\}} \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {e}}\\ U_{\mathrm {Q}} F^\varGamma _\varSigma= & {} 0 \quad \hbox { for every } {\mathrm {Q}} \hbox { in } T-S_{\mathrm {P}},\\ T_{\mathrm {Q}} F^\varGamma _\varSigma= & {} \gamma _{\mathrm {Q}} F^\varGamma _\varSigma \quad \hbox { for every } {\mathrm {Q}} \hbox { not in } T \end{aligned}$$

where $\alpha$’s and $\beta$’s are all assumed non-zero. Then, for $\mathfrak {P}$ in $S_{\mathrm {P}}-\varGamma$ which we fix, the family $\{F_\varSigma \}_\varSigma$ of eigenforms define a family of eigenforms $\{F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}\}_\varSigma$ defined over $X_{K{\mathrm {Iw}}}^{+, \varGamma } [0, f]$ with $\varSigma =\varSigma _{\mathrm {d}}\times \varSigma _{\mathrm {e}}$ ranging amongst the subsets of $S_{\mathrm {P}}-(\varGamma \cup \{\mathfrak {P} \})$ such that, if $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}}$,

$$\begin{aligned} U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_{\varSigma }= & {} \alpha _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {\mathfrak {P}}\}}_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in }\\&(S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}}-\{\mathfrak {P}\})-\varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {\mathfrak {p}}\}}_\varSigma= & {} \beta _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {d}},\\ (U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma -\alpha _\mathfrak {p}) F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} 0 \quad \hbox { for every } \mathfrak {p} \hbox { in } (S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}})-\varSigma _{\mathrm {e}}\\ U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \alpha _\mathfrak {p}F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma +F^{\varGamma \cup \{\mathfrak {P}\}}_{\varSigma -\{\mathfrak {p}\}} \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {e}}\\ U_{\mathrm {Q}} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} 0 \quad \hbox { for every } {\mathrm {Q}} \hbox { in } T-S_{\mathrm {P}},\\ T_{\mathrm {Q}} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \gamma _{\mathrm {Q}} F^\varGamma _\varSigma \quad \hbox { for every } {\mathrm {Q}} \hbox { not in } T, \end{aligned}$$

or if $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}}$

$$\begin{aligned} U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_{\varSigma }= & {} \alpha _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } (S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}})-\varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \beta _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {d}},\\ U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \alpha _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma \quad \hbox { for every } \mathfrak {p} \hbox { in } (S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}}-\{\mathfrak {P}\})-\varSigma _{\mathrm {e}}\\ U_\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \alpha _\mathfrak {p} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma +F^{S\cup \{\mathfrak {P}\}}_{\varSigma -\{\mathfrak {p}\}} \quad \hbox { for every } \mathfrak {p} \hbox { in } \varSigma _{\mathrm {e}}\\ U_{\mathrm {Q}} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} 0 \hbox { for every } {\mathrm {Q}} \hbox { in } T-S_{\mathrm {P}},\\ T_{\mathrm {Q}} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma= & {} \gamma _{\mathrm {Q}} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma \hbox { for every } {\mathrm {Q}} \hbox { not in } T. \end{aligned}$$

Furthermore, when $f>1$ (resp. $f=1$), if the equality

$$\begin{aligned} F_\varSigma ^\varGamma ((A, C))=F_\varSigma ^\varGamma ((A, D)) \end{aligned}$$

holds for any pair of points (A, C) and (A, D) of $\varSigma _{K{\mathrm {Iw}}}^{+}\cap X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$ (resp. $\varSigma _{K{\mathrm {Iw}}}^{+}\cap X_{K{\mathrm {Iw}}}^{+, \varGamma }[(e-1)/e, 1)$) satisfying $C[\mathfrak {p}]\ne D[\mathfrak {p}]$ for all $\mathfrak {p}$ in $\varGamma$, then

$$\begin{aligned} F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}((A, C))=F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}((A, D)) \end{aligned}$$

holds for any pair of points (A, C) and (A, D) of $\varSigma _{K{\mathrm {Iw}}}^{+}\cap X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$ satisfying $C[\mathfrak {p}]\ne D[\mathfrak {p}]$ for every $\mathfrak {p}$ in $\varGamma \cup \{\mathfrak {P}\}$.

Proof

We shall prove the case $e>1$ and $f>1$. The case $f=1$ follows similarly. Fix $\varSigma \subset S_{\mathrm {P}}-(\varGamma \cup \{\mathfrak {P}\})$.

Suppose firstly that $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}}$. By definition, the sections $F^\varGamma _\varSigma$ and $F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ are both thought of as being defined over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)\subset X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f]$ and are eigenforms with the same eigenvalues except at $\mathfrak {P}$. For brevity, let $U_\mathfrak {P} F^\varGamma _\varSigma =\alpha F^\varGamma _\varSigma$ and $U_{\mathfrak {P}} F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}=\beta F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$; we shall also let $F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}=\alpha F^\varGamma _{\varSigma }-\beta F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ and $H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}=-( F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}} -F^\varGamma _{\varSigma })$, both of which are defined over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$ but are no longer $U_{\mathfrak {P}}$-eigenforms. We shall think of $H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}$ as a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, 1/e)\subset X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)$ (since $f>1$ is assumed).

Suppose that $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}}$. The sections $F^\varGamma _\varSigma$ and $F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ are eigenforms with the same eigenvalues for Hecke operators away from $S_{\mathrm {P}}$ and for $U_\mathfrak {p}$ for $\mathfrak {p}$ in $S_{\mathrm {P}}-\varGamma$; furthermore, $F^\varGamma _\varSigma$ is an $U_{\mathfrak {P}}$-eigenform with eigenvalue $\alpha$ (which we may assume to be 1 but continues to write $\alpha$) while $F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ is a multiplicity 2 generalised $U_\mathfrak {P}$-eigenvector and $U_{\mathfrak {P}}F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}=\alpha F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}+F^\varGamma _{\varSigma }$. We let $F^{\varGamma \cup \{\mathfrak {P}\}}_{\varSigma }=F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ and $H^{\varGamma \cup \{\mathfrak {P}\}}_{\varSigma }=\alpha F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}+F^\varGamma _{\varSigma }$.

Let $w=w_\mathfrak {P}$ denote the map of sections defined as above. We shall glue $w (H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}})$ defined over $w( X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, 1/e))=X_{K{\mathrm {Iw}}}^{+, \varGamma }(f-1/e, f]$ and $F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}$ at the intersection

$$\begin{aligned} X_{K{\mathrm {Iw}}}^{+, \varGamma }(f-1/e, f)= X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)\cap X_{K{\mathrm {Iw}}}^{+, \varGamma }(f-1/e, f] \end{aligned}$$

to construct a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f)\cup X_{K{\mathrm {Iw}}}^{+, \varGamma }(f-1/e, f]= X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f].$

For the fractional ideal $J=\ell ^{-1}$ for some fixed representative $\ell$ , let ${\mathrm {Tate}}_J(q)=\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^J$ denote the algebrified (rigid analytic) quotient over a $[F:\mathbf {Q}]$-dimensional polydisc over L by the $O_F$-linear morphism $q: J\rightarrow \mathbb {G}\otimes _{\mathbf {Z}} D^{-1}$.

The (semi)abelian variety ${\mathrm {Tate}}_J(q)$ comes naturally equipped with real multiplication and is naturally $J^{-1}$-polarisable. We suppose that ${\mathrm {Tate}}_J(q)$ is equipped with a n-level structure $\eta$ and (when appropriate) with choices of isomorphisms:

• $O_F/\mathfrak {p}\simeq (\mathbb {G}\otimes _\mathbf {Z} D^{-1})[\mathfrak {p}]$

• and $O_F/\mathfrak {p}\simeq \mathfrak {p}^{-1} J/J$ (and let $q^{\mathfrak {p}^{-1}}$ denote a lifting in $q^{\mathfrak {p}^{-1}}$ of the generator of $q^{\mathfrak {p}^{-1}J/J}$ defined by this isomorphism)

for every $\mathfrak {p}$ above p, and these define cusps of $X_{K{\mathrm {Iw}}}^{\mathrm {PR}}$ and $X_{K{\mathrm {Iw}}, {\mathrm {Iw}}_\mathfrak {p}}^{\mathrm {PR}}$.

For an overconvergent cuspidal modular form F of weight $\lambda =(1, w)$ and of level $K{\mathrm {Iw}}$, let $F_{J}$ denote the restriction of F over $X^{{\mathrm {PR}}, {\mathrm {R}}\text {-}{\mathrm {a}}}_{K{\mathrm {Iw}}, \ell }$ and let $\sum _{\nu \in J_+} c_J(\nu , F)q^\nu$ denote the q-expansion obtained by evaluating F (or $F_J$) at ${\mathrm {Tate}}_J(q)$. By slight abuse of notation, by

$$\begin{aligned} (\mathbb {G}\otimes _\mathbf {Z}D^{-1})[\mathfrak {P}]/q^J\subset (\mathbb {G}\otimes _\mathbf {Z}D^{-1})[p]/q^J \end{aligned}$$

we shall also mean the ‘full’ multiplicative Raynaud vector subspace of ${\mathrm {Tate}}_J(q)$ (as only the $\mathfrak {P}$-part is relevant to the calculations that follow). Then, fixing $J=\ell ^{-1}$ as above,

$$\begin{aligned} (U_\mathfrak {P}F)({\mathrm {Tate}}_J(q), \mathbb {G}\otimes _\mathbf {Z}D^{-1}[\mathfrak {P}]/p^J)=\sum _{\nu \in J_+} c_{J_\mathfrak {P}}(r\nu , F)q^\nu \end{aligned}$$

where r is a totally positive element satisfying $\mathfrak {P}J^{-1}=r J^{-1}_\mathfrak {P}$ with $J_\mathfrak {P}^{-1}=\ell _\mathfrak {P}$ a member of the fixed representative for the class of the fractional ideal $\mathfrak {P} J^{-1}$.

More generally, for any non-zero integer $\lambda$, let $J_{\mathfrak {P}^\lambda }$ denote a member of the fixed set of representatives satisfying $\mathfrak {P}^\lambda J^{-1}=r_\lambda J_{\mathfrak {P}^\lambda }$ for some totally positive element $r_\lambda =r^J_{\mathfrak {P}^\lambda }$. We often write r for $r_1$.

Lemma 30

Over $X_{K{\mathrm {Iw}}}^{+, \varGamma }(f-1/e, f)$ if $e>1$, over $X^{+, \varGamma }_{K{\mathrm {Iw}}}(f-1, f-r)$ if $e=1$ and $f>1$ and over $X^{+, \varGamma }_{K{\mathrm {Iw}}}(f-1, f-r)$ if $e=1$ and $f=1$,

$$\begin{aligned} F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}=w ( H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}). \end{aligned}$$

Proof

Firstly we prove the case when $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {d}}}-\varGamma _{\mathrm {d}}$. As in Proposition 6.9, [26], it suffices to prove the equality

$$\begin{aligned} \pi _{1, \mathfrak {P}}^*F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}=\pi ^*\pi _{2, \mathfrak {P}}^*H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}} \end{aligned}$$

of sections over the admissible open subset $\pi _{1, \mathfrak {P}}^{-1}( X^{+, \varGamma }_{K{\mathrm {Iw}}}[0, f))$ in the generic fibre $X^{\mathrm {PR}}_{K{\mathrm {Iw}}, {\mathrm {Iw}}_{\mathfrak {P}}}$, where $\pi$ is the map of invertible sheaves $\pi _{2, \mathfrak {P}}^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}\rightarrow \pi _{1, \mathfrak {P}}^*\mathscr {A}_{\lambda , {\mathrm {R}}\text{- }{\mathrm {a}}}$ where $\lambda =(1, 1)$.

We may and will normalise Fourier q-expansions to assume $\alpha c_J(\nu , F_{\varSigma }^{\varGamma })=c_{J_\mathfrak {P}}(r\nu , F_{\varSigma }^{\varGamma })$ and $\beta c_J(\nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma })=c_{J_\mathfrak {P}}(r\nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma })$, for r in $F_+$ such that $\mathfrak {P}J^{-1}=rJ_\mathfrak {P}^{-1}$, hold for all $\nu$ in $J_+$. On one hand,

$$\begin{aligned}&\pi _{1, \mathfrak {P}}^*F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}(\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{J}, \mathbb {G}\otimes _{\mathbf {Z}} D^{-1}[\mathfrak {P}]/q^{J}, q^{\mathfrak {P}^{-1}})\\&\quad =(\alpha F_{\varSigma }^\varGamma -\beta F_{\varSigma \cup \{\mathfrak {P}\}}^\varGamma )(\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{J})\\&\quad =\sum _{\nu \in J_+} (\alpha c_J( \nu , F_{\varSigma }^{\varGamma })- \beta c_J(\nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma }))q^\nu \\&\quad =\sum _{\nu \in J_+} ( c_{J_\mathfrak {P}}( r\nu , F_{\varSigma }^{\varGamma })-c_{J_\mathfrak {P}}(r\nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma }))q^{ \nu }. \end{aligned}$$

On the other hand,

$$\begin{aligned}&\pi ^*\pi _{2, \mathfrak {P}}^*H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}(\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{J}, \mathbb {G}\otimes _{\mathbf {Z}} D^{-1}[\mathfrak {P}]/q^{J}, q^{\mathfrak {P}^{ -1}}) \\&\quad =-(F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}-F^\varGamma _{\varSigma }) (\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{\mathfrak {P}^{ -1}J})\\&\quad =(F^\varGamma _{\varSigma }-F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}) (\mathbb {G}\otimes _\mathbf {Z}D^{-1}/q^{J_\mathfrak {P}})\\&\quad =\sum _{\nu \in J_+} ( c_{J_\mathfrak {P}}( r\nu , F^\varGamma _{\varSigma })-c_{J_\mathfrak {P}} (r\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}) ) q^{ \nu } \end{aligned}$$

We shall prove the case when $\mathfrak {P}$ is in $S_{{\mathrm {P}}, {\mathrm {e}}}-\varGamma _{\mathrm {e}}$. We may normalise the Fourier q-expansion to assume, for every $\nu$ in $J_+$, that $\alpha c_J(\nu , F_\varSigma ^\varGamma )=c_{J_\mathfrak {P}} (r \nu , F_\varSigma ^\varGamma )$ holds.

Since

$$\begin{aligned} U_\mathfrak {P}( F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}-c F^\varGamma _{\varSigma })=\alpha F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}+F^\varGamma _{\varSigma }-c\alpha F^\varGamma _{\varSigma }=\alpha (F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}-cF^\varGamma _{\varSigma })+F^\varGamma _{\varSigma } \end{aligned}$$

for a constant c, one may subtract a constant multiple of $F_{\varSigma , J}^\varGamma$ from $F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}, J}$ if necessary to assume, for every J that

$$\begin{aligned} c_J(1 , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}, J})=0 \end{aligned}$$

from now onwards. Since $F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}$ is an eigenform for all Hecke operator $T_{\mathrm {Q}}$ for ${\mathrm {Q}}$ not in T, we may therefore further assume that

$$\begin{aligned} c_J (\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}, J})=0 \end{aligned}$$

for every J and $\nu$ in $J_+$ such that $\nu J^{-1}$ is coprime to the primes of T, or indeed to p by making the tame level K sufficiently smaller, if necessary.

Sublemma 1

For $\lambda \ge 1$, $c_{J_{\mathfrak {P}^\lambda }} ( r_\lambda \nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})= \lambda \alpha ^{\lambda -1} c_{J} ( \nu , F^\varGamma _{\varSigma })$ for $\nu J^{-1}$ coprime to p.

Proof

Evaluating $U_{\mathfrak {P}}F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}= \alpha F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}+F^\varGamma _{\varSigma }$ at $({\mathrm {Tate}}_J(q), \mathbb {G}\otimes _\mathbf {Z}D^{-1})[\mathfrak {P}]/q^J)$, we have

$$\begin{aligned} \sum _{\nu \in J_+} c_{J_\mathfrak {P}}(r\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})q^\nu =\sum _{\nu \in J_+} \alpha c_J(\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})q^\nu +\sum _{\nu \in J_+} c_J(\nu , F^\varGamma _{\varSigma })q^\nu \end{aligned}$$

i.e.,

$$\begin{aligned} c_{J_\mathfrak {P}}(r\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})=\alpha c_J(\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})+c_J(\nu , F^\varGamma _{\varSigma }). \end{aligned}$$

Similarly, since $U_\mathfrak {P}^\lambda F_{\varSigma \cup \{\mathfrak {P}\}}^\varGamma =\alpha ^\lambda F_{\varSigma \cup \{\mathfrak {P}\}}^\varGamma +\lambda \alpha ^{\lambda -1} F_{\varSigma }^\varGamma$, evaluating at $({\mathrm {Tate}}_J(q), \mathbb {G}\otimes _\mathbf {Z}D^{-1})[\mathfrak {P}]/q^J)$, we have

$$\begin{aligned} \sum _{\nu \in J_+} c_{J_{\mathfrak {P}^\lambda }}( r_\lambda \nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})q^\nu= & {} \sum _{\nu \in J_+} \alpha ^\lambda c_J(\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})q^\nu \\&+\lambda \alpha ^{\lambda -1}\sum _{\nu \in J_+} c_J(\nu , F^\varGamma _{\varSigma })q^\nu , \end{aligned}$$

which proves the assertion, as $c_J(\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})=0$. $\square$

As $\alpha$ is a unit, we may and will explicitly assume $\alpha =1$.

Sublemma 2

For $\lambda \ge 1$, $c_{J_{\mathfrak {P}^\lambda }} (r_\lambda \nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}})=\lambda c_J(\nu , F^\varGamma _{\varSigma })$ for $\nu$ in $J_+$.

Proof

Clear. $\square$

We now prove the assertion of the lemma, by comparing q-expansions at $({\mathrm {Tate}}_{J}(q), \mathbb {G}\otimes _\mathbf {Z}D^{-1}[\mathfrak {P}]/q^{J})$. On one hand,

$$\begin{aligned}&F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}(\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{J}, \mathbb {G}\otimes _\mathbf {Z} D^{-1}[\mathfrak {P}]/q^{J})\\&\quad =\sum _{\nu \in J_+}c_{J} ( \nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma }) q^{\nu }. \end{aligned}$$

In particular, the coefficient of $r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}} \nu$-power of q, where $\nu$ lies in $J_+$, is

$$\begin{aligned} c_{J} (r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}} \nu , F_{\varSigma \cup \{\mathfrak {P}\}}^{\varGamma })=\lambda c_{J_{\mathfrak {P}^{-\lambda }}}(\nu , F_\varSigma ^\varGamma ) \end{aligned}$$

by the lemma.

On the other hand,

$$\begin{aligned}&w(H_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}})(\mathbb {G}\otimes _{\mathbf {Z}} D^{-1}/q^{J}, \mathbb {G}\otimes _{\mathbf {Z}} D^{-1}[\mathfrak {P}]/q^{J})\\&\quad =\sum _{\nu \in J_{+}} c_{J_{\mathfrak {P}^{-1}}} ( (r^{J_{\mathfrak {P}^{-1}}})^{-1}\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}) q^{ \nu }+\sum _{\nu \in J_{+}} c_{J_{\mathfrak {P}^{-1}}} ( (r^{J_{\mathfrak {P}^{-1}}})^{-1} \nu , F^\varGamma _{\varSigma }) q^{ \nu }. \end{aligned}$$

Because $r^{J_{\mathfrak {P}^{-1}}}= r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}} / r_{\lambda -1}^{J_{\mathfrak {P}^{-\lambda }}}$ by definition, the coefficient of the $r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}}\nu$-power of q, where $\nu$ lies in $J_+$, is

$$\begin{aligned}&c_{J_{\mathfrak {P}^{-1}}} ( ( r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}} / r_{\lambda -1}^{J_{\mathfrak {P}^{-\lambda }}})^{-1} r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}}\nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}) \\&\quad +c_{J_{\mathfrak {P}^{-1}}} ( ( r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}} / r_{\lambda -1}^{J_{\mathfrak {P}^{-\lambda }}})^{-1} r_\lambda ^{J_{\mathfrak {P}^{-\lambda }}}\nu , F^\varGamma _{\varSigma })\\&\quad =c_{J_{\mathfrak {P}^{-1}}} ( r_{\lambda -1}^{J_{\mathfrak {P}^{-\lambda }}} \nu , F^\varGamma _{\varSigma \cup \{\mathfrak {P}\}}) +c_{J_{\mathfrak {P}^{-1}}} (r_{\lambda -1}^{J_{\mathfrak {P}^{-\lambda }}}\nu , F^\varGamma _{\varSigma })\\&\quad =(\lambda -1) c_{J_{\mathfrak {P}^{-\lambda }}} (\nu , F^\varGamma _{\varSigma })+ c_{J_{\mathfrak {P}^{-\lambda }}} (\nu , F^\varGamma _{\varSigma })\\&\quad =\lambda c_{J_{\mathfrak {P}^{-\lambda }}} (\nu , F^\varGamma _{\varSigma }) \end{aligned}$$

by the sub-lemma. The coefficients of the ${r_\lambda \nu }$-power of q for all $\lambda \ge 1$ on both sides coincide, and therefore the lemma follows. $\square$

It remains to establish the last assertion of Proposition 24. Suppose that (A, C) is a point of $\varSigma _{K{\mathrm {Iw}}}^{+}\cap X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f]$, and D is a Raynaud submodule scheme of A[p] such that $C[\mathfrak {p}]\ne D[\mathfrak {p}]$ for every prime $\mathfrak {p}$ in $\varGamma \cup \{\mathfrak {P}\}$. By the assumptions, it is only necessary to deal with the case at $\mathfrak {P}$. To this end, let G be a Raynaud submodule scheme of $A[\mathfrak {P}]$ distinct from $C[\mathfrak {P}]$ and $D[\mathfrak {P}]$. In which case, (A, C, G) (resp. (A, D, G)) defines a point $\pi _{1, \mathfrak {P}}^{-1}( X^{+, \varGamma }_{K{\mathrm {Iw}}}[0, f))$ lying above (A, C) (resp. (A, D)) along $\pi _{1, \mathfrak {P}}$ respectively. It then follows from the identity of sheaves over $\pi _{1, \mathfrak {P}}^{-1}( X^{+, \varGamma }_{K{\mathrm {Iw}}}[0, f))$, established in Lemma 30 that

$$\begin{aligned} F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A, C))= & {} \pi _{1, \mathfrak {P}}^*F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A, C, G))=\pi ^*H^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A/G, A[\mathfrak {P}]/G))\\= & {} w_\mathfrak {P}( H^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma )((A, G)). \end{aligned}$$

On the other hand, one can similarly deduce the equality $F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A, D))= w_\mathfrak {P}( H^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma )((A, G))$, we then deduce $F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A, C))=F^{\varGamma \cup \{\mathfrak {P}\}}_\varSigma ((A, D))$. $\square$

Corollary 5

$F_\varSigma ^{\varGamma \cup \{\mathfrak {P}\}}$ extends to a section over $X_{K{\mathrm {Iw}}}^{+, \varGamma }[0, f]$.

Proof of the main theorem

By Theorem 5, we have a family of overconvergent eigenforms $\{F_\varSigma \}$, one for every $\varSigma \subseteq S_{\mathrm {P}}$. Inductively apply Proposition 24 on $\varGamma$ to construct a section $F^+=F_\varnothing$ over $X_{K{\mathrm {Iw}}}^{{\mathrm {PR}}, +}$ which is an eigenform for all Hecke operators corresponding to the ideals not in T. Indeed, $F^+$ descends to the level K and write $F^-$ for $\pi _*F^+$ where $\pi$ is the forgetful morphism $\pi : X^{{\mathrm {PR}}, +}_{K{\mathrm {Iw}}}\rightarrow X^{{\mathrm {PR}}, +}_{K}$ which is finite flat of degree $1+p^{\sum _\mathfrak {p} f_\mathfrak {p}}$. Hence $\pi ^*F^-=\pi ^*\pi _*F^+=(p^{\sum _\mathfrak {p} f_\mathfrak {p}}+1) F^+$. Since $F^-$ is a section over $X_{K}^{{\mathrm {PR}}, +}$, it follows from the Riemann extension theorem (Proposition 2.10 in [26] for example) that it extends to a section over $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K}$. It then follows that the equality $(p^{\sum _\mathfrak {p} f_\mathfrak {p}}+1) F^+=\pi ^*F^-$ of sections over $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ holds. To see this, it suffices to observe that the equality $(p^{\sum _\mathfrak {p} f_\mathfrak {p}}+1) F^+=\pi ^*F^-$ holds at the admissible open subset $\varSigma _{K{\mathrm {Iw}}}^{+}$. This, in turn, follows from the last assertion in Proposition 24 that, if (A, C) / S is a (non-cuspidal) S-point of the set, the equality

$$\begin{aligned} (\pi ^*F^-)((A, C)/S)= & {} F^-(A/S)=(\pi _*F^+)(A/S)=\sum _{D} F^+((A, D)/S)\\= & {} (p^{\sum _\mathfrak {p} f_\mathfrak {p}}+1) F^+((A, C)/S) \end{aligned}$$

holds, where the sum ranges over all Raynaud submodule schemes $D\subset A[p]$ such that (A, D) / S is in the pre-image by $\pi$ of $\pi (A, C)$. Hence $F^+$ is a section over $X^{{\mathrm {PR}}, {{\mathrm {R}}\text{- }{\mathrm {a}}}}_{K{\mathrm {Iw}}}$ which is a classical cuspidal Hilbert modular eigenform of weight 1 of level old at p. $\square$

6.6 Modularity of Artin representations and the strong Atrin conjecture

Proposition 25

Let F be a totally real field. Let

$$\begin{aligned} \overline{\rho }: {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(\overline{\mathbf {F}}_5) \end{aligned}$$

be a continuous representation of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of F satisfying the following conditions.

• $\overline{\rho }$ is totally odd.

• The projective image of $\overline{\rho }$ is $A_5$.

Then there exists a finite soluble totally real field extension K of F such that $\overline{\rho }$, when restricted to ${\mathrm {Gal}}(\overline{F}/K)$, is of the form in Sect. 2.1. Furthermore, the restriction is modular in the sense of Sect. [2.4].

Proof

This can be proved as in Section 2 in [43]. Indeed, as the projective image of $\overline{\rho }$ is $A_5$, one firstly replaces F by its finite soluble totally real extension to assume that $\overline{\rho }$ takes values in ${\mathrm {GL}}_2(\mathbf {F}_5)$ with mod 5 cyclotomic determinant. We may and will choose a finite soluble totally real field extension $K\subset \overline{F}$ of F such that the restriction of $\overline{\rho }$ to ${\mathrm {Gal}}(\overline{F}/K)$ is unramified at every place of K above 3. We then find an elliptic curve E over K whose 5-torsion representation of ${\mathrm {Gal}}(\overline{F}/K)$ is isomorphic to the restriction of $\overline{\rho }$ to ${{\mathrm {Gal}}(\overline{F}/K)}$, whose 3-torsion representation of ${\mathrm {Gal}}(\overline{F}/K)$ is absolutely irreducible when restricted to $K(\sqrt{-3})$, and whose 3-adic Tate module representation $T_3E$ of ${\mathrm {Gal}}(\overline{F}/K)$ is ordinary at every place of K above 3. We use the degree 24 cover of the $\overline{\rho }|_{{\mathrm {Gal}}(\overline{F}/K)}$-twisted ‘modular curve’ of $X_5$ over K constructed by Shepherd-Barron-Taylor in Section 1 of [46], and make appeal to Ekedahl’s Hilbert irreducibility theorem (Theorem 1.3 in [16]) to find a K-point of the twisted curve.

By the Langlands-Tunnell theorem and a result of Kisin [31] (the weight two specialisation of the Hida family passing though the weight one cusp eigenform corresponding to E[3] renders $T_3E$ strongly residually modular in the sense of [31]), one deduces $T_3E$ is modular, hence E and, by extension the restriction of $\overline{\rho }$ to ${{\mathrm {Gal}}(\overline{F}/K)}$, is modular. Finally, apply the main theorem of [2]. $\square$

As a corollary,

Corollary 6

The strong Artin conjecture for two-dimensional, totally odd, continuous representations $\rho : {\mathrm {Gal}}(\overline{F}/F)\rightarrow {\mathrm {GL}}_2(\mathbf {C})$ of the absolute Galois group ${\mathrm {Gal}}(\overline{F}/F)$ of a totally real field F holds.

Proof

This follows from Proposition 24 and the preceding proposition. $\square$