Forcing theory for transverse trajectories of surface homeomorphisms

Abstract

This paper studies homeomorphisms of surfaces isotopic to the identity by means of purely topological methods and Brouwer theory. The main development is a novel theory of orbit forcing using maximal isotopies and transverse foliations. This allows us to derive new proofs for some known results as well as some new applications, among which we note the following: we extend Franks and Handel’s classification of zero entropy maps of $\mathbb {S}^2$ for non-wandering homeomorphisms; we show that if f is a Hamiltonian homeomorphism of the annulus, then the rotation set of f is either a singleton or it contains zero in the interior, proving a conjecture posed by Boyland; we show that there exist compact convex sets of the plane that are not the rotation set of some torus homeomorphisms, proving a first case of the Franks–Misiurewicz conjecture; we extend a bounded deviation result relative to the rotation set to the general case of torus homeomorphisms.

1 Introduction

Let us begin by recalling some facts about Sharkovski’s theorem, which can be seen as a typical example of an orbit forcing theory in dynamical systems. In this theorem, an explicit total order $\preceq$ on the set of natural integers is given that satisfies the following: every continuous transformation f on [0, 1] that contains a periodic orbit of period m contains a periodic orbit of period n if $n\preceq m$. Much more can be said. If f admits a periodic orbit of period different from a power of 2, one can construct a Markov partition and codes orbits with the help of the associated finite subshift. In particular one can prove that the topological entropy of f is positive. There exists a forcing theory about periodic orbits for surface homeomorphisms related to Nielsen–Thurston classification of surface homeomorphisms, with many interesting dynamical applications (see for example [5] or [33] for survey articles). In case of homeomorphisms isotopic to the identity, this theory deals with the braid types associated to the periodic orbits. A more subtle theory (homotopic Brouwer theory) was introduced by Handel for surface homeomorphisms and developed by Franks and Handel to become a very efficient tool in two-dimensional dynamics.

The goal of the article is to give a new orbit forcing theory for surface homeomorphisms that are isotopic to the identity, theory that will be expressed in terms of maximal isotopy, transverse foliations and transverse trajectories. Note first that the class of surface homeomorphisms isotopic to the identity contains the time one maps of time dependent vector fields. Consequently, what is proved in this article can be applied to the dynamical study of a time dependent vector field on a surface, periodic in time. In what follows, a surface M is orientable and furnished with an orientation. If f is a homeomorphism of M isotopic to the identity, the choice of an isotopy $I=(f_t)_{t\in [0,1]}$ from the identity to M should not be very important, as we are looking at the iterates of f. What looks like the trajectory of a point z, that means the path $I(z):t\mapsto f_t(z)$ seems useless. It appears that this is not the case: there are isotopies that are better than the other ones. This is clear if f is the time one map of a complete time independent vector field $\xi$. The isotopy $(f_t)_{[0,1]}$ defined by the restriction of the flow $(f_t)_{t\in \mathbb {R}}$ is clearly better than any other choice of an isotopy, in the sense that it will be useful while studying the dynamics of f. It is easy to see that in this last case, there is no fixed point of f in the complement of the singular set of the vector field whose trajectory is contractible relative to this same singular set. In this situation, the singular points correspond to the fixed points of I, which means the points whose trajectory is constant.

In general, let us say that an isotopy $I=(f_t)_{t\in [0,1]}$, that joins the identity to a homeomorphism f, is a maximal isotopy if there is no fixed point of f whose trajectory is contractible relative to the fixed point set of I. A very recent result of Béguin et al. [4] asserts that such an isotopy always exists if f is isotopic to the identity (a slightly weaker result was previously proved by Jaulent [21]). A fundamental result [27] asserts that a maximal isotopy always admits a transverse foliation. This is a singular oriented foliation $\mathcal {F}$ whose singular set coincides with the fixed point set of I and such that every non trivial trajectory is homotopic (relative to the endpoints) to a path that is transverse to the foliation (which means that it locally crosses every leaf from the right to the left). This path $I_{\mathcal {F}}(z)$, the transverse trajectory, is uniquely defined up to a natural equivalence relation (meaning that the induced path in the space of leaves is unique). In the case where f is the time one map of a complete time independent vector field $\xi$, it is very easy to construct a transverse foliation by taking the integral curves of any vector field $\eta$ that is transverse to $\xi$, and in that case the trajectories I(z) are transverse. In a certain sense, maximal isotopies are isotopies that are as close as possible to isotopies induced by flows.

Maximal isotopies and transverse foliations are known to be efficient tools for the dynamical study of surface homeomorphisms (see [9, 10, 26,27,28,29, 32, 39] for example). Usually they are used in the following way. Properties of f are transposed “by duality” to properties of $\mathcal {F}$, then one studies the dynamics of the foliation and comes back to f. Roughly speaking, the leaves of the foliation are pushed along the dynamics. This property is cleverly used in the articles of Dávalos [9, 10]. Our original goal was a boundedness displacement result (Theorem H of this introduction) which needed a formalization of the ideas of Dávalos. This was nothing but a forcing theory for transverse trajectories. For every integer $n\geqslant 1$, let us define by concatenation the paths $I^n(z)=\prod _{0\leqslant k<n} I(f^k(z))$ and $I_{\mathcal {F}}^n(z)=\prod _{0\leqslant k<n} I_{\mathcal {F}}(f^k(z))$. The basic question can be formulated as follows: from the knowledge of a finite family $(I_{\mathcal {F}}^{n_i}(z_i))_{1\leqslant i\leqslant p}$ of transverse trajectories, can we deduce the existence of other transverse trajectories $I^n_{\mathcal {F}}(z)$? The key result (Proposition 20), which is new and whose proof is very simple, can be stated as follows: if two paths $I_{\mathcal {F}}^{n_1}(z_1)$ and $I_{\mathcal {F}}^{n_2}(z_2)$ intersect transversally relative to $\mathcal {F}$ (the precise definition will be given later in the article) then one can construct two other paths $I_{\mathcal {F}}^{n_1+n_2}(z_3)$ and $I_{\mathcal {F}}^{n_1+n_2}(z_4)$ by a natural change of direction at the intersection point. It becomes possible, in many situations to code transverse trajectories with the help of a Bernouilli shift or in other situations to construct transverse trajectories that are multiples of the same loop.

In order to obtain applications of this forcing theory, we need to relate the information obtained by the knowledge of these new sets of transverse trajectories to other properties of the dynamics. To do so, one can define the whole trajectory $I^{\mathbb {Z}}(z)=\prod _{k\in \mathbb {Z}} I(f^k(z))$ and the whole transverse trajectory $I_{\mathcal {F}}^{\mathbb {Z}}(z)=\prod _{k\in \mathbb {Z}} I_{\mathcal {F}}(f^k(z))$ of a point z. The properties of the dynamics are recovered by three structural results that, together with Proposition 20, form the core of the theory. The first of these results is a realization result, Proposition 26, showing that in many cases, the existence of finite transverse trajectories that are equivalent to multiples of a given transverse loop implies the existence of a periodic point whose transverse trajectory for one period is equivalent to the same transverse loop. The second of these results, Theorem 29, shows that if there exist two recurrent points z and $z'$ such that $I_{\mathcal {F}}^{\mathbb {Z}}(z)$ and $I_{\mathcal {F}}^{\mathbb {Z}}(z')$ intersect transversally relative to $\mathcal {F}$ (with a self intersection if $z=z'$) the number of periodic points of period n for some iterate of f grows exponentially in n. The third result, Theorem 36, shows that if in the previous result we assume that the surface is closed, then the topological entropy of f is strictly positive. This final result presents, to our knowledge, an entirely new mechanism to detect positive entropy, one that bypasses any requirement of smoothness of the map. Consequently, our applications are for general homeomorphisms isotopic to the identity, and include both new entropy theorems for maps of the annulus and generalizations of results known only for $C^1$-diffeomorphisms (sometimes for $C^{1+\varepsilon }$-diffeomorphisms, sometimes for $C^{\infty }$-diffeomorphisms). There is no doubt that they are many similarities with Franks–Handel methods. Looking more carefully at the links between the two methods should be a project of high interest.

Let us display now more precisely the main applications, beginning with the case of annulus homeomorphisms. Here, $\mathcal {M}(f)$ is the set of invariant Borel probability measures $\mu$ of f, the set ${\mathrm {supp}}(\mu )$ the support of $\mu$, the rotation number ${\mathrm {rot}}(\mu )$ the integral $\int _{\mathbb {A}} \varphi \, d\mu$, where $\varphi :\mathbb {A}\rightarrow \mathbb {R}$ is the map lifted by $\pi _1\circ \check{f}- \pi _1$ (the map $\pi _1:(x,y)\mapsto x$ being the first projection), the segment ${\mathrm {rot}}(\check{f})$ the set of rotation numbers of invariant measures.

Theorem A

Let f be a homeomorphism of $\mathbb {A}=\mathbb {T}^1\times [0,1]$ that is isotopic to the identity and $\check{f}$ a lift to $\mathbb {R}\times [0,1]$. Suppose that ${\mathrm {rot}}(\check{f})$ is a non trivial segment and that $\rho$ is an endpoint of ${\mathrm {rot}}(\check{f})$ that is rational. Define

$$\begin{aligned} {\mathcal {M}}_{\rho }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, {\mathrm {rot}}(\mu )=\rho \right\} , \, {X}_{\rho }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\rho }} {\mathrm {supp}}(\mu )}. \end{aligned}$$

Then every invariant measure supported on ${X}_{\rho }$ belongs to ${\mathcal {M}}_{\rho }.$

We deduce immediately the following positive answer to a question of Boyland:

Corollary B

Let f be a homeomorphism of $\mathbb {A}$ that is isotopic to the identity and preserves a probability measure $\mu$ with full support. Let us fix a lift $\check{f}$. Suppose that ${\mathrm {rot}}(\check{f})$ is a non trivial segment. The rotation number ${\mathrm {rot}}(\mu )$ cannot be an endpoint of ${\mathrm {rot}}(\check{f})$ if this endpoint is rational.

Let us explain what happens for torus homeomorphisms. Here again $\mathcal {M}(f)$ is the set of invariant Borel probability measures $\mu$ of f, the set ${\mathrm {supp}}(\mu )$ the support of $\mu$ and the rotation vector ${\mathrm {rot}}\mu )$ the integral $\int _{\mathbb {T}^2} \varphi \, d\mu$, where $\varphi :\mathbb {T}^2\rightarrow \mathbb {R}^2$ is the map lifted by $\check{f}-{\mathrm {Id}}$. The set of rotation vectors of invariant measures ${\mathrm {rot}}(\check{f})$ is a compact and convex subset of $\mathbb {R}^2$. Nothing is known about the plane subsets that can be written as such a rotation set. The following result gives the first obstruction:

Theorem C

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. The frontier of ${\mathrm {rot}}(\check{f})$ does not contain a segment with irrational slope that contains a rational point in its interior.

It was previously conjectured by Franks and Misiurewicz [15] that a line segment L could not be realized as a rotation set of a torus homeomorphism in the following conditions: (i) L has irrational slope and a rational point in its interior, (ii) L has rational slope but no rational points and (iii) L has irrational slope and no rational points. While Theorem C implies the conjecture for case (i), Ávila has given a counter-example for case (iii).

The second result is a boundedness result:

Theorem D

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. If ${\mathrm {rot}}(\check{f})$ has a non empty interior, then there exist a constant L such that for every $z\in \mathbb {R}^2$ and every $n\geqslant 1$, one has $d(\check{f}^n(z)-z, n{\mathrm {rot}}(\check{f}))\leqslant L$.

Note that by definition of the rotation set one knows that

$$\begin{aligned} \lim _{n\rightarrow +\infty } {1\over n}\left( \max _{z\in \mathbb {R}^2} d(\check{f}^n(z)-z, n{\mathrm {rot}}(\check{f}))\right) =0 \end{aligned}$$

Theorem D clarifies the speed of convergence. It was already known for homeomorphisms in the special case of a polygon with rational vertices (see Dávalos [10]) and for $\mathcal {C}^{1+\epsilon }$ diffeomorphisms (see Addas-Zanata [2]). As already noted in [2], we can deduce an interesting result about maximizing measures, which means measure $\mu \in \mathcal {M}(f)$ whose rotation vector belongs to the frontier of ${\mathrm {rot}}(\check{f})$. The rotation number of such a measure belongs to at least one supporting line of ${\mathrm {rot}}(\check{f})$. Such a line admits the equation $\psi (z)=\alpha (\psi )$ where $\psi$ is a non trivial linear form on $\mathbb {R}^2$ and

$$\begin{aligned} \alpha (\psi )=\max _{\mu \in {\mathcal {M}}(f)} \psi ({\mathrm {rot}}(\mu ))=\max _{\mu \in {\mathcal {M}}(f)}\int _{\mathbb {T}^2}\psi \circ \varphi \, d\mu . \end{aligned}$$

Set

$$\begin{aligned} {\mathcal {M}}_{\psi }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, \psi ({\mathrm {rot}}(\mu ))=\alpha (\psi )\right\} , \, {X}_{\psi }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\psi }} {\mathrm {supp}}(\mu )}. \end{aligned}$$

The following result, that can be easily deduced from Theorem 63 and Atkinson’s Lemma in Ergodic Theory (see [1]), tells us that the sets $X_{\psi }$ behave like the Mather sets of the Tonelli Lagrangian systems.

Proposition E

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. Assume that ${\mathrm {rot}}(\check{f})$ has a non empty interior. Then, every measure $\mu$ supported on ${X}_{\psi }$ belongs to ${\mathcal {M}}_{\psi }$. Moreover, if z lifts a point of $X_{\psi }$, then for every $n\geqslant 1$, one has $\vert \psi (\check{f}^n(z))-\psi (z)-n\beta (\psi )\vert \leqslant L\Vert \psi \Vert$, where L is the constant given by Theorem D.

It admits as an immediate corollary the torus version of Boyland’s question:

Corollary F

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity, preserving a measure $\mu$ of full support, and $\check{f}$ a lift of f to $\mathbb {R}^2$. Assume that ${\mathrm {rot}}(\check{f})$ has a non empty interior. Then ${\mathrm {rot}}(\mu )$ belongs to the interior of ${\mathrm {rot}}(\check{f})$.

This result was known for $\mathcal {C}^{1+\epsilon }$ diffeomorphisms (see [2]).

The next resut is due to Llibre and MacKay, see [30]. Its original proof uses Thurston–Nielsen theory of surface homeomorphisms, more precisely the authors prove that there exists a finite invariant set X such that $f\vert _{\mathbb {T}^2\setminus X}$ is isotopic to a pseudo-Anosov map. We will give here an alternative proof by exhibiting $(n,\varepsilon )$ separated sets constructed with the help of transverse trajectories.

Theorem G

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. If ${\mathrm {rot}}(\check{f})$ has a non empty interior, then the topological entropy of f is positive.

Our original goal, while writing this article, was to prove the following boundedness displacement result:

Theorem H

We suppose that M is a compact orientable surface furnished with a Riemannian structure. We endow the universal covering space $\check{M}$ with the lifted structure and denote by d the induced distance. Let f be a homeomorphism of M isotopic to the identity and $\check{f}$ a lift to $\check{M}$ naturally defined by the isotopy. Assume that there exists an open topological disk $U\subset M$ such that the fixed points set of $\check{f}$ projects into U. Then;

• either there exists $K>0$ such that $d(\check{f}^n(\check{z}), \check{z})\leqslant K$, for all $n\geqslant 0$ and all bi-recurrent point $\check{z}$ of $\check{f}$;

• or there exists a nontrivial covering automorphism T and $q>0$ such that, for all $r/s\in (-1/q,1/q)$, the map $\check{f}^{q}\circ T^{-p}$ has a fixed point. In particular, f has non-contractible periodic points of arbitrarily large prime period.

Theorem H has an interesting consequence for torus homeomorphisms. Say a homeomorphism f of $\mathbb {T}^2$ is Hamiltonian if it preserves a measure $\mu$ with full support and it has a lift $\check{f}$ (called the Hamiltonian lift of f) such that the rotation vector of $\mu$ is null.

Corollary I

Let f be a Hamiltonian homeomorphism of $\mathbb {T}^2$ such that all its periodic points are contractible, and such that it fixed point set is contained in a topological disk. Then there exists $K>0$ such that if $\check{f}$ is the Hamiltonian lift of f, then for every z and every $n\geqslant 1$, one has $\Vert \check{f}^n(z)-z\Vert \leqslant K$.

The study of non-contractible periodic orbits for Hamiltonian maps of sympletic manifolds has been receiving increased attention (see for instance [16]). A natural question in the area, posed by V. Ginzburg, is to determine if the existence of non-contractible periodic points is generic for smooth Hamiltonians. A consequence of Corollary I is an affirmative answer for the case of the torus:

Proposition J

Let ${\mathrm {Ham}}_{\infty }(\mathbb {T}^2)$ be the set of Hamiltonian $C^{\infty }$ diffeomorphisms of $\mathbb {T}^2$ endowed with the Whitney $C^{\infty }$-topology. There exists a residual subset $\mathcal {A}$ of ${\mathrm {Ham}}_{\infty }(\mathbb {T}^2)$ such that every f in $\mathcal {A}$ has non-contractible periodic points.

Let us explain now the results related to the entropy. For example we can give a short proof of the following improvement of a result due to Handel [19].

Theorem K

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that the complement of the fixed point set is not an annulus. If f is topologically transitive then the number of periodic points of period n for some iterate of f grows exponentially in n. Moreover, the entropy of f is positive.

Another entropy result we obtain is related to the existence and continuous variation of rotation numbers for homeomorphisms of the open annulus. A stronger version of this result for diffeomorphisms was already proved in an unpublished paper of Handel [20]. Given a homeomorphism of $\mathbb {T}^1\times \mathbb {R}$ and a lift $\check{f}$ to $\mathbb {R}^2$, we say that a point $z\in \mathbb {T}^1\times \mathbb {R}$ has a rotation number ${\mathrm {rot}}(z)$ if the $\omega$-limit of its orbit is not empty, and if for any compact set $K\subset \mathbb {T}^1\times \mathbb {R}$ and every increasing sequence of integers $n_k$ such that $f^{n_k}(z)\in K$ and any $\check{z}\in \pi ^{-1}(z)$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{1}{n_k}\left( \pi _1(\check{f}^{n_k}(\check{z})- \pi _1(\check{z})\right) ={\mathrm {rot}}(z), \end{aligned}$$

where $\pi$ is the covering projection from $\mathbb {R}^2$ to $\mathbb {T}^1\times \mathbb {R}$ and $\pi _1:\mathbb {R}^2\rightarrow \mathbb {R}$ is the projection on the first coordinate.

Theorem L

Let f be a homeomorphism of the open annulus $\mathbb {T}^1\times \mathbb {R}$ isotopic to the identity, $\check{f}$ a lift of f to the universal covering and $f_{{\mathrm {sphere}}}$ be the natural extension of f to the sphere obtained by compactifying each end with a point. If the topological entropy of $f_{{\mathrm {sphere}}}$ is zero, then each bi-recurrent point (meaning forward and backward recurrent) has a rotation number, and the function $z\mapsto {\mathrm {rot}}(z)$ is continuous on the set of bi-recurrent points.

Let us finish with a last application. Franks and Handel recently gave a classification result for area preserving diffeomorphisms of $\mathbb {S}^2$ with entropy 0 (see [14]). Their proofs are purely topological but the $C^1$ assumption is needed to use a Thurston–Nielsen type classification result relative to the fixed point set (existence of a normal form) and the $C^{\infty }$ assumption to use Yomdin results on arcs whose length growth exponentially by iterates. We will give a new proof of the fundamental decomposition result (Theorem 1.2 of [14]) which is the main building block in their structure theorem. In fact we will extend their result to the case of homeomorphisms and replace the area preserving assumption by the fact that every point is non wandering.

Theorem M

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that $\Omega (f)=\mathbb {S}^2$ and $h(f)=0$. Then there exists a family of pairwise disjoint invariant open sets $(A_{\alpha })_{\alpha \in \mathcal {A}}$ whose union is dense such that:

i) :

each $A_{\alpha }$ is an open annulus;

ii) :

the sets $A_{\alpha }$ are the maximal fixed point free invariant open annuli;

iii) :

the $\alpha$-limit set of a point $z\not \in \bigcup _{\alpha \in \mathcal {A}}A_{\alpha }$ is included in a single connected component of the fixed point set ${\mathrm {fix}}(f)$ of f, and the same holds for the $\omega$-limit set of z;

iv) :

let C be a connected component of the frontier of $A_{\alpha }$ in $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$, then the connected components of ${\mathrm {fix}}(f)$ that contain $\alpha (z)$ and $\omega (z)$ are independent of $z\in C$.

Let us explain now the plan of the article. In the second section we will introduce the definitions of many mathematical objects, including precise definitions of rotation vectors and rotation sets. The third section will be devoted to the study of transverse paths to a surface foliation. We will introduce the notion of a pair of equivalent paths, of a recurrent transverse path and of $\mathcal {F}$-transverse intersection between two transverse paths. An important result, which will be very useful in the proofs of Theorems K and M is Proposition 2 which asserts that a transverse recurrent path to a singular foliation on $\mathbb {S}^2$ that has no $\mathcal {F}$-transverse self-intersection is equivalent to the natural lift of a transverse simple loop (i.e. an adapted version of Poincaré-Bendixson theorem). We will recall the definition of maximal isotopies, transverse foliations and transverse trajectories in Sect. 4. We will state the fundamental result about $\mathcal {F}$-transverse intersections of transverse trajectories (Proposition 20) and its immediate consequences. An important notion that will be introduced is the notion of linearly admissible transverse loop. To any periodic orbit is naturally associated such a loop. A realization result (Proposition 26) will give us sufficient conditions for a linearly admissible transverse loop to be associated to a periodic orbit. Section 5 will be devoted to the proofs of Theorem 29 (about exponential growth of periodic orbits) and Theorem 36 (about positiveness of the entropy). We will give the proofs of Theorems H, A and K in Sect. 6 while Sect. 7 will be almost entirely devoted to the proof of Theorem M (we will prove Theorem L at the end of it).We will begin by stating a “local version” relative to a given maximal isotopy (Theorem 53). We will study torus homeomorphisms in Sect. 8 and will give there the proofs of Theorems C, D and G.

We would like to thank Frédéric Le Roux for informing us of some important gaps in the original proofs of Theorems 29 and 36. We would also like to thank Andrés Koropecki for his useful comments and for discussions regarding Proposition J, and to Victor Ginzburg for presenting us the question on the genericity of non-contractible periodic points for Hamiltonian diffeomorphisms. Finally, we would like to thank the anonymous referee for the careful work and suggestions which greatly improved our text.

2 Notations

We will endow $\mathbb {R}^2$ with its usual scalar product $\langle \,\rangle$ and its usual orientation. We will write $\Vert \,\Vert$ for the associated norm. For every point $z\in \mathbb {R}^2$ and every set $X\subset \mathbb {R}^2$ we write $d(z,X)=\inf _{z'\in X} \Vert z-z'\Vert$. We denote by $\pi _1:(x,y)\mapsto x$ and $\pi _2:(x,y)\mapsto y$ the two projections. If $z=(x,y)$, we write $z^{\perp }=(-y,x)$.

The r-dimensional torus $\mathbb {R}^r/\mathbb {Z}^r$ will be denoted $\mathbb {T}^r$, the 2-dimensional sphere will be denoted $\mathbb {S}^2$. A subset X of a surface M is called an open disk if it is homeomorphic to $\mathbb {D}=\{z\in \mathbb {R}^2\, ,\, \Vert z\Vert <1\}$ and a closed disk if it is homeomorphic to $\overline{\mathbb {D}}=\{z\in \mathbb {R}^2\, ,\, \Vert z\Vert \leqslant 1\}$. It is called an annulus if it homeomorphic to $\mathbb {T}^1\times J$, where J is a non trivial interval of $\mathbb {R}$. In case where $J=[0,1]$, $J=(0,1)$, $J=[0,1)$, we will say that X is a closed annulus, an open annulus, a semi-closed annulus respectively.

Given a homeomorphism f of a surface M and a point $z\in M$ we define the $\alpha$-limit set of z by $\bigcap _{n\geqslant 0}\overline{\bigcup _{k\geqslant n} f^{-k}(z)}$ and we denote it $\alpha (z)$. We also define the $\omega$-limit set of z by $\bigcap _{n\geqslant 0}\overline{\bigcup _{k\geqslant n} f^{k}(z)}$ and we denote it $\omega (z)$.

2.1 Paths, lines, loops

A path on a surface M is a continuous map $\gamma :J\rightarrow M$ defined on an interval $J\subset \mathbb {R}$. In absence of ambiguity its image will also be called a path and denoted by $\gamma$. We will denote $\gamma ^{-1}:-J\rightarrow M$ the path defined by $\gamma ^{-1}(t)=\gamma (-t)$. If X and Y are two disjoint subsets of M, we will say that a path $\gamma :[a,b]\rightarrow M$ joins X to Y if $\gamma (a)\in X$ and $\gamma (b)\in Y$. A path $\gamma :J\rightarrow M$ is proper if J is open and the preimage of every compact subset of M is compact. A line is an injective and proper path $\lambda :J\rightarrow M$, it inherits a natural orientation induced by the usual orientation of $\mathbb {R}$. If $M=\mathbb {R}^2$, the complement of $\lambda$ has two connected components, $R(\lambda )$ which is on the right of $\lambda$ and $L(\lambda )$ which is on its left. More generally, if M is a non connected surface with connected components homeomorphic to $\mathbb {R}^2$, and if $M'$ is the connected component of M containing $\lambda$, the two connected components of $M'\setminus \lambda$ will similarly be denoted $R(\lambda )$ and $L(\lambda )$.

Let us suppose that $\lambda _0$ and $\lambda _1$ are two disjoint lines of $\mathbb {R}^2$. We will say that they are comparable if their right components are comparable for the inclusion. Note that $\lambda _0$ and $\lambda _1$ are not comparable if and only if $\lambda _0$ and $(\lambda _1)^{-1}$ are comparable.

Let us consider three lines $\lambda _0$, $\lambda _1$, $\lambda _2$ in $\mathbb {R}^2$. We will say that $\lambda _2$ is above $\lambda _1$ relative to $\lambda _0$ (and $\lambda _1$ is below $\lambda _2$ relative to $\lambda _0$) if:

• the three lines are pairwise disjoint;

• none of the lines separates the two others;

• if $\gamma _1$, $\gamma _2$ are two disjoints paths that join $z_1=\lambda _0(t_1)$, $z_2=\lambda _0(t_2)$ to $z'_1\in \lambda _1$, $z'_2=\lambda _2$ respectively, and that do not meet the three lines but at the ends, then $t_2>t_1$.

Fig. 1

Order of lines relative to $\lambda _0$

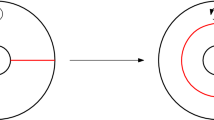
This notion does not depend on the orientation of $\lambda _1$ and $\lambda _2$ but depends of the orientation of $\lambda _0$ (see Fig. 1).¹ If $\lambda _0$ is fixed, note that we get in that way an anti-symmetric and transitive relation on every set of pairwise disjoint lines that are disjoint from $\lambda _0$.

A proper path $\gamma$ of $\mathbb {R}^2$ induces a dual function $\delta$ on its complement, defined up to an additive constant as follows: for every z and $z'$ in $\mathbb {R}^2\setminus \gamma$, the difference $\delta (z')-\delta (z)$ is the algebraic intersection number $\gamma \wedge \gamma '$ where $\gamma '$ is any path from z to $z'$. If $\gamma$ is a line, there is a unique dual function $\delta _{\gamma }$ that is equal to 0 on $R(\gamma )$ and to 1 on $L(\gamma )$.

Consider a unit vector $\rho \in \mathbb {R}^2,\, \Vert \rho \Vert =1$. Say that a proper path $\gamma :\mathbb {R}\rightarrow \mathbb {R}^2$ is directed by $\rho$ if

$$\begin{aligned} \lim _{t\rightarrow \pm \infty }\Vert \gamma (t)\Vert =+\infty , \, \lim _{t\rightarrow +\infty }\gamma (t)/\Vert \gamma (t)\Vert =\rho , \, \lim _{t\rightarrow -\infty }\gamma (t)/\Vert \gamma (t)\Vert =-\rho . \end{aligned}$$

Observe that if $\gamma$ is directed by $\rho$, then $\gamma ^{-1}$ is directed by $-\rho$ and that for every $z\in \mathbb {R}^2$, the translated path $\gamma +z: t\mapsto \gamma (t)+z$ is directed by $\rho$. Among the connected components of $\mathbb {R}^2\setminus \gamma$, two of them $R(\gamma )$ and $L(\gamma )$ are uniquely determined by the following: for every $z\in \mathbb {R}^2$, one has $z-s\rho ^{\perp }\in R(\gamma )$ and $z+s\rho ^{\perp }\in L(\gamma )$ if s is large enough. In the case where $\gamma$ is a line, the definitions agree with the former ones. Note that two disjoint lines directed by $\rho$ are comparable.

Instead of looking at paths defined on a real interval we can look at paths defined on an abstract interval J, which means a one dimensional oriented manifold homeomorphic to a real interval. If $\gamma : J\rightarrow M$ and $\gamma ': J'\rightarrow M$ are two paths, if J has a right end b and $J'$ a left end $a'$ (in the natural sense), and if $\gamma (b)=\gamma '(a')$, we can concatenate the two paths and define the path $\gamma \gamma '$ defined on the interval $J''=J\sqcup J'/b\sim a'$ coinciding with $\gamma$ on J and $\gamma '$ on $J'$. One can define in a same way the concatenation $\prod _{l\in L} \gamma _{l}$ of paths indexed by a finite or infinite interval of $\mathbb {Z}$.

A path $\gamma :\mathbb {R}\rightarrow M$ such that $\gamma (t+1)=\gamma (t)$ for every $t\in \mathbb {R}$ lifts a continuous map $\Gamma :\mathbb {T}^1\rightarrow M$. We will say that $\Gamma$ is a loop and $\gamma$ its natural lift. If $n\geqslant 1$, we denote $\Gamma ^n$ the loop lifted by the path $t\mapsto \gamma (nt)$. Here again, if M is oriented and $\Gamma$ homologous to zero, one can define a dual function $\delta$ defined up to an additive constant on $M\setminus \Gamma$ as follows: for every z and $z'$ in $\mathbb {R}^2\setminus \Gamma$, the difference $\delta (z')-\delta (z)$ is the algebraic intersection number $\Gamma \wedge \gamma '$ where $\gamma '$ is any path from z to $z'$.

2.2 Rotations vectors

Let us recall the notion of rotation vector and rotation set for a homeomorphism of a closed manifold, introduced by Schwartzman [37] (see also Pollicott [36]). Let M be an oriented closed connected manifold and I an identity isotopy on M, which means an isotopy $(f_t)_{t\in [0,1]}$ such that $f_0$ is the identity. The trajectory of a point $z\in M$ is the path $I(z): z\mapsto f_t(z)$. If $\omega$ is a closed 1-form on M, one can define the integral $\int _{I(z)}\omega$ on every trajectory I(z). Write $f_1=f$ and denote $\mathcal {M}(f)$ the set of invariant Borel probability measures. For every $\mu \in \mathcal {M}(f)$, the integral $\int _M \left( \int _{I(z)}\omega \right) \, d\mu (z)$ vanishes when $\omega$ is exact. One deduces that $\omega \rightarrow \int _M\left( \int _{I(z)}\omega \right) \, d\mu (z)$ defines a natural linear form on the first cohomology group $H^1(M,\mathbb {R})$, and by duality an element of the first homology group $H_1(M,\mathbb {R})$, which is called the rotation vector of $\mu$ and denoted ${\mathrm {rot}}(\mu )$. The set $\mathcal {M}(f)$, endowed with the weak$^*$ topology, being convex and compact and the map $\mu \mapsto {\mathrm {rot}}(\mu )$ being affine, one deduces that the set ${\mathrm {rot}}(I)=\{{\mathrm {rot}}(\mu )\, ,\, \mu \in \mathcal {M}(f)\}$ is a convex compact subset of $H_1(M,\mathbb {R})$. If M is a surface of genus greater than 1 and $I'$ is a different identity isotopy given by $(f'_t)_{t\in [0,1]}$ such that $f'_1=f$, then for all $z\in M$ the trajectories I(z) and $I'(z)$ are homotopic with fixed endpoints. Therefore the rotation vectors (and the rotation set) are independent of the isotopy, depending only on f. If M is a torus, it depends on a given lift of f. Let us clarify this case (see Misiurewicz and Zieman [34]). Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\widetilde{f}$ a lift of f to the universal covering space $\mathbb {R}^2$. The map $\widetilde{f}-{\mathrm {Id}}$ is invariant by the integer translations $z\mapsto z+p$, $p\in \mathbb {Z}^2$, and lifts a continuous map $\varphi :\mathbb {T}^2\rightarrow \mathbb {R}$. The rotation vector of a Borel probability measure invariant by f is the integral $\int _{\mathbb {T}^2} \varphi \, d\mu$. If $\mu$ is ergodic, then for $\mu$-almost every point z, the Birkhoff means converge to ${\mathrm {rot}}(\mu )$. If $\widetilde{z}\in \mathbb {R}^2$ is a lift of z, one has

$$\begin{aligned} \lim _{n\rightarrow +\infty } {\widetilde{f}^n(\widetilde{z})- \widetilde{z}\over n}= \lim _{n\rightarrow +\infty }{1\over n}\sum _{k=0}^{n-1}\varphi (f^k(z))={\mathrm {rot}}(\mu ). \end{aligned}$$

We will say that z (or $\widetilde{z}$) has a rotation vector ${\mathrm {rot}}(\mu )$. The rotation set ${\mathrm {rot}}(\widetilde{f})$ is a non empty compact convex subset of $\mathbb {R}^2$. It is easy to prove that every extremal point of ${\mathrm {rot}}(\widetilde{f})$ is the rotation vector of an ergodic measure. Indeed the set of Borel probability measures of rotation vector $\rho \in {\mathrm {rot}}(f)$ is convex and compact, moreover its extremal points are extremal in ${\mathcal {M}}(f)$ if $\rho$ is extremal in ${\mathrm {rot}}(f)$. Observe also that for every $p\in \mathbb {Z}^2$ and every $q\in \mathbb {Z}$, the map $\widetilde{f}^q+p$ is a lift of $f^q$ and one has ${\mathrm {rot}}(\widetilde{f}^q+p)=q{\mathrm {rot}}(\widetilde{f})+p$.

We will also be concerned with annulus homeomorphisms. Let f be a homeomorphism of $\mathbb {A}=\mathbb {T}^1\times [0,1]$ that is isotopic to the identity and $\widetilde{f}$ a lift of f to the universal covering space $\mathbb {R}\times [0,1]$. The map $\pi _1\circ f-\pi _1$ is invariant by the translation $T: z\mapsto z+(1,0)$ and lifts a continuous map $\varphi :\mathbb {A}\rightarrow \mathbb {R}$. The rotation number ${\mathrm {rot}}(\mu )$ of a Borel probability measure invariant by f is the integral $\int _{\mathbb {A}} \varphi \, d\mu$. If $\mu$ is ergodic, then for $\mu$-almost every point z, the Birkhoff means converge to ${\mathrm {rot}}(\mu )$. If $\widetilde{z}\in \mathbb {R}\times [0,1]$ is a lift of z, one has

$$\begin{aligned} \lim _{n\rightarrow +\infty } {\pi _1\circ \widetilde{f}^n(\widetilde{z})- \pi _1(\widetilde{z})\over n}= \lim _{n\rightarrow +\infty }{1\over n}\sum _{k=0}^{n-1}\varphi (f^k(z))={\mathrm {rot}}(\mu ). \end{aligned}$$

Here again we will say that $\widetilde{z}$ (or z) has a rotation number ${\mathrm {rot}}(\mu )$. The rotation set ${\mathrm {rot}}(\widetilde{f})$ is a non empty compact real segment and every endpoint of ${\mathrm {rot}}(\widetilde{f})$ is the rotation number of an ergodic measure. Here again, for every $p\in \mathbb {Z}$ and every $q\in \mathbb {Z}$, the map $\widetilde{f}^q\circ T^p$ is a lift of $f^q$ and one has ${\mathrm {rot}}(\widetilde{f}^q\circ T^p)=q{\mathrm {rot}}(\widetilde{f})+p$.

Note that if J is a real interval, one can also define the rotation number of an invariant probability measure of a homeomorphism of $\mathbb {T}^1\times J$ isotopic to the identity, for a given lift to $\mathbb {R}\times J$, provided the support of the measure is compact.

3 Transverse paths to surface foliations

3.1 General definitions

Let us begin by introducing some notations that will be used throughout the whole text. A singular oriented foliation on an oriented surface M is an oriented topological foliation $\mathcal {F}$ defined on an open set of M. We will call this set the domain of $\mathcal {F}$ and denote it ${\mathrm {dom}}(\mathcal {F})$, its complement will be called the singular set (or set of singularities) and denoted ${\mathrm {sing}}(\mathcal {F})$. If the singular set is empty, we will say that $\mathcal {F}$ is non singular. A subset of M is saturated if it is the union of singular points and leaves. A trivialization neighborhood is an open set $W\subset {\mathrm {dom}}(\mathcal {F})$ endowed with a homeomorphism $h:W\rightarrow (0,1)^2$ that sends the restricted foliation $\mathcal {F}\vert _W$ onto the vertical foliation. If $\check{M}$ is a covering space of M and $\check{\pi }: \check{M}\rightarrow M$ the covering projection, $\mathcal {F}$ can be naturally lifted to a singular foliation $\check{\mathcal {F}}$ of $\check{M}$ such that ${\mathrm {dom}}(\check{\mathcal {F}})=\check{\pi }^{-1}({\mathrm {dom}}(\mathcal {F}))$. If $\check{N}$ is a covering space of ${\mathrm {dom}}(\mathcal {F})$, then the restriction of $\mathcal {F}$ to ${\mathrm {dom}}(\mathcal {F})$ can also be naturally lifted to a non singular foliation of $\check{N}$. We will denote $\widetilde{{\mathrm {dom}}}(\mathcal {F})$the universal covering space of ${\mathrm {dom}}(\mathcal {F})$ and $\widetilde{\mathcal {F}}$ the foliation lifted from $\mathcal {F}\mid _{{\mathrm {dom}}(\mathcal {F})}$. For every $z\in {\mathrm {dom}}(\mathcal {F})$ we will write $\phi _z$ for the leaf that contains z, $\phi ^+_z$ for the positive half-leaf and $\phi _z^-$ for the negative one. One can define the $\alpha$-limit and $\omega$-limit sets of $\phi$ as follows:

$$\begin{aligned} \alpha (\phi )=\bigcap _{z\in \phi } \overline{\phi _z^-},\, \omega (\phi )=\bigcap _{z\in \phi } \overline{\phi _z^+}. \end{aligned}$$

Suppose that a point $z\in \phi$ has a trivialization neighborhood W such that each leaf of $\mathcal {F}$ contains no more than one leaf of $\mathcal {F}\vert _W$. In that case every point of $\phi$ satisfies the same property. If furthermore no closed leaf of $\mathcal {F}$ meets W, we will say that $\phi$ is wandering. Recall the following facts, in the case where $M=\mathbb {R}^2$ and $\mathcal {F}$ is non singular (see Haefliger and Reeb [18]):

• every leaf of $\mathcal {F}$ is a wandering line;

• the space of leaves $\Sigma$, furnished with the quotient topology, inherits a structure of connected and simply connected one-dimensional manifold;

• $\Sigma$ is Hausdorff if and only if $\mathcal {F}$ is trivial (which means that it is the image of the vertical foliation by a plane homeomorphism) or equivalently if all the leaves are comparable.

A path $\gamma :J\rightarrow M$ is positively transverse ² to $\mathcal {F}$ if its image does not meet the singular set and if, for every $t_0\in J$, there exists a (continuous) chart $h:W\rightarrow (0,1)^2$ at $\gamma (t_0)$ compatible with the orientation and sending the restricted foliation ${\mathcal {F}}_W$ onto the vertical foliation oriented downward such that the map $\pi _1\circ h\circ \gamma$ is increasing in a neighborhood of $t_0$. Let $\check{M}$ be a covering space of M and $\check{\pi }: \check{M}\rightarrow M$ the covering projection. If $\gamma :J\rightarrow {\mathrm {dom}}({\mathcal {F}})$ is positively transverse to $\mathcal {F}$, every lift $\check{\gamma }:J\rightarrow \check{M}$ is transverse to the lifted foliation $\check{\mathcal {F}}$. Moreover, every lift ${\widetilde{\gamma }}:J\rightarrow \widetilde{{\mathrm {dom}}}({\mathcal {F}})$ to the universal covering space $\widetilde{{\mathrm {dom}}}({\mathcal {F}})$ is transverse to the lifted non singular foliation $\widetilde{\mathcal {F}}$.

Suppose first that $M=\mathbb {R}^2$ and that $\mathcal {F}$ is non singular. Say that two transverse paths $\gamma :J\rightarrow \mathbb {R}^2$ and $\gamma ':J'\rightarrow \mathbb {R}^2$ are equivalent for $\mathcal {F}$ or $\mathcal {F}$ -equivalent if they satisfy the three following equivalent conditions:

• there exists an increasing homeomorphism $h:J\rightarrow J'$ such that $\phi _{\gamma '(h(t))}=\phi _{\gamma (t)}$, for every $t\in J$;

• the paths $\gamma$ and $\gamma '$ meet the same leaves;

• the paths $\gamma$ and $\gamma '$ project onto the same path of $\Sigma$.

Moreover, if $J=[a,b]$ and $J'=[a',b']$ are two segments, these conditions are equivalent to this last one:

• one has $\phi _{\gamma (a)}=\phi _{\gamma '(a')}$ and $\phi _{\gamma (b)}=\phi _{\gamma '(b')}$.

In that case, note that the leaves met by $\gamma$ are the leaves $\phi$ such that $R(\phi _{\gamma (a)})\subset R(\phi )\subset R(\phi _{\gamma (b)}).$ If the context is clear, we just say that the paths are equivalent and omit the dependence on $\mathcal {F}$.

If $\gamma :J\rightarrow \mathbb {R}^2$ is a transverse path, then for every $a<b$ in J, the set $L(\phi _{ \gamma (a)})\cap R(\phi _{\gamma (b)})$ is a topological plane and $\gamma \vert _{(a,b)}$ a line of this plane. Let us say that $\gamma$ has a leaf on its right if there exists $a<b$ in J and a leaf $\phi$ in $L(\phi _{ \gamma (a)})\cap R(\phi _{\gamma (b)})$ that lies in the right of $\gamma \vert _{(a,b)}$. Similarly, one can define the notion of having a leaf on its left (Fig. 2).

Fig. 2

$\gamma :[a,b]\rightarrow \mathbb {R}^2$ has both a leaf on its right ($\phi _0$) and a leaf on its left ($\phi _1)$. $\gamma \vert _{(a,b)}$ is also a line in $L(\phi _{\gamma (a)})\cap R(\phi _{\gamma (b)})$

All previous definitions can be naturally extended in case every connected component of M is a plane and $\mathcal {F}$ is not singular. Let us return to the general case. Two transverse paths $\gamma :J\rightarrow {\mathrm {dom}}(\mathcal {F})$ and $\gamma ':J'\rightarrow {\mathrm {dom}}(\mathcal {F})$ are equivalent for $\mathcal {F}$ or $\mathcal {F}$ -equivalent if they can be lifted to the universal covering space $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ of ${\mathrm {dom}}(\mathcal {F})$ as paths that are equivalent for the lifted foliation $\widetilde{\mathcal {F}}$. This implies that there exists an increasing homeomorphism $h:J\rightarrow J'$ such that, for every $t\in J$, one has $\phi _{\gamma '(h(t))}=\phi _{\gamma (t)}$. Nevertheless these two conditions are not equivalent. In Fig. 3, such a homeomorphism can be constructed but the two loops are not equivalent. Nonetheless, one can show that $\gamma$ and $\gamma '$ are equivalent for $\mathcal {F}$ if, and only if, there exists a holonomic homotopy between $\gamma$ and $\gamma '$, that is, if there exists a continuous transformation $H:J\times [0,1]\rightarrow {\mathrm {dom}}(\mathcal {F})$ and an increasing homeomorphism $h:J\rightarrow J'$ satisfying:

• $H(t,0) = \gamma (t), \, H(t,1)=\gamma '(h(t))$;

• for all $t\in J$ and $s_1, s_2\in [0,1]$, $\phi _{H(t, s_1)}=\phi _{H(t, s_2)}$.

Fig. 3

The paths $\gamma _1$ and $\gamma _2$ are not equivalent for $\mathcal {F}$, even though they cross the same leafs

By definition, a transverse path has a leaf on its right if it can be lifted to $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ as a path with a leaf of $\widetilde{\mathcal {F}}$ on its right (in that case every lift has a leaf on its right) and has a leaf on its left if it can be lifted as a path with a leaf on its left. Note that if $\gamma$ and $\gamma '$ have no leaf on their right and $\gamma \gamma '$ is well defined, then $\gamma \gamma '$ has no leaf on its right. Note also that if $\gamma$ and $\gamma '$ are $\mathcal {F}$-equivalent, and if $\gamma$ has a leaf on its right, then $\gamma '$ has a leaf on its right. We say that an $\mathcal {F}$-equivalence class has a leaf on its right (on its left) if some representative of the class has a leaf on its right (on its left).

Similarly, a loop $\Gamma :\mathbb {T}^1\rightarrow {\mathrm {dom}}(\mathcal {F})$ is called positively transverse to $\mathcal {F}$ if it is the case for its natural lift $\gamma :\mathbb {R}\rightarrow {\mathrm {dom}}(\mathcal {F})$. It has a leaf on its right or its left if it is the case for $\gamma$. Two transverse loops $\Gamma :\mathbb {T}^1\rightarrow {\mathrm {dom}}(\mathcal {F})$ and $\Gamma ':\mathbb {T}^1\rightarrow {\mathrm {dom}}(\mathcal {F})$ are equivalent if there exists two lifts ${\widetilde{\gamma }}:\mathbb {R}\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ and ${\widetilde{\gamma }}':\mathbb {R}\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ of $\Gamma$ and $\Gamma '$ respectively, a covering automorphism T and an orientation preserving homeomorphism $h:\mathbb {R}\rightarrow \mathbb {R}$, such that, for every $t\in \mathbb {R}$, one has

$$\begin{aligned} \widetilde{\gamma }(t+1)= & {} T(\widetilde{\gamma }(t)), \, \widetilde{\gamma }'(t+1)=T(\widetilde{\gamma }'(t)),\, h(t+1)\\= & {} h(t)+1, \,\phi _{\widetilde{\gamma }'(h(t))}=\phi _{{\widetilde{\gamma }}(t)}. \end{aligned}$$

Of course $\Gamma ^n$ and $\Gamma '^n$ are equivalent transverse loops, for every $n\geqslant 1$, if it is the case for $\Gamma$ and $\Gamma '$. A transverse loop $\Gamma$ will be called prime if there is no transverse loop $\Gamma '$ and integer $n\geqslant 2$ such that $\Gamma$ is equivalent to $\Gamma '{}^n$.

If two transverse loops $\Gamma$ and $\Gamma '$ are equivalent, there exists a holonomic homotopy between them and therefore they are freely homotopic in ${\mathrm {dom}}(\mathcal {F})$, but the converse does not need to hold, as Fig. 4 shows.

Fig. 4

The transversal loops $\Gamma$ and $\Gamma '$ are not equivalent for $\mathcal {F}$, even though they are freely homotopic

A transverse path $\gamma :\mathbb {R}\rightarrow M$ will be called $\mathcal {F}$-positively recurrent if for every segment $J\subset \mathbb {R}$ and every $t\in \mathbb {R}$ there exists a segment $J'\subset [t,+\infty )$ such that $\gamma \vert _{J'}$ is equivalent to $\gamma \vert _J$. It will be called $\mathcal {F}$-negatively recurrent if for every segment $J\subset \mathbb {R}$ and every $t\in \mathbb {R}$ there exists a segment $J'\subset (-\infty , t]$ such that $\gamma \vert _{J'}$ is equivalent to $\gamma \vert _J$. It is $\mathcal {F}$-bi-recurrent if it is both $\mathcal {F}$-positively and $\mathcal {F}$-negatively recurrent. Note that, if $\gamma :\mathbb {R}\rightarrow M$ and $\gamma ':\mathbb {R}\rightarrow M$ are $\mathcal {F}$-equivalent and if $\gamma$ is $\mathcal {F}$-positively recurrent (or $\mathcal {F}$-negatively recurrent), then so is $\gamma '$. We say that an $\mathcal {F}$-equivalence class is positively recurrent (negatively recurrent, bi-recurrent) if some representative of the class is $\mathcal {F}$-positively recurrent (resp. $\mathcal {F}$-negatively recurrent, $\mathcal {F}$-bi-recurrent).

We will very often use the following remarks. Suppose that $\Gamma$ is a transverse loop homologous to zero and $\delta$ a dual function. Then $\delta$ decreases along each leaf with a jump at every intersection point. One deduces that every leaf met by $\Gamma$ is wandering. In particular, $\Gamma$ does not meet any set $\alpha (\phi )$ or $\omega (\phi )$, which implies that for every leaf $\phi$, there exist $z_-$ and $z_+$ on $\phi$ such that $\Gamma$ does not meet neither $\phi _{z_-}^-$ nor $\phi _{z_+}^+$. Writing $n_+$ and $n_-$ for the value taken by $\delta$ on $\phi _{z_-}^-$ and $\phi _{z_+}^+$ respectively, one deduces that $n_+-n_-$ is the number of times that $\Gamma$ intersect $\phi$. Note that $n_+-n_-$ is uniformly bounded. Indeed, the fact that every leaf that meets $\Gamma$ is wandering implies that $\mathbb {T}^1$ can be covered by open intervals where $\Gamma$ is injective and does not meet any leaf more than once. By compactness, $\mathbb {T}^1$ can be covered by finitely many such intervals, which implies that there exists N such that $\Gamma$ meets each leaf at most N times. We have similar results for a multi-loop $\Gamma =\sum _{1\leqslant i\leqslant p}\Gamma _i$ homologous to zero. In case where $M=\mathbb {R}^2$, we have similar results for a proper transverse path with finite valued dual function. In case of an infinite valued dual function, everything is true but the existence of $z_-$, $z_+$, $n_-$, $n_+$ and the finiteness condition about intersection with a given leaf. In particular a transverse line $\lambda$ meets every leaf at most once (because the dual function takes only two values) and one can define the sets $r(\lambda )$ and $l(\lambda )$, union of leaves included in $R(\lambda )$ and $L(\lambda )$ respectively. They do not depend on the choice of $\lambda$ in the equivalence class. Note that if the diameter of the leaves of $\mathcal {F}$ are uniformly bounded, every path equivalent to $\lambda$ is still a line. We have similar results for directed proper paths. If $\gamma$ is a proper path directed by a unit vector $\rho$, one can define the sets $r(\gamma )$ and $l(\gamma )$, union of leaves included in $R(\gamma )$ and $L(\gamma )$ respectively. They do not depend on the choice of $\gamma$ in the equivalence class. Moreover, if the leaves of $\mathcal {F}$ are uniformly bounded, every path equivalent to $\gamma$ is still a path directed by $\rho$.

3.2 $\mathcal {F}$-transverse intersection for non singular plane foliations

We suppose here that $M=\mathbb {R}^2$ and that $\mathcal {F}$ is non singular.

Let $\gamma _1:J_1\rightarrow \mathbb {R}^2$ and $\gamma _2:J_2\rightarrow \mathbb {R}^2$ be two transverse paths. The set

$$\begin{aligned} X=\left\{ (t_1,t_2)\in J_1\times J_2\,\vert \phi _{\gamma _1(t_1)}=\phi _{\gamma _2(t_2)}\right\} , \end{aligned}$$

if not empty, is an interval that projects injectively on $J_1$ and $J_2$ as does its closure. Moreover, for every $(t_1,t_2) \in \overline{X}\setminus X$, the leaves $\phi _{\gamma _1(t_1)}$ and $\phi _{\gamma _2(t_2)}$ are not separated in $\Sigma$. To be more precise, suppose that $J_1$ and $J_2$ are real intervals and that $\phi _{\gamma _1(t_1)}=\phi _{\gamma _2(t_2)}$. Set $J_1^-=J_1\cap (-\infty , t_1]$ and $J_2^-=J_2\cap (-\infty , t_2]$. Then either one of the paths $\gamma _1\vert _{J_1^-}$, $\gamma _2\vert _{J_2^-}$ is equivalent to a subpath of the other one, or there exist $a_1<t_1$ and $a_2<t_2$ such that:

• $\gamma _1\vert _{(a_1,t_1]}$ and $\gamma _2\vert _{(a_2,t_2]}$ are equivalent;

• $\phi _{\gamma _1(a_1)}\subset L(\phi _{\gamma _2(a_2)}),\, \phi _{\gamma _2(a_2)}\subset L(\phi _{\gamma _1(a_1)})$

• $\phi _{\gamma _1(a_1)}$ and $\phi _{\gamma _2(a_2)}$ are not separated in $\Sigma$.

Observe that the second property (but not the two other ones) is still satisfied when $a_1$, $a_2$ are replaced by smaller parameters. Note also that $\phi _{\gamma _2(a_2)}$ is either above or below $\phi _{\gamma _1(a_1)}$ relative to $\phi _{\gamma _1(t_1)}$ and that this property remains satisfied when $a_1$, $a_2$ are replaced by smaller parameters and $t_1$ by any parameter in $(a_1,t_1]$. We have a similar situation on the possible right end of X.

Let $\gamma _1:J_1\rightarrow \mathbb {R}^2$ and $\gamma _2:J_2\rightarrow \mathbb {R}^2$ be two transverse paths such that $\phi _{\gamma _1(t_1)}=\phi _{\gamma _2(t_2)}=\phi$. We will say that $\gamma _1$ and $\gamma _2$ intersect $\mathcal {F}$ -transversally and positively at $\phi$ (and $\gamma _2$ and $\gamma _1$ intersect $\mathcal {F}$ -transversally and negatively at $\phi$) if there exist $a_1$, $b_1$ in $J_1$ satisfying $a_1<t_1<b_1$, and $a_2$, $b_2$ in $J_2$ satisfying $a_2<t_2<b_2$, such that:

• $\phi _{\gamma _2(a_2)}$ is below $\phi _{\gamma _1(a_1)}$ relative to $\phi$;

• $\phi _{\gamma _2(b_2)}$ is above $\phi _{\gamma _1(b_1)}$ relative to $\phi$.

See Fig. 5.

Fig. 5

$\mathcal {F}$-transverse intersection. The tangency point is also a point of $\mathcal {F}$-transverse intersection

Note that, if $\gamma _1$ intersects $\mathcal {F}$-transversally $\gamma _2$, if $\gamma _1'$ is equivalent to $\gamma _1$ and $\gamma _2'$ is equivalent to $\gamma _2$, then $\gamma _1'$ intersects $\mathcal {F}$-transversally $\gamma _2'$, and we say that the equivalence class of $\gamma _1$ intersect transversally the equivalence class of $\gamma _2$.

As none of the leaves $\phi$, $\phi _{\gamma _1(a_1)}$, $\phi _{\gamma _2(a_2)}$ separates the two others, one deduces that

$$\begin{aligned} \phi _{\gamma _1(a_1)}\subset L(\phi _{\gamma _2(a_2)}),\, \phi _{\gamma _2(a_2)}\subset L(\phi _{\gamma _1(a_1)}) \end{aligned}$$

and similarly that

$$\begin{aligned} \phi _{\gamma _1(b_1)}\subset R(\phi _{\gamma _2(b_2)}),\, \phi _{\gamma _2(b_2)}\subset R(\phi _{\gamma _1(b_1)}). \end{aligned}$$

As explained above, these properties remain true when $a_1$, $a_2$ are replaced by smaller parameters, $b_1$, $b_2$ by larger parameters and $\phi$ by any other leaf met by $\gamma _1$ and $\gamma _2$. Note that $\gamma _1$ and $\gamma _2$ have at least one intersection point and that one can find two transverse paths $\gamma '_1$, $\gamma '_2$ equivalent to $\gamma _1$, $\gamma _2$ respectively, such that $\gamma '_1$ and $\gamma '_2$ have a unique intersection point, located on $\phi$, with a topologically transverse intersection. Note that, if $\gamma _1$ and $\gamma _2$ are two paths that meet the same leaf $\phi$, then either they intersect $\mathcal {F}$-transversally, or one can find two transverse paths $\gamma '_1$, $\gamma '_2$ equivalent to $\gamma _1$, $\gamma _2$, respectively, with no intersection point.

3.3 $\mathcal {F}$-transverse intersection in the general case

Here again, the notion of $\mathcal {F}$-transverse intersection can be naturally extended in case every connected component of M is a plane and $\mathcal {F}$ is not singular. Let us return now to the general case of a singular foliation $\mathcal {F}$ on a surface M. Let $\gamma _1:J_1\rightarrow M$ and $\gamma _2:J_2\rightarrow M$ be two transverse paths that meet a common leaf $\phi =\phi _{\gamma _1(t_1)}=\phi _{\gamma _2(t_2)}$. We will say that $\gamma _1$ and $\gamma _2$ intersect $\mathcal {F}$ -transversally at $\phi$ if there exist paths ${\widetilde{\gamma }}_1:J_1\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ and ${\widetilde{\gamma }}_2:J_2\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$, lifting $\gamma _1$ and $\gamma _2$, with a common leaf ${\widetilde{\phi }}=\phi _{{\widetilde{\gamma }}_1(t_1)}=\phi _{{\widetilde{\gamma }}_2(t_2)}$ that lifts $\phi$, and intersecting $\widetilde{\mathcal {F}}$-transversally at $\widetilde{\phi }$. If $\phi$ is closed the choices of ${\widetilde{\gamma }}_1$ and ${\widetilde{\gamma }}_2$ do not need to be unique, see Fig. 6.

Fig. 6

Given a lift ${\widetilde{\gamma }}_1$ of $\gamma _1$, there are two different lifts of $\gamma _2$ intersecting $\widetilde{\mathcal {F}}$-transversally ${\widetilde{\gamma }}_1$

Here again, we can give a sign to the intersection. As explained in the last subsection, there exist $t'_1$ and $t'_2$ such that $\gamma _1(t'_1)= \gamma _2(t'_2)$ and such that $\gamma _1$ and $\gamma _2$ intersect $\mathcal {F}$-transversally at $\phi _{\gamma _1(t'_1)}=\phi _{\gamma _2(t'_2)}$. In this case we will say that $\gamma _1$ and $\gamma _2$ intersect $\mathcal {F}$-transversally at $\gamma _1(t'_1)=\gamma _2(t'_2)$. In the case where $\gamma _1=\gamma _2$ we will talk of an $\mathcal {F}$-transverse self-intersection. A transverse path $\gamma$ has an $\mathcal {F}$-transverse self-intersection if for every lift ${\widetilde{\gamma }}$ to the universal covering space of the domain, there exists a non trivial covering automorphism T such that ${\widetilde{\gamma }}$ and $T({\widetilde{\gamma }})$ have a $\widetilde{\mathcal {F}}$-transverse intersection. We will often use the following fact. Let $\gamma _1:J_1\rightarrow M$ and $\gamma _2:J_2\rightarrow M$ be two transverse paths that meet a common leaf $\phi =\phi _{\gamma _1(t_1)}=\phi _{\gamma _2(t_2)}$. If $J'_1$, $J'_2$ are two sub-intervals of $J_1$, $J_2$ that contain $t_1$, $t_2$ respectively and if $\gamma _1\vert _{J'_1}$ and $\gamma _2\vert _{J'_2}$ intersect $\mathcal {F}$-transversally at $\phi$, then $\gamma _1$ and $\gamma _2$ intersect $\mathcal {F}$-transversally at $\phi$.

Similarly, let $\Gamma$ be a loop positively transverse to $\mathcal {F}$ and $\gamma$ its natural lift. If $\gamma$ intersects $\mathcal {F}$-transversally a transverse path $\gamma '$ at a leaf $\phi$, we will say that $\Gamma$ and $\gamma '$ intersect $\mathcal {F}$-transversally at $\phi$. Moreover if $\gamma '$ is the natural lift of a transverse loop $\Gamma '$ we will say that $\Gamma$ and $\Gamma '$ intersect $\mathcal {F}$-transversally at $\phi$. Here again we can talk of self-intersection.

As a conclusion, note that if two transverse paths have an $\mathcal {F}$-transverse intersection, they both have a leaf on their right and a leaf on their left.

3.4 Some useful results

In this section, we will state different results that will be useful in the rest of the article. Observe that the finiteness condition for the next proposition is satisfied if every leaf of $\mathcal {F}$ is wandering, or when M has genus 0.

Proposition 1

Let $\mathcal {F}$ be an oriented singular foliation on a surface and $(\Gamma _i)_{1\leqslant i\leqslant m}$ a family of prime transverse loops that are not pairwise equivalent. We suppose that the leaves met by the loops $\Gamma _i$ are never closed and that there exists an integer N such that no loop $\Gamma _i$ meets a leaf more than N times. Then, for every $i\in \{1,\ldots , m\}$, there exists a transverse loop $\Gamma '_i$ equivalent to $\Gamma _i$ such that:

i) :

$\Gamma '_i$ and $\Gamma '_j$ do not intersect if $\Gamma _i$ and $\Gamma _j$ have no $\mathcal {F}$-transverse intersection;

ii) :

$\Gamma '_i$ is simple if $\Gamma _i$ has no $\mathcal {F}$-transverse self-intersection.

Proof

There is a natural partial order on ${\mathrm {dom}}({\mathcal {F}})$ defined as follows: write $z\leqslant z'$ if $\phi _{z}$ is not closed and $z'\in \phi _{z}^+$. One can suppose, without loss of generality, that the loops $\Gamma _i$ are included in the same connected component W of ${\mathrm {dom}}({\mathcal {F}})$. One can lift ${\mathcal {F}}\vert _{W}$ to an oriented foliation $\widetilde{\mathcal {F}}$ on the universal covering space ${\widetilde{W}}$ of W. We will parameterize $\Gamma _i$ by a copy $\mathbb {T}^1_i$ of $\mathbb {T}^1$ and consider the $\mathbb {T}^1_i$ as disjoint circles. We will endow the set $\mathbb {T}_*=\sqcup _{1\leqslant i\leqslant m} \mathbb {T}^1_i$ with the natural topology generated by the open sets of the $\mathbb {T}^1_i$. We get a continuous map $\Gamma :\mathbb {T}_*\rightarrow W$ (a multi-loop) by setting $\Gamma (t)=\Gamma _{i(t)}(t)$, where $t\in \mathbb {T}^1_{i(t)}$. Suppose that $t\not =t'$ and $\phi _{\Gamma (t)}=\phi _{\Gamma (t')}$. One can lift the loops $\Gamma _{i(t)}$ and $\Gamma _{i(t')}$ to lines ${\widetilde{\gamma }}_{i(t)}:\mathbb {R}\rightarrow {\widetilde{W}}$ and ${\widetilde{\gamma }}_{i(t')}:\mathbb {R}\rightarrow {\widetilde{W}}$ transverse to $\widetilde{\mathcal {F}}$ such that ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t)}({\widetilde{t}})}={\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t')}({\widetilde{t}}')}={\widetilde{\phi }}$, where ${\widetilde{t}}$ and ${\widetilde{t}}'$ lift t and $t'$ respectively. The fact that the loops are prime and not equivalent implies that ${\widetilde{\gamma }}_{i(t)}\vert _{[{\widetilde{t}},+\infty )}$ and ${\widetilde{\gamma }}_{i(t')}\vert _{[{\widetilde{t}}',+\infty )}$ are not equivalent and similarly that ${\widetilde{\gamma }}_{i(t)}\vert _{(-\infty , {\widetilde{t}}]}$ and ${\widetilde{\gamma }}_{i(t')}\vert _{(-\infty , {\widetilde{t}}']}$ are not equivalent. So, ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t')}}({\widetilde{t}}'')$ is above or below ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t)}}({\widetilde{t}}'')$ relative to ${\widetilde{\phi }}$ if $\left|{{\widetilde{t}}''}\right|$ is sufficiently large. Moreover the option does not depend on the choice of the lifts. We will write $t\prec t'$ in the case where ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t')}}({\widetilde{t}}'')$ is above ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t)}}({\widetilde{t}}'')$ and ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t')}}(-{\widetilde{t}}'')$ is above ${\widetilde{\phi }}_{{\widetilde{\gamma }}_{i(t)}}(-{\widetilde{t}}'')$ for ${\widetilde{t}}''$ sufficiently large. Observe that one has $t\prec t'$ or $t'\prec t$ in the two following cases:

• $i(t)\not =i(t')$ and $\Gamma _{i(t)}$ and $\Gamma _{i(t')}$ have no $\mathcal {F}$-transverse intersection;

• $i(t)=i(t')$ and $\Gamma _{i(t)}$ has no $\mathcal {F}$-transverse self-intersection.

We will say that $t\in \mathbb {T}_*$ is a good parameter of $\Gamma$, if for every $t'\in \mathbb {T}_*$, one has

$$\begin{aligned} t\prec t'\Rightarrow \Gamma (t)<\Gamma (t'). \end{aligned}$$

To get the proposition it is sufficient to construct, for every $i\in \{1,\ldots , m\}$, a transverse loop $\Gamma '_i$ equivalent to $\Gamma _i$ such that the induced multi-loop $\Gamma '$ has only good parameters. Let us define the order o(t) of $t\in \mathbb {T}_*$ to be the number of $t'\in \mathbb {T}_*$ such that $t\prec t'$. Note that every parameter of order 0 is a good parameter. We will construct $\Gamma '$ by induction, supposing that every parameter of order $\leqslant r$ is good and constructing $\Gamma '$ such that every parameter of order $\leqslant r+1$ is good. Note that for every s, the set $\mathbb {T}_{\leqslant s}$ of parameters of order $\leqslant s$ is closed and the set $\mathbb {T}_{\mathrm {good}}$ of good parameters is open. The set $\mathbb {T}_{\mathrm {bad}} =\mathbb {T}_{\leqslant r+1}\setminus \mathbb {T}_{\mathrm {good}}$ is closed and disjoint from $\mathbb {T}_{\leqslant r}$: it contains only parameters of order $r+1$. Let us fix an open neighborhood O of $\mathbb {T}_{\mathrm {bad}}$ disjoint from $\mathbb {T}_{\leqslant r}$. By hypothesis, for every $t\in \mathbb {T}_{\mathrm {bad}}$, one can find $r+1$ points $\theta _0(t)$, ..., $\theta _{r}(t)$ in $\mathbb {T}_{*}$ such that $t\prec \theta _{i}(t)$ for every $i\in \{0,\ldots , r\}$ and among the $\Gamma (\theta _i(t))$ a smallest one $\Gamma (\theta (t))$ (for the order $\leqslant$). Each $\theta _i(t)$ belongs to $\mathbb {T}_{\leqslant r}$ and therefore is disjoint from O. Note that each function $\theta _i$ can be chosen continuous in a neighborhood of a point t, which implies that $t\mapsto \Gamma (\theta (t))$ is continuous on $\mathbb {T}_{\mathrm {bad}}$. It is possible to make a perturbation of $\Gamma$ supported on O by sliding continuously each point $\Gamma (t)$ on $\phi _{\Gamma (t)}^-$ to obtain a transverse multi-loop $\Gamma '$ such that $\Gamma '(t)<\Gamma (\theta (t))$. Since the perturbation is a holonomic homotopy, $\Gamma '$ must be equivalent to $\Gamma$.

Since $\theta _{i}(t) \in \mathbb {T}_{\leqslant r}$ for every $i\in \{0,\ldots , r\}$ , we have $\Gamma (\theta _i (t))=\Gamma '( \theta _{i}(t))$ and so $\Gamma '(t)< \Gamma '( \theta (t))$. $\square$

Let us continue with the following adapted version of Poincaré-Bendixson Theorem.

Proposition 2

Let $\mathcal {F}$ be an oriented singular foliation on $\mathbb {S}^2$ and $\gamma :\mathbb {R}\rightarrow \mathbb {S}^2$ an $\mathcal {F}$-bi-recurrent transverse path. The following properties are equivalent:

i) :

$\gamma$ has no $\mathcal {F}$-transverse self-intersection;

ii) :

there exists a transverse simple loop $\Gamma '$ such that $\gamma$ is equivalent to the natural lift $\gamma '$ of $\Gamma '$;

iii) :

the set $U=\bigcup _{t\in \mathbb {R}}\phi _{\gamma (t)}$ is an open annulus.

Proof

To prove that ii) implies iii), just note that a dual function of $\Gamma '$ takes only two consecutive values, which implies that every leaf of $\mathcal {F}$ meets $\Gamma '$ at most once.

To prove that iii) implies i) it is sufficient to note that if $\bigcup _{t\in \mathbb {R}}\phi _{\gamma (t)}$ is an annulus, each connected component of its preimage in the universal covering space of ${\mathrm {dom}}({\mathcal {F}})$ is an open set, union of leaves, where the lifted foliation $\widetilde{\mathcal {F}}$ is trivial. This implies that $\gamma$ has no $\mathcal {F}$-transverse self-intersection.

It remains to prove that i) implies ii). The path $\gamma$ being $\mathcal {F}$-bi-recurrent, one can find $a<b$ such that $\phi _{\gamma (a)}=\phi _{\gamma (b)}$. Replacing $\gamma$ by an equivalent transverse path, one can suppose that $\gamma (a)=\gamma (b)$. Let $\Gamma$ be the loop naturally defined by the closed path $\gamma \vert _{[a,b]}$. As explained previously, every leaf that meets $\Gamma$ is wandering and consequently, if t and $t'$ are sufficiently close, one has $\phi _{\Gamma (t)}\not =\phi _{\Gamma (t')}$. Moreover, because $\Gamma$ is positively transverse to $\mathcal {F}$, one cannot find an increasing sequence $(a_n)_{n\geqslant 0}$ and a decreasing sequence $(b_n)_{n\geqslant 0}$, such that $\phi _{\gamma (a_n)}=\phi _{\gamma (b_n)}$. So, there exist $a\leqslant a'<b'\leqslant b$ such that $t\mapsto \phi _{\gamma (t)}$ is injective on $[a',b')$ and satisfies $\phi _{\gamma (a')}=\phi _{\gamma (b')}$. Replacing $\gamma$ by an equivalent transverse path, one can suppose that $\gamma (a')=\gamma (b')$. The set $U=\bigcup _{t\in [a',b']}\phi _{\gamma (t)}$ is an open annulus and the loop $\Gamma '$ naturally defined by the closed path $\gamma \vert _{[a',b']}$ is a simple loop.

Let us prove now that $\gamma$ is equivalent to the natural lift $\gamma '$ of $\Gamma '$. Being $\mathcal {F}$-bi-recurrent it cannot be equivalent to a strict subpath of $\gamma '$. So it is sufficient to prove that it is included in U. We will give a proof by contradiction. We denote the two connected components of the complement of U as $X_1,\, X_2$. Suppose that there exists $t\in \mathbb {R}$ such that $\gamma (t)\not \in U$. The path $\gamma$ being $\mathcal {F}$-bi-recurrent and the sets $X_i$ saturated, there exists $t'\in \mathbb {R}$ separated from t by $[a',b']$ such that $\gamma (t')$ is in the same component $X_i$ than $\gamma (t)$. More precisely, one can find real numbers

$$\begin{aligned} t_1<a''\leqslant a'<b'\leqslant b''<t_2 \end{aligned}$$

and an integer $k\geqslant 1$, uniquely determined such that

• $\gamma \vert _{[a'',b'']}$ is equivalent to $\gamma \vert _{[a',b']}^k$;

• $\gamma \vert _{(t_1,a'')}$ and $\gamma \vert _{(b'',t_2)}$ are included in U but do not meet $\phi _{\gamma (a')}$;

• $\gamma (t_1)$ and $\gamma (t_2)$ do not belong to U.

Moreover, if $\gamma (t_2)$ does not belong to the same component $X_i$ than $\gamma (t_1)$, one can find real numbers $t_2\leqslant t_3<t_4$ uniquely determined such that

• $\gamma (t_4)$ belongs to the same component $X_i$ than $\gamma (t_1)$;

• $\gamma \vert _{[t_2, t_4)}$ does not meet this component,

• $\gamma \vert _{(t_3, t_4)}$ is included in U;

• $\gamma (t_3)$ does not belong to U.

Observe now that if $\gamma (t_1)$ and $\gamma (t_2)$ belong to the same component $X_i$, then $\gamma _{[t_1, b'']}$ and $\gamma _{[a'', t_2]}$ intersect $\mathcal {F}$-transversally at $\phi _{\gamma (a'')}=\phi _{\gamma (b'')}$. Suppose now that $\gamma (t_1)$ and $\gamma (t_2)$ do not belong to the same component $X_i$. Fix $t\in (t_3,t_4)$. There exists $t'\in [a',b']$ such that $\phi _{\gamma (t')}=\phi _{\gamma (t)}$. Observe that $\gamma \vert _{[t_1, t_2]}$ and $\gamma \vert _{[t_3, t_4]}$ intersect $\mathcal {F}$-transversally at $\phi _{\gamma (t')}=\phi _{\gamma (t)}$ (See Fig. 7). $\square$

Remark 3

Note that the proof above tells us that if $\gamma$ is $\mathcal {F}$-positively or $\mathcal {F}$-negatively recurrent, there exists a transverse simple loop $\Gamma '$ such that $\gamma$ is equivalent to a subpath of the natural lift $\gamma '$ of $\Gamma '$.

Fig. 7

Proof of Proposition 2

The next result is a slight modification.

Proposition 4

Let $\mathcal {F}$ be an oriented singular foliation on $\mathbb {R}^2$ with leaves of uniformly bounded diameter and $\gamma$ be a transverse proper path. The following properties are equivalent:

i) :

$\gamma$ has no $\mathcal {F}$-transverse self-intersection;

ii) :

$\gamma$ meets every leaf at most once;

iii) :

$\gamma$ is a line.

Proof

The fact that ii) implies iii) is obvious, as is the fact that iii) implies i). It remains to prove that (i) implies ii). Let us suppose that $\phi _{\gamma (a)}=\phi _{\gamma (b)}$, where $a<b$. We will prove that $\gamma$ has a transverse self-intersection. Like in the proof of the previous proposition, replacing $\gamma$ by an equivalent transverse path, one can find $a\leqslant a'<b'\leqslant b$ such that $\gamma (a')=\gamma (b')$, such that $U=\bigcup _{t\in [a',b']}\phi _{\gamma (t)}$ is an open annulus and such that the loop $\Gamma '$ naturally defined by the closed path $\gamma \vert _{[a',b']}$ is a simple loop. Write $X_1$ for the unbounded connected component of $\mathbb {R}^2\setminus \Gamma '$ and $X_2$ for the bounded one. The path $\gamma$ being proper, one can find real numbers

$$\begin{aligned} t_1<a''\leqslant a'<b'\leqslant b''<t_2 \end{aligned}$$

and an integer $k\geqslant 1$, uniquely determined such that

• $\gamma \vert _{[a'',b'']}$ is equivalent to $\gamma \vert _{[a',b']}^k$;

• $\gamma \vert _{(t_1,a'')}$ and $\gamma \vert _{(b'',t_2)}$ are included in U but do not meet $\phi _{\gamma (a')}$;

• $\gamma (t_1)$ and $\gamma (t_2)$ do not belong to U.

As seen in the proof of the previous proposition, if $\gamma (t_1)$ and $\gamma (t_2)$ belong to the same component $X_i$, then $\gamma _{[t_1, b'']}$ and $\gamma _{[a'', t_2]}$ intersect $\mathcal {F}$-transversally at $\phi _{\gamma (a'')}=\phi _{\gamma (b'')}$. If $\gamma (t_1)\in X_1$ and $\gamma (t_2)\in X_2$, using the fact that $\gamma$ is proper, one can find real numbers $t_2\leqslant t_3<t_4$ uniquely determined such that

• $\gamma (t_4)$ belongs to $X_1$;

• $\gamma \vert _{[t_2, t_4)}$ does not meet $X_1$,

• $\gamma \vert _{(t_3, t_4)}$ is included in U;

• $\gamma (t_3)$ belongs to $X_2$.

As seen in the proof of the previous proposition, $\gamma \vert _{[t_1, t_2]}$ and $\gamma \vert _{[t_3, t_4]}$ intersect $\mathcal {F}$-transversally. The case where $\gamma (t_1)\in X_2$ and $\gamma (t_2)\in X_1$ can be treated analogously. $\square$

Let us add another result describing paths with no $\mathcal {F}$-transverse self-intersection:

Proposition 5

Let $\mathcal {F}$ be an oriented singular foliation on $\mathbb {R}^2$, $\gamma$ a transverse proper path and $\delta$ a dual function of $\gamma$. If $\gamma '$ is a transverse path that does not intersect $\mathcal {F}$-transversally $\gamma$, then $\delta$ takes a constant value on the union of the leaves met by $\gamma '$ but not by $\gamma$.

Proof

Let us suppose that $\gamma '$ meets two leaves $\phi _0$ and $\phi _1$, disjoint from $\gamma$ and such that $\delta$ does not take the same value on $\phi _0$ and on $\phi _1$. One can suppose that $\gamma '$ joins $\phi _0$ to $\phi _1$. Let W be the connected component of ${\mathrm {dom}}({\mathcal {F}})$ that contains $\gamma$. Write $\widetilde{W}$ for the universal covering space of W and $\widetilde{\mathcal {F}}$ for the lifted foliation. Every lift of $\gamma$ is a line. Fix a lift ${\widetilde{\gamma }}'$, it joins a leaf ${\widetilde{\phi }}_0$ that lifts $\phi _0$ to a leaf ${\widetilde{\phi }}_1$ that lifts $\phi _1$. By hypothesis, there exists a lift ${\widetilde{\gamma }}$ of $\gamma$ such that the dual function $\delta _{{\widetilde{\gamma }}}$ do not take the same value on ${\widetilde{\phi }}_0$ and ${\widetilde{\phi }}_1$. One can suppose that ${\widetilde{\phi }}_0\subset r({\widetilde{\gamma }})$ and ${\widetilde{\phi }}_1\subset l({\widetilde{\gamma }})$ for instance (recall that $r({\widetilde{\gamma }})$ is the union of leaves included in the connected component of ${\widetilde{W}}\setminus {\widetilde{\gamma }}$ on the right of ${\widetilde{\gamma }}$ and $l({\widetilde{\gamma }})$ the union of leaves included in the other component). The foliation $\widetilde{\mathcal {F}}$ being non singular, the sets $r({\widetilde{\gamma }})$ and $l({\widetilde{\gamma }})$ are closed. Consequently, there exists a subpath ${\widetilde{\gamma }}''$ of ${\widetilde{\gamma }}'$ that joins a leaf of $r({\widetilde{\gamma }})$ to a leaf of $l({\widetilde{\gamma }})$ and that is contained but the ends in the open set ${\widetilde{U}}$, union of leaves met by ${\widetilde{\gamma }}$. Observe now that ${\widetilde{\gamma }}$ and ${\widetilde{\gamma }}''$ intersect $\widetilde{\mathcal {F}}$-transversally and positively. $\square$

We deduce immediately

Corollary 6

Let $\mathcal {F}$ be an oriented singular foliation on $\mathbb {R}^2$, $\gamma$ a transverse path that is either a line or a proper path directed by a unit vector $\rho$ and $\gamma '$ a transverse path. If $\gamma$ and $\gamma '$ do not intersect $\mathcal {F}$-transversally, then $\gamma '$ cannot meet both sets $r(\gamma )$ and $l(\gamma )$.

Given a transverse loop $\Gamma$ with a $\mathcal {F}$-transverse self-intersection and its natural lift $\gamma$, there exists some integer K for which $\gamma \vert _{[0, K]}$ also has an $\mathcal {F}$-transverse self-intersection. Let us continue this section with an estimate of the minimal such K when $\Gamma$ is homologous to zero.

Proposition 7

Let $\mathcal {F}$ be an oriented singular foliation on M and $\Gamma :\mathbb {T}^1\rightarrow M$ a transverse loop homologous to zero in M with an $\mathcal {F}$-transverse self-intersection. If $\gamma :\mathbb {R}\rightarrow M$ is the natural lift of $\Gamma$, then $\gamma \vert _{[0,2]}$ has an $\mathcal {F}$-transverse self-intersection.

Proof

Write $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ for the universal covering space of ${\mathrm {dom}}(\mathcal {F})$. If ${\widetilde{\gamma }}:J\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ is a path and T a covering automorphism, write $T({\widetilde{\gamma }}):J\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ for the path satisfying $T({\widetilde{\gamma }})(t)=T({\widetilde{\gamma }}(t))$ for every $t\in J$. Choose a lift ${\widetilde{\gamma }}$ of $\gamma$ to $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ and write T for the covering automorphism such that ${\widetilde{\gamma }}(t+1)=T({\widetilde{\gamma }})(t)$, for every $t\in \mathbb {R}$. Since $\gamma$ has an $\mathcal {F}$-transverse self-intersection and is periodic of period 1, there exist a covering automorphism S and

$$\begin{aligned} a_1<t_1<b_1, \, a_2<t_2<b_2, \end{aligned}$$

such that

• ${\widetilde{\gamma }}\vert _{(a_1,b_1)}$ is equivalent to $S({\widetilde{\gamma }})\vert _{(a_2,b_2)}$;

• ${\widetilde{\gamma }}\vert _{[a_1,b_1]}$ and $S({\widetilde{\gamma }})\vert _{[a_2,b_2]}$ have a $\widetilde{\mathcal {F}}$-transverse intersection at ${\widetilde{\gamma }}(t_1)=S({\widetilde{\gamma }})(t_2)$,

• both $a_1, a_2$ belong to [0, 1).

We will show that $b_1\leqslant a_1+1$ and $b_2 \leqslant a_2+1$ , which implies that $\gamma \vert _{[0, 2]}$ has an $\mathcal {F}$-transverse self-intersection. Assume for a contradiction that $b_1>a_1+1$ (the case where $b_2> a_2+1$ is treated similarly). Then we can find $a_1', a_2', b_2'$ with

$$\begin{aligned} a_1<a_1'<t_1, \, a_2<a_2'<t_2<b_2'<b_2 \end{aligned}$$

such that ${\widetilde{\gamma }}\vert _{[a_1', a_1'+1]}$ is equivalent to $S({\widetilde{\gamma }})\vert _{[a_2', b_2']}$.

Consider first the case where $b_2'=a_2'+1$. In that situation there exists an increasing homeomorphism $h:[a_1', a_1'+1] \rightarrow [a_2', a_2'+1],$ such that $h(t_1)=t_2$ and $\phi _{{\widetilde{\gamma }}(t)}=\phi _{S({\widetilde{\gamma }})(h(t))}$. This implies that

$$\begin{aligned} T(\phi _{{\widetilde{\gamma }}(a'_1)})=\phi _{{\widetilde{\gamma }}(a'_1+1)}=\phi _{S({\widetilde{\gamma }})(a'_2+1)}=STS^{-1}\phi _{{\widetilde{\gamma }}(a'_2)}=STS^{-1}\phi _{{\widetilde{\gamma }}(a'_1)}. \end{aligned}$$

In case $STS^{-1}=T$, one can extend h to a homeomorphism of the real line that commutes with the translation $t\mapsto t+1$ such that $\phi _{{\widetilde{\gamma }}(t)}=\phi _{S({\widetilde{\gamma }})(h(t))}$, for every $t\in \mathbb {R}$. If K is large enough, then $[-K,K]$ contains $[a_1,b_1]$ and $h([-K,K])$ contains $[a_2,b_2]$. This contradicts the fact that ${\widetilde{\gamma }}\vert _{[a_1,b_1]}$ and $S({\widetilde{\gamma }})\vert _{[a_2,b_2]}$ have a $\widetilde{\mathcal {F}}$-transverse intersection at ${\widetilde{\gamma }}(t_1)= S({\widetilde{\gamma }})(t_2)$. In case $STS^{-1}\not =T$, the leaf $\phi _{{\widetilde{\gamma }}(a'_1)}$ is invariant by the commutator $T^{-1}STS^{-1}$ and so projects into a closed leaf of $\mathcal {F}$ that is homological to zero in ${\mathrm {dom}}(\mathcal {F})$, which means that it bounds a closed surface in this domain. This closed surface, being a subsurface of ${\mathrm {dom}}(\mathcal {F})$, is naturally foliated by $\mathcal {F}$, a non singular foliation, and one gets a contradiction by Poincaré-Hopf formula. One also gets a contradiction since this closed leaf has a non zero intersection number with the loop $\Gamma$.

Now assume that $b_2'< a_2'+1$. Let $s \in (b_2', a_2'+1)$ and consider $\phi _{\gamma (s)}$. As noted in the last paragraph of Sect. 3.1, since $\Gamma$ is homologous to zero, it intersects every given leaf a finite number of times. Let n be the number of times it intersects $\phi _{\gamma (s)}$. It is equal to the number of times $\gamma \vert _{[a_1', a_1'+1)}$ or $\gamma \vert _{[a_2', a_2'+1)}$ intersect $\phi _{\gamma (s)}$. On the other hand, since $\gamma \vert _{[a_2', b_2')}$ is equivalent to $\gamma \vert _{[a_1', a_1'+1)}$, it must also intersect $\phi _{\gamma (s)}$ exactly n times, and since $s \in (b_2', a_2'+1)$, $\gamma \vert _{[a_2', a_2'+1)}$ needs to intersect $\phi _{\gamma (s)}$ at least $n+1$ times, a contradiction (see Fig. 8).

Finally, if $b_2'>a_2'+1$, then $\gamma \vert _{[a_2', a_2'+1]}$ is equivalent to $\gamma \vert _{[a_1', b_1']}$ for some $b_1'<a_1'+1$ and the same reasoning as above may be applied. $\square$

Fig. 8

Contradiction from Proposition 7. $\widetilde{\gamma }\mid _{[a_1', a_1'+1]}$ and $S\widetilde{\gamma }\mid _{[a_2', a_2'+1]}$ must cross the same finite number of lifts of $\phi _{\gamma (s)}$

We will finish this subsection with a result (Proposition 9) that will be useful later. Let us begin with this simple lemma.

Lemma 8

Let $\mathcal {F}$ be an oriented singular foliation on M and $\widetilde{\mathcal {F}}$ the lifted foliation on the universal covering space $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ of ${\mathrm {dom}}(\mathcal {F})$. Let ${\widetilde{\gamma }}$ and ${\widetilde{\gamma }}'$ be two lines of $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ transverse to $\widetilde{\mathcal {F}}$, invariant by T and $T'$ respectively, where T and $T'$ are non trivial covering automorphisms. Up to a right composition by a power of T and a left composition by a power of $T'$ there are finitely many covering automorphisms S such that ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }}')$ intersect $\widetilde{\mathcal {F}}$-transversally.

Proof

Suppose ${\widetilde{\gamma }}:\mathbb {R}\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ and ${\widetilde{\gamma }}':\mathbb {R}\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ parameterized such that ${\widetilde{\gamma }}(t+1)=T({\widetilde{\gamma }}(t))$ and ${\widetilde{\gamma }}'(t+1)=T'({\widetilde{\gamma }}(t))$, for every $t\in \mathbb {R}$. The group of covering automorphisms acts freely and properly. So there exists $L<+\infty$ automorphisms S such that ${\widetilde{\gamma }}\vert _{[0,1]}\cap S({\widetilde{\gamma }}'\vert _{[0,1]})\not =\emptyset$. If ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }}')$ intersect $\widetilde{\mathcal {F}}$-transversally, there exist t and $t'$ such that ${\widetilde{\gamma }}(t)=S({\widetilde{\gamma }}')(t')$. Write [x] for the integer part of a real number x. One has ${\widetilde{\gamma }}(t-[t])=T^{-[t]}ST'{}^{[t']}({\widetilde{\gamma }})(t'-[t'])$, which implies that $T^{-[s]}ST'{}^{[t]}$ is one of the L previous automorphisms. $\square$

Let $\mathcal {F}$ be an oriented singular foliation on M and $\widetilde{\mathcal {F}}$ the lifted foliation on the universal covering space $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ of ${\mathrm {dom}}(\mathcal {F})$. Let $\Gamma$ be a loop on M transverse to $\mathcal {F}$ and ${\widetilde{\gamma }}$ a lift of $\Gamma$ to $\widetilde{{\mathrm {dom}}}(\mathcal {F})$. Write T for the covering automorphism such that ${\widetilde{\gamma }}(t+1)=T({\widetilde{\gamma }}(t))$ for every $t\in \mathbb {R}$. If $\delta :J\rightarrow \widetilde{{\mathrm {dom}}}(\mathcal {F})$ is a transverse path equivalent to a subpath of ${\widetilde{\gamma }}$ we define its width (relative to ${\widetilde{\gamma }}$) to be the largest integer l (possibly infinite) such that $\delta$ meets l translates of a leaf by a power of T. More precisely, ${\mathrm {width}}_{{\widetilde{\gamma }}}(\delta )=\infty$ if there exists a leaf $\phi$ such that $\delta$ meets infinitely many translates of $\phi$ by a power of T, and ${\mathrm {width}}(\delta )=l<+\infty$ if there exists a leaf $\phi$ such that $\delta$ meets every leaf $T^k(\phi )$, $0\leqslant k<l$, and if $l+1$ does not satisfy this property. By Lemma 8, up to a left composition by a power of T there are finitely many lifts $S({\widetilde{\gamma }})$ such that ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }})$ intersect $\widetilde{\mathcal {F}}$-transversally. This number is clearly independent of the chosen lift ${\widetilde{\gamma }}$, we denote it ${\mathrm {self}}(\Gamma )$. Saying that $\Gamma$ has a $\mathcal {F}$-transverse self-intersection means that ${\mathrm {self}}(\Gamma )\not =0$. If ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }})$ intersect $\widetilde{\mathcal {F}}$-transversally, one can consider the maximal subpath of $S({\widetilde{\gamma }})$ that is equivalent to a subpath of ${\widetilde{\gamma }}$. Note that its width (relative to ${\widetilde{\gamma }}$) is finite. Looking at all the $S({\widetilde{\gamma }})$ that intersect $\widetilde{\mathcal {F}}$-transversally ${\widetilde{\gamma }}$ and taking the supremum, one gets a finite number because the $S({\widetilde{\gamma }})$ are finite up to a composition by a power of T. This number is independent of the choice of ${\widetilde{\gamma }}$, we denote it ${\mathrm {width}}(\Gamma )$. One gets a total order $\preceq _{{\widetilde{\gamma }}}$ on the set of leaves met by a lift ${\widetilde{\gamma }}$, where

$$\begin{aligned} {\widetilde{\phi }}\preceq _{{\widetilde{\gamma }}}{\widetilde{\phi }}'\,\Leftrightarrow \, R({\widetilde{\phi }})\subset R({\widetilde{\phi }}'). \end{aligned}$$

Note that if ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }})$ intersect transversally and ${\widetilde{\phi }}$ is a leaf met by ${\widetilde{\gamma }}$, then there exist at most ${\mathrm {width}}(\Gamma )$ translates of ${\widetilde{\phi }}$ by a power of T that meet $S({\widetilde{\gamma }})$. Moreover, there exists $k\in \mathbb {Z}$ such that every leaf ${\widetilde{\phi }}'$ met by ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }})$ satisfies $T^{k}({\widetilde{\phi }})\prec _{{\widetilde{\gamma }}} {\widetilde{\phi }}'\prec _{{\widetilde{\gamma }}}T^{{\mathrm {width}}(\Gamma )+1+k}({\widetilde{\phi }})$ and consequently that ${\widetilde{\phi }}$ and $T^{{\mathrm {width}}(\Gamma )+1} ({\widetilde{\phi }})$ are separated by $T^{-k}S({\widetilde{\gamma }})$.

Proposition 9

Let $\mathcal {F}$ be an oriented singular foliation on M, let $\Gamma$ be a transverse loop with a $\mathcal {F}$-self-transverse intersection and $\gamma$ its natural lift. Write

$$\begin{aligned} M(\Gamma )=\,{\mathrm {self}}(\Gamma ) {\mathrm {width}}(\Gamma )({\mathrm {width}}(\Gamma )+1)+1. \end{aligned}$$

Consider two points z and $z'$ disjoint from $\Gamma$ and look at the set of homotopy classes, with fixed endpoints, of paths starting at z and ending at $z'$. There are at most $2M(\Gamma )$ classes which are represented both by a path disjoint from $\Gamma$ and by a (possibly different) transverse path equivalent to a subpath of $\gamma$.

Proof

Fix a lift $\widetilde{z}$ of z in $\widetilde{{\mathrm {dom}}}(\mathcal {F})$ and denote ${\widetilde{X}}$ the set of lifts $\widetilde{z}'$ of $z'$ such that there exists a path from $\widetilde{z}$ to $\widetilde{z}'$ disjoint from all lifts of $\gamma$ and such that there exists a transverse path from $\widetilde{z}$ to $\widetilde{z}'$ that is $\widetilde{\mathcal {F}}$-equivalent to a subpath of at least one lift of $\gamma$. The proposition is equivalent to showing that ${\widetilde{X}}$ does not contain more than $2M(\Gamma )$ points.

By definition, for every $\widetilde{z}'\in {\widetilde{X}}$, there exists a transverse path ${\widetilde{\delta }}_{\widetilde{z}'}$ from $\widetilde{z}$ to $\widetilde{z}'$, unique up to equivalence. Moreover the set ${\widetilde{X}}\cup \{\widetilde{z}\}$ is included in a connected component ${\widetilde{W}}$ of the complement of the union of lifts of $\gamma$. There is no lift ${\widetilde{\gamma }}$ of $\gamma$ that separates points of ${\widetilde{X}}$: for each lift ${\widetilde{\gamma }}$, the set ${\widetilde{X}}$ is included in $R({\widetilde{\gamma }})$ or in $L({\widetilde{\gamma }})$. One can write ${\widetilde{X}}={\widetilde{X}}_r\cup {\widetilde{X}}_l$, where $\widetilde{z}'\in {\widetilde{X}}_r$ if there exists a lift ${\widetilde{\gamma }}$ of $\gamma$ satisfying ${\widetilde{X}}\subset R({\widetilde{\gamma }})$ such that ${\widetilde{\delta }}_{\widetilde{z}'}$ is a subpath of ${\widetilde{\gamma }}$ (up to equivalence). One define similarly ${\widetilde{X}}_l$ replacing the condition ${\widetilde{X}}\subset R({\widetilde{\gamma }})$ by ${\widetilde{X}}\subset L({\widetilde{\gamma }})$. We will prove that ${\widetilde{X}}_r$ and ${\widetilde{X}}_l$ do not contain more than $M(\Gamma )$ points. The two situations being similar, we will study the first one.

Lemma 10

If $\widetilde{z}'_1$ and $\widetilde{z}'_2$ are two different points in ${\widetilde{X}}$, then $\phi _{{\widetilde{z}'_1}}\not =\phi _{{\widetilde{z}'_2}}$.

Proof

See Fig. 9 for the following construction. Suppose for example that $\widetilde{z}'_1\in \phi ^+_{{\widetilde{z}'_2}}$ and denote by S the covering automorphism such that $\widetilde{z}'_1=S(\widetilde{z}'_2)$. There exists a lift ${\widetilde{\gamma }}$ of $\gamma$ such that ${\widetilde{\delta }}_{\widetilde{z}'_1}$ is a subpath of ${\widetilde{\gamma }}$ (up to equivalence). Note that there exists $k\in \mathbb {Z}$ such that $\widetilde{z}'_1\in R(S^k({\widetilde{\gamma }}))$ and $\widetilde{z}'_2\in L(S^k({\widetilde{\gamma }}))$. The lift $S^k({\widetilde{\gamma }})$ separates $\widetilde{z}'_1$ and $\widetilde{z}'_2$, we have a contradiction. $\square$

Fig. 9

Cases described in Lemma 10 (left) and Lemma 11 (right)

Lemma 11

If $\widetilde{z}'_1$ and $\widetilde{z}'_2$ are two different points in ${\widetilde{X}}_r$, then up to equivalence, one of the paths ${\widetilde{\delta }}_{\widetilde{z}'_1}$, ${\widetilde{\delta }}_{\widetilde{z}'_2}$ is a subpath of the other one.

Proof

Each path ${\widetilde{\delta }}_{\widetilde{z}'_i}$, $i\in \{1,2\}$, joins $\phi _{\widetilde{z}}$ to $\phi _{{\widetilde{z}'_i}}$. We claim that either $L(\phi _{{\widetilde{z}'_1}})\subset L(\phi _{{\widetilde{z}'_2}})$ or $L(\phi _{{\widetilde{z}'_2}})\subset L(\phi _{{\widetilde{z}'_1}})$. If this is not the case, one of the leaves $\phi _{{\widetilde{z}'_1}}$, $\phi _{{\widetilde{z}'_2}}$ is above the other one relative to $\phi _{\widetilde{z}}$. Suppose that it is $\phi _{{\widetilde{z}'_1}}$. By definition of ${\widetilde{X}}_r$, there exists a lift ${\widetilde{\gamma }}$ of $\gamma$ satisfying ${\widetilde{X}}_r\subset R({\widetilde{\gamma }})$ such that ${\widetilde{\delta }}_{\widetilde{z}'_1}$ is a subpath of ${\widetilde{\gamma }}$ (up to equivalence). Note now that $\phi _{{\widetilde{z}'_2}}\subset L({\widetilde{\gamma }})$ which contradicts the fact that $\widetilde{z}'_2\in R({\widetilde{\gamma }})$.

Since $L(\phi _{\widetilde{z}})$ contains both $L(\phi _{{\widetilde{z}'_1}})$ and $L(\phi _{{\widetilde{z}'_2}})$, and since, by the previous lemma, $\phi _{\widetilde{z}}, \, \phi _{{\widetilde{z}'_1}}$, and $\phi _{{\widetilde{z}'_2}}$ are all distinct, either $\phi _{{\widetilde{z}'_1}}$ separates $\phi _{\widetilde{z}}$ from $\phi _{{\widetilde{z}'_2}}$, or $\phi _{{\widetilde{z}'_2}}$ separates $\phi _{\widetilde{z}}$ from $\phi _{{\widetilde{z}'_1}}$. In the first case, ${\widetilde{\delta }}_{\widetilde{z}'_1}$ is equivalent to a subpath of ${\widetilde{\delta }}_{\widetilde{z}'_2}$, and in the second case ${\widetilde{\delta }}_{\widetilde{z}'_2}$ is equivalent to a subpath of ${\widetilde{\delta }}_{\widetilde{z}'_1}$. $\square$

We will suppose that ${\widetilde{X}}_r$ has at least K points, and we will show that $K\leqslant M(\Gamma )$, which proves the proposition. Using Lemmas 10 and 11, one can find a family $(\widetilde{z}'_i)_{0\leqslant i\leqslant {K-1}}$ of points of ${\widetilde{X}}_r$ such that ${\widetilde{\delta }}_{\widetilde{z}'_i}$ is a strict subpath of ${\widetilde{\delta }}_{\widetilde{z}_j}$ (up to equivalence) if $i<j$. One knows that there exists a lift ${\widetilde{\gamma }}$ of $\gamma$ such that ${\widetilde{\delta }}_{\widetilde{z}'_{M(\Gamma )}}$ is equivalent to a subpath of ${\widetilde{\gamma }}$. One deduces that every leaf $\phi _{\widetilde{z}'_i}$, $0\leqslant i\leqslant {K-1}$, is met by ${\widetilde{\gamma }}$ and that $\phi _{\widetilde{z}'_i} \prec _{{\widetilde{\gamma }}}\phi _{\widetilde{z}'_j}$ if $i<j$. Write $\widetilde{z}'_i=T_i(\widetilde{z}'_0)$ and note that $T_i$ belongs to ${\mathrm {stab}}({\widetilde{W}})$, the stabilizer of ${\widetilde{W}}$ in the group of covering automorphisms.

Fig. 10

Final case of Lemma 12

Lemma 12

The lifts ${\widetilde{\gamma }}$ and $T_i({\widetilde{\gamma }})$ intersect transversally for every $i\in \{1,\ldots , {K-1}\}$.

Proof

Fix $i\in \{1,\ldots , {K-1}\}$. One can find a transverse line ${\widetilde{\beta }}$ invariant by $T_i$ passing through $\widetilde{z}'_0$ and $\widetilde{z}'_i$. Write ${\widetilde{\delta }}$ for the maximal subpath of ${\widetilde{\gamma }}$ that is equivalent to a subpath of ${\widetilde{\beta }}$. If ${\widetilde{\gamma }}$ and ${\widetilde{\beta }}$ intersect $\widetilde{\mathcal {F}}$-transversally, then ${\widetilde{\gamma }}$ separates $T_i^{-k}(\phi _{\widetilde{z}'_0})$ and $T_i^{k}(\phi _{\widetilde{z}'_0})$ if k is large enough. So, it separates $T_i^{-k}(\widetilde{z}'_0)$ and $T_i^{k}(\widetilde{z}'_0)$. This contradicts the fact that $T_i\in {\mathrm {stab}}({\widetilde{W}})$. If ${\widetilde{\delta }}$ is unbounded or equivalently if ${\mathrm {width}}_{\beta }(\gamma )=+\infty$, then ${\widetilde{\delta }}$ is forward or backward invariant by $T_i$. Look at the first case. Since $\gamma$ has a $\mathcal {F}$-transverse self-intersection, there exists a covering automorphism S such that ${\widetilde{\gamma }}$ and $S({\widetilde{\gamma }})$ intersect $\widetilde{\mathcal {F}}$-transversally. For every integer n, the lines $T^nS({\widetilde{\gamma }})$ and ${\widetilde{\gamma }}$ intersect $\widetilde{\mathcal {F}}$-transversally. One deduces that if n is large enough, then $T^nS({\widetilde{\gamma }})$ and ${\widetilde{\delta }}$ intersect $\widetilde{\mathcal {F}}$-transversally and consequently $T^nS({\widetilde{\gamma }})$ and ${\widetilde{\beta }}$ intersect $\widetilde{\mathcal {F}}$-transversally. So, if k is large enough, $T^nS({\widetilde{\gamma }})$ separates $T_i^{-k}(\phi _{\widetilde{z}'_0})$ and $T_i^{k}(\phi _{\widetilde{z}'_0})$. This again contradicts the fact that $T_i\in {\mathrm {stab}}({\widetilde{W}})$. The case where ${\widetilde{\delta }}$ is backward invariant can be treated analogously. It remains to study the case where $\delta$ is bounded and ${\widetilde{\gamma }}$ and ${\widetilde{\beta }}$ do not intersect $\widetilde{\mathcal {F}}$-transversally.

See Fig. 10 for the following construction. Write ${\widetilde{\delta }}'$ for the maximal subpath of ${\widetilde{\beta }}$ that is equivalent to ${\widetilde{\delta }}$. There exist $a<b$ such that ${\widetilde{\delta }}={\widetilde{\gamma }}\vert _{(a,b)}$ and $a'<b'$ such that ${\widetilde{\delta }}'={\widetilde{\beta }}\vert _{(a',b')}$. The sets $R({\widetilde{\gamma }}(a))$ and $R({\widetilde{\beta }}(a'))$ are disjoint, as are the sets $L({\widetilde{\gamma }}(b))$ and $L({\widetilde{\beta }}(b'))$. There exists a leaf $\phi _0$ such that ${\widetilde{\delta }}$ and ${\widetilde{\delta }}'$ meet $\phi _0$ and $T_i(\phi _0)$. In particular $T_i(\phi _0)$ is met by ${\widetilde{\gamma }}\vert _{[a,b]}$ and $T_i({\widetilde{\gamma }})\vert _{[a,b]}$. By assumption, ${\widetilde{\gamma }}$ and ${\widetilde{\beta }}$ do not intersect $\widetilde{\mathcal {F}}$-transversally. There is no loss of generality by supposing that $\phi _{{\widetilde{\beta }}(a')}$ is below $\phi _{{\widetilde{\gamma }}(a)}$ and $\phi _{{\widetilde{\beta }}(b')}$ below $\phi _{{\widetilde{\gamma }}(b)}$ relative to $\phi _0$ or $T_i(\phi _0)$. The leaf $T_i(\phi _{{\widetilde{\beta }}(a')})$ is above $T_i(\phi _{{\widetilde{\gamma }}(a)})= \phi _{T_i({\widetilde{\gamma }})(a)}$ relative to $T_i(\phi _0)$. Moreover, since $T_i$ preserves ${\widetilde{\beta }}$, one has that $T_i(\phi _{{\widetilde{\beta }}(a')})$ separates $\phi _{{\widetilde{\beta }}(a')}$ and $T_i(\phi _0)$, and therefore it is crossed by both ${\widetilde{\delta }}$ and ${\widetilde{\delta }}'$. This implies that there exists a transverse path that joins $\phi _{{\widetilde{\gamma }}(a)}$ to $T_i(\phi _{{\widetilde{\beta }}(a')})$. Consequently, $\phi _{{\widetilde{\gamma }}(a)}$ belongs to $R(T_i(\phi _{{\widetilde{\beta }}(a')}))$ and is above $\phi _{T_i({\widetilde{\gamma }})(a)}$ relative to $T_i(\phi _0)$. Similarly, there exists a transverse path that joins $\phi _{{\widetilde{\beta }}(b')}$ to $\phi _{T_i({\widetilde{\gamma }})(b)}$. Consequently, $\phi _{T_i({\widetilde{\gamma }})(b)}$ belongs to $L(\phi _{{\widetilde{\beta }}(b')})$ and is above $\phi _{{\widetilde{\gamma }}(b)}$ relative to $T_i(\phi _0)$. We have proved that the paths ${\widetilde{\gamma }}_{[a,b]}$ and $T_i({\widetilde{\gamma }})_{[a,b]}$ intersect $\widetilde{\mathcal {F}}$-transversally. $\square$

By the definition of ${\mathrm {self}}(\Gamma )$ and Lemma 12, there exists covering automorphisms $(S_l)_{0\leqslant l <{\mathrm {self}}(\Gamma )}$ such that ${\widetilde{\gamma }}$ and $S_l({\widetilde{\gamma }})$ intersect $\widetilde{\mathcal {F}}$-transversally, a family $(l_i)_{1\leqslant i\leqslant {K-1}}$ in $\{0, \ldots , {\mathrm {self}}(\Gamma )-1\}$ and families of relative integers $(n_i)_{1\leqslant i\leqslant {K-1}}$, $(m_i)_{1\leqslant i\leqslant {K-1}}$, such that $T_{i}=T^{n_i}S_{l_i}T^{m_i}$. Note that, if $1\leqslant i, j \leqslant {K-1}$, and $i\not =j$, then $T_i\not =T_j$, and the function that assigns for each i the triple $(n_i, l_i, m_i)$ is injective.

Define, for $0\leqslant l <{\mathrm {self}}(\Gamma )$ the set $I_l=\{1\leqslant i\leqslant {K-1}, \, l_i=l \}$ and fix some l in $\{1, \ldots , {\mathrm {self}}(\Gamma )\}$. If $i\in I_l$, each leaf $T^{m_i}(\phi _{\widetilde{z}'_{0}})= S_{l}^{-1}T^{-n_i}(\phi _{\widetilde{z}'_{i}})$ is met both by ${\widetilde{\gamma }}$ and by $S_{l}^{-1}({\widetilde{\gamma }})$, and since ${\widetilde{\gamma }}$ and $S_{l}^{-1}({\widetilde{\gamma }})$ also intersect $\widetilde{\mathcal {F}}$-transversally, we deduce that there are at most ${\mathrm {width}}(\Gamma )$ possible values for $m_{i}$ with $i\in I_l$. Fix such a value m and consider the set $I_{l, m}=\{1\leqslant i\leqslant {K-1}, \, l_i=l,\, m_i=m \}$. Note that, if $i\in I_{l, m}$, then the leaf $\phi _{\widetilde{z}'_{i}}= T^{n_i}S_{l}T^{m}(\phi _{\widetilde{z}'_{0}})$ is met by both ${\widetilde{\gamma }}$ and $S^{l}({\widetilde{\gamma }})$. The fact that no line $T^kS{\widetilde{\gamma }}$, $k\in \mathbb {Z}$ separates the leaves $\phi _{\widetilde{z}'_{i}}, i\in I_{l, m}$ implies, as noted just before Proposition 9, that there at most ${\mathrm {width}}(\Gamma )+1$ such leaves, that means at most ${\mathrm {width}}(\Gamma )+1$ possible values of $n_i$ and elements in $I_{l, m}$. One deduces that

$$\begin{aligned} {K\leqslant {\mathrm {self}}(\Gamma ){\mathrm {width}}(\Gamma )({\mathrm {width}}(\Gamma )+1)=M(\Gamma ),} \end{aligned}$$

as desired. $\square$

3.5 Transverse homology set

For any loop $\Gamma$ on M, let us denote $[\Gamma ]\in H_1(M,\mathbb {Z})$ its singular homology class. The transverse homology set of ${\mathcal {F}}$ is the smallest set ${\mathrm {THS}}({\mathcal {F}})$ of $H_1(M,\mathbb {Z})$, that is stable by addition and contains all classes of loops positively transverse to $\mathcal {F}$. The following result will also be useful:

Proposition 13

Let $\mathcal {F}$ be a singular oriented foliation on $\mathbb {T}^2$ and $\widetilde{\mathcal {F}}$ its lift to $\mathbb {R}^2$. If one can find finitely many classes $\kappa _i\in {\mathrm {THS}}({\mathcal {F}})$, $1\leqslant i\leqslant r$, that linearly generate the whole homology of the torus and satisfy $\sum _{1\leqslant i\leqslant r}\kappa _i=0$, then the diameters of the leaves of $\widetilde{\mathcal {F}}$ are uniformly bounded.

Proof

Decomposing each class $\kappa _i$ and taking out all the loops homologous to zero, one can suppose (changing r is necessary) that for every $i\in \{1,\ldots ,r\}$, there exists a transverse loop $\Gamma _i$ such that $[\Gamma _i]=\kappa _i$. The fact that the $\kappa _i$ linearly generate the whole homology of the torus implies that the multi-loop $\Gamma =\sum _{1\leqslant i\leqslant p}\Gamma _i$ is connected (as a set) and that the connected components of its complement are simply connected. Moreover, these components are lifted in uniformly bounded simply connected domains of $\mathbb {R}^2$, let us say by a constant K. The multi-loop $\Gamma$ being homologous to zero induces a dual function $\delta$ on its complement. It has been explained before that $\delta$ decreases on each leaf of $\mathcal {F}$ and is bounded. Consequently, there exists an integer N such that every leaf meets at most N components. If one lifts it to $\mathbb {R}^2$, one find a path of diameter bounded by NK. $\square$

4 Maximal isotopies, transverse foliations, admissible paths

4.1 Singular isotopies, maximal isotopies

Let us begin by introducing mathematical objects related to isotopies. Let f be a homeomorphism of an oriented surface M. An identity isotopy of f is a path joining the identity to f in the space of homeomorphisms of M, furnished with the $C^0$ topology (defined by the uniform convergence of maps and their inverse on every compact set). We will write $\mathcal {I}$ for the set of identity isotopies of f and will say that f is isotopic to the identity if this set is not empty. If $I=(f_t)_{t\in [0,1]}\in \mathcal {I}$ is such an isotopy, we can define the trajectory of a point $z\in M$, which is the path $I(z): t\mapsto f_t(z)$. More generally, for every $n\geqslant 1$ we define $I^n(z)=\prod _{0\leqslant k<n} I(f^k(z))$ by concatenation. We will also use the following notations

$$\begin{aligned} I^{\mathbb {N}} (z)= & {} \prod _{0\leqslant k<+\infty } I (f^k(z)),\, I^{-\mathbb {N}} (z)=\prod _{-\infty<k<0} I(f^k(z)), \\ I^{\mathbb {Z}}(z)= & {} \prod _{-\infty<k<+\infty } I(f^k(z)). \end{aligned}$$

The last path will be called the whole trajectory of z.

One can define the fixed point set ${\mathrm {fix}}(I)=\bigcap _{t\in [0,1]}{\mathrm {fix}}(f_t)$ of I, which is the set of points with trivial trajectory.

A wider class of isotopies is the class of singular isotopies. Such an object I is an identity isotopy defined on an open set invariant by f, the domain of I, whose complement, the singular set, is included in the fixed point set of f. We will write ${\mathrm {dom}}(I)$ for the domain and ${\mathrm {sing}}(I)$ for the singular set. Like in the case of a global isotopy, one can define the trajectory I(z) of a point $z\in {\mathrm {dom}}(I)$ and the fixed point set, which is included in the domain. Note that any isotopy $I\in \mathcal {I}$ is itself a singular isotopy with empty singular set and induces by restriction to the complement of the fixed point set a singular isotopy such that ${\mathrm {sing}}(I)={\mathrm {fix}}(I)$.

If $\check{M}$ is a covering space of M and $\check{\pi }:\check{M}\rightarrow M$ the covering projection, every identity isotopy I can be lifted to $\check{M}$ as an identity isotopy $\check{I}=(\check{f}_t)_{t\in [0,1]}$. The homeomorphism $\check{f}=\check{f}_1$ is the lift of f associated to I or induced by I. Similarly, every singular isotopy can be lifted as a singular isotopy $\check{I}$ of $\check{f}$ such that ${\mathrm {dom}}(\check{I})=\check{\pi }^{-1}({\mathrm {dom}}(I))$.

Let us recall now some results due to Jaulent [21]. Denote the set of singular isotopies by $\mathcal {I}_{{\mathrm {sing}}}$. It is not difficult to show that one gets a preorder $\preceq$ on $\mathcal {I}_{{\mathrm {sing}}}$, writing $I\preceq I'$ if:

i) :

${\mathrm {dom}}(I')\subset {\mathrm {dom}}(I)$;

ii) :

for every $z\in {\mathrm {dom}}(I')$, the trajectories $I'(z)$ and I(z) are homotopic in ${\mathrm {dom}}(I)$;

iii) :

for every $z\in {\mathrm {dom}}(I)\setminus {\mathrm {dom}}(I')$, the trajectory I(z) is homotopic to zero in ${\mathrm {dom}}(I)$.

We will say that I and $I'$ are equivalent if $I\preceq I'$ and $I'\preceq I$. We will say that I is maximal if there is no singular isotopy $I'$ such that $I\preceq I'$ and ${\mathrm {dom}}(I')\not ={\mathrm {dom}}(I)$. If I is a singular isotopy and if there is no point $z\in {\mathrm {fix}}(f)\cap {\mathrm {dom}}(I)$ such that I(z) is homotopic to zero in ${\mathrm {dom}}(I)$, then I is maximal by iii). The converse is true. If there is a point $z\in {\mathrm {fix}}(f)\cap {\mathrm {dom}}(I)$ such that I(z) is homotopic to zero in ${\mathrm {dom}}(I)$, one can find an isotopy $I'$ on ${\mathrm {dom}}(I)$ that is homotopic to I (as a path in the space of homeomorphisms of M and relative to the ends) and that fixes z. Taking the restriction of $I'$ on ${\mathrm {dom}}(I)\setminus \{z\}$, one finds a singular isotopy strictly larger than I. The main result of [21] is the fact that every singular isotopy is smaller than a maximal singular isotopy. In fact, the result is more precise and can be stated for hereditary singular isotopies (we will explain later the interest of looking at this class of singular isotopies). By definition, such an isotopy I satisfies the following condition: for every open set U containing ${\mathrm {dom}}(I)$, there exists $I'\in \mathcal {I}_{{\mathrm {sing}}}$ such that $I'\preceq I$ and ${\mathrm {dom}}(I')=U$. Writing $\mathcal {I}_{{\mathrm {her}}}$ for the set of hereditary singular isotopies, we have the following result due to Jaulent [21]:

Theorem 14

For every $I\in \mathcal {I}_{{\mathrm {her}}}$ there exists $I'\in \mathcal {I}_{{\mathrm {her}}}$, maximal in $\mathcal {I}_{{\mathrm {her}}}$, satisfying $I\preceq I'$. Such an isotopy $I'$ is maximal in $\mathcal {I}_{{\mathrm {sing}}}$ and so there is no point $z\in {\mathrm {fix}}(f)\cap {\mathrm {dom}}(I')$ such that $I'(z)$ is homotopic to zero in ${\mathrm {dom}}(I')$

Note that if $\check{M}$ is a covering space of M and $\check{\pi }:\check{M}\rightarrow M$ the covering projection, then for every singular isotopies I, $I'$ satisfying $I\preceq I'$, the respective lifts $\check{I}$, $\check{I}'$ satisfy $\check{I}\preceq \check{I}'$. Note also that a singular isotopy I is maximal if and only if its lift $\check{I}$ is maximal.

Let us explain the reason why hereditary singular isotopies are important. It is related to the following problem. If I is a singular isotopy, does there exists a global isotopy $I'\in \mathcal {I}$ such that ${\mathrm {fix}}(I')= {\mathrm {sing}}(I)\cup {\mathrm {fix}}(I)$ and $I'\vert _{M\setminus {\mathrm {fix}}(I')}$ equivalent to I ? Such an isotopy $I'$ always exists in the case where ${\mathrm {fix}}(f)$ is totally disconnected. Indeed, in that case, I naturally extends to an isotopy on M that fixes the ends of ${\mathrm {dom}}(I)$ corresponding to points of M. The problem is much more difficult in the case where ${\mathrm {fix}}(f)$ is not totally disconnected. The fact that I is a hereditary singular isotopy is necessary because the restriction of a global isotopy to the complement of its fixed point set is obviously hereditary. It appears that this condition is sufficient. This is the purpose of a recent work by Béguin et al. [4]. Following [4], Jaulent’s theorem about existence of maximal isotopies can be stated in the following much more natural form: for every $I\in \mathcal {I}$, there exists $I'\in \mathcal {I}$ such that:

i) :

${\mathrm {fix}}(I)\subset {\mathrm {fix}}(I')$;

ii) :

$I'$ is homotopic to I relative to ${\mathrm {fix}}(I)$;

iii) :

there is no point $z\in {\mathrm {fix}}(f)\setminus {\mathrm {fix}}(I')$ whose trajectory $I'(z)$ is homotopic to zero in $M\setminus {\mathrm {fix}}(I')$.

The last condition can be stated in the following equivalent form:

• if ${\widetilde{I}}'=(\widetilde{f}'_t)_{t\in [0,1]}$ is the identity isotopy that lifts $I'\vert _{M\setminus {\mathrm {fix}}(I')}$ to the universal covering space of $M\setminus {\mathrm {fix}}(I')$, then $\widetilde{f}'_1$ is fixed point free.

The typical example of an isotopy $I\in {\mathcal {I}}$ verifying iii) is the restricted family $I=(f_t)_{t\in [0,1]}$ of a topological flow $(f_t)_{t\in \mathbb {R}}$ on M. Indeed, one can lift the flow $(f_t\vert _{M\setminus {\mathrm {fix}}(I)})_{t\in \mathbb {R}}$ as a flow $(\widetilde{f}_t)_{t\in \mathbb {R}}$ on the universal covering space of $M\setminus {\mathrm {fix}}(I)$. This flow has no fixed point and consequently no periodic point. So $\widetilde{f}_1$ is fixed point free, which exactly means that the condition iii) is fulfilled. In particular, the restriction of f to $M\setminus {\mathrm {fix}}(I)$ is a hereditary maximal isotopy. To construct a maximal singular isotopy that is not hereditary, let us consider the flow $(f_t)_{t\in \mathbb {R}}$ on $\mathbb {R}^2$ defined as follows in polar coordinates

$$\begin{aligned} f_t(r,\theta )=( r, \theta + 2\pi t h(r)) \end{aligned}$$

where

$$\begin{aligned} {h(r) = {\left\{ \begin{array}{ll} r(1-r), &{}\text{ if } r\in [0,1], \\ r^{-1}(1-r^{-1}), &{} \text{ if } r\in [1,+\infty ). \end{array}\right. } } \end{aligned}$$

and set $f=f_1$. The fixed point set of the flow is the union of the origin and the unit circle $\mathbb {S}^1$ and so, the restriction of the isotopy $(f_t)_{t\in [0,1]}$ to the complement of this fixed point set is a maximal hereditary singular isotopy. The isotopy $I'=(f'_t)_{t\in [0,1]}$, whose domain is the complement of $\{(0,0)\}\cup \mathbb {S}^1$, that coincides with $(f_t)_{t\in [0,1]}$ on the set of points such that $0<r<1$ and defined on the set of points such that $r>1$ by:

$$\begin{aligned} f'_t(r,\theta ) = {\left\{ \begin{array}{ll} ( r, \theta +4\pi tr), &{}\text{ if } t\in [0,1/2], \\ ( r, \theta +4\pi (t-1/2)h(r)), &{} \text{ if } t\in [1/2,1]. \end{array}\right. } \end{aligned}$$

is not a hereditary singular isotopy. There is no singular isotopy $I''$ of f whose domain is the complement of $\{(0,0), (1,0)\}$ such that $I''\preceq I'$ for the following reason. If ${\widetilde{I}}''$ is the lift of $I''$ to the universal covering of ${\mathrm {dom}}(I'')$, and if $\ z$ is a lift of $(0, -1)$, and $\widetilde{z}_n$ are lifts of $(0, -1-1/n)$ such that $\widetilde{z}_n$ converges to $\widetilde{z}$, then the trajectory of ${\widetilde{I}}''(\widetilde{z})$ would be a closed loop, but the endpoints of the trajectories of ${\widetilde{I}}''(\widetilde{z}_n)$ do not converge to $\widetilde{z}$, since the trajectories of $I'(z_n)$ and $I''(z_n)$ are homotopic in ${\mathrm {dom}}(I)$.

Since the proof of [4] is not published yet, we will use the formalism of singular isotopies in the article.

4.2 Transverse foliations

Let f be an orientation preserving plane homeomorphism. By definition, a Brouwer line of f is a topological line $\lambda$ such that $f(\overline{L(\lambda )})\subset L(\lambda )$ (or equivalently a line $\lambda$ such that $f(\lambda )\subset L(\lambda )$ and $f^{-1}(\lambda )\subset R(\lambda ))$. The classical Brouwer Plane Translation Theorem asserts that $\mathbb {R}^2$ can be covered by Brouwer lines in case f is fixed point free (see [7]). Let us recall now the equivariant foliated version of this theorem (see [28]). Suppose that f is a homeomorphism isotopic to the identity on an oriented surface M. Let I be a maximal singular isotopy and write ${\widetilde{I}}=(\widetilde{f}_t)_{t\in [0,1]}$ for the lifted identity defined on the universal covering space $\widetilde{{\mathrm {dom}}}(I)$ of ${\mathrm {dom}}(I)$. Recall that $\widetilde{f}=\widetilde{f}_1$ is fixed point free. Suppose first that ${\mathrm {dom}}(I)$ is connected. In that case, $\widetilde{{\mathrm {dom}}}(I)$ is a plane and we have [28]:

Theorem 15

There exists a non singular topological oriented foliation $\widetilde{\mathcal {F}}$ on $\widetilde{{\mathrm {dom}}}(I)$, invariant by the covering automorphisms, whose leaves are Brouwer lines of $\widetilde{f}$.

Consequently, for every point $\widetilde{z}\in \widetilde{{\mathrm {dom}}}(I)$, one has

$$\begin{aligned} \widetilde{f}(\widetilde{z})\in L(\phi _{\widetilde{z}}), \,\widetilde{z}\in R(\phi _{\widetilde{f}(\widetilde{z})}). \end{aligned}$$

This implies that there exists a path ${\widetilde{\gamma }}$ positively transverse to $\widetilde{\mathcal {F}}$ that joins $\widetilde{z}$ to $\widetilde{f}(\widetilde{z})$. As noted in Sect. 3.1, this path is uniquely defined up to $\widetilde{\mathcal {F}}$-equivalence, provided the endpoints remain the same. The leaves of the lifted foliation $\widetilde{\mathcal {F}}$ met by ${\widetilde{\gamma }}$ are the leaves $\phi$ such that $R(\phi _{\widetilde{z}})\subset R(\phi )\subset R(\phi _{\widetilde{f}(\widetilde{z})})$. In particular, every leaf met by ${\widetilde{\gamma }}$ is met by ${\widetilde{I}}(\widetilde{z})$. Of course, $\widetilde{\mathcal {F}}$ lifts a singular foliation ${\mathcal {F}}$ such that ${\mathrm {dom}}(\mathcal {F})={\mathrm {dom}}(I)$. We immediately get the following result, still true in case ${\mathrm {dom}}(I)$ is not connected:

Corollary 16

There exists a singular topological oriented foliation ${\mathcal {F}}$ satisfying ${\mathrm {dom}}({\mathcal {F}})={\mathrm {dom}}(I)$ such that for every $z\in {\mathrm {dom}}(I)$ the trajectory I(z) is homotopic, relative to the endpoints, to a path $\gamma$ positively transverse to ${\mathcal {F}}$ and this path is uniquely defined up to equivalence.

We will say that a foliation $\mathcal {F}$ satisfying the conclusion of Corollary 16 is transverse to I. Observe that if $\check{M}$ is a covering space of M and $\check{\pi }:\check{M}\rightarrow M$ the covering projection, a foliation $\mathcal {F}$ transverse to a maximal singular isotopy I lifts to a foliation $\check{\mathcal {F}}$ transverse to the lifted isotopy $\check{I}$.

We will write $I_{\mathcal {F}} (z)$ for the class of paths that are positively transverse to ${\mathcal {F}}$, that join z to f(z) and that homotopic in ${\mathrm {dom}}(I)$ to I(z), relative to the endpoints. We will also use the notation $I_{\mathcal {F}} (z)$ for every path in this class and called it the transverse trajectory of z. Similarly, for every $n\geqslant 1$, one can define $I_{\mathcal {F}}^n (z)=\prod _{0\leqslant k<n} I_{\mathcal {F}} (f^k(z))$, that is either a transverse path passing through the points z, f(z), ..., $f^n(z)$, or a set of such paths. Similarly we will define

$$\begin{aligned} I_{\mathcal {F}}^{\mathbb {N}} (z)= & {} \prod _{0\leqslant k<+\infty } I_{\mathcal {F}} (f^k(z)),\, I_{\mathcal {F}}^{-\mathbb {N}} (z)=\prod _{-\infty<k<0} I_{\mathcal {F}} (f^k(z)), \, I_{\mathcal {F}}^{\mathbb {Z}} (z)\\= & {} \prod _{-\infty<k<+\infty } I_{\mathcal {F}} (f^k(z)). \end{aligned}$$

The last object will be called the whole transverse trajectory of z.

If z is a periodic point of period q, there exists a transverse loop $\Gamma$ whose natural lift $\gamma$ satisfies $\gamma \vert _{[0,1]}= I_{\mathcal {F}}^q (z)$. By definition a transverse loop is associate to z if it is $\mathcal {F}$-equivalent to $\Gamma$ (the definition was given in Sect. 3.1). Of course this does not depend on the choices of the $I_{\mathcal {F}} (f^k(z)), 0\leqslant k<q$.

Let us state two results that will be useful in Sect. 5.2.

Lemma 17

Fix $z \in {{\mathrm {dom}}(I)}$, $n\geqslant 1$, and parameterize $I_{\mathcal {F}}^n (z)$ by [0, 1]. For every $0<a<b<1$, there exists a neighborhood V of z such that, for every $z'\in V$, the path $I_{\mathcal {F}}^n(z)\vert _{[a,b]}$ is equivalent to a subpath of $I_{\mathcal {F}}^n (z')$. Moreover, there exists a neighborhood W of z such that, for every $z'$ and $z''$ in W, the path $I_{\mathcal {F}}^n(z')$ is equivalent to a subpath of $I_{\mathcal {F}}^{n+2} (f^{-1}(z''))$

Proof

Keep the notations introduced above. Fix a lift $\widetilde{z} \in \widetilde{{\mathrm {dom}}(I)}$ of z and denote by $\phi$ and $\phi '$ the leaves of $\widetilde{\mathcal {F}}$ containing ${\widetilde{I}}_{\widetilde{\mathcal {F}}}^n(\widetilde{z})(a)$ and ${\widetilde{I}}_{\widetilde{\mathcal {F}}}^n(\widetilde{z})(b)$ respectively. One has

$$\begin{aligned} \overline{R(\phi _{\widetilde{z} })}\subset R(\phi )\subset \overline{R(\phi )}\subset R(\phi ')\subset \overline{R(\phi ')}\subset R(\phi _{\widetilde{f}^n(\widetilde{z}) }). \end{aligned}$$

If $V\subset {\mathrm {dom}}(I)$ is a topological disk, small neighborhood of z, the lift $\widetilde{V}$ that contains $\widetilde{z}$ satisfies

$$\begin{aligned} {\widetilde{V}} \subset R(\phi ), \,\widetilde{f}^n({\widetilde{V}}) \subset L(\phi '). \end{aligned}$$

Consequently, for every $z'\in V$, the path $I_{\mathcal {F}}^n(z)\vert _{[a,b]}$ is equivalent to a subpath of $I_{\mathcal {F}}^n (z')$.

Let us prove the second assertion. One can find a leaf $\phi$ of the lifted foliation such that

$$\begin{aligned} \overline{R(\phi _{\widetilde{f}^{-1}( \widetilde{z} )})}\subset R(\phi )\subset \overline{R(\phi )}\subset R(\phi _{\widetilde{z} }) \end{aligned}$$

and a leaf $\phi '$ such that

$$\begin{aligned} \overline{R(\phi _{\widetilde{f}^n( \widetilde{z} )})}\subset R(\phi ')\subset \overline{R(\phi ')}\subset R(\phi _{\widetilde{f}^{n+1}(\widetilde{z} )}). \end{aligned}$$

If $W\subset {\mathrm {dom}}(I)$ is a topological disk, small neighborhood of z, the lift ${\widetilde{W}}$ that contains $\widetilde{z}$ satisfies

$$\begin{aligned} \widetilde{f}^{-1}({\widetilde{W}}) \subset R(\phi ), \,{\widetilde{W}}\subset L(\phi ), \,\widetilde{f}^n({\widetilde{W}}) \subset R(\phi '), \widetilde{f}^{n+1}({\widetilde{W}})\subset L(\phi '). \end{aligned}$$

Consequently, for every $z'$ and $z''$ in W, the path $I^n_{\mathcal {F}}(z')$ is equivalent to a subpath of $I_{\mathcal {F}}^{n+2}(f^{-1}(z''))$. $\square$

Say that $z\in M$ is positively recurrent if $z\in \omega (z)$, which means that there is a subsequence of the sequence $(f^n(z))_{n\geqslant 0}$ that converges to z. Say that $z\in M$ is negatively recurrent if $z\in \alpha (z)$, which means that there is a subsequence of the sequence $(f^{-n}(z))_{n\geqslant 0}$ that converges to z. Say that $z\in M$ is bi-recurrent if it is positively and negatively recurrent. An immediate consequence of the previous lemma is the fact that if $z\in {\mathrm {dom}}(I)$ is positively recurrent, negatively recurrent or bi-recurrent, then $I_{\mathcal {F}}^{\mathbb {Z}} (z)$ is $\mathcal {F}$-positively recurrent, $\mathcal {F}$-negatively recurrent or $\mathcal {F}$-bi-recurrent respectively.

Fig. 11

Lemma 18, construction of $V_a$ and $V_b$

Lemma 18

Suppose that $\gamma :[a,b]\rightarrow {\mathrm {dom}}(I)$ is a transverse path that has a leaf on its right and a leaf on its left. Then, there exists a compact set $K\subset {\mathrm {dom}}(I)$ such that for every $n>0$ and for every transverse trajectory $I^n_{\mathcal {F}}(z)$ that contains a subpath equivalent to $\gamma$, there exists $k\in \{0,\ldots , n-1\}$ such that $f^k(z)$ belongs to K.

Proof

Lifting our path to the universal covering space of the domain, it is sufficient to prove the result in the case where ${\mathrm {dom}}(I)$ is a plane.

Figure 11 illustrates the following construction. Suppose that $\phi _0$ is on the right of $\gamma$ and $\phi _1$ on its left and write W for the connected component of the complement of $\phi _0\cup \phi _1$ that contains $\gamma$. Since $\phi _0$ and $\phi _1$ are Brouwer lines, every orbit that goes from $\overline{R(\phi _{\gamma (a)})}$ to $\overline{L(\phi _{\gamma (b)})}$ is contained in W. Let $\delta$ be a simple path that joins a point $z_0$ of $\phi _0$ to a point $z_1$ of $\phi _1$, that is contained in W but the endpoints and that does not meet neither $\overline{R(\phi _{\gamma (a)})}$ nor $\overline{L(\phi _{\gamma (b)})}$. Write $V_b$ for the connected component of $W\setminus \delta$ that contains $\overline{L(\phi _{\gamma (b)})}$. We will extend $\delta$ as a line $\alpha _0\beta _0\delta \beta _1\alpha _1$ as follows. If W is contained in $R(\phi _0)$, set $\alpha _0=f^{2}(\phi _{z_0}^-)$ and choose for $\beta _0$ a simple path that joins $f^{2} (z_0)$ to $z_0$ and is contained in $R(f^{2}(\phi _0))\cap L(\phi _0)$ but the endpoints. If W is contained in $L(\phi _0)$, set $\alpha _0=(\phi _{z_0}^{+})^{-1}$ and $\beta _0=\{z_0\}$. Similarly, if W is contained in $R(\phi _1)$, choose for $\beta _1$ a simple path that joins $z_1$ to $f^{2} (z_1)$ and is contained in $L(\phi _1)\cap R(f^{2}(\phi _1))$ but the endpoints and set $\alpha _1=f^{2}(\phi _{z_1}^{+})$. Otherwise, if W is contained in $L(\phi _1)$, set $\beta =\{z_1\}$ and $\alpha _1=(\phi _{z_1}^{-})^{-1}$. Note that $\lambda =\alpha _0\beta _0\delta \beta _1\alpha _1$ is a line.

The image of $\beta _0\delta \beta _1$ by $f^{-1}$ is compact and the images of $\alpha _0$ and $\alpha _1$ by $f^{-1}$ are disjoint from W. So, one can find a simple path $\delta '$ that joins a point $z'_0$ of $\phi _0$ to a point $z'_1$ of $\phi _1$, that is contained in W but the endpoints, that does not meet $\overline{V_b}$ and such that the connected component $V_a$ of $W\setminus \delta$ that does not contain $V_b$ (and that meets $\overline{R(\phi _{\gamma (a)})}$), does not intersect $f^{-1}(\lambda )$. This implies that $f(V_a)$ and $V_b$ are separated by $\lambda$ and satisfy $f(V_a)\cap V_b=\emptyset$. So, every orbit that goes from $\overline{R(\phi _{\gamma (a)})}$ to $\overline{L(\phi _{\gamma (b)})}$ has to meet both sets $V_a$ and $V_b$ but is not included in the union of these sets. It must meet the compact set $K=\overline{W\setminus (V_a\cup V_b)}$. $\square$

4.3 Admissible paths

Until the end of the whole section, we suppose given a homeomorphism f isotopic to the identity on an oriented surface M and a maximal singular isotopy I. We write ${\widetilde{I}}=(\widetilde{f}_t)_{t\in [0,1]}$ for the lifted identity defined on the universal covering space $\widetilde{{\mathrm {dom}}}(I)$ of ${\mathrm {dom}}(I)$ and set $\widetilde{f}=\widetilde{f}_1$ for the lift of $f\vert _{{\mathrm {dom}}(I)}$ induced by the isotopy. We suppose that $\mathcal {F}$ is a foliation transverse to I and write $\widetilde{\mathcal {F}}$ for the lifted foliation on $\widetilde{{\mathrm {dom}}}(I)$.

We will say that a path $\gamma :[a,b]\rightarrow {{\mathrm {dom}}}(I)$, positively transverse to $\mathcal {F}$, is admissible of order n if it is equivalent to a path $I_{\mathcal {F}}^n (z)$, $z\in {\mathrm {dom}}(I)$, in the sense defined in Sect. 3.1. It means that if ${\widetilde{\gamma }}:[a,b]\rightarrow \widetilde{{\mathrm {dom}}}(I)$ is a lift of $\gamma$, there exists a point $\widetilde{z}\in \widetilde{{\mathrm {dom}}}(I)$ such that $\widetilde{z}\in \phi _{{\widetilde{\gamma }} (a)}$ and $\widetilde{f}^n(\widetilde{z})\in \phi _{{\widetilde{\gamma }} (b)}$, or equivalently, that

$$\begin{aligned} \widetilde{f}^n(\phi _{{\widetilde{\gamma }} (a)})\cap \phi _{{\widetilde{\gamma }}(b)}\not =\emptyset . \end{aligned}$$

We will say that $\gamma$ is admissible of order $\leqslant n$ if it is a subpath of an admissible path of order n. If ${\widetilde{\gamma }}:[a,b]\rightarrow \widetilde{{\mathrm {dom}}}(I)$ is a lift of $\gamma$, this means that

$$\begin{aligned} \widetilde{f}^n(\overline{R(\phi _{{\widetilde{\gamma }}(a)})})\cap \overline{L(\phi _{{\widetilde{\gamma }}(b)})}\not =\emptyset . \end{aligned}$$

More generally, we will say that a transverse path $\gamma :J\rightarrow {{\mathrm {dom}}}(I)$ defined on an interval is admissible if for every segment $[a,b]\subset J$, there exists $n\geqslant 1$ such that $\gamma \vert _{[a,b]}$ is admissible of order $\leqslant n$. If ${\widetilde{\gamma }}:J\rightarrow \widetilde{{\mathrm {dom}}}(I)$ is a lift of $\gamma$, this means that for every $a<b$ in J, there exists $n\geqslant 1$ such that

$$\begin{aligned} \widetilde{f}_1^n(\overline{R(\phi _{{\widetilde{\gamma }}(a)})})\cap \overline{L(\phi _{{\widetilde{\gamma }}(b)})}\not =\emptyset . \end{aligned}$$

Similarly, we will say that a transverse loop $\Gamma$ is admissible if its natural lift is admissible. If the context is clear, we will say that a path is of order n (order $\leqslant n$) if it is admissible of order n (resp. admissible of order $\leqslant n$).

Let us finish this subsection with a useful result which says that except in some particular trivial cases, there is no difference between being of order $\leqslant n$ and being of order n (and so of being of order $\leqslant n$ and being of order m for every $m\geqslant n$).

Proposition 19

Let $\gamma : [a,b]\rightarrow {{\mathrm {dom}}}(I)$ be a transverse path of order $\leqslant n$ but not of order n, then $\gamma$ has no leaf on its right and no leaf on its left.

Proof

Lifting the path to the universal covering space of the domain, it is sufficient to prove the result in case where ${{\mathrm {dom}}}(I)$ is a plane. By hypothesis, one has:

$$\begin{aligned} f^n(\phi _{ \gamma (a)})\cap \phi _{\gamma (b)}=\emptyset , \, f^n(\overline{R(\phi _{\gamma (a)})})\cap \overline{L(\phi _{\gamma (b)})}\not =\emptyset . \end{aligned}$$

This implies that $f^n(\overline{L(\phi _{\gamma (a)})})\subset L(\phi _{\gamma (b)})$ and $f^{-n}(\overline{R(\phi _{\gamma (b)})})\subset R(\phi _{\gamma (a)})$. Suppose that there exists a leaf $\phi$ in $\overline{L(\phi _{ \gamma (a)})})\cap \overline{R(\phi _{\gamma (b)})}$ that does not meet $\gamma$. Recall that $\phi$ is a Brouwer line. One of the sets $R(\phi )$ or $L(\phi )$ is included in $\overline{L(\phi _{ \gamma (a)})})\cap \overline{R(\phi _{ \gamma (b)})}$. It cannot be $R(\phi )$, because $f^{-n}(R(\phi ))$ would be contained both in $R(\phi )$ and in $R(\phi _{\gamma (a)})$; it cannot be $L(\phi )$, because $f^{n}(L(\phi ))$ would be contained both in $L(\phi )$ and in $L(\phi _{\gamma (b)})$. We have a contradiction.

$\square$

4.4 The fundamental proposition

The next proposition is a new result about maximal isotopies and transverse foliations. It gives us an operation that permits to construct admissible paths from a pair of admissible paths and its proof is very simple. Nevertheless, this fundamental result will have many interesting consequences.

Proposition 20

Suppose that $\gamma _1: [a_1,b_1]\rightarrow M$ and $\gamma _2: [a_2,b_2]\rightarrow M$ are transverse paths that intersect $\mathcal {F}$-transversally at $\gamma _1(t_1)=\gamma _2(t_2)$. If $\gamma _1$ is admissible of order $n_1$ and $\gamma _2$ is admissible of order $n_2$, then $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ and $\gamma _2\vert _{[a_2,t_2]}\gamma _1\vert _{[t_1,b_1]}$ are admissible of order $n_1+n_2$. Furthermore, either one of these paths is admissible of order $\min (n_1, n_2)$ or both paths are admissible of order $\max (n_1, n_2)$.

Proof

Please see Fig. 12 for the following construction. By lifting to the universal covering space of the domain, it is sufficient to prove the result in the case where M is a plane and $\mathcal {F}$ is non singular.

By Proposition 19, each path $\gamma _1$, $\gamma _2$, $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ and $\gamma _2\vert _{[a_2,t_2]}\gamma _1\vert _{[t_1,b_1]}$, having a leaf on its right or on its left, will be admissible of order m if it is admissible of order $\leqslant m$. Note first that for every integers $k_1$, $k_2$ in $\mathbb {Z}$, one has

$$\begin{aligned} f^{k_1}(\overline{R(\phi _{ \gamma _1(a_1)})})\cap \ f^{k_2}(\overline{R(\phi _{ \gamma _2(a_2)})})= f^{k_1}(\overline{L(\phi _{ \gamma _1(b_1)})})\cap f^{k_2}(\overline{L(\phi _{ \gamma _2(b_2)})})=\emptyset . \end{aligned}$$

For every $i\in \{1,2\}$ define the sets

$$\begin{aligned} X_i= f^{n_i}(\overline{R(\phi _{ \gamma _i(a_i)})})\cup \overline{L(\phi _{\gamma _i(b_i)})}, \, Y_i= f^{-n_i}(\overline{L(\phi _{ \gamma _i(b_i)})})\cup \overline{R(\phi _{\gamma _i(a_i)})}, \end{aligned}$$

which are connected according to the admissibility hypothesis.

If $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is not admissible of order $n_1$, then $X_1\cap \overline{L(\phi _{\gamma _2(b_2)})}=\emptyset$ and so $X_1$ separates $\overline{R(\phi _{\gamma _2(a_2)})}$ and $\overline{L(\phi _{\gamma _2(b_2)})}$. This implies that none of the sets $X_1\cap X_2$ and $X_1\cap Y_2$ is empty. The first property implies that $f^{n_2}(\overline{R(\phi _{ \gamma _i(a_2)})})\cap \overline{L(\phi _{\gamma _1(b_1)})}\not =\emptyset$, which means that $\gamma _2\vert _{[a_2,t_2]}\gamma _1\vert _{[t_1,b_1]}$ is admissible of order $n_2$. The second one implies that $f^{-n_2}(\overline{L(\phi _{ \gamma _2(b_2)})})\cap f^{n_1}(\overline{R(\phi _{ \gamma _1(a_1)})})\not =\emptyset$, which means that $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is admissible of order $n_1+n_2$.

Fig. 12

Fundamental lemma, the case where $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is not admissible of order $n_1$

If $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is not admissible of order $n_2$, then $Y_2\cap \overline{R(\phi _{\gamma _1(b_1)})}=\emptyset$ and so $Y_2$ separates $\overline{R(\phi _{\gamma _1(a_1)})}$ and $\overline{L(\phi _{\gamma _1(b_1)})}$. This implies that none of the sets $Y_2\cap Y_1$ and $Y_2\cap X_1$ is empty. The first property implies that $\gamma _2\vert _{[a_2,t_2]}\gamma _1\vert _{[t_1,b_1]}$ is admissible of order $n_1$. The second one implies that $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is admissible of order $n_1+n_2$.

In conclusion, $\gamma _1\vert _{[a_1,t_1]}\gamma _2\vert _{[t_2,b_2]}$ is admissible of order $n_1+n_2$ . Moreover, if it is not admissible of order $\min (n_1,n_2)$ then $\gamma _2\vert _{[a_2,t_2]}\gamma _1\vert _{[t_1,b_1]}$ is admissible of order $\max (n_1,n_2)$. The paths $\gamma _1$ and $\gamma _2$ playing the same role, we get the proposition. $\square$

One deduces immediately the following:

Corollary 21

Let $\gamma _i: [a_i,b_i]\rightarrow M$, $1\leqslant i\leqslant r$, be a family of $r\geqslant 2$ transverse paths. We suppose that for every $i\in \{1,\ldots ,r\}$ there exist $s_i\in [a_i,b_i]$ and $t_i\in [a_i,b_i]$, such that:

i) :

$\gamma _i\vert _{[s_i,b_i]}$ and $\gamma _{i+1}\vert _{[a_{i+1},t_{i+1}]}$ intersect $\mathcal {F}$-transversally at $\gamma _i(t_i)=\gamma _{i+1}(s_{i+1})$ if $i<r$;

ii) :

one has $s_1=a_1<t_1<b_1$, $a_r<s_r<t_r=b_r$ and $a_i<s_i<t_i<b_i$ if $1<i<r$;

iii) :

$\gamma _i$ is admissible of order $n_i$.

Then $\prod _{1\leqslant i\leqslant r} \gamma _i\vert _{[s_i,t_i]}$ is admissible of order $\sum _{1\leqslant i\leqslant r} n_i$.

Proof

Here again, it is sufficient to prove the result when $M=\mathbb {R}^2$ and $\mathcal {F}$ is not singular. One must prove by induction on $q\in \{2,\ldots , r\}$ that

$$\begin{aligned} \left( \prod _{1\leqslant i<q} \gamma _i\vert _{[s_i,t_i]}\right) \gamma _q\vert _{[s_q,b_q]} \end{aligned}$$

is admissible of order $\sum _{1\leqslant i\leqslant q} n_i$. The result for $q=2$ is nothing but Proposition 20. Suppose that it is true for $q<r$ and let us prove it for $q+1$. The paths

$$\begin{aligned} \left( \prod _{1\leqslant i<q} \gamma _i\vert _{[s_i,t_i]}\right) \gamma _q\vert _{[s_q,b_q]} \end{aligned}$$

and $\gamma _{q+1}$ intersect $\mathcal {F}$-transversally at $\gamma _q(t_q)=\gamma _{q+1}(s_{q+1})$ because this is the case for the subpaths $\gamma _q\vert _{[s_q,b_q]}$ and $\gamma _{q+1}\vert _{[a_{q+1},t_{q+1}]}$. One deduces that

$$\begin{aligned} \left( \prod _{1\leqslant i\leqslant q} \gamma _i\vert _{[s_i,t_i]}\right) \gamma _{q+1}\vert _{[s_{q+1},b_{q+1}]} \end{aligned}$$

is admissible of order $\sum _{1\leqslant i\leqslant q+1} n_i$. $\square$

The following result is more subtle. The $\mathcal {F}$-transverse intersection property is stated on the paths $\gamma _i$ and not on subpaths but the signs of intersection are the same.

Corollary 22

Let $\gamma _i: [a_i,b_i]\rightarrow M$, $1\leqslant i\leqslant r$, be a family of $r\geqslant 2$ transverse paths. We suppose that for every $i\in \{1,\ldots ,r\}$ there exist $s_i\in [a_i,b_i]$ and $t_i\in [a_i,b_i]$, such that:

i) :

$\gamma _i$ and $\gamma _{i+1}$ intersect $\mathcal {F}$-transversally and positively at $\gamma _i(t_i)=\gamma _{i+1}(s_{i+1})$ if $i<r$;

ii) :

one has $s_1=a_1<t_1<b_1$, $a_r<s_r<t_r=b_r$ and $a_i<s_i<t_i<b_i$ if $1<i<r$;

iii) :

$\gamma _i$ is admissible of order $n_i$.

Then $\prod _{1\leqslant i\leqslant r} \gamma _i\vert _{[s_i,t_i]}$ is admissible of order $\sum _{1\leqslant i\leqslant r} n_i$.

Proof

Here again, it is sufficient to prove the result when $M=\mathbb {R}^2$ and $\mathcal {F}$ is not singular. Here again, one must prove by induction on $q\in \{2,\ldots , r\}$ that

$$\begin{aligned} \left( \prod _{1\leqslant i<q} \gamma _i\vert _{[s_i,t_i]}\right) \gamma _q\vert _{[s_q,b_q]} \end{aligned}$$

is admissible of order $\sum _{1\leqslant i\leqslant q} n_i$ and here again, the case $q=2$ is nothing but Proposition 20. Supposing that it is true for $q<r$, one must prove that

$$\begin{aligned} \left( \prod _{1\leqslant i<q} \gamma _i\vert _{[s_i,t_i]}\right) \gamma _q\vert _{[s_q,b_q]} \end{aligned}$$

and $\gamma _{q+1}$ intersect $\mathcal {F}$-transversally and positively at $\gamma _q(t_q)=\gamma _{q+1}(s_{q+1})$. By hypothesis, one knows that $\phi _{\gamma _{q+1}(b_{q+1})}$ is above $\phi _{\gamma _q(b_q)}$ relative to $\phi _{\gamma _q(t_q)}$. It remains to prove that $\phi _{\gamma _{q+1}(a_{q+1})}$ is below $\phi _{\gamma _1(a_1)}$ relative to $\phi _{\gamma _q(t_q)}$. For every $i\in \{1,\ldots , q-1\}$, the leaves $\phi _{\gamma _i(a_i)}$ and $\phi _{\gamma _{i+1}(a_{i+1})}$ belong to $R(\phi _{\gamma _i(t_i)})$ and $\phi _{\gamma _{i+1}(a_{i+1})}$ is below $\phi _{\gamma _i(a_i)}$ relative to $\phi _{\gamma _i(t_i)}$. So, each $\phi _{\gamma _i(a_i)}$ belongs to $R(\phi _{\gamma _q(t_q)})$ and $\phi _{\gamma _{i+1}(a_{i+1})}$ is below $\phi _{\gamma _i(a_i)}$ relative to $\phi _{\gamma _q(t_q)}$. One deduces that $\phi _{\gamma _{q+1}(a_{q+1})}$ is below $\phi _{\gamma _1(a_1)}$ relative to $\phi _{\gamma _q(t_q)}$. $\square$

Let us finish by explaining the interest of this result in the case where an admissible transverse path has an $\mathcal {F}$-transverse self-intersection.

Proposition 23

Suppose that $\gamma :[a,b]\rightarrow M$ is a transverse path admissible of order n and that $\gamma$ intersects itself $\mathcal {F}$-transversally at $\gamma (s)=\gamma (t)$ where $s<t$. Then $\gamma \vert _{[a,s]}\gamma \vert _{[t,b]}$ is admissible of order n and $\gamma \vert _{[a,s]}\left( \gamma \vert _{[s,t]}\right) ^{q}\gamma \vert _{[t,b]}$ is admissible of order qn for every $q\geqslant 1$.

Proof

See Fig. 13 illustrating the construction below. Applying Corollary 22 to the family

$$\begin{aligned} \gamma _i=\gamma , \,s_i=s \,{\mathrm {if}}\, 1<i\leqslant q \, , \,t_i=t \,{\mathrm {if}}\, \, 1\leqslant i<q , \end{aligned}$$

one knows that

$$\begin{aligned} \gamma \vert _{[a,t]}\left( \gamma \vert _{[s,t]}\right) ^{q-2}\gamma \vert _{[s,b]}=\gamma \vert _{[a,s]}\left( \gamma \vert _{[s,t]}\right) ^{q}\gamma \vert _{[t,b]} \end{aligned}$$

is admissible of order qn for every $q\geqslant 2$. Moreover the induction argument and the last sentence of Proposition 20 tell us either that $\gamma \vert _{[a,s]}\gamma \vert _{[t,b]}$ is admissible of order n, or that $\gamma \vert _{[a,s]}\left( \gamma \vert _{[s,t]}\right) ^{q}\gamma \vert _{[t,b]}$ is admissible of order n for every $q\geqslant 1$. To get the proposition, one must prove that the last case is impossible.

Fig. 13

Proof of Proposition 23

We do not lose any generality by supposing that ${\mathrm {dom}}(I)$ is connected. Fix a lift ${\widetilde{\gamma }}$ of $\gamma$ and denote T the covering automorphism such that ${\widetilde{\gamma }}(t)=T({\widetilde{\gamma }}(s))$. The quotient space $\widehat{{\mathrm {dom}}}({I})=\widetilde{{\mathrm {dom}}}({I})/T$ is an annulus and one gets an identity isotopy ${\widehat{I}}=({\widehat{f}}_t)_{\in [0,1]}$ on $\widehat{{\mathrm {dom}}}(I)$ by projection, as a homeomorphism ${\widehat{f}}={\widehat{f}}_1$ and a transverse foliation $\widehat{\mathcal {F}}$. The path ${\widetilde{\gamma }}$ projects onto a transverse path ${\widehat{\gamma }}$. The path ${\widetilde{\gamma }}'=\prod _{k\in \mathbb {Z}} T^k({\widetilde{\gamma }}\vert _{[s,t]})$ is a line that lifts a loop ${\widehat{\Gamma }}'$ of $\widehat{{\mathrm {dom}}}(I)$ transverse to $\widehat{\mathcal {F}}$. The union of leaves that meet ${\widetilde{\gamma }}'$ is a plane ${\widetilde{U}}$ that lifts an annulus $\widehat{U}$ of $\widehat{{\mathrm {dom}}}(I)$. The fact that $\gamma$ intersects itself $\mathcal {F}$-transversally at $\gamma (t)=\gamma (s)$ means that ${\widetilde{\gamma }}$ and $T({\widetilde{\gamma }})$ intersect $\widetilde{\mathcal {F}}$-transversally at ${\widetilde{\gamma }}(t)=T({\widetilde{\gamma }}(s))$. One deduces the following:

• the paths ${\widetilde{\gamma }}_{[a,s]}$ and ${\widetilde{\gamma }}_{[t,b]}$ are not contained in ${\widetilde{U}}$;

• if $a'\in [a,s)$ is the largest value such that ${\widetilde{\gamma }}(a')\not \in {\widetilde{U}}$ and $b'\in (t,b]$ the smallest value such that ${\widetilde{\gamma }}(b')\not \in {\widetilde{U}}$, then ${\widetilde{\gamma }}(a')$ and ${\widetilde{\gamma }}(b')$ are in the same connected component of $\widetilde{{\mathrm {dom}}}(I)\setminus {\widetilde{\gamma }}'$.

The fact that $\gamma \vert _{[a,s]}\left( \gamma \vert _{[s,t]}\right) ^{q}\gamma \vert _{[t,b]}$ is admissible of order n implies that

$$\begin{aligned} {\widetilde{\gamma }}\vert _{[a,s]}\prod _{0\leqslant k<q} T^k({\widetilde{\gamma }}\vert _{[s,t]})\,T^{q-1}({\widetilde{\gamma }}\vert _{[t,b]}) \end{aligned}$$

is admissible of order n or equivalently that $\widetilde{f}^{n}(\phi _{{\widetilde{\gamma }}(a')})\cap T^{q-1}(\phi _{{\widetilde{\gamma }}(b')})\not =\emptyset$. So one must prove that this cannot happen if q is large enough.

There is no loss of generality by supposing that the leaves $\phi _{{\widetilde{\gamma }}(a')}$ and $\phi _{{\widetilde{\gamma }}(b')}$ are on the right of ${\widetilde{\gamma }}'$. The projected leaves $\phi _{{\widehat{\gamma }}(a')}$ and $\phi _{{\widehat{\gamma }}(b')}$ are lines contained in the boundary of ${\widehat{U}}$. One can compactify the annulus $\widehat{{\mathrm {dom}}}(I)$ with a point S at the end on the right of ${\widehat{\Gamma }}'$ and a point N at the end on the left of ${\widehat{\Gamma }}'$. We know that the $\alpha$-limit and $\omega$-limit sets of $\phi _{{\widehat{\gamma }}(a')}$ and $\phi _{{\widehat{\gamma }}(b')}$ are reduced to S. Let us fix $\widetilde{z}_0\in \phi _{{\widetilde{\gamma }}(a')}$. The sets $T^k(\widetilde{f}^n (\overline{R( \phi _{{\widetilde{\gamma }}(a')})}))$, $k\in \mathbb {Z}$, are pairwise disjoint and one can choose a simple path $\alpha$ joining $T(\widetilde{f}^n( \widetilde{z}_0))$ to $\widetilde{f}^n( \widetilde{z}_0)$ and disjoint from $\widetilde{f}^n(\overline{R(\phi _{{\widetilde{\gamma }}(a')})})$ and $T(\widetilde{f}^n(\overline{R(\phi _{{\widetilde{\gamma }}(a')})}))$ but at its ends. One can extend $\alpha$ in $\overline{L(\phi _{{\widetilde{\gamma }}(a')})}\cap T(\overline{L(\phi _{{\widetilde{\gamma }}(a')})})$ to a simple path $\alpha '$ joining $T(\widetilde{z}_0)$ to $\widetilde{z}_0$ and disjoint from $\overline{R(\phi _{{\widetilde{\gamma }}(a')})}$ and $T(\overline{R( \phi _{{\widetilde{\gamma }}(a')})})$ but at its ends. The path $\alpha ''=T(\phi _{\widetilde{z}_0}^-)\,\alpha '\, \phi _{\widetilde{z}_0}^+$ is a line and $L(\alpha '')$ contains $T(\widetilde{f}^n(\phi _{\widetilde{z}_0}^-))$ and $\widetilde{f}^n( \phi _{\widetilde{z}_0}^+)$. Let us choose a real parameterization $t\mapsto \phi _{{\widetilde{\gamma }}(b')}(t)$ of $\phi _{{\widetilde{\gamma }}(b')}$. The fact that the $\alpha$-limit and $\omega$-limit sets of $\phi _{{\widehat{\gamma }}(b')}$ are reduced to S implies that there exists $K>0$ such that for every $q\geqslant 0$, $\alpha '$ does not meet neither $T^q(\phi _{{\widetilde{\gamma }}(b')}\vert _{(-\infty , -K]})$ nor $T^q( \phi _{{\widetilde{\gamma }}(b')}\vert _{[K, +\infty )})$. One deduces that there exists $q_0$ such that for every $q\geqslant q_0$, $\alpha '$ does not meet $T^q(\phi _{{\widetilde{\gamma }}(b')})$. This implies that if $q\geqslant q_0$, then $T^q(\phi _{{\widetilde{\gamma }}(b')})$ does not meet $\alpha ''$ and so is included in $R(\alpha '')$. In particular it cannot intersect neither $T(\widetilde{f}^n(\phi _{\widetilde{z}_0}^-))$ nor $\widetilde{f}^n( \phi _{\widetilde{z}_0}^+)$. Consequently, this implies that $\widetilde{f}^n(\phi _{{\widetilde{\gamma }}(a')})$ does not meet $T^q({\widetilde{\phi }}_{{\widetilde{\gamma }}(b')})$, if $q\geqslant q_0$. $\square$

Corollary 24

Let $\gamma :[a,b]\rightarrow M$ be a transverse path admissible of order n. Then, there exists a transverse path of order n, $\gamma ':[a,b]\rightarrow M$ such that $\gamma '$ has no $\mathcal {F}$-transverse self-intersections, and $\phi _{\gamma '(a)}=\phi _{\gamma (a)},\, \phi _{\gamma '(b)}=\phi _{\gamma (b)}$.

Proof

Note first that there exists a transverse path $\gamma ':[a,b]\rightarrow M$ equivalent to $\gamma$ with finitely many self-intersections (not necessarily $\mathcal {F}$-transverse). Indeed, choose for every z on $\gamma$, a trivialization neighborhood $W_z$. Divide the interval in n intervals $J_i=[a_i,b_i]$ of equal length and set $\gamma _i=\gamma _{J_i}$, so that $\gamma =\prod _{1\leqslant i\leqslant n}\gamma _i$. If n is large enough, then for every i, the union of $\gamma _i$ and all paths $\gamma _j$ that meet $\gamma _i$ is contained in a set $W_{z}$. Let us begin by perturbing each $\gamma _i$ to find an equivalent path $\gamma '_i$, such that $\gamma '_i(b_i)=\gamma '_{i+1}(a_i)$, if $i<n$, and such that the $\gamma '_i(b_i)$ are all distinct. One can also suppose that that for every i, the union of $\gamma '_i$ and all $\gamma '_j$ that meet $\gamma '_i$ is contained in a set $W_{z}$. Suppose that for every $i<i_0$ and every $j\not =i$, the paths $\gamma '_i$ and $\gamma '_j$ have finitely many points of intersection. One can perturb in an equivalent way each $\gamma '_j$ on $(a_j,b_j)$, $j>i_0$, such that it intersects $\gamma _{i_0}$ finitely many often, without changing the intersection points with $\gamma _i$ if $i<i_0$ and such that condition concerning the trivialization neighborhoods is still satisfied. One knows that for every $i\leqslant i_0$ and every $j\not =i$, the new paths $\gamma '_i$ and $\gamma '_j$ have finitely many points of intersection.

Let $\mathcal {G}$ be the collection of all transverse paths that are admissible of order n whose initial leaf is $\phi _{\gamma (a)}$ and whose final leaf is $\phi _{\gamma (b)}$. Let $\gamma ':[a, b]\rightarrow M$ be a path in $\mathcal {G}$ that is minimal with regards to the number of self-intersections. Then $\gamma '$ has no $\mathcal {F}$-transverse self-intersections. Indeed, if $\gamma '$ had an $\mathcal {F}$-transverse self-intersection at $\gamma '(t)=\gamma '(s)$ where $s<t$, by the Proposition 23 the path $\gamma '\mid _{[a, s]}\gamma '\mid _{[t, b]}$ would also be also contained in $\mathcal {G}$ and it would have a strictly smaller number of self-intersections. $\square$

4.5 Realizability of transverse loops

Let $\Gamma$ be a transverse loop associated to a periodic point z of period q. Recall that it means that $\Gamma$ is equivalent to a transverse loop $\Gamma '$ whose natural lift $\gamma '$ is equivalent to the whole transverse trajectory of z. In particular, if $\gamma$ is the natural lift of $\Gamma$, there exists $t\in (-1,0]$ such that $\phi _{\gamma (t)}=\phi _z$ and such that for every $n\geqslant 1$, $\gamma _{[t,t+n]}$ is equivalent to $I_{\mathcal {F}} ^{nq}(z)$. So, the loop satisfies the following:

$$\begin{aligned} (P_q): \,\,{\mathrm {for \, every}} \, n\geqslant 1,\gamma \vert _{[0,n-1]} \,\mathrm {is} \,{\mathrm {admissible\, of \, order}} \, \leqslant nq. \end{aligned}$$

The following question is natural:

Let $\Gamma$ be a transverse loop that satisfies $(P_q)$. Is $\Gamma$ associated to a periodic orbit of period q?

We will see that in many situations, it is the case. In such situations, f will have infinitely many periodic orbits. More precisely, for every rational number $r/s\in (0,1/q]$ written in an irreducible way, the loop $\Gamma ^r$ will be associated to a periodic orbit of period s. In fact the weaker following property will be sufficient:

$(Q_q):$ there exist two sequences $(r_k)_{k\geqslant 0}$ and $(s_k)_{k\geqslant 0}$ of natural integers satisfying

$$\begin{aligned} \lim _{k\rightarrow +\infty }r_k=\lim _{k\rightarrow +\infty }s_k=+\infty ,\, \limsup _{k\rightarrow +\infty }{r_k/s_k}\geqslant 1/q \end{aligned}$$

such that $\gamma \vert _{[0, r_k]}$ is admissible of order $\leqslant s_k$.

We will say that a transverse loop $\Gamma$ is linearly admissible of order q if it satisfies $(Q_q)$ (note that every equivalent loop will satisfy the same condition).

Let us define now the natural covering associated to $\Gamma$ (or to its natural lift $\gamma$) and introduce some useful notations. Fix a lift ${\widetilde{\gamma }}$ of $\gamma$ and denote T the covering automorphism such that ${\widetilde{\gamma }}(t+1)=T({\widetilde{\gamma }}(t))$ for every $t\in \mathbb {R}$. The path ${\widetilde{\gamma }}$ is a line and the union of leaves that it crosses is a topological plane ${\widetilde{U}}$. Moreover it projects onto the natural lift of a loop ${\widehat{\Gamma }}$ in the quotient space $\widehat{{\mathrm {dom}}}(I)=\widetilde{{\mathrm {dom}}}(I)/T$. One gets an identity isotopy ${\widehat{I}}=({\widehat{f}}_t)_{\in [0,1]}$ on $\widehat{{\mathrm {dom}}}(I)$ by projection, as a homeomorphism ${\widehat{f}}={\widehat{f}}_1$ and a transverse foliation $\widehat{\mathcal {F}}$. The loop ${\widehat{\Gamma }}$ is transverse to $\widehat{\mathcal {F}}$ and the union of leaves that it crosses is a topological annulus ${\widehat{U}}$.

Before stating the realization result, let us recall the following lemma (for example, see [28], Theorem 9.1, for a proof that uses maximal isotopies and transverse foliations). A loop in an annulus will be called essential if it is not homotopic to zero.

Lemma 25

Let J be a real interval, f a homeomorphism of $\mathbb {T}^1\times J$ isotopic to the identity and $\widetilde{f}$ a lift of f to $\mathbb {R}\times J$. We suppose that:

• every essential simple loop $\Gamma \subset \mathbb {T}^1\times J$ meets its image by f;

• there exist two probability measures $\mu _1$ and $\mu _2$ with compact support, invariant by f, such that their rotation numbers (for $\widetilde{f}$) satisfy ${\mathrm {rot}}(\mu _1)<{\mathrm {rot}}(\mu _2)$.

Then, for every $r/s\in [{\mathrm {rot}}(\mu _1),{\mathrm {rot}}(\mu _2)]$ written in an irreducible way, there exists a point $z\in \mathbb {R}\times J$ such that $\widetilde{f}^s(z)=z+(r,0).$

Let us state now the principal result of this subsection.

Proposition 26

Let $\Gamma$ be a linearly admissible transverse loop of order q that satisfies one of the three following conditions. Then for every rational number $r/s\in (0,1/q]$ written in an irreducible way, $\Gamma ^r$ is associated to a periodic orbit of period s.

i) :

The loop $\Gamma$ has a leaf on its left and a leaf on its right, and the annulus ${\widehat{U}}$ does not contain a simple loop homotopic to ${\widehat{\Gamma }}$ disjoint from its image by ${\widehat{f}}$.

ii) :

There exists both an admissible transverse path that intersects $\Gamma$ $\mathcal {F}$-transversally and positively, and an admissible transverse path that intersects $\Gamma$ $\mathcal {F}$-transversally and negatively.

iii) :

The loop $\Gamma$ has an $\mathcal {F}$-transverse self-intersection.

Proof

The condition iii) is stronger than ii) because $\Gamma$ intersects itself $\mathcal {F}$-transversally positively and negatively. The condition ii) tells us that there is an admissible transverse path that intersects ${\widehat{\Gamma }}$ $\widehat{\mathcal {F}}$-transversally and positively, and an admissible transverse path that intersects ${\widehat{\Gamma }}$ $\widehat{\mathcal {F}}$-transversally and negatively. But this implies that i) is satisfied because there exists orbits that cross ${\widehat{U}}$ in both ways. It remains to prove the result under the assumption i).

We do not lose any generality by supposing that ${\mathrm {dom}}(I)$ is connected, which means that $\widetilde{{\mathrm {dom}}}(I)$ is a plane and $\widehat{{\mathrm {dom}}}(I)$ an annulus. By assumption, we know that there exists a leaf on the left of ${\widetilde{\gamma }}$ and a leaf on its right. One can compactify $\widehat{{\mathrm {dom}}}(I)$ with a point S at the end on the right of ${\widehat{\Gamma }}$ and a point N at the end on the left of ${\widehat{\Gamma }}$. We will denote by $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ this compactification and still write ${\widehat{f}}$ for the extension that fixes the added points. The $\omega$-limit set $\omega ({\widehat{\phi }})$ in $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ of a leaf ${\widehat{\phi }}\subset {\widehat{U}}$ does not depend on ${\widehat{\phi }}$.

Lemma 27

The set $\omega ({\widehat{\phi }})$ is reduced to S.

Proof

If not, $\omega ({\widehat{\phi }})$ is either a closed leaf that bounds ${\widehat{U}}$ or the union of S and of leaves homoclinic to S (which means that the two limit sets are reduced to S). In the first case, the closed leaf that bounds ${\widehat{U}}$ is homotopic to ${\widehat{\Gamma }}$ and disjoint from its image by ${\widehat{f}}$. A simple loop included in ${\widehat{U}}$ sufficiently close will satisfy the same properties. This contradicts the assumptions of the proposition.

Let us study now the second case. Choose a point ${\widehat{z}}^*\in \omega ({\widehat{\phi }})\setminus \{S\}$ and denote by ${\widehat{\phi }}^*$ the leaf that contains ${\widehat{z}}^*$. One can suppose that ${\widehat{\Gamma }}$ is on the right of ${\widehat{\phi }}^*$. This is independent of the choice of ${\widehat{z}}^*$ and in that case, the leaf ${\widehat{\phi }}$ is on the right of ${\widehat{\phi }}^*$. Let us present two arguments to deal with this situation. The first argument is the following: As $\widehat{{\mathrm {dom}}}(I)$ has only finitely many ends and $\widehat{\mathcal {F}}$ is transversal to ${\widehat{I}}$, one could adapt the proof of Lemma 3.3 of [29] to show that, given any point ${\widehat{y}}$ in $\widehat{{\mathrm {dom}}}(I)$, there exists a neighborhood $V_{{\widehat{y}}}$ of ${\widehat{y}}$ such that, if $\widehat{\mathcal {F}}'$ is an oriented foliation of $\widehat{{\mathrm {dom}}}(I)$ that is equal to $\widehat{\mathcal {F}}$ in the complement of $V_{{\widehat{y}}}$, then $\widehat{\mathcal {F}}'$ is also transversal to ${\widehat{I}}$. Let $V'$ be a neighborhood of ${\widehat{z}}^*$ as given by this result, and we further assume that there exists a homeomorphism $h:V'\rightarrow [-1,1]\times [-1,1]$ sending the leafs of $\widehat{\mathcal {F}}\cap V'$ onto horizontal line segments oriented from right to left, and such that $h({\widehat{z}}^*)=(0,0)$. Note that $h^{-1}([-1, 1]\times (0,1])\subset {\widehat{U}}$, and since ${\widehat{z}}^*\in \omega ({\widehat{\phi }})$, there exist $t_1<t_2$ such that ${\widehat{\phi }}(t_1), {\widehat{\phi }}(t_2)$ both belong to $V'$, and such that ${\widehat{\phi }}(s)$ is disjoint from $V'$ if $t_1< s< t_2$. This implies that there exists $x_1, x_2$ in (0, 1) such that $h( {\widehat{\phi }}(t_1))=(-1, x_1)$ and $h( {\widehat{\phi }}(t_2))=(1, x_2)$. One can find then an oriented foliation $\widehat{\mathcal {F}}'$ of $\widehat{{\mathrm {dom}}(I)}$ that agrees with $\widehat{\mathcal {F}}$ in the complement of $h^{-1}([-1, 1]\times (0,1])$, and such that, if $\sigma$ is the line segment in $h(V')$ connecting $(-1, x_1)$ to $(1, x_2)$, then $h^{-1}(\sigma )$ is contained in a single leaf of the foliation. In particular, the leaf ${\widehat{\phi }}'$ of $\widehat{\mathcal {F}}'$ that contains $h^{-1}(\sigma )$ is a closed leaf contained in ${\widehat{U}}$. Since $\widehat{\mathcal {F}}'$ is also transversal to the isotopy ${\widehat{I}}$, one obtains again a contradiction as in the first case.

Fig. 14

Construction of ${\widetilde{\gamma }}_n$ in Lemma 27

Since Lemma 3.3 of [29] is not stated in the form we used above, let us present a complete argument for the second case: We have the following result; for every neighborhood V of S, there exists a neighborhood W of $\omega ({\widehat{\phi }})$ in $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ such that ${\widehat{f}}(W\setminus V)\cap \overline{{\widehat{U}}}=\emptyset$. Let us consider a simple path ${\widehat{\beta }}$ joining a point ${\widehat{z}}^{**}\in {\widehat{U}}$ to ${\widehat{z}}^*$ positively transverse to $\widehat{\mathcal {F}}$, included (but the end ${\widehat{z}}^*$) in ${\widehat{U}}$ and sufficiently small that its image by ${\widehat{f}}$ will be included in the connected component of $\widehat{{\mathrm {dom}}}(I)\setminus {\widehat{\phi }}^*$ that is on the left of ${\widehat{\phi }}^*$. The leaf ${\widehat{\phi }}$ meets ${\widehat{\beta }}$ in a“monotone” sequence $({\widehat{z}}_n)_{n\geqslant 0}$, where $\lim _{n\rightarrow +\infty } {\widehat{z}}_n={\widehat{z}}^{*}.$ More precisely, for every real parameterization of ${\widehat{\phi }}$, one has ${\widehat{z}}_n={\widehat{\phi }} (t_n)$, where $t_{n+1}>t_n$, and $\lim _{n\rightarrow +\infty } t_n=+\infty$. Moreover, ${\widehat{z}}_{n+1}$ is “closer” to ${\widehat{z}}^{*}$ than ${\widehat{z}}_{n}$ on ${\widehat{\beta }}$. We will prove that if n is large enough, the simple loop ${\widehat{\Gamma }}_n$ obtained by concatenating the segment ${\widehat{\alpha }}_n\subset {\widehat{\phi }}$ joining ${\widehat{z}}_{n}$ to ${\widehat{z}}_{n+1}$ and the subpath ${\widehat{\xi }}_n$ of ${\widehat{\beta }}^{-1}$ joining ${\widehat{z}}_{n+1}$ to ${\widehat{z}}_{n}$ is disjoint from its image by ${\widehat{f}}$, see Fig. 14 for the following construction. We will begin by extending ${\widehat{\beta }}$ in a simple proper path (with the same name) contained in $\widehat{{\mathrm {dom}}}(I)\setminus \omega ({\widehat{\phi }})$ “joining” the end N to ${\widehat{z}}^*$. One can find a neighborhood $W'$ of $\omega ({\widehat{\phi }})$ in $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ that intersects ${\widehat{\beta }}$ only between ${\widehat{z}}_0$ and ${\widehat{z}}^*$. If n is large enough, ${\widehat{\alpha }}_n$ will be contained in $W'$ and so will intersect ${\widehat{\beta }}$ only at the points ${\widehat{z}}_{n}$ and ${\widehat{z}}_{n+1}$. We will suppose n large enough to satisfy this property. Fix a lift $\widetilde{z}_0$ of ${\widehat{z}}_0$, write ${\widetilde{\beta }}_0$ for the lift of ${\widehat{\beta }}$ that contains $\widetilde{z}_0$, write $\widetilde{z}^*_0$ for its end and ${\widetilde{\phi }}^*_0$ for the lift of ${\widehat{\phi }}^*$ that contains $\widetilde{z}^*_0$. For every $n\geqslant 0$ define

$$\begin{aligned} \widetilde{z}^*_n=T^{-n}(\widetilde{z}^*_0), \, {\widetilde{\beta }}_n=T^{-n}({\widetilde{\beta }}_0), \, {\widetilde{\phi }}^*_n=T^{-n}({\widetilde{\phi }}^*_0). \end{aligned}$$

Write $\widetilde{z}_n$ for the lift of ${\widehat{z}}_n$ that lies on ${\widetilde{\beta }}_n$, write ${\widetilde{\zeta }}_n$ for the segment of ${\widetilde{\beta }}_n$ that joins $\widetilde{z}_n$ to $\widetilde{z}^*_n$ and ${\widetilde{\alpha }}_n$ for the lift of ${\widehat{\alpha }}_n$ that joins $\widetilde{z}_n$ to $\widetilde{z}_{n+1}$. Choose a parameterization ${\widehat{\phi }}^*:\mathbb {R}\rightarrow \widehat{{\mathrm {dom}}}(I)$ of ${\widehat{\phi }}^*$ sending 0 onto $\widetilde{z}^*$ and lift it to parameterize the leaves ${\widetilde{\phi }}^*_n$. We will prove that the line

$$\begin{aligned} {\widetilde{\lambda }}_n={\widetilde{\phi }}^*_n\vert _{(-\infty ,0]}\,{\widetilde{\zeta }}_n^{-1}\,{\widetilde{\alpha }}_n\,\widetilde{\zeta }_{n+1}\,{\widetilde{\phi }}^*_{n+1}\vert _{[0,+\infty ]} \end{aligned}$$

is a Brouwer line if n is large enough. Observe first that one has

$$\begin{aligned} L({\widetilde{\phi }}^*_n)\cup L({\widetilde{\phi }}^*_{n+1})\subset L({\widetilde{\lambda }}_n)\subset L\left( {\widetilde{\phi }}^*_n\vert _{(-\infty ,0]}\,{\widetilde{\beta }}_n^{-1}\right) \cap L\left( {\widetilde{\beta }}_{n+1}\, {\widetilde{\phi }}^*_{n+1}\vert _{[0,+\infty )}\right) , \end{aligned}$$

then note that if K is large enough one has

$$\begin{aligned}&\widetilde{f}^{-1}\left( {\widetilde{\phi }}^*_n\vert _{(-\infty ,-K]}\right) \subset R\left( {\widetilde{\phi }}^*_n\vert _{(-\infty ,0]}\,{\widetilde{\beta }}_n^{-1}\right) , \, \widetilde{f}^{-1}\left( {\widetilde{\phi }}^*_{n+1}\vert _{[K,+\infty ]}\right) \\&\quad \subset R\left( {\widetilde{\beta }}_{n+1}\, {\widetilde{\phi }}^*_{n+1}\vert _{[0,+\infty )}\right) . \end{aligned}$$

Let V be a neighborhood of S such that ${\widehat{f}}(V)\cap \left( {\widehat{\phi }}^*([-K,K])\cup {\widehat{\beta }}\right) =\emptyset$ and W a neighborhood of $\omega ({\widehat{\phi }})$ such that $f(W\setminus V) \cap \overline{{\widehat{U}}}=\emptyset$. If n is large enough, then ${\widehat{\Gamma }}_n$ is included in W. Let us prove that ${\widetilde{\lambda }}_n$ is a Brouwer line of $\widetilde{f}$ and then that ${\widehat{\Gamma }}_n$ is disjoint from its image by ${\widehat{f}}$. The leaves ${\widetilde{\phi }}^*_n$ and ${\widetilde{\phi }}^*_{n+1}$ being Brouwer lines of $\widetilde{f}$, one has

$$\begin{aligned} \widetilde{f}({\widetilde{\phi }}^*_n\vert _{(-\infty ,0]})\subset L({\widetilde{\phi }}^*_n) \subset L({\widetilde{\lambda }}_n),\, \widetilde{f}({\widetilde{\phi }}^*_{n+1}\vert _{[0,+\infty )})\subset L({\widetilde{\phi }}^*_{n+1}) \subset L({\widetilde{\lambda }}_n). \end{aligned}$$

By hypothesis on ${\widehat{\beta }}$, one knows that

$$\begin{aligned} \widetilde{f}(\widetilde{\zeta }_n)\subset L({\widetilde{\phi }}^*_n) \subset L({\widetilde{\lambda }}_n), \, \widetilde{f}(\widetilde{\zeta }_{n+1})\subset L({\widetilde{\phi }}^*_{n+1}) \subset L({\widetilde{\lambda }}_n). \end{aligned}$$

The path ${\widetilde{\alpha }}_n$ being included in a leaf of $\widetilde{\mathcal {F}}$ and each leaf being a Brouwer line of $\widetilde{f}$, one knows that

$$\begin{aligned} \widetilde{f}({\widetilde{\alpha }}_n)\cap {\widetilde{\alpha }}_n=\emptyset . \end{aligned}$$

To prove that ${\widetilde{\lambda }}_n$ is a Brouwer line, it remains to prove that $\widetilde{f}({\widetilde{\alpha }}_n)$ does not meet any of the paths

$$\begin{aligned} {\widetilde{\phi }}^*_n\vert _{(-\infty ,0]}, \, {\widetilde{\phi }}^*_{n+1}\vert _{[0, +\infty )},\, \widetilde{\zeta }_n,\,\widetilde{\zeta }_{n+1}. \end{aligned}$$

By hypothesis, one knows that ${\widehat{f}}({\widehat{\alpha }}_n)$ does not meet neither ${\widehat{\phi }}^*([-K,K])$, nor ${\widehat{\zeta }}_0$. Moreover, one knows that ${\widetilde{\alpha }}_n$ does not meet neither $\widetilde{f}^{-1}({\widetilde{\phi }}^*_n\vert _{(-\infty ,K]})$, nor $\widetilde{f}^{-1}({\widetilde{\phi }}^*_{n+1}\vert _{[K, +\infty )})$. So, we are done.

To prove that ${\widehat{\Gamma }}_n$ is disjoint from its image by ${\widehat{f}}$, one must prove that ${\widehat{\Gamma }}_n$ is lifted to a path that is disjoint from its image by $\widetilde{f}$. This path will be included in the union of the images by the iterates of T of the path ${\widetilde{\zeta }}_n^{-1}\,{\widetilde{\alpha }}_n\,\widetilde{\zeta }_{n+1}$. So it is sufficient to prove that the union of these translates is disjoint from its image by $\widetilde{f}$. Observe now that every path $T^k( {\widetilde{\zeta }}_n^{-1}\,{\widetilde{\alpha }}_n\,\widetilde{\zeta }_{n+1})$, $k\in \mathbb {Z}$, is disjoint from $L({\widetilde{\lambda }}_n)$, which implies that it is disjoint from $\widetilde{f}( {\widetilde{\zeta }}_n^{-1}\,{\widetilde{\alpha }}_n\,\widetilde{\zeta }_{n+1})$. $\square$

Lemma 28

There is no simple loop included in $\widehat{{\mathrm {dom}}}(I)$ homotopic to ${\widehat{\Gamma }}$ that is disjoint from its image by ${\widehat{f}}$.

Proof

Suppose that there exists a simple loop ${\widehat{\Gamma }}_0$ included in $\widehat{{\mathrm {dom}}}(I)$ that is homotopic to ${\widehat{\Gamma }}$ and disjoint from its image by ${\widehat{f}}$. One can suppose for instance that ${\widehat{f}}({\widehat{\Gamma }}_0)$ is included in the component of $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}\setminus {\widehat{\Gamma }}_0$ that contains N, and orient ${\widehat{\Gamma }}_0$ in such a way that this component, denoted by $L({\widehat{\Gamma }}_0)$, is on the left of ${\widehat{\Gamma }}_0$. The loop ${\widehat{\Gamma }}_0$ meets finitely many leaves of $\widehat{\mathcal {F}}$ homoclinic to S that are on the frontier of ${\widehat{U}}$. We denote them ${\widehat{\phi }}_i$, $1\leqslant i\leqslant p$. Let us prove first that ${\widehat{\Gamma }}$ is on the left side of each ${\widehat{\phi }}_i$. Indeed, if ${\widehat{\Gamma }}$ is on the right side of ${\widehat{\phi }}_i$, writing ${\widetilde{\Gamma }}_0$ for the lift of ${\widehat{\Gamma }}_0$ and ${\widetilde{\phi }}_i$ for a lift of ${\widehat{\phi }}_i$, one finds a non empty compact subset $\overline{L({\widetilde{\Gamma }}_0))}\cap \overline{L({\widetilde{\phi }}_i)}$ of $\widetilde{{\mathrm {dom}}}(I)$ that is forward invariant by $\widetilde{f}$. But such a set does not exist because $\widetilde{f}$ is fixed point free.

Each loop ${\widehat{\phi }}_i\cup \{S\}$ bounds a Jordan domain ${\widehat{L}}_i$ of $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ that contains N. By a classical result of Kerékjártó [22], one knows that the connected component of $L({\widehat{\Gamma }}_0)\cap (\bigcap _{1\leqslant i\leqslant p} {\widehat{L}}_i)$ that contains N is a Jordan domain whose boundary ${\widehat{\Gamma }}_1$ is a simple loop homotopic to ${\widehat{\Gamma }}$ in $\widehat{{\mathrm {dom}}}(I)$, disjoint from its image by ${\widehat{f}}$, and included in $\overline{{\widehat{U}}}\cup L(\Gamma )$ (see Fig. 15). By intersecting ${\widehat{\Gamma }}_1$ with the leaves of $\widehat{\mathcal {F}}$ homoclinic to N that are on the frontier of ${\widehat{U}}$, one constructs similarly a simple loop ${\widehat{\Gamma }}_2$ included in $\widehat{{\mathrm {dom}}}(I)\cap \overline{{\widehat{U}}}$ that is homotopic to ${\widehat{\Gamma }}$ in ${\widehat{M}}$ and disjoint from its image by ${\widehat{f}}$. It remains to approximate ${\widehat{\Gamma }}_2$ by a simple loop included in ${\widehat{U}}$ and we get a contradiction since we are assuming condition i) in Proposition 26. $\square$

Fig. 15

Construction of $\widehat{\Gamma }_1$ in Lemma 28

End of the proof of Proposition 26

One must prove that for every rational number $r/s\in (0,1/q]$ written in an irreducible way, there exists a point $\widetilde{z}\in \widetilde{{\mathrm {dom}}}(I)$ such that $\widetilde{f}^s(\widetilde{z})=T^r(\widetilde{z})$. Indeed, the orbit of $\widetilde{z}$ should be contained in ${\widetilde{U}}$, the point $\widetilde{z}$ will project in ${{\mathrm {dom}}}(I)$ onto a periodic point z of f of period s, finally the loop $\Gamma ^r$ will be associated to z.

Write ${\widetilde{\phi }}_0$ for the leaf containing ${\widetilde{\gamma }}(0)$ and ${\widehat{\phi }}_0$ for its projection in $\widehat{{\mathrm {dom}}}(I)$. Using the analogous of Lemma 27 for $\alpha$-limit sets, one can suppose that ${\widehat{\phi }}_0$ is a line. Let us fix a leaf ${\widehat{\phi }}_N$ homoclinic to N and a leaf ${\widehat{\phi }}_S$ homoclinic to S, which exists since we are assuming that the loop $\Gamma$ has a leaf on its right and a leaf on its left. Each of them is disjoint from all its images by the (non trivial) iterates of ${\widehat{f}}$. By a result of Béguin, Crovisier, Le Roux (see [29], Proposition 2.3.3) one knows that there exists a compactification $\widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ obtained by blowing up the two ends N and S replaced by circles ${\widehat{\Sigma }}_N$ and ${\widehat{\Sigma }}_S$ such that ${\widehat{f}}$ extends to a homeomorphism ${\widehat{f}}_{\mathrm {ann}}$ that admits fixed points on each added circle with a rotation number equal to zero for the lift that extends $\widetilde{f}$. Moreover, one can suppose that each set $\omega ({\widehat{\phi }}_N)$ and $\omega ({\widehat{\phi }}_S)$ is reduced to a unique point on ${\widehat{\Sigma }}_N$ and ${\widehat{\Sigma }}_S$ respectively. One can join a point of ${\widehat{\phi }}_N$ to a point of ${\widehat{\phi }}_S$ by a segment disjoint from ${\widehat{\phi }}_0$. Consequently, one can construct a line ${\widehat{\lambda }}$ in $\widehat{{\mathrm {dom}}}(I)$, disjoint from ${\widehat{\phi }}_0$, that admits a limit on each added circle. Write $\widetilde{{\mathrm {dom}}}(I)_{\mathrm {ann}}=\widetilde{{\mathrm {dom}}}(I)\sqcup {\widetilde{\Sigma }}_N\sqcup {\widetilde{\Sigma }}_S$ for the universal covering space of $\widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ and keep the notation T for the natural covering automorphism. Write ${\widetilde{\lambda }}$ for the lift of ${\widehat{\lambda }}$ located between ${\widetilde{\phi }}_0$ and $T({\widetilde{\phi }}_0)$. One can construct a continuous real function ${\widetilde{g}}$ on $\widetilde{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ that satisfies ${\widetilde{g}}(T(\widetilde{z})) ={\widetilde{g}}(z)+1$ and vanishes on ${\widetilde{\lambda }}$. The function ${\widetilde{h}}={\widetilde{g}}\circ \widetilde{f}- {\widetilde{g}}$ is invariant by T and lifts a continuous function ${\widehat{h}}:\widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}\rightarrow \mathbb {R}$. If $\mu$ is a Borel probability measure invariant by ${\widehat{f}}$, the quantity $\int _{\widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}} h\, d\mu$ is the rotation number of the measure $\mu$ for the lift $\widetilde{f}_{\mathrm {ann}}$. Let us consider now the real function ${\widetilde{g}}_0$ on $\widetilde{{\mathrm {dom}}}(I)_{\mathrm {ann}}$, that coincides with ${\widetilde{g}}$ on ${\widetilde{\Sigma }}_N\cup {\widetilde{\Sigma }}_S$, that satisfies ${\widetilde{g}}_0(T(\widetilde{z})) ={\widetilde{g}}_0(\widetilde{z})+1$ and that vanishes on ${\widetilde{\phi }}_0$ and at every point located between ${\widetilde{\phi }}_0$ and $T({\widetilde{\phi }}_0)$. Note that ${\widetilde{g}}-{\widetilde{g}}_0$ is uniformly bounded by a certain number K and invariant by T. The property $(Q_q)$ satisfied by $\Gamma$ tells us that for every $k\geqslant 0$, one can find a point $\widetilde{z}_k\in R({\widetilde{\phi }}_0)$ such that $\widetilde{f}^{s_k}(\widetilde{z}_k)\in L(T^{r_k}({\widetilde{\phi }}_0))$. Write ${\widehat{z}}_k$ for its projection in $\widehat{{\mathrm {dom}}}(I)$. Observe that

$$\begin{aligned} {\widetilde{g}}_0(f^{s_k}(\widetilde{z}_k))-{\widetilde{g}}_0(\widetilde{z}_k)\geqslant r_k. \end{aligned}$$

By taking a subsequence, one can suppose that

$$\begin{aligned} \lim _{k\rightarrow +\infty } {1\over s_k}\left( {\widetilde{g}}_0(f^{s_k}(\widetilde{z}_k))-{\widetilde{g}}_0(\widetilde{z}_k)\right) =\rho \in \left[ {1\over q}, +\infty \right] \end{aligned}$$

and so that

Write $\delta _{{\widehat{z}}}$ for the Dirac measure at a point ${\widehat{z}}\in \widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ and choose a measure $\mu$ that is the limit of a subsequence of $\left( {1\over s_k} \sum _{i=0}^{s_k-1}\delta _{{\widehat{f}}^{i}_{\mathrm {ann}}({\widehat{z}}_{k})}\right) _{k\geqslant 0}$ for the weak$^*$ topology. One knows that $\mu$ is an invariant measure of rotation number $\rho$. As the rotation number induced on the boundary circles are equal to 0, one deduces that the rotation set ${\mathrm {rot}}(\widetilde{f}_{\mathrm {ann}})$ contains $[0,\rho ]$. The intersection property supposed in i) implies by Lemma 25 that for every rational number $r/s\in (0,1/q]$ written in an irreducible way, there exists a point $\widetilde{z}\in \widetilde{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ such that $\widetilde{f}_{{\mathrm {ann}}}^s(\widetilde{z})=T^r(\widetilde{z})$. But this point does not belong to the boundary circles because the induced rotation numbers are equal to 0. So its belongs to $\widetilde{{\mathrm {dom}}}({I})$. $\square$

5 Exponential growth of periodic points and entropy

In this section we give a sufficient condition for the exponential growth of periodic points of a surface homeomorphism. This condition will imply that the topological entropy is positive in the compact case. We will make use of these criteria later.

We assume here, as in the previous section, that f is a homeomorphism isotopic to the identity on an oriented surface M and that $I=(f_t)_{t\in [0,1]}$ is a maximal hereditary singular isotopy, which implies that $f_1=f\vert _{{\mathrm {dom}}(I)}$. We write ${\widetilde{I}}=(\widetilde{f}_t)_{t\in [0,1]}$ for the lifted identity defined on the universal covering space $\widetilde{{\mathrm {dom}}}(I)$ of ${\mathrm {dom}}(I)$ and set $\widetilde{f}=\widetilde{f}_1$ for the lift of $f\vert _{{\mathrm {dom}}(I)}$ induced by the isotopy. We suppose that $\mathcal {F}$ is a foliation transverse to I and write $\widetilde{\mathcal {F}}$ for the lifted foliation on $\widetilde{{\mathrm {dom}}}(I)$.

5.1 Exponential growth of periodic points

The main result of this section is

Theorem 29

Let $\gamma _1, \gamma _2 :\mathbb {R}\rightarrow M$ be two admissible positively recurrent transverse paths (possibly equal) with an $\mathcal {F}$-transverse intersection. Then the number of periodic points of period n for some iterate of f grows exponentially in n.

Theorem 29 is a direct consequence of Lemma 30 and Proposition 31.

Lemma 30

Let $\gamma _1,\, \gamma _2$ be two admissible $\mathcal {F}$-positively recurrent transverse paths (possibly equal) with an $\mathcal {F}$-transverse intersection, and let $I_1$ and $I_2$ be two real segments. Then there exists a linearly admissible transverse loop $\Gamma$ with an $\mathcal {F}$-transverse self-intersection, such that $\gamma _1\vert _{I_1}$ and $\gamma _2\vert _{I_2}$ are equivalent to subpaths of the natural lift of $\Gamma$.

Proof

As explained at the end of Sect. 3.3, we can find $a_1, b_1, t_1, a_2, b_2, t_2$ such that $I_1\subset [a_1, b_1]$, $I_2\subset [a_2,b_2]$ and such that $\gamma _1\vert _{[a_1,b_1]}$ intersects $\mathcal {F}$-transversally $\gamma _2\vert _{[a_2, b_2]}$ at $\gamma _1(t_1)=\gamma _2(t_2)$. Since $\gamma _1$ is $\mathcal {F}$-positively recurrent, we can find

$$\begin{aligned} b_1<a'_1<b'_1<a''_1<b''_1 \end{aligned}$$

such that $\gamma _1\vert _{[a_1,b_1]}$, $\gamma _1\vert _{[a'_1,b'_1]}$ and $\gamma _1\vert _{[a''_1,b''_1]}$ are equivalent. In particular, there exists

$$\begin{aligned} a'_1<t'_1<b'_1<a''_1<t''_1<b''_1 \end{aligned}$$

such that

• $\gamma _1\vert _{[a_1,t_1]}$, $\gamma _1\vert _{[a'_1,t'_1]}$ and $\gamma _1\vert _{[a''_1,t''_1]}$ are equivalent;

• $\gamma _1\vert _{[t_1,b_1]}$, $\gamma _1\vert _{[t'_1,b'_1]}$ and $\gamma _1\vert _{[t''_1,b''_1]}$ are equivalent.

Moreover, replacing $\gamma _1$ by an equivalent path, one can suppose that $\gamma _1(t_1)=\gamma _1(t'_1)=\gamma _1(t''_1)$. Since $\gamma _2$ is $\mathcal {F}$-positively recurrent, we can also find

$$\begin{aligned} b_2<a'_2<t'_2<b'_2<a''_2<t''_2<b''_2 \end{aligned}$$

and replace $\gamma _2$ by an equivalent path such that a similar statement holds with the necessary changes. Note that this implies that $\gamma _1$ is $\mathcal {F}$-transverse to $\gamma _2$ at both $\gamma _1(t''_1)=\gamma _2(t_2)$ and $\gamma _1(t_1)=\gamma _2(t''_2)$. Suppose that $\gamma _1\vert _{[a_1,b''_1]}$ and $\gamma _2\vert _{[a_2,b''_2]}$ are admissible of order $\leqslant q$ and apply Corollary 21 to the families $(\gamma _i)_{1\leqslant i\leqslant 2n}$, $(s_i)_{1\leqslant i\leqslant 2n}$, $(t_i)_{1\leqslant i\leqslant 2n}$ where

$$\begin{aligned} \gamma _{2j+1}= \gamma _1\vert _{[a_1,b''_1]}, \,\gamma _{2j}= \gamma _2\vert _{[a_2,b''_2]} \end{aligned}$$

and

$$\begin{aligned} s_{2j+1}= t_1\,{\mathrm {if}}\, j>0 \,,\,s_{2j}= t_2\,, \,t_{2j+1}= t''_1 \,,\,t_{2j}= t''_2 \,{\mathrm {if}}\, j<n. \end{aligned}$$

One deduces that for every $n\geqslant 1$,

$$\begin{aligned} \gamma _1\vert _{[a_1, t_1]}\left( \gamma _1\vert _{[t_1, t''_1]}\gamma _2\vert _{[t_2, t''_2]}\right) ^n\gamma _2\vert _{[t''_2, b_2]} \end{aligned}$$

is admissible of order 2nq and consequently that $\left( \gamma _1\vert _{[t_1, t''_1]}\gamma _2\vert _{[t_2, t''_2]}\right) ^n$ is admissible of order $\leqslant 2nq$. So, the closed path $\gamma '=\gamma _1\vert _{[t_1, t''_1]}\gamma _2\vert _{[t_2, t''_2]}$ defines a loop that is linearly admissible: it satisfies the condition $(Q_{2q})$ stated in the previous section. Furthermore, since both $\gamma _1\vert _{[a'_1,b'_1]}$ and $\gamma _2\vert _{[a'_2, b'_2]}$ are subpaths of $\gamma '$, the induced loop has an $\mathcal {F}$-transverse self-intersection. $\square$

Proposition 31

If there exists a linearly admissible transverse loop $\Gamma$ with an $\mathcal {F}$-transverse self-intersection, then the number of periodic points of period n for some iterate of f grows exponentially in n.

Proof

The proof of Proposition 31 will last until the end of this subsection. Suppose that $\Gamma$ satisfies the condition $(Q_{q_0})$ and denote $\gamma$ its natural lift. By assumption, there exist $s<t$ such that $\gamma$ has an $\mathcal {F}$-transverse self-intersection at $\gamma (s)=\gamma (t)$. So, one can apply the realization result (Proposition 26) and deduce that $\Gamma$ is associated to a fixed point of $f^{q_0}$. Modifying $\Gamma$ in its equivalence class if necessary, one can suppose that for every $r\geqslant 1$, the path $\gamma \vert _{[0,r]}$ is admissible of order $rq_0$. Adding the same positive integer to both s and t, one can find a positive integer K such that $\gamma \vert _{[0, K]}$ has an $\mathcal {F}$-transverse self-intersection at $\gamma (s)=\gamma (t)$ and one knows that $\gamma \vert _{[0, mK]}$ is admissible of order $mKq_0$ for every $m\geqslant 1$. To get our proposition, one needs a preliminary result. Set

$$\begin{aligned} \gamma _1=\gamma \vert _{[s,t]},\,\gamma _2=\gamma _{[t, K+s]}. \end{aligned}$$

$\square$

Lemma 32

For every sequence $(\varepsilon _i)_{i\in \mathbb {N}}\in \{1,2\}^{\mathbb {N}}$, every $n\geqslant 1$, and every $m\geqslant 1$ the path

$$\begin{aligned} \gamma \vert _{[0, s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i}\, \gamma _{[t, mK]} \end{aligned}$$

is admissible of order $(n+m)Kq_0$.

Proof

We will give a proof by induction on n.

Let us begin with the case where $n=1$. If $\varepsilon _0=1$, we must prove that $\gamma \vert _{[0,s]}\gamma \vert _{[s,t]}\gamma \vert _{[t,mK]}=\gamma \vert _{[0,mK]}$ is admissible of order $(m+1){Kq_0}$, which is true by Proposition 19 as it is admissible of order $m{Kq_0}$). If $\varepsilon _0=2$, we must prove that

$$\begin{aligned} \gamma \vert _{[0,s]}\gamma \vert _{[t,s+K]} \gamma \vert _{[t,mK]}=\gamma \vert _{[0,s]}\gamma \vert _{[t,s+K]}\gamma \vert _{[t+K,(m+1)K]} \end{aligned}$$

is admissible of order $(m+1){Kq_0}$. The path $\gamma \vert _{[0,(m+1)K]}$ having an $\mathcal {F}$-transverse self-intersection at $\gamma (t)=\gamma (s)$ and being admissible of order $\leqslant (m+1){Kq_0}$, one deduces by Proposition 23 that $\gamma \vert _{[0,s]}\gamma \vert _{[t,(m+1)K]}$ is admissible of order $(m+1){Kq_0}$. This last path has an $\mathcal {F}$-transverse self-intersection at $\gamma (t+K)=\gamma (s+K)$. Applying Proposition 23 again, one deduces that $\gamma \vert _{[0,s]}\gamma \vert _{[t,s+K]}\gamma \vert _{[t+K,(m+1)K]}$ is admissible of order $(m+1){Kq_0}$.

Suppose now the result proved for n. There are three cases to consider.

The first case is if the sequence $(\varepsilon _i)_{0\leqslant i\leqslant n}$ is constant equal to 1. We apply Corollary 22 to the families $(\gamma _i)_{1\leqslant i\leqslant n+1}$, $(s_i)_{1\leqslant i\leqslant n+1}$, $(t_i)_{1\leqslant i \leqslant n+1}$, where

$$\begin{aligned} \gamma _{i}= \gamma \vert _{[0,K]}\,{\mathrm {if }}\, i\leqslant n, \, \gamma _{n+1}=\gamma \vert _{[0,mK]} \end{aligned}$$

and

$$\begin{aligned} s_{i}= s \,{\mathrm {if}}\, i>0 \,,\,t_{i}= t \,{\mathrm {if}}\, i\leqslant n \, \end{aligned}$$

One deduces that

$$\begin{aligned} \gamma \vert _{[0,t]} \left( \gamma \vert _{[s,t]}\right) ^{n-1}\gamma _{[s,mK]}=\gamma \vert _{[0,s]} \left( \gamma \vert _{[s,t]}\right) ^{{n}}\gamma \vert _{[t,mK]} \end{aligned}$$

is admissible of order $(m+n){Kq_0}$ and so is admissible of order $(m+n+1){Kq_0}$.

The second case to consider is if there exists $n'<n$ such that $\varepsilon _{n'}=2$ and $\varepsilon _i=1$ if $i>n'$. We apply Corollary 22 to the families $(\gamma _i)_{1\leqslant i\leqslant n-n'+1}$, $(s_i)_{1\leqslant i\leqslant n-n'+1}$, $(t_i)_{1\leqslant i \leqslant n-n'+1}$ where

$$\begin{aligned} \gamma _{0}= & {} \gamma \vert _{[0,s]}\prod _{0\leqslant i<n'} \gamma _{\varepsilon _i} \gamma \vert _{[t,2K]}\,,\,\\ \gamma _{i}= & {} \gamma \vert _{[K,2K]}\,{\mathrm {if }}\, 1<i\leqslant n-n', \, \gamma _{n-n'+1}=\gamma \vert _{[K,(m+1)K]} \end{aligned}$$

and

$$\begin{aligned} s_{i}= s+K \,{\mathrm {if}}\, i>0 \,,\,t_{i}= t +K\,{\mathrm {if}}\, i \leqslant n-n' \, \end{aligned}$$

The induction hypothesis tells us that $\gamma _{0}= \gamma \vert _{[0,s]}\prod _{0\leqslant i<n'} \gamma _{\varepsilon _i} \gamma _{[t,2K]}$ is admissible of order $(n'+2){Kq_0}$, so

$$\begin{aligned}&\gamma \vert _{[0,s]}\prod _{0\leqslant i<n'} \gamma _{\varepsilon _i} \gamma \vert _{[t,s+K]} \left( \gamma \vert _{[s+K,t+K]}\right) ^{n-n'+1}\gamma \vert _{[t+K,(m+1)K]}\\&\quad =\gamma \vert _{[0,s]}\prod _{0\leqslant i\leqslant n} \gamma _{\varepsilon _i} \gamma \vert _{[t,mK]} \end{aligned}$$

is admissible of order $(n'+2){Kq_0}+(n-n'-1){Kq_0} +m{Kq_0}=(m+n+1){Kq_0}$.

The final case to consider is if $\varepsilon _n=2$. We must prove that

$$\begin{aligned} \gamma \vert _{[0,s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i} \gamma \vert _{[t,s+K]}\gamma \vert _{[t,mK]}=\gamma \vert _{[0,s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i} \gamma \vert _{[t,s+K]}\gamma \vert _{[t+K,(m+1)K]} \end{aligned}$$

is admissible of order $(m+n+1){Kq_0}$. The path $\gamma \vert _{[K,(m+1)K]}$ having an $\mathcal {F}$-transverse self-intersection at $\gamma (t+K)=\gamma (s+K)$, the same is true when we extend this path on the left by adding $\gamma \vert _{[0,s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i}\gamma \vert _{[t,K]}$. Moreover by induction hypothesis, one knows that

$$\begin{aligned} \gamma \vert _{[0,s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i}\gamma \vert _{[t,K]}\gamma \vert _{[K,(m+1)K]} \end{aligned}$$

is admissible of order $(m+n+1){Kq_0}$. Applying Proposition 23, one deduces that

$$\begin{aligned} \gamma \vert _{[0,s]}\prod _{0\leqslant i<n} \gamma _{\varepsilon _i} \gamma \vert _{[t,s+K]}\gamma \vert _{[t+K,(m+1)K]} \end{aligned}$$

is admissible of order $(m+n+1){Kq_0}$. $\square$

Lemma 33

Let $\mathbf {e}= (\varepsilon _i)_{i\in \mathbb {N}}\in \{1,2\}^{\mathbb {N}}$ be a periodic word of period q which is not periodic of period 1. Then the loop $\Gamma _{{\mathbf {e}}}$, defined by the closed path $\prod _{0\leqslant i<q} \gamma _{\varepsilon _i}$, is equivalent to a transverse loop associated to a fixed point of $f^{qKq_0}$.

Proof

Lemma 32 tells us that, for every n, the path

$$\begin{aligned} \gamma \vert _{[0, s]}\left( \prod _{0\leqslant i< q} \gamma _{\varepsilon _i}\right) ^n\, \gamma _{[t, K]} \end{aligned}$$

is admissible of order $(1+qn)Kq_0$ and consequently that $\left( \prod _{0\leqslant i<q} \gamma _{\varepsilon _i}\right) ^n$ is admissible of order $(1+qn)Kq_0$. So $\Gamma _{{\mathbf {e}}}$ is linearly admissible: it satisfies the condition ${(Q_{qKq_0})}$. Note that, since $\Gamma _{\mathbf {e}}$ is not a constant sequence, it has a self-intersection. The lema follows by applying the realization result (Proposition 26). $\square$

Consider now the paths

$$\begin{aligned} \gamma _1'=\gamma _1\gamma _2=\gamma _{[s, K+s]}, \,\,\, \gamma _2'=\gamma _2\gamma _1=\gamma \vert _{[t, K+t]}. \end{aligned}$$

Since $\gamma \vert _{[0,K]}$ has a $\mathcal {F}$-transverse self-intersection at $z^*=\gamma (s)=\gamma (t)$, then for every lift ${\widetilde{\gamma }}$ of $\gamma$, there exists a covering automorphism T such that ${\widetilde{\gamma }}\vert _{[0,K]}$ and $T({\widetilde{\gamma }})\vert _{[0,K]}$ have a $\widetilde{\mathcal {F}}$-transverse intersection at ${\widetilde{\gamma }}(t)=T({\widetilde{\gamma }})(s)$. Consequently, ${\widetilde{\gamma }}\vert _{[0,K+t]}$ and $T({\widetilde{\gamma }})\vert _{[0,K+s]}$ have a $\widetilde{\mathcal {F}}$-transverse intersection at ${\widetilde{\gamma }}(t)=T({\widetilde{\gamma }})(s)$. This implies that among the leaves $\phi _{{\widetilde{\gamma }}(K+t)}$ and $\phi _{T({\widetilde{\gamma }})(K+s)}$, one is above the other one relative to $\phi _{{\widetilde{\gamma }}(t)}=\phi _{T({\widetilde{\gamma }})(s)}$. This means that if ${\widetilde{\gamma }}'_1$ and ${\widetilde{\gamma }}'_2$ lift $\gamma '_1$ and $\gamma '_2$ respectively and start from the same point $\widetilde{z}^*$, then the leaf containing the ending point of ${\widetilde{\gamma }}'_1$ is either above or below the leaf containing the ending point of ${\widetilde{\gamma }}'_2$ (relative to $\phi _{\widetilde{z}}$), see Fig. 16. We do not loose any generality by supposing it is the former, which means that ${\widetilde{\gamma }}\vert _{[0,K]}$ and $T({\widetilde{\gamma }})\vert _{[0,K]}$ have a positive $\widetilde{\mathcal {F}}$-transverse intersection at $\gamma (t)=T({\widetilde{\gamma }})(s)$. In this situation $\phi _{{\widetilde{\gamma }}(0)}$ is above $\phi _{T({\widetilde{\gamma }})(0)}$ relative to $\phi _{{\widetilde{\gamma }}(t)}$, so $\phi _{{\widetilde{\gamma }}(t-K)}$ is above $\phi _{T({\widetilde{\gamma }})(s-K)}$ relative to $\phi _{{\widetilde{\gamma }}(t)}$.

Fig. 16

Relative position of the leafs of the endpoints of ${\widetilde{\gamma }}_1$ and ${\widetilde{\gamma }}_2$, when both start at $\widetilde{z}^*$ in Lemma 33

This means that, if ${\widetilde{\gamma }}'_1$ and ${\widetilde{\gamma }}'_2$ lift ${\widetilde{\gamma }}_1$ and ${\widetilde{\gamma }}_2$ respectively and end at the same point $\widetilde{z}^*$, then the leaf containing the starting point of ${\widetilde{\gamma }}'_1$ is below the leaf containing the ending point of ${\widetilde{\gamma }}'_2$ (relatively to $\phi _{\widetilde{z}}$).

We say that a finite word ${\mathbf {e}}= (\varepsilon _i)_{0\leqslant i < 2n}\in \{1,2\}^{2n}$ is a palindromic word of length 2n if it satisfies $\varepsilon _{n+j}=\varepsilon _{n-j-1},\, 0\leqslant j < n$. Let us fix a base point $\widetilde{z}^*$ projecting on $z^*$. To each palindromic word ${\mathbf {e}}$ of length 2n, we associate the loop $\Gamma '_{{\mathbf {e}}}$ naturally defined by the closed path $\prod _{0\leqslant i< 2n} \gamma '_{\varepsilon _i}$ and the lift ${\widetilde{\gamma }}'_{{\mathbf {e}}}={\widetilde{\gamma }}'_{{\mathbf {e}}}{}^{-}{\widetilde{\gamma }}'_{{\mathbf {e}}}{}^{+}$ of $\prod _{0\leqslant i< 2n} \gamma '_{\varepsilon _i}$, where ${\widetilde{\gamma }}'_{{\mathbf {e}}}{}^{-}$ is the lift of $\prod _{0\leqslant i< n} \gamma '_{\varepsilon _i}$ ending at $\widetilde{z}^*$ and ${\widetilde{\gamma }}'_{{\mathbf {e}}}{}^{+}$ the lift of $\prod _{n\leqslant i< 2n-1} \gamma '_{\varepsilon _i}$ starting at $\widetilde{z}^*$. The ending point of ${\widetilde{\gamma }}'_{{\mathbf {e}}}$ is the image of its starting point by a covering automorphism that we denote $T_{{\mathbf {e}}}$. We define the path ${\widetilde{\gamma }}'{}^2_{{\mathbf {e}}}= {\widetilde{\gamma }}'_{{\mathbf {e}}}T_{{\mathbf {e}}}({\widetilde{\gamma }}'_{{\mathbf {e}}})$ and the line ${\widetilde{\gamma }}'{}^{\infty }_{{\mathbf {e}}}=\prod _{k\in \mathbb {Z}}T^k_{{\mathbf {e}}}({\widetilde{\gamma }}'_{\mathbf {e}})$, which is a lift of $\Gamma '_{{\mathbf {e}}}$.

Lemma 34

If ${\mathbf {e}}\not =\mathbf {e'}$ are two palindromic words of the same length, then the paths ${\widetilde{\gamma }}'_{{\mathbf {e}}}$ and ${\widetilde{\gamma }}'_{\mathbf { e'}}$ intersect $\widetilde{\mathcal {F}}$-transversally at $\widetilde{z}$.

Proof

If $\mathbf{e}\not =\mathbf{e'}$, there exists $k\in \{0,\ldots , n-1\}$ such that $\varepsilon _{n+j}=\varepsilon '_{n+j}$ if $0\leqslant j<k$ and $\varepsilon _{n+k}\not =\varepsilon '_{n+k}$. Let us suppose for example that $\varepsilon _{n+k}=1$ and $\varepsilon '_{n+k}=2$. The paths $\prod _{0\leqslant j<k}\gamma '_{\varepsilon _{n+j}}$ and $\prod _{0\leqslant j<k}\gamma '_{\varepsilon '_{n+j}}$ are equal, as are the lifts starting from $\widetilde{z}^*$. Let us write $\widetilde{z}$ for the ending point of the common lift. The leaf containing the ending point of the lift of $\prod _{0\leqslant j\leqslant k}\gamma '_{\varepsilon _{n+j}}$ starting from $\widetilde{z}^*$ is above (relative to $\phi _{\widetilde{z}}$ but also relative to $\phi _{\widetilde{z}^*}$) the leaf containing the ending point of the lift of $\prod _{0\leqslant j\leqslant k}\gamma '_{\varepsilon '_{n+j}}$ starting from $\widetilde{z}^*$. So, we have a similar result replacing $\prod _{0\leqslant j\leqslant k}\gamma '_{\varepsilon _{n+j}}$ with the extension ${\widetilde{\gamma }}_{{\mathbf {e}}}^{+}$ and $\prod _{0\leqslant j\leqslant k}\gamma '_{\varepsilon '_{n+j}}$ with the extension ${\widetilde{\gamma }}_{{\mathbf {e}}'}^{+}$. One proves similarly that the leaf containing the starting point of ${\widetilde{\gamma }}_{{\mathbf {e}}}^{-}$ is below (relative to $\phi _{\widetilde{z}^*}$) the leaf containing the starting point of ${\widetilde{\gamma }}_{{\mathbf {e}}'}^{-}$. $\square$

By Lemma 33, for every palindromic word ${\mathbf {e}}$ of length 2n, there exists a fixed point $z_{{\mathbf {e}}}$ of $f^{4nKq_0}$ such that $\Gamma '_{{\mathbf {e}}}$ is associated to $z_{{\mathbf {e}}}$.

Lemma 35

There exists a constant $L>0$ such that, given a palindromic word ${\mathbf {e}}$ of length 2n, there are at most $L n^2$ different palindromic words $\mathbf {e'}$ of length 2n such that $\Gamma '_{{\mathbf {e}}}$ and $\Gamma '_{{\mathbf {e}}'}$ are equivalent.

Proof

Let ${\widetilde{\gamma }}'_1$ and ${\widetilde{\gamma }}'_2$ be two respective lifts of $\gamma '_1$ and $\gamma '_2$ to $\widetilde{{\mathrm {dom}}}(I)$. The group of covering automorphisms acts freely and properly. So there exists a constant $L'$ such that there are at most $L'$ automorphisms S such that ${\widetilde{\gamma }}'_1\cap S({\widetilde{\gamma }}'_1)\not =\emptyset$, at most $L'$ automorphisms S such that ${\widetilde{\gamma }}'_2\cap S({\widetilde{\gamma }}'_2)\not =\emptyset$ and at most $L'$ automorphisms S such that ${\widetilde{\gamma }}'_1\cap S({\widetilde{\gamma }}'_2)\not =\emptyset$. Of course, $L'$ is independent of the choices of ${\widetilde{\gamma }}'_1$ and ${\widetilde{\gamma }}'_2$. We deduce that for every palindromic word $\mathbf{e}$ of length 2n, there are at most $8L'n^2$ automorphisms S such that ${\widetilde{\gamma }}'_\mathbf{e}\cap S({\widetilde{\gamma }}'{}^2_\mathbf{e})\not =\emptyset$. This implies that there are at most $8L'n^2$ automorphisms S such that ${\widetilde{\gamma }}'_\mathbf{e}$ and $S({\widetilde{\gamma }}'{}^2_\mathbf{e})$ have a $\widetilde{\mathcal {F}}$-transverse intersection.

Suppose that ${\mathbf {e}}$ and ${\mathbf {e}}'$ are two palindromic words of length 2n such that $\Gamma '_{{\mathbf {e}}}$ and $\Gamma '_{{\mathbf {e}}'}$ are equivalent. There exists a covering automorphism $S_{{\mathbf {e}}'}$ such that ${\widetilde{\gamma }}'{}^{\infty }_{{\mathbf {e}}'}$ is equivalent to $S_{{\mathbf {e}}'}({\widetilde{\gamma }}'{}^{\infty }_{{\mathbf {e}}})$ and such that $S_{{\mathbf {e}}'}\circ T_{{\mathbf {e}}}\circ S_{{\mathbf {e}}'}^{-1}= T_{{\mathbf {e}}'}$. Composing $S_{{\mathbf {e}}'}$ on the left by a power of $T_{{\mathbf {e}}'}$ if necessary, one can suppose that ${\widetilde{\gamma }}'_{{\mathbf {e}}'}$ is equivalent to a subpath of $S_{{\mathbf {e}}'}({\widetilde{\gamma }}'{}^2_{{\mathbf {e}}})$. By Lemma 34, one deduces that ${\widetilde{\gamma }}'_{{\mathbf {e}}}$ and $S_{{\mathbf {e}}'}({\widetilde{\gamma }}'{}^2_{{\mathbf {e}}})$ intersect $\widetilde{\mathcal {F}}$-transversally. It remains to prove that $S_{{\mathbf {e}}'}\not =S_{{\mathbf {e}}''}$ if ${\mathbf {e}}'\not ={\mathbf {e}}''$. But if this the case, then ${\widetilde{\Gamma }}'_{{\mathbf {e}}'}$ and ${\widetilde{\Gamma }}'_{{\mathbf {e}}''}$ are equivalent, which is impossible because this two paths intersect $\widetilde{\mathcal {F}}$-transversally at $\widetilde{z}$. $\square$

Since there exists $2^{n}$ different palindromic words of length 2n, one concludes by Lemmas 33 and 35 that $f^{4nKq_0}$ has at least $\frac{2^{n}}{L n^2}$ distinct fixed points, proving Proposition 31.

5.2 Topological entropy

By the previous result, it is natural to believe that the topological entropy is positive, in case M is compact. The next result asserts that this is the case:

Theorem 36

Let M be a compact surface, $\gamma _1, \gamma _2 :\mathbb {R}\rightarrow M$ be two admissible $\mathcal {F}$-positively recurrent transverse paths (possibly equal) with an $\mathcal {F}$-transverse intersection. Then the topological entropy of f is positive.

Remark 37

As we will see in the proof, Theorem 36 will be stated even in case where M is not compact by proving that its Alexandrov extension has positive entropy. More precisely, write ${\mathrm {dom}}(I)_{{\mathrm {alex}}}$ for the Alexandrov compactification of ${\mathrm {dom}}(I)$ if it is not compact, and $f_{{\mathrm {alex}}}$ for the extension of $f\vert _{{\mathrm {dom}}(I)}$ that fixes the point at infinity (otherwise set ${\mathrm {dom}}(I)_{{\mathrm {alex}}}= {\mathrm {dom}}(I)$ and $f_{{\mathrm {alex}}}=f\vert _{{\mathrm {dom}}(I)}$ in what follows). Of course, $f_{{\mathrm {alex}}}$ is a factor of f and so $h(f)\geqslant h(f_{{\mathrm {alex}}})$ if M is compact.

Theorem 36 will be the direct consequence of Lemma 30 and the following result:

Proposition 38

Let $\Gamma$ be a transverse loop with an $\mathcal {F}$-transverse self-intersection, and $\gamma$ its natural lift. Assume that there exists integers K, r such that $\gamma \vert _{[0, K]}$ has an $\mathcal {F}$-transverse self-intersection, and such that $\gamma \vert _{[0, mK]}$ is admissible of order mr for every $m\geqslant 1$. Then the topological entropy of $f_{{\mathrm {alex}}}$ is at least equal to $\log 2/(4r)$.

Before proving the proposition, we will need the following lemma:

Lemma 39

There exists a covering $(V_z)_{z\in {\mathrm {dom}}(I)}$ of ${\mathrm {dom}}(I)$ satisfying the following properties:

i) :

$V_z$ is an open disk that contains z;

ii) :

for every $z_1$, $z_2$ in ${\mathrm {dom}}(I)$, for every integer $p\geqslant 1$ and for every $z\in V_{z_1}\cap f^{-p}(V_{z_2})$ there exists a transverse path joining $z_1$ to $z_2$ equivalent to a subpath of $I_{\mathcal {F}}^{p+2}(f^{-1}(z))$, that is homotopic, with endpoints fixed, to the path $\alpha _1 I^p(z)\alpha _2^{-1}$, where $\alpha _1$ is a path in $V_{z_1}$ that joins $z_1$ to z and $\alpha _2$ is a path in $V_{z_2}$ that joins $z_2$ to $f^p(z)$;

iii) :

in the previous assertion, if $p=1$, the homotopy class of the path that joins $z_1$ to $z_2$ does not depend on $z\in V_{z_1}\cap f^{-1}(V_{z_2})$.

Proof

One can construct an increasing sequence $(K_i)_{i\geqslant 1}$ of compact sets of ${\mathrm {dom}}(I)$ that cover ${\mathrm {dom}}(I)$ and such $K_{i+1}$ is a neighborhood of $K_i\cup f(K_{i})\cup f^{-1}(K_{i})$, a distance on $\widetilde{{\mathrm {dom}}}(I)$, denoted by d, that is invariant under the action of the group of covering transformations, and an equivariant family of leaves $(\phi ^*_{\widetilde{z}})_{\widetilde{z} \in \widetilde{{\mathrm {dom}}}(I)}$, where $\phi ^*_{\widetilde{z}}$ separates $\widetilde{z}$ and $\widetilde{f}(\widetilde{z})$ and consequently is met by ${\widetilde{I}}_{\widetilde{ \mathcal {F}}}(\widetilde{z})$ (equivariant means that $\phi ^*_{T(\widetilde{z})}=T(\phi ^*_{\widetilde{z}})$ for every covering transformation T). Then one can construct an equivariant family of relatively compact open sets $(W_{\widetilde{z}})_{\widetilde{z} \in \widetilde{{\mathrm {dom}}}(I)}$, where $W_{\widetilde{z}}$ contains $\widetilde{z}$, projects onto an open disk of ${{\mathrm {dom}}(I)}$ and satisfies

$$\begin{aligned} \widetilde{f}^{-1}(W_{\widetilde{z}}) \subset R\left( \phi ^*_{\widetilde{f}^{-1}(z) }\right) , \, \widetilde{f}(W_{\widetilde{z}}) \subset L\left( \phi ^*_{\widetilde{z}}\right) . \end{aligned}$$

Note that, given $\widetilde{z}, \phi ^{*}_{\widetilde{z}}$ and $W_{\widetilde{z}}$ as above, if $\widetilde{z}'$ is sufficiently close to $\widetilde{z}$, then one could choose $\phi ^{*}_{\widetilde{z}'}$ to be equal to $\phi ^{*}_{\widetilde{z}}$ and also $W_{\widetilde{z}'}=W_{\widetilde{z}}$. Therefore we may assume that the family $(W_{\widetilde{z}})_{\widetilde{z} \in \widetilde{{\mathrm {dom}}}(I)}$ is locally finite.

Set $K_i=\emptyset$ if $i\leqslant 0$. One knows that $f(\overline{K_i\setminus K_{i-1}})\subset {\mathrm {int}}(K_{i+1}\setminus K_{i-2})$. By a compactness argument, there exists a positive and decreasing sequence $(\eta _{i})_{i\geqslant 1}$ such that for every $\widetilde{z}\in \pi ^{-1}(\overline{K_i\setminus K_{i-1}})$, the open ball $B(\widetilde{z}, \eta _{i})$ is included in $W_{\widetilde{z}}\cap \pi ^{-1}({\mathrm {int}}(K_{i+1}\setminus K_{i-2}))$ and its image $\widetilde{f}(B(\widetilde{z}, \eta _{i}))$ included in $\pi ^{-1}({\mathrm {int}}(K_{i+1}\setminus K_{i-2}))$, the ball $B(\widetilde{z}, \eta _{i})$ being defined with respect to d. Then, one considers a decreasing and positive sequence $(\eta '_{i})_{i\geqslant 1}$ satisfying $\eta '_i<\eta _{i+4}/4$ and such that for every $\widetilde{z}\in \pi ^{-1}(\overline{K_i\setminus K_{i-1}})$, one has

$$\begin{aligned} \widetilde{f}\left( B\left( \widetilde{z}, \eta '_i\right) \right) \subset B(\widetilde{f}(\widetilde{z}), \eta _{i+1}/2). \end{aligned}$$

Finally, one constructs an equivariant family of open sets $(V_{\widetilde{z}})_{\widetilde{z} \in \widetilde{{\mathrm {dom}}}(I)}$, where $V_{\widetilde{z}}$ contains $\widetilde{z}$, is included in $B(\widetilde{z}, \eta '_i)$ if $\widetilde{z}\in \pi ^{-1}(K_i\setminus K_{i-1})$ and projects onto an open disk of ${{\mathrm {dom}}(I)}$. Note that $V_{\widetilde{z}}\subset W_{\widetilde{z}}$.

By projection on ${\mathrm {dom}}(I)$, one gets a family $(V_{z})_{z \in {{\mathrm {dom}}(I)}}$ satisfying i). To prove that it satisfies ii), one must prove that if there exists a point $\widetilde{z} \in V_{\widetilde{z}_1}$ such that $\widetilde{f}^p(\widetilde{z}) \in V_{\widetilde{z}_2}$, then there exists a transverse path from $\widetilde{z}_1$ to $\widetilde{z}_2$ that is equivalent to a subpath of ${\widetilde{I}}^{p+2}_{\widetilde{\mathcal {F}}}(\widetilde{f}^{-1}(\widetilde{z}))$. As $V_{\widetilde{z}_i}\subset W_{\widetilde{z}_i}, i\in \{1, 2\}$, by the properties of the chosen family $(W_{{\widetilde{y}}})_{{\widetilde{y}} \in \widetilde{{\mathrm {dom}}}(I)}$,

$$\begin{aligned} R\left( \phi _{\widetilde{f}^{-1}(\widetilde{z} )}\right) \subset R\left( \phi ^*_{\widetilde{f}^{-1}(\widetilde{z}_1)}\right) \subset R\left( \phi _{\widetilde{z}_1}\right) \subset R\left( \phi ^*_{\widetilde{z}_1}\right) \subset R\left( \phi _{\widetilde{f}(\widetilde{z})}\right) \end{aligned}$$

and

$$\begin{aligned} R\left( \phi _{\widetilde{f}^{p-1}(\widetilde{z} )}\right) \subset R\left( \phi ^*_{\widetilde{f}^{-1}(\widetilde{z}_2)}\right) \subset R\left( \phi _{\widetilde{z}_2}\right) \subset R\left( \phi ^*_{\widetilde{z}_2}\right) \subset R\left( \phi _{\widetilde{f}^{p+1}(\widetilde{z})}\right) . \end{aligned}$$

One deduces that ${\widetilde{I}}^{p+2}_{\widetilde{\mathcal {F}}} (\widetilde{f}^{-1}(\widetilde{z}))$ meets $\phi _{\widetilde{z}_1}$ and $\phi _{\widetilde{z}_2}$. It remains to prove that $R(\phi _{\widetilde{z}_1})\subset R(\phi _{\widetilde{z}_2})$ to ensure that $\phi _{\widetilde{z}_1}$ is met before $\phi _{\widetilde{z}_2}$ and to prove the existence of a transverse path from $\widetilde{z}_1$ to $\widetilde{z}_2$. The case where $p\geqslant 2$ is easy because

$$\begin{aligned} R(\phi _{\widetilde{z}_1})\subset R(\phi _{\widetilde{f}(\widetilde{z}))})\subset R(\phi _{\widetilde{f}^{p-1}(\widetilde{z} )})\subset R(\phi _{\widetilde{z}_2}). \end{aligned}$$

To prove the result in the case where $p=1$ it is sufficient to prove that $V_{\widetilde{z}_2}$ is included in $W_{{\widetilde{f}}(\widetilde{z}_1)}$ because every point in $W_{\widetilde{f}(\widetilde{z}_1)}$ belongs to $L(\phi ^*_{\widetilde{z}_1})$. Moreover one will get iii) because $W_{\widetilde{f}(\widetilde{z}_1)}$ is disjoint from its images by the non trivial covering transformations. Set $\eta _j=\eta _1$ and $\eta '_j=\eta '_1$ if $j\leqslant 0$, and let i be such that $z_1\in K_i\setminus K_{i-1}$. One knows that $\widetilde{z}\in \pi ^{-1}({\mathrm {int}}(K_{i+1}\setminus K_{i-2}))$, so $\widetilde{f}(\widetilde{z})\in \pi ^{-1}({\mathrm {int}}(K_{i+2}\setminus K_{i-3}))$ and $\widetilde{z}_2 \in \pi ^{-1}({\mathrm {int}}(K_{i+3}\setminus K_{i-4}))$. One also knows that $\widetilde{f}(\widetilde{z}_1)\in \pi ^{-1}({\mathrm {int}}(K_{i+1}\setminus K_{i-2}))$. Using the fact that $\eta '_{i-3}<\eta _{i+1}/4$, that $d(\widetilde{f}(\widetilde{z}), \widetilde{f}(\widetilde{z}_1))<\eta _{i+1}/2$, and that $d(\widetilde{f}(\widetilde{z}), \widetilde{z}_2)<\eta '_{i-3}$, one deduces that

$$\begin{aligned} V_{\widetilde{z}_2}\subset B\left( \widetilde{z}_2,\eta '_{i-3}\right) \subset {B(\widetilde{f}(\widetilde{z}_1),\eta _{i+1})\subset W_{\widetilde{f}(\widetilde{z}_1)}.} \end{aligned}$$

$\square$

Proof of Proposition 38

We keep the notations of Proposition 31. Since, by Lemma 34 applied to $n=1$, the paths $(\gamma _1')^2$ and $(\gamma _2')^2$ intersect $\mathcal {F}$-transversally, one deduces that $\gamma '{}_1^2$ has a leaf on its right and a leaf on its left, which implies that $\gamma '_1$ satisfies the same property. One proves similarly that $\gamma '_2$ has a leaf on its right and a leaf on its left. By Lemma 18, there exists a compact set K such that for every $n\geqslant 1$ and every $z\in {\mathrm {dom}}(I)\setminus \bigcup _{0\leqslant k<n}f^{-k}(K)$, none of the paths $\gamma '_1$ and $\gamma '_2$ is equivalent to a subpath of $I_{\mathcal {F}}^n(z)$. We can find a compact set $K'$ larger than K such that for all $z\in {\mathrm {dom}}(I)\setminus K'$, the trajectory I(z) is disjoint from $\gamma _1'$ and $\gamma _2'$, as is every open set $V_{z'}$ given by Lemma 39 that contains z. Adding $\infty$ to ${\mathrm {dom}}(I)\setminus K'$, one gets a neighborhood $V_{\infty }$ of $\infty$ in ${\mathrm {dom}}(I)_{{\mathrm {alex}}}$. Define $V_{\infty ,p}=\bigcap _{\vert k\vert \leqslant p} f^{-k}(V_{\infty })$ and consider the covering ${\mathcal {V}}_p$ of ${\mathrm {dom}}(I)_{{\mathrm {alex}}}$ that consists of $V_{\infty ,p}$ added to the covering $(V_z)_{z\in {\mathrm {dom}}(I)}$ of ${\mathrm {dom}}(I)$ given by Lemma 39. Write $\Gamma '$ for the loop naturally defined by the closed path $(\gamma _1')^2(\gamma _2')^2$ and $\gamma '$ for its natural lift. Recall that $M(\Gamma ')$ has been defined in Proposition 9 . Proposition 38 is an immediate consequence of the following: $\square$

Lemma 40

The entropy of $f_{{\mathrm {alex}}}$ relative to the covering ${\mathcal {V}}_p$ is at least equal to $\log 2/(4r)-\log M(\Gamma ')/2p$.

Proof

As seen in the proof of Theorem 29, to every palindromic word $\mathbf {e}=(\varepsilon _i)_{0\leqslant i<2n}$ of length 2n is associated a fixed point $z_{{\mathbf {e}}}$ of $f^{4nr}$ and an associate $\mathcal {F}$-transverse loop defined by $\prod _{0\leqslant j<2n} \gamma '_{\varepsilon _{i}}$. Moreover, by Lemma 35, there exists $L>0$, independent of n, such that there are at least $2^n/Ln^2$ different equivalent classes among the associated loops. We will prove that every open set of the covering $\bigvee _{0\leqslant k< 4nr} f^{-k}({\mathcal {V}}^p)$ contains at most $Ln^2M(\Gamma ')^{ 2nr/p}$ points $z_{{\mathbf {e}}}$. We deduce that every finite sub-covering of $\bigvee _{0\leqslant k< 4nr} f^{-k}({\mathcal {V}}^p)$ has at least $2^{n}/Ln^2M(\Gamma ')^{2nr/p}$ open sets and so

$$\begin{aligned}&h(f_{{\mathrm {alex}}}, {\mathcal {V}}_p)\geqslant \lim _{n\rightarrow +\infty } {1\over 4nr} \log (2^{n}/Ln^2M(\Gamma ')^{2nr/p})\\&\quad =\log 2/(4r)-\log M(\Gamma ')/2p. \end{aligned}$$

Let us consider an element $W=\bigcap _{0\leqslant j< 4nr}f^{-j}(V^j)$ of ${\mathcal {V}}_p$. We suppose that it contains at least one point $z_{{\mathbf {e}}}$. Denote $J_{\infty }$ the set of $j\in \{0, \ldots ,4nr-1\}$ such that there exists $j'\in \{0, \ldots ,4nr\}$ satisfying $\vert j-j'\vert <p$ and $V^{j'}=V_{\infty ,p}$ and denote $J_{<\infty }$ the complement of $J_{\infty }$. Note that $f^j(z_{{\mathbf {e}}})\in V_{\infty }$ if $j\in J_{\infty }$. By Lemma 18, one knows that the orbit of $z_{{\mathbf {e}}}$ cannot be contained in $V_{\infty }$. So $J_{<\infty }\not =\emptyset$.

Let us begin with the case where $0\in J_{<\infty }$ and write $J_{<\infty }=\{j_0,\ldots , j_{l^*}\}$, where $j_0=0<j_1\cdots < j_{l^*}$, and add $j_{l^*+1}=4nr$. Every open set $V^{j_l}$ can be written $V^{j_l}=V_{z_{j_l}}$. For every l, choose a path $\delta _l$ in $V_{z_{j_l}}$ from $z_{j_l}$ to $f^{j_l}(z_{{\mathbf {e}}})$. By Lemma 39, there exists a $\mathcal {F}$-transverse path $\beta _l$ from $z_{j_l}$ to $z_{j_{l+1}}$ equivalent to a subpath of $I^{j_{l+1}-j_l+2}_{\mathcal {F}}(f^{j_l-1}(z_{{\mathbf {e}}}))$ and homotopic to $\delta _l I^{j_{l+1}-j_j} (f^{j_l}(z_{{\mathbf {e}}}))\delta ^{-1}_{l+1}$. In the case where $j_{l+1}-j_l=1$, the homotopy class of $\beta _i$ (with endpoints $z_{i_l}$ and $z_{i_{l+1}}$ fixed) is uniquely determined. Let us explain now why there are at most $M(\Gamma ')$ possible homotopy classes if $j_{l+1}-j_l\geqslant 2$. Note first that $j_{l+1}-j_l\geqslant 2p$ in that case, and that all points $f^j(z_{{\mathbf {e}}})$, $j_{l}-1\leqslant j\leqslant j_{l+1}+1$ belong to $V_{\infty }$. This implies that neither $\gamma _1'$ nor $\gamma _2'$ are equivalent to subpaths of $I^{j_{l+1}-j_l+2}_{\mathcal {F}}(f^{j_l-1}(z_{{\mathbf {e}}}))$. Note that the latter is equivalent to a subpath of $I^{4nr}_{\mathcal {F}}(z_{{\mathbf {e}}})$, which is equivalent to $\prod _{0\leqslant j<2n} \gamma '_{\varepsilon _{i}}$. We remark that, if $\sigma$ is any transverse path that is equivalent to a subpath of $\prod _{0\leqslant j<2n} \gamma '_{\varepsilon _{i}}$, but that does not contain a subpath that is equivalent to either $\gamma _1'$ or $\gamma _2'$, then $\sigma$ must be equivalent to a subpath of one the six possible following paths:

$$\begin{aligned} \gamma '_1, \,\gamma '_2, \,\gamma '_1\gamma '_1, \,\gamma '_1\gamma '_2,\,\gamma '_2\gamma '_1,\,\gamma '_2\gamma '_2 \end{aligned}$$

and therefore $\sigma$ (and thus $I^{j_{l+1}-j_l+2}_{\mathcal {F}}(f^{j_l-1}(z_{{\mathbf {e}}}))$) must equivalent to a subpath of $\gamma '$. Furthermore $\beta _i=\delta _l I^{j_{l+1}-j_j} (f^{j_l}(z_{{\mathbf {e}}}))\delta ^{-1}_{l+1}$ is disjoint from $\Gamma '$ by definition of $V_{\infty }$ because it is the case for $I^{j_{l+1}-j_j} (f^{j_l}(z_{{\mathbf {e}}}))$ and for the disks $V_{z_{j_l}}$ and $V_{z_{j_{l+1}}}$. One can apply Proposition 9 and obtain that $\beta _i$ must belong to one of the at most $M(\Gamma ')$ different homotopy classes of paths connecting $z_{i_l}$ and $z_{i_{l+1}}$, as claimed before. The path $\prod _{0\leqslant l\leqslant l^*} \beta _l$ is a closed path based at $z_0$. Noting that there exist at most $4nr/2p=2nr/p$ integers l such that $j_{l+1}-j_l\not =1$, we deduce that there exist at most $M(\Gamma ')^{2nr/p}$ homotopy classes (with fixed base point) possible. The loop defined by $\prod _{0\leqslant l\leqslant l^*} \beta _l$ is freely homotopic to $\Gamma '_{{\mathbf {e}}}$. So there exist at most $M(\Gamma ')^{2nr/p}$ free homotopy classes defined by the loops $\Gamma '_{{\mathbf {e}}}$ such that $z_\mathbf{e}\in W$. By Lemma 35, to prove that there is at most $Ln^2M(\Gamma ')^{2nr/p}$ points $z_\mathbf{e}$ in W, it is sufficient to prove the following stronger result: there exist at most $M(\Gamma ')^{2nr/p}$ classes defined by the loops $\Gamma '_{{\mathbf {e}}}$ that are equivalent as transverse paths and such that $z_\mathbf{e}\in W$. Suppose that $z_\mathbf{e}$ and $z_\mathbf{e'}$ belong to W and that the paths $\beta _l$, $0\leqslant l\leqslant l^*$, constructed with $z_\mathbf{e}$ and $z_\mathbf{e'}$ are all homotopic. Fix a lift $V_{\widetilde{z}_0}$ of $V_{z_0}$ and note $\widetilde{z}_\mathbf{e}$ and $\widetilde{z}_\mathbf{e'}$ the respective lifts of $z_\mathbf{e}$ and $z_\mathbf{e'}$ that belongs to $V_{\widetilde{z}_0}$. The whole $\widetilde{\mathcal {F}}$-transverse trajectories of $\widetilde{z}_\mathbf{e}$ and $\widetilde{z}_\mathbf{e'}$ are invariant by the same non trivial covering automorphism T, which is naturally defined by the lift $\prod _{0\leqslant l\leqslant l^*} {\widetilde{\beta }}_l$ of $\prod _{0\leqslant l\leqslant l^*} \beta _l$. Moreover, ${\widetilde{\beta }}_0$ is $\widetilde{\mathcal {F}}$-equivalent to a subpath of ${\widetilde{I}}_{\widetilde{\mathcal {F}}}(\widetilde{z}_\mathbf{e})$ and to a subpath of ${\widetilde{I}}_{\widetilde{\mathcal {F}}}(\widetilde{z}_\mathbf{e'})$. So these two lines meet a common leaf ${\widetilde{\phi }}$. One deduces that they meet $T^k({\widetilde{\phi }})$, for every $k\in \mathbb {Z}$ and consequently that they meet the same leaves. So there are equivalent.

The case where $0\in J_{\infty }$ can be reduced to the case where $0\in J_{<\infty }$ after a cyclic permutation on $\{0,\ldots , 4nr-1\}$ because the points $z_\mathbf{e}$ are all fixed by $f^{4nr}$. $\square$

As a direct application of Proposition 38 we can obtain the following result, which is connected to the study of the minimal entropy of pure braids in $\mathbb {S}^2$. There are sharper results with a larger lower bound for the entropy (see [38]), but they use very different techniques.

Theorem 41

Let f be an orientation preserving homeomorphism on $\mathbb {S}^2$ and I a maximal hereditary singular isotopy. Assume that there exists $z\in {\mathrm {dom}}(I)\cap {\mathrm {fix}}(f)$ such that the loop naturally defined by the trajectory I(z) is not homotopic in ${\mathrm {dom}}(I)$ to a multiple of a simple loop. Then the entropy of f is at least equal to $\log (2)/(4)$.

Proof

Let $\mathcal {F}$ be a foliation transverse to the isotopy. By hypothesis, the transverse loop $\Gamma$ associated to z is not a multiple of a simple loop, so by Proposition 2, it has an $\mathcal {F}$-transverse self-intersection. If $\gamma$ is the natural lift of $\Gamma$, then for all integers $K, \,\gamma \vert _{[0, K]}$ is admissible of order K. Furthermore, by Proposition 7, $\gamma \vert _{[0,2]}$ has an $\mathcal {F}$-transverse self-intersection. The theorem then follows directly from Proposition 38. $\square$

5.3 Associated subshifts

Let us give a natural application of Corollaries 21, 22 and the results of this section. We keep the assumptions and notations given at the beginning of the section. Consider a transverse path $\gamma :[a,b]\rightarrow {\mathrm {dom}}(\mathcal {F})$ with finitely many double points, none of them corresponding to an end of the path and no triple points (by a slight modification of the argument given in the proof of Corollary 24 one can show that every transverse path is equivalent to such a path). There exists real numbers $a<t_1<\cdots<t_{2r}<b$ and a fixed point free involution $\sigma$ on $\{1,\ldots , 2r\}$ such that $\gamma (t_i)=\gamma (t_{\sigma (i)})$, for every $i\in \{1,\ldots , 2r\}$ and such that $\gamma$ is injective on the complement of $\{t_1,\ldots , t_{2r}\}$. Set $t_0=a$ and $t_{2r+1}=b$ and define for every $i\in \{0,\ldots , 2r\}$ the path $\gamma _i=\gamma \vert _{[t_i,t_{i+1}]}$. Consider the incidence matrix $P\in M_{2r+1}(\mathbb {Z})$ (indexed by $\{0,\ldots , 2r\}$) such that $P_{i,j}=1$ if $j=i+1$ or $j=\sigma (i+1)$ and 0 otherwise (in particular if $i=2r$). Note that the first column and the last row only contain 0. For every P-admissible word $(i_s)_{1\leqslant s\leqslant s_0}$, which means that $P_{i_s,i_{s+1}}=1$ if $s<s_0$, the path $\prod _{1\leqslant s\leqslant s_0}\gamma _{i_s}$ is transverse to $\mathcal {F}$. Note that every transverse path $\gamma :[a',b']\rightarrow {\mathrm {dom}}(\mathcal {F})$ whose image is contained in the image of $\gamma$ is a subpath of such a path $\prod _{1\leqslant s\leqslant s_0}\gamma _{i_s}$.

Suppose now that $\gamma$ is admissible of order n. Can we decide when a path $\prod _{1\leqslant s\leqslant s_0}\gamma _{i_s}$ is admissible and what is its order? More precisely, do there exist other incidence matrices $P'$ smaller than P (which means that $P'_{i,j}=0$ if $P_{i,j}=0$) such that $\prod _{1\leqslant s\leqslant s_0}\gamma _{i_s}$ is admissible if $(i_s)_{1\leqslant s\leqslant s_0}$ is $P'$-admissible?

Corollaries 21 and 22 imply that the following three matrices satisfy this property:

• the matrix $P^{{\mathrm {strong}}}$, where $P^{{\mathrm {strong}}}_{i,j}=1$ if and only if $j=i+1$, or if $j=\sigma (i+1)$ and $\gamma _{i}\gamma _{i+1}$ and $\gamma _{j-1}\gamma _j$ have an $\mathcal {F}$-transverse intersection at $\gamma (t_{i+1})=\gamma (t_j)$;

• the matrix $P^{{\mathrm {left}}}$, where $P^{{\mathrm {left}}}_{i,j}=1$ if and only if $j=i+1$, or if $j=\sigma (i+1)$ and $\gamma$ has an $\mathcal {F}$-transverse positive self-intersection at $\gamma (t_{i+1})=\gamma (t_j)$;

• the matrix $P^{{\mathrm {right}}}$, where $P^{{\mathrm {right}}}_{i,j}=1$ if and only if $j=i+1$, or if $j=\sigma (i+1)$ and $\gamma$ has an $\mathcal {F}$-transverse negative self-intersection at $\gamma (t_{i+1})=\gamma (t_j)$.

More precisely, if $P'$ is one of the three previous matrices, then for every $P'$-admissible word $(i_s)_{1\leqslant s\leqslant s_0}$, the path $\prod _{1\leqslant s\leqslant s_0}\gamma _{i_s}$ is admissible of order kn, where k is the number of $s<s_0$ such that $i_{s+1}=\sigma (i_s+1)$. As explained in Proposition 23, its order can be less. One can adapt the proof of Theorem 36 to give a lower bound to the topological entropy of $f_{{\mathrm {alex}}}$. For example it is at least equal to 1 / n times the logarithm of the spectral radius of $P'$ if the paths $\gamma _{i}$ have a leaf on their right and a leaf on their left, otherwise one has to replace these paths by finite admissible words. One can adapt the proof of Theorem 29 to show that for every $P'$-admissible word $(i_s)_{1\leqslant s\leqslant s_0}$ such that $i_1=i_{s_0}$, the loop naturally defined by $\prod _{1\leqslant s<s_0}\gamma _{i_s}$ is associated to a periodic orbit (except for some exceptional cases).

Let us illustrate this procedure with four examples, where we start with an admissible path of order 1:

For the first example, see Fig. 17, the admissibility matrices are

$$\begin{aligned} P^{{\mathrm {strong}}}_1= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) ,\\ P^{{\mathrm {left}}}_1= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \, P^{{\mathrm {right}}}_1 = \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$

The matrix $P^{{\mathrm {strong}}}_1$ does not tell us anything, the only admissible paths are subpaths of $\gamma =\gamma _0\ldots \gamma _4$. The only interesting informations got from $P^{{\mathrm {left}}}_1$ and $P^{{\mathrm {right}}}_1$ respectively are the facts that the loops naturally defined by $\gamma _2\gamma _3$ and $\gamma _1\gamma _2$ are linearly admissible of order 2. Nevertheless the first loop has no leaf on its left while the second one has no leaf on its right. So, one cannot apply Proposition 26 and deduce that the loops are equivalent to transverse loops associated to periodic points of period 2. Note also that the spectral radius of $P^{{\mathrm {left}}}_1$ and $P^{{\mathrm {right}}}_1$ are equal to 1. In this example, one cannot deduce neither the positivity of entropy, nor the existence of periodic orbits.

Fig. 17

Example 1: Leafs of the foliation are represented as dashed lines, while transverse paths are solid

For the second example, see Fig. 18, the admissibility matrices are

$$\begin{aligned} P^{{\mathrm {strong}}}_2= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) ,\\ P^{{\mathrm {left}}}_2= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0&{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \, P^{{\mathrm {right}}}_2 = \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$

The matrix $P^{{\mathrm {strong}}}_2$ does not tell us anything. The matrix $P^{{\mathrm {right}}}_2$ is nilpotent and the only admissible paths are $\gamma _0\gamma _4,\, \gamma _0\gamma _1\gamma _3\gamma _4$ and $\gamma$, all of them admissible of order 1 by Proposition 23. The matrix $P^{{\mathrm {left}}}_2$ is much more interesting: its spectral radius, the real root of the polynomial $X^3-X^2-1$, is larger than 1. The loop naturally defined by $\gamma _2$ is linearly admissible of order 1 but has no leaf on its left: one cannot deduce that it is equivalent to a transverse loop associated to a fixed point. If $p\geqslant 1$, the loop naturally defined by $\gamma _1\gamma _2^p\gamma _3$ is linearly admissible of order p and has leaf on its right and a leaf on its left. More precisely, it has a transverse self-intersection, so one can apply Proposition 26 and deduce that it is equivalent to a transverse loop associated to a periodic point of period p. In particular, the loop defined by $\gamma _1\gamma _2\gamma _3$ is equivalent to a transverse loop associated to a fixed point: one can apply Theorem 41 and deduce that the entropy of f is at least $\log 2/4$.

Fig. 18

Example 2: Leafs of the foliation are represented as dashed lines, while transverse paths are solid

In third example, see Fig. 19, the trajectory is the same as in the first example but the foliation is different. The admissibility matrices are

$$\begin{aligned} P^{{\mathrm {strong}}}_3= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) ,\\ P^{{\mathrm {left}}}_3= & {} \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \, P^{{\mathrm {right}}}_3 = \left( \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$

The matrices $P^{{\mathrm {right}}}_3$ and $P^{{\mathrm {left}}}_3$ are the same as in the first example. Nevertheless, one can say more. Indeed the loops defined by $\gamma _2\gamma _3$ and $\gamma _1\gamma _2$, which are linearly admissible of order 2, now have a leaf on their left and a leaf on their right. They intersect $\mathcal {F}$-transversally and negatively the paths $\gamma _0\gamma _1$ and $\gamma _3\gamma _4$ respectively but they do not interest $\mathcal {F}$-transversally and positively a path drawn on $\gamma$. So, one cannot apply the second item of Proposition 26. However, by the first item of the same proposition, if they are not equivalent to transverse loops associated to periodic points of period 2, they are homotopic in the domain to a simple loop that does not meet its image by f. In particular, if $\Omega (f)=\mathbb {S}^2$, they must be equivalent to transverse loops associated to periodic points of period 2. The matrix $P^{{\mathrm {strong}}}_3$ is much more interesting: its spectral radius is equal to $\sqrt{2}$. Every path defined by a word of length n in the alphabet $\{\gamma _1\gamma _2, \gamma _3\gamma _2\}$ is admissible of order 2n and intersect $\gamma$ transversally. The proofs of Theorems 36 and 29 tell us that the topological entropy of f is at least equal to $\log 2/2$, and that the number of fixed point of $f^{2n}$ in the domain is at least equal to $e^n$ if $\Omega (f)=\mathbb {S}^2$.

Fig. 19

Example 3: Leafs of the foliation are represented as dashed lines, while transverse paths are solid

Fig. 20

Example 4: Leafs of the foliation are represented as dashed lines, while transverse paths are solid

In the fourth example, see Fig. 20, the foliation is the same as in the first example but the trajectory is different. In particular, there are three points of self-intersection of $\gamma$, and all are $\mathcal {F}$-transverse. The admissibility matrices are:

$$\begin{aligned} P^{{\mathrm {strong}}}_1= & {} \left( \begin{array}{ccccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) ,\\ P^{{\mathrm {left}}}_1= & {} \left( \begin{array}{ccccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) , \\ P^{{\mathrm {right}}}_1= & {} \left( \begin{array}{ccccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right) . \end{aligned}$$

By inspection of $P^{{\mathrm {left}}}_1$ one assures the existence of a single admissible loop $\gamma _4\gamma _5$, while inspection of $P^{{\mathrm {right}}}_1$ we see that both loops $\gamma _2$ and $\gamma _2\gamma _3\gamma _4\gamma _1$ are admissible and that the entropy of f must be positive.

6 First applications

In this section we give two applications for homeomorphisms of compact oriented surfaces. The first one is a new proof of Handel’s result on transitive homeomorphisms of the sphere. The second application provides sufficient conditions for the existence of non-contractible periodic orbits, and has as a consequence a positive answer to a problem posed by Boyland for the annulus.

6.1 Transitive maps of surfaces of genus 0

In [19], Handel prove that a transitive orientation preserving homeomorphism f of $\mathbb {S}^2$ with at least three fixed points, but finitely many, has infinitely many periodic orbits: more precisely the number of periodic points of period n for some iterate of f grows exponentially in n. We will improve this result as follows, with Theorem K of the introduction:

Theorem 42

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that the complement of the fixed point set is not an annulus. If f is topologically transitive then the number of periodic points of period n for some iterate of f grows exponentially in n. Moreover, the entropy of f is positive.

Proof

Recall that, in our case, the transitivity implies the existence of a point z whose $\omega$-limit and $\alpha$-limit sets are the whole sphere. One knows that every connected component of $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$ is invariant(see Brown and Kister [8]). Since f has a dense orbit, this complement must be connected. Moreover it cannot be a disk because f has a dense orbit. Indeed the Brouwer Plane Translation Theorem implies that every fixed point free orientation preserving homeomorphism of the plane has only wandering points. One deduces that the fixed point set has at least three connected components. Choose three fixed points in different connected components and an isotopy $I'$ from identity to f that fixes these three fixed points (this is always possible). The restriction of $I'$ to the complement of these three points is a hereditary singular isotopy. Using Theorem 14 one can find a maximal hereditary singular isotopy I larger than $I'$. Let $\mathcal {F}$ be a foliation transverse to this isotopy. It has the same domain as I, and this domain is not an annulus because I is larger than $I'$. The fact that $\omega (z)= \alpha (z)=\mathbb {S}^2$ implies that $I_{\mathcal {F}}^{\mathbb {Z}} (z)$ is an admissible $\mathcal {F}$-bi-recurrent transverse path that contains as a subpath (up to equivalence) every admissible segment and consequently that crosses all leaves of $\mathcal {F}$. Since ${\mathrm {dom}}(I)$ is not a topological annulus, this implies that $I_{\mathcal {F}}^{\mathbb {Z}} (z)$ has an $\mathcal {F}$-transverse self-intersection by Proposition 2. The result follows from Theorems 29 and 36. $\square$

6.2 Existence of non-contractible periodic orbits

Let f be a homeomorphism isotopic to identity on an oriented connected surface M and $I'$ an identity isotopy of f. A periodic point $z\in M$ of period q is said to have a contractible orbit if $I'^q(z)$ naturally defines a homotopically trivial loop, otherwise it is said to be non-contractible. In this subsection we examine some conditions that ensure the existence of non-contractible periodic orbits of arbitrarily high period. Through this subsection we assume that $\check{M}$ is the universal covering space of M and write $\check{\pi }: \check{M}\rightarrow M$ for the covering projection. Write $\check{I}'$ for the lifted identity isotopy and $\check{f}$ for the associated lift of f. One can find a maximal hereditary singular isotopy I larger than $I'$. It can be lifted to an identity isotopy $\check{I}$ on $\check{{\mathrm {dom}}}(I)=\check{\pi }^{-1}({\mathrm {dom}}(I))$. This isotopy is a maximal singular isotopy of $\check{f}$ larger than $\check{I}'$. Let $\mathcal {F}$ be a foliation transverse to I, its lift to $\check{{\mathrm {dom}}}(I)$, denoted by $\check{\mathcal {F}}$ is transverse to $\check{I}$.

The main technical result is the following proposition:

Proposition 43

Suppose that there exist an admissible $\check{\mathcal {F}}$-bi-recurrent path $\check{\gamma }$ for $\check{f}$, a leaf $\check{\phi }$ of $\check{\mathcal {F}}$ and three distinct covering automorphisms $T_i$, $1\leqslant i\leqslant 3$, such that $\check{\gamma }$ crosses each $T_i(\check{\phi })$. Then there exists $q>0$ and a non trivial covering automorphism $T=T_i\circ T_j^{-1}$ such that for all $r/s\in (0,1/q]$, the maps $\check{f}^{s}\circ T^{-r}$ and $\check{f}^{s}\circ T^{r}$ have fixed points. In particular, f has non-contractible periodic points of arbitrarily large prime period.

Proof

By assumptions, there are non trivial covering automorphisms. So M is not simply connected and $\check{M}$ is a topological plane. For every loop $\check{\Gamma }$ in $\check{M}$, we will denote $\delta _{\check{\Gamma }}$ the dual function that vanishes on the unbounded connected component of $\check{M}\setminus \check{\Gamma }$. It is usually called the winding number of $\check{\Gamma }$. $\square$

Sub-lemma 44

If $\check{\Gamma }$ is a loop positively transverse to $\check{\mathcal {F}}$, the set of singular points $\check{z}$ of $\check{\mathcal {F}}$ such that $\delta _{\check{\Gamma }}(\check{z})\not =0$ is a non empty compact subset $\Sigma _{\check{\Gamma }}$ of $\check{M}$. Furthermore $\Sigma _{\check{\Gamma }}=\Sigma _{\check{\Gamma }'}$ if $\check{\Gamma }$ and $\check{\Gamma }'$ are equivalent transverse loops.

Proof

The fact that $\Sigma _{\check{\Gamma }}=\Sigma _{\check{\Gamma }'}$ if $\check{\Gamma }$ and $\check{\Gamma }'$ are equivalent transverse loops is obvious as is the fact that $\Sigma _{\check{\Gamma }}$ compact. To prove that this set is not empty, let us consider a leaf $\check{\phi }$ that meets $\check{\Gamma }$. As recalled in the first section, at least one the two following assertions is true:

• the set $\alpha (\check{\phi })$ is a non empty compact set and $\delta _{\check{\Gamma }}$ takes a constant positive value on it;

• the set $\omega (\check{\phi })$ is a non empty compact set and $\delta _{\check{\Gamma }}$ takes a constant negative value on it.

Suppose for instance that we are in the first situation. If $\alpha (\check{\phi })$ contains a singular point, we are done. If not, it is a closed leaf disjoint from $\check{\Gamma }$. More precisely, $\alpha (\check{\phi })$ is contained in a bounded connected component of $\check{M}\setminus \check{\Gamma }$ where $\delta _{\check{\Gamma }}$ takes a constant positive value. This component contains the bounded component of the complement of $\alpha (\check{\phi })$ and so contains a singular point. $\square$

Let us prove first that there exists an admissible loop $\check{\Gamma }$ that crosses each $T_i(\check{\phi })$. Suppose first that $\check{\gamma }$ has a $\check{\mathcal {F}}$-transverse self-intersection and choose $a_1, b_1, t_1, a_2, b_2, t_2$ be such that $\check{\gamma }_1\vert _{[a_1,b_1]}$ intersects $\check{\mathcal {F}}$-transversally $\check{\gamma }_2\vert _{[a_2, b_2]}$ at $\check{\gamma }_1(t_1)=\check{\gamma }_2(t_2)$ and such that $\check{\gamma }_1\vert _{[a_1,b_1]}$ crosses each $T_i(\check{\phi })$. The construction done in the proof of Lemma 30 gives us such a loop $\check{\Gamma }$. Suppose now that $\check{\gamma }$ has no $\check{\mathcal {F}}$-transverse self-intersection. By Proposition 2, one knows that $\check{\gamma }$ is equivalent to the natural lift of a simple loop $\check{\Gamma }$ and this loop satisfies the desired property.

Let us prove now that one can find at least two distinct loops among the $T_i^{-1}(\check{\Gamma })$ that have a $\check{\mathcal {F}}$-transverse intersection. If not, by Proposition 1, one can find for every $i\in \{1,2,3\}$ a transverse loop $\check{\Gamma }'_i$ equivalent to $T_i^{-1}(\check{\Gamma })$ such that the $\check{\Gamma }'_i$ are pairwise disjoint. The three functions $\delta _{\check{\Gamma }'_i}$ are decreasing on the leaf $\check{\phi }$. For each i, either $\delta _{\check{\Gamma }'_i}$ is not null in $\alpha (\check{\phi })$ or $\delta _{\check{\Gamma }'_i}$ is not null in $\omega (\check{\phi })$, and therefore either there exists two different indices i and j such that for all points in $\alpha (\check{\phi }),\, \delta _{\check{\Gamma }'_i}\not =0$ and $\delta _{\check{\Gamma }'_j}\not =0$, or there exists two different indices i and j such that for all points in $\omega (\check{\phi }),\, \delta _{\check{\Gamma }'_i}\not =0$ and $\delta _{\check{\Gamma }'_j}\not =0$. In any case, there exists a point $\check{z}\in \check{\phi }$ and two different indices i and j such that $\delta _{\check{\Gamma }'_i}(\check{z})\not =0$ and $\delta _{\check{\Gamma }'_j}(\check{z})\not =0$. The fact that there exists a point where the two dual functions do not vanish tells us that one of the loops, let us say $\check{\Gamma }'_i$, is included in a bounded connected component of the complement of the other one $\check{\Gamma }'_j$, and that $\check{\Gamma }'_j$ is included in the unbounded connected component of the complement of $\check{\Gamma }'_i$. One deduces that $\Sigma _{\check{\Gamma }'_i}\subset \Sigma _{\check{\Gamma }'_j}$. Setting $T=T_j\circ (T_{i})^{-1}$, one gets the inclusion $T(\Sigma _{\check{\Gamma }})\subset \Sigma _{\check{\Gamma }}$, where $\Sigma _{\check{\Gamma }}$ is a non empty compact set. We have found a contradiction because T is a non trivial covering automorphism.

We have proved that there exist $i\not =j$ such that $T_i^{-1}(\check{\Gamma })$ and $T_j^{-1}(\check{\Gamma })$ intersect $\check{\mathcal {F}}$-transversally. This implies that $\check{\Gamma }$ and $T(\check{\Gamma })$ intersect $\check{\mathcal {F}}$-transversally, where $T=T_j\circ (T_{i})^{-1}$. Write $\check{\gamma }$ for the natural lift of $\check{\Gamma }$ and choose an integer L sufficiently large, so that $\check{\gamma }\vert _{[0, L]}$ has a $\check{\mathcal {F}}$-transverse intersection with $T(\check{\gamma })\vert _{[0,L]}$ at $\check{\gamma }(t)=T(\check{\gamma })(s)$, with $s<t$. The loop $\check{\Gamma }$ being admissible, there exists $q>0$ such that $\check{\gamma }\vert _{[-L,2L]}$ is admissible of order q. It follows from Corollary 22 and Proposition 19 that, for any $n>1$, the paths

$$\begin{aligned} \prod _{i=0}^{n-1}T^{i}\left( \check{\gamma }\vert _{[s-L,t+L]}\right) , \, \prod _{i=0}^{n-1}T^{-i}\left( \check{\gamma }\vert _{[t-L,s+l]}\right) \end{aligned}$$

are admissible of order nq, and both have $\check{\mathcal {F}}$-transverse self-intersections. Therefore the paths $\check{\gamma }\vert _{[s-L,t+L]}$ and $\check{\gamma }\vert _{[t-L,s+l]}$ project onto closed paths of M and the two loops naturally defined have $\mathcal {F}$-transverse self-intersection and are linearly admissible. So, one can deduce Proposition 43 from Proposition 26. $\square$

Let us state a first application of Proposition 43. In [39] conditions are given for a homeomorphism f, isotopic to the identity, of a compact surface M to have only contractible periodic points. There it is shown, using Nielsen–Thurston theory, that for such f, under a suitable condition on the size of its fixed point set, there exists an uniform bound on the diameter of the orbits of periodic points. The next theorem improves the main result of that note, by extending the uniform bound on the diameter of orbits from $\check{f}$ periodic points to $\check{f}$ recurrent points. Note that the hypothesis that the fixed point set of $\check{f}$ project in a disk cannot be removed. There exists an example of a $\mathcal {C}^{\infty }$ diffeomorphism f of $\mathbb {T}^2$ preserving the Lebesgue measure and ergodic such that every periodic orbit of f is contractible, and such that almost all points in the lift have orbits unbounded in every direction (see [25]). The following is Theorem H of the introduction:

Theorem 45

We suppose that M is compact and furnished with a Riemannian structure. We endow the universal covering space $\check{M}$ with the lifted structure and denote by d the induced distance. Let f be a homeomorphism of M isotopic to the identity and $\check{f}$ a lift to $\check{M}$ naturally defined by the isotopy. Assume that there exists an open topological disk $U\subset M$ such that the fixed point set of $\check{f}$ projects into U. Then;

• either there exists $K>0$ such that $d(\check{f}^n(\check{z}), \check{z})\leqslant K$, for all $n\geqslant 0$ and all bi-recurrent point $\check{z}$ of $\check{f}$;

• or there exists a nontrivial covering automorphism T and $q>0$ such that, for all $r/s\in (-1/q,1/q)$, the map $\check{f}^{s}\circ T^{-r}$ has a fixed point. In particular, f has non-contractible periodic points of arbitrarily large prime period.

Proof

Let I be a maximal hereditary singular isotopy larger than the given isotopy and $\mathcal {F}$ a foliation transverse to I. Denote $\check{M}$ the universal covering space of M and $\check{\pi }: \check{M}\rightarrow M$ the covering projection. Write $\check{I}'$ for the lifted identity isotopy on $\check{{\mathrm {dom}}}(I)=\check{\pi }^{-1}({\mathrm {dom}}(I))$ and $\check{\mathcal {F}}$ for the lifted foliation. The theorem follows directly from the next lemma and Proposition 43. $\square$

Lemma 46

There exists $K>0$ such that, for all $\check{z}$ in $\check{M}$ and all $n\geqslant 0$, if $d(\check{f}^n(\check{z}),\check{z})\geqslant K$, then there exists a leaf $\check{\phi }$ and three distinct covering automorphisms $T_i$, $1\leqslant i\leqslant 3$, such that $I_{\check{\mathcal {F}}}^n(\check{z})$ crosses each $T_i(\check{\phi })$.

Proof

One can find a neighborhood $V\subset U$ of ${\mathrm {sing}}(I)$ such that for every point $\check{z}\in \pi ^{-1}(V)$, the points $\check{z}$ and $\check{f}(\check{z})$ belong to the same connected component of $\pi ^{-1}(U)$. For reasons explained in the proof of Lemma 18, one knows that for every $z\in M\setminus V$, there exists a small open disk $O_z\subset {\mathrm {dom}}(\mathcal {F})$ containing z such that $I_{\mathcal {F}}^2(f^{-1}(z'))$ crosses $\phi _{z}$ if $z'\in O_z$. By compactness of $M\setminus V$, one can cover this set by a finite family $(O_{z_i})_{1\leqslant i\leqslant r}$. One constructs easily a partition $(X_{z_i})_{1\leqslant i\leqslant r}$ of $M\setminus V$ such that $X_{z_i}\subset O_{z_i}$. We have a unique partition $(\check{X}_{\alpha })_{\alpha \in \mathcal {A}}$ of $\check{M}$ such that, either $\check{X}_{\alpha }$ is contained in a connected component of $\pi ^{-1}(U)$ and projects onto V, or there exists $i\in \{1,\ldots ,r\}$ such that $\check{X}_{\alpha }$ is contained in a connected component of $\pi ^{-1}(O_{z_i})$ and projects onto $X_{z_i}$. Write $\alpha (\check{z})=\alpha$ if $\check{z}\in \check{X}_{\alpha }$. Let us define

$$\begin{aligned} K_0=\max _{\check{z}\in \check{M}} d( \check{f}( \check{z}), \check{z})),\, K_1=\max _{\alpha \in \mathcal {A}}{\mathrm {diam}}(\check{X}_{\alpha }) . \end{aligned}$$

Fix $\check{z}\in \check{M}$, $n\geqslant 1$ and define a sequence $n_0<n_1<\cdots <n_s$ in the following inductive way:

$$\begin{aligned} n_0= & {} 0, \, n_{j+1}= 1+ \sup \{k\in \{n_j, \ldots , n-1\}\,\vert \,\alpha (\check{f}^k(\check{z}))=\alpha (\check{f}^{n_j}(\check{z}))\}, \,\\ n_s= & {} n. \end{aligned}$$

Note that $d(\check{f}^{n_j}(\check{z}),\check{f}^{n_{j+1}}(\check{z})) \leqslant K_0+K_1$, if $j<s$. Note also that, if $\check{X}_{\alpha (\check{f}^{n_j}(\check{z}))}$ projects on V, then $f^{n_{j+1}-1}(z)$ also belongs to V and by the choice of V both $\check{f}^{n_{j+1}-1}(\check{z})$ and $\check{f}^{n_{j+1}}(\check{z})$ belong to the same connected component of $\pi ^{-1}(U)$. As $\alpha (\check{f}^{n_j}(\check{z}))\not =\alpha (\check{f}^{n_{j+1}}(\check{z}))$, one gets that $\check{X}_{\alpha (\check{f}^{n_j+1}(\check{z}))}$ do not project on V. Fix $K>(6r+1)(K_0+K_1 )$. If $d(\check{f}^n(\check{z}),\check{z})\geqslant K$, then $s\geqslant 6r+1$ and there exist at least 3r sets $\check{X}_{\alpha (\check{f}^{n_j}(\check{z}))}$, $0<j<s$, that do not project on V. This implies that there exist three points $f^{n_{j_l}}(\pi (z))$ that belong to the same $X_{z_i}$, and therefore one finds that there exist a point $\check{z}_i\in \pi ^{-1}(z_i)$ and two distinct nontrivial covering automorphisms $T_1, T_2$ such that the orbit of $\check{z}$ intersects the three distinct connected components of $\pi ^{-1}(O_{z_i})$ that contain $\check{z}_i,T_1(\check{z}_i)$ and $T_2(\check{z}_i)$, respectively. By the choice of $O_{z_i}$, this implies that $I_{\check{\mathcal {F}}}^n(\check{z})$ intersect $\phi _{\check{z}_i}, T_1(\phi _{\check{z}_i})$ and $T_2(\phi _{\check{z}_i})$. $\square$

Proposition 43 is also fundamental in solving the following conjecture posed by Boyland (see, for instance, [3] where the conjecture is shown to be true generically for sufficiently smooth diffeomorphisms): Let f be a homeomorphism of the closed annulus preserving a probability measure $\mu$ with full support, and let $\check{f}$ be a lift of f to the universal covering space of the annulus. If the rotation set of f is a non trivial segment and the rotation number of $\mu$ is null, is it true that ${\mathrm {rot}}(\mu )$ belongs to the interior of the rotation set?

We recall first Atkinson’s Lemma on ergodic theory, that will be very useful in this paper (see [1]).

Proposition 47

Let $(X,\mathcal {B},\mu )$ be a probability space, and let $T:X\rightarrow X$ be an ergodic automorphism. If $\varphi : X\rightarrow \mathbb {R}$ is an integrable map such that $\int \varphi \, d\mu =0$, then for every $B\in \mathcal {B}$ and every $\varepsilon >0$, one has

$$\begin{aligned} \mu \left( \left\{ x\in B, \exists n\geqslant 0, \, T^n(x)\in B\, and \,\left| \sum _{k=0}^{n-1}\varphi (T^k(x))\right| < \varepsilon \right\} \right) = \mu (B). \end{aligned}$$

We have the following, Theorem A of the introduction:

Theorem 48

Let f be a homeomorphism of $\mathbb {A}=\mathbb {T}^1\times [0,1]$ that is isotopic to the identity and $\check{f}$ a lift to $\mathbb {R}\times [0,1]$. Suppose that ${\mathrm {rot}}(f)$ is a non trivial segment and that one of its endpoint $\rho$ is rational. Define

$$\begin{aligned} {\mathcal {M}}_{\rho }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, {\mathrm {rot}}(\mu )=\rho \right\} , \, {X}_{\rho }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\rho }} {\mathrm {supp}}(\mu )}. \end{aligned}$$

Then every invariant measure supported on ${X}_{\rho }$ belongs to ${\mathcal {M}}_{\rho }$.

Proof

Replacing f by a power $f^q$ and $\check{f}$ by a lift $\check{f}^q\circ T^p$, one can assume that $\rho =0$ and ${\mathrm {rot}}(f)=[0,a]$, where $a>0$. The fact that 0 is extremal implies that for every $\mu \in {\mathcal {M}}_{0}$, each ergodic measure $\mu '$ that appears in the ergodic decomposition of $\mu$ also belongs to ${\mathcal {M}}_{0}$. Atkinson’s Lemma, with $T=f$ and $\varphi$ the map lifted by $\check{\varphi }: z\mapsto \pi _1(\check{f}(\check{z})-\check{z})$, tells us that $\mu '$-almost every point of $\mathbb {A}$ is lifted to a recurrent point of $\check{f}$. The union of the supports of such ergodic measures being dense in ${\mathrm {supp}}(\mu )$, one deduces that the recurrent set of $\check{f}$ is dense in $\pi ^{-1}(X_0)$. Writing $f=(f_1,f_2)$, one can extend f to a homeomorphism of $\mathbb {T}^1\times \mathbb {R}$ such that $f(x,y)=(f_1(x,1), y)$ if $y\geqslant 1$ and $f(x,y)=(f_1(x,0), y)$ if $y\leqslant 0$ and still denote by $\check{f}$ the lift that extends the initial lift. Let $I'$ be an identity isotopy of f that is lifted to an identity isotopy $\check{I}'$ of $\check{f}$. Let I be a maximal hereditary singular isotopy larger than $I'$ and $\mathcal {F}$ a foliation transverse to I. Consider the lift $\check{I}$ of I and the lifted foliation $\check{\mathcal {F}}$. If there exists an invariant measure supported on ${X}_{0}$ whose rotation number is positive, there exists a recurrent point z of rotation number strictly larger than 0. Let us fix a lift $\check{z}$. As $\check{z}$ is not fixed by $\check{f}$, it belongs to the domain of $\check{I}$ and the path ${\mathcal {I}}_{\check{\mathcal {F}}}^{\mathbb {Z}}(\check{z})$ meets infinitely many translates of $\phi _{\check{z}}$. But $\check{z}$ can be approximated by a recurrent point $\check{z}'$ of $\check{f}$ because we have seen that the recurrent set of $\check{f}$ was dense in $\pi ^{-1}(X_0)$. So we can suppose that ${\mathcal {I}}_{\check{\mathcal {F}}}^{\mathbb {Z}}(\check{z}')$ meets at least three translates of $\phi _{\check{z}}$. The result now follows from Proposition 43. Indeed, one finds some power n of T such that for any pair of integers r, s with $s>0$ and such that $\left|{r/s}\right|$ is sufficiently small, there exists a fixed point $\check{z}_{r,s}$ of $\check{f}^{r}\circ T^{-ns}$. The points $\check{z}_{r,s}$ project to periodic points $z_{r,s}$ in $\mathbb {A}$ such that the rotation number of $z_{r,s}$ is r / ns. In particular both 1 / sn and $-1/sn$ belong to the rotation set of $\check{f}$ if s is sufficiently large, in contradiction with the fact that 0 is an end of ${\mathrm {rot}}(f)$. $\square$

We deduce immediately the positive answer to Boyland’s question, Corollary B of the introduction:

Corollary 49

Let f be a homeomorphism of $\mathbb {A}$ that is isotopic to the identity and preserves a probability measure $\mu$ with full support. Let us fix a lift $\check{f}$. Suppose that ${\mathrm {rot}}(f)$ is a non trivial segment. The rotation number ${\mathrm {rot}}(\mu )$ cannot be an endpoint of ${\mathrm {rot}}(f)$ if this endpoint is rational.

Proof

If ${\mathrm {rot}}(f)$ is an endpoint of ${\mathrm {rot}}(f)$ and this endpoint is a rational $\rho$, by Theorem 48 we get that, if $X_{\rho }= {\mathrm {supp}}(\mu )$ is the whole annulus $\mathbb {A}$, then every invariant measure supported on $\mathbb {A}$ has rotation vector $\rho$, which implies that ${\mathrm {rot}}(f)=\{\rho \}$. $\square$

7 Entropy zero conservative homeomorphisms of the sphere

We will prove in this section the improvement of Franks–Handel’s result about area preserving diffeomorphisms of $\mathbb {S}^2$ with entropy zero, stated in the introduction as Theorem M. Let us begin by introducing an important notion due to Franks and Handel: let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism, a point z is free disk recurrent if there exist an integer $n>1$ and a topological open disk D containing z and $f^n(z)$ such that $f(D)\cap D=\emptyset$. We will also need the notion of heteroclinic point, which means that its $\alpha$-limit and $\omega$-limit sets are included in connected subsets of ${\mathrm {fix}}(f)$.

Let us state first some easy but useful facts. By definition if f is a homeomorphism of a topological space X, a subset Y is free if $f(Y)\cap Y=\emptyset$.

Proposition 50

One has the following results:

i) :

the set of free disk recurrent points is an invariant open set ${\mathrm {fdrec}}(f)$;

ii) :

it contains every positively or negatively recurrent point outside ${\mathrm {fix}}(f)$;

iii) :

every point in $\mathbb {S}^2\setminus {\mathrm {fdrec}}(f)$ is heteroclinic;

iv) :

every periodic connected component of ${\mathrm {fdrec}}(f)$ is fixed.

Proof

If D is a free disk that contains z and $f^n(z)$, it contains $z'$ and $f^n(z')$ if $z'$ is close to z. Moreover $f^k(D)$ is a free disk that contains $f^k(z)$ and $f^{k+n}(z)$, for every $k\in \mathbb {Z}$. So i) is true.

For every $z\in \mathbb {S}^2\setminus {\mathrm {fix}}(f)$, one can choose a free disk D that contains z. If z is positively recurrent, there exists $n>1$ such that $f^n(z)\in D$. If z is negatively recurrent, there exist $n>1$ such that $f^{-n}(z)\in D$, which implies that $f^n(D)$ is a free disk that contains z and $f^n(z)$. In both cases, z belongs to ${\mathrm {fdrec}}(f)$, which means that ii) is true.

It is sufficient to prove iii) for the $\omega$-limit set, the proof for the $\alpha$-limit set being similar. Let us prove first that $\omega (z)\subset {\mathrm {fix}}(f)$ if $z\not \in {\mathrm {fdrec}}(f)$. Indeed, if $z'\in \omega (z)\setminus {\mathrm {fix}}(f)$, one can choose a free disk D containing $z'$ and two integers $n'>n$ such that $f^n(z)$ and $f^{n'}(z)$ belong to D. It implies that $f^{-n}(D)$ is a free disk that contains z and $f^{n'-n}(z)$. This contradicts the fact that $z\not \in {\mathrm {fdrec}}(f)$. To prove that $\omega (z)$ is included in a connected component of ${\mathrm {fix}}(f)$, it is sufficient to prove that it is contained in a connected component of O, for every neighborhood O of ${\mathrm {fix}}(f)$. If O is such a neighborhood,there exists a neighborhood $O'\subset O$ of ${\mathrm {fix}}(f)$ such that for every $z\in O'\cap f^{-1}(O')$, the points z and f(z) belong to the same connected component of O. There exists N such that $f^n(z)\in O'$ for every $n\geqslant N$. This implies that the $f^n(z)$, $n\geqslant N$, belong to the same connected component of O.

It remains to prove iv). If W is a connected component of ${\mathrm {fdrec}}(f)$ of period $q>1$, it is not a connected component of $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$ (see Brown and Kister [8]) and so one can find a path $\alpha$ in $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$ joining a point $z\in W$ to a point $z'\not \in W$. Taking a subpath if necessary, one can suppose that $\gamma$ is included in W but the endpoint $z'$ (which is in the frontier of W and not fixed). Let us choose a path $\beta$ in W joining z to $f^q(z)$. It is a classical fact that there exists a simple path $\gamma$ joining $z'$ to $f^q(z')$ whose image is included in the image of $\alpha ^{-1}\beta f^q(\alpha )$. The point $z'$ is not periodic because it is neither in ${\mathrm {fix}}(f)$ nor in ${\mathrm {fdrec}}(f)$ and so the points $z'$, $f(z')$, $f^{q}(z')$ and $f^{q+1}(z')$ are distinct (recall that $q>1$). More precisely, since $\gamma \subset W$ and W is free, the path $\gamma$ is free and so one can find a free disk that contains it, which contradicts the fact that $z'$ is not in ${\mathrm {fdrec}}(f)$. $\square$

Suppose now that the set of positively recurrent points is dense. It is equivalent to say that $\Omega (f)=\mathbb {S}^2$ and in that case the set of positively recurrent points is a dense $G_{\delta }$ set, as is the set of bi-recurrent points (these conditions are satisfied in the particular case of an area preserving homeomorphism). Note that, in this case, every connected component of ${\mathrm {fdrec}}(f)$ is periodic and so is fixed. Write $(W_{\alpha })_{\alpha \in \mathcal {A}_f}$ for the family of connected components of ${\mathrm {fdrec}}(f)$ and define $A_{\alpha }$ to be the interior in $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$ of the closure of $W_{\alpha }$. Note that

$$\begin{aligned} A_{\alpha }= \mathbb {S}^2\setminus \overline{\bigcup _{\alpha '\in \mathcal {A}_f\setminus \{\alpha \}} A_{\alpha '}}\cup {\mathrm {fix}}(f) \end{aligned}$$

because the recurrent points are dense in $\mathbb {S}^2$ and contained in ${\mathrm {fdrec}}(f)$ if not fixed.

We will prove the following result, which implies Theorem M of the introduction, and that extends Theorem 1.2 of [14].

Theorem 51

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that $\Omega (f)=\mathbb {S}^2$ and $h(f)=0$. Then one has the following results:

i) :

each $A_{\alpha }$ is an open annulus;

ii) :

the sets $A_{\alpha }$ are the maximal fixed point free invariant open annuli;

iii) :

every point that is not in a $A_{\alpha }$ is heteroclinic;

iii) :

let C be a connected component of the frontier of $A_{\alpha }$ in $\mathbb {S}^2\setminus {\mathrm {fix}}(f)$, then the connected components of ${\mathrm {fix}}(f)$ that contain $\alpha (z)$ and $\omega (z)$ are independent of $z\in C$.

We will begin by stating a local version of this result, which means a version relative to a given maximal hereditary singular isotopy I. We denote $\widetilde{I}$ the lifted identity isotopy to the universal covering space $\widetilde{\mathrm {dom}}(I)$ of ${\mathrm {dom}}(I)$ and $\widetilde{f}$ the induced lift of $f\vert _{ {\mathrm {dom}}(I)}$. Say that a point $z\in {\mathrm {dom}}(I)$ is free disk recurrent relative to I or I free disk recurrent if there exists an integer $n>0$ and a topological open disk $D\subset {\mathrm {dom}}(I)$ containing z and $f^n(z)$, such that each lift to $\widetilde{\mathrm {dom}}(I)$ is disjoint from its image by $\widetilde{f}$ (we will say that D is I-free). Let us state the local version of Proposition 50.

Proposition 52

One has the following results:

i) :

the set of I-free disk recurrent points is an invariant open set ${\mathrm {fdrec}}(I)$;

ii) :

it contains every positively or negatively recurrent point in ${\mathrm {dom}}(I)$;

iii) :

every point in $\mathbb {S}^2\setminus {\mathrm {fdrec}}(I)$ is heteroclinic and its $\alpha$-limit and $\omega$-limit sets are included in connected subsets of ${\mathrm {sing}}(I)$;

iv) :

every periodic connected component of ${\mathrm {fdrec}}(I)$ is fixed and lifted to fixed subsets of $\check{f}$.

Proof

Replacing free disks by I-free disks, one proves the three first assertions exactly like in the global situation. Similarly, one can prove that every periodic connected component of ${\mathrm {fdrec}}(I)$ is fixed. Writing $\pi :\widetilde{\mathrm {dom}}(I)\rightarrow {\mathrm {dom}}(I)$ for the universal covering projection, it remains to prove that the connected components of $\pi ^{-1}(W)$ are fixed by $\widetilde{f}$, if W is a fixed connected component of ${\mathrm {fdrec}}(I)$. If they are not fixed, they are not connected components of $\widetilde{\mathrm {dom}}(I)$, which means that W is not a connected component of $\mathrm {dom}(I)$. So one can find a simple path $\alpha$ joining a point $z\in W$ to a point $z'\in \partial W\cap \mathrm {dom}(I)$ and included in W but the endpoint $z'$, and then construct a simple path $\gamma$ joining $z'$ to $f^2(z')$ included in W but the two endpoints. It will lift to a $\widetilde{f}$-free simple path and so one can find a I-free disk that contains $\gamma$. This contradicts the fact that $z'$ is not in ${\mathrm {fdrec}}(I)$. $\square$

Suppose now that $\Omega (f)=\mathbb {S}^2$. Write $(W_{\beta })_{\beta \in \mathcal {B}_I}$ for the family of connected components of ${\mathrm {fdrec}}(I)$ and define $A_{\beta }$ to be the interior in ${\mathrm {dom}}(I)$ of the closure of $W_{\beta }$. One knows that the sets $W_{\beta }$, $A_{\beta }$ are fixed and lifted to fixed subsets of $\widetilde{f}$. Here again, one has

$$\begin{aligned} A_{\beta }={\mathrm {dom}}(I)\setminus \overline{\bigcup _{\beta '\in \mathcal {B}_I\setminus \{\beta \}} A_{\beta '}}. \end{aligned}$$

The local version of Theorem 51 is the following:

Theorem 53

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that $\Omega (f)=\mathbb {S}^2$ and $h(f)=0$, and I a hereditary singular maximal isotopy. Then one has the following results:

i) :

each $A_{\beta }$ is an open annulus;

ii) :

the sets $A_{\beta }$ are the maximal invariant open annuli contained in ${\mathrm {dom}}(I)$;

iii) :

every point that is not in a $A_{\beta }$ is heteroclinic and its $\alpha$-limit and $\omega$-limit sets are included in connected subsets of ${\mathrm {sing}}(I)$;

iv) :

let C be connected component of the frontier of $A_{\beta }$ in ${\mathrm {dom}}(I)$, then the connected components of ${\mathrm {sing}}(I)$ that contain $\alpha (z)$ and $\omega (z)$ are independent of $z\in C$.

Let us explain first why the local theorem implies the global one. If A is a topological annulus, an open set will be called essential if it contains an essential loop and inessential otherwise. A closed set will be called inessential if there exists a connected component of its complement that is a neighborhood of the two ends in the case where A is open, that meets the two boundary circle in the case where A is closed, and that is a neighborhood of the unique end and meets the boundary circle in the remaining case. Otherwise, we will say that this set is essential.

Proof of Theorem 51, first part, proof of assertions (i), (ii), and (iii)

Let us explain first why every fixed point free invariant open annulus A is contained in an $A_{\alpha }$, $\alpha \in \mathcal {A}_f$. It is sufficient to prove that ${\mathrm {fdrec}}(f)\cap A$ is connected. Indeed ${\mathrm {fdrec}}(f)\cap A$ will be contained in a $W_{\alpha }$, $\alpha \in \mathcal {A}_f$, and consequently A will be contained in $A_{\alpha }$. Let W be a connected component of ${\mathrm {fdrec}}(f)\cap A$. Applying Proposition 50 to the end compactification of A, one knows that W is fixed. If it is inessential, one gets an invariant open disk $D\subset A$ by filling W, which means adding the inessential components of its complement. By Brouwer’s plane translation Theorem, since the restriction of f to D has non wandering points, there must exist a fixed point in this disk, which is impossible. So, every connected component of ${\mathrm {fdrec}}(f)\cap A$ is essential. Suppose now that ${\mathrm {fdrec}}(f)\cap A$ has at least two connected components. The complement in A of the union of two such components has a unique compact connected component. It is located “between” these components. This last set is invariant (by uniqueness) and contains points that are not free disk recurrent. But one knows that the $\alpha$-limit and $\omega$-limit sets of such points contain fixed points and A is fixed point free. We have a contradiction.

Let us prove now that each $A_{\alpha }$, $\alpha \in {\mathcal {A}}_f$, is an annulus. It is sufficient to prove that it is contained in a fixed point free invariant annulus. Let us consider a sequence $(z_i)_{i\geqslant 0}$ dense in ${\mathrm {fix}}(f)$, sequence which will be finite if there are finitely many fixed points. Let us fix $A_{\alpha }$. Let $I_0$ be a maximal hereditary singular isotopy whose singular set contains $z_0$, $z_1$, $z_2$. The set $W_{\alpha }$ is connected and included in ${\mathrm {fdrec}}(I_0)$ so it is contained in a connected component $W_{\beta _0}$, $\beta _0\in \mathcal {B}_{I_0}$. One deduces that $A_{\alpha }\subset A_{\beta _0}$. If $A_{\beta _0}$ is fixed point free, we stop the process. If not, we consider the first $z_{k_1}$ that belongs to $A_{\beta _0}$ and consider a maximal hereditary singular isotopy $I_1$ of $f\vert _{A_{\beta _0}}$ whose singular set contains $z_{k_1}$. Similarly, there exists $\beta _1\in \mathcal {B}_{I_1}$ such that $A_{\alpha }\subset A_{\beta _1}$. If $A_{\beta _1}$ is fixed point free, we stop the process. If not, we consider the first $z_{k_2}$ that belongs to $A_{\beta _1}$ and we continue. If the process stops, the last annulus will be fixed point free. If the process does not stop, $A_{\alpha }$ is contained in the interior of $\bigcap _{i\geqslant 0} A_{\beta _i}$. The connected component W of the interior of $\bigcap _{i\geqslant 0} A_{\beta _i}$ that contains $A_{\alpha }$ is invariant. Moreover, it is fixed point free because it is open and because the sequence $(z_i)_{i\geqslant 0}$ is dense in ${\mathrm {fix}}(f)$ and away from W. Let us prove that for i large enough, $A_{\beta _{i+1}}$ is essential in $A_{\beta _{i}}$ and that W is an annulus. Let us suppose that $A_{\beta _{i+1}}$ is inessential in $A_{\beta _{i}}$ for infinitely many i. Consider a simple loop $\Gamma$ in W. It bounds a disk (uniquely determined) included in $A_{\beta _{i}}$, every time $A_{\beta _{i+1}}$ is inessential in $A_{\beta _{i}}$, which implies that it bounds a disk included in $\bigcap _{i\geqslant 0} A_{\beta _i}$, and so included in W. This means that W is a disk, which contradicts the fact it is fixed point free. Suppose now that $A_{\beta _{i+1}}$ is essential in $A_{\beta _{i}}$ for every $i\geqslant i_0$. By the same reasoning, if $\Gamma \subset W$ is a simple loop such that $\Gamma$ is inessential in the $A_{\beta _i}$, $i\geqslant i_0$, then $\Gamma$ bounds a disk in W. This implies that W is an open annulus, that is essential in the $A_{\beta _i}$, $i\geqslant i_0$.

The assertion iii) is obvious because every free disk recurrent point is contained in a $W_{\alpha }$ and so in an $A_{\alpha }$. We will postpone the proof of iv) to the end of this section because we need a little bit more than what is stated in the local theorem. $\square$

Before proving Theorem 53, we will state a result relative to a couple $(I, \mathcal {F})$, where $\mathcal {F}$ is a foliation transverse to I. By Theorem 36 and the density of the set of recurrent points, one knows that two transverse trajectories never intersect $\mathcal {F}$-transversally. In particular, there is no transverse trajectory with $\mathcal {F}$-transverse self-intersection and by Proposition 2 every whole transverse trajectory of an $\mathcal {F}$-bi-recurrent point is equivalent to the natural lift of a transverse simple loop $\Gamma$. We denote by ${\mathcal {G}}_{I,\mathcal {F}}$ the set of such loops (well defined up to equivalence) and ${\mathrm {rec}}(f)_{\Gamma }$ the set of bi-recurrent points whose whole transverse trajectory is equivalent to the natural lift of $\Gamma$. Consider a point $z\in {\mathrm {dom}}(I)$. For any given segment of $I_{\mathcal {F}}^{\mathbb {Z}}(z)$ there exists a neighborhood of z such that this segment is equivalent to a subpath of $I_{\mathcal {F}}^{\mathbb {Z}}(z')$ if $z'$ belongs to this neighborhood. Suppose now that this segment meets a leaf more than once. The transverse simple loop $\Gamma$ associate to $z'$ does not depend on $z'$, if $z'$ is chosen bi-recurrent (remind that the set of bi-recurrent points is dense). Summarizing, we have stated that any segment of $I_{\mathcal {F}}^{\mathbb {Z}}(z)$ is equivalent to a subpath of the natural lift of a transverse simple loop, but this loop is uniquely defined (up to equivalence) if this segment meets a leaf more than once. Consequently, if $I_{\mathcal {F}}^{\mathbb {Z}}(z)$ meets a leaf more than once, it is equivalent to a subpath of the natural lift of a uniquely defined transverse simple loop. One deduces that the set of points whose whole transverse trajectory meets a leaf more than once, admits a partition $\bigsqcup _{\Gamma \in \mathcal {G}_{I,\mathcal {F}}} W_{\Gamma }$ in disjoint invariant open sets, where $z\in W_{\Gamma }$ if $I_{\mathcal {F}}^{\mathbb {Z}}(z)$ meets a leaf at least twice and is a subpath of the natural lift of $\Gamma$. Define $A_{\Gamma }={\mathrm {int}}(\overline{W_{\Gamma }})$. Note that

$$\begin{aligned} A_{\Gamma }={\mathrm {int}}(\overline{{\mathrm {rec}}(f)_{\Gamma }})= {\mathrm {dom}}(I)\setminus \overline{\bigcup _{\Gamma '\in \mathcal {G}_{I,\mathcal {F}}\setminus \{\Gamma \}} A_{\Gamma '}}. \end{aligned}$$

Recall that $U_{\Gamma }$ is the union of leaves that meet $\Gamma$.

Proposition 54

One has the following results:

i) :

the set $A_{\Gamma }$ is an essential open annulus of $U_{\Gamma }$;

ii) :

every point in ${\mathrm {dom}}(I)\setminus \bigcup _{\Gamma \in \mathcal {G}_{I,F}} A_{\Gamma }$ is heteroclinic and its $\alpha$-limit and $\omega$-limit sets are included in connected subsets of ${\mathrm {sing}}(I)$;

iii) :

let C be a connected component of the frontier of $A_{\Gamma }$ in ${\mathrm {dom}}(I)$, then the connected components of ${\mathrm {sing}}(I)$ that contain $\alpha (z)$ and $\omega (z)$ are independent of $z \in C$.

7.1 Proof of Proposition 54

This subsection is devoted entirely to the proof of Proposition 54.

The assertion ii) is an immediate consequence of the following: if $z' \in {\mathrm {dom}}(I)$ belongs to the $\alpha$-limit or $\omega$-limit set of $z\in {\mathrm {dom}}(I)$, then the whole transverse trajectory of z meets infinitely often the leaf $\phi _{z'}$ and so z belongs to $\bigcup _{\Gamma \in \mathcal {G}_{I,\mathcal {F}}} W_{\Gamma }$.

Let us prove i). One can always suppose that ${\mathrm {dom}}(I)$ is connected, otherwise one must replace ${\mathrm {dom}}(I)$ by its connected component that contains $\Gamma$ in what follows. Fix a lift ${\widetilde{\gamma }}$ of $\Gamma$ in $\widetilde{{\mathrm {dom}}}(I)$, write T for the covering automorphism such that ${\widetilde{\gamma }}(t+1)=T({\widetilde{\gamma }}(t))$, write $\widehat{{\mathrm {dom}}}(I)=\widetilde{{\mathrm {dom}}}(I)/T$ for the annular covering space associated to $\Gamma$. Denote by ${\widehat{\pi }}: \widehat{{\mathrm {dom}}}(I)\rightarrow {\mathrm {dom}}(I)$ the covering projection, by ${\widehat{I}}$ the induced identity isotopy, by ${\widehat{f}}$ the induced lift of f, by $\widehat{\mathcal {F}}$ the induced foliation. The line ${\widetilde{\gamma }}$ projects onto the natural lift of a loop ${\widehat{\Gamma }}$. The union of leaves that meet ${\widehat{\Gamma }}$, denoted by $U_{{\widehat{\Gamma }}}$, is the annular component of ${\widehat{\pi }}^{-1}(U_{\Gamma })$. We note that there cannot be an essential simple closed curve ${\widehat{\Gamma }}'$ contained in $U_{{\widehat{\Gamma }}}$ whose image by ${\widehat{f}}$ is disjoint from itself, otherwise the region bounded by ${\widehat{\pi }}({\widehat{\Gamma }}')$ and ${\widehat{\pi }}({\widehat{f}}({\widehat{\Gamma }}'))$ would be wandering for any f. In particular, by the same reasoning as in Lemma 27, one gets that the $\alpha$ and $\omega$ limit of any given leaf of $\widehat{\mathcal {F}}$ that is contained in $U_{{\widehat{\Gamma }}}$ must be different ends of $\widehat{{\mathrm {dom}}}(I)$, and every leaf of $\widehat{\mathcal {F}}$ that does not intersect $U_{{\widehat{\Gamma }}}$ disconnects $\widehat{{\mathrm {dom}}}(I)$. One gets a sphere $\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}$ by adding the end N of $\widehat{{\mathrm {dom}}}(I)$ at the left of $\Gamma$ and the end S at the right. The complement of $U_{{\widehat{\Gamma }}}$ has two connected components $l({\widehat{\Gamma }})\cup \{N\}$ and $r({\widehat{\Gamma }})\cup \{S\}$. Note that ${\widehat{\Gamma }}$ is the unique simple loop (up to equivalence) that is transverse to $\widehat{\mathcal {F}}$. Like in ${\mathrm {dom}}(I)$, transverse trajectories do not intersect $\widehat{\mathcal {F}}$-transversally. The set of points that lift a bi-recurrent point of f is dense. If the trajectory of such a point z meets a leaf at least twice, then ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ is the natural lift of ${\widehat{\Gamma }}$. Denote ${\mathrm {rec}}(f)_{{\widehat{\Gamma }}}$ the set of such points. Otherwise ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ meets either $l({\widehat{\Gamma }})$ or $r({\widehat{\Gamma }})$, the two situations being excluded, because ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ does not intersect ${\widehat{\Gamma }}$ $\widehat{\mathcal {F}}$-transversally. Denote ${\mathrm {rec}}(f)_N$ and ${\mathrm {rec}}(f)_S$ the set of points z that lift a bi-recurrent point of f and such that ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ meets $l({\widehat{\Gamma }})$ and $r({\widehat{\Gamma }})$ respectively. Note that the intersection of the complete transverse trajectory of $z\in {\mathrm {rec}}(f)_N$ and $U_{{\widehat{\Gamma }}}$, when not empty is equivalent to ${\widehat{\Gamma }}\vert _J$ where J is an open interval of $\mathbb {T}^1$, and a similar statement holds if $z\in {\mathrm {rec}}(f)_S$. In particular there exists $n\geqslant 0$ such that ${\widehat{I}}^{\mathbb {N}}_{ \widehat{\mathcal {F}}}({\widehat{f}}^n(z))\subset l({\widehat{\Gamma }})$ and ${\widehat{I}}^{-\mathbb {N}}_{ \widehat{\mathcal {F}}}({\widehat{f}}^{-n}(z))\subset l({\widehat{\Gamma }})$. Write $W_{{\widehat{\Gamma }}}$ for the set of points such that ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ meets a leaf at least twice, write $W_N$ for the set of points $z\in \widehat{{\mathrm {dom}}}(I)$ such that ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ meets $l({\widehat{\Gamma }})$, write $W_S$ for the set of points such that ${\widehat{I}}^{\mathbb {Z}}_{ \widehat{\mathcal {F}}}(z)$ meets $r({\widehat{\Gamma }})$. We get three disjoint invariant open sets, that contain ${\mathrm {rec}}(f)_{{\widehat{\Gamma }}}$, ${\mathrm {rec}}(f)_N$, ${\mathrm {rec}}(f)_S$ respectively and whose union is dense. Note that the $\alpha$-limit and $\omega$-limit sets of a point $z\not \in W_{{\widehat{\Gamma }}}$ are reduced to one of the ends. These ends are both equal to N if $z\in {\mathrm {rec}}(f)_N$ and both equal to S if $z\in {\mathrm {rec}}(f)_S$. We will see later that they are both equal to N if $z\in \overline{W_N}$ and both equal to S if $z\in \overline{W_S}$. Note also that

$$\begin{aligned} W_N=\bigcup _{k\in \mathbb {Z}} f^{-k}\left( l(\Gamma )\right) , \, W_S=\bigcup _{k\in \mathbb {Z}} f^{-k}\left( r(\Gamma )\right) . \end{aligned}$$

Indeed, every leaf $\phi$ that is not in $U_{{\widehat{\Gamma }}}$ bounds a disk disjoint from $U_{{\widehat{\Gamma }}}$. So, if ${\widehat{I}}_{ \widehat{\mathcal {F}}}(z)$ meets $\phi$ and $\phi \subset l(\Gamma )$, then one of the point z or ${\widehat{f}}(z)$ is in $l(\Gamma )$, and if $\phi \subset r(\Gamma )$, then one of the point z or ${\widehat{f}}(z)$ is in $r(\Gamma )$.

Observe that $W_{{\widehat{\Gamma }}}$ projects homeomorphically on $W_{\Gamma }$ and that $A_{{\widehat{\Gamma }}}={\mathrm {int}}(\overline{W_{{\widehat{\Gamma }}}})=\widehat{{\mathrm {dom}}}(I)_{\mathrm {sph}}\setminus \overline{W_N}\cup \overline{W_S}$ projects homeomorphically on $A_{\Gamma }$. We want to prove that $A_{{\widehat{\Gamma }}}$ is an annulus.

Lemma 55

There exists a leaf $\phi _S$ in $U_{{\widehat{\Gamma }}}$ that does not meet $\overline{W_N}$.

Proof

Recall that the intersection of the whole transverse trajectory of $z\in {\mathrm {rec}}(f)_N$ and $U_{{\widehat{\Gamma }}}$, when not empty is equivalent to ${\widehat{\Gamma }}\vert _J$ where J is an open interval of $\mathbb {T}^1$. Consider the set $\mathcal {J}$ of such intervals. The fact that there are no transverse intersection tells us that these intervals do not overlap: if two intervals intersect, one of them contains the other one. One deduces that there exists $t\in \mathbb {T}^1$ that does not belong to any J. Indeed, by a compactness argument, if $\mathbb {T}^1$ can be covered by the intervals of $\mathcal {J}$, there exists $r\geqslant 2$ such that it can be covered by r such intervals but not less. By connectedness, at least two of the intervals intersect and one can lower the number r. Set $\phi _{S}=\phi _{{\widehat{\Gamma }}(t)}$. The set ${\mathrm {rec}}(f)_N$ being dense in $\overline{W_N}$, the leaf $\phi _S$ does not meet the whole transverse trajectories of points in $\overline{W_N}$. In particular, it does not meet $\overline{W_N}$. $\square$

Lemma 56

The set $O_S$ of points whose whole transverse trajectory meets $\phi _S$ is a connected essential open set.

Proof

Fix a lift ${\widetilde{\phi }}$ of $\phi _S$ in $\widetilde{{\mathrm {dom}}}(I)$. The set ${\widetilde{O}}$ of points whose trajectory meets ${\widetilde{\phi }}$ is equal to $\bigcup _{k\in \mathbb {Z}} \widetilde{f}^{-k}\left( \overline{ L({\widetilde{\phi }})\cap R(\widetilde{f}({\widetilde{\phi }}))}\right)$, it its connected and simply connected. So its projection $O_S$ is connected. Every lift of a point in ${\mathrm {rec}}(f)_{{\widehat{\Gamma }}}$ belongs to all the translates $T^k({\widetilde{O}})$, $k\in \mathbb {Z}$. So the union of the translates is connected, which means that $O_S$ is essential. $\square$

Lemma 57

The set $\overline{W_{N}}$ does not contains S and for every $z\in \overline{W_{N}}$, one has $\alpha (z)=\omega (z)=\{N\}$.

Proof

The set $\overline{W_{N}}$ is connected because it can be written

$$\begin{aligned} \overline{W_N}=\overline{\bigcup _{k\in \mathbb {Z}} f^{-k}\left( l(\Gamma )\cup \{N\}\right) }. \end{aligned}$$

It does not contain S because it is connected and does not intersect the essential open set $O_S$. Moreover, one knows that the $\alpha$-limit and $\omega$-limit sets of points in $\overline{W_{N}}$ are reduced to one of the ends. They both are equal to N, because $S\not \in \overline{W_{N}}$. $\square$

Similarly, there exists a leaf $\phi _N$ in $U_{{\widehat{\Gamma }}}$ that does not meet $\overline{W_S}$ and the set $O_N$ of points whose whole transverse trajectory meets $\phi _N$ is a connected essential open set. Moreover, $N\not \in \overline{W_{S}}$ and for every $z\in \overline{W_{S}}$, one has $\alpha (z)=\omega (z)=\{S\}$. Consequently $\overline{W_{N}}$ and $\overline{W_{S}}$ do not intersect. Two points in $O_S\cap O_N$ are not separated neither by $\overline{W_{N}}$ nor by $\overline{W_{S}}$, because $O_S$ and $O_N$ are connected and disjoint from $\overline{W_{N}}$ and $\overline{W_{S}}$ respectively. So they are not separated by $\overline{W_{S}}\cup \overline{W_{N}}$ because $\overline{W_{S}}\cap \overline{W_{N}}=\emptyset$. One deduces that $O_S\cap O_N$ is contained in a connected component O of the complement of $\overline{W_S}\cup \overline{W_N}$, which is nothing but $A_{{\widehat{\Gamma }}}$. So we have

$$\begin{aligned} W_{{\widehat{\Gamma }}}\subset O_S\cap O_N\subset O\subset A_{{\widehat{\Gamma }}}\subset \overline{W_{{\widehat{\Gamma }}}}. \end{aligned}$$

We deduce that the sets appearing in the inclusions have the same closure and that $A_{{\widehat{\Gamma }}}$ is connected because $O\subset A_{{\widehat{\Gamma }}}\subset \overline{O}$. To conclude that $A_{{\widehat{\Gamma }}}$ is an essential annulus, it is sufficient to use the connectedness of $\overline{W_N}$ and $\overline{W_S}$, they are the two connected components of the complement of $A_{{\widehat{\Gamma }}}$.

It remains to prove iii). Note first that every leaf of $\mathcal {F}$ is met by a transverse simple loop and so is wandering. It implies that the $\alpha$-limit and $\omega$-limit sets of a leaf are included in two different connected components of ${\mathrm {sing}}(I)$. Let us fix $\Gamma \in \mathcal {G}_{I,{\mathcal {F}}}$. The complement of $A_{\Gamma }$ has two connected components. One of them contains all singularities at the left of $\Gamma$ and all leaves in $l(\Gamma )$, denote it by $L(A_{\Gamma })$. One defines similarly $R(A_{\Gamma })$. Write $\Xi$ for the union of intervals $J\in \mathcal {J}$ defined in the proof of Lemma 55. A point $t\in \mathbb {T}^1$ belongs to $\Xi$ if and only if there exists $z\in {\mathrm {rec}}(f)\cap L(A_{\Gamma })$ whose whole transverse trajectory meets $\phi _{\Gamma (t)}$ or equivalently, if there exists $z\in L(A_{\Gamma })$ whose whole transverse trajectory meets $\phi _{\Gamma (t)}$. Note that if C is a connected component of $\left( \partial A_{\Gamma }\setminus {\mathrm {sing}}(I)\right) \cap L(A_{\Gamma })$, then the set

$$\begin{aligned} J_C=\{t\in \mathbb {T}^1, \, C\cap \phi _{\Gamma (t)}\not =\emptyset \} \end{aligned}$$

is an interval contained in $\Xi$. Denote by $(t_-,t_+)$ the connected component of $\Xi$ that contains this interval. The assertion iii) is an immediate consequence of the following:

Lemma 58

The interval $J_C$ is equal to $(t_-,t_+)$. Moreover, for every $z\in C$, the connected components of ${\mathrm {sing}}(I)$ that contain $\alpha (z)$ and $\omega (z)$ coincide with the connected components of ${\mathrm {sing}}(I)$ that contain $\omega (\phi _{\Gamma (t_-)})$ and $\omega (\phi _{\Gamma (t_+)})$ respectively.

Proof

Fix $z\in C$. Every point $f^k(z)$ belongs to a leaf $\phi _{\Gamma (t_k)}$, where $t_k\in \mathbb {T}^1$. By definition of $\Xi$, one knows that the whole transverse trajectory of z never meets a leaf $\phi _{\Gamma (t)}$, $t\not \in \Xi$, and so $t\in (t_-,t_+)$ if $\phi _{\Gamma (t)}$ meets this trajectory. In particular, the sequence $(t_k)_{k\in \mathbb {Z}}$ is an increasing sequence in $(t_-,t_+)$. We set $t'_-=\lim _{k\rightarrow -\infty } t_k$ and $t'_+=\lim _{k\rightarrow +\infty } t_k$. We write $F'_+$ for the connected component of ${\mathrm {sing}}(I)$ that contains $\omega (\phi _{\Gamma (t'_+)})$. We will prove first that the connected component of ${\mathrm {sing}}(I)$ that contains $\omega (z)$ is $F'_+$ and then that $t'_+=t_+$. We can do the same for the $\alpha$-limit set. One knows that $\omega (z)$ is contained in $L(A_{\Gamma })\cap {\mathrm {sing}}(I)$. So, there exists a sequence $(z'_k)_{k\geqslant 0}$ such that $z'_k\in \phi ^-(z_k)$ for every $k\geqslant 0$, that “converges to $F'_+$” in the following sense: every neighborhood of $F'_+$ contains $z'_k$ for k sufficiently large. Let us prove now that every neighborhood of $F'_+$ contains the segment $\gamma _k$ of $\phi _{\Gamma (t_k)}$ between $z'_k$ and $z_k$, for k sufficiently large. If not, there exists a subsequence of $(\gamma _k)_{k\geqslant 0}$ that converges for the Hausdorff topology to a set that contains a point $z\not \in {\mathrm {sing}}(I)$. This point belongs to $l(\Gamma )$ and the leaf $\phi _{z}$ is met by a loop $\Gamma '\in \mathcal {G}_{I,{\mathcal {F}}}$. For convenience choose the loop passing through z, so that we know that $z_k$ belongs to $L(\Gamma ')$, for infinitely many k. One deduces that the connected component of ${\mathrm {sing}}(I)$ that contains $\omega (z)$ belongs to $L(\Gamma ')$. But this implies that it also belongs to $L(A_{\Gamma '})$. This connected component being included in the open disk $A_{\Gamma '}\cup L(A_{\Gamma '})$, every point $z_k$ belongs to this disk for k large enough. This contradicts the fact that $z\in \partial A_{\Gamma }$, because $A_{\Gamma '}\cup L(A_{\Gamma '})$ is in the interior of $L(A_{\Gamma })$. It remains to prove that $t'_+=t_+$. If $t'_+<t_+$, then $\phi _{\Gamma (t'_+)}$ is met by a loop $\Gamma '\in \mathcal {G}_{I,{\mathcal {F}}}$ such that $A_{\Gamma '}\subset L(A_{\Gamma })$ and we prove similarly that for k large enough $z_k$ belongs to the open disk $A_{\Gamma '}\cup L(A_{\Gamma '})$ getting the same contradiction. $\square$

7.2 Proofs of Theorems 53 and 51

Proof of Theorem 53

Note that if $\Gamma$ and $\Gamma '$ are two distinct elements of ${\mathcal {G}}_{I,\mathcal {F}}$, then $\Gamma$ is not freely homotopic to $\Gamma '$ in ${\mathrm {dom}}(I)$. Indeed, there exists a leaf $\phi \in U_{\Gamma }\setminus U_{\Gamma '}$. The two sets $\alpha (\phi )$ and $\omega (\phi )$ are separated by $\Gamma$ but not by $\Gamma '$ which implies that these two loops are not freely homotopic. Let us explain now why the families $({\mathrm {rec}}(f)_{\Gamma })_{\Gamma \in \mathcal {G}_{I,\mathcal {F}}}$ and $(A_{\Gamma })_{\Gamma \in \mathcal {G}_{I,\mathcal {F}}}$ are independent of $\mathcal {F}$ (up to reindexation), they depend only on I. In particular, if ${\mathcal {F}}'$ is another foliation transverse to I, then every $\Gamma \in {\mathcal {G}}_{I,\mathcal {F}}$ is freely homotopic to a unique $\Gamma '\in {\mathcal {G}}_{I,{\mathcal {F}}'}$ and one has ${\mathrm {rec}}(f)_{\Gamma }={\mathrm {rec}}(f)_{\Gamma '}$. Let z be a recurrent point and $D\subset {\mathrm {dom}}(I)$ an open disk containing z. For every couple of points $(z',z'')$ in D, choose a path $\gamma _{z',z''}$ in D joining $z'$ to $z''$. Let $(n_k)_{k\geqslant 0}$ be an increasing sequence of integers such that $\lim _{k\rightarrow +\infty } f^{n_k}(z)=z$. For k large enough, the path $I^{n_k}(z)\gamma _{f^{n_k}(z),z}$ defines a loop whose homotopy class is independent of the choices of D and $\gamma _{f^{n_k}(z),z}$. If z belongs to ${\mathrm {rec}}(f)_{\Gamma }$, this class is a multiple of the class of $\Gamma$. This means that the family of classes of loops $\Gamma \in {\mathcal {G}}_{I,\mathcal {F}}$ does not depend on $\mathcal {F}$. It implies that the family of sets ${\mathrm {rec}}(f)_{\Gamma }$ does not depend on $\mathcal {F}$ either. We will denote $(A_{\kappa })_{\kappa \in \mathcal {K}_I}$ and $({\mathrm {rec}}(f)_{\kappa })_{\kappa \in \mathcal {K}_I}$ our families indexed by homotopy classes.

The fact that every invariant annulus contained in ${\mathrm {dom}}(I)$ is contained in an $A_{\beta }$, $\beta \in \mathcal {B}_I$, can be proven exactly like in the global case. So, to prove Theorem 53, particularly the fact that every $A_{\beta }$ is an annulus, it is sufficient to prove that it is equal to an $A_{\kappa }$, $\kappa \in \mathcal {K}_I$. Note that an $A_{\kappa }$ is an invariant annulus contained in ${\mathrm {dom}}(I)$ and so is contained in an $A_{\beta }$. If we prove that every I-free disk recurrent point is contained in an $A_{\kappa }$, we will deduce that each $A_{\beta }$ is a union of $A_{\kappa }$, which implies that it is equal to one $A_{\kappa }$ because it is connected. We will prove in fact that for every I-free disk recurrent point z, there exists a transverse foliation $\mathcal {F}$ such that z belongs to a $W_{\Gamma }$, $\Gamma \in \mathcal {G}_{I,\mathcal {F}}$. Let us give the reason. In the construction of transverse foliations we have the following: if X is a finite set included in an I-free disk D, one can construct a transverse foliation such that X is included in a leaf (see Proposition 59 at the next subsection). Consequently, if D contains two points z and $f^n(z)$, $n>0$, one can construct a transverse foliation such that z and $f^n(z)$ are on the same leaf, which implies that z belongs to a $W_{\Gamma }$. $\square$

Proof of Theorem 51, second part, proof of assertion iv). Fix $\alpha _0\in {\mathcal {A}}_f$. The assertion iv) is obviously true if the complement of $A_{\alpha _0}$ is the union of two fixed points. Let us prove it in case exactly one the connected components of the complement of $A_{\alpha _0}$ is a fixed point $z_0$. By assertion iii) there exists at least one connected component $X_1\not =\{z_0\}$ of ${\mathrm {fix}}(f)$ that meets the frontier of $A_{\alpha _0}$. If $\{z_0\}$ and $X_1$ are the only connected components of ${\mathrm {fix}}(f)$, the result is also obviously true. If not, choose a third component $X_2$, then choose $z_1\in X_1\cap \partial (A_{\alpha _0})$ and $z_2\in X_2$ and finally a maximal hereditary singular isotopy I whose singular set contains $z_0$, $z_1$ and $z_2$. We will prove that the connected component $A_{\beta _0}$, $\beta _0\in {\mathcal {B}}_I$, that contains $A_{\alpha _0}$ is reduced to $A_{\alpha _0}$. This will imply iv). Suppose that $A_{\beta _0}$ is not reduced to $A_{\alpha _0}$. In that case it contains other $A_{\alpha }$, $\alpha \in {\mathcal {A}}_f$, and the union of such sets is dense in $A_{\beta _0}$ and contain all the recurrent points. The two ends of $A_{\beta _0}$ are adjacent to $A_{\alpha _0}$ because $z_1\in {\mathrm {sing}}(I)$. It implies that $A_{\alpha _0}$ is the unique $A_{\alpha }$ that is essential in $A_{\beta _0}$. So, if $A_{\alpha }$ is included in $A_{\beta _0}$ and $\alpha \not =\alpha _0$, the union of $A_{\alpha }$ and of the connected component of its complement that are included in $A_{\beta _0}$ is an invariant open disk $D_{\alpha }\subset A_{\beta _0}$ disjoint from $A_{\alpha _0}$. Let us consider a foliation $\mathcal {F}$ transverse to I and the loop $\Gamma \in \mathcal {G}_{I,\mathcal {F}}$ such that $A_{\Gamma }=A_{\beta }$. We will work in the annular covering space, where $A_{{\widehat{\Gamma }}}$ is homeomorphic to $A_{\Gamma }$ and will write $D_{{\widehat{\alpha }}}\subset A_{{\widehat{\Gamma }}}$ for the disk corresponding to $D_{\alpha }$ and $A_{{\widehat{\alpha }}_0}$ for the annulus corresponding to $A_{\alpha _0}$.

The fact that $\{z_0\}$ is a connected component of $\mathbb {S}^2\setminus A_{\alpha _0}$ and that the singular set of I contains $z_0$ and two other points in different components of the fixed point set of f, implies that one of the sets $r({\widehat{\Gamma }})$ or $l({\widehat{\Gamma }})$ is empty and the other one is not. We will assume for instance that $r({\widehat{\Gamma }})=\emptyset$ and $l({\widehat{\Gamma }})\not =\emptyset$. We have seen in the proof of Proposition 26 that there exists a compactification $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$ obtained by blowing up the end N at the left of ${\widehat{\Gamma }}$ by a circle ${\widehat{\Sigma }}_N$ such that ${\widehat{f}}$ extends to a homeomorphism ${\widehat{f}}_{\mathrm {ann}}$ that admits fixed points on the added circle with a rotation number equal to zero for the lift $\widetilde{f}_{\mathrm {ann}}$ that extends $\widetilde{f}$. Note now that every recurrent point of ${\widehat{f}}$ that belongs to a $D_{{\widehat{\alpha }}}$ has a rotation number (for the lift $\widetilde{f}$) and that this number is a positive integer because $D_{{\widehat{\alpha }}}$ is fixed and included in $A_{{\widehat{\Gamma }}}$. So, every periodic orbit whose rotation number is not an integer belongs to $A_{{\widehat{\alpha }}_0}$.

There are different ways to get a contradiction. Let us begin by the following one. The closure of $A_{{\widehat{\beta }}_0}$ in $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$ is an invariant essential closed set that contains $A_{{\widehat{\alpha }}_0}$ and meets $\Sigma _N$. In particular it contains fixed points of rotation number 0 on $\Sigma _N$. Denote by K the complement of $A_{{\widehat{\alpha }}_0}$ in the closure of $A_{{\widehat{\beta }}_0}$ in $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$. It contains the fixed points located on $\Sigma _N$ and all the $D_{{\widehat{\alpha }}}$, which means that it contains fixed points of positive rotation number. It is an essential compact set, because $A_{{\widehat{\alpha }}_0}$ is an essential annulus which is a neighborhood of the end of $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$. All points in K being non wandering, one can apply a result of S. Matsumoto [32] saying that K contains a periodic orbit of period q and rotation number p / q for every $p/q\in (0,1)$. But one knows that all such periodic points must belong to $A_{{\widehat{\alpha }}_0}$. We have a contradiction.

Let us give another explanation. We will need the following intersection property: every essential simple loop in $\widehat{{\mathrm {dom}}}(I)_{\mathrm {ann}}$ meets its image by ${\widehat{f}}_{\mathrm {ann}}$. The reason is very simple. Perturbing our loop, it is sufficient to prove that every essential simple loop in $\widehat{{\mathrm {dom}}}({I})$ meets its image by ${\widehat{f}}$. Such a loop meets $A_{{\widehat{\beta }}_0}$ because the two ends of $\widehat{{\mathrm {dom}}}({I})$ are adjacent to $A_{{\widehat{\beta }}_0}$ and so contains a non wandering point (every point of $A_{{\widehat{\beta }}_0}$ is non wandering). This implies that the loop meets its image by ${\widehat{f}}$.

Using the fact that the entropy of $f^2$ is zero, one can consider the family of annuli $(A_{\alpha '})_{\alpha '\in {\mathcal {A}}(f^2)}$, and denote by $A_{{\widehat{\alpha }}'}$ the annulus of $A_{{\widehat{\beta }}_0}$ that corresponds to an annulus $A_{\alpha '}$ contained in $A_{\beta _0}$. Every periodic point z of period 3 and rotation number 1 / 3 or 2 / 3 belongs to an annulus $A_{{\widehat{\alpha }}'}$ and this annulus is ${\widehat{f}}^2$-invariant. It must be essential in $A_{{\widehat{\beta }}_0}$, otherwise the rotation number of z should be a multiple of 1 / 2. But if it is essential, it must be ${\widehat{f}}$-invariant, its ${\widehat{f}}$-period cannot be 2. It is included in $A_{{\widehat{\alpha }}_0}$, otherwise it would be included in a non essential $A_{{\widehat{\alpha }}}$. Being given such an essential annulus, note that the set of periodic points of period 3 and rotation 1 / 3 or 2 / 3 strictly above (which means on the same side as ${\widehat{\Sigma }}_N$) is compact. Indeed, the rotation number induced on the added circle is 0. One deduces that there are finitely many annuli $A_{{\widehat{\alpha }}'}$ that contains periodic points of period 3 and rotation number 1 / 3 or 2 / 3 above a given one and so there exists an highest essential annulus $A_{{\widehat{\alpha }}'_0}$ that contains periodic points of period 3 and rotation number 1 / 3 or 2 / 3. If one adds the connected component of $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}\setminus A_{{\widehat{\alpha }}'_0}$ containing ${\widehat{\Sigma }}_N$ to $A_{{\widehat{\alpha }}'_0}$, one gets an invariant semi-open annulus A that contains ${\widehat{\Sigma }}_N$ and all disks $D_{{\widehat{\alpha }}}$. The restriction ${\widehat{f}}_{\mathrm {ann}}\vert _A$ satisfies the intersection property stated in Lemma 25 because A is essential in $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$. The annulus A contains a fixed point of rotation number 0 and a fixed point of positive rotation number, so, by Lemma 25, it contains at least one periodic orbit of period 3 and rotation number 1 / 3 and one periodic orbit of period 3 and rotation number 2 / 3. These two orbits must be included in $A_{{\widehat{\alpha }}'_0}$ by definition of this set. But ${\widehat{f}}\vert _{A_{{\widehat{\alpha }}'_0}}$ satisfies the intersection property because $A_{{\widehat{\alpha }}'_0}$ is essential in $\widehat{{\mathrm {dom}}}({I})_{\mathrm {ann}}$. So $A_{{\widehat{\alpha }}'_0}$ contains a periodic point of period 2 and rotation number 1 / 2, which is impossible.

In the case where none of the connected components of the complement of $A_{\alpha _0}$ is a fixed point, one can crush one of these components to a point and used what has been done in the new sphere. $\square$

Let us add some comments on the boundary of the annuli $A_{\alpha }$.

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that $\Omega (f)=\mathbb {S}^2$ and $h(f)=0$. Suppose moreover than the fixed point set is totally disconnected. Every annulus $A_{\alpha }$, $\alpha \in \mathcal {A}_{f}$, admits accessible fixed points on its boundary. More precisely, if X is a connected component of $\mathbb {S}^2\setminus A_{\alpha }$, there exists a simple path $\gamma$ joining a point $z\in A_{\alpha }$ to a point $z'\in {\mathrm {sing}}(f)\cap X$ and contained in $A_{\alpha }$ but the end $z'$. Indeed, one can always suppose that the other connected component of $\mathbb {S}^2\setminus A_{\alpha }$ is reduced to a point $z_0$ and that f has least three fixed points (otherwise the result is obvious). What has been done in the previous proof tells us that there exists a maximal hereditary singular isotopy I, a transverse foliation $\mathcal {F}$ and $\Gamma \in \mathcal {G}_{I, \mathcal {F}}$ such that $A_{\alpha }=A_{\Gamma }$. There exists a leaf $\phi \subset U_{\Gamma }$ that is not met by any transverse trajectory that intersects X. This leaf (or the inverse of the leaf) joins $z_0$ to a fixed point $z\in X$ and is contained in $A_{\Gamma }$.

Let $f:\mathbb {S}^2\rightarrow \mathbb {S}^2$ be an orientation preserving homeomorphism such that $\Omega (f)=\mathbb {S}^2$ and $h(f)=0$. Let I be a maximal hereditary singular isotopy and $\mathcal {F}$ a transverse foliation. Every annulus $A_{\Gamma }$, $\Gamma \in \mathcal {G}_{I, \mathcal {F}}$, that meets $\phi$ is such that the connected components of ${\mathrm {Fix}}(I)$ that contains $\alpha (\phi )$ and $\omega (\phi )$ are separated by $A_{\Gamma }$. One deduces immediately that a point $z\in {\mathrm {dom}}(I)$ belongs to the frontier of at most two annuli $A_{\Gamma }$, $\Gamma \in \mathcal {G}_{I, \mathcal {F}}$. Of course this means that a point $z\in {\mathrm {dom}}(I)$ belongs to the frontier of at most two annuli $A_{\beta }$, $\beta \in \mathcal {B}_{I}$, but it also implies that a point $z\not \in {\mathrm {fix}}(f)$ belongs to the frontier of at most two annuli $A_{\alpha }$, $\alpha \in \mathcal {A}_{f}$. Indeed, suppose that $z\not \in {\mathrm {fix}}(f)$ belongs to the frontier of $A_{\alpha _i}$, $0\leqslant i\leqslant 2$. If $X_i$ is the connected component of $\mathbb {S}^2\setminus A_{\alpha _i}$ that does not contain z, then the three sets $X_i$ are disjoint. Choose a fixed point $z_i$ in each $X_i$ (such a fixed point exists because $X_i\cup A_{\alpha _i}$ is an invariant disk and $A_{\alpha _i}$ has no fixed points). Choose a maximal hereditary singular isotopy I that fixes the $z_i$ and denote $A_{\beta _i}$, $\beta _i\in \mathcal {B}_I$, the annulus that contains $A_{\alpha _i}$. Note that the three annuli $A_{\beta _i}$ are distinct and that z belongs to their frontier. We have a contradiction. $\square$

7.3 Transverse foliation and free disks

We conclude this section by justifying a point used above in the proof of Theorem 53.

Proposition 59

Let $f:M\rightarrow M$ be a homeomorphism isotopic to the identity on a surface M and I a maximal singular isotopy. Let X be a finite set contained in an I-free disk. Then, there exists a transverse foliation $\mathcal {F}$ such that X is contained in a leaf of $\mathcal {F}$.

Proof

The proof can be deduced immediately from the construction of transverse foliations, that we recall now (see [28]). A brick decomposition ${\mathcal {D}}=(V,E,B)$ on a surface is given by a one dimensional stratified set, the skeleton $\Sigma ({\mathcal {D}})$, with a zero-dimensional submanifold V such that any vertex $v\in V$ is locally the extremity of exactly three edges $e\in E$. A brick $b\in B$ is the closure of a connected component of the complement of $\Sigma ({\mathcal {D}})$. Say that a brick decomposition ${\mathcal {D}}=(V,E,B)$ on ${\mathrm {dom}}(I)$ is I-free, if every brick is I-free, or equivalently, if its lifts to a brick decomposition $\widetilde{\mathcal {D}}=({\widetilde{V}},{\widetilde{E}}, {\widetilde{B}})$ on the universal covering $\widetilde{{\mathrm {dom}}}(I)$, whose bricks are $\widetilde{f}$-free, where $\widetilde{f}$ is the lift associated to ${\widetilde{I}}$. Say that ${\mathcal {D}}$ is minimal if there is no I-free brick decomposition whose skeleton is strictly included in the skeleton of ${\mathcal {D}}$. Such a decomposition always exists.

Write G for the group of automorphisms of the universal covering space. Using the classical Franks’ lemma on free disk chains [11], one constructs a natural order $\leqslant$ on ${\widetilde{B}}$ that satisfies the following:

• it is G-invariant;

• if ${\widetilde{f}}({\widetilde{\beta }})$ meets $\beta '$, then $\beta '\leqslant \beta$;

• two adjacent bricks are comparable.

One can define an orientation on $\Sigma (\widetilde{\mathcal {D}})$ (inducing an orientation on $\Sigma ({\mathcal {D}})$) such that the brick on the left of an edge ${\widetilde{e}}\in {\widetilde{E}}$ is smaller than the brick on the right. Moreover, every vertex ${\widetilde{v}}\in {\widetilde{V}}$ is the ending point of at least one oriented edge and the starting point of at least one oriented edge. In other words there is no sink and no source on the oriented skeleton. We have three possibilities for the bricks of ${\widetilde{B}}$:

• it can be a closed disk with a sink and a source on the boundary (seen from inside);

• it can be homeomorphic to $[0,+\infty [\times \mathbb {R}$ with a sink on the boundary and a source at infinity;

• it can be homeomorphic to $[0,+\infty [\times \mathbb {R}$ with a source on the boundary and a sink at infinity;

• it can be homeomorphic to $[0,1]\times \mathbb {R}$ with a sink and a source at infinity (in this case it can project onto a closed annulus).

Let us state now the fundamental result, easy to prove in the case where G is abelian and much more difficult in the case it is not (see Proposition 3.2 of [28]): one can cover $\Sigma (\widetilde{\mathcal {D}})$ with a G-invariant family of Brouwer lines of $\widetilde{f}$, such that two lines never intersect transversally in the following sense: if $\lambda$ and $\lambda '$ are two lines in this family, either they do not intersect, or one of the sets $R(\lambda )$, $R(\lambda ')$ contains the other one.

Such family of lines inherits a natural order $\leqslant$, where

$$\begin{aligned} \lambda \leqslant \lambda ' \Leftrightarrow R(\lambda )\subset R(\lambda '). \end{aligned}$$

One can “complete” this family to get a larger family, with the same properties, that possesses the topological properties of a lamination (in particular every line admits a compact and totally ordered neighborhood). Then one can arbitrarily foliate each brick $b\in B$ such that, when lifted to a foliation on a brick ${\widetilde{b}}\in {\widetilde{B}}$, every leaves goes from the source to the sink. We obtain then, in a natural way, a decomposition of $\widetilde{{\mathrm {dom}}}(I)$ by a G-invariant family of Brouwer lines that do not intersect transversally, and that possesses the topological structure of a plane foliation (it is a non Hausdorff one dimensional manifold).

It remains to blow up each vertex, by a desingularization process (see [27]) to obtained a G-invariant foliation by Brouwer lines. $\square$

7.4 Zero entropy annulus homeomorphisms

In this subsection we prove some results for a general open annulus homeomorphism whose extension to the ends compactification has zero topological entropy. A stronger version of the first result for diffeomorphisms was already proved in an unpublished paper of Handel [20].

As noted in the introduction, given a homeomorphism of an open annulus $\mathbb {T}^1\times \mathbb {R}$ and a lift $\check{f}$ to $\mathbb {R}^2$, denote by $\pi : \mathbb {R}^2\rightarrow \mathbb {T}^1\times \mathbb {R}$ the covering projection, and by $\pi _1:\mathbb {R}^2 \rightarrow \mathbb {R}$ the projection in the first coordinate. For any point $z\in \mathbb {T}^1\times \mathbb {R}$ such that its $\omega$-limit set is not empty, we say that z has a rotation number ${\mathrm {rot}}(z)$ if, for any compact set $K\subset \mathbb {T}^1\times \mathbb {R}$, any increasing sequence of integers $n_k$ such that $f^{n_k}(z)\in K$ and any $\check{z}\in \pi ^{-1}(z)$,

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{1}{n_k}\left( \pi _1(\check{f}^{n_k}(\check{z})- \pi _1(\check{z})\right) ={\mathrm {rot}}(z). \end{aligned}$$

In general it is not expected that every point will have a rotation number, but if we assume that f has zero entropy this must be the case, at least for recurrent points, as shown by the following theorem, which is a restatement of Theorem L

Theorem 60

Let f be a homeomorphism of $\mathbb {T}^1\times \mathbb {R}$ isotopic to the identity, $\check{f}$ a lift of f to the universal covering space, and let $f_{{\mathrm {sphere}}}$ be the natural extension of f to the sphere obtained by compactifying each end with a point. If the topological entropy of $f_{{\mathrm {sphere}}}$ is zero, then each bi-recurrent point has a rotation number ${\mathrm {rot}}(z)$. Moreover, the function $z\mapsto {\mathrm {rot}}(z)$ is continuous on the set of bi-recurrent points.

Proof

For every compact set K of $\mathbb {T}^1\times \mathbb {R}$ define the set ${\mathrm {rot}}_{\check{f}, K}(z)\subset \mathbb {R}\cup \{-\infty , \infty \}$ as following: $\rho$ belongs to ${\mathrm {rot}}_{\widetilde{f}, K}(z)$ if there exists an increasing sequence of integers $n_k$ such that $f^{n_k}(z)\in K$ and such that for any $\check{z}\in \pi ^{-1}(z)$, one has

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{1}{n_k}\left( \pi _1(\check{f}^{n_k}(\check{z})- \pi _1(\check{z})\right) =\rho . \end{aligned}$$

Writing $T:(x,y)\mapsto (x+1,y)$ for the fundamental covering automorphism, one immediately gets ${\mathrm {rot}}_{\check{f}\circ T^p, K}(z)={\mathrm {rot}}_{\check{f}, K}(z)+p$ for every $p\in \mathbb {Z}$. One can prove quite easily that ${\mathrm {rot}}_{\check{f}^q, K_q}(z)=q{\mathrm {rot}}_{\check{f}, K}(z)$, for every $q\geqslant 1$, where $K_q=\bigcup _{0\leqslant k<q} f^{-k}(K)$. Finally, note that ${\mathrm {rot}}_{\check{f}, K}(z)={\mathrm {rot}}_{\check{f}, \overline{O}(f,z)\cap K}(z)$, where O(f, z) is the f-orbit of z.

Now, recall why every positively recurrent point z of f is a positively recurrent point of $f^q$, for every $q\geqslant 1$. The set R of integers r such that there exists a subsequence of $(f^{nq}(z))_{n\geqslant 0}$ that converges to $f^r(z)$ or equivalently a subsequence of $(f^{nq-r}(z))_{n\geqslant 0}$ that converges to z, is non empty because z is positively recurrent. Note that R is stable by addition. Indeed if r and $r'$ belong to R, one can approximate $f^{r+r'}(z)=f^r(f^{r'}(z))$ by a point $f^r(f^{n'q}(z))=f^{r+n'q}(z)$ as close as we want, and then approximate $f^{r+n'q}(z)= f^{n'q}(f^r(z))$ by a point $f^{n'q}(f^{nq}(z))=f^{(n+n')q}(z)$ as close as we want. One deduces that qr belongs to R if it is the case for r, which implies that z is a positively recurrent point of $f^q$. Similarly, every bi-recurrent point z of f is a bi-recurrent point of $f^q$, for every $q\geqslant 1$.

For every couple (p, q) of integers relatively prime ($q\geqslant 1$), one can choose an identity isotopy $I^*_{p,q}$ of $f^q$ that is lifted to an identity isotopy of $\check{f}^q\circ T^{-p}$, then a maximal hereditary singular isotopy $I_{p,q}$ such that $I'_{p,q}\preceq I_{p,q}$, and finally a singular foliation ${\mathcal {F}}_{p,q}$ transverse to $I_{p,q}$. The singular points of $I_{p,q}$ are periodic points of period q and rotation number p / q. Let z be a bi-recurrent point of f that is not a singular point of $I_{p,q}$. By Theorem 36 and Proposition 2, the whole trajectory $(I_{p,q})^{\mathbb {Z}}_{{\mathcal {F}}_{p,q}}(z)$ is the natural lift of a simple loop $\Gamma _{p,q}(z)$ (uniquely defined up to equivalence). In particular, one has $\Gamma _{p,q}(z)=\Gamma _{p,q}(f^q(z))$. Write $U_{\Gamma _{p,q}(z)}$ for the open annulus, union of leaves met by $\Gamma _{p,q}(z)$. Every leaf containing a point of $\overline{O(f^q,z)}$ is met by $(I_{p,q})^{\mathbb {Z}}_{{\mathcal {F}}_{p,q}}(z)$. It implies that $\overline{O(f^q,z)}\subset U_{\Gamma _{p,q}(z)}\cup {\mathrm {sing}}(I_{p,q})$. Note also that the function $z\mapsto \Gamma _{p,q}(z)$ is locally constant on the set of bi-recurrent points. Indeed if z is a bi-recurrent point and $\gamma :[0,1]\rightarrow {\mathrm {dom}}(I_{p,q})$ a non simple transverse subpath of the natural lift of $\Gamma _{p,q}(z)$, then $\gamma$ is a subpath of the whole trajectory of $z'$, if $z'$ is a bi-recurrent point sufficiently close to z, which implies that $\Gamma _{p,q}(z')=\Gamma _{p,q}(z)$.

One can lift the isotopy $I_{p,q}$ to a singular maximal isotopy $\check{I}_{p,q}$ of $\check{f}^q\circ T^{-p}$ and the foliation ${\mathcal {F}}_{p,q}$ to a foliation $\check{\mathcal {F}}_{p,q}$ transverse to $\check{I}_{p,q}$. Fix a lift $\check{z}\in \mathbb {R}^2$ of z. In the case where $\Gamma _{p,q}(z)$ is not essential, then $(\check{I}_{p,q})^{\mathbb {Z}}_{\check{\mathcal {F}}_{p,q}}(\check{z})$ is the natural lift of a transverse simple loop $\Gamma _{p,q}(\check{z})$ that lifts $\Gamma _{p,q}(z)$. The $\widetilde{f}^q\circ T^{-p}$-orbit of $\check{z}$ stays in the annulus $U_{\Gamma _{p,q}(\check{z})}$, union of leaves met by $\Gamma _{p,q}(\check{z})$. In the case where $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the left of $\Gamma _{p,q}(z)$, then $(\check{I}_{p,q})^{\mathbb {Z}}_{\check{\mathcal {F}}_{p,q}}(\check{z})$ is the natural lift of a transverse line $\gamma _{p,q}(\check{z})$ that lifts $\Gamma _{p,q}(z)$. The $\widetilde{f}^q\circ T^{-p}$-orbit of $\check{z}$ stays in the strip $U_{\gamma _{p,q}(\check{z})}$, union of leaves met by $\gamma _{p,q}(\check{z})$. Fix a parameterization $\gamma _{p,q}(\check{z}):\mathbb {R}\rightarrow {\mathrm {dom}}(\check{I}_{p,q})$ such that $\gamma _{p,q}(\check{z})(t+1)=T(\gamma _{p,q}(\check{z})(t))$. For every $\check{z}'\in U_{\gamma _{p,q}(\check{z})}$ there exist a unique real number, denoted by $\pi _{ \gamma _{p,q}(\check{z})}(\check{z}')$ such that $\check{z}'$ and $\gamma _{p,q}(\check{z})(t)$ are on the same leaf. One gets a map $\pi _{ \gamma _{p,q}(\check{z})}: U_{\gamma _{p,q}(\check{z})}\rightarrow \mathbb {R}$, such that the sequence $(\pi _{ \gamma _{p,q}(\check{z})}(\check{f}^{q}\circ T^{-p})^k(\check{z}))_{k\in \mathbb {Z}}$ is increasing. In the case where $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma _{p,q}(z)$, one proves by the same argument that the sequence $(\pi _{ \gamma _{p,q}(\check{z})}(\check{f}^{q}\circ T^{-p})^k(\check{z}))_{k\in \mathbb {Z}}$ is decreasing.

Let z be a periodic point that is not a singular point of $I_{p,q}$. If $\Gamma _{p,q}(z)$ is not essential, then the rotation number of z (defined for the lift $\widetilde{f}^q\circ T^{-p}$ of $f^q$) is equal to zero, which implies that ${\mathrm {rot}}(z)=p/q$. If $\Gamma _{p,q}(z)$ is essential and if the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the left of $\Gamma _{p,q}(z)$, the rotation number of z (defined for the lift $\widetilde{f}^q\circ T^{-p}$ of $f^q$) is positive, which implies that ${\mathrm {rot}}(z)>p/q$. If $\Gamma _{p,q}(z)$ is essential and if the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma _{p,q}(z)$, then ${\mathrm {rot}}(z)<p/q$.

Let us prove now that if z is bi-recurrent, the periodic points that belong to the closure of O(f, z) have the same rotation number. Otherwise, one can find a couple (p, q) of integers relatively prime ($q\geqslant 1$), and two periodic points $z_1$, $z_2$ in the closure of $O(f^q,z)$ such that ${\mathrm {rot}}(z_1)<p/q<{\mathrm {rot}}(z_2)$. One deduces that $\Gamma _{p,q}(z_1)=\Gamma _{p,q}(z_2)=\Gamma _{p,q}(z)$, which is impossible because the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma _{p,q}(z_1)$ and on the left of $\Gamma _{p,q}(z_2)$.

Let K be a compact subset of $\mathbb {T}^1\times \mathbb {R}$ and z a bi-recurrent point. Let us suppose first that the closure of O(f, z) has no periodic points. For every couple (p, q) of integers relatively prime ($q\geqslant 1$), the set $\overline{O(f,z)}\cap K_q$ is a compact subset of the annulus $U_{\Gamma _{p,q}(z)}$. In the case where $\Gamma _{p,q}(z)$ is not essential, one deduces that ${\mathrm {rot}}_{\widetilde{f}^q\circ T^{-p},K_q}(z)$ is reduced to $\{0\}$ and so ${\mathrm {rot}}_{\widetilde{f},K}(z)$ is reduced to $\{p/q\}$. In the case where $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the left of $\Gamma _{p,q}(z)$, there exits a real number M such that for every point $\widetilde{z}'$ that lifts a point of $(\overline{O(f,z)}\cap K_q)\cup \{z\}$, one has $\vert \pi _1(\check{z}')-\pi _{ \gamma _{p,q}(\check{z})}(\check{z}')\vert \leqslant M$. Using this property and the fact that the sequence $(\pi _{ \gamma _{p,q}(\check{z})}(\check{f}^{q}\circ T^{-p})^k(\check{z}))_{k\in \mathbb {Z}}$ is increasing, one deduces that ${\mathrm {rot}}_{\widetilde{f}\circ T^{-p},K_q}(z)\subset [0,+\infty ]$ and consequently that ${\mathrm {rot}}_{\widetilde{f},K}(z)\subset [p/q,+\infty ]$. Similarly, in the case where $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma _{p,q}(z)$, one gets ${\mathrm {rot}}_{\widetilde{f},K}(z)\subset [-\infty ,p/q]$.

One immediately concludes that ${\mathrm {rot}}_{\widetilde{f},K}(z)$ is reduced to a number in $\mathbb {R}\cup \{-\infty ,\infty \}$ if not empty. Of course, this number is independent of K, we denote it ${\mathrm {rot}}(z)$. Suppose now that the closure of O(f, z) contains periodic points. As said before, they have the same rotation number $p_0/q_0$. The argument above is still valid if $p/q\not =p_0/q_0$ and permit us to concluded that ${\mathrm {rot}}_{\widetilde{f},K}(z)$ is reduced to a number in $\mathbb {R}\cup \{-\infty ,\infty \}$ independent of K. Of course the number is nothing but $p_0/q_0$. Note that in both situations ${\mathrm {rot}}(z)$ is uniquely defined by the following property:

• if $p/q<{\mathrm {rot}}(z)$, then $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma (z)$,

• if $p/q>{\mathrm {rot}}(z)$, then $\Gamma _{p,q}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the left of $\Gamma (z)$.

Using the fact that each function $z\mapsto \Gamma _{p,q}(z)$ is locally constant on the set of bi-recurrent points, one deduces immediately that the function $z\mapsto {\mathrm {rot}}(z)$ is continuous on the set of bi-recurrent points.

It remains to prove that ${\mathrm {rot}}(z)$ is finite. Of course one can suppose that the closure of O(f, z) does not contain a periodic orbit (otherwise as said before ${\mathrm {rot}}(z)$ is rational). By assumption, z is not periodic, so let us choose a free disk D containing z. There exists an integer $s>0$ such that $f^s(z)\in D$ and an integer $r\in \mathbb {Z}$ such that $\check{f}^s(\check{z})\in T^r(\check{D})$, if $\check{D}\subset \mathbb {R}^2$ is a lift of D and $\check{z}$ is the lift of z contained in $\check{D}$. Let us consider the singular isotopy $I_{k,1}$, where $k>r/s$. As explained above the two points z and $f^s(z)$ belong to the free disk D. So, by Proposition 59 one can choose the foliation ${\mathcal {F}}_{k,1}$ such that z and $f^s(z)$ belong to the same leaf $\phi$. This implies that $\Gamma _{k,1}(z)$ is essential and the upper end of $\mathbb {T}^1\times \mathbb {R}$ is on the right of $\Gamma _{k,1}(z)$. Consequently, one deduces that ${\mathrm {rot}}(z)\leqslant k$. One proves similarly that ${\mathrm {rot}}(z)\geqslant k'$ if $k'$ is an integer smaller than r / s. $\square$

An interesting consequence is:

Proposition 61

Let f be an orientation preserving homeomorphism of $S^2$. Suppose that there exists a bi-recurrent point z such that the closure of its orbit contains periodic points of minimal period $q_1<q_2$, where $q_1$ does not divide $q_2$. Then the entropy of f is positive.

Proof

We suppose that the closure of the f-orbit O(f, z) of z contains a periodic point $z_1$ of period $q_1$ and a periodic point $z_2$ of period $q_2$. One can choose $z_1$ and $z_2$ in $\overline{O(f^{q_2},z)}$. Writing r for the remainder of the Euclidean division of $q_2$ by $q_1$, one knows that $f^{q_2}(z_1)=f^r(z_1)$. Since $q_2$ is not a multiple of $q_1$, it is larger than 2 and $f^{q_2}$ must have at least three distinct fixed points. Choose a maximal hereditary identity isotopy I of $f^{q_2}$ whose singular set contains $z_2$, $f^{r}(z_2)$ and at least a third fixed point of $f^{q_2}$, then consider a singular foliation $\mathcal {F}$ transverse to I. Since f has zero topological entropy, $f^{q_2}$ has zero topological entropy, and the path $I_{\mathcal {F}}^{\mathbb {Z}}(z_1)$ is equivalent to the natural lift of a simple transverse loop $\Gamma$. Using the fact that there exist at least there singular points, one can find two singular points $z'_2$ and $z''_2$ of I that are separated by $\Gamma$ and such that $\{z'_2,z''_2\}\not =\{z_2,f^r(z_2)\}$. The isotopy I defines a natural lift of $f^q\vert _{S^2\setminus \{z'_2,z''_2\}}$ and for this lift, the rotation number of every point of the $f^{q_2}$-orbit of $z_1$ is a non vanishing number, while the rotation number of every singular point different from $z'_2$ and $z''_2$ is zero. As seen in the previous proposition, the points z and $f^r(z)$ are bi-recurrent points of $f^{q_2}$. In the case where $z_2\not \in \{z'_2,z''_2\}$, the closure of $O(f^{q_2},z)$ contains two periodic points $z_1$ and $z_2$ with different rotation numbers. In the case where $f^r(z_2)\not \in \{z'_2,z''_2\}$, the closure of $O(f^{q_2},f^r(z))$ contains two periodic points $f^r(z_1)=f^{q_2}(z_1)$ and $f^r(z_2)$ with different rotation numbers. We have seen in the proof of the previous proposition that in both cases, the entropy of f is positive. $\square$

8 Applications to torus homeomorphims

In this section an element of $\mathbb {Z}^2$ will be called an integer and an element of $\mathbb {Q}^2$ a rational. If K is a convex compact subset of $\mathbb {R}^2$, a supporting line is an affine line that meets K but does not separate two points of K, a vertex is a point that belongs to infinitely many supporting lines.

Let us begin by stating the main results of this section, that are nothing but Theorems C, D and G from the introduction.

Theorem 62

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. The frontier of ${\mathrm {rot}}(\check{f})$ does not contain a segment with irrational slope that contains a rational point in its interior.

Theorem 63

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. If ${\mathrm {rot}}(\check{f})$ has a non empty interior, then there exists $L\geqslant 0$ such that for every $z\in \mathbb {R}^2$ and every $n\geqslant 1$, one has $d(\check{f}^n(z)-z, n{\mathrm {rot}}(\check{f}))\leqslant L$.

Theorem 64

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. If ${\mathrm {rot}}(\check{f})$ has a non empty interior, then the topological entropy of f is positive.

Recall that Theorem 64 has been known for a long time and is due to Llibre and MacKay, see [30] and that Theorem 63 was known for homeomorphisms in the special case of a polygon with rational vertices, see Davalos [10], and for $\mathcal {C}^{1+\epsilon }$ diffeomorphisms, see Addas-Zanata [2].

Let us state first some consequences of these results. Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. We suppose that ${\mathrm {rot}}(\check{f})$ has non empty interior. For every non trivial linear form $\psi$ on $\mathbb {R}^2$, define

$$\begin{aligned} \alpha (\psi )=\max \{ \psi ({\mathrm {rot}}(\mu ))\,,\, \mu \in {\mathcal {M}}(f)\}. \end{aligned}$$

The affine line of equation $\psi (z)=\alpha (\psi )$ is a supporting line of ${\mathrm {rot}}(\check{f})$. Set

$$\begin{aligned} {\mathcal {M}}_{\psi }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, \psi ({\mathrm {rot}}(\mu ))=\alpha (\psi )\right\} , \, {X}_{\psi }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\psi }} {\mathrm {supp}}(\mu )}. \end{aligned}$$

As already noted in [2], we can deduce from Theorem 63 and Proposition 47 (Atkinson’s Lemma) the following result, Proposition E of the introduction.

Proposition 65

Every measure $\mu$ supported on ${X}_{\psi }$ belongs to ${\mathcal {M}}_{\psi }$. Moreover, if z lifts a point of $X_{\psi }$, then for every $n\geqslant 1$, one has $\vert \psi (\check{f}^n(z))-\psi (z)-n\alpha (\psi )\vert \leqslant L\Vert \psi \Vert$, where L is the constant given by Theorem 63.

Proof

We will prove the second statement, it obviously implies the first one. Note first that the ergodic components of a measure $\mu \in {\mathcal {M}}_{\psi }$ also belong to ${\mathcal {M}}_{\psi }$. Furthermore, the set of points $A'$ having a lift z satisfying that $\vert \psi (\check{f}^n(z))-\psi (z)-n\alpha (\psi )\vert \leqslant L\Vert \psi \Vert$ for every $n\geqslant 1$ is a closed set. It is then sufficient to prove that for every ergodic measure $\mu \in {\mathcal {M}}_{\psi }$ there exists a set $A\subset A'$ of full measure. As seen before, since $\mu \in {\mathcal {M}}_{\psi }$, the function lifted by $\psi \circ \check{f}-\psi -\alpha (\psi )$ has null mean, and we can apply Atkinson’s lemma to obtain that there exists a set A of full measure such that, for every point z lifting a point of A, there exists a subsequence $(n_l)_{l\in \mathbb {N}}$ such that

$$\begin{aligned} \lim _{l\rightarrow +\infty } \psi (\check{f}^{n_l}(z))-\psi (z)-n_l\alpha (\psi )=0. \end{aligned}$$

By Theorem 63, one knows that for every $z\in \mathbb {R}^2$ and every $n\geqslant 1$, one has $\psi (\check{f}^n(z))-\psi (z)-n\alpha (\psi )\leqslant L\Vert \psi \Vert .$ It remains to prove that $\psi (\check{f}^n(z))-\psi (z)-n\alpha (\psi )\geqslant -L\Vert \psi \Vert$ if z lifts a point of A. If $n_l$ is greater than n one can write

Letting l tend to $+\infty$, one gets our inequality. $\square$

Let us state two corollaries. The first one, Corollary F of the introduction, as already noted in [2], follows immediately from the previous proposition.

Corollary 66

Let f be a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity, preserving a measure $\mu$ of full support, and $\check{f}$ a lift of f to $\mathbb {R}^2$. Assume that ${\mathrm {rot}}(\check{f})$ has a non empty interior. Then ${\mathrm {rot}}(\mu )$ belongs to the interior of ${\mathrm {rot}}(\check{f})$.

Boyland had conjectured that, for a given f and $\check{f}$ in the hypotheses of Corollary 66, if ${\mathrm {rot}}(\mu )$ was an integer then it belonged to the interior of ${\mathrm {rot}}(\check{f})$. The previous result shows that the conjecture is true, and that the hypothesis on the rationality of the rotation vector of $\mu$ is superfluous.

The second corollary shows that, for points in the lift of the support of measures with rotation vector in a vertex, the displacement from the corresponding rigid rotation is uniformly bounded.

Corollary 67

Let $\rho$ be a vertex of ${\mathrm {rot}}(\check{f})$, and set

$$\begin{aligned} {\mathcal {M}}_{\rho }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, {\mathrm {rot}}(\mu )=\rho \right\} , \, {X}_{\rho }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\rho }} {\mathrm {supp}}(\mu )}. \end{aligned}$$

There exists a constant $L_{\rho }$ such that if z lifts a point of $X_{\rho }$, then for every $n\geqslant 1$, one has $d(\check{f}^n(z))-z-n\rho ) \leqslant L_{\rho }$.

Proof

One can find two forms $\psi$ and $\psi '$, linearly independent such that $\rho$ belongs to the supporting lines defined by these forms. Note that $X_{\rho }=X_{\psi }\cap X_{\psi '}$ and apply Proposition 65. $\square$

We remark that the conclusion from Corollary 67 does not hold if instead of requiring that $\rho$ is a vertex of ${\mathrm {rot}}(\check{f})$ we assume that $\rho$ is an extremal point of ${\mathrm {rot}}(\check{f})$, see Boyland et al. [6].

Write $\partial \left( {\mathrm {rot}}(\check{f})\right)$ for the frontier of ${\mathrm {rot}}(\check{f})$. Let us define now

$$\begin{aligned} {\mathcal {M}}_{\partial }=\left\{ \mu \in {\mathcal {M}}(f)\,,\, {\mathrm {rot}}(\mu )\in \partial \left( {\mathrm {rot}}(\check{f}) \right) \right\} ,\, {X}_{\partial }= \overline{\bigcup _{\mu \in {\mathcal {M}}_{\partial }} {\mathrm {supp}}(\mu )} =\overline{\bigcup _{\psi \not =0} X_{\psi }}. \end{aligned}$$

Similarly, we have:

Proposition 68

Every ergodic measure $\mu$ supported on ${X}_{\partial }$ belongs to ${\mathcal {M}}_{\partial }$. Moreover, if z lifts a point of $X_{\partial }$, then for every $n\geqslant 1$, one has $d\left( \check{f}^n(z)-z, n\,\partial \left( {\mathrm {rot}}(\check{f})\right) \right) \leqslant L$, where L is the constant given by Theorem 63.

Proof

Here again, it is sufficient to prove the second statement. To do so, let us choose a non trivial linear form $\psi$ and let us prove that for every $n\geqslant 1$, and for every point z lifting a point of $X_{\psi }$, one has

$$\begin{aligned} d\left( \check{f}^n(z)-z, n\,\partial \left( {\mathrm {rot}}(\check{f})\right) \right) \leqslant L. \end{aligned}$$

The fact that, by Proposition 65,

$$\begin{aligned} \vert \psi (\check{f}^n(z))-\psi (z)-n\beta (\psi )\vert \leqslant L\Vert \psi \Vert \end{aligned}$$

implies that $d(\check{f}^n(z)-z, \Delta )\leqslant L$ where $\Delta$ is the affine line of equation $\psi (z)=n\alpha (z)$. So, if $f^n(z)-z$ does not belong to $n \,{\mathrm {rot}}(\check{f})$, one has

$$\begin{aligned} d\left( \check{f}^n(z)-z, n\,\partial \left( {\mathrm {rot}}(\check{f})\right) \right) =d(\check{f}^n(z)-z, n \,{\mathrm {rot}}(\check{f}))\leqslant L, \end{aligned}$$

and if $\check{f}^n(z)-z$ belongs to $n\, {\mathrm {rot}}(\check{f})$, one has

$$\begin{aligned} d\left( \check{f}^n(z)-z, n\,\partial \left( {\mathrm {rot}}(\check{f})\right) \right) \leqslant d(\check{f}^n(z)-z, \Delta )\leqslant L. \end{aligned}$$

$\square$

Another application is a classification result about Hamiltonian homeomorphisms. In our setting, a Hamiltonian homeomorphism is a torus homeomorphism preserving a probability measure $\mu$ which has a lift $\check{f}$ (the Hamiltonian lift) such that that ${\mathrm {rot}}(\mu )=(0,0).$ An illustrative example is given by the time one map of a time dependent Hamiltonian flow, 1 periodic in time, and its natural lift.

We will need the following result, which can be found in [26]:

Proposition 69

Let f be a homeomorphism of $\mathbb {T}^2$ isotopic to the identity and $\check{f}$ a lift of f. If (0, 0) is a vertex of ${\mathrm {rot}}(\check{f})$ then, for any measure $\mu \in \mathcal {M}(f)$ such that ${\mathrm {rot}}(\mu )=(0,0)$, almost every point lifts to a recurrent point of $\check{f}$ .

We have:

Theorem 70

Let f be a Hamiltonian homeomorphism of $\mathbb {T}^2$ such that its fixed point set is contained in a topological disk, and let $\check{f}$ be its Hamiltonian lift. Then one of the following three conditions holds:

• The set ${\mathrm {rot}}(\check{f})$ does not have empty interior: in that case the origin lies in its interior.

• The set ${\mathrm {rot}}(\check{f})$ is a non trivial segment: in that case ${\mathrm {rot}}(\check{f})$ generates a line with rational slope, the origin is not an end of ${\mathrm {rot}}(\check{f})$, furthermore, there exists an invariant essential open annulus in $\mathbb {T}^2$.

• The set ${\mathrm {rot}}(\check{f})$ is reduced to the origin: in that case, there exists $K>0$ such that, for every $z\in \mathbb {R}^2$ and every $k\in \mathbb {Z}$, one has $\Vert \check{f}^k(z)-z\Vert \leqslant K.$

Proof

Suppose first that ${\mathrm {rot}}(\check{f})$ is reduced to the origin. The origin being a vertex, one knows by Proposition 69 that the recurrent set of $\check{f}$ is dense in $\mathbb {R}^2$. So the assertion comes from Theorem 45.

Suppose now that ${\mathrm {rot}}(\check{f})$ is a non trivial segment. If the origin was an end of ${\mathrm {rot}}(\check{f})$ its would be a vertex and we would have a contradiction, still from from Proposition 69 and Theorem 45. The fact that ${\mathrm {rot}}(\check{f})$ generates a line with rational slope is a consequence of Theorem 62. The existence of an essential open annulus which is left invariant by the dynamics whenever ${\mathrm {rot}}(\check{f})$ is a non trivial segment that generates a line with rational slope is the main result of [17].

The case where ${\mathrm {rot}}(\check{f})$ has non empty interior is nothing but Corollary 66. $\square$

Here again, as in Theorem 45, the requirement that the fixed point set is contained in a topological disk cannot be removed. As a consequence, we obtain the following boundedness result for area preserving homeomorphisms of the torus with restriction on its rotational behaviour, Corollary I of the introduction:

Corollary 71

Let f be a Hamiltonian homeomorphism of $\mathbb {T}^2$ such that all its periodic points are contractible, and such that its fixed point set is contained in a topological disk. Then there exists $K>0$ such that if $\check{f}$ is the Hamiltonian lift of f, then for every $z\in \mathbb {R}^2$ and every $k\in \mathbb {Z}$, one has $\Vert \check{f}^k(z)-z\Vert \leqslant K$.

Proof

By Theorem 70, f must belong to one of the three described possibilities. If f is a homeomorphism of $\mathbb {T}^2$ such that all its periodic points are contractible, then by the main result of [12] the rotation set of any lift of f must have empty interior (see also Remark 74 later in the paper), and so the first possibility in Theorem 70 is excluded. Furthermore, it was shown in [13] that, if g is an area preserving homeomorphism with lift $\check{g}$ and the rotation set of $\check{g}$ is a line segment, then for every point in ${\mathrm {rot}}(\check{g})$ with bi-rational coordinates there exists a periodic point for f with the same rotation vector. Since f has no periodic points that are not contractible, the second possibility is also excluded. $\square$

As a consequence we obtain the Proposition J:

Proposition 72

Let ${\mathrm {Ham}}_{\infty }(\mathbb {T}^2)$ be the set of Hamiltonian $C^{\infty }$ diffeomorphisms of $\mathbb {T}^2$ endowed with the Whitney $C^{\infty }$-topology. There exists a residual subset $\mathcal {A}$ of ${\mathrm {Ham}}_{\infty }(\mathbb {T}^2)$ such that f has non-contractible periodic points if $f\in \mathcal {A}$.

Proof

We will prove that f has non contractible periodic points if the following properties are satisfied:

• if $f^q(z)=z$, then 1 is not an eigenvalue of $Df^q(z)$;

• if z is an elliptic periodic point of period q (which means that the eigenvalues of $Df^q(z)$ are on the unit circle), then z is Moser stable (which means that z is surrounded by $f^q$-invariant curves arbitrarily close to z);

• if z, $z'$ are hyperbolic periodic points of period q, $q'$ respectively (which means that the eigenvalues of $Df^q(z)$ and $Df^{q'}(z')$ are real), then the stable and unstable manifolds of z and $z'$ are either disjoint or they intersect transversally.

The first property implies that the fixed point set of f is finite and so included in a topological disk. By Corollary 71, to get our result it remains to prove that there is no $K>0$ such that if $\check{f}$ is the Hamiltonian lift of f, then for every $z\in \mathbb {R}^2$ and every $k\in \mathbb {Z}$, one has $\Vert \check{f}^k(z)-z\Vert \leqslant K$. If such K exists, choose a bounded open set W containing the fundamental domain $[0,1]^2$. The set $\bigcup _{k\in \mathbb {Z}} \check{f}^k(W)$ is an invariant bounded open set. One finds an invariant bounded open disk V containing $[0,1]^2$ by looking at the complement of the unbounded component of the complement of W. Let us show first that $\partial V$ has no periodic points. Since V is bounded, we may take a sufficiently large integer L such that, if ${\hat{\mathbb {T}}}=\mathbb {R}^2/(L\mathbb {Z})^2$ is the torus that finitely covers $\mathbb {T}^2$, ${\hat{f}}$ is the induced homeomorphism and ${\hat{\pi }}:\mathbb {R}^2\rightarrow {\hat{\mathbb {T}}}^2$ is the projection, then ${\hat{\pi }}(\overline{V})$ is contained in a topological disk. The diffeomorphism ${\hat{f}}$ satisfies the following properties:

• if ${\hat{f}}^q(z)=z$, then 1 is not an eigenvalue of $D{\hat{f}}^q(z)$;

• every elliptic periodic point of ${\hat{f}}$ is Moser stable;

• the stable and unstable manifolds of hyperbolic periodic points of ${\hat{f}}$ are either disjoint or they intersect transversally.

By a theorem of Mather (see [31]), one knows that the prime-end rotation number of ${\hat{\pi }}(V)$ is irrational. The main result from [24] shows that the frontier $\partial {\hat{\pi }}(V)$ has no periodic point because the prime-end rotation number of ${\hat{\pi }}(V)$ is irrational. This implies that $\partial V$ has no periodic points.

In fact it is not necessary to use [24]. Indeed, working directly with V and $\check{f}$, the boundedness condition implies that the stable and unstable manifolds of every hyperbolic periodic point z are bounded. Mather’s arguments implies that, under our generic conditions, the branches of z have all the same closure. By a result of Pixton [35], every stable branch of z intersect every unstable branch and one can find surrounding curves arbitrarily close to z contained in the union of the stable and unstable manifolds. By Mather’s argument again, one knows that such a point z cannot be contained in $\partial V$. Moreover there is no elliptic periodic point on $\partial V$.

The fact that V contains $[0,1]^2$ implies that $\bigcup _{p\in \mathbb {Z}^2} (\partial V+p)$ is connected. Moreover, the interior of $\bigcup _{p\in \mathbb {Z}^2} (\partial V+p)$ is empty. This set projects onto a compact subset of $\mathbb {T}^2$ whose interior is empty, which is totally essential (the connected components of its complement are open disks) and which does not contain periodic points of f. This contradicts a result of A. Koropecki (see [23]) that states the following: if K is an invariant closed connected subset of a homeomorphism defined on a closed orientable surface and having no wandering points, and if K has no periodic point, then either M is a torus and K coincides with M, or K is a decreasing sequence of compact annuli. $\square$

Before proving our three theorems, let us state some introductory results. In what follows (Proposition 73 and Proposition 75) f is a homeomorphism of $\mathbb {T}^2$ that is isotopic to the identity and $\check{f}$ a lift of f to $\mathbb {R}^2$. We consider an identity isotopy $I'$ of f that is lifted to an identity isotopy $\check{I}'$ of $\check{f}$. We consider a maximal hereditary singular isotopy I larger than $I'$ and its lift $\check{I}$ to $\mathbb {R}^2$. We consider a foliation $\mathcal {F}$ transverse to I an its lift $\check{\mathcal {F}}$ to $\mathbb {R}^2$.

Proposition 73

If (0, 0) belongs to the interior of ${\mathrm {rot}}(\check{f})$ or to the interior of a segment with irrational slope included in $\partial \left( {\mathrm {rot}}(\check{f})\right)$, then the leaves of $\check{\mathcal {F}}$ are uniformly bounded.

Proof

Suppose first that (0, 0) belongs to the interior of ${\mathrm {rot}}(\check{f})$. One can find finitely many extremal points $\rho _i$ of ${\mathrm {rot}}(\check{f})$, $1\leqslant i\leqslant r$, that linearly generate the plane and positive numbers $t_i$, $1\leqslant i\leqslant r$, such that:

$$\begin{aligned} \sum _{1\leqslant i\leqslant r} t_i=1,\, \sum _{1\leqslant i\leqslant r} t_i\rho _i=(0,0). \end{aligned}$$

Each $\rho _i$ is the rotation number of an ergodic measure $\mu _i\in {\mathcal {M}}(f)$. Applying Poincaré Recurrence Theorem and Birkhoff Ergodic Theorem, one can find a positively recurrent point $z_i$ of f having $\rho _i$ as a rotation number. Fix a lift $\check{z}_i$ of $z_i$ and a small neighborhood $\check{W}_i$ of $\check{z}_i$ that trivializes $\check{\mathcal {F}}$. One can find a subsequence $(\check{f}^{n_l}(z_i))_{l\geqslant 0}$ of $\check{f}^{n}(z_i)_{n\geqslant 1}$ and a sequence $(p_{i,l})_{l\geqslant 0}$ of integers such that $\check{f}^{n_l}(\check{z}_i)\in \check{W}_i+p_{i,l}$ and such that $\lim _{l\rightarrow +\infty } p_{i,l}/n_l=\rho _i$. One deduces that the transverse homological space ${\mathrm {THS}}({\mathcal {F}})$ contains $p_{i,l}$. If l is large enough, the $p_{i,l}$ generate the plane and (0, 0) is contained in the interior of the polygonal defined by these points. By Proposition 13, we deduce that the leaves of $\check{\mathcal {F}}$ are uniformly bounded.

Suppose now that (0, 0) belongs to the interior of a segment with irrational slope included in $\partial \left( {\mathrm {rot}}(\check{f})\right)$. If this segment $[\rho _1,\rho _2]$ is chosen maximal, then $\rho _1$ and $\rho _2$ are extremal points of ${\mathrm {rot}}(\check{f})$ and respectively equal to the rotation number of ergodic measures $\mu _1$ and $\mu _2$ in ${\mathcal {M}}(f)$. Let $W_i\subset \mathbb {T}^2$ be a trivializing box of $\mathcal {F}$ such that $\mu _i(W_i)\not =0$ and $\check{W}_i\subset \mathbb {R}^2$ a lift of $W_i$. The first return map $\Phi _i:W_i\rightarrow W_i, z\mapsto f^{\tau _i}(z)$ (where $\tau _i: W_i\rightarrow \mathbb {N}$) is defined $\mu _i$-almost everywhere on $W_i$ as the displacement function $\xi _i: W_i\rightarrow \mathbb {Z}^2$, where $\check{f}^{\tau _i(z)}(\check{z})\in \check{W}_i+\xi _i(z)$, if $\check{z}$ is the lift of z that belongs to $\check{W}_i$. Let $\psi :\mathbb {R}^2\rightarrow \mathbb {R}$ be a non trivial linear form that vanishes on our segment. Using Birkhoff Ergodic Theorem, one knows that $\mu _i$-almost every point z has a rotation number $\rho _i$, and so

$$\begin{aligned} \lim _{n\rightarrow +\infty } {\sum _{k=0} ^{n-1} \xi _i (\Phi _i ^k(z))\over \sum _{k=0} ^{n-1} \tau _i(\Phi _i^k(z))} =\rho _i. \end{aligned}$$

By Kac’s theorem, one knows that $\tau _i$ is $\mu _i$-integrable and satisfies $\int _{W_i} \tau _i \,d\mu _i =\mu _i(\bigcup _{k\in \mathbb {Z}} f^k(W_i))\in {(0,1]}$. One can note that $\xi _i/\tau _i$ is bounded, which implies that $\xi _i$ is $\mu _i$-integrable. Consequently, one has

$$\begin{aligned} \lim _{n\rightarrow +\infty } {\sum _{k=0} ^{n-1}\xi _i (\Phi _i ^k(z))\over \sum _{k=0} ^{n-1} \tau _i(\Phi _i^k(z))} = {\int _{W_i} \xi _i \,d\mu _i\over \int _{W_i} \tau _i \,d\mu _i}, \end{aligned}$$

which implies that

$$\begin{aligned} \int _{W_i} \xi _i \,d\mu _i=\left( \int _{W_i} \tau _i \,d\mu _i\right) \rho _i\not =0 \end{aligned}$$

and

$$\begin{aligned} \int _{W_i} \psi \circ \xi _i \,d\mu _i=\psi \left( \int _{W_i} \xi _i \,d\mu _i\right) =0. \end{aligned}$$

Note that $\psi \circ \xi _i (z)\not =0$ if $\xi _i ( z)\not =0$, because $\xi _i (z)$ is an integer and the kernel of $\psi$ is generated by a segment with irrational slope. We deduce that there exists $z_1$, $z'_1$ in $W_1$ such that

$$\begin{aligned} \psi \circ \xi _1 ( z_1)<0<\psi \circ \xi _1\left( z'_1\right) . \end{aligned}$$

Consequently, one can find $z''_1\in W_1$, $z''_2\in W_2$ and integers $n_1$, $n_2$ such that (0, 0) is in the interior of the quadrilateral determined by

$$\begin{aligned} \xi _1 ( z_1),\, \xi _1\left( z'_1\right) ,\, {\sum _{k=0} ^{n_1-1} \xi _1\left( \Phi _1^k\left( z''_1\right) \right) \over \sum _{k=0} ^{n_1-1} \tau _1 \left( \Phi _1^k\left( z''_1\right) \right) }, \, {\sum _{k=0} ^{n_2-1} \xi _2\left( \Phi _2 ^k( z_2)\right) \over \sum _{k=0} ^{n_2-1} \tau _2\left( \Phi _2^k\left( z''_2\right) \right) }, \end{aligned}$$

because the last two points may be chosen arbitrarily close to $\rho _1$ and $\rho _2$. The set ${\mathrm {THS}}({\mathcal {F}})$ containing the integers

$$\begin{aligned} \xi _1 ( z_1),\, \xi _1\left( z'_1\right) ,\, \sum _{k=0} ^{n_1-1} \xi _1\left( \Phi _1 ^k( z''_1)\right) , \sum _{k=0} ^{n_2-1} \xi _2\left( \Phi _2 ^k( z_2)\right) , \end{aligned}$$

one can apply Proposition 13 to conclude that the leaves of $\check{\mathcal {F}}$ are uniformly bounded. $\square$

Remark 74

As a corollary, one deduces that $\mathcal {F}$ is singular and that $\check{f}$ is not fixed point free. Applying this to $\check{f}^q-p$, for every rational $p/q\in {\mathrm {int}}( {\mathrm {rot}}(\check{f}))$, one deduces that there exists a point $z\in \mathbb {R}^2$ such that $\check{f}^q(z)=z+q$. This result was already well known, due to Franks [12].

Proposition 75

We suppose that the leaves of $\check{\mathcal {F}}$ are uniformly bounded. If there exists an admissible transverse path $\check{\gamma }:[a,b]\rightarrow {\mathrm {dom}}(\check{\mathcal {F}})$ of order q and an integer $p\in \mathbb {Z}^2$ such that $\check{\gamma }$ and $\check{\gamma }+p$ intersect $\check{\mathcal {F}}$-transversally at $\phi _{\check{\gamma }(t)}=\phi _{(\check{\gamma }+p)(s)}$, where $s<t$, then p / q belongs to ${\mathrm {rot}}(\check{f})$.

Proof

By Corollary 22 one deduces that for every $k\geqslant 2$ the path

$$\begin{aligned} \check{\gamma }\vert _{[a,t]}\left( \prod _{0<i<k-1} (\check{\gamma }+ip)\vert _{[s,t]}\right) (\check{\gamma }+(k-1)p)\vert _{[s,b]} \end{aligned}$$

is admissible of order kq. This implies that there exists a point $\check{z}_k\in \phi _{\check{\gamma }(a)}$ such that $\check{f}^{kq}(\check{z}_k)\in \phi _{(\check{\gamma }+(k-1)p)(b)}= \phi _{ \check{\gamma }(b)}+(k-1)p$. The fact that the leaves of $\check{\mathcal {F}}$ are uniformly bounded tells us that there exists K such that for every $k\geqslant 1$, one has $\Vert \check{f}^{kq}(\check{z}_k)-\check{z}_k-(k-1)p\Vert \leqslant K$. Denote $z_k$ the projection of $\check{z}_k$ in $\mathbb {T}^2$. Choose a measure $\mu$ that is the limit of a subsequence of $\left( {1\over kq} \sum _{i=0}^{kq-1}\delta _{f^{i}(z_{k})}\right) _{k\geqslant 2}$ for the weak$^*$ topology. It is an invariant measure of f of rotation number p / q for $\check{f}$. $\square$

Let us state the following improved version of Atkinson’s Lemma:

Proposition 76

Let $(X,\mathcal {B},\mu )$ be a probability space and $T:X\rightarrow X$ an ergodic automorphism. If $\varphi : X\rightarrow \mathbb {R}$ is an integrable map such that $\int \varphi \, d\mu =0$, then for every $B\in \mathcal {B}$ and every $\varepsilon >0$, one has

$$\begin{aligned} \mu \left( \left\{ x\in B, \, \exists n\geqslant 0, \, T^n(x)\in B\, and \,0\leqslant \sum _{k=0}^{n-1}\varphi (T^k(x))< \varepsilon \right\} \right) = \mu (B). \end{aligned}$$

Proof

Let us consider $B\in {\mathcal {B}}$ and set

$$\begin{aligned} A=B\setminus \left\{ x\in B, \, \exists n\geqslant 0, \, T^n(x)\in B\, and \,0\leqslant \sum _{k=0}^{n-1}\varphi (T^k(x))< \varepsilon \right\} \}. \end{aligned}$$

Atkinson’s result directly implies that there exists a set $A'\subset A$ with $\mu (A')=\mu (A)$ such that, for every $x\in A'$, there exists a subsequence $(n_l)_{l\in \mathbb {N}}$ such that $T^{n_l}(x)\in A$ and $\lim _{l\rightarrow \infty } \sum _{k=0} ^{n_l-1} \varphi (T^k(x))=0$. Assume, for a contradiction, that $\mu (A)>0$. There exists some $x\in A'$ and $n_0>0$ such that $y=T^{n_0}(x) \in A$ and $a=\sum _{k=0}^{n_0-1}\varphi (T^{k}(x)) \in (-\varepsilon , \varepsilon )$, and since $x\in A$ we know that $a<0$. Since $x \in A'$ there exists some $n_{1}>n_0$ such that $T^{n_{1}}(x)\in A$ and $a< \sum _{k=0}^{n_1-1}\varphi (T^{k}(x))< \varepsilon +a$. This implies that $T^{n_{1}-n_0}(y) \in A$ and that $0<\sum _{k=0}^{n_l-n_0-1}\varphi (T^{k}(y))<\varepsilon$, which is a contradiction since $y \in A$ proving the claim. $\square$

Proof of Theorem 62

We will give a proof by contradiction. Replacing f by $f^q$ and $\check{f}$ by $\check{f}^q-p$, where $q\in \mathbb {N}$ and $p\in \mathbb {Z}^2$, we can suppose that the frontier of ${\mathrm {rot}}(\check{f})$ contains a segment $[\rho _0,\rho _1]$ with irrational slope, that (0, 0) is in its interior and that $\rho _0$ and $\rho _1$ are extremal points of ${\mathrm {rot}}(\check{f})$. We can suppose moreover than for every $\rho \in {\mathrm {rot}}(\check{f})$, one has $\langle \rho _0^{\perp },\rho \rangle \leqslant 0\leqslant \langle \rho _1^{\perp },\rho \rangle$. We consider two ergodic measures $\mu _0$ and $\mu _1$ in ${\mathcal {M}}(f)$ whose rotation vectors are $\rho _0$ and $\rho _1$ respectively. We know that there exists a point $z_0\in \mathbb {R}^2$ such that ${\mathrm {rot}}(z_0)=\rho _0$ and that projects onto a bi-recurrent point of f. By Proposition 76, we have a stronger result: $\square$

Lemma 77

There exists a point $z_0$, projecting to a bi-recurrent point and with ${\mathrm {rot}}(z_0)=\rho _0$, such that for every $\varepsilon \in \{-1,1\}$ one can find a sequence $(p_l,q_l)_{l\geqslant 0}$ in $\mathbb {Z}^2\times \mathbb {N}$ satisfying:

$$\begin{aligned} \lim _{l\rightarrow +\infty } q_l= & {} +\infty , \, \lim _{l\rightarrow +\infty }\check{f}^{q_l}(z_0)-z_0-p_l=0, \, \\&{\lim _{l\rightarrow +\infty } \left\langle \rho _0^{\perp },p_l\right\rangle =0,} \, \varepsilon \left\langle \rho _0^{\perp },p_l\right\rangle >0 \end{aligned}$$

and a sequence $(p'_l,q'_l)_{l\geqslant 0}$ in $\mathbb {Z}^2\times \mathbb {N}$ satisfying:

$$\begin{aligned} \lim _{l\rightarrow +\infty } q'_l= & {} +\infty , \, \lim _{l\rightarrow +\infty }\check{f}^{-q'_l}(z_0)-z_0-p'_l=0,\, \\&\quad {\lim _{l\rightarrow +\infty } \left\langle \rho _0^{\perp },p'_l\right\rangle =0,} \,\varepsilon \left\langle \rho _0^{\perp },p'_l\right\rangle >0. \end{aligned}$$

Proof

Let $W_0$ be a small disk such that $\mu _0(W_0)\not =0$ and $\check{W}_0$ a lift of $W_0$. Define the maps $\tau _0$ and $\xi _0$ like in Proposition 73. The measure $\mu _0$ being ergodic, one knows that $\int _{W_0} \tau _0\, d\mu _0=1$ and that $\int _{W_0} \xi _0\, d\mu _0 =\rho _0$. Let us define on $W_0$ the first return map $T: z\mapsto f^{\tau _0(z)}(z)$ and the function $\varphi :z\mapsto \varepsilon \langle \rho _0^{\perp }, \xi _0(z)\rangle$.

For each integer $i\geqslant 1$, let $(B_{i,j})_{1\leqslant j\leqslant k_i}$ be a covering of $W_0$ by open sets with diameter smaller than 1 / i, and define

$$\begin{aligned} C_{i,j}=\left\{ x\in B_{i,j}\cap W_0, \, \exists n\geqslant 0, \, T^n(x)\in B_{i,j}\cap W_0\,{\mathrm {and}}\,0 \leqslant \sum _{k=0}^{n-1}\varphi (T^k(x))< 1/i\right\} \end{aligned}$$

Set $C_i= \bigcup _{j=1}^{k_i} C_{i,j}$ and $C= \bigcap _{i\geqslant 1} C_i$. By Proposition 76, one knows that $\mu _0(C_i)=\mu _0(C)=\mu _0(W_0)$, and if $C'$ is the subset of the bi-recurrent points of C with rotation vector $\rho _0$, then $\mu _0(C')=\mu _)(C)$.. If $z_0$ belongs to $C'$, one can find an increasing integer sequence $(m_l)_{l\geqslant 0}$ such that

$$\begin{aligned}&\lim _{l\rightarrow +\infty } T^{m_l}(z_0)=z_0, \, \lim _{l\rightarrow +\infty }\sum _{k=0}^{m_l-1} \varepsilon \left\langle \rho _0^{\perp },\xi _0(T^k(z_0)\right\rangle = 0, \\&\quad \, \sum _{k=0}^{m_l-1} \varepsilon \left\langle \rho _0^{\perp },\xi _0(T^k(z_0)\right\rangle \geqslant 0. \end{aligned}$$

Setting $p_l=\sum _{k=0}^{m_l-1} \xi _0(T^k(z_0))$ and $q_l=\sum _{k=0}^{m_l-1} \tau _0(T^k(z_0))$, one gets the first assertion of the lemma, with a large inequality instead of a strict one. Noting that $\lim _{l\rightarrow +\infty } \Vert p_l\Vert =+\infty$ and that the line generated by $\rho _0$ has irrational slope, one deduces that the inequality is strict. The second assertion can be proved analogously. $\square$

We note that, by Proposition 73, the leaves of $\check{\mathcal {F}}$ are uniformly bounded. Let us choose $z_0$ as in the previous lemma. The fact that ${\mathrm {rot}}(z_0)=\rho _0$ tells us that the whole trajectory $\check{I}^{\mathbb {Z}}(z_0)$ is a proper path directed by $\rho _0$. The fact that the leaves of $\check{\mathcal {F}}$ are uniformly bounded and that every leaf met by $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$ is also met by $\check{I}^{\mathbb {Z}}(z_0)$ implies that $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$ is a transverse proper path directed by $\rho _0$. We parameterize $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$ in such a way that $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) \vert _{[l,l+1]}=\check{I}_{\check{\mathcal {F}}}(\check{f}^l(z_0))$. We consider sequences $(p_l,q_l)_{l\geqslant 0}$ and $(p'_l,q'_l)_{l\geqslant 0}$ given by the previous lemma (the sign $\varepsilon$ has no importance at the beginning).

Lemma 78

For every closed segment $[a,b]\subset \mathbb {R}$ and every positive real numbers L, $\varepsilon$, there exists $p\in \mathbb {Z}^2$ and a segment $[a',b']\subset \mathbb {R}$ satisfying $a'-b>L$ such that $\vert \langle \rho _0^{\perp },p\rangle \vert <\varepsilon$ and such that the paths $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) \vert _{[a,b]}$ and $(\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) +p)\vert _{[a',b']}$ are equivalent. One has a similar result replacing the inequality $a'-b>L$ by $a-b'>L$.

Proof

Let us choose integers q and $q'$ such that $[a,b]\subset (q, q')$. As $z_0$ projects to a bi-recurrent point, one can find l, using Lemma 77, sufficiently large, such that $q_l>q'-q+L$ and such that $\check{f}^{q_l}(\check{f}^q(z_0))-p_l$ is so close to $\check{f}^q(z_0)$ that we can affirm that $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) \vert _{[a,b]}$ is equivalent to a path $(\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) -p_l)\vert _{[a',b']}$, where $[a',b']\subset (q+q_l, q'+q_l)$. Note that $\vert \langle \rho _0^{\perp },p_l\rangle \vert <\varepsilon$ if l is sufficiently large. The version with the inequality $a-b'>L$ can be proven similarly by using the sequences $(p'_l)_{l\geqslant 0}$ and $(q'_l)_{l\geqslant 0}$. $\square$

Lemma 79

There is no $p\in \mathbb {Z}^2\setminus \{0\}$ such that $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$ and $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) +p$ intersect $\check{\mathcal {F}}$-transversally.

Proof

Write $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) =\gamma _0$ for convenience. Suppose that $\gamma _0$ and $\gamma _0+p$ intersect $\check{\mathcal {F}}$-transversally at $\phi = \phi _{\gamma _0(t)}=\phi _{(\gamma _0 +p)(s)}$. The leaves being uniformly bounded, one knows that $\phi _{\gamma _0(t)}\not =\phi _{\gamma _0(t)}+p$ and so $t\not =s$. Replacing p with $-p$ if necessary, one can suppose that $s<t$. By Proposition 75, there exists $q\geqslant 1$ such that $p/q\in {\mathrm {rot}}(\check{f})$. Consequently, one has $\langle \rho ^{\perp }_0,p\rangle \leqslant 0$. By assumption, the segment $[0,\rho _0]$ has irrational slope and $p\not =0$, so one deduces that $\langle \rho _0^{\perp },p\rangle <0$.

We know that there exists a sufficiently large N such that $\gamma _0\vert _{[-N, N]}$ and $(\gamma _0+p)\vert _{[-N, N]}$ intersect $\check{\mathcal {F}}$-transversally at $\phi$. By Lemma 78, we can find some $p'\in \mathbb {Z}^2$ such that $\vert \langle \rho _0^{\perp },p'\rangle \vert$ is sufficiently small as to get $\langle \rho _0^{\perp },p+p'\rangle <0$, and such that there exists some $a',b'$ with $N<a'<b'$, where $(\gamma _0+p')\vert _{[a', b']}$ is equivalent to $\gamma _0\vert _{[-N, N]}$. This implies that $(\gamma _0+p+p')\vert _{[a', b']}$ is equivalent to $(\gamma _0+p)\vert _{[-N, N]}$, and so $\gamma _0$ and $\gamma _0+p+p'$ intersect $\check{\mathcal {F}}$-transversally at $\phi _{\gamma _0(t)}=\phi _{(\gamma _0 +p+p')(s')}$ where $s'>t$. So, one knows that $\gamma _0$ and $\gamma _0-p-p'$ intersect $\check{\mathcal {F}}$-transversally at $\phi _{\gamma _0 (s')}=\phi _{(\gamma _0 -p-p')(t)}$. We deduce as before, by Proposition 75, that for some $q'>1$ the vector $\frac{-p-p'}{q'}\in {\mathrm {rot}}(\check{f})$, a contradiction since $\langle \rho _0^{\perp },-p-p'\rangle <0$. $\square$

Lemma 80

The path $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$ is a line

Proof

Here again, write $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0) =\gamma _0$. If $\gamma _0$ is a not a line, by Proposition 4 one knows that there exist two segments $[a_0,b_0]$ and $[a_1,b_1]$ such that $\gamma _0\vert _{[a_0,b_0]}$ and $\gamma _0\vert _{[a_1,b_1]}$ intersect $\check{\mathcal {F}}$-transversally. By Lemma 78, one deduces that there exist $p\in \mathbb {Z}^2\setminus \{0\}$ and a segment $[a'_1,b'_1]$ such that $\gamma _0\vert _{[a_0,b_0]}$ and $(\gamma _0+p)\vert _{[a'_1,b'_1]}$ intersect $\check{\mathcal {F}}$-transversally. This contradicts Lemma 79. $\square$

Similarly, we can find a point $z_1$ of rotation number $\rho _1$ that projects onto a recurrent point of f and such that $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_1)$ is a line directed by $\rho _1$ that does not meet transversally its integer translated.

Lemma 81

The line $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_1)$ intersects $\check{\mathcal {F}}$-transversally one of the translates of $\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$.

Proof

Let us prove by contradiction that $\gamma _1=\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_1)$ intersects $\check{\mathcal {F}}$-transversally one of the translates of $\gamma _0=\check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_0)$. If not, let us denote by $U_0$ the union of leaves that are met by $\gamma _0$. Its complement can be written $R(U_0)\sqcup L(U_0)$ where $R(U_0)=R(\gamma _0)\setminus U_0$ is the union of $r(\gamma _0)$ and of the set of singularities at the right of $\gamma _0$ and $L(U_0)=L(\gamma _0)\setminus U_0$ is the union of $l(\gamma _0)$ and of the set of singularities at the left of $\gamma _0$. If $\gamma _1$ and $\gamma _0$ do not intersect $\check{\mathcal {F}}$-transversally, then by Corollary 6, one knows that either $\gamma _1\cap R(U_0)=\emptyset$ or $\gamma _1\cap L(U_0)=\emptyset$. As $\gamma _0$ is directed by $\frac{\rho _0}{\Vert \rho _0\Vert }$ and $\gamma _1$ is directed by the opposite vector $\frac{\rho _1}{\Vert \rho _1\Vert }=-\frac{\rho _0}{\Vert \rho _0\Vert }$, one knows that if $\gamma _1\cap R(U_0)=\emptyset$, then $R(\gamma _1)\cap R(U_0)=\emptyset$, and if $\gamma _1\cap L(U_0)=\emptyset$, then $L(\gamma _1)\cap L(U_0)=\emptyset$. Consequently, $\gamma _0$ and $\gamma _1$ cannot meet a common leaf. Indeed if $\phi$ is such a leaf, one knows by Proposition 4 that it is met once by $\gamma _0$ and $\gamma _1$. So, the $\alpha$-limit set of $\phi$ is contained in $L(U_0)\cap \overline{L(\gamma _1)}$ and the $\omega$-limit set is included in $R(U_0)\cap \overline{R(\gamma _1)}$, which is impossible.

So, if the conclusion of our lemma is not true, there exists a partition $\mathbb {Z}^2=A^-\sqcup A^+$, where

Also, by Lemma 79 and the fact that $\gamma _0$ is directed by $\rho _0$, one knows that $l(\gamma _0+p)\subset l(\gamma _0)$ if $0\leqslant \langle \rho _0^{\perp },p\rangle$ and one deduces this partition is a cut of the order on $\mathbb {Z}^2$ defined as follows

$$\begin{aligned} p\preceq p'\Leftrightarrow \left\langle \rho _0^{\perp },p\right\rangle \leqslant \left\langle \rho _0^{\perp },p'\right\rangle . \end{aligned}$$

Let us fix a leaf $\phi$ that intersects $\gamma _1$. By Lemma 78, one knows that there exists $p_0\not =(0,0)$ such that $\phi$ intersects $\gamma _1+p_0$. One deduces that $A^-+p_0=A^-$ and $A^++p_0=A^+$, which of course is impossible. $\square$

End of the proof of Theorem 62

Replacing $\gamma _0$ by a translate if necessary, we can always suppose that $\gamma _0$ and $\gamma _1$ intersect $\check{\mathcal {F}}$-transversally at $\gamma _0(t_0)=\gamma _1(t_1)$ and we define $\gamma =\gamma _0\vert _{[-\infty ,t_0]}\gamma _1\vert _{[t_1,+\infty ]}$ which is an admissible transverse proper path. There exist two segments $[a_0,b_0]$ and $[a_1,b_1]$ containing $t_0$ and $t_1$ respectively in their interior, such that $\gamma _0\vert _{[a_0,b_0]}$ and $\gamma _1\vert _{[a_1,b_1]}$ intersect transversally at $\gamma _0(t_0)=\gamma _1(t_1)$. Using Lemma 78, one can find $p_0$ and $p_1$ in $\mathbb {Z}^2$ distinct, and segments $[a'_0,b'_0]\subset (-\infty , t_0)$ and $[a'_1,b'_1]\subset (t_1,+\infty )$ such that $(\gamma _0+p_0)\vert _{[a'_0,b'_0]}$ is equivalent to $\gamma _0\vert _{[a_0,b_0]}$ and $(\gamma _1+p_1)\vert _{[a'_1,b'_1]}$ is equivalent to $\gamma _1\vert _{[a_1,b_1]}$. We deduce that there exists $t'_0\in (a'_0,b'_0)$ and $t'_1\in (a'_1+t_0-t_1,b'_1+t_0-t_1)$ such that $\gamma +p_0$ and $\gamma +p_1$ intersect $\check{\mathcal {F}}$-transversally at $\phi = \phi _{(\gamma +p_0)(t'_0)}=\phi _{(\gamma +p_1)(t'_1)}$. So $\gamma$ and $\gamma +p_1-p_0$ intersect $\check{\mathcal {F}}$-transversally at $\phi -p_0= \phi _{\gamma (t'_0)}=\phi _{(\gamma +p_1-p_0)(t'_1)}$. Observing that $t'_0<t'_1$, one deduces, by Proposition 75, that there exists $q\geqslant 1$ such that $(p_1-p_0)/q\in {\mathrm {rot}}(\check{f})$ and thus $\langle \rho _0^{\perp },p_1-p_0\rangle <0$. But Lemma 77 tells us that $p_0$ and $p_1$ can be chosen so that $\langle \rho _0^{\perp },p_0\rangle <0$ and $\langle \rho _0^{\perp },p_1\rangle >0$. We have found a contradiction. $\square$

Proof of Theorem 63

In the proof, we will use the sup norm $\Vert \,\Vert _{\infty }$ where $\Vert (x_1,x_2)\Vert _{\infty }=\max (\vert x_1\vert , \vert x_2\vert )$ which will be more convenient that the Euclidean norm and will write $d_{\infty }(z,X)=\inf _{z'\in X} \Vert z-z'\Vert _{\infty }$. Replacing f by $f^q$ and $\check{f}$ by $\check{f}^q-p$, where $q\in \mathbb {N}$ and $p\in \mathbb {Z}^2$, we can suppose that (0, 0) is in the interior of ${\mathrm {rot}}(\check{f})$. Here again, we consider an identity isotopy $I'$ of f that is lifted to an identity isotopy $\check{I}'$ of $\check{f}$. We consider a maximal hereditary singular isotopy I larger than $I'$ and its lift $\check{I}$ to $\mathbb {R}^2$. We consider a foliation $\mathcal {F}$ transverse to I an its lift $\check{\mathcal {F}}$ to $\mathbb {R}^2$. One knows by Proposition 73 that the leaves of $\check{\mathcal {F}}$ are uniformly bounded. In the remainder of the proof we will usually work in the universal covering space of $\mathbb {T}^2$, with paths transversal to the lifted foliation $\check{\mathcal {F}}$. The theorem is an immediate consequence of the following, where the direction $D(\gamma )$ of a path $\gamma : [a,b]\rightarrow \mathbb {R}^2$ is defined as $D(\gamma )=\gamma (b)-\gamma (a)$:

Proposition 82

There exists a constant L such that for every transverse admissible path $\gamma$ of order n, one has $d_{\infty }(D(\gamma ), n\,{\mathrm {rot}}(f))\leqslant L$.

We will begin by proving:

Lemma 83

There exist a transverse admissible path $\gamma ^*:[0,3]\rightarrow \mathbb {R}^2$, a real number $K^*$ and an integer $p^*\in \mathbb {Z}^2$ such that:

• every transverse path $\gamma$ whose diameter is larger than $K^*$ intersects $\check{\mathcal {F}}$-transversally an integer translate of $\gamma ^*_{\vert [1,2]}$;

• $\gamma ^*_{\vert [2,3]}$ and $\gamma ^*_{\vert [0,1]}+p^*$ intersect $\check{\mathcal {F}}$-transversally.

Proof

Let us choose N large enough such (1 / N, 0) and (0, 1 / N) belong to the interior of ${\mathrm {rot}}(\check{f})$. As previously noted in Remark 74, there exists a point $z_0$ satisfying $\check{f}^N(z_0)=z_0+(1,0)$ and a point $z_1$ satisfying $\check{f}^N(z_1)=z_1+(0,1)$. The transverse trajectories $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0)$ and $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)$ are parameterized, such that $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0)(t+1)=\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0)(t)+(1,0)$ and $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)(t+1)=\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)(t)+(0,1)$.

$\square$

Sub-lemma 84

There exists a real number K such that if $\gamma$ is a transverse path that does not intersect $\check{\mathcal {F}}$-transversally $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0)$ , then either $\pi _2(\gamma (t))> -K$ or $\pi _2(\gamma (t))<K$ and if it does not intersect $\check{\mathcal {F}}$-transversally $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)$, then either $\pi _1(\gamma (t))>-K$ or $\pi _1(\gamma (t))<K$.

Proof

There exists $K_0>0$ such that the diameter of each leaf of $\mathcal {F}$ is bounded by $K_0$ and there exists $K'_0>0$ such that $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0) \subset \mathbb {R}\times (-K'_0,K'_0)$. Setting $K=K_0+K'_0$, note that every leaf that intersects $\mathbb {R}\times (-\infty , -K]$ belongs to $r(\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0) )$ and every leaf that intersects $\mathbb {R}\times [K,+\infty )$ belongs to $l(\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0))$. It remains to apply Corollary 6. We have a similar argument for $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)$. $\square$

Setting $K^*=2K+1$, one deduces immediately:

Corollary 85

If $\gamma$ is a transverse path and if the diameter of $\pi _2\circ \gamma$ is larger than $K^*$, there exists $p_0\in \mathbb {Z}^2$ such that $\gamma$ intersects $\check{\mathcal {F}}$-transversally $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0) +p_0$ and if the diameter of $\pi _1\circ \gamma$ is larger than $K^*$, there exists $p_1\in \mathbb {Z}^2$ such that $\gamma$ intersects $\check{\mathcal {F}}$-transversally $\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1) +p_1$.

In particular $\gamma _0=\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_0)$ intersects $\gamma _1=\check{I}_{{\check{\mathcal {F}}}}^{\mathbb {Z}}(z_1)$ $\check{\mathcal {F}}$-transversally at a point $\gamma _0(t_0)=\gamma _1(t_1)$. One can find an integer $r>0$ such that $\gamma _0\vert _{[t_0-r,t_0+r]}$ and $\gamma _1\vert _{[t_1-r,t_1+r]}$ intersect $\check{\mathcal {F}}$-transversally at $\gamma _0(t_0)=\gamma _1(t_1)$. Let $\gamma ^*:[0,3]\rightarrow \mathbb {R}^2$ be a path such that

• $\gamma ^*_{[0,1]}$ is a reparameterization of $\gamma _0\vert _{[t_0-(4r+2),t_0-(2r+2)]}$;

• $\gamma ^*_{[1,2]}$ is a reparameterization of $\gamma _0\vert _{[t_0-(2r+2),t_0]}\gamma _1\vert _{[t_1,t_1+(2r+2)]}$;

• $\gamma ^*_{[2,3]}$ is a reparameterization of $\gamma _1\vert _{[t_1+(2r+2),t_1+(4r+2)]}$.

Let us prove that $\gamma ^*$ satisfies the proposition. Observe first that $\gamma ^*$ is admissible of order $(8r+4)N$ by Corollary 21 and that the paths $\gamma ^*\vert _{[0,2]}$ and $\gamma ^*\vert _{[1,3]}$ are admissible of order $(6r+2)N$. Note first that $\gamma ^*_{\vert [2,3]}$ and $\gamma ^*_{\vert [0,1]}+(3r+2,3r+2)$ intersect $\check{\mathcal {F}}$-transversally. One can set $p^*=(3r+2,3r+2)$. Let $\gamma$ be a transverse path such that the diameter of $\pi _2\circ \gamma$ is larger than $K^*$. By Sub-lemma 84 one knows that there exists $p_0\in \mathbb {R}^2$ such that $\gamma$ intersects $\check{\mathcal {F}}$-transversally $\gamma _0+p_0$. This means that there exist two real segments J and $J_0$ such that

• $\gamma \vert _{J}$ intersects $\check{\mathcal {F}}$-transversally $\gamma _0\vert _{J_0}+p_0$;

• $\gamma \vert _{{\mathrm {int}} J}$ and $\gamma _0\vert _{{\mathrm {int }}J_0}+p_0$ are equivalent.

If the length of $J_0$ is smaller than $2r+1$, then $J_0$ is included in an interval $[t_0-(2r+2)+l_0, t_0+l_0]$. This implies that $\gamma$ intersects $\check{\mathcal {F}}$-transversally $\gamma ^*\vert _{[1,2]}+p_0+(l_0,0)$. If the length is at least equal to $2r+1$, then $J_0$ contains an interval $[t_0-r+l_0, t_0+r+ l_0]$. This implies that $\gamma$ intersects $\check{\mathcal {F}}$-transversally $\gamma _1\vert _{[t_1-r, t_1+r]}+ p_0+(l_0,0)$ and so intersects $\check{\mathcal {F}}$-transversally $\gamma ^*\vert _{[1,2]}+p_0+(l_0,-r)$. We get the same conclusion for a transverse path such that the diameter of $\pi _1\circ \gamma$ is larger than $K^*$. $\square$

Proof of the Proposition 82

We denote by $K^{**}$ the diameter of $\gamma ^*$ and by $K^{***}$ the diameter of ${\mathrm {rot}}(f)$. Let $\gamma : [a,b]\rightarrow \mathbb {R}^2$ be a transverse path such that $\Vert D(\gamma )\Vert >2K^*$. One can find c, d in (a, b) with $c<d$ such that $\Vert D(\gamma \vert _{[a,c]})\Vert =\Vert D(\gamma \vert _{[d,b]})\Vert =K^*$. Note that, if c is chosen to be minimal with this property, and d is chosen to be maximal, then the diameter of both $\gamma \vert _{[a,c]}$ and $\gamma \vert _{[d,b]}$ are at most $2K^*$. There exist p and $p'$ in $\mathbb {Z}^2$ such that

• $\gamma \vert _{[a,c]}$ and $\gamma ^*\vert _{[1,2]}+p$ intersect $\check{\mathcal {F}}$-transversally at $\gamma (t)=\gamma ^*(s)+p$;

• $\gamma \vert _{[d,b]}$ and $\gamma ^*\vert _{[1,2]}+p'$ intersect $\check{\mathcal {F}}$-transversally at $\gamma (t')=\gamma ^*(s')+p'$.

If $\gamma$ is admissible of order n, then the path

$$\begin{aligned} \gamma '=(\gamma ^*\vert _{[0,s]}+p)\gamma \vert _{[t,t']}(\gamma ^*\vert _{[s',3]}+p') \end{aligned}$$

is admissible of order $n+(12r+4)N$ by Corollary 21 and one has

$$\begin{aligned} \Vert D(\gamma ')-D(\gamma )\Vert \leqslant {4K^*}+2K^{**}. \end{aligned}$$

Recall that $\gamma ^*_{[2,3]}$ intersects $\check{\mathcal {F}}$-transversally $\gamma ^*_{[0,1]}+p^*$. One deduces that $(\gamma ^*\vert _{[s',3]}+p')$ intersects $\check{\mathcal {F}}$-transversally $(\gamma ^*\vert _{[0,s]}+p)+p''$, where $p''=p'-p+p^*$ and so that $\gamma '$ intersects $\check{\mathcal {F}}$-transversally $\gamma '+p''$. Proposition 75 tells us that $p''/(n+(12r+4)N)$ belongs to ${\mathrm {rot}}(\check{f})$, which implies

$$\begin{aligned} d(p'', n\,{\mathrm {rot}}(\check{f}))\leqslant (12r+4)N K^{***}. \end{aligned}$$

Observe now that $\Vert p''-D(\gamma ')\Vert \leqslant 2K^{**}$ and so $\Vert p''-D(\gamma )\Vert \leqslant {4K^*+4K^{**}}$. So, one gets

$$\begin{aligned} d(D(\gamma ), n\,{\mathrm {rot}}(\check{f}))\leqslant {4K^*+4K^{**}}+(12r+4)NK^{***}. \end{aligned}$$

$\square$

Proof of Theorem 64

Here again, using the fact that for every $q\geqslant 1$ and every $p\in \mathbb {Z}^2$, one has ${\mathrm {rot}}(\check{f}^q+p)=q{\mathrm {rot}} (\check{f})+p$, it is easy to see that it is sufficient to prove the result in the case where (0, 0) belongs to the interior of ${\mathrm {rot}}(\check{f})$. Here again, we consider an identity isotopy $I'$ of f that is lifted to an identity isotopy $\check{I}'$ of $\check{f}$. We consider a maximal hereditary singular isotopy I larger than $I'$ and its lift $\check{I}$ to $\mathbb {R}^2$. We consider a foliation $\mathcal {F}$ transverse to I an its lift $\check{\mathcal {F}}$ to $\mathbb {R}^2$. We know that the leaves of $\check{\mathcal {F}}$ are uniformly bounded. We can immediately deduce the theorem from what has been done in the previous proof and Theorem 36. Indeed, we know that there are two transverse loops associated to periodic points that have a transverse intersection. We will give a proof that does not use Theorem 36 by exhibiting separated sets. $\square$

Let us begin with the following lemma:

Lemma 86

There exists a constant K such that for every point $z\in {\mathrm {dom}}(\check{\mathcal {F}})$ and any $z'$ for which $\phi _{z'}$ intersects $I_{\check{\mathcal {F}}}(z)$, one has $d(z, z')\leqslant K$.

Proof

There exists $K'>0$ such that the diameter of each leaf of $\check{\mathcal {F}}$ is bounded by $K'$. Moreover, the set $\bigcup _{t\in [0,1], z\in [0,1]^2}I(z)$, being compact, is included in $[-K'',K''+1]^2$,for some $K''>0$. The leaves that $\check{I}_{\check{\mathcal {F}}}(z)$ intersects, are also intersected by $\check{I}(z)$ (see the beginning of Sect. 3). One deduces that $K=K'+K''$ satisfies the conclusion of the lemma. $\square$

We consider the paths $\gamma _0= \check{I}_{\check{\mathcal {F}}}(z_0)$ and $\gamma _1= \check{I}_{\check{\mathcal {F}}}^{\mathbb {Z}}(z_1)$ defined in the proof of Theorem 63. We keep the same notations and set $z^*=\gamma _0(t_0)=\gamma _1(t_1)$. Let us define

$$\begin{aligned} K'''=\max \left( {\mathrm {diam}}( \gamma _0\vert _{[t_0,t_0+r]}), \,{\mathrm {diam}}( \gamma _1\vert _{[t_1,t_1+r]})\right) \end{aligned}$$

and choose an integer $m\geqslant 1$ such that $mr\geqslant K'''+2K_0+K+1$. Set

$$\begin{aligned} \gamma '_0=\gamma _0\vert _{[t_0,t_0+mr]},\, \gamma '_1=\gamma _1\vert _{[t_1,t_1+mr]}. \end{aligned}$$

Fix n and for every $\mathbf {e}=(\varepsilon _1,\ldots ,\varepsilon _n)\in \{0,1\}^{n}$ define

$$\begin{aligned} \gamma '_{\mathbf {e}}= \prod _{1\leqslant i\leqslant n} (\gamma '_{\varepsilon _i}+p_{i-1}), \end{aligned}$$

where the sequence $(p_i)_{0\leqslant i\leqslant n}$ satisfies $k_0=0$ and is defined inductively by the relation:

$$\begin{aligned} p_{i+1}= {\left\{ \begin{array}{ll} p_i+(mr,0) &{} \text{ if } \varepsilon _i=0, \\ p_i+(0, mr) &{} \text{ if } \varepsilon _i=1. \end{array}\right. } \end{aligned}$$

The path $\gamma '_{\omega }$ is admissible of order $l=nmrN$. More precisely, there exists a point $z_{\mathbf {e}}\in \phi _{z^*}$ such that $\check{f}^{l}(z_{\mathbf {e}})\in \phi _{z^*}+k_n$, and such that $\gamma '_{\mathbf {e}}= \check{I}_{\check{\mathcal {F}}}^{l}(z_{\mathbf {e}})$.

Lemma 87

If $\mathbf {e}$ and $\mathbf {e}'$ are two different sequences in $\{0,1\}^{n}$, there exists $j\in \{0, \ldots , l-1\}$ such that $\Vert \check{f}^j (z_{\mathbf {e}})- \check{f}^j (z_{\mathbf {e}'})\Vert \geqslant 1$.

Proof

Consider the integer $i^*$ such that $\varepsilon _{i^*}\not = \varepsilon '_{i^*}$ and $\varepsilon _{i}= \varepsilon '_{i}$ if $i<i^*$. The leaf $\phi _{z^*}+p_{i^*}$ is intersected by $\gamma '_{\mathbf {e}}$ but not by $\gamma '_{\mathbf {e}'}$. More precisely $d(\phi _{z^*}+p_{i^*}, \gamma '_{\mathbf {e}'})\geqslant mr-K'-K_0$. Using Lemma 86, one deduces that there exists $j\in \{0, \ldots , l\}$ such that $d(\check{f}^j(z_{\omega }), \phi _{z^*}+p_{i^*})\leqslant K$. Moreover, one knows that $d(\check{f}^j(z_{\mathbf {e}'}), \gamma '_{\mathbf {e}'})\leqslant K_0$ because $\gamma '_{\mathbf {e}}$ intersects $\phi _{\check{f}^j(z_{\mathbf {e}'})}$. One deduces that

$$\begin{aligned} \Vert \check{f}^j (z_{\mathbf {e}})- \check{f}^j (z_{\mathbf {e}'})\Vert \geqslant mr-K'-2K_0-K\geqslant 1. \end{aligned}$$

$\square$

To finish the proof of the proposition, let us define on $\mathbb {T}^2$ the distance

$$\begin{aligned} d(Z,Z')=\inf _{\pi (z)=Z,\,\pi (z')=Z'}\Vert z-z'\Vert , \end{aligned}$$

where

is the projection. Note that for every $Z\in \mathbb {T}^2$, one has

$$\begin{aligned} \pi ^{-1}(B(Z,1/4))=\bigsqcup _{\pi (z)=Z} B(z, 1/4) \end{aligned}$$

and every map $\pi \vert _{B(z,1/4)}$ is an isometry from B(z, 1 / 4) onto B(Z, 1 / 4).

Fix $\varepsilon \in (0,1/4)$ such that for every z, $z'$ in $\mathbb {R}^2$, one has

$$\begin{aligned} \Vert z-z'\Vert<\varepsilon \Rightarrow \Vert \check{f}(z)-\check{f}(z')\Vert <1/4. \end{aligned}$$

One deduces that two points Z and $Z'$ such that $d(f^j(Z), f^j(Z))<\varepsilon$, for every $j\in \{0, \ldots l-1\}$ are lifted by points z, $z'$ such that $\Vert \check{f}^j(z)-\check{f}^j(z)\Vert <\varepsilon$, for every $j\in \{0, \ldots l-1\}$.

Consequently, the points $z_{\mathbf {e}}$ project on a $(nmrN, \varepsilon )$-separated set of cardinality $2^n$. One deduces that $h(f)>\log 2/mrN$. $\square$