Quivers with relations for symmetrizable Cartan matrices I: Foundations

Abstract

We introduce and study a class of Iwanaga–Gorenstein algebras defined via quivers with relations associated with symmetrizable Cartan matrices. These algebras generalize the path algebras of quivers associated with symmetric Cartan matrices. We also define a corresponding class of generalized preprojective algebras. For these two classes of algebras we obtain generalizations of classical results of Gabriel, Dlab–Ringel, and Gelfand–Ponomarev. In particular, we obtain new representation theoretic realizations of all finite root systems without any assumption on the ground field.

1 Introduction and main results

1.1 Quivers, Coxeter functors and preprojective algebras

Let Q be a finite connected acyclic quiver, and let $H = KQ$ be the path algebra of Q with coefficients in a field K. The following five results, all proved in the 1970’s, form an essential part of the foundations of modern representation theory of finite-dimensional algebras.

• (1) Gabriel’s Theorem [30]: The quiver Q is representation-finite if and only if Q is a Dynkin quiver of type $A_n, D_n, E_6, E_7, E_8$. In this case, there is a bijection between the isomorphism classes of indecomposable representations of Q and the set of positive roots of the corresponding simple complex Lie algebra.

• (2) Bernstein, Gelfand and Ponomarev’s [11] discovery of Coxeter functors

  $$\begin{aligned} C^\pm (-) = F_{i_n}^\pm \circ \cdots \circ F_{i_1}^\pm : {\text {rep}}(H) \rightarrow {\text {rep}}(H), \end{aligned}$$

  which are defined as compositions of reflection functors. They lead to a more conceptual proof of Gabriel’s Theorem. Applied to the indecomposable projective (resp. injective) representations they yield a family of indecomposable representations, called preprojective (resp. preinjective) representations.

• (3) Gabriel’s Theorem [32] saying that there are functorial isomorphisms $TC^\pm (-) \cong \tau ^\pm (-)$, where T is a twist functor and $\tau (-)$ is the Auslander–Reiten translation (see also the comment below on an earlier result by Brenner and Butler).

• (4) Auslander, Platzeck and Reiten’s Theorem [3] saying that the functors $F_k^+$ and ${\text {Hom}}_H(T,-)$, where $F_k^+$ is a BGP-reflection functor and T is the associated APR-tilting module, are equivalent. This result can be considered as the starting point of tilting theory.

• (5) Gelfand and Ponomarev’s [35] discovery of the preprojective algebra $\Pi (Q)$ of a quiver, and their result that $\Pi (Q)$, seen as a module over H, is isomorphic to the direct sum of all preprojective H-modules, hence the name preprojective algebra. The algebra $\Pi (Q)$ is isomorphic to the tensor algebra $T_H({\text {Ext}}_H^1({\text {D}}(H),H))$, where ${\text {D}}$ denotes the duality with respect to the base field K, see [7, 22, 48].

The above results hold for arbitrary ground fields K. At the price of quite strong assumptions on K they were generalized from quivers to the more general setup of modulated graphs. (One needs to assume the existence of finite field extensions of K with prescribed degrees.) For the finite type situation, this extended the theory from the simply laced root systems of types $A_n, D_n, E_6, E_7$ and $E_8$ to the non-simply laced root systems $B_n, C_n, F_4$ and $G_2$. The definition of a modulated graph (also called species) and of its representations is due to Gabriel [31]. The theory itself has been developed by Dlab and Ringel, who generalized (1), (2) and (5) to modulated graphs [25,26,27,28, 46]. Brenner and Butler [14] proved an earlier result closely related to (3), which is also valid for modulated graphs. (They don’t treat $C^\pm$ as endofunctors, and the twist automorphism T does not appear.)

1.2 Hereditary, selfinjective and Iwanaga–Gorenstein algebras

In this section, by an algebra we mean a finite-dimensional K-algebra.

An algebra A is hereditary if all A-modules have projective and injective dimension at most 1. The representation theory of quivers and species corresponds to the representation theory of finite-dimensional hereditary algebras.

An algebra A is selfinjective if the classes of projective and injective A-modules coincide. This implies that all modules (except the projective-injectives) have infinite projective and injective dimension. Despite being opposite homological extremes, hereditary and selfinjective algebras are often intimately linked. For example the path algebra KQ is always hereditary, and in contrast, if Q is a Dynkin quiver, then the closely related preprojective algebra $\Pi (Q)$ is selfinjective. Also, the classification of representation-finite selfinjective algebras shows striking similarities to the classification of representation-finite hereditary algebras.

An algebra A is m-Iwanaga–Gorenstein if

These algebras were first studied by Iwanaga [39, 40]. In this case, [4, Lemma 6.9] implies that ${\text {inj.~dim}}(A) = {\text {proj.~dim}}({\text {D}}(A))$, and by [40, Theorem 5] for any A-module M the following are equivalent:

• (i) ${\text {proj.~dim}}(M) \le m$;

• (ii) ${\text {inj.~dim}}(M) \le m$;

• (iii) ${\text {proj.~dim}}(M) < \infty$;

• (iv) ${\text {inj.~dim}}(M) < \infty$.

Note that with this definition a given algebra can be m-Iwanaga–Gorenstein for different values of m. An algebra is selfinjective if and only if it is 0-Iwanaga–Gorenstein. All hereditary algebras and also all selfinjective algebras are 1-Iwanaga–Gorenstein. Now let A be a 1-Iwanaga–Gorenstein algebra. Then there are two subcategories of the category ${\text {rep}}(A)$ of finite-dimensional A-modules which are of interest:

• (a) The subcategory

  

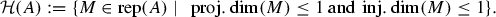
• (b) The subcategory

  $$\begin{aligned} {{\mathcal G}{\mathcal P}}(A) := \{ M \in {\text {rep}}(A) \mid {\text {Ext}}_A^1(M,A) = 0 \} \end{aligned}$$

  of Gorenstein-projective modules.

Let ${\mathcal P}(A)$ be the subcategory of projective A-modules. We have

$$\begin{aligned} {\mathcal P}(A) = {\mathcal H}(A) \cap {\mathcal G}{\mathcal P}(A). \end{aligned}$$

For each $M \in {\text {rep}}(A)$ there are short exact sequences

$$\begin{aligned} 0 \rightarrow H_M \rightarrow G_M \rightarrow M \rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} 0 \rightarrow M \rightarrow H^M \rightarrow G^M \rightarrow 0 \end{aligned}$$

with $H_M,H^M \in {\mathcal H}(A)$ and $G_M,G^M \in {\mathcal G}{\mathcal P}(A)$, see [2, 8.1].

The category ${\mathcal H}(A)$ carries the homological features of module categories of hereditary algebras, whereas ${\mathcal G}{\mathcal P}(A)$ is a Frobenius category, thus displaying the homological features of module categories of selfinjective algebras. We have ${\mathcal G}{\mathcal P}(A) = {\mathcal P}(A)$ and ${\mathcal H}(A) = {\text {rep}}(A)$ if and only if A is hereditary, and in the other extreme we have ${\mathcal G}{\mathcal P}(A) = {\text {rep}}(A)$ and ${\mathcal H}(A) = {\mathcal P}(A)$ if and only if A is selfinjective.

The stable category of ${\mathcal G}{\mathcal P}(A)$ is a triangulated category, which is triangle equivalent to the singularity category

$$\begin{aligned} D_\mathrm{sg}(A) := D^b(A)/K^b({\text {proj}}(A)) \end{aligned}$$

defined and studied by Buchweitz [17], see also [45]. (Here $D^b(A)$ denotes the derived category of bounded complexes of finite-dimensional A-modules, and $K^b({\text {proj}}(A))$ is the homotopy category of bounded complexes of finite-dimensional projective A-modules.) It follows that $D_\mathrm{sg}(A) = 0$ if and only if A is hereditary.

Thus the class of 1-Iwanaga–Gorenstein algebras can be seen as an intermediary class sitting between the hereditary and the selfinjective algebras, and the singularity category $D_\mathrm{sg}(A)$ can be considered as a measure of how far A is from being hereditary.

1.3 1-Iwanaga–Gorenstein algebras attached to Cartan matrices

To each symmetrizable generalized Cartan matrix C and an orientation $\Omega$ of C we attach an infinite series of 1-Iwanaga–Gorenstein algebras $H = H(C,D,\Omega )$ indexed by the different symmetrizers D of C. These algebras are defined by quivers with relations over an arbitrary field K.

If C is symmetric and connected, then $(C,\Omega )$ corresponds to a connected acyclic quiver Q, and the series of algebras H consists of the algebras of the form

$$\begin{aligned} A_m \otimes _K KQ,\qquad (m\ge 1), \end{aligned}$$

where $A_m := K[X]/(X^m)$ is a truncated polynomial ring. Representations of such algebras are nothing else than representations of Q over the ground rings $A_m$.

In the general case of a symmetrizable matrix C, the algebras H can be identified with tensor algebras of modulations of the oriented valued graph $\Gamma$ corresponding to $(C,\Omega )$. However, in contrast to the classical notion of a modulation, the rings attached to vertices of $\Gamma$ are truncated polynomial rings instead of division rings.

We also introduce a series of algebras $\Pi = \Pi (C,D)$, again defined by quivers with relations, which can be regarded as preprojective algebras of quivers (or more generally of modulated graphs) over truncated polynomial rings.

We show that analogues of all five results mentioned in Sect. 1.1 also hold for our algebras H and $\Pi$. However certain definitions must be adapted. For example, we say that H has finite $\tau$ -representation type if its Auslander–Reiten quiver has only finitely many $\tau$-orbits consisting entirely of modules of finite homological dimension. The analogue of (1) states that H has finite $\tau$-representation type if and only if C is of Dynkin type. In this case, there is a bijection between the isomorphism classes of indecomposable modules sitting on these $\tau$-orbits and the positive roots of the simple Lie algebra associated with C. So for each Cartan matrix C of Dynkin type we get an infinite family of new representation theoretic incarnations of the root system of C. Let us stress that even in the non-simply laced case these incarnations are defined without any assumption on the ground field K. To prove this theorem, we define analogues of the reflection functors and Coxeter functors of (2), and we give an analogue of Gabriel’s Theorem (3) for the subcategory of H-modules of finite homological dimension. This yields alternative descriptions of the preprojective algebra $\Pi$ similar to (5). We also obtain an analogue of (4) describing the reflection functors in terms of certain tilting H-modules.

In the rest of this section we give precise definitions of the algebras H and $\Pi$, and we state our main results in more detail. We then point out previous appearances of some of the algebras H and $\Pi$ in the literature.

1.4 Definition of H and $\Pi$

A matrix $C = (c_{ij}) \in M_n(\mathbb {Z})$ is a symmetrizable generalized Cartan matrix provided the following hold:

• (C1) $c_{ii} = 2$ for all i;

• (C2) $c_{ij} \le 0$ for all $i \not = j$;

• (C3) $c_{ij} \not = 0$ if and only if $c_{ji} \not = 0$.

• (C4) There is a diagonal integer matrix $D = {\text {diag}}(c_1,\ldots ,c_n)$ with $c_i \ge 1$ for all i such that DC is symmetric.

The matrix D appearing in (C4) is called a symmetrizer of C. The symmetrizer D is minimal if $c_1 + \cdots + c_n$ is minimal. From now on, by a Cartan matrix we always mean a symmetrizable generalized Cartan matrix. In this case, define for all $c_{ij} < 0$

$$\begin{aligned} g_{ij} := |\gcd (c_{ij},c_{ji})|,\quad f_{ij} := |c_{ij}|/g_{ij},\quad k_{ij} := \gcd (c_i,c_j). \end{aligned}$$

Note that we have

$$\begin{aligned} g_{ij} = g_{ji}, \quad k_{ij} = k_{ji}, \quad c_i = k_{ij}f_{ji}. \end{aligned}$$

Let $C = (c_{ij}) \in M_n(\mathbb {Z})$ be a Cartan matrix. An orientation of C is a subset $\Omega \subset \{ 1,2,\ldots ,n \} \times \{ 1,2,\ldots ,n \}$ such that the following hold:

• (i) $\{ (i,j),(j,i) \} \cap \Omega \not = \varnothing$ if and only if $c_{ij}<0$;

• (ii) For each sequence $((i_1,i_2),(i_2,i_3),\ldots ,(i_t,i_{t+1}))$ with $t \ge 1$ and $(i_s,i_{s+1}) \in \Omega$ for all $1 \le s \le t$ we have $i_1 \not = i_{t+1}$.

For an orientation $\Omega$ of C let $Q := Q(C,\Omega ) := (Q_0,Q_1,s,t)$ be the quiver with the set of vertices $Q_0 := \{ 1,\ldots , n\}$ and with the set of arrows

$$\begin{aligned} Q_1 := \{ \alpha _{ij}^{(g)}:j \rightarrow i \mid (i,j) \in \Omega , 1 \le g \le g_{ij} \} \cup \{ \varepsilon _i:i \rightarrow i \mid 1 \le i \le n \}. \end{aligned}$$

(Thus we have $s(\alpha _{ij}^{(g)}) = j$ and $t(\alpha _{ij}^{(g)}) = i$ and $s(\varepsilon _i) = t(\varepsilon _i) = i$, where s(a) and t(a) denote the starting and terminal vertex of an arrow a, respectively.) If $g_{ij}=1$, we also write $\alpha _{ij}$ instead of $\alpha _{ij}^{(1)}$. We call Q a quiver of type C. Let $Q^\circ := Q^\circ (C,\Omega )$ be the quiver obtained from Q by deleting all loops $\varepsilon _i$. Clearly, $Q^\circ$ is an acyclic quiver. Having said that, one might want to call $\Omega$ an acyclic orientation. Future research might require to modify the definition of an orientation and drop the acyclicity assumption.

Throughout let K be a field. For a quiver $Q = Q(C,\Omega )$ and a symmetrizer $D = {\text {diag}}(c_1,\ldots ,c_n)$ of C, let

$$\begin{aligned} H := H(C,D,\Omega ) := KQ/I \end{aligned}$$

where KQ is the path algebra of Q, and I is the ideal of KQ defined by the following relations:

• (${\mathbf {H}}1$) For each i we have the nilpotency relation

  $$\begin{aligned} \varepsilon _i^{c_i} = 0. \end{aligned}$$

• (${\mathbf {H}}2$) For each $(i,j) \in \Omega$ and each $1 \le g \le g_{ij}$ we have the commutativity relation

  $$\begin{aligned} \varepsilon _i^{f_{ji}}\alpha _{ij}^{(g)} = \alpha _{ij}^{(g)}\varepsilon _j^{f_{ij}}. \end{aligned}$$

The following remarks are straightforward.

• (i) H is a finite-dimensional K-algebra.

• (ii) H depends on the chosen symmetrizer D. But note that the relation (H2) does not depend on D.

• (iii) The relation (H2) becomes redundant for all $(i,j) \in \Omega$ with $k_{ij} = 1$.

• (iv) If C is symmetric and if D is minimal, then H is isomorphic to the path algebra $KQ^\circ$.

The behaviour of H under change of the symmetrizer D is studied in [33].

The opposite orientation of an orientation $\Omega$ is defined as $\Omega ^* := \{ (j,i) \mid (i,j) \in \Omega \}$. Let $\overline{\Omega } := \Omega \cup \Omega ^*$. For later use, let us define

$$\begin{aligned} \Omega (i,-)&:= \{ j \in Q_0 \mid (i,j) \in \Omega \},&\Omega (-,j)&:= \{ i \in Q_0 \mid (i,j) \in \Omega \},\\ \overline{\Omega }(i,-)&:= \{ j \in Q_0 \mid (i,j) \in \overline{\Omega } \},&\overline{\Omega }(-,j)&:= \{ i \in Q_0 \mid (i,j) \in \overline{\Omega } \}. \end{aligned}$$

Observe that $\overline{\Omega }(i,-) = \overline{\Omega }(-,i)$.

For $(i,j) \in \overline{\Omega }$ define

$$\begin{aligned} {\text {sgn}}(i,j) := {\left\{ \begin{array}{ll} 1 &{} \text {if } (i,j) \in \Omega ,\\ -1 &{} \text {if } (i,j) \in \Omega ^*. \end{array}\right. } \end{aligned}$$

For $Q = Q(C,\Omega )$ and a symmetrizer $D = {\text {diag}}(c_1,\ldots ,c_n)$ of C, we define an algebra

$$\begin{aligned} \Pi := \Pi (C,D,\Omega ) := K\overline{Q}/\overline{I} \end{aligned}$$

as follows. The double quiver $\overline{Q} = \overline{Q}(C)$ is obtained from Q by adding a new arrow $\alpha _{ji}^{(g)}:i \rightarrow j$ for each arrow $\alpha _{ij}^{(g)}:j \rightarrow i$ of $Q^\circ$. (Note that we did not add any new loops to the quiver Q.) The ideal $\overline{I}$ of the path algebra $K\overline{Q}$ is defined by the following relations:

• (P1) For each i we have the nilpotency relation

  $$\begin{aligned} \varepsilon _i^{c_i} = 0. \end{aligned}$$

• (P2) For each $(i,j) \in \overline{\Omega }$ and each $1 \le g \le g_{ij}$ we have the commutativity relation

  $$\begin{aligned} \varepsilon _i^{f_{ji}}\alpha _{ij}^{(g)} = \alpha _{ij}^{(g)}\varepsilon _j^{f_{ij}}. \end{aligned}$$

• (P3) For each i we have the mesh relation

  $$\begin{aligned} \sum _{j\in \overline{\Omega }(-,i)} \sum _{g=1}^{g_{ji}} \sum _{f=0}^{f_{ji}-1} {\text {sgn}}(i,j) \varepsilon _i^f\alpha _{ij}^{(g)} \alpha _{ji}^{(g)} \varepsilon _i^{f_{ji}-1-f} = 0. \end{aligned}$$

We call $\Pi$ a preprojective algebra of type C. Here are again some straightforward remarks:

• (i) Up to isomorphism, the algebra $\Pi := \Pi (C,D) := \Pi (C,D,\Omega )$ does not depend on the orientation $\Omega$ of C.

• (ii) In general, $\Pi$ can be infinite-dimensional.

• (iii) $\Pi$ depends on the chosen symmetrizer D. But note that the relations (P2) and (P3) do not depend on D.

• (iv) If C is symmetric and if D is minimal, then $\Pi$ is isomorphic to the classical preprojective algebra $\Pi (Q^\circ )$ associated with $Q^\circ$.

For an example illustrating the above definitions, see below Sect. 13.1.

1.5 Main results

Let $e_1,\ldots ,e_n$ be the idempotents in H (resp. $\Pi$) corresponding to the vertices of Q (resp. $\overline{Q}$). Define $H_i := e_iHe_i$. Clearly, $H_i$ is isomorphic to the truncated polynomial ring $K[\varepsilon _i]/(\varepsilon _i^{c_i})$. For each representation M of H or $\Pi$ we get an $H_i$-module structure on $M_i := e_iM$. The following definition is of central importance.

Definition 1.1

A module $M \in {\text {rep}}(H)$ or $M \in {\text {rep}}(\Pi )$ is called locally free if $M_i$ is a free $H_i$-module for every i.

Let ${\text {rep}}_\mathrm{l.f.}(H)$ (resp. ${\text {rep}}_\mathrm{l.f.}(\Pi )$) be the subcategory of all locally free $M \in {\text {rep}}(H)$ (resp. $M \in {\text {rep}}(\Pi )$).

Theorem 1.2

The algebra H is a 1-Iwanaga–Gorenstein algebra. For $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) ${\text {proj.~dim}}(M) \le 1$;

• (ii) ${\text {inj.~dim}}(M) \le 1$;

• (iii) ${\text {proj.~dim}}(M) < \infty$;

• (iv) ${\text {inj.~dim}}(M) < \infty$;

• (v) M is locally free.

Let M be a locally free module. For each $i\in Q_0$ let $r_i$ be the rank of the free $H_i$-module $M_i$. Thus $\dim _K(M_i) = r_ic_i$. We put

$$\begin{aligned} \underline{{\text {rank}}}(M) := (r_1,\ldots ,r_n). \end{aligned}$$

Let $\tau$ be the Auslander–Reiten translation for the algebra H, and let $\tau ^-$ be the inverse Auslander–Reiten translation. An indecomposable H-module M is preprojective (resp. preinjective) if there exists some $k \ge 0$ such that $M \cong \tau ^{-k}(P)$ (resp. $M \cong \tau ^k(I)$) for some indecomposable projective H-module P (resp. indecomposable injective H-module I). Let us warn the reader that the usual definition of a preprojective or preinjective module M requires some additional conditions on the Auslander–Reiten component containing M.

In general, the Auslander–Reiten translates $\tau ^k(M)$ of an indecomposable locally free H-module M are not locally free, see the example in Sect. 13.5. An indecomposable H-module M is called $\tau$-locally free, if $\tau ^k(M)$ is locally free for all $k \in \mathbb {Z}$.

A module M over an algebra A is called rigid if ${\text {Ext}}_A^1(M,M) = 0$.

The following result is an analogue for the algebras $H=H(C,D,\Omega )$ of Gabriel’s Theorem (1) for quivers and of its generalization by Dlab and Ringel to modulated graphs.

Theorem 1.3

There are only finitely many isomorphism classes of $\tau$-locally free H-modules if and only if C is of Dynkin type. In this case, the following hold:

• (i) The map $M \mapsto \underline{{\text {rank}}}(M)$ yields a bijection between the set of isomorphism classes of $\tau$-locally free H-modules and the set $\Delta ^+(C)$ of positive roots of the semisimple complex Lie algebra associated with C.

• (ii) For an indecomposable H-module M the following are equivalent:

  • (a) M is preprojective;

  • (b) M is preinjective;

  • (c) M is $\tau$-locally free;

  • (d) M is locally free and rigid.

Crawley-Boevey [21] studied representations of quivers over principal ideal domains. There are some striking analogies between Theorem 1.3 and his results.

Note that the algebras H are usually representation infinite, even if C is a Cartan matrix of Dynkin type with a minimal symmetrizer D. Already for C of type $B_3$ with minimal symmetrizer, there exist indecomposable locally free H-modules M with $\underline{{\text {rank}}}(M) \notin \Delta ^+(C)$, see Sect. 13.7. Furthermore, for C of type $B_5$ with minimal symmetrizer there exists a $K^*$-family of pairwise non-isomorphic indecomposable locally free H-modules, all having the same dimension vector.

Inspired by the classical theory for path algebras and modulated graphs we define Coxeter functors

$$\begin{aligned} C^+,C^-:{\text {rep}}(H) \rightarrow {\text {rep}}(H) \end{aligned}$$

as products of reflection functors, see Sect. 8. Let

$$\begin{aligned} T:{\text {rep}}(H) \rightarrow {\text {rep}}(H) \end{aligned}$$

be the twist automorphism induced from the algebra automorphism $H \rightarrow H$ defined by $\varepsilon _i \mapsto \varepsilon _i$ and $\alpha _{ij}^{(g)} \mapsto -\alpha _{ij}^{(g)}$. In other words, T sends a representation $(M_i,M(\alpha _{ij}^{(g)}),M(\varepsilon _i))$ of H to $(M_i,-M(\alpha _{ij}^{(g)}),M(\varepsilon _i))$. The following theorem, analogous to Gabriel’s Theorem (3), relates Coxeter functors to the Auslander–Reiten translation, and provides the main step in proving Theorem 1.3.

Theorem 1.4

For $M \in {\text {rep}}(H)$ there are functorial isomorphisms

$$\begin{aligned} {\text {D}}{\text {Ext}}_H^1(M,H) \cong TC^+(M) \text { and } {\text {Ext}}_H^1({\text {D}}(H),M) \cong TC^-(M). \end{aligned}$$

Furthermore, if $M \in {\text {rep}}_\mathrm{l.f.}(H)$, then there are functorial isomorphisms

$$\begin{aligned} \tau (M) \cong TC^+(M) \text { and } \tau ^{-}(M) \cong TC^-(M). \end{aligned}$$

Vice versa, if $\tau (M) \cong TC^+(M)$ or $\tau ^{-}(M) \cong TC^-(M)$ for some $M \in {\text {rep}}(H)$, then $M \in {\text {rep}}_\mathrm{l.f.}(H)$.

Recall that H is a 1-Iwanaga–Gorenstein algebra, and that ${\mathcal G}{\mathcal P}(H)$ denotes the subcategory of Gorenstein-projective H-modules.

Corollary 1.5

For $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) $C^+(M) = 0$;

• (ii) $M \in {\mathcal G}{\mathcal P}(H)$.

For an algebra A and an A-A-bimodule M, let $T_A(M)$ denote the corresponding tensor algebra. Theorem 1.4 implies the following description of the preprojective algebra $\Pi =\Pi (C,D)$ associated with H.

Theorem 1.6

$\Pi \cong T_H({\text {Ext}}_H^1({\text {D}}(H),H))$.

The algebra $\Pi$ contains H as a subalgebra in an obvious way. Let ${_H}\Pi$ be the algebra $\Pi$ considered as a left module over H. The following result says that ${_H}\Pi$ is isomorphic to the direct sum of all preprojective H-modules. This justifies that $\Pi$ is called a preprojective algebra.

Theorem 1.7

We have ${_H}\Pi \cong \bigoplus _{m \ge 0} \tau ^{-m}({_H}H)$. In particular, $\Pi$ is finite-dimensional if and only if C is of Dynkin type.

Finally, we obtain the following analogue for locally free $\Pi$-modules of the classical important Ext-symmetry of preprojective algebras.

Theorem 1.8

For $M,N \in {\text {rep}}_\mathrm{l.f.}(\Pi )$ we have a functorial isomorphism

$$\begin{aligned} {\text {Ext}}_\Pi ^1(M,N) \cong {\text {D}}{\text {Ext}}_\Pi ^1(N,M). \end{aligned}$$

1.6 Previous appearances of $H(C,D,\Omega )$

1.6.1. Let Q be a quiver without oriented cycles. Ringel and Zhang [51] study representations of Q over the algebra $A:=K[X]/(X^2)$ of dual numbers. This can be interpreted as the category of $\Lambda$-modules with $\Lambda := A\otimes _K KQ$. It is shown in [51] that $\Lambda$ is a 1-Iwanaga–Gorenstein algebra, and that the stable category of ${\mathcal G}{\mathcal P}(\Lambda )$ is triangle equivalent to the orbit category $D^b(KQ)/[1]$ of the bounded derived category $D^b(KQ)$ of the path algebra KQ modulo the shift functor [1]. In our setup, if we take symmetric Cartan matrices C with symmetrizer $D = {\text {diag}}(2,\ldots ,2)$, then the class of algebras $H(C,D,\Omega )$ coincides with the class of algebras studied by Ringel and Zhang. Fan [29] studies the Hall algebra of representations of Q over $K[X]/(X^m)$ with $m \ge 1$. Again this is a special case of our setup with C symmetric and $D = {\text {diag}}(m,\ldots ,m)$. For Q a quiver of type $A_2, A = K[X]/(X^m)$ and $\Lambda := A\otimes _K KQ$ the category ${\mathcal G}{\mathcal P}(\Lambda )$ is studied in work of Ringel and Schmidmeier [50]. Note also that in this case we have $\Lambda \cong T_2(A)$, where $T_2(A)$ is the algebra of upper triangular $2 \times 2$-matrices with entries in A. More generally, the algebras $T_2(A)$ with A a Nakayama algebra have been studied by Skowroński [53], and the algebras $T_n(A)$ have been studied by Leszczyński and Skowroński [42].

1.6.2. A general framework for studying cluster structures arising from 2-Calabi–Yau categories with loops has been provided by [16]. As an example they study the cluster category ${\mathcal C}:= D^b({\mathcal T}_n)/\tau ^-[1]$ of the mesh category of a tube ${\mathcal T}_n$ of rank $n \ge 2$. The endomorphism algebras of the maximal rigid objects in ${\mathcal C}$ have been studied by Vatne and Yang [54, 56]. It turns out that there exists a maximal rigid object T in ${\mathcal C}$ such that ${\text {End}}_{\mathcal C}(T)$ is isomorphic to one of our algebras $H(C,D,\Omega )$, where C is of Dynkin type $C_{n-1}$ and D is minimal. (We identify the types $C_1 = A_1$ and $C_2 = B_2$.)

1.6.3 Let Q be a Dynkin quiver of type $E_8$, and let $F := S^4\Sigma ^{-4}$, where S is the Serre functor and $\Sigma$ is the translation functor for the bounded derived category $D^b(KQ)$ of the path algebra KQ. Ladkani [41, Section 2.6] studies the orbit category ${\mathcal C}:= D^b(KQ)/F$. He shows that ${\mathcal C}$ is a triangulated 2-Calabi–Yau category containing exactly 6 cluster-tilting objects. Ladkani shows that ${\mathcal C}$ categorifies a cluster algebra of Dynkin type $G_2$. He also shows that the cluster tilting-objects in ${\mathcal C}$ have an endomorphism algebra isomorphic to $A = KQ/I$, where Q is a quiver of the form

and I is generated by $\varepsilon ^3$. Note that the algebras A are isomorphic to the algebras $H(C,D,\Omega )$ with C of type $G_2$ and D minimal.

1.7 Previous appearances of $\Pi (C,D)$

1.7.1 Let C be a Cartan matrix of Dynkin type. In [38], an algebra $A=A(C)$ was introduced, by means of an infinite quiver with potential. Certain finite-dimensional A-modules (the generic kernels $K^{(i)}_{k,m}$, see [38, Definition 4.5]) were shown to encode the q-characters of the Kirillov–Reshetikhin modules of the quantum loop algebra $U_q(L\mathfrak {g})$, where $\mathfrak {g}$ is the complex simple Lie algebra with Cartan matrix C. The connection with the algebras considered in this article is the following: Let $\widetilde{\Pi }(C)$ denote the algebra $K\overline{Q}/\widetilde{I}$, where $\widetilde{I}$ is the two-sided ideal defined by the relations (P2) and (P3) only. (Thus, the nilpotency relation (P1) is omitted.) Then A(C) is a truncation of a $\mathbb {Z}$-covering of $\widetilde{\Pi }(C^*)$, where $C^*$ is the transposed Cartan matrix, in other words, the Cartan matrix of the Langlands dual $\mathfrak {g}^L$ of $\mathfrak {g}$. In particular, for $m\ll 0$ the generic kernels $K^{(i)}_{c_i,m}$ of A(C) coincide with the indecomposable projective $\Pi (C^*,D)$-modules regarded as $\mathbb {Z}$-graded $\widetilde{\Pi }(C^*)$-modules (compare for instance [38, Section 6.5] to Fig. 11 below). This generalizes [38, Example 4.7].

1.7.2 The algebras $\widetilde{\Pi }(C)$ mentioned in Sect. 1.7.1 were defined and studied independently by Cecotti [18, Section 3.4] and Cecotti and del Zotto [19, Section 5.1]. In [18] they are called generalized preprojective algebras.

1.7.3 For $(C,\Omega )$ let

$$\begin{aligned} W(C,\Omega ) := \sum _{(j,i) \in \overline{\Omega }} \sum _{g=1}^{g_{ji}} {\text {sgn}}(i,j) \varepsilon _i^{f_{ji}}\alpha _{ij}^{(g)} \alpha _{ji}^{(g)}. \end{aligned}$$

Then the cyclic derivatives of the potential $W(C,\Omega )$ yield the defining relations (P2) and (P3) of $\Pi (C,D)$, compare [18, 19, 38], where these relations are also encoded via potentials.

1.7.4 After the first version of this article appeared on arXiv, we were informed by D. Yamakawa of the following connection between $\Pi (C,D)$ and some quiver varieties for quivers with multiplicities introduced in [55]. Suppose that C is a generalized Cartan matrix of the form $C = (c_{ij}) = 2I_n - AD$, where $I_n$ is the unit matrix, $A=(a_{ij})$ is a symmetric matrix with $a_{ij}\in \mathbb {N}$ and $a_{ii}=0$, and $D = {\text {diag}}(c_1,\ldots ,c_n)$ with positive integers $c_i$. Then C is symmetrizable with symmetrizer D. (Note that not every symmetrizable Cartan matrix is of this form. For instance Cartan matrices of type $C_n$ are of this form, but not Cartan matrices of type $B_n$.) Assume further that $k_{ij} = \gcd (c_i,c_j) = 1$ whenever $c_{ij} < 0$. Then the defining relations (P2) of $\Pi (C,D)$ are redundant, and the mesh relations (P3) can be regarded as the vanishing of the moment map of some Hamiltonian space considered in [55]. As a result, in this case, the isomorphism classes of locally free $\Pi (C,D)$-modules of rank vector ${\mathbf r}$ are parametrized by the set theoretical quotient $\mathcal {N}^{\mathrm set}(\mathbf {r},0)$ of [55].

1.8 Future directions

This article intends to provide the foundation for generalizing many of the connections between path algebras, preprojective algebras, Lie algebras and cluster algebras from the symmetric to the symmetrizable case.

In particular, since the algebras H and $\Pi$ are defined via quivers with relations, one can study their module varieties over an arbitrary field K. Taking $K=\mathbb {C}$, one can hope to generalize Lusztig’s nilpotent varieties and Nakajima quiver varieties from the symmetric to the symmetrizable case.

As a first step in this direction, in [34] we construct the enveloping algebra of the positive part of an arbitrary simple finite-dimensional complex Lie algebra as an algebra of constructible functions on varieties of locally free H-modules.

1.9 Outline

The article is organized as follows. In Sect. 2 we recall some definitions and basic facts on Cartan matrices, quadratic forms and Weyl groups. A description of the projective and injective H-modules and some fundamental results on locally free H-modules are obtained in Sect. 3. In particular, Sect. 3 contains the proof of Theorem 1.2 (combine Proposition 3.5 and Corollary 3.7). In Sect. 4 we show that the quadratic form $q_C$ associated with a Cartan matrix C coincides with the restriction of the homological Euler form of H to the subcategory of locally free H-modules. The representation theory of the algebras H and $\Pi$ can be reformulated in terms of a generalization of the representation theory of modulated graphs. This point of view, which is of central importance for proving (and in part also for formulating) our main results, is explained in Sect. 5. An interpretation of H and $\Pi$ as tensor algebras is discussed in Sect. 6. Section 7 provides a bimodule resolution of H. In Sect. 8 we introduce a trace pairing for $H_i$-modules and relate it with the adjunction isomorphisms. Section 9 contains some fundamental properties of generalizations of BBK-reflection functors to our algebras $\Pi$. (The letters BBK stand for Baumann and Kamnitzer [8, 9] and Bolten [12]. Independently from each other they introduced reflection functors for the classical preprojective algebras associated with quivers.) The reflection functors for $\Pi$ restrict to reflection functors for H. We show that the latter are generalized versions of APR-tilting functors. The intimate relation between Coxeter functors and the Auslander–Reiten translation for H is studied in Sect. 10. Theorem 1.4 follows from Theorem 10.1 and Proposition 11.9. We also prove some crucial properties of the algebras $\Pi$. In particular, Theorem 1.6 corresponds to Corollary 10.6. In Sect. 11 we use the previous constructions for proving Theorem 1.3 (see Theorem 11.10). The proof of Theorem 1.7 can be found in Sect. 11.3. We also obtain some first results on the Auslander–Reiten theory of H. Section 12 contains the construction of a bimodule resolution for $\Pi$. This resolution plays an important part in the study of locally free representations. In particular, Sect. 12.2 contains the proof of Theorem 1.8 (see Theorem 12.6). Finally, Sect. 13 contains a collection of examples.

1.10 Notation

By a subcategory we always mean a full subcategory which is closed under isomorphisms and direct summands. By an algebra we mean an associative K-algebra with 1. For a K-algebra A let ${\text {mod}}(A)$ be the category of finite-dimensional left A-modules. If $A = KQ/I$ is the path algebra of a quiver Q modulo some ideal I, then ${\text {rep}}(A)$ denotes the category of finite-dimensional representations of (Q, I). By definition these are the representations of Q which are annihilated by I. We often identify ${\text {mod}}(A)$ and ${\text {rep}}(A)$. Let ${\text {proj}}(A)$ and ${\text {inj}}(A)$ be the full subcategories of ${\text {rep}}(A)$ with objects the projective and injective A-modules, respectively. Let ${\text {D}}:= {\text {Hom}}_K(-,K)$ be the usual K-duality. For a finite-dimensional algebra A let $\tau (-) = \tau _A(-)$ be the Auslander–Reiten translation of A. For a module X we denote by ${\text {add}}(X)$ the subcategory of modules which are isomorphic to finite direct sums of direct summands of X. As a general reference for the representation theory of finite-dimensional algebras we refer to the books [5, 47]. The composition of maps $f:X \rightarrow Y$ and $g:Y \rightarrow Z$ is denoted by $gf:X \rightarrow Z$. For arrows $\alpha :i \rightarrow j$ and $\beta :j \rightarrow k$ in a quiver, we write their composition as $\beta \alpha :i \rightarrow k$. By $\mathbb {N}$ we denote the natural numbers including 0.

2 Cartan matrices and the Weyl group

2.1 Cartan matrices and valued graphs

Let $C = (c_{ij}) \in M_n(\mathbb {Z})$ be a Cartan matrix, and let $D = {\text {diag}}(c_1,\ldots ,c_n)$ be a symmetrizer of C. The valued graph $\Gamma (C)$ of C has vertices $1,\ldots ,n$ and an (unoriented) edge between i and j if and only if $c_{ij} < 0$. An edge has value $(|c_{ji}|,|c_{ij}|)$. In this case, we display this valued edge as

and we just write if $(|c_{ji}|,|c_{ij}|) = (1,1)$.

A Cartan matrix C is connected if $\Gamma (C)$ is a connected graph. In this case, the symmetrizer D is uniquely determined up to multiplication with a positive integer. More precisely, if D is a minimal symmetrizer of a connected Cartan matrix C, then the other symmetrizers of C are given by mD with $m \ge 1$.

2.2 The quadratic form

Define the quadratic form $q_C:\mathbb {Z}^n \rightarrow \mathbb {Z}$ of C by

$$\begin{aligned} q_C := \sum _{i=1}^n c_i X_i^2 - \sum _{i<j} c_i|c_{ij}| X_iX_j. \end{aligned}$$

(Recall that $c_i|c_{ij}| = c_j|c_{ji}|$.) The quadratic form $q_C$ plays a crucial role in the representation theory of the quivers of Cartan type C and more generally of the species (see for example [26]) of type C.

A Cartan matrix C is of Dynkin or Euclidean type if $q_C$ is positive definite or positive semidefinite, respectively. It is well known that C is of Dynkin type if and only if $\Gamma (C)$ is a disjoint union of Dynkin graphs. (The Dynkin graphs are listed in Sect. 13.2.)

2.3 The Weyl group

As before let $C = (c_{ij})$ be a Cartan matrix, and let $\alpha _1,\ldots ,\alpha _n$ be the positive simple roots of the Kac–Moody algebra $\mathfrak {g}(C)$ associated with C. For $1 \le i,j \le n$ define

$$\begin{aligned} s_i(\alpha _j) := \alpha _j - c_{ij} \alpha _i. \end{aligned}$$

This yields a reflection $s_i:\mathbb {Z}^n \rightarrow \mathbb {Z}^n$ on the root lattice

$$\begin{aligned} \mathbb {Z}^n = \sum _{i=1}^n \mathbb {Z}\alpha _i \end{aligned}$$

where we identify $\alpha _i$ with the ith standard basis vector of $\mathbb {Z}^n$. The Weyl group W(C) of $\mathfrak {g}(C)$ is the subgroup of $\mathrm{Aut}(\mathbb {Z}^n)$ generated by $s_1,\ldots ,s_n$. The Weyl group is finite if and only if C is of Dynkin type.

2.4 Roots

Let

$$\begin{aligned} \Delta _\mathrm{re}(C) := \bigcup _{i=1}^n W(\alpha _i) \end{aligned}$$

be the set of real roots of C.

Let

$$\begin{aligned} (-,-)_C:\mathbb {Z}^n \times \mathbb {Z}^n \rightarrow \mathbb {Z}\end{aligned}$$

be the symmetric bilinear form of C defined by $(\alpha _i,\alpha _j)_C := c_ic_{ij}$. The fundamental region of C is defined by

$$\begin{aligned} F := \{ d \in \mathbb {N}^n \mid d \not = 0,\; \mathrm{supp}(d) \text { connected}, (d,\alpha _i)_C \le 0 \text { for all } 1 \le i \le n \}, \end{aligned}$$

where $\mathrm{supp}(d)$ is the full subgraph of $\Gamma (C)$ given by the vertices i with $d_i \not = 0$. Then

$$\begin{aligned} \Delta _\mathrm{im}(C) := W(F) \cup W(-F) \end{aligned}$$

is the set of imaginary roots of C.

Let

$$\begin{aligned} \Delta _\mathrm{re}^+(C) := \Delta _\mathrm{re}(C) \cap \mathbb {N}^n\quad \text {and}\quad \Delta _\mathrm{im}^+(C) := \Delta _\mathrm{im}(C) \cap \mathbb {N}^n \end{aligned}$$

be the set of positive real roots and positive imaginary roots, respectively. It turns out that

$$\begin{aligned} \Delta _\mathrm{re}(C) = \Delta _\mathrm{re}^+(C) \cup -\Delta _\mathrm{re}^+(C) \quad \text {and}\quad \Delta _\mathrm{im}(C) = \Delta _\mathrm{im}^+(C) \cup -\Delta _\mathrm{im}^+(C). \end{aligned}$$

Finally, let

$$\begin{aligned} \Delta (C) := \Delta _\mathrm{re}(C) \cup \Delta _\mathrm{im}(C) \end{aligned}$$

be the set of roots of C, and

$$\begin{aligned} \Delta ^+(C) := \Delta (C) \cap \mathbb {N}^n = \Delta _\mathrm{re}^+(C) \cup \Delta _\mathrm{im}^+(C) \end{aligned}$$

is the set of positive roots.

By definition, for $w \in W(C)$ and $d \in \Delta (C)$ we have $w(d) \in \Delta (C)$. We have $q_C(d) = c_i$ if $d \in W(\alpha _i)$ is a real root, and $q_C(d) \le 0$ if d is an imaginary root. The following are equivalent:

• (i) C is of Dynkin type;

• (ii) $\Delta (C)$ is finite;

• (iii) $\Delta _\mathrm{re}(C) = \Delta (C)$.

2.5 Coxeter transformations

For an orientation $\Omega$ of C and some $1 \le i \le n$ let

$$\begin{aligned} s_i(\Omega ) := \{ (r,s) \in \Omega \mid i \notin \{r,s\} \} \cup \{ (s,r) \in \Omega ^* \mid i \in \{r,s\} \}. \end{aligned}$$

If i is a sink or source in $Q^\circ (C,\Omega )$, then $s_i(\Omega )$ is again an orientation of C. A sequence ${\mathbf i}= (i_1,\ldots ,i_n)$ is a $+$-admissible sequence for $(C,\Omega )$ if $\{i_1,\ldots ,i_n\} = \{1,\ldots ,n\}, i_1$ is a sink in $Q^\circ (C,\Omega )$ and $i_k$ is a sink in the acyclic quiver $Q^\circ (C,s_{i_{k-1}} \cdots s_{i_1}(\Omega ))$ for $2 \le k \le n$. For such a sequence ${\mathbf i}$ let

$$\begin{aligned} \beta _{{\mathbf i},k} := \beta _k := {\left\{ \begin{array}{ll} \alpha _{i_1} &{} \quad \text {if }\quad k=1,\\ s_{i_1}s_{i_2} \cdots s_{i_{k-1}}(\alpha _{i_k}) &{} \quad \text {if } \quad 2 \le k \le n \end{array}\right. } \end{aligned}$$

where $s_1,\ldots ,s_n \in W(C)$. Similarly, define

$$\begin{aligned} \gamma _{{\mathbf i},k} := \gamma _k := {\left\{ \begin{array}{ll} s_{i_n} \cdots s_{i_{k+1}}(\alpha _{i_k}) &{} \quad \text {if } \quad 1 \le k \le n-1,\\ \alpha _{i_n} &{} \quad \text {if } \quad k=n. \end{array}\right. } \end{aligned}$$

Let

$$\begin{aligned} c^+ : = s_{i_n}s_{i_{n-1}} \cdots s_{i_1}:\mathbb {Z}^n \rightarrow \mathbb {Z}^n \text { and } c^- : = s_{i_1}s_{i_2} \cdots s_{i_n}:\mathbb {Z}^n \rightarrow \mathbb {Z}^n. \end{aligned}$$

be the Coxeter transformations. For $k \in \mathbb {Z}$ we set

$$\begin{aligned} c^k := {\left\{ \begin{array}{ll} (c^+)^k&{} \quad \text {if }\quad k > 0,\\ (c^-)^{-k}&{} \quad \text {if } \quad k < 0,\\ {\text {id}}&{} \quad \text {if } k=0. \end{array}\right. } \end{aligned}$$

We get

$$\begin{aligned} c^+(\beta _{{\mathbf i},k})&= (s_{i_n}s_{i_{n-1}} \cdots s_{i_1})(s_{i_1}s_{i_2} \cdots s_{i_{k-1}}(\alpha _{i_k}))\\&= s_{i_n}s_{i_{n-1}} \cdots s_{i_k}(\alpha _{i_k})\\&= - s_{i_n}s_{i_{n-1}} \cdots s_{i_{k+1}}(\alpha _{i_k})\\&= - \gamma _{{\mathbf i},k}. \end{aligned}$$

The following two lemmas are well known. For example, they are a consequence of the study of preprojective and preinjective representations of species without oriented cycles.

Lemma 2.1

Suppose C is not of Dynkin type. Then the elements $c^{-r}(\beta _i)$ and $c^s(\gamma _j)$ with $r,s \ge 0$ and $1 \le i,j \le n$ are pairwise different elements in $\Delta _\mathrm{re}^+(C)$.

Let C be of Dynkin type. For $1 \le i \le n$ let $p_i \ge 1$ be minimal with $c^{-{p_i}}(\beta _i) \notin \mathbb {N}^n$, and let $q_j \ge 1$ be minimal such that $c^{q_j}(\gamma _j) \notin \mathbb {N}^n$. It is well known that such $p_i$ and $q_j$ exist. The elements $c^{-r}(\beta _i)$ with $1 \le i \le n$ and $0 \le r \le p_i-1$ are pairwise different, and the elements $c^s(\gamma _j)$ with $1 \le j \le n$ and $0 \le s \le q_j-1$ are pairwise different.

Lemma 2.2

Assume that C is of Dynkin type. Then

$$\begin{aligned} \Delta ^+(C)= & {} \{ c^{-r}(\beta _i) \mid 1 \le i \le n,\, 0 \le r \le p_i-1 \} = \{ c^s(\gamma _j) \mid 1\nonumber \\&\le j \le n,\, 0 \le s \le q_j-1 \}. \end{aligned}$$

3 Locally free H-modules

For the whole section, let $H = H(C,D,\Omega )$ and $Q = Q(C,\Omega )$ as defined in Sect. 1.4.

3.1 Modules defined by idempotents

Let $M \in {\text {rep}}(H)$. For $1 \le i \le n$ let $M_i := e_iM$. The H-module structure on M is described by the spaces $M_i$ with $1 \le i \le n$ and by K-linear maps $M(\alpha ):M_{s(\alpha )} \rightarrow M_{t(\alpha )}$ with $\alpha$ running through the arrows of the quiver Q. (Of course, these maps need to satisfy the defining relations for H.)

For a non-empty subset J of $\{ 1,\ldots ,n \}$ let $e := \sum _{j \in J} e_j$. Thus e is an idempotent in H. We get a vector space decomposition

$$\begin{aligned} eM = \bigoplus _{j \in J} M_j. \end{aligned}$$

For $1 \le i \le n$ we set

$$\begin{aligned} (eM)_i := {\left\{ \begin{array}{ll} M_i &{} \quad \text {if } \quad i \in J, \\ 0 &{} \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

and for each arrow $\alpha$ of Q we define a map $(eM)(\alpha ):(eM)_{s(\alpha )} \rightarrow (eM)_{t(\alpha )}$ by

$$\begin{aligned} (eM)(\alpha ) := {\left\{ \begin{array}{ll} M(\alpha ) &{} \quad \text {if } s(\alpha ), \quad t(\alpha ) \in J, \\ 0 &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

This defines an H-module structure on eM. This follows from the nature of the defining relations for H. Namely, for a given i, there are no relations passing through i, i.e. any of the relations either starts in i, ends in i, or does not involve i.

3.2 Description of the projective and injective modules

The algebra H is by definition a path algebra modulo an admissible ideal generated by zero relations and commutativity relations. This implies that each indecomposable projective H-module $P_i := He_i$ has a basis $B_i$ with the following properties: For each path p in Q and each $b \in B_i$ we have $p \cdot b \in B_i \cup \{0\}$. In particular, we can visualize $P_i$ by drawing a graph with vertices the elements in $B_i$, and an arrow $b \xrightarrow {a} b'$ if for an arrow $a \in Q_1$ and $b,b' \in B_i$ we have $a \cdot b = b'$. We say that $P_i$ has a multiplicative basis. Similarly, the indecomposable injective H-modules $I_i := {\text {D}}(e_iH)$ have a multiplicative basis.

Let i be a vertex of Q. We define an H-module ${_-}H_i$ as follows: A basis of $e_i{_-}H_i$ is given by vectors $a_{i,c}$ with $1 \le c \le c_i$, and for $j \in \Omega (-,i)$ a basis of $e_j{_-}H_i$ is given by vectors $b_{j,c}^{f,g}$ with $1 \le c \le c_j, 1 \le f \le f_{ji}$ and $1 \le g \le g_{ji}$, and for $s \notin \Omega (-,i)$ define $e_s{_-}H_i := 0$. The arrows of Q act as follows:

$$\begin{aligned} \varepsilon _ia_{i,c}&:= {{\left\{ \begin{array}{ll} a_{i,c-1} &{} \quad \text {if } \quad c\ge 2,\\ 0 &{} \quad \text {if } \quad c=1, \end{array}\right. }}\\ \varepsilon _jb_{j,c}^{f,g}&:= {{\left\{ \begin{array}{ll} b_{j,c-1}^{f,g} &{} \quad \text {if } \quad c\ge 2,\\ 0 &{} \quad \text {if } \quad c=1, \end{array}\right. }} \end{aligned}$$

and for $0 \le k< k_{ji}, 0 \le f < f_{ji}$ and $1 \le g \le g_{ji}$ we have

$$\begin{aligned} \alpha _{ji}^{(g)} a_{i,c_i-f-kf_{ji}} := b_{j,c_j-kf_{ij}}^{f_{ji}-f,g}. \end{aligned}$$

For $c_i=9, c_j=6, f_{ji}=3, f_{ij}=2$ (and therefore $k_{ji} = 3$) we display a part of the module $(e_i+e_j){_-}H_i$ in Fig. 1.

Fig. 1

Construction of the H-module $(e_i+e_j){_-}H_i$ with $c_i=9, c_j=6, f_{ji}=3, f_{ij}=2$ and $k_{ji} = 3$

The module ${_-}H_i$ has one i-column with basis $(a_{i,1},\ldots ,a_{i,c_i})$, and for each $j \in \Omega (-,i)$ it has a j-column with basis $(b_{j,1}^{f,g},\ldots ,b_{j,c_j}^{f,g})$ for each $1 \le f \le f_{ji}$ and each $1 \le g \le g_{ji}$. By definition we have

$$\begin{aligned} \dim {_-}H_i = c_i + \sum _{j \in \Omega (-,i)} f_{ji}g_{ji}c_j. \end{aligned}$$

The number of j-columns of ${_-}H_i$ is $f_{ji}g_{ji} = |c_{ji}|$.

Suppose j is a sink in $Q^\circ$. The module $P_j = e_jP_j$ has a basis $a_{j,1},\ldots ,a_{j,c_j}$ such that

$$\begin{aligned} \varepsilon _ja_{j,c} := {\left\{ \begin{array}{ll} a_{j,c-1} &{} \quad \text {if } \quad c\ge 2,\\ 0 &{} \quad \text {if } c=1, \end{array}\right. }. \end{aligned}$$

Then $(a_{j,1},\ldots ,a_{j,c_j})$ is the j-column of $P_j$.

Next, assume that i is a vertex of Q such that for each $j \in \Omega (-,i)$ the projective module $P_j$ is already constructed, and $P_j$ has a distinguished basis including a j-column $(a_{j,1},\ldots ,a_{j,c_j})$, which forms a basis of $e_jP_j$.

Then $P_i$ is constructed as follows: We take for each $j \in \Omega (-,i), 1 \le f \le f_{ji}$ and $1 \le g \le g_{ji}$ a copy $P_j^{f,g}$ of $P_j$ and identify the j-column $(b_{j,1}^{f,g},\ldots ,b_{j,c_j}^{f,g})$ of ${_-}H_i$ with the j-column $(a_{j,1},\ldots ,a_{j,c_j})$ of $P_j^{f,g}$. The resulting module is our indecomposable projective H-module $P_i$, and by definition its i-column is the i-column $(a_{i,1},\ldots ,a_{i,c_i})$ of the module ${_-}H_i$.

The indecomposable injective H-modules $I_j$ are constructed dually by gluing modules ${_j}H_-$, which are dual to the modules ${_-}H_i$. Again, for $c_i=9, c_j=6, f_{ji}=3, f_{ij}=2$ and $k_{ji} = 3$ we display a part of the module $(e_i+e_j){_j}H_-$ in Fig. 2.

Fig. 2

Construction of the H-module $(e_i+e_j){_j}H_-$ with $c_i=9, c_j=6, f_{ji}=3, f_{ij}=2$ and $k_{ji} = 3$

Recall that the notion of a locally free module can be found in Definition 1.1. Let $S_1,\ldots ,S_n$ be the simple H-modules with $\underline{\dim }(S_i) = \alpha _i$, and let $E_1,\ldots ,E_n$ be the (indecomposable) locally free H-modules with $\underline{{\text {rank}}}(E_i) = \alpha _i$. (Here $\alpha _1,\ldots ,\alpha _n$ is the standard basis of $\mathbb {Z}^n$.) We refer to the $E_i$ as the generalized simple H-modules. Thus $E_i$ corresponds to the regular representation of $H_i$. More precisely, we have $E_i = e_iE_i$, and $e_iE_i$ has a basis $a_{i,1},\ldots ,a_{i,c_i}$ such that

$$\begin{aligned} \varepsilon _ia_{i,c} := {\left\{ \begin{array}{ll} a_{i,c-1} &{} \quad \text {if } \quad c\ge 2,\\ 0 &{} \quad \text {if } c=1. \end{array}\right. } \end{aligned}$$

In particular, if i is a sink in $Q^\circ (C,\Omega )$, then $E_i = P_i$. Dually, if i is a source in $Q^\circ (C,\Omega )$, then $E_i = I_i$.

It follows from our construction of $P_i$ and $I_i$ that these modules are locally free. Furthermore, we get the following result, which again follows directly from our construction.

Proposition 3.1

For every $i\in Q_0$, the canonical exact sequence

$$\begin{aligned} 0 \rightarrow \bigoplus _{j \in \Omega (-,i)} P_j^{|c_{ji}|} \rightarrow P_i \rightarrow E_i \rightarrow 0 \end{aligned}$$

is a minimal projective resolution of $E_i$, and the canonical exact sequence

$$\begin{aligned} 0 \rightarrow E_i \rightarrow I_i \rightarrow \bigoplus _{j \in \Omega (i,-)} I_j^{|c_{ji}|} \rightarrow 0 \end{aligned}$$

is a minimal injective resolution of $E_i$.

3.3 Example

Let

with symmetrizer $D = {\text {diag}}(4,2,2)$ and $\Omega = \{ (2,1), (3,2) \}$. Thus C is a Cartan matrix of type $C_3$. Then $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1^4 = 0, \varepsilon _2^2 = \varepsilon _3^2 = 0, \varepsilon _2\alpha _{21} = \alpha _{21}\varepsilon _1^2$ and $\varepsilon _3\alpha _{32} = \alpha _{32}\varepsilon _2$. The indecomposable projective H-module $P_1$ and the indecomposable injective H-module $I_3$ are displayed in Fig. 3. The modules $P_2$ and $P_3$ are submodules of $P_1$, and $I_1$ and $I_2$ are factor modules of $I_3$.

Fig. 3

A projective and an injective H-module for type $C_3$

3.4 The rank vectors of projective and injective modules

Assume that ${\mathbf i}= (i_1,\ldots ,i_n)$ is a $+$-admissible sequence for $(C,\Omega )$. Without loss of generality, assume that $i_k = k$ for $1 \le k \le n$. Recall that we defined some positive roots $\beta _k,\gamma _k \in \Delta _\mathrm{re}^+(C)$ in Sect. 2.5.

Lemma 3.2

We have $\underline{{\text {rank}}}(P_k) = \beta _k$.

Proof

By our construction of the indecomposable projective H-modules $P_i$ we get

$$\begin{aligned} \underline{{\text {rank}}}(P_k)&= \underline{{\text {rank}}}(E_k) + \sum _{j \in \Omega (-,k)} g_{jk}f_{jk} \underline{{\text {rank}}}(P_j) \\&= \underline{{\text {rank}}}(E_k) + \sum _{j \in \Omega (-,k)} |c_{jk}| \underline{{\text {rank}}}(P_j). \end{aligned}$$

For $k=1$ we have $P_k \cong E_k$. Thus we have $\underline{{\text {rank}}}(P_k) = \alpha _1 = \beta _1$. For $k \ge 2$ we have

$$\begin{aligned} \beta _k&= s_1 \cdots s_{k-2}(\alpha _k-c_{k-1,k}\alpha _{k-1})\\&= s_1 \cdots s_{k-2}(\alpha _k) - c_{k-1,k}\beta _{k-1}\\&= \alpha _k - \sum _{j \in \Omega (-,k)} c_{jk} \beta _j\\&= \alpha _k + \sum _{j \in \Omega (-,k)} |c_{jk}| \beta _j \end{aligned}$$

The claim follows by induction. $\square$

The proof of the next result is similar to the proof of Lemma 3.2.

Lemma 3.3

We have $\underline{{\text {rank}}}(I_k) = \gamma _k$.

As a consequence of Lemmas 3.2 and 3.3 we get the following result.

Proposition 3.4

We have $\underline{{\text {rank}}}(P_i),\underline{{\text {rank}}}(I_i) \in \Delta _\mathrm{re}^+(C)$.

3.5 The Coxeter matrix

The Cartan matrix $C_H$ of H is the $(n\times n)$-matrix with kth column the dimension vector $\underline{\dim }(P_k), 1 \le k \le n$. (This is not to be confused with the Cartan matrix C.) It follows that the kth row of $C_H$ is $\underline{\dim }(I_k), 1 \le k \le n$, see for example [48, Section 2.4, p.70]. The matrix $C_H$ is invertible over $\mathbb {Q}$ (but not necessarily over $\mathbb {Z}$). (We can choose a numbering of the vertices of $Q(C,\Omega )$ such that $C_H$ is an upper triangular matrix with only non-zero entries on the diagonal.) The Coxeter matrix of H is defined as

$$\begin{aligned} \Phi _H := -C_H^TC_H^{-1} \end{aligned}$$

where $C_H^T$ denotes the transpose of $C_H$. It follows that

$$\begin{aligned} \Phi _H(\underline{\dim }(P_k)) = - \underline{\dim }(I_k) \end{aligned}$$

(Here we treat $\underline{\dim }(P_k)$ as a column vector.)

Next, let $C_{H,P}$ be the $(n\times n)$-matrix with kth column the rank vector $\underline{{\text {rank}}}(P_k)$, and let $C_{H,I}$ be the $(n\times n)$-matrix with kth row the rank vector $\underline{{\text {rank}}}(I_k), 1 \le k \le n$. We have

$$\begin{aligned} C_{H,P} = D^{-1}C_H \text { and } C_{H,I} = C_HD^{-1}. \end{aligned}$$

We get

$$\begin{aligned} D^{-1}\Phi _HD = -D^{-1}C_H^TC_H^{-1}D = - C_{H,I}^TC_{H,P}^{-1} \end{aligned}$$

and this matrix satisfies

$$\begin{aligned} D^{-1}\Phi _HD(\underline{{\text {rank}}}(P_k)) := -\underline{{\text {rank}}}(I_k). \end{aligned}$$

Thus by Lemmas 3.2 and 3.3 we can identify $D^{-1}\Phi _HD$ with the Coxeter transformation $c^+$.

3.6 Homological characterization of locally free modules

Proposition 3.5

For $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) ${\text {proj.~dim}}(M) \le 1$;

• (ii) ${\text {inj.~dim}}(M) \le 1$;

• (iii) ${\text {proj.~dim}}(M) < \infty$;

• (iv) ${\text {inj.~dim}}(M) < \infty$;

• (v) M is locally free.

Proof

For $M= 0$, all properties $\mathrm{(i)},\ldots ,\mathrm{(v)}$ hold. Thus we assume that M is non-zero.

Let M be locally free. Then there exists a vertex i of the quiver $Q(C,\Omega )$ of H such that $e_iM \not = 0$ and $e_jM = 0$ for all $j \in \Omega (-,i)$. (Here we used that $Q^\circ (C,\Omega )$ is acyclic.) It follows that $e_iM$ is a submodule of M, and $(1-e_i)M$ is isomorphic to the factor module $M/e_iM$ of M. So we get a short exact sequence

$$\begin{aligned} 0 \rightarrow e_iM \rightarrow M \rightarrow (1-e_i)M \rightarrow 0 \end{aligned}$$

of H-modules. Note that $e_iM$ and $(1-e_i)M$ are both locally free. If $(1-e_i)M = 0$, then $e_iM = M$. In this case, we have $M \cong E_i^m$ for some $m \ge 1$, and Proposition 3.1 yields that $\mathrm{(i)},\ldots ,\mathrm{(iv)}$ hold for M. If $(1-e_i)M \not = 0$, then by induction on the dimension we get that $\mathrm{(i)},\ldots ,\mathrm{(iv)}$ hold for $e_iM$ and for $(1-e_i)M$. Now one uses long exact homology sequences associated with the short exact sequence above to show that $\mathrm{(i)},\ldots ,\mathrm{(iv)}$ also hold for M.

Next, assume that M is not locally free. Let i be a vertex of Q such that $e_iM$ is not a free $H_i$-module. Any projective resolution

$$\begin{aligned} \cdots \rightarrow P_2 \rightarrow P_1 \rightarrow P_0 \rightarrow M \rightarrow 0 \end{aligned}$$

(3.1)

of M yields a projective resolution of $H_i$-modules

$$\begin{aligned} \cdots \rightarrow e_iP_2 \rightarrow e_iP_1 \rightarrow e_iP_0 \rightarrow e_iM \rightarrow 0. \end{aligned}$$

(3.2)

But $H_i$ is a selfinjective algebra, and $e_iM$ is not a projective $H_i$-module. Thus the resolution (3.2) and therefore also the resolution (3.1) has to be infinite. This implies ${\text {proj.~dim}}(M) = \infty$. Dually, one shows that ${\text {inj.~dim}}(M) = \infty$. $\square$

For a finite-dimensional algebra A, let $\tau = \tau _A$ denote its Auslander–Reiten translation. Recall that for $X,Y \in {\text {mod}}(A)$ there are functorial isomorphisms

$$\begin{aligned} {\text {Ext}}_A^1(X,Y) \cong {\text {D}}\overline{{\text {Hom}}}_A(Y,\tau (X)) \cong {\text {D}}\underline{{\text {Hom}}}_A(\tau ^-(Y),X), \end{aligned}$$

see for example [48, Section 2.4] for details. These isomorphisms are often referred to as Auslander–Reiten formulas. If ${\text {proj.~dim}}(X) \le 1$, we get a functorial isomorphism

$$\begin{aligned} {\text {Ext}}_A^1(X,Y) \cong {\text {D}}{\text {Hom}}_A(Y,\tau (X)), \end{aligned}$$

and if ${\text {inj.~dim}}(Y) \le 1$, then

$$\begin{aligned} {\text {Ext}}_A^1(X,Y) \cong {\text {D}}{\text {Hom}}_A(\tau ^-(Y),X). \end{aligned}$$

Recall that an A-module X is $\tau$-rigid (resp. $\tau ^-$-rigid) if ${\text {Hom}}_A(X,\tau (X)) = 0$ (resp. ${\text {Hom}}_A(\tau ^-(X),X) = 0$) [1]. Clearly, if X is $\tau$-rigid or $\tau ^-$-rigid, then X is rigid.

Corollary 3.6

For $M \in {\text {rep}}_\mathrm{l.f.}(H)$ the following are equivalent:

• (i) M is rigid;

• (ii) M is $\tau$-rigid;

• (iii) M is $\tau ^-$-rigid.

Combining Propositions 3.1 and 3.5 yields the following result.

Corollary 3.7

The algebra H is a 1-Iwanaga–Gorenstein algebra.

Lemma 3.8

The subcategory ${\text {rep}}_\mathrm{l.f.}(H)$ is closed under extensions, kernels of epimorphisms and cokernels of monomorphisms.

Proof

Let

$$\begin{aligned} 0 \rightarrow X \xrightarrow {f} Y \xrightarrow {g} Z \rightarrow 0 \end{aligned}$$

be a short exact sequence in ${\text {rep}}(H)$. For each $1 \le i \le n$ this induces a short exact sequence

$$\begin{aligned} 0 \rightarrow e_iX \rightarrow e_iY \rightarrow e_iZ \rightarrow 0 \end{aligned}$$

of $H_i$-modules. Recall that $M \in {\text {rep}}(H)$ is locally free if and only if $e_iM$ is a projective (and therefore also an injective) $H_i$-module for all i. It follows that if any two of the three modules $e_iX, e_iY$ and $e_iZ$ are projective $H_i$-modules, then the third module is also projective as an $H_i$-modules. This finishes the proof. $\square$

For the following definitions, see for example [6]. Let A be a finite-dimensional K-algebra, and let ${\mathcal U}$ be a subcategory of ${\text {mod}}(A)$. Then ${\mathcal U}$ is a resolving subcategory if the following hold:

• (i) ${_A}A \in {\mathcal U}$;

• (ii) ${\mathcal U}$ is closed under extensions (i.e. for a short exact sequence $0 \rightarrow X \rightarrow Y \rightarrow Z \rightarrow 0$ of A-modules, if $X,Z \in {\mathcal U}$, then $Y \in {\mathcal U}$);

• (iii) ${\mathcal U}$ is closed under kernels of epimorphisms.

Dually, ${\mathcal U}$ is coresolving if

• (i) ${\text {D}}(A_A) \in {\mathcal U}$;

• (ii) ${\mathcal U}$ is closed under extensions;

• (iii) ${\mathcal U}$ is closed under cokernels of monomorphisms.

For $X \in {\text {mod}}(A)$ a homomorphism $f:X \rightarrow U$ is a left ${\mathcal U}$ -approximation of X if $U \in {\mathcal U}$ and

$$\begin{aligned} {\text {Hom}}_A(U,U') \xrightarrow {{\text {Hom}}_A(f,U')} {\text {Hom}}_A(X,U') \rightarrow 0 \end{aligned}$$

is exact for all $U' \in {\mathcal U}$. Dually, a homomorphism $g:U \rightarrow X$ is a right ${\mathcal U}$-approximation of X if $U \in {\mathcal U}$ and

$$\begin{aligned} {\text {Hom}}_A(U',U) \xrightarrow {{\text {Hom}}_A(U',g)} {\text {Hom}}_A(U',X) \rightarrow 0 \end{aligned}$$

is exact for all $U' \in {\mathcal U}$. The subcategory ${\mathcal U}$ is covariantly finite if every $X \in {\text {mod}}(A)$ has a left ${\mathcal U}$-approximation. Dually, ${\mathcal U}$ is contravariantly finite if every $X \in {\text {mod}}(A)$ has a right ${\mathcal U}$-approximation. Finally, ${\mathcal U}$ is functorially finite if ${\mathcal U}$ is covariantly and contravariantly finite.

Theorem 3.9

The subcategory ${\text {rep}}_\mathrm{l.f.}(H)$ is resolving, coresolving and functorially finite. In particular, ${\text {rep}}_\mathrm{l.f.}(H)$ has Auslander–Reiten sequences.

Proof

By Lemma 3.8 and Proposition 3.1 we get that ${\text {rep}}_\mathrm{l.f.}(H)$ is a resolving and coresolving subcategory of ${\text {rep}}(H)$. Furthermore, by Proposition 3.5 we know that ${\text {rep}}_\mathrm{l.f.}(H)$ coincides with the subcategory of all H-modules with projective dimension 1. Thus ${\text {rep}}_\mathrm{l.f.}(H)$ is covariantly finite by [4, Proposition 4.2]. Since ${\text {rep}}_\mathrm{l.f.}(H)$ also coincides with the subcategory of all H-modules with injective dimension 1, the dual of [4, Proposition 4.2] yields that ${\text {rep}}_\mathrm{l.f.}(H)$ is contravariantly finite. Thus ${\text {rep}}_\mathrm{l.f.}(H)$ is functorially finite in ${\text {rep}}(H)$. Now it follows from [6, Theorem 2.4] that ${\text {rep}}_\mathrm{l.f.}(H)$ has Auslander–Reiten sequences. $\square$

4 The homological bilinear form

As before, let $H = H(C,D,\Omega )$. For $M,N \in {\text {rep}}_\mathrm{l.f.}(H)$ define

$$\begin{aligned} \langle M,N\rangle _H&:= \dim {\text {Hom}}_H(M,N) - \dim {\text {Ext}}_H^1(M,N),\\ (M,N)_H&:= \langle M,N\rangle _H + \langle N,M\rangle _H,\\ q_H(M)&:= \langle M,M\rangle _H. \end{aligned}$$

Proposition 4.1

For $M,N \in {\text {rep}}_\mathrm{l.f.}(H)$ we have

$$\begin{aligned} \langle M,N\rangle _H = \sum _{i=1}^n c_ia_ib_i - \sum _{(j,i) \in \Omega } c_i|c_{ij}| a_ib_j \end{aligned}$$

where $\underline{{\text {rank}}}(M) = (a_1,\ldots ,a_n)$ and $\underline{{\text {rank}}}(N) = (b_1,\ldots ,b_n)$.

Proof

Let $Q = Q(C,\Omega )$. Let $i_1$ be a sink in $Q^\circ$, and let $i_n$ be a source of $Q^\circ$. We get short exact sequences

$$\begin{aligned} 0 \rightarrow E_{i_1}^{a_{i_1}} \xrightarrow {f_1} M \xrightarrow {f_2} M' \rightarrow 0 \end{aligned}$$

(4.1)

and

$$\begin{aligned} 0 \rightarrow N' \xrightarrow {g_1} N \xrightarrow {g_2} E_{i_n}^{b_{i_n}} \rightarrow 0 \end{aligned}$$

(4.2)

where $f_1$ is the obvious canonical inclusion, $f_2$ is the canonical projection onto ${\text {Cok}}(f_1), g_2$ is the obvious canonical projection, and $g_1$ is the canonical inclusion of ${\text {Ker}}(g_2)$. Applying ${\text {Hom}}_H(-,N)$ to sequence (4.1) and ${\text {Hom}}_H(M,-)$ to the sequence (4.2) yields the long exact cohomology sequences

$$\begin{aligned}&0 \rightarrow {\text {Hom}}_H(M',N) \rightarrow {\text {Hom}}_H(M,N) \rightarrow {\text {Hom}}_H(E_{i_1}^{a_{i_1}},N) \nonumber \\&\quad \rightarrow {\text {Ext}}_H^1(M',N) \rightarrow {\text {Ext}}_H^1(M,N) \rightarrow {\text {Ext}}_H^1(E_{i_1}^{a_{i_1}},N) \rightarrow 0 \end{aligned}$$

(4.3)

and

$$\begin{aligned}&0 \rightarrow {\text {Hom}}_H(M,N') \rightarrow {\text {Hom}}_H(M,N) \rightarrow {\text {Hom}}_H(M,E_{i_n}^{b_{i_n}}) \nonumber \\&\quad \rightarrow {\text {Ext}}_H^1(M,N') \rightarrow {\text {Ext}}_H^1(M,N) \rightarrow {\text {Ext}}_H^1(M,E_{i_n}^{b_{i_n}}) \rightarrow 0. \end{aligned}$$

(4.4)

For the exactness of the first cohomology sequence we used that ${\text {inj.~dim}}(N) \le 1$, and for the second sequence we needed that ${\text {proj.~dim}}(M) \le 1$, compare Proposition 3.5. The first sequence implies that

$$\begin{aligned} \langle M,N\rangle _H = \langle M',N\rangle _H + \langle E_{i_1}^{a_{i_1}},N\rangle _H, \end{aligned}$$

and the second sequence yields

$$\begin{aligned} \langle M,N\rangle _H = \langle M,N'\rangle _H + \langle M,E_{i_n}^{b_{i_n}}\rangle _H. \end{aligned}$$

Thus by induction we get

$$\begin{aligned} \langle M,N\rangle _H = \sum _{1 \le i,j \le n} a_ib_j \langle E_i,E_j\rangle _H. \end{aligned}$$

For $1 \le j \le n$ we have

$$\begin{aligned} \dim {\text {Hom}}_H(E_i,E_j) = \dim {\text {Hom}}_H(P_i,E_j) = {\left\{ \begin{array}{ll} c_i &{} \quad \text {if } \quad i=j,\\ 0 &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

Recall that the minimal projective resolution of $E_i$ has the form

$$\begin{aligned} 0 \rightarrow \bigoplus _{j \in \Omega (-,i)} P_j^{|c_{ji}|} \rightarrow P_i \rightarrow E_i \rightarrow 0. \end{aligned}$$

(4.5)

Applying ${\text {Hom}}_H(-,E_j)$ for $1 \le j \le n$ yields

$$\begin{aligned} \dim {\text {Ext}}_H^1(E_i,E_j) = {\left\{ \begin{array}{ll} c_j|c_{ji}| &{} \text {if } j \in \Omega (-,i),\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Since $c_jc_{ji} = c_ic_{ij}$, the result follows. $\square$

Proposition 4.1 shows that for $M, N \in {\text {rep}}_\mathrm{l.f.}(H)$ the number $\langle M,N\rangle _H$ depends only on the rank vectors $\underline{{\text {rank}}}(M)$ and $\underline{{\text {rank}}}(N)$. This implies:

Corollary 4.2

The map $(M,N) \mapsto \langle M,N\rangle _H$ descends to the Grothendieck group $\mathbb {Z}^n$ of ${\text {rep}}_\mathrm{l.f.}(H)$ and induces a bilinear form $\mathbb {Z}^n \times \mathbb {Z}^n \rightarrow \mathbb {Z}$ still denoted by $\langle -,-\rangle _H$. This bilinear form is characterized by $\langle \alpha _i,\alpha _j\rangle _H = \langle E_i,E_j\rangle _H$, where $\alpha _1,\ldots ,\alpha _n$ is the standard basis of $\mathbb {Z}^n$.

Let

$$\begin{aligned} (-,-)_H:\mathbb {Z}^n \times \mathbb {Z}^n \rightarrow \mathbb {Z}\end{aligned}$$

be the symmetrization of $\langle -,-\rangle _H$ defined by $(a,b)_H := \langle a,b\rangle _H + \langle b,a\rangle _H$, and let $q_H:\mathbb {Z}^n \rightarrow \mathbb {Z}$ be the quadratic form defined by $q_H(a) := \langle a,a\rangle _H$. The forms $q_H$ and $\langle -,-\rangle _H$ are called the homological bilinear forms of H.

Corollary 4.3

We have $q_H = q_C$ and $(-,-)_H = (-,-)_C$.

Proof

By definition we have

$$\begin{aligned} q_C := \sum _{i=1}^n c_i X_i^2 - \sum _{i<j} c_i|c_{ij}| X_iX_j, \end{aligned}$$

and we know from Proposition 4.1 that

$$\begin{aligned} q_H = \sum _{i=1}^n c_iX_i^2 - \sum _{(j,i) \in \Omega } c_i|c_{ij}| X_iX_j. \end{aligned}$$

Note that $q_H$ does not depend on the orientation $\Omega$, since $c_ic_{ij} = c_jc_{ji}$ for all i, j. Thus we have $q_H = q_C$. Similarly, one also shows easily that $(-,-)_H = (-,-)_C$. $\square$

5 An analogy to the representation theory of modulated graphs

The constructions and results of this section form a crucial part of this article. For example, it contains the foundation for defining reflection functors and Coxeter functors for the algebras $H(C,D,\Omega )$.

5.1 The bimodules ${_j}H_i$

Let $C = (c_{ij}) \in M_n(\mathbb {Z})$ be a Cartan matrix with symmetrizer $D = {\text {diag}}(c_1,\ldots ,c_n)$, and let $\Omega$ be an orientation of C, and let $\Omega ^*$ be the opposite orientation. Let $H := H(C,D,\Omega )$ and $H^* := H(C,D,\Omega ^*)$. Recall that for $1 \le i \le n$ we have

$$\begin{aligned} H_i := e_iHe_i = K[\varepsilon _i]/(\varepsilon _i^{c_i}). \end{aligned}$$

In the following we write $\otimes _i$ for a tensor product $\otimes _{H_i}$ over $H_i$. If there is no danger of misunderstanding, we also just write $\otimes$ instead of $\otimes _i$.

For $(j,i) \in \Omega$ we define

$$\begin{aligned} {_j}H_i:= & {} H_j \mathrm{Span}_K(\alpha _{ji}^{(g)} \mid 1 \le g \le g_{ji})H_i\\= & {} \mathrm{Span}_K(\varepsilon _j^{f_j}\alpha _{ji}^{(g)}\varepsilon _i^{f_i} \mid f_j,f_i \ge 0, 1 \le g \le g_{ji}). \end{aligned}$$

Our considerations in Sect. 3.2 show that ${_j}H_i$ is an $H_j$-$H_i$-bimodule, which is free as a left $H_j$-module and free as a right $H_i$-module. Let ${_i}H_j$ be the corresponding $H_i$-$H_j$-bimodule coming from $H^*$. We get

$$\begin{aligned} {_j}H_i = \bigoplus _{g=1}^{g_{ij}} \bigoplus _{f=0}^{f_{ji}-1} H_j(\alpha _{ji}^{(g)}\varepsilon _i^f) = \bigoplus _{g=1}^{g_{ij}}\bigoplus _{f=0}^{f_{ij}-1} (\varepsilon _j^f\alpha _{ji}^{(g)})H_i \end{aligned}$$

and

$$\begin{aligned} {_i}H_j = \bigoplus _{g=1}^{g_{ij}} \bigoplus _{f=0}^{f_{ij}-1} H_i(\alpha _{ij}^{(g)}\varepsilon _j^f) = \bigoplus _{g=1}^{g_{ij}}\bigoplus _{f=0}^{f_{ji}-1} (\varepsilon _i^f\alpha _{ij}^{(g)})H_j. \end{aligned}$$

So we have

$$\begin{aligned} {_{H_j}}({_j}H_i)&\cong H_j^{|c_{ji}|} \cong ({_i}H_j)_{H_j}, \\ {_{H_i}}({_i}H_j)&\cong H_i^{|c_{ij}|} \cong ({_j}H_i)_{H_i}. \end{aligned}$$

Define

$$\begin{aligned} {_j}L_i&:= \{ \alpha _{ji}^{(g)}, \alpha _{ji}^{(g)}\varepsilon _i,\ldots , \alpha _{ji}^{(g)}\varepsilon _i^{f_{ji}-1} \mid 1 \le g \le g_{ij} \}, \\ {_i}L_j&:= \{ \alpha _{ij}^{(g)}, \alpha _{ij}^{(g)}\varepsilon _j,\ldots , \alpha _{ij}^{(g)}\varepsilon _j^{f_{ij}-1} \mid 1 \le g \le g_{ij} \}, \\ {_j}R_i&:= \{ \alpha _{ji}^{(g)}, \varepsilon _j\alpha _{ji}^{(g)},\ldots , \varepsilon _j^{f_{ij}-1}\alpha _{ji}^{(g)} \mid 1 \le g \le g_{ij} \}, \\ {_i}R_j&:= \{ \alpha _{ij}^{(g)}, \varepsilon _i\alpha _{ij}^{(g)},\ldots , \varepsilon _i^{f_{ji}-1}\alpha _{ij}^{(g)} \mid 1 \le g \le g_{ij} \}. \end{aligned}$$

Then ${_j}L_i$ (resp. ${_j}R_i$) is a basis of ${_j}H_i$ as a left $H_j$-modules (resp. as a right $H_i$-module). We have $|{_j}L_i| = |{_i}R_j| = |c_{ji}|$ and $|{_i}L_j| = |{_j}R_i| = |c_{ij}|$.

Let $({_j}L_i)^*$ and $({_j}R_i)^*$ be the dual basis of ${\text {Hom}}_{H_j}({_j}H_i,H_j)$ and ${\text {Hom}}_{H_i}({_j}H_i,H_i)$, respectively. For $b \in {_j}L_i$ or $b \in {_j}R_i$ let $b^*$ be the corresponding dual basis vector. Similarly, define $({_i}L_j)^*$ and $({_i}R_j)^*$.

There is an $H_i$-$H_j$-bimodule isomorphism

$$\begin{aligned} \rho :{_i}H_j \rightarrow {\text {Hom}}_{H_j}({_j}H_i,H_j) \end{aligned}$$

given by

$$\begin{aligned} \rho \left( \varepsilon _i^{f_{ji}-1-f}\alpha _{ij}^{(g)}\right) = (\alpha _{ji}^{(g)}\varepsilon _i^f)^* \end{aligned}$$

for $0 \le f \le f_{ji}-1$ and $1 \le g \le g_{ij}$. Indeed, for the left $H_i$-module structure on ${\text {Hom}}_{H_j}({_j}H_i,H_j)$ one has

$$\begin{aligned} \varepsilon _i \cdot (\alpha _{ji}^{(g)}\varepsilon _i^f)^* = {\left\{ \begin{array}{ll} (\alpha _{ji}^{(g)}\varepsilon _i^{f-1})^*&{} \quad \text {if } \quad f>0,\\ (\alpha _{ji}^{(g)}\varepsilon _i^{f_{ji}-1})^*\cdot \varepsilon _j^{f_{ij}} &{} \quad \text {if } \quad f=0. \end{array}\right. } \end{aligned}$$

Similarly there is an $H_i$-$H_j$-bimodule isomorphism

$$\begin{aligned} \lambda :{_i}H_j \rightarrow {\text {Hom}}_{H_i}({_j}H_i,H_i) \end{aligned}$$

given by

$$\begin{aligned} \lambda \left( \alpha _{ij}^{(g)}\varepsilon _j^{f_{ij}-1-f}\right) = (\varepsilon _j^f\alpha _{ji}^{(g)})^* \end{aligned}$$

for $0 \le f \le f_{ij}-1$ and $1 \le g \le g_{ij}$. In particular, we get $\rho ({_i}R_j) = ({_j}L_i)^*$ and $\lambda ({_i}L_j) = ({_j}R_i)^*$. In the following, we sometimes identify the spaces ${\text {Hom}}_{H_j}({_j}H_i,H_j), {_i}H_j$ and ${\text {Hom}}_{H_i}({_j}H_i,H_i)$ via $\rho$ and $\lambda$. For example, for $b \in {_j}L_i$, we consider $b^* \in {\text {Hom}}_{H_j}({_j}H_i,H_j)$ as an element in ${_i}H_j$.

If $N_j$ is an $H_j$-module, then we have a natural isomorphism of $H_i$-modules

$$\begin{aligned} {\text {Hom}}_{H_j}({_j}H_i,N_j) \rightarrow {_i}H_j \otimes _j N_j \end{aligned}$$

defined by

$$\begin{aligned} f \mapsto \sum _{b \in {_j}L_i} b^* \otimes _j f(b). \end{aligned}$$

Now, if in addition $M_i$ is an $H_i$-module, the adjunction map gives an isomorphism of K-vector spaces:

$$\begin{aligned} {\text {Hom}}_{H_j}({_j}H_i\otimes _i M_i, N_j) \rightarrow {\text {Hom}}_{H_i}(M_i, {\text {Hom}}_{H_j}({_j}H_i,N_j)). \end{aligned}$$

Combining these two maps we get a functorial isomorphism of K-vector spaces

$$\begin{aligned} {\text {ad}}_{ji} := {\text {ad}}_{ji}(M_i,N_j):{\text {Hom}}_{H_j}({_j}H_i \otimes _i M_i,N_j) \rightarrow {\text {Hom}}_{H_i}(M_i,{_i}H_j \otimes _j N_j) \end{aligned}$$

given by

$$\begin{aligned} f \mapsto \left( f^\vee :m \mapsto \sum _{b \in {_j}L_i} b^* \otimes _j f(b \otimes _i m)\right) . \end{aligned}$$

The inverse ${\text {ad}}_{ji}^{-1}$ of ${\text {ad}}_{ji}$ is given by

$$\begin{aligned} g \mapsto \left( g^\vee :h \otimes _i m \mapsto \sum _{b \in {_j}L_i} b^*(h) (g(m))_b\right) \end{aligned}$$

where the elements $(g(m))_b \in N_j$ are uniquely determined by

$$\begin{aligned} g(m) = \sum _{b \in {_j}L_i} b^* \otimes _j (g(m))_b. \end{aligned}$$

Here we used that each element x in ${_i}H_j \otimes _j N_j$ can be written uniquely as a sum of the form

$$\begin{aligned} x = \sum _{b \in {_j}L_i} b^* \otimes _j x_b. \end{aligned}$$

5.2 Representation theory of modulated graphs

The tuple $(H_i,{_i}H_j,{_j}H_i)$ defined in Sect. 5.1 is called a modulation of C and is denoted by ${\mathcal M}(C,D)$.

For an orientation $\Omega$ of C, a representation $M \!=\! (M_i,M_{ij})$ of $({\mathcal M}(C,D),\Omega )$ is given by a finite-dimensional $H_i$-module $M_i$ for each $1 \le i \le n$ and an $H_i$-linear map

$$\begin{aligned} M_{ij}:{_i}H_j \otimes _j M_j \rightarrow M_i \end{aligned}$$

for each $(i,j) \in \Omega$. A morphism $f:M \rightarrow N$ of representations $M = (M_i,M_{ij})$ and $N = (N_i,N_{ij})$ of $({\mathcal M}(C,D),\Omega )$ is a tuple $f = (f_i)_i$ of $H_i$-linear maps $f_i:M_i \rightarrow N_i$ for $1 \le i \le n$ such that for each $(i,j) \in \Omega$ the diagram

commutes. One easily checks that the representations of $({\mathcal M}(C,D),\Omega )$ form an abelian category ${\text {rep}}(C,D,\Omega )$.

For $(M_i,M_{ij}) \in {\text {rep}}(C,D,\Omega )$ define a representation

$$\begin{aligned} (M_i,M(\alpha _{ij}^{(g)}),M(\varepsilon _i)) \end{aligned}$$

of $H(C,D,\Omega )$ as follows: Define a K-linear map $M(\varepsilon _i):M_i \rightarrow M_i$ by

$$\begin{aligned} M(\varepsilon _i)(m) := \varepsilon _i m. \end{aligned}$$

(Here we use that $M_i$ is an $H_i$-module.) Let $(i,j) \in \Omega$. Recall that ${_i}H_j$ has an $H_i$-basis

$$\begin{aligned} {_i}L_j = \{ \alpha _{ij}^{(g)}, \alpha _{ij}^{(g)}\varepsilon _j,\ldots , \alpha _{ij}^{(g)}\varepsilon _j^{f_{ij}-1} \mid 1 \le g \le g_{ij} \}. \end{aligned}$$

Define a K-linear map $M(\alpha _{ij}^{(g)}):M_j \rightarrow M_i$ by

$$\begin{aligned} M(\alpha _{ij}^{(g)})(m) := M_{ij}(\alpha _{ij}^{(g)} \otimes _j m). \end{aligned}$$

Now one can check that the relations (H1) and (H2) are satisfied. In other words, $(M_i,M(\alpha _{ij}^{(g)}),M(\varepsilon _i))$ is a representation of $H(C,D,\Omega )$.

Conversely, let $(M_i,M(\alpha _{ij}^{(g)}),M(\varepsilon _i))$ be a representation of $H(C,D,\Omega )$. Note that $M_i$ is an $H_i$-module via the map $M(\varepsilon _i)$. For $(i,j) \in \Omega$ define an $H_i$-linear map

$$\begin{aligned} M_{ij}:{_i}H_j \otimes _j M_j \rightarrow M_i \end{aligned}$$

by

$$\begin{aligned} M_{ij}(\alpha _{ij}^{(g)}\varepsilon _j^f \otimes m) := (M(\alpha _{ij}^{(g)}) \circ M(\varepsilon _j)^f)(m). \end{aligned}$$

Then $(M_i,M_{ij}) \in {\text {rep}}(C,D,\Omega )$.

These two constructions yield obviously mutually inverse bijections between the representations of $({\mathcal M}(C,D),\Omega )$ and $H(C,D,\Omega )$. It is also clear how to associate to a morphism in ${\text {rep}}(C,D,\Omega )$ a morphism in ${\text {rep}}(H(C,D,\Omega ))$ and vice versa. Now it is straightforward to verify the following statement.

Proposition 5.1

The categories ${\text {rep}}(C,D,\Omega )$ and ${\text {rep}}(H(C,D,\Omega ))$ are isomorphic.

Thus the representation theory of the algebras $H(C,D,\Omega )$ shows a striking analogy to the representation theory of modulated graphs in the sense of Dlab and Ringel [26]. The main difference is that in Dlab and Ringel’s theory, the rings $H_i$ would be division rings, whereas in our case they are commutative symmetric algebras, or more precisely, truncations of polynomial rings. Generalizations of the representation theory of modulated graphs have been formulated already in [43].

5.3 Representations of $\Pi (C,D)$

Next, we want to interpret the category ${\text {rep}}(\Pi (C,D))$ of finite-dimensional representations of $\Pi (C,D)$ as a category of representations of modulated graphs. Let ${\text {rep}}(C,D,\overline{\Omega })$ be the category with objects $M = (M_i,M_{ij},M_{ji})$ with $(i,j) \in \Omega$ such that $(M_i,M_{ij}) \in {\text {rep}}(C,D,\Omega )$ and $(M_i,M_{ji}) \in {\text {rep}}(C,D,\Omega ^*)$. Given two such objects M and N a tuple $f = (f_i)_i$ is a homomorphism $f:M \rightarrow N$ if f is both a homomorphism $(M_i,M_{ij}) \rightarrow (N_i,N_{ij})$ in ${\text {rep}}(C,D,\Omega )$ and a homomorphism $(M_i,M_{ji}) \rightarrow (N_i,N_{ji})$ in ${\text {rep}}(C,D,\Omega ^*)$.

For an object $M = (M_i,M_{ij},M_{ji})$ in ${\text {rep}}(C,D,\overline{\Omega })$ let

$$\begin{aligned} M_{i,\mathrm in} := ({\text {sgn}}(i,j)M_{ij})_j:\bigoplus _{j \in \overline{\Omega }(i,-)} {_i}H_j \otimes M_j \rightarrow M_i \end{aligned}$$

and

$$\begin{aligned} M_{i,\mathrm out} := (M_{ji}^\vee )_j:M_i \rightarrow \bigoplus _{j \in \overline{\Omega }(-,i)} {_i}H_j \otimes M_j. \end{aligned}$$

These are both $H_i$-module homomorphisms. (Recall that $M_{ji}^\vee = {\text {ad}}_{ji}(M_{ji})$, see Sect. 5.1.) Set

$$\begin{aligned} \widetilde{M_i} := \bigoplus _{j \in \overline{\Omega }(i,-)} {_i}H_j \otimes M_j. \end{aligned}$$

Since $\overline{\Omega }(i,-) = \overline{\Omega }(-,i)$, we have

$$\begin{aligned} \bigoplus _{j \in \overline{\Omega }(i,-)} {_i}H_j \otimes M_j = \bigoplus _{k \in \overline{\Omega }(-,i)} {_i}H_k \otimes M_k. \end{aligned}$$

Thus we get a diagram

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} M_i \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i}. \end{aligned}$$

Proposition 5.2

The category ${\text {rep}}(\Pi (C,D))$ is isomorphic to the full subcategory of ${\text {rep}}(C,D,\overline{\Omega })$ with objects $M = (M_i,M_{ij},M_{ji})$ such that

$$\begin{aligned} M_{i,\mathrm in} \circ M_{i,\mathrm out} = 0 \end{aligned}$$

for all i.

Proof

For an object $M = (M_i,M_{ij},M_{ji})$ in ${\text {rep}}(C,D,\overline{\Omega })$, the composition

$$\begin{aligned} M_{i,\mathrm in} \circ M_{i,\mathrm out} = \sum _{j \in \overline{\Omega }(-,i)} {\text {sgn}}(i,j)M_{ij} \circ M_{ji}^\vee \end{aligned}$$

is in ${\text {End}}_{H_i}(M_i)$ and maps an element $m \in M_i$ to

$$\begin{aligned} M_{i,\mathrm in} \circ M_{i,\mathrm out}(m) = \sum _{j \in \overline{\Omega }(-,i)} {\text {sgn}}(i,j)\sum _{b \in {_j}L_i} M_{ij}\left( b^* \otimes _j M_{ji}(b \otimes _i m)\right) . \end{aligned}$$

Let $b \in {_j}L_i$. Thus we have $b = \alpha _{ji}^{(g)}\varepsilon _i^{f_{ji}-1-f}$ for some $0 \le f \le f_{ji}-1$. This implies that $b^* = \varepsilon _i^f\alpha _{ij}^{(g)} \in {_i}R_j$. It follows that

$$\begin{aligned}&{\text {sgn}}(i,j)M_{ij}\left( b^* \otimes _j M_{ji}(b \otimes _i m)\right) \\&\quad = {\text {sgn}}(i,j)M(\varepsilon _i)^fM(\alpha _{ij}^{(g)})M(\alpha _{ji}^{(g)})M(\varepsilon _i)^{f_{ji}-1-f}(m). \end{aligned}$$

In view of the defining relation (P3) of $\Pi (C,D)$, this yields the result. $\square$

6 The algebras H and $\Pi$ are tensor algebras

Let A be a K-algebra, and let $M = {_A}M_A$ be an A-A-bimodule. The tensor algebra $T_A(M)$ is defined as

$$\begin{aligned} T_A(M) := \bigoplus _{k \ge 0} M^{\otimes k} \end{aligned}$$

where $M^0 := A$, and $M^{\otimes k}$ is the k-fold tensor product of M for $k \ge 1$. The multiplication of $T_A(M)$ is defined as follows: For $r,s \ge 1, m_i,m_i' \in M$ and $a,a' \in A$ let

$$\begin{aligned} (m_1 \otimes \cdots \otimes m_r) \cdot (m_1' \otimes \cdots \otimes m_s') := (m_1 \otimes \cdots \otimes m_r \otimes m_1' \otimes \cdots \otimes m_s') \end{aligned}$$

and

$$\begin{aligned} a(m_1 \otimes \cdots \otimes m_r)a' := (am_1 \otimes \cdots \otimes m_ra'). \end{aligned}$$

Recall that the modules over a tensor algebra $T_A(M)$ are given by the A-module homomorphisms $M \otimes _A X \rightarrow X$, where X is an A-module.

Let A be a K-algebra, $A_0$ a subalgebra and $A_1$ an $A_0$-$A_0$-subbimodule of A. Following [10] we say that A is freely generated by $A_1$ over $A_0$ if the following holds: For every K-algebra B and any pair $(f_0,f_1)$ with $f_0:A_0 \rightarrow B$ an algebra homomorphism, and $f_1:A_1 \rightarrow B$ an $A_0$-$A_0$-bimodule homomorphism (with the $A_0$-$A_0$-bimodule structure on B given by $f_0$) there exists a unique K-algebra homomorphism $f:A \rightarrow B$ which extends $f_0$ and $f_1$. The following two lemmas can be found in [10, Section 1].

Lemma 6.1

For any K-algebra A and any A-A-bimodule M the tensor algebra $T_A(M)$ is freely generated by M over A.

Lemma 6.2

Let A be a K-algebra which is freely generated by $A_1$ over $A_0$. Then A is isomorphic to the tensor algebra $T_{A_0}(A_1)$.

Let Q be a finite quiver, and let $w:Q_1 \rightarrow \{0,1\}$ be a map assigning to each arrow of Q a degree. Then the path algebra KQ is naturally $\mathbb {N}$-graded: Each path gets as degree the sum of the degrees of its arrows. By definition the paths of length 0 have degree 0. Let $r_1,\ldots ,r_m$ be a set of relations for KQ which are homogeneous with respect to this grading. Suppose that there is some $1 \le l \le m$ such that $\deg (r_i) = 0$ for $1 \le i \le l$ and $\deg (r_j) = 1$ for $l+1 \le j \le m$.

Let $A := KQ/I$, where I is the ideal generated by $r_1,\ldots ,r_m$. Clearly, A is again $\mathbb {N}$-graded. Let $A_i$ be the subspace of elements with degree i. Observe that $A_1$ is naturally an $A_0$-$A_0$-bimodule. Now Lemmas 6.1, 6.2 yield the following result.

Proposition 6.3

A is isomorphic to the tensor algebra $T_{A_0}(A_1)$.

As before, let $H = H(C,D,\Omega )$. Define

$$\begin{aligned} S := \prod _{i=1}^n H_i \text { and } B := \bigoplus _{(i,j) \in \Omega } {_i}H_j. \end{aligned}$$

Clearly, B is an S-S-bimodule.

Proposition 6.4

$H \cong T_S(B)$.

Proof

The algebra H is graded by defining $\deg (\varepsilon _i) := 0$ and $\deg (\alpha _{ij}^{(g)}) := 1$ for all $(i,j) \in \Omega$ and all g. The defining relations for H are homogeneous, S is the subalgebra of elements of degree 0, and B is the subspace of elements of degree 1. Now we can apply Proposition 6.3. $\square$

Let $\Pi = \Pi (C,D,\Omega )$ be the preprojective algebra. Define $\deg (\varepsilon _i) := 0$ for all i, and for $(i,j) \in \Omega$ let $\deg (\alpha _{ij}^{(g)}) := 0$ and $\deg (\alpha _{ji}^{(g)}) := 1$ for all g. Let

$$\begin{aligned} \Pi _1 := \Pi (C,D,\Omega )_1 \end{aligned}$$

be the subspace of $\Pi$ consisting of the elements of degree 1. Note that $\Pi _1$ is an H-H-bimodule. Again we can apply Proposition 6.3 and get the following result.

Proposition 6.5

$\Pi \cong T_H(\Pi _1)$.

Define

$$\begin{aligned} \overline{B} := \bigoplus _{(i,j) \in \overline{\Omega }} {_i}H_j. \end{aligned}$$

Next, for $1 \le i \le n$ let

$$\begin{aligned} \rho _i := \sum _{j \in \overline{\Omega }(-,i)} {\text {sgn}}(i,j)\sum _{b \in {_j}L_i} b^* \otimes _j b \in T_S(\overline{B}). \end{aligned}$$

Every $b \in {_j}L_i$ is of the form $b = \alpha _{ji}^{(g)}\varepsilon _i^{f_{ji}-1-f}$ for some $0 \le f \le f_{ji}-1$ and $1 \le g \le g_{ij}$. Then $b^* \in {_i}R_j$ is equal to $\varepsilon _i^f\alpha _{ij}^{(g)}$. Thus $\rho _i$ translates to the defining relation (P3)

$$\begin{aligned} \sum _{j\in \overline{\Omega }(-,i)} \sum _{g=1}^{g_{ij}} \sum _{f=0}^{f_{ji}-1} {\text {sgn}}(i,j) \varepsilon _i^f\alpha _{ij}^{(g)} \alpha _{ji}^{(g)} \varepsilon _i^{f_{ji}-1-f} = 0. \end{aligned}$$

of $\Pi$.

The algebra $T_S(\overline{B})/(\rho _1,\ldots ,\rho _n)$ is an analogue of Dlab and Ringel’s [28] definition of a preprojective algebra of a modulated graph.

Proposition 6.6

$\Pi \cong T_S(\overline{B})/(\rho _1,\ldots ,\rho _n)$.

Proof

Similarly as in the proof of Proposition 6.4 one shows that $T_S(\overline{B})$ is isomorphic to the path algebra $K\overline{Q}$ modulo the defining relations (P1) and (P2) of $\Pi$.

Let M be a module over the tensor algebra $T_S(\overline{B})$. Then M is defined by the structure maps

$$\begin{aligned} M_{ij}:{_i}H_j \otimes _j M_j \rightarrow M_i \end{aligned}$$

for each $(i,j) \in \overline{\Omega }$. This yields maps

$$\begin{aligned} M_{iji} := M_{ij} \circ ({\text {id}}_{{_i}H_j} \otimes _j M_{ji}):{_i}H_j \otimes _j {_j}H_i \otimes _i M_i \rightarrow M_i. \end{aligned}$$

Now M is a module over $T_S(\overline{B})/(\rho _1,\ldots ,\rho _n)$ if and only if for each vertex i and each $m \in M_i$ we have $\rho _im = 0$. This is equivalent to

$$\begin{aligned} \sum _{j \in \overline{\Omega }(-,i)} {\text {sgn}}(i,j)M_{iji}(\sum _{b\in {_j}L_i} b^* \otimes _j b \otimes _i m) = 0. \end{aligned}$$

It follows from the definitions that

$$\begin{aligned} \sum _{j \in \overline{\Omega }(-,i)} {\text {sgn}}(i,j)M_{iji}(\sum _{b\in {_j}L_i} b^* \otimes _j b \otimes _i m) = (M_{i,\mathrm in} \circ M_{i,\mathrm out})(m). \end{aligned}$$

Now Proposition 5.2 yields the result. $\square$

7 Projective resolutions of H-modules

Proposition 7.1

We have a short exact sequence of H-H-bimodules

$$\begin{aligned} P_\bullet : \;\;\;\;\;\; 0 \rightarrow \bigoplus _{(j,i) \in \Omega } He_j \otimes _j {_j}H_i \otimes _i e_iH \xrightarrow {d} \bigoplus _{k=1}^n He_k \otimes _k e_kH \xrightarrow {\mathrm{mult}} H \rightarrow 0 \end{aligned}$$

(7.1)

where

$$\begin{aligned} d(p \otimes _j h \otimes _i q) := ph \otimes _i q - p \otimes _j hq. \end{aligned}$$

Proof

We know that $H = T_S(B)$. The sequence $P_\bullet$ is isomorphic to the sequence

$$\begin{aligned} 0 \rightarrow H \otimes _S B \otimes _S H \xrightarrow {d} H \otimes _S H \xrightarrow {\mathrm{mult}} H \rightarrow 0 \end{aligned}$$

of H-H-bimodules, where $d(h \otimes b \otimes h') := (hb \otimes h' - h \otimes bh')$. Now the statement follows from [52, Theorems 10.1 and 10.5]. $\square$

The components of $P_\bullet$ are projective as left H-modules and as right H-modules. However, the components are not projective as H-H-bimodules. (Except, if S is semisimple, then the first two components are in fact projective bimodules.) In any case, viewed as a short exact sequence of left or right modules, $P_\bullet$ splits as an exact sequence of projective modules.

Corollary 7.2

If $M \in {\text {rep}}_\mathrm{l.f.}(H)$, then $P_\bullet \otimes _H M$ is a projective resolution of M. Explicitly, $P_\bullet \otimes _H M$ looks as follows

$$\begin{aligned} 0 \rightarrow \bigoplus _{(j,i) \in \Omega } H e_j \otimes _j {_j}H_i \otimes _i M_i \xrightarrow {d \otimes M} \bigoplus _{k=1}^n He_k \otimes _k M_k \xrightarrow {\mathrm{mult}} M \rightarrow 0 \end{aligned}$$

(7.2)

where

$$\begin{aligned} (d \otimes M)(p \otimes _j h \otimes _i m) = ph \otimes _i m - p \otimes _j M_{ji}(h \otimes _i m). \end{aligned}$$

(Here $M_{ji}:{_j}H_i \otimes _i M_i \rightarrow M_j$ is the $H_j$-linear structure map of M associated with $(j,i) \in \Omega$.)

Proof

By the remarks above, $P_\bullet \otimes _H M$ is always exact. If M is locally free, then $e_kH \otimes _H M = e_kM$ and ${_j}H_i \otimes _i e_iH \otimes _H M = {_j}H_i \otimes _i M_i$ are free $H_k$- resp. $H_j$-modules. Thus the relevant components of $P_\bullet \otimes _H M$ are indeed projective. $\square$

8 The trace pairing

8.1 The trace pairing for homomorphisms between free $H_i$-modules

For each $i=1,2,\ldots , n$ we have the K-linear map

$$\begin{aligned} t_i^\mathrm{max}:H_i \rightarrow K \end{aligned}$$

defined by

$$\begin{aligned} \sum _{j=0}^{c_i-1} \lambda _j\varepsilon _i^j \mapsto \lambda _{c_i-1}. \end{aligned}$$

For free $H_i$-modules U and V, with V finitely generated, the trace pairing is the non-degenerate, bilinear form

$$\begin{aligned} {\text {tr}}:= {\text {tr}}_{U,V}:{\text {Hom}}_{H_i}(U,V) \times {\text {Hom}}_{H_i}(V,U) \rightarrow K \end{aligned}$$

defined by

$$\begin{aligned} (f,g) \mapsto t_i^\mathrm{max}({\text {Tr}}_{H_i}(f \circ g)). \end{aligned}$$

It induces an isomorphism

$$\begin{aligned} {\text {Hom}}_{H_i}(U,V) \rightarrow {\text {D}}{\text {Hom}}_{H_i}(V,U), f\mapsto {\text {tr}}(f,-). \end{aligned}$$

Note, that for $U=\bigoplus _{j\in J} H_i u_j$ and $V=\bigoplus _{k=1}^r H_i v_k$ we have

$$\begin{aligned} {\text {Hom}}_{H_i}(U,V)&=\prod _{j\in J}\bigoplus _{k=1}^r{\text {Hom}}_{H_i}(H_iu_j,H_iv_k) \text { and}\\ {\text {D}}{\text {Hom}}_{H_i}(V,U)&= {\text {D}}\left( \bigoplus _{j\in J}\bigoplus _{k=1}^r{\text {Hom}}_{H_i}(H_i v_k, H_iu_j)\right) \\ {}&= \prod _{j\in J}\bigoplus _{k=1}^r{\text {D}}{\text {Hom}}_{H_i}(H_i v_k, H_iu_j). \end{aligned}$$

Let W be another finitely generated free $H_i$-module. The following lemma is easily verified:

Lemma 8.1

For $f \in {\text {Hom}}_{H_i}(V,W)$ the following diagram of natural morphisms commutes:

In other words, under the trace pairing the transpose of ${\text {Hom}}_{H_i}(f,U)$ is identified with ${\text {Hom}}_{H_i}(U,f)$.

8.2 Adjunction and trace pairing

Recall from Sect. 5.1 that for $(j,i)\in \overline{\Omega }$ we have isomorphisms of $H_i\text {-}H_j$-bimodules

$$\begin{aligned} {\text {ad}}_{ji}:{\text {Hom}}_{H_j}({_jH_i}, H_j) \rightarrow {\text {Hom}}_{H_i}(H_i,{_iH_j}), \end{aligned}$$

where we abbreviate ${_jH_i}\otimes _i H_i={_jH_i}$ and ${_iH_j}\otimes _j H_j = {_iH_j}$.

Lemma 8.2

The diagram of natural isomorphisms

with the vertical isomorphisms induced by the respective trace pairings, commutes.

Proof

We have to show that for any $\phi \in {\text {Hom}}_{H_j}({_jH_i},H_j)$ and $\psi \in {\text {Hom}}_{H_i}({_iH_j},H_i)$ we have

$$\begin{aligned} {\text {tr}}_{H_i,{_iH_j}}({\text {ad}}_{ji}(\phi ),\psi )= {\text {tr}}_{{_jH_i},H_j}(\phi ,{\text {ad}}_{ij}(\psi )) \end{aligned}$$

(8.1)

To this end, write

$$\begin{aligned} \phi= & {} \sum _{g=1}^{g_{ij}} \sum _{k=0}^{f_{ji}-1} (\alpha _{ji}^{(g)}\epsilon _i^k)^*\phi ^{(g,k)} \quad \text {with }\quad \phi ^{(g,k)}=\sum _{l=0}^{c_j-1} \phi ^{(g,k)}_l \epsilon _j^l\in H_j \quad \text { and}\\ \psi= & {} \sum _{g=1}^{g_{ij}}\sum _{k'=0}^{f_{ij}-1} (\alpha _{ij}^{(g)}\epsilon _j^{k'})^*\psi ^{(g,k')} \quad \text {with } \quad \psi ^{(g,k')} = \sum _{l'=0}^{c_i-1} \psi ^{(g,k')}_{l'} \epsilon _i^{l'}\in H_i, \end{aligned}$$

where we use heavily the notation from Sects. 1.4 and 5.1. Now a straightforward, though tedious, calculation shows that both sides of (8.1) yield

$$\begin{aligned} \sum _{g=1}^{g_{ij}} \sum _{k'=0}^{f_{ij}-1}\sum _{k=0}^{f_{ji}-1} \sum _{l=0}^{k_{ij}-1} \psi ^{(g,k')}_{k+f_{ji}l}\; \phi ^{(g,k)}_{k'+f_{ij}(k_{ij}-1-l)}. \end{aligned}$$

$\square$

As a direct consequence we obtain the following:

Proposition 8.3

Let M be a free $H_i$-module, and N a finitely generated free $H_j$-module, and denote by ${\text {D}}({\text {ad}}_{ij}):{\text {D}}{\text {Hom}}_{H_j}(N,{_j}H_i\otimes _i M) \rightarrow {\text {D}}{\text {Hom}}_{H_i}({_i}H_j\otimes _j N, M)$ the transpose of ${\text {ad}}_{ij}={\text {ad}}_{ij}(N,M)$. We have a commutative diagram

where the vertical arrows are the isomorphisms induced by the trace pairings.

Proof

In fact, this follows from Lemma 8.2 since ${\text {ad}}_{ji}$ and the isomorphisms induced by the trace pairing are in fact natural transformations between the corresponding bifunctors defined on pairs of free modules. $\square$

9 Reflection functors

In this section, let $H = H(C,D,\Omega )$ and $\Pi = \Pi (C,D)$.

9.1 Reflection functors for $\Pi$

We keep the notations of Sect. 5.3. Let $M \in {\text {rep}}(\Pi )$. Thus we have $M = (M_i,M_{ij},M_{ji})$, where (i, j) runs over $\Omega$, such that $M_{i,\mathrm in} \circ M_{i,\mathrm out} = 0$ for each i. Hence for every i, we have $M_{i,\mathrm out}(M_i) \subseteq {\text {Ker}}(M_{i,\mathrm in})$.

Generalizing the construction in [8, Section 2.2], see also [12], we fix some vertex i and construct a new $\Pi$-module by replacing the diagram

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} M_i \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i} \end{aligned}$$

by

$$\begin{aligned} \widetilde{M_i} \xrightarrow {\overline{M}_{i,\mathrm out}M_{i,\mathrm in}} {\text {Ker}}(M_{i,\mathrm in}) \xrightarrow {\mathrm{can}} \widetilde{M_i} \end{aligned}$$

where $\overline{M}_{i,\mathrm out}:M_i \rightarrow {\text {Ker}}(M_{i,\mathrm in})$ is induced by $M_{i,\mathrm out}$ and $\mathrm{can}$ is the canonical inclusion. Gluing this new datum with the remaining part of M gives a new $\Pi$-module $\Sigma _i^+(M)$.

Similarly, replacing

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} M_i \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i} \end{aligned}$$

by

$$\begin{aligned} \widetilde{M_i} \xrightarrow {\mathrm{can}} {\text {Cok}}(M_{i,\mathrm out}) \xrightarrow {M_{i,\mathrm out}\overline{M}_{i,\mathrm in}} \widetilde{M_i} \end{aligned}$$

where $\overline{M}_{i,\mathrm in}:{\text {Cok}}(M_{i,\mathrm out}) \rightarrow M_i$ is induced by $M_{i,\mathrm in}$ and $\mathrm{can}$ is the canonical projection. Gluing this new datum with the remaining part of M gives a new $\Pi$-module denoted by $\Sigma _i^-(M)$.

The above constructions are obviously functorial. It is straightforward to show that $\Sigma _i^+$ is left exact, and $\Sigma _i^-$ is right exact. Both functors are covariant, K-linear and additive.

The commutative diagram

of $H_i$-module homomorphisms summarizes the situation and also shows the existence of canonical homomorphisms $\Sigma _i^-(M) \rightarrow M \rightarrow \Sigma _i^+(M)$.

For $M \in {\text {rep}}(\Pi )$ let ${\text {sub}}_i(M)$ be the largest submodule U of M such that $e_iU = U$, and let ${\text {soc}}_i(M)$ be the largest submodule V of M such that V is isomorphic to a direct sum of copies of $S_i$. For example, we have ${\text {sub}}_i(E_i) = E_i$ and ${\text {soc}}_i(E_i) \cong S_i$. Dually, let ${\text {fac}}_i(M)$ be the largest factor module M / U of M such that $e_i(M/U) = M/U$, and let ${\text {top}}_i(M)$ be the largest factor module M / V of M such that M / V is isomorphic to a direct sum of copies of $S_i$. All these constructions are functorial.

The proof of the following proposition follows almost word by word the proof of Baumann and Kamnitzer [8, Proposition 2.5], who deal with classical preprojective algebras associated with Dynkin quivers. One difference is that we need to work with ${\text {sub}}_i$ and ${\text {fac}}_i$ instead of ${\text {soc}}_i$ and ${\text {top}}_i$.

Proposition 9.1

For each i the following hold:

• (i) The pair $(\Sigma _i^-,\Sigma _i^+)$ is a pair of adjoint functors, i.e. there is a functorial isomorphism

  $$\begin{aligned} {\text {Hom}}_\Pi (\Sigma _i^-(M),N) \cong {\text {Hom}}_\Pi (M,\Sigma _i^+(N)). \end{aligned}$$

• (ii) The adjunction morphisms ${\text {id}}\rightarrow \Sigma _i^+\Sigma _i^-$ and $\Sigma _i^-\Sigma _i^+ \rightarrow {\text {id}}$ can be inserted in functorial short exact sequences

  $$\begin{aligned} 0 \rightarrow {\text {sub}}_i \rightarrow {\text {id}}\rightarrow \Sigma _i^+\Sigma _i^- \rightarrow 0 \end{aligned}$$

  and

  $$\begin{aligned} 0 \rightarrow \Sigma _i^-\Sigma _i^+ \rightarrow {\text {id}}\rightarrow {\text {fac}}_i \rightarrow 0. \end{aligned}$$

Proof

To establish (i), it is enough to define a pair of mutually inverse bijections between ${\text {Hom}}_\Pi (\Sigma _i^-(M),N)$ and ${\text {Hom}}_\Pi (M,\Sigma _i^+(N))$ for any $\Pi$-modules M and N, which are functorial in M and N. The construction looks as follows. Consider a morphism $f:M \rightarrow \Sigma _i^+(N)$. By definition, this is a collection of $H_j$-module homomorphisms

$$\begin{aligned} f_j:M_j \rightarrow (\Sigma _i^+(N))_j \end{aligned}$$

with $1 \le j \le n$ such that the diagram

commutes for all $(i,j) \in \overline{\Omega }$. Recall that

$$\begin{aligned} \widetilde{M}_i = \bigoplus _{j \in \overline{\Omega }(i,-)} {_i}H_j \otimes _j M_j. \end{aligned}$$

Set

$$\begin{aligned} \widetilde{f_i} := \bigoplus _{j \in \overline{\Omega }(i,-)} 1 \otimes f_j :\widetilde{M_i} \rightarrow \widetilde{N_i}. \end{aligned}$$

In the diagram

the two left squares commute.

There is thus a unique map $g_i$ making the third square commutative. (Observe that $N_{i,\mathrm in}\widetilde{f_i}M_{i,\mathrm out} = N_{i,\mathrm in}\iota f_i = 0$. Thus $N_{i,\mathrm in}\widetilde{f_i}$ factors through the cokernel of $M_{i,\mathrm out}$.)

The fourth square also commutes. Thus if we set $g_j := f_j$ for all vertices $j \not = i$ we get a homomorphism $g:\Sigma _i^-(M) \rightarrow N$. Conversely, consider a homomorphism $g:\Sigma _i^-(M) \rightarrow N$ and set

$$\begin{aligned} \widetilde{g_i} := \bigoplus _{j \in \overline{\Omega }(-,i)} 1 \otimes g_j:\widetilde{M_i} \rightarrow \widetilde{N_i}. \end{aligned}$$

In the diagram

the two right squares commute. Thus there is a unique map $f_i$ making the second square commutative. The first square then also commutes. Thus if we set $f_j := g_j$ for all the vertices $j \not = i$, we get a morphism $f:M \rightarrow \Sigma _i^+(N)$. To establish (ii), one checks that $\Sigma _i^-\Sigma _i^+(M)$ is the $\Pi$-module obtained by replacing in M the part

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} M_i \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i} \end{aligned}$$

with

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} {\text {Im}}(M_{i,\mathrm in}) \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i} \end{aligned}$$

and that $\Sigma _i^+\Sigma _i^-(M)$ is the $\Pi$-module obtained by replacing in M the part

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} M_i \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i} \end{aligned}$$

with

$$\begin{aligned} \widetilde{M_i} \xrightarrow {M_{i,\mathrm in}} {\text {Im}}(M_{i,\mathrm out}) \xrightarrow {M_{i,\mathrm out}} \widetilde{M_i}. \end{aligned}$$

It remains to observe that as vector spaces, ${\text {fac}}_i(M) \cong {\text {Cok}}(M_{i,\mathrm in})$ and ${\text {sub}}_i(M) \cong {\text {Ker}}(M_{i,\mathrm out})$. $\square$

For the following corollary, observe that ${\text {sub}}_i(M) = 0$ if and only if ${\text {soc}}_i(M) = 0$. Dually, ${\text {fac}}_i(M) = 0$ if and only if ${\text {top}}_i(M) = 0$.

Corollary 9.2

The functors $\Sigma _i^+:{\mathcal T}_i \rightarrow {\mathcal S}_i$ and $\Sigma _i^-:{\mathcal S}_i \rightarrow {\mathcal T}_i$ define inverse equivalences of the subcategories

$$\begin{aligned} {\mathcal T}_i := \left\{ M \in {\text {rep}}(\Pi ) \mid {\text {top}}_i(M) = 0 \right\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal S}_i := \left\{ M \in {\text {rep}}(\Pi ) \mid {\text {soc}}_i(M) = 0 \right\} . \end{aligned}$$

Corollary 9.3

For $M,N \in {\text {rep}}(\Pi )$ the following hold:

• (i) If $M,N \in {\mathcal T}_i$, then $\Sigma _i^+$ induces an isomorphism

  $$\begin{aligned} {\text {Ext}}_\Pi ^1(M,N) \cong {\text {Ext}}_\Pi ^1(\Sigma _i^+(M),\Sigma _i^+(N)). \end{aligned}$$

• (ii) If $M,N \in {\mathcal S}_i$, then $\Sigma _i^-$ induces an isomorphism

  $$\begin{aligned} {\text {Ext}}_\Pi ^1(M,N) \cong {\text {Ext}}_\Pi ^1(\Sigma _i^-(M),\Sigma _i^-(N)). \end{aligned}$$

Proposition 9.4

For $M \in {\text {rep}}(\Pi )$ the following are equivalent:

• (i) ${\text {top}}_i(M) = 0$;

• (ii) $M \cong \Sigma _i^-\Sigma _i^+(M)$.

Furthermore, if $M \in {\text {rep}}_\mathrm{l.f.}(\Pi )$, then (i) and (ii) are equivalent to the following:

• (iii) $\underline{{\text {rank}}}(\Sigma _i^+(M)) = s_i(\underline{{\text {rank}}}(M))$.

Dually, the following are equivalent:

• (i) ${\text {soc}}_i(M) = 0$;

• (ii) $M \cong \Sigma _i^+\Sigma _i^-(M)$.

Furthermore, if $M \in {\text {rep}}_\mathrm{l.f.}(\Pi )$, then (i) and (ii) are equivalent to the following:

• (iii) $\underline{{\text {rank}}}(\Sigma _i^-(M)) = s_i(\underline{{\text {rank}}}(M))$.

Proof

The equivalence of (i) and (ii) follows directly from Proposition 9.1 and Corollary 9.2.

Suppose (i) holds for some vertex i of $Q(C,\Omega )$. Let $a = (a_1,\ldots ,a_n) = \underline{{\text {rank}}}(M)$. Recall that we have the $H_i$-module homomorphism

$$\begin{aligned} M_{i,\mathrm in}:\bigoplus _{j \in \overline{\Omega }(i,-)} {_i}H_j \otimes _j M_j \rightarrow M_i. \end{aligned}$$

Since ${\text {top}}_i(M) = 0$, the map $M_{i,\mathrm in}$ is surjective. This implies that $\Sigma _i^+(M)$ is again locally free with

$$\begin{aligned} \left( \underline{{\text {rank}}}(\Sigma _i^+(M)))_i = \sum _{j \in \overline{\Omega }(i,-)} |c_{ij}|a_j - a_i = (s_i(\underline{{\text {rank}}}(\Sigma _i^+(M)))\right) _i. \end{aligned}$$

(Here we used that ${_i}H_j \otimes _j M_j$ is a free $H_i$-module of rank $|c_{ij}|a_j$.) Thus (iii) holds.

Vice versa, the equality

$$\begin{aligned} (\underline{{\text {rank}}}(\Sigma _i^+(M)))_i = (s_i(\underline{{\text {rank}}}(\Sigma _i^+(M))))_i \end{aligned}$$

implies that $M_{i,\mathrm in}$ is surjective. Thus (iii) implies (i). $\square$

Let $M = (M_i,M_{ij},M_{ji}) \in {\text {rep}}(C,D,\overline{\Omega })$. We say that $M_{i,\mathrm in}$ (resp. $M_{i,\mathrm out}$) splits if the image of $M_{i,\mathrm in}$ (resp. $M_{i,\mathrm out}$) is a free $H_i$-module. The following lemma is straightforward.

Lemma 9.5

Let $M \in {\text {rep}}(\Pi )$ be locally free. For each i the following hold:

• (i) $\Sigma _i^+(M)$ is locally free if and only if $M_{i,\mathrm in}$ splits.

• (ii) $\Sigma _i^-(M)$ is locally free if and only if $M_{i,\mathrm out}$ splits.

9.2 Reflection functors for H

We keep the notations of Sect. 5.2. Recall that for an orientation $\Omega$ of C and some $1 \le i \le n$ we defined

$$\begin{aligned} s_i(\Omega ) := \{ (r,s) \in \Omega \mid i \notin \{r,s\} \} \cup \{ (s,r) \in \Omega ^* \mid i \in \{r,s\} \}. \end{aligned}$$

Define

$$\begin{aligned} s_i(H) := s_i(H(C,D,\Omega )) := H(C,D,s_i(\Omega )). \end{aligned}$$

(9.1)

Now let k be a sink in $Q^\circ (C,\Omega )$. Then $\Sigma _k^+$ obviously restricts to a reflection functor

$$\begin{aligned} F_k^+:{\text {rep}}(H) \rightarrow {\text {rep}}(s_k(H)) \end{aligned}$$

which can also be described as follows. Let $M = (M_i,M_{ij}) \in {\text {rep}}(C,D,\Omega )$. Recall that

$$\begin{aligned} M_{k,\mathrm in} = ({\text {sgn}}(k,j)M_{kj})_j:\bigoplus _{j \in \Omega (k,-)} {_k}H_j \otimes M_j \rightarrow M_k. \end{aligned}$$

(Note that $\Omega (k,-) = \overline{\Omega }(k,-)$, since k is a sink.) Let $N_k := {\text {Ker}}(M_{k,\mathrm in})$. We obtain an exact sequence

$$\begin{aligned} 0 \rightarrow N_k \rightarrow \bigoplus _{j \in \Omega (k,-)}{_k}H_j \otimes _j M_j \xrightarrow {M_{k,\mathrm in}} M_k. \end{aligned}$$

Let us denote by $(N_{jk}^\vee )_j$ the inclusion map $N_k \rightarrow \bigoplus _{j \in \Omega (k,-)}{_k}H_j \otimes _j M_j$. Then we have $F_k^+(M) = (N_r,N_{rs})$ with $(r,s) \in s_k(\Omega )$, where

$$\begin{aligned}&N_r := {\left\{ \begin{array}{ll} M_r &{} \quad \text {if } \quad r \not = k,\\ N_k &{} \quad \text {if } \quad r=k \end{array}\right. } \quad \text{ and } \quad \\&N_{rs} := {\left\{ \begin{array}{ll} M_{rs} &{} \quad \text {if } \quad (r,s) \in \Omega \quad \text { and } \quad r \not = k,\\ (N_{rs}^\vee )^\vee &{} \quad \text {if } \quad (r,s) \in \Omega ^* \quad \text { and } \quad s=k. \end{array}\right. } \end{aligned}$$

Similarly, if k is a source in $Q^\circ (C,\Omega )$, then $\Sigma _k^-$ restricts to a reflection functor

$$\begin{aligned} F_k^-:{\text {rep}}(H) \rightarrow {\text {rep}}(s_k(H)). \end{aligned}$$

Proposition 9.6

Let M be locally free and rigid in ${\text {rep}}(H)$. Then $F_k^\pm (M)$ is locally free and rigid.

Proof

Without loss of generality assume that 1 is a sink and n is a source in $Q^\circ (C,\Omega )$. Let M be a locally free and rigid H-module. To get a contradiction, assume that $F_1^+(M)$ is not locally free and that M is of minimal dimension with this property. Recall that $F_1^+(E_1) = 0$. Thus by the minimality of its dimension, M does not have any direct summand isomorphic to $E_1$. We can also assume that $e_iM \not = 0$ for all $1 \le i \le n$. (Otherwise M can be considered as a module over an algebra $H(C',D',\Omega ')$ with fewer vertices.) Since $F_1^+(M)$ is not locally free, we get ${\text {Hom}}_H(M,E_1) \not = 0$, see Lemma 9.5.

We have a short exact sequence

$$\begin{aligned} 0 \rightarrow M' \rightarrow M \rightarrow e_nM \rightarrow 0 \end{aligned}$$

(9.2)

where $M' := (e_1 + \cdots + e_{n-1})M$. Clearly, $M'$ and $e_nM$ are both locally free. In particular, $e_nM \cong E_n^s$ for some $s \ge 1$. We have ${\text {Hom}}_H(M',e_nM) = 0$. Thus applying ${\text {Hom}}_H(M',-)$ to (9.2) we get an embedding ${\text {Ext}}_H^1(M',M') \rightarrow {\text {Ext}}_H^1(M',M)$. Applying ${\text {Hom}}_H(-,M)$ to (9.2) and using that ${\text {Ext}}_H^2(e_nM,M) = 0$ we get ${\text {Ext}}_H^1(M',M) = 0$. This shows that $M'$ is rigid. Applying ${\text {Hom}}_H(-,E_1)$ to the sequence (9.2) yields that ${\text {Hom}}_H(M',E_1) \not = 0$. Since $M'$ is locally free and rigid, the minimality of M implies that $M' \cong E_1^r \oplus U$ for some $r \ge 1$ and some locally free and rigid module U with ${\text {Hom}}_H(U,E_1) = 0$. This yields short exact sequences

$$\begin{aligned} 0 \rightarrow U \xrightarrow {f} M \xrightarrow {g} V \rightarrow 0 \end{aligned}$$

(9.3)

and

$$\begin{aligned} 0 \rightarrow E_1^r \rightarrow V \rightarrow e_nM \rightarrow 0 \end{aligned}$$

(9.4)

where f is the obvious embedding, and g is the obvious projection onto $V := {\text {Cok}}(f)$. Note that V is also locally free, and that ${\text {Hom}}_H(U,E_n) = 0$. Applying ${\text {Hom}}_H(U,-)$ to (9.4) implies that ${\text {Hom}}_H(U,V) = 0$. Now we apply ${\text {Hom}}_H(M,-)$ and ${\text {Hom}}_H(-,V)$ to (9.3) and get similarly as before that V is rigid. Applying ${\text {Hom}}_H(-,E_1)$ to (9.3) implies ${\text {Hom}}_H(M,E_1) \cong {\text {Hom}}_H(V,E_1) \not = 0$. By the minimality of M it now follows that $U=0$ and $V=M$. Thus we have $n=2$.

Since M is locally free, Proposition 3.5 implies that it has a minimal projective resolution of the form

$$\begin{aligned} 0 \rightarrow P'' \rightarrow P' \rightarrow M \rightarrow 0. \end{aligned}$$

Since M is rigid and locally free, we know that M is also $\tau$-rigid, see Corollary 3.6. Thus by [1, Proposition 2.5] we get that ${\text {add}}(P') \cap {\text {add}}(P'') = 0$. (It can be easily checked that [1, Proposition 2.5] is true for arbitrary ground fields.) We obviously have ${\text {Hom}}_H(M,E_2) \not = 0$, since 2 is a source in $Q^\circ (C,\Omega )$. By assumption we have ${\text {Hom}}_H(M,E_1) \not = 0$. This implies that ${\text {Hom}}_H(M,S_i) \not = 0$ for the simple H-modules $S_i$, where $i = 1,2$. Thus $P'$ contains both $P_1$ and $P_2$ as direct summands. Since ${\text {add}}(P') \cap {\text {add}}(P'') = 0$, it follows that $P'' = 0$. In other words, M is projective. But $P=E_1$ is the only indecomposable projective H-module with ${\text {Hom}}_H(P,E_1) \not = 0$. Thus M contains a direct summand isomorphic to $E_1$, a contradiction.

Altogether we proved that ${\text {Hom}}_H(M,E_1) = 0$ for any locally free and rigid H-module M, which does not have a direct summand isomorphic to $E_1$. In this case, we have ${\text {top}}_1(M) = 0$ and $M_{1,\mathrm in}$ is surjective. Thus $F_1^+(M)$ is rigid by Corollary 9.3, and $F_1^+(M)$ is locally free by Lemma 9.5. The corresponding statement for $F_n^-(M)$ is proved dually. This finishes the proof. $\square$

9.3 Reflection functors and APR-tilting

As before, let $H = H(C,D,\Omega )$ and $Q = Q(C,\Omega )$. Let i be a sink in $Q^\circ$, and define

$$\begin{aligned} T := {_H}H/E_i \oplus \tau _H^-(E_i) \text { and } B := {\text {End}}_H(T)^\mathrm{op}. \end{aligned}$$

We also assume that i is not a source in $Q^\circ$. We have $E_i = He_i$. For $1 \le j \le n$ set $P_j := He_j$ and $I_j := {\text {D}}(e_jH)$. Let $S_j$ be the corresponding simple H-module with $S_j \cong {\text {top}}(P_j) \cong {\text {soc}}(I_j)$. Furthermore, let

$$\begin{aligned} T_j := {\left\{ \begin{array}{ll} He_j &{} \quad \text {if } \quad j \not = i, \\ \tau _H^-(E_i) &{} \quad \text {if } \quad j=i. \end{array}\right. } \end{aligned}$$

Thus we have $T = T_1 \oplus \cdots \oplus T_n$. The indecomposable projective B-modules are (up to isomorphism) ${\text {Hom}}_H(T,T_j)$ where $1 \le j \le n$. Let $e_j$ denote the primitive idempotent in B obtained by composing the canonical projection $T \rightarrow T_j$ with the canonical inclusion $T_j \rightarrow T$. Then ${\text {Hom}}_H(T,T_j) \cong Be_j$. Finally, let $S_j$ denote the simple B-module associated with $e_j$. We are using the same notation for the idempotents in $H, s_i(H)$ and B and also for the associated simple modules. However, the context will always save us from confusion.

Recall that a finite-dimensional module T over a finite-dimensional algebra A is a tilting module if the following hold:

• (i) ${\text {proj.~dim}}(T) \le 1$;

• (ii) ${\text {Ext}}_A^1(T,T) = 0$;

• (iii) The number of isomorphism classes of indecomposable direct summands of T is equal to the number of isomorphism classes of simple A-modules.

The following result is inspired by Auslander, Platzeck and Reiten’s [3] ground breaking interpretation of BGP-reflection functors as homomorphism functors of certain tilting modules. Their result can be seen as the beginning of tilting theory.

Theorem 9.7

With the notation above, the H-module T is a tilting module, and the functors

$$\begin{aligned} F_i^+(-):{\text {rep}}(H) \rightarrow {\text {rep}}(s_i(H)) \text { and } {\text {Hom}}_H(T,-):{\text {rep}}(H) \rightarrow {\text {rep}}(B) \end{aligned}$$

are equivalent, i.e. there exists an equivalence

$$\begin{aligned} S:{\text {rep}}(s_i(H)) \rightarrow {\text {rep}}(B) \end{aligned}$$

such that we have an isomorphism of functors $S \circ F_i^+ \cong {\text {Hom}}_H(T,-)$.

As a preparation for the proof of Theorem 9.7 we construct a minimal injective resolution of the H-module $E_i$, see (9.6) below. This yields via the inverse Nakayama functor a minimal projective resolution (9.7) of $\tau _H^-(E_i)$.

Let $E_i'$ be the right H-module such that ${\text {D}}(E_i') \cong E_i$. Similarly to Proposition 3.1 there is a minimal projective resolution

$$\begin{aligned} 0 \rightarrow \bigoplus _{j \in \Omega (i,-)} {_i}H_j \otimes _j e_jH \xrightarrow {\mu } e_iH \rightarrow E_i' \rightarrow 0 \end{aligned}$$

(9.5)

of the right H-module $E_i'$, where the map $e_iH \rightarrow E_i'$ is the canonical projection, and for $j \in \Omega (i,-)$ the jth component of the map $\mu$ is just the multiplication map

$$\begin{aligned} H_{ij}:{_i}H_j \otimes _j e_jH \rightarrow e_iH. \end{aligned}$$

(The maps $H_{ij}$ are the structure maps of the (left) H-module structure on H.) Note that ${_i}H_j \otimes _j e_jH \cong e_jH^{|c_{ji}|}$.

There is a chain of $H_j$-$H_i$-bimodule isomorphisms

$$\begin{aligned} {_j}H_i \cong {\text {Hom}}_{H_i}({_i}H_j,H_i) \cong {\text {D}}{\text {Hom}}_{H_j}({_j}H_i,H_j) \cong {\text {D}}({_i}H_j), \end{aligned}$$

where the first and third isomorphisms are constructed as in Sect. 5.1, and the second isomorphism is defined as in Lemma 8.2. Thus for $r \in {_i}R_j$ we can consider $r^*$ now as an element in ${\text {D}}({_i}H_j)$.

Under the isomorphism

$$\begin{aligned} {\text {D}}(e_jH) \otimes _j {\text {D}}({_i}H_j) \rightarrow {\text {D}}({_i}H_j \otimes _j e_jH) \end{aligned}$$

defined by

$$\begin{aligned} \iota \otimes \eta \mapsto \left( h \otimes e_jh' \mapsto \eta (h)\iota (e_jh')\right) \end{aligned}$$

the dual of the multiplication map $H_{ij}$ is identified with the map

$$\begin{aligned} H_{ij}^*:{\text {D}}(e_iH) \rightarrow {\text {D}}(e_jH) \otimes _j {\text {D}}({_i}H_j) \end{aligned}$$

defined by

$$\begin{aligned} \varphi \mapsto \sum _{r \in {_i}R_j} \varphi (r \cdot -) \otimes r^*. \end{aligned}$$

We have ${\text {D}}(e_iH) = I_i$ and ${\text {D}}(e_jH) \otimes _j {\text {D}}({_i}H_j) \cong I_j \otimes _j {_j}H_i \cong I_j^{|c_{ji}|}$. Applying the duality ${\text {D}}$ to (9.5) we get a minimal injective resolution

$$\begin{aligned} 0 \rightarrow E_i \rightarrow I_i \xrightarrow {(H_{ij}^*)_{j \in \Omega (i,-)}} \bigoplus _{j \in \Omega (i,-)} I_j \otimes _j {_j}H_i \rightarrow 0. \end{aligned}$$

(9.6)

For $j \in \Omega (i,-)$ set

$$\begin{aligned} \theta _{ij} := \nu _H^{-1}(H_{ij}^*) :E_i \rightarrow P_j \otimes _j {_j}H_i \end{aligned}$$

which is given by $he_i \mapsto \sum _{r \in {_i}R_j} hr \otimes r^*$. Here $\nu _H^{-1}:{\text {inj}}(H) \rightarrow {\text {proj}}(H)$ is the inverse Nakayama functor obtained via restriction from ${\text {Hom}}_H({\text {D}}(H_H),-)$. Let $\theta := (\theta _{ij})_j$ where $j \in \Omega (i,-)$. Recall that $E_i = P_i$, since i is a sink in $Q^\circ$. We get that the exact sequence

$$\begin{aligned} 0 \rightarrow E_i \xrightarrow {\theta } \bigoplus _{j \in \Omega (i,-)} P_j \otimes _j {_j}H_i \rightarrow \tau _H^-(E_i) \rightarrow 0 \end{aligned}$$

(9.7)

is a minimal projective resolution of $\tau _H^-(E_i)$. Note that (9.7) is not an Auslander–Reiten sequence if $E_i$ is not simple.

Lemma 9.8

The following hold:

• (i) $\tau _H^-(E_i)$ is locally free;

• (ii) ${\text {Hom}}_H(\tau _H^-(E_i),H) = 0$;

• (iii) ${\text {End}}_H(\tau _H^-(E_i)) \cong {\text {End}}_H(E_i) \cong H_i$.

Proof

The existence of the exact sequence (9.7) implies that $\tau _H^-(E_i)$ is locally free. Since ${\text {inj.~dim}}(E_i) \le 1$, we have ${\text {Hom}}_H(\tau _H^-(E_i),H) = 0$. The H-module $E_i$ is indecomposable non-injective with ${\text {proj.~dim}}(\tau _H^-(E_i)) = 1$ and ${\text {inj.~dim}}(E_i) = 1$. Thus by the Auslander–Reiten formulas we get ${\text {End}}_H(\tau _H^-(E_i)) \cong {\text {End}}_H(E_i) \cong H_i$. This finishes the proof. $\square$

Lemma 9.9

The H-module T is a tilting module.

Proof

By the above considerations we know that

$$\begin{aligned} 0 \rightarrow E_i \xrightarrow {\theta } \bigoplus _{j \in \Omega (i,-)} P_j \otimes _j {_j}H_i \rightarrow \tau _H^-(E_i) \rightarrow 0 \end{aligned}$$

is a minimal projective resolution of $\tau _H^-(E_i)$. It follows that ${\text {proj.~dim}}(T) = 1$. Furthermore, we have

$$\begin{aligned} {\text {Ext}}_H^1(T,T)&= {\text {Ext}}_H^1(\tau _H^-(E_i),T)\\&\cong {\text {D}}{\text {Hom}}_H(T,E_i)\\&= {\text {D}}{\text {Hom}}_H(\tau _H^-(E_i),E_i)\\&= 0. \end{aligned}$$

The equality in the first line of the above equations holds since $\tau _H^-(E_i)$ is the only non-projective indecomposable direct summand of T. The isomorphism in the second line follows by the Auslander–Reiten formulas and the fact that ${\text {proj.~dim}}(\tau _H^-(E_i)) \le 1$. The equality in the third line holds since i is a sink. Finally, the equality in the fourth line follows from Lemma 9.8(ii). The module H has exactly n pairwise non-isomorphic indecomposable direct summands. This finishes the proof. $\square$

Lemma 9.10

We have ${_B}{\text {D}}(T) \cong {\text {D}}(B)/{\text {D}}(e_iB) \oplus \tau _B({\text {D}}(e_iB))$.

Proof

We have

$$\begin{aligned} {_B}{\text {D}}(T) \cong {\text {Hom}}_H(T,{\text {D}}(H)) = \bigoplus _{j=1}^n {\text {Hom}}_H(T,{\text {D}}(e_jH)). \end{aligned}$$

For $j \not = i$ there are B-module isomorphisms

$$\begin{aligned} {\text {Hom}}_H(T,{\text {D}}(e_jH)) \cong {\text {D}}{\text {Hom}}_H(He_j,T) = {\text {D}}{\text {Hom}}_H(T_j,T) \cong {\text {D}}(e_jB). \end{aligned}$$

It follows that

$$\begin{aligned} {_B}{\text {D}}(T) \cong {\text {D}}(B)/{\text {D}}(e_iB) \oplus {\text {Hom}}_H(T,{\text {D}}(e_iH)). \end{aligned}$$

Since ${\text {Ext}}_H^1(T,E_i) \not = 0$, the Connecting Lemma [36, Section 2.3] implies that

$$\begin{aligned} {\text {Hom}}_H(T,{\text {D}}(e_iH)) \cong \tau _B({\text {Ext}}_H^1(T,E_i)). \end{aligned}$$

We have

$$\begin{aligned} {\text {Ext}}_H^1(T,E_i) \cong {\text {D}}{\text {Hom}}_H(\tau _H^-(E_i),T) \cong {\text {D}}(e_iB). \end{aligned}$$

The first isomorphism is obtained from the Auslander–Reiten formulas and the fact that ${\text {inj.~dim}}(E_i) \le 1$. The second isomorphism is obvious. Note that both isomorphism are B-module isomorphisms. This finishes the proof. $\square$

For any of the algebras $A \in \{ H, s_i(H), B \}$ and any simple A-module $S_j$ let

$$\begin{aligned} {\mathcal T}_j^A := \{ M \in {\text {rep}}(A) \mid {\text {Hom}}_A(M,S_j) = 0 \}, \\ {\mathcal S}_j^A := \{ M \in {\text {rep}}(A) \mid {\text {Hom}}_A(S_j,M) = 0 \}. \end{aligned}$$

Using the notation from Sect. 9.1, for $A \in \{ H,s_i(H) \}$ we have ${\mathcal T}_j^A = {\mathcal T}_j \cap {\text {rep}}(A)$ and ${\mathcal S}_j^{A} = {\mathcal S}_j \cap {\text {rep}}(A)$.

Lemma 9.11

The functors $F := {\text {Hom}}_H(T,-)$ and $G := T \otimes _{B} -$ induce mutually quasi-inverse equivalences $F:{\mathcal T}\rightarrow {\mathcal Y}$ and $G:{\mathcal Y}\rightarrow {\mathcal T}$, where

$$\begin{aligned} {\mathcal T}&:= \{ M \in {\text {rep}}(H) \mid {\text {Ext}}_H^1(T,M) = 0\} \\&= \{ M \in {\text {rep}}(H) \mid {\text {D}}{\text {Hom}}_H(M,E_i) = 0 \} \\&= {\mathcal T}_i^H \end{aligned}$$

and

$$\begin{aligned} {\mathcal Y}&:= \{ N \in {\text {rep}}(B) \mid \mathrm{Tor}_B^1(T,N) = 0 \} \\&= \{ N \in {\text {rep}}(B) \mid {\text {D}}{\text {Ext}}_B^1(N,{\text {D}}(T)) = 0 \} \\&= \{ N \in {\text {rep}}(B) \mid {\text {Hom}}_B({\text {D}}(e_iB),N) = 0 \} \\&= {\mathcal S}_i^B. \end{aligned}$$

Furthermore, we have $F({\text {rep}}(H)) \subseteq {\mathcal Y}$ and $G({\text {rep}}(B)) \subseteq {\mathcal T}$.

Proof

This follows mainly from classical tilting theory (Brenner-Butler Therorem, see for example [36, Section 2]) and the Auslander–Reiten formulas. The third equality in the description of ${\mathcal Y}$ uses the Auslander–Reiten formulas in combination with Lemma 9.10. For $j \not = i$ we have

$$\begin{aligned} {\text {Hom}}_B({\text {D}}(e_iB),{\text {D}}(e_jB)) \cong {\text {D}}{\text {Ext}}_B^1({\text {D}}(e_jB),{\text {D}}(T)) = 0. \end{aligned}$$

Thus every composition factor of ${\text {D}}(e_iB)$ is isomorphic to $S_i$. This implies the fourth equality in the description of ${\mathcal Y}$. $\square$

Corollary 9.12

Via restriction of the functors $F_i^+, F \circ F_i^-$ and F we get a commutative diagram

of equivalences of subcategories.

Proof

Combine Lemma 9.11 and Corollary 9.2. $\square$

Corollary 9.13

Via restriction of the functor $F \circ F_i^-$ we get a commutative diagram

with $F \circ F_i^-$ an equivalence of subcategories.

Proof

This follows from Corollary 9.12, the definition of $F_i^+$ and the last statement in Lemma 9.11. $\square$

Lemma 9.14

The following hold:

• (i) ${\text {proj}}(s_i(H)) \subseteq {\mathcal S}_i^{s_i(H)}$;

• (ii) ${\text {proj}}(B) \subseteq {\mathcal S}_i^B$.

Proof

Since i is a source in $Q(C,s_i(\Omega ))^\circ$, we get that ${\text {proj}}(s_i(H)) \subseteq {\mathcal S}_i^{s_i(H)}$. Part (ii) is obvious, since the modules ${\text {Hom}}_T(T,T_j)$ are (up to isomorphism) the indecomposable projective B-modules. $\square$

Theorem 9.7 follows now from [3, Lemma 2.2]. (Corollary 9.13 and Lemma 9.14 and the fact that ${\mathcal S}_i^A$ is closed under submodules for $A \in \{ s_i(H),B\}$ ensure that the assumptions of [3, Lemma 2.2] are satisfied.)

As a consequence, via restriction of $F \circ F_i^-$, we get an equivalence of subcategories

$$\begin{aligned} {\text {proj}}(s_i(H)) \rightarrow {\text {proj}}(B). \end{aligned}$$

In particular, we have $F_i^+(T_j) \cong s_i(H)e_j$ for all $1 \le j \le n$. We also get an algebra isomorphism $s_i(H) \cong B$.

We leave it as an exercise to formulate a dual version of Theorem 9.7.

9.4 Coxeter functors

Let $Q = Q(C,\Omega )$.

Given a $+$-admissible sequence $(i_1,\ldots ,i_n)$ for $(C,\Omega )$ let

$$\begin{aligned} C^+ := F_{i_n}^+ \circ \cdots \circ F_{i_1}^+:{\text {rep}}(H) \rightarrow {\text {rep}}(H). \end{aligned}$$

Dually, one defines −-admissible sequences $(j_1,\ldots ,j_n)$ and $C^- := F_{j_n}^- \circ \cdots \circ F_{j_1}^-$. We call $C^+$ and $C^-$ Coxeter functors. Similarly as in the classical case one proves the following result, compare [11].

Lemma 9.15

The functors $C^+$ and $C^-$ do not depend on the chosen admissible sequences for $(C,\Omega )$.

The next lemma is a consequence of Proposition 9.1, Corollary 9.2 and Lemma 9.5.

Lemma 9.16

Let M be an indecomposable locally free H-module. Let $(i_1,\ldots ,i_n)$ be a $+$-admissible sequence for $(C,\Omega )$. Assume that $F_{i_s}^+ \cdots F_{i_1}^+(M)$ is locally free and non-zero for some $1 \le s \le n$. Then we have

$$\begin{aligned} F_{i_k}^+ \cdots F_{i_1}^+(M) \cong (F_{i_{k+1}}^- \cdots F_{i_s}^-)(F_{i_s}^+ \cdots F_{i_{k+1}}^+) F_{i_k}^+ \cdots F_{i_1}^+(M) \end{aligned}$$

for $1 \le k \le s-1$, and $F_{i_k}^+ \cdots F_{i_1}^+(M)$ is indecomposable and locally free for $1 \le k \le s$.

There is also an obvious dual of Lemma 9.16.

10 Coxeter functors and Auslander–Reiten translations

10.1 Overview

As before we fix $H=H(C,D,\Omega )$. Our aim is to compare the Coxeter functors $C^+$ and $C^-$ introduced in Sect. 9.4 with the Auslander–Reiten translations $\tau$ and $\tau ^-$.

Without loss of generality we assume that for each $(i,j) \in \Omega$ we have $i<j$. Thus,

$$\begin{aligned} C^+ = F_n^+ \circ \cdots \circ F_1^+. \end{aligned}$$

Recall that we defined the twist automorphism T of H by

$$\begin{aligned} T(\varepsilon _i) = \varepsilon _i,\qquad T(\alpha _{ij}^{(g)}) = -\alpha _{ij}^{(g)}, \qquad (i\in Q_0,\ (i,j)\in \Omega ,\ 1\le g \le g_{ij}). \end{aligned}$$

The twist by T defines an automorphism of ${\text {rep}}(H)$ which we denote also by T. More explicitly, for $M = (M_i,M_{ij}) \in {\text {rep}}(H)$ we have $(TM)_i = M_i$ and $(TM)_{ij} = -M_{ij}$.

Following [32, Section 5], we start in Sect. 10.2 by constructing a new algebra $\widetilde{H}$ containing two subalgebras $H_{(0)}$ and $H_{(1)}$ canonically isomorphic to H. Denoting by

$$\begin{aligned} {\text {Res}}_a :{\text {rep}}(\widetilde{H}) \rightarrow {\text {rep}}(H_{(a)}), \quad (a\in \{0,1\}) \end{aligned}$$

the corresponding restriction functors, we will show that $C^+ \cong {\text {Res}}_1\circ {\text {Res}}_0^*$, where

$$\begin{aligned} {\text {Res}}_0^*:{\text {rep}}(H_{(0)})\rightarrow {\text {rep}}(\widetilde{H}) \end{aligned}$$

is right adjoint to ${\text {Res}}_0$. This will follow from a factorization

$$\begin{aligned} {\text {Res}}_0^* = {\text {Res}}^*_{(n-1,n)}\circ \cdots \circ {\text {Res}}^*_{(1,2)}\circ {\text {Res}}^*_{(0,1)} \end{aligned}$$

similar to the definition of $C^+$, and from a comparison of the functors ${\text {Res}}^*_{(i-1,i)}$ and $F^+_i$ obtained in Lemma 10.2.

After that, we will give a different description of the adjoint functor ${\text {Res}}_0^*$, which will allow to show that, for $M\in {\text {rep}}_\mathrm{l.f.}(H)$, the H-module ${\text {Res}}_1\circ {\text {Res}}_0^*(M)$ is the kernel of a certain map $d^*_M$. On the other hand, it follows from Corollary 7.2 that $\tau (TM)$ is the kernel of the map ${\text {D}}{\text {Hom}}_H(d\otimes TM,H)$. We will then show that, under the trace pairings, the maps $d^*_M$ and ${\text {D}}{\text {Hom}}_H(d\otimes TM,H)$ can be identified, hence

$$\begin{aligned} C^+(M) \cong {\text {Res}}_1\circ {\text {Res}}_0^*(M) \cong \tau (TM). \end{aligned}$$

A more detailed statement of our results will be given in Theorem 10.1, whose proof is carried out in Sects. 10.3–10.5.

The remaining sections present direct applications of Theorem 10.1. In 10.6 we give another description of the preprojective algebra $\Pi =\Pi (C,D)$ as a tensor algebra. In 10.7 we adapt to our setting a description of the category ${\text {rep}}(\Pi )$ due to Ringel in the classical case, in terms of H-module homomorphisms $M\rightarrow TC^+(M)$. Finally, in Sect. 10.8 we show that the subcategory of Gorenstein-projective H-modules coincides with the kernel of the Coxeter functor $C^+$.

10.2 An analogue of the Gabriel–Riedtmann construction

The following is an adaptation of [32, Section 5] to our situation.

10.2.1 The algebra $\widetilde{H}$

To our fixed datum $(C,D,\Omega )$ we attach a new algebra $\widetilde{H}$ defined by a quiver with relations. The quiver $\widetilde{Q}$ has set of vertices

$$\begin{aligned} \widetilde{Q}_0 := \{(i,a)\mid i\in Q_0,\ a\in \{0,1\}\}, \end{aligned}$$

and set of arrows

$$\begin{aligned} \widetilde{Q}_1 :=&\ \{\alpha _{(i,a)(j,a)}^{(g)}:(j,a) \rightarrow (i,a) \mid (i,j)\in \Omega ,\ 1\le g \le g_{ij},\ a\in \{0,1\}\}\\&\ \cup \ \{\alpha _{(j,0)(i,1)}^{(g)}:(i,1) \rightarrow (j,0) \mid (i,j)\in \Omega ,\ 1\le g \le g_{ij}\}\\&\ \cup \ \{\varepsilon _{(i,a)}:(i,a) \rightarrow (i,a) \mid (i,a) \in \widetilde{Q}_0\}. \end{aligned}$$

Accordingly we put

$$\begin{aligned} \widetilde{\Omega }:= \{((i,a),(j,a)), ((j,0),(i,1))\mid (i,j)\in \Omega , a\in \{0,1\}\}. \end{aligned}$$

Let

$$\begin{aligned} \widetilde{H} := K\widetilde{Q}/\widetilde{I} \end{aligned}$$

where $\widetilde{I}$ is the ideal of $K\widetilde{Q}$ defined by the following relations:

• ($\widetilde{\mathbf {H}}1$) For each $(i,a)\in \widetilde{Q}_0$ we have

  $$\begin{aligned} \varepsilon _{(i,a)}^{c_i} = 0. \end{aligned}$$

• ($\widetilde{\mathbf {H}}2$) For each $((i,a),(j,b)) \in \widetilde{\Omega }$ and each $1 \le g \le g_{ij}$ we have

  $$\begin{aligned} \varepsilon _{(i,a)}^{f_{ji}}\alpha _{(i,a)(j,b)}^{(g)} = \alpha _{(i,a)(j,b)}^{(g)}\varepsilon _{(j,b)}^{f_{ij}}. \end{aligned}$$

• ($\widetilde{\mathbf {H}}3$) For each $i\in Q_0$ we have

  $$\begin{aligned} \sum _{j\in \Omega (i,-)}\sum _{g=1}^{g_{ij}}\sum _{f=0}^{f_{ji}-1} \varepsilon _{(i,0)}^f\alpha _{(i,0)(j,0)}^{(g)}\alpha _{(j,0)(i,1)}^{(g)} \varepsilon _{(i,1)}^{f_{ji}-1-f}\qquad&\\ \qquad + \sum _{j\in \Omega (-,i)}\sum _{g=1}^{g_{ij}}\sum _{f=0}^{f_{ji}-1} \varepsilon _{(i,0)}^f\alpha _{(i,0)(j,1)}^{(g)}\alpha _{(j,1)(i,1)}^{(g)} \varepsilon _{(i,1)}^{f_{ji}-1-f}&= 0. \end{aligned}$$

When C is symmetric and D is minimal the algebra $\widetilde{H}$ coincides with the bounded quiver denoted by $\widetilde{QQ}$ in [32, Section 5.3].

10.2.2 Example

Let $H = H(C,D,\Omega )$ be defined by the quiver

with relations $\varepsilon _2 = 0, \varepsilon _1^2 = \varepsilon _3^2 = 0$ and $\varepsilon _1\alpha _{13} = \alpha _{13} \varepsilon _3$. Here C is a Cartan matrix of Dynkin type $B_3$, and D is the minimal symmetrizer. Then $\widetilde{H}$ is defined by the quiver

bound by the relations

$$\begin{aligned}&\varepsilon _{(2,a)} = 0,\\&\varepsilon _{(1,a)}^2 = \varepsilon _{(3,a)}^2 = 0,\\&\varepsilon _{(1,a)} \alpha _{(1,a)(3,a)} = \alpha _{(1,a)(3,a)}\varepsilon _{(3,a)},\\&\varepsilon _{(3,0)} \alpha _{(3,0)(1,1)} = \alpha _{(3,0)(1,1)}\varepsilon _{(1,1)}, \end{aligned}$$

with $a \in \{0,1\}$, and

$$\begin{aligned}&\alpha _{(2,0)(1,1)}\alpha _{(1,1)(2,1)} = 0,\\&\varepsilon _{(1,0)}\alpha _{(1,0)(2,0)}\alpha _{(2,0)(1,1)} + \alpha _{(1,0)(2,0)}\alpha _{(2,0)(1,1)}\varepsilon _{(1,1)}\\&+\ \varepsilon _{(1,0)}\alpha _{(1,0)(3,0)}\alpha _{(3,0)(1,1)} + \alpha _{(1,0)(3,0)}\alpha _{(3,0)(1,1)}\varepsilon _{(1,1)} =0,\\&\varepsilon _{(3,0)}\alpha _{(3,0)(1,1)}\alpha _{(1,1)(3,1)} + \alpha _{(3,0)(1,1)}\alpha _{(1,1)(3,1)}\varepsilon _{(3,1)} =0. \end{aligned}$$

10.2.3 $\widetilde{H}$ as a quotient of a tensor algebra

It will be useful to have a more intrinsic description of $\widetilde{H}$ in the spirit of Sect. 6. Define $\widetilde{C} = (\widetilde{c}_{(i,a),(j,b)}) \in \mathbb {Z}^{\widetilde{Q}_0\times \widetilde{Q}_0} = M_{2n}(\mathbb {Z})$ by

$$\begin{aligned} \widetilde{c}_{(i,a),(j,b)} := {\left\{ \begin{array}{ll} c_{ij} &{} \quad \text {if } \quad (a=b),\\ &{}\text {or }(a,b)=(0,1) \quad \text { and } \quad (i,j)\in \Omega ^*,\\ &{}\text {or }(a,b)=(1,0) \quad \text { and } \quad (i,j)\in \Omega ,\\ 0 &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

Clearly, $\widetilde{C}$ is a Cartan matrix with symmetrizer $\widetilde{D} = {\text {diag}}(c_1,\ldots ,c_n,c_1,\ldots ,c_n)$, where $D = {\text {diag}}(c_1,\ldots ,c_n)$ is our symmetrizer for C, and $\widetilde{\Omega }$ is an orientation of $\widetilde{C}$. Moreover, if $\widetilde{c}_{(i,a),(j,b)} < 0$ then

$$\begin{aligned} \widetilde{g}_{(i,a),(j,b)} = g_{ij}, \quad \widetilde{f}_{(i,a),(j,b)} = f_{ij}, \quad \widetilde{k}_{(i,a),(j,b)} = k_{ij}. \end{aligned}$$

As before, one defines the corresponding algebra $H(\widetilde{C},\widetilde{D},\widetilde{\Omega })$. Let

$$\begin{aligned} H_{(i,a)} = K[\varepsilon _{(i,a)}]/(\varepsilon _{(i,a)}^{c_i}). \end{aligned}$$

We have isomorphisms

$$\begin{aligned} \eta _{(i,a)}:H_i\rightarrow H_{(i,a)} \end{aligned}$$

defined by $\varepsilon _i\mapsto \varepsilon _{(i,a)}$, and as before for each $((i,a),(j,b)) \in \widetilde{\Omega }$ we get an $H_{(i,a)}$-$H_{(j,b)}$-bimodule ${_{(i,a)}}H_{(j,b)}$ and an $H_{(j,b)}$-$H_{(i,a)}$-bimodule ${_{(j,b)}}H_{(i,a)}$. There are bimodule isomorphisms

$$\begin{aligned} {_{(i,a)}}H_{(j,b)} \cong {\left\{ \begin{array}{ll} {_i}H_j &{} \text {if } a=b \text { and } (i,j) \in \Omega ,\\ {_i}H_j &{} \text {if } (a,b)=(0,1) \text { and } (i,j) \in \Omega ^*. \end{array}\right. } \end{aligned}$$

via $\eta _{(i,a)}$ and $\eta _{(j,b)}$.

Set

$$\begin{aligned} \widetilde{S} := \prod _{(i,a) \in \widetilde{Q}_0} H_{(i,a)}. \end{aligned}$$

Then

$$\begin{aligned} \widetilde{B} := \bigoplus _{({\mathbf i},{\mathbf j}) \in \widetilde{\Omega }} {_{\mathbf i}}H_{\mathbf j}\end{aligned}$$

is an $\widetilde{S}$-$\widetilde{S}$-bimodule, and we have an isomorphism

$$\begin{aligned} T_{\widetilde{S}}(\widetilde{B}) \cong H(\widetilde{C},\widetilde{D},\widetilde{\Omega }). \end{aligned}$$

In case $(i,j)\in \Omega$ we abbreviate ${_iR_j^0}$ for the standard right basis of ${_{(i,0)}}H_{(j,0)}$ and ${_i}L^1_j$ for the standard left basis of ${_{(i,1)}H_{(j,1)}}$. Moreover, in this case we can identify in a obvious way ${_{(j,0)}H_{(i,1)}}$ with ${\text {Hom}}_{H_{(j,0)}}(_{(i,0)}H_{(j,0)},H_{(j,0)})$ and obtain an $H_{(j,0)}$-basis $(r^*_+)_{r\in {_iR_j^0}}$ of ${_{(j,0)}H_{(i,1)}}$ which is under this identification dual to ${_iR_j^0}$. Similarly, we obtain a dual $H_{(i,1)}$-basis $(\ell ^*_-)_{\ell \in {_iL_j^1}}$ of ${_{(j,0)}H_{(i,1)}}$.

For $j\in Q_0$, define

$$\begin{aligned} \widetilde{\rho }_j := \sum _{\begin{array}{c} i \in \Omega (-,j) \\ \ell \in {_i}L^1_j \end{array}} \ell _-^* \otimes \ell + \sum _{\begin{array}{c} k \in \Omega (j,-) \\ r \in {_j}R^0_k \end{array}} r \otimes r_+^*. \end{aligned}$$

(10.1)

We have $\widetilde{\rho }_j\in e_{(j,0)}\widetilde{B}\otimes _{\widetilde{S}}\widetilde{B}e_{(j,1)}$. Now, arguing as in Sect. 6, we obtain:

$$\begin{aligned} \widetilde{H} \cong T_{\widetilde{S}}(\widetilde{B})/(\widetilde{\rho }_j \mid j \in Q_0). \end{aligned}$$

Similarly to the case of preprojective algebras, for $M\in {\text {rep}}(H(\widetilde{C},\widetilde{D},\widetilde{\Omega }))$ and $j\in Q_0$ we can define maps

$$\begin{aligned} \widetilde{M}_{j,\mathrm in}&\!=\! (M_{(j,0),(k,c)})_{(k,c)} :\bigoplus _{(k,c)\in \widetilde{\Omega }((j,0),-)} {_{(j,0)}H_{(k,c)}}\otimes _{H_{(k,c)}} M_{(k,c)}\rightarrow M_{(j,0)}, \\ \widetilde{M}_{j,\mathrm out}&= ({\text {ad}}_{(i,a),(j,1)}(M_{(i,a),(j,1)}))_{(i,a)} :M_{(j,1)}\rightarrow \\&\quad \bigoplus _{(i,a)\in \widetilde{\Omega }(-,(j,1))} {_{(j,1)}H_{(i,a)}} \otimes _{H_{(i,a)}} M_{(i,a)}. \end{aligned}$$

Note that $\widetilde{\Omega }((j,0),-) = \widetilde{\Omega }(-,(j,1))$ and thus, if we identify by a slight abuse $H_{(j,0)}$ with $H_{(j,1)}$, we can write

$$\begin{aligned}&\bigoplus _{(k,c)\in \widetilde{\Omega }((j,0),-)} {_{(j,0)}H_{(k,c)}}\otimes _{H_{(k,c)}} M_{(k,c)}\\&\quad = \bigoplus _{(i,a)\in \widetilde{\Omega }(-,(j,1))} {_{(j,1)}H_{(i,a)}}\otimes _{H_{(i,a)}} M_{(i,a)}. \end{aligned}$$

With this setup $M\in {\text {rep}}(H(\widetilde{C},\widetilde{D},\widetilde{\Omega }))$ belongs to ${\text {rep}}(\widetilde{H})$ if and only if

$$\begin{aligned} \widetilde{M}_{j,\mathrm in}\circ \widetilde{M}_{j,\mathrm out}=0 \end{aligned}$$

(10.2)

for all $j\in Q_0$.

10.2.4 The subalgebras $H_{(0)}$ and $H_{(1)}$

For $a=0,1$ set

$$\begin{aligned} \mathbbm {1}_a:= \sum _{i\in I}{e_{(i,a)}},\qquad H_{(a)} := \mathbbm {1}_a \widetilde{H} \mathbbm {1}_a. \end{aligned}$$

Clearly, $H_{(a)}$ is a (non-unitary) subalgebra of $\widetilde{H}$, and we have natural isomorphisms $\eta _a:H\rightarrow H_{(a)}$ with $\eta _a(\varepsilon _i)=\varepsilon _{(i,a)}$ and $\eta _a(\alpha _{ij}^{(g)})=\alpha _{(i,a)(j,a)}^{(g)}$.

We obtain for $a\in \{0,1\}$ exact restriction functors

$$\begin{aligned} {\text {Res}}_a:{\text {rep}}(\widetilde{H}) \rightarrow {\text {rep}}(H_{(a)}), \quad M\mapsto \mathbbm {1}_a\widetilde{H}\otimes _{\widetilde{H}} M= \mathbbm {1}_a M. \end{aligned}$$

We will use several times the elementary fact that the functor

$$\begin{aligned} {\text {Res}}_0^*:{\text {rep}}(H_{(0)})\rightarrow {\text {rep}}(\widetilde{H}), \quad N\mapsto {\text {Hom}}_{H_{(0)}}(\mathbbm {1}_0\widetilde{H},N) \end{aligned}$$

is uniquely characterized up to isomorphism as the right adjoint of ${\text {Res}}_0$. It is not hard to see that

$$\begin{aligned} {\text {Res}}_0\circ {\text {Res}}_0^* \cong {\text {id}}_{{\text {rep}}(H_{(0)})}. \end{aligned}$$

10.2.5 The H-H-bimodule X

Define

$$\begin{aligned} X = X(C,D,\Omega ) := \mathbbm {1}_0\widetilde{H}\mathbbm {1}_1. \end{aligned}$$

We regard X as an H-H-bimodule via the maps $\eta _0$ and $\eta _1$, that is,

$$\begin{aligned} hxh' := \eta _0(h)x\eta _1(h'),\qquad (h, h' \in H,\ x\in X). \end{aligned}$$

Similarly, using $\eta _0$ and $\eta _1$ we can regard ${\text {Res}}_1\circ {\text {Res}}_0^*$ as a functor from ${\text {rep}}(H)$ to ${\text {rep}}(H)$. Then it is easy to see that we have an isomorphism of functors:

$$\begin{aligned} {\text {Res}}_1\circ {\text {Res}}_0^* \cong {\text {Hom}}_{H}(X,-). \end{aligned}$$

Theorem 10.1

The following hold:

• (a) For each $M \in {\text {rep}}(H)$ we have a functorial isomorphism

  $$\begin{aligned} {\text {Hom}}_H(X,M)\cong C^+(M). \end{aligned}$$

• (b) For each $M \in {\text {rep}}_\mathrm{l.f.}(H)$ we have functorial isomorphisms

  $$\begin{aligned} {\text {Hom}}_H(X,TM) \cong TC^+(M)\cong \tau (M). \end{aligned}$$

• (c) For each $M \in {\text {rep}}(H)$ we have a functorial isomorphism

  $$\begin{aligned} X\otimes _H M \cong C^-(M). \end{aligned}$$

• (d) For each $M \in {\text {rep}}_\mathrm{l.f.}(H)$ we have functorial isomorphisms

  $$\begin{aligned} X\otimes _H TM \cong TC^-(M) \cong \tau ^-(M). \end{aligned}$$

10.3 Proof of Theorem 10.1(a)

We follow the hints from [32, Section 5.5]. For $l\in Q_0\cup \{0\}$ we define idempotents in $\widetilde{H}$

$$\begin{aligned} \mathbbm {1}^{(l)} := \sum _{i>l} e_{(i,0)} + \sum _{i\le l} e_{(i,1)},\qquad \mathbbm {1}^{(l)}_0:= \mathbbm {1}_0+ \sum _{i\le l} e_{(i,1)}, \end{aligned}$$

and the corresponding (non-unitary) subalgebras

$$\begin{aligned} H^{(l)}:= \mathbbm {1}^{(l)} \widetilde{H}\mathbbm {1}^{(l)}, \qquad \widetilde{H}^{(l)}:= \mathbbm {1}^{(l)}_0 \widetilde{H}\mathbbm {1}^{(l)}_0. \end{aligned}$$

Clearly, $H^{(0)}=\widetilde{H}^{(0)}=H_{(0)}, H^{(n)}=H_{(1)}, \widetilde{H}^{(n)}=\widetilde{H}$, and an easy calculation shows that, using the notation of Eq. (9.1),

$$\begin{aligned} H^{(l)}= s_l \cdots s_2s_1(H^{(0)}), \qquad (l\in Q_0). \end{aligned}$$

Moreover $\mathbbm {1}^{(l)}\in \widetilde{H}^{(l)}$ and thus $H^{(l)}\subset \widetilde{H}^{(l)}\supset \widetilde{H}^{(l-1)}$ for $l\in Q_0$. We study the corresponding restriction functors:

$$\begin{aligned} {\text {Res}}^{(l)}&:{\text {rep}}(\widetilde{H})\rightarrow {\text {rep}}(H^{(l)}), \ \qquad M\mapsto \mathbbm {1}^{(l)}\widetilde{H}\otimes _{\widetilde{H}} M, \\ {\text {Res}}_{(l,m)}&:{\text {rep}}(\widetilde{H}^{(m)})\rightarrow {\text {rep}}(\widetilde{H}^{(l)}), \quad M\mapsto \mathbbm {1}_0^{(l)}\widetilde{H}^{(m)}\otimes _{\widetilde{H}^{(m)}} M, \quad (l<m). \end{aligned}$$

Obviously, ${\text {Res}}_{(l,m)}$ admits a right adjoint

$$\begin{aligned} {\text {Res}}_{(l,m)}^*(-) = {\text {Hom}}_{\widetilde{H}^{(l)}}(\mathbbm {1}_0^{(l)}\widetilde{H}^{(m)},-) \end{aligned}$$

and

$$\begin{aligned} {\text {Res}}_0={\text {Res}}_{(0,1)}\circ {\text {Res}}_{(1,2)}\circ \cdots \circ {\text {Res}}_{(n-1,n)}. \end{aligned}$$

Thus we have

$$\begin{aligned} {\text {Res}}_0^* = {\text {Res}}^*_{(n-1,n)}\circ \cdots \circ {\text {Res}}^*_{(1,2)}\circ {\text {Res}}^*_{(0,1)}. \end{aligned}$$

Lemma 10.2

With the above notations we have functorial isomorphisms

$$\begin{aligned} {\text {Res}}^{(i)}\circ {\text {Res}}^*_{(i-1,i)}(M)\cong F_i^+\circ {\text {Res}}^{(i-1)}(M) \end{aligned}$$

for all $M\in {\text {rep}}(\widetilde{H}^{(i-1)})$ and $i\in Q_0 = \{1,\ldots ,n\}$.

Proof

Note that naturally

$$\begin{aligned} {\text {Res}}_{(i-1,i)}\circ {\text {Res}}^*_{(i-1,i)}(M) \cong M \end{aligned}$$

for all $M\in {\text {rep}}(\widetilde{H}^{(i-1)})$. Now there is a unique functor

$$\begin{aligned} R^*_{(i-1,i)}:{\text {rep}}(\widetilde{H}^{(i-1)}) \rightarrow {\text {rep}}(\widetilde{H}^{(i)}) \end{aligned}$$

satisfying the two following conditions for all $M\in {\text {rep}}(\widetilde{H}^{(i-1)})$:

$$\begin{aligned} {\text {Res}}_{(i-1,i)}\circ R^*_{(i-1,i)}(M) = M, \qquad {\text {Res}}^{(i)}\circ R^*_{(i-1,i)}(M) = F_i^+\circ {\text {Res}}^{(i-1)}(M). \end{aligned}$$

Indeed, the first condition fixes the restriction of $R^*_{(i-1,i)}(M)$ to $\widetilde{H}^{(i-1)}$ and the second one fixes the restriction of $R^*_{(i-1,i)}(M)$ to $H^{(i)}$. Because of the definitions of $H^{(i)}$ and $\widetilde{H}^{(i-1)}$, this determines completely the structure of $R^*_{(i-1,i)}(M)$, and gives uniqueness. Note that the quivers of $\widetilde{H}^{(i-1)}$ and of $H^{(i)}$ contain some common arrows, but the representations M and $F_i^+ \circ {\text {Res}}^{(i-1)}(M)$ are the same for those arrows, by definition of $F_i^+$. So $R^*_{(i-1,i)}(M)$ is indeed a representation of $H(\widetilde{C},\widetilde{D},\widetilde{\Omega })$, supported on the vertices and arrows of $\widetilde{H}^{(i)}$. Finally, this representation satisfies the relation (10.2) for $j=i$, because again of the definition of $F_i^+$, so $R^*_{(i-1,i)}(M)\in {\text {rep}}(\widetilde{H}^{(i)})$.

To prove the lemma, we have to show that the above functor $R^*_{(i-1,i)}$ is isomorphic to ${\text {Res}}^*_{(i-1,i)}$, or equivalently, that $R^*_{(i-1,i)}$ is right adjoint to ${\text {Res}}_{(i-1,i)}$. To do so, let $N\in {\text {rep}}(\widetilde{H}^{(i)})$ and $M\in {\text {rep}}(\widetilde{H}^{(i-1)})$, and consider the natural map

$$\begin{aligned} {\text {Hom}}_{\widetilde{H}^{(i)}}(N, R^*_{(i-1,i)}(M)) \rightarrow {\text {Hom}}_{\widetilde{H}^{(i-1)}}({\text {Res}}_{(i-1,i)}(N), M) \end{aligned}$$

obtained by restricting $f:N \rightarrow R^*_{(i-1,i)}(M)$ to ${\text {Res}}_{(i-1,i)}(N)$. We have to show that this restriction is in fact bijective. That is, for $g \in {\text {Hom}}_{\widetilde{H}^{(i-1)}}({\text {Res}}_{(i-1,i)}(N), M)$ we have to show that there exists a unique $g_{(i,1)} \in {\text {Hom}}_{H_i} (N_{(i,1)}, {\text {Ker}}(\widetilde{M}_{i,\mathrm in}))$ which lifts g to an element of ${\text {Hom}}_{\widetilde{H}^{(i)}}(N, R^*_{(i-1,i)}(M))$.

Now, let

$$\begin{aligned} N_{i,+}:= \bigoplus _{(k,c)\in \widetilde{\Omega }((i,0),-)} {}_{(i,0)}H_{(k,c)}\otimes _{H_{(k,c)}} N_{(k,c)} \end{aligned}$$

denote the domain of $\widetilde{N}_{i,\mathrm in}$, and similarly let $M_{i,+}$ denote the domain of $\widetilde{M}_{i,\mathrm in}$. By the definition of $\widetilde{H}^{(i-1)}$-homomorphisms, we have a commutative diagram

where the bottom row is exact by construction, and in the top row the composition is zero since N is a $\widetilde{H}^{(i)}$-module. Thus $\widetilde{M}_{i,\mathrm in} \circ g_{i,+} \circ \widetilde{N}_{i,\mathrm out} = 0$. By the universal property of ${\text {Ker}}(\widetilde{M}_{i,\mathrm in})$ there exists a unique morphism of $H_i$-modules $g_{(i,1)}:N_{(i,1)} \rightarrow {\text {Ker}}(\widetilde{M}_{i,\mathrm in})$ which makes the left-hand square commutative. $\square$

We can now finish the proof of Theorem 10.1(a). Using n times Lemma 10.2, for $M\in {\text {rep}}(H)$ (regarded as a representation of $H_0$) we have

$$\begin{aligned} {\text {Hom}}_H(X,M)&= {\text {Res}}_1\circ {\text {Res}}_0^*(M)\\&= {\text {Res}}^{(n)}\circ {\text {Res}}_{(n-1,n)}^*\circ \cdots \circ {\text {Res}}_{(0,1)}^*(M)\\&= F_n^+\circ {\text {Res}}^{(n-1)}\circ {\text {Res}}_{(n-2,n-1)}^*\circ \cdots \circ {\text {Res}}_{(0,1)}^*(M)\\&= \quad \cdots \\&= F_n^+\circ F_{n-1}^+ \circ \cdots \circ F_1^+ \circ {\text {Res}}^{(0)}(M) \\&= C^+(M). \end{aligned}$$

10.4 Proof of Theorem 10.1(b)

We follow the idea of [32, Section 5.4], and start by giving an alternative description of ${\text {Res}}_0^*$. This is done by constructing in two steps a functor $R_0^*:{\text {rep}}(H_{(0)})\rightarrow {\text {rep}}(\widetilde{H})$, and then showing that $R_0^*$ is right adjoint to ${\text {Res}}_0$.

Let $M\in {\text {rep}}(H_{(0)})$. We first define $\widetilde{M}\in {\text {rep}}(H(\widetilde{C},\widetilde{D},\widetilde{\Omega }))$ by requiring that

$$\begin{aligned} {\text {Res}}_0(\widetilde{M})&= M, \\ {\text {Res}}_1(\widetilde{M})&= \bigoplus _{(k,l)\in \Omega } {\text {Hom}}_{H_{(l,0)}}({_{(l,0)}H_{(k,1)}}\otimes _{H_{(k,1)}}e_{(k,1)}H_1, M_{(l,0)}). \end{aligned}$$

(Note that $H_{(0)}$ and $H_{(1)}$ can also be regarded as subalgebras of $H(\widetilde{C},\widetilde{D},\widetilde{\Omega })$, so we allow ourselves, by some abuse of notation, to continue to denote the restriction functors ${\text {rep}}(H(\widetilde{C},\widetilde{D},\widetilde{\Omega })) \rightarrow {\text {rep}}(H_{(a)})$ by ${\text {Res}}_a$.) It remains to define, for $(i,j)\in \Omega$, the structure map

$$\begin{aligned} \widetilde{M}_{(j,0),(i,1)}:{_{(j,0)}H_{(i,1)}}\otimes _{H_{(i,1)}} \widetilde{M}_{(i,1)}\longrightarrow \widetilde{M}_{(j,0)}=M_{(j,0)}. \end{aligned}$$

This is given by the following composition:

$$\begin{aligned}&{_{(j,0)}H_{(i,1)}}\otimes _{H_{(i,1)}} \left( \bigoplus _{(k,l)\in \Omega } {\text {Hom}}_{H_{(l,0)}}({_{(l,0)}H_{(k,1)}}\otimes e_{(k,1)}H_1 e_{(i,1)},M_{(l,0)})\right) \\&\quad \overset{\text {proj.}}{\longrightarrow } {_{(j,0)}H_{(i,1)}}\otimes _{H_{(i,1)}} {\text {Hom}}_{H_{(j,0)}}({_{(j,0)}H_{(i,1)}}\otimes e_{(i,1)}H_1 e_{(i,1)},M_{(j,0)})\\&\quad = {_{(j,0)}H_{(i,1)}}\otimes _{H_{(i,1)}} {\text {Hom}}_{H_{(j,0)}}({_{(j,0)}H_{(i,1)}},M_{(j,0)}) \overset{\text {eval.}}{\longrightarrow } M_{(j,0)}, \end{aligned}$$

where the first map is the projection on the direct summand indexed by $(k,l) = (i,j)$ and the second map is the evaluation $h\otimes \varphi \mapsto \varphi (h)$.

Secondly, we define a subrepresentation $R_0^*(M)$ of $\widetilde{M}$ as follows. We set

$$\begin{aligned} (R_0^*(M))_{(i,0)} =\widetilde{M}_{(i,0)}=M_{(i,0)}, \qquad (i\in Q_0), \end{aligned}$$

and we define $(R_0^*(M))_{(h,1)}$ as the subspace of $\widetilde{M}_{(h,1)}$ consisting of all

$$\begin{aligned} (\mu _{k,l}^h)_{(k,l)\in \Omega } \in \bigoplus _{(k,l)\in \Omega } {\text {Hom}}_{H_{(l,0)}}({_{(l,0)}H_{(k,1)}}\otimes e_{(k,1)}H_{(1)} e_{(h,1)},M_{(l,0)}) \end{aligned}$$

such that, for all $l\in Q_0$ and $n^{(1)}\in e_{(l,1)} H_{(1)} e_{(h,1)}$ the following relation holds:

$$\begin{aligned} \sum _{\begin{array}{c} k\in \Omega (-,l)\\ \ell \in {_{k}L^1_{l}} \end{array}} \mu _{k,l}^h(\ell ^*_-\otimes \ell \cdot n^{(1)}) + \sum _{\begin{array}{c} m \in \Omega (l,-)\\ r\in {_{l}R^0_{m}} \end{array}} M_{(l,0),(m,0)} (r\otimes \mu _{l,m}^h(r^*_+\otimes n^{(1)})) = 0. \end{aligned}$$

(10.3)

Here, we use the notation from Sect. 10.2.3. It is straightforward to check that $R_0^*(M)$ is an $H(\widetilde{C},\widetilde{D},\widetilde{\Omega })$-subrepresentation of $\widetilde{M}$. Moreover, $R^*_0(M)$ is in fact a representation of $\widetilde{H}$. To see this, we check the defining relations (10.1) with the help of the special case $n^{(1)}=e_{(l,1)}$ of Eq. (10.3). In fact, if we apply $\widetilde{\rho }_j$ to $\mu ^{(j)}=(\mu _{k,l}^j)_{(k,l)\in \Omega }\in R_0^*(M)_{(j,1)}$ we deduce from the definitions that

$$\begin{aligned}&\sum _{\begin{array}{c} i\in \Omega (-,j)\\ \ell \in {_iL^1_j} \end{array}}\!\! \widetilde{M}_{(j,0),(i,1)}(\ell _-^*\otimes \widetilde{M}_{(i,1),(j,1)}(\ell \otimes \mu ^{(j)}))\nonumber \\&\qquad +\sum _{\begin{array}{c} k\in \Omega (j,-)\\ r\in {_jR^0_k} \end{array}} M_{(j,0),(k,0)}(r\otimes \widetilde{M}_{(k,0),(j,1)}(r^*_+ \otimes \mu ^{(j)}))\\&\quad =\sum _{\begin{array}{c} i\in \Omega (-,j)\\ \ell \in {_iL^1_j} \end{array}}\!\mu _{i,j}^j(\ell _-^*\otimes \ell \cdot e_{(j,1)})\\&\qquad +\sum _{\begin{array}{c} k\in \Omega (j,-)\\ r\in {_jR^0_k} \end{array}} M_{(j,0),(k,0)}(r\otimes \mu _{j,k}^j(r_+^*\otimes e_{(j,1)})) =0, \end{aligned}$$

as required.

Thus, we have obtained a functor $R_0^*:{\text {rep}}(H_{(0)}) \rightarrow {\text {rep}}(\widetilde{H}), \ M\mapsto R_0^*(M)$. It will follow from the next lemma that $R_0^*$ is isomorphic to ${\text {Res}}_0^*$.

Lemma 10.3

$R_0^*$ is right adjoint to ${\text {Res}}_0$.

Proof

Let $N\in {\text {rep}}(\widetilde{H})$ and $M\in {\text {rep}}(H_{(0)})$. Consider $\chi \in {\text {Hom}}_{\widetilde{H}}(N, R_0^*(M))$. Thus, $\chi$ is given by a family of maps

$$\begin{aligned} \chi ^{(i,a)}\in {\text {Hom}}_{H_{(i,a)}}(N_{(i,a)}, (R_0^*(M))_{(i,a)}), \quad ((i,a)\in \widetilde{Q}_0), \end{aligned}$$

subject to the usual commutativity relations. By the construction of $R_0^*(M)$ we have more explicitly for all $i\in Q_0$ and $n_{(i,1)}\in N_{(i,1)}$:

$$\begin{aligned}&\chi ^{(i,0)} \in {\text {Hom}}_{H_{(i,0)}}(N_{(i,0)},M_{(i,0)}), \\&\chi ^{(i,1)}(n_{(i,1)}) \in \bigoplus _{(k,l)\in \Omega } {\text {Hom}}_{H_{(l,0)}}({_{(l,0)}H_{(k,1)}}\otimes e_{(k,1)} H_1 e_{(i,1)}, M_{(l,0)}). \end{aligned}$$

Let us denote by $\chi ^{(i,1)}_{k,l}(-,n_{(i,1)})$ the (k, l)-component of $\chi ^{(i,1)}(n_{(i,1)})$. These maps are subject to the following relations for $(i,j)\in \Omega , \ell ^{(a)}\in {_iL_j^a}, r\in {_iR_j^0}$:

$$\begin{aligned} \chi ^{(i,0)}(N_{(i,0),(j,0)}(\ell ^{(0)}\otimes n_{(j,0)}))&= M_{(i,0),(j,0)}(\ell ^{(0)}\otimes \chi ^{(j,0)}(n_{(j,0)})), \end{aligned}$$

(10.4)

$$\begin{aligned} \chi ^{(j,0)}(N_{(j,0),(i,1)}(r_+^*\otimes n_{(i,1)}))&= \chi _{i,j}^{(i,1)}(r_+^*\otimes e_{(i,1)},n_{(i,1)}), \end{aligned}$$

(10.5)

$$\begin{aligned} \chi _{k,l}^{(i,1)}(-, N_{(i,1),(j,1)}(\ell ^{(1)}\otimes n_{(j,1)}))&= \chi _{k,l}^{(j,1)}(-\cdot \ell ^{(1)}, n_{(j,1)}). \end{aligned}$$

(10.6)

Equation (10.4) means that we have indeed a well-defined restriction

$$\begin{aligned} r_{N,M}:{\text {Hom}}_{\widetilde{H}}(N, R_0^*(M))\rightarrow {\text {Hom}}_{H_{(0)}}({\text {Res}}_0(N), M). \end{aligned}$$

Combining (10.5) and (10.6) we see that the maps $\chi _{k,l}^{(j,1)}$ for $(k,l)\in \Omega$ and $j\in Q_0$ are determined by the maps $\chi ^{(i,0)}$ with $i\in Q_0$, in other words $r_{N,M}$ is injective.

By the same token we see that for each $\chi ^{(0)}\in {\text {Hom}}_{H_{(0)}}({\text {Res}}_0(N), M)$ there exists $\widetilde{\chi }\in {\text {Hom}}_{H(\widetilde{C},\widetilde{D},\widetilde{\Omega })}(N,\widetilde{M})$ which restricts to $\chi ^{(0)}$. We leave it as an exercise to show that if $N\in {\text {rep}}(\widetilde{H})$ then ${\text {Im}}(\widetilde{\chi })\subset R_0^*(M)$. Thus, $r_{N,M}$ is bijective. $\square$

Proposition 10.4

For $M \in {\text {rep}}_\mathrm{l.f.}(H)$ we have

$$\begin{aligned} \tau (TM) \cong {{\text {Res}}_1}\circ R_0^*(M), \end{aligned}$$

where in the right-hand side $H_{(0)}$ and $H_{(1)}$ are identified with H by means of the isomorphisms $\eta _0$ and $\eta _1$.

Proof

Since M is locally free, TM is also locally free and Corollary 7.2 provides a projective resolution:

$$\begin{aligned} 0 \rightarrow \bigoplus _{(j,i) \in \Omega } H e_j \otimes {_j}H_i \otimes (TM)_i \xrightarrow {d \otimes TM} \bigoplus _{k=1}^n He_k \otimes (TM)_k \xrightarrow {\mathrm{mult}} TM \rightarrow 0 \end{aligned}$$

Therefore, by definition of the Auslander–Reiten translation $\tau$, we know that $\tau (TM)$ is isomorphic to ${\text {Ker}}({\text {D}}{\text {Hom}}_H(d \otimes _H TM,H))$.

On the other hand, the construction of $R_0^*(M)$ shows that ${{\text {Res}}_1}\circ R_0^*(M)$ can be identified with the kernel of the map

$$\begin{aligned} d_M^*:\bigoplus _{(j,i) \in \Omega } {\text {Hom}}_{H_i}({_j}H_i^* \otimes e_jH,M_i) \quad \longrightarrow \quad \bigoplus _{k=1}^n {\text {Hom}}_{H_k}(e_kH,M_k) \end{aligned}$$

whose (j, i)-component is defined by

$$\begin{aligned} \varphi _{(j,i)} \mapsto \sum _{\ell \in {_j}L_i} \varphi _{(j,i)}(\ell ^* \otimes _j \ell \cdot -) + \sum _{r \in {_j}R_i} M_{ji}(r \otimes \varphi _{(j,i)}(r^* \otimes _j -)). \end{aligned}$$

(10.7)

Indeed, ${{\text {Res}}_1}\circ R_0^*(M)$ is the subspace of ${{\text {Res}}_1}(\widetilde{M})$ defined by Eq. (10.3). Our goal is to identify under the trace pairing the map ${\text {D}}{\text {Hom}}_H(d \otimes TM,H)$ with $d_M^*$. For $(j,i)\in \Omega$, the restriction $d\otimes TM :He_j\otimes {}_jH_i\otimes M_i \rightarrow He_i\otimes M_i \oplus He_j\otimes M_j$ is given by

$$\begin{aligned} (d\otimes TM)(p\otimes h\otimes m) = ph\otimes m + p\otimes M_{ji}(h\otimes m). \end{aligned}$$

(10.8)

(Note the plus sign, coming from the twist map T). Using adjunction we have

$$\begin{aligned} {\text {Hom}}_H(He_i\otimes M_i,H) \cong {\text {Hom}}_{H_i}(M_i,{\text {Hom}}_H(He_i,H)) \cong {\text {Hom}}_{H_i}(M_i,e_iH), \end{aligned}$$

so under the trace pairing we get

$$\begin{aligned}&{\text {D}}{\text {Hom}}_H(He_i\otimes M_i \oplus He_j\otimes M_j,H) \\&\quad \cong {\text {Hom}}_{H_i}(e_iH,M_i) \oplus {\text {Hom}}_{H_j}(e_jH,M_j). \end{aligned}$$

Similarly,

$$\begin{aligned}&{\text {D}}{\text {Hom}}_H(He_j\otimes {}_jH_i\otimes M_i) \\&\quad \cong {\text {Hom}}_{H_j}(e_jH,{}_jH_i\otimes M_i) \cong {\text {Hom}}_{H_i}({}_iH_j \otimes e_jH, M_i), \end{aligned}$$

where the second isomorphism is given by ${\text {ad}}_{ij}^{-1}$. Hence ${\text {D}}{\text {Hom}}_H(d \otimes TM,H)$ can be identified with a map from $\oplus _{(j,i)\in \Omega } {\text {Hom}}_{H_i}({}_iH_j \otimes e_jH, M_i)$ to $\oplus _k {\text {Hom}}_{H_k}(e_kH,M_k)$, and comparison between (10.7) and (10.8) shows that this map is indeed $d_M^*$. $\square$

Now we are ready to prove part (b) of Theorem 10.1. By Lemma 10.3 and the uniqueness of adjoint functors we have a functorial isomorphism $R_0^*(-) \cong {\text {Res}}_0^* (-)$. Hence, by Proposition 10.4, if $M\in {\text {rep}}_\mathrm{l.f.}(H)$ we have

$$\begin{aligned} {\text {Hom}}_{H}(X,TM) = {\text {Res}}_1\circ {\text {Res}}_0^*(TM) \cong {{\text {Res}}_1}\circ R_0^*(TM)\cong \tau (T^2M)=\tau (M). \end{aligned}$$

This proves Theorem 10.1 (b).

10.5 Proof of Theorem 10.1(c),(d)

Clearly, (c) follows from (a) since $C^-$ is left adjoint to $C^+$. In order to show (d), let $M,N \in {\text {rep}}_\mathrm{l.f.}(H)$. Recall, that this implies that both, M and N, have projective and injective dimension at most 1. We obtain functorial isomorphisms

$$\begin{aligned} {\text {Hom}}_{H}(\tau ^-(M), N)&\cong {\text {Hom}}_H(M,\tau (N))\\&\cong {\text {Hom}}_H(M,C^+(TN))\\&\cong {\text {Hom}}_H(C^-(TM),N). \end{aligned}$$

The first isomorphism is obtained from the Auslander–Reiten formulas, the second follows from (b), and the third isomorphism is just the adjunction map.

With the usual H-H-bimodule structure on ${\text {D}}(H)$ we obtain a functorial isomorphism of right H-modules

$$\begin{aligned} {\text {D}}(X) \cong {\text {Hom}}_H(X,{\text {D}}(H)) \end{aligned}$$

for all (left) H-modules X. Now, in our situation ${\text {D}}(H)$ is locally free, thus taking $N={\text {D}}(H)$ in the above chain of functorial isomorphisms we get

$$\begin{aligned} \tau ^-(M) \cong C^{-}(TM) \cong X^T\otimes _H M \end{aligned}$$

where the last isomorphism comes from (c). This proves Theorem 10.1 (d).

10.6 Another description of $\Pi (C,D)$ as a tensor algebra

Let $\Pi = \Pi (C,D)$. Recall from Sect. 6 that $\Pi _1$ is the subspace of $\Pi$ of elements of degree 1. Let $X^T$ be the twisted version of the H-H-bimodule X, where the bimodule structure is defined by

$$\begin{aligned} hxh' := h xT(h'),\qquad (h, h' \in H,\ x\in X). \end{aligned}$$

Theorem 10.5

We have isomorphisms of H-H-bimodules

$$\begin{aligned} \Pi _1 \cong X^T \cong {\text {Ext}}^1_H({\text {D}}(H),H). \end{aligned}$$

Proof

Note that the bimodule isomorphism $\Pi _1 \cong X^T$ follows directly from the definitions. On the other hand, we have by Theorem 10.1(d) for locally free modules M a functorial isomorphism

$$\begin{aligned} X^T\otimes _H M \cong \tau ^-(M) \cong {\text {Ext}}^1_H({\text {D}}(H),M). \end{aligned}$$

(10.9)

Note that the functor

$$\begin{aligned} {\text {Ext}}_H^1({\text {D}}(H),-):{\text {rep}}(H)\rightarrow {\text {rep}}(H) \end{aligned}$$

is right exact since ${\text {proj.~dim}}({\text {D}}(H)) \le 1$. For $M \in {\text {rep}}(H)$ let

$$\begin{aligned} P_1 \rightarrow P_0 \rightarrow M \rightarrow 0 \end{aligned}$$

(10.10)

be a projective presentation of M. Applying the right exact functors $X^T \otimes _H -$ and ${\text {Ext}}_H^1({\text {D}}(H),-)$ to (10.10) yields a functorial commutative diagram

with exact rows. Since the restrictions of $X^T \otimes _H -$ and ${\text {Ext}}_H^1({\text {D}}(H),-)$ to ${\text {rep}}_\mathrm{l.f.}(H)$ are isomorphic, we get that $\eta _{P_0}$ and $\eta _{P_1}$ are isomorphisms. This implies that $\eta _M$ is an isomorphism as well. It follows that the functors $X^T \otimes _H -$ and ${\text {Ext}}_H^1({\text {D}}(H),-)$ are isomorphic. From the canonical isomorphism of H-H-bimodules ${\text {Ext}}^1_H({\text {D}}(H),H)\otimes _H H\cong {\text {Ext}}_H^1({\text {D}}(H),H)$ we conclude that the right exact functors ${\text {Ext}}_H^1({\text {D}}(H),-)$ and ${\text {Ext}}^1_H({\text {D}}(H),H)\otimes _H-$ are isomorphic. This implies that ${\text {Ext}}_H^1({\text {D}}(H),H)$ and $X^T$ are isomorphic as H-H-bimodules. $\square$

Corollary 10.6

We have K-algebra isomorphisms

$$\begin{aligned} \Pi \cong T_H(X^T) \cong T_H({\text {Ext}}_H^1({\text {D}}(H),H)). \end{aligned}$$

Proof

Combine Theorem 10.5 and Proposition 6.5. $\square$

Corollary 10.7

For $M \in {\text {rep}}(H)$ there are functorial isomorphisms

$$\begin{aligned} {\text {Hom}}_H(X^T,M) \cong {\text {D}}{\text {Ext}}_H^1(M,H) \text { and } X^T \otimes _H M \cong {\text {Ext}}_H^1({\text {D}}(H),M). \end{aligned}$$

Proof

We get the second isomorphism from the proof of Theorem 10.5. The first isomorphism follows then by adjunction. $\square$

10.7 The morphism categories ${\mathcal C}(1,TC^+)$ and ${\mathcal C}(TC^-,1)$

Let $\Pi = \Pi (C,D)$. Following a definition due to Ringel [49] , we define a category ${\mathcal C}(1,TC^+)$ as follows. Its objects are the H-module homomorphims $M \rightarrow TC^+(M)$, where $M \in {\text {rep}}(H)$ and the morphisms in ${\mathcal C}(1,TC^+)$ are given by commutative diagrams

Similarly, let ${\mathcal C}(TC^-,1)$ be the category with objects the H-module homomorphisms $TC^-(M) \rightarrow M$.

Theorem 10.8

The categories ${\text {rep}}(\Pi ), {\mathcal C}(1,TC^+)$ and ${\mathcal C}(TC^-,1)$ are isomorphic.

Proof

It follows from Proposition 9.1 that $(TC^-,TC^+)$ is a pair of adjoint functors ${\text {rep}}(H) \rightarrow {\text {rep}}(H)$. Now [49, Lemma 1] implies that the categories ${\mathcal C}(1,TC^+)$ and ${\mathcal C}(TC^-,1)$ are isomorphic. It follows from Theorem 10.1(c) that there is a functorial isomorphism $X^T \otimes _H - \cong TC^-(-)$, and by Corollary 10.6 we have $\Pi \cong T_H(X^T)$. Now [49, Lemma 12] gives an isomorphism of categories ${\mathcal C}(TC^-,1) \cong {\text {rep}}(\Pi (C,D))$. $\square$

One can also adapt Ringel’s proof of [49, Theorem B] to obtain a more direct proof of Theorem 10.8.

10.8 The kernel of the Coxeter functor

As before, let $H = H(C,D,\Omega )$. Recall that H is a 1-Iwanaga–Gorenstein algebra with the subcategory

$$\begin{aligned} {\mathcal G}{\mathcal P}(H) = \{ M \in {\text {rep}}(H) \mid {\text {Ext}}_H^1(M,H) = 0 \} \end{aligned}$$

of Gorenstein-projective modules.

As an immediate consequence of Theorem 10.1(a), Corollary 10.7, and the definition of $C^+(-)$ we get the following result. Here, the map $M_{i,\mathrm in}$ is defined as in Sect. 5.3, since we can regard the H-module M also as a module over $\Pi (C,D)$.

Theorem 10.9

For an H-module M the following are equivalent:

• (i) $M \in {\mathcal G}{\mathcal P}(H)$;

• (ii) $C^+(M) = 0$;

• (iii) $M_{i,\mathrm in}$ is injective for all $1 \le i \le n$.

If C is symmetric, then the equivalence of (i) and (iii) in Theorem 10.9 is a special case of [44, Theorem 5.1]. For C symmetric and $D = {\text {diag}}(2,\ldots ,2)$ the category ${\mathcal G}{\mathcal P}(H)$ has been studied in detail in [51].

11 $\tau$-Locally free H-modules

11.1 Preprojective, preinjective, and regular H-modules

Let M be an indecomposable H-module. Recall that M is $\tau$-locally free if $\tau ^k(M)$ is locally free for all $k \in \mathbb {Z}$. Furthermore, M is called preprojective (resp. preinjective) if there exists some $k \ge 0$ such that $M \cong \tau ^{-k}(P)$ (resp. $M \cong \tau ^k(I)$) for some indecomposable projective H-module P (resp. indecomposable injective H-module I). A $\tau$-locally free H-module M is $\tau$ -locally free regular if M is neither preprojective nor preinjective. (An indecomposable module M over a finite-dimensional algebra is called regular if $\tau ^k(M) \not = 0$ for all $k \in \mathbb {Z}$.)

Let ${\mathcal C}$ be a K-linear category. The stable category $\underline{{\mathcal C}}$ (resp. $\overline{{\mathcal C}}$) is the quotient category of ${\mathcal C}$ modulo the ideal of all morphisms factoring through projective (resp. injective) objects.

Proposition 11.1

The restriction of $\tau (-)$ yields an equivalence of stable categories

$$\begin{aligned} \underline{{\text {rep}}}_\mathrm{l.f.}(H) \rightarrow \overline{{\mathcal F}}(H) \end{aligned}$$

where ${\mathcal F}(H) := \{ M \in {\text {rep}}(H) \mid {\text {Hom}}_H({\text {D}}(H),M) = 0 \}$, and $\tau ^-(-)$ yields an equivalence of stable categories

$$\begin{aligned} \overline{{\text {rep}}}_\mathrm{l.f.}(H) \rightarrow \underline{{\mathcal G}}(H) \end{aligned}$$

where ${\mathcal G}(H) := \{ M \in {\text {rep}}(H) \mid {\text {Hom}}_H(M,H) = 0 \}$.

Proof

Combine Proposition 3.5 with [4, Lemma 4.1] and its dual. $\square$

Corollary 11.2

For an indecomposable $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) $M \in {\text {rep}}_\mathrm{l.f.}(H)$;

• (ii) ${\text {Hom}}_H(\tau ^-(M),H) = 0$;

• (iii) ${\text {Hom}}_H({\text {D}}(H),\tau (M)) = 0$.

Corollary 11.3

For an indecomposable $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) M is $\tau$-locally free;

• (ii) ${\text {Hom}}_H(\tau ^-(\tau ^k(M)),H) = 0$ for all $k \in \mathbb {Z}$;

• (iii) ${\text {Hom}}_H({\text {D}}(H),\tau (\tau ^k(M))) = 0$ for all $k \in \mathbb {Z}$.

Proof

Recall that for an indecomposable module M we have $\tau (\tau ^-(M)) \cong M$ if and only if M is not injective, and $\tau ^-(\tau (M)) \cong M$ if and only if M is not projective. Now the statement is a direct consequence of Corollary 11.2. $\square$

Proposition 11.4

Let $M \in {\text {rep}}_\mathrm{l.f.}(H)$ be indecomposable and rigid. Then M is $\tau$-locally free and $\tau ^k(M)$ is rigid for all $k \in \mathbb {Z}$.

Proof

By Theorem 10.1 we know that $\tau ^k(M) \cong T^kC^k(M)$. Now the result follows from Proposition 9.6. $\square$

Recall from Sect. 3.5 the Coxeter matrix $\Phi _H$.

Proposition 11.5

For a $\tau$-locally free module $M \in {\text {rep}}(H)$ the following hold:

• (i) If $\tau ^k(M) \not = 0$ for some $k \in \mathbb {Z}$, then $\underline{{\text {rank}}}(\tau ^k(M)) = (D^{-1}\Phi _HD)^k(\underline{{\text {rank}}}(M))$.

• (ii) If $\tau ^k(M) \not = 0$ for some $k \in \mathbb {Z}$ and $\underline{{\text {rank}}}(M)$ is contained in $\Delta _\mathrm{re}^+(C)$ or $\Delta _\mathrm{im}^+(C)$, then $\underline{{\text {rank}}}(\tau ^k(M))$ is in $\Delta _\mathrm{re}^+(C)$ or $\Delta _\mathrm{im}^+(C)$, respectively.

Proof

Part (i) follows from [48, Section 2.4, p.75] combined with Corollary 11.3 and the fact that $\tau$-locally free H-modules and their $\tau ^k$-translates have projective and injective dimension at most 1. To prove (ii), let i be a sink (resp. source) in $Q^\circ (C,\Omega )$. Then for a $\tau$-locally free module M with $M \not \cong E_i$ the map $M_{i,\mathrm in}$ is surjective (resp. $M_{i,\mathrm out}$ is injective). Now the result follows from Proposition 9.4 and Theorem 10.1(b),(d). $\square$

Proposition 11.6

Let M be a preprojective or preinjective H-module. Then the following hold:

• (i) M is $\tau$-locally free and rigid;

• (ii) $\underline{{\text {rank}}}(M) \in \Delta ^+_\mathrm{re}(C)$;

• (iii) If M and N are preprojective or preinjective H-modules with $\underline{\dim }(M) = \underline{\dim }(N)$, then $M \cong N$.

Proof

By definition we have $M \cong \tau ^{-k}(P_i)$ or $M \cong \tau ^k(I_i)$ for some $k \ge 0$ and some $1 \le i \le n$. The modules $P_i$ and $I_i$ are indecomposable, locally free and rigid. Thus by Proposition 11.4 the module M is $\tau$-locally free and rigid. We know from Sect. 3.4 that $\underline{{\text {rank}}}(P_i),\underline{{\text {rank}}}(I_i) \in \Delta _\mathrm{re}^+(C)$. Now part (ii) follows from Proposition 11.5(ii), and (iii) is a consequence of Lemmas 2.1 and 2.2. $\square$

Lemma 11.7

Assume C is connected and not of Dynkin type. Let X be a preprojective, Y a $\tau$-locally free regular and Z a preinjective H-module. Then we have ${\text {Hom}}_H(Z,Y) = 0, {\text {Hom}}_H(Y,X) = 0$ and ${\text {Hom}}_H(Z,X) = 0$.

Proof

We have $X \cong \tau ^{-k}(P_i)$ for some $1 \le i \le n$ and some $k \ge 0$. We get ${\text {Hom}}_H(Y,X) \cong {\text {Hom}}_H(\tau ^k(Y),P_i)$ and ${\text {Hom}}_H(Z,X) \cong {\text {Hom}}_H(\tau ^k(Z),P_i)$. Now Corollary 11.3 yields that these homomorphism spaces are zero. Similarly, one shows that ${\text {Hom}}_H(Z,Y) = 0$. $\square$

A sequence $((i_1,p_1),\ldots ,(i_t,p_t))$ with $1 \le i_k \le n$ and $p_i \in \{+,-\}$ is admissible for $(C,\Omega )$ if the following hold:

• (i) Either $i_1$ is a sink in $Q^\circ (C,\Omega )$ and $p_1 = +$, or $i_1$ is a source in $Q^\circ (C,\Omega )$ and $p_1 = -$;

• (ii) For each $2 \le k \le n$, either $i_k$ is a sink in $Q^\circ (C,s_{i_{k-1}} \cdots s_{i_1}(\Omega ))$ and $p_k = +$, or $i_k$ is a source in $Q^\circ (C,s_{i_{k-1}} \cdots s_{i_1}(\Omega ))$ and $p_k = -$.

Proposition 11.8

For an indecomposable locally free $M \in {\text {rep}}(H)$ the following are equivalent:

• (i) M is $\tau$-locally free;

• (ii) For each admissible sequence $((i_1,p_1),\ldots ,(i_t,p_t))$ for $(C,\Omega )$ the module

  $$\begin{aligned} F_{i_t}^{p_t} \cdots F_{i_1}^{p_1}(M) \end{aligned}$$

  is locally free.

Proof

Assume M is $\tau$-locally free. Let i be a sink in $Q^\circ (C,\Omega )$. We want to show that $F_i^+(M)$ is $\tau$-locally free. If $M \cong P_i = E_i$, then $F_i^+(M) = 0$, which is trivially $\tau$-locally free. Thus we can assume that $M \not \cong E_i$. If $M \cong P_j$ for some $j \not = i$, then ${\text {top}}_i(M) = 0$. In particular, $M_{i,\mathrm in}$ is surjective. Thus $F_i^+(M)$ is locally free. Now Lemma 9.16 yields that $F_i^+(M)$ is indecomposable. Next, assume that M is not projective. In other words, we have $\tau (M) \not = 0$. There clearly exists a $+$-admissible sequence $(i_1,\ldots ,i_n)$ for $(C,\Omega )$ with $i_1=i$. Using that M is $\tau$-locally free and applying Theorem 10.1 we get

$$\begin{aligned} \tau (M) \cong TC^+(M) \cong TF_{i_n}^+ \cdots F_{i_1}^+(M). \end{aligned}$$

By Lemma 9.16, the module $F_i^+(M)$ is indecomposable and locally free. We can now assume that $\tau ^k(F_i^+(M)) \not = 0$ for all $k \in \mathbb {Z}$. (Otherwise, the indecomposable module $F_i^+(M)$ is preprojective or preinjective and therefore $\tau$-locally free.)

Let $k > 0$. There exists a $+$-admissible sequence $(j_1,\ldots ,j_n)$ for $(C,s_i(\Omega ))$ with $j_n=i$. It follows that $(i,j_1,\ldots ,j_{n-1})$ is a $+$-admissible sequence for $(C,\Omega )$. We have

$$\begin{aligned} \tau (F_i^+(M)) \cong T(F_{j_n}^+ \cdots F_{j_1}^+(F_i^+(M)) \cong F_i^+(\tau (M)), \end{aligned}$$

and this module is indecomposable and locally free since $\tau (M)$ is $\tau$-locally free. Now it follows by induction that $\tau ^k(F_i^+(M)) \cong F_i^+(\tau ^k(M))$ is indecomposable and locally free for each $k > 0$.

Next, let $k < 0$. Then there exists a −-admissible sequence $(j_1,\ldots ,j_n)$ for $(C,s_i(\Omega ))$ with $j_1=i$. Then $(j_2,\ldots ,j_n,i)$ is a −-admissible sequence for $(C,\Omega )$. We get

$$\begin{aligned} \tau ^-(F_i^+(M)) \cong F_{j_n}^- \cdots F_{j_2}^-F_i^-F_i^+(M) \cong F_{j_n}^- \cdots F_{j_2}^-(M) \end{aligned}$$

and

$$\begin{aligned} F_i^+(\tau ^-(M)) \cong F_i^+F_i^-F_{j_n}^- \cdots F_{j_2}^-(M) \cong F_{j_n}^- \cdots F_{j_2}^-(M). \end{aligned}$$

(For the last isomorphism we used the dual of Lemma 9.16.) Again by induction we get that $\tau ^k(F_i^+(M)) \cong F_i^+(\tau ^k(M))$ is indecomposable and locally free for each $k<0$.

Altogether we showed that $F_i^+(M)$ is $\tau$-locally free. Dually, one shows that $F_j^-(M)$ is $\tau$-locally free for each source j in $Q^\circ (C,\Omega )$. This implies (ii).

To show the other direction, assume that (ii) holds. It follows that $T^kC^k(M)$ is locally free for all $k \in \mathbb {Z}$. Now we can apply Theorem 10.1 and get $\tau ^k(M) \cong T^kC^k(M)$. Thus M is $\tau$-locally free. $\square$

Proposition 11.9

For an H-module M the following are equivalent:

• (i) M is locally free;

• (ii) $\tau (M) \cong TC^+(M)$;

• (iii) $\tau ^-(M) \cong TC^-(M)$.

Proof

By Theorem 10.1(b) we know that (i) implies (ii). Now suppose that (ii) holds. Let $f:M \rightarrow N$ be a monomorphism from M to a locally free H-module N. (For example we could just take the injective envelope of M.) Since $TC^+$ is a left exact functor we get an exact sequence

$$\begin{aligned} 0 \rightarrow TC^+(M) \rightarrow TC^+(N). \end{aligned}$$

By Theorem 10.1(b) and assumption (ii) we get an exact sequence

$$\begin{aligned} 0 \rightarrow \tau (M) \rightarrow \tau (N). \end{aligned}$$

By Proposition 11.1 we have ${\text {Hom}}_H({\text {D}}(H),\tau (N)) = 0$, since N is locally free. Applying ${\text {Hom}}_H({\text {D}}(H),-)$ to the exact sequence above gives ${\text {Hom}}_H({\text {D}}(H),\tau (M)) = 0$. Again by Proposition 11.1 this implies that M is locally free. The equivalence of (i) and (iii) is proved dually. $\square$

11.2 Finite type classification for $\tau$-locally free modules

Theorem 11.10

For a Cartan matrix C of Dynkin type the following hold:

• (i) The map $M \mapsto \underline{{\text {rank}}}(M)$ yields a bijection between the set of isomorphism classes of $\tau$-locally free H-modules and the set $\Delta ^+(C)$ of positive roots of the Lie algebra associated with C.

• (ii) For an indecomposable H-module M the following are equivalent:

  • (a) M is preprojective;

  • (b) M is preinjective;

  • (c) M is $\tau$-locally free;

  • (d) M is locally free and rigid.

Proof

Let ${\mathbf i}= (i_1,\ldots ,i_n)$ be a $+$-admissible sequence for $(C,\Omega )$. We have $\underline{{\text {rank}}}(P_{i_k}) = \beta _{{\mathbf i},k}$ for $1 \le k \le n$, compare Sect. 3.4. Since C is of Dynkin type, we get all elements of $\Delta ^+(C)$ by applying the Coxeter transformation $c^{-s}$ to the $\beta _{{\mathbf i},k}$ with $s \ge 0$ and $1 \le k \le n$, compare Lemma 2.2. In particular, the preprojective H-modules and the preinjective H-modules coincide. Now Proposition 11.6 implies part (i). We also get that (a) and (b) in part (ii) are equivalent, and that (a) and (b) implies (c) and (d). By Proposition 11.4 we know that (d) implies (c). Now let $M \in {\text {rep}}(H)$ be $\tau$-locally free. Then there exists an injective H-module $I_i$ with ${\text {Hom}}_H(M,I_i) \not = 0$. Since C is of Dynkin type, we know that $P_j = \tau ^k(I_i)$ for some $k \ge 0$ and some $1 \le j \le n$. If $\tau ^s(M) = 0$ for some $s \ge 0$, then M is preprojective and we are done. Thus assume that $\tau ^s(M) \not = 0$ for all $s \ge 0$. Then we have ${\text {Hom}}_H(M,I_i) \cong {\text {Hom}}_H(\tau ^k(M),\tau ^k(I_i)) = {\text {Hom}}_H(\tau ^k(M),P_j) \not = 0.$ (Note that all modules appearing here have projective and injective dimension at most one. Thus the stable homomorphism spaces are equal to the ordinary homomorphism spaces.) It follows that ${\text {Hom}}_H(\tau ^-(\tau ^{k+1}(M)),P_j) \not = 0$, a contradiction to Corollary 11.3. This finishes the proof. $\square$

Combining the results in Sect. 11.1, Theorem 11.10 and Lemmas 2.1 and 2.2 we get the following result.

Theorem 11.11

There are finitely many isomorphism classes of $\tau$-locally free H-modules if and only if C is of Dynkin type.

11.3 The algebra $\Pi$ as a module over H

Let $\Pi = \Pi (C,D)$.

Theorem 11.12

${_H}\Pi \cong \bigoplus _{m \ge 0} \tau ^{-m}({_H}H)$.

Proof

By Proposition 11.6 we know that $\tau ^{-m}(H)$ is locally free for all $m \ge 0$. Thus we have $\tau ^-(H) \cong {\text {Ext}}_H^1({\text {D}}(H),H)$ and

$$\begin{aligned} \tau ^-(\tau ^{-(m-1)}(H))&\cong {\text {Ext}}_H^1({\text {D}}(H),\tau ^{-(m-1)}(H)) \\&\cong {\text {Ext}}_H^1({\text {D}}(H),H) \otimes _H \tau ^{-(m-1)}(H)\\&\cong {\text {Ext}}_H^1({\text {D}}(H),H) \otimes _H {\text {Ext}}_H^1({\text {D}}(H),H)^{\otimes (m-1)} \end{aligned}$$

where the last isomorphism follows by induction. By Corollary 10.6 we know that $\Pi \cong T_H({\text {Ext}}_H^1({\text {D}}(H),H))$. The result follows. $\square$

Corollary 11.13

$\Pi$ is finite-dimensional if and only if C is of Dynkin type.

Proof

This follows directly from Theorems 11.10 and 11.12 and the fact that $\Delta ^+(C)$ is finite if C is of Dynkin type. $\square$

11.4 Regular components of the Auslander–Reiten quiver

A connected component ${\mathcal C}$ of the Auslander–Reiten quiver of H is $\tau$ -locally free regular if it consists only of $\tau$-locally free regular modules. (A connected component of the Auslander–Reiten quiver of a finite-dimensional algebra is called regular if it consists only of regular modules.)

Proposition 11.14

For a connected component ${\mathcal C}$ of the Auslander–Reiten quiver of H the following are equivalent:

• (i) ${\mathcal C}$ contains a $\tau$-locally free regular module;

• (ii) ${\mathcal C}$ is $\tau$-locally free regular.

Proof

Trivially, (ii) implies (i). For the other direction assume that M is a $\tau$-locally free regular module in ${\mathcal C}$. Let $0 \rightarrow \tau (M) \rightarrow E \rightarrow M \rightarrow 0$ be the Auslander–Reiten sequence ending in M. Applying $\tau ^k(-)$ yields again an Auslander–Reiten sequence

$$\begin{aligned} 0 \rightarrow \tau ^{k+1}(M) \rightarrow \tau ^k(E) \rightarrow \tau ^k(M) \rightarrow 0 \end{aligned}$$

for each $k \in \mathbb {Z}$. Here we used that $\tau ^{k+1}(M)$ and $\tau ^k(M)$ and therefore also $\tau ^k(E)$ have projective and injective dimension equal to 1. It follows that $\tau ^k(N)$ is locally free for each indecomposable direct summand N of E. Now (ii) follows by induction. $\square$

Let ${\mathcal C}$ be a connected component of the Auslander–Reiten quiver of H. Suppose ${\mathcal C}$ contains an indecomposable projective module $P_i$ with $c_i \ge 2$. Then ${\text {rad}}(P_i)$ is obviously not locally free. Thus ${\text {rad}}(P_i)$ contains an indecomposable direct summand R, which is not locally free. Since the inclusion ${\text {rad}}(P_i) \rightarrow P_i$ is a sink map, there is an arrow $[R] \rightarrow [P_i]$ in the Auslander–Reiten quiver of H. Thus ${\mathcal C}$ contains a module, which is not locally free.

Ringel [47] proved that the regular components of the Auslander–Reiten quiver of a wild hereditary algebra are always of type $\mathbb {Z}A_\infty$. An alternative proof is due to Crawley-Boevey [20, Section 2] and can easily be adapted to obtain the following theorem.

Theorem 11.15

Assume that C is connected and neither of Dynkin nor of Euclidean type. Let ${\mathcal C}$ be a $\tau$-locally free regular component of the Auslander–Reiten quiver of H. Then ${\mathcal C}$ is a component of type $\mathbb {Z}A_\infty$.

12 Projective resolutions and Ext-group symmetries of $\Pi$-modules

12.1 Projective resolutions of $\Pi (C,D)$-modules

Let $H = H(C,D,\Omega )$ and $\Pi = \Pi (C,D)$. Let ${\text {Rep}}_\mathrm{l.f.}(\Pi )$ denote the category of all locally free $\Pi$-modules, possibly of infinite rank. For typographic reasons we use in this section the convention $I=\{1,2,\ldots , n\}$. Recall that we have defined the S-S-bimodule

$$\begin{aligned} \overline{B} := \bigoplus _{(i,j)\in \overline{\Omega }} {_iH_j}, \end{aligned}$$

and that we can identify $\Pi$ and $T_S(\overline{B})/J$, where J is the ideal of $T_S(\overline{B})$ which is generated by the elements $\rho _i\in \overline{B}\otimes _S\overline{B}$ for $i\in I$. For the next result we follow closely the ideas from [24, Lemma 3.1].

Proposition 12.1

There is an exact sequence of $\Pi$-$\Pi$-bimodules

$$\begin{aligned} \underbrace{\bigoplus _{i\in I} \Pi e_i \otimes e_i\Pi \xrightarrow {f} \bigoplus _{(j,i) \in \overline{\Omega }} \Pi e_j \otimes _j {_j}H_i \otimes _i e_i\Pi \xrightarrow {g} \bigoplus _{i\in I} \Pi e_i \otimes _i e_i\Pi }_{P_\bullet } \xrightarrow {h} \Pi \rightarrow 0 \end{aligned}$$

(12.1)

where

$$\begin{aligned} f(e_i \otimes e_i)&:= \rho _i \otimes e_i + e_i \otimes \rho _i,\\ g(e_j \otimes h \otimes e_i)&:= he_i \otimes e_i - e_j \otimes e_jh,\\ h(m \otimes m')&:= mm'. \end{aligned}$$

Proof

Observe first, that the above complex can be written more compactly as

$$\begin{aligned} \Pi \otimes _S \Pi \xrightarrow {f} \Pi \otimes _S\otimes \overline{B}\otimes _S\Pi \xrightarrow {g}\Pi \otimes _S\Pi \xrightarrow {h}\Pi \rightarrow 0 \end{aligned}$$

Note that we have a surjective $\Pi$-$\Pi$-bimodule homomorphism

$$\begin{aligned} \bigoplus _{i=1}^n \Pi e_i \otimes _i e_i\Pi \xrightarrow {r} J/J^2 \end{aligned}$$

defined by $e_i \otimes e_i \mapsto \rho _i$. Moreover, we have a canonical map

$$\begin{aligned} J/J^2 \xrightarrow {\mathrm{can}} \Pi \otimes _S \overline{B} \otimes _S \Pi \end{aligned}$$

given by $\overline{x} \mapsto \tilde{x}_l \otimes 1 + 1 \otimes \tilde{x}_r$ coming from the compositions of

$$\begin{aligned} J \xrightarrow {i_{J,l}} \bigoplus _{k \ge 1}(\overline{B}^{\otimes k} \otimes _S \overline{B}) \xrightarrow {\mathrm{proj} \otimes {\text {id}}} \Pi \otimes _S \overline{B} \end{aligned}$$

and

$$\begin{aligned} J \xrightarrow {i_{J,r}} \bigoplus _{k \ge 1} (\overline{B} \otimes _S \overline{B}^{\otimes k}) \xrightarrow {{\text {id}}\otimes \mathrm{proj}} \overline{B} \otimes _S \Pi , \end{aligned}$$

respectively, where the maps $i_{J,l}$ and $i_{J,r}$ are the obvious inclusions. Note that both compositions vanish on $J^2$. It is easy to see that $f = \mathrm{can} \circ r$. Thus we only have to show that the sequence

$$\begin{aligned} J/J^2 \xrightarrow {\mathrm{can}} \Pi \otimes _S \overline{B} \otimes _S \overline{B} \xrightarrow {u} \Pi \otimes _S \Pi \xrightarrow {\mathrm{mult}} \Pi \rightarrow 0 \end{aligned}$$

where $u(1 \otimes b \otimes 1) := b \otimes 1 - 1 \otimes b$ is exact. This is a special case of a combination of results by Schofield [52, Theorems 10.1,10.3,10.5]. $\square$

Corollary 12.2

For each $M \in {\text {Rep}}_\mathrm{l.f.}(\Pi )$ the complex $P_\bullet \otimes _\Pi M$ is the beginning of a projective resolution of M.

Proof

The components of $P_\bullet$ are projective as left and as right modules. In fact, for example $H_i^m\otimes _i e_i\Pi \cong (e_i\Pi )^m$ is a projective right $\Pi$-module. Now, ${_jH_i}$ is a free right $H_i$-module and $\Pi e_j$ is a free right $H_j$-module and thus $\Pi e_j\otimes _j {_jH_i}$ is also a free right $H_i$-module. Altogether, $\Pi e_j\otimes _j {_jH_i}\otimes _i e_i \Pi$ is a projective right $\Pi$-module. A similar argument shows that $\Pi e_i\otimes _{H_i} e_i\Pi$ is projective as a right $\Pi$-module. Thus as a sequence of right modules the sequence $P_\bullet$ splits. This implies that the sequence $P_\bullet \otimes _\Pi M$ is exact. Now, if $M \in {\text {Rep}}_\mathrm{l.f.}(\Pi )$, then the relevant components of $P_\bullet \otimes _\Pi M$ are evidently projective. $\square$

Let us write the complex $P_\bullet \otimes _\Pi M$ explicitly:

$$\begin{aligned} \bigoplus _{i\in I} \Pi e_i \otimes _i e_i M&\xrightarrow {f_M }&\bigoplus _{(j,i)\in \overline{\Omega }} \Pi e_j \otimes _j {_j}H_i \otimes _i e_iM\nonumber \\&\xrightarrow {g_M }&\bigoplus _{i\in I} \Pi e_i \otimes _i e_i M \xrightarrow { h_M} M \rightarrow 0 \end{aligned}$$

(12.2)

and the maps $f_M, g_M, h_M$ act on generators as follows:

$$\begin{aligned} f_M(e_j\otimes m_j)&= \sum _{\begin{array}{c} i\in \Omega (-,j)\\ l\in {_iL_j} \end{array}} \left( l^*\otimes l\otimes m_j+e_j\otimes l^*\otimes M_{ij}(l\otimes m_j)\right) \\&\quad -\sum _{ \begin{array}{c} k\in \Omega (j,-)\\ r\in {_jR_k} \end{array}} \left( r\otimes r^*\otimes m_j+e_j\otimes r\otimes M_{kj}(r^*\otimes m_j)\right) ,\\ g_M(e_i\otimes h\otimes m_j)&= h\otimes m_j - e_i\otimes M_{ij}(h\otimes m_j),\\ h_M(e_i\otimes m_i)&= m_i. \end{aligned}$$

Proposition 12.3

Suppose that the Cartan matrix C has no components of Dynkin type. Then in the complex $P_\bullet$ for $\Pi$ we have ${\text {Ker}}(f)=0$. In particular, for all $M \in {\text {Rep}}_\mathrm{l.f.}(\Pi )$ we have ${\text {proj.~dim}}(M) \le 2$.

Proof

In a first step we show that ${\text {Ker}}(E'_i\otimes _\Pi f)=0$ for the generalized simple right $\Pi$-modules $E'_i$ concentrated at the vertex $i \in I$. To this end we adapt the relevant part of the proof of [15, Proposition 4.2] to our setting: Choose an orientation $\Omega$ such that in $H=H(C,D,\Omega )$ the projective H-module $P_i = He_i$ is the generalized simple H-module $E_i$. We have a short exact sequence of H-modules

$$\begin{aligned} 0\rightarrow P_i \rightarrow \oplus _{j\in \Omega (i,-)}P_j\otimes _j{_jH_i} \rightarrow \tau ^-(P_i) \rightarrow 0, \end{aligned}$$

(12.3)

see the proof of Theorem 9.7. Note, that this sequence is possibly not an Auslander–Reiten sequence. Applying ${\text {Hom}}_H(-,\Pi )$ to (12.3) we obtain the sequence of right $\Pi$-modules

$$\begin{aligned}&0\rightarrow {\text {Hom}}_H(\tau ^-(P_i),\Pi )\rightarrow \oplus _{j\in \Omega (i,-)} {_iH_j}\otimes _j\Pi \nonumber \\&\quad \rightarrow e_i\Pi \rightarrow {\text {Ext}}^1_H(\tau ^-(P_i),\Pi )\rightarrow 0 \end{aligned}$$

(12.4)

Now, by Theorem 11.12

$$\begin{aligned} {_H\Pi }=\oplus _{j\in I}\oplus _{k\in \mathbb {N}} \tau ^{-k}(P_j), \end{aligned}$$

with all summands indecomposable, locally free preprojective modules. In particular, in our situation all summands have injective dimension 1. Thus, ${\text {Ext}}^1_H(\tau ^-(P_i),\tau ^{-k}(P_j))={\text {D}}{\text {Hom}}_H(\tau ^{-k}(P_j),P_i)=0$ unless $(j,k)=(i,0)$. We conclude that we have an isomorphism of right $\Pi$-modules ${\text {Ext}}^1_H(\tau ^-(P_i),\Pi )\cong E_i'$. Next

$$\begin{aligned} {\text {Hom}}_H(\tau ^-(P_i),\Pi )\cong {\text {Hom}}_H(P_i,\tau ({_H}\Pi ))=e_i \Pi \end{aligned}$$

where the last equality holds since by our hypothesis on C we have $\tau ({_H}\Pi ) = {_H}\Pi$. Alltogether, we can identify now the exact sequence (12.4) with

$$\begin{aligned} 0 \rightarrow e_i\Pi \xrightarrow {E'_i\otimes f}\oplus _{j\in \Omega (i,-)} {_iH_j}\otimes _j \Pi \xrightarrow {E'_i\otimes g} e_i \Pi \rightarrow E'_i \rightarrow 0 \end{aligned}$$

Now, let $U:={\text {Ker}}(f)$. Then U is projective as a left $\Pi$-module since $P_\bullet \xrightarrow {h}\Pi \rightarrow 0$ is a (split) exact sequence of projective left modules. Next we observe that $E'_i\otimes _\Pi U=0$ since ${\text {Cok}}(f)$ is projective as a left module. Now, let $\mathfrak {m}\subset \Pi$ be the ideal which is generated by $\overline{B}$. Thus $\Pi /\mathfrak {m}^j\in {\text {rep}}_{\mathrm{l.f.}}(\Pi )$ is filtered by the generalized simples $E'_i$ for all $j \ge 1$ and $\Pi \subset \varprojlim _j(\Pi /\mathfrak {m}^j)$. Thus, since U is projective as a left module we get

$$\begin{aligned} U=\Pi \otimes _\Pi U\subset (\varprojlim _j(\Pi /\mathfrak {m}^j))\otimes _\Pi U\subset \varprojlim _j(\Pi /\mathfrak {m}^j\otimes _\Pi U)=0. \end{aligned}$$

This finishes the proof. $\square$

12.2 Symmetry of extension groups

Let $\Pi = \Pi (C,D)$, and let $M = (M_i,M_{ij},M_{ji})$ and $N = (N_i,N_{ij},N_{ji})$ be in ${\text {Rep}}_\mathrm{l.f.}(\Pi )$. Let $Q_\bullet (M,N)$ be the complex

$$\begin{aligned} \bigoplus _{k\in I} {\text {Hom}}_{H_k}(M_k,N_k)&\xleftarrow {\tilde{f}_{M,N}}&\bigoplus _{(i,j)\in \overline{\Omega }} {\text {Hom}}_{H_i}({_iH_j} \otimes _j M_j,N_i)\nonumber \\&\xleftarrow {\tilde{g}_{M,N}}&\bigoplus _{k\in I} {\text {Hom}}_{H_k}(M_k,N_k) \end{aligned}$$

(12.5)

where $\tilde{f}_{M,N}$ is defined by

$$\begin{aligned}&\left( \tilde{f}_{M,N}((\psi _{ij})_{(i,j)\in \overline{\Omega }})\right) _k \\&\quad := \sum _{j\in \overline{\Omega }(-,k)} {\text {sgn}}(j,k) (N_{kj} \circ {\text {ad}}_{j,k}(\psi _{j,k}) - \psi _{k,j} \circ {\text {ad}}_{j,k}(M_{jk})) \end{aligned}$$

and $\tilde{g}_{M,N}$ is defined by

$$\begin{aligned} (\tilde{g}_{M,N}((\phi _k)_{k\in I}))_{(i,j)} := N_{ij} \circ ({\text {id}}_{{_iH_j}} \otimes \phi _j) - \phi _i \circ M_{ij}. \end{aligned}$$

If N is of finite rank, via the trace pairing from Sect. 8.1, we can identify the K-dual of the shifted complex $Q_\bullet (N,M)[2]$ with the following complex $Q_\bullet (N,M)^*$:

$$\begin{aligned}&\bigoplus _{k\in I} {\text {Hom}}_{H_k}(M_k,N_k) \xleftarrow {\tilde{g}^*_{N,M}} \bigoplus _{(i,j)\in \overline{\Omega }} {\text {Hom}}_{H_i}(M_i, {_iH_j} \otimes _j N_j)\nonumber \\&\quad \xleftarrow {\tilde{f}^*_{N,M}} \bigoplus _{k\in I} {\text {Hom}}_{H_k}(M_k,N_k) \end{aligned}$$

(12.6)

(Recall that we have for example natural isomorphisms

$$\begin{aligned} {\text {Hom}}_{H_k}(M_k,N_k)\cong {\text {D}}{\text {Hom}}_{H_k}(N_k,M_k) \end{aligned}$$

since $N_k$ is free of finite rank by hypothesis.) We define moreover

$$\begin{aligned}&{\text {ad}}_{M,N}:\bigoplus _{(i,j)\in \overline{\Omega }}{\text {Hom}}_{H_j}({_jH_i}\otimes _i M_i,N_j)\nonumber \\&\quad \xrightarrow {\oplus _{(i,j)\in \overline{\Omega }}\;{\text {sgn}}(i,j){\text {ad}}_{ji}} \bigoplus _{(i,j)\in \overline{\Omega }}{\text {Hom}}_{H_i}(M_i,{_iH_j}\otimes _j N_j). \end{aligned}$$

We know that ${\text {ad}}_{M,N}$ is an isomorphism.

Lemma 12.4

For $M,N \in {\text {Rep}}_\mathrm{l.f.}(\Pi )$ the following hold:

• (a) The complex ${\text {Hom}}_\Pi (P_\bullet \otimes _\Pi M,N)$ is isomorphic to $Q_\bullet (M,N)$.

• (b) If N is of finite rank

  $$\begin{aligned} ({\text {id}}_{\oplus {\text {Hom}}_{H_k}{(M_k,N_k)}},{\text {ad}}_{M,N}, {\text {id}}_{\oplus {\text {Hom}}_{H_k}(M_k,N_k)}) \end{aligned}$$

  is an isomorphism between the complexes $Q_\bullet (M,N)$ and $Q_\bullet (N,M)^*$.

Proof

Part (a) is straightforward. For (b) we show that $\tilde{f}^*_{N,M}={\text {ad}}_{M,N}\circ \tilde{g}_{M,N}$. To this end we evaluate for $(i,j)\in \overline{\Omega }$ the (i, j)-component of $\tilde{f}^*_{N,M}$ on $(\lambda _k)_{k\in I}\in \oplus _{k\in I} {\text {Hom}}_{H_k}(M_k,N_k)$, according to our discussion of the trace pairing in Sects. 8.1 and 8.2:

$$\begin{aligned} (\tilde{f}_{N,M}^*((\lambda _k)_k))_{ij}&= {\text {sgn}}(i,j)({\text {ad}}_{i,j}^*(\lambda _j\circ M_{ji}) -{\text {ad}}_{j,i}(N_{ji})\circ \lambda _i)\\&={\text {sgn}}(i,j)({\text {ad}}_{j,i}(\lambda _j\circ M_{ji})-{\text {ad}}_{j,i}(N_{ji})\circ \lambda _i)\\&={\text {sgn}}(i,j)({\text {ad}}_{j,i}(\lambda _j\circ M_{ji}-N_{ji}\circ ({\text {id}}_{H_i}\otimes \lambda _i))) \end{aligned}$$

where the second equality follows from Proposition 8.3, and the third equality is just the definition of ${\text {ad}}_{ji}$. The proof of $\tilde{g}^*_{N,M} \circ {\text {ad}}_{M,N}=\tilde{f}_{M,N}$ is similar. $\square$

Proposition 12.5

For $M,N \in {\text {Rep}}_\mathrm{l.f.}(\Pi )$ we have the following functorial isomorphisms:

• (a) ${\text {Ker}}(\tilde{g}_{M,N}) = {\text {Hom}}_\Pi (M,N)$ and ${\text {Ker}}(\tilde{f}_{M,N})/{\text {Im}}(\tilde{g}_{M,N}) \cong {\text {Ext}}_\Pi ^1(M,N)$.

• (b) ${\text {Cok}}{\tilde{f}_{M,N}}={\text {Ext}}^2_\Pi (M,N)$ if C has no component of Dynkin type.

• (c) ${\text {Hom}}_\Pi (N,M)\cong {\text {D}}{\text {Cok}}(\tilde{f}_{M,N})$ if M is of finite rank.

Proof

Part (a) follows from the functorial isomorphism of (12.5) with ${\text {Hom}}_\Pi (P_\bullet \otimes _\Pi M,N)$. Part (b) follows by the same token since in this situation by Proposition 12.3 the map $f_M$ in (12.2) is injective.

For (c) we just note that by (a) and Lemma 12.4 (b) we have ${\text {Ker}}(\tilde{f}^*_{M,N})={\text {Ker}}(\tilde{g}_{N,M})={\text {Hom}}_\Pi (N,M)$. $\square$

Theorem 12.6

Let $M\in {\text {Rep}}_{\mathrm{l.f.}}(\Pi )$ and $N\in {\text {rep}}_{\mathrm{l.f.}}(\Pi )$.

• (a) There is a functorial isomorphism

  $$\begin{aligned} {\text {Ext}}^1_\Pi (M,N)\cong {\text {D}}{\text {Ext}}^1_\Pi (N,M). \end{aligned}$$

• (b) If the Cartan matrix C has no component of Dynkin type, we have more generally functorial isomorphisms

  $$\begin{aligned} {\text {Ext}}^{2-i}_\Pi (M,N)\cong {\text {D}}{\text {Ext}}^i_\Pi (N, M) \text { for } i=0,1,2. \end{aligned}$$

• (c) If M is also of finite rank we have

  $$\begin{aligned} \dim {\text {Ext}}_\Pi ^1(M,N) = \dim {\text {Hom}}_\Pi (M,N) + \dim {\text {Hom}}_\Pi (N,M) - (M,N)_H. \end{aligned}$$

Proof

Recall, that by Proposition 12.5 (a) and (b) we have naturally $H^i(Q_\bullet (M,N)) \cong {\text {Ext}}^i_\Pi (M,N)$ for $i=0,1$ and also for $i=2$ in case C has no Dynkin component. In our situation (N of finite rank), the complex $Q_\bullet (N,M)^*$ is, via the trace pairing, identified to the K-dual shifted complex ${\text {D}}Q_\bullet (N,M)[2]$. Thus, by the same token we have $H^{2-i}(Q_\bullet (N,M)^*)\cong {\text {D}}{\text {Ext}}^i_\Pi (N,M)$ for $i=0,1$, and also for $i=2$ in the Dynkin-free case. Now, by Lemma 12.4 (b) the complexes $Q_\bullet (M,N)$ and $Q_\bullet (N,M)^*$ are naturally isomorphic, which implies (a) and (b). For (c), we observe that by Proposition 12.5 we obtain from the complex (12.5) the equality

$$\begin{aligned}&\dim {\text {Hom}}_\Pi (N,M)-\dim {\text {Ext}}^1_\Pi (M,N)+\dim {\text {Hom}}_\Pi (M,N)\\&\quad = 2\cdot \sum _{k\in I}\dim {\text {Hom}}_{H_k}(M_k,N_k) - \sum _{(i,j)\in \overline{\Omega }}\dim {\text {Hom}}_{H_j} ({_jH_i}\otimes _i M_i,N_j)\\&\quad =(M,N)_H, \end{aligned}$$

which is equivalent to our claim. $\square$

The last statement in Theorem 12.6 generalizes Crawley-Boevey’s formula in [23, Lemma 1].

Corollary 12.7

Suppose that the Cartan matrix C is connected of Dynkin type. Then $\Pi$ is a selfinjective algebra. Moreover, in this situation we have ${\text {Ker}}(f)={\text {Hom}}_\Pi ({\text {D}}(\Pi ),\Pi )$ as a $\Pi$-$\Pi$-bimodule, where f is the last morphism in the complex $P_\bullet$ of Proposition 12.1.

Proof

By Corollary 11.13, $\Pi$ is in this situation a finite-dimensional basic K-algebra. So, for the first claim we have to show only that $\Pi$, as a left module, is injective. In any case, we can find a short exact sequence of left $\Pi$-modules

$$\begin{aligned} 0\rightarrow \Pi \xrightarrow {\iota } Q \xrightarrow {\pi } R \rightarrow 0 \end{aligned}$$

with Q injective. Since $\Pi$ and Q are locally free, R is also locally free. Now, ${\text {Hom}}_\Pi (\iota ,\Pi )$ is surjective since ${\text {Ext}}^1_\Pi (R,\Pi )={\text {D}}{\text {Ext}}^1_\Pi (\Pi ,R)=0$ by Theorem 12.6. Thus, there exists $\rho \in {\text {Hom}}_\Pi (Q,\Pi )$ with $\rho \iota ={\text {id}}_\Pi$. In other words, $\Pi$ is a direct summand of the injective module Q.

For the second claim we note that we have here natural identifications $f= {\text {D}}(\tilde{f}_{\Pi ,{\text {D}}(\Pi )}) = \tilde{g}_{{\text {D}}(\Pi ),\Pi }$. Now, ${\text {Ker}}(\tilde{g}_{{\text {D}}(\Pi ),\Pi })={\text {Hom}}_\Pi ({\text {D}}(\Pi ),\Pi )$ by Proposition 12.5 (a). $\square$

Remark 12.8

For (classical) preprojective algebras $\Pi$ associated to a Dynkin quiver it seems to be folklore that ${\text {Ker}}(f)\cong {\text {D}}(\Pi )$. This is not in contradiction with the above statement. In fact, the Nakayama automorphism, viewed as an element of the group of outer automorphism has order 2 (except for a few cases over fields of characteristic 2 when it is the identity), see [15, Theorem 4.8]. and thus ${\text {D}}(\Pi ) \cong {\text {Hom}}_\Pi ({\text {D}}(\Pi ),\Pi )$ as a bimodule. We expect that for our generalized preprojective algebras a similar statement holds.

13 Examples

13.1. The algebras H(C, D) and $\Pi (C,D)$

is a Cartan matrix, and $D = {\text {diag}}(9,6,2)$ is the minimal symmetrizer of C. Let $\Omega = \{(1,2),(2,3)\}$. This is an orientation of C. We have $f_{12} = 2, f_{21} = 3$, $f_{23} = 1, f_{32} = 3, g_{12} = 2$ and $g_{23} = 3$. The algebra $H = H(C,D,\Omega )$ is given by the quiver

with relations

$$\begin{aligned} \varepsilon _1^9&= 0, \varepsilon _2^6 = 0, \varepsilon _3^2 = 0,\\ \varepsilon _1^3\alpha _{12}^{(g)}&= \alpha _{12}^{(g)}\varepsilon _2^2,\quad (g=1,2),\\ \varepsilon _2^3\alpha _{23}^{(g)}&= \alpha _{23}^{(g)}\varepsilon _3,\quad (g =1,2,3). \end{aligned}$$

(Recall that $\alpha _{ij}^{(g)}$ denotes an arrow $j \rightarrow i$.)

The preprojective algebra $\Pi = \Pi (C,D)$ is given by the double quiver $\overline{Q}(C)$ with relations

$$\begin{aligned}&\varepsilon _1^9 = 0, \quad \varepsilon _2^6 = 0,\quad \varepsilon _3^2 = 0,\\&\varepsilon _1^3\alpha _{12}^{(g)} = \alpha _{12}^{(g)}\varepsilon _2^2,\quad \varepsilon _2^2\alpha _{21}^{(g)} = \alpha _{21}^{(g)}\varepsilon _1^3,\quad (g=1,2), \\&\varepsilon _2^3\alpha _{23}^{(g)} = \alpha _{23}^{(g)}\varepsilon _3,\quad \varepsilon _3\alpha _{32}^{(g)} = \alpha _{32}^{(g)}\varepsilon _2^3, \quad (g =1,2,3),\\&\sum _{g=1}^2 \left( \alpha _{12}^{(g)}\alpha _{21}^{(g)}\varepsilon _1^2 + \varepsilon _1\alpha _{12}^{(g)}\alpha _{21}^{(g)}\varepsilon _1 + \varepsilon _1^2\alpha _{12}^{(g)}\alpha _{21}^{(g)}\right) = 0, \\&\sum _{g=1}^2\left( -\alpha _{21}^{(g)}\alpha _{12}^{(g)}\varepsilon _2 -\varepsilon _2\alpha _{21}^{(g)}\alpha _{12}^{(g)} \right) \\&\quad + \sum _{g=1}^3\left( \alpha _{23}^{(g)}\alpha _{32}^{(g)}\varepsilon _2^2+ \varepsilon _2\alpha _{23}^{(g)}\alpha _{32}^{(g)}\varepsilon _2+ \varepsilon _2^2\alpha _{23}^{(g)}\alpha _{32}^{(g)} \right) = 0,\\&\sum _{g=1}^3 -\alpha _{32}^{(g)}\alpha _{23}^{(g)} = 0. \end{aligned}$$

13.1 Cartan matrices of Dynkin type

Figure 4 shows a list of valued graphs called Dynkin graphs. By definition each of the graphs $A_n, B_n, C_n$ and $D_n$ has n vertices. The graphs $A_n, D_n, E_6, E_7$ and $E_8$ are the simply laced Dynkin graphs. A Cartan matrix C is of Dynkin type if the valued graph $\Gamma (C)$ is isomorphic (as a valued graph) to a disjoint union of Dynkin graphs.

Fig. 4

Dynkin graphs

13.2 Finite representation type

Let $H = H(C,D,\Omega )$ with $D = {\text {diag}}(c_1,\ldots ,c_n)$. Without loss of generality assume that C is connected. We only sketch the proof of the following proposition.

Proposition 13.1

The algebra H is representation-finite if and only if we are in one of the following cases:

• (i) C is of Dynkin type $A_n, C_n, D_n, E_6, E_7, E_8, B_2, B_3$ or $G_2$, and D is minimal;

• (ii) C is of Dynkin type $A_1$;

• (iii) C is of Dynkin type $A_2$, and we have $(c_1,c_2) = (2,2)$ or $(c_1,c_2) = (3,3)$;

• (iv) C is of Dynkin type $A_3$, and we have $(c_1,c_2,c_3) = (2,2,2)$.

Proof

Assume that D is minimal. For Dynkin types $A_n, D_n, E_6, E_7, E_8$, the algebra H is representation-finite by Gabriel’s Theorem. For type $C_n$, the algebra H is a representation-finite string algebra. The Auslander–Reiten quiver of H for types $B_2, B_3$ and $G_2$ can be computed by covering theory and the knitting algorithm for preprojective components. They all turn out to be finite.

If C is of type $A_1$, then the symmetrizers are $D = (m)$ with $m \ge 1$. Then $H \cong K[\varepsilon _1]/(\varepsilon _1^m)$ is just a truncated polynomial ring, which is obviously representation-finite.

If C is of type $A_2$ and $(c_1,c_2) = (2,2)$ or $(c_1,c_2) = (3,3)$, then H is a representation-finite algebra, see Bongartz and Gabriel’s list Maximal algebras with 2 simples modules in [13, Section 7].

If C is of type $A_3$ with $(c_1,c_2,c_3) = (2,2,2)$, then one can again use covering theory and the knitting algorithm to check that H is representation-finite.

It is straightforward to check that these are all representation-finite cases. (One first compiles the list of all minimal algebras H, which are not mentioned in (i), (ii), (iii) and (iv). These are the algebras $H = H(C,D,\Omega )$ of types

• $A_2$ with $D = {\text {diag}}(4,4)$;

• $A_3$ with $D = {\text {diag}}(3,3,3)$;

• $A_4$ with $D = {\text {diag}}(2,2,2,2)$;

• $B_2$ with $D = {\text {diag}}(4,2)$;

• $B_4$ with D minimal;

• $D_4$ with $D = {\text {diag}}(2,2,2,2)$;

• $F_4$ with D minimal.

Then one uses covering theory and the Happel–Vossieck list (see [37]) to check that these minimal algebras are representation infinite.) $\square$

13.3 Notation

In the following sections we discuss several examples. We also display the Auslander–Reiten quivers of some representation-finite algebras H. The $\tau$-locally free H-modules are marked with a double frame, the locally free H-modules, which are not $\tau$-locally free, are marked with a single solid frame, and the Gorenstein-projective H-modules, which are not projective, have a dashed frame.

13.4 Dynkin type $A_2$

Let

with symmetrizer $D = {\text {diag}}(2,2)$ and $\Omega = \{ (1,2)\}$. Thus C is a Cartan matrix of Dynkin type $A_2$ with a non-minimal symmetrizer. We have $f_{12} = f_{21} = 1$. Thus $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1^2 = \varepsilon _2^2 = 0$ and $\varepsilon _1\alpha _{12} = \alpha _{12}\varepsilon _2$. The Auslander–Reiten quiver of H is displayed in Fig. 5. The numbers in the figure correspond to composition factors and basis vectors. (The three modules in the left most column have to be identified with the three modules in the right most column.) Note that $P_2 \cong I_1$ is projective-injective.

Fig. 5

The Auslander–Reiten quiver of $H(C,D,\Omega )$ of type $A_2$ with $D = {\text {diag}}(2,2)$

The preprojective algebra $\Pi = \Pi (C,D)$ is given by the quiver

with relations $\varepsilon _1^2 = \varepsilon _2^2 = 0, \varepsilon _1\alpha _{12} = \alpha _{12}\varepsilon _2, \varepsilon _2\alpha _{21} = \alpha _{21}\varepsilon _1, \alpha _{12}\alpha _{21} = 0$ and $-\alpha _{21}\alpha _{12} = 0$. The indecomposable projective $\Pi$-modules are shown in Fig. 6. (The arrows indicate when an arrow of the algebra $\Pi$ acts with a non-zero scalar on a basis vector.)

Fig. 6

The indecomposable projective $\Pi (C,D)$-modules for type $A_2$ with $D = (2,2)$

13.5 Dynkin type $B_2$

Let

with symmetrizer $D = {\text {diag}}(2,1)$ and $\Omega = \{ (1,2) \}$. The graph $\Gamma (C)$ looks as follows:

Thus C is a Cartan matrix of Dynkin type $B_2$. We have $f_{12} = 1$ and $f_{21} = 2$. Then $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1^2 = 0$ and $\varepsilon _2 = 0$. The Auslander–Reiten quiver of H is shown in Fig. 7. The numbers in the figure correspond to composition factors and basis vectors. (In the last two rows the two modules on the left have to be identified with the corresponding two modules on the right.)

Fig. 7

The Auslander–Reiten quiver of $H(C,D,\Omega )$ of type $B_2$ with D minimal

The preprojective algebra $\Pi = \Pi (C,D)$ is given by the quiver

with relations $\varepsilon _1^2 = 0, \varepsilon _2 = 0, \alpha _{12}\alpha _{21}\varepsilon _1 + \varepsilon _1\alpha _{12}\alpha _{21} = 0$ and $-\alpha _{21}\alpha _{12} = 0$. The indecomposable projective $\Pi$-modules are shown in Fig. 8. (The arrows indicate when an arrow of the algebra $\Pi$ acts with a non-zero scalar on a basis vector.)

Fig. 8

The indecomposable projective $\Pi (C,D)$-modules for type $B_2$ with D minimal

13.6 Dynkin type $B_3$

Let

with symmetrizer $D = {\text {diag}}(2,2,1)$ and $\Omega = \{(1,2),(2,3)\}$. The graph $\Gamma (C)$ looks as follows:

Thus C is a Cartan matrix of Dynkin type $B_3$. We have $f_{12} = f_{21} = 1, f_{23} = 1$ and $f_{32} = 2$. Thus $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1^2 = \varepsilon _2^2 = 0, \varepsilon _3 = 0$ and $\varepsilon _1\alpha _{12} = \alpha _{12}\varepsilon _2$. The Auslander–Reiten quiver of H is shown in Fig. 9. As vertices we have the graded dimension vectors (arising from the obvious $\mathbb {Z}$-covering of H) of the indecomposable H-modules. (In the last three rows the three modules on the left have to be identified with the corresponding three modules on the right.) The indecomposable H-module M with graded dimension vector

$$\begin{aligned} {\begin{matrix}1&{}1&{}0\\ 1&{}2&{}1\\ 0&{}1&{}0\end{matrix}}\end{aligned}$$

is locally free. (It is a direct summand of an extension of locally free modules.) We have $\underline{{\text {rank}}}(M) = (1,2,1)$. In the root lattice of C this corresponds to $\alpha _1+2\alpha _2+\alpha _3$. Thus we have $\underline{{\text {rank}}}(M) \notin \Delta ^+(C)$.

Fig. 9

The Auslander–Reiten quiver of $H(C,D,\Omega )$ of type $B_3$ with D minimal

13.7 Dynkin type $C_3$

Let

with symmetrizer $D = {\text {diag}}(1,1,2)$ and $\Omega = \{ (1,2),(2,3) \}$. The graph $\Gamma (C)$ looks as follows:

Thus C is a Cartan matrix of Dynkin type $C_3$. We have $f_{12} = f_{21} = 1, f_{23} = 2$ and $f_{32} = 1$. Then $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1 = \varepsilon _2 = 0$ and $\varepsilon _3^2 = 0$. The Auslander–Reiten quiver of H is shown in Fig. 10. The numbers in the figure correspond to composition factors and basis vectors. (In the last three rows the three modules on the left have to be identified with the corresponding three modules on the right.)

Fig. 10

The Auslander–Reiten quiver of $H(C,D,\Omega )$ of type $C_3$ with D minimal

The preprojective algebra $\Pi = \Pi (C,D)$ is given by the quiver

with relations $\varepsilon _1 = \varepsilon _2 = 0, \varepsilon _3^2 = 0, \alpha _{12}\alpha _{21} = 0, -\alpha _{21}\alpha _{12} + \alpha _{23}\alpha _{32} = 0$ and $-\alpha _{32}\alpha _{23}\varepsilon _3 - \varepsilon _3\alpha _{32}\alpha _{23} = 0$. The indecomposable projective $\Pi$-modules are shown in Fig. 11.

Fig. 11

The indecomposable projective $\Pi (C,D)$-modules for type $C_3$ with D minimal

Fig. 12

The Auslander–Reiten quiver of $H(C,D,\Omega )$ of type $G_2$ with D minimal

13.8 Dynkin type $G_2$

Let

with symmetrizer $D = {\text {diag}}(1,3)$ and $\Omega = \{ (1,2) \}$. The graph $\Gamma (C)$ looks as follows:

Thus C is a Cartan matrix of Dynkin type $G_2$. We have $f_{12} = 3$ and $f_{21} = 1$. Thus $H = H(C,D,\Omega )$ is given by the quiver

with relations $\varepsilon _1 = 0$ and $\varepsilon _2^3 = 0$. The Auslander–Reiten quiver of H is displayed in Fig. 12. As vertices we have the graded dimension vectors (arising from the obvious $\mathbb {Z}$-covering of H) of the indecomposable H-modules. (The three modules in the left most column have to be identified with the three modules in the right most column.)