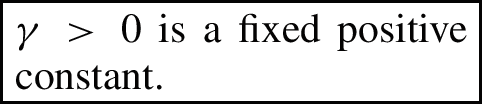Vanishing of Long Time average p-enstrophy Dissipation Rate in the Inviscid Limit of the 2D Damped Navier–Stokes Equations

Abstract

In Constantin and Ramos (Commun Math Phys 275(2), 529–551, 2007), Constantin and Ramos proved a result on the vanishing long time average enstrophy dissipation rate in the inviscid limit of the 2D damped Navier–Stokes equations. In this work, we prove a generalization of this for the p-enstrophy, $1< p < \infty$, sequences of distributions of initial data and sequences of strongly converging right-hand sides. We simplify their approach by working with invariant measures on the global attractors which can be characterized via bounded complete solution trajectories. Then, working on the level of trajectories allows us to directly employ some recent results on strong convergence of the vorticity in the inviscid limit.

1 Introduction and Main Results

We consider the two-dimensional damped Navier–Stokes equations

$$\begin{aligned} \begin{aligned} \partial _t u^\nu + (u^\nu \cdot \nabla )u^\nu + \gamma u^\nu + \nabla p^\nu - \nu \Delta u^\nu&= f^\nu ,\\ {{\,\textrm{div}\,}}u^\nu&= 0, \end{aligned} \end{aligned}$$

(1.1)

in velocity $u^\nu = (u_1^\nu ,u_2^\nu ):\mathbb {R}^2 \times [0,M) \rightarrow \mathbb {R}^2$ and pressure $p^\nu :\mathbb {R}^2 \times [0,M) \rightarrow \mathbb {R}$ with stationary right-hand side $f^\nu :\mathbb {R}^2 \rightarrow \mathbb {R}^2$ and constants $\nu , \gamma > 0$. Then $\omega ^\nu :=\omega (u^\nu ) :={{\,\textrm{curl}\,}}u^\nu = \partial _{x_1}u^\nu _2 - \partial _{x_2}u^\nu _1$ is called the vorticity of $u^\nu$ and formally satisfies

$$\begin{aligned} \begin{aligned} \partial _t \omega ^\nu + u^\nu \cdot \nabla \omega ^\nu + \gamma \omega ^\nu - \nu \Delta \omega ^\nu&= g^\nu ,\\ u^\nu&= K*\omega ^\nu , \end{aligned} \end{aligned}$$

(1.2)

where $g^\nu :={{\,\textrm{curl}\,}}f^\nu$ and $K(x) :=\frac{1}{2\pi }\nabla ^{\perp }\log |x|, x \in \mathbb {R}^2$.

The square of the $L^2(\mathbb {R}^2)$ norm of the vorticity $\omega ^\nu (t)$ at some time t is called enstrophy and by testing (1.2) with $\omega ^\nu (t)$, one obtains

$$\begin{aligned}\frac{d}{dt}\Vert \omega ^\nu (t)\Vert ^2_{L^2} + 2\gamma \Vert \omega ^\nu (t)\Vert _{L^2}^2 + 2\nu \Vert \nabla \omega ^\nu (t)\Vert _{L^2}^2 = (g^\nu ,\omega ^\nu (t))_{L^2}\end{aligned}$$

so that $-2\nu \Vert \nabla \omega ^\nu (t)\Vert _{L^2}^2$ represents the enstrophy dissipation rate at time t by viscous effects.

In the inviscid analogue ($\nu = 0$) of (1.2), the so-called damped Euler equations, this term is not present and it is reasonable to ask if this dissipation rate by viscous effects vanishes in the inviscid limit $(\nu \rightarrow 0)$ of the Navier–Stokes equations.

Enstrophy and its behaviour in the inviscid limit is an important topic in classical 2D turbulence theory, see Sect. 9.7 in [15]. An attempt to reconcile aspects of this theory with the more modern study of the Euler equations was initiated by Eyink [14], see also [21].

One particularly important and useful notion of solution in this context is that of renormalized solutions to the vorticity formulation of the Euler equations, which we are going to define in our situation in Definition 2.2. These renormalized solutions satisfy a balance equation for the p-enstrophy, by which we mean the p-th power of the $L^p(\mathbb {R}^2)$ norm of the vorticity. In the class of vorticity in $L^\infty ((0,M);L^p(\mathbb {R}^2))$, $p \ge 2$, it is well-known that all weak vorticity solutions to the Euler equations are automatically renormalized [12, 21]. For $p < 2$, such renormalized solutions can at least be obtained as weak-* limits in $L^\infty ((0,M);L^p(\mathbb {R}^2))$ of subsequences of (smooth) exact solutions to the Euler equations or the Navier–Stokes equations with vanishing viscosity [10, 11, 21].

In fact, this weak-* convergence has been recently improved in [6, 27] to strong convergence in $C([0,M];L^p(\mathbb {R}^2))$, $1\le p < \infty$. As a consequence, the p-enstrophy dissipation rate can be seen to vanish in $L^1(0,M)$ in the inviscid limit of the full sequence (by a sub-subsequence argument).

Remark 1.1

Most of the referenced articles in this introduction so far only consider the standard Euler and Navier–Stokes equations without damping ($\gamma = 0$). For weak solutions to the damped equations, one can generally show the exact same or analogous results, for which we list the main reasons here:

• (i) The standard a priori estimates for the kinetic energy and enstrophy hold analogously and can even be improved as the damping introduces (further) dissipation to the system.

• (ii) The linearity of the damping term in combination with i) yields that all weak convergence arguments work likewise.

• (iii) The linear damping term does not destroy the parabolic structure of the first equation in the Navier–Stokes equations in vorticity (1.2).

Physically, the terms $\gamma u$ and $\gamma \omega$ often arise in the study of large scale two-dimensional oceanic or atmospheric models describing friction forces. As an example which is very similar to the damped Euler equations, we refer to the Stommel–Charney model of the gulf stream considered in [1] and thoroughly derived in Sect. 5.2 of [28].

In the above mentioned references, the final time M is typically fixed. Here, however, likewise to [8] and the related work [9] on the surface quasi-geostrophic equations, we do not study the inviscid limit on a finite time interval, but study it in the stationary situation that is obtained by first considering long times averages. More precisely, in [8], Constantin and Ramos proved that the long time average of the enstrophy dissipation rate of the 2D damped Navier–Stokes equations vanishes in the inviscid limit, i.e.,

$$\begin{aligned} \lim _{\nu \rightarrow 0}\nu \limsup _{M \rightarrow \infty } \frac{1}{M}\int _{\mathbb {R}^2}|\nabla \omega ^\nu |^2\,dx\,dt = 0. \end{aligned}$$

(1.3)

under the assumptions of $f, u_0 \in (W^{1,1}\cap W^{1,\infty })(\mathbb {R}^2)$ being independent of $\nu$, weakly-divergence free and $\gamma > 0$ being a positive constant.

Our main result generalizes this for the p-enstrophy, $1< p < \infty$, and relaxes the assumptions. We will comment more on this right after stating the main result in the following theorem. Beforehand, we define the space

$$\begin{aligned} \mathcal {E}_q :=\lbrace F = (F_1,F_2) \in L^2(\mathbb {R}^2): F \text { is weakly divergence-free and } {{\,\textrm{curl}\,}}F \in L^q(\mathbb {R}^2)\rbrace \end{aligned}$$

(1.4)

for every $1 \le q \le \infty$. Note that $\mathcal {E}_q$ is a Banach space with norm $\Vert F\Vert _{\mathcal {E}_q} :=\Vert F\Vert _{L^2} + \Vert {{\,\textrm{curl}\,}}F\Vert _{L^q}$, $F \in \mathcal {E}_q$. On the space $\mathcal {E}_1 \cap \mathcal {E}_p$, $1 < p \le \infty$, we consider the norm $\Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p} :=\Vert \cdot \Vert _{\mathcal {E}_1} + \Vert \cdot \Vert _{\mathcal {E}_p}$.

Theorem 1.2

Let $1< p < \infty$ and $\gamma > 0$ be fixed. Consider a bounded family $(f^\nu )_{\nu > 0} \subset \mathcal {E}_1 \cap \mathcal {E}_r$ with $r = \max \lbrace 2,p\rbrace$, where $({{\,\textrm{curl}\,}}f^\nu )_{\nu > 0}$ is precompact in $L^r(\mathbb {R}^2)$. For every $\nu > 0$ denote by $\lbrace S^\nu (t)\rbrace _{t \ge 0}:\mathcal {E}_1 \cap \mathcal {E}_p \rightarrow \mathcal {E}_1 \cap \mathcal {E}_p$ the solution semigroup of the associated damped Navier–Stokes equations (1.1). Moreover, let $(\mu _0^{\nu })_{\nu > 0}$ be a family of Borel probability measures on $\mathcal {E}_1 \cap \mathcal {E}_p$ satisfying

$$\begin{aligned} \int _{\mathcal {E}_1 \cap \mathcal {E}_p} \Vert \omega (u_0)\Vert _{L^p}^p\,d\mu ^{\nu }_0(u_0) < \infty \end{aligned}$$

(1.5)

for every $\nu > 0$. Then,

$$\begin{aligned} \lim _{\nu \rightarrow 0} \limsup _{M \rightarrow \infty } \frac{1}{M}\int _0^M\int _{\mathcal {E}_1 \cap \mathcal {E}_p} \nu \int _{\mathbb {R}^2}|\nabla |\omega (S^\nu (t) u_0)|^\frac{p}{2}|^2\,dx\,d\mu _0^\nu (u_0)\,dt = 0. \end{aligned}$$

(1.6)

Remark 1.3

• (i) In comparison to (1.3) and the assumptions of fixed integrable and uniformly bounded $u_0,f$ with integrable and bounded weak derivatives, here:

  • (a) We consider the dissipation rate of p-enstrophy by viscous effects (up to a constant factor) $\nu \Vert \nabla |\omega (S^\nu (t) u_0)|^\frac{p}{2}\Vert _{L^2(\mathbb {R}^2)}^2$.

  • (b) For the weakly divergence-free right-hand side f in (1.1), we only require it to be in $L^2(\mathbb {R}^2)$ with curl in $(L^1 \cap L^r)(\mathbb {R}^2)$, $r= \max \lbrace 2,p\rbrace$, rather than being in $(W^{1,1} \cap W^{1,\infty })(\mathbb {R}^2)$. Moreover, the right-hand side may depend on $\nu$ as long as $(f^\nu )_{\nu > 0}$ is bounded in $\mathcal {E}_1 \cap \mathcal {E}_r$ and $({{\,\textrm{curl}\,}}f^\nu )_{\nu > 0}$ is precompact in $L^r(\mathbb {R}^2)$.

  • (c) The enstrophy dissipation rate is not necessarily associated to one fixed initial datum but is more generally considered in the mean with respect to a probability distribution on the space of admissible initial data $\mathcal {E}_1 \cap \mathcal {E}_p$. In this way, the result states that the long time averages of the p-enstrophy dissipation rate of a whole ensemble of weak solutions associated to this distribution of initial data vanishes in the inviscid limit. Moreover, these distributions of initial data may depend on $\nu$ as long as (1.5) is satisfied. Note that we do not require a bound in ( 1.5) uniformly in $\nu$. This comes from the fact that in (1.6) we first consider long time averages after which all arguments to follow take place on the attractor of the system, which, due to the damping term, can be bounded independently from the viscosity parameter $\nu$. Note that $\mu ^\nu = \delta _{u_0}$ (independently of $\nu > 0$) for $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$ is admissible and the previous result by Constantin and Ramos corresponds to $\mu ^\nu = \delta _{u_0}$ for weakly divergence-free $u_0 \in (W^{1,1} \cap W^{1,\infty })(\mathbb {R}^2)$.

• (ii) As indicated in c) in part i) of this remark, the primary role mathematically of the linear damping lies in providing a bound for the attractor of the damped Navier–Stokes equations independently of the viscosity parameter $\nu$ (but depending on the fixed damping parameter $\gamma > 0$). Therefore, it would be possible in Theorem 1.2 to also allow for a bounded family $(\gamma ^\nu )_{\nu > 0} \subset (0,\infty )$ that is bounded away from 0. However, to keep things a little bit more simple and avoid needing to discuss the limit of the equations in the parameter $\gamma ^\nu$, we make the standing assumption throughout that

  

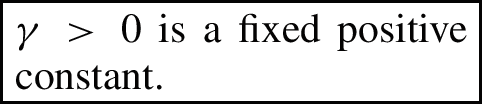
• (iii) A recurring theme throughout this article will be the assumption of the initial data to be in $\mathcal {E}_1 \cap \mathcal {E}_p$ and the right-hand side to be in $\mathcal {E}_1 \cap \mathcal {E}_r$ with $r = \max \lbrace p,2 \rbrace$. This is weaker than assuming $p \ge 2$ but only so by a slight margin: Even if $1< p < 2$, this assumption on the right-hand side will guarantee that the vorticity of the associated weak solution of the Navier–Stokes equations is instantaneously in $L^2(\mathbb {R}^2)$, see Lemma 2.9.

The proof of this main theorem follows the same approach as [8] by first considering measures associated to long time averages for fixed $\nu > 0$ and to then pass on to the limit $(\nu \rightarrow 0)$. However, we will employ that these measures are necessarily concentrated on the global attractor of the solution semigroup of the damped Navier–Stokes equations and use its characterization via bounded, complete (sometimes called ancient) solution trajectories, which allows us to work on the level of trajectories subsequently. In contrast, Constantin and Ramos work with what are called statistical solutions in phase space. This leads to a notion of renormalized stationary statistical solutions and to the adaptation of some more or less technical arguments of the seminal work [12] on renormalization theory by DiPerna and Lions to the context of phase space statistical solutions. Also, stronger assumptions on the right-hand side were made for these constructions as pointed out in Remark 1.3.

Moreover, by working on the level of trajectories, we may employ some recent results on the inviscid limit of solutions to the Navier–Stokes equations. In particular, the improvement to convergence in $C([0,M];L^p(\mathbb {R}^2))$, $1 \le p < \infty$, in the inviscid limit to renormalized solutions of the corresponding damped Euler equations [6, 27], which we already mentioned above, will be of use.

After this introduction, in Sect. 2, we briefly recall some classical and recent theory on renormalized solutions of the damped Euler and Navier–Stokes equations and the inviscid limit. We continue on in Sect. 3 with a discussion on the global attractor of the damped Navier–Stokes equations based on [3, 4, 19, 20]. Next, in Sect. 4, we glimpse over a Krylov–Bogolioubov type construction of invariant measures that are concentrated on the global attractor. In particular, we rely on work in [24]. Finally, in Sect. 5, we prove the main theorem.

2 Weak and Renormalized Solutions of the Damped Euler and Navier–Stokes Equations

For $1 \le p \le \infty$ and $m \in \mathbb {N}$, we denote by $L^p(\mathbb {R}^2)$ and $W^{m,p}(\mathbb {R}^2)$ the standard Lebesgue and Sobolev spaces of functions on $\mathbb {R}^2$ with values in $\mathbb {R}$ or $\mathbb {R}^2$, depending on the context. By $L^{p,\infty }(\mathbb {R}^2)$, we denote the weak $L^p$ spaces with seminorms $\Vert \cdot \Vert _{L^{p,\infty }}$, see [18, chapter 1].

Let us also mention here that the subscript loc in our notation for spaces of continuous functions means that we endow this space with the topology of uniform convergence on compact intervals, while in the notation for Lebesgue spaces, this denotes integrability and the topology of convergence on compact subsets.

We now review some results on the damped Euler and Navier–Stokes equations. We recall our standing assumption of the damping parameter

We now state the following lemma from [17, Lemma 2.2], which summarizes a few standard results on the Biot-Savart law. Recall the definition of the spaces $\mathcal {E}_q, 1 \le q \le \infty$, in (1.4).

Lemma 2.1

Let $1 \le p < \infty$ and $F \in \mathcal {E}_1 \cap \mathcal {E}_p$. Then F is determined by its curl via the Biot-Savart law $F = K * {{\,\textrm{curl}\,}}F$ with kernel $K(x) = \frac{1}{2\pi } \frac{x^\perp }{|x|^2} \in L^{2,\infty }(\mathbb {R}^2)$. Moreover,

• (i) there exists a constant $C_1 > 0$ such that

  $$\begin{aligned}\Vert F\Vert _{L^{2,\infty }} \le C_1 \Vert K\Vert _{L^{2,\infty }}\Vert {{\,\textrm{curl}\,}}F\Vert _{L^1},\end{aligned}$$

• (ii) if $p > 1$, then $F \in W^{1,p}_{loc}(\mathbb {R}^2)$ and there exists a constant $C_2 = C_2(p) > 0$ such that

  $$\begin{aligned}\Vert \nabla F\Vert _{L^p} \le C_2 \Vert {{\,\textrm{curl}\,}}F\Vert _{L^p},\end{aligned}$$

• (iii) if $1< p < 2$, then there exists $C_3 = C_3(p)$ s.t.

  $$\begin{aligned}\Vert F\Vert _{L^{p*}} \le C_3 \Vert {{\,\textrm{curl}\,}}F\Vert _{L^p} \text { with } p* = \frac{2p}{2-p}.\end{aligned}$$

We next provide some brief motivation for the upcoming definition of renormalized solutions. In order for (1.2) and its inviscid analogue ($\nu$ = 0) to be well-defined in the sense of distributions, the non-linear term $u \cdot \nabla \omega = {{\,\textrm{div}\,}}(u\omega )$ requires that $u\omega \in L^1_{loc}((0,M) \times \mathbb {R}^2)$. For $\omega \in (L^1 \cap L^p)(\mathbb {R}^2)$, Lemma 2.1 and the Sobolev-embedding theorem yield that

$$\begin{aligned} u = K * \omega \text { is in } {\left\{ \begin{array}{ll} L^{\frac{2p}{2-p}}(\mathbb {R}^2) &{}: 1< p < 2\\ L^q_{loc}(\mathbb {R}^2) \text { for all } q \in [1,\infty ) &{}: p \ge 2 \end{array}\right. } \end{aligned}$$

Hence, for $1< p < 2$, $u\omega \in L^1_{loc}(\mathbb {R}^2)$ leads to the condition

$$\begin{aligned}\frac{1}{p} + \frac{1}{\frac{2p}{2-p}} \le 1 \Leftrightarrow p \ge \frac{4}{3}.\end{aligned}$$

Therefore, the vorticity formulation of the Euler equations has to be interpreted in a different way when $p < \frac{4}{3}$. The frequently used notion of renormalized solutions is the one we consider here and define next.

Beforehand, we remark that for the Navier–Stokes equations and any $p\ge 1$, in contrast, the local integrability of $u\omega$ is generally satisfied due to better a priori estimates being available thanks to the Laplacian in the equation. The Navier–Stokes equations with initial vorticity in $L^1(\mathbb {R}^2)$ have been considered in [2, 16, 17].

Definition 2.2

Let $1< p < \infty$, $\omega _0 \in (L^1\cap L^p)(\mathbb {R}^2)$, $g \in (L^1 \cap L^p)(\mathbb {R}^2)$. Then $\omega \in C_{loc}([0,\infty );(L^1 \cap L^p)(\mathbb {R}^2))$ is called a renormalized solution of the vorticity formulation of the damped Euler equations with initial data $\omega _0$ and right-hand side g if for every $\beta \in C^1(\mathbb {R}^2)$, bounded with bounded derivative and vanishing in a neighbourhood of 0,

$$\begin{aligned}\int _0^\infty \int _{\mathbb {R}^2} \beta (\omega )(\partial _t\varphi + u\cdot \nabla \varphi )-\gamma \omega \beta '(\omega )\varphi \,dx\,dt + \int _{\mathbb {R}^2} \beta (\omega _0)\varphi (0)\,dx\\ = -\int _0^\infty \int _{\mathbb {R}^2}\beta '(\omega )g\varphi \,dx\,dt,\end{aligned}$$

where $\varphi \in C^\infty _c([0,\infty )\times \mathbb {R}^2)$ and

$$\begin{aligned}u(t,x) = (K * \omega (t))(x) \text { for } a.e.\, (t,x) \in (0,\infty )\times \mathbb {R}^2.\end{aligned}$$

Remark 2.3

• (i) Under a mild decay assumption at infinity, the consistency result [12, Theorem II.3] states that weak and renormalized solutions coincide when for the functions in the non-linear term $u\cdot \nabla \omega = {{\,\textrm{div}\,}}(u\omega )$, we have $\omega \in L^\infty ((0,M);L^p(\mathbb {R}^2))$ and $u \in L^1((0,M);W^{1,q}_{loc}(\mathbb {R}^2))$ with $\frac{1}{p} + \frac{1}{q} = 1$. For the (damped) Euler equations, Lemma 2.1 implies that for u given by the Biot-Savart law, this is generally the case when $p \ge 2$, which has already been noted in [21, Proposition 1].

• (ii) It was proved in [11] and [10] that renormalized solutions to the vorticity formulation of the Euler equations can be constructed as weak-* limits in $L([0,\infty );L^p(\mathbb {R}^2))$, $1 \le p < \infty$, of solutions of the vorticity formulation of the Navier–Stokes equations in the inviscid limit. We also state this fact in Theorem 2.7 in the situation that $1< p < \infty$. The weak solutions of the Navier–Stokes equations on the other hand can be constructed by standard methods such as Galerkin approximations or approximations by solving related smoothed equations from which, in either case, the (unique) weak solution to the Cauchy problem inherits several properties that we state in Theorem 2.4.

Theorem 2.4

Let $1< p < \infty$, $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$, $f \in \mathcal {E}_1 \cap \mathcal {E}_p$ and define $g :={{\,\textrm{curl}\,}}f$. Then there exists a unique weak solution $u \in C_{loc}([0,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ of the damped Navier–Stokes equations (1.1) with viscosity $\nu > 0$, initial data $u_0$ and right-hand side f. Moreover,

• the vorticity $\omega (u) \in C_{loc}([0,\infty );(L^1 \cap L^p)(\mathbb {R}^2))$ is a weak solution of the vorticity formulation of the damped Navier–Stokes equations (1.2) with initial data $\omega (u_0)$ and right-hand side g,

• a.e. on $[0,\infty )$, with equality for $p \ge 2$,

  $$\begin{aligned} \begin{aligned}&\frac{d}{dt}\!\!\int _{\mathbb {R}^2} |\omega (u)|^pdx \!+\! \gamma p \int _{\mathbb {R}^2}|\omega (u)|^p\,dx \!\le \! -4\nu \frac{p-1}{p}\!\int _{\mathbb {R}^2} |\nabla |\omega (u)|^\frac{p}{2}|^2\,dx \!+\! p\int _{\mathbb {R}^2}g\omega (u)|\omega (u)|^{p-2}\,dx, \end{aligned} \end{aligned}$$

  (2.1)

• for all $t \ge 0$,

  $$\begin{aligned} \begin{aligned}&\Vert u(t)\Vert _{L^2}^2 + 2\nu \Vert \nabla u\Vert _{L^2(0,t;L^2)}^2 \le \Vert u_0\Vert _{L^2}^2 + \frac{t}{\gamma } \Vert f\Vert _{L^2}^2\\&\Vert \omega (u)(t)\Vert _{L^p}^p + 4\nu \frac{p-1}{p}\Vert \nabla |\omega (u)|^\frac{p}{2}\Vert _{L^2(0,t;L^2)}^2 \le \Vert \omega (u_0)\Vert _{L^p}^p + \frac{t}{\gamma } \Vert g\Vert _{L^p}^p, \end{aligned} \end{aligned}$$

  (2.2)

• for all $t \ge 0$ and $1 \le q \le p$ (independently of $\nu > 0$!),

  $$\begin{aligned} \begin{aligned}&\Vert u(t)\Vert _{L^2} \le e^{-\gamma t}(\Vert u_0\Vert _{L^2} - \frac{1}{\gamma }\Vert f\Vert _{L^2}) + \frac{1}{\gamma }\Vert f\Vert _{L^2},\\&\Vert \omega (u)(t)\Vert _{L^q} \le e^{-\gamma t}(\Vert \omega (u_0)\Vert _{L^q} - \frac{1}{\gamma }\Vert g\Vert _{L^q}) + \frac{1}{\gamma }\Vert g\Vert _{L^q}. \end{aligned} \end{aligned}$$

  (2.3)

Theorem 2.5

Let $1< p < \infty$, $\omega _0,g \in (L^1 \cap L^p)(\mathbb {R}^2)$ and consider a renormalized solution $\omega \in C_{loc}([0,\infty );(L^1 \cap L^p)(\mathbb {R}^2))$ of the vorticity formulation of the damped Euler equations with initial data $\omega _0$ and right-hand side g. Then

$$\begin{aligned} \frac{d}{dt} \int _{\mathbb {R}^2} |\omega |^p\,dx + \gamma p \int _{\mathbb {R}^2}|\omega |^p\,dx = p\int _{\mathbb {R}^2}g\omega |\omega |^{p-2}\,dx \end{aligned}$$

(2.4)

a.e. on $[0,\infty )$.

The weak-* convergence in $L^\infty ([0,\infty );L^p(\mathbb {R}^2))$ of weak vorticity solutions of the Navier–Stokes equations in the inviscid limit $(\nu \rightarrow 0)$ to renormalized solutions of the Euler equations was improved recently in [6, 27] for $1< p < \infty$, which we state in the following theorem. We remark that while [6] also treats the case $p = 1$, this case is still problematic for our arguments as we sometimes use reflexivity for weak compactness. Moreover, and perhaps even more importantly, the enstrophy (in-)equality (2.1), which is usually obtained by an approximation argument and testing (1.2) with $|\omega |^{p-2}\omega$ (see for instance [12, Theorem IV.1] and the proof thereof for more details) becomes problematic in the case $p = 1$ (for $p=1$, $|\omega |^{p-2}\omega$ does not have any Sobolev regularity in general even for smooth or smoothed $\omega$).

We note that the results in [6, 27] remain true in our case of an additional constant coefficient damping term (recall Remark 1.1), strongly converging right-hand sides and in case one considers viscosity $\nu$ which converges to some positive number, i.e., better behaved convergence of Navier–Stokes solutions to Navier–Stokes solutions.

Theorem 2.6

Let $1< p <\infty$, $(\nu ^k)_{k\in \mathbb {N}} \subset (0,1)$ be a sequence converging to some $\nu \ge 0$ and let $(u_0^{\nu ^k})_{k\in \mathbb {N}}, (f^{\nu ^k})_{k\in \mathbb {N}}$ be bounded sequences of initial data and right-hand sides in $\mathcal {E}_1 \cap \mathcal {E}_p$ with associated weak solutions $(u^{\nu ^k})_{k\in \mathbb {N}}$ as in Theorem 2.4, where $\nu ^k$ is the viscosity constant for every $k \in \mathbb {N}$. We suppose that for some $u_0^\nu ,f^\nu \in \mathcal {E}_1 \cap \mathcal {E}_p$,

$$\begin{aligned} \omega (u_0^{\nu ^k}) \rightarrow \omega (u_0^\nu )\,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2) \end{aligned}$$

and for $g^{\nu ^k} :={{\,\textrm{curl}\,}}f^{\nu ^k}$, $g^\nu :={{\,\textrm{curl}\,}}f^\nu$,

$$\begin{aligned} g^{\nu ^k} \rightarrow g^\nu \,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2). \end{aligned}$$

Then, after passing to a subsequence, there exists $u^\nu$ such that

$$\begin{aligned}&u^{\nu ^k} \overset{*}{\rightharpoonup }\ u^\nu \,(k \rightarrow \infty ) \text { in } L^\infty ([0,\infty );L^2(\mathbb {R}^2)),\\&\omega (u^{\nu ^k}) \rightarrow \omega (u^\nu ) \,(k \rightarrow \infty )\text { in } C_{loc}([0,\infty );L^p(\mathbb {R}^2)), \end{aligned}$$

where $\omega (u^\nu )$ satisfies (in the renormalized sense) the vorticity formulation of the damped Euler $(\nu = 0)$ or Navier-Stokes $(\nu > 0)$ equations with initial data $\omega (u_0^\nu )$ and right-hand side $g^\nu$.

We also state the related main theorem from [11], adapted to our situation. Although it appears to be weaker than Theorem 2.6, we give the theorem in a slightly improved and very useful form of only requiring weak convergence of the initial data opposed to strong convergence as originally stated in [11], which we explain below.

Theorem 2.7

Let $1< p <\infty$, $(\nu ^k)_{k\in \mathbb {N}} \subset (0,1)$ be a sequence converging to 0 and let $(u_0^{\nu ^k})_{k\in \mathbb {N}},(f^{\nu ^k})_{k\in \mathbb {N}}$ be bounded sequences of initial data and right-hand sides in $\mathcal {E}_1 \cap \mathcal {E}_p$ with associated weak solutions $(u^{\nu ^k})_{k\in \mathbb {N}}$ as in Theorem 2.4, where $\nu ^k$ is the viscosity constant for every $k \in \mathbb {N}$. We suppose that for some $u_0,f \in \mathcal {E}_1 \cap \mathcal {E}_p$,

$$\begin{aligned} \omega (u_0^{\nu ^k}) \rightharpoonup \omega (u_0)\,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2) \end{aligned}$$

and for $g^{\nu ^k} :={{\,\textrm{curl}\,}}f^{\nu ^k}$, $g :={{\,\textrm{curl}\,}}f$,

$$\begin{aligned} g^{\nu ^k} \rightarrow g\,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2). \end{aligned}$$

Then, after passing to a subsequence, there exists u such that

$$\begin{aligned}&u^{\nu ^k} \overset{*}{\rightharpoonup }\ u\,(k \rightarrow \infty ) \text { in } L^\infty ([0,\infty );L^2(\mathbb {R}^2)),\\&\omega (u^{\nu ^k}) \overset{*}{\rightharpoonup }\ \omega (u)\,(k \rightarrow \infty ) \text { in } L^\infty ([0,\infty );L^p(\mathbb {R}^2)), \end{aligned}$$

where $\omega (u)$ satisfies the vorticity formulation of the damped Euler equations in the renormalized sense with initial data $\omega (u_0)$ and right-hand side g.

Proof

(sketch) The idea of the proof in [11, Theorem 1.1] is based on the duality argument by DiPerna and Lions in [12, Theorem II.6] and applies here step by step in the same way. Therefore, we only sketch the part in their argument where we can see that weak convergence $\omega (u_0^{\nu ^k}) \rightharpoonup \omega (u_0)\,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2)$, rather than strong convergence, suffices. Let $q = \frac{p}{p-1}$ and denote by $\phi ^{\nu ^k} \in L^\infty ((0,M);L^q(\mathbb {R}^2))$ the unique weak solution to the backward damped transport-diffusion problem

$$\begin{aligned} \begin{aligned} -\partial _t\phi ^{\nu ^k} -\nu ^k\Delta \phi ^{\nu ^k} - {{\,\textrm{div}\,}}(\phi ^{\nu ^k} u^{\nu ^k}) + \gamma \phi ^{\nu ^k}&= \chi ,\\ \phi ^{\nu ^k}(M,\cdot )&= 0, \end{aligned} \end{aligned}$$

with right-hand side $\chi \in C_c^\infty ((0,M) \times \mathbb {R}^2)$. Then, following the arguments in step 1 and 2 in the proof of [11, Theorem 1.1], one obtains that a subsequence of $(\phi ^{\nu ^k})_{k\in \mathbb {N}}$, which we generally do not relabel, converges in $C([0,M],L^q_w(\mathbb {R}^2))$ to the solution $\phi$ of the corresponding backward damped transport equation

$$\begin{aligned} \begin{aligned} -\partial _t\phi - {{\,\textrm{div}\,}}(\phi u) + \gamma \phi&= \chi ,\\ \phi (M,\cdot )&= 0, \end{aligned} \end{aligned}$$

where u is the weak-* limit in $L^\infty ([0,\infty );L^2(\mathbb {R}^2))$ of a subsequence of $(u^{\nu ^k})_{k\in \mathbb {N}}$. Note that if we let $\psi ^{\nu ^k}(t,x) = \phi ^{\nu ^k}(M-t,x), \psi (t,x) = \phi (M-t,x), \tilde{u}^{\nu ^k}(t,x) = u^{\nu ^k}(M-t,x), \tilde{u}(t,x) = u(M-t,x)$ and $\tilde{\chi }(t,x) = \chi (M-t,x)$, then $\psi ^{\nu ^k}$ and $\psi$ solve the corresponding forward damped transport-diffusion and damped transport problems

$$\begin{aligned} \begin{aligned} \partial _t\psi ^{\nu ^k} - \nu ^k\Delta \psi ^{\nu ^k} - {{\,\textrm{div}\,}}(\psi ^{\nu ^k} \tilde{u}^{\nu ^k}) + \gamma \psi ^{\nu ^k}&= \tilde{\chi },\\ \psi ^{\nu ^k}(0,\cdot )&= 0, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \partial _t\psi - {{\,\textrm{div}\,}}(\psi \tilde{u}) + \gamma \psi&= \tilde{\chi },\\ \psi (0,\cdot )&= 0, \end{aligned} \end{aligned}$$

as well as $\psi ^{\nu ^k} \rightarrow \psi$ in $C([0,T];L^q_w(\mathbb {R}^2))$. Then we may apply Proposition 1 in [27] (or alternatively Lemma 3.3 in [6]), both of which imply that by strong convergence of the initial data $\psi ^{\nu ^k}(0,\cdot ) = 0 \rightarrow 0 = \psi (0,\cdot )$ in $L^q(\mathbb {R}^2)$, we also have strong convergence

$$\begin{aligned}\psi ^{\nu ^k} \rightarrow \psi \text { in } C([0,M];L^q(\mathbb {R}^2)).\end{aligned}$$

This particularly implies

$$\begin{aligned} \phi ^{\nu ^k} \rightarrow \phi \text { in } C([0,M];L^q(\mathbb {R}^2)). \end{aligned}$$

(2.5)

Testing the damped Navier–Stokes equations for $\omega ^{\nu ^k}$ with $\phi ^{\nu ^k}$ and integrating by parts yields

$$\begin{aligned} \int _0^M\int _{\mathbb {R}^2} \omega ^{\nu ^k} \chi \,dx\,dt = \int _0^M\int _{\mathbb {R}^2} f^{\nu ^k} \phi ^{\nu ^k}\,dx\,dt + \int _{\mathbb {R}^2} \omega (u_0^{\nu ^k})\phi ^{\nu ^k}(0)\,dx. \end{aligned}$$

(2.6)

Letting $\omega \in L^\infty ([0,\infty );L^p(\mathbb {R}^2))$ be the weak-* limit of a subsequence of $(\omega ^{\nu ^k})_{k\in \mathbb {N}}$, we obtain

$$\begin{aligned}\int _0^M\int _{\mathbb {R}^2} \omega \chi \,dx\,dt = \int _0^M\int _{\mathbb {R}^2} f \phi \,dx\,dt + \int _{\mathbb {R}^2} \omega (u_0)\phi (0)\,dx.\end{aligned}$$

From there on, one may again proceed as in step 4 in [11, Theorem 1.1] to show that $\omega$ is indeed a renormalized solution to the vorticity formulation of the damped Euler equations. $\square$

Remark 2.8

In the formulation in [11, Theorem 1.1], the strong convergence $\omega (u_0^{\nu ^k}) \rightarrow \omega (u_0^\nu )\,(k \rightarrow \infty )$ in $L^p(\mathbb {R}^2)$ was assumed to have convergence of the integrals $\int _{\mathbb {R}^2} \omega (u_0^{\nu ^k})\phi ^{\nu ^k}(0)\,dx$ in (2.6), as it was only known that $(\phi ^{\nu ^k})_{k\in \mathbb {N}}$ converges in $C([0,M],L^q_w(\mathbb {R}^2))$ to $\phi$. However, having used the later and independently from one another proved Proposition 1 in [27] (or alternatively Lemma 3.3 in [6]), we obtained the strong convergence (2.5).

Finally, let us close this section with a result on the vorticity of solutions to the Navier–Stokes equations being instantaneously in $L^2(\mathbb {R}^2)$ with a bound on the corresponding norm for positive times bounded away from 0, even for initial data of lower integrability. Our estimates are derived as in the proof of Theorem B in [2] but with the inclusion of a damping term and a right-hand side $g \in (L^1 \cap L^2)(\mathbb {R}^2)$.

Lemma 2.9

Let $1 \le p < \infty$ and consider the unique solution $u \in C_{loc}([0,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ of the damped Navier–Stokes equations with initial data $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$, right-hand side $f \in \mathcal {E}_1 \cap \mathcal {E}_{\max \lbrace 2,p\rbrace }$ and define $g :={{\,\textrm{curl}\,}}f$. Then, for fixed $t_0 > 0$, $\Vert \omega (u)(t)\Vert _{L^2}$ is bounded in $t \ge t_0$ by a constant $C = C(t_0,\gamma ,\nu ,\Vert g\Vert _{L^1 \cap L^2}, \Vert \omega (u_0)\Vert _{L^1 \cap L^p})$.

Proof

We first note that if $\omega (u_0) \in L^2(\mathbb {R}^2)$, then the lemma follows immediately from (2.3). Therefore, we assume $\omega (u_0) \in L^1(\mathbb {R}^2) \setminus L^2(\mathbb {R}^2)$. In fact, by an approximation argument, it suffices to consider smooth and compactly supported data $u_0$ and g with

$$\begin{aligned} \Vert \omega (u_0)\Vert _{L^2} \ge \lambda , \end{aligned}$$

(2.7)

where $\lambda > 0$ can be chosen arbitrarily large and will be specified later. Equation (2.1) then yields

$$\begin{aligned} \frac{d}{dt} \Vert \omega (u)(t)\Vert _{L^2}^2 \le -2\nu \Vert \nabla \omega (u)(t)\Vert _{L^2}^2 + \frac{\Vert g\Vert _{L^2}^2}{\gamma } \end{aligned}$$

(2.8)

for $t \ge 0$. The right-hand side in (2.3) for $q = 1$ can be bounded by a constant $1 \le c = c(\gamma ,\Vert \omega (u_0)\Vert _{L^1},\Vert g\Vert _{L^1})$ so that the Nash inequality [26, pp. 935, 936] yields

$$\begin{aligned}\Vert \omega (u)(t)\Vert ^2_{L^2} \le \eta \Vert \omega (u)(t)\Vert _{L^1}\Vert \nabla \omega (u)(t)\Vert _{L^2} \le c\eta \Vert \nabla \omega (u)(t)\Vert _{L^2},\end{aligned}$$

for some constant $\eta > 0$. Then (2.8) yields

$$\begin{aligned}\frac{d}{dt}\Vert \omega (u)(t)\Vert _{L^2}^2 \le -\frac{2\nu }{c^2\eta ^2}\Vert \omega (u)(t)\Vert _{L^2}^4 + \frac{\Vert g\Vert _{L^2}^2}{\gamma }.\end{aligned}$$

Therefore, to estimate $\Vert \omega (u)(t)\Vert _{L^2}^2$, we consider the corresponding Riccati differential equation

$$\begin{aligned} \dot{x} = -\frac{2\nu }{c^2\eta ^2} x^2 + \frac{\Vert g\Vert _{L^2}^2}{\gamma }. \end{aligned}$$

(2.9)

We remark that generally for $a,b > 0$ and $x_0 > 0$ large enough such that $\sqrt{\frac{b}{a}}x_0 > 1$, the solution to

$$\begin{aligned} \dot{x} = -ax^2 +b, x(0) = x_0 \end{aligned}$$

(2.10)

is given by

$$\begin{aligned} x(t) = \sqrt{\frac{b}{a}}\coth (\sqrt{ab}(z+t)) \underset{(t \ge t_0)}{\le }\ \sqrt{\frac{b}{a}}\coth (\sqrt{ab}t_0) \end{aligned}$$

(2.11)

for some $z > 0$, where $\coth (s) = \frac{e^{2\,s}+1}{e^{2\,s}-1}$ for $s > 0$. If $x_0, a > 0$ and $b=0$, then the solution to (2.10) is given by

$$\begin{aligned} x(t) = \frac{1}{1/x_0+at} \underset{(t \ge t_0)}{\le }\ \frac{1}{at_0}. \end{aligned}$$

(2.12)

We now choose a and b to match (2.9) and let $\lambda$ in (2.7) be large enough so that in both cases, (2.11) or (2.12) yields the claim. $\square$

3 Attractors of the Damped Navier–Stokes Equations

The global attractor of the solution semigroup of the damped Navier–Stokes equations on H without assumptions on the vorticity was constructed in [19]. We recall the necessary definitions and slightly enhance the attraction and compactness property of the attractor for $L^p$ bounded vorticities. All these arguments blend in with the work in [3, 4, 19, 20].

With exception of Proposition 3.6, the viscosity $\nu > 0$ is fixed and we will not explicitly note the dependence of the solutions to (1.1), (1.2) on $\nu$.

Definition 3.1

Let $\lbrace \theta (t) \rbrace _{t \ge 0}$ be a semigroup on a complete metric space X. A set $\mathcal {U}\subset X$ is called global attractor of $\lbrace \theta (t) \rbrace _{t \ge 0}$ if

• (i) $\mathcal {U}$ is compact in X,

• (ii) $\mathcal {U}$ is attracting in the sense that for any bounded set $B \subset X$ and every open neighbourhood $\mathcal {O}$ of $\mathcal {U}$, there exists $t_0 = t_0(B,\mathcal {O}) > 0$ such that $\theta (t)B \subset \mathcal {O}$ for all $t \ge t_0$,

• (iii) $\mathcal {U}$ is invariant, that is, $\theta (t)\mathcal {U}= \mathcal {U}$ for every $t \ge 0$.

Definition 3.2

Let $1< p < \infty$ and $f \in \mathcal {E}_1 \cap \mathcal {E}_p$. Then $u \in C_{loc}(\mathbb {R};\mathcal {E}_1 \cap \mathcal {E}_p)$ is called complete (or sometimes ancient) solution of the damped Navier–Stokes equations with right-hand side f if it is a weak solution of the damped Navier-Stokes equations with right-hand side f on the time-interval $[t_0,\infty )$ for every $t_0 \in \mathbb {R}$.

Theorem 3.3

[19] Let $\lbrace S(t) \rbrace _{t\ge 0}$ be the solution semigroup of the damped Navier–Stokes equations on

$$\begin{aligned}H :=\lbrace u \in L^2(\mathbb {R}^2): u \text { is weakly divergence-free}\rbrace \end{aligned}$$

with right-hand side $f \in H$ and fixed viscosity $\nu > 0$. Then $\lbrace S(t) \rbrace _{t \ge 0}$ has a global attractor $\mathcal {A}$.

Moreover, if we let $\mathcal {K}\subset C_b(\mathbb {R};L^2(\mathbb {R}^2))$ be the set of complete solution trajectories of the damped Navier–Stokes equations with right-hand side f that are bounded in $L^2(\mathbb {R}^2)$, then

$$\begin{aligned} \mathcal {A}= \lbrace u(0): u \in \mathcal {K}\rbrace . \end{aligned}$$

(3.1)

Lemma 3.4

Let $\mathcal {K}\subset C_b(\mathbb {R};L^2(\mathbb {R}^2))$ be the set of $L^2(\mathbb {R}^2)$ bounded complete solution trajectories of the damped Navier–Stokes equations with right-hand side $f \in H$ and fixed viscosity $\nu > 0$ as in Theorem 3.3. Then $\mathcal {K}$ is bounded by $\frac{\Vert f\Vert _{L^2}}{\gamma }$ in $C_b(\mathbb {R};H)$, independently of $\nu$.

Proof

Let $u \in \mathcal {K}$ and $R > 0$ s.t. $\sup _{t\in \mathbb {R}}\Vert u(t)\Vert _{L^2} \le R$. Then, for any $t\in \mathbb {R}$ and arbitrary $s > 0$, (2.3) implies

$$\begin{aligned} \begin{aligned} \Vert u(t)\Vert _{L^2}&\le e^{-\gamma s}\left( \Vert u(t-s)\Vert _{L^2} - \frac{\Vert f\Vert _{L^2}}{\gamma }\right) + \frac{\Vert f\Vert _{L^2}}{\gamma }\\&\le e^{-\gamma s}\left( R - \frac{\Vert f\Vert _{L^2}}{\gamma }\right) + \frac{\Vert f\Vert _{L^2}}{\gamma }\\&\rightarrow \frac{\Vert f\Vert _{L^2}}{\gamma }\,(s\rightarrow \infty ) \end{aligned} \end{aligned}$$

and we conclude

$$\begin{aligned}\sup _{t\in \mathbb {R}} \Vert u(t)\Vert _{L^2} \le \frac{\Vert f\Vert _{L^2}}{\gamma }.\end{aligned}$$

$\square$

In preparation to the following proposition, for $f \in \mathcal {E}_1 \cap \mathcal {E}_p$, $1< p < \infty$, with $g :={{\,\textrm{curl}\,}}f$ and viscosity $\nu > 0$, we define

$$\begin{aligned} \mathcal {K}_p :=\lbrace u \in \mathcal {K}: \sup _{t \in \mathbb {R}} \Vert \omega (u)(t)\Vert _{L^q} \le \frac{\Vert g\Vert _{L^q}}{\gamma }, q \in \lbrace 1,p \rbrace \rbrace . \end{aligned}$$

(3.2)

Proposition 3.5

Let $1< p < \infty$, $f \in \mathcal {E}_1 \cap \mathcal {E}_{\max \lbrace 2,p\rbrace }$, define $g :={{\,\textrm{curl}\,}}f$ and consider $\mathcal {K}_p$ as in (3.2) for fixed viscosity $\nu > 0$. Then, for every bounded set $B \subset \mathcal {E}_1 \cap \mathcal {E}_p$, the set

$$\begin{aligned} \mathcal {A}_p :=\lbrace u(0): u \in \mathcal {K}_p\rbrace \end{aligned}$$

is both compact and attracts B w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$ and the solution semigroup $\lbrace S(t) \rbrace _{t \ge 0}$ of the damped Navier–Stokes equtions with right-hand side f and viscosity $\nu$.

Proof

We only show the attraction property. The compactness follows similarly. Describing the attraction property in terms of sequences, this means that for an arbitrary bounded sequence $(u_0^n)_{n\in \mathbb {N}} \subset \mathcal {E}_1 \cap \mathcal {E}_p$ and a sequence of times $t^n \rightarrow \infty \,(n \rightarrow \infty )$, there exists a subsequence of $(S(t^n)u_0^n)_{n\in \mathbb {N}}$ converging to some $u_0 \in \mathcal {A}_p$ w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$.

Step 1: First of all, consider solutions $(u^n)_{n\in \mathbb {N}} \subset C_{loc}([-t^n,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ of the damped Navier–Stokes equations satisfying the initial condition $u^n(-t^n) = u_0^n$ for every $n \in \mathbb {N}$. Then $S(t^n)u_0^n = u^n(0)$ for every $n \in \mathbb {N}$ and it suffices to show that $(u^n(0))_{n\in \mathbb {N}}$ converges w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$ to an element of $\mathcal {A}_p$.

Since we already know that $\mathcal {A}$ is the attractor of $\lbrace S(t) \rbrace _{t \ge 0}$ as a semigroup on H, due to (3.1), there exists $u \in \mathcal {K}$ such that for $u_0 :=u(0) \in \mathcal {A}$ and a subsequence, which we do not relabel,

$$\begin{aligned} u^n(0) \rightarrow u_0\,(n\rightarrow \infty ) \text { in } L^2(\mathbb {R}^2). \end{aligned}$$

(3.3)

As $(\omega (u_0^n))_{n\in \mathbb {N}}$ is bounded in $(L^1 \cap L^p)(\mathbb {R}^2)$, we may also assume due to the bound (2.3),

$$\begin{aligned} \omega (u^n)(0) \rightharpoonup \omega (u_0)\,(n\rightarrow \infty ) \text { in } L^p(\mathbb {R}^2) \end{aligned}$$

(3.4)

and $\omega (u_0) \in (L^1 \cap L^p)(\mathbb {R}^2)$ so that $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$.

Step 2: It now remains to show that $u \in \mathcal {K}_p$ and that we have strong convergence in (3.4) for which it suffices to show convergence of the norms $\lim _{n \rightarrow \infty } \Vert \omega (u^n)(0)\Vert _{L^p} = \Vert \omega (u_0)\Vert _{L^p}$.

Step 2.1: We first argue that $u \in \mathcal {K}_p$ or that u can be appropriately redefined so on $(-\infty ,0)$. Since $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$, $u|_{[0,\infty )} \in C_{loc}([0,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ is the unique solution of the damped Navier–Stokes equations as in Theorem 2.4 with this initial datum. Now, let $m \in \mathbb {N}$ and repeat the argument with $(t^n-m)_{n\in \mathbb {N}}$ so that there exists $v \in \mathcal {K}$ s.t.

$$\begin{aligned}S(t^n-m)u_0^n \rightarrow v(0) \,(n\rightarrow \infty ) \text { in } L^2(\mathbb {R}^2).\end{aligned}$$

Likewise, $v(0) \in \mathcal {E}_1 \cap \mathcal {E}_p$. Since $S(t):H \rightarrow H$ is continuous for every $t \ge 0$ [23, Theorem 7.1],

$$\begin{aligned}u_0 = \lim _{n\rightarrow \infty } S(t^n)u_0^n = \lim _{n\rightarrow \infty } S(m)S(t^n-m)u_0^n = S(m)v(0)= v(m) \text { in } L^2(\mathbb {R}^2)\end{aligned}$$

so that $v(m) = u_0$ and by uniqueness of the weak solution,

$$\begin{aligned} u(t) = v(t+m), t \ge 0. \end{aligned}$$

(3.5)

By redefining u via (3.5) on $[-m,0)$, $u(-m) = v(0) \in \mathcal {E}_1 \cap \mathcal {E}_p$ implies that $u|_{[-m,\infty )}$ in $C_{loc}([-m,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ is a solution of the damped Navier–Stokes equations as in Theorem 2.4 still satisfying (3.3) and (3.4). Since $m \in \mathbb {N}$ was arbitrary, one can inductively redefine u and obtain a bounded complete solution $u \in C_b(\mathbb {R};\mathcal {E}_1 \cap \mathcal {E}_p)$ with (3.3) and (3.4).

The bound on the vorticity in the definition of $\mathcal {K}_p$ can then be derived for $\omega (u)$ from (2.3) as in the proof for velocity in Lemma 3.4 so that $u \in \mathcal {K}_p$.

Step 2.2: Now we show that we have strong convergence in (3.4). First, we note that from (3.3) it follows (see the relative energy argument in [23, Theorem 7.1]),

$$\begin{aligned} u^n \rightarrow u \text { in } C_{loc}([0,\infty );L^2(\mathbb {R}^2)) \end{aligned}$$

(3.6)

and with $(\omega (u^n))_{n\in \mathbb {N}}$ being bounded in $C_b([0,\infty );(L^1 \cap L^p)(\mathbb {R}^2))$, we may assume

$$\begin{aligned} \omega (u^n) \overset{*}{\rightharpoonup }\ \omega (u)\,(n \rightarrow \infty ) \text { in } L^\infty ([0,\infty );L^p(\mathbb {R}^2)). \end{aligned}$$

(3.7)

As we redefined u inductively earlier for $m \in \mathbb {N}$ so that

$$\begin{aligned}u(-m) = v(0) = \lim _{n \rightarrow \infty } S(t^n-m)u_0^n = \lim _{n \rightarrow \infty }S(t^n-m)u(-t^n) = \lim _{n \rightarrow \infty } u^n(-m)\end{aligned}$$

in $L^2(\mathbb {R}^2)$, we can actually assume (3.6), (3.7) to hold on $[-m,\infty )$ and ultimately by induction,

$$\begin{aligned} u^n \rightarrow u \text { in } C_{loc}(\mathbb {R};L^2(\mathbb {R}^2)) \text { and } \omega (u^n) \overset{*}{\rightharpoonup }\ \omega (u)\,(n \rightarrow \infty ) \text { in } L^\infty (\mathbb {R};L^p(\mathbb {R}^2)). \end{aligned}$$

(3.8)

Now, for every $n \in \mathbb {N}$, by (2.4),

$$\begin{aligned} \begin{aligned}&\Vert \omega (u^n)(0)\Vert _{L^p}^p- \Vert \omega (u^n)(-t^n)\Vert ^p_{L^p}e^{-p\gamma t^n}\\ \le&- 4\nu \frac{p-1}{p}\int _{-t^n}^0 e^{p\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u^n)|^\frac{p}{2}|^2\,dx\,dt\\&+ p\int _{-t^n}^0 e^{p\gamma t}\int _{\mathbb {R}^2} g\omega (u^n)|\omega (u^n)|^{p-2}\,dx\,dt. \end{aligned} \end{aligned}$$

(3.9)

As $\Vert \omega (u^n)(-t^n)\Vert _{L^p} = \Vert \omega (u^n_0)\Vert _{L^p}$ is bounded in $n \in \mathbb {N}$, it follows that $\Vert \omega (u^n)(-t^n)\Vert _{L^p}^p e^{-p\gamma t^n} \rightarrow 0\,(n \rightarrow \infty )$.

To treat the two terms on the right-hand side, we first differ between the cases $p = 2$ and $p > 2$. By our assumption on the right-hand side, $g \in L^r(\mathbb {R}^2)$ for $r = \max \lbrace 2,p\rbrace$, it is easy to trace the case $1< p < 2$ back to the case $p = 2$. Case $p = 2$: From weak-* convergence (3.8), that is, $\omega (u^n) \overset{*}{\rightharpoonup } \omega (u)\,(n\rightarrow \infty )$ in $L^\infty (\mathbb {R};L^2(\mathbb {R}^2))$, we obtain

$$\begin{aligned}2\int _{-t^n}^0 e^{2\gamma t}\int _{\mathbb {R}^2}g \omega (u^n) \,dx\,dt \rightarrow 2\int _{-\infty }^0e^{2\gamma t}\int _{\mathbb {R}^2} g\omega (u)\,dx\,dt\,(n\rightarrow \infty ).\end{aligned}$$

Due to (2.2), we may also assume $\nabla \omega (u^n) \rightharpoonup \nabla \omega (u)\,(n\rightarrow \infty )$ in $L^2_{loc}(\mathbb {R};L^2(\mathbb {R}^2))$. Using weak lower semi-continuity of the norm, we obtain for every $M>0$,

$$\begin{aligned} \begin{aligned} \liminf _{n \rightarrow \infty } \int _{-t^n}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u^n)||^2\,dx\,dt&= \liminf _{n \rightarrow \infty } \int _{-t^n}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla \omega (u^n)|^2\,dx\,dt\\&\ge \liminf _{n \rightarrow \infty }\int _{-M}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla \omega (u^n)|^2\,dx\,dt\\&\ge \int _{-M}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla \omega (u)|^2\,dx\,dt\\&= \int _{-M}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u)||^2\,dx\,dt \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \liminf _{n \rightarrow \infty } \int _{-t^n}^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u^n)||^2\,dx\,dt \ge \int _{-\infty }^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u)||^2\,dx\,dt. \end{aligned}$$

Combining these results yields

$$\begin{aligned} \limsup _{n \rightarrow \infty } \Vert \omega (u^n)(0)\Vert _{L^2}\le & {} -2\nu \int _{-\infty }^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u)||^2\,dx\,dt + 2\int _{-\infty }^0 e^{2\gamma t}\int _{\mathbb {R}^2}g \omega (u)\,dx\,dt. \end{aligned}$$

On the other hand, the vorticity $\omega (u)$ of the complete trajectory u satisfies (2.1) almost everywhere on $\mathbb {R}$ from which we obtain

$$\begin{aligned} \Vert \omega (u_0)\Vert _{L^2} = -2\nu \int _{-\infty }^0 e^{2\gamma t}\int _{\mathbb {R}^2}|\nabla |\omega (u)||^2\,dx\,dt+ 2\int _{-\infty }^0 e^{2\gamma t}\int _{\mathbb {R}^2}g \omega (u)\,dx\,dt. \end{aligned}$$

Note that even though the right-hand side in (2.2) depends on the length of the time interval, the exponential function in the integrals above guarantees their convergence on $(-\infty ,0]$.

We finally arrive at

$$\begin{aligned}\limsup _{n\rightarrow \infty } \Vert \omega (u^n)(0)\Vert _{L^2} \le \Vert \omega (u_0)\Vert _{L^2} \le \liminf _{n\rightarrow \infty }\Vert \omega (u^n)(0)\Vert _{L^2}.\end{aligned}$$

Case $p > 2$: We note that as we have boundedness of the initial vorticities $(\omega (u^n_0))_{n\in \mathbb {N}}$ in $L^1(\mathbb {R}^2)$, by interpolation, we are also in the situation of the previous case $p = 2$. This means that along with weak-* convergence (3.8), that is, $\omega (u^n) \overset{*}{\rightharpoonup }\ \omega (u)\,(n\rightarrow \infty )$ in $L^\infty (\mathbb {R};L^p(\mathbb {R}^2))$, we may also assume $\omega (u^n)(0) \rightarrow \omega (u)(0)\,(n \rightarrow \infty )$ in $L^2(\mathbb {R}^2)$. By Theorem 2.6, this yields strong convergence

$$\begin{aligned} \omega (u^n) \rightarrow \omega (u)\,(n \rightarrow \infty ) \text { in } C_{loc}([0,\infty );L^2(\mathbb {R}^2)). \end{aligned}$$

(3.10)

As in the arguments before, we can inductively obtain strong convergence on any compact subset of $\mathbb {R}$, not just of $[0,\infty )$, and (3.10) holds in $C_{loc}(\mathbb {R};L^2(\mathbb {R}^2))$.

The first term on the right-hand side in (3.9) involving the gradients may again be estimated in the limit by employing an argument of weak lower-semicontinuity.

For the other term, note that due to boundedness of $(\omega (u^n))_{n\in \mathbb {N}}$ in $C_b(\mathbb {R};(L^1 \cap L^p)(\mathbb {R}^2))$, we may assume that $(\omega (u^n)|\omega (u^n)|^{p-2})_{n\in \mathbb {N}}$ converges weakly-* in $L^\infty (\mathbb {R};L^{\frac{p}{p-1}}(\mathbb {R}^2))$ to some $\Psi$. We can then conclude the argument as in the previous case if we can prove that

$$\begin{aligned} \Psi = \omega (u)|\omega (u)|^{p-2}. \end{aligned}$$

(3.11)

Due to (3.10), interpolating between $L^1(\mathbb {R}^2)$ and $L^2(\mathbb {R}^2)$ or $L^2(\mathbb {R}^2)$ and $L^p(\mathbb {R}^2)$, depending on whether $p-1 < 2$ or $p-1 \ge 2$, yields

$$\begin{aligned}|\omega (u^n)|^{p-2} \rightarrow |\omega (u)|^{p-2}\,(n \rightarrow \infty )\text { in } L^\infty _{loc}(\mathbb {R};L^{\frac{p-1}{p-2}}(\mathbb {R}^2)).\end{aligned}$$

As we may also assume $\omega (u^n) \overset{*}{\rightharpoonup } \omega (u)\,(n \rightarrow \infty )$ in $L^\infty (\mathbb {R};L^{p-1}(\mathbb {R}^2))$ and $\frac{1}{p-1} + \frac{p-2}{p-1} = 1$, we can conclude (3.11).

$1< p < 2$: In this case, we argue that we are actually in the situation of the case $p=2$, i.e., we have strong convergence $\Vert \omega (u^n)(0)\Vert _{L^2} \rightarrow \Vert \omega (u_0)\Vert _{L^2}\,(n\rightarrow \infty )$, which along with a uniform $L^1$ bound implies $\Vert \omega (u^n)(0)\Vert _{L^p} \rightarrow \Vert \omega (u_0)\Vert _{L^p}\,(n\rightarrow \infty )$ as desired.

As seen in Lemma 2.9, $\omega (u^n)(t)$ is instantaneously bounded in $L^2(\mathbb {R}^2)$ for t bounded away from the initial time $-t^n$. Therefore, assuming $t^n > 1$ for all $n \in \mathbb {N}$ and simply using the sequence $\tilde{t}^n :=t^n -1$, $n \in \mathbb {N}$, instead of $(t^n)_{n\in \mathbb {N}}$ in (3.9) and the arguments to follow, we obtain as in the case $p = 2$ that $\Vert \omega (u^n)(0)\Vert _{L^2} \rightarrow \Vert \omega (u_0)\Vert _{L^2}\,(n\rightarrow \infty )$ as desired. $\square$

Proposition 3.6

We assume that $p \ge 2$. Let $(\nu ^k)_{k\in \mathbb {N}} \subset (0,1)$ be a sequence converging to 0 and let $(f^{\nu ^k})_{k\in \mathbb {N}}$ be a bounded sequence in $\mathcal {E}_1 \cap \mathcal {E}_p$. Suppose that there exists $f \in \mathcal {E}_1 \cap \mathcal {E}_p$ s.t. for $g^{\nu ^k} :={{\,\textrm{curl}\,}}f^{\nu ^k}$ and $g :={{\,\textrm{curl}\,}}f$,

$$\begin{aligned}g^{\nu ^k} \rightarrow g \,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2).\end{aligned}$$

Consider a bounded sequence $(u^{\nu ^k})_{k\in \mathbb {N}} \subset C_b(\mathbb {R};\mathcal {E}_1 \cap \mathcal {E}_p)$ of complete weak solutions of the damped Navier–Stokes equations with right-hand sides $(f^{\nu ^k})_{k\in \mathbb {N}}$ with $\nu ^k$ being the viscosity parameter associated to $u^{\nu ^k}$ for every $k \in \mathbb {N}$. After passing to a subsequence, there exists $u \in L^\infty ([0,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$ whose vorticity $\omega (u)$ satisfies the damped Euler equations with right-hand side g in the renormalized sense and

$$\begin{aligned} \omega (u^{\nu ^k}) \rightarrow \omega (u)\,(k\rightarrow \infty )\text { in } C_{loc}([0,\infty );L^p(\mathbb {R}^2)). \end{aligned}$$

(3.12)

Proof

(sketch) We follow the proof of Proposition 3.5. Due to boundedness of $(u^{\nu ^k}(0))_{n\in \mathbb {N}}$ in $\mathcal {E}_1 \cap \mathcal {E}_p$, there exists $u_0 \in \mathcal {E}_1 \cap \mathcal {E}_p$ s.t. after passing to a subsequence,

$$\begin{aligned}u^{\nu ^k}(0) \rightharpoonup u_0 \,(k \rightarrow \infty ) \text { in } L^2(\mathbb {R}^2) \text { and } \omega (u^{\nu ^k})(0) \rightharpoonup \omega (u_0) \,(k \rightarrow \infty ) \text { in } L^p(\mathbb {R}^2).\end{aligned}$$

By Theorem 2.7, after passing to yet another subsequence, there exists u such that

$$\begin{aligned}&u^{\nu ^k} \overset{*}{\rightharpoonup }\ u\,(k \rightarrow \infty ) \text { in } L^\infty ([0,\infty );L^2(\mathbb {R}^2)), \nonumber \\&\omega (u^{\nu ^k}) \overset{*}{\rightharpoonup }\ \omega (u) \,(k \rightarrow \infty )\text { in } L^\infty ([0,\infty );L^p(\mathbb {R}^2)), \end{aligned}$$

(3.13)

where $\omega (u)$ is a renormalized solution of the damped Euler equations with initial data $\omega (u_0)$ and right-hand side g. Then, in order to obtain the strong convergence (3.12) using Theorem 2.6, it suffices again to derive strong convergence of the initial data

$$\begin{aligned} \omega (u^{\nu ^k})(0) \rightarrow \omega (u_0) \text { in } L^p(\mathbb {R}^2). \end{aligned}$$

(3.14)

For this, we consider a sequence $t^k \rightarrow \infty$ and note that (3.9) holds again, so that by dropping the viscous term we obtain

$$\begin{aligned} \Vert \omega (u^{\nu ^k})(0)\Vert _{L^p}^p- \Vert \omega (u^{\nu ^k})(-t^k)\Vert ^p_{L^p}e^{-p\gamma t^k} \le p\int _{-t^k}^0 e^{p\gamma t}\int _{\mathbb {R}^2} g\omega (u^{\nu ^k})|\omega (u^{\nu ^k})|^{p-2}\,dx\,dt. \end{aligned}$$

Moreover, by a diagonal sequence argument, the weak-* convergences in (3.13) can be obtained on the domain $\mathbb {R}$ instead of just $[0,\infty )$ and $\omega (u)$ is a (complete) renormalized solution of the damped Euler equations on $\mathbb {R}$ with right-hand side g, satisfying $\omega (u)(0) = \omega (u_0)$.

From there on, we can argue as in the cases $p = 2$ and $p > 2$ in the proof of Proposition 3.5 by replacing (2.1) with (2.4) to obtain (3.14). $\square$

Proposition 3.6 is going to be useful in combination with the following lemma.

Lemma 3.7

Let $1< p < \infty$, $f \in \mathcal {E}_1 \cap \mathcal {E}_{\max \lbrace 2,p\rbrace }$ and define $g :={{\,\textrm{curl}\,}}f$. Then, $\mathcal {A}_p \subset \mathcal {A}_2$ and $\mathcal {K}_p \subset \mathcal {K}_2$ (see Proposition 3.5 for the definitions of $\mathcal {A}_p,\mathcal {A}_2$ and $\mathcal {K}_p, \mathcal {K}_2$) so that in particular every $u \in \mathcal {K}_p$ satisfies

$$\begin{aligned} \sup _{t \in \mathbb {R}} \Vert \omega (u)(t)\Vert _{L^2(\mathbb {R}^2)} \le \frac{\Vert g\Vert _{L^2}}{\gamma }. \end{aligned}$$

Proof

Let B be a bounded subset of $\mathcal {E}_1 \cap \mathcal {E}_p$ and consider the solution semigroup $\lbrace S(t) \rbrace _{t \ge 0}$ associated to the right-hand side f and some fixed viscosity $\nu > 0$. Since $g \in L^2(\mathbb {R}^2)$, S(t)B is bounded in $L^2(\mathbb {R}^2)$ for positive t bounded away from 0 by Lemma 2.9. Therefore, $\mathcal {A}_2$ attracts B for $\lbrace S(t) \rbrace _{t \ge 0}$ w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_2}$. If we particularly consider the set $B = \mathcal {A}_p$, attraction of $\mathcal {A}_2$ and invariance of $\mathcal {A}_p$ w.r.t. $\lbrace S(t) \rbrace _{t \ge 0}$ already imply

$$\begin{aligned}\mathcal {A}_p \subset \mathcal {A}_2.\end{aligned}$$

Using the definition of $\mathcal {A}_p, \mathcal {A}_2$ and estimate (2.3), one also obtains $\mathcal {K}_p \subset \mathcal {K}_2$ from this.

$\square$

4 Long Time Average Invariant Measures

In this section, we are concerned with the construction of invariant measures from probability distributions of initial data via long time averages.

The main theorem of this section, Theorem 4.1, is essentially an application of Theorem 7 in [24]. We remark, however, that the stated assumptions are note quite satisfied here. The major discrepancy comes from working on $\mathbb {R}^2$, where $\mathcal {E}_1 \not \subset \mathcal {E}_p$: We showed in Proposition 3.5 that $\mathcal {A}_p$ is compact and attracting w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$ instead of $\Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p}$, while we would like to regard the solution semigroup of the damped Navier–Stokes equations $\lbrace S(t) \rbrace _{t \ge 0}$ as a semigroup on $\mathcal {E}_1 \cap \mathcal {E}_p$.

Nevertheless, the proof of [24, Theorem 7] still applies and we give it here for the convenience of the reader.

Theorem 4.1

Let $\mu _0$ be a Borel probability measure on $\mathcal {E}_1 \cap \mathcal {E}_p$. Then, for any sequence $t^j \rightarrow \infty \,(j \rightarrow \infty )$, there exists a subsequence $t^{j^k} \rightarrow \infty \,(k \rightarrow \infty )$ and a Borel probability measure $\mu$ on $\mathcal {E}_p$, concentrated on $\mathcal {A}_p$, which is invariant w.r.t. $\lbrace S(t) \rbrace _{t \ge 0}$ (when $\mu$ is restricted to $\mathcal {E}_1 \cap \mathcal {E}_p$) s.t. for any $\varphi \in C(\mathcal {E}_p)$,

$$\begin{aligned} \lim _{k \rightarrow \infty } \frac{1}{t^{j^k}} \int _0^{t^{j^k}}\int _{\mathcal {E}_1 \cap \mathcal {E}_p} \varphi (S(t)u_0)\,d\mu _0(u_0)\,dt = \int _{\mathcal {A}_p} \varphi (u)\,d\mu (u). \end{aligned}$$

(4.1)

Proof

We begin the proof by making some observations on measurability.

First of all, we note that $\mathcal {E}_1 \cap \mathcal {E}_p$ is a Borel subset of $(\mathcal {E}_p,\Vert \cdot \Vert _{\mathcal {E}_p})$ since it can be written as

$$\begin{aligned}\mathcal {E}_1 \cap \mathcal {E}_p = \bigcup _{l \in \mathbb {N}} \bigcap _{m\in \mathbb {N}} \lbrace u \in \mathcal {E}_p: \Vert \omega (u)\Vert _{L^1(B_m)} \le l\rbrace ,\end{aligned}$$

which is a countable union of countable intersections of closed sets in $(\mathcal {E}_p,\Vert \cdot \Vert _{\mathcal {E}_p})$. Moreover, on $\mathcal {E}_1 \cap \mathcal {E}_p$, the Borel-$\sigma$-algebras generated by the standard norm $\Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p}$ on that space and the subspace norm $\Vert \cdot \Vert _{\mathcal {E}_p}$ coincide: Since $\Vert \cdot \Vert _{\mathcal {E}_p} \le \Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p}$, open sets in $\mathcal {E}_1 \cap \mathcal {E}_p$ w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$ are also open w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p}$.

Conversely, since $(\mathcal {E}_1 \cap \mathcal {E}_p,\Vert \cdot \Vert _{\mathcal {E}_1 \cap \mathcal {E}_p})$ is separable, it suffices to note that an arbitrary open ball $B = \lbrace v \in \mathcal {E}_1 \cap \mathcal {E}_p: \Vert u-v\Vert _{\mathcal {E}_1 \cap \mathcal {E}_p} < r \rbrace$ with center $u \in \mathcal {E}_1 \cap \mathcal {E}_p$ and radius $r > 0$ is Borel-measurable w.r.t. the Borel-$\sigma$-algebra on $\mathcal {E}_1 \cap \mathcal {E}_p$, generated by $\Vert \cdot \Vert _{\mathcal {E}_p}$. This holds since

$$\begin{aligned}B = \bigcup _{l \in \mathbb {N}} \bigcap _{m\in \mathbb {N}} \lbrace v \in \mathcal {E}_1 \cap \mathcal {E}_p: \Vert u-v\Vert _{\mathcal {E}_p} + \Vert \omega (u)- \omega (v)\Vert _{L^1(B_m)} \le r - \frac{1}{l}\rbrace ,\end{aligned}$$

which is a countable union of countable intersections of subsets of $\mathcal {E}_1 \cap \mathcal {E}_p$ which are (relatively) closed w.r.t. $\Vert \cdot \Vert _{\mathcal {E}_p}$.

We now define the average measure $\overline{\mu }^{j}$ for every $j \in \mathbb {N}$ as the Borel probability measure on $\mathcal {E}_1 \cap \mathcal {E}_p$ given by

$$\begin{aligned}\overline{\mu }^{j}(A) :=\frac{1}{t^j}\int _0^{t^j} \mu _0(S(t)^{-1}A)\,dt\end{aligned}$$

for every Borel measurable $A \subset \mathcal {E}_1 \cap \mathcal {E}_p$ so that, equivalently, for every $\varphi \in C_b(\mathcal {E}_1 \cap \mathcal {E}_p)$,

$$\begin{aligned}\int _{\mathcal {E}_1 \cap \mathcal {E}_p} \varphi (u)\,d\overline{\mu }^{j}(u) = \frac{1}{t^j}\int _0^{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p} \varphi (S(t)u)\,d\mu _0(u)\,dt. \end{aligned}$$

Due to the above considerations, we may also view $(\overline{\mu }^j)_{j \in \mathbb {N}}$ as a measure on the Borel-$\sigma$-algebra of $\mathcal {E}_p$ via the formula $\overline{\mu }_j = \overline{\mu }_j(\cdot \cap (\mathcal {E}_1 \cap \mathcal {E}_p))$. We then argue that the sequence of measures $(\overline{\mu }^j)_{j \in \mathbb {N}}$ on $\mathcal {E}_p$ is asymptotically tight, which, by Prokhorov’s theorem (cf. Theorem 1.3.9 in [29]), implies (4.1) for $\varphi \in C_b(\mathcal {E}_p)$.

We first note that $\mu _0$, as a finite Borel measure on the separable Banach space $\mathcal {E}_1 \cap \mathcal {E}_p$, is automatically tight so that there exist compact sets $(K^n)_{n\in \mathbb {N}} \subset \mathcal {E}_1 \cap \mathcal {E}_p$ satisfying

$$\begin{aligned}\mu _0(K^n) \ge 1 - \frac{1}{n}\end{aligned}$$

for every $n \in \mathbb {N}$. Fix $\delta > 0$ and consider the open $\delta$-enlargement

$$\begin{aligned}\mathcal {A}_{p,\delta } :=\lbrace u \in \mathcal {E}_p: {{\,\textrm{dist}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(u,\mathcal {A}_p) < \delta \rbrace .\end{aligned}$$

Due to the attraction property of $\mathcal {A}_p$ proved in Proposition 3.5, for every $n \in \mathbb {N}$ there exists $t_0^n = t_0^n(\delta )$ s.t. for every $t \ge t_0^n$,

$$\begin{aligned}S(t)K^n \subset \mathcal {A}_{p,\delta }.\end{aligned}$$

This particularly implies for $t \ge t_0^n$,

$$\begin{aligned}S(t)^{-1}(\mathcal {A}_{p,\delta } \cap (\mathcal {E}_1 \cap \mathcal {E}_p)) \supset S(t)^{-1}(S(t)K^n \cap (\mathcal {E}_1 \cap \mathcal {E}_p)) = S(t)^{-1}(S(t)K^n) \supset K^n.\end{aligned}$$

Hence, $\mu _0(S(t)^{-1}(\mathcal {A}_{p,\delta }\cap (\mathcal {E}_1 \cap \mathcal {E}_p))) \ge 1 - \frac{1}{n}$ for $t \ge t_0^n$. Therefore, if $t^j \ge t_0^n$,

$$\begin{aligned} \overline{\mu }^j(\mathcal {A}_{p,\delta })&= \overline{\mu }^j(\mathcal {A}_{p,\delta } \cap (\mathcal {E}_1 \cap \mathcal {E}_p))\\&= \frac{1}{t^j}\Bigg (\int _0^{t^n_0} \mu _0(S(t)^{-1}(\mathcal {A}_{p,\delta } \cap (\mathcal {E}_1 \cap \mathcal {E}_p)))\,dt \\ {}&\quad + \int _{t^n_0}^{t^j} \mu _0(S(t)^{-1}(\mathcal {A}_{p,\delta } \cap (\mathcal {E}_1 \cap \mathcal {E}_p)))\,dt\Bigg )\\&\ge \frac{t^j-t_0^n}{t^j}\left( 1 - \frac{1}{n}\right) , \end{aligned}$$

which implies asymptotic tightness. The Borel probablity measure $\mu$ on $\mathcal {E}_p$, obtained as weak limit of an adequate subsequence $(\overline{\mu }^{j^k})_{k\in \mathbb {N}}$ is clearly concentrated on $\mathcal {E}_1 \cap \mathcal {E}_p$ since every measure $\overline{\mu }^{j^k}$ is. Invariance w.r.t. $\lbrace S(t) \rbrace _{t \ge 0}$ can be seen from (4.1), cf. the arguments in [24, Theorem 7] for details.

Denoting the closure of a set A in $(\mathcal {E}_p,\Vert \cdot \Vert _{\mathcal {E}_p})$ by ${{\,\textrm{cl}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(A)$, we also obtain from the above considerations that for every $\delta > 0$,

$$\begin{aligned}\mu ({{\,\textrm{cl}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(A_{p,\delta })) \ge \limsup _{k \rightarrow \infty } \overline{\mu }^{j^k}({{\,\textrm{cl}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(A_{p,\delta })) \ge 1 - \frac{1}{n}.\end{aligned}$$

Since $n \in \mathbb {N}$ can be chosen arbitrarily, this implies $\mu ({{\,\textrm{cl}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(A_{p,\delta })) = 1$. Due to $\bigcap _{\delta > 0} {{\,\textrm{cl}\,}}_{\Vert \cdot \Vert _{\mathcal {E}_p}}(A_{p,\delta })= \mathcal {A}_p$, we conclude $\mu (\mathcal {A}_p) = 1$.

The fact that in (4.1) we may consider all continuous functions and not just bounded continuous functions follows from $\mathcal {A}_p$ being compact in $\mathcal {E}_p$ and can be seen as in [31, Theorem 4.1]. $\square$

5 Vanishing of Long Time Average p-Enstrophy Dissipation Rate

In this concluding part of the article, we prepare and prove Theorem 1.2. As we consider the inviscid limit $(\nu \rightarrow 0)$ in this section, from now on, we will indicate the dependence of the solutions, the attractors, etc. on the viscosity parameter $\nu > 0$ by adding it as a superscript.

Since we do not have a well-defined solution semigroup for the damped Euler equations, we work on the level of trajectories in the next lemma and consider the semigroup of time-shifts $\lbrace T(t) \rbrace _{t \ge 0}$ on $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$, i.e., $T(t)u = u(\cdot + t)$ for all $u \in C_{loc}([0,\infty );L^p(\mathbb {R}^2))$ and $t \ge 0$.

Lemma 5.1

Let $1< p < \infty$ and $\rho$ be a Borel probability measure on the space $V_p :=C_{loc}([0,\infty );L^p(\mathbb {R}^2))$ with support in the subset $\mathcal {F}_p^0$ of all renormalized solutions of the vorticity formulation of the damped Euler equations with right-hand side $g \in (L^1 \cap L^p)(\mathbb {R}^2)$ as in Theorem 2.5, invariant w.r.t. $\lbrace T(t) \rbrace _{t \ge 0}$ and satisfying

$$\begin{aligned} \int _{V_p}\int _{\mathbb {R}^2} |\omega (0)|^p\,dx\,d\rho (\omega ) < \infty . \end{aligned}$$

(5.1)

Then,

$$\begin{aligned} \int _{V_p} \int _{\mathbb {R}^2} -\gamma |\omega (t)|^p + g\omega (t)|\omega (t)|^{p-2}\,dx\,d\rho (\omega ) = 0 \end{aligned}$$

(5.2)

for every $t \ge 0$.

Proof

Due to the invariance of $\rho$ w.r.t. $\lbrace T(t) \rbrace _{t \ge 0}$, (5.1) holds for every $t \ge 0$ and we have

$$\begin{aligned} \begin{aligned}&\int _{V_p} \int _{\mathbb {R}^2} -\gamma |\omega (t)|^p + g\omega (t)|\omega (t)|^{p-2}\,dx\,d\rho (\omega ) \\&\quad = \int _{V_p}\int _{\mathbb {R}^2} -\gamma |\omega (0)|^p + g\omega (0)|\omega (0)|^{p-2}\,dx\,d\rho (\omega ) \end{aligned} \end{aligned}$$

so that the left-hand side is finite and constant in t. Then, by taking the time average and applying both Fubini’s theorem and (2.4), we obtain for all $0 \le t \le M$,

$$\begin{aligned} \begin{aligned}&\int _{V_p} \int _{\mathbb {R}^2} -\gamma |\omega (t)|^p + g\omega (t)|\omega (t)|^{p-2}\,dx\,d\rho (\omega )\\&\quad = \frac{1}{M}\int _0^M\int _{V_p} \int _{\mathbb {R}^2} -\gamma |\omega (t)|^p + g\omega (t)|\omega (t)|^{p-2}\,dx\,d\rho (\omega )\,dt\\&\quad = \frac{1}{M}\int _{V_p}\int _0^M \int _{\mathbb {R}^2} -\gamma |\omega (t)|^p + g\omega (t)|\omega (t)|^{p-2}\,dx\,dt\,d\rho (\omega )\\&\quad = \frac{1}{M}\int _{V_p} (\Vert \omega (M)\Vert _{L^p}^p - \Vert \omega (0)\Vert _{L^p}^p)\,d\rho (\omega ), \end{aligned} \end{aligned}$$

which is 0 due to invariance of $\rho$ w.r.t. $\lbrace T(t) \rbrace _{t \ge 0}$. $\square$

Consider the situation of the main theorem, Theorem 1.2, where we have a bounded family of right-hand sides $(f^\nu )_{\nu > 0} \subset \mathcal {E}_1 \cap \mathcal {E}_r$, $r = \max \lbrace 2, p\rbrace$, for which $(g^\nu :={{\,\textrm{curl}\,}}f^\nu )_{\nu > 0}$ is precompact in $L^r(\mathbb {R}^2)$. Then we define for every viscosity parameter $\nu > 0$ the set of vorticity of associated bounded complete solutions with right-hand side $f^\nu$ (see Definition 3.2 and (3.2)), restricted to non-negative times

$$\begin{aligned} \mathcal {F}^\nu _p :=\lbrace \omega (u)|_{[0,\infty )} \in C_{loc}([0,\infty );(L^1 \cap L^p)(\mathbb {R}^2)): u \in \mathcal {K}^\nu _p\rbrace . \end{aligned}$$

Let $\nu ^n \rightarrow 0\,(n \rightarrow \infty )$ s.t. for some $f \in \mathcal {E}_1 \cap \mathcal {E}_r$, $r = \max \lbrace 2, p\rbrace$, with $g :={{\,\textrm{curl}\,}}f$,

$$\begin{aligned} g^{\nu ^n} \rightarrow g \text { in } L^r(\mathbb {R}^2). \end{aligned}$$

(5.3)

Lemma 5.2

Under the assumptions of Theorem 1.2, consider a sequence $\nu ^n \rightarrow 0\,(n\rightarrow \infty )$ so that (5.3) holds. Then

$$\begin{aligned} \mathcal {F}_p :=\bigcup _{n \in \mathbb {N}} \mathcal {F}^{\nu ^n}_p \end{aligned}$$

(5.4)

is precompact in $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$.

Proof

For fixed $n \in \mathbb {N}$, we first argue that $\mathcal {F}^{\nu ^n}_p$ is precompact in $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$. Consider any sequence $(\omega ^k)_{k\in \mathbb {N}} \subset \mathcal {F}_p^{\nu ^n}$ and $(u^{k})_{k\in \mathbb {N}} \subset \mathcal {K}_p^{\nu ^n}$ with $\omega (u^k)|_{[0,\infty )} = \omega ^k$ for every $k \in \mathbb {N}$. In the proof of Proposition 3.5, we argued that there exists $u \in \mathcal {K}^{\nu ^n}_p$ so that for $u_0 :=u(0)$ and appropriate subsequences,

$$\begin{aligned}u^k \rightarrow u\,(k \rightarrow \infty )\text { in } C_b([0,\infty );L^2(\mathbb {R}^2)) \text { and } \omega (u^n)(0) \rightarrow \omega (u_0) \,(k \rightarrow \infty )\text { in } L^p(\mathbb {R}^2).\end{aligned}$$

Then, by Theorem 2.6, we obtain the desired convergence of a subsequence

$$\begin{aligned}\omega (u^n) \rightarrow \omega (u)\,(k \rightarrow \infty )\text { in } C_{loc}([0,\infty );L^p(\mathbb {R}^2)).\end{aligned}$$

As a consequence, also $\bigcup _{n =1}^N \mathcal {F}^{\nu ^n}_p$ is precompact in $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$ for every $N \in \mathbb {N}$.

Now, it only remains to consider sequences in $\mathcal {F}_p$ associated to a vanishing sequence of viscosity, where convergence of a subsequence in $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$ (to a renormalized solution to the vorticity formulation of the damped Euler equations) follows from Proposition 3.6, which is applicable since $\mathcal {K}_p^{\nu ^k} \subset \mathcal {K}_2^{\nu ^k}$ by Lemma 3.7, whereby $\mathcal {K}_p^{\nu ^k}$ is bounded in $C_b(\mathbb {R};\mathcal {E}_1 \cap \mathcal {E}_r)$, $r = \max \lbrace 2,p\rbrace ,$ independently of $\nu ^k$. $\square$

We may proceed to prove Theorem 1.2 by a similar approach as [8], but with the simplifications described in the introduction to this article and prepared in the previous sections.

Proof of Theorem 1.2

Suppose that (1.6) is false. Then there exists a sequence $(\nu ^n)_{n\in \mathbb {N}} \subset (0,1)$ converging to 0 and some $\delta > 0$ s.t. for every $n \in \mathbb {N}$, there exists a sequence of times $(t^j = t^j(n))_{j\in \mathbb {N}}$ with $t^j \rightarrow \infty \,(j \rightarrow \infty )$ and

$$\begin{aligned}\nu ^n \frac{1}{t^j}\int _0^{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\int _{\mathbb {R}^2} |\nabla |\omega (S^{\nu ^n}(t) u_0)|^\frac{p}{2}|^2\,dx\,d\mu _0^{\nu ^n}(u_0)\,dt \ge \delta ,\end{aligned}$$

$n,j \in \mathbb {N}$. By (2.1) and Fubini’s theorem, the left-hand side is bounded by

$$\begin{aligned} \begin{aligned}&\frac{p^2}{4(p-1)}\frac{1}{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\int _0^{t^j}\int _{\mathbb {R}^2} -\gamma |\omega (S^{\nu ^n}(t) u_0)|^p\\ +&g^{\nu ^n}\omega (S^{\nu ^n}(t) u)|\omega (S^{\nu ^n}(t) u)|^{p-2}\,dx\,dt\,d\mu _0^{\nu ^n}(u_0)\\ +&\frac{1}{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\frac{p}{4(p-1)}(\Vert \omega (u_0)\Vert _{L^p}^p \ \Vert \omega (S^{\nu ^n}(t^j) u_0)\Vert _{L^p}^p)\,d\mu _0^{\nu ^n}(u_0). \end{aligned} \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned}&\frac{1}{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\frac{p}{4(p-1)}(\Vert \omega (u_0)\Vert _{L^p}^p - \Vert \omega (S^{\nu ^n}(t) u)\Vert _{L^p}^p)\,d\mu _0^{\nu ^n}(u_0)\\ \le&\frac{1}{t^j}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\frac{p}{4(p-1)}\Vert \omega (u_0)\Vert _{L^p}^p \,d\mu ^{\nu ^n}_0(u_0)\\ \rightarrow&0\, (j \rightarrow \infty ) \end{aligned} \end{aligned}$$

due to (1.5). The integrals

$$\begin{aligned}u \mapsto \int _{\mathbb {R}^2}-\gamma |\omega (u)|^p\,dx\text { and } u \mapsto \int _{\mathbb {R}^2}g^{\nu ^n} \omega (u)|\omega (u)|^{p-2}\,dx\end{aligned}$$

may be seen as continuous mappings on $(\mathcal {E}_p,\Vert \cdot \Vert _{\mathcal {E}_p})$. Therefore, by Theorem 4.1, after passing to a subsequence $t^{j^k} \rightarrow \infty$, there exists an invariant Borel probability measure $\mu ^{\nu ^n}$ on $\mathcal {E}_p$, concentrated on $\mathcal {A}_p^{\nu ^n}$ so that

$$\begin{aligned} \frac{4(p-1)}{p^2}\delta \nonumber&\le \lim _{k \rightarrow \infty } \frac{1}{t^{j^k}} \int _0^{t^{j^k}}\int _{\mathcal {E}_1 \cap \mathcal {E}_p}\int _{\mathbb {R}^2} -\gamma |\omega (S^{\nu ^n}(t) u_0)|^p\nonumber \\ {}&\qquad + g^{\nu ^n}\omega (S^{\nu ^n}(t) u_0)|\omega (S^{\nu ^n}(t) u_0)|^{p-2}\,dx\,d\mu _0^{\nu ^n}(u_0)\,dt\nonumber \\ {}&= \int _{\mathcal {A}_p^{\nu ^n}} \int _{\mathbb {R}^2} -\gamma |\omega (u)|^p + g^{\nu ^n}\omega (u)|\omega (u)|^{p-2}\,dx\,d\mu ^{\nu ^n}(u). \end{aligned}$$

(5.5)

We denote the solution operator to the Cauchy problem of the damped Navier–Stokes equations with viscosity $\nu > 0$ and right-hand side $f^\nu$ by $\Sigma ^\nu :\mathcal {E}_1 \cap \mathcal {E}_p \rightarrow C_{loc}([0,\infty );\mathcal {E}_1 \cap \mathcal {E}_p)$. The vorticity may be interpreted as a continuous mapping from $\mathcal {E}_1\cap \mathcal {E}_p$ to $L^p(\mathbb {R}^2)$ and we then denote the composition of $\Sigma ^\nu$ with the vorticity mapping (pointwise in time) by

$$\begin{aligned}\Sigma ^\nu _\omega :\mathcal {E}_1 \cap \mathcal {E}_p \rightarrow C_{loc}([0,\infty );L^p(\mathbb {R}^2)).\end{aligned}$$

Then we can pass to a subsequence s.t. the convergence of the curl of the right-hand sides (5.3) holds and define for every $n\in \mathbb {N}$ the pushforward measures

$$\begin{aligned}\rho ^{\nu ^n} :={\Sigma _\omega ^{\nu ^n}}_\sharp \mu ^{\nu ^n}\end{aligned}$$

on $\mathcal {F}^{\nu ^n}_p \subset \mathcal {F}_p \subset C_{loc}([0,\infty );L^p(\mathbb {R}^2))$, with $\mathcal {F}_p$ as in (5.4). We fix some time $\tau \ge 0$ s.t. due to invariance of $\mu ^{\nu ^n}$ w.r.t. $\lbrace S^{\nu ^n}(t) \rbrace _{t \ge 0}$, the right-hand side in (5.5) is equal to

$$\begin{aligned} \int _{\mathcal {F}_p} \int _{\mathbb {R}^2} -\gamma |\omega (\tau )|^p + g^{\nu ^n}\omega (\tau )|\omega (\tau )|^{p-2}\,dx\,d\rho ^{\nu ^n}(\omega ). \end{aligned}$$

We can view every $\rho ^{\nu ^n}$ as a measure on the closure $\overline{\mathcal {F}_p}$ of $\mathcal {F}_p$ in $C_{loc}([0,\infty );L^p(\mathbb {R}^2))$, which is compact by Lemma 5.2. Then, a subsequence of $(\rho ^{\nu ^n})_{n \in \mathbb {N}}$ converges weakly-* to a Borel probability measure $\rho$, i.e.,

$$\begin{aligned}\int _{\overline{\mathcal {F}_p}} \Psi (\omega )\,d\rho ^{\nu ^n}(\omega ) \rightarrow \int _{\overline{\mathcal {F}_p}} \Psi (\omega )\,d\rho (\omega )\,(n \rightarrow \infty )\end{aligned}$$

for every continuous $\Psi :\overline{\mathcal {F}_p} \rightarrow \mathbb {R}$. Passing to the limit $(n \rightarrow \infty )$ in (5.5) then yields

$$\begin{aligned} \frac{4(p-1)}{p^2}\delta \le \int _{\overline{\mathcal {F}_p}} \int _{\mathbb {R}^2}-\gamma |\omega (\tau )|^p + g\omega (\tau )|\omega (\tau )|^{p-2}\,dx\,d\rho (\omega ). \end{aligned}$$

(5.6)

We now derive the contradiction from this. For every $\omega \in {{\,\textrm{supp}\,}}\rho$, there exists a sequence $\tilde{u}^{\nu ^n} \in \mathcal {K}_p^{\nu ^n}, n\in \mathbb {N},$ s.t. (after restricting the time domain to $[0,\infty )$) $\omega (\tilde{u}^{\nu ^n}) \in {{\,\textrm{supp}\,}}\rho ^{\nu ^n} \subset \mathcal {F}_p^{\nu ^n}$ for every $n \in \mathbb {N}$ and

$$\begin{aligned}\omega (\tilde{u}^{\nu ^n}) \rightarrow \omega \,(n\rightarrow \infty ) \text { in }C_{loc}([0,\infty );L^p(\mathbb {R}^2)),\end{aligned}$$

cf. [30, Lemma 2.20]. In particular, $\omega (\tilde{u}^{\nu ^n})(0) \rightarrow \omega (0)\,(n\rightarrow \infty )$ in $L^p(\mathbb {R}^2)$ so that by Theorem 2.6, $\omega \in \mathcal {F}_p^0$, see Lemma 5.1. This means that ${{\,\textrm{supp}\,}}\rho \subset \mathcal {F}_p^0$ and we may apply Lemma 5.1. Note that (5.1) is satisfied as $\rho$ is concentrated on $\overline{\mathcal {F}_p}$, which is bounded in $C_b([0,\infty );L^p(\mathbb {R}^2))$. But then (5.2) contradicts (5.6). $\square$