Abstract
We construct Birkhoff cones for dispersing billiards, which are contracted by the action of the transfer operator. This construction permits the study of statistical properties not only of regular dispersing billiards but also of sequential billiards (the billiard changes at each collision in a prescribed manner), open billiards (the dynamics exits some region or dies when hitting some obstacle) and many other examples. In particular, we include applications to chaotic scattering and the random Lorentz gas.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Billiards are a ubiquitous source of models in physics, in particular in Statistical Mechanics. The study of the ergodic properties of billiards is of paramount importance for such applications and also a source of innovative ideas in Ergodic Theory. In particular, starting with at least [Kry], it has become clear that a quantitive estimate of the speed of convergence to equilibrium is pivotal for this research program. The first strong result of this type dates back to Bunimovich et al. [BSC] in 1990, but it relies on a Markov-partition-like technology that is not very well suited to producing optimal results. The next breakthrough is due to Young [Y98, Y99] who put forward two techniques, towers and coupling, well suited to study the decay of correlations for a large class of systems, billiards included. The idea of coupling was subsequently refined by Dolgopyat [Do04a, Do04b, Do05] who introduced the notion of standard pairs, which have proved a formidable tool to study the statistical properties of dynamical systems in general and billiards in particular [C1, C2, CD, CZ]. See [CM, Chapter 7] for a detailed exposition of these ideas and related references.
In the meantime another powerful idea has appeared, following the seminal work of Ruelle [RS, Ru76] and Lasota–Yorke [LY], to study the spectral properties of the associated transfer operator acting on spaces of functions adapted to the dynamics. After some preliminary attempts [Fr86, Ru96, Ki99], the functional approach for hyperbolic systems was launched by the seminal paper [BKL], which was quickly followed and refined by a series of authors, including [B1, GL, BT, GL2]. Such an approach, when applicable, has provided the strongest results so far, see [B2] for a recent review. In particular, building on a preliminary result by Demers and Liverani [DL], it has been applied to billiards by Demers and collaborators [DZ1, DZ2, DZ3, D2, BD1, BD2]. This has led to manifold results, notably the proof of exponential decay of correlations for certain billiard flows [BDL].
Yet, lately there has been a growing interest in non-stationary systems, when the dynamical system changes with time. Since most systems of interest are not isolated, not even in first approximation, the possibility of a change to the system due to external factors clearly has physical relevance. Another important scenario in which non-stationarity appears is in dynamical systems in random media, e.g. [AL]. The functional approach as such seems not to be well suited to treat these situations since it is based on the study of an operator via spectral theory. In the non-stationary case a single operator is substituted by a product of different operators and spectral theory does not apply.
There exist several approaches that can be used to overcome this problem, notably:
-
1.
Consider random systems; in this case, especially in the annealed case, it is possible to recover an averaged transfer operator to which the theory applies. More recently, the idea has emerged to study quenched systems via infinite dimensional Oseledets theory, see e.g. [DFGV1, DFGV2] and references therein;
-
2.
Consider only slowly changing systems that can be treated using the perturbation theory in [KL99, GL]. For example, see [DS], and references therein, for some recent work in this direction;
-
3.
Use the technology of standard pairs, which has the advantage of being very flexible and applicable to the non-stationary case [SYZ]. Note that the standard pair technology and the above perturbation ideas can be profitably combined together, see [DeL1, DeL2, DLPV];
-
4.
Use the cone and Hilbert metric technology introduced in [Bir, L95a, L95b, LM], which has also been extended to the random setting [AL, AFGV].
The first two approaches, although effective, impose severe limitations on the class of nonstationary systems that can be studied. The second two approaches are more general and seem more or less equivalent. However, coupling arguments are often cumbersome to write in detail and usually provide weaker quantitative estimates compared to the cone method.
Therefore, in the present article we develop the cone method and demonstrate that it can be successfully applied to billiards. Indeed, we introduce a relatively simple cone that is contracted by a large class of billiards. This implies that one can easily prove a loss of memory result for sequences of billiard maps. To show that the previous results have concrete applications we devote one third of this paper to developing applications to several physically relevant classes of models.
We emphasize that the present paper does not exhaust the possible applications of the present ideas. To have a more complete theory one should consider, to mention just a few, billiards with corner points, billiards with electric or magnetic fields, billiards with more general reflection laws, measures different from the SRB measure (that is transfer operators with generalized potentials as in [BD1, BD2]), etc. We believe that most of these cases can be treated by small modifications of the present theory; however, the precise implementation does require a non-negligible amount of work and hence exceeds the scope of this presentation, which aims only at introducing the basic ideas and producing a viable cone for dispersing billiards.
The plan of the paper is as follows. In Sect. 2 we introduce the class of billiards from which we will draw our sequential dynamics and summarize our main analytical results regarding cone contraction. In Sect. 3 we present the uniform properties of hyperbolicity and singularity sets enjoyed by our class of maps, listed as (H1)–(H5); we also prove a Growth Lemma for our sequences of maps and introduce one of our main characters, the transfer operator. In Sect. 4 we introduce our protagonist, the cone (see Sect. 4.3). Section 5 is devoted to showing that the cone so defined is invariant under the action of the transfer operators of the billiards in question. In Sect. 6 we show that in fact the cone is eventually strictly invariant (the image has finite diameter in the associated Hilbert metric) thanks to some mixing properties of the dynamics on a finite scale. The strict cone contraction implies exponential mixing for a very large class of observables and densities as is explained in Sect. 7. Finally, Sect. 8 contains the announced applications, first to sequential systems with holes (open systems), then to chaotic scattering and finally to the random Lorentz gas.
2 Setting and Summary of Main Results
Since we are interested in studying sequential billiards, below we define a set of billiard tables that will have uniform hyperbolicity constants, following [DZ2]. Other classes of billiards are also studied in [DZ2], such as infinite horizon billiards, billiards under small external forces and some types of nonelastic reflections. While such classes of billiards are amenable to the present technique, we do not treat the most general case here since the greater number of technicalities would obscure the main ideas we are trying to present.
2.1 Families of billiard tables with uniform properties
We first choose \(K \in {\mathbb {N}}\) and numbers \(\ell _i >0\), \(i = 1, \ldots K\). Let \(M = \cup _{i=1}^{K^{}} I_i \times [- \frac{\pi }{2}, \frac{\pi }{2}]\), where for each i, \(I_i=[0, \ell _i]/\sim \) is an interval of length \(\ell _i\) with endpoints identified. M will be the phase space common to our collection of billiard maps.
Given K and \(\{ \ell _i \}_{i=1}^K\), we use the notation \(Q = Q(\{ B_i \}_{i=1}^K)\) to denote the billiard table \({\mathbb {T}}^2 \setminus (\cup _{i=1}^K B_i)\), where each \(B_i\) is a closed, convex set whose boundary has arclength \(\ell _i\). We assume that the scatterers \(B_i\) are pairwise disjoint and that each \(\partial B_i\) is a \(C^3\) curve with strictly positive curvature.
The billiard flow is defined by the motion of a point particle traveling at unit speed in \(Q := {\mathbb {T}}^2 \setminus (\cup _i B_i)\) and reflecting elastically at collisions. The associated billiard map T is the discrete-time collision map which maps a point on \(\partial Q\) to its next collision. Parameterizing \(\partial Q\) according to an arclength parameter r (oriented clockwise on each obstacle \(B_i\)) and denoting by \(\varphi \) the angle made by the post-collision velocity vector and the outward pointing normal to the boundary yields the canonical coordinates for the phase space M of the billiard map. In these coordinates, \(M = \cup _i I_i \times [-\frac{\pi }{2}, \frac{\pi }{2}]\), as defined previously.
For \(x = (r,\varphi ) \in M\), let \(\tau (x)\) denote the time until the next collision for x under the flow. We assume that \(\tau \) is bounded on M, i.e. the billiard has finite horizon. Thus since the scatterers are disjoint, there exist constants \(\tau _{\min }(Q), \tau _{\max }(Q) > 0\) depending on the configuration Q such that \(\tau _{\min }(Q) \le \tau (x) \le \tau _{\max }(Q) < \infty \) for all \(x \in M\). Moreover, by assumption there exists \({\mathcal {K}}_{\min }(Q), {\mathcal {K}}_{\max }(Q) >0\) such that if \({\mathcal {K}}(r)\) denotes the curvature of the boundary at coordinate r, then \({\mathcal {K}}_{\min }(Q) \le {\mathcal {K}}(r) \le {\mathcal {K}}_{\max }(Q)\). Finally, let \(E_{\max }(Q)\) denote the maximum value of the \(C^3\) norm of the curves comprising \(\partial Q\) when parametrized according to arclength.
Now fix \(\tau _*, {\mathcal {K}}_*, E_* \in {\mathbb {R}}^+\), and let \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) denote the collection of all billiard tables \(Q( \{ B_i \}_{i=1}^K )\) such that
To each table in \(Q \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) corresponds a billiard flow and hence a billiard map \(T = T(Q)\) and associated collision times. Let \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) denote the collection of billiard maps induced by configurations in \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\), i.e.,
Thus each \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) is identified withFootnote 1 a table \(Q \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\), which we denote by Q(T). Note that all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) have the same phase space M since we have fixed K and the arclengths \(\{ \ell _i \}_{i=1}^K\).
It is a standard fact that all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) preserve the same smooth invariant probability measure, \(d\mu _{\tiny {\text{ SRB }}}= c \cos \varphi \, dr \, d\varphi \), where \(c = \frac{1}{2|\partial Q|} = \frac{1}{2 \sum _{i=1}^K \ell _i}\) is the normalizing constant [CM]. In addition, all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) are mixing with respect to \(\mu _{\tiny {\text{ SRB }}}\) and so are topologically mixing [S] (see also, [CM, Section 6.7]).
It is provedFootnote 2 in [DZ2, Theorem 2.7] that all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) satisfy properties (H1)–(H5) of that paper with uniform constants depending only on \(\tau _*, {\mathcal {K}}_*\) and \(E_*\). We recall the relevant properties in Sect. 3 that we shall use throughout the paper and label them (H1)–(H5).
Remark 2.1
The assumption that all scatterers have the same arclength is made for convenience so that there is a single cone \({\mathcal {C}}\) on which all our operators \({\mathcal {L}}_T\), \(T \in {\mathcal {F}}\), act. This can be relaxed slightly once the hyperbolicity constant \(\Lambda := 1 + 2{\mathcal {K}}_* \tau _*\) has been introduced in (H1) by allowing the arclength of the boundary of each scatterer to change by no more than \(\varepsilon _1\), where \(\varepsilon _1< \frac{\Lambda -1}{\Lambda +1}\), since then rescaling the arclength parametrization of \(\partial B_i\) to be again \([0, \ell _i]\) yields a map with similar properties (H1)–(H5), but with slightly weakened hyperbolicity constant \({\tilde{\Lambda }} = \Lambda \frac{1-\varepsilon _1}{1+\varepsilon _1}>1\) (and \(\theta _0\) from (H3) is weakened accordingly.)
To change the arclengths drastically would force us to consider a sequence of cones \({\mathcal {C}}_n\) on a sequence of phase spaces \(M_n\). This would require further suitable assumptions on the maps \(T_n : M_n \rightarrow M_{n+1}\) in order to ensure hyperbolicity, and such assumptions could be tailored to specific applications. We do not pursue this generality here, but remark that for example, it would be possible to formulate such a generalization for the random Lorentz gas with gates described in Sect. 8.5, in which the central scatterer in each cell is allowed to change arclength and the resulting billiard map between cells would still satisfy (H1)–(H5) (albeit the normalization in (H5) would vary).
Next, we define a notion of distance in \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) as follows. Each table Q comprises K obstacles \(B_i\). Each \(\partial B_i\) can be parametrized according to arclength by a function \(u_i : I_i \rightarrow {\mathbb {R}}^2\) (unfolding \({\mathbb {T}}^2\)). Since two arclength parametrizations of \(\partial B_i\) can differ only in their starting point, the collection \(u_{i,\theta }\), \(\theta \in [0, \ell _i)\), denotes the set of parametrizations associated with \(\partial B_i\). Similarly, for a configuration \({{\widetilde{Q}}}\), denote the parametrizations of obstacles by \({\tilde{u}}_{i, \theta }\), \(\theta \in [0, {\tilde{\ell }}_i)\). Let \(\Pi _K\) denote the set of permutations \(\pi \) on \(\{ 1, \ldots K \}\) which satisfy \({\tilde{\ell }}_{\pi (i)} = \ell _i\). Then define
Fix \(Q_0 \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) and choose \(\kappa \le \frac{1}{2} \min \{ \tau _*, {\mathcal {K}}_* \}\). Let \({\mathcal {Q}}(Q_0, E_*; \kappa )\) denote the set of billiard tables Q withFootnote 3\(\mathbb {d}(Q, Q_0) < \kappa \) and \(E_{\max }(Q) \le E_*\), \(\tau _{\max } \le 2/\tau _*\). Let \({\mathcal {F}}(Q_0, E_*; \kappa )\) denote the corresponding set of billiard maps. The following result is [DZ2, Theorem 2.8 and Section 6.2].
Proposition 2.2
Let \(Q_0 \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\). For all \(\kappa \le \frac{1}{2} \min \{ \tau _*, {\mathcal {K}}_* \}\), we have \({\mathcal {Q}}(Q_0, E_*; \kappa ) \subset {\mathcal {Q}}(\frac{\tau _*}{2}, \frac{{\mathcal {K}}_*}{2}, E_*)\). Moreover, there exists \(C>0\) such that for any \(T_1, T_2 \in {\mathcal {F}}(Q_0, E_*; \kappa )\),
-
(a)
\(d_H({\mathcal {S}}_{-1}^{T_1}, {\mathcal {S}}_{-1}^{T_1}) \le C \kappa ^{1/2}\), where \(d_H\) is the Hausdorff metric and \({\mathcal {S}}_{-1}^T\) is the singularity set for \(T^{-1}\) defined in (H1);
-
(b)
for \(x \notin N_{C\kappa ^{1/2}}(S_{-1}^{T_1}, {\mathcal {S}}_{-1}^{T_2})\), \(d(T_1^{-1}(x), T_2^{-1}(y)) \le C \kappa ^{1/2}\), where \(N_\varepsilon (\cdot )\) denotes the \(\varepsilon \)-neighborhood of a set in M in the Euclidean metric.
We use an (uncountable) index set \({\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), identifying \(\iota \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\) with a map \(T_\iota \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). Choosing a sequence \((\iota _j)_{j \in {\mathbb {N}}} \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), we will be interested in the dynamics of
If we choose \(\iota _j = \iota \) for each j, then \(T_n = T_\iota ^n\), the iterates of a single map. For convenience, denote \(T_0 = \) Id.
2.2 Main analytical results: Cone contraction and loss of memory
As announced in the introduction, the main analytical tool developed in this paper is the construction of a convex cone of functions \({\mathcal {C}}_{c,A,L}(\delta )\), depending on parameters \(\delta >0\), \(c, A, L > 1\), as defined in Sect. 4.3, that is contracted under the sequential action of the transfer operators \({\mathcal {L}}f = f \circ T^{-1} \), defined in Sect. 3.3 for \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). For a sequence of maps \(T_n\) as in (2.2), define \({\mathcal {L}}_n f = f \circ T_n^{-1}\).
In order to state our main result on cone contraction, we define open neighborhoods in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) using the distance \(\mathbb {d}\) between tables defined in (2.1). Let \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), and for \(0< \kappa < \frac{1}{2} \min \{ \tau _*, {\mathcal {K}}_* \}\), define
Remark that since \({\mathcal {F}}(T, \kappa ) \subset {\mathcal {F}}(Q(T), E_*; \kappa )\), the conclusions of Proposition 2.2 apply as well to maps in \({\mathcal {F}}(T, \kappa )\). We will denote the index set corresponding to \({\mathcal {F}}(T, \kappa )\) by \({\mathcal {I}}(T, \kappa ) \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\). Thus \(\iota \in {\mathcal {I}}(T, \kappa )\) if and only if \(T_\iota \in {\mathcal {F}}(T, \kappa )\).
Theorem 2.3
Suppose c, A and L satisfy the conditions of Sect. 5.3, and that \(\delta >0\) satisfies (6.7) and (6.18). Let \(N_{{\mathcal {F}}} := N(\delta )^- + k_*n_*\) be from Theorem 6.12 and let \(\kappa >0\) be from Lemma 6.6(b).
-
(a)
There exists \(\chi \in (0,1)\) such that if \(n \ge N_{{\mathcal {F}}}\), \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T, \kappa )\), then \({\mathcal {L}}_n {\mathcal {C}}_{ c, A, L}(\delta ) \subset {\mathcal {C}}_{ \chi c, \chi A, \chi L}(\delta ) \).
-
(b)
For any \(\chi \in \left( \max \{ \frac{1}{2}, \frac{1}{L}, \frac{1}{\sqrt{A-1}} \}, 1 \right) \), the cone \({\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) has diameter at most
$$\begin{aligned} \log \left( \frac{(1+\chi )^2}{(1-\chi )^2} \chi L \right) < \infty \end{aligned}$$in the Hilbert metric associated to \({\mathcal {C}}_{c, A, L}(\delta )\) (see (4.1) for a precise definition), provided \(\delta >0\) is chosen sufficiently small to satisfy (6.21).
The first statement of this theorem is proved in two steps: first, Proposition 5.1 shows that the parameters c and A contract due to the uniform hyperbolicity properties (H1)–(H5) of the maps in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), subject to the constraints listed in Sect. 5.3 (all that is needed is \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), and not the stronger assumption \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T, \kappa )\)); second, Theorem 6.12 proves the contraction of L using the uniform mixing property of maps \({\widetilde{T}}\in {\mathcal {F}}(T, \kappa )\) as expressed by Lemma 6.6. The second statement of Theorem 2.3 is proved by Proposition 6.13.
From this theorem follow our results on exponential loss of memory for sequential systems of billiard maps. In the case that \(T_{\iota _j} = T\) for each j, these results read as exponential decay of correlations and convergence to equilibrium. Since our maps \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) all preserve the measure \(\mu _{\tiny {\text{ SRB }}}\), we also obtain a type of convergence to equilibrium in the sequential case (see Theorem 2.8).
In order to state our result for the sequential system, we define the notion of an admissible sequence of maps from \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). As before, let \(\kappa >0\) be from Lemma 6.6(b).
Definition 2.4
For \(N \in {\mathbb {N}}\), we call a sequence \(( \iota _j )_{j \ge 1}\), \(\iota _j \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), N-admissible if there exist sequences \((T_k)_{k \ge 1} \subset {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and \((N_k)_{k \ge 1}\) with \(N_k \ge N\), such that \(T_{\iota _j} \in {\mathcal {F}}(T_k, \kappa )\) for all \(k \ge 1\) and \(j \in [1 + \sum _{i=1}^{k-1} N_i, \sum _{i=1}^k N_i]\).
Thus an N-admissible sequence is a sequence which remains in a \(\kappa \) neighborhood of a fixed map \(T_k\) for \(N_k \ge N\) iterates at a time, but which may undergo a large change between such blocks.
Remark 2.5
One can generalize the definition of N-admissible sequence to include short blocks where maps are not required to be close to a fixed map. As long as these short blocks can be grouped to contain at least \(n_0\) iterates, where \(n_0\) is from Proposition 5.1, and they are interspersed regularly with long blocks of length at least \(N = N_{{\mathcal {F}}}\) then one can still set up a regular contraction using Theorem 6.12 on the long blocks.
We first state our results regarding loss of memory, both with respect to \(\mu _{\tiny {\text{ SRB }}}\) and leafwise: the difference of integrals along individual stable curves converge to 0 exponentially fast along any \(N_{{\mathcal {F}}}\)-admissible sequence. Let \({\mathcal {W}}^s(\delta )\) denote the set of homogeneous cone stable curves \({\mathcal {W}}^s\) defined in Sect. 3.1, having length between \(\delta \) and \(2\delta \). We denote by \(\mu _{\tiny {\text{ SRB }}}(f) = \int _M f \, d\mu _{\tiny {\text{ SRB }}}\) and by |W| the (Euclidean) length of a stable curve W in M.
Also, we denote the average value of \(\psi \) on W by  , where \(m_W\) denotes the arclength measure on W induced by the Euclidean metric in M.
, where \(m_W\) denotes the arclength measure on W induced by the Euclidean metric in M.
In Lemma 7.6, we prove that our cone \({\mathcal {C}}_{c,A,L}(\delta )\) contains translations of piecewise Hölder continuous functions, as long as the discontinuities are transverse to the stable cone defined in (H1). We make this precise as follows.
Definition 2.6
We call a countable (mod 0) partition \({\mathcal {P}}= \{ P_i \}_i\) of M regular if each \(P_i\) is an open, simply connected set, and there exist constants \(K, C_{\mathcal {P}}>0\) such that for all \(W \in {\mathcal {W}}^s\), \(W \setminus \partial {\mathcal {P}}\) comprises at most K connected components and for any \(\varepsilon > 0\), \(m_W(N_\varepsilon (\partial {\mathcal {P}})) \le K C_{\mathcal {P}}\varepsilon \), where \(N_\varepsilon (A)\) denotes the \(\varepsilon \)-neighborhood of a set A in M.
For \(t>0\), denote by \(C^t({\mathcal {P}})\) the set of functions on M that are Hölder continuous on each element of \({\mathcal {P}}\) and such that
We recall again \(N_{{\mathcal {F}}} = N(\delta )^- + k_*n_*\) from Theorem 6.12.
Theorem 2.7
Let \({\mathcal {P}}\) be a regular partition of M and letFootnote 4\(t \ge \gamma \). There exist \(C>0\) and \(\vartheta <1\) such that for all \(N_{{\mathcal {F}}}\)-admissible sequences \((\iota _j)_j\), all \(n \ge 0\), and all \(f, g \in C^t({\mathcal {P}})\) with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\):
-
(a)
For all \(W \in {\mathcal {W}}^s(\delta )\) and all \(\psi \in C^1(W)\), we have
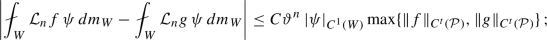
-
(b)
For all \(\psi \in C^1(M)\),
$$\begin{aligned} \left| \int _M {\mathcal {L}}_n f \, \psi \, d\mu _{\tiny {\text{ SRB }}}- \int _M {\mathcal {L}}_n g \, \psi \, d\mu _{\tiny {\text{ SRB }}}\right| \le C \vartheta ^n |\psi |_{C^1(M)} \max \{ \Vert f \Vert _{C^t({\mathcal {P}})}, \Vert g \Vert _{C^t({\mathcal {P}})} \} \, . \end{aligned}$$
We remark that the regularity of \(\psi \in C^1(M)\) can be relaxed to \(\psi \in C^\varsigma (M)\) for any \(\varsigma >0\) by a standard approximation argument, but at the expense of obtaining a weaker rate \(\vartheta \).
Since all our maps preserve the same invariant measure \(\mu _{\tiny {\text{ SRB }}}\), we obtain additionally an equidistribution result for stable curves as well as convergence to equilibrium along admissible sequences.
Theorem 2.8
Under the hypotheses of Theorem 2.7, there exists \(C>0\) such that for all \(N_{{\mathcal {F}}}\)-admissible sequences \((\iota _j)_j \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), all \(f, g \in C^t({\mathcal {P}})\) with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\), and all \(n \ge 0\),
-
(a)
For all \(W_1, W_2 \in {\mathcal {W}}^s(\delta )\) and all \(\psi _i \in C^1(W_i)\) with
 , we have
, we have 
in particular, for all \(W \in {\mathcal {W}}^s(\delta )\) and \(\psi \in C^1(W)\),

-
(b)
for all \(\psi \in C^1(M)\),
$$\begin{aligned} \left| \int _M f \, \psi \circ T_n \, d\mu _{\tiny {\text{ SRB }}}- \int _M f \, d\mu _{\tiny {\text{ SRB }}}\int _M \psi \, d\mu _{\tiny {\text{ SRB }}}\right| \le C \vartheta ^n |\psi |_{C^1(M)}\max \{ \Vert f \Vert _{C^t({\mathcal {P}})}, \Vert g \Vert _{C^t({\mathcal {P}})} \} \, . \end{aligned}$$
Theorems 2.7 and 2.8 are proved in Sect. 7, specifically in Theorems 7.3 and 7.4 and Corollary 7.5.
Remark 2.9
Theorem 2.7 has some overlap with [SYZ], which also considers sequential billiards in which scatterers shift slightly between collisions. Note, however, that our definition of admissible sequence allows abrupt and large changes in the configuration of scatterers within the family \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) every \(N_{{\mathcal {F}}}\) iterates, compared to the slowly changing requirement throughout [SYZ]. This may seem like merely a technical difference due to the cone technique, yet it is precisely this ability to introduce occasional large changes in the dynamics that allows us to apply our results to the chaotic scattering problem and random Lorentz gas described in Sect. 8.
With these convergence results in hand, we are able to provide three applications to concrete problems of physical interest: sequential open systems in Sect. 8.3, a chaotic scattering problem without assuming a no-eclipse condition in Sect. 8.4, and a variant of the random Lorentz gas in Sect. 8.5.
3 Uniform Hyperbolicity, Singularities and Transfer Operators
3.1 Uniform properties for \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\)
Fixing K and \(\{ \ell _i \}_{i=1}^K\), we recall some fundamental properties of billiard maps \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) that depend only on the quantities \(\tau _*\), \({\mathcal {K}}_*\) and \(E_*\). Although many of these properties are well known, a proof of their dependence on \(\tau _*\), \({\mathcal {K}}_*\), \(E_*\) can be found, for example, in [DZ2, Section 6.1].
In order to better align with the abstract framework in [DZ2], we also label our properties (H1)–(H5), although our set-up here is simpler than in [DZ2]. We recall the corresponding index set \({\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\) from Sect. 2.1 and the notation \(T_n\) from (2.2).
(H1) Hyperbolicity and Singularities. The (constant) family of cones
is strictly invariant, \(DT^{-1}C^s(x) \subset C^s(T^{-1}x)\), for all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). Moreover, \(T^{-1}\) enjoys uniform expansion of vectors in the stable cone: set \(\Lambda = 1 + 2{\mathcal {K}}_* \tau _* > 1\); then there exists \(C_1 \in (0,1]\) such that,
where \(\Vert \cdot \Vert \) denotes the Euclidean norm given by \(dr^2 + d\varphi ^2\). There is a family of unstable cones \(C^u\) defined similarly, but with \({\mathcal {K}}_* \le d\varphi /dr \le {\mathcal {K}}_*^{-1} + \tau _*^{-1}\), which is strictly invariant under DT for all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
Due to the unbounded expansion of DT near tangential collisions, we define the standard homogeneity strips, following [BSC]. For some \(k_0 \in {\mathbb {N}}\), to be chosen later in (3.4), define
Set \({\mathcal {S}}_0 = \{ (r, \varphi ) \in M : \varphi = \pm \frac{\pi }{2} \}\). For \(n \ge 1\), the singularity set for \(T_n\) is denoted by \({\mathcal {S}}_n^{T_n} = \cup _{i=0}^{n} T_i^{-1} ({\mathcal {S}}_0)\), while the singularity set for \(T_n^{-1}\) is denoted by \({\mathcal {S}}_{-n}^{T_n} = \cup _{i=0}^n T_i ( {\mathcal {S}}_0)\). On \(M \setminus {\mathcal {S}}_n^{T_n}\), \(T_n\) is a \(C^2\) diffeomorphism onto its image.
There exists a constant, which we still call \(C_1>0\), such that
In order to achieve bounded distortion, we will consider the boundaries of the homogeneity strips as an extended singularity set for T. To this end, define \({\mathcal {S}}_0^{{\mathbb {H}}} = {\mathcal {S}}_0 \cup (\cup _{k \ge k_0} (\partial {\mathbb {H}}_k \cup \partial {\mathbb {H}}_{-k}))\), and for \(n \ge 1\),
(H2) Families of Stable and Unstable Curves. We call a curve \(W \subset M\) a stable curve if for each \(x \in W\), the tangent vector to W at x belongs to \(C^s\). A stable curve is called homogeneous if it lies in one homogeneity strip or outside their union. Denote by \({\mathcal {W}}^s\) the set of homogeneous stable curves with length at most \(\delta _0\in (0,1/2)\) (defined by (3.4)) and with curvature at most \({{\bar{B}}}\).
By [CM, Proposition 4.29], we may choose \({{\bar{B}}}\) sufficiently large that \(T^{-1} {\mathcal {W}}^s \subset {\mathcal {W}}^s\), up to subdividing the curves of length larger than \(\delta _0\), for all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
Similarly, we define an analogous set of homogeneous unstable curves by \({\mathcal {W}}^u\).
(H3) One-Step Expansion. Defining the adapted norm \(\Vert v \Vert _*\), \(v = (dr, d\varphi )\) as in [CM, Sect. 5.10], we have \(\Vert DT^{-1}(x) v \Vert _* \ge \Lambda \Vert v \Vert _*\) for all \(v \in C^s(x)\), wherever \(DT^{-1}\) is defined. For \(W \in {\mathcal {W}}^s\), let \(V_i\) denote the maximal homogeneous components of \(T^{-1}W\). Then by [CM, Lemma 5.56], there exists \(\theta _0 \in (\Lambda , 1)\), a choice of \(k_0\) for the homogeneity strips and \(\delta _0\in (0,1/2)\) such that,
where \(| J_{V_i}T |_*\) denotes the supremum of the Jacobian of T along \(V_i\) in the adapted metric.
Since the stable/unstable cones are global and bounded away from one another, the adapted metric can be extended so that it is uniformly equivalent to the Euclidean metric: There exists \(C_0 \ge 1\) such that \(C_0^{-1} \Vert v \Vert \le \Vert v \Vert _* \le C_0 \Vert v \Vert \) for all \(v \in {\mathbb {R}}^2\).
(H4) Distortion Bounds. Suppose \(W \in {\mathcal {W}}^s\) and for \(n \ge 1\), \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\) are such that \(T_jW \in {\mathcal {W}}^s\) for \(j=0, \ldots n\). There exists \(C_d>0\), independent of W, n and \(\{ \iota _j \}_{j=1}^n\), such that for all \(x, y \in W\),
where \(J_WT_n\) is the (stable) Jacobian of \(T_n\) along W and \(d(\cdot , \cdot )\) denotes arclength on W with respect to the metric \(dr^2+d\varphi ^2\).
Similar bounds hold for stable Jacobians lying on the same unstable curve. Suppose, for \(n \ge 1\), that \(V_1\), \(V_2 \in {\mathcal {W}}^s\) are such that \(T_jV_1\), \(T_jV_2 \in {\mathcal {W}}^s\) for \(0 \le j \le n\), in particular they are not cut by any singularity, and there exists a foliation of unstable curves \(\{ \ell _x \}_{x \in V_1} \subset {\mathcal {W}}^u\) creating a one-to-one correspondence between \(V_1\) and \(V_2\) and such that \(\{ T_n( \ell _x) \}_{x \in V_1} \subset {\mathcal {W}}^u\) creates a one-to-one correspondence between \(T_nV_1\) and \(T_nV_2\). For \(x \in V_1\), define \({\bar{x}}= \ell _x \cap V_2\). Then there exists \(C_d>0\), independent of n, \(\{ \iota _j \}_{j=1}^n\), \(V_1\), \(V_2\), and x, such that,
where \(\phi (x, {\bar{x}})\) denotes the angle between the tangent vectors to \(V_1\) and \(V_2\) at x and \({\bar{x}}\), respectively. For simplicity, we use the same symbol \(C_d\) to represent the distortion constants in (3.5) and (3.6). The proofs for these distortion bounds in this form for a single map can be found in [DZ1, Appendix A] (see also [CM, Section 5.8]). The analogous bounds for sequences of maps in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) are proved in [DZ2, Lemma 3.3]. The constant \(C_d\) depends only on the choice of \(k_0\) from (H3) and the hyperbolicity constants \(C_1\) and \(\Lambda \) from (H1).
(H5) Invariant measure. All \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) preserve the same invariant measure, \(d\mu _{\tiny {\text{ SRB }}}= c \cos \varphi \, dr \, d\varphi \), where \(c = \frac{1}{2|\partial Q|} = \frac{1}{2 \sum _{i=1}^K \ell _i}\) is the normalizing constant [CM].
Remark 3.1
Property (H5) is enjoyed by the class of maps we have chosen, but it is not necessary for this technique to work. Indeed, [DZ2] replaces this condition by: There exists \(\eta >0\) so that \(1+\eta \) is sufficiently small compared to the hyperbolicity constant \(\Lambda \) from (H1), such that \((J_{\mu _{\tiny {\text{ SRB }}}}T)^{-1} \le 1+\eta \), where \(J_{\mu _{\tiny {\text{ SRB }}}}T\) is the Jacobian of \(\mu _{\tiny {\text{ SRB }}}\) with respect to T.
Thus T does not have to preserve \(\mu _{\tiny {\text{ SRB }}}\), but in this sense must be close to a map that does. This permits the application of the current technique to billiards under small external forces and nonelastic reflections, as described in [DZ2, Section 2.4]. See also [C2, Z]. Note however, that while Theorem 2.7 will continue to hold in this generalized context, Theorem 2.8 will not hold once there is no common invariant measure.
3.2 Growth lemma
Although all maps in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) enjoy the uniform properties (H1)–(H5), in Sect. 6.1, we will find it convenient to increase the contraction provided in (3.4) by replacing T with a higher iterate \(T_n\) and choosing \(\delta _0\) sufficiently small so that (3.4) holds for \(T _*:= T_n\) with constant \(\theta _0^n\). This is possible since if W is a stable curve, then there exists \(C>0\), depending only on the family \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), such that, for each \(T\in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), \(|T^{-1}W| \le C|W|^{1/2}\) [CM, Exercise 4.50]. Thus we may redefine \(\delta _0\) so small that no connected component of \(T_k^{-1}(W)\) is longer than \(\delta _0\), from hypothesis (H1), for \(k=0, \ldots , n\). Since no artificial subdivisions are necessary, we apply (3.4) inductively in k to obtain the desired contraction.
Choose \({{\bar{n}}}\) such that \(\theta _1 := \theta _0^{{{\bar{n}}}}\) satisfies
where \(C_0 \ge 1\) is from (H3), and then fix \(\delta _0\), as explained above, such that
where \(V_i\) are the homogeneous components of \(T_{{{\bar{n}}}}^{-1}W\). Note that if we shrink \(\delta _0\) further, then (3.8) will continue to hold for the same value of \({{\bar{n}}}\).
We shall work with the map \(T_*:= T_{{{\bar{n}}}}\) throughout the following. To simplify notation we will call \(T_*\) again T as no confusion can arise. Note, however, that the definition of N-admissible sequence must be modified since the length \(N_{{\mathcal {F}}}\) of the blocks comprising the sequence, for example in Theorem 2.7, is computed for the map \(T_*\). Thus a single block in an N-admissible sequence should comprise at least \({{\bar{n}}} N\) billiard maps that are close in the sense of Definition 2.4.
Definition 3.2
For \(W \in {\mathcal {W}}^s\), for \(T_n\) as in (2.2) we denote by \({\mathcal {G}}_n(W)\) the homogeneous components of \(T_n^{-1}W\), where we have subdivided the elements of \(T_n^{-1}W\) longer than \(\delta _0\) into elements with length between \(\delta _0/2\) and \(\delta _0\) so that \({\mathcal {G}}_n(W)\subset {\mathcal {W}}^s\). We call \({\mathcal {G}}_n(W)\) the nth generation of W.
Let \({\mathcal {I}}_n(W)\) denote the set of curves \(W_i \in {\mathcal {G}}_n(W)\) such that \(T_j(W_i)\) is not contained in an element of \({\mathcal {G}}_{n-j}(W)\) having length at least \(\delta _0/2\) for all \(j = 0, \ldots , n\).
The following growth lemma is contained in [DZ2, Lemma 5.5], but we include the proof of item (b) here for convenience and to draw out the explicit dependence on the constants.
Lemma 3.3
There exists \({\bar{C}}_0 > 0\) such that for all \(W \in {\mathcal {W}}^s\) and \(n \ge 0\) and \(\{ \iota _j \}_{j=1}^n\),
-
(a)
\(\displaystyle \sum _{W_i \in {\mathcal {I}}_n(W)} |J_{W_i}T_n|_{C^0(W_i)} \le C_0 \theta _1^n\);
-
(b)
\(\displaystyle \sum _{W_i \in {\mathcal {G}}_n(W)} |J_{W_i}T_n|_{C^0(W_i)} \le {\bar{C}}_0 \delta _0^{-1} |W| + C_0 \theta _1^n\).
Proof
Item (a) follows by induction on n from (3.8) and the constant \(C_0\) from (H3) comes from translating from the adapted metric to the Euclidean metric at the last step. We focus on proving item (b).
For \(W \in {\mathcal {W}}^s\), let \(L_k(W) \subset {\mathcal {G}}_k(W)\) denote those elements of \({\mathcal {G}}_k(W)\) having length at least \(\delta _0/2\). For \(k \le n\) and \(W_i \in {\mathcal {G}}_n(W)\), we say that \(V_j \in L_k(W)\) is the most recent long ancestor of \(W_i\) if \(k \le n\) is the largest time that \(T_{n-k}W_i\) is contained in an element of \(L_k(W)\). Then by definition, \(W_i \in {\mathcal {I}}_{n-k}(V_j)\). Note that if \(W_i \in L_n(W)\), then \(k=n\) and \(W_i = V_j\). Now we estimate,
where we have used item (a) of the lemma to sum over \(W_i \in {\mathcal {I}}_{n-k}(W)\) and (3.5) to replace \(|J_{V_j}T_k|_{C^0(V_j)}\) with \(\frac{|T_kV_j|}{|V_j|}\). Now since \(\cup _{V_j \in L_k(W)} T_kV_j \subset W\), and \(|V_j| \ge \delta _0/2\), we have
which proves the lemma with \({{\bar{C}}}_0 := \frac{ 2 C_0}{1-\theta _1} e^{C_d \delta _0^{1/3}}\). \(\square \)
Remark 3.4
It is not necessary to work with \(T = T_{\bar{n}}\) in Lemma 3.3. It follows equally well from (3.4) with \(\theta _1\) replaced by \(\theta _0\). However, the stronger contraction provided by (3.8) is useful for Lemma 6.1 and the arguments following it.
Observe that if \(|W| \ge \delta _0/2\), then all pieces \(W_i \in {\mathcal {G}}_n(W)\) have a long ancestor and can be included in the sum over k; in this case, the second term on the right side of item (b) is not needed, and the value of \({{\bar{C}}}_0\) remains unchanged.
3.3 Transfer operator
We define the transfer operator \({\mathcal {L}}\) associated with T acting on scales of spaces of distributions as in [DZ1]. For \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), we denote by \(T_n^{-1}{\mathcal {W}}^s\) the set of curves \(W \in {\mathcal {W}}^s\) such that \(T_jW \in {\mathcal {W}}^s\) for all \(j = 0, \ldots n\). For \(\alpha \le 1/3\), let \(C^\alpha (T_n^{-1}{\mathcal {W}}^s)\) denote the set of complex valued functions on M that are Hölder continuous on elements of \(T_n^{-1}{\mathcal {W}}^s\). Then for \(\psi \in C^\alpha ({\mathcal {W}}^s)\), we have \(\psi \circ T_n \in C^\alpha (T_n^{-1}{\mathcal {W}}^s)\) (see Lemma 5.2(a)). Define
This defines \({\mathcal {L}}_{T_{\iota _n}} : (C^\alpha (T_n^{-1}{\mathcal {W}}^s))^* \rightarrow (C^\alpha (T_{n-1}^{-1}{\mathcal {W}}^s))^*\) for any \(n \ge 1\). See [DZ1] for details.
Recall that by (H5), all our maps T preserve the smooth invariant measure \(d\mu _{\tiny {\text{ SRB }}}= c \cos \varphi dr d\varphi \), where c is the normalizing constant. When \(d\mu = f d\mu _{\tiny {\text{ SRB }}}\) is a measure absolutely continuous with respect to \(\mu _{\tiny {\text{ SRB }}}\), we identify \(\mu \) with its density f. With this identification, the transfer operator acting on densities has the following familiar expression,
and so \({\mathcal {L}}_n f = {\mathcal {L}}_{T_{\iota _n}} \cdots {\mathcal {L}}_{T_{\iota _1}} f\), pointwise. We choose this identification of functions in order to simplify our later work: using the reference measure \(\mu _{\tiny {\text{ SRB }}}\), the Jacobian of the transformation is 1, making \({\mathcal {L}}\) simpler to work with.
4 Cones and Projective Metrics
Given a closed,Footnote 5 convex cone \({\mathcal {C}}\) satisfying \({\mathcal {C}}\cap - {\mathcal {C}}= \emptyset \), we define an order relation by \(f \preceq g\) if and only if \(g - f \in {\mathcal {C}}\cup \{0\}\). We can then define a projective metric by
4.1 A cone of test functions
For \(W \in {\mathcal {W}}^s\), \(\alpha \in (0, 1]\) and \(a \ge 1\), define a cone of test functions by
where \(d(\cdot , \cdot )\) is the arclength distance along W.
The Hilbert metric associated with this cone and defined by (4.1) depends on the constant a and the exponent \(\alpha \) determining the regularity of the functions. For each such choice, the Hilbert metric has the following convenient representation.
Lemma 4.1
([L95a, Lemma 2.2]). Choose \(\alpha \in (0,1]\). For \(\psi _1, \psi _2 \in {\mathcal {D}}_{a,\alpha }(W)\), the corresponding metric \(\rho _{W, a, \alpha }(\cdot , \cdot )\) is given by
A corollary of this lemma is that \({\mathcal {D}}_{a,\alpha }(W)\) has finite diameter in \({\mathcal {D}}_{a,\beta }(W)\) if \(\beta < \alpha \) and \(|W| < 1\) (the proof is similar to [L95a, Lemma 2.3] noting that \(d(x,y)^\alpha \le |W|^{\alpha -\beta }d(x,y)^\beta \)).
The next two lemmas are simple consequences of the regularity of functions in \({\mathcal {D}}_{a, \alpha }(W)\) for \(W \in {\mathcal {W}}^s\). We denote by \(m_W\) the measure induced by arclength along W.
Lemma 4.2
For any \(\alpha \in (0,1]\) and \(W \in {\mathcal {W}}^s\) with \(|W| \in [\delta , 2 \delta ]\), any \(\psi \in {\mathcal {D}}_{a, \alpha }(W)\) and \(x \in W\), we have
Proof
The estimate is immediate since \(\inf _{y \in W} \psi (y)\ge \psi (x)e^{-a|W|^\alpha }\). \(\square \)
Lemma 4.3
Given \(\alpha \in (0,1]\), \(W \in {\mathcal {W}}^s\), \(\psi _1, \psi _2 \in {\mathcal {D}}_{a, \alpha (W)}\) and \(x, y \in W\),
Proof
According to (4.1), we must have,
This in turn implies that
\(\square \)
4.2 Distances between curves and functions
Due to the global stable cones \(C^s\) defined in (H1), we may consider stable curves \(W \in {\mathcal {W}}^s\) as graphs of \(C^2\) functions over an interval \(I_W\) in the r-coordinate:
Using this representation, we define a notion of distance between \(W^1, W^2 \in {\mathcal {W}}^s\) by
if \(W^1\) and \(W^2\) lie in the same homogeneity strip and \(|I_{W^1} \cap I_{W^2}| > 0\); otherwise, we set \(d_{{\mathcal {W}}^s}(W^1, W^2) = \infty \). Note that \(d_{{\mathcal {W}}^s}\) is not a metric, but this is irrelevant for our purposes.
We will also find it necessary to compare between test functions on two different stable curves. Given \(W^1, W^2 \in {\mathcal {W}}^s\) with \(d_{{\mathcal {W}}^s}(W^1, W^2) < \infty \), and \(\psi _i \in {\mathcal {D}}_{a, \beta }(W^i)\), define
to be the (Hölder) distance between \(\psi _1\) and \(\psi _2\), where \(\Vert G_W' \Vert = \sqrt{1+ (d\varphi _W/dr)^2}\). Note that \(d_*\) depends on \(\beta \).
Also, by the bound \({{\bar{B}}}\) on the curvature of elements of \({\mathcal {W}}^s\), there exists \(B_*>0\) such that
Remark 4.4
Note that if \(d_*(\psi _1,\psi _2)=0\), then
where \({\overline{W}}^k = G_{W^k}(I_{W^1} \cap I_{W^2})\), \(k=1,2\).
4.3 Definition of the cone
In order to define a cone of functions adapted to our dynamics, we will fix the following exponents, \(\alpha , \beta , \gamma , q > 0\) and constant \(a>1\) large enough. Choose \(q \in (0, 1/2)\), \(\beta < \alpha \le 1/3\) and finally \(\gamma \le \min \{ \alpha - \beta , q \}\).
For a length scale \(\delta \le \delta _0/3\), define
Let \({\mathcal {A}}_*\) denote the set of functions on M whose restriction to each \(W \in {\mathcal {W}}^s\) is integrable with respect to the arclength measure \(dm_W\). For \(f \in {\mathcal {A}}_*\) define,
Setting \({\mathcal {A}}_0=\{f\in {\mathcal {A}}_*\;:\; {|||}f {|||}_+^{\sim } < \infty \}\), we have that \({|||}\cdot {|||}_+^{\sim }\) is a seminorm on the vector space \({\mathcal {A}}_0\).
Definition 4.5
As usual, we consider the vector space of the classes of equivalence determined by the semi-norm (\(f\sim g\) iff \({|||}f-g {|||}_+^{\sim }=0\)) and call \({\mathcal {A}}\) the resulting normed vector space. Remark that if \(f\sim g\), then f and g are equal almost everywhere both with respect to Lebesgue and to SRB measure \(\mu _{\tiny {\text{ SRB }}}\). In the following, we can then safely ignore the issue of equivalence classes and we will not mention it explicitly.
We will find it convenient to measure the average of functions in our cone on long stable curves, i.e. elements of \({\mathcal {W}}^s(\delta )\). To this end, define for \(f \in {\mathcal {A}}\),
Recall that we denote the average value of \(\psi \) on W by  . Since all of our integrals in this section and the next will be taken with respect to the arclength \(dm_W\), to keep our notation concise, we will drop the measure from our integral notation in what follows.
. Since all of our integrals in this section and the next will be taken with respect to the arclength \(dm_W\), to keep our notation concise, we will drop the measure from our integral notation in what follows.
Now for \(a, c, A, L >1\), and \(\delta \in (0, \delta _0/3]\), define the cone



We write the constants c, A, L explicitly as subscripts in our notation for the cone since these will be the parameters which are contracted by the dynamics. By contrast, the exponents \(\alpha , \beta , \gamma , q\) are fixed and will not be altered by the dynamics, while the constant a, which will be chosen in Lemma 5.2, will not appear directly in the contraction constant of the cone.
Intuitively, (4.6) requires that the ‘mass’ of functions in the cone be evenly distributed throughout the phase space, while (4.7) implies that, even though the functions in the cone are not necessarily bounded, their average on a short stable curve W cannot be larger than some constant times \(|W|^{q-1}\). Condition (4.8) says that, once you integrate along stable curves, you get an object which is morally \(\gamma \)-Hölder on the space of curves with the ‘metric’ \(d_{{\mathcal {W}}^s}\). That is, (4.8) implies some form of weak Hölder regularity for f transverse to the stable cone.
Remark 4.6
The above cone is a considerable simplification of the one introduced in [L95a, Section 4.1]. The parameter \(\zeta \) in [L95a, Section 4.1] plays the role of the parameter q here: it allows one to control the integral of an element of the cone on short stable curves. By contrast, the introduction of the new Hölder exponents \(\alpha ,\beta ,\gamma \) is necessary, as already evident in [DZ1] and [DZ2], to allow for the wilder singularities present in billiard maps with respect to the ones treated in [L95a, Section 4]. In particular, the requirement \(\alpha \le 1/3\) is forced by the distortion bound (H4), which in turn depends on the choice of homogeneity strips. The relation between the above cone and the norms in [DZ1] and [DZ2] is very close: the cone has a natural norm associated to it (see [DKL1, Appendix D.2 and, in particular, equation (D.2.1)]) which is very similar to the norms in [DZ1] and [DZ2].
For convenience, we require \(\delta _0\) to be sufficiently small so that
This will imply similar bounds in terms of \(\delta \) since \(\delta \le \delta _0/3\).
Remark 4.7
Note that, by definition, \({|||}\cdot {|||}_+\) decreases when \(\delta \) decreases, while \({|||}\cdot {|||}_-\) increases. Thus if (4.6) holds for some \(\delta >0\), it will hold automatically for all smaller \(\delta \). We will see that cone invariance has the same property. In fact, as will become clear from our estimates in Sects. 5 and 6, in order to prove that the parameters contract, we will need to choose A large compared to L, and c large compared to A. This yields the compatible set of restrictions, \(1< L< A < c\).
By contrast, the exponents are fixed by the regularity properties of the maps in question: \(\alpha \le 1/3\) due to (3.5), and \(\beta < \alpha \) so that \({\mathcal {D}}_{a, \beta }(W)\) has finite diameter in \({\mathcal {D}}_{a, \alpha }(W)\), while \(\gamma \le \alpha - \beta \) is convenient to obtain the required contraction in Lemma 5.5. See Sect. 5.3 for all the conditions the constants must satisfy for Proposition 5.1. Several further conditions are specified in Theorem 6.12 to prove the strict contraction of the cone.
Remark 4.8
Note that, since \(0 \notin {\mathcal {C}}_{c,A,L}(\delta )\), condition (4.6) implies \({|||}f {|||}_- > 0\), hence for all \(W \in {\mathcal {W}}^s(\delta ), \psi \in {\mathcal {D}}_{a, \beta }(W)\),
In particular, this implies
In addition, condition (4.7) implies
However condition (4.6) is not vacuous since we assume \(A>L\).
Remark 4.9
To have an idea of which functions can belong to the cone note that a function that is strictly negative on a ball of size \(2\delta \) cannot satisfy (4.6) and hence does not belong to the cone. On the other hand each \(f\in C^1\) such that \(\inf f\ge L\Vert f\Vert _\infty \) and \(\Vert f\Vert _{C^1}\le c \inf f\) belongs to the cone. See also Lemma 7.6 for a more detailed description of functions that belong to the cone.
We will need the following lemma in Sect. 6.2.
Lemma 4.10
For all \(f \in {\mathcal {C}}_{c,A, L}(\delta )\), \(W \in {\mathcal {W}}^s(\delta )\) and all \(\psi _1, \psi _2 \in {\mathcal {D}}_{a, \beta }(W)\),

Proof
Let \(f \in {\mathcal {C}}_{c, A, L}(\delta )\), \(W \in {\mathcal {W}}^s(\delta )\) and \(\psi _1, \psi _2 \in {\mathcal {D}}_{a, \beta }(W)\). For each \(\lambda , \mu >0\) such that \(\lambda \psi _1\preceq \psi _2\preceq \mu \psi _1\), hence also \(\lambda \psi _1\le \psi _2\le \mu \psi _1\), we have

where we have dropped the second term above due to (4.10) since \(\psi _2 - \lambda \psi _1 \in {\mathcal {D}}_{a, \beta }(W)\). Taking the sup on \(\lambda \) and the inf on \(\mu \), and recalling (4.1), yields

Then, since \(|W| \ge \delta \), we use (4.6) to estimate,

Reversing the roles of \(\psi _1\) and \(\psi _2\) completes the proof of the lemma. \(\square \)
5 Cone Estimates: Contraction of c and A
In this section, fixing \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), we will prove the following proposition. Let \(n_0 \ge 1\) be such that \(A C_0 \theta _1^{n_0} \le 1/16\).
Proposition 5.1
If the conditions on \(\delta , n_0, a, c, A,L\) specified in Sect. 5.3 are satisfied, then there exists \(\chi < 1\), independent of the cone parameters,Footnote 6 such that for all \(n \ge n_0\) and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\),
Note that the parameter L is not contracted, although it cannot grow too much. To have a contraction of L we need to use the global properties of the map (some kind of topological mixing, see Sect. 6 for details), while the proof of Proposition 5.1 is based only on local arguments.
Before proving Proposition 5.1 we need some facts concerning the behaviour of the test functions under the dynamics.
5.1 Contraction of test functions
For \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), \(W \in {\mathcal {W}}^s\), \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), and \(W_i \in {\mathcal {G}}_n(W)\), define
where \(J_{W_i}T_n\) denotes the Jacobian of \(T_n\) along \(W_i\) with respect to arclength.
The following lemma is a consequence of (H1).
Lemma 5.2
Let \(n\ge 0\) be such that \(C_1^{-\beta } \Lambda ^{-\beta n}<1\), where \(C_1 \le 1\) is from (3.1), and fix \(a > (1- C_1^{-\beta } \Lambda ^{-\beta n})^{-1}C_d \delta _0^{1/3 - \beta }\). For each \(\beta \in (0, 1/3]\), there exist \(\sigma , {\bar{\xi }} < 1\) such that for all \(W \in {\mathcal {W}}^s\) and \(W_i \in {\mathcal {G}}_n(W)\),
-
(a)
\({\widehat{T}}_{n,i} ({\mathcal {D}}_{a, \beta }(W)) \subset {\mathcal {D}}_{\sigma a, \beta }(W_i)\);
-
(b)
\(\rho _{W_i,a, \beta } ({\widehat{T}}_{n,i} \psi _1, {\widehat{T}}_{n,i} \psi _2) \le {\bar{\xi }} \rho _{W, a , \beta }(\psi _1, \psi _2)\) for all \(\psi _1, \psi _2 \in {\mathcal {D}}_{a, \beta }(W)\).
Proof
(a) We need to measure the log-Hölder norm of \({\widehat{T}}_{n,i} \psi \) for \(\psi \in {\mathcal {D}}_{a, \beta }(W)\). For \(x, y \in W_i\), recalling (3.1), we estimate,
where we have used (3.1) and (3.5) as well as the fact that \(\beta \le 1/3\). This proves the first statement of the lemma with \(\sigma = C_1^{-\beta } \Lambda ^{-\beta n} + a^{-1} C_d \delta _0^{1/3-\beta }\).
(b) Using Lemma 4.1, if \(\psi _1, \psi _2 \in {\mathcal {D}}_{\sigma a, \beta }(W_i)\), then,
Thus the diameter of \({\mathcal {D}}_{\sigma a, \beta }(W_i)\) is finite in \({\mathcal {D}}_{a, \beta }(W_i)\). Part (b) of the lemma then follows from [L95a, Theorem 1.1], with \({\bar{\xi }} = \tanh (K/4) < 1\). \(\square \)
Corollary 5.3
Let \(n_1\) denote the least positive integer satisfying \(C_1^{-\beta } \Lambda ^{-\beta n_1}<1\) and \(a C_1^{-\beta } \Lambda ^{-\beta n_1} + C_d \delta _0^{1/3 - \beta } < a\). Define \(\xi = {\bar{\xi }}^{\frac{1}{2n_1}}<1\). Then for \(W \in {\mathcal {W}}^s\), \(n \ge n_1\) and \(W_i \in {\mathcal {G}}_n(W)\),
Proof
The proof follows immediately from Lemma 5.2 once we decompose \(n = kn_1 + r\), where \( r \in [0, n_1)\) and write
Each of the operators \({\widehat{T}}_{n_1, T_{jn_1+r}(W_i)}\) satisfies Lemma 5.2 with the same \(\sigma \) and \({\bar{\xi }}\). The corollary then follows using the observation that \({\bar{\xi }}^{\lfloor n/n_1 \rfloor } \le \xi ^n\), \(\forall n \ge n_1\). \(\square \)
It is important for what follows that the contractive factor \({\bar{\xi }}<1\) is explicitly given in terms of the diameter K, which depends only on a, \(\sigma \), \(\delta _0\) and \(\beta \), but not on \(\delta \). While \(n_1\) depends on the parameter choice \(\beta \), it also is independent of \(\delta \).
In what follows, we require \(n_0 \ge n_1\) by definition, so that Lemma 5.2 and Corollary 5.3 will hold for all \(n \ge n_0\).
5.2 Proof of Proposition 5.1
This section is devoted to the proof of Proposition 5.1.
5.2.1 Preliminary estimate on L
For \(W\in {\mathcal {W}}^s\), recalling Defintion 3.2, we denote by \(Sh_n(W; \delta )\) the elements of \({\mathcal {G}}_n(W)\) of length less than \(\delta \) and by \(Lo_n(W; \delta )\) the elements of \({\mathcal {G}}_n(W)\) of length at least \(\delta \).
Lemma 5.4
Fix \(\delta \in (0, \delta _0/3)\) so that \(4A \delta \delta _0^{-1} {{\bar{C}}}_0 \le 1/4\), then, for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(n \ge n_0\),
Proof
Let \(W \in {\mathcal {W}}^s(\delta )\), \(\psi \in {\mathcal {D}}_{a,\beta }(W)\). Then,
Now since \(\psi \circ T_n J_{W_i}T_n \in {\mathcal {D}}_{a, \beta }(W_i)\) by Lemma 5.2, we subdivide elements \(W_i \in Lo_n(W; \delta )\) into curves \(U^i_\ell \) having length between \(\delta \) and \(2\delta \) and use the definition of \({|||}f {|||}_+\) on each such curve to estimate,
To estimate the short pieces, we apply (4.7), change variables again and use \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), and finally apply Lemma 3.3(b) since \(Sh_n(W;\delta ) \subset {\mathcal {G}}_n(W)\), to estimate

Putting these estimates together in (5.2) and since \(|W| \ge \delta \) implies  , we obtain,
, we obtain,
Now (4.9) implies \(e^{a(2\delta )^\beta } \le 2\), and our choices of \(n_0\) and \(\delta \) imply \(2A\max \{ {{\bar{C}}}_0 \delta \delta _0^{-1} , C_0 \theta _1^{n_0} \} \le 1/4\), which yields the required estimate on \({|||}{\mathcal {L}}_n f {|||}_+\) for all \(n \ge n_0\).
For the bound on \({|||}{\mathcal {L}}_n f {|||}_-\), we perform a similar estimate, except noting that for \(W_i \in Lo_n(W; \delta )\),
we follow (5.2) to estimate,
Again using our choice of \(n_0\) and \(\delta \), we have \(4AC_0 \theta _1^n \le 1/4\) and \(4A \delta \delta _0^{-1} {{\bar{C}}}_0 \le 1/4\), which yields \({|||}{\mathcal {L}}_n f {|||}_- \ge \frac{1}{2} {|||}f {|||}_-\). \(\square \)
In particular the above implies the estimate: for all \(n \ge n_0\),
5.2.2 Contraction of the parameter A.
We prove that the parameter A contracts in (4.7). Choose \(f \in {\mathcal {C}}_{c, A, L}(\delta )\). Let \(W \in {\mathcal {W}}^s\) with \(|W| \le 2\delta \), \(\psi \in {\mathcal {D}}_{a,\beta }(W)\) and \(x \in W\). From now on, we will refer to \(Lo_n(W; \delta )\) and \(Sh_n(W; \delta )\) as simply \(Lo_n(W)\) and \(Sh_n(W)\). We follow (5.2) to write

where in the second line we have used (4.7) for the sum on short pieces. Since \(|W| \le 2\delta \), the first sum above is bounded by

For the sum on short pieces, we use Lemma 3.3(b) and the Hölder inequality to estimateFootnote 7
Combining these two estimates with Lemma 4.2 yields,

This contracts the parameter A if \(2L A^{-1} + e^{a(2\delta )^\beta } ( 2{{\bar{C}}}_0 \delta \delta _0^{-1} + C_0 \theta _1^n )^{1-q} <1\), which we can achieve if \(e^{a(2\delta )^\beta } \le 2\),
Remark that since \(L \ge 1\), we have \(A > 4\), and so according to the assumption of Lemma 5.4, \(2 {{\bar{C}}}_0 \delta \delta _0^{-1} \le 1/32\). Moreover, \(C_0 \theta _1^{n_0} \le 1/64\) by choice of \(n_0\), and since \(1-q \ge 1/2\), the second condition in (5.5) is always satisfied under the assumption of Lemma 5.4.
5.2.3 Contraction of the parameter c
Finally, we verify the contraction of c via (4.8). Let \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(W^1, W^2 \in {\mathcal {W}}^s\) with \(|W^k| \le 2 \delta \) and \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \). Take \(\psi _k \in {\mathcal {D}}_{a, \alpha }(W^k)\) with \(d_*(\psi _1, \psi _2) = 0\).
Without loss of generality we can assume \(|W^2|\ge |W^1|\) and  . Next, note that cone condition (4.7) implies (see Lemma 5.4)
. Next, note that cone condition (4.7) implies (see Lemma 5.4)

It follows that the contraction of the parameter c is trivial for \( |W^2|^q \le \delta ^{q-\gamma } \frac{d_{{\mathcal {W}}^s}(W^1,W^2)^{\gamma }c}{8}\). Thus it suffices to consider the case
Remark that by definition, \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \) implies \(I_{W_1} \cap I_{W_2} \ne \emptyset \). To proceed, define \(C_s := \sqrt{1 + ({\mathcal {K}}_*^{-1} + \tau _*^{-1})^2 }\), which depends on the maximum absolute value of the slopes of curves in the stable cone defined in (3.1). We assume,
Next, for any two manifolds \(U^i\in {\mathcal {W}}^s_-(\delta )\) defined on the intervals \(I_i\) with \(J=I_1\cap I_2\), by the distance Definition (4.2) we have,
Since  , we have \(|\psi _1|_\infty \le e^{a(2\delta )^\alpha }\). On the other hand, since \(I_{W^1} \cap I_{W^2} \ne \emptyset \) and \(d_*(\psi _1, \psi _2)=0\), there must exist \(r \in I_{W^1} \cap I_{W^2}\) such that \(\psi _1 \circ G_{W^1}(r) \Vert G_{W^1}'(r) \Vert = \psi _2 \circ G_{W^2}(r) \Vert G_{W^2}'(r) \Vert \). Thus since,
, we have \(|\psi _1|_\infty \le e^{a(2\delta )^\alpha }\). On the other hand, since \(I_{W^1} \cap I_{W^2} \ne \emptyset \) and \(d_*(\psi _1, \psi _2)=0\), there must exist \(r \in I_{W^1} \cap I_{W^2}\) such that \(\psi _1 \circ G_{W^1}(r) \Vert G_{W^1}'(r) \Vert = \psi _2 \circ G_{W^2}(r) \Vert G_{W^2}'(r) \Vert \). Thus since,
where we use \(\delta < 1\), we estimate,
Then recalling Remarks 4.4 and (4.9), it follows that
Putting this together with (5.8) and using \(\int _{W_1} \psi _1 = |W_1|\), we estimate,
where we have used (4.9), \(3\delta \le \delta _0\le 1/2\le C_s/2\) and \(\alpha >\beta \).
Hence, recalling Lemmas 5.4 and (5.4), \(d_{{\mathcal {W}}^s}(W^1,W^2)\le \delta \) and using (5.6), (5.7) and (5.10), we have

To conclude it suffices then to compare \(\int _{W^1} {\mathcal {L}}_n f \, \psi _1\) and \(\int _{W^2} {\mathcal {L}}_n f \, \psi _2\). To this end, define \({\mathcal {G}}_n^\delta (W^k)\) as the nth generation of pieces in \(T_n^{-1}W^k\) as in Definition 3.2, but with pieces subdivided between length \(\delta \) and \(2\delta \) rather than \(\delta _0/2\) and \(\delta _0\). We create partitions of \({\mathcal {G}}_n^\delta (W^k)\) into ‘matched’ and ‘unmatched’ pieces as follows (see Fig. 1). For each curve \(W^1_i \in {\mathcal {G}}_n^\delta (W^1)\), we construct a foliation of vertical line segments \(\{ \ell _x \}_{x \in W^1_i}\) centered at x and having length at most \(3C_1 \Lambda ^{-n+1} d_{{\mathcal {W}}^s}(W^1, W^2)\) such that their images under \(T_n\) either end on a singularity curve in \({\mathcal {S}}_{-n}^{{\mathbb {H}}}\) or, if not cut by a singularity, have length \(3 d_{{\mathcal {W}}^s}(W^1, W^2)\), with length at least \(d_{{\mathcal {W}}^s}(W^1, W^2)\) on each side of \(T_n(x)\).
In the latter case, this implies that \(\ell _x\) intersects a unique homogeneous element of \(T_n^{-1}W^2\). Let the subcurve \(U^1_{i,+}\subset W^1_i\) be the union of the points x for which this happens and let \(U^2_{i,+}=\{\ell _x\cap T_n^{-1}W^2\}_{x\in U_{i,+}}\) be the corresponding subcurve in \(T_n^{-1}W^2\).Footnote 8 Since \(U^k_{i,+}\) has length at most \(2\delta \), then \(U^2_{i,+}\) can intersect at most 3 elements of \({\mathcal {G}}_n^\delta (W^2)\), due to the possible different ways in which long pieces have been split in \({\mathcal {G}}_n^\delta (W^1)\) and \({\mathcal {G}}_n^\delta (W^2)\). We call \(U^2_j\) the elements of \(\{U^2_{i,+}\cap W^2_l\}_{W^2_l\in {\mathcal {G}}_n^\delta (W^2)}\) and set \(U^1_j=\{x\in U^1_{i,+}\;:\; \ell _x\cap U^2_j\ne \emptyset \}\). We call the subcurves \(U^k_j\), \(k=1,2\) ‘matched’, while we call the remaining subcurves \(V^k_j\) ‘unmatched’. Note that, by construction, each \(W_i^k\in {\mathcal {G}}_n^\delta (W^k)\) can contain at most two unmatched elements and at most 3 matched elements. In addition, for \(x \in V^1_j\), either \(T_n(\ell _x)\) intersects \({\mathcal {S}}^{{\mathbb {H}}}_{-n}\) or \(T_n(x)\) is near an end point of \(W^1\). In either case, due to the uniform transversality of stable and unstable cones, \(|T_n(V^1_j)|\) is short in a sense we will make precise below.
Thus we have defined a decomposition of \({\mathcal {G}}_n^\delta (W^k) = \cup _j U^k_j \cup \cup _j V^k_j\), such that \(U^1_j\) and \(U^2_j\) are defined as the graphs of functions \(G_{U^k_j}\) over the same r-interval \(I_j\) for each j.
Using this decomposition, writing \({\widehat{T}}_{n, U^k_j} \psi _k = \psi _k \circ T_n J_{U^k_j}T_n\) and similarly for \({\widehat{T}}_{n, V^k_j}\psi _k\), we have
We estimate the contribution from unmatched pieces first. To do so, we group the \(V^k_j\) as follows. We say \(V^k_j\) is ‘created’ at time \(0 \le i \le n-1\) if i is the smallest t such that either an endpoint of \(T_{n-t}(V^k_j)\) intersects \(T_{\iota _{t+1}}({\mathcal {S}}_0^{\mathbb {H}})\), or \(T_{n-t}(V^k_j)\) is contained in a larger unmatched piece with this property (this second case can happen when both endpoints of \(V^k_j\) do not belong to \({\mathcal {S}}_{T_n}^{{\mathbb {H}}}\)). Due to the uniform transversality of the stable cone with curves in \(T_{\iota _{i+1}}({\mathcal {S}}_0^{\mathbb {H}})\) as well as the uniform transversality of the stable and unstable cones, we have \(|T_{n-i}V^k_j| \le {{\bar{C}}}_3 \Lambda ^{-i} d_{{\mathcal {W}}^s}(W^1, W^2)\), for some constant \({{\bar{C}}}_3 > 0\). Define \(P(i) = \{ j : V^1_j \text{ created } \text{ at } \text{ time } i \}\).
For ease of notation, when we change variables, we will adopt the following notation for \(n \ge 1\), \(k \ge 0\),
In this notation, \(T_{n,0} = T_n\) and \(T_n = T_{n, n-k} \circ T_{n-k}\).
Although we would like to change variables to estimate the contribution on the curves \(T_{n-i}(V^1_j)\) for \(j \in P(i)\), this is one time step before such cuts would be introduced according to our definition of \({\mathcal {G}}_n^\delta (W)\), so Lemma 3.3 would not apply since there may be many such \(T_{n-i}(V^1_j)\) for each \(W^1_\ell \in {\mathcal {G}}_i^\delta (W^1)\). However, there can be at most two curves \(T_{n-i-1}(V^1_j)\), \(j \in P(i)\), per element of \(W^1_\ell \in {\mathcal {G}}_{i+1}^\delta (W^1)\), so we will change variables to estimate the contribution from curves of the form \(T_{n-i-1}(V^1_j)\) instead. We have two cases.
Case 1. The curve in \(T_{\iota _{i+1}}({\mathcal {S}}_0^{\mathbb {H}})\) that creates \(V^1_j\) at time i is the preimage of the boundary of a homogeneity strip. Then \(T_{n-i-1}V^1_j\) still enjoys uniform transversality with the boundary of the homogeneity strip and the unstable cone, and so \(|T_{n-i-1}V^1_j| \le {{\bar{C}}}_3 \Lambda ^{-i-1} d_{{\mathcal {W}}^s}(W^1, W^2)\) as before.
Case 2. The curve in \(T_{\iota _{i+1}}({\mathcal {S}}_0^{\mathbb {H}})\) that creates \(V^1_j\) at time i is not the preimage of the boundary of a homogeneity strip. Then \(V^1_j\) undergoes bounded expansion from time \(n-i\) to time \(n-i-1\). Thus \(|T_{n-i-1}(V^1_j)| \le C {{\bar{C}}}_3 \Lambda ^{-i} d_{{\mathcal {W}}^s}(W^1, W^2)\), where \(C>0\) depends only on our choice of \(k_0\), the minimum index of homogeneity strips.
In either case, we conclude that \(|T_{n-i-1}(V^1_j)| \le C_3 \Lambda ^{-i} d_{{\mathcal {W}}^s}(W^1, W^2)\), for a uniform constant \(C_3>0\). Also, since \(T_{n-i-1}(V^k_j)\) is contained in an element of \({\mathcal {G}}_{n-i-1}^\delta (W)\), it follows that all such curves have length at most \(2 \delta \), thus we may apply (4.7),
where we have used Lemma 3.3-(b) for the sum over \(j \in P(i)\) since there are at most two curves \(T_{n-i-1}(V^1_j)\) for each element \(W^1_\ell \in {\mathcal {G}}_{i+1}^\delta (W)\).Footnote 9
Since \(n \ge 2n_0\), we have either that \(i+1 \ge n_0\) or \(n - (i+1) \ge n_0\). In the former case, \({|||}{\mathcal {L}}_{n-i-1}f {|||}_- \le 2 {|||}{\mathcal {L}}_n f {|||}_-\) by Lemma 5.4. In the latter case,
where we have used Lemma 5.4 twice, once on \({|||}{\mathcal {L}}_{n-i-1}f {|||}_+\) and once on \({|||}f {|||}_-\). Since the latter estimate (5.14) is the larger of the two, we may use it for all i.
Also, using the assumption that \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \) and (5.7) yields,
Collecting these estimates and summing over the exponential factors yields (since the estimate for \(V^2_j\) is the same),
for some uniform constant \(C_4\) depending only on \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and not on the parameters of the cone.
Next, we estimate the contribution on matched pieces \(U^k_j\). To do this, we will need to change test functions on the relevant curves. Define the following functions on \(U^1_j\),
Note that \(d_*({\widehat{T}}_{n, U^2_j} (\psi _2), {\widetilde{T}}_{n, U^2_j} (\psi _2))=0\) by construction. Also we define
We will need the following lemma to proceed.
Lemma 5.5
If \(c> 4(1+M_0)^q\), \(M_0\) is defined in (5.28), then there exists \(C_5 \ge 1\), independent of n, \(W^1\) and \(W^2\) satisfying (5.6), such that for each j,
-
(a)
\(\displaystyle d_{{\mathcal {W}}^s}(U^1_j, U^2_j) \le C_5 \Lambda ^{-n} d_{{\mathcal {W}}^s}(W^1, W^2) \,\) ;
-
(b)
\(\displaystyle e^{-C_5 d_{{\mathcal {W}}^s}(W^1, W^2)^\alpha }\le \frac{{\widehat{T}}_{n, U^1_j} \psi _1(x)}{{\widetilde{T}}_{n, U^2_j} \psi _2(x)} \le e^{C_5 d_{{\mathcal {W}}^s}(W^1, W^2)^\alpha }\quad \forall x \in U^1_j \,\) ;
-
(c)
setting \(B= 8 \left[ C_5a^{-1}\right] ^{\frac{\alpha -\beta }{\alpha }}d_{{\mathcal {W}}^s}(W^1, W^2)^{\alpha -\beta }\) we have \(\psi ^\Delta _{i,j}+B\psi _j^-\in {\mathcal {D}}_{a,\beta }(U^1_j)\), \(i =1, 2\).
Moreover, \({\widetilde{T}}_{n, U^2_j} \psi _2\) and \(\psi _j^-\) belong to \({\mathcal {D}}_{a,\alpha }(U^1_j)\).
We postpone the proof of the lemma and use it to conclude the estimates of this section.
For future use note that Lemma 5.5(b) implies
Observe that since \(\psi _{k,j}^\Delta + B \psi _j^-, \psi _j^- \in {\mathcal {D}}_{a,\beta }(U^1_j)\), \(k=1,2\), recalling (4.10) we may estimate,

Since \(d_*({\widehat{T}}_{n, U^2_j} \psi _2, {\widetilde{T}}_{n, U^2_j} \psi _2) =0\) by construction, and recalling Remark 4.4, Lemma 5.5(c), condition (4.7), and (5.17), (5.18),

where for the first term, we have used that \(|{\widehat{T}}_{n, U^1_j} \psi _1 - {\widetilde{T}}_{n, U^2_j} \psi _2 | = \psi _{1, j}^\Delta + \psi _{2,j}^\Delta \) in order to apply (5.19), and for the second and third terms we used that \({\widetilde{T}}_{n, U^2_j}\psi _2 \in {\mathcal {D}}_{a,\alpha }(U^1_j)\) by Lemma 5.5 to apply cone conditions (4.8) and (4.7), respectively. Then, recalling Lemma 3.3(b), (5.9) and (4.9), and using that by construction, there are at most 3 curves \(U^2_j\) in each element of \({\mathcal {G}}_n^{\delta }(W^2)\), we can estimate

Next, recalling (5.8), we haveFootnote 10
provided we impose
where \(C_5\) is from Lemma 5.5-(a) and \(\Lambda \) is defined in (3.1). Moreover, remembering the definition of B in Lemma 5.5-(c) and Eq. (5.18),

where we have used the assumptions \(\alpha -\beta \ge \gamma \) and \(a>1\).
Again using (5.8) and Lemma 5.5-(a) we have
Inserting (5.21), (5.23) and (5.24) in (5.20) and recalling Lemmas 5.4 and 5.5-(a) yields,
Then using this estimate in (5.11), and recalling (5.12) and (5.15) yields

which yields the wanted estimate, provided
5.2.4 Proof of Lemma 5.5
Proof
(a) This is [DZ2, Lemma 3.3].
(b) Recall that \(U^k_j\) is defined as the graph of a function \(G_{U^k_j}(r) = (r, \varphi _{U^k_j}(r))\), for \(r \in I^k_j\), \(k = 1,2\). Due to the vertical matching, we have \(I^1_j = I^2_j\).
Now for \(x \in U^1_j\), let \(r \in I^1_j\) be such that \(G_{U^1_j}(r) = x\). Set \({\bar{x}}= G_{U^2_j}(r)\) and note that x and \({\bar{x}}\) lie on the same vertical line in M since \(U^1_j\) and \(U^2_j\) are matched. Thus by (3.6),
where \(M_0\) is a constant depending only on the maximum and minimum slopes in \(C^s\) and \(C^u\).
Next, for \(x \in U^1_j\) consider
Let \(T_n(x)=(r,G_{W^1}(r))\) and \(T_n({{\bar{x}}})=({{\bar{r}}},G_{W^2}({{\bar{r}}}))\), then
If \(r\in I_{W^2}\), then since \(d_*(\psi _1, \psi _2)=0\),
Next, since \(\Vert G_{W^1}' - G_{W^2}' \Vert = |\varphi '_{W^1} - \varphi '_{W^2}|\) and \(\Vert G_{W^k}' \Vert \ge 1\), we have
Similarly, \(\frac{\Vert G'_{U^1_j} \Vert \circ G_{U^1_j}^{-1}(x)}{\Vert G'_{U^2_j} \Vert \circ G_{U^1_j}^{-1}(x)} \le e^{d_{{\mathcal {W}}^s}(U^1_j, U^2_j)}\). Hence, using part (a) of the lemma and assuming
yields
The same estimate holds if \({{\bar{r}}} \in I_{W^1}\). Otherwise it must be that
but then, since \(|I_{W^1}\Delta I_{W^2}|\le d_{{\mathcal {W}}^s}(W^1,W^2)\) we would have \(|W^2|\le (1+M_0) d_{{\mathcal {W}}^s}(W^1,W^2)\), which violates (5.6) together with the assumption, provided
The estimates with the opposite sign follow similarly. Putting together these estimates yields part (b) of the lemma with \(C_5 = M_0C_d \delta ^{1/3 - \alpha } + aM_0^\alpha + 2\).
(c) As noted in (5.18), by (b) it immediately follows that
Next, for \(x, y \in U^1_j\), let \({\bar{x}}= G_{U^2_j} \circ G_{U^1_j}^{-1}(x)\), \({\bar{y}}= G_{U^2_j} \circ G_{U^1_j}^{-1}(y)\), and note these are well-defined due to the vertical matching between \(U^1_j\) and \(U^2_j\). Let \(r = G_{U^1_j}^{-1}(x)\) and \(s = G_{U^1_j}^{-1}(y)\). Recalling (4.4), we have
and similarly for \(\Vert G'_{U^2_j} \Vert \). Using this estimate together with the proof of Lemma 5.2(a),
since \(d({\bar{x}}, {\bar{y}}) \le M_0 d(x,y)\) and provided
To abbreviate what follows, let us denote \(g_1 = {\widehat{T}}_{n, U^1_j} \psi _1\) and \(g_2 = {\widetilde{T}}_{n, U^2_j} \psi _2\). Then, given \(x,y\in U^1_j\), we have \(\psi _j^-(x)=g_{k(x)}\), \(\psi _j^-(y)=g_{k(y)}\). If \(k(x)=k(y)\), then, by Lemma 5.2(a) and (5.31),
If \(k(x)\ne k(y)\), then without loss of generality, we can take \(k(x)=1\) and \(k(y)=2\). By definition, \(g_1(x) \le g_2(x)\) and \(g_2(y) \le g_1(y)\). Hence,
It follows that \(\psi _j^-\in {\mathcal {D}}_{a,\alpha }(U^1_j)\), and by (5.31), \({\widetilde{T}}_{n, U^2_j} \psi _2 \in {\mathcal {D}}_{a, \alpha }(U^1_j)\).
Then, for each \(1>B\ge 2 C_5 d_{{\mathcal {W}}^s}(W^1, W^2)^\alpha \) and \(x,y\in U^1_j\),
provided \(8 B^{-1}C_5 d_{{\mathcal {W}}^s}(W^1, W^2)^\alpha \le a d(x,y)^\beta \) and
It remains to consider the case \(8 B^{-1}C_5 d_{{\mathcal {W}}^s}(W^1, W^2)^\alpha \ge a d(x,y)^\beta \). Again we must split into two cases. If \(k(x)=k(y)=k\), then, setting \(\{\ell \}=\{1,2\}\setminus \{k\}\),
provided that
That is,
The second case is \(k=k(x)\ne k(y)=\ell \). In this case, there must exist \({{\bar{x}}} \in [x,y]\) such that \(\psi _j^-({\bar{x}}) = g_1({\bar{x}}) = g_2({\bar{x}})\). Then,
by the estimate (5.34). A similar estimate holds for \(\psi _{k,j}^\Delta \). It follows that we can choose
and have \(\psi ^\Delta _{i,j}+B\psi _j^-\in {\mathcal {D}}_{a,\beta }(U^1_j)\). \(\square \)
5.3 Conditions on parameters
In this section, we collect the conditions imposed on the cone parameters during the proof of Proposition 5.1. Recall the conditions on the exponents stated before the definition of \({\mathcal {C}}_{c,A,L}(\delta )\): \(\alpha \in (0, 1/3]\), \(q \in (0,1/2)\), \(\beta < \alpha \) and \(\gamma \le \min \{ \alpha - \beta , q \}\).
From (4.9) and Lemma 5.4 we require,
From the proof of Lemma 5.4 and Lemma 5.2, we require the following conditions on \(n_0\),
From Lemma 5.2, Corollary 5.3 and the proof of Lemma 5.5, we require
(recall that we have chosen \(n_0 \ge n_1\) after Corollary 5.3).
From the bound on (4.7), we require in (5.5),
For the contraction of c, we require (see (5.7), the proof of Lemmas 5.5 and (5.27))
Finally, in anticipation of (6.21), we require,
These are all the conditions we shall place on the parameters for the cone, except for \(\delta \), which we will take as small as required for the mixing arguments of Sect. 6. Indeed, note that if the above conditions are satisfied for some \(\delta =\delta _*\), then they are satisfied also for all \(\delta \in (0,\delta _*)\).
6 Contraction of L and Finite Diameter
Proposition 5.1 proves that the parameters c and A of the cone \({\mathcal {C}}_{c,A,L}(\delta )\) contract simply as a consequence of the uniform properties (H1)–(H5) for any sequence of maps \((T_{\iota _j})_j \subset {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). In this section, however, we will restrict our sequence of maps to be drawn from a sufficiently small neighborhood of a single map \(T_0 \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) in order to use the uniform mixing properties of maps T close to \(T_0\) to prove that the parameter L also contracts under the sequential dynamics. This is done in two steps. First, in Sect. 6.1, we use a length scale \(\delta _0 \ge \sqrt{\delta }\) and compare averages on the two length scales, \(\delta \) and \(\delta _0\), culminating in Proposition 6.3. This step does not yet require us to restrict our class of maps. Second, in Sect. 6.2, restricting our sequential system to a neighborhood of a fixed map \(T_0\), we obtain a bound on averages in the length scale \(\delta _0\) as expressed in Lemma 6.8. This leads to the strict contraction of L established in Theorem 6.12, which proves Theorem 2.3(a). We prove Theorem 2.3(b) in Sect. 6.3, showing that the cone \({\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) has finite diameter in the cone \({\mathcal {C}}_{c,A,L}(\delta )\) (Proposition 6.13).
6.1 Comparing averages on different length scales
Recall the length scale \(\delta _0\in (0,1/2)\) from (3.8) and that \(\delta < \delta _0/2\). Also, recall that \({\mathcal {W}}^s(\delta _0/2)\) denotes those curves in \({\mathcal {W}}^s\) with length between \(\delta _0/2\) and \(\delta _0\). We choose \(\delta \le \delta _0^2\) and define
By subdividing curves of with length in \([\delta _0/2,\delta _0]\) into curves with length in \([\delta , 2\delta ]\), we immediately deduce the relations,
Lemma 6.1
Assume \(e^{a \delta _0^\beta } \le 2\), from (4.9), and \(A\delta \le \delta _0/4\), from Lemma 5.4.
For all \(n \in {\mathbb {N}}\), \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\) and \(f\in {\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) we have,Footnote 11
Proof
We prove (6.2) by induction on n. It holds trivially for \(n = 0\). We assume the inequality holds for \(0 \le k \le n-1\) and prove the statement for n.
Let \(W \in {\mathcal {W}}^s(\delta _0/2)\). Define \({\widehat{L}}_1(W)\) to be those elements of \({\mathcal {G}}_1(W)\) having length at least \(\delta _0/2\). For \(k > 1\), let \({\widehat{L}}_k(W)\) denote those curves of length at least \(\delta _0/2\) in \({\mathcal {G}}_k(W)\) whose images are not already contained in an element of \({\widehat{L}}_i(W)\) for any \(i = 1, \ldots , k-1\). For \(V_j \in {\widehat{L}}_k(W)\), let \(P_k(j)\) be the collection of indices i such that \(W_i \in {\mathcal {G}}_n(W)\) satisfies \(T_{n-k}W_i \subset V_j\). Denote by \({\mathcal {I}}^0_n(W)\) those indices i for which \(T_{n-k}W_i\) is never contained in an element of \({\mathcal {G}}_k(W)\) of length at least \(\delta _0/2\), \(1 \le k \le n\), and \(\delta \le |W_i| < \delta _0/2\). Let \({\mathcal {I}}_n(W)\) denote the remainder of the indices i for curves in \({\mathcal {G}}_n(W)\), i.e. those curves \(W_i\) of length shorter than \(\delta \) and for which \(T_{n-k}W_i\) is not contained in an element of \({\mathcal {G}}_k(W)\) of length at least \(\delta _0/2\). By construction, each \(W_i \in {\mathcal {G}}_n(W)\) belongs to precisely one \(P_k(j)\) or \({\mathcal {I}}^0_n(W)\) or \({\mathcal {I}}_n(W)\).
Now, for \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), recalling (5.13), we have,
Using this equality, we estimate,
where for the second inequality we have used the inductive hypothesis, and for the second and third we have used Lemmas 3.3(a) and 4.2. This proves the required inequality if \(\delta _0\) is small enough that \(e^{a\delta _0^\beta } \le 2\) and \(\delta \) is small enough that \(A \delta \le \delta _0 /4\), both of which we have assumed.
We prove (6.3) similarly, although now the inductive hypothesis is \({|||}{\mathcal {L}}_k f {|||}_-^0 \ge (1 - 3\sum _{i=1}^{k} C_0 \theta _1^i)\) for each \(k = 0, \ldots , n-1\). We begin with the same decompostion of \({\mathcal {G}}_n(W)\), although we simply drop the terms in \({\mathcal {I}}_n^0(W)\) since they are all positive (see Remark 4.8).
where again we have used Lemmas 3.3(a) and 4.2 as well as the bound \( {|||}f {|||}_- \le {|||}f {|||}_-^0\). This proves the inductive claim, and from this, (6.3) follows from (3.8). \(\square \)
To continue it is useful to set
Next, we have a partial converse of Lemma 6.1.
Lemma 6.2
For all \(n \ge N(\delta )^- \) and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), we have
Proof
The proof follows along the lines of the proof of Lemma 6.1, using the same decomposition into \({\hat{L}}_k(W)\), \({\mathcal {I}}_n^0(W)\) and \({\mathcal {I}}_n(W)\), except that now we begin with \(W \in {\mathcal {W}}^s(\delta )\) and \(\psi \in {\mathcal {D}}_{a, \beta }(W)\). We have,
which proves the first inequality, given our assumed bound on n. Note that the ratio \(\delta _0/\delta \) appears in the second term since \(|W_i| \le \delta _0/2\), while \(|W| \ge \delta \).
The second inequality follows similarly, again along the lines of Lemma 6.1.
and our bound on n suffices to complete the proof of the lemma. \(\square \)
Proposition 6.3
For all \(n \ge N(\delta )^-\) and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), either,
or
Proof
Since \(n \ge N(\delta )^- \ge n_0\), we may apply both Lemmas 5.4 and 6.2. Now, by Lemma 6.2,
applying Lemma 6.1 to the first term and Lemma 5.4 to the second. This yields immediately, \({|||}{\mathcal {L}}_n f {|||}_- \ge \frac{9}{20} {|||}f {|||}_-^0\), which is the final inequality in the statement of the lemma.
Now consider the following alternatives. If \({|||}{\mathcal {L}}_n f {|||}_+ \le \frac{2}{5} {|||}f {|||}_+\), then
proving the first alternative. On the other hand, if \({|||}{\mathcal {L}}_n f {|||}_+ \ge \frac{2}{5} {|||}f {|||}_+\), then using Lemmas 6.2, 6.1 and 5.4,
which yields the second alternative. \(\square \)
6.2 Mixing implies contraction of L
The importance of Proposition 6.3 is that either L contracts within \(N(\delta )^-\) iterates or we can compare ratios of integrals on the length scale \(\delta _0\) (which is fixed independently of \(\delta \)). In the latter case we will use the uniform mixing property of maps \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) in order to compare the value of \(\int _W {\mathcal {L}}_n f \psi \) for different W of length approximately \(\delta _0\). To this end, we will define a Cantor set \(R_*\) comprised of local stable and unstable manifolds of a certain length in order to make our comparison when curves cross this set.
We begin by recalling the open neighborhoods in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) defined by (2.3).
Let \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), and for \(0< \kappa < \frac{1}{2} \min \{ \tau _*, {\mathcal {K}}_* \}\), define
Recall the index set corresponding to \({\mathcal {F}}(T, \kappa )\) is \({\mathcal {I}}(T, \kappa ) \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\). Thus \(\iota \in {\mathcal {I}}(T, \kappa )\) if and only if \(T_\iota \in {\mathcal {F}}(T, \kappa )\).
Lemma 6.4
For any \(\kappa \in \big (0, \frac{1}{2} \{ \tau _*, {\mathcal {K}}_* \} \big )\), the set \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) can be covered by finitely many sets \({\mathcal {F}}(T, \kappa )\), \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
Proof
Each \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) is associated with a billiard table \(Q \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\). Such billiard tables have exactly K boundary curves with \(C^3\) norm uniformly bounded by \(E_*\). Since the torus is compact and the distance \( \mathbb {d}(Q, {\widetilde{Q}})\) defined in Sect. 2.1 measures distance only in the \(C^2\) norm, the set \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) is compact in the distance \(\mathbb {d}\). Thus for each \(\kappa >0\), there exists \(N_\kappa \in {\mathbb {N}}\) and a set \(\{ Q_{\iota _j} \}_{j =1}^{N_\kappa } \subset {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) such thatFootnote 12\(\cup _j {\mathcal {Q}}(Q_{\iota _j}, E_*; \kappa ) \supset {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\). Since \({\mathcal {F}}(Q_{\iota _j}, E_*; \kappa ) \cap {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*) = {\mathcal {F}}(T_{\iota _j}, \kappa )\), this yields the required covering. \(\square \)
Remark 6.5
The primary reason we restrict to \({\widetilde{T}}\in {\mathcal {F}}(T, \kappa )\) is to conclude Lemma 6.6(b) for a fixed time \(n_*\) and rectangle \(R_*\). This will enable us to make a type of ‘matching’ argument for our sequential system, the main comparison being established in Lemma 6.8.
The reader familiar with the subject will notice that the matching described here requires weaker properties than the usual arguments used in coupling. After stable curves are forced to cross a fixed rectangle by Lemma 6.6, the ‘matched’ pieces are not Cantor sets, but rather full curves. The cone technique thus enables us to bypass the use of real stable/unstable manifolds used in classical coupling arguments for billiards (see [CM, Section 7]), and even the modified coupling developed for sequential systems which only couples for a finite time along approximate invariant manifolds, as in [SYZ], both of which require a more delicate use of the structure of invariant manifolds, in particular control of the gaps in the Cantor sets used for coupling.
For a fixed \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), we construct an approximate rectangle D in M, contained in a single homogeneity strip, whose boundaries are comprised of two local stable and two local unstable manifolds for T as follows. Choose \(\bar{\delta }_0>0\) and \(x \in M\) such that dist\((T^{-n}x, {\mathcal {S}}_1^{{\mathbb {H}}}) \ge {\bar{\delta }}_0 \Lambda ^{- |n|}\) for all \(n \in {\mathbb {Z}}\). This implies that the homogenous local stable and unstable manifoldsFootnote 13 of x, \(W^s_{{\mathbb {H}}}(x)\) and \(W^u_{{\mathbb {H}}}(x)\), have length at least \(\bar{\delta }_0\) on either side of x. By the Sinai Theorem applied to homogeneous unstable manifolds (see, for example, [CM, Theorem 5.70]), we may choose \(\delta _0 < \bar{\delta }_0\) such that more than 0.99 of the measure of points in \(W^u_{{\mathbb {H}}}(x) \cap B_{2.1\delta _0}(x)\) have homogeneous local stable manifolds having length at least \(2.1\delta _0\) on both sides of \(W^u_{{\mathbb {H}}}(x)\), and analogously for the points in \(W^s_{{\mathbb {H}}}(x) \cap B_{2.1 \delta _0}(x)\). Since these subsets of \(W^{s/u}_{{\mathbb {H}}}(x)\) are closed, there exist two extreme points on each manifold whose unstable/stable manifolds define a solid rectangle, which we will denote by \(D'_{2\delta _0}\). By choice of \(\delta _0\), the stable and unstable manifolds comprising \(\partial D'_{2\delta _0}\) have length at least \(4 \delta _0\). There must exist a rectangle \(D_{2\delta _0}\) fully crossing \(D'_{2\delta _0}\) in the stable direction and with boundary comprising two stable and two unstable manifolds, such that the unstable diameter of \(D_{2\delta _0}\) is between \(\delta _0^4\) and \(2\delta _0^4\),Footnote 14 and the set of local homogeneous stable and unstable manifolds fully crossing \(D_{2\delta _0}\) comprise at least 9/10 of the measure of \(D_{2\delta _0}\) with respect to \(\mu _{\tiny {\text{ SRB }}}\); otherwise, at most 9/10 of the measure of \(W^u_{{\mathbb {H}}}(x) \cap B_{2.1\delta _0}(x)\) would have long stable manifolds on either side of \(W^u_{{\mathbb {H}}}(x)\), contradicting our choice of \(\delta _0\). Similarly, define \(D_{\delta _0} \subset D_{2\delta _0}\) to have precisely the same stable boundaries, but stable diameter between \(1.8 \delta _0\) and \(2 \delta _0\) rather than \(4 \delta _0\), still centered at \(W^u_{\mathbb {H}}(x)\). See Fig. 2 for a pictorial illustration of the above construction.
Let \({\mathfrak {S}}^{s/u}(D_{\delta _0})\) denote the maximal set of stable/unstable manifolds that fully cross \(D_{\delta _0}\), including its boundary curves. Define \(R_*^{\delta _0} = {\mathfrak {S}}^s(D_{\delta _0}) \cap {\mathfrak {S}}^u(D_{\delta _0})\) to be the Cantor rectangle defined by the intersection of those maximal families. Define \(R_*^{2\delta _0}\) analogously with respect to \({\mathfrak {S}}^{s/u}(D_{2\delta _0})\).
By construction, \(\mu _{\tiny {\text{ SRB }}}(R_*^{\delta _0}) > (0.9)^2 \mu _{\tiny {\text{ SRB }}}(D_{\delta _0}) \approx \delta _0^5\). Below, we denote \(D_{\delta _0}\) by \(D(R_*^{\delta _0})\) since it is the minimal solid rectangle that defines \(R_*^{\delta _0}\).
We say that a stable curve \(W \in {\mathcal {W}}^s\) properly crosses a Cantor rectangle R (in the stable direction) if W intersects the interior of the solid rectangle D(R), but does not terminate in D(R), and does not intersect the two stable manifolds contained in \(\partial D(R)\).
Lemma 6.6
For \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), let \(R_*^{\delta _0} = R_*^{\delta _0}(T)\) be the Cantor rectangle constructed above.
-
(a)
There exists \(n_* \in {\mathbb {N}}\), depending only on \(\delta _0\) and \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), such that for all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and all \(W \in {\mathcal {W}}^s\) withFootnote 15\(|W| \ge \delta _0/(6 {{\bar{C}}}_0)\), and all \(n \ge n_*\), \(T^{-n}W\) contains a connected, homogeneous component that properly crosses \(R_*^{\delta _0}(T)\).
-
(b)
There exists \(\kappa >0\) such that for all \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and all \(\{ \iota _j \}_{j=1}^{n_*} \subset {\mathcal {I}}(T, \kappa )\), \(T_{n_*}^{-1}W\) contains a connected, homogeneous component that properly crosses \(R_*^{\delta _0}(T)\).
Proof
First we fix \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and prove items (a) and (b) of the lemma for this T, i.e. we demonstrate that such an \(n_*\) and \(\kappa \) exist depending on T. Then we show how Lemma 6.4 implies that \(n_*\) and \(\kappa \) can be chosen uniformly for \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
a) Fix \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). By [CM, Lemma 7.87], there exist finitely many Cantor rectanglesFootnote 16\({\mathcal {R}}(\delta _0) = \{ R_1, \ldots , R_k \}\), with \(\mu _{\tiny {\text{ SRB }}}(R_i) > 0\) for each i, such that any stable curve \(W \in {\mathcal {W}}^s\) with \(|W| \ge \delta _0/(6{{\bar{C}}}_0)\) properly crosses at least one of them. Let \(\varepsilon _{{\mathcal {R}}}\) be the minimum length of an unstable manifold in \(R_i\), for any \(R_i \in {\mathcal {R}}(\delta _0)\).
Consider the solid rectangle \({{\bar{D}}}(R_*^{2\delta _0}) \subset D(R_*^{2\delta _0})\) which crosses \(D(R_*^{2\delta _0})\) fully in the stable direction, but comprises the approximate middle 2/3 of \(D(R_*^{2\delta _0})\) in the unstable direction, with approximately 1/3 of the unstable diameter of \(D(R_*^{2\delta _0})\) on each side of \({{\bar{D}}}(R_*^{2\delta _0})\). Similarly, let \(\widetilde{D}(R_*^{2\delta _0}) \subset {{\bar{D}}}(R_*^{2\delta _0})\) denote the approximate middle 1/3 of \(D(R_*^{2\delta _0})\) in the unstable direction. Let \({{\bar{R}}}_*^{2\delta _0} := R_*^{2\delta _0} \cap {\bar{D}}(R_*^{2\delta _0})\) and let \({{\widetilde{R}}}_*^{2\delta _0} := R_*^{2\delta _0} \cap {{\widetilde{D}}}(R_*^{2\delta _0})\). Note that \(\mu _{\tiny {\text{ SRB }}}({{\bar{R}}}_*^{2\delta _0})> \mu _{\tiny {\text{ SRB }}}( {{\widetilde{R}}}_*^{2\delta _0}) > 0\) since \(\mu _{\tiny {\text{ SRB }}}(R_*^{2\delta _0}) > (0.9)^2 \mu _{\tiny {\text{ SRB }}}(D(R_*^{2\delta _0}))\) by construction.
Now given \(W \in {\mathcal {W}}^s\) with \(|W| \ge \delta _0/(6{{\bar{C}}}_0)\), let \(R_i \in {\mathcal {R}}(\delta _0)\) denote the Cantor rectangle which W crosses properly. By the mixing property of T, there exists \(n_i^* > 0\) such that for all \(n \ge n_i^*\), \(T^n(\widetilde{R}_*^{2\delta _0} ) \cap R_i \ne \emptyset \). We may increase \(n_i^*\) if necessary so that \(C_1 \Lambda ^{n_i^*} \delta _0^4/12 \ge \varepsilon _{{\mathcal {R}}}\). We claim that \(T^n({{\bar{R}}}_*^{2\delta _0})\) properly crosses \(R_i\) in the unstable direction for all \(n \ge n_i^*\). If not, then the unstable manifolds comprising \({{\bar{R}}}_*^{2\delta _0}\) must be cut by a singularity curve in \({\mathcal {S}}_1^{{\mathbb {H}}}\) before time \(n_i^*\) (since otherwise they would be longer than \(2 \varepsilon _{{\mathcal {R}}}\) by choice of \(n_i^*\)), and the images of those unstable manifolds must terminate on the unstable manifolds in \(R_i\). But this implies that some unstable manifolds in \(R_i\) will be cut under \(T^{-n}\), a contradiction.
Since \(T^n({{\bar{R}}}_*^{2\delta _0})\) properly crosses \(R_i\) in the unstable direction, it follows that \(T^n(D ({{\bar{R}}}_*^{2\delta _0}))\) contains a solid rectangle \(D_*\) that fully crosses \(D(R_i)\) in the unstable direction (here we use the fact that the stable manifolds of \({{\bar{R}}}_*^{2\delta _0}\) cannot be cut under \(T^n\), as well as that the singularity curves of \(T^n\) can only terminate on other elements of \({\mathcal {S}}_n^{{\mathbb {H}}}\) [CM, Proposition 4.47]). Define \(V = W \cap D_*\) and note that V fully crosses \(D_*\) in the stable direction. In particular, V lies between two stable manifolds in \(R_i\) and thus between two stable manifolds in \(T^n({{\bar{R}}}_*^{2\delta _0})\). Thus \(T^{-n}V\) properly crosses \({{\bar{R}}}_*^{2\delta _0}\), and also \(R_*^{2\delta _0}\), in the stable direction. Since \(R_*^{\delta _0}\) has the same stable boundaries as \(R_*^{2\delta _0}\), but half the stable diameter, then \(T^{-n}V\) also properly crosses \(R_*^{\delta _0}\), as required. Since \({\mathcal {R}}(\delta _0)\) is finite, setting \(n_* = \max _{1 \le i \le k} \{ n_i^* \} < \infty \) completes the proof of part (a) with \(n_* = n_*(T)\) depending on T.
(b) In the proof of part (a), for \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) we constructed a rectangle \({\bar{{\mathcal {R}}}}_*^{2\delta _0}\) and a time \(n_*\) so that for any \(W \in {\mathcal {W}}^s\) and \(n \ge n_*\), there exists \(V \subset W\) such that \(T^{-n}\) is smooth on V and \(T^{-n}V\) properly crosses \({\bar{{\mathcal {R}}}}_*^{2\delta _0}\). Now for \(\{ \iota _j \}_{j=1}^{n_*} \in {\mathcal {I}}(T, \kappa )\), Proposition 2.2(b) guarantees that \(T_{n_*}^{-1}V\) is close to \(T^{-n_*}V\) for \(\kappa \) sufficiently small, except possibly when iterates land in a neighborhood \(N_{C\kappa ^{1/2}}({\mathcal {S}}_{-1}^T \cup {\mathcal {S}}_{-1}^{T_{\iota _j}})\). But in this case, Proposition 2.2(a) implies that for \(T_\iota \in {\mathcal {F}}(T, \kappa )\), the singularity sets \({\mathcal {S}}_{-1}^T\) and \({\mathcal {S}}_{-1}^{T_\iota }\) either differ by at most \(C\kappa ^{1/2}\) or new components are formed in a \(C\kappa ^{1/2}\) neighborhood of \({\mathcal {S}}_0\). By construction, since \({\bar{{\mathcal {R}}}}_*^{2\delta _0}\) has 2/3 the unstable diameter and twice the stable diameter as \({\mathcal {R}}_*^{\delta _0}\), then there exists \(\kappa \), depending only on \(\delta _0\) and \(n_*\), such that \(T_{n_*}^{-1}V\) properly crosses \({\mathcal {R}}_*^{\delta _0}\), as required.
Finally, we show how \(n_*\) and \(\kappa \) can be chosen uniformly in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\). For each \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), parts (a) and (b) yield \(n_*(T)\) and \(\kappa (T)\) with the stated properties. Then the set of open neighborhoods \(\{ {\mathcal {Q}}(Q(T), E_*; \kappa (T)/2) \}_{T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)}\) forms an open cover of \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\), where Q(T) is the billiard table associated with T. By compactness (see the proof of Lemma 6.4) there exists a finite subcover \(\{ {\mathcal {Q}}(Q(T_{\iota _j}), E_*; \kappa (T_{\iota _j})/2 ) \}_{j=1}^{N_\varepsilon }\). For any \(T \in {\mathcal {F}}(T_{\iota _j}, \kappa (T_{\iota _j})/2)\), we have \({\mathcal {F}}(T, \kappa (T_{\iota _j})/2) \subset {\mathcal {F}}(T_{\iota _j}, \kappa (T_{\iota _j}))\). Thus \(n_*(T_{\iota _j})\) and \(\frac{1}{2} \kappa (T_{\iota _j})\) have the desired properties for this T. Setting \(n_* = \max _j n_*(T_{\iota _j})\) proves part (a) and \(\kappa = \frac{1}{2} \min _j \kappa (T_{\iota _j})\) proves part (b) of the lemma. \(\square \)
From this point forward, we fix \(T_0 \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and let \(R_* = R_*^{\delta _0}(T_0)\) as constructed above. We will consider sequences \(\{ \iota _j \}_j \subset {\mathcal {I}}(T_0, \kappa )\), where \(\kappa \) is from Lemma 6.6(b), i.e. we will draw from maps \(T \in {\mathcal {F}}(T_0, \kappa )\).
Lemma 6.7
Let \(W^1, W^2 \in {\mathcal {W}}^s\), \(n \ge 0\) and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T_0, \kappa )\). Suppose \(U_1 \in {\mathcal {G}}_n(W^1)\) and \(U_2 \in {\mathcal {G}}_n(W^2)\) properly cross \(R_*\) and define \({{\bar{U}}}_i = U_i \cap D(R_*)\), \(i=1,2\). Then there exists \(C_7 >0\), depending only on the maximum slope and maximum curvature \(\bar{B}\) of curves in \({\mathcal {W}}^s\), such that \(d_{{\mathcal {W}}^s}({{\bar{U}}}_1, {{\bar{U}}}_2) \le C_7 \delta _0^2\).
Proof
Define a foliation of vertical line segments covering \(D(R_*)\). Due to the uniform transversality of the stable cone with the vertical direction, it is clear that the length of the segments connecting \({{\bar{U}}}_1\) and \({{\bar{U}}}_2\) have length at most \(C_3 \delta _0^4\), where \(C_3>0\) depends only on the maximum slope in \(C^s(x)\). Moreover, the unmatched parts of \({{\bar{U}}}_1\) and \(\bar{U}_2\) near the boundary of \(D(R_*)\) also have length at most \(C_3 \delta _0^4\). See Fig. 3 for an illustration.
Recalling the definition of \(d_{{\mathcal {W}}^s}(\cdot , \cdot )\), it remains to estimate the \(C^1\) distance between the graphs of \({{\bar{U}}}_1\) and \({{\bar{U}}}_2\). Denote by \(\varphi _1(r)\) and \(\varphi _2(r)\) the functions defining \({{\bar{U}}}_1\) and \({{\bar{U}}}_2\) on a common interval \(I = I_{{{\bar{U}}}_1} \cap I_{{{\bar{U}}}_2}\). Let \(\varphi _i' = \frac{d \varphi _i}{dr}\). For \(x \in {{\bar{U}}}_1\) over I, let \({{\bar{x}}} \in {{\bar{U}}}_2\) denote the point on the same vertical line segment as x.
Suppose there exists \(x \in {{\bar{U}}}_1\) over I such that \(|\varphi _1'(r(x)) - \varphi _2'(r({{\bar{x}}}))| > C \delta _0^2\) for some \(C>0\), where r(x) denotes the r-coordinate of \(x = (r,\varphi )\). Since the curvature of each \(U_i\) is bounded by \({{\bar{B}}}\) by definition, we have \(|\varphi _i''| \le {{\bar{B}}} (1+(K_{\max } + \tau _{\min }^{-1})^2)^{3/2} =: {{\bar{C}}}_7\).
Now consider an interval \(J \subset I\) of radius \(\delta _0^2\) centered at r(x). Then \(|\varphi _1'(r) - \varphi _1'(r(x))| \le {{\bar{C}}}_7 |r-r(x)|\) for all \(r \in J\), and similarly for \(\varphi _2'\). Thus,
This in turn implies that there exists \(r \in J\) such that \(|\varphi _1(r) - \varphi _2(r) | \ge (C - 2{{\bar{C}}}_7) \delta _0^4\), which is a contradiction if \(C - 2{{\bar{C}}}_7 > C_3\). This proves the lemma with \(C_7 = 2 {{\bar{C}}}_7 + C_3\). \(\qquad \square \)
Recall that by Lemma 4.1, for \(W\in {\mathcal {W}}^s\) the cone \({\mathcal {D}}_{a, \alpha }(W)\) has finite diameter in \({\mathcal {D}}_{a, \beta }(W)\) for \(\alpha > \beta \), so that
for some constant \(D_0 > 0\) depending only on \(a, \alpha \) and \(\beta \). Without loss of generality, we take \(D_0 \ge 1\).
Lemma 6.8
Suppose \(W^1, W^2 \in {\mathcal {W}}^s\) with \(|W^1|, |W^2| \in [\delta _0/2, \delta _0]\) and \(d_{{\mathcal {W}}^s}(W^1, W^2) \le C_7\delta _0^2\). Assume \(\psi _\ell \in {\mathcal {D}}_{a,\alpha }(W^\ell )\) with \(\int _{W^1} \psi _1 = \int _{W^2} \psi _2 =1\).
Recall that \(\delta \le \delta _0^2\) and let \(\kappa >0\) be from Lemma 6.6. Let \(C>0\) be such that if \(n \ge C \log (\delta _0/\delta )\) then \(C_5 \Lambda ^{-n} \le \delta /\delta _0^2\), where \(C_5\) is from Lemma 5.5. For all n such that \(n \ge C \log (\delta _0/\delta ) \ge 2n_0\) and all \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T_0, \kappa )\), we have
for all \(f\in {\mathcal {C}}_{c, A, L}(\delta )\), provided
Remark 6.9
Since \(\delta \le \delta _0^2\), the condition of Lemma 6.8 will be satisfied if
This will determine our choice of \(\delta _0\).
Proof
We will change variables to integrate on \(T_n^{-1}W^\ell \), \(\ell = 1, 2\). As in Sect. 5.2.3, we split \({\mathcal {G}}_n(W^\ell )\) into matched pieces \(\{ U^\ell _j \}_j\) and unmatched pieces \(\{ V^\ell _j \}_j\). Corresponding matched pieces \(U^1_j\) and \(U^2_j\) are defined as graphs \(G_{U^\ell _j}\) over the same r-interval \(I_j\) and are connected by a foliation of vertical line segments. Following (5.12), we write,
where \({\widehat{T}}_{n,U^\ell _j} \psi _\ell := \psi _\ell \circ T_n \, J_{U^\ell _j}T_n\), and similarly for \({\widehat{T}}_{n,V^\ell _j} \psi _\ell \), \(\ell = 1, 2\).
We perform the estimate over unmatched pieces first, following the same argument as in Sect. 5.2.3 to conclude that \(|T_{n-i-1}V^1_j| \le C_3 \Lambda ^{-i} d_{{\mathcal {W}}^s}(W^1, W^2) \le C_3 C_7 \Lambda ^{-i} \delta _0^2\), for any curve \(V^1_j\) created at time i, \(0 \le i \le n-1\).
Recalling the sets P(i) from Sect. 5.2.3 of unmatched pieces created at time i, we split the estimate into curves P(i; S) if \(|T_{n-i-1}V^1_j| < \delta \) and curves P(i; L) if \(|T_{n-i-1}V^1_j| \ge \delta \).
The estimate over short unmatched pieces is given by (recalling the notation from (5.13)),
where we have used Lemma 3.3-(b), \(|W^1| \in [\delta _0/2, \delta _0]\), and Remark 3.4 to estimate the sum over the Jacobians, as well as (5.14) to estimate \({|||}{\mathcal {L}}_{n-i-1} f {|||}_- \le 3L {|||}{\mathcal {L}}_n f {|||}_-\).
For the estimate over long pieces, we subdivide them into curves of length between \(\delta \) and \(2\delta \) and estimate them by \({|||}{\mathcal {L}}_{n-i-1} f {|||}_+\), then we recombine them to obtain,
where, in third line we used (5.14), and in the fourth line, since \(|W^1| \ge \delta _0/2\), we used Remark 3.4 to drop the second term in Lemma 3.3(b).
Next, we estimate the integrals over the matched pieces \(U^1_j\). We argue as in Sect. 5.2.3, but our estimates here are somewhat simpler since we do not need to show that parameters contract.
We first treat the matched short pieces with \(|U^1_j| < \delta \) much as we did the unmatched ones. By Lemma 5.5, \(d_{{\mathcal {W}}^s}(U^1_j, U^2_j) \le C_5 \Lambda ^{-n} d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \), since we have chosen \(n \ge C \log (\delta _0/\delta )\). Thus if \(|U^1_j| < \delta \) then \(|U^2_j| < 2\delta \), and the analogous fact holds for short curves \(|U^2_j| < \delta \). With this perspective, we call \(U^\ell _j\) short if either \(|U^1_j| < \delta \) or \(|U^2_j| < \delta \). On short pieces, we apply (4.7)
where we have again used Lemmas 3.3(b) and 5.4 for the second inequality. Remark that the same argument holds for \(U^2_j\) with test function \(\psi _2\).
Finally, to estimate the integrals over matched curves with \(|U^1_j|, |U^2_j| \ge \delta \) we follow equation (5.20), recalling (5.16), although we no longer have Lemma 5.5(c) at our disposal,

where we have used (5.24) to estimate \(\left| \frac{|U^2_j|-|U^1_j|}{|U^1_j|}\right| \).
To estimate the first term on the right side above, we use (4.7) and Lemma 4.10,

where we have used \(|U^1_j| \le \delta _0\) in the last line. We may apply (6.6) since \({\widehat{T}}_{n,U^1_j} \psi _1, {\widetilde{T}}_{n,U^2_j} \psi _2 \in {\mathcal {D}}_{a, \alpha }(U^1_j)\) by Lemma 5.5. Now putting the above estimate together with (6.11), recalling \(d_{{\mathcal {W}}^s}(U^1_j, U^2_j) \le \delta \), and using Lemma 3.3-(b) and Remark 3.4 as well as Lemma 5.4, we sum over j to obtain,
Collecting (6.8), (6.9), (6.10) and (6.12), and recalling \(D_0 \ge 1\) and \(A > 4 L\), yields
Now since \(\int _{W^i} \psi _i = 1\), we have \(e^{- a \delta _0^\alpha } \le |W^i| \psi _i \le e^{a \delta _0^\alpha }\). Thus since \(|W^i| \ge \delta _0/3\),
which proves the lemma. \(\square \)
Our strategy will be the following. For \(W^1\), \(W^2 \in {\mathcal {W}}^s(\delta _0/2)\), n sufficiently large and \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T_0, \kappa )\), we wish to compare \(\int _{W^1} {\mathcal {L}}_n f \, \psi _1\) with \(\int _{W^2} {\mathcal {L}}_n f \, \psi _2\), where we normalize \(\int _{W^1} \psi _1 = \int _{W^2} \psi _2 = 1\). By Lemmas 6.6 and 6.7, we find \(U^\ell _i \in {\mathcal {G}}_{n_*}(W^\ell )\), \(\ell = 1, 2\), such that \(U^\ell _i\) properly crosses \(R_*\), and \(d_{{\mathcal {W}}^s}({{\bar{U}}}^1_i, {{\bar{U}}}^2_i) \le C_7 \delta _0^2\), where \({{\bar{U}}}^\ell _i = U^\ell _i \cap D(R_*)\).
Next, for each i, we wish to compare \(\int _{{{\bar{U}}}^1_i} {\mathcal {L}}_{n-n_*} f \, {\widehat{T}}_{n_*, U^1_i} \psi _1\) with \(\int _{{{\bar{U}}}^2_i} {\mathcal {L}}_{n-n_*} f \, {\widehat{T}}_{n_*, U^2_i} \psi _2 \), where, to abbreviate notation, \({\widehat{T}}_{n_*, U^\ell _i} \psi _\ell = \psi _\ell \circ T_{n, n-n_*} J_{U^\ell _i}T_{n, n-n_*}\). However, the weights \(\int _{{\bar{U}}^\ell _i} {\widehat{T}}_{n_*, U^\ell _i} \psi _\ell \) may be very different for \(\ell = 1,2\) since the stable Jacobians along the respective orbits before time \(n_*\) may not be comparable. To remedy this, we adopt the following strategy for matching integrals on curves.
For each curve \(U^\ell _i \in {\mathcal {G}}_{n_*}(W)\) which properly crosses \(R_*\), we redefine \({{\bar{U}}}^\ell _i\) to denote the middle third of \(U^\ell _i \cap D(R_*)\) (and so having length at least \(2\delta _0/3\)). Let \(M^\ell \) denote the index set of such i.
Let \(p^{(\ell )}_i = \int _{{{\bar{U}}}^\ell _i} {\widehat{T}}_{n_*, U^\ell _i} \psi _\ell \), and let \(m_\ell = \sum _{i \in M^\ell } p^{(\ell )}_i\). Without loss of generality, assume \(m_2 \ge m_1\).
We will match the integrals \(\sum _{i \in M^1} \int _{{{\bar{U}}}^1_i} {\mathcal {L}}_{n-n_*}f \, {\widehat{T}}_{n_*, U^1_i} \psi _1\) with \(\sum _{j \in M^2} \frac{m_1}{m_2} \int _{{{\bar{U}}}^2_j} {\mathcal {L}}_{n-n_*}f \, {\widehat{T}}_{n_*, U^2_j} \psi _2\). The remainder of the integrals \(\sum _{j \in M^2} \frac{m_2 - m_1}{m_2} \int _{{{\bar{U}}}^2_j} {\mathcal {L}}_{n-n_*}f \, {\widehat{T}}_{n_*, U^2_j} \psi _2\) as well as any unmatched pieces (including the outer two-thirds of each \(U^\ell _i\)) we continue to iterate until such time as they can be matched as the middle third of a curve that properly crosses \(R_*\).
Set \({\widehat{T}}_{n_*, U^2_j} {\tilde{\psi }}_2 = \frac{m_1}{m_2} {\widehat{T}}_{n_*, U^2_j} \psi _2\), and consider the following decomposition of the integrals we want to match,
For each pair i, j in the first sum, the test function has integral weight \(\frac{p^{(1)}_i p^{(2)}_j}{m_2}\), and the same is true for the corresponding pair in the second sum. Thus these integrals are paired precisely according to the assumptions of Lemma 6.8. It follows that if \(n - n_* \ge C\log (\delta _0/\delta )\), then
We want to repeat the above construction until most of the mass has been compared. To this end we set up an inductive scheme. Consider the family of curves \(W^\ell _i \in {\mathcal {G}}_{n_*}(W^\ell )\) that have not been matched. Each carries a test function \(\psi _{\ell , i} := {\widehat{T}}_{n_*, W^\ell _i} {\tilde{\psi }}_\ell \), where to keep our notation uniform, we set \({{\tilde{\psi }}}_1 = \psi _1\). Renormalizing by a factor \({\mathfrak {r}}_{\ell ,1} < 1\), we have \(\sum _i \int _{W^\ell _i} \psi _{\ell ,i} = 1\).
Definition 6.10
Given a countable collection of curves and test functions, \({\mathfrak {F}} = \{ W_i, \psi _i \}_i\), with \(W_i \in {\mathcal {W}}^s\), \(|W_i| \le \delta _0\), \(\psi _i \in {\mathcal {D}}_{a, \alpha }(W_i)\) and \(\sum _i \int _{W_i} \psi _i = 1\), we call \({\mathfrak {F}}\) an admissible family if

Notice that any stable curve \(W \in {\mathcal {W}}^s(\delta _0/2)\) together with test function \(\psi \in {\mathcal {D}}_{a,\alpha }(W)\) normalized so that \(\int _W \psi = 1\) forms an admissible family since \(|W| \ge \delta _0/2\). The content of the following lemma is that an admissible family can be iterated and remain admissible; moreover, a family with larger average integral in (6.14) can be made admissible under iteration.
Lemma 6.11
Let \(\{ W_i, \psi _i \}_i\) be a countable collection of curves \(W_i \in {\mathcal {W}}^s\), \(|W_i| \le \delta _0\), with functions \(\psi _i \in {\mathcal {D}}_{a,\alpha }(W_i)\), normalized so that \(\sum _i p_i = 1\), where \(p_i = \int _{W_i} \psi _i\). Suppose that \(\sum _i |W_i|^{-1} p_i = C_\sharp \).
Choose \(n_\sharp \in {\mathbb {N}}\) so that \(C_0 \theta _1^{n_\sharp } \frac{C_\sharp }{C_*} \le 1/6\). Then for all \(n \ge n_\sharp \), and all \(\{ \iota _k \}_{k=1}^n \subset {\mathcal {I}}(T_0, \kappa )\), the dynamically iterated family \(\{ V^i_j \in {\mathcal {G}}_n(W_i), {\widehat{T}}_{n,V^i_j} \psi _i \}_{i,j}\) is admissible.
Proof
Setting \(p^{(i)}_j {=} \int _{V^i_j} {\widehat{T}}_{n,V^i_j} \psi _i {=} \int _{V^i_j} \psi _i \circ T_n J_{V^i_j}T_n\), it is immediate that \(\sum _{i,j} p^{(i)}_j {=} 1\).
Now fix \(W_i\) and consider \(V^i_j \in {\mathcal {G}}_n(W_i)\). Then using Lemmas 3.3 and 4.2 we estimate,

Using that \(e^{a \delta _0^\alpha } \le 2\), we sum over i and use the assumption on the family \(\{ W_i, \psi _i \}_i\) to obtain,
Thus if \(n \ge n_\sharp \), the above expression is bounded by \(C_*\), as required. \(\square \)
Theorem 6.12
Let \(L \ge 60\). Suppose a, c, A and L satisfy the conditions of Sect. 5.3, and that in addition, \(\delta \le \delta _0^2\) satisfy (6.7) and (6.18). Then there exists \(\chi < 1\), independent of the cone parameters,Footnote 17 and \(k_*\in {\mathbb {N}}\) such that if \(n \in {\mathbb {N}}\) satisfies \(n \ge N_{\mathcal {F}}:= N(\delta )^- + k_*n_*\),Footnote 18 with \(k_*\) depending only on \(\delta _0, L \, and \, n_*\) (see Eq. (6.17)), and if \(\{ \iota _j \}_{j=1}^n \subset {\mathcal {I}}(T_0, \kappa )\), where \(\kappa >0\) is from Lemma 6.6(b), then \({\mathcal {L}}_n {\mathcal {C}}_{ c, A, L}(\delta ) \subset {\mathcal {C}}_{ \chi c, \chi A, \chi L}(\delta ) \).
Proof
As before, we take \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), \(W^1\), \(W^2 \in {\mathcal {W}}^s(\delta _0/2)\) and test functions \(\psi _\ell \in {\mathcal {D}}_{a,\beta }(W^\ell )\) such that \(\int _{W^1} \psi _1 = \int _{W^2} \psi _2 = 1\). In order to iterate the matching argument described above, we need upper and lower bounds on the amount of mass matched via the process described by (6.13).
Upper Bound on Matching. By definition of \({{\bar{U}}}^\ell _i\), for each curve \(U^\ell _i\) that properly crosses \(R_*\) at time \(n_*\), at least 2/3 of the length of that curve remains not matched. Thus if \(p_i = \int _{U^\ell _i} {\widehat{T}}_{n,U^\ell _i} {\tilde{\psi }}_\ell \), then at least \((1- e^{a \delta _0^\alpha }/3) p_i\) remains unmatched. Using \(e^{a \delta _0^\alpha } \le 2\), we conclude that at least \((1/3) p_i\) of the mass remains unmatched. Thus if \({\mathfrak {r}}\) denotes the total mass remaining after matching at time \(n_*\), we have \({\mathfrak {r}} \ge 1/3\). Renormalizing the family by \({\mathfrak {r}}\), we have \(\sum _i |W_i|^{-1} \frac{p_i}{{\mathfrak {r}}} \le 3 C_*\).
By the proof of Lemma 6.11 with \(C_\sharp = 3C_*\), we see that choosing \(n_\sharp \) such that \(6C_0 \theta _1^{n_\sharp } \le 1/3\), then the bound in (6.15) is less than \(C_*\), and the family recovers its regularity in the sense of Lemma 6.11 after this number of iterates.
Lower Bound on Matching. By definition of admissible family, for each \(\varepsilon > 0\), \(\sum _{|W_i| < \varepsilon } p_i \le C_* \varepsilon \). So choosing \(\varepsilon = \delta _0 / (6{{\bar{C}}}_0)\), we have that
On each \(W_i\) with \(|W_i| \ge \delta _0/(6 {{\bar{C}}}_0)\), we have at least one \(U^i_j \in {\mathcal {G}}_{n_*}(W_i)\) that properly crosses \(R_*\) by Lemma 6.6. Then denoting by \({{\bar{U}}}^i_j\) the matched part (middle third) of \(U^i_j\) and setting
we have
where we have used the fact that if \(W \in {\mathcal {W}}^s\) and \(T_{\iota _j}^{-1}W\) is a homogeneous stable curve, then \(|T_{\iota _j}^{-1}W| \le C^{-1} |W|^{3/5}\) for some constant \(C>0\) by (H1) (see, for example [DZ3, eq. (6.9)]).
Thus a lower bound on the amount of mass coupled at time \(n_*\) is \(\frac{\varepsilon _{n_*}}{2} > 0\).
We are finally ready to put these elements together. For \(k_* \in {\mathbb {N}}\) and \(k = 1, \ldots k_*\), let \(M^\ell (k)\) denote the index set of curves in \({\mathcal {G}}_{kn_*}(W^\ell )\) which are matched at time \(kn_*\). By choosing \(\delta _0\) small, we can ensure that \(n_\sharp \le n_*\), where \(n_\sharp \) from Lemma 6.11 corresponds to \(C_\sharp = 3 C_*\). Thus the family of remaining curves is always admissible at time \(kn_*\). Let \(M^\ell (\sim )\) denote the index set of curves that are not matched by time \(k_*n_*\). We estimate using (6.13) at each time \(n=k n_*\),
We estimate the sum over unmatched pieices \(M^\ell (\sim )\) by splitting the estimate in curves longer than \(\delta \), \(M^\ell (\sim ; Lo)\), and curves shorter than \(\delta \), \(M^\ell (\sim ; Sh)\).
where we have used (5.14) and the fact that \(k_*n_* \ge n_0\). For the sum over long pieces, we used that the total mass of unmatched pieces decays exponentially in k, while for the sum over short pieces, we used Lemma 3.3 and Remark 3.4 to sum over the Jacobians since \(|W^1| \ge \delta _0/2\). Finally, since  , we conclude,
, we conclude,
using the fact that \(\int _{W^2} \psi _2 = 1\). A similar estimate holds for the sum over curves in \(M^2(\sim )\). Finally, we put together this estimate with (6.16) to obtain,
We choose \(k_*\) such that
Note that this choice of \(k_*\) depends only on \(\delta _0\) via \(\varepsilon _{n_*}\), and not on \(\delta \). Next, choose \(\delta >0\) sufficiently small that
These choices imply that
Finally, we prove that L must contract by at least \(\frac{8}{9}\). This is implied directly by the first alternative of Proposition 6.3. So suppose instead that the second alternative holds. Since (6.19) holds for all \(W^1, W^2 \in {\mathcal {W}}^s(\delta _0/2)\) and test functions \(\psi _1, \psi _2\) with \(\int _{W^1} \psi _1 = \int _{W^2} \psi _2 = 1\), we conclude that, for \(k \ge k_*\) and \(m\ge N(\delta )^-\),
if we choose \(L \ge 60\). \(\square \)
6.3 Finite diameter
In this section we prove the following proposition, which completes the proof of Theorem 2.3.
Proposition 6.13
For any \(\chi \in \left( \max \{ \frac{1}{2}, \frac{1}{L}, \frac{1}{\sqrt{A-1}} \} , 1\right) \), the cone \({\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) has diameter less than \(\Delta := \log \left( \frac{(1+\chi )^2}{(1-\chi )^2} \chi L \right) <\infty \) in \({\mathcal {C}}_{c,A,L}(\delta )\), assuming \(\delta >0\) is sufficiently small to satisfy (6.21).
Proof
For brevity, we will denote \({\mathcal {C}}= {\mathcal {C}}_{c,A,L}(\delta )\) and \({\mathcal {C}}_\chi = {\mathcal {C}}_{ \chi c, \chi A, \chi L}(\delta )\). For \(f \in {\mathcal {C}}_\chi \), we will show that \(\rho (f, 1) < \infty \), where \(\rho \) denotes distance in the cone \({\mathcal {C}}\). Fix \(f \in {\mathcal {C}}_\chi \) throughout.
According to (4.1) if we find \(\lambda >0\) such that \(f-\lambda \succeq 0\), then \({\bar{\alpha }}(1,f)\ge \lambda \).
Notice that \({|||}f- \lambda {|||}_\pm = {|||}f {|||}_\pm - \lambda \). Hence \(f - \lambda \) satisfies (4.6) if
where we have used that \(f \in {\mathcal {C}}_\chi \).
Similarly, \(f - \lambda \) satisfies (4.7) if, for all \(W \in {\mathcal {W}}^s_-(\delta )\) and \(\psi \in {\mathcal {D}}_{a,\beta }(W)\),

Next, notice that for any \(\lambda \ge 0\), \(W^1, W^2 \in {\mathcal {W}}^s_-(\delta )\) and \(\psi _\ell \in {\mathcal {D}}_{a,\alpha }(W^\ell )\),

where we have used (5.8), so that \(f - \lambda \) satisfies (4.8) if
This occurs whenever
provided that \(\delta \) is chosen sufficiently small that
which is possible since \(cA > 2C_s\) by (5.36) and \(\chi > 1/2\).
Note that \({\bar{\alpha }}_2 \le {\bar{\alpha }}_3 \le \bar{\alpha }_1\), so that \({\bar{\alpha }}_2 = \min _i \{ {\bar{\alpha }}_i \}\). Thus if \(\lambda \le {\bar{\alpha }}_2\), then \(f - \lambda \in {\mathcal {C}}\), i.e. \({\bar{\alpha }}(1, f) \ge {\bar{\alpha }}_2\).
Next, we proceed to estimate \({\bar{\beta }}(1,f)\) for \(f \in {\mathcal {C}}_\chi \). If we find \(\mu > 0\) such that \(\mu - f \in {\mathcal {C}}\), this will imply that \({\bar{\beta }}(1,f) \le \mu \). Remarking that \({|||}\mu - f {|||}_{\pm } = \mu - {|||}f {|||}_{\mp }\), we have that \(\mu - f\) satisfies (4.6) if
while \(\mu - f\) satisfies (4.7) if for all \(W \in {\mathcal {W}}^s_-(\delta )\), \(\psi \in {\mathcal {D}}_{a,\beta }(W)\),

Finally, recalling (6.20) and again (5.8), we have that \(\mu -f\) satisfies (4.8) whenever
This is implied by,
where again we have assumed (6.21).
Defining \({\bar{\beta }} = \max _i \{ {\bar{\beta }}_i \}\), it follows that if \(\mu \ge {\bar{\beta }}\), then \(\mu - f \in {\mathcal {C}}\). Thus \(\bar{\beta }\ge {\bar{\beta }}(1, f)\). Since \(\chi > 1/L\) and \(\chi ^2 > 1/(A-1)\), it holds that \({\bar{\beta }}_3 \ge {\bar{\beta }}_2 \ge {\bar{\beta }}_1\). Thus \({\bar{\beta }} = {\bar{\beta }}_3\). Our assumption also implies \(\chi > 1/A\), so that \({\bar{\alpha }}_2 \ge \frac{1-\chi }{1+\chi } {|||}f {|||}_-\).
Finally, recalling (4.1), we have
for all \(f \in {\mathcal {C}}_\chi \), completing the proof of the proposition. \(\square \)
Remark 6.14
Note that, setting \(\chi _*=\max \{ \frac{1}{2}, \frac{1}{L}, \frac{1}{\sqrt{A-1}} \} \), for \(\chi \le \chi _*\) Proposition 6.13 implies only that the diameter of \({\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\subset {\mathcal {C}}_{\chi _* c, \chi _* A, \chi _* L}(\delta )\), in \({\mathcal {C}}_{c,A,L}(\delta )\), is bounded by \( \log \left( \frac{(1+\chi _*)^2}{(1-\chi _*)^2} \chi _* L \right) \). If needed, a more accurate formula can be easily obtained, but it would be more cumbersome.
7 Loss of Memory and Convergence to Equilibrium
In this section we show how Theorem 2.3 (i.e. Theorem 6.12 and Proposition 6.13) imply the loss of memory and convergence to equilibrium stated in Theorems 2.7 and 2.8. For a single map, the loss of memory is simply decay of correlations and the results are comparable to the ones obtained in [DZ1] since they apply to a similar (very) large class of observables (and possibly even distributions). Our loss of memory result is new for our class of billiards, although see Remark 2.9 and [SYZ] for loss of memory in a related billiards model. Before proving the main results of this section (Theorem 7.3 and Corollary 7.5 prove Theorem 2.7 while Theorem 7.4 and Corollary 7.5 prove Theorem 2.8), we establish a key lemma that integration with respect to \(\mu _{\tiny {\text{ SRB }}}\) against suitable test functions respects the ordering in our cone. Recall the vector space of functions \({\mathcal {A}}\) defined in Sect. 4.3.
The parameters \(a, q, \alpha , \beta , \gamma , c, A, L,\delta _0\) are fixed as to satisfy the relations described in Sect. 5.3, hence Theorem 2.3 holds true. With Proposition 5.1 in mind, we prove our next lemma with respect to the slightly larger cone \({\mathcal {C}}_{c,A,3L}(\delta ) \supset {\mathcal {C}}_{c,A,L}(\delta )\).
Lemma 7.1
Let \(\delta >0\) be small enough that \(2 C_\ell C_h (1+A) ( \delta ^{4/3} + \delta ^{1/3 + \beta } a \ell _{\max } ) < 1\), where \(C_\ell , C_h>0\) are from (7.4) and \(\ell _{\max }\) is the maximum diameter of the connected components of M.
Suppose \(\psi \in C^1(M)\) satisfies \(2(2\delta )^{1-\beta } |\psi '|_{C^0(M)} \le a \min _M \psi \). If \(f, g \in {\mathcal {A}}\) with \(g-f \in {\mathcal {C}}_{c,A,3L}(\delta )\), then \(\int f \, \psi \, d\mu _{\tiny {\text{ SRB }}}\le \int g \, \psi \, d\mu _{\tiny {\text{ SRB }}}\).
Proof
Let \(\psi _{\min } = \min _M \psi \). The assumption on \(\psi \) implies that \(\psi \in {\mathcal {D}}_{\frac{a}{2},\beta }(W)\) for each \(W \in {\mathcal {W}}^s_-(\delta )\) since,
Suppose \(f, g \in {\mathcal {A}}\) satisfy \(g-f \in {\mathcal {C}}_{c,A,3L}(\delta )\). Then according to (4.5) and (4.7), for all \(\psi \in {\mathcal {D}}_{a,\beta }(W)\),


Next, we disintegrate \(\mu _{\tiny {\text{ SRB }}}\) according to a smooth foliation of stable curves as follows. Since the stable cones defined in (H1) are globally constant and uniform in the family \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), we fix a direction in the stable cone and consider stable curves in the form of line segments with this slope. Let \(k_\delta \ge k_0\) denote the minimal index k of a homogeneity strip \({\mathbb {H}}_k\) such that the stable line segments in \({\mathbb {H}}_k\) have length less than \(\delta \). Due to the fact that the minimum slope in the stable cone is \({\mathcal {K}}_{\min } > 0\), we have
for some constant \(C_h >0\) independent of \(\delta \).
Now for \(k < k_\delta \), we decompose \({\mathbb {H}}_k\) into horizontal bands \(B_{k,i}\) such that every maximal line segment of the chosen slope in \(B_{k,i}\) has equal length between \(\delta \) and \(2\delta \). We do the same on \({\mathbb {H}}_0 := M \setminus (\cup _{k \ge k_0} {\mathbb {H}}_k)\). On each \(B_{k,i}\), define a foliation of such parallel line segments \(\{ W_\xi \}_{\xi \in \Xi _{k,i}} \subset {\mathcal {W}}^s(\delta )\). Using the smoothness of this foliation, we disintegrate \(\mu _{\tiny {\text{ SRB }}}\) into conditional measures \(\cos \varphi (x) dm_{W_\xi }\) on \(W_\xi \) and a factor measure \({{\hat{\mu }}}\) on the index set \(\Xi _{k,i}\). Note that our conditional measures are not normalized - we include this factor in \({{\hat{\mu }}}\). Finally, on each homogeneity strip \({\mathbb {H}}_k\), \(k \ge k_\delta \), we carry out a similar decomposition, but using homogeneous parallel line segments of maximal length in \({\mathbb {H}}_k\) (which are necessarily shorter than length \(\delta \)). We use the notation \(\{ W_\xi \}_{\xi \in \Xi _{k,1}} \subset {\mathcal {W}}^s_-(\delta )\) for the foliations in these homogeneity strips since there is only one band in each of these \({\mathbb {H}}_k\). Note that for all k and i, we have \({{\hat{\mu }}}(\Xi _{k,i}) \le C_\ell \), for some constant \(C_\ell \) depending only on the chosen slope and spacing of homogeneity strips.
Also, it follows as in (3.5), that for \(x, y \in W \in {\mathcal {W}}^s_-(\delta )\),
so that \(\cos \varphi \in {\mathcal {D}}_{\frac{a}{2}, \beta }(W)\) by the assumption of Lemma 5.2. Thus \(\psi \cos \varphi \in {\mathcal {D}}_{a, \beta }(W)\) for all \(W \in {\mathcal {W}}^s_-(\delta )\).
Using this fact and our disintegration of \(\mu _{\tiny {\text{ SRB }}}\), we estimate the integral applying (7.1) on \(\Xi _{k,i}\) for \(k< k_\delta \) and (7.2) on \(\Xi _{k,1}\) for \(k \ge k_{\delta }\),

where we have estimated \(\sum _{k \ge k_\delta } k^{-2} \le 2 k_\delta ^{-1} \le 2 C_h \delta ^{1/3}\) and \(\mu _{\tiny {\text{ SRB }}}(\cup _{k \ge k_\delta } {\mathbb {H}}_k) \le 2 C_\ell C_h \delta ^{4/3}\).
Now \(|\psi |_{C^0} \le \psi _{\min } + \ell _{\max } |\psi '|_{C^0}\), where \(\ell _{\max }\) is the maximum diameter of the connected components of M. Then by the assumption on \(\psi \), we have
where for the last inequality we have used the assumption on \(\delta \) in the statement of the lemma. We conclude that the lower bound in (7.4) cannot be less than 0. \(\square \)
Remark 7.2
Since Remark 4.8 applies equally well to \({\mathcal {C}}_{c,A,3L}(\delta )\), Lemma 7.1 implies there exists \({{\bar{C}}} \ge 1\) such that \(\int _M f \, d\mu _{\tiny {\text{ SRB }}}\ge \bar{C}^{-1} {|||}f {|||}_- > 0\) for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\).
Using instead the upper bound in (7.1) and following the estimate of (7.4) yields,
for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(\psi \) as in the statement of Lemma 7.1. Since any \(\psi \in C^1(M)\) can be made to satisfy the condition of Lemma 7.1 by adding a constant (see the definition of \(C_\psi \) in (7.8) below), the estimate can be extended to all \(\psi \in C^1(M)\) to obtain,
Loss of memory and convergence to equilibrium, including equidistribution, readily follow from the contraction in the projective metric \(\rho _{{\mathcal {C}}}(\cdot , \cdot )\) of the cone \({\mathcal {C}}_{c, A, L}(\delta )\). Set \(\mu _{\tiny {\text{ SRB }}}(f) = \int _M f \, d\mu _{\tiny {\text{ SRB }}}\).
Recall \(N_{\mathcal {F}}:= N(\delta )^- + k_*n_*\) from Theorem 6.12 and the definition of an \(N_{{\mathcal {F}}}\)-admissible sequence from Sect. 2.2: A sequence \(( \iota _j )_j\), \(\iota _j \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), is \(N_{{\mathcal {F}}}\)-admissible if there exist sequences \((T_k)_{k \ge 1} \subset {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and \((N_k)_{k \ge 1}\) with \(N_k \ge N_{\mathcal {F}}\), such that \(T_{\iota _j} \in {\mathcal {F}}(T_k, \kappa )\) for all \(k \ge 1\) and \(j \in [1 + \sum _{i=1}^{k-1} N_i, \sum _{i=1}^k N_i]\).
That is, an admissible sequence remains in a \(\kappa \) neighborhood of \(T_k\) for \(N_k \ge N_{\mathcal {F}}\) iterates at a time, but may undergo large changes between such blocks.
Our first theorem concerns loss of memory for functions in our cone, both with respect to \(\mu _{\tiny {\text{ SRB }}}\) and with respect to the iteration of individual stable curves. It does not use property (H5), although it does use that \(\mu _{\tiny {\text{ SRB }}}\) is a conformal measure for \({\mathcal {L}}_n\), i.e. \(\mu _{\tiny {\text{ SRB }}}({\mathcal {L}}_n f) = \mu _{\tiny {\text{ SRB }}}(f)\).
Theorem 7.3
Let \(\delta >0\) satisfy the assumption of Lemma 7.1. There exists \(C>0\) and \(\vartheta <1\) such that for all admissible sequences \((\iota _j)_j\), all \(n \ge 0\), and all \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\) with \(\int _M f \, d\mu _{\tiny {\text{ SRB }}}= \int _M g \, d\mu _{\tiny {\text{ SRB }}}\):
-
(a)
For all all \(W \in {\mathcal {W}}^s(\delta )\) and all \(\psi \in C^1(W)\), we have

-
(b)
For all \(\psi \in C^1(M)\),
$$\begin{aligned} \left| \int _M {\mathcal {L}}_n f \, \psi \, d\mu _{\tiny {\text{ SRB }}}- \int _M {\mathcal {L}}_n g \, \psi \, d\mu _{\tiny {\text{ SRB }}}\right| \le C \vartheta ^n |\psi |_{C^1(M)} \min \{ {|||}f {|||}_+ , {|||}g {|||}_+ \} \, .\nonumber \\ \end{aligned}$$(7.5)
Proof
(a) Recall the definition of \({|||}\cdot {|||}_+ \) for elements of \({\mathcal {A}}\) from Definition 4.5 and (4.5),
and note that by (4.10), \({|||}\cdot {|||}_+ \) is an order-preserving semi-norm in \({\mathcal {A}}\).Footnote 19 One can check directly that \({\mathcal {A}}\) is an integrally closed vector lattice. Also \( \mu _{\tiny {\text{ SRB }}}(f) := \int _M f \, d\mu _{\tiny {\text{ SRB }}}\) is homogeneous and order preserving in \({\mathcal {C}}_{c,A,3L}(\delta )\) by Lemma 7.1 applied to \(\psi \equiv 1\).
We would like to apply Theorem 6.12 to each block of \(N_{\mathcal {F}}\) iterates in the admissible sequence; however, at time n, the sequence may have completed fewer than \(N_{\mathcal {F}}\) iterates in its current block so it may be that \({\mathcal {L}}_n f, {\mathcal {L}}_n g \notin {\mathcal {C}}_{c,A,L}(\delta )\). But since \(n \ge N_{\mathcal {F}}> n_0\), it follows from Proposition 5.1 that \({\mathcal {L}}_n f, {\mathcal {L}}_n g \in {\mathcal {C}}_{c,A,3L}(\delta )\). Then denoting by \(\rho _{{\mathcal {C}}'}\) the metric in the larger cone \({\mathcal {C}}_{c,A,3L}(\delta )\), [LSV, Lemma 2.2] implies that, for all \(f,g \in {\mathcal {C}}_{c,A,L}(\delta )\) with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\),Footnote 20
Using the definition of admissible sequence, we may peel off the most recent j iterates, where \(j < n_0 + N_{\mathcal {F}}\), such that \({\mathcal {L}}_{n-j} f ,{\mathcal {L}}_{n-j} g \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(n-j\) is chosen so that we have undergone at least \(N_{\mathcal {F}}\) iterates in the current block at time \(n-j\). Then applying Theorem 6.12 to each block of \(N_k\) iterates, and using Proposition 6.13 and [L95a, Theorem 1.1 and Remark 1.2], for all \(n \ge N_{\mathcal {F}}\),
where \(\vartheta =\left[ \tanh (\Delta /4)\right] ^{ 1/(2 N_{\mathcal {F}})}\), and \(k \in [N_{\mathcal {F}}, 2N_{\mathcal {F}}-1]\) is the least integer \(\ge N_{\mathcal {F}}\) so that \({\mathcal {L}}_{n-j-k}\) ends in a contracting block.
Finally, we use the fact that \({\mathcal {L}}_k f, {\mathcal {L}}_k g \in {\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) together with Proposition 6.13 to conclude \(\rho _{{\mathcal {C}}}({\mathcal {L}}_k f, {\mathcal {L}}_k g) \le \Delta \). Combining these estimates with Lemma 5.4 yields,
where \(C = \frac{3}{2} \Delta e^\Delta \vartheta ^{-3 N_{\mathcal {F}}- n_0}\). This proves (a) for any \(W \in {\mathcal {W}}^s(\delta )\) and \(\psi \in {\mathcal {D}}_{a,\beta }(W)\).
To extend this estimate to more general \(\psi \in C^1(W)\), define \({\tilde{\psi }}= \psi + C_\psi \), where
Then \({\tilde{\psi }}' = \psi '\) and \(\min _W {\tilde{\psi }}\ge \frac{2}{a} |{\tilde{\psi }}'|_{C^0} (2\delta )^{1-\beta }\), so that \({\tilde{\psi }}\in {\mathcal {D}}_{\frac{a}{2}, \beta }(W)\) by the proof of Lemma 7.1. Then since also \(C_\psi \in {\mathcal {D}}_{a, \beta }(W)\), the required estimate follows by writing \(\psi = {\tilde{\psi }}- C_\psi \) and using the triangle inequality.
(b) Following the same strategy as above, given \(\psi \in C^1(M)\) satisfying the assumption of Lemma 7.1, we define a pseudo-norm for \(f \in {\mathcal {A}}\) by
By Lemma 7.1, \(\Vert \cdot \Vert _\psi \) is an order-preserving semi-norm, and as in (7.6), invoking again [LSV, Lemma 2.2], Theorem 6.12, Proposition 6.13 and [L95a, Theorem 1.1], we have for \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\) with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\) and \(n \ge N_{\mathcal {F}}\),
where we applied Remark 7.2. This proves (b) for \(\psi \) satisfying the assumption of Lemma 7.1. We extend to more general \(\psi \in C^1(M)\) by defining \({\tilde{\psi }}= \psi + C_\psi \), where \(C_\psi \) is given by (7.8), and arguing as in the proof of part (a). \(\square \)
Since our maps all preserve \(\mu _{\tiny {\text{ SRB }}}\), the loss of memory also implies equidistribution of measures supported on stable curves and convergence to equilibrium, both of which are summarized in the following theorem.
Theorem 7.4
Let \(\delta >0\) satisfy the assumption of Lemma 7.1. There exists \(C>0\) such that for all \(n \ge 0\) and admissible sequences \((\iota _j)_j \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), \(\vartheta \) as in Theorem 7.3, and all \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\), with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\):
-
(a)
For all \(W_1, W_2 \in {\mathcal {W}}^s(\delta )\) and all \(\psi _i \in C^1(W_i)\) with
 , we have
, we have 
in particular, for all \(W \in {\mathcal {W}}^s(\delta )\) and \(\psi \in C^1(W)\),
 (7.10)
(7.10) -
(b)
for all \(\psi \in C^1(M)\),
$$\begin{aligned} \left| \int _M f \, \psi \circ T_n \, d\mu _{\tiny {\text{ SRB }}}- \int _M f \, d\mu _{\tiny {\text{ SRB }}}\int _M \psi \, d\mu _{\tiny {\text{ SRB }}}\right| \le C \vartheta ^n |\psi |_{C^1(M)} \mu _{\tiny {\text{ SRB }}}(f) \, . \end{aligned}$$
Proof
(a) Since \({\mathcal {L}}_n 1 = 1\) and \({|||}\mu _{\tiny {\text{ SRB }}}(f) {|||}_+ = \mu _{\tiny {\text{ SRB }}}(f)\), applying (7.7) with \(g = \mu _{\tiny {\text{ SRB }}}(f)\) implies,

which proves (7.10) for \(\psi \in {\mathcal {D}}_{a, \beta }(W)\). We extend this estimate to more general \(\psi \in C^1(W)\) by defining \({\tilde{\psi }}= \psi + C_\psi \) as in (7.8) and arguing as in the proof of Theorem 7.3(a). Finally, the first inequality of part (a) follows from an application of the triangle inequality.
(b) Since \(\mu _{\tiny {\text{ SRB }}}\) is conformal with respect to \({\mathcal {L}}_{T}\) for each \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), and using that \({\mathcal {L}}_n 1 = 1\), we have
Thus applying (7.5) to \(g = \mu _{\tiny {\text{ SRB }}}(f)\) proves part (b) since \({|||}\mu _{\tiny {\text{ SRB }}}(f) {|||}_+ = \mu _{\tiny {\text{ SRB }}}(f)\). \(\square \)
We may extend Theorems 7.3 and 7.4 to piecewise Hölder continuous functions, as long as the discontinuities are transverse to the stable cone. Recall the definition of a regular partition \({\mathcal {P}}\) from Definition 2.6 and the set \(C^t({\mathcal {P}})\) of functions which are t-Hölder continuous on each element of \({\mathcal {P}}\), i.e. which satisfy
Corollary 7.5
Let \({\mathcal {P}}\) be a regular partition of M and let \(t \ge \gamma \). Then the convergence in Theorems 7.3 and 7.4 extend to all \(f, g \in C^t({\mathcal {P}})\), with \(\max \{|f|_{C^t({\mathcal {P}})}, |g|_{C^t({\mathcal {P}})}\}\) in place of \(\min \{ {|||}f {|||}_+, {|||}g {|||}_+ \}\) on the right hand side in Theorem 7.3 and in place of \(\mu _{\tiny {\text{ SRB }}}(f)\) on the right hand side in Theorem 7.4.
The proof of this corollary relies on the following lemma.
Lemma 7.6
If \({\mathcal {P}}\) is a regular partition of M and \(f \in C^t({\mathcal {P}})\) with \(t \ge \gamma \), then \(\lambda + f \in {\mathcal {C}}_{c, A, L}(\delta )\) for any
Proof of Corollary 7.5
Let \(f, g \in C^t({\mathcal {P}})\) with \(\mu _{\tiny {\text{ SRB }}}(f) = \mu _{\tiny {\text{ SRB }}}(g)\) and let \(\psi \in C^1(M)\). Let \(\lambda _f, \lambda _g\) be the constants from Lemma 7.6 corresponding to f and g, respectively, and set \(\lambda = \max \{ \lambda _f, \lambda _g \}\). Then \(f + \lambda , g + \lambda \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(\mu _{\tiny {\text{ SRB }}}(f+\lambda ) = \mu _{\tiny {\text{ SRB }}}(g + \lambda )\), so that by Theorem 7.3(b), for all \(n \ge 0\),
since \({|||}f+ \lambda {|||}_+ \le \lambda + |f|_\infty \), and by Lemma 7.6, \(\lambda _f \ge C'' |f|_{C^t({\mathcal {P}})}\), with analogous estimates for g. This proves the analog of part (b) Theorem 7.3 and the proof of part (a) follows similarly, replacing the integral over M by the integral over \(W \in {\mathcal {W}}^s\).
The extension of Theorem 7.4 to \(f, g \in C^t({\mathcal {P}})\) follows analogously, replacing f and g in (7.11) with \(f+\lambda \) and \(g+\lambda \), respectively to prove the analogue of (7.10), and then using the triangle inequality to deduce the first inequality of part (a). Finally, part (b) follows immediately once f is replaced by \(f+\lambda \) since \(\int _M \psi \circ T_n \, d\mu _{\tiny {\text{ SRB }}}= \int _M \psi \, d\mu _{\tiny {\text{ SRB }}}\) due to (H5). \(\square \)
Proof of Lemma 7.6
We must show that \(\lambda + f\) satisfies conditions (4.6)–(4.8) in the definition of \({\mathcal {C}}_{c,A,L}(\delta )\). Since
to guarantee (4.6), we need

Next, to guarantee (4.7), for \(W \in {\mathcal {W}}^s_-(\delta )\), \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), we need,

Lastly, we need to show that (4.8) is satisfied. For this, we prove the claim:

for \(W^1, W^2, \psi _1, \psi _2\) as in (4.8). As in Sect. 5.2.3, we partition \(W^k\) into matched pieces \(U^k_j\) and unmatched pieces \(V^k_i\) such that \(U^1_j\), \(U^2_j\) belong to the same element \(P \in {\mathcal {P}}\) and are defined over the same r-interval \(I_j\) for each j. By assumption on \({\mathcal {P}}\), \(\# \{ U^k_j \}_j \le K\), \(\# \{ V^k_j \}_{k,j} \le 2K\), and \(|V^k_j| \le C_s C_{{\mathcal {P}}} d_{{\mathcal {W}}^s}(W^1, W^2)\).
Recalling the notation from Sect. 4.2, we express the matched pieces as graphs over their common r-interval, \(U^k_j = \{ G_{U^k_j}(r) = (r, \varphi _{U^k_j}(r)) : r \in I_j \}\), for \(k=1,2\).
As in Sect. 5.2.3, we assume without loss of generality that \(|W_2| \ge |W_1|\) and  . Also, we may assume \(|W_2| \ge 2 C_s \delta ^{1-\gamma } d_{{\mathcal {W}}^s}(W_1, W_2)^\gamma \); otherwise, (7.13) is trivially bounded by \(2 |W_2| |f|_\infty \le 4 C_s \delta ^{1-\gamma } d_{{\mathcal {W}}^s}(W_1, W_2)^\gamma |f|_\infty \).
. Also, we may assume \(|W_2| \ge 2 C_s \delta ^{1-\gamma } d_{{\mathcal {W}}^s}(W_1, W_2)^\gamma \); otherwise, (7.13) is trivially bounded by \(2 |W_2| |f|_\infty \le 4 C_s \delta ^{1-\gamma } d_{{\mathcal {W}}^s}(W_1, W_2)^\gamma |f|_\infty \).
Next,

To estimate the first term on the right hand side, recalling (4.3) and \(d_*(\psi _1, \psi _2) = 0\), we have for \(r \in I_j\),
where \(H^t_P(f)\) denotes the Hölder constant of f on \(P \in {\mathcal {P}}\). Integrating over \(I_j\) yields,
For the second term on the right side of (7.14), \(|V^k_i| \le C_s C_{\mathcal {P}}d_{{\mathcal {W}}^s}(W^1, W^2)\) plus (5.9) implies
while for the third term, (5.10) implies
Collecting this estimate together with (7.15) and (7.16) in (7.14), and recalling (4.9), we obtain

proving the bound in (7.13) since \(d_{{\mathcal {W}}^s}(W_1, W_2) \le \delta \) and \(t \ge \gamma \).
With the claim proved, we proceed to verify (4.8). Using (5.8) we estimate,

Thus (4.8) will be verified if
which is implied by the final condition on \(\lambda \) in the statement of the lemma since \(d_{{\mathcal {W}}^s}(W_1, W_2) \le \delta \) and \(cA > 2C_s\) by (5.36). \(\square \)
8 Applications
Suppose that we have a billiard table \(Q = {\mathbb {T}}^2 \setminus \cup _i B_i\) and that the particle can escape from the table by entering certain sets \({\mathbb {G}}\subset Q\), which we call gates or holes, but only at times kN for some \(N\in {\mathbb {N}}\). One could easily consider also the case of \({\mathbb {G}}\subset Q\times S^1\) (i.e. some velocity directions are forbidden, as studied in [D2]), but we prefer to keep things simple. In the literature, one often takes \(N=1\), i.e. the particle can escape at each iterate of the map, but then the holes are required to be very small, see for example [DWY, D1, D2]. By contrast, in this paper we will be interested in relatively large holes and so we will replace the assumption of smallness with an assumption of occasional escape through possibly large sets. This will facilitate the application of this method to two situations we have in mind: chaotic scattering (Sect. 8.4) and a random Lorentz gas (Sect. 8.5).
We begin with the same setup as in Sect. 2.1, fixing K numbers \(\ell _1, \ldots , \ell _K >0\) and identifying them as the arclengths of scatterers belonging to \({\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\) for some fixed choice of \(\tau _*, {\mathcal {K}}_*, E_* \in {\mathbb {R}}^+\). As in Sect. 3.1, we fix an index set \({\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), identifying \(\iota \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\) with a map \(T_\iota \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) induced by the table \(Q_\iota \in {\mathcal {Q}}(\tau _*, {\mathcal {K}}_*, E_*)\).
A hole \({\mathbb {G}}_\iota \subset Q_\iota \) induces a hole \(H_\iota \subset M\) in the phase space of the billiard map \(T_\iota \). We formulate here two abstract conditions on the set \(H_\iota \), and then provide examples of concrete, physically relevant situations which induce holes satisfying our conditions in Sect. 8.3.
-
(O1)
(Complexity) There exists \(P_0 >0\) such that any stable curve of length at most \(\delta \) can be cut into at most \(P_0\) pieces by \(\partial H_\iota \), where \(\delta \) is the length scale of the cone \({\mathcal {C}}_{c, A, L}(\delta )\).
-
(O2)
(Uniform transversality) There exists \(C_t > 0\) such that, for any stable curve \(W \in {\mathcal {W}}^s\) and \(\varepsilon >0\), \(m_W(N_\varepsilon (\partial H_\iota )) \le C_t \varepsilon \), where \(N_\varepsilon (A)\) is the \(\varepsilon \)-neighborhood of A in M.
Remark 8.1
Assumption (O2) can be weakened to, e.g., \(m_W(N_\varepsilon (\partial H_\iota )) \le C_t \varepsilon ^{1/2}\), but this would then require \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta ^2\) in our definition of cone condition (4.8). Similar modifications are made to weaken the transversality assumption in the Banach space setting, see for example [DZ3, D2].
For \(H \subset M\) satisfying (O1) and (O2), we let \(\text{ diam}^s(H)\) denote the maximal length of a stable curve in H, which we call the stable diameter.
As in Sect. 6.2, we fix \(T_0 \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, \tau _*)\) and consider sequences \(\{ \iota _j \}_j \subset {\mathcal {I}}(T_0, \kappa )\), where \(\kappa >0\) is from Lemma 6.6(b). Recalling (6.5), this means we will initially consider sequential open systems comprised of maps \(T \in {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) with \(\mathbb {d}(Q(T), Q(T_0)) < \kappa \). We will then extend this to \(n_\star \)-admissible sequences for appropriate \(n_\star \) depending on H.
Denote by \(\mathbb {1}_{A}\) the characteristic function of the set A. The relevant transfer operator for the open sequential system (opening once every \(n_\star \) iterates) is given by \({\mathcal {L}}_{H, n_\star }={\mathcal {L}}_{n_\star } \mathbb {1}_{H^c}\), where \(H^c\) denotes the complement of H in M, and \({\mathcal {L}}_{n_\star } = {\mathcal {L}}_{T_{\iota _{n_\star }}} \cdots {\mathcal {L}}_{T_{\iota _1}}\) is the usual transfer operator for the \(n_\star \)-step sequential dynamics. The main objective is to control the action of the multiplication operator \(\mathbb {1}_{H^c}\) on the cone \({\mathcal {C}}_{c,A,L}(\delta )\).
Remark 8.2
From now on we will consider parameters c, A, L fixed so that all the conditions of Sect. 5.3 apply for all \(\delta \) smaller that some fixed \(\delta _*\).
8.1 Relatively small holes
First we consider holes H whose stable diameter is short compared to the length scale \(\delta \).
Lemma 8.3
If \(H \subset M\) satisfies (O1) and (O2), and if \(\text{ diam}^s(H) \le \delta \left[ \frac{1}{4P_0A } \right] ^{1/q}\), then
where
Proof
Letting \(f \in {\mathcal {C}}_{c, A, L}(\delta )\), we must control the cone conditions one by one. We begin with (4.6). Given \(W\in {\mathcal {W}}^s(\delta )\), let \({\mathcal {G}}_0\) denote the collection of connected curves in \(W\setminus H\). Then applying (4.7) to each \(W' \in {\mathcal {G}}_0\), for \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), we estimate

where, in the last line, we have used the Hölder inequality to estimate the sum on \(W'\), recalling that, by (O1), the sum has, at most, \(P_0\) elements. On the other hand, if the collection of disjoint curves \(\{W_i\}\) is such that \(\cup _i W_i=W\cap H\),

Hence, for \(\text{ diam}^s(H)\) small enough,
Accordingly, taking the supremum over \(W,\psi \) in (8.1),
Next, to verify (4.7), if \(W\in {\mathcal {W}}^s_-(\delta )\), then estimating as in (8.1),

where we have used (8.2) for the third inequality.
We are left with the last cone condition, (4.8). We take \(W^1, W^2 \in {\mathcal {W}}^s_-(\delta )\) with \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \), and \(\psi _i \in {\mathcal {D}}_{a,\alpha }(W_i)\) with \(d_*(\psi _1, \psi _2) = 0\).
As in Sect. 5.2.3, we may assume without loss of generality that \(|W^2|\ge |W^1|\) and  . First of all note that, by condition (4.7) and our estimate above,
. First of all note that, by condition (4.7) and our estimate above,

for \(k=1,2\), provided \( |W^2|^q \le \delta ^{q- \gamma } \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^{\gamma }\). Accordingly, it suffices to consider the case \(|W^2|^q \ge \delta ^{q-\gamma } \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^{\gamma }\).
It follows from (5.8) that \(|W^1|^q \ge \frac{1}{2} \delta ^{q-\gamma } \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^\gamma \), recalling that \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \) and (5.7). By (O2), we may decompose \(W^k \cap H^c\) into at most \(P_0\) ‘matched’ pieces \(W_j^k\) such that \(d_{{\mathcal {W}}^s}(W_j^1,W_j^2)\le d_{{\mathcal {W}}^s}(W^1,W^2)\) and \(I_{W^1_j} = I_{W^2_j}\), and at mostFootnote 21\(P_0 + 2\) ‘unmatched’ pieces \({{\overline{W}}}^k_i\), which satisfy,
Then, using condition (4.7) and noticing that \(d_*(\psi _1|_{W^1_j},\psi _2|_{W^2_j})=0\),

using (8.2). Next, since \(I_{W^1_j} = I_{W^2_j}\), recalling Remark 4.4 and (5.8) we have \(\int _{W^1_j} \psi _1 = \int _{W^2_j} \psi _2\) andFootnote 22\(||W^1_j| - |W^2_j|| \le |W^1_j| d_{{\mathcal {W}}^s}(W^1, W^2)\). Then applying (4.7) and recalling  ,
,

Next, recalling \(|W^2| \ge \delta ^{1 - \frac{\gamma }{q} } [c/2]^{\frac{1}{q}} d_{{\mathcal {W}}^s}(W^1, W^2)^{\frac{\gamma }{q}}\) and using (5.10) yields,
where we have again used (5.7) and \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \). Using this estimate and the fact that \(q \le 1/2\) in (8.5) and summing over j yields,

Finally, using this estimate in (8.4) concludes the proof of the lemma,

where we have again used (8.2). \(\square \)
Remark that, by Theorem 6.12, we know that there exists \(N_{{\mathcal {F}}}\in {\mathbb {N}}\), \(N_{{\mathcal {F}}}\le k_*n_*+C_{\star }|\ln \delta |\) where \(n_*\), defined in Lemma 6.6, and \(k_*\) from Theorem 6.12, are uniform in \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), while \(C_\star \) depends only on c, A, L, such that \({\mathcal {L}}_{N_{{\mathcal {F}}}} {\mathcal {C}}_{c,A,L}(\delta ) \subset {\mathcal {C}}_{\chi c, \chi A, \chi L} (\delta )\), for all \(\{ \iota _j \}_{j=1}^{N_{\mathcal {F}}} \subset {\mathcal {I}}(T_0, \kappa )\).
To state the next result we need to make explicit the coice of the cone parameters. Let \(c', A', L'\) be given by Lemma 8.3. Choose (minimal) \(c'' \ge c'\), \(A'' \ge A'\) and \(L'' \ge L'\) satisfying the conditions in Sect. 5.3, and \(\delta '' \le \delta \) satisfying (6.7) and (6.18) with respect to \(A''\) and \(L''\).
Define \(N_{{\mathcal {F}}}' = k_*n_* + C'_\star |\ln \delta ''|\), where \(C'_\star \), \(k_*\) and \(n_*\) are from Theorem 6.12 applied to the cone \({\mathcal {C}}_{c'',A'',L''}(\delta '')\). Since, as remarked in Proposition 5.1 and Theorem 6.12, \(\chi \) is independent of the cone parameters, we have \({\mathcal {L}}_n {\mathcal {C}}_{c'',A'',L''}(\delta '') \subset {\mathcal {C}}_{\chi c'', \chi A'', \chi L''}(\delta '')\) for all \(n \ge N_{{\mathcal {F}}}'\).
Recall that \(\kappa >0\) from Lemma 6.6 depends only on the family \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
Proposition 8.4
Let \(n_\star = N_{{\mathcal {F}}}'\). There exists \(J \in {\mathbb {N}}\), depending only on \(c,A,L, P_0,C_t\), such that if assumptions (O1) and (O2) are satisfied and \(\text{ diam}^s(H) \le {\delta ''} \left[ \frac{1}{4P_0A} \right] ^{1/q}\), then there exists \(\chi ' \in (0,1)\) such that for all \(n\ge J n_\star \), and all \(n_\star \)-admissible sequences \((\iota _j )_{j \ge 1}\), \([{\mathcal {L}}_n\mathbb {1}_{H^c}]{\mathcal {C}}_{c,A,L}(\delta '')\subset {\mathcal {C}}_{\chi ' c,\chi ' A,\chi ' L}(\delta '')\).
Proof
For \(n = m N_{{\mathcal {F}}}'\), we may apply both Lemma 8.3 and Theorem 6.12 to obtain,
for as long as \(\chi ^m c'' > c\), \(\chi ^m A'' > A\) or \(\chi ^m L'' > L\). Letting \(m_1\) denote the greatest m such that \(\chi ^m c'' > c\) or \(\chi ^m A'' > A\) or \(\chi ^m L'' > L\), and setting \(J = m_1+1\) produces the required contraction. \(\square \)
Remark 8.5
Taking \(\kappa =0\) we can also consider the case of a single map, \(T_{\iota _j} = T_0\) for each j. Then once we know the transfer operator for the open system acts as a strict contraction on the cone, it is straightforward to recover the usual full set of results for open systems with exponential escape, including a unique escape rate and limiting conditional invariant measure for all elements of the cone. See Theorem 8.16 for an example.
8.2 Large holes
The preceding pertains to relatively small holes. For many applications, large holes must be considered. To do so requires either a much closer look at the combinatorics of the trajectories or requiring the holes to open at even longer time intervals than what was needed before. We will pursue the second, much easier, option with the intent to show that large holes are not out of reach. To work with large holes it is convenient to strengthen hypothesis (O1):
- (O\(1'\)):
-
(Complexity) There exists \(P_0 >0\) such that any stable curve of length at most \(\delta _0\) can be cut into at most \(P_0\) pieces by \(\partial H\).
The main difference between small and large holes is that, according to Lemma 8.3, for holes with sufficiently small stable diameter, multiplication by \(\mathbb {1}_{H^c}\) maps \({\mathcal {C}}_{c,A,L}(\delta )\) into a cone with larger parameters; by contrast, for large holes, multiplying by the indicator function may produce functions that do not belong to any cone and we must use mixing to recover this property, as detailed in Lemma 8.8. To avoid trivialities, we only consider holes with \(\mu _{\tiny {\text{ SRB }}}(H) < 1\).
When iterating \(T^{-1}_nW\) for \(W \in {\mathcal {W}}^s\), we will need to distinguish between elements of \({\mathcal {G}}_n(W)\) which intersect H and those that do not. Recall that \({\mathcal {G}}_n(W)\) subdivides long homogeneous connected components of \(T^{-1}_nW\) into curves of length between \(\delta _0\) and \(\delta _0/3\). We let \({\mathcal {G}}_n^H(W)\) denote the connected components of \(W_i \cap H^c\), for \(W_i \in {\mathcal {G}}_n(W)\), where \(H^c = M \setminus H\). Following the notation of Sect. 5.2, let \(Lo_n^H(W; \delta )\) denote those elements of \({\mathcal {G}}_n^H(W)\) having length at least \(\delta \) and let \(Sh_n^H(W; \delta )\) denote those elements having length at most \(\delta \).
Without the small hole condition, hypotheses (O\(1'\)) and (O2) are insufficient to prove Lemma 8.3; however, one can recover the results of Proposition 8.4 and its consequences provided one is willing to wait for a longer time. To prove the following result, we recall again Definition 2.4 of admissible sequence. We call a sequence \(( \iota _j )_{j \ge 1}\), \(\iota _j \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), N-admissible if there exist sequences \((T_k)_{k \ge 1} \subset {\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and \((N_k)_{k \ge 1}\) with \(N_k \ge N\), such that \(T_{\iota _j} \in {\mathcal {F}}(T_k, \kappa )\) for all \(k \ge 1\) and \(j \in [1 + \sum _{i=1}^{k-1} N_i, \sum _{i=1}^k N_i]\).
Lemma 8.6
If (O1\('\)) and (O2) are satisfied, then for each \(\delta >0\) small enough (depending on \(\mu _{\tiny {\text{ SRB }}}(H)\)) there exists \(n_\delta \in {\mathbb {N}}\), \(n_\delta \le C\ln \delta ^{-1}\) for some constant \(C>0\), such that for all \(n_\delta \)-admissible sequences \((\iota _j)_j\), all \(W\in {\mathcal {W}}^s(\delta )\) and \(n\ge n_\delta \),
Proof
Arguing exactly as in Lemma 8.3 it follows that if (O\(1'\)) and (O2) are satisfied, then there exists \(c'\ge c,A'\ge A, L'\ge L\) such that \(\mathbb {1}_{H^c}+ 1 \in {\mathcal {C}}_{c',A',L'}(\delta )\) and we may choose \(c', A', L'\) and \(\delta >0\) such that the conditions of Theorem 6.12 are satisfied. Setting \(n_\delta := N_{{\mathcal {F}}}'\) from Theorem 6.12 for these cone parameters, we apply Eq. (7.10) of Theorem 7.4 to this larger cone,

On the other hand, recalling Lemma 3.3,

which implies the lemma. \(\square \)
We are now able to state the analogue of Proposition 8.4 without the small hole condition. Note, however, that now \(n_\star \) has a worse dependence on \(\delta \) that we refrain from making explicit. We recall from Remark 8.2 that we have fixed the parameters c, A, L of the cone, but we may choose \(\delta \) smaller as needed.
Proposition 8.7
Under assumptions (O1\('\)) and (O2), for each \(\delta >0\) small enough there exist \(\chi ' \in (0,1)\) and \(J, n_\star \in {\mathbb {N}}\) depending on (O\(1'\)), (O2), \(\mu _{\tiny {\text{ SRB }}}(H)\) and \(\delta \), such that, for all \(n_\star \)-admissible sequences \((\iota _j)_j\) and for all \(n\ge J n_\star \), \([{\mathcal {L}}_n\mathbb {1}_{H^c}]{\mathcal {C}}_{c,A,L}(\delta )\subset {\mathcal {C}}_{\chi ' c,\chi ' A,\chi ' L}(\delta )\).
Before proving Proposition 8.7, we state an auxiliary lemma, similar to Lemma 8.3.
Lemma 8.8
If H satisfies (O\(1'\)) and (O2), there existsFootnote 23\({{\bar{n}}}_\delta \ge n_\delta \) such that for \(n \ge {{\bar{n}}}_\delta \) and all \(n_\delta \)-admissible sequences \((\iota _j)_j\), we have \([{\mathcal {L}}_n\mathbb {1}_{H^c}] {\mathcal {C}}_{c,A,L}(\delta ) \subset {\mathcal {C}}_{c', A', L'}(\delta )\), where
Proof of Proposition 8.7
As in Sect. 8.1, we may choose minimal \(c'' \ge c'\), \(A'' \ge A'\) and \(L'' \ge L'\) and \(\delta >0\) sufficiently small to satisfy the hypotheses of Theorem 6.12. Then letting \(n_\star = \max \{ N_{{\mathcal {F}}}' , {{\bar{n}}}_\delta \}\), withFootnote 24\( N_{{\mathcal {F}}}' = C'_\star |\ln \delta | + k_*n_*\) as before, we may apply both Lemma 8.8 and Theorem 6.12 to obtain,
for as long as \(\chi ^m c'' > c\) or \(\chi ^m A'' > A\) or \(\chi ^m L'' > L\). Letting \(m_1\) denote the greatest m such that \(\chi ^m c'' > c\), \(\chi ^m A'' > A\) or \(\chi ^m L'' > L\), and setting \(J = m_1+1\) produces the required contraction. \(\square \)
Proof of Lemma 8.8
Let \(n\ge n_\delta \) (from Lemma 8.6) and \(f \in {\mathcal {C}}_{c, A, L}(\delta )\). For each \(W\in {\mathcal {W}}^s(\delta )\) and \(\psi \in {\mathcal {D}}_{a,\beta }(W)\), we have
where we are using the notation of Sect. 5.1 for the test functions. Since any element of \({\mathcal {G}}_n(W)\) may produce up to \(P_0\) elements of \(Sh^H_{n}(W; \delta )\) according to assumption (O\(1'\)), we estimate
where we have used \(|W| \ge \delta \) and cone condition (4.7), as well as Lemma 3.3(b) to sum over elements of \(Sh^H_n(W; \delta )\).
Analogously, using Lemma 8.6,
Let \(n_2\) be such that \(2AP_0C_0\theta _1^{n_2}\le \frac{1}{24} (1- \mu _{\tiny {\text{ SRB }}}(H))\), then for \(n\ge n_2\) and \(\delta \) small enough we have
Accordingly, for \(n \ge \max \{n_2, n_\delta \} =: {{\bar{n}}}_\delta \) and \(\delta \) small enough, we obtain
The contraction of A follows step-by-step from our estimates in Sect. 5.2.2. Taking \(W \in {\mathcal {W}}^s_-(\delta )\) and grouping terms as in (8.6) we treat both long and short pieces precisely as in Sect. 5.2.2 with the additional observation that each element of \({\mathcal {G}}_n(W)\) produces at most \(P_0\) elements of \(Sh_n^H(W; \delta )\) by assumption (O\(1'\)). Thus (5.4) becomes,

where we have applied (8.7) and assumed \(n \ge \max \{n_2, n_\delta \}\).
Finally, we show how the parameter c contracts from cone condition (4.8). Following Sect. 5.2.3, we take \(W^1, W^2 \in {\mathcal {W}}^s_-(\delta )\) with \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \), and \(\psi _k \in {\mathcal {D}}_{a,\alpha }(W^k)\) with \(d_*(\psi _1, \psi _2) = 0\). As before, we assume without loss of generality that \(|W^2|\ge |W^1|\) and  .
.
We begin by recording that, by (8.9),

for \(k=1,2\), provided \(|W^2|^q \le \delta ^{q-\gamma } \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^{\gamma }\). Accordingly, it suffices to consider the case \(|W^2|^q \ge \delta ^{\gamma - q} \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^{\gamma }\).
It follows from (5.8) that \(|W^1|^q \ge \frac{1}{2} \delta ^{q-\gamma } \frac{c}{2} d_{{\mathcal {W}}^s}(W^1,W^2)^\gamma \), recalling that \(d_{{\mathcal {W}}^s}(W^1, W^2) \le \delta \) and (5.7).
Next, following (5.11), we decompose elements of \({\mathcal {G}}_n^H(W^k)\) into matched and unmatched pieces, as in (5.12). We estimate the unmatched pieces precisely as in (5.15), noting that by (O\(1'\)) and the transversality condition (O2), each previously unmatched element of \({\mathcal {G}}_n(W^k)\) may be subdivided into at most \(P_0\) additional unmatched pieces \(V^k_j\), while each matched element may produce up to \(P_0\) additional unmatched pieces each having length at most,
by Lemma 5.5(a). Thus,
where we have used (8.7) in (5.14) to estimate
The estimate on matched pieces proceeds precisely as in (5.20), and with an additional factor of \(P_0\) in (5.21), we arrive at (5.25), again applying (8.7),
Combining this estimate together with (8.10) in (5.11) (with \(A'\) in place of A in (5.11)), and recalling (5.12), yields by (5.26),

where we have applied (5.27) to simplify the expression. Setting \(c' = P_0 c\) and recalling the definition of \(A'\) from (8.9) completes the proof of the lemma. \(\square \)
8.3 Loss of memory for sequential open billiards
We conclude the section by illustrating several physically relevant models to which our results apply. Admittedly, we cannot treat the most general cases, yet we believe the following shows convincingly that the techniques developed here can be the basis of a general theory.
Dispersing billiards with small holes have been studied in [DWY, D1, D2], and results obtained regarding the existence and uniqueness of limiting distributions in the form of SRB-like conditionally invariant measures, and singular invariant measures supported on the survivor set. In the present context, we are interested in generalizing these results to the non-stationary setting. Analogous results for sequences of expanding maps with holes have been proved in [MO, GO].
For concreteness, we give two example of physical holes that satisfy our hypotheses, following [DWY, D2].
Holes of Type I. Let \({\mathbb {G}}\subset \partial Q\) be an arc in the boundary of one of the scatterers. Trajectories of the billiard flow are absorbed when they collide with \({\mathbb {G}}\). This induces a hole H in the phase space M of the billiard map of the form \((a,b) \times [-\pi /2, \pi /2]\). Note that \(\partial H\) consists of two vertical lines, so that H satisfies assumption (O2) since the vertical direction is uniformly transverse to the stable cone, as well as assumptions (O1) and (O1\('\)) with \(P_0 = 3\).
Holes of Type II. Let \({\mathbb {G}}\subset Q\) be an open convex set bounded away from \(\partial Q\) and having a \(C^3\) boundary. Such a hole induces a hole H in M via its ‘forward shadow.’
We define H to be the set of \((r,\varphi ) \in M\) whose backward trajectory under the billiard flow enters \({\mathbb {G}}\) before it collides with \(\partial Q\). Thus points in M which are about to enter \({\mathbb {G}}\) before their next collision under the forward billiard flow are considered still in the open system, while those points in M which would have passed through \({\mathbb {G}}\) on the way to their current collision are considered to have been absorbed by the hole.
With this definition, the geometry of H is simple to state: if we view \({\mathbb {G}}\) as an additional scatterer in Q, then H is simply the image of \({\mathbb {G}}\) under the billiard map. Thus H will have connected components on each scatterer that has a line of sight to \({\mathbb {G}}\), and \(\partial H\) will comprise curves of the form \({\mathcal {S}}_0 \cup T({\mathcal {S}}_0)\), which are positively sloped curves, all uniformly transverse to the stable cone. Thus holes of Type II satisfy (O2) as well as (O1) and (O1\('\)) with \(P_0=3\). (See the discussion in [D2, Section 2.2].)
Still other holes are presented in [D2] such as side pockets, or holes that depend on both position and angle, which satisfy (O1), (O1\('\)) and (O2), but for the sake of brevity, we do not repeat those definitions here.
As noted, both holes of Type I and Type II satisfy (O1) and (O1\('\)) with \(P_0=3\). Moreover, holes of Type I satisfy (O2) with \(C_t\) depending only on the maximum slope of curves in the stable cone, which is uniform in the family \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) according to (H1): this (negative) slope is bounded below by \(-{\mathcal {K}}_{\max } - \frac{1}{\tau _{\min }}\), so choosing \(C_t \ge {\mathcal {K}}_* + \tau _*^{-1}\) suffices. Since \(\partial H\) for holes of Type II have positive slope, the same choice of \(C_t\) will suffice for such holes to satisfy (O2).
Fix \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\) and define \({\mathcal {H}}(P_0, C_t)\) to be the collection of holes \(H \subset M\) with \(\mu _{\tiny {\text{ SRB }}}(H) \le 1/2\) and satisfying (O1) or (O\(1'\)) and (O2) with the given constants \(P_0\) and \(C_t\). We define a non-stationary open billiard by fixing a sequence of holes \(H_k \in {\mathcal {H}}(P_0, C_t)\), \(k \in {\mathbb {Z}}^+\), satisfying either (O1) and (O2) or (O\(1'\)) and (O2). In the first case, let \(n_\star \) be from Proposition 8.4, while in the second, let \(n_\star \) be from Proposition 8.7.Footnote 25 Next, choose an \(n_\star \)-admissible sequence \((\iota _j )_j\), \(\iota _j \in {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\).
Recall (5.13): For \(u, v \in {\mathbb {N}}\), \(v > u\), let \(T_{v,u} = T_{\iota _v} \circ \cdots \circ T_{\iota _{u+1}}\). For each \(k \ge 1\), the open system relative to \(H_k\) is defined by \(\mathring{T}_k : (T_{k n_\star , (k-1)n_\star })^{-1}(M \setminus H_k) \rightarrow M \setminus H_k\), where
To concatenate these open maps into a sequential system, define
thus we allow escaping once every \(n_\star \) iterates along the admissible sequence. The transfer operator for the sequential open system is defined by
We will be interested in the evolution of probability densities under the sequential system, given by \(\frac{\mathring{{\mathcal {L}}}_{n,k} f}{ \int _M \mathring{{\mathcal {L}}}_{n,k} f \, d\mu _{\tiny {\text{ SRB }}}}\). Note that if \(f\in {\mathcal {C}}_{c,A,L}(\delta )\) then \(\int _M \mathring{{\mathcal {L}}}_{n,k} f \, d\mu _{\tiny {\text{ SRB }}}> 0\) for each n (thus the normalization is well defined). When \(f \ge 0\), this normalization coincides with the \(L^1(\mu _{\tiny {\text{ SRB }}})\) norm; however, we use the integral rather than the \(L^1\) norm as the normalization since the integral is order preserving with respect to our cone, while the \(L^1\) norm is not. We conclude the section with a result regarding exponential loss of memory for the sequence of open billiards.
Theorem 8.9
Fix \(\tau _*, {\mathcal {K}}_*>0\) and \(E_* <\infty \), and let \(a,c, A, L, \delta \) and \(\delta _0\) satisfy the conditions of Theorem 6.12 and Lemma 7.1. Let \(P_0, C_t > 0\). There exist \(C>0\) and \(\vartheta <1\) such that for all sequences \((H_i)_i \subset {\mathcal {H}}(P_0, C_t)\) satisfying either (O1) and (O2) or (O\(1'\)) and (O2), all \(n_\star \)-admissible sequences \((\iota _j)_j \subset {\mathcal {I}}(\tau _*, {\mathcal {K}}_*, E_*)\), for all \(\psi \in C^1(M)\), all \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\), all \(n\ge 1\) and all \(1 \le k \le n\),
Proof
Remark that the constants appearing in Propositions 8.4 and 8.7 are uniform, depending only on \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\), \(P_0\) and \(C_t\). Hence, if \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\), then for each \(k\le n\in {\mathbb {N}}\), \(\mathring{{\mathcal {L}}}_{n,k} f\), \(\mathring{{\mathcal {L}}}_{n,k} g \in {\mathcal {C}}_{c,A,L}(\delta )\). Since \(\int _M \frac{\mathring{{\mathcal {L}}}_{n,k} f}{ \mu _{\tiny {\text{ SRB }}}(\mathring{{\mathcal {L}}}_{n,k} f ) } d\mu _{\tiny {\text{ SRB }}}= \int _M \frac{\mathring{{\mathcal {L}}}_{n,k} g}{\mu _{\tiny {\text{ SRB }}}( \mathring{{\mathcal {L}}}_{n,k} g ) } d\mu _{\tiny {\text{ SRB }}}=1\), the theorem follows arguing exactly as in the proof of Theorem 7.3(b), using again the order preserving semi-norm \(\Vert \cdot \Vert _\psi \), as well as the fact that by Remark 7.2,
When invoking (7.6), it holds that \(\rho _{{\mathcal {C}}}( \mathring{{\mathcal {L}}}_{n,k} f/ \mu _{\tiny {\text{ SRB }}}( \mathring{{\mathcal {L}}}_{n,k} f ), \mathring{{\mathcal {L}}}_{n,k} g/ \mu _{\tiny {\text{ SRB }}}( \mathring{{\mathcal {L}}}_{n,k} g) ) = \rho _{{\mathcal {C}}} (\mathring{{\mathcal {L}}}_{n,k} f, \mathring{{\mathcal {L}}}_{n,k} g)\) due to the projective nature of the metric. \(\square \)
Note that, by changing variables, \(\int _M \mathring{{\mathcal {L}}}_{n,k} f \, \psi \, d\mu _{\tiny {\text{ SRB }}}= \int _{\mathring{M}_{n,k}} f \, \psi \circ \mathring{T}_{n,k} \, d\mu _{\tiny {\text{ SRB }}}\), where \(\mathring{M}_{n,k} = \cap _{i=k}^n \mathring{T}_k^{-1} \circ \cdots \circ \mathring{T}_i^{-1}(M \setminus H_i)\). Thus the conclusion of the theorem is equivalent to the expression,
Next we show that sequential systems with holes allow us to begin investigating some physical problems that have attracted much attention: chaotic scattering and random Lorentz gasses.
8.4 Chaotic scattering (boxed)
Consider a collection of strictly convex pairwise disjoint obstacles \(\{B_i\}\) in \({\mathbb {R}}^2\) for which the non-eclipsing condition may fail.Footnote 26 Assume that there exists a closed rectangular box \(R=[a,b]\times [c,d]\) such that if an obstacle does not intersect its boundary, then it is contained in the box. In addition, if an obstacle intersects the boundary of R, then it is symmetrical with respect to a reflection across all the linear pieces of the boundary which the obstacle intersects (see Fig. 4 for a picture). Finally, we will assume a finite horizon condition on the cover \(\widetilde{Q}\) defined after Remark 8.12.
Remark 8.10
The restriction regarding symmetrical reflections on the configuration of obstacles is necessary only because we did not develop the theory in the case of billiards in a polygonal box (see Remark 8.12 and the following text to see why this is relevant). Such an extension is not particularly difficult and should eventually be done. Other extensions that should be within reach of our technology are more general types of holes and billiards with corner points. Here, however, we are interested in presenting the basic ideas; addressing all possible situations would make our message harder to understand.
Lemma 8.11
If a particle exits R at time \(t_0\in {\mathbb {R}}\), then, in the time interval \((t_0,\infty )\), it will experience only a finite number of collisions and it will never enter R again.
Proof
Recall that \(R=[a,b]\times [c,d]\). Of course, the lemma is trivially true if, after exiting R, the particle has no collisions. Let us imagine that the particle, after exiting from the vertical side \((b,c)-(b,d)\), collides instead with the obstacle \(B_i\) at the point \(p=(p_1,p_2)\). Note that \(B_i\) must then intersect the same boundary, otherwise it would be situated to the left of the line \(x=b\) and the particle could not collide since necessarily \(p_1>b\). Our hypothesis that \(B_i\) be symmetric with respect to reflection across \(x=b\) implies that also \(( 2b - p_1, p_2 )\in \partial B_i\). Thus, by the convexity of \(B_i\), the horizontal segment joining p and \((2b - p_1, p_2)\) is contained in \(B_i\). This implies that, calling \(\eta =(\eta _1,\eta _2)\) the normal to \(\partial B_i\) in p, it must be \(\eta _1\ge 0\). In addition, if \(v=(v_1,v_2)\) denotes the particle’s velocity just before collision, it must be that \(v_1>0\) since the particle has crossed a vertical line to exit R. Finally, \(\langle v,\eta \rangle \le 0\), otherwise the particle would not collide with \(B_i\). But since the velocity after collision is given by \(v^+=v-\langle v,\eta \rangle \eta \), it follows \(v^+_1=v_1-\langle v,\eta \rangle \eta _1\ge v_1\). That is, the particle cannot come back to the box R. Since all the obstacles are contained in a larger box \(R_1\) and since there is a minimal distance between obstacles, the above also implies that the particle can have only finitely many collisions in the future. The other cases can be treated exactly in the same manner. \(\square \)
Remark 8.12
We want to consider a scattering problem: the particles enter the box coming from far away and with random position and/or velocity, interact and, eventually, leave the box. The basic question is how long they stay in the box or, better, what is the probability that they stay in the box longer than some time t. This is nothing other than an open billiard with holes. Unfortunately, the holes are large and our current theory allows us to deal with large holes only if enough hyperbolicity is present. To extend the result to systems with small hyperbolicity is a very important (and hard) problem as one needs to understand the combinatorics of the trajectories for long times.
An alternative is to study the scattering problem under the non-eclipsing condition. Such an assumption avoids the technicalities associated with billiards and results in Axiom A dynamics with a natural finite Markov partition for the collision map on the survivor set. This problem has been studied and strong results proving exponential escape as well as exponential mixing on the survivor set have been obtained in both discrete [Mo91, LoM, Mo07] as well as continuous [St] time. There are also recent results on the rigidity problem for such open billiards [BDKL, DKL2]. Yet the condition is artificial once there are more than 2 scatterers, hence the importance of developing an alternative approach.
Given the above remark we modify the system in order to have the needed hyperbolicity. This is not completely satisfactory, yet it shows that our machinery can deal with large holes and illustrates exactly what further work is necessary to address the general case.
Fixing N sufficiently large, we suppose that when a particle enters the box, the boundaries of the box become reflecting and are transparent again only between the collisions kN and \(kN+1\), \(k\in {\mathbb {N}}\), counting only collisions with the convex obstacles.
More precisely, consider the billiard in R with elastic reflection at \(\partial R\). We call such a billiard table Q. Let \(M= \big ( \cup _i\partial B_i \cap R \big ) \times [-\frac{\pi }{2},\frac{\pi }{2}]\) be the Poincaré section,Footnote 27 and consider the Poincaré map \(T:M\rightarrow M\) describing the dynamics from one collision with a convex body to the next. Unfortunately, this is not a type of billiard that fits our assumptions since the table has corner points. Yet, when the particle collides with \(\partial R\) we can reflect the box and imagine that the particle continues in a straight line. Note that, by our hypothesis, the image of the obstacles that intersect the boundary are the obstacles themselves; this is the reason why we restrict the obstacle configuration. We can then reflect the box three times, say across its right and top sides and then once more to make a full rectangle with twice the width and height of R, and identify the opposite sides of this larger rectangle. In this way we obtain a torus \({\mathbb {T}}^2\) containing pairwise disjoint convex obstacles. Such a torus is covered by four copies of R, let us call them \(\{R_i\}_{i=1}^4\). We call such a billiard \({{\widetilde{Q}}}\), and we consider the Poincaré map \({{\widetilde{T}}}\) which maps from one collision with a convex body to the next, and denote its phase space by \({{\widetilde{M}}} = \cup _{i=1}^4 {\widetilde{M}}_i\).
Our final assumption on the obstacle configuration is that \({{\widetilde{Q}}}\) is a Sinai billiard with finite horizon. Hence \({{\widetilde{T}}} : {{\widetilde{M}}} \circlearrowleft \) falls within the scope of our theory. By construction there is a map \(\pi :{{\widetilde{M}}} \rightarrow M\) which sends the motion on the torus to the motion in the box. Indeed, if \({{\tilde{x}}}\in {{\widetilde{M}}}\) and \(x=\pi ({{\tilde{x}}})\), then \(T^n(x)=\pi ({\widetilde{T}}^n({{\tilde{x}}}))\), for all \(n\in {\mathbb {N}}\).
We then consider the maps \({{\tilde{S}}}={{\widetilde{T}}}^N\) and \(S=T^N\), again \(\pi ({{\widetilde{S}}}({{\tilde{x}}}))=S(\pi ({{\tilde{x}}}))\). Define also the projections \({{\tilde{\pi }}}_1 : {{\widetilde{M}}} \rightarrow {{\widetilde{Q}}}\) and \(\pi _1 : M \rightarrow Q\), which map a point in the Poincaré section to its position on the billiard table. For \({{\tilde{x}}} \in {{\widetilde{M}}}\), let us call \({{\widetilde{O}}}({{\tilde{x}}})\) the straight trajectory in \({\mathbb {T}}^2\) between \({{\tilde{\pi }}}_1({{\tilde{x}}})\) and \(\tilde{\pi }_1({{\widetilde{T}}}({{\tilde{x}}}))\), and setting \(x = \pi ({{\tilde{x}}})\), O(x) the trajectory between \(\pi _1(x)\) and \(\pi _1(T((x))\). Note that the latter trajectory can consist of several straight segments joined at the boundary of R, where a reflection takes place. By construction, if \(\widetilde{O}({{\tilde{x}}})\) intersects m of the sets \(\partial R_i\), then the trajectory O(x) experiences m reflections with \(\partial R\). Accordingly, we introduce, in our billiard system \((\widetilde{M},{{\widetilde{S}}})\), the following holes : \({{\widetilde{H}}}={{\widetilde{T}}} \{{{\tilde{x}}}\in {{\widetilde{M}}}\;:\; {{\widetilde{O}}}({{\tilde{x}}}) \cap (\cup _i \partial R_i)\ne \emptyset \}\) and set \(H=\pi ({{\widetilde{H}}})\).
The above makes precise the previous informal statement: the system (M, S) with hole H, describes the dynamics of the billiard (M, T) in which the particle can exit R only at the times kN, \(k\in {\mathbb {Z}}\). The transfer operator associated with the open system (M, S; H) is \(\mathbb {1}_{H^c} {\mathcal {L}}_S \mathbb {1}_{H^c}\), yet since \((\mathbb {1}_{H^c} {\mathcal {L}}_S \mathbb {1}_{H^c})^n = \mathbb {1}_{H^c} ({\mathcal {L}}_S \mathbb {1}_{H^c})^n\), it is equivalent to study the asymptotic properties of \(\mathring{{\mathcal {L}}}_S :={\mathcal {L}}_S \mathbb {1}_{H^c}\).
For a function \(f : M \rightarrow {\mathbb {C}}\), we define its lift \({\tilde{f}}: {\widetilde{M}}\rightarrow {\mathbb {C}}\) by \({\tilde{f}}= f \circ \pi \). The pointwise identity then follows,
While \({{\widetilde{H}}}\) is not exactly a hole of Type II, its boundary nevertheless comprises increasing curves since it is a forward image under the flow of a wave front with zero curvature (a segment of \(\partial R_i\)). Hence condition (O\(1'\)) of Sect. 8.2 holds with \(P_0 =3\) and condition (O2) holds with \(C_t\) depending only on the uniform angle between the stable cone and the vertical and horizontal directions in \({{\widetilde{M}}}\). Thus Proposition 8.7 applies to \(\mathring{{\mathcal {L}}}_{{\tilde{S}}}\) with \(n_\star \) depending on \(C_t\) and \(P_0 = 3\). In fact, our next result shows that also \(\mathring{{\mathcal {L}}}_S\) contracts \({\mathcal {C}}_{c, A, L}(\delta )\) on M.
Proposition 8.13
Let \(n_\star \in {\mathbb {N}}\) be from Proposition 8.7 corresponding to \(P_0=3\) and \(C_t>0\). Then for each small enough \(\delta >0\), there exist \(c, A, L >0\), \(\chi \in (0,1)\) such that choosing \(N \ge n_\star \), \(\mathring{{\mathcal {L}}}_S({\mathcal {C}}_{c,A, L}(\delta )) \subset {\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\), where \(S = T^N\).
Proof
As already noted above, Proposition 8.7 implies the existence of \(\delta , c, A, L\) and \(\chi \) such that \(\mathring{{\mathcal {L}}}_{{\tilde{S}}}({\widetilde{{\mathcal {C}}}}_{c,A, L}(\delta )) \subset {\widetilde{{\mathcal {C}}}}_{\chi c, \chi A, \chi L}(\delta )\) if we choose \(N \ge n_\star \). Note that the constant \(C_t\) is the same on \({\widetilde{M}}\) and M. In fact the same choice of parameters for the cone works for \(\mathring{{\mathcal {L}}}_S\).
For any stable curve W, \(\pi ^{-1}W = \cup _{i=1}^4 {\widetilde{W}}_i\) where each \({\widetilde{W}}_i\) is a stable curve satisfying \(\pi ({\widetilde{W}}_i) = W\). Since \(\pi \) is invertible on each \({\widetilde{M}}_i\), we may define the restriction \(\pi _i = \pi |_{{\widetilde{M}}_i}\) such that \(\pi _i^{-1}(W) = {\widetilde{W}}_i\). Conversely, the projection of any stable curve \({\widetilde{W}}\) in \({\widetilde{M}}\) is also a stable curve in M.
Since each \(\pi _i\) is an isometry, and recalling (8.13), for any stable curve \(W \subset M\), each \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), and all \(n \ge 0\),
where \({\tilde{f}}= f \circ \pi \). Moreover, if \(\psi \in {\mathcal {D}}_{a, \beta }(W)\), then \(\psi \circ \pi \in {\mathcal {D}}_{a, \beta }({\widetilde{W}}_i)\), for each \(i = 1, \ldots , 4\). This implies in particular that \({|||}\mathring{{\mathcal {L}}}_S^n f {|||}_{\pm } = {|||}\mathring{{\mathcal {L}}}_{{\tilde{S}}}^n {\tilde{f}}{|||}_{\pm }\) for all \(n \ge 0\), and that \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) if and only if \({\tilde{f}}= f \circ \pi \in {\widetilde{{\mathcal {C}}}}_{c,A,L}(\delta )\). Consequently, \(\mathring{{\mathcal {L}}}_S f \in {\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) if and only if \(\mathring{{\mathcal {L}}}_{{\tilde{S}}} {\tilde{f}}\in {\widetilde{{\mathcal {C}}}}_{\chi c, \chi A, \chi L}(\delta )\), which proves the proposition. \(\square \)
In contrast to the sequential systems studied in Sect. 8.3, the open billiard in this section corresponds to a fixed billiard map T (and its lift \(\widetilde{T}\)). Thus we can expect the (normalized) iterates of \(\mathring{{\mathcal {L}}}_{S}\) to converge to a type of equilibrium for the open system. Such an equilibrium is termed a limiting or physical conditionally invariant measure in the literature, and often corresponds to a maximal eigenvalue for \(\mathring{{\mathcal {L}}}_{S}\) on a suitable function space. Unfortunately, conditionally invariant measures for open ergodic invertible systems are necessarily singular with respect to the invariant measure and so will not be contained in our cone \({\mathcal {C}}_{c, A, L}(\delta )\), which is a set of functions. However, we will show that for our open billiard, the limiting conditional invariant measure is contained in the completion of \({\mathcal {C}}_{c,A,L}(\delta )\) with respect to the following norm.
Definition 8.14
Let \({\mathbb {V}}= \text {span} \big ( {\mathcal {C}}_{c,A,L}(\delta ) \big )\). For all \(f \in {\mathbb {V}}\) we define
Lemma 8.15
The function \(\Vert \cdot \Vert _\star \) has the following properties:
-
(a)
The function \(\Vert \cdot \Vert _\star \) is an order-preserving norm, that is: \(- g \preceq f \preceq g\) implies \(\Vert f \Vert _\star \le \Vert g \Vert _\star \).
-
(b)
There exists \(C>0\) such that for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(\psi \in C^1(M)\),
$$\begin{aligned} \left| \int _{M} f \, \psi \, d\mu _{\tiny {\text{ SRB }}}\right| \le C {|||}f {|||}_+ | \psi |_{C^1(M)} \le C \Vert f \Vert _{\star } | \psi |_{C^1(M)} \, . \end{aligned}$$
Proof
In this proof, for brevity we write \({\mathcal {C}}\) in place of \({\mathcal {C}}_{c,A,L}(\delta )\).
a) First, we show that \(\Vert f \Vert _\star < \infty \) for any \(f \in {\mathbb {V}}\), i.e. for any \(f \in {\mathbb {V}}\) we can find \(\lambda >0\) such that \(\lambda + f, \lambda - f \in {\mathcal {C}}\). By the proof of Proposition 6.13, we claimFootnote 28 that for any \(f \in {\mathcal {C}}\), we can find \(\mu >0\) such that \(\mu - f\) belongs to \({\mathcal {C}}\). This follows since the second part of the proof with \(\chi = 1\) yields that \(\mu - f\) satisfies (4.6) if \(\mu \ge \frac{L}{L-1} {|||}f {|||}_+\), it satisfies (4.7) if \(\mu \ge \frac{2A}{A- 2^{1-q}} {|||}f {|||}_+\), and it satisfies (4.8) if \(\mu \ge \frac{2cA}{cA - \delta - C_s} {|||}f {|||}_+\). Taking \(\mu \) large enough to satisfy these 3 conditions proves the claim.
Next, consider \(f = \alpha g + \beta h\) with \(g, h \in {\mathcal {C}}\) and \(\alpha , \beta \in {\mathbb {R}}\). If \(\alpha , \beta >0\), then since \({\mathcal {C}}\) is closed under addition, the above claim yields \(\mu >0\) such that \(\mu - f\) and \(\mu + f\) are in \({\mathcal {C}}\) and thus \(\Vert f \Vert _\star \le \mu \). It remains to consider the case \(\alpha < 0\), \(\beta >0\) since the remaining cases are similar. Let \(\mu _g >0\) satisfy \(\mu _g - g\) belongs to \({\mathcal {C}}\). Set \(A = \mu _g |\alpha |\). Then \(A + f = |\alpha | (\mu _g - g) + \beta h\) is the sum of elements in \({\mathcal {C}}\) and thus is in \({\mathcal {C}}\). Similarly, let \(\mu _h >0\) satisfy \(\mu _h - h\) belongs to \({\mathcal {C}}\) and set \(B = \mu _h \beta \). Then \(B - f = |\alpha | g + \beta (\mu _h - h)\) is again in \({\mathcal {C}}\). Thus \(\Vert f \Vert _\star \le \max \{ A, B \}\).
Next, if \(\Vert f \Vert _\star = 0\), then there exists a sequence \(\lambda _n \rightarrow 0\) such that \(- \lambda _n \preceq f \preceq \lambda _n\), and so \(\lambda _n + f, \lambda _n - f \in {\mathcal {C}}\) for each n. Since \({\mathcal {C}}\) is closed (see footnote 5), this yields \(f, -f \in {\mathcal {C}}\cup \{ 0 \}\) and so \(f = 0\) since \({\mathcal {C}}\cap - {\mathcal {C}}= \emptyset \) by construction.
Since \(f \preceq g\) is equivalent to \(\nu f \preceq \nu g\) for \(\nu \in {\mathbb {R}}_+\), it follows immediately that \(\Vert \nu f\Vert _\star =\nu \Vert f \Vert _\star \).
To prove the triangle inequality, let \(f, g\in {\mathbb {V}}\). For each \(\varepsilon >0\), there exists a, b, \(a\le \varepsilon +\Vert f\Vert _\star \), \(b\le \varepsilon +\Vert g\Vert _\star \) such that \(-a \preceq f\preceq a\) and \(-b \preceq g\preceq b\). Then
implies the triangle inequality by the arbitrariness of \(\varepsilon \). We have thus proven that \(\Vert \cdot \Vert _\star \) is a norm.
Next, suppose that \(-g\preceq f\preceq g\) and let b be as above. Then
which implies \(\Vert f\Vert _\star \le \Vert g\Vert _\star \), again by the arbitrariness of \(\varepsilon \). Hence, the norm is order preserving.
(b) The first inequality is contained in Remark 7.2. For the second inequality, we will prove that
To see this, note that if \(-\lambda \preceq f \preceq \lambda \), then \({|||}\lambda - f {|||}_- \ge 0\) by Remark 4.8. Thus for any \({\widetilde{W}}\in {{\widetilde{{\mathcal {W}}}}}^s\) and \(\psi \in {\mathcal {D}}_{a,\beta }({\widetilde{W}})\),
and taking suprema over W and \(\psi \) yields \({|||}f {|||}_+ \le \lambda \), which implies (8.14). \(\square \)
Define \({\mathbb {V}}_\star \) to be the completion of \({\mathbb {V}}\) in the \(\Vert \cdot \Vert _\star \) norm. \({\mathbb {V}}_\star \) is a Banach space. Let \({\mathcal {C}}_\star \) be the closure of \({\mathcal {C}}_{c, A, L}(\delta )\) in \({\mathbb {V}}\).
We remark that by Lemma 8.15(b), \({\mathcal {C}}_\star \) embeds naturally into \((C^1(M))'\), where \((C^1(M))'\) is the closure of \(C^0(M)\) with respect to the norm \(\Vert f \Vert _{-1} = \sup _{| \psi |_{C^1}\le 1} \int _{M} f \psi \, d\mu _{\tiny {\text{ SRB }}}\). We shall show that the conditionally invariant measure for the open system (M, T; H) belongs to \({\mathcal {C}}_\star \).
Theorem 8.16
Let (M, S; H) be as defined above, where \(S = T^N\). If \(N \ge n_\star \), where \(n_\star \) is from Proposition 8.7, then:
-
(a)
\(\displaystyle h := \lim _{n \rightarrow \infty } \frac{\mathring{{\mathcal {L}}}_S^n 1}{\mu _{\tiny {\text{ SRB }}}( \mathring{{\mathcal {L}}}_S^n 1 ) }\) is an element of \({\mathcal {C}}_\star \). Moreover, h is a nonnegative probability measure satisfying \(\mathring{{\mathcal {L}}}_S h = \nu h\) for some \(\nu \in (0,1)\) such that
$$\begin{aligned} \log \nu = \lim _{n \rightarrow \infty } \frac{1}{n} \log \mu _{\tiny {\text{ SRB }}}(\cap _{i=0}^n S^{-i}(M \setminus H)) \, , \end{aligned}$$i.e. \(- \log \nu \) is the escape rate of the open system.
-
(b)
There exists \(C>0\) and \(\vartheta \in (0,1)\) such that for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(n \ge 0\),
$$\begin{aligned} \left\| \frac{\mathring{{\mathcal {L}}}_S^n f}{ \mu _{\tiny {\text{ SRB }}}(\mathring{{\mathcal {L}}}_S^n f)} - h \right\| _\star \le C \vartheta ^n\, . \end{aligned}$$In addition, there exists a linear functional \(\ell : {\mathcal {C}}_{c, A, L}(\delta ) \rightarrow {\mathbb {R}}\) such that for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), \(\ell (f) > 0\) and
$$\begin{aligned} \Vert \nu ^{-n}\mathring{{\mathcal {L}}}^n_{S} f- \ell ( f) h \Vert _\star \le C \vartheta ^n \ell ( f ) \Vert h \Vert _\star . \end{aligned}$$The constant C depends on \({\mathcal {C}}_{c,A,L}(\delta )\), but not on f.
Remark 8.17
(a) The conclusions of Theorem 8.16 apply equally well to the open system \(({\widetilde{M}}, {\tilde{S}}; {\widetilde{H}})\).
(b) By Lemma 8.15(b), the convergence in the \(\Vert \cdot \Vert _\star \) norm given by Theorem 8.16(b) implies convergence when integrated against smooth functions \(\psi \in C^1(M)\). As usual, by standard approximation arguments, the same holds for Hölder functions.
(c) Also by Lemma 8.15(b), the above convergence in \(\Vert \cdot \Vert _\star \) implies leafwise convergence as well. First note that for \(W \in {\mathcal {W}}^s(\delta )\), each \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) induces a leafwise distribution on W defined by \(f_W(\psi ) = \int _W f \, \psi \, dm_W\), for \(\psi \in {\mathcal {D}}_{a,\beta }(W)\). This extends by density to \(f \in {\mathcal {C}}_\star \). Since \(h \in {\mathcal {C}}_\star \) by Theorem 8.16(a), let \(h_W\) denote the leafwise measure induced by h on \(W \in {\mathcal {W}}^s(\delta )\). Then by Lemma 8.15(b) and Theorem 8.16(b), there exists \(C>0\) such that for all \(n \ge 0\),
and also,
In particular, the escape rate with respect to \(f dm_W\) on each \(W \in {\mathcal {W}}^s(\delta )\) equals the escape rate with respect to \(\mu _{\tiny {\text{ SRB }}}\).
Proof of Theorem 8.16
We argue as in the proof of Theorem 7.3. Recalling that \(\Vert \cdot \Vert _\star \) is an order-preserving norm, we can apply [LSV, Lemma 2.2], taking the homogeneous function \(\rho \) to also be \(\Vert \cdot \Vert _\star \) and obtain that, as in (7.6), for all \(f,g\in {\mathcal {C}}_{c,A,L}(\delta )\),
since \(\left\| \frac{\mathring{{\mathcal {L}}}^n_{S} f}{ \Vert \mathring{{\mathcal {L}}}^n_{S} f \Vert _\star } \right\| _* = 1\) and similarly for g. This implies that \(\left( \frac{\mathring{{\mathcal {L}}}^n_{S} f}{\Vert \mathring{{\mathcal {L}}}^n_{S} f \Vert _\star } \right) _{n \ge 0}\) is a Cauchy sequence in the \(\Vert \cdot \Vert _\star \) norm, and in addition, the limit is independent of f. Hence, defining \(h_0 = \lim _{n \rightarrow \infty } \frac{\mathring{{\mathcal {L}}}_{S}^n 1}{\Vert \mathring{{\mathcal {L}}}_{S}^n 1\Vert _\star }\), we have \(h_0 \in {\mathcal {C}}_\star \) with \(\Vert h_0 \Vert _\star = 1\) such thatFootnote 29 for all \(\psi \in C^1(M)\),
where all integrals are taken with respect to \(\mu _{\tiny {\text{ SRB }}}\). Thus, \(\mathring{{\mathcal {L}}}_{S} h_0=\nu h_0\). Moreover, the definition of \(h_0\) implies that,
thus \(h_0\) is a measure. In addition, by the positivity of \(\mathring{{\mathcal {L}}}_{S}\), \(h_0\) is a nonnegative measure and since \(\Vert h_0 \Vert _\star = 1\), it must be that \(h_0(1) \ne 0\). Thus we may renormalize and define
Then \(\frac{\mathbb {1}_{H^c} h}{h(H^c)}\) represents the limiting conditionally invariant probability measure for the open system (M, S; H). However, we will work with h rather than its restriction to \(H^c\) because h contains information about entry into H, which we will exploit in Proposition 8.18 below.
Due to the equality in (8.16), h has the alternative characterization,
as required for item (a) of the theorem, where \(\mathring{M}^n = \cap _{i=0}^n S^{-i} (M \setminus H)\) and convergence is in the \(\Vert \cdot \Vert _\star \) norm.
Remark that (8.15) implies \(\frac{\mathring{{\mathcal {L}}}_{S}^n f}{\Vert \mathring{{\mathcal {L}}}_{S}^n f \Vert _\star }\) converges to \(h_0\) at the exponential rate \(\vartheta ^n\). Integrating this relation and using Lemma 8.15(b), we conclude that in addition the normalization ratio \(\frac{\mu _{\tiny {\text{ SRB }}}( \mathring{{\mathcal {L}}}_{S}^n f)}{\Vert \mathring{{\mathcal {L}}}_{S}^n f \Vert _\star }\) converges to \(h_0(1)\) at the same exponential rate. Putting these two estimates together and using the triangle inequality yields for all \(n \ge 0\),
proving the first inequality of item (b).
Next, for each, \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) let
Note that \(\ell \) is bounded, homogeneous of degree one and order preserving. By Lemma 8.15 (b), \(\ell \) can be extended to \({\mathcal {C}}_\star \). Since \(\ell (h)=1\), \(\nu ^{-n} \mathring{{\mathcal {L}}}_{S}^n h = h\) and \(\ell (\nu ^{-n}\mathring{{\mathcal {L}}}^n_{S} f)=\ell (f)\) we can apply, again, [LSV, Lemma 2.2] as in (7.6) to f and \(\ell (f)h\) and obtain
proving the second inequality of item (b) of the theorem. Note that (8.18) also implies (integrating and applying Lemma 8.15(b) ) that the limsup in (8.17) is, in fact, a limit, and hence \(\ell \) is linear. Remark that \(\ell \) is also nonnegative for \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) by Remark 7.2.
By definition, if \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) and \(\lambda > \Vert f \Vert _\star \) then \(\lambda + f, \lambda - f \in {\mathcal {C}}_{c,A,L}(\delta )\), so that using the linearity and nonnegativity of \(\ell \) yields,
Thus either \(\ell (f) = 0\) for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) or \(\ell (f) \ne 0\) for all \(f \in {\mathcal {C}}_{c,AL}(\delta )\). But if the first alternative holds, then by the continuity of \(\ell \) with respect to the \(\Vert \cdot \Vert _\star \) norm (Lemma 8.15(b)), \(\ell \) is identically 0 on \({\mathcal {C}}_\star \), which is a contradiction since \(\ell (h) =1\). Thus \(\ell (f) > 0\) for all \(f \in {\mathcal {C}}_{c,A,L}(\delta )\).
Finally, applying (8.18) to \(f \equiv 1\) integrated with respect to \(\mu _{\tiny {\text{ SRB }}}\) and using again Lemma 8.15(b), we obtain
which in turn implies that \(\log \nu = \lim _{n \rightarrow \infty } \frac{1}{n} \log \mu _{\tiny {\text{ SRB }}}(\mathring{M}^n)\) since \(\ell (1) \ne 0\), as required for the remaining item of part (a) of the theorem. Note that \(\nu \ne 0\) by Remark 7.2 and (8.7), while \(\nu \ne 1\) by monotonicity since the escape rate for this class of billiards is known to be exponential for arbitrarily small holes [DWY, D2]. \(\square \)
We can use Theorem 8.16 to obtain exit statistics from the open billiard in the plane. As an example, for \(\theta \in [0, 2\pi )\) let us define \(H_\theta \) to be the set of \(x \in H\) such that the first intersection of \(O(T^{-1} x)\) with \(\partial R\) has velocity making an angle of \(\theta \) with the positive horizontal axis. Note that \(H_\theta \) is a finite union of increasing curves since it is the image of a wave front with zero curvature moving with parallel velocities. The fact that \(H_\theta \) comprises increasing curves is not altered by the fact that the flow in R may reflect off of \(\partial R\) several times before arriving at a scatterer because such collisions are neutral; also, since the corners of R are right angles, the flow remains continuous at these corner points.
Suppose the incoming particles at time zero are distributed according to a probability measure \(f d\mu _{\tiny {\text{ SRB }}}\) with density \(f \in {\mathcal {C}}_{c,A,L}(\delta )\). The probability that a particle leaves the box at time nN with a direction in the interval \(\Theta =[\theta _1, \theta _2]\), call it \({\mathbb {P}}_f(x_n\in [\theta _1, \theta _2])\), can be expressed as
where \(H_\Theta := \cup _{\theta \in \Theta } H_\theta \). Although the boundary of \(H_\Theta \) comprises increasing curves as already mentioned, the restriction on the angle may prevent \(\partial H_\Theta \) from enjoying the property of continuation of singularities common to billiards. See Fig. 5 (see also [D2, Sect. 8.2.2] for other examples of holes without the continuation of singularities property).
Similarly, for \(p \in \partial R\), define \(H_p\) to be the set of \(x \in H\) such that the last intersection of \(O(T^{-1}x)\) with \(\partial R\) is p. Then for an interval \(P \subset \partial R\), we define \(H_P = \cup _{p \in P} H_p\), and \(\int _M \mathbb {1}_{H_P} \mathring{{\mathcal {L}}}_S^n f\) denotes the probability that a particle leaves the box at time nN through the boundary interval P.
a Sample rays with \(\theta = \theta _1\) and \(\theta =\theta _2\) striking the scatterer \(B_2\). The point p is the topmost point of \(\partial B_3\). b Component of \(H_\Theta \) on the scatterer \(B_2\). In this configuration, \(H_{\theta _1}\) intersects the singularity curve \(T{\mathcal {S}}_0\) coming from \(B_1\) while \(H_{\theta _2}\) reaches \({\mathcal {S}}_0\) directly; however, the left boundary of \(H_{\Theta }\) is an arc of \(H_p\) and the continuation of singularities properties fails for a hole of this type since \(\theta _1 > 0\)
Proposition 8.18
For any intervals of the form \(\Theta = [\theta _1, \theta _2]\), or \(P = [p_1, p_2]\), any \(f \in C^1(M)\) with \(f \ge 0\) and \(\int f \, d\mu _{\tiny {\text{ SRB }}}= 1\), and all \(n \ge 0\), we haveFootnote 30
Remark 8.19
If \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), then \(\ell (f) > 0\) by Theorem 8.16(b), and Proposition 8.18 provides a precise asymptotic for the escape of particles through \(H_{\Theta }\) and \(H_P\). For more general \(f \in C^1(M)\), it may be that \(\ell (f) =0\), in which case Proposition 8.18 merely gives an upper bound on the exit statistic compared to the rate of escape given by \(\nu \).
Proof
We prove the statement for \(\mathbb {1}_{\Theta }\). The statement for \(\mathbb {1}_P\) is similar.
To start with we assume \(f\in {\mathcal {C}}_{c,A,L}(\delta )\), and \(f \ge 0\) with \(\int f \, d\mu _{\tiny {\text{ SRB }}}= 1\). As already mentioned, \(\partial H_\Theta \) comprises finitely many increasing curves in M and so \(H_\Theta \) satisfies (O\(1'\)) and (O2) with \(P_0=3\) and \(C_t\) depending only on the uniform angle between the stable cone and \(\partial H_\Theta \), which is strictly positive due to (H1). Since \(\mathbb {1}_{H_\Theta }\) is not in \(C^1(M)\), we cannot apply Lemma 8.15(b) directly; we will use a mollification to bypass this problem.
Let \(\rho : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) be a nonnegative, \(C^\infty \) function supported in the unit disk with \(\int \rho = 1\), and define \(\rho _\varepsilon (\cdot ) = \varepsilon ^{-2} \rho ( \cdot \, \varepsilon ^{-1} )\). For \(\varepsilon > 0\), define the mollification,
We have \(| \psi _\varepsilon |_{C_0} \le 1\) and \(| \psi _\varepsilon ' |_{C^0} \le C\varepsilon ^{-1}\). Note that \(\psi _\varepsilon = \mathbb {1}_{H_\Theta }\) outside an \(\varepsilon \)-neighborhood of \(\partial H_\theta \) (including \({\mathcal {S}}_0\)). Letting \({\tilde{\psi }}_\varepsilon \) denote a \(C^1\) function with \(|{\tilde{\psi }}_\varepsilon |_{C^0} \le 1\), which is 1 on \(N_\varepsilon (\partial H_\Theta )\) and 0 on \(M \setminus N_{2 \varepsilon }(\partial H_\Theta )\), we have \(| \mathbb {1}_{H_\Theta } - \psi _\varepsilon | \le {\tilde{\psi }}_\varepsilon \). Due to (O2), for any \(W \in {\mathcal {W}}^s\) such that \(W \cap N_\varepsilon (\partial H_{\Theta }) \ne \emptyset \), using first the fact that \(f \ge 0\) and then applying cone condition (4.7),
where we have used the fact that \(W \cap N_{2\varepsilon }(\partial H_{\Theta })\) has at most 2 connected components of length \(2C_t \varepsilon \). Then integrating over M and disintegrating \(\mu _{\tiny {\text{ SRB }}}\) as in the proof of Lemma 7.1, we obtain,
By Remark 7.2, \(\mu _{\tiny {\text{ SRB }}}(\mathring{{\mathcal {L}}}_S^n f) \ge {{\bar{C}}}^{-1} {|||}\mathring{{\mathcal {L}}}_S^n f {|||}_-\), so the bound is uniform in n. Since \({\tilde{\psi }}_\varepsilon \in C^1(M)\) the bound carries over to \(h({\tilde{\psi }}_\varepsilon )\), and since h is a nonnegative measure, to \(h(\mathbb {1}_{H_\Theta } - \psi _\varepsilon )\). Thus for each \(n \ge 0\) and \(\varepsilon >0\),
where we have applied (8.22) to the first and third terms and Theorem 8.16(b) and Lemma 8.15(b) to the second term. Since \(|\psi _\varepsilon |_{C^1} \le \varepsilon ^{-1}\), choosing \(\varepsilon = \vartheta ^{n/(q+1)}\) yields the required estimate for \(f\in {\mathcal {C}}_{c,A,L}(\delta )\).
To conclude, note that by Lemma 7.6, there exists \(C_\flat >0\) such that, if \(f\in C^1(M)\), then, for each \(\lambda \ge C_\flat \Vert f\Vert _{{\mathcal {C}}^1}\), \(\lambda +f\in {\mathcal {C}}_{c,A,L}(\delta )\). Hence, by the linearity of the integral, \(\ell (f)\) as defined in (8.17) can be extended to \(f \in C^1\) by \(\ell (f) = \ell (\lambda + f) - \ell (\lambda )\), and the limsup is in fact a limit since since the limit exists for \(\lambda + f, \lambda \in {\mathcal {C}}_{c,A,L}(\delta )\) (see (8.18) and following).
Now take \(f \in C^1\) with \(\int f \, d\mu _{\tiny {\text{ SRB }}}=1\) and \(\lambda \ge C_\flat \Vert f \Vert _{C^1}\) as above. Then, necessarily \(\lambda + f \ge 0\), and so recalling (8.20), we have
Hence by (8.23),
\(\square \)
8.5 Random Lorentz gas (lazy gates)
Consider a Lorentz gas as described in [AL, Section 2]. That is, we have a lattice of cells of size one with circular obstacles of fixed radius r at their corners and a random obstacle B(z) of fixed radius \(\rho \) and center in a set \({\mathcal {O}}\) at their interior.Footnote 31 The central obstacle is small enough not to intersect with the other obstacles but large enough to prevent trajectories from crossing the cell without colliding with an obstacle. We call the openings between different cells gates, see Fig. 6b, and require that no trajectory can cross two gates without making at least one collision with the obstacles. Thus we fix r and \(\rho \) satisfyingFootnote 32 the following conditions:
With r and \(\rho \) fixed, the set of possible configurations of the central obstacle are described by \(\omega \in \Omega ={\mathcal {O}}^{{\mathbb {Z}}^2}\). In order to ensure that particles cannot cross directly from \({{\hat{R}}}_1\) to \({{\hat{R}}}_3\) or from \({{\hat{R}}}_2\) to \({{\hat{R}}}_4\) without colliding with an obstacle, and to ensure a minimum distance between scatterers, we fix \(\varepsilon _* > 0\) and require the center \(c = (c_1, c_2)\) of the random obstacle \(B_\omega \), \(\omega \in \Omega \), (the central obstacle \(C_5\) in Figure 6b) to satisfy,
Note that (8.24) and (8.25) imply that all possible positions of the central scatterer \(B_\omega \) result in a billiard table with \(\tau _{\min } \ge \tau _* := \min \{ \varepsilon _*, 1-2r \} > 0\).
On \(\Omega \) the space of translations \(\xi _z\), \(z\in {\mathbb {Z}}^2\), acts naturally as \([\xi _z(\omega )]_x=\omega _{z+x}\), see Fig. 6a. We assume that the obstacle configurations are described by a measure \({\mathbb {P}}_e\) which is ergodic with respect to the translations.
Exactly as in the Sect. 8.4, we assume that the gates are reflecting and become transparent only after N collisions with the obstacles. Thus when the particle enters a cell it will stay in that cell for at least N collisions with the obstacles, hence the lazy adjective.
As described in Sect. 8.4, when the particle reflects against a gate one can reflect the table three times and see the flow (for the times at which the gates are closed) as a flow in a finite horizon Sinai billiard on the two torus. Note that the Poincaré section \(M=\cup _{i=1}^5 C_i\times [-\frac{\pi }{2},\frac{\pi }{2}]\) in each cell is exactly the same for each \(\omega \) and z since the arclength of the boundary is always the same, while the Poincaré map \(T_z\) changes depending on the position of the central obstacle, see Fig. 6b. Let us call \({\mathcal {F}}(\tau _*)\) the collection of the different resulting billiard maps corresponding to tables that maintain a minimum distance \(\tau _*>0\) between obstacles, as required by (8.24) and (8.25). (Note that the parameters \({\mathcal {K}}_*\) and \(E_*\) of Sect. 8.3 are fixed in this class once r and \(\rho \) are fixed.) The only difference with Sect. 8.4, as far as the dynamics in a cell is concerned, consists in the fact that we have to be more specific about which cell the particle enters, as now exiting from one cell means entering into another.
Recalling the notation of Sect. 8.4, if we call R(z) the cell at the position \(z\in {\mathbb {Z}}^2\), then the gates \({{\hat{R}}}_i\) are subsets of \(\partial R(z)\). We denote by \({\widetilde{R}}(z)\) the lifted cell (viewed as a subset of \({\mathbb {T}}^2\)) after reflecting R(z) three times, and by \(({\widetilde{M}}, {\widetilde{T}}_z)\) the corresponding billiard map. As before, the projection \(\pi : {\widetilde{M}}\rightarrow M\) satisfies \(\pi \circ {\widetilde{T}}= T \circ \pi \). Then the hole \({{\widetilde{H}}}(z)\) can be written as \({{\widetilde{H}}}(z)=\cup _{i=1}^4 {{\widetilde{H}}}_i(z)\), where \(\pi ({\widetilde{H}}_i(z))=: H_i(z)\) are the points \(x \in M\) such that \(O(T^{-1}x) \cap \partial R(z) \in {{\hat{R}}}_i\).Footnote 33 Due to our Assumption (8.24), this point of intersection is unique for each x since consecutive collisions with \(\partial R\) cannot occur. Then \(H(z) = \pi ({\widetilde{H}}(z)) = \cup _{i=1}^4 H_i(z)\).
As discussed in Sect. 8.4, the holes are neither of Type I nor of Type II, yet they satisfy (O1\('\)) and (O2) with \(P_0 = 3\) and \(C_t\) depending only on the uniform angle between the stable cone for the induced billiard map and the horizontal and vertical directions.
Yet for our dynamics, when a particle changes cell at the Nth collision, it is because after \(N-1\) collisions, that particle is in \(G_i(z) := T_z^{-1}H_i(z)\), and in fact it will never reach \(H_i(z)\). Unfortunately, the geometry of \(G(z) := \cup _{i=1}^4 G_i(z)\) is not convenient for our machinery since \(\partial G(z)\) may contain stable curves, yet we will be able reconcile this difficulty after defining the dynamics precisely as follows.
The phase space is \({\mathbb {Z}}^2\times M\). For \(x \in M\), denote by p(x) the position of x in R(z) and by \(\theta (x)\) the angle of its velocity with respect to the positive horizontal axis in R(z). We define
Also we set \({\mathfrak {W}}=\{w_0,\dots , w_4\}\). If \( x \in G_i(z)\), then we call \({{\bar{q}}}(x)=(q,\theta ) \in {{\hat{R}}}_i\times [0, 2\pi )\) the point \({{\bar{q}}}\) such that \(q=O(x)\cap {{\hat{R}}}_i\) and \(\theta = \theta (x)\), i.e. without reflection at \({{\hat{R}}}_i\). We then consider \({{\bar{q}}}\) as a point in the cell \(z+w(z,x) = z + w_i\) and call \(T_{z,i}(x)\) the post-collisional velocity at the next collision with an obstacle under the flow starting at \({{\bar{q}}}\). Note that in the cell \(R(z+w_i)\), \({{\bar{q}}} \in {{\hat{R}}}_{{\bar{i}}}\), where \({{\bar{i}}} = i + 2 \text{(mod } \text{4*) }\).Footnote 34 Thus if \(\Phi _t^z\) denotes the flow in R(z), then with this notation, \(G_i(z)\) is the projection on M of \({{\hat{R}}}_i\) under the inverse flow \(\Phi _{-t}^z\) while \(H_{{{\bar{i}}}}(z+w(z,x))\) is the projection on M of \({{\hat{R}}}_{{{\bar{i}}}}\) under the forward flow \(\Phi _t^{z+w_i}\). Thus,
which is a relation we shall use to control the action of the relevant transfer operators below.
Differing slightly from the previous section, here it is convenient to set \(S_z=T_z^{N-1}\), and define
We set \((z_n,x_n)=F^n(z,x)\) and we call n the macroscopic time, which corresponds to Nn collisions with the obstacles. The above corresponds to a dynamics in which when the particle enters a cell, it is trapped in the cell for N collisions with the obstacles; then the gates open and until the next collision the particle can change cells, after which it is trapped again for N collisions and so on.
We want to compute the probability that a particle visits the sets \(G_{k_0}(z_0),\cdots G_{k_{n-1}}(z_{n-1})\), in this order, where we have set \(G_0(z)=M\setminus \cup _{i=1}^4 G_i(z)\). Similarly, we define \(H_0(z) = M \setminus \cup _{i=1}^4 H_i(z)\). This itinerary corresponds to a particle that at time i changes its position in the lattice by \(w_{k_i}\). Following the notation of [AL], we call \({\mathbb {P}}_\omega \) the probability distribution in the path space \({\mathfrak {W}}^{\mathbb {N}}\) conditioned on the central obstacles being in the positions specified by \(\omega \in \Omega \). Hence, if the particle starts from the cell \(z_0 = (0,0)\) with x distributed according to a probability measure \(f d\mu _{\tiny {\text{ SRB }}}\) with density \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), then we haveFootnote 35\(z_n= \sum _{k=0}^{n-1} w_{k_i}\) and, for each obstacle distribution \(\omega \in \Omega \),
where \(\mathring{{\mathcal {L}}}_{G_{k_j}(z_j)} := {\mathcal {L}}_{T_{z_{j+1}}}^{N-1}{\mathcal {L}}_{T_{z_j,k_j}}\mathbb {1}_{G_{k_j}(z_j)}\), and we have set \(T_{z,0}:=T_z\). See [AL] for more details. We will prove below that if N is sufficiently large, then Theorem 8.9 applies to each operator \(\mathring{{\mathcal {L}}}_{G_{k}}\). This suffices to obtain an exponential loss of memory property (the analogue of the result obtained for piecewise expanding maps in [AL, Theorem 6.1]), that is property Exp in [AL, Section 4.1]. This is the content of the following theorem.
Theorem 8.20
There exist \(C_*>0\), \(\vartheta \in (0,1)\) and \(N \in {\mathbb {N}}\) such that for \({\mathbb {P}}\)-a.e. \(\omega \in \Omega \), if x is distributed according to \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), with \(f \ge 0\) and \(\int _M f \, d\mu _{\tiny {\text{ SRB }}}= 1\), \(z_0=(0,0)\), and the gates open only once every N collisions, then for all \(n > m \ge 0\) and all \(w \in {\mathfrak {W}}^{\mathbb {N}}\),
Proof
Note that for \(m \ge 0\), \(\xi _{z_m}\omega \) sends the cell at \(z_m\) to (0,0). Thus according to Eq. (8.27), for x distributed according to \(f \in {\mathcal {C}}_{c,A,L}(\delta )\) with \(z_0 = (0,0)\), we have
As remarked earlier, the sets \(G_i(z)\) do not satisfy assumption (O2) so that Proposition 8.7 does not apply directly. Yet, it follows from (8.26) that for \(g \in {\mathcal {C}}_{c,A,L}(\delta )\),
where, as before, \({{\bar{k}}}_j = k_j + 2\) (mod 4*). Then, just as in the proof of Proposition 8.7, it may be the case that \({\mathcal {L}}_{T_{z_j, k_j}}g\) is not in \({\mathcal {C}}_{c,A,L}(\delta )\). Yet, it is immediate from our estimates in Sect. 5 that \({\mathcal {L}}_{T_{z_j, k_j}}g \in {\mathcal {C}}_{c',A', 3L}(\delta )\) for any billiard map \(T_{z_j, k_j} \in {\mathcal {F}}(\tau _*)\) for some constants \(c', A'\) depending only on \({\mathcal {F}}(\tau _*)\). As in the proof of Proposition 8.7, we may choose constants \(c'' \ge c'\), \(A'' \ge A'\) and \(L'' \ge 3L\) and \(\delta >0\) sufficiently small to satisfy the hypotheses of Theorem 6.12. Then since the sets \(H_i(z)\) do satisfy (O\(1')\) and (O2) with \(P_0 = 3\) and \(C_t\) depending only on the angle between the stable cone and the vertical and horizontal directions, which has a uniform minimum in the family \({\mathcal {F}}(\tau _*)\), there exists \(\chi <1\) and N sufficiently large as in Proposition 8.7 so thatFootnote 36\(\big [ {\mathcal {L}}_{T_{z_{j+1}}}^{N-1} \mathbb {1}_{H_{{{\bar{k}}}_j}(z_{j+1})} \big ] {\mathcal {C}}_{c',A', 3L}(\delta ) \subset {\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\), and both \(\chi \) and N are independent of \(z_{j+1}\) and \(k_j\). This implies in particular that
Now the assumption that the gates only open every N collisions implies that for every \(\omega \in \Omega \), every path is the result of an N-admissible sequence.
As in the proof of Theorem 7.3, using the fact that \(\mu _{\tiny {\text{ SRB }}}( \cdot )\) is homogeneous and order preserving on \({\mathcal {C}}_{c,A,L}(\delta )\) and that \(\mu _{\tiny {\text{ SRB }}}({\bar{{\mathcal {L}}}}_m f) = \mu _{\tiny {\text{ SRB }}}(f) =1\), where \({\bar{{\mathcal {L}}}}_m f = \frac{\mathring{{\mathcal {L}}}_{G_{k_m-1}(z_{m-1})} \cdots \mathring{{\mathcal {L}}}_{G_{k_0}(z_0)} f}{\int _M \mathring{{\mathcal {L}}}_{G_{k_m-1}(z_{m-1})} \cdots \mathring{{\mathcal {L}}}_{G_{k_0}(z_0)} f} \in {\mathcal {C}}_{c,A,L}(\delta )\), we estimate as in (7.6) and (7.7),
for some \(\vartheta <1\) depending on the diameter of \({\mathcal {C}}_{\chi c, \chi A, \chi L}(\delta )\) in \({\mathcal {C}}_{c,A,L}(\delta )\).
Finally, the left hand side of (8.28) reads
where we have applied (8.29) twice and used the fact that \(\frac{\int _M\mathring{{\mathcal {L}}}_{G_{k_{n-1}}(z_{n-1})}\cdots \mathring{{\mathcal {L}}}_{G_{k_m}(z_m)} g}{\int _M\mathring{{\mathcal {L}}}_{G_{k_{n-2}}(z_{k_{n-2}})}\cdots \mathring{{\mathcal {L}}}_{G_{k_m}(z_m)}g } \le 1\) for any \(g \in {\mathcal {C}}_{c,A,L}(\delta )\). \(\square \)
In particular, Theorem 8.20, together withFootnote 37 [AL, Theorem 6.4], implies that \(\lim _{n\rightarrow \infty } \frac{1}{n}z_n =0\) for \({\mathbb {P}}_e\) almost all \(\omega \), that is, the walker has, \({\mathbb {P}}_e\)-almost-surely, no drift. See [AL, Section 6] for details.Footnote 38 This latter fact could be deduced also from the ergodicity result in [Le06, Theorem 5.4]; however, Theorem 8.20 is much stronger (indeed, by [AL, Theorem 6.4], it implies [Le06, Theorem 5.4]) since it proves some form of memory loss that is certainly not implied by ergodicity alone. It is therefore sensible to expect that more information on the random walk will follow from Theorem 8.20, although this will require further work.
We conclude with a corollary of Theorem 8.20 which implies the same exponential loss of memory for particles distributed according to two different initial distributions. For \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), let \({\mathbb {P}}_{\omega , f}( \cdot )\) denote the probability in the path space \({\mathfrak {W}}^{\mathbb {N}}\) conditioned on the central obstacles being in position \(\omega \in \Omega \) and with x initially distributed according to \(f d\mu _{\tiny {\text{ SRB }}}\).
Corollary 8.21
There exist \(C>0\) and \(\vartheta \in (0,1)\) such that for all \(f, g \in {\mathcal {C}}_{c,A,L}(\delta )\) with \(\int _M f = \int _M g =1\) and \({\mathbb {P}}\)-a.e. \(\omega \in \Omega \), if \(z_0=(0,0)\), then for all \(n \ge 0\) and all \(w \in {\mathfrak {W}}^{\mathbb {N}}\),
Proof
The proof is the same as that of Theorem 8.20 since (8.29) holds as well with \({\bar{{\mathcal {L}}}}_m f\) replaced by g. \(\square \)
Data Availibility
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
We do not claim that each such T is unique. It may be that \(T(Q) = T(Q')\) pointwise (consider a \(90^\circ \) rotation of a given configuration Q), yet for our purposes they will be considered distinct elements of \({\mathcal {F}}(\tau _*, {\mathcal {K}}_*, E_*)\).
The abstract set-up in [DZ2] also allows billiard tables with infinite horizon and those subjected to external forces, but we are not concerned with the most general case here.
Indeed, the distance \(\mathbb {d}\) allows configurations to move from finite to infinite horizon (see [DZ2, Section 6.2]), but we will not need that here as we will restrict ourselves to finite horizon configurations.
The parameter \(\gamma \in (0,1)\) is from the cone condition (4.8).
Closed here means that for all \(f,g \in {\mathcal {C}}\) and sequence \(\{\alpha _n\}\subset {\mathbb {R}}\) such that \(\lim _{n\rightarrow \infty }\alpha _n=\alpha \) and \(g+\alpha _n f\in {\mathcal {C}}\) for all \(n\in {\mathbb {N}}\) we have \(g+\alpha f\in {\mathcal {C}}\cup \{0\}\).
By independent of the cone parameters, we mean that we may first fix \(\chi < 1\), and then choose \(c,A,L, \delta \) satisfying the conditions of Sect. 5.3 so that the contraction by \(\chi \) is obtained for all choices of \(c' > c\), \(A'>A\), \(L'>L\) and \(\delta ' < \delta \) that satisfy those conditions. Note, however, that larger \(A'>A\) requires \(n_0\) to increase in size.
Note that \(\sum _i |T_nW_i| \le |W|\) and \( \frac{|T_nW_i|}{|W_i|}\le |J_{W_i}T_n|_{C^0(W_i)}\).
Note that, by [CM, Proposition 4.47], given two maximal homogeneous subcurves of \(T_n^{-1}W^k\) that are connected by a vertical segment disjoint from \({\mathcal {S}}_{n}^{{\mathbb {H}}}\), there must exist two piecewise smooth curves in \({\mathcal {S}}_{n}^{{\mathbb {H}}}\) that connect the boundaries of such two subcurves forming a rectangle that does not contain any element of \({\mathcal {S}}_{n}^{{\mathbb {H}}}\) in its interior. Thus \(U^2_{i,+}\) must be a connected subcurve.
Notice that since we subdivide curves in \({\mathcal {G}}_n^\delta (W)\) according to length \(\delta \) and not \(\delta _0\), the estimate of Lemma 3.3(b) becomes \({{\bar{C}}}_0 \delta ^{-1} |W| + C_0 \theta _1^n \le 2 {{\bar{C}}}_0 + C_0 \theta _1^n\), since \(|W| \le 2\delta \).
Since the \(U^k_j\) are vertically matched, the term on the right hand side of (5.8) proportional to \(C_s\) is absent here.
Although the stable/unstable directions in M vary, they always belong to the global stable/unstable cones defined in (H1) and so are uniformly transverse.
The choice of \(\delta _0^4\) will be needed in Lemma 6.7.
Recall that \({{\bar{C}}}_0\) is from Lemma 3.3.
These Cantor rectangles \(R_i\) are maximal in the sense that they are the intersection of the maximal families of local invariant manifolds \({\mathfrak {S}}^{s/u}(D(R_i))\) that fully cross the solid rectangle \(D(R_i)\).
Indeed, using Proposition 5.1 and choosing \(L \ge 60\), we can always choose \(\chi = \frac{8}{9}\), although this will affect the choice of \(N_{\mathcal {F}}\).
A semi-norm \(\Vert \cdot \Vert \) is order preserving if \(-g\preceq f\preceq g\) implies \(\Vert f\Vert \le \Vert g\Vert \).
According to (O1), \(W^k\) is divided into at most \(P_0\) pieces, and \(W^k \cap H^c\) comprises at most \(\frac{P_0}{2}+1\) of them. Each such piece can give rise to at most 2 unmatched pieces.
Since \(I_{W^1_j} = I_{W^2_j}\), the term on the right side of (5.8) proportional to \(C_s\) is absent in this case.
Since we have fixed the cone constants c, A, L, the number \({{\bar{n}}}_\delta \) depends on the constants appearing in (O\(1'\)) and (O2) as well as \(\mu _{\tiny {\text{ SRB }}}(H)\) and the choice of \(\delta \), from Lemma 8.6.
\(N_{{\mathcal {F}}}'\) is number from Theorem 6.12 applied to the cone with larger constants \(c'', A'', L''\).
Requiring \(\mu _{\tiny {\text{ SRB }}}(H) \le 1/2\) enables a uniform choice of \(n_\star \) for all \(H \in {\mathcal {H}}(P_0, C_t)\).
Remember that the non-eclipsing condition is the requirement that the convex hull of any two obstacles does not intersect any other obstacle.
Recall that \(\varphi \in [-\frac{\pi }{2},\frac{\pi }{2}]\) is the angle made by the post-collision velocity vector and the outward pointing normal to the boundary.
This claim implies that the cone is Archimedean.
Note that \(\mathring{{\mathcal {L}}}_{S}\) extends naturally to \(({\mathcal {C}}^1(M))'\) and therefore to \({\mathcal {C}}_\star \).
If instead \(f \in {\mathcal {C}}_{c,A,L}(\delta )\), \(f \ge 0\) and \(\int f \, d\mu _{\tiny {\text{ SRB }}}=1\), then \(\Vert f \Vert _{C^1}\) can be dropped from the right hand side.
The assumption that all obstacles are circular is not essential and can be relaxed by requiring that the obstacles at the corners are symmetric with respect to reflections as described in Sect. 8.4.
Finite horizon requires \(r \ge \frac{1}{1+\sqrt{2}}\), yet our added condition that a particle cannot cross diagonally from, say, \({{\hat{R}}}_1\) to \({{\hat{R}}}_2\) without making a collision requires further that \(r \ge \frac{1}{3}\).
The hole depends on the trajectory of x, which is different in different cells and hence depends on z, while the gates \({{\hat{R}}}_i\) are independent of z.
By (mod 4*) we mean cyclic addition on 1, 2, 3, 4 rather than 0, 1, 2, 3.
Since \(z_0 = (0,0)\), it is equivalent to specify \(z_1, \ldots z_n\) or \(w_{k_0}, \ldots w_{k_{n-1}}\) since \(w_{k_j}\) can be recovered as \(w_{k_j} = z_{j+1} - z_j\).
Here in fact our operators are of the form \({\mathcal {L}}^n\mathbb {1}_H\) while in Proposition 8.7 they have the form \({\mathcal {L}}_n \mathbb {1}_{H^c}\) for some set H. Yet, this is immaterial since the boundaries of H and \(H^c\) in M are the same so that (O\(1'\)) and (O2), and in particular Lemma 8.6, apply equally well to both sets.
Remark that [AL, Theorem 6.4] requires \(\mu _{\tiny {\text{ SRB }}}(G_i(z))\) to be the same for each i and z, independently of \(\omega \). This is precisely the case here since \(G_i(z)\) is defined as the projection of \({{\hat{R}}}_i\) under the inverse flow \(\Phi ^z_{-t}\), and Leb\(({{\hat{R}}}_i \times [0, 2\pi ))\) in the phase space of the flow is independent of i, while \(\mu _{\tiny {\text{ SRB }}}\) is the projection onto M of Lebesgue measure, which is invariant under the flow.
The arguments in [AL, Section 6] are developed for expanding maps, but the relevant parts apply verbatim to the present context.
References
Aimino, R., Liverani, C.: Deterministic walks in random environment. Ann. Probab. 48(5), 2212–2257 (2020)
Atnip, J., Froyland, G., González-Tokman, C., Vaienti, S.: Thermodynamic formalism for random weighted covering systems. Commun. Math. Phys. 386(2), 819–902 (2021)
Baladi, V.: Anisotropic Sobolev spaces and dynamical transfer operators: \({\cal{C} }^\infty \) foliations, algebraic and topological dynamics. In: Kolyada, S., Manin, Y., Ward, T. (eds.) Contemporary Mathematics, pp. 123–136. American Mathematical Society (2005)
Baladi, V.: Dynamical Zeta Functions and Dynamical Determinants for Hyperbolic Maps, a Functional Approach, Results in Mathematics and Related Areas, 3rd Series, A Series of Modern Surveys in Mathematics, vol. 68, Springer, Ergebnisse (2018)
Baladi, V., Demers, M.F.: On the measure of maximal entropy for finite horizon Sinai billiard maps. J. Am. Math. Soc. 33, 381–449 (2020)
Baladi, V., Demers, M.F.: Thermodynamic formalism for dispersing billiards, preprint (2020)
Baladi, V., Demers, M.F., Liverani, C.: Exponential decay of correlations for finite horizon Sinai billiard flows. Invent. Math. 211(1), 39–177 (2018)
Baladi, V., Tsujii, M.: Anisotropic Hölder and Sobolev spaces for hyperbolic diffeomorphisms. Ann. Inst. Fourier. 57, 127–154 (2007)
Balint, P., De Simoi, J., Kaloshin, V., Leguil, M.: Marked length spectrum, homoclinic orbits and the geometry of open dispersing billiards. Commun. Math. Phys. 374, 1531–1575 (2020)
Birkhoff, G.: Extensions of Jentzsch’s theorem. Trans. Am. Math. Soc. 85, 219–227 (1957)
Blank, M., Keller, G., Liverani, C.: Ruelle–Perron–Frobenius spectrum for Anosov maps. Nonlinearity 15(6), 1905–1973 (2002)
Bunimovich, L., Sinai, Y.G., Chernov, N.: Markov partitions for two-dimensional hyperbolic billiards. Russ. Math. Surv. 45, 105–152 (1990)
Chernov, N.: Advanced statistical properties of dispersing billiards. J. Stat. Phys. 122, 1061–1094 (2006)
Chernov, N.: Sinai billiards under small external forces II. Ann. Henri Poincaré 9, 91–107 (2008)
Chernov, N., Dolgopyat, D.: Brownian Brownian Motion—I, vol. 198, p. 927. Memoirs of American Mathematical Society (2009)
Chernov, N., Markarian, R.: Chaotic Billiards, Mathematical Surveys and Monographs, vol. 127. American Mathematical Society (2006)
Chernov, N., Zhang, H.-K.: On statistical properties of hyperbolic systems with singularities. J. Stat. Phys. 136, 615–642 (2009)
Demers, M.F.: Escape rates and physical measures for the infinite horizon Lorentz gas with holes. Dyn. Syst. Int. J. 28(3), 393–422 (2013)
Demers, M.F.: Dispersing billiards with small holes. In: Ergodic Theory, Open Dynamics and Coherent Structures, vol. 70, pp. 137–170. Springer Proceedings in Mathematics (2014)
Demers, M.F., Liverani, C.: Stability of statistical properties in two-dimensional piecewise hyperbolic maps. Trans. Am. Math. Soc. 360(9), 4777–4814 (2008)
Demers, M.F., Wright, P., Young, L.-S.: Escape rates and physically relevant measures for billiards with small holes. Commun. Math. Phys. 294(2), 353–388 (2010)
Demers, M.F., Zhang, H.-K.: Spectral analysis of the transfer operator for the Lorentz gas. J. Mod. Dyn. 5(4), 665–709 (2011)
Demers, M.F., Zhang, H.-K.: A functional analytic approach to perturbations of the Lorentz gas. Commun. Math. Phys. 324(3), 767–830 (2013)
Demers, M.F., Zhang, H.-K.: Spectral analysis of hyperbolic systems with singularities. Nonlinearity 27, 379–433 (2014)
Demers, M.F., Kiamari, N., Liverani, C.: Transfer operators in hyperbolic dynamics. An introduction. 33 Colloquio Brasilero de Matematica. Brazilian Mathematics Colloquiums series, Editora do IMPA, p 252 (2021). ISBN 978-65-89124-26-9
De Simoi, J., Liverani, C.: Statistical properties of mostly contracting fast-slow partially hyperbolic systems. Invent. Math. 206(1), 147–227 (2016)
De Simoi, J., Liverani, C.: Limit theorems for fast-slow partially hyperbolic systems. Invent. Math. 213(3), 811–1016 (2018)
De Simoi, J., Liverani, C., Poquet, C., Volk, D.: Fast-slow partially hyperbolic systems versus Freidlin–Wentzell random systems. J. Stat. Phys. 166(3–4), 650–679 (2017)
De Simoi, J., Kaloshin, V., Leguil, M.: Marked length spectral determination of analytic chaotic billiards with axial symmetries. Invent. Math. (to appear)
Dobbs, N., Stenlund, M.: Quasistatic dynamical systems. Ergod. Theory Dyn. Syst. 37(8), 2556–2596 (2017)
Dolgopyat, D.: Limit theorems for partially hyperbolic systems. Trans. Am. Math. Soc. 356(4), 1637–1689 (2004)
Dolgopyat, D.: On differentiability of SRB states for partially hyperbolic systems. Invent. Math. 155(2), 389–449 (2004)
Dolgopyat, D.: Averaging and invariant measures. Mosc. Math. J. 5(3), 537–576, 742 (2005)
Dragičević, D., Froyland, G., González-Tokman, C., Vaienti, S.: A spectral approach for quenched limit theorems for random expanding systems. Commun. Math. Phys. 360(3), 1121–1187 (2018)
Dragičević, D., Froyland, G., González-Tokman, C., Vaienti, S.: A spectral approach for quenched limit theorems for random hyperbolic dynamical systems. Trans. Am. Math. Soc. 373(1), 629–664 (2020)
Fried, D.: The zeta functions of Ruelle and Selberg. I. Ann. Sci. École Norm. Sup. (4) 19(4), 491–517 (1986)
Geiger, B., Ott, W.: Nonstationary open dynamical systems, arXiv:1808.05315v4 (2019)
Gouëzel, S., Liverani, C.: Banach spaces adapted to Anosov systems. Ergod. Theorem Dyn. Syst. 26(1), 189–217 (2006)
Gouëzel, S., Liverani, C.: Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Differ. Geom. 79(3), 433–477 (2008)
Keller, G., Liverani, C.: Stability of the spectrum for transfer operators. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 28(1), 141–152 (1999)
Kitaev, A.Y.: Fredholm determinants for hyperbolic diffeomorphisms of finite smoothness. Nonlinearity 12, 141–179 (1999)
Krylov, N.S.: Works on the foundations of statistical physics. Translated from the Russian by A. B. Migdal, Ya. G. Sinai and Yu. L. Zeeman. With a preface by A. S. Wightman. With a biography of Krylov by V. A. Fock. With an introductory article "The views of N. S. Krylov on the foundations of statistical physics” by Migdal and Fok. With a supplementary article "Development of Krylov’s ideas” by Sinai. Princeton Series in Physics. Princeton University Press, Princeton (1979)
Lasota, A., Yorke, J.: On the existence of invariant measures for piecewise monotonic transformations. Trans. Am. Math. Soc. 186(1973), 481–488 (1974)
Lenci, M.: Typicality of recurrence for Lorentz gases. Ergod. Theory Dyn. Syst. 26(3), 799–820 (2006)
Liverani, C.: Decay of correlations. Ann. Math. 142, 239–301 (1995)
Liverani, C.: Decay of correlations for piecewise expanding maps. J. Stat. Phys. 78(3–4), 1111–1129 (1995)
Liverani, C., Saussol, B., Vaienti, S.: Conformal measure and decay of correlation for covering weighted systems. Ergod. Theory Dyn. Syst. 18(6), 1399–1420 (1998)
Liverani, C., Maume-Deschamps, V.: Lasota–Yorke maps with holes: conditionally invariant probability measures and invariant probability measures on the survivor set. Ann. Inst. H. Poincaré Probab. Stat. 39(3), 385–412 (2003)
Lopes, A., Markarian, R.: Open billiards: invariant and conditionally invariant probabilities on Cantor sets. SIAM J. Appl. Math. 56(2), 651–680 (1996)
Mohapatra, A., Ott, W.: Memory loss for nonequilibrium open dynamical systems. Discrete Contin. Dyn. Syst. (Ser. A) 34(9), 3747–3759 (2014)
Morita, T.: The symbolic representation of billiards without boundary condition. Trans. Am. Math. Soc. 325(2), 819–828 (1991)
Morita, T.: Meromorphic extensions of a class of zeta functions for two-dimensional billiards without eclipse. Tohoku Math. J. (2) 59(2), 167–202 (2007)
Ruelle, D., Sullivan, D.: Currents, flows and diffeomorphisms. Topology 14(4), 319–327 (1975)
Ruelle, D.: Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34, 231–242 (1976)
Rugh, H.H.: Generalized Fredholm determinants and Selberg zeta functions for Axiom A dynamical systems. Ergod. Theorem Dyn. Syst. 16, 805–819 (1996)
Sinai, Y.G.: Dynamical systems with elastic reflections. Ergodic properties of dispersing billiards. Russ. Math. Surv. 25, 137–189 (1970)
Stoyanov, L.: Spectrum of the Ruelle operator and exponential decay of correlations for open billiard flows. Am. J. Math. 123(4), 715–759 (2001)
Stenlund, M., Young, L.-S., Zhang, H.-K.: Dispersing billiards with moving scatterers. Commun. Math. Phys. 332(3), 909–955 (2013)
Young, L.-S.: Statistical properties of dynamical systems with some hyperbolicity. Ann. Math. (2) 147(3), 585–650 (1998)
Young, L.-S.: Recurrence times and rates of mixing. Israel J. Math. 110, 153–188 (1999)
Zhang, H.-K.: Current in periodic Lorentz gases with twists. Commun. Math. Phys. 306, 747–776 (2011)
Acknowledgements
This work was supported by the PRIN Grant “Regular and stochastic behavior in dynamical systems" (PRIN 2017S35EHN). C. Liverani acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. M. Demers was partially supported by NSF grants DMS 1800321 and DMS 2055070. C. Liverani is a member of the Editorial Board of Communications in Mathematical Physics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by S. Dyatlov.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Jochen Broecker, Tobias Kuna and especially Lea Oljaca for pointing out to us the possibility to prove Lemma 4.10. This work was supported by the PRIN Grant “Regular and stochastic behaviour in dynamical systems” (PRIN 2017S35EHN). C.L. acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. M.D. was partially supported by NSF grants DMS 1800321 and DMS 2055070.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Demers, M.F., Liverani, C. Projective Cones for Sequential Dispersing Billiards. Commun. Math. Phys. 401, 841–923 (2023). https://doi.org/10.1007/s00220-023-04657-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04657-1



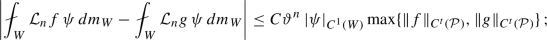
 , we have
, we have 





 , we have
, we have 



