Continuous-Variable Nonlocality and Contextuality

Abstract

Contextuality is a non-classical behaviour that can be exhibited by quantum systems. It is increasingly studied for its relationship to quantum-over-classical advantages in informatic tasks. To date, it has largely been studied in discrete-variable scenarios, where observables take values in discrete and usually finite sets. Practically, on the other hand, continuous-variable scenarios offer some of the most promising candidates for implementing quantum computations and informatic protocols. Here we set out a framework for treating contextuality in continuous-variable scenarios. It is shown that the Fine–Abramsky–Brandenburger theorem extends to this setting, an important consequence of which is that Bell nonlocality can be viewed as a special case of contextuality, as in the discrete case. The contextual fraction, a quantifiable measure of contextuality that bears a precise relationship to Bell inequality violations and quantum advantages, is also defined in this setting. It is shown to be a non-increasing monotone with respect to classical operations that include binning to discretise data. Finally, we consider how the contextual fraction can be formulated as an infinite linear program. Through Lasserre relaxations, we are able to express this infinite linear program as a hierarchy of semi-definite programs that allow to calculate the contextual fraction with increasing accuracy.

1 Introduction

Contextuality is one of the principal markers of non-classical behaviour that can be exhibited by quantum systems. The Heisenberg uncertainty principle identified that certain pairs of quantum observables are incompatible, e.g. position and momentum. In operational terms, observing one will disturb the outcome statistics of the other. This is sometimes cited as evidence that not all observables can simultaneously be assigned definite values. Taking the mathematical formalism of quantum mechanics at face value, that is indeed the case, in stark contrast with classical physical theories. However, one may wonder whether it is possible to build a (presumably more fundamental) theory more in accordance with our classical intuitions, but which still matches the empirical predictions of quantum mechanics. Put briefly, the fundamental question is then whether such quantum oddities are a necessary property of any theory that accurately describes nature, and thus have empirical content, or mere artifices of the mathematical formalism of quantum theory.

This question might be answered by attempting to build a hidden-variable model reproducing quantum-mechanical empirical predictions but with the further assumption that it be noncontextual. Roughly speaking, the latter imposes that the model must respect the basic assumptions that (i) hidden variables assign definite values to all the observable properties, and (ii) jointly performing compatible observables does not disturb the hidden variable. That these apparently simple assumptions are at odds with the empirical predictions of quantum mechanics is the content of the seminal theorems by Bell [19] and by Kochen & Specker [52].

Separately to its foundational importance, contextuality also has a more practical significance. A major application of quantum theory today is in quantum information and computation. There, one is primarily interested in what can be done with quantum systems and is beyond the capabilities of any classical implementation. So one is interested in the properties of the correlations realisable by quantum systems when compared to the kind of correlations that could arise from any classical theory. In this sense, aside from whatever foundational or physical significance one may wish (or not) to ascribe to contextuality, it has an undeniable practical significance in relation to quantum information and computation. In particular, it has now been identified as the essential ingredient for enabling a range of quantum-over-classical advantages in informatic tasks, which include the onset of universal quantum computing in certain computational models [6, 7, 20, 46, 74].

It is notable that to date the study of contextuality has largely focused on discrete variable scenarios and that the main frameworks and approaches to contextuality are tailored to modelling these, e.g. [8, 13, 26, 33]. In such scenarios, observables can only take values in discrete, and usually finite, sets. Discrete variable scenarios typically arise in finite-dimensional quantum mechanics, e.g. when dealing with quantum registers in the form of systems of multiple qubits as is common in quantum information and computation theory.

Yet, from a practical perspective, continuous-variable quantum systems are emerging as some of the most promising candidates for implementing quantum informational and computational tasks [25, 84]. The main reason for this is that they offer unrivalled possibilities for deterministic generation of large-scale resource states [86] and for highly-efficient measurements of certain observables. Together these cover many of the basic operations required in the one-way or measurement-based model of quantum computing [76], for example. Typical implementations are in optical systems where the continuous variables correspond to the position-like and momentum-like quadratures of the quantised modes of an electromagnetic field. Indeed position and momentum, as mentioned previously in relation to the uncertainty principle, are the prototypical examples of continuous variables in quantum mechanics.

Since quantum mechanics itself is infinite dimensional, it also makes sense from a foundational perspective to extend analyses of the key concept of contextuality to the continuous-variable setting. Furthermore, continuous variables can be useful when dealing with iteration, even when attention is restricted to finite-variable actions at discrete time steps, as is traditional in informatics. An interesting question, for example, is whether contextuality arises and is of interest in such situations as the infinite behaviour of quantum random walks.

The main contributions of this article are the following:

• We present a robust framework for contextuality in continuous-variable scenarios that follows along the lines of the discrete-variable framework introduced by Abramsky and Brandenburger [8] (Sect. 3). We thus generalise this framework to deal with outcomes being valued on general measurable spaces, as well as to arbitrary (infinite) sets of measurement labels.

• We show that the Fine–Abramsky–Brandenburger theorem [8, 36] extends to continuous variables (Sect. 4). This establishes that noncontextuality of an empirical behaviour, originally characterised by the existence of a deterministic hidden-variable model [19, 52], can equivalently be characterised by the existence of a factorisable hidden-variable model, and that ultimately both of these are subsumed by a canonical form of hidden-variable model—a global section in the sheaf-theoretic perspective. An important consequence is that Bell nonlocality may be viewed as a special case of contextuality in continuous-variable scenarios just as for discrete-variable scenarios.

• The contextual fraction, a quantifiable measure of contextuality that bears a precise relationship to Bell inequality violations and quantum advantages [6], can also be defined in this setting using infinite linear programming (Sect. 5). It is shown to be a non-increasing monotone with respect to the free operations of a resource theory for contextuality [4, 6]. Crucially, these include the common operation of binning to discretise data. A consequence is that any witness of contextuality on discretised empirical data also witnesses and gives a lower bound on genuine continuous-variable contextuality.

• While the infinite linear programs are of theoretical importance and capture exactly the quantity and Bell-like inequalities in which we are interested, they are not directly useful for actual numerical computations. To get around this limitation, we introduce a hierarchy of semi-definite programs which are relaxations of the original problem and whose values converge monotonically to the contextual fraction (Sect. 8). This applies in the restricted setting where there is a finite set of measurement labels.

Related work. Note that we are specifically interested in scenarios involving observables with continuous spectra, or in more operational language, measurements with continuous outcome spaces. We still consider scenarios featuring only discrete sets of observables or measurements, as is typical in continuous-variable quantum computing. The possibility of considering contextuality in settings with continuous measurement spaces has also been evoked in [30]. We also note that several prior works have explicitly considered contextuality in continuous-variable systems [14, 42, 50, 57, 64, 71, 82]. Our approach is distinct from these in that it provides a genuinely continuous-variable treatment of contextuality itself as opposed to embedding discrete-variable contextuality arguments into, or extracting them from, continuous-variable systems.

2 Continuous-Variable Behaviours

In this section we provide a brief motivational example for the kind of continuous-variable empirical behaviour we are interested in analysing. The approach applies generally to any hypothetical empirical data, including those that do not admit a quantum realisation (e.g. the PR box from Ref. [72]). But also, in particular, it does of course apply to empirical data arising from quantum mechanics, in that the statistics arise from a state and measurements on a quantum system according to the Born rule. Indeed, quantum theory provides the main motivation for this study and more broadly for the sheaf-theoretic approach, because of a feature that may arise in empirical models having quantum but not classical realisations: which we refer to as contextuality.

Suppose that we can interact with a system by performing measurements on it and observing their outcomes. A feature of quantum systems is that not all observables commute, so that certain combinations of measurements are incompatible.

At best, we can obtain empirical observational data for contexts in which only compatible measurements are performed, which can be collected by running the experiment repeatedly. As we shall make more precise in Sects. 3 and 4, contextuality arises when the empirical data obtained is inconsistent with the assumption that for each run of the experiment the system has a global and context-independent assignment of values to all of its observable properties.

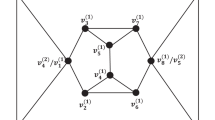
To take an operational perspective, a typical example of an experimental setup or scenario that we consider is the one depicted in Fig. 1 [left]. In this scenario, a system is prepared in some fixed bipartite state, following which parties A and B may each choose between two measurement settings, $m_A \in \mathopen { \{ } a, a'\mathclose { \} }$ for A and $m_B \in \mathopen { \{ } b, b'\mathclose { \} }$ for B. We assume that outcomes of each measurement live in ${{\varvec{R}}}$, which typically will be a bounded measurable subspace of the real numbers $\mathbb {R}$ (with its Borel $\sigma$-algebra). Depending on which choices of inputs were made, the empirical data might for example be distributed according to one of the four hypothetical probability density plots in ${{\varvec{R}}}^2$ depicted in Fig. 1 [right]. This scenario and hypothetical empirical behaviour has been considered elsewhere [50] as a continuous-variable version of the Popescu–Rohrlich (PR) box [72].

Fig. 1

[Left] operational depiction of a typical bipartite experimental scenario. [Right] Hypothetical probability density plots for empirical data arising from such an experiment. Cf. the discrete-variable probability tables of [60, 62]

3 Preliminaries on Measures and Probability

In order to properly treat probability on continuous-variable spaces, it is necessary to introduce a modicum of measure theory. This section serves to recall some basic ideas and to fix notation. The reader may choose to skip the section and consult it as reference for the remainder of the article.

A measurable space is a pair ${{\varvec{X}}}= \left\langle X,\mathcal {F} \right\rangle$ consisting of a set X and a $\sigma$-algebra (or $\sigma$-field) $\mathcal {F}$ on X, i.e. a family of subsets of X containing the empty set and closed under complementation and countable unions. In some sense, this specifies the subsets of X that can be assigned a ‘size’, and which are therefore called the measurable sets of ${{\varvec{X}}}$. Throughout this paper, we follow the convention of using boldface to denote the measurable space and the same symbol in regular face for its underlying set.

A trivial example of a $\sigma$-algebra over any set X is its powerset $\mathcal {P}(X)$, which gives the discrete measurable space $\left\langle X,\mathcal {P}(X) \right\rangle$, where every set is measurable. This is typically used when X is countable (finite or countably infinite), in which case this discrete $\sigma$-algebra is generated by the singletons. Another example, of central importance in measure theory, is $\left\langle \mathbb {R},\mathcal {B}_\mathbb {R} \right\rangle$, where $\mathcal {B}_\mathbb {R}$ is the $\sigma$-algebra generated from the open sets of $\mathbb {R}$, whose elements are called the Borel sets. Working with Borel sets avoids the problems that would arise if we naively attempted to measure or assign probabilities to points in the continuum. More generally, any topological space gives rise to a Borel measurable space in this fashion.

A measurable function between measurable spaces ${{\varvec{X}}}= \left\langle X,\mathcal {F}_X \right\rangle$ and ${{\varvec{Y}}}= \left\langle Y, \mathcal {F}_Y \right\rangle$ is a function $f :X \longrightarrow Y$ between the underlying sets whose preimage preserves measurable sets, i.e. such that, for any $E \in \mathcal {F}_Y$, ${f^{-1}(E) \in \mathcal {F}_X}$. This is analogous to the definition of a continuous function between topological spaces. Clearly, the identity function is measurable and measurable functions compose. We will denote by $\textsf {Meas}$ the category whose objects are measurable spaces and whose morphisms are measurable functions.

The product of two measurable spaces ${{\varvec{X}}}_1 = \left\langle X_1,\mathcal {F}_1 \right\rangle$ and ${{\varvec{X}}}_2 = \left\langle X_2,\mathcal {F}_2 \right\rangle$ is the measurable space

$$\begin{aligned} {{\varvec{X}}}_1 \times {{\varvec{X}}}_2 = \left\langle X_1 \times X_2, \mathcal {F}_1 \otimes \mathcal {F}_2 \right\rangle \text { ,}\end{aligned}$$

(1)

where the Cartesian product of the underlying sets, $X_1 \times X_2$, is equipped with the so-called tensor product $\sigma$-algebra $\mathcal {F}_1 \otimes \mathcal {F}_2$, which is the $\sigma$-algebra generated by the ‘rectangles’, subsets of the form $E_1 \times E_2$ with $E_1 \in \mathcal {F}_1$ and $E_2 \in \mathcal {F}_2$. This is the categorical (binary) product in $\textsf {Meas}$.

We shall also need to deal with infinite products of measurable spaces. The generalisation is analogous to that for products of topological spaces, where the box topology (generated by ‘rectangles’) is no longer the most natural choice when dealing with infinite families, but rather the topology generated by ‘cylinders’. Let I be an arbitrary index set. The product of measurable spaces $({{\varvec{X}}}_i = \left\langle X_i,\mathcal {F}_i \right\rangle )_{i \in I}$ is the measurable space

$$\begin{aligned} \prod _{i \in I} {{\varvec{X}}}_i = \left\langle \prod _{i \in I} X_i, \bigotimes _{i \in I} \mathcal {F}_i \right\rangle \text { ,} \end{aligned}$$

(2)

where $X_I = \prod _{i \in I} X_i$ is the Cartesian product of the underlying sets, and $\mathcal {F}_I = \bigotimes _{i \in I} \mathcal {F}_i$ is the $\sigma$-algebra generated by subsets of $\prod _{i \in I} X_i$ of the form $\prod _{i \in I} E_i$ where $E_i \subseteq X_i$ for all $i \in I$ and $E_i \ne X_i$ for only finitely many $i \in I$. This is the smallest $\sigma$-algebra that makes the projection maps $\pi _k :\prod _{i \in I} X_i \longrightarrow X_k$ measurable. It therefore corresponds to the categorical (arbitrary) product in $\textsf {Meas}$.

A measure on a measurable space ${{\varvec{X}}}= \left\langle X,\mathcal {F} \right\rangle$ is a function $\mu :\mathcal {F} \longrightarrow \overline{\mathbb {R}}$ from the $\sigma$-algebra to the extended real numbers $\overline{\mathbb {R}}= \mathbb {R}\cup \mathopen { \{ }-\infty ,+\infty \mathclose { \} }$ satisfying:

• (i) [nonnegativity] $\mu (E)\ge 0$ for all $E\in \mathcal {F}$;

• (ii) [null empty set] $\mu (\emptyset )=0$;

• (iii) [$\sigma$-additivity] for any countable family $({E_i})_{i=1}^\infty$ of pairwise disjoint measurable sets, it holds that $\mu (\bigcup _{i=1}^\infty E_i) = \sum _{i=1}^\infty \mu (E_i)$.

A measure on ${{\varvec{X}}}$ allows one to integrate well-behaved¹ measurable functions $f :{{\varvec{X}}} \longrightarrow \left\langle \mathbb {R},\mathcal {B}_\mathbb {R} \right\rangle$ to obtain a real value, denoted $\int _{{{\varvec{X}}}}f\;\,\mathrm {d}\,\mu$ or $\int _{x\in {{\varvec{X}}}}f(x)\;\,\mathrm {d}\,\mu (x)$. The simplest example of such a measurable function is the indicator function of a measurable set $E \in \mathcal {F}$:

$$\begin{aligned} \chi _{_E}(x) :={\left\{ \begin{array}{ll} 1 &{} \hbox { if}\ x \in E \\ 0 &{} \text {if }x \not \in E.\end{array}\right. } \end{aligned}$$

For any measure $\mu$ on ${{\varvec{X}}}$, its integral yields

$$\begin{aligned} \int _{{{\varvec{X}}}}\chi _{_E}\;\,\mathrm {d}\,\mu = \mu (E) \text { .}\end{aligned}$$

(3)

A measure $\mu$ is finite if $\mu (X)<\infty$ and in particular it is a probability measure if $\mu (X)=1$. We will denote by $\mathbb {M}({{\varvec{X}}})$ and $\mathbb {P}({{\varvec{X}}})$, respectively, the sets of measures and probability measures on the measurable space ${{\varvec{X}}}$.

A measurable function $f :{{\varvec{X}}} \longrightarrow {{\varvec{Y}}}$ carries any measure $\mu$ on ${{\varvec{X}}}$ to a measure $f_*\mu$ on ${{\varvec{Y}}}$. This push-forward measure is given by $f_*\mu (E) = \mu (f^{-1}(E))$ for any set E measurable in ${{\varvec{Y}}}$. An important use of push-forward measures is that for any integrable function $g :{{\varvec{Y}}} \longrightarrow \left\langle \mathbb {R},\mathcal {B}_\mathbb {R} \right\rangle$, it allows us to write the following change-of-variables formula

$$\begin{aligned} \int _{{{\varvec{Y}}}}g\;\,\mathrm {d}\,f_*\mu = \int _{{{\varvec{X}}}}g \circ f\;\,\mathrm {d}\,\mu \text { .}\end{aligned}$$

(4)

The push-forward operation preserves the total measure, hence it takes $\mathbb {P}({{\varvec{X}}})$ to $\mathbb {P}({{\varvec{Y}}})$.

A case that will be of particular interest to us is the push-forward of a measure $\mu$ on a product space ${{\varvec{X}}}_1 \times {{\varvec{X}}}_2$ along a projection $\pi _i :{{\varvec{X}}}_1 \times {{\varvec{X}}}_2 \longrightarrow {{\varvec{X}}}_i$: this yields the marginal measure $\mu |_{{{\varvec{X}}}_i}={\pi _i}_*\mu$, where e.g. for E measurable in ${{\varvec{X}}}_1$, $\mu |_{{{\varvec{X}}}_1}(E) = \mu (\pi _1^{-1}(E)) = \mu (E \times X_2)$.

In the opposite direction, given measures $\mu _1$ on ${{\varvec{X}}}_1$ and $\mu _2$ on ${{\varvec{X}}}_2$, a product measure $\mu _1 \times \mu _2$ is a measure on the product measurable space ${{\varvec{X}}}_1 \times {{\varvec{X}}}_2$ satisfying $(\mu _1 \times \mu _2)(E_1 \times E_2) = \mu _1(E_1)\mu _2(E_2)$ for all $E_1 \in \mathcal {F}_1$ and $E_2 \in \mathcal {F}_2$. For probability measures, there is a uniquely determined product measure.² The analogous, much more general statement also holds for arbitrary products of probability measures (see e.g. [83, section 11.2]).

We can view $\mathbb {M}$ as a map that takes a measurable space to the set of measures on that space, and similarly for $\mathbb {P}$. These become functors $\textsf {Meas}\longrightarrow \textsf {Set}$ if we define the action on morphisms to be the push-forward operation. Explicitly we set $\mathbb {M}(f) := f_* :\mathbb {M}({{\mathbf {X}}}) \longrightarrow \mathbb {M}({{\mathbf {Y}}}) {:}{:} \mu \longmapsto f_*\mu$, where $f :{{\varvec{X}}} \longrightarrow {{\varvec{Y}}}$ is a measurable function, and similarly for $\mathbb {P}$.

Remarkably, the set $\mathbb {P}({{\varvec{X}}})$ of probability measures on ${{\varvec{X}}}$ can itself be made into a measurable space by equipping it with the least $\sigma$-algebra that makes the evaluation functions

$$\begin{aligned} \begin{aligned} \mathsf {ev}_E :\mathbb {P}({{\mathbf {X}}}) \longrightarrow [0,1] {:}{:} \mu \longmapsto \mu (E) \end{aligned}\end{aligned}$$

measurable for all $E \in \mathcal {F}_X$.³ This yields an endofunctor $\mathbb {P} :\textsf {Meas} \longrightarrow \textsf {Meas}$, which moreover has the structure of a monad, called the Giry monad [39]. The unit of this monad is given by

$$\begin{aligned} \begin{aligned} \eta _{{{\mathbf {X}}}} :{{\mathbf {X}}} \longrightarrow \mathbb {P}({{\mathbf {X}}}) {:}{:} x \longmapsto \delta _x \end{aligned}\end{aligned}$$

where $\delta _x$ is the Dirac measure, or point mass, at x given by $\delta _x(E) := \chi _{_E}(x)$. Multiplication of the monad is given by

$$\begin{aligned} \mu _{{\varvec{X}}} :\mathbb {P}(\mathbb {P}({{\varvec{X}}})) \longrightarrow \mathbb {P}({{\varvec{X}}}) \end{aligned}$$

which takes a probability measure P on $\mathbb {P}({{\varvec{X}}})$ to its ‘average’, a probability measure $\mu _{{\varvec{X}}}(P)$ on ${{\varvec{X}}}$, $\mu _{{\varvec{X}}}(P) :\mathcal {F}_X \longrightarrow [0,1]$, whose value on a measurable set $E \in \mathcal {F}_X$ is given by $\mu _{{\mathbf {X}}}(P)(E) := \int _{\mathbb {P}({{\mathbf {X}}})}\mathsf {ev}_E\;\,\mathrm {d}\,P$.

The Kleisli category of this monad is the category of Markov kernels, which represent continuous-variable probabilistic maps and generalise the discrete notion of stochastic matrix. Concretely, a Markov kernel between measurable spaces ${{\varvec{X}}}= \left\langle X,\mathcal {F}_X \right\rangle$ and ${{\varvec{Y}}}= \left\langle Y, \mathcal {F}_Y \right\rangle$ is a function $k :X \times \mathcal {F}_Y \longrightarrow [0,1]$ such that:

• (i) for all $E \in \mathcal {F}_Y$, $k(-,E) :X \longrightarrow [0,1]$ is a measurable function;⁴

• (ii) for all $x \in X$, $k(x,-) :\mathcal {F}_Y \longrightarrow [0,1]$ is a probability measure.

4 Framework

In this section, we follow closely the discrete-variable framework of [8] in more formally describing the kinds of experimental scenarios in which we are interested and the empirical behaviours that arise on these, although some extra care is required for dealing with continuous variables.

Measurement scenarios

Definition 1

A measurement scenario is a triple $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ whose elements are specified as follows.

–:

X is a (possibly infinite) set of measurement labels.

–:

$\mathcal {M}$ is a covering family of subsets of X, i.e. such that $\bigcup \mathcal {M}= X$. The elements $C \in \mathcal {M}$ are called maximal contexts and represent maximal sets of compatible observables. We therefore require that $\mathcal {M}$ be an anti-chain with respect to subset inclusion, i.e. that no element of this family is a proper subset of another. Any subset of a maximal context also represents a set of compatible measurements, and we refer to elements of ${\mathcal {U} :=\left\{ U \subseteq C \mid C \in \mathcal {M}\right\} }$ as contexts.⁵

–:

${{\varvec{O}}}= ({{{\varvec{O}}}_x})_{x \in X}$ specifies a measurable space of outcomes ${{\varvec{O}}}_x = \left\langle O_x,\mathcal {F}_x \right\rangle$ for each measurement $x \in X$.

Measurement scenarios can be understood as providing a concise description of the kind of experimental setup that is being considered. For example, the setup represented in Fig. 1 is described by the measurement scenario:

$$\begin{aligned} X=\mathopen { \{ }a,a',b,b'\mathclose { \} } \, , \quad \quad \mathcal {M}= \mathopen { \{ } \, \mathopen { \{ }a,b\mathclose { \} }, \, \mathopen { \{ }a,b'\mathclose { \} }, \, \mathopen { \{ }a',b\mathclose { \} }, \, \mathopen { \{ }a',b'\mathclose { \} } \, \mathclose { \} } \, , \quad \quad {{\varvec{O}}}_x = {{\varvec{R}}}\, , \end{aligned}$$

(5)

where ${{\varvec{R}}}$ is a bounded measurable subspace of $\left\langle \mathbb {R},\mathcal {B}_\mathbb {R} \right\rangle$.

If some set of measurements $U \subseteq X$ is considered together, there is a joint outcome space given by the product of the respective outcome spaces (see Eq. (2)),

$$\begin{aligned} \begin{aligned} {{\mathbf {O}}}_U := \prod _{x \in U} {{\mathbf {O}}}_x = \left\langle O_U, \mathcal {F}_U \right\rangle = \left\langle \prod _{x \in U} O_x \; , \; \bigotimes _{x \in U} \mathcal {F}_x \right\rangle \text{. }\end{aligned}\end{aligned}$$

The map $\mathcal {E}$ that maps $U \subseteq X$ to $\mathcal {E}(U) = {{\varvec{O}}}_U$ is called the event sheaf as concretely it assigns to any set of measurements information about the outcome events that could result from jointly performing them. Note that as well as applying the map to valid contexts $U \in \mathcal {U}$ we will see that it can also be of interest to consider hypothetical outcome spaces for sets of measurements that do not necessarily form valid contexts, in particular $\mathcal {E}(X) = {{\varvec{O}}}_X$, the joint outcome space for all measurements. Moreover, as we will briefly discuss, this map satisfies the conditions to be a sheaf ${\mathcal {E} :\mathcal {P}(X)^\mathsf {op} \longrightarrow \textsf {Meas}}$, where $\mathcal {P}(X)$ denotes the powerset of X, similarly to its discrete-variable analogue in [8].

The language of sheaves

Sheaves are widely used in modern mathematics. They might roughly be thought of as providing a means of assigning information to the open sets of a topological space in such a way that information can be restricted to smaller open sets and consistent information on a family of open sets can be uniquely ‘glued’ on their union.⁶ In this work we are concerned with discrete topological spaces whose points represent measurements, and the information that we are interested in assigning has to do with outcome spaces for these measurements and probability measures on these outcome spaces. Sheaves can be defined concisely in category-theoretic terms as contravariant functors (presheaves) satisfying an additional gluing condition, though in what follows we will also give a more concrete description in terms of restriction maps. Categorically, the event sheaf is a functor $\mathcal {E} :\mathcal {P}(X)^\mathsf {op} \longrightarrow \textsf {Meas}$ where $\mathcal {P}(X)$ is viewed as a category in the standard way for partial orders, with morphisms corresponding to subset inclusions.

Sheaves come with a notion of restriction. In our example, restriction arises in the following way: whenever $U, V \in \mathcal {P}(X)$ with $U \subseteq V$ we have an obvious restriction map $\rho ^V_U :\mathcal {E}(V) \longrightarrow \mathcal {E}(U)$ which simply projects from the product outcome space for V to that for U. Note that $\rho ^U_U$ is the identity map for any $U \in \mathcal {P}(X)$ and that if $U \subseteq V \subseteq W$ in $\mathcal {P}(X)$ then $\rho ^V_U \circ \rho ^W_V = \rho ^W_U$. Already this is enough to show that $\mathcal {E}$ is a presheaf. In categorical terms it establishes functoriality. Our map assigns outcome spaces $\mathcal {E}(U) = {{\varvec{O}}}_U$ to sets of measurements $U \in \mathcal {P}(X)$, and in sheaf-theoretic terminology elements of these outcome spaces are called sections over U. Sections over X are called global sections. For an inclusion $U \subseteq V$ and a section $\mathbf {o}\in \mathcal {E}(V) = O_V$, it is often more convenient to use the notation $\mathbf {o}|_U$ to denote $\rho ^V_U (\mathbf {o}) \in \mathcal {E}(U) = O_U$, the restriction of $\mathbf {o}$ to U.

Additionally, the unique gluing property holds for $\mathcal {E}$. Suppose that $\mathcal {N}\subseteq \mathcal {P}(X)$ and we have an $\mathcal {N}$-indexed family of sections $({\mathbf {o}_U \in O_U})_{U \in \mathcal {N}}$ that is compatible in the sense that its elements agree on overlaps, i.e. that for all $U, V \in \mathcal {N}$, $\mathbf {o}_U|_{U \cap V} = \mathbf {o}_V|_{U \cap V}$. Then these sections can always be ‘glued’ together in a unique fashion to obtain a section $\mathbf {o}_{N}$ over $N :=\cup \mathcal {N}$ such that $\mathbf {o}_N|_U = \mathbf {o}_U$ for all $U \in \mathcal {N}$. This makes $\mathcal {E}$ a sheaf.

We will primarily be concerned with probability measures on outcome spaces. For this, we recall that the Giry monad $\mathbb {P} :\textsf {Meas} \longrightarrow \textsf {Meas}$ takes a measurable space and returns the probability measures over that space. Composing it with the event sheaf yields the map $\mathbb {P}\circ \mathcal {E}$ that takes any context and returns the probability measures on its joint outcome space. In fact, this is a presheaf $\mathbb {P}\circ \mathcal {E} :\mathcal {P}(X)^\mathsf {op} \longrightarrow \textsf {Meas}$, where restriction on sections is given by marginalisation of probability measures. Note that marginalisation simply corresponds to the push-forward of a measure along projections to a component of the product space, which are precisely the restriction maps of $\mathcal {E}$. Note, however, that this presheaf does not satisfy the gluing condition and thus it crucially is not a sheaf.

Empirical models

Definition 2

An empirical model on a measurement scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ is a compatible family for the presheaf $\mathbb {P}\circ \mathcal {E}$ on the cover $\mathcal {M}$. Concretely, it is a family $e = ({e_C})_{C \in \mathcal {M}}$, where $e_C$ is a probability measure on the space $\mathcal {E}(C)={{\varvec{O}}}_C$ for each maximal context $C \in \mathcal {M}$, which satisfies the compatibility condition:

$$\begin{aligned} e_C|_{C \cap C'} = e_{C'}|_{C \cap C'} \text { .}\end{aligned}$$

Empirical models capture in a precise way the probabilistic behaviours that may arise upon performing measurements on physical systems. The compatibility condition ensures that the empirical behaviour of a given measurement or compatible subset of measurements is independent of which other compatible measurements might be performed along with them. This is sometimes referred to as the no-disturbance condition. A special case is no-signalling, which applies in multi-party or Bell scenarios such as that of Fig. 1 and Eq. (5). In that case, contexts consist of measurements that are supposed to occur in space-like separated locations, and compatibility ensures for instance that the choice of performing a or $a'$ at the first location does not affect the empirical behaviour at the second location, i.e. $e_{\mathopen { \{ }a,b\mathclose { \} }}|_{\mathopen { \{ }b\mathclose { \} }} = e_{\mathopen { \{ }a',b\mathclose { \} }}|_{\mathopen { \{ }b\mathclose { \} }}$.

Note also that while empirical models may arise from the predictions of quantum theory, their definition is theory-independent. This means that empirical models can just as well describe hypothetical behaviours beyond what can be achieved by quantum mechanics such as the well-studied Popescu–Rohrlich box [72]. This can be useful in probing the limits of quantum theory and in singling out what distinguishes and characterises quantum theory within larger spaces of probabilistic theories, both well-established lines of research in quantum foundations.

Sheaf-theoretically. An empirical model is a compatible family of sections for the presheaf $\mathbb {P}\circ \mathcal {E}$ indexed by the maximal contexts of the measurement scenario. A natural question that may occur at this point is whether these sections can be glued to form a global section, and this is what we address next.

Extendability and contextuality

Definition 3

An empirical model e on a scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ is extendable (or noncontextual⁷) if there is a probability measure $\mu$ on the space $\mathcal {E}(X)={{\varvec{O}}}_X$ such that $\mu |_C = e_C$ for every $C \in \mathcal {M}$.⁸

Recall that ${{\varvec{O}}}_X$ is the global outcome space, whose elements correspond to global assignments of outcomes to all the measurements in the given scenario. Of course, it is not always the case that X is a valid context, and if it were then $\mu = e_X$ would trivially extend the empirical model. The question of the existence of such a probability measure that recovers the context-wise empirical content of e is particularly significant. When it exists, it amounts to a way of modelling the observed behaviour as arising stochastically from the behaviours of underlying states, identified with the elements of $O_X$, each of which deterministically assigns outcomes to all the measurements in X independently of the measurement context that is actually performed. If an empirical model is not extendable it is said to be contextual. Furthermore, we will say that it is Bell nonlocal in the special setting of so-called Bell scenarios, where the compatibility structure of observables is obtained from space-like separation.

Sheaf-theoretically. A contextual empirical model is a compatible family of sections for the presheaf $\mathbb {P}\circ \mathcal {E}$ over the contexts of the measurement scenario that cannot be glued into a global section. Contextuality thus arises as the tension between local consistency and global inconsistency.

5 A FAB Theorem

Quantum theory presents a number of non-intuitive features. For instance, Einstein, Podolsky and Rosen (EPR) identified early on that if the quantum description of the world is taken as fundamental then entanglement poses a problem of “spooky action at a distance” [35]. Their conclusion was that quantum theory should be consistent with a deeper or more complete description of the physical world, in which such problems would disappear. The import of seminal foundational results like the Bell [18] and Bell–Kochen–Specker [19, 52] theorems is that they identify such non-intuitive behaviours and then rule out the possibility of finding any underlying model for them that would not suffer from the same issues. Incidentally, we note that the EPR paradox was originally presented in terms of continuous variables, whereas Bell’s theorem addressed a discrete variable analogue of it.

In the previous section, we characterised contextuality of an empirical model by the absence of a global section for that empirical model. We also saw that global sections capture one kind of underlying model for the behaviour, namely via deterministic global states that assign predefined outcomes to all measurements. This is precisely the kind of model referred to in the Kochen–Specker theorem [52]. Bell’s theorem, on the other hand, pertains to a different kind of hidden-variable model, where the salient feature—Bell locality—is a kind of factorisability rather than determinism. Fine [36] showed that in one important measurement scenario (that of the concrete example from Fig. 1) the existence of one kind of model is equivalent to existence of the other. Abramsky and Brandenburger [8] proved in full generality that this existential equivalence holds for any discrete-variable measurement scenario, and that global sections of $\mathbb {P}\circ \mathcal {E}$ provide a canonical form of hidden-variable model.

In this section, we prove a Fine–Abramsky–Brandenburger theorem in the continuous-variable setting. It establishes that in this setting there is also an unambiguous, unified description of Bell locality and noncontextuality, which is captured in a canonical way by the notion of extendability.

We will begin by introducing hidden-variable models in a more precise way. The idea is that there exists some space ${\varvec{\varLambda }}$ of hidden variables, which determine the empirical behaviour. However, elements of this space may not be directly empirically accessible themselves, so we allow that we might only have probabilistic information about them in the form of a probability measure p on ${\varvec{\varLambda }}$. The empirically observable behaviour should then arise as an average over the hidden-variable behaviours.

Definition 4

Let $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ be a measurement scenario. A hidden-variable model⁹ on this scenario consists of the following ingredients:

• A measurable space ${\varvec{\varLambda }}= \left\langle \varLambda ,\mathcal {F}_\varLambda \right\rangle$ of hidden variables.

• A probability measure p on ${\varvec{\varLambda }}$.

• For each maximal context $C \in \mathcal {M}$, a probability kernel $k_C :{\varvec{\varLambda }} \longrightarrow \mathcal {E}(C)$,¹⁰ satisfying the following compatibility condition: for any maximal contexts $C, C' \in \mathcal {M}$,

  $$\begin{aligned} \forall {\lambda \in \varLambda }\varvec{.}\; \quad k_C(\lambda ,-)|_{C \cap C'} = k_{C'}(\lambda ,-)|_{C \cap C'} \text { .}\end{aligned}$$

  (6)

Remark 1

Equivalently, we can regard Eq. (6) as defining a function ${\underline{k}}$ from $\varLambda$ to the set of empirical models over $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$. The function assigns to each $\lambda \in \varLambda$ the empirical model ${\underline{k}}(\lambda ) :=({{\underline{k}}(\lambda )_C})_{C \in \mathcal {M}}$, where the correspondence with the definition above is via ${\underline{k}}(\lambda )_C = k_C(\lambda ,-)$. This function must be ‘measurable’ in ${\varvec{\varLambda }}$ in the sense that ${\underline{k}}(-)_C(B) :\varLambda \longrightarrow [0,1]$ is a measurable function for all $C \in \mathcal {M}$ and $B \in \mathcal {F}_C$.

Definition 5

Let $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ be a measurement scenario and $\left\langle {\varvec{\varLambda }},p,k \right\rangle$ be a hidden-variable model. Then the corresponding empirical model e is given as follows: for any maximal context $C \in \mathcal {M}$ and measurable set of joint outcomes $B \in \mathcal {F}_C$,

$$\begin{aligned} e_C(B) = \int _{\varLambda }k_C(-,B)\;\,\mathrm {d}\,p = \int _{\lambda \in \varLambda }k_C(\lambda ,B)\;\,\mathrm {d}\,p(\lambda )\text { .}\end{aligned}$$

Note that our definition of hidden-variable model assumes the properties known as $\lambda$-independence [31] and parameter-independence [47, 78]. The former corresponds to the fact that the probability measure p on the hidden-variable space is independent of the measurement context to be performed, while the latter corresponds to the compatibility condition (6), which also ensures that the corresponding empirical model satisfies no-signalling [23]. We refer the reader to [24] for a detailed discussion of these and other properties of hidden-variable models specifically in the case of multi-party Bell scenarios.

The idea behind the introduction of hidden variables is that they could explain away some of the more non-intuitive aspects of the empirical predictions of quantum mechanics, which would then arise as resulting from an incomplete knowledge of the true state of a system rather than being a fundamental feature. There is some precedent for this in physical theories: for instance, statistical mechanics—a probabilistic theory—admits a deeper, albeit usually unwieldily complex, description in terms of classical mechanics, which is purely deterministic. Therefore, it is desirable to impose conditions on hidden-variable models which amount to requiring that they behave in some sense classically when conditioned on each particular value of the hidden variable $\lambda$. This motivates the notions of deterministic and of factorisable hidden-variable models.

Definition 6

A hidden-variable model $\left\langle {\varvec{\varLambda }},p,k \right\rangle$ is deterministic if the probability kernel $k_C(\lambda ,-) :\mathcal {F}_C \longrightarrow [0,1]$ is a Dirac measure for every $\lambda \in \varLambda$ and for every maximal context $C \in \mathcal {M}$; in other words, there is an assignment $\mathbf {o}\in O_C$ such that $k_C(\lambda ,-) = \delta _{\mathbf {o}}$.

In general discussions on hidden-variable models (e.g. [24]), the condition above, requiring that each hidden variable determines a unique joint outcome for each measurement context, is sometimes referred to as weak determinism. This is contraposed to strong determinism, which demands not only that each hidden variable fix a deterministic outcome to each individual measurement, but that this outcome be independent of the context in which the measurement is performed. Note, however, that since our definition of hidden-variable models assumes the compatilibity condition (6), i.e. parameter-independence, both notions of determinism coincide [23].

Definition 7

A hidden-variable model $\left\langle {\varvec{\varLambda }},p,k \right\rangle$ is factorisable if $k_C(\lambda ,-) :\mathcal {F}_C \longrightarrow [0,1]$ factorises as a product measure for every $\lambda \in \varLambda$ and for every maximal context $C \in \mathcal {M}$. That is, for any family of measurable sets $({B_x \in \mathcal {F}_x})_{x \in C}$ with $B_x \ne O_x$ only for finitely many $x \in C$,

$$\begin{aligned} k_C(\lambda ,\prod _{x\in C} B_x) = \prod _{x\in C} k_C|_{\mathopen { \{ }x\mathclose { \} }}(\lambda ,B_x) \end{aligned}$$

where $k_C|_{\mathopen { \{ }x\mathclose { \} }}(\lambda ,-)$ is the marginal of the probability measure $k_C(\lambda ,-)$ on ${{\varvec{O}}}_C=\prod _{x \in C}{{\varvec{O}}}_x$ to the space ${{\varvec{O}}}_{\mathopen { \{ }x\mathclose { \} }} = {{\varvec{O}}}_x$.¹¹

Remark 2

In other words, if we consider elements of $\varLambda$ as inaccessible ‘empirical’ models—i.e. if we use the alternative definition of hidden-variable models using the map ${\underline{k}}$ (see Remark 1)—then factorisability is the requirement that each of these be factorisable in the sense that

$$\begin{aligned} {\underline{k}}_C(\lambda )\left( \prod _{x\in C} B_x\right) = \prod _{x\in C} \, {\underline{k}}_C(\lambda )|_{\mathopen { \{ }x\mathclose { \} }}(B_x) \end{aligned}$$

where ${\underline{k}}_C|_{\mathopen { \{ }x\mathclose { \} }}(\lambda )$ is the marginal of the probability measure ${\underline{k}}_C(\lambda )$ on ${{\varvec{O}}}_C=\prod _{x \in C}{{\varvec{O}}}_x$ to the space ${{\varvec{O}}}_x$.

We now prove the continuous-variable analogue of the theorem proved in the discrete probability setting by Abramsky and Brandenburger [8, Proposition 3.1 and Theorem 8.1], generalising the result of Fine [36] to arbitrary measurement scenarios.

In particular, this result shows that the measurable space $\mathcal {E}(X) = {{\varvec{O}}}_X$ provides a canonical hidden-variable space. The proof that (1) $\Rightarrow$ (2) in the Theorem below shows how a global probability measure extending an empirical model e can be understood as giving a deterministic hidden-variable model with ${\varvec{\varLambda }}= \mathcal {E}(X)$. Canonicity is then established together with the proof that (3) $\Rightarrow$ (1), to the effect that if a given empirical model admits any factorisable hidden-variable model then it admits a deterministic model of the form just mentioned (with $\mathcal {E}(X)$ being the hidden-variable space).

Theorem 1

Let e be an empirical model on a measurement scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$. The following are equivalent:

• (1) e is extendable;

• (2) e admits a realisation by a deterministic hidden-variable model;

• (3) e admits a realisation by a factorisable hidden-variable model.

Proof

We prove the sequence of implications (1) $\Rightarrow$ (2) $\Rightarrow$ (3) $\Rightarrow$ (1).

(1) $\Rightarrow$ (2). The idea is that $\mathcal {E}(X)={{\varvec{O}}}_X$ provides a canonical deterministic hidden-variable space. Suppose that e is extendable to a global probability measure $\mu$. Let us set

$$\begin{aligned} {\varvec{\varLambda }}:= & {} {{\varvec{O}}}_X \\ p:= & {} \mu \\ k_C(\mathbf {g},-):= & {} \delta _{\mathbf {g}|_C} \end{aligned}$$

for all global outcome assignments $\mathbf {g}\in O_X$. This is by construction a deterministic hidden-variable model, which we claim gives rise to the empirical model e.

Let $C \in \mathcal {M}$ and write $\rho :{{\varvec{O}}}_X \longrightarrow {{\varvec{O}}}_C$ for the measurable projection which, in the event sheaf, is the restriction map $\rho ^X_C = \mathcal {E}(C \subseteq X) :\mathcal {E}(X) \longrightarrow \mathcal {E}(C)$.

For any $E \in \mathcal {F}_C$, we have

$$\begin{aligned} k_C(\mathbf {g},E) = \delta _{\mathbf {g}|_C}(E) = \delta _{\rho (\mathbf {g})}(E) = \chi _{_E}(\rho (\mathbf {g})) = (\chi _{_E} \circ \rho )(\mathbf {g}) \end{aligned}$$

(7)

and therefore, as required,

(2) $\Rightarrow$ (3). It is enough to show that if a hidden-variable model $\left\langle {\varvec{\varLambda }},p,k \right\rangle$ is deterministic then it is also factorisable. For this, it is sufficient to notice that a Dirac measure $\delta _{\mathbf {o}}$ with $\mathbf {o}\in O_C$ on a product space ${{\varvec{O}}}_C=\prod _{x \in C}{{\varvec{O}}}_x$ factorises as the product of Dirac measures

$$\begin{aligned}\delta _{\mathbf {o}} = \prod _{x \in C}\delta _{\mathbf {o}(x)} = \prod _{x \in C}\delta _{\mathbf {o}|_{\mathopen { \{ }x\mathclose { \} }}} \text { .}\end{aligned}$$

(3) $\Rightarrow$ (1). Suppose that e is realised by a factorisable hidden-variable model $\left\langle {\varvec{\varLambda }},p,k \right\rangle$. Write $k_x$ for $k_C|_{\mathopen { \{ }x\mathclose { \} }}$ as in the definition of factorisability. Define a measure $\mu$ on ${{\varvec{O}}}_X$ as follows: given a family of measurable sets $({E_x \in \mathcal {F}_x})_{x\in X}$ with $E_x = O_x$ for all but finitely many $x \in X$, the value of $\mu$ on the corresponding cylinder, $\prod _{x\in X}E_x$, is given by

$$\begin{aligned} \mu \left( \prod _{x\in X}E_x\right) :=\int _{\varLambda }\left( \prod _{x\in X} k_x(-,E_x)\right) \;\,\mathrm {d}\,p = \int _{\lambda \in \varLambda }\left( \prod _{x\in X} k_x(\lambda ,E_x)\right) \;\,\mathrm {d}\,p(\lambda ) \text { ,}\end{aligned}$$

(13)

where the product on the right-hand side is a product of finitely many real numbers in the interval [0, 1], since $k_x(\lambda ,O_x) = 1$ and so $k_x(\lambda ,E_x) \ne 1$ for only finitely many $x \in X$. Note that the $\sigma$-algebra of ${{\varvec{O}}}_X$ is the tensor product $\sigma$-algebra $\mathcal {F}_X = \bigotimes _{x \in X}\mathcal {F}_x$, which is generated by such cylinders; hence the equation above uniquely determines $\mu$ as a measure on ${{\varvec{O}}}_X$.

Now, we show that this is a global section for the empirical probabilities. Let $C \in \mathcal {M}$ and consider a ‘cylinder’ set $F = \prod _{x\in C}F_x$ with $F_x \in \mathcal {F}_X$ and $F_x \ne O_x$ only for finitely many $x \in C$. Then

Since the $\sigma$-algebra $\mathcal {F}_C$ of ${{\varvec{O}}}_C$ is generated by the cylinder sets of the form above and we have seen that $\mu |_C$ agrees with $e_C$ on these sets, we conclude that $\mu |_C = e_C$ as required. $\quad \square$

6 Quantifying Contextuality

Beyond questioning whether a given empirical behaviour is contextual or not, it is also interesting to ask to what degree it is contextual. In discrete-variable scenarios, a very natural measure of contextuality is the contextual fraction [8]. This measure was shown in [6] to have a number of very desirable properties. It can be calculated using linear programming, an approach that subsumes the more traditional approach to quantifying nonlocality and contextuality using Bell and noncontextuality inequalities in the sense that we can understand the (dual) linear program as optimising over all such inequalities for the scenario in question and returning the maximum normalised violation of any Bell or noncontextuality inequality achieved by the given empirical model. Crucially, the contextual fraction was also shown to quantifiably relate to quantum-over-classical advantages in specific informatic tasks [6, 63, 85]. Moreover it has been demonstrated to be a monotone with respect to the free operations of resource theories for contextuality [4, 6, 32].

In this section, we consider how to carry those ideas to the continuous-variable setting. The formulation as a linear optimisation problem and the attendant correspondence with Bell inequality violations requires special care as one needs to use infinite linear programming, necessitating some extra assumptions on the outcome measurable spaces.

6.1 The contextual fraction

Asking whether a given behaviour is noncontextual amounts to asking whether the empirical model is extendable, or in other words whether it admits a deterministic hidden-variable model. However, a more refined question to pose is what fraction of the behaviour admits a deterministic hidden-variable model? This quantity is what we call the noncontextual fraction. Similarly, the fraction of the behaviour that is left over and that can thus be considered irreducibly contextual is what we call the contextual fraction.

Definition 8

Let e be an empirical model on the scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$. The noncontextual fraction of e, written $\textsf {NCF}(e)$, is defined as

$$\begin{aligned} \sup \left\{ \mu (O_X) \mid \mu \in \mathbb {M}({{\varvec{O}}}_X), \, \forall {C \in \mathcal {M}}\varvec{.}\; \mu |_C \le e_C\right\} \text { .}\end{aligned}$$

Note that since $e_C \in \mathbb {P}({{\varvec{O}}}_C)$ for all $C \in \mathcal {M}$ it follows that $\textsf {NCF}(e) \in [0,1]$. The contextual fraction of e, written $\textsf {CF}(e)$, is given by $\textsf {CF}(e) :=1 - \textsf {NCF}(e)$.

6.2 Monotonicity under free operations including binning

In the discrete-variable setting, the contextual fraction was shown to be a monotone under a number of natural classical operations that transform and combine empirical models and control their use as resources, therefore constituting the ‘free’ operations of a resource theory of contextuality [4, 6, 32].

All of the operations defined for discrete variables in [6]—viz. translations of measurements, transformation of outcomes, probabilistic mixing, product, and choice—carry almost verbatim to our current setting. One detail is that one must insist that the coarse-graining of outcomes be achieved by (a family of) measurable functions. A particular example of practical importance is binning, which is widely used in continuous-variable quantum information as a method of discretising data by partitioning the outcome space ${{\varvec{O}}}_x$ for each measurement $x \in X$ into a finite number of ‘bins’, i.e. measurable sets. Note that a binned empirical model is obtained by pushing forward along a family $({t_x})_{x\in X}$ of outcome translations $t_x :{{\varvec{O}}}_x \longrightarrow {{\varvec{O}}}'_x$ where ${{\varvec{O}}}'_x$ is finite for all $x \in X$.

For the conditional measurement operation introduced in [4], which allows for adaptive measurement protocols such as those used in measurement-based quantum computation [76], one must similarly insist that the map determining the next measurement to perform based on the observed outcome of a previous measurement be a measurable function. Since, for the quantification of contextuality, we are only considering scenarios where the measurements are treated as constituting a discrete set, this amounts to a partition of the outcome space ${{\varvec{O}}}_x$ of the first measurement, x, into measurable subsets labelled by measurements compatible with x, indicating which will be subsequently performed depending on the outcome observed for x.

The inequalities establishing monotonicity from [6, Theorem 2] also hold for continuous variables. There is a caveat for the equality formula for the product of two empirical models:

$$\begin{aligned} \textsf {NCF}(e_1 \otimes e_2) = \textsf {NCF}(e_1)\textsf {NCF}(e_2). \end{aligned}$$

Whereas the inequality establishing monotonicity ($\ge$) stills holds in general, the proof establishing the other direction ($\le$) makes use of duality of linear programs. Therefore, it only holds under the assumptions we will impose in the remainder of this section.

Proposition 1

If e is an empirical model, and $e^\text {bin}$ is any discrete-variable empirical model obtained from e by binning, then contextuality of $e^\text {bin}$ witnesses contextuality of e, and quantifiably gives a lower bound $\textsf {CF}(e^\text {bin}) \le \textsf {CF}(e)$.

6.3 Assumptions on the outcome spaces

In order to phrase the problem of contextuality as an (infinite) linear programming problem and establish the connection with violations of Bell inequalities, we need to impose some conditions on the measurement scenarios, and in particular on the measurable spaces of outcomes.

First, from now on we assume that we have a finite number of measurement labels i.e. that X is finite.

Moreover, we restrict attention to the case where the outcome space ${{\varvec{O}}}_x$ for each measurement $x \in X$ is the Borel measurable space for a compact Hausdorff space, i.e. that the set $O_x$ is a compact space and $\mathcal {F}_x$ is the $\sigma$-algebra generated by its open sets, written $\mathcal {B}(O_x)$. Note that this includes most situations of interest in practice. In particular, it includes the case of measurements with outcomes in a bounded subspace of $\mathbb {R}$ or $\mathbb {R}^n$. This is also experimentally motivated since measurement devices are energetically bounded. The central missing piece is the case of locally compact spaces, in order to include the measurements with outcomes in $\mathbb {R}$ or $\mathbb {R}^n$, which is theoretically relevant ($\mathbb {R}$ would be the canonical outcome space for the quadratures of the electromagnetic field, for instance). We address this issue in the next section and show that it reduces to the compact case.

To summarise we make the following two assumptions here (we will slightly relax the second one later):

• (i) X is a finite set of measurement labels,

• (ii) for each $x \in X$, the outcome space ${{\varvec{O}}}_x$ is a compact Hausdorff space.

To obtain an infinite linear program, we need to work with vector spaces. However, probability measures, or even finite or arbitrary measures, do not form one. We will therefore consider the set $\mathbb {M}_{\pm }({{\varvec{Y}}})$ of finite signed measures (a.k.a. real measures) on a measurable space ${ {{\varvec{Y}}}= \left\langle Y,\mathcal {F}_Y \right\rangle }$. These are functions $\mu :\mathcal {F}_Y \longrightarrow \mathbb {R}$ such that $\mu (\emptyset )=0$ and $\mu$ is $\sigma$-additive. In comparison to the definition of a measure, one drops the nonnegativity requirement, but insists that the values be finite. The set $\mathbb {M}_{\pm }({{\varvec{Y}}})$ forms a real vector space which includes the probability measures $\mathbb {P}({{\varvec{Y}}})$, and total variation gives a norm on this space. When Y is a compact Hausdorff space and ${{\varvec{Y}}}= \left\langle Y,\mathcal {B}(Y) \right\rangle$, the Riesz–Markov–Kakutani representation theorem [48] says that $\mathbb {M}_{\pm }({{\varvec{Y}}})$ is a concrete realisation of the topological dual space of $C(Y,\mathbb {R})$, the space of continuous real-valued functions on Y. The duality is given by $\left\langle \mu ,f \right\rangle :=\int _{{{\varvec{Y}}}}f\;\,\mathrm {d}\,\mu$ for $\mu \in \mathbb {M}_{\pm }({{\varvec{Y}}})$ and $f \in C(Y,\mathbb {R})$.

6.4 Linear programming

Consider an empirical model $e = ({e_C})_{C \in \mathcal {M}}$ on a scenario $\left\langle X,\mathcal {M},O \right\rangle$ satisfying the assumptions discussed above. Calculation of its noncontextual fraction can be expressed as the infinite linear programming problem (P-CF). This is our primal linear program; its dual linear program is given by (D-CF). In what follows, we will see how to derive the dual and show that the optimal solutions of both programs coincide. We also refer the interested reader to Appendix A where the programs are expressed in the standard form of infinite linear programming [17].

$$\begin{aligned} \hbox {(P-CF)}\left\{ \begin{aligned}&\quad \text {Find } \mu \in \mathbb {M}_{\pm }({\varvec{O}}_X) \\&\quad \text {maximising } \mu (O_X) \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\forall C \in \mathcal {M},\; \mu |_C \;\le \; e_C \\&\mu \;\ge \; 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

$$\begin{aligned} \hbox {(D-CF)}\left\{ \begin{aligned}&\quad \text {Find } ({f_C})_{C \in \mathcal {M}} \in \prod _{C \in \mathcal {M}} C(O_C) \\&\quad \text {minimising } \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \;\ge \; \mathbf {1}_{O_X} \\&\forall C \in \mathcal {M},\; f_C \;\ge \; \mathbf {0}_{O_C} \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

We have written $\rho ^X_C$ for the projection ${O_X}\longrightarrow {O_C}$ as before, and $\mathbf {1}_D$ (resp. $\mathbf {0}_D$) for the constant function $D \longrightarrow \mathbb {R}$ that assigns the number 1 (resp. 0) to all elements of its domain D; in the above instance, to all $\mathbf {g}\in O_X$ (resp. all $\mathbf {o}\in O_C$).¹² We denote the optimal values of problems (P-CF) and (D-CF), respectively, as ${\text {val(P-CF)}}$ and ${\text {val(D-CF)}}$. They both equal $\textsf {NCF}(e)$ due to strong duality (see Proposition 24 and Appendix B).

Analogues of these programs have been studied in the discrete-variable setting [6]. Note however that, in general, these continuous-variable linear programs are over infinite-dimensional spaces and thus not practical to compute directly. For this reason, in Sect. 8 we will introduce a hierarchy of finite-dimensional semi-definite programs that approximate the solution of (P-CF) to arbitrary precision.

Deriving the dual via the Lagrangian

We now give an explicit derivation of (D-CF) as the dual of (P-CF) via the Lagrangian method. To simplify notation, we set $E_1 :=\mathbb {M}_{\pm }({{\varvec{O}}}_X)$ and $F_2 :=\prod _{C \in \mathcal {M}} C(O_C,\mathbb {R})$ and their convex cones $K_1$ and $K_2^*$ (see Appendix A). This matches the standard form notation for infinite linear programming of [17], in which we present our programs in Appendix A. Hence we introduce $|\mathcal {M}|$ dual variables, and one continuous map $f_C \in C(O_C,\mathbb {R})$ for each $C\in \mathcal {M}$ to account for the constraints $\mu |_{C} \le e_C$. From (P-CF), we then define the Lagrangian $\mathcal {L}: K_1 \times K_2^* \longrightarrow \mathbb {R}$ as

(21)

The primal program (P-CF) corresponds to

$$\begin{aligned} \sup _{\mu \in K_1} \; \inf _{(f_C) \in K_2^*} \; \mathcal {L}(\mu ,(f_C)) \text { ,}\end{aligned}$$

(22)

as the infimum here imposes the constraints that $\mu |_C \le e_C$ for all $C \in \mathcal {M}$, for otherwise the Lagrangian diverges. If these constraints are satisfied, then because of the infimum, the second term of the Lagrangian vanishes yielding the objective of the primal problem. To express the dual, which amounts to permuting the infimum and the supremum, we need to rewrite the Lagrangian:

$$\begin{aligned} \mathcal {L}(\mu ,(f_C)) \quad&=\quad \mu (O_X) + \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,(e_C - \mu |_C) \\ \quad&=\quad \int _{O_X}\mathbf {1}\;\,\mathrm {d}\,\mu + \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C - \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,\mu |_C \\ \quad&=\quad \int _{O_X}\mathbf {1}\;\,\mathrm {d}\,\mu + \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C - \sum _{C \in \mathcal {M}} \int _{O_X}f_C \circ \rho ^X_C\;\,\mathrm {d}\,\mu \\ \quad&=\quad \int _{O_X}\mathbf {1}\;\,\mathrm {d}\,\mu + \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C - \int _{O_X}\left( \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \right) \;\,\mathrm {d}\,\mu \\ \quad&=\quad \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C + \int _{O_X}\left( \mathbf {1} - \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \right) \;\,\mathrm {d}\,\mu \text { .}\end{aligned}$$

The dual program (D-CF) indeed corresponds to

$$\begin{aligned} \inf _{(f_C) \in K_2^*} \; \sup _{\mu \in K_1} \; \mathcal {L}(\mu ,(f_C)) \text { .}\end{aligned}$$

(23)

The supremum imposes that $\sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \ge \mathbf {1}$ on $O_X$, since otherwise the Lagrangian diverges. If this constraint is satisfied, then the supremum makes the second term vanish yielding the objective of the dual problem (D-CF).

Zero duality gap

A key result about the noncontextual fraction, which is essential in establishing the connection to Bell inequality violations, is that (P-CF) and (D-CF) are strongly dual, in the sense that no gap exists between their optimal values. Strong duality always holds in finite linear programming, but it does not hold in general for the infinite case.

Proposition 2

Problems (P-CF) and (D-CF) have zero duality gap and their optimal values satisfy

$$\begin{aligned} {\text {val(P-CF)}} = {\text {val(D-CF)}} = \textsf {NCF}(e) \end{aligned}$$

(24)

Proof

This proof relies on [17, Theorem 7.2]. The complete proof is provided in Appendix B. Here, we only provide a brief outline. Let $E_1 :=\mathbb {M}_{\pm }({{\varvec{O}}}_X) \times \prod _{C \in \mathcal {M}} \mathbb {M}_{\pm }({{\varvec{O}}}_C)$ and $E_2 :=\prod _{C \in \mathcal {M}} \mathbb {M}_{\pm }({{\varvec{O}}}_C)$. Strong duality between (P-CF) and (D-CF) amounts to showing that the cone

$$\begin{aligned} \mathcal {K}= \left\{ \left( \, (\mu |_C + \nu _C)_{C\in \mathcal {M}}, \mu (O_X)\, \right) \mid (\mu ,(\nu _C)_{C\in \mathcal {M}}) \in E_{1+}\right\} \end{aligned}$$

is weakly closed in $E_2 \oplus \mathbb {R}$, where:

$$\begin{aligned} E_{1+} :=\left\{ (\mu ,(\nu _C)_{C \in \mathcal {M}}) \in E_1 \mid \mu \ge 0 \text { and } \forall {C \in \mathcal {M}}\varvec{.}\; \nu _C \ge 0\right\} \subset E_1. \end{aligned}$$

We do so by considering a sequence $(\mu ^k,(\nu _C^k)_C)_{k \in \mathbb {N}}$ in $E_{1+}$ and showing that the accumulation point

$$\begin{aligned} \lim _{k \rightarrow \infty } \left( (\mu ^k|_C+\nu ^k)_{C\in \mathcal {M}}, \mu ^k(O_X) \right) \end{aligned}$$

belongs to $\mathcal {K}$. $\quad \square$

7 The Case of Local Compactness

We now focus on cases where the outcome space might be only locally compact. These include most theoretical situations that are of interest in practice. For instance $\mathbb {R}$ could be the outcome space for the position and momentum operators.

For each measurement $x \in X$, ${\varvec{O}}_x$ is supposed to be the Borel measurable space for a second-countable locally compact Hausdorff space, i.e. that the set $O_x$ is equipped with a second-countable locally compact Hausdorff topology and $\mathcal {F}_x$ is the $\sigma$-algebra generated by its open sets, written $\mathcal {B}(O_x)$. Second countability and Hausdorffness of two spaces Y and Z suffice to show that the Borel $\sigma$-algebra of the product topology is the tensor product of the Borel $\sigma$-algebras, i.e. $\mathcal {B}(Y \times Z) = \mathcal {B}(Y) \otimes \mathcal {B}(Z)$ [22, Lemma 6.4.2 (Vol. 2)]. Hence, these assumptions guarantee that ${\varvec{O}}_U$ for $U \in \mathcal {P}(X)$ is the Borel $\sigma$-algebra of the product topology on $O_U= \prod _{x \in U}O_x$. These product spaces are also second-countable, locally compact, and Hausdorff as all three properties are preserved by finite products. When Y is a second-countable locally compact Hausdorff space and ${\varvec{Y}} = \left\langle Y,\mathcal {B}(Y) \right\rangle$, the Riesz–Markov–Kakutani representation theorem [48] says that $\mathbb {M}_{\pm }({\varvec{Y}})$ is a concrete realisation of the topological dual space of $C_0(Y)$, the space of continuous real-valued functions on Y that vanish at infinity.¹³ The duality is given by $\left\langle \mu ,f \right\rangle :=\int _{{\varvec{Y}}}f\;\,\mathrm {d}\,\mu$ for $\mu \in \mathbb {M}_{\pm }({\varvec{Y}})$ and $f \in C_0(Y)$.¹⁴ Note that when Y is compact (as treated above), $C_0(Y) = C(Y)$ as every closed subspace of a compact space is compact.

Next, we show that we can approximate the linear program (P-CF)¹⁵ by a slightly modified linear program defined on the space of finite measures on a measurable compact subspace of ${\varvec{O}}_X$. The idea is to approximate to any desired error the mass of a finite measure on a locally compact set by the mass of the same measure on a compact subset. This naturally comes from the notion of tightness of a measure.

Definition 9

(tightness of a measure). A measure $\mu$ on a metric space U is said to be tight if for each $\varepsilon > 0$ there exists a compact set $U_{\varepsilon } \subseteq U$ such that $\mu (U \setminus U_{\varepsilon }) < \varepsilon$.

Then we need to argue that every measure we will consider is tight. This is a result of the following theorem.

Theorem 2

[70]. If S is a complete separable metric space, then every finite measure on S is tight.

For $x \in X$, ${\varvec{O}}_x$ is a second-countable locally compact Hausdorff space, thus a Polish space i.e. a separable completely metrisable topological space. For this reason, the above theorem applies. We are now ready to state and prove the main theorem of this subsection.

Theorem 3

The linear program (PC-F$^{\mathrm{CV},\varepsilon })$, defined over finite-signed measures on a locally compact space can be approximated to any desired precision $\varepsilon$ by a linear program $(\text {P-CF}^{\text {CV},\varepsilon })$ defined over finite signed measures on a compact space.

Proof

Fix $\varepsilon > 0$. Let $C \in \mathcal {M}$ be a given context and $x \in C$ a given measurement label within that context. Because $e_C$ is a probability measure on $O_C$, the marginal measure $e_C|_{\{x \}}$ is a finite measure on $O_x$. Following Theorem 2, $e_C|_{\{x \}}$ is tight and there exists a compact subset $K_x^{\varepsilon ,C} \subseteq O_x$ such that: $e_C|_{\{x \}}(O_x \setminus K_x^{\varepsilon ,C}) \le \varepsilon$. Importantly there exist proofs that explicitly construct the approximating sets $K_x^{\varepsilon ,C}$ (see [67]) based on the separability of the underlying spaces. It makes this construction feasible in practice and justifies this approach.

We apply this procedure for every context and for all measurements in a context. We now define the compact set

$$\begin{aligned} O_x^{\varepsilon } :=\bigcup \limits _{C | x \in C} K_x^{\varepsilon ,C}. \end{aligned}$$

The previous definition is essential to ensure a noncontextual cut off of the outcome set which ensures the good definition of a compact subset for each measurement label independent of the context. For some subset of measurement labels $U \subseteq X$, we define the compact set $O_U^{\varepsilon } :=\prod _{x \in U} O_x^{\varepsilon }$. For every context $C \in \mathcal {M}$ and for every measurement label $x \in C$, we now have that $K_x^{\varepsilon ,C} \subseteq O_x^{\varepsilon }$ and thus $e_C|_{\{x \}}(O_x \setminus O_x^{\varepsilon }) \le \varepsilon$. Note that due to the compatibility condition, we can write $e_C|_{\{x\}}$ as $e_{\{x\}}$ for any context.

Let $\mu$ be any feasible solution of (P-CF) defined over finite-signed measures on a locally compact space. Due to the constraints of (P-CF) we have that $\forall x \in X, \, \mu |_{\{x\}} \le e_{\{x\}}$. Then:

$$\begin{aligned} \mu (O_X \setminus O^{\varepsilon }_X)&= \mu \left( \prod _{x \in X } O_{x} \setminus \prod _{x \in X } O_{x}^{\varepsilon } \right) \end{aligned}$$

(25)

$$\begin{aligned}&= \mu \left( \prod _{x \in X } ( O_{x} \setminus O_{x}^{\varepsilon } ) \right) \end{aligned}$$

(26)

$$\begin{aligned}&= \prod _{x \in X} \mu |_{\{x\}} (O_x \setminus O_x^\varepsilon ) \end{aligned}$$

(27)

$$\begin{aligned}&\le \prod _{x \in X} e_{\{x\}} (O_x \setminus O_x^\varepsilon ) \end{aligned}$$

(28)

$$\begin{aligned}&\le \varepsilon ^{\vert X \vert } \text { .}\end{aligned}$$

(29)

We now define the linear program $(\text {P-CF}^{\text {CV},\varepsilon })$ which has the same form as (P-CF) though the unknown measures are taken from $\mathbb {M}_{\pm }({\varvec{O}}_X^{\varepsilon })$ where ${\varvec{O}}_X^{\varepsilon } = \left\langle O_X^{\varepsilon },\mathcal {B}(O_X^{\varepsilon }) \right\rangle$. We would like to state that $(\text {P-CF}^{\text {CV},\varepsilon })$ approximates (P-CF) up to $\varepsilon$; i.e. that their values are $\varepsilon$-close. The missing ingredient from the previous chain of inequalities is that given an optimal measure $\mu ^*$ satisfying (P-CF), we do not know whether an optimal solution $\mu ^*_{\varepsilon }$ of $(\text {P-CF}^{\text {CV},\varepsilon })$ is necessarily the restriction of $\mu ^*$ to $O_X^{\varepsilon }$. In fact, it is possible that we do not even have a unique optimal solution. However we only need to prove that they have the same mass on $O_X^\varepsilon$, i.e. $\mu _{\varepsilon }^*(O_X^{\varepsilon }) = \mu ^*|_{O_X^{\varepsilon }}(O_X^{\varepsilon })$. For a contradiction, suppose this does not hold. Then because $\mu ^*_{\varepsilon }$ is an optimal value of $(\text {P-CF}^{\text {CV},\varepsilon })$, we must have $\mu _{\varepsilon }^*(O_X^{\varepsilon }) > \mu ^*|_{O_X^{\varepsilon }}(O_X^{\varepsilon })$. From this we construct a new measure ${\tilde{\mu }}$ on ${\varvec{O}}_X$ which equals $\mu ^*_{\varepsilon }$ on ${\varvec{O}}_X^{\varepsilon }$ and $\mu ^*$ on ${\varvec{O}}_X \setminus O_X^{\varepsilon }$. It satisfies all constraints and furthermore ${\tilde{\mu }}(O_X) > \mu ^*(O_X)$. This contradicts the fact that $\mu ^*$ is an optimal solution of (P-CF). Thus necessarily $\mu _{\varepsilon }^*(O_X^{\varepsilon }) = \mu ^*|_{O_X^{\varepsilon }}(O_X^{\varepsilon })$.

The linear program $(\text {P-CF}^{\text {CV},\varepsilon })$ defined on a compact space has indeed a value $\varepsilon$-close to the original program (P-CF). $\quad \square$

In conclusion to this section, we can approximate the problem of finding the noncontextual fraction in measurement scenarios whose outcome spaces are locally compact by the same problem defined on compact subspace. It thus suffices to restrict the study to the case of compact outcome spaces.

8 Continuous Generalisation of Bell Inequalities

The dual program (D-CF) is of particular interest in its own right. As we now show, it can essentially be understood as computing a continuous-variable ‘Bell inequality’ that is optimised to the empirical model. Making the change of variables $\beta _C :=|\mathcal {M}|^{-1} \mathbf {1}_{O_C}-f_C$ for each $C \in \mathcal {M}$, the dual program (D-CF) transforms to the following.

$$\begin{aligned} \hbox {(B-CF)}\left\{ \begin{aligned}&\quad \text {Find } ({\beta _C})_{C \in \mathcal {M}} \in \prod \limits _{C \in \mathcal {M}} C(O_C) \\&\quad \text {maximising } \sum _{C \in \mathcal {M}} \int _{O_C}\beta _C\;\,\mathrm {d}\,e_C \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\sum _{C \in \mathcal {M}} \beta _C \circ \rho ^X_C \;\le \; \mathbf {0}_{O_X} \\&\forall C \in \mathcal {M},\; \beta _C \;\le \; \vert \mathcal {M}\vert ^{-1} \mathbf {1}_{O_C} \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

This program directly computes the contextual fraction $\textsf {CF}(e)$ instead of the noncontextual fraction. It maximises, subject to constraints, the total value obtained by integrating these functionals context-wise against the empirical model in question. The first set of constraints—a generalisation of a system of linear inequalities determining a Bell inequality — ensures that, for noncontextual empirical models, the value of the program is at most 0, since any such model extends to a measure $\mu$ on ${\varvec{O}}_X$ such that $\mu (O_X) = 1$. The final set of constraints acts as a normalisation condition on the value of the program, ensuring that it takes values in the interval [0, 1] for any empirical model. Any family of functions $\beta = (\beta _C) \in F_2$ satisfying the constraints will thus result in what can be regarded as a generalised Bell inequality,

$$\begin{aligned} \sum _{C \in \mathcal {M}} \int _{O_C}\beta _C\;\,\mathrm {d}\,e_C \le 0 \, , \end{aligned}$$

(30)

which is satisfied by all noncontextual empirical models.

Definition 10

A form $\mathbf {\beta }$ on a measurement scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ is a family $\mathbf {\beta } = (\beta _C)_{C \in \mathcal {M}}$ of functions $\beta _C \in C(O_C)$ for all $C \in \mathcal {M}$. Given an empirical model e on $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$, the value of $\mathbf {\beta }$ on e is¹⁶

$$\begin{aligned} \langle \beta , e \rangle _{_2} :=\sum _{C \in \mathcal {M}} \int _{O_C}\beta _C\;\,\mathrm {d}\,e_C \text { .}\end{aligned}$$

The norm of $\mathbf {\beta }$ is given by

$$\begin{aligned} \Vert \beta \Vert :=\sum _{C \in \mathcal {M}}\Vert \beta _C\Vert = \sum _{C\in \mathcal {M}}\sup \left\{ \beta _C(\mathbf {o}) \mid \mathbf {o}\in O_C\right\} \text { .}\end{aligned}$$

Definition 11

An inequality $(\mathbf {\beta },R)$ on a measurement scenario $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$ is a form $\mathbf {\beta }$ together with a bound $R \in \mathbb {R}$. An empirical model e is said to satisfy the inequality if the value of $\mathbf {\beta }$ on e is below the bound, i.e. $\langle \mathbf {\beta }, e \rangle _{_2} \le R$.

Definition 12

An inequality $(\mathbf {\beta },R)$ is said to be a generalised Bell inequality if it is satisfied by all noncontextual empirical models, i.e. if for any noncontextual model d on $\left\langle X,\mathcal {M},{{\varvec{O}}} \right\rangle$, it holds that $\langle \mathbf {\beta }, d \rangle _{_2} \le R$.

A generalised Bell inequality $(\beta ,R)$ establishes a bound $\langle e,\beta \rangle _{2}$ amongst noncontextual models e. For more general models, the value of $\beta$ on e is only limited by the algebraic bound $\left\Vert \beta \right\Vert$. In the following, we will only consider inequalities $(\beta ,R)$ for which $R < \left\Vert \beta \right\Vert$ excluding inequalities trivially satisfied by all empirical models.

Definition 13

The normalised violation of a generalised Bell inequality $(\mathbf {\beta },R)$ by an empirical model e is

$$\begin{aligned} \frac{\max \mathopen { \{ }0,\langle \beta , e \rangle _{_2} - R\mathclose { \} }}{\Vert \beta \Vert -R} \text { ,}\end{aligned}$$

the amount by which its value $\langle \beta , e \rangle _{_2}$ exceeds the bound R normalised by the maximal ‘algebraic’ violation.

The above definition restricts to the usual notions of Bell inequality and noncontextual inequality in the discrete-variable case and is particularly close to the presentation in [6]. The following theorem also generalises to continuous variables the main result of [6].

Theorem 4

Let e be an empirical model. (i) The normalised violation by e of any generalised Bell inequality is at most $\textsf {CF}(e)$; (ii) if $\textsf {CF}(e) > 0$ then for every $\varepsilon > 0$ there exists a generalised Bell inequality whose normalised violation by e is at least $CF(e)-\varepsilon$.

Proof

The proof follows directly from the definitions of the linear programs, and from strong duality, i.e. the fact that their optimal values coincide (Proposition 2 below). $\quad \square$

Item (ii) is slightly modified compared to the discrete analogue because there is no guarantee that there exists an optimal solution for the dual program (D-CF). In particular, its optimal value might be achieved by a discontinuous function that can be approximated by continuous ones. Hence the modification of (ii) with a normalised violation $\varepsilon$-close to $\textsf {CF}(e)$.

9 Approximating the Contextual Fraction with SDPs

In Sect. 5, we presented the problem of computing the noncontextual fraction as an infinite linear program. Although this is of theoretical importance, it does not allow one to directly perform the actual numerical computation of this quantity. Here we exploit the link between measures and their sequence of moments to derive a hierarchy of truncated finite-dimensional semidefinite programs which are a relaxation of the original primal problem (P-CF). Dual to this vision, we can equivalently exploit the link between positive polynomials and their sum-of-squares representation to derive a hierarchy of semidefinite programs which are a restriction of the dual problem (D-CF). We further prove that the optimal values of the truncated programs converge monotonically to the noncontextual fraction. This makes use of global optimisation techniques developed by Lasserre and Parrilo [54, 69] and further developed in [55]. We introduce them in Appendix C and strongly recommend reading this appendix to readers unfamiliar with these notions. We will use the same notation throughout this section. Another extensive and well-presented reference on the subject is [56]. We start by deriving a hierarchy of SDPs to approximate the contextual fraction and then show that it provides a sequence of optimal values that converge to the noncontextual fraction.

Notation and terminology

We first fix some notation that is also used in Appendix C. Let $\mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ denote the ring of real polynomials in the variables ${\varvec{x}} \in \mathbb {R}^d$, and let $\mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}\subset \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ contain those polynomials of total degree at most k. The latter forms a vector space of dimension $s(k) :=\left( {\begin{array}{c}d+k\\ k\end{array}}\right)$, with a canonical basis consisting of monomials ${\varvec{x}}^{{\varvec{\alpha }}} = x_1^{\alpha _1}\cdots x_d^{\alpha _d}$ indexed by the set $\mathbb {N}^d_k :=\left\{ {\varvec{\alpha }}\in \mathbb {N}^d \mid |{\varvec{\alpha }}|\le k\right\}$ where $|{\varvec{\alpha }}|:=\sum _{i=1}^d\alpha _i$. Any $p \in \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$ can be expanded in this basis as $p({\varvec{x}}) = \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} p_{\alpha }{\varvec{x}}^{{\varvec{\alpha }}}$ and we write $\mathbf{p}:=(p_{{\varvec{\alpha }}}) \in \mathbb {R}^{s(k)}$ for the resulting vector of coefficients.

9.1 Hierarchy of semidefinite relaxations for computing $\textsf {NCF}(e)$

We fix a measurement scenario $\left\langle X,\mathcal {M},{\varvec{O}} \right\rangle$ and an empirical model e on this scenario. We will restrict our attention to outcome spaces of the form detailed in Sect. 5.3. Let $d = \vert X \vert \in \mathbb {N}_{>0}$ so that $O_X$ is a Borel subset of $\mathbb {R}^d$. As a prerequisite, we first need to compute the sequences of moments associated to measures $(e_C)_{C \in \mathcal {M}}$ derived from the empirical model. For $C \in \mathcal {M}$, let ${\varvec{y}}^{e,C} = (y^{e,C}_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d}$ be the sequence of all moments of $e_C$. For a given $k \in \mathbb {N}$, which will fix the level of the hierarchy, we only need to compute a finite number s(k) of moments for all contexts. These will be the inputs to the program.

Below, we derive a hierarchy of SDP relaxations for the primal program (P-CF) such that their optimal values converge monotonically to ${\text {val(P-CF)}} = \textsf {NCF}(e)$. We start by discussing the assumptions we have to make on the outcome space. Then we derive the hierarchy based first on the primal program and then on the dual program and we further show that these formulations are indeed dual. Finally, we prove convergence of the hierarchy.

Further assumptions on the outcome space?

We already made the assumptions mentioned in Sect. 5.3 for the outcome spaces ${\varvec{O}} = ({\varvec{O}}_x)_{x \in X}$ noting that they are not restrictive when considering actual applications. However we would like to meet the assumptions detailed in Assumption 1 for the global outcome space $O_X$ so that both Theorems 6 and 8 apply in our setting (see Appendix C).

Assumption 1 (ii) is already met because we have assumed that for all $x \in X$, $O_x \subset \mathbb {R}$ is compact. Recall that the more general case of locally compact can be reduced to the compact case, as seen in Sect. 6.

Let us discuss Assumption 1 (i). We have that $O_X = \prod _{x \in X} O_x$ with $O_x \subset \mathbb {R}$ compact. If $O_x$ is disconnected, we can always complete it into a connected space by attributing measure zero to the added parts for all measures $e_C$ whenever $x \in C$. Then because $O_x$ is compact, it is bounded and it can be described by two constant polynomials: there exists $a_x,b_x \in \mathbb {R}$ such that $O_x = \left[ a_x,b_x\right]$. This makes $O_X$ a polytope so in particular, it is semi-algebraic. We write it as

$$\begin{aligned} O_X = \left\{ {\varvec{x}} \in \mathbb {R}^d \mid \forall j = 1,\dots ,m, \; g_j({\varvec{x}}) \ge 0\right\} \end{aligned}$$

(31)

for some polynomials $g_j \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ of degree 1.

As noted in [54], Assumption 1 (iii) is not very restrictive. For instance, it is satisfied when the set is a polytope. This is the case for $O_X$.

Thus there is no need for further assumptions beyond those already assumed in Sect. 5.3 in order to apply the results presented in Appendix C.

Relaxation of the primal program

The program (P-CF) can be relaxed so that a converging hierarchy of SDPs can be derived. The program (P-CF) is essentially a maximisation problem on finite-signed Borel measures with additional constraints such as the fact that these are proper measures (i.e. they are nonnegative). We will represent a measure by its moment sequence and use conditions for which this moment sequence has a (unique) representing Borel measure (see Appendix C.2). We recall the expression of the primal program (P-CF):

$$\begin{aligned} \hbox {(P-CF)}\left\{ \begin{aligned}&\quad \text {Find } \mu \in \mathbb {M}_{\pm }({\varvec{O}}_X) \\&\quad \text {maximising } \mu (O_X) \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\qquad \forall C \in \mathcal {M},\; \mu |_C \;\le \; e_C \\&\qquad \mu \;\ge \; 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

From Appendix C.2 which culminates at Theorem 8, it can be relaxed for $k\in \mathbb {N}_{>0}$ as:

The moment matrices $M_k({\varvec{y}})$ and the localising matrices $M_{k-1}(g_j {\varvec{y}})$ are defined in Appendix C. We consider localising matrices of order $k-1$ rather than k because all $g_j$’s are of degree exactly 1. In this way, the maximum degree matches with that of the moment matrices. In general we have to deal with localising matrices of order $k- \lceil \frac{\text {deg}(g_j)}{2} \rceil$. If $\mu$ is a representing measure on ${\varvec{O}}_X$ for ${\varvec{y}}$ then for all contexts $C \in \mathcal {M}$, ${\varvec{y}}|_C$ can be defined through ${\varvec{y}}$ by requiring that ${\varvec{y}}|_C$ has representing measure $\mu |_C$. The two last constraints state necessary conditions on the variable ${\varvec{y}}$ to be moments of some finite Borel measure supported on ${\varvec{O}}_X$. The first constraint is a relaxation of the constraint $\mu |_C \le e_C$ for $C \in \mathcal {M}$. As expected, (SDP-$\hbox {CF}^k$) is a semidefinite relaxation of the problem (P-CF) so that $\forall k \in \mathbb {N}_{>0}$, $\textsf {NCF}(e) = {\text {val(P-CF)}} \le {\text {val}}{(\text {SDP-CF}^{k})}$. Moreover $(\mathrm{val}(\text {SDP-CF}^k))_k$ is a monotone nonincreasing sequence because more constraints are added as k increases (so that the relaxations are tighter and tighter).

Restriction of the dual program

The program (D-CF) can be restricted so that we can derive a converging hierarchy of SDPs. It is essentially the minimisation of continuous functions for which we require additional constraints such as the fact that they are nonnegative. We will exploit the link between positive polynomials and sum-of-squares representation that is presented in Appendix C.1. We recall the expression of the dual program (D-CF):

$$\begin{aligned} \hbox {(D-CF)}\left\{ \begin{aligned}&\quad \text {Find } ({f_C})_{C \in \mathcal {M}} \in \prod _{C \in \mathcal {M}} C(O_C) \\&\quad \text {minimising } \int _{O_C}f_C\;\,\mathrm {d}\,e_C \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\qquad \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \;\ge \; \mathbf {1}_{O_X} \\&\qquad \forall C \in \mathcal {M},\; f_C \;\ge \; \mathbf {0}_{O_C} \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

As this point we could derive the dual of program (SDP-$\hbox {CF}^k$) and show that this is indeed a restriction of the above program. For a more symmetric treatment, we restrict the dual program building on Appendix C.1 and Theorem 6. Instead of optimising over positive continuous functions, we restrict them to belong to the quadratic module Q(g) and then further to $Q_k(g)$ for some $k \in \mathbb {N}_{>0}$. This requires that the degrees of SOS polynomials are fixed. For $k \in \mathbb {N}_{>0}$, we have

(DSDP-$\hbox {CF}^{k}$) is a restriction of (D-CF) so that for all $k \in \mathbb {N}_{> 0}$, we have that $\textsf {NCF}(e) = {\text {val(D-CF)}} \le {\text {val}}{(\text {SDP-CF}^{k})}$. Furthermore, $(\text {val(SDP-CF}^k))_k$ is a monotone nonincreasing sequence.

Problems (SDP-$\hbox {CF}^k$) and (DSDP-$\hbox {CF}^{k}$) are indeed dual programs (see Proposition 5 in Appendix D).

8.2 Convergence of the hierarchy of SDPs

Finally, we prove that the constructed hierarchy provides a sequence of objective values that converges to the noncontextual fraction $\textsf {NCF}(e)$.

Theorem 5

The optimal values of the hierarchy of semidefinite programs (SDP-$\hbox {CF}^k$) (resp. (DSDP-$\hbox {CF}^{k}$)) provide monotonically decreasing upper bounds converging to the noncontextual fraction $\textsf {NCF}(e)$ which is the value of (P-CF). That is

$$\begin{aligned} {\text {val}}({\text {SDP-CF}^\text {k}})&\downarrow&{\text {val(P-CF)}} = \textsf {NCF}(e) \quad \,\text { as } k \rightarrow \infty \, , \end{aligned}$$

(32)

$$\begin{aligned} {\text {val}}({\text {DSDP-CF}^\text {k}})&\downarrow&{\text {val(D-CF)}} = \textsf {NCF}(e) \quad \text { as } k \rightarrow \infty \text { .}\end{aligned}$$

(33)

Proof

Because of the strong duality between the original infinite-dimensional linear programs we have

$$\begin{aligned} {\text {val(P-CF)}} = {\text {val(D-CF)}} = \textsf {NCF}(e). \end{aligned}$$

(34)

Moreover, for all $k \ge 1$ (SDP-$\hbox {CF}^k$) is a relaxation of (P-CF):

$$\begin{aligned} {\text {val}}{(\text {SDP-CF}^\text {k})} \ge {\text {val}}({\text {P-CF}}). \end{aligned}$$

(35)

And for all $k \ge 1$, (DSDP-$\hbox {CF}^{k}$) is a restriction of (D-CF):

$$\begin{aligned} {\text {val}}{(\text {DSDP-CF}^\text {k})} \ge {\text {val(D-CF)}}. \end{aligned}$$

(36)

Also for all $k \ge 1$, we have weak duality between (SDP-$\hbox {CF}^k$) and (DSDP-$\hbox {CF}^{k}$) (see Proposition 5):

$$\begin{aligned} {\text {val}}{(\text {DSDP-CF}^\text {k})} \ge {\text {val}}{(\text {SDP-CF}^\text {k})}. \end{aligned}$$

(37)

Thus for all $k \ge 1$:

$$\begin{aligned} {\text {val}}{(\text {DSDP-CF}^\text {k})} \ge {\text {val}}{(\text {SDP-CF}^\text {k})} \ge \textsf {NCF}(e). \end{aligned}$$

(38)

We already saw that $(\text {val(SDP-CF}^k))_k$ and $({\text {val}}({\text {DSDP-CF}^{k}}))_k$ form monotone nonincreasing sequences. We now show that $(\text {val}(\text {DSDP-CF}^k))_K$ converges to $\textsf {NCF}(e)$. This is equivalent to showing that we can approximate any feasible solution¹⁷ of program (D-CF) with a solution of (DSDP-$\hbox {CF}^{k}$) for a high enough rank k.

Fix $\varepsilon > 0$ and a feasible solution $(f_C)_{C \in \mathcal {M}} \in \prod _{C \in \mathcal {M}} C(O)$ of (D-CF). Then for all $C \in \mathcal {M}$, $f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert }$ is a positive continuous function on $O_C$. Because $O_C$ is compact (see Sect. 5.3) by the Stone–Weierstrass theorem, $f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert }$ can be approximated by a positive polynomial. Thus there exist positive polynomials $p_C^{\varepsilon } \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ such that for all contexts $C \in \mathcal {M}$ we have (in sup norm) that

$$\begin{aligned} \left\Vert f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } - p_C^{\varepsilon }\right\Vert \le \frac{\varepsilon }{\vert \mathcal {M}\vert } \end{aligned}$$

(39)

and also

$$\begin{aligned} \left\Vert \left( f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } - p_C^{\varepsilon } \right) \circ \rho ^X_C \right\Vert < \frac{1}{\vert \mathcal {M}\vert } \underset{{\varvec{x}} \in O_X}{\text {min}} \left( \sum _{C \in \mathcal {M}} \left( f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } \right) \circ \rho ^X_C({\varvec{x}}) - {\varvec{x}} \right) , \quad \end{aligned}$$

(40)

where the minimum is strictly positive as $\sum _C (f_C +\frac{\varepsilon }{\vert \mathcal {M}\vert }) \circ \rho ^X_C > {\varvec{1}}_{O_X}$.

From Eq. (39), the objective derived with $(p_C^{\varepsilon })_C$ is $\varepsilon$-close to the original objective:

$$\begin{aligned} \left| \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,e_C - \sum _{C \in \mathcal {M}} \int _{O_C}p_C^{\varepsilon }\;\,\mathrm {d}\,e_C\right|&\le \sum _{C \in \mathcal {M}} \int _{O_C}\left| f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } - p_C^{\varepsilon }\right| \;\,\mathrm {d}\,e_C \end{aligned}$$

(41)

$$\begin{aligned}&\le \varepsilon \text { .}\end{aligned}$$

(42)

Also from Eq. (40):

$$\begin{aligned} \sum _{C \in \mathcal {M}}&p_C^{\varepsilon } \circ \rho ^X_C - {\varvec{1}} \end{aligned}$$

(43)

$$\begin{aligned}&> \sum _{C \in \mathcal {M}} \left( f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } \right) \circ \rho ^X_C - \underset{{\varvec{x}} \in O_X}{\text {min}} \left( \sum _{C \in \mathcal {M}} \left( f_C + \frac{\varepsilon }{\vert \mathcal {M}\vert } \right) \circ \rho ^X_C({\varvec{x}}) - {\varvec{x}} \right) - {\varvec{1}} \end{aligned}$$

(44)

$$\begin{aligned}&\ge 0, \end{aligned}$$

(45)

so that $\sum _{C \in \mathcal {M}} p_C^{\varepsilon } \circ \rho ^X_C - {\varvec{1}}_{O_X}$ is a positive polynomial on $O_X$. Next, because $O_X$ is of the form required in Assumption 1, by Putinar’s Positivellensatz(see Theorem 6), $\sum _{C \in \mathcal {M}} p_C^{\varepsilon } \circ \rho ^X_C - {\varvec{1}}_{O_X}$ belongs to the quadratic module Q(g). Therefore, for a high enough rank $k \in \mathbb {N}$, it is a feasible solution of (DSDP-$\hbox {CF}^{k}$) and thus:

$$\begin{aligned} |\textsf {NCF}(e) - {\text {val}}({\text {DSDP-CF}^\text {k}}) |\le \varepsilon \text { .}\end{aligned}$$

(46)

$\square$

10 Outlook

Logical forms of contextuality, which are present at the level of the possibilistic rather than probabilistic information contained in an empirical model, remain to be considered (e.g. [2, 8, 38, 62]). In the discrete setting, these can be treated by analysing ‘possibilistic’ empirical models obtained by considering the supports of the discrete-variable probability distributions [8], which indicate the elements of an outcome space that occur with non-zero probability. In general, the notion of support of a measure is not as straightforward, and the naïve approach is not viable since typically all singletons have measure 0. Nevertheless, supports can be defined in the setting of Borel measurable spaces, for instance, which in any case are the kind of spaces in which we are practically interested, in Sects. 5 and 8.

Approaches to contextuality that characterise obstructions to global sections using cohomology have had some success [5, 11, 27,28,29, 65, 66, 75, 77] and typically apply to logical forms of contextuality. An interesting prospect is to explore how the present framework may be employed to these ends, and to see whether the continuous-variable setting can open the door to new techniques that can be applied, or whether qualitatively new forms of contextual behaviour may be uncovered. A related direction to be developed is to understand how our treatment of contextuality can be further extended to continuous measurement spaces as proposed in [30].

Another direction to be explored is how our continuous-variable framework for contextuality can be extended to apply to more general notions of contextuality that relate not only to measurement contexts but also more broadly to contexts of preparations and transformations as well [63, 81], noting that these also admit quantifiable relationships to quantum advantage [43, 63].

Indeed, a major motivation to study contextuality is for its connections to quantum-over-classical advantages in informatic tasks. An important line of questioning is to ask what further connections can be found in the continuous-variable setting, and whether continuous-variable contextuality might offer advantages that outstrip those achievable with discrete-variable contextual resources. Note that it is known that infinite-dimensional quantum systems can offer certain additional advantages beyond finite-dimensional ones [80], though the empirical model that arises in that example is still a discrete-variable one in our sense.

The present work sets the theoretical basis for computational exploration of continuous-variable contextuality in quantum-mechanical empirical models. This, we hope, can provide new insights and inform other avenues to be developed in future work. It can also be useful in verifying the non-classicality of empirical models. Numerical implementation of the programs of Sect. 8 is of particular interest. The hierarchy of semi-definite programs can be used numerically to witness contextuality in continuous-variable experiments. Even if the time-complexity of the semi-definite program may increase drastically with its degree, a low-degree program can already provide a first witness of contextual behaviour.

Since our framework for continuous-variable contextuality is independent of quantum theory itself, it can equally be applied to ‘empirical models’ that arise in other, non-physical settings. The discrete-variable framework of [8] has led to a number of surprising connections and cross-fertilisations with other fields [3], including natural language [12], relational databases [1, 16], logic [5, 10, 51], constraint satisfaction [7, 9] and social systems [34]. It may be hoped that similar connections and applications can be found for the present framework to fields in which continuous-variable data is of central importance. For instance probability kernels of the kind we have used are also widely employed in machine learning (e.g. [45]), inviting intriguing questions about how our framework might be used or what advantages contextuality may confer in that setting.

Appendices

Appendices

Linear Programs in Standard Form

This appendix may be of particular interest to readers familiar with global optimisation. We express the problems (P-CF) and (D-CF) in the standard form of infinite linear programming [17, IV–(7.1)]. We recall them below:

$$\begin{aligned} \hbox {(P-CF)}\left\{ \begin{aligned}&\quad \text {Find } \mu \in \mathbb {M}_{\pm }({\varvec{O}}_X) \\&\quad \text {maximising } \mu (O_X) \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\qquad \forall C \in \mathcal {M},\; \mu |_C \;\le \; e_C \\&\qquad \mu \;\ge \; 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

$$\begin{aligned} \hbox {(D-CF)}\left\{ \begin{aligned}&\quad \text {Find } ({f_C})_{C \in \mathcal {M}} \in \prod _{C \in \mathcal {M}} C(O_C) \\&\quad \text {minimising } \int _{O_C}f_C\;\,\mathrm {d}\,e_C \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\qquad \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \;\ge \; \mathbf {1}_{O_X} \\&\qquad \forall C \in \mathcal {M},\; f_C \;\ge \; \mathbf {0}_{O_C} \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

Problems (P-CF) and (D-CF) are indeed infinite linear programs as both the objective and the constraints are linear with respect to the unknown measure $\mu \in \mathbb {M}_{\pm }({{\varvec{O}}}_X)$. To write (P-CF) in the standard form [17], we introduce the following spaces:

• $\displaystyle E_1 :=\mathbb {M}_{\pm }({\varvec{O}}_X)$.

• $\displaystyle F_1 :=C(O_X)$, the dual space of $E_1$.

• $\displaystyle E_2 :=\prod _{C \in \mathcal {M}} \mathbb {M}_{\pm }({\varvec{O}}_C)$.

• $\displaystyle F_2 :=\prod _{C \in \mathcal {M}} C(O_C)$, the dual space of $E_2$.

The dualities $\langle - , - \rangle _1 : E_1 \times F_1 \longrightarrow \mathbb {R}$ and $\langle - , - \rangle _2 : E_2 \times F_2 \longrightarrow \mathbb {R}$ are defined as follows:

$$\begin{aligned}&\forall \mu \in E_1, \; f \in F_1,&\langle \mu ,f \rangle _1 :=\int _{O_X}f\;\,\mathrm {d}\,\mu \\&\forall (\nu _C) \in E_2, \; (f_C) \in F_2,&\langle (\nu _C),(f_C) \rangle _2 :=\sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,\nu _C\, , \end{aligned}$$

where, for simplicity, we have omitted $C \in \mathcal {M}$ as a subscript for the families of functions. We fix $K_1$ to be the convex cone of positive measures in $E_1 = \mathbb {M}_{\pm }({\varvec{O}}_C)$ and $K_2$ to be the convex cone of families of positive measures in $E_2 = \prod _{C \in \mathcal {M}} \mathbb {M}_{\pm }({\varvec{O}}_C)$. Then $K_1^*$ is the convex cone of positive function in $F_1 = C(O_X)$ and $K_2^*$ is the convex cone of families of positive functions in $F_2 = \prod _{C \in \mathcal {M}} C(O_C)$.

Let $A :E_1 \longrightarrow E_2$ be the following linear transformation: for $\mu \in E_1$

$$\begin{aligned} A(\mu ) := (\mu |_C)_{C \in \mathcal {M}} \in E_2 \text{. } \end{aligned}$$

We also define the linear transformation $A^* :F_2 \longrightarrow F_1$ as follows: for $(f_C) \in F_2$,

$$\begin{aligned} A^*((f_C)) := \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \in F_1 \text{. } \end{aligned}$$

We can verify that $A^*$ is the dual transformation of A: given $\mu \in E_1$ and $(f_C) \in F_2$, we have

$$\begin{aligned} \langle A(\mu ), (f_C) \rangle _2&= \langle (\mu |_C), (f_C) \rangle _2 \end{aligned}$$

(47)

$$\begin{aligned}&= \sum _{C \in \mathcal {M}} \int _{O_C}f_C\;\,\mathrm {d}\,\mu |_C \end{aligned}$$

(48)

$$\begin{aligned}&= \int _{O_X}\sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \;\,\mathrm {d}\,\mu \end{aligned}$$

(49)

$$\begin{aligned}&= \langle \mu , \sum _{C \in \mathcal {M}} f_C \circ \rho ^X_C \rangle _1 \end{aligned}$$

(50)

$$\begin{aligned}&= \langle \mu , A^*((f_C)) \rangle _1 \text { .}\end{aligned}$$

(51)

Now fixing the vector function in the objective to be $c :=- {\varvec{1}}_{O_X} \in F_1$ and the vector in the constraints to be $b := (-e_C)_{C \in \mathcal {M}} \in E_2$, the program (P-CF) (resp. (D-CF)) can be expressed as in the standard form given in [17]:

$$\begin{aligned} \hbox {LP}\left\{ \begin{aligned}&\quad \text {Find } e_1 \in E_1 \\&\quad \text {minimising } \langle e_1,c \rangle _1 \\&\quad \text {subject to:} \\&\quad \begin{aligned}&A(e_1) \ge _{K_2} b \\&e_1 \ge _{K_1} 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

$$\begin{aligned} \hbox {(D-LP)}\left\{ \begin{aligned}&\quad \text {Find } f_2 \in F_2 \\&\quad \text {maximising } \langle b,f_2 \rangle _2 \\&\quad \text {subject to:} \\&\quad \begin{aligned}&A^*(f_2) \le _{K_1^*} c \\&f_2 \ge _{K_2} 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

Note that the minus sign in the vectors c and b was added because we chose the primal program in the standard form to be a minimisation problem while the primal program (P-CF) at hand is a maximisation problem.

Proof of Proposition 2: Zero Duality Gap

In this appendix we give a full proof of Proposition 2; i.e. that strong duality holds between problems (P-CF) and (D-CF).

Proof

To show strong duality, we rely on [17, Theorem 7.2]. Because $\mu _0= {\varvec{0}}_{{\varvec{O}}_X}$—the measure that assigns 0 to every measurable set of ${\varvec{O}}_X$— is a feasible solution for (P-CF) and the noncontextual fraction lies between 0 and 1, (P-CF) is consistent with finite value. Thus it suffices to show that the following cone

$$\begin{aligned} \mathcal {K}= \{ \left( A(\mu ), \langle \mu ,c \rangle _1 \right) \, \mid \, \mu \in K_1 \} = \{ \left( \, (\mu |_C)_C, \mu (O_X)\, \right) \, \mid \, \mu \in K_{1} \} \end{aligned}$$

(52)

is weakly closed in $E_2 \oplus \mathbb {R}$ (i.e. closed in the weak topology of $K_1$) where we recall that $K_1$ is the convex cone of positive measures in $E_1 = \mathbb {M}_{\pm }({\varvec{O}}_X)$.

We first notice that the linear transformation A is a bounded linear operator and thus continuous. Boundedness comes from the fact that for all $\mu \in K_1$,

$$\begin{aligned} \left\Vert A(\mu )\right\Vert _{E_2}&= \left\Vert (\mu |_C)_C\right\Vert _{E_2} \end{aligned}$$

(53)

$$\begin{aligned}&= \sum _{C \in \mathcal {M}} \left\Vert \mu |_C\right\Vert _{\mathbb {M}_{\pm }({\varvec{O}}_C)} \end{aligned}$$

(54)

$$\begin{aligned}&\le \sum _{C \in \mathcal {M}} \left\Vert \mu \right\Vert _{E_1} \end{aligned}$$

(55)

$$\begin{aligned}&= \vert \mathcal {M}\vert \left\Vert \mu \right\Vert _{E_1} \text { ,}\end{aligned}$$

(56)

where we take the strong topology—i.e. the norm induced by the total variation distance—on finite-signed measure spaces. It is defined as:

$$\begin{aligned} \left\Vert \mu \right\Vert _{\mathbb {M}_{\pm }({\varvec{U}})} = \vert \mu \vert (U)\text { .}\end{aligned}$$

We also equip the finite product space $E_2 = \prod _{C \in \mathcal {M}} \mathbb {M}_{\pm }({\varvec{O}}_C)$ with the norm obtained by summing¹⁸ the individual total variation norms. The inequality in Eq. (55) is due to the fact that $\mu \in K_1$ so this is a positive measure and thus $\left\| \mu |_C\right\| _{\mathbb {M}_{\pm }({\varvec{O}}_C)} \le \left\| \mu \right\| _{E_1}$. This, of course, extends to the weak topology.

Secondly, we consider a sequence $(\mu ^k)_{k \in \mathbb {N}}$ in $K_1$ and we want to show that the accumulation point $((\varTheta _C)_C,\lambda ) = \lim _{k \rightarrow \infty } \left( A(\mu ^k), \langle \mu ^k,c \rangle _1 \right)$ belongs to $\mathcal {K}$, where $\varTheta = (\varTheta _C)_C \in E_2$ and $\lambda \in \mathbb {R}$. If we consider the product of indicator functions $(\mathbf {1}_{O_C})_C \in F_2$ then $\langle A(\mu ^k), (\mathbf {1}_{O_C}) \rangle _2 = \sum _{C \in \mathcal {M}} \mu |_C^k(O_C) \longrightarrow _{k} \sum _{C \in \mathcal {M}} \varTheta _C(O_C) < \infty$ as $\varTheta _C$ is a finite measure for all maximal contexts $C \in \mathcal {M}$. Then, because $\mathcal {M}$ is a covering family of X, we have that, for all $k \in \mathbb {N} \ \mu ^k(O_X) \le \sum _{C \in \mathcal {M}} \mu ^k|_C(O_C) < \infty$. Since $(\mu ^k) \in K_1^{\mathbb {N}^{}}$ is a sequence of positive measures, this implies that $(\mu ^k)$ is bounded. Next, by weak-$*$ compactness of the unit ball (Alaoglu’s theorem [58]), there exists a subsequence $(\mu ^{k_i})_{i}$ that converges weakly to an element $\omega \in K_1$. By continuity of A, we obtain that the accumulation point is such that $((\varTheta _C)_C,\lambda ) = \left( A(\omega ), \langle \omega ,c \rangle _1 \right) \in \mathcal {K}$. $\quad \square$

The Lasserre–Parrilo Hierarchy

Below we introduce the Lasserre–Parrilo hierarchy for relaxing infinite-dimensional linear programs known as Generalised Moment Problems [53, 54, 69]. We start by giving insightful results: Sect. C.1 provides results concerning the representation of positive polynomials while Sect. C.2 provides results to understand when a sequence can be represented by a Borel measure.

Notation, terminology

We work in $\mathbb {R}^d$ for $d \in \mathbb {N}^*$. We fix ${\varvec{K}}$ to be a generic Borel measurable subspace of ${\varvec{\mathbb {R}}}^d$. Below we fix some multi-index notations. Let $\mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ denote the ring of real polynomials in the variables ${\varvec{x}} \in \mathbb {R}^d$, and let $\mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}\subset \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ contain those polynomials of total degree at most k. The latter forms a vector space of dimension $s(k) :=\left( {\begin{array}{c}d+k\\ k\end{array}}\right)$, with a canonical basis consisting of monomials ${\varvec{x}}^{{\varvec{\alpha }}} :=x_1^{\alpha _1}\cdots x_d^{\alpha _d}$ indexed by the set $\mathbb {N}^d_k :=\left\{ {\varvec{\alpha }}\in \mathbb {N}^d \mid |{\varvec{\alpha }}|\le k\right\}$ where $|{\varvec{\alpha }}|:=\sum _{i=1}^d\alpha _i$. For $k \in \mathbb {N}$, ${\varvec{x}} \in \mathbb {R}^d$, we define ${\varvec{\mathrm {v}}}_k({\varvec{x}}) :=({\varvec{x}}^{{\varvec{\alpha }}})_{\vert {\varvec{\alpha }}\vert \le d} = (1,x_1,\dots ,x_n,x_1^2,x_1x_2,\dots ,x_n^k)^T$ the vector of monomials of total degree less or equal than k.

Any $p \in \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$ is associated with a vector of coefficients ${\varvec{p}} :=(p_{{\varvec{\alpha }}}) \in \mathbb {R}^{s(k)}$ via expansion in the canonical basis as $p({\varvec{x}}) = \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} p_{{\varvec{\alpha }}}{\varvec{x}}^{{\varvec{\alpha }}}$.

Moment problem in probability

Given a finite set of indices $\varGamma$, a set of reals $\mathopen { \{ }\gamma _j : j \in \varGamma \mathclose { \} }$ and functions $h_j :K \longrightarrow \mathbb {R}$, $j \in \varGamma$, that are integrable with respect to every measure $\mu \in \mathbb {M}_{\pm }({\varvec{K}})$, the corresponding Global Moment Problem (GMP) can be expressed as:

$$\begin{aligned} \hbox {(GMP)}\left\{ \begin{aligned}&\quad \text {Find } \mu \in \mathbb {M}_{\pm }({\varvec{K}}) \\&\quad \text {maximising } \mu ({\varvec{K}}) \\&\quad \text {subject to:} \\&\qquad \qquad \begin{aligned}&\forall j \in \varGamma ,\quad \int _{K}h_j\;\,\mathrm {d}\,\mu \le \gamma _j \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

It dual program can be expressed as:

$$\begin{aligned} \hbox {(D-GMP)}\left\{ \begin{aligned}&\quad \text {Find } {\varvec{\lambda }}\in \mathbb {R}^\varGamma \\&\quad \text {minimising } \sum _{j \in \varGamma } \gamma _j \lambda _j \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\qquad \forall {\varvec{x}} \in K,\quad \sum _{j \in \varGamma } \lambda _j h_j({\varvec{x}}) - {\varvec{x}} \ge 0 \\&\qquad \forall j \in \varGamma , \quad \lambda _j \ge 0 \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

1.1 Positive polynomials and sum-of-squares

Here we present the link between positive polynomials and sum-of-squares representation so that we can derive a converging hierarchy of restriction problems for program (D-GMP).

Definition 14

A polynomial $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ is a sum-of-squares (SOS) polynomial if there exists a finite family of polynomials $({q_i})_{i \in I}$ such that $p = \sum _{i\in I} q_i^2$.

SOS polynomials are widely used in convex optimisation. We will denote by $\varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}\subset \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ the set of (multivariate) SOS polynomials, and $\varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}\subset \varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}$ the set of SOS polynomials of degree at most 2k. The following proposition hints towards the reason why it is desirable to be able to look for a sum-of-squares decomposition: it can be cast as a semidefinite optimisation problem.

Proposition 3

(Prop. 2.1, [54]). A polynomial $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}_{2k}$ has a sum-of-squares decomposition if and only if there exists a real symmetric positive semidefinite matrix $Q \in \textsf {Sym}_{s(k)}$ such that $\forall {\varvec{x}} \in \mathbb {R}^d$, $p({\varvec{x}}) = {\varvec{\mathrm {v}}}_k({\varvec{x}})^T Q {\varvec{\mathrm {v}}}_k({\varvec{x}})$.

Then we will be looking at conditions under which a nonnegative polynomial can be expressed as a sum-of-squares polynomial. This is in essence the question raised by Hilbert in his 17$^\text {th}$ conjecture [44].

Definition 15

For a family $q = (q_j)_{j\in \mathopen { \{ }1, \ldots , m\mathclose { \} }}$ of polynomials, the set:

$$\begin{aligned} Q(q) :=\left\{ \sum _{j=0}^m \sigma _j q_j \mid (\sigma _j)_{j\in \mathopen { \{ }0,\ldots , m\mathclose { \} }} \subset \varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}\right\} \end{aligned}$$

(57)

is a convex cone in $\mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ called the quadratic module generated by the family q with, for convenience, $q_0 = 1$ added. For $k \in \mathbb {N}$, we define $Q_k(q)$ to be the quadratic module Q(q) where we further impose that $(\sigma _j)_{j\in \mathopen { \{ }0,\ldots , m\mathclose { \} }} \subset \varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$ i.e. we limit the degree of SOS polynomials.

In the family of polynomials $(g_j)_{j\in \mathopen { \{ }1, \ldots , m\mathclose { \} }}$ we add $g_0 = 1$ for convenience.

Assumptions 1

Let $K \subset \mathbb {R}^d$. We make the following three assumptions on K.

• (i) Suppose K is a basic semi-algebraic set i.e. there exists a family of polynomials $g = (g_j)_{j\in \mathopen { \{ }1, \ldots , m\mathclose { \} }} \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}^m$ of degrees deg($g_j$) respectively such that:

  $$\begin{aligned} K :=\left\{ {\varvec{x}} \in \mathbb {R}^d \mid \forall j = 1,\dots ,m, \; g_j({\varvec{x}}) \ge 0\right\} . \end{aligned}$$

  (58)

• (ii) Further suppose that K is compact.

• (iii) Finally suppose that there exists $u \in Q(q)$ such that the level set $\left\{ {\varvec{x}} \in \mathbb {R}^d \mid u({\varvec{x}}) \ge 0\right\}$ is compact.

The following theorem is the key result that we will exploit for deriving the hierarchy of SDP restrictions for the dual program (GMP).

Theorem 6

(Putinar’s Positivellensatz [73]). Let $K \subset \mathbb {R}^d$ satisfy Assumptions 1. If $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ is strictly positive on K then $p \in Q(g)$, that is

$$\begin{aligned} p = \sum _{j=0}^m \sigma _j g_j \end{aligned}$$

(59)

for some sum-of-squares polynomials $\sigma _j \in \varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}$ for $j=0,1,\dots ,m$.

A proof can also be found in [56].

Using the results above and Assumption 1, one can derive a hierarchy of SDPs [54] which provide a converging sequence of optimal values towards the value of program (D-GMP):

1.2 Moment sequences and moment matrices

In this subsection, we want to understand why the program (P-CF) can be relaxed so that a converging hierarchy of SDPs can be derived. The program (P-CF) is essentially a maximisation problem on finite-signed Borel measures with additional constraints such as the fact that these are proper measures (i.e. they are nonnegative). We will represent a measure by its moment sequence and find conditions for which this moment sequence has a (unique) representing Borel measure.

Definition 16

Given a sequence ${\varvec{y}} = (y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d}\in \mathbb {R}^{\mathbb {N}^d}$, we define the linear functional $L_{{\varvec{y}}} :\mathbb {R}[1]{[}{\varvec{x}}[1]{]} \longrightarrow \mathbb {R}$ by

$$\begin{aligned} L_{{\varvec{y}}}(p) :=\sum _{{\varvec{\alpha }}\in \mathbb {N}^d}p_{{\varvec{\alpha }}} y_{{\varvec{\alpha }}}. \end{aligned}$$

(60)

Definition 17

Given a measure $\mu \in \mathbb {M}({\varvec{K}})$, its moment sequence ${\varvec{y}} = (y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d} \in \mathbb {R}^{\mathbb {N}^d}$ is given by

$$\begin{aligned} y_{{\varvec{\alpha }}} :=\int _{{\varvec{K}}}{\varvec{x}}^{{\varvec{\alpha }}}\;\,\mathrm {d}\,\mu ({\varvec{x}}) \text { .} \end{aligned}$$

(61)

We say that ${\varvec{y}}$ has a unique representing measure $\mu$ when there exists a unique $\mu$ such that Eq. (61) holds. If $\mu$ is unique then we say it is determinate (i.e. determined by its moments).

The linear functional $L_{{\varvec{y}}}$ then gives integration of polynomials with respect to $\mu$ i.e. for any $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$:

$$\begin{aligned} \begin{aligned} L_{{\varvec{y}}}(p)&= \sum _{{\varvec{\alpha }}\in \mathbb {N}^d}p_{{\varvec{\alpha }}} y_{{\varvec{\alpha }}} = \sum _{{\varvec{\alpha }}\in \mathbb {N}^d}p_{{\varvec{\alpha }}} \int _{{\varvec{K}}}{\varvec{x}}^{{\varvec{\alpha }}}\;\,\mathrm {d}\,\mu ({\varvec{x}}) = \int _{{\varvec{K}}}\sum _{{\varvec{\alpha }}\in \mathbb {N}^d}p_{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}}\;\,\mathrm {d}\,\mu ({\varvec{x}}) \\&= \int _{{\varvec{K}}}p({\varvec{x}})\;\,\mathrm {d}\,\mu ({\varvec{x}}) \\&= \int _{{\varvec{K}}}p\;\,\mathrm {d}\,\mu , \end{aligned} \end{aligned}$$

(62)

where we reversed summation and integration because the sum is finite since p is a polynomial.

The following theorem is often used in optimisation theory over measures as it provides a necessary and sufficient condition for a sequence to have a representing measure.

Theorem 7

(Riesz-Haviland [41]). Let ${\varvec{y}} = (y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d} \in \mathbb {R}^{\mathbb {N}^d}$ and suppose that $K \subseteq \mathbb {R}^d$ is closed. Then ${\varvec{y}}$ has a representation (nonnegative) measure i.e. there exists $\mu$ a measure on K such that:

$$\begin{aligned} \forall {\varvec{\alpha }}\in \mathbb {N}^d, \; \int _{K}{\varvec{x}}^{{\varvec{\alpha }}}\;\,\mathrm {d}\,\mu = y_{{\varvec{\alpha }}} \end{aligned}$$

if and only if $L_{{\varvec{y}}}(p) \ge 0$ for all polynomials $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ nonnegative on K.

We recall that for $k \in \mathbb {N}$, $s(k) = \left( {\begin{array}{c}d+k\\ k\end{array}}\right)$.

Definition 18

For each $k \in \mathbb {N}$, the moment matrix of order k, $M_k({\varvec{y}}) \in \textsf {Sym}_{s(k)}$, of a truncated sequence $(y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d_{2k}}$ is the $s(k) \times s(k)$ symmetric matrix with rows and columns indexed by $\mathbb {N}^d_k$ (i.e. by the canonical basis for $\mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$) defined as follows: for any ${\varvec{\alpha }}, {\varvec{\beta }}\in \mathbb {N}^d_k$,

$$\begin{aligned} \left( M_k({\varvec{y}})\right) _{{\varvec{\alpha }},{\varvec{\beta }}} :=L_{{\varvec{y}}}({\varvec{x}}^{{\varvec{\alpha }}+ {\varvec{\beta }}}) = y_{{\varvec{\alpha }}+ {\varvec{\beta }}} \text { .}\end{aligned}$$

(63)

Definition 19

Given a polynomial $p \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$, the localising matrix $M_k(p {\varvec{y}}) \in \textsf {Mat}_{s(k)}(\mathbb {R})$ of a moment sequence $(y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d} \in \mathbb {R}^{\mathbb {N}^d}$ is defined by: for all ${\varvec{\alpha }}, {\varvec{\beta }}\in \mathbb {N}^d_{k}$,

$$\begin{aligned} \left( M_k(p {\varvec{y}})\right) _{{\varvec{\alpha }}, {\varvec{\beta }}} :=L_{{\varvec{y}}}(p(x) x^{{\varvec{\alpha }}+ {\varvec{\beta }}}) = \sum _{\gamma \in \mathbb {N}^d} p_{\gamma } y_{{\varvec{\alpha }}+ {\varvec{\beta }}+ \gamma } \text { .}\end{aligned}$$

(64)

The localising matrix reduces to the moment matrix for $p=1$. For well-defined moment sequences, i.e. sequences that have a representing finite Borel measure, moment matrices and localising matrices are positive semidefinite, which provides insight on the reason why problem (P-CF) can be relaxed to a problem with positive semidefiniteness constraints.

Proposition 4

Let ${\varvec{y}} = (y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d} \in \mathbb {R}^{\mathbb {N}^d}$ be a sequence of moments for some finite Borel measure $\mu$ on ${\varvec{K}}$. Then for all $k\in \mathbb {N}$, $M_k({\varvec{y}}) \succeq 0$. If $\mu$ has support contained in the set $\left\{ {\varvec{x}} \in K \mid g({\varvec{x}}) \ge 0\right\}$ for some polynomial $g \in \mathbb {R}[1]{[}{\varvec{x}}[1]{]}$ then, for all $k \in \mathbb {N}$, $M_k(g {\varvec{y}}) \succeq 0$.

Proof

Let ${\varvec{y}} = (y_{{\varvec{\alpha }}})$ be the moment sequence of a given Borel measure $\mu$ on ${\varvec{K}}$. Fix $k \in \mathbb {N}$. For any vector ${\varvec{v}} \in \mathbb {R}^{s(k)}$ (noting that ${\varvec{v}}$ is canonically associated with a polynomial $v \in \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$ in the basis $({\varvec{x}}^{{\varvec{\alpha }}})$):

$$\begin{aligned} {\varvec{v}}^T M_k({\varvec{y}}) {\varvec{v}}&= \sum _{{\varvec{\alpha }},{\varvec{\beta }}\in \mathbb {N}^d_k} v_{{\varvec{\alpha }}} y_{{\varvec{\alpha }}+ {\varvec{\beta }}} v_{{\varvec{\beta }}} \end{aligned}$$

(65)

$$\begin{aligned}&= \sum _{{\varvec{\alpha }}, {\varvec{\beta }}\in \mathbb {N}^d_k} v_{{\varvec{\alpha }}} v_{{\varvec{\beta }}} \int _{K}{\varvec{x}}^{{\varvec{\alpha }}+ {\varvec{\beta }}}\;\,\mathrm {d}\,\mu \end{aligned}$$

(66)

$$\begin{aligned}&= \int _{K}\left( \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} v_{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} \right) ^2\;\,\mathrm {d}\,\mu \end{aligned}$$

(67)

$$\begin{aligned}&= \int _{K}v^2({\varvec{x}})\;\,\mathrm {d}\,\mu \ge 0 \text { .} \end{aligned}$$

(68)

Thus $M_{k}({\varvec{y}}) \succeq 0$.

Similarly we can prove that the localising matrix $M_k(g {\varvec{y}})$ is positive semidefinite when g is a nonnegative polynomial on the support of $\mu$. Indeed for all ${\varvec{v}} \in \mathbb {R}^{s(k)}$:

$$\begin{aligned} {\varvec{v}}^T M_k(g {\varvec{y}}) {\varvec{v}} = \int _{K}v^2({\varvec{x}}) g({\varvec{x}})\;\,\mathrm {d}\,\mu \ge 0 \text { ,}\end{aligned}$$

(69)

which concludes the proof. $\quad \square$

The following theorem, which is the dual facet of Theorem 6, is the key result for deriving the hierarchy of SDP relaxations for the primal problem (P-CF). It provides a necessary and sufficient condition for a sequence to have a representing measure.

Theorem 8

(Theorem 3.8 [54]). Let ${\varvec{y}} = (y_{{\varvec{\alpha }}})_{{\varvec{\alpha }}\in \mathbb {N}^d} \in \mathbb {R}^{\mathbb {N}^d}$ be a given infinite sequence in $\mathbb {R}$. Let $K \subset \mathbb {R}^d$ satisfy Assumptions 1. Then ${\varvec{y}}$ has a finite Borel representing measure with support contained in K if and only if:

$$\begin{aligned}&M_k({\varvec{y}}) \succeq 0, \; \forall k \in \mathbb {N}, \end{aligned}$$

(70)

$$\begin{aligned}&M_k(g_j {\varvec{y}}) \succeq 0, \; \forall j=1,\dots ,m , \; \forall k \in \mathbb {N}. \end{aligned}$$

(71)

Using the results above and Assumption 1, one can derive a hierarchy of SDPs [54] which provide a converging sequence of optimal values towards the value of program (GMP):

We refer readers to [54] for the proof of convergence of the hierarchies given by programs ($\hbox {GMP}^k$) and (D-$\hbox {GMP}^k$).

Duality between programs (SDP-$\hbox {CF}^k$) and (DSDP-$\hbox {CF}^k$)

As mentioned above, we chose to derive programs (SDP-$\hbox {CF}^k$) and (DSDP-$\hbox {CF}^{k}$) using dual arguments. These programs should therefore be dual to one another, which will immediately provide weak duality. We prove this for completeness.

Proposition 5

The program (DSDP-$\hbox {CF}^{k}$) is the dual formulation of the program (SDP-$\hbox {CF}^k$).

Proof

We start by rewriting $M_k({\varvec{y}})$ as $\sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} {\varvec{y}}_{{\varvec{\alpha }}} A_{{\varvec{\alpha }}}$ and $M_{k-1}(g_j {\varvec{y}})$ as $\sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} y_{{\varvec{\alpha }}} B^j_{{\varvec{\alpha }}}$ for $1 \le j \le m$ and for appropriate real symmetric matrices $A_{{\varvec{\alpha }}}$ and $(B^j_{{\varvec{\alpha }}})_j$. For instance, in the basis $({\varvec{x}}^{{\varvec{\alpha }}})$:

$$\begin{aligned} ( A_{{\varvec{\alpha }}} )_{{\varvec{s}}, {\varvec{t}}} = \bigg ( {\left\{ \begin{array}{ll} 1 \text { if } {\varvec{s}}+{\varvec{t}} = {\varvec{\alpha }}\\ 0 \text { otherwise} \end{array}\right. } \bigg )_{{\varvec{s}}, {\varvec{t}}} \text { .}\end{aligned}$$

From $A_{{\varvec{\alpha }}}$, we also extract $A_{{\varvec{\alpha }}}^C$ for $C \in \mathcal {M}$ in order to rewrite $M_k({\varvec{y}}|_C)$ as $\sum _{\alpha \in \mathbb {N}^d_k} {\varvec{y}}_{{\varvec{\alpha }}} A_{{\varvec{\alpha }}}^C$. This amounts to identifying which matrices $(A_{{\varvec{\alpha }}})$ contribute to a given context $C \in \mathcal {M}$. Then (SDP-$\hbox {CF}^k$) can be rewritten as:

Via the Lagrangian method, this is equivalent to:

$$\begin{aligned} \sup _{{\varvec{y}} \in \mathbb {R}^{s(k)}} \; \inf _{ \begin{array}{c} (X^C), (Y_j), Z \\ \text { SDP matrices} \end{array}} \; \mathcal {L}({\varvec{y}},(X_C),Y,(Z_j)), \end{aligned}$$

(72)

with

$$\begin{aligned} \begin{aligned} \mathcal {L}({\varvec{y}},(X^C),(Y_j),Z)&= y_{{\varvec{0}}} \\&\quad + \sum _{C \in \mathcal {M}} \text {Tr}(M_k({\varvec{y}}^{e,C}) X^C) - \sum _{C \in \mathcal {M}} \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} y_{{\varvec{\alpha }}} \text {Tr}(A_{{\varvec{\alpha }}}^C X^C) \\&\quad + \sum _{j=1}^m \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} y_{{\varvec{\alpha }}} \text {Tr}(B_{{\varvec{\alpha }}}^j Y_j) \\&\quad + \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} y_{{\varvec{\alpha }}} \text {Tr}(A_{{\varvec{\alpha }}} Z) \text { .}\end{aligned} \end{aligned}$$

(73)

The dual program corresponds to

$$\begin{aligned} \inf _{ \begin{array}{c} (X^C), (Y_j), Z \\ \text { SDP matrices} \end{array}} \; \sup _{{\varvec{y}} \in \mathbb {R}^{s(k)}} \; \mathcal {L}({\varvec{y}},(X^C),(Y_j),Z) \text { .}\end{aligned}$$

(74)

We rewrite the Lagrangian as:

$$\begin{aligned} \mathcal {L}({\varvec{y}},(X_C),Y,(Z_j))= & {} \sum _{C \in \mathcal {M}} \text {Tr}(M_k({\varvec{y}}^{e,C}) X^C) \nonumber \\&+ \sum _{{\varvec{\alpha }}\in \mathbb {N}^d_k} y_{{\varvec{\alpha }}} \left( \delta _{{\varvec{\alpha }}, {\varvec{0}}} - \sum _{C \in \mathcal {M}} \text {Tr}(A_{{\varvec{\alpha }}}^C X^C) + \sum _{j=1}^m \text {Tr}(B_{{\varvec{\alpha }}}^j Y_j) + \text {Tr}(A_{{\varvec{\alpha }}} Z) \right) \text { .}\quad \quad \end{aligned}$$

(75)

Then the dual program of (SDP-$\hbox {CF}^k$) reads:

$$\begin{aligned} \left\{ \begin{aligned}&\quad \text {Find } ({X^C})_{C \in \mathcal {M}}, ({Y_j})_{j=1,\dots ,m} \text { and } Z \text { SDP matrices } \\&\quad \text {maximising } \sum _{C \in \mathcal {M}} \text {Tr}(M_k({\varvec{y}}^{e,C}) X^C) \\&\quad \text {subject to:} \\&\quad \begin{aligned}&\forall {\varvec{\alpha }}\in \mathbb {N}^d_k, \; \sum _{C \in \mathcal {M}} \text {Tr}(A_{{\varvec{\alpha }}}^C X^C) - \sum _{j=1}^m \text {Tr}(B_{{\varvec{\alpha }}}^j Y_j) - \text {Tr}(A_{{\varvec{\alpha }}} Z) = \delta _{{\varvec{\alpha }}, {\varvec{0}}} \text { .}\end{aligned} \end{aligned} \right.&\end{aligned}$$

We finally show that the above program exactly corresponds to (DSDP-$\hbox {CF}^{k}$). We start with the objective. For all $C \in \mathcal {M}$, with $X^C$ a positive semidefinite matrix:

$$\begin{aligned} \text {Tr}(M_k({\varvec{y}}^{e,C}) X^C)&= \sum _{{\varvec{\alpha }}} \sum _{{\varvec{\beta }}} (M_k({\varvec{y}}^{e,C}))_{{\varvec{\alpha }}{\varvec{\beta }}} (X^C)_{{\varvec{\beta }}{\varvec{\alpha }}} \end{aligned}$$

(76)

$$\begin{aligned}&= \sum _{{\varvec{\alpha }}} \sum _{{\varvec{\beta }}} {\varvec{y}}^{e,C}_{{\varvec{\alpha }}+ {\varvec{\beta }}} (X^C)_{{\varvec{\alpha }}{\varvec{\beta }}} \end{aligned}$$

(77)

$$\begin{aligned}&= \sum _{{\varvec{\alpha }}} \sum _{{\varvec{\beta }}} \int _{\mathcal {O}_C}{\varvec{x}}^{{\varvec{\alpha }}+ {\varvec{\beta }}}\;\,\mathrm {d}\,e_C (X^C)_{{\varvec{\alpha }}{\varvec{\beta }}} \end{aligned}$$

(78)

$$\begin{aligned}&= \int _{\mathcal {O}_C} {\varvec{\mathrm {v}}}_k({\varvec{x}})^T X^C {\varvec{\mathrm {v}}}_k({\varvec{x}})\;\,\mathrm {d}\,e_C \end{aligned}$$

(79)

$$\begin{aligned}&= \int _{\mathcal {O}_C} p_C \;\,\mathrm {d}\,e_C, \end{aligned}$$

(80)

with for all $C \in \mathcal {M}$, $p_C \in \varSigma ^2 \mathbb {R}[1]{[}{\varvec{x}} [1]{]}_{k}$ a sum-of-squares polynomial via Proposition 3 and where we used ${\varvec{\mathrm {v}}}_k({\varvec{x}})$ the vectors of monomials of maximal total degree k.

Now, to retrieve the constraint, we multiply each side by ${\varvec{x}}^{{\varvec{\alpha }}}$ and we sum for all ${\varvec{\alpha }}$:

$$\begin{aligned} \sum _{C \in \mathcal {M}} \text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} A^C_{{\varvec{\alpha }}} X^C) - {\varvec{1}} = \sum _{j=1}^m \text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} B_{{\varvec{\alpha }}}^j Y_j) + \text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} A_{{\varvec{\alpha }}} Z) \end{aligned}$$

(81)

Recalling the definition of moment and localising matrices:

$$\begin{aligned}&\sum _{{\varvec{\alpha }}} A^C_{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} = {\varvec{\mathrm {v}}}_k({\varvec{x}}) {\varvec{\mathrm {v}}}_k({\varvec{x}})^T \end{aligned}$$

(82)

$$\begin{aligned}&\sum _{{\varvec{\alpha }}} B_{{\varvec{\alpha }}}^j \mathrm {v}_k({\varvec{x}}) \mathrm {v}_k({\varvec{x}})^T = g_j({\varvec{x}}) {\varvec{\mathrm {v}}}_{k-1}({\varvec{x}}) {\varvec{\mathrm {v}}}_{k-1}({\varvec{x}})^T, \; \forall j=1,\dots ,m \end{aligned}$$

(83)

Thus, by Proposition 3, for appropriate sum-of-squares polynomials $(\sigma _j)_{j=0,1,\dots ,m} \subset \mathbb {R}[1]{[}{\varvec{x}}[1]{]}_{k-1}$:

$$\begin{aligned}&\text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} A^C_{{\varvec{\alpha }}} X^C) = p_C \circ \rho _C^X ({\varvec{x}}) \end{aligned}$$

(84)

$$\begin{aligned}&\text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} B_{{\varvec{\alpha }}}^j Y_j) = g_j({\varvec{x}}) \sigma _j({\varvec{x}}) \end{aligned}$$

(85)

$$\begin{aligned}&\text {Tr}(\sum _{{\varvec{\alpha }}} {\varvec{x}}^{{\varvec{\alpha }}} A_{{\varvec{\alpha }}} Z) = \sigma _0({\varvec{x}}) \end{aligned}$$

(86)

This is exactly the constraint in (DSDP-$\hbox {CF}^{k}$) with, for convenience, $g_0 = 1$. $\quad \square$