On the Light Ray Transform of Wave Equation Solutions

Abstract

We study the light ray transform on Minkowski space-time and its small metric perturbations acting on scalar functions which are solutions to wave equations. We show that the light ray transform uniquely determines the function in a stable way. The problem is of particular interest because of its connection to inverse problems of the Sachs–Wolfe effect in cosmology.

1 Introduction

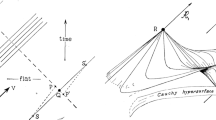
Let $M = [t_0, t_1]\times {\mathbb R}^3$ and $(t, x), t\in [t_0, t_1], x\in {\mathbb R}^3$ be the local coordinates. Let $g_M = -dt^2 + dx^2$ be the Minkowski metric on M. Consider the Lorentzian manifold $(M, g_M)$. We denote the interior by $M^\circ = (t_0, t_1)\times {\mathbb R}^3$ and the boundaries by ${\mathscr {S}}_0 = \{t_0\}\times {\mathbb R}^3$ and ${\mathscr {S}}= \{t_1\}\times {\mathbb R}^3.$ See Fig. 1.

Consider light-like geodesics on $(M, g_M)$ which are straight lines. We parametrize the set of light rays ${\mathscr {C}}$ as follows: let $x_0\in {\mathscr {S}}_0$ and $v \in {\mathbb S}^2$ the unit sphere in ${\mathbb R}^3$. Then a light ray from $x_0$ in direction (1, v) is $\gamma (\tau ) = (t_0, x_0) + \tau (1, v), \tau \in [0, t_1 - t_0].$ See Fig. 1. In particular, we can identify ${\mathscr {C}}= {\mathbb R}^3\times {\mathbb S}^2.$ The light ray transform for scalar functions on $(M, g_M)$ is defined by

$$\begin{aligned} X_M(f)(\gamma ) = \int _{0}^{t_1-t_0}f(\gamma (\tau )) d\tau , \ \ f\in C_0^\infty (M). \end{aligned}$$

(1.1)

Of course, one can regard $X_M$ as the restriction of the light ray transform $X_{{\mathbb R}^4}$ of the Minkowski spacetime $({\mathbb R}^4, g_M)$ acting on functions supported in M. However, it is perhaps better to think of $X_M$ as the compact version of the transform, which is similar to the geodesic ray transform on a compact Riemannian manifold with boundary, see for instance [20].

In this work, we study $X_M$ acting on scalar functions which are solutions to the Cauchy problem of wave equations on M. Let $c > 0$ be a constant. Denote $\square _c = \partial _t^2 + c^2 \Delta$ where $\Delta$ is the positive Laplacian on ${\mathbb R}^3,$ namely $\Delta = \sum _{i = 1}^3 D_{x_i}^2, D_{x_i} = -\sqrt{-1} \frac{\partial }{\partial x_i}.$ Here, c is the wave speed. On $(M, g_M)$, $c = 1$ is the speed of light, and $\square _c$ is the d’Alembert operator. Consider the Cauchy problem

$$\begin{aligned} \begin{aligned} \begin{gathered} \square _c f = 0 \ \ \text{ on } M^\circ \\ f= f_1, \ \ \partial _t f = f_2, \ \ \text{ on } {\mathscr {S}}_0. \end{gathered}\end{aligned} \end{aligned}$$

(1.2)

The problem we address in this paper is the determination of f or equivalently $f_1, f_2$ from $X_M(f)$ with the constraint (1.2). Let $\mathcal {N}^s {\mathop {=}\limits ^{{\text {def}}}}H_{{\text {comp}}}^{s+1}({\mathscr {S}}_0) \times H_{{\text {comp}}}^s({\mathscr {S}}_0)$. Our main result is

Theorem 1.1

Suppose $0 < c \le 1$ is constant. Assume that $(f_1, f_2)\in \mathcal {N}^s, s\ge 0$, and $f_1, f_2$ are supported in a compact set ${\mathscr {K}}$ of ${\mathscr {S}}_0$. Then $X_M f$ uniquely determines f and $f_1, f_2$ which satisfy (1.2). Moreover, there exists $C> 0$ such that

$$\begin{aligned} \Vert (f_1, f_2)\Vert _{\mathcal {N}^s} \le C \Vert X_M f\Vert _{H^{s+ 2}({\mathscr {C}})} \text { and } \Vert f\Vert _{H^{s+1}(M)} \le C \Vert X_M f\Vert _{H^{s+ 2}({\mathscr {C}})} \end{aligned}$$

where ${\mathscr {C}}$ is the set of light rays on M.

We will prove stronger versions of the theorem including lower order terms in the wave equation in Theorem 8.3 in Sect. 8. However, for ease of presentation, we use the standard wave equation on Minkowski spacetime throughout the paper until the final sections where the necessary changes are indicated.

Fig. 1

The setup of the problem for the Minkowski space-time

Next, we consider the generalization of Theorem 1.1 corresponding to $c = 1$. We remark that it is not difficult to formulate the result corresponding to $c<1$ although we do not discuss it. We consider metric perturbations $g_\delta = g_M + h$ where h satisfies assumptions (A1), (A2) in Sect. 9, which says that h is a suitably smooth small perturbation of the Minkowski spacetime. In this case, light rays may not be straight lines. Let $X_\delta$ be the light ray transform on $(M, g_\delta )$ see (9.6). Let $\square _{g_\delta }$ be the d’Alembert operator on $(M, g_\delta )$. Consider the Cauchy problem

$$\begin{aligned} \begin{aligned} \begin{gathered} \square _{g_\delta } f = 0 \ \ \text{ on } M^\circ \\ f = f_1, \ \ \partial _t f = f_2, \ \ \text{ on } {\mathscr {S}}_0.\end{gathered} \end{aligned} \end{aligned}$$

(1.3)

Our result is

Theorem 1.2

Consider $(M, g_\delta )$ satisfying assumptions (A1), (A2) to be stated in Sect. 9. Assume that $(f_1, f_2)\in \mathcal {N}^s, s \ge 0$, and $f_1, f_2$ are supported in a compact set ${\mathscr {K}}$ of ${\mathscr {S}}_0$. For $\delta \ge 0$ sufficiently small, $X_\delta f$ uniquely determines f and $f_1, f_2$ which satisfy (1.3). Moreover, there exists $C> 0$ such that

$$\begin{aligned} \Vert (f_1, f_2)\Vert _{\mathcal {N}^s} \le C \Vert X_\delta f\Vert _{H^{s+ 2}({\mathscr {C}}_\delta )} \text { and } \Vert f\Vert _{H^{s+1}(M)} \le C \Vert X_\delta f\Vert _{H^{s+ 2}({\mathscr {C}}_\delta )} \end{aligned}$$

where ${\mathscr {C}}_\delta$ is the set of light rays on $(M, g_\delta )$, see Sect. 9.

Our motivation for this setup of the light ray transform comes from some inverse problems in cosmology. We are particularly interested in the determination of gravitational perturbations such as primordial gravitational waves from the anisotropies of the Cosmic Microwave Background (CMB), see for example [2, 4, 11]. Sachs and Wolfe in their 1967 paper [19] discovered the connection of the CMB anisotropy and the light ray transform of the gravitational perturbations, now called the Sachs–Wolfe effects. We discuss the background in Sects. 2 and 3. Physically, $c< 1$ and $c =1$ in Theorem 1.1 correspond to different Universe models driven by hydrodynamical perturbations and scalar field perturbations, respectively. Moreover, Theorem 1.2 covers some cases of variable wave speeds.

The reason that we are able to get a stable determination is the restriction of singularities of f. In general, it is known that time-like singularities in f, namely all $(z, \zeta ) \in T^*M$ in the wave front set $\text {WF}(f)$ of f with $\zeta$ time-like, are lost after taking the light ray transform, although the light ray transform $X_M$ is injective on $C_0^\infty (M)$. In particular, we do not expect Theorem 1.1 to hold for $c>1$. There is a fundamental difference in our treatment between the $c < 1$ and $c = 1$ cases. The former requires a good understanding of the normal operator $X_M^*X_M$ which was considered in [12] and further generalized in [13], while the latter relies on a thorough analysis of the operator $X_M E$ where E is the fundamental solution or parametrix for the Cauchy problem.

The paper is organized as follows. In Sects. 2 and 3, we discuss the (integrated) Sachs–Wolfe effects and explain how the inverse problem is related to our theorems. In Sect. 4, we review some properties of the light ray transform. Then we consider the Cauchy problem in Sect. 5. In Sects. 6 and 7, we construct the microlocal parametrix for the light ray transform with the wave constraint for $c< 1$ and $c = 1$ respectively. We prove Theorem 1.1 and the version including lower order terms in the wave equation in Sect. 8. Finally, we address the small metric perturbations of Minkowski space-time in Sect. 9.

2 The Integrated Sachs–Wolfe Effect

Consider the flat Friedman–Lemaîte–Robertson–Walker (FLRW) model for the cosmos:

$$\begin{aligned} \mathscr {M}= (0, \infty )\times {\mathbb R}^3, \ \ g_0 = dt^2 - a^2(t) \delta _{ij} dx^i dx^j \end{aligned}$$

where $(t, x), t \in (0, \infty ), x\in {\mathbb R}^3$ are coordinates and $\delta _{ij} = 1$ if $i = j$ and otherwise 0. Here, the signature of $g_0$ is $(+, -, -, -)$ because we will refer to some results in [16] later. The factor a(t) is assumed to be positive and smooth in t. It represents the rate of expansion of the Universe.

We assume that the actual cosmos is a metric perturbation $g = g_0 + \delta g$ on $\mathscr {M}$ where $\delta g$ is a small perturbation compared to $g_0.$ Here, we follow the convention of [16] that $\delta A$ denotes the perturbation of quantity A (not $\delta$ times A). We introduce the conformal time s such that $ds = a^{-1}(t)dt$. Then we get

$$\begin{aligned} g_0 = a^2(s) \left( ds^2 - \delta _{ij} dx^i dx^j\right) = a^2(s) g_{M} \end{aligned}$$

where $g_{M}$ is the Minkowski metric on $\mathscr {M}= (0, \infty )$ and we used a(s) to denote a(t(s)). We write $g = a^2(s) (g_{M} + \delta g)$ where $\delta g$ denotes the corresponding perturbation in conformal time. In the literature, the metric perturbations are classified to scalar, vector and tensor type. We consider the scalar type perturbations. In the longitudinal gauge, also called the conformal Newtonian gauge, the metric g is of the form

$$\begin{aligned} g = a^2(s)\left[ (1+ 2\Phi ) ds^2 - (1-2\Psi ) dx^2\right] \end{aligned}$$

(2.1)

see [16, Section 2]. Here, $\Phi , \Psi$ are scalar functions on M. We remark that there is a gauge invariant formulation of cosmological perturbations. However, in the longitudinal gauge, the gauge invariant variables are equal to $\Phi , \Psi$, see [16]. In this work, we fix the gauge and work with $\Phi , \Psi$ for simplicity.

Consider the Cosmic Microwave Background (CMB) measurement. Our main references are [2, 4, 19]. Let ${\mathscr {S}}_0 = \{s_0\}\times {\mathbb R}^3$ be the surface of last scattering. This is the moment after which photons stopped interaction and started to travel freely in $\mathscr {M}.$ Let ${\mathscr {S}}= \{s_1\}\times {\mathbb R}^3$ be the surface where we make observation of the photons. Let $\gamma (\tau )$ be a light ray from ${\mathscr {S}}_0$ to ${\mathscr {S}}$. It represents the trajectory of photons in $\mathscr {M}.$ Explicitly, we have

$$\begin{aligned} \gamma (\tau ) = \left( s_0, x_0\right) + \tau (1, v), \ \ \left( s_0, x_0\right) \in {\mathscr {S}}_0, v\in {\mathbb S}^2, \tau \in \left[ 0, s_1-s_0\right] . \end{aligned}$$

Then we consider the photon energies observed at ${\mathscr {S}}_0, {\mathscr {S}}$ denoted by $E_0 = g_0(\dot{\gamma }(s_0), \partial _s), E = g_0(\dot{\gamma }(s_1), \partial _s).$ Here, the observer is represented by the flow of the vector field $\partial _s.$ The redshift z is defined by

$$\begin{aligned} 1 + z = E/E_0. \end{aligned}$$

In [19], Sachs and Wolfe derived that to the first order linearization, $1+ z$ is represented by a light ray transform of the metric perturbations, see [19, equation (39)]. In cosmological literatures, one often connects this to the CMB temperature anisotropies. Let T be the temperature observed at ${\mathscr {S}}$ in the isotropic background $g_0$. Let $\delta T$ be the temperature fluctuation from the isotropic background. One can compute $\delta T/T$ in terms of the energies $E_0, E$. One component of $\delta T/T$ is the integrated Sachs–Wolfe (ISW) effects

$$\begin{aligned} \begin{aligned} (\frac{\delta T}{T})^{ISW}(\gamma )&= \int _{0}^{s_1-s_0}(\partial _s \Phi \left( \gamma (\tau )\right) + \partial _s \Psi \left( \gamma (\tau )\right) d\tau = X_M (\partial _s \Phi + \partial _s \Psi )(\gamma ) \end{aligned} \end{aligned}$$

(2.2)

see [4, Section 2.5]. Note that this quantity depends on the light ray $\gamma$ which indicates the anisotropy. We remark that another component of $\delta T/T$ is the ordinary Sachs–Wolfe effect (OSW) which only involves $\Phi , \Psi$ at ${\mathscr {S}}_0$. The integrated Sachs–Wolfe effect can be extracted from the CMB and other astrophysical data, see for example [14].

The inverse Sachs–Wolfe problem we study is to determine $\Phi , \Psi$ on M from $(\delta T/T)^{ISW}$, which in particular includes the initial value of $\Phi , \Psi$ on ${\mathscr {S}}_0$. Before we proceed, we observe that there are natural obstructions to the unique determination from (2.2). If $\Phi + \Psi$ is a constant, then the integrated Sachs–Wolfe effect is always zero. So the goal is to determine $\Phi , \Psi$ up to such natural obstructions.

3 Dynamical Equations for Perturbations

For the Sachs–Wolfe problem, we should take into account that g satisfies the Einstein equations with certain source fields and initial perturbations at ${\mathscr {S}}_0$ from $g_0$. On the linearization level, this puts the perturbation $\delta g$ under some wave equation constraint as we discuss in this section. The derivations of the equations for the perturbation take some amount of work and they are mostly done in the literature, see for example [2, Section 5.1] and [4]. We follow the presentation and the notations in [16, Section 4–6] closely. Instead of the gauge invariant approach, we choose to work in the longitudinal gauge for simplicity. It is not hard to transform back and forth and our analysis works for the gauge invariant formulation as well.

Let $R^\mu _{\ \ \nu }$ be the Ricci curvature tensor and R the scalar curvature on $(\mathscr {M}, g)$ (in conformal time). Let $T^\mu _{ \ \ \nu }$ denote the stress-energy tensor of certain source fields. The Einstein equations are

$$\begin{aligned} G^\mu _{\ \ \nu } = 8\pi G T^\mu _{\ \ \nu }, \ \ G^\mu _{\ \ \nu } = R^\mu _{\ \ \nu } - \frac{1}{2}\delta ^\mu _{\ \ \nu } R \end{aligned}$$

where G is Newton’s gravitational constant. We assume that $T^\mu _{\ \ \nu } = {}^{(0)}T^\mu _{\ \ \nu } + \delta T^\mu _{\ \ \nu }$ where ${}^{(0)}T$ denotes the stress-energy tensor of the background field and $\delta T$ denotes the perturbation. We also have $g = a^2 (g_M + \delta g)$. Then we can write $G^\mu _{\ \ \nu } = {}^{(0)}G^\mu _{\ \ \nu } + \delta G^\mu _{\ \ \nu } + \cdots .$ From the asymptotic expansion, one finds that the Einstein tensor for the background metric $g_M$ are

$$\begin{aligned} \begin{aligned} {}^{(0)}G_0^{\ \ 0} = 3a^{-2} H^2, \ \ {}^{(0)}G_{\ \ i}^0 = 0, \ \ {}^{(0)}G_{\ \ j}^i = a^{-2}(2H' + H^2) \delta ^i_{\ \ j}, \end{aligned} \end{aligned}$$

(3.1)

where $i, j = 1, 2, 3,$ $H(s) = \partial _s a(s)/a(s)$, see [16, equation (4.2)]. Here, $H' = \partial _s H$ denotes the derivative in the conformal time variable. We emphasize that we work with a flat Universe and we get the equation ${}^{(0)}G^\mu _{\ \ \nu } = 8\pi G {}^{(0)}T^\mu _{\ \ \nu }$.

For the first order perturbation term, we get $\delta G^\mu _{\ \ \nu } = 8\pi G \delta T^\mu _{\ \ \nu }$. After lengthy calculations, one obtains (see [16, equation (4.15)]) the following equations for $\Phi , \Psi$

$$\begin{aligned} \begin{aligned}&-3H \left( H \Phi + \Psi '\right) + \Delta \Psi = 4\pi G a^2 \delta T^0_{\ \ 0}\\&\quad \partial _i (H \Phi + \Psi ') = 4\pi G a^2 \delta T^0_{\ \ i}\\&\quad [(2 H' + H^2)\Phi + H \Phi ' + \Psi '' + 2H \Psi ' + \frac{1}{2}\Delta (\Phi - \Psi ) ] \delta ^i_{\ \ j}\\&\qquad - \frac{1}{2}\delta ^{ik}(\Phi - \Psi )_{|kj} = -4\pi Ga^2 \delta T^i_{\ \ j}, \end{aligned} \end{aligned}$$

(3.2)

where $i, j = 1, 2, 3$, $\partial _i$ denotes the ith component of the covariant derivative with respect to the background metric $g_M$, $\Delta$ denotes the standard Laplacian on ${\mathbb R}^3$, and as in (3.1), prime denotes $\partial _s$ derivative.

Now we need to specify the source field. We consider two important examples: the perfect fluid and the scalar field. We first consider Universe dominated by perfect fluid sources. Let u be the four fluid velocity of a fluid source. The stress-energy tensor for a perfect fluid is

$$\begin{aligned} T^\alpha _{\ \ \beta } = (\epsilon + p) u^\alpha u_\beta - p\delta ^\alpha _{\ \ \beta } \end{aligned}$$

see [16, equation (5.2)], Here, $\epsilon$ is the energy density and p is the pressure of the fluid. We assume that $\epsilon = \epsilon _0 + \delta \epsilon , p = p_0 + \delta p$ where 0 denotes the quantity for the background and $\delta$ denotes the perturbations. For fluid source, from (3.2) one deduces that the perturbations $\Phi = \Psi$. In the case of adiabatic perturbations, $\Phi$ satisfies the following equation, called Bardeen’s equation

$$\begin{aligned} \Phi '' + 3H(1 + c_s^2)\Phi ' - c_s^2 \Delta \Phi + [2H' + (1 + 3c_s^2)H^2 ]\Phi = 0, \end{aligned}$$

(3.3)

see [16, equation (5.22)]. In general, the right hand side of the equation is a non-zero term related to the entropy perturbations. The fluid velocity u also satisfies a wave equation with speed $c_s$, see [16, equation (5.25)]. Here, $c_s < 1$ is the speed of sound. Prescribing Cauchy data of $\Phi$ at ${\mathscr {S}}_0$, one can solve the Cauchy problem of (3.3) to get $\Phi$ in $\mathscr {M}$. We formulate the inverse Sachs–Wolfe problem in this case as

Problem 3.1

Determining $\Phi$ from (2.2) where $\Phi$ satisfies the Cauchy problem of (3.3).

Commuting equation (3.3) with $\partial _s$, we see that $\partial _s\Phi$ also satisfies a wave equation. Hence, we arrived at the model problem we proposed in the introduction.

Next, let’s consider Universe governed by a scalar field $\phi$. The stress energy tensor is

$$\begin{aligned} T^\mu _{\ \ \nu } = \nabla ^\mu \phi \nabla _\nu \phi - [\frac{1}{2}\nabla ^\alpha \phi \nabla _\alpha \phi - V(\phi )]\delta ^\mu _{\ \ \nu } \end{aligned}$$

see [16, equation (6.2)]. Here, V is the potential function for the scalar field $\phi$. The field itself satisfies the Klein-Gordon equation $\square \phi + \partial _\phi V(\phi ) = 0.$ Now assume that $\phi = \phi _0 + \delta \phi$ where $\phi _0$ is the scalar field which drives the background model and $\delta \phi$ denotes the perturbation. Then we can split $T^\mu _{\ \ \nu } = {}^{(0)}T^\mu _{\ \ \nu } + \delta T^{\mu }_{\ \ \nu }$. Again, one finds that $\Phi = \Psi$ and it satisfies the equation

$$\begin{aligned} \Phi '' + 2(H - \phi _0''/\phi _0') \Phi ' - \Delta \Phi + 2(H' - H \phi _0''/\phi _0)\Phi = 0 \end{aligned}$$

(3.4)

see [16, equation (6.48)]. This is a damped wave equation with wave speed $c = 1$. We can formulate the inverse Sachs–Wolfe problem in this case as

Problem 3.2

Determining $\Phi$ from (2.2) in which $\Phi$ satisfies the Cauchy problem of (3.4).

Again, we arrived at the model problem in the introduction with $c = 1.$ We do not need it but record that the scalar field perturbation also satisfies a wave equation, see [16, equation (6.47)].

Applying our main result of the paper, in particular Theorem 8.3 which allows lower order terms in the wave equation, we obtain the following result.

Corollary 3.3

For the inverse Sachs–Wolfe effect Problems 3.1 and 3.2, one can uniquely determine $\Phi$ in $\mathscr {M}$ (and the initial conditions at ${\mathscr {S}}_0$) in the longitudinal gauge up to a constant in a stable way.

4 The Light Ray Transform on Functions

We recall some facts about the light ray transform on scalar functions. Consider the Lorentzian manifold $(M, g_M)$ and hereafter we change the signature of $g_M$ to $(-, +, +, +).$ For $(t, x)\in M^\circ , t\in (t_0, t_1), x\in {\mathbb R}^3$, we use $\Xi = (\tau , \xi ), \tau \in {\mathbb R}, \xi \in {\mathbb R}^3$ for the coordinate in $T_{(t, x)}M^\circ$ so that tangent vectors are represented by $\tau \partial _t + \sum _{j = 1}^3 \xi ^j\partial _{x^j}$. We divide the tangent vectors in $T_{(t, x)}M^\circ$ into time-like vectors $\Omega ^-_{(t, x)} M^\circ = \{\Xi \in {\mathbb R}^4: g_M(\Xi , \Xi ) = -\tau ^2+ |\xi |^2 < 0 \}$, space-like vectors $\Omega ^+_{(t, x)} M^\circ = \{\Xi \in {\mathbb R}^4: g_M(\Xi , \Xi ) > 0 \}$ and light-like vectors $L_{(t, x)} M^\circ = \{\Xi \in {\mathbb R}^4: g_M(\Xi , \Xi ) = 0 \}$. We denote the corresponding fiber bundles by $\Omega ^-M^\circ , \Omega ^+M^\circ , LM^\circ .$ The cotangent vectors can be classified similarly using the dual metric $g_M^*$ on $T^*M^\circ .$ The corresponding bundles are denoted by $\Omega ^{*,-}M^\circ , \Omega ^{*, +}M^\circ , L^*M^\circ .$

From now on, without loss of generality, we take $t_0 = 0$ in M, which amounts to a translation in the t variable. Let ${\mathscr {C}}$ be the set of light rays on $(M, g_M)$. As M has a global coordinate system, we can parametrize ${\mathscr {C}}$ as follows. Let $y\in {\mathbb R}^3, v \in {\mathbb S}^2 {\mathop {=}\limits ^{{\text {def}}}}\{z \in {\mathbb R}^3: |z| = 1\}$ with $|\cdot |$ the Euclidean norm. We denote $\theta = (1, v)$ so that $\theta$ is a (future pointing) light-like vector. Then all the light rays are given by $\gamma _{y, v}(\tau ) = (\tau , y + \tau v), \tau \in (0, t_1), (y, v)\in {\mathbb R}^3\times {\mathbb S}^2$. Thus, we can identify ${\mathscr {C}}= {\mathbb R}^3\times {\mathbb S}^2.$ For $f\in C_0^\infty (M^\circ )$ and $y\in {\mathbb R}^3, v\in {\mathbb S}^2$, we have

$$\begin{aligned} \begin{aligned} X_{M}f(y, v)&= \int _0^{t_1} f(\tau , y + \tau v)d\tau \\&= (2\pi )^{-3}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _{0}^{t_1} e^{i ( (y - x)\cdot \eta + t v\cdot \eta )} f(t, x) dt dx d\eta . \end{aligned} \end{aligned}$$

(4.1)

The Schwartz kernel of $X_{M}$ is $\delta _Z$ the delta distribution on ${\mathscr {C}}\times M^\circ$ supported on the point-line relation Z defined by

$$\begin{aligned} \begin{aligned} Z = \{(\gamma , q)\in {\mathscr {C}}\times M^\circ : q\in \gamma \} = \{(y, v, (t, x)) \in {\mathbb R}^3 \times {\mathbb S}^2 \times M^\circ : x = y+ t v\}. \end{aligned} \end{aligned}$$

We know (see e.g. [12]) that $X_{M}$ is an Fourier integral operator of order $-3/4$ associated with the canonical relation $(N^*Z)'$, where $N^*Z$ denotes the conormal bundle of Z minus the zero section. Hence $X_{M}: \mathcal {E}'(M^\circ )\rightarrow \mathcal {D}'({\mathscr {C}})$ is continuous. Here, $\mathcal {D}'(M^\circ ), \mathcal {E}'(M^\circ )$ denotes the space of distributions and compactly supported distributions on $M^\circ$.

It is known that on ${\mathbb R}^4$, the light ray transform is injective on $C_0^\infty ({\mathbb R}^4)$, see [10, 17], but not injective on $\mathcal {S}({\mathbb R}^4)$ (Schwartz functions on ${\mathbb R}^4$). It is proved in [10, Corollary 7] that the kernel of the transform consists of $\mathcal {S}({\mathbb R}^4)$ functions whose Fourier transforms are supported in the time-like cone. One can obtain analogous results for $X_M$. The point is that after taking the light ray transform, time-like singularities in the functions are lost.

To see the difference in the treatment between space-like and light-like singularities, consider the normal operator $X_{M}^*X_{M}.$ For the light ray transform on ${\mathbb R}^4$, the Schwartz kernel of the normal operator can be computed explicitly using Fourier transforms, see [17]. Let’s look at the microlocal structure. The canonical relation $C = N^*Z'$ is

$$\begin{aligned} \begin{aligned} C =&\{((y, v, \eta , w); (t, x, \tau , \xi )) \in (T^*{\mathscr {C}}\backslash 0) \times (T^*M^\circ \backslash 0) : y = x- t v,\ \ \eta = \xi , \\ w =&t \xi |_{T_v{\mathbb S}^2},\ \ \tau = -\xi \cdot v, \ \ y\in {\mathbb R}^3, v\in {\mathbb S}^2, \eta \in {\mathbb R}^3, (t, x) \in M^\circ \}, \end{aligned} \end{aligned}$$

(4.2)

see [12, equation (39)]. In the expression of w, $\xi$ is regarded as a co-tangent vector to $T_v{\mathbb S}^2.$ If $\Xi = (\tau , \xi )$ is light-like, then $\xi |_{T_v{\mathbb S}^2} = 0$, see [12, Lemma 10.1]. We look at the double fibration picture

If $\rho$ is an injective immersion, the double fibration satisfies the Bolker condition, and the normal operator $X_{M}^*\circ X_{M}$ belongs to the clean intersection calculus so that the normal operator is a pseudo-differential operator, see [6]. As shown in [12, Lemma 10.1], $\rho$ fails to be injective on the set ${\mathcal {L}}\cap C$ where

$$\begin{aligned} {\mathcal {L}}= \{(y, v, \eta , w; t, x, \Xi ) \in (T^*{\mathscr {C}}\backslash 0) \times (T^*M^\circ \backslash 0): \,\Xi \, \text {is light-like}\}. \end{aligned}$$

In particular, the normal operator is an elliptic pseudo-differential operator when restricted to space-like directions, see [17] and [12]. In general, it is proved in [23] that the Schwartz kernel of the normal operator $X_M^*X_M$ is a paired Lagrangian distribution and a parametrix can be constructed within the framework of [5]. However, the picture near light-like directions is still not so clear. We remark that Guillemin [7] considered the structure of $X_M X_M^*$ for $2+1$ dimensional Minkowski spacetime.

5 Solution of the Cauchy Problem

We find a representation of the solution of the Cauchy problem in this section. Consider

$$\begin{aligned} \begin{aligned} \square _c u&= 0, \quad \text { on } M^\circ = \left( t_0, t_1\right) \times {\mathbb R}^3 \\ u =&f_1, \quad \partial _t u = f_2, \text { on } {\mathscr {S}}_0 = \{t_0\}\times {\mathbb R}^3. \end{aligned} \end{aligned}$$

(5.1)

The fundamental solution can be written down quite explicitly. However, it will be more convenient to look at its microlocal structure. For (5.1), all we need is the Fourier transform, see for example Trèves [21, Chapter VI, Section 1]. For general strictly hyperbolic equations, Duistermaat-Hörmander (see [3, Chaper 5]) constructed a parametrix for the Cauchy problem. So one can find a parametrix for (5.1) even when the equation contains lower order terms which will be used in Sect. 8.

Let $(\tau , \xi ), \xi \in {\mathbb R}^3$ be the dual variables in $T^*M^\circ$ to $(t, x), x\in {\mathbb R}^3$. Taking the Fourier transform of (5.1) in the x variable, we get (for $t_0 = 0$)

$$\begin{aligned} \begin{aligned}&\partial _t^2 \hat{u}(t, \xi ) + c^2 |\xi |^2 \hat{u}(t, \xi ) = 0, \\&\quad \hat{u}(0, \xi ) = \hat{f}_1(\xi ), \quad \partial _t \hat{u}(0, \xi ) = \hat{f}_2(\xi ) . \end{aligned} \end{aligned}$$

Solving this ODE, we get

$$\begin{aligned} \hat{u}(t, \xi ) = \frac{1}{2}e^{i t c |\xi |}(\hat{f}_1 +\frac{1}{ic|\xi |}\hat{f}_2) +\frac{1}{2}e^{-itc |\xi |} (\hat{f}_1 -\frac{1}{ic|\xi |}\hat{f}_2). \end{aligned}$$

Taking the inverse Fourier transform, we get

$$\begin{aligned} \begin{aligned} u(t, x)&= (2\pi )^{-3}\frac{1}{2}\int _{{\mathbb R}^3} e^{i\left( x\cdot \xi + ct |\xi |\right) } (\hat{f}_1 + \frac{1}{ic|\xi |}\hat{f}_2) d\xi + (2\pi )^{-3}\frac{1}{2}\int _{{\mathbb R}^3} e^{i\left( x\cdot \xi - tc |\xi |\right) }(\hat{f}_1\\&\quad - \frac{1}{ic|\xi |}\hat{f}_2) d\xi \\&= (2\pi )^{-3}\int _{{\mathbb R}^3} e^{i(x\cdot \xi + ct |\xi |)} \hat{h}_1(\xi ) d\xi + (2\pi )^{-3}\int _{{\mathbb R}^3} e^{i\left( x\cdot \xi - tc |\xi |\right) } \hat{h}_2(\xi ) d\xi \\&= E_+ h_1 + E_- h_2, \end{aligned} \end{aligned}$$

(5.2)

where

$$\begin{aligned} \hat{h}_1 = \frac{1}{2}(\hat{f}_1 + \frac{1}{ic|\xi |}\hat{f}_2), \ \ \hat{h}_2 = \frac{1}{2}(\hat{f}_1 - \frac{1}{ic|\xi |}\hat{f}_2). \end{aligned}$$

We see that $E_\pm$ are represented by oscillatory integrals

$$\begin{aligned} E_\pm (f) =(2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i\left( (x-y)\cdot \xi \pm ct |\xi |\right) } f(y) dy d\xi . \end{aligned}$$

(5.3)

The phase functions are $\phi _\pm (t, x, y, \xi ) = (x - y) \cdot \xi \pm ct |\xi |$ and amplitude function $a(t, x, \xi ) = 1.$ In Hörmander’s notation, we conclude that $E_\pm \in I^{-\frac{1}{4}}({\mathbb R}^3\times M^\circ ; (C^\pm )')$ are Fourier integral operators where the canonical relations are

$$\begin{aligned}&C^\pm = \{\left( t, x, \zeta _0, \zeta '; y, \xi \right) \in T^*M^\circ \backslash 0\times T^*{\mathbb R}^3\backslash 0:\nonumber \\&y = x - c t \left( \pm \xi /|\xi |\right) , \zeta ' = \xi , \zeta _0 = \pm c |\xi |\}. \end{aligned}$$

(5.4)

It suffices to regard $h_1, h_2$ as the reparametrized initial conditions for the Cauchy problem and represent $u = E_+ h_1 + E_- h_2$ in (5.2). Once we find $h_1, h_2$, we can easily find $f_1, f_2$ from

$$\begin{aligned} f_1 = h_1 + h_2, \ \ f_2 = i c\Delta ^\frac{1}{2}\left( h_1 - h_2\right) . \end{aligned}$$

(5.5)

6 The Microlocal Inversion: $c < 1$

For $0< c < 1$, it is important to observe that singularities (or the wave front set) of the solution u to (5.1) are all in space-like directions for $(M, g_M).$ From the canonical relation $C^\pm$ in (5.4), we know that for u in (5.1)

$$\begin{aligned} \text {WF}(u) \subset \{(t, x, \xi _0, \xi ') \in T^*M^\circ \backslash 0: \xi _0 = \pm c |\xi '|\}, \end{aligned}$$

and $|(\xi _0, \xi ')|^2_{g^*_M} = -\xi _0^2 + |\xi '|^2 = (-c^2+1)|\xi '|^2 > 0$ for $c<1$. For such $(\xi _0, \xi ')$, the corresponding vector in $TM^\circ$ is time-like. So these singularities correspond to trajectories of particles moving slower than photons in $(M, g_M)$.

Now we can use the fact that in space-like directions, the normal operator $X_M^*\circ X_M$ is actually a pseudo-differential operator as shown in [12]. The symbol of $\square _c$ is $p_c(\xi _0, \xi ') = -\xi ^2_0 + c^2 |\xi '|^2.$ Let $\chi (t)$ be a smooth cut-off function with $\chi (t) = 1, |t|< 1$ and $\chi (t) = 0, |t|> 1/c^2$ for $c<1$. Then we define

$$\begin{aligned} \chi _1\left( \xi _0, \xi '\right) = \chi (\frac{\xi _0^2}{c^2|\xi '|^2}) \end{aligned}$$

so $\chi _1(\xi _0, \xi ') = 1$ on $\{(\xi _0, \xi ') \in {\mathbb R}^4: p_c(\xi _0, \xi ') > 0\}$ and $\chi _1(\xi _0, \xi ') = 0$ on $\Omega ^{*, -}M^\circ$. Let $\chi _1(D)$ be the pseudo-differential operator with symbol $\chi _1$. We have

Lemma 6.1

$\chi _1(D) X_M^*\circ X_M \chi _1(D)$ is a pseudo-differential operator of order $-1$ on $M^\circ$. The principal symbol at $(t, x, \xi _0, \xi ') \in T^*M^\circ$ is

$$\begin{aligned} \frac{4\pi ^2}{|\xi '|}\chi _1^2\left( \xi _0, \xi '\right) . \end{aligned}$$

Proof

It follows from Theorem 2.1 of [13] that $\chi _1(D) X_M^*\circ X_M \chi _1(D)$ is a pseudo-differential operator on $M^\circ$ with an oscillatory integral representation. The symbol is

$$\begin{aligned} \begin{aligned} \sigma \left( t, x, \xi _0, \xi '\right) = 2\pi |{\mathbb S}^1| \chi _1^2\left( \xi _0, \xi '\right) |\xi '|^{-1} \end{aligned} \end{aligned}$$

(6.1)

We remark that the symbol is singular at $\xi = 0$ but this can be removed by introducing a smooth cut-off function supported near $\xi = 0$ and noticing that $|\xi |^{-1}$ is integrable near $\xi = 0$. Since it only changes $\chi _1(D) X_M^*\circ X_M \chi _1(D)$ by a smoothing operator, we will not show it for simplicity. $\square$

Now we show that

Lemma 6.2

The normal operator $E_+^*X_M^*\circ X_M E_+, E_-^*X_M^*\circ X_M E_-$ are elliptic pseudo-differential operators of order $-1$ on ${\mathbb R}^3$, and $E_+^*X_M^*\circ X_M E_-$ and $E_-^*X_M^*\circ X_M E_+$ are smoothing operators on ${\mathbb R}^3.$

Proof

First of all, we know that $(X_M^*\circ X_M) E_+ = (\chi _1(D) X_M^*\circ X_M \chi _1(D)) E_+$ modulo a smoothing operator, thus $(X_M^*\circ X_M) E_+ \in I^{-\frac{5}{4}}(M^\circ \times {\mathbb R}^3; (C^+)')$ from the composition of a pseudo-differential operator and an FIO. The principal symbol is non-vanishing. We also know that $E_+^* \in I^{-\frac{1}{4}}(M^\circ \times {\mathbb R}^3; (C^{+, -1})')$. To compose these two operators, we would like to apply the clean composition theorem [8, Theorem 25.2.3], however, the operators are not properly supported. But this can be justified using the oscillatory integral representation. We have (modulo a pseudo-differential operator of a lower order)

$$\begin{aligned} \begin{aligned}&E_+^*\left( X_M^*\circ X_M E_+\right) f(z)\\&\quad = (2\pi )^{-6} \int _{{\mathbb R}^3}\int _{0}^{t_1}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i\left( (z-x)\cdot \eta - c t |\eta |\right) } e^{i((x-y)\cdot \xi + ct |\xi |)}a(\xi ) f(y) dy d\xi dx dt d\eta \\&\quad = (2\pi )^{-6} \int _{{\mathbb R}^3}\int _{0}^{t_1}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i\left( z\cdot \eta - y\cdot \xi + x(\xi - \eta ) - c t |\eta | + ct |\xi |\right) } a(\xi ) f(y) dy d\xi dx dt d\eta \\&\quad = (2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3 } e^{i\left( z\cdot \xi - y\cdot \xi \right) } t_1 a(\xi ) f(y) dy d\xi . \end{aligned} \end{aligned}$$

This is a pseudo-differential operator of order $-1$ on ${\mathbb R}^3.$ The same proof works for the minus sign.

To see that $E_+^*X_M^*\circ X_M E_-$ is smoothing, we just need to observe that the canonical relations $C^+, C^-$ in (5.4) are disjoint. So a wave front analysis using e.g. [3, Theorem 1.3.7] tells that the operator is smoothing. $\square$

We finished the proof but we mention the following alternative argument. Essentially, we want to consider the operator $E_+$ for fixed t, denoted by $E_+(t)$. We know that $E_+(t): \mathcal {E}'({\mathbb R}^3)\rightarrow \mathcal {D}'({\mathbb R}^3)$ is a Fourier integral operator

$$\begin{aligned} E_+(t)f(x) =(2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3 } e^{i((x-y)\cdot \xi + ct |\xi |)} f(y) dy d\xi \end{aligned}$$

with canonical relation $C_t = \{(y, \eta ; x, \xi )\in T^*{\mathbb R}^3\backslash 0 \times T^*{\mathbb R}^3\backslash 0 : y = x + ct \xi /|\xi |, \xi = \eta \}.$ Then $E_+(t)\in I^{0}({\mathbb R}^3\times {\mathbb R}^3; C_t')$ is properly supported. The canonical relation $C_t$ is a graph of a symplectic transformation, thus the composition $E_+^{*}(t)E_+(t)$ is a pseudo-differential operator of order 0 on ${\mathbb R}^3$. In our case, $E_+^{*}(t)X_M^*X_M E_+(t)$ is a pseudo-differential operator of order $-1$ and the symbols are smooth in $t \in [t_0, t_1]$. Finally, integrating the symbols in t produces a symbol and we get the result.

Now we construct a parametrix for the transform.

Proposition 6.3

For $c< 1,$ there exist operators $A_1, A_2$ such that

$$\begin{aligned} A_1 X_M f = f_1 + R_1 f_1 + R_1'f_2, \ \ A_2 X_M f = f_2 + R_2 f_1 + R_2'f_2 \end{aligned}$$

where $R_1, R_2, R_1', R_2'$ are smoothing operators and $A_i = \widetilde{A}_i \circ X_M^*, i = 1, 2$ in which $\widetilde{A}_i$ are Fourier integral operators.

Proof

First, we represent $f = E_+ h_1 + E_- h_2$ and write

$$\begin{aligned} X_M f = X_M E_+ h_1 + X_M E_- h_2. \end{aligned}$$

(6.2)

We apply $E_+^* X_M^*$ to get

$$\begin{aligned} E_+^* X_M^*X_M f =E_+^* X_M^* X_M E_+ h_1 + E_+^* X_M^*X_M E_- h_2 = E_+^* X_M^* X_M E_+ h_1 + R_1 h_2. \end{aligned}$$

Since $E_+^* X_M^* X_M E_+$ is an elliptic pseudo-differential operator of order $-1$, we can find a parametrix $B_+$ which is a pseudo-differential operator of order 1 on ${\mathbb R}^3$ and

$$\begin{aligned} B_+\circ E_+^* X_M^*X_M f = h_1 + R_1 h_1 + R_1' h_2 \end{aligned}$$

where $R_1, R_1'$ are smoothing. We repeat the argument for the minus sign. Apply $E_-^*X_M^*$ to (6.2), we get

$$\begin{aligned} E_-^* X_M^*X_M f =E_-^* X_M^* X_M E_+ h_1 + E_-^* X_M^*X_M E_- h_2 = E_-^* X_M^* X_M E_- h_2 + R_2 h_2. \end{aligned}$$

Apply the parametrix $B_-$ for $E_-^* X_M^* X_M E_-$ and we get

$$\begin{aligned} B_-\circ E_-^* X_M^*X_M f = h_2+ R_2 h_1 + R_2' h_2. \end{aligned}$$

Finally, we get

$$\begin{aligned} \begin{aligned}&f_1 + R_1 f_1 + R_2 f_2 = \left( B_+\circ E_+^* + B_- \circ E_-^*\right) X_M^*X_M f \\&\quad \text { and } f_2 + R_1' f_1 + R_2' f_2 = ic\Delta ^\frac{1}{2}\left( B_+\circ E_+^* + B_- \circ E_-^*\right) X_M^*X_M f \end{aligned} \end{aligned}$$

as claimed. We set $\widetilde{A}_1 = B_+\circ E_+^* + B_- \circ E_-^*$ which is a sum of two FIOs in $I^{3/4}(M^\circ \times {\mathbb R}^3; (C^{+, -1})')$ and $I^{3/4}(M^\circ \times {\mathbb R}^3; (C^{-, -1})')$, and $\widetilde{A}_2 = ic\Delta ^\frac{1}{2}(B_+\circ E_+^* + B_- \circ E_-^*)$ which is a sum of two FIOs in $I^{7/4}(M^\circ \times {\mathbb R}^3; (C^{+, -1})')$ and $I^{7/4}(M^\circ \times {\mathbb R}^3; (C^{-, -1})')$. This completes the proof. $\square$

For convenience, we formulate a microlocal inversion result for determining f.

Corollary 6.4

For $c < 1$, there exist operators A such that

$$\begin{aligned} A X_M f = f + R_1 f_1 + R_2f_2, \end{aligned}$$

where $R_1, R_2$ are smoothing operators.

Proof

Again, we simply solve the wave equation (5.1) using the parametrix. In fact, it is easier to use $h_1, h_2$.

$$\begin{aligned} \begin{aligned} f&= E_+ h_1 + E_-h_2 = E_+ B_+ \circ E_+^* X_M^*X_M f + E_-B_-\circ E_-^* X_M^*X_M f + \widetilde{R}_1 h_1 +\widetilde{R}_2 h_2 \\&= \left( E_+ B_+ \circ E_+^* + E_-B_-\circ E_-^*\right) X_M^*X_M f + R_1 f_1 + R_2 f_2 \end{aligned} \end{aligned}$$

as claimed, where $\widetilde{R}_1, \widetilde{R}_2, R_1, R_2$ are smoothing operators and $A = (E_+ B_+ \circ E_+^* + E_-B_-\circ E_-^*) X_M^*.$ $\square$

7 The Microlocal Inversion: c = 1

For $c = 1$, the singularities of the solutions of (5.1) are all in light-like directions. As explained in the end of Sect. 4, the Schwartz kernel of $X_M^* \circ X_M$ is more complicated and the previous argument does not work directly. We will take a different approach by considering the composition $X_M\circ E_\pm$. Let $\varphi$ be a smooth function on ${\mathbb S}^2$, and $I^\varphi$ be the integration operator on $C^\infty ({\mathbb R}^3\times {\mathbb S}^2)$ defined by

$$\begin{aligned} I^\varphi f(y) = \int _{{\mathbb S}^2} \varphi (v) f(y, v)dv. \end{aligned}$$

Then we consider the composition $I^\varphi \circ X_M \circ E_\pm$ as an operator from $C^\infty ({\mathscr {S}}_0)$ to $C^\infty ({\mathscr {S}}_0)$. For technical reasons, we introduce a smooth cut-off function. For $\epsilon >0$ small, let $\chi _\epsilon (t)$ be a smooth cut-off function on ${\mathbb R}$ such that $\chi _\epsilon (t) = 1$ for $2\epsilon< t < t_1 - 2\epsilon$ and $\chi _\epsilon (t) = 0$ for $t<\epsilon$ and $t > t_1 - \epsilon .$ We prove

Proposition 7.1

$K_\pm \doteq I^\varphi X_M \chi _\epsilon E_\pm \in \Psi ^{-1}({\mathscr {S}}_0)$ are pseudo-differential operators of order $-1$ with complete symbol $k_\pm (\xi ), \xi \in {\mathbb R}^3\backslash 0$ and the principal symbols are given by

$$\begin{aligned} \begin{aligned} k_{+, -1}(\xi )&= 2\pi i c_\epsilon |\xi |^{-1} \varphi (-\xi /|\xi |), \quad k_{-, -1}(\xi ) = -2\pi i c_\epsilon |\xi |^{-1}\varphi (\xi /|\xi |), \\&\text {where } c_\epsilon = \int _0^{t_1}t^{-1} \chi _\epsilon (t)dt \end{aligned} \end{aligned}$$

Proof

We start with $K_+.$ We recall from (4.1) that

$$\begin{aligned} \begin{aligned} X_{M}f(y, v) = (2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _{0}^{t_1} e^{i ( (y-x)\cdot \eta + t v\cdot \eta )} f(t, x) dt dx d\eta \end{aligned} \end{aligned}$$

and from Sect. 5 that

$$\begin{aligned} E_+(f)(t, x) =(2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i((x-z)\cdot \xi + t |\xi |)} f(z) dz d\xi . \end{aligned}$$

Consider the oscillatory integral integral representation of the Schwartz kernel $K_+$

$$\begin{aligned}&K_+(y, z)\nonumber \\&\quad = (2\pi )^{-6} \int _{{\mathbb S}^2} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _{0}^{t_1}\int _{{\mathbb R}^3 } e^{i \left( (y - x)\cdot \eta + t v\cdot \eta + (x-z)\cdot \xi + t |\xi |\right) } \varphi (v) \chi _\epsilon (t) d\xi dt dx d\eta dv\nonumber \\ \end{aligned}$$

(7.1)

In this case, the oscillatory integral can be computed explicitly. But before we proceed with the calculation, we examine the phase function

$$\begin{aligned} \phi \left( y, z, \xi , t; \eta , x, v\right) = (y - x)\cdot \eta + t v\cdot \eta + (x-z)\cdot \xi + t |\xi | \end{aligned}$$

Consider $\phi$ in $\eta , x, v$ variables. We have

$$\begin{aligned} \phi _\eta = y - x + tv, \quad \phi _x = \xi - \eta , \quad \phi _v = t\eta |_{T_v{\mathbb S}^2}, \end{aligned}$$

so the critical points are given by

$$\begin{aligned} \xi = \eta , \quad v = \pm \xi /|\xi |, \quad x = y - t \xi /|\xi | \end{aligned}$$

Here, we remark that $t\xi |_{T_v{\mathbb S}^2} = 0$ implies that $\xi$ is parallel to v so $v = \pm \xi /|\xi |$. Also, we have

$$\begin{aligned} \partial ^2_{(\eta , x, v)} \phi = \begin{pmatrix} 0 &{}\quad -{\text {Id}}&{}\quad t \\ {\text {Id}}&{}\quad 0&{}\quad 0\\ *&{}\quad 0 &{}\quad *\end{pmatrix} \end{aligned}$$

To compute $*$, we introduce local coordinates on ${\mathbb S}^2$ near the critical point. By using an orthogonal transformation, we can assume that $\xi /|\xi | = (0, 0, 1).$ We use $v = (v_1, v_2, \pm \sqrt{1 - v_1^2 -v_2^2})$ near $\pm \xi /|\xi |$ where $v_1^2 + v_2^2 <1$ . Then we have

$$\begin{aligned} \partial _v \phi = \partial _{\left( v_1, v_2\right) }\left( t v\cdot \eta \right) = t \begin{pmatrix} \eta _1 \pm \eta _3 \frac{-v_1}{\sqrt{1 - v_1^2 - v_2^2}}\\ \eta _2 \pm \eta _3 \frac{-v_2}{\sqrt{1 - v_1^2 - v_2^2}} \end{pmatrix}. \end{aligned}$$

On the set of critical point, $v = \pm (0, 0, 1)$ and $\eta = (0, 0, |\xi |)$. We observe that $\partial _v \phi = 0.$ Next,

$$\begin{aligned} \partial _{\eta }\left( \frac{\partial \phi }{\partial v}\right) = t\begin{pmatrix} 1 &{} 0 &{} \pm \frac{-v_1}{\sqrt{1 - v_1^2 - v_2^2}} \\ 0 &{} 1 &{} \pm \frac{-v_2}{\sqrt{1 - v_1^2 - v_2^2}} \end{pmatrix} \text { and } \partial _{v}\left( \frac{\partial \phi }{\partial v}\right) = \pm t \eta _3 \begin{pmatrix} \frac{-1 + v_2^2}{\left( 1 - v_1^2 - v_2^2\right) ^{\frac{3}{2}}} &{} \frac{-v_1 v_2}{\left( 1 - v_1^2 - v_2^2\right) ^{\frac{3}{2}}} \\ \frac{-v_1 v_2}{\left( 1 - v_1^2 - v_2^2\right) ^{\frac{3}{2}}} &{} \frac{-1 + v_1^2}{\left( 1 - v_1^2 - v_2^2\right) ^{\frac{3}{2}}} \end{pmatrix}. \end{aligned}$$

On critical points,

$$\begin{aligned} \begin{aligned} \partial _{v}\left( \frac{\partial \phi }{\partial v}\right) = \pm t|\xi | \begin{pmatrix} -1&{}0\\ 0 &{} -1 \end{pmatrix}. \end{aligned} \end{aligned}$$

This shows that the phase function is non-degenerate in $\eta , x, v$. We can apply stationary phase argument so the phase becomes

$$\begin{aligned} \begin{aligned} \phi (y, z, \xi , t)&= (y - z)\cdot \xi + 2t |\xi | \text { when } v = \xi /|\xi |\\ \phi (y, z, \xi , t)&= (y - z)\cdot \xi \text { when } v = -\xi /|\xi | \end{aligned} \end{aligned}$$

Finally, after integrating in t, we will get a pseudo-differential operator. This will be shown explicitly in the follows.

First, in (7.1), we integrate in $x, \eta$ to get

$$\begin{aligned} \begin{aligned} K_+(y, z) = (2\pi )^{-3} \int _{{\mathbb S}^2} \int _{0}^{t_1}\int _{{\mathbb R}^3} e^{i \left( y\cdot \xi + t v\cdot \xi -z \cdot \xi + t |\xi |\right) } \varphi (v)\chi _\epsilon (t) d\xi dt dv \end{aligned} \end{aligned}$$

Consider the integral in v. For t non-zero, the v integral is non-degenerate with stationary points at $v=\pm \xi /|\xi |$. Applying stationary phase argument see e.g. [15, Lemma 1.2], we get

$$\begin{aligned} \begin{aligned} K_+(y, z)&= (2\pi )^{-3} \int _{0}^{t_1}\int _{{\mathbb R}^3} e^{i \left( (y-z) \cdot \xi + 2 t |\xi |\right) } \left( \varphi (\xi /|\xi |)\right. \\&\quad \left. + \varphi ^+(t, \xi )\right) \chi _\epsilon (t) \left( t|\xi |\right) ^{-1} e^{-\frac{1}{2}i\pi }(2\pi ) d\xi dt \\&\quad + (2\pi )^{-3} \int _{0}^{t_1}\int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi } \left( \varphi (-\xi /|\xi |)\right. \\&\quad \left. + \varphi ^-(t, \xi )\right) \chi _\epsilon (t) (t|\xi |)^{-1} e^{\frac{1}{2}i\pi }(2\pi ) d\xi dt \\&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi } k_+(\xi ) d\xi \end{aligned} \end{aligned}$$

(7.2)

where $\varphi ^\pm$ come from the stationary phase argument and they have asymptotic expansions

$$\begin{aligned} \varphi ^\pm (t, \xi ) \sim \sum _{k = 1}^\infty a_k^\pm (\xi /|\xi |) (t|\xi |)^{-k} \end{aligned}$$

(7.3)

in which $a_k^\pm$ are smooth functions on ${\mathbb S}^2$. Also,

$$\begin{aligned} \begin{aligned} k_+(\xi )&= + 2\pi i|\xi |^{-1} \varphi (-\xi /|\xi |) \int _{0}^{t_1} t^{-1}\left( 1 + \varphi ^-(t, \xi )\right) \chi _\epsilon (t)dt\\&\quad - 2\pi i|\xi |^{-1} \varphi (\xi /|\xi |) \int _0^{t_1}e^{2it|\xi |}t^{-1}(1 +\varphi ^+(t, \xi ))\chi _\epsilon (t)dt \end{aligned} \end{aligned}$$

(7.4)

The second integral in t is $O(|\xi |^{-\infty })$ for $|\xi |$ large because t is away from 0 and $\chi _\epsilon$ is smooth. For the first integral, the integral of each asymptotic term of $\varphi ^-$ in (7.3) in t is finite. Thus $k_+(\xi )$ is a symbol of order $-1$ and the leading order term is

$$\begin{aligned} k_{+, -1}(\xi ) = 2\pi i |\xi |^{-1} \varphi (-\xi /|\xi |) \int _0^{t_1}t^{-1} \chi _\epsilon (t)dt. \end{aligned}$$

This shows that $K_+$ in (7.2) is a pseudo-differential operator of order $-1$ on ${\mathbb R}^3.$

For $K_-$, the calculation is similar and we look for the symbol.

$$\begin{aligned} \begin{aligned} K_-(y, z)&= (2\pi )^{-3} \int _{t_0}^{t_1}\int _{{\mathbb R}^3} e^{i \left( y\cdot \xi + t v\cdot \xi -z \cdot \xi - t |\xi |\right) } \chi _\epsilon (t) d\xi dt dv\\&= - i(2\pi )^{-2} \int _{t_0}^{t_1}\int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi } (t|\xi |)^{-1} \left( \varphi (\xi /|\xi |) + \widetilde{\varphi }^+(t, \xi )\right) \chi _\epsilon (t)d\xi dt \\&+i (2\pi )^{-2} \int _{t_0}^{t_1}\int _{{\mathbb R}^3} e^{i ((y-z) \cdot \xi - 2t|\xi |)} (t|\xi |)^{-1}\left( \varphi (-\xi /|\xi |) + \widetilde{\varphi }^-(t, \xi )\right) \chi _\epsilon (t) d\xi dt \\&= (2\pi )^{-3}\int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi } k_-(\xi ) d\xi \end{aligned} \end{aligned}$$

where $\widetilde{\varphi }^\pm$ have similar asymptotic expansion as (7.3), and $k_-(\xi )$ is given by

$$\begin{aligned} \begin{aligned} k_-(\xi )&= - 2\pi i |\xi |^{-1} \int _0^{t_1}\left( \varphi \left( \xi /|\xi |\right) + \widetilde{\varphi }^+(t, \xi )\right) t^{-1} \chi _\epsilon (t)dt \\&\quad + 2\pi i |\xi |^{-1} \int _{0}^{t_1} e^{-2it|\xi |}\left( \varphi (-\xi /|\xi |) + \widetilde{\varphi }^-(t, \xi )\right) t^{-1}\chi _\epsilon (t)dt \end{aligned} \end{aligned}$$

(7.5)

This is a symbol of order $-1$ and the leading order term is

$$\begin{aligned} k_{-, -1}(\xi ) = -2\pi i |\xi |^{-1}\varphi (\xi /|\xi |) \int _0^{t_1} t^{-1} \chi _\epsilon (t)dt \end{aligned}$$

This completes the proof of the proposition. $\square$

Next we discuss what needs to be changed when the smooth cut-off function $\chi _\epsilon$ is replaced by the characteristic function $\chi _{[\epsilon , t_1]}$ of the interval $[\epsilon , t_1]$ in ${\mathbb R}$. All the calculations in Proposition 7.1 hold up to (7.4) which is now

$$\begin{aligned} \begin{aligned} k_+(\xi )&= + 2\pi i|\xi |^{-1} \varphi (-\xi /|\xi |) \int _{\epsilon }^{t_1} t^{-1}\left( 1 + \varphi ^-(t, \xi )\right) dt\\&\quad - 2\pi i|\xi |^{-1} \varphi (\xi /|\xi |) \int _{\epsilon }^{t_1}e^{2it|\xi |}t^{-1}\left( 1 +\varphi ^+(t, \xi )\right) dt \end{aligned} \end{aligned}$$

(7.6)

The first integral, denoted by $I_1$ below, still gives a symbol of order $-1$. For the second integral denoted by $I_2$ below, integration by parts gives

$$\begin{aligned} \begin{aligned} I_2(\xi )&= - 2\pi i|\xi |^{-1} \varphi (\xi /|\xi |) \{ \frac{1}{2i|\xi |} (e^{2it_1|\xi |} t_1^{-1} (1 + \varphi ^+(t_1, \xi ))) \\&\quad - \frac{1}{2i|\xi |} e^{2i \epsilon |\xi |} \epsilon ^{-1} (1 + \varphi ^+(\epsilon , \xi )) \\&\quad - \frac{1}{2i|\xi |} \int _{\epsilon }^{t_1}e^{2it|\xi |}\frac{d}{dt}[t^{-1}(1 +\varphi ^+(t, \xi )) ]dt \} \end{aligned} \end{aligned}$$

We can repeat the integration by parts and get

$$\begin{aligned} I_2(\xi ) = e^{2it_1|\xi |} a(\xi ) + e^{2i\epsilon |\xi |}b(\xi ) \end{aligned}$$

where $a(\xi ), b(\xi )$ are symbols of order $-2.$ Using these in (7.2), we get

$$\begin{aligned} \begin{aligned} K_+(y, z) =&(2\pi )^{-3} \int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi } I_1(\xi ) d\xi + (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi + 2it_1|\xi |} a(\xi ) d\xi \\&+ (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i (y-z) \cdot \xi + 2i\epsilon |\xi |} b(\xi ) d\xi . \end{aligned} \end{aligned}$$

Thus, we can write $K_+ = K_+^0 + K_+^{\epsilon } + K_+^{t_1}$ where $K_+^0 \in \Psi ^{-1}({\mathbb R}^3)$, and $K_+^\epsilon \in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_\epsilon ), K_+^{t_1}\in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_{t_1})$ are Fourier integral operators of order $-2.$ The canonical relation $C_\epsilon , C_{t_1}$ can be described as follows. For $\alpha \in {\mathbb R}$, we define

$$\begin{aligned} \begin{aligned} C_\alpha = \{\left( y, \eta , z, \zeta \right) \in T^*{\mathbb R}^3\backslash 0\times T^*{\mathbb R}^3\backslash 0: y = z + 2 \alpha \xi /|\xi |, \xi = \eta \}. \end{aligned} \end{aligned}$$

We see that $C_\alpha$ is a graph of a canonical transformation, see [8, Section 25.3]. The same argument shows that $K_-$ is also a sum of $K_-^0 \in \Psi ^{-1}({\mathbb R}^3)$ and $K_-^\epsilon \in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_{-\epsilon }), K_-^{t_1} \in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_{-t_1})$.

Now we are ready to obtain a parallel result of Proposition 6.3 about the microlocal inversion.

Proposition 7.2

For $c = 1$ and any $N\in {\mathbb N}$, there exist operators $A_1, A_2$ such that

$$\begin{aligned} A_1 X_M \chi _{\left[ \epsilon , t_1\right] } f = h_1 + R_1h_1 + R_1'h_2, \ \ A_2 X_M \chi _{\left[ \epsilon , t_1\right] } f = h_2 + R_2 h_1 + R_2'h_2 \end{aligned}$$

where $h_1, h_2$ are defined in Sect. 5 and $R_1, R_1', R_2, R_2' \in I^{-N}({\mathbb R}^3, {\mathbb R}^3; C^N_{\epsilon , t_1})$ which is the N-fold composition of elements in $I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{\pm \epsilon })$ and $I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{\pm t_1})$, more explicitly

$$\begin{aligned} \begin{aligned} I^{-N}({\mathbb R}^3, {\mathbb R}^3; C^N_{\epsilon , t_1})&= \{A_1 \circ A_2\cdots A_N: A_i \in I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{\epsilon }) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{t_1})\\&\quad + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-\epsilon }) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-t_1}) \}. \end{aligned} \end{aligned}$$

Proof

We divide the proof in two steps.

Step 1: Let’s replace $\chi _{[\epsilon , t_1]}$ with the smooth cut-off $\chi _\epsilon$ as in Proposition 7.1 and see how to get $h_1, h_2$ using Proposition 7.1. We write

$$\begin{aligned} X_M \chi _\epsilon f = X_M\chi _\epsilon E_+ h_1 + X_M \chi _\epsilon E_- h_2. \end{aligned}$$

Let $\varphi$ be a smooth function on ${\mathbb S}^2$. Applying $I^\varphi$ we get

$$\begin{aligned} I^\varphi X_M\chi _\epsilon f = I^\varphi X_M \chi _\epsilon E_+ h_1 + I^\varphi X_M \chi _\epsilon E_- h_2 = K^{\varphi , +} h_1 + K^{\varphi , -}h_2 \end{aligned}$$

(7.7)

where we added $\varphi$ to the notation of $K_\pm$ to emphasize the dependency because we will choose different $\varphi$ below.

First, let $\varphi _1 = 1$. From Proposition 7.1, we see that $K^{\varphi _1}_\pm \in \Psi ^{-1}({\mathbb R}^3)$ and the principal symbols are given by

$$\begin{aligned} \begin{aligned} k^{\varphi _1}_{+, -1}(\xi ) = -k^{\varphi _1}_{-, -1}(\xi ) = 2\pi i c_\epsilon |\xi |^{-1}. \end{aligned} \end{aligned}$$

We let $Q^1_+$ be a parametrix of $K^{\varphi _1}_+$ and get

$$\begin{aligned} \begin{aligned} Q^{1}_+ I^{\varphi _1} X_M\chi _\epsilon f = h_1 + Q^1_+ K^{\varphi _1}_-h_2 + R_1 h_1 \end{aligned} \end{aligned}$$

(7.8)

where $R_1, R_2$ are smoothing operators. From the composition of pseudo-differential operators, we know that $Q^1_+ K^{\varphi _1}_- \in \Psi ^{0}({\mathbb R}^3)$ with principal symbol equal to $-1.$

Next, we change the function $\varphi$. Ideally, we will take an odd function $\varphi (-v) = -\varphi (v)$ but then $\varphi$ vanishes somewhere on ${\mathbb S}^2$ so we proceed as follows. Let $x = (x_1, x_2, x_3)$ be the coordinate for ${\mathbb R}^3$. For $\delta >0$, let ${\mathscr {U}}_k = \{v: v = (x_1, x_2, x_3), \Vert x\Vert = 1, |x_k| > \delta /2\}, k = 1, 2, 3.$ For $\delta$ sufficiently small, ${\mathscr {U}}_k, k = 1, 2, 3$ form an open covering of ${\mathbb S}^2.$ Let $\chi _k(v), k = 1, 2, 3$ be a partition of unity subordinated to this covering and $\chi _k(v) = 1$ on ${\mathscr {V}}_k = \{v: v = (x_1, x_2, x_3), \Vert x\Vert = 1, |x_k| > \delta \}, k = 1, 2, 3.$ Here, by possibly taking $\delta$ smaller, we can assume that ${\mathscr {V}}_k$ also form an open covering of ${\mathbb S}^2.$ For $v\in {\mathbb S}^2$, we let

$$\begin{aligned} \varphi _{2, k}(v) = \chi _k(x) x_k + 2, \quad k = 1, 2, 3 \end{aligned}$$

Then $\varphi _{2}(v)\ne 0$ and $\varphi _{2, k}(-v) - \varphi _{2}(v, k) \ne 0$ for $v\in {\mathscr {U}}_k.$ From Proposition 7.1, we know that $K^{\varphi _{2, k}}_\pm \in \Psi ^{-1}({\mathbb R}^3)$ with principal symbols

$$\begin{aligned} \begin{aligned} k^{\varphi _{2, k}}_{+, -1}(\xi ) = 2\pi i c_\epsilon |\xi |^{-1} \varphi _{2, k}(-\xi /|\xi |), \quad k^{\varphi _{2, k}}_{-, -1}(\xi ) = -2\pi i c_\epsilon |\xi |^{-1} \varphi _{2, k}(\xi /|\xi |). \end{aligned} \end{aligned}$$

We consider $k = 1$ in the follows as the other cases are similar. Let $Q^{2, 1}_{+}$ be a parametrix for $K^{\varphi _{2, 1}}_+$. We get

$$\begin{aligned} \begin{aligned} Q^{2, 1}_+ I^{\varphi _{2, 1}} X_M\chi _\epsilon f = h_1 + Q^{2, 1}_+ K^{\varphi _{2, 1}}_-h_2 + R_3 h_1 \end{aligned} \end{aligned}$$

where $R_3$ is a smoothing operator, and $Q^{2, 1}_+ K^{\varphi _{2, 1}}_-\in \Psi ^{0}({\mathbb R}^3)$ with principal symbol

$$\begin{aligned} \sigma _0\left( Q^{2, 1}_+ K^{\varphi _{2, 1}}_-\right) (x, \xi ) = -\frac{\varphi _{2, 1}(\xi /|\xi |)}{\varphi _{2, 1}\left( -\xi /|\xi |\right) } \ne -1 \end{aligned}$$

(7.9)

when $\xi /|\xi |\in {\mathscr {U}}_1.$ Now we consider

$$\begin{aligned} \begin{aligned} Q^{1}_+ I^{\varphi _1} X_M\chi _\epsilon f - Q^{2, 1}_+ I^{\varphi _{2, 1}} X_M\chi _\epsilon f = ( Q^1_+ K^{\varphi _1}_- - Q^{2, 1}_+ K^{\varphi _{2, 1}}_-)h_2 + R_{1} h_1+ R_{2} h_1 - R_3 h_1 \end{aligned} \end{aligned}$$

We observe that $A = Q^1_+ K^{\varphi _1}_- - Q^{2, 1}_+ K^{\varphi _{2, 1}}_-$ is a pseudo-differential operator of order 0 and the principal symbol does not vanish on ${\mathscr {U}}_1.$ Let $\widetilde{\chi }_k, k = 1, 2, 3$ be a smooth partition of unity subordinated to ${\mathscr {V}}_k$. Then $\chi _1\widetilde{\chi }_1 = \widetilde{\chi }_1$. Let $B_1$ be a pseudo-differential operator of order 0 with principal symbol $\sigma _0(B_1)(\xi ) = \widetilde{\chi }_1(\xi /|\xi |)/\sigma _0(A)(\xi )$. We can improve $B_1$ to a parametrix for A so that $B_1\circ A = \widetilde{\chi }_1(D) + R_4$ with $R_4$ smoothing. So we get

$$\begin{aligned} \begin{aligned} B_1(Q^{1}_+ I^{\varphi _1} X_M\chi _\epsilon - Q^{2, 1}_+ I^{\varphi _{2, 1}} X_M\chi _\epsilon )f = \widetilde{\chi }_1(D)h_2 + R_3 h_2 + R_4 h_1 \end{aligned} \end{aligned}$$

where by abusing notations, $R_3, R_4$ are smoothing operators. We can repeat the construction for $k = 2, 3$ to get the corresponding $B_2, B_3 \in \Psi ^0({\mathbb R}^3)$. Then we arrive at

$$\begin{aligned} \begin{aligned} \sum _{k = 1}^3B_k(Q^{1}_+ I^{\varphi _1} X_M\chi _\epsilon - Q^{2, k}_+ I^{\varphi _{2, k}} X_M\chi _\epsilon )f = h_2 + R_5 h_2 + R_6 h_1 \end{aligned} \end{aligned}$$

(7.10)

with $R_5, R_6$ smoothing. This gives $A_2 = \sum _{k = 1}^3B_k(Q^{1}_+ I^{\varphi _1} - Q^{2, k}_+ I^{\varphi _{2, k}} )$ so that $A_2 X_M \chi _{\epsilon } f = h_2 + R_6 h_1 + R_5h_2$. For $A_1$, we can use (7.8) and (7.10) to get

$$\begin{aligned} Q^{1}_+ I^{\varphi _1} X_M\chi _\epsilon f = h_1 + Q^1_+ K^{\varphi _1, -} A_2 X_M\chi _\epsilon f + R_5' h_1 + R_6' h_2 \end{aligned}$$

where $R_5', R_6'$ are smoothing operators. So we obtain $A_1 = Q^{1}_+ I^{\varphi _1} - Q^1_+ K^{\varphi _1}_- A_2$ so that $A_1 X_M \chi _{\epsilon } f = h_1 + R_5'h_1 + R_6'h_2$.

Step 2: Now we deal with the characteristic function $\chi _{[\epsilon , t_1]}$. We start with

$$\begin{aligned} X_M \chi _{\left[ \epsilon , t_1\right] } f = X_M \chi _{\left[ \epsilon , t_1\right] } E_+ h_1 + X_M \chi _{\left[ \epsilon , t_1\right] } E_- h_2. \end{aligned}$$

Applying $I^\varphi$, we get

$$\begin{aligned} I^\varphi X_M \chi _{\left[ \epsilon , t_1\right] } f = K^{\varphi }_+ h_1 + K^{\varphi }_- h_2 \end{aligned}$$

where $K^{\varphi }_\pm = I^\varphi X_M \chi _{[\epsilon , t_1]} E_\pm$. According to the arguments after Proposition 7.1, we can write the above as

$$\begin{aligned} \begin{aligned} I^\varphi X_M \chi _{\left[ \epsilon , t_1\right] } f = (K^{\varphi , 0}_+ + K^{\varphi , \epsilon }_+ + K^{\varphi , t_1}_+) h_1 + (K^{\varphi , 0}_- + K^{\varphi , \epsilon }_- + K^{\varphi , t_1}_-)h_2 \end{aligned} \end{aligned}$$

(7.11)

where $K^{\varphi , 0}_\pm \in \Psi ^{-1}({\mathbb R}^3)$, $K^{\varphi , \epsilon }_\pm \in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_{\pm \epsilon })$ and $K^{\varphi , t_1}_\pm \in I^{-2}({\mathbb R}^3, {\mathbb R}^3; C_{\pm t_1})$. As in Step 1, we can apply pseudo-differential operators $Q_+^1, Q_+^{2,k}, k = 1, 2, 3$ to (7.11). The arguments for $K^{\varphi , 0}_\pm$ are the same as before. As for $K^{\varphi , \epsilon }_\pm , K^{\varphi , t_1}_\pm$, we notice that the composition $Q_+^1 K^{\varphi , j}_\pm , Q_+^{2,k}K^{\varphi , j}_\pm , k = 1, 2, 3, j = \epsilon , t_1$ are all Fourier integral operators of order $-1$ with canonical relation $C_{\pm \epsilon }$ or $C_{\pm t_1}$. Therefore, using the same $A_1, A_2$ in Step 1, we obtain

$$\begin{aligned} A_1 X_M \chi _{\left[ \epsilon , t_1\right] } f = h_1 + R_1h_1 + R_1'h_2, \ \ A_2 X_M \chi _{\left[ \epsilon , t_1\right] } f = h_2 + R_2 h_1 + R_2'h_2 \end{aligned}$$

(7.12)

where $R_1, R_1', R_2, R_2' \in I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_\epsilon ) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{t_1}) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-\epsilon }) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-t_1})$.

Finally, we improve the remainder term using the Neumann series. We write (7.12) in matrix form

$$\begin{aligned} \begin{pmatrix} A_1 X_M \chi _{\left[ \epsilon , t_1\right] } f \\ A_2 X_M \chi _{\left[ \epsilon , t_1\right] } f \end{pmatrix} = {\text {Id}}\begin{pmatrix} h_1\\ h_2 \end{pmatrix} +R \begin{pmatrix} h_1\\ h_2 \end{pmatrix}, \ \ R = \begin{pmatrix} R_1 &{} R_1'\\ R_2 &{} R_2' \end{pmatrix}. \end{aligned}$$

For $N \in {\mathbb N}$, we let $W = \sum _{n = 0}^{N-1} (-R)^n$ and get

$$\begin{aligned} W \begin{pmatrix} A_1 X_M \chi _{\left[ \epsilon , t_1\right] } f \\ A_2 X_M \chi _{\left[ \epsilon , t_1\right] } f \end{pmatrix} = {\text {Id}}\begin{pmatrix} h_1\\ h_2 \end{pmatrix} +R^N \begin{pmatrix} h_1\\ h_2 \end{pmatrix} \end{aligned}$$

Because $R_1, R_1', R_2, R_2'$ are FIOs of the canonical graph type, we can apply the composition result in [8, Section 25.3] to conclude that the terms in $R^N$ belongs to $I^{-N}({\mathbb R}^3, {\mathbb R}^3; C^N_{\epsilon , t_1})$. Finally, we set

$$\begin{aligned} \begin{pmatrix} \widetilde{A}_1\\ \widetilde{A}_2 \end{pmatrix} = W \begin{pmatrix} A_1 \\ A_2 \end{pmatrix} \end{aligned}$$

Changing notations of $\widetilde{A}_1, \widetilde{A}_2$ to $A_1, A_2$ finishes the proof. $\square$

8 The Stable Determination

We prove Theorem 1.1, starting with the injectivity of the light ray transform. It is known, see for instance [10, 17], that the light ray transform on ${\mathbb R}^{n+1}$ is injective on $C_0^\infty$ functions. This also holds for $L^1_{{\text {comp}}}$ functions and the proof is similar, see [17].

Theorem 8.1

Suppose $f\in L^1_{{\text {comp}}}({\mathbb R}^{n+1}), n \ge 2$ and $X_{{\mathbb R}^{n+1}}f = 0$. Then $f = 0.$

Proof

For $f\in L^1_{{\text {comp}}}({\mathbb R}^{n+1})$, the Fourier transform $\hat{f}$ is analytic. Let $\theta \in {\mathbb S}^{n-1}$ and $\Theta = (1, \theta )$ be a light-like vector. Let $z = (s, y + s\theta ) \in {\mathbb R}^{n+1}, s\in {\mathbb R}, y\in {\mathbb R}^n$. We parametrize the light ray transform as

$$\begin{aligned} X_{{\mathbb R}^{n+1}} f(z, \Theta ) = \int _{{\mathbb R}} f\left( t, y + t\theta \right) d t. \end{aligned}$$

From the standard Fourier Slice Theorem for geodesic ray transforms on ${\mathbb R}^{n+1}$, we get

$$\begin{aligned} \hat{f}(\zeta ) = \int _{\Theta ^\perp } e^{-iy\cdot \zeta } X_{{\mathbb R}^{n+1} } f(z, \Theta ) dS_z \end{aligned}$$

where the integration is over the hyperplane $\Theta ^\perp$ perpendicular to $\Theta$ with respect to the Euclidean inner product in ${\mathbb R}^{n+1}$ and $\zeta = (\tau , \xi )\in {\mathbb R}^{n+1}, \xi \in {\mathbb R}^n, \xi \ne 0$ is perpendicular to $\Theta$. We notice that if $|\tau |\le |\xi |$, then there is a null vector $(1, \theta )$ which is Euclidean orthogonal to $\zeta$. Actually, $\tau + \theta \cdot \xi = 0$ so $\theta \cdot (\xi /|\xi |) = -\tau /|\xi | \in [-1, 1]$ and we can find $\theta \in {\mathbb S}^{n-1}$. We conclude that $\hat{f}(\zeta ) = 0$ for $|\tau | \le |\xi |$. By analyticity, $\hat{f} = 0$ and thus $f = 0.$ $\square$

Corollary 8.2

Suppose $X_Mf = 0$ where f satisfies the wave equation constraint (1.2) in which $f_1 \in H_{{\text {comp}}}^{s+1}({\mathbb R}^3), f_2\in H_{{\text {comp}}}^{s}({\mathbb R}^3), s\ge 0$ are compactly supported. Then $f = f_1 = f_2 = 0.$

Proof

Let $K = \text {supp }f_1 \cup \text {supp }f_2 \subset {\mathbb R}^3$. Let $I^+_c(K)$ be the chronological future of K with respect to the Lorentzian metric induced by c. We know that there is a unique solution $f \in H^{s+1}(M)$ of (1.2). By finite speed of propagation (or strong Huygens principle), the solution f is supported in $I^+_c(K)\cap M$. Now we extend f trivially to $\widetilde{f}\in L^1_{{\text {comp}}}({\mathbb R}^4)$ and we regard $X_M$ as the light ray transform $X_{{\mathbb R}^4}$ on ${\mathbb R}^4$. We still have $X_{{\mathbb R}^4} \widetilde{f} = 0.$ By Theorem 8.1, we conclude that $f = 0$ on ${\mathbb R}^4$ so that $f = 0$ on M and $f_1 = f_2 = 0$ on ${\mathscr {S}}_0.$ $\square$

Proof of Theorem 1.1

The uniqueness part is done in Corollary 8.2. So we prove the stability estimate below. We divide the proof into three steps.

Step 1: Consider $c<1.$ From Proposition 6.3, we know that there are operators $A_1, A_2$ such that

$$\begin{aligned} A_1 X_M f = f_1 + R_1 f_1 + R_1'f_2, \ \ A_2 X_M f = f_2 + R_2 f_1 + R_2'f_2 \end{aligned}$$

and $R_i, R_i', i =1, 2$ are all smoothing operators. We denote

$$\begin{aligned} T \begin{pmatrix} f_1\\ f_2 \end{pmatrix} = {\text {Id}}\begin{pmatrix} f_1\\ f_2 \end{pmatrix} +K \begin{pmatrix} f_1\\ f_2 \end{pmatrix}, \ \ K = \begin{pmatrix} R_1 &{}\quad R_1'\\ R_2 &{}\quad R_2' \end{pmatrix}. \end{aligned}$$

We consider T acting on $\mathcal {N}^s, s\ge 0.$ Then K is compact from $\mathcal {N}^s$ to $\mathcal {N}^{s - \rho }, \rho \in {\mathbb R}$. So we have the estimate

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le \Vert A_1 X_M f\Vert _{H^{s+1}\left( {\mathbb R}^3\right) } + \Vert A_2 X_Mf\Vert _{H^{s}\left( {\mathbb R}^3\right) } + C_\rho \Vert (f_1, f_2)\Vert _{\mathcal {N}^{s-\rho }} \end{aligned}$$

for some constant $C_\rho$. Recall from Proposition 6.3 that $A_1 = B_+ \circ (X_M\circ E_+)^* + B_- (X_M\circ E_-)^*$ and $A_2 = ic\Delta ^\frac{1}{2}(B_+\circ (X_M\circ E_+)^* + B_- \circ (X_M\circ E_-)^*)$. Since the normal operator $(X_M E_\pm )^*X_M E_\pm$ are pseudo-differential operators of order $-1$. By the $L^2$ estimate of pseudo-differential operators, we conclude that $X_M \circ E_\pm : H^s_{{\text {comp}}}({\mathbb R}^3)\rightarrow H^{s+\frac{1}{2}}_{\text {loc}}({\mathscr {C}})$ is bounded. Also, $(X_M \circ E_\pm )^*: H^{s}_{{\text {comp}}}({\mathscr {C}}) \rightarrow H^{s+\frac{1}{2}}_{\text {loc}}({\mathbb R}^3)$ is bounded. Therefore, $A_1: H^{s+ \frac{1}{2}}_{{\text {comp}}}({\mathscr {C}})\rightarrow H^{s}_{\text {loc}}({\mathbb R}^3)$ and $A_2: H^{s+ \frac{1}{2}}_{{\text {comp}}}({\mathscr {C}})\rightarrow H^{s-\frac{1}{2}}_{\text {loc}}({\mathbb R}^3)$ are bounded. For $(f_1, f_2)\in \mathcal {N}^s$, we know from (5.2) that $X_Mf = X_M E_+ h_1 + X_M E_- h_2$ and $h_1, h_2\in H^{s+1}({\mathbb R}^3)$. Thus, $X_Mf \in H^{s+ 3/2}({\mathscr {C}})$ so we get

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le C \Vert X_M f\Vert _{H^{s+3/2}({\mathscr {C}})} + C_\rho \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^{s-\rho }} \end{aligned}$$

(8.1)

where $C_\rho > 0$ is a constant depending on $\rho .$ Note that the order is better than what claimed in the theorem for this case.

Step 2: Consider $c = 1.$ It is convenient to work with $t_0>0$ which can be always arranged. For the Cauchy problem in Sect. 3 with initial condition on $t = t_0$

$$\begin{aligned} \begin{aligned}&\qquad \qquad \square f = 0, \quad \text{ on } {\mathbb R}\times {\mathbb R}^3 \\&f= f_1, \quad \partial _t f = f_2, \text{ on } \{t_0\}\times {\mathbb R}^3, \end{aligned} \end{aligned}$$

(8.2)

it is known that

$$\begin{aligned} U(t): \left( f_1, f_2\right) \rightarrow \left( f(t), \partial _t f(t)\right) , \quad t\in {\mathbb R}\end{aligned}$$

is bijective on $H^{s+1}({\mathbb R}^3)\times H^s({\mathbb R}^3)$. In fact, for (8.2), U(t) is a unitary operator with respect to the energy norm. We consider $(\widetilde{f}_1, \widetilde{f}_2) = U(-t_0)(f_1, f_2)$ which is the Cauchy data at $t = 0$ corresponding to $(f_1, f_2)$ at $t = t_0.$ Then we have

$$\begin{aligned} \begin{aligned} C_1 (\Vert \widetilde{f}_1\Vert _{H^{s+1}({\mathbb R}^3)} + \Vert \widetilde{f}_2\Vert _{H^{s}({\mathbb R}^3)}) \le&\Vert f_1\Vert _{H^{s+1}({\mathbb R}^3)} + \Vert f_2\Vert _{H^{s}({\mathbb R}^3)} \\ \le&C_2 (\Vert \widetilde{f}_1\Vert _{H^{s+1}({\mathbb R}^3)} + \Vert \widetilde{f}_2\Vert _{H^{s}({\mathbb R}^3)}) \end{aligned} \end{aligned}$$

(8.3)

for some $C_1, C_2 > 0$, which follows from the energy estimate of the wave equation. We observe that the solution of (8.2) on $[t_0, t_1]\times {\mathbb R}^3$ can be expressed as

$$\begin{aligned} f = \chi _{\left[ t_0, t_1\right] } E\left( \widetilde{f}_1, \widetilde{f}_2\right) \end{aligned}$$

where $E(\widetilde{f}_1, \widetilde{f}_2) = E_+ \widetilde{h}_1 + E_-\widetilde{h}_2$ is the solution operator for the Cauchy problem from $t = 0$ in (5.2) and $\widetilde{h}_1, \widetilde{h}_2$ correspond to $\widetilde{f}_1, \widetilde{f}_2$, see Sect. 5. Therefore, we can apply Proposition 7.2 to the operator $X_M\chi _{[t_0, t_1]}E_\pm$ with $t_0>0$.

From Proposition 7.2, for any $\rho \in {\mathbb N}$, there are operators $A_1, A_2$ such that

$$\begin{aligned} A_1 X_M \chi _{\left[ t_0, t_1\right] } f = \widetilde{h}_1 + R_1 \widetilde{h}_1 + R_1' \widetilde{h}_2, \ \ A_2 X_M \chi _{\left[ t_0, t_1\right] } f = \widetilde{h}_2 + R_2 \widetilde{h}_1 + R_2' \widetilde{h}_2 \end{aligned}$$

and $R_i, R_i', i =1, 2$ are FIOs of order $-\rho$. By the same argument in Step 1 and using Sobolev estimate of FIOs of canonical graph type, we have

$$\begin{aligned} \begin{aligned} \Vert \widetilde{h}_1\Vert _{H^s({\mathbb R}^3)} + \Vert \widetilde{h}_2\Vert _{H^s({\mathbb R}^3)} \le&\Vert A_1 X_M f\Vert _{H^{s+1}({\mathbb R}^3)} + \Vert A_2 X_M f\Vert _{H^{s}({\mathbb R}^3)} \\&\quad + C_\rho (\Vert \widetilde{h}_1\Vert _{H^{s-\rho }({\mathbb R}^3)} + \Vert \widetilde{h}_2\Vert _{H^{s-\rho }({\mathbb R}^3)}) \end{aligned} \end{aligned}$$

for some constant $C_\rho$. Using (5.5), we can change the estimate of $\widetilde{h}_1, \widetilde{h}_2$ to that of $\widetilde{f}_1, \widetilde{f}_2$ and get

$$\begin{aligned} \begin{aligned} \Vert \left( \widetilde{f}_1, \widetilde{f}_2\right) \Vert _{\mathcal {N}^s}&\le \Vert A_1 X_M \chi _{\left[ t_0, t_1\right] } f\Vert _{H^{s+1}\left( {\mathbb R}^3\right) }\\&+ \Vert A_2 X_M \chi _{\left[ t_0, t_1\right] } f\Vert _{H^{s}\left( {\mathbb R}^3\right) } + C_\rho \Vert \left( \widetilde{f}_1, \widetilde{f}_2\right) \Vert _{\mathcal {N}^{s-\rho }} \end{aligned} \end{aligned}$$

Finally, using (8.3), we get

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le \Vert A_1 X_M f\Vert _{H^{s+1}\left( {\mathbb R}^3\right) } + \Vert A_2 X_M f\Vert _{H^{s}\left( {\mathbb R}^3\right) } + C_\rho \Vert (f_1, f_2)\Vert _{\mathcal {N}^{s-\rho }} \end{aligned}$$

Now recall from the proof of Proposition 7.2 that

$$\begin{aligned}&\begin{pmatrix} A_1\\ A_2 \end{pmatrix} = W\begin{pmatrix} \widetilde{A}_1\\ \widetilde{A}_2 \end{pmatrix} \text { where } \widetilde{A}_1 = Q^{1}_+ I^{\varphi _1} - Q^1_+ K^{\varphi _1, -} \widetilde{A}_2,\\&\quad \widetilde{A}_2 = \sum _{k = 1}^3B_k(Q^{1}_+ I^{\varphi _1} - Q^{2, k}_+ I^{\varphi _{2, k}} ) \end{aligned}$$

in which $Q_+^1, Q_+^{2, k}\in \Psi ^1({\mathbb R}^3), k = 1, 2, 3$, $B_k \in \Psi ^0({\mathbb R}^3), K^{\varphi _1, -}\in \Psi ^{-1}({\mathbb R}^3)$ and $W = \sum _{n = 0}^{\rho - 1}(-R)^n$ with elements of R belonging to $I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{t_0}) + I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{t_1})+ I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-t_0})$ $+ I^{-1}({\mathbb R}^3, {\mathbb R}^3; C_{-t_1})$. Using the estimate for pseudo-differential operators and FIOs of canonical graph type, we get

$$\begin{aligned} \begin{aligned}&\Vert A_1 X_M f\Vert _{H^{s+1}\left( {\mathbb R}^3\right) } + \Vert A_2 X_M f\Vert _{H^{s}\left( {\mathbb R}^3\right) }\\&\quad \le C \Vert I^{\varphi _1} X_M f\Vert _{H^{s+2}\left( {\mathbb R}^3\right) } + C \sum _{k = 1}^3\Vert I^{\varphi _2, k} X_M f\Vert _{H^{s+1}\left( {\mathbb R}^3\right) } \le C\Vert X_M f\Vert _{H^{s+2}} \end{aligned} \end{aligned}$$

So in this case, we get

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le C \Vert X_M f\Vert _{H^{s+2}({\mathscr {C}})} + C_\rho \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^{s-\rho }}, \quad \rho \in {\mathbb N}. \end{aligned}$$

(8.4)

Step 3: We get rid of the last term in (8.1) and (8.4). Let ${\mathscr {K}}$ be a compact subset of ${\mathbb R}^3$ and denote by $\mathcal {N}^s({\mathscr {K}})$ the function space consisting of $(f_1, f_2) \in \mathcal {N}^s$ supported in ${\mathscr {K}}.$ Then the inclusion of $\mathcal {N}^s({\mathscr {K}})$ into $\mathcal {N}^{s-\rho }({\mathscr {K}}), \rho >0$ is compact. We claim that

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s({\mathscr {K}})} \le C \Vert X_M f\Vert _{H^{s+2}({\mathscr {C}})} \end{aligned}$$

for some $C >0$. We argue by contradiction. Assume the estimate without the error term is not true. We can get a sequence $(f^{(j)}_1, f^{(j)}_2), j = 1, 2, \ldots$ with unit norm in $\mathcal {N}^s({\mathscr {K}})$ such that $X_M f^{(j)}$ goes to 0 in $H^{s+2}({\mathscr {C}})$ as $j\rightarrow \infty$. By (8.1) (for $(f_1, f_2)$ supported in ${\mathscr {K}}$), we conclude that $1=\Vert (f_1^{(j)},f_2^{(j)})\Vert _{\mathcal {N}^s({\mathscr {K}})}\le C_\rho \Vert (f_1^{(j)},f_2^{(j)})\Vert _{\mathcal {N}^{s-\rho }({\mathscr {K}})}$. This gives a weak limit $(f_1,f_2)$ in $\mathcal {N}^s({\mathscr {K}})$ along a subsequence, which thus converges strongly in $\mathcal {N}^{s-\rho }({\mathscr {K}})$. Therefore, $\Vert (f_1, f_2)\Vert _{\mathcal {N}^{s-\rho }({\mathscr {K}})}$ is bounded below by $1/C_\rho$, thus non-zero. However, $X_M f = 0$ so $f = 0$ by the injectivity of $X_M$. So $(f_1, f_2) = 0$ a contradiction. This finishes the proof. $\square$

Finally, we prove a stronger version of Theorem 1.1 which allows lower order terms in the wave equation. We consider differential operators of the form

$$\begin{aligned} P\left( x, t, D_x, \partial _t\right) = \partial _t^2 + c^2 \sum _{i = 1}^3D_{x_i}^2 + P_1\left( x, t, iD_x, \partial _t\right) + P_0(x, t) \end{aligned}$$

where $P_1$ is a first order differential operator with real valued smooth coefficients and $P_0$ is smooth. Then we consider the Cauchy problem

$$\begin{aligned} \begin{aligned}&P\left( x, t, D_x, \partial _t\right) f= 0 \ \ \text { on } M^\circ \\&\quad f = f_1, \ \ \partial _t f = f_2, \ \ \text { on } {\mathscr {S}}_0. \end{aligned} \end{aligned}$$

(8.5)

We remark that the equations for $\Phi$ in Sect. 3 are of this type. We prove

Theorem 8.3

Under the same assumptions as in Theorem 1.1, $X_M f$ uniquely determines f and $f_1, f_2$ which satisfy (8.5). Moreover, there exists a $C> 0$ such that

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le C \Vert X_M f\Vert _{H^{s+ 2}({\mathscr {C}})} \text { and } \Vert f\Vert _{H^{s+1}(M)} \le C \Vert X_M f\Vert _{H^{s+ 2}({\mathscr {C}})} \end{aligned}$$

where ${\mathscr {C}}$ is the set of light rays on M.

Proof

The proof follows the same arguments as for Theorem 1.1. So we just point out what needs to be modified. When the wave equation contains lower order terms, one can construct parametrices $E_\pm$ for the Cauchy problem, see [3, Chapter 5]. These are Fourier integral operators and can be represented by oscillatory integrals. So the construction in Sect. 5 works through, and the analysis for $X_ME_\pm$ is the same as the standard wave equation case. However, we do need to justify the ellipticity of the involved operators in Lemma 6.2 and Proposition 7.1. We remark that ellipticity of the solution itself is standard, and follows simply from the principal symbol satisfying a transport equation.

We follow the parametrix construction in Trèves [21, Section 1, Chapter VI] to check this in a transparent manner.

We look for operators $E_j, j = 0, 1$ such that

$$\begin{aligned} \begin{aligned}&P\left( x, t, D_x, \partial _t\right) E_j = 0 \ \ \text { on } M^\circ \\&\quad \partial _t^k E_j = \delta _{kj}, k = 0, 1, \ \ \text { on } {\mathscr {S}}_0 . \end{aligned} \end{aligned}$$

Here, for $j = 0, 1$ we have

$$\begin{aligned} \begin{aligned} E_j f(x)=&{} (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\phi _0\left( x, t, \xi \right) } a_{j0}(x, t, \xi ) \hat{f}(\xi ) d\xi \\ {}&+ (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\phi _1(x, t, \xi )} a_{j1}(x, t, \xi ) \hat{f}(\xi ) d\xi + R_j(t)f(x) \end{aligned} \end{aligned}$$

where $R_j$ are smoothing operators, see [21, (1.37)]. The phase functions are

$$\begin{aligned} \phi _0(x, t, \xi ) = x\cdot \xi + ct |\xi |, \ \ \phi _1\left( x, t, \xi \right) = x\cdot \xi - ct|\xi |. \end{aligned}$$

The amplitude can be written as $a_{jk}(x, t, \xi ) = \sum _{l = 0}^\infty a_{jkl}(x, t, \xi )$ and each $a_{jkl}$ is homogeneous of degree $-j-l$ for $|\xi |$ large. Before we look into the structures that we need of the amplitude, we find the initial values of the leading order term $a_{jk0}$ at $t = t_0$. They satisfy (see [21, (1.53)])

$$\begin{aligned} a_{000}(x, t, \xi ) = \frac{1}{2}, \ \ a_{010}(x, t, \xi ) = \frac{1}{2}, \ \ a_{100}(x, t, \xi ) = \frac{1}{2ic|\xi |}, \ \ a_{110}(x, t, \xi ) = -\frac{1}{2ic|\xi |}. \end{aligned}$$

The amplitudes satisfy first order equations which are deduced from (see [21, (1.39)])

$$\begin{aligned} P\left( x, t, D_x + \partial _x \phi _k, \partial _t + i\partial _t \phi _k\right) a_{jk}(x, t, \xi ) = 0. \end{aligned}$$

For the leading order term, we get

$$\begin{aligned}&\partial _\tau P_2\left( x, t, \partial _x \phi _k, i\partial _t \phi _k\right) \partial _t a_{jk0}\nonumber \\&+ \sum _{\nu = 1}^3 \partial _{\xi _\nu }P_2\left( x, t, \partial _x\phi _k, i\partial _t\phi _k\right) D_{x^\nu } a_{jk0} + C\left( \phi _k; x, t, \xi \right) a_{jk0} = 0 \end{aligned}$$

(8.6)

and the C term in this case is (the sub-principal symbol of P)

$$\begin{aligned} C\left( \phi _k; x, t, \xi \right) = P_1\left( x, t, i\partial _x \phi _k, i\partial _t \phi _k\right) . \end{aligned}$$

Note that $P_1$ has real valued coefficients and is homogeneous of degree one in $i\partial _x\phi _k, i\partial _t\phi _k$. Dividing by $i = \sqrt{-1}$, we see that equation (8.6) is a first order linear equation with real valued coefficients. Solving the equation amounts to solving a ODE along the integral curve and the solution $a_{jk0}$ will be positive scalar multiples of the initial conditions hence not only non-vanishing, but is real or purely imaginary depending on its initial value.

Finally, we can represent the solution to (8.5) as

$$\begin{aligned} f(x, t) = E_0 f_1 + E_1 f_2 = E_{+} h_1 + E_-{h_2} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} E_{+}h&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\left( x\cdot \xi + ct|\xi |\right) } \left( a_{00}(x, t, \xi ) + 2ic|\xi | a_{10}(x, t, \xi )\right) \hat{h}(\xi ) d\xi \\&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i(x\cdot \xi + ct|\xi |)} a_+(x, t, \xi ) \hat{h}(\xi ) d\xi \\ E_{-}h&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\left( x\cdot \xi - ct|\xi |\right) } \left( a_{01}(x, t, \xi ) - 2ic|\xi | a_{11}(x, t, \xi )\right) \hat{h}(\xi ) d\xi \\&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\left( x\cdot \xi - ct|\xi |\right) } a_-(x, t, \xi ) \hat{h}(\xi ) d\xi \end{aligned} \end{aligned}$$

(8.7)

and

$$\begin{aligned} h_1 = f_1 + \frac{1}{2ic}\Delta ^{-\frac{1}{2}} f_2, \ \ h_2 = f_1 - \frac{1}{2ic}\Delta ^{-\frac{1}{2}} f_2. \end{aligned}$$

We see that the leading order terms of $a_+, a_-$ are all positive. From these oscillatory integral representations, it is easy to see that Lemma 6.2 holds for $c<1$. For Proposition 7.1, we see that the principal symbol of $k_+$ is given by

$$\begin{aligned} k_{+, -1}(x, \xi ) = 2\pi i |\xi |^{-1} \varphi \left( -\xi /|\xi |\right) \int _0^{t_1}t^{-1} \chi _\epsilon (t) a_{+, 0}(t, x)dt \end{aligned}$$

where $a_{+, 0}$ is the in the expansion $a_+\sim \sum _{k = 0}^\infty a_{+, k}(t, \xi ) |\xi |^{-1-k}$. So $k_{+, -1}(x, \xi )$ is non-vanishing. Thus the operator $I^\varphi X_M\chi _\epsilon E_+$ is elliptic. The rest of the proof is the same as for Theorem 1.1. $\square$

9 Small Perturbations of the Minkowski Spacetime

We consider metric perturbations $g_\delta = g_M + h$ with $h = \sum _{i, j = 0}^3 h_{ij} dx^idx^j$. We assume that

• (A1) h is a symmetric two tensor smooth on M;

• (A2) for $\delta > 0$ small, the seminorm $\Vert h_{ij}\Vert _{C^{3}}$ $= \sup _{(t, x)\in M}\sum _{|\alpha |\le 3}|\partial ^\alpha h_{ij}(t, x)| < \delta , i, j = 0, 1, 2, 3.$

Without loss of generality, we can assume that h is extended to some larger manifold $\widetilde{M} = (\widetilde{t}_0, \widetilde{t}_1)\times {\mathbb R}^3$ such that $M\subset \widetilde{M}$ and (A2) holds on $\widetilde{M}$. In this section, we study the inverse problem on $(M, g_\delta )$ for $\delta$ sufficiently small. Note that in this case, light rays may not follow straight lines and the injectivity of the light ray transform on scalar functions is not known. We will show that by using a perturbation argument on the Fourier integral operator level, one can obtain the same determination result as for the Minkowski case.

We start with the light-like geodesics on $(M, g_\delta )$ and their parametrizations. Let $\gamma (s)$ denote a light-like geodesic from ${\mathscr {S}}_0$. It satisfies

$$\begin{aligned} \begin{aligned}&\partial _s^2 \gamma ^k(s) + \Gamma ^{k}_{ij} \partial _s\gamma ^i(s) \partial _s\gamma ^j(s) = 0\\&\quad \gamma (0) = (0, y), \partial _s \gamma (0) = (\beta , v) \end{aligned} \end{aligned}$$

(9.1)

where $\Gamma ^{k}_{ij}$ is the Christoffel symbol for $g_\delta$, $v\in {\mathbb S}^2$ and $\beta$ is such that $g_\delta (\beta , v) = 0$ and $(\beta , v)$ future pointing. It is known, see for example [1], that (9.1) is equivalent to a first order system on $T^*M.$ Here, M is regarded as a submanifold of $\widetilde{M}.$ We use (t, x) and $(\tau , \xi )$ for the local coordinates on $T^*M.$ Consider the Hamiltonian

$$\begin{aligned} p\left( t, x, \tau , \xi \right)= & {} \frac{1}{2}g^*_\delta (\tau , \xi ) = \frac{1}{2}g_M^*(\tau , \xi ) + H(t, x, \tau , \xi )\\= & {} \frac{1}{2}\left( -|\tau |^2 + \sum _{i = 1}^3|\xi _i|^2\right) + H(t, x, \tau , \xi ). \end{aligned}$$

Here, 2H is the perturbation of the dual metric corresponding to the perturbation h. Let $\Xi = (\tau , \xi )$, then $H(t, x, \Xi ) = \sum _{i, j = 0, 1, 2, 3} H_{ij}(t, x) \Xi _i\Xi _j$ is homogeneous of degree two in $\Xi$ and the seminorm $\Vert H_{ij}\Vert _{C^{3}} < C\delta$ for some constants C. We denote the Hamilton vector field by $H_p$. Let $(t(s), x(s), \tau (s), \xi (s))$ be an integral curve of $H_p$ in the characteristic set $\Sigma _p = \{(t, x, \tau , \xi ) \in T^*M: p(t, x, \tau , \xi ) = 0\}$, called null-bicharacteristics. With $\gamma (s) = (t(s), x(s))$, (9.1) can be converted to

$$\begin{aligned} \begin{aligned} \frac{d t}{ds}&= \frac{\partial p}{\partial \tau } = - \tau + \partial _\tau H\left( t, x, \tau , \xi \right) ; \quad \frac{d x_i}{ds} = \frac{\partial p}{\partial \xi _i} = \xi _i + \partial _{\xi _i} H\left( t, x, \tau , \xi \right) \\ \frac{d \tau }{ds}&= -\partial _{t} H\left( t, x, \tau , \xi \right) ; \quad \frac{d \xi _i}{ds} = -\partial _{x_i}H\left( t, x, \tau , \xi \right) , \quad i = 1, 2, 3\\ t(0)&= t_0= 0, \quad x_i(0) = y_i, \quad \tau (0) = \tau _0, \quad \xi _i(0) = \xi _{0, i}. \end{aligned} \end{aligned}$$

(9.2)

Here, $(\tau _0, \xi _0)$ is the cotangent vector obtained from $(\beta , v)$ using $g_\delta$ and we also denote it by $(\tau _0, \xi _0) = (\beta , v)^\flat$. If we consider the system for the Minkowski metric namely $H = 0$, then $\beta = 1$ and the covector $(\tau _0, \xi _0) = (-1, v)$. (9.2) becomes

$$\begin{aligned} \begin{aligned} \frac{dt}{ds}&= - \tau , \quad \frac{d x_i}{ds} = \xi _i, \quad \frac{d \tau }{ds} = 0, \quad \frac{d \xi _i}{ds} = 0, \quad i = 1, 2, 3\\ t(0)&= 0, \quad x_i(0) = y_i, \quad \tau (0) = -1, \quad \xi _i(0) = v_i. \end{aligned} \end{aligned}$$

(9.3)

We see that $x(s) = (s, y + s v), t(s) = s$, which agrees with our parametrization used previously. Now we have the following result.

Lemma 9.1

For $\delta > 0$ sufficiently small, the set of light rays on $(M, g_\delta )$ is given by ${\mathscr {C}}_\delta = \{\gamma = (t, x(t, y, v)): (y, v)\in {\mathscr {S}}_0 \times {\mathbb S}^2, t\in [t_0, t_1]\}$, where x is a smooth function of t, y, v. Moreover, we have

$$\begin{aligned} \Vert x(t, y, v) - (y + tv) \Vert _{C^2} < C \delta \end{aligned}$$

for some constant C.

Proof

For $v\in {\mathbb S}^2$, the co-vectors $(\tau _0, \xi _0) = (\beta , v)^\flat$ are in a bounded set of ${\mathbb R}^4$. We assume that $|(\tau _0, \xi _0)| < M_1$. We also notice that $\tau _0$ is away from zero, say $|\tau _0|> M_0 > 0$. Then we consider $(\tau , \xi )$ such that $|(\tau , \xi ) - (\tau _0, \xi _0)| < M_0/2$ so that $|(\tau , \xi )|< M\doteq M_1 + M_0/2$ and $|\tau | > M_0/2$. Consider the system (9.2). Because H is homogeneous of degree two in $(\tau , \xi )$, for $|(\tau , \xi )|< M$ and for $\delta > 0$ sufficiently small, we see that $\frac{dt}{ds} \ne 0$. Therefore, we can take t as the parameter and convert (9.2) to

$$\begin{aligned} \begin{aligned} \frac{d s}{dt}&= \frac{1}{- \tau + \partial _\tau H(t, x, \tau , \xi )}; \quad \frac{d x_i}{dt} = \frac{\xi _i + \partial _{\xi _i} H\left( t, x, \tau , \xi \right) }{- \tau + \partial _\tau H\left( t, x, \tau , \xi \right) }\\ \frac{d \tau }{dt}&= \frac{-\partial _{t} H\left( t, x, \tau , \xi \right) }{- \tau + \partial _\tau H(t, x, \tau , \xi )}; \quad \frac{d \xi _i}{dt} = \frac{-\partial _{x_i}H\left( t, x, \tau , \xi \right) }{- \tau + \partial _\tau H(t, x, \tau , \xi )}, \quad i = 1, 2, 3\\ s(0)&= 0, \quad x_i(0) = y_i, \quad \tau (0) = \tau _0, \quad \xi _i(0) = \xi _{0, i}. \end{aligned} \end{aligned}$$

(9.4)

The system corresponding to (9.3) is

$$\begin{aligned} \begin{aligned} \frac{d s}{dt}&=\frac{1}{- \tau }; \quad \frac{d x_i}{dt} = \frac{\xi _i }{- \tau }, \quad \frac{d \tau }{dt} = 0; \quad \frac{d \xi _i}{dt} = 0 , \quad i = 1, 2, 3\\ s(0)&= 0, \quad x_i(0) = y_i, \quad \tau (0) = -1, \quad \xi _i(0) = v. \end{aligned} \end{aligned}$$

(9.5)

Let $(\widetilde{t}, \widetilde{x}, \widetilde{\tau }, \widetilde{\xi })$ be the solution of (9.5) and $(t, x, \tau , \xi )$ satisfy (9.4). Then let $u = (t - \widetilde{t}, x - \widetilde{x}, \tau - \widetilde{\tau }, \xi - \widetilde{\xi })$. We see that u satisfies the system

$$\begin{aligned} \begin{aligned} \frac{d u}{ds}= F(u)\\ u(0) = u_0,\end{aligned} \end{aligned}$$

where F is smooth and $|F(u)| < C\delta$, $|u_0|< C\delta$ for generic constant C. Now it follows from standard ODE theorems, see for instance [9, Theorem 1.2.3] that for $\delta$ sufficiently small, there is a unique $C^\infty$ solution u on $[t_0, t_1]$ and $|u| \le C\delta .$ Higher order estimates can be obtained similarly. This finishes the proof. $\square$

Now we consider the light ray transform $X_\delta$ on $(M, g_\delta )$. The parametrization of the light rays is not unique, although all choices give rise to equivalent analysis for our purpose. Perhaps the most natural parameterization is to use the cosphere bundle on ${\mathscr {S}}_0$ of the induced metric. Let $\bar{g}_\delta$ be the induced Riemannian metric of $g_\delta$ on ${\mathscr {S}}_0$. For $y\in {\mathscr {S}}_0,$ let ${\mathbb S}_{\delta , y}^2 = \{v \in T{\mathscr {S}}_0: \bar{g}_\delta (v, v) = 1\}$. For $v\in {\mathbb S}_{\delta , y}^2$, there is a unique future pointing light-like vector $(v_0, v)$ at y. In particular, $v_0$ is close to 1 for $\delta$ small. Then the light ray from (0, y) in direction $(v_0, v)$ is parametrized by $\gamma _{y, v}(s) = \exp _{(0, y)} s(v_0, v), s\in [0, s_1]$ where s is the affine parameter such that $\gamma _{y, v}(0) = (0, y)\in {\mathscr {S}}_0$ and $\gamma _{y, v}(s_1)\in {\mathscr {S}}_1$. In this parametrization, we can write

$$\begin{aligned} \begin{aligned} X_{\delta }f(y, v) = \int _0^{s_1} f\left( \gamma _{y, v}(s)\right) d s. \end{aligned} \end{aligned}$$

(9.6)

Now we can identify ${\mathbb S}_{\delta , y}^2$ with ${\mathbb S}_{y}^2$ via a diffeomorphism. By the above Lemma 9.1, s is a smooth function of y, t and $v\in {\mathbb S}^2$ so we can use t variable to parametrize the light rays. We have

$$\begin{aligned} \begin{aligned} X_{\delta }f(y, v) = \int _0^{t_1} w(y, v, t) f(t, x(t, y, v))dt, \quad y\in {\mathscr {S}}_0, v\in {\mathbb S}^2, \end{aligned} \end{aligned}$$

where w is a weight coming from the change of variables. In fact, w is smooth and close to 1 for $\delta$ sufficiently small. w only mildly affects the argument, changing the elliptic principal symbol of the final operator $X_\delta \circ E_+$ in (9.14), thus maintaining ellipticity. For simplicity, we will ignore it in the follows and take

$$\begin{aligned} \begin{aligned} X_{\delta }f(y, v)&= \int _0^{t_1} f(t, x(t, y, v))d t \\&= (2\pi )^{-3}\int _{{\mathbb R}^3} \int _{{\mathbb R}^3}\int _{0}^{t_1} e^{i ( (x(t, y, v) - z)\cdot \eta )} f(t, z) dt dz d\eta . \end{aligned} \end{aligned}$$

(9.7)

This is the parametrization of $X_\delta$ we work with in the rest of this section. The Schwartz kernel of $X_{\delta }$ is the delta distribution on ${\mathscr {C}}\times M^\circ$ supported on the point-line relation $Z_\delta$ defined by

$$\begin{aligned} \begin{aligned} Z_\delta = \left\{ (\gamma , q)\in {\mathscr {C}}\times M^\circ : q\in \gamma \right\} = \left\{ (y, v, (t, x)) \in {\mathbb R}^3 \times {\mathbb S}^2 \times M^\circ : x = x(t, y, v)\right\} . \end{aligned} \end{aligned}$$

Next, let $\square _{g_\delta }$ be the d’Alembert operator on $(M, g_\delta )$ and we consider the second order operator

$$\begin{aligned} P_\delta \left( x, t, D_x, \partial _t\right) = \square _{g_\delta } + P_1\left( x, t, iD_x, \partial _t\right) + P_0(x, t) \end{aligned}$$

(9.8)

where $P_1$ is a first order differential operator with real valued smooth coefficients and $P_0$ is smooth. Then we consider the Cauchy problem

$$\begin{aligned} \begin{aligned}&P_\delta \left( x, t, D_x, \partial _t\right) f= 0 \ \ \text { on } M^\circ \\&\quad f = f_1, \ \ \partial _t f = f_2, \ \ \text { on } {\mathscr {S}}_0. \end{aligned} \end{aligned}$$

(9.9)

We remark that for sufficiently small metric perturbations, the operators $\square _{g_\delta }$ and $P_\delta$ are both strictly hyperbolic with respect to ${\mathscr {S}}_0.$ Therefore, as in previous sections, the parametrix construction of Duistermaat-Hörmander can be applied. In general, the parametrix does not have a global oscillatory integral representation on M. However, we show below that for sufficiently small perturbations of the Minkowski spacetime, this is possible.

The parametrix construction is the same as in the previous section. We look for operators $E_j, j = 0, 1$ such that

$$\begin{aligned} \begin{aligned}&P_\delta \left( x, t, D_x, \partial _t\right) E_j = 0 \ \ \text { on } M^\circ \\&\quad \partial _t^k E_j = \delta _{kj}, k = 0, 1, \ \ \text { on } {\mathscr {S}}_0 . \end{aligned} \end{aligned}$$

For $j = 0, 1$ we have

$$\begin{aligned} E_j f(x)= & {} (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\phi _+(x, t, \xi )} a_{j,+}(x, t, \xi ) \hat{f}(\xi ) d\xi \\&+ (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i\phi _-(x, t, \xi )} a_{j, -}(x, t, \xi ) \hat{f}(\xi ) d\xi + R_j(t)f(x) \end{aligned}$$

where $R_j$ are smoothing operators, see [21, (1.37)]. We follow Trèves [21] to find the phase functions $\phi (t, x, \xi )$ for $(t, x)\in (t_0, t_1) \times {\mathbb R}^3$, $\xi \in {\mathbb R}^3$. The phase function should satisfy the eikonal equation

$$\begin{aligned} \begin{aligned} p(\nabla \phi ) = -|\partial _t\phi |^2 + |\partial _x \phi |^2 + H\left( \partial _t \phi , \partial _x \phi \right) = 0. \end{aligned} \end{aligned}$$

By the strict hyperbolicity, there are two solutions for $\partial _t\phi$ denoted by $\partial _t \phi = \lambda _\pm (t, x, \partial _x \phi )$ and $\lambda _\pm$ are smooth functions and homogeneous of degree one in $\partial _x \phi$. We take initial conditions $\partial _t \phi = x\cdot \xi , \xi \in {\mathbb R}^3$ at $t = 0$. Below, we consider $\lambda _+$. The treatment for $\lambda _-$ is identical. We consider the Hamilton-Jacobi equation

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&= - \partial _\eta \lambda _{+}(t, x, \eta ), \quad \frac{d \eta }{dt} = \partial _x \lambda _+(t, x, \eta )\\ x(0)&= y, \quad \eta (0) = \xi , \quad y \in {\mathbb R}^3, \xi \in {\mathbb R}^3\backslash 0. \end{aligned} \end{aligned}$$

(9.10)

We denote the solution by $x(t, y, \xi ), \xi (t, y, \xi )$. Then the phase function is

$$\begin{aligned} \phi _+(t, x, \xi ) = x\cdot \xi + \int _0^t \lambda _+(s, x, \eta (s, y, \xi ))ds. \end{aligned}$$

(9.11)

Here, one can express y in terms of x, see [21, Section 2, Chapter VI] for more details. For the Minkowski spacetime, we know $\lambda _+ = -|\xi |$ so that (9.10) becomes

$$\begin{aligned} \begin{aligned} \frac{dx}{dt} =&\xi /|\xi |, \quad \frac{d \eta }{dt} = 0\\ x(0)&= y, \quad \eta (0) = \xi . \end{aligned} \end{aligned}$$

(9.12)

The solution is simply $x(t) = y + t\xi /|\xi |, \eta (t) = \xi$ and the phase function is $\phi _0(t, x, \xi ) = x\cdot \xi + t|\xi |$. Using the same argument as for Lemma 9.1, we get

Lemma 9.2

For $\delta > 0$ sufficiently small, there is a unique smooth solution $(x(t, y, \xi ), \eta (t, y, \xi ))$ to (9.10) for $t\in [t_0, t_1], y\in {\mathbb R}^3, \xi \in {\mathbb R}^3\backslash 0$, and they satisfy

$$\begin{aligned} \Vert x\left( t, y, \xi \right) - \left( y - t \xi /|\xi |\right) \Vert _{C^2}< C\delta , \quad \Vert \eta (t, y, \xi )/|\xi | - \xi /|\xi |\Vert _{C^2} < C \delta \end{aligned}$$

for some constant $C > 0.$ It follows that the phase function $\phi _+$ in (9.11) is also smooth and satisfies

$$\begin{aligned} \Vert \phi _+\left( t, x, \xi \right) - \left( x\cdot \xi + t|\xi |\right) \Vert _{C^2} < C\delta |\xi |. \end{aligned}$$

We remark that similar argument was used in [18] for a backscattering problem. Using this lemma, we can represent the solution to (9.9) as

$$\begin{aligned} f(x, t) = E_0 f_1 + E_1 f_2 = E_{+} h_1 + E_-{h_2} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} E_{+}h&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i \phi _+(t, x, \xi ) } a_+(x, t, \xi ) \hat{h}(\xi ) d\xi \\ E_{-}h&= (2\pi )^{-3} \int _{{\mathbb R}^3} e^{i \phi _-(t, x, \xi )} a_-(x, t, \xi ) \hat{h}(\xi ) d\xi . \end{aligned} \end{aligned}$$

(9.13)

The $a_\pm$ and $h_1, h_2$ are the same as in (8.7).

With these preparations, we now state and prove our main result in this section.

Theorem 9.3

Consider $(M, g_\delta )$ which satisfy the assumptions (A1), (A2) in the beginning of this section. Assume that $(f_1, f_2)\in \mathcal {N}^s, s \ge 0$, and $f_1, f_2$ are supported in a compact set ${\mathscr {K}}$ of ${\mathscr {S}}_0$. For $\delta \ge 0$ sufficiently small, $X_\delta f$ uniquely determines f and $f_1, f_2$ which satisfy (9.9). Moreover, there exists $C> 0$ such that

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le C \Vert X_\delta f\Vert _{H^{s+ 2}\left( {\mathscr {C}}_\delta \right) } \text { and } \Vert f\Vert _{H^{s+1}(M)} \le C \Vert X_\delta f\Vert _{H^{s+ 2}\left( {\mathscr {C}}_\delta \right) } \end{aligned}$$

where ${\mathscr {C}}_\delta$ is the set of light rays on $(M, g_\delta )$.

Proof

We examine the arguments in Sects. 7 and 8 and point out what needs to be modified. We consider the composition of $X_\delta$ and $E_+$ defined in (9.13). We have

$$\begin{aligned} \begin{aligned} X_{\delta }f(y, v) = (2\pi )^{-3}\int _{{\mathbb R}^3} \int _{{\mathbb R}^3} \int _{0}^{t_1} e^{i ( (x(t, y, v) - x')\cdot \eta )} f(t, x') dt dx' d\eta \end{aligned} \end{aligned}$$

and

$$\begin{aligned} E_+(f)(t, x') =(2\pi )^{-3} \int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i\left( \phi _+(t, x', \xi ) - z \cdot \xi \right) } a_+(t, x', \xi ) f(z) dz d\xi . \end{aligned}$$

Consider the integral operator $I^\varphi$ defined in Sect. 7. Using the oscillatory integral representations, we have

$$\begin{aligned} \begin{aligned}&I^\varphi X_{\delta } \chi _\epsilon E_+ f(y, v) \\&\quad = (2\pi )^{-6} \int _{{\mathbb S}^2}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3}\int _0^{t_1}\int _{{\mathbb R}^3}\int _{{\mathbb R}^3} e^{i \left( x(t, y, v)\cdot \eta - x'\cdot \eta + \phi _+(t, x', \xi ) - z\cdot \xi \right) }\\&\qquad \varphi (v) a(t, x', \xi ) \chi _\epsilon (t) f(z) dz d\xi dt dx' d\eta dv \\ \end{aligned} \end{aligned}$$

(9.14)

We write the phase function as $\Phi = \phi + \psi$ in which

$$\begin{aligned} \phi \left( y, z; \xi , \eta , x', t, v\right) = (y - x')\cdot \eta + t v\cdot \eta + (x' -z)\cdot \xi + t |\xi | \end{aligned}$$

and $\psi$ is a smooth function and homogeneous of degree one in $\xi , \eta$. In particular, $\Phi$ is a small perturbation of $\phi$. As in Proposition 7.1, we first consider the integration in $x', \eta , v$ in (9.14). As shown in Proposition 7.1, the phase function $\phi$ in these variables is non-degenerate. Since $\psi$ is a small perturbation of $\phi$, for $\delta$ sufficiently small, we see that $\Phi$ in $x', \eta , v$ variables is also non-degenerate. Note that

$$\begin{aligned} \partial _{x'}\Phi = -\eta + \partial _{x'}\phi _+(t, x', \xi ), \quad \partial _{\eta } \Phi = x(t, y, v) - x', \quad \partial _{v}\Phi = \partial _vx(t, y, v)\cdot \eta \end{aligned}$$

(9.15)

For the stationary points, we see that $x' = x(t, y, v)$ so (t, x) is on the light ray from (0, y) in direction (1, v). Let $\tau$ satisfy $p_\delta (t, x, \tau , \eta ) = 0$. From $\eta = \partial _{x'}\phi _{+}(t, x', \xi )$ we see that $(t, x', \tau , \eta )$ is on the bicharactersitics from $(y, \xi )$. Since there is no conjugate points, we get $v = \pm \xi /|\xi |$. Thus at the stationary points, the phase function becomes

$$\begin{aligned} \Phi (y, z, t, \xi ) = \phi _+(t, x(t, y, \pm \xi /|\xi |), \xi ) - z\cdot \xi \end{aligned}$$

After integrating in $x', \eta , v$, the Schwartz kernel becomes

$$\begin{aligned} \begin{aligned} I^\varphi X_{\delta } \chi _\epsilon E_+ (y, z)&= (2\pi )^{-3} \int _0^{t_1}\int _{{\mathbb R}^3} e^{i \left( \phi _+\left( t, x\left( t, y, \xi /|\xi |\right) , \xi \right) - z\cdot \xi \right) } k^\delta _+(t, \xi ) d\xi dt\\&\quad + (2\pi )^{-3} \int _0^{t_1}\int _{{\mathbb R}^3} e^{i \left( \phi _+(t, x(t, y, - \xi /|\xi |), \xi ) - z\cdot \xi \right) } k^\delta _-(t, \xi ) d\xi dt \end{aligned} \end{aligned}$$

(9.16)

where $k^\delta _\pm$ are small perturbations of $k_\pm$ in (7.4) and (7.5) of Proposition 7.1. Finally, we integrate in t. For the second integral in (9.16), the phase function is a small perturbation of

$$\begin{aligned} (y - z) \cdot \xi + 2t|\xi | \end{aligned}$$

thus as in Proposition 7.1, the integral is $O(|\xi |^{-\infty })$. For the first integral of (9.16), we need to examine the phase function at the stationary points. Using (9.11), we get

$$\begin{aligned} \Phi (y, z, t, \xi ) = x\cdot \xi + \int _0^t \lambda _+(s, x, \xi )ds - z\cdot \xi \end{aligned}$$

where $x = x(t, y, \xi /|\xi |)$. Taking $\xi$ derivative, we get

$$\begin{aligned} \begin{aligned} \partial _\xi \Phi (y, z, t, \xi )&= (x - z) + \partial _\xi x \cdot \xi + \int _0^t \left( \partial _\eta \lambda _+(s, x(s, y, \xi /|\xi |), \xi )\partial _\xi x + \partial _\eta \lambda _+\right) ds \\&= (x - z) + \partial _\xi x \cdot \xi + \int _0^t -\frac{dx}{ds}(s, x, \xi ) ds \end{aligned} \end{aligned}$$

where we used the stationary point condition (9.15) and $\partial _\eta \lambda _+ = -dx/dt$. Note that $\partial _\xi x$ is the Jacobi field, and because $x(t, y, \xi /|\xi |)$ is a light-like geodesic, $\partial _\xi x\cdot \xi = 0$, see Lemma 3.1 and Lemma 3.4 of [13]. Therefore, $\partial _\xi \Phi (y, z, t, \xi ) = (x - z)$ and $\Phi (y, z, t, \xi ) = (y - z)\cdot \xi + \widetilde{\Phi }(y, z, t)$ where $\widetilde{\Phi }$ is small. Finally, integrating in t of the first integral of (9.16) gives a pseudo-differential operator of order $-1$ and the principal symbol $k^\delta _{+, -1}$ is a small perturbation of $k_{+, -1}(\xi )$ in Proposition 7.1. This implies that Proposition 7.1 hold for the small perturbations.

To see that the analogous result of Proposition 7.2 holds for small perturbations, it suffices to examine the kernel (9.16) in which $\chi _\epsilon$ is replaced by $\chi _{[\epsilon , t_1]}$

$$\begin{aligned} \begin{aligned} I^\varphi X_{\delta } \chi _{\left[ \epsilon , t_1\right] } E_+ (y, z)&= (2\pi )^{-3} \int _\epsilon ^{t_1}\int _{{\mathbb R}^3} e^{i \left( \phi _+\left( t, x\left( t, y, \xi /|\xi |\right) , \xi \right) - z\cdot \xi \right) } k^\delta _+(t, \xi ) d\xi dt \\&\quad + (2\pi )^{-3} \int _\epsilon ^{t_1}\int _{{\mathbb R}^3} e^{i \left( \phi _+\left( t, x\left( t, y, - \xi /|\xi |\right) , \xi \right) - z\cdot \xi \right) } k^\delta _-(t, \xi ) d\xi dt \end{aligned} \end{aligned}$$

(9.17)

The first integral still gives a pseudo-differential operator as shown above. For the second integral, integration by parts in t gives an oscillatory integral of the form

$$\begin{aligned} \int _{{\mathbb R}^3} e^{i (\phi _+(\epsilon , x(\epsilon , y, - \xi /|\xi |), \xi ) - z\cdot \xi )} a(\xi ) d\xi + \int _{{\mathbb R}^3} e^{i (\phi _+(t_1, x(t_1, y, - \xi /|\xi |), \xi ) - z\cdot \xi )} b(\xi ) d\xi \end{aligned}$$

(9.18)

where a, b are symbols of order $-2$. Here, we used that $\phi _+$ is homogeneous of degree one in $\xi .$ To see that these are FIOs of canonical graph type, we use the characterization in [8, page 26] which says that an oscillatory integral with phase $\phi (x, \eta ) - x \cdot \eta$ is an FIO whose canonical relation is a canonical graph if and only if $\det \frac{\partial ^2\phi }{\partial x\partial \eta } \ne 0.$ Since $\phi _+(\epsilon , x(\epsilon , y, - \xi /|\xi |), \xi )$ is a small perturbation of $y\cdot \xi + 2 \epsilon |\xi |$ and $\det \frac{\partial ^2 }{\partial y\partial \xi } (y\cdot \xi + 2 \epsilon |\xi |) = -1 \ne 0$, we conclude that for $\delta$ sufficiently small, the first integral in (9.18) gives an FIO of canonical graph type. The same is true for the second integral. Thus Proposition 7.2 holds for small perturbations.

Now, the proof of Theorem 1.1 in Sect. 8 go through line by line, except the injectivity of $X_\delta$. In particular, we have the estimate as (8.1)

$$\begin{aligned} \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^s} \le C \Vert X_\delta f\Vert _{H^{s+2}({\mathscr {C}}_\delta )} + C_\rho \Vert \left( f_1, f_2\right) \Vert _{\mathcal {N}^{s-\rho }} \end{aligned}$$

where $C_\rho$ is a constant depending on $\rho .$ To get rid of the last term, we use the following argument, see [22, Section 2.7]. Notice that given $s,\rho$ and for some fixed small $\delta _0$, if we consider all metric g such that $\Vert g - g_M\Vert _{C^{3}} \le \delta _0$ , then the above estimate is uniform (a fixed constant $C_\rho$ works for all such metrics) by the uniformity of the construction. Now suppose there is no $\delta$ such that for all metrics within $\delta$ of the Minkowski metric $g_M$ (in the Fréchet space sense) the transform is injective. Let $F^j=(f^j_1,f^j_2), j = 1, 2, \ldots$ be such that the corresponding $f^j$ is in the null-space of $X_{g_j} =X_j$ and $\Vert F^j\Vert _{\mathcal {N}^s} = 1$, with $g_j$ within 1/j of the Minkowski metric. By the above inequality, $1\le C_\rho \Vert F^j\Vert _{\mathcal {N}^{s-\rho }}.$ Now, $F^j$ has a $\mathcal {N}^s$-weakly convergent subsequence, not shown in notation, to some $F\in \mathcal {N}^s$, which thus strongly converges in $\mathcal {N}^{s-\rho }$. By the above inequality, $F\ne 0$. But $0 = X_j f$ converges to $X_M f$ e.g. in the sense of distributions. So $X_M f =0$ which by the injectivity of $X_M$, implies that $f = 0$. So we get $F = 0$ a contradiction. This shows the injectivity of $X_\delta$ and finishes the proof of Theorem 9.3. $\square$