Abstract
We prove that any one-dimensional (1D) quantum state with small quantum conditional mutual information in all certain tripartite splits of the system, which we call a quantum approximate Markov chain, can be well-approximated by a Gibbs state of a short-range quantum Hamiltonian. Conversely, we also derive an upper bound on the (quantum) conditional mutual information of Gibbs states of 1D short-range quantum Hamiltonians. We show that the conditional mutual information between two regions A and C conditioned on the middle region B decays exponentially with the square root of the length of B. These two results constitute a variant of the Hammersley–Clifford theorem (which characterizes Markov networks, i.e. probability distributions which have vanishing conditional mutual information, as Gibbs states of classical short-range Hamiltonians) for 1D quantum systems. The result can be seen as a strengthening—for 1D systems—of the mutual information area law for thermal states. It directly implies an efficient preparation of any 1D Gibbs state at finite temperature by a constant-depth quantum circuit.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A sequence of discrete random variables \(X_1, \ldots , X_n\) forms a Markov chain if \(X_{i+1}\) is uncorrelated from \(X_{1}, \ldots , X_{i-1}\) conditioned on the value of \(X_i\). Markov chains are a central concept in probability theory, statistics and beyond. In this paper we consider a combination of two natural generalizations of the concept of a Markov chain.
In the first we only require approximate independence from previous random variables, i.e. \(X_{i+1}\) should only be almost independent from \(X_{1}, \ldots , X_{i-1}\) conditioned on \(X_i\). One way to make this notion quantitative is to use the conditional mutual information, defined for every three random variables X, Y, Z drawn from the distribution p(X, Y, Z) as
where \(H(X)_p:=-\sum _{x_i\in X} p_X(x_i)\log p_X(x_i)\) is the Shannon entropy of the marginal distribution on X.Footnote 1 In terms of the conditional mutual information, \(X_1, \ldots , X_n\) is a Markov chain if
The conditional mutual information can also be written as
where \(I(X:Z)_{p_y}\) is the mutual information:
with \(p_{y}(X, Z)\) which is the conditional distribution of X and Z for given \(Y = y\). Thus if \(I(X : Z|Y)_p\) is small, X and Z are almost uncorrelated conditioned on Y. For \(\varepsilon >0\), we say \(X_1, \ldots , X_n\) is a \(\varepsilon \)-approximate Markov chain if
In the second, instead of considering random variables, we consider a n-partite quantum state given by a density matrix \(\rho _{A_1 \ldots A_n} \in {{\mathcal {D}}}({{\mathcal {H}}}_{A_1} \otimes \cdots \otimes {{\mathcal {H}}}_{A_n})\).Footnote 2 The quantum conditional mutual information of a tripartite state \(\rho _{ABC}\) is defined as
where \(S(X)_{\rho } := - {\mathrm {Tr}}(\rho _X \log \rho _X)\) is the von Neumann entropy of the reduced state on subsystem X. Quantum states satisfying \(I(A:C|B)_\rho = 0\) are analogues of Markov chains of three random variables. As in the classical case (I), a multipartite quantum state \(\rho _{A_1, \ldots , A_n}\) is a quantum Markov chain if
In this paper, we are interested in quantum approximate Markov chains, a combination of both generalizations. Such concept is already non-trivial for tripartite quantum states \(\rho _{ABC}\). We can say \(\rho _{ABC}\) forms a quantum \(\varepsilon \)-approximate Markov chain if
However there is no quantum analogue of Eq. (1) (see Ref. [1]) and therefore it is unclear if the definition in the above has a nontrivial meaning. A recent result in quantum information theory reveals its meaning [2]. It shows that
where the minimum is over all completely-positive and trace-preserving (CPTP) map \(\Delta _{B \rightarrow BC}\) mapping \(\mathcal {D}({{\mathcal {H}}}_B)\) to \(\mathcal {D}({{\mathcal {H}}}_B \otimes {{\mathcal {H}}}_C)\), and \(F(\rho , \sigma ) := {\mathrm {Tr}}((\sigma ^{1/2} \rho \sigma ^{1/2})^{1/2})\) is the fidelity. Thus if the conditional mutual information is small, A is only correlated to C through B up to a small error, in the sense that C can be approximately recovered given the information contained in B only (see Refs. [3,4,5]). More generally, we say \(\rho _{A_1, \ldots , A_n}\) is a quantum \(\varepsilon \)-approximate Markov chain if
1.1 The Hammersley–Clifford theorem
In this paper we will be interested in finding a structural characterization of quantum approximate Markov chains. Our motivation is a powerful result in statistics called the Hammersley–Clifford Theorem [6]. It states that Markov chains (and more generally Markov networksFootnote 3), in which all elements of the distribution are non-zero, are equivalent to the set of Gibbs (thermal) states of nearest-neighbor Hamiltonians on a 1D open spin chainFootnote 4:
for functions \(h_i : \mathbb {R}^{2} \rightarrow \mathbb {R}\), where
is the partition function. Here, the “temperature” is included in the interaction terms.
In Refs. [7, 8], the Hammersley–Clifford theorem was generalized to quantum Markov chains (and Markov networks): A full-rank quantum state \(\rho _{A_1 \ldots A_n}\) is a quantum Markov chain if, and only if, it can be written as
where \(Z={\mathrm {Tr}}(\exp (-\sum _i h_{i, i+1}))\) and each \(h_{i, i+1}\) only acts on subsystems \(A_iA_{i+1}\), such that \([h_{i, i+1}, h_{j, j+1}] = 0\) for all i, j. Therefore we have a characterization of full-rank quantum Markov chains as Gibbs states of 1D commuting short-range quantum Hamiltonians.Footnote 5 Conversely, this result also clarifies that correlations in Gibbs states of 1D commuting short-range Hamiltonians are always mediated through interactions between neighboring regions.
The characterization above only involves exact quantum Markov chains and a special set of short-range Hamiltonians. A natural question is whether there is a similar relation between quantum approximate Markov chains and more general quantum Gibbs states. The main result of this paper answers the question in the affirmative: we prove that quantum approximate Markov chains are equivalent to Gibbs states of 1D short-range quantum Hamiltonians, which we also call local Gibbs states in short.
Notation: In the following, we consider a quantum spin system \(\Lambda \) on a graph \(G=(V,E)\), where \(V=\{1,\ldots ,n\}\) and \(E=\{(i,i+1)\}_{i=1}^{n-1}\) for \(n\in {\mathbb {Z}}_{>0}\), i.e., a 1D open spin chain. Sometimes we also consider a closed chain by adding additional edge (n, 1). The Hilbert space of a local subsystem \(\mathcal {H}_i\) corresponding to spin i is associated to each \(i\in V\), which has finite dimension \(d<\infty \). For a subsystem specified by subregion \(X\subset V\) (we abuse the notation by using same X to denote both a subsystem and a subregion), we denote \(\mathcal {H}_X:=\bigotimes _{i\in X}\mathcal {H}_{i}\). The logarithm of \(\dim \mathcal {H}_{X}\) is simply denoted by |X|. We denote the operator norm of an operator O by \(\Vert O\Vert \), and the trace norm of O by \(\Vert O\Vert _1\). We say that the support of O is X if an operator O on \(\Lambda \) can be written as

i.e., the tensor product of some operator \(O_X\) on region X and the identity operator  acting on the complement of X (which we denoted by \(X^c\)). We will denote the support of an operator O by \(\text {supp}(O)\), unless explicitly mentioned.
acting on the complement of X (which we denoted by \(X^c\)). We will denote the support of an operator O by \(\text {supp}(O)\), unless explicitly mentioned.
A short-range Hamiltonian H is a bounded Hermitian operator on \(\mathcal {H}_\Lambda \) which can be decomposed into
where each \(\Vert h_i\Vert \) is bounded by a constant and \(\text {supp}(h_i)\) only contains spins within graph distance \(r<\infty \) from the spin i. We also consider a restricted Hamiltonian \(H_X\) on a region X, defined as
i.e., the sum of interactions acting on spins sitting inside of X. The Gibbs state \(\rho ^{H_X}\) of the Hamiltonian \(H_X\) at (inverse) temperature \(\beta >0\) is defined as
where \(Z_X={\mathrm {Tr}}[e^{-\beta H_X}]\). Note that we will omit \(\beta \) in the notations and simply denote \(\rho ^{H_X}\) and \(Z_X\), while they depend on \(\beta \). The reduced state of the Gibbs state on a subregion \(Y\subset X\) is denoted by \(\rho ^{H_X}_Y\).
Throughout the paper, we often consider a disjoint tripartition ABC of \(\Lambda \). We say B shields A from C if A and C are indirectly connected through B. We denote by d(A, C) the graph distance between A and C. \(d(A, C)=|B|\) if B shields A from C and is connected.
2 Results
In this section we present the main results of this paper. For two quantum states \(\rho , \sigma \), we denote their (quantum) relative entropy as
if \(\text {supp}(\rho )\subset \text {supp}(\sigma )\), and \(S(\rho \Vert \sigma ) :=+\infty \) otherwise (Here “\(\text {supp}(\rho )\)” means the subspace spanned by eigenvectors of \(\rho \) with nonzero eigenvalues).
2.1 Approximation of quantum approximate Markov states by local Gibbs states
Let us divide 1D spin chain \(\Lambda \) into m connected regions \(A_1A_2\ldots A_m\). We denote the coarse-grained 1D spin chain \(A_1A_2\ldots A_m\) by A. Our first result is the following theorem (see Sect. 3 for the proof):
Theorem 1
Let \(\rho _{A_1 \ldots A_m}\) be a quantum \(\varepsilon \)-approximate Markov chain on a 1D open chain for \(\varepsilon >0\). Then there exists a short-range Hamiltonian \(H = \sum _{i=1}^{m-1} h_{A_i, A_{i+1}}\) with \( \text {supp}(h_{A_i, A_{i+1}})=A_iA_{i+1}\), such that
where \(Z={\mathrm {Tr}}e^{-H}\).
From the relation
we find that the state \(\rho \) is also close in fidelity to a local Gibbs state. Note that Theorem 1 is not restricted to full-rank states.
It is natural to expect that there exists a similar bound for 1D closed chains. In this paper, we say a state \(\rho _{A_1\ldots A_m}\) is a quantum \(\varepsilon \)-approximate Markov chain on a 1D closed chain if
in analogy with a quantum Markov network.Footnote 6 Here, we imposed the periodic boundary condition on labels, e.g., \(m+1\equiv 1\). In this situation, the proof of Theorem 1 does not work straightforwardly. To solve this difficulty, we consider two sufficient conditions as assumptions which show the closeness to local Gibbs states respectively.
The first assumption is that the existence of the finite correlation length in terms of the quantum mutual information, which is obtained by replacing the Shannon entropy by the von Neumann entropy in Eq. (2). The second assumption is called the uniform Markov property [9] requiring that the reduced states of the state are also approximately Markov chains. Note that the second assumption may be derived from the definition of the quantum approximate Markov chains while we have not had any result on it.
Theorem 2
Let \(\rho _{A_1 \ldots A_m}\) be a quantum \(\varepsilon \)-approximate Markov chain on a 1D closed chain for \(\varepsilon >0\).
-
(i)
Assume that \(\rho _{A_1\ldots A_m}\) also satisfies
$$\begin{aligned} I(A_i:A\backslash A_{i-1}A_iA_{i+1})_\rho \le \varepsilon \,\,\forall i\in [1,m]. \end{aligned}$$Then there exists a short-range Hamiltonian \(H = \sum _{i} h_{A_{i-1},A_i, A_{i+1}}\), with \(\text {supp}(h_{A_{i-1},A_i, A_{i+1}})=A_{i-1}A_i A_{i+1}\), such that
$$\begin{aligned} S \left( \rho \left\| \frac{e^{-H}}{Z} \right. \right) \le \varepsilon m. \end{aligned}$$ -
(ii)
Assume that for any \(i\in [1,m]\), \({\mathrm {Tr}}_{A_i}(\rho _{A_1\ldots A_m})\) is a quantum \(\varepsilon \)-approximate Markov chain for the 1D open chain \(A_{i+1}A_{i+2}\ldots A_{i-1}\) (we used \(m+1\equiv 1\)). Then there exists a short-range Hamiltonian \(H = \sum _{i} h_{A_{i-1},A_i, A_{i+1}}\), with \(\text {supp}(h_{A_{i-1},A_i, A_{i+1}})=A_{i-1}A_i A_{i+1}\), such that
$$\begin{aligned} S \left( \rho \left\| \frac{e^{-H}}{Z} \right. \right) \le \varepsilon m. \end{aligned}$$
The approximate Markov property appears in analysis of gapped ground states of many-body systems (see e.g., Refs. [10, 11]). In these cases, the additional assumptions seem to be satisfied for certain choice of subsystems. Interestingly, there exists a class of states which are locally quantum approximate Markov chains but globally not. A simple example is the n-qubit GHZ state
on a spin chain (either open or closed). When we trace out one qubit from the chain, the reduced state exactly become a quantum Markov chain. However, this state has \(I(A:C|B)=1\) for any tripartition ABC of the whole system where B shields A from C. Therefore, it is not a quantum Markov chain globally. A similar situation arises when considering a ring-like regions in systems with topological order [12]. We show that for these cases, the value of the conditional mutual information for the whole system approximately represents the distance from the set of local Gibbs states. We will discuss an application of this result for analysis of entanglement spectrum in 2D topologically ordered phases in a complementary work [13].
Theorem 3
Consider a 1D spin chain \(X=X_1X_2\ldots X_m\) with the size \(N=|X_1\ldots X_m|\). Let \(\rho _{X_1\ldots X_m}\) be a state such that the reduced state obtained by tracing out \(X_i\) is a quantum \(\varepsilon \)-approximate Markov chain for all \(i\in [1, m]\). Define the set of Gibbs states of short-range Hamiltonians with interaction strength K as
Note that here we include the normalization factor in the Hamiltonians. Then, for \(K=\Theta (N)\) and sufficiently small \(\varepsilon >0\), there exists a constant \(c>0\) such that for any tripartition ABC of the whole system such that B shields A from C, it holds that
and
where \(\delta =8\sqrt{\varepsilon }+2^{-N}\).
Here we used \(X_i\) to label subsystems instead of \(A_i\) to avoid confusion with \(A\subset X\).
2.2 Quantum approximate Markov property of 1D Gibbs states
Our second main result is a kind of converse to Theorems 1 and 2. (see Sect. 4 for the proof):
Theorem 4
Let \(H = \sum _i h_i\) be a short-range 1D Hamiltonian with \(\Vert h_i \Vert \le 1\) and \(l_0, c, c'>0\) be universal constants. For an inverse temperature \(\beta > 0\) and any partition ABC with \(d(A, C)\ge l_0\), there exists a CPTP-map \(\Lambda _{B\rightarrow BC} : \mathcal {D}({{\mathcal {H}}}_B) \rightarrow \mathcal {D}({{\mathcal {H}}}_B \otimes {{\mathcal {H}}}_C)\) such that
where \(q(\beta ) = ce^{- c' \beta }\) if the correlation length of \(\rho ^{H_{ABC}}\) is \(\xi =e^{\mathcal {O}(\beta )}\).
The theorem above states that if we choose the region B sufficiently large, the Gibbs state can be approximately recovered from the partial trace over C by performing a recovery map on B. In turn, the statement implies the corresponding conditional mutual information decays similarly:
Corollary 5
Under the setting of Theorem 4,
Therefore, \(I(A:C|B)_\rho \le \mathcal {O}(e^{-\Theta (\sqrt{d(A,C)})})\) and thus any 1D local Gibbs state is a quantum approximate Markov chain with small \(\varepsilon \) after certain coarse-graining. Conversely, Theorem 1 shows that any quantum approximate Markov chain can be well-approximated by some 1D local Gibbs state. Therefore the combination of the two results can be regarded as a variant of the Hammersley–Clifford theorem for quantum approximate Markov chains. Below we discuss two implications of our results:
2.3 Saturation rate of area law for 1D Gibbs states
A Gibbs state of a short-range Hamiltonian obeys an area law in terms of the mutual information. For instance, for any Gibbs state \(\rho ^H\) of a short-range Hamiltonian on a lattice, it holds that [14]
where \(J>0\) is a constant only depending on the locality of H and the norm of the local interactions. The upper bound is a constant when the system is 1D.
The area law represented by Eq. (9) implies a decay of the conditional mutual information. Consider a 1D spin chain system and let A be a simply connected region. We divide \(A^c\) into \(\{b_i\}_i\) so that \(b_1\) shields \(b_2\) from A, \(b_2\) shields \(b_3\) from \(Ab_1\) and so on. We set \(B_l=b_1b_2\ldots b_l\). By the monotonicity of the mutual information under the partial trace, we have
Since the upper bound is independent of l, \(I(A:b_{l+1}|B_{l})_{\rho ^H}=I(A:B_{l+1})_{\rho ^H}-I(A:B_l)_{\rho ^H}\) eventually vanishes when l grows. Corollary 5 goes one step further and quantifies the rate at which \(I(A:B_l)_{\rho ^H}\) saturates when l grows. Indeed if each size of \(b_i\) and l are sufficiently large, we have
for some constants \(C, c > 0\). Therefore, the mutual information of a 1D local Gibbs state saturates the upper bound of the area law at least subexponentially fast in l.
2.4 A short depth representation of 1D Gibbs states
Theorem 4 ensures that there exist local CPTP-maps which approximately recover a 1D Gibbs state from tracing out operations on local regions. In other words, the Gibbs state can be prepared by local operations on reduced states on separated subregions (Fig. 1).
Corollary 6
A Gibbs state of any 1D short-range Hamiltonian at constant (inverse) temperature \(\beta >0\) can be well-approximated by a depth-two (mixed) circuit with each gate acting on \(O(\log ^2(n))\) qubits.
In more detail, there is a CPTP-map (corresponding to the circuit) of the form
with each local CPTP-map \(\Delta _{k, i}\) acting on \(O(e^{O(\beta )} \log ^2(n/\varepsilon ))\) sites, with \(\Delta _{k, i}\) and \(\Delta _{k, j}\) acting on non-overlapping sites for \(i \ne j\), such that
with \(\tau \) the maximally mixed state.
The proof is given in Sect. 4.4. An earlier result [15] proved that 1D Gibbs states of local Hamiltonians at finite constant temperature can be approximated by a matrix product operator of polynomial bond dimension, which implies they can be constructed efficiently on a quantum computer. However this result does not give that the state can be constructed by a short depth quantum circuit, as Corollary 6 shows. A similar construction methods appear in Refs. [16, 17] under certain assumptions on the approximate Markov property.
A schematic picture of the preparation algorithm for 1D Gibbs states. At the first step (upside), we perform CPTP-map \(\bigotimes _i\Delta _{1,i}\) on a product state (black dots). Each \(\Delta _{1,i}\) acts on a small set of spins (dotted circle) and produces the reduced state of the target Gibbs state on the set (connected dots). At the second step (downside), we perform another CPTP-map to concatenate these reduced states locally. Due to the approximate Markov property of the Gibbs state, the output state is close to the Gibbs state
3 Gibbs State Representations of 1D States with the Approximate Markov Property
In this section, we prove Theorems 1 and 2 which states that quantum approximate Markov chains can be approximated by 1D local Gibbs states. We also prove Theorem 3. In these proofs, a relationship between Gibbs states and the maximum entropy principle plays an important role. We first review the relationship and then turn to the proofs.
3.1 The maximum entropy state and Gibbs states
The maximum entropy principle, introduced by E. T. Jaynes in classical statistical mechanics [18, 19], is a method to choose an inference under partial information represented by some linear constraints. According to the maximum entropy principle, the most “unbiased” inference is given by the probability distribution with maximum entropy among all distributions satisfying the linear constraints. The solution of this optimization problem is given by a Gibbs distribution, as can be shown by the method of Lagrange multipliers.
This framework has been generalized to quantum systems (see, e.g., Refs. [20, 21]). Especially we are interested in the case where the linear constraints are given by reduced density matrices. Let \(\rho \) be a quantum state in \(\mathcal {D}(\mathcal {H}_1\otimes \cdots \otimes \mathcal {H}_n)\). Consider sets of subsystems labeled by \(X_1,\ldots ,X_m\) with \(X_i\subset \{1,\ldots ,n\}\) and let \(\mathbf{X}=\{X_1,\ldots ,X_m\}\). We define the set \(R_\rho (\mathbf{X})\) by
\(R_\rho (\mathbf{X})\) is the set of all states with the same reduced states as \(\rho \) for all \(X_i\). Since \(R_\rho (\mathbf{X})\) is a closed convex set, there exists a unique state such that
We call \(\sigma _{\max }\)the maximum entropy state in \(R_\rho (\mathbf X)\). Similar to the classical setting, \(\sigma _{\max }\) is given by a Gibbs state of a Hamiltonian with a specific structure. Let us consider the set of Gibbs states \(E(\mathbf{X})\) defined as
where \(\text {supp}(H_{X_i})=X_i\). For any \(\omega \in E(\mathbf{X})\), it is proven that the Pythagorean theorem
holds (Corollary 3.7 & Theorem 6.16, [20]). The maximum entropy state \(\sigma _{\max }\) is the unique element of the intersection of \(R_\rho (\mathbf{X})\) and \(\overline{E(\mathbf{X})}\): the closure of \(E(\mathbf{X})\) in the reverse-information topology [20] defined as
Therefore, the Pythagorean theorem (12) implies that
since \(\inf _{\omega \in {E(\mathbf{X})}}S(\sigma _{\max }\Vert \omega )=0\). By choosing \(\omega \) in Eq. (12) as the completely mixed state, which is always contained in \(E(\mathbf{X})\), we have
and therefore
We will use these formulas in the proof of theorems.
3.2 Proof of Theorem 1
We now prove:
Theorem 1
Let \(\rho _{A_1 \ldots A_m}\) be a quantum \(\varepsilon \)-approximate Markov chain on a 1D open chain for \(\varepsilon >0\). Then there exists a short-range Hamiltonian \(H = \sum _{i=1}^{m-1} h_{A_i, A_{i+1}}\) with \( \text {supp}(h_{A_i, A_{i+1}})=A_iA_{i+1}\), such that
Proof
Let \(\sigma _{A_1 \ldots A_m}\) be the maximum entropy state such that
for all \(i \in [1, m-1]\). We will show
The result then follows from Eq. (15), since \(\sigma _{A_1\ldots A_m}\) is an element of \(\overline{E(\mathbf{X})}\) for \(\mathbf{X}=\{A_iA_{i+1}\}_{i=1}^{m-1}\) which is a (closure of) set of local Gibbs states.
By strong subadditivity, we find
The last equality follows from Eq. (16). Since \(\rho _{A_1\ldots A_m}\) is a quantum \(\varepsilon \)-approximate Markov chain,
which can be rewritten as
i.e., the strong subadditivity is saturated up to error \(\varepsilon \). Therefore we obtain
where \(S(A|B)_\rho :=S(AB)_\rho -S(B)_\rho \) is the conditional entropy. Combining Eqs. (17) and (18) we have
Since \(\sigma _A\in \overline{E(\mathbf{X})}\), there exists a Gibbs state
which satisfies
Using the Pythagorean theorem, we obtain
which completes the proof. \(\quad \square \)
3.3 Proof of Theorem 2
Let us first restate the theorem:
Theorem 2
Let \(\rho _{A_1 \ldots A_m}\) be a quantum \(\varepsilon \)-approximate Markov chain on a 1D closed chain for \(\varepsilon >0\).
-
(i)
Assume that \(\rho _{A_1\ldots A_m}\) also satisfies
$$\begin{aligned} I(A_i:A\backslash A_{i-1}A_iA_{i+1})_\rho \le \varepsilon \,\,\forall i\in [1,m]. \end{aligned}$$Then there exists a short-range Hamiltonian \(H = \sum _{i} h_{A_{i-1},A_i, A_{i+1}}\), with \(\text {supp}(h_{A_{i-1},A_i, A_{i+1}})=A_{i-1}A_i A_{i+1}\), such that
$$\begin{aligned} S \left( \rho \left\| \frac{e^{-H}}{Z} \right. \right) \le \varepsilon m. \end{aligned}$$ -
(ii)
Assume that for any \(i\in [1,m]\), \({\mathrm {Tr}}_{A_i}(\rho _{A_1\ldots A_m})\) is a quantum \(\varepsilon \)-approximate Markov chain for the 1D open chain \(A_{i+1}A_{i+2}\ldots A_{i-1}\) (we used \(m+1\equiv 1\)). Then there exists a short-range Hamiltonian \(H = \sum _{i} h_{A_{i-1},A_i, A_{i+1}}\), with \(\text {supp}(h_{A_{i-1},A_i, A_{i+1}})=A_{i-1}A_i A_{i+1}\), such that
$$\begin{aligned} S \left( \rho \left\| \frac{e^{-H}}{Z} \right. \right) \le \varepsilon m. \end{aligned}$$
Proof
Theorem 2(i) can be shown in the following way. Let \(\sigma _{A_1 \ldots A_m}\) be the maximum entropy state such that
for all \(i \in [1, m]\) (with the periodic boundary condition). As in the previous section, we recursively use the strong subadditivity and obtain
where we used subadditivity \(S(A_iA_j)\le S(A_i)+S(A_j)\) in the second inequality. From the additional assumption on the mutual information,
By using this type of inequalities, we obtain that
Since \(\rho _{A_1\ldots A_n}\) is a quantum \(\varepsilon \)-approximate Markov chain on a closed chain, one can further show that
The rest part of the proof is the same as the proof of Theorem 1.
To prove Theorem 2(ii), we use the strong subadditivity to the maximum entropy state \(\sigma _{A_1\ldots A_m}\) to obtain:
Recall that \(\rho _{A_2\ldots A_m}\) is a quantum \(\varepsilon \)-approximate Markov chain by assumption. Therefore, we have
from which we complete the proof in the same way as in the proof of Theorem 1. \(\quad \square \)
3.4 Proof of Theorem 3
Finally, we prove Theorem 3:
Theorem 3
Consider a 1D spin chain \(X=X_1X_2\ldots X_m\) with the size \(N=|X_1\ldots X_m|\). Let \(\rho _{X_1\ldots X_m}\) be a state such that the reduced state obtained by tracing out \(X_i\) is a quantum \(\varepsilon \)-approximate Markov chain for all \(i\in [1, m]\). Define the set of Gibbs states of short-range Hamiltonians with interaction strength K as
Then, for \(K=\Theta (N)\) and sufficiently small \(\varepsilon >0\), there exists a constant \(c>0\) such that for any tripartition ABC of the whole system such that B shields A from C, it holds that
and
where \(\delta =8\sqrt{\varepsilon }+2^{-N}\).
The strategy of the proof is as follows. We first construct a global state \({\tilde{\rho }}'_{ABC}\) on ABC from a reduced state of \(\rho _{ABC}\) by using recovery maps. We then introduce \({\tilde{\rho }}_{ABC}\), a modification of \({\tilde{\rho }}'_{ABC}\) and define a Gibbs state of a nearest-neighbor Hamiltonian \({\tilde{\pi }}_{ABC}\) from its reduced states. Finally we show that this Gibbs state is almost the closest state in the set of Gibbs states of bounded nearest-neighbor Hamilntonians.
Proof
Without loss of generality, we consider a system defined on a 1D closed spin chain, e.g., \(X_1\equiv X_{m+1}\), and assume that \(|X_1|=\max _i|X_i|\). Let \(A\equiv X_1\), \(B_1\equiv X_mX_2\), \(B_2\equiv X_{m-1}X_3\) and \(C\equiv X_4X_5\ldots X_{m-2}\). In the following, we use both notations \(X_1\ldots X_m\) and ABC interchangeably. Note that if we choose another tripartition \(A^{\prime }{}B^{\prime }{}C^{\prime }{}\) satisfying the condition instead of ABC, the chain rule of the conditional mutual information:
and the assumption imply that
From the results in Ref. [2], there exist CPTP maps called (approximate) recovery maps such that
where we omitted the identity maps for simplicity. By using these maps, we define a global state
Since the CPTP-maps recover reduced states with good accuracy, \(\rho _{ABC}^{\prime }{}\) has almost same bipartite marginals on, e.g., AB.
The first inequality follows from the triangle inequality of the trace norm, and the second inequality follows from the monotonicity of the trace-norm under \({\mathrm {Tr}}_C\). The same bound holds for marginals on BC as well. Equations (20) and (22) imply that \({\tilde{\rho }}_{ABC}^{\prime }{}\) is approximately recoverable state:
For two quantum states \(\rho _{AB}, \sigma _{AB}\) satisfying \(\Vert \rho _{AB}-\sigma _{AB}\Vert _1<\delta \le 1\), the (Alicki-)Fannes inequality [22]
holds with the binary entropy \(h_2(\delta )=H(p=\{\delta ,1-\delta \})\). This inequality and Eq. (23) yields
where we denote \({\tilde{\rho }}''_{ABC}:=\Lambda _{B_2\rightarrow B_2C}({\tilde{\rho }}_{AB}^{\prime }{})\) in the second line which follows from the data processing inequality for \(\Lambda _{B_2 \rightarrow B_2C}\). Therefore, \({\tilde{\rho }}_{ABC}'\) is a quantum approximate Markov chain for small \(\varepsilon >0\).
Next, define a full-rank modification of \({\tilde{\rho }}_{ABC}^{\prime }{}\), that is,
where \(\tau _{ABC}\) is the completely mixed state on ABC (recall that N represents the logarithm of the total dimension). Since by definition
the Fannes inequality implies that
Therefore \({\tilde{\rho }}_{ABC}\) is still an approximate Markov chain for large N.
Then, we construct a Gibbs state \({\tilde{\pi }}_X\)
from the reduced states of \({\tilde{\rho }}_{ABC}\), where Z is the normalizer and
\({\tilde{\pi }}_X\) is an element of \(E^K_{nn}\) with \(K=\Theta (N)\). In the following, we show that \({\tilde{\pi }}\) is close to \({\tilde{\rho }}\).
By definition of \(H_X^{\tilde{\rho }}\), it holds that
Note that \(\sum _{i=1}^mS(X_{i}|X_{i+1})_{{\tilde{\rho }}}=\sum _{i=1}^mS(X_{i+1}|X_{i})_{{\tilde{\rho }}}\) by \(X_{m+1}=X_1\). By an iterative calculation, we have
By using the subadditivity \(S(X_2X_m)\le S(X_2)+S(X_m)\), we obtain that
Therefore, we have
where we used the chain rule (19). The first three terms only depend on marginals of \({\tilde{\rho }}_{ABC}\) on AB or BC. Since \({\tilde{\rho }}_{ABC}\) is close to \({\tilde{\rho }}'_{ABC}\) (25), \({\tilde{\rho }}_{ABC}\) also has marginals close to \(\rho _{ABC}\) on these regions:
Thus, as in Eq. (26), the Fannes inequality implies that
Combining with Eq. (27), we obtain
where we used \(m|X_1|=\Theta (N)\) and the asymptotic notation \(\mathcal {O}(f(N,\varepsilon ))\) as \(N\rightarrow \infty \) and \(\varepsilon \rightarrow 0\) (and therefore \(\delta \rightarrow 0\)).
Let us estimate the partition function \(Z={\mathrm {Tr}}e^{-H^{{\tilde{\rho }}}_X}\). By Pinsker inequality, the above bound implies
where we used the inequality \(\left| \Vert A\Vert _1-\Vert B\Vert _1\right| \le \Vert A-B\Vert _1\). For given N, we assume \(\delta \) is sufficiently small so that Eq. (31) is smaller than 1. We then obtain
Thus, the difference between \({\tilde{\rho }}_X\) and \({\tilde{\pi }}_X\) is bounded as
Again, by the Fannes inequality, the conditional mutual information of \({\tilde{\pi }}_X\) is bounded as
The marginal of \({\tilde{\pi }}\) on AB satisfy
Here, we used Eqs. (22), (25) and (32) in the second inequality. In the same way, we also obtain
Finally, we show that \(I(A:C|B)_\rho \) approximates the distance between \(\rho \) and the set of Gibbs states \(E_{nn}^K\) in terms of the relative entropy. By combining Eqs. (33) and (34) with the Fannes inequality, we have that
By definition, it holds that
Here, \(\log \mu \propto H_{AB}+H_{BC}\) for some bounded Hermitian operators \(H_{AB}\) and \(H_{BC}\) satisfying \(\Vert H_{AB}\Vert +\Vert H_{BC}\Vert \le \mathcal {O}(mK)\). Equations (33) and (34) yield that
for \(Y=AB,BC\). Therefore, we can approximate \({\mathrm {Tr}}(\rho \log \mu )\) by \({\mathrm {Tr}}({\tilde{\pi }}\log \mu )\), and we have
where we used \(mK=\Theta (N^2)\) and Eq. (35) in the secondline. The third inequality follows from Eq. (35) and the last line follows from \({\tilde{\pi }}\in E_{nn}^K\). \(\quad \square \)
4 1D Quantum Gibbs states are Quantum Approximate Markov Chain
In this section, we provide a proof of Theorem 4, Corollaries 5 and 6. A key point of the proof is that if a short-range Hamiltonian changes locally, the corresponding Gibbs state also changes quasi-locally. To obtain operators representing changes of the Gibbs state, we employ quantum belief propagation equations which have been studied in Refs. [23, 24]. We first introduce these technical tools, and then show the proofs. We discuss another approach to prove Theorem 4 based on the results of Ref. [25] in Appendix A.
4.1 Perturbative analysis of Gibbs states
Let us consider an one-parameter family of a Hamiltonian H on a spin lattice with a perturbation operator V
where \(s\in [0,1]\). The change of the corresponding Gibbs state due to a small change of s can be computed through a quantum belief propagation equation [23, 24]:
where the operator \(\Phi _\beta ^{H(s)}(V)\) is given by [24]
in the energy eigenbasis of \(H(s)=\sum _iE_i(s)|i\rangle \langle i|\),Footnote 7 with \({{\tilde{f}}}_\beta (\omega )=\frac{\mathrm{tanh}(\beta \omega /2)}{\beta \omega /2}\). Using the Fourier transform \(f_\beta (t)=\frac{1}{2\pi }\int d\omega {{\tilde{f}}}_\beta (\omega )e^{i\omega t}\), \(\Phi _\beta ^{H(s)}(V)\) can be written as the integral form:
Taking the formal integration of Eq. (38), we obtain
where the operator O is defined as
with \({{\mathcal {T}}}\) the time-ordering operation. Since we have \(dtf_\beta (t)=\frac{dt}{\beta }f_1(\frac{t}{\beta })\), it holds that
The integral in the last equality can be calculated through the series expansion:
The upper bound of \(\Vert \Phi _\beta ^{H(s)}(V)\Vert \) implies the upper bound of \(\Vert O\Vert \) that is given by
When the Hamiltonian defined on a many-body system is short-ranged, time-evolutions of a local operator is restricted by using the Lieb-Robinson bound [26]. Suppose that H is a Hamiltonian obeying the Lieb-Robinson bound, and \(O_A\) and \(O_B\) are observables supported on local regions A and B, respectively. Then, the Lieb-Robinson bound for these operators is formulated as
where \(c,v\ge 0\), \(c^{\prime }{}>0\) are constants. Assume that H(0) is a short-range Hamiltonian and supp(V) is a simply-connected local region. Then H(s) obeys the Lieb-Robinson bound for all \(s\in [0,1]\). Since \(f_\beta (t)\) decays fast in |t|, the Lieb-Robinson bound implies that the effective support of \(\Phi _\beta ^{H(s)}(V)\) can be restricted to a local region \(\mathcal {V}_l\), which contains all sites within distance l from supp(V). More precisely, there exist positive constants \(c^{\prime }{} \) and v, which is determined by H(s), such that [24]

where \(d_{\mathcal {V}_l^c}:=\dim \mathcal {H}_{\mathcal {V}_l^c}\). We also define the integral of the restricted operator in Eq. (46) as

This operator is also localized on \(\mathcal {V}_l\) and approximates O with good accuracy. Let us choose \(c^{\prime }{}\) and v so that Eq. (46) holds for all \(s\in [0,1]\). Then, we obtain that
To see this, consider some parametrized operators Q(s) and \({{\tilde{Q}}}(s)\) satisfying \(\Vert Q(s)\Vert ,\Vert {{\tilde{Q}}}(s)\Vert \le C\) and \(\Vert Q(s)-{{\tilde{Q}}}(s)\Vert \le \Delta \) for all \(s\in [0,1]\). From the simple calculation, we obtain
where \(\Delta _j=Q(s_j)-{{\tilde{Q}}}(s_j)\) and \(\Vert \Delta _j\Vert \le \Delta \). Therefore, we obtain that
In our case, \(Q(s)=\Phi _\beta ^{H(s)}(V)\) and  . We can choose \(\Delta =c^{\prime }{}e^{-\frac{c^{\prime }{}l}{1+c^{\prime }{}v\beta /\pi }}\Vert V\Vert \). From Eqs. (42) and (46), their norms can be bounded as
. We can choose \(\Delta =c^{\prime }{}e^{-\frac{c^{\prime }{}l}{1+c^{\prime }{}v\beta /\pi }}\Vert V\Vert \). From Eqs. (42) and (46), their norms can be bounded as
Therefore, Eq. (49) holds for \(C=(1+c^{\prime }{})\Vert V\Vert \). By inserting Eq. (49) to the definition of O, we obtain Eq. (48).
4.2 Proof of Theorem 4
For the convenience of the reader, we restate Theorem 4 below.
Theorem 4
Let \(H = \sum _i h_i\) be a short-range 1D Hamiltonian with \(\Vert h_i \Vert \le 1\) and \(l_0, C, c>0\) be universal constants. For an inverse temperature \(\beta > 0\) and any partition ABC with \(d(A, C)\ge l_0\), there exists a CPTP-map \(\Lambda _{B\rightarrow BC} : \mathcal {D}({{\mathcal {H}}}_B) \rightarrow \mathcal {D}({{\mathcal {H}}}_B \otimes {{\mathcal {H}}}_C)\) such that
where \(q(\beta ) = ce^{- c' \beta }\) if the correlation length of \(\rho ^{H_{ABC}}\) is \(\xi =e^{(\mathcal {O}(\beta )}\).
The proof of Theorem 4 consists of three steps. In the first step, we show that there exists a CP-map which recovers the Gibbs state from the reduced state with exponentially good accuracy (Lemma 7). In the second, we normalize the CP-map to make it trace non-increasing i.e. we show the existence of a quantum operation which succeed to recover the Gibbs state with some probability (Lemma 9). We also show that the success probability is a constant of system size. Finally, we construct a CPTP-map from the probabilistic operation by employing a repeat-until-success strategy in the third step.
Let us begin with the following lemma.
Lemma 7
For any 1D Gibbs state \(\rho ^{H_{ABC}}\) of a short-range Hamiltonian on a system with a partition ABC such that \(l:=d(A,C)/2>r\), there exists a CP map \(\kappa _{B\rightarrow BC}\), non-negative constants \(c^{\prime }{}\) and v such that
where \(C_1(\beta )\) is a non-negative constant and \(q_1(\beta )=\frac{c^{\prime }{}}{1+c^{\prime }{}v\beta /\pi }\), as defined in Eq. (46).
Proof
Let us consider a short-range Hamiltonian \(H=\sum _{i}h_{i}\) with the range r. Without loss of generality, we introduce a tripartition ABC of a 1D system so that each subsystem is simply connected and d(A, C) is chosen to be 2l for some integer \(l>r\). We then split region B into the left half \(B^L\), which touches A, and the right half \(B^R\) which touches C (Fig. 2). We denote the sum of the all interactions \(h_{i}\) acting on both \(B^L\) and \(B^R\) by \(H_{B^M}=\sum _{j:i\in {\mathrm{supp}}(h_j)}h_{j}\). By assumption, \(\Vert H_{B^M}\Vert \le J\) for some constant \(J\ge 0\).
Remark 8
When B consists of a fixed number of simply connected regions, each connected component neighboring both A and C is divided into two halves as in the same way. Then, \(H_{B^M}\) is the sum of all interaction terms acting on both such divided regions.
We apply the technical tools discussed in the previous section to a parametrized Hamiltonian \(H_{ABC}(s)=H_{AB^L}+H_{B^RC}+sH_{B^M}\). Here, \(H_{B^M}\) corresponds to the perturbation operator V in the previous section. Then, we introduce an operator \(O_{ABC}\) defined as
Equations (41) implies that
We also introduce the inverse operator \({\tilde{O}}_{ABC}\), that is given by
where \({\bar{{\mathcal {T}}}}\) denotes the inverse time-ordering operator. \(O_{ABC}\) and \({\tilde{O}}_{ABC}\) satisfies the following relation (see e.g., [27])

From Eq. (44), the operator norms of \(O_{ABC}\) and \({\tilde{O}}_{ABC}\) can be bounded as
Importantly, the upper bound is independent of size of A, B and C. From the definitions of \(O_{ABC}\) and its inverse, it is not difficult to see that
From Eq. (48), we know that there exist operators \(O_B\) and \({\tilde{O}}_B\) whose supports are restricted on B. For simplicity, let us denote
Then, \(O_B\) and \({\tilde{O}}_B\) satisfy
where \(q_1(\beta )=\frac{c^{\prime }{}}{1+c^{\prime }{}v\beta /\pi }\) for non-negative constants \(c^{\prime }{}\) and v which are chosen as in Eq. (48). Then, the operator norm of the local operators \(O_B\) and \({\tilde{O}}_B\) can be bounded by
which is independent of the size of B. Let \({{\tilde{O}}}_{B|B}\) be the non-trivial part of \({{\tilde{O}}}_B\) acting on B, i.e.,

By using this notation, we define a CP-map \(\kappa _{B\rightarrow BC}\) by replacing \(O_{ABC}({\tilde{O}}_{ABC})\) by local operators \(O_B({\tilde{O}}_B)\) and removing partial trace over C in Eq. (51), i.e.,
Let us denote
and
We have
We used the monotonicity of the trace-norm in the last inequality. To address the calculation, we use the following spacial case of the H\(\ddot{\mathrm{o}}\)lder’s inequality:
It implies that
The first and second lines follow from Eq. (56) and \(\Vert \rho ^{H_{ABC}}\Vert _1=1\). In the last line, we used Eqs. (52) and (53).
By using the above bound, we bound the difference between the original Gibbs state \(\rho ^{H_{ABC}}\) and \(\kappa _{B\rightarrow BC}(\rho ^{H_{ABC}}_{AB})\) as
Here we used the fact that \(\Vert X_1\Vert _1\le \Vert \rho ^{H_{ABC}}\Vert _1\Vert {\tilde{O}}_{ABC}\Vert ^2=\Vert {\tilde{O}}_{ABC}\Vert ^2\) in the fourth line. Choosing \(C_1(\beta )=4K(\beta )\left( e^{\frac{\beta J}{2}}+K(\beta )\right) ^3\) completes the proof. \(\quad \square \)
Unfortunately, the map \(\kappa _{B\rightarrow BC}\) is not a trace non-increasing map in general. Thus, we normalize \(\kappa _{B\rightarrow BC}\) to obtain a CP and trace non-increasing map, which corresponds to a probabilistic process.
Lemma 9
Under the setting of Lemma 7, there exists a CP and trace non-increasing map \({\tilde{\Lambda }}_{B\rightarrow BC}\) for any \(l\ge l_0(\beta )\equiv \left\lceil \frac{\log C_1(\beta )+1}{q_1(\beta )}\right\rceil =\mathcal {O}(\beta ^2)\) such that
where \(C_2(\beta )=\frac{2C_1(\beta )}{(1-e^{-1})}\). Moreover, \(p={\mathrm {Tr}}[{\tilde{\Lambda }}_{B\rightarrow BC}(\rho ^{H_{ABC}}_{AB})]\) is a strictly positive constant which is independent of the size of subsystems A, B and C.
Proof
We denote the maximum eigenvalue of \(O_B^\dagger O_B\) (\({\tilde{O}}_B^\dagger {\tilde{O}}_B\)) by \(\lambda _{\max }^{O_B}\) (\(\lambda _{\max }^{{\tilde{O}}_B}\)). From Eq. (53)and inequality \(\Vert A^\dagger A\Vert \le \Vert A\Vert ^2\), these eigenvalues are bounded as
Define \(\lambda _{\max }:=\lambda _{\max }^{O_B}\lambda _{\max }^{{\tilde{O}}_B}\). Then, we define the normalized map \({\tilde{\Lambda }}_{B\rightarrow BC}\) as
By definition, \({\tilde{\Lambda }}_{B\rightarrow BC}\) is CP and trace non-increasing. After the normalization, the output state for the input \(\rho ^{H_{ABC}}_{AB}\) is
Let us introduce \(l_0(\beta )=\frac{\ln C_1(\beta )+1}{q_1(\beta )}\). For any \(l\ge l_0(\beta )\), \(C_1(\beta )e^{-q_1(\beta )l}\le e^{-1}<1\). For such l, the probability p for the input \(\rho ^{H_{ABC}}_{AB}\) is then estimated as
where we used Eq. (58) in the line before the last.
The approximation error of the output is then estimated as
In the third line, we used the fact
which follows from
Thus, we conclude that Lemma 9 holds by choosing \(C_2(\beta )=\frac{2C_1(\beta )}{1-e^{-1}}\). \(\quad \square \)
We are now in position to prove Theorem 1. Without loss of generality, let us assume that \(d(A,C)=|B|=3l^2-l\) for \(l\in {{\mathbb {N}}}\). We divide B into \(B=B_l{{\bar{B}}}_{l-1}B_{l-1}\ldots {{\bar{B}}}_1B_1\) as shown in Fig. 3, where for each i, \(|B_i|=2l\) and \(|{{\bar{B}}_i}|=l\). From Lemma 9, there exists a CP and trace non-increasing map \({\tilde{\Lambda }}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\) for each i which approximately recovers \(\rho ^{H_{ABC}}\) from the reduced state on \(AB_l\ldots {{\bar{B}}}_iB_i\) (here, we choose \(B_i\) as “B” and \(B_{i-1}\ldots B_1C\) as “C” in the lemma). We then introduce a CP and trace non-increasing map \({\tilde{E}}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\) for each \({\tilde{\Lambda }}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\) so that \(\{{\tilde{\Lambda }}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}, {\tilde{E}}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\}\) forms a quantum instrument.Footnote 8 We simply denote \({\tilde{\Lambda }}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\) by \({\tilde{\Lambda }}_i\) and its complementary map \({\tilde{E}}_{B_i\rightarrow B_i{{\bar{B}}_{i-1}}\ldots B_1C}\) by \({\tilde{E}}_i\). We also denote the tracing operation over \({{\bar{B}}_i}B_i\ldots B_1C\) by \({\mathrm {Tr}}_i\). We define a CPTP-map \(\Lambda _{B\rightarrow BC}\) as
based on the repeat-until-success method (Fig. 3).
A schematic picture of the repeat-until-success method. We introduced buffer systems \(\{{{\bar{B}}}_i\}\) to suppress the effect of failure. The “failure” output at the end corresponds to the CP-map \({\tilde{E}}_l\circ {\mathrm {Tr}}_{l-1}{\tilde{E}}_{l-1}\cdots \circ {\mathrm {Tr}}_1{\tilde{E}}_1\)
When we input \(\rho ^{H_{ABC}}_{AB}\) to \(\Lambda _{B\rightarrow BC}\), the output of each map \({\tilde{\Lambda }}_i\) corresponds to the success of the recovery process at the ith step (with probability \(p_i\)) and \({\tilde{E}}_i\) corresponds to the failure of the recovery process (with probability \(1-p_i\)). If it fails, we trace out both the recovered system and the “buffer” system \({{\bar{B}}}_i\), and then, the effect of the failure can be almost neglected. Thus, we can repeat the probabilistic process to obtain the success outcome. The effect of the failure is estimated by the following lemma, which utilizes the exponential decay of correlation of 1D Gibbs states [25].
Lemma 10
Under the setting of Lemma 7, there exists a constant \(\xi \ge 0\) such that
Proof
Define a correlation function \(\mathrm{Cor}(X:Y)_\rho \) of regions X and Y by
Consider some CP and trace-decreasing map  . By lemma 9 of Ref. [28], it holds that
. By lemma 9 of Ref. [28], it holds that
where \(M_Y=\sum _iE_i^\dagger E_i\) and
It has been shown that any 1D Gibbs states with a short-range Hamiltonian have exponentially decaying \(\mathrm{Cor}(X:Y)_\rho \) [25], i.e., there exist constants \(c,\xi \ge 0\) such that
Choosing \(X=AB_l\ldots B_{i+1}\), \(Y=B_i\), \(Z=B_i\ldots B_1C\) and \({{\mathcal {E}}}_{Y\rightarrow Z}={\tilde{E}}_i\) prove Lemma 10. \(\quad \square \)
Without loss of generality, let us assume
for all i.Footnote 9 Lemma 10 allows an iterative calculation. First we have
Here, we used Lemma 10 for \({\mathrm {Tr}}_1{\tilde{E}}_1(\rho _{AB}^{H_{ABC}})\) and \(\rho _{AB_l\ldots B_2}^{H_{ABC}}\). Then we can obtain
We can proceed in a similar way, where at each ith step, we replace \({\mathrm {Tr}}_i{\tilde{E}}_i(\rho _{AB}^{H_{ABC}})\) by \({\mathrm {Tr}}_i(\rho ^{H_{ABC}})\) by using the triangle inequality. After iterating \(l-1\) steps, we obtain
Since \(\left( \sum _{i=1}^{l}p(1-p)^{i-1}\right) +(1-p)^l=1\), it follows
and thus
Therefore, by combining Eqs. (62) and (63), we conclude
Here, the probability p can be bounded as in Eq. (59), and thus we have
where the last inequality follows from \(\log (1-x)\le -x\) for any \(x\in [0,1]\). If \(\xi = e^{\mathcal {O}(\beta )}\), Eq. (64) can be bounded by
where \(q^{\prime }{}(\beta )=\Omega ( e^{-\Theta (\beta )})\). Since \(d(A,C)=3l^2-l\), Eq. (65) is \(\Theta (e^{-\Theta (\sqrt{d(A,C)})})\). Therefore, for sufficiently large l, there exists a constant \(q(\beta )=\Omega ( e^{-\Theta (\beta )})\) such that \(e^{-q^{\prime }{}(\beta )l+\ln (2C_2(\beta )l)}\le e^{-q(\beta )\sqrt{d(A,C)}}\).
4.3 Proof of Corollary 5
Proof
Let us first consider a 1D open spin chain with a tripartition ABC so that a simply connected region B shields A from C. Then, \(d(A,C)=|B|\). Without loss of generality, we assume \(|A|\le |B|\le |C|\). Divide C into \(C=C_1\cup C_2\cup \ldots \cup C_m\), where m is the maximum number such that \(|C_i|=|B|\) for \(1\le i< m\) and each \(C_i\) shields \(C_{i-1}\) from \(C_{i+1}\) (here, \(C_0\equiv B\)).
Theorem 4 and the Fannes inequality imply
with a constant \(q(\beta )\ge 0\) for any \(i\in [1, m]\) and sufficiently large |B|. By the chain rule
we have
Again, the upper bound is \(e^{-\Theta (\sqrt{d(A,C)})}\). The same strategy works for a more complicated tripartition ABC of both 1D open chains and closed chains. \(\quad \square \)
4.4 Proof of Corollary 6
Proof
Let us consider 1D open spin chain without loss of generality. We first divide the whole chain into consecutive regions \(A_1B_1C_1A_2B_2C_2{\ldots } A_kB_kC_k\), where we choose \(|A_i|=|B_j|=l\ge l_0\) and \(|C_i|=5\xi (\ln d) l\) for all i, where \(l_0\) is the constant given in Theorem 4, the correlation length \(\xi \) is given in Eq. (61) and d is a constant bounding the dimension of the Hilbert space of one spin from above. Let us consider region \((A_1B_1C_1\ldots C_{i-1}A_iB_{i+1})(B_iA_{i+1})C_i\), where \(B_iA_{i+1}\) shields \(A_1B_1\ldots B_{i+1}\) from \(C_i\). From Theorem 4, there exists a CPTP-map \(\delta _i:\mathcal {D}(\mathcal {H}_{B_iA_{i+1}})\rightarrow \mathcal {D}(\mathcal {H}_{B_iC_iA_{i+1}})\) such that
Since the Gibbs state has exponentially decaying correlations, after tracing out \(C_i\), the two remained connected components are almost uncorrelated. By using Lemma 20 of Ref. [28], it follows that
Each \(\Delta _i\) acts on different sets of spins and therefore does not overlap. Then we have
The first inequality follows from the triangle inequality, the second from the monotonicity of the trace norm under quantum operations, the third from Eq. (67), and the fourth from Eq. (66) and \(e^{-(\ln d)l}\le e^{- q(\beta )\sqrt{l}}\) for large l.
Iterating the argument above, we find
Since \(k \le n\), choosing \(l = \mathcal {O}(\log ^2(n/\varepsilon ))\) gives an error bounded by \(\varepsilon \). We denote a CPTP-map which construct \(\rho _{A_iB_i}\) by \(\Delta _{1,i}\) and relabel \(\Delta _i\) in the above by \(\Delta _{2,i}\). The CPTP-map \(\bigotimes _i\Delta _{1,i}\) creates product state of the form of \(\rho _{A_1B_1}\otimes \rho _{A_2B_2}\otimes \cdots \otimes \rho _{A_kB_k}\), and then \(\bigotimes _i\Delta _{2, i}\) approximately creates the target state from this product state. \(\quad \square \)
5 Extension to More General Graphs and a Conjecture for Higher Dimension
Our proof for 1D spin chains can be generalized to more general graphs with appropriate partitions. For instance, let us consider a tree graph \(G=(E, V)\) with a partition ABC as depicted in Fig. 4. Since G is a tree, there is a unique path connecting A and C. Then, all spins in B are classified as (i) spins belonging to the path (ii) descendants of spins on the path (iii) the rest spins which are separated from the path. We can obtain a coarse grained 1D chain by regarding each spin on the path and its descendants as one system, and removing all spins in (iii). Therefore, we can apply the proof in the previous section to this situation as well. Note that the norm of an interaction term connecting spins on the path is irrelevant to the size of the coarse grained spins.
An important point of the above argument is that the success probability of the recovery map in lemma 9 is bounded by a constant of d(A, C). In general cases, we can consider a partition ABC which cannot be reduced to 1D systems, such as depicted in Fig. 5. Remember that the success probability p is in the order \(\Omega (e^{\beta \Vert H_{B^M}\Vert })\). In the case of Fig. 5, \(H_{B^M}\) is the sum of all interactions along the perimeter of \(B^L\), which is proportional to l. When considering the repeat-until-success method, the success probability decays too rapidly, and therefore our strategy does not work.
The quantum Hammersley–Clifford theorem holds for more general class of Markov networks such as regular D-dimensional lattices. In this case, a partition ABC of the system is chosen so that B shields A from C (Fig. 5). Due to this observation, we expect that Gibbs states of short-ranged Hamiltonians obey fast decay of the conditional mutual information in D-dimensional systems as well. We have the following conjecture:
Conjecture 1
Let \(\rho \) be a Gibbs state of a short-ranged Hamiltonian defined on a D-dimensional spin lattice. Then, there exist constants \(C, c>0\) such that for every three regions A, B, C with B shielding A from C,
Note that when \(D=1\), this conjecture gives an improved bound. It turns out that the area law for mutual information implies a weak version of the conjecture, as discussed in Sect. 2.3. Consider a Gibbs state in the infinite volume limit (as a KMS state). Let A be a region of the lattice and \(B_l\) be a ring around A of width l. Then, because of the area law [14], for every \(\varepsilon >0\) there is an integer l s.t.
which can be written as
with \(C := B_{l+1} \backslash B_{l}\).
We can also ask whether Theorem 1 can be extended to higher dimensions, i.e. is any state on a D-dim lattice with small I(A : C|B) for B shielding A from C close to thermal? As displayed in Theorem 2, we may need additional conditions for general graphs. Although we do not know any counter-example, we also could not find any partial result whether the additional conditions in those theorems are necessary.
Notes
In the following we always use 2 as the base of log.
\({{\mathcal {D}}}({{\mathcal {H}}}_{A_1} \otimes \cdots \otimes {{\mathcal {H}}}_{A_n})\) is the set of density matrices over the finite-dimensional Hilbert space \({{\mathcal {H}}}_{A_1} \otimes \cdots \otimes {{\mathcal {H}}}_{A_n}\).
A Markov network is a generalization of a Markov chain given by random variables \(X_{1}, \ldots , X_{n}\) defined on the vertices \(1, \ldots , n\in V\) of a graph \(G=(V,E)\), such that \(X_{i}\) is uncorrelated from all other random variables conditioned on the random variables \(\{ X_{j} \}_{(i,j)\in E }\) associated to neighboring vertices.
For Markov networks, in turn, the Hamiltonian is a sum of local functions of variables on all cliques of the graph.
In Ref. [8] a more general result was shown for quantum Markov networks. In contrast to the classical case, positive (i.e. full-rank) quantum Markov networks are only equivalent to Gibbs states of commuting Hamiltonians with terms on the cliques of the graph if the graph is triangle free.
Any quantum \(\varepsilon \)-approximate Markov chain \(\rho _{A_1\ldots A_m}\) satisfies \(I(A_i: A\backslash A_{i-1}A_iA_{i+1} | A_{i-1}A_{i+1})_\rho \le 2\varepsilon \) for all \(i \in [3,m-2]\).
Each \(|i\rangle \) depends on s as well as the eigenvalues \(E_i(s)\).
For instance, \({\tilde{E}}_{B \rightarrow BC}\) can be chosen to be
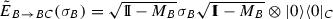 , where
, where 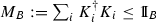 with \(\{K_i\}\) the Kraus operators of \({\tilde{\Lambda }}_{B\rightarrow BC}\).
with \(\{K_i\}\) the Kraus operators of \({\tilde{\Lambda }}_{B\rightarrow BC}\).Otherwise, we just pick the smallest p among \(p_i,i=1,\ldots ,l\) and redefine \({\tilde{\Lambda }}_i\) to be \(\frac{p}{p_i}{\tilde{\Lambda }}_i\) and \({\tilde{E}}_i\) to be \({\tilde{E}}_i+(1-\frac{p}{p_i}){\tilde{\Lambda }}_i\).
References
Ibinson, B., Linden, N., Winter, A.: Robustness of quantum markov chains. Commun. Math. Phys. 277(2), 289–304 (2008)
Fawzi, O., Renner, R.: Quantum conditional mutual information and approximate markov chains. Commun. Math. Phys. 340(2), 575–611 (2015)
Devetak, I., Yard, J.: Exact cost of redistributing multipartite quantum states. Phys. Rev. Lett. 100, 230501 (2008)
Berta, M., Brandao, F.G.S.L., Majenz, C., Wilde, M.M.: Deconstruction and conditional erasure of quantum correlations (2016). arXiv e-prints arXiv:1609.06994
Sharma, K., Wakakuwa E., Wilde, M.M.: Conditional quantum one-time pad (2017). arXiv e-prints arXiv:1703.02903
Hammersley, J.M., Clifford, P.E.: Markov field on finite graphs and lattices (1971). http://www.statslab.cam.ac.uk/grg/books/hammfest/hamm-cliff.pdf
Leifer, M.S., Poulin, D.: Quantum graphical models and belief propagation. Ann. Phys. 323(8), 1899–1946 (2008)
Brown, W., Poulin D.: Quantum Markov networks and commuting Hamiltonians (2012). arXiv e-prints arXiv:1206.0755
Brandao, F.G.S.L., Kastoryano, M.J.: Finite correlation length implies efficient preparation of quantum thermal states (2016). arXiv e-prints arXiv:1609.07877
Kim, I.H.: Determining the structure of the real-space entanglement spectrum from approximate conditional independence. Phys. Rev. B 87, 155120 (2013)
Flammia, S.T., Haah, J., Kastoryano, M.J., Kim, I.H.: Limits on the storage of quantum information in a volume of space. Quantum 1, 4 (2017)
Levin, M., Wen, X.-G.: Detecting topological order in a ground state wave function. Phys. Rev. Lett. 96, 110405 (2006)
Kato, K., Brandao, F.G.S.L.: Locality of edge states and entanglement spectrum from strong subadditivity (2018). arXiv preprints arXiv:1804.05457
Wolf, M.M., Verstraete, F., Hastings, M.B., Cirac, J.I.: Area laws in quantum systems: mutual information and correlations. Phys. Rev. Lett. 100, 070502 (2008)
Hastings, M.B.: Solving gapped Hamiltonians locally. Phys. Rev. B 73(8), 085115 (2006)
Swingle, B., McGreevy, J.: Mixed \(s\)-sourcery: building many-body states using bubbles of nothing. Phys. Rev. B 94(15), 155125 (2016)
Brandao, F.G.S.L.: Finite correlation length implies efficient preparation of quantum thermal states (2016). arXiv prepromts arXiv:1609.07877
Jaynes, E.T.: Information theory and statistical mechanics. Phys. Rev. 106, 620–630 (1957)
Jaynes, E.T.: Information theory and statistical mechanics. II. Phys. Rev. 108, 171–190 (1957)
Weis, S.: Information topologies on non-commutative state spaces. J. Conv. Anal. 21(2), 339–399 (2014)
Weis, S.: The MaxEnt extension of a quantum Gibbs family, convex geometry and geodesics. In: AIP Conference Proceedings, vol. 1641 (2015)
Alicki, R., Fannes, M.: Continuity of quantum conditional information. J. Phys. A: Math. Gen. 37, L55 (2004)
Hastings, M.B.: Quantum belief propagation: an algorithm for thermal quantum systems. Phys. Rev. B 76, 201102 (2007)
Kim, I.H.: Perturbative analysis of topological entanglement entropy from conditional independence. Phys. Rev. B 86, 245116 (2012)
Araki, H.: Gibbs states of a one dimensional quantum lattice. Commun. Math. Phys. 14(2), 120–157 (1969)
Lieb, E.H., Robinson, D.W.: The finite group velocity of quantum spin systems. Commun. Math. Phys. 28(3), 251–257 (1972)
Araki, H.: Expansional in banach algebras. Ann. Sci. Ecole Norm. S. 6(1), 67–84 (1973)
Brandao, F.G.S.L., Horodecki, M.: Exponential decay of correlations implies area law. Commun. Math. Phys. 333(2), 761–798 (2015)
Acknowledgements
Part of this work was done when both of us were working in the QuArC group of Microsoft Research. KK thanks Advanced Leading Graduate Course for Photon Science (ALPS) and JSPS KAKENHI Grant Number JP16J05374 for financial support. We thank Matthew Hastings and Michael Kastoryano for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. M. Wolf.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Another approach to prove Theorem 4
Appendix A: Another approach to prove Theorem 4
In Sect. 4, we employ a perturbative method to obtain a local operator O determined by the Hamiltonian and a local operator V such that
The existence of such operator plays a central role in the proof of Theorem 4. In this appendix, we introduce another approach to obtain similar operators, which is based on the previous work by Araki [25]. The main difference between these approaches is the origins of locality of the operator O. In the perturbative approach, the locality is originated in Lieb-Robinson bounds, which restrict real time evolutions of operators. Instead, in Araki’s approach, locality of O is originated in a restriction on imaginary-time evolutions of V.
Let us consider a 1D spin chain \(\Lambda =[-n,n]\), a short-range Hamiltonian H on \(\Lambda \), and a local operator V. We denote the maximum strength of H by J. A simple algebra show the following relation holds.
where we denote \(e^{-\frac{\beta }{2}(H+V)}e^{\frac{\beta }{2}H}\) by \(E_r(V; H)\). By denoting \(V(\beta )=e^{-\beta H}Ve^{\beta H}\), \(E_r(V; H)\) has another form written as [25]
Actually, \(E_r(V; H)\) can be approximated by a local operator.
Lemma 11
[25] The following statements hold for any region \(X\subset [-n,n]\) and any bounded operator V with \(supp(V)=[a,b]\subset [-n,n]\).
-
(i)
There exists a constant \(C\ge 0\) depending on \(\beta \), J and \(\Vert V\Vert \)such that
$$\begin{aligned} \Vert E_r(V; H_X)\Vert \le C\, \end{aligned}$$ -
(ii)
There exist constants \(C, q\ge 0\) depending on \(\beta \), J and \(\Vert V\Vert \) such that
$$\begin{aligned} \left\| E_r(V; H_X)-E_r(V; H_{X\cap [a-l,b+l]})\right\| \le C\frac{q^{1+\lfloor \frac{l}{2}\rfloor }}{(1+\lfloor \frac{l}{2}\rfloor )!}. \end{aligned}$$
Since \(\log x!\approx x\log x-x\), the denominator grows faster than the numerator with respect to l, and thus, the accuracy of the above approximation is exponentially good with respect to l. Note that similar properties hold for the inverse of \(E_r(V; H_X)\), \(E_l(V;H_X)\equiv e^{-\frac{\beta }{2}H_X}e^{\frac{\beta }{2}(H_X+V)}\). Therefore, by choosing \(V=H_{B^M}\), \(E_r(V; H)\) and its local approximation play the same role as \(O_{ABC}\) and \(O_B\) in Sect. 4.2.
Rights and permissions
About this article
Cite this article
Kato, K., Brandão, F.G.S.L. Quantum Approximate Markov Chains are Thermal. Commun. Math. Phys. 370, 117–149 (2019). https://doi.org/10.1007/s00220-019-03485-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-019-03485-6








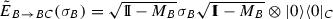 , where
, where 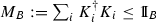 with
with