1 Introduction

First-principle electronic structure calculations, with particular emphasis on density functional theory (DFT), have revolutionized molecular structure determination in chemistry over the last three decades. The accuracy and reliability of first-principle electronic structure optimized geometrical parameters have reached a similar level as corresponding single crystal X-ray diffraction data [1]. However, a severe restriction for first-principle methods is still system size. The structure determination of small proteins and enzymes with first-principle electronic structure methods remains challenging or even impossible. To overcome these limitations, the variational fitting of the Coulomb and Fock potentials has been proposed in the literature [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. A computationally particularly efficient implementation of density fitting in the framework of DFT is realized by auxiliary density functional theory [17] (ADFT). In parallel ADFT calculations of molecular systems with several thousands of atoms, the computational demand is dominated by linear algebra tasks associated with the density fitting and the self-consistent field (SCF) calculation [18]. For the density fitting, we recently proposed a Krylov subspace method that eliminates the corresponding computational and random access memory (RAM) bottlenecks [19]. As a result, the ADFT Kohn-Sham matrix transformation and diagonalization in the SCF remains as the critical linear algebra bottleneck in large-scale parallel ADFT calculations. A possible solution to this problem is given by so-called linear scaling methods [20], mainly developed in the context of semi-empirical quantum chemistry programs. Typical examples are the density matrix minimization (DMM) [21,22,23,24], the Fermi operator expansion [25, 26], conjugate gradient density matrix search [27] (CGDMS), Chebyshev expansion method [28] (CEM), purification of density matrix [29] (PDM) and pseudo-diagonalization [30, 31](PD). In this work, we will focus on the PD algorithm. It is based on the annihilation of the occupied-virtual Kohn-Sham or Fock matrix elements, which is a necessary and sufficient condition for a stationary SCF solution. In order to obtain a linear scaling approach, localized molecular orbitals (LMOs) must be used in PD SCF implementations. We note that this not only reduces the scaling of the computational demand but also, if appropriate sparse matrix storage is used, the scaling of RAM demand. In fact, within the framework of semi-empirical methods it has been shown by Stewart and others [27, 30,31,32] that LMOs in PD SCF iterations grow only to around 100 atoms independent of systems size. Thus, not only the computational demand but also the RAM demand becomes linear scaling with system size.

These literature reports have motivated us to implement a PD SCF algorithm in the framework of ADFT. Because our goal is to use PD for the solution of the Roothaan-Hall (RH)-type ADFT Kohn-Sham equation systems, the focus of this study lies on the PD ADFT SCF convergence behavior and the propagation of the LMOs within the corresponding iterations. To this end, we have implemented a parallel PD ADFT SCF using LMOs in a developer version of the deMon2k program [33]. The initial LMOs are obtained by the localization of the start density tight-binding MOs. The article is organized as follows. In Section 2, the theoretical background of our PD ADFT SCF is outlined alongside with implementation details. The computational details are given in the next section. In Section 4, the propagation of LMOs during PD ADFT SCF iterations is analyzed. Furthermore, the PD and RH single-point SCF calculations are compared for selected fullerenes, hydrogen-saturated graphene sheets and diamond blocks. Final conclusions are given in the last section.

2 Theoretical background

ADFT as implemented in deMon2k possesses a linear scaling for the calculation of energies and Kohn-Sham matrix elements when employing the local density approximation (LDA) or the generalized gradient approximation (GGA). Take for example an ADFT Kohn-Sham matrix element given by:

$$\begin{aligned} K_{\mu \nu } = H_{\mu \nu } + \sum _{{\bar{k}}}\langle \mu \nu \Vert {\bar{k}}\rangle (x_{{\bar{k}}}+z_{{\bar{k}}}), \end{aligned}$$
(1)

In Eq. 1, \( H_{{\mu v}} \) denotes an element of the core Hamiltonian that possesses a formal quadratic scaling. However, if integral screening due to the atomic orbital overlap is introduced, the number of non-vanishing \(H_{\mu \nu }\) elements increases linearly with system size. The three-center electron repulsion integral (ERI),

$$\begin{aligned} \langle \mu \nu \Vert {\bar{k}}\rangle = \iint \frac{\mu (\mathbf{r}_1)\nu (\mathbf{r}_1){\bar{k}}(\mathbf{r}_2)}{|\mathbf{r}_1 - \mathbf{r}_2|}d\mathbf{r}_1d\mathbf{r}_2, \end{aligned}$$
(2)

introduces a formal cubic scaling into the calculation of the ADFT Kohn-Sham matrix elements. However, with overlap integral screening and the double asymptotic ERI expansion [34] the calculation of this term becomes linear scaling with system size, too. Furthermore, the Coulomb, \(x_{{\bar{k}}}\), and exchange correlation, \(z_{{\bar{k}}}\), fitting coefficients are linear scaling by construction. Thus, the LDA and GGA ADFT Kohn-Sham matrix calculation scales linearly with increasing system size. However, cubic scaling linear algebra tasks in the form of matrix multiplication and diagonalization appear due to density fitting and RH type SCF iterations. To overcome these bottlenecks, we have recently developed a Krylov subspace method in form of MINRES [35] for the density fitting in our research group and implemented it in deMon2k [19]. This has eliminated cubic scaling linear algebra tasks in the density fitting. Therefore, only the Kohn-Sham matrix transformation and diagonalization remain as cubic scaling bottlenecks for ADFT SCF iterations. Here, the transformation refers to multiplication of the Kohn-Sham matrix with \(S^{-1/2}\) in deMon2k. Although extremely well optimized and parallelized linear algebra algorithms for matrix multiplications and diagonalization are available in deMon2k through LAPACK and ScaLAPACK routines, we observe ultimately a cubic scaling with system size. To overcome this scaling bottleneck, we have implemented the pseudo-diagonalization of the molecular orbital (MO) Kohn-Sham matrix using LMOs. As was outlined by Stewart and Pulay in the context of Hartree-Fock SCF calculations, a necessary and sufficient condition for SCF convergence, based on Brillouin’s theorem [36], is that all molecular orbital Fock matrix elements connecting occupied and virtual (L)MOs are zero [30, 31]. As our results show, this condition yields in the here implemented form of PD within ADFT convergence to ground states that are indistinguishable, within the given SCF tolerance, from corresponding RH calculations. The necessary ADFT Kohn-Sham matrix elements in MO representation are given by:

$$\begin{aligned} {\mathcal {K}}_{ov} = \sum _{\mu ,\nu }C_{\mu o}K_{\mu \nu }C_{\nu v} \qquad \forall \quad o \in occ \quad \wedge \quad v \in vir \end{aligned}$$
(3)

In Eq. 3, occ and vir refer to occupied and virtual (L)MOs, respectively. Our PD implementation annihilates the occupied-virtual block of the (L)MO ADFT Kohn-Sham matrix. To this end, we apply MO rotations analog to Jacobi rotations to the (L)MO ADFT Kohn-Sham matrix:

$$\begin{aligned} {\mathcal {K}}^{I+1} = {\mathcal {R}}^{T}{\mathcal {K}}^{I}{\mathcal {R}} \end{aligned}$$
(4)

In Eq. 4, \({\mathcal {R}}\) is an orthogonal (L)MO rotation matrix and the superscripts I and \(I+1\) denote rotation indices. These elementary rotations are collected into a swap, which rotates all \({\mathcal {K}}_{ov}\) matrix elements above a certain threshold. The rotation matrix of a swap is the product of all elementary rotation matrices that belong to the swap. A description of an elementary rotation of the MO Kohn-Sham matrix is described in the supporting information (SI). The corresponding rotations of the (L)MOs are given by:

$$\begin{aligned} \mathbf{C}_{i}^{I+1}= & {} \mathbf{C}_{i}^{I}\cos \theta - \mathbf{C}_{a}^{I}\sin \theta \end{aligned}$$
(5a)
$$\begin{aligned} \mathbf{C}_{a}^{I+1}= & {} \mathbf{C}_{i}^{I}\sin \theta + \mathbf{C}_{a}^{I}\cos \theta \end{aligned}$$
(5b)

Here the sine and cosine functions are evaluated as [37]:

$$\begin{aligned} \cos \theta= & {} \sqrt{\frac{1}{2} + \alpha } \end{aligned}$$
(6a)
$$\begin{aligned} \sin \theta= & {} -sgn({{\mathcal {K}}^{I}_{ia}})\sqrt{\frac{1}{2} - \alpha } \end{aligned}$$
(6b)

with

$$\begin{aligned} \alpha = \frac{1}{\sqrt{4+\left( \frac{4{\mathcal {K}}^{I}_{ia}}{{\mathcal {K}}^{I}_{aa}-{\mathcal {K}}^{I}_{ii}}\right) ^2}} \end{aligned}$$
(7)

Eqs. 5, 6 and 7 are the working equations implemented in deMon2k for elementary rotations in the PD procedure. The superscript \(I+1\) in Eqs. 5 denotes a rotated (L)MO vector. A swap is finished when all elementary rotations are applied to all \({\mathcal {K}}_{ia}\) matrix elements above a certain threshold. For the corresponding threshold definition see section 2.1. In general, the complete annihilation of the \({\mathcal {K}}_{ov}\) matrix will usually require many swaps. However, for SCF convergence it is sufficient to diminish the absolute values of the \({\mathcal {K}}_{ia}\) matrix elements successively in each SCF step. In our implementation, we are performing 2 swaps in each SCF cycle. At SCF convergence, the converged occupied and virtual (L)MOs are decoupled, i.e., the corresponding \({\mathcal {K}}_{ia}\) matrix elements are below the convergence threshold. Here we analyze the SCF convergence behavior of this approach in the framework of ADFT. To this end, we compare converged SCF energies and numbers of SCF cycles between the outlined PD approach and conventional RH calculations. Furthermore, we monitor the spread of the localized MOs in the PD ADFT SCF.

2.1 Practical implementation

Following the algorithmic outline in the previous section, we now need to define thresholds for the rotation of \({\mathcal {K}}_{ia}\) matrix elements. A straightforward brute force approach is to calculate the rotation angles for all \({\mathcal {K}}_{ia}\) matrix elements and sort them from largest to smallest. According to this list, the matrix elements are annihilated in the first swap. The same procedure is applied for the second swap in the same SCF iteration. This approach is computationally very demanding due to the sorting of the \({\mathcal {K}}_{ia}\) matrix elements at the beginning of each swap and large number of rotations. The sorting can be avoided by defining a fixed threshold for the rotational angle [38]. This reduces the number of necessary rotations, too, according to the selected threshold. Nevertheless, the rotation angles must be still calculated. To avoid this drawback, we define here thresholds directly via the \({\mathcal {K}}_{ia}\) matrix elements. The following two threshold definitions are tested in this work:

  1. 1.

    In the adaptative threshold definition, the maximum absolute value of the \({\mathcal {K}}_{ia}\) matrix elements in a SCF iteration is determined. Then the threshold \(\tau \) for the LMO rotations in the 2 swaps of this SCF cycle is defined as:

    $$\begin{aligned} \tau = \beta {|{\mathcal {K}}_{ia}|}_{max} \end{aligned}$$
    (8)

    All \({\mathcal {K}}_{ia}\) matrix elements above \(\tau \) are annihilated. We present results for \(\beta =0.04\) and \(\beta =0.4\) in this work.

  2. 2.

    In the fixed threshold definition, \(\tau \) is calculated in each SCF cycle, \(N_{S\!C\!F}\), according to:

    $$\begin{aligned} \tau = 10e^{-(N_{S\!C\!F}+4)} \end{aligned}$$
    (9)

    Only those \({\mathcal {K}}_{ia}\) are annihilated in the 2 swaps of the given SCF cycle that are above this threshold. For large molecules, the fixed threshold approach is particularly attractive because the search for the maximum \(|{\mathcal {K}}_{ia}|\) element in each SCF cycle is avoided.

2.2 PD ADFT SCF Algorithm

We need a set of initial localized orbitals for our LMO-based PD ADFT. To this end, we localize the SCF start density MOs with a two-step localization procedure [14] consisting of a pivoted Cholesky decomposition of the density matrix [39] followed by a Foster-Boys MO localization [40, 41]. At this point, it is important to note that during the PD ADFT SCF no other MO localization is applied. The SCF proceeds the standard route, except for the Kohn-Sham matrix orthogonalization and successive diagonalization. Instead, the calculated Kohn-Sham matrix in atomic orbital representation of the current SCF step, which possesses a sparse matrix structure, is transformed with the available LMO coefficients from the previous SCF cycle into molecular orbital representation. Because LMOs are used, this matrix remains sparse, as Stewart pointed out first [31]. This is a marked difference to the orthogonalization transformation in RH ADFT SCF calculations. This sparsity also reduces the number of rotations needed to diminish the \({\mathcal {K}}_{ov}\) matrix elements. The pseudocode of our PD algorithm is depicted in Fig. 1.

Fig. 1
figure 1

Pseudo-diagonalization algorithm for ADFT SCF calculations

Full size image

According to the threshold definition, the pseudo-diagonalization in Fig. 1 starts either with the search for the largest absolute \(|{\mathcal {K}}_{ia}|\) matrix element and the corresponding threshold definition given by Eq. 8 or with the fixed threshold given by Eq. 9. Then, the diagonal elements of the Kohn-Sham matrix in MO representation are calculated since they are needed for the \(\alpha \) calculation in Eq. 7. In Fig. 1, superscript I denotes quantities that change with elementary rotations, whereas superscript J denotes quantities that change with swaps. Quantities without superscript are SCF cycle specific. As the pseudocode in Fig. 1 shows, each of the 2 swaps in a SCF cycle contains loops over the virtual and occupied orbitals. Once a virtual orbital is addressed, a parallel matrix-vector multiplication for the calculation of \(X^J_{\mu a}\) is performed. An example of this multiplication is depicted in Fig. 2, where a \(5\times 5\) Kohn-Sham matrix is distributed over 3 threads. In Fig. 2, the rows of the Kohn-Sham matrix elements in atomic orbital representation are distributed over the threads and the \(C^{I}_{\mu a}\) LMO coefficient vector is sent completely to each of the 3 threads. Then, each thread multiplies its partial \({\mathcal {K}}_{\mu \nu }\) block with the \(C^{I}_{\mu a}\) vector and the results are obtained in the \(X^J_{\mu a}\) block vector on each thread as can be seen from Fig. 2. These \(X^J_{\mu a}\) vectors have the dimension of the number of basis functions distributed to a thread and remain unchanged in the following loop over occupied LMOs.

Fig. 2
figure 2

A \(5\times 5\) example for the \({\mathcal {K}}_{\mu \nu }\) and \(C^I_{\nu a}\) block distribution over 3 threads and the distributed construction of the \(X^J_{\mu a}\) vectors in parallel calculations

Full size image

In order to calculate the \({\mathcal {K}}_{ia}\) matrix elements, a dot product between the \(X^J_{\mu a}\) and the \(C^I_{\mu i}\) LMO coefficient vector must be calculated. To this end, the \(C^I_{\mu i}\) vector is distributed by rows over the threads according to the \(X^J_{\mu a}\) distribution given in Fig. 2. The scalar dot product of these two vectors is calculated in parallel. If the absolute value of the resulting \({\mathcal {K}}_{ia}\) matrix element is above the threshold \(\tau \), the rotation between the \(i^{th}\) occupied LMO and the \(a^{th}\) virtual LMO coefficient vector is performed. Equations 5, 6 and 7 (See SI for details) are needed for this rotation of the \(C^I_{\mu i}\) and \(C^I_{\mu a}\) LMO coefficient vectors. Note that the occupied MO coefficients are used for the calculation of the next \({\mathcal {K}}^{I}_{ia}\) element according to line 12 in Fig. 1. This distinguishes our algorithm from the implementations described in [30] and [31]. The use of LMOs significantly reduces the number of rotations because the \({\mathcal {K}}_{ov}\) matrix is sparse.

3 Computational details

The results presented here were obtained with a modified 6.1.2 version of the deMon2k program [42]. In the ADFT calculations, the variational fitting of the Coulomb potential [8, 43] was used and the numerical calculations of the exchange-correlation energy and potential were performed with the fitted density. Therefore, no four-center ERIs nor quadratic scaling density evaluations on the grid are needed. The three-center ERIs were recalculated twice in each SCF step (direct SCF) utilizing the double asymptotic expansion for long-range ERIs [34]. As a result, the calculation of the ADFT energy and Kohn-Sham matrix becomes linear scaling with respect to system size already for moderate large molecules with a few hundred atoms. To avoid cubic scaling linear algebra operations in the density fitting, the MINRES approach was used [19]. The calculations are performed with the PBE [44] GGA and PBE0 [45, 46] hybrid functionals. For the linear combination of Gaussian-type orbital (LCGTO) approximation the DZVP [47] and aug-cc-pVTZ [48] basis sets with Cartesian orbitals are employed. If not otherwise stated, the GEN-A2* auxiliary function set was used for the variational density fitting. In the validation calculations listed in Tables 1, 2 and SI-1, the RH and PD SCF convergence thresholds were set to \(10^{-6}\) and \(10^{-5}\) a.u. for the total energy and the variational density fitting, respectively. For the calculations in Table 3, the default deMon2k SCF convergence thresholds of \(10^{-5}\) and \(5\times 10^{-4}\) a.u. for the total energy and density fitting were used. All calculations were performed in parallel on 24 Intel® Xeon® CPU E5-2650 v4 @ 2.20GHz cores.

To analyze the LMO propagation during PD ADFT SCF iterations, we calculate the square root of the orbital variance:

$$\begin{aligned} \sigma _i = \sqrt{Q_i - D_i^2} \end{aligned}$$
(10)

Here the \(Q_i\) and \(D^2_i\) are defined as [49, 50]:

$$\begin{aligned} Q_i\equiv & {} \langle i |x^2| i \rangle + \langle i |y^2| i \rangle + \langle i |z^2| i \rangle \nonumber \\ D^2_i\equiv & {} \langle i |x| i \rangle ^2 + \langle i |y| i \rangle ^2 + \langle i |z| i \rangle ^2 \end{aligned}$$
(11)

In the literature [50], \(\sigma _i\) is introduced as the spread of the orbital i, and closely related to the so-called Boys localization function [40, 41]. Therefore, we use \(\sigma _i\) to monitor the spread of the (L)MOs during the SCF. To this end, we calculated the occupied and virtual molecular orbital maximum spreads, denoted by OMS and VMS, respectively, in each SCF step.

4 Results

4.1 LMO propagation analysis

In order to analyze the SCF convergence and the (L)MO propagation during SCF iterations, we performed single-point energy calculations of small alkane chains with 6, 10, 18, 22 and 30 carbon atoms as well as of water clusters with 4, 8, 12, 16, 20 and 38 \(\text {H}_2\text {O}\) molecules (\(\text {W}_4\) to \(\text {W}_{38}\)). We chose these systems as typical examples for MO localizable covalent bonded molecules and molecular assemblies.

Table 1 Comparison of RH and PD ADFT single-point energies [a.u.] and SCF cycles
Full size table
Table 2 Comparison of RH and PD ADFT single-point energies [a.u.] and SCF cycles
Full size table
Table 3 Comparison of single-point energies [a.u.] for the test systems of Fig. 5 obtained from RH and PD ADFT SCF calculations. The number of basis, \(N_{bas}\), and auxiliary functions, \(N_{aux}\), of the test systems are given, too. Calculations were performed with the PBE/DZVP/GEN-A2 level of theory
Full size table

Tables 1 and 2 show results from these calculations for the more compact DZVP basis set using the PBE and PBE0 functionals. Table SI−1 in the supporting information shows the corresponding results for the more extended aug-cc-pVTZ basis with the PBE functional. For each system, the converged SCF energy (a.u.) along with the number of SCF cycles is listed. The OMS and VMS entries denote the occupied maximum spread and virtual maximum spread, respectively, for the converged (L)MOs except for the column Guess. Here OMS and VMS refer to the maximum spreads of the tight-binding start MOs after localization. The studied SCF methods in Tables 1 and 2 as well as SI-1 are the standard RH ADFT method (RH), the adaptative threshold pseudo-diagonalization (PD) ADFT method with \(\beta =0.04\) and \(\beta =0.4\) as well as the fixed sequential threshold PD ADFT method, PD(fixed).

The following general trends can be observed from these three tables. The occupied tight-binding start density MOs can be well localized for all systems independently of the used basis set and functional. In the RH SCF calculations, this MO localization is lost for all systems at SCF convergence. In fact, it is already lost in the first SCF step. Moreover, Tables 1, 2 and SI-1 show that the OMS values increase with system size in RH SCF calculations. This is well documented in the literature, too. RH MOs are most delocalized according to the Heisenberg uncertainty principle [51]. Therefore, RH SCF calculations delocalize valence MOs even for molecules or molecular assemblies that are intuitively localizable such as the here presented alkanes and water clusters. For the PD SCF, the situation is different. For all presented calculations in Tables 1, 2 and SI-1, the OMS and VMS values of the converged PD SCF MOs are very similar to the initial localized start density values. In general, we observe during PD ADFT SCF iterations only moderate relaxations of the initial localized tight-binding start density MOs. Although certain LMOs might increase slightly their extension, all MOs remain localized until SCF convergence in PD ADFT SCF calculations. Despite this marked difference in MO localization, the converged PD ADFT SCF energies show fair to excellent agreement with the corresponding RH ADFT SCF energies. Closer inspection of Tables 1, 2 and SI-1 reveals that the converged energies of the adaptative threshold PD SCF calculations with \(\beta =0.04\) and the fixed sequence threshold PD SCF calculations are within the used SCF convergence threshold of \(10^{-6}\) a.u., in excellent agreement with the corresponding RH converged results. Because the fixed threshold PD SCF needs usually significantly more SCF cycles for convergence than the \(\beta =0.04\) adaptative PD SCF, we used the latter one for all following calculations.

Fig. 3
figure 3

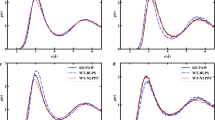
Plot of OMS (upper 3 chains) and VMS (lower 3 chains) (L)MOs of \(\text {C}_{60}\text {H}_{122}\). Each graph shows from top to bottom the OMS/VMS guess LMO, the RH converged OMS/VMS canonical MO and the PD converged OMS/VMS LMO. The calculations were performed with the PBE/DZVP/GEN-A2* level of theory

Full size image

To gain more insight into the presented OMS and VMS values, we plot the (L)MOs of selected systems. Figure 3 plots the OMS and VMS (L)MOs of \(\text {C}_{60}\text {H}_{122}\) for the localized tight-binding guess, the converged RH ADFT SCF and the converged PD(0.04) ADFT SCF. The OMS for the localized tight-binding is 1.839. This value increases for the converged RH ADFT SCF to 51.719, whereas it decreases for the converged PD(0.04) ADFT to 1.634. The plots in Fig. 3 show the corresponding localization and delocalization of the (L)MOs. For the VMS, similar situations are found. Note that the large VMS value for the converged RH ADFT SCF (lower graph, middle chain) of 68.680 arises from a canonical MO that is localized at the ends of the chain. Figure 4 shows the same plots for a water cluster of 50 \(\text {H}_{2}\text {O}\) molecules. The tight-binding OMS LMO (top left) is localized on one water molecule. As a result, the localized tight-binding OMS value is only 1.530. Again this localization is destroyed in the RH ADFT SCF, and the converged canonical OMS MO, with an OMS value of 9.781, is delocalized over several \(\text {H}_2\text {O}\) molecules (Fig. 4, top middle). On the other hand, the PD ADFT SCF conserves the localization of the start density tight-binding LMOs. As a result, the PD(0.04) ADFT SCF converged LMO is localized on one \(\text {H}_2\text {O}\) molecule (Fig. 4, top right) with an OMS value of only 1.510. The VMS MOs, Fig. 4 bottom, show the same qualitative trend but are slightly more delocalized.

Fig. 4
figure 4

Plot of OMS (top) and VMS (bottom) (L)MOs of a water cluster with 50 \(\text {H}_2\text {O}\) molecules. Each graph shows from left to right the OMS/VMS LMOs of the tight-binding start density, the converged canonical OMS/VMS MOs of the RH ADFT SCF and the converged OMS/VMS LMOs of the PD ADFT SCF. Calculations were performed with the PBE/DZVP/GEN-A2* level of theory

Full size image

4.2 Single-point energy calculations

After the calculations of simple naturally localizable test systems have shown that the PD(0.04) ADFT SCF algorithm with LMOs proposed here converges to the same results as corresponding RH ADFT SCF calculations, we now turn to the study of more challenging molecules. To this end, we performed single-point energy calculations of the \(\text {C}_{60}\), \(\text {C}_{180}\) and \(\text {C}_{540}\) fullerenes, of hydrogen saturated graphene sheets with 42, 80 and 150 carbon atoms and of hydrogen saturated diamond-like structures with 54, 200 and 360 carbon atoms. The structures of these test systems are shown in Fig. 5.

Fig. 5
figure 5

Structures of test systems for single-point energy calculations listed in Table 3. The graphs show fullerene cages (top), saturated graphene sheets (middle) and saturated diamond-like structures (bottom)

Full size image

Table 3 compares the converged SCF energies for RH and PD(0.04) ADFT SCF calculations. For these calculations, we used the PBE/DZVP/GEN-A2 level of theory and the default deMon2k convergence thresholds typically used in production runs. As Table 3 shows, the converged RH and PD(0.04) SCF energies agree in the range of \(10^{-4}\) a.u. for all systems. The largest deviation of around 2.8\(\times {10}^{-4}\) a.u. between the RH and PD(0.04) converged energies was found for the \(\text {C}_{150}\text {H}_{30}\) graphene sheet. Because further tightening of the PD(0.04) SCF convergence did not reduce this difference, we account it to restrictions in our PD algorithm, in particular to the swap restriction per SCF cycle. This assumption is further supported by the fact that the converged RH energies in Table 3 are always lower than the corresponding PD(0.04) energies. Thus, for larger molecules more than 2 swaps per SCF cycle might be needed in the PD ADFT SCF method. Another interesting detail from Table 3 is the convergence of \(\text {C}_{60}\). It was pointed out in the literature that this fullerene converges with a PD SCF implementation to an excited state [32]. Table 3 shows that this problem does not occur in the here presented PD(0.04) ADFT SCF. Altogether, the study of the here presented carbon systems shows that PD(0.04) ADFT SCF calculations converge to the same result as corresponding RH ADFT SCF calculations.

After we have established the correct SCF convergence of the PD algorithm for the more challenging carbon systems depicted in Fig. 5, we now turn to the analysis of the (L)MO propagation in these systems. To this end, we plot in Fig. 6 the OMS and VMS (L)MOs of the \(\text {C}_{60}\) fullerene, the hydrogen-saturated \(\text {C}_{42}\text {H}_{16}\) graphene sheet and the hydrogen-saturated \(\text {C}_{54}\text {H}_{54}\) diamond−like structure. Already visual inspection of Fig. 6 shows that the tight−binding start density LMOs of \(\text {C}_{60}\) (Fig. 6 top, left) and of \(\text {C}_{42}\text {H}_{16}\) (Fig. 6 middle, left) are more extended than the ones of the \(\text {C}_{60}\text {H}_{122}\) alkane chain in Fig. 3 or the ones of the water cluster in Fig. 4. This is confirmed by the corresponding OMS/VMS values for these LMOs of 2.478/4.390 for the fullerene and 2.531/6.001 for the graphene sheet, respectively. Thus, the here used localization procedure yields for these \(\pi \) delocalized systems LMOs with larger extension than for saturated molecules, including the \(\text {C}_{54}\text {H}_{54}\) diamond-like structure depicted at the bottom of Fig. 6 (Guess OMS/VMS is 2.279/3.882). We note that these findings are in agreement with previous studies [16, 52]. With the RH ADFT SCF, this localization is destroyed (Fig. 6 top and middle, center). The resulting OMS/VMS values for the converged canonical MOs are 7.048/9.387 for the fullerene and 10.386/12.423 for the graphene sheet, respectively. On the other hand, the converged PD(0.04) ADFT SCF MOs are localized (Fig. 6 top and middle, right) with OMS/VMS values of 2.478/4.388 for the fullerene and 2.460/6.000 for the graphene sheet. This demonstrates that the here presented PD ADFT SCF algorithm conserves MO localization in molecules with delocalized \(\pi \) systems, albeit with LMOs of larger extension. The (L)MOs of the diamond-like \(\text {C}_{54}\text {H}_{54}\) system depicted at the bottom of Fig. 6 are very similar to those for the \(\text {C}_{60}\text {H}_{122}\) alkane shown in Fig. 3. Also the corresponding OMS/VMS values of 2.279/3.882, 13.099/12.779 and 2.165/3.886 for the LMOs of the tight-binding start-density, the converged canonical MOs of the RH ADFT SCF and the converged LMOs of the PD(0.04) ADFT SCF, respectively, are similar to corresponding data for alkane chains in Table 1.

Fig. 6
figure 6

Plot of OMS (upper structures) and VMS (lower structures) (L)MOs of the \(\text {C}_{60}\) fullerene (top), the \(\text {C}_{42}\text {H}_{16}\) graphene sheet (middle) and the \(\text {C}_{54}\text {H}_{54}\) diamond-like structure (bottom). Each graph shows from left to right the OMS/VMS LMOs of the tight-binding start density, the converged canonical OMS/VMS MOs of the RH ADFT SCF and the converged OMS/VMS LMOs of the PD ADFT SCF. Calculations were performed with the PBE/DZVP/GEN-A2* level of theory

Full size image

5 Conclusions

A parallel pseudo-diagonalization (PD) algorithm was implemented in the framework of ADFT. Our test calculations show that the ADFT SCF with the PD converges for all systems to the same result as the standard Roothaan-Hall ADFT SCF implementation. For the \(\text {C}_{150}\text {H}_{30}\) saturated graphene sheet, we found the largest difference in the converged SCF energies in the range of 2.8\(\times 10^{-4}\) atomic units. Our analysis indicates that this difference is due to the limited number of swaps permitted in the here proposed PD implementation. Certainly, there is room for improvement of this algorithm, Nevertheless, we experienced no SCF convergence problems in the PD ADFT SCF for the here studied systems. At least for \(\text {C}_{60}\), this is different to previous studies. We attribute this to the use of our PD in the framework of a MinMax SCF [53] that drives the ADFT SCF convergence through the Coulomb fitting coefficients instead of the molecular orbital (MO) coefficients.

Another interesting result of this study arises from the monitoring of the localized MO coefficients in the ADFT SCF employing PD. For all systems we found that the extension of the localized MOs remains stable during the PD ADFT SCF. Thus, relocalization between SCF steps [54] was not performed. This opens up the possibility of sparse matrix storage in PD ADFT SCF, which is currently under investigation in out laboratory.