1 Introduction

Structural effects are of paramount importance in organometallics, and in particular in homogeneous catalysis since they can account for ligand substitution kinetics. Actually, the links between these geometric (that can be also characterized as static) and these kinetic effects (measured in terms of substitution rate constants), while certain, are not fully equivalent. In this paper, we will only focus on the structural effects (SE), evaluated through the evolution of bond lengths due to ligand nature.

In case of square planar or tetrahedral complexes, two main SE have been identified: the so-called structural trans effect (STE) [1,2,3] (sometimes also coined “trans influence”) [4] and the structural cis effect (SCE) [5,6,7]. STE (respectively, SCE) refers to the increase of the metal–ligand bond length in trans (resp. in cis) to a considered ligand, which impacts, among others, on the catalytic activity and selectivity. It is most frequently observed in transition metal complexes [8, 9], but it has also been found in lanthanide [10], actinide [11, 12], and iodine species [13, 14], and is significant besides catalysis [15,16,17,18,19] to rationalize metalloprotein [20,21,22,23] and anti-tumoral properties [24,25,26].

Several scales for common ligands have been proposed over the last decades, initially from experimental data, but also from a pure theoretical point of view since the advent of the electrostatic [27,28,29,30] and of the celebrated Chatt–Dewar–Duncanson [31, 32] (CDD) models. More generally, the tools used to unravel the physicochemical factors responsible for structural effects can be classified into two main categories: those based on the wavefunction properties through mainly a molecular orbital approach (like CDD) grounded on the relevant abstract Hilbert space, and those rooted on real space analysis. This last one encompasses several techniques, like conceptual density functional theory [33, 34] (CDFT) and quantum chemical topology [35, 36] (QCT).

CDFT has been recently advocated by the Geerlings–De Proft’s group [37] and recently by us. It was indeed suggested in Ref. [13] that the dual descriptor (whether in its standard [38] or state-specific [39] formulation) was able to discriminate cis and trans positions, a proposal that we implemented in a quantitative way [40] through the use of the constant sign domain partition [41].

The aim of this article is instead to investigate what QCT may bring to the field. More specifically, we will rely on the electron density topology, as pioneered by Richard Bader who founded the quantum theory of atoms-in-molecules [42, 43] (QTAIM). It enables us to partition the 3D real space into non-overlapping volumes called “atomic basins”. When dealing with organometallic complexes, it henceforth becomes possible to isolate a space region that univocally defines the metallic center within the molecule. This metal basin can be subsequently analyzed and characterized by an extensive arsenal of descriptors (some of them will be defined in the next section) that are able to account for the metal center reactivity.

In this paper, we will focus on d 6 octahedral carbonyl complexes, but our methodology can be straightforwardly extended to other systems. Our choice has been dictated by the following reasons: (1) it is in direct continuation of our previous study [40], (2) trans effects in octahedral complexes appear almost only for d 0 and d 6 configurations [9], (3) carbonyl ligands are ubiquitous, well experimentally characterized, and lead to subtle effects since they are both σ donors and π acceptors. In fact, in the CDD framework, they are known to participate to bonding through both donation and backdonation.

More explicitly, we will explore M(CO)5Lig compounds, where Lig is a cis or trans orienting ligand. Depending on the Lig nature, the trans M-CO and cis M-CO bond lengths will differ and will reflect the ability of Lig to induce structural effects. Note that only two parameters will be varied in our study, making comparisons unequivocal: the d 6 metal (we retained cobalt and rhodium) and Lig. Many complexes of this type have been reported in the literature (see for instance Ref. [44] for the synthesis of Rh(CO)5Cl). Noteworthy is also the theoretical work [45] from the Frenking’s group on M(CO)5L complexes for M = Cr, Mo, and W.

We emphasize that we will not investigate the nature of bonding. The interested reader could look for instance at Bader’s seminal study [46], at Refs. [47, 48] for the analysis of bonding in (mainly homoleptic) carbonyl complexes through the interaction quantum atoms decomposition, and Ref. [49] from the electron localization function perspective, as well as at Frenking’s review [50] for a more global approach of transition metal–ligand bonding. Here we will instead concentrate on the metal atom properties when the cis or trans ligand is missing. Indeed, we conjecture that these atomic properties may explain (or at least be correlated to) the equilibrium bond length when the missing carbonyl coordinates.

To this purpose, this paper will be divided as follows: in the next section, we will provide an overview of all considered descriptors. We will then give details about our computational protocol, before discussing the geometries of the complexes and the possible correlations between the selected bond lengths and the above-mentioned descriptors.

2 Descriptors

The investigated descriptors can be divided into two main categories: the first ones are local, that-is-to-say they are evaluated at one particular real space point (for instance at critical points). The second family corresponds to atomic properties obtained by the numerical integration of the relevant local functions over the metal atomic basin Ω M . Note that a given function of \(\vec{r}\) can be fruitfully analyzed locally by displaying maps on isosurfaces or by inspecting its critical points, and integrated over a domain, giving rise to so-called condensed values. We think that both approaches are clearly complementary.

More specifically, two main types of local properties have been scrutinized. The first ones are built on the molecular electrostatic potential (MEP) [51, 52] defined (in atomic units) by:

$${\text{MEP}}\left( {\vec{r}} \right) = \sum\limits_{A} {\frac{{Z_{A} }}{{\left\| {\vec{r} - \vec{R}_{A} } \right\|}} - \int\limits_{{R^{3} }} {\frac{{\rho \left( {\vec{r}^{\prime}} \right)}}{{\left\| {\vec{r} - \vec{r}^{\prime}} \right\|}}{\text{d}}^{3} r^{\prime}} } ,$$
(1)

where ρ denotes the electron density, \(\vec{R}_{A}\) the location of nucleus A, and Z A its charge.

It is common practice to report MEP values on selected isodensity surfaces as we recently did to investigate amphiphilic ligands [53]. As the metal is expected to mainly behave as an electrophilic center, it is natural to focus on positive values. Following the numerous works by Politzer and coworkers [51, 52], we will thus concentrate on the maximal MEP values on three different standard isodensity surfaces (namely 0.0004 a.u., 0.001 a.u., 0.002 a.u.) in the vacancy region (outer electrophilic part of the metal atom pointing toward the missing ligand), which we will denote \({\text{MEP}}_{\hbox{max} }^{0.0004} ,\;{\text{MEP}}_{\hbox{max} }^{0.001} ,\;{\text{MEP}}_{\hbox{max} }^{0.002}\), respectively.

In addition, we included the so-called MEP at the nucleus value (often used [54, 55] to predict proton affinities) evaluated by:

$${\text{MEP}}\left( {\vec{R}_{M} } \right) = \sum\limits_{A \ne M} {\frac{{Z_{A} }}{{\left\| {\vec{R}_{M} - \vec{R}_{A} } \right\|}} - \int\limits_{{R^{3} }} {\frac{{\rho \left( {\vec{r}^{\prime}} \right)}}{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R}_{M} - \vec{r}^{\prime}} \right\|}}{\text{d}}^{3} r^{\prime}} } .$$
(2)

It is worthy remarking that, from a topological perspective, the real space points where \({\text{MEP}}_{\hbox{max} }^{0.0004} ,\;{\text{MEP}}_{\hbox{max} }^{0.001} ,\;{\text{MEP}}_{\hbox{max} }^{0.002}\) are computed are not critical points, since they correspond to maximal value on the considered isodensity surface but are not in general extremal in the orthogonal direction. While the topology of MEP has been recently discussed [56], we will not consider it in this paper.

The second type of local properties is related to the electron density Laplacian field, which has been reviewed by Popelier [57] and that has found many applications in organometallics both from experimental or theoretical electron densities [58,59,60,61,62,63,64]. Let us recall that negative laplacian values indicate local charge concentration, while positive ones reveal local charge depletion. These epithets should be understood in the sense of spherically average differences: there is depletion (resp. accumulation) when the density value at the considered point is lower (resp. higher) than the average value around it.

This should not be confused with the same words sometimes used for instance in X-ray crystallography when it can refer to the decrease or increase of electron density with respect to a reference electron density (that can be built by a superposition of atomic densities), important discrepancies being possible between these two descriptions [65].

Critical points (CPs) for this field correspond to points where \(\vec{\nabla }\left( {\nabla^{2} \rho \left( {\vec{r}} \right)} \right) = \vec{0}\). Of particular interest are the maxima, which correspond to (3,−3) CP type in the (rank, signature) typology. Three descriptors associated to this (3,−3) CP will be considered: the value (local maxima) of the laplacian at this point (\(\nabla^{2} \rho_{(3, - 3)}\)), the density value at this point (\(\rho_{(3, - 3)}\)), and the distance between this point and the metal nucleus (\(d_{(3, - 3)}\)).

We now make a survey of the integrated descriptors. The two first are basic QTAIM ones: the atomic charge of the metal atom (q(M)), and the volume (\({\text{Vol}}(M)\)) of the region defined by the intersection of the atomic basin and the \(\rho \left( {\vec{r}} \right) \ge 0.001\;a.u.\) zone (let us recall that QTAIM basins are of infinite size). Then comes an idiosyncratic QTAIM concept: the atomic dipole [66,67,68,69]. Indeed, QTAIM enables to exactly decompose the total molecular dipole moment into atomic contributions, \(\vec{\mu }(A)\), each one being the sum of a monopolar term (the one that appears in the context of pure point charges) and linked to interatomic charge transfer, and of an intraatomic one that is linked to the anisotropy of the electron distribution inside the atomic basin (that vanishes for spherical densities as in free atoms). This is this last term, denoted \(\vec{\mu }^{p} (M)\), that we will include in our descriptors list: it gives insight onto the density polarization inside the atom.

Another relevant quantity derived from the atomic dipole moment is the atomic polarizability tensor \(\underline{\underline{\alpha }}\) whose components are defined by [70,71,72,73]:

$$\alpha_{ij} \left( A \right) = \left. {\frac{{\partial \mu_{i} (A)}}{{\partial F_{j} }}} \right|_{{F_{j} = 0}} .$$
(3)

where F j denotes a static homogenous external electric field applied along axis j.

The main polarizability of the metal atom is then obtained by:

$$\bar{\alpha }\left( M \right) = \frac{1}{3}{\text{Trace}}\left( {\underline{\underline{\alpha }} (M)} \right) .$$
(4)

One can even go further by considering the quadrupole moment, here in its traceless form. Once diagonalized and its eigenvalues Q i obtained, one can evaluate [74]:

$$Q\left( M \right) = \sqrt {\frac{2}{3}\sum\nolimits_{i = 1}^{3} {Q_{i}^{2} } } .$$
(5)

Then, energetic atomic quantities will be incorporated. The first one is the Kohn–Sham (KS) kinetic energy Ks:

$$K_{S} (M) = \int\limits_{{\varOmega_{M} }} {\left( {\frac{1}{2}\sum\limits_{i = 1}^{N} {\left\| {\vec{\nabla }\varphi_{i}^{KS} \left( {\vec{r}} \right)} \right\|^{2} } } \right){\text{d}}^{3} r} = \int\limits_{{\varOmega_{M} }} {\left( { - \frac{1}{2}\sum\limits_{i = 1}^{N} {\varphi_{i}^{KS} \left( {\vec{r}} \right)\nabla^{2} \varphi_{i}^{KS} \left( {\vec{r}} \right)} } \right){\text{d}}^{3} r} .$$
(6)

As discussed in detail by Matta, Arabi, and Keith [75] and in our recent work [76], this is not the “true” atomic kinetic energy K(M) since the correlation kinetic contribution is missing. However, it is expected to give semiquantitative insight into the atom reactivity. Besides, the two following atomic potential energies will be taken into consideration:

$$\left\{ \begin{array} {ll} E_{\text{en}} (M) = - \int\limits_{{\varOmega_{M} }} {\left( {\rho \left( {\vec{r}} \right)\sum\limits_{A} {\frac{{Z_{A} }}{{\left\| {\vec{r} - \vec{R}_{A} } \right\|}}} } \right){\text{d}}^{3} r} \hfill \\ E_{{{\text{en}}M}} (M) = - \int\limits_{{\varOmega_{M} }} {\left( {\rho \left( {\vec{r}} \right)\frac{{Z_{M} }}{{\left\| {\vec{r} - \vec{R}_{M} } \right\|}}} \right){\text{d}}^{3} r} \hfill \\ \end{array} \right. .$$
(7)

The last line in Eq. (7) represents the attraction energy of the electrons inside the metal basin by their own nucleus, while the first equation includes the contribution of all nuclei and constitutes one component of the Interacting Quantum Atoms (IQA) decomposition scheme [77,78,79,80] that we have extensively used for the last years (for instance in Refs. [81,82,83,84]). Note that, contrarily to \(K(M) \approx K_{s} (M)\), Eq. (7) is exact but will be applied to an approximate electron density [85]. From a qualitative point of view, they both could provide hints on the “availability” of the electrons to be engaged in new bonds. Similarly, this propensity could depend on the atomic electronic localization index λ(A) that measures the average number of electrons pairs inside the basin [86]:

$$\lambda (A) = N(A)^{2} - 2D_{2} (A,A) \approx 2\sum\limits_{i} {\sum\limits_{j} {S_{ij} (A)^{2} } } ,$$
(8)

where N(A) is the atomic electron population, D 2 (A,A) the integrated electron pair density, S ij the overlap matrix elements, having made, for closed-shell species, the approximation of computing D 2 from the KS wavefunction (that-is-to-say that of the uncorrelated fictitious wavefunction), a widespread approximation that was discussed in detail by Matta [87] and Poater et al. [88].

The atomic energies previously discussed are only one part of the molecular energy, so that their sum does not recover the molecular energy. For the exact wavefunctions at an equilibrium geometry, the virial theorem actually states that [89]:

$$E_{\text{mol}} = \sum\limits_{A} { - K\left( A \right)} ,$$
(9)

affording an exact atomic decomposition of the molecular energy and leading to Bader’s original definition of atomic virial energies that have been extensively used to account for energy storage and energy transfers [90, 91]. Matta and coworkers [75, 92] have commented on the use of such approach at a non-stationary point on the potential energy surface and for a non-exact wavefunction. The following scaling strategy,

$$E_{\text{mol}} = \underbrace {{\frac{{E_{\text{mol}} }}{{\sum\limits_{A} {K(A)} }}}}_{\tau }\sum\limits_{A} {K(A)} = \sum\limits_{A} {\underbrace {{\left( {\tau K(A)} \right)}}_{{E_{\text{sc}} (A)}}} = \sum\limits_{A} {E_{\text{sc}} (A)} ,$$
(10)

is formally exact and readily applicable even if its interpretation can be arguable. E sc(M) will thus be reported (in conjunction with the \(K(M) \approx K_{s} (M)\) already mentioned approximation).

The last atomic descriptors that we will consider stem from conceptual DFT (CDFT) [33, 34], a framework that shares the same fundamental ingredient as QTAIM, namely the electron density. One can notably define the electronegativity of an atom in a molecule in the Kohn–Sham approach [93]:

$$\chi (M) = \frac{1}{N}\left[ {\left( {1 - \kappa } \right)K_{S} (M) + V_{I} (M)} \right] ,$$
(11)

where N is the total number of electrons, V I the atomic local ionization potential, and κ is Tozer’s [94] homogeneity parameter. We refer the interested reader to our recent paper [93] for a thorough discussion of this expression. In CDFT, local electrophilicity is defined from one of the celebrated Fukui function that reads [95, 96], (using finite difference linearization at constant external potential \(v\left( {\vec{r}} \right)\)):

$$f^{ + } \left( {\vec{r}} \right) = \left( {\frac{{\partial \rho \left( {\vec{r}} \right)}}{\partial N}} \right)_{{v\left( {\vec{r}} \right)}} = \rho_{N + 1} \left( {\vec{r}} \right) - \rho_{N} \left( {\vec{r}} \right) ,$$
(12)

where \(\rho_{N \pm 1}\) denotes the ground state electron densities when adding or removing one electron at fixed geometry.

This local function can be condensed onto any atomic basin by integration. It should be noticed that there are practical subtleties depending whether basin relaxation is considered or not upon vertical electron addition (leading to the so-called Response of Molecular Fragment (RMF) and Fragment of Molecular Response (FMR) formulations) [97], an issue we discussed in Ref. [98]. Here, we have chosen the simplest approach (basins are relaxed) that is equivalent to the popular Yang–Mortier [99] condensation scheme. As we want to compare systems with different number of electrons, one has to shift to the grand-canonical ensemble through the appropriate Legendre transform [33]. This is easily achieved by multiplying the Fukui function by the global softness S. The following descriptor is thus defined by:

$$s^{ + } \left( M \right) = S\left[ {\int\limits_{{\varOmega_{M} (N + 1)}} {\rho_{N + 1} \left( {\vec{r}} \right){\text{d}}^{3} r} - \int\limits_{{\varOmega_{M} (N)}} {\rho_{N} \left( {\vec{r}} \right){\text{d}}^{3} r} } \right] = S\left[ {q_{N} (M) - q_{N + 1} (M)} \right] .$$
(13)

As the metal center can be partially nucleophilic through the backdonation process, it is meaningful to look at the dual descriptor [38] that summarizes the two possible reactive behaviors:

$$\Delta f\left( {\vec{r}} \right) = \left( {\frac{{\partial^{2} \rho \left( {\vec{r}} \right)}}{{\partial N^{2} }}} \right)_{{v\left( {\vec{r}} \right)}} = \rho_{N + 1} \left( {\vec{r}} \right) + \rho_{N - 1} \left( {\vec{r}} \right) - 2\rho_{N} \left( {\vec{r}} \right) .$$
(14)

Its grand-canonical version is straightforward if ones neglect the hyper-hardness and lead to the following atomic descriptor [40]:

$$\Delta s\left( M \right) = S^{2} \left[ {2q_{N} (M) - q_{N + 1} (M) - q_{N - 1} (M)} \right] .$$
(15)

An alternative is the multiphilic descriptor [100, 101]:

$$\omega \left( M \right) = \omega \left[ {2q_{N} (M) - q_{N + 1} (M) - q_{N - 1} (M)} \right] ,$$
(16)

where \(\mu_{\text{pot}}^{2} /\left( {2\eta } \right)\) is the electrophilicity index [102, 103], \(\mu_{\text{pot}}\) and η stand for the molecular (electronic) chemical potential and hardness, respectively.

The very last CDFT descriptor we will consider is the static linear response kernel, which is non-local, but that can also be condensed into any atomic basin:

$${\text{LR}}\left( M \right) = \int\limits_{{\varOmega_{M} }} {\int\limits_{{\varOmega_{M} }} {\left( {\frac{{\delta^{2} E}}{{\delta \rho \left( {\vec{r}} \right)\delta \rho \left( {\vec{r}^{\prime}} \right)}}} \right)}}_{N} {\text{d}}^{3} r{\text{d}}^{3} r^{\prime} ,$$
(17)

which is instrumental in the calculation of the polarization energy (see also Ref. [104] for its physical meaning) and whose use in chemistry has been pioneered by Geerlings et al. [105,106,107,108,109,110]. Note that they used Hirshfeld partition for condensation, so that, from the best of our knowledge, it is the first time that QTAIM is used to get QTAIM atomic linear response values. In the frozen orbital approximation, LR(M) can be expressed in terms of the occupied ε a and virtual ε i KS orbital energies, and of the atomic overlap matrix elements (in the spirit of Eq. 8 in restricted cases) [111]:

$${\text{LR}}\left( M \right) = - 4\sum\limits_{i} {\sum\limits_{a} {\frac{{S_{ia}^{2} }}{{\varepsilon_{a} - \varepsilon_{i} }}} } .$$
(18)

In total, 22 descriptors have thus been computed: \({\text{MEP}}_{max}^{0.0004} ,\;{\text{MEP}}_{max}^{0.001} ,\;{\text{MEP}}_{max}^{0.002}\), \(MEP\left( {\vec{R}_{M} } \right)\), \(\nabla^{2} \rho_{(3, - 3)}\), \(\rho_{(3, - 3)}\), \(d_{(3, - 3)}\), \({\text{Vol}}(M)\) , q(M), \(\left\| {\vec{\mu }^{p} (M)} \right\|\), \(\bar{\alpha }\left( M \right)\), \(Q\left( M \right)\), \(K\left( M \right)\), \(E_{\text{en}} (M),\;E_{{{\text{en}}M}} (M)\), E sc(M), \(\lambda \left( M \right),\) \({\text{LR}}\left( M \right),\) \(\chi (M)\), \(s^{ + } \left( M \right)\), \(\Delta s\left( M \right)\), \(\omega \left( M \right)\).

3 Computational details

All optimized geometries, wavefunctions, and electron densities were obtained using the Gaussian 09 program [112] with the PBE0 global hybrid exchange–correlation functional [113] that has been shown by Bühl and coworkers [114] to provide accurate geometries for organometallic complexes involving transition metal of both first and second rows. All ligand atoms were described by the all-electron triple-ζ 6-311++G(3df,3pd) basis set, while cobalt and rhodium were described with the standard Stuttgart-Dresden (SDD) pseudopotential in conjunction with the associated valence basis set. No symmetry constraints were imposed for optimization, and the nature of the obtained stationary points was confirmed by computing analytical harmonic frequencies.

Laplacian critical points search and standard QTAIM analysis were performed with the AIMAll software [115]. Basin integration was monitored by inspecting integrated laplacian values (that should be equal to zero in principle). Nonstandard QTAIM descriptors, such as atomic electronegativities, atomic polarizabilities, and atomic linear responses, were obtained by homemade Fortran routines that extract the requested information from the various AIMAll output files.

In order to avoid inexact topologies (for instance existence of spurious critical points in the electron density topology) due to the use of a pseudopotential for the metal atom, a core electron density is added, represented as a linear combination of primitive S-type Gaussian functions [115, 116].

The derivatives in Eq. (3) have been evaluated through a symmetric two-point approximation at the zero-field geometry (\(\alpha_{ij} \left( A \right) \approx \frac{{\left. {\mu_{i} (A)} \right|_{{F_{j} }} - \left. {\mu_{i} (A)} \right|_{{ - F_{j} }} }}{{2F_{j} }}\)), implying that 6 single-point calculations are necessary to reconstruct the full polarizability tensor. The value for F j should be small enough so that the finite difference tends to the derivative, but not too small so that the difference in the SCF energy induced by the field is consequently higher than the SCF convergence criteria. Consistently with Macchi [73], we selected F j  = 0.005 a.u. and checked that the molecular polarizability is close to that given by Gaussian 09. For instance, the mean absolute deviation for the trans rhodium subgroup is equal to 0.1 a.u. Note, however, that due to some integration errors, atomic polarizabilities will not be reported for cis rhodium compounds.

As for the electronegativity, the Tozer’s homogeneity parameter has been fixed equal to 1.0 for all systems (von–Weizsäcker type behavior). Note that such a choice insures that all metal electronegativities are positive. Finally, global hardness and electrophilicity index were computed using the frontier orbital energies following the Koopmans’ type approach used in our previous work [40].

All complexes have been considered in their lowest spin state (in general, singlet in the octahedral case, as supported by usual molecular orbital theory for d 6 complexes). All distances are given in Angströms, while all other values are reported in atomic units unless otherwise explicitly stated. Tables with computed values for all descriptors are gathered in the supplementary information file.

4 Results and discussion

All studied complexes feature a formal d 6 metal configuration (oxidation state: +III) and correspond either to the [Co(CO)5Lig]n+ or [Rh(CO)5Lig]n+ formulas. (21) typical ligands have been considered (in the alphabetical order): Br−, CF3 −, CH3 −, CN−, C2H4, Cl−, F−, H−, H2O, NC−, NH3, NO2 −, OH−, O .−2 , PH3, PMe3, Ph−, C5H5N−, SCN−, and SH2. This dataset gathers main ligands types (X and L in the Green’s nomenclature), involving heteroatoms and common substituents, both σ or π donor/acceptors, aliphatic or aromatic, covering a large diversity of bonding schemes. They include for instance compounds like [Co(CO)5Br]2+ and [Rh(CO)5NH3]3+. Lig will thus be considered as the trans or cis orienting ligand, while the five carbonyl ligands can be classified into four cis and one trans with respect to Lig. In the following, by convention, we will only consider the CO cis ligand that displays the longest bond to the metal center.

Firstly, we will look at the Co-CO bond length in trans to Lig. The smallest values are obtained (in increasing order) for Lig = H2O (1.917), Br− (1.929), Cl− (1.932), C2H4 (1.938), while the highest ones correspond to (in decreasing order) O .−2 , (2.035), CF3 − (2.028), NO2 − (2.023), PMe3 (1.996). For rhodium, the following order is found: H2O (1.975), F− (2.016), NH3 (2.031), Cl− (2.040), and CF3 − (2.202), NO2 − (2.185), Ph− (2.174), O .−2 (2.171). It appears that there is no universal ranking possible (that-is-to-say independent of the metal). From a more qualitative point of view, the Co-CO trans bond length (1.97 in average) is, as expected from atomic radii, always shorter than the Rh-CO trans one (2.09 in average), the mean value for the d(Rh-CO trans )-d(Co-CO trans ) difference being equal to 0.12.

The same analysis can be carried out on the M-CO cis bond length. As previously, it is always higher for M = Rh (average value: 2.02) than for Co (average: 1.90), the mean value for d(Rh-CO cis )-d(Co-CO cis ) being equal to 0.11. One can wonder whether, for a given ligand, d(M-CO trans ) and d(M-CO cis ) are linearly correlated. The coefficients of determination definitely exclude it, since the corresponding r 2 values are equal to 0.20 for Co and to 0.50 for Rh.

One can now inspect the Δd M-CO = d(M-CO trans )-d(M-CO cis ) difference for a fixed ligand. It generally takes positive values, with the following average values: +0.07 (Co) and +0.08 (Rh). However, some negative values can be identified: only one for cobalt complexes (−0.032 with H2O), and three for rhodium, but two of them are negligible (−0.001 and −0.003 for F− and NH3, respectively), the only relevant one being also in the water case with an enhanced effect (−0.070). Consistently with our previous remark, no significant correlation can be found between Δd M-CO and d(M-CO trans ) or d(M-CO cis ).

We now depict our approach that is the very same as in our recent contribution [40]. Once a given octahedral complex has been geometrically optimized, the CO ligand in cis or trans to Lig is removed, affording the incomplete (unsaturated) [M(CO)4Lig]n+ species. QTAIM properties are then evaluated without geometry reoptimization. This is a reasonable and cheap computational approach that we briefly justified in our previous paper (“The validity of these approaches is supported by the fact that ligand substitution in octahedral complexes generally proceeds via dissociative mechanisms, these moieties therefore bear some chemical meaning as potential intermediates”).

Considering the formal \([{{\text{M}}\left( {\text{CO}} \right)_{4} {\text{Lig}}}]^{n+} + {\text{CO}}\mathop \to \limits_{{cis\,\, {\text{ or }}\,\, trans \, {\text{to}} \, Lig}} [ {{\text{M}}\left( {\text{CO}} \right)_{5} {\text{Lig}}}]^{n + }\) reactions, one can first look at charge transfers. If the variation of the metal atom charge upon CO coordination, Δq(M), is positive (decrease of its electronic population), one can conclude that the metal has globally acted as a nucleophile (backdonation). On the other hand, if Δq(M) is negative, the metal has been subject to an overall electron gain, indicating that it mainly acted as an electrophile (electron donation from ligands).

For cobalt complexes, we found that it is negative in all cases, with the following statistics: average (resp. minimal) value is equal to −0.06 (resp. −0.15) for trans complexes, while for cis compounds, the mean (resp. minimal) value equals −0.09 (resp. −0.19). Besides, for a given ligand, the charge transfer is always (except one negligible case) higher in cis than in trans (average value of the difference equal to 0.04), which is consistent with the fact that cis bond lengths are shorter than in trans. Quite similar trends are obtained for the rhodium complexes: the average cis value is equal to −0.06 with only negative Δq(Rh) values, and equal to −0.03 for trans cases for which six small positive values have been obtained.

One may now wonder whether this charge transfer can be predicted by the electrophilic Fukui function, f +, condensed on the metal atom when one CO ligand is missing. Let us recall that it is evaluated using finite difference linearization (Eq. 13) that involves adding one electron to the full complex. In general, condensed values are expected to be positive: atoms are reduced when the entire molecule is reduced. Interestingly, we actually identified two cases with negative condensed f +(Co) values in the trans PMe3 and phosphinine cases. However, the corresponding oxidation of the metal induced by the reduction of the whole molecule remains very small (q(Co) is equal to 0.936 before and to 0.941 after reduction, numbers that were confirmed using the most robust integration scheme consisting in extended capture and in the “sculpt” algorithm).

The existence of such negative Fukui functions (a general topic that has been studied, among others, by the groups of Ayers and Toro-Labbé [117,118,119,120]) may suggest that s +(M) (condensed grand-canonical Fukui function) is not a suitable descriptor to quantify charge transfer upon CO coordination. This conjecture is confirmed by the very low r 2 values between s +(M) and Δq(M): 0.15 for the trans CO family, 0.07 for cis CO, 0.05 for trans Rh, and 0.28 for cis Rh. One may nevertheless argue that it is compulsory to take also into account the partial nucleophilic character of the metal that manifests itself in the backdonation process.

This balance can be in principle achieved by considering the condensed dual descriptor. Positive values indicate an overall electrophilic atom, while negative values imply that the studied atom is mainly nucleophilic. From our charge analysis, one thus expects Δs(M) and ω(M) to be positive. It is the case in only 38% of the cases (8 over 21) for the trans Co species, the application of Eqs. (14–16) predicting a counterintuitive nucleophilic propensity of the metal atom. This fact is actually consistent with our previous analysis [40] based on the natural orbitals for chemical valence (NOCV) [121] analysis that clearly makes metallic electron loss domains appear.

The situation is otherwise “improved” for cis Co since positive values (overall electrophilic character) now represent 80%. Interestingly, only positive values are obtained for the Rh complexes, for which the dual descriptor may seem a promising tool. However, no correlation at all between Δs(M) or ω(M) and Δq are observed (all r 2 values are below 0.10). This result shows that neither Fukui functions nor the dual descriptor (and its avatars) are able to retrieve charge transfer upon CO coordination. This failure can be partly ascribed to the excessive averaging caused by the condensation procedure, a point that we discussed in Refs.  [41, 53].

Obviously, such bonding could be studied using other functions. To this aim, it is instructive to display some maps of the [M(CO)4Lig]n+ species, like those for the MEP function. As evidenced by Fig. 1, in case of [M(CO4)Br]2+ with a trans vacancy (left: cobalt, right: rhodium), the zone that shows the most positive MEP value (represented in blue in Fig. 1) is the one that is directly along the Br-M axis, an observation that is quite reminiscent of the celebrated σ-hole concept [122,123,124,125], which is a cornerstone for the study of noncovalent interactions (with the important difference that, for the chosen isodensity surface, MEP values are here everywhere positive due to the global positive charge of the complex).

Fig. 1
figure 1

Views of the molecular electrostatic potential (MEP) mapped on the 0.001 electron isodensity surface for the [Co(CO4)Br]2+ (left) and [Rh(CO)4Br]2+ (right) complexes featuring a coordination vacancy in trans of bromine. Atomic units are used

Full size image

These σ-holes are present in both trans and cis cases and for all of the studied complexes. From the crudest point of view, the bonding of the sixth ligand can be described as resulting from the coordination of a CO electron lone pair to these holes. As illustrated in Fig. 1, the most positive MEP value is always lower (for a given Lig) for rhodium than for cobalt (the average value for the \({\text{MEP}}_{max}^{0.001} (Rh)/{\text{MEP}}_{max}^{0.001} (Co)\) ratio is equal to 0.92 for trans cases and to 0.95 for cis ones). This is qualitatively consistent with the fact that bond lengths in rhodium complexes are longer than in cobalt ones.

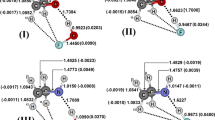
This picture can be complemented by analyzing the laplacian topology. As illustrated in Fig. 2, a myriad of critical points exist around the metal center as a consequence of the shell structure around it. In any case, we located a (3,−3) CP in the metal-missing ligand axis (which is also the furthest one from the metal), drawn in violet. From the qualitative point of view and in the light of our recent work on the tight connection between MEP and laplacian [126], this is an expected result since the σ-hole can also be characterized in terms of electron density laplacian (defining the “lump-hole” paradigm) [127, 128]. In line with our previous remarks, and as expected, the \(d_{(3, - 3)} ({\text{Rh}})/d_{(3, - 3)} ({\text{Co}})\) ratio is always higher than 1 (1.41 in average) due to the different atom size, and the density and laplacian values at this (3,−3) CP are always lower in rhodium than in cobalt complexes (mean values for the \(\nabla^{2} \rho_{(3, - 3)}\), \(\rho_{(3, - 3)}\), \(d_{(3, - 3)}\), respectively are equal to 0.28 and 0.42), suggesting a weaker coordination of the missing carbonyl ligand.

Fig. 2
figure 2

Views of the critical points (CPs) for the electron density Laplacian field inside the cobalt (left) and rhodium (right) atomic basin for the [Co(CO4)Br]2+ and [Rh(CO)4Br]2+ complexes featuring a coordination vacancy in trans of bromine. The following color code is used: yellow = (3, +3), green = (3, +1), pink = (3, −1), purple = (3,−3). The \(\nabla^{2} \rho_{(3, - 3)}\), \(\rho_{(3, - 3)}\), \(d_{(3, - 3)}\) values discussed in this paper are related to the CP designated by arrows

Full size image

One may wonder if these three laplacian descriptors are actually independent. It turned out that there exists a high correlation between \(\nabla^{2} \rho_{(3, - 3)}\) and \(d_{(3, - 3)}\). Indeed, gathering the 42 cobalt complexes (21 trans and 21 cis) (as represented in the left part of Fig. 3) provides a very robust model (with r 2 higher than 0.99) that is valid for any ligand and any position (both cis and trans). A similar model can also be built (r 2 = 0.98, right part of Fig. 3) for rhodium, according to (in atomic units):

Fig. 3
figure 3

Variations of \(\nabla^{2} \rho_{(3, - 3)}\) with respect to \(d_{(3, - 3)}\) for the cobalt (left) and rhodium (right) complexes evaluated at the (3,−3) laplacian critical point in trans (black squares) or cis (red circles) position relatively to the orienting ligand. Corresponding regression curves in dashed lines. Atomic units are used

Full size image
$$\left\{ \begin{aligned} \nabla^{2} \rho_{(3, - 3)} (Co) = 62.53 - 56.02\;d_{(3, - 3)} ({\text{Co}}) \hfill \\ \nabla^{2} \rho_{(3, - 3)} (Rh) = 34.29 - 24.85\;d_{(3, - 3)} ({\text{Rh}}) \hfill \\ \end{aligned} \right. .$$
(19)

On the other hand, no correlation at all has been found between \(\nabla^{2} \rho_{(3, - 3)}\) and \(\rho_{(3, - 3)}\). This can be explained by the fact that the density value is much less sensitive than the other descriptors to the ligand pattern. For instance, for the cis Rh complexes, it varies between 0.558 and 0.570, spanning a very narrow range.

We now seek correlations between bond lengths and the values of the MEP-associated descriptors evaluated on [M(CO)4Lig]n+ once the trans or cis CO has been removed. The correlations were unfortunately found to be low (lower than 0.60). Besides, it was shown that the four descriptors are not fully equivalent. More precisely, for each family, the correlations between \({\text{MEP}}_{max}^{0.0004}\), \({\text{MEP}}_{max}^{0.001}\), and \({\text{MEP}}_{max}^{0.002}\) are very high (with r 2 > 0.98 in general) but that \({\text{MEP}} ( {\vec{R}_{Co} })\) is sometimes nicely correlated to \({\text{MEP}}_{max}^{0.001}\) (r 2 = 0.95 for the trans Co cases) but sometimes not. For instance, for the cis Co group, the coefficient of determination is equal to 0.81, showing important discrepancies.

Moreover, the overall correlation between local descriptors and bond lengths is not significantly better (see r 2 values in the supplementary information) with laplacian descriptors, the r 2 values being lower than 0.60 in both rhodium and cobalt cases. Interestingly, for rhodium complexes, the distance between the nucleus and the furthest (3,−3) CP (\(d_{(3, - 3)}\)) shows a not negligible correlation (r 2 = 0.84) for trans position, but not anymore for the cis ones (r 2 = 0.40). From these results, one can conclude that albeit MEP and electron density laplacian provide a qualitative explanation for bonding in such complexes (the reason why they have been used in practice for many years to compare few compounds), they fail to be quantitative in a more general way.

One could ascribe this failure to the fact that all these descriptors are local: the information on one point may be not sufficient to account for bonding that includes non-local effects. We can thus now assess the performances of atomic descriptors. The best ones are represented in the supplementary information (see Figure S1 for cobalt and Figure S2 for rhodium), but the associated numbers prove that none of these descriptors is enough general. We also looked for some bilinear regressions based on physical combinations, by mixing, for instance, atomic charges and condensed electrophilic Fukui functions in the spirit of Ayers’ “general purpose” descriptor [129], but no significant improvement was obtained.

One may, however, wonder whether relative differences (in contrast to absolute) values can be accounted for, in particular between cis and trans coordination schemes. For each property P, the P trans  − P cis quantity can be easily evaluated. The corresponding values are collected in Tables S5 and S6 in the supplementary information file. As stated above, bond lengths in trans position are in almost all cases higher than in cis. From a qualitative point of view, this could result from the fact that the metal atom is more electrophilic in the cis cases. One thus expects the ΔMEP(M) = MEP(M) trans  − MEP(M) cis , Δ(q(M)) = q(M) trans  − q(M) cis (not to be confused with the previous Δq(M) descriptor used to quantify charge transfer), and the Δ(s +(M)) = s +(M) trans  − s +(M) cis differences to be negative.

This is actually the case for \(\Delta {\text{MEP}}( {\vec{R}_{M} } )\) since we noticed only two very small negative values among the 42 complexes (for Lig = H2O with Co and Rh, which are the only two significant complexes for which the bond is longer in cis than in trans positions). The dichotomy is less valid when looking at \(\Delta {\text{MEP}}_{max}^{0.001}\) since almost half of the computed values are positive for cobalt complexes (a ratio equal to 29% when considering \(\Delta {\text{MEP}}_{max}^{0.002}\)), proving once more that \({\text{MEP}}( {\vec{R}_{M} } )\) and \(\Delta {\text{MEP}}_{max}^{x}\) descriptions are not fully equivalent.

The situation is more clear for Δ(q(M)) (only two values are positive), Δs +(M) (4 positive values among the 42 differences), and \(\Delta\bar{\alpha }\left( {Co} \right)\) (all values except one are negative). In other words, the metal atom in cis cases is more positively charged, more electrophilic, and more polarizable, which can account for shorter bonds. One can also wonder what laplacian critical points may describe. Qualitatively, the more depletion, the more electrophilic, so that \(\Delta \nabla^{2} \rho_{(3, - 3)}\) is expected to exhibit negative values, which is true in 88% of the cases. Interestingly, the \(\Delta \rho_{(3, - 3)}\) quantity is more difficult to interpret: it is almost always negative for cobalt complexes, but always positive for rhodium. In conclusion, from the qualitative point of view, \(\Delta {\text{MEP}}( {\vec{R}_{M} })\), Δq(M), Δ(s +(M)), and \(\Delta \nabla^{2} \rho_{(3, - 3)}\) are consistent with the shorter M-CO cis bonds.

However, such descriptors are not quantitative since they are not well correlated to the difference in bond lengths. Conversely, consequent correlations were obtained using ΔE en with r 2 equal to 0.93 (cobalt complexes) and 0.94 (rhodium), respectively, the corresponding models (represented in Fig. 4) being given by:

Fig. 4
figure 4

Views of the best linear models for the metal-CO bond length differences (trans with respect to cis position, in Angströms) for cobalt (left) and rhodium (right) complexes. ΔE en(M) values are given in atomic units. Corresponding regression curves in dashed lines

Full size image
$$\left\{ \begin{array} {ll} \Delta d_{\text{Co--CO}} = - 0.0035 - 0.0294\;\Delta E_{\text{en}} \left( {\text{Co}} \right) \hfill \\ \Delta d_{\text{Rh--CO}} = - 0.013 - 0.0376\;\Delta E_{\text{en}} ({\text{Rh}}) \hfill \\ \end{array} \right. .$$
(20)

Noteworthy is also the fact that the only two cases where Δd M-CO is significantly negative (Lig = H2O with cobalt and rhodium) are also the two only cases for which ΔE en(M) is positive. Furthermore, it is possible to build a general model (r 2 = 0.92) valid for both metals (using all 42 points) as depicted in the left part of Fig. 5:

Fig. 5
figure 5

Left view of the best linear model for the metal-CO bond length differences (in Angströms) for all complexes. ΔE en(M) values are given in atomic units. Corresponding regression curve in dashed line. Right comparisons between ΔE en(M) values (in atomic units) obtained with the SDD pseudopotential + associated valence basis set and the Wachters + f all-electron basis set. Corresponding regression curve in dashed line

Full size image
$$\Delta d_{\text{M--CO}} = - 0.0098 - 0.0342\;\Delta E_{\text{en}} \left( M \right) .$$
(21)

Finally, from the methodological point of view, the influence of the pseudopotential on the pivotal \(\Delta E_{\text{en}} (M)\) atomic descriptor values can be briefly commented on. To this aim, we performed single-point calculations (to disentangle pure electronic from structural effects) on cobalt complexes using the all-electron Wachters + f basis set [130] (that was recommended by Bühl and Kabrede [131] for first row transition metals). The results are shown in the right part of Fig. 5 and prove that both descriptions are almost fully equivalent (r 2 > 0.99). This means that \(\Delta E_{\text{en}} (M)\) can be surely used to predict trans/cis preferences, almost independently of the computational protocol.

5 Conclusions

In this paper, we tackled the description of organometallic compounds within the QTAIM framework, focusing on the ability of both local and atomic descriptors to account for cis and trans structural effects in cobalt and rhodium octahedral carbonyl complexes. We found that common descriptors, like the molecular electrostatic potential and the properties of laplacian critical points, provide a satisfying qualitative approximation for the observed differences. Nevertheless, they fail in being enough quantitative. However, a promising model based on the attraction energy of the electrons inside the metal atom basin by all nuclei was reported. Such an encouraging result constitutes, from our viewpoint, incentive reasons to foster the use of QTAIM energy components for chemical rationalization and for building a fruitful dialogue between experimentalists and theoreticians in organometallics. Other applications of such descriptors will be reported in due course.