Introduction

The prediction of reactive behaviors through quantified descriptors has focused great interest in the last decades inside the theoretical chemistry community, leading to the publication of many models not only to account for experimental observations, but also to predict new chemical tendencies. Such an approach requires that models are confronted with experimental data, and that both theoretical approximations and experimental protocols are assessed. Among these approaches, the quantitative structure properties relationship (QSPR) [1, 2] framework has achieved a widespread popularity in chemoinformatics and has been used to predict a wide variety of physicochemical properties [3–5].

The chemical descriptors that enter such models can stem from various theories: some can be obtained only using chemical formulas, while others require the knowledge of the geometrical structure which can be obtained from experimental data or from theoretical calculations. Other molecular descriptors can only be obtained at the quantum level, such as ones stemming from conceptual density functional theory (CDFT) [6, 7] or Bader’s quantum theory of atoms-in-molecules (QTAIM) [8, 9]. These descriptors present, from our viewpoint, the advantage of being deeply grounded in physics and are directly derived from the electron density, which is the primary physical observable in quantum chemistry.

In this paper, we will use these descriptors for the study of the reactivity of some Brønsted acids and bases. Historically, sorting and comparing these systems through scales of pKa values stand as one of the early successes in the quantification of chemical reactivity. However, the prediction of pKa in solution are notoriously known to be difficult in computational chemistry [10, 11], as solvent effects are important and cannot often be correctly described using a genuine implicit model. Even if considerable progress has been made in the modeling of such effects, they still remain a challenge [12].

On the contrary, gas-phase basicity is a candidate of choice to assess the ability of quantum chemical descriptors to rationalize such reactions. CDFT, which can be described as a perturbative approach, has been successfully exploited to provide quantified indexes of reactivity. For instance, linear dependence between experimental pKa values and such theoretical indexes were observed across various types of small inorganic [13] and organic molecular systems [14, 15]. Similarly, the use of QTAIM was advocated to quantify the basicity of the lone pairs of basic hereroatoms [16]. Obviously, alternative computational methods exist, also giving realiable results [17–20].

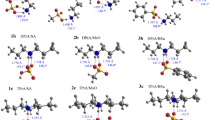
The present work will focus on the pyridine and phosphinine derivatives (see Scheme 1) studied in one of your previous works [21], featuring typical organic substituents (carbonyl, halogens, amines, thiols, alkyl chains…). It was shown that both cycle types exhibit different donor-acceptor properties [22], and ambivalent reactivity was reported [23]. They are thus well suited to scrutinize the efficiency of the pertubative model on which CDFT is grounded. Besides, charge transfers and electron density reorganization will be in particular discussed within Bader’s theory, aiming at providing thorough insights regarding the basicity of pyridines and phosphonines.

Scheme 1
scheme 1

The studied molecules

Full size image

Computational details and theory

All calculations were carried out at the DFT level with the Gaussian 09 package [24], using the B3LYP exchange-correlation functional and the 6-311++G(3d,3p) basis set. All geometries were fully optimized without symmetry constraints. QTAIM atomic charges, delocalization indexes and bond critical point (BCP) properties were obtained with Keith’s AIMAll software [25].

In the canonical E[N,v] ensemble, the energy variation of a chemical system can be expanded using a Taylor expansion:

$$ \varDelta E=\underset{\varDelta {E}_{\varDelta N}}{\underbrace{\mu \varDelta N}}+\underset{\varDelta {E}_{\varDelta v}}{\underbrace{{\displaystyle \int \rho \left(\overrightarrow{r}\right)\varDelta v\left(\overrightarrow{r}\right){d}^3r}}}+ higher\kern0.5em order\kern0.5em terms, $$
(1)

where μ is the (electronic) chemical potential. Local Fukui functions are then defined by:

$$ f\left(\overrightarrow{r}\right)\overset{ def}{=}{\left(\frac{\delta \mu}{\delta v\left(\overrightarrow{r}\right)}\right)}_N. $$
(2)

Due to the energy discontinuity for integer values of N [26, 27], it is necessary to distinguish electrophilic (\( {f}^{+}\left(\overrightarrow{r}\right) \)) and nucleophilic (\( {f}^{-}\left(\overrightarrow{r}\right) \)) local reactive behaviors. The dual descriptor [28] is then defined as:

$$ {f}^{(2)}\left(\overrightarrow{r}\right)\overset{ def}{=}{\left(\frac{\partial f\left(\overrightarrow{r}\right)}{\partial N}\right)}_{v\left(\overrightarrow{r}\right)}\approx {f}^{+}\left(\overrightarrow{r}\right)-{f}^{-}\left(\overrightarrow{r}\right). $$
(3)

Predominant electrophilic and nucleophilic local tendencies are thus characterized at once according to the sign and magnitude of the dual descriptor [29].

When comparing two different molecules (and not two different sites on the same molecule), one has to switch to the grand canonical ensemble [30], considering the local softnesses:

$$ {s}^{+/-}\left(\overrightarrow{r}\right)\overset{ def}{=}{\left(\frac{\partial \rho \left(\overrightarrow{r}\right)}{\partial \mu}\right)}_{v\left(\overrightarrow{r}\right)}^{+/-}={\left(\frac{\partial \rho \left(\overrightarrow{r}\right)}{\partial N}\right)}_{v\left(\overrightarrow{r}\right)}^{+/-}{\left(\frac{\partial N}{\partial \mu}\right)}_{v\left(\overrightarrow{r}\right)}=S{f}^{+/-}\left(\overrightarrow{r}\right), $$
(4)

where S is the chemical softness, computed using a finite difference linearization involving the SCF energies of the N and N±1 species (at fixed geometry):

$$ S\overset{ def}{=}{\left(\frac{\partial N}{\partial \mu}\right)}_{v\left(\overrightarrow{r}\right)}\approx \frac{1}{E\left(N-1\right)+E\left(N+1\right)-2E(N)}. $$
(5)

Similarly, the \( {S}^2{f}^{(2)}\left(\overrightarrow{r}\right) \) function should be considered instead of the dual descriptor.

When Bader’s basins are used, condensed (atomic) descriptors are obtained by integration on the considered basin Ω:

$$ {s}^{+/-}\left(\varOmega \right)={\displaystyle \underset{\varOmega }{\int }{s}^{+/-}\left(\overrightarrow{r}\right){d}^3r}. $$
(6)

Condensed Fukui functions and condensed dual functions were computed thanks to AIMgrid, a local highly-parallelized code based on Cartesian grid principle [21].

Results and discussion

First of all, we will discuss the geometries of the acidic form. It must be noticed that we will restrain our analysis to the protonation of the heteroatom A in the cycle (even if other protonation sites might be considered). After describing the main structural parameters of the acidic form (cationic minimum obtained with the creation of the N-H or P-H bonds), we will briefly discuss the shape of the potential energy surface corresponding to this proton attack.

The main structural parameters are gathered in Table 1. As expected, the N-H bond lies in the ring plane: all C1NH angles are equal to 180°. It is not any longer the case for the phosphinine derivatives for which only six compounds have a C1PH angle close to 180° (H, NO, HCO, COOH, COCl substituents).

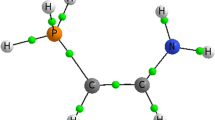
Table 1 Selected geometrical parameters for the optimized protonated compounds (bond lengths in angström, angles in °), and activation barriers (in kcal mol−1) for the crossing of the phosphinines planes
Full size table

This out-of-plane hydrogen position cannot be ascribed to sterical hindrance between this hydrogen and the B substituents, since COCl or COOH belong to the “plane” category whereas the CH3 or CN cases, less bulky, do not. The deviation from the planarity can be considerable: for instance, for fluorine, the angle is equal to 125.6°. Interestingly, when this is replaced by a less electronegative halogen (respectively Cl and Br), the P-H comes closer to the plane (respectively 133.5° and 136.2°). In order to account for this out-of-plane P,N-proton bond, the nature of the lone pairs in the basic forms was investigated using a natural bond orbital (NBO) [31] analysis: the lone pair on P importantly differs from the one on N, the first one having a strong s character (about 60 %, with respect to 28 %). However, there exists no correlation between the s percentage and the C1PH angle.

We now examine if the C1PH angle in the optimized geometry for the basic form can give insight into the trajectory followed during the capture process. To study these non-planar proton attacks, energy scans were performed. Graph 1 represents the energy variations depending on the C1PH angle for selected phosphinines. These curves correspond to relaxed energy scans for the acidic form. For the H and COOH subsitutents, the energy is decreasing when θ=C1PH increases, exhibiting only one energy minimum at 180° (the corresponding angle value being denoted θ eq ).

Graph 1
figure 1

Relaxed energy scans on the C1PH angle for the protonated phosphinine, dicarboxyphosphinine, dibromophosphinine and diaminophosphinine. Energies differences (in kcal mol−1) are computed with respect to the equilibrium ones

Full size image

Conversely, for the B=NH2 and B=Br substituents, 180° is maximum and corresponds to a transition state (TS) connecting the two symmetric minima at θ eq and –θ eq . Accordingly, the energy at 180° enables to evaluate the isomerization barrier, denoted ΔE ZPE iso , required for the proton to cross the plane, whose values are collected in Table 1. All barriers are lower than 13.5 kcal mol−1, a value which is not negligible but that is accessible at room temperature.

Qualitatively, the closest θ eq is to 180°, the lower the isomerization barrier. We thus propose the following fit, using all points and constraining the curve to intersect the X axis at θ eq  = 180° (R 2 = 0.94):

$$ \varDelta {E}_{iso}^{ZPE}=0.061\left(180-{\theta}_{eq}\right)-0.0048{\left(180-{\theta}_{eq}\right)}^2+0.00010{\left(180-{\theta}_{eq}\right)}^3. $$
(7)

One may now wonder if these θ eq angles represent the optimal angle of attack, that-is-to-say: does the proton adopt and keep this angular orientation during its approach? Graph 2 shows that it is not actually the case. For instance, for B=Br, the equilibrium angle is 136°. The dark green curve shows that, whatever the P-H distance, this approach is lower in energy than the 180° approach. But, the light green curve indicates, however, that when the proton is beyond 2.1 Å, the system is more stable perpendicular to the ring (θ = 90°). In the same vein, the equilibrium orientation for the diaminophosphinine (θeq = 112°) is less stable than the 90° one for P-H>1.9 Å. All these curves prove that the minimal energy path for the proton coordination does not occur at constant angle, and that the potential energy surface is more complicated in case the proton is not in the cycle plane for the minimum structure (note that for large separation distances, the use of a monodeterminantal scheme as the KS one becomes questionable).

Graph 2
figure 2

Relaxed energy scans on the P-H bond length for the dibromophosphinine and the diaminophosphinine. The θ=C1PH angles are frozen. Energies differences (in kcal mol−1) are computed with respect to the points obtained for the equilibrium θ eq value

Full size image

We now discuss the importance of charge transfer upon proton capture, measured in terms of variations of QTAIM atomic charges (in electrons, see Table 2):

Table 2 Variations of the QTAIM atomic charges (in e) between the basic and acidic forms
Full size table
$$ \varDelta q(X)=q{(X)}_{acid}-q{(X)}_{base}. $$
(8)

The results are very homogeneous for the pyridines. The variation for the H charge lies inside the [−0.64; −0.55] range, showing that the final charge on hydrogen is partly independent on the substituents, whatever they are electron donating or electron withdrawing groups.

Similarly, the variation of the nitrogen charge is very low in absolute value (lower than 0.10). It is worth noticing that this variation is negative, that-is-to-say that N gains electrons when it binds to the proton. This can seem counterintuitive since one expects that some electrons from nitrogen are transferred to hydrogen. Even if this phenomenon is small in magnitude, it cannot be neglected. This is due to the fact that the formation of the N-H bond induces a full rearrangement of the electron density inside the aromatic ring, so that electrons are also transferred from the carbon atoms of the cycle.

This can be measured in terms of the Δq(N)+Δq(H) sum. Indeed, if the charge transfer was occurring only between N and H, this sum would be equal to zero. On the contrary, it is strongly negative (about −0.60 electrons), proving the role of all other atoms when the covalent bond is formed.

Once more, the observed situation is different for the phosphinines. The variation of the phosphorus charge is highly positive, in the [0.53; 0.89] range. Interestingly, the variation for the hydrogen atom charge is higher (in absolute value) than one electron. In other words, the final charge on hydrogen is negative, contrarily to what was obtained for the pyridine derivatives. Thus, this hydrogen in the phosphine series changes its nature, from a proton to a hydride.

This can be rationalized in terms of electronegativites. Whereas N is much more electronegative than H, P has almost the same electronegativity as H (2.2 in Pauling’s scale). Interestingly, while the charge transfers for each atom are very different between pyridines and phosphinines, the total electron fluxes Δq(N)+Δq(H) and Δq(P)+Δq(H) can be similar and do not really reflect these atomic discrepancies.

In order to illustrate more precisely how the residual charge is redistributed on the whole molecule, we represented, in Scheme 2, the atomic charge variations for the pyridine and the phosphinine disubstituted by the carboxylic acid group. It immediately appears that, except the H and the N, P atoms, the variations for pyridine and phosphinine are very similar. For instance, the para-hydrogen has the same variation (+0.07). It can be noticed that the carbons on the cycle have various behaviors: the meta and para ones are enriched in electrons, while the ortho looses electrons. The total variation of the charge for each COOH group is respectively 0.17 and 0.19 for the pyridine and phosphinine derivatives, so that the two substituents on the ring recovers about 35 % of the total charge, showing how large the charge delocalization can be.

Scheme 2
scheme 2

Variation of the atomic charges and of delocalization indexes upon protonation (in atomic units)

Full size image

A complementary approach of this phenomenon is to look at BCP properties. We will first investigate more deeply the nature of the N-H and P-H bonds (Table 3). The BCP density, denoted ρ c , is quite high in both cases, as a consequence of the covalent nature of such bonds [32], a nature that is confirmed by the negative values of the BCP laplacian values (traducing an electron accumulation around the BCP). The values of these descriptors are not highly sensitive to the substitution patterns: the BCP density is in the [0.337; 0.352] a.u. range for pyridines and in [0.174; 0.185] a.u. for the phosphinines set.

Table 3 Selected bond critical points (BCPs) properties for the whole set. All values are given in atomic units
Full size table

As previously cast in light, the formation of the N-H or P-H bond also impact the other bonds, in particular the two N-C or P-C bonds, which will be denoted X-C3 and X-C4. Δρ c (not to be confused with the laplacian ∇2 ρ c ) measures the variation of the BCP density for these two bonds, according to:

$$ \varDelta {\rho}_c={\left\{{\rho}_c\left(X-{C}_3\right)+{\rho}_c\left(X-{C}_4\right)\right\}}_{acid}-{\left\{{\rho}_c\left(X-{C}_3\right)+{\rho}_c\left(X-{C}_4\right)\right\}}_{base}. $$
(9)

These quantities are all negative for the pyridine family, indicating a slight weakening of these N-C bonds (in favor of the newly created N-H one). The situation for the phosphinines is more balanced, since there are many more cases (12/16) with an increase of the P-C BCP densities (corresponding to positive values for Δρ c ). For instance, the maximum value for Δρ c is equal to 0.038 a.u. (for B=COOH). This is not at all negligible since it is a value that corresponds to the BCP density value for quite strong hydrogen bonds [33] and for several agostic ones [34]. So, these results suggest that the formation of the P-H bond can strengthen the P-C bonds in a non-negligible way.

It is intuitively expected that this density variation is higher when the proton strongly interacts with the heteroatom, so that we can speculate that the lowest is the N,P-H distance, the higher is Δρ c . Interestingly, we found that, for phosphinines, such a trend is observed. A linear correlation gives (with R 2 = 0.91):

$$ {\left.\varDelta {\rho}_c\right|}_{a.u.}=3.651-2.597{\left.\left(P-H\right)\right|}_{\AA}. $$
(10)

However, it is not at all the case for the pyridine derivatives since R 2 = 0.05! Once more, phosphinines and pyridines strongly differ in the way they redistribute charges.

Such a study can also be envisioned by inspecting delocalization indexes (DIs) [35–37] that were previously used as a kind of bond order [38]. As we did for charges analyses, we represented in Scheme 2 the variation of the DI for all bonds for the carboxylic acid derivatives. The DIs are substantially higher for P-H (about 0.8–0.9) than for N-H (0.7–0.8). As was previously enlightened, the C-N bond is considerably weakened (DI variation equal to −0.16) which is consistent with the conclusion drawn from the BCP density values, while the P-C one is very slightly strengthened (+0.01). On the contrary, all other DIs are similar between phosphine and pyridine derivatives. Interestingly, the variation is positive for the Cortho-Cmeta bond (+0.03 for the pyridine case), while negative for the Cmeta-Cpara (−0.03), confirming the non-equivalence of these positions already observed on the atomic charges analysis.

It can be noticed however that the two viewpoints (charges and DIs) are complementary and not fully equivalent: for instance, the total variation of the DIs for the COOH group is almost null (0.00 and 0.02) while charges variations are consequent.

Finally, to conclude this part, it must be stressed that the use of QTAIM to study inductive and mesomeric effects is a vivid and still developing subject, which can be not only tackled from atomic charges or BCP properties viewpoints [39, 40], but also using more sophisticated tools [41–43].

We now consider the reaction energy of the proton attachment reaction:

$$ \varDelta {\xi}_H={\xi}_{acid}-{\xi}_{base}, $$
(11)

where ξ stands either for the SCF energy with the zero-point energy correction, or for the Gibbs enthalpy (see Table 4). It immediately follows from the results that distinguishing SCF energy and Gibbs energies is irrelevant, confirming, with other examples, the remark of Huang et al. [15]: “there exists a near perfect correlation between ΔE and ΔH (proton affinity) or between ΔE and ΔG (gas-phase basicity)”.

Table 4 Reaction energies (in kcal mol−1) for protonation
Full size table

From a chemical perspective, the coming proton can be considered as an electrophilic species. P and N can be viewed on the other hand as nucleophiles. We introduced in the Computational details and theory section the condensed Fukui functions that enable to quantify how nucleophilic and how electrophilic an atom is, as reported in Table 5. Both atoms have an ambivalent behavior (at the same time nucleophilic and electrophilic). Thanks to the dual descriptor, it is possible to determine what the predominant reactive trend is: the considered atom will be predominantly nucleophilic if the condensed value for f (2) is negative. It is the case in 56 % of the cases for pyridines and in 44 % for phosphinines.

Table 5 Nitrogen and phosphorus condensed Fukui functions and dual descriptors, and values of the electrostatic potential at nuclei calculated on the basic forms. All values are in atomic units
Full size table

These low percentages explain why the condensed Fukui functions and the dual descriptor are not correlated to the reaction energies: all of the correlation coefficients R 2 (for s + (N), s − (N), S 2 f (2) (N), s + (P), s − (P), 2 Sf (2) (P)) are lower than 0.20. One can wonder whether such a result is surprising or not. On the one hand, condensed Fukui functions were successfully used to predict protonation sites in anilines and derivatives molecules by Fuentealba and coworkers [44]. On the other hand, Fukui functions were shown to fail to describe hard-hard interactions, as demonstrated by Melin et al. [45] and recently confirmed by Ayers and coworkers [12]: “For the amines the hardness and Fukui function did not show any correlation to the pK a”. More generally, local descriptors derived from Fukui functions often “can not describe any charge-controlled process because they have not been designed to explain these reactions” [46].

From our results, we can say that the Fukui functions are truly useful to locate the protonation sites (P and N atoms correctly revealing nucleophilic from our condensed values), but are not relevant to predict the corresponding bonding energy. They actually give insight into the beginning of the reaction (where proton attacks), but not to the thermodynamic product final stability.

On the contrary, electrostatic potential is often useful to quantify them. It can thus be concluded that the descriptors that revealed efficient to predict electro/nucleophilic attacks [47] in organic chemistry may not be suited to model acido-basic reactions. In other words, descriptors derived from the chemical potential may appear not adequate.

However, one cannot fully exclude that the finite different approximation may partly account for this failure. From this perspective, the work of Chattaraj and coworkers [48–50] of the pKa predictions based on philicity indexes, where nice correlations are obtained, deserves to be cited.

Coming back to our systems, Eq. 1 shows that the energy variation not only depends on μ (associated to charge transfers), but also on the response to the external potential variation ΔE Δv . Following Liu and coworkers [15, 51], this contribution can be approximated by the electrostatic potential at the nucleus of the heteroatom X:

$$ \varDelta {E}_{\varDelta v}\propto EP(X)={\displaystyle \sum_{nuclei\kern0.5em i\ne X}}{\displaystyle \left(\frac{Z_i}{\Vert {\overrightarrow{R}}_i-{\overrightarrow{R}}_X\Vert }-{\displaystyle \int \frac{\rho \left(\overrightarrow{r}\right)}{\Vert \overrightarrow{r}-{\overrightarrow{R}}_X\Vert }}\right)}{d}^3r. $$
(12)

Graph 3 shows that these EP X enable to evaluate quite accurately the reaction energies: the correlation coefficients R 2 are equal to 0.89 (pyridines) and 0.92 (phosphinines) according to:

Graph 3
figure 3

Evolution of ΔG 0 H (in kcal mol−1) with respect to the electrostatic potential on the hetereoatom nucleus (in a.u.) for pyridines (black squares) and phosphinines (red circles). The solid lines correspond to the obtained linear regressions. Please note the break at the middle of the X axis

Full size image
$$ \left\{\begin{array}{l}\varDelta {G}_H^0\left|\mathrm{kcal}/\mathrm{mol}\right.=8178.7+456.56 EP(N)\left|a.u.\right.\\ {}\varDelta {G}_H^0\left|\mathrm{kcal}/\mathrm{mol}\right.=29647.6+550.75 EP(P)\left|a.u.\right.\end{array}\right. $$
(13)

As expected, the more negative the electrostatic potential, the more negative the reaction energy. Interestingly, the best model is obtained for the set where the charge transfer is the most important (phosphinines), which is the one for which the electrostatic potential is expected to be the least relevant. Actually, the linear regression enables to artificially take into account the missing part due to the variation of the atomic populations inside the basic moiety.

Finally, it should be noticed that Eq. 13 proves that it is not possible to build a simple universal model: the protonation of pyridines and phosphinines cannot be simultaneously described by a reduced subgroup of common atomic descriptors.

Conclusions

In this paper, we studied the protonation of some pyridines and phosphinine derivatives. We showed that the behavior of the two families is different upon proton attack. In particular, this attack can occur outside the cycle plane in the case of phosphinines, due to the spherical character of the phosphorus’ lone pair. We then carried a detailed analysis of the charge transfers, emphasizing that they must not be neglected and that they involve the atoms of the aromatic cycle. Lastly, we revisited the relationship between the reaction energies and some atomic molecular descriptors. The electrostatic potential calculated on the binding heteroatoms is revealed well correlated to these energies, contrarily to condensed Fukui functions, and thus constitutes a powerful tool for the rationalization of such chemical transformations, even if it cannot be universal.