On numerical approximations to fluid–structure interactions involving compressible fluids

Abstract

In this paper we introduce a numerical scheme for fluid–structure interaction problems in two or three space dimensions. A flexible elastic plate is interacting with a viscous, compressible barotropic fluid. Hence the physical domain of definition (the domain of Eulerian coordinates) is changing in time. We introduce a fully discrete scheme that is stable, satisfies geometric conservation, mass conservation and the positivity of the density. We also prove that the scheme is consistent with the definition of continuous weak solutions.

1 Introduction

In the recent decades, there is an increasing attendance of mathematicians on the subject of fluid–structure interaction (FSI) problems due to their numerous applications. This includes blood flow through a vessel, oil flows through an elastic pipe, oscillations of suspension bridges, lifting of airplanes, bouncing of elastic balls or the rotation of wind turbines, see [2, 5, 10, 40] and the references therein.

We will consider the particular setting where the solid (or the structure) is a shell or a plate. This means that it is modeled as a thin object of one dimension less than the fluid. For related up-to-date modeling and model reductions on plates and shells see [16, 17, 41] and references therein. The fluid will be considered to be governed by the compressible Navier–Stokes equations. We are interested in the development of Galerkin schemes which are connected to the setting of weak solutions. Most of the mathematical effort in this setting so far was devoted to incompressible fluids for weak solutions with a fixed prescribed scalar direction of displacement of the shell. Well posedness results commonly show that a weak solution exists until a self-touching of the solid is approached. For incompressible Newtonian fluids we name the following results [3, 9, 20, 21, 32, 33, 37, 45,46,47]. On the other hand, the theory for compressible flows is much less developed. Only recently the existence of weak solutions in the above setting was shown [4], see also [50] for the existence of a weak solution where the structure is a thermoelastic plate.

The numerical results of fluid–structure interactions are rich and diverse. The numerical analysis for the incompressible flows is developed in accordance with the existence theory; see the kinematic splitting schemes developed in [9, 11, 12, 38], see also [10, 29, 36, 48] for more simulation results. The numerical theory for compressible fluids interacting with shells or plates is rather sparse. We mention [1, 19] for the stability analysis with a given variable geometry and [28, 42] for some numerical simulations. It seems that a numerical strategy for compressible flows interacting with an elastic structure stays undeveloped due to the high nonlinearity of the problem originating from the fluid and its sensitive coupling to the motion of solid structure.

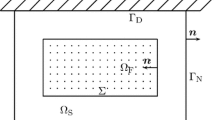
This paper aims to fill that gap and enrich the theory on fluid–structure interactions by introducing a (fully discrete) numerical approximation scheme which is in coherence with the known continuous existence theory. In particular we study numerics for the interaction between a compressible barotropic fluid flow with an elastic shell in the time-space domain $Q_T= I \times \Omega$, where $\Omega =\Omega (t)\subset \mathbb {R}^{d}$ ($d\in \{2,3\}$, $t\in I=[0,T])$ is a time dependent domain defined by its unsteady boundary. The boundary of $\Omega$ consists of a time dependent elastic shell $\Gamma _S(t)$ on the top surface of the fluid (whose projection in $d^{th}$- space direction is $\Sigma$ given below), and fixed solid walls $\Gamma _D=\partial \Omega \backslash \Gamma _S$ for the other parts of the boundary. Throughout the paper we reserve $r=(x_1,\ldots , x_{d-1})$ as the coordinates for the plate displacement $\eta =\eta (t, r) : \Sigma \rightarrow \mathbb {R}$, i.e. the distance of the shell above the horizontal plane $x_d=H$. We define $x= (r,x_d)$ as the Eulerian coordinates in the domain

Moreover, we denote by $\widehat{\Omega }= \Sigma \times [0,H]$ the reference domain. The mapping from the reference domain $\widehat{\Omega }$ to the current domain $\Omega$ reads

$$\begin{aligned} \mathcal {A}:\widehat{\Omega }\mapsto \Omega , \quad \widehat{x}\mapsto x=\mathcal {A}(t,\widehat{x})=\mathcal {A}(t, \widehat{r},\widehat{x}_d) = \left( \widehat{r}, \widehat{x}_d\frac{H+\eta (t,r)}{H}\right) . \end{aligned}$$

(1.1)

Note that $\mathcal {A}$ is invertible as long as $\eta (t,r)>-H$. Here and hereafter, we distinguish the functions on the reference domain by the superscript “ $\widehat{ }$ ” with the exception of the ALE mapping denoted by $\mathcal {A}$ instead of $\widehat{\mathcal {A}}$. Further, we denote $\mathbb {J}$ and $\mathcal {F}$ as the Jacobian of the mapping $\mathcal {A}$ and its determinant:

We present Fig. 1 for a two dimensional example of the domain and ALE mapping.

Fig. 1

Time dependent domain and the ALE mapping

The evolution of the fluid flow is modelled by the Navier–Stokes system

(1.2a)

(1.2b)

where $\varrho = \varrho (t,x)$ is the fluid density, $\mathbf {u}= \mathbf {u}(t, x)$ is the fluid velocity, $\mathbf {f}$ is an external force, $\varvec{\tau }$ is the Cauchy stress

Here, $a>0$, $\gamma >1$, the viscosity coefficients satisfy $\mu >0$ and $2 \mu +d\lambda \ge 0$. The motion of the shell is given by

$$\begin{aligned} \varepsilon _0\varrho _S\partial _t^2 \eta + K'(\eta )&= g+\mathbf {e}_d \cdot \mathbf {F}, \quad \text {on } I\times \Sigma , \end{aligned}$$

(1.2c)

where $\varrho _S>0$ is the density of the shell, $\mathbf {e}_d=(0,0,1)^T$ for $d=3$ ($\mathbf {e}_d=(0,1)^T$ for $d=2$), $g=g(t,r)$ is a given function, $\mathbf {F}= - \big (\varvec{\tau }\cdot \mathbf {n}\big )\circ \mathcal {A}\ \mathcal {F}$, $\mathbf {n}$ is the outer normal vector. For the sake of simplicity, we assume throughout the paper that $\varepsilon _0\varrho _S=1$. As the elastic energy $K(\eta )$ we use the following linearised energy functional $K(\eta )= \frac{\alpha |\nabla ^2 \eta |^2}{2}+\frac{\beta |\nabla \eta |^2}{2}, \; \alpha > 0,\; \beta \ge 0$, which leads to the following $L^2$-gradient:

Throughout the paper, for the sake of a concise presentation we denote by $z=\partial _t\eta$ the function representing the speed of the shell deformation.

We refer to Ciarlet and Roquefort [16] and references therein for the details of the model and also other choices of $K(\eta )$. To close the system we propose the following boundary conditions and initial data

$$\begin{aligned} \mathbf {u}|_{\Gamma _D}= & {} 0, \; \eta |_{\partial \Sigma }=0,\; \nabla \eta |_{\partial \Sigma }=0, \quad \varrho (0)=\varrho _0,\; (\varrho \mathbf {u})(0) =\mathbf {q}_0 \text { in } \Omega (0), \nonumber \\ \eta (0,\cdot )= & {} \eta _0,\; z (0,\cdot )=z_0 \; \text {in}\; \Sigma . \end{aligned}$$

(1.3)

We also need a compatibility condition between the shell-motion and the fluid

$$\begin{aligned} \mathbf {u}(t,x)|_{\Gamma _S}\circ \mathcal {A}= z (t,r) \mathbf {e}_d. \end{aligned}$$

(1.4)

The purpose of the present paper is to introduce a fully discrete numerical scheme that is equipped with suitable physical and mathematical properties. By that we mean that it satisfies in particular:

• (a) A weak continuity equation that can be renormalized in the sense of DiPerna and Lions on the discrete level, such that the error for convex renormalizations is positive.

• (b) Mass conservation and positivity of the discrete density is preserved.

• (c) A fully coupled momentum equation in the spirit of Definition 1 on the discrete level.

• (d) A discrete energy inequality for the coupled system (analogous to the continuous energy inequality (2.1)).

• (e) The scheme is consistent with the continuous weak solutions introduced in [4] (See also Definition 1). This means in particular, that if the discrete deformation, density and velocity converge (strongly) to some limit triple, this limit triple is indeed a weak solution of the continuous problem.

• (f) The scheme exists for a minimal time-interval. I.e. for every $\delta _0\in (0,H/2)$ there is a minimal time $T_0$, such that a-priori $\hbox {inf}_{[0,T_0]}\eta (t,r)\ge \delta _0-H$.

The existence of weak solutions for compressible viscous barotropic fluids interacting with an elastic plate has only recently been shown in [4]. It follows the seminal existence proof for weak solutions of the compressible Navier–Stokes equations [27, 44]. Note that the existence approach introduced in [4] can not be adapted to numerical approximations in a straight forward manner since it uses fixed point theorems and regularization operators on the continuous level. Indeed, the introduction of a numerical scheme that satisfies all conditions above turns out to be rather sophisticated. In particular, in order to capture the material time-derivative at the interacting interface, we have to introduce a background geometric flow field (the function $\mathbf {w}$, below) that depends (linearly) on the elastic deformation $\eta$ which allows to approximate the material derivative of the deformation of the domain.

The main result of the present paper is the existence of numerical solutions which satisfy (a)–(f) stated above. We illustrate our methodology for the proofs of (a)–(f) first by studying a semi-discrete numerical scheme (discrete in time but continuous in space). In the second part of the paper we study the fully discrete case for which (a)–(f) hold. For the better readability we state here where the respective results are shown:

• (a) See Lemma 2 (semi-discrete) and Lemma 8 (fully discrete) for the renormalized equation.

• (b) See (3.3) and Lemma 3 for conservation of mass and non-negativity of the density for the semi-discrete case; see (4.18) and Lemma 9 for conservation of mass and positivity of the density for the fully discrete case.

• (c) See Definition 2 (semi-discrete) and Definition 3 (fully discrete) for the fully coupled momentum problem.

• (d) See Theorem 1 (semi-discrete) and Theorem 4 (fully discrete) for the energy inequality.

• (e) See Theorem 2 (semi-discrete) and Theorem 5 (fully discrete) for the consistency of the schemes.

• (f) See Theorem 3 for the existence of a numerical solution to the fully discrete scheme. See Lemma 5 (semi-discrete) and Corollary 6 (fully discrete) for the minimal time interval of existence.

The critical property of the schemes introduced are Theorem 4 (resp. Theorem 1) where it is shown that the introduced fully discrete (resp. semi-discrete) scheme satisfies a discrete version of the energy inequality. It turns out that for compressible fluids only a fully implicit and nonlinear scheme does satisfy the energy inequality (see Remark 4). This is in contrast to incompressible fluids, which can be linearized (see e.g. [9]). Though the strategy to get energy stable schemes for the compressible barotropic Navier–Stokes system is quite standard if the fluid domain $\Omega$ is fixed, see e.g. [30, 34, 39], it becomes rather difficult when a time dependent domain is considered. We would like to mention here the stability results of [1, 19] where the moving domain is defined by a given function. As far as we know, this is the first result on energy stable and mass conservative numerical solutions for the FSI problem with compressible fluids.

The technical highlight is the consistency of solutions, see Theorem 2 and Theorem 5. This is due to the fact that the definition of the space of test function is a part of the weak solution for fluid–structure interaction problems (see Definition 1). One has to ensure that the space of test functions of the limit weak solution (that depends on the limit geometry) can indeed be approximated. For that reason, the consistency of solutions is sensitive to the regularity of solutions in particular the regularity of the (discrete) deformation $\eta$.

The plan of the paper is the following. In Section 2 we introduce the necessary analysis for the incremental time-stepping approximation, Section 3 is dedicated to a semi-discrete scheme, which means that all functions are assumed to be continuous in space. This is (to some extent) a preparation of Section 4 where the fully time and space discrete scheme is introduced and the respective results are proven.

Finally wish to point out that the scheme is built in such a way that one may prove that any subsequence of a numerical approximation converges weakly to a continuous solution. The convergence result for the scheme will be the content of an independent paper.

2 Preliminaries

In this section, we introduce the necessary notations, the time discretization and time difference operators.

Weak solutions We begin by introducing the following concept of weak solutions developed in [4] where the existence of weak solutions (until a self-contact of the boundary) under appropriate initial conditions was shown. Indeed, existence could be shown in the following continuous spaces:

• The deformation is usually assumed to be in the following Bochner space¹$\eta \in W^I:=L^2(0,T;W^{2,2}_0(\Sigma )) \cap W^{1,2}(0,T;L^2(\Sigma ))$.

• The density $\varrho \in Q^I$, were $Q^I:=L^\infty (0,T;L^\gamma (\Omega (t))$. This means that $\varrho (t)\in L^\gamma (\Omega (t))$ for almost every t and that the essential supremum over the respective norms is bounded.

• The velocity $\mathbf {u}\in V^I:=\{\mathbf {u}\in L^2(0,T;W^{1,2}(\Omega (t)), \, \mathbf {u}(r,H+\eta (r))=\partial _t \eta (r)\mathbf {e}_d\text { for all }r\in \Sigma \text { and } \mathbf {u}\equiv 0 \text { on }\Gamma _D\}.$ Here let us point out that the space $V^I$ does depend on the deformation map $\eta$ in two ways. Firstly it defines the domain of definition and secondly its time-derivative defines the (no-slip) boundary conditions. In particular the compatibility (1.4) holds.

Note that the space of the velocity depends sensitively on the deformation in two ways, by the shape of the domain and the boundary values at the moving part of the domain.

Definition 1

(Weak solution) A weak solution to the problem (1.2) with the initial data (1.3) is a triple $(\eta ,\varrho , \mathbf {u})\in W^I\times Q^I\times V^I$ that satisfies the following for all $\varphi \in C^\infty _0 \left( (-\infty ,T)\times \mathbb {R}^d \right)$

and for all $(\varvec{\Psi }, \psi ) \in C^\infty _0 ((-\infty ,T) \times \mathbb {R}^d) \times C^\infty _0 ((-\infty ,T) \times \Sigma )$ with $\varvec{\Psi }(t,r,H+\eta )=\psi (t,r)\mathbf {e}_d$ on $(-\infty ,T) \times \Sigma$ and $\varvec{\Psi }\equiv 0$ on $\Gamma _D$ that

In particular the boundary condition (1.4) is satisfied the sense of traces for a.e. $t\in [0,T]$. Moreover, the solution satisfies the energy estimates

(2.1)

where $\mathcal {H}(\varrho ) = \frac{a }{\gamma -1}\varrho ^\gamma$ represents the pressure potential of the fluid and $c(\mathbf {f},g)$ is a positive constant depending on the right-sides f, g.

Time discretization We divide the time interval I into $N_T$ subintervals and set $\tau = T/ N_T {\; \in (0,1)}$ as the size of the time step. For simplicity, we write $t^k=k\tau$ and $I^k=(t^{k-1}, t^k]$ for all $k=1,\ldots ,N_T$. Moreover, we denote $v_\tau ^k$ as the approximation of v at time $t^k$ for $v\in \{ \varrho , \mathbf {u}, p, \eta , z, \mathbf {w}, \varphi , \varvec{\Psi }, \psi , \Omega , \mathcal {A}\}$, where $\mathbf {w}$ represents the deformation rate of the fluid domain $\mathbf {w}$, see (2.6). Further, it is convenient to extend the set of point-wise-in-time functions $\{v_\tau ^1, \cdots , v_\tau ^{N_T}\}$ as a piecewise constant in time function on the whole time interval I, i.e.

$$\begin{aligned} v_\tau (t,\cdot ):= & {} \sum _{k=1}^{N_T} 1_{I^k}(t) v_\tau ^k \; \text{ for } \text{ any } \; t\in I, \; \nonumber \\&v_\tau \in \{ \varrho _\tau , \mathbf {u}_\tau , p_\tau , \eta _\tau , z_\tau , \mathbf {w}_\tau , \varphi _\tau , \varvec{\Psi }_\tau , \psi _\tau , \Omega _\tau \}, \end{aligned}$$

(2.2)

where $1_{I^k}(t)$ is the characteristic function

Analogously, we denote on the fixed reference domain $\widehat{\Omega }$

$$\begin{aligned} \widehat{v}_{\tau }(t,\cdot ) := \sum _{k=1}^{N_T} 1_{I^k}(t) \widehat{v}_{\tau }^k \; \text{ for } \text{ any } \; t\in I, \; \widehat{v}_{\tau }\in \{ \widehat{\varrho }_{\tau }, \widehat{\mathbf {u}}_{\tau }, \widehat{p}_\tau , \widehat{\mathbf {w}}_{\tau }, \widehat{\mathbf {f}}_{\tau }, \widehat{\varphi }_\tau , \widehat{\varvec{\Psi }}_\tau , \mathcal {A}\}.\qquad \end{aligned}$$

(2.3)

Here we would like to point out that

$$\begin{aligned} v_\tau = \widehat{v}_{\tau }\circ \mathcal {A}_{\tau }^{-1} \quad \text{ and } \quad v_\tau ^k = \widehat{v}_{\tau }^k \circ (\mathcal {A}_{\tau }^{k})^{-1}, \quad \text{ for } v\in \{ \varrho , \mathbf {u}, p, \mathbf {w}, \varphi , \varvec{\Psi }\}. \end{aligned}$$

(2.4)

Finally, we define a projection operator mapping a continuous-in-time function to a time-discrete function:

$$\begin{aligned} \Pi _t [v] = \sum _{k=1}^{N_T} \frac{1_{I^k}(t)}{\tau } \int _{I^k} v \,{\mathrm{d}} t . \end{aligned}$$

(2.5)

ALE mapping In consistency with the ALE mapping (1.1) and (2.4), we define the deformation rate of the fluid domain on the reference domain $\widehat{\Omega }$ and current domain $\Omega _\tau$ respectively by

$$\begin{aligned}&\widehat{\mathbf {w}}_{\tau }^{k}= \frac{\mathcal {A}_{\tau }^{k}-\mathcal {A}_{\tau }^{k-1}}{\tau } = \left( \mathbf{0}_{d-1}, \frac{\eta _\tau ^{k} -\eta _\tau ^{k-1}}{\tau }\frac{\widehat{x}_d}{H } \right) ^T \text{ and } \nonumber \\&\mathbf {w}_\tau ^k = \widehat{\mathbf {w}}_{\tau }^k \circ (\mathcal {A}_{\tau }^k)^{-1} = \left( \mathbf{0}_{d-1}, \frac{\eta _\tau ^{k} -\eta _\tau ^{k-1}}{\tau }\frac{x_d}{\eta _\tau ^{k} +H } \right) ^T, \end{aligned}$$

(2.6)

for $k\in \{1,\ldots , N_T\}$, where $\mathbf{0}_{d-1}$ is $(d-1)$-dimensional zero vector. For convenience, we introduce ${X}_i^j$ as the mapping from $\Omega _\tau ^i$ at time interval $I^i$ to $\Omega _\tau ^j$ at time interval $I^j$, i.e.,

$$\begin{aligned} {X}_i^j: \quad \Omega _\tau ^i \mapsto \Omega _\tau ^j, \qquad x^i \mapsto {X}_i^j(x^i) = \mathcal {A}_{\tau }^j \circ (\mathcal {A}_{\tau }^i)^{-1}(x^i). \end{aligned}$$

(2.7)

Recalling again the definition of the ALE mapping (1.1), the Jacobian of ${X}_i^j$ and its determinant read

$$\begin{aligned} \mathbb {J}_i^j = \frac{\partial {X}_i^j(x^i)}{\partial x^i} \quad \text{ and } \quad \mathcal {F}_i^j =\det \left( \mathbb {J}_i^j \right) = \frac{\eta ^{j} +H }{\eta ^i +H} , \end{aligned}$$

(2.8)

respectively. From the above notations it is easy to check

(2.9)

Further, if $\eta _\tau ^k(r)\in (\delta _0-H, \delta _{\max } -H )$, $\delta _{\max }>\delta _0 >0$, we observe for all $k\in \{1,...,N_T\}$ and $r\in \Sigma$ that

In order to transfer between the current domain and the reference domain, we recall the chain-rule and properties of the Piola transformation from [14]

(2.10)

for a scalar function q and a vector filed $\mathbf {q}$, where we have denoted by $\widehat{\nabla }\equiv \nabla _{\widehat{x}}$ and . Finally we denote for simplicity

(2.11)

Time difference operators First, we introduce the standard backward Euler method

$$\begin{aligned} \delta _t \eta _\tau ^{k}({r}) = \frac{ \eta _\tau ^{k}({r})-\eta _\tau ^{k-1}({r}) }{\tau }, \; \delta _t^2 \eta _\tau ^{k}({r})= \delta _t(\delta _t \eta _\tau ^{k}({r}))=\frac{\delta _t \eta _\tau ^{k}({r})- \delta _t \eta _\tau ^{k-1}({r})}{\tau }.\nonumber \\ \end{aligned}$$

(2.12a)

Next, we define the material derivative

$$\begin{aligned} D_t^\mathcal {A}q_\tau ^k = \frac{ q_\tau ^k - q_\tau ^{k-1} \circ {X}_k^{k-1}}{\tau }, \end{aligned}$$

(2.12b)

where ${X}_k^{k-1}=\mathcal {A}_{\tau }^{k-1}\circ (\mathcal {A}_{\tau }^{k})^{-1}$ is the mapping from $\Omega _\tau ^k$ to $\Omega _\tau ^{k-1}$, see (2.7). Further, we define a “conservative²" time derivative

$$\begin{aligned} D_t q_\tau ^k = \frac{ q_\tau ^k - q_\tau ^{k-1} \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau }. \end{aligned}$$

(2.12c)

Thanks to (2.9) it is easy to observe that

$$\begin{aligned} D_t q_\tau ^k= & {} \frac{ q_\tau ^k - q_\tau ^{k-1} \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } = \frac{ q_\tau ^k - q_\tau ^{k-1} \circ {X}_k^{k-1}}{\tau } +\frac{ (1-\mathcal {F}_k^{k-1}) }{\tau } q_\tau ^{k-1} \circ {X}_k^{k-1}\nonumber \\= & {} D_t^\mathcal {A}q_\tau ^k + \mathrm{div}\mathbf {w}_\tau ^{k} \; q_\tau ^{k-1}\circ {X}_k^{k-1}, \end{aligned}$$

(2.13)

which, as can be seen below, turns out to be the suitable deviation for getting the following discrete version of the Reynolds transport theorem.

Lemma 1

(Discrete Reynolds transport) Let the discrete operators $\delta _t$, $D_t^\mathcal {A}$ and $D_t$ be given in (2.12). Then we have the following discrete analogy of the Reynolds transport theorem.

where ${X}_k^{k-1}$ is given in (2.7) and $\mathbf {w}_\tau$ is given in (2.6).

Proof

Recalling the definitions (2.7) and (2.12) together with the equality (2.13), we derive

$\square$

Note that the discrete Reynolds transport holds also for any subdomain of $\Omega _\tau (t)$. Consequently, we obtain the following corollary by taking $q_\tau \equiv 1$ in Lemma 1, which is well known as the geometric conservation law.

Corollary 1

(Geometric conservation law) Let $C_\tau \subset \Omega _\tau$ be an arbitrary d-dimensional subdomain of $\Omega _\tau$. Then it holds for all $k=1,\dots , N_T$ that

(2.14)

where $|C_\tau |$ is the volume of the domain $C_\tau$.

3 Semi-discrete scheme

This section introduces the necessary tools and observations with respect to a time discretization scheme for the approximation of the problem (1.2). Due to the overwhelming technical notations in the fully discrete case we decided to include this semi-discrete section and leave the space discretization to the next section. We emphasize that the main objective of this section is to explain the methodology.

3.1 The scheme

Before giving the semi-discrete scheme, let us denote $W= W^{2,2}_0(\Sigma )$, $Q_\tau ^k = L^\gamma (\Omega _\tau ^k)$ and $V_\tau ^k = \{v\in W^{1,2}(\Omega _\tau ^k)\,:\,v|_{\Gamma _D}=0\}$ for all $k\in \{1,\dots ,N_T\}$. Moreover, we denote piecewise-constant-in-time function spaces $Q_\tau = L^\gamma (\Omega _\tau )$ and $V_\tau = W^{1,2}(\Omega _\tau )$ in the sense of (2.2).

Definition 2

(Semi-discrete scheme on the current domain) For all $k \in \{ 1,\ldots , N_T \}$ we say that $(\eta _\tau ^{k} ,\varrho _\tau ^{k}, \mathbf {u}_\tau ^{k} ) \in W\times Q_\tau ^k\times V_\tau ^k$ such that $\varrho _\tau ^{k}\mathbf {u}_\tau ^{k}\in L^1(\Omega _\tau ^k)$ is a weak solution to the semi-discrete scheme (on the current domain), if for all $\varphi _\tau \in C^\infty (\mathbb {R}^d)$ we find that

$$\begin{aligned} \int _{\Omega _\tau ^k} D_t \varrho _\tau ^{k} \varphi _\tau \,\mathrm{d} {x} - \int _{\Omega _\tau ^k} \varrho _\tau ^{k} \mathbf {v}_\tau ^{k} \cdot \nabla \varphi _\tau \,\mathrm{d} {x} = 0; \end{aligned}$$

(3.1a)

and for all $(\psi _\tau ,\varvec{\Psi }_\tau ) \in C^\infty _0(\Sigma ) \times C^\infty (\mathbb {R}^d;\mathbb {R}^d)$ with $\varvec{\Psi }_\tau |_{\Gamma _S}\circ \mathcal {A}_{\tau }= \psi _\tau \mathbf {e}_d$ and $\varvec{\Psi }_\tau |_{\Gamma _D}=0$ we find that

$$\begin{aligned}&\int _{\Omega _\tau ^k} ( D_t \left( \varrho _\tau ^{k} \mathbf {u}_\tau ^{k} \right) \cdot \varvec{\Psi }_\tau - (\varrho _\tau ^{k} \mathbf {u}_\tau ^{k}\otimes \mathbf {v}_\tau ^{k} ) :\nabla \varvec{\Psi }_\tau ) \,\mathrm{d} {x} \nonumber \\&\qquad + \int _{\Omega _\tau ^k} \mathbf {S}(\nabla \mathbf {u}_\tau ^{k}) : \nabla \varvec{\Psi }_\tau \,\mathrm{d} {x} - \int _{\Omega _\tau ^k} p(\varrho _\tau ^{k}) \mathrm{div}\varvec{\Psi }_\tau \,\mathrm{d} {x} + \int _{\Sigma } \delta _t z_\tau ^{k} \psi _\tau \mathrm{d}r \nonumber \\&\qquad + \alpha \int _{\Sigma } \Delta \eta _\tau ^{k} \Delta \psi _\tau \mathrm{d}r + \beta \int _{\Sigma } \nabla \eta _\tau ^{k} \cdot \nabla \psi _\tau \mathrm{d}r\nonumber \\&\quad = \int _{\Omega _\tau ^k} \varrho _\tau ^k \mathbf {f}_\tau ^{k}\cdot \varvec{\Psi }_\tau \,\mathrm{d} {x} + \int _{\Sigma } g_\tau ^{k} \psi _\tau \mathrm{d}r \end{aligned}$$

(3.1b)

with

where the initial data and boundary conditions are given by

We will discuss the solvability of the scheme later in Theorem 3, where a fully discrete scheme is analyzed.

3.2 Stability

In this subsection, we aim to show some stability properties for the scheme (3.1). The stability properties are only shown formally. The methodology is justified in Section 4 where all arguments can be rigorously repeated for the fully discrete approximation scheme. In principle the assumptions vary from statement to statement. It is however always enough to assume

$$\begin{aligned} \varrho _\tau ^k\in W^{1,\infty }(\Omega _\tau ^k)\quad \text { for all }k\in \{1,...,N_T\}. \end{aligned}$$

(3.2)

In particular this assumption implies that all below used test-function for the semi-discrete scheme introduced in Definition 2 are admissible.

First, we remark that the scheme (3.1) preserves the total mass. Indeed, by setting $\varphi _\tau \equiv 1$ in (3.1a) and applying the discrete Reynolds transport Lemma 1, we derive $\delta _t \left( \int _{\Omega _\tau ^k} \varrho _\tau ^k \,\mathrm{d} {x} \right) =\int _{\Omega _\tau ^k} D_t \varrho _\tau ^k \,\mathrm{d} {x}=0$ for all $k=1,\ldots ,N_T$, which implies

$$\begin{aligned} \int _{\Omega _\tau ^k} \varrho _\tau ^k \,\mathrm{d} {x} = \int _{\Omega _\tau ^{k-1}} \varrho _\tau ^{k-1} \,\mathrm{d} {x} = \cdots = \int _{\Omega _\tau ^0} \varrho _\tau ^0 \,\mathrm{d} {x} =:M_0, \; \text{ for } \text{ all } k=1,\ldots ,N_T.\nonumber \\ \end{aligned}$$

(3.3)

Next, we show the renormalization of the discrete density problem.

Lemma 2

(Renormalized continuity equation)

Let $(\varrho _\tau ,\mathbf {u}_\tau )\in Q_\tau \times V_\tau$ satisfy the discrete continuity equation (3.1a) with the boundary condition $\mathbf {u}_\tau |_{\partial \Omega _\tau } = \mathbf {w}_\tau |_{\partial \Omega _\tau }$ and let (3.2) hold. Then for any $B \in C^1({ \mathbb {R}})$ it holds

where $D_0= \frac{1}{\tau }\int _{\Omega _\tau ^k} \mathcal {F}_k^{k-1}\left( B(\varrho _\tau ^{k-1}\circ {X}_k^{k-1}) {-} B(\varrho _\tau ^k) {-} B'(\varrho _\tau ^{k}) \big ( \varrho _\tau ^{k-1}\circ {X}_k^{k-1}{-}\varrho _\tau ^k \big ) \right) \,\mathrm{d} {x}.$ Obviously, $D_0\ge 0$ if B is convex.

Proof

We set $\varphi _\tau =B'(\varrho _\tau ^k)$ in the discrete density equation (3.1a) and obtain

First, by direct computation we have

(3.4)

where we have used the relation between the Jacobian and the deformation rate of the domain given in (2.9). Next, noticing the equality $\nabla \Big (\varrho B'(\varrho ) -B{ (\varrho ) } \Big ) = \varrho \nabla B'(\varrho )$ and thanks to integration by parts, we reformulate the convective term as

Consequently, summing up the above equations and seeing $\mathbf {v}_\tau = \mathbf {u}_\tau -\mathbf {w}_\tau$, we complete the proof. $\square$

With the renormalized continuity equation in hand, we are ready to show non-negativity of the discrete density and the internal energy balance.

Lemma 3

(Non-negativity of density) Let $\varrho _\tau ^0 \ge 0$ and (3.2) hold. Then any solution to the scheme (3.1) preserves non-negativity of the density. It mean $\varrho _\tau ^{k} \ge 0$ for all $k=1,\ldots , N_T$.

Proof

We show the proof by mathematical induction and it is enough to show $\varrho _\tau ^k \ge 0$ given $\varrho _\tau ^{k-1} \ge 0$. The rough idea is to set $B(\varrho ) = \max \{0,-\varrho \} \ge 0$ in Lemma 2. More precisely, we adopt the idea of [34, Lemma 3.2] and construct an approximate sequence $B_\delta (\varrho ) \in C^1(\mathbb {R})$ such that

for $\delta >0$. Note that $B_\delta (\varrho ) \rightarrow B(\varrho )=\max \{-\varrho , 0\}$ and $\varrho B'_\delta (\varrho ) - B_\delta { (\varrho )} =\delta (-\varrho )^{\delta +1} \rightarrow 0 \text{ as } \delta \rightarrow 0^+ \text{ for } \varrho <0$, as well as $\varrho B'_\delta (\varrho ) - B_\delta { (\varrho )}=0$ for $\varrho \ge 0$. Collecting the above information we apply Lemma 2 with the choice of $B\in C^1(\mathbb {R})$ as $\varrho \mapsto B(\varrho )=B_\delta (\varrho )$. Then passing $\delta \rightarrow 0^+$ in the estimate we find $\int _{\Omega _\tau ^k} B(\varrho _\tau ^k) \,\mathrm{d} {x} \le 0$. Realizing B is a non-negative function we know that $B(\varrho _\tau ^k)=0$ holds for all $x\in \Omega _\tau ^k$ which implies $\varrho _\tau ^k \ge 0$. $\square$

Further discussion on the strict positivity of the discrete density will be shown for the fully discrete scheme in Lemma 9 in the next section.

Next, we recall the pressure potential $\mathcal {H}(\varrho ) =\frac{p(\varrho )}{\gamma -1}$ defined in Definition 1. By setting $B=\mathcal {H}(\varrho )$ in Lemma 2 and realizing $p=\varrho \mathcal {H}'(\varrho ) -\mathcal {H}(\varrho )$, we derive the following relation on the pressure potential that plays the role of the internal energy.

Corollary 2

(Internal energy balance) Let $(\eta _\tau ^k, \varrho _\tau ^k,\mathbf {u}_\tau ^k)$ be a solution of the semi-discrete scheme (3.1) for all $k=1,\ldots ,N_T$ and let (3.2) hold. Then

$$\begin{aligned}&\frac{ 1}{\tau } \left( \int _{\Omega _\tau ^k} \mathcal {H}(\varrho _\tau ^k) \,\mathrm{d} {x} - \int _{\Omega _\tau ^{k-1}} \mathcal {H}(\varrho _\tau ^{k-1}) \,\mathrm{d} {x} \right) + \int _{\Omega _\tau ^k} p(\varrho _\tau ^{k}) \mathrm{div}\mathbf {u}_\tau ^{k} \,\mathrm{d} {x} + D_1 =0,\quad \text{ with } \nonumber \\&D_1 = \frac{1}{\tau }\int _{\Omega _\tau ^k} \mathcal {F}_k^{k-1}\left( \mathcal {H}(\varrho _\tau ^{k-1}\circ {X}_k^{k-1}) - \mathcal {H}(\varrho _\tau ^k) - \mathcal {H}'(\varrho _\tau ^{k}) \big ( \varrho _\tau ^{k-1}\circ {X}_k^{k-1}-\varrho _\tau ^k \big ) \right) \,\mathrm{d} {x}\nonumber \\&\qquad = \int _{\Omega _\tau ^k} \tau \mathcal {F}_k^{k-1}\frac{\mathcal {H}''(\xi )}{2} \left| D_t^\mathcal {A}\varrho _\tau ^{k} \right| ^2 \,\mathrm{d} {x} \ge 0, \end{aligned}$$

(3.5)

where $\xi \in \mathrm{co}\{ \varrho _\tau ^{k-1}\circ {X}_k^{k-1} , \varrho _\tau ^{k} \}$. Here, we have denoted $\mathrm{co}\{ a , b \} = [\min (a,b), \max (a,b)]$.

Finally, we proceed to show the energy stability of the scheme (3.1).

Theorem 1

(Energy estimates) Let $\left( \varrho _\tau ^{k}, \mathbf {u}_\tau ^{k}, \eta _\tau ^{k}\right)$ be a solution of the semi-discrete scheme (3.1) for all $k=1,\ldots , N_T$ and let (3.2) hold. Then the following energy estimate holds for any $N=1,\dots ,N_T$

$$\begin{aligned}&\left( \int _{ \Omega _\tau ^N}{ E_f^{N} }\,\mathrm{d} {x}+ \int _{\Sigma } E_s^{N} \mathrm{d}r \right) - \left( \int _{\Omega _{\tau }^0}{ E_f^{0} }\,\mathrm{d} {x}+ \int _{\Sigma } E_s^{0} \mathrm{d}r \right) \nonumber \\&\qquad + \frac{\tau ^2}{2} \sum _{k=1}^N \int _{\Sigma } \left( |\delta _t z_\tau ^{k} |^2+ \alpha \left| \Delta z_\tau ^{k} \right| ^2 + \beta \left| \nabla z_\tau ^{k}\right| ^2 \right) \mathrm{d}r\nonumber \\&\qquad + \tau \sum _{k=1}^N \int _{\Omega _\tau ^k} \left( 2\mu |\mathbf {D}(\mathbf {u}_\tau ^{k}) |^2 + \lambda |\mathrm{div}\mathbf {u}_\tau ^{k} |^2 \right) \,\mathrm{d} {x}\nonumber \\&\qquad + \frac{\tau ^2}{2} \sum _{k=1}^N \int _{\Omega _\tau ^k} \mathcal {F}_k^{k-1}\left( \mathcal {H}''(\xi ) \left| D_t^\mathcal {A}\varrho _\tau ^{k} \right| ^2 + \varrho _\tau ^{k-1} \circ {X}_k^{k-1}\left| D_t^\mathcal {A}\mathbf {u}_\tau ^{k} \right| ^2 \right) \,\mathrm{d} {x}\nonumber \\&\quad = \tau \sum _{k=1}^N \left( \int _{\Omega _\tau ^k} \varrho _\tau ^k \mathbf {f}_\tau ^{k}\cdot \mathbf {u}_\tau ^{k} \,\mathrm{d} {x} + \int _{\Sigma } g_\tau ^{k} z_\tau ^{k} \mathrm{d}r \right) , \end{aligned}$$

(3.6)

where $\quad E_f^{k}= \frac{1}{2} \varrho _\tau ^{k} \left| \mathbf {u}_\tau ^{k}\right| ^2 + \mathcal {H}(\varrho _\tau ^{k}) , \quad E_s^{k} =\frac{1}{2} (|z_\tau ^{k}|^2 + \alpha |\Delta \eta _\tau ^{k}|^2 + \beta |\nabla \eta _\tau ^{k}|^2)$.

Proof

Setting $\varphi _\tau = - \frac{\left| \mathbf {u}_\tau ^{k}\right| ^2}{2}$ in (3.1a), and $(\varvec{\Psi }_\tau , \psi _\tau ) =( \mathbf {u}_\tau ^{k},z_\tau ^k)$ in (3.1b), we have $\sum _{i=1}^2 I_i=0$, and $\sum _{i=3}^{9} I_i=0$, respectively, where

Now we proceed with the summation of all the $I_i$ terms for $i=1,\ldots ,9$.

Term $I_1+I_3+I_{8}$. Applying the equality $a(a-b) =\frac{a^2-b^2}{2}+\frac{(a-b)^2}{2}$ we get

Term $I_2+I_4$. For the convective terms, we have

Pressure term $I_{5}$. Recalling the discrete internal energy equation (3.5), we can rewrite the pressure term as

Term $I_6+I_7$. These terms don’t change.

Term $I_{9}$. Applying again $a(a-b) =\frac{a^2-b^2}{2}+\frac{(a-b)^2}{2}$, we deduce

Collecting all the above terms, we find

Finally, summing up the above equality from $k=1$ to N and multiplying with $\tau$ complete the proof. $\square$

3.3 Some a-priori estimates

Let us recall that all unknowns including the domain and the test functions are piecewise constant in time, see (2.3). We define $\overline{\eta _\tau }(t,r)$ as the affine linear interpolant of $\eta _\tau$ meaning that $\overline{\eta _\tau }\in C^0([0,T];\Sigma )$, such that $\overline{\eta _\tau }(t^k,r)=\eta _\tau ^k(r)$ and $\partial _t\overline{\eta _\tau }(t,r)=z_\tau ^k(r)$ for $t\in I^k= (t^{k-1},t^{k}]$.

With a little abuse of notation we use $[0,T]\times \Omega _\tau =\bigcup _{k=1}^{N_T}(t^{k-1},t^k]\times \Omega _\tau ^k$. Accordingly we define for $s\in [0,\infty )$, $q\in [1,\infty ]$ and $p\in [1,\infty )$

Note that the expressions above bound the respective norms for both the piecewise constant functions in time as well as the piecewise affine linear functions in time.

Then the energy estimate Theorem 1 implies the following a-priori estimates (for the piecewise constant in time functions $\eta _\tau ,\varrho _\tau ,\mathbf {u}_\tau$) that are uniform in $\tau$:

Corollary 3

(A-priori estimates)

Let $(\eta _\tau ,\varrho _\tau ,\mathbf {u}_\tau )$ be a solution of the semi-discrete scheme (3.1) with $\gamma >1$. Further, assume that the right hand side in (3.6) is bounded in the sense that $\mathbf {f}\in L^\infty ([0,T]\times \Omega _\tau )$ and $g\in L^2([0,T]\times \Sigma )$. Then we have the following estimates:

where c depends on the external force $\mathbf {f}$ and g as well as the initial data.

Proof

We find by Hölder’s and Young’s inequality that

This allows to estimate the right hand side of (3.6)

Choosing $\delta <\frac{1}{c}$ in the last term of the above inequality allows us to absorb this term by the left-hand side of the energy balance (3.6), that implies the a-priori estimates. $\square$

In order to prove the consistency of the scheme (3.1) we need some additional a-priori estimates.

Lemma 4

For all $s\in [0,\frac{1}{2})$ and all $q\in [1,4)$ there is a constant independent of $\tau$ such that

The constant C depends on the initial values and the bounds of the energy estimates alone. Moreover, for all $\theta \in [0,\frac{1}{2})$ there exists a constant $C_\theta$ depending on the energy estimates and $\theta$, such that

$$\begin{aligned} \max _{k}\left\Vert \eta _\tau ^k-\eta _\tau ^{k-1}\right\Vert _{L^\infty (\Sigma )}\le C_\theta \tau ^\theta . \end{aligned}$$

(3.7)

Proof

Since $z_\tau ^k$ is the trace of $\mathbf {u}_\tau ^k$ which is in $L^2(0,T;W^{1,2}(\Omega _\tau ^k))$, we find by the trace-theorem (see the related estimate in [37, Corollary 2.9]) and by change of variable that for for all $s\in [0,\frac{1}{2})$

which can be bounded by the energy as well, see the second and the third line of the estimates stated in Corollary 3. Due to the fact that for any $q\in [1,4)$ there is an $s<\frac{1}{2}$ such that $W^{s,2}\hookrightarrow L^q$ the first inequality is completed.

The second inequality follows by the very definition of $\mathbf {w}_\tau$.

Finally, we proceed to show the last inequality. We extend $\eta _\tau ^k, \eta _\tau ^{k-1}$ by zero to $\mathbb {R}^{ d-1}$ and take $\sigma >0$. We use the notation of for the mean value integral. We fix $\alpha \in (0,1)$, such that $\theta =\frac{\alpha }{1+\alpha }$. Then by Sobolev embedding, we find that $\eta _\tau ^k\in C^\alpha (\Sigma )$ (with uniform bounds in k) and so for all $\sigma >0$

(3.8)

Now the result follows by choosing $\sigma =\tau ^\frac{1}{\alpha +1}$.

$\square$

The regularity can be used to guarantee a minimal existence interval in time in which the shell is not touching the bottom of the fluid domain. At first we have the following observation which is a direct consequence of (3.7) above.

Corollary 4

(Inductive prolongation principle) Let the parameters C and $\theta \in [0,\frac{1}{2})$ be given in Lemma 4. Let $\tau ^\theta \le \frac{\delta _0}{C}$ and $\delta _1\ge 2\delta _0$. Then $\hbox {inf}_{r} \eta _\tau ^{k}(r)\ge \delta _1-\delta _0-H$ for any $k\in \{1,...,N_T\}$ provided $\hbox {inf}_{r} \eta _\tau ^{k-1}(r)\ge \delta _1-H$.

Moreover, we have the following lemma:

Lemma 5

For every $\delta _0\in (0,H/2)$ there exists a $T_0$ just depending on the bounds of the energy inequality and H, such that $\hbox {inf}_{[0,T_0]}\eta _\tau (t,r)\ge \delta _0-H$.

Proof

The result essentially follows from (3.7) from which we import the bound $C_\theta$ to a given exponent $\theta =\frac{\alpha }{\alpha +1}$. Let $(T_0+\tau )^\theta \le \frac{H-\delta _0}{C_\theta }$. Then we choose N such that $(N-1)\tau <T_0\le N\tau$. For $k\in \{1,...,N\}$ we find by the fact that $\eta _\tau ^0\equiv 0$ analogous to (3.8) for $t\in ((k-1)\tau ,k\tau )$ (using the 0 extension of $\eta _\tau ^k$ again) that

where we have chosen $\sigma =(T_0+\tau )^\frac{1}{1+\alpha }$ in the last equality. $\square$

3.4 Consistency

In this subsection, we aim to show the consistency of the scheme, meaning the if the numerical solution converges, then it satisfies the weak formulation (1) in the limit of $\tau \rightarrow 0$.

Usually, for that one takes a fixed test function and shows that the error produced by the discretization vanishes in the limit. Due to the geometric coupling we have to approximate the test function space as well. Indeed, due to the non-linear coupling the consistency can only be shown provided the numerically approximated geometry is close enough to a limit geometry. Recall that $\overline{\eta }_\tau :[0,T]\times \Sigma \rightarrow [\delta _0-H,\infty )$ is defined as the affine linear function in time which satisfies $\overline{\eta }_\tau (k \tau )=\eta _\tau ^k$ for all k. Then, the a-priori estimates imply the following lemma:

Lemma 6

For any $\alpha \in [0,\frac{1}{2})$ and any of the above approximation sequences there exists a sub-sequence, $\{\overline{\eta }_{\tau _j}\}_{j\in \mathbb {N}}\in C^\alpha ([0,T]\times \Sigma )$ and an $\eta \in C^\alpha ([0,T]\times \Sigma )$, such that $\overline{\eta }_{\tau _j}\rightarrow \eta \text { with }j\rightarrow \infty$ uniformly in $C^\alpha ([0,T]\times \Sigma )$.

Proof

Sobolev embedding implies that $\overline{\eta }_\tau (t)$ is bounded in $C^{\alpha }(\Sigma )$ for all $\alpha \in (0,1)$ uniformly in $t,\tau$ thanks to the uniform bounds stated in Corollary 3. Combining that with (3.7) implies that $\overline{\eta }_\tau$ is bounded in $C^{\alpha }([0,T]\times \Sigma )$ for all $\alpha \in (0,\frac{1}{2})$ uniformly in $\tau$. Hence the theorem of Arzela–Ascoli implies the result. $\square$

The above lemma motivates us to assume that $\overline{\eta }_{\tau }\rightarrow \eta$ uniformly (omitting the index j of $\tau _j$). Now, we take a coupled test function on the limit domain for a potential limit equation (see Definition 1):

(3.9)

The strategy of consistency is as follows: We first fix an approximation parameter $\epsilon \in (0,1)$ which introduces a sub-class of test-functions that satisfy the coupling condition not only on the (variable in time) limit-boundary determined by the limit function $\eta$ but in a neighborhood of the (variable in time) limit boundary. In particular, these test functions will satisfy the coupling conditions for all geometries that are close enough to the limit geometry–which is the case for our strongly converging subsequence $\overline{\eta }_\tau$ for $\tau$ small enough.

In particular, we require for a given $\epsilon \in (0,1)$ that³

(3.10)

Since the uniform convergence of $\overline{\eta }_{\tau }\rightarrow \eta$ in $C^\alpha$ implies in particular that there exists a $\tau _\epsilon$ such that $\left\Vert \overline{\eta }_{\tau }-\eta \right\Vert _\infty <\epsilon$ for $\tau \in (0,\tau _\epsilon )$ we find that $(\psi ,\Psi _{\epsilon })$ is an admissible test function for Definition 2 for all $\tau \in (0,\tau _\epsilon )$.

The next theorem is a consistency theorem in the following sense. If the numeric scheme converges (by which we means that $\eta _\tau , \varrho _\tau ,\mathbf {u}_\tau$ converge to some limit functions in an appropriate sense), then one may pass to the limit first with $\tau \rightarrow 0$ and then with $\epsilon \rightarrow 0$, which would imply that those limit functions satisfy Definition 1. Note further that for the continuity equation we do not need the extra approximation parameter $\epsilon$ for the space of test-functions since no coupled boundary values are requested.

Theorem 2

(Consistency of the semi-discrete scheme (3.1)) Let $(\eta _\tau ,\varrho _\tau , \mathbf {u}_\tau )$ be a solution of the scheme (3.1) with $\tau \in (0,1)$ and $\gamma >1$. Then for any $\varphi \in C^2([0,T]\times \mathbb {R}^d)$ there exists $\vartheta >0$ that

$$\begin{aligned} - \int _{\Omega _\tau ^0} \varrho _\tau ^0 \varphi ^0 \,\mathrm{d} {x} - \int _0^T \int _{\Omega _\tau } \left( \varrho _\tau \partial _t\varphi + \varrho _\tau \mathbf {u}_\tau \cdot \nabla \varphi \right) \,\mathrm{d} {x} \,{\mathrm{d}} t = \mathcal {O}(\tau ^\vartheta ), \end{aligned}$$

(3.11)

Assume moreover, that $\overline{\eta }_\tau \rightarrow \eta$ in $C^\alpha ([0,T]\times \Sigma )$ (for some $\alpha \in (0,1)$, see Lemma 6). There exists $\vartheta \in (0,1]$, such that for $\epsilon \in (0,1)$ and $\tau \in (0,1)$ with $\left\Vert \overline{\eta }_{\tau }-\eta \right\Vert _\infty <\epsilon$ we find

$$\begin{aligned}&-\int _{\Omega _\tau ^0} \varrho _\tau ^0 \mathbf {u}_\tau ^0 \cdot \Psi _{\epsilon }^0 \,\mathrm{d} {x} - \int _0^T \int _{\Omega _\tau } \left( \varrho _\tau \mathbf {u}_\tau \cdot \partial _t\Psi _{\epsilon }+ \varrho _\tau \mathbf {u}_\tau \otimes \mathbf {u}_\tau : \nabla \Psi _{\epsilon }\right) \,\mathrm{d} {x}\,{\mathrm{d}} t \nonumber \\&\qquad + \int _0^T \int _{\Omega _{\tau }}{ \left( \mathbf {S}(\nabla \mathbf {u}_\tau ) : \nabla \Psi _{\epsilon }- p(\varrho _\tau ) \mathrm{div}\Psi _{\epsilon }\right) } \mathrm{d}x\,{\mathrm{d}} t \nonumber \\&\qquad -\int _{\Sigma } \partial _t\eta (0) \psi ^0 \mathrm{d}r - \int _0^T \int _{\Sigma } \delta _t \eta _\tau \partial _t\psi \mathrm{d}r\,{\mathrm{d}} t \nonumber \\&\qquad + \int _0^T \int _{\Sigma } {\left( \alpha \Delta \eta _\tau \Delta \psi + \beta \nabla \eta _\tau \cdot \nabla \psi \right) } \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\quad = \int _0^T \int _{\Sigma } g_\tau \psi \mathrm{d}r + \int _0^T \int _{\Omega _\tau } \mathbf {f}_\tau \cdot \Psi _{\epsilon } \,\mathrm{d} {x} \,{\mathrm{d}} t + \mathcal {O}(\tau ^\vartheta )\,{\mathrm{d}} t \end{aligned}$$

(3.12)

for all pairs $(\Psi _{\epsilon },\psi ) \in C^2_0(0,T\times \mathbb {R}^d) \times C^2_0([0,T]\times \Sigma )$ satisfying the coupling condition (3.10).

Proof

To prove the consistency, we must test the discrete problem (3.1) with piecewise constant in time test functions. Thus we apply the piecewise constant projection operator $\Pi _t$ introduced in (2.5) to the smooth test functions $\varphi$, $\Psi$ and $\psi$. Note that for any $\phi _\tau = \Pi _t [\phi ]$, $\phi \in \{\varphi , \Psi _{\epsilon }, \psi \}$ and for any piecewise constant in time function $q_\tau$ it holds

Thanks to this equality, hereafter, we will directly use smooth (in time) test functions to show the consistency of our numerical scheme.

As we are dealing with functions that are continuous in space, we only need to treat the consistency error of the time derivative terms.

First, for the time derivative term of the shell displacement, we have

$$\begin{aligned}&\int _0^T \int _{\Sigma } \delta _t z_\tau \psi _\tau \mathrm{d}r \,{\mathrm{d}} t = \int _0^{T} \int _{\Sigma } \frac{ z_\tau (t) - z_\tau (t-\tau )}{\tau } \psi (t) \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\quad =\frac{1}{\tau } \int _0^T \int _{\Sigma } z_\tau (t) \psi (t) \mathrm{d}r \,{\mathrm{d}} t - \frac{1}{\tau } \int _{-\tau }^{T-\tau } \int _{\Sigma } z_\tau (t) \psi (t+\tau ) \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\quad = \int _0^{T} \int _{\Sigma } z_\tau (t) \frac{ \psi (t) - \psi (t+\tau )}{\tau } \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\qquad + \frac{1}{\tau } \int _{T-\tau }^T \int _{\Sigma } z_\tau (t) \underbrace{\psi (t+\tau )}_{=0} \mathrm{d}r \,{\mathrm{d}} t - \frac{1}{\tau } \int _{-\tau }^{0} \int _{\Sigma } z_\tau (t) \psi (t+\tau ) \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\quad =\int _0^T \int _{\Sigma } z_\tau \partial _t\psi \mathrm{d}r \,{\mathrm{d}} t - \int _{\Sigma } \psi ^{0} \partial _t\eta (0) \mathrm{d}r +e_0, \end{aligned}$$

(3.13)

where $\partial _t\eta (0) =z_\tau ^0$ due to the initial condition and $e_0$ reads

which is the consistency of the time derivative term for the shell displacement.

Next, we show the consistency of the time derivative terms of the density and momentum. In the following we use $q_\tau$ as a substitute for either $\varrho _\tau$ or $\varrho _\tau \mathbf {u}_\tau$. Analogously to (3.13), we find

It is easy to derive

where

Concerning the estimate of $I_1$, we begin by the observation

where $\xi \in \mathrm{co}\{ x_d , x_d \frac{\eta ^{k+1}- \eta ^k}{\eta ^{k}+H} \}$ and the term $\mathcal {R}^k$ reads

By Taylor’s expansion, the fact $x_d\in [0, \eta ^k+H]$ and the bounds on $\eta _\tau$ we find

which implies by Lemma 4 that

for $\tau <1$. Hence

Now we calculate using Taylor’s expansion (using the uniform bounds on $\left\Vert \partial _t^2\Psi _{\epsilon }\right\Vert _\infty \tau \left\Vert q_\tau \right\Vert _{L^1(0,T;L^1(\Omega _\tau ))}$ and find for a suitable $\theta >0$ that

$$\begin{aligned} I_1=&\sum _{k=1}^{N_T}\int _{I^k}\int _{\Omega _\tau ^k} \Bigg (q_\tau ^k\frac{\Psi _{\epsilon }(t,r,x_d)-\Psi _{\epsilon }\Big (t+\tau ,r, x_d\Big )}{\tau } \\&+ q_\tau ^k\frac{\Psi _{\epsilon }(t+\tau ,r,x_d) -\Psi _{\epsilon }\Big (t+\tau ,r, x_d\frac{\eta ^{k+1}+H}{\eta ^{k}+H}\Big )}{\tau }\Bigg ) \,\mathrm{d} {x} \,{\mathrm{d}} t \\ =&-\sum _{k=1}^{N_T} \int _{I^k}\int _{\Omega _\tau ^k}q_\tau ^k\partial _t\Psi _{\epsilon }\,\,\mathrm{d} {x}\,{\mathrm{d}} t +O(\tau )\\&- \sum _{k=1}^{N_T}\int _{I^k}\int _{\Omega _\tau ^k}q_\tau ^k\mathbf {w}_\tau ^{k} \cdot \nabla \Psi _{\epsilon }(t+\tau )\,\,\mathrm{d} {x}\,{\mathrm{d}} t + O(\tau ^\theta ). \end{aligned}$$

Consequently we derive

$$\begin{aligned}&\int _0^T \int _{\Omega _\tau } D_t q_\tau \Psi _{\epsilon } \,\mathrm{d} {x} \,{\mathrm{d}} t + \int _{\Omega _\tau ^0} q_\tau ^0\Psi ^0 \,\mathrm{d} {x}\,{\mathrm{d}} t + \int _0^T \int _{\Omega _\tau } q_\tau (t) \partial _t\Psi _{\epsilon }(t) \,\mathrm{d} {x} \,{\mathrm{d}} t \nonumber \\&\quad + \int _0^T \int _{\Omega _\tau } q_\tau (t) \mathbf {w}_\tau (t) \cdot \nabla \Psi _{\epsilon }(t) \,\mathrm{d} {x} = \mathcal {O}(\tau ^\vartheta ), \; \vartheta >0, \end{aligned}$$

(3.14)

for $q_\tau$ being $\varrho _\tau$ we may take $\Psi _{\epsilon }\equiv \varphi$ in case $q_\tau$ = $\varrho _\tau \mathbf {u}_\tau$ we have to take the $\epsilon$-approximation.

Finally, substituting (3.14) into the continuity method, (3.14) and (3.13) into the coupled momentum and structure method (3.1b), we finish the proof. $\square$

Remark 1

In variable domain analysis (in particular in fluid structure interaction involving elastic solids) it is unavoidable to approximate the space of test functions at some point. In our case we do this by introducing the parameter $\epsilon$. We wish to indicate what are the next steps in order to prove that a subsequence converges to a weak solution, which will be the content of a second paper (relaying on this work). The energy estimate allows to take weakly converging sub-sequences (in $\tau$). In order to pass with $\tau \rightarrow 0$ one has to prove that the various non-linearities as the pressure and the convective terms do indeed decouple in the limit. This is a sophisticated analysis introduced in [4] and goes back to seminal works of Lions [44]. The last step is then to pass with $\epsilon \rightarrow 0$. This limit passage is how ever not as dramatic (essentially it uses Taylor expansion); but it depends sensitively on the regularity of $\partial _t\eta$ and in particular on the fact that $\gamma > \frac{12}{7}$. $\square$

Remark 2

We have assumed for simplicity that the boundary $\Gamma _D$ consists of solid walls only. The extension of our (stability and consistency) analysis to more general boundary conditions on $\Gamma _D$ would be an interesting future task. Here, we would like to invite the reader to a very recent work of Kwon and Novotný [43], where the authors analyzed the consistency, convergence and error estimates for a mixed finite volume–finite element approximation of the compressible Navier-Stokes equations with general inflow/outflow boundary data.

4 Fully discrete scheme

In this section, we propose a fully discrete scheme for the FSI problem (1.2). For the time discretization, we use the method introduced in Section 3. Further, for the space discretization, we adopt a mixed finite volume–finite element method proposed by Karper [39] for the compressible Navier– Stokes part (1.2a)–(1.2b) and a standard finite element method for the shell part (1.2c). Following Section 3 we keep $\tau$ as the time discretization parameter. Moreover, we introduce h as the spatial discretization parameter, which is assumed to be coupled to $\tau$ in a convenient manner⁴. In the following we will use the subscripts $(h,\tau )$ for all discrete functions. We shall write $a{\mathop {\sim }\limits ^{<}}b$ if $a\le c b$ for some positive constant c (independent of h and $\tau$), and $a \approx b$ if $a {\mathop {\sim }\limits ^{<}}b$ and $b {\mathop {\sim }\limits ^{<}}a$.

4.1 Discretization

For the discretization in time, we follow the previous section and approximate all unknowns including the mesh and test functions by piecewise constant in time functions. For the space discretization, we start with the notations on the fixed reference domain.

Mesh for the fluid part Let the reference domain $\widehat{\Omega }$ be a closed polygonal domain, and $\widehat{\mathcal {T}}_h$ be a triangulation of $\widehat{\Omega }$: $\overline{\widehat{\Omega }} = \cup _{K \in \widehat{\mathcal {T}}_h} K$. The time dependent domain (or mesh) at time $t^k$ is described by the ALE mapping

where the ALE mapping $\mathcal {A}_{h,\tau }^{k}$ will be given in (4.9) below. Further, we take the following notations and assumptions:

• By $\mathcal {E}(K)$ we denote the set of the edges $\sigma$ of an element $K \in \mathcal {T}_{h,\tau }$. The set of all edges is denoted by $\mathcal {E}$. We distinguish exterior and interior edges: $\mathcal {E}= \mathcal {E}_{\mathrm{I}}\cup \mathcal {E}_{\mathrm{E}},\ \mathcal {E}_{\mathrm{E}}= \left\{ \sigma \in \mathcal {E}\ \Big | \ \sigma { \subset } \partial \Omega _{h,\tau }\right\} ,\ \mathcal {E}_{\mathrm{I}}= \mathcal {E}\setminus \mathcal {E}_{\mathrm{E}}.$

• We denote the set of all faces on the top boundary by $\mathcal {E}_{\mathrm{S}}$ $(\subset \mathcal {E}_{\mathrm{E}})$.

• For each $\sigma \in \mathcal {E}$ we denote $\mathbf {n}$ as the outer normal and write it as $\mathbf {n}_{\sigma ,K}$ if $\sigma \in \mathcal {E}(K)$. Moreover, for any $\sigma =K|L$ being a common edge of elements K and L, we have $\mathbf {n}_{\sigma , K}=-\mathbf {n}_{\sigma ,L}$.

• We denote by |K| and $|\sigma |$ the d and $(d-1)$-dimensional Hausdorff measure of the element K and edge $\sigma$, respectively. Further, we remark $h_K$ as the diameter of K and $h=\max _{K \in \mathcal {T}_{h,\tau }} h_K$ as the size of the triangulation. The mesh is regular and quasi-uniform in the sense of [15], i.e. there exist positive real numbers $\theta _0$ and $c_0$ independent of h such that $\theta _0 \le \inf \left\{ \frac{\xi _K}{h_K}, K \in \mathcal {T}_{h,\tau }^0\right\}$ and $c_0 h \le h_K$, where $\xi _K$ stands for the diameter of the largest ball included in K.

• The mesh is built by an extension of the $(d-1)$-dimensional bottom surface mesh in the $d^{\mathrm{th}}$ direction, i.e., the projection of any element in the $d^{\mathrm{th}}$ direction must coincide with an edge $\sigma \in \mathcal {E}_{\mathrm{E}}$ on the bottom surface. We give an example in two dimensions for illustrating such kind of mesh, see Fig. 2. In particular $\mathcal {T}_{h,\tau }^k$ is assumed to be a conformal triangulation.

Mesh for the structure part The mesh discretization of the time independent $(d-1)$-dimensional domain $\Sigma$ coincides with bottom edges of $\partial \Omega _{h,\tau }$ such that $\Sigma _h= \mathcal {E}_{\mathrm{E}}\cap \{x_d=0\}$.

Fig. 2

An example of mesh in two dimensions: left is the reference mesh and right is the deformed current mesh

Remark 3

On one hand, the mesh is constructed by the extension of the mesh of the $(d-1)$-dimensional bottom boundary. On the other hand, we will define a linear function for the discrete ALE mapping $\mathcal {A}_{h,\tau }$, see (4.8) below. As a consequence, any triangle on the reference mesh is kept to be a triangle in the current mesh, see a two dimensional mesh discretization in Fig. 2.

Function spaces Our scheme utilizes spaces of piecewise smooth functions, for which we define the traces

Note that, $v^{\mathrm{out}}$ is set according to the boundary condition for an exterior edges $\sigma \in \mathcal {E}_{\mathrm{E}}$. We also define

Next, we introduce on the reference mesh the space of piecewise constant functions

and the space of the linear Crouzeix–Raviart finite element

and the space of piecewise polynomial functions of degree $\ell \in \mathbb {N}$ on the shell domain $\Sigma$

for some $\ell \ge 3$. For the case of $d=2$ one can use the standard Hermit elements with any $\ell \ge 3$ (since $\Sigma$ is one dimensional in this case), and for the case of $d=3$ we refer to [15] for the Hsieh-Clough-Tocher macro finite elements with $\ell =3$.

In accordance with (2.4) we denote the piece-wise constant function $v_{h,\tau }= \widehat{v}_{h,\tau }\circ \mathcal {A}_{h,\tau }^{-1}$ for all $t\in (0,T)$ and for all unknowns including the test functions $v\in \{ \varrho , \mathbf {u}, p, \eta , z , \mathbf {w}, \varphi , \varvec{\Psi }, \psi \}$ as well as the function spaces

Thus it is clearly that

The associated projections of the function spaces are

and (the uniquely defined interpolation operator [22])

Coupling at the boundary and ALE mapping Following the previous notations we denote by $\Gamma _S^k=\Gamma _S(t^k)$ the piecewise polynomial boundary produced by $\eta _{h,\tau }^k$. Namely $\Gamma _S^k=\left\{ (r,x_d)\in [0,L]^{d-1}\times \{H+\eta _{h,\tau }^k(r)\} \right\}$ is a $C^1$ boundary since we have used a $C^1$ finite element space for the approximation of $\eta _{h,\tau }$. In order to get automatically a piecewise linear discretization of $\Gamma _S$ we shall introduce a projection operator on $\eta _{h,\tau }$. To this end, we first introduce a piecewise linear function space on $\Sigma _h$

(4.1)

Then we use the following projection

$$\begin{aligned}&\Pi _p :W^{1,2}_0(\Sigma )\mapsto W_h^* \text { satisfying }\nonumber \\&\int _{\Sigma _h} \nabla \Pi _p v \cdot \nabla \phi _h \mathrm{d}r = \int _{\Sigma _h} \nabla v \cdot \nabla \phi _h \mathrm{d}r \quad \text {for all }\phi _h\in W_h^*. \end{aligned}$$

(4.2)

Thanks to this projection we obtain a polygonal computational domain given by

$$\begin{aligned} \mathcal {T}_{h,\tau }^k :=\{(r,x_d)\in \Sigma \times [0,H+\Pi _p (\eta _{h,\tau }^k)(r))]\}. \end{aligned}$$

(4.3)

Here, let us derive the estimates related to the above projection operator $\Pi _p$, which will be used later and which indicate that its use is suitable. Upon setting $\phi _h =\Pi _p v$ in (4.2) and using Hölder’s inequality we find

$$\begin{aligned} \left\Vert \nabla \Pi _p v\right\Vert _{L^2(\Sigma )}\le \left\Vert \nabla v\right\Vert _{L^2(\Sigma )} \quad \text { for all } v \in W^{1,2}_0(\Sigma ) . \end{aligned}$$

(4.4)

Next, we introduce $\xi _h\in W^*_h$ as the $L^2$ projection of $-\Delta v$ for $v \in W_h$, meaning

$$\begin{aligned} \int _{\Sigma _h}(\xi _h+\Delta v)\phi _h\, dr=0 \text { for all } \phi _h\in W^*_h. \end{aligned}$$

(4.5)

Then we find $\int _{\Sigma _h} \nabla \Pi _p v \cdot \nabla \phi _h \mathrm{d}r\, =\int _{\Sigma _h} \xi _h\phi _h \mathrm{d}r$ for all $v \in W_h$. By setting $\phi _h = \xi _h$ in (4.5) and using Hölder’s inequality we find that $\left\Vert \xi _h\right\Vert _{L^2(\Sigma _h)}\le \left\Vert \Delta v\right\Vert _{L^2(\Sigma _h)}$. This implies for instance by [49, equation (5.10)] and Sobolev-Poincare’s inequality that

$$\begin{aligned} \left\Vert \nabla \Pi _p v\right\Vert _{L^p(\Sigma )}\le c\left\Vert \Delta v\right\Vert _{L^{2}(\Sigma )} \text { for all } p \in [1,\infty ) \quad \text {and } \left\Vert \Pi _p v\right\Vert _{L^\infty (\Sigma )}\le c\left\Vert \Delta v\right\Vert _{L^{2}(\Sigma )}. \end{aligned}$$

(4.6)

Moreover, by the standard projector error (see for instance [49, equation (6.3)]), we have

This together with the inverse estimate stated later in (4.14) imply that

$$\begin{aligned} \left\Vert \Pi _p v-v\right\Vert _{L^\infty (\Sigma )}&\le c h^{-(d-1)/s}\left\Vert \Pi _p v-v\right\Vert _{L^s(\Sigma )} \nonumber \\&\le c h^{-(d-1)/s}\left\Vert \nabla (\Pi _p v-v)\right\Vert _{L^2(\Sigma )} \nonumber \\&\le c h^{s_0}\left\Vert \Delta v\right\Vert _{L^2(\Sigma )}, \end{aligned}$$

(4.7)

where $s_0 = 1-(d-1)/s>0$ for all $s\in (d-1,\infty )$.

In consistency with (4.3), the discrete ALE mapping (1.1) is redefined due to the space discretization preceddingly introduced

$$\begin{aligned}&x:=\mathcal {A}_{h,\tau }(\widehat{x}) \equiv \left( \widehat{r}, \frac{ \Pi _p (\eta _{h,\tau }) +H}{H}\widehat{x}_d \right) , \text { with } \nonumber \\&r= \widehat{r}, \; x_d= \frac{\Pi _p (\eta _{h,\tau }) +H}{H}\widehat{x}_d \text{ for } x=(r,x_d). \end{aligned}$$

(4.8)

The discrete Jacobian and determinant read $\mathbb {J}^k = \widehat{ \nabla } \mathcal {A}_{h,\tau }^{k}$, $\mathcal {F}^k =\det (\mathbb {J}^k)$, respectively. Moreover, we need to update the definitions in (2.6) and (2.8) due to the ALE mapping.

(4.9)

Note that the domain $\Omega _{h,\tau }$ is defined via $\eta _{h,\tau }$ and its triangulation $\mathcal {T}_{h,\tau }$ is defined by $\Pi _p \eta _{h,\tau }$. Moreover, the Dirichlet boundary values of $\mathbf {u}_{h,\tau }$ will be defined by $\Pi _p z_{h,\tau }= \Pi _p \delta _t \eta _{h,\tau }$.

Upwind divergence To approximate the convective terms, we apply a dissipative upwind operator

$$\begin{aligned} \mathrm{div}^{\mathrm{up}}_{h,\tau }(q_{h,\tau }, \mathbf {v}_{h,\tau })(x) :=\sum _{K \in \mathcal {T}_{h,\tau }}\frac{1_K}{|K|} \sum _{\sigma \in \mathcal {E}(K)} \int _{\sigma } \mathrm{Up}[q_{h,\tau }, \mathbf {v}_{h,\tau }] \mathrm{d}S(x), \end{aligned}$$

(4.10)

where

Here

As pointed out in [23], the artificial diffusion included in the above flux function is . For the consistency we will require

We emphasize that the existence of a numerical solution, its stability, mass conservation and positivity of the density do not depend on the additional artificial diffusion term. However, it is important for deriving the unconditional consistency of our numerical scheme without any assumption on the regularity of the numerical solution, see Theorem 5.

In accordance with the relation (2.10), we introduce the upwind divergence on the reference domain as

Preliminary inequalities We assume the readers are familiar with the techniques in finite element method. For the sake of completeness, we report a few necessary inequalities. As is common the constant c appearing in this paper depends on the regularity of the mesh; i.e. on the constants $\theta _0$ and $c_0$ above. As follows from our estimates (4.25) the numbers $c_0$ and $\theta _0$ can be chosen independently of h and $\tau$. Meaning that $\theta _0 \le \inf \left\{ \frac{\xi _K}{h_K}, K \in \mathcal {T}_{h,\tau }\right\}$ and $c_0 h \le h_K,$ where $\xi _K$ stands for the diameter of the largest ball included in K. Moreover, it follows from (4.25) that $h_K\le c_1 h \text{ for } \text{ all } K \in \mathcal {T}_{h,\tau }$, with a constant uniform in h and $\tau$.

Since these constants can assumed to be uniform w.r.t the change of variables (due to the $L^\infty$ bound on $\eta _{h,\tau }$ (4.24)) the below estimates hold both on the reference domain, as well as on the current domain. For that reason we take $\Omega _{h,\tau }=\bigcup _{K\in \mathcal {T}_{h,\tau }} K$ as a (regular) polygonal domain. We define for the discrete function $\mathbf {u}_{h,\tau }$ the following norms:

Next we would like to introduce the Korn inequality [7, equation (1.19)].

and the Poincaré–Friedrichs inequality [6, equation (1.5)]

respectively for all $\mathbf {u}_{h,\tau }\in V_h$. Thus we deduce the following modified Korn inequality

$$\begin{aligned} \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{1,\mathcal {T}_{h,\tau }} + \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^2(\Omega _{h,\tau })} {\mathop {\sim }\limits ^{<}}\left\Vert \mathbf {D}(\mathbf {u}_{h,\tau })\right\Vert _{L^2(\Omega _{h,\tau })} + \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^2(\partial \Omega _{h,\tau })} + \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{H^1_Y} .\nonumber \\ \end{aligned}$$

(4.11)

Further, we need the following version of Sobolev’s inequality [24, Lemma 2.3]

$$\begin{aligned} \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^6(\Omega _{h,\tau })} {\mathop {\sim }\limits ^{<}}\left\Vert \mathbf {u}_{h,\tau }\right\Vert _{1,\mathcal {T}_{h,\tau }} + \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^1(\Omega _{h,\tau })}^2, \; \forall \; \mathbf {u}_{h,\tau }\in V_h. \end{aligned}$$

(4.12)

Next, due to scaling argument we introduce the trace theorem [24, equation (2.26)]

(4.13)

where $\mathcal {P}^m(K)$ denotes the space of polynomial degree not grater than m. It is worth mentioning the inverse estimate, see [15] and [34, Remark 2.1]

$$\begin{aligned}&\left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^{p_1}(0,T; L^{q_1}(\Omega _{h,\tau }))} {\mathop {\sim }\limits ^{<}}\tau ^{\frac{1}{p_1} - \frac{1}{p_2} } h^{d(\frac{1}{q_1} - \frac{1}{q_2}) } \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{L^{p_2}(0,T; L^{q_2}(\Omega _{h,\tau }))}, \nonumber \\&\quad \forall \; 1 \le p_2 \le p_1 \le \infty , \; 1 \le q_2 \le q_1 \le \infty . \end{aligned}$$

(4.14)

Finally, we recall the standard interpolation error estimates for $\phi \in C^1(\Omega _{h,\tau })$ [8] (see also [31, Appendix]).

(4.15)

for $1\le p \le \infty$, and also from [39, Lemma 2.7] and [18] that

(4.16)

4.2 The scheme

With the above notations, we are ready to present a mixed finite volume–finite element method for the FSI problem (1.2). First we present the scheme in the current domain.

Definition 3

(Fully discrete scheme on the current domain) Let $(\varrho ^0_h, \mathbf {u}_{h,\tau }^0, \eta _{h,\tau }^0, z_{h,\tau }^{0})= (\Pi _\mathcal {T}[\varrho _0], \Pi _\mathcal {T}[\mathbf {u}_0], \Pi _{W}[\eta _0], \Pi _W [z_0])$ be the given initial data. We say $(\eta _{h,\tau }^{k}, \varrho _{h,\tau }^{k}, \mathbf {u}_{h,\tau }^{k})\in W_h\times Q_{h,\tau }^k\times V_{h,\tau }^k$, $k = 1,\ldots , N_T$, is a mixed finite volume–finite element approximation of the problem (1.2) if the following hold for any $({\psi }_{h,\tau }^k, {\varphi }_{h,\tau }^k, {\varvec{\Psi }}_{h,\tau }^k) \in W_h\times Q_{h,\tau }^k\times V_{h,\tau }^k$ with $\Pi _\mathcal {E}[{\varvec{\Psi }}_{h,\tau }^k(r,\eta +H)] = \Pi _\mathcal {E}[\Pi _p {\psi }_{h,\tau }^k(r)]\mathbf {e}_d$ (for all $r\in \Sigma _h$):

$$\begin{aligned}&\int _{\Omega _{h,\tau }^k} D_t \varrho _{h,\tau }^{k} {\varphi }_{h,\tau } \,\mathrm{d} {x} + \int _{\Omega _{h,\tau }^k} \mathrm{div}^{\mathrm{up}}_{h,\tau }( \varrho _{h,\tau }^{k} , \mathbf {v}_{h,\tau }^{k} ) {\varphi }_{h,\tau } \,\mathrm{d} {x} = 0; \end{aligned}$$

(4.17a)

$$\begin{aligned}&\int _{\Omega _{h,\tau }^k} D_t \left( \varrho _{h,\tau }^{k} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}] \right) \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Omega _{h,\tau }^k} \mathrm{div}^{\mathrm{up}}_{h,\tau }(\varrho _{h,\tau }^{k} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}], \mathbf {v}_{h,\tau }^{k} ) \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + 2\mu \int _{\Omega _{h,\tau }^k} \mathbf {D}(\mathbf {u}_{h,\tau }^{k}) : \nabla {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \mathrm{d}S(x) + \lambda \int _{\Omega _{h,\tau }^k} \mathrm{div}\mathbf {u}_{h,\tau }^{k} \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad - \int _{\Omega _{h,\tau }^k} p(\varrho _{h,\tau }^{k}) \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Sigma } \delta _t z_{h,\tau }^{k} {\psi }_{h,\tau } \mathrm{d}r + \int _{\Sigma } \Delta \eta _{h,\tau }^{k} \Delta {\psi }_{h,\tau } \mathrm{d}r\nonumber \\&\quad = \int _{\Omega _{h,\tau }^k} \varrho _{h,\tau }^k \mathbf {f}_{h,\tau }^{k}\cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Sigma } g_{h,\tau }^{k} {\psi }_{h,\tau } \mathrm{d}r ; \end{aligned}$$

(4.17b)

where

Moreover, the boundary conditions are

where $\Pi _W$ is the projection operator from $W^{2,2}(\Sigma )$ to $W_h$.

Here we would like to point out that by construction

Analogously to the semi-discrete case, the fully discrete scheme (4.17) preserves the total mass as well

$$\begin{aligned} \int _{\Omega _{h,\tau }^k} \varrho _{h,\tau }^k \,\mathrm{d} {x}= & {} \int _{\Omega _{h,\tau }^{k-1}} \varrho _{h,\tau }^{k-1} \,\mathrm{d} {x} = \cdots \nonumber \\= & {} \int _{\Omega _{h,\tau }^0} \varrho _{h,\tau }^0 \,\mathrm{d} {x} =:M_0, \; \text{ for } \text{ all } k=1,\ldots ,N_T.\nonumber \\ \end{aligned}$$

(4.18)

Actually, it can be shown by setting ${\varphi }_{h,\tau }\equiv 1$ in (4.17a) and noticing the conservativity of the upwind flux.

Remark 4

We observe that the above scheme is fully implicit and nonlinear. This means that both velocity $\mathbf {u}_{h,\tau }^k$ and density $\varrho _{h,\tau }^k$ are coupled to their domain of definition $\Omega _{h,\tau }^k$, which is determined by the unknown $\eta _{h,\tau }^k$ for each time step $k=1,2,\ldots , N_T$. This is in contrast to the approaches from incompressible flows [9] where the velocity and pressure can be solved for each time step in the domain of the previous step. Here a common problem for compressible fluids reveals itself: The fact that the renormalized density equation that is necessary for deriving an energy inequality makes an implicit and non-linear scheme unavoidable up-to-date. Indeed, even for fixed domains there is no time discretization method known for compressible fluids providing energy estimates which is not both nonlinear and fully implicit. Analogously, the coupling between the velocity fields of the fluid and the shell together with the requirement of an implicit mesh velocity $\mathbf {w}$ in the discrete Reynolds transport theory (Lemma 1) block us to work with a scheme that is explicit with respect to the shell. Conclusively, in our investigations it turned out that also for fluid–structure interactions there is no space to allow explicit in time parts of the solutions. Nevertheless, we can solve the scheme (4.17) by rewriting its equivalent formulation on the reference domain $\widehat{\Omega }$ to avoid the problem of solving unknowns on an unknown domain, see scheme (4.19) given below in Definition 7. Though the scheme (4.19) is also a fully implicit and nonlinear scheme, we can solve the nonlinear system iteratively on the given reference domain. Furthermore, we will show that a full discretization in time and space actually admits a solution, see Theorem 3. In addition, we can assure that for a positive time interval that the fully discrete scheme is well-defined, see Corollary 6.

Recalling (2.4) allows to transfer the scheme in the following way:

Lemma 7

(Fully discrete scheme on reference domain) Let $(\eta _{h,\tau }^{k}, \varrho _{h,\tau }^{k}, \mathbf {u}_{h,\tau }^{k})\in W_h\times Q_{h,\tau }^k\times V_{h,\tau }^k$, $k = 1,\ldots , N_T$, be a solution to the mixed FV-FE method given in Definition 3. Then $(\eta _{h,\tau }^{k}, \widehat{\varrho }_{h,\tau }^{k}, \widehat{\mathbf {u}}_{h,\tau }^{k})$ satisfies:

$$\begin{aligned}&\int _{\widehat{\Omega }} \frac{\widehat{\varrho }_{h,\tau }^k \mathcal {F}^{k}-\widehat{\varrho }_{h,\tau }^{k-1}\mathcal {F}^{k-1}}{\tau } \widehat{\varphi }_{h,\tau } \,\mathrm{d} \widehat{x} + \int _{\widehat{\Omega }} \widehat{\mathrm{div}^{\mathrm{up}}_{h,\tau }( \varrho _{h,\tau }^{k}, \mathbf {v}_{h,\tau }^{k} )} \widehat{\varphi }_{h,\tau }\mathcal {F}^{k} \,\mathrm{d} \widehat{x} = 0;\qquad \end{aligned}$$

(4.19a)

$$\begin{aligned}&\int _{\widehat{\Omega }} \frac{\widehat{\varrho }_{h,\tau }^k \Pi _\mathcal {T}[\widehat{\mathbf {u}}_{h,\tau }^{k}] \mathcal {F}^{k}-\widehat{\varrho }_{h,\tau }^{k-1}\Pi _\mathcal {T}[\widehat{\mathbf {u}}_{h,\tau }^{k-1}]\mathcal {F}^{k-1}}{\tau } \cdot \widehat{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} \widehat{x}\nonumber \\&\quad + \int _{\widehat{\Omega }} \widehat{ \mathrm{div}^{\mathrm{up}}_{h,\tau }(\varrho _{h,\tau }^{k} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}], \mathbf {v}_{h,\tau }^{k} )} \cdot \widehat{\varvec{\Psi }}_{h,\tau }\mathcal {F}^{k} \,\mathrm{d} \widehat{x}\nonumber \\&\quad +2 \mu \int _{\widehat{\Omega }} \widehat{ \mathbf {D}( \mathbf {u}_{h,\tau }^k)} : \widehat{ \nabla {\varvec{\Psi }}_{h,\tau }} \mathcal {F}^{k} \,\mathrm{d} \widehat{x}\nonumber \\&\quad +2 \mu \sum _{\sigma \in \widehat{\mathcal {E}_{\mathrm{I}}}}\int _{\sigma } \frac{1}{ h} \left[ \! \left[ \widehat{\mathbf {u}}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ \widehat{\varvec{\Psi }}_{h,\tau }\right] \! \right] | \mathcal {F}^{k}(\mathbb {J}^k)^{-T} \widehat{\mathbf {n}} | \mathrm{d}S(\widehat{x})\nonumber \\&\quad + \lambda \int _{\widehat{\Omega }} \widehat{ \mathrm{div}\mathbf {u}_{h,\tau }^{k}} \widehat{ \mathrm{div}{\varvec{\Psi }}_{h,\tau }} \mathcal {F}^{k} \,\mathrm{d} \widehat{x}\nonumber \\&\quad - \int _{\widehat{\Omega }} p(\widehat{\varrho }_{h,\tau }^{k}) \widehat{ \mathrm{div}{\varvec{\Psi }}_{h,\tau }} \mathcal {F}^{k} \,\mathrm{d} \widehat{x} + \int _{\Sigma } \delta _t z_{h,\tau }^{k} \psi \mathrm{d}r \nonumber \\&\quad + \int _{\Sigma } \Delta \eta _{h,\tau }^{k} \Delta \psi \mathrm{d}r\quad =\int _{\widehat{\Omega }} \widehat{\varrho }_{h,\tau }^k \widehat{\mathbf {f}}_{\tau }^{k}\cdot \widehat{\varvec{\Psi }}_{h,\tau }\mathcal {F}^{k} \,\mathrm{d} \widehat{x} + \int _{\Sigma } g_\tau ^{k} {\psi }_{h,\tau } \mathrm{d}r \end{aligned}$$

(4.19b)

and boundary conditions

Our numerical scheme is nonlinear, nevertheless we can show that its solution always exists.

Theorem 3

(Existence of a numerical solution and positivity of the density)

Let $0<\varrho _{h,\tau }^{k-1}\in Q_{h,\tau }^{k-1}$, $(\mathbf {u}_{h,\tau }^{k-1}, \eta _{h,\tau }^{k-1}, z_{h,\tau }^{k-1}) \in V_{h,\tau }^{k-1} \times W_h\times W_h$ be given. Then there exist $0<\varrho _{h,\tau }^k\in Q_{h,\tau }$ and $(\mathbf {u}_{h,\tau }^k,\eta _{h,\tau }^k,z_{h,\tau }^k:= \frac{\eta _{h,\tau }^k -\eta _{h,\tau }^{k-1}}{\tau }) \in V_{h,\tau }\times W_h\times W_h$ satisfying the discrete problem (4.17) (or equivalently (4.19)), where $\eta _{h,\tau }^k = \eta _{h,\tau }^{k-1} + \tau z_{h,\tau }^k$.

The proof is an adaption of previous approaches using homotopy arguments (see [30]). For the sake of completeness a rigorous proof can be found in the Appendix A.1.

4.3 Stability

Since the differences of the proofs of the renormalization and the stability between the semi and fully discrete scheme are merely of technical nature we put the respective proofs in the appendix.

First, the fully discrete scheme (4.17) satisfies the renormalized continuity equation.

Lemma 8

(Renormalized continuity equation) Let $(\varrho _{h,\tau },\mathbf {u}_{h,\tau })\in Q_{h,\tau }\times V_{h,\tau }$ satisfy the discrete continuity equation (4.17a). Then for any function $B \in C^1([0,\infty ))$ we have

where

Moreover, $D_1 \ge 0$ and $D_2 \ge 0$ provided B is convex.

Proof

The proof is similar to Lemma 2 but we need to pay attention to the convective terms, see the details of the proof in Appendix A.2. $\square$

Next, we show the strictly positivity of the discrete density.

Lemma 9

(Positivity of density) Let $\varrho _{h,\tau }^0 > 0$. Then any solution to (4.17) satisfies $\varrho _{h,\tau }^{k} > 0$ for all $k=1,\ldots , N_T$.

Proof

We prove via mathematical induction and start with the assumption $\varrho _{h,\tau }^{k-1}>0$. First, by exactly the same argument as in Lemma 3 we know that $\varrho _{h,\tau }^{k} \ge 0$. Second, we assume there exists a $K\in \mathcal {T}_{h,\tau }^{k}$ such that $\varrho _K^{k}=0$. Then a straightforward calculation from the density scheme (4.17a) yields

which contradicts with the assumption $\varrho _{h,\tau }^{k-1}>0$. Thus we know $\varrho _{h,\tau }^k>0$ and finish the proof. $\square$

Further, setting $B=\mathcal {H}(\varrho _{h,\tau })$ in Lemma 8 we get the following corollary on the internal energy balance.

Corollary 5

(Discrete internal energy balance) Let $(\varrho _{h,\tau },\mathbf {u}_{h,\tau })\in Q_{h,\tau }\times V_{h,\tau }$ satisfy the discrete continuity equation (4.17a). Then there exists $\xi \in \mathrm{co}\{ \varrho _{h,\tau }^{k-1}\circ {X}_k^{k-1} , \varrho _{h,\tau }^{k} \}$ and $\zeta \in \mathrm{co}\{ \varrho _K^{k} , \varrho _L^{k} \}$ for any $\sigma =K|L \in \mathcal {E}_{\mathrm{I}}^{k}$ such that

$$\begin{aligned}&\frac{ 1}{\tau } \left( \int _{\Omega _{h,\tau }^k} \mathcal {H}(\varrho _{h,\tau }^k) \,\mathrm{d} {x} - \int _{\Omega _{h,\tau }^{k-1}} \mathcal {H}(\varrho _{h,\tau }^{k-1}) \,\mathrm{d} {x} \right) \nonumber \\&\quad + \int _{\Omega _{h,\tau }^k} p(\varrho _{h,\tau }^{k}) \mathrm{div}\mathbf {u}_{h,\tau }^{k} \,\mathrm{d} {x} = - D_1 - D_2, \text{ where: } \end{aligned}$$

(4.20)

(4.21)

Analogously as the semi-discrete case, the fully discrete scheme (4.17) (or (4.19)) dissipates the total energy.

Theorem 4

(Energy stability of the fully discrete scheme (4.17)) Let $\left( \varrho _{h,\tau }^k, \mathbf {u}_{h,\tau }^k, \eta _{h,\tau }^k\right) _{k=1}^{N_T}$ be a family of numerical solutions obtained by the scheme (4.17) (or (4.19)). Then for any $N=1,\ldots , N_T$ the energy is stable in the following sense

where $D_1, \; D_2$ are given in (4.21), $E_f^{k}= \frac{1}{2} \varrho _{h,\tau }^k \left| \Pi _\mathcal {T}[ \mathbf {u}_{h,\tau }^{k}]\right| ^2 + \mathcal {H}(\varrho _{h,\tau }^k)$ and $E_s^{k} =\frac{1}{2} (|z_{h,\tau }^{k}|^2 + \alpha | \Delta \eta _{h,\tau }^{k}|^2 + \beta |\nabla \eta _{h,\tau }^{k}|^2).$

Proof

The proof is similar to the energy stability of the semi-discrete scheme, see Theorem 1. We leave it to Appendix A.3. $\square$

4.4 A-priori estimates

Before proving the consistency of the scheme (4.17) (or equivalently (4.19)) we derive some useful estimates. Due to the coherence of the argument we use the notation of Subsection 3.4. In particular we use the same definition of the piecewise constant in time functions (as defined in (2.3)) and the piecewise constant domain $\Omega _{h,\tau }$.

Applying the modified Korn inequality (4.11) and the Sobolev inequality (4.12) to the energy estimates (Theorem 4) and the definition of $D_1$ and $D_2$ (see (4.21)) directly imply the following uniform bounds on the numerical solutions:

(4.22)

where c depends on the external force $\mathbf {f}_\tau$ and $g_\tau$ as well as the initial data. Further, we recall the triangular inequality, interpolation error (using the Aubin-Nitsche-duality method), and the above estimates on $z_{h,\tau }$ and $\Delta z_{h,\tau }$ to derive

(4.23)

Next, since the discretization of the displacement $\eta _{h,\tau }$ is conformal in $W^{2,2}_0(\Sigma )\subset C^1_0(\Sigma )$ we find for $\eta _{h,\tau }$ that

$$\begin{aligned}&\left\Vert \eta _{h,\tau }\right\Vert _{ L^\infty (0,T; { W^{2,2}}(\Sigma ))}\le c \hbox { and (by Sobolev embedding) }\nonumber \\&\left\Vert \eta _{h,\tau }\right\Vert _{ L^\infty (0,T; L^\infty (\Sigma ))}+\left\Vert \nabla \eta _{h,\tau }\right\Vert _{ L^\infty (0,T; { L^p}(\Sigma ))} \le c, \end{aligned}$$

(4.24)

where the constant depends on $p<\infty$ but is independent from $\tau ,h$. Thanks to the above estimates, the Sobolev inequality, and (4.6) we have

Moreover, by precisely the same argument as in Lemma 4 combined with (4.7) we find for all $\theta \in [0,{ \frac{1}{2}})$ there exists a constant C depending on the energy estimates and $\theta$, such that

which implies the following corollary by the very same argument as in the semi-discrete case.

Corollary 6

(Exclusion of self-touching) Let $\tau ^\theta \le \frac{\delta _0}{C}$ and $\delta _1\ge 2\delta _0$. Then, if for some $k\in \{1,...,N_T\}$ $\hbox {inf}_r\eta _{h,\tau }^{ k-1}(r)\ge \delta _1-H$, then $\eta _{h,\tau }^{ k}$ satisfies $\hbox {inf}_\sigma \eta _{h,\tau }^k(r)\ge \delta _1-\delta _0-H$. Moreover, for every $\delta _0\in (0,H/2)$ there exists a $T_0$ just depending on the bounds of the energy inequality H, such that $\hbox {inf}_{[0,T_0]}\eta (t,r)\ge \delta _0-H$.

From the above and the $L^\infty$ bound of $\eta _{h,\tau }$ given in (4.24), we may assume in the following that there exist two positive constants $\delta _2> \delta _1 >0$ such that

$$\begin{aligned} 0< \delta _1 \le \mathcal {F}^{k}= \frac{\eta _{h,\tau }^k + H}{H} \le \delta _2 . \end{aligned}$$

(4.25)

Remark 5

Note the uniform upper and lower bounds on the Jacobian (4.25) imply that all uniform bounds in Lebesgue spaces appeared in this paper hold both on the reference domain $\widehat{\Omega }_h$ and the current time-dependent domain $\Omega _{h,\tau }$. We emphasize this fact in the following by denoting $L^p L^{q}$, $L^q$ for the norms $L^p(0,T;L^q(\Omega _{h,\tau })$ and $L^q(\Omega _{h,\tau })$, respectively.

Moreover, by the same reasoning all estimates on integrals over the jumps, as well as on area-integrals that have been shown on the reference mesh are also valid on the push forwarded mesh.

In the following we collect some estimates that we need for the consistency proof. First, we recall the definition of $\mathrm{div}\mathbf {w}_\tau$ and $\mathbf {w}_\tau$ (4.9), the estimates (4.23) and (4.25), and the fact $x_d \le (\Pi _p (\eta _{h,\tau }^k)+H)$ to obtain

$$\begin{aligned}&\left\Vert \mathrm{div}\mathbf {w}_{h,\tau }\right\Vert _{ L^\infty L^2 } = \left\Vert \frac{\Pi _p z_{h,\tau }}{H+\Pi _p \eta _{h,\tau }} \right\Vert _{ L^\infty (0,T; L^2(\Sigma ))} \approx \left\Vert \Pi _p z_{h,\tau } \right\Vert _{ L^\infty (0,T; L^2(\Sigma ))} {\mathop {\sim }\limits ^{<}}1,\nonumber \\&\left\Vert \mathbf {w}_{h,\tau }\right\Vert _{L^\infty L^2} = \left\Vert \frac{\Pi _p z_{h,\tau } x_d}{H+\Pi _p \eta _{h,\tau } } \right\Vert _{L^\infty L^2} {\mathop {\sim }\limits ^{<}}\left\Vert \Pi _p z_{h,\tau }\right\Vert _{L^\infty (0,T; L^2(\Sigma _h))} {\mathop {\sim }\limits ^{<}}1. \end{aligned}$$

(4.26)

The estimate (4.26) together with the velocity bounds stated in (4.22) imply

$$\begin{aligned} \left\Vert \mathrm{div}\mathbf {v}_{h,\tau }\right\Vert _{L^2 L^2} {\mathop {\sim }\limits ^{<}}1 \quad \text {and} \quad \left\Vert \mathbf {v}_{h,\tau }\right\Vert _{L^2 L^2} {\mathop {\sim }\limits ^{<}}1. \end{aligned}$$

(4.27)

Next, we use Sobolev’s inequality, the estimate (4.4), and the estimate of $\nabla z_{h,\tau }$ stated in (4.22) to get

$$\begin{aligned} \left\Vert \Pi _p z_{h,\tau } \right\Vert _{ L^2 (0,T; L^p(\Sigma ))} {\mathop {\sim }\limits ^{<}}\left\Vert \nabla \Pi _p z_{h,\tau } \right\Vert _{ L^2 ((0,T)\times \Sigma )} \le \left\Vert \nabla {z_{h,\tau }} \right\Vert _{ L^2 ((0,T)\times \Sigma )} {\mathop {\sim }\limits ^{<}}\tau ^{-1/2} \end{aligned}$$

for any $p \in [1,\infty )$. Further, recalling (4.9) for the definition of $\mathbf {w}_\tau$ and the velocity bound stated in (4.22) we find for all $\tau \in (0,1)$ that

$$\begin{aligned}&\left\Vert \mathbf {w}_{h,\tau }\right\Vert _{L^2L^p} = \left\Vert \frac{\Pi _p z_{h,\tau } x_d}{H+\Pi _p \eta _{h,\tau } } \right\Vert _{L^2 L^p} {\mathop {\sim }\limits ^{<}}\left\Vert \Pi _p z_{h,\tau }\right\Vert _{L^2(0,T; L^p(\Sigma _h))} {\mathop {\sim }\limits ^{<}}\tau ^{-\frac{1}{2}} \nonumber \\&\text {and } \left\Vert \mathbf {v}_{h,\tau }\right\Vert _{ L^2 L^6}\le \tau ^{-1/2}. \end{aligned}$$

(4.28)

The next lemma collects some estimates related to the errors that appear due to the convective terms. The proof of these estimates goes along the techniques developed by the community of the numerics for compressible fluids, see appendix A.4 for a complete proof.

Lemma 10

(Useful estimates) Let $c>0$ be a constant independent of the parameters $\tau$ and h (may depend on the initial data, the external force $\mathbf {f}$ and g and the mesh regularity).

• 1. Let $\varrho _{h,\tau }, \mathbf {v}_{h,\tau }$ be a solution of (4.17a) with $h \in (0,1)$ and satisfy the estimates

  

  Then the following holds

  

  (4.29)

• 2. Let $\varrho _{h,\tau }, \mathbf {v}_{h,\tau }$ be a solution of (4.17a) with $\gamma \ge 2$ and satisfies the estimates

  

  Then the following holds

  

  (4.30)

• 3. Let $\varrho _{h,\tau }, \mathbf {u}_{h,\tau }, \mathbf {w}_{h,\tau }$ satisfy the estimates in (4.22). Then the following hold

  

  (4.31a)
  

  (4.31b)

  where

  

• 4. Let $r, F \in Q_{h,\tau }, \mathbf {v}\in V_{h,\tau }$ and $\phi \in C^1(\mathcal {T}_{h,\tau })$. Then it holds

  

  (4.32)

4.5 Consistency

With the a-priori estimates derived in the last subsection, we are ready to show the consistency of the fully discrete scheme (4.17) (or equivalently (4.19)). For the momentum equation we have to introduce the $\epsilon$-layer again.

Theorem 5

(Consistency of the fully discrete scheme (4.17)) Let $(\eta _{h,\tau },\varrho _{h,\tau }, \mathbf {u}_{h,\tau })$ be a solution of the scheme (4.17) with $\tau \approx h\, { \in (0,1)}$, $\gamma >\frac{6}{5}$ and the artificial diffusion parameter $\varepsilon$ in the upwind flux (4.10) satisfy $\varepsilon \in (0, 2(\gamma -1))$. Then for any $\varphi \in C^2_0(0,T;\mathbb {R}^d)$ we have

$$\begin{aligned}&- \int _{\Omega _\tau ^0} \varrho _{h,\tau }^0 \varphi ^0 \,\mathrm{d} {x} - \int _0^T \int _{\Omega _{h,\tau }} \left( \varrho _{h,\tau }\partial _t\varphi + \varrho _{h,\tau }\mathbf {u}_{h,\tau }\cdot \nabla \varphi \right) \,\mathrm{d} {x}\nonumber \\&\quad = \mathcal {O}(h^{ \theta }), \text{ for } \text{ some } \theta \, { \in (0,1)}. \end{aligned}$$

(4.33)

If moreover, $\eta _{h,\tau }\rightarrow \eta$ in $L^\infty ([0,T]\times \Sigma )$, then there exists $\theta \in (0,1)$ such that for all $\epsilon \in (0,1)$ and all $\tau \in (0,1)$ with $\left\Vert \Pi _p \eta _{h,\tau }-\eta \right\Vert _\infty <\epsilon$ we find⁵

(4.34)

for all $(\Psi _{\epsilon },\psi ) \in C^2_0(0,T\times \mathbb {R}^d) \times C^2_0([0,T]\times \Sigma )$ satisfying (3.10).

Proof

To show the consistency of the numerical scheme, we take $\Psi _{\epsilon ,h}= \Pi _\mathcal {T}[\Psi _{\epsilon }]$ and the pair $( \Psi _{\epsilon ,h}, {\psi }_{h,\tau })= (\Pi _\mathcal {E}[\Psi _{\epsilon }], \Pi _\mathcal {E}[\psi ])$ as the test functions in the discrete density and momentum equation, respectively. As mentioned already before due to the uniform conformity of the mesh with respect to time change we have bounds on the projection error independent of the time-step. And as before we will use below all quantities that are related to the triangulation like $\mathcal {T}_{h,\tau },K,\sigma , \mathcal {E}$ as quantities that change from time-step to time-step. We deal with each term separately: Step 1 – time derivative terms The consistency of the time derivative terms have been shown in Theorem 2. Indeed, by recalling (3.14) and (3.13) as well as the interpolation estimates (4.15), we find that

$$\begin{aligned}&\int _0^T \int _{\Omega _{h,\tau }} D_t \varrho _{h,\tau }\varphi \ \,\mathrm{d} {x}\,{\mathrm{d}} t + \int _{\Omega _{h,\tau }^0} \varrho _{h,\tau }^0\varphi ^0 \,\mathrm{d} {x}\nonumber \\&\qquad + \int _0^T \int _{\Omega _{h,\tau }} \varrho _{h,\tau }(t) \partial _t\varphi (t) \ \,\mathrm{d} {x}\,{\mathrm{d}} t + \int _0^T \int _{\Omega _{h,\tau }} \varrho _{h,\tau }(t) \mathbf {w}_{h,\tau }(t) \cdot \nabla \varphi (t) \ \,\mathrm{d} {x}\,{\mathrm{d}} t \nonumber \\&\quad = \mathcal {O}(\tau ^\theta )+\mathcal {O}(h), \; \theta { \in (0,1)}, \end{aligned}$$

(4.35a)

$$\begin{aligned}&\int _0^T \int _{\Omega _{h,\tau }} D_t (\varrho _{h,\tau }\mathbf {u}_{h,\tau }) \cdot \Psi _{\epsilon } \ \,\mathrm{d} {x}\,{\mathrm{d}} t + \int _{\Omega _{h,\tau }^0} \varrho _{h,\tau }^0\mathbf {u}_{h,\tau }^0 \cdot \Psi _{\epsilon }^0 \,\mathrm{d} {x}\nonumber \\&\qquad + \int _0^T \int _{\Omega _{h,\tau }} \varrho _{h,\tau }\mathbf {u}_{h,\tau }\cdot \partial _t\Psi _{\epsilon }(t) \ \,\mathrm{d} {x}\,{\mathrm{d}} t \nonumber \\&\qquad + \int _0^T \int _{\Omega _{h,\tau }} (\varrho _{h,\tau }\mathbf {u}_{h,\tau }\otimes \mathbf {w}_{h,\tau }) : \nabla \Psi _{\epsilon }(t) \ \,\mathrm{d} {x}\,{\mathrm{d}} t \nonumber \\&\quad = \mathcal {O}(\tau ^\theta ) + {\; \mathcal {O}(h)}, \; \theta {\;\in (0,1)}, \end{aligned}$$

(4.35b)

$$\begin{aligned}&\int _0^T \int _{\Sigma } \delta _t z_{h,\tau }\psi \mathrm{d}r \,{\mathrm{d}} t \nonumber \\&\quad = \int _0^T \int _{\Sigma } z_{h,\tau }\partial _t\psi \mathrm{d}r \,{\mathrm{d}} t - \int _{\Sigma } \psi ^{0} \partial _t\eta (0) \mathrm{d}r +\mathcal {O}(\tau )+\mathcal {O}(h), \end{aligned}$$

(4.35c)

Step 2 – convective terms We first deal with convective terms of the discrete density problem by setting $r=\varrho _{h,\tau }$, $\mathbf {v}= \mathbf {v}_{h,\tau }$, $\phi = \varphi$, and $F=\Pi _\mathcal {T}[\varphi ]$ in (4.32)

where

Next, we estimate the terms $\sum _{i=1}^4 E_i$.

Term $E_1(\varrho _{h,\tau })$ Applying the estimate (4.31a) we get

where

$$\begin{aligned} \zeta _1 = {\left\{ \begin{array}{ll} \frac{1}{4} &{} \text{ if } \gamma \ge \frac{6}{5}, \\ \frac{3(\gamma -1)}{2\gamma }&{} \text{ if } \gamma \in (1, \frac{6}{5}). \\ \end{array}\right. } \end{aligned}$$

(4.36)

Obviously $\zeta _1 > 0$ for all $\gamma > 1$.

Term $E_2(\varrho _{h,\tau })$ It is easy to get from Hölder’s inequality, the estimates (4.22), the fact that $\varrho _{h,\tau }$ is piece wise constant, Gauss theorem and (4.29) that

where $\zeta _2$ reads

$$\begin{aligned} \zeta _2= {\left\{ \begin{array}{ll} 1-\frac{\varepsilon +2}{2 \gamma } &{} \text{ if } \gamma \in (1,2), \\ 1 &{} \text{ if } \gamma \ge 2. \end{array}\right. } \end{aligned}$$

(4.37)

Obviously $\zeta _2>0$ as $\varepsilon <2(\gamma -1)$.

Term $E_3(\varrho _{h,\tau })$ Applying Hölder’s inequality, the first estimate of the uniform bounds (4.22) and the velocity bound (4.27) we get

where $\zeta _2>0$ is the same as in (4.37).

Term $E_4(\varrho _{h,\tau })$ Applying Hölder’s inequality, the interpolation estimate (4.15), the uniform bounds (4.22), the fact $( | a-b |\le {a} +{b})$ for $a,b \ge 0$, and the trace inequality (4.13) we get

Consequently, we derive

$$\begin{aligned}&\int _0^T \int _{\Omega _{h,\tau }} \varrho _{h,\tau }\mathbf {v}_{h,\tau }\cdot \nabla \varphi \ \,\mathrm{d} {x}\,{\mathrm{d}} t + \int _0^T \sum _{K} \int _{K} \Pi _\mathcal {T}[\varphi ]\mathrm{div}^{\mathrm{up}}_{h,\tau }[\varrho _{h,\tau }, \mathbf {v}_{h,\tau }] \ \,\mathrm{d} {x} \,{\mathrm{d}} t \nonumber \\&\le h^\theta , \quad \theta =\min \{\zeta _1 , \zeta _2, \varepsilon \}. \end{aligned}$$

(4.38)

Clearly, $\theta >0$ for $\varepsilon \in (0, 2(\gamma -1))$ and $\gamma >1$.

Next, we deal with convective terms in the discrete momentum problem. We recall (4.32) with $r=\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }]$, $\mathbf {v}= \mathbf {v}_{h,\tau }$, $\phi = \Psi _{\epsilon }$, $F= \Pi _\mathcal {T}[\Pi _\mathcal {E}[\Psi _{\epsilon }]]$

where

Next, we estimate the terms $\sum _{i=1}^4 E_i(\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }])$.

Term $E_1(\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }])$ By Hölder’s inequality and the interpolation estimate (4.15) we get

where we have also applied the product rule $\left[ \! \left[ uv\right] \! \right] _\sigma = {u}_\sigma ^{\mathrm{in}} \left[ \! \left[ v\right] \! \right] _\sigma +\left[ \! \left[ u\right] \! \right] _\sigma {v}_\sigma ^\mathrm{out} \text{ for } \text{ all } u,v\in Q_\tau .$ Applying the estimate (4.31b) we get the estimates of the first term

where $\zeta _3= {\left\{ \begin{array}{ll}1/4 &{} \text{ if } \gamma \in [\frac{4}{3}, \infty ), \\ {(5\gamma -6)}/(2\gamma ) &{} \text{ if } \gamma \in (1,\frac{4}{3}), \end{array}\right. }\quad \zeta _3>0 \text{ provided } \gamma >\frac{6}{5}.$ The second term $I_2$ can be estimates by

where we have used the estimate (4.22). It is obvious that $I_2 {\mathop {\sim }\limits ^{<}}h^{\frac{1}{4}}$ for $\gamma \ge \frac{6}{5}$. Further by the inverse estimate we derive for $\gamma \in (1, \frac{6}{5})$ that

Consequently, $I_2 {\mathop {\sim }\limits ^{<}}h^{\zeta _1}$, and $\zeta _1>0$ for all $\gamma >1$, see (4.36).

Combining the estimates of the terms $I_1$ and $I_2$ we get

Term We proceed analogously as the estimate of term with the fact that $\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }]$ is constant on each K.

where $\zeta _2 >0$ is given in (4.37). Term $E_3(\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }])$ Employing Hölder’s inequality, the interpolation estimate (4.15) and the estimate (4.22) we derive

where $\zeta _2 >0$ is given in (4.37). Term $E_4(\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }])$ Using Hölder’s inequality, the interpolation estimate (4.15), and the estimate (4.22) we derive

Consequently, we derive

$$\begin{aligned}&\int _0^T \int _{\Omega } (\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }] \otimes \mathbf {v}_{h,\tau }) : \nabla \Psi _{\epsilon } \,\mathrm{d} {x} \,{\mathrm{d}} t \nonumber \\&\quad + \int _0^T \sum _{K \in \mathcal {T}_{h,\tau }}\int _{K} \mathrm{div}^{\mathrm{up}}_{h,\tau }[\varrho _{h,\tau }\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }], \mathbf {v}_{h,\tau }] \cdot \Pi _\mathcal {E}[\Psi _{\epsilon }] \ \,\mathrm{d} {x} \,{\mathrm{d}} t \le h^\theta , \end{aligned}$$

(4.39)

where $\theta = \min \{ \zeta _1, \zeta _2, \zeta _3, \varepsilon \} >0$ provided $\gamma >\frac{6}{5}$ and $\varepsilon \in (0, 2(\gamma -1))$.

Step 3 – pressure and diffusion terms First, it is easy to calculate

$$\begin{aligned}&\int _{\Omega } p_{h,\tau }\mathrm{div}\Pi _\mathcal {E}[\Psi _{\epsilon }] \,\mathrm{d} {x} = \sum _{K \in \mathcal {T}_{h,\tau }}p_K \int _{K} \mathrm{div}\Pi _\mathcal {E}[\Psi _{\epsilon }] \ \,\mathrm{d} {x}\nonumber \\&\quad =\sum _{K \in \mathcal {T}_{h,\tau }}p_K \int _{\mathcal {E}(K)} { \Psi _{\epsilon }\cdot \mathbf {n} } = \int _{\Omega } p_{h,\tau }\mathrm{div}\Psi _{\epsilon } \,\mathrm{d} {x} . \end{aligned}$$

(4.40)

Similarly for the physical diffusion term we have

$$\begin{aligned}&\int _{\Omega _{h,\tau }} \mathrm{div}\mathbf {u}_{h,\tau }\mathrm{div}\Pi _\mathcal {E}[\Psi _{\epsilon }] \,\mathrm{d} {x} =\int _{\Omega _{h,\tau }} \mathrm{div}\mathbf {u}_{h,\tau }\mathrm{div}\Psi _{\epsilon } \,\mathrm{d} {x} , \nonumber \\&\int _{\Omega _{h,\tau }} \mathbf {D}(\mathbf {u}_{h,\tau }) : \nabla \Pi _\mathcal {E}[\Psi _{\epsilon }] \,\mathrm{d} {x} =\int _{\Omega _{h,\tau }} \mathbf {D}(\mathbf {u}_{h,\tau }) : \nabla \Psi _{\epsilon } \,\mathrm{d} {x}. \end{aligned}$$

(4.41)

Concerning the penalty diffusion term, we control it as follows

$$\begin{aligned}&\sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }\right] \! \right] \cdot \left[ \! \left[ \Pi _\mathcal {E}[\Psi _{\epsilon }]\right] \! \right] \mathrm{d}S(x) \\&\quad =\sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }\right] \! \right] \cdot \left[ \! \left[ \Pi _\mathcal {E}[\Psi _{\epsilon }]- \Psi _{\epsilon }\right] \! \right] \mathrm{d}S(x) {\mathop {\sim }\limits ^{<}}\left\Vert \mathbf {u}_{h,\tau }\right\Vert _{H^1_Y} \left\Vert \Pi _\mathcal {E}[\Psi _{\epsilon }]- \Psi _{\epsilon }\right\Vert _{H^1_Y}\\&\quad {\mathop {\sim }\limits ^{<}}h \left\Vert \mathbf {u}_{h,\tau }\right\Vert _{H^1_Y} \left\Vert \Psi _{\epsilon }\right\Vert _{W^{2,2}} \end{aligned}$$

where we have used Hölder’s inequality, the fact $\left[ \! \left[ \Psi _{\epsilon }\right] \! \right] \equiv 0$ and the following estimate

thanks to the trace inequality (4.13) and the interpolation error (4.16), see also [35, Lemma 2.6] for an analogous proof of estimate.

Step – 4 rest of the structure part and external forces By the standard interpolation error and the uniform bounds (4.22) we have

(4.42)

Finally, collecting all the above terms we finish the proof. $\square$

5 Conclusion

We have studied the fluid–structure interaction problem involving compressible viscous fluids. We have firstly proposed an energy stable time discretization scheme (3.1), see Theorem 1. Our discretization fulfils the geometric conservation law, see Corollary (1). Moreover, we have shown that the numerical solutions satisfy the renormalized equation and they are consistent with respect to the weak solutions, see Lemma 2 and Theorem 2, respectively.

Further, we have developed a fully discrete mixed finite volume–finite element method (4.17). We have proven the existence of a numerical solution to the scheme (4.17) in Theorem 3. We have shown that numerical solutions of (4.17) satisfy the renormalized equation, mass conservation, positivity of density, energy dissipation and they are consistent to the weak solutions, see Lemma 8, (4.18), Lemma 9, Theorem 4, and Theorem 5, respectively.

Finally, we would like to emphasize that the time discretization method (3.1) can be used in the design of other numerical methods pursuing the energy stability for compressible fluids interacting with an elastic structure.

A: Appendix

1.1 A.1 Proof of Theorem 3: existence of a numerical solution

We aim to prove Theorem 3 for the existence of a numerical solution. Before that let us first introduce an abstract theorem, see [30, Theorem A.1].

Theorem 6

([30, Theorem A.1]) Let M and N be positive integers. Let $C_2>\epsilon >0$ and $C_1>0$ be real numbers. Let V and W be defined as follows:

where the notation $x > c$ means that each component of x is greater than c, and $\Vert \cdot \Vert$ is a norm defined over $R ^N$. Let F be a continuous function from $V \times [0,1]$ to $R ^M \times R ^N$ satisfying:

• 1. $\forall \, \zeta \in [0,1]$, if $v \in V$ is such that $F(v,\zeta )=0$ then $v \in W$;

• 2. The equation $F (v, 0)=0$ is a linear system on v and has a solution in W.

Then there exists at least a solution $v \in W$ such that $F(v,1) = 0$.

Now we are ready to show Theorem 3.

Proof

Let us denote , and define

It is obvious that the degrees of freedom of the spaces $Q_{h,\tau }$ and $\mathbb {Q}$ are finite. Indeed, the space $Q_{h,\tau }$ can be identified by the set of values $\varrho _K$ for all $K \in \mathcal {T}_{h,\tau }^{k}$, therefore $Q_{h,\tau }\subset \mathbb {R}^M$, where M is the total number of elements of $\mathcal {T}_{h,\tau }^{k}$. Analogously, $\mathbb {Q}\subset \mathbb {R}^N$, where N is the sum of d times degrees of freedom of $\mathcal {E}^k$ and the degrees of freedom of $\Sigma$. Let us consider the mapping

$$\begin{aligned} F : \ V \times [0,1]\longrightarrow Q_h\times \mathbb {Q}. \qquad (\varrho _{h,\tau }^k,U_{h,\tau }^k , \zeta )\longmapsto ( \varrho ^\star , U^\star ) =F(\varrho _{h,\tau }^k,U_{h,\tau }^k ,\zeta ), \end{aligned}$$

where $( \varrho ^\star , U^\star ) \in Q_{h,\tau }\times \mathbb {Q}$ is such that

$$\begin{aligned}&\int _{\Omega _{h,\tau }} \varrho ^\star {\varphi }_{h,\tau } \,\mathrm{d} {x} = \int _{\Omega _{h,\tau }} \frac{\varrho _{h,\tau }^k -\varrho _{h,\tau }^{k-1}\circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } {\varphi }_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + \zeta \int _{\Omega _{h,\tau }} \mathrm{div}^{\mathrm{up}}_{h,\tau }( \varrho _{h,\tau }^{k}, \mathbf {v}_{h,\tau }^{k} ){\varphi }_{h,\tau } \,\mathrm{d} {x} ; \end{aligned}$$

(A.1a)

$$\begin{aligned}&\int _{\Omega _{h,\tau }} U^\star \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\quad = \int _{\Omega _{h,\tau }} \frac{\varrho _{h,\tau }^k \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}] - (\varrho _{h,\tau }^{k-1}\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k-1}]) \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + \int _{\Sigma } \frac{ z_{h,\tau }^{k} - z_{h,\tau }^{k-1} }{\tau }{\psi }_{h,\tau } \mathrm{d}r + \int _{\Sigma } \Delta \eta _{h,\tau }^{k} \Delta {\psi }_{h,\tau } \mathrm{d}r \nonumber \\&\qquad - \int _{\Omega _{h,\tau }} \varrho _{h,\tau }^k \mathbf {f}_\tau ^{k}\cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Sigma } g_\tau ^{k} {\psi }_{h,\tau } \mathrm{d}r\nonumber \\&\qquad +\zeta \int _{\Omega _{h,\tau }} \mathrm{div}^{\mathrm{up}}_{h,\tau }(\varrho _{h,\tau }^{k} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}], \mathbf {v}_{h,\tau }^{k} ) \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} - \zeta \int _{\Omega _{h,\tau }} p(\varrho _{h,\tau }^{k}) \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + \zeta \lambda \int _{\Omega _{h,\tau }} \mathrm{div}\mathbf {u}_{h,\tau }^{k} \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \zeta 2\mu \int _{\Omega _{h,\tau }} \mathbf {D}( \mathbf {u}_{h,\tau }^{k} ) : \nabla {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\qquad + (1-\zeta ) \mu \int _{\Omega _{h,\tau }} \frac{1}{\mathcal {F}^{k}} { \left( \nabla \mathbf {u}_{h,\tau }^k \mathbb {J}^k + (\mathbb {J}^k)^T \nabla ^T\mathbf {u}_{h,\tau }^k \right) : \left( \nabla {\varvec{\Psi }}_{h,\tau }\mathbb {J}^k \right) } \,\mathrm{d} {x}\nonumber \\&\qquad + \zeta 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \mathrm{d}S(x) \nonumber \\&\qquad + (1-\zeta ) 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \frac{1}{ | \mathcal {F}^{k}(\mathbb {J}^k)^{-T} \widehat{\mathbf {n}} | } \mathrm{d}S(x) ; \end{aligned}$$

(A.1b)

where ${\varvec{\Psi }}_{h,\tau }= ({\varvec{\Psi }}_{h,\tau }, {\psi }_{h,\tau }), \quad \eta _{h,\tau }^k = \eta _{h,\tau }^{k-1} + \tau z_{h,\tau }^k, \quad \mathbf {u}_{h,\tau }^k|_{\Sigma } = z_{h,\tau }^k \mathbf {e}_d , \quad \mathcal {F}_k^{k-1}= \left( H + \eta _{h,\tau }^{k-1}\right) /\left( H + \eta _{h,\tau }^{k}\right) .$

It is easy to check that F is continuous. Indeed, it is a one to one mapping, since the values of $\varrho ^\star$ and $U^\star$ can be determined by setting ${\varphi }_{h,\tau }= 1_{K}$ in (A.1a), and $(\Phi _\tau )_i=1_{D_\sigma }, (\Phi _\tau )_j=0$ for $j\ne i$ in (A.1b).

Let $(\varrho _{h,\tau }^k,U_{h,\tau }^k ) \in Q_h\times \mathbb {Q}$ and $\zeta \in [0,1]$ such that $F(\varrho _{h,\tau }^k,U_{h,\tau }^k , \zeta )=(0,0)$ (in particular $\varrho _{h,\tau }^k>0$). Then for any $\big ({\varphi }_{h,\tau }, {\varvec{\Phi }}_{h,\tau }= ({\varvec{\Psi }}_{h,\tau }, {\psi }_{h,\tau }) \big )\in Q_h\times \mathbb {Q}$

$$\begin{aligned}&\int _{\Omega _{h,\tau }} \frac{\varrho _{h,\tau }^k -\varrho _{h,\tau }^{k-1} \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } {\varphi }_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\qquad + \zeta \int _{\Omega _{h,\tau }} \mathrm{div}^{\mathrm{up}}_{h,\tau }( \varrho _{h,\tau }^{k}, \mathbf {v}_{h,\tau }^{k} ){\varphi }_{h,\tau } \,\mathrm{d} {x} =0; \end{aligned}$$

(A.2a)

$$\begin{aligned}&\int _{\Omega _{h,\tau }} \frac{\varrho _{h,\tau }^k \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}] -(\varrho _{h,\tau }^{k-1}\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k-1}]) \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\qquad + \int _{\Sigma } \frac{ z_{h,\tau }^{k} - z_{h,\tau }^{k-1} }{\tau }{\psi }_{h,\tau } \mathrm{d}r\nonumber \\&\qquad + \int _{\Sigma } \Delta \eta _{h,\tau }^{k} \Delta {\psi }_{h,\tau } \mathrm{d}r - \int _{\Omega _{h,\tau }} \varrho _{h,\tau }^k \mathbf {f}_\tau ^{k}\cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Sigma } g_\tau ^{k} {\psi }_{h,\tau } \mathrm{d}r\nonumber \\&\qquad +\zeta \int _{\Omega _{h,\tau }} \mathrm{div}^{\mathrm{up}}_{h,\tau }(\varrho _{h,\tau }^{k} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}], \mathbf {v}_{h,\tau }^{k} ) \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\qquad -\zeta \int _{\Omega _{h,\tau }} p(\varrho _{h,\tau }^{k}) \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \zeta \lambda \int _{\Omega _{h,\tau }} \mathrm{div}\mathbf {u}_{h,\tau }^{k} \mathrm{div}{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\qquad + \zeta 2\mu \int _{\Omega _{h,\tau }} \mathbf {D}( \mathbf {u}_{h,\tau }^{k} ) : \nabla {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} \nonumber \\&\qquad +(1-\zeta ) \mu \int _{\Omega _{h,\tau }} \frac{1}{\mathcal {F}^{k}} { \left( \nabla \mathbf {u}_{h,\tau }^k \mathbb {J}^k + (\mathbb {J}^k)^T \nabla ^T\mathbf {u}_{h,\tau }^k \right) : \left( \nabla {\varvec{\Psi }}_{h,\tau }\mathbb {J}^k \right) } \,\mathrm{d} {x}\nonumber \\&\qquad + \zeta 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \mathrm{d}S(x) \nonumber \\&\qquad + (1-\zeta ) 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \frac{1}{ | \mathcal {F}^{k}(\mathbb {J}^k)^{-T} \widehat{\mathbf {n}} | } \mathrm{d}S(x) . \end{aligned}$$

(A.2b)

Taking ${\varphi }_{h,\tau }=1$ as a test function in (A.2a) we obtain

$$\begin{aligned} \left\Vert \varrho _{h,\tau }^k\right\Vert _{L^1(\Omega _{h,\tau })}= \int _{\Omega _{h,\tau }^k} \varrho _{h,\tau }^k \,\mathrm{d} {x} = \int _{\Omega _{h,\tau }^{k-1}} \varrho _{h,\tau }^{k-1} \,\mathrm{d} {x} >0, \end{aligned}$$

(A.3)

which indicates the boundedness of $\varrho _{h,\tau }^k$ in the $L^1$ norm, and thus in all norms as the problem is of finite dimension. Following the same argument as Lemma 3 we know that $\varrho _{h,\tau }^k \ge 0$ provided $\varrho _{h,\tau }^{k-1} \ge 0$.

Taking ${\varvec{\Phi }}_{h,\tau }=(\mathbf {u}_{h,\tau }^k, z_{h,\tau }^k)$ as the test function in (A.2b) and follow the proof of Theorem (1) gives

$$\begin{aligned} \left\Vert U_{h,\tau }^k \right\Vert := \left\Vert \nabla \mathbf {u}_{h,\tau }^k\right\Vert _{L^2(\Omega _{h,\tau })} + \left\Vert z_{h,\tau }^k\right\Vert _{L^2(\Sigma )} \le C_1 \end{aligned}$$

(A.4)

where $C_1$ depends on the data of the problem.

Further, let $K\in \mathcal {T}_{h,\tau }^{k}$ be such that $\varrho _K^k$ is the smallest, i.e., $\varrho _K^k \le \varrho _L^k$ for all $L\in \mathcal {T}_{h,\tau }^{k}$. We denote $K'= \mathcal {A}_{h,\tau }^{k-1}\circ (\mathcal {A}_{h,\tau }^{k})^{-1}(K)$. Then a straightforward computation gives

Thus $\varrho _{h,\tau }^k \ge \varrho _K^k \ge \frac{ | K' |}{ | K |} \frac{\varrho ^{k-1}_{K'} }{1 + \tau \zeta | (\mathrm{div}\mathbf {v}_{h,\tau }^k)_K | } >0.$ Consequently, by virtue of (A.4) $\varrho _{h,\tau }^k > \epsilon$, where $\epsilon$ depends only on the data of the problem. Further, we get from (A.3) that $\varrho _{h,\tau }^k \le \frac{ \int _{\Omega _{h,\tau }^{k-1}} \varrho _{h,\tau }^{k-1} \,\mathrm{d} {x}}{\min _{K\in \mathcal {T}_{h,\tau }^{k}} |K|}$, which indicates the existence of $C_2>0$ such that $\varrho _{h,\tau }^k <C_2$. Therefore, Hypothesis 1 of Theorem 6 is satisfied.

Next, we proceed to show that Hypothesis 2 of Theorem 6 is satisfied. Let $\zeta =0$ then the system $F(\varrho _{h,\tau }^k,U_{h,\tau }^k )=0$ reads

$$\begin{aligned}&\varrho _{h,\tau }^k = \varrho _{h,\tau }^{k-1} \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}; \end{aligned}$$

(A.5a)

$$\begin{aligned}&\int _{\Omega _{h,\tau }} \frac{\varrho _{h,\tau }^k \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k}] -(\varrho _{h,\tau }^{k-1} \Pi _\mathcal {T}[\mathbf {u}_{h,\tau }^{k-1}] ) \circ {X}_k^{k-1}\mathcal {F}_k^{k-1}}{\tau } \cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x}\nonumber \\&\quad + \int _{\Sigma } \frac{ z_{h,\tau }^{k} - z_{h,\tau }^{k-1} }{\tau }{\psi }_{h,\tau } \mathrm{d}r\nonumber \\&\quad + \mu \int _{\Omega _{h,\tau }} \frac{1}{\mathcal {F}^{k}} { \left( \nabla \mathbf {u}_{h,\tau }^k \mathbb {J}^k + (\mathbb {J}^k)^T \nabla ^T\mathbf {u}_{h,\tau }^k \right) : \left( \nabla {\varvec{\Psi }}_{h,\tau }\mathbb {J}^k \right) } \,\mathrm{d} {x} \nonumber \\&\quad + 2\mu \sum _{\sigma \in \mathcal {E}_{\mathrm{I}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \mathbf {u}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ {\varvec{\Psi }}_{h,\tau }\right] \! \right] \frac{1}{ | \mathcal {F}^{k}(\mathbb {J}^k)^{-T} \widehat{\mathbf {n}} | } \mathrm{d}S(x)\nonumber \\&\quad + \int _{\Sigma } \left( \alpha \Delta \eta _{h,\tau }^{k} \Delta {\psi }_{h,\tau }+ \beta \nabla \eta _{h,\tau }^{k} \nabla {\psi }_{h,\tau }\right) \mathrm{d}r \nonumber \\&\quad - \int _{\Omega _{h,\tau }} \varrho _{h,\tau }^k \mathbf {f}_{h,\tau }^{k}\cdot {\varvec{\Psi }}_{h,\tau } \,\mathrm{d} {x} + \int _{\Sigma } g_\tau ^{k} {\psi }_{h,\tau } \mathrm{d}r =0. \end{aligned}$$

(A.5b)

To solve the above system (A.5), we further reformulate it on the reference domain according to (2.10)

$$\begin{aligned}&\widehat{\varrho }_{h,\tau }^k \mathcal {F}^{k}= \widehat{\varrho }_{h,\tau }^{k-1}\mathcal {F}^{k-1}; \end{aligned}$$

(A.6a)

$$\begin{aligned}&\quad \int _{\widehat{\Omega }} \widehat{\varrho }_{h,\tau }^{k-1}\mathcal {F}^{k-1}\frac{\Pi _\mathcal {T}[\widehat{\mathbf {u}}_{h,\tau }^{k}] -\Pi _\mathcal {T}[\widehat{\mathbf {u}}_{h,\tau }^{k-1}]}{\tau } \cdot \widehat{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} \widehat{x}\nonumber \\&\quad + \int _{\Sigma } \frac{ z_{h,\tau }^{k} - z_{h,\tau }^{k-1} }{\tau }{\psi }_{h,\tau } \mathrm{d}r + 2\mu \sum _{\sigma \in \widehat{\mathcal {E}_{\mathrm{I}}}}\int _{\sigma } \frac{1}{h} \left[ \! \left[ \widehat{\mathbf {u}}_{h,\tau }^k\right] \! \right] \cdot \left[ \! \left[ \widehat{\varvec{\Psi }}_{h,\tau }\right] \! \right] \mathrm{d}S(\widehat{x})\nonumber \\&\quad + 2\mu \int _{\widehat{\Omega }} \widehat{\mathbf {D}}( \widehat{\mathbf {u}}_{h,\tau }^{k} ) : \widehat{ \nabla } \widehat{\varvec{\Psi }}_{h,\tau } \,\mathrm{d} \widehat{x} + \int _{\Sigma } \left( \alpha \Delta \eta _{h,\tau }^{k} \Delta {\psi }_{h,\tau }+ \beta \nabla \eta _{h,\tau }^{k} \nabla {\psi }_{h,\tau }\right) \mathrm{d}r\nonumber \\&\quad - \int _{\widehat{\Omega }} \widehat{\mathbf {f}}_{\tau }^{k}\cdot \widehat{\varvec{\Psi }}_{h,\tau }\widehat{\varrho }_{h,\tau }^{k-1} \mathcal {F}^{k-1} \,\mathrm{d} \widehat{x} + \int _{\Sigma } g^{k} {\psi }_{h,\tau } \mathrm{d}r =0, \end{aligned}$$

(A.6b)

where $\mathcal {F}^{k-1}= 1+ \eta _{h,\tau }^{k-1}/H$ is determined by $\eta _{h,\tau }^{k-1}$. Realizing that (A.6b) is a linear system with a matrix being block-wise symmetric positive definite, we know that there exists exactly one solution $\widehat{U}_{h,\tau }^k =(\widehat{\mathbf {u}}_{h,\tau }^k, z_{h,\tau }^k)$. Then using the fact $\eta _{h,\tau }^k = \eta _{h,\tau }^{k-1} + \tau z_{h,\tau }^k$ we get $\eta _{h,\tau }^k$ and $\mathcal {A}_{h,\tau }^{k}$. Further, it is straightforward that $\mathbf {u}_{h,\tau }^k=\widehat{\mathbf {u}}_{h,\tau }^k\circ \mathcal {A}_{h,\tau }^{k}(\widehat{x})$. Finally, substituting $\eta _{h,\tau }^k$ into (A.6a) we obtain the solution for $\varrho _{h,\tau }^k$. Obviously, $\varrho _{h,\tau }^k>0$ as long as no self touching. Thus the solution $(\varrho _{h,\tau }^k,U_{h,\tau }^k )$ belongs to W, which implies Hypothesis 2 of Theorem 6.

We have shown that both hypotheses of Theorem 6 hold. Applying Theorem 6 finishes the proof. $\square$

1.2 A.2 Proof of Lemma 8: renormalization

Here we show the validity of the discrete renormalized equation stated in Lemma 8 for the discrete continuity problem (4.17a).

Proof

Firstly, we set ${\varphi }_{h,\tau }=B'(\varrho )$ in (4.17a) and obtain

Next, recalling (3.4), we know there exist $\xi \in \mathrm{co}\{ \varrho _{h,\tau }^{k-1}\circ {X}_k^{k-1} , \varrho _{h,\tau }^{k} \}$ such that

where

Further, by recalling the definition of the upwind flux (4.10), and using again the Taylor expansion, we reformulate the convective term as

where

Moreover, using the facts

we obtain

Consequently, we derive

Finally, collecting the above terms and seeing $\mathbf {v}_{h,\tau }^k + \mathbf {w}_{h,\tau }^k= \mathbf {u}_{h,\tau }^k$, we complete the proof, i.e.,

$\square$

1.3 A.3 Proof of Theorem 4: energy stability

Here we prove the energy stability stated in Theorem 4 for the discrete scheme (4.17).

Proof

Setting ${\varphi }_{h,\tau }= - \frac{\left| \Pi _\mathcal {T}[ \mathbf {u}_{h,\tau }^{k}]\right| ^2}{2}$ in (4.17a) and $({\varvec{\Psi }}_{h,\tau },{\psi }_{h,\tau }) = (\mathbf {u}_{h,\tau }^{k}, z_{h,\tau }^{k})$ in (4.17b) we get $\sum _{i=1}^2 I_i=0$ and $\sum _{i=3}^{9} I_i=0$ respectively, where

Now we proceed with the summation of all the $I_i$ terms for $i=1,\ldots ,9$.

Term $(I_1+I_3+I_8)+(I_6+I_7)+I_9$. Firstly, analogously as in the proof of Theorem 1 we have

Term $I_2+I_4$. For the convective terms, we have using the fact that $\Pi _\mathcal {T}[\mathbf {u}_{h,\tau }]$ and $\mathrm{div}^{\mathrm{up}}_{h,\tau }\left( \varrho _{h,\tau }^k \Pi _\mathcal {T}[ \mathbf {u}]^{k}_h , \mathbf {v}_{h,\tau }^{k} \right)$ are constant on each $K\in \mathcal {T}_{h,\tau }$ and the upwind divergence

Pressure term $I_{5}$. Recalling the discrete internal energy equation (4.20), we can rewrite the pressure term as

where $D_1$ and $D_2$ are given in (4.21). Collecting all the above terms, we get

We finish the proof by summing up the above equation for $k=1,\ldots ,N$ and multiplying with $\tau$. $\square$

1.4 A.4 Proof of Lemma 10: useful estimates

Proof

Item 1 has been reported by [23, Lemma 3.5]. Item 2 has been reported by [31, Lemma 4.3]. Item 4 has been reported by [25, Chaper 9, Lemma 7]. We are only left with the proof of Item 3. We start the proof with the a-priori estimates on $\mathbf {v}_{h,\tau }$

where we used (4.14) for $\mathbf {u}_{h,\tau }$ and (4.28) for $\mathbf {w}_{h,\tau }$. On one hand, for $\gamma \ge 2$, we employ (4.30) to get

On the other hand, it is easy to check for $\gamma \in (1,2)$ that $\mathcal {H}''(r)=a r^{\gamma -2} \ge a$ if $r\le 1$ and $r \mathcal {H}''(r)= ar^{\gamma -1} \ge a$ if $r\ge 1$. Therefore

$$\begin{aligned} \mathcal {H}''(r)(1+r) \ge a \text{ for } \text{ all } r \in (0,\infty ) \end{aligned}$$

Applying these inequalities together with Hölder’s inequality, and the estimate (4.22) we derive (by choosing $\varrho _{h,\tau }^\dagger$ conveniently and (4.13)) that

Then, for $\gamma \in [6/5, 2)$ we have $I_1 {\mathop {\sim }\limits ^{<}}h^{-\frac{1}{2}}\tau ^{-\frac{1}{4}}$. Concerning $\gamma \in (1,6/5)$ we deduce by inverse estimate (4.14) that

which completes the proof of the first estimate (4.31a).

Similarly, we prove the second estimate (4.31b) in two steps. First for $\gamma \ge 2$ we may derive it due to Hölder’s inequality, trace theorem, and the inverse estimate (4.14) that

Next, we proceed to show the second estimates for $\gamma \in (1, 2)$.

where we have used the algebraic inequality for $\gamma \in (1,2)$ that . On the other hand, if $1<\gamma < \frac{4}{3}$ we complete the proof by the inverse estimates (4.14) and find

which finishes the estimate. $\square$