Abstract
The paper discusses the following topics: attractions of the real tridiagonal case, relative eigenvalue condition number for matrices in factored form, dqds, triple dqds, error analysis, new criteria for splitting and deflation, eigenvectors of the balanced form, twisted factorizations and generalized Rayleigh quotient iteration. We present our fast real arithmetic algorithm and compare it with alternative published approaches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The dqds algorithm was introduced in [9] as a fast and extremely accurate way to compute all the singular values of a bidiagonal matrix B. This algorithm implicitly performs the Cholesky LR iteration on the tridiagonal matrix \(B^TB\) and it is used in LAPACK. However the dqds algorithm can also be regarded as executing, implicitly, the LR algorithm applied to any tridiagonal matrix with 1’s on the superdiagonal. Our interest here is in real unsymmetric matrices which may, of course, have some complex eigenvalues. In contrast to the QR algorithm, the LR algorithm preserves tridiagonal form and this feature makes dqds attractive. It is natural to try to retain real arithmetic and yet permit complex conjugate pairs of shifts. Our analogue of the double shift QR algorithm of Francis [14] is the triple step dqds algorithm. We explain why three steps are needed. However the main goal of this paper is to derive our implicit implementation (3dqds) of this 3-steps process which relies on the implicit L analogue of the implicit Q theorem. See Sect. 3.4.1 and Theorem 3.1.
In order to focus on our 3dqds algorithm we assume an extensive background for our reader. The unsymmetric eigenvalue problem can be almost ill-posed and such cases are not easily apparent. A tridiagonal matrix requires so little storage that it seems feasible to compute approximate eigenvalues together with an indication of the number of digits that are robust in the presence of computer arithmetic. We decided to provide relative condition numbers (for factored forms) for each computed eigenvalue even when the user does not request it. The extra cost, in storage and arithmetic operations is surprisingly low, 2n storage and \({{\mathcal {O}}}(n)\) computing. See Sect. 7.2 for details. We omit any history of the contributions to the field, even the seminal work of H. Rutishauser who invented the qd algorithm and the LR algorithm [26,27,28]. We must however mention that he also discovered the so-called differential form of qd but did not appreciate its accuracy and never published it. That understanding came much later in the computation of singular values of bidiagonal matrices. See [9]. We do describe the double LR algorithm for complex conjugate shifts because of its relation to our triple dqds algorithm. We say nothing about the need for an eigensolver devoted to tridiagonal matrices because that issue is covered admirably by Bini et al. [1]. We do give pseudocode for a complete program but hope it will not produce distractions from our main concern, the 3dqds algorithm. We provide error analyses for both dqds and 3dqds.
A novel feature of our approach is the usefulness of keeping matrices in factored form. We also acknowledge the preliminary work on this problem by Wu [36].
We do not follow Householder conventions except that we reserve capital Roman letters for matrices. Section 2 describes other relevant methods, Sect. 3 presents standard, but needed, material on LR, dqds, single and double shifts and the implicit L theorem. Section 4 develops our 3dqds algorithm, Sect. 5 is our error analysis, Sect. 6 our splitting, deflation and shift strategy.
Section 7 analyzes applications of factored forms - the computation of eigenvectors using twisted factorizations of the balanced form, relative condition numbers and the generalized Rayleigh quotient iteration. Finally, Sect. 8 presents our numerical tests using Matlab and Sect. 9 gives our conclusions.
2 Other methods relevant to 3dqds
2.1 2 steps of LR = 1 step of QR
For a symmetric positive definite tridiagonal matrix 2 steps of the LR (Cholesky) algorithm produces the same matrix as 1 step of the QR algorithm. Less well known is the article by Xu [37] which extends this result when the symmetric matrix is not positive definite. The catch here is that the LR transform, if it exists, does not preserve symmetry. The remedy is to regard similarities by diagonal matrices as “trivial”, always available, operations. Indeed, diagonal similarities cannot introduce zeros into a matrix. So, when successful, 2 steps of LR are diagonally similar to one step of QR. Even less well known is a short paper by Slemons [31] showing that for a tridiagonal matrix, not necessarily symmetric, 2 steps of of LR are diagonally equivalent to 1 step of HR, see [2]. Note that when symmetry disappears then QR is out of the running because it does not preserve the tridiagonal property.
The point of listing these results is to emphasize that 2 steps of LR gives twice as many shift opportunities as 1 step of QR or HR. Thus convergence can be more rapid with LR (or dqds) than with QR or HR. This is one of the reasons that dqds is faster than QR for computing singular values of bidiagonals. This extra speed is an additional bonus to the fundamental advantage that dqds delivers high relative accuracy in all the singular values. The one drawback to dqds, for bidiagonals, is that the singular values must be computed in monotone increasing order; QR allows the singular values to be found in any order.
In our case, failure is always possible and so there is no constraint on the order in which eigenvalues are found. The feature of having more opportunities to shift leads us to favor dqds over QR and HR. See the list of other methods which follows. We take up the methods in historical order and consider only those that preserve tridiagonal form.
2.2 Cullum’s complex QR algorithm
As part of a program that used the Lanczos algorithm to reduce a given matrix to tridiagonal form in [4], Jane Cullum used the fact that an unsymmetric tridiagonal matrix may always be balanced by a diagonal similarity transformation [18]. She then observed that another diagonal similarity with 1 or i produces a symmetric, but complex, tridiagonal matrix to which the (complex) tridiagonal QR algorithm may be applied. The process is not backward stable because the relation
is not a constraint on \(|\cos \tau |\) and \(|\sin \tau |\) when \(\tau \) is complex. Despite the possibility of breakdown the method proved satisfactory in practice. We have not used it in our comparisons because we are persuaded by 2.1 that it is outperformed by the complex dqds algorithm, described below.
2.3 Liu’s HR algorithm
In [16], Liu found a variation on the HR algorithm of Angelika Bunse–Gerstner that, in exact arithmetic, is guaranteed not to breakdown—but the price is a temporary increase in bandwith. This procedure has only been implemented in Maple and we do not include it in our comparison.
2.4 Complex dqds
In his thesis Day [5] developed a Lanczos-style algorithm to reduce a general matrix to tridiagonal form and, as with Jane Cullum, needed a suitable algorithm to compute its eigenvalues. He knew of the effectiveness of dqds in the symmetric positive definite case and realized that dqds extends formally to any tridiagonal that admits triangular factorization. The code uses complex arithmetic because of the possible presence of complex conjugate pairs of eigenvalues.
We compare our real \(\textit{3dqds}\) algorithm with its explicit version—the three steps of \(\textit{dqds}\) are computed explicitly in complex arithmetic—in a more sophisticated version of David Day’s complex dqds code.
2.5 Ehrlich–Aberth algorithm
This very careful and accurate procedure was presented by Bini et al. [1]. It finds the zeros of the characteristic polynomial \(p(\cdot )\) and exploits the tridiagonal form to evaluate \(p^\prime (z)/p(z)\) for any z. The polynomial solver improves a full set of approximate zeros at each step. Initial approximations are found using a divide-and-conquer procedure that delivers the eigenvalues of the top and bottom halves of the matrix T. The quantity \(p^\prime (z)/p(z)\) is evaluated indirectly as \(\left[ trace(zI-T)^{-1}\right] \) using a QR factorization of \(zI-T\). Since T is not altered there is no deflation to assist efficiency. Very careful tests exhibit the method’s accuracy - but it is very slow compared to dqds-type algorithms.
3 LR and dqds
The reader is expected to have had some exposure to the QR and/or LR algorithms so we will be brief.
3.1 LU factorization
Any \(n\times n\) matrix A permits unique triangular factorization \(A=LD{\widetilde{U}}\) where L is unit lower triangular, D is diagonal, \({\widetilde{U}}\) is unit upper triangular, if and only if the leading principal submatrices of orders \(1,\dots ,n-1\) are nonsingular.
In this paper we follow common practice and write \(U=D{\widetilde{U}}\) so that the “pivots” (entries of D) lie on U’s diagonal. Throughout this paper any matrix L is unit lower triangular while U is simply upper triangular.
3.2 LR transform with shift
Note that U is “right” triangular and L is “left” triangular and this explains the standard name LR. For any shift \(\sigma \) let
Then \({\widehat{A}}\) is the LR\((\sigma )\) transform of A. Note that
We say that the shift is restored (in contrast to dqds—see below). The LR algorithm consists of repeated LR transforms with shifts chosen to enhance convergence to upper triangular form. For the theory see [28, 29, 33, 34].
In contrast to the well known QR algorithm, the LR algorithm can breakdown and can suffer from element growth, \(\Vert L\Vert>>\Vert A\Vert \), \(\Vert U\Vert>>\Vert A\Vert \). However LR preserves the banded form of A while QR does not (except for the Hessenberg form).
When a matrix A is represented by its entries then the shift operation \(A\longrightarrow A-\sigma I\) is trivial. When a matrix is given in factored form the shift operation is not trivial.
3.3 The dqds algorithm
From now on we focus on tridiagonal matrices in J -form which means that entries \((i,i+1)\) are all 1, \(i=1,\ldots ,n-1\). Any tridiagonal matrix \(C=tridiag({\varvec{b}},{\varvec{a}},{\varvec{c}})\) that does not split (unreduced), \(b_ic_i\ne 0\), is diagonally similar to a J-form. Entries \((i+1,i)\) equal \(b_ic_i\). Throughout this paper all J matrices have this form. See [11, Section 2.2] on representations of tridiagonals.
If \(J-\sigma I\) permits triangular factorization
then L and U must have the following form
It is an attractive feature of LR that
is also of J-form. Thus the parameters \(l_i\), \(i=1,\ldots ,n-1\), and \(u_j\), \(j=1,\ldots ,n\), determine the matrices L and U above and implicitly define two tridiagonal matrices LU and UL.
The qds algorithm is equivalent to the LR algorithm but only the factors L, U are formed, not the J matrices. The progressive transformation is from L, U to \({\widehat{L}}, {\widehat{U}}\),
Notice that the shift is not restored and so \({\widehat{U}}{\widehat{L}}\) is not similar to UL,
Equating entries in each side of equation (3.4) gives
The algorithm qds fails when \({\widehat{u}}_{i}=0\) for some \(i<n.\) When \(\sigma =0\) we write simply qd, not qds.
In 1994 a better way was found to implement \(\textit{qds}(\sigma )\). These are called differential qd algorithms. See [21] for more history. This form uses an extra variable d but never forms matrix products.
By definition, dqd=dqds(0). In practice we choose to compute, and store, \({\widehat{u}}_i\) and \({\widehat{l}}_i\) separately from \(u_i\) and \(l_i\). This allows us to reject a transform, choose a new shift, and proceed smoothly to another step. Only when the transform is accepted will we write \({\widehat{u}}_i\) and \({\widehat{l}}_i\) over \(u_i\) and \(l_i\).
A word on terminology. In Rutishauser’s original work \(q_i=u_i\), \(e_i=l_i\); and the \(q_i\)’s were certain quotients and the \(e_i\)’s were called modified differences. In fact the qd algorithm led to the LR algorithm, not vice-versa. The reader can find more information concerning dqds in [21, 23]
One virtue of the dqds and QR transforms is that they work on the whole matrix so that large eigenvalues are converging near the top, albeit slowly, while the small ones are being picked off at the bottom.
We summarize some advantages and disadvantages of the factored form.
3.3.1 Advantages of the factored form
-
1.
L, U determines the entries of J to greater than working-precision accuracy because the addition and multiplication of l’s and u’s is implicit. Thus, for instance, the (i, i) entry of J is given by \(l_{i-1}+u_i\) implicitly but \(fl(l_{i-1}+u_i)\) explicitly.
-
2.
Singularity of J is detectable by inspection when L and U are given, but only by calculation from J. So, LU reveals singularity, J does not.
-
3.
LU defines the eigenvalues better than J does (usually). There is more on this in [7].
-
4.
Solution of \(Jx=b\) takes half the time when L and U are available.
3.3.2 Disadvantages of the factored form
The mapping \(J,\sigma \mapsto L,U\) is not everywhere defined for all pairs \(J,\sigma \) and can suffer from element growth. This defect is not as serious as it was when the new transforms were written over the old ones. For tridiagonals we can afford to double the storage and map L, U into different arrays \({\widehat{L}},{\widehat{U}}\). Then we can decide whether or not to accept \({\widehat{L}},{\widehat{U}}\) and only then would L and U be overwritten. So the difficulty of excessive element growth has been changed from disaster to the non-trivial but less intimidating one of, after rejecting a transform, choosing a new shift that will not spoil convergence and will not cause another rejection.
Now we turn to our main question of \(\textit{dqds}(\sigma )\): how can complex shifts be used without having to use complex arithmetic? This question has a beautiful answer for QR and LR iterations.
3.4 Implicit shifted LR for \({\varvec{J}}\) matrices
3.4.1 Double shift LR algorithm
We use the J, L and U notation from the previous section. Consider two steps of the LR algorithm with shifts \(\sigma _1\) and \(\sigma _2\),
Then, with matrices \(\varvec{{\mathcal {L}}}=L_1L_2\) and \(\varvec{{\mathcal {U}}}=U_2U_1\), we have
and the triangular factorization
An important observation from (3.8) is that column 1 of M is proportional to column 1 of \(\varvec{{\mathcal {L}}}\),
According to the following theorem, matrix \(\varvec{{\mathcal {L}}}\) is determined by its first column and we can compute \(J_3\) from \(J_1\) without using \(J_2\).
Theorem 3.1
[Implicit L theorem] If \(H_1\) and \(H_2\) are unreduced upper Hessenberg matrices and \(H_2=L^{-1}H_1L\), where L is unit lower triangular, then \(H_2\) and L are completely determined by \(H_1\) and column 1 of L.
We omit the proof and refer to [11, pp. 66–68].
So the application to \(J_1\) and \(J_3\), using (3.7), is to choose column 1 of \(\varvec{{\mathcal {L}}}\) (which has only three nonzero entries since \(J_1\) is tridiagonal and \(J_1^2\) is pentadiagonal) to be
where \( {\varvec{m}}_1=\begin{bmatrix} 0&m_{21}/m_{11}&m_{31}/m_{11}&0&\ldots&0 \end{bmatrix}^T\) and perform a first explicit similarity transform on \(J_1\),
Observe that K is not tridiagonal. In the \(6\times 6\) case
Next we apply a sequence of elementary similarity transformations such that each transformation pushes the \(2\times 1\) bulge one row down and one column to the right. Finally the bulge is chased off the bottom to restore the J-form. In exact arithmetic, the implicit L theorem ensures that this technique of bulge chasing gives
In Sect. 4.1 below we will see the details on \(\mathcal {L}_j\), \(j=2,\ldots ,n-1\).
If matrix \(J_1\) and shifts \(\sigma _1\) and \(\sigma _2\) are real then factors \(L_1,U_1,L_2,U_2\) and matrices \(J_2\), \(J_3\) will all be real. Now suppose that \(J_1\) is real and \(\sigma _1\) is complex. Then, by (3.8), \(J_3\) will be real if, and only if, \(\sigma _2={\overline{\sigma }}_1\). The reason is that M is real,
so that \(\varvec{{\mathcal {L}}}\) and \(\varvec{{\mathcal {U}}}\) are real and \(J_3\) is the product of real matrices. Note however that \(J_2,\) and factors \(L_2,U_2\), will be complex, given that \(L_1,U_1\) and shifts \(\sigma _1,\sigma _2\) are all complex. As we have described above, it is possible to skip this complex matrix \(J_2\) and go straight from real \(J_1\) to real \(J_3\). So, in the case of complex eigenvalues (which for real matrices occur in complex conjugate pairs) we will be able to apply a complex conjugate pair of shifts implicitly and avoid complex arithmetic. Recall that we are seeking an algorithm that uses only real arithmetic and converges to real Schur form.
3.4.2 Connection to dqds algorithm
In Fig. 1 we examine the two steps of the LR transform derived in the previous section but with a significant difference. Instead of \(J_1\) being an arbitrary matrix in J-form, we assume that it is given to us in the form \(U_0L_0\). A different way of introducing this factorization is saying that our initial matrix is \(J_0\) (not \(J_1\)) and we always consider an additional unshifted LR step for constructing real factored forms
so that dqds starts with factors \(L_0,U_0\). The dqds algorithm can not start with \(J_1\) unless its UL factorization is available.
The crucial observation in Fig. 1 is that the implicit LR algorithm forms only the J matrices while dqds, on the bottom line, works only on the factors L,U. So with LR the only J matrix which is skipped by an implicit double step is \(J_2\) and we go from \(J_1=U_0L_0\) to \(J_3=L_3U_3\). The dqds algorithm cannot stop with \(L_2,U_2\) because it is only when we take the product \(U_2L_2\) and add back the shift \(\sigma _2\) that we get the matrix \(J_3\); it requires a third step to obtain \(L_3,U_3\) which define \(J_3\). The triple dqds algorithm will skip the factors \(L_1,U_1,L_2,U_2\) and will go from \(L_0,U_0\) to \(L_3,U_3\) performing implicitly three dqds steps.
Here is another way to describe the diagonal arrows in Fig. 1 for the relation between double shift LR and triple dqds:
So the similarity (3.7) corresponds to
and, in contrast to a single dqds step, a triple dqds step (implicit) restores the shifts.
Observe that in the triple dqds step (3.11) we find factors \(L_3,U_3\) such that \(J_3=L_3U_3\) and these factors (different factors) would only occur in LR in the following step with a new shift \(\sigma _3\),
So to make explicit dqds equivalent to LR with shifts \(\sigma _i\) and \(\sigma _{i+1}\) it is necessary to use the differences \((\sigma _{i+1} -\sigma _i)\) with dqds. In other words, successive shifts \(\sigma _i\) and \(\sigma _{i+1}\) in LR lead to the dqds step
3.4.3 Single shift LR and double dqds
Analogously to a double shift, a single shift LR step is equivalent to two steps of dqds when we consider the implicit implementation of these shifted algorithms.
with \(\varvec{{\mathcal {L}}}=L_1\). Here matrix M is tridiagonal,
and matrix K corresponding to (3.10) has only one bulge in entry (3, 1) (instead of a \(2\times 1\) bulge).
Recall from Sect. 3.4.1 that the implicit double LR algorithm uses the technique of bulge chasing. This technique is also applied for implicit single shifts.
The next section develops a form of bulge chasing for the triple dqds algorithm (3dqds). We did not develop this technique for the double dqds algorithm (2dqds) because in our shift strategy we will always use double shifts (only initially we use single dqds with zero shifts). See Sect. 6.3 for details on the shift strategy in our complete algorithm.
4 Triple dqds algorithm
We use the term 3dqds as a shorthand for our triple dqds algorithm which, using bulge chasing, implements implicitly the three dqds steps (3.11) equivalent to an implicit double shift LR step. Although the 3dqds algorithm has been primarily developed to avoid complex arithmetic in the case of consecutive complex shifts \(\sigma _1\) and \(\sigma _2={\overline{\sigma }}_1\) in the presence of complex eigenvalues, it can be applied to the case of two real shifts \(\sigma _1\) and \(\sigma _2\). To cover both cases, all we need is the sum and the product of the pair of shifts, \(\textsf {sum}=\sigma _1+\sigma _2\) and \(\textsf {prod}=\sigma _1\sigma _2\), to form matrix M in (3.8),
Using (3.12) the idea is to transform \(U_0\) into \(L_3\) and \(L_0\) into \(U_3\) by bulge chasing in each matrix,
Notice that we need to transform an upper bidiagonal into a lower bidiagonal and vice-versa. From the uniqueness of the LU factorization, when it exists, it follows, see [20], that there is a unique hidden matrix X such that
The matrix \(\varvec{{\mathcal {L}}}\) is given, from Sect. 3.4.1, as a product
(\(\mathcal {L}_{n}=I\)) and we will gradually construct the matrix X in corresponding factored form \(X_n \cdots X_2X_1\). In fact we will write each \(X_i\) as a product
Matrices \(\mathcal {L}_i\) and \(Y_i\) are elementary matrices, \(\mathcal {L}_i=I+{\varvec{m}}_i{\varvec{e}}_i^T\) and \(Y_i=I+{\varvec{w}}_i{\varvec{e}}_i^T\), but \(Z_i\) is not. The details are quite complicated and will be shown in the following sections.
4.1 Chasing the bulges
Starting with the factors \(L_0\), \(U_0\) and the shifts \(\sigma _1\), \(\sigma _2\), we normalize column 1 of M in (4.1) to form \({{\mathcal {L}}}_1\), spoil the bidiagonal form with
and at each minor step i, \(i=1,\ldots ,n\), matrices \(Z_i\), \(\mathcal {L}_i\) and \(Y_i\) are chosen to chase the bulges. After n minor steps, we obtain \(L_3\) and \(U_3\),
All the work of bulge chasing will be confined to two matrices F and G. Initially,
and, finally,
For a pair of shifts \(\sigma _1\) and \(\sigma _2\) (real or a complex conjugate pair), the triple dqds algorithm has the following matrix formulation:
4.2 Details of 3dqds
In this section we will go into important details of the 3dqds algorithm. Consider \(L_0\) with subdiagonal entries \(l_{1},\ldots ,l_{n-1}\) and \(U_0\) with diagonal entries \(u_1,\ldots ,u_n\), as defined in Sect. 3.3, and consider matrices \(L_3\) and \(U_3\) with subdiagonal entries \({\widehat{l}}_1,\ldots ,{\widehat{l}}_{n-1}\) and diagonal entries \({\widehat{u}}_1,\ldots ,{\widehat{u}}_n\), respectively.
For each iteration of 3dqds, at the beginning of a minor step \(i, \; i=2,\ldots ,n-3,\) the active \(4\times 4\) windows of F and G are
We denote the entries \(F_{i+1,i-1}\) and \(F_{i+2,i-1}\) by \(\begin{bmatrix} x_l&y_l \end{bmatrix}^T\), the \(2 \times 1\) bulge in F, and the entries \(G_{i,i}\), \(G_{i+1,i}\) and \(G_{i+2,i}\) by \(\begin{bmatrix} x_r&y_r&z_r \end{bmatrix}^T\). The bulge in G is \(\begin{bmatrix} y_r&z_r \end{bmatrix}^T\). In practice, as the bulges both change value and position, these 5 auxiliary variables are enough to accomplish all the calculations. The subscripts l and r in x, y and z derive from “left” and “right”, respectively, and observe that these variables are not from matrices X, Y and Z described in Sect. 4.1.
Each minor step i, \(i=2,\ldots ,n-3\), consists of the following 3 parts. The values in \(x_l,y_l,x_r,y_r,z_r\) change and they move one column right and one row down.
\({{\underline{\varvec{{Minor step{i}}}}}}\)
-
(a)
\(F \longleftarrow FZ_i^{-1}\) puts 0 into \(F_{i,i+1}\) and 1 into \(F_{i,i}\) \(G \longleftarrow Z_iG\) turns \(G_{i,i+1}\) into 1 and changes \(G_{i,i}\)
$$\begin{aligned} Z_i^{-1}= \begin{bmatrix} \ddots &{}\quad &{} &{} &{} &{}\\ &{} 1&{} \quad &{} &{} &{} \\ &{} &{}\quad \frac{1}{u_i} &{}\quad -\frac{1}{u_i} &{} &{} \\ &{} &{} \quad 0&{} \quad 1 &{} &{} \\ &{} &{} &{} &{}\quad 1 &{} \\ &{} &{} &{} &{} &{}\quad \ddots \\ \end{bmatrix}, \qquad \qquad Z_i= \begin{bmatrix} \ddots &{} \quad &{} &{} &{} &{} \\ &{} \quad 1 \quad &{} &{} &{} &{} \\ &{} \quad &{}\quad u_i &{}\quad 1 &{} &{} \\ &{} &{}\quad 0 &{}\quad 1 &{} &{} \\ &{} &{} &{} &{}\quad 1 &{}\quad \\ &{} &{} &{} &{} &{}\quad \ddots \end{bmatrix}, \end{aligned}$$$$\begin{aligned} FZ_i^{-1}= \begin{bmatrix} \ddots &{}\quad &{} &{} &{} &{} \\ \ddots &{}\quad 1&{} &{} &{} &{} \\ &{}\quad {\widehat{l}}_{i-1} &{}\quad \varvec{1} &{}\quad \varvec{0} &{} &{} \\ &{}\quad x_l &{} &{}\quad u_{i+1} &{}\quad 1 &{} \\ &{}\quad y_l &{} &{} &{}\quad u_{i+2} &{}\quad \ddots \\ &{} &{} &{} &{} &{}\quad \ddots \end{bmatrix},&\quad Z_iG=\begin{bmatrix} \ddots &{}\quad \ddots &{}\quad &{} &{} &{} \\ &{}\quad {\widehat{u}}_{i-1} &{}\quad 1 &{}\quad &{} &{} \\ &{} \quad &{}\quad x_r &{}\quad \varvec{1} &{} &{} \\ &{} \quad &{}\quad y_r &{}\quad 1 &{} &{} \\ &{} \quad &{}\quad z_r &{}\quad l_{i+1} &{}1\quad &{} \\ &{} \quad &{} &{} &{}\quad \ddots &{}\quad \ddots \end{bmatrix}\\&\quad \qquad x_r \longleftarrow x_r*u_i+y_r \end{aligned}$$ -
(b)
\(F \longleftarrow \mathcal {L}_i^{-1}F\) puts 0 into \(F_{i+1,i-1}\) and \(F_{i+2,i-1}\), and moves the bulge to column i \(G\longleftarrow G\mathcal {L}_i\) creates \({\widehat{u}}_i\) in \(G_{i,i}\) and changes \(G_{i+1,i}\), \(G_{i+2,i}\) and \(G_{i+3,i}\) below it
$$\begin{aligned} \begin{array}{l} x_l \longleftarrow -x_l/{\widehat{l}}_{i-1} \\ y_l \longleftarrow -y_l/{\widehat{l}}_{i-1} \\ \end{array}, \quad \mathcal {L}_i^{-1}= \begin{bmatrix} &{} \ddots &{} &{} &{} &{} \\ &{} &{}1 &{} &{} &{} \\ &{} &{}x_l &{}1 &{} &{} \\ &{} &{}y_l &{} &{}1 &{} \\ &{} &{} &{} &{} &{}\ddots \end{bmatrix}, \quad \mathcal {L}_i= \begin{bmatrix} &{} \ddots &{} &{} &{} &{} \\ &{} &{}1 &{} &{} &{} \\ &{} &{}-x_l &{}1 &{} &{} \\ &{} &{}-y_l &{} &{}1 &{} \\ &{} &{} &{} &{} &{}\ddots \end{bmatrix} \end{aligned}$$$$\begin{aligned} \mathcal {L}_i^{-1}F= \begin{bmatrix} \ddots &{} &{} &{} &{} &{} \\ \ddots &{} 1&{} &{} &{} &{} \\ &{}{\widehat{l}}_{i-1} &{}\varvec{1} &{}\varvec{0} &{} &{} \\ &{}\varvec{0} &{}x_l &{}u_{i+1} &{}1 &{} \\ &{}\varvec{0} &{}y_l &{} &{}u_{i+2} &{}\ddots \\ &{} &{} &{} &{} &{}\ddots \end{bmatrix},&\quad G\mathcal {L}_i= \begin{bmatrix} \ddots &{} \ddots &{} &{} &{} &{} \\ &{}{\widehat{u}}_{i-1} &{}1 &{} &{} &{} \\ &{}&{}\varvec{{\widehat{u}}_i} &{}\varvec{1} &{} &{} \\ &{}&{}x_r &{}1 &{} &{} \\ &{}&{}y_r &{}l_{i+1} &{}1 &{} \\ &{}&{}z_r &{} &{}l_{i+2} &{}1\\ &{}&{} &{} &{} &{}\ddots &{}\ddots \end{bmatrix}\\&\qquad \quad \begin{array}{l} {\widehat{u}}_i \longleftarrow x_r-x_l\\ x_r \longleftarrow y_r-x_l\\ y_r \longleftarrow z_r-y_l-x_l*l_{i+1}\\ z_r \longleftarrow -y_l*l_{i+2}\\ \end{array} \end{aligned}$$ -
(c)
\(G\longleftarrow Y_iG\) puts 0 into \(G_{i+1,i}\), \(G_{i+2,i}\) and \(G_{i+3,i}\), and moves the bulge to column \(i+1\) \(F \longleftarrow FY_i^{-1}\) creates \({\widehat{l}}_i\) in \(F_{i+1,i}\) and changes \(F_{i+2,i}\) and \(F_{i+3,i}\) (bulge in F) below it
$$\begin{aligned} \begin{array}{l} x_r \longleftarrow x_r/{\widehat{u}}_i\\ y_r \longleftarrow y_r/{\widehat{u}}_i\\ z_r \longleftarrow z_r/{\widehat{u}}_i\\ \end{array},\quad Y_i^{-1}= \begin{bmatrix} \ddots &{} &{} &{} &{} &{} \\ &{}1 &{} &{} &{} \\ &{}x_r &{}1 &{} &{} \\ &{}y_r &{} &{}1 &{} \\ &{}z_r &{} &{} &{}1\\ &{} &{} &{} &{} &{}\ddots \end{bmatrix}, \qquad Y_i= \begin{bmatrix} \ddots &{} &{} &{} &{} &{} \\ &{}1 &{} &{} &{} \\ &{}-x_r &{}1 &{} &{} \\ &{}-y_r &{} &{}1 &{} \\ &{}-z_r &{} &{} &{}1\\ &{} &{} &{} &{} &{}\ddots \end{bmatrix} \end{aligned}$$$$\begin{aligned} FY_i^{-1}= \begin{bmatrix} \ddots &{} &{} &{} &{} &{} \\ \ddots &{} 1&{} &{} &{} &{} \\ &{}{\widehat{l}}_{i-1} &{}\varvec{1} &{}\varvec{0} &{} &{} \\ &{}\varvec{0} &{}\varvec{{\widehat{l}}_{i}} &{}u_{i+1} &{}1 &{} \\ &{}\varvec{0} &{}x_l &{} &{}u_{i+2} &{}1 &{} \\ &{} &{}y_l &{} &{} &{} u_{i+3}&{}\ddots \\ &{} &{} &{} &{} &{} &{} \ddots \end{bmatrix},&\quad Y_iG= \begin{bmatrix} \ddots &{} \ddots &{} &{} &{} &{} \\ &{}{\widehat{u}}_{i-1} &{}1 &{} &{} &{} \\ &{}&{}\varvec{{\widehat{u}}_i} &{}\varvec{1} &{} &{} \\ &{}&{}\varvec{0} &{}x_r &{} &{} \\ &{}&{}\varvec{0} &{}y_r &{}1 &{} \\ &{}&{}\varvec{0} &{}z_r &{}l_{i+2} &{}1\\ &{}&{} &{} &{} &{}\ddots &{}\ddots \end{bmatrix}\\\\ \begin{array}{l} {\widehat{l}}_i \longleftarrow x_l+y_r+x_r*u_{i+1}\\ x_l \longleftarrow y_l+z_r+ y_r*u_{i+2}\\ y_l \longleftarrow z_r*u_{i+3} \\ \end{array} \qquad \qquad \quad&\qquad \quad \begin{array}{l} x_r \longleftarrow 1-x_r\\ y_r \longleftarrow l_{i+1}-y_r\\ z_r \longleftarrow -z_r\\ \end{array} \end{aligned}$$
The result of this minor step is that the active windows of F and G shown in (4.2) have been moved down and to the right by one place.
Naturally steps \(1, n-2, n-1,n\) are slightly different and their practical implementation may be found in [11, pp.147–157].
4.3 Comparison of dqds and 3dqds
In this section we present a detailed version of the inner loop of 3dqds and compare one step of 3dqds with three steps of simple dqds in terms of arithmetic effort.
Here is the inner loop of 3dqds. See “AppendixA” for the whole 3dqds algorithm.
In contrast,
In practice, each \(d_{i+1}\) may be written over its predecessor in a single variable d and, using and auxiliary variable t, only one division is needed.
Table 1 below shows that the number of floating point operations required by one step of 3dqds is comparable to three steps of dqds (table expresses only the number of floating point operations in the inner loops).
However to accomplish a complex conjugate pair of shifts these 3 dqds steps will be complex in contrast to our 3dqds which uses only real arithmetic. Thus 3 steps of complex dqds take more time than one step of 3dqds(complex arithmetic raises the cost by a factor of about 4 [6, p.163]).
5 Error analysis
We turn to the effect of finite precision arithmetic on our algorithms. First consider the dqds algorithm.
5.1 dqds
It is well known that even in exact arithmetic the dqds iteration, applied to the factors L, U of a J matrix can break down due to a zero pivot in the new factors. The dqds transform, just like the LR transform, is unstable. In the early days when the new was written over the old immediately breakdown was a disaster. Today all users can afford to store the new factors separately from the old and simply reject a transform with unacceptable element growth, choose a new shift, and continue the iteration. A rejection is a nuisance, not a disaster.
One of the attractions of dqds is that it has high mixed relative stability, to be explained below. One of us proved this in [9] in the context of singular values of bidiagonals and eigenvalues of real symmetric tridiagonals. Since this desired property is independent of symmetry, we take this opportunity to present the result again in the context of J matrices.
To set up notation for the proof we consider real bidiagonal factors L and U of a real J matrix together with a real shift \(\sigma \) and use the dqds transform to obtain output \({\widehat{L}},{\widehat{U}}\) satisfying
We assume no anomalies occur, i.e. no divisions by zero, no overflow/underflow.
Theorem 5.1
([9], Theorem 4) Let \(\textit{dqds}(\sigma )\) map L, U into computed \({\widehat{L}},{\widehat{U}}\) with no anomalies. Then well chosen small relative changes in the entries of both input and output matrices, of at most 3 ulps each, produces new matrices, one pair mapped into the other, in exact arithmetic, by \(\textit{dqds}(\sigma )\).
Our analysis consists to write down the exact relations satisfied by the computed quantities \({\widehat{L}},{\widehat{U}}\) and then to work out among them an exact dqds transform whose input is close to L, U and output is close to \({\widehat{L}},{\widehat{U}}\). The diagram in Fig. 2 is an excellent summary.
The model of arithmetic we assume is that the floating point result of a basic arithmetic operation \(\odot \) (one of the four binary operations \(+\), −, \(*\) and /) satisfies
where \(\varepsilon \) and \(\eta \) depend on x, y, and the operation \(\odot \), and satisfy
The quantity \(\epsilon \) is called variously roundoff unit, machine precision or macheps. We will choose freely the form \((\varepsilon \text { or } \eta )\) that suits the analysis. We will also use the acronym ulp which stands for units in the last place held and it is the natural way to refer to relative differences between numbers.
Our result is possible because of the simple form of the recurrence for the auxiliary variable \(\{d_i\}_{i=1}^n\). In exact arithmetic
Proof
We consider the floating point implementation of dqds in (4.3). The computed quantities \({\widehat{L}},{\widehat{U}}\) are governed by the following exact relations.
The symbol \(\varepsilon _{**}\) represents the rounding error in the second multiplication \(l_i*t_i\). All the \(\varepsilon \)’s obey (5.3) and depend on i but we supress this dependence on i except for the subtraction of the shift \(\sigma \). Here \(\varepsilon _{i+1}\) accounts for the error in subtracting the real shift \(\sigma \). To be consistent we must also use \(d_i(1+\varepsilon _i)\), where \(\varepsilon _i\) is defined in minor step \(i-1\), and \((1+\varepsilon _1)d_1=u_1-\sigma \). Here t is just an auxiliary variable for the analysis.
Now we can write an exact dqds transform using \([\,\cdot \,]\) to surround our chosen variables.
We can read off the perturbations, defining  and
and  on the way to an exact transform:
on the way to an exact transform:

The perturbations are as claimed in the theorem: 3 ulps for \(u_i\) and 1 ulp for \(l_i\), and 2 ulps each for \({\widehat{l}}_i\) and \({\widehat{u}}_i\) as shown in Fig. 2. Notice that our choices of  and
and  are not in general machine representable.
are not in general machine representable.
When \(\sigma =0\) the \((1+\varepsilon _i)\) factors are omitted but still 3 ulps are needed for \(u_{i+1}\).
\(\square \)
The remarkable feature here is that element growth does not impair the result. However,
Theorem 5.1 does not guarantee that dqds returns accurate eigenvalues. For that, an extra requirement is needed such as positivity of all the parameters \(u_j\), \(l_j\) in the computation, as is the case for the eigenvalues of \(B^TB\) where B is upper bidiagonal.
We mention that Yao Yang considered the roundoff in dqds in his dissertation at UC, Berkeley, in 1994 [38]. He had two results. He gave an \(n=4\) example to show that even dqd (no shift in dqds) is not backward stable. He also produced an a posteriori (computable) bound on the error in the exact product \({\widehat{L}}{\widehat{U}}\) of the output matrices. Unfortunatly, his dissertation has not been published but his results are stated and proved in [21].
5.2 3dqds
Each minor step in the algorithm consists of 3 simple transformations on work matrices F and G. All three parts arise from similarities that chase the bulges in the transformation from \(U_0L_0\) to \(L_3U_3\). See Sect. 4. Two of these transformations are elementary transformations of the form \(I+{\varvec{v}}{\varvec{e}}_j^T\), with inverse \(I-{\varvec{v}}{\varvec{e}}_j^T\), and \({\varvec{v}}\) has at most 3 nonzero entries. We examine the condition number of these 3 transforms. Consult Sect. 4.2 to follow the details.
-
The active part of \(Z_i\) is
$$\begin{aligned} \begin{bmatrix} u_i &{}\quad 1\\ 0 &{}\quad 1 \end{bmatrix} \qquad \text {and} \qquad cond(Z_i)\simeq \max \left\{ |u_i|, |u_i|^{-1}\right\} . \end{aligned}$$ -
The active part of \(\mathcal {L}_i\) is
$$\begin{aligned} \begin{bmatrix} 1 &{}\quad \\ -x_l/{\widehat{l}}_{i-1} &{}\quad 1\\ -y_l/{\widehat{l}}_{i-1} &{}\quad 0 &{}\quad 1 \end{bmatrix} \qquad \text {and} \qquad cond(\mathcal {L}_i)\simeq 1+ \left( \frac{x_l}{{\widehat{l}}_{i-1}}\right) ^2 + \left( \frac{y_l}{{\widehat{l}}_{i-1}}\right) ^2. \end{aligned}$$ -
The active part of \(Y_i\) is
$$\begin{aligned} \begin{bmatrix} 1 &{}\quad \\ -x_r/{\widehat{u}}_{i} &{}\quad 1\\ -y_r/{\widehat{u}}_{i} &{}\quad 0 &{}\quad 1\\ -z_r/{\widehat{u}}_{i} &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \end{bmatrix} \qquad \text {and} \qquad cond({Y}_i)\simeq 1+ \left( \frac{x_r}{{\widehat{u}}_{i}}\right) ^2 + \left( \frac{y_r}{{\widehat{u}}_{i}}\right) ^2+\left( \frac{z_r}{{\widehat{u}}_{i}}\right) ^2. \end{aligned}$$
The variables \(x_l,y_l,x_r,y_r,z_r\) are formed from additions and multiplications of previous quantities. Note that \(u_i\) is part of the input and so is assumed to be of acceptable size. We see that it is tiny values of \({\widehat{l}}_{i-1}\) and \({\widehat{u}}_i\) that lead to an ill-conditioned transform at minor step i. In the simple dqds algorithm a small value of \({\widehat{u}}_i\) (relative to \(u_{i+1}\)) leads to a large value of \({\widehat{l}}_{i}\) and \(d_{i+1}\). In 3dqds the effect of 3 consecutive transforms is more complicated. The message is the same: reject any transform that has more then modest element growth. In practice, \(|{\widehat{u}}_i|\) and \(|{\widehat{l}}_{i-1}|\) are monitored and a transform is rejected if either quantity is too big (bigger than \(1/\sqrt{\varepsilon }\)). The computed eigenvalues are used as input for Rayleigh quotient correction in the original balanced matrix (see [19]).
In order to understand the intricate arguments below we have found it essential to absorb the contents of Sects. 4.1 and 4.2, in particular the division of the typical inner loop of 3dqds in three parts \(\mathbf (a) \), \(\mathbf (b) \) and \(\mathbf (c) \). The three dqds similarities have morphed into a sequence of \(n-1\) similarities of FG (implicit) each of which in its turn is composed of three transformations of F and G by matrices \(Z_i\), \(\mathcal {L}_i\), \(Y_i\) (with exact inverses) at minor step, or loop, i where we concentrate our attention.
Minor step \(\varvec{i}\).
Recall that at the start the bulges \(x_l\), \(y_l\) are in column \(i-1\) of F while \(x_r\), \(y_r\), \(z_r\) are in column i of G. See (4.2). The values in these bulges change and they move one column right and one row down. In analysis, not practice, as the bulges both change value and position, new variables are created and denoted by augmentation of the subscripts (See Table 2). By the end of minor step i new values are given to all the bulge variables to be ready for the next step. The most active is \(x_r\), the entry on the diagonal of G. The loop i updates \(x_r\) four times so we find
and the last value \(x_{r_4}\) becomes \(x_r\) at the next loop \(i+1\). Its position changes from \(G_{i,i}\) to \(G_{i+1,i+1}\). This change in position occurs at operation 14 of the 16 arithmetic operations in 3dqds.
To follow the analysis below the reader should have reference to Sect. 4.2. At minor step i the inner loop transforms columns \(i-1\), i of F and i, \(i+1\) of G.
To anticipate our result we are going to show that very small relative, but well chosen, perturbations in the input and output variables of each part, (a), (b), and (c), separately, of loop i yield exact, albeit implicit, transformations of F and G. Of course, the input and output variables are different for each part.
Note that the output variables for Part (b) may be perturbed (again) as input variables of Part (c). We will point out the two (of 16) operations at which our perturbations fail to give an exact implementation of the whole of loop i. That would be a result as strong as the one for real dqds.
As said above, if \({\varvec{e}}_j\) denotes column j of I and \(\varvec{v}\) is a vector satisfying \({\varvec{e}}_j^T\varvec{v}=\varvec{0}\) then the exact inverse of \(I-\varvec{v}{\varvec{e}}_j^T\) is \(I+\varvec{v}{\varvec{e}}_j^T\) since \( (I-\varvec{v}{\varvec{e}}_j^{\textsf {T}})(I+\varvec{v}{\varvec{e}}_j^{\textsf {T}})= I-\varvec{v}{\varvec{e}}_j^{\textsf {T}}\varvec{v}{\varvec{e}}_j^{\textsf {T}}= I-({\varvec{e}}_j^{\textsf {T}}\varvec{v})\varvec{v}{\varvec{e}}_j^{\textsf {T}}=I. \) Hence the attraction of using elementary matrices for Parts \(\varvec{(b)}\) and \(\varvec{(c)}\). The matrix \(Z_i\), whose active part is \(\begin{bmatrix} u_i &{} 1\\ 0 &{} 1 \end{bmatrix}\), is not elementary but the action of its inverse is implicit in creating 0 and 1 in F and it is only \(Z_i\) that acts on G. Thus \(1/u_i\) is never used explicitly and, again, there is no error in the implicit use of \(Z_i^{-1}\) on F. These observations help to explain the welcome accuracy of 3dqds in practice.
In the analysis in each statement we use a subscript on \(\varepsilon \) as an indicator of the operation. For example,
We find it simpler to not name the perturbed variables but to indicate them by judicious use of parentheses and square brackets. We use either a dot or juxtaposition to represent an exact multiplication.


Some comments. In Op. 4, for example, when cancellation occurs (\(x_{r_1}\) and \(x_{l_1}\) have same exponent) there is no error in subtraction but \({\widehat{u}}_i\)’s uncertainty increases (Table 2).
We perturb \(x_{r_2}\) in Op. 5, as an output in Part (b), and also in Op. 8, as an input in Part (c). Similarly, we perturb \(y_{r_1}\) in Op. 6, in Part (b), and also in Op. 9 in Part (c). We use plain \(z_{r_1}\) in Op. 7, as an output in Part (b), and perturb \(z_{r_1}\) in Op. 10, as an input in Part (c).
We did not need to perturb \(x_{l_1}\) nor \(y_{l_1}\) in Ops. 2 and 3 in Part (b) and used \(x_{l_1}\) and \(y_{l_1}\) in Ops. 5 and 6, still Part (b), as well as Op. 11 and 12, in Part (c). So \(x_{l_1}\) and \(y_{l_1}\) did preserve their identities for the whole of loop i.
In Ops. 5 and 6 the perturbations we heaped on \(x_{r_2}\) and \(y_{r_1}\) were to avoid perturbing \(x_{l_1}\) and \(y_{l_1}\). It seemed just too messy to try and carry the perturb \(x_{r_2}\) and \(y_{r_1}\) through the later operations in Part (c) that use them, such as Ops. 8 and 9.
Minor step 1 has a slightly different analysis but we omit the details which may be derived using a similar analysis.
In summary,
Theorem 5.2
If 3dqds is executed in standard floating point IEEE standard arithmetic with no invalid operations then suitable small perturbations (2 ulps maximum) of Parts (a), (b), and (c) produce an exact instance of each part in every minor step.
6 Implementation details
6.1 Deflation \(\varvec{(n \leftarrow n-1)}\)
Some of our criteria for deflating come from [23], others are new. Consider both matrices UL and LU and the trailing \(2\times 2\) blocks,
Deflation \((n \leftarrow n-1)\) removes \(l_{n-1}\) as well as \(u_n\). Looking at entry \((n-1,n-1)\) of UL shows that a necessary condition is that \(l_{n-1}\) be negligible compared to \(u_{n-1}\),
for a certain tolerance tol close to roundoff unit \(\varepsilon \).
The (n, n) entries of UL and LU suggest either \(u_n+acshift\) or \(l_{n-1}+u_n+acshift\) as eigenvalues where acshift is the accumulated shift. Recall that simple dqds is a non-restoring transform (see (3.5)). To make these consistent we require that
Finally we must consider the change \(\delta \uplambda \) in the eigenvalue \(\uplambda \) caused by setting \(l_{n-1}=0\). We estimate \(\delta \uplambda \) by starting from UL with \(l_{n-1}=0\) and then allowing \(l_{n-1}\) to grow. To this end let J be UL with \(l_{n-1}=0\) and \((u_n,{\varvec{y}}^T,{\varvec{x}})\) be the eigentriple for J. Clearly \({\varvec{y}}^T={\varvec{e}}_n^T\). Now we consider perturbation theory with parameter \(l_{n-1}\). The perturbing matrix \(\delta J\), as \(l_{n-1}\) grows, is
By first order perturbation analysis
and \(\Vert {\varvec{y}}\Vert _2=1\) in our case. So,
and we use the crude bound \( \displaystyle \frac{|x_{n-1}|}{\Vert {\varvec{x}}\Vert _2}<1. \) So, we let \(l_{n-1}\) grow until the change
in eigenvalue \(\uplambda =u_n\) is no longer acceptable. Our condition for deflation is then
A similar first order perturbation analysis for LU with \(l_{n-1}=0\) will give our last condition for deflation. For the eigentriple \((u_n,{\varvec{y}}^T,{\varvec{x}})\) we also have \({\varvec{y}}^T={\varvec{e}}_n^T\). The perturbing matrix is now
and
Finally we require
6.2 Splitting and deflation \(\varvec{(n \leftarrow n-2)}\)
Recall that the implicit L theorem was invoked to justify the 3dqds algorithm. This result fails if any \(l_k\), \(k<n-1\) vanishes. Consequently, checking for negligible values among the \(l_k\) is a necessity, not a luxury for increased efficiency. Consider \(J=UL\) in block form

where \(\mu =u_{k+1}l_k\), \(k<n-1\). We can replace \(\mu \) by 0 when
However we are not going to estimate the eigenvalues of \(J_1\) and \(J_2\). Instead we create a local criterion for splitting at \((k+1,k)\) as follows. Focus on the principal \(4\times 4\) window of J given by

Now \(J_1\) and \(J_2\) are both \(2\times 2\) and our local criterion is
Let us see what this yields. Perform block factorization on J and note that the Schur complement of \(J_1\) in J is
with
where
Thus
Since \(\det \) is linear by rows and the second rows are equal
Our criterion reduces to splitting only when
Thus we require
Since
the criterion for splitting J at \((k+1,k)\) is then
Finally, to remove \(l_{k}\) we also need \(l_k\) to be negligible compared to \(u_{k}\),
Deflation \(\varvec{(n \leftarrow n-2)}\)
We use the same criterion for deflation \((n \leftarrow n-2)\), but because \(l_{k+2}=l_n=0\) there is a common factor \(det_2\) on each side of (6.6). Deflate the trailing \(2\times 2\) submatrix when
and
We omit the role of acshift here because it makes the situation more complicated. We have to recall that 3dqds uses restoring shifts and acshift is always real. So, for complex shifts, \(det_2\) is not going to zero. In fact
where \(\uplambda \) is an eigenvalue of \(J_2\).
When \(n=3\) these criteria simplify a lot. Both reduce to
6.3 Shift strategy
As with LR, the dqds algorithm with no shift gradually forces large entries to the top and brings small entries towards the bottom. We want to use a shift as soon as the trailing \(2\times 2\) principal submatrix appears to be converging. We use the size of the last two entries of L to make the judgement. The code executes a dqds transform with a zero shift if
Otherwise, a 3dqds transform is executed with
the trace and the determinant of the trailing \(2\times 2\) submatrix of UL. This will let us converge to either two real eigenvalues in the bottom \(2\times 2\) or a single \(2\times 2\) block with a complex conjugate pair of eigenvalues.
An unexpected reward for having both transforms available is to cope with a rejected transform. Our strategy is simply to use the other transform with the current shift. More precisely, given \(\texttt {sum}\) and \(\texttt {prod}\), if \(\textit{3dqds}(\texttt {sum},\texttt {prod})\) is rejected we try \(\textit{dqds}(u_n)\); if \(\textit{dqds(0)}\) is rejected, we try \(\textit{3dqds}(\delta ,\delta )\) with \(\delta =\sqrt{\varepsilon }\). We have to admit the possibility of a succession of rejections and in this case we don’t want to move away from the previous shift too much, just a small amount so that the transformation does not breakdown. See Algorithm 4 in “AppendixB” for details. The number of rejections is recorded and added to the total number of iterations.
7 Factored forms
7.1 Eigenvectors from twisted factorizations of the balanced form \(\varvec{\Delta T}\)
A salient property of an unreduced real tridiagonal matrix \(C=tridiag({\varvec{b}},{\varvec{a}},{\varvec{c}})\) (no off-diagonal entry vanishes) is that it can be balanced by a diagonal similarity easily and, once the matrix is balanced, it can be made real symmetric by changing the signs of certain rows. However, changing the signs is not a similarity transformation and would not preserve the eigenvalues. It is accomplished by premultiplying by a so-called signature matrix \(\Delta =diag(\delta _1,\ldots ,\delta _n)\), \(\delta _i=\pm 1\). So we can write
where T is real symmetric and S is diagonal positive definite, \(S=diag(s_1,\ldots ,s_n)\) with \(s_1=1\), \(s_i=\big (|c_1c_2\cdots c_{i-1}|/|b_1b_2\cdots b_{i-1}|\big )^{1/2}\), \(i=2, \ldots ,n\). See [11, Section 2.2.3]
Let \(\uplambda \) be a simple eigenvalue of \(\Delta T\) with eigenvector equations
Recall that \(\varvec{x}\), \(\varvec{y}\) and \(\uplambda \) may be complex and \(\varvec{y}^*\varvec{x}\ne 0\), since \(\uplambda \) is simple. An attraction of the \(\Delta T\) representation is that the row eigenvector \(\varvec{y}^*\) is determined by the right (or column) eigenvector \(\varvec{x}\). Transpose \(\Delta T\varvec{x}=\varvec{x}\uplambda \) and insert \(I=\Delta ^2\) to find
Compare with \(\varvec{y}^*\Delta T=\uplambda \varvec{y}^*\) to see that \(\varvec{y}^*=\varvec{x}^{\textsf {T}}\Delta \). See [13, 30].
The so-called twisted factorizations generalize the lower and upper bidiagonal factorizations. These factorizations gained new popularity as they were used for the purpose of computing eigenvectors of symmetric tridiagonal matrices [10, 22]. The idea is to begin both a top-to-bottom and a bottom-to-top factorization until they meet at, say, the k-th row, where they will have to be glued together. The index k is called the twist index or the twist position.
Observe that the eigenvector equations \(\Delta T\varvec{x}=\varvec{x}\uplambda \) and \((\varvec{x}^{\textsf {T}}\Delta )\Delta T=\uplambda (\varvec{x}^{\textsf {T}}\Delta )\) are equivalent to
where \(T-\uplambda \Delta \) is symmetric. Now suppose that we have \({\widetilde{\uplambda }}\) as an approximation to an eigenvalue \(\uplambda \) of \(\Delta T\) and that \(T-{\widetilde{\uplambda }}\Delta \) admits both lower and upper bidiagonal factorizations, starting the Gaussian elimination at the first row and at the last row, respectively,
where L is unit lower bidiagonal and U is unit upper bidiagonal. Matrices D and R are the diagonals holding the pivots of the elimination process. Let \((L)_ {i+1,i}=\ell _i\), \((U)_{i,i+1}=u_i\), \(i=1,\ldots ,n-1\), and \(D=diag(d_1,\ldots ,d_n)\), \(R=diag(r_1,\ldots ,r_n)\), \(i=1,\ldots ,n\). Then, for each twist index \(k=1,\ldots ,n\), we can construct a twisted factorization of \(T-{\widetilde{\uplambda }}\Delta \) as
where
The only new quantity is the twist element \(\gamma _k=(G_k)_{k,k}\) and one formula for it is
and another is
These formulae are not difficult to obtain. See [35].
A very useful feature of these twisted factorizations is that they can deliver a very accurate approximation to the column eigenvector \({\varvec{x}}\) (and row eigenvector \({\varvec{x}}^{\textsf {T}}\Delta \)). Since \(N_k^{-1}\varvec{e}_k=\varvec{e}_k\) and \(G_k^{-1}\gamma _k\varvec{e}_k=\varvec{e}_k\), solving a system of the form
is equivalent to solving
which leads to the recurrence
The above is just inverse iteration to obtain \(\varvec{z}\) (and \(\varvec{z}^{\textsf {T}}\Delta \)) as an approximation to \(\uplambda \)’s eigenvector \(\varvec{x}\) (and \(\varvec{x}^{\textsf {T}}\Delta \)) with residual norm
Therefore a natural choice for the twist index would be k such that
This strategy to choose an initial guess for the eigenvector provides, as a by-product, the diagonal entries of \((T -{\widetilde{\uplambda }}\Delta )^{-1}\) since \(\left[ (T -{\widetilde{\uplambda }}\Delta )^{-1}\right] _{k,k}=\gamma _k^{-1}\). See [35, Lemma 2.3].
If \(\Delta \) is definite, one important result presented in [7, 8] is that we can always find a twist index k such that
Since (7.9) uses only multiplications, the computed vector will be very good provided that \({\widetilde{\uplambda }}\) is accurate enough. In the general case, to judge the accuracy of the eigenvectors, we compute column (and row) residual norm relative to the eigenvalue,
This is a stricter measure than the usual \( \displaystyle \frac{\Vert \Delta T{\varvec{z}}-{\widetilde{\uplambda }}{\varvec{z}}\Vert }{\Vert {\varvec{z}}\Vert \Vert \Delta T\Vert }. \)
In [24] we show that unique tridiagonal “backward error” matrices can be designated for an approximate pair of complex eigenvectors (column and row) or two approximate real eigenvectors.
7.2 Relative eigenvalue condition numbers
The condition number of every eigenvalue of a real symmetric matrix is 1, but only in the absolute sense. The relative condition number can vary. In the unsymmetric case even the absolute condition numbers can rise to \(\infty \) and little is known about relative errors. In [13] several relative condition numbers with respect to eigenvalues were derived. Some of them use bidiagonal factorizations instead of the matrix entries and so they shed light on when eigenvalues are less sensitive to perturbations of factored forms than to perturbations of the matrix entries. These condition numbers are measures of relative sensitivity, i.e., measures of the relative variation of an eigenvalue with respect to the largest relative perturbation of each of the nonzero entries of the representation of the matrix. So the perturbations we consider are of the form \(|\delta p_i|\le \eta |p_i|\), \(0<\eta \ll 1\). In this section we present the relative condition number for the entries of the matrix C and for the LU factorization of the J-form.
Assume that \(\uplambda \ne 0\) is a simple eigenvalue of real tridiagonal matrix \(C=tridiag({\varvec{b}},{\varvec{a}},{\varvec{c}})\). Let \(\Delta T=SCS^{-1}\) be the balanced form (7.1) of C and \(\left( \uplambda ,\varvec{x},\varvec{x}^{\textsf {T}}\Delta \right) \) be an eigentriple of \(\Delta T\),
and recall that \(\Delta T\) and C eigenvectors are simply related by
The relative condition number with respect to \(\uplambda \) for the entries of C is
where \(|M|_{ij}=|M_{ij}|\), for any matrix M. Since S is diagonal it follows that
We have just shown that, in general, for any scaling matrix X invertible and diagonal, the expression for \(relcond(\uplambda ;C)\) yields \(relcond(\uplambda ;XCX^{-1})=relcond(\uplambda ;C)\). See [13, Lemma 6.2].
When C is unreduced it is also diagonally similar to a J-form,
where \(D=diag(1, c_1, c_1c_2, \ldots , c_1c_2\cdots c_{n-1})\) and \(\varvec{\mathfrak {b}}=diag(b_1c_1,b_2c_2,\ldots , b_{n-1}c_{n-1})\). Now assume that J permits bidiagonal factorization \(J=LU\) and write
to obtain
Recall that \(L=I+\mathring{L}\) and \({U}=diag(u_1,\ldots ,u_n) \left( I+\mathring{U}\right) \) with
For the cost of solving two bidiagonal linear systems,
we obtain the following expression of the relative condition number for the entries of L and U,
See [13, Section 6.3]. Next we deal with a case of a simple zero eigenvalue. Although the right hand side of (7.15) is a nonzero finite number for a simple eigenvalue \(\uplambda =0\), observe that the perturbations we consider for U, that is, \(|\delta u_i| \le \eta |u_i|\), produce \(u_n + \delta u_n = 0\) whenever \(u_n =0\). This means that singularity is preserved or, equivalently, that the zero eigenvalue is preserved. Therefore, it seems appropriate to set \(relcond(0;{L}, {U})=0\).
We use eigenvalue approximation \({\widetilde{\uplambda }}\) from Rayleigh Quotient Iteration (RQI) and eigenvector approximations \(\varvec{z}\) and \(\varvec{z}^{\textsf {T}}\Delta \) obtained from (7.8) to compute the relative condition numbers (7.13) and (7.15). The residual norms for \(\Delta T\) are given by (7.10) but for \(J=LU\), with eigenvector approximations \(F^{-1}{\varvec{z}}\) and \({\varvec{z}}^{\textsf {T}}\Delta F\), by
7.3 Generalized Rayleigh quotient iteration
In addition to computing both column and row eigenvector approximations from twisted factorizations of \(\Delta T\), the algorithm described in Sect. 7.1 can also be used to improve the accuracy of the eigenvalue approximation \({\widetilde{\uplambda }}\) by performing a Rayleigh Quotient Iteration. So, our code will return an eigenpair approximation \((S^{-1}{\varvec{z}},\varvec{z}^{\textsf {T}}\Delta S)\) for C together with an improved eigenvalue estimate, the generalized Rayleigh quotient,
Given the twisted factorization in (7.4) and (7.7), the Rayleigh quotient correction is given by
since \(z_k=1\), where \(\gamma _k\) is given in (7.6) and (7.5).
Recall that for \(x\in {\mathbb {C}}\), \(\Re (x)\) denotes the real part of x. The following lemma extends Lemma 12 in [8, pg. 886] to the unsymmetric case.
Lemma 7.1
Let \(T-{\widetilde{\uplambda }} \Delta =N_kG_kN_k^{\textsf {T}}\) and \(N_kG_kN_k^{\textsf {T}}\varvec{z}=\gamma _k\varvec{e}_k\), \(z_k=1\). Then the Rayleigh quotient \(\rho \) with respect to \(\Delta T -{\widetilde{\uplambda }}I\) is
and
where \(\omega _k=2\delta _k \Re (\varvec{z}^{\textsf {T}}\Delta {\varvec{z}})-\Vert \varvec{z}\Vert ^2\).
Proof
Let \(\Delta =diag(\delta _1,\ldots ,\delta _n)\), \(\delta _i=\pm 1\). Since
then
Thus,
Observe that, since \(z_k=1\),
If the easily checked condition
is satisfied, we obtain a decrease in the residual norm by using the Rayleigh quotient; the pair \(({\widetilde{\uplambda }}+\rho , \varvec{z} )\) is a better approximate eigenpair than \(({\widetilde{\uplambda }}, \varvec{z})\). \(\square \)
When \(\Delta =I\) (symmetrizable case) the condition (7.19) reduces to \( 2\Vert \varvec{z}\Vert ^2-\Vert \varvec{z}\Vert ^2=\Vert \varvec{z}\Vert ^2>0 \) and the Rayleigh quotient correction always gives an improvement. In this case (7.18) simplifies to
Given an approximation \({\widetilde{\uplambda }}\) to an eigenvalue \(\uplambda \) of \(\Delta T\) we compute the twisted factorization of \(T-{\widetilde{\uplambda }} \Delta \) and use inverse iteration (7.8) to obtain \(\uplambda \)’s column and row eigenvector approximations, \({\varvec{z}}\) and \({\varvec{z}}^{\textsf {T}}\Delta \). The Rayleigh quotient correction (7.17) gives a new approximation \({\widetilde{\uplambda }}+\rho \) for \(\uplambda \). We may repeat this process until there is no improvement in the residual (7.18). Although RQI can misbehave for non-normal matrices, we can use (7.19) to judge improvement (see [15, 34]). Our code 3dqds examines \(\omega _k\) and whenever it is greater than zero we apply RQI, otherwise not.
8 Numerical examples
The need for a tridiagonal eigensolver is admirably covered in Bini, Gemignani and Tisseur [1], many parts of which have been of great help to us. We refer to the Ehrlich-Aberth algorithm (see Sect. 2.5) as BGT and to our code simply as 3dqds, although we combine 3dqds with real dqds as described in Sect. 6.3.
Here the exact eigenvalue \(\uplambda _i\) is computed in quadruple precision, using Matlab Symbolic Math Toolbox with variable-precision arithmetic, and \({\widetilde{\uplambda }}_i\) denotes the computed eigenvalue in double precision (unit roundoff \(2.2\, 10^{-16}\)). We compare our \(\textit{3dqds}\) algorithm with its explicit version, refered as \(\textit{ex3dqds}\) (the three steps of \(\textit{dqds}\) are computed explicitly in complex arithmetic, see Fig. 1), with a Matlab implementation of BGT and with the QR algorithm on an upper Hessenberg matrix (Matlab function \(\textsf {eig}\)).
All the experiments were performed in Matlab (R2020b) on a LAPTOP-KVSVAUU8 with an Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz and 8 GB RAM, under Windows 10 Home. No parallel operations were used. We acknowledge that the Matlab tests do not reflect Fortran performance, but even in Matlab environment the ratio of elapsed times is an important feature.
8.1 Bessel matrix
Bessel matrices, associated with generalized Bessel polynomials [25], are nonsymmetric tridiagonal matrices defined by \(B_n^{(a,b)}=tridiag (\varvec{\beta },\varvec{\alpha },\varvec{\gamma })\) with
Parameter b is a scaling factor and most authors take \(b=2\) and so do we. The case \(a\in \mathbb {R}\) is the most investigated in literature. The eigenvalues of \(B_n^{(a,b)}\), well separated complex eigenvalues, suffer from ill-conditioning that increases with n - close to a defective matrix. In Pasquini [25] it is mentioned that the ill-conditining seems to reach its maximum when a ranges from \(-8.5\) to \(-4.5\). We pay a lot of attention to these matrices because they are an interesting family for our purposes. Each picture teaches us a lot about the behavior of eigenvalues.
Our examples take \(B_{n}^{(-8.5,2)}\), \(B_{n}^{(-4.5,2)}\) and \(B_{n}^{(12,2)}\) for \(n=40,50\). We show pictures for Matlab (double precison), BGT and 3dqds to illustrate the extreme sensitivity of some of the eigenvalues. The results of ex3dqds are visually identical to 3dqds, so we don’t show them. In exact arithmetic the spectrum lies on an arc in the interior of the moon-shaped region. Our pictures show this region and the eigenvalues computed in quadruple precision (labeled as exact).
Table 3 shows the minimum and maximum relative errors, respectively, \(rel_{min}=\min _i|\uplambda _i-{\widetilde{\uplambda }}_i|/|\uplambda _i|\) and \(rel_{max}=\max _i|\uplambda _i-{\widetilde{\uplambda }}_i|/|\uplambda _i|\). The relative condition numbers \(relcond(\uplambda ;C)\) and \(relcond(\uplambda ;{L},{U})\) (see (7.13) and (7.15)) and residual norms (see (7.10) and (7.16)) are shown in Table 4. We show both condition numbers because Matlab and BGT only use matrix entries and 3dqds uses L, U factors.
The results for \(B_{18}^{(-8.5,2)}\), \(n=18,25\), are shown in Fig. 3, without RQI (Rayleigh Quotient Iteration) and with one RQI. Observe on the real line that our approximations with one RQI (c) lie on top of the BGT approximations. We include the pictures (b) and (d) to show well the extreme sensitivity of the eigenvalues. Note how the eigenvalues move out of the moon-shaped inclusion region.
In Fig. 4 we show the results for \(B_{n}^{(-4.5,2)}\), \(n=20,25\), and \(B_{n}^{(12,2)}\), \(n=40,50\), without RQI. The reader is invited to see the large effect of changing n from 20 to 25, in (a) and (b), and from 40 to 50, in (c) and (d). Notice that our results are slightly but consistently better than those of the other two methods.
8.2 Clement matrix
The so-called Clement matrices (see [3])
with \(b_j=j\) and \(c_j=b_{n-j}\), \(j=1,\ldots ,n-1\), have real eigenvalues,
These matrices posed no serious difficulties. The initial zero diagonal obliges the dqds based methods to take care when finding an initial LU factorization.
The 3dqds and ex3dqds codes use only real shifts as they should and the accuracy (approximately the same) is less than BGT but satisfactory. One RQI reduces errors to \({{\mathcal {O}}}(\varepsilon )\).
Our numerical tests have \(n=50,100,200,400,800\). The relative condition number \(relcond(\uplambda ;C)\) ranges from \(10^0\) to \(4\;10^2\) and it is smaller at the ends of the spectrum. The maximum residual norm for C is \({{\mathcal {O}}}(10^{-11})\). The minimum and maximum relative errors, \(rel_{min}\) and \(rel_{max}\), are shown in Table 5. Note the poor performance of Matlab’s eig (so much for backward stability).
The CPU elapsed times are presented in Table 6. We put \((+)\) whenever a RQI is used. Since we compare Matlab versions of all the codes we acknowledge that the elapsed times are accurate to only about 0.02 seconds. However, this is good enough to show the striking time ratios between BGT and the dqds codes.
We draw the readers attention that for \(n=400\) our algorithm is about 200 times faster than BGT but when n rises to 1000 it is over 600 times faster. This is finding the eigenvalues to the same accuracy, namely \({{\mathcal {O}}}(\varepsilon )\). In addition we provide eigenvectors and condition numbers.
An important further comment which illustrates challenges of the unsymmetric eigenvalue problem is that in these examples for \(n\ge 200\) the scaling matrices F used above (see (7.14)) are not representable. This limitation indicates why we use the \(\Delta T\) form for computing the eigenvectors. The overflow problem, which also arises for \(S^{-1}\) (see (7.12)), although not so quickly, explains why BGT confines its attention to \(n=50\), but we go further because of our approach.
8.3 Matrix with clusters
Matrix in Test 5 in [1],
seems to be a challenging test matrix. It was designed to have large, tight clusters of eigenvalues around \(10^{-5}\), \(-10^5\) and \(10^5\). Half the spectrum is around \(10^{-5}\) and the rest is divided unevenly between \(-10^5\) and \(10^5\). The diagonal alternates between entries of absolute value \(10^5\) and \(10^{-5}\) and so, for dqds codes, there is a lot of rearranging to do. When \(n \ge 100\) it is not clear what is meant by accuracy.
The matrix has a repetitive structure and the diagonal entries are a good guide to the eigenvalues. For \(n=100\) and for the large real eigenvalues near \(\pm 10^5\) the eigenvectors have spikes \((-10^{-5}, -1, 10^{-5})\) (complex conjugate pairs have spikes \((10^{-5}, 1, -10^{-7},-1,10^{-5})\), at the appropriate places, and negligible elsewhere. Hence the numerical supports for many eigenvectors are disjoint. The essential structure of the matrix is exhibited with \(n=10\),
and it has 5 eigenvalues near 0, 3 eigenvalues near \(10^5\) and 2 near \(-10^5\). All the eigenvalues are well-conditioned and the three codes obtain the correct number of eigenvalues in each cluster.
When \(n=20\) there are 10 eigenvalues near \(10^{-5}\), 6 near \(-10^5\) and 4 near \(10^5\); \(relcond(\uplambda ;C)\) and \(relcond(\uplambda ;{L},{U})\) are all less than \(1.2 \;10^{1}\); the maximum residual norm for C and \(J=LU\) is \({{\mathcal {O}}}(10^{-2})\). For the eigenvalues with small modulus, BGT and \(\textit{3dqds}\) (with 2 RQI, in average) compute approximations with relative errors of \({{\mathcal {O}}}(\varepsilon )\), whereas eig yield larger relative errors, as large as \(10^{-6}\). See Table 7.
8.4 Other scaled test matrices
Here we consider other test matrices from [1]. The eigenvalues of these matrices have a variety of distributions, in particular, the eigenvalues in Test 4 and Test 7 are distributed along curves. See Fig. 5. All these matrices are given in the form
The extreme relative errors, condition numbers and residual norms for the three codes, Matlab’s eig, BGT and 3dqds, are shown in Tables 8 and 9.
Table 10 reports the CPU time in seconds required by 3dqds versus the time required by Matlab’s eig, BGT and ex3dqds with n ranging from 400 to 1000. Examples were chosen to represent the best, worst, and average efficiency of BGT.
8.5 Liu matrix
Liu [16] devised an algorithm to obtain one-point spectrum unreduced tridiagonal matrices of arbitrary dimension \(n \times n\). These matrices have only one eigenvalue, zero with multiplicity n, the Jordan form consists of one Jordan block and so the eigenvalue condition number is infinite. Our code 3dqds computes this eigenvalue exactly (and also the generalized eigenvectors) using the following method which is part of the prologue. See [12].
The best place to start looking for eigenvalues of a tridiagonal matrix \(C=tridiag({\varvec{b}},{\varvec{a}},{\varvec{c}})\) is at the arithmetic mean which we know \((\mu =trace(C)/n)\). Before converting to J-form and factoring, we check whether \(\mu \) is an eigenvalue by using the 3-term recurrence to solve
Here
and
If, by chance, \(\upsilon \) vanishes, or is negligible compared to \(\Vert {\varvec{x}}\Vert \), then \(\mu \) is an eigenvalue (to working accuracy) and \({\varvec{x}}\) is an eigenvector. To check its multiplicity we differentiate with respect to \(\mu \) and solve
with \(y_1=0\), \(y_2=1=x_2^\prime \) \((=x_1)\). If
vanishes, or is negligible w.r.t. \(\Vert {\varvec{y}}\Vert \), then we continue the same way until the system is inconsistent or there are n generalized eigenvectors.
Usually \(\upsilon \ne 0\) and the calculation appears to have been a waste. This is not quite correct. In exact arithmetic, triangular factorization of \(\mu I-C\) or \(\mu I-J\), where \(J=D C D^{-1}\), will break down if, and only if, \(x_j\) vanishes for \(1<j<n\). So our code examines \(\min _j |x_j|\) and if it is too small w.r.t. its neighbors and w.r.t. \(\Vert {\varvec{x}}\Vert \) then we do not choose \(\mu \) as our initial shift. Otherwise we do obtain initial L and U from \(J-\mu I=LU\).
For comparison purposes, we ignored our prologue and give to our \(\textit{3dqds}\) code the Liu matrices for \(n=14\) and \(n=28\), \(tridiag({\varvec{1}}, \varvec{\alpha }^n,\varvec{\gamma }^n)\) defined by
and
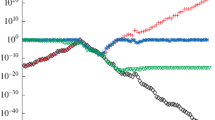
The accuracy of the approximations delivered by \(\textit{3dqds}\) is as good as the accuracy of those provided by Matlab and BGT. The absolute errors are \({{\mathcal {O}}}(10^{-2})\) for \(n=14\) and \({{\mathcal {O}}}(10^{-1})\) for \(n=28\). The number of iterations needed for 3dqds to converge is less than 3n. See Fig. 6a, b. We show the numerical results along with the circles \(z=\root n \of {\varepsilon }\).
We also considered glued Liu matrices which are defined as the direct sum of two Liu matrices, shifting one of them by \(\sqrt{2}\) and letting the glue between them be \(\varepsilon \). Roundoff will give us two clusters, one around 0, the other around \(\sqrt{2}\). This is not a one-point spectrum matrix and all three methods give the results expected by perturbation theory. See Fig. 6c, d. This is a very unstable example, the condition numbers all exceed \(10^{10}\).
9 Conclusions
Following the broad success of the HQR algorithm to compute eigenvalues of real square matrices it seems natural to use a sequence of similarity transforms to reduce an initial real matrix to eventual triangular form and also deflate eigenvalues from the bottom of the matrix as they converge. Any real (unreduced) tridiagonal matrix is easily put into J-form (all superdiagonal entries are 1) and such matrices ask for the use of the LR (not QR) algorithm since it preserves the J-form. The potential breakdown of the LR transform, from a 0 pivot, was a strong deterrent in the early days (1960s) [20] but today is a mild nuisance as explained in Sect. 5.1. A further incentive is that the whole procedure can be carried out in real arithmetic since complex conjugate pairs of eigenvalues are determined from \(2\times 2\) submatrices that converge and may be deflated in a manner similar to real eigenvalues. The more recent success of the dqds transform in computing singular values of bidiagonal matrices encouraged us to keep out J matrices in factored form: \(J - \sigma I= LU\), \({\widehat{J}}=UL\), because, in exact arithmetic, the two algorithms, LR and dqds, are equivalent. In addition the dqds transform of today is numerically superior to the original, and seminal, qd transform discovered by Rutishauser [26] and which gave rise to the LR algorithm itself.
In order to hasten convergence we will need to apply complex conjugate pairs of shifts to our current \(LU = J\) matrix. It is well known how to do this entirely in real arithmetic in the context of the LR algorithm. To the best of our knowledge this has not been tried in the context of dqds. The main contribution of this paper is the solution to this challenge. We realized that three, not two, transforms are required to return to real factors L and U when complex shifts are applied consecutively. This is the nature of our explicit version, a local detour invoking complex arithmetic. We went further and produced a subprogram 3dqds that accomplishes the same goal but in (exact) real arithmetic. This implicit version is more efficient than the explicit but is sensitive to roundoff error in its initial step. Experts will recall the papers on “washout of the shift” in the implicit shift HQR algorithm in the 1980s. We can not prove that our algorithm is backward stable. In fact we dought that it is. However we do show that the three parts of the inner loop separately enjoy high mixed relative stability.
In the process of implementing our new features we were led to a novel and detailed criterion for deciding when our \(J = LU\) matrix has split into two or more unreduced submatrices. We check for splits at every iteration. Our new subprograms must only be applied to unreduced matrices. We also gave attention to the choice of a new shift when a factorization fails and when to start using the bottom \(2\times 2\) submatrix for shifting.
We save a lot of space by confining our eigenvector calculations to the \(\Delta T\) form so that only one vector need be stored. From it we can compute the relative condition numbers that we need. Instructions are given how to generate the eigenvectors for the original and the J-form representions.
References
Bini, D.A., Gemignani, L., Tisseur, F.: The Ehrlich–Aberth method for the nonsymmetric tridiagonal eigenvalue problem. SIAM J. Matrix Anal. Appl. 27(1), 153–175 (2005)
Bunse-Gerstner, A.: An analysis of the HR algorithm for computing the eigenvalues of a matrix. Linear Algebra Appl. 35, 155–173 (1981)
Clement, P.A.: A class of triple-diagonal matrices for test purposes. In: SIAM Review, vol. 1 (1959)
Cullum, J.K.: A QL procedure for computing the eigenvalues of complex symmetric tridiagonal matrices. SIAM J. Matrix Anal. Appl. 17(1), 83–109 (1996)
Day, D.: Semi-duality in the Two-sided Lanczos Algorithm. Ph.D Thesis, University of California, Berkeley (1993)
Demmel, J.W.: Applied Numerical Linear Algebra, Society for Industrial and Applied Mathematics (1997)
Dhillon, I.S., Parlett, B.N.: Multiple representations to compute orthogonal eigenvectors of symmetric tridiagonal matrices. Linear Algebra Appl. 387, 1–28 (2004)
Dhillon, I.S., Parlett, B.N.: Orthogonal eigenvectors and relative gaps. SIAM J. Matrix Anal. Appl. 25, 858–899 (2004)
Fernando, K.V., Parlett, B.: Accurate singular values and differential QD algorithms. Numer. Math. 67, 191–229 (1994)
Fernando, K.V.: On computing an eigenvector of a tridiagonal matrix. Part I: basic results. SIAM J. Matrix Anal. Appl. 18, 1013–1034 (1997)
Ferreira, C.: The Unsymmetric Tridiagonal Eigenvalue Problem. Ph.D Thesis, University of Minho (2007). http://hdl.handle.net/1822/6761
Ferreira, C., Parlett, B.: Convergence of LR algorithm for a one-point spectrum tridiagonal matrix. Numer. Math. 113(3), 417–431 (2009)
Ferreira, C., Parlett, B., Froilán, M.D.: Sensitivity of eigenvalues of an unsymmetric tridiagonal matrix. Numer. Math. (2012). https://doi.org/10.1007/s00211-012-0470-z
Francis, J.G.F.: The QR transformation—a unitary analogue to the LR transformation, parts I and II. Comput. J. 4, 265–272; 332–245 (1961/1962)
Kahan, W., Parlett, B.N., Jiang, E.: Residual bounds on approximate eigensystems of non-normal matrices. SIAM J. Numer. Anal. 19, 470–484 (1982)
Liu, Z.A.: On the extended HR algorithm. Technical Report PAM-564, Center for Pure and Applied Mathematics, University of California, Berkeley, CA, USA (1992)
Parlett, B.N., Reinsch, C.: Balancing a matrix for calculation of eigenvalues and eigenvectors. Numer. Math. 13, 292–304 (1969)
Parlett, B.N.: The Rayleigh quocient iteration and some generalizations for non-normal matrices. Math. Comput. 28(127), 679–693 (1974)
Parlett, B.N.: The contribution of J. H. Wilkinson to numerical analysis. In: Nash, S.G. (ed.), A History of Scientific Computing, ACM Press, p. 25 (1990)
Parlett, B.N.: Reduction to tridiagonal form and minimal realizations. SIAM J. Matrix Anal. Appl. 13, 567–593 (1992)
Parlett, B.N.: The new QD algorithms. Acta Numer 4, 459–491 (1995)
Parlett, B.N., Dhillon, I.S.: Fernandos solution to Wilkinsons problem: an application of double factorization. Linear Algebra Appl. 267, 247–279 (1997)
Parlett, B.N., Marques, O.A.: An implementation of the DQDS algorithm. Linear Algebra Appl. 309, 217–259 (2000)
Parlett, B., Dopico, F.M., Ferreira, C.: The inverse eigenvector problem for real tridiagonal matrices. SIAM J. Matrix Anal. Appl. 37, 577–597 (2016)
Pasquini, L.: Accurate computation of the zeros of the generalized Bessel polynomials. Numerische Mathematic 86, 507–538 (2000)
Rutishauser, H.: Der Quotienten-Differenzen-Algorithmus. Z. Angew. Math. Physik 5, 233–251 (1954)
Rutishauser, H.: Der Quotienten-Differenzen-Algorithmus. Mitt. Inst. Angew. Math. ETH, vol. 7, Birkh\(\ddot{\text{a}}\)user, Basel (1957)
Rutishauser, H.: Solution of eigenvalue problems with the LR-transformation. Natl. Bur. Stand. Appl. Math. Ser. 49, 47–81 (1958)
Rutishauser, H., Schwarz, H.R.: The LR transformation method for symmetric matrices. Numer. Math. 5, 273–289 (1963)
Slemons, J.: Toward the Solution of the Eigenproblem: Nonsymmetric Tridiagonal Matrices. Ph.D Thesis, University of Washington, Seattle (2008)
Slemons, J.: The result of two steps of the LR algorithm is diagonally similar to the result of one step of the HR algorithm. SIAM J. Matrix Anal. Appl. 31(1), 68–74 (2009)
Trefethen, L.N., Embree, M.: Spectra and pseudospectra. In: The Behavior of Nonnormal Matrices and Operators, Princeton University Press (2005)
Watkins, D.S.: QR-like algorithms—an overview of convergence theory and practice. Lect. Appl. Math. 32, 879–893 (1996)
Watkins, D.S., Elsner, L.: Convergence of algorithms of decomposition type for the eigenvalue problem. Linear Algebra Appl. 143, 19–47 (1991)
Willems, P.R., Lang, B.: Twisted factorizations and QD-type transformations for the \(\text{ MR}^3\) algorithm—new representations and analysis. SIAM J. Matrix Anal. Appl. 33(2), 523–553 (2012)
Wu. Z.: The Triple DQDS Algorithm for Complex Eigenvalues. Ph.D Thesis, University of California, Berkeley (1996)
Xu, H.: The relation between the QR and LR algorithms. SIAM J. Matrix Anal. Appl. 19(2), 551–555 (1998)
Yao, Y.: Error Analysis of the QDs and DQDs Algorithms. Ph.D Thesis, University of California, Berkeley (1994)
Acknowledgements
The authors would like to thank Associate Editor Martin H. Gutknecht and the anonymous referees for forcing us to look more deeply into an error analysis of our triple dqds algorithm (first version) and to give a clearer presentation of its mathematical analysis and implemention details (last version).
Author information
Authors and Affiliations
Corresponding author
Additional information
The research of the first author was partially financed by Portuguese Funds through FCT (Fundação para a Ciência e a Tecnologia) within the Projects UIDB/00013/2020 and UIDP/00013/2020.
Appendices
3dqds algorithm


Pseudocode for the whole algorithm






Rights and permissions
About this article
Cite this article
Ferreira, C., Parlett, B. A real triple dqds algorithm for the nonsymmetric tridiagonal eigenvalue problem. Numer. Math. 150, 373–422 (2022). https://doi.org/10.1007/s00211-021-01254-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01254-z