Numerical validation of blow-up solutions with quasi-homogeneous compactifications

Abstract

We provide a numerical validation method of blow-up solutions for finite dimensional vector fields admitting asymptotic quasi-homogeneity at infinity. Our methodology is based on quasi-homogeneous compactifications containing quasi-parabolic-type and directional-type compactifications. Divergent solutions including blow-up solutions then correspond to global trajectories of associated vector fields with appropriate time-variable transformation tending to equilibria on invariant manifolds representing infinity. We combine standard methodology of rigorous numerical integration of differential equations with Lyapunov function validations around equilibria corresponding to divergent directions, which yields rigorous upper and lower bounds of blow-up time as well as rigorous profile enclosures of blow-up solutions.

1 Introduction

Our concern in this paper is blow-up solutions of the following initial value problem of an autonomous system of ordinary differential equations (ODEs) in $\mathbb {R}^n$:

$$\begin{aligned} \frac{dy(t)}{dt}=f (y(t)),\quad y(0)=y_0, \end{aligned}$$

(1.1)

where $t\in [0,T)$ with $0<T\le \infty$, $f:\mathbb {R}^n\rightarrow \mathbb {R}^n$ is a $C^1$ function and $y_0\in \mathbb {R}^n$. We shall call a solution $\{y(t)\}$ of the initial value problem (1.1) a blow-up solution if

$$\begin{aligned} t_{\max }:=\sup \left\{ \bar{t}\mid \text{ a } \text{ solution } y\in C^1([0,\bar{t})) \text{ of } ](1.1) \text{ exists }\right\} < \infty . \end{aligned}$$

The maximal existence time $t_{\max }$ is then called the blow-up time of (1.1). Blow-up solutions can be seen in many dynamical systems generated by (partial) differential equations like nonlinear heat equations or Keller–Segel systems. These are categorized as the presence of finite-time singularity in dynamical systems, and many researchers have broadly studied these phenomena from mathematical, physical, numerical viewpoints and so on (e.g. [9, 12, 18, 23] from theoretical viewpoints and e.g. [1,2,3,4, 24] from numerical viewpoints). Fundamental questions for blow-up problem are whether or not a solution blows up and, if does, when, where, and how it blows up. In general blow-up phenomena depend on initial data. Rigorous concrete detection of fundamental information of blow-up solutions as functions of initial data remains a nontrivial problem.

Recently, authors and their collaborators have provided a numerical validation procedure based on interval and affine arithmetics for calculating rigorous blow-up profiles and their blow-up time [21]. The approach is based on compactification of phase space; embedding the original phase space into a compact manifold M, possibly with boundary. In this methodology, the infinity on the original phase space can correspond to a point on $\mathcal {E} \equiv \partial M$ or a specified point on M called a point at infinity. Combining a compactification with an appropriate time-scale transformation, called time-variable desingularization, suitable for given vector field, divergent solutions including blow-up solutions are characterized as global trajectories of the transformed vector field on M tending to a point, such as an equilibrium $x_*$, on $\mathcal {E}$. Finally, the Lyapunov function validation ([17]) around $x_*\in \mathcal {E}$ is applied to derivation of a re-parameterization of trajectories so that we can validate rigorous lower and upper bounds of blow-up time $t_{\max }$ with numerical validations. In this methodology, (i) rigorous numerical integration of ODEs, (ii) eigenvalue validations, and (iii) polynomial estimates essentially realize numerical validations of blow-up solutions with their blow-up time. A remarkable point of the above methodology is that, unlike the approximation method mentioned above, the final numerical validation results contain mathematically rigorous information of solutions. Therefore the methodology rigorously detect the nature of blow-up solutions. However, applicability of the proposed methodology there is restricted to vector fields which are asymptotically homogeneous at infinity, since applied compactifications are assumed to respect homogeneous scalings. In other words, verifications of blow-ups for differential equations possessing, say quasi-homogeneous scaling laws such as $h(u,v) := u^2-v$ may return meaningless information.¹ If we apply such a numerical validation methodology to a broad class of differential equations, we have to choose appropriate compactifications which appropriately extracts information of dynamics at infinity.

Inspired by the above work, the first author has discussed blow-up solutions for differential equations which are asymptotically quasi-homogeneous at infinity from the viewpoint of dynamical systems [16]. There a new quasi-homogeneous compactification called quasi-Poincaré compactification is defined as a quasi-homogeneous analogue of well-known Poincaré compactifications and as a global compactification alternative of well-known local compactifications which shall be called directional compactifications (e.g., [7] with a terminology Poincaré-Lyapunov disks). By using the same essence as previous works about blow-up solutions [8, 21], several blow-up solutions for asymptotically quasi-homogeneous vector fields can be characterized by trajectories on stable manifolds of “hyperbolic invariant sets” on the boundary $\mathcal {E}$ of a manifold M. Moreover, such blow-up solutions characterize their blow-up rates from the growth rate of original vector fields. The same characterizations also make sense for dynamical systems with directional compactifications. A series of studies involving characterization of blow-up solutions in [16] contain blow-up results in the previous work [8], and the applications to numerical validations of blow-up solutions for systems of asymptotically quasi-homogeneous differential equations are expected.

Our present aim is to provide numerical validation methodology of blow-up solutions for systems of differential equations with asymptotic quasi-homogeneity at infinity. It turns out that fundamental features of a good class of quasi-homogeneous compactifications enable us to apply the same methodology as [21] to the present blow-up validations. Note that there is another direction for characterizing blow-up solutions with computer assistance [5], where the detection of blow-up behavior is reduced to the existence of bounded time-periodic solutions with an appropriate transformation. There the problem is reduced to the zero-finding one for an appropriate equation in functional analytic setting, while our present approach is based on integration of initial value problems for a certain general class of autonomous ODEs as well as topological arguments using Lyapunov functions (e.g. [17]).

The rest of this paper is organized as follows. In Sect. 2, we provide tools for our treatments of blow-up solutions. First we review a class of vector fields called asymptotically quasi-homogeneous vector fields discussed in [16], and define an admissible class of compactifications with given quasi-homogeneous type. We see that our admissible class admits the same asymptotic properties at infinity as quasi-Poincaré compactifications introduced in [16]. As a nontrivial example, we also introduce a concrete compactification which is admissible in our sense, called a quasi-parabolic compactification. This compactification is a quasi-homogeneous analogue of (homogeneous) parabolic compactifications [8, 21]. Directional compactifications, which are defined only in subsets of the whole space, are also reviewed. In Sect. 3, we study vector fields and dynamics on compactified manifolds. Under our admissible compactifications, we have a good correspondence of dynamical systems between on original phase spaces and on compactified manifolds. Moreover, as in the case of quasi-Poincaré compactifications, we can define desingularized vector fields on compactified manifolds so that dynamics at infinity makes sense. Here we have a new essential result that, for $C^1$ vector field f in the original problem, the desingularized vector field g with quasi-parabolic compactifications becomes $C^1$ including the boundary of compactified manifolds corresponding to the infinity. This property is very crucial because the desingularized vector fieldgwith quasi-Poincaré compactifications is not always$C^1$even iffis sufficiently smooth. Details are shown in [16]. The feature of quasi-parabolic compactifications enables us to study stability analysis for dynamical systems without any obstructions of regularity of vector fields. In Sect. 4, we provide criteria for validating blow-up solutions and numerical validation procedure for blow-up solutions with their blow-up time. Our criteria consists of not only pure mathematical arguments but also numerical validation implementations for blow-up solutions. Our arguments indicate that blow-up solutions correspond to trajectories on stable manifolds of asymptotically stable equilibria on$\mathcal {E}$, which can be validated by standard techniques of dynamical systems with computer assistance. We review a fundamental tool called Lyapunov function, which validates level surfaces around equilibria and is essential to estimate explicit enclosures of blow-up time. We conclude Sect. 4 by providing concrete validation steps for blow-up solutions. Finally, we demonstrate several numerical validation examples of blow-up solutions in Sect. 5 to show applicability of our methodology to blow-up solutions with various morphology.

2 Compactifications

In this section, we introduce several compactifications of phase spaces which are appropriate for studying dynamics at infinity. There are mainly two types of compactifications that are defined on the whole phase space $\mathbb {R}^n$ or just on subsets of $\mathbb {R}^n$. The main aim of this section is to introduce a general, globally defined, compactifications of quasi-homogeneous type, while locally defined ones are well known and well applied to various systems for studying complete dynamics through dynamics at infinity (e.g. [7, 14]).

As an example of such appropriate ones, we introduce the quasi-parabolic compactification. This compactification is an alternative of admissible, homogeneous ones discussed in e.g., [8, 10], and of quasi-Poincaré compactifications derived in [16]. Our present compactification is based on an appropriate scaling of vector-valued functions at infinity and quasi-homogeneous desingularization of singularities in dynamical systems (e.g., [6]). Moreover, it overcomes the lack of smoothness of (transformed) vector fields at infinity, which is mentioned later. Firstly, we briefly review quasi-homogeneous vector fields discussed in [16]. Secondly, we introduce a class of compactifications called (admissible global) quasi-homogeneous compactifications which are defined on the whole phase space. Thirdly, we define the quasi-parabolic compactification. Finally, we review a well-known quasi-homogeneous (local) compactification which shall be called directional compactification. Once we know that divergent solutions has an identical sign for some component, the latter type of compactifications make our blow-up problem much simpler than globally defined ones.

2.1 Quasi-homogeneous vector fields

First of all, we review a class of vector fields in our present discussions.

Definition 2.1

(Quasi-homogeneous vector fields, e.g., [6]) Let $f: \mathbb {R}^n \rightarrow \mathbb {R}$ be a smooth function. Let $\alpha _1,\ldots , \alpha _n, k \ge 1$ be natural numbers. We say that f is a quasi-homogeneous function of type$(\alpha _1,\ldots , \alpha _n)$and orderk if

$$\begin{aligned} f(r^{\alpha _1}x_1,\ldots , r^{\alpha _n}x_n) = r^k f(x_1,\ldots , x_n),\quad \forall x\in \mathbb {R}^n,\quad r\in \mathbb {R}. \end{aligned}$$

Next, let $X = \sum _{j=1}^n f_j(x)\frac{\partial }{\partial x_j}$ be a smooth vector field on $\mathbb {R}^n$. We say that X, or simply $f = (f_1,\ldots , f_n)$ is a quasi-homogeneous vector field of type$(\alpha _1,\ldots , \alpha _n)$and order$k+1$ if each component $f_j$ is a quasi-homogeneous function of type $(\alpha _1,\ldots , \alpha _n)$ and order $k + \alpha _j$.

For applications to general vector fields, in particular for dynamics near infinity, we define the following notion.

Definition 2.2

(Asymptotically quasi-homogeneous vector fields at infinity, [16]) Let $f = (f_1,\ldots , f_n):\mathbb {R}^n \rightarrow \mathbb {R}^n$ be a smooth function. We say that $X = \sum _{j=1}^n f_j(x)\frac{\partial }{\partial x_j}$, or simply f is an asymptotically quasi-homogeneous vector field of type$(\alpha _1,\ldots , \alpha _n)$and order$k+1$at infinity if

$$\begin{aligned} \lim _{r\rightarrow +\infty } r^{-(k+\alpha _j)}\left\{ f_j(r^{\alpha _1}x_1, \ldots , r^{\alpha _n}x_n) - r^{k+\alpha _j}(f_{\alpha ,k})_j(x_1, \ldots , x_n) \right\} = 0 \end{aligned}$$

holds uniformly for $(x_1,\ldots , x_n)\in S^{n-1}$ for some quasi-homogeneous vector field $f_{\alpha ,k} = ((f_{\alpha ,k})_1,\ldots , (f_{\alpha ,k})_n)$ of type $(\alpha _1,\ldots , \alpha _n)$ and order $k+1$.

The asymptotic quasi-homogeneity at infinity plays a key role in consideration of (polynomial) vector fields at infinity, which is shown later. Throughout successive sections, consider the (autonomous) polynomial vector field

$$\begin{aligned} y' = f(y), \end{aligned}$$

(2.1)

where $f: \mathbb {R}^n \rightarrow \mathbb {R}^n$ be a smooth function. We further assume that f is an asymptotically quasi-homogeneous vector field of type $\alpha = (\alpha _1,\ldots , \alpha _n)$ and order $k+1$ at infinity. The next step is to determine an appropriate transform of the phase space so that we can consider dynamics at infinity in an appropriate sense. One approach for realizing appropriate transformation of the vector field is based on the choice of appropriate compactifications with the type associated with that for f.

2.2 Admissible global quasi-homogeneous compactifications

Here we define a class of globally defined compactifications.

Definition 2.3

(Admissible global quasi-homogeneous compactification) Fix natural numbers $\alpha _1,\ldots , \alpha _n$. Let $\beta _1,\ldots , \beta _n$ be natural numbers² such that

$$\begin{aligned} \alpha _1 \beta _1 = \alpha _2 \beta _2 = \ldots = \alpha _n \beta _n \equiv c \in \mathbb {N}. \end{aligned}$$

(2.2)

Define a functional p(y) as

$$\begin{aligned} p(y) := \left( y_1^{2\beta _1} + y_2^{2\beta _2} + \cdots + y_n^{2\beta _n} \right) ^{1/2c}. \end{aligned}$$

Define the mapping $T: \mathbb {R}^n \rightarrow \mathbb {R}^n$ as

$$\begin{aligned} T(y) = x,\quad x_i := \frac{y_i}{\kappa (y)^{\alpha _i}}, \end{aligned}$$

where $\kappa = \kappa (y)$ is a $C^1$ positive function. We say that T is an (admissible) global quasi-homogeneous compactification (of type$\alpha$) if all the following conditions hold:

(A0):

$\kappa (y) = q\circ p(y)$ for some positive, smooth function $q = q(R)$ defined on $R\ge 0$ which is strictly increasing in $R>0$, and $\kappa (y) > p(y)$ holds for all $y\in \mathbb {R}^n$,

(A1):

For any sequence $\{y_n\}_{n\ge 1}\subset \mathbb {R}^n$ with $p(y_n)\rightarrow \infty$ as $n\rightarrow \infty$, $\lim _{n\rightarrow \infty } \left\{ p(y_n) / \kappa (y_n)\right\} = 1$ holds,

(A2):

$\nabla \kappa (y) = ((\nabla \kappa (y))_1, \ldots , (\nabla \kappa (y))_n)$ satisfies

$$\begin{aligned} (\nabla \kappa (y))_i \sim \frac{1}{\alpha _i}\frac{y_i^{2\beta _i-1}}{p(y)^{2c-1}}\quad \text { as }\quad p(y)\rightarrow \infty . \end{aligned}$$

(A3):

Letting $y_\alpha = (\alpha _1 y_1,\ldots , \alpha _n y_n)^T$ for $y\in \mathbb {R}^n$, we have $\langle y_\alpha , \nabla \kappa \rangle < \kappa (y)$ holds for any $y\in \mathbb {R}^n$.

In the present argument, the notation $f(x)\sim g(x)$ means that there exists a constant $K>1$ such that $K^{-1}g(x)< f(x)< Kg(x)$ for large x.

The admissibility conditions (A0) $\sim$ (A3) come from fundamental properties of quasi-Poincaré compactifications$T = T_{qP}$ introduced in [16], which is defined by $\kappa (y) = \left( 1+p(y)^{2c}\right) ^{1/2c}$. This definition is also expressed as $\kappa (y) = q\circ p(y)$ with $q(R) = \left( 1+R^{2c}\right) ^{1/2c}$. From (2.2), it immediately holds that $p(y)^{2c} = \kappa (y)^{2c}p(x)^{2c}$ and hence $p(x)\rightarrow 1$ holds as $p(y)\rightarrow \infty$, which follows from the requirement (A1). By the condition (A0), T maps $\mathbb {R}^n$ into

$$\begin{aligned} \mathcal {D} := \{x\in \mathbb {R}^n \mid p(x) < 1\}. \end{aligned}$$

In particular, the following proposition holds.

Proposition 2.4

The admissible global quasi-homogeneous compactification T is a bijection from $\mathbb {R}^n$ onto $\mathcal {D} = \{x\in \mathbb {R}^n \mid p(x) < 1\}$.

Proof

See Appendix C.1.³$\square$

Remark 2.5

The present definition of compactifications is relatively too restrictive to well-known definitions of homogeneous type compactifications due to the requirement $\kappa (y) = q\circ p(y)$ in (A0), which will be categorized as radial-type (cf. [8]). Although this restriction can be ultimately removed, we make this assumption for the following reasons. One is the technical simplicity for arguments below. On the other hand, in many applications, only radial-type (global) compactifications are used, which is the second reason for making the present assumption. If one needs non-radial-type compactifications in future problems, the generalization should be introduced.

Remark 2.6

For given $C>0$, admissible global quasi-homogeneous compactifications onto the set $\mathcal {D}_C\equiv \{x\in \mathbb {R}^n \mid p(x) < C\}$ can be also considered, in which case our requirements in Definition 2.3 are replaced by the following:

$\mathbf{(A0)}_C$:

$\kappa (y) = q_C\circ p(y)$ for some positive, smooth function $q_C = q_C(R)$ defined on $R\ge 0$ which is strictly increasing in $R>0$, and $\kappa (y) > C^{-1}p(y)$ holds for all $y\in \mathbb {R}^n$,

$\mathbf{(A1)}_C$:

For any sequence $\{y_n\}_{n\ge 1}\subset \mathbb {R}^n$ with $p(y_n)\rightarrow \infty$ as $n\rightarrow \infty$, $\lim _{n\rightarrow \infty } \left\{ p(y_n) / \kappa (y_n)\right\} = C$ holds,

$\mathbf{(A2)}_C$:

$\nabla \kappa (y) = ((\nabla \kappa (y))_1, \ldots , (\nabla \kappa (y))_n)$ satisfies

$$\begin{aligned} (\nabla \kappa (y))_i \sim \frac{1}{C\alpha _i}\frac{y_i^{2\beta _i-1}}{p(y)^{2c-1}}\quad \text { as }\quad p(y)\rightarrow \infty . \end{aligned}$$

$\mathbf{(A3)}_C$:

Letting $y_\alpha = (\alpha _1 y_1,\ldots , \alpha _n y_n)^T$ for $y\in \mathbb {R}^n$, we have $\langle y_\alpha , \nabla \kappa \rangle < \kappa (y)$ holds for any $y\in \mathbb {R}^n$.

For example, in case of the quasi-Poincaré compactification, the corresponding functional $\kappa$ is replaced by $\kappa (y) = \left( 1+(C^{-1}p(y))^{2c}\right) ^{1/2c}$.

The infinity in the original coordinate then corresponds to a point on the boundary

$$\begin{aligned} \mathcal {E} = \{x \in \mathbb {R}^n \mid p(x) = 1\}. \end{aligned}$$

Definition 2.7

(cf. [16]). We call the boundary $\mathcal {E}$ the horizon.

The horizon determines directions where solution trajectories diverge.

Definition 2.8

We say that a solution orbit y(t) of (2.1) with the maximal existence time (a, b), possibly $a = -\infty$ and $b = +\infty$, tends to infinity in the direction$x_*\in \mathcal {E}$(associated withT) (as $t\rightarrow a+0$ or $b-0$) if

$$\begin{aligned} p(y(t))\rightarrow \infty ,\quad \left( \frac{y_1}{\kappa (y)^{\alpha _1}}, \ldots , \frac{y_n}{\kappa (y)^{\alpha _n}}\right) \rightarrow x_*\quad \text { as }t\rightarrow a+0 \text { or }b-0. \end{aligned}$$

Note that the above argument is completely parallel to arguments of bijectivity of the quasi-Poincaré compactification [16]. Four properties (A0) $\sim$ (A3) in Definition 2.3 will play central roles in the theory of, which shall be called, global quasi-homogeneous compactifications and associated dynamics. Indeed, in the case of homogeneous compactifications, namely $\alpha _1 = \cdots = \alpha _n = \beta _1 = \cdots = \beta _n = 1$, these conditions describe admissibility of compactifications [8], which play central roles in dynamics at infinity. The Poincaré compactification; namely the quasi-Poincaré compactification of type $(1,\ldots , 1)$, is the prototype of other admissible homogeneous compactifications such as parabolic ones (e.g., [8, 21]), and hence properties (A0) $\sim$ (A3) which quasi-Poincaré compactifications possess will be appropriate to define an “admissible”class of global quasi-homogeneous compactifications.

2.3 Quasi-parabolic compactification

Here we introduce an example of global quasi-homogeneous compactifications other than quasi-Poincaré ones, which is an analogue of parabolic compactifications discussed in [8, 21].

Let the type $\alpha = (\alpha _1,\ldots , \alpha _n)\in \mathbb {Z}_{>0}^n$ fixed. Let $\{\beta _i\}_{i=1}^n$ and c be a collection of natural numbers satisfying (2.2). For any $x\in \mathcal {D}$, define $y\in \mathbb {R}^n$ by

$$\begin{aligned} S(x) = y,\quad y_j = \frac{x_j}{(1- p(x)^{2c})^{\alpha _j}},\quad j=1,\ldots , n. \end{aligned}$$

Let $\tilde{\kappa }_\alpha (x) := (1-p(x)^{2c})^{-1}$, which satisfies $\tilde{\kappa }_\alpha (x) \ge 1$ for all $x\in \mathcal {D}$. Moreover, $y\not = 0$ implies $\tilde{\kappa }_\alpha (x) > 1$. We also have

$$\begin{aligned} p(y)^{2c} = \tilde{\kappa }_\alpha (x)^{2c}p(x)^{2c} = \tilde{\kappa }_\alpha (x)^{2c}\left( 1-\frac{1}{\tilde{\kappa }_\alpha (x)}\right) . \end{aligned}$$

(2.3)

This equality indicates that $p(y) = p(S(x)) < \tilde{\kappa }_\alpha (x)$ holds for all $x\in \mathcal {D}$.

Lemma 2.9

Let $F(\kappa ; R) := \kappa ^{2c} - \kappa ^{2c-1} - R^{2c}$ for $R\ge 0$. Then, for any $R\ge 0$, there is a unique $\kappa = q(R)$ satisfying $q(0) = 1$ such that $F(q(R); R) \equiv 0$. Moreover, $q(R) > 1$ holds for all $R>0$ and q(R) is smooth with respect to $R\ge 0$.

Proof

Observe that $F(1;0) = 0$, $F(1;R) = -R^{2c} < 0$ as long as $R > 0$. Moreover,

$$\begin{aligned} \frac{\partial F}{\partial \kappa }(\kappa ; R) = 2c\kappa ^{2c-1} - (2c-1)\kappa ^{2c-2} > 2c\kappa ^{2c-2}(\kappa - 1) \ge 0\quad (\text {if }\kappa \ge 1), \end{aligned}$$

(2.4)

which shows that $F(\cdot ;R)$ is strictly increasing in $\{\kappa \ge 1\}$. Therefore the Implicit Function Theorem (IFT) shows that there is a small neighborhood⁴U of 0 in $\mathbb {R}$ and the uniquely determined function $\kappa = q(R)$ such that $q(0) = 1$ and that, for any $R\in U$, $F(q(R);R) \equiv 0$ holds. Smoothness property is trivial since $F(\kappa ;R)$ is just a polynomial of $\kappa$. Since c is a positive integer, the positivity in (2.4) holds for sufficiently small U. Here consider the following two cases.

Case 1::

$0 \le R <1$. IfUis chosen sufficiently small, this is the case for$R\in U$.

If a constant $c_R\ge 1$ is chosen sufficiently large, we have

$$\begin{aligned} F(c_R;R) = c_R^{2c} - c_R^{(2c-1)} - R^{2c}> c_R^{2c} - c_R^{(2c-1)} -1 > 0. \end{aligned}$$

Case 2::

$R \ge 1$.

Also in this case, choosing a positive constant $c_R$ sufficiently large we have

$$\begin{aligned} F\left( c_R R^{2c/(2c-1)};R \right) = c_R^{2c} R^{4c^2/(2c-1)} - (c_R^{2c-1}+1)R^{2c} \ge \{c_R^{2c} - (c_R^{2c-1}+1) \} R^{2c} \end{aligned}$$

and $c_R^{2c} - (c_R^{2c-1}+1) >0$, which implies $F\left( c_R R^{2c/(2c-1)}; R \right) > 0$.

In both cases, the Intermediate Theorem can be applied to the existence of a function $\tilde{q} = \tilde{q}(R)$ satisfying $F(\tilde{q}(R); R) = 0$ for each R. Since $F(1;R) = -R^{2c} < 0$ for any $R\not = 0$ and $F(\kappa ;R)$ is increasing for $\kappa \ge 1$, then $\tilde{q}(R)$ has to be greater than 1. Thus the inequality (2.4), and hence IFT is applied to show that $\tilde{q}(R)$ is uniquely determined and is locally smooth for any $R>0$. On the other hand, $\tilde{q}(R) = q(R)$ holds for $R\in U$, and hence we conclude that $\tilde{q}(R) = q(R)$ holds for all $R\ge 0$. $\square$

Now we have $\tilde{\kappa }_\alpha (x)$ satisfies $F(\tilde{\kappa }_\alpha (x);p(y)) = 0$. By the uniqueness of $\kappa (y) = q(R)$ with respect to $R=p(y)$, for any $y\in \mathbb {R}^n\setminus \{\mathbf{0}\}$, $\kappa (y) \equiv \kappa (S(x)) := \tilde{\kappa }_\alpha (x)$ is well defined. We are then ready to introduce the new compactification mapping.

Definition 2.10

(Quasi-parabolic compactification) Let the type $\alpha = (\alpha _1,\ldots , \alpha _n)\in \mathbb {Z}_{>0}^n$ fixed. Let $\{\beta _i\}_{i=1}^n$ and c be a collection of natural numbers satisfying (2.2). Define $T_{para}:\mathbb {R}^n\rightarrow \mathcal {D}$ as

$$\begin{aligned} T_{para}(y) := x,\quad x_i = \frac{y_i}{\kappa (y)^{\alpha _i}}, \end{aligned}$$

where $\kappa = \kappa (y) = \tilde{\kappa }_\alpha (x)$ is the unique zero of $F(\kappa ; p(y))=0$ given in Lemma 2.9. We say $T_{para}$ the quasi-parabolic compactification (with type$\alpha$).

Theorem 2.11

Let the type $\alpha = (\alpha _1,\ldots , \alpha _n)\in \mathbb {Z}_{>0}^n$ fixed. Let $\{\beta _i\}_{i=1}^n$ and c be a collection of natural numbers satisfying (2.2). Then the quasi-parabolic compactification $T_{para}$ is an admissible global quasi-homogeneous compactification. In particular, $T_{para}^{-1}=S$.

Proof

By construction in the proof of Lemma 2.9, $\kappa (y)$ indeed has the form $\kappa (y) = q(p(y))$ satisfying $F(\kappa (y); p(y)) \equiv 0$. For $\kappa \ge \max \{1,p(y)\}$, we have

$$\begin{aligned} \kappa (y)^{2c} - p(y)^{2c} = \kappa (y)^{2c-1} > 0. \end{aligned}$$

Since $p = p(y)$ is smooth, then $\kappa = \kappa (y)$ can be regarded as the composition of smooth functions $R=p(y)$ and $q = q(R)$. In particular, $\kappa =\kappa (y)$ is $C^1$ with respect to y. Moreover, differentiating the identity $F(q(R);R) = q(R)^{2c} - q(R)^{2c-1} - R^{2c}\equiv 0$ with respect to R, we obtain

$$\begin{aligned} 2c q(R)^{2c-1}\frac{dq}{dR} - (2c-1)q(R)^{2c-2}\frac{dq}{dR} = 2c R^{2c-1}, \end{aligned}$$

namely,

$$\begin{aligned} \frac{dq}{dR} = \frac{2c R^{2c-1}}{2cq(R)^{2c-1} - (2c-1)q(R)^{2c-2}}. \end{aligned}$$

The denominator of the right-hand side is positive for $q = q(R) \ge 1$ and hence the above expression makes sense. This expression shows that q is strictly increasing for $R>0$. As a consequence, $\kappa = \kappa (y)$ satisfies (A0).

From (2.3), we have $p(y) \rightarrow \infty$ as $p(x)\rightarrow 1$ and vice versa. Moreover, from the identity $p(y)^{2c} = \kappa (y)^{2c}p(x)^{2c}$, we have $p(y) / \kappa (y) \rightarrow 1$ as $p(x)\rightarrow 1$, equivalently $p(y)\rightarrow \infty$, which shows (A1).

Differentiating $\kappa (y) = q(p(y)) \equiv q(R)$ with respect to y, we have

$$\begin{aligned} (\nabla _y \kappa (y))_j&= \frac{dq}{dR}\frac{\partial p}{\partial y_j} = \frac{2c p^{2c-1}}{2cq(R)^{2c-1} - (2c-1) q(R)^{2c-2}}\cdot \frac{1}{2c} q(R)^{1-2c} \cdot 2\beta _j y_j^{2\beta _j-1}\\&= \frac{2\beta _j y_j^{2\beta _j-1}}{2c q(R)^{2c-1} - (2c-1)q(R)^{2c-2}} = \frac{2\beta _j y_j^{2\beta _j-1}}{2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c} \kappa (y)^{-1}\right) }. \end{aligned}$$

By (A1), we have $R / q(R) \rightarrow 1$ as $R\rightarrow \infty$, equivalently $p(y)/\kappa (y)\rightarrow 1$ as $p(y)\rightarrow \infty$, and hence

$$\begin{aligned} (\nabla _y \kappa (y))_j \sim \frac{2\beta _j y_j^{2\beta _j-1}}{2cp(y)^{2c-1}} = \frac{y_j^{2\beta _j-1}}{\alpha _j p(y)^{2c-1}}\quad \text { as }\quad p(y)\rightarrow \infty , \end{aligned}$$

which shows (A2).

Next, check (A3). We have

$$\begin{aligned} \langle y_\alpha , \nabla _y \kappa \rangle = \sum _{j=1}^n \alpha _j y_j \frac{2\beta _j y_j^{2\beta _j-1}}{2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) } = \frac{2c p(y)^{2c}}{2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) } \end{aligned}$$

and it is sufficient to show $\kappa (y) \left\{ 2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) \right\} > 2c p(y)^{2c}$ for our statement. Let

$$\begin{aligned} G(y) := \kappa (y) \left\{ 2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) \right\} - 2c p(y)^{2c}. \end{aligned}$$

Then

$$\begin{aligned} G(y) = 2c\kappa (y)^{2c} - (2c-1)\kappa (y)^{2c-1} - 2cp(y)^{2c} > 2c\{\kappa (y)^{2c} - \kappa (y)^{2c-1} - p(y)^{2c}\} = 0 \end{aligned}$$

and we obtain (A3).

As a consequence, $T_{para}$ is an admissible global quasi-homogeneous compactification. In particular, $T_{para}:\mathbb {R}^n\rightarrow \mathcal {D}$ is a surjective $C^1$-diffeomorphism by Proposition 2.4. Observe that

$$\begin{aligned} S\circ T_{para}(y)&= S\left( \frac{y_1}{\kappa (y)^{\alpha _1}}, \ldots , \frac{y_n}{\kappa (y)^{\alpha _n}}\right) \\&= \left( \frac{y_1}{\kappa (y)^{\alpha _1}(1-\tilde{p}^{2c})^{\alpha _1}}, \ldots , \frac{y_n}{\kappa (y)^{\alpha _n}(1-\tilde{p}^{2c})^{\alpha _n}}\right) \\&=(y_1,\ldots , y_n) \equiv y, \end{aligned}$$

where

$$\begin{aligned} \tilde{p}^{2c} = \frac{p(y)^{2c}}{\kappa (y)^{2c}} = p(x)^{2c}\quad \text { and }\quad (1-\tilde{p}^{2c})^{-1} = \tilde{\kappa }_\alpha (x) \equiv \kappa (y). \end{aligned}$$

(2.5)

Similarly,

$$\begin{aligned} T_{para}\circ S(x)&= T_{para}\left( \frac{x_1}{(1-p(x)^{2c})^{\alpha _1}}, \ldots , \frac{x_n}{(1-p(x)^{2c})^{\alpha _n}}\right) \\&= \left( \frac{x_1}{(1-p(x)^{2c})^{\alpha _1}\kappa (y)^{\alpha _1}}, \ldots , \frac{x_n}{(1-p(x)^{2c})^{\alpha _n}\kappa (y)^{\alpha _n}}\right) \\&=(x_1,\ldots , x_n)\equiv x, \end{aligned}$$

which follows from the identity (2.5). Consequently, $S=T_{para}^{-1}$ holds and the proof is completed. $\square$

Remark 2.12

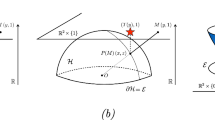
The name quasi-“parabolic” in $T_{para}$ comes from the homogeneous parabolic-type compactification; namely, $T_{para}$ with $(\alpha _1,\ldots , \alpha _n) = (1,\ldots , 1)$ and $c=1$. In the homogeneous case, $T_{para}$ is the composite of the mapping from $\mathbb {R}^n$ to a parabolic hypersurface $\{x_1^2 + \cdots + x_n^2 = x_{n+1}\}\subset \mathbb {R}^{n+1}$ and the projection $(x_1,\ldots , x_n, x_{n+1})\mapsto (x_1,\ldots , x_n)$. In the homogeneous case $\alpha = (1,\ldots , 1)$ and $c=1$, $\kappa = \kappa (y)$ is explicitly given as $\kappa (y) = \frac{1}{2}\left( 1 + \sqrt{1+4\sum _{i=1}^n y_i^2}\right)$, which is also calculated from $F(\kappa ;y) = 0$. See [8, 21] for details. Illustrations of parabolic and quasi-parabolic compactifications in two-dimensional situations are shown in Fig. 1.

The origin of parabolic-type compactifications comes from realization of approximations of unbounded functions discussed in [10]. Parabolic compactification (of homogeneous type, namely of type $\alpha = (1,\ldots , 1)$) is turned out to be a good tool for approximations of unbounded functions by rational functions, like Weierstrass’ approximations of continuous functions on closed intervals. One of the main features for realizing such approximations is that parabolic compactification maps rational functions to rational ones, which is not the case of Poincaré-type ones. The quasi-parabolic compactification is a nontrivial example of admissible global quasi-homogeneous compactifications. The biggest difference from quasi-Poincaré compactification is that the functional $\tilde{\kappa }_\alpha (x)$ does not contain any radicals. This property unconditionally guarantees the$C^1$smoothness of the desingularized vector field of goodfon$\overline{\mathcal {D}}$. In particular, the stability analysis at infinity is available without particular restrictions to f. Details are discussed in Sect. 3.

Fig. 1

Parabolic and quasi-parabolic compactifications with type (2, 1) for $\mathbb {R}^2$ Surfaces drawn here are a$\mathcal {H} = \{(y_1,y_2,\zeta )\mid y_1^2 + y_2^2 = \zeta \}$ (parabolic compactification), and b$\mathcal {H}_\alpha = \{(y_1,y_2,\zeta )\mid y_1^2 + y_2^4 = \zeta \}$ (quasi-parabolic compactification with type (2, 1)). In both figures, the original phase space corresponds to $\mathbb {R}^2\times \{0\}\subset \mathbb {R}^{2+1}$ in the extended space. In the case of a, the type $\alpha$ is chosen to be (1, 1). The point P(M) show the intersection point between (0, 0, 1) and the given point $M\in \mathbb {R}^2$ on $\mathcal {H}$ and $\mathcal {H}_\alpha$ respectively, through the curve $C_\alpha (y) = \{((1-\zeta )^{\alpha _1} y_1, (1-\zeta )^{\alpha _2} y_2, \zeta )\}$. Note that the curve $C_\alpha$ is just a straight line in the case of homogeneous compactification $\alpha = (1,1)$. The projections of P(M) onto the original phase space; (x, 0), are the images of (quasi-)parabolic compactifications, respectively. These observations can be easily generalized to $\mathbb {R}^n$

2.4 Directional compactifications

There are several other compactifications reflecting (asymptotic) quasi-homogeneity of vector fields at infinity. For example, the transform $y = (y_1,\ldots , y_n) \mapsto T_d(y) = (s,\hat{x}) \equiv (s, \hat{x}_1,\ldots , \hat{x}_{i-1}, \hat{x}_{i+1}, \ldots , \hat{x}_n)$ given by

$$\begin{aligned} y_j = \frac{\hat{x}_j}{s^{\alpha _j}}\quad (j\not = i),\quad y_i = \pm \frac{1}{s^{\alpha _i}} \end{aligned}$$

(2.6)

is a kind of compactifications,⁵ which corresponds the infinity to the subspace $\{s=0\}\equiv \mathcal {E}$. We shall call such a compactification a directional compactification with the type$\alpha = (\alpha _1,\ldots , \alpha _n)$, according to [16]. The set $\mathcal {E} = \{s=0\}$ is called the horizon. This compactification is geometrically characterized as a local coordinate of quasi-Poincaré hemisphere of type $\alpha$:

$$\begin{aligned} \mathcal {H}_\alpha := \left\{ (y_1,\ldots , y_n, s)\in \mathbb {R}^{n+1}\mid \frac{1}{(1+p(y)^{2c})} \sum _{i=1}^n y_i^{2\beta _i} + s^{2c} = 1\right\} , \end{aligned}$$

at $(x_1, \ldots , x_n, s) = (0,\ldots , 0, x_i = \pm 1, 0, \ldots , 0, 0)$. See [16] for details. Note that, unlike admissible global quasi-homogeneous compactifications in Definition 2.3, the coordinate representation (2.6) only makes sense in $\{\pm y_i > 0\}$, in which sense directional compactifications are local ones. In particular, whenever we consider trajectories whose $y_i$-component can change the sign, we have to take care of transformations among coordinate neighborhoods, which is quite tough for numerical integration of differential equations. Nevertheless, this compactification is still a very powerful tool if we consider solutions near infinity whose$y_i$-component is known a priori to have identical sign.

3 Dynamics at infinity through compactifications

In this section, we calculate the vector field (2.1) through quasi-homogeneous compactifications. The main idea is twofold. First, we apply quasi-homogeneous compactifications associated with the type of f. Direct calculations then yield a transformed vector field, where the rate of divergence or decay at infinity is completely mapped into those on the horizon. We apply time-scale transformation determined by compactifications and the order $k+1$ of f as the second step. Then we obtain vector fields which are continuous including the horizon, as already mentioned in [16] in several cases. In particular, we can consider dynamics at infinity through such transformed vector fields, which shall be called desingularized vector fields. Moreover, in case of quasi-parabolic compactifications and typical directional compactifications we mention here, the resulting desingularized vector fields are as smooth as f on the horizon. Therefore dynamics at infinity including stability analysis of equilibria or general invariant sets can be studied in the similar way to standard theory of dynamical systems.

3.1 Desingularized vector field with admissible global quasi-homogeneous compactifications

Regard $\kappa$ in the definition of T as a function of y. Integers $\{\beta _i\}_{i=1}^n$ and c in the definition of T are assumed to satisfy (2.2). Differentiating $x = T(y)$ with respect to t, we have

$$\begin{aligned} x_i'&= \left( \frac{y_i}{\kappa ^{\alpha _i}}\right) ' = \frac{y_i'}{\kappa ^{\alpha _i}} - \frac{\alpha _i y_i \kappa ^{\alpha _i-1}}{\kappa ^{2\alpha _i}}\kappa ' \\&= \frac{y_i'}{\kappa ^{\alpha _i}} - \frac{\alpha _i y_i }{\kappa ^{\alpha _i+1}} \langle \nabla \kappa , y'\rangle \\&= \frac{f_i(y)}{\kappa ^{\alpha _i}} - \frac{\alpha _i y_i }{\kappa ^{\alpha _i+1}} \langle \nabla \kappa , f(y)\rangle . \end{aligned}$$

Namely,

$$\begin{aligned} x' = A_\alpha \left( f_i(y) - \kappa ^{-1}\langle f, \nabla \kappa \rangle y_\alpha \right) , \end{aligned}$$

(3.1)

where

$$\begin{aligned} A_\alpha = \mathrm{diag}(\kappa ^{-\alpha _1}, \ldots , \kappa ^{-\alpha _n}),\quad y_\alpha = (\alpha _1 y_1,\ldots , \alpha _n y_n)^T. \end{aligned}$$

We have the one-to-one correspondence of bounded equilibria, which helps us with detecting dynamics at infinity.

Proposition 3.1

An admissible global quasi-homogeneous compactification T maps bounded equilibria of (2.1) in $\mathbb {R}^n$ into equilibria of (3.1) in $\mathcal {D}$, and vice versa.

Proof

See Appendix C.2. $\square$

Next we discuss the dynamics at infinity. Denoting

$$\begin{aligned} \tilde{f}_j(x_1,\ldots , x_n) := \kappa ^{-(k+\alpha _j)} f_j(\kappa ^{\alpha _1}x_1, \ldots , \kappa ^{\alpha _n}x_n),\quad j=1,\ldots , n, \end{aligned}$$

(3.2)

we have

$$\begin{aligned} x_i'&= \frac{\kappa ^{k+\alpha _i} \tilde{f}_i(x)}{\kappa ^{\alpha _i}} - \frac{\alpha _i \kappa ^{\alpha _i}x_i }{\kappa ^{\alpha _i+1}} \sum _{j=1}^n (\nabla \kappa )_j \kappa ^{k+\alpha _j}\tilde{f}_j(x)\nonumber \\&= \kappa ^k \tilde{f}_i(x) - \alpha _i x_i \sum _{j=1}^n (\nabla \kappa )_j \kappa ^{k+\alpha _j - 1}\tilde{f}_j(x). \end{aligned}$$

(3.3)

Since $\kappa \rightarrow \infty$ as $p(x) \rightarrow 1$, then the vector field has singularities at infinity, while $\tilde{f}_j(x)$ themselves are continuous on $\overline{\mathcal {D}}$ because of the asymptotic quasi-homogeneity of f. Nevertheless, admissibility of compactifications yields the following observation.

Lemma 3.2

The right-hand side of (3.3) is $O(\kappa ^k)$ as $\kappa \rightarrow \infty$. In other words, the order with respect to $\kappa$ is independent of i.

Proof

See Appendix C.3. $\square$

Lemma 3.2 leads to introduce the following transformation of time variable.

Definition 3.3

(Time-variable desingularization). Define the new time variable $\tau$ depending on y by

$$\begin{aligned} d\tau = \kappa (y(t))^{k} dt \end{aligned}$$

(3.4)

namely,

$$\begin{aligned} t - t_0 = \int _{\tau _0}^\tau \frac{d\tau }{\kappa (y(\tau ))^k}, \end{aligned}$$

where $\tau _0$ and $t_0$ denote the correspondence of initial times, and $y(\tau )$ is the solution trajectory y(t) under the new time variable $\tau$. We shall call (3.4) the time-variable desingularization of (3.3) of order$k+1$.

$$\begin{aligned} \dot{x}_i \equiv \frac{dx_i}{d\tau } = \tilde{f}_i(x) - \alpha _i x_i \sum _{j=1}^n (\nabla \kappa )_j \kappa ^{\alpha _j - 1}\tilde{f}_j(x) \equiv g_i(x). \end{aligned}$$

(3.5)

Summarizing the above observation, we have the extension of dynamics at infinity.

Proposition 3.4

(Extension of dynamics at infinity). Let $\tau$ be the new time variable given by (3.4). Then the dynamics (2.1) can be extended to the infinity in the sense that the vector field g is continuous on $\overline{\mathcal {D}}$.

Proof

The component-wise desingularized vector field (3.5) is obviously continuous on $\overline{\mathcal {D}}$ since this consists of product and sum of continuous functions $x_i$’s and $\tilde{f}_i$’s on $\overline{\mathcal {D}}$. $\square$

Example 3.5

(Extension of vector fields via quasi-parabolic compactifications). In the case of quasi-parabolic compactification (Definition 2.10), $\nabla \kappa$ is given by

$$\begin{aligned} (\nabla _y \kappa (y))_j&= \frac{2\beta _j y_j^{2\beta _j-1}}{2c\kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) }\\&= \frac{\kappa (y)^{2c - \alpha _j} x_j^{2\beta _j-1}}{\alpha _j \kappa (y)^{2c-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) } = \frac{x_j^{2\beta _j-1}}{\alpha _j \kappa (y)^{\alpha _j-1} \left( 1- \frac{2c-1}{2c}\kappa (y)^{-1}\right) }. \end{aligned}$$

We can see that g in (3.5) can be extended to be $C^0$ on $\mathcal {E} = \overline{\mathcal {D}}$.

Proposition 3.4 shows that the “dynamics and invariant sets at infinity” make sense. For example, “equilibria at infinity” defined below are well-defined.

Definition 3.6

(Equilibria at infinity). We say that the vector field (2.1) has an equilibrium at infinity in the direction $x_*$ if $x_*$ is an equilibrium of (3.5) on $\partial {\mathcal {D}}$.

Now divergent solutions are described in terms of trajectories asymptotic to equilibria on the horizon for desingularized vector fields.

Theorem 3.7

(Divergent solutions and asymptotic behavior). Let y(t) be a solution of (2.1) with the interval of maximal existence time (a, b), possibly $a=-\infty$ and $b=+\infty$. Assume that y tends to infinity in the direction $x_*$ as $t\rightarrow b-0$ or $t\rightarrow a+0$. Then $x_*$ is an equilibrium of (3.5) on $\mathcal {E}$.

Proof

See Appendix C.4. $\square$

This theorem shows that divergent solutions in the direction $x_*$ correspond to trajectories of (3.5) on the stable manifold $W^s(x_*)$⁶ of the equilibrium $x_*$. This correspondence opens the door to applications of various results in dynamical systems to divergent solutions. Several useful properties of dynamics at infinity are shown in Theorem 3.15 in [16], which are also valid for general admissible compactifications through the same arguments.

3.2 Desingularized vector field with quasi-parabolic compactifications

In the case of quasi-parabolic compactifications, there is an alternative time-variable desingularization given below. In what follows, let $\kappa _{para}(y)$ be the functional $\kappa = \kappa (y)$ given in Definition 2.10.

Definition 3.8

(Time-variable desingularization for quasi-parabolic compactifications). Let y(t) be a solution of (2.1) with an asymptotically quasi-homogeneous vector field f of type $\alpha$ and order $k+1$. Let also $x = T_{para}(y)$ be the image of y via the quasi-parabolic compactification of type $\alpha$. Define the new time variable $\tau$ depending on $y = y(t)$ by

$$\begin{aligned} d\tau _{para}&= \kappa _{para}(y)^{k}\left( 1-\frac{2c-1}{2c}\kappa _{para}(y)^{-1}\right) ^{-1} dt\nonumber \\&= (1-p(x)^{2c})^{-k}\left( 1-\frac{2c-1}{2c}(1-p(x)^{2c}) \right) ^{-1}dt. \end{aligned}$$

(3.6)

We shall call (3.6) the quasi-parabolic time-variable desingularization of (3.3).

The resulting desingularized vector field is given as follows:

$$\begin{aligned} \frac{dx_i}{d\tau _{para}} = \left( 1-\frac{2c-1}{2c}(1-p(x)^{2c}) \right) \tilde{f}_i(x) - \alpha _i x_i \sum _{j=1}^n \frac{x_j^{2\beta _j-1}}{\alpha _j}\tilde{f}_j(x) \equiv g_{para,i}(x). \end{aligned}$$

(3.7)

In the case of quasi-Poincaré compactifications, the desingularized vector field g associated with the vector field f is not always$C^1$ even if f is sufficiently smooth because of the presence of radicals in $\kappa$. See Remark 4.2 in [16] for details. On the other hand, in the case of quasi-parabolic compactifications, if f is smooth, the corresponding desingularized vector field $g_{para}$ can be always smooth on $\overline{\mathcal {D}}$ with the alternative time-variable desingularization. This big difference is one of the reasons why we introduce an alternative quasi-homogeneous compactifications, which is mentioned again in Sect. 4.

Proposition 3.9

Let f be an asymptotically quasi-homogeneous, $C^1$ vector field f of type $\alpha$ and order $k+1$. Let $x = T_{para}(y)$ be a new variable through quasi-parabolic compactification. Then the vector field $g_{para}$ given in (3.7), associated with (3.3) and $\tau _{para}$-timescale given in (3.6), is $C^1$ on $\overline{\mathcal {D}}$.

Proof

See Appendix C.5. $\square$

3.3 Desingularized vector field with directional compactifications

The desingularized vector field associated with f is also considered with directional compactifications like (2.6). For simplicity, set $i=n$ in (2.6). Let

$$\begin{aligned} \hat{f}_j(s, \hat{x}_1, \ldots , \hat{x}_{n-1}) := s^{k+\alpha _j} f_j(s^{-\alpha _1}\hat{x}_1, \ldots , s^{-\alpha _{n-1}}\hat{x}_{n-1}, s^{-\alpha _n}),\quad j=1,\ldots , n. \end{aligned}$$

(3.8)

By the similar desingularization process to (3.2), we obtain the desingularized vector field for directional compactifications whose details are shown in [16].

Definition 3.10

(Time-variable desingularization: directional compactification version). Define the new time variable $\tau _d$ by

$$\begin{aligned} d\tau _d = s(t)^{-k} dt \end{aligned}$$

(3.9)

equivalently,

$$\begin{aligned} t - t_0 = \int _{\tau _0}^\tau s(\tau _d)^k d\tau _d, \end{aligned}$$

where $\tau _0$ and $t_0$ denote the correspondence of initial times, and $s(\tau _d)$ is the solution trajectory s(t) under the parameter $\tau$. We shall call (3.9) the time-variable desingularization of order$k+1$.

The desingularized vector field in $\tau _d$-time scale is

$$\begin{aligned} \begin{pmatrix} \frac{ds}{d\tau _d} \\ \frac{dx_1}{d\tau _d} \\ \vdots \\ \frac{dx_{n-1}}{d\tau _d} \end{pmatrix} = \begin{pmatrix} -s &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \ldots &{}\quad 1 \end{pmatrix} B \begin{pmatrix} \hat{f}_1 \\ \hat{f}_2 \\ \vdots \\ \hat{f}_n \end{pmatrix}\equiv g_d(s,\hat{x}_1,\ldots , \hat{x}_{n-1}), \end{aligned}$$

(3.10)

where B is the inverse⁷ of the matrix

$$\begin{aligned} \begin{pmatrix} \alpha _1 \hat{x}_1 &{}\quad 1 &{}\quad 0 &{}\quad \ldots &{}\quad 0\\ \alpha _2 \hat{x}_2 &{}\quad 0 &{}\quad 1 &{}\quad \ldots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \alpha _{n-1} \hat{x}_{n-1} &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 1\\ \alpha _n &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \end{pmatrix}. \end{aligned}$$

Equilibria at infinity under directional compactifications are then characterized as equilibria for (3.10) on the horizon $\mathcal {E} = \{s=0\}$. Note that $g_d$ is smooth on $\{s\ge 0\}\times \mathbb {R}^{n-1}$ if f is smooth.

Remark 3.11

In [16], the topological equivalence among desingularized vector fields with quasi-Poincaré compactifications and with directional compactifications including the horizon is discussed. In other words, dynamics of desingularized vector fields around the horizon is topologically identical among these compactifications. An essence of such a result is the admissibility in the sense of Definition 2.3 for the equivalence, which indicates that the equivalence result is also valid for quasi-parabolic compactifications.

4 Blow-up criterion and numerical validation procedure

Theorem 3.7 indicates that divergent solutions are described as trajectories on stable manifolds of equilibria on the horizon $\mathcal {E}$ for (3.5). On the other hand, Theorem 3.7 itself does not distinguish blow-up solutions from divergent solutions. Under additional assumptions to equilibria on $\mathcal {E}$, we can characterize blow-up solutions from the viewpoint of dynamical systems. In this section, we firstly review a criterion of blow-ups discussed in [16]. Then we provide a methodology for explicit estimates of maximal existence time $t_{\max }$. Finally, we give an algorithm for validating blow-up solutions with computer assistance.

4.1 Blow-up criterion

Firstly we review an abstract result of blow-up criterion via quasi-homogeneous-type compactifications. For a squared matrix A, $\mathrm{Spec}(A)$ denotes the set of eigenvalues of A.

Proposition 4.1

(Stationary blow-up, [16]). Assume that (2.1) has an equilibrium at infinity in the direction $x_*$. Suppose that the desingularized vector field g in (3.5) is $C^1$ on $\overline{\mathcal {D}}$, and that $x_*$ is hyperbolic for (3.5); namely all elements in $\mathrm{Spec}(Dg(x_*))$ are away from the imaginary axis. Then the solution y(t) of (2.1) whose image $x = T(y)$ is on $W^s(x_*)$ in the desingularized vector field (3.5) satisfies $t_{\max } < \infty$; namely, y(t) is a blow-up solution. Moreover,

$$\begin{aligned} p(y(t)) \sim C(t_{\max } - t)^{-1/k}\quad \text { as }\quad t\rightarrow t_{\max }, \end{aligned}$$

where $k+1$ is the order of asymptotically quasi-homogeneous vector field f. Finally, if the i-th component $(x_*)_i$ of $x_*$ is not zero, then we also have

$$\begin{aligned} y_i(t) \sim C(t_{\max } - t)^{-\alpha _i /k}\quad \text { as }\quad t\rightarrow t_{\max }. \end{aligned}$$

In the above original version of blow-up criterion stated as above, the $C^1$-smoothness of the desingularized vector field g in (3.5) is assumed, because such a smoothness is nontrivial for quasi-Poincaré compactifications even if f is sufficiently smooth, as mentioned in Sect. 3.2. On the other hand, Proposition 3.9 shows that stability analysis of equilibria at infinity always makes sense with quasi-parabolic compactifications, because in which case the desingularized vector field $g_{para}$ is always $C^1$ on $\overline{\mathcal {D}}$ if f is $C^1$. Needless to say, the above proposition does not provide information of concrete blow-up time $t_{\max }$ depending on initial data. In the successive subsections, we provide a validation procedure of blow-up solutions with estimates of explicit blow-up time.

4.2 Lyapunov functions around asymptotically stable equilibria

Our main tool for validating blow-up time is Lyapunov function, which describes the monotonous behavior of trajectories in terms of its value. As the general setting, consider the vector field

$$\begin{aligned} \frac{dx}{dt} = f(x),\quad f :\mathbb {R}^n\rightarrow \mathbb {R}^n\text {: smooth}. \end{aligned}$$

(4.1)

For $x\in \mathbb {R}^n$, Df(x) denotes the Jacobian matrix of f at x.

Proposition 4.2

(Lyapunov function for stable equilibria, [17]). Let $x_*$ be an equilibrium for (4.1) in a compact star-shaped set $N \subset \mathbb {R}^n$. Assume that there is a real symmetric matrix Y such that the matrix

$$\begin{aligned} A(x) := Df(x)^TY + YDf(x) \end{aligned}$$

(4.2)

is strictly negative definite for all $x\in N$. Then the functional $L:\mathbb {R}^n\rightarrow \mathbb {R}$ given by

$$\begin{aligned} L(x) := (x-x_*)^TY(x-x_*) \end{aligned}$$

(4.3)

is a Lyapunov function on N such that dL/dt vanishes at $x_*$. In particular, $x_*$ is the unique equilibrium in N. If further the matrix Y is chosen to be positive definite, then the equilibrium $x_*$ is asymptotically stable.

We shall call the compact set N satisfying the assumption in Proposition 4.2 a Lyapunov domain of $x_*$.

Remark 4.3

(The present choice of L(x)). Roughly speaking, the matrix Y contains information of sign of the real part of each $\mathrm{Spec}(Df(x))$ and a matrix representing change of coordinates. In the present case, we only treat asymptotically stable equilibria, which indicates that signs of $\mathrm{Re}\lambda$ for any $\lambda \in \mathrm{Spec}(Df(x))$ should be identically negative. Before validating an equilibrium $x_*$, it should be usually computed in a numerical (i.e., non-rigorous computation) sense with associated eigenvalues for finding candidates of validating equilibrium.

When we numerically compute eigenvalues of a Jacobian matrix, say Df(x), we also compute eigenvectors to construct the eigenmatrix X, which represents change of coordinates to an orthogonal one. In [17], the matrix Y in (4.3) is typically defined as $Y = \mathrm{Re}(X^{-H}X^{-1})$, where $X^{-H} := (X^{-1})^H$ and $*^H$ denotes the Hermitian transpose of the object (vectors or matrices). Note that, in which case, the equilibrium $x_*$ is shown to be asymptotically stable in N. However, there are cases that an eigenvalue has multiplicity larger than 1, in which cases the validation is failed because the computed eigenmatrix X typically becomes singular. Indeed, our example below contains such a case.

One way to avoid such difficulty is to use the real Schur decomposition of the matrix Df(x) instead of eigenpair computations. See Appendix A about a quick review of Schur decompositions of matrices. Let Q be a matrix such that $Q^TDf(x)Q$ is a real upper triangle matrix for some point x. Then we can check the sign of $\mathrm{Re}\lambda$ for all $\lambda \in \mathrm{Spec}(Df(x))$. We then choose the matrix Q as a change of coordinates instead of the eigenmatrix X. In such a case, the corresponding matrix Y is $Y=\mathrm{Re}(Q^{-H}Q^{-1})$. When we use the real Schur decomposition, Q is an orthogonal real matrix. Then we take $Y = I$: the identity matrix, which shows that our Lyapunov function L becomes $L(x) = \Vert x-x_*\Vert ^2$. This fact also shows that $x_*$ is asymptotically stable in N.

There can be another choice of L(x) other than (4.3). The present choice of L(x) shows an example for validating rigorous enclosure of blow-up solutions and their blow-up time, and the other type of Lyapunov functions can be applied provided we can calculate the explicit upper bound of $t_{\max } - t_N$, an example of which is shown below.

Once we have validated a Lyapunov function L as well as the Lyapunov domain $\tilde{N}$ of an asymptotically stable equilibrium $x_*$, we can easily characterize global trajectory asymptotic to $x_*$. For a positive number $\epsilon > 0$, assume that $N := \{x\in \mathbb {R}^n\mid L(x) \le \epsilon \}\subset \tilde{N}$. Let $\{x(t)\}_{t\in [0,t_N]}$ be a trajectory of vector field (4.1) for some $t_N > 0$ and assume that $x(t_N) \in \mathrm{int}\,N$. Then the trajectory x(t) behaves so that it strictly decreasesL. Since $N = \{x\in \mathbb {R}^n \mid L(x) \le \epsilon \}$, then the trajectory can be continued until it tend to a point on $\{L=0\}$, in which case $x=x_*$. Therefore the trajectory $\{x(t)\}_{t\in [0,t_N]}$ is extended to the global trajectory $\{x(t)\}_{t\in [0,\infty )}$ satisfying $x(t)\rightarrow x_*$ as $t\rightarrow \infty$, as desired.

4.3 Estimate of explicit blow-up time with computer assistance

Here we provide an explicit estimate methodology of blow-up time. The basic idea is Lyapunov tracing discussed in [17, 21]; namely, computation of the maximal existence time

$$\begin{aligned} t_{\max } = \int _0^\infty \frac{d\tau }{\kappa (T^{-1}(x(\tau )))^k},\quad \text { or }\quad t_{d,\max } = \int _0^\infty s(\tau )^k d\tau _d, \end{aligned}$$

of trajectory $\{y(t) = T^{-1}(x(t))\}$ in terms of Lyapunov functions around an equilibrium $x_*$ on the horizon $\mathcal {E}$. Theorem 4.1 shows that blow-up solutions correspond to trajectories on stable manifolds of hyperbolic equilibria on$\mathcal {E}$. According to this fact and preceding methodology in [21], we validate asymptotic behavior of blow-up solutions by the following steps. An admissible global quasi-homogeneous compactification $T:\mathbb {R}^n\rightarrow \mathcal {D}$ and time-variable desingularization are assumed to be given in advance.

• 1. Validate an equilibrium $x_*\in \mathcal {E}$.

• 2. Validate a Lyapunov function of the form (4.3) around $x_*$ as well as its Lyapunov domain $\tilde{N}$.

Now we are ready to validate blow-up time with computer assistance. Let T be an admissible global quasi-homogeneous compactification with type $\alpha$. Assume that the desingularized vector field (3.5) is $C^1$ on $\overline{\mathcal {D}}$, which is always the case when $T = T_{para}$ and f is $C^1$. Let $x_*\in \mathcal {E}$ be an equilibrium on the horizon for (3.5). Explicit estimates of maximal existence time $t_{\max }$ actually depend on the choice of compactifications T and time-variable desingularizations. In what follows we fix T as the quasi-parabolic compactification $T_{para}$ (associated with type $\alpha$) and quasi-parabolic time-variable desingularization (3.6).

Assume that we have computed the global trajectory $\{x(\tau _{para})\}_{\tau _{para} \in [0,\infty )}$ for (3.7) such that $x(\tau _{para})\in N = \{x\in \mathcal {D}\mid L(x)\le \epsilon \}\subset \tilde{N}$ for all $\tau _{para}\in [\tau _{para,N},\infty )$ and some $\epsilon > 0$, where $\tau _{para,N} > 0$ and $\tilde{N}$ is a Lyapunov domain of an asymptotically stable equilibrium $x_*\in \mathcal {E}$.⁸ The maximal existence time of $x(\tau )$ in t-timescale is then

$$\begin{aligned} t_{para, \max }&= t_{para,N} + \int _{\tau _{para,N}}^\infty \left( 1-\frac{2c-1}{2c}\kappa _{para}(y)^{-1}\right) \frac{d\tau _{para}}{\kappa _{para}(T^{-1}(x(\tau _{para})))^k}\\&= t_{para,N} + \int _{\tau _{para,N}}^\infty \left( 1-\frac{2c-1}{2c}(1-p(x(\tau ))^{2c})\right) (1-p(x(\tau ))^{2c})^k d\tau _{para}, \end{aligned}$$

where

$$\begin{aligned} t_{para,N} = \int _0^{\tau _{para,N}} \left( 1-\frac{2c-1}{2c}(1-p(x(\tau ))^{2c})\right) (1-p(x(\tau ))^{2c})^k d\tau _{para}. \end{aligned}$$

(4.4)

Then compute an upper bound of $t_{\max }$ by

$$\begin{aligned} 0 < t_{para,\max } - t_{para,N}&\le \frac{1}{c_{\tilde{N}}c_1} \int _0^{L(x(\tau _{para,N}))} \frac{C_{n,\alpha ,N}(L)^{k}}{L}dL\nonumber \\&\le \frac{1}{c_{\tilde{N}}c_1} \int _0^{\epsilon } \frac{C_{n,\alpha ,N}(L)^{k}}{L}dL \equiv \overline{C_{n,\alpha ,k, N}}(\epsilon ), \end{aligned}$$

(4.5)

where $L = L(x)$ is the value of validated Lyapunov function at $x\in N$, $c_1$ and $c_{\tilde{N}}$ are constants involving eigenvalues of Y and A(x) whose details are shown in [21]. This inequality comes from the property of Lyapunov function following the definition:

$$\begin{aligned} \frac{dL}{d\tau _{para}}(x(\tau _{para}))_{\tau _{para}= 0} \le -c_1 c_{\tilde{N}}L(x(0)), \end{aligned}$$

which is strictly negative as long as $x(0)\not = x_*$. See [21] for the detail. A function $C_{n,\alpha ,N}(L)$ depends on the value L of Lyapunov function satisfying

$$\begin{aligned} \left| 1-p(x)^{2c}\right| \le C_{n,\alpha ,N}(L)\quad \text { for }\quad x\in \tilde{N}. \end{aligned}$$

Concrete estimates of the function $C_{n,\alpha , N}(L)$ we have used in practical validations are derived in Appendix B. Since $L(x(\tau _{para,N})) \le \epsilon$, the rightmost side of (4.5) is an integral on a compact interval. If we can estimate the right-hand side of (4.5) being finite, we obtain a finite upper bound of $t_{para,\max }$, which shows that the trajectory $\{y(t)\}_{t\in [0,t_{\max })} = \{T_{para}^{-1}(x(\tau _{para}))\}_{\tau _{para}\in [0,\infty )}$ is a blow-up solution of the original initial value problem (2.1) with blow-up time $t_{para,\max }\in [t_{para,N}, t_{para,N} + \overline{C_{n,\alpha ,k,N}}(\epsilon )]$.

The similar estimate is also derived for directional compactifications. In such a case with the same setting as above, the maximal existence time $t_{\max }$ is computed as

$$\begin{aligned} t_{d,\max } = \int _0^\infty s(\tau _d)^k d\tau _d = t_{d,N} + \int _{\tau _{d,N}}^\infty s(\tau _d)^k d\tau _d, \end{aligned}$$

where $t_{d,N} = \int _0^{\tau _{d,N}} s(\tau _d)^k d\tau _d$. Assume that the trajectory $\{(s(\tau _d), \hat{x}(\tau _d))\}_{\tau _d\in [0,\tau _{d,N}]}$ enters inside $\mathrm{int}N:= \{L(s,\hat{x}) < \epsilon \} \subset \tilde{N}$, where $\tilde{N}$ is a Lyapunov domain of $(0,\hat{x}_*) \in \mathcal {E}$. Then we have

$$\begin{aligned} \int _{\tau _{d,N}}^\infty s(\tau _d)^k d\tau _d&\le \int _{\tau _{d,N}}^\infty (|s|^2 + \Vert \hat{x}-\hat{x}_*\Vert ^2 )^k d\tau _d\nonumber \\&\le \int _{\tau _{d,N}}^\infty \left\{ c_1 L(s(\tau _d),\hat{x}(\tau _d)) \right\} ^{k/2} d\tau _d\nonumber \\&\le - \int _{L(s(\tau _{d,N}),\hat{x}(\tau _{d,N}))}^0 \left\{ c_1 L \right\} ^{k/2} \frac{dL}{\tilde{c}_N c_1 L}\nonumber \\&= \frac{c_1^{k/2-1}}{\tilde{c}_N } \int _0^{L(s(\tau _{d,N}),\hat{x}(\tau _{d,N}))} L^{\frac{k}{2}-1} dL\nonumber \\&\le \frac{c_1^{k/2-1}}{\tilde{c}_N} \left[ 2L^{k/2} \right] _0^{\epsilon } = \frac{2c_1^{k/2-1}}{\tilde{c}_N} \epsilon ^{k/2} \equiv \overline{C_{n,k,N}}(\epsilon ). \end{aligned}$$

(4.6)

The rightmost quantity gives an upper bound of $t_{\max } = t_{d,\max }$. More precisely, the blow-up time $t_{d,\max }$ is a value in $[t_{d,N}, t_{d,N} + \overline{C_{n,k,N}}(\epsilon )]$.

4.4 Validation procedure of blow-up solutions

Now we have obtained an estimate of explicit blow-up time. Theorem 3.7 indicates that blow-up solutions correspond to trajectories on stable manifolds of (hyperbolic) equilibria at infinity, which can be validated by standard numerical validation techniques of dynamical systems (e.g., [13]).

Our algorithm for validating blow-up solutions is the following, which is essentially same as that in the preceding work [21].

Algorithm 1

(Validation of blow-up solutions with quasi-parabolic compactifications). Let $f:\mathbb {R}^n\rightarrow \mathbb {R}^n$ be an asymptotically quasi-homogeneous, smooth vector field of type $\alpha = (\alpha _1,\ldots , \alpha _n)$ and order $k+1$. Choose natural numbers $\beta _1,\ldots , \beta _n, c\in \mathbb {N}$ so that (2.2) holds. Let $T_{para}:\mathbb {R}^n\rightarrow \mathcal {D}$ be a quasi-parabolic compactification and $\frac{dx}{d\tau _{para}} = g_{para}(x)$ be the associated desingularized vector field with time-variable desingularization (3.6).

• 1. Validate an equilibrium at infinity $x_*$; namely, a zero of $g_{para}$ on $\mathcal {E} = \partial \mathcal {D}$.

• 2. Construct a compact, star-shaped set $\tilde{N}\subset \overline{\mathcal {D}}$ containing $x_*$ so that the negative definiteness of (4.2) on $\tilde{N}$ with a positive definite, real symmetric matrix Y is validated as large as possible. If we cannot find such a set $\tilde{N}$, return failed.

• 3. Let $L(x)=(x-x_*)^T Y (x-x_*)$ be the validated Lyapunov function on $\tilde{N}$. Set $\epsilon > 0$ as the maximal value so that $N := \{x\in \mathbb {R}^n \mid L(x)\le \epsilon \} \subset \tilde{N}$. Integrate the ODE $(dx/d\tau _{para}) = g_{para}(x)$ with initial data $x_0\in \mathcal {D}$ until $\tau = \tau _N$ so that $x(\tau _N)\in \mathrm{int}N$. If we cannot find such $x(\tau _N)$, return failed.

• 4. Compute $\overline{C_{n,\alpha ,k, N}}(\epsilon )$. Simultaneously, compute $t_N$ following (4.4). If $\overline{C_{n,\alpha ,k, N}}(\epsilon )$ can be validated to be finite, return succeeded.

The similar algorithm with directional compactifications is derived as follows.

Algorithm 2

(Validation of blow-up solutions with directional compactifications). Let $f:\mathbb {R}^n\rightarrow \mathbb {R}^n$ be an asymptotically quasi-homogeneous, smooth vector field of type $\alpha = (\alpha _1,\ldots , \alpha _n)$ and order $k+1$. Let $T_d:U\rightarrow \{s>0\}\times \mathbb {R}^{n-1}$ be a directional compactification determined by (2.6) and $\frac{d(s,\hat{x})}{d\tau _d} = g_d(s,\hat{x})$ be the associated desingularized vector field with time-variable desingularization (3.4), where U is a domain of definition of $T_d$ chosen so that it is compatible with $T_d$.

• 1. Validate an equilibrium at infinity $(0,\hat{x}_*)$; namely, a zero of $g_d$ on $\mathcal {E} = \{s=0\}$.

• 2. Construct a compact, star-shaped set $\tilde{N}\subset \{s\ge 0\}\times \mathbb {R}^{n-1}$ containing $(0, \hat{x}_*)$ so that the negative definiteness of (4.2) on $\tilde{N}$ with a positive definite, real symmetric matrix Y is validated as large as possible. If we cannot find such a set $\tilde{N}$, return failed.

• 3. Let $L(s,\hat{x})= ((s,\hat{x})- (0,\hat{x}_*))^T Y((s,x)- (0,\hat{x}_*))$ be the validated Lyapunov function on $\tilde{N}$. Set $\epsilon > 0$ as the maximal value so that $N := \{(s,\hat{x})\in \{s\ge 0\}\times \mathbb {R}^{n-1} \mid L(s,\hat{x})\le \epsilon \} \subset \tilde{N}$. Integrate the ODE $(d(s,\hat{x})/d\tau _d) = g_d(s,\hat{x})$ with initial data $(s_0,\hat{x}_0)\in \{s> 0\}\times \mathbb {R}^{n-1}$ until $\tau _d = \tau _{d,N}$ so that $(s(\tau _{d,N}), \hat{x}(\tau _{d,N}))\in \mathrm{int}N$. If we cannot find such $(s(\tau _{d,N}), \hat{x}(\tau _{d,N}))$, return failed.

• 4. Compute $\overline{C_{n,k, N}}(\epsilon )$. Simultaneously, compute $t_{d,N} = \int _0^{\tau _{d,N}} s(\tau _d)^k d\tau _d$. If $\overline{C_{n,k, N}}(\epsilon )$ can be validated to be finite, return succeeded.

Under the successful operations of Algorithm 1 or 2, we have the following results, which show the validation of blow-up solutions. The proofs immediately follow from properties of compactifications and Lyapunov functions.

Theorem 4.4

(Validation of blow-up solutions with quasi-parabolic compactifications) Let $y_0\in \mathbb {R}^n$. Assume that Algorithm 1 returns succeeded with $x_0 = T_{para}(y_0)$. Then the solution $\{y(t) = T_{para}^{-1}(x(t))\}$ of (2.1) with $y(0) = y_0$ such that

$$\begin{aligned} \{x(\tau _{para})\mid \tau _{para} \in [0, \infty ), x(\tau _{para})\rightarrow x_*\text { as }\tau _{para}\rightarrow \infty \} \end{aligned}$$

via a time-variable desingularization (3.6) and an asymptotically stable equilibrium $x_*\in \mathcal {E}$ is a blow-up solution with the blow-up time $t_{para,\max } \in [\tau _{para,N}, \tau _{para,N} + \overline{C_{n,\alpha ,k, N}}(\epsilon )]$.

Theorem 4.5

(Validation of blow-up solutions with directional compactifications). Let $y_0\in \mathbb {R}^n$. Assume that Algorithm 2 returns succeeded with $(s_0, \hat{x}_0) = T_d(y_0)$. Then the solution $\{y(t) = T_d^{-1}(s(t), \hat{x}(t))\}$ of (2.1) with $y(0) = y_0$ such that

$$\begin{aligned} \{(s(\tau _d), \hat{x}(\tau _d))\mid \tau _d \in [0, \infty ), s(\tau _d)\rightarrow 0,\ \hat{x}(\tau _d)\rightarrow \hat{x}_*\text { as }\tau _d\rightarrow \infty \} \end{aligned}$$

via a time-variable desingularization (3.9) and an asymptotically stable equilibrium $(0,\hat{x}_*) \in \mathcal {E}$ is a blow-up solution with the blow-up time $t_{\max } = t_{d,\max } \in [\tau _{d,N}, \tau _{d,N} + \overline{C_{n,k, N}}(\epsilon )]$.

Finally we remark that our validations do not contain those of hyperbolicity for equilibria on $\mathcal {E}$. Indeed, we only verify negative definiteness of the symmetrization of Df(x) or an associated matrix in (4.2). In particular, our validation does not directly provide rigorous blow-up rates of blow-up solutions mentioned in Proposition 4.1. Nevertheless, Proposition 4.1 provides a guideline for focusing on our targeting objects for validations, and Lyapunov function validations yield the asymptotic stability of equilibria and rigorous estimates of blow-up time, as mentioned.

5 Validation examples

In this section, we demonstrate our procedure with several test problems. We have three validation examples, which aim at demonstrating the following, respectively:

• Section5.1 shows an application of quasi-parabolic compactifications for quasi-homogeneous vector fields. In particular, sign-changing profiles are validated. Using the above compactification, we do not need to care about sign-changing nature for computing blow-up profiles.

• Section5.2 shows an application of quasi-parabolic compactifications for asymptotically quasi-homogeneous vector fields. As mentioned in Proposition 3.9, quasi-parabolic compactifications and the associated time-scale desingularizations map the original smooth vector field into the desingularized one with the same smoothness, which is not the case of Poincaré-type compactifications (cf. [16, 21]).

• Section5.3 shows the effectiveness of directional compactifications for blow-up profiles, provided we have a priori knowledge that some components have an identical sign.

All computations were carried out on macOS Sierra (ver. 10.12.5), Intel(R) Xeon(R) CPU E5-1680 v2 @ 3.00 GHz using the kv library [13] ver. 0.4.41 to rigorously compute the trajectories of ODEs.

5.1 Example 1

The first example is the following two-dimensional ODE:

$$\begin{aligned} {\left\{ \begin{array}{ll} u' = u^2 - v, &{} \\ v' = \frac{1}{3}u^3. &{} \end{array}\right. } \end{aligned}$$

(5.1)

This vector field is the special case of (5.3) discussed in the next example. It immediately holds that the vector field (5.1) is quasi-homogeneous of type (1, 2) and order 2. The numerical study of complete dynamics including infinity is shown in [16]. Our purpose here is to validate a blow-up solution observed there. We introduce the quasi-parabolic compactification of type (1, 2) given by

$$\begin{aligned} u = \frac{x_1}{1-p(x)^4},\quad v = \frac{x_2}{(1-p(x)^4)^2},\quad p(x)^4 = x_1^4 + x_2^2. \end{aligned}$$

Then the corresponding desingularized vector field (3.7) is given by the following:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1 = (x_1^2 - x_2) F(x) - x_1G(x) &{} \\ \dot{x}_2 = \frac{1}{3}x_1^3 F(x) - 2x_2 G(x) &{} \end{array}\right. },\quad \dot{~} = \frac{d}{d\tau _{para}}, \end{aligned}$$

(5.2)

where

$$\begin{aligned} F(x) = \frac{1}{4}\left\{ 1 + 3(1-p(x)^4)\right\} ,\quad G(x) = x_1^3 (x_1^2 - x_2) + \frac{1}{6}x_1^3 x_2. \end{aligned}$$

We are then ready to validate blow-up solutions, following Algorithm 1. In the similar way to [16], it turns out that the system (5.2) admits exactly four equilibria at infinity, one of which is a sink,⁹ the other one of which is a source¹⁰ and the rest of two are saddles.¹¹ Here we compute the sink on the horizon satisfying

$$\begin{aligned} x_*\in \left( \begin{array}{c} \left[ 0.98913699589497727,0.98913699589497773\right] \\ \left[ 0.20675855700518036,0.2067585570051809\right] \end{array}\right) , \end{aligned}$$

where $[\cdot ,\cdot ]$ denotes a real interval. In the next step, we validate a Lyapunov function as well as its Lyapunov domain including $N= \{x\in \overline{\mathcal {D}}\mid L(x) \le \epsilon \}$ around the sink and a solution trajectory $x(\tau )$ which enters N in a finite time $\tau _N$. The initial data are given by $(x_1(0),x_2(0))=(-0.1,0.0001)$ and $(-0.1,-0.1)$. Table 1 shows validated results of blow-up solutions for (5.1). See also Fig. 2.

Table 1 Validated results for (5.1): numerical validations prove $x(\tau _{para,N})\in \mathrm{int}\,N$ and (4.5) yields the inclusion of the blow-up time $t_{para,\max }$

Fig. 2

A blow-up trajectory for (5.1) A blow-up trajectory with the initial data $(u(0),v(0)) = T_{para}^{-1}(x)$, $(x_1(0), x_2(0)) = (-0.1, 0.0001)$ are drawn. Horizontal axis is the original time variable t, and vertical axis is the value of variables u and v. a The u-component of the blow-up trajectory. b the u-component of the blow-up trajectory in a vicinity of $u=0$. c The v-component of the blow-up trajectory. d The v-component of the blow-up trajectory in a vicinity of $v=0$

Validated results in this example show the efficiency of quasi-parabolic compactifications for validating sign-changing solutions, compared with directional compactifications. As indicated in [16] and Fig. 2, validated trajectories can change the sign. Numerical computations as well as rigorous validations of trajectories with directional compactifications require the assumption that (at least) one of components never change the sign and that, even if it is the case, one knows such a component in advance. If we deal with sign-changing trajectories, coordinate-change transformations have to be incorporated into the whole computations, which are not easy tasks for numerical integration of differential equations. On the other hand, there is no such worry with quasi-parabolic compactifications because they provide globally defined charts on embedding manifolds. Trajectories can be therefore validated without any assumptions about their signs.

Remark 5.1

Even for non-rigorous computations of divergent solutions of ODEs, treatment of coordinate transform among directional compactifications with different directions is not a trivial task, which can cause lengthy and inefficient arguments, and accumulation of numerical errors. On the other hand, quasi-Poincaré ([16]) and quasi-parabolic compactifications define one global charts including the horizon, and hence they can work effectively for computing divergent solutions for general systems as the first step. Even if the targeting divergent and blow-up solutions turn out to have an identical sign in a certain direction during time evolution, it is still worth applying quasi-Poincaré and quasi-parabolic compactifications to detecting the direction where the sign is identical during evolution.

5.2 Example 2

The second example is the following two-dimensional ODE:

$$\begin{aligned} {\left\{ \begin{array}{ll} u' = u^2 - v -su - c_1, &{} \\ v' = \frac{1}{3}u^3 - u - sv - c_2, &{} \end{array}\right. } \end{aligned}$$

(5.3)

where $(c_1,c_2) = (c_{1L}, c_{2L})$ or $(c_{1R}, c_{2R})$ are constants with

$$\begin{aligned} {\left\{ \begin{array}{ll} c_{1L} = u_L^2 - v_L - su_L, &{} \\ c_{2L} = \frac{1}{3}u_L^3 - u_L - sv_L, &{} \\ \end{array}\right. } \quad {\left\{ \begin{array}{ll} c_{1R} = u_R^2 - su_R - v_R, &{} \\ c_{2R} = \frac{1}{3}u_R^3 - u_R - sv_R. &{} \\ \end{array}\right. } \end{aligned}$$

The system (5.3) is well-known as the traveling wave equation derived from the Keyfitz-Kranser model [15], which is the following initial value problem of the system of conservation laws:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle { \frac{\partial u}{\partial t} + \frac{\partial }{\partial x}(u^2 - v) = 0, } &{} \\ \displaystyle { \frac{\partial v}{\partial t} + \frac{\partial }{\partial x}\left( \frac{1}{3}u^3 - u\right) =0, } &{} \end{array}\right. } \quad (u(x,0), v(x,0)) = {\left\{ \begin{array}{ll} (u_L, v_L) &{} x<0, \\ (u_R, v_R) &{} x>0. \end{array}\right. } \end{aligned}$$

(5.4)

In particular, our attentions are restricted to solutions of the form

$$\begin{aligned} u(x,t) = \tilde{u}(\xi ),\quad v(x,t) = \tilde{v}(\xi ),\quad \xi = x-st \end{aligned}$$

(5.5)

satisfying the following boundary condition:

$$\begin{aligned} \lim _{\xi \rightarrow -\infty } \begin{pmatrix} \tilde{u}(\xi ) \\ \tilde{v}(\xi ) \end{pmatrix} = \begin{pmatrix} u_L \\ v_L \end{pmatrix},\quad \lim _{\xi \rightarrow +\infty } \begin{pmatrix} \tilde{u}(\xi ) \\ \tilde{v}(\xi ) \end{pmatrix} = \begin{pmatrix} u_R \\ v_R \end{pmatrix}. \end{aligned}$$

(5.6)

The governing system with the ansatz (5.5)-(5.6) derives the system (5.3).

Remark 5.2

The system (5.1) in the previous example actually extracts the quasi-homogeneous part of (5.3). Solutions (5.5) of (5.3) satisfying (5.6) correspond to shock waves with speeds for the Riemann (initial value) problem (5.4) satisfying viscosity profile criterion. The boundary condition (5.6) is known as the Rankine-Hugoniot condition which weak solutions of (5.4) admitting discontinuity must be satisfied. On the other hand, it is well-known that the Riemann problem (5.4) admits shock wave solutions with Dirac-delta singularities called singular shock waves. Such solutions satisfy only a part of (5.6); called Rankine-Hugoniot deficit, and such structure corresponds to the presence of blow-up solutions for (5.3) with $(c_1,c_2) = (c_{1L}, c_{2L})$ or $(c_{1R}, c_{2R})$, which inspires our considerations herein. See e.g., [15, 20] for details about (5.4).

It immediately holds that, as in the previous example, the vector field (5.3) turns out to be asymptotically quasi-homogeneous at infinity with type $\alpha = (1,2)$ and order 2. The desingularized vector field with quasi-parabolic compactifications is calculated as follows. Introduce the quasi-parabolic compactification of type (1, 2) given by

$$\begin{aligned} u = \frac{x_1}{1-p(x)^4},\quad v = \frac{x_2}{(1-p(x)^4)^2},\quad p(x)^4 = x_1^4 + x_2^2 \end{aligned}$$

and nonlinear functions $\tilde{f}_1(x), \tilde{f}_2(x)$ by

$$\begin{aligned} \tilde{f}_1(x) := x_1^2 - x_2 - s\kappa ^{-1}x_1 - \kappa ^{-2}c_1,\quad \tilde{f}_2(x) := \frac{1}{3}x_1^3 - \kappa ^{-2}x_1 - s\kappa ^{-1}x_2 - c_2\kappa ^{-3}, \end{aligned}$$

where $\kappa ^{-1} = \kappa (x)^{-1} = (1-p(x)^4)^{1/4}$, the desingularized vector field associated with (5.3) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1 = (x_1^2 - x_2 - s\kappa ^{-1}x_1 - \kappa ^{-2}c_1) F(x) - x_1 \tilde{G}(x) &{} \\ \dot{x}_2 = \left( \frac{1}{3}x_1^3 - \kappa ^{-2}x_1 - s\kappa ^{-1}x_2 - c_2\kappa ^{-3}\right) F(x) - 2x_2 \tilde{G}(x) &{} \end{array}\right. },\quad \dot{~} = \frac{d}{d\tau _{para}}, \end{aligned}$$

where

$$\begin{aligned} F(x)&= \frac{1}{4}\left\{ 1 + 3(1-p(x)^4)\right\} ,\\ \tilde{G}(x)&= x_1^3 (x_1^2 - x_2 - s\kappa ^{-1}x_1 - \kappa ^{-2}c_1) + \frac{1}{2} x_2\left( \frac{1}{3}x_1^3 - \kappa ^{-2}x_1 - s\kappa ^{-1}x_2 - c_2\kappa ^{-3}\right) . \end{aligned}$$

In the present validation, we applied $(c_1, c_2) = (c_{1L}, c_{2L})$ as well as the speed parameter s are set as

$$\begin{aligned}&u_L = [1.46777062491],\quad v_L = [0.238709208571],\quad s\in 0.44819467507505_{461}^{512},\\&c_{1L}\in 1.25779442046144_{35}^{51},\quad c_{2L}\in -0.5207279753417_{6075}^{5985} \end{aligned}$$

following the Rankine-Hugoniot relation (e.g., [15]), where [a] denotes the point interval consisting of a value a, and subscript and superscript numbers denote lower and upper bounds of the interval, respectively. We then compute an equilibrium on the horizon which satisfy

$$\begin{aligned} x_*\in \left( \begin{array}{c} \left[ 0.98913699589497727,0.98913699589497773\right] \\ \left[ 0.20675855700518036,0.2067585570051809\right] \end{array}\right) . \end{aligned}$$

Finally, validate blow-up solutions in the same way as the previous example. Our validation result is listed in Table 2.

Table 2 Validated results for (5.3): numerical validations prove $x(\tau _{para,N})\in \mathrm{int}\,N$ and (4.5) yields the inclusion of the blow-up time $t_{para,\max }$

Validated results in this example show the efficiency of quasi-parabolic compactifications for asymptotically quasi-homogeneous vector fields at infinity. As indicated in [16], quasi-Poincaré compactifications; namely, the case $\kappa (y) = \kappa _{Poin}(y) = (1+p(y)^{2c})^{1/2c}$, require calculations of radicals because of the presence of $\kappa _{Poin}^{-1}$ in desingularized vector fields. Such terms cause the lack of smoothness of desingularized vector fields on the horizon, which indicates that the stability analysis of equilibria there in terms of Jacobian matrices makes no sense. In particular, blow-up arguments cannot be developed within the present argument. Details of this point are discussed in Remark 4.2 in [16]. On the other hand, quasi-parabolic compactifications guarantees the smoothness of desingularized vector fields derived from original ones under their smoothness, including the horizon, by Proposition 3.9. This property can reflect a good correspondence between rational functions through parabolic-type compactifications [10]. Blow-up arguments including numerical validations with quasi-parabolic compactifications can be therefore applied to vector fields which are not quasi-homogeneous but asymptotically quasi-homogeneous, since quasi-parabolic compactifications keep the smoothness of vector fields between the original one and the desingularized one.

5.3 Example 3

The final example is a finite dimensional approximation of the following system of partial differential equations:

$$\begin{aligned} \left\{ \begin{array}{ll} u_t=r^{1-d}\left( r^{d-1}\left( u_r-uv_r\right) \right) _r,&{}r\in (0,L),~t>0,\\ v_t=r^{1-d}\left( r^{d-1}v_r\right) _r-v+u&{}r\in (0,L),~t>0,\\ u_r=v_r=0,&{}r=0,L,~t>0,\\ u(r,0)=u_0(r),~v(r,0)=v_0(r),&{}r\in (0,L) \end{array} \right. \end{aligned}$$

(5.7)

for some $L > 0$, which is the well-known Keller–Segel model on the d-dimensional ball with homogeneous Neumann boundary condition and radially symmetric anzatz:

$$\begin{aligned} \left\{ \begin{array}{ll} u_t=\Delta u-\nabla \cdot (u\nabla v),&{}x\in \Omega ,~t>0,\\ v_t=\Delta v-v+u,&{}x\in \Omega ,~t>0,\\ \frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,&{}x\in \partial \Omega ,~t>0,\\ u(x,0)=u_0(x),~v(x,0)=v_0(x),&{}x\in \Omega , \end{array} \right. \end{aligned}$$

(5.8)

where $\Omega = \{x\in \mathbb {R}^d \mid |x|<L\}$.

Zhou and Saito [24] has proposed a finite volume discretization scheme so that blow-up solutions for (5.7) of the parabolic-elliptic (namely, $v_t=0$) type can be computed.

Remark 5.3

It is known that solutions of the Keller–Segel system (5.8) with positive initial data $u_0(x) > 0$, $v_0(x) > 0$ must be positive. Moreover, the system (5.8) possesses an $L^1$-conservation law for u; namely $\int _\Omega u(x,t)dx = \int _\Omega u_0(x)dx$ holds for all $t\ge 0$. However, $L^1$-conservative discretization schemes for (5.8) are known to possess no numerical blow-up solutions typically. The choice of the present scheme aims at computations of blow-up behavior for Keller–Segel type system. It is reported in [24] that the corresponding scheme provide the positivity of solutions if the spatial grid size h and the temporal grid size $\tau$ are sufficiently small and numerical solutions are far from blow-up profile, while the positivity breaks down as solutions approach to blow-up.

We consider a parabolic-parabolic alternative of the discretization defined below:

$$\begin{aligned} \frac{du_1}{dt}&=\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{u_2-u_1}{h}\right) -\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{v_2-v_1}{h}u_1\right) \\ \frac{du_2}{dt}&= \frac{r_2^{1-d}}{h}\left( r_{2+\frac{1}{2}}^{d-1}\frac{u_3-u_2}{h}-r_{2-\frac{1}{2}}^{d-1}\frac{u_2-u_1}{h}\right) \\&\quad -\frac{r_2^{1-d}}{h}\left( r_{2+\frac{1}{2}}^{d-1}\frac{v_3-v_2}{h}u_2-r_{2-\frac{1}{2}}^{d-1}\frac{v_2-v_1}{h}u_1\right) \\&\vdots \\ \frac{du_i}{dt}&= \frac{r_i^{1-d}}{h}\left( r_{i+\frac{1}{2}}^{d-1}\frac{u_{i+1}-u_{i}}{h}-r_{i-\frac{1}{2}}^{d-1}\frac{u_{i}-u_{i-1}}{h}\right) \\&\quad -\frac{r_i^{1-d}}{h}\left( r_{i+\frac{1}{2}}^{d-1}\frac{v_{i+1}-v_{i}}{h}u_i-r_{i-\frac{1}{2}}^{d-1}\frac{v_{i}-v_{i-1}}{h}u_{i-1}\right) \\&\vdots \\ \frac{du_{N}}{dt}&=\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{u_{N}-u_{N-1}}{h}\right) -\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{v_{N}-v_{N-1}}{h}u_{N}\right) , \end{aligned}$$

and

$$\begin{aligned} \frac{dv_1}{dt}&=\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{v_2-v_1}{h}\right) -v_1+u_1\\ \frac{dv_2}{dt}&=\frac{r_2^{1-d}}{h}\left( r_{2+\frac{1}{2}}^{d-1}\frac{v_3-v_2}{h}-r_{2-\frac{1}{2}}^{d-1}\frac{v_2-v_1}{h}\right) -v_2+u_2\\&\vdots \\ \frac{dv_i}{dt}&=\frac{r_i^{1-d}}{h}\left( r_{i+\frac{1}{2}}^{d-1}\frac{v_{i+1}-v_i}{h}-r_{i-\frac{1}{2}}^{d-1}\frac{v_i-v_{i-1}}{h}\right) -v_i+u_i\\&\vdots \\ \frac{dv_{N}}{dt}&=\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{v_{N}-v_{N-1}}{h}\right) -v_{N}+u_{N}. \end{aligned}$$

We name the system (FvKS). The corresponding spatial discretization is based on the scheme stated in [24]. The precise setting (FvKS) is as follows: letting $N\in \mathbb {N}$ and $h=L/N$, the mesh of the interval $(0,L)\subset \mathbb {R}$ is defined by

$$\begin{aligned} 0=r_{\frac{1}{2}}<r_{1+\frac{1}{2}}<\dots<r_{N-1+\frac{1}{2}}<r_{N+\frac{1}{2}}=L, \end{aligned}$$

where $r_{i+\frac{1}{2}}=ih$ ($i=0,1,\dots ,N$). In this example, we set $L=1$. Here, $(r_{i+\frac{1}{2}},r_{i+1+\frac{1}{2}})$ ($i=0,1,\dots ,N-1$) is called the control volume with its control point $r_{i+1}=(i+\frac{1}{2})h$. The semi-discretization of the space variable yields the approximation satisfying $u_i(t)\simeq u(r_i,t)$ and $v_i(t)\simeq v(r_i,t)$ ($i=1,2,\dots ,N$, $t>0$).

Remark 5.4

We briefly gather several facts about blow-up behavior in the Keller–Segel systems of the parabolic-parabolic type (5.8). In [12], radially symmetric blow-up solutions for (5.7) with $d\ge 2$ are constructed constitutively. In [19], the Keller–Segel system with $d=1$ is proved to admit no blow-up solutions. In [23], criteria for blow-ups of radial-symmetric solutions for (5.7) with $d\ge 3$ are provided. In [18], radially symmetric blow-up solutions for (5.7) with $d=2$ is proved to be of so-called type II; namely, asymptotics near blow-up is not determined only by nonlinearity of vector fields. See references therein and others for more details.

It should be noted that, in the present argument, we cannot discuss that how accurate our present arguments describe the true nature of the Keller–Segel system (5.7). Even if N can be chosen as large as possible, which looks close to the original Keller–Segel system, our problem is considered just as an independent finite-dimensional ODE system because there are non-trivial gaps between the present system and (5.7), such as the choice of scaling or breaking of positivity. Compare Lemma 5.5 with Sect. 5.3.3. Moreover, as seen in our validated results (Fig. 3 below), the blow-up profiles does not possess positivity, which reflect the property of the scheme mentioned in Remark 5.3 and roughness of the grid size which we have succeeded in validations. If a numerical scheme which possess positivity even near blow-up is proposed and if numerical validations are succeeded for sufficiently large N, the validated solutions can approximate the true nature of blow-up profiles for the Keller–Segel system in some sense.

First we observe that (FvKS) is asymptotically quasi-homogeneous in the following sense.

Lemma 5.5

The system (FvKS) is an asymptotically quasi-homogeneous vector field at infinity of the following type and order 2:

$$\begin{aligned} \alpha = (\underbrace{2\dots ,2}_{N}, \underbrace{1\dots ,1}_{N}). \end{aligned}$$

In other words, (FvKS) is asymptotically quasi-homogeneous under the scaling $u_i\mapsto s^2u_i$ and $v_i\mapsto sv_i$ for $i=1,\ldots , N$.

Following Lemma 5.5, we consider two types of quasi-homogeneous compactifications. One is the directional compactification of type $\alpha$:

$$\begin{aligned} u_1 = \frac{1}{s^2},\quad u_i = \frac{\hat{x}_i}{s^2}\ (i=2,\ldots , N),\quad v_j = \frac{\hat{y}_j}{s}\ (j=1,\ldots , N), \end{aligned}$$

(5.9)

and the other is the quasi-parabolic compactification of type $\alpha$:

$$\begin{aligned} y_j = \frac{x_j}{(1-p(x)^{4})^{\alpha _j}}\ (j=1,\ldots , 2N),\quad p(x)^4 = \sum _{j=1}^{N}\tilde{u}_j^2 + \tilde{v}_j^4,\quad \kappa _{para}^{-1} = 1-p(x)^4, \end{aligned}$$

(5.10)

where $x = (x_1,\ldots , x_{2N}) \equiv (\tilde{u}_1,\ldots , \tilde{u}_N, \tilde{v}_1, \ldots , \tilde{v}_N)$.

5.3.1 Directional compactification

Direct computations yield the following transformation of vector fields:

$$\begin{aligned} u_1'&= -2s^{-3} s'\\&= \frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}s^{-2}\frac{\hat{x}_2-1}{h}\right) -\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}s^{-3}\frac{\hat{y}_2-\hat{y}_1}{h}\right) , \end{aligned}$$

namely,

$$\begin{aligned} s' = -\frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} . \end{aligned}$$

Similarly,

$$\begin{aligned} u_2'&= -2s^{-3}\hat{x}_2 s' + s^{-2} \hat{x}_2'\\&= \frac{r_2^{1-d}}{h} s^{-2} \left( r_{2+\frac{1}{2}}^{d-1}\frac{\hat{x}_3 - \hat{x}_2}{h}-r_{2-\frac{1}{2}}^{d-1}\frac{\hat{x}_2-1}{h}\right) \\&\quad - \frac{r_2^{1-d}}{h}s^{-3} \left( r_{2+\frac{1}{2}}^{d-1} \frac{\hat{y}_3 - \hat{y}_2}{h}\hat{x}_2 - r_{2-\frac{1}{2}}^{d-1}\frac{\hat{y}_2 - \hat{y}_1}{h}\right) , \end{aligned}$$

to obtain

$$\begin{aligned} \hat{x}_2'&= 2s^{-1}\hat{x}_2 s' + s^2 u_2'\\&= 2s^{-1}\hat{x}_2 \left[ -\frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_2^{1-d}}{h} \left( r_{2+\frac{1}{2}}^{d-1}\frac{\hat{x}_3 - \hat{x}_2}{h}-r_{2-\frac{1}{2}}^{d-1}\frac{\hat{x}_2-1}{h}\right) \\&\quad - \frac{r_2^{1-d}}{h}s^{-1} \left( r_{2+\frac{1}{2}}^{d-1} \frac{\hat{y}_3 - \hat{y}_2}{h}\hat{x}_2 - r_{2-\frac{1}{2}}^{d-1}\frac{\hat{y}_2 - \hat{y}_1}{h}\right) \\&= -s^{-1}\hat{x}_2 \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_2^{1-d}}{h^2} \left[ r_{2+\frac{1}{2}}^{d-1} \left\{ (\hat{x}_3 - \hat{x}_2) -s^{-1}(\hat{y}_3 - \hat{y}_2) \hat{x}_2 \right\} - r_{2-\frac{1}{2}}^{d-1} \left\{ (\hat{x}_2-1) -s^{-1}(\hat{y}_2 - \hat{y}_1)\right\} \right] . \end{aligned}$$

For $u_i$ with $i= 3,\ldots , N-1$,

$$\begin{aligned} u_i'&= -2s^{-3}\hat{x}_i s' + s^{-2} \hat{x}_i'\\&= \frac{r_i^{1-d}}{h} s^{-2} \left( r_{i+\frac{1}{2}}^{d-1}\frac{\hat{x}_{i+1} - \hat{x}_{i}}{h}-r_{i-\frac{1}{2}}^{d-1} \frac{\hat{x}_{i} - \hat{x}_{i-1}}{h}\right) \\&\quad -\frac{r_i^{1-d}}{h} s^{-3} \left( r_{i+\frac{1}{2}}^{d-1}\frac{\hat{y}_{i+1} - \hat{y}_{i}}{h}\hat{x}_i - r_{i-\frac{1}{2}}^{d-1}\frac{\hat{y}_{i} - \hat{y}_{i-1}}{h}\hat{x}_{i-1}\right) , \end{aligned}$$

to obtain

$$\begin{aligned} \hat{x}_i'&= -2s^{-1}\hat{x}_i s' + s^2 u_i'\\&= -s^{-1}\hat{x}_i \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_i^{1-d}}{h^2} \left[ r_{i+\frac{1}{2}}^{d-1} \left\{ (\hat{x}_{i+1} - \hat{x}_{i}) - s^{-1} (\hat{y}_{i+1} - \hat{y}_{i}) \hat{x}_i \right\} \right. \\&\quad \left. - r_{i-\frac{1}{2}}^{d-1} \left\{ (\hat{x}_{i} - \hat{x}_{i-1}) - s^{-1}(\hat{y}_{i} - \hat{y}_{i-1})\hat{x}_{i-1}\right\} \right] . \end{aligned}$$

Finally,

$$\begin{aligned} u_N'&= -2s^{-3}\hat{x}_N s' + s^{-2} \hat{x}_N'\\&=\frac{r_{N}^{1-d}}{h} s^{-2}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{\hat{x}_{N} - \hat{x}_{N-1}}{h}\right) -\frac{r_{N}^{1-d}}{h} s^{-2} \left( -r_{N-\frac{1}{2}}^{d-1}\frac{\hat{y}_{N} - \hat{y}_{N-1}}{h}\hat{x}_{N}\right) \end{aligned}$$

to obtain

$$\begin{aligned} \hat{x}_N'&= -2s^{-1}\hat{x}_N s' + s^2 u_N'\\&= -s^{-1}\hat{x}_N \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad - \frac{r_{N}^{1-d}}{h^2} r_{N-\frac{1}{2}}^{d-1} \left\{ (\hat{x}_{N} - \hat{x}_{N-1}) - s^{-1}(\hat{y}_{N} - \hat{y}_{N-1})\hat{x}_{N}\right\} . \end{aligned}$$

Next compute $\hat{y}_i'$.

$$\begin{aligned} v_1'= -s^{-2} \hat{y}_1 s' + s^{-1} \hat{y}_1' = \frac{r_1^{1-d}}{h}s^{-1}\left( r_{1+\frac{1}{2}}^{d-1}\frac{\hat{y}_2 - \hat{y}_1}{h}\right) - s^{-1}\hat{y}_1+ s^{-2} \end{aligned}$$

to obtain

$$\begin{aligned} \hat{y}_1'&= s^{-1} \hat{y}_1 s' + s v_1'\\&= -s^{-1}\hat{y}_1 \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] + \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} (\hat{y}_2 - \hat{y}_1)- \hat{y}_1+ s^{-1}. \end{aligned}$$

Similarly,

$$\begin{aligned} v_i'&= -s^{-2} \hat{y}_i s' + s^{-1} \hat{y}_i'\\&= \frac{r_i^{1-d}}{h^2}s^{-1}\left( r_{i+\frac{1}{2}}^{d-1}(\hat{y}_{i+1} - \hat{y}_i) -r_{i-\frac{1}{2}}^{d-1} (\hat{y}_i - \hat{y}_{i-1}) \right) - s^{-1}\hat{y}_i + s^{-2}\hat{x}_i \end{aligned}$$

to obtain

$$\begin{aligned} \hat{y}_i'&= s^{-1} \hat{y}_i s' + s v_i'\\&= -s^{-1}\hat{y}_i \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_i^{1-d}}{h^2} \left( r_{i+\frac{1}{2}}^{d-1}(\hat{y}_{i+1} - \hat{y}_i) -r_{i-\frac{1}{2}}^{d-1} (\hat{y}_i - \hat{y}_{i-1}) \right) - \hat{y}_i + s^{-1}\hat{x}_i,\quad i=2,\ldots , N-1, \end{aligned}$$

and

$$\begin{aligned} v_N'&= -s^{-2} \hat{y}_N s' + s^{-1} \hat{y}_N'\\&= \frac{r_{N}^{1-d}}{h^2}s^{-1}\left( -r_{N-\frac{1}{2}}^{d-1}(\hat{y}_{N} - \hat{y}_{N-1}) \right) - s^{-1}\hat{y}_{N}+ s^{-2}\hat{x}_{N} \end{aligned}$$

to obtain

$$\begin{aligned} \hat{y}_N'&= s^{-1} \hat{y}_N s' + s v_N'\\&= -s^{-1}\hat{y}_N \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_{N}^{1-d}}{h^2} r_{N-\frac{1}{2}}^{d-1}\left( -(\hat{y}_{N} - \hat{y}_{N-1}) \right) - \hat{y}_{N}+ s^{-1}\hat{x}_{N}. \end{aligned}$$

Introducing the time-variable desingularization

$$\begin{aligned} \frac{d\tau _d}{dt} = s^{-1}, \end{aligned}$$

we have the following result.

Lemma 5.6

The desingularized vector field of (FvKS) with respect to the directional compactification (5.9) is the following system:

$$\begin{aligned} \dot{s}&= - s\frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} ,\\ \dot{\hat{x}}_2&= -\hat{x}_2 \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_2^{1-d}}{h^2} \left[ r_{2+\frac{1}{2}}^{d-1} \left\{ s (\hat{x}_3 - \hat{x}_2) - (\hat{y}_3 - \hat{y}_2) \hat{x}_2 \right\} - r_{2-\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) -(\hat{y}_2 - \hat{y}_1)\right\} \right] ,\\ \dot{\hat{x}}_i&= - \hat{x}_i \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + \frac{r_i^{1-d}}{h^2} \left[ r_{i+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_{i+1} - \hat{x}_{i}) - (\hat{y}_{i+1} - \hat{y}_{i}) \hat{x}_i \right\} \right. \\&\qquad \quad \left. - r_{i-\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_{i} - \hat{x}_{i-1}) - (\hat{y}_{i} - \hat{y}_{i-1})\hat{x}_{i-1}\right\} \right] ,\\&\quad \quad (i=3,\ldots , N-1)\\ \dot{\hat{x}}_N&= - \hat{x}_N \left[ \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad - \frac{r_{N}^{1-d}}{h^2} r_{N-\frac{1}{2}}^{d-1} \left\{ s (\hat{x}_{N} - \hat{x}_{N-1}) - (\hat{y}_{N} - \hat{y}_{N-1})\hat{x}_{N-1}\right] ,\\ \dot{\hat{y}}_1&= - \hat{y}_1 \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] + s \frac{r_1^{1-d}}{h^2}r_{1+\frac{1}{2}}^{d-1} (\hat{y}_2 - \hat{y}_1) - s \hat{y}_1+ 1,\\ \dot{\hat{y}}_i&= -\hat{y}_i \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] \\&\quad + s \frac{r_i^{1-d}}{h^2} \left( r_{i+\frac{1}{2}}^{d-1}(\hat{y}_{i+1} - \hat{y}_i) -r_{i-\frac{1}{2}}^{d-1} (\hat{y}_i - \hat{y}_{i-1}) \right) \\&\quad - s \hat{y}_i + \hat{x}_i,\quad (i=2,\ldots , N-1)\\ \dot{\hat{y}}_N&= - \hat{y}_N \left[ \frac{r_1^{1-d}}{2h^2}r_{1+\frac{1}{2}}^{d-1} \left\{ s(\hat{x}_2-1) - (\hat{y}_2 - \hat{y}_1)\right\} \right] + s \frac{r_{N}^{1-d}}{h^2} r_{N-\frac{1}{2}}^{d-1}\left( -(\hat{y}_{N} - \hat{y}_{N-1}) \right) \\&\quad - s \hat{y}_{N}+ \hat{x}_{N}. \end{aligned}$$

Our concerning blow-up solution is a trajectory of the desingularized vector field asymptotic to an equilibrium on the horizon $\{s=0\}$. The initial data is given by

$$\begin{aligned} u_i(0)=100(1+\cos (\pi r_i)),~v_i(0)=0~(i=1,2,\dots ,N). \end{aligned}$$

(5.11)

Then, we derive

$$\begin{aligned} s(0)=\frac{1}{\sqrt{u_1(0)}},~\hat{x}_i(0)=\frac{u_i(0)}{u_1(0)}~(i=2,3,\dots ,N),~\hat{y}_j(0)=\frac{v_j(0)}{\sqrt{u_1(0)}}~(j=1,2,\dots ,N). \end{aligned}$$

Following Algorithm 2, we validate global trajectories for the vector field in Lemma 5.6 asymptotic to $\mathcal {E} = \{s=0\}$ with various (d, N). Validated equilibria are near

$$\begin{aligned}&s = 0,\quad \hat{x}_1 = -0.036653902557231,\quad \hat{x}_2 = -8.275562067652\times 10^{-5},\\&\quad \quad \hat{x}_j = 0\ (j\ge 3),\\&\hat{y}_1 = 0.04910809766161,\quad \hat{y}_2 = 0.001800003426459655,\quad \hat{y}_j = 0\ (j\ge 3),\quad \text {etc.} \end{aligned}$$

Validated results are collected in Table 3, which correspond to rigorous enclosures of a trajectory illustrated in Fig. 3.

Table 3 Validated results for (FvKS) using the directional compactification: numerical validations prove that the solution enclosures at $\tau = \tau _{d,N}$ are included in $\mathrm{int}\,N$ and that (4.6) provides the inclusion of the blow-up time $t_{d,\max }$

Fig. 3

A blow-up trajectory for (FvKS) with $(d,N)=(3,11)$. A blow-up trajectory with the initial data (5.11) are drawn. a The (t, r, u)-plot of the blow-up trajectory. b The (r, u)-plot of the blow-up trajectory near $t=t_{\max } \approx 0.04$. a The (t, r, v)-plot of the blow-up trajectory. b The (r, v)-plot of the blow-up trajectory near $t=t_{\max } \approx 0.04$

Remark 5.7

The statement “Failed” in Table 3 comes from the failure of Step 2 in Algorithm 2. That is, the matrix $A(\cdot )$ could not be validated to be negative definite, although corresponding equilibria admit only eigenvalues with negative real parts (at least in the numerical sense). This might be caused by the change of eigenvalue distributions of matrices $Df(\cdot )$ via their symmetrizations. As long as we have tried, validations have been failed $(d,N) = (4,13), (4,14)$ by the same reason. As for the case $(d,N) = (4,15)$, we have failed computation of eigenvalues even in the non-rigorous sense.

On the other hand, several eigenvalues of $Df(\cdot )$ at equilibria are actually accumulated in the numerical sense, which implies that the computed eigenvectors may be linearly dependent. In such a case, we cannot apply the eigenmatrix diagonalizing the Jacobian matrix to determining the matrix Y in Proposition 4.2. Instead, we apply the Schur decomposition of the Jacobian matrix to checking eigenvalues, and to determining Y; $Y=I$, as indicated in Remark 4.3.

The similar cases occur for the system (FvKS) with quasi-parabolic compactifications.

5.3.2 Quasi-parabolic compactification

Let

$$\begin{aligned} \tilde{f}_j(x_1,\ldots , x_{2N}) := \kappa _{para}^{-(1+\alpha _j)}\tilde{f}_j(\kappa ^2 x_1,\ldots , \kappa ^2 x_N, \kappa x_{N+1}, \ldots , \kappa x_{2N}). \end{aligned}$$

Then we have

$$\begin{aligned} \tilde{f}_1&=\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{\tilde{u}_2 - \tilde{u}_1}{h}\right) \kappa _{para}^{-1} - \frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{\tilde{v}_2 - \tilde{v}_1}{h}\tilde{u}_1\right) ,\\ \tilde{f}_j&= \frac{r_j^{1-d}}{h}\left( r_{j+\frac{1}{2}}^{d-1}\frac{\tilde{u}_{j+1} - \tilde{u}_{j}}{h}-r_{j-\frac{1}{2}}^{d-1}\frac{\tilde{u}_{j} - \tilde{u}_{j-1}}{h}\right) \kappa _{para}^{-1} \\&\quad - \frac{r_j^{1-d}}{h}\left( r_{j+\frac{1}{2}}^{d-1}\frac{\tilde{v}_{j+1} - \tilde{v}_{j}}{h}\tilde{u}_j - r_{j-\frac{1}{2}}^{d-1}\frac{\tilde{v}_{j} - \tilde{v}_{j-1}}{h}\tilde{u}_{j-1}\right) ,\\&\quad \quad (j=2,\ldots , N-1)\\ \tilde{f}_N&=\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{\tilde{u}_{N} - \tilde{u}_{N-1}}{h}\right) \kappa _{para}^{-1} -\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{\tilde{v}_{N} - \tilde{v}_{N-1}}{h}\tilde{u}_{N}\right) , \end{aligned}$$

and

$$\begin{aligned} \tilde{f}_{N+1}&=\frac{r_1^{1-d}}{h}\left( r_{1+\frac{1}{2}}^{d-1}\frac{\tilde{v}_2 - \tilde{v}_1}{h}\right) \kappa _{para}^{-1} - \tilde{v}_1 \kappa _{para}^{-1}+ \tilde{u}_1,\\ \tilde{f}_{N+j}&=\frac{r_j^{1-d}}{h}\left( r_{j+\frac{1}{2}}^{d-1}\frac{\tilde{v}_{j+1}-\tilde{v}_j}{h}-r_{j-\frac{1}{2}}^{d-1}\frac{\tilde{v}_j - \tilde{v}_{j-1}}{h}\right) \kappa _{para}^{-1} - \tilde{v}_j \kappa ^{-1} + \tilde{u}_j,\\&\quad \quad (j=2,\ldots , N-1)\\ \tilde{f}_{2N}&=\frac{r_{N}^{1-d}}{h}\left( -r_{N-\frac{1}{2}}^{d-1}\frac{\tilde{v}_{N} - \tilde{v}_{N-1}}{h}\right) \kappa _{para}^{-1} - \tilde{v}_{N} \kappa _{para}^{-1} + \tilde{u}_{N}. \end{aligned}$$

Recall that the desingularized vector field associated with the vector field $y'=f(y)$ on $\mathbb {R}^{2N}$ with quasi-parabolic compactification of type $\alpha$ is (3.7). The sum $G(x) := \sum _{j=1}^{2N} \frac{x_j^{2\beta _j-1}}{\alpha _j} \tilde{f}_j(x)$ is necessary to be computed. Now we have

$$\begin{aligned} \sum _{j=1}^{N} \frac{x_j^{2\beta _j-1}}{\alpha _j} \tilde{f}_j(x)&= \sum _{j=1}^{N} \frac{\tilde{u}_j}{2} \tilde{f}_j(x)\\&= \frac{1}{2h^2}\sum _{j=1}^{N-1} r_{j+\frac{1}{2}}^{d-1} \{-r_{j+1}^{1-d}\tilde{u}_{j+1} + r_j^{1-d}\tilde{u}_j \}\\&\quad \cdot \{\kappa _{para}^{-1}(\tilde{u}_{j+1} - \tilde{u}_j) - (\tilde{v}_{j+1}-\tilde{v}_j)\tilde{u}_j \},\\ \sum _{j=N+1}^{2N} \frac{x_j^{2\beta _j-1}}{\alpha _j} \tilde{f}_j(x)&= \sum _{j=1}^{N} \tilde{v}_j^3 \tilde{f}_{N+j}(x)\\&= \frac{\kappa _{para}^{-1}}{h^2} \sum _{j=1}^{N-1} r_{j+\frac{1}{2}}^{d-1} \{-r_{j+1}^{1-d}\tilde{v}_{j+1}^3+ r_j^{1-d}\tilde{v}_j^3 \} (\tilde{v}_{j+1} - \tilde{v}_j)\\&\quad - \kappa _{para}^{-1}\sum _{j=1}^N \tilde{v}_j^4 +\sum _{j=1}^N \tilde{v}_j^3 \tilde{u}_j. \end{aligned}$$

Therefore we have

$$\begin{aligned} G(x)&= \frac{1}{2h^2}\sum _{j=1}^{N-1} r_{j+\frac{1}{2}}^{d-1} \{-r_{j+1}^{1-d}\tilde{u}_{j+1} + r_j^{1-d}\tilde{u}_j \}\cdot \{\kappa _{para}^{-1}(\tilde{u}_{j+1} - \tilde{u}_j) - (\tilde{v}_{j+1}-\tilde{v}_j)\tilde{u}_j \}\nonumber \\&\quad + \frac{\kappa _{para}^{-1}}{h^2}\sum _{j=1}^{N-1} r_{j+\frac{1}{2}}^{d-1} \{-r_{j+1}^{1-d}\tilde{v}_{j+1}^3+ r_j^{1-d}\tilde{v}_j^3 \} (\tilde{v}_{j+1} - \tilde{v}_j) - \kappa _{para}^{-1}\sum _{j=1}^N \tilde{v}_j^4 +\sum _{j=1}^N \tilde{v}_j^3 \tilde{u}_j. \end{aligned}$$

(5.12)

Summarizing these arguments, we have the concrete form of the desingularized vector field:

Lemma 5.8

The desingularized vector field for (FvKS) with the quasi-parabolic compactification of type $\alpha$ is the following:

$$\begin{aligned} \frac{d\tilde{u}_i}{d\tau _{para}}&= \frac{1}{4}\left( 1+3\sum _{j=1}^N (\tilde{u}_j^2 + \tilde{v}_j^4)\right) \tilde{f}_i(x) - 2\tilde{u}_i G(x),\quad i=1,\ldots , N,\\ \frac{d\tilde{v}_i}{d\tau _{para}}&= \frac{1}{4}\left( 1+3\sum _{j=1}^N (\tilde{u}_j^2 + \tilde{v}_j^4)\right) \tilde{f}_{N+i}(x) - \tilde{v}_i G(x),\quad i=1,\ldots , N, \end{aligned}$$

where $x=(x_1,\ldots , x_{2N})\equiv (\tilde{u}_1,\ldots , \tilde{u}_N, \tilde{v}_1,\ldots , \tilde{v}_N)$ and G(x) is given in (5.12).

Our concerning blow-up solution is a trajectory of the desingularized vector field asymptotic to an equilibrium on the horizon $\{p(x) = 1\}$, which generally depends on (d, N), while it corresponds to a point validated in Sect. 5.3.1. Following Algorithm 1, we validate global trajectories for the vector field in Lemma 5.8 asymptotic to $\mathcal {E} = \partial \mathcal {D}$. The initial data are set as (5.11) with application of $T_{para}$. As for computations of $\kappa (y)$, we have applied the Krawczyk method (e.g., [22]) to $F(\kappa ;y)= \kappa ^4 - \kappa ^3 - p(y)^4 = 0$ appeared in Lemma 2.9. Final validated results are collected in Table 4.

Table 4 Validated results for (FvKS) using the quasi-parabolic compactification: numerical validations prove $x(\tau _{para,N})\in \mathrm{int}\,N$ and (4.5) yields the inclusion of the blow-up time $t_{para,\max }$

5.3.3 Final remark: scalings for (FvKS)

The scaling derived in Lemma 5.5 does not actually reflect the scaling in the original Keller–Segel system (5.8). Indeed, the following simpler system

$$\begin{aligned} \left\{ \begin{array}{ll} u_t=\Delta u-\nabla \cdot (u\nabla v),&{}x\in \Omega ,~t>0,\\ v_t=\Delta v+u,&{}x\in \Omega ,~t>0,\\ \frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,&{}x\in \partial \Omega ,~t>0,\\ u(x,0)=u_0(x),~v(x,0)=v_0(x),&{}x\in \Omega , \end{array} \right. \end{aligned}$$

(5.13)

namely in the absence of the term $``-v''$ in the second equation, possesses the following scaling invariance:

$$\begin{aligned} u_\lambda (x,t) := \lambda ^2 u(\lambda x, \lambda ^2 t),\quad v_\lambda (x,t) := v(\lambda x, \lambda ^2 t),\quad \lambda > 0. \end{aligned}$$

(5.14)

In particular, the value of v is not scaled, which is different from the type derived in Lemma 5.5. We can consider another scaling to (FvKS) regarding the grid size parameter h as an independent variable. Actually, we have the following scaling law for (FvKS), which will reflect the scaling (5.14).

Lemma 5.9

Regard h as an independent variable with trivial time evolution $dh/dt = 0$. Then the system (FvKS) is asymptotically quasi-homogeneous of the following type and order 3:

$$\begin{aligned} \alpha = \left( \underbrace{2\dots ,2}_{N}, \underbrace{0\dots ,0}_{N}, -1\right) \end{aligned}$$

with natural extension of type for nonpositive integers. In other words, (FvKS) is asymptotically quasi-homogeneous under the scaling $u_i\mapsto s^2u_i$, $v_i\mapsto v_i$ for $i=1,\ldots , N$ and $h\mapsto s^{-1}h$.

The authors have tried computing trajectories asymptotic to the horizon (for directional compactifications) with the above scaling, but they could find no such trajectories. Indeed, the temporal-spatial scaling (5.14) transforms blow-up solutions for (5.13) to bounded solutions. Correspondingly, divergent solutions of the corresponding discretized system can tend to points away from the horizon, and hence compactification approach is not effective in this case. Instead, the scaling $h\mapsto s^{-1}h$ has a potential to link a rescaling algorithm for numerics of partial differential equations (e.g. [2]).

6 Conclusion

In the present paper, we have derived a numerical validation procedure of blow-up solutions for vector fields with asymptotic quasi-homogeneity at infinity. Our proposing numerical validation methodology is essentially the same as the previous study by authors and their collaborators [21] except the mathematical formulation of compactifications as well as time-variable desingularizations. We have applied quasi-homogeneous compactifications, in particular quasi-parabolic and directional ones, to describing the infinity so that the desingularized vector field for asymptotically quasi-homogeneous ones can appropriately describe dynamics at infinity.

We have also introduced a new quasi-homogeneous compactification called quasi-parabolic one, which is an alternative of the quasi-Poincaré compactification [16]. This compactification determines a global chart unlike directional compactifications, and overcomes the lack of smoothness of desingularized vector fields at infinity which arise in cases of Poincaré-type compactifications. The former property enables us to validate blow-up solutions through sign-changing trajectories (Sect. 5.1), and the latter enables us to apply our validation procedure to asymptotically quasi-homogeneous vector fields (Sects. 5.2 and 5.3). Effectiveness of directional compactifications towards validation of blow-up solutions possessing a component with identical sign during time evolutions is demonstrated. Quasi-homogeneous compactifications such as directional and admissible quasi-homogeneous ones will open the door to numerical validations of blow-up solutions for various (asymptotically) polynomial vector fields including finite dimensional approximations of systems of partial differential equations.

Appendices

A Schur decompositions

In this section we review Schur decompositions of squared matrices.

Proposition A.1

(Schur decomposition, e.g., [11]). Let $A\in M_n(\mathbb {C})$: complex $n\times n$ matrix. Then there exists a unitary matrix $Q\in U(n)$ such that

$$\begin{aligned} Q^H A Q = T \equiv D + N, \end{aligned}$$

where $Q^H$ is the Hermitian transpose of Q, $D = \mathrm{diag}(\lambda _1,\ldots , \lambda _n)$ and $N\in M_n(\mathbb {C})$ is strictly upper triangular. Furthermore, Q can be chosen so that the eigenvalues $\lambda _i$ appear in any order along the diagonal. We shall call Ta Schur normal form ofA.

When we treat all computations in real floating number or interval arithmetic, the real version of Schur decompositions can be applied.

Proposition A.2

(Real Schur decomposition, e.g., [11]). Let $A\in M_n(\mathbb {R})$: real $n\times n$ matrix. Then there exists an orthogonal matrix $Q\in O(n)$ such that

$$\begin{aligned} Q^T A Q = T\equiv \begin{pmatrix} R_{11} &{}\quad R_{12} &{}\quad \ldots &{}\quad R_{1m} \\ 0 &{}\quad R_{22} &{}\quad \ldots &{}\quad R_{2m} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \ldots &{}\quad R_{mm} \end{pmatrix}, \end{aligned}$$

where each $R_{ii}$ is either a $1\times 1$ or a $2\times 2$ matrix having complex conjugate eigenvalues. We shall call Ta real Schur normal form ofA.

A merit of Schur decompositions is that we can apply it to arbitrary square matrices. In particular, change of coordinates via Schur decompositions can be realized no matter what the multiplicities of any eigenvalues are.

B concrete calculations of an upper bound of $t_{\max }$ with quasi-parabolic compactifications

In this section, we consider the rigorous validation of the maximal existence time

$$\begin{aligned} t_{para,\max } = \int _0^\infty \kappa _{para}(y)^{-k}\left( 1-\frac{2c-1}{2c}\kappa _{para}(y)^{-1}\right) d\tau _{para} \end{aligned}$$

of solution trajectories with quasi-parabolic compactifications and computer assistance. First of all, we compute the following integral representing the time of integration of computed trajectory for desingularized vector fields int-timescale in advance:

$$\begin{aligned} t_{para,N}=\int _0^{\tau _{para,N}}\left( 1-p(x(\tau _{para}))^{2c}\right) ^{k}\left( 1-\frac{2c-1}{2c}\left( 1-p(x(\tau _{para}))^{2c}\right) \right) d\tau _{para}. \end{aligned}$$

As mentioned in Sect. 4.3, the estimate of $|1-p(x)^{2c}|$ is essential to computation of an upper bound $C_{n,\alpha ,N}(L)$. At first, we derive the estimate with the type $\alpha =(1,2)$ and $c=2$ as an example. Let $x_*= (x^*_1, x^*_2) \in \mathcal {E}$ and assume that a Lyapunov function L(x) is validated in a vicinity of $x_*$. Then

$$\begin{aligned} x_1^4+x_2^2 =&(x_1-x_1^*+x_1^*)^4+(x_2-x_2^*+x_2^*)^2\\ =&(x_1-x_1^*)^4+4(x_1-x_1^*)^3x_1^*+6(x_1-x_1^*)^2(x_1^*)^2+4(x_1-x_1^*)(x_1^*)^3+(x_1^*)^4\\&+(x_2-x_2^*)^2+2(x_2-x_2^*)x_2^*+(x_2^*)^2. \end{aligned}$$

Now $p(x_*)=1$ holds since $x_*\in \mathcal {E}$. Thus we have

$$\begin{aligned} \left| 1-p(x)^{2c}\right| =&\Big |(x_1-x_1^*)^4+4(x_1-x_1^*)^3x_1^*+6(x_1-x_1^*)^2(x_1^*)^2+4(x_1-x_1^*)(x_1^*)^3\\&+(x_2-x_2^*)^2+2(x_2-x_2^*)x_2^*\Big |\\ =&\left| \left[ 4(x_1^*)^3~2x_2^*\right] \left[ \begin{array}{l} x_1-x_1^*\\ x_2-x_2^*\end{array}\right] +\left[ 6(x_1^*)^2~1\right] \left[ \begin{array}{l} (x_1-x_1^*)^2\\ (x_2-x_2^*)^2 \end{array}\right] \right. \\&\left. +\left[ 4x_1^*~0\right] \left[ \begin{array}{l} (x_1-x_1^*)^3\\ (x_2-x_2^*)^3 \end{array}\right] +\left[ 1~0\right] \left[ \begin{array}{l} (x_1-x_1^*)^4\\ (x_2-x_2^*)^4 \end{array}\right] \right| \\ \le&\left\| \left[ \begin{array}{l} 4(x_1^*)^3\\ 2x_2^*\end{array}\right] \right\| \left\| x-x_*\right\| \\&+\max \left\{ 6(x_1^*)^2,1\right\} \left\| x-x_*\right\| ^2+\left| 4x_1^*\right| \left\| x-x_*\right\| ^3+\left\| x-x_*\right\| ^4. \end{aligned}$$

By $\Vert x-x_*\Vert \le \left( c_1L\right) ^{1/2}$ followed by the value of Lyapunov function L(x), we obtain

$$\begin{aligned} \left| 1-p(x)^{2c}\right|&\le \left\{ 16(x_1^*)^6+4(x_2^*)^2\right\} ^{1/2}\left( c_1L\right) ^{1/2}\\&\quad +\max \left\{ 6(x_1^*)^2,1\right\} c_1L+\left| 4x_1^*\right| \left( c_1L\right) ^{3/2}+\left( c_1L\right) ^{2}\\&=:C_{n,\alpha ,N}(L). \end{aligned}$$

Finally we obtain an upper bound of $t_{para,\max }$ as follows:

$$\begin{aligned} t_{para,\max }&=t_{para,N}+\int _{\tau _{para,N}}^\infty \left( 1-p(x(\tau _{para}))^{2c}\right) ^{k}\\&\quad \left( 1-\frac{2c-1}{2c}\left( 1-p(x(\tau _{para}))^{2c}\right) \right) d\tau _{para}\\&=t_{para,N}+\int _{\tau _{para,N}}^\infty \left( 1-p(x(\tau _{para}))^{2c}\right) ^{k}\\&\quad \left( \frac{1}{2c}+\frac{2c-1}{2c}p(x(\tau _{para}))^{2c}\right) d\tau _{para}\\&\le t_{para,N}+\int _{\tau _{para,N}}^\infty \left| 1-p(x(\tau _{para}))^{2c}\right| ^{k}d\tau _{para}\\&\le t_{para,N} +\frac{1}{c_{\tilde{N}}c_1} \int _0^{L(x(\tau _{para,N}))} \frac{C_{n,\alpha ,N}(L)^{k}}{L}dL, \end{aligned}$$

where we have used the estimate $\frac{dL}{d\tau _{para}}\le -c_{\tilde{N}}c_1L$ along the trajectory $\{x(\tau _{para})\}$, which follows from the inequality of Lyapunov functions. The positive constants $c_{\tilde{N}}, c_1$ are shown in [21].

Next we show an estimate of $|1-p(x)^{2c}|$ with compactifications of general type $\alpha =(\alpha _1,\dots ,\alpha _n)$. As in the previous case, let $x_*= (x^*_1, \ldots , x^*_n) \in \mathcal {E}$ and assume that a Lyapunov function L(x) is validated in a vicinity of $x_*$. Then

$$\begin{aligned} \left| 1-p(x)^{2c}\right|&=\left| 1-\sum _{i=1}^nx_i^{2\beta _i}\right| \\&=\left| \sum _{i=1}^n\left( x_i^*\right) ^{2\beta _i}-\sum _{i=1}^n\left( x_i-x_i^*+x_i^*\right) ^{2\beta _i}\right| \\&=\left| \sum _{i=1}^n\sum _{j=1}^{2\beta _i}\left( {\begin{array}{c}2\beta _i\\ j\end{array}}\right) \left( x_i-x_i^*\right) ^{j}\left( x_i^*\right) ^{2\beta _i-j}\right| \\&=\left| \sum _{j=1}^{\max \left\{ 2\beta _i\right\} }v_j^T\left[ \begin{array}{c} (x_1-x_1^*)^j\\ (x_2-x_2^*)^j\\ \vdots \\ (x_n-x_n^*)^j \end{array}\right] \right| , \end{aligned}$$

where $v_j\in \mathbb {R}^n$ is the vector given by

$$\begin{aligned} \left( v_j\right) _i=\left\{ \begin{array}{ll} \left( {\begin{array}{c}2\beta _i\\ j\end{array}}\right) \left( x_i^*\right) ^{2\beta _i-j}&{}(j\le 2\beta _i),\\ 0&{}(j>2\beta _i). \end{array}\right. \end{aligned}$$

Thus we have

$$\begin{aligned} \left| 1-p(x)^{2c}\right|&=\left| \sum _{j=1}^{\max \left\{ 2\beta _i\right\} }v_j^T\left[ \begin{array}{c} (x_1-x_1^*)^j\\ (x_2-x_2^*)^j\\ \vdots \\ (x_n-x_n^*)^j \end{array}\right] \right| \\&\le \Vert v_1\Vert \Vert x-x_*\Vert +\sum _{j=2}^{\max \left\{ 2\beta _i\right\} }\Vert v_j\Vert _\infty \Vert x-x_*\Vert ^j\\&\le \Vert v_1\Vert \left( c_1L\right) ^{1/2}+\sum _{j=2}^{\max \left\{ 2\beta _i\right\} }\Vert v_j\Vert _\infty \left( c_1L\right) ^{j/2}=:C_{n,\alpha ,N}(L), \end{aligned}$$

where we have used $\Vert x-x_*\Vert \le \left( c_1L\right) ^{1/2}$.

If $k=1$, which is the case shown in Sect. 5.3, then an upper bound estimate of $t_{\max }$ is realized as follows, for example:

$$\begin{aligned} t_{para,\max }&\le t_{para,N} +\frac{1}{c_{\tilde{N}}c_1} \int _0^{L(x(\tau _{para,N}))} \frac{C_{n,\alpha ,N}(L)}{L}dL\\&= t_{para,N} +\frac{1}{c_{\tilde{N}}} \int _0^{L(x(\tau _{para,N}))} \left\{ \Vert v_1\Vert \left( c_1L\right) ^{-1/2}+\sum _{j=2}^{\max \left\{ 2\beta _i\right\} }\Vert v_j\Vert _\infty \left( c_1L\right) ^{j/2-1}\right\} dL\\&= t_{para,N} +\frac{1}{c_{\tilde{N}}} \left\{ 2\Vert v_1\Vert c_1^{-1/2}L(x(\tau _{para,N}))^{1/2}+\sum _{j=2}^{\max \left\{ 2\beta _i\right\} }\frac{2}{j}\Vert v_j\Vert _\infty c_1^{j/2-1}L(x(\tau _{para,N}))^{j/2}\right\} . \end{aligned}$$

C Proofs of statements

1.1 C.1 Proof of Proposition 2.4

Now compute the Jacobian matrix of T for verifying its bijectivity. Direct computations yield

$$\begin{aligned} \frac{\partial x_i}{\partial y_j} = \kappa ^{-\alpha _i}\left( \delta _{ij} - \kappa ^{-1} \alpha _i y_i \frac{\partial \kappa }{\partial y_j}\right) \end{aligned}$$

with the matrix form

$$\begin{aligned} J&= \left( \frac{\partial x_i}{\partial y_j}\right) _{i,j = 1,\ldots , n} = A_{\alpha } \left( I_n - \kappa ^{-1} y_\alpha (\nabla \kappa )^T\right) ,\\ A_\alpha&= \mathrm{diag}(\kappa ^{-\alpha _1}, \ldots , \kappa ^{-\alpha _n}),\quad y_\alpha = (\alpha _1 y_1,\ldots , \alpha _n y_n)^T. \end{aligned}$$

We following arguments in [8], for any (column) vectors $y,z\in \mathbb {R}^n$, to have

$$\begin{aligned} (I_n + \beta yz^T)(I_n + \delta yz^T)&= I_n + (\beta + \delta )yz^T + \beta \delta yz^T yz^T\\&= I_n + (\beta + \delta + \beta \delta \langle z,y\rangle )yz^T, \end{aligned}$$

so $I_n+\delta yz^T = (I_n +\beta yz^T )^{-1}$ if $\delta = -\beta / (1 + \beta \langle z,y\rangle )$.

In this case, we choose $\beta = -\kappa ^{-1}, y = y_\alpha , z = \nabla \kappa$ and have

$$\begin{aligned} \left( \frac{\partial y_j}{\partial x_i}\right) = \left( \frac{\partial x_i}{\partial y_j}\right) ^{-1} = \left( I_n - \frac{1}{\kappa - \langle y_\alpha , \nabla \kappa \rangle } y_\alpha (\nabla \kappa )^T\right) A_{\alpha }^{-1} \end{aligned}$$

By (A3) we have $\kappa > \langle y_\alpha , \nabla \kappa \rangle$, which indicates that the transformation T as well as $T^{-1}$ are well-defined and $C^1$ locally bijective including $y=0$. On the other hand, the map T maps any one-dimensional curve $y = (r^{\alpha _1}v_1, \ldots , r^{\alpha _n}v_n)$, $0\le r < \infty$, with some fixed direction $v\in \mathbb {R}^n$, into itself (cf. [16]). For continuous mappings from $\mathbb {R}$ to $\mathbb {R}$, local bijectivity implies global bijectivity. Consequently, (A3) guarantees also the global bijectivity of Tinto$T(\mathbb {R}^n)\subset \mathcal {D}$. Finally we prove that T is onto. First let $y\in \mathbb {R}^n\setminus \{0\}$. Then the correspondence

$$\begin{aligned} \iota : y_i \mapsto \frac{y_i}{p(y)^{\alpha _i}} \end{aligned}$$

maps $\mathbb {R}^n\setminus \{0\}$ onto the set $\{p(y) = 1\}$. If $p(y) = 1$ then $\kappa (y)$ attains a constant $\kappa _1 > 1$ from (A0). From $\kappa (y)^{2c}p(x)^{2c} = p(y)^{2c}$, we know that the compactification T maps the set $\{p(y) = 1\}$ onto the set $\{x\in \mathcal {D} \mid p(x) = 1/\kappa _1\}$. In particular, the set $\mathbb {R}^n\setminus \{0\}$ is mapped onto $\{x\in \mathcal {D} \mid p(x) = 1/\kappa _1\}$ via the map $T\circ \iota$. Therefore the surjectivity of T is reduced to that on the ray $C_y = \{(r^{\alpha _1}y_1, \ldots , r^{\alpha _n}y_n)\mid 0\le r < \infty \}$ for each $(y_1, \ldots y_n)\in \mathbb {R}^n$ with $p(y) = 1$. By definition $T(C_y)$ is

$$\begin{aligned} T(C_y) = \left\{ (x_1, \ldots , x_n) = \left( \frac{r^{\alpha _1}}{q(r)^{\alpha _1}}y_1, \ldots , \frac{r^{\alpha _n}}{q(r)^{\alpha _n}}y_n \right) \mid 0\le r < \infty \right\} . \end{aligned}$$

From $\kappa (y)^{2c}p(x)^{2c} = p(y)^{2c}$, we have $p(x) = r/q(r)$ on $T(C_y)$. From (A0) and (A1), for any value $c_x\in (0,1)$, we can choose the value $r \in (0,1)$ so that $r/q(r) = c_x$. Correspondingly we can define y from x on $T(C_y)$. Obviously, $T(\mathbf{0})=\mathbf{0}$ and hence $T:\mathbb {R}^n\rightarrow \mathcal {D}$ is onto and the proof is completed.

Note that the condition (A2) is not actually used in the present argument.

1.2 C.2 Proof of Lemma 3.1

Suppose that $y_*$ is an equilibrium of (2.1), i.e., $f(y_*) = 0$. Then the right-hand side of (3.1) obviously vanishes at the corresponding $x_*$.

Conversely, suppose that the right-hand side of (3.1) vanishes at a point $x\in \mathcal {D}, p(x) < 1$: namely,

$$\begin{aligned} f(\kappa x) - \kappa (y)^{-1}\langle \nabla \kappa , f(\kappa x) \rangle y_\alpha = 0. \end{aligned}$$

Multiplying $\nabla \kappa$, we have

$$\begin{aligned} \langle \nabla \kappa , f(\kappa x) \rangle \left( 1- \kappa (y)^{-1}\langle \nabla \kappa , y_\alpha \rangle \right) = 0. \end{aligned}$$

Due to (A3), we have $|\kappa (y)^{-1}\langle \nabla \kappa , y_\alpha \rangle | < 1$ and hence $\langle \nabla \kappa , f(\kappa x) \rangle = 0$. Thus we have $f(y) = f(\kappa x) = 0$ by the assumption.

1.3 C.3 Proof of Lemma 3.2

By admissibility (A1)-(A2), we have

$$\begin{aligned} (\nabla \kappa (y))_i \sim \frac{1}{\alpha _i}\frac{y_i^{2\beta _i-1}}{\kappa (y)^{2c-1}} = \frac{1}{\alpha _i}\frac{\kappa ^{\alpha _i(2\beta _i-1)}x_i^{2\beta _i-1}}{\kappa ^{2c-1}} = \frac{1}{\alpha _i}\frac{x_i^{2\beta _i-1}}{\kappa ^{\alpha _i-1}} \quad \text { as }\quad p(y)\rightarrow \infty , \end{aligned}$$

where we used the condition $\alpha _j \beta _j \equiv c$ for all j from (2.2). Therefore the vector field (3.3) near infinity becomes

$$\begin{aligned} x_i'&\sim \kappa ^k \tilde{f}_i(x) - \alpha _i x_i \sum _{j=1}^n \frac{1}{\alpha _j}\frac{x_j^{2\beta _j-1}}{\kappa ^{\alpha _j-1}} \kappa ^{k+\alpha _j - 1}\tilde{f}_j(x)\nonumber \\&= \kappa ^k \left\{ \tilde{f}_i(x) - \alpha _i x_i \sum _{j=1}^n \frac{x_j^{2\beta _j-1}}{\alpha _j} \tilde{f}_j(x)\right\} \quad \text { as }\quad \kappa \rightarrow \infty . \end{aligned}$$

(C.1)

Since $\tilde{f}_i$ is O(1) as $\kappa \rightarrow \infty$, then right-hand side of (C.1) is $O(\kappa ^k)$ as $\kappa \rightarrow \infty$.

1.4 C.4 Proof of Theorem 3.7

The property $b = \sup \{t\mid y(t) \text { is a solution of (2.1)}\}$ corresponds to the property that

$$\begin{aligned} \sup \{\tau \mid x(\tau ) = T(y(t)) \text { is a solution of } (3.5) \text { in the time variable } \tau \} = \infty . \end{aligned}$$

Indeed, if not, then $\tau \rightarrow \tau _0 < \infty$ and $\lim _{\tau \rightarrow \tau _0-0}x(\tau ) = x_*$ as $t\rightarrow b-0$. The condition $x(\tau ) = x_*$ is the regular initial condition of (3.5). The vector field (3.5) with the new initial point $x(\tau ) = x_*$ thus has a locally unique solution $x(\tau )$ in a neighborhood of $\tau _0$, which contradicts the maximality of b. Therefore we know that $\tau \rightarrow +\infty$ as $t\rightarrow b-0$. Since $\lim _{\tau \rightarrow \infty }x(\tau ) = x_*$, then $x_*$ is an equilibrium of (3.5) on $\partial {\mathcal {D}}$. The similar arguments show that $t\rightarrow a+0$ corresponds to $\tau \rightarrow -\infty$ and that the same consequence holds true.

1.5 C.5 Proof of Proposition 3.9

Each $\tilde{f}_j(x)$ given by (3.2) with $\kappa = \kappa _{para}$ is $C^1$ on $\overline{\mathcal {D}}$, since all terms of $\tilde{f}_j$ are multiples of powers of $(1-p(x)^{2c})$ and smooth asymptotically quasi-homogeneous terms in $f_j(y)$. Consequently, we know that the right-hand side of (3.7) is $C^1$ on $\overline{\mathcal {D}}$.