Abstract
This paper introduces a low-order discontinuous Petrov-Galerkin (dPG) finite element method (FEM) for the Stokes equations. The ultra-weak formulation utilizes piecewise constant and affine ansatz functions and piecewise affine and discontinuous lowest-order Raviart–Thomas test search functions. This low-order discretization for the Stokes equations allows for a direct proof of the discrete inf-sup condition with explicit constants. The general framework of Carstensen et al. (SIAM J Numer Anal 52(3):1335–1353, 2014) then implies a complete a priori and a posteriori error analysis of the dPG FEM in the natural norms. Numerical experiments investigate the performance of the method and underline its quasi-optimal convergence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The initial motivation for the discontinuous Petrov-Galerkin (dPG) methodology in [18,19,20] was the design of the optimal test function space in applications of fluid mechanics, when a stabilization appears obligatory for many standard finite element methods (FEMs). Since important examples of this class follow as linearizations of the Navier–Stokes equations, the understanding of simple low-order dPG schemes for the Stokes equations appears to be a necessary step. The first dPG FEMs for the Stokes equations in [25] and [10] utilize polynomials of much higher degrees in the trial and test search space. This paper introduces a much simpler lowest-order dPG FEM with an emphasis on a direct estimation of the discrete inf-sup constant and the discussion of the associated Fortin-type operators for a reliable a posteriori analysis to generalize [10] for low-order test functions. Popular alternative simulation tools for the Stokes equations with optimal convergence rates for adaptive mesh-refining algorithm are the nonconforming (restricted to first-order in 3D) and the pseudostress FEM with a more complicated a posteriori error analysis [8, 16].
The dGP methodology is roughly described as a minimum residual method with discontinuous ansatz and test functions. This leads to piecewise (also called broken) Sobolev spaces with related trace spaces on element boundaries and so requires a careful definition and analysis on the independence of the underlying partition. In return, this results in a local and parallel computation of the underlying dual norms and a simple implementation and allows rather general geometries of the element domains; both regarded as obligatory in particular in higher space dimensions. The detailed description of the ultraweak formulation with piecewise smooth functions and several flux variables on the boundaries of the element domain is cumbersome and follows in Sect. 3. For the sake of this introduction it may suffice to acknowledge that this leads to a continuous formulation in Lebesgue and broken Sobolev spaces X and Y such that the continuous problem of the standard Stokes equation leads to a right-hand side \(F\in Y^*\) and an exact solution \(x\in X\) of the (well-posed) equation
The bounded bilinear form \(b:X\times Y\rightarrow \mathbb {R}\) models the equivalent ultraweak formulation of the Stokes equation as in [10]. This equation is well posed if that b satisfies an inf-sup condition on the continuous level,
With a few and well-spotted exceptions, the least-squares FEMs start with the minimization of the residual \(F-b(x_h,\bullet )\) in subspaces of \(L^2\). For the bilinear form b at hand, this is impossible as Y does not solely contain Lebesgue functions. The dPG schemes first approximate the dual norm in \(Y^*\) of the residual by the dual norm \(Y_h^*\) over a finite-dimensional subspace \(Y_h\subset Y\) of Y and second minimize the residual \(F-b(x_h,\bullet )\) for ansatz functions \(x_h\) in a finite-dimensional subspace \(X_h\subset X\) of X. In other words, the dPG approximation is the minimizer \(x_h\) in
The computational costs are related to the total number \(N+M\) of unknowns with the dimensions \(N:={{\mathrm{dim}}}(X_h)\) for the ansatz function space and \(M:={{\mathrm{dim}}}(Y_h)\) for the test search space. The minimal residual method is not a mixed finite element scheme in that it allows \(N\le M\) with significantly larger M. The benefit is that the test search space \(Y_h\) can be much richer and approximate Y well so that the crucial discrete inf-sup condition
can be made larger to approximate the idealized inf-sup constant \(\beta _h^* \),
which may even be larger than the global inf-sup constant \(\beta \). Hence a sufficiently large test search space \(Y_h\) may stabilize a situation, when a stable pairing does not exist or is at least unknown and a mixed finite element scheme is not available with \(M=N\). It is known that the dPG scheme is equivalent to a mixed scheme with an extended bilinear form \(\mathcal {B} : (X\times Y)\times (X\times Y)\rightarrow \mathbb {R}\), when Y is a Hilbert space [from L. Demkovicz in personal communication]. Moreover, it can even be reduced to the computation of some subspace \(M_h\subset Y_h\) with \({{\mathrm{dim}}}(M_h)=N\) such that \(x_h\) is a solution to a quadratic mixed FEM with b reduced to \(X_h\times Y_h\) [20]. This is all related to the numerical linear algebra of the dPG schemes and the computational costs grow with \(N+M\). It is therefore practically relevant to minimize the test search space \(Y_h\) and so \(M\ge N\), while \(\beta _h>0\) is still uniformly bounded away from zero as the underlying partitions become finer and finer. The first proofs of a stability result of this type [22] involve some linear and bounded Fortin operator \(\varPi :Y\rightarrow Y_h\) with operator norm \(\Vert \varPi \Vert _{}\) and the annulation property
Given such an operator \(\varPi \), the analysis in [22] leads to \(\beta /\Vert \varPi \Vert _{}\le \beta _h\) [6, Proposition 5.4.2] and so is a sufficient condition for stability. Conversely, the stability leads to the existence of some Fortin interpolation operator \(\varPi \) with \(\Vert \varPi \Vert _{}\le \Vert b \Vert _{}/\beta _h\) [14, Lemma 2.10].
The examples in [10, 22] typically involve piecewise polynomials of degree k (and one variable with \(k+1\)) in \(X_h\) and piecewise polynomials of degree \(k+n\) in \(Y_h\) of the underlying partition with J element domains in \(\mathbb {R}^n\) with n space dimensions. This leads to \(N= \mathcal {O}(J(k+1))\) and \(M=\mathcal {O}(J(k+n+1))\), which results in overall computational costs which grow with \(J(2k+n+2)\). The subsequent discussion concerns the same fixed ansatz space \(X_h\) and so N is fixed. The overall costs are then expected to be of a monoton function in M and the precise dependence is less clear for an optimized numerical linear algebra with parallel computation. This paper is motivated in the extreme case \(k=0\) because then the current dPG schemes require \(M=\mathcal {O}(J(1+n))\) which is \(n+1\) times higher than the costs for a (unknown) mixed FEM with \(M=N=\mathcal {O}(J)\) for the space dimension \(n=2,3\). This paper introduces a stable choice of \(Y_h\) with piecewise polynomial degree at most 1 rather than n from [10, 22] for \(k=0\).
The mentioned ultraweak formulation of the well-known Stokes equation with a volume term \(f\in L^2(\varOmega ;\mathbb {R}^{n})\) on the right-hand side leads on the discrete level to the residual \(F(y_h)-b(x_h,y_h)\). Throughout this paper, \({{\mathrm{dev}}}\) denotes the deviatoric part of a matrix, \(D_{\text { NC}}\) is the piecewise functional matrix, \(\cdot \) (resp. : ) denotes the scalar product of two vectors (resp. matrices), cf. Sect. 2 for more details. For some particular \(x_h\) and \(y_h\) in the Stokes equations below, the aforementioned residual reads as
up to modifications for the Dirichlet boundary conditions. Therein, \(\varvec{\sigma }_0\) and \(u_0\) are piecewise constant functions, while \(v_1\) and \(\varvec{\tau }_{\text { RT}}\) are piecewise affine with respect to a triangulation \(\mathcal {T}\). On the skeleton with respect to the sides \(\mathcal {E}\) in \(\mathcal {T}\), \(t_0\) is piecewise constant but, \(s_1\) is piecewise affine and globally continuous.
This paper bounds the inf-sup constants (2) and (4) for arbitrary dimension n explicitly in terms of the Friedrichs, the tr-div-dev constant, and the inf-sup constant of the \(H({{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n})/\mathbb {R}\times L^2(\varOmega ;\mathbb {R}^{n})\) mixed FEM for Stokes equations. This implies the quasi optimal convergence
for the novel low-order dPG FEM. The general a posteriori error analysis of [10] leads to the a posteriori error control for any approximation \(\xi _h\in X_h\) (so it allows an inexact solve of the discrete minimization problem)
The residual term \(\Vert F-b\left( \xi _h,\bullet \right) \Vert _{Y_h^*}\) is computable and the remaining data approximation term \(\Vert F\circ \left( 1-\varPi \right) \Vert _{Y^*}\) involves the Fortin interpolation \(\varPi \). In all the examples of [10] with the aforementioned larger test search spaces, this term is an oscillation and hence the data approximation term may be regarded as a higher-order term and in fact is neglected in many practical calculations.
In the novel low-order dPG scheme, this is not the case and the Fortin interpolation operator is characterized in Theorem 5.2 below. It turns out that the data approximation term is of first order and so, for quasi-uniform meshes and a singular solution possibly of higher-order. For adaptive mesh-refining, this argument is no longer valid and the a posterior error control may fail to be efficient. This leads to the extension \({\hat{Y}}_h\) of the trial search space \(Y_h\subset {\hat{Y}}_h\subset Y\) by three piecewise enrichments by additional cubic bubble functions, piecewise affines or first-order Raviart-Thomas functions in the first component. The resulting overall strategy for guaranteed and effective a posteriori error control assumes an approximation \(x_h\in X_h\) computed by the proposed dPG scheme even with inexact solve from an iterative numerical linear algebra with the test search space \(Y_h\). The a posteriori error control applies to \({\hat{Y_h}}\) and computes the residual \(\Vert F-b(x_h,\bullet ) \Vert _{{\hat{Y}}_h^*}\) in the dual norm \({\hat{Y}}_h^*\) and allows for the reduced data approximation term \(\Vert {F\circ (1-{\hat{\varPi }})}\Vert _{Y^*}\) with respect to the Fortin interpolation \({\hat{\varPi }} : Y \rightarrow {\hat{Y}}_h\). Notice that the inf-sup constant \({\hat{\beta }}_h\ge \beta _h\), where \({{\hat{\beta }}_h =\inf _{x_h\in X_h}\sup _{{\hat{y}}_h\in {\hat{Y}}_h}b(x_h,{\hat{y}}_h)/(\Vert x_h \Vert _{X}\Vert {\hat{y}}_h \Vert _{Y})}\). This leads to \(\Vert {F\circ (1-{\hat{\varPi }})}\Vert _{Y^*}\) as oscillations, which may be negligible at least for piecewise smooth data. The analysis of this strategy and affirmative numerical examples conclude the paper.
The remaining parts of the paper are organized as follows. Section 2 recalls the necessary notation on triangulation and function spaces. Section 3 and 4 investigate the continuous and discontinuous formulation (1)–(3) related to (7) and prove the inf-sup conditions (2) and (4). Section 5 discusses the data approximation error in the two-dimensional case which contains the Fortin interpolator. Numerical experiments for benchmark problems are presented in Sect. 6. The supplement contains some remarks on the Fortin operator and on the implementation.
Standard notation applies to Lebesgue and Sobolev spaces throughout this paper, \(H^1(T)\) abbreviates \(H^1({{\mathrm{int}}}(T))\) for a set T with nonempty interior \({{\mathrm{int}}}(T)\). Furthermore, \(a\lesssim b\) abbreviates, that there exists a generic constant C with \(a\le C b\), while \(a\approx b\) abbreviates \(a\lesssim b\lesssim a\). Given a normed linear space \((X,\,\Vert \bullet \Vert _{X})\), let \(S(X):=\left\{ x\in X:\Vert \bullet \Vert _{X}=1\right\} \) be its unit sphere.
2 Notation
2.1 Vector and matrix notation
This subsection clarifies details on the overall notation of vectors and matrices. For two vectors \(a,\,b \in \mathbb {R}^m\), the dot denotes the scalar product \(a\cdot b=\sum _{j=1}^{ m} a_j b_j\in \mathbb {R},\) while the scalar product A : B of \(m\times m\) matrices \(A,\, B \in \mathbb {R}^{m\times m}\) reads \(A:B=\sum _{j,k=1}^m A_{jk}B_{jk}\in \mathbb {R}.\) The dyadic product of \(a,\,b \in \mathbb {R}^m\) reads \(a\otimes b:= ab^T\in \mathbb {R}^{m\times m}.\) Notice that \(|a\otimes b|=|a||b|\). The identity mapping is denoted by \(\bullet \). The notation \(|\bullet |\) is dependent on context, the norm induced by \(\cdot \) (resp. : ) on \(\mathbb {R}^{n}\) (resp. \(\mathbb {R}^{n\times n}\)), the cardinality of a finite set, the n- or \((n-1)\)-dimensional Lebesgue measure of a subspace of \(\mathbb {R}^{n}\). The linear operators deviator, \({{\mathrm{dev}}}A=A-1/n\left( {{\mathrm{tr}}}A\right) \text {I}_{n\times n}\), and trace, \({{\mathrm{tr}}}A=A_{11}+\dots +A_{nn}\), of any matrix \(A\in \mathbb {R}^{n\times n}\), lead to \({{\mathrm{tr}}}{{\mathrm{dev}}}A=0\) and
(This is the theorem of Pythagoras \(|A|^2=A:A=|{{\mathrm{dev}}}A|^2+ 1/n ({{\mathrm{tr}}}A)^2\) for a matrix \(A\in \mathbb {R}^{n\times n}\) based on the orthogonality of the unit matrix \(\text {I}_{n\times n}\) and the deviatoric part \({{\mathrm{dev}}}\).) Let \(\mathbb {R}^{n\times n}_{{{\mathrm{dev}}}}:={{\mathrm{dev}}}(\mathbb {R}^{n\times n})\) denote the deviatoric (also called trace-free) \(n\times n\) matrices and note \({{\mathrm{dev}}}A:{{\mathrm{dev}}}B={{\mathrm{dev}}}A:B=A:{{\mathrm{dev}}}B \text { for all }A,\,B\in \mathbb {R}^{n\times n}\).
2.2 Triangulation
Given a regular triangulation \(\mathcal {T}\) of \(\varOmega \subseteq \mathbb {R}^{n}\) into closed n-simplices \(T\in \mathcal {T},\mathcal {E}(T)\) denotes the set of all \(n+1\) sides (\((n-1)\)-simplices like edges for \(n=2\) and faces for \(n=3\)) of T and \(\mathcal {N}(T)\) the set of all \(n+1\) vertices of T. The set of all sides and nodes read
the set of all interior (resp. boundary) sides reads \(\mathcal {E}(\varOmega )\) (resp. \(\mathcal {E}({\partial \varOmega })\)) as well as \(\mathcal {N}(\varOmega )\) (resp. \(\mathcal {N}({\partial \varOmega })\)) is the set of all interior (resp. boundary) nodes. The skeleton \(\partial \mathcal {T}:=\bigcup _{T\in \mathcal {T}}\partial T\) is the union of all boundaries of simplices \(T\in \mathcal {T}\). Throughout this paper, \(h_\mathcal {T}\) abbreviates the piecewise constant function with \(h_\mathcal {T}|_T:=h_T:={{\mathrm{diam}}}(T)=\max _{x,y\in T}|x-y|\) the diameter of a simplex \(T\in \mathcal {T}\) and \(h_{\text { max}}:=\max h_\mathcal {T}\) its maximum.
Let \(\nu _T\) denote the outer unit normal vector field along the boundary \(\partial T\) on a fixed element \(T\in \mathcal {T}\). Each side \(E\in \mathcal {E}\) has an assigned orientation of the unit normal \(\nu _E\). For exterior sides \(E\in \mathcal {E}({\partial \varOmega }),\nu _E=\nu _\varOmega \) points outwards. For an interior side \(E=\partial T_+\cap \partial T_-\in \mathcal {E}(\varOmega )\) one orientation of the unit normal \(\nu _E\) is fixed throughout this paper. The neighbouring triangles are named such that \(\nu _E\) points from \(T_+\) to \(T_-\) as in Fig. 1. In this context the following sign-function is defined \( {{\mathrm{sgn}}}(T,E):=\nu _E\cdot \nu _T\in \left\{ \pm 1\right\} \ \text {for all } T\in \mathcal {T},\ E\in \mathcal {E}(T). \) Furthermore, for a function \(v\in L^2(\varOmega ;\mathbb {R}^{m\times n})\) the jump along an interior side \(E\in \mathcal {E}(\varOmega )\) is denoted by \(\left[ v\right] _E:=(v|_{T_+}-v|_{T_-})\big |_{E}\in L^2(E;\mathbb {R}^{m\times n})\) and along an boundary side \(E\in \mathcal {E}({\partial \varOmega })\) by \(\left[ v\right] _E:=v|_E\in L^2(E;\mathbb {R}^{m\times n})\).
For each simplex \(T\in \mathcal {T}\),  denotes the center of gravity and the function \(\bullet -{{\mathrm{mid}}}(\mathcal {T})\in L^\infty (\varOmega ;\mathbb {R}^{n})\) has the value \(x-{{\mathrm{mid}}}(T)\) for \(x\in T\in \mathcal {T}\) and satisfies for all \(T\in \mathcal {T}\)
denotes the center of gravity and the function \(\bullet -{{\mathrm{mid}}}(\mathcal {T})\in L^\infty (\varOmega ;\mathbb {R}^{n})\) has the value \(x-{{\mathrm{mid}}}(T)\) for \(x\in T\in \mathcal {T}\) and satisfies for all \(T\in \mathcal {T}\)
2.3 Function spaces
Standard notation applies to \(L^2(\varOmega ),\,H^1(\varOmega ),\, H({{\mathrm{div}}},\varOmega )\) and their vector- or matrix-valued relatives such as \(L^2(\varOmega ;\mathbb {R}^{n}),L^2(\varOmega ;\mathbb {R}^{n\times n})\), \(H^1(\varOmega ;\mathbb {R}^{n}),H({{\mathrm{div}}},\varOmega ;\) \(\mathbb {R}^{n\times n})\). Let \(\mathcal {T}\) be a regular triangulation of \(\varOmega \). The test search space only exhibits certain piecewise regularity properties on \(T\in \mathcal {T}\),
where \(\tau _j\) denotes the j-th row of \(\varvec{\tau }\). The piecewise application of the divergence operator \({{\mathrm{div}}}\) and the derivative \({{\mathrm{D}}}\) read \({{\mathrm{div}}}_{\text { NC}}\) and \({{\mathrm{D}}}_{\text { NC}}\) and give rise to
The following essential facts about trace spaces are proven in [2, 21]. For any open, bounded Lipschitz domain \(U\subseteq \mathbb {R}^{n}\), there exists exactly one continuous linear mapping \(\gamma _0:\,H^1(U)\rightarrow L^2\left( \partial U\right) \) with \(\gamma _0 w= w|_{\partial U}\) for all \(w\in H^1(U)\cap C^0(\overline{U})\). Let \(H^{1/2}(\partial U):=\gamma _0(H^1\left( U\right) )\) and let \(H^{-1/2}(\partial U)=(H^{1/2}(\partial U))^{*}\) be its dual space. Then there exists exactly one continuous linear mapping \(\gamma _\nu :\,H({{\mathrm{div}}},U)\rightarrow H^{-1/2}\left( \partial U\right) \) with \(\gamma _\nu q= (q|_{\partial U})\cdot \nu \) for all \(q\in H({{\mathrm{div}}},U)\). Moreover, for all \(q\in H({{\mathrm{div}}},U)\) and \(w\in H^1(U)\) it holds
The extension of the \(L^2\)-scalar product on the skeleton is for all \(t=\left( t_T\right) _{T\in \mathcal {T}}\in \prod _{T\in \mathcal {T}}H^{-1/2}\left( \partial T;\mathbb {R}^{n}\right) \) and \(s=\left( s_T\right) _{T\in \mathcal {T}}\in \prod _{T\in \mathcal {T}}H^{1/2}\left( \partial T;\mathbb {R}^{n}\right) \) denoted by
Define the trace operators
on the skeleton \(\partial \mathcal {T}\) by \(\gamma _0^\mathcal {T}w:=\left( s_T\right) _{T\in \mathcal {T}} \text { with } s_T:=\gamma _0\left( w|_T\right) \) and \( \gamma _\nu ^\mathcal {T}{\varvec{q}}:=\left( t_T\right) _{T\in \mathcal {T}}\text { with } t_T:=\gamma _\nu \left( {\varvec{q}}|_T\right) \) for all \(T\in \mathcal {T}\). The associated trace spaces read
These spaces are equipped with the following minimal extension norms
The spaces \(H^{1/2}_0\left( \partial \mathcal {T};\mathbb {R}^{n}\right) \) and \(H^{-1/2}\left( \partial \mathcal {T};\mathbb {R}^{n}\right) \) are subspaces of product spaces and not dual to each other in general.
Lemma 2.1
(Duality Lemma) It holds
Proof
This is contained in [11, Lemma 2.2].\(\square \)
2.4 Discrete function spaces
The finite-dimensional subspaces of the trial space \(X_h\subset X\) and the test search space \(Y_h\subset Y\) are piecewise polynomials. For any \(k\in \mathbb {N}_0\), let \(P_k(T;\mathbb {R}^{m\times n})\) denote polynomials of total degree at most k in each component as functions in \(L^2(T;\mathbb {R}^{m\times n})\) and set
Analogous definitions apply on the skeleton, i.e.,
Let \(\varPi _0\) be the \(L^2\) projection onto \(P_0(\mathcal {T})\) defined for \(f\in L^2(\varOmega ;\mathbb {R}^{m\times n})\) by  . The continuous and piecewise finite element functions \(P_k\) on \(\mathcal {T}\) read
. The continuous and piecewise finite element functions \(P_k\) on \(\mathcal {T}\) read

and on the skeleton
The lowest-order Raviart-Thomas functions read
On each simplex \(T\in \mathcal {T}\) any \(\varvec{q}_{\text { RT}}\in RT_0^\text {pw}(\mathcal {T};\mathbb {R}^{n\times n})\) can be written as \(\varvec{q}_{\text { RT}}|_T=A+1/n \ {{\mathrm{div}}}\varvec{q}_{\text { RT}}\otimes \left( \bullet -{{\mathrm{mid}}}(T)\right) \) for some \(A\in \mathbb {R}^{n\times n}\). Then it holds by (9)
It is useful to regard \(P_0(\mathcal {E};\mathbb {R}^{n})\) as a subspace of \(H^{-1/2}(\partial T;\mathbb {R}^{n})\) via the embedding
where \(\varvec{q}_{\text { RT}}\in RT_0(\mathcal {T};\mathbb {R}^{n\times n})\) satisfies \(\varvec{q}_{\text { RT}}|_E\nu _E=t_0|_E\) for all \(E\in \mathcal {E}\). Notice the norm equivalence
from [13, Lemma 3.2].
3 Continuous problem
Given some \(f\in L^2(\varOmega ;\mathbb {R}^{n})\) on some n-dimensional, bounded Lipschitz domain \(\varOmega \) with polyhedral boundary \(\partial \varOmega \) and Dirichlet boundary data \(g\in H^1({\partial \varOmega };\mathbb {R}^{n})\) with \(\int _{{\partial \varOmega }}g\cdot \nu \,\mathrm{d}s=0\), the Stokes pseudostress formulation seeks \(\varvec{\sigma }\in H({{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n})\) and \(u\in H^1\left( \varOmega ;\mathbb {R}^{n}\right) \) with
There exists a unique solution \((\varvec{\sigma },u)\) to (14) up to a constant multiple of the \(n\times n\) unit matrix \(\text {I}_{n\times n}\) fixed by \(\int _{\varOmega } {{\mathrm{tr}}}\varvec{\sigma }\,\mathrm{d}x=0\) written \(\varvec{\sigma }\in H({{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n})/\mathbb {R}\). The discontinuous Petrov-Galerkin formulation (dPG) is based on a regular triangulation \(\mathcal {T}\) of \(\varOmega \) from Sect. 2.2. On each simplex \(T\in \mathcal {T}\), a multiplication of (14) with the test functions \(\varvec{\tau }\in H({{\mathrm{div}}},T;\mathbb {R}^{n\times n})\) and \(v\in H^1(T;\mathbb {R}^{n})\) followed by an integration by parts leads to
The summation over all \(T\in \mathcal {T}\) results in traces on the skeleton \(\gamma _0^\mathcal {T}u\) and \(\gamma _\nu ^\mathcal {T}\varvec{\sigma }\). Let \(g\in H^{1}(\varOmega ;\mathbb {R}^{n})\) extend the Dirichlet boundary data \(g\in H^1({\partial \varOmega };\mathbb {R}^{n})\). The interface variables \(s:=\gamma _0^\mathcal {T}(u-g)\) and \(t:=\gamma _\nu ^\mathcal {T}\varvec{\sigma }\) circumvent the continuity conditions for \(\varvec{\sigma }\) and u. The sum of the two equations leads to the dPG formulation (on the continuous level). In abstract notation, the dPG formulation seeks \(x\in X\) with
For any \(x=(\varvec{\sigma },u,s,t)\in \, X\) and \(y=(\varvec{\tau },v)\in \, Y\) with
the bilinear form \(b: X\times Y\rightarrow \mathbb {R}\) and the functional \(F\in Y^*\) read
The remaining parts of this section establish the boundedness of b, its non-degeneracy, and the inf-sup condition (2). The weak formulation of (14) leads with \(Z:=H\left( {{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n}\right) /\mathbb {R}\times L^2\left( \varOmega ;\mathbb {R}^{n}\right) \) to a bilinear form \({\tilde{b}}: Z\times Z\rightarrow \mathbb {R}\) defined for \((\varvec{\tau },v),(\varvec{\rho },w)\in Z\) by
The well-posedness of (14) leads to a positive inf-sup constant [9, Thm.2.3]
which allows to describe the dependence of the inf-sup constant \(\beta \) below. The bilinear form b of the ultraweak formulation is a broken form of the established bilinear form \({\tilde{b}}\) with the term broken used in the sense of [11].
Theorem 3.1
The bilinear form b from (18) is bounded with
and satisfies \( N=\left\{ y\in Y:\ b\left( \bullet ,y\right) =0\in X^*\right\} =\left\{ 0\right\} \) as well as
The constant \(\gamma \) involves the Ladyshenskaya constant [7, (11.2.3)] or the constant \(C_{\text {tdd}}\) from the following tr-dev-div lemma.
Lemma 3.2
[6, Thm.9.1.1] There exists a constant \(C_{\text {tdd}}<\infty \) (solely depending on \(\varOmega \)) such that any \(\varvec{\tau }\in H({{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n})/\mathbb {R}\) satisfies
The proof of Theorem 3.1 requires the following splitting argument from [11].
Theorem 3.3
(splitting lemma) Let X and Y be (real) Hilbert spaces with \(X=X_1\times X_2\). Let \(b_1: X_1\times Y\rightarrow \mathbb {R}\) and \(b_2: X_2\times Y\rightarrow \mathbb {R}\), suppose the continuous bilinear form \(b: X\times Y \rightarrow \mathbb {R}\) is their sum, in the sense that for all \(x=(x_1,x_2)\in X_1\times X_2=X\) and all \(y\in Y\),
Set \(Y_1\ :=\left\{ y\in Y: b_2(x_2,y)=0\text { for all }x_2\in X_2\right\} \) and suppose, that
Then it follows \(N:=\left\{ y\in Y:\ b(x,y)=0 \text { for all } x\in X\right\} =\left\{ 0\right\} \) and
Proof
This is essentially [11, Thm.3.1] in different notation, but the constant here is slightly better than \(\beta ={\beta _1\beta _2}/\left( {\beta _1^2+\beta _2^2+\Vert b_1 \Vert _{}^2+2\beta _1\Vert b_1 \Vert _{}}\right) ^{-1/2}\) and this requires the additional condition (24). Set \(Y_2:=Y_1^\perp \) for an orthogonal split \(Y=Y_1\oplus Y_2\). Then \(\beta _2\) from (23) is positive and \(b_2|_{X_2\times Y_2}\) is non-degenerate in the sense that \(b_2(\bullet ,y_2)\not \equiv 0\) in \(X_2^*\) for all \(y_2\in Y_2\setminus \left\{ 0\right\} \). The general theory on bilinear forms [4, Thm.2.1] guarantees, that given any \(x=(x_1,x_2)\in X\), there exists \(y_2\in Y_2\) with \(b_2(\bullet ,y_2)=(x_2,\bullet )_{X_2}\) in \(X_2^*\). Hence \(\beta _2\Vert y_2 \Vert _{Y}\le \Vert x_2 \Vert _{X_2}\). Since \(\beta _1>0\) and \(N_1=\left\{ 0\right\} \), there exists a unique \(y_1\in Y_1\) such that \(b_1(\bullet ,y_1)=(\bullet ,x_1)_{X_1}-b_1(\bullet ,y_2)\) in \(X_1^*\) and \(\beta _1\Vert y_1 \Vert _{Y}\le \Vert x_1 \Vert _{X_1}+\Vert b_1 \Vert _{}\Vert y_2 \Vert _{Y}\). Then
Moreover, \(y=y_1+y_2\in Y\) satisfies
The upper bound is recast as
for the maximal eigenvalue
of the displayed symmetric \(2\times 2\) coefficient matrix. This concludes the proof. \(\square \)
Proof of Theorem 3.1
In the setting of Theorem 3.3, let (equipped with the natural norms)
For all \(x_1=(\varvec{\sigma },u)\in X_1,x_2=(s,t)\in X_2\) and \(y=(\varvec{\tau },v)\in Y\) set
For all \(x_1=(\varvec{\sigma },u)\in X_1\) and \(y=(\varvec{\tau },v)\in Y\), the Cauchy–Schwarz inequality proves
Thus, \(\Vert b_1 \Vert _{}\le \sqrt{2}\). Given \(x_2=(s,t)\in X_2\) and \(y=(\varvec{\tau },v)\in Y\). The substitution of \(s=\gamma _0^\mathcal {T}w\) with \(w\in H^1_0\left( \varOmega ;\mathbb {R}^{n}\right) \) and \(\Vert w \Vert _{H^1(\varOmega )}=\Vert s \Vert _{H^{1/2}\left( \partial \mathcal {T}\right) }\) as well as \(t=\gamma _\nu ^\mathcal {T}{\varvec{q}}\) with \({\varvec{q}}\in H\left( {{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n}\right) \) and \(\Vert {\varvec{q}} \Vert _{H({{\mathrm{div}}})}=\Vert t \Vert _{H^{-1/2}\left( \partial \mathcal {T}\right) }\) allow an integration by parts. Hence,
It follows, \(\Vert b_2 \Vert _{}\le 1\) and so \(\Vert b \Vert _{}\le \sqrt{3}\).
For an arbitrary \(0\not = x_1=\left( \varvec{\sigma }, u\right) \in X_1\), define \({\tilde{F}}\in Z^*\) by
The Cauchy–Schwarz inequality implies \( \Vert {{\tilde{F}}}\Vert _{Z^*} \le \sqrt{2}\Vert x_1 \Vert _{ X_1}. \) Since the formulation (20) for the Stokes equations has unique solutions [9, Thm.2.3], there exists \(\left( \varvec{\tau },-v\right) \in Z\) such that \({\tilde{b}}\left( \left( \varvec{\tau },-v\right) ,\bullet \right) ={\tilde{F}}\) in \(Z^*\). For any \(\left( \varvec{\rho },w\right) \in Z\), this reads
Since \(w\in L^2(\varOmega ;\mathbb {R}^{n})\) and \(\varvec{\rho }\) is arbitrary in \(H({{\mathrm{div}}},\varOmega ;\mathbb {R}^{n\times n})/\mathbb {R}, {{\mathrm{div}}}\varvec{\tau }= u\) and (31) implies \(v\in H^1_0(\varOmega ;\mathbb {R}^{n})\) with \({{\mathrm{D}}}v=\varvec{\sigma }-{{\mathrm{dev}}}\varvec{\tau }\). This test function \(y_1:=(\varvec{\tau },v)\in Y_1\) allows for
Recall \(\gamma \) from (21) the inf-sup constant for \({\tilde{b}}\). Then
The triangle inequality implies \(\Vert {{\mathrm{D}}}v \Vert _{L^2(\varOmega )}^2\le 2\Vert \varvec{\sigma } \Vert _{L^2(\varOmega )}^2+2\Vert \varvec{\tau } \Vert _{L^2(\varOmega )}^2.\) The previous two displayed inequalities prove
Hence, for all \(x_1=(\varvec{\sigma },u)\in X_1\) and \(y_1:=(\varvec{\tau },v)\in Y_1\) as above,
This proves (22) with \((6\gamma ^{-2} +2)^{-1/2}\le \beta _1 \).
The duality Lemma 2.1 shows, that any \(x_2=(s,t)\in X_2\) satisfies
Hence, (23) holds with \(2^{-1/2}\le \beta _2\).
Given any \(y=\left( \varvec{\tau }, v\right) \in Y\) with \(b_2(x_2,y)=-\left\langle \gamma _\nu ^\mathcal {T}\varvec{\tau } , s \right\rangle _{\partial \mathcal {T}}-\left\langle t , \gamma _0^\mathcal {T}v \right\rangle _{\partial \mathcal {T}}=0\) for all \(x_2=(s,t)\in X_2\). This means that all jumps of v and (normal components) of \(\varvec{\tau }\) disappear. Hence, \(y\in Y_1\) as demanded in Theorem 3.3.
Let \(y_1=(\varvec{\tau },v)\in N_1\). With \(x_1=\left( 0,u\right) \in X_1\) for any \(u\in C_0^\infty \left( \varOmega ;\mathbb {R}^{n}\right) \subseteq L^2\left( \varOmega ;\mathbb {R}^{n}\right) ,y_1\in N_1\) implies \({{\mathrm{div}}}\varvec{\tau }\equiv 0\). The boundary conditions and continuity in \(Y_1\) prove
Furthermore, the choice \(x_1=\left( \varvec{\tau },0\right) \in X_1\) results in
whence \({{\mathrm{dev}}}\varvec{\tau }=0\). Lemma 3.2 proves \(\varvec{\tau }\equiv 0\). Further, for all \(\varvec{\sigma }\in C_0^\infty (\varOmega ;\mathbb {R}^{n\times n})\) set  and \(x_1=({{\tilde{\varvec{\sigma }}}},0)\in X_1\). Then
and \(x_1=({{\tilde{\varvec{\sigma }}}},0)\in X_1\). Then

Hence, \({{\mathrm{D}}}v\equiv 0\) for \(v\in H^1_0(\varOmega ;\mathbb {R}^{n})\) and so \(v\equiv 0\). This concludes the proof. \(\square \)
4 Discrete problem
The low-order discrete trial and test search space of the introduced method read
Given b from (18) and F from (19), the discrete problem seeks \(x_h\in X_h\) with (3). This section establishes the discrete inf-sup condition (4) with a constant \(\beta _h\), which depends on the Friedrichs constant \(C_{{F}}\) (with \( ||\bullet ||_{L^2(\varOmega )}\le C_F || D \bullet ||_{L^2(\varOmega )} \) in \(H^1_0(\varOmega )\)) and the tr-div-dev constant \(C_{\text {tdd}}\).
Theorem 4.1
(inf-sup) The discrete spaces (32)–(33) and the bilinear form b from (18) satisfy
Proof of Theorem 3.1
-
Step 1. Discrete test functions. The discrete traces in \(S_0^1(\mathcal {E};\mathbb {R}^{n})\) (resp. \(P_0(\mathcal {E};\mathbb {R}^{n})\)) admit a unique extension by \(S_0^1(\mathcal {T};\mathbb {R}^{n})\) (resp. \(RT_0(\mathcal {T};\mathbb {R}^{n\times n})\)). Thus, given \(x_h=(\varvec{\sigma }_0,u_0,s_1,t_0) \in X_h\) chose \(w_{\text {c}}\in S_0^1(\mathcal {T};\mathbb {R}^{n})\) with \(\gamma _0^\mathcal {T}w_{\text {c}}=s_1\) and \(\varvec{q}_{\text { RT}}\in RT_0(\mathcal {T};\mathbb {R}^{n\times n})\) with \(\gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}}=t_0\). The norm for the trace space in Sect. 2.3 by minimal extension fulfils
$$\begin{aligned} \Vert x_h \Vert _{X}^2&=\Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}^2+\Vert u_0 \Vert _{L^2(\varOmega )}^2+\Vert \gamma _0^\mathcal {T}w_{\text {c}}\Vert _{H^{1/2}(\partial \mathcal {T})}^2+\Vert \gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}}\Vert _{H^{-1/2}(\partial \mathcal {T})}^2\nonumber \\&\le \Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}^2+\Vert u_0 \Vert _{L^2(\varOmega )}^2+\Vert w_{\text {c}} \Vert _{H^1(\varOmega )}^2+\Vert \varvec{q}_{\text { RT}} \Vert _{H({{\mathrm{div}}},\varOmega )}^2. \end{aligned}$$(34)For \(x_h=(\varvec{\sigma }_0,u_0,\gamma _0^\mathcal {T}w_{\text {c}},\gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}})\in X_h\setminus \left\{ 0\right\} \), set \(y_h=(\varvec{\tau }_{\text { RT}},v_1)\in Y_h\)
$$\begin{aligned} \varvec{\tau }_{\text { RT}}&:={{\mathrm{dev}}}\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}+{1}/{n} \ \left( u_0-\varPi _0w_{\text {c}}\right) \otimes \left( \bullet -{{\mathrm{mid}}}(T)\right) ,\\ v_1&:=-{{\mathrm{div}}}\varvec{q}_{\text { RT}}+\left( \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}}\right) \left( \bullet -{{\mathrm{mid}}}(T)\right) . \end{aligned}$$Notice, that \({{\mathrm{div}}}_{\text { NC}}\varvec{\tau }_{\text { RT}}=u_0-\varPi _0w_{\text {c}},{{\mathrm{D}}}_{\text { NC}}v_1=\varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}}\) and \(\varPi _0v_1=-{{\mathrm{div}}}\varvec{q}_{\text { RT}}\). The side restriction \(\int _\varOmega {{{\mathrm{tr}}}\varvec{\sigma }_0}\,\mathrm{d}x=0\) implies \(\int _\varOmega {{{\mathrm{tr}}}\varvec{\tau }_{\text { RT}}}\,\mathrm{d}x=0\).
Furthermore, the substitution of \(s_1\) by \(\gamma _0^\mathcal {T}w_{\text {c}}\) and \(t_0\) by \(\gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}}\) allows an integration by parts. Hence, \(x_h=(\varvec{\sigma }_0,u_0,\gamma _0^\mathcal {T}w_{\text {c}},\gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}})\) and the above test function \(y_h=(\varvec{\tau }_{\text { RT}},v_1)\) satisfy
$$\begin{aligned} b\left( x_h,y_h\right)&= \int _{\varOmega }\varvec{\sigma }_0:{{\mathrm{D}}}_{\text { NC}}v_1\,\mathrm{d}x+\int _{\varOmega }{{\mathrm{dev}}}\varvec{\sigma }_0:\varvec{\tau }_{\text { RT}}\,\mathrm{d}x+\int _{\varOmega }u_0\cdot {{\mathrm{div}}}_{\text { NC}}\varvec{\tau }_{\text { RT}}\,\mathrm{d}x\nonumber \\&\quad -\int _{\varOmega }\left( v_1\cdot {{\mathrm{div}}}\varvec{q}_{\text { RT}}+\varvec{q}_{\text { RT}}:{{\mathrm{D}}}_{\text { NC}}v_1\right) \,\mathrm{d}x\nonumber \\&\quad -\int _{\varOmega }\left( \varvec{\tau }_{\text { RT}}:{{\mathrm{D}}}w_{\text {c}}+w_{\text {c}}\cdot {{\mathrm{div}}}_{\text { NC}}\varvec{\tau }_{\text { RT}}\right) \,\mathrm{d}x\nonumber \\&=\Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2+\Vert {{\mathrm{dev}}}\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2\nonumber \\&\quad +\Vert u_0-\varPi _0w_{\text {c}} \Vert _{L^2(\varOmega )}^2 +\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2. \end{aligned}$$(35) -
Step 2. Key estimates. The test function from Step 1. and (9) prove
$$\begin{aligned} \Vert y_h \Vert _{Y}^2&= \Vert \varvec{\tau }_{\text { RT}} \Vert _{H({{\mathrm{div}}},\mathcal {T})}^2+\Vert v_1 \Vert _{H^1(\mathcal {T})}^2\\&\le \Vert {{\mathrm{dev}}}\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2+\left( h_{\text { max}}^2/(n+1)^2+1\right) \Vert u_0-\varPi _0w_{\text {c}} \Vert _{L^2(\varOmega )}^2\\&\quad +\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2+\left( h_{\text { max}}^2n^2/(n+1)^2+1\right) \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2. \end{aligned}$$The combination with (35) shows for \(C_{y_h}:={1+h_{\text { max}}^2 n^2/(n+1)^2}\) holds \(\Vert y_h \Vert _{Y}^2 \le C_{y_h}\ b\left( x_h,y_h\right) \). The proof of \(\Vert x_h \Vert _{X}\lesssim b\left( x_h,y_h\right) \) requires the computation of \(C_{{w_{\text {c}}}}\) with \(\Vert {{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}=:| | | w_{\text {c}} | | |^2\le C_{{w_{\text {c}}}}b\left( x_h,y_h\right) \). The function
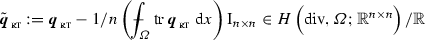 (36)
(36)allows an application of Lemma 3.2. Moreover,
-
(i)
\(\Vert {{\mathrm{dev}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}=\Vert {{\mathrm{dev}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\) and \(\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}=\Vert {{\mathrm{div}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\),
-
(ii)
for \(\varvec{\sigma }_0\in L^2(\varOmega ;\mathbb {R}^{n\times n})/\mathbb {R}\) holds \( \Vert \varvec{\sigma }_0-\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\le \Vert \varvec{\sigma }_0-\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}, \)
-
(iii)
for \(f\in L^2(\varOmega ;\mathbb {R})\) with \(\int _\varOmega f\,\mathrm{d}x=0\) holds \(\int _\varOmega f {{\mathrm{tr}}}\varvec{q}_{\text { RT}}\,\mathrm{d}x=\int _\varOmega f{{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}}\,\mathrm{d}x\).
This verifies
$$\begin{aligned} {C_{\text {tdd}}^{-1}}\Vert {{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\le&\Vert {{\mathrm{dev}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}. \end{aligned}$$(37)It holds
$$\begin{aligned} \Vert {{\mathrm{dev}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}&\le \Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-\varvec{q}_{\text { RT}}) \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}) \Vert _{L^2(\varOmega )}\\&\quad +\Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}. \end{aligned}$$$$\begin{aligned}\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-\varvec{q}_{\text { RT}}) \Vert _{L^2(\varOmega )}\le \Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}}) \Vert _{L^2(\varOmega )}+\frac{h_{\text { max}}}{n+1}\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}.\end{aligned}$$This proves
$$\begin{aligned} {C_{\text {tdd}}}^{-1}\Vert {{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}&\le \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}) \Vert _{L^2(\varOmega )}\\&\quad +\Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}+(1+h_{\text { max}}/(n+1))\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}. \end{aligned}$$On the other hand,
$$\begin{aligned} \Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2&= \int _\varOmega \left( \varPi _0(\varvec{\sigma }_0-\varvec{q}_{\text { RT}})-{{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}})+\varvec{q}_{\text { RT}}\right) :{{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}}\,\mathrm{d}x\\&\le \left( \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}) \Vert _{L^2(\varOmega )}\right) \Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )} \\&\quad +\int _\varOmega \tilde{\varvec{q}}_{\text { RT}}:{{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}}\,\mathrm{d}x. \end{aligned}$$The decomposition of the deviator followed by an integration by parts shows
$$\begin{aligned} \int _\varOmega {{\mathrm{dev}}}\tilde{\varvec{q}}_{\text { RT}}:{{\mathrm{D}}}w_{\text {c}}\,\mathrm{d}x&=\int _\varOmega \tilde{\varvec{q}}_{\text { RT}}:{{\mathrm{D}}}w_{\text {c}}\,\mathrm{d}x-1/n \ \int _\varOmega ({{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}}){{\mathrm{div}}}w_{\text {c}}\,\mathrm{d}x\\&\le -\int _\varOmega w_{\text {c}}\cdot {{\mathrm{div}}}\varvec{q}_{\text { RT}}\,\mathrm{d}x+1/n\ \Vert {{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )} \\&\le C_{{F}}| | | w_{\text {c}} | | |\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}\\&\quad + 1/n\ \Vert {{\mathrm{tr}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}. \end{aligned}$$The combination of the aforementioned estimates leads with
$$\begin{aligned} a&:=\ \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}) \Vert _{L^2(\varOmega )} +C_{\text {tdd}}/n\ \Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}, \\ b&:=\ C_{\text {tdd}}\left( \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+\Vert {{\mathrm{dev}}}(\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}}) \Vert _{L^2(\varOmega )}\right) +\Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}\\&\quad +C_{\text {tdd}}(1+h_{\text { max}}/(n+1))\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )},\text { and } c:=\ C_{{F}}\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}\\&\quad \text { to } | | | w_{\text {c}} | | |^2 \le a\Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}+b/n\Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}+c| | | w_{\text {c}} | | |. \end{aligned}$$This upper bound is the scalar product in \(\mathbb {R}^3\) of the vector \((a,b/\sqrt{n},c)\) with \((\Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )},\ \Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}/\sqrt{n},\ | | | w_{\text {c}} | | |)\). The Cauchy-Schwarz inequality leads to
$$\begin{aligned} | | | w_{\text {c}} | | |^2&\le \sqrt{\Vert {{\mathrm{dev}}}{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2+1/n\Vert {{\mathrm{div}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2+| | | w_{\text {c}} | | |^2}\sqrt{a^2+b^2/n+c^2}\\&= | | | w_{\text {c}} | | |\sqrt{2}\sqrt{a^2+b^2/n+c^2}=:C_1\ | | | w_{\text {c}} | | |{.} \end{aligned}$$The Cauchy-Schwarz inequality, (8), and the abbrevations \(g:=\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}, f:=\Vert {{\mathrm{D}}}w_{\text {c}}-{{\mathrm{dev}}}\varvec{\sigma }_0 \Vert _{L^2(\varOmega )}\) and \(e:=\Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}\) allow to rewrite the pre-factors \(a,\,b,\) and c as
$$\begin{aligned} a&\le \sqrt{2+C_{\text {tdd}}^2/n}\sqrt{e^2+f^2},\\ b&\le \sqrt{e^2+f^2+g^2}\sqrt{n+C_{\text {tdd}}^2 (2+ (1+h_{\text { max}}/(n+1))^2)}\text { and }c =C_{{F}}\ g. \end{aligned}$$Since by (35), \(e^2+f^2+g^2\le b(x_h,y_h)\), it follows
$$\begin{aligned} C_1^2 \le 2\left( \max \left\{ C_{{F}}^2, 2+\frac{C_{\text {tdd}}^2}{n}\right\} +1+\frac{C_{\text {tdd}}^2}{n}\left( 2+\left( 1+\frac{h_{\text { max}}}{n+1}\right) ^2\right) \right) b(x_h,y_h). \end{aligned}$$Therefore, the constant \(C_{w_{\text {c}}}\) with \(| | | w_{\text {c}} | | |^2\le C_{w_{\text {c}}}{b(x_h,y_h)}\) satisfies
$$\begin{aligned} C_{w_{\text {c}}} \le {2}\left( \max \left\{ C_{{F}}^2,\ 2+C_{\text {tdd}}^2/n\right\} +1+C_{\text {tdd}}^2/n(2+(1+h_{\text { max}}/(n+1))^2)\right) . \end{aligned}$$It remains to prove \(\Vert x_h \Vert _{X}^2\lesssim b\left( x_h,y_h\right) \). For \(\varvec{q}_{\text { RT}}\in RT_0(\mathcal {T};\mathbb {R}^{n\times n})\), (13) and (9) imply
$$\begin{aligned} \Vert \varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2&\le \frac{h^2_{\text { max}}}{(n+1)^2}\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2+2\Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2+2\Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}^2. \end{aligned}$$On the other hand, the auxiliary function \(\tilde{\varvec{q}}_{\text { RT}}\) from (36)–(37) allows for
$$\begin{aligned} \Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}&\le \Vert \varvec{\sigma }_0-\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}+\frac{C_{\text {tdd}}}{\sqrt{n}} \Vert {{\mathrm{div}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\\&\quad +\left( 1+\frac{C_{\text {tdd}}}{\sqrt{n}}\right) \Vert {{\mathrm{dev}}}\tilde{\varvec{q}}_{\text { RT}} \Vert _{L^2(\varOmega )}\\&\le (2+C_{\text {tdd}}/\sqrt{n})\Vert \varvec{\sigma }_0-\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+C_{\text {tdd}}/\sqrt{n}\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}\\&\quad +(1+C_{\text {tdd}}/\sqrt{n})\Vert {{\mathrm{dev}}}\varvec{\sigma }_0 \Vert _{L^2(\varOmega )}. \end{aligned}$$Furthermore, it holds
$$\begin{aligned} \Vert \varvec{\sigma }_0-\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}&\le \Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}+h_{\text { max}}/(n+1)\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )} \quad \text { and}\\ \Vert {{\mathrm{dev}}}\varvec{\sigma }_0 \Vert _{L^2(\varOmega )}&\le \Vert {{\mathrm{dev}}}\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}+| | | w_{\text {c}} | | |. \end{aligned}$$Therefore, all terms in the decomposition of \(\Vert x_h \Vert _{X}\) as in (34) are under control,
$$\begin{aligned} \Vert x_h \Vert _{X}^2&\le \Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}^2+\Vert u_0 \Vert _{L^2(\varOmega )}^2+\Vert \varvec{q}_{\text { RT}} \Vert _{H({{\mathrm{div}}},\varOmega )}^2+\Vert w_{\text {c}} \Vert _{H^1(\varOmega )}^2 \\&\le \Vert \varvec{\sigma }_0 \Vert _{L^2(\varOmega )}^2+(1+C_{{F}}^2)\Vert u_0-\varPi _0w_{\text {c}} \Vert _{L^2(\varOmega )}^2\\&\quad +(2+2C_{{F}}^2)| | | w_{\text {c}} | | |^2 +\Vert \varvec{q}_{\text { RT}} \Vert _{H({{\mathrm{div}}},\varOmega )}^2. \end{aligned}$$Careful bookkeeping reveals that
$$\begin{aligned} C_3&:= \frac{3h_{\text { max}}^2}{(n+1)^2}\left( \frac{C_{\text {tdd}}}{\sqrt{n}}+2\right) ^2+\frac{6h_{\text { max}}}{n+1} \left( \frac{C_{\text {tdd}}^2}{n}+2\frac{C_{\text {tdd}}}{\sqrt{n}}\right) \\&\quad +12\left( \frac{C_{\text {tdd}}}{\sqrt{n}}+1\right) ^2+6 \end{aligned}$$satisfies
$$\begin{aligned} \Vert x_h \Vert _{X}^2&\le \left( 1+C_{{F}}^2\right) \Vert u_0-\varPi _0w_{\text {c}} \Vert _{L^2(\varOmega )}^2 +C_3\Vert {{\mathrm{dev}}}\varvec{\sigma }_0-{{\mathrm{D}}}w_{\text {c}} \Vert _{L^2(\varOmega )}^2\\&\quad +(2+C_3)\Vert \varvec{\sigma }_0-\varPi _0\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2+(2+2C_{{F}}^2+C_3)| | | w_{\text {c}} | | |^2\\&\quad +(1+h^2_{\text { max}}/(n+1)^2+C_3)\Vert {{\mathrm{div}}}\varvec{q}_{\text { RT}} \Vert _{L^2(\varOmega )}^2. \end{aligned}$$Therefore, \(\Vert x_h \Vert _{X}^2\le C_{{x_h}}b(x_h,y_h)\) holds for
$$\begin{aligned} C_{{x_h}}&:= \max \Big \{1+C_{{F}}^2,\,C_3+\max \Big \{2,\,1+\frac{h_{\text { max}}^2}{(n+1)^2}\Big \}\Big \} +\left( C_3+2C_{{F}}^2+2\right) C_{{w_{\text {c}}}}. \end{aligned}$$ -
(i)
-
Step 3. Alltogether, for all \( x_h=(\varvec{\sigma }_0,u_0,\gamma _0^\mathcal {T}w_{\text {c}},\gamma _\nu ^\mathcal {T}\varvec{q}_{\text { RT}})\in X_h\setminus \left\{ 0\right\} \) and \(y_h\in Y_h\) as in Step 1 , it holds
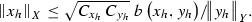
This concludes the proof of
 with \(\beta _h\) from (4).
with \(\beta _h\) from (4).
\(\square \)
5 Data approximation error
The Fortin interpolator (5) is explicitly constructed in [10, 19, 22] with higher-order test search functions. The low order spaces in [13, 14] require a direct verification of the discrete inf-sup condition and allow explicit constants \(\Vert b \Vert _{},\,\beta _h\) in the a posteriori error bound (7). The upper error bound involves the computable residual error \(\Vert {F-b(\xi _h,\bullet )}\Vert _{Y_h^*}\) and the remaining data approximation error \(\Vert {F\circ (1-\varPi )}\Vert _{Y^*}\). The latter is not of higher-order in general as shown in Sect. 5.1. This motivates an extension of the test search space in Sect. 5.2.
5.1 Fortin interpolation
The description of the operator \(\varPi :Y\rightarrow Y_h\) with (5) in 2D with a shape-regular triangulation \(\mathcal {T}\) of the simply-connected bounded polygonal domain \(\varOmega \subset \mathbb {R}^2\) into triangles requires further notation. For \(\beta \in C^1(\varOmega ;\mathbb {R}^{2})\), set
with the piecewise version \({{\mathrm{Curl}}}_{\text { NC}}\) and \({{\mathrm{curl}}}_{\text { NC}}\) (piecewise with respect to \(\mathcal {T}\)). Define
The nonconforming Crouzeix-Raviart functions space reads
The discrete divergence-free Crouzeix-Raviart functions
are well known from the the nonconforming finite element analysis of the Stokes equations. Any \(w_{\text { CR}}\in \mathrm {CR}^1_0(\mathcal {T};\mathbb {R}^{2})\) satisfies \(\int _E \left[ w_{\text { CR}}\right] _E\,\mathrm{d}s=0\) along any edge \(E\in \mathcal {E}\). The local nonconforming interpolant \(I_{\text { NC}}^\text {pw}\) guarantees a similar property: Define \(I_{\text { NC}}^\text {pw}v\in P_1(\mathcal {T};\mathbb {R}^{2})\) for \(v\in H^1(\mathcal {T};\mathbb {R}^{2})\) on any \(T\in \mathcal {T}\) via

For all \(T\in \mathcal {T}\) and \(E\in \mathcal {E}(T)\) holds \(\int _E {I_{\text { NC}}^\text {pw}v|_T}=\int _E v|_T\,\mathrm{d}s\), whence \(\varPi _0{{\mathrm{D}}}_{\text { NC}}v={{\mathrm{D}}}_{\text { NC}}I_{\text { NC}}^\text {pw}v\).
Lemma 5.1
(discrete Helmholtz decompositions) For a simply-connected domain \(\varOmega \), the following decompositions are orthogonal in \(L^2(\varOmega ; \mathbb {R}^{2\times 2})\)
Proof
The paper [17] includes a proof of (39) and (40) is known from [3].\(\square \)
Based on those preliminaries, the Fortin interpolation is characterized in the sequel. Given a simply-connected domain \(\varOmega \) and \(y=(\varvec{\tau },v)\in Y\). Let \(\alpha _{\text { CR}}\in \mathrm {CR}^1(\mathcal {T};\mathbb {R}^2)/\mathbb {R}^2\) satisfy \(\int _{\varOmega } \alpha _{\text { CR}}\,\mathrm{d}x=0\) and
for all \(w_{\text { CR}}\in \mathrm {CR}^1(\mathcal {T};\mathbb {R}^2)\). (This follows from one solve of the Crouzeix-Raviart FEM and \(\int _\varOmega (1-\varPi _0){{\mathrm{div}}}_{\text { NC}}\varvec{\tau }\,\mathrm{d}x=0.\)) Let  The discrete Helmholtz decomposition (39) guarantees the existence of \(z_{\text { CR}}\in Z_{\text { CR}}\) and \(\beta _c\in X_{{{\mathrm{curl}}}}\), such that
The discrete Helmholtz decomposition (39) guarantees the existence of \(z_{\text { CR}}\in Z_{\text { CR}}\) and \(\beta _c\in X_{{{\mathrm{curl}}}}\), such that
Theorem 5.2
Given \((\varvec{\tau },v)\in Y\) and \(\alpha _{\text { CR}}\in \mathrm {CR}^1(\mathcal {T};\mathbb {R}^2)/\mathbb {R}^2,z_{\text { CR}}\in Z_{\text { CR}},\beta _c\in X_{{{\mathrm{curl}}}},\alpha _0\in \mathbb {R}^{2}\) as above with (41)–(42), set
The mapping \(\varPi :Y\rightarrow Y_h,(\varvec{\tau },v)\mapsto (\varvec{\tau }_{\text { RT}},v_1)\) is linear, bounded, idempotent and fulfils (5). The discrete kernel \(N_h:=\left\{ y_h\in Y_h:b(x_h,y_h)=0\ \forall x_h\in X_h\right\} \) of \(B_{2,h}:Y_h\rightarrow X_h^*,\) \(y_h\mapsto b(\bullet ,y_h)|_{Y_h}\) has dimension \({{\mathrm{dim}}}(N_h)=2(|\mathcal {T}|-1)\) and is equal to
Proof
The design of \(\alpha _0\) leads to \(\int _\varOmega {{\mathrm{tr}}}\varvec{\tau }_{\text { RT}}\,\mathrm{d}x=0\). For all \(\varvec{\sigma }_0\in P_0(\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\), the split (42) and \(\varPi _0{{\mathrm{D}}}_{\text { NC}}v={{\mathrm{D}}}_{\text { NC}}I_{\text { NC}}^\text {pw}v\) prove
Since \({{\mathrm{div}}}_{\text { NC}}\varvec{\tau }_{\text { RT}}=\varPi _0{{\mathrm{div}}}_{\text { NC}}\varvec{\tau }\), any \(u_0\in P_0(\mathcal {T};\mathbb {R}^{2})\) satisfies
For all \(s_1\in S^1_0(\mathcal {E};\mathbb {R}^{2})\) on the skeleton \(\partial \mathcal {T}\), consider the linear extension \(w_{\text {c}}\in S^1_0(\mathcal {T};\mathbb {R}^{2})\subseteq \mathrm {CR}^1(\mathcal {T},\mathbb {R}^{2})\) with \(\gamma _0^\mathcal {T}w_{\text {c}}=s_1\) to allow an integration by parts. Thus, \(\int _\varOmega {{\mathrm{D}}}w_{\text {c}}\,\mathrm{d}x=0\), (40)–(41), and \({{\mathrm{div}}}_{\text { NC}}\varvec{\tau }_{\text { RT}}=\varPi _0{{\mathrm{div}}}_{\text { NC}}\varvec{\tau }\) prove
The properties of the Crouzeix-Raviart-functions and \(I_{\text { NC}}^\text {pw}\) (38) prove for all \(t_0\in P_0(\mathcal {E};\mathbb {R}^{2})\),
For the proof, that \(\varPi \) is idempotent (hence a projection), suppose that \((\varvec{\tau },v)\in RT_0^\text {pw}(\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\times P_1(\mathcal {T};\mathbb {R}^{2})\) and decompose \(\varPi _0\varvec{\tau }={{\mathrm{D}}}_{\text { NC}}a_{\text { CR}}+{{\mathrm{Curl}}}b_c\) for unique \(a_{\text { CR}}\in CR^1(\mathcal {T};\mathbb {R}^{2})/\mathbb {R}^{2}\) and \(b_c\in S^1_0(\mathcal {T};\mathbb {R}^{2})\). Since \((1-\varPi _0){{\mathrm{div}}}_{\text { NC}}\varvec{\tau }=0\) a.e. in \(\varOmega \), (41) shows \(a_{\text { CR}}=\alpha _{\text { CR}}\). Since \(b_c=0\) along \({\partial \varOmega }\) and  , (42) reveals that
, (42) reveals that  and \(z_{\text { CR}}=0\). Notice that \(0=\int _\varOmega {{\mathrm{tr}}}\varvec{\tau }\,\mathrm{d}x=\int _\varOmega {{\mathrm{tr}}}\varPi _0\varvec{\tau }\,\mathrm{d}x=\int _\varOmega {{\mathrm{div}}}_{\text { NC}}\alpha _{\text { CR}}\,\mathrm{d}x=0\) implies \(\alpha _0=0\). Altogether, it follows that \(\varvec{\tau }_{\text { RT}}=\varvec{\tau }\) and \(v_1=v\), i.e., \(\varPi ^2=\varPi \).
and \(z_{\text { CR}}=0\). Notice that \(0=\int _\varOmega {{\mathrm{tr}}}\varvec{\tau }\,\mathrm{d}x=\int _\varOmega {{\mathrm{tr}}}\varPi _0\varvec{\tau }\,\mathrm{d}x=\int _\varOmega {{\mathrm{div}}}_{\text { NC}}\alpha _{\text { CR}}\,\mathrm{d}x=0\) implies \(\alpha _0=0\). Altogether, it follows that \(\varvec{\tau }_{\text { RT}}=\varvec{\tau }\) and \(v_1=v\), i.e., \(\varPi ^2=\varPi \).
The discrete Friedrichs and Poincaré inequality [7, Thm.10.6.12], Lemma 3.2, and [12, Thm.4] show that the proposed mapping \(\varPi \) is bounded. A lengthy but straight forward calculation with \(C:=2\max \left\{ 1+C_{\text {tdd}}^2,2+2C_{\text {dF}}^2\right\} \) reveals
It remains to characterize \(N_h\). For all \({\tilde{y}}_h=(\tilde{\varvec{\tau }}_{\text { RT}},\tilde{v}_1)\in N_h\), the condition
implies \(\tilde{v}_1\in \mathrm {CR}_0^1(\mathcal {T};\mathbb {R}^{2})\). Since
it follows \({{\mathrm{div}}}_{\text { NC}}\tilde{\varvec{\tau }}_{\text { RT}}=0\) and \(\varPi _0\tilde{\varvec{\tau }}_{\text { RT}}=\tilde{\varvec{\tau }}_{\text { RT}}\). The linear extension of \(s_1\in S^1_0(\mathcal {E};\mathbb {R}^{2})\) to \(w_{\text {c}}\in S^1_0(\mathcal {T};\mathbb {R}^{2})\) with \(\gamma _0^\mathcal {T}w_{\text {c}}=s_1\) and an integration by parts result in
This and the Helmholtz decomposition (40) reveal \(\tilde{\varvec{\tau }}_{\text { RT}}={{\mathrm{Curl}}}_{\text { NC}}\beta _{\text { CR}}\) for \(\beta _{\text { CR}}\in \mathrm {CR}^1(\mathcal {T};\mathbb {R}^{2})/\mathbb {R}^{2}\). For all \(\varvec{\sigma }_0\in P_0(\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\),
Hence, \({{\mathrm{dev}}}\tilde{\varvec{\tau }}_{\text { RT}}=-{{\mathrm{D}}}_{\text { NC}}\tilde{v}_1\) and so \(v_1\in Z_{\text { CR}}\). This proves the asserted representation of \(N_h\). Let \(M_h:=N_h^\perp \subseteq Y_h\) denote the orthogonal compliment of \(N_h\) in \(Y_h\) with respect to the scalar product in Y. Then the dPG FEM is equivalent to the mixed FEM with \(x_h\in X_h\) and \( b(x_h,\bullet )=F\text { in } M_h^*\) [13, 14]. Its solvability guarantees \({{\mathrm{dim}}}(M_h)={{\mathrm{dim}}}(X_h)=6|\mathcal {T}|+2|\mathcal {N}(\varOmega )|+2|\mathcal {E}|-1\). This and \({{\mathrm{dim}}}(Y_h)=12|\mathcal {T}|-1\) leads to \({{\mathrm{dim}}}(N_h)=2(|\mathcal {T}|-1)\).\(\square \)
Given an extension \(g\in H^{1}(\varOmega ;\mathbb {R}^{2})\) of the Dirichlet data \(g\in H^1({\partial \varOmega };\mathbb {R}^{2})\) the data approximation error contribution reads
In addition, assume that \(g\in H^1(\varOmega ;\mathbb {R}^{2})\cap H^2(\mathcal {T};\mathbb {R}^{2})\) is piecewise divergence free in that \(\varPi _0{{\mathrm{div}}}g=0\) in \(\varOmega \). Let \(\kappa :=\sqrt{1/48+j_{1,1}^{-2}}=0.298234942888\) for the first root \(j_{1,1}\) of the first Bessel function and the discrete Friedrichs constant \(C_{\text {dF}}\) [7, 10.6.14].
Theorem 5.3
The projection \(\varPi \) from Theorem 5.2 satisfies
Proof
First investigate the volume contributions, i.e., the data approximation error in case \(g\equiv 0\). The Cauchy-Schwarz and the discrete Friedrichs inequality [7, 10.6.14] with constant \(C_{\text {dF}}\) prove, for all \(y=(\varvec{\tau },v)\in Y\), that
The first term is bounded as in [12, Thm.4] by
The choice of \(z_{\text { CR}}\) in the Helmholtz decomposition (42), (41) and the Poincaré inequality, prove for the second term
Altogether,
Let \(g\in H^1(\varOmega ;\mathbb {R}^{2})\cap H^2(\mathcal {T};\mathbb {R}^{2})\) be as above and define the nonconforming interpolant \(I_{\text { NC}}g\in \mathrm {CR}^1(\mathcal {T};\mathbb {R}^{2})\) by  for all \(E\in \mathcal {E}\).
for all \(E\in \mathcal {E}\).
The definition of \(\varvec{\tau }_{\text { RT}}\), (9), \({{\mathrm{div}}}_{\text { NC}}g=0\), and (41) lead to
Equation (42), the Cauchy-Schwarz inequality, and (41) lead to
The application of the Poincaré inequality and (44) prove
Finally, for all \((\varvec{\tau },v)\in S(Y_h)\), it holds
The equality \(\Vert 1-\varPi \Vert _{}=\Vert \varPi \Vert _{}\) follows from Kato’s lemma [23, Lemma 4]. \(\square \)
In conclusion, the data approximation term is not necessarily of higher-order, but at least controlled by \(h_{\text { max}}\) even for non homogeneous boundary data.
5.2 Extensions of test spaces
The discrete inf-sup condition (4) also holds for an enlarged discrete test search space. Three examples for an enlarged test search space \({\hat{Y}}_h=Y_{h,j}\) for \(j=1,\,2,\,3\) allow for a decoupling of the Fortin interpolation operator \(\varPi \) and higher-order data approximation error. Here, \(\mathcal {B}_3(\mathcal {T}):=\left\{ v\in P_3(\mathcal {T}): v=0 \text { along } \partial \mathcal {T}\right\} \) denotes the cubic bubble functions, and
-
(i)
\(Y_{h,1}:= Y_h\oplus \left( \mathcal {B}_3(\mathcal {T})\mathbb {R}^{2\times 2}_{{{\mathrm{dev}}}}\times \left\{ 0\right\} \right) \),
-
(ii)
\(Y_{h,2}:= P_1(\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\times P_1(\mathcal {T};\mathbb {R}^{2})\),
-
(iii)
\(Y_{h,3}:= RT_1^\text {pw}(\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\times P_1(\mathcal {T};\mathbb {R}^{2}).\)
Given \(\varvec{\tau }\in H({{\mathrm{div}}},\mathcal {T};\mathbb {R}^{2\times 2})/\mathbb {R}\), there exists \((\hat{\varvec{\tau }}_{\text { RT}},0)\in {\hat{Y}}_h:=Y_{h,j}\) for \(j=1,2,3\) with
In particular (46) implies \(\varPi _0{{\mathrm{div}}}\hat{\varvec{\tau }}_{\text { RT}}=\varPi _0{{\mathrm{div}}}\tau \). Altogether, the definition \({\hat{\varPi }}(\varvec{\tau },v):=(\hat{\varvec{\tau }}_{\text { RT}},I_{\text { NC}}^\text {pw}v)\) with (45)–(46) guarantees \(b(x_h,(1-{\hat{\varPi }}) y)=0\) for all \(x_h\in X_h\). In case \({\hat{Y}}_h=Y_{h,2}\) and \({\hat{Y}}_h=Y_{h,3}\), (45)–(46) allow multiple choices of \(\hat{\varvec{\tau }}_{\text { RT}}\).
Lemma 5.4
In case \({\hat{Y}}_h=Y_{h,1},{\hat{\varPi }}(y)=(\hat{\varvec{\tau }}_{\text { RT}}, I_{\text { NC}}^\text {pw}v)\in RT_0^\text {pw}(\mathcal {T};\mathbb {R}^{2})/R\oplus \mathcal {B}_3(\mathcal {T})\mathbb {R}^{2\times 2}_{{{\mathrm{dev}}}}\times P_1(\mathcal {T};\mathbb {R}^{2})\) is unique and defines a projection. A bound of \(\Vert {\hat{\varPi }}\Vert \le (2+15.5 \sqrt{\cot (\alpha _{\min })}h_{\text { max}}+(3.22+60\cot (\alpha _{\min })) h_{\text { max}}^2)^{1/2}\) depends on \(h_{\text { max}}\) and the smallest angle of the triangulation \(\alpha _{\min }\).
Proof
The proof of Lemma 5.4 is given in the appendix.\(\square \)
The representation \({\hat{\varPi }}(\varvec{\tau },v):=(\hat{\varvec{\tau }}_{\text { RT}},I_{\text { NC}}^\text {pw}v)\) of the operator \({\hat{\varPi }}\) and (43) prove
In case of inhomogeneous boundary data, let \(g\in H^1(\varOmega ,\mathbb {R}^{2})\) be an extension of \(g\in H^{1}({\partial \varOmega };\mathbb {R}^{2})\) with \(g|_E\in P_1(E)\) for all \(E\in \mathcal {E}(\varOmega )\). Let \(I g\in S_1(\mathcal {E};\mathbb {R}^{n})\) denote the conforming interpolation defined by linear interpolation of the nodal values, \(I g(z)=g(z)\) for all \(z\in \mathcal {N}\). Hence, g and Ig coincide along any interior edge \(E\in \mathcal {E}(\varOmega )\). This choice and (46) lead to
Let \(g':=\partial g/\partial s\) denote the arc-length derivative of \(g\in H^1({\partial \varOmega };\mathbb {R}^{2})\) along the boundary, \(\varPi ^\mathcal {E}_{0}g'\) the \(L^2({\partial \varOmega })\)-orthogonal projection of \(g'\) onto \(P_0(\mathcal {E}({\partial \varOmega });\mathbb {R}^{2})\), and \(h_\mathcal {E}\in P_0(\mathcal {E})\) the piecewise constant function with \(h_\mathcal {E}|_E={{\mathrm{diam}}}(\omega _E)={{\mathrm{diam}}}(T_+\cup T_-)\) for every \(E\in \mathcal {E}\) as in Fig. 1. This allows to define the Dirichlet data oscillation
According to [8, Proof of Lemma 2.1], [5] there exists \(w\in H^1(\varOmega ;\mathbb {R}^{2})\) with \(w|_{{\partial \varOmega }}=(1-I)g|_{{\partial \varOmega }}\) and \(\Vert w \Vert _{H^1(\varOmega )}\lesssim {{\mathrm{osc}}}(g',\mathcal {E}({\partial \varOmega }))\). Hence,
Therefore, for each \({\hat{Y}}_h:=Y_{h,j}\) for \(j=1,2,3\), it follows
Hence, a slight enlargement of the test search space guarantees an higher-order data approximation error independent of the given Dirichlet data g. For \(g|_E\in H^2(E)\) for all \(E\in \mathcal {E}({\partial \varOmega })\) with edgewise second surface derivative \(\partial ^2_\mathcal {E}g/\partial s^2\) a better estimate with explicit constants is possible. There exists \(w\in H^1(\varOmega ;\mathbb {R}^{2})\), such that \(w|_{{\partial \varOmega }}= (1-I)g\) and
The constants are computed in [15, Thm.5.1] and [24, Thm.4.2.2]. They depend only on the shape of the triangles of \(\mathcal {T}\) not on the mesh-size, e.g., for right isosceles triangles \(c_1\le 0.4980\) and \(c_2\le 0.0654\).
Lemma 5.5
Let \(\mathcal {T}\) consist of right isosceles triangles and \(g|_E\in H^2(E)\) for all \(E\in \mathcal {E}({\partial \varOmega })\). The data approximation error \(\Vert F\circ \left( 1-\varPi \right) \Vert _{Y^*}\) is explicitly bounded from above by
Proof
This follows directly from (47)–(49), Kato’s Lemma and Lemma 5.4. \(\square \)
6 Numerical examples
Three benchmark examples concern uniform and adaptive mesh-refinement with various choices of the input bulk parameter \(\theta \) in the adaptive algorithm displayed in the convergence history plots.

6.1 Numerical realisation
The implementation has been performed straightforwardly into Matlab and extends the data structures of [1]. The adaptive finite element mesh-refining runs Algorithm 1 with \(\eta _\ell ^2:=\Vert F-b(x_\ell ,\bullet ) \Vert _{Y_\ell ^*}^2\) for the discrete test search space \(Y_\ell \) on level \(\ell \) and the associated discrete solution \(x_\ell \). Let \(Y_\ell (T)\subset Y_\ell \) denote the set of all basis functions with support \(T\in \mathcal {T}\) and use \(\eta ^2_\ell (T):=\Vert F-b(x_\ell ,\bullet ) \Vert _{Y_\ell (T)^*}^2\) as a refinement indicator. The extended test space \({\hat{Y}}_\ell :=Y_\ell \oplus ( \mathcal {B}_3(\mathcal {T})\mathbb {R}^{2\times 2}_{{{\mathrm{dev}}}}\times \left\{ 0\right\} )\) from Sect. 5.2 leads to the error estimator \({\hat{\eta }}_\ell ^2:=\Vert F-b(x_\ell ,\bullet ) \Vert _{{\hat{Y}}_\ell ^*}^2\) and \({\tilde{\eta }}_\ell ^2:={\hat{\eta }}_\ell ^2+{{\mathrm{osc}}}^2(g',\mathcal {E}({\partial \varOmega })).\) The oscillations are computed with the exact derivatives of \(g\in H^1({\partial \varOmega };\mathbb {R}^{2})\) and numerical integration with 7 Gauss points per edge. In the examples \(f\equiv 0\), so that \({\hat{\eta }}_\ell \) is a guaranteed error estimator upto a multiplicative generic constant. Instead of the exact error \(\Vert x-x_\ell \Vert _{X}\) an upper bound is computed and displayed via the unique extensions \(w_{\text {c}}\in S^1_0(\mathcal {T};\mathbb {R}^{2})\) (resp. \(\varvec{q}_{\text { RT}}\in RT_0(\mathcal {T};\mathbb {R}^{2})\)) of \(s_1\in S^1_0(\mathcal {E};\mathbb {R}^{2})\) (resp. \(t_0\in P_0(\mathcal {E};\mathbb {R}^{2})\)) as in (34),
6.2 Colliding flow example
In this benchmark problem \(f\equiv 0\) in \(\varOmega =(-1,1)^2\) with given boundary data from the exact solution (u, p) with, for all \((x_1,x_2)\in \varOmega ,\)
Figure 2 presents the computed error estimator and upper bound for the exact error for uniform refinement. The estimator converges with the optimal rate 0.5 for uniform red-refinement. The exact error is dominated by the error in the pseudostress component.
6.3 Example on L-shaped domain
In this example \(f\equiv 0\) on the L-shaped domain, \(\varOmega =(-1,1)^2\setminus \left( [0,1]\times [-1,0]\right) \), with \(\omega =3\pi /2,\alpha =856399/1572864\), and
The exact solution from [26, p.324] reads, in polar coordinates for the implicit boundary data, for all \((r,\varphi )\in [0,\infty )\times [0,3\pi /2]\),
Figure 3 shows the convergence history plot with an adaptive refinement strategy of optimal empirical convergence rate 0.5. In case of uniform refinement, as expected in a non-convex domain with singularity in the reentrant corner, the empirical convergence rate is 0.25. The computed error shows some pre-asymptotic range, which is typical also for other finite element discretizations (not displayed). The error estimator \({\tilde{\eta }}_\ell \), which includes the boundary oscillation, follows accordingly. The adaptive algorithm resolves the singularity in the reentrant corner first as depicted in Fig. 4.
6.4 Backward facing step example
This benchmark example with \(f\equiv 0\) on a slightly deformed L-shaped domain \(\varOmega =\left( (-2,8)\times (-1,1)\right) \setminus \left( (-2,0)\times (-1,0)\right) \) has the Dirichlet data g for \((x_1,x_2)\in {\partial \varOmega }\)
Figure 5 presents the error estimator for varying bulk parameter \(\theta \). Obviously, a smaller \(\theta \) leads to a better convergence rate. On the other hand, more levels are needed to reach a certain number of degrees of freedom and \(\theta =0.3\) leads to the optimal empirical convergence rate. The choice of different error estimators \(\eta _\ell ,\, {\hat{\eta }}_\ell ,\, {\tilde{\eta }}_\ell \) does not influence the result. The inhomogeneous Dirichlet boundary conditions are resolved in the triangulation in Fig. 6 before the singularity at the reentrant corner becomes significant.
6.5 Conclusion
All the numerical experiments confirm the theoretical results and support the conjectured instant stability of the dPG paradigm: The systematic convergence with a clear empirical convergence rate is visible from the very beginning even for the coarsest meshes. The extensions of the test search space do not affect the approximation of the discrete solution significantly. It is not rewarding to compute with bigger test search spaces. The error estimators \(\eta _\ell \) and \({\hat{\eta }}_\ell \) are almost identical thought \({\tilde{\eta }}_\ell \) leads to a guaranteed error bound. It is utterly an empirical observation that the associated adaptive mesh-refining algorithm improves suboptimal convergence rates in case of singular solutions.
References
Alberty, J., Carstensen, C., Funken, S.: Remarks around 50 lines of Matlab: short finite element implementation. Numer. Algor. 20(2–3), 117–137 (1999)
Alt, H.W.: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung, 5. Auflg (2006)
Arnold, D.N., Falk, R.S.: A uniformly accurate finite element method for the Reissner-Mindlin plate. SIAM J. Numer. Anal. 26(6), 1276–1290 (1989)
Babuška, I.: Error-bounds for finite element method. Numer. Math. 16, 322–333 (1970/1971)
Bartels, S., Carstensen, C., Dolzmann, G.: Inhomogeneous Dirichlet conditions in a priori and a posteriori finite element error analysis. Numer. Math. 99(1), 1–24 (2004)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications. Springer Series in Computational Mathematics. Springer, Berlin, Heidelberg (2013)
Brenner, S., Scott, R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics. Springer, Berlin (2008)
Bringmann, P., Carstensen, C.: An adaptive least-squares FEM for the Stokes equations with optimal convergence rates. Numer. Math. 135(2), 459–492 (2017)
Cai, Z., Tong, C., Vassilevski, P.S., Wang, C.: Mixed finite element methods for incompressible flow: stationary Stokes equations. Numer. Methods Partial Differ. Equ. 26(4), 957–978 (2010)
Carstensen, C., Demkowicz, L., Gopalakrishnan, J.: A posteriori error control for DPG methods. SIAM J. Numer. Anal. 52(3), 1335–1353 (2014)
Carstensen, C., Demkowicz, L., Gopalakrishnan, J.: Breaking spaces and forms for the DPG method and applications including Maxwell equations. Comput. Math. Appl. 72(3), 494–522 (2016)
Carstensen, C., Gallistl, D.: Guaranteed lower eigenvalue bounds for the biharmonic equation. Numer. Math. 126(1), 33–51 (2014)
Carstensen, C., Gallistl, D., Hellwig, F., Weggler, L.: Low-order dPG-FEM for an elliptic PDE. Comput. Math. Appl. 68(11), 1503–1512 (2014)
Carstensen, C., Hellwig, F.: Low-order discontinuous Petrov–Galerkin finite element methods for linear elasticity. SIAM J. Numer. Math. 54(6), 3388–3410 (2016)
Carstensen, C., Merdon, C.: Computational survey on a posteriori error estimators for nonconforming finite element methods for the Poisson problem. J. Comput. Appl. Math. 249, 74–94 (2013)
Carstensen, C., Merdon, C.: Computational survey on a posteriori error estimators for the Crouzeix-Raviart nonconforming finite element method for the Stokes problem. Comput. Methods Appl. Math. 14(1), 35–54 (2014)
Carstensen, C., Peterseim, D., Rabus, H.: Optimal adaptive nonconforming FEM for the Stokes problem. Numer. Math. 123(2), 291–308 (2013)
Demkowicz, L., Gopalakrishnan, J.: A class of discontinuous Petrov–Galerkin methods. Part I: The transport equation. Comput. Methods Appl. Mech. Eng. 199(23), 1558–1572 (2010)
Demkowicz, L., Gopalakrishnan, J.: Analysis of the DPG method for the Poisson equation. SIAM J. Numer. Anal. 49(5), 1788–1809 (2011)
Demkowicz, L., Gopalakrishnan, J.: A class of discontinuous Petrov-Galerkin methods. Part II. Optimal test functions. Numer. Methods Partial Differ. Equ. 27(1), 70–105 (2011)
Girault, V., Raviart, P.A.: Finite element methods for Navier–Stokes equations: theory and algorithms. Springer, Berlin (1986)
Gopalakrishnan, J., Qiu, W.: An analysis of the practical DPG method. Math. Comput. 83(286), 537–552 (2014)
Kato, T.: Estimation of iterated matrices, with application to the von Neumann condition. Numer. Math. 2(1), 22–29 (1960)
Merdon, C.: Aspects of guaranteed error control in computations for partial differential equations. Ph.D. thesis, Humboldt-Universität zu Berlin (2013)
Roberts, N.V., Bui-Thanh, T., Demkowicz, L.: The DPG method for the Stokes problem. Comput. Math. Appl. 67(4), 966–995 (2014). High-order Finite Element Approximation for Partial Differential Equations
Verfürth, R.: A posteriori error estimators for the Stokes equations. Numer. Math. 55(3), 309–325 (1989)
Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) in the Priority Program 1748 ‘Reliable simulation techniques in solid mechanics. Development of non-standard discretization methods, mechanical and mathematical analysis’ under the project CA 151/22-1. The second author is supported by the Berlin Mathematical School.
Author information
Authors and Affiliations
Corresponding author
Appendix: Fortin interpolation in an extended test search space
Appendix: Fortin interpolation in an extended test search space
Proof of Lemma 5.4
For \({\hat{Y}}_h:=({RT_0^\text {pw}(\mathcal {T};\mathbb {R}^{2})/\mathbb {R}\oplus \mathcal {B}_3(\mathcal {T})\mathbb {R}^{2\times 2}_{{{\mathrm{dev}}}}}) \times P_1(\mathcal {T};\mathbb {R}^{2})\) the Fortin interpolator \({\hat{\varPi }}: Y\rightarrow {\hat{Y}}_h\) maps \((\varvec{\tau },v)\mapsto (\hat{\varvec{\tau }}_{\text { RT}}, I_{\text { NC}}^\text {pw}v)\) such that (45)–(46) hold. Recall the edge-based Raviart–Thomas basis \(\psi _{E}\) for \(E\in \mathcal {E}(T)\), the opposite vertex \(P_E\in \mathcal {N}(T)\), and the component \(\kappa =1,\,2\), let \(\varPsi _{E,\kappa }:=e_\kappa \otimes \psi _E :=e_\kappa \otimes \chi (T)(x-P_E)|E|/(2|T|)\). The Crouzeix-Raviart basis functions in two components \(\varPhi _{E,\kappa }\) read \(\varPhi _{E,\kappa }:=\phi _{E}\ e_\kappa :=\chi (T)(1-2\varphi _{P_E})\ e_\kappa \) with nodal basis functions \(\varphi _{z}\) of \(z\in \mathcal {N}\). Given \(T\in \mathcal {T},\varvec{\tau }\in H({{\mathrm{div}}},T;\mathbb {R}^{2\times 2})\), define
Since \(\left( \psi _E\cdot \nu _T\right) |_F=\delta _{EF}\) and \(\int _F \phi _E \,\mathrm{d}s=\delta _{EF}|E|\) for \(E,F\in \mathcal {E}(T),I_F=I_F^2\) is a projection. Moreover, \(\left\langle I_F\varvec{\tau }\nu _T , \varPhi _{E,\kappa } \right\rangle _{\partial T}=\left\langle \varvec{\tau }\nu _T , \varPhi _{E,\kappa } \right\rangle _{\partial T}\) for any \(E\in \mathcal {E}(T)\) and \(\kappa =1,\,2\) implies (46). An integration by parts allows to rewrite \(I_F\varvec{\tau }\). The projection property implies \(I_F q=q\) for all \(q\in P_0(T)\). This and \(\sum _{E\in \mathcal {E}(T)} \varphi _E=1\) reveal

where  . Given \(b_T:=60 \varphi _1\varphi _2\varphi _3\in B_3(T)\), for \(T\in \mathcal {T}\), set
. Given \(b_T:=60 \varphi _1\varphi _2\varphi _3\in B_3(T)\), for \(T\in \mathcal {T}\), set
Since \(b_T|_{\partial T}=0\) and  , this operator \(\varPi _\tau \) satisfies (45)–(46). To compute \(\Vert \varPi _\tau \Vert _{}\) with
, this operator \(\varPi _\tau \) satisfies (45)–(46). To compute \(\Vert \varPi _\tau \Vert _{}\) with
estimate the Frobenius norm \(\Vert Q(T) \Vert _{F}\) of Q(T) as follows. Since \(\vert {{\mathrm{mid}}}(T)-P_E\vert \le 2h_T/3\) and \(\Vert \phi _E \Vert _{L^2(T)}^2=|T|/3\), the Cauchy-Schwarz inequality allows

Moreover, \(\Vert b_T \Vert _{L^2(T)}^2=10|T|/7\) and \(\Vert \nabla b_T \Vert _{L^2(T)}^2=20 |T|\Vert {{\mathrm{G}}}(T) \Vert _{F}^2\), with
and \(\Vert G(T) \Vert _{F}^2=(2|T|)^{-2}\sum _{E\in \mathcal {E}(T)}|E|^2\le 3 h_T^2(2|T|)^{-2}.\) Let \(\alpha _T\) denote the smallest angle in T and recall \(h_T^2\le 4|T|\cot (\alpha _T)\). Hence,
Alltogether,
Set \({\hat{\varPi }}(\varvec{\tau },v)|_T:=(\varPi _\tau (\varvec{\tau }|_T),I_{\text { NC}}^\text {pw}v|_T)\) as in (51). Given \(y=(\varvec{\tau },v)\in Y\), the above computation, the abbreviation \(\alpha _{\min }\) for the smallest angle of the triangulation (which is bounded in a regular triangulation) and [12, Thm. 4] prove

\(\square \)
Rights and permissions
About this article
Cite this article
Carstensen, C., Puttkammer, S. A low-order discontinuous Petrov–Galerkin method for the Stokes equations. Numer. Math. 140, 1–34 (2018). https://doi.org/10.1007/s00211-018-0965-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-018-0965-3
Keywords
- Stokes
- Discontinuous Petrov Galerkin
- Low-order discretization
- A priori
- A posteriori
- Adaptive mesh refinement






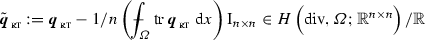
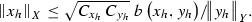
 with
with 



