Residual-based a posteriori error estimation for multipoint flux mixed finite element methods

Abstract

A novel residual-type a posteriori error analysis technique is developed for multipoint flux mixed finite element methods for flow in porous media in two or three space dimensions. The derived a posteriori error estimator for the velocity and pressure error in $L^{2}$-norm consists of discretization and quadrature indicators, and is shown to be reliable and efficient. The main tools of analysis are a locally postprocessed approximation to the pressure solution of an auxiliary problem and a quadrature error estimate. Numerical experiments are presented to illustrate the competitive behavior of the estimator.

1 Introduction

Let $\Omega \subset {\mathbb {R}}^{d}$ be a bounded polygonal ($d=2$) or polyhedral ($d=3$) domain with a Lipschitz continuous boundary $\partial \Omega$. We consider the following first-order system of diffusion-type partial differential equations:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \mathbf{u}=-K\nabla p &{} \text{ in }\ \ \Omega ,\\ \nabla \cdot \mathbf{u}=f &{} \text{ in }\ \Omega ,\\ p=g &{} \text{ on } \Gamma _{D},\\ \mathbf{u}\cdot \mathbf{n}=0 &{} \text{ on }\ \Gamma _{N}.\\ \end{array}\right. \end{aligned}$$

(1.1)

Here $\Gamma _{D}, {\Gamma }_{N}$ are partitions of the boundary $\partial \Omega$ corresponding to the Dirichlet and Neumann conditions, respectively, with $\partial \Omega =\bar{\Gamma }_{D}\cup \bar{\Gamma }_{N}$, ${\Gamma }_{D}\cap {\Gamma }_{N}=\emptyset$ and $meas(\Gamma _{D})>0$, $\mathbf{n}$ is the outward unit normal vector on $\partial \Omega$, and K is a symmetric and uniformly positive definite tensor with

$$\begin{aligned} k_{0}\xi ^\mathrm{T}\xi \le \xi ^\mathrm{T}K(\mathbf{x})\xi \le k_{1}\xi ^\mathrm{T}\xi , \quad \forall \ \mathbf{x}\in \Omega ,\quad \forall \ \xi \in {\mathbb {R}}^{d} \end{aligned}$$

(1.2)

for $0<k_{0}\le k_{1}<\infty$. This system has been widely used in physics to model diffusion processes such as heat or mass transfer and flow in porous media.

In flow in porous media, p denotes the pressure, $\mathbf{u}$ is the Darcy velocity, and K represents the permeability divided by the viscosity.

The main goal of this paper is to derive residual-based a posteriori error estimation for multipoint flux mixed finite element (MFMFE) methods for the model (1.1). The MFMFE approach was developed for single phase flow in porous media in [25, 34, 35]. It is motivated by the multipoint flux approximation (MPFA) approach [1, 2, 22, 27, 28], which is a control volume method developed by the oil industry as a reliable discretization for single-phase Darcy flow. One main advantage of this method lies in that, by introducing sub-edge (or sub-face) fluxes, it provides a local explicit flux with respect to the flow pressure, and allows for local flux elimination around grid vertices and reduction to a cell-centered pressure scheme. The MFMFE method is based on the lowest order Brezzi–Douglas–Marini (BDM1) [14] or Brezzi–Douglas–Duran–Fortin (BDDF1) [13] finite element space. By using special quadrature rules, local velocity elimination is also attained which leads to a symmetric and positive definite cell-centered system for the pressure on quadrilateral, simplicial and hexahedral meshes. In [36], a coupling discretization of MFMFE method and continuous Galerkin finite element method was applied to the poroelasticity system that describes fluid flow in deformable porous media.

It is well-known that adaptive algorithms for the numerical solution of partial differential equations are nowadays standard tools in science and engineering. A posteriori error estimation, as an essential ingredient of adaptivity, provides adaptive mesh refinement strategy and quantitative estimates of the numerical solution obtained. For second-order elliptic problems, the theory of a posteriori error estimation has reaches a degree of maturity for finite element of conforming, nonconforming and mixed types (see [3–12, 16–18, 20, 26, 29, 32] and the references therein). To the authors’ knowledge, no a posteriori estimation for the MFMFE method has been proposed in the literature so far.

In this paper, we develop a novel technique to derive residual-based a posteriori error estimation for the MFMFE method for the porous media model in two or three-dimensional case. Since the MFMFE method employs a special quadrature rule, its a posteriori error estimator should include a term to control the error of quadrature. This is different from the standard analytical technique based on the discrete $L^{2}$-inner product. Moreover, we can not directly utilize the analytical technique developed by Carstensen in [17] for nonconforming finite elements to estimate

$$\begin{aligned} \displaystyle \inf _{\beta \in H^{1}(\Omega )}||\nabla \beta -K^{-1}\mathbf{u}_{h}||, \end{aligned}$$

because the BDM1 finite element for the velocity approximation, $\mathbf{u}_{h}$, does not have the same continuity of mean of trace across the interior sides as the nonconforming finite elements do.

To overcome this difficulty, we shall construct a locally postprocessed approximation to the pressure solution to an auxiliary mixed finite element scheme, and use a derived estimate of quadrature error.

We note that the idea of postprocessing in this contribute follows from the works [29, 33].

The rest of this paper is organized as follows. In Sect. 2, we introduce some notations and the continuous problem. Section 3 shows the MFMFE method. Section 4 includes main results. Sections 5, 6 are respectively devoted to the a posteriori error estimation and the analysis of efficiency. Finally, we illustrate the performance of the obtained estimation in Sect. 7 by numerical experiments.

2 Notations and continuous problem

Let $\mathcal {T}_{h}$ be a shape regular triangulation of $\Omega \subset {\mathbb {R}}^{d}$ in the sense of [19] which satisfies the angle condition, namely there exists a constant $C_{0}>0$ such that for all $T\in \mathcal {T}_{h}$

$$\begin{aligned} C_{0}^{-1}h_{T}^{d}\le |T|\le C_{0}h_{T}^{d}, \end{aligned}$$

where $h_{T} :=\mathrm{diam}(T)$. Let h be a piecewise constant function with $h|_T=h_T$.

We denote by $\varepsilon _{h}$ the set of element sides (or faces) in $\mathcal {T}_{h}$, by $\varepsilon _{T}$ the set of sides (or faces) of element $T\in \mathcal {T}_{h}$ , by $\varepsilon _{h}^{0}$ and $\varepsilon _{D}$ respectively the sets of the interior and Dirichlet boundary sides (or faces) of all elements in $\mathcal {T}_{h}$, by $\omega _{E}$ the union of all elements in $\mathcal {T}_{h}$ sharing side (or face) $E\in \varepsilon _{h}$, and by $\mathcal {N}$ the set of nodes in $\mathcal {T}_{h}$.

For a domain $A\subset \mathbb {R}^{d}$, let $(\cdot ,\cdot )_{A}$ be the $L^{2}$ inner product on A, and $<\cdot ,\cdot >_{\partial A}$ the dual pair between $H^{-1/2}(\partial A)$ and $H^{1/2}(\partial A)$. Let $W_p^{k}(A)$ be the usual Sobolev space consisting of functions defined on A with all derivatives of order up to k belonging to $L^p(A)$, with norm $||\cdot ||_{k,p,A}$. When $p=2$, $W_2^{k}(A)=:H^{k}(A)$ and $||\cdot ||_{k,2,A}=:||\cdot ||_{k,A}$, especially $||\cdot ||_{0,A}=:||\cdot ||_{A}$ for $k=0$. We omit the subscript A if $A=\Omega$. For a tensor-valued function $M=(M_{ij})$, let $||M||_{\alpha }=\max _{i,j}||M_{ij}||_{\alpha }$ for any norm $||\cdot ||_{\alpha }$. Introduce

$$\begin{aligned} \mathbf{H}(\mathrm{div};A):=\{\mathbf{v}\in L^{2}(A)^d:\nabla \cdot \mathbf{v}\in L^{2}(A)\}, \end{aligned}$$

and define the “broken Sobolev space”

$$\begin{aligned} H^{1}(\cup \mathcal {T}_{h}) :=\{\varphi \in L^{2}(\Omega ):\varphi |_{T}\in H^{1}(T), \quad \forall T\in \mathcal {T}_{h}\}. \end{aligned}$$

We denote by $[v]|_{E} :=(v|_{T_{+}})|_{E}-(v|_{T_{-}})|_{E}$ the jump of $v\in H^{1}(\cup \mathcal {T}_{h})$ over an interior side $E :=T_{+}\cap T_{-}$ with diameter $h_{E}: =\mathrm{diam}(E)$, shared by the two neighboring (closed) elements $T_{+},T_{-}\in \mathcal {T}_{h}$. Especially, $[v]|_{E} :=(v|_{T})|_{E}$ if $E\in \varepsilon _{T}\cap \Gamma _{D}$.

Since we consider two and three-dimensional cases ($d=2,3$) simultaneously, the Curl of a function $\psi \in H^{1}(\Omega )^{k}$ with $k =1$ if $d=2$ and $k =3$ if $d=3$ is defined by

$$\begin{aligned} \mathrm{Curl}\psi :=(-\partial _{2}\psi ,\partial _{1}\psi ) \ \mathrm{if \ d=2} \quad \mathrm{and} \quad \mathrm{Curl}\mathbf{\psi } :=\nabla \times \mathbf{\psi } \ \mathrm{if\ d=3}, \end{aligned}$$

where $\times$ denotes the usual vector product of two vectors in $\mathbb {R}^{3}$. Given a unit normal vector $\mathbf{n}_{E}=(n_1,\ldots ,n_d)^T$ along the side E, we define the tangential component of a vector $\mathbf{v}\in \mathbb {R}^{d}$ with respect to $\mathbf{n}_{E}$ by

$$\begin{aligned} \gamma _{\mathbf{t}_{E}}(\mathbf{v}) :=\left\{ \begin{array}{ll} \mathbf{v}\cdot (-n_{2},n_{1}) &{}\quad \text{ if }\, d=2,\\ \mathbf{v}\times \mathbf{n}_{E} &{}\quad \text{ if }\, d=3. \end{array}\right. \end{aligned}$$

Throughout the paper, $\nabla _{h} :H^{1}(\cup \mathcal {T}_{h})\rightarrow (L^{2}(\Omega ))^{d}$ denotes the local version of differential operator $\nabla$ defined by $\nabla _{h}\varphi |_{T} :=\nabla (\varphi |_{T})$ for all $\ T\ \in \mathcal {T}_{h}$. We also use the notation $A\lesssim B$ to represent $A\le CB$ where C is a generic, positive constant independent of the mesh size of $\mathcal {T}_{h}$.

Moreover, $A\approx B$ abbreviates $A\lesssim B\lesssim A$.

Denote

$$\begin{aligned} \mathbf{V}:=\{\mathbf{v}\in \mathbf{H}(\mathrm{div};\Omega )\ :\mathbf{v}\cdot \mathbf{n}=0\ \ \mathrm{on}\ \Gamma _{N}\},\quad \ W:=L^{2}(\Omega ), \end{aligned}$$

then the weak formulation of the model (1.1) is as follows: Find $\mathbf{u}\in \mathbf{V}$, $p\in W$ such that

$$\begin{aligned} (K^{-1}\mathbf{u},\mathbf{v})= & {} (p,\nabla \cdot \mathbf{v})-<g,\mathbf{v}\cdot \mathbf{n}>_{\Gamma _{D}},\quad \forall \ \mathbf{v}\in \ \mathbf{V},\end{aligned}$$

(2.1)

$$\begin{aligned} (\nabla \cdot \mathbf{u},w)= & {} (f,w),\quad \forall \ {w}\in \ {W}. \end{aligned}$$

(2.2)

It is well-known that this problem admits a unique solution [15].

3 Multipoint flux mixed finite element method

We follow the notations and definitions employed in [25, 34] to describe the MFMFE method.

Let $\hat{T}$ be the reference element which is a unit triangle in two-dimensional case or unit tetrahedron in three-dimensional case, and $P_{l}$ be the set of polynomials of degree $\le l$. The lowest order $\mathrm{BDM}_{1}$ mixed finite element spaces on $\hat{T}$ are defined as

$$\begin{aligned} \hat{\mathbf{V}}(\hat{T})=P_{1}(\hat{T})^{d},\quad \hat{W}(\hat{T})=P_{0}(\hat{T}). \end{aligned}$$

Since $\hat{\mathbf{v}}\cdot \hat{\mathbf{n}}_{\hat{e}}\in P_1({\hat{e}})$ for any $\hat{\mathbf{v}}\in \hat{\mathbf{V}}(\hat{T})$ and any edge (or face) $\hat{e}$ of $\hat{T}$, the degrees of freedom for $\hat{\mathbf{V}}(\hat{T})$ can be chosen to be the values of $\hat{\mathbf{v}}\cdot \hat{\mathbf{n}}_{\hat{e}}$ at any two points on each edge $\hat{e}$ of $\hat{T}$ if $\hat{T}$ is the unit triangle, or any three points on each face $\hat{e}$ of $\hat{T}$ if $\hat{T}$ is the unit tetrahedron [14, 15]. In the MFMFE method, these points are chosen to be the vertices of $\hat{e}$ for the requirement of accuracy and certain orthogonality for the trapezoidal quadrature rules. Such a choice allows for local velocity elimination and leads to a cell-centered stencil for the pressure [25, 34].

The lowest order $\mathrm{BDM}_{1}$ spaces on $\mathcal {T}_{h}$ are given by

$$\begin{aligned} \begin{array}{lll} \mathbf{V}_{h} &{}:&{}=\{\mathbf{v}\in \mathbf{V}\ : \mathbf{v}|_{T}=\frac{1}{J_{T}}DF_{T}\hat{\mathbf{v}}\circ F_{T}^{-1},\ \ \hat{\mathbf{v}}\in \hat{\mathbf{V}}(\hat{T})\quad \forall \ T\in \mathcal {T}_{h}\},\\ {W}_{h} &{}:&{}=\{w\in {W}\ :\ {w}|_{T}=\hat{w}\circ F_{T}^{-1},\ \ \hat{w}\in \hat{W}(\hat{T})\quad \forall \ T\in \mathcal {T}_{h}\}, \end{array} \end{aligned}$$

where $F_{T}^{-1}$ is the inverse mapping of the bijection $F_{T} : \hat{T}\rightarrow T$, $DF_{T}$ is the Jacobian matrix with respect to $F_{T}$ on the element T with $J_{T}=|det(DF_{T})|$. Note that the vector transformation $\mathbf{v}=\frac{1}{J_{T}}DF_{T}\hat{\mathbf{v}}\circ F_{T}^{-1}$ is known as the Piola transformation.

For $\mathbf{q},\mathbf{v}\in \mathbf{V}_{h}$, it holds

$$\begin{aligned} \begin{array}{lll} \displaystyle \int _{T}K^{-1}\mathbf{q}\cdot \mathbf{v}d\mathbf{x}&{}=&{}\displaystyle \int _{\hat{T}}\hat{K}^{-1}\frac{1}{J_{T}}DF_{T}\hat{\mathbf{q}}\cdot \frac{1}{J_{T}}DF_{T}\hat{\mathbf{v}}J_{T}d\hat{\mathbf{x}}\\ &{}=&{}\displaystyle \int _{\hat{T}}\frac{1}{J_{T}}(DF_{T})^\mathrm{T}\hat{K}^{-1}DF_{T}\hat{\mathbf{q}}\cdot \hat{\mathbf{v}}d\hat{\mathbf{x}}\\ &{}=&{}\displaystyle \int _{\hat{T}}\mathcal {K}^{-1}\hat{\mathbf{q}}\cdot \hat{\mathbf{v}}d\hat{\mathbf{x}} \end{array} \end{aligned}$$

with $\mathcal {K} :=J_{T}DF_{T}^{-1}\hat{K}(DF_{T}^{-1})^\mathrm{T}.$ The quadrature formula on an element T is then defined as [25, 34]

$$\begin{aligned} (K^{-1}\mathbf{q},\mathbf{v})_{Q,T} :=(\mathcal {K}^{-1}\hat{\mathbf{q}},\hat{\mathbf{v}})_{\hat{Q},\hat{T}} :=\frac{|\hat{T}|}{s}\sum \limits _{i=1}^{s}\mathcal {K}^{-1}(\hat{\mathbf{r}}_{i})\hat{\mathbf{q}}(\hat{\mathbf{r}}_{i})\cdot \hat{\mathbf{v}}(\hat{\mathbf{r}}_{i}), \end{aligned}$$

(3.1)

where $\hat{\mathbf{r}}_{i}$ ($i=1,2,\ldots ,s$) are the corresponding vertices of $\hat{T}$ with $s=3$ for the unit triangle and $s=4$ for the unit tetrahedron.

Define the global quadrature formula as

$$\begin{aligned} (K^{-1}\mathbf{q},\mathbf{v})_{Q}=\sum \limits _{T\in \mathcal {T}_{h}}(K^{-1}\mathbf{q},\mathbf{v})_{Q,T}, \end{aligned}$$

(3.2)

then the MFMFE method is formulated as follows: Find $\mathbf{u}_{h}\in \mathbf{V}_{h}$ and $p_{h}\in W_{h}$ such that

$$\begin{aligned} \displaystyle (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{Q}= & {} (p_{h},\nabla \cdot \mathbf{v}_{h})-<g,\mathbf{v}_{h}\cdot \mathbf{n}>_{\Gamma _{D}},\quad \forall \ \mathbf{v}_{h}\in \ \mathbf{V}_{h},\end{aligned}$$

(3.3)

$$\begin{aligned} \displaystyle (\nabla \cdot \mathbf{u}_{h},w_{h})= & {} (f,w_{h}),\quad \forall \ w_{h}\in \ W_{h}. \end{aligned}$$

(3.4)

The existence and uniqueness of the solution to the scheme (3.3)–(3.4) follow from [25, 34].

As shown in [25, 34], the algebraic system that arises from (3.3)–(3.4) is of the form

$$\begin{aligned} \left( \begin{array}{c} \ \ A\ \ \ \ \quad B^\mathrm{T}\\ -B\ \ \ \quad 0 \end{array} \right) \left( \begin{array}{c} \ U\ \\ \ P \end{array} \right) = \left( \begin{array}{c} \ G\\ \ F \end{array} \right) , \end{aligned}$$

(3.5)

where $A=(a_{ij}),\ B=(b_{lj})$ with $a_{ij}=(K^{-1}\mathbf{v}_{j},\mathbf{v}_{i})_{Q}$ and $b_{lj}=-(\nabla \cdot \mathbf{v}_{j}, w_{l})$, and $\{\mathbf{v}_{i}\}$, $\{w_{l}\}$ are respectively the bases of $\mathbf{V}_{h}$ and $W_{h}$. The matrix A is block-diagonal with symmetric and positive definite blocks, and the local elimination of U leads to a system for P with a symmetric and positive definite matrix $BA^{-1}B^{T}$. For the details, we refer to [25, 34].

4 Main results

Let $\eta _{h}$ be the discretization indicator defined by

$$\begin{aligned} \eta _{h}^{2} :=||h(f-\nabla \cdot \mathbf{u}_{h})||^{2}+\sum \limits _{T\in \mathcal {T}_{h}}\sum \limits _{E\in \varepsilon _{T}}h_{E}J_{\mathbf{t}_E}^{2}, \end{aligned}$$

(4.1)

where

$$\begin{aligned} J_{\mathbf{t}_E}^{2} :=\left\{ \begin{array}{ll} ||[\gamma _{\mathbf{t}_{E}}(K^{-1}\mathbf{u}_{h})]||_{E}^{2} &{}\quad \text{ if }\ \ E\in \varepsilon _{h}^{0}\cap \partial T,\\ ||\gamma _{\mathbf{t}_{E}}(K^{-1}\mathbf{u}_{h})-\partial g/\partial s||_{E}^{2}+h_{E}^{2}||\frac{\partial ^{2}g}{\partial s^{2}}||_{E}^{2}&{}\quad \text{ if }\ \ E\in \partial T\cap \varepsilon _{D},\\ 0&{}\quad \text{ if } \ E\in \partial T\cap \Gamma _{N}, \end{array}\right. \end{aligned}$$

(4.2)

and $\partial g/\partial s$ and $\partial ^{2}g/\partial s^{2}$ denote respectively the first and second order tangential derivatives of function $g\in H^{2}(E)$ along side E. Introduce the quadrature indicator

$$\begin{aligned} \eta _{Q}^{2} :=\sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}. \end{aligned}$$

(4.3)

We note this indicator is owing to the use of the special quadrature formula (3.1) in the MFMFE method.

We now state in Theorems 4.1–4.2 a posteriori error estimates for the errors of velocity and pressure in $L^{2}-$norm, respectively.

Theorem 4.1

Let $(\mathbf{u},p)\in \mathbf{V}\times W$ be the weak solution of the continuous problem (2.1)–(2.2), and $(\mathbf{u}_{h},p_{h})\in \mathbf{V}_{h}\times W_{h}$ be the solution of the MFMFE method (3.3)–(3.4). Assume $K^{-1}\in W_{\infty }^{1}(\mathcal {T}_{h})$. Then it holds

$$\begin{aligned} ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||\lesssim (\eta _{h}^{2}+\eta _{Q}^{2})^{1/2}. \end{aligned}$$

(4.4)

Theorem 4.2

Assume $K^{-1}\in W_{\infty }^{2}(\mathcal {T}_{h})$. Under the assumptions of Theorem 4.1, it holds

$$\begin{aligned}&\displaystyle ||Q_{h}p-p_{h}||\lesssim h_\mathrm{max}(\eta _{h}+\eta _{Q})+||h(f-\nabla \cdot \mathbf{u}_{h})||,\end{aligned}$$

(4.5)

$$\begin{aligned}&\displaystyle ||p-p_{h}||\lesssim h_\mathrm{max}(\eta _{h}+\eta _{Q})+||hK^{-1}\mathbf{u}_{h}||+||h(f-\nabla \cdot \mathbf{u}_{h})||. \end{aligned}$$

(4.6)

Here $h_\mathrm{max} :=\max _{T\in \mathcal {T}_{h}}h_{T}$, and $Q_{h}$ denotes the $L^{2}-$projection operator onto $W_{h}$.

Remark 4.1

We note that the two terms $||h(f-\nabla \cdot \mathbf{u}_{h})||$ and $\left\{ \sum \nolimits _{E\in \varepsilon _{D}}h_{E}^{3}||\frac{\partial ^{2}g}{\partial s^{2}}||_{E}^{2}\right\} ^{1/2}$ in the estimator $\eta _{h}$ are of high order with respect to the lowest order scheme, which are usually omitted in computation. In fact, from (3.4) it follows $\nabla \cdot \mathbf{u}_{h}=Q_{h}f$, and $||h(f-\nabla \cdot \mathbf{u}_{h})||=||h(f-Q_hf)||$ turns out to be an oscillation term of high order.

Remark 4.2

The above estimates (4.4)–(4.6) also apply to the original mixed finite element discretization where the special quadrature rule (3.1) is not used in the scheme (3.3)–(3.4). In this case, the estimator $\eta _{Q}$ is not involved, and then $\eta _{Q}=0$ in the estimates (4.4)–(4.6). In this sense, our work can be regarded as a generalization of Carstensen’s [16] to the three-dimensional case. We note that our estimator $\eta _h$ is a bit different from that in [16] due to no occurrence of the term $||h\mathrm{Curl}_{h}(K^{-1}\mathbf{u}_{h})||$ ($\mathrm{Curl}_{h}$ denotes the piecewise $\mathrm{Curl}$ operator acting on element by element in $\mathcal {T}_{h}$). Here we also consider more general boundary conditions.

We finally state in Theorem 4.3 the efficiency of the a posteriori error estimators. Note that the efficiency of a reliable a posteriori error estimator means that its converse estimate holds up to high order terms and different multiplicative constants. For the sake of simplicity, we assume that $K^{-1}$ is a matrix of piecewise polynomial functions.

Theorem 4.3

Under the assumptions of Theorems 4.1–4.2, it holds

$$\begin{aligned} \eta _{h}+\eta _{Q}+h_\mathrm{max}^{-1}||hK^{-1}\mathbf{u}_{h}||\lesssim ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||+||h^{-1}(p-p_{h})||+h.o.t.. \end{aligned}$$

where h.o.t. denotes some high-order term depending on given data.

5 A posteriori error analysis

This section is devoted to the proofs of Theorems 4.1–4.2.

Introduce the global quadrature error $\sigma (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})$ and the element quadrature error $\sigma _{T}(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})$ as follows:

$$\begin{aligned} \sigma (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})|_{T}= & {} \sigma _{T}(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h}) :=(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{T}\nonumber \\&-(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{Q,T} ,\quad \mathrm{for\ all}\quad T\in \mathcal {T}_{h}. \end{aligned}$$

(5.1)

Let $\mathbf{V}_{h}^{0} :=\mathrm{RT}_{0}(\mathcal {T}_{h})$ denote the lowest order $\mathrm{RT}$ element space on $\mathcal {T}_{h}$.

We state two estimates on the quadrature error derived in [25, 34] as follows. If $K^{-1}\in W_{\infty }^{1}(T)$ for all element $T\in \mathcal {T}_{h}$, then it holds

$$\begin{aligned} |\sigma (K^{-1}\mathbf{q}_{h},\mathbf{v}_{h})|\lesssim \sum \limits _{T\in \mathcal {T}_{h}}h_{T}||\mathbf{q}_{h}||_{1,T}||\mathbf{v}_{h}||_{T} \end{aligned}$$

(5.2)

for all $\mathbf{q}_{h}\in \mathbf{V}_{h}$, $\mathbf{v}_{h}\in \mathbf{V}_{h}^{0}$. Moreover, if $K^{-1}\in W_{\infty }^{2}(T)$ for all element $T\in \mathcal {T}_{h}$, then it holds

$$\begin{aligned} |\sigma (K^{-1}\mathbf{q}_{h},\mathbf{v}_{h})|\lesssim \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{q}_{h}||_{1,T}||\mathbf{v}_{h}||_{1,T} \end{aligned}$$

(5.3)

for all $\mathbf{q}_{h},\mathbf{v}_{h}\in \mathbf{V}_{h}$.

Denote respectively by $\Pi$ and $\Pi _{0}$ the standard projection operators from $\mathbf{H}(\mathrm{div};\Omega )\cap (L^{\varrho }(\Omega ))^{d}$ onto $V_{h}$ and $V_{h}^{0}$ for some $\varrho >2$ (cf. [16, 34]). It holds the following estimates:

$$\begin{aligned} ||h^{-1}(\mathbf{q}-\Pi _{0}\mathbf{q})||\lesssim ||\mathbf{q}||_{H^{1}(\cup \mathcal {T}_{h})}\quad \mathrm{for\ all}\quad \mathbf{q}\in (H^{1}(\cup \mathcal {T}_{h}))^{d}\cap \mathbf{H}(\mathrm{div};\Omega ), \end{aligned}$$

(5.4)

$$\begin{aligned} ||\Pi _{0}\mathbf{v}||_{1,T}\lesssim ||\mathbf{v}||_{1,T},||\Pi \mathbf{v}||_{1,T}\lesssim ||\mathbf{v}||_{1,T}\quad \mathrm{for \ all}\quad \mathbf{v}\in (H^{1}(T))^{d},\quad \forall T\in \mathcal {T}_{h}.\nonumber \\ \end{aligned}$$

(5.5)

Note that bound (5.4) can be found in [16], and bounds (5.5) are the direct results of Lemma 3.1 in [34].

To derive a reliable a posteriori error estimate for the velocity error, we need to

introduce an auxiliary problem as following:

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla \cdot (K\nabla \vartheta )=\nabla \cdot \mathbf{u}_{h} &{}\quad \text{ in }\ \ \Omega ,\\ \vartheta =-g &{}\quad \text{ on }\ \ \Gamma _{D},\\ K\nabla \vartheta \cdot \mathbf{n}=0 &{}\quad \text{ on }\ \ \Gamma _{N}. \end{array}\right. \end{aligned}$$

(5.6)

Since K is a symmetric and uniformly positive definite tensor, by the Lax–Milgram theorem there exists a unique solution $\vartheta \in H^{1}(\Omega )$ to this problem, provided that $g\in H^{1/2}(\Gamma _D)$. As $K\nabla \vartheta -\mathbf{u}_{h}$ is divergence-free, a decomposition of two or three-dimensional vector fields (see Theorem 3.4 and Remark 3.10 in [23]) implies that there exists a stream function $\psi \in H^{1}(\Omega )^{k}$ such that

$$\begin{aligned} K\nabla \vartheta -\mathbf{u}_{h}=\mathrm{Curl}\ \psi . \end{aligned}$$

Since $K\nabla \vartheta \cdot \mathbf{n}$ and $\mathbf{u}_{h}\cdot \mathbf{n}$ vanish on $\Gamma _{N}$, we easily know $\mathrm{Curl}\ \psi \cdot \mathbf{n}=0$ on $\Gamma _{N}$.

Introduce $H_{D}^{1}(\Omega ): =\{v\in H^{1}(\Omega ): v=0\ \ \mathrm{on}\ \ \Gamma _{D}\}$, then $z: =-(p+\vartheta )\in H_{D}^{1}(\Omega )$ and it holds

$$\begin{aligned} \mathbf{u}-\mathbf{u}_{h}=-K\nabla p-K\nabla \vartheta +\mathrm{Curl}\ \psi =K\nabla z+\mathrm{Curl}\ \psi . \end{aligned}$$

(5.7)

This relation leads to

$$\begin{aligned} ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||^{2}= & {} \int _{\Omega }K^{-1}(\mathbf{u}-\mathbf{u}_{h})\cdot (\mathbf{u}-\mathbf{u}_{h})\nonumber \\= & {} \int _{\Omega }(\nabla z+K^{-1}\mathrm{Curl}\ \psi )\cdot (K\nabla z+\mathrm{Curl}\ \psi )\nonumber \\= & {} \int _{\Omega }K\nabla z\cdot \nabla z{+}2\int _{\Omega }\nabla z\cdot \mathrm{Curl}\ \psi {+}\int _{\Omega }K^{-1}\mathrm{Curl}\ \psi \cdot \mathrm{Curl}\ \psi .\nonumber \\ \end{aligned}$$

(5.8)

Using integration by parts and noticing $\mathrm{Curl}\ \psi \cdot \mathbf{n}=0$ on $\Gamma _{N}$ and $z=0$ on $\Gamma _{D}$, we have

$$\begin{aligned} \displaystyle \int _{\Omega }\nabla z\cdot \mathrm{Curl}\ \psi =-\displaystyle \int _{\Omega }\nabla \cdot (\mathrm{Curl}\ \psi )z+\int _{\Gamma _{D}\cup \Gamma _{N}}\mathrm{Curl}\ \psi \cdot \mathbf{n}z=0. \end{aligned}$$

(5.9)

Notice that $K\nabla z=(\mathbf{u}-\mathbf{u}_{h})-\mathrm{Curl}\ \psi$, $(\mathbf{u}-\mathbf{u}_{h})\cdot \mathbf{n}=0$ on $\Gamma _{N}$ and $z=0$ on $\Gamma _{D}$. The relation (5.9) and integration by parts yield

$$\begin{aligned} \displaystyle \int _{\Omega }K\nabla z\cdot \nabla z=\displaystyle \int _{\Omega }(\mathbf{u}-\mathbf{u}_{h})\cdot \nabla z =\displaystyle -\int _{\Omega }\nabla \cdot (\mathbf{u}-\mathbf{u}_{h})z. \end{aligned}$$

(5.10)

Let $Q_{h}z$ denote the $L^{2}-$projection of z onto $W_{h}$. From (2.2) and (3.4) it follows

$$\begin{aligned} (\nabla \cdot (\mathbf{u}-\mathbf{u}_{h}),Q_{h}z)=0. \end{aligned}$$

(5.11)

In view of $\nabla \cdot \mathbf{u}=f$, the above two relations, (5.10) and (5.11), imply

$$\begin{aligned} \begin{array}{lll} \displaystyle \int _{\Omega }K\nabla z\cdot \nabla z&{}=&{}\displaystyle -\int _{\Omega }\nabla \cdot (\mathbf{u}-\mathbf{u}_{h})(z-Q_{h}z)\\ &{}=&{}\displaystyle \sum \limits _{T\in \mathcal {T}_{h}}\int _{T}(-f+\nabla \cdot \mathbf{u}_{h})(z-Q_{h}z)\\ &{}\lesssim &{}\displaystyle \sum \limits _{T\in \mathcal {T}_{h}}h_{T}||f-\nabla \cdot \mathbf{u}_{h}||_{T}||\nabla z||_{T}\\ &{}\lesssim &{}||h(f-\nabla \cdot \mathbf{u}_{h})||\ ||K^{1/2}\nabla z||, \end{array} \end{aligned}$$

which results in

$$\begin{aligned} ||K^{1/2}\nabla z|| \lesssim ||h(f-\nabla \cdot \mathbf{u}_{h})||. \end{aligned}$$

(5.12)

By (5.7) and (5.9) we have

$$\begin{aligned} ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||^{2}=||K^{1/2}\nabla z||^{2}+||K^{-1/2}\mathrm{Curl}\ \psi ||^{2}. \end{aligned}$$

(5.13)

Recalling $\displaystyle \int _{\Omega }\mathrm{Curl}\ \psi \cdot \nabla v=0$ for all $v\in H_{D}^{1}(\Omega )$, in light of (5.7) we have, for any $\beta \in H^{1}(\Omega )$,

$$\begin{aligned} \begin{array}{lll} &{} &{}\displaystyle \int _{\Omega }K^{-1}\mathrm{Curl}\ \psi \cdot \mathrm{Curl}\ \psi =\displaystyle \int _{\Omega }(K^{-1}(\mathbf{u}-\mathbf{u}_{h})-\nabla z)\cdot \mathrm{Curl}\ \psi \\ &{} &{}\ =\displaystyle \int _{\Omega }K^{-1}(\mathbf{u}-\mathbf{u}_{h}-K\nabla v)\cdot \mathrm{Curl}\ \psi \\ &{} &{}\ =\displaystyle \int _{\Omega }K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )\cdot \mathrm{Curl}\ \psi +\int _{\Omega }K^{-1}(K\nabla \beta -\mathbf{u}_{h})\cdot \mathrm{Curl}\ \psi \\ &{} &{}\ \le \displaystyle (||K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )||+||\nabla \beta -K^{-1}\mathbf{u}_{h}||)||\mathrm{Curl}\ \psi ||, \end{array} \end{aligned}$$

which implies

$$\begin{aligned} ||K^{-1/2}\mathrm{Curl}\ \psi ||\lesssim & {} \inf _{v\in H_{D}^{1}(\Omega )}||K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )||\nonumber \\&+\inf _{\beta \in H^{1}(\Omega )}||\nabla \beta -K^{-1}\mathbf{u}_{h}||. \end{aligned}$$

(5.14)

Finally, from (5.12)–(5.14) it follows

$$\begin{aligned} ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||\lesssim & {} \left\{ \inf _{v\in H_{D}^{1}(\Omega )}||K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )||\right. \nonumber \\&\left. +\inf _{\beta \in H^{1}(\Omega )}||\nabla \beta -K^{-1}\mathbf{u}_{h}||+||h(f-\nabla \cdot \mathbf{u}_{h})||\right\} .\qquad \end{aligned}$$

(5.15)

In what follows, we shall follow the routines of [17] to estimate the first and second terms on the right-hand side of (5.15). To this end, we assume that $g\in H^{1}(\Gamma _{D})\cap C(\Gamma _{D})$ and $g|_{E}\in H^{2}(E)$ for all $E\in \varepsilon _{h}\cap \Gamma _{D}$ and denote by $g_{h,D}$ the nodal $\varepsilon _{D}-$piecewise linear interpolation of g on $\Gamma _{D}$ which satisfies $g_{h,D}(\mathbf{z})=g(\mathbf{z})$ for all $\mathbf{z}\in \mathcal {N}\cap \Gamma _{D}$. Let $\{\varphi _\mathbf{z}: \mathbf{z}\in \mathcal {N}\}$ be the nodal basis of the lowest order finite element space associated to $\mathcal {T}_{h}$, i.e., $\varphi _\mathbf{z}\in C(\bar{\Omega }), \varphi _\mathbf{z}|_{T}\in P_{1}(T)$ for all $T\in \mathcal {T}_{h}$, $\varphi _\mathbf{z}(\mathbf{x})=0$ for $\mathbf{x}\in \mathcal {N}/\{\mathbf{z}\}$, and $\varphi _\mathbf{z}(\mathbf{z})=1$. Denote by $\omega _\mathbf{z} :=\mathrm{int}(\mathrm{supp}\varphi _\mathbf{z})$. We then introduce a subspace of $H^{1}(\Omega )$, $\tilde{S}$, as follows (see [17]):

$$\begin{aligned} \tilde{S} :==\left\{ \begin{array}{c} \displaystyle \sum \limits _{\mathbf{z}\in \mathcal {N}}\varphi _\mathbf{z}v_\mathbf{z}: \forall \ \mathbf{z} \in \mathcal {N},v_\mathbf{z}\in C(\omega _\mathbf{z}),\ v_\mathbf{z}|_{\omega _\mathbf{z}}\ \mathrm{is\ a\ piecewise} \\ \mathrm{polynomial,\ and}\ v_\mathbf{z}=-g_{h,D}\ \mathrm{on}\ \Gamma _{D}\cap \omega _\mathbf{z}. \end{array}\right\} \end{aligned}$$

Lemma 5.1

For $\beta \in \tilde{S}$, it holds

$$\begin{aligned} \inf _{v\in H_{D}^{1}(\Omega )}||K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )||\lesssim \left\{ \sum \limits _{E\subset \Gamma _{D}}h_{E}^{3}||\partial ^{2}g/\partial s^{2}||_{E}^{2}\right\} ^{1/2}. \end{aligned}$$

(5.16)

Proof

The definition of $\tilde{S}$ shows $\beta =-g_{h,D}$ on $\Gamma _{D}$. Noticing $K^{-1}\mathbf{u}=-\nabla p$, we have

$$\begin{aligned} \inf _{v\in H_{D}^{1}(\Omega )}||K^{-1}(\mathbf{u}-K\nabla v-K\nabla \beta )||=\inf _{w\in H^{1}(\Omega ),w|_{\Gamma _{D}}=g-g_{h,D}}||\nabla w||. \end{aligned}$$

The desired result (5.16) immediately follows from an estimate in the proof of Lemma 3.4 in [17]. $\square$

On the other hand, it holds

$$\begin{aligned} \inf _{\beta \in H^{1}(\Omega )}||\nabla \beta -K^{-1}\mathbf{u}_{h}||\le \inf _{v_{h}\in \tilde{S}}||\nabla v_{h}-K^{-1}\mathbf{u}_{h}||. \end{aligned}$$

(5.17)

It is sophisticated to give a computational upper bound for the right-hand side term of (5.17) with the help of $\mathbf{u}_{h}$ and given data. To this end, let $\overline{K^{-1}}$ denote the piecewise mean value of $K^{-1}$ on $\mathcal {T}_{h}$, i.e. $\overline{K^{-1}}|_T=\frac{1}{|T|}\int _{T} K^{-1}(\mathbf{x}) d\mathbf{x}$ for all $T\in \mathcal {T}_{h}.$ Then

$\overline{K^{-1}}$ is symmetric and has the following $V-$ellipticity:

$$\begin{aligned} k_{1}^{-1}\xi ^\mathrm{T}\xi \le \xi ^\mathrm{T}\overline{K^{-1}}\xi \le k_{0}^{-1}\xi ^\mathrm{T}\xi \ \mathrm{for\ all}\ \mathbf{x}\in \Omega , \quad \xi \in \mathbb {R}^{d}. \end{aligned}$$

Recall that $\mathbf{V}_{h}^{0}$ is the lowest order $\mathrm{RT}$ element space on $\mathcal {T}_{h}$. and $W_{h}$ is the piecewise constant space. Introduce the following auxiliary problem: Find $(\tilde{\mathbf{u}}_{h},\tilde{p}_{h})\in \mathbf{V}_{h}^{0}\times W_{h}$ such that

$$\begin{aligned} (\overline{K^{-1}}\tilde{\mathbf{u}}_{h},\mathbf{v}_{h})= & {} (\tilde{p}_{h},\nabla \cdot \mathbf{v}_{h})-<g,\mathbf{v}_{h}\cdot \mathbf{n}>_{\Gamma _{D}},\quad \forall \ \mathbf{v}_{h}\in \mathbf{V}_{h}^{0},\end{aligned}$$

(5.18)

$$\begin{aligned} (\nabla \cdot \tilde{\mathbf{u}}_{h},w_{h})= & {} (f,w_{h}),\quad \forall w_{h}\in W_{h}. \end{aligned}$$

(5.19)

It is well-known that this problem admits a unique solution (see [15]).

Lemma 5.2

Let $(\tilde{\mathbf{u}}_{h},\tilde{p}_{h})\in \mathbf{V}_{h}^{0}\times W_{h}$ be the solution of the auxiliary problem (5.18)–(5.19), and $(\mathbf{u}_{h},p_{h})\in \mathbf{V}_{h}\times W_{h}$ be the solution of the MFMFEM scheme (3.3)–(3.4). Assume $K^{-1}\in W_{\infty }^{1}(\mathcal {T}_{h})$. Then it holds

$$\begin{aligned} ||\overline{K^{-1}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||\lesssim \left\{ \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}\right\} ^{1/2}, \end{aligned}$$

(5.20)

where $\Pi _{0}$ is the standard projection operator from $\mathbf{H}(\mathrm{div};\Omega )$ onto $\mathbf{V}_{h}^{0}$.

Proof

Notice that $\mathbf{V}_{h}^{0}\subset \mathbf{V}_{h}$. From (3.3) we get

$$\begin{aligned} (\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h},\mathbf{v}_{h})= & {} (p_{h},\nabla \cdot \mathbf{v}_{h})-<g,\mathbf{v}_{h}\cdot \mathbf{n}>_{\Gamma _{D}}\nonumber \\&\ +\,(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h},\mathbf{v}_{h})-(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{Q},\quad \forall \ \mathbf{v}_{h}\in \mathbf{V}_{h}^{0}.\qquad \end{aligned}$$

(5.21)

Using the commuting property of $\Pi _{0}$ and (3.4), we have

$$\begin{aligned} (\nabla \cdot \Pi _{0}\mathbf{u}_{h},w_{h})=(Q_{h}\nabla \cdot \mathbf{u}_{h},w_{h}) =(\nabla \cdot \mathbf{u}_{h},w_{h})=(f,w_{h}), \quad \forall w_{h}\in W_{h}.\nonumber \\ \end{aligned}$$

(5.22)

A combination of (5.19) and (5.22) yields

$$\begin{aligned} (\nabla \cdot (\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h}),w_{h})=0,\quad \forall w_{h}\in W_{h}. \end{aligned}$$

(5.23)

Taking $\mathbf{v}_{h}=\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h} \in \mathbf{V}_{h}^{0}$, subtracting (5.21) from (5.18) and using (5.23), we have

$$\begin{aligned}&\displaystyle ||\overline{K^{-1}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||^{2}=(\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h}),\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})\nonumber \\&\quad =\displaystyle (\tilde{p}_{h}-p_{h},\nabla \cdot (\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h}))+(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{Q}-(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h},\mathbf{v}_{h})\nonumber \\&\quad =\displaystyle (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})_{Q}-(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})+(K^{-1}\mathbf{u}_{h},\mathbf{v}_{h}) -(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h},\mathbf{v}_{h})\nonumber \\&\quad =\displaystyle -\sigma (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h})+((K^{-1}-\overline{K^{-1}})\mathbf{u}_{h},\mathbf{v}_{h})+(\overline{K^{-1}}(\mathbf{u}_{h}-\Pi _{0}\mathbf{u}_{h}),\mathbf{v}_{h}).\qquad \qquad \end{aligned}$$

(5.24)

The work left is to estimate the three terms in the last line of (5.24). Notice that the inequality (5.2) implies

$$\begin{aligned}&|-\sigma (K^{-1}\mathbf{u}_{h},\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})| \lesssim \displaystyle \sum \limits _{T\in \mathcal {T}_{h}}h_{T}||\mathbf{u}_{h}||_{1,T}||\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h}||_{T}\nonumber \\&\displaystyle \lesssim \left\{ \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}\right\} ^{1/2}||{\overline{K^{-1}}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||. \end{aligned}$$

(5.25)

Due to $K^{-1}\in W_{\infty }^{1}(\mathcal {T}_{h})$, it holds

$$\begin{aligned} ((K^{-1}-\overline{K^{-1}})\mathbf{u}_{h},\quad \tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})\lesssim ||h\mathbf{u}_{h}||\ ||{\overline{K^{-1}}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||. \end{aligned}$$

(5.26)

In view of the approximation property (5.4) of $\Pi _{0}$, we have

$$\begin{aligned} (\overline{K^{-1}}(\mathbf{u}_{h}-\Pi _{0}\mathbf{u}_{h}),\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h}) \displaystyle\lesssim & {} \left( \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}\right) ^{1/2}||{\overline{K^{-1}}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||.\nonumber \\ \end{aligned}$$

(5.27)

Combining (5.24)–(5.27) leads to the desired estimate (5.20). $\square$

We now follow the idea of [33] to construct a postprocessed scalar pressure $l_{h}$ which links $\tilde{\mathbf{u}}_{h}$ and $\tilde{p}_{h}$ on each simplicial element in the following way:

$$\begin{aligned}&\displaystyle -\overline{K^{-1}}^{-1}\nabla l_{h}=\tilde{\mathbf{u}}_{h} \ \mathrm{in} \ T,\quad \mathrm{for\ all} \ T\in \mathcal {T}_{h},\end{aligned}$$

(5.28)

$$\begin{aligned}&\displaystyle \frac{1}{|T|}\int _{T}l_{h}d\mathbf{x}=\tilde{p}_{h}|_{T},\quad \,\,\,\, \mathrm{for\ all} \ T\in \mathcal {T}_{h}. \end{aligned}$$

(5.29)

We refer to [33] for the existence of the postprocessed solution $l_{h}$.

As shown in [33], the new quantity $l_{h}$ has the continuity of the mean values of traces across interior sides (or faces), and its mean of trace on any boundary side (or face) equals to that of g. In fact, for an interior side (or face) E shared by $T_{+}$ and $T_{-}$, let $\mathbf{v}_{E}$ denote the side (or face) basis function on E with respect to $\mathbf{V}_{h}^{0}$ with the support set $\omega _{E}$. From (5.18), (5.28)–(5.29) and integration by parts we have

$$\begin{aligned} \begin{array}{lll} 0&{}=&{}\displaystyle (-\nabla _{h}l_{h},\mathbf{v}_{E})_{T_{+}\cup T_{-}}-(\tilde{p}_{h},\nabla \cdot \mathbf{v}_{E})_{T_{+}\cup T_{-}}+<g,\mathbf{v}_{E}\cdot \mathbf{n}>_{\partial \omega _{E}\cap \Gamma _{D}}\\ &{}=&{}\displaystyle \int _{T_{+}}\nabla \cdot \mathbf{v}_{E}(l_{h}-\tilde{p}_{h})+\int _{T_{-}}\nabla \cdot \mathbf{v}_{E}(l_{h}-\tilde{p}_{h})+\int _{E}\mathbf{v}_{E}\cdot \mathbf{n}_{E}(l_{h}|_{T_{+}}-l_{h}|_{T_{-}})\\ &{}=&{}\displaystyle <1,l_{h}|_{T_{+}}-l_{h}|_{T_{-}}>_{E}, \end{array} \end{aligned}$$

which implies the continuity of the means of traces of $l_{h}$ across the interior side. For a boundary side $E\subset \Gamma _{D}$, let $E\subset \partial T$. Similarly, from (5.18) and (5.28)–(5.29) we have

$$\begin{aligned} 0= & {} -(\nabla l_{h},\mathbf{v}_{E})_{T}-(\tilde{p}_{h},\nabla \cdot \mathbf{v}_{E})_{T}+<g,\mathbf{v}_{E}\cdot \mathbf{n}>_{\partial T\cap \Gamma _{D}}\\= & {} <1,g-l_{h}>_{E}. \end{aligned}$$

For $K^{-1}\in W_{\infty }^{1}(\mathcal {T}_{h}),$ from the triangle inequality, the postprocessing (5.28), an interpolation estimate, an inverse inequality, Lemma 5.2 and the Definition (4.3) of the quadrature indicator $\eta _{Q}$ it follows

$$\begin{aligned} \inf \limits _{v_{h}\in \tilde{S}} ||\nabla v_{h}-K^{-1}\mathbf{u}_{h}||\le & {} \inf \limits _{v_{h}\in \tilde{S}}\left\{ \displaystyle ||\nabla v_{h}-\overline{K^{-1}}\tilde{\mathbf{u}}_{h}||+||\overline{K^{-1}}\tilde{\mathbf{u}}_{h}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}||\right. \nonumber \\&\ \ \left. \displaystyle +\,||\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}-\overline{K^{-1}}\mathbf{u}_{h}||+||\overline{K^{-1}}\mathbf{u}_{h}-K^{-1}\mathbf{u}_{h}||\right\} \nonumber \\\lesssim & {} \inf \limits _{v_{h}\in \tilde{S}}\displaystyle \left\{ ||\nabla _{h}(v_{h}+l_{h})||+||\overline{K^{-1}}^{1/2}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||\right. \nonumber \\&\ \ \left. \displaystyle +\left( \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}\right) ^{1/2}+||h\mathbf{u}_{h}||\right\} \nonumber \\\lesssim & {} \inf \limits _{v_{h}\in \tilde{S}}||h^{-1}(v_{h}+l_{h})||+\eta _{Q}. \end{aligned}$$

(5.30)

Following the idea of the proof of Lemma 3.4 in [17], we easily obtain the following conclusion.

Lemma 5.3

Let $l_{h}$ be the postprocessed scalar pressure determined by (5.28)–(5.29), and $g_{h,D}$ be the nodal $\varepsilon _{D}-$piecewise linear interpolation of g on $\Gamma _{D}$. For a side (or face) $E\in \varepsilon _{h}$, denote

$$\begin{aligned} \tilde{J}_{\mathbf{t}_{E}} :=\left\{ \begin{array}{ll} h_{E}^{1/2}||[l_{h}]||_{E}, &{}\quad \text{ if }\ \ E\in \varepsilon _{h}^{0},\\ h_{E}^{1/2}||l_{h}-g_{h,D}||_{E}, &{}\quad \text{ if }\ \ E\in \varepsilon _{D}. \end{array}\right. \end{aligned}$$

Then it holds

$$\begin{aligned} \inf _{v_{h}\in \tilde{S}}||h^{-1}(v_{h}+l_{h})||^{2}\lesssim \displaystyle \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}^{-2}\tilde{J}_{\mathbf{t}_{E}}^{2}. \end{aligned}$$

(5.31)

Using Lemma 5.3, we have a further conclusion as follows.

Lemma 5.4

Let $J_{\mathbf{t}_{E}}$ and $\eta _{Q}$ denote the tangential jump and the quadrature indicator defined in (4.2) and (4.3), respectively. Under the assumption of Lemma 5.2, it holds

$$\begin{aligned} \inf _{v_{h}\in \tilde{S}}||h^{-1}(v_{h}+l_{h})||^{2}\lesssim \displaystyle \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}J_{\mathbf{t}_{E}}^{2}+\eta _{Q}^{2}. \end{aligned}$$

(5.32)

Proof

We only prove the three-dimensional case, since the two-dimensional one is somewhat simpler and can be derived similarly. In the case $E=T_{+}\cap T_{-}\in \varepsilon _{h}^{0}$, since $\int _{E}[l_{h}]ds$ vanishes, a sidewise Poincaré inequality and the postprocessing (5.28) yield that

$$\begin{aligned} \begin{array}{lll} ||[l_{h}]||_{E}&{}\lesssim &{}h_{E}||(\nabla l_{h}|_{T_{+}}-\nabla l_{h}|_{T_{-}})\times \mathbf{n}_{E}||_{E}\\ &{}=&{}h_{E}||(\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{-}}-\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{+}})\times \mathbf{n}_{E}||_{E}. \end{array} \end{aligned}$$

(5.33)

Recall that $\Pi _{0}$ is the projection from $\mathbf{H}(\mathrm{div};\Omega )$ onto $\mathbf{V}_{h}^{0}$, and notice that

$$\begin{aligned}&\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{-}}-\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{+}}\nonumber \\&\quad =(\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{-}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}})+(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}-\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{+}})\nonumber \\&\qquad +\,(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}})\nonumber \\&\quad =(\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{-}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}})+(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}-\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{+}})\nonumber \\&\qquad +\,(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}}-K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{-}})+(K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{-}}-K^{-1}\mathbf{u}_{h}|_{T_{-}})\nonumber \\&\qquad +\,(K^{-1}\mathbf{u}_{h}|_{T_{-}}-K^{-1}\mathbf{u}_{h}|_{T_{+}}) +(K^{-1}\mathbf{u}_{h}|_{T_{+}}-K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{+}})\nonumber \\&\qquad +\,(K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}). \end{aligned}$$

(5.34)

Employing the trace theorem, inverse estimate and the local shape regularity of the mesh, we have

$$\begin{aligned} \begin{array}{lll} &{}||(\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{-}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}})\times \mathbf{n}_{E}||_{E}+||(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}\\ &{}\qquad -\overline{K^{-1}}\tilde{\mathbf{u}}_{h}|_{T_{+}})\times \mathbf{n}_{E}||_{E}\\ &{}\quad \lesssim h_{E}^{-1/2}||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||_{\omega _{E}}. \end{array} \end{aligned}$$

(5.35)

The trace theorem, together with the stable estimate (5.5) on the operator $\Pi _{0}$, also indicates

$$\begin{aligned} \begin{array}{lll} &{} ||(\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{-}}-K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{-}})\times \mathbf{n}_{E}||_{E}\\ &{}\quad \le ||(\overline{K^{-1}}-K^{-1})\Pi _{0}\mathbf{u}_{h}|_{T_{-}}||_{\partial T_{-}}\\ &{}\quad \lesssim ||(\overline{K^{-1}}-K^{-1})\Pi _{0}\mathbf{u}_{h}||_{T_{-}}^{1/2}||(\overline{K^{-1}}-K^{-1})\Pi _{0}\mathbf{u}_{h}||_{1,T_{-}}^{1/2}\\ &{}\quad \lesssim h_{T_{-}}^{1/2}||\mathbf{u}_{h}||_{1,T_{-}}. \end{array} \end{aligned}$$

(5.36)

Similarly, it holds

$$\begin{aligned}&\displaystyle ||(K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{+}}-\overline{K^{-1}}\Pi _{0}\mathbf{u}_{h}|_{T_{+}})\times \mathbf{n}_{E}||_{E}\lesssim h_{T_{+}}^{1/2}||\mathbf{u}_{h}||_{1,T_{+}},\end{aligned}$$

(5.37)

$$\begin{aligned}&\displaystyle ||(K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{-}}-K^{-1}\mathbf{u}_{h}|_{T_{-}})\times \mathbf{n}_{E}||_{E}\lesssim h_{E}^{1/2}||\mathbf{u}_{h}||_{1,T_{-}}, \end{aligned}$$

(5.38)

and

$$\begin{aligned} ||(K^{-1}\mathbf{u}_{h}|_{T_{+}}-K^{-1}\Pi _{0}\mathbf{u}_{h}|_{T_{+}})\times \mathbf{n}_{E}||_{E}\lesssim h_{E}^{1/2}||\mathbf{u}_{h}||_{1,T_{+}}, \end{aligned}$$

(5.39)

where in the latter two inequalities we have also used the estimate (5.4).

As a result, a combination of (5.33)–(5.39) shows

$$\begin{aligned} ||[l_{h}]||_{E}\lesssim & {} h_{E}\{h_{E}^{-1/2}||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||_{\omega _{E}}\nonumber \\&+\,h_{E}^{1/2}||\mathbf{u}_{h}||_{1,\omega _{E}}+||[\gamma _{\mathbf{t}_{E}}(K^{-1}\mathbf{u}_{h})]||_{E}\}. \end{aligned}$$

(5.40)

On the other hand, in the case $E\subset \partial T\cap \varepsilon _{D}$ it holds

$$\begin{aligned} \displaystyle \frac{1}{|E|}\int _{E}(l_{h}-g)ds=0 \end{aligned}$$

due to $\int _{E}l_{h}ds=\int _{E}gds$. Using the triangle inequality, sidewise Poincaré inequality and interpolation estimation, we have

$$\begin{aligned} ||l_{h}-g_{h,D}||_{E}\le & {} ||l_{h}-g||_{E}+||g-g_{h,D}||_{E}\nonumber \\\lesssim & {} h_{E}||\nabla l_{h}\times \mathbf{n}_{E}-\partial g/\partial s||_{E}+h_{E}^{2}||\partial ^{2}g/\partial s^{2}||_{E}. \end{aligned}$$

(5.41)

Similarly it holds

$$\begin{aligned} h_{E}||\nabla l_{h}\times \mathbf{n}_{E}-\frac{\partial g}{\partial s}||_{E}\lesssim & {} h_{E}^{1/2}||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||_{T}+h_{E}^{3/2}||\mathbf{u}_{h}||_{1,T}\nonumber \\&\ +\,h_{E}||K^{-1}\mathbf{u}_{h}\times \mathbf{n}_{E}-\partial g/\partial s||_{E}. \end{aligned}$$

(5.42)

The above two estimates, (5.41) and (5.42), lead to

$$\begin{aligned} ||l_{h}-g_{h,D}||_{E}\lesssim & {} h_{E}^{1/2}||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||_{T}+h_{E}^{3/2}||\mathbf{u}_{h}||_{1,T}\nonumber \\&\ +\,h_{E}||K^{-1}\mathbf{u}_{h}\times \mathbf{n}_{E}-\partial g/\partial s||_{E}+h_{E}^{2}||\partial ^{2}g/\partial s^{2}||_{E}.\qquad \end{aligned}$$

(5.43)

From the definition of $\tilde{J}_{\mathbf{t}_{E}}$ in Lemma 5.3, the estimates (5.40) and (5.43) indicate

$$\begin{aligned}&\sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}^{-2}\tilde{J}_{\mathbf{t}_{E}}^{2}= \sum \limits _{E\in \varepsilon _{h}^{0}}h_{E}^{-2}h_{E}||[l_{h}]||_{E}^{2}+ \sum \limits _{E\in \varepsilon _{D}}h_{E}^{-2}h_{E}||l_{h}-g_{h,D}||_{E}^{2}\nonumber \\&\quad \lesssim \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}^{2}+||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||^{2}+\sum \limits _{E\in \varepsilon _{h}^{0}}h_{E}||[\gamma _{\mathbf{t}_{E}}(K^{-1}\mathbf{u}_{h})]||_{E}^{2}\nonumber \\&\qquad +\sum \limits _{E\in \varepsilon _{D}}(h_{E}||\gamma _{\mathbf{t}_{E}}(K^{-1}\mathbf{u}_{h})-\partial g/\partial s||_{E}^{2}+h_{E}^{3}||\partial ^{2}g/\partial s^{2}||_{E}). \end{aligned}$$

(5.44)

By noticing that Lemma 5.2 implies

$$\begin{aligned} ||\overline{K^{-1}}(\tilde{\mathbf{u}}_{h}-\Pi _{0}\mathbf{u}_{h})||^{2}\lesssim \eta _{Q}^{2}, \end{aligned}$$

the estimate (5.44), together with the definitions of $J_{\mathbf{t}_{E}}$ and $\eta _{Q}$, (4.2) and (4.3), yields

$$\begin{aligned} \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}^{-2}\tilde{J}_{\mathbf{t}_E}^{2}\lesssim \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}J_{\mathbf{t}_{E}}^{2}+\eta _{Q}^{2}. \end{aligned}$$

(5.45)

The desired result (5.32) follows from Lemma 5.3 and (5.45). $\square$

The proof of Theorem 4.1 Collecting (5.17), (5.30) and (5.32), we get

$$\begin{aligned} \inf _{\beta \in H^{1}(\Omega )}||\nabla \beta -K^{-1}\mathbf{u}_{h}||\lesssim \left\{ \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}J_{\mathbf{t}_{E}}^{2}\right\} ^{1/2}+ \eta _{Q}, \end{aligned}$$

(5.46)

which, together with the estimates (5.15)–(5.16), yields

$$\begin{aligned}&||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||\lesssim ||h(f-\nabla \cdot \mathbf{u}_{h})||+\left\{ \sum \limits _{E\in \varepsilon _{D}}h_{E}^{3}||\partial ^{2}g/\partial s^{2}||_{E}^{2}\right\} ^{1/2}\nonumber \\&\qquad +\left\{ \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}J_{\mathbf{t}_{E}}^{2}\right\} ^{1/2}+ \eta _{Q}\nonumber \\&\quad \lesssim ||h(f-\nabla \cdot \mathbf{u}_{h})||+\left\{ \sum \limits _{E\in \varepsilon _{h}^{0}\cup \varepsilon _{D}}h_{E}J_{\mathbf{t}_{E}}^{2}\right\} ^{1/2}+ \eta _{Q}.\qquad \end{aligned}$$

(5.47)

The desired result (4.4) then follows from (5.47) and the definition (4.1) of $\eta _{h}$.

The proof of Theorem 4.2 Recall that $Q_{h}$ is the $L^{2}-$projection operator onto $W_{h}$. Construct the following auxiliary problem: Find $\phi \in H^{1}(\Omega )$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla \cdot (K\nabla \phi )=Q_{h}p-p_{h} &{}\quad \text{ in }\ \ \Omega ,\\ \phi =0 &{}\quad \text{ on }\ \partial \Omega . \end{array}\right. \end{aligned}$$

(5.48)

By the assumptions of K and Lax–Milgram theorem, the operator

$$\begin{aligned} \nabla \cdot (K\nabla \cdot ):H_{0}^{1}(\Omega )\rightarrow H^{-1}(\Omega ) \end{aligned}$$

is invertible and it holds the following regularity estimate:

$$\begin{aligned} ||\phi ||_{1}\lesssim ||Q_{h}p-p_{h}||. \end{aligned}$$

(5.49)

Moreover, if $\Omega$ is convex, $K\in \mathcal {C}^{1,0}(\overline{\Omega })$ implies that

$$\begin{aligned} \nabla \cdot (K\nabla \cdot ):H_{0}^{1}(\Omega )\cap H^{2}(\Omega )\rightarrow L^{2}(\Omega ) \end{aligned}$$

is invertible ([24]) and the regularity estimate

$$\begin{aligned} ||\phi ||_{H^{2}(\bigcup \mathcal {T}_{h})}\lesssim ||Q_{h}p-p_{h}|| \end{aligned}$$

(5.50)

holds. We emphasize that here we only need a regularity estimate on $||\phi ||_{H^{2}(T)}$ for each $T\in \mathcal {T}_{h}$ and then assume a weakened constraint on K such that (5.50) holds. In [16] Carstensen gave an example where K is piecewise constant and $\phi$ satisfies (5.50) but is not $H^{2}$-regular.

Notice that the error equation of the MFMFE method (3.3)–(3.4) can be written as

$$\begin{aligned} (K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\mathbf{v}_{h})=(Q_{h}p-p_{h},\nabla \cdot \mathbf{v}_{h})-\sigma (K^{-1}\mathbf{u}_{h},\mathbf{v}_{h}),\quad \forall \mathbf{v}_{h}\in V_{h}. \end{aligned}$$

(5.51)

Recalling $\Pi$ is the standard projection operator from $\mathbf{H}(\mathrm{div};\Omega )\cap (L^{\varrho }(\Omega ))^{d}$ onto $V_{h}$, and taking $\mathbf{v}_{h}=\Pi (K\nabla \phi )$ in (5.51), from (5.48) and the commuting property $\nabla \cdot (\Pi K\nabla \phi )=Q_h\nabla \cdot ( K\nabla \phi )$, we have

$$\begin{aligned} \begin{array}{lll} ||Q_{h}p-p_{h}||^{2}&{}=&{}(Q_{h}p-p_{h},\nabla \cdot (\Pi K\nabla \phi ))\\ &{}=&{}(K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\Pi (K\nabla \phi ))+\sigma (K^{-1}\mathbf{u}_{h},\Pi K\nabla \phi ). \end{array} \end{aligned}$$

(5.52)

Since $(\nabla \cdot (\mathbf{u}-\mathbf{u}_{h}),w_{h})=0, \forall w_{h}\in W_{h}$, by integration by parts, the approximation property of $\Pi$ and the estimates (5.49)–(5.50), we have

$$\begin{aligned}&(K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\Pi (K\nabla \phi ))\nonumber \\&\quad =(K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\Pi (K\nabla \phi )-K\nabla \phi )+(\mathbf{u}-\mathbf{u}_{h},\nabla \phi )\nonumber \\&\quad =(K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\Pi (K\nabla \phi )-K\nabla \phi )-(\nabla \cdot (\mathbf{u}-\mathbf{u}_{h}),\phi )\nonumber \\&\quad =(K^{-1}(\mathbf{u}-\mathbf{u}_{h}),\Pi (K\nabla \phi )-K\nabla \phi )-(\nabla \cdot (\mathbf{u}-\mathbf{u}_{h}),\phi -Q_{h}\phi )\nonumber \\&\quad \lesssim \left( ||hK^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||+||h\nabla \cdot (\mathbf{u}-\mathbf{u}_{h})||\right) ||Q_{h}p-p_{h}||. \end{aligned}$$

(5.53)

On the other hand, a combination of (5.3), (5.5) and (5.50) yields

$$\begin{aligned} \begin{array}{lll} |\sigma (K^{-1}\mathbf{u}_{h},\Pi K\nabla \phi )|&{}\lesssim &{}\displaystyle \sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{2}||\mathbf{u}_{h}||_{1,T}||\Pi (K\nabla \phi )||_{1,T}\\ &{}\lesssim &{}\displaystyle (\sum \limits _{T\in \mathcal {T}_{h}}h_{T}^{4}||\mathbf{u}_{h}||_{1,T}^{2})^{1/2}||Q_{h}p-p_{h}||. \end{array} \end{aligned}$$

(5.54)

Noticing $\nabla \cdot (\mathbf{u}-\mathbf{u}_{h})=f-Q_{h}f$, from (5.52) to (5.54) and the estimate (4.4) of Theorem 4.1 we obtain the assertion (4.5), i.e.

$$\begin{aligned} ||Q_{h}p-p_{h}||\lesssim h_\mathrm{max}(\eta _{h}+\eta _{Q})+||h(f-\nabla \cdot \mathbf{u}_{h})||. \end{aligned}$$

A triangle inequality, the relation $\mathbf{u}=-K\nabla p$ and the approximation property of $Q_h$ further imply

$$\begin{aligned} \begin{array}{lll} ||p-p_{h}||&{}\le &{}||p-Q_{h}p||+||Q_{h}p-p_{h}||\lesssim ||h\nabla p||+||Q_{h}p-p_{h}||\\ &{}\le &{}||hK^{-1}(\mathbf{u}-\mathbf{u}_{h})||+||hK^{-1}\mathbf{u}_{h}||+||Q_{h}p-p_{h}||. \end{array} \end{aligned}$$

This inequality, together with the estimate (4.5), leads to the conclusion (4.6).

Remark 5.1

Note that the technique developed in this contribution for simplicial elements may not be extended trivially to other types of elements such as quadrilateral (hexahedral) elements, since the analysis depends on a locally postprocessed approximation which fails on the quadrilateral (hexahedral) elements. On the other hand, the MPFA methods are also widely used on quadrilateral/hexahedral and even polygon/polyhedral elements (cf. [1, 2, 22, 27, 28]), so it will be significant to develop similar techniques of a posteriori error analysis for such kinds of meshes.

6 Analysis for the efficiency

This section is devoted to the proof of Theorem 4.3. For the sake of simplicity, we assume that $K^{-1}$ is a matrix of piecewise polynomial functions. Since the two terms $||h(f-\nabla \cdot \mathbf{u}_{h})||$ and $\displaystyle \{\sum \nolimits _{E\in \varepsilon _{D}}h_{E}^{3}||\frac{\partial ^{2}g}{\partial s^{2}}||_{E}^{2}\}^{1/2}$ in $\eta _{h}$ are of high order, they are directly incorporated in h.o.t. as a high order term. Using standard analytical techniques, we easily obtain Lemma 6.1.

Lemma 6.1

Let $\eta _{h}$ denote the discretization indicator given by (4.1). Then it holds

$$\begin{aligned} \displaystyle \eta _{h}\lesssim ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||+h.o.t. \end{aligned}$$

(6.1)

Lemma 6.2

Let $\eta _{Q}$ denote the quadrature indicator given by (4.3). Then it holds

$$\begin{aligned} \eta _{Q}\lesssim ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||+||h^{-1}(p-p_{h})||. \end{aligned}$$

(6.2)

Proof

An inverse inequality and the assumption (1.2) yield

$$\begin{aligned} ||\mathbf{u}_{h}||_{1,T}\lesssim h_{T}^{-1}||\mathbf{u}_{h}||_{T}\lesssim h_{T}^{-1}||K^{-1}\mathbf{u}_{h}||_{T}. \end{aligned}$$

(6.3)

For all $T\in \mathcal {T}_{h}$, let $\psi _{T}$ denote the bubble function on T with $\psi _{T}|_{\partial T}=0$ and $0\le \psi _{T}\le 1$. Then the two norms, $||\psi _{T}^{1/2}\cdot ||_{T}$ and $||\cdot ||_{T}$, are equivalent for polynomials. Since $\nabla p_{h}|_{T}=0$ due to $p_h\in W_h$, it then holds

$$\begin{aligned} ||K^{-1}\mathbf{u}_{h}||_{T}^{2}= & {} ||K^{-1}\mathbf{u}_{h}+\nabla p_{h}||_{T}^{2}\nonumber \\\lesssim & {} ||\psi _{T}^{1/2}(K^{-1}\mathbf{u}_{h}+\nabla p_{h})||_{T}^{2}\nonumber \\= & {} \left( \psi _{T}K^{-1}\mathbf{u}_{h},K^{-1}\mathbf{u}_{h}+\nabla p_{h}\right) _{T}\nonumber \\= & {} \left( \psi _{T}K^{-1}\mathbf{u}_{h},K^{-1}(\mathbf{u}_{h}-\mathbf{u})\right) _{T}+\left( \psi _{T}K^{-1}\mathbf{u}_{h},\nabla (p_{h}-p)\right) _{T}\nonumber \\= & {} \left( \psi _{T}K^{-1}\mathbf{u}_{h},K^{-1}(\mathbf{u}_{h}-\mathbf{u})\right) _{T}-\left( \nabla \cdot (\psi _{T}K^{-1}\mathbf{u}_{h}),p_{h}-p\right) _{T}\nonumber \\\lesssim & {} ||K^{-1}\mathbf{u}_{h}||_{T}\left( ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||_{T}+h_{T}^{-1}||p-p_{h}||_{T}\right) , \end{aligned}$$

(6.4)

where in the fourth and last lines we have used the relation $\mathbf{u}=-K\nabla p$ and an inverse inequality, respectively. This inequality, together with (6.3), shows

$$\begin{aligned} h_{T}||\mathbf{u}_{h}||_{1,T}\lesssim ||K^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||_{T}+h_{T}^{-1}||(p-p_{h})||_{T}, \end{aligned}$$

from which the desired estimate (6.2) follows.

The proof of Theorem 4.3 From (6.4) we obtain

$$\begin{aligned} ||hK^{-1}\mathbf{u}_{h}||\lesssim ||hK^{-1/2}(\mathbf{u}-\mathbf{u}_{h})||+||p-p_{h}||, \end{aligned}$$

(6.5)

which, together with Lemmas 6.1–6.2, leads to the desired efficiency estimate of Theorem 4.3.

7 Numerical experiments

In this section, we use two model problems to test the performance of the developed a posteriori error estimator for the MFMFE method. We consider two types of meshes: uniformly refined meshes and adaptively refined meshes. The latter type of meshes is generated by a standard adaptive algorithm based on the a posteriori error estimation. In the first example, the permeability K equals to identity matrix and $\Omega$ is an L-shape domain. In the second example, K is inhomogeneous and anisotropic. We are thus able to study how meshes adapt to various effect from lack of regularity of solutions to non-convexity of domains.

7.1 Example 7.1

We consider the problem (1.1) in an L-shape domain $\Omega =\{(-1,1)\times (0,1)\}\cup \{(-1,0)\times (-1,0)\}$ with Dirichlet boundary conditions and $K=I$ (identity matrix). The exact solution is given by

$$\begin{aligned} p(\rho ,\theta )=\rho ^{r}\sin (r\theta ), \end{aligned}$$

where $\rho ,\theta$ are the polar coordinates, r is a parameter. We consider two cases for r: $r=0.4$ and $r=0.1$. Some simple calculations show $f=0$.

Fig. 1

A mesh with 347 triangles, iteration 6 (left) and a mesh with 578 triangles, iteration 8 (right) in case $r=0.4$

Fig. 2

A mesh with 1607 triangles, iteration 11 (left) and a mesh with 2618 triangles, iteration 12 (right) in case $r=0.4$

It is well known that this model possesses singularity at the origin and holds $p\in H^{1+r-\epsilon }(\Omega )$ for any $\epsilon >0$. The singularity of the solution in the case $r=0.4$ is weaker than in the case $r=0.1$. The original mesh consists of 6 right-angled triangles.

In the adaptive algorithm we first solve the MFMFE scheme (3.3)–(3.4), then mark elements in terms of Dörfler marking with the marking parameter $\tilde{\theta }=0.5$, and finally use the “longest edge” refinement to recover an admissible mesh. In particular, the uniform refinement means that all elements should be marked.

Fig. 3

A mesh with 245 triangles, iteration 10 (left) and a mesh with 3265 triangles, iteration 24 (right) in case $r=0.1$

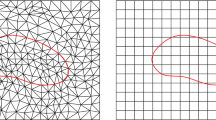
From Figs. 1, 2 with the parameter $r=0.4$ and Fig. 3 with the parameter $r=0.1$, we see that using the adaptive algorithm the refinement concentrates around the origin. This means that the predicted error estimator captures well the singularity of the solution, and that the stronger the solution possesses singularity, the better the a posteriori error estimator can identify.

Fig. 4

The postprocessing approximation to the pressure on the adaptively refined mesh in case $r=0.4$ (left) and in case $r=0.1$ (right)

Figure 4 reports a continuous piecewise-linear postprocessing approximation to the pressure on the adaptively refined mesh in the case $r=0.4$ (left) and in the case $r=0.1$ (right) with 24 iterations. Since the approximation to the pressure of the MFMFE method is piecewise constant, the value of the postprocessing approximation to the pressure on each node is taken as the algorithmic mean of the values of the pressure finite element solution on all the elements sharing the vertex.

Fig. 5

The estimated and actual errors against the number of elements in uniformly/adaptively refined meshes in case $r=0.4$ (left) and in case $r=0.1$ (right) with the marking parameter $\tilde{\theta }=0.5$

Figure 5 reports the estimated and actual errors of the numerical solutions on uniformly and adaptively refined meshes. It can be seen that the error of the velocity in $L^{2}$ norm uniformly reduces with a fixed factor on two successive meshes, and that the error on the adaptively refined meshes decreases more rapidly than the one on the uniformly refined meshes. This means that one can substantially reduce the number of unknowns necessary to obtain the prescribed accuracy by using a posteriori error estimators and adaptively meshes. We note that the exact error is approximated with a 7-point quadrature formula in each triangle.

Fig. 6

The quadrature error $\eta _{Q}$ and discretization error $\eta _{h}$ against the number of elements in adaptively refined meshes in case $r=0.4$ with the marking parameter $\tilde{\theta }=0.5$ (left) and in case $r=0.1$ with the marking parameter $\tilde{\theta }=0.8$ (right)

Figure 6 shows the quadrature error $\eta _{Q}$ and discretization error $\eta _{h}$ in adaptively refined meshes in case $r=0.4$ with the marking parameter $\theta =0.5$ (left) and in case $r=0.1$ with the marking parameter $\theta =0.8$ (right). It can be seen that the error indicator $\eta _{h}$ produced by the discretization is very close to the error indicator $\eta _{Q}$ produced by the quadrature rule as the mesh is refined. This also shows that the quadrature indicator $\eta _{Q}$ is very efficient. We note that this efficiency is not sufficiently demonstrated by Theorem 4.3 due to the appearance of the pressure error term, while this error term usually has the second order accuracy on uniform meshes.

7.2 Example 7.2

We consider the problem (1.1) in a square domain $\Omega =(-1,1)\times (-1,1)$ with Dirichlet boundary conditions, where $\Omega$ is divided into four subdomains $\Omega _{i}$ ($i=1,2,3,4$) corresponding to the axis quadrants (in the counterclockwise direction), and the permeability K is piecewise constant with $K=s_{i}I$ in $\Omega _{i}$. We assume the exact solution of this model has the form

$$\begin{aligned} p(\rho ,\theta )|_{\Omega _{i}}=\rho ^{r}(a_{i}sin(r\theta )+b_{i}cos(r\theta )). \end{aligned}$$

Here $\rho ,\theta$ are the polar coordinates in $\Omega$, $a_{i}$ and $b_{i}$ are constants depending on $\Omega _{i}$, and r is a parameter. This solution is not continuous across the interfaces, and only the normal component of its velocity $\mathbf{u}=-K\nabla p$ is continuous, and it exhibits a strong singularity at the origin. We consider a set of coefficients in the following table:

$s_{1}=s_{3}=5$, $s_{2}=s_{4}=1$

$r=0.53544095$

$a_{1}=\ \ 0.44721360,$ $b_{1}=\ \ 1.00000000$

$a_{2}=-0.74535599,$ $b_{2}=\ \ 2.33333333$

$a_{3}=-0.94411759,$ $b_{3}=\ \ 0.55555555$

$a_{4}=-2.40170264,$ $b_{4}=-0.48148148$

The origin mesh consists of 8 right-angled triangles. We perform the adaptive algorithm described in Example 7 with the marking parameter $\tilde{\theta }=0.5$. Figures 7, 8 report the adaptive meshes generated by 6–8 iterations, and the continuous piecewise-linear postprocessing approximation to the pressure on the adaptively refined mesh. We again see that the refinement concentrates around the origin. This indicates that the predicted error estimator captures well the singularity of the solution.

Fig. 7

A mesh with 740 triangles, iteration 6 (left) and a mesh with 1350 triangles, iteration 7 (right)

Fig. 8

A mesh with 2328 triangles, iteration 8 (left) and the postprocessing approximation to the pressure on the adaptively refined mesh

Figure 9 reports the estimated and actual errors of the numerical solutions on uniformly and adaptively refined meshes (left), and the quadrature indicator $\eta _{Q}$ and discretization indicator $\eta _{h}$ in adaptively refined meshes (right).

Fig. 9

The estimated and actual errors against the number of elements in uniformly/adaptively refined meshes (left) and the quadrature error $\eta _{Q}$ and discretization error $\eta _{h}$ against the number of elements in adaptively refined meshes (right)

We can see that the error of the velocity uniformly reduces with a fixed factor on two successive meshes, that the error on the adaptively refined meshes decreases more rapidly than the one on the uniformly refined meshes, and that the a posteriori error estimators developed in this paper are efficient with respect to inhomogeneities and anisotropy of the permeability. This means that one can substantially reduce the number of unknowns necessary to obtain the prescribed accuracy by using a posteriori error estimators and adaptively refined meshes. We also see that the error indicator $\eta _{h}$ and $\eta _{Q}$ differs at most a constant factor, which shows the quadrature error estimator $\eta _{Q}$ is efficient.

8 Conclusions

In this contribution we have developed a reliable and efficient a posteriori error estimator of residual-type for the multi-point flux mixed finite element methods for flow in porous media in two or three space dimensions. The main tools of our analysis are a locally postprocessed technique and a quadrature error estimation. Numerical experiments are conformable to our theoretical results.