Abstract
The Lanczos method is often used to solve a large scale symmetric matrix eigenvalue problem. It is well-known that the single-vector Lanczos method can only find one copy of any multiple eigenvalue (unless certain deflating strategy is incorporated) and encounters slow convergence towards clustered eigenvalues. On the other hand, the block Lanczos method can compute all or some of the copies of a multiple eigenvalue and, with a suitable block size, also compute clustered eigenvalues much faster. The existing convergence theory due to Saad for the block Lanczos method, however, does not fully reflect this phenomenon since the theory was established to bound approximation errors in each individual approximate eigenpairs. Here, it is argued that in the presence of an eigenvalue cluster, the entire approximate eigenspace associated with the cluster should be considered as a whole, instead of each individual approximate eigenvectors, and likewise for approximating clusters of eigenvalues. In this paper, we obtain error bounds on approximating eigenspaces and eigenvalue clusters. Our bounds are much sharper than the existing ones and expose true rates of convergence of the block Lanczos method towards eigenvalue clusters. Furthermore, their sharpness is independent of the closeness of eigenvalues within a cluster. Numerical examples are presented to support our claims.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Lanczos method [15] is widely used for finding a small number of extreme eigenvalues and their associated eigenvectors of a symmetric matrix (or Hermitian matrix in the complex case). It requires only matrix-vector products to extract enough information to compute the desired solutions, and thus is very attractive in practice when the matrix is sparse and its size is too large to be solved by, e.g., the QR algorithm [8, 21] or the matrix does not exist explicitly but in the form of a procedure that is capable of generating matrix-vector multiplications.
Let \(A\) be an \(N\times N\) Hermitian matrix. Given an initial vector \(v_0\), the single-vector Lanczos method begins by recursively computing an orthonormal basis \(\{q_1,q_2,\ldots , q_n\}\) of the \(n\)th Krylov subspace of \(A\) on \(v_0\):
and at the same time the projection of \(A\) onto \({\mathcal {K}}_n(A,v_0)\): \(T_n=Q_n^{{{\mathrm{H}}}}AQ_n\), where \(Q_n=[q_1,q_2,\ldots , q_n]\) and usually \(n \,{\scriptstyle \ll }\, N\). Afterwards some of the eigenpairs \((\tilde{\lambda },w)\) of \(T_n\):
especially the extreme ones, are used to construct approximate eigenpairs \((\tilde{\lambda }, Q_nw)\) of \(A\). The number \(\tilde{\lambda }\) is called a Ritz value and \(Q_nw\) a Ritz vector. This procedure of computing approximate eigenpairs is not limited to Krylov subspaces but in general works for any given subspace. It is called the Rayleigh–Ritz procedure.
The single-vector Lanczos method may have difficulty in computing all copies of a multiple eigenvalue of \(A\). In fact, only one copy of the eigenvalue can be found unless certain deflating strategy is incorporated. On the other hand, a block Lanczos method with a block size that is no smaller than the multiplicity of the eigenvalue can compute all copies of the eigenvalue at the same time. But perhaps the biggest problem for the single-vector Lanczos method is its effectiveness in handling eigenvalue clusters—slow convergence to each individual eigenvalue in the cluster. The closer the eigenvalues in the cluster are, the slower the convergence will be. It is well-known that a block version with a big enough block size will perform much better.
There are a few block versions, e.g., the ones introduced by Golub and Underwood [9], Cullum and Donath [5], and, more recently, by Ye [25] for an adaptive block Lanczos method (see also Cullum and Willoughby [6], Golub and van Loan [10]). The basic idea is to use an \(N\times n_b\) matrix \(V_0\), instead of a single vector \(v_0\), and accordingly an orthonormal basis of the \(n\)th Krylov subspace of \(A\) on \(V_0\):
will be generated, as well as the projection of \(A\) onto \({\mathcal {K}}_n(A,V_0)\). Afterwards the same Rayleigh-Ritz procedure is applied to compute approximate eigenpairs of \(A\).
There has been a wealth of development, in both theory and implementation, for the Lanczos methods, mostly for the single-vector version. The most complete reference up to 1998 is Parlett [21]. This paper is concerned with the theoretical convergence theory of the block Lanczos method. Related past works include Kaniel [12], Paige [20], Saad [22], Li [18], as well as the potential-theoretic approach in Kuijlaars [13, 14] who, from a very different perspective, investigated which eigenvalues are found first according to the eigenvalue distribution as \(N\rightarrow \infty \), and what are their associated convergence rates as \(n\) goes to \(\infty \) while \(n/N\) stays fixed. Results from these papers are all about the convergence of an individual eigenvalue and eigenvector, even in the analysis of Saad on the block Lanczos method.
The focus in this paper is, however, on the convergence of a cluster of eigenvalues, including multiple eigenvalues, and their associated eigenspace for the Hermitian eigenvalue problem. Our results distinguish themselves from those of Saad [22] in that they bound errors in approximate eigenpairs belonging to eigenvalue clusters together, rather than separately for each individual eigenpair. The consequence is much sharper bounds as our later numerical examples will demonstrate. These bounds are also independent of the closeness of eigenvalues within a cluster.
One of the key steps in analyzing the convergence of Lanczos methods is to pick (sub)optimal polynomials to minimize error bounds. For any eigenpair other than the first one, it is often the standard practice, as in [22], that each chosen polynomial has a factor to annihilate vector components in all proceeding eigenvector directions, resulting in a “bulky” factor in the form of the product involving all previous eigenvalues/Ritz values in the error bound. The factor can be big and likely is an artifact of the analyzing technique. We propose also a new kind of error bounds that do not have such a “bulky” factor, but require knowledge of the distance from the interested eigenspace to a Krylov subspace \({\mathcal {K}}_i\) of a lower order as a tradeoff.
The rest of this paper is organized as follows. Section 2 collects some necessary results on unitarily invariant norms and canonical angles between subspaces for our later use. Section 3 presents the (simplest) block Lanczos method whose convergence analysis that results in error bounds of the eigenspace/eigenvalue cluster type is done in Sect. 4 for eigenspaces and Sect. 5 for eigenvalues. In Sect. 6, we perform a brief theoretical comparison between our results and related results derived from those of Saad [22] and point out when Saad’s bounds will overestimate the true rate of convergence. Numerical examples are given in Sect. 7 to support our comparison analysis. Section 8 establishes more bounds, based on the knowledge of Krylov subspaces of lower orders. Finally, we present our conclusion in Sect. 9.
Throughout this paper, \(A\) is an \(N\times N\) Hermitian matrix, and has

\({\mathbb {C}}^{n\times m}\) is the set of all \(n\times m\) complex matrices, \({\mathbb {C}}^n={\mathbb {C}}^{n\times 1}\), and \({\mathbb {C}}={\mathbb {C}}^1\). \({\mathbb {P}}_k\) is the set of polynomial of degree no bigger than \(k\). \(I_n\) (or simply \(I\) if its dimension is clear from the context) is the \(n\times n\) identity matrix, and \(e_j\) is its \(j\)th column. The superscript “\({\cdot }^{{{\mathrm{H}}}}\)” takes the complex conjugate transpose of a matrix or vector. We shall also adopt MATLAB-like convention to access the entries of vectors and matrices. Let \(i:j\) be the set of integers from \(i\) to \(j\) inclusive. For a vector \(u\) and a matrix \(X\), \(u_{(j)}\) is \(u\)’s \(j\)th entry, \(X_{(i,j)}\) is \(X\)’s \((i,j)\)th entry; \(X\)’s submatrices \(X_{(k:\ell ,i:j)}\), \(X_{(k:\ell ,:)}\), and \(X_{(:,i:j)}\) consist of intersections of row \(k\) to row \(\ell \) and column \(i\) to column \(j\), row \(k\) to row \(\ell \), and column \(i\) to column \(j\), respectively. \({\mathcal {R}}(X)\) is the column space of \(X\), i.e., the subspace spanned by the columns of \(X\), and \({{\mathrm{eig}}}(X)\) denotes the set of all eigenvalues of a square matrix \(X\). For matrices or scalars \(X_i\), both \({{\mathrm{diag}}}(X_1,\ldots ,X_k)\) and \(X_1\oplus \cdots \oplus X_k\) denote the same block diagonal matrix with the \(i\)th diagonal block \(X_i\).
2 Preliminaries
2.1 Unitarily invariant norm
A matrix norm \(\left|\left|\left|\cdot \right|\right|\right|\) is called a unitarily invariant norm on \({\mathbb {C}}^{m\times n}\) if it is a matrix norm and has the following two properties [1, 23]
-
1.
\(\left|\left|\left|X^{{{\mathrm{H}}}}BY\right|\right|\right|=\left|\left|\left|B\right|\right|\right|\) for all unitary matrices \(X\) and \(Y\) of apt sizes and \(B\in {\mathbb {C}}^{m\times n}\).
-
2.
\(\left|\left|\left|B\right|\right|\right|=\Vert B\Vert _2\), the spectral norm of \(B\), if \({{\mathrm{rank}}}(B)=1\).
Two commonly used unitarily invariant norms are
where \(\sigma _1,\sigma _2,\ldots ,\sigma _{\min \{m,n\}}\) are the singular values of \(B\). The trace norm
is a unitarily invariant norm, too. In what follows, \(\left|\left|\left|\cdot \right|\right|\right|\) denotes a general unitarily invariant norm.
In this article, for convenience, any \(\left|\left|\left|\cdot \right|\right|\right|\) we use is generic to matrix sizes in the sense that it applies to matrices of all sizes. Examples include the matrix spectral norm \(\Vert \cdot \Vert _2\), the Frobenius norm \(\Vert \cdot \Vert _{{{\mathrm{F}}}}\), and the trace norm. One important property of unitarily invariant norms is
for any matrices \(X\), \(Y\), and \(Z\) of compatible sizes.
Lemma 2.1
Let \(H\) and \(M\) be two Hermitian matrices, and let \(S\) be a matrix of a compatible size as determined by the Sylvester equation \(HY-YM=S\). If \({{\mathrm{eig}}}(H)\cap {{\mathrm{eig}}}(M)=\emptyset \), then the equation has a unique solution \(Y\), and moreover
where \(\eta =\min |\mu -\omega |\) over all \(\mu \in {{\mathrm{eig}}}(M)\) and \(\omega \in {{\mathrm{eig}}}(H)\), and the constant \(c\) lies between \(1\) and \(\pi /2\), and it is \(1\) for the Frobenius norm, or if either \({{\mathrm{eig}}}(H)\) is in a closed interval that contains no eigenvalue of \(M\) or vice versa.
This lemma for the Frobenius norm and for the case when either \({{\mathrm{eig}}}(H)\) is in a closed interval that contains no eigenvalue of \(M\) or vice versa is essentially in [7] (see also [23]), and it is due to [2, 3] for the most general case: \({{\mathrm{eig}}}(H)\cap {{\mathrm{eig}}}(M)=\emptyset \) and any unitarily invariant norm.
2.2 Angles between subspaces
Consider two subspaces \({\mathcal {X}}\) and \({\mathcal {Y}}\) of \({\mathbb {C}}^N\) and suppose
Let \(X\in {\mathbb {C}}^{N\times k}\) and \(Y\in {\mathbb {C}}^{N\times \ell }\) be orthonormal basis matrices of \({\mathcal {X}}\) and \({\mathcal {Y}}\), respectively, i.e.,
and denote by \(\sigma _j\) for \(1\le j\le k\) in ascending order, i.e., \(\sigma _1\le \cdots \le \sigma _k\), the singular values of \(Y^{{{\mathrm{H}}}}X\). The \(k\) canonical angles \(\theta _j({\mathcal {X}},{\mathcal {Y}})\) from Footnote 1 \({\mathcal {X}}\) to \({\mathcal {Y}}\) are defined by
They are in descending order, i.e., \(\theta _1({\mathcal {X}},{\mathcal {Y}})\ge \cdots \ge \theta _k({\mathcal {X}},{\mathcal {Y}})\). Set
It can be seen that angles so defined are independent of the orthonormal basis matrices \(X\) and \(Y\), which are not unique. A different way to define these angles is through the orthogonal projections onto \({\mathcal {X}}\) and \({\mathcal {Y}}\) [24].
When \(k=1\), i.e., \(X\) is a vector, there is only one canonical angle from \({\mathcal {X}}\) to \({\mathcal {Y}}\) and so we will simply write \(\theta ({\mathcal {X}},{\mathcal {Y}})\).
In what follows, we sometimes place a vector or matrix in one or both arguments of \(\theta _j(\,\cdot \,,\,\cdot \,)\), \(\theta (\,\cdot \,,\,\cdot \,)\), and \(\varTheta (\,\cdot \,,\,\cdot \,)\) with the understanding that it is about the subspace spanned by the vector or the columns of the matrix argument.
Proposition 2.1
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be two subspaces in \({\mathbb {C}}^N\) satisfying (2.1).
-
(a)
For any \(\widehat{{\mathcal {Y}}}\subseteq {{\mathcal {Y}}}\) with \(\dim (\widehat{{\mathcal {Y}}})=\dim ({{\mathcal {X}}})=k\), we have \(\theta _j({{\mathcal {X}}},{{\mathcal {Y}}})\le \theta _j({{\mathcal {X}}}, \widehat{{\mathcal {Y}}})\) for \(1\le j\le k\).
-
(b)
There exist an orthonormal basis \(\{x_1,x_2,\ldots ,x_k\}\) for \({\mathcal {X}}\) and an orthonormal basis \(\{y_1,y_2,\ldots ,y_{\ell }\}\) for \({\mathcal {Y}}\) such that
$$\begin{aligned} \begin{array}{ll} \theta _j({\mathcal {X}},{\mathcal {Y}})=\theta (x_j,y_j)&{}\quad {\text {for }}\quad 1\le j\le k, \hbox {and} \\ x_i^{{{\mathrm{H}}}}y_j=0&{}\quad {\text {for }}\quad 1\le i\le k, k+1\le j\le \ell . \end{array} \end{aligned}$$In particular, \(\varTheta ({{\mathcal {X}}}, {{\mathcal {Y}}})=\varTheta ({{\mathcal {X}}}, \widehat{{\mathcal {Y}}})\), where \(\widehat{{\mathcal {Y}}}={{\mathrm{span}}}\{y_1, y_2,\ldots ,y_k\}\), and the subspace \(\widehat{{\mathcal {Y}}}\) is unique if \(\theta _1({{\mathcal {X}}},{{\mathcal {Y}}})<\pi /2\).
Proof
Let \(X\in {\mathbb {C}}^{N\times k}\) and \(Y\in {\mathbb {C}}^{N\times \ell }\) be orthonormal basis matrices of \({\mathcal {X}}\) and \({\mathcal {Y}}\), respectively. If \(\widehat{{\mathcal {Y}}}\subseteq {\mathcal {Y}}\) with \(\dim (\widehat{{\mathcal {Y}}})=\dim ({{\mathcal {X}}})=k\), then there is \(W\in {\mathbb {C}}^{\ell \times k}\) with orthonormal columns such that \(\widehat{Y}=YW\) is an orthonormal basis matrix of \(\widehat{{\mathcal {Y}}}\). Since \(\cos \theta _j({{\mathcal {X}}},\widehat{{\mathcal {Y}}})\) for \(1\le j\le k\) are the singular values of \(X^{{{\mathrm{H}}}}YW\) which are no bigger than the singular values of \(X^{{{\mathrm{H}}}}Y\), i.e., \(\cos \theta _j({{\mathcal {X}}}, \widehat{{\mathcal {Y}}})\le \cos \theta _j({{\mathcal {X}}},{{\mathcal {Y}}})\) individually, or equivalently, \(\theta _j({\mathcal {X}},\widehat{{\mathcal {Y}}})\ge \theta _j({{\mathcal {X}}},{{\mathcal {Y}}})\) for \(1\le j\le k\). This is item (a).
For item (b), let \(X^{{{\mathrm{H}}}}Y=V\varSigma W^{{{\mathrm{H}}}}\) be the SVD of \(X^{{{\mathrm{H}}}}Y\), where
Then \(XV\) and \(YW\) are orthonormal basis matrices of \({\mathcal {X}}\) and \({\mathcal {Y}}\), respectively, and their columns, denoted by \(x_i\) and \(y_j\), respectively, satisfy the specified requirements in the theorem. If also \(\theta _1({\mathcal {X}},{\mathcal {Y}})<\pi /2\), then all \(\sigma _i>0\) and the first \(k\) columns of \(W\) spans \({\mathcal {R}}(Y^{{{\mathrm{H}}}}X)\) which is unique; so \(\widehat{{\mathcal {Y}}}\) is unique for each given basis matrix \(Y\). We have to prove that \(\widehat{{\mathcal {Y}}}\) is independent of the choosing of \(Y\). Let \(\widetilde{Y}\) be another orthonormal basis matrix of \({\mathcal {Y}}\). Then \(\widetilde{Y}=YZ\) for some \(\ell \times \ell \) unitary matrix \(Z\). Following the above construction for \(\widehat{{\mathcal {Y}}}\), we will have a new \(\widehat{{\mathcal {Y}}}_{{{\mathrm{new}}}}={{\mathcal {R}}}(\widetilde{Y}\widetilde{W}_{(:,1:k)})\), where \(\widetilde{W}\) is from the SVD \(X^{{{\mathrm{H}}}}\widetilde{Y}=\widetilde{V}\varSigma \widetilde{W}^{{{\mathrm{H}}}}\). Notice
which is yet another SVD of \(X^{{{\mathrm{H}}}}\widetilde{Y}\). Thus the columns of \((Z^{{{\mathrm{H}}}}W)_{(:,1:k)}=Z^{{{\mathrm{H}}}}W_{(:,1:k)}\) span the column space of \(\widetilde{Y}^{{{\mathrm{H}}}}X\) which is also spanned by the columns of \(\widetilde{W}_{(:,1:k)}\). Hence \(\widetilde{W}_{(:,1:k)}=Z^{{{\mathrm{H}}}}W_{(:,1:k)}M\) for some nonsingular matrix \(M\), and
which implies \(\widehat{{\mathcal {Y}}}_{{{\mathrm{new}}}}={{\mathcal {R}}}(\widetilde{Y}\widetilde{W}_{(:,1:k)})={\mathcal {R}}(YW_{(:,1:k)})=\widehat{{\mathcal {Y}}}\), as expected. \(\square \)
Proposition 2.2
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be two subspaces in \({\mathbb {C}}^N\) satisfying (2.1), and let \(X\in {\mathbb {C}}^{N\times k}\) be an orthonormal basis matrix of \({\mathcal {X}}\), i.e., \(X^{{{\mathrm{H}}}}X=I_k\). Then
Proof
Let \(Y_{\bot }\in {\mathbb {C}}^{N\times (N-\ell )}\) be an orthonormal basis matrix of the orthogonal complement of \({\mathcal {Y}}\) in \({\mathbb {C}}^N\). We observe that \(\sin \theta _j({\mathcal {X}},{\mathcal {Y}})\) for \(1\le j\le k\) are the singular values of \(X^{{{\mathrm{H}}}}Y_{\bot }\) and thus \(\left|\left|\left|\sin \varTheta ({\mathcal {X}},{\mathcal {Y}})\right|\right|\right|=\left|\left|\left|X^{{{\mathrm{H}}}}Y_{\bot }\right|\right|\right|\). Observe also \(\sin \theta (X_{(:,j)},{\mathcal {Y}})=\left|\left|\left|X_{(:,j)}^{{{\mathrm{H}}}}Y_{\bot }\right|\right|\right|=\Vert X_{(:,j)}^{{{\mathrm{H}}}}Y_{\bot }\Vert _2\). Therefore
They yield both (2.4) and (2.5). For (2.6), we notice
for \(1\le j\le k\). \(\square \)
Proposition 2.3
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be two subspaces in \({\mathbb {C}}^N\) with equal dimension: \(\dim ({\mathcal {X}})=\dim ({\mathcal {Y}})=k\), and let \(X\in {\mathbb {C}}^{N\times k}\) be an orthonormal basis matrix of \({\mathcal {X}}\), i.e., \(X^{{{\mathrm{H}}}}X=I_k\), and \(Y\) be a (not necessarily orthonormal) basis matrix of \({\mathcal {Y}}\) such that each column of \(Y\) is a unit vector, i.e., \(\Vert Y_{(:,j)}\Vert _2=1\) for all \(j\). Then
Proof
Since \(\sin ^2\theta _j({\mathcal {X}},{\mathcal {Y}})\) for \(1\le j\le k\) are the eigenvalues of
we have
as was to be shown. In obtaining (2.8), we have used
because \(X_{(:,j)}^{{{\mathrm{H}}}}Y_{(:,j)}\) is the \(j\)th entry of the vector \(X^{{{\mathrm{H}}}}Y_{(:,j)}\). \(\square \)
Remark 2.1
The inequality (2.7) is about controlling the subspace angle \(\varTheta ({\mathcal {X}},{\mathcal {Y}})\) by the individual angles between corresponding basis vectors. These individual angles depend on the selection of the basis vectors as well as their labelling. By Proposition 2.1(b), it is possible to find basis vectors for both \({\mathcal {X}}\) and \({\mathcal {Y}}\) and match them perfectly such that \(\theta _j({\mathcal {X}},{\mathcal {Y}})\) collectively is the same as all individual angles between corresponding basis vectors. But, on the other hand, it is possible that for two close subspaces in the sense that \(\varTheta ({\mathcal {X}},{\mathcal {Y}})\) is tiny there are unfortunately chosen and labelled basis vectors to make one or more individual angles between corresponding basis vectors near or even \(\pi /2\). In fact, this can happen even when \({\mathcal {X}}={\mathcal {Y}}\). Therefore in general the collection \(\{\theta (X_{(:,j)},Y_{(:,j)}),\,1\le j\le k\}\) cannot be controlled by \(\varTheta ({\mathcal {X}},{\mathcal {Y}})\) without additional information.
Proposition 2.4
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be two subspaces in \({\mathbb {C}}^N\) with equal dimension: \(\dim ({\mathcal {X}})=\dim ({\mathcal {Y}})=k\). Suppose \(\theta _1({\mathcal {X}},{\mathcal {Y}})<\pi /2\).
-
(a)
For any \(\widehat{{\mathcal {Y}}}\subseteq {\mathcal {Y}}\) of dimension \(k_1=\dim (\widehat{{\mathcal {Y}}})\le k\), there is a unique \(\widehat{{\mathcal {X}}}\subseteq {\mathcal {X}}\) of dimension \(k_1\) such that \(P_{{\mathcal {Y}}}\widehat{{\mathcal {X}}}=\widehat{{\mathcal {Y}}}\), where \(P_{{\mathcal {Y}}}\) is the orthogonal projection onto \({\mathcal {Y}}\). Moreover
$$\begin{aligned} \theta _{j+k-k_1}({\mathcal {X}},{\mathcal {Y}})\le \theta _j(\widehat{{\mathcal {X}}},\widehat{{\mathcal {Y}}})\le \theta _j({\mathcal {X}},{\mathcal {Y}})\quad \text{ for } 1\le j\le k_1 \end{aligned}$$(2.9)which implies
$$\begin{aligned} \vert \vert \vert \sin \varTheta (\widehat{{\mathcal {X}}},\widehat{{\mathcal {Y}}})\vert \vert \vert \le \left|\left|\left|\sin \varTheta ({\mathcal {X}},{\mathcal {Y}})\right|\right|\right|\!. \end{aligned}$$ -
(b)
For any set \(\{y_1,y_2,\ldots ,y_{k_1}\}\) of orthonormal vectors in \({\mathcal {Y}}\), there is a set \(\{x_1,x_2,\ldots ,x_{k_1}\}\) of linearly independent vectors in \({\mathcal {X}}\) such that \(P_{{\mathcal {Y}}}x_j=y_j\) for \(1\le j\le k_1\). Moreover (2.9) holds for \(\widehat{{\mathcal {X}}}={{\mathrm{span}}}\{x_1,x_2,\ldots ,x_{k_1}\}\) and \(\widehat{{\mathcal {Y}}}={{\mathrm{span}}}\{y_1,y_2,\ldots ,y_{k_1}\}\).
Proof
Let \(X\in {\mathbb {C}}^{N\times k}\) and \(Y\in {\mathbb {C}}^{N\times k}\) be orthonormal basis matrices of \({\mathcal {X}}\) and \({\mathcal {Y}}\), respectively. \(\widehat{{\mathcal {Y}}}\subseteq {\mathcal {Y}}\) can be represented by its orthonormal basis matrix \(Y\widehat{Y}\), where \(\widehat{Y}\in {\mathbb {C}}^{k\times k_1}\) satisfies \(\widehat{Y}^{{{\mathrm{H}}}} \widehat{Y}=I_{k_1}\). We need to find a \(\widehat{{\mathcal {X}}}\subseteq {\mathcal {X}}\) with the desired property. \(\widehat{{\mathcal {X}}}\subseteq {\mathcal {X}}\) can be represented by its basis matrix (not necessary orthonormal) \(X\widehat{X}\), where \(\widehat{X}\in {\mathbb {C}}^{k\times k_1}\) is nonsingular and to be determined. The equation \(P_{{\mathcal {Y}}}\widehat{{\mathcal {X}}}=\widehat{{\mathcal {Y}}}\) is the same as
because \(\theta _1({\mathcal {X}},{\mathcal {Y}})<\pi /2\) implies \(Y^{{{\mathrm{H}}}}X\) is nonsingular. This proves the existence of \(\widehat{{\mathcal {X}}}={\mathcal {R}}(X\widehat{X})\). Following the argument, one can also prove that this \(\widehat{{\mathcal {X}}}\) is independent of how the orthonormal basis matrices \(X\) and \(Y\) are chosen, and thus unique. To prove (2.9), we note that \(\hat{\sigma }_j:=\cos \theta _j(\widehat{{\mathcal {X}}},\widehat{{\mathcal {Y}}})\) for \(1\le j\le k_1\) are the singular values of
So the eigenvalues of \(\widehat{Y}^{{{\mathrm{H}}}} (Y^{{{\mathrm{H}}}}X)^{-{{\mathrm{H}}}} (Y^{{{\mathrm{H}}}}X)^{-1}\widehat{Y}\) are \(\hat{\sigma }_j^{-2}\) for \(1\le j\le k_1\). On the other hand, \(\sigma _j:=\cos \theta _j({\mathcal {X}},{\mathcal {Y}})\) for \(1\le j\le k\) are the singular values of \(Y^{{{\mathrm{H}}}}X\). So the eigenvalues of \((Y^{{{\mathrm{H}}}}X)^{-{{\mathrm{H}}}}(Y^{{{\mathrm{H}}}}X)^{-1}\) are \(\sigma _j^{-2}\) for \(1\le j\le k\). Use the Cauchy interlacing inequalities [21] to conclude that
which yield (2.9). This proves item (a).
To prove item (b), we pick the orthonormal basis matrix \(Y\) above in such a way that its first \(k_1\) columns are \(y_1,y_2,\ldots ,y_{k_1}\). In (2.10), let \(\widehat{Y}=[e_1,e_2,\ldots ,e_{k_1}]\), i.e., \(\widehat{{\mathcal {Y}}}={{\mathrm{span}}}\{y_1,y_2,\ldots ,y_{k_1}\}\), and let \(\widehat{X}=(Y^{{{\mathrm{H}}}}X)^{-1}\widehat{Y}\). Then \([x_1,x_2,\ldots ,x_{k_1}]:=X\widehat{X}\) gives what we need because of (2.10). \(\square \)
Remark 2.2
The part of Proposition 2.4 on the existence of \(\widehat{{\mathcal {X}}}\) in the case of \(k_1=1\) is essentially taken from [22, Lemma 4].
Remark 2.3
The canonical angles are defined under the standard inner product \(\langle x,y\rangle =x^{{{\mathrm{H}}}}y\) in \({\mathbb {C}}^N\). In a straightforward way, they can be defined under any given \(M\)-inner product \(\langle x,y\rangle _M=x^{{{\mathrm{H}}}}My\), where \(M\in {\mathbb {C}}^{N\times N}\) is Hermitian and positive definite. We will call these angles the \(M\) -canonical angles. All results we have proved in this section are valid in slightly different forms for the \(M\)-canonical angles. Details are omitted.
3 Block Lanczos method
Given \(V_0\in {\mathbb {C}}^{N\times n_b}\) with \({{\mathrm{rank}}}(V_0)=n_b\), the block Lanczos process [5, 9] of Algorithm 1 is the simplest version and will generate an orthonormal basis of the Krylov subspace \({\mathcal {K}}_n(A,V_0)\) as well as a projection of \(A\) onto the Krylov subspace. It is simplest because we assume all \(Z\) at Lines 4 and 8 there have full column rank \(n_b\) for all \(j\). Then \(V_j\in {\mathbb {C}}^{N\times n_b}\), and
the direct sum of \({\mathcal {R}}(V_j)\) for \(j=1,2,\ldots ,n\).

A fundamental relation of the process is
where
\(T_n=Q_n^{{{\mathrm{H}}}}AQ_n\) is the so-called Rayleigh quotient matrix with respect to \({\mathcal {K}}_n\) and it is the projection of \(A\) onto \({\mathcal {K}}_n\), too. Let
which is the orthogonal projection onto \({\mathcal {K}}_n\). In particular \(\varPi _1=Q_1Q_1^{{{\mathrm{H}}}}=V_1V_1^{{{\mathrm{H}}}}\) is the orthogonal projection onto \({\mathcal {R}}(V_0)={\mathcal {R}}(V_1)\).
Basically the block Lanczos method is this block Lanczos process followed by solving the eigenvalue problem for \(T_n\) to obtain approximate eigenpairs for \(A\): any eigenpair \((\tilde{\lambda }_j,w_j)\) of \(T_n\) gives an approximate eigenpair \((\tilde{\lambda }_j, Q_nw_j)\) for \(A\). The number \(\tilde{\lambda }_j\) is called a Ritz value and \(\tilde{u}_j:=Q_nw_j\) a Ritz vector.
We introduce the following notation for \(T_n\) that will be used in the next two sections:

Note the dependency of \(\tilde{\lambda }_j,\,w_j,W\) on \(n\) is suppressed for convenience.
As in Saad [22], there is no loss of generality in assuming that all eigenvalues of \(A\) are of multiplicity not exceeding \(n_b\). In fact, let \(P_j\) be the orthogonal projections onto the eigenspaces corresponding to the distinct eigenvalues of \(A\). Then
is an invariant subspace of \(A\), and \(A_{|{\mathcal {U}}}\), the restriction of \(A\) onto \({\mathcal {U}}\), has the same distinct eigenvalues as \(A\) and the multiplicity of any distinct eigenvalue of \(A_{|{\mathcal {U}}}\) is no bigger than \(n_b\). Since \({\mathcal {K}}_n(A,V_0)\subseteq {\mathcal {U}}\), what the block Lanczos method does is essentially to approximate some of the eigenpairs of \(A_{|{\mathcal {U}}}\).
When \(n_b=1\), Algorithm 1 reduces to the single-vector Lanczos process.
4 Convergence of eigenspaces
Recall \(\varPi _n\) in (3.4), and in particular, \(\varPi _1=Q_1Q_1^{{{\mathrm{H}}}}=V_1V_1^{{{\mathrm{H}}}}\). For the rest of this and the next section, each of \(i\), \(k\), and \(\ell \) will be reserved for one assignment only: we are considering the \(i\)th to \((i+n_b-1)\)st eigenpairs of \(A\) among which the \(k\)th to \(\ell \)th eigenvalues may form a cluster as in

where
Recall (1.3). We are interested in bounding
-
1.
the canonical angles from the invariant subspace \({\mathcal {R}}(U_{(:,k:\ell )})\) to the Krylov subspace \({\mathcal {K}}_n\equiv {\mathcal {K}}_n(A,V_0)\),
-
2.
the canonical angles between the invariant subspace \({\mathcal {R}}(U_{(:,k:\ell )})\) and \({{\mathrm{span}}}\{\tilde{u}_k,\ldots ,\tilde{u}_{\ell }\}\) (which we call a Ritz subspace),
-
3.
the differences between the eigenvalues \(\lambda _j\) and the Ritz values \(\tilde{\lambda }_j\) for \(k\le j\le \ell \).
In doing so, we will use the \(j\)th Chebyshev polynomial of the first kind \({\fancyscript{T}}_j(t)\):
It frequently shows up in numerical analysis and computations because of its numerous nice properties, for example \(|{\fancyscript{T}}_j(t)|\le 1\) for \(|t|\le 1\) and \(|{\fancyscript{T}}_j(t)|\) grows extremely fastFootnote 2 for \(|t|>1\). We will also need [17]
where
In the rest of this section and the entire next section, we will always assume
and \(X_{i,k,\ell }\in {\mathbb {C}}^{N\times (\ell -k+1)}\) is to be defined by (4.5) below. Consider an application of Proposition 2.4(b) with \(k_1=\ell -k+1\),
The application yields a unique
such that \({\mathcal {R}}(X_{i,k,\ell })\subseteq {\mathcal {R}}(V_0)\) and
Moreover, by Proposition 2.4(a),
They show that the chosen \({\mathcal {R}}(X_{i,k,\ell })\) has a significant component in the eigenspace \({\mathcal {R}}(U_{(:,k:\ell )})\) of interest if the initial \({\mathcal {R}}(V_0)\) has a significant component in the eigenspace \({\mathcal {R}}(U_{(:,i:i+n_b-1)})\).
The matrix \(X_{i,k,\ell }\) defined in (4.5) obviously depends on \(n_b\) as well. This dependency is suppressed because \(n_b\) is reserved throughout this article. The idea of picking such \(X_{i,k,\ell }\) is essentially borrowed from [22, Lemma 4] (see Remark 2.2).
Theorem 4.1
For any unitarily invariant norm \(\left|\left|\left|\cdot \right|\right|\right|\), we have
where \(X_{i,k,\ell }\) is defined by (4.5), \(\widetilde{U}\) by (3.5), andFootnote 3
and the constant \(c\) lies between \(1\) and \(\pi /2\), and it isFootnote 4 \(1\) for the Frobenius norm or if \(\tilde{\lambda }_{k-1}>\lambda _k\), and
For the Frobenius norm, \(\gamma \) in (4.13) can be improved to
Proof
Write

For convenience, let’s drop the subscripts to \(X_{i,k,\ell }\) because \(i,k,\ell \) do not change in this proof. We have
by (4.6). Let \(X_0=X(X^{{{\mathrm{H}}}}X)^{-1/2}\) which has orthonomal columns. We know that
since \({\mathcal {R}}(X_0)={\mathcal {R}}(X)\subseteq {\mathcal {R}}(V_0)\). By (4.17),
By (4.6), \(\check{U}_2^{{{\mathrm{H}}}}X=I_{\ell -k+1}\) and thus \(\check{U}_2^{{{\mathrm{H}}}}X_0\) is nonsingular. Now if also \(f(\check{\varLambda }_2)\) is nonsingular (which is true for the selected \(f\) later), then
and consequently by Proposition 2.1
We need to pick an \(f\in {\mathbb {P}}_{n-1}\) to make the right-hand side of (4.20) as small as we can. To this end for the case \(i=1\), we choose
for which
This, together with (4.20), concludes the proof of (4.9) for \(i=1\).
In general for \(i>1\), we shall consider polynomials of form
and search a \(g\in {\mathbb {P}}_{n-i}\) such that \(\max _{i+n_b\le j\le N}|g(\lambda _j)|\) is made as small as we can while \(\min _{k\le j\le \ell }|g(\lambda _j)| =g(\lambda _{\ell })=1\). To this end, we choose
for which
This, together with (4.20) and (4.23), concludes the proof of (4.9) for \(i>1\).
Next we prove (4.10) with an argument influenced by [11]. Recall (4.16). Let \(Q_{\bot }\in {\mathbb {C}}^{N\times (N-nn_b)}\) such that \([Q_n,Q_{\bot }]\) is unitary, and write
where \(Z=Q_n^{{{\mathrm{H}}}}\check{U}_2\), \(Z_{\bot }=Q_{\bot }^{{{\mathrm{H}}}}\check{U}_2\). Then
Keeping in mind that \(A\check{U}_2=\check{U}_2\check{\varLambda }_2\), \(Q_n^{{{\mathrm{H}}}}AQ_n=T_n\), and \(T_nW=W\varOmega \) from (3.5), we have
Similarly to (4.16), partition \(W\) and \(\varOmega \) as

and set \(W_{1,3}:=[W_1,W_3]\) and \(\varOmega _{1,3}:=\varOmega _1 \oplus \varOmega _3\). Multiply (4.28) by \(W^{{{\mathrm{H}}}}\) from the left to get \(\varOmega W^{{{\mathrm{H}}}}Z-W^{{{\mathrm{H}}}}Z \check{\varLambda }_2=-W^{{{\mathrm{H}}}}Q_n^{{{\mathrm{H}}}}AQ_{\bot }Z_{\bot }\), and thus we have
By Lemma 2.1, we conclude that
Let \(\widetilde{U}_{1,3}=Q_nW_{1,3}\). It can be verified that
by (4.26). Therefore
which, for the Frobenius norm, can be improved to an identity
The inequality (4.10) is now a consequence of (4.27), (4.30), and (4.31). \(\square \)
Remark 4.1
Although the appearance of three integers, \(i\), \(k\), and \(\ell \) makes Theorem 4.1 awkward and more complicated than simply taking \(i=k\) or \(i+n_b-1=\ell \), it provides the flexibility when it comes to apply (4.9) with balanced \(\xi _{i,k}\) (which should be made as small as possible) and \(\delta _{i,\ell ,n_b}\) (which should be made as large as possible). In fact, for given \(k\) and \(\ell \), both \(\xi _{i,k}\) and \(\delta _{i,\ell ,n_b}\) increase with \(i\). But the right-hand side of (4.9) increases as \(\xi _{i,k}\) increases and decreases (rapidly) as \(\delta _{i,\ell ,n_b}\) increases. So we would like to make \(\xi _{i,k}\) as small as we can and \(\delta _{i,\ell ,n_b}\) as large as we can. In particular, if \(k\le \ell \le n_b\), one can always pick \(i=1\) so that (4.9) gets used with \(\xi _{1,k}=1\); but then if \(\delta _{1,\ell ,n_b}\) is tiny, (4.9) is better used with some \(i>1\). A general guideline is to make sure \(\{\lambda _j\}_{j=k}^{\ell }\) is a cluster and the rest of \(\lambda _j\) are relatively far away.
5 Convergence of eigenvalues
In this section, we will bound the differences between the eigenvalues \(\lambda _j\) and the Ritz values \(\tilde{\lambda }_j\) for \(k\le j\le \ell \).
Theorem 5.1
Let \(k=i\). For any unitarily invariant norm, we have
where \(\kappa _{i,\ell ,n_b}\) is the same as the one in (4.12), and
In particular, if also \(\tilde{\lambda }_{i-1}\ge \lambda _i\), then
Proof
Upon shifting \(A\) by \(\lambda _iI\) to \(A-\lambda _i I_N\), we may assume \(\lambda _i=0\). Doing so doesn’t change the Krylov subspace \({\mathcal {K}}_n(A,V_0)={\mathcal {K}}_n(A-\lambda _iI,V_0)\) and doesn’t change any eigenvector and any Ritz vector of \(A\), but it does shift all eigenvalues and Ritz values of \(A\) by the same amount, i.e., \(\lambda _i\), and thus all differences \(\lambda _p-\lambda _j\) and \(\lambda _p-\tilde{\lambda }_j\) remain unchanged. Suppose \(\lambda _i=0\) and thus \(\lambda _{i-1}\ge \lambda _i=0\ge \lambda _{i+1}\).
Recall (3.5), and adopt the proof of Theorem 4.1 up to (4.19). Take \(f\) as
where \(g\in {\mathbb {P}}_{n-i}\). We claim \(Y^{{{\mathrm{H}}}}Q_nw_j=0\) for \(1\le j\le i-1\). This is because \(Y\) can be represented by \(Y=(A-\tilde{\lambda }_jI)\widehat{Y}\) for some matrix \(\widehat{Y}\in {\mathbb {C}}^{N\times (\ell -i+1)}\) with \({\mathcal {R}}(\widehat{Y}) \subseteq {\mathcal {K}}_n\) which further implies \(\widehat{Y}=Q_n\check{Y}\) for some matrix \(\check{Y}\in {\mathbb {C}}^{nn_b\times (\ell -i+1)}\). Thus \(Y=(A-\tilde{\lambda }_jI)Q_n\check{Y}\) and
Set
where \(R_j=f(\varLambda _j)U_j^{{{\mathrm{H}}}}X_0\left( \check{U}_2^{{{\mathrm{H}}}} X_0\right) ^{-1}[f(\check{\varLambda }_2)]^{-1}\).
Let \(Z=Y_0(Y_0^{{{\mathrm{H}}}}Y_0)^{-1/2}\), and denote by \(\mu _1\ge \cdots \ge \mu _{\ell -i+1}\) the eigenvalues of \(Z^{{{\mathrm{H}}}}AZ\) which depends on \(f\) in (5.4) to be determined for best error bounds. Note
Write \(Z=Q_n\widehat{Z}\) because \({\mathcal {R}}(Z)\subseteq {\mathcal {K}}_n\), where \(\widehat{Z}\) has orthonormal columns. Apply Cauchy’s interlace inequalities to \(Z^{{{\mathrm{H}}}}AZ=\widehat{Z}^{{{\mathrm{H}}}}(Q_n^{{{\mathrm{H}}}}AQ_n)\widehat{Z}\) and \(Q_n^{{{\mathrm{H}}}}AQ_n\) to get \(\tilde{\lambda }_{i+j-1}\ge \mu _j\) for \(1\le j\le \ell -i+1\), and thus
In particular, this implies \(\mu _j\le \lambda _{i+j-1}\le \lambda _i\le 0\) and consequently \(Y_0^{{{\mathrm{H}}}}AY_0\) is negative semidefinite. Therefore for any nonzero vector \(y\in {\mathbb {C}}^{\ell -i+1}\),
where we have used \(y^{{{\mathrm{H}}}}R_1^{{{\mathrm{H}}}}\varLambda _1R_1y\ge 0\), \(y^{{{\mathrm{H}}}}R_1^{{{\mathrm{H}}}}R_1y\ge 0\), and \(y^{{{\mathrm{H}}}}R_3^{{{\mathrm{H}}}}R_3y\ge 0\). Therefore
Denote by \(\hat{\mu }_1\ge \cdots \ge \hat{\mu }_{\ell -i+1}\) the eigenvalues of \(\check{\varLambda }_2+R_3^{{{\mathrm{H}}}}\varLambda _3R_3\). By (5.8), we know \(\mu _j\ge \hat{\mu }_j\) for \(1\le j\le \ell -i+1\) which, together with (5.7), lead to
Hence for any unitarily invariant norm [16, 23]
where the last inequality is true because (1) \(R_3^{{{\mathrm{H}}}}\varLambda _3R_3\) is negative semi-definite, (2) we shifted \(A\) by \(\lambda _iI\), and (3) the \(j\)th largest eigenvalue of \(R_3^{{{\mathrm{H}}}}(\lambda _iI-\varLambda _3)R_3\) which is positive semi-definite is bounded by the \(j\)th largest eigenvalue of \((\lambda _i-\lambda _N)R_3^{{{\mathrm{H}}}}R_3\).
Denote by \(\sigma _j\) (in descending order) for \(1\le j\le \ell -i+1\) the singular values of \(R_3=f(\varLambda _3)U_3^{{{\mathrm{H}}}}X_0 \left( \check{U}_2^{{{\mathrm{H}}}}X_0\right) ^{-1}[f(\check{\varLambda }_2)]^{-1}\), and by \(\hat{\sigma }_j\) (in descending order) for \(1\le j\le \ell -i+1\) the singular values of \(U_3^{{{\mathrm{H}}}}X_0\left( \check{U}_2^{{{\mathrm{H}}}}X_0\right) ^{-1}\). Then \(\hat{\sigma }_j\) is less than or equal to the \(j\)th largest singular value of \(\begin{bmatrix} U_1^{{{\mathrm{H}}}}X_0\left( \check{U}_2^{{{\mathrm{H}}}}X_0\right) ^{-1} \\ U_3^{{{\mathrm{H}}}}X_0\left( \check{U}_2^{{{\mathrm{H}}}}X_0\right) ^{-1} \end{bmatrix}\), which is \(\tan \theta _j(\check{U}_2,X)\). We have
What remains to be done is to pick \(f\in {\mathbb {P}}_{n-1}\) to make the right-hand side of (5.11) as small as we can.
For the case of \(i=1\), we choose \(f\) as in (4.21), and then (4.22) holds. Finally combining (5.10) and (5.11) with (4.22) leads to (5.1) for the case \(i=1\).
In general for \(i>1\), we take \(f(t)\) as in (5.4) with \(g(t)\) given by (4.24) satisfying (4.25), together again with (5.10) and (5.11), to conclude the proof. \(\square \)
Remark 5.1
In Theorem 5.1, \(k=i\) always, unlike lin Theorem 4.1, because we need the first equation in (5.6) for our proof to work.
6 A comparison with the existing results
The existing results related to our results in the previous two sections include those by Kaniel [12], Paige [20], and Saad [22] (see also Parlett [21]). The most complete and strongest ones are in Saad [22].
In comparing ours with Saad’s results, the major difference is that ours are of the eigenspace/eigenvalue cluster type while Saad’s results are of the single-vector/eigenvalue type. When specialized to an individual eigenvector/eigenvalue, our results reduce to those of Saad. Specifically, for \(k=\ell =i\) the inequality (4.9) becomes Saad [22, Theorem 5] and Theorem 5.1 becomes Saad [22, Theorem 6]. Certain parts of our proofs bear similarities to Saad’s proofs for the block case, but there are subtleties in our proofs that cannot be handled in a straightforward way following Saad’s proofs.
It is well-known [7] that eigenvectors associated with eigenvalues in a tight cluster are sensitive to perturbations/rounding errors while the whole invariant subspace associated with the cluster is not so much. Therefore it is natural to treat the entire invariant subspace as a whole, instead of each individual eigenvectors in the invariant subspace separately.
In what follows, we will perform a brief theoretical comparison between our results and those of Saad, and point out when Saad’s bounds may be too large. Numerical examples in the next section support this comparison.
As mentioned, Saad’s bounds are of the single-vector/eigenvalue type. So a direct comparison cannot be done. But it is possible to derive some bounds for eigenspaces/eigenvalue clusters from Saad’s bounds, except that these derived bounds are less elegant and (likely) less sharp (which we will demonstrate numerically in Sect. 7). One possible derivation based on [22, Theorem 5] may be as follows. By Proposition 2.2,
These inequalities imply that the largest \(\sin \theta (u_j,{\mathcal {K}}_n)\) is comparable to \(\sin \varTheta (U_{(:,k:\ell )},{\mathcal {K}}_n)\), and thus finding good bounds for all \(\sin \theta (u_j,{\mathcal {K}}_n)\) is comparably equivalent to finding a good bound for \(\sin \varTheta (U_{(:,k:\ell )},{\mathcal {K}}_n)\).
The right-most sides of (6.1) and (6.2) can be bounded, using [22, Theorem 5] (i.e., the inequality (4.9) for the case \(k=\ell =i\)). In the notation of Theorem 4.1, we have, for \(k\le j\le \ell \),
and use \(\sin \theta \le \tan \theta \) to get
where \(X_{j,j,j}\in {\mathbb {C}}^N\) are as defined right before Theorem 4.1, and \(\kappa _{j,j,n_b}\) are as defined in Theorem 4.1. If \(\theta _1(U_{(:,k:\ell )},{\mathcal {K}}_n)\) is not too close to \(\pi /2\) which we will assume, the left-hand sides of (4.9), (6.4), and (6.5) are comparable by Proposition 2.2, but there isn’t any easy way to compare their right-hand sides. Nevertheless, we argue that the right-hand side of (4.9) is preferable. First it is much simpler; Second, it is potentially much sharper for two reasons:
-
1.
One or more \(\xi _{j,j}\) for \(k\le j\le \ell \) in (6.4) and (6.5) may be much bigger than \(\xi _{i,k}\) in (4.9).
-
2.
By Proposition 2.3, \(\varTheta (U_{(:,k:\ell )},[X_{k,k,k},\ldots ,X_{\ell ,\ell ,\ell }])\) can be bounded in terms of the angles in \(\{\theta (u_j,X_{j,j,j}),\,k\le j\le \ell \}\) but not the other way around, i.e., together \(\{\theta (u_j,X_{j,j,j}),\,k\le j\le \ell \}\) cannot be bounded by something in terms of
$$\begin{aligned} \varTheta (U_{(:,k:\ell )},[X_{k,k,k},\ldots ,X_{\ell ,\ell ,\ell }]) \end{aligned}$$in general as we argued in Remark 2.1.
For bounding errors between eigenvectors \(u_j\) and Ritz vectors \(\tilde{u}_j\), the following inequality was established in [22, Theorem3] (which is also true for the block Lanczos method as commented there [22, p. 703]):
This inequality can grossly overestimate \(\sin \theta (u_{j},\tilde{u}_j)\) even with the “exact” (i.e., computed) \(\sin \theta (u_{j},\mathcal {K}_n)\) for the ones associated with a cluster of eigenvalues due to possibly extremely tiny gap \(\min _{p\ne j}|\lambda _j-\tilde{\lambda }_p|\), not to mention after using (6.3) to bound \(\sin \theta (u_{j},\mathcal {K}_n)\). By Proposition 2.3, we have
Inherently any bound derived from bounds for all \(\sin ^2\theta (u_{j},\tilde{u}_j)\) likely very much overestimates \(\Vert \sin \varTheta (U_{(:,k:\ell )},\widetilde{U}_{(:,k:\ell )})\Vert _{{{\mathrm{F}}}}^2\) because there is no simply way to bound \(\sum _{j=k}^{\ell }\sin ^2\theta (u_{j},\tilde{u}_j)\) in terms of \(\Vert \sin \varTheta (U_{(:,k:\ell )},\widetilde{U}_{(:,k:\ell )})\Vert _{{{\mathrm{F}}}}^2\), i.e., the former may already be much bigger than the latter, as we argued in Remark 2.1. So we anticipate the bounds of (6.7) and (6.8) to be bad when \(\lambda _j\) with \(k\le j\le \ell \) form a tight cluster.
Saad [22, Theorem 6] provides a bound on \(\lambda _j-\tilde{\lambda }_j\) individually. The theorem is the same as our Theorem 5.1 for the case \(k=\ell =i\). Concerning the eigenvalue cluster \(\{\lambda _k,\ldots ,\lambda _{\ell }\}\), Saad’s theorem gives
This bound, too, could be much bigger than the one of (5.1) because of one or more \(\zeta _j\) with \(k=i\le j\le \ell \) are much bigger than \(\zeta _i\).
7 Numerical examples
In this section, we shall numerically test the effectiveness of our upper bounds on the convergence of the block Lanczos method in the case of a cluster. In particular, we will demonstrate that our upper bounds are preferable to those of the single-vector/eigenvalue type in Saad [22], especially in the case of a tight cluster. Specifically,
-
(a)
the subspace angle \(\varTheta (U_{(:,k:\ell )},X_{i,k,\ell })\) used in our bounds is more reliable than the individual angles in \(\{\theta (u_j,X_{j,j,j}),\,k\le j\le \ell \}\) together to bound \(\varTheta (U_{(:,k:\ell )},\mathcal {K}_n)\) (see remarks in Sect. 6), and
-
(b)
our upper bounds are much sharper than those derived from Saad’s bounds in the presence of tight clusters of eigenvalues.
We point out that the worst individual bound of (6.3) or (6.6) or for \(\lambda _j-\tilde{\lambda }_j\) is at the same magnitude as the derived bound of (6.5) or (6.8) or (6.9), respectively. So if a derived bound is bad, the worst corresponding individual bound cannot be much better. For this reason, we shall focus on comparing our bounds to the derived bounds in Sect. 6.
Our first example below is intended to illustrate the first point (a), while the second example supports the second point (b). The third example is essentially taken from [22], again to show the effectiveness of our upper bounds.
We implemented the block Lanczos method within MATLAB, with full reorthogonalization to simulate the block Lanczos method in exact arithmetic. This is the best one can do in a floating point environment. In our tests, without loss of generality, we take
with special eigenvalue distributions to be specified later. Although we stated our theorems in unitarily invariant norms for generality, our numerical results are presented in terms of the Frobenius norm for easy understanding (and thus for Theorem 4.1, \(\gamma \) by (4.15) is used). No breakdown was encountered during all Lanczos iterations.
We will measure the following errors: (in all examples, \(k=i=1\) and \(\ell =n_b=3\))
for their numerically observed values (considered as “exact”), bounds of Theorems 4.1 and 5.1, and derived bounds of (6.9), (6.8) and (6.5) considered as “Saad’s bounds” for comparison purpose. Rigorously speaking, these are not Saad’s bounds.
For very tiny \(\theta _1(U_{(:,k:\ell )},{\mathcal {K}}_n)\), \(\epsilon _3\approx \epsilon _4\) since
Indeed in the examples that follows, the difference between \(\epsilon _3\) and \(\epsilon _4\) is so tiny that we can safely ignore their difference. Therefore we will be focusing on \(\epsilon _1\), \(\epsilon _2\), and \(\epsilon _3\), but not \(\epsilon _4\).
Example 7.1
We take \(N=600\), the number of Lanczos steps \(n=20\), and
and set \(i=k=1,\ell =3\) and \(n_b=3\). There are two eigenvalue clusters: \(\{\lambda _1,\lambda _2,\lambda _3\}\) and \(\{\lambda _4,\dots ,\lambda _N\}\). We are seeking approximations related to the first cluster \(\{\lambda _1,\lambda _2,\lambda _3\}\). The gap \(0.5\) between eigenvalues within the first cluster is to ensure that our investigation for our point (a) will not be affected too much by the eigenvalue closeness in the cluster. The effect of the closeness is, however, the subject of Example 7.2.
Our first test run is with a special \(V_0\) given by
Table 1 reports \(\epsilon _1\), \(\epsilon _2\), and \(\epsilon _3\) and their bounds. Our bounds are very sharp—comparable to the observed ones, but the ones by (6.9), (6.8) and (6.5) overestimate the true errors too much to be of much use. Looking at (6.5) carefully, we find two contributing factors that make the resulting bound too big. The first contributing factor is the constants
The second contributing factor is the angles \(\theta (u_j,X_{j,j,j})\) for \(k\le j\le \ell \):

What we see is that the canonical angles \(\theta _j(U_{(:,k:\ell )}, X_{i,k,\ell })\) are bounded away from \(\pi /2\) but the last two of the angles \(\theta (u_{j},X_{j,j,j})\) are nearly \(\pi /2=1.57080\). This of course has something to do with the particular initial \(V_0\) in (7.2). But given the exact eigenvectors are \(e_1,e_2,e_3\), this \(V_0\) should not be considered a deliberate choice so as to simply make our bounds look good.
Similar reasons explain why the upper bounds of (6.9) and (6.8) are poor as well. In fact, now the first contributing factor is
and then again the set of angles \(\theta (u_j,X_{j,j,j})\) for \(k\le j\le \ell \) is the second contributing factor.
Next we test random initial \(V_0\) as generated by randn \((N,n_b)\) in MATLAB. Table 2 reports the averages of the same errors/bounds as reported before over \(20\) test runs. The bounds of (6.9), (6.8) and (6.5) are much better now, but still about 1,000 times bigger than ours. The following table displays the canonical angles \(\theta _j(U_{(:,k:\ell )},X_{i,k,\ell })\) as well as \(\theta (u_{j},X_{j,j,j})\).

It shows that the randomness in \(V_0\) makes none of \(\theta (u_{j},X_{j,j,j})\) for \(k\le j\le \ell \) as close to \(\pi /2\) as \(V_0\) in (7.2) does. In fact, they are about at the same level as the canonical angles \(\theta _j(U_{(:,k:\ell )},X_{i,k,\ell })\). Therefore, the sole contributing factor that makes the bounds of (6.9), (6.8), and (6.5), worse than ours are the \(\xi \)’s and \(\zeta \)’s in (7.3) and (7.4).
Example 7.2
Let \(N=1{,}000, n=25\), and
and again set \(i=k=1,\ell =3\), \(n_b=3\). We will adjust the parameter \(\delta >0\) to control the tightness among eigenvalues within the cluster \(\{\lambda _1,\lambda _2,\lambda _3\}\) and to see how it affects the upper bounds and the convergence rate of the block Lanczos method. We will demonstrate that our bounds which are of the eigenspace/eigenvalue cluster type are insensitive to \(\delta \) and barely change as \(\delta \) goes to \(0\), while “Saad’s bounds” are very sensitive and quickly become useless as \(\delta \) goes to \(0\). We randomly generate initial \(V_0\) and investigate the average errors/bounds over \(20\) test runs. Since the randomness will reduce the difference in contributions by \(\varTheta (U_{(:,k:\ell )}, X_{i,k,\ell })\) and by \(\theta (u_{j},X_{j,j,j})\) as we have seen in Example 7.1, the gap \(\delta \) within the cluster and the gap between the cluster and the rest of the eigenvalues are the only contributing factor for approximation errors \(\epsilon _i\).
Table 3 reports the averages of the errors defined in 7.1 and the averages of their bounds of Theorems 4.1 and 5.1 and “Saad’s bounds” of (6.9), (6.8) and (6.5) over 20 test runs. From the table, we observed that
-
(i)
all of our bounds which are of the eigenspace/eigenvalue cluster type are rather sharp—comparable to the observed (“exact”) errors, and moreover, they seem to be independent of the parameter \(\delta \) as it becomes tinier and tinier;
-
(ii)
as \(\delta \) gets tinier and tinier, the “Saad’s bounds” of (6.9), (6.8), and (6.5) increase dramatically and quickly contain no useful information for \(\delta =10^{-3}\) or smaller.
To explain the observation (ii), we first note that \(\xi _{j,j}\) in (6.5) are given by
They grow uncontrollably to \(\infty \) as \(\delta \) goes to \(0\). Therefore, the “Saad’s bound” of (6.5) is about \(\mathcal {O}(\delta ^{-2})\) for tiny \(\delta \). Similarly, since \(\xi _{j,j}\) and \(\zeta _j\) are almost of the same level, it can be seen from (6.9) that the “Saad’s bound” for \(\epsilon _1\) is about \(\mathcal {O}(\delta ^{-4})\). For (6.8), when \(n\) is moderate, \(\chi _j\) is about \(\mathcal {O}(\delta ^{-1})\), and therefore, “Saad’s bound” for \(\epsilon _2\) is about \(\mathcal {O}(\delta ^{-3})\) for tiny \(\delta \).
We argued in Sect. 6 that Saad’s bound on \(\theta (u_{j},\tilde{u}_j)\) can be poor in a tight cluster of eigenvalues. Practically, it is also unreasonable to expect it to go as tiny as the machine’s unit roundoff \(\varvec{u}\) as the number of Lanczos steps increases. For this example, by the Davis-Kahan \(\sin \theta \) theorem [7] (see also [23]), we should expect, for \(1\le j\le 3\),
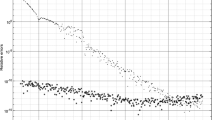
where \({\mathcal {O}}({\varvec{u}}/{\delta })\) is due to machine’s roundoff and can dominate the Lanczos approximation error after certain number of Lanczos steps. To illustrate this point, we plot, in Fig. 1,
as \(\delta \) varies from \(10^{-1}\) down to \(10^{-11}\). Also plotted are its two upper bounds \(\beta _1\) and \(\beta _2\) of (6.7) and (6.8)
as well as the observed values of \(\epsilon _2=\Vert \sin \varTheta (U_{(:,k: \ell )},\widetilde{U}_{(:,k:\ell )})\Vert _{{{\mathrm{F}}}}\) defined in (7.1b) and its upper bounds of (4.11). From the figure, we see that the observed \(\epsilon _5\) is about \(10^{-7}\) for \(\delta \ge 10^{-7}\) and then starts to deteriorate from about \(10^{-7}\) up to \(10^{-3}\) as \(\delta \) goes down to \(10^{-8}\) or smaller. At the same time, the magnitudes of \(\epsilon _2\) and its bound of (4.11) remain unchanged around \(10^{-7}\). This supports our point that one should measure the convergence of the entire invariant subspace corresponding to tightly clustered eigenvalues rather than their each individual eigenvector within the subspace.
Observed \(\epsilon _5\) deteriorates as \(\delta \) goes to \(0\) while \(\epsilon _2\) seems to remain unchanged in magnitude. “Saad’s bounds” on \(\epsilon _5\) are not included in the left plot in order not to obscure the radical difference between \(\epsilon _2\) and \(\epsilon _5\) for tiny \(\delta \)
Example 7.3
Our last example is from [22]:

Since the first three eigenvalues are in a cluster, we take \(i=k=1,\ell =3\) and \(n_b=3\). Saad [22] tested this problem for \(N=60\) and \(n=12\). We ran our code with various \(N\), including \(N=60\) and saw little variations in observed errors and their bounds. What we report in Table 4 is for \(N=900\) and \(n=12\).
The table shows that our bounds very much agree with the corresponding observed values but “Saad’s bounds” are much bigger — about the square roots of the observed values and our bounds. This is due mainly to the small gap between \(\lambda _2\) and \(\lambda _3\) since we observed that \(\theta _j(U_{(:,k:\ell )}, X_{i,k,\ell })\approx \theta (u_{j}, X_{j,j,j})\approx 1.51303\) for \(j=1,2,3\).
8 More bounds
The numerical examples in the previous section indicate that \(\xi _{i,k}\) in Theorem 4.1 and \(\zeta _i\) in Theorem 5.1 can worsen the error bounds, especially in the case of tightly clustered eigenvalues. However, both can be made \(1\) if only the first \(n_b\) eigenpairs are considered (see Remark 4.1). To use Theorems 4.1 or 5.1 for eigenvalues/eigenvectors involving eigenpairs beyond the first \(n_b\) ones, we have to have \(\xi _{i,k}\) or \(\zeta _i\) in the mix. Thus potentially the resulting bounds may overestimate too much to be indicative.
Another situation in which the bounds of Theorems 4.1 or 5.1 would overestimate the actual quantities (by too much) is when there are clustered eigenvalues with cluster sizes bigger than \(n_b\), because then \(\delta _{i,\ell ,n_b}\) is very tiny for any choices of \(i\), \(k\), and \(\ell \). Ye [25] proposed an adaptive strategy to use variable \(n_b\) aiming at updating \(n_b\) adaptively so that it is bigger than or equal to the biggest cluster size of interest.
In what follows, we propose more error bounds with \(\xi _{i,k}\) and \(\zeta _i\) always \(1\). However, it requires the knowledge of the canonical angles from the interested eigenspace to \({\mathcal {K}}_i(A,V_0)\), where \(i<n\) is a positive integer. Roughly speaking, the new results show that if the eigenspace is not too far from \({\mathcal {K}}_i(A,V_0)\) for some \(i<n\) (in the sense that no canonical angle is too near \(\pi /2\)), the canonical angles from the eigenspace to \({\mathcal {K}}_n(A,V_0)\) are reduced by a factor purely depending upon the optimal polynomial reduction.
To proceed, we let \(i<n\). Now we are considering the \(1\)st to \((in_b)\)th eigenpairs of \(A\) among which the \(k\)th to \(\ell \)th eigenvalues may form a cluster as in

where
Suppose \(\theta _1(U_{(:,1:in_b)},Q_i)=\theta _1(U_{(:, 1:in_b)},{\mathcal {K}}_i(A,V_0))<\pi /2\), i.e.,
Consider an application of Proposition 2.4(b) with \(k_1=\ell -k+1\),
The application yields a unique
such that \({\mathcal {R}}(Z_{i,k,\ell })\subseteq {\mathcal {R}}(Q_i)\) and
Moreover
Finally, we observe that
The rest is the straightforward application of Theorems 4.1 and 5.1 to \({\mathcal {K}}_{n-i+1}(A,Q_i)\).
Theorem 8.1
For any unitarily invariant norm \(\left|\left|\left|\cdot \right|\right|\right|\), we have
where \(Z_{i,k,\ell }\) is defined by (8.2), \(\widetilde{U}\) by (3.5), and
and \(\gamma \) takes the same form as in (4.13) with, again, the constant \(c\) lying between \(1\) and \(\pi /2\) and being \(1\) for the Frobenius norm or if \(\tilde{\lambda }_{k-1}>\lambda _k\), and with \(\eta \) being the same as the one in (4.14). For the Frobenius norm, \(\gamma \) can be improved to the one in (4.15).
Theorem 8.2
Let \(k=1\). For any unitarily invariant norm, we have
where \(\hat{\kappa }_{i,\ell ,n_b}\) is the same as the one in (8.10).
9 Conclusions
We have established a new convergence theory for solving large scale Hermitian eigenvalue problem by the block Lanczos method from a perspective of bounding approximation errors in the entire eigenspace associated with all eigenvalues in a tight cluster, in contrast to bounding errors in each individual approximate eigenvector as was done in Saad [22]. In a way, this is a natural approach to follow because the block Lanczos method is known to be capable of computing multiple/cluster eigenvalues much faster than the single-vector Lanczos method (which will miss all but one copy of each multiple eigenvalue). The outcome is three error bounds on
-
1.
the canonical angles from the eigenspace to the generated Krylov subspace,
-
2.
the canonical angles between the eigenspace and its Ritz approximate subspace,
-
3.
the total differences between the eigenvalues in the cluster and their corresponding Ritz values.
These bounds are much sharper than the existing ones and expose true rates of convergence of the block Lanczos method towards eigenvalue clusters, as illustrated by numerical examples. Furthermore, their sharpness is independent of the closeness of eigenvalues within a cluster.
As is well-known, the (block) Lanczos method favors the eigenvalues at both ends of the spectrum. So far, we have only focused on the convergence of the few largest eigenvalues and their associated eigenspaces, but as is usually done, applying what we have established to the eigenvalue problem for \(-A\) will lead to various convergence results for the few smallest eigenvalues and their associated eigenspaces.
All results are stated in terms of unitarily invariant norms for generality, but specializing them to the spectral norm and the Frobenius norm will be sufficient for all practical purposes. Those results can also be extended to the generalized eigenvalue problem without much difficulty [19, Sect. 9].
Notes
If \(k=\ell \), we may say that these angles are between \({\mathcal {X}}\) and \({\mathcal {Y}}\).
In fact, a result due to Chebyshev himself says that if \(p(t)\) is a polynomial of degree no bigger than \(j\) and \(|p(t)|\le 1\) for \(-1\le t\le 1\), then \(|p(t)|\le |{\fancyscript{T}}_j(t)|\) for any \(t\) outside \([-1,1]\) [4, p. 65].
By convention, \(\prod _{j=1}^0(\cdots )\equiv 1\).
A by-product of this is that \(c=1\) if \(k=\ell \).
References
Bhatia, R.: Matrix Analysis. Graduate Texts in Mathematics, vol. 169. Springer, New York (1996)
Bhatia, R., Davis, C., Koosis, P.: An extremal problem in Fourier analysis with applications to operator theory. J. Funct. Anal. 82, 138–150 (1989)
Bhatia, R., Davis, C., McIntosh, A.: Perturbation of spectral subspaces and solution of linear operator equations. Linear Algebra Appl. 52–53, 45–67 (1983)
Cheney, E.W.: Introduction to Approximation Theory, 2nd edn. Chelsea Publishing Company, New York (1982)
Cullum, J.K., Donath, W.E.: A block Lanczos algorithm for computing the \(q\) algebraically largest eigenvalues and a corresponding eigenspace of large, sparse, real symmetric matrices. In: Decision and Control including the 13th Symposium on Adaptive Processes, 1974 IEEE Conference on, vol. 13, pp. 505–509 (1974)
Cullum, J.K., Willoughby, R.A.: Lanczos Algorithms for Large Symmetric Eigenvalue Computations, vol. I: Theory. SIAM, Philadelphia (2002)
Davis, C., Kahan, W.: The rotation of eigenvectors by a perturbation. III. SIAM J. Numer. Anal. 7, 1–46 (1970)
Demmel, J.: Applied Numerical Linear Algebra. SIAM, Philadelphia (1997)
Golub, G.H., Underwood, R.R.: The block Lanczos method for computing eigenvalues. In: Rice, J.R. (ed.) Mathematical Software III, pp. 361–377. Academic Press, New York (1977)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore (1996)
Jia, Z., Stewart, G.W.: An analysis of the Rayleigh–Ritz method for approximating eigenspaces. Math. Comput. 70, 637–647 (2001)
Kaniel, S.: Estimates for some computational techniques in linear algebra. Math. Comput. 20(95), 369–378 (1966)
Kuijlaars, A.B.J.: Which eigenvalues are found by the Lanczos method? SIAM J. Matrix Anal. Appl. 22(1), 306–321 (2000)
Kuijlaars, A.B.J.: Convergence analysis of Krylov subspace iterations with methods from potential theory. SIAM Rev. 48(1), 3–40 (2006)
Lanczos, C.: An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Nat. Bur. Standards 45, 255–282 (1950)
Li, R.C.: Matrix perturbation theory. In: Hogben, L., Brualdi, R., Greenbaum, A., Mathias, R. (eds.) Handbook of Linear Algebra, p. Chapter 15. CRC Press, Boca Raton (2006)
Li, R.C.: On Meinardus’ examples for the conjugate gradient method. Math. Comput. 77(261), 335–352 (2008). Electronically published on September 17, 2007
Li, R.C.: Sharpness in rates of convergence for symmetric Lanczos method. Math. Comput. 79(269), 419–435 (2010)
Li, R.C., Zhang, L.H.: Convergence of block Lanczos method for eigenvalue clusters. Technical Report 2013–03, Department of Mathematics, University of Texas at Arlington (2013). Available at http://www.uta.edu/math/preprint/
Paige, C.C.: The computation of eigenvalues and eigenvectors of very large sparse matrices. Ph.D. thesis, London University, London, England (1971)
Parlett, B.N.: The symmetric eigenvalue problem. SIAM, Philadelphia (1998). This SIAM edition is an unabridged, corrected reproduction of the work first published by Prentice-Hall Inc. Englewood Cliffs, New Jersey (1980)
Saad, Y.: On the rates of convergence of the Lanczos and the block-Lanczos methods. SIAM J. Numer. Anal. 15(5), 687–706 (1980)
Stewart, G.W., Sun, J.G.: Matrix Perturbation Theory. Academic Press, Boston (1990)
Wedin, P.Å.: On angles between subspaces. In: Kågström, B., Ruhe, A. (eds.) Matrix Pencils, pp. 263–285. Springer, New York (1983)
Ye, Q.: An adaptive block Lanczos algorithm. Numer. Algoritm. 12, 97–110 (1996)
Acknowledgments
The authors are grateful to both reviewers for their constructive comments/suggestions that improve the presentation considerably. Li is supported in part by NSF grants DMS-1115834 and DMS-1317330, and a Research Gift grant from Intel Corporation, and and NSFC grant 11428104. Zhang is supported in part by NSFC grants 11101257, 11371102, and the Basic Academic Discipline Program, the 11th five year plan of 211 Project for Shanghai University of Finance and Economics.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, RC., Zhang, LH. Convergence of the block Lanczos method for eigenvalue clusters. Numer. Math. 131, 83–113 (2015). https://doi.org/10.1007/s00211-014-0681-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-014-0681-6