Abstract
In this paper, we present a new variational integrator for problems in Lagrangian mechanics. Using techniques from Galerkin variational integrators, we construct a scheme for numerical integration that converges geometrically, and is symplectic and momentum preserving. Furthermore, we prove that under appropriate assumptions, variational integrators constructed using Galerkin techniques will yield numerical methods that are arbitrarily high-order. In particular, if the quadrature formula used is sufficiently accurate, then the resulting Galerkin variational integrator has a rate of convergence at the discrete time-steps that is bounded below by the approximation order of the finite-dimensional function space. In addition, we show that the continuous approximating curve that arises from the Galerkin construction converges on the interior of the time-step at half the convergence rate of the solution at the discrete time-steps. We further prove that certain geometric invariants also converge with high-order, and that the error associated with these geometric invariants is independent of the number of steps taken. We close with several numerical examples that demonstrate the predicted rates of convergence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There has been significant recent interest in the development of structure-preserving numerical methods for variational problems. One of the key points of interest is developing high-order symplectic integrators for Lagrangian systems. The generalized Galerkin framework has proven to be a powerful theoretical and practical tool for developing such methods. This paper presents a high-order Galerkin variational integrator for Lagrangian systems on vector spaces that exhibits geometric convergence. In addition, this method is symplectic, momentum-preserving, and stable even for very large time-steps.
Galerkin variational integrators fall into the general framework of discrete mechanics. For a general and comprehensive introduction to the subject, the reader is referred to Marsden and West [35]. Discrete mechanics develops mechanics from discrete variational principles, and, as Marsden and West demonstrated, gives rise to many discrete structures which are analogous to structures found in classical mechanics. By taking these structures into account, discrete mechanics suggests numerical methods which often exhibit excellent long-term stability and qualitative behavior. Because of these qualities, much recent work has been done on developing numerical methods from the discrete mechanics viewpoint. See, for example, Hairer et al. [17] for a broad overview of the field of geometric numerical integration, and Marsden and West [35]; Müller and Ortiz [38]; Patrick and Cuell [40] discuss the error analysis of variational integrators. Various extensions have also been considered, including, Lall and West [22]; Leok and Zhang [31] for Hamiltonian systems; Fetecau et al. [15] for nonsmooth problems with collisions; Lew et al. [32]; Marsden et al. [36] for Lagrangian PDEs; Cortés and Martínez [9]; Fedorov and Zenkov [14]; McLachlan and Perlmutter [37] for nonholonomic systems; Bou-Rabee and Owhadi [5, 6] for stochastic Hamiltonian systems; Bou-Rabee and Marsden [4]; Lee et al. [25, 26] for problems on Lie groups and homogeneous spaces.
The fundamental object in discrete mechanics is the discrete Lagrangian \(L_{d}: Q \times Q \times {\mathbb {R}} \rightarrow {\mathbb {R}}\), where \(Q\) is a configuration manifold. Denoting points in the configuration manifold as \(q\), and time dependent curves through the configuration manifold as \(q(t)\), the discrete Lagrangian is chosen to be an approximation to the action of a Lagrangian over the time-step \([0,h]\),
or simply \(L_{d}(q_{0},q_{1})\) when \(h\) is assumed to be constant. Discrete mechanics is formulated by finding stationary points of a discrete action sum based on the sum of discrete Lagrangians,
For Galerkin variational integrators specifically, the discrete Lagrangian is induced by constructing a discrete approximation of the action integral over the interval \([0,h]\) based on an \((n+1)\)-dimensional function space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\), and quadrature rule, \(h\sum _{j=1}^{m} b_{j}f\left( c_{j}h\right) \approx \int _{0}^{h}f(t)\hbox {d}t\). Once this discrete action is constructed, the discrete Lagrangian can be recovered by solving for stationary points of the discrete action subject to fixed endpoints, and then evaluating the discrete action at these stationary points,
Because the rate of convergence of the approximate flow to the true flow is related to how well the discrete Lagrangian approximates the true action, this type of construction gives a method for constructing and analyzing high-order methods. The hope is that the discrete Lagrangian inherits the accuracy of the function space used to construct it, much in the same way as standard finite-element methods. We will show that for certain Lagrangians, Galerkin constructions based on high-order approximation spaces do in fact result in correspondingly high-order methods.
Significant work has already been done constructing and analyzing high-order variational integrators. In Leok [28], a number of different possible constructions based on the Galerkin framework are presented. In Leok and Shingel [29], piecewise Hermite polynomials are used to construct high-order methods using a collocation method on the prolongation of the Euler–Lagrange vector field. In Leok and Shingel [30], a general construction is presented for converting a one-step method of a given order into a variational integrator of the same order. What separates this work from the work that precedes it is
-
(1)
the use of the spectral approximation paradigm, which induces methods that exhibit geometric convergence;
-
(2)
theorems establishing lower bounds on the rate of convergence for a general class of Galerkin variational integrators, and providing explicit conditions under which convergence is guaranteed;
-
(3)
an examination of the rate of convergence of continuous approximations on the interior of the time-step;
-
(4)
an examination of the behavior of geometric invariants along these continuous approximations on the interior of the time-step.
We summarize our major results below:
-
(1)
If \(Q\) is a vector space, for Lagrangians of the canonical form
$$\begin{aligned} L\left( q,\dot{q}\right) = \frac{1}{2}\dot{q}^{T}M\dot{q} - V\left( q\right) \!, \end{aligned}$$Galerkin methods can be used to construct variational integrators of arbitrarily high-order.
-
(2)
If \(Q\) is a vector space, for an arbitrary Lagrangian \(L:TQ\rightarrow {\mathbb {R}}\), if the Lagrangian is sufficiently smooth and the stationary point of the action is a minimizer, Galerkin methods can be used to construct variational integrators of arbitrarily high-order.
-
(3)
If \(Q\) is a vector space, for Lagrangians of the form
$$\begin{aligned} L\left( q,\dot{q}\right) = \frac{1}{2}\dot{q}^{T}M\dot{q} - V\left( q\right) \!, \end{aligned}$$spectral Galerkin methods can be used to construct variational integrators which converge geometrically.
-
(4)
If \(Q\) is a vector space, for an arbitrary Lagrangian \(L:TQ\rightarrow {\mathbb {R}}\), if the Lagrangian is sufficiently smooth and the stationary point of the action is a minimizer, spectral Galerkin methods can be used to construct variational integrators which converge geometrically.
-
(5)
If \(Q\) is a vector space, it is possible to recover a continuous approximation to the flow on the interior of the time-step from a Galerkin variational integrator which has error \({\mathcal {O}}(h^{\frac{p}{2}})\) for a Galerkin variational integrator with local error \({\mathcal {O}}(h^{p})\), or which converges geometrically for a spectral Galerkin variational integrator with geometric convergence.
-
(6)
If the Galerkin variational integrator shares a symmetry with the Lagrangian \(L\), then the geometric invariant resulting from that symmetry is preserved up to a fixed error along the continuous approximation on the interior of the time-step. This error is independent of the number of time-steps taken.
We will present these results with greater precision once we have introduced the necessary background and presented the construction of our methods. Furthermore, we will present numerical evidence of our results with several examples, and discuss possible extensions of this work.
1.1 Background: structure-preserving numeric integration, Galerkin methods, and spectral methods
1.1.1 Structure-preserving numeric integration
Structure-preserving numeric integration has become an important tool in scientific computing. Broadly speaking, structure-preserving methods are numerical methods for differential equations which preserve or approximately preserve important invariants of the underlying problem. Classic examples of invariants in a differential equation include the energy, linear, and angular momentum in certain mechanical systems. However, the study of geometric mechanics has revealed structure in many important mechanical systems which is much more subtle than these classical examples, including the symplectic form for mechanical systems, which is particularly relevant to the discussion here. One can think of the symplectic form as an area form in the phase space of a mechanical system; it will not be discussed in great detail here but the interested reader is referred to many of the classic texts on geometric integration and geometric mechanics for a comprehensive overview, particularly Marsden and Ratiu [34] and Hairer et al. [17]. Methods which preserve the symplectic form are known as symplectic integrators, and they comprise a particularly important class of geometric numerical methods.
The structure associated with differential equations is important because it reveals much about the behavior of the system described by the differential equations. Invariants of physical systems can be viewed as constraints on the evolution of the system. Structure-preserving integrators tend to outperform classical methods for simulating systems with structure over long time-scales because the evolution of the approximate solutions is constrained in a similar way to the true solution.
As a simple illustrative example, consider a pendulum of length \(1\) and mass \(1\) under the influence of gravity. The equations of motion for the pendulum can be given in terms of an angle, \(\theta \), as illustrated in Fig. 1a, and are
where \(g\) is the gravitational constant. An example of an invariant for the pendulum is its energy, or Hamiltonian. The Hamiltonian (which can be thought of as a generalized energy function),
remains constant for all time on the trajectory of the system. Because of this, if we consider all possible positions and velocities of the pendulum, we know that the entire trajectory of the pendulum is constrained to level sets of the Hamiltonian. When we plot the evolution of the position and velocity of the approximations produced by two different standard first-order numerical methods, we see that one of the methods wanders away from these level sets, while one essentially follows it. The one that wanders away from the level sets is a classical method, and the one that is constrained is the structure-preserving symplectic Euler method. Because it is constrained in a similar way to the true solution, the symplectic Euler method vastly outperforms the classical method for long-term integration of this system (Figs. 1(b) and 1(c)).
The pendulum (a), is a classic example of a mechanical system with geometric structure. The level sets of the Hamiltonian function, \(H\), are plotted in b and c in black. The evolution of \((\theta ,\dot{\theta })\) produced by two different numerical methods are plotted on these level sets. The classical numerical method (b) quickly crosses the level sets, while the structure-preserving method (c) approximately follows them
Because of these favorable qualities, structure-preserving methods often perform very well where standard methods do very poorly; for example, in numerical simulations over very long time spans or for unstable systems. They facilitate numerical simulations that are extremely difficult or impossible with classical numerical methods, and structure-preserving integrators have been applied with great success to a number of different applications, including astrophysics, for example Laskar [24] or Sussman and Wisdom [42], control theory, as in Leyendecker et al. [33] and Bloch et al. [3], computational physics, as in Biesiadecki and Skeel [1] and Stern et al. [41], and engineering as in Lew et al. [32] and Lee et al. [27].
1.1.2 Galerkin methods
Galerkin methods, and their extensions, have become a standard tool in the numerical solution of partial differential equations. At their core, Galerkin methods are methods where a variational principle is discretized by replacing the function space of the problem with a finite-dimensional approximation space, and solving the resulting finite-dimensional problem. Galerkin methods have become ubiquitous in a vast number of scientific and engineering applications, and as such the literature about them is vast. The interested reader is referred to Larsson and Thomée [23] as a starting point.
This is not the first work that suggests a Galerkin approach to discretizing ordinary differential equations. Both Hulme [20] and Estep and French [11] discuss using the weak formulation of an ordinary differential equation as the foundation for Galerkin type integration schemes. In the classic work on variational integrators, Marsden and West [35] suggest a Galerkin approach for constructing structure-preserving methods. However, this work is the first that establishes broad estimates on a variety of different possible Galerkin constructions from the discrete mechanics standpoint. While the works that preceded this one have established error estimates for Galerkin constructions, they are either for very specific methods or non-geometric methods. Furthermore, they do not consider the spectral approach to convergence, as we do here. While we drew much of our inspiration for this work from these important works, spectral variational integrators represent an important next step in the development of structure-preserving numerical methods.
1.1.3 Spectral Methods
Like Galerkin methods, spectral methods have enjoyed great success in a variety of applications. Spectral methods are a large class of methods that make use of high-dimensional, global approximation spaces to achieve convergence. The works of Trefethen [43] and Boyd [7] provide excellent introductions to both the theoretical and practical aspects of spectral methods, as well as many of their applications.
One of the attractive characteristics of spectral methods is that they often achieve geometric convergence, that is, convergence at a rate which is faster than any polynomial order. Specifically, we say that a sequence of approximations \(\{f_{n}\}_{n=1}^{\infty }\) converges to \(f\) geometrically in a norm \(\Vert \cdot \Vert \) if,
for some \(K < 1\) which is independent of \(n\). This type of convergence is achieved by enriching the function space on which the numerical method is constructed, as opposed to standard methods, where convergence is achieved by shrinking the size domain of each local function, often measured by \(h\).
As far as we can tell, there has been little work done on the construction of structure-preserving methods using the spectral paradigm. What makes this paradigm attractive for structure-preserving methods is that highly accurate methods that do not require changing the step-size can be constructed using spectral techniques. For symplectic methods, development of accurate methods for fixed step-sizes is particularly important, as standard methods of error control through adaptive time-stepping can destroy the structure-preserving qualities of a symplectic integrator, as discussed in Biesiadecki and Skeel [1], Gladman et al. [16], and Calvo and Sanz-Serna [8].
1.2 A brief review of discrete mechanics
Before discussing the construction and convergence of spectral variational integrators, it is useful to review some of the fundamental results from discrete mechanics that are used in our analysis. This is only a brief introduction, we recommend Marsden and West [35] for a thorough introduction. We have already introduced the discrete Lagrangian (1), which we recall here, \(L_{d}:Q \times Q \times {\mathbb {R}} \rightarrow {\mathbb {R}}\),
and the discrete action sum (2), which is
Taking variations of the discrete action sum and using discrete integration by parts leads to the discrete Euler–Lagrange equations,
for \(k = 2,..,N-1\) and where \(D_{1}\) and \(D_{2}\) denote partial derivatives with respect to the first and second variables, respectively, i.e.,
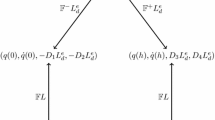
Given \((q_{k-1},q_{k})\), these equations implicitly define an update map, known as the discrete Lagrangian flow map, \(F_{L_{d}}: Q \times Q \rightarrow Q \times Q\), given by \(F_{L_{d}}(q_{k-1},q_{k}) = (q_{k},q_{k+1})\), where \((q_{k-1},q_{k}),(q_{k},q_{k+1})\) satisfy (6). This update map defines a numerical method, as the pairs \(\{(q_{k},q_{k+1})\}_{k=1}^{N-1}\) can be viewed as samplings of an approximation to the flow of the Lagrangian vector field. Additionally, the discrete Lagrangian defines the discrete Legendre transforms, \({\mathbb {F}}^{\pm }L_{d}: Q\times Q \rightarrow T^{*}Q\):
Using the discrete Legendre transforms, we define the discrete Hamiltonian flow map, \(\tilde{F}_{L_{d}}: T^{*}Q \rightarrow T^{*}Q\),
The following commutative diagram illustrates the relationship between the discrete Hamiltonian flow map, discrete Lagrangian flow map, and the discrete Legendre transforms,
This diagram also describes how one converts initial conditions expressed in terms of \((q_0,p_0)\in T^*Q\) into initial conditions \((q_0,q_1)\in Q\times Q\), i.e., \((q_0,q_1)=({\mathbb {F}}^-L_d)^{-1}(q_0,p_0)\). Furthermore, if the initial conditions are given using initial position and velocity, \((q_0,v_0)\in TQ\), then one can convert it into initial position and momentum conditions by using the continuous Legendre transform, \({\mathbb {F}}L:TQ \rightarrow T^*Q,\, (q_0,v_0)\rightarrow (q_0,p_0)= (q_0,\frac{\partial L}{\partial \dot{q}}(q_0,v_0))\).
We now introduce the exact discrete Lagrangian \(L^{E}_{d}\),
An important theoretical result for the error analysis of variational integrators is that the discrete Hamiltonian and Lagrangian flow maps associated with the exact discrete Lagrangian produces an exact sampling of the true flow, as was shown in Marsden and West [35]. Using this result, Marsden and West [35] show that there is a fundamental relationship between how well a discrete Lagrangian \(L_{d}\) approximates the exact discrete Lagrangian \(L_{d}^{E}\) and how well the corresponding discrete Hamiltonian flow maps, discrete Lagrangian flow maps and discrete Legendre transforms approximate their continuous analogues. This relationship is described in the following theorem, found in Marsden and West [35], which is critical to the error analysis of our work:
Theorem 1.1
(Variational error analysis) Given a regular Lagrangian \(L\) and corresponding Hamiltonian \(H\), the following are equivalent for a discrete Lagrangian \(L_{d}\):
-
(1)
the discrete Hamiltonian flow map for \(L_{d}\) has error \({\mathcal {O}}(h^{p+1})\),
-
(2)
the discrete Legendre transforms of \(L_{d}\) have error \({\mathcal {O}}(h^{p+1})\),
-
(3)
\(L_{d}\) approximates the exact discrete Lagrangian with error \({\mathcal {O}}(h^{p+1})\).
In addition, in Marsden and West [35], it is shown that integrators constructed in this way, which are referred to as variational integrators, have significant geometric structure. Most importantly, variational integrators always conserve the canonical symplectic form, and a discrete Noether’s Theorem guarantees that a discrete momentum map is conserved for any continuous symmetry of the discrete Lagrangian. The preservation of these discrete geometric structures underlie the excellent long-term behavior of variational integrators.
2 Construction
2.1 Generalized Galerkin variational integrators
The construction of spectral variational integrators falls within the framework of generalized Galerkin variational integrators, discussed in Leok [28] and Marsden and West [35]. The motivating idea is to replace the generally non-computable exact discrete Lagrangian \(L_{d}^{E}(q_{k},q_{k+1})\) with a highly accurate computable discrete analogue, \(L_{d}(q_{k},q_{k+1})\). Galerkin variational integrators are constructed by using a finite-dimensional function space to discretize the action of a Lagrangian. Specifically, given a Lagrangian \(L:TQ \rightarrow {\mathbb {R}}\), to construct a Galerkin variational integrator:
-
(1)
choose an \((n+1)\)-dimensional function space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\subset C^{2}(\left[ 0,h\right] \!,Q)\), with a finite set of basis functions \(\{\phi _{i}(t)\}_{i=0}^{n}\),
-
(2)
choose a quadrature rule \({\mathcal {G}}(\cdot ):F ([0,h],{\mathbb {R}})\rightarrow {\mathbb {R}}\), so that \({\mathcal {G}}(f) = h\sum _{j=1}^{m} b_{j}f(c_{j}h) \approx \int _{0}^{h} f(t) \hbox {d}t\), where \(F\) is some appropriate function space,
and then construct the discrete action \(\mathbb {S}_{d}(\{q^{i}_{k}\}_{i=0}^{n}):\prod _{i=0}^{n} Q_{i} \rightarrow {\mathbb {R}}\), (not to be confused with the discrete action sum \(\mathbb {S}(\{q_{k}\}_{k=1}^{N})\)),
where we use superscripts to index the weights associated with each basis function, as in Marsden and West [35]. The reader should note that we have chosen the slightly awkward notation of calling the \((n+1)\)-dimensional function space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\), and have chosen to index the \(n+1\) basis functions of \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\) from \(0\) to \(n\); this is because we will use polynomial spaces extensively in later sections, and following this convention \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\) will denote the polynomials of degree at most \(n\). Likewise, while we have made no assumption about the number of quadrature points \(m\) used in our quadrature rule, we will later establish that the choice of quadrature rule has significant implications for the accuracy of the method. An example of an element of the \((n+1)\)-dimensional function space \(\mathbb {M}^n([0,h],Q)\) is given in Fig. 2.
A visual schematic of the curve \(\tilde{q}_{n}(t) \in \mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\). The points marked with crosses represent the quadrature points, which may or may not be the same as interpolation points \(d_{i}h\). In this figure we have chosen to depict a curve constructed from interpolating basis functions, but this is not necessary in general
Once the discrete action has been constructed, a discrete Lagrangian can be induced by finding stationary points \(\tilde{q}_{n}(t) = \sum _{i=0}^{n}q_{k}^{i}\phi _{i}(t)\) of the action under the conditions \(\tilde{q}_{n}(0) = q_{k}\) and \(\tilde{q}_{n}(h) = q_{k+1}\) for some given \(q_{k}\) and \(q_{k+1}\),
A discrete Lagrangian flow map that results from this type of discrete Lagrangian is referred to as a Galerkin variational integrator.
It should be noted that this construction is only valid if \(Q\) is a vector space. If \(Q\) is not a vector space, there is no guarantee that the finite-dimensional approximation space, \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\), is contained in \(C^{2}(\left[ 0,h\right] \!,Q)\), as the linear combinations of elements in \(Q\) may not be elements of \(Q\). Hence, for the remainder of the paper, we will restrict our attention to configuration spaces \(Q\) that are vector spaces. Our results are only valid for such configuration spaces, and the construction of Galerkin variational integrators for configuration spaces which are not vector spaces, and the extension of our error analysis to such spaces, is still an area of active research. A generalization of our approach to the setting of Lie groups is described in Hall and Leok [19].
2.2 Spectral variational integrators
There are two defining features of spectral variational integrators. The first is the choice of function space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\), and the second is that convergence is achieved not by shortening the time-step \(h\), but by increasing the dimension \(n\) of the function space.
2.2.1 Choice of function space
Restricting our attention to the case where \(Q\) is a linear space, spectral variational integrators are constructed using the basis functions \(\phi _{i}(t) = l_{i}(t)\), where \(l_{i}(t)\) are Lagrange interpolating polynomials based on the points \(h_{i} = \frac{h}{2}\cos (\frac{(i+1) \pi }{n}) + \frac{h}{2}\) which are the Chebyshev points \(t_{i} = \cos (\frac{(i+1) \pi }{n})\), rescaled and shifted from \([-1,1]\) to \([0,h]\). The resulting finite-dimensional function space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\) is simply the polynomials of degree at most \(n\) on \(Q\). However, the choice of this particular set of basis functions offer several advantages over other possible bases for the polynomials:
-
(1)
the condition \(\tilde{q}_{n}(0) = q_{k}\) reduces to \(q_{k}^{0} = q_{k}\) and \(\tilde{q}_{n}(h) = q_{k+1}\) reduces to \(q_{k}^{n} = q_{k+1}\),
-
(2)
the induced numerical methods have generally better stability properties because of the excellent approximation properties of the interpolation polynomials at the Chebyshev points.
Using this choice of basis functions, for any chosen quadrature rule, the discrete Lagrangian becomes
Requiring the curve \(\tilde{q}_{n}(t)\) to be a stationary point of the discretized action provides \(n-1\) internal stage conditions:
Combining these internal stage conditions with the discrete Euler–Lagrange equations,
and the continuity condition \(q_{k}^{0} = q_{k}\) yields the following set of \(n+1\) nonlinear equations:
where \(p_{k} = D_{2} L_d(q_{k-1},q_{k})\) is obtained using the data from the previous time-step, and the momentum condition,
defines the right hand side of (9) for the next time-step. Evaluating \(q_{k+1} = \tilde{q}_{n}\left( h\right) \) defines the next step for the discrete Lagrangian flow map,
and because of the choice of basis functions, this is simply \(q_{k+1} = q_{k}^{n}\).
In practice, the initial conditions for the Galerkin variational integrator are typically given directly in terms of position and momentum, \((q_0,p_0) \in T^*Q\). By solving Eqs. (7)–(9) for \(q_0^0,\ldots q_0^n\), we obtain \(q_1=q_0^n\). Then, \(p_1\) can be computed using Eq. (10), and this yields the discrete Hamiltonian flow map, \(\tilde{F}_{L_d}:(q_0,p_0)\mapsto (q_1,p_1)\). This procedure can then be iterated to time-march the discrete solution forward. If instead, the initial conditions are expressed in terms of position and velocity, \((q_0,v_0)\in TQ\), then one can use the continuous Legendre transform, \({\mathbb {F}}L:TQ \rightarrow T^*Q\), \((q_0,v_0)\rightarrow (q_0,p_0)= (q_0,\frac{\partial L}{\partial \dot{q}}(q_0,v_0))\), to convert this into initial position and momentum.
2.2.2 \(n\)-Refinement
As is typical for spectral numerical methods (see, for example, Boyd [7]; Trefethen [43]), convergence for spectral variational integrators is achieved by increasing the dimension of the function space, \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\). Furthermore, because the order of the discrete Lagrangian also depends on the order of the quadrature rule \({\mathcal {G}}\), we must also refine the quadrature rule as we refine \(n\). Hence, for examining convergence, we must also consider the quadrature rule as a function of \(n\), \({\mathcal {G}}_{n}\). Because of the dependence on \(n\) instead of \(h\), we will often examine the discrete Lagrangian \(L_{d}\) as a function of \(Q \times Q \times \mathbb {N}\),
as opposed to the more conventional
This type of refinement is the foundation for the exceptional convergence properties of spectral variational integrators.
3 Existence, uniqueness and convergence
In this section, we will discuss the major important properties of Galerkin variational integrators and spectral variational integrators. The first will be the existence of unique solutions to the internal stage equations (7), (8), (9) for certain types of Lagrangians. The second is the convergence of the one-step map that results from the Galerkin and spectral variational constructions, which we will show can be either arbitrarily high-order or have geometric convergence. The third and final is the convergence of continuous approximations to the Euler–Lagrange flow which can easily be constructed from Galerkin and spectral variational integrators, and the behavior of geometric invariants associated with the approximate continuous flow. We will show a number of different convergence results associated with these quantities, which demonstrate that Galerkin and spectral variational integrators can be used to compute continuous approximations to the exact solutions of the Euler–Lagrange equations which have excellent convergence and structure-preserving behavior.
3.1 Existence and uniqueness
In general, demonstrating that there exists a unique solution to the internal stage equations for a spectral variational integrator is difficult, and depends on the properties of the Lagrangian. However, assuming a Lagrangian of the form
it is possible to show the existence and uniqueness of the solutions to the implicit equations for the one-step method under appropriate assumptions. We will establish existence and uniqueness using a contraction mapping argument, making several assumptions about the Eqs. (7), (8), and (9), and then establish that these assumptions hold for polynomial bases.
Theorem 3.1
(Existence and uniqueness of solutions to the internal stage equations) Given a Lagrangian \(L:TQ \rightarrow {\mathbb {R}}\) of the form
if \(\nabla V\) is Lipschitz continuous, \(b_{j}> 0\) for every \(j\) and \(\sum _{i=1}^{m} b_{j}= 1\), and \(M\) is symmetric positive-definite, then there exists an interval \([0,h]\) where there exists a unique solution to the internal stage equations for a spectral variational integrator.
Proof
We will consider only the case where \(q(t)\in {\mathbb {R}}\), but the argument generalizes easily to higher dimensions. To begin, we note that for a Lagrangian of the form
the internal stage Euler–Lagrange equations (8), momentum condition (9), and continuity condition (7) yield a set of equations of the form
where \(q^{i}\) is the vector of internal weights, \(q^{i} = (q_{k}^{0},q_{k}^{1},\ldots ,q_{k}^{n})^{T}\), \(A\) is an \((n +1) \times (n+1)\) matrix with entries defined by
and \(f\) is a vector-valued function defined by
It is important to note that the entries of \(A\) depend on \(h\). For now we will assume \(A\) is invertible, and that \(\Vert A^{-1}\Vert < \Vert A_{1}^{-1}\Vert \), where \(A_{1}\) is the matrix \(A\) generated on the interval \([0,1]\). Of course, the properties of \(A\) depend on the choice of basis functions \(\{\phi _{i}\}_{i=0}^{n}\), but we will establish these properties for a polynomial basis later. Defining the map:
it is easily seen that (11) is satisfied if and only if \(q^{i} = \Phi \left( q^{i}\right) \), that is, \(q^{i}\) is a fixed-point of \(\Phi \left( \cdot \right) \). If we establish that \(\Phi \left( \cdot \right) \) is a contraction mapping,
for some \(k < 1\), we can establish the existence of a unique fixed-point, and thus show that the steps of the one-step method are well-defined. Here, and throughout this section, we use \(\left\| \cdot \right\| _{p}\) to denote the vector or matrix \(p\)-norm, as appropriate.
To show that \(\Phi \left( \cdot \right) \) is a contraction mapping, we consider arbitrary \(w^{i}\) and \(v^{i}\):
Considering \(\Vert f(w^{i}) - f(v^{i})\Vert _{\infty }\), we see that
for some appropriate index \(r^{*} \in \{0,\ldots ,n\}\). Note that the first and last terms of \(\left\| f(w^{i}) - f(v^{i})\right\| _{\infty }\) will vanish, so the maximum element must take the form of (15). Let \(\phi ^{i}(t) = (\phi _{0}(t),\phi _{1}(t),\ldots ,\phi _{n}(t))\) and \(C_{L}\) be the Lipschitz constant for \(\nabla V(q)\). Now,
Hence, we derive the inequality
and since by assumption \(\left\| A^{-1}\right\| _{\infty } \le \left\| A_{1}^{-1}\right\| _{\infty }\),
Thus, if
then
where \(k < 1\), which establishes that \(\Phi (\cdot )\) is a contraction mapping, and establishes the existence of a unique fixed-point, and thus the existence of unique steps of the one-step method. \(\square \)
A critical assumption made during the proof of existence and uniqueness is that the matrix \(A\) is nonsingular. This property depends on the choice of basis functions \(\phi _{i}\). However, using a polynomial basis, like Lagrange interpolation polynomials, it can be shown that \(A\) is invertible.
Lemma 3.1
(\(A\) is invertible) If \(\{\phi _{i}\}_{i=0}^{n}\) is a polynomial basis of \(P_{n}\), the space of polynomials of degree at most \(n\), M is symmetric positive-definite, and the quadrature rule is order at least \(2n - 1\), then \(A\) defined by (12)–(14) is invertible.
Proof
We begin by considering the equation
Let \(\tilde{q}_{n}(t) = \sum _{i=1}^{n} q_{k}^{i} \phi _{i}(t)\). Considering the definition of \(A\), \(Aq^{i} = 0\) holds if and only if the following equations hold:
It can easily be seen that \(\{\dot{\phi }_{i}\}_{i=0}^{n-1}\) is a basis of \(P_{n-1}\). Using the assumption that the quadrature rule is of order at least \(2n-1\) and that \(M\) is symmetric positive-definite, we can see that (16) implies
and this implies
where \(\langle \cdot ,\cdot \rangle \) is the standard \(L^{2}\) inner product on \([0,h]\). Since \(\{\dot{\phi }_{i}\}_{i=0}^{n-1}\) forms a basis for \(P_{n-1}\), \(\dot{\tilde{q}}_{n}\in P_{n-1}\), and \(\langle \cdot ,\cdot \rangle \) is non-degenerate, this implies that \(\dot{\tilde{q}}_{n}(t) = 0\). Thus,
which implies that \(\tilde{q}_{n}(t) = 0\) and hence \(q^{i} = 0\). Thus, if \(Aq^{i} = 0\) then \(q^{i} = 0\), from which it follows that \(A\) is non-singular. \(\square \)
Another subtle difficulty is that the matrix \(A\) is a function of \(h\). Since we assumed that \(\Vert A^{-1}\Vert _{\infty }\) is bounded to prove Theorem 3.1, we must show that for any choice of \(h\), the quantity \(\Vert A^{-1}\Vert _{\infty }\) is bounded. We will do this by establishing \(\Vert A^{-1}\Vert _{\infty } \le \left\| A_{1}^{-1}\right\| _{\infty }\), where \(A_{1}\) is \(A\) defined with \(h=1\). By Lemma 3.1, we know that \(\left\| A_{1}^{-1}\right\| _{\infty } < \infty \), which establishes the upper bound for \(\left\| A^{-1}\right\| _{\infty }\). This argument is easily generalized for a higher upper bound on \(h\).
Lemma 3.2
\((\Vert A^{-1}\Vert _{\infty } \le \Vert A_{1}^{-1}\Vert _{\infty })\) For the matrix \(A\) defined by (12)–(14), if \(h < 1\), \(\Vert A^{-1}\Vert _{\infty } < \Vert A_{1}^{-1} \Vert _{\infty }\) where \(A_{1}\) is \(A\) defined on the interval \([0,1]\).
Proof
We begin the proof by examining how \(A\) changes as a function of \(h\). First, let \(\{\phi _{i}\}_{i=0}^{n}\) be the basis for the interval \([0,1]\). Then for the interval \([0,h]\), the basis functions are
and hence the derivatives are
Thus, if \(A_{1}\) is the matrix defined by (12)–(14) on the interval \([0,1]\), then for the interval \([0,h]\),
where \(I_{n\times n}\) is the \(n\times n\) identity matrix. This gives
which gives
which proves the statement. The reader should note that we have used the fact that
when \(h \le 1\) to obtain the rightmost equality in (17). \(\square \)
3.2 Arbitrarily high-order and geometric convergence
To determine the rate of convergence for spectral variational integrators, we will utilize Theorem 1.1 and a simple extension of Theorem 1.1:
Theorem 3.2
(Extension of Theorem 1.1 to geometric convergence) Given a regular Lagrangian \(L\) and corresponding Hamiltonian \(H\), the following are equivalent for a discrete Lagrangian \(L_{d}\left( q_{0},q_{1},n\right) \):
-
(1)
there exist a positive constant \(K\), where \(K < 1\), such that the discrete Hamiltonian map for \(L_{d}(q_{0},q_{h},n)\) has error \({\mathcal {O}}(K^{n})\),
-
(2)
there exists a positive constant \(K\), where \(K < 1\), such that the discrete Legendre transforms of \(L_{d}(q_{0},q_{h},n)\) have error \({\mathcal {O}}(K^{n})\),
-
(3)
there exists a positive constant \(K\), where \(K < 1\), such that \(L_{d}(q_{0},q_{h},n)\) approximates the exact discrete Lagrangian \(L_{d}^{E}(q_{0},q_{h},h)\) with error \({\mathcal {O}}(K^{n})\).
This theorem provides a fundamental tool for the analysis of Galerkin variational methods. Its proof is almost identical to that of Theorem 1.1, and can be found in the appendix. The critical result is that the order of the error of the discrete Hamiltonian flow map, from which we construct the discrete flow, has the same order as the discrete Lagrangian from which it is constructed. Thus, in order to determine the order of the error of the flow generated by spectral variational integrators, we need only determine how well the discrete Lagrangian approximates the exact discrete Lagrangian. This is a key result which greatly reduces the difficulty of the error analysis of Galerkin variational integrators. Furthermore, while this theorem deals only with local error estimates, this local estimate extends to a global error estimate so long as the Lagrangian vector field is sufficiently well-behaved. This issue is addressed in both Marsden and West [35] and Hairer et al. [18].
Naturally, the goal of constructing spectral variational integrators is constructing a variational method that has geometric convergence. To this end, it is essential to establish that Galerkin type integrators inherit the convergence properties of the spaces which are used to construct them. The arbitrarily high-order convergence result is related to the problem of \(\Gamma \)-convergence (see, for example, Dal Maso [10]), as the Galerkin discrete Lagrangians are given by extremizers of an approximating sequence of variational problems, and the exact discrete Lagrangian is the extremizer of the limiting variational problem. The \(\Gamma \)-convergence of variational integrators was studied in Müller and Ortiz [38], and our approach involves a refinement of their analysis. We now state our results, which establish not only the geometric convergence of spectral variational integrators, but also order of convergence of all Galerkin variational integrators under appropriate smoothness assumptions.
The general techniques for establishing these bounds are the same for both \(n\)-refinement and \(h\)-refinement: we establish that as long as stationary points of both the discrete and continuous actions are minimizers, then the difference between the value of the exact discrete Lagrangian evaluated at any two points and the Galerkin discrete Lagrangian evaluated at these points is controlled by the accuracy of the quadrature rule and the quality of approximations in the approximation space. Hence, so long as the quadrature rule is sufficiently accurate and the approximation space can produce high-order approximations to the true solution, a Galerkin variational integrator will produce a high-order approximation to the true dynamics. We then demonstrate that, for the canonical Lagrangian, stationary points of both the true and discrete actions are minimizers, up to a time-step restriction, which makes these bounds immediately applicable to Galerkin variational integrators for systems with canonical Lagrangians.
Theorem 3.3
(Arbitrarily high-order Convergence of Galerkin variational integrators) Given an interval \([0,h]\) and a Lagrangian \(L:TQ \rightarrow {\mathbb {R}}\), let \(\bar{q}\) be the exact solution to the Euler–Lagrange equations subject to the conditions \(\bar{q}(0) = q_{0}\) and \(\bar{q}(h) = q_{1}\), and let \(\tilde{q}_{n}\) be the stationary point of a Galerkin variational discrete action, i.e. if \(L_{d}:Q\times Q \times {\mathbb {R}} \rightarrow {\mathbb {R}}\),
then
If:
-
(1)
there exists a constant \(C_{A}\) independent of \(h\), such that for each \(h\), there exists a curve \(\hat{q}_{n}\in \mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\), such that,
$$\begin{aligned} \left\| \left( \hat{q}_{n}\left( t\right) ,\dot{\hat{q}}_{n}\left( t\right) \right) - \left( \bar{q}\left( t\right) ,\dot{\bar{q}}\left( t\right) \right) \right\| _1&\le C_{A}h^{n},\qquad \text {for all }t\in [0,h], \end{aligned}$$ -
(2)
there exists a closed and bounded neighborhood \(U \subset TQ\), such that \((\bar{q}(t),\dot{\bar{q}}(t)) \in U\), \((\hat{q}_{n}(t),\dot{\hat{q}}_{n}(t)) \in U\) for all \(t\), and all partial derivatives of \(L\) are continuous on \(U\),
-
(3)
for the quadrature rule \({\mathcal {G}}(f) = h\sum _{j=1}^{m} b_{j}f(c_{j}h) \approx \int _{0}^{h}f(t)\hbox {d}t\), there exists a constant \(C_{g}\), such that,
$$\begin{aligned} \left| \int _{0}^{h} L\left( q_{n}\left( t\right) , \dot{q}_{n}\left( t\right) \right) \hbox {d}t- h\sum _{j=1}^{m} b_{j} L\left( q_{n}\left( c_{j}h\right) ,\dot{q}_{n}\left( c_{j}h\right) \right) \right| \le C_{g}h^{n+1}, \end{aligned}$$for any \(q_{n} \in \mathbb {M}^{n}(\left[ 0,h\right] ,Q)\),
-
(4)
and the stationary points \(\bar{q}\), \(\tilde{q}_{n}\) minimize their respective actions,
then
for some constant \(C_{op}\) independent of \(h\), i.e. discrete Lagrangian \(L_{d}\) has at most error \({\mathcal {O}}(h^{n+1})\), and hence the discrete Hamiltonian flow map has at most error \({\mathcal {O}}(h^{n+1})\).
Proof
First, we rewrite both the exact discrete Lagrangian and the Galerkin discrete Lagrangian:
where in the last line, we have suppressed the \(t\) argument, a convention we will continue throughout the proof. Now we introduce the action evaluated on the \(\hat{q}_{n}\) curve, which is an approximation with error \({\mathcal {O}}(h^{n})\) to the exact solution \(\bar{q}\):
Considering the first term (18a):
By assumption, all partials of \(L\) are continuous on \(U\), and since \(U\) is closed and bounded, this implies \(L\) is Lipschitz on \(U\). Let \(L_{\alpha }\) denote that Lipschitz constant. Since, again by assumption, \((\bar{q},\dot{\bar{q}}) \in U\) and \((\hat{q}_{n},\dot{\hat{q}}_{n}) \in U\), we can rewrite:
where we have made use of the best approximation estimate. Hence,
Next, considering the second term (18b),
since \(\tilde{q}_{n}\), the stationary point of the discrete action, minimizes its action and \(\hat{q}_{n}\in \mathbb {M}^{n}([0,h],Q)\),
where the inequalities follow from the assumptions on the order of the quadrature rule. Furthermore,
where the inequalities follow from (19), the order of the quadrature rule, and the assumption that \(\bar{q}\) minimizes its action. Putting (20) and (21) together, we can conclude that
Now, combining the bounds (19) and (22) in (18a) and (18b), we can conclude that
which, combined with Theorem 1.1, establishes the order of the error of the integrator.
\(\square \)
The above proof establishes a significant convergence result for Galerkin variational integrators, namely that for sufficiently well-behaved Lagrangians, one can construct Galerkin variational integrators that will produce discrete approximate flows that converge to the exact flow as \(h\rightarrow 0\), and that arbitrarily high order can be achieved provided the quadrature rule is of sufficiently high-order.
We will discuss assumption 4 in Sect. 3.3. While in general we cannot assume that stationary points of the action are minimizers, it can be shown that for Lagrangians of the canonical form
under some mild assumptions on the derivatives of \(V\) and the accuracy of the quadrature rule, there always exists an interval \([0,h]\) over which stationary points are minimizers. In Sect. 3.3 we will show the result extends to the discretized action of Galerkin variational integrators. A similar result was established in Müller and Ortiz [38].
Geometric convergence of spectral variational integrators is not strictly covered under the proof of arbitrarily high-order convergence. While the above theorem establishes convergence of Galerkin variational integrators by shrinking \(h\), the interval length of each discrete Lagrangian, spectral variational integrators achieve convergence by holding the interval length of each discrete Lagrangian constant and increasing the dimension of the approximation space \(\mathbb {M}^{n}(\left[ 0,h\right] \!,Q)\). Thus, for spectral variational integrators, we have the following analogous convergence theorem:
Theorem 3.4
(Geometric convergence of spectral variational integrators) Given an interval \([0,h]\) and a Lagrangian \(L:TQ \rightarrow {\mathbb {R}}\), let \(\bar{q}\) be the exact solution to the Euler–Lagrange equations, and \(\tilde{q}_{n}\) be the stationary point of the spectral variational discrete action:
If:
-
(1)
there exists constants \(C_{A},K_{A}\), \(K_{A}< 1\), independent of \(n\), such that for each \(n\), there exists a curve \(\hat{q}_{n}\in \mathbb {M}^{n}([0,h],Q)\), such that,
$$\begin{aligned} \left\| \left( \hat{q}_{n}\left( t\right) ,\dot{\hat{q}}_{n}\left( t\right) \right) - \left( \bar{q}\left( t\right) ,\dot{\bar{q}}\left( t\right) \right) \right\| _1&\le C_{A}K_{A}^{n},\qquad \text {for all }t\in [0,h], \end{aligned}$$ -
(2)
there exists a closed and bounded neighborhood \(U \subset TQ\), such that \((\bar{q}(t),\dot{\bar{q}}(t)) \in U\) and \((\hat{q}_{n}(t),\dot{\hat{q}}_{n}(t)) \in U\) for all \(t\) and \(n\), and all partial derivatives of \(L\) are continuous on \(U\),
-
(3)
for the sequence of quadrature rules \({\mathcal {G}}_{n}(f) = \sum _{j=1}^{m_{n}} b_{j_{n}}f(c_{j_{n}}h) \approx \int _{0}^{h}f(t)\hbox {d}t\), there exists constants \(C_{g}\), \(K_{g}\), \(K_{g}< 1\), independent of \(n\), such that,
$$\begin{aligned} \left| \int _{0}^{h} L\left( q_{n}\left( t\right) , \dot{q}_{n}\left( t\right) \right) \hbox {d}t- h\sum _{j=1}^{m_{n}} b_{j_{n}}L\left( q_{n}\left( c_{j_{n}}h\right) ,\dot{q}_{n}\left( c_{j_{n}}h\right) \right) \right| \le C_{g}K_{g}^{n}, \end{aligned}$$for any \(q_{n}\in \mathbb {M}^{n}(\left[ 0,h\right] ,Q)\),
-
(4)
and the stationary points \(\bar{q}\), \(\tilde{q}_{n}\) minimize their respective actions,
then
for some constants \(C_{s},K_{s}\), \(K_{s}< 1\), independent of \(n\), and hence the discrete Hamiltonian flow map has at most error \({\mathcal {O}}(K_{s}^{n})\).
The proof of the above theorem is very similar to that of arbitrarily high-order convergence, and would be tedious to repeat here. It can be found in the appendix. The main differences between the proofs are the assumption of the sequence of converging functions in the increasingly high-dimensional approximation spaces, and the assumption of a sequence of increasingly high-order quadrature rules. These assumptions are used in the obvious way in the modified proof.
3.3 Minimization of the action
One of the major assumptions made in the convergence Theorems 3.3 and 3.4 is that the stationary points of both the continuous and discrete actions are minimizers over the interval \([0,h]\). This type of minimization requirement is similar to the one made in the paper on \(\Gamma \)-convergence of variational integrators by Müller and Ortiz [38]. In fact, the results in Müller and Ortiz [38] can easily be extended to demonstrate that for sufficiently well-behaved Lagrangians of the form
where \(q \in C^{2}(\left[ 0,h\right] \!,Q)\), there exists an interval \([0,h]\), such that stationary points of the Galerkin action are minimizers.
Theorem 3.5
Consider a Lagrangian of the form
where \(q \in C^{2}(\left[ 0,h\right] \!,Q)\) and each component \(q^{d}\) of \(q\), \(q^{d} \in C^{2}(\left[ 0,h\right] \!,Q)\), is a polynomial of degree at most \(n\). Assume \(M\) is symmetric positive-definite and all second-order partial derivatives of \(V\) exist, and are continuous and bounded. Then, there exists a time interval \([0,h]\), such that stationary points of the discrete action,
on this time interval are minimizers if the quadrature rule used to construct the discrete action is of order at least \(2n+1\).
We quickly note that the assumption that each component of \(q\), \(q^{d}\), is a polynomial of degree at most \(n\) allows for discretizations where different components of the configuration space are discretized with polynomials of different degrees. This allows for more efficient discretizations where slower evolving components are discretized with lower-degree polynomials than faster evolving ones.
Proof
Let \(\tilde{q}_{n}\) be a stationary point of the discrete action \(\mathbb {S}_{d}(\cdot )\), and let \(\delta q\) be an arbitrary perturbation of the stationary point \(\tilde{q}_{n}\), under the conditions \(\delta q\) is a polynomial of the same degree as \(\tilde{q}_{n}\), \(\delta q(0) = \delta q(h) = 0\). Any such arbitrary perturbation is uniquely defined by a set \(\{\delta q_{k}^{i}\}_{i=1}^{n} \subset Q\). Then, perturbing the stationary point by \(\delta q_{k}^{i}\) yields
Making use of Taylor’s remainder theorem, we expand:
where \(|R_{lm}| \le \sup _{l,m}|\frac{\partial ^{2}V}{\partial q_{l} \partial q_{m}}|\). Using this expansion, we rewrite
which, given the symmetry in \(M\), rearranges to:
Now, it should be noted that the stationarity condition for the discrete Euler–Lagrange equations is
for arbitrary \(\delta q\), which allows us to simplify the expression to
Now, using the assumption that the partial derivatives of \(V\) are bounded, \(|R_{lm}| \le |\frac{\partial ^{2} V}{\partial q_{l}\partial q_{m}}| < C_{R}\), and standard matrix inequalities, we get the inequality:
where \(D\) is the number of spatial dimensions of \(Q\). Thus,
Because \(M\) is symmetric positive-definite, there exists \(m > 0\), such that \(x^{T}Mx \ge mx^{T}x\) for any \(x\). Hence,
Now, we note that since each component of \(\delta q\) is a polynomial of degree at most \(n\), \(\delta q^{T} \delta q\) and \(\delta \dot{q}^{T} \delta \dot{q}\) are both polynomials of degree less than or equal to \(2n\). Since our quadrature rule is of order \(2n+1\), the quadrature rule is exact, and we can rewrite
From here, we note that \(\delta q \in H_{0}^{1}(\left[ 0,h\right] \!,Q)\), and make use of the Poincaré inequality to conclude that
Since \(\int _{0}^{h} \delta q^{T} \delta q \hbox {d}t> 0\),
so long as \(h < \sqrt{\frac{m \pi ^{2}}{DC_{R}}}\). \(\square \)
We conclude our discussion of the error associated with the one-step map with two theorems that synthesize the results of Theorems 3.1, 3.3, 3.4, and 3.5 into unified results that give a lower bound on the order of convergence for Galerkin variational integrators for canonical Lagrangians.
Theorem 3.6
(Arbitrarily high order convergence of Galerkin variational integrators for canonical Lagrangians) For a canonical Lagrangian and a sufficiently small time-step \(h\), a Galerkin variational integrator constructed from a basis \(\{\phi _{i}\}_{i=0}^{n}\) or polynomials of degree at most \(n\) and a quadrature rule of at least order \(2n+1\) will have error at most \({\mathcal {O}}(h^{n +1})\). The internal stage Euler–Lagrange equations needed to construct the Galerkin variational integrator will also have a unique solution.
Theorem 3.7
(Geometric convergence of Galerkin variational integrators for canonical Lagrangians) For a canonical Lagrangian and a sufficiently small time-step \(h\), a Galerkin variational integrator constructed from a basis \(\{\phi _{i}\}_{i=0}^{n}\) or polynomials of degree at most \(n\) and a quadrature rule of at least order \(2n+1\) will have error at most \({\mathcal {O}}(K^{n})\) for some \(K\) independent of \(n\) and less than \(1\). The internal stage Euler–Lagrange equations needed to construct the Galerkin variational integrator will also have a unique solution.
These results follow easily by combining Theorems 3.1, 3.3, 3.4, and 3.5. Furthermore, while these theorems are more unified than our preceding results, they are also less general; they establish convergence for a special set of Galerkin variational integrators for a specific class of Lagrangians. We emphasize the constituent theorems earlier because individually they are less restrictive in their assumptions and hence may be used to expand error bounds to constructions based on approximation spaces beyond the polynomials.
Furthermore, while Theorems 3.6 and 3.7 both provide lower bounds on the order of the error, these bounds are not sharp for specific constructions. For example, in [35], Galerkin variational integrators based on polynomials of degree \(n\) and \(n\)-order Gauss–Legendre quadrature rules are shown to result in the collocation Gauss–Legendre methods of order \(2n\), which is a rate of convergence significantly higher than our bound. Also, when the \(n\)-order Lobatto quadrature rule is used instead, the Lobatto IIIA–IIIB partitioned Runge–Kutta method of order \(2n-2\) is obtained. However, our results are general across different polynomial bases and different quadrature rules. A deeper exploration of the precise order for other specific constructions, and the relationship between different polynomial bases, quadrature rules, and the sharp order of convergence of the resulting method would be an interesting avenue of investigation, but is beyond the scope of this paper.
3.4 Convergence of Galerkin curves and Noether quantities
3.4.1 Galerkin curves
In order to construct the one-step method, spectral variational integrators determine a curve
which satisfies
Evaluating this curve at \(h\) defines the next step of the one-step method, \(q_{k+1} = \tilde{q}_{n}(h)\), but the curve itself has many desirable properties which makes it a good continuous approximation to the true solution of the Euler–Lagrange equations \(\bar{q}(t)\). In this section, we will examine some of the favorable properties of \(\tilde{q}_{n}(t)\), hereafter referred to as the Galerkin curve.
However, before discussing the properties of the Galerkin curve, it is useful to review the different curves with which we are working. We have already defined the Galerkin curve, \(\tilde{q}_{n}(t)\), and we will also be making use of the local solution to the Euler–Lagrange equations \(\bar{q}(t)\), where
However, while for each interval \(\bar{q}\) satisfies the Euler–Lagrange equations exactly, it is not the exact solution of the Euler–Lagrange equations globally, as \(q_{k} \ne \Phi _{kh}(q_{0},\dot{q}_{0})\), where \(\Phi _{t}(q_{0},\dot{q}_{0})\) is the flow of the Euler–Lagrange vector field. That is to say, while the local solution is exact for the time interval \([kh,(k+1)h]\), since the \(q_{k}\) at the beginning of this interval only approximates the true global solution, the local exact solution is not the same as the exact global solution. This is particularly important when discussing invariants, where the invariants of \(\bar{q}\) remain constant within a time-step, but not from time-step to time-step.
The first property of the Galerkin curve that we will examine is its rate of convergence to the true flow of the Euler–Lagrange vector field. There are two general sources of error that affect the convergence of these curves, the first being the accuracy to which the curves approximate the local solution to the Euler–Lagrange equations over the interval \([0,h]\) with the boundary conditions \((q_{k},q_{k+1})\), and the second being the accuracy of the boundary conditions \((q_{k},q_{k+1})\) as approximations to a true sampling of the exact flow. Numerical experiments will show that often the second source of error dominates the first, causing the Galerkin curves to converge at the same rate as the one-step map. However, the accuracy to which the Galerkin curves approximate the true minimizers independent of the error of the boundary can also be established under appropriate assumptions about the action. Two theorems which establish this convergence are presented below.
Our technique for determining the accuracy of the Galerkin curves is to establish that, so long as the second Frechet derivative of the discrete action is coercive, the error between the discrete action evaluated on the Galerkin curve and and the discrete action on the local exact solution bounds the error between the curves. The error analysis of the one-step map established bounds on the error between the discrete action evaluated on the Galerkin curve and the discrete action on the local exact solution, and we apply this to bound the error between the local exact solution and the Galerkin curve. We then establish that the second Frechet derivative is coercive for an action based on the canonical Lagrangian, which makes our result immediately applicable to problems with canonical Lagrangians.
Before we state the theorems, we quickly recall the definitions of the Sobolev Norm \(\left\| \cdot \right\| _{W^{1,p}(\left[ 0,h\right] )}\),
We will make extensive use of this norm when examining convergence of Galerkin curves.
Theorem 3.8
(Geometric convergence of Galerkin curves with \(n\)-refinement) Under the same assumptions as Theorem 3.4, if at \(\bar{q}\), the action is twice Frechet differentiable, and if the second Frechet derivative of the action \(\text {D}^{2}\mathfrak {S}(\cdot )[\cdot ,\cdot ]\) is coercive in a neighborhood \(U\) of \(\bar{q}\), that is,
for all curves \(\delta q \in H_{0}^{1}(\left[ 0,h\right] \!,Q)\) and all \(\nu \in U\), then the curves which minimize the discrete action converge to the true solution geometrically with \(n\)-refinement with respect to \(\left\| \cdot \right\| _{W^{1,1}(\left[ 0,h\right] )}\). Specifically, if the discrete Hamiltonian flow map has error \({\mathcal {O}}(K_{s}^{n})\), \(K_{s}< 1\), then the Galerkin curves have error \({\mathcal {O}}({\sqrt{K_{s}}}^{n})\).
Proof
We start with the bound (23) given at the end of Theorem 3.4,
and expand using the definitions of \(L_{d}^{E}(q_{k},q_{k+1})\) and \(L_{d}(q_{k},q_{k+1},n)\), as well as the assumed accuracy of the quadrature rule \({\mathcal {G}}_{n}\) to derive
which implies:
because \(K_{s}\ge K_{g}\), (see the proof of Theorem 3.4 in the appendix). Using this inequality, we make use of a Taylor expansion of \(\mathfrak {S}\left( \tilde{q}_{n}\right) \),
for some \(\nu \in U\), to see that
The reader should note that we have used \(\text {D}^{n}\mathfrak {S}\) here to denote the \(n\)-th Frechet derivative of the functional \(\mathfrak {S}\). Now, we see that
where the boundary term in the integration by parts vanished because \(\tilde{q}_{n}(0) = \bar{q}(0)\) and \(\tilde{q}_{n}(h) = \bar{q}(h)\), by definition (note that this implies \((\tilde{q}_{n}- \bar{q}) \in H^{1}_{0}([0,h],Q)\)). Then,
where \(C = \sqrt{\frac{2(C_{s}+ C_{g})}{C_{f}}}\). \(\square \)
This result shows that Galerkin curves converge to the true solution geometrically with \(n\)-refinement, albeit with a larger geometric constant, and hence a slower rate. By simply replacing the bounds (25) and (26) from Theorem 3.4 with those from Theorem 3.3 and the term \(C_{s}K_{s}^{n}\) with \(C_{op}h^{p}\), an identical argument shows that Galerkin curves converge at half the rate with \(h\)-refinement.
Theorem 3.9
(Convergence of Galerkin curves with \(h\)-refinement) Under the same assumptions as Theorem 3.3, if at \(\bar{q}\), the action is twice Frechet differentiable, and if the second Frechet derivative of the action \(\text {D}^{2}\mathfrak {S}(\cdot )[\cdot ,\cdot ]\) is coercive with a constant \(C_{f}\) independent of \(h\) in a neighborhood \(U\) of \(\bar{q}\), for all curves \(\delta q \in H^{1}_{0}([0,h],Q)\), then if the discrete Lagrange map has error \({\mathcal {O}}(h^{p+1})\), the Galerkin curves have error at most \({\mathcal {O}}(h^{\frac{p+1}{2}})\) in \(\left\| \cdot \right\| _{W^{1,1}(\left[ 0,h\right] )}\). If \(C_{f}\) is a function of \(h\), this bound becomes \({\mathcal {O}}\left( C_{f}\left( h\right) ^{-1}h^{\frac{p+1}{2}}\right) \).
Like the requirement that the stationary points of the actions are minimizers, the requirement that the second Frechet derivative of the action is coercive may appear quite strong at first. Again, the coercivity will depend on the properties of the Lagrangian \(L\), but we can establish that for Lagrangians of the canonical form
there exists a time-step \([0,h]\) over which the action is coercive on \(H_{0}^{1}(\left[ 0,h\right] \!,Q)\).
Theorem 3.10
(Coercivity of the action) For Lagrangians of the form
where \(M\) is symmetric positive-definite, and the second derivatives of \(V(q)\) are bounded, there exists an interval \([0,h]\) over which the action is coercive over \(H_{0}^{1}(\left[ 0,h\right] \!,Q)\), that is,
for any \(\delta q \in H_{0}^{1}(\left[ 0,h\right] \!,Q)\) and any \(\nu \in C^{2}(\left[ 0,h\right] \!,Q)\).
Proof
First, we note that if
then
where \(H(\nu )\) is the Hessian of V(\(\cdot \)) at the point \(\nu \). Since \(M\) is symmetric positive-definite, and the second derivatives of \(V(\cdot )\) are bounded, then there exists \(C_{r}\) and \(m\), such that,
[see (24) for a derivation of (27)]. Hence,
Considering the last two terms in (28), and noting that \(\delta q \in H_{0}^{1}(\left[ 0,h\right] \!,Q)\), we make use of the Poincaré inequality to derive:
Thus, substituting (29) in for the last two terms of (28), we conclude:
and making use of Hölder’s inequality, we see that \(\left\| \delta q\right\| _{L^{2}(\left[ 0,h\right] )} \ge h^{\frac{1}{2}}\left\| \delta q\right\| _{L^{1}(\left[ 0,h\right] )}\), thus,
which establishes the coercivity result. \(\square \)
3.4.2 Noether quantities
One of the great advantages of using variational integrators for problems in geometric mechanics is that, by construction, they have a rich geometric structure which helps lead to excellent long-term and qualitative behavior. An important geometric feature of variational integrators is the preservation of discrete Noether quantities, which are invariants that are derived from symmetries of the action. These are analogous to the more familiar Noether quantities of geometric mechanics in the continuous case. We quickly recall Noether’s theorem in both the discrete and continuous case, which will also help define the notation used throughout the proofs that follow. The proofs of both these theorems can be found in Hairer et al. [17].
Theorem 3.11
(Noether’s Theorem) Consider a system with Hamiltonian \(H(p,q)\) and Lagrangian \(L(q,\dot{q})\). Suppose \(\{g_{s}:s\in {\mathbb {R}}\}\) is a one-parameter group of transformations which leaves the Lagrangian invariant. Let
be defined as the vector field with flow \(g_{s}(q)\), referred to as the infinitesimal generator, and define the canonical momentum
Then
is a first integral of the Hamiltonian system.
Theorem 3.12
(Discrete Noether’s Theorem) Suppose the one-parameter group of transformations leaves the discrete Lagrangian \(L_{d}(q_{k},q_{k+1})\) invariant for all \((q_{k},q_{k+1})\). Then:
where
For the remainder of this section, we will refer to \(I(q,p)\) as the Noether quantity and \(p_{k}^{T}a(q_{k}) = p_{k+1}^{T}a(q_{k+1})\) as the discrete Noether quantity.
For Galerkin variational integrators, it is possible to bound the error of the Noether quantities along the Galerkin curve from the behavior of the analogous discrete Noether quantities of the discrete problem and, more importantly, this bound is independent of the number of time-steps that are taken in the numerical integration. This is significant because it offers insight into the excellent behavior of spectral variational integrators even over long periods of integration. The significance of conserved Noether quantities is illustrated in Fig. 3, as conserved quantities act as constraints on the evolution of system.
Conserved and approximately conserved Noether quantities and the resulting constrained solution space. Suppose that both \(p^{T}q = 1\) and \(p^{2} + q^{2} = 5\) were conserved quantities for a certain Lagrangian. Then the solutions of the Euler–Lagrange equations would be constrained to the intersections of these two constant surfaces in phase space; in the figure, this is the intersection of the dashed and solid lines. If these quantities were conserved up to a fixed error along a numerical solution, then the numerical solution would be constrained to the intersection of the shaded regions in the above figure. By construction, variational integrators produce approximation solutions that automatically remain in these regions, which is what leads to many of their excellent qualities
The proof of convergence and near preservation of Noether quantities is broken into three major parts. First, we note that on step \(k\) of a numerical integration, the discrete Noether quantity arises from a function of the Galerkin curve and the initial point of the one-step map \((q_{k-1},q_{k})\), and that a bound exists for the difference of this discrete Noether quantity evaluated on the Galerkin curve and evaluated on the local exact solution to the Euler–Lagrange equations \(\bar{q}\). Second, we show that a bound exists for the difference of the discrete Noether quantity on the local exact solution of the Euler–Lagrange equations and the value of the Noether quantity of the local exact solution, which is conserved along the flow of the Euler–Lagrange vector field. Finally, we show that under certain smoothness conditions, there exists a point-wise bound between the Noether quantity evaluated on the Galerkin curve and the Noether quantity evaluated on the local exact solution. Thus, we establish a point-wise bound between the Noether quantity evaluated on the Galerkin curve and the discrete Noether quantity, and a bound between the discrete Noether quantity and the Noether quantity, which leads to a point-wise bound between the Noether quantity evaluated on the Galerkin curve, and the Noether quantity which is conserved along the global flow of the Euler–Lagrange vector field.
Throughout this section we will make the simplifying assumptions that
where \(q_{k}^{0} = q_{k}\), and thus,
This assumption significantly simplifies the analysis.
We begin by bounding the discrete Noether quantity by a function of the local exact solution of the Euler–Lagrange equations.
Lemma 3.3
(Bound on discrete Noether quantity) Define the Galerkin Noether map as:
and note that the discrete Noether quantity is given by
where \(p_{k}\) is given by the standard definition of the discrete Legendre transform for a variational integrator,
which for a Galerkin variational integrator takes the form
Assuming the quadrature accuracy of Theorem 3.4 with \(n\)-refinement and Theorem 3.3 with \(h\)-refinement, if \(\frac{\partial L}{\partial q}(q,\dot{q})\), \(\frac{\partial L}{\partial \dot{q}}(q,\dot{q})\) and \(\frac{\text{ d }}{\hbox {d}t}\frac{\partial L}{\partial \dot{q}}\) are Lipschitz continuous, \(\left\| \phi _{0}\right\| _{L^{\infty }(\left[ 0,h\right] )}\) is bounded with \(n\)-refinement, and \(\left\| \tilde{q}_{n}- \bar{q}\right\| _{W^{1,1}(\left[ 0,h\right] )}\) is bounded below by the quadrature error, then
for some \(C\) independent of \(n\) and \(h\).
Proof
We begin by expanding the definitions of the discrete Noether quantity:
Now we introduce the function \(e_{q}(\cdot ,\cdot )\) which gives the error of the quadrature rule, and thus,
Integrating by parts, we get:
Introducing the Lipschitz constants \(L_{1}\) for \(\frac{\partial L}{\partial q}\), \(L_{2}\) for \(\frac{\partial L}{\partial \dot{q}}\), and \(L_{3}\) for \(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\),
We now make the simplification that the quadrature error \(|e_{q}(\cdot ,\cdot )|\) serves as a lower bound for \(\left\| \tilde{q}_{n}- \bar{q}\right\| _{W^{1,1}(\left[ 0,h\right] )}\). While this may not strictly hold, all of our estimates on the convergence for \(\tilde{q}_{n}\) imply this bound, and hence it is a reasonable simplification for establishing convergence in this case. Now, note that \(\left\| \phi _{0}\right\| _{L^{\infty }(\left[ 0,h\right] )}\) is invariant under \(h\) rescaling, and let
to get
which establishes the result. \(\square \)
Lemma 3.3 establishes a bound between the discrete Noether quantity and \(I_{d}(\bar{q},q_{k})\). The next step is to establish a bound between \(I_{d}(\bar{q},q_{k})\) and the Noether quantity.
Lemma 3.4
(Error between discrete Noether quantity and true Noether quantity) Assume that \(\phi _{0}(0) = 1\) and \(\phi _{0}(h) = 0 \), and that the sequence \(\{|a(q_{k})|\}_{k=1}^{N}\) is bounded by a constant \(C_{a}\) which is independent of \(N\). Let
Once again, let the error of the quadrature rule be given by \(e_{q}(\cdot ,\cdot )\). Then,
for any \(t \in [0,h]\).
Proof
First, we note that since \(\bar{q}\) solves the Euler–Lagrange equations exactly, \(I(\bar{p}(t),\bar{q}(t))\) is a conserved quantity along the flow, so it suffices to show the inequality holds for \(t=0\). We begin by expanding:
Since \(\bar{q}(t)\) solves the Euler–Lagrange equations, \(\phi _{0}(0) = 1\) and \(\phi _{0}(h) = 0\), and \(\bar{q}(0) = q_{k}\),
which yields the desired bound. \(\square \)
Once again, if we assume that the quadrature error serves as a lower bound for the Sobolev error, combining the bounds from Lemmata 3.3 and 3.4 yields:
This bound serves two purposes; the first is to establish a bound between the discrete Noether quantity and the Noether quantity computed on the local exact solution \(\bar{q}\). The second is to establish a bound between the discrete Noether quantity after one-step and the Noether quantity computed on the initial data:
since for \((q_{1},q_{2})\), \(\bar{q}\) is the global exact flow of the Euler–Lagrange equations.
The difference between these two bounds is subtle but important; by establishing a bound between the discrete Noether quantity and the Noether quantity associated with the initial conditions, on any step of the method we can bound the error between the discrete Noether quantity and the Noether quantity associated with the global exact flow. By establishing the bound between the discrete Noether quantity and the Noether quantity associated with \(\bar{q}\) at any step, we can bound the error between the Noether quantity associated with the local exact flow \(\bar{q}\) and the true Noether quantity conserved along the global exact flow:
for any \(t \in [0,h]\) on any time-step \(k\). Because the local exact flow \(\bar{q}\) is generated from boundary conditions \((q_{k},q_{k+1})\) which only approximate the boundary conditions of the true flow, there is no guarantee that the Noether quantity associated with \(\bar{q}\) will be the same step to step, only that it will be conserved within each time-step. However, because there is a bound between the Noether quantity associated with \(\bar{q}\) and the discrete Noether quantity at every time-step, the discrete Noether quantity and the Noether quantity associated with the exact flow, and because the Noether quantity is conserved point-wise along \(\bar{q}\) on each time-step, there exists a bound between the Noether quantity associated with each point of the local exact flow and the Noether quantity associated with the true solution.
We finally arrive at the desired result, which is a theorem that bounds the error between the Noether quantity along the Galerkin curve and the true Noether quantity. It is significant because not only does it bound the error of the Noether quantity, but the bound is independent of the number of steps taken, and hence will not grow even for extremely long numerical integrations.
Theorem 3.13
(Convergence of conserved Noether quantities) Define
Under the assumptions of Lemmata 3.3 and 3.4, if the Noether map \(I(p,q)\) is Lipschitz continuous in both its arguments, then there exists a constant \(C_{v}\) independent of \(N\), the number of method steps, such that,
for any \(t \in [0,Nh]\).
Proof
We begin by introducing the Noether quantity evaluated at \(t\) on the local exact flow, \(\bar{q}\):
Considering the first term in (31), let \(L_{4}\) be the Lipschitz constant for \(I(\cdot ,\cdot )\). Then,
The second term in (31) is exactly the bound given by (30) and thus combining (32) and (30) in (31) and defining \(C_{v}= 4CC_{a}+ L_{4}(L_{2}+1)\), we have:
which completes the result. \(\square \)
The convergence and bounds of the Noether quantity evaluated on the Galerkin curve to that of the true solution is hampered by one issue. While Theorems 3.8 and 3.9 provide estimates for convergence in the Sobolev norm \(\left\| \cdot \right\| _{W^{1,1}(\left[ 0,h\right] )}\), Theorem 3.13 requires estimates in the \(L^{\infty }\) norm. We can establish a bound for \(\left\| \tilde{q}_{n}(t) - \bar{q}(t)\right\| _{L^{\infty }(\left[ 0,h\right] )}\), but it is much more difficult to establish a general estimate for \(\left\| \dot{\tilde{q}}_{n}(t) - \dot{\bar{q}}(t)\right\| _{L^{\infty }(\left[ 0,h\right] )}\).
Lemma 3.5
(Bound on \(L^{\infty }\) norm from Sobolev norm) For any \(t \in [0,h]\), the following bound holds:
and thus,
Proof
This is a basic extension of the arguments from Lemma A.1. in Larsson and Thomée [23], generalizing the lemma from the interval \([0,1]\) to an interval of arbitrary length, \([0,h]\). We note that for any \(t, s \in [0,h]\), \(q(t) = q(s) + \int _{s}^{t} \dot{q}(u)\hbox {d}u\). Thus:
Now, we integrate with respect to \(s\):
which yields the desired result. \(\square \)
Under certain assumptions about the behavior of \(\dot{\tilde{q}}_{n}- \dot{\bar{q}}\), it is possible to establish bounds on the point-wise error of \(\dot{\tilde{q}}_{n}\) from the Sobolev error \(\left\| \tilde{q}_{n}- \bar{q}\right\| _{W^{1,1}(\left[ 0,h\right] )}\). For example, if the length of time that the error is within a given fraction of the max error is proportional to the length of the interval \([0,h]\), i.e. there exists \(C_{1},C_{2}\) independent of \(h\): i.e.,
where \(m\) is the Lebesgue measure, then it can easily be seen that:
While we will not establish here that the \(\dot{\tilde{q}}_{n}\) converges in the \(L^{\infty }\) norm with the same rate that the Galerkin curve converges in the Sobolev norm, our numerical experiments will show that the Noether quantities tend to converge at the same rate as the Galerkin curve.
4 Numerical experiments
To support the results in this paper, several numerical experiments were conducted by applying spectral variational techniques to well-known mechanical problems. For each problem, the spectral variational integrator was constructed using Lagrange interpolation polynomials at \(n\) Chebyshev points with the Gauss–Legendre quadrature rule at \(2n\) points. Convergence of both the one-step map and the Galerkin curves was measured using the \(\ell ^{\infty }\) and \(L^{\infty }\) norms respectively, although we record them on the same axis labeled \(L^{\infty }\) error in a slight abuse of notation. The experiments strongly support the results of this paper, and suggest topics for further investigation.
There are several remarks we wish to make regarding our numerical results. First, we will omit a discussion of the efficiency of our results compared with other methods for now. This is a large topic, and is highly implementation-dependent. In particular, determining efficient and stable implementations of our proposed method is an area of active research, and we will discuss this in greater detail in Sect. 5. On a similar note, in many of our figures, the methods converge to a relatively high roundoff error. This is almost certainly a product of the current implementation of the methods, and the error tolerance of our nonlinear solver. We present our numerical experiments mainly to provide supporting evidence for the error analysis of this paper. In practice, one would use compensated summation techniques [21] to mitigate the effect of roundoff errors.
4.1 Harmonic oscillator
The first and simplest numerical experiment conducted was the harmonic oscillator. Starting from the Lagrangian,
where \(q\in {\mathbb {R}}\), the corresponding spectral variational integrators have discrete Euler–Lagrange equations that are linear. Choosing the large time-step \(h=20\) over 100 steps yields the expected geometric convergence as can be seen in Fig. 4. It should be noted that the \(L^{\infty }\) error, denoted by \(e\), obeys the bound
Geometric convergence of the spectral variational integration of the harmonic oscillator problem, for 100 steps at step-size \(h = 20.0\)
which corresponds to geometric convergence with \(K = 0.21\). The two different markers in the plot, \(\bigcirc \) and \(\times \), correspond to the error of the one-step map and along the continuous Galerkin curve, respectively. While our theory predicts a possible lower rate of convergence for the Galerkin curve, we do not observe it here. It will be apparent in later numerical experiments. In addition, the max error of the energy also decays geometrically, see Fig. 5. Here, and in all future plots, we measure the error of the invariants along the Galerkin curve, and hence there will be some error in the invariants even though they are conserved at the steps of the one-step map. That is, when we examine the behavior of invariants, we are measuring the invariants of the original continuous Lagrangian evaluated along the Galerkin curve, \(I(\frac{\partial L}{\partial q}(\tilde{q}_{n},\dot{\tilde{q}}_{n}),\tilde{q}_{n})\). These experiments illustrate that these errors are bounded, converge at the predicted rates, and do not grow over the time of integration, as is illustrated in Fig. 6 for the harmonic oscillator.
Geometric convergence of the energy error of the spectral variational integration of the harmonic oscillator problem for 100 steps at step-size \(h = 20.0\)
Energy stability of the spectral variational integration of the harmonic oscillator problem. This energy was computed for the integration using \(n = 14\) for step-size \(h = 20.0\)
4.2 N-body problems
We now turn our attention towards Kepler \(N\)-body problems, which are both good benchmark problems and are interesting in their own right. The general form of the Lagrangian for these problems is
where \(q_{i} \in {\mathbb {R}}^{D}\) is the center of mass for body \(i\), \(G\) is a gravitational constant, and \(m_{i}\) is a mass constant associated with the body described by \(q_{i}\).
4.2.1 2-Body problem
The first experiment we will conduct has parameters \(D = 2\), \(m_{1} = m_{2} = 1\). Centering the coordinate system at \(q_{1}\), we choose \(q_{2}(0) = (0.4,0)\), \(\dot{q}_{2}(0) = (0, 2)\), which has a known closed form solution which is a stable closed elliptical orbit with eccentricity \(0.6\). Knowing the closed form solution allows us to examine the rate of convergence to the true solution, and when solved with the large time time-step \(h = 2.0\), over 100 steps, the error of the one-step map is \({\mathcal {O}}(0.56^{n})\) with \(n\)-refinement and \({\mathcal {O}}(h^{2\lceil \frac{n}{2}\rceil })\) with \(h\)-refinement, as can be seen in Figs. 7 and 8, respectively. The numerical evidence suggests that our bound for the one-step map with \(h\)-refinement is not sharp, as the convergence of the one-step map is always even. Interestingly, it is also possible to observe the different convergence rates of the one-step map and the Galerkin curves with \(n\)-refinement, as eventually the Galerkin curves have error approximately \({\mathcal {O}}(0.74^{n})\) while the one-step map has error approximately \({\mathcal {O}}(0.56^{n})\), and \(\sqrt{0.56} \approx 0.7483\). However, it appears that the error from the one-step map dominates until very high choices of \(n\), and thus it is difficult to observe the error of the Galerkin curves directly with \(h\)-refinement, roundoff error becomes a problem before the error of the Galerkin curves does for smaller choices of \(n\).
Geometric convergence of the Kepler 2-body problem with eccentricity 0.6 over 100 steps of \(h = 2.0\). Note that around \(n=32\), the error for the Galerkin curves becomes \({\mathcal {O}}(0.74^{n})\), while the error for the one-step map is always \({\mathcal {O}}(0.56^{n})\)
Convergence of the Kepler 2-body problem with eccentricity 0.6 over 100 steps with \(h\) refinement. Here we use \(N\) in the legend to denote the number of Chebyshev points used to construct the method. Note our bound is not sharp, as the error is \({\mathcal {O}}(h^{2 \lceil \frac{n}{2} \rceil })\), where \(\lceil \cdot \rceil \) is the ceiling function
The N-body Lagrangian is invariant under the action of \(\text{ SO }(D)\), which yields the conserved Noether quantity of angular momentum. For the two-body problem, this is
where \(q = (q_{x},q_{y})\). Numerical experiments show that the error of the angular momentum evaluated along the continuous Galerkin curve, \(I(\tilde{q}_{n},\dot{\tilde{q}}_{n})\), does not grow with the number of steps taken in the integration, Fig. 9, but that the error is of the same order as the error of Galerkin curve with \(n\)-refinement, as can be seen in Fig. 10. Numerical experiments show similar convergence for the energy error with \(n\)-refinement, Fig. 11. With \(h\)-refinement, the angular momentum appears to have error \({\mathcal {O}}(h^{\frac{n}{2} + 2})\) in Fig. 12. This is interesting because the theoretical bound on the error of the Galerkin curves is \({\mathcal {O}}(h^\frac{n}{2})\), and the error of the Noether quantities is theoretically a factor \(C(h)\) times the error of the Galerkin curves, where \(C\) is the factor that arises in the proof of the convergence of the conserved Noether quantities. Numerical experiments suggest \(C\) is \({\mathcal {O}}(h^{2})\) for this problem, but that the Galerkin curves do converge at a rate of \({\mathcal {O}}(h^{\frac{n}{2}})\), which is consistent with of the Galerkin curve error estimate. Numerical experiments suggest similar convergence behavior for energy with \(h\)-refinement (Fig. 13), and likewise, the energy error does not grow with time (Fig. 14). While this evidence is not conclusive, it is suggestive that the error analysis provides a plausible bound. A careful analysis of the factor \(C\) would be an interesting direction for further investigation.
Stability of angular momentum for the Kepler 2-body problem
Geometric convergence of the angular momentum of the Kepler 2-body problem with eccentricity 0.6 over 100 steps of \(h = 2.0\). Again, the error is of the same order as it was the Galerkin curves
Geometric convergence of the Energy Error of the Kepler 2-body problem with eccentricity 0.6 over 100 steps of \(h = 2.0\). Note that the error is \({\mathcal {O}}(0.74^{n})\), the same as it was for the Galerkin curves
Convergence of the angular momentum of the Kepler 2-body problem with eccentricity 0.6 over 100 steps of \(h = 2.0\). Here we use \(N\) in the legend to denote the number of Chebyshev points used to construct the method
Convergence of the Kepler 2-body problem energy with eccentricity 0.6 over 100 steps with \(h\) refinement. Here we use \(N\) in the legend to denote the number of Chebyshev points used to construct the method
Stability of the energy for the Kepler 2-body problem
4.2.2 The solar system
To illustrate a potential application of spectral variational integrators, we let \(D = 3\), \(N = 10\), and use the velocities, positions, and masses of the sun, 8 planet, and the dwarf planet Pluto on January 1, 2000 (as provided by the JPL Solar System ephemeris [39]) as initial configuration parameters for the Kepler system. Taking \(100\) time-steps of \(h = 100\) days, the \(n = 25\) spectral variational integrator produces a highly stable flow in Fig. 15. It should be noted that orbits are closed, stable, and exhibit almost none of the “precession” effects that are characteristic of symplectic integrators (as can be seen for a low-order symplectic integrator in Fig. 16), even though the time-step is larger than the orbital period of Mercury. Additionally, considering just the outer solar system (Jupiter, Saturn, Uranus, Neptune, Pluto), and aggregating the inner solar system (Sun, Mercury, Venus, Earth, Mars) to a point mass, an \(N = 25\) spectral variational integrator taking 100 time-steps \(h = 1{,}825\) days (5 year steps) produces the orbital flow seen in Fig. 17. Again, these are highly stable, precession-free orbits. As can be clearly seen, the spectral variational integrator produces extremely stable flows, even for very large time-steps.
Orbital diagram for the inner solar system produced by an \(n = 25\) point spectral variational integrator using all 8 planets, the sun, and Pluto with 100 time-steps with \(h=100\) days
For comparison, orbital diagram for the inner solar system produced by the symplectic Euler method (a first order method) using all 8 planets, the sun, and Pluto with 500 time-steps with \(h=5\) days. Notice the precession of Mercury’s orbit
Orbital diagram for the outer solar system produced by an \(n = 25\) spectral variational integrator using the 4 outer planets, Pluto, with the sun and 4 inner planets aggregated to a point with 100 time-steps at \(h=1{,}825\) days
Because high-order Galerkin integrators can take such large time-steps, it is possible to use them to compute very high-order long-term integrations. In Fig. 18, we present a 10 million year integration of the solar system using a 25 point numerical method. This simulation was performed on a single processor in less than 72 h, and incorporates the Sun and the 8 planets of the solar system. While the specifics of the implementation of these high-order methods remains an area of investigation, our numerical experiments suggest that with the proper implementation, spectral variational integrators could be a valuable tool in scientific computing.
A ten million year simulation of the solar system (the Sun and all planets Mercury through Neptune) using an \(n = 25\) Galerkin variational integrator with 100 day time-steps. Note that 100 days is longer than the orbital period of Mercury. The dots are samplings of the positions of the planets every 2,000 years
5 Conclusions and future work
In this paper, a new numerical method for variational problems was introduced, specifically a symplectic momentum-preserving integrator that exhibits geometric convergence to the true flow of a system under the appropriate conditions. These integrators were constructed under the general framework of Galerkin variational integrators, and made use of the global function paradigm common to many different spectral methods.
Additionally, a general convergence theorem was established for Galerkin type variational integrators, establishing the important result that, under suitable hypotheses, Galerkin variational integrators can be constructed of arbitrarily high-order. This result provides a powerful tool for both constructing and analyzing variational integrators, it provides a methodology for constructing methods of very high-order of accuracy, and it also establishes order of convergence for methods that can be formulated as Galerkin variational integrators. For example, the popular Störmer–Verlet method can be formulated as a Galerkin variational integrator using a linear approximation space and the trapezoidal rule for quadrature. It was shown that from the one-step map, a continuous approximation to the solution of the Euler–Lagrange equations can be easily recovered over each time-step. The error of these continuous approximations was shown to be related to the error of the one-step map. Furthermore, the Noether quantities along this continuous approximation approximate the true Noether quantity up to a small error which does not grow with the number of steps taken. It was also shown that the error of the Noether quantities converges to zero with \(n\)-refinement or \(h\)-refinement at a predictable rate.
In addition to the convergence results, another interesting feature of spectral variational integrators is the construction of very high-order methods that remain accurate using time-steps that are orders of magnitude larger than can be tolerated by traditional integrators. The trade-off is that the computational effort required to compute each time-step is much greater than that of other methods. However, a mitigating factor of this trade-off is that the approach of solving a short sequence of large problems, as opposed to a large sequence of small problems, lends itself much better to parallelization and computational acceleration. The literature on methods for acceleration of the construction and solution of structured systems of linear and nonlinear problems for PDE problems is extensive, and it is likely that such methods could be applied to spectral variational integrators to greatly improve their computation efficiency.
5.1 Future work
Future directions for this work are numerous. Because of generality of the construction of Galerkin variational integrators, there exists many possible directions for further exploration.
5.2 Efficient implementation
A common criticism of high-order variational integrators is that they often require the solution of a large set of nonlinear equations at every time-step, which greatly curtails their efficiency. For Galerkin variational integrators, this problem is exasperated by the fact that high-order quadrature rules must be used to construct high-order methods. However, for Galerkin variational integrators applied to Lagrangians of the canonical form, it is possible to solve the nonlinear system of equations efficiently using a contraction mapping method inspired by the proof of existence and uniqueness of solutions to the internal stage Euler–Lagrange equations. There are two major advantages to this approach,
-
(1)
there are many quantities used in the contraction mapping that can be pre-computed, which reduces the computational cost of solving the nonlinear system of equations to \({\mathcal {O}}(n^{2}D^{2})\), where \(n\) is the order of the integrator and \(D\) is the number of spatial dimensions of the problem,
-
(2)
applying the contraction mapping can be decomposed into several largely independent subproblems, which can be efficiently solved in parallel.
Making use of these advantages in concert with the fact that high-order Galerkin variational integrators are capable of taking time-steps that are orders of magnitude larger than lower-order integrators, it may be possible to efficiently compute long-term high-order integrations using Galerkin variational integrators. An in depth study of efficient implementations and a comparison of computational costs is a critical future direction of research.
5.2.1 Lie group spectral variational integrators
Following the approach of Leok and Shingel [30] or Bou-Rabee and Marsden [4], it is relatively straight forward to extend spectral variational integrators to Lie groups using natural charts. A systematic investigation of the resulting Lie group methods, including convergence and near conservation of Noether quantities, would be a natural extension of the work done here.
5.2.2 Multiple time-scale and small perturbation variational integrators
It is often very difficult to construct efficient numerical methods for problems where different components are evolving at radically different time-scales, as quickly evolving dynamics severely restrict the maximum stable step-size of the numerical method. One approach to alleviating this restriction is to construct integrators based on function spaces that capture the fast dynamics over long intervals, as discussed in Leok [28]. This technique is even more effective when the fast dynamics only have a small influence on the other components, as was shown in Farr [12]. Such an approach naturally extends to Galerkin variational integrators, through the choice of the approximation space \(\mathbb {M}([0,h],Q)\). Early work on constructing and analyzing Galerkin variational integrators for multiple time-scales has been promising, and once a complete theory is developed, such constructions could provide a critical tool in the behavior of long-term dynamics of systems with multiple time-scale evolutions.
A particular problem of interest is the study of the long-term dynamics of the solar system. In this system, Mercury’s rapid orbital period is currently the limiting factor on the maximum step-size for many state of the art methods, see for example Blanes et al. [2] or Farrés et al. [13]. By using Galerkin variational integrators as the basis for a numerical averaging technique, in conjunction with specially developed high-order splitting methods, it may be possible to alleviate the step-size restriction without compromising the accuracy or efficiency of the numerical method.
5.2.3 Multisymplectic variational integrators
Multisymplectic geometry (see Marsden et al. [36]) has become an increasingly popular framework for extending much of the geometric theory from classical Lagrangian mechanics to Lagrangian PDEs. The foundations for a discrete theory have been laid, and there have been significant results achieved in geometric techniques for structured problems such as elasticity, fluid mechanics, nonlinear wave equations, and computational electromagnetism. However, there is still significant work to be done in the areas of construction of numerical methods, analysis of discrete geometric structure, and especially error analysis. Galerkin type methods have become a standard method in classical numerical PDE methods, such as Finite-Element Methods, Spectral, and Pseudospectral methods. The variational Galerkin framework could provide a natural framework for extending these classical methods to structure-preserving geometric methods for PDEs, and the analysis of such methods will rely on the notion of the boundary Lagrangian (see Vankerschaver et al. [44]), which is the PDE analogue of the exact discrete Lagrangian.
References
Biesiadecki, J.J., Skeel, R.D.: Dangers of multiple time step methods. J. Comput. Phys. 109(2), 318–328 (1993)
Blanes, S., Casas, F., Farres, A., Laskar, J., Makazaga, J., Murua, A.: New families of symplectic splitting methods for numerical integration in dynamical astronomy. Appl. Numer. Math. (2013)
Bloch, A.M., Leok, M. Marsden, J.E., Zenkov, D.V.: Controlled lagrangians and stabilization of the discrete cart-pendulum system. In: 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference. CDC-ECC’05, pp. 6579–6584. IEEE (2005)
Bou-Rabee, N., Marsden, J.E.: Hamilton-Pontryagin integrators on Lie groups. I. Introduction and structure-preserving properties. Found. Comput. Math. 9(2), 197–219 (2009)
Bou-Rabee, N., Owhadi, H.: Stochastic variational integrators. IMA J. Numer. Anal. 29(2), 421–443 (2009)
Bou-Rabee, N., Owhadi, H.: Long-run accuracy of variational integrators in the stochastic context. SIAM J. Numer. Anal. 48(1), 278–297 (2010)
Boyd, J.P.: Chebyshev and Fourier Spectral Methods, 2nd edn. Dover Publications Inc., Mineola (2001)
Calvo, M.P., Sanz-Serna, J.M.: The development of variable-step symplectic integrators, with application to the two-body problem. SIAM J. Sci. Comput. 14(4), 936–952 (1993)
Cortés, J., Martínez, S.: Non-holonomic integrators. Nonlinearity 14(5), 1365–1392 (2001)
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Progress in Nonlinear Differential Equations and their Applications, 8. Birkhäuser Boston Inc., Boston (1993)
Estep, D., French, D.: Global error control for the continuous Galerkin finite element method for ordinary differential equations. RAIRO Modél. Math. Anal. Numér. 28(7), 815–852 (1994)
Farr, W.M.: Variational integrators for almost-integrable systems. Celestial Mech. Dyn. Astron. 103(2), 105–118 (2009)
Farrés, A., Laskar, J., Blanes, S., Casas, F., Makazaga, J., Murua, A.: High precision symplectic integrators for the solar system. Celestial Mechanics and Dynamical Astronomy, pp. 1–34 (2013)
Fedorov, Y.N., Zenkov, D.V.: Discrete nonholonomic LL systems on Lie groups. Nonlinearity 18(5), 2211–2241 (2005)
Fetecau, R., Marsden, J.E., Ortiz, M., West, M.: Nonsmooth Lagrangian mechanics and variational collision integrators. SIAM J. Appl. Dyn. Syst. 2(3), 381–416 (2003)
Gladman, B., Duncan, M., Candy, J.: Symplectic integrators for long-term integrations in celestial mechanics. Celestial Mech. Dyn. Astron. 52(3), 221–240 (1991)
Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration, Springer Series in Computational Mathematics, vol. 31, 2nd edn. Springer, Berlin (2006)
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems. Solving Ordinary Differential Equations. Springer, Berlin (2008). ISBN 9783540788621
Hall, J., Leok, M.: Lie group spectral variational integrators. Found. Comput. Math. (2014) (submitted, arXiv:1402.3327[math.NA])
Hulme, B.L.: One-step piecewise polynomial Galerkin methods for initial value problems. Math. Comput. 26, 415–426 (1972)
Kahan, W.: Pracniques: further remarks on reducing truncation errors. Commun. ACM 8(1), 40–48 (1965)
Lall, S., West, M.: Discrete variational Hamiltonian mechanics. J. Phys. A 39(19), 5509–5519 (2006)
Larsson, S., Thomée, V.: Partial Differential Equations with Numerical Methods, Texts in Applied Mathematics, vol. 45. Springer, Berlin (2003)
Laskar, J.: A numerical experiment on the chaotic behaviour of the solar system. Nature 338, 237–238 (1989)
Lee, T., Leok, M., McClamroch, N.H.: Lie group variational integrators for the full body problem. Comput. Methods Appl. Mech. Eng. 196(29–30), 2907–2924 (2007)
Lee, T., Leok, M., McClamroch, N.H.: Lagrangian mechanics and variational integrators on two-spheres. Int. J. Numer. Methods Eng. 79(9), 1147–1174 (2009)
Lee, T., Leok, M., McClamroch, N.H.: Geometric numerical integration of complex dynamics of tethered spacecraft. In; Proc. American Control Conf., pp. 1885–1891 (2011)
Leok, M.: Generalized Galerkin variational integrators: Lie group, multiscale, and pseudospectral methods. (preprint, arXiv:math.NA/0508360) (2004)
Leok, M., Shingel, T.: Prolongation-collocation variational integrators. IMA J. Numer. Anal. 32(3), 1194–1216 (2012a)
Leok, M., Shingel, T.: General techniques for constructing variational integrators. Front. Math. China 7(2), 273–303 (2012b). (special issue on computational mathematics, invited paper)
Leok, M., Zhang, J.: Discrete Hamiltonian variational integrators. IMA J. Numer. Anal. 31(4), 1497–1532 (2011)
Lew, A., Marsden, J.E., Ortiz, M., West, M.: Asynchronous variational integrators. Arch. Ration. Mech. Anal. 167(2), 85–146 (2003)
Leyendecker, S., Ober-Blöbaum, S., Marsden, J.E., Ortiz, M.: Discrete mechanics and optimal control for constrained systems. Optim. Control Appl. Methods 31(6), 505–528 (2010)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Texts in Applied Mathematics. Springer, New York (1999). ISBN 9780387986432
Marsden, J.E., West, M.: Discrete mechanics and variational integrators. Acta Numer. 10, 357–514 (2001)
Marsden, J.E., Patrick, G.W., Shkoller, S.: Multisymplectic geometry, variational integrators, and nonlinear PDEs. Commun. Math. Phys. 199(2), 351–395 (1998)
McLachlan, R., Perlmutter, M.: Integrators for nonholonomic mechanical systems. J. Nonlinear Sci. 16(4), 283–328 (2006)
Müller, S., Ortiz, M.: On the \(\Gamma \)-convergence of discrete dynamics and variational integrators. J. Nonlinear Sci. 14(3), 279–296 (2004)
NASA. JPL Horizons system online solar system data and ephemeris (2012). http://ssd.jpl.nasa.gov/?horizons
Patrick, G.W., Cuell, C.: Error analysis of variational integrators of unconstrained Lagrangian systems. Numer. Math. 113(2), 243–264 (2009)
Stern, A., Tong, Y., Desbrun, M., Marsden, J.E.: Geometric computational electrodynamics with variational integrators and discrete differential forms. In: Geometry, Mechanics, and Dynamics: The Legacy of Jerry Marsden, Fields Inst. Commun. Springer, Berlin (2014, to appear)
Sussman, G.J., Wisdom, J.: Chaotic evolution of the solar system. Technical report, DTIC Document (1992)
Trefethen, L.N.: Spectral Methods in MATLAB, Software, Environments, and Tools, vol. 10. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2000)
Vankerschaver, J., Liao, C., Leok, M.: Generating functionals and Lagrangian PDEs. J. Math. Phys. 54(8), 082901 (2013). (22 pages)
Acknowledgments
We are very grateful to the referee of this paper, whose comments and observations significantly improved our exposition. This work was supported in part by NSF Grants CMMI-1029445, DMS-1065972, CMMI-1334759, DMS-1411792, and NSF CAREER Award DMS-1010687.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs of geometric convergence of spectral variational integrators
Appendix: Proofs of geometric convergence of spectral variational integrators
As stated in Sect. 3.2, it can be shown that spectral variational integrators converge geometrically to the true flow associated with a Lagrangian under the appropriate conditions. The proof is similar to that of arbitrarily high-order convergence, and is offered below.
However, before we offer a proof of the theorem, we must establish a result that extends Theorem 1.1. Specifically, we must show:
Theorem 6.1
(Extension of Theorem 1.1 to geometric convergence) Given a regular Lagrangian \(L\) and corresponding Hamiltonian \(H\), the following are equivalent for a discrete Lagrangian \(L_{d}(q_{0},q_{1},n)\):
-
(1)
there exist a positive constant \(K\), where \(K < 1\), such that the discrete Hamiltonian map for \(L_{d}(q_{0},q_{h},n)\) has error \({\mathcal {O}}(K^{n})\),
-
(2)
there exists a positive constant \(K\), where \(K < 1\), such that the discrete Legendre transforms of \(L_{d}(q_{0},q_{h},n)\) have error \({\mathcal {O}}(K^{n})\),
-
(3)
there exists a positive constant \(K\), where \(K < 1\), such that \(L_{d}(q_{0},q_{h},n)\) approximates the exact discrete Lagrangian \(L_{d}^{E}(q_{0},q_{h},h)\) with error \({\mathcal {O}}(K^{n})\).
The proof of this theorem is a simple modification of the proof of Theorem 1.1, and is included here for completeness. For details, the interested reader is referred to [35].
Proof
Since we are assuming that the time-step \(h\) is being held constant, we will suppress it as an argument to the exact discrete Lagrangian, writing \(L^{E}_{d}(q_{0},q_{h})\) for \(L^{E}_{d}(q_{0},q_{h},h)\). First, we will assume that \(L_{d}(q_{0},q_{h},n)\) approximates \(L^{E}_{d}(q_{0},q_{h})\) with error \({\mathcal {O}}(K^{n})\) and show this implies the discrete Legendre transforms have error \({\mathcal {O}}(K^{n})\). By assumption, if \(L_{d}(q_{0},q_{h},n)\) has error \({\mathcal {O}}(K^{n})\), there exists a function which is smooth in its first two arguments \(e_{v}: Q \times Q \times \mathbb {N} \rightarrow {\mathbb {R}}\), such that,
with \(|e_{v}(q_{0},q_{h},n)| \le C_{v}\) on \(U_{v}\). Taking derivatives with respect to the first argument yields:
and with respect to the second yields:
Since \(e_{v}\) is smooth and bounded over the closed set \(U\), so are \(D_{1}e_{v}\) and \(D_{2}e_{v}\), yielding that the discrete Legendre transforms have error \({\mathcal {O}}(K^{n})\). Now, to show that if the discrete Legendre transforms have error \({\mathcal {O}}(K^{n})\), the discrete Lagrangian has error \({\mathcal {O}}(K^{n})\), we write:
Since \(D_{1}e_{v}\) and \(D_{2}e_{v}\) are smooth and bounded on a bounded set, this implies there exists a function \(d(n)\), such that,
for some constant \(C_{v}\). This shows that the discrete Lagrangian is equivalent to a discrete Lagrangian with error \({{{\mathcal {O}}}}(K^{n})\). We note that the equivalence is a consequence of the fact that one can add a function of \(h\) or \(n\) to any discrete Lagrangian and the resulting discrete Euler–Lagrange equations and discrete Legendre Transforms are unchanged, hence the function \(d(n)\).
To show the equivalence of the discrete Hamiltonian map having error \({\mathcal {O}}(K^{n})\) and the discrete Legendre transforms having error \({\mathcal {O}}(K^{n})\), we recall expressions for the discrete Hamiltonian map for the discrete Lagrangian \(L_{d}\) and exact discrete Lagrangian \(L^{E}_{d}\):
Now, we make use of the following consequence of the implicit function theorem: If we have smooth functions \(g_{1},g_{2}\) and the sequences of functions \(\{f_{1_{n}}\}_{n=1}^{\infty }\), \(\{f_{2_{n}}\}_{n=1}^{\infty }\), \(\{e_{1_{n}}\}_{n=1}^{\infty }\) and \(\{e_{2_{n}}\}_{n=1}^{\infty }\), such that,
where \(\sup {\{\Vert e_{1_{n}}\Vert \}_{n=1}^{\infty }} < C_{1}\) and \(\sup {\{\Vert e_{2_{n}}\Vert \}_{n=1}^{\infty }} < C_{2}\) on compact sets, then,
for some sequences of functions \(\{e_{12_{n}}\}_{n=1}^{\infty }\), \(\{\bar{e}_{1_{n}}\}_{n=1}^{\infty }\) where \(\sup {\{\Vert e_{12_{n}}\Vert \}_{n=1}^{\infty }} < C_{1}\) and \(\sup {\{\Vert \bar{e}_{1_{n}}\Vert \}_{n=1}^{\infty }} < C_{2}\) on compact sets.
It follows from (33) and (34) that if the discrete Legendre transforms have error \({\mathcal {O}}(K^{n})\), the discrete Hamiltonian map does as well. Finally, if we have a discrete Hamiltonian map with error \({\mathcal {O}}(K^{n})\), we use the identity
where \(\pi _{Q}\) is the projection map \(\pi _{Q}:(q,p) \rightarrow q\) and (34) to see that \({\mathbb {F}}^{-}L_{d}\) has error \({\mathcal {O}}(K^{n})\), and the identity:
along with (33) to establish that \({\mathbb {F}}^{+}L_{d}\) also has error \({\mathcal {O}}(K^{n})\), which completes the proof. \(\square \)
This simple extension is a critical tool for establishing the geometric convergence of spectral variational integrators, and leads to the following theorem concerning the accuracy of spectral variational integrators.
Theorem 6.2
(Geometric convergence of spectral variational integrators) Given an interval \([0,h]\) and a Lagrangian \(L:TQ \rightarrow {\mathbb {R}}\), let \(\bar{q}\) be the exact solution to the Euler–Lagrange equations, and \(\tilde{q}_{n}\) be the stationary point of the spectral variational discrete action
If:
-
(1)
there exists constants \(C_{A},K_{A},\, K_{A}< 1\), independent of \(n\), such that for each \(n\), there exists a curve \(\hat{q}_{n}\in \mathbb {M}^{n}([0,h],Q)\), such that,
$$\begin{aligned} \left\| \left( \hat{q}_{n}\left( t\right) \!,\dot{\hat{q}}_{n}\left( t\right) \right) - \left( \bar{q}\left( t\right) \!,\dot{\bar{q}}\left( t\right) \right) \right\| _1&\le C_{A}K_{A}^{n},\qquad \text {for all }t\in [0,h], \end{aligned}$$ -
(2)
there exists a closed and bounded neighborhood \(U \subset TQ\), such that \((\bar{q}(t),\dot{\bar{q}}(t)) \in U\) and \((\hat{q}_{n}(t),\dot{\hat{q}}_{n}(t)) \in U\) for all \(t\) and \(n\), and all partial derivatives of \(L\) are continuous on \(U\),
-
(3)
for the sequence of quadrature rules \({\mathcal {G}}_{n}(f) = h\sum _{j=1}^{m_{n}} b_{j_{n}}f(c_{j_{n}}h) \approx \int _{0}^{h}f(t)\hbox {d}t\), there exists constants \(C_{g}\), \(K_{g}\), \(K_{g}< 1\), independent of \(n\), such that,
$$\begin{aligned} \left| \int _{0}^{h} L\left( q_{n}\left( t\right) \!, \dot{q}_{n}\left( t\right) \right) \hbox {d}t- h\sum _{j=1}^{m_{n}} b_{j_{n}}L\left( q_{n}\left( c_{j_{n}}h\right) \!,\dot{q}_{n}\left( c_{j_{n}}h\right) \right) \right| \le C_{g}K_{g}^{n}, \end{aligned}$$for any \(q_{n}\in \mathbb {M}^{n}([0,h],Q)\),
-
(4)
and the stationary points \(\bar{q}\), \(\tilde{q}_{n}\) minimize their respective actions,
then
for some constants \(C_{s},K_{s}\), \(K_{s}< 1\), independent of \(n\), and hence the discrete Hamiltonian flow map has error \({\mathcal {O}}(K_{s}^{n})\).
Proof
As before, we rewrite both the exact discrete Lagrangian and the spectral discrete Lagrangian:
with suppression of the \(t\) argument. We introduce the action evaluated on the curve \(\hat{q}_{n}\):
Considering the first term in (36):
By assumption, all partials of \(L\) are continuous on \(U\), and since \(U\) is closed and bounded, this implies \(L\) is Lipschitz on \(U\), so let \(L_{\alpha }\) denote the Lipschitz constant. Since, again by assumption, \((\bar{q},\dot{\bar{q}}) \in U\) and \((\hat{q}_{n},\dot{\hat{q}}_{n}) \in U\), we can obtain:
Hence,
Next, considering the second term in (36),
since \(\tilde{q}_{n}\) minimizes its action,
where the inequalities follow from the assumptions on the order of the quadrature rule and (39). Furthermore,
where the inequalities follow from (39), the order of the sequence of quadrature rules, and the assumption that \(\bar{q}\) minimizes its action. Putting (40) and (41) together, we can conclude:
where \(K_{s}= \max (K_{A},K_{g})\). Now, combining the bounds (39) and (42) in (36), we can conclude
which, combined with Theorem 6.1, establishes the rate of convergence. \(\square \)
