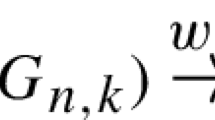The mod 2 cohomology rings of oriented Grassmannians via Koszul complexes

Abstract

We study the structure of mod 2 cohomology rings of oriented Grassmannians $\widetilde{{\text {Gr}}}_k(n)$ of oriented k-planes in ${\mathbb {R}}^n$. Our main focus is on the structure of the cohomology ring $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2)$ as a module over the characteristic subring C, which is the subring generated by the Stiefel–Whitney classes $w_2,\ldots ,w_k$. We identify this module structure using Koszul complexes, which involves the syzygies between the relations defining C. We give an infinite family of such syzygies, which results in a new upper bound on the characteristic rank of $\widetilde{{\text {Gr}}}_k(2^t)$, $k<2^t$, and formulate a conjecture on the exact value of the characteristic rank of $\widetilde{{\text {Gr}}}_k(n)$. For the case $k=3$, we use the Koszul complex to compute a presentation of the cohomology ring $H=\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2)$ for $2^{t-1}<n\le 2^t-4$ for $t\ge 4$, complementing existing descriptions in the cases $n=2^t-i$, $i=0,1,2,3$ for $t\ge 3$. More precisely, as a C-module, H splits as a direct sum of the characteristic subring C and the anomalous module H/C, and we compute a complete presentation of H/C as a C-module from the Koszul complex. We also discuss various issues that arise for the cases $k>3$, supported by computer calculation.

1 Introduction

The cohomology of real Grassmannians is by now fairly well understood, both with mod 2 and with integral coefficients, by ways of Schubert calculus. It might then be very surprising that something as innocuous as taking a double cover can produce something as little understood as the oriented Grassmannians. While the mod 2 and rational Betti numbers are known, the mod 2 cohomology ring structure as well as the integral cohomology are still fairly mysterious. In this paper, we study the mod 2 cohomology ring of the oriented Grassmannians $\widetilde{{\text {Gr}}}_3(n)$ of oriented 3-planes in an oriented real n-dimensional vector space, using Koszul complexes.

1.1 Question and known results

To give an idea of the context and known results pertaining to the cohomology ring structure for the oriented Grassmannians, we give a brief overview before formulating our results in the next section.

Before even getting to the ring structure, recall that the mod 2 Betti numbers for the oriented Grassmannians are known by work of Ozawa [15], using Morse theory.

Turning to the ring structure, there are some general approaches that can be used for homogeneous spaces, e.g. the Eilenberg–Moore spectral sequence for the fibration $G/H\rightarrow \textrm{B}H\rightarrow \textrm{B}G$, combined with information on the cohomology rings of classifying spaces. Many results have been achieved with this technique, see e.g. the papers of Borel [3], Baum [2] and Franz [6]. Such techniques work very well for the additive structure. For the multiplicative structure, there are extension problems, but in [6] these extension problems are solved under the assumption that 2 is invertible in the coefficients. The case of mod 2 coefficients seems to be the most difficult, as examples are known where the passage from the $E_\infty$-page to the actual cohomology involves nontrivial extensions.

This means that some additional information is necessary to investigate the ring structure in the oriented Grassmannian case. In [12], Korbaš and Rusin determined the ring structure for $\widetilde{{\text {Gr}}}_2(n)$ using the Gysin sequence combined with information on the characteristic rank and the image of the pullback along the double cover from [13].

Beyond the case $\widetilde{{\text {Gr}}}_2(n)$, no complete information on cohomology rings has been available so far. In the cases $\widetilde{{\text {Gr}}}_k(n)$, $k=3$ or 4, information on the characteristic rank and the image of the pullback has been obtained using Gröbner bases in [16, 18] (for $k=3$) and [11, 17] (for $k=4$). Computations of cohomology rings have been made in some cases: Basu and Chakraborty [1] partially computed the cohomology ring structures for $\widetilde{{\text {Gr}}}_k(n)$ with $k=3$ and $n=2^t-i$, where $t\ge 3$ and $i=0,1,2,3$, and remaining ambiguities in the relations were recently resolved by Colović–Prvulović [4] and Jovanović–Prvulović [9]. Our focus in this paper is the description of the remaining cases for $k=3$, when $2^{t-1}<n\le 2^t-4$ and $t\ge 4$.

For a few more known computations, Jovanović also recently determined integral cohomology for some $\widetilde{{\text {Gr}}}_3(n)$ cases in [8], and Rusin computed some mod 2 cohomology rings for $\widetilde{{\text {Gr}}}_4(n)$ in [19].

1.2 The general setup

After the overview of the literature, we now turn to describe a simple framework for computing the mod 2 cohomology of $\widetilde{{\text {Gr}}}_k(n)$. Before we can formulate our results, we need to set up some background and notation, which is discussed in more detail in Sect. 2 below. The first thing to note is that the Gysin sequence for the double cover $\widetilde{{\text {Gr}}}_k(n)\rightarrow {\text {Gr}}_k(n)$ produces an exact sequence of C-modules

(1.1)

where C and K are the cokernel and kernel of the map $w_1:\textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)\rightarrow \textrm{H}^{*+1}({\text {Gr}}_k(n),{\mathbb {F}}_2)$ given by multiplication with the first Stiefel–Whitney class of the tautological subbundle. This immediately poses three questions:

• a) describe C as a ring using generators and relations,

• b) describe K as a C-module using generators and relations, and

• c) determine the extension class in ${\text {Ext}}_C(K,C)$ given by the exact sequence (1.1).

For step a), the ring C has a well-known [7] explicit description as follows:

$$\begin{aligned} C={\mathbb {F}}_2[w_2,\ldots ,w_k]/(q_{n-k+1},\ldots ,q_n), \end{aligned}$$

(1.2)

with $w_i=w_i(S)$ and $q_i=w_i(\ominus S)$ where $\ominus S$ is the formal inverse of the tautological bundle $S\rightarrow \textrm{BSO}(k)$. The $q_i$ can be expressed in terms of $w_i$ via a Giambelli type formula (3.1), (3.3) or a recursion, see 3.4. A lot of information on the structure of C as a commutative ring can be obtained via Gröbner basis methods used in many papers, e.g. [4, 7, 16, 17].

The next step b) – and the one this paper is really focused on – is to compute a presentation for K as a C-module. To determine C and K, we note that they appear as 0th and 1st Koszul homology groups for the ideal $I=(q_{n-k+1},\dots ,q_n)$ over the ring $W_2={\mathbb {F}}_2[w_2,\dots ,w_k]$. The generators of K are directly related to the syzygies between generators of the ideal I in $W_2$, see the discussion in Sect. 5.

After determining the extension class in step c), most of the information relevant for the mod 2 cohomology ring is available, namely all products where one factor is in C. We settle this description for $k=3$, in the cases that are not covered in the literature.

1.3 The case $k=3$

Next, we summarize our computations of the mod 2 cohomology rings of $\widetilde{{\text {Gr}}}_3(n)$. As detailed above, the cases $n=2^t-i$, with $i=0,1,2,3$ and $t\ge 3$, have been mostly settled in the literature, and we will focus on the remaining cases $2^{t-1}<n\le 2^t-4$ in the present paper.

The reason for the distinction between the two cases $n=2^t-i$, $i=0,1,2,3$ and $2^{t-1}<n\le 2^t-4$ is that in the former case, the one dealt with in the literature, the C-module K is free of rank one, so the extension automatically splits, answering both questions b) and c). In the cases $2^{t-1}<n\le 2^t-4$ that we are dealing with here, K is no longer free, and it is generated by two elements $a_n$ and $d_n$. The degrees of the generators were already determined in [1], but the relations in the presentation of K have not been determined before. Our key computation in Sect. 6 is based on a detailed investigation of the Koszul complex for the ideal $I=(q_{n-2},q_{n-1},q_n)$ over the ring $W_2={\mathbb {F}}_2[w_2,w_3]$. The main results of the paper give a presentation for K as a C-module, answering question b). Having that, it turns out that the above exact sequence splits as an extension of C-modules for degree reasons, see Proposition 7.1, which settles the extension problem. In conclusion, we obtain the following description of the cohomology ring of $\widetilde{{\text {Gr}}}_3(n)$ for $2^{t-1}<n\le 2^t-4$.

Theorem 1.1

Let $t\ge 4$, $2^{t-1}<n\le 2^t-4$, let C be defined as in (1.2) and set $i=2^t-3-n$ and $j=n-2^{t-1}+1$.

Then we have an isomorphism of C-modules

$$\begin{aligned} \textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2)\cong C\langle 1,a_n,d_n\rangle /(q_ia_n+r_{j-1}d_n, q_{i+1}a_n+w_3r_{j-2}d_n, w_3q_{i-1}a_n+r_jd_n),\nonumber \\ \end{aligned}$$

(1.3)

where $\deg a_n=3n-2^t-1$ and $\deg d_n=2^t-4$. Here $q_i$ are polynomials in ${\mathbb {F}}_2[w_2,w_3]$ defined by the recursion $q_{i}=w_2q_{i-2}+w_3q_{i-3}$ with $q_0=1$, $q_{<0}=0$, and $r_j$ are polynomials in ${\mathbb {F}}_2[w_2,w_3]$ defined by the recursion

$$\begin{aligned} r_{j+1}=w_2r_j+w_3^2r_{j-2}. \end{aligned}$$

with $r_0=1$, $r_{<0}=0$. Closed-form expressions for $q_j$ and $r_j$ can be found in (3.5) and (4.15), respectively.

The remaining ring structure of $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n),{\mathbb {F}}_2)$ is determined by

$$\begin{aligned} a_n^2=a_nd_n=d_n^2=0. \end{aligned}$$

(1.4)

The proof proceeds in the following steps:

• (I) In Proposition 6.3 we show that the kernel of the differential in the Koszul complex is a free $W_2$-module on two elements:

  $$\begin{aligned} \ker \left( d_1:W_2^{\oplus 3}\rightarrow W_2\right) =W_2\langle u_{3n-2^t},v_{2^t-3}\rangle , \end{aligned}$$

• (II) we compute the relations in the presentation of K as a C-module (using the Koszul differential $d_2$) in Proposition 6.5,

• (III) we show that we have a splitting of C-modules $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n),{\mathbb {F}}_2)=C\oplus K$ in Proposition 7.1,

• (IV) and we compute the remaining products (1.4) in Proposition 8.1.

1.4 The general method, and the case $k=4$

The approach used for $k=3$ can also help computations and get some mileage in the cases $k>3$. It should be noted, however, that already the situation for $k=4$ differs in a significant number of aspects from the $k=3$ case, which really appears to be unusually smooth. Part of the difficulty of computing the cohomology rings $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2)$ for $k>3$ is related to the difficulty of computing a presentation of the first Koszul homology group as a C-module. We briefly outline the general method and mention some aspects that fail for $k>3$ here. For a more detailed discussion, see Sect. 2 for the general method and Sect. 9 for a description of the phenomena in the $k>3$ cases.

1.4.1 The Koszul complex

The short exact sequence (1.1) derived from the Gysin sequence as well as the description of C and K as the zeroth and first homology of the Koszul complex works in complete generality. From this description, the generators of K are directly related to the syzygies between generators of the ideal $I=(q_{n-k+1},\dots ,q_n)$ in $W_2={\mathbb {F}}_2[w_2,\dots ,w_k]$, see the discussion in Sect. 5.

We find some such syzygies in Theorem 4.6:

Theorem 1.2

For $n=2^t$ and $0<k<2^t$, the following relation holds between $q_{n-k},\ldots ,q_n$:

$$\begin{aligned} \sum _{k\ge i\ge 0 \text { even}}q_{n-i}w_{i}=\sum _{k\ge i>1 \text { odd}} q_{n-i}w_{i}=0. \end{aligned}$$

(1.5)

The relation (1.5) is a generalization of a result of Fukaya and Korbaš about the vanishing of $q_{2^t-3}$ in the cases $k=3,4$, see [7, 11], which is crucial in understanding the characteristic rank in these cases. The above result provides a C-module generator of the anomalous module K, and thus provides a new upper bound on the characteristic rank of $\widetilde{{\text {Gr}}}_k(2^t)$ for general k and t, see Theorem 5.6.

We also develop a general technique of “ascending” and “descending” such relations between the $q_j$ in Sect. 4, which allows to obtain such relations for $\widetilde{{\text {Gr}}}_k(n)$ from similar relations for $\widetilde{{\text {Gr}}}_k(n-1)$ or $\widetilde{{\text {Gr}}}_k(n+1)$. In the case $k=3$, all syzygies (and thus all generators of K) are obtained from the vanishing $q_{2^t-3}=0$ via ascending and descending relations. This is already not true for $k=4$, as we demonstrate in Sect. 9. However, the technique of ascending and descending relations provides syzygies for arbitrary n. Combining the fundamental relation in Theorem 1.2 with the technique of ascending and descending relations, we formulate a general conjecture on the characteristic rank in Conjecture 5.8 which is supported by computer experiments for small k and n, see the discussion in Sect. 9.

An intermediate step in the computation of K as a C-module — viewed as the first homology of the Koszul complex — is the computation of the kernel of the differential $d_1:{\mathcal {K}}_1\rightarrow {\mathcal {K}}_0$, cf. Definition 5.1. In the case $k=3$, this kernel is free of rank 2, generated exactly by the ascended and descended relations. This fails for $k=4$: more generators are necessary to generate the kernel, which is also no longer free. Computational experiments suggest that the kernel (as a $W_2$-module) always has a free resolution of length $k-2$. Nevertheless, it seems possible to obtain presentations for the kernel in the $k=4$ case, and once this is done, the relations in a presentation of K as C-module can be extracted from the differential $d_2:{\mathcal {K}}_2\rightarrow {\mathcal {K}}_1$ much as in the present paper.

1.4.2 The extension class

Once a presentation of K as a C-module has been obtained, we can ask how to determine the class of the extension $0\rightarrow C\rightarrow \textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)\rightarrow K\rightarrow 0$ as an element in $\textrm{Ext}^1_C(K,C)$. In the $k=3$ case, the degree zero part of the Ext-group vanishes for degree reasons, see the discussion in Sect. 7. However, computer algebra experiments show that the Ext-group is not generally trivial already for some $k=4$ cases. This non-vanishing of the Ext-group means that determining the C-module structure on $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ is potentially much more complicated for $k>3$, a level of difficulty that seems to have not been noticed before. Nevertheless, one could imagine that the explicit description of the Koszul complex and kernel as in the previous step will help in computing the Ext-group more conceptually (at least in the $k=4$ case). This computation, and the question how to determine the class of the extension for $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ in this Ext-group (which is equivalent to computing a presentation of the cohomology as a C-module), will be the focus of future research.

1.4.3 Remaining ambiguities

Once we understand $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ as a C-module, most of the product structure is described. All that remains is to compute products between (lifts of) generators of K as elements in $\textrm{H}^*$. In the case $k=3$, there are only three products that need to be determined, one of which is trivial for degree reasons. The squares are shown to be zero via a similar induction as the one used for the relations, cf. Propositions 8.4 and 8.7. For $k>3$, one can well imagine to use integral cohomology information or cohomology operations to remove the remaining ambiguities as was done in recent papers [4, 9]. There are also some $k=4,5,6$ cases where the Ext-group vanishes and the remaining ambiguities can be removed easily, which we discuss in Sect. 9.

1.5 Structure of the paper

We begin in Sect. 2 with a review of possible techniques that have been employed to compute the cohomology of the oriented Grassmannians. We also emphasize the questions of extensions and module structures over the characteristic subring. Section 3 provides information on the characteristic subring and its properties. In Sect. 4 we give a syzygy between the Stiefel–Whitney polynomials defining the characteristic subring and a new inductive procedure to obtain further relations. Then Sect. 5 recalls Koszul complexes and provides the concrete identification of the anomalous module K as first Koszul homology. This allows to compute an explicit presentation of K as a module over the characteristic subring in Sect. 6. A general discussion of Ext-groups and the vanishing result for the $k=3$ case is provided in Sect. 7, and the remaining products of anomalous generators are investigated in Sect. 8. We also include an extensive discussion of the differences in the $k>3$ cases in Sect. 9. We include three appendices with information we think might be helpful: Appendix A provides the Macaulay2 code used for the experiments, Appendix B provides some recollection on graded Ext-groups, and Appendix c explains how our presentation of the cohomology ring $\widetilde{{\text {Gr}}}_3(n)$ leads to significantly simplified formulas for Betti numbers.

2 General method and notations

In this section we describe our general approach as well as introduce some notation and terminology. We also recall some other possible approaches and show how Poincaré duality completely settles the C-module question in cases when K is generated by a single element.

2.1 The Gysin sequence and setup of notation

We denote by ${\text {Gr}}_k(n)$ the real Grassmannian of k-planes in ${\mathbb {R}}^n$ and by $\widetilde{{\text {Gr}}}_k(n)$ the Grassmannian of oriented k-planes in ${\mathbb {R}}^n$, where $0<k<n$. At the core of the upcoming algebraic computations is the Gysin sequence associated to the degree 2 covering $\pi :\widetilde{{\text {Gr}}}_k(n)\rightarrow {\text {Gr}}_k(n)$:

In particular, the cohomology of $\widetilde{{\text {Gr}}}_k(n)$ sits in the short exact sequence

(2.1)

where each map is a homomorphism of graded ${\text {coker}}w_1$-modules and $\delta$ is a map of degree 0. Since they will appear so often in the text, we introduce the shorthand notation

$$\begin{aligned} C:={\text {coker}}w_1,\qquad H:=\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2),\qquad K:= \ker w_1, \end{aligned}$$

(2.2)

where k and n are usually fixed beforehand and clear from context. When k and n are not fixed, we use the notation $C_k(n)$ and $K_k(n)$.

For k fixed, we will denote $W_1={\mathbb {F}}_2[w_1,\ldots ,w_k]$ and $W_2={\mathbb {F}}_2[w_2,\ldots ,w_k]$ (in most of the paper $k=3$). Then $\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$ has a presentation as $W_1/(Q_{n-k+1},\ldots ,Q_n)$ where $Q_i$ are some quotient Stiefel–Whitney classes (which can be expressed as Giambelli determinants) recalled in Sect. 3, and

$$\begin{aligned} C=\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)/(w_1)=W_2/(q_{n-k+1},\ldots ,q_n), \end{aligned}$$

where $q_j=Q_j|_{w_1=0}$. Before proceeding further, let us fix some practical terminology.

Definition 2.1

The subring $\pi ^*C\subseteq \textrm{H}^*(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2)$ is called the characteristic subring, since it is the subring generated by the Stiefel–Whitney classes of the tautological bundle $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$. In the terminology of [13], a class $x\in H$ is anomalous, if $x\not \in {\text {Im}}\pi ^*$, equivalently, if its image under the projection $\delta :H\rightarrow K$ is nonzero. In abuse of terminology, we will therefore also call K the anomalous module.

Remark 2.2

We will be careful to distinguish between anomalous classes in H and their image in K in cases where it matters (such as for questions of the ring structure, since $\delta$ is only a C-module homomorphism). Namely, for $k=3$ and $2^{t-1}<n<2^t-3$ for $t\ge 4$, we will see in Proposition 6.5 that $K_3(n)$ is generated by two elements $A_n$ and $D_n$; note that these denote elements of $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$. We will use $a_n$ and $d_n$ to denote lifts of these elements to $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2)$, i.e. these are elements satisfying $\delta (a_i)=A_i$ and $\delta (d_i)=D_i$.

In connection with the question of computing the ring structure for H, we can ask what the C-module structure of H is. Since (2.1) is a short exact sequence of graded C-modules, the C-module structure determines all products where at least one factor is in the image of the characteristic subring C. Knowing the C-module structure of H, all that remains to determine the ring structure of H is the computation of products of anomalous classes in H. In fact, it suffices to compute products of classes which map to C-module generators of K – in the cases $k\le 3$, there are at most two such generators.

To determine the C-module structure on the cohomology H using the exact sequence (2.1), one is faced with the following questions:

• a) describe C as a ring using generators and relations,

• b) describe K as a C-module using generators and relations, and

• c) determine the extension class in ${\text {Ext}}_C(K,C)$ given by the exact sequence (1.1).

Question a) has been much addressed in the literature, often in terms of Gröbner bases. For the case $k=3$, we will answer question b) in Sect. 6. Question c) also turns out to have a simple answer for $k=3$ as the Ext-group actually vanishes in this case, cf. Sect. 7. However, we will see in Sect. 9 that the Ext-group is in general non-trivial for $k\ge 4$, making question c) significantly more difficult to answer in general.

We will need the following compatibility of Steenrod squares with (2.1). The following proposition and its proof appear in [14]. We reproduce them here for the convenience of the reader.

Proposition 2.3

In the short exact sequence (2.1), $C={\text {coker}}w_1$ and $K=\ker w_1$ are Steenrod-modules, and the maps are Steenrod-module homomorphisms.

Proof

For the first half of the statement, it is enough to note that the ideal K is a Steenrod submodule by the Cartan formula. The compatibility of Steenrod operations with pullback is immediate. The second morphism (projection to K) factors as a composition of a boundary map and a Thom isomorphism $\textrm{Th}$. Stability of Steenrod operations implies that ${\text {Sq}}^k$ commutes with the boundary map, but in general, Steenrod operations don’t commute with the Thom isomorphism, instead the following holds: $\textrm{Th}\circ \textrm{Sq}\circ \textrm{Th}^{-1}=w\cdot \textrm{Sq}$, where w denotes the total Stiefel–Whitney class and $\textrm{Sq}$ denotes the total Steenrod square. The key point in our case is that the total Stiefel–Whitney class is $w=1+w_1$, and any element in the image of $\delta$ is in $K=\ker (w_1)\subseteq \textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$. This implies that the Thom isomorphism commutes with Steenrod squares for elements in the image of $\delta$, and consequently the projection $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2)\rightarrow K$ is compatible with Steenrod operations. $\square$

2.2 Comparison to spectral sequence methods

While for the present, we will focus on using the Gysin sequence as a way to determine the cohomology of $\widetilde{{\text {Gr}}}_k(n)$, we briefly discuss other approaches that have been considered in the literature.

First, we note that complete information on the additive structure, i.e., information on the mod 2 Betti numbers, is available, cf. [15]. All the ways we know to compute the mod 2 Betti numbers eventually boil down to understanding the multiplication with $w_1$ on $\textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)$ in terms of Young diagram combinatorics. Note, however, that the presentation of the cohomology ring of $\widetilde{{\text {Gr}}}_3(n)$ given in Theorem 1.1 allows for much simpler formulas describing the Betti numbers. We discuss this in Appendix c.

One way to understand the multiplicative structure is by use of suitable spectral sequences. First, note that the oriented Grassmannian $\widetilde{{\text {Gr}}}_k(n)$ also has the structure of a homogeneous space $\textrm{SO}(n)/\left( \textrm{SO}(k)\times \textrm{SO}(n-k)\right)$. To compute cohomology of a general homogeneous space G/H with coefficients in a field k, one can use the Eilenberg–Moore spectral sequence

$$\begin{aligned} E_2^{*,*}=\textrm{Tor}_{\textrm{H}^*(\textrm{B}H,k)}^{*,*}(\textrm{H}^*(\textrm{B}G,k);k)\Rightarrow \textrm{H}^*(G/H,k) \end{aligned}$$

associated to the fiber sequence $G/H\rightarrow \textrm{B}H\rightarrow \textrm{B}G$ combined with the computation of cohomology of classifying spaces of Lie groups. This is the approach taken e.g. by Baum [2] and Franz [6].

However, there are still problems with the cohomology ring structure. While the spectral sequence has a multiplicative structure, this only implies that there is a filtration on $\textrm{H}^*(G/H,{\mathbb {F}}_p)$ whose associated graded is computed by the $E_\infty$-page. As shown in [2] and [6], these extension problems can be solved (and the extensions are split) in many cases, but for the particular case of $p=2$ there seem to be no general methods to solve the extension problems at this point. In the context of the spectral sequences, what we do in this paper is compute the multiplicative structure of the $E_\infty$-page (that’s the C-module structure of K) and solve the extension problem (that’s the vanishing of the Ext-group) for the specific case of $\widetilde{{\text {Gr}}}_3(n)$.

Alternatively, one could also use the Serre spectral sequence associated to the degree 2 covering $\widetilde{{\text {Gr}}}_k(n)\rightarrow {\text {Gr}}_k(n)$ to compute the cohomology of $\widetilde{{\text {Gr}}}_k(n)$. However, in this case, the Serre spectral sequence in fact degenerates to the Gysin sequence. Similarly, in the case of the Eilenberg–Moore spectral sequence, the filtration on cohomology only has one nontrivial step. This means that in the case $\widetilde{{\text {Gr}}}_k(n)$, the spectral sequences available don’t have more information than the Gysin sequence, and solving the extension problem requires different methods anyway. For this reason, we will work with the Gysin sequence throughout.

2.3 Poincaré duality

In some simpler cases, we can also exploit the Poincaré duality structure to establish relations between C and K.

Proposition 2.4

Poincaré duality on ${\text {Gr}}_k(n)$ induces a perfect pairing between $K=\ker w_1$ and $C={\text {coker}}w_1$. In particular, if $c_d$, $k_d$ denote the Betti numbers of C and K in degree d, respectively, then $c_i=k_{N-i}$, where N is the dimension of ${\text {Gr}}_k(n)$.

Proof

We denote by

$$\begin{aligned} b:\textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)\otimes \textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)\rightarrow {\mathbb {F}}_2:(x,y)\mapsto \pi _!(x\cup y) \end{aligned}$$

the perfect pairing of Poincaré duality. Restrict b to $\ker w_1\otimes \textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)$. The orthogonal complement of $\ker w_1$ under b is $(w_1)$: by definition, $(w_1)\subset (\ker w_1)^\perp$, but then we have $\dim _{{\mathbb {F}}_2}\ker (w_1)+\dim _{{\mathbb {F}}_2}(w_1)=\dim _{{\mathbb {F}}_2}\textrm{H}^*({\text {Gr}}_k(n),{\mathbb {F}}_2)$, forcing equality. Thus b descends to a perfect pairing $\ker w_1\otimes {\text {coker}}w_1\rightarrow {\mathbb {F}}_2$. $\square$

Remark 2.5

This is a purely algebraic and a more general statement; we just need a Poincaré duality algebra and an element in it.

Corollary 2.6

In the situation $\widetilde{{\text {Gr}}}_k(n)$, if the anomalous module K is generated by one element, then K is free of rank one. Consequently, $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)\cong C\oplus K\cong C^{\oplus 2}$ as C-modules (with the second isomorphism ignoring the grading).

Proof

We can consider the total dimension of K as ${\mathbb {F}}_2$-vector space. Since by assumption K is cyclic, this is at most the total dimension of C as ${\mathbb {F}}_2$-vector space. The perfect pairing from Proposition 2.4 then implies that K needs to be free: any relation divided out would reduce the total dimension. From this, we deduce that the extension (2.1) splits and the second claim follows. $\square$

Remark 2.7

This covers many situations considered in the literature, such as the cases $n=2^t-i$, $i=0,1,2,3,$ for $\widetilde{{\text {Gr}}}_3(n)$ in [1, 4, 9], or the cases $\textrm{Gr}_4(n)$ for $n=8,9$ in [19]. We also find several further situations in Sect. 9 such as $\widetilde{{\text {Gr}}}_5(16)$, $\widetilde{{\text {Gr}}}_5(32)$ and $\widetilde{{\text {Gr}}}_4(n)$ for $n=13,\dots ,17,29,\dots ,33$. One could conjecture that this generalizes to $\widetilde{{\text {Gr}}}_5(2^t)$ and $\widetilde{{\text {Gr}}}_4(n)$ with $2^t-3\le n\le 2^t+1$.

3 The characteristic subring and its properties

In this short section, we will recall some information on the characteristic subring $C={\text {coker}}(w_1)$ as a ring and its presentation in terms of Giambelli determinants $q_i$.

3.1 Presentation of the characteristic subring

Recall that the cohomology of the (unoriented) real Grassmannian ${\text {Gr}}_k(n)$ has a presentation as

$$\begin{aligned} \textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)={\mathbb {F}}_2[w_1,\ldots ,w_k]/(Q_{n-k+1},\ldots ,Q_n), \end{aligned}$$

where the $Q_j$ are uniquely determined by the Whitney sum formula (since $Q_j$ lives in degree j):

$$\begin{aligned} 1+w_1+\ldots +w_k=\frac{1}{1+Q_1+Q_2+\ldots }. \end{aligned}$$

More explicitly, the $Q_j$ can be written as the following Giambelli determinant:

$$\begin{aligned} Q_j=\det \left( \begin{array}{ccccc} w_1 &{} w_2 &{} \ldots &{} w_{j-1} &{} w_j \\ 1 &{} w_1 &{} w_2 &{} \ldots &{} w_{j-1} \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \ldots &{} 1 &{} w_1 &{} w_2 \\ 0 &{} \ldots &{} 0 &{} 1 &{} w_1 \end{array}\right) \end{aligned}$$

(3.1)

where $Q_1=w_1$, $Q_2=w_1^2+w_2$ and so on. In these formulas, if $l>k$, $w_l=0$, since these are Stiefel–Whitney classes of a rank k bundle.

For the cokernel $C={\text {coker}}(w_1)$, being the quotient by $w_1$, we get a similar presentation

$$\begin{aligned} C={\mathbb {F}}_2[w_2,\ldots ,w_k]/(q_{n-k+1},\ldots ,q_n), \end{aligned}$$

where now the relations $q_j$ of degree j are determined by

$$\begin{aligned} 1+w_2+\ldots +w_k=\frac{1}{1+q_1+q_2+\ldots }. \end{aligned}$$

(3.2)

Alternatively, we obtain $q_j$ explicitly by setting $w_1=0$ in the above Giambelli determinant:

$$\begin{aligned} q_j=Q_j|_{w_1=0}. \end{aligned}$$

(3.3)

This implies that the $q_j$ satisfy the following recursive formula (with $q_j=0$ for $j<0$ and $q_0=1$):

$$\begin{aligned} q_j=\sum _{l=2}^k w_lq_{j-l}. \end{aligned}$$

(3.4)

Via a standard computation, [4, (2.8)], we can also write even more explicitly

$$\begin{aligned} q_j=\sum _{j=2a_2+\ldots + ka_k} \left( {\begin{array}{c}|a|\\ a\end{array}}\right) w^a, \end{aligned}$$

(3.5)

where $a=(a_2,\ldots ,a_k)$, $w^a=\prod _{i=2}^k w_i^{a_i}$, $|a|=\sum _{i=2}^k a_i$ and $\left( {\begin{array}{c}|a|\\ a\end{array}}\right)$ is the mod 2 multinomial coefficient corresponding to a. We will use the following statement in the description of Koszul homology.

Proposition 3.1

For $2\le k< n$ we have the following equality of ideals in $W_2={\mathbb {F}}_2[w_2,\dots ,w_k]$:

$$\begin{aligned} \sqrt{(q_{n-k+1},\dots ,q_n)}=(w_2,\dots ,w_k) \end{aligned}$$

Proof

The ring C is the quotient of the cohomology ring $\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$ by the ideal $(w_1)$. Since $\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$ is bounded above, C is also bounded from above. Since $C=W_2/I$ where $I=(q_{n-k+1},\ldots ,q_n)$, $W_2$ and I agree in high enough degrees. Therefore the radical of I is the irrelevant ideal. $\square$

4 Syzygies of the characteristic subring

In this section, we give a system of syzygies between $(q_{n-k},\ldots ,q_n)$ over $W_2={\mathbb {F}}_2[w_2,\ldots ,w_k]$. First, we will describe one such relation for arbitrary k and $n=2^t$ which plays a fundamental role. More precisely, we prove in Theorem 4.6 (with the convention that $w_l=0$ for $l>k$):

$$\begin{aligned} \sum _{i\ge 0} w_{2i}q_{n-2i}=0. \end{aligned}$$

From this relation we recover the relations discovered by Fukaya [7] and Korbaš [11] in their study of the cohomological properties of $\widetilde{{\text {Gr}}}_3(n)$ and $\widetilde{{\text {Gr}}}_4(n)$.

In the second half of this section, we will examine how these relations give further relations as n increases or decreases - we call this method ascending and descending relations. In this way we obtain relations between $(q_{n-k},\ldots ,q_n)$ for all n, cf. (4.3) and (4.9). We will use this method in our computation of the Koszul homology of the $\widetilde{{\text {Gr}}}_3(n)$ case. The discussion in Sect. 9 suggests that the fundamental syzygy and the procedure of ascending and descending relations might play a key role also in $k>3$ cases.

4.1 Multinomial coefficients mod 2

We first review some properties of multinomial coefficients mod 2 which will be relevant for the proof of the fundamental syzygy in Theorem 4.6.

For a sequence of non-negative integers $a=(a_2,\ldots ,a_k)$¹ we say that their base-2 expansions are disjoint if each power of 2 appears in the base-2 expansion of at most one of the $a_j$. We will denote the multinomial coefficient corresponding to the sequence a by $\left( {\begin{array}{c}|a|\\ a\end{array}}\right)$, where $|a|=\sum _{i=2}^k a_i$. The following characterization of mod 2 multinomial coefficients is also known as Lucas’ theorem.

Lemma 4.1

For a tuple $a=(a_2,\dots ,a_k)$, denote $|a|=\sum _{i=2}^k a_i$. Then the 2-adic valuation of the multinomial coefficient $\left( {\begin{array}{c}|a|\\ a_2,\dots ,a_k\end{array}}\right)$ equals the number of carrying operations in the addition $|a|=a_2+\cdots +a_k$. As a consequence, the following are equivalent:

• (1)
  $$\begin{aligned} \left( {\begin{array}{c}|a|\\ a_2,\dots ,a_k\end{array}}\right) \equiv 1\bmod 2 \end{aligned}$$

• (2) There is no carrying in the addition $|a|=a_2+\cdots +a_k$ in base 2.

• (3) The base 2 expansions of the $a_i$ are disjoint.

Proof

The Legendre formula for the 2-adic valuation of a factorial n! states that $\nu _2(n!)=n-s_2(n)$ where $s_2$ is the sum of the digits in the base-2 expansion of n. The latter is simply the number of 1 s in the base-2 expansion of n. So, for the multinomial coefficient, we compute the 2-adic valuation as follows:

$$\begin{aligned} \nu _2\left( {\begin{array}{c}|a|\\ a_2,\dots ,a_k\end{array}}\right)&=\nu _2\left( \frac{|a|!}{a_2!\cdots a_k!}\right) =\nu _2(|a|!)-\nu _2(a_2!\cdots a_k!)\\&=|a|-s_2(|a|)-\left( |a|-s_2(a_2)-\cdots -s_2(a_k)\right) =\sum _{i=2}^ks_2(a_i)-s_2(|a|). \end{aligned}$$

We see that the 2-adic valuation of the multinomial coefficient is the sum of nonzero digits in the $a_2,\dots ,a_k$ minus the nonzero digits in |a|. But this is equal to the number of carry operations (since each carry operation reduces the number of nonzero digits by 1). The equivalent characterizations of mod 2 nonvanishing of the multinomial coefficient follows directly from this. $\square$

Example 4.2

The base-2 expansion of $a=(2,5,8)$ is $[a]_2=(10,101,1000)$. Their sum is 1111, which needs no carrying. The corresponding multinomial coefficient is $\left( {\begin{array}{c}|a|\\ a\end{array}}\right) =135135$ which is odd.

For a given sequence $a=(a_2,\ldots ,a_k)$, let ${\hat{a}}_j$ denote the sequence

$$\begin{aligned} \hat{a}_j=(a_2,\ldots ,a_j-1,\ldots ,a_k). \end{aligned}$$

We will need a lemma about ‘consecutive’ multinomial coefficients mod 2:

Lemma 4.3

The following relations hold for consecutive multinomial coefficients mod 2:

• (1) If $\left( {\begin{array}{c}|a|\\ a\end{array}}\right) \equiv 1\bmod 2$, then there is a unique l, such that $\left( {\begin{array}{c}|a|-1\\ {\hat{a}}_l\end{array}}\right) \equiv 1\bmod 2$. If $2^p$ is the largest two-power dividing all $a_i$, then l is the unique index for which $2^{p+1}$ does not divide $a_l$.

• (2) If $\left( {\begin{array}{c}|a|\\ a\end{array}}\right) \equiv 0\bmod 2$, then there are either exactly two indices j such that $\left( {\begin{array}{c}|a|-1\\ {\hat{a}}_j\end{array}}\right) \equiv 1\bmod 2$ or there are none. If there are two such indices j, then they are characterized as follows: if $2^p$ is the largest two-power dividing all $a_i$, then these are the indices j for which $2^{p+1}$ does not divide $a_j$.²

Proof

(1) By Lemma 4.1, the numbers $a_2,\dots ,a_k$ have disjoint base-2 expansions. Decreasing one such number by 1 means changing the right-most digit 1 in the base-2 expansion to a 0, and changing all the zeros to the right of this position to 1 s. The only way this doesn’t destroy disjointness between the base-2 expansions is if we do this to the (unique) overall right-most digit 1 in the base-2 expansions of $a_2,\dots ,a_k$. Since by assumption the base-2 expansions of the $a_2,\dots ,a_k$ are disjoint, there is a unique j where the right-most digit 1 appears. This argument also implies the statement about the largest two-power dividing $a_i$.

(2) Assume that there exists an index j, such that $\left( {\begin{array}{c}|a|-1\\ {\hat{a}}_j\end{array}}\right) \equiv 1\bmod 2$. We will show that there exists a unique $l\ne j$ such that $\left( {\begin{array}{c}|a|-1\\ {\hat{a}}_l\end{array}}\right) \equiv 1\bmod 2$. By Lemma 4.1, the base-2 expansions of $(a_2,\ldots ,a_j-1,\ldots ,a_k)$ are disjoint, but the base-2 expansions of $(a_2,\ldots ,a_j,\ldots ,a_k)$ are not. In $a_j$, there is exactly one nonzero bit which was zero in $a_j-1$ (this holds for any number, the nonzero bit is the last carry). Since the $(a_2,\ldots ,a_j-1,\ldots ,a_k)$ are disjoint, but $(a_2,\ldots ,a_j,\ldots ,a_k)$ are not, the new nonzero bit in $a_j$ is nonzero in exactly one other $a_l$. So the largest two-power $2^p$ dividing $a_j$ also divides $a_l$, but $2^{p+1}$ does not. Therefore $(a_2,\ldots ,a_l-1,\ldots ,a_k)$ are also disjoint. For any other $i\not \in \{j,l\}$, $\left( {\begin{array}{c}|a|-1\\ {\hat{a}}_i\end{array}}\right) \equiv 0\bmod 2$, since $a_j$ and $a_l$ are not disjoint. $\square$

Example 4.4

In the base-2 expansions of $a=(2,5,8)$, if we decrease 10, we get overlap between 1 and 101 and the corresponding multinomial coefficient is even. If we decrease 1000, we get 111 and overlap with both 10 and 101, and an even multinomial coefficient. Only if we decrease 101, we get 100 which doesn’t overlap with any of the others.

From the lemma, for any nonzero multinomial coefficient we get a unique chain of decreasing multinomial coefficients which are nonzero mod 2:

$$\begin{aligned} (2,5,8)\rightarrow (2,4,8)\rightarrow (1,4,8)\rightarrow (4,8)\rightarrow (3,8)\rightarrow (2,8)\rightarrow (1,8)\rightarrow (8)\rightarrow (7)\rightarrow \ldots \end{aligned}$$

The following proposition is the key step in proving the relation between the $q_i$’s.

Proposition 4.5

If for a sequence $a=(a_2,\ldots ,a_k)$ we have $\sum _{i=2}^kia_i=2^t$, then

$$\begin{aligned} \left( {\begin{array}{c}|a|\\ a\end{array}}\right) = \sum _{j=1}^{\lfloor k/2 \rfloor }\left( {\begin{array}{c}|a|-1\\ \hat{a}_{2j}\end{array}}\right) \end{aligned}$$

Proof

There are two cases depending on the parity of $\left( {\begin{array}{c}|a|\\ a\end{array}}\right)$.

If $\left( {\begin{array}{c}|a|\\ a\end{array}}\right) \equiv 1\bmod 2$, then by part (1) of Lemma 4.3, there is a unique l such that $\left( {\begin{array}{c}|a|-1\\ \hat{a}_{l}\end{array}}\right)$ is also $\equiv 1\bmod 2$. We claim that l is even, so that a unique term on the right-hand side is nonzero. If $2^p$ is the largest 2-power dividing all $a_i$, then $a_l$ is the unique $a_i$ not divisible by $2^{p+1}$ by Lemma 4.3. If l is odd, then $\sum _{i=2}^k ia_i\equiv 2^p\bmod 2^{p+1}$. Since the left-hand side is equal to $2^t$, this implies $2^p=2^t$, but this is impossible since $l>1$.

Assume now that $\left( {\begin{array}{c}|a|\\ a\end{array}}\right) \equiv 0\bmod 2$. It is enough to show that if $\left( {\begin{array}{c}|a|-1\\ \hat{a}_{2j}\end{array}}\right) \equiv 1$, then there is a unique l, such that $\left( {\begin{array}{c}|a|-1\\ \hat{a}_{l}\end{array}}\right) \equiv 1$ and that l is even. The unique existence of l is given by part (2) of Lemma 4.3. We now show that l is even. By part (2) of Lemma 4.3, $2^p$ divides both $a_{2j}$ and $a_l$, but $2^{p+1}$ does not. If l is odd, then since 2j is even, $\sum _{i=2}^kia_i\equiv 2^p$ mod $2^{p+1}$, and we can conclude as above. $\square$

4.2 Explicit relations between $q_i$

For the description of the Koszul homology, we need to understand the $W_2={\mathbb {F}}_2[w_2,\ldots ,w_k]$-relations between the $q_j$. Using the above results on mod 2 multinomial coefficients, we now obtain the following syzygy between the $q_i$’s for $n=2^t$ and arbitrary k:

Theorem 4.6

The following relation between the $q_j$ holds in $W_2={\mathbb {F}}_2[w_2,\ldots ,w_k]$ if $n=2^t$:

$$\begin{aligned} \sum _{0\le i\le k\text { even}}q_{n-i}w_{i}=\sum _{1<i\le k \text { odd}} q_{n-i}w_{i}=0. \end{aligned}$$

(4.1)

If $k\ge n$, then relation (4.1) holds only if $n=2^t$.

Proof

Assume that $n=2^t$. By the recursion (3.4), we have $\sum _{i=0}^k w_iq_{n-i}=0$ (with $w_1=0$), so it is enough to prove the statement about the even part. Since $q_j=\sum _{j=2a_2+\ldots +ka_k} \left( {\begin{array}{c}|a|\\ a\end{array}}\right) w^a$, the relation (4.1) reduces to a statement about multinomial coefficients, which is Proposition 4.5.

For the other direction, let $k\ge n$. We first assume that n is odd. We can check that the sum in question is $w_3$ in case $n=3$, so we may assume $n\ge 5$. In that case, we can write $n=i+j$ for $i\ge 2$ even and $j\ge 3$ odd. We claim that the monomial $w_iw_j$ appears in the sum in question. Note that the monomial is nonzero by our assumption $k\ge n$. Since $a_i=a_j=1$ and all other $a_l$ are 0, the multinomial coefficient is $0\bmod 2$, hence $w_iw_j$ doesn’t appear in $q_n$. Now $w_j$ appears in $q_j$ in the sum in question, but $w_i$ doesn’t appear in any $q_{n-2i}$ because j is odd. So the sum in question contains the monomial $w_iw_j$ and is therefore not 0.

For any m which is not a power of 2, we can write $m=2^tn$ for n odd. Now we know from the previous argument that the monomial $w_iw_j$ (with $n=i+j$) appears in the sum for n. But then the monomial $w_i^{2^t}w_j^{2^t}$ appears in the sum for $m=2^ti+2^tj$ and we are done. $\square$

We can consider specializations of this formula to different k’s via the substitutions $w_{>k}=0$. The following proposition can be found in [7, Proposition 3.2] and [11, Lemma 2.3 (ii)]. We will show how the statements follow from Theorem 4.6:

Proposition 4.7

 

• (1) For $k=2$, $q_{2t+1}=0$ for all t.

• (2) For $k=3$, $q_{2^t-3}=0$ for all t.

• (3) For $k=4$, $q_{2^t-3}=0$ for all t.

Proof

Statement (1) is trivial, since $q_i=w_2q_{i-2}$ by (3.4) and $q_{-1}=0$. For $k=3$, Theorem 4.6 implies

$$\begin{aligned} q_{2^t}+w_2q_{2^t-2}=w_3q_{2^t-3}=0. \end{aligned}$$

Since ${\mathbb {F}}_2[w_2,w_3]$ is an integral domain, $q_{2^t-3}=0$. For $k=4$, Theorem 4.6 implies

$$\begin{aligned} q_{2^t}+w_2q_{2^t-2}+w_4q_{2^t-4}=w_3q_{2^t-3}=0, \end{aligned}$$

which implies $q_{2^t-3}=0$ as before. $\square$

We will show in the next sections that for $k=3$, all the syzygies between $(q_{n-2},q_{n-1},q_n)$ are obtained from the vanishing statement in Proposition 4.7 via ascending and descending relations. However, in the cases $n=2^t-3,\dots ,2^t$, one of these relations is “inessential”, i.e., is contained in the image of the boundary map of the Koszul complex and therefore doesn’t contribute to the presentation of K as C-module. As we will discuss in Sect. 9, the $k=4$ case is somewhat similar in that most of the time we have two relations produced from Proposition 4.7 via ascending and descending relations.

4.3 Descending relations

In what follows, k is fixed, and we will assume that $(q_i)_{i\in {\mathbb {Z}}}$ is a sequence in $W_2$ (or a $W_2$-module) satisfying the recursive relationship:

$$\begin{aligned} q_{i}=\sum _{j=2}^k w_j q_{i-j}. \end{aligned}$$

(4.2)

Then given a relation between $(q_{n-k+1},\ldots ,q_n)$, there is also a relation between $(q_{n-k},\ldots ,q_{n-1})$ as the following proposition describes. For our application, these $q_i$’s are the relations defining the characteristic subrings $C_k(n)$ and $C_k(n-1)$, respectively.

Proposition 4.8

If $(q_i)$ satisfies (4.2) and

$$\begin{aligned} \sum _{j=0}^{k-1}\alpha _j^0 q_{n-j}=0 \end{aligned}$$

is a homogeneous relation in $W_2$ in degree d between $(q_{n-k+1},\ldots ,q_n)$, then

$$\begin{aligned} \sum _{j=0}^{k-1}\alpha _j^i q_{n-i-j}=0 \end{aligned}$$

(4.3)

is a homogeneous relation in $W_2$ in degree d between $(q_{n-i-k+1},\ldots ,q_{n-i})$. Here, the sequence of doubly-indexed polynomials $\alpha _r^i\in W_2$ is defined by a double recursion starting with $\alpha _0^{<0}=0$, a recursion for the $\alpha _0^i$ given by

$$\begin{aligned} \alpha _{0}^{i+1}=\sum _{r=1}^{k-1}w_{k+1-r}\alpha _0^{i+r-k}, \end{aligned}$$

(4.4)

and finally, the $\alpha _r^i$ are defined by

$$\begin{aligned} \alpha _{k-j}^{i}=\sum _{r=0}^{j-1}w_{k-r}\alpha _0^{i+r-j}. \end{aligned}$$

(4.5)

Proof

Using the recursion (4.2) for $q_n$, write

$$\begin{aligned} \sum _{j=0}^{k-1}\alpha _j^0 q_{n-j}= \sum _{j=1}^{k}(\alpha _0^0w_j+\alpha _j^0)q_{n-j}=\sum _{j=0}^{k-1}(\alpha _0^0w_{j+1}+\alpha _{j+1}^0)q_{n-1-j} \end{aligned}$$

with $w_1=0$ and $\alpha ^0_k=0$. By induction, setting

$$\begin{aligned} \alpha ^{i+1}_j=w_{j+1}\alpha ^{i}_0+\alpha ^i_{j+1} \end{aligned}$$

(4.6)

for $j=0,\ldots ,k-1$ and $\alpha _k^{i+1}=0$ we get a relation between $(q_{n-i},\ldots ,q_{n-i-k+1})$:

$$\begin{aligned} \sum _{j=0}^{k-1}\alpha _j^i q_{n-i-j}=0. \end{aligned}$$

Using (4.6), the coefficients $\alpha _j^i$ can also be expressed recursively from the sequence $(\alpha _0^i)$:

$$\begin{aligned} \alpha _{k-1}^{i+1}=w_k\alpha _0^i,\qquad \alpha _{k-2}^{i+1}=w_{k-1}\alpha _0^i+\alpha _{k-1}^{i}=w_{k-1}\alpha _0^i+w_{k}\alpha _{0}^{i-1}, \end{aligned}$$

and by induction, we obtain (4.5). $\square$

Corollary 4.9

For $k=3$, the following relation in degree $m=2^t-3$ holds for all $n\le m$ and $i=m-n$:

$$\begin{aligned} q_iq_{n}+q_{i+1}q_{n-1}+w_3q_{i-1}q_{n-2}=0 \end{aligned}$$

(4.7)

This is a relation between the relations $(q_n,q_{n-1}, q_{n-2})$ defining the characteristic subring $C_3(n)$.

Proof

For $k=3$, by Fukaya’s theorem (Proposition 4.7), $q_{2^t-3}=0$ is a relation. We set $\alpha _0^0=1=q_0$, $\alpha _1^0=\alpha _2^0=0$, $\alpha _0^{<0}=0$. The recursion (4.4) is $\alpha _{0}^{i}=w_3\alpha _0^{i-3}+w_2\alpha _0^{i-2}$. The same recursion defines $(q_i)$, cf. (4.2), so that $\alpha _0^i=q_i$ for all i. Then by (4.5),

$$\begin{aligned} \alpha _1^i=w_3\alpha _0^{i-2}+w_2\alpha _0^{i-1}=w_3q_{i-2}+w_2q_{i-1}=q_{i+1}, \end{aligned}$$

and

$$\begin{aligned} \alpha _2^i=w_3\alpha _0^{i-1}=w_3q_{i-1} \end{aligned}$$

Therefore the relation (4.3) is of the form (4.7). $\square$

Corollary 4.10

For $k=4$, the following relation in degree $m=2^t-3$ holds for all $n\le m$ and $i=m-n$:

$$\begin{aligned} q_iq_{n}+q_{i+1}q_{n-1}+(q_{i+2}+w_2q_{i})q_{n-2}+(q_{i+3}+w_2q_{i+1}+w_3q_i)q_{n-3}=0 \end{aligned}$$

(4.8)

This is a relation between the relations $(q_n,q_{n-1}, q_{n-2}, q_{n-3})$ defining the characteristic subring $C_4(n)$.

Proof

For $k=4$, by Proposition 4.7, $q_{2^t-3}=0$ is a relation, so set $\alpha _0^0=1=q_0$, $\alpha _1^0=\alpha _2^0=\alpha _3^0=0$, $\alpha _0^{<0}=0$. The recursion (4.4) is $\alpha _{0}^{i}=w_4\alpha _0^{i-4}+w_3\alpha _0^{i-3}+w_2\alpha _0^{i-2}$. Again, the same recursion defines $(q_i)$, cf. (4.2), so that $\alpha _0^i=q_i$ for all i. By (4.5)

$$\begin{aligned} \alpha _1^i= & {} w_4\alpha _0^{i-3}+w_3\alpha _0^{i-2}+w_2\alpha _0^{i-1}=w_4q_{i-3}+w_3q_{i-2}+w_2q_{i-1}=q_{i+1}, \\ \alpha _2^i= & {} w_4\alpha _0^{i-2}+w_3\alpha _0^{i-1}=w_4q_{i-2}+w_3q_{i-1}=q_{i+2}+w_2q_{i}, \end{aligned}$$

and

$$\begin{aligned} \alpha _3^i=w_4\alpha _0^{i-1}=q_{i+3}+w_2q_{i+1}+w_3q_{i}. \end{aligned}$$

Therefore the relation (4.3) is of the form (4.8). $\square$

4.4 Ascending relations

Given a relation between $(q_{n-k+1},\ldots ,q_n)$, we can also get a relation between $(q_{n-k+2},\ldots , q_{n+1})$ from the recursion $q_i=\sum _{j=2}^kw_jq_{i-j}$, as the following proposition describes. Again, for our application, the $q_i$’s are the relations defining the characteristic subrings $C_k(n)$ and $C_k(n+1)$.

Proposition 4.11

If $(q_i)$ satisfies (4.2) and

$$\begin{aligned} \sum _{j=0}^{k-1}\beta _j^0 q_{n-j}=0 \end{aligned}$$

is a homogeneous relation in degree D between $(q_{n-k+1},\ldots ,q_n)$, then

$$\begin{aligned} \sum _{j=0}^{k-1}\beta _j^i q_{n+i-j}=0 \end{aligned}$$

(4.9)

is a homogeneous relation in degree $D+ki$ between $(q_{n+i-k+1},\ldots ,q_{n+i})$, where the sequence of doubly-indexed polynomials $(\beta _j^i)$ is defined by a double recursion starting with $\beta ^{<0}_j=0$ for all j:

$$\begin{aligned} \beta ^{i+1}_j=\sum _{r=0}^jw_{j-r}w_k^r\beta _{k-1}^{i-r} \end{aligned}$$

(4.10)

Note that $w_1=0$ and that (4.10) for $j=k-1$ is a recursive definition of $(\beta _{k-1}^i)$:

$$\begin{aligned} \beta ^{i+1}_{k-1}=\sum _{r=0}^{k-1}w_{k-1-r}w_k^r\beta _{k-1}^{i-r} \end{aligned}$$

Proof

We multiply the given relation with $w_k$, and use the recursion (4.2) in the form $w_kq_{n-k+1}=\sum _{j=0}^{k-1}w_jq_{n+1-j}$ (with $w_1=0$ and $w_0=1$) to get

$$\begin{aligned} 0= & {} w_k\sum _{j=0}^{k-1}\beta _j^0 q_{n-j}=\beta _{k-1}^0\left( \sum _{j=0}^{k-1}w_jq_{n+1-j}\right) +w_k\sum _{j=1}^{k-1}\beta _{j-1}^0 q_{n+1-j}\\= & {} \sum _{j=0}^{k-1}\left( \beta _{k-1}^0w_j+w_k\beta _{j-1}^0\right) q_{n+1-j} \end{aligned}$$

with $w_1=0$ and $\beta ^0_{-1}=0$. By induction, setting

$$\begin{aligned} \beta ^{i+1}_j=w_{j}\beta ^{i}_{k-1}+w_k\beta ^i_{j-1} \end{aligned}$$

(4.11)

for $j=0,1,\ldots ,k-1$ and $\beta _{-1}^{i+1}=0$ we get a relation between $(q_{n+i-k+1},\ldots ,q_{n+i})$:

$$\begin{aligned} \sum _{j=0}^{k-1}\beta _j^i q_{n+i-j}=0. \end{aligned}$$

Using (4.11), the coefficients $\beta _j^i$ can also be expressed recursively from the sequence $(\beta _0^i)$, starting with

$$\begin{aligned} \beta _0^{i+1}=\beta _{k-1}^i,\qquad \beta _1^{i+1}=w_1\beta _{k-1}^i+w_k\beta _{k-1}^{i-1}. \end{aligned}$$

By induction on j, we obtain (4.10). $\square$

Applying this to Fukaya’s relations $q_{2^t-3}=0$ in the case $k=3$, we directly get the following syzygy between the relations $(q_n,q_{n-1}, q_{n-2})$ defining the characteristic subring $C_3(n)$. To alleviate notation, for $k=3$ we introduce

$$\begin{aligned} r_j=\beta _2^j. \end{aligned}$$

(4.12)

Corollary 4.12

For $k=3$, let $d=2^{t}-1$, $n\ge d$ and $j=n-d$. Then we have the following relation between $(q_{n},q_{n-1}, q_{n-2})$ in degree $(d-2)+3j$:

$$\begin{aligned} r_{j-1}q_{n}+w_3r_{j-2}q_{n-1}+r_jq_{n-2}=0 \end{aligned}$$

(4.13)

where $r_i$ satisfy the recursion

$$\begin{aligned} r_{i+1}=w_2r_i+w_3^2r_{i-2}. \end{aligned}$$

(4.14)

with $r_0=1$, $r_{<0}=0$.

Proof

We first check the degrees in the statement. Assuming the recursion, we see that the degree of $r_j$ is 2j, and then the relation has degree $2j-2+n=2n-2d-2=(d-2)+3j$.

Now we prove the statement by induction. The induction start is $n=d$, $j=0$. In this case, $r_{-1}q_n+w_3r_{-2}q_{n-1}+r_0q_{n-2}=0$ holds because $r_{<0}=0$ and $q_{2^t-3}=0$ from Proposition 4.7. The recursion $r_{i+1}=w_2r_i+w_3^2r_{i-2}$ is exactly the last recursion from Proposition 4.11. To see that the claim follows by induction, there is some reindexing necessary so that we can write the starting relation as $\beta _0^0q_n+w_3\beta _1^0q_{n-1}+\beta _2^0q_{n-2}=0$ and use Proposition 4.11. In particular, we start with $\beta _0^0=\beta _1^0=0$ and $\beta _2^0=1$. From (4.10), we get $\beta _0^j=w_0w_3^0r_{j-1}$ and $\beta _1^j=w_0w_3r_{j-2}$ (using $w_1=0$). In particular, we find

$$\begin{aligned} \beta _0^jq_n+\beta _1^jq_{n-1}+\beta _2^jq_{n-2}=r_{j-1}q_n+w_3r_{j-2}q_{n-1}+r_jq_{n-2}. \end{aligned}$$

This finishes the proof. $\square$

We remark that from the recursion (4.13), via a standard computation, $r_j$ can also be given in a closed form as follows:

$$\begin{aligned} r_j=\sum _{2j=2b_2+6b_3}\left( {\begin{array}{c}b_2+b_3\\ b_2\end{array}}\right) w_2^{b_2}w_3^{2b_3} \end{aligned}$$

(4.15)

Similarly, for $k=4$, we get the following syzygy between the relations $(q_n,\dots ,q_{n-3})$ defining the characteristic subring $C_4(n)$.

Corollary 4.13

For $k=4$, let $d=2^r$, $n\ge d$ and $i=n-d$. Then we have the following relation between $(q_{n},q_{n-1}, q_{n-2},q_{n-3})$ in degree $(d-3)+4i$:

$$\begin{aligned} \beta _{3}^{i-1}q_{n}+w_4\beta _3^{i-2}q_{n-1}+\left( w_2\beta _3^{i-1}+w_4^2\beta _3^{i-3}\right) q_{n-2}+\beta _3^iq_{n-3}=0 \end{aligned}$$

(4.16)

where $\beta _3^i$ satisfy the recursion

$$\begin{aligned} \beta _3^{i+1}=w_3\beta _3^i+w_2w_4\beta _3^{i-1}+w_4^3\beta _3^{i-3} \end{aligned}$$

with $\beta _3^0=1$ and $\beta _3^{<0}=0$.

Proof

We first consider the degrees of the relation in the statement. From the recursion for $\beta _3^i$, we find that the degree of $\beta _3^i$ is 3i. The relation then has degree $3i-3+n=2n-3d-3=d-3+4i$.

We start with the base case $n=d$, $i=0$. In this case, the first three terms have $\beta _3^{<0}=0$ while the last term is $q_{2n-3}$, so the relation holds.

For general $n=d+i$, Proposition 4.11 implies a relation of the form

$$\begin{aligned} \beta _0^iq_n+\beta _1^iq_{n-1}+\beta _2^iq_{n-2}+\beta _3^iq_{n-3}=0. \end{aligned}$$

Now we can rewrite the coefficients using the recursions from Proposition 4.11, omitting the terms containing $w_1=0$:

$$\begin{aligned} \beta _0^i&=w_0w_4^0\beta _3^{i-1}\\ \beta _1^i&=w_0w_4^1\beta _3^{i-2}\\ \beta _2^i&=w_2w_4^0\beta _3^{i-1}+w_0w_4^2\beta _3^{i-3} \end{aligned}$$

Writing out the last recursion in Proposition 4.11 produces $\beta _3^{i+1}=w_3w_4^0\beta _3^i+w_2w_4^1\beta _3^{i-1}+w_0w_4^3\beta _3^{i-3}$. The claims follow from this. $\square$

5 Generalities on Koszul homology and the anomalous module

In this section, we prepare for the computation of the C-module presentation of K by interpreting K as first Koszul homology for the sequence $(q_{n-k+1},\dots ,q_n)$ in $W_2$. That Koszul homology should play a role for the computation is already apparent in Baum’s computation of cohomology of homogeneous spaces in [2].

5.1 Recollections on Koszul homology

Definition 5.1

For a commutative ring R, and an R-linear map $f:R^n\rightarrow R$, the associated Koszul complex ${\mathcal {K}}(f)$ is the complex

with boundary maps

$$\begin{aligned} \wedge ^jf(\alpha _1\wedge \cdots \wedge \alpha _j)=\sum _{i=1}^j(-1)^{i+1}f(\alpha _i)\cdot \alpha _1\wedge \cdots \wedge {\hat{\alpha }}_i\wedge \cdots \wedge \alpha _j. \end{aligned}$$

(5.1)

If $Q=(Q_1,\ldots ,Q_n)\in R$ is a sequence of elements in R, then the associated Koszul complex ${\mathcal {K}}(Q)$ is the Koszul complex of the R-linear map $(r_1,\ldots ,r_n)\mapsto \sum _{i=1}^nQ_ir_i$.

For an R-module M, we then define the Koszul homology as the homology of the complex ${\mathcal {K}}_M(f):={\mathcal {K}}(f)\otimes _R M$. Below, we will only consider the situation where f is given by a sequence $Q=(Q_1,\dots ,Q_n)$, and the Koszul homology will be denoted by $H_i(Q,M)$.

Actually, for what follows, we will consider the Koszul complex in a graded setting. If R is a ${\mathbb {Z}}$-graded ring and $f:\bigoplus _{i=1}^n R[d_i]\rightarrow R$ a linear map of graded R-modules, there is a Koszul complex of free graded R-modules, of the form given above. The only change is that we replace $\bigwedge ^j R^n$ by its graded version

$$\begin{aligned} \bigwedge ^j\left( \bigoplus _{i=1}^nR[d_i]\right) \cong \bigoplus _{1\le i_1\le \cdots \le i_j\le n} R[d_{i_1}+\cdots +d_{i_j}]. \end{aligned}$$

The boundary maps (5.1) then preserve the grading. Moreover, for a sequence of homogeneous elements $Q=(Q_1,\dots ,Q_n)\in R$, we get a graded Koszul complex ${\mathcal {K}}(Q)$ associated to the map

$$\begin{aligned} \bigoplus _{i=1}^n R[-\deg Q_i]\rightarrow R:(r_1,\dots ,r_n)\mapsto \sum _{i=1}^nQ_ir_i. \end{aligned}$$

Here $R[-\deg Q_i]$ is the free rank one R-module shifted in such a way that $R[-\deg Q_i]_j=R_{-\deg Q_i+j}$, i.e., the degree 0 component of R is shifted to lie in degree $\deg Q_i$ of $R[-\deg Q_i]$. The linear map above is then a degree 0 map. Some explicit examples of the graded Koszul complexes can be found in the Betti number computation in Appendix c.

5.2 Relation of Koszul homology to K

Let $W_1:={\mathbb {F}}_2[w_1,\ldots ,w_k]$ and $W_2:={\mathbb {F}}_2[w_2,\ldots ,w_k]$. We consider both rings with a grading given by $\deg w_i=i$. Then $W_2$ is naturally a graded $W_1$-module (where $w_1$ acts by 0) and there is a short exact sequence of $W_1$-modules:

(5.2)

The first entry is shifted to account for multiplication with $w_1$ being a degree 1 map on $W_1$.

Let $H:=\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$, which has the presentation $H=W_1/(Q)$ with $Q=(Q_{n-k+1},\dots ,Q_n)$. Since Q is a regular sequence of homogeneous elements in $W_1$, all Koszul homologies $H_i(Q, W_1)$ vanish for $i>0$. In general, for a graded $W_1$-module M,

$$\begin{aligned} H_0(Q, M)=M/(Q)M \end{aligned}$$

(this is one of the defining properties of Koszul homology). Therefore

$$\begin{aligned} H_0(Q,W_2)=W_2/(Q){W_2}=C,\qquad H_0(Q,W_1)=W_1/(Q){W_1}=H \end{aligned}$$

The short exact sequence of $W_1$-modules (5.2) induces a long exact sequence of $W_1$-modules in Koszul homology:

Therefore

$$\begin{aligned} K[-1]=\ker (w_1:H[-1]\rightarrow H)\cong \delta (H_1(Q,W_2)), \end{aligned}$$

and the exactness of the sequence also proves that $H_i(Q,W_2)=0$ for $i>1$.

In particular, the identification of zeroth and first Koszul homology with characteristic subring C and the anomalous module K, respectively, respects the gradings from cohomological degree. Taking the grading into account as above also makes explicit the shift appearing when translating between Koszul homology $H_1(Q,W_2)$ and $K=\ker (w_1)$.

Remark 5.2

In fact, $H_i(Q,W_2)={\text {Tor}}_i^{W_1}(H,W_2)$, see e.g. [20, Corollary 4.5.5.] and (5.3) is the long exact sequence of ${\text {Tor}}_i^{W_1}(H,\cdot )$ associated to (5.2).

The way to unravel the boundary map $\delta$ is via the snake lemma: take a relation $r_i\in H_1(Q,W_2)$ (between $q_i$), and represent it by some 1-chain $R_i$ in the Koszul complex $({\mathcal {K}}_{W_1}(Q))_1$. Then take its boundary $d_1(R_i)\in ({\mathcal {K}}_{W_1}(Q))_0=W_1$, take a preimage in $W_1$ via $w_1$ (i.e., divide by $w_1$) and take its reduction to $H=W_1/(Q)$. Since the sequence (5.3) is exact, the resulting element is in the kernel of $w_1$.

This procedure gives explicit $W_1$-generators of K in terms of the syzygies (relations between relations) in C. Also, the presentation of K as a $W_1$-module provides a presentation as a C-module, by base extension. Indeed, $K\otimes _{W_1}C\cong K$, since ${\text {Ann}}_{W_1}(K)=(w_1,Q_{n-k+1},\ldots ,Q_n)$ – in other words, this is just the statement that K is a C-module.

Remark 5.3

We can make this boundary map even more explicit. For ease of notation, we are omitting full documentation of the relevant degrees. Let $Q_i\in W_1$ be the relations (the complete homogeneous symmetric polynomials expressed in terms of elementary symmetric ones) and let

$$\begin{aligned} q_i:=Q_i|_{w_1=0}\in W_2,\qquad P_i:=Q_i+q_i\in (w_1). \end{aligned}$$

Since $P_i\in (w_1)\subseteq W_1$, it has a unique preimage $p_i$ via $w_1$, i.e., $w_1p_i=P_i$. That is,

If $\sum f_iq_i=0\in W_2$ is a relation, then since $Q_i=0$ in H, we have the following equality in H:

$$\begin{aligned} \sum f_iP_i=\sum f_i q_i=0, \end{aligned}$$

since $\sum f_iq_i=0\in W_2\subseteq W_1$, and using that H is a quotient of $W_1$. The boundary map in the long exact sequence (5.3) maps such a relation $\sum f_iq_i$ in the Koszul complex to

$$\begin{aligned} \delta \left( \sum f_iq_i\right) =\sum f_ip_i\in H. \end{aligned}$$

(5.4)

Note that since $w_1p_i=P_i$, $\sum f_i p_i$ is an element in $\ker w_1\subseteq H$. Also note that $\delta$ decreases the degrees by one; $\deg \delta (\xi )=\deg \xi -1$ for $\xi \in \ker (d_1)$.

The classes $P_i$ and $p_i$ also satisfy recursive identities: since $Q_i=\sum _{r=1}^k w_rQ_{i-r}$ and $q_i=\sum _{r=2}^k w_rq_{i-r}$,

$$\begin{aligned} P_i=Q_i+q_i=w_1Q_{i-1}+\sum _{r=2}^k w_rP_{i-r} \end{aligned}$$

and since $Q_{i-1}=P_{i-1}+q_{i-1}$:

$$\begin{aligned} P_i=w_1q_{i-1}+\sum _{r=1}^k w_rP_{i-r} \end{aligned}$$

(5.5)

So

$$\begin{aligned} p_i=q_{i-1}+\sum _{r=1}^kw_rp_{i-r} \end{aligned}$$

(5.6)

Remark 5.4

The Koszul homology of $(q_{n-2},q_{n-1},q_n)\subseteq W_2={\mathbb {F}}_2[w_2,w_3]$ is the same as the Koszul homology of $(w_1,Q_{n-2},Q_{n-1},Q_n)\subseteq W_1={\mathbb {F}}_2[w_1,w_2,w_3]$.

Remark 5.5

The Koszul homology description generalizes to the cohomology of the sphere bundle S of a rank n vector bundle $E\rightarrow X$, whenever $\textrm{H}^*(X)$ is a complete intersection ring ${\mathbb {F}}_2[x_1,\ldots ,x_r]/(Q_1,\ldots ,Q_p)$ for some regular sequence $Q_i$. Then the first homology of the Koszul complex of $(w_n(E),Q_1,\ldots ,Q_p)$ over ${\mathbb {F}}_2[x_1,\ldots ,x_r]$ is $\ker w_n(E)\subseteq \textrm{H}^*(X)$.

5.3 The characteristic rank of $\widetilde{{\text {Gr}}}_k(2^t)$

The characteristic rank of a vector bundle $E\rightarrow X$ over an n-dimensional manifold X, is the maximal degree $0\le r\le n$, such that $\textrm{H}^{\le r}(X;{\mathbb {F}}_2)$ is generated by the Stiefel–Whitney classes of E. Then for the tautological bundle $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$, $\textrm{crk}(S)$ is the maximal degree r such that the inclusion $C^{\le r}\subset \textrm{H}^{\le r}(\widetilde{{\text {Gr}}}_k(n);{\mathbb {F}}_2)$ is an isomorphism. So a nonzero class in the Koszul homology $H_1(Q,W_2)$ in degree d gives the upper bound $\textrm{crk}(S)\le d-2$. The characteristic ranks $\textrm{crk}(S)$ for $k=3$ and $k=4$ have been determined in [16, Theorem 1] and [17, Theorem 6.6]. The characteristic rank $\textrm{crk}(S)$ is not known besides these cases, though upper and lower bounds have been developed in the literature, see the discussion below. Using Theorem 4.6 we can give a new upper bound for $\textrm{crk}(S)$ when $n=2^t$.

Theorem 5.6

Assume $2^t-5\ge k\ge 5$. The characteristic rank of the tautological bundle $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$ for $n=2^t$ satisfies

$$\begin{aligned} \textrm{crk}(S)\le 2^t-2. \end{aligned}$$

In other words, there is a nonzero anomalous class in the cohomology $\textrm{H}^{2^t-1}(\widetilde{{\text {Gr}}}_k(2^t);{\mathbb {F}}_2)$ of the oriented Grassmannian.

Proof

We can assume $k\le 2^{t-1}$ by the duality $\widetilde{{\text {Gr}}}_k(2^t)\cong \widetilde{{\text {Gr}}}_{2^t-k}(2^t)$. Since $n=2^t$, the following relation from Theorem 4.6 holds:

$$\begin{aligned} \sum _{i=1}^{\lfloor {k/2}\rfloor -1} q_{n-2i-1}w_{2i+1}=0, \end{aligned}$$

which gives a generator of $\ker (d_1)$ in the Koszul complex:

$$\begin{aligned} v=(0,0,0,w_3,0,w_5,0,\ldots )\in \wedge ^1W_2^{\oplus k}. \end{aligned}$$

We claim that this is not in the image of the differential $d_2$ which has the following form:

$$\begin{aligned} \wedge ^2(W_2^{\oplus k})\ni A=\left( \begin{array}{ccccc} 0 &{} \lambda _{12} &{} \lambda _{13} &{} \ldots &{} \lambda _{1k} \\ \lambda _{12} &{} 0 &{} \lambda _{23} &{} \ldots &{} \lambda _{2k} \\ \vdots &{} \vdots &{} \ddots &{} \ldots &{} \vdots \\ \lambda _{1k} &{} \lambda _{2k} &{} \lambda _{3k} &{} \ldots &{} 0 \end{array}\right) \mapsto A \left( \begin{array}{c} q_{n-k+1} \\ q_{n-k+2} \\ \vdots \\ q_n \end{array} \right) \in \wedge ^1(W_2^{\oplus k}) \end{aligned}$$

Since all entries of Aq are homogeneous and the lowest degree nonzero term in q is of degree $n-k+1\ge 2^t-2^{t-1}+1\ge 3$, this implies that $v\in \ker (d_1)$ is not in ${\text {Im}}(d_2)$, and defines a nontrivial element in the Koszul homology $H_1(Q,W_2)$. Via the long exact sequence (5.3), this defines a nonzero element of K, which in turn lifts to an anomalous class in $\textrm{H}^{2^t-1}(\widetilde{{\text {Gr}}}_k(2^t);{\mathbb {F}}_2)$. Therefore the characteristic rank is at most $2^t-2$, by definition. $\square$

Remark 5.7

The nonzero element of K in the above proof can be identified more explicitly, it is the highest nonzero power of $w_1$, cf. the discussion in Section 6 of [14]. The proof uses exactly the translation between Koszul homology and K outlined above.

This anomalous class in $\widetilde{{\text {Gr}}}_k(2^t)$ provides further anomalous classes for $\widetilde{{\text {Gr}}}_k(n)$ by ascending and descending the relation of Theorem 4.6. Sometimes these ascended and descended relations vanish in Koszul homology, as they fall into the image of the Koszul boundary, as we illustrate in Sect. 6.4. However, these classes always seem to be responsible for the characteristic rank of $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$, cf. Sect. 9. We formulate our observations in the following conjecture:

Conjecture 5.8

The characteristic rank of the tautological bundle $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$ is equal to

$$\begin{aligned} \textrm{crk}(S)=\min (2^t-2,k(n-2^{t-1})+2^{t-1}-2). \end{aligned}$$

(5.7)

for $5\le k\le 2^{t-1}<n\le 2^t$ and $t\ge 5$.

We verified this conjecture by computer calculations for $k=5$, $n\le 32$ and $k=6$, $n\le 23$, cf. Sect. 9. Further cases of the conjecture are established in [14].

Remark 5.9

We comment on the assumptions made in this conjecture.

In the $k\le 4$ cases the syzygies follow a different pattern than in the $k\ge 5$ cases, which gives rise to different characteristic ranks, cf. Proposition 4.7 and Corollaries 4.9 to 4.13, which is why we make the $k\ge 5$ assumption. This different behaviour also influences the characteristic ranks via the duality $\widetilde{{\text {Gr}}}_k(n)\cong \widetilde{{\text {Gr}}}_{n-k}(n)$ in the range $8<n\le 16$ for $k=5,6$, which is why we make the $t\ge 5$ assumption. The explicit examples not satisfying (5.7) with $5\le k\le 8<n\le 16$ are $\textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_5(10))=10$, $\textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_5(11))=13$ and $\textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_6(12))=13$, see Sect. 9.

Remark 5.10

We briefly summarize what else is known about the characteristic rank of $S\rightarrow \widetilde{{\text {Gr}}}_k(n)$. There is a simple lower bound $\textrm{crk}(S)\ge n-k-1$; this amounts to the obvious statement that there cannot be a $W_2$-relation between $(q_{n-k+1},\ldots ,q_n)$ in degree $n-k$. The best known lower bounds have been obtained in [17] using Gröbner basis techniques; for $k\ge 6$:

$$\begin{aligned} \textrm{crk}(S)\ge (n-k)+\lfloor k/3\rfloor -1, \end{aligned}$$

as well as some stronger estimates for certain pairs (k, n). The authors also note [17, Remark 6.8] that “there are reasons to believe that for $k \ge 5$, there is some n such that $\textrm{crk}(S) > 2(n-k) - 1$”.³ From the tables in Sect. 9, we see that

$$\begin{aligned} \textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_6(18))=2(n-k)+4,\qquad \textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_6(19))=2(n-k)+6. \end{aligned}$$

More generally, Conjecture 5.8 would imply that for any r, there is a choice of k and n, such that $\textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_k(n))>2(n-k)+r$.

Remark 5.11

In the literature, often the characteristic rank of a manifold is considered, which is the characteristic rank of its tangent bundle $\textrm{crk}(TM)$. Whenever the total Stiefel–Whitney class of the tangent bundle w(TM) can be expressed in terms of w(E), there is an obvious upper bound $\textrm{crk}(TM)\le \textrm{crk}(E)$. In general, these are not equal; for example $\textrm{crk}(T{\mathbb {R}}P^{2r+1})=0$, but $\textrm{crk}(S\rightarrow {\mathbb {R}}P^{2r+1})=2r+1$. On the other hand, $\textrm{crk}(T{\mathbb {R}}P^{2r})=\textrm{crk}(S\rightarrow {\mathbb {R}}P^{2r})=2r$. By a result of Korbaš [10, p. 72], $\textrm{crk}(T\widetilde{{\text {Gr}}}_{k}(2n+1))=\textrm{crk}(S\rightarrow \widetilde{{\text {Gr}}}_{k}(2n+1))$ — this is due to the fact that w(S) can also be expressed from $w(T\widetilde{{\text {Gr}}}_{k}(2n))$.

6 Presentation of the anomalous module for $k=3$

For $k=3$, we exhibited certain $W_2$-relations between $(q_{n-2},q_{n-1}, q_n)$ in Corollaries 4.9 and 4.12. These involved the polynomials $q_i$ themselves and the polynomials $r_l$ of degree 2l defined by the recursion $r_{l+1}=w_2r_l+w_3^2r_{l-2}$. The goal of this section is to prove the following Theorem:

Theorem 6.1

For $t\ge 4$, let $2^{t-1}<n\le 2^t-4$, and set $i=2^t-3-n$ and $j=n-2^{t-1}+1$. Then the anomalous module $K\subseteq \textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$ is isomorphic (as a graded C-module) to

$$\begin{aligned} K=C\langle A_n,D_n\rangle /(q_iA_n+r_{j-1}D_n, q_{i+1}A_n+w_3r_{j-2}D_n, w_3q_{i-1}A_n+r_jD_n), \end{aligned}$$

(6.1)

where $A_n$ and $D_n$ are explicit elements (6.3), (6.2) of K of degrees $\deg A_n=3n-2^t-1$ and $\deg D_n=2^t-4$.

We will derive this presentation of K using its identification with the first Koszul homology of the ideal $(q_{n-2},q_{n-1},q_n)\subseteq W_2={\mathbb {F}}_2[w_2,w_3]$ described in Sect. 5.2. Throughout this section, given $t\ge 4$ and $2^{t-1}-1\le n\le 2^t-3$, we will use the notation $j=n-(2^{t-1}-1)$ and $i=2^t-3-n$, cf. Fig. 1.

Fig. 1

Notations

6.1 Relations between $q_l$ and $r_l$

The following equalities connect the coefficients of the ascended and descended relations, and will play a crucial role for the proofs in this section:

Lemma 6.2

With the indexing conventions set up above, the following equations hold in $W_2={\mathbb {F}}_2[w_2,w_3]$ for all $2^{t-1}-1\le n\le 2^t-3$:

$$\begin{aligned} w_3r_{j-2}q_i+r_{j-1}q_{i+1}&=q_{n-2}\\ r_jq_i+w_3r_{j-1}q_{i-1}&=q_{n-1}\\ r_jq_{i+1}+w_3^2r_{j-2}q_{i-1}&=q_n \end{aligned}$$

Proof

The start of the induction is the case $n=2^{t-1}-1$, $j=0$ and $i=2^{t-1}-2$, where we can make use of $r_{<0}=0$ and $r_0=1$. In this case, the first equality reduces to $q_{2^{t-1}-3}=0$ from Proposition 4.7. The second and third equality both reduce to $q_i=q_{n-1}$ which follows from the $i=n-1$ of the assumption.

For the induction step, assume that the three equations are satisfied for n, with $i=2^t-n-3$ and $j=n-2^{t-1}-1$. We want to show that the equations for $n+1$, $i-1$ and $j+1$ are also satisfied.

We first show $r_{j+1}q_i+w_3^2r_{j-1}q_{i-2}=q_{n+1}$:

$$\begin{aligned} q_{n+1}&=w_2r_jq_i+w_2w_3r_{j-1}q_{i-1}+w^2_3r_{j-2}q_i+w_3r_{j-1}q_{i+1}\\&=r_{j+1}q_i+w_2w_3r_{j-1}q_{i-1}+w_3r_{j-1}q_{i+1}\\&=r_{j+1}q_i+w_2w_3r_{j-1}q_{i-1}+w_2w_3r_{j-1}q_{i-1}+w_3^2r_{j-1}q_{i-2}\\&=r_{j+1}q_i+w_3^2r_{j-1}q_{i-2} \end{aligned}$$

The first equality uses the recursion $q_{n+1}=w_2q_{n-1}+w_3q_{n-2}$, combined with the equations for the inductive assumption. The second equality combines the first and third summand using the recursion for $r_{j+1}$, and the third equality uses the recursion $q_{i+1}=w_2q_{i-1}+w_3q_{i-2}$. The two middle terms cancel and we have established the claim.

Next, we show $r_{j+1}q_{i-1}+w_3r_{j}q_{i-2} =q_{n}$:

$$\begin{aligned} q_{n}&=r_jq_{i+1}+w_3^2r_{j-2}q_{i-1}\\&=w_2r_jq_{i-1}+w_3r_jq_{i-2}+w_3^2r_{j-2}q_{i-1}\\&=r_{j+1}q_{i-1}+w_3r_jq_{i-2} \end{aligned}$$

The first equality is the inductive assumption, the second uses the recursion $q_{i+1}=w_2q_{i-1}+w_3q_{i-2}$, and the third uses the recursion for $r_{j+1}$, on the first and third summand in the second line. So the second equation is established.

Finally, the relation $w_3r_{j-1}q_{i-1}+r_{j}q_{i}=q_{n-1}$ is one of the equations in the inductive assumptions. $\square$

6.2 The kernel of the Koszul differential $d_1$

In this part we show that $\ker (d_1)$ is a free $W_2$-module of rank 2 and explicitly identify a $W_2$-basis.

Proposition 6.3

For $\widetilde{{\text {Gr}}}_3(n)$ with $2^{t-1}<n\le 2^t-4$, $i=2^t-3-n$ and $j=n-2^{t-1}+1$, the following equality holds in $W_2={\mathbb {F}}_2[w_2,w_3]$ for $x,y,z\in W_2$:

$$\begin{aligned} \left( \begin{array}{ccc}q_{n-2}&q_{n-1}&q_n\end{array}\right) \left( \begin{array}{c}x\\ y\\ z\end{array}\right) =\det \left( \begin{array}{ccc}x &{} r_j&{}w_3q_{i-1}\\ y&{}w_3r_{j-2}&{}q_{i+1}\\ z&{}r_{j-1}&{}q_i\end{array}\right) \end{aligned}$$

In particular, the 2nd and 3rd column vectors on the right-hand side form a basis for the kernel $\ker (d_1)$ in the Koszul complex, and so $\ker (d_1)$ is a free graded $W_2$-module of rank 2.

Proof

Before we embark on the proof, we recall from Sect. 5 that the Koszul complex is a complex of graded modules. In particular, kernels of differentials as well as homology groups will inherit a grading, and all linear algebra arguments below will be with homogeneous elements.

(1) The matrix equation claimed in the proposition is equivalent to the following three equations, which follow from Lemma 6.2:

$$\begin{aligned} q_{n-2}&=\det \left( \begin{array}{cc}w_3r_{j-2}&{}q_{i+1}\\ r_{j-1}&{}q_{i}\end{array}\right) \\ q_{n-1}&=\det \left( \begin{array}{cc}r_{j}&{}w_3q_{i-1}\\ r_{j-1}&{}q_{i}\end{array}\right) \\ q_{n}&=\det \left( \begin{array}{cc}r_{j}&{}w_3q_{i-1}\\ w_3r_{j-2}&{}q_{i+1}\end{array}\right) \end{aligned}$$

For ease of reference in the next two steps, we denote the 2nd and 3rd column vectors on the right-hand side by $u=(r_j, w_3r_{j-2}, r_{j-1})^{\textrm{t}}$ and $v=(w_3q_{i-1}, q_{i+1},q_i)^{\textrm{t}}$.

(2) Now we consider the graded $W_2$-submodule ${\text {span}}\langle u,v\rangle \subseteq W_2^{\oplus 3}$. For a homogeneous prime ideal $\mathfrak {p}\subseteq W_2$ not containing the irrelevant ideal, denote by ${\mathbb {F}}$ the fraction field of $W_2/\mathfrak {p}$. Our goal in this step is to show that the ${\mathbb {F}}$-submodule of ${\mathbb {F}}^{\oplus 3}=W_2^{\oplus 3}\otimes _{W_2}{\mathbb {F}}$ generated by (the images of) u and v is of rank 2. This shows, in particular, that u and v are independent and that ${\text {span}}\langle u,v\rangle$ is a free $W_2$-submodule of $W_2^{\oplus 3}$.⁴ To prove the claim, it is enough to show that at least one of the minors $q_{n-2}, q_{n-1}, q_n$ does not vanish in ${\mathbb {F}}$. But if all three minors vanished in ${\mathbb {F}}$, then they would already vanish in $W_2/\mathfrak {p}$, i.e., $(q_{n-2},q_{n-1},q_n)\subseteq \mathfrak {p}$. Since $\sqrt{(q_{n-2},q_{n-1},q_n)}=(w_2,w_3)$, cf. Proposition 3.1, this implies that $\mathfrak {p}$ contains the irrelevant ideal, a contradiction, showing that the images of u and v are linearly indepedent over ${\mathbb {F}}$.

(3) Finally, we need to show that u and v actually span $\ker (d_1)$. It is easy to check that ${\text {span}}\langle u,v\rangle \subseteq \ker (d_1)$. As submodules of the finitely generated graded $W_2$-module $W_2^{\oplus 3}$, they both are finitely generated graded $W_2$-modules. We want to show that the inclusion $\iota :{\text {span}}\langle u,v\rangle \hookrightarrow \ker (d_1)$ is in fact surjective, i.e., that the quotient module ${\text {coker}}(\iota )$ vanishes. It suffices to check the vanishing locally at points of the homogeneous prime spectrum. By the graded Nakayama lemma, it suffices to check vanishing at residue fields of homogeneous prime ideals.

This means the following. For a homogeneous prime ideal $\mathfrak {p}\subseteq W_2$ not containing the irrelevant ideal, denote by ${\mathbb {F}}$ the fraction field of $W_2/\mathfrak {p}$. Then we want to show that ${\text {span}}_{{\mathbb {F}}}\langle {\overline{u}},{\overline{v}}\rangle \supseteq \ker (d_1\otimes {\mathbb {F}})$. For $s=(x,y,z)^{\textrm{t}}\in \ker (d_1\otimes {\mathbb {F}})$, the matrix equation established in step (1) shows that $\{s,{\overline{u}},{\overline{v}}\}$ is linearly dependent, i.e., there are $\alpha ,\lambda ,\mu \in {\mathbb {F}}$ such that $\alpha s+\lambda {\overline{u}}+\mu {\overline{v}}=0$. From step (2), we have that ${\overline{u}}$ and ${\overline{v}}$ are linearly independent over ${\mathbb {F}}$, i.e., at least one of the determinants of the $(2\times 2)$-minors is nonzero in ${\mathbb {F}}$. In particular, we get $\alpha \ne 0$, meaning that $s\in {\text {span}}_{{\mathbb {F}}}\langle {\overline{u}},{\overline{v}}\rangle$. This finishes the proof. $\square$

Remark 6.4

The proof actually shows that all the coefficients $r_{\ge 0}$ appearing in the relation are in fact nonzero. If one of them was zero, the basis u, v would not span the kernel. But then some u would be divisible by $w_3$, leading to a linear expression $w_3s+u=0$. The last step in the proof shows that this is not possible, and we in fact do get all the elements in the kernel.

6.3 Presentation of the anomalous module

Using Proposition 6.3, we can name explicit elements $A_n,D_n\in K_3(n)$ via the boundary map $\delta$ of the long exact sequence of Koszul homologies (5.3), as described in Remark 5.3, in particular (5.4). The first generator of $\ker (d_1)$ is the descended relation:

$$\begin{aligned} q_iq_n+q_{i+1}q_{n-1}+w_3q_{i-1}q_{n-2}=0. \end{aligned}$$

Denote by $D_n\in W_1$ the image of this relation via $\delta$:

$$\begin{aligned} D_n=q_ip_n+q_{i+1}p_{n-1}+w_3q_{i-1}p_{n-2}. \end{aligned}$$

(6.2)

Similarly, denote by $A_n\in W_1$ the image of the ascended relation via $\delta$:

$$\begin{aligned} A_n=r_{j-1}p_n+w_3r_{j-2}p_{n-1}+r_jp_{n-2}. \end{aligned}$$

(6.3)

In order not to overburden notation, we will also denote by $A_n,D_n$ the reductions of these classes from $W_1$ to $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)=W_1/(Q_{n-2},Q_{n-1},Q_n)$. From Proposition 6.3 and the long exact sequence (5.3) it follows that $K_3(n)$ is generated by these two elements as a C-module, however so far one of these elements could just as well be 0. In this section, we will show that this is not the case, and compute the relations between these elements.

Proposition 6.5

The graded $W_2$-module K has a presentation by 2 generators $A_n$ and $D_n$ in degrees $\deg A_n=3n-2^t-1$ and $\deg D_n=2^t-4$. These two generators satisfy 3 relations of degrees $2n-4, 2n-3$ and $2n-2$, respectively, given as follows:

$$\begin{aligned} q_iA_n+r_{j-1}D_n, \qquad q_{i+1}A_n+w_3r_{j-2}D_n, \qquad w_3q_{i-1}A_n+r_jD_n. \end{aligned}$$

A similar presentation holds for K as graded C-module.

Proof

We first note that the degrees actually are as claimed: this follows from (6.2), (6.3), $\deg (p_l)=\deg (q_l)-1=l-1$ and $\deg (r_l)=2\,l$.

The differential $d_2$ for the Koszul complex is given by the following matrix, cf. Definition 5.1:

$$\begin{aligned} \left( \begin{array}{ccc} q_{n-1}&{}q_n&{}0\\ q_{n-2}&{}0&{}q_n\\ 0&{}q_{n-2}&{}q_{n-1} \end{array}\right) \end{aligned}$$

From Proposition 6.3, we know that $\ker d_1$ is a free rank 2 module. A presentation of K, as the first homology of the Koszul complex, can thus be obtained by writing the columns of the above matrix in terms of the basis vectors given in Proposition 6.3. We thus need to solve the following system of $W_2$-linear equations:

$$\begin{aligned} \left( \begin{array}{ccc} q_{n-1}&{}q_n&{}0\\ q_{n-2}&{}0&{}q_n\\ 0&{}q_{n-2}&{}q_{n-1} \end{array}\right) =\left( \begin{array}{cc} r_j&{}w_3q_{i-1}\\ w_3r_{j-2}&{}q_{i+1}\\ r_{j-1}&{}q_i \end{array}\right) \cdot \left( \begin{array}{ccc} \lambda _{11}&{}\lambda _{12}&{}\lambda _{13}\\ \lambda _{21}&{}\lambda _{22}&{}\lambda _{23} \end{array}\right) \end{aligned}$$

The columns in the right-most matrix will then describe the coefficients of the three relations between the two generators.

The claim in the proposition is that the following matrix is a solution of the system:

$$\begin{aligned} \left( \begin{array}{ccc} \lambda _{11}&{}\lambda _{12}&{}\lambda _{13}\\ \lambda _{21}&{}\lambda _{22}&{}\lambda _{23} \end{array}\right) = \left( \begin{array}{ccc} q_i&{}q_{i+1}&{}w_3q_{i-1}\\ r_{j-1}&{}w_3r_{j-2}&{}r_j \end{array}\right) \end{aligned}$$

One easily checks that the product has the symmetric structure required for the $d_2$-differential of the Koszul complex. It remains to check the following three equations, which are established in Lemma 6.2:

$$\begin{aligned} w_3r_{j-2}q_i+r_{j-1}q_{i+1}&=q_{n-2}\\ r_jq_i+w_3r_{j-1}q_{i-1}&=q_{n-1}\\ r_jq_{i+1}+w_3^2r_{j-2}q_{i-1}&=q_n \end{aligned}$$

$\square$

This concludes the proof of Theorem 6.1.

6.4 Koszul boundary

In this section we show how at the boundary of the interval $2^{t-1}<n<2^t-3$ the ascended and descended relations fall into the image of the Koszul boundary $d_2$. In other words we explain why there is only one generator in these cases.

Proposition 6.6

For $n=2^{t-1}$ and the corresponding $i=2^{t-1}-3$, the vector $(q_i,q_{i+1},w_3q_{i-1})\in W_2^{\oplus 3}$ corresponding to the descended relation (4.7)

$$\begin{aligned} q_iq_{n}+q_{i+1}q_{n-1}+w_3q_{i-1}q_{n-2}=0 \end{aligned}$$

is in the image of the Koszul boundary $d_2$.

For $n=2^t-3$ and the corresponding $j=2^{t-1}-2$, the vector $(r_{j-1},w_3r_{j-2},r_j)\in W_2^{\oplus 3}$ corresponding to the ascended relation (4.13)

$$\begin{aligned} r_{j-1}q_{n}+w_3r_{j-2}q_{n-1}+r_jq_{n-2}=0 \end{aligned}$$

is in the image of the Koszul boundary $d_2$.

Proof

The descended relation is

$$\begin{aligned} q_{2^{t-1}-3}q_{2^{t-1}}+q_{2^{t-1}-2}q_{2^{t-1}-1}+w_3q_{2^{t-1}-4}q_{2^{t-1}-2}=0. \end{aligned}$$

Using $w_3q_{2^{t-1}-4}=q_{2^{t-1}-1}$ and $q_{2^{t-1}-3}=0$, we can rewrite this as

$$\begin{aligned} q_{2^{t-1}-2}q_{2^{t-1}-1}+q_{2^{t-1}-1}q_{2^{t-1}-2}=0, \end{aligned}$$

which is clearly an element in the image of $d_2$. The ascended relation is the following (using $q_{2^t-3}=0$):

$$\begin{aligned} w_3r_{2^{t-1}-4}q_{2^t-4}+r_{2^{t-1}-2}q_{2^t-5}=0 \end{aligned}$$

We can conclude, since the coefficients are $q_{2^t-5}$ and $q_{2^t-4}$, by the following lemma. $\square$

Lemma 6.7

For all $t\ge 2$, the following relations hold in $W_2$:

$$\begin{aligned} r_{2^{t-1}-2}=q_{2^t-4},\qquad w_3r_{2^{t-1}-4}=q_{2^t-5}. \end{aligned}$$

The recursion on $r_n$ also implies $r_{2^{t-1}-1}=q_{2^t-2}$.

Proof

Using the recursion (3.4), one can show that the $q_j$ satisfy [11, (2.6)]

$$\begin{aligned} q_j=w_2^{2^s}q_{j-2\cdot 2^s}+w_3^{2^s}q_{j-3\cdot 2^s}, \end{aligned}$$

for all s such that $j\ge 1+3\cdot 2^s$. By a similar inductive argument on s using the recursion (4.14), one can show

$$\begin{aligned} r_j=w_2^{2^s}r_{j-2^s}+w_3^{2^{s+1}}r_{j-3\cdot 2^{s}} \end{aligned}$$

and similarly

$$\begin{aligned} r_{3\cdot 2^{t}-2}=w_2^{2^{t}}r_{2^{t+1}-2}. \end{aligned}$$

(6.4)

Using this, we can show the first equality $r_{2^{t-1}-2}=q_{2^t-4}$ by induction. The first step for $t=2,3$ states that $r_0=q_0=1$ and $r_2=q_4=w_2^2$. Using the recursions (3.4), (4.14) and (6.4), the induction step is

$$\begin{aligned} q_{2^t-4}=w_2^{2^{t-2}}q_{2^{t-1}-4}+w_3^{2^{t-2}}q_{2^{t-2}-4} =w_2^{2^{t-3}}\underbrace{w_2^{2^{t-3}}r_{2^{t-2}-2}}_{r_{3\cdot 2^{t-3}-2}}+w_3^{2^{t-2}}r_{2^{t-3}-2}=r_{2^{t-1}-2}. \end{aligned}$$

The other case can be obtained by an entirely analogous argument. $\square$

7 Vanishing of Ext-groups for $k=3$

Given the presentation of K as a C-module established in Sect. 6, we will now show that the ${\text {Ext}}$-group $\textrm{Ext}^1_C(K,C)$ always vanishes in the $k=3$ case, basically for degree reasons. This implies, in particular, that the extension (1.1) always splits, and $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ is, as a C-module, simply isomorphic to $K\oplus C$. Some basics on Ext-groups, how to compute them and how they relate to extensions can be found in Appendix B. Note that we are interested in graded degree 0 extensions, i.e., extensions of graded C-modules where all the maps preserve degrees.

Proposition 7.1

For all $n\ge 3$, we have that $\textrm{Ext}^1_C(K,C)=0$ (the graded, degree zero part is trivial).

Proof

In the cases $n=2^t-3,\dots ,2^t$, K is a cyclic C-module by [1, Theorem A], and therefore free by the Corollary 2.6. This implies the triviality of the Ext-group.

We can thus focus on the cases $2^{t-1}<n\le 2^t-4$. In these cases, K is generated by two elements of degrees $3n-2^t-1$ and $2^t-4$, again by [1, Theorem A] or Theorem 6.1. The smallest-degree anomalous generator is Poincaré dual to the top degree class of C. The dimension of $\widetilde{{\text {Gr}}}_3(n)$ being $3n-9$, the top degree of C is therefore the maximum of $2^t-8$ and $3n-2^t-5$.

On the other hand, K has 3 relations in degrees $2l+2=2n-4,2l+3,2l+4$, by Proposition 6.5. If we can show that the degrees of the relations are always bigger than the top degree of C, the Ext-group is trivial for degree reasons, cf. the discussion in Appendix B. But the assumption $n>2^{t-1}$ implies $2n-4>2^t-4>2^t-8$, and the assumption $n\le 2^t-4<2^t+1$ implies $2n-4>3n-2^t-5$. So we are done. $\square$

8 Removing remaining ambiguities

Using the splitting of Proposition 7.1, we know that $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n),{\mathbb {F}}_2)$ in the range $2^{t-1}<n\le 2^t-4$ is a C-module generated by lifts $a_n$ and $d_n$ of the elements $A_n$ and $D_n$, and we have computed the C-module relations in Theorem 6.1. This determines the cohomology $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)\cong C\oplus K$ as a C-module. To determine the complete ring structure, the only ambiguities left are the products $a_n^2, d_n^2$ and $a_nd_n$. We prove:

Proposition 8.1

Let $a_n, d_n\!\in \! \textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2)$ be lifts of the elements $A_n,D_n\in \textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$ defined in (6.3) and (6.2), i.e. $\delta (a_n)=A_n$ and $\delta (d_n)=D_n$. Then

$$\begin{aligned} a_n^2=d_n^2=a_nd_n=0. \end{aligned}$$

Proof

The product $a_nd_n$ vanishes for degree reasons:

$$\begin{aligned} \deg (a_nd_n)=(3n-2^t-1)+(2^t-4)=3n-5>3n-9=\dim \widetilde{{\text {Gr}}}_3(n). \end{aligned}$$

We will show that $\delta (a_n)^2=A_n^2=0$ and $\delta (d_n)^2=D_n^2=0$ in $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$ in Propositions 8.7 and 8.4. Then we can conclude by the following Lemma 8.2. $\square$

Lemma 8.2

$a_n^2=d_n^2=0$ in $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2)$ if and only if $A_n^2=D_n^2=0$ in $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$.

Proof

Boundary morphisms commute with Steenrod squares by Proposition 2.3. For the other direction, it is enough to show that $\deg (A_n^2)$ and $\deg (D_n^2)$ are above the top degree of C. As in Proposition 7.1, the top degree of C is $\max \{2^t-8,3n-2^t-5\}$. In the following lines, we will check that (under the standing assumptions) the degrees of the squares are always bigger than the top degree of C, so we are done. The inequality $\deg (D_n^2)=2(2^t-4)=2^{t+1}-8>2^t-8$ is straightforward. To show $\deg (D_n^2)=2(2^t-4)=2^{t+1}-8>3n-2^t-5$, we use

$$\begin{aligned} 2^{t+1}+2^t-3=3\cdot 2^t-3>3(2^t-4)\ge 3n. \end{aligned}$$

Next, $\deg (A_n^2)=2(3n-2^t-1)>3n-2^t-5$ follows from

$$\begin{aligned} 3n-2^{t+1}+2^t+3>3\cdot 2^{t-1}-2^{t+1}+2^t+3=2^{t-1}+3>0. \end{aligned}$$

Similarly, $\deg (A_n^2)=2(3n-2^t-1)>2^t-8$ follows from $3n-2^t-1>2^{t-1}-1>2^{t-1}-4$.

$\square$

In the remainder of this section, we complete the proof of Proposition 8.1 by showing that the squares of the $A_n$ and $D_n$ vanish in $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$.

8.1 The descended square

Recall that $P_i=Q_i+q_i$ and $P_i=w_1p_i$, and that they satisfy the following recursive formulas in $W_1={\mathbb {F}}_2[w_1,\ldots ,w_k]$:

$$\begin{aligned} P_i=w_1q_{i-1}+\sum _{r=1}^k w_rP_{i-r},\qquad p_i=q_{i-1}+\sum _{r=1}^kw_rp_{i-r}. \end{aligned}$$

(8.1)

To prove $D_n^2=0$ in $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$, we will use the following recursive identity for $D_n$:

Lemma 8.3

The $D_n$ satisfy the following recursion in $W_1$:

$$\begin{aligned} D_{n-1}=q_iQ_{n-1}+D_n, \end{aligned}$$

with the usual notation $i=2^t-3-n$.

Proof

Recall from (6.2) that

$$\begin{aligned} D_n=q_ip_n+q_{i+1}p_{n-1}+w_3q_{i-1}p_{n-2}. \end{aligned}$$

Using the recursion on $q_l$ and $w_2p_{n-2}+w_3p_{n-3}=w_1p_{n-1}+q_{n-1}+p_{n}$ – see (5.6) – we have

$$\begin{aligned} D_{n-1}&=q_{i+1}p_{n-1}+q_{i+2}p_{n-2}+w_3q_{i}p_{n-3}\\&=q_{i+1}p_{n-1}+(w_2q_i+q_{i-1}w_3)p_{n-2}+w_3q_{i}p_{n-3}\\&=\underbrace{q_ip_n+q_{i+1}p_{n-1}+q_{i-1}w_3p_{n-2}}_{D_n}+q_i(\underbrace{w_1p_{n-1}+q_{n-1}}_{Q_{n-1}}). \end{aligned}$$

$\square$

We now show that the square of the descended generator is always zero in $\textrm{H}^*({\text {Gr}}_3(n);{\mathbb {F}}_2)$.

Proposition 8.4

For $2^{t-1}<n\le 2^{t}-3$,

$$\begin{aligned} D_n^2\in (Q_n,Q_{n-1},Q_{n-2})\subseteq W_1. \end{aligned}$$

Proof

We prove this by downwards induction on n. For $n=2^t-3$, the reduction of $D_{n}^2\in W_1$ to

$$\begin{aligned} \textrm{H}^*({\text {Gr}}_3(2^t-3);{\mathbb {F}}_2)=W_1/(Q_{2^t-3},Q_{2^t-4}, Q_{2^t-5}) \end{aligned}$$

vanishes by the results of [9, Theorem 1.1. (c)]. Indeed, $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(2^t-3);{\mathbb {F}}_2)=C[d_n]/d_n^2$ and since $\delta (d_n)=D_n$ and $\delta$ is a ${\text {Sq}}$-module homomorphism by Proposition 2.3, it follows that

$$\begin{aligned} D_n^2={\text {Sq}}^{\deg d_n}\delta (d_n)=\delta (d_n^2)=0. \end{aligned}$$

Therefore

$$\begin{aligned} D_{2^t-3}^2\in (Q_{2^t-3},Q_{2^t-4}, Q_{2^t-5}). \end{aligned}$$

The induction step is then stated in the following lemma. $\square$

Lemma 8.5

If $D_n^2\in (Q_n,Q_{n-1},Q_{n-2})\subseteq W_1$, then $D_{n-1}^2\in (Q_{n-1},Q_{n-2},Q_{n-3})\subseteq W_1$.

Proof

Write for some coefficients $d_0,d_1,d_2\in W_1$,

$$\begin{aligned} D_n^2=d_2Q_{n-2}+d_1Q_{n-1}+d_0Q_n. \end{aligned}$$

We would like to show that there exist $d'_0,d'_1,d'_2\in W_1$, such that

$$\begin{aligned} D_{n-1}^2=d'_2Q_{n-3}+d'_1Q_{n-2}+d'_0Q_{n-1}. \end{aligned}$$

By Lemma 8.3, the induction hypothesis and the recursion for $Q_n$ analogous to (3.4), we have

$$\begin{aligned} D_{n-1}^2&=D_n^2+q_i^2Q_{n-1}^2=d_2Q_{n-2}+(d_1+q_i^2Q_{n-1})Q_{n-1}+d_0Q_n\\&=d_0w_3Q_{n-3}+(d_0w_2+d_2)Q_{n-2}+(d_1+q_i^2Q_{n-1}+w_1d_0)Q_{n-1} \end{aligned}$$

which tells us the coefficients $d_i'$. $\square$

8.2 The ascended square

Similarly, set $p=2^{t-1}-1$ and $j=n-p=n-2^{t-1}+1$. Recall that the $r_j$ are defined by the recursion

$$\begin{aligned} r_{j+1}=w_2r_j+w_3^2r_{j-2}. \end{aligned}$$

The $A_n$’s also satisfy a recursion:

Lemma 8.6

The $A_n$ satisfy the following recursion in $W_1$:

$$\begin{aligned} A_{n+1}=w_3A_n+r_jQ_n, \end{aligned}$$

with the usual notation $j=n-2^{t-1}+1$.

Proof

By definition (6.3),

$$\begin{aligned} A_n=r_{j-1}p_n+w_3r_{j-2}p_{n-1}+r_jp_{n-2}, \end{aligned}$$

Since $Q_{n}=w_1p_n+q_{n}$ (see Remark 5.3), the recursion (5.6) can be written as $p_{n+1}=Q_n+w_2p_{n-1}+w_3p_{n-2}$, and we have

$$\begin{aligned} A_{n+1}&=r_{j}p_{n+1}+w_3r_{j-1}p_{n}+r_{j+1}p_{n-1}\\&=r_j(Q_n+w_2p_{n-1}+w_3p_{n-2})+w_3r_{j-1}p_n+(w_2r_j+w_3^2r_{j-2})p_{n-1}\\&=w_3\underbrace{(r_{j-1}p_n+w_3r_{j-2}p_{n-1}+r_jp_{n-2})}_{A_n}+r_jQ_n \end{aligned}$$

$\square$

Proposition 8.7

For $2^{t-1}\le n<2^{t}-3$,

$$\begin{aligned} A_n^2\in (Q_n,Q_{n-1},Q_{n-2})\subseteq W_1. \end{aligned}$$

Proof

We prove this by induction on n. For $n=2^{t-1}$, the reduction of $A_{n}^2\in W_1$ to

$$\begin{aligned} \textrm{H}^*({\text {Gr}}_3(2^{t-1});{\mathbb {F}}_2)=W_1/(Q_{2^{t-1}},Q_{2^{t-1}-1}, Q_{2^{t-1}-2}) \end{aligned}$$

vanishes by the results of [4, Theorem 1.1.] and the same arguments as in Proposition 8.4. The induction step is contained in the following lemma. $\square$

Lemma 8.8

If $A_n^2\in (Q_n,Q_{n-1},Q_{n-2})\subseteq W_1$, then $A_{n+1}^2\in (Q_{n+1},Q_{n},Q_{n-1})\subseteq W_1$.

Proof

Assume that in $W_1$ we can write

$$\begin{aligned} A_n^2=a_2Q_{n-2}+a_1Q_{n-1}+a_0Q_n. \end{aligned}$$

Then we want to show that increasing n and j, there exist $a'_0,a'_1,a'_2$, such that

$$\begin{aligned} A_{n+1}^2=a'_2Q_{n-1}+a'_1Q_{n}+a'_0Q_{n+1}. \end{aligned}$$

By Lemma 8.6, $Q_{n+1}=w_1Q_{n}+w_2Q_{n-1}+w_3Q_{n-2}$ and the induction hypothesis:

$$\begin{aligned} A_{n+1}^2&=w_3^2A_n^2+(r_jQ_n)^2=w_3^2(a_2Q_{n-2}+a_1Q_{n-1}+a_0Q_n)+(r_jQ_n)^2\\&=w_3a_2(Q_{n+1}+w_1Q_n+w_2Q_{n-1})+w_3^2(a_1Q_{n-1}+a_0Q_n)+(r_jQ_n)^2\\&=(w_2w_3a_2+w_3^2a_1)Q_{n-1}+\big (r_j^2Q_n+w_3^2a_0+w_1w_3a_2\big )Q_n+(w_3a_2)Q_{n+1} \end{aligned}$$

which tell us the coefficients $a_i'$. $\square$

This concludes the proof of Proposition 8.1 and thus the proof of Theorem 1.1.

9 Discussion of the $k>3$ cases

In this final section, we want to outline some of the issues that arise when we go beyond the $k=3$ case. Some of these issues are well-known, but some haven’t been noticed because the module structure over the characteristic subring hasn’t been investigated much.

9.1 Ascending and descending relations

The technique of ascending and descending relations works rather generally, as we discussed in Sect. 4. However, starting from $k=4$, there are many further syzygies besides the ones obtained from Theorem 4.6. For now, it is not clear what to expect. As a first glance, we can use the Macaulay2 code in Appendix A to check the degrees of generators of the anomalous module K for $k=5$, starting with $n=10$:

n	Degrees	n	Degrees	n	Degrees	n	Degrees
10	11, 13	16	15	22	31, 39, 40, 41, 42, 45	28	31, 48, 51
11	14, 15, 16	17	20, 24	23	31, 40, 42, 42, 50	29	31, 48
12	15, 16, 19	18	25, 27, 29	24	31, 40, 42, 47, 55	30	31, 53
13	15, 16	19	30, 30, 31, 32	25	31, 40, 42	31	31, 54
14	15, 21	20	31, 33, 35, 35, 40	26	31, 43, 45	32	31
15	15, 22	21	31, 36, 38, 40, 40	27	31, 46, 48	33	36, 56

We make some observations:

• In the two cases $n=16$ and $n=32$, the module K is free of rank 1 on the generator described in Theorem 5.6 (which subsequently implies that $\textrm{H}^*(\widetilde{{\text {Gr}}}_5(2^t),{\mathbb {F}}_2)$ is a free C-module of rank 2 for $t=4$ and $t=5$).

• These generators provide generators for other values of n as predicted by the ascending and descending relations. Between $n=16,\ldots ,24$, the ascending generators live in the following degrees: $(15,20,25,\ldots ,55)$. The situation is similar as the one described for $k=3$: the ascended relation for $n=25$ in degree 60 is in the image of the Koszul boundary, and therefore represents 0, which is why it is not visible in this table. Similarly, we have descending generators for $n=32,31,\ldots ,18$ in degree 31. However, these generators describe only a small portion of all the generators of the anomalous module.

We can make a similar table for $k=6$, recording the degrees of the generators of K for $n=12$ to $n=21$:

n	Degrees	n	Degrees
12	14, 15, 16	17	21, 26, 28
13	15, 16	18	27, 28, 30, 32, 36
14	15, 16	19	31, 33, 34, 34, 36, 38, 38, 40, 42
15	15, 22	20	31, 38, 38, 38, 39, 40, 40, 40, 42, 42
16	15, 22	21	31, 40, 42, 42, 44, 44, 44, 45, 46, 46

The previous phenomenon of a single generator for the case $n=2^t$ seems to disappear beyond $k=5$. The number of generators seems to grow. Some stabilization patterns (both for varying n with fixed k and with varying k) are discernible, but the rules of the game seem unclear for now. Nevertheless, the prevalence of one generator in degree $2^t-1$ seems to persist and the picture supports Conjecture 5.8.

The ascending relations would move k steps each time. One family of such generators for $k=5$ is visible, starting with the degree 20 generator for $n=17$, another one for $k=6$ starting with degree 21 in $n=17$. But most of the degrees do not seem to follow easy patterns compatible with ascending and descending relations.

9.2 The kernel of the differential

For our results in the case $\widetilde{{\text {Gr}}}_3(n)$, one of the key steps was that the kernel of $d_1$ in the Koszul complex was a free $W_2$-module, cf. Proposition 6.3. For $k\ge 4$, it is no longer the case that $\ker (d_1)$ is a free $W_2$-module, but we can compute a resolution for $\ker (d_1)$ as $W_2$-module using the Macaulay2 code from Appendix A, simply by running the line (after specifying k and n):

Again, we can record a couple of observations:

• Computing this for a number of examples with $k=4,5,6$, suggests that in general $\ker (d_1)$ has a free resolution of length $k-2$.

• The ranks of the free modules in the resolution seem to be fairly complicated for $k>4$, but for $k=4$, most of the time, the resolution has the form $0\rightarrow W_2^{\oplus n}\rightarrow W_2^{\oplus (n+3)}\rightarrow \ker (d_1)\rightarrow 0$ for $n=1,2,3$.

It seems conceivable that the techniques of Sect. 6 could possibly be adapted (in the case $k=4$) to provide a general formula for the resolution of $\ker (d_1)$ in the Koszul complex, as a $W_2$-module. To get an idea of what we could possibly expect, we compute the degrees of generators for $\ker (d_1)$ using presentation kernel kosz(4,n).dd_1, for $n=17,\dots ,32$:

n	Degrees	n	Degrees
17	17, 29, 30, 31	25	29, 41, 46, 47, 49
18	21, 29, 31, 33, 34	26	29, 45, 47, 49, 50
19	25, 29, 33, 34, 35	27	29, 49, 49, 50, 51
20	29, 29, 33, 37, 38, 39	28	29, 49, 53, 54, 55
21	29, 33, 37, 37, 38, 39	29	29, 53, 54, 55
22	29, 37, 37, 39, 41, 42	30	29, 55, 57, 57
23	29, 37, 41, 42, 43	31	29, 58, 59, 61
24	29, 37, 45, 46, 47	32	29, 61, 62, 63

Compared to the previous table, here we consider $\ker (d_1)$ instead of K. We also record here the degrees of elements in the Koszul complex, where in the previous subsection, we considered the degrees of generators of K. These two things differ by a shift of 1, i.e., the degrees for K are the Koszul degrees minus 1, see the discussion in Sect. 5.

By Corollary 4.10, the descended relation for this stretch has degree 29, and that is prominently visible. By Corollary 4.13, the ascended relation for given n would have degree $(d-3)+4i$ for $d=16$ and $i=n-d$. The sequence starts with degree 17 for $n=17$, degree 21 for $n=18$, and so on. The stretch, however, ends prematurely at $n=25$, as there is no degree 53 generator for $\ker (d_1)$ in the case $n=26$.

However, another phenomenon is observable. The last three degrees of generators of $\ker (d_1)$ appearing in the above table are always degrees appearing in degree 2 of the Koszul complex, making it likely that these are coming from the image of $d_2$. But then there are some additional degrees not appearing from ascended/descended relations or the Koszul complex: degree 33 for $n=20$, one of the degree 37 relations for $n=21,\dots ,24$, degree 41 for $n=25$, degree 45 for $n=26$, degree 49 for $n=27,28$. Currently there is no explanation for the appearance of these relations.

9.3 The presentation of K

After discussing the presentation or the resolution of $\ker (d_1)$ in the Koszul complex, we now come to the presentation of K as a C-module for the case $k=4$. The following table collects the degrees of the generators of K for $\widetilde{{\text {Gr}}}_4(n)$ with $n=17,\dots ,28$.

n	Degrees	n	Degrees	n	Degrees
17	17	23	29, 37	29	29
18	21, 29	24	29, 37	30	29
19	25, 29	25	29, 41	31	29
20	29, 29, 33	26	29, 45	32	29
21	29, 33, 37	27	29, 49
22	29, 37, 37	28	29, 49

Again, we can make some observations:

• The generators whose degree we identified as appearing in the degree 2 part of the Koszul complex have vanished. This supports the previously formulated assumption that these generators of $\ker (d_1)$ are also already in the image of $d_2$.

• Contrary to the case $k=3$, not all relations are ascended or descended from the relations $q_{2^t-3}=0$. There is an ascending relation between $n=17,\ldots ,22$ and the descending relation persists between $n=18,\ldots ,32$. There is a new relation appearing between $n=20,\ldots ,28$, which also follows an ascending pattern, but this pattern is broken; sometimes the relation stays in the same degree, possibly due to the vanishing of some coefficients (to compare with $k=3$, cf. Remark 6.4).

We also include one more experiment concerning the degrees of the relations in the presentation of K. We check degrees relations prune K where K has been constructed as anomalous module from the Koszul complex, using the code from Appendix A. The following table collects the degrees of relations in the presentation for K, for $\widetilde{{\text {Gr}}}_4(n)$ with $n=17,\dots ,28$.

n	Degrees	n	Degrees
17	–	23	43, 44, 45
18	32, 33, 35	24	43, 44, 45
19	35, 36, 37	25	45, 47, 48
20	35, 36, 37, 41, 45, 45	26	48, 49, 51
21	39, 40, 41, 41, 45, 49	27	51, 52, 53
22	40, 41, 43, 45, 45, 53	28	51, 52, 53

To state the observation here, we note that the Koszul complex for $k=4$ always has the form

$$\begin{aligned} 0\rightarrow W_2\rightarrow W_2^{\oplus 4}\rightarrow W_2^{\oplus 6}\xrightarrow {d_2} W_2^{\oplus 4}\xrightarrow {d_1} W_2. \end{aligned}$$

The middle degree always has six generators. The observation we record here is that three of those appeared in the presentation of $\ker (d_1)$ before, and the other three appear now in the above table, as the first three degrees.

As a final observation, checking resolution prune HH_1 kosz(4,n) suggests that it is possible to get a fairly reasonably-looking and small free resolution of K as a $W_2$-module by modifying the Koszul complex with the short free resolution of $\ker (d_1)$.

The study of the presentation of K as C-module for $\widetilde{{\text {Gr}}}_4(n)$ will be subject of future study.

9.4 Nontrivial Ext groups

We now come to one of the bigger problems when going beyond the $k=3$ case. What simplified the presentation of $\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n),{\mathbb {F}}_2)$ as a C-module significantly, was the triviality of the Ext-group as discussed in Proposition 7.1. This is no longer true for $k\ge 4$, and we will discuss a couple of examples where the Ext-group is nontrivial below, making again use of the Macaulay2-code from Appendix A.

Above, we made an observation about getting a resolution of K as a $W_2$-module from a modification of the Koszul complex by the free resolution of $\ker (d_1)$. This could be a more conceptual way to determine the Ext-group ${\text {Ext}}_C^1(K,C)$ for $\widetilde{{\text {Gr}}}_4(n)$ generally. But even with that, it remains a significant challenge to actually determine the class of the extension

as an element in ${\text {Ext}}_C^1(K,C)$ (or even the triviality or nontriviality of this element). We also hope to return to this question in future investigations. Lifts of generators and relations of K to integral cohomology could potentially prove helpful.

In the following, we list the examples of non-trivial Ext-groups for $k=4,5,6$ and small n. Here, “small” is essentially determined by patience vs running time of the Macaulay2-computation. More computational power or patience can easily extend the list.

• For $k=4$ and $n\le 36$, the following examples have non-trivial Ext-group: $n=18$ of rank 1, $n=24$ of rank 2, $n=25$ of rank 1, $n=34$ of rank 1, $n=35$ of rank 2, $n=36$ of rank 4.

• For $k=5$ and $n\le 21$, the following examples have nontrivial Ext-group: $n=13$ of rank 1, $n=14$ of rank 1, $n=15$ of rank 1, $n=17$ of rank 3, and $n=18$ of rank 5.

• For $k=6$, and $n\le 18$, the following examples have nontrivial Ext-group: $n=12$ of rank 1, $n=13$ of rank 1, $n=14$ of rank 1, $n=15$ of rank 1, $n=16$ of rank 1, $n=17$ of rank 10, and $n=18$ of rank 26.

For examples that fall within the scope (k, n) listed above but have trivial Ext-group, i.e., are not mentioned in the above list, a presentation of $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ can be obtained using our Macaulay2-code: simply get a presentation of K as C-module, and then $\textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)\cong C\oplus K$ as C-module. Note, however, that even if the Ext-group is non-trivial, it could still be possible that the cohomology of $\widetilde{{\text {Gr}}}_k(n)$ splits as $C\oplus K$; for now, we cannot make any more definite statements on nontriviality of the Ext-class.

To conclude, we discuss what the Ext-group calculation by hand could look like in two specific cases:

Example 9.1

We consider the case $\widetilde{{\text {Gr}}}_4(18)$ in which there is a nontrivial Ext-group. The module $K=\ker w_1$ is generated by two elements $a_{20}$ and $a_{28}$ with three relations

$$\begin{aligned} w_2^4w_3a_{20}+w_3a_{28}, \qquad (w_2^6+w_3^4+w_2^4w_4)a_{20}+w_4a_{28}, \qquad w_2^5w_4a_{20}+(w_3^2+w_2w_4)a_{28} \end{aligned}$$

There are six relations between relations in degrees 35, 37, 38, 43, 45 and 46, where $C^{35}=0$ and all of the remaining degrees are above the top degree of C. In particular, the Ext-group is the quotient of the differential $d_0:C^{20}\times C^{28}\rightarrow C^{31}\times C^{32}\times C^{34}$ given by the above relations. Note that the ${\mathbb {F}}_2$-dimensions of $C^{31}$ and $C^{34}$ are one and the ${\mathbb {F}}_2$-dimension of $C^{32}$ is two, i.e., the target of $d_0$ has ${\mathbb {F}}_2$-dimension 4. Using the diffrank-function from the appendix, we can compute that the differential has rank 3, with a basis for the image given by

$$\begin{aligned} d_0(0,w_2^3w_3^6w_4)&=(0,w_2w_3^2w_4^6,0),\\ d_0(0,w_2^3w_3^2w_4^4)&=(0,w_2^2w_4^7,w_3^2w_4^7), \\ d_0(0,w_4^7)&=(w_3w_4^7,0,w_3^2w_4^7). \end{aligned}$$

We see that by adding suitable degree 28 elements, we can always achieve that the relations in degrees 31 and 32 are trivial. In such a normal form, the extension is determined by the relation in degree 34. For example, one representative of the non-trivial extension of K by C in this case is the C-module generated by $\alpha _0,\alpha _{20}$ and $\alpha _{28}$ subject to the relations

$$\begin{aligned} w_2^4w_3\alpha _{20}+w_3\alpha _{28}= & {} (w_2^6+w_3^4+w_2^4w_4)\alpha _{20}+w_4\alpha _{28}=0, w_2^5w_4\alpha _{20}+(w_3^2+w_2w_4)\alpha _{28}\\ {}= & {} w_3^2w_4^7\alpha _0. \end{aligned}$$

Example 9.2

We consider the case $\widetilde{{\text {Gr}}}_6(12)$ with a non-trivial Ext-group. The module $K=\ker w_1$ is generated by three elements $a_{14}$, $a_{15}$ and $a_{16}$ with six relations

$$\begin{aligned}{} & {} w_3a_{14}, \quad w_5a_{14}+w_3a_{16}, \quad w_2^2a_{15}+w_3a_{16}, \\{} & {} \quad (w_2w_4+w_6)a_{14}+(w_2w_3+w_5)a_{15}+w_4a_{16}, \quad w_2^2a_{16}, \quad w_3^2a_{15}+(w_2w_3+w_5)a_{16}. \end{aligned}$$

There are 13 relations between relations in degrees between 21 and 27. Of these, only the two relations

$$\begin{aligned} w_2^2R_{17}, \qquad w_5R_{17}+w_3(R_{19,1}+R_{19,2}) \end{aligned}$$

in degree 21 and 22 matter, all the others are above the top degree of C which is 22. The differential $d_1$ has rank 1, and the differential $d_0$ has rank 7, and the dimension of the space of 1-cocycles is 9. The Ext-group therefore is a 1-dimensional ${\mathbb {F}}_2$-vector space.

Appendices

Computing Koszul resolutions, presentations and Ext-groups with Macaulay2

In this appendix, we include some Macaulay2 code that allows to compute Koszul complexes and presentations for the anomalous module K as well as the relevant Ext-groups for the oriented Grassmannian computations. We briefly indicate what the code is doing, how it is used and how to compute one of the examples discussed in Sect. 9.

We start off with a couple of lines containing the preliminary definitions of Giambelli determinants. The function giambrow produces the rows of the matrix $Q_j$ in (3.1) starting with a number of zeroes zs and the list of Stiefel–Whitney classes ws. Then giambmx puts together the matrix, and giambdet returns the relevant Giambelli determinant.

Next, we have a couple lines to construct the Koszul complex for the ideal $(q_{n-k+1},\dots ,q_n)$ in $W_2$. The function q(k,j) encodes the recursive definition of $q_j$ in $W_2={\mathbb {F}}_2[w_2,\dots ,w_k]$ from (3.4), and then kosz constructs the Koszul complex (after turning the $q_i$ into a matrix to be used by the Macaulay2 function constructing the Koszul complex). Note that kosz(k,l) constructs the Koszul complex relevant for $\widetilde{{\text {Gr}}}(k,k+l)$.

After this, the Koszul homology can be accessed. As we discussed in Sect. 5, the characteristic subring and the anomalous module appear as 0th and 1st Koszul homology, respectively. Note, however, that HH_i cplx would return the i-th homology of the complex as a $W_2$-module. The following lines then do some conversion: charsubring takes the presentation of HH_0 cplx as a $W_2$-module and uses it to actually construct C as a quotient ring of $W_2$. The function anomalous converts the description of HH_1 cplx as $W_2$-module to a description as C-module. Using prune everywhere helps cut down the complexity of the resulting presentations to human-readable size and form.

Having C and K, it is now easy to compute the Ext-group (or its rank) as follows. It is important to note that would compute a graded Ext-group for K and C as graded modules over the graded ring C (with the grading coming from the grading of $W_2$ where $w_i$ has degree i). As explained in Sect. 5, K is actually the shift of the first homology of the Koszul complex by one. The command takes that into account, actually computing a basis of the Ext-group that classifies degree 0 extensions of C by a shifted copy of K.

Finally, some mystery code to compute information pertaining to the rank of the differential of the Koszul complex in a specified degree:

Basics on (graded) Ext-groups

In the following section, we recall some basics on Ext-groups and how they relate to extensions. This is to support our discussion in Sect. 7 (where we show triviality of Ext-groups for $k=3$) and Sect. 9 (where we exhibit examples of nontrivial Ext-groups in some $k>3$ cases). For our application to the cohomology of oriented Grassmannians we are actually interested in Ext-groups and extensions for graded modules over the graded ring C. A discussion of some of the relevant graded homological algebra can be found e.g. in the rational homotopy book by Félix, Halperin and Thomas [5, Chapter 20]; for the situation without grading, one of the standard references is [20].

Fix a ${\mathbb {Z}}$-graded ring R, for our purposes we can assume R commutative. Recall that for two graded R-modules A and B, the Ext-groups $\textrm{Ext}^i_R(A,B)=\textrm{RHom}^i_R(A,B)$ can be computed as the cohomology groups of the complex $\textrm{Hom}_R(P_\bullet ,B)$ where $P_\bullet \rightarrow A$ is a chosen projective resolution of A (in the category of graded R-modules). Graded free resolutions of graded modules exist and behave much like ordinary free resolutions of modules over rings. Since $P_\bullet$ is a graded resolution and B is a graded module, $\textrm{Hom}_R(P_\bullet ,B)$ is a complex of graded modules, and the Ext-groups $\textrm{Ext}^i_R(A,B)$ therefore inherit a grading.

Remark B.1

For a graded R-module K, the start of a projective graded resolution looks like

$$\begin{aligned} \cdots \rightarrow P_2\rightarrow P_1\rightarrow P_0\rightarrow K\rightarrow 0. \end{aligned}$$

We can choose $P_0$ to be the free graded R-module on a chosen set of homogeneous R-generators of K, with $P_0\rightarrow K$ mapping the elements corresponding to the generators to the respective generators in K. Note that the summand of $P_0$ corresponding to a degree d generator x of K is $R[-d]$, so that mapping $1\in R[-d]_d$ to x is a degree 0 homomorphism of graded modules. Similarly, we can then choose $P_1$ to be the free graded R-module on a chosen set of homogeneous R-relations between the generators, with the morphism $P_1\rightarrow P_0$ mapping the generator corresponding to a relation in K to “itself”, written out in terms of the generators of $P_0$ (which correspond to the generators of K). Again, the summand corresponding to a relation of degree d has to be shifted appropriately. Then we choose $P_2$ to be the free R-module on relations between relations, and so on. Given the resolution, we can compute $\textrm{Ext}^1_R(K,C)$ as the first cohomology of the complex

$$\begin{aligned} 0\rightarrow \textrm{Hom}_R(P_0,C)\rightarrow \textrm{Hom}_R(P_1,C)\rightarrow \textrm{Hom}_R(P_2,C)\rightarrow \cdots \end{aligned}$$

The differentials for this complex are induced by composition $P_{i+1}\rightarrow P_i\rightarrow C$.

In terms of the above description of a resolution in terms of generators and (higher) relations of K, a class in $\textrm{Ext}^1(K,C)$ is described by a choice of homogeneous elements $r_1,\dots ,r_m$ of C corresponding to the relations in K. The cycle condition translates into the requirement that these elements satisfy the “relations between relations” in K. The Ext-class is a coboundary if there is a choice of homogeneous elements $g_1,\dots ,g_n$ of C corresponding to the generators of K, such that $r_1,\dots ,r_m$ are actually the relations of K written in terms of the $g_1,\dots ,g_n$.

As mentioned above, the Ext-group $\textrm{Ext}^1(K,C)$ inherits a grading. We have that $P_1\cong \bigoplus _{i=1,\dots ,r} R[-d_i]$ is a direct sum of shifted copies of R, one for each homogeneous R-relation in a presentation of K. The summand corresponding to a relation of degree $d_i$ is shifted so that it starts in degree $d_i$. An element in $\textrm{Ext}^1(K,C)$, represented by a homomorphism $P_1\rightarrow C$ is of degree 0 in the Ext-group, if the representing homomorphism is of degree 0, i.e., it maps a generator of $P_1$ corresponding to a relation of degree i to a degree i element of C. Shifting of K and C respectively has the effect of shifting the grading on the Ext-group, i.e.,

$$\begin{aligned} \textrm{Ext}^1(K[-1],C)\cong \textrm{Ext}^1(K,C)[1]\cong \textrm{Ext}^1(K,C[1]). \end{aligned}$$

The degree 0 elements of each of the above groups are represented by degree 1 maps $P_1\rightarrow C$.

We also briefly recall how $\textrm{Ext}^1(A,B)$ classifies equivalence classes of extensions

$$\begin{aligned} 0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0 \end{aligned}$$

of R-modules. In the ungraded setting, the class $[E]\in \textrm{Ext}^1(A,B)$ associated to the extension is given as the image of $\textrm{id}_A$ under the boundary map $\partial :\textrm{Hom}_R(A,A)\rightarrow \textrm{Ext}^1(A,B)$ in the long exact Ext-group sequence associated to the given extension.

In the graded setting, we want to classify extensions $0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0$ of graded R-modules where the maps in the extension are degree 0. As in the ungraded setting, an extension produces a long exact sequence of Ext-groups, and the image of $\textrm{id}_A$ under the boundary map produces a degree 0 element in $\textrm{Ext}^1(A,B)$. This induces a bijection between equivalence classes of graded extensions and degree 0 elements in $\textrm{Ext}^1(A,B)$.

Remark B.2

The boundary map can be computed as usual in the exact sequence of complexes

$$\begin{aligned} 0\rightarrow \textrm{Hom}_R(P_\bullet ,B)\rightarrow \textrm{Hom}_R(P_\bullet ,E)\rightarrow \textrm{Hom}_R(P_\bullet ,A)\rightarrow 0, \end{aligned}$$

where $P_\bullet \rightarrow A$ is a graded free resolution. The class of $\textrm{id}_A$ in $\textrm{Hom}_R(A,A)=\textrm{Ext}^0_R(A,A)$ is represented by the map $P_0\rightarrow A$ in the projective resolution of A. Lift this to $\textrm{Hom}_R(P_0,E)$ by lifting the generators of A to E (along the degree 0 map $E\rightarrow A$). Apply the boundary map $\textrm{Hom}_R(P_0,E)\rightarrow \textrm{Hom}_R(P_1,E)$ by writing out the relations in the presentation of A in terms of the lifts of generators to E. By construction, the composition $P_1\rightarrow E\rightarrow A$ will be 0, so that the morphism $P_1\rightarrow E$ is in the image of $\textrm{Hom}_R(P_1,B)\rightarrow \textrm{Hom}_R(P_1,E)$. The resulting 1-cochain represents $[E]\in \textrm{Ext}^1(A,B)$, and it is represented by a degree 0 homomorphism $P_1\rightarrow B$. In particular, the Ext-class can be computed explicitly from the R-module structure of E and an R-module presentation of A.

From the class [E] in the degree 0 part of $\textrm{Ext}^1(A,B)$, we can indeed completely recover the extension of A by B. Starting from the extension $0\rightarrow M\rightarrow P_0\rightarrow A\rightarrow 0$ arising from a projective resolution of A, we obtain an exact sequence

$$\begin{aligned} \textrm{Hom}_R(P_0,B)\rightarrow \textrm{Hom}_R(M,B)\rightarrow \textrm{Ext}^1_R(A,B)\rightarrow 0 \end{aligned}$$

by applying $\textrm{Ext}^\bullet _R(-,B)$ (and noting that $P_0$ is projective). We choose a preimage $e:M\rightarrow B$ of $[E]\in \textrm{Ext}^1_R(A,B)$ and obtain an extension

$$\begin{aligned} 0\rightarrow B\rightarrow P_0\cup _M B\rightarrow A\rightarrow 0 \end{aligned}$$

by pushout of $M\rightarrow P_0$ along $e:M\rightarrow B$. Since we started with a degree 0 element in $\textrm{Ext}^1(A,B)$, the morphism $e:M\rightarrow B$ will have degree 0, and so will the maps in the extension constructed.

Remark B.3

In the concrete situation of the cohomology rings of oriented Grassmannians, we can get an explicit presentation for the cohomology ring $H\cong \textrm{H}^*(\widetilde{{\text {Gr}}}_k(n),{\mathbb {F}}_2)$ as a C-module from the Ext-class $[H]\in \textrm{Ext}^1_C(K,C)$. We again take the free graded resolutions starting with a presentation of K as C-module. This provides an injection $P_1/P_2=M\hookrightarrow P_0$, where M is the submodule of relations in $P_0$. The Ext-class [H] is represented by a 1-cocycle $e:P_1\rightarrow C$, where the cocycle property means that the 1-cocycle factors through a morphism $P_1/P_2\rightarrow C$. Then $H\cong P_0\cup _{P_1/P_2} C$. Spelling this out, we can present H as a C-module generated by 1 and the generators $g_1,\dots ,g_m$ of K, and for each relation R in K, we have a relation identifying the relation spelled out in terms of the $g_1,\dots ,g_m$ with the image of the corresponding relation element under the map $e:P_1\rightarrow C$. The fact that all of this is built in a graded setting basically means that we present H as graded C-module, with generators and relations of appropriate degrees as determined by a homogeneous presentation of K.

Remark B.4

The reason for focusing on graded Ext-groups and in particular their degree 0 part is that we are really only interested in graded degree 0 extensions for the description of the cohomology of $\widetilde{{\text {Gr}}}_3(n)$. We only care about extensions $0\rightarrow C\rightarrow H\rightarrow K\rightarrow 0$ where all maps have degree 0, because this is the situation of the Gysin sequence. We want to point out that in many of the examples in Sect. 9, the full graded Ext-group $\textrm{Ext}^1_C(K,C)$ is quite non-trivial while the degree 0 part is actually trivial. This means that generally there are extensions $0\rightarrow C\rightarrow H\rightarrow K\rightarrow 0$ where the maps $C\rightarrow H$ or $H\rightarrow K$ are of degree different from 0, but these have little relevance for the description of the cohomology of $\widetilde{{\text {Gr}}}_3(n)$.

Consequences for Betti numbers of oriented Grassmannians $\widetilde{{\text {Gr}}}_3(n)$

As indicated in Sect. 2, information on mod 2 Betti numbers of oriented Grassmannians is available in the literature, cf. [15]. However, the computations basically involve understanding kernel and cokernel of multiplication with $w_1$ on $\textrm{H}^*({\text {Gr}}_k(n);{\mathbb {F}}_2)$ and are therefore not easy to do. In this appendix, we sketch how our results on the $k=3$ case, more specifically the information on the presentation of K in Propositions 6.3 and 6.5, allow to prove significantly simpler closed formulas for Betti numbers of oriented Grassmannians $\widetilde{{\text {Gr}}}_3(n)$.

In the following, we will focus on computing the Betti numbers of the anomalous module K. We’ll outline at the end of the section how to obtain Betti numbers for $\widetilde{{\text {Gr}}}_3(n)$ from this. For a ${\mathbb {Z}}$-graded ${\mathbb {F}}_2$-vector space $M_*$ such that all $M_i$ are finite dimensional, we consider the Hilbert–Poincaré series

$$\begin{aligned} \textrm{HP}(M_*,T)=\sum _{i\in {\mathbb {Z}}}\dim _{{\mathbb {F}}_2}M_i\cdot T^i. \end{aligned}$$

The Hilbert–Poincaré series for the ring $W_2={\mathbb {F}}_2[w_2,w_3]$ is then

$$\begin{aligned} \textrm{HP}(W_2,T)=\frac{1}{(1-T^2)(1-T^3)}=1+T^2+T^3+T^4+T^5+2T^6+T^7+2T^8+2T^9+\cdots \end{aligned}$$

To compute the Hilbert–Poincaré series for the anomalous module K, we realize it as the homology of a complex of free $W_2$-modules, built from the Koszul complex for the sequence $(q_{n-2},q_{n-1},q_n)$ in $W_2$. The Koszul complex ${\mathcal {K}}_*$ has the form

$$\begin{aligned} 0\rightarrow W_2[-3n+3]\rightarrow W_2[-2n+3,-2n+2,-2n+1]\rightarrow W_2[-n+2,-n+1,-n]\rightarrow W_2\rightarrow 0, \end{aligned}$$

where we denote by $W_2[-m_1,\dots ,-m_j]$ the free graded $W_2$-module of rank j, where the i-th summand is shifted to start in degree $m_i$. From this complex ${\mathcal {K}}_*$, we can already compute the difference of Betti numbers of C and K by

$$\begin{aligned} \sum _{i=0}^k(-1)^i\textrm{HP}({\mathcal {K}}_i,T)=\textrm{HP}(C,T)-T\textrm{HP}(K,T). \end{aligned}$$

This follows, since the Hilbert–Poincaré series of the complex agrees with the Hilbert–Poincaré series of its homology, and we have $H_0({\mathcal {K}}_*)=C$ and $H_1({\mathcal {K}}_*)=K[-1]$ (with a degree shift), cf. Sect. 5.

To isolate the Hilbert–Poincaré series of K, we need to modify the Koszul complex by truncation: we cut off ${\mathcal {K}}_0=W_2$ and replace ${\mathcal {K}}_1=W_2[-n+2,-n+1,-n]$ by the kernel of $d_1:{\mathcal {K}}_1\rightarrow {\mathcal {K}}_0$. The resulting complex has $H_1=K[-1]$, with all other homology groups trivial, and it is still a complex of free $W_2$-modules, by Proposition 6.3. Consequently, we get a free resolution of K of the form

$$\begin{aligned} 0\rightarrow W_2[-3n+3]\rightarrow W_2[-2n+3,-2n+2,-2n+1]\rightarrow W_2[-\deg a_n-1,-\deg d_n-1]\rightarrow K[-1]\!\rightarrow \! 0. \end{aligned}$$

Here $a_n$ and $d_n$ are the ascended and descended generators, with the degrees as elements of $\ker w_1$. This necessitates a shift by 1 to get the correct degrees for the Koszul homology generators.

From the modified Koszul complex, resp. the free resolution of $K[-1]$ as a $W_2$-module, we can immediately read off the Hilbert–Poincaré series for $K[-1]$:

$$\begin{aligned} \textrm{HP}(K[-1],T)=\frac{T^{3n-3}-T^{2n-3}-T^{2n-2}-T^{2n-1}+T^{\deg a_n+1}+T^{\deg d_n+1}}{(1-T^2)(1-T^3)} \end{aligned}$$

(C.1)

where $\deg a_n=3n-2^{t}-1$ and $\deg d_n=2^t-4$.

Example C.1

For $\widetilde{{\text {Gr}}}_3(19)$, the resolution of the first Koszul homology as $W_2$-module has the form

$$\begin{aligned} 0\rightarrow W_2[-54]\rightarrow W_2[-35]\oplus W_2[-36]\oplus W_2[-37]\rightarrow W_2[-25]\oplus W_2[-29]\rightarrow K[-1]\rightarrow 0 \end{aligned}$$

The resulting Hilbert–Poincaré polynomial is

$$\begin{aligned} \textrm{HP}(K[-1],T)&=\frac{T^{54}-T^{35}-T^{36}-T^{37}+T^{25}+T^{29}}{(1-T^2)(1-T^3)}\\&=T^{25} + T^{27} + T^{28} + 2T^{29} + T^{30} + 3T^{31} + 2T^{32} + 3T^{33}\\&+ 3T^{34} + 3T^{35} + 2T^{36} + 3T^{37} + 2T^{38} + 2T^{39} + 2T^{40} \\&+ 2T^{41} + T^{42} + 2T^{43} + T^{44} + T^{45} + T^{46} + T^{47} + T^{49} \end{aligned}$$

This agrees with an explicit computation of Hilbert–Poincaré polynomial for $\ker w_1$, with the degrees shifted by 1.

Finally, to obtain the Hilbert–Poincaré series encoding the Betti numbers of $\widetilde{{\text {Gr}}}_3(n)$, we note that the sequence of Betti numbers of C is just a mirrored version of the one for K, suitably shifted. In our usual setting $2^{t-1}<n\le 2^t-4$, with $d=3n-9$ denoting the top non-zero degree of K (equal to the dimension of $\widetilde{{\text {Gr}}}_3(n)$), we get the Hilbert–Poincaré series

$$\begin{aligned} \begin{aligned} \textrm{HP}(C,T)&=T^d\textrm{HP}(K,1/T)=\\&= \frac{ T^{2^t-3}+T^{3n-2^t}-T^n-T^{n-1}-T^{n-2}+1}{(1-T^2)(1-T^3)}. \end{aligned} \end{aligned}$$

Consequently, the Betti numbers of $\widetilde{{\text {Gr}}}_3(n)$ for $2^{t-1}<n\le 2^t-4$ are

$$\begin{aligned} \begin{aligned}&\textrm{HP}(\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2),T)\\&\quad =\textrm{HP}(C,T)+\textrm{HP}(K,T)\\&\quad = \frac{1-(1+T^{n-2})(T^n+T^{n-1}+T^{n-2})+(1+T)(T^{3n-2^t-1}+T^{2^t-4})+T^{3n-4}}{(1-T^2)(1-T^3)} \end{aligned} \end{aligned}$$

In the end, we obtain a completely explicit closed-form expression for the Betti numbers of $\widetilde{{\text {Gr}}}_3(n)$ that requires only simply numerical input dependent on n and no computations related to Young diagrams or cohomology of Grassmannians.

Example C.2

For $\widetilde{{\text {Gr}}}_3(19)$, we get the Hilbert–Poincaré series $\textrm{HP}(\textrm{H}^*(\widetilde{{\text {Gr}}}_3(n);{\mathbb {F}}_2),T)$ as follows:

$$\begin{aligned} \frac{1-T^{17}-T^{18}-T^{19}+T^{24}+T^{25}+T^{28}+T^{29}-T^{34}-T^{35}-T^{36}+T^{53}}{(1-T^2)(1-T^3)}. \end{aligned}$$