A transcendental Hénon map with an oscillating wandering Short ${\mathbb {C}}^2$

Abstract

Short ${\mathbb {C}}^2$’s were constructed in [5] as attracting basins of a sequence of holomorphic automorphisms whose rate of attraction increases superexponentially. The goal of this paper is to show that such domains also arise naturally as autonomous attracting basins: we construct a transcendental Hénon map with an oscillating wandering Fatou component that is a Short ${\mathbb {C}}^2$. The superexponential rate of attraction is not obtained at single iterations, but along consecutive oscillations.

1 Introduction

In [5] Fornæss proved the existence of so-called Short ${\mathbb {C}}^k$’s. Such domains are increasing union of balls whose Kobayashi metric vanishes identically, but which allow for the existence of non-constant bounded plurisubharmonic functions, and are thus not equivalent to ${\mathbb {C}}^k$. In the construction by Fornæss the Short ${\mathbb {C}}^k$ arises as an attracting basin for a non-autonomous dynamical systems, given by compositions of a sequence of holomorphic automorphisms, see Proposition 3 below. We prove here that a Short ${\mathbb {C}}^k$ can also arise naturally as a Fatou component of a single holomorphic automorphism.

It is clear that we cannot work with the basin of an attracting fixed point: such domains are always biholomorphic to ${\mathbb {C}}^k$ [11, 12]. We note that the attracting basins of neutral or semi-neutral fixed points are often known to be biholomorphic to ${\mathbb {C}}^k$, see for example [13] for the semi-parabolic case, and [7, 14] for maps tangent to the identity. In contrast, in the recent paper [4] examples of attracting basins of neutral fixed points were constructed that are not biholomorphic to ${\mathbb {C}}^k$ but to ${\mathbb {C}} \times \mathbb ({\mathbb {C}}^\star )^{k-1}$. Whether the basin of attraction of a neutral fixed point can be a Short ${\mathbb {C}}^k$ is not known, but we consider it unlikely.

Instead we will prove that there exist holomorphic automorphisms with wandering Fatou components equivalent to a Short ${\mathbb {C}}^2$. It immediately follows that such maps give rise to infinitely many disjoint Short ${\mathbb {C}}^2$’s, giving an alternative construction to an observation from [2]. Recall that a Fatou component ${\mathcal {F}}_0$ of a map F is wandering if $F^k({\mathcal {F}}_0)\cap F^j({\mathcal {F}}_0)=\varnothing$ for all $k\ne j$. A wandering Fatou component ${\mathcal {F}}_0$ is oscillating if some subsequence $F^{k_n}$ has bounded orbits in ${\mathcal {F}}_0$, while a different subsequence has orbits converging to infinity.

The first construction of a holomorphic automorphism of ${\mathbb {C}}^2$ with a wandering Fatou component is due to Fornæss-Sibony [6], although the complex structure of the domain has not been studied in the literature. Recently Arosio–Benini–Fornæss–Peters [1] constructed a transcendental Hénon map, i.e. a holomorphic automorphism of ${\mathbb {C}}^2$ of the form $F(z,w)=(f(z)+aw,az)$ with $f:{\mathbb {C}}\rightarrow {\mathbb {C}}$ a transcendental function, which admits an oscillating wandering Fatou component biholomorphic to ${\mathbb {C}}^2$. In this paper we will modify the construction from [1] to obtain the following:

Theorem 1

There exist a transcendental Hénon map with an oscillating wandering Fatou component biholomorphic to a Short ${\mathbb {C}}^2$.

Remark 1.1

Our proof in fact guarantees that the constructed wandering Fatou component is biholomorphic to one of the Short ${\mathbb {C}}^2$’s constructed by Fornæss. Little has been written about the possible equivalence classes of Short ${\mathbb {C}}^k$’s, although it is clear from the results in [5] that there are at least countably many. Recall from the recent paper of Forstnerič and the second author [3] that there are in fact uncountably many equivalent classes of complex manifolds with vanishing Kobayashi pseudometric that can be written as an increasing union of balls; a more general notion sometimes taken as the definition of a Short ${\mathbb {C}}^k$.

We note that a transcendental Hénon map F has constant Jacobian determinant, thus the rate of contraction cannot increase, even as orbits escape to infinity. Using Runge approximation we recursively construct an oscillating orbit $P_n$ in such a way that the number of iterates of the consecutive oscillations increases superexponentially fast. This guarantees the rate of contraction to increase superexponentially fast when one considers the iterations from a point $P_{n_j}$ in one oscillation to a point $P_{n_{j+1}}$ in the next, allowing the construction of maps that are, after a suitable rescaling, arbitrarily close to the non-autonomous sequence of maps constructed by Fornæss in [5].

We construct a sequence of corresponding balls $B(P_{n_j}, \beta _{n_j})$, with $\beta _{n_j} \rightarrow 0$, each mapped by $F^{n_{j+1} - n_j}$ into the next ball $B(P_{n_{j+1}}, \beta _{n_{j+1}})$. The construction guarantees that the calibrated basin is a Short ${\mathbb {C}}^2$; see [10] and the appendix of this paper for a discussion of calibrated basins.

The calibrated basin is necessarily contained in the corresponding Fatou component ${\mathcal {F}}_0$. To prove that the calibrated basin is in fact equal to the Fatou component, we use a method introduced in [1]: we construct a non-positive plurisubharmonic function on ${\mathcal {F}}_0$ that is strictly negative at some point in the calibrated basin, and constantly equal to 0 on its complement. It follows that the Fatou component cannot be larger than the calibrated basin. In the appendix we show how the plurisubharmonic method can be applied to arbitrary calibrated basins, clarifying the main result from [10].

2 Preparatory results

If $(H_{n})_{n\ge 1}$ is a sequence of automorphisms of ${\mathbb {C}}^2$, then for all $0\le n\le m$ we write

$$\begin{aligned} H_{m,n}:=H_{m}\circ \dots \circ H_{n+1}. \end{aligned}$$

Notice that with these notations we have for all $n\ge 0$,

$$\begin{aligned} H_{n+1,n}=H_{n+1}, \quad H_{n,n}=\mathsf{id}. \end{aligned}$$

If for all $n\ge 1$ we have $H_{n}({\mathbb {B}})\subset {\mathbb {B}}$, where ${\mathbb {B}}$ represents the unit ball, then we define the basin of the sequence $(H_n)$ as the domain

$$\begin{aligned} \Omega _H:=\bigcup _{n\ge 0} H_{n,0}^{-1}({\mathbb {B}}). \end{aligned}$$

Lemma 2

To every finite family $(F_1, \dots , F_n)$ of holomorphic automorphisms of ${\mathbb {C}}^2$ satisfying $F_{j}({\mathbb {B}})\subset \subset {\mathbb {B}}$ for all $0\le j\le n$ we can associate $\varepsilon (F_1, \dots , F_n)>0$ such that the following holds:

Given any two sequences $(H_{n})_{n\ge 1}$ and $(G_{n})_{n\ge 1}$ of holomorphic automorphisms of ${\mathbb {C}}^2$ satisfying $H_{n}({\mathbb {B}})\subset \subset {\mathbb {B}}$ and $G_{n}({\mathbb {B}})\subset {\mathbb {B}}$ for all $n\ge 1$, and moreover satisfying

$$\begin{aligned} \Vert H_{n}-G_{n}\Vert _{{\overline{{\mathbb {B}}}}}\le \varepsilon (H_1, \dots , H_n),\quad \forall n\ge 1, \end{aligned}$$

the basins $\Omega _{G}$ and $\Omega _H$ are biholomorphically equivalent.

Proof

Let $(H_{n})_{n\ge 1}$ and $(G_{n})_{n\ge 1}$ be sequences as above. We will show how to choose the constants $(\varepsilon (H_1, \dots , H_n))_{n\ge 1}$ to obtain a biholomorphism between $\Omega _{G}$ and $\Omega _H$.

For all $n\ge 0$ write $U_n:=G_{n,0}^{-1}(\overline{{\mathbb {B}}})$, and $V_n:=H_{n,0}^{-1}(\overline{{\mathbb {B}}})$, and define

$$\begin{aligned} \Phi _n:=H_{n,0}^{-1}\circ G_{n,0}. \end{aligned}$$

Notice that $\Phi _n$ is a holomorphic automorphisms of ${\mathbb {C}}^2$ satisfying $\Phi _n(U_n)=V_n$. We have that

$$\begin{aligned} \Phi _{n+1}\circ \Phi _n^{-1}=H_{n,0}^{-1}\circ (H_{n+1}^{-1}\circ G_{n+1})\circ H_{n,0}. \end{aligned}$$

Thus

$$\begin{aligned} \Vert \Phi _{n+1}-\Phi _{n}\Vert _{ U_n}&=\Vert \Phi _{n+1}\circ \Phi _n^{-1}-\mathsf{id}\Vert _{V_n}\le M_{n+1}\Vert H_{n+1}^{-1}\circ G_{n+1}-\mathsf{id}\Vert _{{\overline{{\mathbb {B}}}}}\\&\le M_{n+1}N_{n+1}\Vert H_{n+1}-G_{n+1}\Vert _{{\overline{{\mathbb {B}}}}} \le M_{n+1}N_{n+1}\varepsilon (H_1, \dots , H_{n+1}), \end{aligned}$$

where $M_{n+1}>0$ is the Lipschitz constant of $H_{n,0}^{-1}$ on $H^{-1}_{n+1}({\overline{{\mathbb {B}}}})$ and $N_{n+1}>0$ is the Lipschitz constant of $H_{n+1}^{-1}$ on ${\overline{{\mathbb {B}}}}$. Hence if for all $n\ge 0$ we choose

$$\begin{aligned} \varepsilon (H_1, \dots , H_{n+1})\le \frac{1}{2^{n+1}M_{n+1}N_{n+1}}, \end{aligned}$$

the sequence $(\Phi _n)$ converges to a holomorphic map $\Phi$ on $\Omega _G$.

Recall that there exist ${\tilde{\delta }}>0$ such that for every holomorphic map $F:{\overline{{\mathbb {B}}}}\rightarrow {\mathbb {C}}^2$ which satisfies $\Vert F-\mathsf{id}\Vert _{{\overline{{\mathbb {B}}}}}\le {{\tilde{\delta }}}$ we have that the differential $d_0F$ is nonsingular. By Hurwitz’s theorem the map $\Phi$ is either injective or degenerate. Assuming that

$$\begin{aligned} \varepsilon (H_1, \dots , H_{n+1})\le \frac{{{\tilde{\delta }}}}{2^{n+1} M_{n+1}N_{n+1}} \end{aligned}$$

we have, since $\Phi _0:= \mathsf{id}$,

$$\begin{aligned} \Vert \Phi -\mathsf{id}\Vert _{{\overline{{\mathbb {B}}}}}\le \sum _{k=0}^{\infty }\Vert \Phi _{k+1}-\Phi _k\Vert _{{\overline{{\mathbb {B}}}}}\le {{\tilde{\delta }}}, \end{aligned}$$

and thus $\Phi$ is injective.

To prove surjectivity, observe that since for every $n\ge 1$ we have $H_{n}({\mathbb {B}})\subset \subset {\mathbb {B}}$ it follows that $V_{n-1}\subset \mathrm{int}( V_{n})$ hence there exist $\delta _n>0$ such that for every injective holomorphic map $F:\overline{{\mathbb {B}}}\rightarrow {\mathbb {C}}^2$ which satisfies $\Vert F-H_{n,0}^{-1}\Vert _{{\overline{{\mathbb {B}}}}}\le \delta _n$ it follows that $V_{n-1}\subset F({\overline{{\mathbb {B}}}})$. Clearly the choice of $\delta _n$ depends only on $H_1,\ldots , H_{n}$. Let us assume that

$$\begin{aligned} \varepsilon (H_1, \dots , H_{n+1})\le \frac{\min _{1\le j\le n}\delta _j}{2^{n+1} M_{n+1}N_{n+1}}. \end{aligned}$$

We have

$$\begin{aligned} \Vert \Phi -\Phi _n\Vert _{U_n}\le \sum _{k=n}^{\infty }\Vert \Phi _{k+1}-\Phi _k\Vert _{U_n}\le \delta _n \end{aligned}$$

(1)

or equivalently

$$\begin{aligned} \Vert \Phi \circ G_{n,0}^{-1}-H_{n,0}^{-1}\Vert _{{\overline{{\mathbb {B}}}}}\le \delta _n \end{aligned}$$

which implies $V_{n-1}\subset \Phi (U_n)$. Since this holds for every n it follows that $\Phi :\Omega _G\rightarrow \Omega _H$ is surjective.

$\square$

The following result is slightly modified version of [5, Theorem 1.4], we sketch the proof for the reader’s convenience.

Proposition 3

Let $(d_k)$ be a sequence of integers with $d_k\ge 2$, and let us define $H_n(z,w)=((\frac{z}{2})^{d_n}+2^{-d_n\cdots d_1}w,2^{-d_n\cdots d_1}z)$. Then $\Omega _H:=\bigcup _{k\ge 0} H_{k,0}^{-1}({\mathbb {B}})$ is a Short ${\mathbb {C}}^2$.

Proof

We prove the following:

• (1) $\Omega _H$ is non-empty, open, connected set in ${\mathbb {C}}^2$,

• (2) $\Omega _H$ is the increasing union of its subdomains $\Omega _j:=H_{j,0}^{-1}({\mathbb {B}})$ which are biholomorphic to the unit ball ${\mathbb {B}}$,

• (3) the infinitesimal Kobayashi metric of $\Omega _H$ vanishes identically,

• (4) there is a non-constant plurisubharmonic function $\psi$ on ${\mathbb {C}}^2$ satisfying $\Omega _H=\{\psi <0\}$.

First observe that $H_k$ is fixing the origin and $H_k({\mathbb {B}})\subset \subset {\mathbb {B}}$ for every $k\ge 1$. Since $H_k$ are holomorphic automorphisms of ${\mathbb {C}}^2$ we immediately obtain (1) and (2).

For (3) let us fix $(p,\zeta )$, where $p\in \Omega _H$ and $\zeta \in T_p\Omega _H$. Pick $R>0$. Since $p\in \Omega _H$ we have $p_k:=H_{k,0}(p)\rightarrow 0$. Next we write $\zeta _k:= d_pH_{k,0}(\zeta )$. Since $(H_{k,0})_k$ converge on $\Omega _H$ to a constant map it follows that $\zeta _k\rightarrow 0$. Now we can find $k>0$ such that the map $\eta _k(w):=p_k+wR\zeta _k$ satisfies $\eta _k({\mathbb {D}})\subset {\mathbb {B}}$, where ${\mathbb {D}}\subset {\mathbb {C}}$ represents the unit disk. Finally we define $\eta :{\mathbb {D}}\rightarrow \Omega _H$ as $\eta (w):=H_{k,0}^{-1}\circ \zeta _k (w)$. It follows from the definition of $\eta$ that $\eta (0)=p$ and $\eta '(0)=d_{p_k}H^{-1}_{k,0}(R\zeta _n)=R\zeta$, hence (3) is proved.

It remains to show that also property (4) holds. Let us write $H_{k,0}=(h_1^k,h_2^k)$ and $\eta _k:=2^{-d_k\cdots d_1}$. We define $\varphi _k(z):=\max \{|h_1^k|,|h_2^k|,\eta _k\}$ and

$$\begin{aligned} \psi _k:=\frac{\log {\varphi _k}}{d_k\cdots d_1}. \end{aligned}$$

Claim 1: The functions $\psi _k$ converge on ${\mathbb {C}}^2$ to a plurisubharmonic function $\psi$.

We show first that $\varphi _{k+1}\le 2\varphi _k^{d_{k+1}}$ on ${\mathbb {C}}^2$. Assume that $\varphi _k\le 1$. Then

$$\begin{aligned} \varphi _{k+1}(z)&=\max \left\{ \left| \left( \frac{h^k_1}{2}\right) ^{d_{k+1}} +\eta _{k+1}h_2^{k}\right| ,\eta _{k+1}\left| h_1^k\right| ,\eta _{k+1}\right\} \\&\le \max \{\varphi _k^{d_{k+1}}+\eta _k^{d_{k+1}},\eta _k^{d_{k+1}}\}\\&\le 2\varphi _k^{d_{k+1}}. \end{aligned}$$

If $\varphi _k> 1$, then

$$\begin{aligned} \varphi _{k+1}(z)&=\max \left\{ \left| \left( \frac{h^k_1}{2}\right) ^{d_{k+1}} +\eta _{k+1}h_2^{k}\right| ,\eta _{k+1}\left| h_1^k\right| ,\eta _{k+1}\right\} \\&\le \max \{\varphi _k^{d_{k+1}}+\eta _k^{d_{k+1}}\varphi _k,\eta _k^{d_{k+1}}\varphi _k,\eta _k^{d_{k+1}}\}\\&\le \varphi _k^{d_{k+1}}+\varphi _k\\&\le 2\varphi _k^{d_{k+1}}. \end{aligned}$$

This way we obtain $\psi _{k+1}\le \psi _k+\frac{\log 2}{d_{k+1}\cdots d_{1}}$. Now define ${\tilde{\psi }}_k:=\psi _k+\sum _{j>k}\frac{\log 2}{d_j\cdots d_1}$ and observe that ${\tilde{\psi }}_{k+1}\le {\tilde{\psi }}_{k}$. The plurisubharmonic functions ${\tilde{\psi }}_k$ form a monotonically decreasing sequence, whose limit $\psi$ is therefore also plurisubharmonic. Since ${\tilde{\psi }}_k-\psi _k\rightarrow 0$, it follows that $\psi _k\rightarrow \psi .$

Claim 2: We have $\Omega _H=\{\psi <0\}$.

Let us assume that $\psi (z_0)<0$, then there exist $k>0$ and $s<0$ such that $\frac{\log \varphi _k(z_0)}{d_k\cdots d_1}<s<0$, hence $\varphi _k(z_0)<e^{s\cdot d_k\cdots d_1}$. From the definition of $\varphi _k$ it follows that $\Vert H_{k,0}(z_0)\Vert <2e^{s\cdot d_k\cdots d_1}$, hence $H_{k,0}(z_0)\rightarrow 0$ and therefore $z_0\in \Omega _H$.

Next we assume that $z_0\in \Omega _H$. Then there exist $k_0>0$ such that $H_{k,0}(z_0)\in {\mathbb {B}}$ for all $k>k_0$. But this implies that $\psi _k(z_0)<0$, hence $\psi (z_0)\le 0$. Since $H_{k,0}(0)=0$ for all k it follows that $\psi _k(0)=-\log 2$ for all k, hence $\psi (0)=-\log 2<0$. We have seen that $\psi \le 0$ on $\Omega _H$ and $\psi <0$ at some point in $\Omega _H$, therefore it follows from the maximum principle that $\psi <0$ on $\Omega _H$.

Claim 3: $\psi$ is not constant on $\Omega _H$.

Suppose that the contrary is true, i.e. $\psi |_{\Omega _H}\equiv s <0$. First observe that $\Vert H_{k,0}(8,0)\Vert \rightarrow \infty$, hence $\Omega _H$ is not all ${\mathbb {C}}^2$. Pick $R>0$ such that ${\mathbb {B}}(0,R)\subset \Omega _H$ and there exist a point $p\in \partial {\mathbb {B}}(0,R)\cap \partial \Omega _H$. Since $\Omega _H=\{\psi <0\}$ it follows that $\psi (p)\ge 0$. By subaveraging property of plurisubharmonic functions, $\psi (p)$ is bounded above by the average on any small ball ${\mathbb {B}}(p,\varepsilon )$. If $\varepsilon$ small enough then $\psi =s<0$ on more than one third of the ball ${\mathbb {B}}(p,\varepsilon )$, and since $\psi$ is upper semicontinuous, this leads to a contradiction. $\square$

3 Proof of Theorem 1

The proof of Theorem 1 is based on the iterative construction contained in the following proposition, whose proof is postponed to Sect. 4.

Proposition 4

Let $a=\frac{1}{2}$. There exists a sequence of automorphims of ${\mathbb {C}}^2$

$$\begin{aligned} F_k(z,w)=(f_k(z)+aw,az),\qquad f_k(z)=z+O(z^2),\qquad k=0,1,2,\ldots \end{aligned}$$

a sequence of points $P_n=(z_n,w_n)$ where $n=0,1,2,\ldots$, sequences $(\beta _n)_{n\ge 0}\rightarrow 0$, $(R_k)_{k\ge 0}\nearrow \infty$, strictly increasing sequences of integers $(n_k)_{k\ge 0}$ and $(N_k)_{k\ge 0}$ satisfying $n_0=0$ and $N_{k-1}\le n_k\le N_k$, and a sequence of odd integers $(d_k)_{k\ge 1}$, $d_k\ge 2$ such that the following properties are satisfied:

• (a) $\Vert F_{k}-F_{k-1}\Vert _{D(0,R_{k-1})\times {\mathbb {C}}}\le 2^{-k}$ for all $k\ge 1$,

• (b) $F_{k}(P_n)=P_{n+1}$ for all $0\le n< N_k$,

• (c) $\Vert P_{n_k}\Vert \le \frac{1}{k}$ for all $k\ge 1$,

• (d) $|z_{N_{k}}|> R_{k}+3$ and $|z_n|+\beta _n< R_k$ for every $0\le n<N_{k}$,

• (e) for all $k\ge 1$, $\beta _n=\frac{1}{k}$ if $N_{k-1}<n< n_{k}$, and $\beta _n=\frac{1}{k+1}$ if $n_k< n\le N_k,$ and $\beta _{n_k}< \frac{1}{k+1}$ is of the form $\beta _{n_k}=a^{2q_k}$, for some integer $q_k$,

• (f) $k|\log {\beta _{n_k}}|\le d_k\cdots d_1$ for all $k\ge 1$,

• (g) for all $0\le s\le k$,

  $$\begin{aligned} F_{k}^j({\mathbb {B}}(P_{n_s},\beta _{n_s}))\subset \subset {\mathbb {B}}(P_{n_s+j},\beta _{n_s+j}), \quad \forall \,1\le j\le N_{k}-n_s, \end{aligned}$$

• (h) for all $1\le s\le k$,

  $$\begin{aligned} \Vert \Phi _{n_{s}}^{-1}\circ F_k^{n_{s}-n_{s-1}}\circ \Phi _{n_{s-1}}-H_{s}\Vert _{\overline{{\mathbb {B}}}}<\min \{\varepsilon (H_1,\dots , H_s),a^{d_s\cdots d_1}\}, \end{aligned}$$

  where $\Phi _n(z,w):=P_n+(z\beta _n, w\beta _n)$, $H_j(z,w)=((az)^{d_j}+a^{d_j\cdots d_1}w,a^{d_j\cdots d_1}z)$.

Using this proposition we can now prove our main theorem.

Proof of Theorem 1

Let $(F_k)$ be a sequence of automorphisms of ${\mathbb {C}}^2$ satisfying conditions $(a)-(h)$ of Proposition 4. The sequence $(F_k)$ converges uniformly on compact subsets to a transcendental Hénon map $F\in \mathrm{Aut}({\mathbb {C}}^2)$ with a saddle fixed point at the origin and with an unbounded orbit $(P_n)$, a sequence $\beta _n\rightarrow 0$, a strictly increasing sequences of integers $(n_k)$ and a sequence of odd integers $(d_k)$, $d_k\ge 2$ such that the following properties are satisfied:

• (i) $P_{n_k}\rightarrow 0$,

• (ii) for all $k\ge 0$,

  $$\begin{aligned} F^j({\mathbb {B}}(P_{n_k},\beta _{n_k}))\subset {\mathbb {B}}(P_{n_k+j},\beta _{n_k+j}),\quad \forall \, j\ge 0. \end{aligned}$$

  (2)

• (iii) $\lim _{k\rightarrow \infty }\frac{\log {\beta _{n_k}}}{d_k\cdots d_1}=0$,

• (iv) if for all $k\ge 1$ we write

  $$\begin{aligned} G_{k}:=\Phi _{n_{k}}^{-1}\circ F^{n_{k}-n_{k-1}}\circ \Phi _{n_{k-1}}\in \mathrm{Aut}({\mathbb {C}}^2), \end{aligned}$$

  then by combining conditions (g) and (h) it follows that $G_{k}({\mathbb {B}})\subset {\mathbb {B}}$ for all k, and

  $$\begin{aligned} \Vert G_{k}-H_{k}\Vert _{\overline{{\mathbb {B}}}}\le \min \{\varepsilon (H_1,\dots , H_k),a^{d_k\cdots d_1}\},\quad \forall \,k\ge 1, \end{aligned}$$

  (3)

  where $H_k$ represents the holomorphic automorphism

  $$\begin{aligned} H_{k}(z,w):=((az)^{d_k}+a^{d_k\cdots d_1}w, a^{d_k\cdots d_1}z). \end{aligned}$$

It follows from Lemma 3 that $\Omega _H:=\bigcup _{k\ge 0} H_{k,0}^{-1}({\mathbb {B}})$ is a Short ${\mathbb {C}}^2$. By Lemma 2 the basin $\Omega _G:=\bigcup _{k\ge 0} G_{k,0}^{-1}({\mathbb {B}})$ is biholomorphic to $\Omega _H$. Define

$$\begin{aligned} \Omega _F:=\bigcup _{k=0}^{\infty } F^{-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k})). \end{aligned}$$

Notice that $\Omega _F=\Phi _{0}(\Omega _G),$ and hence $\Omega _F$ is a Short ${\mathbb {C}}^k$. We now show that $\Omega _F$ is contained in an oscillating Fatou component.

First of all, the set $\Omega _F$ is contained in the Fatou set of F. Indeed, by the invariance of the Fatou set it is enough to prove that for all $k\ge 0$, the ball ${\mathbb {B}}(n_k,\beta _{n_k})$ is contained in the Fatou set. But this follows from (2) since the euclidean diameter of $F^j({\mathbb {B}}(P_{n_k},\beta _{n_k}))$ is bounded for $j\ge 0$ (in fact, it goes to 0 as $j\rightarrow \infty$). For all $j\ge 0$ let ${\mathcal {F}}_{n_j}$ be the Fatou component containing ${\mathbb {B}}(P_{n_j},\beta _{n_j})$. Since $\Omega _F$ is connected, it is contained in the Fatou component ${\mathcal {F}}_{0}$.

Since $\beta _n\rightarrow 0$, by (2) and by the identity principle it follows that all limit functions on each ${\mathcal {F}}_{n_j}$ are constants. We claim that for all $j\ge 0$, if $i>j$, then ${\mathcal {F}}_{n_i}\ne {\mathcal {F}}_{n_j}$, which implies that they are all oscillating wandering Fatou component. Assume by contradiction that ${\mathcal {F}}_{n_j}={\mathcal {F}}_{n_i}$, and set $k:=n_i-n_j$. Since the origin is a saddle point, there exists a neighborhood U of the origin that contains no periodic points of order less than or equal to k. Since the sequence $(P_n)$ oscillates, there exists a subsequence $(P_{m_\ell })$ of $(P_n)$ such that $P_{m_\ell }\rightarrow z \in U{\setminus }\{0\}.$ But then

$$\begin{aligned} F^{m_\ell -n_j}(P_{n_i})=F^{n_i-n_j}(P_{m_\ell })\rightarrow F^k(z)\ne z, \end{aligned}$$

which contradicts $F^{m_\ell -n_j}(P_{n_j})=P_{m_\ell }\rightarrow z$.

We complete the proof by showing that $\Omega _F={\mathcal {F}}_0$. Suppose by contradiction that $\Omega _F\ne {\mathcal {F}}_0$. For all $k\ge 1$, let us define the plurisubharmonic function $\psi _k$ as follows

$$\begin{aligned} \begin{aligned} \psi _k(z)&:=\frac{\log ({\max \{\Vert F^{n_k}(z)-P_{n_k}\Vert ,\beta _{n_k}\eta _k\}})}{d_k\cdots d_1}\\&=\frac{\log ({\max \{\Vert \Phi _{n_{k}}\circ G_{k,0} \circ \Phi _{0}^{-1}(z) -P_{n_k}\Vert ,\beta _{n_k}\eta _k\}})}{d_k\cdots d_1}, \end{aligned} \end{aligned}$$

where $\eta _k:=a^{d_k\cdots d_1}$.

By (2) the limit functions of the sequence $F^k$ are constant on ${\mathcal {F}}_0$. Since the sequence $(P_{n_k})$ is bounded, it follows that for all compact subsets $K \subset {\mathcal {F}}_0$ we have

$$\begin{aligned} \Vert F^{n_k}(z)-P_{n_k}\Vert _K\rightarrow 0. \end{aligned}$$

As a consequence, we have that $(\psi _k)$ is locally uniformly bounded from above on ${\mathcal {F}}_0$ and that for all $z\in {\mathcal {F}}_0$, $\limsup _{k\rightarrow \infty }\psi _{k}(z)\le 0.$ For all $k\ge 1$ define the plurisubharmonic function as

$$\begin{aligned} \varphi _k(w):=\psi _k\circ \Phi _{0}(w)=\frac{\log ({\max \{\Vert G_{k,0} (w)\Vert ,\eta _k\}})+ \log {\beta _{n_k}}}{d_k\cdots d_1}. \end{aligned}$$

The sequence $(\varphi _k)$ is clearly locally uniformly bounded from above on $\Phi _{0}^{-1}({\mathcal {F}}_0)$ and

$$\begin{aligned} \limsup _{k\rightarrow \infty }\varphi _{k}(z)\le 0, \quad \forall z\in \Phi _{0}^{-1}({\mathcal {F}}_0). \end{aligned}$$

(4)

We now show that the sequence $(\varphi _k)$ converges on $\Phi _{0}^{-1}({\mathcal {F}}_0)$ to a function $\varphi$ (which has to satisfy $\varphi \le 0$ by (4)) which is plurisubharmonic on $\Omega _G=\Phi _{0}^{-1}({\Omega _F})$, strictly negative at the origin, and identically zero on $\Phi _{0}^{-1}({{\mathcal {F}}_0}){\setminus }\Omega _G$.

Once this is done, we conclude the proof in the following way: such function $\varphi$ is upper semicontinuous on the whole $\Phi _{0}^{-1}({{\mathcal {F}}_0})$ since it is identically zero on $\Phi _{0}^{-1}({{\mathcal {F}}_0}){\setminus }\Omega _G$, and thus it coincides with its upper semicontinuous regularization, which is plurisubharmonic on $\Phi _{0}^{-1}({{\mathcal {F}}_0})$ since $(\varphi _k)$ is locally uniformly bounded from above on $\Phi _{0}^{-1}({{\mathcal {F}}_0})$ (see [8, Proposition 2.9.17]). But this contradicts the maximum principle.

Since $\lim _{k\rightarrow \infty }\frac{\log {\beta _{n_k}}}{d_k\cdots d_1}=0$ we only need to prove that the sequence

$$\begin{aligned} \tilde{\varphi }_k(w):=\frac{\log ({\max \{\Vert G_{k,0} (w)\Vert ,\eta _k\}})}{d_k\cdots d_1} \end{aligned}$$

converges to such a function $\varphi$.

Recall that $\Vert G_k-H_k\Vert \le \eta _k$ on ${\overline{{\mathbb {B}}}}$ by (3). For all $w \in \Omega _G$ define $\theta _k(w):=\max \{\Vert G_{k,0} (w)\Vert ,\eta _k\}$. Recall that $\Omega _G=\bigcup _{j\in {\mathbb {N}}}G_{j,0}^{-1}({\mathbb {B}})$. Fix $j\ge 0$ and let $w\in G_{j,0}^{-1}({\mathbb {B}})$. Then for all $k\ge j$ we have that $G_{k,0}(w)\in {\mathbb {B}}$, and

$$\begin{aligned} \theta _{k+1}(w)&=\max \{\Vert G_{k+1,0} (w)\Vert ,\eta _{k+1}\}\\&\le \max \{\Vert H_{k+1}(G_{k,0} (w))\Vert +\eta _{k+1},\eta _{k+1}\}\\&\le \max \{\Vert G_{k,0} (w)\Vert ^{d_{k+1}}+ \eta _{k+1} \Vert G_{k,0} (w)\Vert +\eta _{k+1},\eta _{k+1} \}\\&\le \max \{\theta _k^{d_{k+1}}(w)+ 2\eta _{k}^{d_{k+1}} ,\eta _{k}^{d_{k+1}} \}\\&\le 3\theta _k^{d_{k+1}}(w). \end{aligned}$$

Hence for $k\ge j$ we have, for all $w\in G_{j,0}^{-1}({\mathbb {B}})$,

$$\begin{aligned} {{\tilde{\varphi }}}_{k+1}(w)\le {{\tilde{\varphi }}}_k(w)+\frac{\log 3}{d_{k+1}\cdots d_1}. \end{aligned}$$

This implies that the sequence of plurisubharmonic functions on $G_{j,0}^{-1}({\mathbb {B}})$

$$\begin{aligned} {{\tilde{\varphi }}}_k+\sum _{j>k}\frac{\log 3}{d_{j}\cdots d_1} \end{aligned}$$

is monotonically decreasing, hence its limit $\varphi$ exists and is plurisubharmonic on $G_{j,0}^{-1}({\mathbb {B}})$. Since this holds for every $j\ge 0$ we obtain that the limit $\varphi$ exists and is plurisubharmonic on $\Omega _G.$ Notice that $\varphi (0)=-\log 2<0$. If $w\in \Phi _{0}^{-1}({{\mathcal {F}}_0})\setminus \Omega _G$, then we have that $\Vert G_{k,0}(w)\Vert \ge 1$ for all $k\in {\mathbb {N}}$, which implies ${{\tilde{\varphi }}}_k(w)\ge 0$ and thus $\liminf _{k\rightarrow \infty }{{\tilde{\varphi }}}_k(w)\ge 0$. But then (4) implies that ${{\tilde{\varphi }}}_k(w)$ converges to 0. $\square$

4 Proof of Proposition 4

We prove this proposition by induction on k. We start the induction by letting $R_0=1$, $n_0=N_0=0$, $\beta _0=1$, $q_0=0$, $P_0=(z_0,w_0)$ with $|z_0|>6$ and $F_0(z,w)=(z+aw,az)$, such that all conditions are satisfied for $k =0$. Let us suppose that conditions (a)—(h) hold for certain k, and proceed with the constructions satisfying the conditions for $k+1$.

By Lemma 7.5 from [1], which relies on the Lambda Lemma, there exist a finite $F_k$ orbit $(Q_j)=(z_j',w_j')_{0\le j \le M}$ such that:

• $\Vert Q_{\ell }\Vert <\frac{1}{k+1}$ for some $0<\ell <M$,

• for small enough $0<\theta <\frac{1}{k+2}$ the three disks

  $$\begin{aligned} {\overline{D}}(z_{N_k},\beta _{N_k}),\qquad {\overline{D}}(w_0'/a, \theta ), \qquad {\overline{D}}(z_M', \theta ) \end{aligned}$$

  are pairwise disjoint, and disjoint from the polynomially convex set

  $$\begin{aligned} K:={\overline{D}}(0,R_k)\cup \bigcup _{0\le i<M} {\overline{D}}(z_i',\theta ). \end{aligned}$$

  (5)

By continuity of $F_k$ there exists $0<s_\ell <\frac{\theta }{2}$ small enough such that for all $0< j\le M-\ell$,

$$\begin{aligned} F_k^j({\mathbb {B}}(Q_\ell ,s_\ell ))\subset \subset {\mathbb {B}}\Big (Q_{\ell +j},\frac{\theta }{2}\Big ) \end{aligned}$$

and such that for all $0< j\le \ell$,

$$\begin{aligned} F_k^{-j}({\mathbb {B}}(Q_\ell ,s_\ell ))\subset \subset {\mathbb {B}}\big (Q_{\ell -j}, \frac{\theta }{2}\big ). \end{aligned}$$

Moreover we can assume that

$$\begin{aligned} s_\ell =a^{2q_{k+1}}\quad {\text{ for } \text{ some }}\quad q_{k+1}\ge \ell +2. \end{aligned}$$

(6)

We define $\Phi _{\ell }=Q_{\ell }+s_{\ell }\cdot z.$

Fig. 1

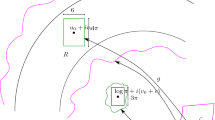
A sketch of the piece of orbit constructed at step $k+1$. In green: the boundary of the cylinder $D(0, R_k) \times {\mathbb {C}}$. In red, the points $Q_n = (z_n^\prime , w_n^\prime )$ constructed using the Lambda Lemma. In blue, the points $T_n = (z_n^{\prime \prime }, w_n^{\prime \prime })$ connecting $T_0 = P_{N_k}$ to $T_N = Q_0$

Our next goal is to construct the map $F_{k+1}$ with a piece of orbit $T_0:=P_{N_k}, T_1,\dots , T_{N}:=Q_0$ such that the iterate $F_{k+1}^{N}$ approximates the composition $F^{-\ell }_k\circ \Phi _{\ell }\circ H_{k+1}\circ \Phi _{n_k}^{-1}\circ F^{n_k -N_k}_k$ arbitrarily well near the point $P_{N_k}$, where

$$\begin{aligned} H_{k+1}(z,w):=((az)^{d_{k+1}}+a^{d_{k+1}\cdots d_1}w, a^{d_{k+1}\cdots d_1}z), \end{aligned}$$

and where $d_{k+1}\ge 2$ is an odd integer to be determined later. See Fig. 1 for a sketch of the piece of orbits constructed in step $k+1$.

Lemma 5

For every sufficiently large odd integer $d_{k+1}\ge 2$ the map

$$\begin{aligned} F^{-\ell }_k\circ \Phi _{\ell }\circ H_{k+1}\circ \Phi _{n_k}^{-1}\circ F^{n_k -N_k}_k \end{aligned}$$

can be written as a finite composition $\psi _{N}\circ \ldots \circ \psi _1$ of maps of the form $\psi _j(z,w)=(\varphi _j(z)+aw,az)$, with $\varphi _j:{\mathbb {C}}\rightarrow {\mathbb {C}}$ holomorphic.

Proof

Let $F_k(z,w)=(f_k(z)+aw,az)$ and $\tau (z,w)=(aw,az)$. The map $\tau$ is clearly of the form $(\varphi (z)+aw,az)$ if we set $\varphi \equiv 0$. A quick computation shows that

$$\begin{aligned} F^{-1}_k(z,w) = \tau ^{-2}\circ \tau \circ \Lambda \circ \tau \circ \tau ^{-2} (z,w). \end{aligned}$$

where $\Lambda (z,w)=(-f_k(z)+aw,az)$. Clearly $\tau ^{-2}$ commutes with $\tau$. The map $\tau ^{-2}$ does not commute with $\Lambda$, but it satisfies the following relations: for all $j\ge 1$,

$$\begin{aligned} \tau ^{-2j}\circ \Lambda ={{\tilde{\Lambda }}}_j\circ \tau ^{-2j},\quad \Lambda \circ \tau ^{-2j}=\tau ^{-2j}\circ {\hat{\Lambda }}_j, \end{aligned}$$

where we write

$$\begin{aligned} {{\tilde{\Lambda }}}_j(z,w):=\Big (-\frac{f_k(a^{2j}z)}{a^{2j}}+aw,az\Big ),\quad {\hat{\Lambda }}_j(z,w):=\Big (-a^{2j}f_k(\frac{z}{a^{2j}})+aw,az\Big ). \end{aligned}$$

Notice that the maps ${{\tilde{\Lambda }}}_j$ and ${\hat{\Lambda }}_j$ are of the required form $(z,w)\rightarrow (\varphi (z)+aw,az)$. If for all $j\ge 1$ we write

$$\begin{aligned} {{\tilde{\Lambda }}}_{0,j}:={{\tilde{\Lambda }}}_1\circ \ldots \circ {{\tilde{\Lambda }}}_j, \quad {\hat{\Lambda }}_{j,0}:= {\hat{\Lambda }}_{j}\circ \ldots \circ {\hat{\Lambda }}_1, \end{aligned}$$

we obtain

$$\begin{aligned} F^{-j}_k=\tau \circ {{\tilde{\Lambda }}}_{0,j}\circ \tau \circ \tau ^{-2(j+1)}=\tau ^{-2(j+1)}\circ \tau \circ {\hat{\Lambda }}_{j,0} \circ \tau . \end{aligned}$$

(7)

Define

$$\begin{aligned} {\mathcal {H}}_{k+1}(z,w):=(a^{(2-d_1\cdots d_{k+1})d_{k+1}}z^{d_{k+1}}+ aw,az), \end{aligned}$$

and notice that

$$\begin{aligned} H_{k+1}={\mathcal {H}}_{k+1}\circ \tau ^{d_1\cdots d_{k+1}-1}. \end{aligned}$$

We remark that from the last formula it follows that the product $d_1\cdots d_{k+1}$ must be odd, as otherwise the linear parts on left and right hand side cannot be equal.

Finally we focus on $\Phi _{\ell }$ and $\Phi _{n_k}^{-1}$. By inductive assumption (e) we know that $\beta _{n_k}=a^{2q_k}$. By (6) we know that $s_{\ell }=a^{2q_{k+1}}$. Let us write $P_{n_k}=(z_{n_k}, w_{n_k})$ and $Q_\ell =(z_{\ell }', w_{\ell }')$ and recall that

$$\begin{aligned} \Phi _{\ell }(z,w)=(s_{\ell }\cdot z+z_{\ell }',s_{\ell }\cdot w+w_{\ell }'). \end{aligned}$$

If we define

$$\begin{aligned} S_1(z,w):=\Big (\frac{w_{\ell }'}{a^{2(q_{k+1}-1)+1}}+aw,az\Big ),\quad S_2(z,w):=\Big (\frac{z_{\ell }'}{a^{2(q_{k+1}-1)}}+aw,az\Big ), \end{aligned}$$

then a quick computation gives us

$$\begin{aligned} \Phi _{\ell }=\tau ^{2(q_{k+1}-1)}\circ S_2\circ S_1. \end{aligned}$$

For the inverse

$$\begin{aligned} \Phi _{n_k}^{-1}(z,w)=\Big (\frac{z-z_{n_k}}{\beta _{n_k}},\frac{w-w_{n_k}}{\beta _{n_k}}\Big ). \end{aligned}$$

we write $R_1(z,w):=(-a w_{n_k}+aw,az)$ and $R_2(z,w):=(-a^2 z_{n_k}+aw,az)$

$$\begin{aligned} \Phi _{n_k}^{-1}=\tau ^{-2(q_k-1)}\circ R_2\circ R_1. \end{aligned}$$

Now we can write

$$\begin{aligned}&F^{-\ell }_k\circ \Phi _{\ell }\circ H_{k+1}\circ \Phi _{n_k}^{-1}\circ F^{n_k-N_k}_k\nonumber \\&\quad =\tau \circ {{\tilde{\Lambda }}}_{0,\ell }\circ \tau ^{2(q_{k+1}-\ell -2)+1}\circ S_2\circ S_1\circ {\mathcal {H}}_{k+1}\circ \tau ^{d_1\cdots d_{k+1}-1-2(q_k-1)}\nonumber \\&\qquad \quad \circ R_2\circ R_1\circ \tau ^{-2(N_k-n_k+1)}\circ \tau \circ {\hat{\Lambda }}_{N_k-n_k,0} \circ \tau \nonumber \\&\quad =\tau \circ {{\tilde{\Lambda }}}_{0,\ell }\circ \tau ^{2(q_{k+1}-\ell -2)+1} \circ S_2\circ S_1 \circ {\mathcal {H}}_{k+1}\circ \tau ^{d_1\cdots d_{k+1}-1 -2(N_k-n_k+q_k)}\nonumber \\&\qquad \quad \circ {\tilde{R}}_2\circ {\tilde{R}}_1\circ \tau \circ {\hat{\Lambda }}_{N_k-n_k,0} \circ \tau , \end{aligned}$$

(8)

where

$$\begin{aligned} {\tilde{R}}_1(z,w)&=\Big (-a^{2(N_k-n_k+1)+1} w_{n_k}+aw,az\Big ),\\ {\tilde{R}}_2(z,w)&=\Big (-a^{2(N_k-n_k+1)+2} z_{n_k}+aw,az\Big ). \end{aligned}$$

Since $q_{k+1}\ge \ell + 2$ it follows that $2(q_{k+1}-\ell -2)+1\ge 0$. If we choose the positive odd integer $d_{k+1}$ in such a way that

$$\begin{aligned} d_{k+1}\ge \frac{2(N_k-n_k+q_k)+1}{d_1\cdots d_n}, \end{aligned}$$

then $d_1\cdots d_{k+1}-1 -2(N_k-n_k+q_k)\ge 0$, and hence the lemma is proven. $\square$

Let $\psi _{N}\circ \ldots \circ \psi _1$ be the maps given by Lemma 5. Let us write $P_{N_k}:=(x_0,y_0)$, and, for all $1\le n\le N$,

$$\begin{aligned} X_n:=(x_n,y_n):=\psi _n\circ \ldots \circ \psi _1(x_0,y_0). \end{aligned}$$

Notice that $X_N:= Q_0$, and that $y_n=ax_{n-1}$.

Lemma 6

Define $W:=F_k^{N_k-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k}))$. If $d_{k+1}$ is sufficiently large then for every $1\le n\le N$ we have

$$\begin{aligned} \psi _n\circ \ldots \circ \psi _1(W)\subset \subset {\mathbb {B}}\Big (X_n,\frac{1}{k+1}\Big ). \end{aligned}$$

Proof

By condition (g) of the inductive process we have that for all $0\le j\le N_k-n_k$,

$$\begin{aligned} F_k^{-j}(W)\subset \subset {\mathbb {B}}\Big (P_{N_k-j},\frac{1}{k+1}\Big ). \end{aligned}$$

(9)

Notice that $F_k^{-N_k+n_k}(W)={\mathbb {B}}\Big (P_{n_k},\beta _{n_k}\Big )$.

By (7) we have $F_k^{-1}=\tau ^{-4}\circ \tau \circ \hat{\Lambda }_{1,0}\circ \tau$. Since $\tau (z,w)=(aw,az)$, it follows that $\psi _1(W)=\tau (W)\subset {\mathbb {B}}(X_1,\frac{1}{k+1})$. By (9) we obtain

$$\begin{aligned} \tau ^{-3}\circ {\hat{\Lambda }}_{1}\circ \tau (W)\subset \subset {\mathbb {B}}(P_{N_k-1},\frac{1}{k+1}), \end{aligned}$$

and thus

$$\begin{aligned} \psi _2\circ \psi _1(W)={\hat{\Lambda }}_{1}\circ \tau (W)\subset \subset \tau ^3({\mathbb {B}}\Big (P_{N_k-1},\frac{1}{k+1})\Big )\subset {\mathbb {B}}\Big (X_2, \frac{1}{k+1}\big ). \end{aligned}$$

Since $F_k^{-2}= \tau ^{-5}\circ \hat{\Lambda }_2\circ \hat{\Lambda }_1\circ \tau$, by (9) we obtain

$$\begin{aligned} \tau ^{-5}\circ \hat{\Lambda }_2\circ \hat{\Lambda }_1\circ \tau (W)\subset \subset {\mathbb {B}}(P_{N_k-2},\frac{1}{k+1}), \end{aligned}$$

and thus

$$\begin{aligned} \psi _3\circ \psi _2\circ \psi _1(W)=\hat{\Lambda }_{2}\circ \hat{\Lambda }_{1}\circ \tau ( W) \subset \subset {\mathbb {B}}(X_3,\frac{1}{k+1}). \end{aligned}$$

Repeating this argument we obtain, for all $1\le n\le N_{k}-n_k+1$,

$$\begin{aligned} \psi _n\circ \dots \circ \psi _1(W)={\hat{\Lambda }}_{n-1,0}\circ \tau (W)\subset \subset {\mathbb {B}}\Big (X_n,\frac{1}{k+1}\Big ). \end{aligned}$$

The maps ${\tilde{R}}_1$, ${\tilde{R}}_2$, $\tau$ are affine contractions, hence after applying these maps the image of W will still be contained in the respective balls of radius $\frac{1}{k+1}$. Let us look at what happens if we now apply the map ${\mathcal {H}}_{k+1}$. Notice that

$$\begin{aligned} {\mathcal {H}}_{k+1}\circ \tau ^{d_1\cdots d_{k+1}-1 -2(N_k-n_k+q_k)}\circ {\tilde{R}}_2\circ {\tilde{R}}_1\circ \tau \circ \hat{\Lambda }_{N_k-n_k,0} \circ \tau = H_{k+1}\circ \Phi _{n_k}^{-1}\circ F^{n_k-N_k}_k, \end{aligned}$$

hence

$$\begin{aligned} {\mathcal {H}}_{k+1}\circ \tau ^{d_1\cdots d_{k+1}-1 -2(N_k-n_k+q_k)}\circ {\tilde{R}}_2\circ {\tilde{R}}_1\circ \tau \circ \hat{F}_{k,(N_k-n_k)} \circ \tau (W)= H_{k+1}({\mathbb {B}}). \end{aligned}$$

By choosing $d_{k+1}$ sufficiently large we can make sure that $H_{k+1}({\mathbb {B}})$ and all remaining images of W are contained in the balls of radius $\frac{1}{k+1}$. $\square$

Let us write $P_{N_k}:=(z_0'',w_0'')$, $Q_0:=(z_N'',w_N'')$, let $z_1'',\ldots , z_{N-2}''\in {\mathbb {C}}$ be some sequence of points to be determined later, and let $z_{N-1}'':=\frac{w_{0}'}{a}=\frac{w_{N}''}{a}$. Next we define for all $0\le n \le N$, $w_{n}'':=az_{n-1}''$, $T_n:=(z_{n}'',w_{n}'')$ and $\Theta _n(z,w):=(z-z_n''+x_n, w-w_n''+y_n)$. For all $1\le n \le N$,

$$\begin{aligned} G_n(z,w)&:=\Theta _{n}^{-1}\circ \psi _n\circ \Theta _{n-1}\\&=(z_{n}''+\varphi _n(z-z_{n-1}''+x_{n-1})-\varphi _{n}(x_{n-1})-aw_{n-1}''+aw ,az), \end{aligned}$$

which is of the form $G_n(z,w)=(g_n(z)+aw,az),$ where

$$\begin{aligned} g_n(z):=z_{n}''+\varphi _n(z-z_{n-1}''+x_{n-1})-\varphi _{n}(x_{n-1})-aw_{n-1}''. \end{aligned}$$

(10)

Notice that for every $1\le n \le N$ we have $G_n(T_{n-1})=T_n,$ since $\Theta _j(T_j)=X_j$ for all $0\le j\le N$. Notice also that $\Theta _N=\Theta _0=\mathsf{id}$, and thus

$$\begin{aligned} G_N\circ \ldots \circ G_1=F^{-\ell }_k\circ \Phi _{\ell }\circ H_{k+1}\circ \Phi _{n_k}^{-1}\circ F^{n_k-N_k}_k. \end{aligned}$$

Since the maps $\Theta _{n}$ are just translations, and $\Theta _0$ is the identity, it follows from Lemma 6 that

$$\begin{aligned} G_n\circ \ldots \circ G_1(W)=\Theta _n^{-1}\circ \psi _n\circ \dots \circ \psi _1\circ \Theta _0\subset \subset {\mathbb {B}}\Big (T_n,\frac{1}{k+1}\Big ). \end{aligned}$$

Remark 4.1

Observe that $G_N=\Theta _{N}^{-1}\circ \tau \circ \Theta _{N-1}=(a(y_{N-1}-w_{N-1}'') +aw,az)$. We know that $G_N\circ \ldots \circ G_1(W)\subset \subset {\mathbb {B}}(Q_0,\frac{\theta }{2})$, hence

$$\begin{aligned} G_{N-1}\circ \ldots \circ G_1(W)\subset \subset {\mathbb {B}}(T_{N-1},\theta ). \end{aligned}$$

Fix $d_{k+1}$ such that $\frac{\log {s_{\ell }}}{d_1\ldots d_{k+1}}\le \frac{1}{k+1}$ and such that Lemma 5 and Lemma 6 hold. We now have complete freedom of choosing points $z_1'',\ldots , z_{N-2}''\in {\mathbb {C}}$ such that the disks

$$\begin{aligned} {\overline{D}}(z_{N_k},\beta _{N_k}),\qquad {\overline{D}}(w_0'/a, \theta ), \qquad {\overline{D}}(z_M', \theta ),\qquad ({\overline{D}}(z_j'',\frac{1}{k+1}))_{1\le j\le N-2 } \end{aligned}$$

are pairwise disjoint, and disjoint from the polynomially convex set K defined by (5). Let H represent the union of these disks, and define $R_{k+1}>0$ sufficiently large so that $K\cup H\subset D(0,R_{k+1})$.

We define a holomorphic function h on the polynomially convex set $K\cup H$ in the following way:

• (1) h coincides with $f_k$ on K

• (2) $h|_{{\overline{D}}(z_{N_k},\beta _{N_k})}$ coincides with $g_1$, where the $g_j$ are defined in (10),

• (3) $h|_{{\overline{D}}\Big (z_j'',\frac{1}{k+1}\Big )}$ coincides with $g_{j+1}$ for all $1\le j \le N-2$,

• (4) $h|_{{\overline{D}}(w_0'/a, \theta )}$ coincides with $g_N$,

• (5) $h|_{{\overline{D}}(z_M',\theta )}$ is constantly equal to some value $A\in {\mathbb {C}}$ such that $|A+aw'_M|>R_{k+1} +3$.

By the Runge Approximation Theorem there exists a function $f_{k+1}\in {\mathcal {O}}({\mathbb {C}})$ satisfying:

• (1) $f_{k+1}(0)=h(0)=0$ and $f_{k+1}'(0)=h'(0)=1$,

• (2) $f_{k+1}$ coincides with h on all the points $z_j,z_j', z_j''$,

• (3) $\Vert f_{k+1}-h\Vert _{K\cup H}<\delta _{k+1}\le 2^{-k-1}$, with $\delta _{k+1}$ to be chosen later.

We define $F_{k+1}:=(f_{k+1}(z)+aw,az)$, so that the sequences of points

$$\begin{aligned} (P_j)_{0\le j\le N_k},\qquad (T_j)_{1\le j\le N-1},\qquad (Q_j)_{0\le j\le M} \end{aligned}$$

together form the start of an $F_{k+1}$-orbit.

Set $n_{k+1}:=N_k+N+\ell$ and $N_{k+1}:=N_k+N+M+1$, $P_{N_{k+1}}:=F_{k+1}(Q_M)$. Define $\beta _j:=\frac{1}{k+1}$ if $N_k\le j< n_{k+1}$, $\beta _{n_{k+1}}:=s_\ell$ and $\beta _j:=\frac{1}{k+2}$ if $n_{k+1}<j\le N_{k+1}$.

It is immediate that conditions (a) — (f) are satisfied for the $(k+1)$-th step. We claim that $\delta _{k+1}$ can be chosen sufficiently small enough such that conditions (g) and (h) are satisfied for the $(k+1)$-th step. We start with (g), that is we show that for all $0\le s\le k+1$,

$$\begin{aligned} F_{k+1}^j({\mathbb {B}}(P_{n_s},\beta _{n_s}))\subset \subset {\mathbb {B}}(P_{n_s+j},\beta _{n_s+j}), \quad \forall \,1\le j\le N_{k+1}-n_s, \end{aligned}$$

(11)

We have

$$\begin{aligned}&F_k^{j}({\mathbb {B}}(P_{n_k},\beta _{n_k})\subset \subset {\mathbb {B}}(P_{n_k+j},\beta _{n_k+j}),\quad \forall 1\le j\le N_{k}-n_k,\\&G_{j}\circ \dots \circ G_1\circ F_k^{N_k-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k}))\subset \subset {\mathbb {B}}(T_j,\frac{1}{k+1}),\quad \forall 1\le j\le N-2,\\&G_{N-1}\circ \dots \circ G_1 \circ F_k^{N_k-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k}))\subset \subset {\mathbb {B}}(T_{N-1},\theta ),\\&F_k^j\circ G_{N}\circ \dots \circ G_1\circ F_k^{N_k-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k}))\subset \subset {\mathbb {B}}(Q_j,\theta ), \quad \forall 0\le j\le M. \end{aligned}$$

Notice that all these sets are contained in $(K\cup H)\times {\mathbb {C}}$, and that

$$\begin{aligned} (A+aw,az)\circ F_k^M\circ G_{N}\circ \dots \circ G_1\circ F_k^{N_k-n_k}({\mathbb {B}}(P_{n_k},\beta _{n_k}))\subset \subset {\mathbb {B}}\Big (P_{N_{k+1}},\frac{1}{k+2}\Big ). \end{aligned}$$

Hence we can choose $\delta _{k+1}>0$ small enough such that (11) holds for $s=k$. Similarly one obtains (11) for $0\le s\le k+1$, and hence (h), completing the proof of Proposition 4.

Appendix: Calibrated basins and the plurisubharmonic method

As a further illustration of using the plurisubharmonic method to prove that an attracting basin equals the Fatou component containing the basin, we take a closer look at the calibrated basins constructed in [10]. Let $f_0, f_1,f_2 \ldots$ be a sequence of automorphisms of ${\mathbb {C}}^k$, all having an attracting fixed point at the origin. For all $j\ge 0$ there exists a radius $r_j>0$, a constant $0<\mu _j<1$ and a constant $C_j>0$ such that

$$\begin{aligned} \Vert f_j^n(z)\Vert \le C_j\mu _j^n\Vert z\Vert ,\quad \forall z\in B(0,r_j), n\ge 0. \end{aligned}$$

We can choose $n_j$ large enough to obtain

$$\begin{aligned} f_j^{n_j} (B(0, r_j)) \subset B(0,r_{j+1}), \end{aligned}$$

and $r_j\rightarrow 0$. We then define the calibrated basin $\Omega _{(r_j), (n_j)}$ by

$$\begin{aligned} \Omega _{(r_j),(n_j)} := \bigcup _{j \in {\mathbb {N}}} (f_{j-1}^{n_{j-1}}\circ \dots \circ f_0^{n_0})^{-1} (B(0, r_j)). \end{aligned}$$

It is easy to see that the calibrated basin may depend on the sequences $(r_j)$ and $(n_j)$ chosen.

Recall the following result from [10]:

Theorem 7

Fix the sequence $(r_j)$. For $n_0, n_1, \ldots$ sufficiently large, where each $n_j$ may depend on the choices of $n_0, \ldots , n_{j-1}$, the calibrated basin of the sequence $f_0^{n_0}, f_1^{n_1}, \ldots$ is biholomorphic to ${\mathbb {C}}^k$.

Recall that it may be necessary to replace the maps $f_j$ by large iterates: all assumptions (with $r_j = \frac{1}{2}$) are satisfied by the maps in [5], see Proposition 3, but in this case the calibrated basin is a Short ${\mathbb {C}}^k$, and hence not equivalent to ${\mathbb {C}}^k$.

One may wonder whether it is necessary to work with the calibrated basin instead of the basin that contains all points whose orbits converge to 0. It turns out that this may indeed be necessary: for suitable choices of the sequence $f_0, f_1, \ldots$ the full basin may not be open, even when replacing the maps with arbitrarily high iterates $f_0^{n_0}, f_1^{n_1}, \ldots$, see [10]. This raises another natural question: is the calibrated basin equal to the Fatou component ${\mathcal {F}}_0$ containing the origin, that is, the largest connected open set with locally uniform convergence to 0? Here we prove that this is indeed the case.

Theorem 8

Fix the sequence $(r_j)$. For $n_0, n_1, \ldots$ sufficiently large we have

$$\begin{aligned} {\mathcal {F}}_0 = \Omega _{(r_j),(n_j)}. \end{aligned}$$

Proof

Define

$$\begin{aligned} G_j(z) := \frac{\log \Vert f_j^{n_j} \circ \cdots \circ f_0^{n_0}(z)\Vert }{-n_j \log \mu _j}. \end{aligned}$$

Observe that, given a compact $K\subset {\mathcal {F}}_0$, for big j we have that $f_j^{n_j} \circ \cdots \circ f_0^{n_0}(K)\subset {\mathbb {B}}^k$, and thus that $G_j|_K\le 0$. Let

$$\begin{aligned} G = \limsup _{j\rightarrow \infty } G_j, \end{aligned}$$

and write $G^\star$ for the upper semi-continuous regularization of G. It follows that $G^\star$ is plurisubharmonic on ${\mathcal {F}}_0$.

If we choose $n_j$ sufficiently large we may assume that

$$\begin{aligned} \frac{\log r_{j+1}}{ n_j\log \mu _j}\longrightarrow 0, \end{aligned}$$

hence for any point $z \in {\mathcal {F}}_0{\setminus } \Omega _{(r_j),(n_j)}$ we have $G^\star (z) = G(z) = 0$.

On the other hand, let $z\in \Omega _{(r_j),(n_j)},$ and let $j\ge 0$ be large enough such that $z_j:=f_{j-1}^{n_{j-1}} \circ \cdots \circ f_0^{n_0}(z)\in B(0,r_j)$. Then

$$\begin{aligned} G_j(z)=\frac{\log \Vert f_j^{n_j}(z_j)\Vert }{-n_j\log \mu _j}\le \frac{\log C_j+\log \Vert z_j\Vert +n_j\log \mu _j}{-n_j\log \mu _j}. \end{aligned}$$

Choosing the $n_j$’s large enough we thus obtain $G(z)\le -1$ for all $z \in \Omega _{(r_j),(n_j)}$, which implies that $G^\star (z)\le -1$ for all $z \in \Omega _{(r_j),(n_j)}$. Since ${\mathcal {F}}_0$ is open and connected, it follows from the maximum principle that ${\mathcal {F}}_0{\setminus }\Omega _{(r_j),(n_j)}$ must be empty, which completes the proof. $\square$