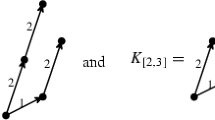Quasi-hereditary algebras via generator–cogenerators of local self-injective algebras and transfer of Ringel duality

Abstract

The dominant dimension of algebras in the class $\mathbf A$ of 1-quasi-hereditary algebras introduced in Pučinskaitė (J Lond Math Soc (2) 87(2):478–496, 2013) is at least two. By the Morita–Tachikawa Theorem this implies that $\mathbf A$ is related to a certain class $\mathbf B$ of pairs consisting of an (another) algebra and a module satisfying the double centralizer condition. In this paper we determine the class $\mathbf B$, and show the connection between the partial order of a 1-quasi-hereditary algebra and the structure of the related pair in $\mathbf B$ (see Theorem A). If the first component of a pair in $\mathbf B$ is a commutative algebra, then the corresponding algebra in $\mathbf A$ receives additional features described in Theorem B. Finally we introduce the Ringel dual for objects in $\mathbf B$. Of particular interest are those pairs in $\mathbf B$ which occur as Ringel dual (see Theorem C).

1 Introduction

Let $\mathcal {A}$, $\mathcal {B}$ be algebras. An $\mathcal {A}$-$\mathcal {B}$-bimodule ${}_{\mathcal {A}}\mathcal {M}_{\mathcal {B}}$ satisfying the double centralizer condition $\mathcal {A}\cong {{\mathrm{End}}}_{\mathcal {B}}(\mathcal {M}_{\mathcal {B}})$ and $\mathcal {B}\cong {{\mathrm{End}}}_{\mathcal {A}}({}_{\mathcal {A}}\mathcal {M})$ provides a relationship between the representation theories of the algebras $\mathcal {A}$ and $\mathcal {B}$ that may differ in terms of their homological properties. Soergel’s ’Struktursatz’ relating an algebra $\mathcal {A}_{\Theta }(\mathfrak {g})$ corresponding to a block $\Theta$ of the Bernstein-Gelfand-Gelfand category $\mathcal {O}(\mathfrak {g})$ of a complex semisimple Lie algebra $\mathfrak {g}$ with a subalgebra of the corresponding coinvariant algebra as well as the Schur-Weyl duality between the Schur algebra $S(n,r)$ for $n\ge r$ and the group algebra $K\Sigma _r$ of the symmetric group are prominent examples for this connection (see for instance [10]).

In this paper we present a further example for this situation which relates a 1-quasi-hereditary algebra $A$ defined in [11] with a local self-injective algebra $B$ via an $A$-$B$-bimodule $L$ whose structure has a precise description: The $A$-module $L$ is a projective-injective indecomposable and the ${{\mathrm{End}}}_A(L)^{{op}}$-module $L$ decomposes into a direct sum of local ideals of $B:={{\mathrm{End}}}_A(L)$ generated by the endomorphisms corresponding to certain paths in the quiver of $A$ (see Proposition  3.4). The $B$-module $L$ is a generator–cogenerator of ${{\mathrm{mod}}}B$ (i.e., any projective and any injective indecomposable $B$-module is a direct summand of $L$). Thus, any 1-quasi-hereditary algebra can be defined as an endomorphism algebra of a generator–cogenerator of a local self-injective algebra.

The algebras $\mathcal {A}_{\Theta }(\mathfrak {g})$ and $S(n,r)$ belong to the class $\fancyscript{A}$ of quasi-hereditary algebras with a duality (induced by an anti-automorphism) and with dominant dimension at least two (see [10] and [6]). The class of 1-quasi-hereditary algebras has a non-empty intersection with $\fancyscript{A}$. Many factor algebras of $\mathcal {A}_{\Theta }(\mathfrak {g})$ related to certain saturated subsets of weights are 1-quasi-hereditary. Note that a 1-quasi-hereditary algebra does not have a duality in general. The results in this paper clarify the connection between $\mathcal {A}_{\Theta }(\mathfrak {g})$ and the coinvariant algebras (see Remark 5.7).

Throughout this paper $K$ is an algebraically closed field. Our first result presents a one-to-one correspondence (up to isomorphism) between the class of 1-quasi-hereditary algebras and the class of pairs $(B,L)$ yielding 1-quasi-hereditary algebras via the double centralizer condition. There $B$ is a local self-injective algebra and $L\in {{\mathrm{mod}}}B$ satisfies certain properties. Any algebra $\mathcal {A}$ in this paper is basic, thus given by a quiver and relations $(Q(\mathcal {A}),\mathcal {I}(\mathcal {A}))$.

Theorem A

Let $A$, $B$ be finite dimensional basic $K$-algebras and $L$ be a $B$-module. Let $n\in \mathbb {N}$ and $(\Lambda :=\left\{ 1,\ldots , n\right\} ,\leqslant )$ be a partially ordered set. The following statements are equivalent:

• (i) $A$ with $\left( \Lambda , \leqslant \right)$ is 1-quasi-hereditary (here we identify $\Lambda$ with the vertices in $Q(A)$), i.e., $A\cong {{\mathrm{End}}}_B(L)^{op}$, where $L$ is a multiplicity-free generator–cogenerator of ${{\mathrm{mod}}}B$.

• (ii) $B$ is local, self-injective with ${{\mathrm{dim}}}_KB=n$ and $\displaystyle L\cong \bigoplus \nolimits _{i\in \Lambda } L(i)$ where $L(i)$ are local submodules of $B$ and $L(1)=B$, moreover, for all $i, j\in \Lambda$ the following properties  hold:

  • (a) There exists an epimorphisms $L(i)\twoheadrightarrow L(j)$ if and only if $i\leqslant j$,

  • (b) $\displaystyle {{\mathrm{rad}}}(L(i))=\sum \nolimits _{i<j}L(j)$.

Recall that an algebra of the form $A_{\Theta }(\mathfrak {g})$ is 1-quasi-hereditary if $\hbox {rank} (\mathfrak {g})\le 2$, hence Theorem A is applicable for these algebras.

Dlab, Heath and Marko have shown in [3] that a pair $(B,L)$ with the properties in $(ii)$ and if $B$ is commutative yields a quasi-hereditary BGG-algebra (defined by Irving in [8]). The next theorem strengthens the main theorem in [3] by determining the properties of a 1-quasi-hereditary algebra $A\cong {{\mathrm{End}}}_B(L)^{op}$ for which $B$ is commutative.

In the quiver $Q$ of a 1-quasi-hereditary algebra $(A,\leqslant )$ between two vertices $i$ and $j$ either there are no arrows or two arrows pointing in opposite directions $i \leftrightarrows j$ and $i,j$ are neighbours with respect to $\leqslant$ (see [11, Theorem 2.7]). Thus for any path $p$ in $Q$ there exists an uniquely determined path $p^{op}$ running through the same vertices in the opposite direction.

Theorem B

Let $B$ be an algebra and $L$ a $B$-module with the conditions $(ii)$ in Theorem  A, and $A\cong {{\mathrm{End}}}_B(L)^{op}$. The following statements are equivalent:

• (i) $B$ is commutative.

• (ii) If $\rho \in I(A)$ is a relation of $A$, then $\rho ^{op}$ is also a relation of $A$.

• (iii) $A$ has a duality induced by the anti-automorphism $p\mapsto p^{op}$.

Theorem B implies that for a 1-quasi-hereditary algebra $A\cong {{\mathrm{End}}}_B(L)^{op} \cong KQ/\mathcal {I}$ with $B$ is commutative there exists a set $\mathfrak {R}$ of relations with $\mathcal {I}=\left\langle \mathfrak {R}\right\rangle$ such that $\rho \in \mathfrak {R}$ if and only if $\rho ^{op}\in \mathfrak {R}$. The coinvariant algebra $\mathcal {B}:=\mathcal {B}_{\Theta }(\mathfrak {g})$ related to the algebra $\mathcal {A}:=\mathcal {A}_{\Theta }(\mathfrak {g})$ is commutative. Moreover, $\mathcal {A}\cong {{\mathrm{End}}}_{\mathcal {B}}(\mathcal {M})^{op}$ for a $\mathcal {B}$-module $\mathcal {M}$ (Soergel’s ’Struktursatz’). Note that the properties $(ii)$ and $(iii)$ in Theorem B are satisfied for all algebras $\mathcal {A}_{\Theta }(\mathfrak {g})$ that have been computed in the literature so far, also for some algebras which are not 1-quasi-hereditary, for example $\mathcal {A}_{0}(\mathfrak {sl}_4)$ (see [15]).

Moreover, according to [5], any 1-quasi-hereditary algebra $A={{\mathrm{End}}}_B(L)^{op}$, where $B$ is commutative, is isomorphic to ${{\mathrm{Hom}}}_A(\mathcal {D}(A),A)$ as an $A$-$A$-bimodule (here $\mathcal {D}$ denotes the standard duality), $A$ is also a Morita algebra in the sense of Kerner and Yamagata (see [9]).

The concept of Ringel duality introduced in [13] is essential in the theory of quasi-hereditary algebras: For a (basic) quasi-hereditary algebra $\mathcal {A}$ there exists another quasi-hereditary algebra $R(\mathcal {A})$ such that $R(R(\mathcal {A}))\cong \mathcal {A}$. In this paper we show how the Ringel duality induces a corresponding concept $R(-)$ on the class of pairs $(B,L)$ with the properties $(ii)$ in Theorem A: For a pair $(B,L)$ there exists another pair $(R(B),B(L))$ such that $R(R(B))\cong B$ and $R(R(L))\cong L$ (we will show $B\cong R(B)$, see Lemma 5.2). The class of 1-quasi-hereditary algebras is not closed under Ringel duality thus the pair $(R(B),R(L))$ do not satisfies the conditions $(ii)$ in Theorem A. However the ”Ringel dual” of $(R(B),R(L))$ yields a pair with properties $(ii)$ in Theorem A. I would like to emphasize that the consideration of the structure of $L(R)$ is related to the consideration of the algebras $\mathcal {A}_{\Theta }(\mathfrak {g})$ because they also come from an algebra $\mathcal {B}$ and a $\mathcal {B}$-module $\mathcal {M}$.

Our next result explicitly determines the aforementioned correspondence for those 1-quasi-hereditary algebras, whose Ringel duals are also 1-quasi-hereditary.

Theorem C

Let $(A,\leqslant )$ and $(R(A),\geqslant )$ be 1-quasi-hereditary algebras as well as $(B,L)$ and $( R(B), R(L))$ the corresponding pairs (w.r.t. Theorem A (ii)), where $\displaystyle L\cong \bigoplus \nolimits _{i\in \Lambda }L(i)$ and $\displaystyle R(L)\cong \bigoplus \nolimits _{i\in \Lambda }R(L(i))$. Then $B\cong R(B)$ and for every $i\in \Lambda$ we have

$$\begin{aligned} \displaystyle R(L(i))\cong B/\left( \sum _{j\not \leqslant i}L(j)\right) \cong \bigcap _{j\not \leqslant i} \ker \left( B\twoheadrightarrow L(j)\right) \!. \end{aligned}$$

In particular, if a 1-quasi-hereditary algebra is Ringel self-dual, then $L \cong R(L)$. There exists a permutation $\sigma \in \hbox {Sym}({{\mathrm{dim}}}_KB)$ with $L(\sigma (i))\cong R(L(i))$. The algebras of the form $\mathcal {A}_{\Theta }(\mathfrak {g})$ are Ringel self-dual. In case of $\hbox {rank}(\mathfrak {g})\le 2$ the algebra $\mathcal {A}_{\Theta }(\mathfrak {g})$ is 1-quasi-hereditary, we have for them the situation described in Theorem C. (See Example 2.6 and Remark 5.6 for the pairs $(B,L)$ and $(B, R(L))$ corresponding to the algebra $\mathcal {A}_{0}(\mathfrak {sl}_3)$.)

The paper is organized as follows: In Sect. 1, we introduce the Morita–Tachikawa Theorem which shows that a minimal faithful module over an algebra of dominant dimension at least two has the double centralizer property. The results of this paper build upon on this theorem. We also recall the relevant definitions and give some examples which show the diversity of modules over a local self-injective algebra satisfying the double centralizer condition.

Section 2 is devoted to the proof of Theorem A. The paths in the quiver of a 1-quasi-hereditary algebra of the form $p(j,i,k)$ defined in [11, Section 3] play an important role. The other part of the proof is based on the structure of the $B$-module $L$ which will be analyzed in Lemma  3.5. We also determine an easier transition from the $B$-maps of $L$ to the relations of the algebra $A={{\mathrm{End}}}_B(L)^{op}$ (see Remark 3.10).

This is used in the proof of Theorem B in Sect. 3.

In Sect. 4 we describe the transfer of Ringel duality. Consequently we obtain a decomposition of the class of 1-quasi-hereditary algebras with their Ringel duals into subclasses which are closed under Ringel duality. Moreover, the algebras in a fixed subclass arise from the same local self-injective algebra. Subsequently we present the proof of Theorem C.

2 Preliminaries

Unless otherwise specified, any algebra $\mathcal {A}$ is an associative, finite dimensional, basic $K$-algebra over an algebraically closed field $K$. Thus $\mathcal {A}$ is determined by a quiver $Q:=Q(\mathcal {A})=(Q_0,Q_1)=(\left\{ \hbox {the set of vertices}\right\} \!, \left\{ \hbox {the set of arrows}\right\} )$ and relations $\mathcal {I}$, or in other words, $\mathcal {A}=KQ/\mathcal {I}$ is a quotient algebra of the path algebra $KQ$ by an admissible ideal $\mathcal {I}$ (Theorem of Gabriel). The algebra $KQ/\mathcal {I}$ is is said to be a bound quiver algebra. The product of arrows $(k\rightarrow i)$ and $(i\rightarrow j)$ is given by the path $(k\rightarrow i\rightarrow j)=(i \rightarrow j )\cdot (k \rightarrow i)$. If we say that $p$ is a path in $Q$ (resp. in $\mathcal {A}$), then this means that $p$ is an element in $KQ$ (resp. $p$ the corresponding residue class in $KQ/\mathcal {I}$). The relevant material can be found in [1, Chapter III]. Furthermore, ${{\mathrm{mod}}}\mathcal {A}$ is the category of finite dimensional left $\mathcal {A}$-modules. For $\mathcal {M}\in {{\mathrm{mod}}}\mathcal {A}$ we denote by ${{\mathrm{soc}}}\mathcal {M}$, ${{\mathrm{rad}}}\mathcal {M}$ and ${{\mathrm{top}}}\mathcal {M}$ the socle, the radical and the top of $\mathcal {M}$, respectively, and ${{\mathrm{add}}}(\mathcal {M})$ is the full subcategory of ${{\mathrm{mod}}}\mathcal {A}$ whose objects are the direct sums of direct summands of $\mathcal {M}$ (for references see [1]).

We repeat some notations and facts about bound quiver algebras $\mathcal {A}=KQ/\mathcal {I}$. Throughout, we identify the set of vertices $Q_0:=Q_0(\mathcal {A})$ with the set $\Lambda =\left\{ 1, \ldots , \left| Q_0\right| \right\}$. We denote by $P(i)$, $I(i)$, $S(i)$ and $e_i$ the projective indecomposable, injective indecomposable, simple $\mathcal {A}$-module and the primitive idempotent, respectively, corresponding to $i\in \Lambda$. The module $P(i)$ as a vector space is generated by all paths in $\mathcal {A}$ which start in the vertex $i$. Let $\mathcal {M}\in {{\mathrm{mod}}}\mathcal {A}$, then for $\mathcal {M}$ as a $K$-space we have $\mathcal {M}\cong \bigoplus _{i\in \Lambda }\mathcal {M}_i$ with $\mathcal {M}_i\cong {{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\mathcal {M})$ via $m\mapsto f_{(m)}:P(i)\rightarrow \mathcal {M}$, where $f_{(m)}(a\cdot e_i)=a\cdot m$ for all $a\in \mathcal {A}$. In particular, $P(j)_i \cong {{\mathrm{Hom}}}_{\mathcal {A}}(P(i),P(j))= {{\mathrm{span}}}_{K}\left\{ f_{(p)}\mid p \hbox { is a path in } \mathcal {A}, \ p \hbox { starts in } j \hbox { and ends in } i \right\}$. Recall that ${{\mathrm{End}}}_{\mathcal {A}}(\mathcal {M})^{op}$ is a $K$-algebra with the product $F\circ G=\left( \mathcal {M}\mathop {\rightarrow }\limits ^{G}\mathcal {M}\mathop {\rightarrow }\limits ^{F}\mathcal {M}\right)$. The (left) ${{\mathrm{End}}}_{\mathcal {A}}(\mathcal {M})^{op}$-module $\mathcal {M}$ is isomorphic to $\bigoplus _{i\in \Lambda }{{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\mathcal {M})$, written ${}_{{{\mathrm{End}}}_{\mathcal {A}}(\mathcal {M})^{op}}\mathcal {M}$. The Jordan-Hölder multiplicity of $S(i)$ in $\mathcal {M}$ is denoted by $[ \mathcal {M}:S(i) ]$. In particular, we have ${{\mathrm{dim}}}_K{{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\mathcal {M})=[ \mathcal {M}:S(i) ]$.

2.1 Theorem of Morita–Tachikawa

Based on various works by Morita and Tachikawa (see [16, 17]), in [14] is described a relationship between the algebras $\mathcal {A}$ and ${{\mathrm{End}}}_{\mathcal {A}}(\mathcal {M})^{op}$ via an $\mathcal {A}$-module $\mathcal {M}$ having the double centralizer condition. We recall some notations and terminology needed in the statement of the theorem below.

The dominant dimension of $\mathcal {A}$ is at least $2$ (written ${{\mathrm{dom.dim}}}\mathcal {A}\ge 2$), if there exists an exact sequence $0\rightarrow {}_{\mathcal {A}}\mathcal {A}\rightarrow \mathcal {M}_1 \rightarrow \mathcal {M}_2$ such that $\mathcal {M}_1,\mathcal {M}_2$ are projective and injective $\mathcal {A}$-modules. An $\mathcal {A}$-module $\mathcal {M}$ is called faithful if ${}_{\mathcal {A}}\mathcal {A}$ can be embedded into a direct sum of copies of $\mathcal {M}$. An $\mathcal {A}$-module $\mathcal {M}$ is minimal faithful if $\mathcal {M}$ is faithful, and $\mathcal {M}$ is a direct summand of any faithful $\mathcal {A}$-module. A minimal faithful $\mathcal {A}$-module is unique up to isomorphism and will be denoted by $\fancyscript{M}(\mathcal {A})$. An $\mathcal {A}$-module $\fancyscript{G}$ is a generator–cogenerator of ${{\mathrm{mod}}}\mathcal {A}$ if every projective indecomposable as well as every injective indecomposable $\mathcal {A}$-module is a direct summand of $\mathcal {M}$. We denoted by $[\mathcal {A}]$ resp. $[\mathcal {A},\fancyscript{G}]$ the isomorphism class of $\mathcal {A}$ and a $\mathcal {A}$-module $\fancyscript{G}$.

Theorem 2.1

(Morita–Tachikawa) There are bijections $\Psi$ and $\Phi$ between

$$\begin{aligned}&\mathbf X {:=} \left\{ [\mathcal {A}] \ \ \ \ \left| \begin{array}{ll} \mathcal {A}\hbox { is a basic artin algebra,} {{\mathrm{dom.dim}}}\mathcal {A}\ge 2 \end{array} \right. \right\} \quad and\\&\mathbf Y {:=} \left\{ [\mathcal {B},\fancyscript{G}] \ \left| \begin{array}{l} \mathcal {B}\hbox { is a basic artin algebra, }\\ \fancyscript{G} \hbox { is a multiplicity-free, generator--cogenerator of }{{\mathrm{mod}}}\mathcal {B}\end{array} \right. \right\} \end{aligned}$$

defined as follows:

$$\begin{aligned} \begin{array}{ccl} \mathbf X &{} \mathop {\longrightarrow }\limits ^{\Phi } &{} \mathbf Y \\ \left[ \mathcal {A}\right] &{} \mapsto &{} \bigl [ \mathcal {B}(\mathcal {A}):={{\mathrm{End}}}_{\mathcal {A}}\left( \fancyscript{M}(\mathcal {A})\right) ^{op},{}_{\mathcal {B}(\mathcal {A})}\fancyscript{M}(\mathcal {A})\bigr ] \end{array} \qquad and \qquad \begin{array}{ccl} \mathbf Y &{} \mathop {\longrightarrow }\limits ^{\Psi } &{} \mathbf X \\ \left[ \mathcal {B},\fancyscript{G}\right] &{} \mapsto &{} \left[ {{\mathrm{End}}}_{\mathcal {B}}(\fancyscript{G})^{op}\right] \end{array}, \end{aligned}$$

such that $\Psi \circ \Phi = {{\mathrm{Id}}}_\mathbf{X }$ and $\Phi \circ \Psi = {{\mathrm{Id}}}_\mathbf{Y }$.

This theorem also provides correspondences between the subsets of $\mathbf X$ and their image under $\Phi$ in $\mathbf Y$. By the Theorem of König et al. [10, Theorem 1.3] the algebras of blocks of the BGG-categoy $\mathcal {O}$ as well as Schur algebras $S(n,r)$ (with $n>r$) have dominant dimension at least two. The Theorem  2.1 covers this kind of algebras. Especially the module $\fancyscript{M}(\mathcal {A})$ has the double centralizer condition.

Note that the Theorem of Morita–Tachikawa provides some connections between a finite dimensional algebra $\mathcal {A}=KQ/\mathcal {I}$ with ${{\mathrm{dom.dim}}}\mathcal {A}\ge 2$ and a pair $(\mathcal {B},\fancyscript{G})$ with $\Phi [A]=[\mathcal {B},\fancyscript{G}]$. Because $\mathcal {A}\hookrightarrow \fancyscript{M}(\mathcal {A})^m$ for some $m\in \mathbb {N}$, we have $[\fancyscript{M}(\mathcal {A}):S(i)]\ne 0$ and consequently ${{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\fancyscript{M}(\mathcal {A}))\ne 0$ for all $i\in \Lambda (=Q_0)$. Obviously $\mathcal {B}\cong {{\mathrm{End}}}_{\mathcal {A}}(\fancyscript{M}(\mathcal {A}))^{op}$ and ${}_{\mathcal {B}}\fancyscript{M}(\mathcal {A})\cong \bigoplus _{i\in \Lambda }{{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\fancyscript{M}(\mathcal {A}))$. Since $\mathcal {A}\cong {{\mathrm{End}}}_{\mathcal {B}}({}_{\mathcal {B}}\fancyscript{M}(\mathcal {A}))^{op}$ is basic, the number of vertices of the quiver of $\mathcal {A}$ is the number of indecomposable summands of ${}_{\mathcal {B}}\fancyscript{M}(\mathcal {A})$. Therefore ${{\mathrm{Hom}}}_{\mathcal {A}}(P(i),\fancyscript{M}(\mathcal {A}))$ is indecomposable for any $i\in \Lambda$. The $\mathcal {B}$-module $\fancyscript{G}$ has $\left| \Lambda \right|$ pairwise non-isomorphic, indecomposable direct summands.

2.2 Quasi-hereditary algebras and local self-injective algebras

In this paper we consider a subclass of quasi-hereditary algebras with dominant dimension at least 2 which are related to local self-injective algebras. We recall some definitions.

Quasi-hereditary algebras were defined by Cline et al. in [2]. We use the equivalent definition and terminology given by Dlab and Ringel in [4]: Let $\mathcal {A}$ be a bound quiver algebra and $(\Lambda ,\leqslant )$ a poset (so $\Lambda$ is the set of vertices). For every $i\in \Lambda$ the standard module $\Delta (i)$ is the largest factor module of $P(i)$ such that $[\Delta (i):S(k)]=0$ for all $k\in \Lambda$ with $k\not \leqslant i$. We denote by $\mathfrak {F}(\Delta )$ the full subcategory of ${{\mathrm{mod}}}\mathcal {A}$ consisting of modules having a filtration such that each subquotient is isomorphic to a standard module. The modules in $\mathfrak {F}(\Delta )$ are called $\Delta$-good and these filtrations are $\Delta$-good filtrations. For $M\in \mathfrak {F}(\Delta )$ we denote by $\left( M:\Delta (i)\right)$ the (well-defined) number of subquotients isomorphic to $\Delta (i)$ in a $\Delta$-good filtration of $M$.

An algebra $\mathcal {A}$ with $(\Lambda ,\leqslant )$ is quasi-hereditary if for all $i,k\in \Lambda$ the following conditions are satisfied:

• $[\Delta (i):S(i)]=1$,

• $P(i)$ is a $\Delta$-good module with $\left( P(i):\Delta (k)\right) =0$ for all $k\not \geqslant i$ and $\left( P(i):\Delta (i)\right) =1$.

Throughout, $(\mathcal {A},\leqslant )$ denotes an algebra $\mathcal {A}$ with a partial order $\leqslant$ on $\Lambda$.

We can identify the vertices of the quivers of $\mathcal {A}$ and $\mathcal {A}^{op}$. An algebra $(\mathcal {A},\leqslant )$ is quasi-hereditary if and only if $\left( \mathcal {A}^{op},\leqslant \right)$ is quasi-hereditary (see [4]). The standard duality $\mathcal {D}:={{\mathrm{Hom}}}_K(-,K)$ provides the costandard $\mathcal {A}$-module $\nabla (i)\cong \mathcal {D}(\Delta _{\mathcal {A}^{op}}(i))$ corresponding to $i\in \Lambda$ and also the subcategory $\mathfrak {F}(\nabla )$ of ${{\mathrm{mod}}}\mathcal {A}$ of all $\nabla$-good modules.

We recall the definition of a 1-quasi-hereditary algebra from [11] and we will show that the dominant dimension of them is at least two. To distinguish between an arbitrary algebra $\mathcal {A}$ and a 1-quasi-hereditary algebra, we denote the latter by $A$.

Definition 2.2

(1-Quasi-hereditary) A quasi-hereditary algebra $A$ with $(\Lambda ,\leqslant )$ is called 1-quasi-hereditary if for all $i,j\in \Lambda =\left\{ 1, \ldots , n\right\}$ the following conditions are satisfied:

• (1) There is a smallest and a largest element with respect to $\leqslant$, without loss of generality we will assume them to be $1$ and $n$, respectively,

• (2) $[\Delta (i):S(j)]=\big (P(j):\Delta (i)\big )=1$ for $j\leqslant i$,

• (3) ${{\mathrm{soc}}}P(j) \cong {{\mathrm{top}}}I(j)\cong S(1)$,

• (4) $\Delta (i) \hookrightarrow \Delta (n)$ and $\nabla (n)\twoheadrightarrow \nabla (i).$

Proposition 2.3

Let $(\mathcal {A},\leqslant )$ be a quasi-hereditary algebra and let $I$ be a projective-injective $\mathcal {A}$-module. For any $i\in \Lambda$ assume that

• ${{\mathrm{soc}}}(\Delta (i))\in {{\mathrm{add}}}\left( {{\mathrm{soc}}}I\right)$ and

• $P(i)\hookrightarrow I$ with $I/P(i)\in \mathfrak {F}(\Delta )$.

Then ${{\mathrm{dom.dim}}}\mathcal {A}\ge 2$.

Proof

Let $0=D_0\subset D_1\subset \cdots \subset D_r=I/P(i)$ be a $\Delta$-good filtration with $D_k/D_{k-1}\cong \Delta (j_k)$. Then ${{\mathrm{soc}}}\left( I/P(i)\right) \in {{\mathrm{add}}}\left( \bigoplus _{k=1}^r{{\mathrm{soc}}}(\Delta (j_k))\right) \subseteq {{\mathrm{add}}}\left( {{\mathrm{soc}}}I\right)$. Therefore $I/P(i)$ can be embedded into some copies of $I$ for any $i\in \Lambda$. There exists an exact sequence $0\rightarrow P(i)\rightarrow I\rightarrow I^{r(i)}$ for some $r(i)\in \mathbb {N}$. Since ${}_{\mathcal {A}}\mathcal {A}\cong \bigoplus _{i\in \Lambda }P(i)$, there exist $m,r\in \mathbb {N}$ such that the sequence $0\rightarrow {}_{\mathcal {A}}\mathcal {A}\rightarrow I^m\rightarrow I^r$ is exact. $\square$

Lemma 2.4

Let $(A,\leqslant )$ be a 1-quasi-hereditary algebra with $\left\{ 1\right\} =\min (\Lambda ,\leqslant )$. Then $P(1)$ is a minimal faithful $A$-module and ${{\mathrm{dom.dim}}}A\ge 2$.

Proof

According to [11, 2.6] we have $P(1)\cong I(1)$ and $\Delta (i)\hookrightarrow P(i)\hookrightarrow P(1)$ for every $i\in \Lambda$. Thus we have ${{\mathrm{soc}}}\Delta (i)\in {{\mathrm{add}}}\left( {{\mathrm{soc}}}I(1)\right)$. Moreover, $P(1)/P(i)\in \mathfrak {F}(\Delta )$ for any $i\in \Lambda$ (see [11, 4.3]). Therefore ${{\mathrm{dom.dim}}}A\ge 2$ according to Proposition 2.3.

In particular, $P(1)$ is a minimal faithful $A$-module because $P(1)$ is indecomposable, and ${}_AA\hookrightarrow P(1)^{\left| \Lambda \right| }$. We have $\fancyscript{M}(A)\cong P(1)$. $\square$

To distinguish between an arbitrary algebra and a local, self-injective algebra, we denote the latter by $B$. Recall that an (finite dimensional, basic) algebra $B$ is local and self-injective if and only if the socle and the top of ${}_{B}B$ are simple. An ideal $I$ of $B$ is a two-sided, local ideal if $B \cdot I \subseteq I$ as well as $I\cdot B\subseteq I$ and ${{\mathrm{rad}}}(I)$ is the unique maximal submodule of $I$.

Definition 2.5

${(\boxed {\leqslant })}$. Let $B$ be an algebra, $L\in {{\mathrm{mod}}}B$ and $\left( \Lambda =\left\{ 1,\ldots ,n\right\} ,\leqslant \right)$ be a poset. We say that the pair $(B,L)$ satisfies the condition $\boxed {\leqslant }$ if

• (1) $B$ is a local, self-injective algebra, ${{\mathrm{dim}}}_K B=n$,

• (2) $\displaystyle L= \bigoplus \nolimits _{i\in \Lambda }^{} L(i)$, where $L(1),\ldots , L(n)$ are two-sided local ideals of $B$ such that $L(1)=B$ and for all $i, j\in \Lambda$ the following is satisfied:

  • (a) $L(i)\twoheadrightarrow L(j)$ if and only if $i\leqslant j$,          (b) $\displaystyle {{\mathrm{rad}}}\left( L(i)\right) =\sum \nolimits _{i<j}L(j)$.

If $(B,L)$ satisfies the condition $\boxed {\leqslant }$, then $[B,L]\in \mathbf Y$: Since $B$ is local and self-injective, any projective (resp. injective) indecomposable $B$-module is isomorphic to $_{B}B$. Hence $L$ is a generator–cogenerator of ${{\mathrm{mod}}}B$, because ${}_BB (=L(1))$ is a direct summand of $L$. The condition $(a)$ implies $L(i)\cong L(j)$ if and only if $i=j$, therefore $L$ is multiplicity-free. The quiver of $B$ consists of one vertex and finitely many loops. To distinguish between an arbitrary generator–cogenerator $\fancyscript{G}$ of ${{\mathrm{mod}}}B$ and a generator–cogenerator related to $\boxed {\leqslant }$, we denote the latter by $L$.

It should be noted that for a fixed local, self-injective algebra $B$, the poset $(\Lambda ,\leqslant )$ and the $B$-module $L$ which satisfy the condition $\boxed {\leqslant }$ are not uniquely determined.

Example 2.6

The algebra $B=\mathbb {C}[x,y]/\left\langle xy, \ x^3-y^3\right\rangle$ is local and self-injective with ${{\mathrm{dim}}}_{\mathbb {C}}B=6$. The next diagrams present the partial orders $\leqslant _{(k)}$ on $\Lambda =\left\{ 1,\ldots , 6\right\}$ and the generators-cogenerators $L_k=\bigoplus _{i=1}^6L_k(i)$ of ${{\mathrm{mod}}}B$ for $k=1,2,3.$ The arrow $L_{k}(i)\rightarrow L_{k}(i')$ means $i <_{(k)}i'$ and $i,i'$ are neighbours. In the diagram on the right-hand side, $\omega = \frac{1}{2}+\mathtt i \frac{\sqrt{3}}{2}$ is a 6th root of unity, where $\mathtt i ^2=-1$.

It is easy to check that $(B,L_k)$ satisfies the condition $\boxed {\leqslant _{(k)}}$. Therefore, $[B,L_{k}]\in \mathbf Y$. In view of Theorem A, the module $L_{k}$ is an $A_k$-$B$-bimodule, where $A_k={{\mathrm{End}}}_B(L_{k})^{op}$ is a 1-quasi-hereditary algebra for $k=1,2,3$. Note that the algebra $A_3$ is associated to a regular block of the ${{\mathrm{BGG}}}$-category $\mathcal {O}(\mathfrak {sl}_3)$. The quiver and relations of $A_3$ are presented in  [12, Example 1].

The Morita–Tachikawa Theorem  2.1 and Lemma  2.4 yield that for any 1-quasi-hereditary algebra $A$ there exists an (up to isomorphism) uniquely determined pair $(\mathcal {B},\fancyscript{G})$ with $A\cong {{\mathrm{End}}}_{\mathcal {B}}(\fancyscript{G})^{op}$, where $\mathcal {B}$ is an algebra and $\fancyscript{G}$ a generator–cogenerator of ${{\mathrm{mod}}}\mathcal {B}$. In other words when $A\cong {{\mathrm{End}}}_{\mathcal {B}}(\fancyscript{G})^{op}$ for some generator–cogenerator $\fancyscript{G}$ of ${{\mathrm{mod}}}\mathcal {B}$, then $A$ and $\mathcal {B}$ are related by double centralizer properties.

In the next section we prove Theorem A which can be rewritten as follows:

Theorem A. Let $A$, $B$ be finite dimensional basic $K$-algebras and $n\in \mathbb {N}$. Moreover, let $\left( \Lambda :=\left\{ 1,\ldots , n\right\} ,\leqslant \right)$ be partially ordered. The following statements are equivalent:

• (i) The algebra $(A,\leqslant )$ is 1-quasi-hereditary, i.e., $A\cong {{\mathrm{End}}}_B(L)^{op}$ and $L$ is a (multiplicity-free) generator–cogenerator of ${{\mathrm{mod}}}B$,

• (ii) The pair $(B,L)$ satisfies the condition $\boxed {\leqslant }$.

Theorem A provides bijections between the isomorphism classes of 1-quasi-hereditary algebras and the pairs defined in  2.5. In the Example 2.6 the algebra $B$ is commutative. In the next subsection we consider this situation. In general $B$ does not have to be commutative.

Example 2.7

Let $n\ge 3$ and $C=\left( c_{ij}\right) _{2\le i,j\le n-1}\in \hbox {GL}_{n-2}(K)$. We define $B:= B_n(C)= K\left\langle x_2,\ldots , x_{n-1}\right\rangle /\mathtt I$ with $\mathtt I := \left\langle \left\{ c_{mk}\cdot x_i\cdot x_j-c_{ij}\cdot x_m\cdot x_k, \ \ x_i^3 \mid 2\le j,i,k,m\le n-1\right\} \right\rangle$.

Let $X_k=x_k+\mathtt I$ for any $k\in \Gamma := \left\{ 2,\ldots ,n-1\right\}$. Since $\hbox {det} \ C\ne 0$, for every $i\in \Gamma$ there exist $l(i),r(i)\in \Gamma$ such that $c_{l(i)i}\ne 0$ and $c_{ir(i)}\ne 0$, therefore $c_{l(j)j} X_{i} X_{r(i)} =c_{ir(i)} X_{l(j)} X_j$ Furthermore, we have $c_{ik}=0$ iff $X_iX_k=0$. For any $j\in \Lambda$ there exists $\lambda _j\in K$ such that $X_iX_j= \lambda _j X_iX_{r(i)}$. Since $X_m^3=0$ for all $m\in \Gamma$, we have $X_i X_j X_k=0$ for all $i,j,k\in \Gamma$.  Thus

$$\begin{aligned} \left\langle X_i\right\rangle = B\cdot X_i={{\mathrm{span}}}_K\left\{ X_i,X_{l(i)} X_i\right\} ={{\mathrm{span}}}_K\left\{ X_i,X_i X_{r(i)}\right\} =X_i\cdot B \end{aligned}$$

is a two-sided local ideal of $B$ and ${{\mathrm{soc}}}B= \left\langle X_{i} X_{r(i)}\right\rangle$ for all $i\in \Gamma$. The algebra $B$ is self-injective and ${{\mathrm{dim}}}_KB=n$. Let $\left( \Lambda =\left\{ 1,\ldots , n\right\} ,\leqslant \right)$ be the poset given by $1\triangleleft i\triangleleft n$ for all $2\le i\le n-1$ and let the $B$-module $L:= \bigoplus _{i=1}^{n} L(i)$ be given by $L(1)=B$, $L(i)=\left\langle X_i\right\rangle$ for all $i\in \Gamma$ and $L(n)={{\mathrm{soc}}}B$. The pair $(B,L)$ satisfies the property $\boxed {\leqslant }$. The quiver and relations of the 1-quasi-hereditary algebra $A_{n}(C):={{\mathrm{End}}}_B(L)^{op}$ can by found in [12, Example 3]. The algebra $B$ is commutative if and only if $C=C^{t}$.

2.3 BGG-algebras

We refer to the definition of ${{\mathrm{BGG}}}$-algebras given by Xi in [18]: A quasi-hereditary algebra $\mathcal {A}$ is called a BGG-algebra if there is a duality $\delta$ of ${{\mathrm{mod}}}\mathcal {A}$ such that $\delta (S(i))\cong S(i)$ for all $i\in Q_0(\mathcal {A})$.

Recall that an anti-automorphism $\bar{\epsilon }:\mathcal {A}\rightarrow \mathcal {A}$ of $\mathcal {A}$ is a $K$-map such that $\bar{\epsilon } (a\cdot a')=\bar{\epsilon }(a')\cdot \bar{\epsilon }(a)$ and $\bar{\epsilon }^2(a)=a$ for all $a,a'\in \mathcal {A}$.

Moreover, Xi has shown that if there is an anti-automorphism $\bar{\epsilon }$ of $\mathcal {A}$ such that $\mathcal {A}\cdot \bar{\epsilon }(e_i)\cong \mathcal {A}\cdot e_i$ for all $i\in Q_0(\mathcal {A})$, then $\mathcal {A}$ is a ${{\mathrm{BGG}}}$-algebra (see [18, Theorem 1.5]).

We recall some properties of 1-quasi-hereditary algebras which we need. According to [11, Theorem 2.7], the quiver $Q(A)$ of a 1-quasi-hereditary algebra $(A,\leqslant )$ is the double of the quiver of the incidence algebra of $(\Lambda ,\leqslant )$: Let $i,j\in \Lambda$, we write

$$\begin{aligned} i \triangleleft j\hbox { and }i\triangleright j \end{aligned}$$

if $i$ is a smaller neighbour of $j$ and $i$ is a larger neighbour of $j$, respectively. We have $\left| \left\{ \alpha \in Q_1(A)\mid i\mathop {\rightarrow }\limits ^{\alpha }j\right\} \right| = \left\{ \begin{array}{cl} 1 &{} \hbox {if } i\triangleleft j, \\ 1 &{} \hbox {if } i\triangleright j, \\ 0 &{} \hbox {else.} \end{array} \right.$

Thus for any path $p=(i_1\rightarrow i_2 \rightarrow \cdots \rightarrow i_m)$ there exists a uniquely determined path $p^{op}:=(i_m \rightarrow \cdots \rightarrow i_2 \rightarrow i_1)$ in $Q(A)$ running

through the same vertices in the opposite direction. Obviously, $(p^{op})^{op}=p$. Since the set of paths is a $K$-basis of $KQ$, the map $p\mapsto p^{op}$ can be lifted to the $K$-linear map $\epsilon : KQ \rightarrow KQ$. Note that in general $\epsilon$ do not induces a $K$-map $\bar{\epsilon }:A\rightarrow A$ given by $\bar{\epsilon }(p+\mathcal {I})=p^{op}+\mathcal {I}$. In the Example 2.7 for the algebra $A:=A_4(C)$ with $C= {\left( \begin{array}{cc} 1 &{} q \\ 0 &{} 1 \end{array} \right) }$ and $q \ne 0$, we have that the residue class of the path $p=(3\rightarrow 1\rightarrow 2)$ is zero, but the residue class of $p^{op}$ is non-zero.  In general, 1-quasi-hereditary algebras are not BGG-algebras  (see [12, Example 3]).

Definition 2.8

We say that a 1-quasi-hereditary algebra $A=KQ/\mathcal {I}$ is a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$ -algebra, if the map $\bar{\epsilon }:A\rightarrow A$ with $\bar{\epsilon }(p+\mathcal {I})=p^{op}+\mathcal {I}$, induced by $K$-map $KQ \rightarrow KQ$, $p\mapsto p^{op}$, is an anti-automorphism of $A$.

It should be noted that it is not known in general whether a duality $\delta$ of ${{\mathrm{mod}}}\mathcal {A}$ comes from an anti-automorphism of $\mathcal {A}$. It is also not known how an anti-automorphism with the properties in [18, Theorem 1.5] does look like (the condition $\mathcal {A}\cdot \bar{\epsilon }(e_i)\cong \mathcal {A}\cdot e_i$ does not imply $\bar{\epsilon }(e_i)=e_i$). It is not known in general whether a 1-quasi-hereditary BGG-algebra is a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$-algebra. In the Example  2.7 the algebra $A_n(C)$ is a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$-algebra if and only if $C=C^{\hbox {tr}}$.

Theorem B. Let $A\cong {{\mathrm{End}}}_B(L)^{op} \cong KQ/\mathcal {I}$ with $(\Lambda ,\leqslant )$ be a 1-quasi-hereditary algebra such that $(B,L)$ satisfies the condition $\boxed {\leqslant }$. The following statements are equivalent:

• (i) $B$ is commutative.

• (ii) $A$ is a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$-algebra.

• (iii) $\displaystyle \sum \nolimits _{t=1}^{r}c_t\cdot p_t\in \mathcal {I}$ if and only if $\displaystyle \sum \nolimits _{t=1}^{r}c_t \cdot p_t^{op} \in \mathcal {I}$.

Note that for a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$-algebra $A=KQ/\mathcal {I}$ there exists a set $\mathfrak {R}$ of relations generating $\mathcal {I}$ such that $\rho \in \mathfrak {R}$ implies $\rho ^{op}\in \mathfrak {R}$. This set can be written as $\mathfrak {R}= \mathfrak {R}_0\dot{\cup } \mathfrak {R}_1\dot{\cup } \mathfrak {R}_2$, where the starting and ending vertex of the paths $p_t$ in a relation $\rho =\sum _{t=1}^{r}c_t\cdot p_t$ of $\mathfrak {R}_0$ is the same. The paths of a relation in $\mathfrak {R}_1$ start and end in different vertices such that $\mathfrak {R}_2=\left\{ \rho ^{op}\mid \rho \in \mathfrak {R}_1\right\}$.

Dlab, Heath and Marko have shown in [3] that if for a commutative algebra $B$ and a $B$-module $L$ the pair $(B,L)$ satisfies the condition $\boxed {\leqslant }$, then the algebra ${{\mathrm{End}}}_B(L)^{op}$ is a ${{\mathrm{BGG}}}$-algebra as defined by Irving in [8]. Our Theorem B provides a strong form of the main Theorem [3].

The correspondence between the isomorphism classes of 1-quasi-hereditary algebras and the pairs satisfying the property $\boxed {\leqslant }$ is a restriction of the Morita–Tachikawa correspondence  2.1 which is unrelated to the statements of Theorems A and B. For the subsets $\mathbf X (1)\!:=\!\left\{ [A]\mid A \hbox { is a 1-quasi-hereditary algebra}\right\}$, $\mathbf X '\!:=\!\left\{ [A]\mid A\hbox { is a }{{\mathrm{BGG}}}_{(\leftrightarrows )}\hbox {-algebra}\right\}$ and $\mathbf Y (1)\!:=\!\left\{ [B,L]\!\mid \! (B,L) \hbox { has the property } \, \boxed {\leqslant } \right\} , \mathbf Y '\!:=\! \left\{ [B,L]\!\in \! \mathbf Y (1)\! \mid \! B\hbox {is commutative}\right\}$ of $\mathbf X$ and $\mathbf Y$, respectively, (defined in  2.1) we have $\Phi \left( \mathbf X (1)\right) =\mathbf Y (1)$ and $\Psi \left( \mathbf Y (1)\right) =\mathbf X (1)$ as well as $\Phi \left( \mathbf X '\right) =\mathbf Y '$ and $\Psi \left( \mathbf Y '\right) =\mathbf X '$. The function $\Phi$ restricted to $\mathbf X (1)$ maps $[A,\leqslant ]$ to $\left[ {{\mathrm{End}}}_A(P(1))^{op},P(1)\right]$, where $\left\{ 1\right\} =\min (\Lambda ,\leqslant )$. The relation between $\mathbf X (1)$ and $\mathbf Y (1)$ as well as $\mathbf X '$ and $\mathbf Y '$ yields the precise version of the Morita–Tachikawa correspondence. It may be visualised as follows.

3 Proof of the Theorem A

In this section let $(\Lambda ,\leqslant )$ be a poset. Until the end of this paper for any $j\in \Lambda$ we denote by $\Lambda _{(j)}$ and $\Lambda ^{(j)}$ the following subsets of $\Lambda$:

$$\begin{aligned} \Lambda _{(j)}{:=}\left\{ i\in \Lambda \mid i\leqslant j\right\} \hbox { and }\ \Lambda ^{(j)}:=\left\{ i\in \Lambda \mid i\geqslant j\right\} . \end{aligned}$$

We also adopt all notation of the previous section.

3.1 Proof of the Theorem A $(i)\Rightarrow (ii)$

In this subsection the algebra $A$ with the ordering $(\Lambda ,\leqslant )$ denotes a 1-quasi-hereditary algebra. We assume $1$ is the unique minimal element in $(\Lambda ,\leqslant )$. Then $P(1)$ is a minimal faithful $A$-module, and Morita–Tachikawa Theorem 2.1 as well as Lemma  2.4 imply that for any $[\mathcal {B},\fancyscript{G}]\in \mathbf Y$ with $A\cong {{\mathrm{End}}}_{\mathcal {B}}\left( \fancyscript{G}\right) ^{op}$ we obtain $\mathcal {B}\cong {{\mathrm{End}}}_A(P(1))^{op}$ and $\fancyscript{G}\cong {}_{{{\mathrm{End}}}_A(P(1))^{op}}P(1) \cong \bigoplus _{k\in \Lambda } {{\mathrm{Hom}}}_A(P(k),P(1))$. Until the end of this section we write

$$\begin{aligned} B={{\mathrm{End}}}_A(P(1))^{op} \hbox { and }\ \fancyscript{G}(k)= {{\mathrm{Hom}}}_A(P(k),P(1))\hbox { for any }k\in \Lambda . \end{aligned}$$

Remark 3.1

We recall some notations and properties of 1-quasi-hereditary algebras from [11] and [12]: Let $Q$ be the quiver of $A$ and $\mathcal {I}$ be the corresponding ideal of $KQ$ generated by the relations of $A$. The structure of $Q$ (see Subsection 1.3.2) shows that for all $j,i,k \in \Lambda$ with $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$ there exists a path $(j\rightarrow \lambda _1\rightarrow \cdots \rightarrow \lambda _m\rightarrow i)$ with $j\leqslant \lambda _1\leqslant \cdots \leqslant \lambda _m\leqslant i$ and a path $(i\rightarrow \mu _1\rightarrow \cdots \rightarrow \mu _r\rightarrow k)$ with $i\geqslant \mu _1\geqslant \cdots \geqslant \mu _m\geqslant k$. We write $p^{\uparrow }(j,i)$ resp. $p^{\downarrow }(i,k)$ for the residue class $A$ of a such path. If $i\ne j$ then a path of the form $p^{\uparrow }(j,i)$ runs strictly increasing from $j$ to $i$ and $p^{\downarrow }(i,j)$ runs strictly decreasing from $i$ to $j$ (the arrows $\downarrow$ and $\uparrow$ in the notations accent the shape of these paths). The concatenation of these two paths is denoted by $p(j,i,k)=p^{\downarrow }(i,k)\cdot p^{\uparrow }(j,i)$. For any $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$ we fix a path of the form $p^{\uparrow }(j,i)$ and $p^{\downarrow }(i,k)$. Note that for $i=k$ we have $p(j,i,k)=p^{\uparrow }(j,i)$, and for $j=i$ we have $p(j,i,k)= p^{\downarrow }(i,k)$. By $\mathfrak {f}^{\uparrow }_{(j,i)}$, $\mathfrak {f}^{\downarrow }_{(i,k)}$ and $\mathfrak {f}_{(j,i,k)}$ we denote the $A$-maps corresponding to $p^{\uparrow }(j,i)$, $p^{\downarrow }(i,k)$ and $p(j,i,k)$ respectively. In particular, the map $\mathfrak {f}^{\uparrow }_{(j,i)}$ is injective (see [11, 3.1(a)]).

$$\begin{aligned} \mathfrak {f}_{(j,i,k)}=\mathfrak {f}^{\uparrow }_{(j,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)}:\left( P(k) \mathop {\longrightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(i,k)}} P(i) \mathop {\hookrightarrow }\limits ^{\mathfrak {f}^{\uparrow }_{(j,i)}} P(j)\right) ;\ \ e_k\!\mapsto \! p(j,i,k)\!=\!p^{\downarrow }(i,k)\cdot p^{\uparrow }(j,i). \end{aligned}$$

Remark 3.2

According to [11, Theorem 3.2], the set $\left\{ p(j,i,k)\mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\}$ is a $K$-basis of the $K$-subspace $P(j)_k$ of $P(j)$, thus for all $j,k\in \Lambda$ we have

• (1) $\left\{ \mathfrak {f}_{(j,i,k)} \mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\}$ is a $K$-basis of ${{\mathrm{Hom}}}_A(P(k),P(j))$.

• (2) $\displaystyle \dot{\bigcup _{k\in \Lambda }}\left\{ \mathfrak {f}_{(1,i,k)} \mid i\in \Lambda ^{(k)}\right\}$ is a $K$-basis of the $B$-module $\displaystyle {}_BP(1) \cong \bigoplus _{k\in \Lambda }{{\mathrm{Hom}}}_A(P(k),P(1))$.

The proof of of Theorem A 1.2.6 $(i)\Rightarrow (ii)$ is based on the following properties of $B$-modules generated by the maps $\mathfrak {f}_{(1,i,k)}$.

Lemma 3.3

Let $i\in \Lambda$. The following statements hold.

• (1) $B\circ \mathfrak {f}_{(1,i,k)}={{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,k)}\mid t\in \Lambda ^{(i)}\right\}$ where $k\in \Lambda _{(i)}$.

• (2) $B \circ \mathfrak {f}^{\uparrow }_{(1,i)} \cong B \circ \mathfrak {f}_{(1,i,1)}$.

• (3) $B\circ \mathfrak {f}_{(1,i,1)} = \mathfrak {f}_{(1,i,1)} \circ B = {{\mathrm{span}}}_{K}\left\{ \mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\right\}$.

Proof

(1) We have $F \circ \mathfrak {f}^{\uparrow }_{(1,i)}\in {{\mathrm{Hom}}}_A(P(i),P(1)) \mathop {\in }\limits ^{2.1.2(1)} {{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,i)}\mid t\in \Lambda ^{(i)}\right\}$ for any $F\in B$. Thus $F\circ \mathfrak {f}^{\uparrow }_{(1,i)} = \sum _{t\in \Lambda ^{(i)}} c_t\cdot \mathfrak {f}_{(1,t,i)}$ for some $c_t\in K$. Since $p(1,t,k)=p^{\downarrow }(i,k)\cdot p(1,t,i)$, this implies $\mathfrak {f}_{(1,t,k)}= \mathfrak {f}_{(1,t,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)}$ (we may visualise the situation as in the following picture).

Thus we obtain $B\circ \mathfrak {f}_{(1,i,k)} \subseteq {{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,k)} \mid t\in \Lambda ^{(i)}\right\}$ because

$$\begin{aligned} F \circ \mathfrak {f}_{(1,i,k)}&= \displaystyle F\circ \left( \mathfrak {f}^{\uparrow }_{(1,i)} \circ \mathfrak {f}^{\downarrow }_{(i,k)}\right) = \sum \limits _{t\in \Lambda ^{(i)}} c_t\cdot \left( \mathfrak {f}_{(1,t,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)} \right) \\&= \displaystyle \sum \limits _{t\in \Lambda ^{(i)}} c_t\cdot \mathfrak {f}_{(1,t,k)}\in {{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,k)} \mid t\in \Lambda ^{(i)}\right\} \end{aligned}$$

Since $\mathfrak {f}^{\uparrow }_{(1,i)}:P(i)\hookrightarrow P(1)\cong I(1)$, the universal property of injective modules implies that for any $t\in \Lambda ^{(i)}$ there exists $F(t)\in B$ such that $F(t)\circ \mathfrak {f}^{\uparrow }_{(1,i)} = \mathfrak {f}_{(1,t,i)}$. Let $k\in \Lambda _{(i)}$, then $\mathfrak {f}^{\uparrow }_{(1,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)} = \mathfrak {f}_{(1,i,k)}$ provides the commutative diagram

$$\begin{aligned} \begin{array}{rcclccc} \mathfrak {f}_{(1,t,k)}:&{} P(k)&{} \mathop {\longrightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(i,k)}} &{} P(i)&{} \mathop {\longrightarrow }\limits ^{\mathfrak {f}_{(1,t,i)}} &{} P(1) &{} \\ &{} || &{} &{} \ \ \downarrow \overset{\mathfrak {f}^{\uparrow }_{(1,i)}}{}&{} &{} || &{} \\ F(t)\circ \mathfrak {f}_{(1,i,k)}:&{} P(k)&{} \mathop {\longrightarrow }\limits ^{\mathfrak {f}_{(1,i,k)}} &{} P(1) &{} \mathop {\longrightarrow }\limits ^{F(t)}&{} P(1) &{} \end{array} \end{aligned}$$

$F(t)\circ \mathfrak {f}_{(1,i,k)} = \mathfrak {f}_{(1,t,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)}=\mathfrak {f}_{(1,t,k)}$ for any $t\in \Lambda ^{(i)}$ implies $B\circ \mathfrak {f}_{(1,i,k)}\supseteq {{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,k)}\mid t\in \Lambda ^{(i)}\right\}$.

(2) We consider the map $\left( -\circ \mathfrak {f}^{\downarrow }_{(i,1)}\right) : B \circ \mathfrak {f}^{\uparrow }_{(1,i)} \rightarrow B \circ \mathfrak {f}_{(1,i,1)}$, $F\circ \mathfrak {f}^{\uparrow }_{(1,i)} \mapsto F \circ \mathfrak {f}_{(1,i,1)}$. Obviously, this map is a surjective $B$-map. The set $\left\{ \mathfrak {f}_{(1,t,k)} \mid t\in \Lambda ^{(i)}\right\}$ (as a subset of a $K$-basis) is $K$-independent for any $k\in \Lambda _{(i)}$ (see  3.2(1)). Thus for $k=1$ and $k=i$ we have ${{\mathrm{dim}}}_K\left( B \circ \mathfrak {f}^{\uparrow }_{(1,i)}\right) \mathop {=}\limits ^{\textit{(1)}} {{\mathrm{dim}}}_K\left( B \circ \mathfrak {f}_{(1,i,1)}\right) = \left| \Lambda ^{(i)}\right|$. This implies $B \circ \mathfrak {f}^{\uparrow }_{(1,i)} \cong B \circ \mathfrak {f}_{(1,i,1)}$.

(3) Since $B \circ \mathfrak {f}_{(1,i,1)} \mathop {=}\limits ^{\textit{(1)}} {{\mathrm{span}}}_{K}\big \{\mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\big \}$, it is enough to show $\mathfrak {f}_{(1,i,1)} \circ B = {{\mathrm{span}}}_{K}\big \{\mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\big \}$: We have $\mathfrak {f}^{\downarrow }_{(i,1)}\circ F\in {{\mathrm{Hom}}}_A\left( P(1),P(i)\right) \mathop {=}\limits ^{2.1.2}{{\mathrm{span}}}_K\big \{\mathfrak {f}_{(i,t,1)}\mid t\in \Lambda ^{(i)}\big \}$ for all $F\in B$. With similar arguments as in the proof of (1) we obtain $\mathfrak {f}_{(1,t,1)}=\mathfrak {f}^{\uparrow }_{(1,i)}\circ \mathfrak {f}_{(i,t,1)}$. This yields $\mathfrak {f}_{(1,i,1)}\circ F =\mathfrak {f}^{\uparrow }_{(1,i)} \circ \left( \mathfrak {f}^{\downarrow }_{(i,1)} \circ F\right) \in {{\mathrm{span}}}_K\big \{\mathfrak {f}^{\uparrow }_{(1,i)}\circ \mathfrak {f}_{(i,t,1)} \mid t\in \Lambda ^{(i)}\big \}= {{\mathrm{span}}}_K\left\{ \mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\right\}$ for every $F\in B$. We obtain $\mathfrak {f}_{(1,i,1)} \circ B \subseteq {{\mathrm{span}}}_{K}\left\{ \mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\right\}$.

The $A$-module $A\cdot p(1,t,1)$ is a submodule of $A\cdot p(1,i,1)$ for any $t\in \Lambda ^{(i)}$ (see [12], 2.2 (a)]). There exists $p(t)\in P(1)_1$ with $p(1,t,1)=p(t)\cdot p(1,i,1)$. Let $F(t)\in B$ be given by $F(t)(e_1)=p(t)$, then $\mathfrak {f}_{(1,t,1)} = \mathfrak {f}_{(1,i,1)}\circ F(t)$. Thus $\mathfrak {f}_{(1,i,1)} \circ B \supseteq {{\mathrm{span}}}_{K}\left\{ \mathfrak {f}_{(1,t,1)} \mid t\in \Lambda ^{(i)}\right\}$.

$\square$

For the implication $(i)\Rightarrow (ii)$ in Theorem A we have to show that the pair $(B,\bigoplus _{i\in \Lambda } \fancyscript{G}(i))$ satisfies the property  $\boxed {\leqslant }$, where $\fancyscript{G}(i)={{\mathrm{Hom}}}_A(P(i),P(1))$. We have to show

• 1. The algebra $B$ is local, self-injective, and ${{\mathrm{dim}}}_KB=\left| \Lambda \right|$.

• 2. $\fancyscript{G}(j) \twoheadrightarrow \fancyscript{G}(i)$ if and only if $j\leqslant i$, and ${}_BB\in \left\{ \fancyscript{G}(i) \mid i\in \Lambda \right\}$.

• 3. $\fancyscript{G}(i) = B \circ \mathfrak {f}^{\uparrow }_{(1,i)}$ for any $i\in \Lambda$.

• 4. $\displaystyle {{\mathrm{rad}}}\left( B \circ \mathfrak {f}_{(1,i,1)}\right) =\sum \nolimits _{i<t}\left( B \circ \mathfrak {f}_{(1,t,1)}\right)$ for any $i\in \Lambda$.

Recall that an (left) ideal $I$ of an (basic local) algebra $B$ is local if and only if it is generated by some non-zero element in $B$. Moreover, ${{\mathrm{dim}}}_K({{\mathrm{rad}}}I)= {{\mathrm{dim}}}_K(I)-1$. According to Lemma  3.3 (2) and (3) the statement $\fancyscript{G}(i) = B \circ \mathfrak {f}^{\uparrow }_{(1,i)}$ implies that $\fancyscript{G}(i)\cong B \circ \mathfrak {f}_{(1,i,1)}=\mathfrak {f}_{(1,i,1)} \circ B$ is a two-sided local ideal of $B$.

Proof

1. The algebra $B = {{\mathrm{End}}}_A(P(1))^{op}$ is local, since $P(1)$ is indecomposable. According to Remark  3.2(1) for $j=k=1$ we have ${{\mathrm{dim}}}_KB=\left| \Lambda \right|$. It is enough to show that ${{\mathrm{soc}}}({}_BB)$ is simple: Since $P(1)\cong I(1)$ there exists $\mathcal {S}\in B$ with ${{\mathrm{im}}}(\mathcal {S})={{\mathrm{soc}}}P(1) \cong S(1)$. For any non-invertible $h \in B$ we have ${{\mathrm{soc}}}P(1) \subseteq \ker (h)$. Since $h\circ \mathcal {S}=0$ for all non-invertible $h \in B$, the submodule $B\circ \mathcal {S}$ of $_BB$ is simple.

Let $f\in B\backslash \left\{ 0\right\}$ and $\tilde{f}\in {{\mathrm{Hom}}}_A(P(1),{{\mathrm{im}}}(f))$ with $\tilde{f}(p)=f(p)$ for all $p\in P(1)$. Since ${{\mathrm{top}}}({{\mathrm{im}}}f)\cong S(1)$, there exist a surjective $A$-map $\tilde{g}:{{\mathrm{im}}}(f)\twoheadrightarrow S(1)$. The $A$-module $P(1)\cong I(1)$ is an injective envelope of $P(1)$, ${{\mathrm{im}}}(f)$ and $S(1)$, because the socles of these modules are $S(1)$. Thus there exist $g\in B$ and inclusions $\iota _1$, $\iota _2$ such that the diagram

$$\begin{aligned} \begin{array}{rcclccc} \tilde{g}\circ \tilde{f}:&{} P(1)&{} \mathop {\twoheadrightarrow }\limits ^{\tilde{f}} &{} {{\mathrm{im}}}(f) &{} \mathop {\twoheadrightarrow }\limits ^{\tilde{g}}&{} S(1) &{} \\ &{} || &{} &{} \ \ \downarrow \iota _1 &{} &{} \downarrow \iota _2 &{} \\ g\circ f:&{} P(1)&{} \mathop {\longrightarrow }\limits ^{f} &{} P(1)&{} \mathop {\longrightarrow }\limits ^{g} &{} P(1) &{} \\ \end{array} \end{aligned}$$

is commutative. The map $\iota _2\circ \tilde{g} \circ \tilde{f} =g\circ f$ is a scalar multiple of the map $\mathcal {S}$. This implies $B\circ \mathcal {S} \subseteq B\circ f$. Thus $B\circ \mathcal {S}$ is a submodule of any non-zero submodule of $_BB$. Therefore $B\circ \mathcal {S}$ is the socle of $_BB$.

2. Since the map $\mathfrak {f}^{\uparrow }_{(j,i)}:P(i) \rightarrow P(j)$ is an inclusion and $P(1)\cong I(1)$, the contravariant functor ${{\mathrm{Hom}}}_A(-, P(1)): {{\mathrm{mod}}}A \rightarrow {{\mathrm{mod}}}B$ is exact. Therefore $\mathfrak {f}^{\uparrow }_{(j,i)}$ induces a surjective $B$-map $\underbrace{{{\mathrm{Hom}}}_A(P(j), P(1))}_{\fancyscript{G}(j)} \twoheadrightarrow \underbrace{{{\mathrm{Hom}}}_A(P(i), P(1))}_{\fancyscript{G}(i)}$ with $g\mapsto g\circ \mathfrak {f}^{\uparrow }_{(j,i)}$. We have $P(i)\hookrightarrow P(j)$ if and only if $i\in \Lambda ^{(j)}$ (see [11, 2.2]). Thus $\fancyscript{G}(j)\twoheadrightarrow \fancyscript{G}(i)$ if and only if $j\leqslant i$. Moreover, ${}_BB=\fancyscript{G}(1)\in \left\{ \fancyscript{G}(i) \mid i\in \Lambda \right\}$.

3. The surjection $\fancyscript{G}(1) \twoheadrightarrow \fancyscript{G}(i)$, $f\mapsto f\circ \mathfrak {f}^{\uparrow }_{(1,i)}$ provides $\fancyscript{G}(i)= B\circ \mathfrak {f}^{\uparrow }_{(1,i)}$ for any $i\in \Lambda$.

4. The $B$-module $B\circ \mathfrak {f}_{(1,i,1)}$ is local and $B\circ \mathfrak {f}_{(1,t,1)}\subset B\circ \mathfrak {f}_{(1,i,1)}$ for all $t\in \Lambda ^{(i)}\backslash \left\{ i\right\} =\left\{ t\in \Lambda \mid i<t\right\}$ (see Lemma 3.3 (1)). This implies $\sum _{i<t}\left( B\circ \mathfrak {f}_{(1,t,1)}\right) \subseteq {{\mathrm{rad}}}\left( B\circ \mathfrak {f}_{(1,i,1)}\right)$. Since the set $\left\{ \mathfrak {f}_{(1,t,1)}\mid i<t\right\}$ is linearly independent and $\left\{ \mathfrak {f}_{(1,t,1)}\mid i<t\right\} \subseteq \sum _{i<t}\left( B\circ \mathfrak {f}_{(1,t,1)}\right)$, we have ${{\mathrm{dim}}}_K\left( \sum _{i<t}\left( B\circ \mathfrak {f}_{(1,t,1)}\right) \right) \ge \left| \Lambda ^{(i)}\right| -1 = {{\mathrm{dim}}}_K \left( B\circ \mathfrak {f}_{(1,i,1)}\right) -1={{\mathrm{dim}}}_K {{\mathrm{rad}}}\left( B\circ \mathfrak {f}_{(1,i,1)}\right)$. We obtain $\sum _{i<t}\left( B\circ \mathfrak {f}_{(1,t,1)}\right) = {{\mathrm{rad}}}\left( B\circ \mathfrak {f}_{(1,i,1)}\right)$ for all $i\in \Lambda$.

$\square$

Moreover, there is the following explicit expression of the $B$-module $P(1)$:

Proposition 3.4

For a 1-quasi-hereditary algebra $(A,\leqslant )$ with $\left\{ 1\right\} =\min \left( Q_0(A),\leqslant \right)$ and $B={{\mathrm{End}}}_A(P(1))^{op}$ we have ${}_{B}P(1)\cong \bigoplus _{i\in \Lambda }B\circ \mathfrak {f}_{(1,i,1)}$, where $\mathfrak {f}_{(1,i,1)}$ is the endomorphism of $P(1)$ as described in Remark 3.1.

3.2 Proof of the Theorem A $(ii)\Rightarrow (i)$

In this subsection let $B$ be a local, self-injective $K$-algebra with ${{\mathrm{dim}}}_KB=n$. Let the set $(\Lambda =\left\{ 1,\ldots , n\right\} ,\leqslant )$ be partially ordered. For any $i\in \Lambda$ let $L(i)$ be a two-sided local ideal of $B$ with $L(1)=B$. Moreover, let $L(j)\twoheadrightarrow L(i)$ if and only if $j\leqslant i$, and ${{\mathrm{rad}}}L(j)=\sum _{j<i}L(i)$. In other words $B$ and $L:=\bigoplus _{i\in \Lambda }L(i)$ satisfy the condition $\boxed {\leqslant }$ (see Definition 2.5). The letter $L$ is used to accent the property ”local” of a generator–cogenerator $L$ of ${{\mathrm{mod}}}B$.

Recall that $L(i)=B\cdot x_i$ for some $x_i\in B\backslash \left\{ 0\right\}$ and $L(i)={{\mathrm{span}}}_{K}\left\{ x_i \dot{\cup } {{\mathrm{rad}}}L(i)\right\}$ for any $i\in \Lambda$. Moreover, for a submodule $N$ of $B$, any $B$-map $g:L(i)\rightarrow N$ is induced by right multiplication by an element $b\in B$ (in this case we write $L(i)\mathop {\rightarrow }\limits ^{\cdot b}N$). The element $g(x_i)=x_i\cdot b$ generates ${{\mathrm{im}}}(g)=B\cdot g(x)$. In particular, we have ${{\mathrm{Hom}}}_{B}(L(i),B)=\left\{ L(i)\mathop {\rightarrow }\limits ^{\cdot b}B\mid b\in B\right\}$. The annihilator of $L(i)$ is ${{\mathrm{Ann}}}(L(i)):=\left\{ b\in B\mid b\cdot L(i)=0\right\}$.

The proof of Theorem A 1.2.6 $(ii) \Rightarrow (i)$ is based on some properties of the $B$-module $L$ which we consider in the next Lemma.

Lemma 3.5

Then for all $i,j,k\in \Lambda$ the following properties are satisfied:

• (1) There exists a uniquely determined minimal element and a unique determined maximal element in $(\Lambda ,\leqslant )$ (without loss of generality, $1$ is the minimal and $n=|\Lambda |$ is the maximal element).

• (2) Let $x_j\in B$ be a generator of $L(j)$ and $W(j):=\left\{ x_i\mid i\in \Lambda ^{(j)}\right\}$. Then we have:

  • (2.1) The set $W(j)$ is a $K$-basis of $L(j)$. In particular, for any subset $\Gamma \subseteq \Lambda$ the set $\displaystyle \bigcup \nolimits _{j\in \Gamma }W(j)$ is a $K$-basis of $\displaystyle \sum \nolimits _{j\in \Gamma }L(j)$, and $\displaystyle \bigcap \nolimits _{j\in \Gamma }W(j)$ is a $K$-basis of $\displaystyle \bigcap \nolimits _{j\in \Gamma }L(j)$.

  • (2.2) $L(j)=B\cdot x_j=x_j\cdot B$.

• (3) Let $N$ be a submodule of $B$, then ${{\mathrm{im}}}(g)\subseteq L(j)\cap N$ for all $g\in {{\mathrm{Hom}}}_B(L(j),N)$.

• (4) We have $L(i)\hookrightarrow L(j)$ resp. $L(j)\twoheadrightarrow L(i)$ if and only if $i\in \Lambda ^{(j)}$. Moreover,

  • (4.1) ${{\mathrm{im}}}\left( L(i)\hookrightarrow L(j)\right) =L(i)$ for any injective $B$-map from $L(i)$ to $L(j)$,

  • (4.2) $\ker \left( L(j)\twoheadrightarrow L(i)\right) = {{\mathrm{Ann}}}(L(i))\cdot L(j)$ for any surjective $B$-map from $L(j)$ to $L(i)$.

• (5) For $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$ let $g_{(i\hookrightarrow k)}:L(i)\hookrightarrow L(k)$ be an injective, $g_{(j\twoheadrightarrow i)}:L(j)\twoheadrightarrow L(i)$ a surjective $B$-map and $\displaystyle g_{(k,i,j)}:= g_{(i\hookrightarrow k)}\circ g_{(j\twoheadrightarrow i)}:\left( L(j)\mathop {\twoheadrightarrow }\limits ^{g_{(j\twoheadrightarrow i)}}L(i)\mathop {\hookrightarrow }\limits ^{g_{(i\hookrightarrow k)}}L(k)\right)$. Then

  • (5.1) $\mathfrak {B}(j,k):= \left\{ g_{(k,i,j)} \mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\}$ is a $K$-basis of ${{\mathrm{Hom}}}_B(L(j), L(k))$,

  • (5.2) every map $g\in {{\mathrm{Hom}}}_B(L(j), L(k))$ factors through $\bigoplus _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} L(i)$.

Proof

(1) Since $B(=L(1))$ is a projective cover of any local $B$-module, we have $L(1)\twoheadrightarrow L(i)$. The condition ”$L(j)\twoheadrightarrow L(i)$ if and only if $j\leqslant i$” implies $1\leqslant i$ for all $i\in \Lambda$. Let $n\in \Lambda$ be maximal, then the condition ${{\mathrm{rad}}}L(n)=\sum _{n<i}L(i)$ yields ${{\mathrm{rad}}}L(n)=0$. The local submodule $L(n)$ of $B$ is simple. Thus $L(n)={{\mathrm{soc}}}(B)$, because the socle of a local self-injective algebra is simple, and $L(n)$ belongs to any non-zero submodule of $B$. Therefore $L(n)\subseteq L(j)$ for every $j\in \Lambda$. Since $L(n)\cong L(j)$ if $k=j$, we have $L(n)\subseteq {{\mathrm{rad}}}L(j)$ for all $j\in \Lambda$ with $j\ne n$. The condition ${{\mathrm{rad}}}L(j)=\sum _{j<i}L(i)$ implies $j\leqslant n$ for all $j\in \Lambda$.

(2.1) This is proved by induction on ${{\mathrm{dim}}}_K (L(j))$: If ${{\mathrm{dim}}}_K(L(j))=1$, then $L(j)$ is simple, thus $j=n$ and $W(n)=\left\{ x_n\right\}$ is a $K$-basis of $L(n)={{\mathrm{soc}}}B$. Let $j\in \Lambda$ with ${{\mathrm{dim}}}_K(L(j))=m+1$, then for any $i\in \Lambda ^{(j)}\backslash \left\{ j\right\} =\left\{ i\in \Lambda \mid j<i\right\}$ we have $L(i)\subseteq {{\mathrm{rad}}}L(j)$. This implies ${{\mathrm{dim}}}_KL(i)\le {{\mathrm{dim}}}_K\left( {{\mathrm{rad}}}L(j)\right) =m$. The induction assumption implies $L(i)={{\mathrm{span}}}_KW(i)$. Thus ${{\mathrm{rad}}}L(j)=\sum _{j<i}L(i)$ is spanned by $\bigcup _{j<i}W(i)=\left\{ x_i\mid j <i\right\}$ and consequently $W(j)=\left\{ x_j\right\} \cup \bigcup _{j<i}W(i)$ spans the $K$-space $L(j)$. Since $W(1)=\left\{ x_1,\ldots , x_n\right\}$ spans $B=L(1)$ and ${{\mathrm{dim}}}_KB=n$, the set $W(1)$ is a $K$-basis of $B$. Consequently, the subset $W(j)$ of $W(1)$ is linearly independent.

Let $\Gamma \subseteq \Lambda$. The subsets $\bigcup _{j\in \Gamma }W(j) =\left\{ x_k\mid k\in \Lambda ^{(i)}, \hbox { for some } i\in \Gamma \right\}$ and $\bigcap _{j\in \Gamma }W(j) =\left\{ x_k\mid k\in \bigcap _{j\in \Gamma }\Lambda ^{(j)} \right\}$ of $W(1)$ generate $\sum _{j\in \Gamma }L(j)$ and $\bigcap _{j\in \Gamma }L(j)$ as $K$-spaces, respectively.

(2.2) Since $L(j)\twoheadrightarrow L(i)$, there exists $b_i\in B$ with $L(j)\mathop {\twoheadrightarrow }\limits ^{\cdot b_i} L(i)$ and $x_i= x_j \cdot b_i$ for any $i\in \Lambda ^{(j)}$. Let $y\in L(j)=B \cdot x_j$, then $y\mathop {=}\limits ^{\textit{(2.1)}}\sum _{i\in \Lambda ^{(j)}}c_i\cdot x_i = \sum _{i\in \Lambda ^{(j)}}c_i\cdot x_j\cdot b_i = x_j\cdot \left( \sum _{i\in \Lambda ^{(j)}}c_i\cdot b_i\right)$ (here $c_i\in K$). We obtain $B \cdot x_j\subseteq x_j \cdot B$. Since $L(j)$ is a two-sided ideal, we have $B\cdot x_j \cdot B\subseteq B\cdot x_j$, thus $x_j \cdot B\subseteq B \cdot x_j$ and consequently $L(j)= B\cdot x_j = x_j \cdot B$.

(3) For $g\in {{\mathrm{Hom}}}_B(L(j),N)$ there exists some $b\in B$ with $g:L(j)\mathop {\rightarrow }\limits ^{\cdot b}N$. Let $x_j$ be a generator of $L(j)$, then $g(x_j)=x_j\cdot b=\widetilde{b} \cdot x_j$ for some $\widetilde{b}\in B$ by (2.2). Thus $g(x_j)\in L(j)$ and consequently ${{\mathrm{im}}}(g)\subseteq L(j)\cap N$.

(4.1) Let $N$ be a submodule of $L(k)$ with $N\cong L(i)$ and $g\in {{\mathrm{Hom}}}_B(L(i),N)$ be an isomorphism, then $g(L(i))= N \subseteq L(i) \cap N$ (see (3)). We obtain $g(L(i))=L(i)=N$.

(4.2) Let $\pi _i:L(j)\twoheadrightarrow L(i)$ be a surjection and $x_j$ a generator of $L(j)$. Then $x_i:=\pi _i(x_j)$ generates $L(i)$. Let $x\in L(j)$, then $x=b\cdot x_j$ for some $b\in B$. Obviously, $x\in \ker \left( \pi _i\right)$ if and only if $\pi _i(x)= b\cdot x_i =0$ and this holds if and only if $b\cdot x_i\cdot B \mathop {=}\limits ^{\textit{(2.2)}} b\cdot L(i)=0$. We obtain $\ker (\pi _i)=\left\{ b\cdot x_j\in L(j)\mid b\in {{\mathrm{Ann}}}(L(i))\right\} = {{\mathrm{Ann}}}(L(i))\cdot L(j)$.

(5.1) Let $x_j$ be a generator of $L(j)$. Then $x_i:= g_{(k,i,j)}(x_j)$ generates the submodule $L(i)$ of $L(j)\cap L(k)$. The set $\left\{ x_i\mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\} \mathop {=}\limits ^{\textit{(2.1)}} W(j)\cap W(k)$ is a $K$-basis of $L(j)\cap L(k)$. Let $g\in {{\mathrm{Hom}}}_B(L(j),L(k))$, then ${{\mathrm{im}}}(g)\subseteq L(j)\cap L(k)$ (see (3)). Thus $g(x_j)=\sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}c_i\cdot x_i$ and consequently $g=\sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}c_i\cdot g_{(k,i,j)}$.

(5.2) Let $h_1, h_2$ be the $B$-maps given by $h_1:\left( \begin{array}{ccl} L(j)&{}\longrightarrow &{}\bigoplus _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}L(i) \\ x_j &{} \mapsto &{} \left( g_{(j\twoheadrightarrow i)}(x_j)\right) _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} \end{array}\right)$ and $h_2:\left( \begin{array}{ccl} \bigoplus _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}L(i) &{}\longrightarrow &{} L(k) \\ \left( y_i\right) _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} &{} \mapsto &{} \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} c_i\cdot g_{(i\hookrightarrow j)}(y_i) \end{array}\right) .$ We have $g=h_2\circ h_1$. Thus $g$ factors through $\bigoplus _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}L(i)$. $\square$

Remark 3.6

Let the pair $(B,L)$ be as above. We denote by $\mathtt B$ the algebra $B^{op}$ and by $\mathtt L (i)$ the $\mathtt B$-module $\mathcal {D}(L(i))$, where $\mathcal {D}:{{\mathrm{mod}}}B \rightarrow {{\mathrm{mod}}}\mathtt B$ is the standard duality functor. Since ${{\mathrm{top}}}L(i)$ and ${{\mathrm{soc}}}L(i)$ are simple, we obtain that ${{\mathrm{soc}}}\mathtt L (i)$ and ${{\mathrm{top}}}\mathtt L (i)$ are simple. In particular, $\mathtt B$ is a local, self-injective algebra ince as a module $\mathtt B =\mathtt L (1)$, and ${{\mathrm{dim}}}_K\mathtt B ={{\mathrm{dim}}}_KB=n$. For any $i\in \Lambda$ the module $\mathtt L (i)$ can by considered as a local (left) ideal of $\mathtt B$.

We denote by $\mathtt g _{(j,i,k)}$ the $\mathtt B$-map $\mathcal {D}\left( g_{(k,i,j)}\right) :\mathtt L (k)\rightarrow \mathtt L (j)$ for all $i,j,k\in \Lambda$ with $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$, where $g_{(k,i,j)}$ is the $B$-map described in  3.5 (5). As $\mathcal {D}$ is duality, we have $\mathtt g _{(k\twoheadrightarrow i)}=\mathcal {D}(g_{(i\hookrightarrow k)})$ and $\mathtt g _{(i \hookrightarrow j)}=\mathcal {D}(g_{(j\twoheadrightarrow i)})$ as well as

Proposition 3.7

A pair $(B,L)$ satisfies the condition $\boxed {\leqslant }$ if and only if $\left( B^{op},\mathcal {D}(L)\right)$ satisfies the condition $\boxed {\leqslant }$.

Proof

Any two injections $\iota _1$, $\iota _2:\mathtt L (i)\hookrightarrow \mathtt L (j)$ are induced by some surjections $\pi _1, \pi _2:L(j)\twoheadrightarrow L(i)$. Since $\ker (\pi _1)\mathop {=}\limits ^{2.2.1\textit{(4)}} \ker (\pi _2)$, we obtain ${{\mathrm{im}}}(\iota _1)={{\mathrm{im}}}(\iota _2)=\mathtt L (i)$ for all $i\in \Lambda ^{(j)}$.

Let $\mathtt 1 :=\mathtt 1 _\mathtt{B }$ , then $\mathtt y _i:=\mathtt g _{(j,i,1)}(\mathtt 1 )$ is a generator of the submodule $\mathtt L (i)$ of $\mathtt L (j)$ for any $i\in \Lambda ^{(j)}$. The set $\left\{ \mathtt g _{(j,i,1)} \mid i\in \Lambda ^{(j)}\right\}$ is a $K$-basis of ${{\mathrm{Hom}}}_\mathtt{B }(\mathtt L (1),\mathtt L (j))$ (see Lemma  3.5 (5)). Thus $\mathtt W (j):=\left\{ \mathtt y _i\mid i\in \Lambda ^{(j)}\right\}$ is a $K$-basis of $\mathtt L (j)$, since ${{\mathrm{dim}}}_K\mathtt L (j)={{\mathrm{dim}}}_KL(j)\mathop {=}\limits ^{2.2.1\textit{(2)}}\left| \mathtt W (j)\right|$.

Now we show $\mathtt L (k)=\mathtt B \cdot \mathtt y _k=\mathtt y _k\cdot \mathtt B$. Let $\mathtt g _{(k\twoheadrightarrow i)}:\mathtt L (k)\mathop {\twoheadrightarrow }\limits ^{\cdot b_i}\mathtt L (i)$ such that $\mathtt y _i=\mathtt y _k\cdot b_i$ for any $i\in \Lambda ^{(k)}$. Let $\mathtt y \in \mathtt B \cdot \mathtt y _k$, then $\mathtt y =\sum _{i\in \Lambda ^{(k)}}c_i\cdot \mathtt y _i=\mathtt y _k\cdot \left( \sum _{i\in \Lambda ^{(k)}}c_i\cdot b_i\right) \in \mathtt y _k\cdot \mathtt B$, thus $\mathtt B \cdot \mathtt y _k\subseteq \mathtt y _k\cdot \mathtt B$. On the other hand, if $\mathtt y \in \mathtt y _k\cdot \mathtt B$, then $\mathtt y =\mathtt y _k \cdot b$ for some $b\in \mathtt B$. Let $\mathtt g \in {{\mathrm{Hom}}}_\mathtt{B }\left( \mathtt L (k), \mathtt L (1)\right) = {{\mathrm{span}}}_K\left\{ \mathtt g _{(1,i,k)}\mid i\in \Lambda ^{(k)}\right\}$ be given by $\mathtt g :\mathtt L (k)\mathop {\rightarrow }\limits ^{\cdot b}\mathtt L (1)=\mathtt B$, then $\mathtt y \in {{\mathrm{im}}}(\mathtt g )$. Since ${{\mathrm{im}}}\left( \mathtt g _{(1,i,k)}\right) = \mathtt L (i) \subseteq \mathtt L (k)$, we have ${{\mathrm{im}}}(\mathtt g )\subseteq \mathtt L (k)$. Thus $\mathtt y \in \mathtt L (k)=\mathtt B \cdot \mathtt y _k$. Therefore $\mathtt B \cdot \mathtt y _k \supseteq \mathtt y _k\cdot \mathtt B$. This implies that $\mathtt L (k)$ is a two-sided local ideal of $\mathtt B$ for any $k\in \Lambda$.

If $i\ne j$, then $\mathtt L (i)\ne \mathtt L (j)$, thus $\mathtt L (i)\subseteq {{\mathrm{rad}}}(\mathtt L (j))$ for any $i\in \Lambda ^{(j)}\backslash \left\{ j\right\}$. Consequently, $\sum _{j<i}\mathtt L (i)\subseteq {{\mathrm{rad}}}(\mathtt L (j))$. The set $\bigcup _{j<i}\mathtt W (i)= \left\{ \mathtt y _i\mid i\in \Lambda ^{(j)}\backslash \left\{ j\right\} \right\}$ is a $K$-basis of $\sum _{j<i}\mathtt L (i)$, since $\mathtt W (i)$ is a $K$-basis of $\mathtt L (i)$. Thus ${{\mathrm{dim}}}_K\left( \sum _{j<i}\mathtt L (i)\right) = \left| \Lambda ^{(j)}\backslash \left\{ j\right\} \right| = \left| \Lambda ^{(j)}\right| -1= {{\mathrm{dim}}}_K\mathtt L (j)-1 = {{\mathrm{dim}}}_K\left( {{\mathrm{rad}}}\mathtt L (j)\right)$ and we obtain $\sum _{j<i}\mathtt L (i)= {{\mathrm{rad}}}(\mathtt L (j))$ for all $j\in \Lambda$. $\square$

Furthermore, we consider the algebra $A:= {{\mathrm{End}}}_B(L)^{op}\cong {{\mathrm{End}}}_\mathtt{B }\left( \mathtt L \right)$. Because $L$ is multiplicity-free and has $n$ direct summands, $A$ is basic and the quiver $Q(A)$ has $n$ vertices. We identify these with the elements in $\Lambda$. The evaluation functor ${{\mathrm{Hom}}}_\mathtt{B }(\mathtt L ,-):{{\mathrm{mod}}}\mathtt B \rightarrow {{\mathrm{mod}}}A$ provides an isomorphism ${{\mathrm{Hom}}}_\mathtt{B }(\mathtt L (i),\mathtt L (j))\cong {{\mathrm{Hom}}}_A(P(i),P(j))$ (see [1, Proposition 2.1]). Moreover, because ${{\mathrm{Hom}}}_\mathtt{B }(\mathtt L ,-)$ is left exact, an injective $\mathtt B$-map $\mathtt L (i)\hookrightarrow \mathtt L (j)$ induces an injective $A$-map $P(i)\hookrightarrow P(j)$.

The properties described in Lemma 3.5 are also satisfied for the $\mathtt B$-ideals $\mathtt L (i)$ (see Proposition 3.7). Since ${{\mathrm{im}}}\left( \mathtt L (i)\hookrightarrow \mathtt L (j)\right) = \mathtt L (i)$ for any injective $\mathtt B$-map (see  3.5 (4)), a submodule of $P(j)$ isomorphic to $P(i)$ is uniquely determined for any $i\in \Lambda ^{(j)}$. We consider $\sum _{i\in \Gamma }P(i)$ as a submodule of $P(j)$ for any subset $\Gamma$ of $\Lambda ^{(j)}$.

Remark-Notations 3.8

By $\mathfrak {f}^{\uparrow }_{(j,i)}$ and $\mathfrak {f}^{\downarrow }_{(i,k)}$ we denote the $A$-maps induced by $\mathtt B$-maps $\mathtt g _{(i\hookrightarrow j)}$ and $\mathtt g _{(k\twoheadrightarrow i)}$ respectively (described in  3.6). And the $A$-map $\mathfrak {f}_{(j,i,k)}$ is induced by $\mathtt g _{(j,i,k)} \in {{\mathrm{Hom}}}_\mathtt{B }(\mathtt L (k),\mathtt L (j))$. Since $\mathtt g _{(j,i,k)}= \mathtt g _{(i\hookrightarrow j)}\circ \mathtt g _{(k\twoheadrightarrow i)}$ and $\mathtt g _{(i\hookrightarrow j)}$ is injective, we obtain

$$\begin{aligned} \mathfrak {f}_{(j,i,k)}=\mathfrak {f}^{\uparrow }_{(j,i)}\circ \mathfrak {f}^{\downarrow }_{(i,k)}:\left( P(k)\mathop {\longrightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(i,k)}}P(i) \mathop {\hookrightarrow }\limits ^{\mathfrak {f}^{\uparrow }_{(j,i)}}P(j)\right) . \end{aligned}$$

Obviously, ${{\mathrm{im}}}\left( \mathfrak {f}_{(j,i,k)}\right)$ belongs to the submodule $P(i)$ of $P(j)$. For any $f\in {{\mathrm{Hom}}}_{A}(P(k),P(j))$ we have ${{\mathrm{im}}}(f)\subseteq \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} {{\mathrm{im}}}\left( \mathfrak {f}_{(j,i,k)}\right) \subseteq \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}}P(i)$. In particular, if $k\not \leqslant j$ we have ${{\mathrm{im}}}(f)\subseteq \sum _{j<i}P(i)$ for all $f\in {{\mathrm{Hom}}}_A(P(k),P(j))$.

Recall that for any $A$-module $M$ the $K$-subspaces $M_k =\left\{ f(e_k)\mid f\in {{\mathrm{Hom}}}_A(P(k),M)\right\}$ of $M$ yield a direct decomposition $M = \bigoplus _{k\in \Lambda }M_k$ as a vector space.

Lemma 3.9

Let $i,j,k\in \Lambda$ with $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$. Let $p(j,i,k):= \mathfrak {f}_{(j,i,k)}(e_k)$ and $\mathbf B _j(i, k):= \left\{ p(j,t,k)\mid t\in \Lambda ^{(i)}\cap \Lambda ^{(k)}\right\}$. For any subset $\Gamma$ of $\Lambda ^{(j)}$ the following hold:

• (1) $\mathbf B _j(\Gamma , k):= \bigcup _{i\in \Gamma } \mathbf B _j(i,k)$ is a $K$-basis of the subspace $\left( \sum _{i\in \Gamma }P(i)\right) _k$ of $P(j)_k$.

• (2) $\mathbf B _j(\Gamma ):= \bigcup _{k\in \Lambda } \mathbf B _j(\Gamma , k)$ is a $K$-basis of the submodule $\sum _{i\in \Gamma }P(i)$ of $P(j)$.

Proof

(1) Note that $\mathbf B _j\left( \{i\}, k\right) =\mathbf B _j(\Lambda ^{(i)}, k)$. According to Lemma 3.5 (5) the set $\left\{ \mathfrak {f}_{(j,i,k)} \mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\}$ is a $K$-basis of ${{\mathrm{Hom}}}_A(P(k),P(j))$ for each $j,k\in \Lambda$. Since the $K$-map ${{\mathrm{Hom}}}_A(P(k),P(j)) \rightarrow P(j)_k$ with $f \mapsto f(e_k)$ is an isomorphism, the set $\mathbf B _j(\{j\}, k)=\left\{ \mathfrak {f}_{(j,i,k)}(e_k)=p(j,i,k)\mid i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}\right\}$ is a $K$-basis of $P(j)_k$. By applying ${{\mathrm{Hom}}}_A(P(k),-)$ to $\mathfrak {f}^{\uparrow }_{(j,i)}:P(i)\hookrightarrow P(j)$, $e_i \mapsto \mathfrak {f}^{\uparrow }_{(j,i)}(e_i)$, we obtain

$$\begin{aligned} {{\mathrm{Hom}}}_A(P(k),P(i)) \hookrightarrow {{\mathrm{Hom}}}_{A}(P(k),P(j)) \hbox { with }\ \mathfrak {f}_{(i,t,k)}\mapsto \mathfrak {f}^{\uparrow }_{(j,i)}\circ \mathfrak {f}_{(i,t,k)} =\mathfrak {f}_{(j,t,k)} \end{aligned}$$

or, equivalently, $P(i)_k\hookrightarrow P(j)_k$ with $p(i,t,k)\mapsto p(j,t,k)$. This injection maps $\mathbf B _i(\{i\}, k)$ to $\mathbf B _j(\{i\}, k)$. Thus $\mathbf B _j(\{i\}, k)$ is a $K$-basis of the subspace $P(i)_k$ of $P(j)_k$.

Obviously, $\mathbf B _j(\Gamma , k)= \left\{ p(j,t,k)\mid t\in \bigcup _{i\in \Gamma }\left( \Lambda ^{(i)}\cap \Lambda ^{(k)}\right) \right\}$. Since $\Lambda ^{(i)}\cap \Lambda ^{(k)}\subseteq \Lambda ^{(j)}\cap \Lambda ^{(k)}$ for all $i\in \Gamma$, we have $\mathbf B _j(\Gamma , k)\subseteq \mathbf B _j(\{j\}, k)$. Thus $\mathbf B _j(\Gamma , k)$ is linearly independent and the subspace $\left( \sum _{i\in \Gamma }P(i)\right) _k$ of $P(j)_k$ is spanned by $\mathbf B _j(\Gamma , k)$.

(2) The union $\bigcup _{k\in \Lambda } \mathbf B _j(\Gamma , k)$ is disjoint, thus $\mathbf B _j(\Gamma )$ is a $K$-basis of $\sum _{i\in \Gamma } P(i)$.$\square$

The poset $(\Lambda ,\leqslant )$ has a uniquely determined minimal element and a uniquely determined maximal element (see  3.5 (1)). In order to prove that $(A,\leqslant )$ is a 1-quasi-hereditary algebra (see Definition  2.2) we have to show that for all $j\in \Lambda$ the following holds:

• 1. $[\Delta (j):S(k)]=1$ for all $k\in \Lambda _{(j)}$,

• 2. $P(j)$ has a $\Delta$-good filtration with $\left( P(j):\Delta (i)\right) = \left\{ \begin{array}{cl} 1 &{}\quad \hbox {if } \ i\in \Lambda ^{(j)} ,\\ 0&{} \quad \hbox {else}, \end{array} \right.$

• 3. ${{\mathrm{soc}}}P(j)\cong {{\mathrm{top}}}I(j) \cong S(1)$,

• 4. $\Delta (j)\hookrightarrow \Delta (n)$ and $\nabla (n)\twoheadrightarrow \nabla (j)$.

Proof

1. The definition of the standard modules provides $\Delta (j)=P(j)/N(j)$, where $N(j)= \sum _{k\not \leqslant j}\sum _{\mathfrak {f}\in {{\mathrm{Hom}}}_{A}(P(k),P(j))}{{\mathrm{im}}}(\mathfrak {f})\mathop {\subseteq }\limits ^{2.2.4} \sum _{j<i}P(i)$. Since $P(i)={{\mathrm{im}}}\left( \mathfrak {f}^{\uparrow }_{(j,i)}\right) \subseteq N(j)$ for any $j<i$, we obtain $N(j)\supseteq \sum _{j<i}P(i)$, thus $\Delta (j)=P(j)/\left( \sum _{j<i}P(i) \right)$.

Lemma 3.9 (1) yields $P(j)_k ={{\mathrm{span}}}_K\mathbf B _j\left( \Lambda ^{(j)},k\right)$ and $\left( \sum _{j<i}P(i) \right) _k={{\mathrm{span}}}_K\mathbf B _j(\Lambda ^{(j)}\backslash \left\{ j\right\} ,k)$. By assumption $k\in \Lambda _{(j)}$ (i.e., $\Lambda ^{(j)}\cap \Lambda ^{(k)}=\Lambda ^{(j)}$), hence we obtain $\left| \mathbf B _j(\Lambda ^{(j)},k)\right| =\left| \mathbf B _j(\Lambda ^{(j)}\backslash \left\{ j\right\} ,k)\right| +1$. Thus $[\Delta (j):S(k)]={{\mathrm{dim}}}_K\Delta (j)_k={{\mathrm{dim}}}_K\left( P(j)_k/\left( \sum _{j<i}P(i)\right) _k\right) =1$.

2. Let $\mathbf i \in \mathcal {L}(j):=\left\{ (i_1, i_2, \ldots , i_r) \mid i_m\in \Lambda ^{(j)} , \ i_{l}\not \geqslant i_{t}, \ 1\le l < t \le r :=\left| \Lambda ^{(j)}\right| \right\}$ (see [11, 4.2]). Obviously, $P(i_t)\subseteq P(j)=P(i_1)$ for all $1\le t\le r$. Denote by $\fancyscript{D}(\mathbf i )$ the filtration $0=D(r+1)\subset D(r)\subset \cdots \subset D(t) \subset \cdots \subset D(1)$ with $D(t):=\sum _{m=t}^{r}P(i_m)$. It is easy to check that $\mathbf B _j\left( \Lambda ^{(i_t)}\backslash \left\{ i_t\right\} \right) = \mathbf B _j\left( \left\{ i_t\right\} \right) \cap \mathbf B _j\left( \left\{ i_{t+1},\ldots , i_r\right\} \right)$ for all $1\le t\le r-1$. This implies $\sum _{i_t<k}P(k)= P(i_t)\cap \left( \sum _{m=t+1}^rP(i_m)\right)$ (see  3.9 (2)) and consequently $D(t)/D(t+1)\cong P(i_t)/\left( \sum _{i_t<k}P(k)\right) \cong \Delta (i_t)$ for all $1\le t\le r$. The filtration $\fancyscript{D}(\mathbf i )$ of $P(j)$ is $\Delta$-good. Since $\left\{ i_1, i_2, \ldots , i_r\right\} =\Lambda ^{(j)}$ and $l\ne t$ implies $i_l\ne i_t$, we obtain $\left( P(j):\Delta (i)\right) =1$ for any $i\in \Lambda ^{(j)}$ and $\left( P(j):\Delta (i)\right) =0$ if $i\in \Lambda \backslash \Lambda ^{(j)}$.

3. Since $P(i)\hookrightarrow P(1)$ for all $i\in \Lambda$, it is enough to show that ${{\mathrm{soc}}}P(1)\cong S(1)$. We consider the map $\mathfrak {f}_{(1,n,1)}:P(1)\rightarrow P(1)$ induced by $\mathtt g _{(1,n,1)}:\mathtt L (1)\twoheadrightarrow \mathtt L (n)\hookrightarrow \mathtt L (1)$, here $\mathtt L (n)={{\mathrm{soc}}}\mathtt L (1)$ since $n$ is maximal. We show that ${{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right) \subseteq {{\mathrm{im}}}\left( \mathfrak {f}\right)$ for all $\mathfrak {f}\in {{\mathrm{Hom}}}_A(P(i),P(1))\backslash \left\{ 0\right\}$ and all $i\in \Lambda$ (this implies that ${{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right)$ is contained in every local submodule of $P(1)$ and therefore in every non-zero submodule of $P(1)$): Let $\mathfrak {f}$ be induced by $\mathtt g \in {{\mathrm{Hom}}}_\mathtt{B }\left( \mathtt L (i),\mathtt L (1)\right)$, then $\mathtt g \ne 0$ and consequently $\mathtt L (n)\subseteq {{\mathrm{im}}}\left( \mathtt g \right)$. There exists some $\mathtt x \in \mathtt L (i)$ with $\mathtt g (\mathtt x )=\mathtt b _n$, where $\mathtt b _n$ is a generator of $\mathtt L (n)$. Let $\mathfrak {h}\in {{\mathrm{Hom}}}_A(P(1),P(i))$ be induced by $\mathtt h :\mathtt L (1)\mathop {\rightarrow }\limits ^{\cdot \mathtt x }\mathtt L (i)$. We have $\mathtt g \circ \mathtt h =\mathtt g _{(1,n,1)}$. This implies $\mathfrak {f}\circ \mathfrak {h}=\mathfrak {f}_{(1,n,1)}$ and consequently ${{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right) \subseteq {{\mathrm{im}}}\left( \mathfrak {f}\right)$. Thus ${{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right)$ is the uniquely determined simple submodule of $P(1)$. Since ${{\mathrm{top}}}\left( {{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right) \right) \cong S(1)$, we have ${{\mathrm{im}}}\left( \mathfrak {f}_{(1,n,1)}\right) \cong S(1)$.

According to  3.7 for the algebra $A^{op}\cong {{\mathrm{End}}}_{B}(L)\cong {{\mathrm{End}}}_\mathtt{B ^{op}}(\mathcal {D}(\mathtt L ))$ we have ${{\mathrm{soc}}}P_{A^{op}}(i)\cong S_{A^{op}}(1)$, thus ${{\mathrm{top}}}I(i)\cong S(1)$ holds for all $i\in \Lambda$.

4. Let $\mathfrak {f}^{\downarrow }_{(n,j)}:P(j)\rightarrow P(n)$ be the $A$-map induced by the $\mathtt B$-map $\mathtt g _{(j\twoheadrightarrow n)}:\mathtt L (j)\twoheadrightarrow \mathtt L (n)$. It is enough to show $\sum _{j<i}P(i)= {{\mathrm{ker}}}\left( \mathfrak {f}^{\downarrow }_{(n,j)}\right)$, because this implies $P(j)/\left( \sum _{j<i}P(i)\right) \mathop {=}\limits ^{1} \Delta (j)\hookrightarrow P(n)=\Delta (n)$ for any $j\in \Lambda$: Let $i\in \Lambda ^{(j)}\backslash \left\{ j\right\}$, then the functor ${{\mathrm{Hom}}}_\mathtt{B }(\mathtt L ,-)$ maps a $\mathtt B$-map $\mathtt g :\left( \mathtt L (i)\mathop {\hookrightarrow }\limits ^\mathtt{g _{(i\hookrightarrow j)}}\mathtt L (j)\mathop {\twoheadrightarrow }\limits ^\mathtt{g _{(j\twoheadrightarrow n)}}\mathtt L (n)\right)$ to the $A$-map $\mathfrak {f}:\left( P(i)\mathop {\hookrightarrow }\limits ^{\mathfrak {f}^{\uparrow }_{(j,i)}}P(j)\mathop {\rightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(n,j)}}P(n)\right)$. Since $\mathtt L (n)={{\mathrm{soc}}}\mathtt B$ is simple, we have ${{\mathrm{ker}}}\left( \mathtt g _{(j\twoheadrightarrow n)}\right) ={{\mathrm{rad}}}\mathtt L (j)$. Because $j<i$, we have $\mathtt L (i)\subseteq {{\mathrm{rad}}}\mathtt L (j)$. Hence $\mathtt g$ and therefore $\mathfrak {f}$ are zero-maps. Consequently, the submodule $P(i)$ of $P(j)$ belongs to $\ker \left( \mathfrak {f}^{\downarrow }_{(n,j)}\right)$ for any $j < i$. We obtain $\sum _{j<i}P(i)\subseteq \ker \left( \mathfrak {f}^{\downarrow }_{(n,j)}\right)$.

Because $\Delta (j)=P(j)/\left( \sum _{j<i}P(i)\right)$, there exists a submodule $U$ of $\Delta (j)$ such that $P(j)/\left( \ker \mathfrak {f}^{\downarrow }_{(n,j)}\right) \cong \Delta (j)/U$. For the $K$-subspace ${{\mathrm{im}}}\left( \mathfrak {f}^{\downarrow }_{(n,j)}\right) _k$ of ${{\mathrm{im}}}\left( \mathfrak {f}^{\downarrow }_{(n,j)}\right)$ we have

$$\begin{aligned} {{\mathrm{dim}}}_K \left( {{\mathrm{im}}}\mathfrak {f}^{\downarrow }_{(n,j)}\right) _k = {{\mathrm{dim}}}_K\left( P(j)/\ker \mathfrak {f}^{\downarrow }_{(n,j)}\right) _k = {{\mathrm{dim}}}_K\left( \Delta (j)/U \right) _k \le {{\mathrm{dim}}}_K\left( \Delta (j)\right) _k. \end{aligned}$$

Let $k\in \Lambda _{(j)}$, then the $\mathtt B$-map $\mathtt g :\left( \mathtt L (k) \mathop {\twoheadrightarrow }\limits ^\mathtt{g _{(k\twoheadrightarrow j)}}\mathtt L (j)\mathop {\twoheadrightarrow }\limits ^\mathtt{g _{(j\twoheadrightarrow n)}}\mathtt L (n)\right)$ is non-zero. Thus the induced $A$-map $\mathfrak {f}:\left( P(k) \mathop {\longrightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(j,k)}}P(j)\mathop {\longrightarrow }\limits ^{\mathfrak {f}^{\downarrow }_{(n,j)}}P(n)\right)$ is non-zero. Hence $0\ne \mathfrak {f}(e_k)\in \left( {{\mathrm{im}}}\mathfrak {f}^{\downarrow }_{(n,j)}\right) _k$, thus ${{\mathrm{dim}}}_K\left( {{\mathrm{im}}}\mathfrak {f}^{\downarrow }_{(n,j)}\right) _k\ne 0$ and consequently for all $k\in \Lambda$ we have ${{\mathrm{dim}}}_K\left( {{\mathrm{im}}}\mathfrak {f}^{\downarrow }_{(n,j)}\right) _k={{\mathrm{dim}}}_K\left( \Delta (j)\right) _k\mathop {=}\limits ^{\hbox {1}}\left\{ \begin{array}{cl} 1 &{} \hbox {if } k\in \Lambda _{(j)},\\ 0 &{} \hbox {else} \end{array} \right.$. We obtain $U=0$ and therefore $\sum _{j<i}P(i)= {{\mathrm{ker}}}\left( \mathfrak {f}^{\downarrow }_{(n,j)}\right)$.

Proposition 3.7 implies that the functor ${{\mathrm{Hom}}}_{B}(L,-):{{\mathrm{mod}}}B\rightarrow {{\mathrm{mod}}}A^{op}$ yields an inclusion $\Delta _{A^{op}}(j)\hookrightarrow \Delta _{A^{op}}(n)$. By applying the duality we get a surjection $\nabla (n)\twoheadrightarrow \nabla (j)$ for each $j\in \Lambda$.

This finishes the proof of Theorem A 1.2.6. $\square$

The features of the $B$-module $L=\bigoplus _{i\in \Lambda }L(i)$, for a pair $(B,L)$ with $\boxed {\leqslant }$, imply some properties for the quiver and relations of the 1-quasi-hereditary algebra $A={{\mathrm{End}}}_B(L)^{op}$.

Remark-Notations 3.10

For every $i\in \Lambda$ we fix a generator $\mathbf x _i\in B$ of the direct summand $L(i)$ of $L$ and $\mathbf x _1=\mathtt 1 :=\mathtt 1 _B$, here $\left\{ 1\right\} =\min \left( \Lambda ,\leqslant \right)$. For all $i,j\in \Lambda$ with $j<i$ there exists $\mathbf b _{ij}\in B$ with $\mathbf x _j\cdot \mathbf b _{ij}=\mathbf x _i$, because $\mathbf x _i\in L(i)\subset L(j)=B\cdot \mathbf x _j=\mathbf x _j\cdot B$ (see  3.5 (2)). We define an injective and a surjective $B$-map between $L(i)$ and $L(j)$ by

$$\begin{aligned} \mathbf g _{(i\hookrightarrow j)}:L(i)\mathop {\hookrightarrow }\limits ^{\cdot \mathtt 1 } L(j)\qquad \hbox { and } \qquad \mathbf g _{(j\twoheadrightarrow i)}:L(j)\mathop {\twoheadrightarrow }\limits ^{\cdot \mathbf b _{ij}} L(i) \end{aligned}$$

Note that for an inclusion $g_{(i\hookrightarrow j)}$ described in Lemma 3.5 (5) there exist $c\in K\backslash \left\{ 0\right\}$ and $r\in {{\mathrm{rad}}}L(i)\subseteq L(j)$ such that $g_{(i\hookrightarrow j)}(\mathbf x _i)=c\cdot \mathbf x _i+ r$. In other words $g_{(i\hookrightarrow j)} = c\cdot \mathbf g _{(i\hookrightarrow j)} + g$ where $g:L(i)\mathop {\rightarrow }\limits ^{\cdot \overline{r}}L(j)$ with $\mathbf x _i\cdot \overline{r}=r$. The maps $\mathbf g _{(j\twoheadrightarrow i)}$ and $g_{(j\twoheadrightarrow i)}$ are related in a similar way.

For any $l,t\in \Lambda$ let $\mathfrak {X}(L(l),L(t))$ be the space of non-invertible maps $g\in {{\mathrm{Hom}}}_{B}\left( L(l),L(t)\right)$ with the property ” if $g =g_2\circ g_1$ factors through ${{\mathrm{add}}}L$, then either $g_1$ is a split monomorphism or $g_2$ is a split epimorphism”. The number of arrows from $l$ to $t$ in the quiver of the algebra $A$ is ${{\mathrm{dim}}}_K\mathfrak {X}(L(l),L(t))$ (see [1]).

According to  3.5 (5), any map $g\in {{\mathrm{Hom}}}_{B}\left( L(l),L(t)\right)$ factors through $\bigoplus _{i\in \Lambda ^{(l)}\cap \Lambda ^{(t)}}L(i)$. If $l$ and $t$ are incomparable, then $l,t\not \in \Lambda ^{(l)}\cap \Lambda ^{(t)}$, thus $\mathfrak {X}(L(l),L(t))=0$. Assume $l<t$ and $g:L(l) \rightarrow L(t)$. There exists $b\in B$ with $\mathbf x _t\cdot b = g(\mathbf x _l)$, since $L(t)=B\cdot \mathbf x _t\mathop {=}\limits ^{2.2.1\textit{(2)}}\mathbf x _t\cdot B$ and hence $g:\left( L(l) \twoheadrightarrow L(t) \mathop {\rightarrow }\limits ^{ \cdot b}L(t) \right)$. If $g$ is not surjective, then $b$ is not invertible and consequently $g\not \in \mathfrak {X}(L(l),L(t))$. If $g$ is surjective but $l$ and $t$ are not adjacent, then $g:L(l)\twoheadrightarrow L(j) \twoheadrightarrow L(t)$ for some $j\in \Lambda$ with $l<j<t$ and therefore $g\not \in \mathfrak {X}(L(l),L(t))$. Let $l\triangleleft t$ and $h: L(l)\twoheadrightarrow L(t)$ with $h:\left( L(l)\twoheadrightarrow L(t) \mathop {\twoheadrightarrow }\limits ^{\cdot b}L(t)\right)$, then $L(t) \mathop {\twoheadrightarrow }\limits ^{\cdot b}L(t)$ is a split epimorphism if $b= c\cdot \mathtt 1$ for some $c\in K\backslash \left\{ 0\right\}$, in other words $h=c\cdot \mathbf g _{(l\twoheadrightarrow t)}$. Using analogous arguments also for $j> t$, we obtain $\mathfrak {X}(L(l),L(t))= \left\{ \begin{array}{cl} {{\mathrm{span}}}_K\left\{ \mathbf g _{(l\hookrightarrow t)}\right\} &{} \hbox {if } l\triangleright t, \\ {{\mathrm{span}}}_K\left\{ \mathbf g _{(t \twoheadrightarrow l)}\right\} &{} \hbox {if } l\triangleleft t, \\ 0 &{} \hbox {else}. \end{array} \right.$

(1) In the quiver of a 1-quasi-hereditary algebra $A$ two vertices $i$ and $j$ are connected by an arrow if they are neighbours with respect to $\leqslant$. More precisely, we have $i \rightleftarrows j$. Assume $j\triangleleft i$, then the $B$-maps $\mathbf g _{(i\hookrightarrow j)}$ and $\mathbf g _{(j\twoheadrightarrow i)}$ can by considered as the maps corresponding to the arrows $i\rightarrow j$ and $j\rightarrow i$ respectively. In this case we use the notation $L(i) \overset{\cdot \mathtt 1 }{\underset{\cdot \mathbf b _{ij}}{\rightleftarrows }} L(j)$. In general the notation $L(i) \overset{\cdot \mathtt a }{\underset{\cdot \mathtt b }{\rightleftarrows }} L(j)$ means that $i$ and $j$ are neighbours and $(\mathtt a ,\mathtt b )=\left\{ \begin{array}{ll} (\mathtt 1 ,\mathbf b _{ij}) &{} \hbox {if } j\triangleleft i, \\ (\mathbf b _{ji}, \mathtt 1 ) &{} \hbox {if } j\triangleright i. \end{array} \right.$ We always have $(\mathbf x _i \cdot \mathtt a , \mathbf x _j\cdot \mathtt b )=\left\{ \begin{array}{ll} (\mathbf x _i, \mathbf x _i) &{} \hbox {if } j\triangleleft i, \\ (\mathbf x _j, \mathbf x _j) &{} \hbox {if } j\triangleright i. \end{array} \right.$

(2) Let $p_t=(i,i_1^{(t)},\ldots , i_{m_t}^{(t)},j)$ for $1\le t\le r$ be some paths in $Q(A)$ (obviously, $i_{k}^{(t)}$ and $i_{k+1}^{(t)}$ are neighbours). Then $\sum _{t=1}^r c_t\cdot p_t\in \mathcal {I}(A)$ if and only if

$$\begin{aligned} \displaystyle \sum _{t=1}^{r}c_t\cdot \left( L(i)\mathop {\longrightarrow }\limits ^{\cdot \mathbf b _0^{(t)}} L(i_1^{(t)}) \mathop {\longrightarrow }\limits ^{\cdot \mathbf b _1^{(t)}} \cdots \mathop {\longrightarrow }\limits ^{\cdot \mathbf b _{m_t-1}^{(t)}} L(i_{m_t}^{(t)}) \mathop {\longrightarrow }\limits ^{\cdot \mathbf b _{m_t}^{(t)}} L(j) \right) = 0, \end{aligned}$$

here the maps $L(i_{k}^{(t)}) \mathop {\longrightarrow }\limits ^{\cdot \mathbf b _{k}^{(t)}}L(i_{k+1}^{(t)})$ are of the form $\mathbf g _{(l\hookrightarrow t)}$ or $\mathbf g _{(t \twoheadrightarrow l)}$.

Lemma 3.11

Let $A\cong {{\mathrm{End}}}_B\left( L\right) ^{op}\cong KQ/\mathcal {I}$ with $(\Lambda ,\leqslant )$ be a 1-quasi-hereditary algebra, where $\left( B,L=\bigoplus _{i\in \Lambda }L(i)\right)$ satisfies the property $\boxed {\leqslant }$.

• (1) If $p$ and $q$ are some paths in $Q$ of the form $p(j,i,k)$ (see Subsection 2.1), then $p-q\in \mathcal {I}$. In particular, $p(j,i,k)^{op}=p(k,i,j)$.

• (2) Let $\Gamma$ be the set of (larger) neighbours of $1$, where $\left\{ 1\right\} =\min (\Lambda ,\leqslant )$ and $x_i$ be some generator of $L(i)$ for any $i\in \Gamma$. Then the set $\left\{ x_i\mid i\in \Gamma \right\}$ is a generating system of $B$. In particular, $B$ is a factor algebra of $K\left\langle y_1,\ldots ,y_m\right\rangle$, where $m=\left| \Gamma \right|$.

Proof

(1) Let $j<i$ and $v$, $w$ be some increasing paths from $j$ to $i$. There exists $i=i_0\triangleleft i_1\triangleleft \cdots \triangleleft i_m=j$ and $i=j_0\triangleleft j_1 \triangleleft \cdots \triangleleft j_r=j$ with $v=(i,i_1,\ldots , i_m,j)$ and $w=(i,j_1,\ldots , j_r,j)$ as well as $v^{op}=(j,i_m,\ldots , i_1,i)$ and $w^{op}=(j,j_r,\ldots ,j_1,i)$. For the corresponding $B$-maps $\mathbf g _{(v)}:=\mathbf g _{(i_m\hookrightarrow j)} \circ \cdots \circ \mathbf g _{(i_1\hookrightarrow i_2)} \circ \mathbf g _{(i\hookrightarrow i_1)}$ and $\mathbf g _{(w)}:=\mathbf g _{(j_r\hookrightarrow j)} \circ \cdots \circ \mathbf g _{(j_1\hookrightarrow j_2)} \circ \mathbf g _{(i\hookrightarrow j_1)}$ as well as $\mathbf g _{(v^{op})}=\mathbf g _{( i_1\twoheadrightarrow i)} \circ \mathbf g _{(i_2\twoheadrightarrow i_1)} \circ \cdots \circ \mathbf g _{(j\twoheadrightarrow i_m)}$ and $\mathbf g _{(w^{op})}=\mathbf g _{(j_1\twoheadrightarrow i)} \circ \mathbf g _{(j_2 \twoheadrightarrow j_1)} \circ \cdots \circ \mathbf g _{(j \twoheadrightarrow j_r)}$ we obtain $\mathbf g _{(v)}- \mathbf g _{(w)}=0$ and $\mathbf g _{(v^{op})}-\mathbf g _{(w^{op})}=0$.

For some $i,j,k\in \Lambda$ with $i \leqslant j,k$ let $p$ and $q$ be some paths in $Q$ of the form $p(j,i,k)$, then $p=v_1^{op}\cdot v_2$ and $q=w_1^{op}\cdot w_2$ with some increasing paths $v_1,w_1$ from $k$ to $i$ and $v_2,w_2$ from $j$ to $i$. For the corresponding $B$-maps we have $\mathbf g _{(p)}=\mathbf g _{(v_1^{op})}\circ \mathbf g _{(v_2)}$ and $\mathbf g _{(w)}=\mathbf g _{(w_1^{op})}\circ \mathbf g _{(w_2)}$. Since $\mathbf g _{(v_2)}=\mathbf g _{(w_2)}$ and $\mathbf g _{(v_1^{op})}=\mathbf g _{(w_1^{op})}$, we obtain $\mathbf g _{(p)}= \mathbf g _{(q)}$. This implies $p-q\in \mathcal {I}$.

(2) For any $i\in \Lambda$ with $i\ne 1$ there exists $j\in \Gamma$ with $j\leqslant i$. Thus $L(i)\subseteq L(j)$ and consequently ${{\mathrm{rad}}}B= \sum _{i\in \Lambda \backslash \left\{ 1\right\} }L(i)\mathop {=}\limits ^{1.2.4(2)(b)}\sum _{i\in \Gamma }L(i)$. The set $\left\{ x_i\mid i\in \Gamma \right\}$ generates ${{\mathrm{rad}}}B$. Since $B$ is local, we obtain that $B$ is a factor algebra of $K\left\langle y_1,\ldots , y_{\left| \Gamma \right| }\right\rangle$. $\square$

4 Proof of Theorem B

In this section let $(\Lambda ,\leqslant )$ be a poset, $(B,L=\bigoplus _{i\in \Lambda }L(i))$ is a pair with the property $\boxed {\leqslant }$, and let $A\cong {{\mathrm{End}}}_B(L)^{op}\cong KQ/\mathcal {I}$ be the corresponding 1-quasi-hereditary algebra.

Recall that two vertices in the quiver of $A$ are connected by an arrow iff they are neighbours with respect to $\leqslant$, and in this case there is a pair of arrows, $i \leftrightarrows j$. For any path $p$ in the quiver of $A$ there exists a uniquely determined path $p^{op}$ running through the same vertices in the opposite direction.

For a relation $\rho = \sum _{t=1}^{r}c_t\cdot p_t$ in $\mathcal {I}$ we can define $\rho ^{op}=\sum _{t=1}^{r}c_t\cdot p_t^{op}$. Recall that $A$ is a ${{\mathrm{BGG}}}_{(\leftrightarrows )}$-algebra if $(-)^{op}:A\rightarrow A$, $p+\mathcal {I}\mapsto p^{op}+\mathcal {I}$ is an anti-automorphism.

For the proof of Theorem B we have to show the equivalence of the following statements:

$$\begin{aligned} 1.\, B\hbox { is commutative},\qquad 2.\, A\hbox { is a }{{\mathrm{BGG}}}_{(\leftrightarrows )}-\hbox {algebra}, \qquad 3.\, \rho \in \mathcal {I}\hbox {if and only if }\rho ^{op} \in \mathcal {I}\end{aligned}$$

For every $i\in \Lambda$ we fix a generator $\mathbf x _i\in B$ of $L(i)$ and $\mathbf x _1=\mathtt 1 := \mathtt 1 _{B}$. For $i,j\in \Lambda$ with $i\triangleleft j$ or $i\triangleright j$ we denote by $L(i) \overset{\cdot \mathtt a }{\underset{\cdot \mathtt b }{\rightleftarrows }} L(j)$ the $B$-maps described in  3.10(1). Note, if $i\triangleleft j$, the map $L(i)\mathop {\rightarrow }\limits ^{\cdot \mathtt a }L(j)$ is surjective with $\mathbf x _i\cdot \mathtt a =\mathbf x _j$, and the map $L(j)\mathop {\rightarrow }\limits ^{\cdot \mathtt b }L(i)$ is injective with $\mathtt b =\mathbf 1$, because $\mathbf x _j\cdot \mathtt b =\mathbf x _j$. In particular, if $i=1$ we have $\mathtt a = \mathtt 1 \cdot \mathtt a =\mathbf x _j$.

Lemma 4.1

The following statements are equivalent:

• (i) $B$ is commutative.

• (ii) Let $p=(i_0,i_1,\ldots , i_m)$ be some path in $Q$ and $L(i_0) \overset{\cdot \mathtt a _1}{\underset{\cdot \mathtt b _1}{\rightleftarrows }} L(i_1) \overset{\cdot \mathtt a _2}{\underset{\cdot \mathtt b _2}{\rightleftarrows }} \cdots \overset{\cdot \mathtt a _{m}}{\underset{\cdot \mathtt b _{m}}{\rightleftarrows }} L(i_{m})$ be the corresponding $B$-maps. Then $\mathbf x _{i_0}\cdot \mathtt a _1\cdot \mathtt a _2\cdots \mathtt a _{m} = \mathbf x _{i_m}\cdot \mathtt b _{m} \cdots \mathtt b _2\cdot \mathtt b _1$.

• (iii) Statement $(ii)$ holds for $m=4$.

Proof

$(i)\Rightarrow (ii)$ We show this by induction on $m$: If $m=1$, then for $L(i_0)\overset{\cdot \mathtt a _1}{\underset{\cdot \mathtt b _1}{\rightleftarrows }} L(i_1)$ we have $\left( \mathbf x _{i_0}\cdot \mathtt a _1, \mathbf x _{i_1}\cdot \mathtt b _1\right) \in \Big \{\left( \mathbf x _{i_0},\mathbf x _{i_0}\right) , \left( \mathbf x _{i_1},\mathbf x _{i_1}\right) \Big \}$ (see  3.10(1)), thus $\mathbf x _{i_0}\cdot \mathtt a _1 = \mathbf x _{i_1}\cdot \mathtt b _1$. Assume $\mathbf x _{i_0}\cdot \mathtt a _1\cdot \mathtt a _2\cdots \mathtt a _{m-1} = \mathbf x _{i_{m-1}}\cdot \mathtt b _{m-1} \cdots \mathtt b _2\cdot \mathtt b _1$, then by multiplication with $\mathtt a _m$ we obtain

because $B$ is commutative. If $i_{m-1}\triangleright i_{m}$, then $\mathtt a _m=\mathtt 1$ and $\mathbf x _{i_{m-1}}= \mathbf x _{i_m}\cdot \mathtt b _m$. The equation $(\circledast )$ yields $\mathbf x _{i_0}\cdot \mathtt a _1\cdot \mathtt a _2\cdots \mathtt a _{m-1}\cdot \mathtt a _m = \mathbf x _{i_m}\cdot \mathtt b _m\cdot \mathtt b _{m-1} \cdots \mathtt b _2\cdot \mathtt b _1$. If $i_{m-1} \triangleleft i_{m}$, we obtain $\mathbf x _{i_{m-1}}\cdot \mathtt a _m= \mathbf x _{i_m}$ and $\mathtt b _m=\mathtt 1$, thus the equation $(\circledast )$ is $\mathbf x _{i_0}\cdot \mathtt a _1\cdot \mathtt a _2\cdots \mathtt a _{m-1}\cdot \mathtt a _m = \mathbf x _{i_m}\cdot \mathtt b _m\cdot \mathtt b _{m-1} \cdots \mathtt b _2\cdot \mathtt b _1$.

$(ii)\Rightarrow (iii)$ This is trivial.

$(iii)\Rightarrow (i)$ Let $i,j\in \left\{ l\in \Lambda \mid 1\triangleleft l\right\}$ and $L(1) \overset{\cdot \mathtt a _1}{\underset{\cdot \mathtt b _1}{\rightleftarrows }} L(i) \overset{\cdot \mathtt a _2}{\underset{\cdot \mathtt b _2}{\rightleftarrows }} L(1) \overset{\cdot \mathtt a _3}{\underset{\cdot \mathtt b _3}{\rightleftarrows }} L(j) \overset{\cdot \mathtt a _4}{\underset{\cdot \mathtt b _4}{\rightleftarrows }} L(1)$. Since $1\triangleleft i \triangleright 1 \triangleleft j \triangleright 1$, we have $(\mathtt a _1, \mathtt b _1)=(\mathbf x _i,\mathtt 1 )$, $(\mathtt a _2, \mathtt b _2)=(\mathtt 1 ,\mathbf x _i)$, $(\mathtt a _3, \mathtt b _3)=(\mathbf x _j,\mathtt 1 )$, and $(\mathtt a _4, \mathtt b _4)=(\mathtt 1 ,\mathbf x _j)$. By the assumption, we have $\mathbf x _1\cdot \mathtt a _1 \cdot \mathtt a _2 \cdot \mathtt a _3 \cdot \mathtt a _4 = \mathbf x _1\cdot \mathtt b _4 \cdot \mathtt b _3 \cdot \mathtt b _2\cdot \mathtt b _1$, in other words, $\mathtt 1 \cdot \mathbf x _i \cdot \mathtt 1 \cdot \mathbf x _j\cdot \mathtt 1 =\mathtt 1 \cdot \mathbf x _j\cdot \mathtt 1 \cdot \mathbf x _i\cdot \mathtt 1$. This implies $\mathbf x _i\cdot \mathbf x _j=\mathbf x _j\cdot \mathbf x _i$. The algebra $B$ is commutative, because $\left\{ \mathbf x _k\mid 1\triangleleft k\right\}$ is a generating system of $B$ (see Lemma 3.11(2)).

$\square$

Proof

1$\Rightarrow$3 Let $\rho =\sum _{t=1}^{r}c_t\cdot \left( i_0^{(t)}, i_1^{(t)}, \ldots , i_{m_t}^{(t)} \right)$ be a relation with $i=i_0^{(t)}$, $j = i_{m_t}^{(t)}$, and $L(i_{v-1}^{(t)}) \overset{\cdot \mathtt a _v^{(t)}}{\underset{\cdot \mathtt b _v^{(t)}}{\rightleftarrows }} L(i_{v}^{(t)})$ the corresponding $B$-map for $1\le t\le r$. We obtain $\sum _{t=1}^{r}c_t\cdot \left( L(i)\mathop {\rightarrow }\limits ^{\cdot \mathtt a _1^{(t)}} L(i_1^{(t)}) \mathop {\rightarrow }\limits ^{\cdot \mathtt a _2^{(t)}} \cdots \mathop {\rightarrow }\limits ^{\cdot \mathtt a _{m_t}^{(t)}} L(j) \right) = 0$ (see  3.10(2)). Hence, $\sum _{t=1}^{r}c_t\cdot \left( \mathbf x _i\cdot \mathtt a _1^{(t)} \cdots \mathtt a _{m_t}^{(t)}\right) = 0$. We have $\sum _{t=1}^{r}c_t\cdot \left( \mathbf x _j\cdot \mathtt b _{m_t}^{(t)} \cdots \mathtt b _{1}^{(t)}\right) \mathop {=}\limits ^{3.1} 0$. This implies $\rho ^{op}=\sum _{t=1}^{r}c_t\cdot \left( i_{m_t}^{(t)}, \cdots , i_{1}^{(t)}, i_{0}^{(t)} \right) \in \mathcal {I}$, because $\sum _{t=1}^{r}c_t\cdot \left( L(j)\mathop {\longrightarrow }\limits ^{\cdot \mathtt b _{m_t}^{(t)}} \cdots \mathop {\longrightarrow }\limits ^{\cdot \mathtt b _{2}^{(t)}} L(i_{1}^{(t)}) \mathop {\longrightarrow }\limits ^{\cdot \mathtt b _1^{(t)}} L(i) \right) = 0$.

3$\Rightarrow$1 Let $\Gamma :=\left\{ k\in \Lambda \mid 1\triangleleft k\right\}$. It is enough to show $\mathbf x _k\cdot \mathbf x _j=\mathbf x _j\cdot \mathbf x _k$ for all $k,j \in \Gamma$ (see  3.11): Let $k,j\in \Gamma$, then we have $L(1) \overset{\cdot \mathbf x _k}{\underset{\cdot \mathtt 1 }{\rightleftarrows }} L(k) \overset{\cdot \mathtt 1 }{\underset{\cdot \mathbf x _k}{\rightleftarrows }} L(1) \overset{\cdot \mathbf x _j}{\underset{\cdot \mathtt 1 }{\rightleftarrows }} L(j) \overset{\cdot \mathtt 1 }{\underset{\cdot \mathbf x _j}{\rightleftarrows }} L(1)$, since $1\triangleleft k, j \triangleright 1$. Let $\mathbf g$ and $\mathbf h$ be the composition of the maps which goes from left to right and from right to left, respectively, i.e., $\mathbf g :\left( L(1)\mathop {\twoheadrightarrow }\limits ^{\cdot \mathbf x _k} L(k)\mathop {\hookrightarrow }\limits ^{\cdot 1} L(1)\mathop {\twoheadrightarrow }\limits ^{\cdot \mathbf x _j} L(j)\mathop {\hookrightarrow }\limits ^{\cdot 1} L(1)\right)$ and $\mathbf h :\left( L(1)\mathop {\twoheadrightarrow }\limits ^{\cdot \mathbf x _j} L(j)\mathop {\hookrightarrow }\limits ^{\cdot 1} L(1)\mathop {\twoheadrightarrow }\limits ^{\cdot \mathbf x _k} L(k)\mathop {\hookrightarrow }\limits ^{\cdot 1} L(1)\right)$. We obtain $\mathbf x _k\cdot \mathbf x _j= \mathbf g (\mathtt 1 )=\mathbf h (\mathtt 1 )=\mathbf x _j\cdot \mathbf x _k$ if and only if $\mathbf g =\mathbf h$. Since $\mathbf g$ and $\mathbf h$ correspond to the paths $(1,k,1,j,1)$ and $(1,j,1,k,1)$ respectively, we have to show that $(1,j,1,k,1)=(1,k,1,j,1)$ in $A$.

According to [11, Theorem 3.2] for the path $(j,1,k)$ there exists some $c_i\in K$ with $\rho =(j, 1, k)-\sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} c_i \cdot p(j,i,k)\in \mathcal {I}$. Since $(j,1,k)^{op}=(k,1,j)$ and $p(j,i,k)^{op}=p(k,i,j)$, by our assumption we obtain $\rho ^{op}=(k,1,j) - \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} c_i \cdot p(k,i,j)\in \mathcal {I}$. Obviously, $(1,j,1,k,1)= (k\rightarrow 1)\cdot (j, 1, k) \cdot (1\rightarrow j)$ and $(1,k,1,j,1)= (1,j,1,k,1)^{op}= (j\rightarrow 1)\cdot (k, 1, j) \cdot (1\rightarrow k)$. The relations $\rho$ and $\rho ^{op}$ imply the following equations in $A$:

$$\begin{aligned} \begin{array}{ccl} (1,j,1,k,1) &{} = &{} \displaystyle \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} c_i \cdot \left( (k\rightarrow 1)\cdot p(j,i,k)\cdot (1\rightarrow j)\right) \\ (1,k,1,j,1) &{} = &{} \displaystyle \sum _{i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}} c_i \cdot \left( (j\rightarrow 1)\cdot p(k,i,j)\cdot (1\rightarrow k)\right) \\ \end{array} \end{aligned}$$

For every $i\in \Lambda ^{(j)}\cap \Lambda ^{(k)}$ the paths $p_{(i)}= (k\rightarrow 1)\cdot p(j,i,k)\cdot (1\rightarrow j)$ and $q_{(i)}=(j\rightarrow 1)\cdot p(k,i,j)\cdot (1\rightarrow k)$ are of the form $p(1,i,1)$ (in the picture below the black and the inner gray path respectively). Thus Lemma  3.11(1) implies $p_{(i)}=q_{(j)}$ in $A$, hence $(1,j,1,k,1)=(1,k,1,j,1)$.

2$\Leftrightarrow$3 Assume the $K$-map $(-)^{op}:A\rightarrow A$ with $p\mapsto p^{op}$ is an anti-automorphism of $A$. If for some paths $p_1,\ldots , p_r$, which start in $i$ and end in $j$ we have $\sum _{t=1}^rc_t\cdot p_t=0$, then $\left( \sum _{t=1}^rc_t\cdot p_t\right) ^{op}=\sum _{t=1}^rc_t\cdot p_t^{op}=0$ (in other words, if $\rho \in \mathcal {I}$, then $\rho ^{op}\in \mathcal {I}$ ). On the other hand, if $\mathcal {I}=\left\{ \rho ^{op}\mid \rho \in \mathcal {I}\right\}$, then $(-)^{op}:A\rightarrow A$ is obviously an anti-automorphism. $\square$

5 Ringel-duality on generators-cogenerators of local self-injective algebras

Let $(\mathcal {A},\leqslant )$ be a quasi-hereditary algebra, then for any $i\in Q_0(\mathcal {A})$ there exists a (up to isomorphism) uniquely determined indecomposable module $T(i)\in \mathfrak {F}(\Delta )\cap \mathfrak {F}(\nabla )$ with the following properties: For all $j\in Q_0(\mathcal {A})$ with $j\not \leqslant i$ we have $[T(i):S(j)]=0$ and $[T(i):S(i)]=\left( T(i):\Delta (i)\right) =\left( T(i):\nabla (i)\right) =1$, moreover, $\mathfrak {F}(\Delta )\cap \mathfrak {F}(\nabla )={{\mathrm{add}}}\left( \bigoplus _{i\in Q_0(\mathcal {A})}T(i)\right)$. Note that for a minimal vertex $\mathtt i$ we always have $T(\mathtt i )\cong \Delta (\mathtt i )\cong \nabla (\mathtt i ) \cong S(\mathtt i )$.

For any 1-quasi-hereditary algebra $(A,\leqslant )$ with $1\leqslant i\leqslant n$ we have $T(1)\cong S(1)$, and $P(1)\cong I(1)\cong T(n)$, since $P(1)\in \mathfrak {F}(\Delta )\cap \mathfrak {F}(\nabla )$ is indecomposable and $\left( P(1):\Delta (n)\right) =(I(1):\nabla (n))=1$.

The module $T:=\bigoplus _{i\in Q_0(\mathcal {A})}T(i)$ is called the characteristic tilting module. The Ringel-dual $R(\mathcal {A}):= {{\mathrm{End}}}_{\mathcal {A}}(T)^{op}$ of $\mathcal {A}$ is a basic algebra on the same vertex set $Q_0(R(\mathcal {A}))=Q_0(\mathcal {A})$. Also, $R(\mathcal {A})$ is quasi-hereditary with the opposite order $\geqslant$ (we use the notation $\leqslant _{(R)}$). Moreover, $R(R(\mathcal {A}))\cong \mathcal {A}$ as quasi-hereditary algebras. The functor $\fancyscript{R}:={{\mathrm{Hom}}}_{A}(T, -): {{\mathrm{mod}}}A \longrightarrow {{\mathrm{mod}}}R(A)$ yields an exact equivalence between the subcategories $\mathfrak {F}(\nabla _{\mathcal {A}})$ and $\mathfrak {F}(\Delta _{R(\mathcal {A})})$. Moreover, $P_{R(\mathcal {A})}(i)\cong \fancyscript{R}(T(i))$, $T_{R(\mathcal {A})}(i)\cong \fancyscript{R}(I(i))$ and $\Delta _{R(\mathcal {A})}(i)\cong \fancyscript{R}(\nabla (i))$ for all $i\in Q_0(\mathcal {A})$ (for more details, see [13]).

The class of 1-quasi-hereditary algebras is not closed under Ringel duality. Example  4 in [12] presents a 1-quasi-hereditary algebra $A$ for which $R(A)$ is not 1-quasi-hereditary. However, the properties of $R(A)$ for a 1-quasi-hereditary algebra $A$ considered in  [11, Lemma 6.2] yield the following lemma. (For $R(A)$-modules we will use the index $(R)$, note that $1\leqslant i\leqslant n$ implies $n\leqslant _{(R)} i\leqslant _{(R)} 1$ for all $i\in \Lambda :=Q_0(R(A))= Q_0(A)$.)

Lemma 5.1

Let $(A,\leqslant )$ be a 1-quasi-hereditary algebra with $1\leqslant i \leqslant n$ for any $i\in \Lambda$ and let $(R(A),\leqslant _{(R)} )$ be the Ringel dual of $(A,\leqslant )$. Then ${{\mathrm{dom.dim}}}R(A)\ge 2$ and $P_{(R)}(n)$ is a minimal faithful $R(A)$-module.

Proof

Since $\left\{ 1\right\} =\max \left( \Lambda ,\leqslant _{(R)}\right)$, the definition of standard modules implies $P_{(R)}(1)=\Delta _{(R)}(1)$. According to [11, Lemma 6.2] we obtain $\Delta _{(R)}(i) \hookrightarrow \Delta _{(R)}(1)=P_{(R)}(1)\hookrightarrow P_{(R)}(n)\cong I_{(R)}(n)$. We have ${{\mathrm{soc}}}\left( \Delta _{(R)}(i)\right) \in {{\mathrm{add}}}\left( {{\mathrm{soc}}}I_{(R)}(n)\right)$ for all $i\in \Lambda$. According to Proposition  2.3, it is enough to show $P_{(R)}(i) \hookrightarrow P_{(R)}(n)^{r_i}$ (for some $r_i\in \mathbb {N}$) and $P_{(R)}(n)^{r_i}/P_{(R)}(i) \in \mathfrak {F}(\Delta _{(R)})$ for any $i\in \Lambda$.

Since $T(i)\in \mathfrak {F}(\Delta )$, we have ${{\mathrm{soc}}}T(i)\in {{\mathrm{add}}}\left( \bigoplus _{j\in \Lambda }{{\mathrm{soc}}}\Delta (j)\right) \mathop {=}\limits ^{1.2.1}{{\mathrm{add}}}\left( S(1)\right)$. Let ${{\mathrm{soc}}}T(i)\cong S(1)^{r_i}$, then $T(i)\hookrightarrow T(n)^{r_i}$ since $T(n)\cong I(1)$ (see [11, 5.3]). The exact sequence $\xi :0\rightarrow T(i)\rightarrow T(n)^{r_i}\rightarrow T(n)^{r_i}/T(i)\rightarrow 0$ yields $T(n)^{r_i}/T(i)\in \mathfrak {F}(\nabla )$, because $\mathfrak {F}(\nabla )$ is closed under cokernels of injective maps (see [13]). By applying $\fancyscript{R}(-)$ to $\xi$ we obtain an exact sequence $0\rightarrow P_{(R)}(i)\rightarrow P_{(R)}(n)^{r_i}\rightarrow P_{(R)}(n)^{r_i}/P_{(R)}(i) \rightarrow 0$ with $P_{(R)}(n)^{r_i}/P_{(R)}(i)\in \mathfrak {F}(\Delta _{(R)})$ for any $i\in \Lambda$.$\square$

5.1 Transfer of Ringel duality

Throughout, we keep the notation for the sets $\mathbf X$, $\mathbf Y$, $\mathbf X (1)$, $\mathbf Y (1)$ and for the functions $\mathbf X \overset{\Phi }{\underset{\Psi }{\rightleftarrows }} \mathbf Y$ used in Sect. 1. Moreover, we denote by $\mathbf X (R(1))$ the set of isomorphism classes of Ringel-duals of 1-quasi-hereditary algebras. Lemma  5.1 implies that $\mathbf X (R(1))\subseteq \mathbf X$. We denote by $\mathbf Y (R(1))$ the image of $\Phi |_\mathbf{X (R(1))}$. Moreover, let $\mathcal {X}:=\mathbf X (1)\cup \mathbf X (R(1))$ and $\mathcal {Y}:=\mathbf Y (1)\cup \mathbf Y (R(1))$ as well as $\widehat{\mathcal {X}}:=\mathbf X (1)\cap \mathbf X (R(1))$ and $\widehat{\mathcal {Y}}:=\mathbf Y (1)\cap \mathbf Y (R(1))$.

Note that the second component of a pair in $\mathcal {Y}$ is not necessarily a direct sum of local modules. We use again the notation $\fancyscript{G}$ for a generator–cogenerator.

The map $\mathcal {R}: \mathcal {X}\rightarrow \mathcal {X}$ with $\mathcal {R}\left( \left[ A\right] \right) = \left[ R(A)\right]$ is obviously bijective and $\mathcal {R}^2={{\mathrm{id}}}_{\mathcal {X}}$. The Morita–Tachikawa Theorem  2.1 and Theorem A 1.2.6 yield the transfer of Ringel-duality for $\mathcal {X}$ on $\mathcal {Y}$ (we may visualise the situation as in the following picture).

Obviously, for any pair $[\mathcal {B},\fancyscript{G}]\in \mathcal {Y}$ with $[A]=\Psi \left( [\mathcal {B},\fancyscript{G}]\right)$, the algebra $(A,\leqslant )$ or $(R(A),\leqslant _{(R)})$ is 1-quasi-hereditary. Without loss of generality assume that $A$ with partial order $(\Lambda ,\leqslant )$ by 1-quasi-hereditary. Since $\fancyscript{G}$ has $\left| \Lambda \right| ={{\mathrm{dim}}}_K\mathcal {B}$ (pairwise non-isomorphic, indecomposable) direct summands, the quiver of the algebra $A$ as well as the quiver of $R(A)$ has $\left| \Lambda \right|$ vertices. Thus for $\mathbf R [\mathcal {B},\fancyscript{G}]=[R(\mathcal {B}), R(\fancyscript{G})]$ we obtain that the generator–cogenerator $R(\fancyscript{G})$ of $R(\mathcal {B})$ has also $\left| \Lambda \right|$ direct summands, which are denoted by $R(\fancyscript{G}(i))$ for $i\in \Lambda$.

Lemma 5.2

Let $[B,L]\in \mathbf Y (1)$ and $[A]=\Psi \left( [B,L]\right) \in \mathbf X (1)$. Then for $\mathbf R ( [B,L]) = \left[ R(B),R(L)\right]$ with $R(L) \cong \bigoplus _{i\in \Lambda }R(L(i))$ we have

$$\begin{aligned} B\cong R(B) \quad \hbox { and }\quad \displaystyle R(L(i)) \cong {{\mathrm{Hom}}}_{A}(T(i),T(n)). \end{aligned}$$

Proof

The Morita–Tachikawa Theorem  2.1 and Lemma  5.1 yield $B\cong {{\mathrm{End}}}_{A}(P(1))^{op}$ and $R(B)\cong {{\mathrm{End}}}_{R(A)}(P_{(R)}(n))^{op}$. Since $R(A)={{\mathrm{End}}}_A(T)^{op}$ and $P_{(R)}(i)\cong {{\mathrm{Hom}}}_A(T, T(i))$, the functor ${{\mathrm{Hom}}}_{A}(T,-):{{\mathrm{mod}}}A\rightarrow {{\mathrm{mod}}}R(A)$ yields an isomorphism ${{\mathrm{Hom}}}_{A}(T(i),T(n)) \cong {{\mathrm{Hom}}}_{R(A)}(P_{(R)}(i),P_{(R)}(n))$ for all $i\in \Lambda$ (see [1, 2.1]). Since $T(n)\cong P(1)$, we have

$$\begin{aligned} B\cong {{\mathrm{End}}}_{A}(P(1))^{op}\cong {{\mathrm{End}}}_{R(A)}(P_{(R)}(n))^{op}\cong R(B). \end{aligned}$$

Since $P_{(R)}(n)$ is the minimal faithful $R(B)$-module, $R(L)$ is isomorphic to ${}_{R(B)}P_{(R)}(n)$. Thus

$$\begin{aligned} R(L)\cong \bigoplus \nolimits _{i\in \Lambda }{{\mathrm{Hom}}}_{R(A)}(P_{(R)}(i),P_{(R)}(n))\cong \bigoplus \nolimits _{i\in \Lambda }{{\mathrm{Hom}}}_{A}(T(i),T(n)). \end{aligned}$$

$\square$

Lemma  5.2 implies that for any $[\mathcal {B},\fancyscript{G}]\in \mathcal {Y}$ we have $\mathbf R ([\mathcal {B},\fancyscript{G}])=[\mathcal {B},R(\fancyscript{G})]$. Since $[\mathcal {B},\fancyscript{G}] \in \mathbf Y (1)$ or $\mathbf R ([\mathcal {B},\fancyscript{G}]) \in \mathbf Y (1)$, the algebra $\mathcal {B}$ is a local self-injective algebra having a module with the property $\boxed {\leqslant }$ in Definition 2.5 for some $(\Lambda ,\leqslant )$. Let $B$ be an algebra and

$$\begin{aligned} \mathfrak {M}(B){:=} \left\{ M\in {{\mathrm{mod}}}B\mid (B,M) \hbox { or } (B,R(M)) \hbox { has the property } \boxed {\leqslant }, \hbox { for some } (\Lambda ,\leqslant )\right\} . \end{aligned}$$

Obviously, there exist finitely many partial orders on $\Lambda$. However, $\mathfrak {M}(B)$ has infinitely many pairwise non-isomorphic $B$-modules.

Proposition 5.3

Let $\mathbf L \!:=\!\left\{ [B] \!\mid \! \mathfrak {M}(B) \!\ne \! \emptyset \right\}$ and $[B]\in \mathbf L$. Then $\mathcal {Y}(B)\!:=\!\left\{ [B,M]\!\mid \! M\!\in \! \mathfrak {M}(B)\right\}$ and $\mathcal {X}(B):=\left\{ \left[ {{\mathrm{End}}}_B(M)^{op}\right] \mid M\in \mathfrak {M}(B)\right\}$ is closed under Ringel-duality $\mathbf R$ and $\mathcal {R}$, respectively. Moreover, $\mathcal {Y}=\overset{\cdot }{\bigcup }_{[B]\in \mathbf L }\mathcal {Y}(B)$ and $\mathcal {X}=\overset{\cdot }{\bigcup }_{[B]\in \mathbf L }\mathcal {X}(B)$.

Proof

It is easy to see that for all $\left[ B\right] ,\left[ B'\right] \in \mathbf L$ with $\left[ B\right] \ne \left[ B'\right]$ we have $\mathcal {Y}(B) \cap \mathcal {Y}(B')=\emptyset$, and any pair in $\mathcal {Y}$ belongs to $\mathcal {Y}(B)$ for some $[B]\in \mathbf L$.

Let $M\in \mathfrak {M}(B)$, then there exists $\leqslant$ on $\Lambda$ such that $(B,M)$ or $(B,R(M))$ has the property $\boxed {\leqslant }$. Since $\mathbf R [B,R(M)]=[B,R(R(M))]=[B,M]$, the pair $(B,R(M))$ or $(B,R(R(M)))$ has the property $\boxed {\leqslant }$. Thus $R(M)\in \mathfrak {M}(B)$, and consequently $\mathbf R [B,R(M)]\in \mathfrak {M}(B)$. The Morita–Tachikawa Theorem  2.1 yields that for any $[A]\in \mathcal {X}(B)$ we have $[\mathcal {R}(A)]\in \mathcal {X}(B)$. Obviously, $[B]\ne [B']$ implies $\mathcal {X}(B) \cap \mathcal {X}(B')$, and any $[A]\in \mathcal {X}$ belongs to $\mathcal {X}(B)$ for some $[B]\in \mathbf L$.$\square$

Note that the function $\mathbf X (1) \rightarrow \mathbf L$ with $[A]\mapsto \left[ {{\mathrm{End}}}_A(P(1))\right]$ is surjective, non-injective. The set $\mathbf L$ is not finite (for example we have $[B_1\otimes B_2]\in \mathbf L$ for all $[B_1],[B_2]\in \mathbf L$). In the picture the sets $\mathcal {X}$ and $\mathcal {Y}$ are presented as the disjoint union of $\mathcal {X}(B)$ and $\mathcal {Y}(B)$ (symbolized by the circles, they are closed under the Ringel-duality $\mathbf R$ and $\mathcal {R}$) respectively.

The dark circles inside the circle corresponding to $\mathcal {X}(B)$ symbolize $\mathcal {X}(B)\cap \widehat{\mathcal {X}}$. Similarly, a pair $[B,M]$ in the dark circle of $\mathcal {Y}(B)$ has the property $\boxed {\leqslant }$ and $\mathbf R ([B,M])$ has the property $\boxed {\geqslant }$, i.e., $[B,M]\in \widehat{\mathcal {Y}}$. In particular, $\widehat{\mathcal {X}}$ and $\widehat{\mathcal {Y}}$ are the disjoint unions of the dark circles. They are also closed under $\mathcal {R}$ resp. $\mathbf R$. The observation of Ringel-duality on $\mathcal {X}$ and $\mathcal {Y}$ can by restricted to $\mathcal {X}(B)$ and $\mathcal {Y}(B)$ respectively.

Remark 5.4

In general for a fixed poset $(\Lambda ,\leqslant )$ the number of pairs $[B,L]$ with the property $\boxed {\leqslant }$ is not finite. For example, the algebra $B=K[x,y]/\left\langle x^2,y^2\right\rangle$ is a local and self-injective algebra of dimension $4$. The poset $\left( \left\{ 1,2,3,4\right\} ,\leqslant \right)$ is given by $1\triangleleft 2,3\triangleleft 4$. Let $L(1)=\left\langle \mathtt 1 _{B}\right\rangle$, $L(2)=\left\langle X\right\rangle$, $L(4)=\left\langle XY\right\rangle$ and $L_{\lambda }(3)=\left\langle Y+\lambda \cdot X\right\rangle$ for $\lambda \in K$. The pair $[B,L_{\lambda }]$ with has the property $\boxed {\leqslant }$ for all $\lambda \in K$, but $L_{\lambda }(3)\not \cong L_{\mu }(3)$ if $\lambda \ne \mu$.

Moreover, if $(B,L)$ and $(B,L')$ satisfy the condition $\boxed {\leqslant }$, then the property $[B,L]\in \widehat{\mathcal {Y}}$ does not imply $[B,L']\in \widehat{\mathcal {Y}}$.

5.2 Ringel-duality on $\widehat{\mathcal {Y}}$

In [11, Sec. 5 and 6] 1-quasi-hereditary algebras whose isomorphism classes belong to $\widehat{\mathcal {X}}$ have been considered. These results yield a precise description of the Ringel-duality $\mathbf R$ on $\widehat{\mathcal {Y}}$.

Let $[B,L]$ be in $\mathbf Y (1)$ and $A={{\mathrm{End}}}_B(L)^{op}\cong KQ/\mathcal {I}$ be the corresponding 1-quasi-hereditary algebra with $(\Lambda ,\leqslant )$ (here $1\leqslant i\leqslant n$ for all $i\in \Lambda$). Then $B\cong {{\mathrm{End}}}_A(P(1))^{op}$ and $L\cong \bigoplus _{i\in \Lambda }B\circ \mathfrak {f}_{(i)}$, where $\mathfrak {f}_{(i)}:=\mathfrak {f}_{(1,i,1)}$ is the endomorphism of $P(1)$ corresponding to the path $p(1,i,1)$ of $A$ (see Proposition 3.4). Assume that $R(A)={{\mathrm{End}}}_A(T)^{op}$ with $(\Lambda ,\leqslant _{(R)})$ is also 1-quasi-hereditary. According to Theorem 6.1 in [11], the direct summand $T(i)$ of $T$ is a submodule and a factor module of $P(1)\cong I(1)$ for any $i\in \Lambda$. More precisely,

$$\begin{aligned} T(i)\cong P(1)/\left( \sum \limits _{j\in \Lambda \backslash \Lambda _{(i)}}P(j)\right) \cong \bigcap \nolimits _{j\in \Lambda \backslash \Lambda _{(i)}}\ker \left( P(1)\twoheadrightarrow I(j)\right) \end{aligned}$$

(using the notations of Sect. 2, we have $\Lambda \backslash \Lambda _{(i)} =\left\{ j\in \Lambda \mid j\not \leqslant i\right\} =\left\{ j\in \Lambda \mid i\not \leqslant _{(R)}j\right\}$). Consequently, the subspace $P(1)_1\mathop {=}\limits ^{2.1.2}{{\mathrm{span}}}_K\left\{ p(1,j,1)\mid j\in \Lambda \right\}$ of $P(1)$ contains an element $\mathfrak {t}(i)$ which generates $T(i)(= A\cdot \mathfrak {t}(i))$. For any $i\in \Lambda$ we denote by $\theta _{(i)}$ the following endomorphism of $P(1)$: $\theta _{(i)}=(\iota _{(i)}\circ \pi _{(i)}):\left( P(1)\mathop {\twoheadrightarrow }\limits ^{\pi _{(i)}} T(i)\mathop {\hookrightarrow }\limits ^{\iota _{(i)}} P(1)\right)$ with $e_1\mathop {\mapsto }\limits ^{\pi _{(i)}} \mathfrak {t}(i)$ and $\mathfrak {t}(i)\mathop {\mapsto }\limits ^{\iota _{(i)}} \mathfrak {t}(i)$

Using Lemma 3.2 [12] it is easy to show, that the pair $(B,\mathcal {L})$ with $\mathcal {L}\cong \bigoplus _{i\in \Lambda }B\circ \theta _{(i)}$ satisfies the condition $\boxed {\leqslant _{(R)}}$.

The Ringel duality $\mathbf R$ on $\widehat{\mathcal {Y}}$ provides a relationship between the endomorphisms $\theta _{(1)}, \ldots , \theta _{(n)}$ and $\mathfrak {f}_{(1)},\ldots , \mathfrak {f}_{(n)}$ of $P(1)$. The following statement yields Theorem C from the introduction.

Theorem C. Let $(A,\leqslant )$ be a 1-quasi-hereditary algebra, $B={{\mathrm{End}}}_A(P(1))^{op}$ and $L\cong \bigoplus _{i\in \Lambda }L(i)$ where $L(i)= B\circ \mathfrak {f}_{(i)}$ for any $i\in \Lambda$ (i.e., $[(B,L),\leqslant ]$ is the corresponding pair in $\mathbf Y (1)$). Let $[B,R(L)]$ with $R(L)\cong \bigoplus _{i\in \Lambda } R(L(i))$ be the Ringel-dual of $[B,L]$. Then the following statements are equivalent:

• (i) $[B,L]\in \widehat{\mathcal {Y}}$.

• (ii) $\displaystyle R(L(i))\cong B \circ \theta _{(i)}$, where ${{\mathrm{im}}}\left( \theta _{(i)}\right) =T(i)$ for every $i\in \Lambda$.

• (iii) $R(L(i))\cong B/\left( \sum _{j\in \Lambda \backslash \Lambda _{(i)}}L(j)\right) \cong \bigcap _{j\in \Lambda \backslash \Lambda _{(i)}} \ker \left( B\twoheadrightarrow L(j)\right)$ for every $i\in \Lambda$.

Proof

According to Lemma 5.2 for any $i\in \Lambda$ we have $R(L(i))\cong {{\mathrm{Hom}}}_{A}(T(i),T(n))$.

$(i)\Rightarrow (ii)$ The assumption $[B,L]\in \widehat{\mathcal {Y}}$ implies $[A]\in \widehat{\mathcal {X}}$. As already explained, we can define endomorphisms $\theta _{(i)}=(\iota _{(i)}\circ \pi _{(i)})$ for any $i\in \Lambda$. Since ${{\mathrm{Hom}}}_A(-,P(1))$ is exact, the inclusion $T(i)\mathop {\hookrightarrow }\limits ^{\iota _{(i)}} P(1)$ yields a surjective $B$-map ${{\mathrm{Hom}}}_{A}(P(1),P(1))\twoheadrightarrow {{\mathrm{Hom}}}_A(T(i),P(1))$ with $F\mapsto F\circ \iota _{(i)}$. Thus ${{\mathrm{Hom}}}_A(T(i),P(1))= B\circ \iota _{(i)}$. The map $(-\circ \pi _{(i)}): B\circ \iota _{(i)} \rightarrow B\circ \theta _{(i)}$ is obviously a $B$-module isomorphism. We obtain $R(L(i))\cong B\circ \iota _{(i)} \cong B\circ \theta _{(i)}$ for all $i\in \Lambda$.

$(ii)\Rightarrow (i)$ Since ${{\mathrm{im}}}\left( \theta _{(i)}\right) =T(i)$ for every $i\in \Lambda$, the top of any direct summand of the characteristic tilting $A$-module is simple. According to Theorem 5.1 and 6.1 in [11] the algebra $(R(A),\leqslant _{(R)})$ is 1-quasi-hereditary. This implies $\mathbf R [B,L]\in \mathbf Y (1)$.

$(i) \Rightarrow (iii)$ For any $i\in \Lambda$ the map $\Upsilon _{(i)}:B\twoheadrightarrow L(i)$ with $F \mapsto F\circ \mathfrak {f}_{(i)}$ is a surjective $B$-map. The properties of $T(i)$ yield ${{\mathrm{dim}}}_K{{\mathrm{Hom}}}_A(P(i),T(j))=[T(j):S(i)]=0$ for any $j\in \Lambda \backslash \Lambda ^{(i)}$. Thus (in the notations of Subsection 2.1) we have

$$\begin{aligned} \left( \theta _{(j)}\circ \mathfrak {f}_{(i)}\right) :\left( P(1)\mathop {\rightarrow }\limits ^{f^{\downarrow }_{(i,1)}}P(i)\mathop {\hookrightarrow }\limits ^{f^{\uparrow }_{(1,i)}} P(1)\mathop {\twoheadrightarrow }\limits ^{\pi (j)} T(j)\mathop {\hookrightarrow }\limits ^{\iota (j)} P(1)\right) =0 \end{aligned}$$

For all $i,j\in \Lambda$ with $i\not \leqslant j$ we have $\theta _{(j)} \in \ker (\Upsilon _{(i)})$, thus $R(L(j)) = B\circ \theta _{(j)} \subseteq \ker (\Upsilon _{(i)})$ and

$$\begin{aligned} \sum \nolimits _{j\in \Lambda \backslash \Lambda ^{(i)}}R(L(j)) \subseteq \ker (\Upsilon _{(i)}) \ \ \hbox {as well as} \ \ R(L(j)) \subseteq \bigcap \nolimits _{i\in \Lambda \backslash \Lambda _{(j)}}\ker (\Upsilon _{(i)}). \end{aligned}$$

By our assumption the pairs $(B,L)$ and $(B,R(L))$ satisfy the properties $\boxed {\leqslant }$ and $\boxed {\leqslant _{(R)}}$ respectively. Therefore ${{\mathrm{dim}}}_KL(i)\mathop {=}\limits ^{2.2.1\textit{(2)}}\left| \Lambda ^{(i)}\right|$ implies ${{\mathrm{dim}}}_K\ker \left( \Upsilon _{(i)}\right) = \left| \Lambda \backslash \Lambda ^{(i)}\right|$. Moreover, . This implies $\sum _{j\in \Lambda \backslash \Lambda ^{(i)}}R(L(j))= \ker (\Upsilon _{(i)})$. Because $R(L(k))\subseteq R(L(j))$ for all $k\in \Lambda$ with $j\leqslant _{(R)}k$, we obtain $\bigcap _{i\in \Lambda \backslash \Lambda _{(j)}}\ker (\Upsilon _{(i)})= \sum _{j\leqslant _{(R)}k}R(L(k))=R(L(j))$. Therefore $L(i) \cong B/\ker (\Upsilon _{(i)}) \cong B/\left( \sum _{j\in \Lambda \backslash \Lambda ^{(i)}}R(L(j)) \right) = B/\left( \sum _{j\not \leqslant _{(R)}i}R(L(j)) \right)$. Using the dual arguments we obtain $R(L(i))\cong B/\left( \sum _{j\in \Lambda \backslash \Lambda _{(i)}}L(j)\right)$ for any $i\in \Lambda$

$(iii)\Rightarrow (i)$ We have to show that $(B,\bigoplus _{i\in \Lambda }R(L(i)))$ satisfies the property $\boxed {\leqslant _{(R)}}$: Since $L(i)=B\circ \mathfrak {f}_{(i)} \mathop {=}\limits ^{2.2.1\textit{(2)}} \mathfrak {f}_{(i)} \circ B$, for $f,g\in B$ there exists $h\in B$ with $g\circ f \circ \mathfrak {f}_{(i)} = g\circ \mathfrak {f}_{(i)}\circ h$.

Therefore, $g\in \ker \left( B \mathop {\twoheadrightarrow }\limits ^{-\circ \mathfrak {f}_{(i)}} L(i)\right)$ implies $g\circ f\in \ker \left( B \mathop {\twoheadrightarrow }\limits ^{-\circ \mathfrak {f}_{(i)}} L(i)\right)$. The assumption $R(L(j))\cong \bigcap _{i\in \Lambda \backslash \Lambda _{(i)}}\ker \left( B\twoheadrightarrow L(i)\right)$ implies $R(L(j))\circ B\subseteq R(L(j))$. Thus $R(L(j))$ is a two-sided local ideal of $B$, since $R(L(j))$ is a factor module and a submodule of $B$.

The property $\boxed {\leqslant }$ of $L(i)$ implies $R(L(k))\twoheadrightarrow R(L(j))$ and also $R(L(j)) \subseteq R(L(k))$ if and only if $k\leqslant _{(R)} j$, because $\Lambda \backslash \Lambda _{(k)}\subseteq \Lambda \backslash \Lambda _{(j)}$ if and only if $j\leqslant k$. We have ${{\mathrm{rad}}}R(L(k)) = \sum _{k<_{(R)}j}R(L(j))$ for all $k\in \Lambda$ because $R(L(k))/\left( \sum _{k<_{(R)}j}R(L(j))\right)$ is simple. $\square$

Example 5.5

Let $B:=B_n(C)$ be the algebra given in Example 2.7 and $L=B\oplus \bigoplus _{i=2}^{n-1}\left\langle X_i\right\rangle \oplus ({{\mathrm{soc}}}B)$. The Ringel dual of the corresponding 1-quasi-hereditary algebra $A_n(C)$ is also 1-quasi-hereditary (see [12, Lemma 1.2]). Thus $[B,L]\in \widehat{\mathcal {Y}}$, in particular, $R(L(1))\cong {{\mathrm{soc}}}B$, $R(L(n))\cong B$ and for $2\le j\le n-1$, where the $d_{ij}$ are given by inverse of $C$, i.e. $C^{-1}=(d_{ij})_{2\le i,j\le n-1}$.

Remark 5.6

If a 1-quasi-hereditary algebra $A$ is Ringel self-dual, then $(A,\leqslant )\cong (R(A),\leqslant _{(R)})$ implies $[B,L]=\Phi ([A])=\Phi ([R(A)])=[B,R(L)]$. In other words: The pair $[B,L]$ satisfies the property $\boxed {\leqslant }$ and the property $\boxed {\leqslant _{(R)}}$. Thus, there exists a permutation $\sigma \in \hbox {Sym}({{\mathrm{dim}}}_KB)$ with $L(\sigma (i))\cong R(L(i))$.

The algebras associated with blocks of the category $\mathcal {O}(\mathfrak {g})$ are Ringel self-dual. In the Example 2.6 the 1-quasi-hereditary algebra $(A_3,\leqslant _{(3)})$ corresponding to the pair $(B,L_3)$ is related to a regular block of $\mathcal {O}(\mathfrak {sl}_3)$. It is easy to check that the permutation $\sigma =(\sigma (1),\ldots , \sigma (6))= (6,5,4,3,2,1) \in \hbox {Sym}(6)$ yields $L_3(\sigma (i))\cong R(L_3(i))$.

In the same example the algebra $(A_1,\leqslant _{(1)})$ is also Ringel self-dual. The permutation $\tau \in \hbox {Sym}(6)$ with $L_1(\tau (i))\cong R(L_1(i))$ is given by $\tau =(6,4,5,2,3,1)$.

If $[B,L]\in \widehat{\mathcal {Y}}$, then the socle of $B/\left( \sum _{j\in \Lambda \backslash \Lambda _{(i)}}L(j)\right)$ is simple for all $i\in \Lambda$, because these factor modules of $B$ are also submodules of $B$ (see Theorem 4.2.1). In the Example 2.6 the algebra $R(A_2)$ is not 1-quasi-hereditary, because ${{\mathrm{soc}}}(B/\left( \sum _{j\in \Lambda \backslash \Lambda _{(4)}}L_2(j)\right) )\cong {{\mathrm{soc}}}\left( B/L_2(5)\right)$ is not simple. Thus $[A_2]\not \in \widehat{\mathcal {X}}$.

In general, for some $[B,L]\in \widehat{\mathcal {Y}}$ the equation $[B,L]= [B,R(L)]$ is not satisfied (see Example 5.5). Consequently a 1-quasi-hereditary algebra $A$ with $[A]\in \widehat{\mathcal {X}}$ is not Ringel self-dual, in general.

Remark 5.7

The class of Ringel self-dual, 1-quasi-hereditary algebras is a subclass of

The most important examples in $\mathbf O$ are the algebras of the form $\mathcal {A}_{\Theta }(\mathfrak {g})$ (for simplicity, let $\Theta$ be a regular block)(see [6] and [7]). The vertices of the quiver of $\mathcal {A}_{\Theta }(\mathfrak {g})$ correspond to the elements of the Weyl group $W$ of $\mathfrak {g}$ and $\leqslant$ conforms to the Bruhat ordering.

For any $[\mathcal {A}]\in \mathbf O$ we have $[\mathcal {A}]=[{{\mathrm{End}}}_{\mathcal {B}}({}_{\mathcal {B}}P(1))^{op}]$, where $\mathcal {B}\cong {{\mathrm{End}}}_{\mathcal {A}}(P(1))^{op}$. In the case $\mathcal {A}= \mathcal {A}_{\Theta }(\mathfrak {g})$, the algebra $\mathcal {B}$ is the coinvariant algebra of $W$.

The methods used in the proofs for 1-quasi-hereditary algebras can be carried over to the proofs of some properties of $(\mathcal {B}, {}_{\mathcal {B}}P(1))$. In Subsect. 3.1 (proof of 1) we have seen that $\mathcal {B}={{\mathrm{End}}}_{\mathcal {A}}(P(1))^{op}$ is a local and self-injective algebra. The proof uses only the fact that $P(1)$ is a projective-injective indecomposable $\mathcal {A}$-module. The same argument yields that the coinvariant algebra of $W$ is a local self-injective algebra. Moreover, BGG reciprocity and $(P(1):\Delta (j))=1$ for all $j\in \Lambda$ implies ${{\mathrm{dim}}}_KP(1)_1 ={{\mathrm{dim}}}_K\mathcal {B}=\left| W\right|$.

As shown in this paper, the structure of the pair $(B,L)$ depends on the structure of the poset $(\Lambda ,\leqslant )$ of a 1-quasi-hereditary algebra $A={{\mathrm{End}}}_B(L)^{op}$. This raises the questions how the structure of the coinvariant algebra depends on $W$ and its Bruhat ordering, and what influence the commutativity of coinvariant algebra has on the relations of $\mathcal {A}_{\Theta }(\mathfrak {g})$.

The algebras in $\mathbf O$ are BGG-algebras, thus the number of arrows from $i$ to $j$ is the same as the number the arrows from $j$ to $i$ (see [18, Corollary 2.6]). But this number is in general not equal to 1, and $i,j$ are not necessary adjacent. For adjacent vertices we have $i\leftrightarrows i'$. Thus for any three vertices $j, i,k$ with $j,k\leqslant i$ we can construct the paths of the form $p(j,i,k)$ running through adjacent vertices strictly increasing from $j$ to $i$ and strictly decreasing from $i$ to $k$, as described in Remark 3.1. Using the same arguments as in the proof of [11, Lemma 3.3] it is possible to show that the set $\left\{ \left. \mathfrak {f}_{(i)}:\left( \begin{array}{ccl} P(1)&{} \rightarrow &{} P(1)\\ e_i &{} \mapsto &{} p(1,i,1) \end{array} \right) \right| i\in \Lambda \right\}$ of $\mathcal {B}$-maps is a $K$-basis of $\mathcal {B}$. Furthermore, the arguments used in the proof of Lemma 3.3 (2) yield that if ${{\mathrm{soc}}}P(i)$ is simple $\mathcal {B}\circ \mathfrak {f}_{(i)}$ is a direct summand of the $\mathcal {B}$-module $P(1)$. This raises the question of the remaining direct summands of the $\mathcal {B}$-module $P(1)$ and their dependence on the given partial order.

Furthermore, since $\mathcal {A}=\mathcal {A}_{\Theta }(\mathfrak {g})$ is Ringel self-dual, for the $\mathcal {B}$-module $P(1)$ we have ${}_{\mathcal {B}}P(1)\cong \bigoplus _{i\in W}{{\mathrm{Hom}}}_{\mathcal {A}}(P(i),P(1)) \cong \bigoplus _{i\in W}{{\mathrm{Hom}}}_{\mathcal {A}}(T(i),T(n))$. Thus there exists $\sigma \in \hbox {Sym}(|W|)$ with ${{\mathrm{Hom}}}_{\mathcal {A}}(P(i),P(1)) \cong {{\mathrm{Hom}}}_{\mathcal {A}}(T(\sigma (i)),T(n))$. If ${{\mathrm{soc}}}P(i)$ is simple, then $\mathcal {B}\circ \mathfrak {f}_{(i)}\cong {{\mathrm{Hom}}}_{\mathcal {A}}(P(i),P(1)) \cong {{\mathrm{Hom}}}_{\mathcal {A}}(T(\sigma (i)),T(n))$ and ${{\mathrm{im}}}(\mathfrak {f}_{(i)}) \cong T(\sigma (i))$. For each $i$ with ${{\mathrm{soc}}}P(i)$ simple we obtain one indecomposable direct summand $T(\sigma (i))$ of the characteristic tilting module. The module theoretical structure of those $T(\sigma (i))$ where $i$ is such that ${{\mathrm{soc}}}P(i)$ is not simple appears to be unknown.

For example, when $\mathfrak {g}=\mathfrak {sl}_4(\mathbb {C})$, the Weyl group (so the set of vertices of the quiver of $\mathcal {A}_{\Theta }(\mathfrak {g})$) is $\hbox {Sym}(4)$ and $P(4321)$ is minimal faithful. All indecomposable projective $\mathcal {A}_{\Theta }(\mathfrak {g})$-modules, except those who corresponds to $(3412)$ and $(4231)$, have simple socle. The map $\sigma :\hbox {Sym}(4) \rightarrow \hbox {Sym}(4)$ with $\sigma (i_1i_2i_3i_4)= (4321)(i_1i_2i_3i_4)$ induces a permutation such that ${{\mathrm{im}}}(\mathfrak {f}_{(i_1i_2i_3 i_4)})\cong T(\sigma (i_1i_2i_3i_4))$ for all $(i_1i_2i_3i_4)\in \hbox {Sym}(4)\backslash \left\{ (3412),(4231)\right\}$. A set of the relations of $\mathcal {A}_{\Theta }(\mathfrak {g})$, calculated in [15], can be transformed in a set $\mathfrak {R}$ such that $\rho \in \mathfrak {R}$ implies $\rho ^{op}\in \mathfrak {R}$. This computation has been carried out and is not given here.