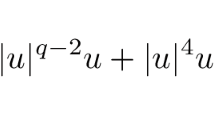Normalized solutions for Kirchhoff equations with Sobolev critical exponent and mixed nonlinearities

Abstract

This paper focuses on the existence of normalized solutions for the following Kirchhoff equation:

$$\begin{aligned} \left\{ \begin{array}{ll} -\left( a+b\int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x\right) \Delta u+\lambda u=u^5+\mu |u|^{q-2}u, & x\in {\mathbb {R}}^3, \\ \int _{{\mathbb {R}}^3}u^2\textrm{d}x=c, \\ \end{array} \right. \end{aligned}$$

where $a,b,c>0$, $\mu \in {\mathbb {R}}$ and $2<q<6$, $\lambda \in {\mathbb {R}}$ will arise as a Lagrange multiplier that is not a priori given. By using new analytical techniques, the paper establishes several existence results for the case $\mu >0$:

• (1) The existence of two solutions, one being a local minimizer and the other of mountain-pass type, under explicit conditions on c when $2<q<\frac{10}{3}$.

• (2) The existence of a mountain-pass type solution under explicit conditions on c when $\frac{10}{3}\le q<\frac{14}{3}$.

• (3) The existence of a ground state solution for all $c>0$ when $\frac{14}{3}\le q<6$.

Furthermore, the paper presents the first non-existence result for the case $\mu \le 0$ and $2<q<6$. In particular, refined estimates of energy levels are proposed, suggesting a new threshold of compactness in the $L^2$-constraint. This study addresses an open problem for $2<q<\frac{10}{3}$ and fills a gap in the case $\frac{10}{3}\le q<\frac{14}{3}$. We believe that our approach can be applied to a broader range of nonlinear terms with Sobolev critical growth, and the underlying ideas have potential for future development and applicability.

1 Introduction

In this paper, we study the existence of normalized solutions for the following Kirchhoff equation:

$$\begin{aligned} \left\{ \begin{array}{ll} -\left( a+b\int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x\right) \Delta u+\lambda u=u^5+\mu |u|^{q-2}u, & x\in {\mathbb {R}}^3, \\ \int _{{\mathbb {R}}^3}u^2\textrm{d}x=c, \\ \end{array} \right. \end{aligned}$$

(1.1)

where $a,b>0$ and $c>0$ are given constants, $\lambda \in {\mathbb {R}}$ will arise as a Lagrange multiplier and is not a priori given, $\mu \in {\mathbb {R}}$ and $2<q<6$. Here 6 is the Sobolev critical exponent. Normalized solutions to (1.1) can be obtained as critical points of the energy functional $\Phi : H^1({\mathbb {R}}^3) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \Phi (u) = \frac{a}{2}\int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x +\frac{b}{4}\left( \int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x\right) ^2 -\frac{1}{6}\int _{{\mathbb {R}}^3}u^6\textrm{d}x-\frac{\mu }{q}\int _{{\mathbb {R}}^3}|u|^q\textrm{d}x\nonumber \\ \end{aligned}$$

(1.2)

restricted on

$$\begin{aligned} {\mathcal {S}}_c=\left\{ u\in H^1({\mathbb {R}}^3):\Vert u\Vert _2^2=c\right\} . \end{aligned}$$

(1.3)

The first equation of (1.1) is a special form of the Kirchhoff type equation

$$\begin{aligned} -\left( a+b\int _{{\mathbb {R}}^N}|\nabla u|^2\textrm{d}x\right) \Delta u+\lambda u=f(u), \end{aligned}$$

(1.4)

where $N\ge 1$ and $f\in {\mathcal {C}}({\mathbb {R}},{\mathbb {R}})$, which was proposed by Kirchhoff as an extension of the classical D’Alembert’s wave equations, describing free vibrations of elastic strings. Mathematically, (1.4) is often referred to be nonlocal as the appearance of the term $\left( \int _{\mathbb {R}^N}\nabla u|^{2}dx\right) \Delta u$ implies that (1.4) is no longer a pointwise identity. This phenomenon causes some mathematical difficulties, which make the study of (1.4) particularly interesting. After the pioneering work of Lions [13], where a functional analysis approach was proposed, the Kirchhoff type equations began to call attention of researchers.

For the study of (1.4), there exist two distinct options regarding the frequency parameter $\lambda$, leading to two different research fields. A possible choice is fixing $\lambda \in {\mathbb {R}}$, or even with an additional external and fixed potential V(x). This direction has been extensively studied in the last ten years, there are numerous relevant literature sources, and we will not list them here.

Alternatively, it is of great interest to investigate solutions to (1.4) that possess a prescribed $L^2$-norm, which are commonly referred to as normalized solutions. In this situation, the frequency $\lambda \in {\mathbb {R}}$ is an unknown parameter and acts as a Lagrange multiplier with respect to the constraint ${\mathcal {S}}_N(c)=\left\{ u\in H^1({\mathbb {R}}^N):\Vert u\Vert _2^2=c\right\}$. Normalized solutions to (1.4) can be obtained as critical points of the energy functional $\Phi _N: H^1({\mathbb {R}}^N) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \Phi _N(u) = \frac{a}{2}\int _{{\mathbb {R}}^N}|\nabla u|^2\textrm{d}x +\frac{b}{4}\left( \int _{{\mathbb {R}}^N}|\nabla u|^2\textrm{d}x\right) ^2 -\int _{{\mathbb {R}}^N}F(u)\textrm{d}x \end{aligned}$$

(1.5)

on the constraint ${\mathcal {S}}_N(c)$, where $F(u):=\int _0^uf(t)\textrm{d}t$. From the physical point of view, finding normalized solutions seems to be particularly meaningful because the $L^2$-norm of such solutions is a preserved quantity of the evolution and their variational characterization can help to analyze the orbital stability or instability, see, for example, [2, 14]. Despite its physical relevance, there have been few works available on this topic. In particular, when considering the critical growth case, we are only aware of the papers [11, 12, 21]. Before delving into the results motivate our research, let us highlight some novel aspects in the study of (1.4) with an $L^2$-constraint in the next subsection.

1.1 Previous developments and some perspectives

From a variational point of view, besides the Sobolev critical exponent $2^*:=\frac{2N}{N-2}$ for $N\ge 3$ and $2^*=\infty$ for $N=1,2$, a new $L^2$-critical exponent $q_N:=2+\frac{8}{N}$ arises that plays a pivotal role in the study of normalized solutions to (1.4). This threshold determines whether the constrained functional $\Phi _N$ remains bounded from below on ${\mathcal {S}}_N(c)$ and consequently influences our choice of approaches when searching for constrained critical points. As far as we know, in this regard, the first results for (1.4) with $f(u)=|u|^{q-2}u$ can be attributed to the work by Ye in a sequence of papers [18,19,20]. These results are summarized in Table 1.

Table 1 Results on (1.4) with $f(u)=|u|^{q-2}u$

In particular, for $q>2+\frac{8}{N}$, $\Phi _N$ is always unbounded from below on ${\mathcal {S}}_N(c)$ since it can be easily derived that $\Phi _{N}\left( t^{N/2}u_{t}(x)\right) \rightarrow -\infty$ as $t\rightarrow \infty$, where

$$\begin{aligned} u_t(x):=u(tx),\quad \forall \ x\in {\mathbb {R}}^N, \ t>0 \end{aligned}$$

(1.6)

is a dilation preserving the $L^2$-norm, that is $\Vert t^{N/2}u_t\Vert _2=\Vert u\Vert _2$ for $t>0$, and this situation corresponds to what is termed as an $L^2$-supercritical case. In this case, more efforts are always needed since one cannot search for a global minimum of $\Phi _{N}$ restricted on ${\mathcal {S}}_N(c)$ and only identify a suspected critical level. Later, the results in the case $2+\frac{8}{N}<q<2^*$ of Table 1 were further extended in [6] to the more general $L^2$-supercritical case with Sobolev subcritical growth, where $f(u)\sim \sum _{i=1}^{m}|u|^{q_i-2}u$ ($2+\frac{8}{N}<q_i<2^*$ and $m\ge 2$). Furthermore, as observed from Table 1, when $p \in (2, 2 + \frac{8}{N})$, the exponent $2 + \frac{4}{N}$ also plays an important role in the investigation of normalized solutions. In fact, it corresponds to the $L^2$-critical exponent in the study of normalized solutions to the Schrödinger equation, specifically (1.4) with $b=0$. It is worth emphasizing that for the Schrödinger equation (1.4) with $b=0$, the $L^2$-critical exponent is always strictly smaller than the Sobolev critical exponent, specifically $2+\frac{4}{N}<\frac{2N}{N-2}$. However, for the Kirchhoff equation (1.4) with $b>0$, the $L^2$-critical exponent is strictly smaller than the Sobolev critical exponent only when $N\le 3$, that is, $q_N=2+\frac{8}{N}<2^*=\frac{2N}{N-2}$ if and only if $N\le 3$. This explains why the research on normalized solutions for the Kirchhoff equation is predominantly focused on the case of $N\le 3$, and when the nonlinearity exhibits Sobolev critical growth, it suffices to consider the case of $N=3$.

It is well-known that compared to the subcritical growth case, the Sobolev critical growth case of (1.4) presents additional challenges in terms of the compactness analysis, especially when considering the $L^2$-constraint. To the best of our knowledge, the first work on the Sobolev critical growth case is due to Zhang–Han [21]. They established the existence of normalized solutions to (1.1) when $\mu =1$ and $\frac{14}{3}\le q<6$ by calculating the threshold of the mountain pass level. Subsequently, Li–Nie–Zhang [12] obtained similar results in the $L^2$-supercritical case $\frac{14}{3}<q<6$ using a different method that relies on the Sobolev subcritical approximation. However, their results require $\mu >0$ to be large enough in (1.1). More recently, Li–Luo–Yang [11] further extended these results on (1.1). However, their work is restricted to the power ranges: $2<q<\frac{10}{3}$ or $\frac{14}{3}\le q<6$, and leaves a gap: $\frac{10}{3}\le q<\frac{14}{3}$. The significant findings from their research are summarized in Table 2.

Table 2 Existence results on (1.1) in [11]

In Table 2, despite explicitly identifying the range of existence for local minima with respect to $\mu$ for $2<q<\frac{10}{3}$, the expression for the upper bound $\mu _*(c,q)$ is excessively convoluted. Moreover, two open problems, labeled as (Q1) and (Q2), remain unaddressed. It is noteworthy that $\frac{10}{3}$ and $\frac{14}{3}$ are the $L^2$-critical exponents in the case of $N=3$ to (1.4) with $b=0$ and (1.4) with $b>0$, respectively. When $b=0$, Eq. (1.1) reduces to the three-dimensional scenario ($N=3$) of the Schrödinger equation with Sobolev critical growth:

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+\lambda u=\mu |u|^{q-2}u+|u|^{2^*-2}u, & x\in {\mathbb {R}}^N, \ N\ge 3, \\ \int _{{\mathbb {R}}^N}u^2\textrm{d}x=c, \ \end{array} \right. \end{aligned}$$

(1.7)

which can be viewed as a counterpart of the classical Brezis–Nirenberg problem in the context of $L^2$-constraint. In addition to the Sobolev critical growth, an important feature of this kind of problem lies in the fact that the presence of multiple powers destroys the scale invariance of the homogeneous equation, and thus it is called a mixed problem. Such a problem has become an active research topic, as seen in references such as [5, 8,9,10, 15, 16]. In these references, some existence results were established for certain small values of $c>0$, some of which are summarized in Table 3.

Table 3 Existing results on (1.7)

Here and in the rest of the paper, ${\mathcal {S}}$ denotes the best constant for the Sobolev inequality, i.e., for any $N \ge 3$ there exists an optimal constant ${\mathcal {S}} > 0$ depending only on N, such that

$$\begin{aligned} {\mathcal {S}}\Vert u\Vert _{2^*}^{2}\le \Vert \nabla u\Vert _2^{2},\ \ \forall \ u\in {\mathcal {D}}^{1,2}({\mathbb {R}}^N). \ \ \text{(Sobolev } \text{ inequality) } \end{aligned}$$

(1.8)

Remark that the existence of a second solution to (1.7) when $2<q<2+\frac{4}{N}$ had been raised as an open problem in [15], subsequently, it was addressed, as presented in Table 3.

Compared to the case $b=0$, the study of (1.1) with $b>0$ is much more challenging, due to the additional difficulties caused by the combined effect of the nonlocal term of $(\Vert \nabla u\Vert _2^2)\Delta u$ and multiple powers. For example,

• (i) The functional $\Phi$ is comprised of four distinct terms that exhibit varying scaling behavior with respect to the dilation $t^{3/2}u(t\cdot )$. The intricate interplay among these terms makes it more difficult to ascertain the types of critical points for $\Phi$ on ${\mathcal {S}}_c$.

• (ii) It is widely recognized that establishing the compactness in critical growth problems hinges on obtaining rigorous upper bound estimates for the minimax levels. This has only been achieved when $b=0$, specifically:

  $$\begin{aligned} M(c)< \left\{ \begin{array}{ll} m_c+ \frac{1}{3}{\mathcal {S}}^{\frac{3}{2}}, & \ \hbox {if}\ 2<q<\frac{10}{3}, \ \hbox {where}\ m_c \ \hbox {is defined in Table\ }3,\\ \frac{1}{3}{\mathcal {S}}^{\frac{3}{2}}, & \ \hbox {if}\ \frac{10}{3}\le q<6.\\ \end{array} \right. \end{aligned}$$

  In the case of $b>0$, there is also a need to establish a similar inequality. However, at present, only one result is available for the range $\frac{14}{3}\le q<6$, while the cases of $2<q<\frac{10}{3}$ and $\frac{10}{3}\le q<\frac{14}{3}$ remain unresolved due to the strong competitive effect of the term $\Vert \nabla u\Vert _2^4$ in $\Phi$, more precisely,

  $$\begin{aligned} M(c)< \left\{ \begin{array}{lll} ?, & \ \hbox {if}\ 2<q<\frac{10}{3},\\ ?, & \ \hbox {if}\ \frac{10}{3}\le q<\frac{14}{3},\\ \Theta ^*:=\frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24}+\frac{\left( b^2{\mathcal {S}}^4+4a{\mathcal {S}}\right) ^{\frac{3}{2}}}{24}, & \ \hbox {if}\ \frac{14}{3}\le q<6.\\ \end{array} \right. \end{aligned}$$

  (1.9)

  Hence, the crucial outstanding matter is how to ascertain the compactness threshold for the problem when $2<q<\frac{10}{3}$ and $\frac{10}{3}\le q<\frac{14}{3}$, and subsequently develop the appropriate energy estimates to mitigate the unavoidable competitive impact of the term $\Vert \nabla u\Vert _2^4$ in the functional $\Phi$.

• (iii) Even when the aforementioned difficulties can be addressed, establishing the compactness of (PS) sequences becomes more complicated compared to the case when $b=0$. This is primarily due to the presence of the term $\Vert \nabla u\Vert _2^4$ in $\Phi$, which implies that the weak convergence $u_n\rightharpoonup u$ in $H^1({\mathbb {R}}^3)$ does not guarantee the convergence

  $$\begin{aligned} \Vert \nabla u_n\Vert _2^2\int _{{\mathbb {R}}^3}\nabla u_n \cdot \nabla \varphi \textrm{d}x \rightarrow \Vert \nabla u\Vert _2^2\int _{{\mathbb {R}}^3}\nabla u \cdot \nabla \varphi \textrm{d}x\ \text {for all}\ \varphi \in {\mathcal {C}}_0^{\infty }({\mathbb {R}}^3). \end{aligned}$$

  Consequently, when $b>0$, it becomes even more intricate to rule out the possibility of vanishing and dichotomy for (PS) sequences, preventing its strong convergence in $H^1({\mathbb {R}}^3)$.

1.2 Highlights of the paper and main results

Motivated by the aforementioned work, this paper aims to thoroughly investigate the existence and multiplicity of normalized solutions for (1.1), covering the complete range of subcritical perturbations within the interval $2<q<6$. In the study of (1.1), we classify the power q into three intervals: $2<q<\frac{10}{3}$, $\frac{10}{3}\le q<\frac{14}{3}$, and $\frac{14}{3}\le q<6$, taking into account the combined effect of $\Delta u$ and $(\Vert \nabla u\Vert _2^2)\Delta u$. Notably, we use new analytical techniques and ideas to overcome the aforementioned challenges and address two open problems, denoted as (Q1) and (Q2) in Table 3, while also filling the research gap for the interval $\frac{10}{3}\le q<\frac{14}{3}$. Specifically, for $\mu >0$ and under suitable conditions on the mass c, we establish the following results:

• (i) When $2<q<\frac{10}{3}$, $\Phi$ exhibits a geometry of local minima on ${\mathcal {S}}_c$, suggesting the existence of an additional mountain pass geometry originating from the local minimizer.

• (ii) When $\frac{10}{3}\le q<\frac{14}{3}$ and $\frac{14}{3}\le q<6$, $\Phi$ possesses a mountain pass geometry on ${\mathcal {S}}_c$.

Based on these observations, our research is divided into two parts, which are summarized in Tables 4 and 5. Additionally, we establish the non-existence result for $\mu \le 0$ and $2<q<6$.

Table 4 Geometry of local minima

Table 5 Mountain pass geometry

Here the number $\Theta ^*$ is defined by (1.9), the numbers $s_0,c_0,c_1,c_2$ and $c_3$ are defined by:

$$\begin{aligned} s_0&:=\left[ \frac{(10-3q)a{\mathcal {S}}^{3}}{6-q}\right] ^{\frac{1}{2}}, \end{aligned}$$

(1.10)

$$\begin{aligned} c_0&:= \left[ \frac{4aq}{3(6-q)\mu {\mathcal {C}}_q^q} \left( \frac{4q}{3(10-3q)\mu {\mathcal {C}}_{q}^q{\mathcal {S}}^{3}}\right) ^{\frac{3q-10}{3(6-q)}}\right] ^{\frac{3}{2}}, \end{aligned}$$

(1.11)

$$\begin{aligned} c_1&:= \left\{ \left[ \frac{4q}{\mu (6-q){\mathcal {C}}_q^q}\right] \left[ \left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^3}{6} +\frac{b{\mathcal {S}}\sqrt{b^2{\mathcal {S}}^4+4(a+bs_0){\mathcal {S}}}}{12}\right) s_0^{(10-3q)/4}\right. \right. \nonumber \\&\qquad \left. \left. +\frac{b}{12}s_0^{(14-3q)/4}\right] \right\} ^{\frac{4}{6-q}}, \end{aligned}$$

(1.12)

$$\begin{aligned} c_2&:=\left( \frac{5a}{3\mu {\mathcal {C}}_{10/3}^{10/3}}\right) ^{\frac{3}{2}} \end{aligned}$$

(1.13)

and

$$\begin{aligned} & c_3 := \left[ \frac{4q}{\mu (6-q){\mathcal {C}}_q^q}\right] ^{\frac{4}{6-q}}\left[ \frac{b}{3(3q-10)}\right] ^{\frac{3q-10}{6-q}}\nonumber \\ & \times \left[ \frac{4}{14-3q}\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^{3}}{6} +\frac{b{\mathcal {S}}}{12}\sqrt{b^2S^4+4a{\mathcal {S}}}\right) \right] ^{\frac{14-3q}{6-q}},\nonumber \\ \end{aligned}$$

(1.14)

the functional $\Psi : H^1({\mathbb {R}}^3) \rightarrow {\mathbb {R}}$ is defined by

$$\begin{aligned} \Psi (u)&:= \frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b}{b^2{\mathcal {S}}^3+4a}\Vert \nabla u\Vert _2^2\right) ^{\frac{3}{2}}-1\right] +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \Vert \nabla u\Vert _2^2\nonumber \\&\quad \ \ \ \ +\frac{b}{4}\Vert \nabla u\Vert _2^4 -\frac{1}{6}\Vert u\Vert _{6}^{6}-\frac{\mu }{q}\Vert u\Vert _q^q, \end{aligned}$$

(1.15)

and the set $A_{\rho }$ is defined by

$$\begin{aligned} A_{\rho }:=\left\{ u\in H^1({\mathbb {R}}^3): \Vert \nabla u\Vert _2^2<\rho \right\} , \end{aligned}$$

where, and in the rest of the paper, ${\mathcal {C}}_s$, determined by s, denotes the best constant for the Gagliardo–Nirenberg inequality in ${\mathbb {R}}^3$ (see [1]),

$$\begin{aligned} \Vert u\Vert _s\le {\mathcal {C}}_s\Vert u\Vert _2^{(6-s)/2s}\Vert \nabla u\Vert _2^{3(s-2)/2s} \ \text{ for }\ \ 2<s<6. \ \ \text{(Gagliardo-Nirenberg } \text{ inequality) }\nonumber \\ \end{aligned}$$

(1.16)

To state our main results, we define the $L^2$-Pohozaev functional

$$\begin{aligned} {\mathcal {P}}(u) = a\int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x +b\left( \int _{{\mathbb {R}}^3}|\nabla u|^2\textrm{d}x\right) ^2-\int _{{\mathbb {R}}^3}u^6\textrm{d}x -\frac{3\mu (q-2)}{2q}\int _{{\mathbb {R}}^3}|u|^q\textrm{d}x.\nonumber \\ \end{aligned}$$

(1.17)

It is well known that any solution to (1.1) belongs to the $L^2$-Pohozaev manifold defined by

$$\begin{aligned} {\mathcal {M}}(c):=\{u\in {\mathcal {S}}_c: {\mathcal {P}}(u)=0\}. \end{aligned}$$

(1.18)

We recall a solution u to be a ground state solution on ${\mathcal {S}}_c$ if u minimizes the functional $\Phi$ among all the solutions to (1.1), i.e.,

$$\begin{aligned} \Phi \big |_{{\mathcal {S}}_c}'(u)=0\ \ \hbox {and}\ \ \Phi (u)=\inf \left\{ \Phi (u): \Vert u\Vert _2^2=c, \ \ \Phi \big |_{{\mathcal {S}}_c}'(u)=0\right\} . \end{aligned}$$

Our results are as follows.

Theorem 1.1

Let $2<q<\frac{10}{3}$, $\mu >0$ and $c\in (0,c_0)$. Then (1.1) has a couple solution $({\tilde{u}}_c,{\tilde{\lambda }}_c) \in ({\mathcal {S}}_c\cap H^1 ({\mathbb {R}}^3)) \times (0, +\infty )$ such that

$$\begin{aligned} {\tilde{u}}_c\in {\mathcal {S}}_c\cap A_{s_0}, \ \ \ \ {\tilde{u}}_c> 0, \ \ \ \ \Phi ({\tilde{u}}_c)=m(c):=\inf _{{\mathcal {S}}_c\cap A_{s_0}} \Phi <0. \end{aligned}$$

(1.19)

Theorem 1.2

Let $2<q<\frac{10}{3}$, $\mu >0$ and $c\in (0,\min \{c_0,c_1\})$. Then (1.1) has a second couple solution $({\bar{u}}_c,{\bar{\lambda }}_c) \in ({\mathcal {S}}_c\cap H_{\textrm{rad}}^1({\mathbb {R}}^3)) \times (0, +\infty )$ such that

$$\begin{aligned} 0<\Phi ({\bar{u}}_c) < \inf _{{\mathcal {S}}_c\cap A_{s_0}} \Psi +\Theta ^*. \end{aligned}$$

(1.20)

Theorem 1.3

Let $\frac{10}{3}\le q<\frac{14}{3}$, $\mu >0$ and $c\in (0,\min \{c_2,c_3\})$. Then (1.1) has a couple solution $({\bar{u}}_c,\lambda _c) \in ({\mathcal {S}}_c\cap H_{\textrm{rad}}^1 ({\mathbb {R}}^3)) \times (0, +\infty )$ such that

$$\begin{aligned} 0<\Phi ({\bar{u}}_c) < \Theta ^*. \end{aligned}$$

(1.21)

Theorem 1.4

Let $\frac{14}{3}\le q<6$, $\mu >0$ and $c\in (0,+\infty )$. Then (1.1) has a couple solution $({\bar{u}}_c,\lambda _c) \in H^1 ({\mathbb {R}}^3) \times (0, +\infty )$ such that

$$\begin{aligned} \Phi ({\bar{u}}_{c})=\inf _{{\mathcal {M}}(c)}\Phi . \end{aligned}$$

(1.22)

Theorem 1.5

Let $2< q<6$, $\mu \le 0$ and $c\in (0,+\infty )$. Then (1.1) has no solutions in $H^1 ({\mathbb {R}}^3) \times (0, +\infty )$.

Remark 1.6

Our research can be considered as a counterpart of the Brezis-Nirenberg problem in the context of normalized solutions to Kirchhoff equations, and appears to be a significant contribution in this regard. This is particularly noteworthy because our study covers the entire interval of $2<q<6$ with subcritical lower exponents. To be more specific, Theorems 1.2 and 1.3 address the open problems (Q1) and (Q2) mentioned in Table 2, respectively, while filling the research gap in the interval $\frac{10}{3}\le q<\frac{14}{3}$. The statements highlighted in red in Tables 4 and 5 further illustrate this point. Additionally, Theorem 1.5 establishes the first result of nonexistence for (1.1) when $\mu <0$.

Remark 1.7

(i) Our approach to constructing (PS) sequences in the proofs of Theorems 1.1–1.4 is fundamentally different from the work of [11]. It is based on several critical point theorems on manifolds that we have recently developed in [5] for the study of (1.7). Our method offers several advantages over Ghoussoub’s minimax approach introduced in [7], as it is technically simpler and does not rely on the decomposition of Pohozaev manifolds. Consequently, it is applicable to a wider range of nonlinear terms.

(ii) From Theorem 1.2, one might wonder why it is necessary to introduce a new functional $\Psi$ defined by (1.15). In fact, it plays a crucial role in proving the compactness of (PS) sequences. By using new analytical techniques and refined energy estimates, we establish rigorous inequalities concerning the energy levels, which are given as follows:

$$\begin{aligned} M(c)< \left\{ \begin{array}{lll} \inf _{{\mathcal {S}}_c\cap A_{s_0}} \Psi +\Theta ^*, & \ \hbox {if}\ 2<q<\frac{10}{3},\\ \Theta ^*, & \ \hbox {if}\ \frac{10}{3}\le q<\frac{14}{3},\\ \Theta ^*, & \ \hbox {if}\ \frac{14}{3}\le q<6,\\ \end{array} \right. \end{aligned}$$

(1.23)

complementing the corresponding result from previous studies, namely the inequality (1.9). The right-hand side of the inequalities represents the compactness threshold of the problem, below which the (PS) condition holds. The derivation of these inequalities is one of the noteworthy highlights of this paper. The argument in the case where $2< q < \frac{10}{3}$ is the most delicate, making it the key and pivotal element in proving Theorem 1.2.

Let us now highlight the key difficulties encountered and outline our research strategy for proving Theorem 1.2, which we believe is the most inspiring part of this paper.

Motivated by the results on (1.7) in Table 3, it is natural to expect that (1.1) has a second solution of the mountain pass type when $2<q<\frac{10}{3}$. However, achieving this result poses the greatest challenge, as mentioned in Remark 1.7-(ii). Drawing upon our experience studying (1.7) in [5], we conjecture that the value $m(c)+\Theta ^*$ may serve as a potential candidate for the compactness threshold in the case $2< q < \frac{10}{3}$, where m(c) is given by (1.19). Following our ideas in [5], in order to establish the strict inequality $M(c) < m(c)+\Theta ^*$, we consider a superposition of the minimizer of m(c) and the Aubin-Talenti bubbles associated with the Sobolev inequality, while ensuring that the resulting function remains constrained to ${\mathcal {S}}_c$ through appropriate technical modifications. The interplay between these components is expected to lead to a decrease in the corresponding energy value, ultimately yielding $M(c) < m(c)+\Theta ^*$. Unfortunately, unlike in the study of (1.7), the additional term $\Vert \nabla u\Vert _2^4$ in $\Phi$ causes the energy value to exceed the anticipated compactness threshold. Specifically, considering $\Phi (u):=\phi (u)+\frac{b}{4}\Vert \nabla u\Vert _2^4$, we can observe from (1.24) that controlling the mountain pass level from above using $m(c)+\Theta ^*$ is not feasible due to the presence of undesirable cross-term interferences:

$$\begin{aligned} \Phi (u_1+u_2)&= \phi (u_1+u_2)+\frac{b}{4}\left( \Vert \nabla u_1\Vert _2^4+\Vert \nabla u_2\Vert _2^4\right) \nonumber \\&\qquad { {+b\left( \Vert \nabla u_1\Vert _2^2+\Vert \nabla u_2\Vert _2^2+\int _{{\mathbb {R}}^3}\nabla u_1\cdot \nabla u_2\textrm{d}x\right) \int _{{\mathbb {R}}^3}\nabla u_1\cdot \nabla u_2\textrm{d}x}}\nonumber \\&\qquad { {+\frac{b}{2}\Vert \nabla u_1\Vert _2^2\Vert \nabla u_2\Vert _2^2}}, \quad \forall \ u_1,u_2\in H^1({\mathbb {R}}^3). \end{aligned}$$

(1.24)

This observation indicates that the aforementioned conjecture does not hold, necessitating the implementation of new ideas to address this problem. Precisely, instead of starting from the local minimizer of m(c), we introduce the auxiliary functional $\Psi$ and search for a local minimizer of $\Psi$ as the first step, as follows:

• Step 1: Prove the existence of ${\hat{u}}_c\in H^1_{\textrm{rad}}({\mathbb {R}}^3)$ such that $\Psi ({\hat{u}}_c)={\hat{m}}(c):=\inf _{{\mathcal {S}}_c\cap A_{s_0}} \Psi$.

• Step 2: Using the function ${\hat{u}}_c$ obtained in Step 1 as the starting point, construct a path set of the mountain pass type:

  $$\begin{aligned} \Gamma _{c}=\left\{ \gamma \in {\mathcal {C}}([0,1], {\mathcal {S}}_c): \gamma (0)={\hat{u}}_c, \Phi (\gamma (1))<2m(c)\right\} , \end{aligned}$$

  and prove that for $c\in (0,c_0)$, there exists $\kappa >0$ such that

  $$\begin{aligned} M(c) =\inf _{\gamma \in \Gamma _{c}}\max _{t\in [0, 1]}\Phi (\gamma (t))\ge \kappa >\sup _{\gamma \in \Gamma _{c}}\max \left\{ \Phi (\gamma (0)), \Phi (\gamma (1))\right\} . \end{aligned}$$

Remarkably, the combination of this inequality and the next step will allow us to obtain a good (PS) sequence $\{u_n\} \subset {\mathcal {S}}_c$ such that

$$\begin{aligned} \Phi (u_n)\rightarrow M(c)\in (0,{\hat{m}}(c)+\Theta ^*), \ \ \Phi |_{{\mathcal {S}}_c}'(u_n) \rightarrow 0\ \ \text{ and }\ \ {\mathcal {P}}(u_n)\rightarrow 0. \end{aligned}$$

(1.25)

• Step 3: For each $n\in {\mathbb {N}}$ and $t>0$, construct a family of new sequences of testing functions restricted on ${\mathcal {S}}_c$:

  $$\begin{aligned} W_{n,t}(x):=\sqrt{\tau }[{\hat{u}}_{c}(\tau x)+tU_n(\tau x)] \end{aligned}$$

  with $\tau =\tau _{n,t}:=\Vert {\hat{u}}_{c}+tU_n\Vert _2/\sqrt{c}$ and $U_n(x):=\Theta _n(|x|)$ and

  $$\begin{aligned} \Theta _n(r)=\root 4 \of {3} {\left\{ \begin{array}{ll} \sqrt{\frac{n}{1+n^2r^2}}, \ \ & 0\le r< 1;\\ \sqrt{\frac{n}{1+n^2}}(2-r), \ \ & 1\le r< 2;\\ 0, \ \ & r\ge 2, \end{array}\right. } \end{aligned}$$

  and prove that

  $$\begin{aligned} \Phi (W_{n,t})< \Theta ^*+\Psi ({\hat{u}}_{c})-O\left( \frac{1}{\sqrt{n}}\right) , \quad \forall \ t>0. \end{aligned}$$

  This novel inequality allows us to find large two numbers ${\bar{n}}\in {\mathbb {N}}$ and ${\hat{t}}>0$ such that

  $$\begin{aligned} W_{{\bar{n}},0}={\hat{u}}_c \ \ \hbox {and}\ \ \Phi (W_{{\bar{n}},{\hat{t}}}) <2m(c). \end{aligned}$$

  In this way, we find a suitable path $\gamma _{{\bar{n}}}(t):=W_{{\bar{n}},t{\hat{t}}}$ such that $\gamma _{{\bar{n}}}\in \Gamma _{c}$, and thus $M(c)\le \max _{t\in [0,1]}\Phi (\gamma _{{\bar{n}}}(t)) < {\hat{m}}(c)+\Theta ^*$, see Lemmas 3.11 and 3.12 for more details.

• Step 4: Prove the compactness of the (PS) sequence $\{u_n\}$ obtained in (1.25). The boundedness of $\{u_n\}$ can be deduced from the additional property ${\mathcal {P}}(u_n)\rightarrow 0$. By contradiction and using the strict inequality $M(c)< {\hat{m}}(c)+\Theta ^*<\Theta ^*$, we establish two key elements: (i) excluding the possibility of vanishing, which implies the existence of ${\bar{u}}\in H_{\textrm{rad}}^1({\mathbb {R}}^3)$ with $0<\Vert {\bar{u}}\Vert _2^2\le c$ such that $u_n\rightharpoonup {\bar{u}}$ in $H_{\textrm{rad}}^1({\mathbb {R}}^3)$; (ii) showing $\Vert \nabla (u_n- {\bar{u}})\Vert _2^2\rightarrow 0$, which is necessary to verify that ${\bar{u}}\in {\mathcal {S}}_c$ is a second solution of (1.1). The proof of the former is not difficult since, if ${\bar{u}} = 0$, a standard argument yields $M(c)+o(1)=\Phi (u_n)\ge \Theta ^*$, contradicting the strict inequality. The essential difficulty lies in deducing $\Vert \nabla (u_n - {\bar{u}})\Vert _2^2 \rightarrow 0$. To derive a contradiction with $M(c)< {\hat{m}}(c)+\Theta ^*$, we need to establish the relationship between $\Phi ({\bar{u}})$, $\Psi ({\bar{u}})$, and $\Theta ^*$ based on the definition of ${\hat{m}}(c)$. To accomplish this, we employ fresh analytical techniques by distinguishing two cases: $\Vert \nabla {\bar{u}}\Vert _2^2< s_0$ and $\Vert \nabla {\bar{u}}\Vert _2^2\ge s_0$. This process also sheds light on why the value ${\hat{m}}(c) + \Theta ^*$ appears as the compactness threshold of the problem.

The paper is organized as follows. Section 2 is devoted to some preliminary results, which will be used in the rest of paper. In Sect. 3, we study the case $2<q<\frac{10}{3}$, and give the proofs of Theorems 1.1 and 1.2. In Sect. 4, we study the case $\frac{10}{3}\le q<\frac{14}{3}$, and finish the proof of Theorem 1.3. In Sect. 4, we study the case $\frac{14}{3}\le q<6$, and finish the proof of Theorem 1.4, moreover, Theorem 1.5 is proved in this section.

Throughout the paper, we make use of the following notations:

• $H_{\textrm{rad}}^1({\mathbb {R}}^3):=\{u\in H^1({\mathbb {R}}^3)\ \big |\ u(x)=u(|x|)\ \hbox {a.e. in } {\mathbb {R}}^3\}$;

• $L^s({\mathbb {R}}^3) (1\le s< \infty )$ denotes the Lebesgue space with the norm $\Vert u\Vert _s =\left( \int _{{\mathbb {R}}^3}|u|^s\textrm{d}x\right) ^{1/s}$;

• For any $u\in H^1({\mathbb {R}}^3)$ and $t>0$, we set $u_t(x):=u(tx)$;

• For any $x\in {\mathbb {R}}^3$ and $r>0$, $B_r(x):=\{y\in {\mathbb {R}}^3: |y-x|<r \}$ and $B_r=B_r(0)$;

• $C_1, C_2,\ldots$ denote positive constants possibly different in different places.

2 Preliminary results

Let H be a real Hilbert space whose norm and scalar product will be denoted respectively by $\Vert \cdot \Vert _H$ and $(\cdot , \cdot )_H$. Let E be a real Banach space with norm $\Vert \cdot \Vert _E$. We assume throughout this section that

$$\begin{aligned} E\hookrightarrow H \hookrightarrow E^* \end{aligned}$$

(2.1)

with continuous injections, where $E^*$ is the dual space of E. Thus H is identified with its dual space. We will always assume in the sequel that E and H are infinite dimensional spaces. We consider the manifold

$$\begin{aligned} M:=\{u\in E: \Vert u\Vert _H=1\}. \end{aligned}$$

(2.2)

M is the trace of the unit sphere of H in E and is, in general, unbounded. Throughout the paper, M will be endowed with the topology inherited from E. Moreover M is a submanifold of E of codimension 1 and its tangent space at a given point $u\in M$ can be considered as a closed subspace of E of codimension 1, namely

$$\begin{aligned} T_uM:=\{v\in E: (u,v)_H=0\}. \end{aligned}$$

(2.3)

We consider a functional $\varphi : E\rightarrow {\mathbb {R}}$ which is of class ${\mathcal {C}}^1$ on E. We denote by $\varphi |_{M}$ the trace of $\varphi$ on M. Then $\varphi |_{M}$ is a ${\mathcal {C}}^1$ functional on M, and for any $u\in M$,

$$\begin{aligned} \langle \varphi |_{M}'(u), v\rangle =\langle \varphi '(u), v\rangle , \quad \forall \ v\in T_uM. \end{aligned}$$

(2.4)

In the sequel, for any $u\in M$, we define the norm $\left\| \varphi |_{M}'(u)\right\|$ by

$$\begin{aligned} \left\| \varphi |_{M}'(u)\right\| =\sup _{v\in T_uM,\Vert v\Vert _E=1}|\langle \varphi '(u), v\rangle |. \end{aligned}$$

(2.5)

Let $E\times {\mathbb {R}}$ be equipped with the scalar product

$$\begin{aligned} ((u,\tau ),(v,\sigma ))_{E\times {\mathbb {R}}}:=(u,v)_{H}+\tau \sigma , \quad \forall \ (u,\tau ), (v,\sigma )\in E\times {\mathbb {R}}, \end{aligned}$$

and corresponding norm

$$\begin{aligned} \Vert (u,\tau )\Vert _{E\times {\mathbb {R}}}:=\sqrt{\Vert u\Vert ^2_{H}+\tau ^2}, \quad \forall \ (u,\tau )\in E\times {\mathbb {R}}. \end{aligned}$$

Next, we consider a functional ${\tilde{\varphi }}: E\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ which is of class ${\mathcal {C}}^1$ on $E\times {\mathbb {R}}$. We denote by ${\tilde{\varphi }}|_{M\times {\mathbb {R}}}$ the trace of ${\tilde{\varphi }}$ on $M\times {\mathbb {R}}$. Then ${\tilde{\varphi }}|_{M\times {\mathbb {R}}}$ is a ${\mathcal {C}}^1$ functional on $M\times {\mathbb {R}}$, and for any $(u,\tau ) \in M\times {\mathbb {R}}$,

$$\begin{aligned} \langle {\tilde{\varphi }}|_{M\times {\mathbb {R}}}'(u,\tau ), (v,\sigma )\rangle :=\langle {\tilde{\varphi }}'(u,\tau ), (v,\sigma )\rangle , \quad \forall \ (v,\sigma )\in {\tilde{T}}_{(u,\tau )}(M\times {\mathbb {R}}), \end{aligned}$$

(2.6)

where

$$\begin{aligned} {\tilde{T}}_{(u,\tau )}(M\times {\mathbb {R}}):=\{(v,\sigma )\in E\times {\mathbb {R}}: (u,v)_H=0\}. \end{aligned}$$

(2.7)

In the sequel, for any $(u,\tau )\in M\times {\mathbb {R}}$, we define the norm $\left\| {\tilde{\varphi }}|_{M\times {\mathbb {R}}}'(u,\tau )\right\|$ by

$$\begin{aligned} \left\| {\tilde{\varphi }}|_{M\times {\mathbb {R}}}'(u,\tau )\right\| =\sup _{(v,\sigma )\in {\tilde{T}}_{(u,\tau )}(M\times {\mathbb {R}}),\Vert (v,\sigma )\Vert _{E\times {\mathbb {R}}}=1}|\langle {\tilde{\varphi }}'(u,\tau ), (v,\sigma )\rangle |. \end{aligned}$$

(2.8)

Lemma 2.1

[5] Let $\varphi \in {\mathcal {C}}^1(E,{\mathbb {R}})$, $S\subset M$, ${\tilde{a}}\in {\mathbb {R}}$, $\varepsilon ,\delta >0$ such that

$$\begin{aligned} u\in M\cap \varphi ^{-1}([{\tilde{a}}-2\varepsilon ,{\tilde{a}}+2\varepsilon ])\cap S_{2\delta }\Rightarrow \left\| \varphi |_{M}'(u)\right\| \ge \frac{8\varepsilon }{\delta }. \end{aligned}$$

(2.9)

Then, there exists $\eta \in {\mathcal {C}}([0,1]\times M, M)$ such that

• (i) $\eta (t,u)=u$, if $t=0$, or if $u\notin M\cap \varphi ^{-1}([{\tilde{a}}-2\varepsilon ,{\tilde{a}}+2\varepsilon ])\cap S_{2\delta }$;

• (ii) $\eta \left( 1,\varphi ^{{\tilde{a}}+\varepsilon }\cap S\right) \subset \varphi ^{{\tilde{a}}-\varepsilon }$;

• (iii) for every $t\in [0,1]$, $\eta (t,\cdot ): M\rightarrow M$ is a homeomorphism;

• (iv) $\Vert \eta (t,u)-u\Vert \le \delta ,\ \forall \ u\in M,\ t\in [0,1]$;

• (v) for every $u\in M$, $\varphi (\eta (t,u))$ is non-increasing on $t\in [0,1]$;

• (vi) $\varphi (\eta (t,u))<{\tilde{a}},\ \forall \ u\in M\cap \varphi ^{{\tilde{a}}}\cap S_{\delta },\ t\in [0,1]$.

Lemma 2.2

[3] Let $\{u_n\}\subset M$ be a bounded sequence in E. Then the following are equivalent:

• (i) $\Vert \varphi |_{M}'(u_n)\Vert \rightarrow 0$ as $n\rightarrow \infty$;

• (ii) $\varphi '(u_n)-\langle \varphi '(u_n),u_n\rangle u_n\rightarrow 0$ in $E'$ as $n\rightarrow \infty$.

Lemma 2.3

[5] Let $\varphi \in {\mathcal {C}}^1(E,{\mathbb {R}})$ and $K\subset E$. If there exists $\rho >0$ such that

$$\begin{aligned} {\tilde{a}}:=\inf _{v\in M\cap K}\varphi (v) <{\tilde{b}}:=\inf _{v\in M\cap (K_{\rho }{\setminus } K)}\varphi (v), \end{aligned}$$

(2.10)

where $K_{\rho }:=\{v\in E:\Vert v-u\Vert _E<\rho , \ u\in K\}$, then, for every $\varepsilon \in (0,({\tilde{b}}-{\tilde{a}})/2)$, $\delta \in (0,\rho /2)$ and $w\in M\cap K$ such that

$$\begin{aligned} \varphi (w)\le {\tilde{a}}+\varepsilon , \end{aligned}$$

(2.11)

there exists $u\in M$ such that

• (i) ${\tilde{a}}-2\varepsilon \le \varphi (u)\le {\tilde{a}}+2\varepsilon$;

• (ii) $\Vert u-w\Vert _{E}\le 2\delta$;

• (iii) $\left\| \varphi |_{M}'(u)\right\| \le 8\varepsilon /\delta$.

Corollary 2.4

[4] Let $\varphi \in {\mathcal {C}}^1(E,{\mathbb {R}})$ and $K\subset E$. If there exist $\rho >0$ and ${\bar{u}}\in M\cap K$ such that

$$\begin{aligned} \varphi ({\bar{u}})=\inf _{v\in M\cap K}\varphi (v) <\inf _{v\in M\cap (K_{\rho }{\setminus } K)}\varphi (v), \end{aligned}$$

(2.12)

then $\varphi |_{M}'({\bar{u}})=0$.

Lemma 2.5

[5] Assume that $\theta _1,\theta _2\in {\mathbb {R}}$ and ${\tilde{\varphi }}\in {\mathcal {C}}^1(E\times {\mathbb {R}},{\mathbb {R}})$ satisfies

$$\begin{aligned} {\tilde{a}}:=\inf _{{\tilde{\gamma }}\in {\tilde{\Gamma }}}\max _{t\in [0, 1]}{\tilde{\varphi }}({\tilde{\gamma }}(t)) >{\tilde{b}}:=\sup _{{\tilde{\gamma }}\in {\tilde{\Gamma }}}\max \left\{ {\tilde{\varphi }}({\tilde{\gamma }}(0)), {\tilde{\varphi }}({\tilde{\gamma }}(1))\right\} , \end{aligned}$$

(2.13)

where

$$\begin{aligned} {\tilde{\Gamma }}:=\left\{ {\tilde{\gamma }}\in {\mathcal {C}}([0,1], M\times {\mathbb {R}}): {\tilde{\varphi }}({\tilde{\gamma }}(0))\le \theta _1, {\tilde{\varphi }}({\tilde{\gamma }}(1)) < \theta _2\right\} . \end{aligned}$$

Let $\{{\tilde{\gamma }}_n\}\subset {\tilde{\Gamma }}$ be such that

$$\begin{aligned} \sup _{t\in [0, 1]}{\tilde{\varphi }}({\tilde{\gamma }}_n(t))\le {\tilde{a}}+\frac{1}{n}, \quad \forall \ n\in {\mathbb {N}}. \end{aligned}$$

(2.14)

Then there exists a sequence $\{(v_n,\tau _n)\}\subset M\times {\mathbb {R}}$ satisfying

• (i) ${\tilde{a}}-\frac{2}{n}\le {\tilde{\varphi }}(v_n,\tau _n)\le {\tilde{a}}+\frac{2}{n}$;

• (ii) $\min _{t\in [0,1]}\Vert (v_n,\tau _n)-{\tilde{\gamma }}_n(t)\Vert _{E\times {\mathbb {R}}}\le \frac{2}{\sqrt{n}}$;

• (iii) $\left\| {\tilde{\varphi }}|_{M\times {\mathbb {R}}}'(v_n,\tau _n)\right\| \le \frac{8}{\sqrt{n}}$.

3 The Case when $2<q<\frac{10}{3}$

In this section, we study the case $2<q<\frac{10}{3}$, and give the proofs of Theorems 1.1 and 1.2.

For any $c>0$, we consider the function $g_c(s)$ defined on $s\in (0,+\infty )$ by

$$\begin{aligned} g_c(s)&:= \frac{a}{2}-\frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4}s^{(3q-10)/4} -\frac{s^2}{6{\mathcal {S}}^{3}}. \end{aligned}$$

(3.1)

By some simple calculations, we easily verify the following lemma.

Lemma 3.1

There hold

• (i) $(1+st)^{\frac{3}{2}}-1 \le t^{\frac{3}{2}}\left[ (1+s)^{\frac{3}{2}}-1\right] , \ \ \forall \ s\ge 0, \ t\ge 1$;

• (ii) $(1+s+t)^{\frac{3}{2}}-1\ge \left[ (1+s)^{\frac{3}{2}}-1\right] +\left[ (1+t)^{\frac{3}{2}}-1\right] , \ \ \forall \ s,t\ge 0$.

Similar to [8, Lemma 2.1], we can prove the following lemma.

Lemma 3.2

Let $2<q<\frac{10}{3}$ and $\mu > 0$. Then for each $c > 0$, the function $g_c(s)$ has a unique global maximum and the maximum value satisfies

$$\begin{aligned} \max _{0<s<+\infty }g_c(s)=g_c(s_c) \left\{ \begin{array}{ll}>0, \ \text{ if } & c<c_0, \\ =0, \ \text{ if } & c=c_0, \\ <0, \ \text{ if } & c>c_0, \end{array} \right. \end{aligned}$$

(3.2)

where $c_0$ is defined by (1.11), and

$$\begin{aligned} s_c:=\left[ \frac{3(10-3q)\mu {\mathcal {C}}_{q}^q{\mathcal {S}}^{3}}{4q}\right] ^{\frac{4}{3(6-q)}}c^{\frac{1}{3}}. \end{aligned}$$

(3.3)

In particular, we have $s_{c_0}=s_0$.

Lemma 3.3

Let $2<q<\frac{10}{3}$ and $\mu > 0$. Then for each $c > 0$, we have that

$$\begin{aligned} \Psi (u)\ge \Phi (u)\ge \Vert \nabla u\Vert _2^2\ g_c(\Vert \nabla u\Vert _2^2), \ \ \forall \ u\in {\mathcal {S}}_c. \end{aligned}$$

(3.4)

Proof

From (1.2), (1.8), (1.15), (1.16) and (3.1), one has

$$\begin{aligned} \Psi (u)\ge & \Phi (u)\\= & \frac{a}{2}\Vert \nabla u\Vert _2^2+\frac{b}{4}\Vert \nabla u\Vert _2^4-\frac{1}{6}\Vert u\Vert _6^6-\frac{\mu }{q}\Vert u\Vert _q^q \\\ge & \frac{a}{2}\Vert \nabla u\Vert _2^2 -\frac{1}{6{\mathcal {S}}^3}\Vert \nabla u\Vert _2^6-\frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4} \Vert \nabla u\Vert _2^{3(q-2)/2} \\= & \Vert \nabla u\Vert _2^2\ g_c(\Vert \nabla u\Vert _2^2), \quad \forall \ u\in {\mathcal {S}}_c. \end{aligned}$$

$\square$

Set

$$\begin{aligned} A_{\rho }:= & \left\{ u\in H^1({\mathbb {R}}^3): \Vert \nabla u\Vert _2^2 < \rho \right\} , \ \ \\ m(c):= & \inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Phi (u), \ \ {\hat{m}}(c):=\inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Psi (u). \end{aligned}$$

Lemma 3.4

Let $2<q<\frac{10}{3}$ and $\mu > 0$. Then for any $c \in (0, c_0)$, the following properties hold,

$$\begin{aligned} m(c)=\inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Phi (u)<0<\inf _{u\in \partial ({\mathcal {S}}_c\cap A_{s_0})}\Phi (u) \end{aligned}$$

(3.5)

and

$$\begin{aligned} {\hat{m}}(c)=\inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Psi (u)<0<\inf _{u\in \partial ({\mathcal {S}}_c\cap A_{s_0})}\Psi (u). \end{aligned}$$

(3.6)

Proof

For any $u\in {\mathcal {S}}_c$, since $t^{3/2}u_t\in {\mathcal {S}}_c$ and $\Vert \nabla (t^{3/2}u_t)\Vert _2^2=t^2\Vert \nabla u\Vert _2^2<s_0$ for small $t>0$, it follows that $t^{3/2}u_t\in {\mathcal {S}}_c\cap A_{s_0}$ for small $t>0$. Furthermore, we have

$$\begin{aligned} \Phi (t^{3/2}u_t)&\le \Psi (t^{3/2}u_t)\nonumber \\&= \frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4bt^{2}}{b^2{\mathcal {S}}^3+4a}\Vert \nabla u\Vert _2^2\right) ^{\frac{3}{2}}-1\right] \nonumber \\&\quad +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) t^2\Vert \nabla u\Vert _2^2\nonumber \\&\quad +\frac{bt^4}{4}\Vert \nabla u\Vert _2^4-\frac{t^6}{6}\Vert u\Vert _{6}^{6} -\frac{\mu t^{3(q-2)/2}}{q}\Vert u\Vert _q^q\nonumber \\&\le \left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}+\frac{b{\mathcal {S}}\sqrt{b^2{\mathcal {S}}^4+4a{\mathcal {S}}}}{3}\right) t^2\Vert \nabla u\Vert _2^2+\frac{bt^4}{4}\Vert \nabla u\Vert _2^4\nonumber \\&\quad -\frac{t^6}{6}\Vert u\Vert _{6}^{6}-\frac{\mu t^{3(q-2)/2}}{q}\Vert u\Vert _q^q < 0, \quad \text{ for } \text{ small } \quad t>0, \end{aligned}$$

(3.7)

due to $2<q<\frac{10}{3}$. In the above second inequality, we have used the following fact:

$$\begin{aligned} (1+s)^{\frac{3}{2}}\le 1+2s, \quad \text{ for } \text{ small }\quad s>0. \end{aligned}$$

(3.7) shows that $\inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Phi (u)\le \inf _{u\in {\mathcal {S}}_c\cap A_{s_0}}\Psi (u)<0$. Therefore, (3.5) and (3.6) follow from Lemmas 3.2 and 3.3. $\square$

Lemma 3.5

Let $2<q<\frac{10}{3}$ and $\mu > 0$. Then it holds that

• (i) Let $c\in (0,c_0)$. Then for all $\alpha \in (0, c)$, we have $m(c)\le m(\alpha ) + m(c-\alpha )$, and if $m(\alpha )$ or $m(c-\alpha )$ is reached then the inequality is strict.

• (ii) The function $c\mapsto m(c)$ is continuous on $(0, c_0)$.

Lemma 3.5 can be proved by the similar arguments as the following lemma, so we omit it.

Lemma 3.6

Let $2<q<\frac{10}{3}$ and $\mu > 0$. Then it holds that

• (i) Let $c\in (0,c_0)$. Then for all $\alpha \in (0, c)$, we have ${\hat{m}}(c)\le {\hat{m}}(\alpha ) + {\hat{m}}(c-\alpha )$, and if ${\hat{m}}(\alpha )$ or ${\hat{m}}(c-\alpha )$ is reached then the inequality is strict.

• (ii) The function $c\mapsto {\hat{m}}(c)$ is continuous on $(0, c_0)$.

Proof

(i) Fix $\alpha \in (0,c)$. By (3.1) and (3.2), we have

$$\begin{aligned} g_{\alpha }\left( \frac{\theta \alpha }{c}s_0\right)&= \frac{a}{2}-\frac{\mu {\mathcal {C}}_q^q}{q}\alpha ^{(6-q)/4}\left( \frac{\theta \alpha }{c}s_0\right) ^{(3q-10)/4} -\frac{(\theta \alpha )^2s_0^2}{6c^2{\mathcal {S}}^{3}}\nonumber \\&\ge \frac{a}{2}-\frac{\mu {\mathcal {C}}_q^q}{q}\left( \frac{\alpha }{c}\right) ^{(q-2)/2}c^{(6-q)/4}s_0^{(3q-10)/4} -\frac{(\theta \alpha )^2s_0^2}{6c^2{\mathcal {S}}^{3}}\nonumber \\&\ge g_c(s_0)=g_c(s_{c_0})>g_{c_0}(s_{c_0})=0, \ \ \forall \ \theta \in [1,c/\alpha ]. \end{aligned}$$

(3.8)

Let $\{u_n\}\subset {\mathcal {S}}_{\alpha }\cap A_{s_0}$ be such that $\lim _{n\rightarrow \infty }\Psi (u_n) ={\hat{m}}(\alpha )$. Since ${\hat{m}}(\alpha )<0$, it follows from (3.4) that for large $n\in {\mathbb {N}}$,

$$\begin{aligned} 0>\Psi (u_n)\ge \Vert \nabla u_n\Vert _2^2g_{\alpha }(\Vert \nabla u_n\Vert _2^2), \end{aligned}$$

which, together with (3.8), implies that for large $n\in {\mathbb {N}}$,

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2<\frac{\alpha }{c}s_0. \end{aligned}$$

(3.9)

For any $\theta \in (1,c/\alpha ]$. Set $v_n(x):=u_n(\theta ^{-1/3}x)$. Then $\Vert v_n\Vert _2^2=\theta \Vert u_n\Vert _2^2=\theta \alpha$, $\Vert v_n\Vert _p^p=\theta \Vert u_n\Vert _p^p$ for $2\le p\le 6$, and

$$\begin{aligned} \Vert \nabla v_n\Vert _2^2=\theta ^{\frac{1}{3}}\Vert \nabla u_n\Vert _2^2\le \left( \frac{c}{\alpha }\right) ^{\frac{1}{3}}\frac{\alpha }{c}s_0<s_0. \end{aligned}$$

(3.10)

Hence, it follows from (1.15), (3.6), (3.10) and Lemma 3.1 (i) that

$$\begin{aligned} {\hat{m}}(\theta \alpha )&\le \Psi (v_n)\nonumber \\&= \frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b\theta ^{\frac{1}{3}}}{b^2{\mathcal {S}}^3+4a}\Vert \nabla u_n\Vert _2^2\right) ^{\frac{3}{2}}-1\right] \nonumber \\&\quad +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \theta ^{\frac{1}{3}}\Vert \nabla u_n\Vert _2^2\nonumber \\&\quad +\frac{b\theta ^{\frac{2}{3}}}{4}\Vert \nabla u_n\Vert _2^4-\frac{\theta }{6}\Vert u_n\Vert _{6}^{6} -\frac{\mu \theta }{q}\Vert u_n\Vert _q^q\nonumber \\&< \frac{\theta (b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b}{b^2{\mathcal {S}}^3+4a}\Vert \nabla u_n\Vert _2^2\right) ^{\frac{3}{2}}-1\right] \nonumber \\&\quad +\theta \left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \Vert \nabla u_n\Vert _2^2\nonumber \\&\quad +\frac{b\theta }{4}\Vert \nabla u_n\Vert _2^4-\frac{\theta }{6}\Vert u_n\Vert _{6}^{6} -\frac{\mu \theta }{q}\Vert u_n\Vert _q^q\nonumber \\&= \theta \Psi (u_n)=\theta {\hat{m}}(\alpha )+o(1), \end{aligned}$$

(3.11)

which implies that

$$\begin{aligned} \theta \in \left( 1,\frac{c}{\alpha }\right] \Rightarrow {\hat{m}}(\theta \alpha )\le \theta {\hat{m}}(\alpha ). \end{aligned}$$

(3.12)

If ${\hat{m}}(\alpha )$ is reached by $u\in {\mathcal {S}}_{\alpha }\cap A_{s_0}$, then we choose $u_n\equiv u$ in (3.11), and thus the strict inequality follows. Hence, it follows from (3.12) that

$$\begin{aligned} {\hat{m}}(c)=\frac{c-\alpha }{c}{\hat{m}}(c)+\frac{\alpha }{c}{\hat{m}}(c)\le {\hat{m}}(c-\alpha )+{\hat{m}}(\alpha ), \end{aligned}$$

with a strict inequality if ${\hat{m}}(\alpha )$ or ${\hat{m}}(c-\alpha )$ is reached.

(ii) Let $c\in (0, c_0)$ be arbitrary and $\{{\tilde{c}}_n\}\subset (0, c_0)$ be such that ${\tilde{c}}_n \rightarrow c$. For any $\alpha \in (0,c_0)$, by the definition of ${\hat{m}}(\alpha )$ and Lemma 3.4, one has ${\hat{m}}(\alpha )<0$. If ${\tilde{c}}_n<c$, then it follows from (i) that

$$\begin{aligned} {\hat{m}}(c)\le {\hat{m}}({\tilde{c}}_n)+{\hat{m}}(c-{\tilde{c}}_n)<{\hat{m}}({\tilde{c}}_n). \end{aligned}$$

(3.13)

If ${\tilde{c}}_n\ge c$, we let $u_n\in {\mathcal {S}}_{{\tilde{c}}_n}\cap A_{s_0}$ be such that $\Psi (u_n)\le {\hat{m}}({\tilde{c}}_n)+\frac{1}{n}$. Set $v_n=\sqrt{\frac{c}{{\tilde{c}}_n}}u_n$. Then $v_n\in {\mathcal {S}}_{c}\cap A_{s_0}$. Furthermore, we have

$$\begin{aligned} {\hat{m}}(c)&\le \Psi (v_n)=\Psi (u_n)+[\Psi (v_n)-\Psi (u_n)]\nonumber \\&= \Psi (u_n)\nonumber \\&\quad +\frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4bc\Vert \nabla u_n\Vert _2^2}{{\tilde{c}}_n\left( b^2{\mathcal {S}}^3+4a\right) }\right) ^{\frac{3}{2}} -\left( 1+\frac{4b\Vert \nabla u_n\Vert _2^2}{b^2{\mathcal {S}}^3+4a}\right) ^{\frac{3}{2}}\right] \nonumber \\&\quad +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \frac{c-{\tilde{c}}_n}{{\tilde{c}}_n} \Vert \nabla u_n\Vert _2^2+\frac{b\left( c^2-{\tilde{c}}_n^2\right) }{4{\tilde{c}}_n^2}\Vert \nabla u_n\Vert _2^4\nonumber \\&\quad -\frac{c^3-{\tilde{c}}_n^3}{6{\tilde{c}}_n^3}\Vert u_n\Vert _{6}^{6} -\frac{\mu \left( c^{q/2}-{\tilde{c}}_n^{q/2}\right) }{q{\tilde{c}}_n^{q/2}}\Vert u_n\Vert _q^q\nonumber \\&= \Psi (u_n)+o(1)\le {\hat{m}}({\tilde{c}}_n)+o(1). \end{aligned}$$

(3.14)

Combining (3.13) with (3.14), we have

$$\begin{aligned} {\hat{m}}(c)\le {\hat{m}}({\tilde{c}}_n)+o(1). \end{aligned}$$

(3.15)

Now, for any $\varepsilon > 0$ sufficiently small, there exists $u\in {\mathcal {S}}_{c}\cap A_{s_0}$ such that

$$\begin{aligned} \Psi (u)<{\hat{m}}(c)+\varepsilon . \end{aligned}$$

(3.16)

Set $w_n=\sqrt{\frac{{\tilde{c}}_n}{c}}u$. Then $w_n\in {\mathcal {S}}_{{\tilde{c}}_n}\cap A_{s_0}$ for n large enough. Since $\Psi (w_n)\rightarrow \Psi (u)$, then

$$\begin{aligned} {\hat{m}}({\tilde{c}}_n)\le \Psi (w_n)=\Psi (u)+[\Psi (w_n)-\Psi (u)]=\Psi (u)+o(1)<{\hat{m}}(c)+\varepsilon +o(1). \end{aligned}$$

Therefore, since $\varepsilon > 0$ is arbitrary, we deduce that ${\hat{m}}({\tilde{c}}_n) \rightarrow {\hat{m}}(c)$ from the above inequality and (3.15). $\square$

Proof of Theorem 1.1

Let $\{u_n\}\subset {\mathcal {S}}_c\cap A_{s_0}$ be a minimizing sequence for m(c). Since $\{|u_n|\}\subset {\mathcal {S}}_c\cap A_{s_0}$ is also a minimizing sequence for m(c), so we can assume that $u_n\ge 0$. Then by Lemma 3.4, we have

$$\begin{aligned} \Vert u_n\Vert _2^2 = c, \quad \Vert \nabla u_n\Vert _2^2< s_0< +\infty , \quad \Phi (u_n)= m(c)+o(1)<0. \end{aligned}$$

(3.17)

To obtain the existence of solutions for (1.1), we split the proof into several steps.

Step 1. Set $\delta :=\limsup _{n\rightarrow \infty }\sup _{y\in {\mathbb {R}}^3}\int _{B_1(y)}|u_n|^2\textrm{d}x$. If $\delta =0$, then by Lions’ concentration compactness principle [17, Lemma 1.21], we have $u_n\rightarrow 0$ in $L^{s}({\mathbb {R}}^3)$ for $2<s<6$. It follows that

$$\begin{aligned} \int _{{\mathbb {R}}^3}|u_n|^q\textrm{d}x=o(1). \end{aligned}$$

(3.18)

From (1.2), (1.8), (3.1), (3.2), (3.17) and (3.18), one has

$$\begin{aligned} m(c)+o(1)&= \frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4-\frac{\mu }{q}\Vert u_n\Vert _q^q -\frac{1}{6}\Vert u_n\Vert _6^6\nonumber \\&\ge \frac{a}{2}\Vert \nabla u_n\Vert _2^2-\frac{1}{6{\mathcal {S}}^3}\Vert \nabla u_n\Vert _2^6+o(1)\nonumber \\&\ge \Vert \nabla u_n\Vert _2^2\left( \frac{a}{2}-\frac{s_0^2}{6{\mathcal {S}}^3}\right) +o(1)\nonumber \\&= \Vert \nabla u_n\Vert _2^2\left[ g_c(s_0) +\frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4}s_0^{(3q-10)/2}\right] +o(1)\nonumber \\&\ge o(1). \end{aligned}$$

(3.19)

This contradiction shows that $\delta >0$ due to $m(c)<0$.

Going if necessary to a subsequence, we may assume the existence of $y_n\in {\mathbb {R}}^3$ such that

$$\begin{aligned} \int _{B_1(y_n)}|u_n|^2\textrm{d}x> \frac{\delta }{2}. \end{aligned}$$

(3.20)

Let ${\tilde{u}}_n(x)=u_n(x+y_n)$. Then

$$\begin{aligned} \int _{B_1(0)}|{\tilde{u}}_n|^2\textrm{d}x> \frac{\delta }{2}, \end{aligned}$$

(3.21)

and so there exists ${\tilde{u}}\in H^1({\mathbb {R}}^3){\setminus }\{0\}$ with ${\tilde{u}}\ge 0$ such that, passing to a subsequence,

$$\begin{aligned} {\tilde{u}}_n\rightharpoonup {\tilde{u}}\ \ \text{ in }\ H^1({\mathbb {R}}^3), \ \ {\tilde{u}}_n\rightarrow {\tilde{u}}\ \ \text{ in }\ L_{\textrm{loc}}^s({\mathbb {R}}^3) \ \text{ for } \ s\in (1,6), \ \ {\tilde{u}}_n\rightarrow {\tilde{u}}\ \text{ a.e. } \text{ on }\ {\mathbb {R}}^3. \end{aligned}$$

(3.22)

Moreover, (3.17) gives

$$\begin{aligned} 0<\Vert {\tilde{u}}\Vert _2^2\le \Vert {\tilde{u}}_n\Vert _2^2= c, \quad \Vert \nabla {\tilde{u}}_n\Vert _2^2 < s_0, \quad \Phi ({\tilde{u}}_n)= m(c)+o(1). \end{aligned}$$

(3.23)

Step 2. Set $v_n:={\tilde{u}}_n-{\tilde{u}}$. By (3.22), we have

$$\begin{aligned} \Vert \nabla {\tilde{u}}_n\Vert _2^2=\Vert \nabla {\tilde{u}}\Vert _2^2+\Vert \nabla v_n\Vert _2^2+o(1) \end{aligned}$$

(3.24)

and

$$\begin{aligned} \Vert \nabla {\tilde{u}}_n\Vert _2^4=\Vert \nabla {\tilde{u}}\Vert _2^4+\Vert \nabla v_n\Vert _2^4 +2\Vert \nabla {\tilde{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.25)

Hence, by (1.2), (3.24), (3.25) and the Brezis–Lieb lemma, we have

$$\begin{aligned} \Phi ({\tilde{u}}_n)=\Phi ({\tilde{u}})+\Phi (v_n)+\frac{b}{2}\Vert \nabla {\tilde{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.26)

Step 3. By (3.22) and (3.23), we have

$$\begin{aligned} \Vert v_n\Vert _2^2=\Vert {\tilde{u}}_n\Vert _2^2-\Vert {\tilde{u}}\Vert _2^2+o(1)=c-\Vert {\tilde{u}}\Vert _2^2+o(1). \end{aligned}$$

(3.27)

Now, we claim that $\Vert v_n\Vert _2^2\rightarrow 0$. In order to prove this, let us denote ${\tilde{c}}:= \Vert {\tilde{u}}\Vert _2^2>0$. By (3.27), if we show that ${\tilde{c}} = c$ then the claim follows. We assume by contradiction that ${\tilde{c}} < c$. In view of (3.24) and (3.27), for $n\in {\mathbb {N}}$ large enough, we have

$$\begin{aligned} \alpha _n:=\Vert v_n\Vert _2^2\le c, \quad \Vert \nabla v_n\Vert _2^2\le \Vert \nabla {\tilde{u}}_n\Vert _2^2< s_0. \end{aligned}$$

(3.28)

Hence, we obtain that

$$\begin{aligned} v_n\in {\mathcal {S}}_{\alpha _n}\cap A_{s_0}, \quad \Phi (v_n)\ge m(\alpha _n):=\inf _{u\in {\mathcal {S}}_{\alpha _n}\cap A_{s_0}}\Phi (u). \end{aligned}$$

(3.29)

From (3.23), (3.26) and (3.29), we have

$$\begin{aligned} m(c)+o(1)&= \Phi ({\tilde{u}}_n)=\Phi ({\tilde{u}})+\Phi (v_n) +\frac{b}{2}\Vert \nabla {\tilde{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1)\nonumber \\&\ge \Phi ({\tilde{u}})+m(\alpha _n)+\frac{b}{2}\Vert \nabla {\tilde{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.30)

Since the map $c \mapsto m(c)$ is continuous (see Lemma 3.5 (ii)) and in view of (3.27), we deduce

$$\begin{aligned} m(c) \ge \Phi ({\tilde{u}})+ m(c-{\tilde{c}}). \end{aligned}$$

(3.31)

We also have that ${\tilde{u}}\in {\mathcal {S}}_{{\tilde{c}}}\cap \overline{A_{s_0}}$ by the weak limit. This implies that $\Phi ({\tilde{u}})\ge m({\tilde{c}})$. If $\Phi ({\tilde{u}})> m({\tilde{c}})$, then it follows from (3.31) and Lemma 3.5 (i) that

$$\begin{aligned} m(c) > m({\tilde{c}})+ m(c-{\tilde{c}})\ge m(c), \end{aligned}$$

which is impossible. Hence, we have $\Phi ({\tilde{u}})= m({\tilde{c}})$. So, using Lemma 3.5 (i) with the strict inequality, we deduce from (3.31) that

$$\begin{aligned} m(c) \ge m({\tilde{c}})+ m(c-{\tilde{c}}) > m(c), \end{aligned}$$

which is impossible. Thus, the claim follows and from (3.27) we deduce that $\Vert {\tilde{u}}\Vert _2^2=c$ and so ${\tilde{u}}\in {\mathcal {S}}_{c}\cap \overline{A_{s_0}}$ by the weak limit. It follows from (1.8), (3.1), (3.2), (3.23), (3.26) and $\Phi ({\tilde{u}}) \ge m(c)$ that

$$\begin{aligned} o(1)&\ge \frac{a}{2}\Vert \nabla v_n\Vert _2^2+\frac{b}{4}\Vert \nabla v_n\Vert _2^4-\frac{\mu }{q}\Vert v_n\Vert _q^q -\frac{1}{6}\Vert v_n\Vert _6^6+\frac{b}{2}\Vert \nabla {\tilde{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2\nonumber \\&\ge \frac{a}{2}\Vert \nabla v_n\Vert _2^2-\frac{1}{6{\mathcal {S}}^3}\Vert \nabla v_n\Vert _2^6+o(1)\nonumber \\&\ge \Vert \nabla v_n\Vert _2^2\left( \frac{a}{2}-\frac{s_0^2}{6{\mathcal {S}}^3}\right) +o(1)\nonumber \\&= \Vert \nabla v_n\Vert _2^2\left[ g_c(s_0)+\frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4}s_0^{(3q-10)/2}\right] +o(1). \end{aligned}$$

(3.32)

It follows from that $\Vert \nabla v_n\Vert _2^2=o(1)$. Since $\Vert v_n\Vert _2^2=o(1)$, we have ${\tilde{u}}_n\rightarrow {\tilde{u}}$ in $H^1({\mathbb {R}}^3)$. Hence,

$$\begin{aligned} \Vert {\tilde{u}}\Vert _2^2= c, \quad \Vert \nabla {\tilde{u}}\Vert _2^2 \le s_0,\quad \Phi ({\tilde{u}})= m(c), \end{aligned}$$

which, together with Lemma 3.4, implies $\Vert \nabla {\tilde{u}}\Vert _2^2 < s_0$. Hence, Corollary 2.4 implies that $\Phi |_{{\mathcal {S}}_c}'({\tilde{u}})=0$, and so there exists a Lagrange multiplier ${\tilde{\lambda }}_c\in {\mathbb {R}}$ such that

$$\begin{aligned} -\left( a+b\Vert \nabla {\tilde{u}}\Vert _2^2\right) \Delta {\tilde{u}}+{\tilde{\lambda }}_c {\tilde{u}}={\tilde{u}}^5 +\mu |{\tilde{u}}|^{q-2}{\tilde{u}},\ \ x\in {\mathbb {R}}^3. \end{aligned}$$

It is easy to verify that $\tilde{\lambda }_{c}>0$. Since ${\tilde{u}}\ge 0$ and ${\tilde{u}}\ne 0$, the strong maximum principle implies that ${\tilde{u}}>0$. $\square$

Lemma 3.7

Let $2<q<\frac{10}{3}$, $\mu > 0$ and $c\in (0,c_0)$. Then ${\hat{m}}(c)$ is reached by a positive, radially symmetric function, denoted ${\hat{u}}_c\in {\mathcal {S}}_c\cap A_{s_0}$ that satisfies, for a $\lambda _c\in {\mathbb {R}}$,

$$\begin{aligned}&-\left[ a+\frac{b^2{\mathcal {S}}^{3}}{2}+b\Vert \nabla {\hat{u}}_c\Vert _2^2 +\frac{b{\mathcal {S}}}{2}\sqrt{b^2{\mathcal {S}}^4+4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) {\mathcal {S}}}\right] \Delta {\hat{u}}_c+\lambda _c{\hat{u}}_c \nonumber \\&\quad = {\hat{u}}_c^5+\mu |{\hat{u}}_c|^{q-2}{\hat{u}}_c. \end{aligned}$$

(3.33)

Proof

Let $\{u_n\}\subset {\mathcal {S}}_c\cap A_{s_0}$ be a minimizing sequence for ${\hat{m}}(c)$. It is not restrictive to assume that $\{u_n\}$ is radially decreasing for every n (if this is not the case, we can replace $u_n$ with $|u_n|^*$, the Schwarz rearrangement of $|u_n|$). Then by Lemma 3.4, we have

$$\begin{aligned} \Vert u_n\Vert _2^2 = c, \quad \Vert \nabla u_n\Vert _2^2< s_0,\quad \Psi (u_n)= {\hat{m}}(c)+o(1)<0. \end{aligned}$$

(3.34)

Since $\{u_n\}\subset H_{\textrm{rad}}^1({\mathbb {R}}^3)$ is bounded, we may thus assume, passing to a subsequence if necessary, that

$$\begin{aligned} \left\{ \begin{array}{ll} u_n\rightharpoonup {\hat{u}}, & \text{ in } \ H_{\textrm{rad}}^1({\mathbb {R}}^3); \\ u_n\rightarrow {\hat{u}}, & \text{ in } \ L^s({\mathbb {R}}^3), \ \forall \ s\in (2,6);\\ u_n\rightarrow {\hat{u}}, & \text{ a.e. } \text{ on } \ {\mathbb {R}}^3. \end{array} \right. \end{aligned}$$

(3.35)

To prove the lemma, we split the proof into several steps.

Step 1. ${\hat{u}}\ne 0$. Otherwise, we have $u_n\rightarrow 0$ in $L^{s}({\mathbb {R}}^3)$ for $s\in (2,6)$. It follows that

$$\begin{aligned} \int _{{\mathbb {R}}^3}|u_n|^q\textrm{d}x=o(1). \end{aligned}$$

(3.36)

From (1.8), (1.15), (3.1), (3.2), (3.34), (3.35) and (3.36), one has

$$\begin{aligned} {\hat{m}}(c)+o(1)&= \Psi (u_n)\nonumber \\&\ge \frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4 -\frac{1}{6}\Vert u_n\Vert _6^6-\frac{\mu }{q}\Vert u_n\Vert _q^q\nonumber \\&\ge \frac{a}{2}\Vert \nabla u_n\Vert _2^2-\frac{1}{6{\mathcal {S}}^3}\Vert \nabla u_n\Vert _2^6+o(1)\nonumber \\&\ge \Vert \nabla u_n\Vert _2^2\left( \frac{a}{2}-\frac{s_0^2}{6{\mathcal {S}}^3}\right) +o(1)\nonumber \\&= \Vert \nabla u_n\Vert _2^2\left[ g_c(s_0) +\frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4}s_0^{(3q-10)/2}\right] +o(1)\nonumber \\&\ge o(1). \end{aligned}$$

(3.37)

This contradiction shows that ${\hat{u}}\ne 0$ due to ${\hat{m}}(c)<0$.

Step 2. Set $v_n:=u_n-{\hat{u}}$. By (3.35), we have

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2=\Vert \nabla {\hat{u}}\Vert _2^2+\Vert \nabla v_n\Vert _2^2+o(1) \end{aligned}$$

(3.38)

and

$$\begin{aligned} \Vert \nabla u_n\Vert _2^4=\Vert \nabla {\hat{u}}\Vert _2^4+\Vert \nabla v_n\Vert _2^4 +2\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.39)

Hence, by (1.15), (3.38), (3.39), Lemma 3.1 (ii) and the Brezis-Lieb lemma, we have

$$\begin{aligned} \Psi (u_n)\ge \Psi ({\hat{u}})+\Psi (v_n)+\frac{b}{2}\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.40)

Step 3. By (3.34) and (3.35), we have

$$\begin{aligned} \Vert v_n\Vert _2^2=\Vert u_n\Vert _2^2-\Vert {\hat{u}}\Vert _2^2+o(1)=c-\Vert {\hat{u}}\Vert _2^2+o(1). \end{aligned}$$

(3.41)

Now, we claim that $\Vert v_n\Vert _2^2\rightarrow 0$. In order to prove this, let us denote ${\tilde{c}}:= \Vert {\hat{u}}\Vert _2^2>0$. By (3.41), if we show that ${\tilde{c}} = c$ then the claim follows. We assume by contradiction that ${\tilde{c}} < c$. In view of (3.38) and (3.41), for $n\in {\mathbb {N}}$ large enough, we have

$$\begin{aligned} \alpha _n:=\Vert v_n\Vert _2^2\le c, \quad \Vert \nabla v_n\Vert _2^2\le \Vert \nabla u_n\Vert _2^2< s_0. \end{aligned}$$

(3.42)

Hence, we obtain that

$$\begin{aligned} v_n\in {\mathcal {S}}_{\alpha _n}\cap A_{s_0}, \quad \Psi (v_n)\ge {\hat{m}}(\alpha _n):=\inf _{u\in {\mathcal {S}}_{\alpha _n}\cap A_{s_0}}\Psi (u). \end{aligned}$$

(3.43)

From (3.34), (3.40) and (3.43), we have

$$\begin{aligned} {\hat{m}}(c)+o(1)&= \Psi (u_n)\nonumber \\&\ge \Psi ({\hat{u}})+\Psi (v_n) +\frac{b}{2}\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1)\nonumber \\&\ge \Psi ({\hat{u}})+{\hat{m}}(\alpha _n)+\frac{b}{2}\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1). \end{aligned}$$

(3.44)

Since the map $c \mapsto {\hat{m}}(c)$ is continuous (see Lemma 3.6 (ii)) and (3.41), we deduce

$$\begin{aligned} {\hat{m}}(c) \ge \Psi ({\hat{u}})+ {\hat{m}}(c-{\tilde{c}}). \end{aligned}$$

(3.45)

We also have that ${\hat{u}}\in {\mathcal {S}}_{{\tilde{c}}}\cap \overline{A_{s_0}}$ by the weak limit. This implies that $\Psi ({\hat{u}})\ge {\hat{m}}({\tilde{c}})$. If $\Psi ({\hat{u}})> {\hat{m}}({\tilde{c}})$, then

$$\begin{aligned} {\hat{m}}(c) > {\hat{m}}({\tilde{c}})+ {\hat{m}}(c-{\tilde{c}})\ge {\hat{m}}(c), \end{aligned}$$

which is impossible. Hence, we have $\Psi ({\hat{u}})= {\hat{m}}({\tilde{c}})$. So, using Lemma 3.6 (i) with the strict inequality, we deduce from (3.45) that

$$\begin{aligned} {\hat{m}}(c) \ge {\hat{m}}({\tilde{c}})+ {\hat{m}}(c-{\tilde{c}}) > {\hat{m}}(c), \end{aligned}$$

which is impossible. Thus, the claim follows and from (3.41) we deduce that $\Vert {\hat{u}}\Vert _2^2=c$ and so ${\hat{u}}\in {\mathcal {S}}_{c}\cap \overline{A_{s_0}}$ by the weak limit. It follows from (1.8), (3.1), (3.2), (3.34), (3.40), (3.41) and $\Psi ({\hat{u}}) \ge$ ${\hat{m}}(c)$ that

$$\begin{aligned} o(1)&\ge \Psi (v_n)+\frac{b}{2}\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+o(1)\nonumber \\&\ge \frac{a}{2}\Vert \nabla v_n\Vert _2^2+\frac{b}{4}\Vert \nabla v_n\Vert _2^4-\frac{\mu }{q}\Vert v_n\Vert _q^q -\frac{1}{6}\Vert v_n\Vert _6^6\nonumber \\&\ge \frac{a}{2}\Vert \nabla v_n\Vert _2^2 -\frac{1}{6{\mathcal {S}}^3}\Vert \nabla v_n\Vert _2^6+o(1)\nonumber \\&\ge \Vert \nabla v_n\Vert _2^2\left( \frac{a}{2}-\frac{s_0^2}{6{\mathcal {S}}^3}\right) +o(1)\nonumber \\&= \Vert \nabla v_n\Vert _2^2\left[ g_c(s_0)+ \frac{\mu {\mathcal {C}}_q^q}{q}c^{(6-q)/4}s_0^{(3q-10)/2}\right] +o(1). \end{aligned}$$

(3.46)

It follows from that $\Vert \nabla v_n\Vert _2^2=o(1)$. Since $\Vert v_n\Vert _2^2=o(1)$, we have $u_n\rightarrow {\hat{u}}$ in $H_{\textrm{rad}}^1({\mathbb {R}}^3)$. Hence,

$$\begin{aligned} \Vert {\hat{u}}\Vert _2^2= c, \quad \Vert \nabla {\hat{u}}\Vert _2^2 \le s_0,\quad \Psi ({\hat{u}})= {\hat{m}}(c), \end{aligned}$$

which, together with Lemma 3.4, implies $\Vert \nabla {\hat{u}}\Vert _2^2 < s_0$. Hence, Corollary 2.4 implies that $\Psi |_{{\mathcal {S}}_c}'({\hat{u}})=0$, and so there exists a Lagrange multiplier $\lambda _c\in {\mathbb {R}}$ such that $\Psi '({\hat{u}})+\lambda _c{\hat{u}}=0$, which implies (3.33) holds with ${\hat{u}}_c={\hat{u}}$. Since ${\hat{u}}_c\ge 0$ and ${\hat{u}}_c\ne 0$, the strong maximum principle implies that ${\hat{u}}_c>0$. $\square$

Since $\Psi '({\hat{u}}_c)+\lambda _c{\hat{u}}_c=0$, by a standard argument, we have the following lemma immediately.

Lemma 3.8

Let $2<q<\frac{10}{3}$, $\mu > 0$ and $c\in (0,c_0)$. Then there holds

$$\begin{aligned}&\left[ a+\frac{b^2{\mathcal {S}}^{3}}{2} +\frac{b{\mathcal {S}}}{2}\sqrt{b^2{\mathcal {S}}^4+4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) {\mathcal {S}}}\right] \Vert \nabla {\hat{u}}_c\Vert _2^2\nonumber \\&\quad +b\Vert \nabla {\hat{u}}_c\Vert _2^4 -\Vert {\hat{u}}_c\Vert _{6}^{6}-\frac{3\mu (q-2)}{2q}\Vert {\hat{u}}_c\Vert _q^q=0. \end{aligned}$$

(3.47)

To apply Lemma 2.5, we let $E=H_{\textrm{rad}}^1({\mathbb {R}}^3)$ and $H=L^2({\mathbb {R}}^3)$. Define the norms of E and H by

$$\begin{aligned} \Vert u\Vert _E:= \left[ \int _{{\mathbb {R}}^3}\left( |\nabla u|^{2}+u^2\right) \textrm{d}x\right] ^{1/2},\quad \Vert u\Vert _H:=\frac{1}{\sqrt{c}}\left( \int _{{\mathbb {R}}^3}u^2\textrm{d}x\right) ^{1/2},\quad \forall \ u\in E.\nonumber \\ \end{aligned}$$

(3.48)

After identifying H with its dual, we have $E\hookrightarrow H \hookrightarrow E^*$ with continuous injections. Set

$$\begin{aligned} M:= \left\{ u\in E: \Vert u\Vert _2^2=\int _{{\mathbb {R}}^3}u^2\textrm{d}x=c\right\} . \end{aligned}$$

(3.49)

Let us define a continuous map $\beta : H_{\textrm{rad}}^1({\mathbb {R}}^3)\times {\mathbb {R}}\rightarrow H^1({\mathbb {R}}^3)$ by

$$\begin{aligned} \beta (v, t)(x):=e^{3t/2}v(e^tx)\ \ \text{ for }\ v\in H_{\textrm{rad}}^1({\mathbb {R}}^3),\ \ \ \ \forall \ t\in {\mathbb {R}},\ x\in {\mathbb {R}}^3, \end{aligned}$$

(3.50)

and consider the following auxiliary functional:

$$\begin{aligned} {\tilde{\Phi }}(v,t):= & \Phi (\beta (v,t))\nonumber \\= & \frac{ae^{2t}}{2}\Vert \nabla v\Vert _2^2+\frac{be^{4t}}{4}\Vert \nabla v\Vert _2^4-\frac{e^{6t}}{6}\Vert v\Vert _6^6 -\frac{\mu e^{3(q-2)t/2}}{q}\Vert v\Vert _q^q. \end{aligned}$$

(3.51)

We see that ${\tilde{\Phi }}$ is of class ${\mathcal {C}}^1$, and for any $(w,s)\in H_{\textrm{rad}}^1({\mathbb {R}}^3)\times {\mathbb {R}}$,

$$\begin{aligned} \left\langle {\tilde{\Phi }}'(v,t),(w,s)\right\rangle&= \left\langle {\tilde{\Phi }}'(v,t),(w,0)\right\rangle +\left\langle {\tilde{\Phi }}'(v,t), (0,s)\right\rangle \nonumber \\&= e^{2t}\left( a+e^{2t}b\Vert \nabla v\Vert _2^2\right) \int _{{\mathbb {R}}^3}\nabla v\cdot \nabla w\textrm{d}x\nonumber \\&\quad +e^{2t}s\left( a+e^{2t}b\Vert \nabla v\Vert _2^2\right) \Vert \nabla v\Vert _2^2\nonumber \\&\quad -\int _{{\mathbb {R}}^3}\left[ e^{6t}v^5w+\mu e^{3(q-2)t/2}|v|^{q-2}vw\right] \textrm{d}x\nonumber \\&\quad -s\int _{{\mathbb {R}}^3}\left[ e^{6t}v^6+\frac{3\mu (q-2)}{2q} e^{3(q-2)t/2}|v|^{q}\right] \textrm{d}x\nonumber \\&= \left\langle \Phi '(\beta (v,t)),\beta (w,t)\right\rangle +s{\mathcal {P}}(\beta (v,t)). \end{aligned}$$

(3.52)

Let

$$\begin{aligned} u(x):=\beta (v,t)(x)=e^{3t/2}v(e^tx),\ \ \phi (x):=\beta (w,t)(x)=e^{3t/2}w(e^tx).\nonumber \\ \end{aligned}$$

(3.53)

Then

$$\begin{aligned} (u,\phi )_H=\frac{1}{c}\int _{{\mathbb {R}}^3}u(x)\phi (x)\textrm{d}x=\frac{1}{c}\int _{{\mathbb {R}}^3}v(x)w(x)\textrm{d}x =(v,w)_H. \end{aligned}$$

(3.54)

This shows that

$$\begin{aligned} \phi \in T_u({\mathcal {S}}_c)\ \Leftrightarrow \ (w,s)\in {\tilde{T}}_{(v,t)}({\mathcal {S}}_c\times {\mathbb {R}}), \quad \forall \ t,s\in {\mathbb {R}}. \end{aligned}$$

(3.55)

It follows from (3.52), (3.53) and (3.55) that

$$\begin{aligned} |{\mathcal {P}}(u)|=\left| \left\langle {\tilde{\Phi }}'(v,t),(0,1)\right\rangle \right| \le \left\| {\tilde{\Phi }}|_{{\mathcal {S}}_c\times {\mathbb {R}}}'(v,t)\right\| \end{aligned}$$

(3.56)

and

$$\begin{aligned} \left\| \Phi |_{{\mathcal {S}}_c}'(u)\right\|= & \sup _{\phi \in T_u({\mathcal {S}}_c)}\frac{1}{\Vert \phi \Vert _E} \left| \left\langle \Phi '(u),\phi \right\rangle \right| \nonumber \\= & \sup _{\phi \in T_u({\mathcal {S}}_c)}\frac{1}{\sqrt{\Vert \nabla \phi \Vert _2^2+\Vert \phi \Vert _2^2}} \left| \left\langle \Phi '(\beta (v,t)),\beta (w,t)\right\rangle \right| \nonumber \\= & \sup _{\phi \in T_u({\mathcal {S}}_c)}\frac{1}{\sqrt{\Vert \nabla \phi \Vert _2^2+\Vert \phi \Vert _2^2}} \left| \left\langle {\tilde{\Phi }}'(v,t),(w,0)\right\rangle \right| \nonumber \\\le & \sup _{(w,0)\in {\tilde{T}}_{(v,t)}({\mathcal {S}}_c\times {\mathbb {R}})}\frac{e^{|t|}}{\Vert (w,0)\Vert _{E\times {\mathbb {R}}}} \left| \left\langle {\tilde{\Phi }}'(v,t),(w,0)\right\rangle \right| \nonumber \\\le & e^{|t|}\left\| {\tilde{\Phi }}|_{{\mathcal {S}}_c\times {\mathbb {R}}}'(v,t)\right\| . \end{aligned}$$

(3.57)

Lemma 3.9

Let $2<q<\frac{10}{3}$, $\mu > 0$ and $c\in (0,c_0)$. Then there exists $\kappa >0$ such that

$$\begin{aligned} M(c):=\inf _{\gamma \in \Gamma _{c}}\max _{t\in [0, 1]}\Phi (\gamma (t))\ge \kappa >\sup _{\gamma \in \Gamma _{c}}\max \left\{ \Phi (\gamma (0)), \Phi (\gamma (1))\right\} , \end{aligned}$$

(3.58)

where

$$\begin{aligned} \Gamma _{c}=\left\{ \gamma \in {\mathcal {C}}([0,1], {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)): \gamma (0)={\hat{u}}_c, \Phi (\gamma (1))<2m(c)\right\} . \end{aligned}$$

(3.59)

Proof

Set $\kappa :=\inf _{u\in \partial ({\mathcal {S}}_c\cap A_{s_0})}\Phi (u)$. By (3.5), $\kappa >0$. Let $\gamma \in \Gamma _{c}$ be arbitrary. By Lemma 3.7, $\gamma (0)={\hat{u}}_c\in ({\mathcal {S}}_c\cap A_{s_0}) {\setminus } (\partial ({\mathcal {S}}_c\cap A_{s_0}))$, and $\Phi (\gamma (1))<2\,m(c)<m(c)<0$, necessarily in view of (3.5), $\gamma (1)\not \in {\mathcal {S}}_c\cap \overline{A_{s_0}}$. By continuity of $\gamma (t)$ on [0, 1], there exists a $t_0 \in (0,1)$ such that $\gamma (t_0)\in \partial ({\mathcal {S}}_c\cap A_{s_0})$, and so $\max _{t\in [0, 1]}\Phi (\gamma (t))\ge \kappa$. Since $\Phi (\gamma (0)) =\Phi ({\hat{u}}_c)<\Psi ({\hat{u}}_c)={\hat{m}}(c)<0$. Thus, (3.58) holds. $\square$

Remark 3.10

In Lemma 3.9, one may wonder why the starting point of the path set $\Gamma _{c}$, defined by (3.59), is chosen as ${\hat{u}}_c$ (the solution of the auxiliary problem (3.33)), rather than the solution of the original constraint problem (1.1) as we did previously in the case of $b=0$ ( [5, Lemma 4.2]). It is worth noting that when $2<q<\frac{10}{3}$, the new compactness threshold for the constraint problem (1.1) is ${\hat{m}}(c)+\Theta ^*$, not $m(c)+\Theta ^*$ as in the case of $b=0$, as we mentioned in Remark 1.7 and subsequent remarks after it. Importantly, ${\hat{u}}_c$ is precisely the minimizer of ${\hat{m}}(c)$, which will be crucial in our subsequent proof of Lemma 3.12 that the mountain pass level is below the compactness threshold. Therefore, the solution of the original constraint problem (1.1) is not suitable as the starting point of the path set. This reveals an essential difference between the constraint problem (1.1) in the case of $b=0$ and $b>0$, and also explains why the methods developed for the study of the case $b=0$ cannot be directly applied to the case $b>0$.

Lemma 3.11

Let $2<q<\frac{10}{3}$, $\mu > 0$ and $c\in (0,c_0)$. Then there exists a sequence $\{u_n\}\subset {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$ such that

$$\begin{aligned} \Phi (u_n)\rightarrow M(c)>0, \ \ \Phi |_{{\mathcal {S}}_c}'(u_n) \rightarrow 0\ \ \text{ and }\ \ {\mathcal {P}}(u_n)\rightarrow 0. \end{aligned}$$

(3.60)

Proof

By Lemma 3.7, ${\hat{u}}_c\in {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$. Let ${\tilde{\Phi }}$ be defined by (3.51),

$$\begin{aligned} {\tilde{\Gamma }}_{c}:= & \left\{ {\tilde{\gamma }}\in {\mathcal {C}}([0,1], ({\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3))\times {\mathbb {R}}): {\tilde{\gamma }}(0)=({\hat{u}}_c,0), {\tilde{\Phi }}({\tilde{\gamma }}(1))<2m(c)\right\} \nonumber \\ \end{aligned}$$

(3.61)

and

$$\begin{aligned} {\tilde{M}}(c):=\inf _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t)). \end{aligned}$$

(3.62)

For any ${\tilde{\gamma }}\in {\tilde{\Gamma }}_c$, it is easy to see that $\gamma =\beta \circ {\tilde{\gamma }}\in \Gamma _c$ defined by (3.59). By (3.58), there exists $\kappa _c'>0$ such that

$$\begin{aligned} \max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t))= & \max _{t\in [0, 1]}\Phi (\gamma (t))\ge \kappa _c>\kappa _c' >\max \left\{ \Phi (\gamma (0)), \Phi (\gamma (1))\right\} \\= & \max \left\{ {\tilde{\Phi }}({\tilde{\gamma }}(0)), {\tilde{\Phi }}({\tilde{\gamma }}(1))\right\} . \end{aligned}$$

It follows that ${\tilde{M}}(c)\ge M(c)$, and

$$\begin{aligned} \inf _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t))\ge \kappa _c >\kappa _c'\ge \sup _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max \left\{ {\tilde{\Phi }}({\tilde{\gamma }}(0)), \Phi ({\tilde{\gamma }}(1))\right\} . \end{aligned}$$

(3.63)

This shows that (2.13) holds with ${\tilde{\varphi }}={\tilde{\Phi }}$.

On the other hand, for any $\gamma \in \Gamma _c$, let ${\tilde{\gamma }}(t):=(\gamma (t),0)$. It is easy to verify that ${\tilde{\gamma }}\in {\tilde{\Gamma }}_c$ and $\Phi (\gamma (t))={\tilde{\Phi }}({\tilde{\gamma }}(t))$, and so, we trivially have ${\tilde{M}}(c)\le M(c)$. Thus ${\tilde{M}}(c) = M(c)$.

For any $n\in {\mathbb {N}}$, (3.59) implies that there exists $\gamma _n\in \Gamma _c$ such that

$$\begin{aligned} \max _{t\in [0,1]}\Phi (\gamma _n(t)) \le M(c)+\frac{1}{n}. \end{aligned}$$

(3.64)

Set ${\tilde{\gamma }}_n(t):=(\gamma _n(t),0)$. Then applying Lemma 2.5 to ${\tilde{\Phi }}$, there exists a sequence $\{(v_n,t_n)\}\subset ({\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3))\times {\mathbb {R}}$ satisfying

• (i) $M(c)-\frac{2}{n}\le {\tilde{\Phi }}(v_n,t_n)\le M(c)+\frac{2}{n}$;

• (ii) $\min _{t\in [0,1]}\Vert (v_n,t_n)-(\gamma _n(t),0)\Vert _{E\times {\mathbb {R}}}\le \frac{2}{\sqrt{n}}$;

• (iii) $\left\| {\tilde{\Phi }}|_{{\mathcal {S}}_c\times {\mathbb {R}}}'(v_n,t_n)\right\| \le \frac{8}{\sqrt{n}}$.

Let $u_n=\beta (v_n,t_n)$. It follows from (3.56), (3.57) and (i)–(iii) that (3.60) holds. $\square$

Now we define functions $U_n(x):=\Theta _n(|x|)$, where

$$\begin{aligned} \Theta _n(r)=\root 4 \of {3} {\left\{ \begin{array}{ll} \sqrt{\frac{n}{1+n^2r^2}}, \ \ & 0\le r< 1;\\ \sqrt{\frac{n}{1+n^2}}(2-r), \ \ & 1\le r< 2;\\ 0, \ \ & r\ge 2. \end{array}\right. } \end{aligned}$$

(3.65)

Computing directly, we have

$$\begin{aligned} \Vert U_n\Vert _2^2= & \int _{{\mathbb {R}}^3}|U_n|^2\textrm{d}x=4\pi \int _{0}^{+\infty }r^{2}|\Theta _n(r)|^2\textrm{d}r\nonumber \\= & 4\sqrt{3}\pi \left[ \int _{0}^{1}\frac{nr^{2}}{\left( 1+n^2r^2\right) }\textrm{d}r +\left( \frac{n}{1+n^2}\right) \int _{1}^{2}r^{2}(2-r)^2\textrm{d}r\right] \nonumber \\= & 4\sqrt{3}\pi \left[ \frac{n-\arctan n}{n^2} +\frac{8}{15}\left( \frac{n}{1+n^2}\right) \right] = O\left( \frac{1}{n}\right) ,\ \ n\rightarrow \infty , \end{aligned}$$

(3.66)

$$\begin{aligned} \Vert \nabla U_n\Vert _2^2= & \int _{{\mathbb {R}}^3}|\nabla U_n|^2\textrm{d}x =4\pi \int _{0}^{+\infty }r^2|\Theta _n'(r)|^2\textrm{d}r\nonumber \\= & 4\sqrt{3}\pi \left[ \int _{0}^{1}\frac{n^5r^4}{\left( 1+n^2r^2\right) ^3}\textrm{d}r +\frac{n}{1+n^2}\int _{1}^{2}r^2\textrm{d}r\right] \nonumber \\= & {\mathcal {S}}^{3/2}+4\sqrt{3}\pi \left[ -\int _{n}^{+\infty }\frac{s^4}{\left( 1+s^2\right) ^3}\textrm{d}s+\frac{7n}{3(1+n^2)}\right] \nonumber \\= & {\mathcal {S}}^{3/2}+O\left( \frac{1}{n}\right) ,\ \ n\rightarrow \infty \end{aligned}$$

(3.67)

and

$$\begin{aligned} \Vert U_n\Vert _{6}^{6}= & \int _{{\mathbb {R}}^3}|U_n|^{6}\textrm{d}x =4\pi \int _{0}^{+\infty }r^2|\Theta _n(r)|^{6}\textrm{d}r\nonumber \\= & 12\sqrt{3}\pi \left[ \int _{0}^{1}\frac{n^3r^2}{\left( 1+n^2r^2\right) ^3}\textrm{d}r +\left( \frac{n}{1+n^2}\right) ^3 \int _{1}^{2}r^2(2-r)^{6}\textrm{d}r\right] \nonumber \\= & 12\sqrt{3}\pi \left[ \int _{0}^{n}\frac{s^2}{\left( 1+s^2\right) ^3}\textrm{d}s +\left( \frac{n}{1+n^2}\right) ^3\int _{0}^{1}s^{6}(2-s)^2\textrm{d}s\right] \nonumber \\= & {\mathcal {S}}^{3/2}+O\left( \frac{1}{n^3}\right) ,\ \ n\rightarrow \infty . \end{aligned}$$

(3.68)

Both (3.66) and (3.67) imply that $U_n\in H_{\textrm{rad}}^1({\mathbb {R}}^3)$.

Lemma 3.12

Let $2<q<\frac{10}{3}$, $\mu > 0$ and $c\in (0,c_0)$. Then there holds:

$$\begin{aligned} M(c) < {\hat{m}}(c)+\Theta ^*. \end{aligned}$$

(3.69)

Proof

Let ${\hat{u}}_c\in {\mathcal {S}}_c\cap H_{\textrm{rad}}^1({\mathbb {R}}^3)$ be given in Lemma 3.7. Then by Lemmas 3.7 and 3.8, we have

$$\begin{aligned} \Vert {\hat{u}}_c\Vert _2^2=c,\ \ \Psi ({\hat{u}}_c)={\hat{m}}(c), \ \ \lambda _c\Vert {\hat{u}}_c\Vert _2^2=\frac{\mu (6-q)}{2q}\Vert {\hat{u}}_c\Vert _q^q, \ \ {\hat{u}}_c(x)> 0, \ \ \forall \ x\in {\mathbb {R}}^3\nonumber \\ \end{aligned}$$

(3.70)

and

$$\begin{aligned}&\left[ a+\frac{b^2{\mathcal {S}}^3}{2}+b\Vert \nabla {\hat{u}}_c\Vert _2^2+\frac{b{\mathcal {S}}}{2}\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) {\mathcal {S}}}\right] \int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c \cdot \nabla U_n\textrm{d}x\nonumber \\&\quad = \int _{{\mathbb {R}}^3}\left( {\hat{u}}_c^5+\mu {\hat{u}}_c^{q-1}-\lambda _c{\hat{u}}_c\right) U_n\textrm{d}x. \end{aligned}$$

(3.71)

Set $B:=\inf _{|x|\le 1}{\hat{u}}_c(x)$. Then $B>0$. Hence, it follows from (3.65), (3.66) and (3.71) that

$$\begin{aligned} \int _{{\mathbb {R}}^3}\hat{u}_{c}U_n\textrm{d}x =O\left( \frac{1}{\sqrt{n}}\right) , \ \ n\rightarrow \infty , \end{aligned}$$

(3.72)

$$\begin{aligned} \left| \int _{{\mathbb {R}}^3}\nabla \hat{u}_{c}\cdot \nabla U_n\textrm{d}x\right| = \left| \int _{{\mathbb {R}}^3}U_n\Delta \hat{u}_{c}\textrm{d}x\right| = O\left( \frac{1}{\sqrt{n}}\right) , \ \ n\rightarrow \infty , \end{aligned}$$

(3.73)

$$\begin{aligned} \int _{\mathbb {R}^{3}} \hat{u}_{c}^{q-1}U_{n}\textrm{d}x\le & \left[ \int _{{\mathbb {R}}^3}\hat{u}_{c}^{2(q-1)}\textrm{d}x\int _{|x|\le 2}U_n^2\textrm{d}x\right] ^{\frac{1}{2}} =O\left( \frac{1}{\sqrt{n}}\right) , \ \ n\rightarrow \infty \nonumber \\ \end{aligned}$$

(3.74)

and

$$\begin{aligned} \int _{{\mathbb {R}}^3}\hat{u}_{c}U_n^{5}\textrm{d}x\ge & 4\pi B\int _{0}^{1}r^2|\Theta _n(r)|^{5}\textrm{d}r\nonumber \\= & 12\pi \root 4 \of {3}B\int _{0}^{1}\frac{n^{5/2}r^2}{\left( 1+n^2r^2\right) ^{5/2}}\textrm{d}r\nonumber \\\ge & \frac{12\pi \root 4 \of {3}B}{\sqrt{n}}\int _{0}^{1}\frac{s^2}{\left( 1+s^2\right) ^{5/2}}\textrm{d}s:= \frac{B_0}{\sqrt{n}}. \end{aligned}$$

(3.75)

By (3.66) and (3.70), one has

$$\begin{aligned} \Vert {\hat{u}}_c+tU_n\Vert _2^2= & c+t^2\Vert U_n\Vert _2^2+2t\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x\nonumber \\= & c+2t\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x +t^2\left[ O\left( \frac{1}{n}\right) \right] , \ \ n\rightarrow \infty . \end{aligned}$$

(3.76)

Let $\tau =\tau _{n,t}:=\Vert {\hat{u}}_c+tU_n\Vert _2/\sqrt{c}$. Then

$$\begin{aligned} \tau ^2 = 1+\frac{2t}{c}\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x +t^2\left[ O\left( \frac{1}{n}\right) \right] , \ \ n\rightarrow \infty . \end{aligned}$$

(3.77)

Now, we define

$$\begin{aligned} W_{n,t}(x):=\sqrt{\tau }[{\hat{u}}_c(\tau x)+tU_n(\tau x)]. \end{aligned}$$

(3.78)

Then one has

$$\begin{aligned} \Vert \nabla W_{n,t}\Vert _2^2=\Vert \nabla ({\hat{u}}_c+tU_n)\Vert _2^2,\ \ \Vert W_{n,t}\Vert _{6}^{6}=\Vert {\hat{u}}_c+tU_n\Vert _{6}^{6} \end{aligned}$$

(3.79)

and

$$\begin{aligned} \Vert W_{n,t}\Vert _2^2=\tau ^{-2}\Vert {\hat{u}}_c+tU_n\Vert _2^2=c,\ \ \Vert W_{n,t}\Vert _q^q=\tau ^{(q-6)/2}\Vert {\hat{u}}_c+tU_n\Vert _q^q. \end{aligned}$$

(3.80)

Set

$$\begin{aligned} t_*^2=\frac{1}{2}\left[ b{\mathcal {S}}^{\frac{3}{2}}+\sqrt{b^2S^3+4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) }\right] . \end{aligned}$$

(3.81)

Then (3.71) can be rewritten as

$$\begin{aligned} \left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2+b{\mathcal {S}}^{\frac{3}{2}}t_*^2\right) \int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c \cdot \nabla U_n\textrm{d}x = \int _{{\mathbb {R}}^3}\left( {\hat{u}}_c^5+\mu |{\hat{u}}_c|^{q-2}{\hat{u}}_c -\lambda _c {\hat{u}}_c\right) U_n\textrm{d}x. \end{aligned}$$

(3.82)

By (1.9) and (3.81), we can deduce

$$\begin{aligned}&{\mathcal {S}}^{\frac{3}{2}}\left[ \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{2}t^2 +\frac{b{\mathcal {S}}^{\frac{3}{2}}}{4}t^4-\frac{1}{6}t^{6}\right] \nonumber \\&\quad < {\mathcal {S}}^{\frac{3}{2}}\left[ \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{2}t_*^2 +\frac{b{\mathcal {S}}^{\frac{3}{2}}}{4}t_*^4-\frac{1}{6}t_*^{6}\right] \nonumber \\&\quad = {\mathcal {S}}^{\frac{3}{2}}\left[ \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{3}t_*^2 +\frac{b{\mathcal {S}}^{\frac{3}{2}}}{12}t_*^4\right] \nonumber \\&\quad = \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{6}{\mathcal {S}}^{\frac{3}{2}} \left[ b{\mathcal {S}}^{\frac{3}{2}}+\sqrt{b^2S^3 +4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) }\right] \nonumber \\&\qquad +\frac{b{\mathcal {S}}^{3}}{48}\left[ b{\mathcal {S}}^{\frac{3}{2}} +\sqrt{b^2S^3+4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) }\right] ^2\nonumber \\&\quad = \frac{b{\mathcal {S}}^3\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{4}+\frac{b^3{\mathcal {S}}^6}{24} +\frac{\left[ b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2\right) {\mathcal {S}}\right] ^{\frac{3}{2}}}{24}\nonumber \\&\quad = \Theta ^*+\frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b}{b^2{\mathcal {S}}^3+4a}\Vert \nabla {\hat{u}}_c\Vert _2^2\right) ^{\frac{3}{2}}-1\right] \nonumber \\&\qquad +\frac{b^2{\mathcal {S}}^3}{4}\Vert \nabla {\hat{u}}_c\Vert _2^{2},\forall \ t\in (0,t_*)\cup (t_*,+\infty ). \end{aligned}$$

(3.83)

It is easy to verify that

$$\begin{aligned} (1+t)^p\ge 1+pt+pt^{p-1}+t^p, \quad \forall p\ge 3, \ \ t\ge 0 \end{aligned}$$

(3.84)

and

$$\begin{aligned} (1+t)^p\ge 1+pt^{p-1}+t^p, \ \ \forall p\ge 2, \ \ t\ge 0. \end{aligned}$$

(3.85)

From (1.2), (1.15), (3.66)–(3.68), (3.70) and (3.72)–(3.85), we have

$$\begin{aligned}&\Phi (W_{n,t})\nonumber \\&\quad = \frac{a}{2}\Vert \nabla W_{n,t}\Vert _2^{2}+\frac{b}{4}\Vert \nabla W_{n,t}\Vert _2^{4} -\frac{1}{6}\Vert W_{n,t}\Vert _{6}^{6}-\frac{\mu }{q}\Vert W_{n,t}\Vert _q^q\nonumber \\&\quad = \frac{a}{2}\Vert \nabla ({\hat{u}}_c+tU_n)\Vert _2^{2}+\frac{b}{4}\Vert \nabla ({\hat{u}}_c+tU_n)\Vert _2^{4} -\frac{1}{6}\Vert {\hat{u}}_c+tU_n\Vert _{6}^{6}-\frac{\mu \tau ^{(q-6)/2}}{q}\Vert {\hat{u}}_c+tU_n\Vert _q^q\nonumber \\&\quad \le \frac{a}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}+\frac{b}{4}\Vert \nabla {\hat{u}}_c\Vert _2^{4}-\frac{1}{6}\Vert {\hat{u}}_c\Vert _{6}^{6} -\frac{\mu \tau ^{(q-6)/2}}{q}\Vert {\hat{u}}_c\Vert _q^q +\frac{at^2}{2}\Vert \nabla U_n\Vert _2^{2}\nonumber \\&\qquad +\frac{bt^4}{4}\Vert \nabla U_n\Vert _2^{4}-\frac{t^{6}}{6}\Vert U_n\Vert _{6}^{6} -t\int _{{\mathbb {R}}^3}{\hat{u}}_c^5U_n\textrm{d}x-t^5\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n^5\textrm{d}x\nonumber \\&\qquad -\mu \tau ^{(q-6)/2}t\int _{{\mathbb {R}}^3}{\hat{u}}_c^{q-1}U_n\textrm{d}x +\frac{bt^2}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}\Vert \nabla U_n\Vert _2^{2}\nonumber \\&\qquad +\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^2+bt^2\Vert \nabla U_n\Vert _2^2\right) t \int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c\cdot \nabla U_n\textrm{d}x +bt^2\left( \int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c\cdot \nabla U_n\textrm{d}x\right) ^2\nonumber \\&\quad = \frac{a}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}+\frac{b}{4}\Vert \nabla {\hat{u}}_c\Vert _2^{4}-\frac{1}{6}\Vert {\hat{u}}_c\Vert _{6}^{6} -\frac{\mu }{q}\Vert {\hat{u}}_c\Vert _q^q+\frac{at^2}{2}\Vert \nabla U_n\Vert _2^{2} +\frac{bt^4}{4}\Vert \nabla U_n\Vert _2^{4}-\frac{t^{6}}{6}\Vert U_n\Vert _{6}^{6}\nonumber \\&\qquad +\frac{\mu \left( 1-\tau ^{(q-6)/2}\right) }{q}\Vert {\hat{u}}_c\Vert _q^q +\mu \left( 1-\tau ^{(q-6)/2}\right) t\int _{{\mathbb {R}}^3}{\hat{u}}_c^{q-1}U_n\textrm{d}x -\lambda _ct\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x\nonumber \\&\qquad +\frac{bt^2}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}\Vert \nabla U_n\Vert _2^{2} +b\left( t^2\Vert \nabla U_n\Vert _2^2-t_*^2{\mathcal {S}}^{\frac{3}{2}}\right) t \int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c\cdot \nabla U_n\textrm{d}x-t^5\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n^5\textrm{d}x\nonumber \\&\qquad +t^2\left[ O\left( \frac{1}{n}\right) \right] \nonumber \\&\quad \le \frac{a}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}+\frac{b}{4}\Vert \nabla {\hat{u}}_c\Vert _2^{4}-\frac{1}{6}\Vert {\hat{u}}_c\Vert _{6}^{6} -\frac{\mu }{q}\Vert {\hat{u}}_c\Vert _q^q+{\mathcal {S}}^{\frac{3}{2}}\left[ \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{2}t^2+\frac{b{\mathcal {S}}^{\frac{3}{2}}}{4}t^4-\frac{1}{6}t^{6}\right] \nonumber \\&\qquad +\frac{\mu \Vert {\hat{u}}_c\Vert _q^q}{q}\left\{ 1-\left[ 1+\frac{2t}{c}\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x +t^2\left( O\left( \frac{1}{n}\right) \right) \right] ^{(q-6)/2}\right\} -\lambda _ct\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x\nonumber \\&\qquad +\mu \left\{ 1-\left[ 1+\frac{2t}{c}\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n\textrm{d}x +t^2\left( O\left( \frac{1}{n}\right) \right) \right] ^{(q-6)/2}\right\} t\int _{{\mathbb {R}}^3}{\hat{u}}_c^{q-1}U_n\textrm{d}x\nonumber \\&\qquad +b{\mathcal {S}}^{\frac{3}{2}}\left( t^2-t_*^2\right) t\int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c\cdot \nabla U_n\textrm{d}x -t^5\int _{{\mathbb {R}}^3}{\hat{u}}_cU_n^5\textrm{d}x +\left( t^2+t^6\right) \left[ O\left( \frac{1}{n}\right) \right] \nonumber \\&\quad \le \frac{a}{2}\Vert \nabla {\hat{u}}_c\Vert _2^{2}+\frac{b}{4}\Vert \nabla {\hat{u}}_c\Vert _2^{4}-\frac{1}{6}\Vert {\hat{u}}_c\Vert _{6}^{6} -\frac{\mu }{q}\Vert {\hat{u}}_c\Vert _q^q+{\mathcal {S}}^{\frac{3}{2}}\left[ \frac{\left( a+b\Vert \nabla {\hat{u}}_c\Vert _2^{2}\right) }{2}t^2+\frac{b{\mathcal {S}}^{\frac{3}{2}}}{4}t^4-\frac{1}{6}t^{6}\right] \nonumber \\&\qquad -\frac{B_0t^5}{\sqrt{n}}+b{\mathcal {S}}^{\frac{3}{2}}\left( t^2-t_*^2\right) t\left[ O\left( \frac{1}{\sqrt{n}}\right) \right] +\left( t^2+t^6\right) \left[ O\left( \frac{1}{n}\right) \right] \end{aligned}$$

(3.86)

$$\begin{aligned}&\quad \le \Theta ^*+\frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b}{b^2{\mathcal {S}}^3+4a}\Vert \nabla {\hat{u}}_c\Vert _2^2\right) ^{\frac{3}{2}}-1\right] +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \Vert \nabla {\hat{u}}_c\Vert _2^2\nonumber \\&\qquad +\frac{b}{4}\Vert \nabla {\hat{u}}_c\Vert _2^4 -\frac{1}{6}\Vert {\hat{u}}_c\Vert _{6}^{6}-\frac{\mu }{q}\Vert {\hat{u}}_c\Vert _q^q-O\left( \frac{1}{\sqrt{n}}\right) \nonumber \\&\quad = \Theta ^*+\Psi ({\hat{u}}_c)-O\left( \frac{1}{\sqrt{n}}\right) \nonumber \\&\quad = {\hat{m}}(c)+\Theta ^*-O\left( \frac{1}{\sqrt{n}}\right) , \ \ \forall \ t>0. \end{aligned}$$

(3.87)

Hence, it follows from (3.87) that there exists ${\bar{n}}\in {\mathbb {N}}$ such that

$$\begin{aligned} \sup _{t>0}\Phi (W_{{\bar{n}},t})< {\hat{m}}(c)+\Theta ^*. \end{aligned}$$

(3.88)

Next, we prove that (3.69) holds. Let ${\bar{n}}\in {\mathbb {N}}$ be given in (3.88). By (3.76), (3.78), (3.79) and (3.80), we have

$$\begin{aligned} W_{{\bar{n}},t}(x):={\bar{\tau }}^{1/2}[{\hat{u}}_c({\bar{\tau }} x)+tU_{{\bar{n}}}(\tau x)],\ \ \Vert W_{{\bar{n}},t}\Vert _2^2=c \end{aligned}$$

(3.89)

and

$$\begin{aligned} \Vert \nabla W_{{\bar{n}},t}\Vert _2^2= & \Vert \nabla ({\hat{u}}_c+tU_{{\bar{n}}})\Vert _2^2\nonumber \\= & \Vert \nabla {\hat{u}}_c\Vert _2^2+t^2\Vert \nabla U_{{\bar{n}}}\Vert _2^2 +2t\int _{{\mathbb {R}}^3}\nabla {\hat{u}}_c\cdot \nabla U_{{\bar{n}}}\textrm{d}x, \end{aligned}$$

(3.90)

where

$$\begin{aligned} {\bar{\tau }}^2=\Vert {\hat{u}}_c+tU_{{\bar{n}}}\Vert _2^2/c= & 1+\frac{2t}{c}\int _{{\mathbb {R}}^3}{\hat{u}}_cU_{{\bar{n}}}\textrm{d}x +t^2\Vert U_{{\bar{n}}}\Vert _2^2. \end{aligned}$$

(3.91)

It follows from (3.86), (3.89) and (3.90) that $W_{{\bar{n}},t}\in {\mathcal {S}}_c$ for all $t>0$, $W_{{\bar{n}},0}={\hat{u}}_c$ and $\Phi (W_{{\bar{n}},t}) <2m(c)$ for large $t>0$. Thus, there exists ${\hat{t}}>0$ such that

$$\begin{aligned} \Phi (W_{{\bar{n}},{\hat{t}}}) <2m(c). \end{aligned}$$

(3.92)

Let $\gamma _{{\bar{n}}}(t):=W_{{\bar{n}},t{\hat{t}}}$. Then $\gamma _{{\bar{n}}}\in \Gamma _{c}$ defined by (3.59). Hence, it follows from (3.58) and (3.88) that (3.69) holds. $\square$

Proof of Theorems 1.2

In view of Lemmas 3.11 and 3.12, there exists $\{u_n\}\subset {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$ such that

$$\begin{aligned} \Vert u_n\Vert _2^2=c, \ \ \Phi (u_n)\rightarrow M(c)\in (0,{\hat{m}}(c)+\Theta ^*), \ \ \Phi |_{{\mathcal {S}}_c}'(u_n)\rightarrow 0, \ \ {\mathcal {P}}(u_n)\rightarrow 0.\nonumber \\ \end{aligned}$$

(3.93)

It follows from (1.2), (1.17) and (3.93) that

$$\begin{aligned} M(c)+o(1)=\frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4 -\frac{1}{6}\Vert u_n\Vert _6^6-\frac{\mu }{q}\Vert u_n\Vert _q^q \end{aligned}$$

(3.94)

and

$$\begin{aligned} o(1)=a\Vert \nabla u_n\Vert _2^2+b\Vert \nabla u_n\Vert _2^4-\Vert u_n\Vert _6^6-\frac{3\mu (q-2)}{2q}\Vert u_n\Vert _q^q. \end{aligned}$$

(3.95)

Both (3.94) and (3.95), together with (1.16), show that

$$\begin{aligned} M(c)+o(1)&= \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert u_n\Vert _q^q\nonumber \\&\ge \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4 -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\Vert \nabla u_n\Vert _2^{3(q-2)/2}. \end{aligned}$$

(3.96)

Since $2<q<\frac{10}{3}$, it follows that $\{\Vert u_n\Vert \}$ is bounded. By Lemma 2.2, one has

$$\begin{aligned} \Phi '(u_n)+\lambda _nu_n\rightarrow 0, \end{aligned}$$

(3.97)

where

$$\begin{aligned} -\lambda _n=\frac{1}{\Vert u_n\Vert _2^2}\langle \Phi '(u_n),u_n\rangle =\frac{1}{c}\left[ \left( a+b\Vert \nabla u_n\Vert _2^2\right) \Vert \nabla u_n\Vert _2^2-\mu \Vert u_n\Vert _q^q-\Vert u_n\Vert _{6}^{6}\right] .\nonumber \\ \end{aligned}$$

(3.98)

Since $\{\Vert u_n\Vert \}$ is bounded, it follows from (3.98) that $\{|\lambda _n|\}$ is also bounded. Thus, we may thus assume, passing to a subsequence if necessary, that

$$\begin{aligned} \left\{ \begin{array}{ll} \lambda _n\rightarrow \lambda _c, \ \ & \Vert \nabla u_n\Vert _2^2\rightarrow A^2;\\ u_n\rightharpoonup {\bar{u}}, & \text{ in } \ H_{\textrm{rad}}^1({\mathbb {R}}^3); \\ u_n\rightarrow {\bar{u}}, & \text{ in } \ L^s({\mathbb {R}}^3), \ \forall \ s\in (2,6);\\ u_n\rightarrow {\bar{u}}, & \text{ a.e. } \text{ on } \ {\mathbb {R}}^3. \end{array} \right. \end{aligned}$$

(3.99)

First, we prove that ${\bar{u}}\ne 0$. Otherwise, we assume that ${\bar{u}} =0$. Then $\Vert u_n\Vert _q^q\rightarrow 0$. It follows from (3.95) that

$$\begin{aligned} o(1)=a\Vert \nabla u_n\Vert _2^2+b\Vert \nabla u_n\Vert _2^4-\Vert u_n\Vert _6^6. \end{aligned}$$

(3.100)

Up to a subsequence, we assume that

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2\rightarrow {\hat{l}}_1\ge 0, \ \ \Vert u_n\Vert _6^6\rightarrow {\hat{l}}_2\ge 0. \end{aligned}$$

(3.101)

Then it follows from (1.8), (3.100) and (3.101) that $a{\hat{l}}_1+b{\hat{l}}_1^2={\hat{l}}_2\le {\mathcal {S}}^{-3}{\hat{l}}_1^3$. If ${\hat{l}}_1 > 0$, an elementary calculation yields that

$$\begin{aligned} {\hat{l}}_1\ge \frac{{\mathcal {S}}}{2}\left[ b{\mathcal {S}}^2+\sqrt{b^2S^4+4a{\mathcal {S}}}\right] . \end{aligned}$$

(3.102)

From (3.94), (3.100), (3.101) and (3.102), we obtain

$$\begin{aligned} M(c)+o(1)&= \frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4-\frac{1}{6}\Vert u_n\Vert _6^6\\&= \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4\nonumber \\&\ge \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{\left( b^2S^4+4a{\mathcal {S}}\right) ^{3/2}}{24}+o(1)=\Theta ^*+o(1), \end{aligned}$$

which contradicts with (3.93). Thus, $\Vert \nabla u_n\Vert _2^2\rightarrow 0$, and so it follows from (3.94) that $M(c)=0$, which contradicts with (3.93) also. Therefore, ${\bar{u}}\ne 0$.

Define I(u) as follows:

$$\begin{aligned} I(u):= \frac{a+bA^2}{2}\Vert \nabla u\Vert _2^2-\frac{1}{6}\Vert u\Vert _6^6-\frac{\mu }{q}\Vert u\Vert _q^q. \end{aligned}$$

(3.103)

By (3.97), (3.98), (3.99) and (3.103) and a standard argument, we can deduce

$$\begin{aligned} I'({\bar{u}})+\lambda _c{\bar{u}}=0. \end{aligned}$$

(3.104)

It follows that

$$\begin{aligned} \left( a+bA^2\right) \Vert \nabla {\bar{u}}\Vert _2^2+\lambda _c\Vert {\bar{u}}\Vert _2^2-\mu \Vert {\bar{u}}\Vert _q^q-\Vert {\bar{u}}\Vert _{6}^{6}=0. \end{aligned}$$

(3.105)

By the Pohozaev type identity for the functional (3.103), one has

$$\begin{aligned} \left( a+bA^2\right) \Vert \nabla {\bar{u}}\Vert _2^2+3\lambda _c\Vert {\bar{u}}\Vert _2^2-\frac{6\mu }{q}\Vert {\bar{u}}\Vert _q^q-\Vert {\bar{u}}\Vert _{6}^{6}=0. \end{aligned}$$

(3.106)

Combining (3.105) with (3.106), one has

$$\begin{aligned} {\mathcal {P}}_I({\bar{u}}):= (a+bA^2)\Vert \nabla {\bar{u}}\Vert _2^2-\Vert {\bar{u}}\Vert _6^6-\frac{3\mu (q-2)}{2q}\Vert {\bar{u}}\Vert _q^q=0 \end{aligned}$$

(3.107)

and

$$\begin{aligned} \lambda _c\Vert {\bar{u}}\Vert _2^2=\frac{\mu (6-q)}{2q}\Vert {\bar{u}}\Vert _q^q. \end{aligned}$$

(3.108)

Let $v_n:=u_n-{\bar{u}}$. Then $v_n\rightharpoonup 0$ in $H_{\textrm{rad}}^1({\mathbb {R}}^3)$ and $v_n\rightarrow 0$ in $L^s({\mathbb {R}}^3)$ for all $s\in (2,6)$. Using Brezis–Lieb lemma, one has

$$\begin{aligned} \left\{ \begin{array}{ll} \Vert v_n\Vert _2^2=\Vert u_n\Vert _2^2-\Vert {\bar{u}}\Vert _2^2+o(1); \\ \Vert v_n\Vert _6^6=\Vert u_n\Vert _6^6-\Vert {\bar{u}}\Vert _6^6+o(1); \\ A^2=\Vert \nabla u_n\Vert _2^2+o(1)=\Vert \nabla {\bar{u}}\Vert _2^2+\Vert \nabla v_n\Vert _2^2+o(1). \end{array} \right. \end{aligned}$$

(3.109)

From (3.95), (3.107), and (3.109), we deduce

$$\begin{aligned} o(1)&= \left( a+b\Vert \nabla u_n\Vert _2^2\right) \Vert \nabla u_n\Vert _2^2-\Vert u_n\Vert _6^6-\frac{3\mu (q-2)}{2q}\Vert u_n\Vert _q^q\nonumber \\&= \left( a+bA^2\right) \Vert \nabla {\bar{u}}\Vert _2^2-\Vert {\bar{u}}\Vert _6^6-\frac{3\mu (q-2)}{2q}\Vert {\bar{u}}\Vert _q^q\nonumber \\&\quad +\left( a+bA^2\right) \Vert \nabla v_n\Vert _2^2-\Vert v_n\Vert _6^6+o(1)\nonumber \\&= \left( a+bA^2\right) \Vert \nabla v_n\Vert _2^2-\Vert v_n\Vert _6^6+o(1)\nonumber \\&= \left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) \Vert \nabla v_n\Vert _2^2+b\Vert \nabla v_n\Vert _2^4 -\Vert v_n\Vert _6^6+o(1). \end{aligned}$$

(3.110)

Up to a subsequence, we assume that

$$\begin{aligned} \Vert \nabla v_n\Vert _2^2\rightarrow l_1\ge 0, \ \ \Vert v_n\Vert _6^6\rightarrow l_2\ge 0. \end{aligned}$$

(3.111)

Then it follows from (3.110) and (3.111) that

$$\begin{aligned} \left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) l_1+bl_1^2=l_2. \end{aligned}$$

(3.112)

If $l_1 > 0$, by (1.8), (3.111) and (3.112), we have

$$\begin{aligned} l_1\ge {\mathcal {S}}\left[ \left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) l_1+bl_1^2\right] ^{1/3}, \end{aligned}$$

which implies

$$\begin{aligned} l_1\ge \frac{{\mathcal {S}}}{2}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] . \end{aligned}$$

(3.113)

From (1.2), (3.94), (3.109) and (3.110), we obtain

$$\begin{aligned} M(c)+o(1)&= \frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4-\frac{1}{6}\Vert u_n\Vert _6^6 -\frac{\mu }{q}\Vert u_n\Vert _q^q\nonumber \\&= \frac{a}{2}\Vert \nabla v_n\Vert _2^2+\frac{b}{4}\Vert \nabla v_n\Vert _2^4 -\frac{1}{6}\Vert v_n\Vert _6^6+\frac{b}{2}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2 +\Phi ({\bar{u}})+o(1)\nonumber \\&= \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{3}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+\Phi ({\bar{u}})+o(1). \end{aligned}$$

(3.114)

There are two cases to distinguish.

Case 1). $\Vert \nabla {\bar{u}}\Vert _2^2<s_0$. Then it follows from Lemmas 3.4 and 3.6 that

$$\begin{aligned} \Psi ({\bar{u}})\ge {\hat{m}}(\Vert {\bar{u}}\Vert _2^2)\ge {\hat{m}}(c). \end{aligned}$$

(3.115)

From (1.15), (3.111), (3.113), (3.114) and (3.115), we obtain

$$\begin{aligned}&M(c)+o(1)\\&\quad = \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{3}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+\Phi ({\bar{u}})+o(1)\nonumber \\&\quad { { = \frac{a+b\Vert \nabla {\bar{u}}\Vert _2^2}{3}l_1+\frac{b}{12}l_1^2+\Phi ({\bar{u}})+o(1)}}\nonumber \\&\quad { {\ge \frac{(a+b\Vert \nabla {\bar{u}}\Vert _2^2){\mathcal {S}}}{6}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] }}\nonumber \\&\qquad { { +\frac{b{\mathcal {S}}^2}{48}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] ^2+\Phi ({\bar{u}})+o(1)}}\nonumber \\&\quad { { = }} \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{\left[ b^2S^4+4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}\right] ^{3/2}}{24} +\frac{b^2{\mathcal {S}}^{3}}{4}\Vert \nabla {\bar{u}}\Vert _2^2+\Phi ({\bar{u}})+o(1)\nonumber \\&\quad = \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{\left( b^2S^4+4a{\mathcal {S}}\right) ^{3/2}}{24}\nonumber \\&\qquad +\frac{(b^2{\mathcal {S}}^4+4a{\mathcal {S}})^{\frac{3}{2}}}{24} \left[ \left( 1+\frac{4b}{b^2{\mathcal {S}}^3+4a}\Vert \nabla {\bar{u}}\Vert _2^2\right) ^{\frac{3}{2}}-1\right] \nonumber \\&\qquad +\left( \frac{a}{2}+\frac{b^2{\mathcal {S}}^3}{4}\right) \Vert \nabla {\bar{u}}\Vert _2^2 +\frac{b}{4}\Vert \nabla {\bar{u}}\Vert _2^4 -\frac{1}{6}\Vert {\bar{u}}\Vert _6^6-\frac{\mu }{q}\Vert {\bar{u}}\Vert _q^q+o(1)\nonumber \\&\quad = \Theta ^*+\Psi ({\bar{u}})+o(1)\ge \Theta ^*+{\hat{m}}(c)+o(1), \end{aligned}$$

which contradicts with (3.93).

Case 2). $\Vert \nabla {\bar{u}}\Vert _2^2\ge s_0$. Then it follows from (1.2), (1.12), (1.16), (3.107), (3.109), (3.111) and (3.114) that

$$\begin{aligned}&M(c)+o(1)\nonumber \\&\quad = \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{3}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+\Phi ({\bar{u}})+o(1)\nonumber \\&\quad = \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{6}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2 +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4\nonumber \\&\qquad -\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)\nonumber \\&\quad { {= \frac{2a+b\Vert \nabla {\bar{u}}\Vert _2^2}{6}l_1+\frac{b}{12}l_{1}^{2} +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)}}\nonumber \\&\quad { {\ge \frac{(2a+b\Vert \nabla {\bar{u}}\Vert _2^2){\mathcal {S}}}{12}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] }}\nonumber \\&\qquad { { +\frac{b{\mathcal {S}}^2}{48}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] ^2 +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4}}\nonumber \\&\qquad { { -\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)}}\nonumber \\&\quad = \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{b^2S^4+2\left( 2a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}{24} \sqrt{b^2S^4+4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\nonumber \\&\qquad +\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^{3}}{6}\right) \Vert \nabla {\bar{u}}\Vert _2^2 +\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)\nonumber \\&\quad \ge \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{\left( b^2S^4+4a{\mathcal {S}}\right) ^{3/2}}{24}\nonumber \\&\qquad +\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^3}{6} +\frac{b{\mathcal {S}}\sqrt{b^2S^4+4(a+bs_0){\mathcal {S}}}}{12}\right) \Vert \nabla {\bar{u}}\Vert _2^2\nonumber \\&\qquad +\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4 -\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)\nonumber \\&\quad \ge \Theta ^*+\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^3}{6} +\frac{b{\mathcal {S}}\sqrt{b^2S^4+4(a+bs_0){\mathcal {S}}}}{12}\right) \Vert \nabla {\bar{u}}\Vert _2^2 +\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4\nonumber \\&\qquad -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\Vert \nabla {\bar{u}}\Vert _2^{3(q-2)/2} +o(1)\nonumber \\&\quad \ge \Theta ^*+\left[ \left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^3}{6} +\frac{b{\mathcal {S}}\sqrt{b^2S^4+4(a+bs_0){\mathcal {S}}}}{12}\right) s_0^{(10-3q)/4} +\frac{b}{12}s_0^{(14-3q)/4}\right. \nonumber \\&\qquad \left. -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\right] \Vert \nabla {\bar{u}}\Vert _2^{3(q-2)/2} +o(1)\nonumber \\&\quad \ge \Theta ^*+o(1), \end{aligned}$$

which contradicts with (3.93). Both Cases 1) and 2) show that $l_1=0$, i.e. $\Vert \nabla v_n\Vert \rightarrow 0$, and so

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2\rightarrow \Vert \nabla {\bar{u}}\Vert _2^2, \ \ \Vert u_n\Vert _6^6\rightarrow \Vert {\bar{u}}\Vert _6^6. \end{aligned}$$

(3.116)

Now from (1.2), (3.93), (3.94), (3.97), (3.98), (3.99), (3.105), (3.108) and (3.116), it is easy to deduce that

$$\begin{aligned} \lambda _c>0, \ \ \Vert {\bar{u}}\Vert _2^2=c, \ \ { {\Phi '({\bar{u}})+\lambda _c{\bar{u}}=0}}, \ \ \Phi ({\bar{u}})=M(c). \end{aligned}$$

$\square$

4 The case when $\frac{10}{3}\le q<\frac{14}{3}$

In this section, we study the case $\frac{10}{3}\le q<\frac{14}{3}$, and finish the proof of Theorem 1.3.

Lemma 4.1

Let $\frac{10}{3}\le q<\frac{14}{3}$, $\mu > 0$ and $c\in (0,c_2]$. Then

• (i) there exist $\vartheta _c'>\vartheta _c>0$ such that $\Phi (u)>0$ if $u\in A_{\vartheta _c'}$, and

  $$\begin{aligned} 0<\sup _{u\in A_{\vartheta _c}}\Phi (u)<\inf \left\{ \Phi (u): u\in {\mathcal {S}}_c, \ \Vert \nabla u\Vert _2^2= \vartheta _c' \right\} , \end{aligned}$$

  (4.1)

  where

  $$\begin{aligned} A_{\vartheta _c}=\left\{ u\in {\mathcal {S}}_c: \Vert \nabla u\Vert _2^2< \vartheta _c\right\} \ \ \hbox {and} \ \ { { A_{\vartheta _c'}=\left\{ u\in {\mathcal {S}}_c: \Vert \nabla u\Vert _2^2 < \vartheta _c'\right\} }}; \end{aligned}$$

  (4.2)

• (ii) ${\hat{\Gamma }}_{c}=\{\gamma \in {\mathcal {C}}([0,1],{\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)):\Vert \nabla \gamma (0)\Vert _2^2< \vartheta _c, \Phi (\gamma (1))<0\}\ne \emptyset$ and

  $$\begin{aligned} {\hat{M}}(c)&:= \inf _{\gamma \in {\hat{\Gamma }}_{c}}\max _{t\in [0,1]}\Phi (\gamma (t)) \ge {\hat{\kappa }}_{c}:=\inf \left\{ \Phi (u): u\in {\mathcal {S}}_c, \Vert \nabla u\Vert _2^2 = { {\vartheta _c' }}\right\} \nonumber \\&> \max _{\gamma \in {\hat{\Gamma }}_{c}}\max \{\Phi (\gamma (0)),\Phi (\gamma (1))\}. \end{aligned}$$

  (4.3)

Proof

(i) We distinguish two cases.

Case 1). $\frac{10}{3}< q<\frac{14}{3}$. In this case, one has $0<\frac{3q-10}{2}<2$. By (1.2), (1.8) and (1.16), one has

$$\begin{aligned} \Phi (u)= & \frac{a}{2}\Vert \nabla u\Vert _2^2+\frac{b}{4}\Vert \nabla u\Vert _2^4-\frac{\mu }{q}\Vert u\Vert _q^q -\frac{1}{6}\Vert u\Vert _6^6\nonumber \\\le & \Vert \nabla u\Vert _2^2\left( \frac{a}{2}+\frac{b}{4}\Vert \nabla u\Vert _2^2\right) ,\ \ \forall \ u\in {\mathcal {S}}_{c} \ \ \ \end{aligned}$$

(4.4)

and

$$\begin{aligned} \Phi (u)= & \frac{a}{2}\Vert \nabla u\Vert _2^2+\frac{b}{4}\Vert \nabla u\Vert _2^4-\frac{\mu }{q}\Vert u\Vert _q^q -\frac{1}{6}\Vert u\Vert _6^6\nonumber \\\ge & \Vert \nabla u\Vert _2^2\left[ \frac{a}{2}-\frac{\mu c^{(6-q)/4}{\mathcal {C}}_q^q}{q}\Vert \nabla u\Vert _2^{(3q-10)/2} -\frac{1}{6{\mathcal {S}}^{3}}\Vert \nabla u\Vert _2^{4}\right] ,\ \ \forall \ u\in {\mathcal {S}}_{c}. \end{aligned}$$

Since $0<\frac{3q-10}{2}<2$, the above inequalities show that there exist $\vartheta _c'>\vartheta _c>0$ such that (i) holds.

Case 2). $q=\frac{10}{3}$. By (1.2), (1.8) and (1.16), one has

$$\begin{aligned} \Phi (u)= & \frac{a}{2}\Vert \nabla u\Vert _2^2+\frac{b}{4}\Vert \nabla u\Vert _2^4-\frac{3\mu }{10}\Vert u\Vert _{10/3}^{10/3} -\frac{1}{6}\Vert u\Vert _6^6\nonumber \\\ge & \Vert \nabla u\Vert _2^2\left( \frac{a}{2}+\frac{b}{4}\Vert \nabla u\Vert _2^2 -\frac{3\mu }{10} {\mathcal {C}}_{10/3}^{10/3}c^{2/3} -\frac{1}{6{\mathcal {S}}^{3}}\Vert \nabla u\Vert _2^{4}\right) ,\ \ \forall \ u\in {\mathcal {S}}_{c}. \end{aligned}$$

Since $c\le c_2$, the above inequality and (4.4) show that there exist $\vartheta _c'>\vartheta _c>0$ such that (i) holds also.

(ii) For any given $w\in {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$, we have $\Vert t^{3/2}w_t\Vert _2=\Vert w\Vert _2$, and so $t^{3/2}w_t\in {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$ for every $t>0$. Then (1.2) yields

$$\begin{aligned} \Phi \left( t^{3/2}w_t\right)= & \frac{at^2}{2}\Vert \nabla w\Vert _2^{2}+\frac{bt^4}{4}\Vert \nabla w\Vert _2^{4} -\frac{\mu t^{3(q-2)/2}}{q}\Vert w\Vert _q^q\nonumber \\ & -\frac{t^{6}}{6}\Vert w\Vert _{6}^{6} \rightarrow -\infty \ \ \hbox {as}\ \ t\rightarrow +\infty . \end{aligned}$$

(4.5)

Thus we can deduce that there exist $t_1>0$ small enough and $t_2>0$ large enough such that

$$\begin{aligned} \left\| \nabla \left( t_1^{3/2}w_{t_1}\right) \right\| _2^2=t_1^2\Vert \nabla w\Vert _2^2< \vartheta _c, \ \ \hbox {and}\ \ \Phi \left( t_2^{3/2}w_{t_2}\right) <0. \end{aligned}$$

(4.6)

Let $\gamma _0(t):=[t_1+(t_2-t_1)t]^{3/2}w_{t_1+(t_2-t_1)t}$. Then $\gamma _0\in {\hat{\Gamma }}_{c}$, and so ${\hat{\Gamma }}_{c}\ne \emptyset$. Now using the intermediate value theorem, for any $\gamma \in {\hat{\Gamma }}_{c}$, there exists $t_0\in (0,1)$, depending on $\gamma$, such that $\Vert \nabla \gamma (t_0)\Vert _2^2=\vartheta _c'$ and

$$\begin{aligned} \max _{t\in [0,1]}\Phi (\gamma (t))\ge \Phi (\gamma (t_0))\ge \inf \left\{ \Phi (u): u\in {\mathcal {S}}_c, \Vert \nabla u\Vert _2^2= \vartheta _c' \right\} , \end{aligned}$$

which, together with the arbitrariness of $\gamma \in {\hat{\Gamma }}_{c}$, implies

$$\begin{aligned} {\hat{M}}(c)=\inf _{\gamma \in {\hat{\Gamma }}}\max _{t\in [0,1]}\Phi (\gamma (t))\ge \inf \left\{ \Phi (u): u\in {\mathcal {S}}_c, \Vert \nabla u\Vert _2^2= \vartheta _c' \right\} . \end{aligned}$$

(4.7)

Hence, (4.3) follows directly from (4.1) and (4.7), and the proof is completed. $\square$

Lemma 4.2

Let $\frac{10}{3}\le q<\frac{14}{3}$, $\mu > 0$ and $c\in (0,c_2]$. Then there exists a sequence $\{u_n\}\subset {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$ such that

$$\begin{aligned} \Phi (u_n)\rightarrow {\hat{M}}(c)>0, \ \ \Phi |_{{\mathcal {S}}_c}'(u_n) \rightarrow 0\ \ \text{ and }\ \ {\mathcal {P}}(u_n)\rightarrow 0. \end{aligned}$$

(4.8)

Proof

Let ${\tilde{\Phi }}$ be defined by (3.51),

$$\begin{aligned} {\tilde{\Gamma }}_{c}:= & \left\{ {\tilde{\gamma }}\in {\mathcal {C}}([0,1], ({\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3))\times {\mathbb {R}}): {\tilde{\gamma }}(0)=({\tilde{\gamma }}_1(0),0), \Vert \nabla {\tilde{\gamma }}_1(0)\Vert _2^2< \vartheta _c, \right. \nonumber \\ & \quad \left. {\tilde{\Phi }}({\tilde{\gamma }}(1))<0\right\} \end{aligned}$$

(4.9)

and

$$\begin{aligned} {\tilde{M}}(c):=\inf _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t)). \end{aligned}$$

(4.10)

For any ${\tilde{\gamma }}\in {\tilde{\Gamma }}_c$, it is easy to see that $\gamma =\beta \circ {\tilde{\gamma }}\in {\hat{\Gamma }}_c$. By (4.3), there exists ${\hat{\kappa }}_c'\in (0,{\hat{\kappa }}_c)$ such that

$$\begin{aligned} \max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t))= & \max _{t\in [0, 1]}\Phi (\gamma (t))\ge {\hat{\kappa }}_c>{\hat{\kappa }}_c' >\max \left\{ \Phi (\gamma (0)), \Phi (\gamma (1))\right\} \nonumber \\= & \max \left\{ {\tilde{\Phi }}({\tilde{\gamma }}(0)), {\tilde{\Phi }}({\tilde{\gamma }}(1))\right\} . \end{aligned}$$

It follows that ${\tilde{M}}(c)\ge {\hat{M}}(c)$, and

$$\begin{aligned} \inf _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max _{t\in [0, 1]}{\tilde{\Phi }}({\tilde{\gamma }}(t))\ge \kappa _c >\kappa _c'\ge \sup _{{\tilde{\gamma }}\in {\tilde{\Gamma }}_c}\max \left\{ {\tilde{\Phi }}({\tilde{\gamma }}(0)), {\tilde{\Phi }}({\tilde{\gamma }}(1))\right\} . \end{aligned}$$

(4.11)

This shows that (2.13) holds with ${\tilde{\varphi }}={\tilde{\Phi }}$.

On the other hand, for any $\gamma \in {\hat{\Gamma }}_c$, let ${\tilde{\gamma }}(t):=(\gamma (t),0)$. It is easy to verify that ${\tilde{\gamma }}\in {\tilde{\Gamma }}_c$ and $\Phi (\gamma (t))={\tilde{\Phi }}({\tilde{\gamma }}(t))$, and so, we trivially have ${\tilde{M}}(c)\le {\hat{M}}(c)$. Thus ${\tilde{M}}(c) = {\hat{M}}(c)$.

For any $n\in {\mathbb {N}}$, (4.3) implies that there exists $\gamma _n\in {\hat{\Gamma }}_c$ such that

$$\begin{aligned} \max _{t\in [0,1]}\Phi (\gamma _n(t)) \le {\hat{M}}(c)+\frac{1}{n}. \end{aligned}$$

(4.12)

Set ${\tilde{\gamma }}_n(t):=(\gamma _n(t),0)$. Then applying Lemma 2.5 to ${\tilde{\Phi }}$, there exists a sequence $\{(v_n,t_n)\}\subset ({\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3))\times {\mathbb {R}}$ satisfying

• (i) ${\hat{M}}(c)-\frac{2}{n}\le {\tilde{\Phi }}(v_n,t_n)\le {\hat{M}}(c)+\frac{2}{n}$;

• (ii) $\min _{t\in [0,1]}\Vert (v_n,t_n)-(\gamma _n(t),0)\Vert _{E\times {\mathbb {R}}}\le \frac{2}{\sqrt{n}}$;

• (iii) $\left\| {\tilde{\Phi }}|_{{\mathcal {S}}_c\times {\mathbb {R}}}'(v_n,t_n)\right\| \le \frac{8}{\sqrt{n}}$.

Let $u_n=\beta (v_n,t_n)$. It follows from (3.56), (3.57) and (i)–(iii) that (4.8) holds. $\square$

Next, we give a precise estimation for the energy level ${\hat{M}}(c)$ given by (4.3) when $\frac{10}{3}\le q<\frac{14}{3}$. To this end, for any fixed $c>0$, we choose $\max \{(14-3q)/8,0\}<\alpha <1$ and $R_n> n^{\alpha }$ to be such that

$$\begin{aligned} c = 4\sqrt{3}\pi \left\{ \frac{n^{1+\alpha }-\arctan \left( n^{1+\alpha }\right) }{n^2} +\frac{R_n^{5}n-[10R_n^2-15R_nn^{\alpha }+6n^{2\alpha }]n^{1+3\alpha }}{30(R_n-n^{\alpha })^2(1+n^{2(1+\alpha }))}\right\} .\nonumber \\ \end{aligned}$$

(4.13)

From (4.13), one can deduce that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{R_n}{n^{(1+2\alpha )/3}}= \root 3 \of {\frac{15c}{2\sqrt{3}\pi }}. \end{aligned}$$

(4.14)

Now, we define function ${\tilde{U}}_n(x):={\tilde{\Theta }}_n(|x|)$, where

$$\begin{aligned} {\tilde{\Theta }}_n(r)=\root 4 \of {3} {\left\{ \begin{array}{ll} \sqrt{\frac{n}{1+n^2r^2}}, \ \ & 0\le r< n^{\alpha };\\ \sqrt{\frac{n}{1+n^{2(1+\alpha )}}}\frac{R_n-r}{R_n-n^{\alpha }}, \ \ & n^{\alpha }\le r< R_n;\\ 0, \ \ & r\ge R_n. \end{array}\right. } \end{aligned}$$

(4.15)

Computing directly, we have

$$\begin{aligned} \Vert {\tilde{U}}_n\Vert _2^2= & \int _{{\mathbb {R}}^3}|{\tilde{U}}_n|^2\textrm{d}x =4\pi \int _{0}^{+\infty }r^2|{\tilde{\Theta }}_n(r)|^2\textrm{d}r\nonumber \\= & 4\sqrt{3}\pi \left[ \int _{0}^{n^{\alpha }}\frac{nr^2}{1+n^2r^2}\textrm{d}r +\frac{n}{1+n^{2(1+\alpha )}} \int _{n^{\alpha }}^{R_n}\frac{r^2(R_n-r)^2}{(R_n-n^{\alpha })^2}\textrm{d}r\right] \nonumber \\= & 4\sqrt{3}\pi \left\{ \frac{1}{n^2}\int _{0}^{n^{1+\alpha }}\frac{s^2}{1+s^2}\textrm{d}s +\frac{n}{1+n^{2(1+\alpha )}}\frac{R_n^{5}-[10R_n^2-15R_nn^{\alpha }+6n^{2\alpha }]n^{3\alpha }}{30(R_n-n^{\alpha })^2}\right\} \nonumber \\= & 4\sqrt{3}\pi \left\{ \frac{n^{1+\alpha }-\arctan \left( n^{1+\alpha }\right) }{n^2} +\frac{R_n^{5}n-[10R_n^2-15R_nn^{\alpha }+6n^{2\alpha }]n^{1+3\alpha }}{30(R_n-n^{\alpha })^2(1+n^{2(1+\alpha }))}\right\} \nonumber \\= & c, \end{aligned}$$

(4.16)

$$\begin{aligned} \Vert \nabla {\tilde{U}}_n\Vert _2^2= & \int _{{\mathbb {R}}^3}|\nabla {\tilde{U}}_n|^2\textrm{d}x =4\pi \int _{0}^{+\infty }r^2|{\tilde{\Theta }}_n'(r)|^2\textrm{d}r\nonumber \\= & 4\sqrt{3}\pi \left[ \int _{0}^{n^{\alpha }}\frac{n^{5}r^{4}}{\left( 1+n^2r^2\right) ^{3}}\textrm{d}r +\frac{n}{1+n^{2(1+\alpha )}} \int _{n^{\alpha }}^{R_n}\frac{r^2}{(R_n-n^{\alpha })^2}\textrm{d}r\right] \nonumber \\= & 4\sqrt{3}\pi \left[ \int _{0}^{n^{1+\alpha }}\frac{s^4}{\left( 1+s^2\right) ^3}\textrm{d}s +\frac{R_n^3-n^{3\alpha }}{3(R_n-n^{\alpha })^2}\frac{n}{1+n^{2(1+\alpha )}}\right] \nonumber \\= & {\mathcal {S}}^{\frac{3}{2}}+4\sqrt{3}\pi \left[ -\int _{n^{1+\alpha }}^{+\infty }\frac{s^4}{\left( 1+s^2\right) ^3}\textrm{d}s +\frac{n(R_n^3-n^{3\alpha })}{3(R_n-n^{\alpha })^2(1+n^{2(1+\alpha )})}\right] \nonumber \\= & {\mathcal {S}}^{\frac{3}{2}}+O\left( \frac{1}{n^{2(1+2\alpha )/3}}\right) , \ \ \ \ n\rightarrow \infty , \end{aligned}$$

(4.17)

$$\begin{aligned} \Vert {\tilde{U}}_n\Vert _{6}^{6}= & \int _{{\mathbb {R}}^3}|{\tilde{U}}_n|^{6}\textrm{d}x =4\pi \int _{0}^{+\infty }r^{2}|{\tilde{\Theta }}_n(r)|^{6}\textrm{d}r\nonumber \\= & 12\sqrt{3}\pi \left[ \int _{0}^{n^{\alpha }}\frac{n^3r^2}{\left( 1+n^2r^2\right) ^3}\textrm{d}r +\left( \frac{n}{1+n^{2(1+\alpha )}}\right) ^3 \int _{n^{\alpha }}^{R_n}\frac{r^2(R_n-r)^{6}}{(R_n-n^{\alpha })^{6}}\textrm{d}r\right] \nonumber \\= & 12\sqrt{3}\pi \left[ \int _{0}^{n^{1+\alpha }}\frac{s^{2}}{\left( 1+s^2\right) ^3}\textrm{d}s +\left( \frac{n}{1+n^{2(1+\alpha )}}\right) ^3 \int _{0}^{R_n-n^{\alpha }}\frac{s^{6}(R_n-s)^2}{(R_n-n^{\alpha })^{6}}\textrm{d}s\right] \nonumber \\= & {\mathcal {S}}^{\frac{3}{2}}+12\sqrt{3}\pi \left[ -\int _{n^{1+\alpha }}^{+\infty }\frac{s^2}{\left( 1+s^2\right) ^3}\textrm{d}s\right. \nonumber \\ & \ \ \left. +R_n^3\left( \frac{n}{1+n^{2(1+\alpha )}}\right) ^3 \int _{0}^{1-n^{\alpha }/R_n}\frac{s^{6}(1-s)^2}{(1-n^{\alpha }/R_n)^{6}}\textrm{d}s\right] \nonumber \\= & {\mathcal {S}}^{\frac{3}{2}}+O\left( \frac{1}{n^{2(1+2\alpha )}}\right) , \ \ \ \ n\rightarrow \infty \end{aligned}$$

(4.18)

and

$$\begin{aligned} \Vert {\tilde{U}}_n\Vert _q^q= & \int _{{\mathbb {R}}^3}|{\tilde{U}}_n|^q\textrm{d}x=4\pi \int _{0}^{+\infty }r^2 |{\tilde{\Theta }}_n(r)|^q\textrm{d}r\nonumber \\\ge & 4\cdot 3^{q/4}\pi \int _{0}^{n^{\alpha }}\frac{n^{q/2}r^2}{\left( 1+n^2r^2\right) ^{q/2}}\textrm{d}r\nonumber \\\ge & \frac{4\cdot 3^{q/4}\pi }{n^{(6-q)/2}}\int _{0}^{1}\frac{s^2}{\left( 1+s^2\right) ^{q/2}}\textrm{d}s:= \frac{K_0}{n^{3-q/2}}. \end{aligned}$$

(4.19)

Both (4.16) and (4.18) imply that ${\tilde{U}}_n\in {\mathcal {S}}_c$.

Lemma 4.3

Let $\frac{10}{3}\le q<6$, $\mu >0$ and $c>0$. Then there exists ${\bar{n}}\in {\mathbb {N}}$ such that

$$\begin{aligned} \sup _{t>0}\Phi \left( t^{3/2}({\tilde{U}}_{{\bar{n}}})_{t}\right) < \Theta ^*. \end{aligned}$$

(4.20)

Proof

Set

$$\begin{aligned} t_{**}^2=\frac{1}{2}\left[ b{\mathcal {S}}^{\frac{3}{2}}+\sqrt{b^2S^3+4a}\right] . \end{aligned}$$

(4.21)

By (1.9) and (4.21), we can deduce

$$\begin{aligned} \frac{{\mathcal {S}}^{\frac{3}{2}}}{2}\left( at^2+\frac{b{\mathcal {S}}^{\frac{3}{2}}}{2}t^4 -\frac{1}{3}t^{6}\right)&< \frac{{\mathcal {S}}^{\frac{3}{2}}}{2}\left( at_{**}^2+\frac{b{\mathcal {S}}^{\frac{3}{2}}}{2}t_{**}^4 -\frac{1}{3}t_{**}^{6}\right) \nonumber \\&= \Theta ^*, \ \ \forall \ t\in (0,t_{**})\cup (t_{**},+\infty ). \end{aligned}$$

(4.22)

From (1.2), (4.17), (4.18) and (4.19), we have

$$\begin{aligned} \Phi \left( t^{3/2}({\tilde{U}}_{n})_{t}\right)&= \frac{at^2}{2}\Vert \nabla {\tilde{U}}_n\Vert _2^{2}+\frac{bt^4}{4}\Vert \nabla {\tilde{U}}_n\Vert _2^{4} -\frac{\mu t^{3(q-2)/2}}{q}\Vert {\tilde{U}}_n\Vert _q^q-\frac{t^{6}}{6}\Vert {\tilde{U}}_n\Vert _{6}^{6}\nonumber \\&\le \frac{at^2}{2}\left[ {\mathcal {S}}^{\frac{3}{2}}+O\left( \frac{1}{n^{2(1+2\alpha )/3}}\right) \right] +\frac{bt^4}{4}\left[ {\mathcal {S}}^{\frac{3}{2}}+O\left( \frac{1}{n^{2(1+2\alpha )/3}}\right) \right] ^2 \nonumber \\&\quad -\frac{t^{6}}{6}\left[ {\mathcal {S}}^{\frac{3}{2}} +O\left( \frac{1}{n^{2(1+2\alpha )}}\right) \right] -\frac{K_0\mu t^{3(q-2)/2}}{qn^{3-q/2}}\nonumber \\&= \frac{{\mathcal {S}}^{\frac{3}{2}}}{2}\left( at^2+\frac{b{\mathcal {S}}^{\frac{3}{2}}}{2}t^4 -\frac{1}{3}t^{6}\right) +\frac{2at^2+bt^4}{4}\left[ O\left( \frac{1}{n^{2(1+2\alpha )/3}}\right) \right] \nonumber \\&\quad -\frac{t^{6}}{6}\left[ O\left( \frac{1}{n^{2(1+2\alpha )}}\right) \right] -\frac{K_0\mu t^{3(q-2)/2}}{qn^{3-q/2}}, \ \ \forall \ t>0. \end{aligned}$$

(4.23)

Hence, it follows from (4.22), (4.23) and the fact $\max \{(14-3q)/8,0\}<\alpha <1$ that there exists ${\bar{n}}\in {\mathbb {N}}$ such that (4.20) holds. $\square$

Lemma 4.4

Let $\frac{10}{3}\le q<\frac{14}{3}$, $\mu >0$ and $c\in (0,c_2]$. Then there holds

$$\begin{aligned} {\hat{M}}(c)< \Theta ^*. \end{aligned}$$

(4.24)

Proof

Let ${\bar{n}}\in {\mathbb {N}}$ be given by (4.20). Then it follows from (1.2) that

$$\begin{aligned} \Phi \left( t^{3/2}({\tilde{U}}_{{\bar{n}}})_{t}\right)&= \frac{at^2}{2}\Vert \nabla {\tilde{U}}_{{\bar{n}}}\Vert _2^{2}+\frac{bt^4}{4}\Vert \nabla {\tilde{U}}_{{\bar{n}}}\Vert _2^{4}\nonumber \\&\quad -\frac{\mu t^{3(q-2)/2}}{q}\Vert {\tilde{U}}_{{\bar{n}}}\Vert _q^q-\frac{t^{6}}{6}\Vert {\tilde{U}}_{{\bar{n}}}\Vert _{6}^{6}, \ \ \forall \ t>0. \end{aligned}$$

(4.25)

By (4.25), we can deduce that there exist $t_1>0$ small enough and $t_2>0$ large enough such that

$$\begin{aligned} \left\| \nabla \left( t_1^{3/2}({\tilde{U}}_{{\bar{n}}})_{t_1}\right) \right\| _2^2=t_1^2\Vert \nabla {\tilde{U}}_{{\bar{n}}}\Vert _2^2< \vartheta _c, \ \ \hbox {and}\ \ \Phi \left( t_2^{3/2}({\tilde{U}}_{{\bar{n}}})_{t_2}\right) <0. \end{aligned}$$

(4.26)

Let $\gamma _0(t):=[t_1+(t_2-t_1)t]^{3/2}({\tilde{U}}_{{\bar{n}}})_{t_1+(t_2-t_1)t}$. Then $\gamma _0\in {\hat{\Gamma }}_{c}$ which is defined by Lemma 4.1. Therefore, we have by Lemma 4.3

$$\begin{aligned} {\hat{M}}(c)\le \sup _{t>0}\Phi \left( t^{3/2}({\tilde{U}}_{{\bar{n}}})_{t}\right) < \Theta ^*. \end{aligned}$$

This shows (4.24) holds. $\square$

Proof of Theorems 1.3

In view of Lemmas 4.2 and 4.4, there exists $\{u_n\}\subset {\mathcal {S}}_c\cap H^1_{\textrm{rad}}({\mathbb {R}}^3)$ such that

$$\begin{aligned} \Vert u_n\Vert _2^2=c, \ \ \Phi (u_n)\rightarrow {\hat{M}}(c)\in (0,\Theta ^*), \ \ \Phi (u_n)|_{{\mathcal {S}}_c}'\rightarrow 0, \ \ {\mathcal {P}}(u_n)\rightarrow 0. \end{aligned}$$

(4.27)

It follows from (1.2), (1.16), (1.17) and (4.27) that

$$\begin{aligned} {\hat{M}}(c)+o(1)&= \Phi (u_n)-\frac{1}{6}{\mathcal {P}}(u_n)\nonumber \\&= \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert u_n\Vert _q^q\nonumber \\&\ge \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4 -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\Vert \nabla u_n\Vert _2^{3(q-2)/2}. \end{aligned}$$

(4.28)

Since $\frac{10}{3}\le q<\frac{14}{3}$, it follows that $\{\Vert u_n\Vert \}$ is bounded. Similar to the proof of Theorem 1.2, one has (3.96)–(3.114) instead of M(c) by ${\hat{M}}(c)$. From (1.14), (3.107), (3.110), (3.113) and (3.114), we have

$$\begin{aligned}&{\hat{M}}(c)+o(1)\nonumber \\&\quad = \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{3}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2+\Phi ({\bar{u}})+o(1)\nonumber \\&\quad = \frac{a}{3}\Vert \nabla v_n\Vert _2^2+\frac{b}{12}\Vert \nabla v_n\Vert _2^4 +\frac{b}{6}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla v_n\Vert _2^2\nonumber \\&\qquad +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4 -\frac{\mu }{4q}(6-q)\Vert {\bar{u}}\Vert _q^q+o(1)\nonumber \\&\quad { {= \frac{2a+b\Vert \nabla {\bar{u}}\Vert _2^2}{6}l_1+\frac{b}{12}l_2^2 +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)}}\nonumber \\&\quad { {\ge \frac{(2a+b\Vert \nabla {\bar{u}}\Vert _2^2){\mathcal {S}}}{12}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] }}\nonumber \\&\qquad { {+\frac{b{\mathcal {S}}^2}{48}\left[ b{\mathcal {S}}^2+\sqrt{b^2{\mathcal {S}}^4 +4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\right] ^2 +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4}}\nonumber \\&\qquad { {-\frac{\mu (6-q)}{4q}\Vert {\bar{u}}\Vert _q^q+o(1)}}\nonumber \\&\quad { { =}} \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{b^2S^4+4a{\mathcal {S}}}{24} \sqrt{b^2S^4+4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}} +\frac{b^2{\mathcal {S}}^{3}}{6}\Vert \nabla {\bar{u}}\Vert _2^2\nonumber \\&\qquad +\frac{b{\mathcal {S}}}{12}\sqrt{b^2S^4+4\left( a+b\Vert \nabla {\bar{u}}\Vert _2^2\right) {\mathcal {S}}}\ \Vert \nabla {\bar{u}}\Vert _2^2 +\frac{a}{3}\Vert \nabla {\bar{u}}\Vert _2^2+\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4\nonumber \\&\qquad -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\Vert \nabla {\bar{u}}\Vert _2^{3(q-2)/2}+o(1)\nonumber \\&\quad { {\ge }} \frac{ab{\mathcal {S}}^{3}}{4}+\frac{b^3{\mathcal {S}}^{6}}{24} +\frac{\left( b^2S^4+4a{\mathcal {S}}\right) ^{3/2}}{24} +\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^{3}}{6}+\frac{b{\mathcal {S}}}{12}\sqrt{b^2S^4+4a{\mathcal {S}}}\right) \Vert \nabla {\bar{u}}\Vert _2^2\nonumber \\&\qquad +\frac{b}{12}\Vert \nabla {\bar{u}}\Vert _2^4-\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\Vert \nabla {\bar{u}}\Vert _2^{3(q-2)/2}{ {+o(1)}}\nonumber \\&\quad \ge \Theta ^*+\left\{ \left[ \frac{4}{14-3q}\left( \frac{a}{3}+\frac{b^2{\mathcal {S}}^{3}}{6} +\frac{b{\mathcal {S}}}{12}\sqrt{b^2S^4+4a{\mathcal {S}}}\right) \right] ^{\frac{14-3q}{4}} \left[ \frac{b}{3(3q-10)}\right] ^{\frac{3q-10}{4}}\right. \nonumber \\&\qquad \left. -\frac{\mu (6-q)}{4q}{\mathcal {C}}_q^qc^{(6-q)/4}\right\} \Vert \nabla {\bar{u}}\Vert _2^{3(q-2)/2}+o(1)\nonumber \\&\quad \ge \Theta ^*+o(1), \end{aligned}$$

(4.29)

which contradicts with (4.27). This shows that $l_1=0$, i.e. $\Vert \nabla v_n\Vert \rightarrow 0$, and so

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2\rightarrow \Vert \nabla {\bar{u}}\Vert _2^2, \ \ \Vert u_n\Vert _6^6\rightarrow \Vert {\bar{u}}\Vert _6^6. \end{aligned}$$

(4.30)

Now from (1.2), (3.97), (3.98), (3.99), (3.105), (3.108), (4.27) and (4.30), it is easy to deduce that

$$\begin{aligned} \lambda _c>0, \ \ \Vert {\bar{u}}\Vert _2^2=c, \ \ { {\Phi '({\bar{u}})+\lambda _c{\bar{u}}=0}}, \ \ \Phi ({\bar{u}})={\hat{M}}(c). \end{aligned}$$

$\square$

5 The case when $\frac{14}{3}\le q<6$

In this section, we study the case $\frac{14}{3}\le q<6$, and finish the proofs of Theorems 1.4 and 1.5.

Let us define the following function

$$\begin{aligned} h(t):=\frac{1-t^4}{4}-\frac{1-t^{6}}{6}, \quad \forall \ t\ge 0. \end{aligned}$$

(5.1)

It is easy to see that $h(t)>h(1)=0$ for all $t\in [0,1)\cup (1,+\infty )$. With it, we establish the following crucial inequality,

Lemma 5.1

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then there holds

$$\begin{aligned} \Phi (u)\ge & \Phi \left( t^{3/2}u_t\right) +\frac{1-t^4}{4}{\mathcal {P}}(u)+\frac{a(1-t^2)^2}{4}\Vert \nabla u\Vert _2^2\nonumber \\ & +h(t)\Vert u\Vert _{6}^{6}, \quad \forall \ u\in {\mathcal {S}}_c, \ t>0. \end{aligned}$$

(5.2)

Proof

Since $\frac{14}{3} \le q < 6$, it is easy to see that

$$\begin{aligned} \frac{3(q-2)(1-t^{4})}{8q}-\frac{1-t^{3(q-2)/2}}{q}\ge 0, \ \ \forall \ t\ge 0. \end{aligned}$$

(5.3)

From (1.2), (1.17), (5.1) and (5.3), one has

$$\begin{aligned} \Phi (u)-\Phi \left( t^{3/2}u_t\right)&= \frac{a(1-t^2)}{2}\Vert \nabla u\Vert _2^2+\frac{b(1-t^4)}{4}\Vert \nabla u\Vert _2^4\nonumber \\&\quad -\frac{\mu (1-t^{3(q-2)/2})}{q}\Vert u\Vert _q^q-\frac{1-t^{6}}{6}\Vert u\Vert _6^6\nonumber \\&= \frac{1-t^4}{4}\left[ a\Vert \nabla u\Vert _2^2+b\Vert \nabla u\Vert _2^4-\frac{3\mu (q-2)}{2q}\Vert u\Vert _q^q-\Vert u\Vert _6^6\right] \nonumber \\&\quad +\frac{a(1-t^2)^2}{4}\Vert \nabla u\Vert _2^2 +\mu \left( \frac{3(q-2)(1-t^{4})}{8q}-\frac{1-t^{3(q-2)/2}}{q}\right) \Vert u\Vert _q^q\nonumber \\&\quad +\left( \frac{1-t^{4}}{4}-\frac{1-t^{6}}{6}\right) \Vert u\Vert _6^6\nonumber \\&\ge \frac{1-t^4}{4}{\mathcal {P}}(u)+\frac{a(1-t^2)^2}{4}\Vert \nabla u\Vert _2^2+h(t)\Vert u\Vert _6^6. \end{aligned}$$

$\square$

From Lemma 5.1, we have the following corollary.

Corollary 5.2

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then for $u\in {\mathcal {M}}(c)$, there holds

$$\begin{aligned} \Phi (u) = \max _{t> 0}\Phi \left( t^{3/2}u_t\right) . \end{aligned}$$

(5.4)

Lemma 5.3

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then for any $u\in {\mathcal {S}}_c$, there exists a unique $t_u>0$ such that $t_u^{3/2}u_{t_u}\in {\mathcal {M}}(c)$.

The proof of Lemma 5.3 is standard, so we omit it.

From Corollary 5.2 and Lemma 5.3, we have the following lemma.

Lemma 5.4

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then

$$\begin{aligned} \inf _{u\in {\mathcal {M}}(c)}\Phi (u):={\tilde{m}}(c)=\inf _{u\in {\mathcal {S}}_c}\max _{t > 0}\Phi \left( t^{3/2}u_t\right) . \end{aligned}$$

(5.5)

By the Brezis–Lieb lemma, we have the following lemma.

Lemma 5.5

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. If $u_n\rightharpoonup {\bar{u}}$ in $H^1({\mathbb {R}}^3)$, then

$$\begin{aligned} \Phi (u_n)=\Phi ({\bar{u}})+\Phi (u_n-{\bar{u}})+\frac{b}{2}\Vert \nabla {\bar{u}}\Vert _2^2\Vert \nabla (u_n-{\bar{u}})\Vert _2^2+o(1) \end{aligned}$$

(5.6)

and

$$\begin{aligned} {\mathcal {P}}(u_n)={\mathcal {P}}({\bar{u}})+{\mathcal {P}}(u_n-{\bar{u}})+2b\Vert \nabla {\bar{u}}\Vert _2^2 \Vert \nabla (u_n-{\bar{u}})\Vert _2^2+o(1). \end{aligned}$$

(5.7)

Lemma 5.6

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then

• (i) there exists $\vartheta _0>0$ such that $\Vert \nabla u\Vert _2\ge \vartheta _0, \ \forall \ u\in {\mathcal {M}}(c)$;

• (ii) ${\tilde{m}}(c)>0$.

Proof

(i) Since ${\mathcal {P}}(u)=0, \ \forall \ u\in {\mathcal {M}}(c)$, by (1.8), (1.16) and (1.17), one has

$$\begin{aligned} a\Vert \nabla u\Vert _2^2+b\Vert \nabla u\Vert _2^4= & \Vert u\Vert _{6}^{6}+\frac{3\mu (q-2)}{2q}\Vert u\Vert _q^q\nonumber \\\le & \frac{1}{{\mathcal {S}}^{3}}\Vert \nabla u\Vert _2^{6}\nonumber \\ & +\frac{3\mu (q-2)}{2q}{\mathcal {C}}_{q}^qc^{(6-q)/4} \Vert \nabla u\Vert _2^{3(q-2)/2}, \ \ \forall \ u\in {\mathcal {M}}(c), \ \ \ \nonumber \\ \end{aligned}$$

(5.8)

which implies

$$\begin{aligned} a\le \frac{1}{{\mathcal {S}}^{3}}\Vert \nabla u\Vert _2^{4}+\frac{3\mu (q-2)}{2q}{\mathcal {C}}_{q}^qc^{(6-q)/4} \Vert \nabla u\Vert _2^{(3q-10)/2}, \quad \forall \ u\in {\mathcal {M}}(c). \end{aligned}$$

Since $\frac{14}{3}\le q<6$, then the above inequality shows there exists $\vartheta _0>0$ such that

$$\begin{aligned} \Vert \nabla u\Vert _2\ge \vartheta _0, \quad \forall \ u\in {\mathcal {M}}(c). \end{aligned}$$

(5.9)

(ii) From (1.2), (1.17) and (5.9), we have

$$\begin{aligned} \Phi (u)&= \Phi (u)-\frac{2}{3(q-2)}{\mathcal {P}}(u)\nonumber \\&= \frac{a(3q-10)}{6(q-2)}\Vert \nabla u\Vert _2^2+\frac{b(3q-14)}{12(q-2)}\Vert \nabla u\Vert _2^4 +\frac{6-q}{6(q-2)}\Vert u\Vert _{6}^{6}\nonumber \\&\ge \frac{a(3q-10)}{6(q-2)}\vartheta _0^2, \quad \forall \ u\in {\mathcal {M}}(c). \end{aligned}$$

(5.10)

This shows that ${\tilde{m}}(c)=\inf _{u\in {\mathcal {M}}(c)}\Phi (u)>0$. $\square$

Lemma 5.7

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then the function $c \mapsto {\tilde{m}}(c)$ is nonincreasing on $(0,+\infty )$. In particular, if ${\tilde{m}}(c_0')$ is achieved, then ${\tilde{m}}(c_0') > {\tilde{m}}(c_2')$ for any $c_2' > c_0'$.

Proof

For any $c_2'> c_0' > 0$, it follows from the definition of ${\tilde{m}}(c_0')$ that there exists $\{u_n\} \subset {\mathcal {M}}(c_0')$ such that

$$\begin{aligned} \Phi (u_n)<{\tilde{m}}(c_0')+\frac{1}{n}, \quad \forall \ n\in {\mathbb {N}}. \end{aligned}$$

(5.11)

Let $\theta :=\sqrt{c_2'/c_0'}$ and $v_n(x):=\theta ^{-1/2}u_n\left( x/\theta \right)$. Then $\Vert \nabla v_n\Vert _2^2=\Vert \nabla u_n\Vert _2^2$, $\Vert v_n\Vert _{6}^{6}=\Vert u_n\Vert _{6}^{6}$, $\Vert v_n\Vert _{q}^{q}=\theta ^{3-q/2}\Vert u_n\Vert _{q}^{q}$ and $\Vert v_n\Vert _2^2=c_2'$. By Lemma 5.3, there exists $t_n > 0$ such that $t_n^{3/2}(v_n)_{t_n}\in {\mathcal {M}}(c_2')$. Then it follows from (1.2), (5.11) and Corollary 5.2 that

$$\begin{aligned} {\tilde{m}}(c_2')\le & \Phi \left( t_n^{3/2}(v_n)_{t_n}\right) \nonumber \\= & \frac{at_n^2}{2}\Vert \nabla v_n\Vert _2^2+\frac{bt_n^4}{4}\Vert \nabla v_n\Vert _2^4-\frac{t_n^{6}}{6}\Vert v_n\Vert _{6}^{6} -\frac{\mu t_n^{3(q-2)/2}}{q}\Vert v_n\Vert _{q}^{q}\nonumber \\= & \frac{at_n^2}{2}\Vert \nabla u_n\Vert _2^2+\frac{bt_n^4}{4}\Vert \nabla u_n\Vert _2^4 -\frac{t_n^{6}}{6}\Vert u_n\Vert _{6}^{6}-\frac{\mu \theta ^{3-q/2} t_n^{3(q-2)/2}}{q}\Vert u_n\Vert _{q}^{q}\nonumber \\< & \Phi \left( t_n^{3/2}(u_n)_{t_n}\right) \le \Phi (u_n)<{\tilde{m}}(c_0')+\frac{1}{n}, \end{aligned}$$

(5.12)

which shows that ${\tilde{m}}(c_2') \le {\tilde{m}}(c_0')$ by letting $n\rightarrow \infty$.

If ${\tilde{m}}(c_0')$ is achieved, i.e., there exists ${\tilde{u}}\in {\mathcal {M}}(c_0')$ such that $\Phi ({\tilde{u}})={\tilde{m}}(c_0')$. By the same argument as in (5.12), we can obtain that ${\tilde{m}}(c_2')<{\tilde{m}}(c_0')$. $\square$

By Lemma 4.3, we have the following lemma.

Lemma 5.8

Let $\frac{14}{3}\le q<6$, $\mu >0$ and $c>0$. Then there holds

$$\begin{aligned} {\tilde{m}}(c)< \Theta ^*. \end{aligned}$$

(5.13)

Lemma 5.9

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. Then ${\tilde{m}}(c)$ is achieved.

Proof

In view of Lemmas 5.3 and 5.6, we have ${\mathcal {M}}(c) \ne \emptyset$ and ${\tilde{m}}(c)>0$. Let $\{u_n\}\subset {\mathcal {M}}(c)$ be such that $\Phi (u_n)\rightarrow {\tilde{m}}(c)$. It follows from (1.2) and (1.17) that

$$\begin{aligned} {\tilde{m}}(c)+o(1)=\frac{a}{2}\Vert \nabla u_n\Vert _2^2+\frac{b}{4}\Vert \nabla u_n\Vert _2^4 -\frac{1}{6}\Vert u_n\Vert _6^6-\frac{\mu }{q}\Vert u_n\Vert _q^q \end{aligned}$$

(5.14)

and

$$\begin{aligned} 0=a\Vert \nabla u_n\Vert _2^2+b\Vert \nabla u_n\Vert _2^4-\Vert u_n\Vert _6^6-\frac{3\mu (q-2)}{2q}\Vert u_n\Vert _q^q. \end{aligned}$$

(5.15)

From (5.14) and (5.15), one has

$$\begin{aligned} {\tilde{m}}(c)+o(1)\ge \frac{a}{4}\Vert \nabla u_n\Vert _2^2. \end{aligned}$$

(5.16)

This shows that $\{\Vert \nabla u_n\Vert _2\}$ is bounded, and so $\{u_n\}$ is bounded in $H^1({\mathbb {R}}^3)$.

Let $\delta :=\limsup _{n\rightarrow \infty }\sup _{y\in {\mathbb {R}}^3}\int _{B_1(y)}|u_n|^2\textrm{d}x$. We show that $\delta >0$. Otherwise, in light of Lions’ concentration compactness principle [17, Lemma 1.21], $\Vert u_n\Vert _q \rightarrow 0$. Hence, it follows from (5.15) that

$$\begin{aligned} a\Vert \nabla u_n\Vert _2^2+b\Vert \nabla u_n\Vert _2^4 = \Vert u_n\Vert _{6}^{6}+\frac{3\mu (q-2)}{2q}\Vert u_n\Vert _{q}^{q} = \Vert u_n\Vert _{6}^{6}+o(1). \end{aligned}$$

(5.17)

Up to a subsequence, we assume that

$$\begin{aligned} \Vert \nabla u_n\Vert _2^2\rightarrow l, \ \ \Vert u_n\Vert _6^6\rightarrow al+bl^2. \end{aligned}$$

(5.18)

If $l = 0$, then it follows from (5.14) and (5.18) that ${\tilde{m}}(c)=0$, a contradiction. If $l > 0$, by Sobolev inequality (1.8) and (5.18), we have

$$\begin{aligned} l\ge \frac{{\mathcal {S}}}{2}\left[ b{\mathcal {S}}^2+\sqrt{b^2S^4+4a{\mathcal {S}}}\right] . \end{aligned}$$

(5.19)

Hence, it follows from (5.14), (5.15), (5.18), (5.19), the definition of $\{u_n\}$ and $\Vert u_n\Vert _q\rightarrow 0$ that

$$\begin{aligned} {\tilde{m}}(c)+o(1)&= \Phi (u_n)-\frac{1}{6}{\mathcal {P}}(u_n)\nonumber \\&= \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4-\frac{\mu (6-q)}{4q}\Vert u_n\Vert _q^q+o(1)\nonumber \\&= \frac{a}{3}\Vert \nabla u_n\Vert _2^2+\frac{b}{12}\Vert \nabla u_n\Vert _2^4+o(1)\nonumber \\&\ge \Theta ^*+o(1), \end{aligned}$$

(5.20)

which contradicts (5.13). Thus $\delta >0$. Without loss of generality, we may assume the existence of $y_n\in {\mathbb {R}}^3$ such that $\int _{B_{1}(y_n)}|u_n|^2\textrm{d}x> \frac{\delta }{2}$. Let ${\hat{u}}_n(x)=u_n(x+y_n)$. Then we have

$$\begin{aligned} \Vert {\hat{u}}_n\Vert _2^2=c, \quad {\mathcal {P}}({\hat{u}}_n)= 0, \quad \Phi ({\hat{u}}_n)\rightarrow {\tilde{m}}(c), \quad \int _{B_1(0)}|{\hat{u}}_n|^2\textrm{d}x> \frac{\delta }{2}. \end{aligned}$$

(5.21)

Therefore, there exists ${\hat{u}}\in H^1({\mathbb {R}}^3)\setminus \{0\}$ such that, passing to a subsequence,

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{u}}_n\rightharpoonup {\hat{u}}, & \text{ in } \ H^1({\mathbb {R}}^3); \\ {\hat{u}}_n\rightarrow {\hat{u}}, & \text{ in } \ L_{\textrm{loc}}^s({\mathbb {R}}^3), \ \forall \ s\in [1, 6);\\ {\hat{u}}_n\rightarrow {\hat{u}}, & \text{ a.e. } \text{ on } \ {\mathbb {R}}^3. \end{array} \right. \end{aligned}$$

(5.22)

Let $w_n={\hat{u}}_n-{\hat{u}}$. Then (5.22) and Lemma 5.5 yield

$$\begin{aligned} \Phi ({\hat{u}}_n) = \Phi ({\hat{u}})+\Phi (w_n)+\frac{b}{2}\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla w_n\Vert _2^2+o(1) \end{aligned}$$

(5.23)

and

$$\begin{aligned} {\mathcal {P}}({\hat{u}}_n) = {\mathcal {P}}({\hat{u}})+{\mathcal {P}}(w_n)+2b\Vert \nabla {\hat{u}}\Vert _2^2 \Vert \nabla w_n\Vert _2^2+o(1). \end{aligned}$$

(5.24)

Set

$$\begin{aligned} Q(u):=\frac{a}{4}\Vert \nabla u\Vert _2^2+\frac{1}{12}\Vert u\Vert _{6}^{6}+\frac{\mu (3q-14)}{8q}\Vert u\Vert _{q}^{q}. \end{aligned}$$

(5.25)

Then it follows from (1.2), (1.17), (5.21), (5.23), (5.24) and (5.25) that

$$\begin{aligned} {\tilde{m}}(c)-Q({\hat{u}})+o(1)=Q(w_n) \end{aligned}$$

(5.26)

and

$$\begin{aligned} {\mathcal {P}}(w_n) = -{\mathcal {P}}({\hat{u}})-2b\Vert \nabla {\hat{u}}\Vert _2^2\Vert \nabla w_n\Vert _2^2+o(1). \end{aligned}$$

(5.27)

If there exists a subsequence $\{w_{n_i}\}$ of $\{w_n\}$ such that $w_{n_i}=0$, then going to this subsequence, we have

$$\begin{aligned} \Vert {\hat{u}}\Vert _2^2=c, \quad \Phi ({\hat{u}})={\tilde{m}}(c), \quad {\mathcal {P}}({\hat{u}})=0, \end{aligned}$$

(5.28)

which implies the conclusion of Lemma 5.9 holds. Next, we assume that $w_n\ne 0$. By (5.21) and (5.22), one has

$$\begin{aligned} c=\Vert {\hat{u}}_n\Vert _2^2=\Vert {\hat{u}}\Vert _2^2+\Vert w_n\Vert _2^2+o(1). \end{aligned}$$

(5.29)

This implies that $\Vert {\hat{u}}\Vert _2^2:={\hat{c}}\le c$ and $\Vert w_n\Vert _2^2:={\tilde{c}}_n\le c$ for large $n\in {\mathbb {N}}$. We claim that ${\mathcal {P}}({\hat{u}})\le 0$. Otherwise, if ${\mathcal {P}}({\hat{u}})>0$, then (5.27) implies ${\mathcal {P}}(w_n) < 0$ for large n. In view of Lemma 5.3, there exists $t_n>0$ such that $t_n^{3/2}(w_n)_{t_n}\in {\mathcal {M}}({\tilde{c}}_n)$. From (1.2), (1.17), (5.2), (5.26), (5.27), Lemma 5.1 and Lemma 5.7, we obtain

$$\begin{aligned} {\tilde{m}}(c)-Q({\hat{u}})+o(1)= & Q(w_n)= \Phi (w_n)-\frac{1}{4}{\mathcal {P}}(w_n)\\\ge & \Phi \left( t_n^{3/2}{(w_n)}_{t_n}\right) -\frac{t_n^4}{4}{\mathcal {P}}(w_n) \ge {\tilde{m}}(c), \end{aligned}$$

which implies ${\mathcal {P}}({\hat{u}})\le 0$ due to $Q({\hat{u}})>0$. Since ${\hat{u}}\ne 0$ and ${\mathcal {P}}({\hat{u}})\le 0$, in view of Lemma 5.3, there exists ${\hat{t}}>0$ such that ${\hat{t}}^{3/2}{\hat{u}}_{{\hat{t}}}\in {\mathcal {M}}({\hat{c}})$. From (1.2), (1.17), (5.2), (5.26), (5.27), Lemmas 5.1, 5.7, Fatou’s lemma and the weak semicontinuity of norm, one has

$$\begin{aligned} {\tilde{m}}(c) = \lim _{n\rightarrow \infty }Q({\hat{u}}_n) \ge Q({\hat{u}}) = \Phi ({\hat{u}})-\frac{1}{4}{\mathcal {P}}({\hat{u}}) \ge \Phi \left( \hat{t}^{3/2}{{\hat{u}}}_{{\hat{t}}}\right) -\frac{{\hat{t}}^4}{4}{\mathcal {P}}({\hat{u}}) \ge {\tilde{m}}(c), \end{aligned}$$

(5.30)

which implies

$$\begin{aligned} \Vert {\hat{u}}\Vert _2^2={\hat{c}}, \quad \Phi ({\hat{u}})={\tilde{m}}({\hat{c}})={\tilde{m}}(c), \quad {\mathcal {P}}({\hat{u}})=0. \end{aligned}$$

(5.31)

This shows ${\tilde{m}}({\hat{c}})$ is achieved. In view of Lemma 5.7, ${\hat{c}}=c$. Thus, (5.28) holds also, i.e. the conclusion of Lemma 5.9 holds. $\square$

Lemma 5.10

Let $\frac{14}{3}\le q < 6$, $\mu >0$ and $c>0$. If ${\bar{u}}\in {\mathcal {M}}(c)$ and $\Phi ({\bar{u}})={\tilde{m}}(c)$, then ${\bar{u}}$ is a critical point of $\Phi$ on ${\mathcal {S}}_c$, i.e. $\Phi |_{{\mathcal {S}}_c}'({\bar{u}})=0$.

Proof

Assume that $\Phi |_{{\mathcal {S}}_c}'({\bar{u}})\ne 0$. Then there exist $\delta >0$ and $\varrho >0$ such that

$$\begin{aligned} \Vert u-{\bar{u}}\Vert \le 3\delta \Rightarrow \Vert \Phi |_{{\mathcal {S}}_c}'(u)\Vert \ge \varrho . \end{aligned}$$

(5.32)

It is easy to see that

$$\begin{aligned} \left\| \nabla \left( t^{\frac{3}{2}}{\bar{u}}_{t}\right) -\nabla {\bar{u}}\right\| _2^2= & \int _{{\mathbb {R}}^3}\left| \nabla \left( t^{\frac{3}{2}}{\bar{u}}_{t}\right) -\nabla {\bar{u}}\right| ^2\textrm{d}x \nonumber \\= & (t^2+1)\int _{{\mathbb {R}}^3}|\nabla {\bar{u}}|^2\textrm{d}x -2t^{\frac{3}{2}}\int _{{\mathbb {R}}^3}\nabla {\bar{u}}_{t}\cdot \nabla {\bar{u}}\textrm{d}x \rightarrow 0, \ \ t\rightarrow 1. \nonumber \\ \end{aligned}$$

(5.33)

Thus, there exists $\delta _1\in (0, 1/4)$ such that

$$\begin{aligned} |t-1|<\delta _1\Rightarrow \left\| t^{\frac{3}{2}}{\bar{u}}_t-{\bar{u}}\right\| < \delta . \end{aligned}$$

(5.34)

In view of Lemma 5.1, one has

$$\begin{aligned} \Phi \left( t^{\frac{3}{2}}{\bar{u}}_t\right)\le & \Phi ({\bar{u}})-h(t)\Vert {\bar{u}}\Vert _{6}^{6} = {\tilde{m}}(c)-h(t)\Vert {\bar{u}}\Vert _{6}^{6}, \quad \forall \ t> 0. \end{aligned}$$

(5.35)

It follows from (1.17) that there exist $T_1\in (0,1/2)$ and $T_2\in (3/2, +\infty )$ such that

$$\begin{aligned} {\mathcal {P}}\left( T_1^{\frac{3}{2}}{\bar{u}}_{T_1}\right) >0,\quad {\mathcal {P}}\left( T_2^{\frac{3}{2}}{\bar{u}}_{T_2}\right) <0. \end{aligned}$$

(5.36)

Let

$$\begin{aligned} \varepsilon :=\min \left\{ \frac{1}{4}h(T_1)\Vert {\bar{u}}\Vert _{6}^{6}, \frac{1}{4}h(T_2)\Vert {\bar{u}}\Vert _{6}^{6}, 1, \frac{\varrho \delta }{8}\right\} , \quad S:=\{v\in {\mathcal {S}}_c: \Vert v-{\bar{u}}\Vert <\delta \}. \end{aligned}$$

Then Lemma 2.1 yields a deformation $\eta \in {\mathcal {C}}([0, 1]\times {\mathcal {S}}_c, {\mathcal {S}}_c)$ such that

• (i) $\eta (1, u)=u$ if $\Phi (u)<{\tilde{m}}(c)-2\varepsilon$ or $\Phi (u)>{\tilde{m}}(c)+2\varepsilon$;

• (ii) $\eta \left( 1, \Phi ^{{\tilde{m}}(c)+\varepsilon }\cap S\right) \subset \Phi ^{{\tilde{m}}(c)-\varepsilon }$;

• (iii) $\Phi (\eta (1, u))\le \Phi (u), \ \forall \ u\in {\mathcal {S}}_c$;

• (iv) $\eta (1, u)$ is a homeomorphism of ${\mathcal {S}}_c$.

By Corollary 5.2, $\Phi \left( t^{\frac{3}{2}}{\bar{u}}_t\right) \le \Phi ({\bar{u}}) ={\tilde{m}}(c)$ for $t> 0$, then it follows from (5.34) and ii) that

$$\begin{aligned} \Phi \left( \eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) \right) \le {\tilde{m}}(c)-\varepsilon , \quad \forall \ t> 0, \ \ |t-1|< \delta _1. \end{aligned}$$

(5.37)

On the other hand, by iii) and (5.35), one has

$$\begin{aligned} \Phi \left( \eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) \right)\le & \Phi \left( t^{\frac{3}{2}}{\bar{u}}_t\right) \le {\tilde{m}}(c)-h(t)\Vert {\bar{u}}\Vert _{6}^{6} \nonumber \\\le & {\tilde{m}}(c)-\delta _2\Vert {\bar{u}}\Vert _{6}^{6}, \quad \forall \ t> 0, \ \ |t-1|\ge \delta _1, \end{aligned}$$

(5.38)

where

$$\begin{aligned} \delta _2:=\min \{h(1-\delta _1), h(1+\delta _1)\}>0. \end{aligned}$$

Combining (5.37) with (5.38), we have

$$\begin{aligned} \max _{t\in [T_1, T_2]}\Phi \left( \eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) \right) <{\tilde{m}}(c). \end{aligned}$$

(5.39)

Define $\Psi _0(t):={\mathcal {P}}\left( \eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) \right)$ for $t> 0$. It follows from (5.35) and (i) that $\eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) =t^{\frac{3}{2}}{\bar{u}}_t$ for $t=T_1$ and $t=T_2$, which, together with (5.36), implies

$$\begin{aligned} \Psi _0(T_1)={\mathcal {P}}\left( T_1^{\frac{3}{2}}{\bar{u}}_{T_1}\right) >0, \quad \Psi _0(T_2)={\mathcal {P}}\left( T_2^{\frac{3}{2}}{\bar{u}}_{T_2}\right) <0. \end{aligned}$$

Since $\Psi _0(t)$ is continuous on $(0, \infty )$, then we have that $\eta \left( 1, t^{\frac{3}{2}}{\bar{u}}_t\right) \cap {\mathcal {M}}(c)\ne \emptyset$ for some $t_0\in [T_1, T_2]$, contradicting the definition of ${\tilde{m}}(c)$. $\square$

Proof of Theorem 1.4

It follows directly combining Lemmas 5.9 and 5.10. $\square$

6 The case when $\mu \le 0$

In this section, we shall prove Theorem 1.5.

Proof of Theorem 1.5

Assume that $(u,\lambda ) \in H^1 ({\mathbb {R}}^3) \times (0, +\infty )$ is a solution of Eq. (1.1). Then it follows from (1.1) and the Pohozaev type identity that

$$\begin{aligned} \left( a+b\Vert \nabla u\Vert _2^2\right) \Vert \nabla u\Vert _2^2+\lambda \Vert u\Vert _2^2-\mu \Vert u\Vert _q^q-\Vert u\Vert _{6}^{6}=0 \end{aligned}$$

(6.1)

and

$$\begin{aligned} \left( a+b\Vert \nabla u\Vert _2^2\right) \Vert \nabla u\Vert _2^2+3\lambda \Vert u\Vert _2^2-\frac{6\mu }{q}\Vert u\Vert _q^q-\Vert u\Vert _{6}^{6}=0. \end{aligned}$$

(6.2)

Combining (6.1) with (6.2), we have

$$\begin{aligned} 0<\lambda c=\lambda \Vert u\Vert _2^2=\frac{(6-q)\mu }{2q}\Vert u\Vert _q^q\le 0, \end{aligned}$$

which is a contradiction. $\square$