Abstract
We study a 3D fluid–rigid body interaction problem. The fluid flow is governed by 3D incompressible Navier–Stokes equations, while the motion of the rigid body is described by a system of ordinary differential equations describing conservation of linear and angular momentum. Our aim is to prove that any weak solution satisfying certain regularity conditions is smooth. This is a generalization of the classical result for the 3D incompressible Navier–Stokes equations, which says that a weak solution that additionally satisfy Prodi–Serrin \(L^r-L^s\) condition is smooth. We show that in the case of fluid–rigid body the Prodi–Serrin conditions imply \(W^{2,p}\) and \(W^{1,p}\) regularity for the fluid velocity and fluid pressure, respectively. Moreover, we show that solutions are \(C^{\infty }\) if additionally we assume that the rigid body acceleration is bounded almost anywhere in time variable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Fluid–rigid body system
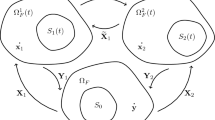
Let \(\Omega \subset {{\mathbb {R}}}^3\) be a smooth bounded domain, and \(S_0\subset \Omega \) be smooth such that \(d(\partial \Omega ,\overline{S_0})>0\). \(S_0\) represents part of the domain occupied by the rigid body at the initial state. \(\Omega _F=\Omega \setminus \overline{S_0}\) is the fluid domain at the initial state which we will use as the reference domain. The unknowns of the system are fluid velocity \(\textbf{u}:[0,T]\times \Omega _F(t)\rightarrow {{\mathbb {R}}}^3\), fluid pressure \(p:[0,T]\times \Omega _F(t)\rightarrow {{\mathbb {R}}}\), position of the center of mass of the rigid body \(\textbf{q}:[0,T]\rightarrow {{\mathbb {R}}}^3\) and angular velocity of the rigid body \(\varvec{\omega }:[0,T]\rightarrow {{\mathbb {R}}}^3\). Here we used the following abuse of notation which is standard in analysis of moving boundary problems:
where \(\Omega _F(t)=\Omega \setminus \overline{S(t)}\) is the fluid domain at time t, and S(t) is a part of the domain occupied by the rigid body at time t and is defined by \(\textbf{q}\) and \(\varvec{\omega }\) in the following way. Let \({{\mathbb {P}}}\) be a skew-symmetric matrix such that \({{\mathbb {P}}}(t)\textbf{x}=\varvec{\omega }(t)\times \textbf{x},\; \textbf{x}\in {{\mathbb {R}}}^{3}.\) Then rotation of the rigid body \({{\mathbb {Q}}}:[0,T]\rightarrow SO(3)\) is defined by relation
The domain S(t) is defined by an orientation preserving isometry
as the set
The Eulerian velocity of the rigid body is given by:
where \(\textbf{a}=\frac{\textrm{d} }{\textrm{d} t }\textbf{q}\) is the translation velocity of the rigid body.
The equations modelling dynamics of the fluid–rigid body system read as follows:
Here \({{\mathbb {T}}}(\textbf{u},p) = -p{{\mathbb {I}}}+ 2{{\mathbb {D}}}\textbf{u}\) is the fluid Cauchy stress tensor, where \({{\mathbb {D}}}\textbf{u}= \frac{1}{2}\left( \nabla \textbf{u}+\nabla \textbf{u}^T\right) \) is symmetric part of the gradient, and \({{\mathbb {J}}}\) is the inertial tensor defined as follows:
Notice that for simplicity we normalized all physical constants since their concrete values do not influence our analysis.
Remark 1.1
(About the notation) Throughout the paper, we will denote by \(\textbf{u}\) both the fluid velocity defined on \(\Omega _F\) and the global velocity defined on \(\Omega \). The global velocity is obtained by extending the fluid velocity by setting \(\textbf{u}=\textbf{u}_S\) on S(t). To avoid confusion we will always write the domain of definition.
1.2 Statement of the results
The goal of the paper is to study the regularity of weak solution to fluid–rigid body problem (1.6). Definition and existence of finite energy weak solutions (i.e. of Leray–Hopf type) are well-known (see e.g. [6]). Here for the convenience of reader, we recall the definition of weak solution: first we define a function space
and a weak solution is given by the following definition
Definition 1.1
[21] The couple \(\left( \textbf{u}, \textbf{B}\right) \) is a weak solution to the system (1.6) if the following conditions are satisfied:
-
1.
The function \(\textbf{B}(t,\cdot ):{{\mathbb {R}}}^{3}\rightarrow {{\mathbb {R}}}^{3}\) is an orientation preserving isometry given by the formula (1.3), which defines a time-dependent set \(S(t)=\textbf{B}(t,S)\). The isometry \(\textbf{B}\) is compatible with \(\textbf{u}=\textbf{u}_S\) on S(t) in the following sense: the rigid part of velocity \(\textbf{u}\), denoted by \(\textbf{u}_S\), satisfies condition (1.5), and \(\textbf{q},\; {{\mathbb {Q}}}\) are absolutely continuous on \(\left[ 0,T\right] \) and satisfy (1.2) with \(\textbf{a}=\frac{\textrm{d} }{\textrm{d} t }\textbf{q}\).
-
2.
The function \(\textbf{u}\in L^{2}(0,T;V(t))\cap L^{\infty }(0,T;L^2(\Omega ))\) satisfies the integral equality
$$\begin{aligned}{} & {} \int _{0}^{T}\int _{\Omega }\{ \textbf{u}\cdot \partial _{t}\varvec{\varphi }+ (\textbf{u}\otimes \textbf{u}) :{{\mathbb {D}}}\varvec{\varphi }-2\,{{\mathbb {D}}}\textbf{u}:{{\mathbb {D}}}\varvec{\varphi }\,\}\, \textrm{d} \textbf{x}\textrm{d} t - \int _{\Omega }\textbf{u}(T)\varvec{\varphi }(T)\,\textrm{d} \textbf{x}\nonumber \\{} & {} \quad = - \int _{\Omega }\textbf{u}_{0}\varvec{\varphi }(0)\,\textrm{d} \textbf{x}, \end{aligned}$$(1.8)which holds for any test function \(\varvec{\varphi }\in H^1(0,T;V(t))\).
-
3.
The energy inequality
$$\begin{aligned} \frac{1}{2}\Vert \textbf{u}(t)\Vert _{L^2(\Omega )}^2 + 2\int _{0}^{t} \int _{\Omega _{F}(\tau )}\,|{{\mathbb {D}}}\textbf{u}|^{2} \,\textrm{d} \textbf{x}\,\textrm{d} \tau \le \frac{1}{2}\Vert \textbf{u}_0\Vert _{L^2(\Omega )}^2. \end{aligned}$$holds for almost every \(t\in (0,T)\).
Now we state the main result of the paper.
Theorem 1.1
Let \((\textbf{u},\textbf{B})\) be a weak solution to the system (1.6). Assume that \(d(S(t),\partial \Omega )>\delta \), for some constant \(\delta >0\). If \(\frac{\textrm{d} }{\textrm{d} t }\textbf{a},\frac{\textrm{d} }{\textrm{d} t }\varvec{\omega }\in L^{\infty }(0,T)\), and \(\textbf{u}\) satisfies Prodi–Serrin condition
then
It is a classical result in the theory of Navier–Stokes equations that any weak solution to 3D Navier–Stokes equations satisfying condition (1.9) is smooth (see e.g. [11] where also critical case \(s=\infty \) and \(r=3\) was solved, and references within). Our result is generalization of this classical result to the fluid–rigid body system (1.6). Notice that we have two extra assumptions. The first assumption says that rigid body do not touch the boundary of \(\Omega \), i.e. the fluid domain does not degenerate. It is well known (e.g. [30]) that this condition is necessary since the domain degeneration leads to non-smooth solutions. The second condition, i.e. boundedness of the rigid body acceleration, is somewhat unexpected, and we will later elaborate more on technical reasons that give rise to that condition. In absence of this condition we can show that solutions are strong:
Theorem 1.2
Let \((\textbf{u},\textbf{B})\) be a weak solution to the system (1.6). Assume that \(d(S(t),\partial \Omega )>\delta \), for some constant \(\delta >0\). If \(\textbf{u}\) satisfies Prodi–Serrin condition (1.9) then
for all \(\varepsilon >0\) and for all \(1\le p<\infty \).
1.3 Literature review
The global regularity of the incompressible Navier–Stokes equations in dimension 2 is a well-known result which was first proved by by Leray [25] and Ladyzhenskaya [24], but in dimension 3 it is a famous open problem. However, there are regularity results for weak solutions that additionally satisfy Prodi–Serrin condition proved by Leray [26] for \(\Omega ={{\mathbb {R}}}^3\), including the case \(s=\infty \), and by Fabes, Lewis and Riviere [12, 13], and Sohr [29] for domains with a bounded boundary. These regularity results were extended to the case \(s=3\) by von Wahl [33] on the bounded domain, and by Giga [19] on the domain with a bounded boundary. There are also plenty of conditional regularity results with other types of conditions, e.g. on gradient of the fluid velocity or the pressure (see e.g. Remarks 5.6 and 5.9 in [16]).Footnote 1
In the case of the fluid–rigid body system theory is much less developed. 2D case is studied in [2, 3, 20] where existence and uniqueness of global weak solution is proved provided that rigid body does not touch the boundary. Moreover, they show that these solutions are strong away from \(t=0\). In the three dimensional case there are results of local-in-time strong solutions or global-in time solutions for small initial data [7, 8, 10, 17, 27, 31]. Moreover, global-in-time existence (or existence up to the time of contact) of Leray–Hopf type weak solution were studied in [6, 9, 14, 15, 22]. We also mention the existence results in the case of slip boundary conditions [2, 3, 5, 18, 34]. Uniqueness of weak solutions is still an open problem, but results of weak-strong uniqueness type were proved in both slip and no-slip case [4, 21] which state that the weak solution satisfying additional condition on the fluid velocity is unique in the larger class of weak solutions.
Our regularity result stated in Theorem 1.1 is motivated by the classical regularity result for the incompressible Navier–Stokes case [16, Theorem 5.2]). To the best of our knowledge, this is the first result on the regularity of weak solution for the fluid-rigid body interaction problem. Inspired by works [17, 31, 32] we use fixed point theorem in combination with the maximal regularity result for the Stokes problem. The proof strategy in more details is outline in the next Section.
2 Proof strategy
Here we follow the classical approach to linearize problem (1.6) around a solution that satisfies the Prodi–Serrin condition, and to analyse the regularity properties of the solution to the linear system. Since the linearized problem has a unique solution and a solution to the nonlinear problem is the solution to the linearized problem, proving the regularity for the linearized problem is enough. This approach has also been used to prove a conditional regularity result for the incompressible Navier–Stokes equations (see e.g. [16, Section 5]). However, adapting this strategy to the fluid–rigid body system is very technically challenging as outlined below. The main steps of the proof are:
-
Linearization Let \((\widetilde{\textbf{u}},\widetilde{p},\widetilde{\textbf{q}},\widetilde{\varvec{\omega }})\) be a weak solution to the problem (1.6) which satisfies Prodi–Serrin condition. We linearize around that solution and obtain a linear fluid–rigid body problem where the movement of the rigid body is prescribed by \(\widetilde{\textbf{q}}\) and \(\widetilde{\varvec{\omega }}\). We show that the obtained linear problem has a unique weak solution which we denote by \(({\textbf{u}},{p},{\textbf{a}},{\varvec{\omega }})\).
-
Transformation to the fixed reference domain Since the linear problem is posed in the moving domain it is convenient to transform it a cylindrical domain, i.e. to the reference domain that does not depend on time. We use a change of variable that preserves the divergence free condition and is rigid near the rigid body. This change of variables was introduced in [23] and by now is a standard tool in analysis of the fluid–rigid body system. Solution to the linearized problem on the cylindrical domain is denoted by \((\textbf{U},P,\textbf{A},\varvec{\Omega })\).
-
Strong solution We show that if \(\widetilde{\textbf{u}}\) satisfied the Prodi–Serrin condition then \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) is the strong solution, i.e. equations (1.6) are satisfied in the \(L^p\) sense. The main technical tool is the fixed point theorem and a maximal regularity result for the fluid–rigid body operator. This finishes the proof of Theorem 1.2.
-
Higher regularity In this step the goal is to bootstrap the argument from the previous step to get the higher regularity estimates. Therefore, first we need to prove regularity of the time derivatives. This is achieved by analysing the system obtained by formally differentiating in time the linearized system from the previous steps. The main issue here is to prove that the solution to the system obtained by taking the time derivative is exactly the time derivative of the solution. This is a nontrivial step because we do not have any a priori estimates for time derivatives and our solution is obtained by the fixed point procedure and thus it is not possible to directly justify the formal estimates. In this step we need an additional regularity condition on the rigid body acceleration \(\frac{\textrm{d} ^2}{\textrm{d} t ^2}\widetilde{\textbf{q}},\frac{\textrm{d} }{\textrm{d} t }\widetilde{\varvec{\omega }}\in L^{\infty }(0,T)\).
The paper is organized as follows. In Sect. 2.1, we introduce the linearized problem and show that it admits a unique weak solution which is equal to the solution of (1.6). The second step, transformation to the fixed reference domain is done in Sect. 2.2. There we also state Proposition 2.1 (which corresponds to third step of the proof), and Propositions 2.2 and 2.3 which correspond to the last step of the proof. The proofs of these Propositions will be presented in Sects. 3, 4 and 5, respectively. The technical core of the paper are Sects. 3 and 4. The additional condition on the boundedness of the rigid body acceleration is needed in Sect. 4. Here we want to point out that even though formal estimates do not require this condition, this condition is needed in rigorous justification of the estimates. Namely, the standard methods for construction of the solutions, such as Galerkin method or the regularization method, do not seem to work in this context because of the presence of the moving boundary. Finally, few technical proofs are relegated to the Appendix. Since the proof involves a lot of notation, for the convenience of the reader we have summarized all notations used in the paper in table at the end of Appendix.
2.1 Linear problem
Let \((\widetilde{\textbf{u}},\widetilde{p},\widetilde{\textbf{q}},\widetilde{\varvec{\omega }})\) be a weak solution to the problem (1.6) in a sense of Definition 1.1 which additionally satisfies the Prodi–Serrin condition. Let the rigid body domain S(t) be defined by \((\widetilde{\textbf{q}},\widetilde{\varvec{\omega }})\) through formulas (1.3) and (1.4) as well as the fluid domain \(\Omega _{F}(t) = \Omega \setminus \overline{S(t)}\). We define the following linear problem:
Find \(({\textbf{u}},{p},{\textbf{a}},{\varvec{\omega }})\) such that
Note that the problem is linear since the motion of the domain is a priori given and is not computed via \((\textbf{a},\varvec{\omega })\).
Definition 2.1
A weak solution for (2.1) is a function \({\textbf{u}}\in L^{2}(0,T;V(t))\cap L^{\infty }(0,T;L^2(\Omega ))\) which satisfies
for all \(\varvec{\varphi }\in H^1(0,T;V(t))\), where
First, we show the uniqueness result for the linearized problem (2.1).
Lemma 2.1
Let \(\widetilde{\textbf{u}}\) be a weak solution to the (1.6) which additionally satisfies the Prodi–Serrin condition, and let \({\textbf{u}}\) be a weak solution for (2.1). Then \(\textbf{u}=\widetilde{\textbf{u}}\) almost everywhere in \((0,T)\times \Omega \).
Proof
Let us denote \(\bar{\textbf{u}}=\widetilde{\textbf{u}}-\textbf{u}\), \(\bar{\textbf{a}}=\widetilde{\textbf{a}}-\textbf{a}\), \(\bar{\varvec{\omega }}=\widetilde{\varvec{\omega }}-\varvec{\omega }\). By subtracting the equations
we get
We substitute \(\varvec{\varphi }= \bar{\textbf{u}}^h\) and let \( h \rightarrow 0 \). Here \(\textbf{u}^{h}\) is a regularization of \(\textbf{u}\) as defined in [21, Section 2.3]. We use [21, Lemma 2.4] to pass to the limit and get:
To estimate the third term we use the Prodi–Serrin condition as in [21], and in the end we get the inequality of the form
where \(f\in L^1(0,t)\), so Gronwall lemma implies that \(\bar{\textbf{u}}=0\). \(\square \)
Therefore, by Lemma 2.1 it follows that \(\widetilde{\textbf{u}}\) is a unique weak solution to the linearized problem (2.1). Therefore, in the rest of the paper we will consider linear problem (2.1) and prove that the solution to the linear problem is regular.
2.2 The transformed problem
In order to transform the problem to the cylindrical domain we use a change of variables inspired by Inoue and Wakimoto [23], i.e. we define the mapping \((\textbf{u},p,\textbf{a},\varvec{\omega })\mapsto (\textbf{U},P,\textbf{A},\varvec{\Omega })\) with
where \(\textbf{X}(t)\) is a volume-preserving diffeomorphism from initial to the physical domain described in [21], Appendix A.1, and \(\textbf{Y}(t)\) is its inverse. By construction, \(\textbf{X}\), \(\textbf{Y}\) belong to \(W^{1,\infty }(0,T;C_c^{\infty }(\Omega ))\) and depend on the domain of given solution, i.e. translation velocity \(\widetilde{\textbf{a}}\) and angular velocity \(\widetilde{\varvec{\omega }}\). In the following, \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) and \((\widetilde{\textbf{U}},\widetilde{P},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\) denote the transformations of solutions \((\textbf{u},p,\textbf{a},\varvec{\omega })\) and \((\widetilde{\textbf{u}},\widetilde{p},\widetilde{\textbf{a}},\widetilde{\varvec{\omega }})\) to the cylindrical domain by mapping (2.3). Notice that lowercase letters refer to the solutions defined on the physical moving domain and uppercase letters to the solutions defined on the fixed reference domain. Therefore \((\widetilde{\textbf{U}},\widetilde{P},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\) is the solution to the following system (which is equivalent to (2.1)):
where
The operator \(\mathcal {L}\) is the transformed Laplace operator and it is given by
the convection term is transformed into
the transformation of time derivative and gradient is given by
and the gradient of pressure is transformed as follows:
Here we have denoted the metric covariant tensor
the metric covariant tensor
and the Christoffel symbol (of the second kind)
Note that operators \(\mathcal {L},\mathcal {M},\mathcal {N}\) and \(\mathcal {G}\) are linear and depend on transformation \(\textbf{X}\), i.e. on functions \(\widetilde{\textbf{A}}\) and \(\widetilde{\varvec{\Omega }}\).
The first step of the proof is to show that the linear problem (2.4) admits a unique strong solution, which by Lemma 2.1 means that the solution to the original nonlinear problem is also a strong solution. Therefore Theorem 1.2 follows from the following result:
Proposition 2.1
Let \((\widetilde{\textbf{U}},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\in (L^{2}(0,T;V(0))\cap L^{\infty }(0,T;L^2(\Omega )))\times L^{\infty }(0,T)\times L^{\infty }(0,T)\) be a weak solution to the problem (1.6) that satisfies the Prodi–Serrin condition. Then there exists a unique solution \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) of (2.4) in the sense of Definition 2.1 satisfying the following regularity properties
for all \(\varepsilon >0\) and for all \(1\le p<\infty \). Moreover, by Lemma 2.1, \((\widetilde{\textbf{U}}, \widetilde{P},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})=({\textbf{U}}, P, {\textbf{A}},{\varvec{\Omega }})\) and thus satisfies the same regularity properties. In particular, \((\widetilde{\textbf{U}},\widetilde{P},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\) is a strong solution to problem (1.6).
We relegate the proof to Sect. 3. Next, we state two Propositions which provide higher regularity of the solution and thus finish the proof of Theorem 1.1. The proofs of these Propositions are given in Sects. 4 and 5.
Proposition 2.2
Let \(\widetilde{\textbf{U}}\) be a weak solution satisfying the assumption of Lemma 2.1 and \(\frac{\textrm{d} }{\textrm{d} t }\widetilde{\textbf{A}}, \frac{\textrm{d} }{\textrm{d} t }\widetilde{\varvec{\Omega }}\in L^{\infty }(0,T)\). Then
for all \(\varepsilon >0, l\ge 0\) and for all \(1\le p<\infty \).
Proposition 2.3
Let \(\widetilde{\textbf{U}}\) be a weak solution satisfying the assumption of Proposition 2.2. Then
3 Strong Solution
This section deals with the proof of Proposition 2.1. Since \(\textbf{X},\textbf{Y}\in W^{1,\infty }(0,T;C_c^{\infty }(\Omega ))\), the transformation (2.3) preserves integrability of functions, so we have
and \(\widetilde{\textbf{U}}\) satisfies Prodi–Serrin condition. Since we are interested in the regularity excluding \(t=0\) we multiply (2.4) by t and define
which satisfy the following problem on a cylindrical domain with vanishing initial conditions
where
It is sufficient to show that there is a unique strong solution to the problem (3.1)–(3.2), with
are given functions. Then the problem (2.4) also has a unique strong solution on the interval \((\varepsilon ,T)\), for all \(\varepsilon >0\). Finally, by change of variables, i.e. returning to the physical domain, follows that \((\widetilde{\textbf{u}},\widetilde{\textbf{a}},\widetilde{\varvec{\omega }})\) is the strong solution of (1.6).
First we prove the following result:
Proposition 3.1
Let
where operators F, G and H are defined by (2.5)–(2.6).
-
a)
Let
$$\begin{aligned} (\widetilde{\textbf{U}},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\in (L^{2}(0,T;V(0))\cap L^{\infty }(0,T;L^2(\Omega )))\times L^{\infty }(0,T)\times L^{\infty }(0,T) \end{aligned}$$satisfy Prodi–Serrin condition (1.9) and
$$\begin{aligned} \mathcal {R}\in L^2(0,T;L^2(\Omega _F)),\quad \mathcal {R}_{\textbf{a}},\mathcal {R}_{\varvec{\omega }}\in {L^2(0,T)}. \end{aligned}$$(3.4)Then there is a unique solution \((\textbf{U}^{*},P^{*},\textbf{A}^{*},\varvec{\Omega }^{*})\) for (3.1) satisfying
$$\begin{aligned} \begin{aligned}&\textbf{U}^{*}\in H^1(0,T;L^2(\Omega _F))\cap L^2(0,T;H^{2}(\Omega _F)), \\&P^{*}\in L^2(0,T;H^{1}(\Omega _F)\,/\,{{\mathbb {R}}}), \\&\textbf{A}^{*},\varvec{\Omega }^{*}\in H^{1}(0,T). \end{aligned} \end{aligned}$$ -
b)
If in addition we assume
$$\begin{aligned}{} & {} (\widetilde{\textbf{U}},\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }})\in (L^{2m}(0,T;W^{2,2m}(\Omega _F))\cap W^{1,2m}(0,T;L^{2m}(\Omega _F)))\\{} & {} \quad \times W^{1,2m}(0,T)\times W^{1,2m}(0,T) \end{aligned}$$and
$$\begin{aligned} \mathcal {R}\in L^{2m}(0,T;L^{2m}(\Omega _F)),\quad \mathcal {R}_{\textbf{a}},\mathcal {R}_{\varvec{\omega }}\in {L^{2m}(0,T)}, \end{aligned}$$(3.5)for \(m\in {{\mathbb {N}}}\). Then
$$\begin{aligned} \begin{aligned}&\textbf{U}^{*}\in W^{1,2m}(0,T;L^{2m}(\Omega _F))\cap L^{2m}(0,T;W^{2,2m}(\Omega _F)), \\&P^{*}\in L^{2m}(0,T;W^{1,2m}(\Omega _F)\,/\,{{\mathbb {R}}}), \\&\textbf{A}^{*},\varvec{\Omega }^{*}\in W^{1,2m}(0,T). \end{aligned} \end{aligned}$$
Especially, for
we obtain the right hand side (3.2) which satisfies (3.4).
We will prove Proposition 3.1 by using the fixed point theorem and the following maximal regularity result
Theorem 3.1
[17, Theorem 4.1] Let \(\varvec{\Omega }\) be a domain with boundary of class \(C^{2,1}\) and \(p,q\in (1,\infty )\). Let \(F^{*}\in L^{p}(0,T;L^{q}(\Omega _F))\), and \(G^{*}, H^{*}\in L^{p}(0,T)\). Then for every \(T > 0\), problem (3.1) admits a unique solution
which satisfies the estimate
where the constant C depends only on the geometry of the rigid body and on T.
Remark 3.1
From the proof of the above Theorem it can be seen that the constant C is non-decreasing with respect to T.
For fixed \(R>0\), which we will choose later, we define a set
and a function
where \(({\textbf{U}}^{*}, {P}^{*}, {\textbf{A}}^{*}, {\varvec{\Omega }}^{*})\) is solution to the problem (3.1) with the right hand side which depends on \((\widehat{\textbf{U}}, \widehat{P}, \widehat{\textbf{A}}, \widehat{\varvec{\Omega }})\), i.e. we consider problem (3.1) with
We will prove that S is a contraction and will use the Banach’s fixed point theorem. More precisely, we will show that:
-
\(\mathcal {S}\) is well defined on \(\mathcal {K}_R\) and \(\mathcal {S}(\mathcal {K}_R)\subset \mathcal {K}_R\),
-
\(\mathcal {S}\) is a contraction,
which yields a unique fixed point of \(\mathcal {S}\), i.e. a unique solution \(({\textbf{U}}^{*}, {P}^{*}, {\textbf{A}}^{*}, {\varvec{\Omega }}^{*})\in \mathcal {K}_R\) to problem (3.1)–(3.2).
3.1 Estimates on the right hand side
In order to use Theorem 3.1 we have to estimate the right hand side (3.6)–(3.7).
First, we state an auxiliary Lemma which directly follows form the basic properties of the transformations \(\textbf{X}\) and \(\textbf{Y}\). Since these estimates follow by direct calculations in the standard way (see e.g. [31, Section 6.2]) we omit the proof.
Lemma 3.1
If \(\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }}\in W^{l,p}(0,T)\), for \(l\ge 0\) and \(1< p\le \infty \), then
for all \(t\in [0,T]\), where \( \frac{1}{p}+\frac{1}{p'}=1 \) and constant C depends on \( K_p = \Vert \widetilde{\textbf{A}}\Vert _{W^{l,p}(0,T)}+\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{l,p}(0,T)} \) nondecreasingly.
For the convective term we have the following result.
Lemma 3.2
Assume that \( \widehat{\textbf{U}}\in X_{2,2}^T \) and \( \widetilde{\textbf{U}}\in L^{r}(0,T;L^{s}(\Omega _F)), \) such that \(\frac{3}{s}+\frac{2}{r}=1\), \(s\in (3,\infty )\). Then
Proof
By using the following embeddings
for \( \frac{1}{r} + \frac{1}{r'} = \frac{1}{2}, \frac{1}{s} + \frac{1}{s'} = \frac{1}{2}, \) we conclude that \( \nabla \widehat{\textbf{U}}\in L^{r'}(0,T;L^{s'}(\Omega _F)), \) and therefore we have
\(\square \)
Now, we can show the following Lemma to estimate the right-hand side given by (3.6).
Lemma 3.3
Assume that \( \widetilde{\textbf{A}},\widetilde{\varvec{\Omega }}\in L^{p}(0,T) \), for all \(1\le p<\infty \) and \( \widetilde{\textbf{U}}\in L^{r}(0,T;L^{s}(\Omega _F)), \) such that \(\frac{3}{s}+\frac{2}{r}=1\), \(s\in (3,\infty )\). Then for \(\widehat{\textbf{U}}\in X_{2,2}^T , \widehat{P}\in Y_{2,2}^T \) the following estimates hold:
for \(T\le 1\), where constant \(C>0\) depends on T nondecreasingly.
Proof
Lemma 3.1 and 3.2 imply the estimate for the convective term.
The second estimate comes from Lemma 3.1
since \( L^2(0,T;H^2(\Omega _{F}))\cap H^1(0,T;L^2(\Omega _{F})) \hookrightarrow H^{\frac{1}{2}}(0,T;H^{1}(\Omega _{F})) \hookrightarrow L^{4}(0,T;H^{1}(\Omega _{F})) \) and \(\widetilde{\textbf{A}},\widetilde{\varvec{\Omega }}\in L^{\infty }(0,T)\).
Finally, for the pressure term we get
\(\square \)
Corollary 3.1
Assume that \( \widetilde{\textbf{A}},\widetilde{\varvec{\Omega }}\in L^{p}(0,T)\), for all \(1\le p<\infty \) and \( \widetilde{\textbf{U}}\in X_{2m,2m}^T, \) for some \(m\in {{\mathbb {N}}}\). Then for \(\widehat{\textbf{U}}\in X_{2(m+1),2(m+1)}^T , \widehat{P}\in Y_{2(m+1),2(m+1)}^T \) the following estimates hold:
for \(T\le 1\), where a constant \(C>0\) depends on T nondecreasingly.
Proof
Let \(m\in {{\mathbb {N}}}\). By using the interpolation result in [1, Theorem 5.2] for \(s_0=1, s_1=0\), \(p_0=p_1=2m\) we conclude that
for all \(\theta \in (0,1)\) and \(s<1-\theta \). Now for \( \theta =\frac{3}{4m(m+1)}, \) we can choose \(\frac{1}{2m}<s<1-\theta \) since
and get
Therefore, we have
and by Lemma 3.1 we get
Next, we have
The last inequality follows by embedding
The other terms can be estimated in a similar way as before. In the same way, we can get estimates for arbitrary \(m\in {{\mathbb {N}}}\). \(\square \)
3.2 Proof of Proposition 3.1
Now, we can finish the proof of Proposition 3.1. First we are going to show that \(\mathcal {S}(\mathcal {K}_R)\subset \mathcal {K}_R\) for suitably chosen R and T. For \((\widehat{\textbf{U}},\widehat{P},\widehat{\textbf{A}},\widehat{\varvec{\Omega }})\in \mathcal {K}_R\), Lemma 3.3 implies that
and since
we obtain
for \(R>0\) large enough, where \(C_0>0\) is the constant form Theorem 3.1. Also, we can choose \(T=T_0>0\) small enough, i.e. such that
and, therefore we get
By Theorem 3.1 we conclude that \(\mathcal {S}\) is well defined on \(\mathcal {K}_R\), and \(\mathcal {S}(\mathcal {K}_R)\subset \mathcal {K}_R\). It remains to show that \(\mathcal {S}\) is a contraction.
For \((\widehat{\textbf{U}},\widehat{P},\widehat{\textbf{A}},\widehat{\varvec{\Omega }})\in \mathcal {K}_R \) and
we have
Hence,
and, again, for \(T=T_0>0\) small enough, we get
for some \(0<\mu <1\), so \(\mathcal {S}\) i contraction. Banach fixed point theorem implies that \(\mathcal {S}\) has a unique fixed point \(({\textbf{U}}^{*},{P}^{*},{\textbf{A}}^{*},{\varvec{\Omega }}^{*})\in \mathcal {K}_R\), which is a unique solution to the problem (3.1)–(3.2). Therefore, we have shown part a) of Proposition 3.1.
Remark 3.2
The choice of the time \(T_0\) does not depend on the solution itself, but only on the norms \( \Vert {\widetilde{\textbf{U}}}\Vert _{L^r(0,T_0;L^s(\Omega _F))}, \Vert {\widetilde{\textbf{A}}}\Vert _{L^2(0,T_0)} \) and \( \Vert {\widetilde{\varvec{\Omega }}}\Vert _{L^2(0,T_0)}. \) Since the norms \( \Vert {\widetilde{\textbf{U}}}\Vert _{L^r(0,T;L^s(\Omega _F))}, \Vert {\widetilde{\textbf{A}}}\Vert _{L^2(0,T)} \) and \( \Vert {\widetilde{\varvec{\Omega }}}\Vert _{L^2(0,T)} \) are given, we can split the interval \(\left[ 0,T\right] \) into smaller ones \(\left[ T_{i-1},T_i\right] \), such that
repeat the procedure at each interval.
For part b) of Proposition 3.1 we can proceed as in part a) by using Corollary 3.1 instead of Lemma 3.3.
Notice that Theorem 1.2 follows directly from our construction and Proposition 3.1. Namely, Proposition 3.1 a), change of coordinates and Lemma 2.1 implies
for all \(\varepsilon >0\). By induction and using Proposition 3.1 b) we get property (1.10).
4 Higher time derivatives estimates
To summarize, in the previous section we proved that:
for all \(\varepsilon >0\) and all \(1\le p<\infty \). Now, we want to show inductively that all time derivatives of the solution has the following regularity properties:
for all \(l\ge 1\) and all \(\varepsilon >0\).
In this section, for simplicity of presentation, we prove (4.2) for \(l=1\) and \(p=2\), while the general case is done in Appendix, see Sect. 6.1. We consider the problem (3.1) with right hand side
where
and \(\mathcal {L}_1\), \(\mathcal {M}_1\), \(\mathcal {N}_1\) and \(\mathcal {G}_1\) denote operators obtained by taking time derivative of the coefficients in operators \(\mathcal {L}\), \(\mathcal {M}\), \(\mathcal {N}\) and \(\mathcal {G}\)
Remark 4.1
This problem is obtained by formal differentiation of (2.4) w.r.t. time variable, multiplication by t (to cut-off initial condition), and setting
To have vanishing initial data, the time derivative \(\partial _t\textbf{U}\) should not explode too fast at \(t=0\). Since
it is better to multiply by \(t-\varepsilon '\) and look at the solution for \( t>\varepsilon '\). Here, for \(\varepsilon >0\) arbitrary small, we can chose \(\varepsilon<\varepsilon '<2\varepsilon \) such that \(\partial _t^{l}\textbf{U}(\varepsilon ')\in L^2(\Omega _F)\). After the translation \(t\mapsto t+\varepsilon '\), we obtain (3.1) with right hand side (4.3). Therefore, in the following we can replace \(\varepsilon \) with 0 in the assumption (4.1).
In what follows we show that described problem has a unique solution \((\textbf{U}^{*},P^{*},\textbf{A}^{*},\varvec{\Omega }^{*})\) such that
and that it equals \( \left( t\partial _t\textbf{U},t\partial _t P,t\frac{\textrm{d} }{\textrm{d} t }\textbf{A},t\frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }\right) . \) Then it follows that
for all \(\varepsilon >0\). We use Proposition 3.1 with
Therefore, it is sufficient to show that
The critical term is (4.6) which comes from the convective term. By Theorem 1.2 and Remark 4.1 we have
Therefore
All other terms can be estimated as in Sect. 3, so by Proposition 3.1 we conclude that there exists a unique strong solution \((\textbf{U}_1^{*},P_1^{*},\textbf{A}_1^{*},\varvec{\Omega }_1^{*})\) satisfying
It remains to prove that the obtained solution equals \( \left( t\partial _t\textbf{U},t\partial _t P,t\frac{\textrm{d} }{\textrm{d} t }\textbf{A},t\frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }\right) , \) which will imply the statement of Proposition 2.2 for \(l=1\) and \(p=2\).
4.1 \((\textbf{U}_1^{*},P_1^{*},\textbf{A}_1^{*},\varvec{\Omega }_1^{*})=\left( t\partial _t\textbf{U},t\partial _t P,t\frac{\textrm{d} }{\textrm{d} t }\textbf{A},t\frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }\right) \)
So far we have shown that there is a unique strong solution \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) of problem (2.4) satisfying (4.1), and a unique strong solution \((\textbf{U}_1^{*},P_1^{*},\textbf{A}_1^{*},\varvec{\Omega }_1^{*})\) of (3.1) with right hand side (4.3) satisfying (4.10). In order to complete the proof of Proposition 2.2, it is necessary to show that
Notice that while the above equality formally holds, it is delicate to prove it because we do not have any information on \(\partial _t P\). We consider problem (2.4) in the form
where
and the problem (3.1) with the right hand side (4.3)
Operators \(\mathcal {L}\), \(\mathcal {M}\), \(\mathcal {N}\) and \(\mathcal {G}\) are defined by formulas (2.7)–(2.10), operators \(F_1, G_1\) and \(H_1\) by (4.4)–(4.5).
In order to compare solutions of (4.11) and (4.13) we would like to differentiate (4.11) with respect to time, but the right-hand side is not regular enough, since \(\partial _t\textbf{U}\in L^2(\varepsilon ,T;L^2(\Omega _F))\) and the pressure P is not regular enough in time variable. This means that we have to use some regular approximations of the solution for (4.11). The idea is to use Galerkin’s method. First we will multiply the equation (4.11)\(_1\) by
and obtain pressure term \(\nabla P\) on the right-hand side in the equation
since \( \mathbb {G}\mathcal {G}(P)=\nabla P. \) Then we can get rid of the pressure by using a divergence-free test function, write down an approximative problem and to show that it has a unique solution which is a good approximation for \(\textbf{U}\). That allows us to differentiate the approximative problem with respect to time and get estimates for \(\partial _t \textbf{U}\). Finally, we will show that \(\textbf{U}_1^{*} = t\partial _t \textbf{U}\) by using the equation for approximative problem and the equation for \(\textbf{U}_1^{*}\). The point is that in this way we will avoid the term with \(\partial _t P\).
We are going to use following function spaces
-
\( \mathbb {H}(\Omega _{F}) = \left\{ (\textbf{v},\textbf{a},\varvec{\omega })\in L^2(\Omega )\times {{\mathbb {R}}}^3\times {{\mathbb {R}}}^3 : \mathop {\textrm{div}}\nolimits \textbf{v}=0, \textbf{v}\cdot \textbf{n}|_{\partial \Omega } = 0, \textbf{v}|_{S_0}(\textbf{y})= \textbf{a}+ \varvec{\omega }\times \textbf{y}\right\} \)
-
\( \mathbb {V}(\Omega _{F}) = \left\{ (\textbf{v},\textbf{a},\varvec{\omega })\in H_0^1(\Omega )\times {{\mathbb {R}}}^3\times {{\mathbb {R}}}^3 \,:\, \mathop {\textrm{div}}\nolimits \textbf{v}=0,\, \textbf{v}|_{S_0}(\textbf{y})=\textbf{a}+ \varvec{\omega }\times \textbf{y}\right\} \)
Let \( \left\{ \, \left( {\varvec{\Psi }}_i, {\varvec{\Psi }}^{\textbf{a}}_i, {\varvec{\Psi }}^{\varvec{\omega }}_i \right) , i\in {{\mathbb {N}}}\,\right\} \) be an orthonormal basis for \(\mathbb {H}(\Omega _{F})\) with scalar product
We define finite-dimensional space
For \(m\in {{\mathbb {N}}}\) we observe the following approximate problem
for \(i=1,\ldots ,m\), where
and
Equation (4.16) is obtained by summing the equation (4.14) multiplied by the test function \({\varvec{\Psi }}_i\) and integrated over \(\Omega _{F}\) with the equations (4.11)\(_3\) and (4.11)\(_4\) multiplied by the test functions \({\varvec{\Psi }}_i^{\textbf{a}}\) and \({\varvec{\Psi }}_i^{\varvec{\omega }}\), respectively. Then from (4.18) using integration by parts we obtain
and therefore,
for regular enough and divergence-free functions \(\textbf{U}, \varvec{\psi }\).
Together with the initial conditions
there exists a unique solution \((\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)\) for (4.16) on some interval \([0,T_m]\), \(T_m\le T\) (\(c_{jm}\in H^1(0,T_k)\)).
To show that \((\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)\) converges to the solution \((\textbf{U},\textbf{A},\varvec{\Omega })\), we have to derive the energy estimates. We multiply (4.16) by \(c_{jm}\), and sum over j from 1 to m, and if we go back to physical domain \(\Omega _F(t)\) with
we will obtain
Since
it follows that
By integrating the equality on (0, t) we obtain the estimate
from which we conclude that \(|c_{jm}(t)|<\Vert \textbf{u}_0\Vert _{L^2(\Omega )}\), so the inequality holds for all \(t\in [0,T]\). Hence, \(\textbf{u}^m\) is bounded in \(L^{\infty }(0,T;L^2(\Omega ))\cap L^2(0,T;H^1(\Omega ))\) which implies that \(\textbf{u}^m\rightarrow \bar{\textbf{u}}\) weakly in \(L^2(0,T;H^1(\Omega ))\) and weakly-* in \(L^{\infty }(0,T;L^2(\Omega ))\).
Let us show that \(\bar{\textbf{u}}\) is a weak solution for (1.6). We take test function
multiply (4.16) by h(t) and write the equation in the physical domain \(\Omega _F(t)\)
with
By integrating on (0, T) and using the integration by parts we obtain
Now, we let \(m\rightarrow \infty \)
and go to the cylindrical domain
with
By taking \(\varvec{\psi }=h_i(t){\varvec{\Psi }}_i\) and summing up over i from 1 to m the equality holds for all test functions in \(\mathbb {V}_m\) which is dense in \(\mathbb {V}(\Omega _F)\). It is not difficult to show that the equation (4.20) is equivalent to (2.2) from Definition 2.1 and therefore we call the function \(\bar{\textbf{U}}\) a weak solution for (4.11). Finally, the uniqueness of weak solution implies \(\bar{\textbf{U}}=\textbf{U}\in L^2(0,T;H^2(\Omega ))\cap H^1(0,T;L^2(\Omega ))\). Then, since \(\bar{\textbf{U}}=\bar{\textbf{A}}+\bar{\varvec{\Omega }}\times \textbf{y}\) and \({\textbf{U}}={\textbf{A}}+{\varvec{\Omega }}\times \textbf{y}\) on \(\overline{S_0}\), we conclude that \(\bar{\textbf{A}}=\textbf{A}\) and \(\bar{\varvec{\Omega }}=\varvec{\Omega }\) belong to \(H^{1}(0,T)\).
4.1.1 Estimates for time derivatives
In this step we would like to show that
By (4.16) solution \((\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)\) satisfies
for \(i=1,\ldots m\). This is a consequence of \(\mathbb {G}={{\mathbb {I}}}\) on \(\overline{S_0}\) and equality
We differentiate the equation in time
We recall that operators G, H are defined by (2.6), and \(G_1\) and \(H_1\) by (4.5). We multiply the above equation by \(\frac{\textrm{d} }{\textrm{d} t }c_{im}\) and sum over i form 1 to m to obtain
Then we integrate the equation on \([t_1,t_2]\subset (0,T]\) and estimate each term. For the first term we have
which implies
By the definition of \(\left\langle \mathbb {G}\mathcal {F}(\textbf{U}),\varvec{\psi }\right\rangle \) and Lemma 3.1 we get
for arbitrary \(\mu >0\) and \(\textbf{u}_t^m=\nabla \textbf{X}\partial _t\textbf{U}^m\). Hence, for the second term in (4.22) we obtain
where constant \(C>0\) depends on T non-decreasingly.
Now, for the third term we compute
Hence,
for arbitrary \(\mu >0\), where constant \(C>0\) depends on T non-decreasingly, since \(\partial _t\widetilde{\textbf{U}}\in L^8(\varepsilon ,T;L^4(\Omega )),\) \(\forall \varepsilon >0\) by (4.1) and since \(\frac{\textrm{d} }{\textrm{d} t }\widetilde{\textbf{A}}, \frac{\textrm{d} }{\textrm{d} t }\widetilde{\varvec{\Omega }}\in L^{\infty }(0,T)\) by the assumption of Proposition 2.2. Here we emhasize that this assumption was necessary for bounding term involving \(\partial _t(\mathbb {G}\mathcal {M})(\textbf{U}^m)\).
Note that
since \(\nabla \textbf{Y}\nabla \textbf{X}={{\mathbb {I}}}\), so all together, we get
where \(\Vert (g_{ik}g^{jl}-\delta _{ik}\delta _{jl})\Vert _{L^{\infty }(0,T;L^{\infty }(\Omega ))}\) is small for small T, by Lemma 3.1.
Now, we take sufficiently small T, integrate the inequality on \(t_1\in (\varepsilon ,t_2)\) and by Gronwall’s Lemma we find
for all \(t\in (\varepsilon ,t)\), where constant \(M>0\) depends on the norms \(\Vert \partial _t\widetilde{\textbf{U}}\Vert _{L^{8}(\varepsilon ,T;L^4(\Omega ))}\), \(\Vert \widetilde{\textbf{U}}\Vert _{L^{2}(\varepsilon ,T;H^1(\Omega ))}\), \(\Vert \textbf{U}^m\Vert _{L^{2}(0,T;H^1(\Omega ))}\), \(\Vert \widetilde{\textbf{A}}\Vert _{W^{1,\infty }(0,T)}\) and \(\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{1,\infty }(0,T)}\). Finally, since \(\Vert \textbf{U}^m\Vert _{L^{2}(0,T;H^1(\Omega ))}\) is bounded, on the limit we get that \(\partial _t\textbf{U}\in L^2(\varepsilon ,T;H^1(\Omega ))\cap L^{\infty }(\varepsilon ,T;L^2(\Omega ))\).
4.1.2 Uniqueness for time-derivative system
Now we are able to show that \(\textbf{U}_1^{*}=t\partial _t\textbf{U}\). \((\textbf{U}, P)\) satisfies the following weak formulation
for all \(\varvec{\psi }\in V(0)\), and \((\textbf{U}^{*}, P^{*},\textbf{A}^{*},\varvec{\Omega }^{*})\) satisfies
where
with \( \mathcal {F}_1 = \mathcal {L}_1 - \mathcal {M}_1 - \mathcal {N}_1 \) and operators \(\mathcal {L}_1\), \(\mathcal {M}_1\), \(\mathcal {N}_1\), \(\mathcal {G}_1\) are defined by (4.6)–(4.9). For \(j\in {{\mathbb {N}}}\) and \((\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})=h(t)({\varvec{\Psi }}_j,{\varvec{\Psi }}_j^{\textbf{a}},{\varvec{\Psi }}_j^{\varvec{\omega }})\) we have
where
Note that the second row in (4.25) is the time derivative of \(\left\langle \mathbb {G}\mathcal {F}(\textbf{U}^m),\varvec{\psi }\right\rangle \), for time independent \(\varvec{\psi }\), which holds from (4.19) since \(\mathbb {G}={{\mathbb {I}}}\) on \(\overline{S_0}\) and \(\textbf{U}^m\) is regular enough. We multiply the above equation by t and subtract from the previous one with
Then, by using (4.23), we obtain
Since
terms with the pressure cancels, and after integrating above equation on (0, t), we get
We let \(m\rightarrow \infty \) and obtain the equation
where
By linearity and density, the above equality holds for all \((\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})\in \mathbb {V}\). Then we substitute
and get the equality
Now, as before, we can get the estimate
for all \(\mu >0\) and for sufficiently small \(\mu \) we get
Finally, Gronwall’s Lemma implies \( \widehat{\textbf{U}}_1=0\) which means that \(\textbf{U}_1^{*}=t\partial _t\textbf{U}\). Then the equations (4.11)\(_1\) and (4.13)\(_1\) give \(\nabla P_1^{*}=t\nabla \partial _t P\). Moreover, since \(\textbf{U}_1^{*}=\textbf{A}_1^{*}+ \varvec{\Omega }_1^{*}\times \textbf{y}\) and \(\partial _t\textbf{U}=\frac{\textrm{d} }{\textrm{d} t }\textbf{A}+ \frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }\times \textbf{y}\) on \(\overline{S_0}\), it follows that \(\textbf{A}_1^{*}=t\frac{\textrm{d} }{\textrm{d} t }\textbf{A}\) and \(\varvec{\Omega }_1^{*}=t\frac{\textrm{d} }{\textrm{d} t }\varvec{\Omega }\).
5 Spatial derivatives estimates
Let \((\widetilde{\textbf{U}},\widetilde{P},\widehat{\textbf{A}},\widetilde{\varvec{\Omega }})\) be a weak solution satisfying the assumption of Lemma 2.1. We want to show that
for all \(l\ge 0, k\ge 2\). The case \(k=2\) is exactly the statement of Proposition 2.2.
As in previous sections, we consider a linear problem on cylindrical domain (2.4) and follow the proof for the Navier–Stokes case (see eg. [16, Section 5]). Let \(k\ge 2\) and let us assume that solution \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) to the system (2.4) satisfies
and by uniqueness
which by Sobolev embeddings means that
We want to show that
The solution for (2.4) satisfies the following system
for all \(l\ge 0\), where operators F and \(F_l\) are defined by (2.5) and (4.6)–(4.9) respectively, and if we define \(F_0(\textbf{U},P)=0\).
The idea is to use the following well known result for the steady Stokes system (see [16, Lemma 5.2]).
Lemma 5.1
Let \(\Omega \) be a bounded domain of \({{\mathbb {R}}}^n\), of class \(C^{k+2}\). For any \(F\in W^{k,q}(\Omega )\), there exists one and only one solution \((\textbf{U},P)\) to the following Stokes problem
such that
and
This solution satisfies the estimate:
Therefore, first for \(l=0\) by Lemma 5.1 and fixed point argument we will obtain that
and by uniqueness
Then for \(l\ge 1\) if we assume that
we will conclude that
First we define a smooth divergence-free extension of the rigid velocity
Operator \({\text {Ext}}(\cdot )\) extends a function from solid domain \(S_0\) to the domain \(\Omega \) such that it preserves regularity of function and the divergence-free property. The construction of the operator can be found in [21, Appendix A.1]. Since \(\mathop {\textrm{div}}\nolimits b_{\textbf{A},\varvec{\Omega }} = 0\), functions \( \bar{\textbf{U}}_l = \partial _t^l\textbf{U}- \partial _t^{l}b_{\textbf{A},\varvec{\Omega }} \) and \( \bar{P}_l=\partial _t^l P \) satisfy
for all \(l\ge 0\), where
and \(\mathcal {L}\), \(\mathcal {M}\), \(\mathcal {N}\) are defined by (2.7), (2.9), (2.8) respectively. Now, for \(l\ge 0\), we use fixed point argument, and consider the following problem
with
By Lemma 5.1, it is enough to show that
since \(\partial _t^{l}b_{\textbf{A},\varvec{\Omega }}\in C^{\infty }((0,T)\times \Omega )\), and \(\partial _{t}^{l+1}\textbf{U}\in C^{\infty }((0,T];H^{k}(\Omega _F))\) by assumption. The only critical terms are derivatives of the convective term. For \(k=2,l=1\) we have
and in the general case the estimates can be obtained in the same way.
Data availability
There are no associated data corresponding to the manuscript.
Notes
Let us mention also the conditional regularity of the type that one component of the velocity field is more regular, see [28].
References
Amann, H.: Compact embeddings of vector valued Sobolev and Besov spaces. Glasnik Mat. 35(1), 161–177 (2000)
Bravin, M.: Energy Equality and Uniqueness of Weak Solutions of a “Viscous Incompressible Fluid + Rigid Body’’ System with Navier Slip-with-Friction Conditions in a 2D Bounded Domain. J. Math. Fluid Mech. 21(2), 21–23 (2019)
Bravin, M.: On the 2D viscous incompressible fluid+ rigid body system with Navier conditions and unbounded energy. Comptes Rendus Math. 358, 303–319 (2020)
Chemetov, N.V., Nečasová, Š, Muha, B.: Weak-strong uniqueness for fluid-rigid body interaction problem with slip boundary condition. J. Math. Phys. 60(1), 011505 (2019)
Chemetov, N.V., Nečasová, Š: The motion of the rigid body in the viscous fluid including collisions. Global solvability result. Nonlinear Anal. Real World Appl. 34, 416–445 (2017)
Carlos, C., Jorge, S.M.H., Marius, T.: Existence of solutions for the equations modelling the motion of a rigid body in a viscous fluid. Commun. Partial Differ. Equ. 25(5–6), 1019–1042 (2000)
Cumsille, P., Takahashi, T.: Well posedness for the system modelling the motion of a rigid body of arbitrary form in an incompressible viscous fluid. Czechoslov. Math. J. 58, 961–992 (2008)
Desjardins, B., Esteban, M.J.: Existence of weak solutions for the motion of rigid bodies in a viscous fluid. Arch. Ration. Mech. Anal. 146(1), 59–71 (1999)
Desjardins, B., Esteban, M.J.: On weak solutions for fluid-rigid structure interaction: compressible and incompressible models. Commun. Partial Differ. Equ. 25(7–8), 1399–1413 (2000)
Dintelmann, E., Geissert, M., Hieber, M.: Strong \({L}^p\)-solutions to the Navier–Stokes flow past moving obstacles: the case of several obstacles and time dependent velocity. Trans. Am. Math. Soc. 361, 653–669 (2009)
Escauriaza, L., Seregin, G.A., Sverak, V.: \(L_{3,\infty }\)-solutions of Navier–Stokes equations and backward uniqueness. Russ. Math. Surv. 58(2), 211–250 (2003)
Fabes, E.B., Lewis, J.E., Riviere, N.M.: Boundary value problems for the Navier–Stokes equations. Am. J. Math. 99, 626–668 (1977)
Fabes, E.B., Lewis, J.E., Riviere, N.M.: Singular integrals and hydrodynamic potentials. Am. J. Math. 99, 601–625 (1977)
Feireisl, E.: On the motion of rigid bodies in a viscous fluid. Appl. Math. 47, 463–484 (2002)
Feireisl, E.: On the motion of rigid bodies in a viscous incompressible fluid. J. Evol. Equ. 3(3), 419–441 (2003)
Galdi, G.P.: An introduction to the Navier–Stokes initial-boundary value problem. In: Fundamental Directions in Mathematical Fluid Mechanics Advances in Mathematical Fluid Mechanics, pp. 1–70. Birkhäuser, Basel (2000)
Geissert, M., Götze, K., Hieber, M.: \(L^p\)-theory for strong solutions to fluid-rigid body interaction in Newtonian and generalized Newtonian fluids. Trans. Am. Math. Soc. 365(3), 1393–1439 (2013)
Gérard-Varet, D., Hillairet, M.: Existence of weak solutions up to collision for viscous fluid-solid systems with slip. Commun. Pure Appl. Math. 67, 2022–2076 (2014)
Giga, Y.: Solutions for semilinear parabolic equations in Lp and regularity of weak solutions of the Navier–Stokes system. J. Differ. Equ. 218(2), 907–944 (2015)
Glass, O., Sueur, F.: Uniqueness results for weak solutions of two-dimensional fluid-solid systems. Arch. Ration. Mech. Anal. 62, 186–212 (1986)
Muha, B., Nečasová, Š, Radošević, A.: A uniqueness result for 3D incompressible fluid-rigid body interaction problem. J. Math. Phys. 23(1), 1–39 (2020)
Gunzburger, M.D., Lee, H.-C., Seregin, G.A.: Global existence of weak solutions for viscous incompressible flows around a moving rigid body in three dimensions. J. Math. Fluid Mech. 2(3), 219–266 (2000)
Inoue, A., Wakimoto, M.: On existence of solutions of the Navier–Stokes equation in a time dependent domain. J. Fac. Sci. Univ. Tokyo Sect. IA Math 24(2), 303–319 (1977)
Ladyzhenskaia, O.: Solution in the large of the nonstationary boundary value problem for the Navier–Stokes system with two space variables. Commun. Pure Appl. Math. 12, 427–433 (1959)
Leray, J.: Essai sur les mouvements plans d’un fluide visqueux que limitent des parois. J. Math. Pures Appl. 13, 331–418 (1934)
Leray, J.: Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248 (1934)
Maity, D., Tucsnak, M.: \(L^p\)-\(L^q\) maximal regularity for some operators associated with linearized incompressible fluid-rigid body problems. In: Mathematical Analysis in Fluid Mechanics—Selected Recent Results, Volume 710 of Contemporary Mathematics, pp. 175–201. American Mathematical Society, Providence (2018)
Neustupa, J., Penel, P.: Regularity of a Suitable Weak Solution to the Navier–Stokes Equations as a Consequence of Regularity of One Velocity Component. Applied Nonlinear Analysis, pp. 391–402. Kluwer, New York (1999)
Sohr, H.: Zur regularitätstheorie der instationären Gleichungen von Navier–Stoke. Math. Z. 184, 359–375 (1983)
Starovoitov, V.N.: Behavior of a rigid body in an incompressible viscous fluid near a boundary. In: Free Boundary Problems, Volume 147 of International Series of Numerical Mathematics, pp. 313–327. Birkhäuser, Basel (2004)
Takahashi, T.: Analysis of strong solutions for the equations modeling the motion of a rigid-fluid system in a bounded domain. Adv. Differ. Equ. 8(12), 1499–1532 (2003)
Takahashi, T., Tucsnak, M.: Global strong solutions for the two dimensional motion of an infinite cylinder in a viscous fluid. J. Math. Fluid Mech. 6, 53–77 (2004)
von Wahl, W.: Regularity of weak solutions of the Navier–Stokes equations. Proc. Symp. Pure Appl. Math. 45, 497 (1986)
Wang, C.: Strong solutions for the fluid-solid systems in a 2-D domain. Asymptot. Anal. 89, 263–306 (2014)
Acknowledgements
The authors express their sincere gratitude to the anonymous referee for providing a detailed and insightful review of the manuscript. The suggestions and comments provided by the referee helped us to improve the clarity and quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Šárka Nečasová as the corresponding author declares on behalf of all authors, that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research of B.M. leading to these results has been supported by Croatian Science Foundation under the project IP-2018-01-3706.
The research of Š.N. leading to these results has received funding from the Czech Sciences Foundation (GAČR), 22-01591S. Moreover, Š. N. has been supported by Praemium Academiae of Š. Nečasová. CAS is supported by RVO:67985840.
The research of A.R. leading to these results has been supported by Croatian Science Foundation under the project IP-2019-04-1140. Moreover, The research of A.R. leading to these results has received funding from the Czech Sciences Foundation (GAČR) 22-01591S, and by Praemium Academiae of Š. Nečasová.
Appendices
Appendix
1.1 Time derivatives-general case
In Sect. 4, we have presented the proof of Proposition 2.2 for case \(l=1\). Here we are going to present the induction step for general \(l\in {{\mathbb {N}}}\). The proof in general case is conceptually the same, but with more complicated expressions in the equations.
Let \(l\ge 1\) and let us assume that
for all \(\varepsilon >0\) and \(1\le p <\infty \). We consider the problem (3.1) with right hand side
where
Subscript \(l-p\) in operators \(\mathcal {L}_{l-p}\), \(\mathcal {M}_{l-p}\), \(\mathcal {N}_{l-p}\) and \(\mathcal {G}_{l-p}\) denotes \((l-p)\)th order time derivative of the coefficients in operators \(\mathcal {L}\), \(\mathcal {M}\), \(\mathcal {N}\) and \(\mathcal {G}\). As for \(l=1\), to show that described problem has a unique solution \((\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})\) such that
it is sufficient to show that
satisfy
All the terms can be estimated as in Sect. 4, so by Proposition 3.1 there exists a unique strong solution \((\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})\) of (3.1) with the right hand side (6.1) satisfying (6.4). Again, we have to prove that the obtained solution equals \( \left( t\partial _t^l\textbf{U},t\partial _t^l P,t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A},t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\right) \).
Lemma 6.1
Let \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) be a unique strong solution for (2.4), and \((\textbf{U}_l^{*},P_l^{*},\textbf{A}_l^{*},\varvec{\Omega }_l^{*})\) be a unique strong solution for (3.1) with the right hand side (6.1) satisfying (6.4). Suppose that
hold for some \(l\in {{\mathbb {N}}}\) and for all \(\varepsilon >0\) and all \(1\le p<\infty \). Then
1.2 Proof of Lemma 6.1
Let \((\textbf{U},P,\textbf{A},\varvec{\Omega })\) be a unique strong solution for (2.4) satisfying (6.5) and let \((\textbf{U}_{l}^{*},P_{l}^{*},\textbf{A}_{l}^{*},\varvec{\Omega }_{l}^{*})\) be a unique strong solution for (3.1) with the right hand side (6.1). We want to show (6.6). Since we have already shown that the statement is valid for \(l=1\) in Sect. 4.1, we can suppose that \(l\ge 2\).
We use Galerkin approximations \((\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)\), as in Sect. 4.1, and assume that
for some constant \(M>0\). This assumption comes from the previous step of the induction.
We want to show that
for some constant \(M>0\), which implies that
By (4.16) approximation \((\textbf{U}^m,\textbf{A}^m,\varvec{\Omega }^m)\) satisfies
for \(i=1,\ldots m\). We differentiate the equation in time l times
multiply by \(\frac{\textrm{d} ^l}{\textrm{d} t ^l}c_{im}\) and sum over i form 1 to m to obtain
Then we integrate the equation on \([t_1,t_2]\subset (0,T]\) and, in the same way as in Sect. 4.1.1, estimate
The only difference from Sect. 4.1.1 is in the following estimate
The last inequality follows from the fact that \( \widetilde{\textbf{A}}, \widetilde{\varvec{\Omega }}\in W^{l,4}(\varepsilon ,T)\cap W^{1,\infty }(\varepsilon ,T) \) and embedding \(W^{l-2,4}(t_1,t_2;H^{1}(\Omega _F))\hookrightarrow H^{l-1}(t_1,t_2;H^{1}(\Omega _F))\) for \(l\ge 2\). Therefore, we get
All together, we get
for arbitrary \(\mu >0\), where \(\Vert g_{ik}g^{il}-\delta _{ik}\delta _{il}\Vert _{L^{\infty }(0,T;L^{\infty }(\Omega ))}\) is small for small T. Now, we take sufficiently small T, integrate the inequality on \(t_1\in (\varepsilon ,t_2)\) and by Gronwall’s Lemma we find
where constant \(M>0\) depends on the norms \(\Vert \widetilde{\textbf{U}}\Vert _{H^{l-1}(\varepsilon ,T;H^1(\Omega ))}\), \(\Vert \textbf{U}^m\Vert _{H^{l-1}(0,T;H^1(\Omega ))}\), \(\Vert \widetilde{\textbf{A}}\Vert _{W^{1,\infty }(\varepsilon ,T)}\), \(\Vert \widetilde{\textbf{A}}\Vert _{W^{l,4}(\varepsilon ,T)}\), \(\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{1,\infty }(\varepsilon ,T)}\), \(\Vert \widetilde{\varvec{\Omega }}\Vert _{W^{l,4}(\varepsilon ,T)}\) and T. Finally, in the limit we get that \(\partial _t^l\textbf{U}\in L^2(\varepsilon ,T;H^1(\Omega ))\cap L^{\infty }(\varepsilon ,T;L^2(\Omega ))\), for all \(\varepsilon >0\).
1.2.1 Uniqueness
In previous section, we showed that \(\partial _t^l\textbf{U}\in L^2(\varepsilon ,T;H^1(\Omega ))\cap L^{\infty }(\varepsilon ,T;L^2(\Omega ))\), for all \(\varepsilon >0\). Now we are able to show that \(\textbf{U}_{l}^{*}=t\partial _t^l\textbf{U}\). We know that \((\textbf{U}, P)\) satisfies
for all \(\varvec{\psi }\in V(0)\), and \((\textbf{U}_{l}^{*}, P_{l}^{*},\textbf{A}_{l}^{*},\varvec{\Omega }_{l}^{*})\) satisfies
where
For \((\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})=h(t)({\varvec{\Psi }}_j,{\varvec{\Psi }}_j^{\textbf{a}},{\varvec{\Psi }}_j^{\varvec{\omega }})\) we have
where
We multiply the above equation by t and subtract from the previous one with
Then, by using (6.7), we obtain
It can be shown that the terms with the pressure cancels, i.e. it holds
and after integrating above equation on (0, t), we get
We let \(m\rightarrow \infty \) and obtain the equation
where
By the linearity and the density, the above equality holds for all \((\varvec{\psi },\varvec{\psi }_{\textbf{a}},\varvec{\psi }_{\varvec{\omega }})\in \mathbb {V}\). Then we can substitute
and get the equality
Now, as in Sect. 4, we can get the estimate
for all \(\mu >0\) and for sufficiently small \(\mu \) we get
Finally, Gronwall’s Lemma implies \(\widehat{\textbf{U}}=0\) which means that \(\textbf{U}_{l}^{*}=t\partial _t^l\textbf{U}\). Then the equations for \(\textbf{U}\) and \(\textbf{U}_l^{*}\) give \(\nabla P_l^{*}=t\nabla \partial _t P\), and since \(\textbf{U}_l^{*}=\textbf{A}_l^{*}+ \varvec{\Omega }_l^{*}\times \textbf{y}\) and \(\partial _t\textbf{U}=\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}+ \frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\times \textbf{y}\) on \(\overline{S_0}\), it follows that \(\textbf{A}_l^{*}=t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\textbf{A}\) and \(\varvec{\Omega }_l^{*}=t\frac{\textrm{d} ^l}{\textrm{d} t ^l}\varvec{\Omega }\).
Notation
Label | Description | Definition/1st appearance |
|---|---|---|
\((\widetilde{\textbf{u}}, \widetilde{p},\widetilde{\varvec{\omega }},\widetilde{\textbf{a}})\) | Solution for the original nonlinear problem (1.6) on physical domain | Section 2.1 |
\((\textbf{u}, p,\varvec{\omega },\textbf{a})\) | Solution for the linear problem (2.1) on the physical domain | Section 2.1 |
\((\widetilde{\textbf{U}}, \widetilde{P},\widetilde{\varvec{\Omega }},\widetilde{\textbf{A}})\) | Solution for the nonlinear problem on the cylindrical domain | |
\((\textbf{U}, P,\varvec{\Omega },\textbf{A})\) | Solution for the linear problem (2.4) on the cylindrical domain | |
\((\varvec{\varphi }, \varvec{\varphi }_{\varvec{\omega }}, \varvec{\varphi }_{\textbf{a}})\) | Test function on the physical domain | Definition 1.1 |
\((\varvec{\psi }, \varvec{\psi }_{\varvec{\omega }}, \varvec{\psi }_{\textbf{a}})\) | Test function on the cylindrical domain | Section 4.1 |
\(\textbf{X}(t,\textbf{y})\) | Changes of variables | Section 2.2 |
\(\textbf{Y}(t,\textbf{x})\) | Changes of variables | Section 2.2 |
\(F(\textbf{U},P)\), \(G(\textbf{A}), H(\varvec{\Omega })\) | Right-hand side of the linear problem (2.4) on the cylindrical domain, | |
\(F(\textbf{U},P) = (\mathcal {L}-\Delta )\textbf{U}-\mathcal {M}\textbf{U}-\mathcal {N}\textbf{U}-(\mathcal {G}-\nabla )P\) | ||
\(\mathcal {L}\textbf{U}\) | The transformed Laplace operator | Equation (2.7) |
\(\mathcal {M}\textbf{U}\) | The transformation of time derivative and gradient | Equation (2.9) |
\(\mathcal {N}\textbf{U}\) | The transformation of the convection term | Equation (2.8) |
\(\mathcal {G}P\) | \(\mathcal {G}P=\nabla \textbf{Y}\nabla \textbf{Y}^T\nabla P\), the transformation of the gradient of the pressure | Equation (2.10) |
\(\mathcal {F}\textbf{U}\) | \(\mathcal {F}\textbf{U}= \mathcal {L}\textbf{U}-\mathcal {M}\textbf{U}-\mathcal {N}\textbf{U}-\mathcal {G}P\) | Equation (4.12) |
\(({\textbf{U}}^{*}, {P}^{*},{\varvec{\Omega }}^{*},{\textbf{A}}^{*})\) | The fixed point, the solution for the transformed problem | Section 3 |
\((\widehat{\textbf{U}}, \widehat{P},\widehat{\varvec{\Omega }},\widehat{\textbf{A}})\) | The fixed point, functions on the right-hand side | Section 3 |
\(F^{*}\), \(G^{*}\), \(H^{*}\) | The right-hand side for the Stokes problem | Section 3 |
\(X_{p,q}^T\), \(Y_{p,q}^T\) | \(X_{p,q}^T :=W^{1,p}(0,T;L^q(\Omega _{F}))\cap L^p(0,T;W^{2,q}(\Omega _F))\) \(Y_{p,q}^T := L^p(0,T; {W}^{1,q}(\Omega _{F}))\) | |
\(F_l(\textbf{U},P)\) | “\(F_l(\textbf{U},P)=\partial _{t}^l(F({\textbf{U}},{P}))-F(\partial _{t}^l{\textbf{U}},\partial _{t}^l{P})\)” | |
\(G_l(\textbf{A})\) | “\(G_l(\textbf{A})=\frac{d^l}{{dt}^l}(G(\textbf{A}))-G\left( \frac{d^l}{{dt}^l}\textbf{A}\right) \)” | |
\(H_l(\varvec{\Omega })\) | “\(H_l(\varvec{\Omega })=\frac{d^l}{{dt}^l}(H(\varvec{\Omega }))-H\left( \frac{d^l}{{dt}^l}\varvec{\Omega }\right) \)” | |
\(\mathcal {G}_l(P)\) | The operator obtained by taking lth order time derivative of the coefficients in operator \(\mathcal {G}\), i.e. \(\mathcal {G}_l(P)=\partial _t^l(\nabla \textbf{Y}\nabla \textbf{Y}^T)\nabla P\) | |
\(\mathcal {F}_l(\textbf{U})\) | \(\mathcal {F}_l(\textbf{U}) = \mathcal {L}_l(\textbf{U})-\mathcal {M}_l(\textbf{U})-\mathcal {N}_l(\textbf{U})-\mathcal {G}_l(P)\), \(\mathcal {L}_l, \mathcal {M}_l, \mathcal {N}_l\) are operators obtained by taking lth order time derivative of the coefficients in operators \(\mathcal {L}, \mathcal {M}, \mathcal {N}\) | |
\(\mathbb {G}\) | \(\mathbb {G}=\nabla \textbf{X}^T\nabla \textbf{X}\) | Section 4.1 |
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Muha, B., Nečasová, Š. & Radošević, A. On the regularity of weak solutions to the fluid–rigid body interaction problem. Math. Ann. 389, 1007–1052 (2024). https://doi.org/10.1007/s00208-023-02664-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-023-02664-0