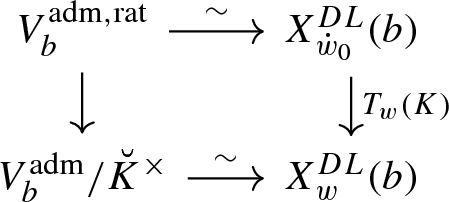Affine Deligne–Lusztig varieties at infinite level

Abstract

We initiate the study of affine Deligne–Lusztig varieties with arbitrarily deep level structure for general reductive groups over local fields. We prove that for ${{\,\mathrm{GL}\,}}_n$ and its inner forms, Lusztig’s semi-infinite Deligne–Lusztig construction is isomorphic to an affine Deligne–Lusztig variety at infinite level. We prove that their homology groups give geometric realizations of the local Langlands and Jacquet–Langlands correspondences in the setting that the Weil parameter is induced from a character of an unramified field extension. In particular, we resolve Lusztig’s 1979 conjecture in this setting for minimal admissible characters.

1 Introduction

In their fundamental paper [13], Deligne and Lusztig gave a powerful geometric approach to the construction of representations of finite reductive groups. To a reductive group G over a finite field ${\mathbb {F}}_q$ and a maximal ${\mathbb {F}}_q$-torus $T \subseteq G$, they attach a variety given by the set of Borel subgroups of G lying in a fixed relative position (depending on T) to their Frobenius translate. This variety has a T-torsor called the Deligne–Lusztig variety. The Deligne–Lusztig variety has commuting actions of G and T, and its $\ell$-adic étale cohomology realizes a natural correspondence between characters of $T({\mathbb {F}}_q)$ and representations of $G({\mathbb {F}}_q)$.

Two possible ways of generalizing this construction to reductive groups over local fields are to consider subsets cut out by Deligne–Lusztig conditions in the semi-infinite flag manifold (in the sense of Feigin–Frenkel [15]) or in affine flag manifolds of increasing level. The first approach is driven by an outstanding conjecture of Lusztig [25] that the semi-infinite Deligne–Lusztig set has an algebro-geometric structure, one can define its $\ell$-adic homology groups, and the resulting representations should be irreducible supercuspidal. This conjecture was studied in detail in the case of division algebras by Boyarchenko and the first named author in [5, 10, 11], and ultimately resolved in this setting in [12]. Prior to the present paper, Lusztig’s conjecture was completely open outside the setting of division algebras.

The second approach is based on Rapoport’s affine Deligne–Lusztig varieties [29], which are closely related to the reduction of (integral models of) Shimura varieties. Affine Deligne–Lusztig varieties for arbitrarily deep level structure were introduced and then studied in detail for ${{\,\mathrm{GL}\,}}_2$ by the second named author in [21,22,23], where it was shown that their $\ell$-adic cohomology realizes many irreducible supercuspidal representations for this group.

The goals of the present paper are to show that these constructions

• (A) are isomorphic for all inner forms of ${{\,\mathrm{GL}\,}}_n$ and their maximal unramified elliptic torus

• (B) realize the local Langlands and Jacquet–Langlands correspondences for supercuspidal representations coming from unramified field extensions

The first goal is achieved by computing both sides and defining an explicit isomorphism between Lusztig’s semi-infinite construction and an inverse limit of coverings of affine Deligne–Lusztig varieties. In particular, this allows us to use the known scheme structure of affine Deligne–Lusztig varieties to define a natural scheme structure on the semi-infinite side, which was previously only known in the case of division algebras. This resolves the algebro-geometric conjectures of [25] for all inner forms of ${{\,\mathrm{GL}\,}}_n$.

To attain the second goal, we study the cohomology of this infinite-dimensional variety using a wide range of techniques. To show irreducibility of certain eigenspaces under the torus action, we generalize a method of Lusztig [26, 31] to quotients of parahoric subgroups which do not come from reductive groups over finite rings. We study the geometry and its behavior under certain group actions to prove an analogue of cuspidality for representations of such quotients. To obtain a comparison to the local Langlands correspondence, we use the Deligne–Lusztig fixed-point formula to determine the character on the maximal unramified elliptic torus and use characterizations of automorphic induction due to Henniart [19, 20]. In particular, for minimal admissible characters, we resolve the remaining part of Lusztig’s conjecture (supercuspidality) for all inner forms of ${{\,\mathrm{GL}\,}}_n$.

We now give a more detailed overview. Let K be a non-archimedean local field with finite residue field ${\mathbb {F}}_q$, let $\breve{K}$ be the completion of the maximal unramified extension of K and let $\sigma$ denote the Frobenius automorphism of ${\breve{K}}/K$. For any algebro-geometric object X over K, we write ${\breve{X} \,{:=}\,X(\breve{K})}$ for the set of its $\breve{K}$-points. Let ${\mathcal {G}}$ be a connected reductive group over K. For simplicity assume that ${\mathcal {G}}$ is split. For $b \in \breve{{\mathcal {G}}}$, let $J_b$ be the $\sigma$-stabilizer of b

$$\begin{aligned} {J_b(R) \,{:=}\,\{ g \in {\mathcal {G}}(R \otimes _K \breve{K}) :g^{-1}b\sigma (g) = b \}} \end{aligned}$$

for any K-algebra R. Then $J_b$ is an inner form of a Levi subgroup of ${\mathcal {G}}$, and if b is basic, $J_b$ is an inner form of ${\mathcal {G}}$. Let ${\mathcal {T}}$ be a maximal split torus in ${\mathcal {G}}$. For an element w in the Weyl group of $({\mathcal {G}}, {\mathcal {T}})$, let

$$\begin{aligned} {T_w(R) \,{:=}\,\{ t \in {\mathcal {T}}(R \otimes _K \breve{K}) :t^{-1}{\dot{w}}\sigma (t) = {\dot{w}} \}} \end{aligned}$$

for any K-algebra R, where ${\dot{w}}$ is a lift of w to $\breve{{\mathcal {G}}}$.

The semi-infinite Deligne–Lusztig set $X_{\dot{w}}^{DL}(b)$ is the set of all Borel subgroups of $\breve{{\mathcal {G}}}$ in relative position w to their $b \sigma$-translate. It has a cover

$$\begin{aligned} {\dot{X}_{\dot{w}}^{DL}(b) \,{:=}\,\{g \breve{U} \in \breve{{\mathcal {G}}}/\breve{U} : g^{-1} b \sigma (g) \in \breve{U} {\dot{w}} \breve{U}\} \subseteq \breve{{\mathcal {G}}}/{\breve{U}}} \end{aligned}$$

with a natural action by $J_b(K) \times T_w(K)$, and this set coincides with Lusztig’s construction [25]. On the other hand, for arbitrarily deep congruence subgroups $J \subseteq \breve{{\mathcal {G}}}$, one can define affine Deligne–Lusztig sets of higher level J,

$$\begin{aligned} {X_x^J(b) \,{:=}\,\{gJ \in \breve{{\mathcal {G}}}/J :g^{-1}b\sigma (g) \in JxJ \} \subseteq \breve{{\mathcal {G}}}/J,} \end{aligned}$$

where x is a J-double coset in $\breve{{\mathcal {G}}}$. Under some technical conditions on x, we prove that these sets can be endowed with a structure of an ${\mathbb {F}}_q$-scheme (Theorem 4.9). We remark that when K has mixed characteristic, $\breve{{\mathcal {G}}}/J$ is a ind-(perfect scheme), so $X_x^J(b)$ will also carry the structure of a perfect scheme.

We now specialize to the following setting. Consider $\breve{{\mathcal {G}}} = {{\,\mathrm{GL}\,}}_n({\breve{K}})$ and $G = J_b(K)$ for some basic $b \in {{\,\mathrm{GL}\,}}_n(\breve{K})$ so that G is an inner form of ${{\,\mathrm{GL}\,}}_n(K)$. Let w be a Coxeter element so that ${T \,{:=}\,T_w(K) \cong L^\times }$ for the degree-n unramified extension L of K. Let $G_{{\mathcal {O}}}$ be a maximal compact subgroup of G and let $T_{{\mathcal {O}}} = T \cap G_{{\mathcal {O}}} \cong {\mathcal {O}}_L^{\times }$. We consider a particular tower of affine Deligne–Lusztig varieties $\dot{X}_{\dot{w}_r}^m(b)$ for congruence subgroups of $\breve{{\mathcal {G}}}$ indexed by m, where the image of each $\dot{w}_r$ in the Weyl group is w. We form the inverse limit $\dot{X}_w^\infty (b) = \varprojlim \nolimits _{r>m\ge 0} \dot{X}_{\dot{w}_r}^m(b)$, which carries a natural action of $G \times T$.

Theorem

() There is a $(G \times T)$-equivariant map of sets

$$\begin{aligned} \dot{X}_w^{DL}(b) {\mathop {\longrightarrow }\limits ^{\sim }} \dot{X}_w^\infty (b). \end{aligned}$$

In particular, this gives $\dot{X}_w^{DL}(b)$ the structure of a scheme over ${{\overline{{\mathbb {F}}}}}_q$.

We completely determine the higher level affine Deligne–Lusztig varieties $\dot{X}_{\dot{w}_r}^m(b)$. They are $({\mathcal {O}}_L/{\mathfrak {p}}_L^{m+1})^{\times }$-torsors over the schemes $X_{\dot{w}_r}^m(b)$, which are interesting in their own right. In particular, $X_{\dot{w}_r}^0(b)$ provide examples of explicitly described Iwahori-level affine Deligne–Lusztig varieties. We prove the following.

Theorem

() The scheme $X_{\dot{w}_r}^m(b)$ is a disjoint union, indexed by $G/G_{\mathcal {O}}$, of classical Deligne–Lusztig varieties for the reductive quotient of $G_{{\mathcal {O}}} \times T_{{\mathcal {O}}}$ times finite-dimensional affine space.

The disjoint union decomposition is deduced from Viehmann [32]. We point out the similarity between the Iwahori level varieties $X_{\dot{w}_r}^0(b)$ and those considered by Görtz and He [16, e.g. Proposition 2.2.1], though in our setting, the elements $\dot{w}_r$ can have arbitrarily large length in the extended affine Weyl group.

One of the key insights throughout our paper is the flexibility of working with different representatives b of a $\sigma$-conjugacy class. For example, when $G = {{\,\mathrm{GL}\,}}_n(K)$, switching between $b = 1$ and b being a Coxeter element allows us to use techniques that are otherwise inaccessible.

Having established the isomorphism $\dot{X}_w^{DL}(b) {\mathop {\longrightarrow }\limits ^{\sim }} \dot{X}_w^\infty (b)$, the main objective in the rest of the paper is to study the virtual G-representation

$$\begin{aligned} {R_T^G(\theta ) \,{:=}\,\textstyle \sum \limits _i (-1)^i H_i(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]} \end{aligned}$$

for smooth characters $\theta :T \rightarrow \overline{{\mathbb {Q}}}_\ell ^\times$, where $[\theta ]$ denotes the subspace where T acts by $\theta$. We write $|R_T^G(\theta )|$ to denote the genuine representation when one of $\pm R_T^G(\theta )$ is genuine.

One could try to calculate $R_T^G(\theta )$ by calculating the cohomology of the affine Deligne–Lusztig varieties $\dot{X}_{\dot{w}_r}^m(b)$. These finite-level varieties have somewhat strange descriptions (see the equivalence relation ${{\dot{\sim }}}_{b,m,r}$ in Sect. 6.2), though it is conceivable that one could use the results of Part 4 to study the cohomology of these higher-level affine Deligne–Lusztig varieties.

Instead of passing through affine Deligne–Lusztig varieties, we approximate our infinite-level object $\dot{X}_w^{DL}(b)$ by using an analogue of Deligne–Lusztig varieties for parahoric subgroups, which are easier to explicitly describe than affine Deligne–Lusztig varieties. Using the decomposition of ${\dot{X}}_w^{\infty }(b)$ into G-translates of $G_{{\mathcal {O}}}$-stable components (as in Theorem 6.17), the computation of the cohomology of ${\dot{X}}_b^{\infty }(b)$ reduces to the computation for one such component, which can in turn be written as an inverse limit $\varprojlim _h X_h$ of finite-dimensional varieties $X_h$, each endowed with an action of level-h quotients $G_h \times T_h$ of $G_{\mathcal {O}}\times T_{\mathcal {O}}$. We write $R_{T_h}^{G_h}(\theta )$ for the virtual $G_h$-representation corresponding to $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$. We note that $X_1$ is a classical Deligne–Lusztig variety for the reductive subquotient of $T_{\mathcal {O}}$ in the reductive quotient of $G_{{\mathcal {O}}}$.

However, the infinite-level object $\dot{X}_w^\infty (b)$ has a very natural description, so we proceed by defining another tower of finite-dimensional objects $X_h$, which are analogues of Deligne–Lusztig varieties for parahoric subgroups. Using the Deligne–Lusztig fixed-point formula, we compute (part of) the character of $R_{T_h}^{G_h}(\theta )$ on $T_h$, which when combined with Henniart’s characterizations [19, 20] of automorphic induction yields:

Theorem

() Let $\theta :T \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be a smooth character. If $|R_T^G(\theta )|$ is irreducible supercuspidal, then the assignment $\theta \mapsto |R_T^G(\theta )|$ is a geometric realization of automorphic induction and the Jacquet–Langlands correspondence.

Proving that $|R_T^G(\theta )|$ is irreducible supercuspidal involves two main steps: proving that $|R_{T_h}^{G_h}(\theta )|$ is irreducible and proving its induction to G (after extending by the center) is irreducible. In [26], Lusztig studies the irreducibility of $R_{T_h}^{G_h}(\theta )$ for reductive groups over finite rings under a regularity assumption on $\theta$. In our setting, this regularity assumption corresponds to $\theta$ being minimal admissible. We extend Lusztig’s arguments to the non-reductive setting to handle the non-quasi-split inner forms of ${{\,\mathrm{GL}\,}}_n(K)$ and prove that $R_{T_h}^{G_h}(\theta )$ is irreducible under the same regularity assumption on $\theta$ (Theorem 8.1). In this context, we prove a cuspidality result (Theorem 9.1) for $|R_{T_h}^{G_h}(\theta )|$, which allows us to emulate the arguments from [27, Proposition 6.6] that inducing classical Deligne–Lusztig representations gives (depth zero) irreducible supercuspidal representations of p-adic groups. This approach was carried out in the ${{\,\mathrm{GL}\,}}_2$ case for arbitrary depth in [21, Propositions 4.10, 4.22]. Note that the $|R_T^G(\theta )|$ can have arbitrarily large depth, depending on the level of the smooth character $\theta$.

Theorem

() If $\theta :T \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ is minimal admissible, then $|R_T^G(\theta )|$ is irreducible supercuspidal.

1.1 Outline

This paper is divided into four parts. The first part of the article is devoted to purely geometric properties of the Deligne–Lusztig constructions for arbitrary reductive groups over local fields. In Sects. 3 and 4, we define and recall the two types of Deligne–Lusztig constructions. The main result of this part is Theorem 4.9, where we prove that, under a technical hypothesis, affine Deligne–Lusztig sets of arbitrarily deep level can be endowed with a scheme structure. After Part 1, we work only in the context of the inner forms of ${{\,\mathrm{GL}\,}}_n(K)$.

We begin Part 2 with a discussion of the group-theoretic constructions we will use at length throughout the rest of the paper (Sect. 5). We emphasize the importance of the seemingly innocuous Sect. 5.2, where we define two representatives b for each basic $\sigma$-conjugacy class of ${{\,\mathrm{GL}\,}}_n(\breve{K})$. In Sect. 6, we define the affine Deligne–Lusztig varieties $\dot{X}_{\dot{w}_r}^m(b)$, construct an isomorphism between $\dot{X}_w^\infty (b)$ and $\dot{X}_{w}^{DL}(b)$ using the isocrystal $(\breve{K}^n, b\sigma )$, and explicate the scheme structure of $\dot{X}_w^\infty (b)$. In Sect. 7, we introduce a family of smooth finite-type schemes $X_h$ whose limit is a component of $\dot{X}_w^\infty (b)$ corresponding to $G_{{\mathcal {O}}}$ and study its geometry. This plays the role of a Deligne–Lusztig variety for subquotients of G (see Proposition 7.12).

In Part 3, we calculate the cohomology $R_{T_h}^{G_h}(\theta )$ under a certain regularity assumption on $\theta$. We prove irreducibility (Theorem 8.1) using a generalization of [26, 31] discussed in Sect. 8.4. We prove a result about the restriction of $R_{T_h}^{G_h}(\theta )$ to the “deepest part” of unipotent subgroups (Theorem 9.1) which can be viewed as an analogue of cuspidality for $G_h$-representations. This is a long calculation using fixed-point formulas.

Finally, in Part 4, we combine the results of the preceding two parts to deduce our main theorems about $R_T^G(\theta )$, the homology of the affine Deligne–Lusztig variety at infinite level $\dot{X}_w^\infty (b)$. We review the methods of Henniart [19, 20] in Sect. 10, define and discuss some first properties of the homology of $\dot{X}_w^\infty (b)$ in Sect. 11, and prove the irreducible supercuspidality of $R_T^G(\theta )$ for minimal admissible $\theta$ in Sect. 12.

2 Notation

Throughout the paper we will use the following notation. Let K be a non-archimedean local field with residue field ${\mathbb {F}}_q$ of prime characteristic p, and let $\breve{K}$ denote the completion of a maximal unramified extension of K. We denote by ${\mathcal {O}}_K$, ${\mathfrak {p}}_K$ (resp. ${\mathcal {O}}$, ${\mathfrak {p}}$) the integers and the maximal ideal of K (resp. of $\breve{K}$). The residue field of $\breve{K}$ is an algebraic closure ${\overline{{\mathbb {F}}}}_q$ of ${\mathbb {F}}_q$. We write $\sigma$ for the Frobenius automorphism of $\breve{K}$, which is the unique K-automorphism of $\breve{K}$, lifting the ${\mathbb {F}}_q$-automorphism $x \mapsto x^q$ of ${\overline{{\mathbb {F}}}}_q$. Finally, we denote by $\varpi$ a uniformizer of K (and hence of $\breve{K}$) and by ${{\,\mathrm{ord}\,}}= {{\,\mathrm{ord}\,}}_{\breve{K}}$ the valuation of $\breve{K}$, normalized such that ${{\,\mathrm{ord}\,}}(\varpi ) = 1$.

If K has positive characteristic, we let ${\mathbb {W}}$ denote the ring scheme over ${\mathbb {F}}_q$ where for any ${\mathbb {F}}_q$-algebra A, ${\mathbb {W}}(A) = A[\![\pi ]\!]$. If K has mixed characteristic, we let ${\mathbb {W}}$ denote the K-ramified Witt ring scheme over ${\mathbb {F}}_q$ so that ${\mathbb {W}}({\mathbb {F}}_q) = {\mathcal {O}}_K$ and ${\mathbb {W}}({{\overline{{\mathbb {F}}}}}_q) = {\mathcal {O}}$. Let ${\mathbb {W}}_h = {\mathbb {W}}/V^h {\mathbb {W}}$ be the truncated ring scheme, where $V :{\mathbb {W}}\rightarrow {\mathbb {W}}$ is the Verschiebung morphism. For any $1 \le r \le h$, we write ${\mathbb {W}}_h^r$ to denote the kernel of the natural projection ${\mathbb {W}}_h \rightarrow {\mathbb {W}}_r$. As the Witt vectors are only well behaved on perfect ${\mathbb {F}}_q$-algebras, algebro-geometric considerations when K has mixed characteristic are taken up to perfection. We fix the following convention.

Convention If K has mixed characteristic, whenever we speak of a scheme (resp. ind-scheme) over its residue field ${\mathbb {F}}_q$, we mean a perfect scheme (resp. ind-(perfect scheme)), that is a set-valued functor on perfect ${\mathbb {F}}_q$-algebras, representable by the perfection of a scheme (resp. ind-scheme).

For results on perfect schemes we refer to [2, 34]. Note that passing to perfection does not affect the $\ell$-adic étale cohomology; thus for purposes of this paper, we could in principle pass to perfection in all cases. However, in the equal characteristic case working on non-perfect rings does not introduce complications, and we prefer to work in this slightly greater generality.

Fix a prime $\ell \ne p$ and an algebraic closure $\overline{{\mathbb {Q}}}_\ell$ of ${\mathbb {Q}}_\ell$. The field of coefficients of all representations is assumed to be ${{\overline{{\mathbb {Q}}}}}_\ell$ and all cohomology groups throughout are compactly supported $\ell$-adic étale cohomology groups.

2.1 List of terminology

Our paper introduces some notions for a general group G (Part 1) and then studies these notions for G an inner form of ${{\,\mathrm{GL}\,}}_n$ (Parts 2 through 4). The investigations for G an inner form of ${{\,\mathrm{GL}\,}}_n$ involve many different methods. For the reader’s reference, we give a brief summary of the most important notation introduced and used in Parts 2 through 4.

L:

The degree-n unramified extension of K. Its ring of integers ${\mathcal {O}}_L$ has a unique maximal ideal $\mathfrak {p}_L$ and its residue field is ${\mathcal {O}}_L/\mathfrak {p}_L \cong {\mathbb {F}}_{q^n}$. For any $h \ge 1$, we write $U_L^h = 1 + \mathfrak {p}_L^h$

[b]:

Fixed basic $\sigma$-conjugacy class of ${{\,\mathrm{GL}\,}}_n(\breve{K})$. Typically we take representatives b of [b] to be either the Coxeter-type or special representative (Sect. 5.2)

$\kappa$:

$\kappa _{{{\,\mathrm{GL}\,}}_n}([b])$, where $\kappa _{{{\,\mathrm{GL}\,}}_n}$ is the Kottwitz map. We assume that $0 \le \kappa \le n-1$ and set $n' = \gcd (n, \kappa )$, $n_0 = n/n'$, $k_0 = \kappa /n'$

F:

Twisted Frobenius morphism $F :{{\,\mathrm{GL}\,}}_n(\breve{K}) \rightarrow {{\,\mathrm{GL}\,}}_n(\breve{K})$ given by $F(g) = b \sigma (g) b^{-1}$

G:

$= J_b(K) = {{\,\mathrm{GL}\,}}_n(\breve{K})^F \cong {{\,\mathrm{GL}\,}}_{n'}(D_{k_0/n_0})$, where $D_{k_0/n_0}$ is the division algebra with Hasse invariant $k_0/n_0$

T:

$= L^\times$, an unramified elliptic torus in G

$g_b^\mathrm {red}(x)$:

$(n \times n)$-matrix whose ith column is $\varpi ^{-\lfloor (i-1) k_0/n_0 \rfloor } (b\sigma )^{i-1}(x)$ with $x \in V$ (Eq. (6.5))

$\dot{X}_{\dot{w}}^{DL}(b)$:

a semi-infinite Deligne–Lusztig variety, with a natural action of $G \times T$ (Sect. 3)

$\dot{X}_{\dot{w}_r}^m(b)$:

an affine Deligne–Lusztig variety with a natural action of $G \times T$ (Sect. 6.2)

$\dot{X}_w^\infty (b)$:

$= \varprojlim \nolimits _{r > m} \dot{X}_{\dot{w}_r}^m(b) = V_b^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \cong V_b^{\mathrm {adm},\mathrm {rat}} = \{x \in V_b^{\mathrm {adm}} : \det g_b(x) \in K^\times \}$ an affine Deligne–Lusztig variety at the infinite level, with a natural $G \times {\mathcal {O}}_L^\times$-action (Corollary 6.18)

$\dot{X}_w^\infty (b)_{{\mathscr {L}}_0}$:

$= {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \cong {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}} = \{ x \in {\mathscr {L}}_0 :\det g_b^{\mathrm {red}}(x) \in {\mathcal {O}}_K^\times \}$ is the union of connected components of $X_w^\infty (b)$ associated to the lattice ${\mathscr {L}}_0$ (Definition 6.10)

$G_h$:

$= {\mathbb {G}}_h({\mathbb {F}}_q) = (\breve{G}_{{\mathbf {x}},0}/\breve{G}_{{\mathbf {x}},(h-1)+})^F$ where $F(g) = b \sigma (g) b^{-1}$ for b the Coxeter-type or special representative. $G_h$ is a subquotient of G (Sect. 5.3)

$T_h$:

$= {\mathbb {T}}_h({\mathbb {F}}_q) \cong {\mathcal {O}}_L^\times /U_L^h$

$X_h$:

A quotient of $\dot{X}_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$ for any $r > m \ge 0$ (Sect. 7.6). It has a $(G_h \times T_h)$-action and is a finite-ring analogue of a Deligne–Lusztig variety (Proposition 7.12)

$R_{T_h}^{G_h}(\theta )$:

$= \sum _i (-1)^i H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$, where $H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] \subset H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )$ is the subspace where $T_h$ acts by $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$

$R_T^G(\theta )$:

$= \sum _i (-1)^i H_i(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] = \sum _i (-1)^i H_i(\dot{X}_w^{DL}(b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$, where the homology groups of the scheme $\dot{X}_w^\infty (b)$ are defined in Sect. 11 and where $[\theta ]$ denotes the subspace where T acts by $\theta :T \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$

${\mathscr {X}}$:

The set of all smooth characters of $L^\times$ that are in general position; i.e., they have trivial stabilizer in ${{\,\mathrm{Gal}\,}}(L/K)$ (Part 4)

${\mathscr {X}}^{\mathrm{min}}$:

The set of all characters of $L^\times$ that are minimal admissible (Sect. 12)

The action of $G \times T$ on each of the schemes $\dot{X}_{\dot{w}_r}^m(b), \dot{X}_w^\infty (b), \dot{X}_w^{DL}(b)$ is given by $x \mapsto g x t$. These actions descend to an action of $G_h \times T_h$ on $X_h$.

3 Part 1. Deligne–Lusztig constructions for p-adic groups

In this part we discuss two analogues of Deligne–Lusztig constructions attached to a reductive group over K: semi-infinite Deligne–Lusztig sets and affine Deligne–Lusztig varieties at higher level. We begin by fixing some notation.

Let G be a connected reductive group over K. Let S be a maximal $\breve{K}$-split torus in G. By [8, 5.1.12] it can be chosen to be defined over K. Let $T = {\mathscr {Z}}_G(S)$ and ${\mathscr {N}}_G(S)$ be the centralizer and normalizer of S, respectively. By Steinberg’s theorem, $G_{\breve{K}}$ is quasi-split, hence T is a maximal torus. The Weyl group W of S in G is the quotient $W = {\mathscr {N}}_G(S)/T$ of the normalizer of S by its centralizer. By [3, Theorem 21.2], every connected component of ${\mathscr {N}}_G(S)$ meets $\breve{G}$, so $W = {\mathscr {N}}_G(S)(\breve{K})/\breve{T}$. In particular, the action of the absolute Galois group of K on W factors through a ${{\,\mathrm{Gal}\,}}(\breve{K}/K)$-action.

For a scheme X over K, the loop space LX of X is the functor on ${\mathbb {F}}_q$-algebras given by $LX(R) = X({\mathbb {W}}(R)[\varpi ^{-1}])$. For a scheme ${\mathfrak {X}}$ over ${\mathcal {O}}$, the space of positive loops $L^+{\mathfrak {X}}$ of ${\mathfrak {X}}$ is the functor on ${\mathbb {F}}_q$-algebras given by $L^+{\mathfrak {X}}(R) = {\mathfrak {X}}({\mathbb {W}}(R))$, and the functor $L^+_h$ of truncated positive loops is given by $L^+_h {\mathfrak {X}} (R) = {\mathfrak {X}}({\mathbb {W}}_h(R))$.

For any algebro-geometric object X over K, we write $\breve{X}$ for the set of its $\breve{K}$-rational points.

4 Semi-infinite Deligne–Lusztig sets in G/B

Assume that G is quasi-split. Pick a K-rational Borel $B \subseteq G$ containing T and let U be the unipotent radical of B. We have the following direct analogue of classical Deligne–Lusztig varieties [13].

Definition 3.1

Let $w \in W$, $\dot{w} \in {\mathscr {N}}_G(S)(\breve{K})$ a lift of w, and $b \in \breve{G}$. The semi-infinite Deligne–Lusztig sets $X_w^{DL}(b), \dot{X}_w^{DL}(b)$ are

$$\begin{aligned} X_w^{DL}(b)&= \{ g \in \breve{G}/ \breve{B} : g^{-1}b\sigma (g) \in \breve{B} w \breve{B}\}, \\ \dot{X}_{{\dot{w}}}^{DL}(b)&= \{ g \in \breve{G}/\breve{U} : g^{-1}b\sigma (g) \in \breve{U} \dot{w} \breve{U} \}. \end{aligned}$$

There is a natural map $\dot{X}_{{\dot{w}}}^{DL}(b) \rightarrow X_w^{DL}(b)$, $g\breve{U} \mapsto g\breve{B}$.

For $b \in \breve{G}$, we denote by $J_b$ the $\sigma$-stabilizer of b, which is the K-group defined by

$$\begin{aligned} {J_b(R) \,{:=}\,\{ g \in G(R \otimes _K \breve{K}) : g^{-1} b \sigma (g) = b \}} \end{aligned}$$

for any K-algebra R (cf. [30, 1.12]). Then $J_b$ is an inner form of the centralizer of the Newton point b (which is a Levi subgroup of G). In particular, if b is basic, i.e., the Newton point of b is central, then $J_b$ is an inner form of G. Let $w \in W$ and let ${\dot{w}} \in {\mathscr {N}}_G(S)(\breve{K})$ be a lift. We denote by $T_w$ the $\sigma$-stabilizer of $\dot{w}$ in T, which is the K-group defined by

$$\begin{aligned} {T_w(R) \,{:=}\,\{ t \in T(R \otimes _K \breve{K}) : t^{-1}{\dot{w}}\sigma (t) = {\dot{w}} \}.} \end{aligned}$$

for any K-algebra R. As T is commutative, this only depends on w, not on ${\dot{w}}$.

Lemma 3.2

Let $b\in \breve{G}$ and let $w \in W$ with lift ${\dot{w}} \in {\mathscr {N}}_G(S)(\breve{K})$.

• (i) Let $g \in \breve{G}$. The map $x\breve{B} \mapsto gx\breve{B}$ defines a bijection $X_w^{DL}(b) {\mathop {\rightarrow }\limits ^{\sim }} X_w^{DL}(g^{-1}b\sigma (g))$.

• (ii) Let $g \in \breve{G}$ and $t \in \breve{T}$. The map $x\breve{U} \mapsto gxt\breve{U}$ defines a bijection $\dot{X}_{{\dot{w}}}^{DL}(b) {\mathop {\rightarrow }\limits ^{\sim }} \dot{X}_{t^{-1}{\dot{w}}\sigma (t)}^{DL}(g^{-1}b\sigma (g))$.

• (iii) There are actions of $J_b(K)$ on $X_w^{DL}(b)$ given by $(g, x\breve{B}) \mapsto gx\breve{B}$ and of $J_b(K) \times T_w(K)$ on $\dot{X}_{{\dot{w}}}^{DL}(b)$ given by $(g,t,x\breve{U}) \mapsto gxt\breve{U}$. They are compatible with $\dot{X}_{{\dot{w}}}^{DL}(b) \rightarrow X_w^{DL}(b)$, and if this map is surjective, then $\dot{X}_{{\dot{w}}}^{DL}(b)$ is a right $T_w(K)$-torsor over $X_w^{DL}(b)$.

Proof

(i) and (ii) follow from the definitions by immediate computations. (iii) follows from (i) and (ii). $\square$

Remark 3.3

• (i) Whereas the classical Deligne–Lusztig varieties are always non-empty, $X_w^{DL}(b)$ is non-empty if and only if the $\sigma$-conjugacy class [b] of b in $G(\breve{K})$ intersects the double coset $\breve{B} w \breve{B}$. For example, if $G = {{\,\mathrm{GL}\,}}_n$ ($n \ge 2$) and b is superbasic, then $X_1^{DL}(b) = \varnothing$, as was observed by E. Viehmann.

• (ii) L. Fargues pointed out the following way to endow the semi-infinite Deligne–Lusztig set $X_w^{DL}(1)$ (and $\dot{X}_{\dot{w}}^{DL}(b)$ if $T_w$ is elliptic) with a scheme structure: assume that G (and B) come from a reductive group over ${\mathcal {O}}_K$ (again denoted G), such that G/B is a projective ${\mathcal {O}}_K$-scheme. Then

  $$\begin{aligned} (G/B)(\breve{K}) = (G/B)({\mathcal {O}}) = \mathop {\underleftarrow{\lim } }_r (G/B)({\mathcal {O}}/{\mathfrak {p}}^r). \end{aligned}$$

  Now $(G/B)({\mathcal {O}}/{\mathfrak {p}}^r) = L^+_r(G/B)({\overline{{\mathbb {F}}}}_q)$ is a finite dimensional ${\mathbb {F}}_q$-scheme via $L^+_r$. For a given element w in the finite Weyl group, the corresponding Deligne–Lusztig condition is given by a finite set of open and closed conditions in G/B which involve $\sigma$. The closed conditions cut a closed, hence projective, subscheme of G/B, and replacing G/B by this closed subscheme Z, we may assume that there are only open conditions. These define an open subscheme $Y_r$ in each $L^+_r Z$. Set ${X_w^{DL}(1)_r \,{:=}\,{{\,\mathrm{pr}\,}}_r^{-1}(Y_r)}$, where ${{\,\mathrm{pr}\,}}_r :L^+Z \rightarrow L^+_rZ$ is the projection. This gives $X_w^{DL}(1)_r$ the structure of an open subscheme of $L^+Z$ and $X_w(1) = \bigcup _{r = 1}^{\infty } X_w^{DL}(1)_r$ is now an (ascending) union of open subschemes of $L^+Z$. Note that since the transition morphisms are not closed immersions, this union does not define an ind-scheme. Now if w is such that $T_w$ is elliptic, then $T_w(K)$ is compact modulo Z(K), where Z is the center of G, and $\dot{X}^{DL}_w(1)$—being a $T_w(K)$-torsor over $X_w^{DL}(1)$—is a scheme. However, this scheme structure appears to be the “correct” one only on the subscheme $X_w^{DL}(1)_1$, as the action of $G(K) = J_1(K)$ on $X_w^{DL}(1)$ cannot in general be an action by algebraic morphisms (whereas the action of $G({\mathcal {O}}_K)$ on $X_w^{DL}(1)_1$ is). This will become clear from the $\mathrm{SL}_2$-example discussed in Sect. 6.5 below. $\Diamond$

Finally we investigate the relation of $\dot{X}_{\dot{w}}^{DL}(b)$ with Lusztig’s constructions from [25, 26]. In fact, consider the map $F :\breve{G} \rightarrow \breve{G}, g \mapsto b \sigma (g) b^{-1}$. Assuming that (w, b) satisfies $w\breve{B} = b\sigma (\breve{B})$, so that $w \breve{B} b^{-1} = F(\breve{B})$,

$$\begin{aligned} X_w^{DL}(b)&= \{ g\breve{B} \in \breve{G}/\breve{B} : g^{-1} b \sigma (g) \in \breve{B}w\breve{B} \} \\&= \{ g\breve{B} \in \breve{G}/\breve{B} : g^{-1}F(g) \in \breve{B}F(\breve{B}) \} \\&= \{ g \in \breve{G} : g^{-1}F(g) \in F(\breve{B})\} / (\breve{B} \cap F(\breve{B})) \\ \end{aligned}$$

Similarly, assuming that $({\dot{w}},b)$ satisfies ${\dot{w}}\breve{U} = b\sigma (\breve{U})$, so that ${\dot{w}}\breve{U}b^{-1} = F(\breve{U})$,

$$\begin{aligned} \dot{X}_{{\dot{w}}}^{DL}(b) = \{g \in \breve{G} : g^{-1}F(g) \in F(\breve{U})\} / (\breve{U} \cap F(\breve{U})). \end{aligned}$$

This is precisely the definition of the semi-infinite Deligne–Lusztig set in [25]. It was studied by Boyarchenko [5] and the first named author [10,11,12] in the case when $G = {{\,\mathrm{GL}\,}}_n$ and b superbasic, i.e., $J_b(K)$ are the units of a division algebra over K, where it admits an ad hoc scheme structure.

In the setting of Part 2 of this paper (see Theorem 6.5), it will turn out that $X_w^{DL}(b) = \{g \in \breve{G} : g^{-1}F(g) \in F(\breve{U})\}/(\breve{T}^F (\breve{U} \cap F(\breve{U}))) = \dot{X}_{\dot{w}}^{DL}(b)/\breve{T}^F$. This is quite nontrivial. In the finite field setting [13, Definition 1.17(i)], this is true because the Lang map $g \mapsto g^{-1}F(g)$ is surjective. In the setting of p-adic groups (even in our ${{\,\mathrm{GL}\,}}_n$ setting), the Lang map is no longer surjective. However, a corollary of Theorem 6.5 is that for any $x \in X_w^{DL}(b)$, there exists a representative $g \in \breve{G}$ such that $g^{-1}F(g) = tu \in F(\breve{B})$ with t in the image of the Lang map on $\breve{T}$.

5 Affine Deligne–Lusztig varieties and covers

Let the notation be as in the beginning of part 1. In this section we recall from [21] the definition of affine Deligne–Lusztig varieties of higher level, and prove that they are locally closed in the affine Grassmannian (Theorem 4.9 and Corollary 4.10).

5.1 Affine Grassmannian

We will use representability results on affine Grassmannians attached to G, which were proven by Pappas–Rapoport [28] in the equal characteristic case, and by Zhu [34] and Bhatt–Scholze [2] in the mixed characteristic case. Let ${\mathcal {G}}$ be a smooth affine ${\mathcal {O}}_K$-scheme with generic fiber G and with connected special fiber. The functor $L^+{\mathcal {G}}$ is represented by an (infinite-dimensional) affine group scheme over ${\mathbb {F}}_q$. The functor LG is represented by a strict ind-scheme of ind-finite type; that is, LG can be written as a direct limit of schemes of finite type, with transition morphisms being closed immersions.

The affine Grassmannian associated with ${\mathcal {G}}$ is the fpqc-sheaf $LG/L^+{\mathcal {G}}$, which is the sheafification for the fpqc-topology of the functor on ${\mathbb {F}}_q$-algebras given by

$$\begin{aligned} R \mapsto LG(R)/L^+{\mathcal {G}}(R). \end{aligned}$$

It possesses the following representability properties.

Theorem 4.1

(cf. [28, Theorem 1.4], [34, Theorem 1.4] and [2, Corollary 9.6]) The fpqc-sheaf $LG/L^+{\mathcal {G}}$ on ${\mathbb {F}}_q$-algebras is represented by a strict ind-scheme. The quotient morphism $LG \rightarrow LG/L^+{\mathcal {G}}$ has sections locally for the étale topology (i.e., $\mathrm{Spec}(R) \times _{LG/L^+{\mathcal {G}}} LG \cong \mathrm{Spec}(R) \times _{\mathrm{Spec}({\mathbb {F}}_q)} L^+{\mathcal {G}}$ for each point of $LG/L^+{\mathcal {G}}$ with values in a strictly henselian ring R).

Moreover, if ${\mathcal {G}}$ is parahoric, then $LG/L^+{\mathcal {G}}$ is ind-proper, but we will not use this in the following. In general, the affine Grassmannian is not reduced. We have $LG/L^+{\mathcal {G}}({\overline{{\mathbb {F}}}}_q) = \breve{G} / {\mathcal {G}}({\mathcal {O}})$.

5.2 Level subgroups

Let $\Phi = \Phi (G_{\breve{K}}, S)$ denote the set of roots of S in $G_{\breve{K}}$ and let $U_{\alpha }$ denote the root subgroup for $\alpha \in \Phi$. Put ${U_0 \,{:=}\,T}$.

Let $\mathbf{x}$ be a point in the apartment of S inside the Bruhat–Tits building of the adjoint group of G over $\breve{K}$. Attached to it, there is a valuation of the root datum of G in the sense of Bruhat–Tits [8]. In particular, for each $\alpha \in \Phi$, it induces a descending filtration $\breve{U}_{\alpha , r}$ on $\breve{U}_{\alpha }$ with $r \in \widetilde{{\mathbb {R}}}$, where ${\widetilde{{\mathbb {R}}} \,{:=}\,{\mathbb {R}} \cup \{r+ :r \in {\mathbb {R}}\} \cup \{\infty \}}$ is the ordered monoid as in [8, 6.4.1]. Further, a choice of an admissible schematic filtration on tori (in the sense of [33, §4]) also defines a descending filtration $\breve{U}_{0, r} := \breve{U}_{0,r}$ on $\breve{U}_0$. (If G is either simply connected or adjoint, or split over a tamely ramified extension, this filtration coincides with the Moy–Prasad filtration, and hence is independent on the choice.) For any concave function $f :\Phi \cup \{0\} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$, let $\breve{G}_f$ denote the subgroup of $\breve{G}$ (depending on $\mathbf{x}$) generated by $U_{\alpha ,f(\alpha )}$ ($\alpha \in \Phi \cup \{0\}$). In [33, Theorem 8.3] it is shown that there exists a smooth affine group scheme ${\mathcal {G}}_f$ over ${\mathcal {O}}$ with generic fiber G, satisfying ${\mathcal {G}}_f({\mathcal {O}}) = \breve{G}_f$. Moreover, assume that $\mathbf{x}$ is stable under the action of $\sigma$ on the adjoint building. Then ${\mathcal {G}}_f$ descends to a smooth affine group scheme over ${\mathcal {O}}_K$, again denoted ${\mathcal {G}}_f$ [33, §9.1].

Proposition 4.2

Let $f,g :\Phi \cup \{0\} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ be two concave functions with $g \ge f$.

• (i) $L^+{\mathcal {G}}_g$ is a closed subgroup scheme of $L^+{\mathcal {G}}_f$.

Assume that ${\mathcal {G}}_g$ is normal in ${\mathcal {G}}_f$, and that $L^+{\mathcal {G}}_g$ is pro-unipotent.

• (ii) The fpqc quotient sheaf $L^+{\mathcal {G}}_f / L^+{\mathcal {G}}_g$ is representable by a smooth affine ${\mathbb {F}}_q$-group scheme. The morphism $L^+{\mathcal {G}}_f \rightarrow L^+{\mathcal {G}}_f / L^+{\mathcal {G}}_g$ splits Zariski-locally on the target.

• (iii) The fpqc sheaf morphism $LG/L^+{\mathcal {G}}_g \rightarrow LG/L^+{\mathcal {G}}_f$ is represented in the category of ind-schemes. It is thus an $L^+{\mathcal {G}}_f / L^+{\mathcal {G}}_g$-torsor in the category of ind-schemes. It admits sections locally for the étale topology on $LG/L^+{\mathcal {G}}_f$.

Proof

When ${\mathcal {G}}_g, {\mathcal {G}}_f$ are parahoric models of G, part (i) is shown in [28, Proposition 8.7(a)]. In the general case, (i) follows by the same argument. To see (ii), first observe that $L^+{\mathcal {G}}_g \hookrightarrow L^+{\mathcal {G}}_f$ is a monomorphism of sheaves (although ${\mathcal {G}}_g \rightarrow {\mathcal {G}}_f$ is not an immersion if $f \ne g$), as ${\mathcal {G}}_g$ is obtained from ${\mathcal {G}}_f$ by a series of dilatations (see [4, §3]) of closed subschemes in the special fiber. Put ${\mathcal {G}}_f^{(0)} = {\mathcal {G}}_f$ and for $h \ge 1$, let ${\mathcal {G}}_f^{(h)}$ be the dilatation of ${\mathcal {G}}_f^{(h-1)}$ along the unit section of the special fiber. Then $L^+{\mathcal {G}}_f^{(h)} = \ker (L^+{\mathcal {G}}_f \rightarrow L^+_h{\mathcal {G}}_f)$ (cf. [34, p. 414]). We can find an $h \ge 1$, such that the natural morphism ${\mathcal {G}}_f^{(h)} \rightarrow {\mathcal {G}}_f$ factors through ${\mathcal {G}}_g \rightarrow {\mathcal {G}}_f$. This gives closed immersions $L^+{\mathcal {G}}_f^{(h)} \hookrightarrow L^+{\mathcal {G}}_g \hookrightarrow L^+{\mathcal {G}}_f$. Applying the natural morphism of functors $L^+ \rightarrow L^+_h$ to the arrow ${\mathcal {G}}_g \rightarrow {\mathcal {G}}_f$, and using that $L^+ \rightarrow L^+_h$ is surjective when evaluated at a flat ${\mathcal {O}}_K$-scheme, we thus obtain the following commutative diagram of fpqc-sheaves on ${\mathbb {F}}_q$-algebras, with exact rows and columns:

Now a diagram chase shows that the right vertical map is a monomorphism. Hence it is an isomorphism. We have presented $L^+{\mathcal {G}}_f/L^+{\mathcal {G}}_g$ as a quotient of two finite dimensional smooth affine group schemes. The last claim of (ii) follows as in the proof of [28, Proposition 8.7(b)].

Finally, we prove (iii). It is clear that the morphism of fpqc sheaves $p :LG / L^+{\mathcal {G}}_g \rightarrow LG/L^+{\mathcal {G}}_f$ is an $L^+{\mathcal {G}}_f/L^+{\mathcal {G}}_g$-torsor. A (sheaf-)torsor under an affine group scheme is always relatively representable, so we deduce from (ii) that for any scheme T and any morphism $t :T \rightarrow LG / L^+{\mathcal {G}}_f$, the pullback $p_t :T \times _{LG/L^+{\mathcal {G}}_f} LG / L^+{\mathcal {G}}_g \rightarrow T$ is a morphism of schemes. This implies that $LG / L^+{\mathcal {G}}_g \rightarrow LG/L^+{\mathcal {G}}_f$ is a morphism of ind-schemes. The last claim follows from Theorem 4.1. $\square$

5.3 Affine Deligne–Lusztig varieties of higher level

Until the end of Sect. 4, we fix a $\sigma$-stable $\mathbf{x}$ as above, and a $\sigma$-stable Iwahori subgroup $I \subseteq \breve{G}$, whose corresponding alcove in the building contains $\mathbf{x}$. There is a function $f_I :\Phi \cup \{0\} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ satisfying $\breve{G}_{\mathbf{x},f_I} = I$, and we have the corresponding integral model ${\mathcal {I}}:= {\mathcal {G}}_{\mathbf{x}, f_I}$. The extended affine Weyl group of S in G is ${\widetilde{W}} = {\mathscr {N}}_G(S)(\breve{F})/{\mathscr {N}}_G(S)(\breve{F}) \cap I$.

In [29] Rapoport introduced an affine Deligne–Lusztig variety attached to elements $w \in {\widetilde{W}}$ and $b \in \breve{G}$,

$$\begin{aligned} X_w(b) = \{ gI \in \breve{G}/I: g^{-1}b\sigma (g) \in IwI \} \subseteq \breve{G}/I = (LG/L^+{\mathcal {I}})({\overline{{\mathbb {F}}}}_q). \end{aligned}$$

It is a locally closed subset of $LG/L^+{\mathcal {I}}$, hence it inherits the reduced induced sub-ind-scheme structure (see also Theorem 4.9 below). It is even a scheme locally of finite type over ${\mathbb {F}}_q$. Covers of $X_w(b)$ were introduced by the second named author in [21]. We recall the definition (cf. [22, Sections 2.1–2.2] for a discussion in a more general setup).

Definition 4.3

Let $b \in \breve{G}$. Let $f :\Phi \cup \{0\} \rightarrow {\widetilde{R}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ be a concave function such that $\breve{G}_f$ is $\sigma$-stable. Let $x \in \breve{G}_f \backslash \breve{G} /\breve{G}_f$ be a double coset. Then we define the corresponding affine Deligne–Lusztig set of level f,

$$\begin{aligned} {X_x^f(b) \,{:=}\,\{g\breve{G}_f \in \breve{G}/\breve{G}_f: g^{-1}b\sigma (g) \in \breve{G}_f x \breve{G}_f \} \subseteq \breve{G}/\breve{G}_f = (LG/L^+{\mathcal {G}}_f)({\overline{{\mathbb {F}}}}_q).} \end{aligned}$$

If $J = \breve{G}_f$ satisfies the assumptions in the definition, we sometimes also write $X_x^J(b)$ for $X_x^f(b)$. We will prove that $X_x^f(b)$ is in certain cases a locally closed subset of $LG/L^+{\mathcal {G}}_f$ (Theorem 4.9). There is a natural $J_b(K)$-action by left multiplication on $X_x^f(b)$ for all f and all x. If $f' \ge f$ and $x^{\prime } \in \breve{G}_{f'}\backslash \breve{G} / \breve{G}_{f'}$ lies over $x \in \breve{G}_f \backslash \breve{G}/\breve{G}_f$, then the natural projection $\breve{G}/\breve{G}_{f'} \twoheadrightarrow \breve{G}/\breve{G}_f$ restricts to a map $X_{x^{\prime }}^{f'}(b) \rightarrow X_x^f(b)$. Concerning the right action, we have the following lemma.

Lemma 4.4

Let $J' = \breve{G}_{f'}$ and $J = \breve{G}_f$ be two subgroups as in Definition 4.3, such that $J'$ is a normal subgroup of J. Let $x' \in J'\backslash \breve{G} / J'$ lie over $x \in J\backslash \breve{G} / J$ and let $b \in \breve{G}$.

• (i) Any $i \in J$ defines an $X_x^J(b)$-isomorphism $X_{x'}^{J'}(b) \rightarrow X_{i^{-1}x'\sigma (i)}^{J'}(b)$ given by $g J' \mapsto g i J'$.

• (ii) If $X_{x'}^{J'}(b) \rightarrow X_x^J(b)$ is surjective, then $X_{x'}^{J'}(b)$ is set-theoretically a $(J/J')_{x'}$-torsor over $X_x^J(b)$, where

  $$\begin{aligned} {(J/J')_{x'} \,{:=}\,\{ i \in J : i^{-1} x' \sigma (i) = x' \}/J'.} \end{aligned}$$

Proof

Since $J'$ is normal in J, we see that $i J' x' J' \sigma (i)^{-1} = J' i x' \sigma (i)^{-1} J'$. This implies (i). For (ii) we need to show that $(J/J')_{x'}$ acts faithfully and transitively on the fibers of $\varphi :X_{x'}^{J'}(b) \rightarrow X_x^J(b)$. By definition, $\varphi ^{-1}(g J) = \{gh J' : h \in J\text { and } (gh)^{-1} b \sigma (gh) \in J' x' J'\}$. The claim follows from normality of $J'$ in J and the definition of $(J/J')_{x'}$. $\square$

5.4 Scheme structure

We need some notation. Write ${{\widehat{\Phi }} \,{:=}\,\Phi \cup \{0\}}$. Let $\Phi _{\mathrm {aff}}$ denote the set of affine roots of S in G and let ${{\widehat{\Phi }}}_\mathrm {aff}$ be the disjoint union of $\Phi _\mathrm {aff}$ with the set of all pairs (0, r) with $r \in \widetilde{{\mathbb {R}}}_{< \infty }$, for which the filtration step $\breve{U}_{0, r}/\breve{U}_{0, r+}$ is non-trivial. There is a natural projection $p :{{\widehat{\Phi }}}_{\mathrm {aff}} \twoheadrightarrow {{\widehat{\Phi }}}$, mapping an affine root to its vector part and (0, r) to 0. We extend the action of ${\widetilde{W}}$ on $\Phi , \Phi _\mathrm {aff}$ to an action on ${\widehat{\Phi }}, {{\widehat{\Phi }}}_\mathrm {aff}$ by letting it act trivially on 0 and all (0, r).

By [33], for any $\alpha \in {\widehat{\Phi }}$ and $r \in \tilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$, there is an ${\mathcal {O}}$-scheme ${\mathcal {U}}_{\alpha ,r}$ satisfying ${\mathcal {U}}_{\alpha ,r}({\mathcal {O}}) = \breve{U}_{\alpha ,r}$ whose generic fibre is $U_{\alpha , \breve{K}}$. If $f :{{\widehat{\Phi }}} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ is concave, the schematic closure of $U_{\alpha }$ in ${\mathcal {G}}_f$ is ${\mathcal {U}}_{\alpha , f(\alpha )}$. If $r < s$ in $\widetilde{{\mathbb {R}}}_{< \infty }$, there is a unique morphism of group schemes ${\mathcal {U}}_{\alpha ,s} \rightarrow {\mathcal {U}}_{\alpha ,r}$ which induces the natural inclusion $\breve{U}_{\alpha , s} \hookrightarrow \breve{U}_{\alpha , r}$ on ${\mathcal {O}}$-points. Let $L_{[r,s)}{\mathcal {U}}_{\alpha }$ be the fpqc quotient sheaf

$$\begin{aligned} L_{[r,s)}{\mathcal {U}}_{\alpha } = L^+{\mathcal {U}}_{\alpha ,r}/L^+{\mathcal {U}}_{\alpha ,s}. \end{aligned}$$

It is represented by a finite-dimensional group scheme over ${\overline{{\mathbb {F}}}}_q$.

Lemma 4.5

Let $f :{\widehat{\Phi }} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ be a concave function such that $\breve{G}_f \subseteq I$ is a normal subgroup. Then there is an isomorphism of ${\overline{{\mathbb {F}}}}_q$-schemes

$$\begin{aligned} \textstyle \prod \limits _{\alpha \in {{\widehat{\Phi }}}} L_{[f_I(\alpha ),f(\alpha ))}{\mathcal {U}}_{\alpha } \rightarrow L^+{\mathcal {I}}/L^+{\mathcal {G}}_f, \end{aligned}$$

which on geometric points is given by $(a_{\alpha })_{\alpha \in {{\widehat{\Phi }}}} \rightarrow \prod _{\alpha } {\tilde{a}}_{\alpha }$, where ${\tilde{a}}_{\alpha }$ is any lift of $a_{\alpha }$ to $\breve{U}_{\alpha ,f_I(\alpha )}$ and the product can be taken in any order.

Proof

The conclusion of [8, 6.4.48] also holds for the Iwahori subgroup, i.e., for the function $f_I$ (this follows from the Iwahori decomposition). Thus there is a bijection

$$\begin{aligned} \textstyle \prod \limits _{\alpha \in {{\widehat{\Phi }}}} L^+{\mathcal {U}}_{\alpha ,f_I(\alpha )}({\overline{{\mathbb {F}}}}_q) \rightarrow I, \quad (a_{\alpha })_{\alpha \in \Phi \cup \{0\}} \rightarrow \prod _{\alpha } a_{\alpha }, \end{aligned}$$

given by multiplication in any order, and a similar statement for $I,f_I$ replaced by $\breve{G}_f,f$. The statement of the lemma on geometric points follows from these bijections by normality of $\breve{G}^f$ in I. Now, the map $(a_{\alpha })_{\alpha \in {{\widehat{\Phi }}}} \rightarrow \prod _{\alpha } {\tilde{a}}_{\alpha }$ in the lemma is an algebraic morphism between smooth varieties that is bijective on geometric points and hence an isomorphism. $\square$

Let $x \in {\widetilde{W}}$. We give an explicit parametrization of the set of double cosets $\breve{G}_f \backslash IxI / \breve{G}_f$ in certain cases. For simplicity, we abuse the notation in the following few lemmas and write x again for any lift of x to $\breve{G}$. We say also that $(\alpha ,m) \in \widehat{\Phi }_\mathrm {aff}$ occurs in a subgroup J of $\breve{G}$, if $\breve{U}_{\alpha ,m}$ is contained in J. Then $(\alpha ,m)$ occurs in $\breve{G}_f$ if and only if $m \ge f(\alpha )$. Let $\widehat{\Phi }_\mathrm {aff}(J) \subseteq {{\widehat{\Phi }}}_\mathrm {aff}$ denote the set of all pairs $(\alpha ,m)$ occurring in J. If $J^{\prime } \subseteq J$ is a normal subgroup, let ${\widehat{\Phi }_\mathrm {aff}(J/J^{\prime }) \,{:=}\,\widehat{\Phi }_\mathrm {aff}(J) {\,\smallsetminus \,}{{\widehat{\Phi }}}_\mathrm {aff}(J^{\prime })}$.

Let $f :{{\widehat{\Phi }}} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ be a concave function such that $\breve{G}_f \subseteq I$ is a normal subgroup. For $x \in {\widetilde{W}}$, we can divide the set of all affine roots $\Phi _\mathrm {aff}(I/\breve{G}_f)$ into three disjoint parts $A_x$, $B_x$, $C_x$:

$$\begin{aligned} A_x&= \{(\alpha ,m) \in {{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f) :x.(\alpha ,m) \not \in {{\widehat{\Phi }}}_\mathrm {aff}(I) \} \nonumber \\ B_x&= \{ (\alpha ,m) \in {{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f) :x.(\alpha ,m) \in {{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f) \} \nonumber \\ C_x&= \{ (\alpha ,m) \in \widehat{\Phi }_\mathrm {aff}(I/\breve{G}_f) :x.(\alpha ,m) \in \widehat{\Phi }_\mathrm {aff}(\breve{G}_f) \} \end{aligned}$$

(4.1)

Lemma 4.6

Let $f :{{\widehat{\Phi }}} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{\infty \}$ be a concave, such that $\breve{G}_f \subseteq I$ is a normal subgroup. Let $x \in {\widetilde{W}}$. Assume that $p(A_x)$, $p(B_x)$ and $p(C_x)$ are mutually disjoint, and that the same is true for $p(A_{x^{-1}}), p(B_{x^{-1}}), p(C_{x^{-1}})$. Then there is a well-defined bijective map

$$\begin{aligned}&\textstyle \prod \limits _{\alpha \in p(A_{x^{-1}})} L_{[f_I(\alpha ),f(\alpha ))} {\mathcal {U}}_{\alpha }({\overline{{\mathbb {F}}}}_q) \\&\quad \times \prod \limits _{\alpha \in p(B_x)} L_{[f_I(\alpha ),f(\alpha ))} {\mathcal {U}}_{\alpha }({\overline{{\mathbb {F}}}}_q) \\&\quad \times \prod \limits _{\alpha \in p(A_x)} L_{[f_I(\alpha ),f(\alpha ))} {\mathcal {U}}_{\alpha }({\overline{{\mathbb {F}}}}_q) \rightarrow \breve{G}_f \backslash IxI / \breve{G}_f \\ \end{aligned}$$

given by $((a_{\alpha })_{\alpha \in p(A_{x^{-1}})}, (b_{\alpha })_{\alpha \in p(B_x)}, (a_{\alpha })_{\alpha \in p(A_x)}) \mapsto \prod _{\alpha \in p(A_{x^{-1}})} {\tilde{a}}_{\alpha } \cdot x \cdot \prod _{\alpha \in p(B_x)} {\tilde{b}}_{\alpha } \cdot \prod _{\alpha \in p(A_x)} {\tilde{a}}_{\alpha }$, where ${\tilde{a}}_{\alpha }$ is any lift of $a_{\alpha }$ to an element of $\breve{U}_{\alpha ,f_I(\alpha )}$, and similarly for $\tilde{b}_{\alpha }, b_{\alpha }$. This endows the set $\breve{G}_f \backslash IxI/\breve{G}_f$ with the structure of a reduced ${\overline{{\mathbb {F}}}}_q$-scheme of finite type.

Proof

That the claimed map is well-defined follows from Lemma 4.5. We have an obvious surjective map $I/\breve{G}_f \times I/\breve{G}_f \rightarrow \breve{G}_f \backslash IxI / \breve{G}_f$, given by $(i \breve{G}_f, j \breve{G}_f) \mapsto \breve{G}_f i x j \breve{G}_f$. By Lemma 4.5, we may write any element of the left $I/\breve{G}_f$ as product $a_{x^{-1}} b_{x^{-1}} c_{x^{-1}}$, where $a_{x^{-1}} = \prod _{\alpha \in p(A_{x^{-1}})} a_{\alpha }$, etc. Thus any element of $\breve{G}_f \backslash IxI / \breve{G}_f$ may be written in the form

$$\begin{aligned} \breve{G}_f {\tilde{a}}_{x^{-1}} {\tilde{b}}_{x^{-1}} {\tilde{c}}_{x^{-1}} \cdot x \cdot j \breve{G}_f, \end{aligned}$$

(4.2)

for some $j \in I$, where $\tilde{(\cdot )}$ denotes an arbitrary lift of an element to the root subgroup. Bringing ${\tilde{b}}_{x^{-1}} {\tilde{c}}_{x^{-1}}$ to the right side of x changes it to $x^{-1}{\tilde{b}}_{x^{-1}} {\tilde{c}}_{x^{-1}} x$, which is a product of elements of certain filtration steps of root subgroups, all of which lie in I by definition of $B_{x^{-1}}, C_{x^{-1}}$. Thus we may eliminate ${\tilde{b}}_{x^{-1}} {\tilde{c}}_{x^{-1}}$ from (4.2). Now, by Lemma 4.5, we may write any element of the right $I/\breve{G}_f$ as the product $c_x b_x a_x$, with $c_x = \prod _{\alpha \in p(C_x)} c_{\alpha }$, etc. That is, any element of $\breve{G}_f \backslash IxI / \breve{G}_f$ may be written as

$$\begin{aligned} \breve{G}_f {\tilde{a}}_{x^{-1}} \cdot x \cdot {\tilde{c}}_x {\tilde{b}}_x {\tilde{a}}_x \breve{G}_f, \end{aligned}$$

(4.3)

for some lifts ${\tilde{c}}_x, {\tilde{b}}_x, {\tilde{a}}_x$ of $c_x, b_x, a_x$. Bringing ${\tilde{c}}_x$ to the left side of x in (4.3), makes it to $x^{-1} {\tilde{c}}_x x$, which is a product of elements of certain filtration steps of root subgroups, all of which lie in $\breve{G}_f$ by definition of $C_{x}$. By normality of $\breve{G}_f$, we may eliminate ${\tilde{c}}_{x}$ from the (4.3). It finally follows that we may write any element of $\breve{G}_f \backslash IxI / \breve{G}_f$ as a product

$$\begin{aligned} \breve{G}_f {\tilde{a}}_{x^{-1}} \cdot x \cdot {\tilde{b}}_x {\tilde{a}}_x \breve{G}_f, \end{aligned}$$

(4.4)

with ${\tilde{a}}_{x^{-1}}$, ${\tilde{b}}_x$, ${\tilde{a}}_x$ as above. This shows the surjectivity of the map in the lemma. It remains to show injectivity.

Suppose there are tuples $(a_{x^{-1}}, b_x, a_x)$ and $(a_{x^{-1}}^{\prime }, b_x^{\prime }, a_x^{\prime })$ giving the same double coset, i.e., ${\tilde{a}}_{x^{-1}} x {\tilde{b}}_x {\tilde{a}}_x = i {\tilde{a}}_{x^{-1}}^{\prime } x {\tilde{b}}_x^{\prime } {\tilde{a}}_x^{\prime } j$ for some $i,j \in \breve{G}_f$. This equation is equivalent to

$$\begin{aligned} x^{-1} ({\tilde{a}}_{x^{-1}}^{\prime })^{-1} i {\tilde{a}}_{x^{-1}} x = {\tilde{b}}_x^{\prime } {\tilde{a}}_x^{\prime } j {\tilde{a}}_x^{-1} {\tilde{b}}_x^{-1}. \end{aligned}$$

Here, the right hand side lies in I, hence it follows that $({\tilde{a}}_{x^{-1}}^{\prime })^{-1} i {\tilde{a}}_{x^{-1}} \in I \cap xIx^{-1}$. We now apply Lemma 4.5: any element of $I/\breve{G}_f$ can be written uniquely as a product $s_{x^{-1}} r_{x^{-1}}$ with $s_{x^{-1}} = \prod _{\alpha \in p(A_{x^{-1}})} s_{\alpha }$ and $r_{x^{-1}} = \prod _{\alpha \in p(B_{x^{-1}} \cup C_{x^{-1}})} r_{\alpha }$ with $s_{\alpha }, r_{\alpha } \in L_{[f_I(\alpha ),f(\alpha ))}U_{\alpha }(\overline{{\mathbb {F}}_q})$. By definition, the affine roots in $A_{x^{-1}}$ are precisely those affine roots in ${{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f)$ which do not occur in $I \cap xIx^{-1}$. Hence we see that the image of the composed map $I \cap xIx^{-1} \hookrightarrow I \twoheadrightarrow I/\breve{G}_f$ is equal to the set of all elements of $I/\breve{G}_f$ with $s_{x^{-1}} = 1$ in the above decomposition. Now we have inside $I/\breve{G}_f$ (so in particular, the element $i \in \breve{G}_f$ can be ignored)

$$\begin{aligned} a_{x^{-1}} = a_{x^{-1}} \cdot 1 = a_{x^{-1}}^{\prime } \cdot (a_{x^{-1}}^{\prime })^{-1} i a_{x^{-1}}, \end{aligned}$$

which gives two decompositions of the element $a_{x^{-1}} \in I/\breve{G}_f$. By uniqueness of such a decomposition, we must have $a_{x^{-1}}^{\prime } = a_{x^{-1}}$. Now analogous computations (first done for $a_x^{\prime }, a_x$ and then for $b_x^{\prime }, b_x$) show that we also must have $a_x^{\prime } = a_x$ and $b_x^{\prime } = b_x$. This finishes the proof of injectivity. $\square$

The Schubert cell attached to $x \in {\widetilde{W}}$ is the reduced subscheme of $LG/L^+{\mathcal {I}}$ whose underlying set of ${\overline{{\mathbb {F}}}}_q$-points is $IxI/I \subseteq \breve{G}/I$. We denote it by C(x). As ${\overline{{\mathbb {F}}}}_q$-schemes $C(x) \cong {\mathbb {A}}^{\ell (x)}$, where $\ell (x)$ is the length of the element x in ${\widetilde{W}}$. We now consider the reduced subscheme of $LG/L^+{\mathcal {G}}_f$, whose underlying set of ${\overline{{\mathbb {F}}}}_q$-points is $IxI/\breve{G}_f \subseteq \breve{G}/\breve{G}_f$ and we denote it by $C_f(x)$. The étale $L^+{\mathcal {I}}/L^+{\mathcal {G}}_f$-torsor $LG/L^+{\mathcal {G}}_f \rightarrow LG/L^+{\mathcal {I}}$ pulls back to the étale $L^+{\mathcal {I}}/L^+{\mathcal {G}}_f$-torsor $C_f(x) \rightarrow C(x)$.

Lemma 4.7

Let $f :{{\widehat{\Phi }}} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{ \infty \}$ be a concave function such that $\breve{G}_f \subseteq I$ is a normal subgroup. Let $x \in {\widetilde{W}}$. The étale $L^+{\mathcal {I}}/L^+{\mathcal {G}}_f$-torsor $C_f(x) \rightarrow C(x)$ is trivial. If $p^{-1}(p(A_{x^{-1}})) \cap {{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f) = A_{x^{-1}}$, then there is an isomorphism of ${\overline{{\mathbb {F}}}}_q$-schemes

$$\begin{aligned} \textstyle \prod \limits _{\alpha \in p(A_{x^{-1}})} L_{[f_I(\alpha ),f(\alpha ))} {\mathcal {U}}_{\alpha } \times L^+{\mathcal {I}}/L^+{\mathcal {G}}_f \rightarrow C_f(x) \end{aligned}$$

given by $((a_{\alpha })_{\alpha \in p(A_{x^{-1}})}, i) \mapsto \prod _{\alpha \in p(A_{x^{-1}})} {\tilde{a}}_{\alpha } \cdot x \cdot i\breve{G}_f$, where ${\tilde{a}}_{\alpha } \in \breve{U}_{\alpha , f_I(\alpha )}$ is any lift of $a_{\alpha }$.

Proof

The group $L^+{\mathcal {I}}/L^+{\mathcal {G}}_f$ has a composition series with all subquotients either ${\mathbb {G}}_a$ or ${\mathbb {G}}_m$. The cohomology of both vanishes on an affine space. This proves that $C_f(x) \rightarrow C(x)$ is a trivial torsor. The explicit isomorphism is proven in the same way as in Lemma 4.6. $\square$

Lemma 4.8

Under the assumptions of Lemma 4.6, the projection $p :C_f(x) \twoheadrightarrow \breve{G}_f \backslash I x I / \breve{G}_f$ is a geometric quotient in the sense of Mumford for the left multiplication action of $L^+{\mathcal {G}}_f$ on $C_f(x)$. Here $\breve{G}_f \backslash IxI/\breve{G}_f$ is endowed with the structure of an ${\mathbb {F}}_q$-scheme using the parametrization from Lemma 4.6.

Proof

First note that from the assumptions of Lemma 4.6 it follows that $p^{-1}(p(A_{x^{-1}})) \cap {{\widehat{\Phi }}}_\mathrm {aff}(I/\breve{G}_f) = A_{x^{-1}}$ (as $A_{x^{-1}} {{\dot{\cup }}} B_{x^{-1}} {{\dot{\cup }}} C_{x^{-1}} = {{\widehat{\Phi }}}_{\mathrm{aff}}(I/\breve{G}_f)$), so we may use Lemma 4.7. The action of $L^+{\mathcal {G}}_f$ on $C_f(x)$ factors through a finite-dimensional quotient (any subgroup $J \subseteq \breve{G}_f \cap x \breve{G}_f x^{-1}$ which is normal in $\breve{G}_f$ acts trivially on $C_f(x)$). Now, since p is a surjective orbit map, $\breve{G}_f \backslash I x I / \breve{G}_f$ is normal and the irreducible components of $C_x(f)$ are open. Thus by [3, Proposition 6.6], it remains to show that p is a separable morphism of varieties. But this is true since, in terms of the parameterizations given in Lemmas 4.6 and 4.7, it is given by $(a_{x^{-1}}, i = c_x b_x a_x) \mapsto (a_{x^{-1}}, b_x, a_x)$. $\square$

Theorem 4.9

Assume G is split. Let $f :{{\widehat{\Phi }}} \rightarrow \widetilde{{\mathbb {R}}}_{\ge 0} {\,\smallsetminus \,}\{ \infty \}$ be a concave function such that $\breve{G}_f \subseteq I$ is a normal subgroup. Let ${\dot{x}}$ be an $\breve{G}_f$-double coset in $\breve{G}$ with image x in ${\widetilde{W}}$. Assume that $p(A_x)$, $p(B_x)$ and $p(C_x)$ are mutually disjoint, and that the same is true for $p(A_{x^{-1}}), p(B_{x^{-1}}),p(C_{x^{-1}})$, where A, B, C are as in (4.1). For $b \in \breve{G}$ arbitrary, $X_{{\dot{x}}}^f(b)$ is locally closed in $\breve{G}/\breve{G}_f$.

Proof

By Lemma 4.8, the theorem is now a special case of [22, Proposition 2.4]. We recall the proof. It is well known that the Iwahori-level sets $X_x^I(b) = X_x(b)$ are locally closed in $LG/L^+{\mathcal {I}}$. Let ${{\widetilde{X}}}$ be the pullback of $X_x^I(b)$ along $LG/L^+{\mathcal {G}}_f \rightarrow LG/L^+{\mathcal {I}}$. As $X_w(b)$ are schemes locally of finite type over ${\overline{{\mathbb {F}}}}_q$, the same is true for ${\widetilde{X}}$. By Theorem 4.1, the map $\beta :LG \rightarrow LG/L^+{\mathcal {G}}_f$ admits sections étale locally. Let $U \rightarrow {{\widetilde{X}}}$ be étale such that there is a section $s :U \rightarrow \beta ^{-1}(U)$ of $\beta$. Consider the composition

$$\begin{aligned} \psi :U \rightarrow \beta ^{-1}(U) \times U \rightarrow LG/L^+{\mathcal {G}}_f, \end{aligned}$$

where the first map is $g \mapsto (s(g^{-1}),b\sigma (g))$ and the second map is the restriction of the left multiplication action of LG on $LG/L^+{\mathcal {G}}_f$. As U lies over ${\widetilde{X}}$, this composition factors through $C_f(x) \rightarrow LG/L^+{\mathcal {G}}_f$. Denote the resulting morphism by $\psi _0 :U \rightarrow C_f(x)$. Let $p :C_f(x) \rightarrow \breve{G}_f \backslash I x I / \breve{G}_f$ denote the geometric quotient from Lemma 4.8. The composition $p \circ \psi _0$ is independent of the choice of the section s. It sends an ${\overline{{\mathbb {F}}}}_q$-point $g\breve{G}_f$ to the double coset $\breve{G}_f g^{-1} b \sigma (g) \breve{G}_f$. Thus étale locally, $X_{{\dot{x}}}^f(b)$ is just the preimage of the point ${\dot{x}}$ under $p \circ \psi _0$. The theorem now follows by using étale descent for closed subschemes. $\square$

Corollary 4.10

Under the assumptions as in Theorem 4.9, $X_{\dot{x}}^f(b)$ endowed with the induced reduced sub-ind-scheme structure is a scheme locally of finite type over ${\overline{{\mathbb {F}}}}_q$.

Proof

$X_w^I(b)$ is a scheme locally of finite type over ${\overline{{\mathbb {F}}}}_q$. Since $p :LG/L^+{\mathcal {G}}_f \rightarrow LG/L^+{\mathcal {I}}$ is a morphism of ind-schemes which is a torsor under the finite-dimensional affine group scheme $L^+{\mathcal {I}}/L^+{\mathcal {G}}_f$ (by Proposition 4.2), it follows that ${\widetilde{X}} := p^{-1}(X_w^I(b))$ is also a scheme locally of finite type over ${\overline{{\mathbb {F}}}}_q$. Now the proof of Theorem 4.9 shows that $X_x^f(b)$ has the same property. $\square$

6 Part 2. Geometry of Deligne–Lusztig varieties for inner forms of ${{\,\mathrm{GL}\,}}_n$

From now and until the end of the paper, we fix an integer $n \ge 1$ and study in detail the constructions in Part 1 for ${{\,\mathrm{GL}\,}}_n(K)$ and its inner forms. Inner forms of ${{\,\mathrm{GL}\,}}_n$ over K can be naturally parametrized by $\frac{1}{n} {\mathbb {Z}}/{\mathbb {Z}}$. Fix an integer $0 \le \kappa < n$, put $n^{\prime } = \gcd (\kappa ,n),$ and let $n_0$, $k_0$ be the non-negative integers such that

$$\begin{aligned} n = n' n_0, \qquad \kappa = n' k_0. \end{aligned}$$

The group of K-points of the inner form corresponding to $\kappa /n$ is isomorphic to ${G \,{:=}\,{{\,\mathrm{GL}\,}}_{n^{\prime }}(D_{k_0/n_0})}$, where $D_{k_0/n_0}$ denotes the central division algebra over K with invariant $k_0/n_0$. Let ${\mathcal {O}}_{D_{k_0/n_0}}$ denote the ring of integers of $D_{k_0/n_0}$ and set ${G_{\mathcal {O}}\,{:=}\,{{\,\mathrm{GL}\,}}_{n'}({\mathcal {O}}_{D_{k_0/n_0}})}$. Note that $G_{\mathcal {O}}$ is a maximal compact subgroup of G.

We let L denote the unramified extension of K of degree n, and write ${\mathcal {O}}_L$ for its integers, ${\mathfrak {p}}_L$ for the maximal ideal in ${\mathcal {O}}_L$. For $h\ge 1$, we write $U_L^h = 1 + {\mathfrak {p}}_L^h$ for the h-units of L.

Up to conjugacy there is only one maximal unramified elliptic torus $T \subseteq G$. We have $T \cong L^\times$. Moreover, we say a smooth character $\theta :L^{\times } \rightarrow \overline{{\mathbb {Q}}}_{\ell }$ has level $h \ge 0$, if $\theta$ is trivial on $U_L^{h+1}$ and non-trivial on $U_L^h$.

We let V be an n-dimensional vector space over $\breve{K}$ with a fixed K-rational structure $V_K$. Fix a basis $\{e_1, \ldots , e_n\}$ of $V_K$. This gives an identification of ${{\,\mathrm{GL}\,}}(V_K)$ with ${{\,\mathrm{GL}\,}}_n$ over K. Set ${\mathscr {L}}_0$ to be the ${\mathcal {O}}$-lattice generated by $\{e_1, \ldots , e_n\}$.

7 Inner forms of ${{\,\mathrm{GL}\,}}_n$

7.1 Presentation as $\sigma$-stabilizers of basic elements

For $b \in {{\,\mathrm{GL}\,}}_n(\breve{K})$, recall from Sect. 3 the $\sigma$-stabilizer $J_b$ of b. Then $J_b$ is an inner form of the centralizer of the Newton point b (which is a Levi subgroup of ${{\,\mathrm{GL}\,}}_n$). In particular, if b is basic, i.e. the Newton point of b is central, then $J_b$ is an inner form of ${{\,\mathrm{GL}\,}}_n$, and every inner form of ${{\,\mathrm{GL}\,}}_n$ arises in this way. If

$$\begin{aligned} {\kappa = \kappa _{{{\,\mathrm{GL}\,}}_n}(b) \,{:=}\,{{\,\mathrm{ord}\,}}\circ \det (b),} \end{aligned}$$

then $J_b$ is the inner form corresponding to $\kappa /n$ modulo ${\mathbb {Z}}$. Note that $\kappa _{{{\,\mathrm{GL}\,}}_n}$ is the Kottwitz map

$$\begin{aligned} {\kappa _{{{\,\mathrm{GL}\,}}_n} :B({{\,\mathrm{GL}\,}}_n(\breve{K})) \,{:=}\,\{\sigma \text {-conj classes in }{{\,\mathrm{GL}\,}}_n(\breve{K})\} \rightarrow {\mathbb {Z}}} \end{aligned}$$

and induces a bijection between the set of basic $\sigma$-conjugacy classes and ${\mathbb {Z}}$. Consider

$$\begin{aligned} F :{{\,\mathrm{GL}\,}}_n(\breve{K}) \rightarrow {{\,\mathrm{GL}\,}}_n(\breve{K}), \qquad g \mapsto b\sigma (g)b^{-1}. \end{aligned}$$

This is a twisted Frobenius on ${{\,\mathrm{GL}\,}}_n(\breve{K})$ and $J_b$ is the K-group corresponding to this Frobenius on ${{\,\mathrm{GL}\,}}_n(\breve{K})$. In particular, if b is in the basic $\sigma$-conjugacy class with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$, then

$$\begin{aligned} G = {{\,\mathrm{GL}\,}}_{n'}(D_{k_0/n_0}) \cong {{\,\mathrm{GL}\,}}_n(\breve{K})^F = J_b(K). \end{aligned}$$

7.2 Two different choices for b

We will need to choose representatives b of the basic $\sigma$-conjugacy class [b] with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$. Depending on the context, we will work with either a Coxeter-type representative or a special representative.

7.2.1 Coxeter-type representatives

Set

$$\begin{aligned} {b_0 \,{:=}\,\left( \begin{matrix} 0 &{}\quad 1 \\ 1_{n-1} &{}\quad 0 \end{matrix}\right) , \qquad \text {and} \qquad t_{\kappa ,n} \,{:=}\,{\left\{ \begin{array}{ll} {{\,\mathrm{diag}\,}}(\underbrace{1, \ldots , 1}_{n-\kappa },\underbrace{\varpi , \ldots , \varpi }_{\kappa }) &{}\quad \text {if }(\kappa ,n) = 1, \\ {{\,\mathrm{diag}\,}}(\underbrace{t_{k_0,n_0}, \ldots , t_{k_0,n_0}}_{n'}) &{}\quad \text {otherwise.} \end{array}\right. }} \end{aligned}$$

Fix an integer $e_{\kappa ,n}$ such that $(e_{\kappa ,n},n)=1$ and $e_{\kappa ,n} \equiv k_0$ mod $n_0$. (It is clear that $e_{\kappa ,n}$ exists.) If $\kappa$ divides n, (i.e. $k_0 = 1$), always take $e_{\kappa ,n} = 1$.

Definition 5.1

The Coxeter-type representative attached to $\kappa$ is $b_0^{e_{\kappa ,n}} \cdot t_{\kappa ,n}.$

The main advantage of this choice is that the maximal torus of ${{\,\mathrm{GL}\,}}_n(\breve{K})$ consisting of diagonal matrices gives an unramified elliptic torus of $J_b$ (as the image of b in the Weyl group of the diagonal torus is a cycle of length n). Thus when we use the explicit presentation $G = J_b(K)$ for the Coxeter-type b, then our unramified elliptic torus $T \subseteq G$ is the diagonal torus.

7.2.2 Special representatives

Definition 5.2

The special representative attached to $\kappa$ is the block-diagonal matrix of size $n \times n$ with $(n_0 \times n_0)$-blocks of the form $\begin{pmatrix} 0&{}\quad \varpi \\ 1_{n_0 - 1} &{}\quad 0 \end{pmatrix}^{k_0}$.

Note that the special representative and the Coxeter-type representative agree if $(\kappa ,n) = 1$ (see the proof of Lemma 5.6), though in general they may differ (for example, when $\kappa = 0$, the special representative is the identity and the Coxeter representative is $b_0$).

Remark 5.3

If b is the special representative, $b\sigma$ acts on the standard basis $\{\mathbf {e}_i\}_{i=1}^n$ of V in the same way as in [32, Section 4.1] the operator F considered there acts on the basis $\{e_{j,i,l}\}_{j,i,l}$. To be more precise, in our situation, there is only one j (that is $j=1$) as the isocrystal $(V, b\sigma )$ is isoclinic. Then our basis element $\mathbf {e}_i$ for $1\le i \le n$ corresponds to Viehmann’s basis element $e_{1,i'+1,l}$, where $i = i'n_0 + l$ for $0 \le i' < n'$, $0\le l < n_0$. $\Diamond$

Remark 5.4

If $(\kappa , n) = 1$, the special representative b is a length-0 element of the extended affine Weyl group of ${{\,\mathrm{GL}\,}}_n$ and therefore is a standard representative in the sense of [17, Section 7.2]. In general, b is block-diagonal with blocks consisting of the standard representative of size $n_0 \times n_0$ and determinant $k_0$. $\Diamond$

7.2.3 Properties of the representatives

Lemma 5.5

Let $\breve{T}_{\mathrm{diag}}$ denote the maximal torus of ${{\,\mathrm{GL}\,}}_n(\breve{K})$ given by the subgroup of diagonal matrices. Then the Coxeter-type and special representatives lie in the normalizer $N_{{{\,\mathrm{GL}\,}}_n(\breve{K})}(\breve{T}_{\mathrm{diag}})$. Moreover, both representatives are basic elements whose Newton polygon has slope $\kappa /n$.

Proof

The first statement is clear. For $b \in N_{{{\,\mathrm{GL}\,}}_n(\breve{K})}(\breve{T}_{\mathrm{diag}})$, the Newton point can be computed as $\frac{1}{a} v_{b^a}$, where $a \in {\mathbb {Z}}_{>0}$ is appropriate such that $b^a \in \breve{T}_{\mathrm{diag}}$. Thus the second statement follows from an easy calculation (for the Coxeter type, it uses the condition on $e_{\kappa ,n}$). $\square$

Let $b,b' \in {{\,\mathrm{GL}\,}}_n(\breve{K})$. We say $b, b'$ are integrally $\sigma$-conjugate if there is $g \in {{\,\mathrm{GL}\,}}_n({\mathcal {O}})$ such that $g^{-1}b\sigma (g) = b'$.

Lemma 5.6

The Coxeter-type and special representatives attached to $\kappa /n$ are integrally $\sigma$-conjugate.

Proof If $\kappa$ is coprime to n, then necessarily $e_{\kappa ,n} = \kappa$. We have $b_0^{-1}{{\,\mathrm{diag}\,}}(1,\ldots , 1, \varpi ) b_0 = {{\,\mathrm{diag}\,}}(1, \ldots , 1, \varpi , 1)$ and it follows that $(b_0 \cdot t_{1,n})^\kappa = b_0^\kappa \cdot t_{\kappa ,n}$, so the special representative and the Coxeter representative agree. Now assume that $(\kappa ,n) = n' > 1$. For convenience of notation, let b denote the Coxeter-type representative and let $b'$ denote the special representative. Recall that $b = b_0^{e_{\kappa ,n}} \cdot t_{\kappa ,n} = \left( {\begin{matrix} 0 &{} 1 \\ 1_{n-1} &{} 0 \end{matrix}}\right) ^{e_{\kappa ,n}} \cdot {{\,\mathrm{diag}\,}}(t_{k_0,n_0}, \ldots , t_{k_0,n_0})$ and that $b'$ is the block-diagonal matrix with $\left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0-1} &{} 0 \end{matrix}}\right) ^{k_0}$ in each block. We would like to produce a $g \in {{\,\mathrm{GL}\,}}_n({\mathcal {O}})$ such that $b \sigma (g) = g b'$. Write

$$\begin{aligned} g = \Big ( g_1 \, \big | \, g_2 \, \big | \, \cdots \, \big | \, g_n\Big ), \text {where}\, g_i = \left( {\begin{matrix} g_{i,1} \\ g_{i,2} \\ \vdots \\ g_{i,n} \end{matrix}}\right) . \end{aligned}$$

Then the first $n_0$ columns of the equation $b \sigma (g) = g b'$ is the equality of $n \times n_0$ matrices

$$\begin{aligned} \Big ( b \sigma (g_1) \big | b\sigma (g_2) \big | \cdots \big | b\sigma (g_{n_0})\Big ) = \Big (g_{k_0+1} \big | g_{k_0+2} \, \big | \, \cdots \, \big | \, g_{n_0} \, \big | \, \varpi g_{1} \, \big | \, \varpi g_2 \big | \cdots \big | \varpi g_{k_0}\Big ). \end{aligned}$$

In other words, we have

$$\begin{aligned} g_i = {\left\{ \begin{array}{ll} \varpi ^{-1} \cdot b\sigma (g_{[i-k_0]_{n_0}}) &{} \text {if}\, 1 \le i \le k_0, \\ b\sigma (g_{[i-k_0]_{n_0}}) &{} \text {if}\, k_0 + 1 \le i \le n_0, \end{array}\right. } \end{aligned}$$

(5.1)

and hence

$$\begin{aligned} \varpi ^{k_0} g_{k_0} = \varpi ^{k_0-1} b \sigma (g_{n_0}) = \varpi ^{k_0-1} b^2\sigma ^2(g_{n_0-k_0}) = \cdots = b^{n_0} \sigma ^{n_0}(g_{k_0}), \end{aligned}$$

(5.2)

where the exponent of $\varpi$ changes periodically according to (5.1). Observe that since $b_0^{-1}t_{\kappa ,n}b_0$ is the block-diagonal matrix with blocks equal to $\left( {\begin{matrix} 0 &{} 1 \\ 1_{n_0-1} &{} 0 \end{matrix}}\right) ^{-1}t_{k_0,n_0}\!\left( \!{\begin{matrix} 0 &{} 1 \\ 1_{n_0-1} &{} 0 \end{matrix}}\right)$, we see that $\varpi ^{-k_0} b^{n_0}$ is a permutation matrix of order $n'$; writing $e' \,{:=}\,[e_{\kappa ,n} n_0]_n$, we have $\varpi ^{-k_0}b^{n_0} = \left( {\begin{matrix} 0 &{} 1_{e'} \\ 1_{n-e'} &{} 0 \end{matrix}}\right)$ and $(e',n) = n_0$. Write

$$\begin{aligned} g_{k_0} = \left( {\begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix}}\right) . \end{aligned}$$

Then from (5.2) it follows that

$$\begin{aligned} \left( {\begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_{e'} \\ x_{e'+1} \\ \vdots \\ x_n \end{matrix}}\right) = \left( {\begin{matrix} \sigma ^{n_0}(x_{n-e'+1}) \\ \sigma ^{n_0}(x_{n-e'+2}) \\ \vdots \\ \sigma ^{n_0}(x_n) \\ \sigma ^{n_0}(x_1) \\ \vdots \\ \sigma ^{n_0}(x_{n-e'}) \end{matrix}}\right) . \end{aligned}$$

In particular, the vector $g_{k_0}$ is determined by $x_1, x_2, \ldots , x_{n_0}$.

Let $\overline{\alpha }\in {\mathbb {F}}_{q^n}^\times$ be an element such that $\overline{\alpha }, \sigma (\overline{\alpha }), \ldots , \sigma ^{n-1}(\overline{\alpha })$ are linearly independent over ${\mathbb {F}}_q$. Let $\alpha \in {\mathcal {O}}^\times$ be any lift of $\overline{\alpha }$. Let $g_{k_0}$ be the vector associated to the choice $x_{n_0-k_0+1} = \alpha$ and $x_i = 0$ otherwise. We next show that for this choice of $g_{k_0}$, each of the columns $g_1, \ldots , g_{n_0}$ (all of which are determined by $g_{k_0}$ by (5.1)) have coefficients in ${\mathcal {O}}$ and that moreover the entries are either zero or in ${\mathcal {O}}^\times$. For any positive integer j, we know that

$$\begin{aligned} b\sigma (\mathbf{e}_{[i_0-{e}_{\kappa ,n}j]_{n}}) = {\left\{ \begin{array}{ll} \varpi \cdot \mathbf{e}_{[i_0-e_{\kappa ,n}(j+1)]_{n}} &{} \text {if} [i_0-e_{\kappa ,n}j]_{n_0} \ge n_0 - k_0 + 1 \\ \mathbf{e}_{[i_0-{ e}_{\kappa ,n}(j+1)]_{n}} &{} \text {if} [i_0 - e_{\kappa ,n}j]_{n_0} \le n_0 - k_0 \end{array}\right. } \end{aligned}$$

where $\mathbf {e}_i$ denotes the ith elementary column vector. Comparing this to (5.1), we see that the condition for when the scalar $\varpi ^{-1}$ appears in the equation for $g_{[(j+1)k_0]_{n_0}}$ coincides with the condition for when the scalar $\varpi$ appears in the equation for $b\sigma (\mathbf{e}_{[i_0-{e}_{\kappa ,n}j]_{n}})$ when $[e_{\kappa ,n}(j+1)]_{n_0} = n_0+1-[i_0-e_{\kappa ,n}j]_{n_0}$. Since $e_{\kappa ,n} \equiv k_0$ modulo $n_0$ by definition, this implies $i_0 = n_0-k_0+1$, and it follows now that the entries of $g_1, \ldots , g_{n_0}$ are either zero or in ${\mathcal {O}}^\times$.

We may repeat the above argument for the next $n_0$ columns of the equation $b\sigma (g) = g b'$. We then obtain that for $n_0+1 \le i \le 2n_0$, the columns $g_i$ of g are uniquely determined by $g_{n_0+k_0}$, and that the vector $g_{n_0+k_0}$ is uniquely determined by its first $n_0$ entries $x_1, \ldots , x_{n_0}$. Let $g_{n_0+k_0}$ be the vector associated to the choice $x_{n_0-k_0+1} = \sigma (\alpha )$ and $x_i = 0$ otherwise. Repeating this for the remaining columns of g, with $g_{in_0+k_0}$ being determined by setting $x_{n_0-k_0+1} = \sigma ^i(\alpha )$ for $1 \le i \le n'-1$, we have now obtained an $n \times n$ matrix g satisfying $b\sigma (g) = gb'$ whose entries are either 0 or in ${\mathcal {O}}^\times$.

To complete the proof that $b,b'$ are integrally $\sigma$-conjugate, it remains to show that the ${\mathcal {O}}$-valued $n \times n$ matrix g lies in ${{\,\mathrm{GL}\,}}_n({\mathcal {O}})$; that is, it remains to show that $\det (g) \in {\mathcal {O}}^\times$. To see this, observe that by construction, the rows and columns of g can be permuted so that it is block-diagonal with ith ($1 \le i \le n_0$) block equal to the matrix

$$\begin{aligned} \sigma ^{(i-1)n'}\left( \begin{matrix} \alpha &{} \sigma (\alpha ) &{} \cdots &{} \sigma ^{n'-1}(\alpha ) \\ \sigma (\alpha ) &{} \sigma ^2(\alpha ) &{} \cdots &{} \alpha \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \sigma ^{n'-1}(\alpha ) &{} \alpha &{} \cdots &{} \sigma ^{n'-2}(\alpha ) \end{matrix}\right) . \end{aligned}$$

The reduction-modulo-$\varpi$ of this matrix is a Vandermonde matrix, and since $\overline{\alpha }$ is such that $\overline{\alpha }, \sigma (\overline{\alpha }), \ldots , \sigma ^{n-1}(\overline{\alpha }) \in {\mathbb {F}}_{q^n}$ are linearly dependent over ${\mathbb {F}}_q$, it has nonzero determinant. Hence $\det (g) \in {\mathcal {O}}^\times$.

7.3 Integral models

Let ${{\mathcal {B}}^{{{\,\mathrm{red}\,}}} \,{:=}\,{\mathcal {B}}^{{{\,\mathrm{red}\,}}}({{\,\mathrm{GL}\,}}_n, \breve{K})}$ be the reduced building of ${{\,\mathrm{GL}\,}}_n$ over $\breve{K}$. For any point $x \in {\mathcal {B}}^{{{\,\mathrm{red}\,}}}$, the Moy–Prasad filtration is a collection of subgroups $\breve{G}_{x,r} \subset {{\,\mathrm{GL}\,}}_n(\breve{K})$ indexed by real numbers $r \ge 0$ [27, Section 3.2]. We write $\breve{G}_{x,r+} = \cup _{s > r} \breve{G}_{x,s} \subset {{\,\mathrm{GL}\,}}_n(\breve{K})$.

Let ${\mathcal {A}}^{{{\,\mathrm{red}\,}}}$ denote the apartment of ${\mathcal {B}}^{{{\,\mathrm{red}\,}}}$ associated to the maximal split torus given by the subgroup of diagonal matrices in ${{\,\mathrm{GL}\,}}_n(\breve{K})$ and let b be the Coxeter-type representative so that b acts on ${\mathcal {A}}^{{{\,\mathrm{red}\,}}}$ with a unique fixed point ${\mathbf {x}}\in {\mathcal {A}}^{{{\,\mathrm{red}\,}}}$. By construction, each $\breve{G}_{{\mathbf {x}},r}$ is stable under the Frobenius $F(g) = b \sigma (g) b^{-1}$ and $\breve{G}_{{\mathbf {x}},0}^F \cong G_{\mathcal {O}}$.

We now define ${\mathbb {G}}$ to be the smooth affine group scheme over ${\mathbb {F}}_q$ such that

$$\begin{aligned} {\mathbb {G}}({{\overline{{\mathbb {F}}}}}_q) = \breve{G}_{{\mathbf {x}}, 0}, \qquad {\mathbb {G}}({\mathbb {F}}_q) = \breve{G}_{{\mathbf {x}},0}^F. \end{aligned}$$

For $h \in {\mathbb {Z}}_{\ge 1}$, we define ${\mathbb {G}}_h$ to be the smooth affine group scheme over ${\mathbb {F}}_q$ such that

$$\begin{aligned} {\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q) = \breve{G}_{{\mathbf {x}},0}/\breve{G}_{{\mathbf {x}},(h-1)+}, \qquad {\mathbb {G}}_h({\mathbb {F}}_q) = \breve{G}_{{\mathbf {x}},0}^F/\breve{G}_{{\mathbf {x}},(h-1)+}^F. \end{aligned}$$

We have a well-defined determinant morphism

$$\begin{aligned} \det :{\mathbb {G}}_h \rightarrow {\mathbb {W}}_h^\times . \end{aligned}$$

Define ${\mathbb {T}}_h$ to be the subgroup scheme of ${\mathbb {G}}_h$ defined over ${\mathbb {F}}_q$ given by the diagonal matrices. Set:

$$\begin{aligned} {G_h \,{:=}\,{\mathbb {G}}_h({\mathbb {F}}_q), \qquad T_h \,{:=}\,{\mathbb {T}}_h({\mathbb {F}}_q).} \end{aligned}$$

Note that ${\mathbb {G}}_h({\mathbb {F}}_q)$ is a subquotient of G and ${\mathbb {T}}_h({\mathbb {F}}_q) \cong ({\mathcal {O}}_L/\varpi ^h)^\times \cong {\mathbb {W}}_h^\times ({\mathbb {F}}_{q^n})$ is a subquotient of the unramified elliptic torus T of G.

We remark that each $\breve{G}_{{\mathbf {x}},r}$ is also stable under the Frobenius $F(g) = b \sigma (g) b^{-1}$ for the special representative b and that $\breve{G}_{{\mathbf {x}},0}^F \cong G_{\mathcal {O}}$. Thus we also can regard ${\mathbb {G}}_h$ as a group scheme over ${\mathbb {F}}_q$ as above with ${\mathbb {G}}_h({\mathbb {F}}_q)$ a subquotient of $J_b(K)$ with b being the special representative. However, the induced ${\mathbb {F}}_q$-rational structure on ${\mathbb {T}}_h$ gives that ${\mathbb {T}}_h({\mathbb {F}}_q) \cong ({\mathbb {W}}_h^\times ({\mathbb {F}}_{q^{n_0}}))^{\times n'}$, which is not a subquotient of any elliptic torus in G.

Explicitly, ${\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q)$ is the group of invertible $n \times n$-matrices, whose $n_0\times n_0$-blocks are matrices $(a_{ij})_{1\le i,j \le n_0}$ with $a_{ii} \in {\mathcal {O}}/{\mathfrak {p}}^h$, $a_{ij} \in {\mathcal {O}}/{\mathfrak {p}}^{h-1}$ ($\forall i>j$), $a_{ij} \in {\mathfrak {p}}/{\mathfrak {p}}^h$ ($\forall i<j$). For example, for $n_0=3$, the $n_0 \times n_0$-blocks are

$$\begin{aligned} \left( {\begin{matrix} {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h \\ {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h \\ {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h \end{matrix}}\right) . \end{aligned}$$

The following lemma describes the F-fixed part of the Weyl group of ${\mathbb {T}}_1$ in ${\mathbb {G}}_1$ explicitly. Note that $b^{n_0}\varpi ^{-k_0}$ is a permutation matrix in ${{\,\mathrm{GL}\,}}_n(\breve{K})$.

Lemma 5.7

Let b be the Coxeter-type representative. We have

• (i) We have $\mathrm{N}_{{\mathbb {G}}_h}({\mathbb {T}}_h)/{\mathbb {T}}_h = \mathrm{N}_{{\mathbb {G}}_1}({\mathbb {T}}_1)/{\mathbb {T}}_1 = S_{n'} \times \dots \times S_{n'}$ ($n_0$ copies).

• (ii) $\mathrm{N}_{G_h}(T_h)/T_h = (\mathrm{N}_{{\mathbb {G}}_h}({\mathbb {T}}_h)/{\mathbb {T}}_h)^F = \langle b^{n_0}\varpi ^{-k_0} \rangle \cong {{\,\mathrm{Gal}\,}}(L/K)[n']$, the $n'$-torsion subgroup of ${{\,\mathrm{Gal}\,}}(L/K)$.

Proof

Part (i) is clear by the explicit description of ${\mathbb {G}}_h$. To prove (ii), we need to make the action of F on $\mathrm{N}_{{\mathbb {G}}_h}({\mathbb {T}}_h)/{\mathbb {T}}_h$ explicit. Indeed, F is an automorphism of order n, it permutes the copies of $S_{n'}$ cyclically, and each of the copies is stabilized by $F^{n_0}$. We can think of the first $S_{n'}$ as permutation matrices with entries 0 and 1 in ${{\,\mathrm{GL}\,}}(\langle \mathbf {e}_i :i \equiv 1 \pmod {n_0} \rangle ) \cong {{\,\mathrm{GL}\,}}_{n'}$. Then the $F^{n_0}$-action $S_{n'}$ comes from the conjugation by $b^{n_0}$ on ${{\,\mathrm{GL}\,}}(\langle \mathbf {e}_i :i \equiv 1 \pmod {n_0} \rangle )$. But $b^{n_0}$ is the order-$n'$ cycle $e_1 \mapsto e_{1 + n_0} \mapsto \dots \mapsto e_{1 + n_0(n'-1)} \mapsto e_1$, and the subgroup of $S_{n'}$ stable by it is $\langle b^{n_0}\varpi ^{-k_0} \rangle$. We can identify it with ${{\,\mathrm{Gal}\,}}(L/K)[n']$ by sending $b^{n_0}\varpi ^{-k_0}$ to $\sigma ^{n_0}$ (see also Lemma 5.8). $\square$

7.4 Twisted polynomial rings

Let $L_0$ be the degree-$n_0$ unramified extension of K and consider the twisted polynomial ring $L_0 \langle \Pi _0 \rangle$ determined by the commutation relation $a \cdot \Pi _0 = \Pi _0 \cdot \sigma ^{l_0}(a)$, where $l_0$ is the integer in the range $1 \le l_0 \le n_0$ with $l_0 k_0 = 1$ modulo $n_0$.

On the other hand, consider the Frobenius map $F_0 :M_{n_0}(\breve{K}) \rightarrow M_{n_0}(\breve{K})$ defined by $F_0(g) = \left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0-1} &{} 0 \end{matrix}}\right) ^{k_0} \sigma (g) \left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0-1} &{} 0 \end{matrix}}\right) ^{-k_0}.$ The diagonal matrices in $M_{n_0}(\breve{K})^{F_0}$ are exactly of the form

$$\begin{aligned} {D_0(a) \,{:=}\,{{\,\mathrm{diag}\,}}(a, \sigma ^{l_0}(a), \ldots , \sigma ^{(n_0-1)l_0}(a)), \qquad \text {for }a \in L_0.} \end{aligned}$$

By a direct calculation, we see that we can define an isomorphism

$$\begin{aligned} L_0\langle \Pi _0 \rangle /(\Pi _0^{n_0} - \varpi ^{k_0}) \rightarrow M_{n_0}(\breve{K})^{F_0} = D_{k_0/n_0} \end{aligned}$$

by sending $a \in L_0$ to $D_0(a)$, and sending $\Pi _0$ to $\left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0-1} &{} 0 \end{matrix}}\right)$. Note that under this identification, the ring of integers ${\mathcal {O}}_{D_{k_0/n_0}}$ of $D_{k_0/n_0}$ is ${\mathcal {O}}_{L_0}\langle \Pi _0 \rangle /(\Pi _0^{n_0} - \varpi ^{k_0})$.

7.5 Cartan decomposition

Let b be the special representative and let $\Pi _0 = \left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0-1} &{} 0 \end{matrix}}\right)$. We use the description of $D_{k_0/n_0}$ in Sect. 5.4. Let $\breve{T}_{\mathrm{diag}}$ be the subgroup of diagonal matrices in ${{\,\mathrm{GL}\,}}_n(\breve{K})$. Then the set of F-fixed points of the cocharacters $X_*(\breve{T}_{\mathrm{diag}})^F$ is given by

$$\begin{aligned} X_{*}(\breve{T}_{\mathrm{diag}})^F = \{\nu = (\nu _1,\dots ,\nu _1,\nu _2,\dots ,\nu _2, \dots ,\nu _{n'},\dots ,\nu _{n'}) :\nu _i \in {\mathbb {Z}}\}, \end{aligned}$$

where each $\nu _i$ repeated $n_0$ times. Let $X_{*}(\breve{T}_\mathrm{diag})_{\mathrm{dom}}^F \subset X_*(\breve{T}_{\mathrm{diag}})^F$ be the subset consisting of $\nu$ with $\nu _1 \le \nu _2 \le \dots \le \nu _{n'}$. For $\nu \in X_{*}(\breve{T}_{\mathrm{diag}})^F$, we write $\Pi _0^{\nu }$ for the $n \times n$ block-diagonal matrix whose ith $n_0\times n_0$-block is $\Pi _0^{\nu _i}$. The Cartan decomposition of $G = {{\,\mathrm{GL}\,}}_{n'}(D_{k_0/n_0})$ with respect to the maximal compact subgroup $G_{\mathcal {O}}= {{\,\mathrm{GL}\,}}_{n'}({\mathcal {O}}_{D_{k_0/n_0}})$ is given by

$$\begin{aligned} G = \bigsqcup _{\nu \in X_{*}(\breve{T}_{\mathrm{diag}})_{F,\mathrm{dom}}} G_{\mathcal {O}}\Pi _0^{\nu } G_{\mathcal {O}}\end{aligned}$$

Note that $\Pi _0^\nu$ normalizes $G_{\mathcal {O}}$ if and only if all $\nu _i$ are equal, and $\Pi _0^\nu$ centralizes $G_{\mathcal {O}}$ if and only if all $\nu _i$ are equal and divisible by $n_0$ so that

$$\begin{aligned} N_{G}(G_{\mathcal {O}})/Z_G G_{\mathcal {O}}\cong {\mathbb {Z}}/n_0 {\mathbb {Z}}. \end{aligned}$$

7.6 Reductive quotient ${\mathbb {G}}_1$

Let b be either the Coxeter-type or the special representative. The group ${\mathbb {G}}_1$ is equal to the reductive quotient of ${\mathbb {G}}$. Recall the ${\mathcal {O}}$-lattice ${\mathscr {L}}_0$ and its basis $\{\mathbf {e}_i\}_{i=1}^n$ from the beginning of Part 2. The following lemma describes the reductive quotient in terms of ${\mathscr {L}}_0$. Its proof reduces to some elementary explicit calculations, so we omit it.

Lemma 5.8

Let $c,d \in {\mathbb {Z}}$ with $k_0 c + n_0 d = 1$.

• (i) We have $(b\sigma )^c \varpi ^d({\mathscr {L}}_0) \subseteq {\mathscr {L}}_0$, and $(b\sigma )^c \varpi ^d({\mathscr {L}}_0)$ is independent of the choice of c, d.¹ The quotient space

  $$\begin{aligned} {{\overline{V}} \,{:=}\,{\mathscr {L}}_0/(b\sigma )^c \varpi ^d({\mathscr {L}}_0)} \end{aligned}$$

  is $n^{\prime }$-dimensional ${\overline{{\mathbb {F}}}}_q$-vector space. The images of $\{\mathbf {e}_i\}_{i \equiv 1 \pmod {n_0}}$ form a basis of ${\overline{V}}$.

• (ii) The map $(b\sigma )^{n_0} \varpi ^{-k_0}$ induces a $\sigma ^{n_0}$-linear automorphism $\overline{\sigma _b}$ of ${\overline{V}}$, equipping it with a ${\mathbb {F}}_{q^{n_0}}$-linear structure. If b is the special representative, the $\sigma ^{n_0}$-linear operator $\overline{\sigma _b}$ of ${\overline{V}}$ is given by $\mathbf {e}_i \mapsto \mathbf {e}_i$ for $1 \le i \le n$ with $i \equiv 1 \pmod {n_0}$. If b is Coxeter-type, then it is given by $e_{1 + n_0i} \mapsto e_{1 + n_0(i+e_{\kappa ,n})}$.

• (iii) We have a canonical identification

  $$\begin{aligned}{\mathbb {G}}_1 = \mathrm{Res}_{{\mathbb {F}}_{q^{n_0}}/{\mathbb {F}}_q} {{\,\mathrm{GL}\,}}_{n'}{{\overline{V}}}. \end{aligned}$$

7.7 Isocrystals

We recall that an ${\overline{{\mathbb {F}}}}_q$-isocrystal is an $\breve{K}$-vector space together with an $\sigma$-linear isomorphism. For $b\in {{\,\mathrm{GL}\,}}_n(\breve{K})$, we have the isocrystal $(V,b\sigma )$. Assume now that b is basic with $\kappa _G(b) = \kappa$. Then $(V,b\sigma )$ is isomorphic to the direct sum of $n'$ copies of the simple isocrystal with slope $k_0/n_0$. We observe that $(V,b\sigma )$ up to isomorphy only depends on the $\sigma$-conjugacy class [b], and that its group of automorphisms is $G = J_b(K)$.

8 Comparison in the case ${{\,\mathrm{GL}\,}}_n$, b basic, w Coxeter

We will compare the two Deligne–Lusztig type constructions from Part 1 in this special situation and describe both explicitly using the isocrystal $(V,b\sigma )$. In Sects. 6.1 and 6.2, we let $b \in {{\,\mathrm{GL}\,}}_n(\breve{K})$ be any basic element with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$. From Sect. 6.3 onwards, we take b to be the special representative defined in Sect. 5.2.2.

8.1 The admissible subset of $(V,b\sigma )$

We will describe the various Deligne–Lusztig varieties using certain subsets of V, which we now define. Let $x \in V$. Put

$$\begin{aligned} g_b(x)&= \text {matrix in }M_n(\breve{K})\text { with columns }x, b\sigma (x), \dots , (b\sigma )^{n-1}(x) \\ V_b^\mathrm {adm}&= \{x \in V : \det g_b(x) \in \breve{K}^{\times } \} \\ V_b^{\mathrm {adm}, \mathrm {rat}}&= \{x \in V : \det g_b(x) \in K^{\times } \} \end{aligned}$$

If $g^{-1} b' \sigma (g) = b$, then the isomorphism of isocrystals $(V,b\sigma ) \rightarrow (V,b'\sigma )$, $x \mapsto gx$, maps $V_b^{\mathrm {adm}}$ to $V_{b'}^{\mathrm {adm}}$. In particular, $J_b(K)$ acts on $V_b^{\mathrm {adm}}$ by left multiplication. Moreover, $L^{\times }$ acts on $V_b^{\mathrm{adm, rat}}$ by scaling. Note also that $x \in V$ lies in $V_b^\mathrm {adm}$ if and only if the ${\mathcal {O}}$-submodule of V generated by $x,(b\sigma )(x), \dots , (b\sigma )^{n-1}(x)$ is an ${\mathcal {O}}$-lattice.

We have the following useful lemma, which essentially follows from basic properties of Newton polygons. Its simple proof was explained to the authors by E. Viehmann.

Lemma 6.1

Let $x \in V_b^{\mathrm {adm}}$. The ${\mathcal {O}}$-lattice generated by $\{(b\sigma )^i(x)\}_{i=0}^{n-1}$ is $b\sigma$-stable, i.e., there exist unique elements $\lambda _i \in {\mathcal {O}}$ such that $(b\sigma )^n(x) = \sum _{i = 0}^{n-1} \lambda _i (b\sigma )^i(x)$. Moreover, ${{\,\mathrm{ord}\,}}(\lambda _0) = \kappa _G(b)$.

Proof

The Newton polygon of $(V,b\sigma )$ is the straight line segment connecting the points (0, 0) and $(n,\kappa )$ in the plane. Now, let $K[\Sigma ]$ be the non-commutative ring defined by the relation $a\Sigma = \Sigma \sigma (a)$, and let $\Sigma$ act on V by $b\sigma$. Then the Newton polygon of the characteristic polynomial of x (which is an element of $K[\Sigma ]$) is equal to the Newton polygon of $(V, b\sigma )$ (see e.g. [1]). Observe that any $x \in V_b^\mathrm {adm}$ generates V as a $K[\Sigma ]$-module. Then the point $(i,{{\,\mathrm{ord}\,}}(a_i))$ in the plane, where $a_i$ is the coefficient of $\Sigma ^{n-i}$ in the characteristic polynomial, lies over that Newton polygon. This simply means ${{\,\mathrm{ord}\,}}(a_i) \ge \frac{i\kappa }{n} \ge 0$, as $\kappa \ge 0$. Hence $\Sigma ^n(v) = \sum _{i=1}^n a_i \Sigma ^{n-i}(x)$ lies in the ${\mathcal {O}}$-lattice generated by $x, \Sigma (x), \dots , \Sigma ^{n-1}(x)$. This proves the first assertion. The second statement follows as $(n, {{\,\mathrm{ord}\,}}(a_n))$ has necessarily to be the rightmost vertex of the Newton polygon, which is $(n,\kappa )$. $\square$

Example 6.2

For $b = 1$, the set $V_1^\mathrm {adm}$ is just the Drinfeld upper halfspace. If $(\kappa , n) = 1$, then $V_b^\mathrm {adm}= V {\,\smallsetminus \,}\{0\}$ as $(V,b\sigma )$ has no proper non-trivial sub-isocrystals.

8.2 Set-theoretic description

We need the following notation:

• Let $T_{{{\,\mathrm{diag}\,}}}$ denote the diagonal torus of ${{\,\mathrm{GL}\,}}_n$ and W its Weyl group.

• Let w be the image in W of the element $b_0$ from Sect. 5.2.1. Then the form $T_w := T_{{{\,\mathrm{diag}\,}},w}$ of $T_{diag}$ (as in Sect. 3) is elliptic with $T_w(K) \cong L^{\times }$ and has a natural model over ${\mathcal {O}}_K$, again denoted $T_w$, with $T_w({\mathcal {O}}_K) \cong {\mathcal {O}}_L^{\times }$.

• $I^m$ (with $m \ge 0$) denotes the preimage under the projection ${{\,\mathrm{GL}\,}}_n({\mathcal {O}}) \twoheadrightarrow {{\,\mathrm{GL}\,}}_n({\mathcal {O}}/\varpi ^{m+1}{\mathcal {O}})$, of all lower triangular matrices in ${{\,\mathrm{GL}\,}}_n({\mathcal {O}}/\varpi ^{m+1}{\mathcal {O}})$ whose entries under the main diagonal lie in $\varpi ^m{\mathcal {O}}/\varpi ^{m+1}{\mathcal {O}}$

• ${\dot{I}}^m$ (with $m \ge 0$) denotes the subgroup of $I^m$ consisting of all elements whose diagonal entries are congruent 1 modulo $\varpi ^{m+1}$

• $X_{*}^m(b)$, ${\dot{X}}_{*}^m(b)$ denote affine Deligne–Lusztig varieties of level $I^m$, ${\dot{I}}^m$ respectively (for appropriate $*$)

• For $r \ge 0$ and $x \in V_b^\mathrm {adm}$, let $g_{b,r}(x) \in {{\,\mathrm{GL}\,}}_n(\breve{K})$ denote the matrix whose ith column is $\varpi ^{r(i-1)}(b\sigma )^{i-1}(x)$. We have $g_b(x) = g_{b,0}(x)$.

• For $r, m \ge 0$, define $\sim _{b,m,r}$ and ${\dot{\sim }}_{b,m,r}$ on $V_b^\mathrm {adm}$ by

  $$\begin{aligned} x \,\sim _{b,m,r}\, y \in V_b^\mathrm {adm}\,\Leftrightarrow & {} \, y \in g_{b,r}(x) \cdot \begin{pmatrix} {\mathcal {O}}^{\times }&{\mathfrak {p}}^m&\dots&{\mathfrak {p}}^m \end{pmatrix}^\intercal , \\ x \,{\dot{\sim }}_{b,m,r}\, y \in V_b^\mathrm {adm}\,\Leftrightarrow & {} \, y \in g_{b,r}(x) \cdot \begin{pmatrix} 1+ {\mathfrak {p}}^{m+1}&{\mathfrak {p}}^m&\dots&{\mathfrak {p}}^m \end{pmatrix}^\intercal . \end{aligned}$$

  It follows from Lemma 6.6 that $\sim _{b,m,r}$ and ${\dot{\sim }}_{b,m,r}$ are equivalence relations.

• For $r \ge 0$, set ${\dot{w}}_r = b_0 \varpi ^{(-r,\dots ,-r,\kappa + (n-1)r)} \in {{\,\mathrm{GL}\,}}(\breve{K})$ and denote again by ${\dot{w}}_r$ the image of ${\dot{w}}_r$ in all the sets $I^m\backslash {{\,\mathrm{GL}\,}}_n(\breve{K})/I^m$ and ${\dot{I}}^m\backslash {{\,\mathrm{GL}\,}}_n(\breve{K})/{\dot{I}}^m$ for $m \ge 0$. The image of ${\dot{w}}_r$ in W is the Coxeter element w.

Furthermore, we define

$$\begin{aligned} {V_b^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \,{:=}\,\{x \in V : \sigma (\det g_b(x)) = \det (\dot{w}_0) \det (b)^{-1} \det (g_b(x))\}.} \end{aligned}$$

(6.1)

Observe that $\det (\dot{w}_0) \det (b)^{-1} \in {\mathcal {O}}^\times$, so picking any $\alpha \in {\mathcal {O}}^\times$ such that $\sigma (\alpha \sigma (\alpha ) \sigma ^2(\alpha ) \cdots \sigma ^{n-1}(\alpha )) = \det (\dot{w}_0) \det (b)^{-1}$ induces a $(J_b(K) \times L^\times )$-equivariant isomorphism $V_b^{\mathrm {adm}, \mathrm {rat}} \rightarrow V_b^{\mathrm {adm}, \mathrm {rat}, \dot{w}_0}$ given by $x \mapsto \alpha x$.

Remark 6.3

We will study the scheme structure on $X_{{\dot{w}}_r}^m(b)$, $\dot{X}_{{\dot{w}}_r}^m(b)$ in detail below in Sect. 6.4. But we want to point out already here that both are locally closed in ${{\,\mathrm{GL}\,}}_n(\breve{K})/I^m$, ${{\,\mathrm{GL}\,}}_n(\breve{K})/\dot{I}^m$, hence are reduced ${\mathbb {F}}_q$-schemes locally of finite type. Indeed, $\dot{I}^m$ is normal in I and the image of ${\dot{w}}_r$ in ${\widetilde{W}}$ satisfies the assumptions of Theorem 4.9 (see Lemma 6.4 below), hence it follows that $\dot{X}_{{\dot{w}}_r}^m(b) \subseteq \breve{{{\,\mathrm{GL}\,}}_n}/\dot{I}^m$ is locally closed. The same argument does not apply to $X_{{\dot{w}}_r}^m(b)$ as $I^m \subseteq I$ is not normal. Still $X_{{\dot{w}}_r}^m(b) \subseteq {{\,\mathrm{GL}\,}}_n(\breve{K})/I^m$ is locally closed. Indeed, let $p :{{\,\mathrm{GL}\,}}_n(\breve{K})/I^m \rightarrow {{\,\mathrm{GL}\,}}_n(\breve{K})/I$ denote the natural projection. As we will see below in Proposition 6.12, the Iwahori level variety $X_{\dot{w}_r}^0(b) = \bigsqcup _{G/G_{{\mathcal {O}}}} g.X^0_{\dot{w}_r}(b)_{{\mathscr {L}}_0} \subseteq {{\,\mathrm{GL}\,}}_n(\breve{K})/I$ is the scheme-theoretic disjoint union of translates of a certain locally closed subset $X^0_{\dot{w}_r}(b)_{{\mathscr {L}}_0}$. It thus suffices to show that $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0} = X_{\dot{w}_r}^m(b) \cap p^{-1}(X^0_{\dot{w}_r}(b)_{{\mathscr {L}}_0}) \subseteq p^{-1}(X^0_{\dot{w}_r}(b)_{{\mathscr {L}}_0})$ is locally closed. But this follows from the explicit coordinates on $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$ given in the proof of Theorem 6.17. $\Diamond$

Lemma 6.4

Let $w_r$ denote the image of $\dot{w}_r$ in ${{\widetilde{W}}}$. Then $w_r$ and $\dot{I}_m$ satisfy the assumptions of Theorem 4.9 (with respect to the Iwahori subgroup $I^0)$.

Proof

We use the same notation as in Theorem 4.9. We have to show that the subsets $p(A_{w_r})$, $p(B_{w_r})$, $p(C_{w_r})$ of ${{\widehat{\Phi }}}$ are disjoint and that the same holds for $p(A_{w_r^{-1}})$, $p(B_{w_r^{-1}})$, $p(C_{w_r^{-1}})$. Write ${{\widehat{\Phi }}} = \{\alpha _{i,j} :1\le i \ne j \le n\} \cup \{0\}$ where $\alpha _{i,j}$ corresponds to the i, j-th entry of a matrix. Let w be the image of $w_r$ in the finite Weyl group W. Then w acts on $\Phi$ by $w.\alpha _{i,j} = \alpha _{i+1,j+1}$, $w.0 = 0$, where we consider i, j as elements of ${\mathbb {Z}}/n{\mathbb {Z}}$. Then ${{\widehat{\Phi }}}_{\mathrm{aff}}(I/\dot{I}^m)$ is equal to

$$\begin{aligned}&\{(\alpha _{i,j}, \lambda ) :\alpha _{i,j} \in \Phi \text { and } 0\le \lambda \le m-1 \text { (if }i>j) \text { resp. } 1 \\&\quad \le \lambda \le m \text { (if }i<j) \} \cup \{(0,\lambda ) :0\le \lambda \le m\}. \end{aligned}$$

Now one computes that $w_r.(0,\lambda ) = (0,\lambda )$ and $w_r.(\alpha _{i,j},\lambda ) = (\alpha _{i+1,j+1},\lambda )$ if either ($n> i > j$) or ($n> j > i$). Further, $w_r.(\alpha _{n,j},\lambda ) = (\alpha _{1,j+1}, \lambda +nr+\kappa )$ and $w_r.(\alpha _{i,n},\lambda ) = (\alpha _{i+1,1}, \lambda - nr - \kappa )$. Thus we deduce that $p(B_{w_r}) = \{\alpha _{i,j} \in \Phi :n>i>j \text { or } n>j>i \} \cup \{0\}$, $p(A_{w_r}) = \{\alpha _{i,n} \in \Phi :1\le i\le n-1\}$ and $p(C_{w_r}) = \{\alpha _{n,j} \in \Phi :1\le j\le n-1\}$. Similarly, we compute that $p(B_{w_r}^{-1}) = \{\alpha _{i,j} \in \Phi :i>j>1 \} \cup \{0\}$, $p(A_{w_r^{-1}}) = \{\alpha _{1,j} \in \Phi :1\le j\le n-1\}$ and $p(C_{w_r^{-1}}) = \{\alpha _{i,1} \in \Phi :1\le i\le n-1\}$. $\square$

Recall from Sect. 3 that $G = J_b(K)$ acts on $X_w^{DL}(b)$ and $\dot{X}_{\dot{w}_0}^{DL}(b)$ by left multiplication. By Theorem 6.5 below, the maps $\dot{X}_{\dot{w}_0}^{DL}(b) \rightarrow X_w^{DL}(b)$ and $\dot{X}_{\dot{w}_r}^m(b) \rightarrow X_{\dot{w}_r}^m(b)$ are both surjective. Hence the former is a $T_w(K)$-torsor via the right-multiplication action of $T_w(K)$ on $\dot{X}_{\dot{w}_0}^{DL}(b)$ (by Lemma 3.2(iii)) and the latter is a $(I^m/\dot{I}^m)_{\dot{w}_r} \cong T_w({\mathcal {O}}_K/\varpi ^{m+1})$-torsor via the right-multiplication action of $I^m/\dot{I}^m$ on $\dot{X}_{\dot{w}_r}^m(b)$.

Theorem 6.5

• (i) There is a commutative diagram of sets

  

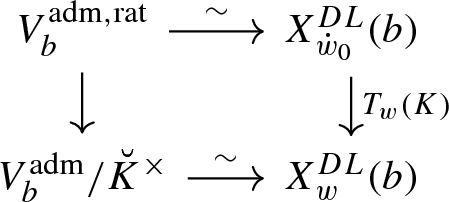
  in which horizontal arrows are $G\times T_w(K)$-equivariant isomorphisms. Moreover, the vertical arrows in the diagram are surjective.

• (ii) Assume that $r \ge m \ge 0$. There is a commutative diagram of sets

  

  in which horizontal arrows are $G \times T_w({\mathcal {O}}_K/\varpi ^{m+1})$-equivariant isomorphisms. Moreover, the vertical arrows in the diagram are surjective.

Before proving the theorem, we need some preparations. Observe that by Lemmas 3.2 and 4.4 in the proof of Theorem 6.5, we may replace b by an $\sigma$-conjugate element of $\breve{G}$.

Lemma 6.6

Let $r > 0$. Let $x,y \in V_b^\mathrm {adm}$. Then

$$\begin{aligned} x \sim _{b,m,r} y\Leftrightarrow & {} g_{b,r}(x)I^m = g_{b,r}(y)I^m, \end{aligned}$$

(6.2)

$$\begin{aligned} x {\dot{\sim }}_{b,m,r} y\Leftrightarrow & {} g_{b,r}(x){\dot{I}}^m = g_{b,r}(y){\dot{I}}^m. \end{aligned}$$

(6.3)

Proof

Indeed, $g_{b,r}(y) \in g_{b,r}(x)I^m$ is equivalent to

$$\begin{aligned} y&\in x {\mathcal {O}}^{\times } + \varpi ^{m+r}b\sigma (x) {\mathcal {O}}+ \dots + \varpi ^{m + r(n-1)} (b\sigma )^{n-1}(x) {\mathcal {O}}\\ \varpi ^r (b\sigma )(y)&\in \varpi ^{m+1} x {\mathcal {O}}+ \varpi ^r b\sigma (x) {\mathcal {O}}^{\times } + \varpi ^{m+2r} (b\sigma )^2(x) {\mathcal {O}}\dots + \varpi ^{m+(n-1)r}(b\sigma )^{n-1}(x) {\mathcal {O}}\\&\;\;\vdots \\ \varpi ^{r(n-1)} (b\sigma )^{n-1}(y)&\in \varpi ^{m+1}x{\mathcal {O}}+ \dots + \varpi ^{m+1+r(n-2)} (b\sigma )^{n-2}(x) {\mathcal {O}}+ \varpi ^{r(n-1)}(b\sigma )^{n-1}(x) {\mathcal {O}}^{\times }. \end{aligned}$$

By definition, the first equation is equivalent to $x \sim _{b,m,r} y$. But once the first equation holds, then the $(i+1)$th equation must also hold by applying $\varpi ^{ri} (b\sigma )^i$ to the first equation and using Lemma 6.1. Hence (6.2) follows, and a similar proof gives (6.3). $\square$

Lemma 6.7

Let $r \ge 0$ and $x \in V_b^\mathrm {adm}$. Then

$$\begin{aligned} b\sigma (g_{b,r}(x)) = g_{b,r}(x) {\dot{w}}_r A, \end{aligned}$$

where $A \in {{\,\mathrm{GL}\,}}_n(\breve{K})$ is a matrix, which can differ from the identity matrix only in the last column. Moreover, the lower right entry of A lies in ${\mathcal {O}}^{\times }$, and if $r > m \ge 0$, then $A \in I^m$.

Proof

By definition, we have

$$\begin{aligned} b \sigma (g_{b,r}(x))&= \begin{pmatrix} b\sigma (x)&\varpi ^r (b\sigma )^2(x)&\cdots&\varpi ^{r(n-2)}(b\sigma )^{n-1}(x)&\varpi ^{r(n-1)} (b\sigma )^n(x) \end{pmatrix}, \\ g_{b,r}(x){\dot{w}}_r&= \begin{pmatrix} b\sigma (x)&\varpi ^r (b\sigma )^2(x)&\cdots&\varpi ^{r(n-2)}(b\sigma )^{n-1}(x)&\varpi ^{r(n-1) + \kappa _G(b)} x \end{pmatrix}, \end{aligned}$$

As the first $n-1$ columns of these matrices coincide, it follows that A can at most differ from the identity matrix in the last column. By Lemma 6.1, we may write

$$\begin{aligned} (b\sigma )^n(x)&= \sum _{i=0}^{n-1} \alpha _i \cdot (b\sigma )^i(x) \\&= \frac{\alpha _0}{\varpi ^{r(n-1)+\kappa _G(b)}} \cdot \varpi ^{r(n-1)+\kappa _G(b)} x + \sum _{i=1}^{n-1} \frac{\alpha _i}{\varpi ^{r(i-1)}} \cdot \varpi ^{r(i-1)} (b\sigma )^i(x), \end{aligned}$$

where $\alpha _0, \ldots , \alpha _{n-1} \in {\mathcal {O}}$ and ${{\,\mathrm{ord}\,}}(\alpha _0) = \kappa$. By construction, the last column of A is

$$\begin{aligned} \left( \varpi ^{r(n-1)} \alpha _1, \varpi ^{r(n-2)} \alpha _2, \varpi ^{r(n-3)} \alpha _3, \ldots , \varpi ^r \alpha _{n-1}, \frac{\alpha _0}{\varpi ^{\kappa _G(b)}}\right) ^\intercal . \end{aligned}$$

We then see that the lower right entry of A is $\frac{\alpha _0}{\varpi ^{\kappa }} \in {\mathcal {O}}^\times$ and that if $r \ge m+1$, then all the entries above $\frac{\alpha _0}{\varpi ^{\kappa }}$ lie in $\varpi ^{m+1} {\mathcal {O}}$ and $A \in I^m$. $\square$

Proof of Theorem 6.5

(i) As in [13, §1], the sets $X_w^{DL}(b)$ do not depend on the choice of the Borel subgroup, so we may choose $B \subseteq {{\,\mathrm{GL}\,}}_n$ to be the Borel subgroup of the upper triangular matrices and U its unipotent radical. Lemma 6.7 for $r = 0$ implies the existence of the map

$$\begin{aligned} V_b^\mathrm {adm}\rightarrow X_w^{DL}(b), \quad x \mapsto g_b(x)\breve{B}. \end{aligned}$$

We claim this map is surjective. Let $g\breve{B} \in X_w^{DL}(b)$, i.e., $g^{-1} b \sigma (g) \in \breve{B} {\dot{w}}_0 \breve{B}$. Replacing g by another representative in $g\breve{B}$ if necessary, we may assume that $b \sigma (g) \in g {\dot{w}}_0 \breve{B}$. Moreover, this assumption does not change, whenever we replace g by another representative $g^{\prime } = gc$ with $c \in \breve{B} \cap {}^{\dot{w}_0} \breve{B}$ (here ${}^{\dot{w}_0} \breve{B} = \dot{w}_0\breve{B}\dot{w}_0^{-1}$). A direct computation shows that replacing g by gc for an appropriate $c \in B \cap {}^{{\dot{w}}_0} \breve{B}$, we find a representative g of $g\breve{B}$ with columns $g_1, g_2, \dots , g_n$ satisfying $g_{i+1} = b\sigma (g_i)$ for $i = 1, \dots , n-1$. This means precisely $g = g_b(x)$. All this shows the surjectivity claim. For $x, y \in V_b^\mathrm {adm}$, one has $g_b(x) \breve{B} = g_b(y) \breve{B}$ if and only if x, y differ by a constant in $\breve{K}^{\times }$. This shows the lower horizontal isomorphism in part (i) of the theorem.

We now construct the upper isomorphism. We may write an element of ${\dot{g}}\breve{U} \in \breve{G}/\breve{U}$ lying over $g_b(x)\breve{B} \in X_w^{DL}(b)$ as ${\dot{g}}\breve{U} = g_b(x)t\breve{U}$ for some $t \in \breve{T}$. Using Lemma 6.7 (and the notation from there) we see that

$$\begin{aligned} {\dot{g}}^{-1} b \sigma ({\dot{g}}) = t^{-1} g_b(x)^{-1}b \sigma (g_b(x)) \sigma (t) = t^{-1} {\dot{w}}_0 A \sigma (t) \end{aligned}$$

Now write $A = \lambda A_0$ with $A_0 \in \breve{U}$ and $\lambda = {{\,\mathrm{diag}\,}}(1,\dots ,1,\lambda _0)$ a diagonal matrix with $\lambda _0 \in {\mathcal {O}}^\times$. We then see that ${\dot{g}}^{-1} b \sigma ({\dot{g}}) = t^{-1}\dot{w}_0 \lambda \sigma (t)\cdot {}^{\sigma (t)}A_0$. Hence $g_b(x)t \in X_{{\dot{w}}_0}^{DL}(b)$ if and only if $\dot{w}_0^{-1}t^{-1}\dot{w}_0 \sigma (t) = \lambda ^{-1}$. Thus, if we write $t_0, t_1, \dots , t_{n-1} \in \breve{K}^{\times }$ for the diagonal entries of t, then we have $t_{i+1} = \sigma (t_i)$ for $0 \le i \le n-2$. We may assume this. In particular, it implies that $g_b(x)t = g_b(xt_0)$. In other words, replacing x by $xt_0$, we may assume that ${\dot{g}} = g_b(x)$. It remains to determine all $x \in V_b^\mathrm {adm}$, for which $g_b(x)\breve{U} \in X_{{\dot{w}}_0}^{DL}(b)$, i.e., $g_b(x)^{-1} b\sigma (g_b(x)) \in \breve{U} {\dot{w}}_0 \breve{U}$. Comparing the determinants on both sides we deduce that $\sigma (\det g_b(x)) = \det (\dot{w}_0) \det (b)^{-1} \det g_b(x)$ (i.e. that $x \in V_b^{\mathrm {adm},\mathrm {rat},\dot{w}_0}$) as a necessary condition. Assume this holds. With notations as in Lemma 6.7, we deduce $\det (A) = 1$. Moreover, since A can differ from the identity matrix in at most the last column by Lemma 6.7, $\det (A) = 1$ is equivalent to $A \in \breve{U}$. All this, together with the fact that $V_b^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \cong V_b^{\mathrm {adm},\mathrm {rat}}$ (see (6.1)) shows the upper isomorphism in part (i). The commutativity of the diagram and $J_b(K)$-equivariance of the involved maps are clear from the construction. The surjectivity claim for the vertical maps is shown in exactly the same way as the analogous claim in part (ii) below.

(ii) Lemma 6.7 for $r > m \ge 0$ implies the existence of the map

$$\begin{aligned} V_b^\mathrm {adm}\rightarrow X_{{\dot{w}}_r}^m(b), \quad x \mapsto g_{b,r}(x)I^m. \end{aligned}$$

We claim it is surjective. Let $gI^m \in X_{{\dot{w}}_r}^m(b)$, i.e., $g^{-1}b\sigma (g) \in I^m {\dot{w}}_r I^m$. Replacing g by another representative of $gI^m$ if necessary, we may assume that $b\sigma (g) \in g {\dot{w}}_r I^m$. Moreover, this assumption does not change, whenever we replace g by another representative $g^{\prime } = gj$ with $j \in I^m \cap {}^{{\dot{w}}_r} I^m$. In the rest of the proof, we call such transformations allowed. We compute

$$\begin{aligned} I^m \cap {}^{\dot{w}_r} I^m = \begin{pmatrix} {\mathcal {O}}^{\times } &{}\quad {\mathfrak {p}}^{rn+m} &{}\quad \cdots &{}\quad \cdots &{}\quad {\mathfrak {p}}^{rn+m} \\ {\mathfrak {p}}^m &{}\quad {\mathcal {O}}^{\times } &{}\quad {\mathfrak {p}}^{m+1} &{}\quad \cdots &{}\quad {\mathfrak {p}}^{m+1} \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ {\mathfrak {p}}^m &{}\quad \cdots &{}\quad {\mathfrak {p}}^m&{}\quad {\mathcal {O}}^{\times }&{}\quad {\mathfrak {p}}^{m+1} \\ {\mathfrak {p}}^m &{}\quad \cdots &{}\quad \cdots &{}\quad {\mathfrak {p}}^m &{}\quad {\mathcal {O}}^{\times } \end{pmatrix} \end{aligned}$$

(on the main diagonal entries can lie in ${\mathcal {O}}^{\times }$, under the main diagonal in ${\mathfrak {p}}^m$, in the first row, beginning from the second entry, in ${\mathfrak {p}}^{rn + m}$, and above the main diagonal, except for the first row, in ${\mathfrak {p}}^{m+1}$). Let $g_1, \dots , g_n$ denote the columns of g, seen as elements of V. Then $g{\dot{w}}_r \in b\sigma (g)I^m$ is equivalent to the following n equations:

$$\begin{aligned} g_2&\in \varpi ^r b\sigma (g_1){\mathcal {O}}^{\times } + \varpi ^{r+m}b\sigma (g_2) {\mathcal {O}}+ \dots + \varpi ^{r+m} b\sigma (g_n) {\mathcal {O}}\\ g_3&\in \varpi ^{r+m+1} b\sigma (g_1) {\mathcal {O}}+ \varpi ^r b\sigma (g_2){\mathcal {O}}^{\times } + \varpi ^{r+m} b\sigma (g_3) {\mathcal {O}}+ \dots + \varpi ^{r+m} b\sigma (g_n) {\mathcal {O}}\\&\;\;\vdots \\ g_n&\in \varpi ^{r+m+1} b\sigma (g_1) {\mathcal {O}}+ \dots + \varpi ^{r+m+1} b\sigma (g_{n-2}){\mathcal {O}}+ \varpi ^r b\sigma (g_{n-1}) {\mathcal {O}}^{\times } + \varpi ^{r+m} b\sigma (g_n) {\mathcal {O}}\\ \varpi ^{rn+m+\kappa } g_1&\in \varpi ^{r + 2m + 1} b\sigma (g_1) {\mathcal {O}}+ \dots + \varpi ^{r + 2m + 1} b\sigma (g_{n-1}){\mathcal {O}}+ \varpi ^{r+m} b\sigma (g_n) {\mathcal {O}}^{\times }. \end{aligned}$$

A linear algebra exercise shows that after some allowed transformations these equations can be rewritten as

$$\begin{aligned} g_2&\in \varpi ^r b\sigma (g_1){\mathcal {O}}^{\times } \\ g_3&\in \varpi ^r b\sigma (g_2){\mathcal {O}}^{\times } \\&\;\;\vdots \\ g_n&\in \varpi ^r b\sigma (g_{n-1}) {\mathcal {O}}^{\times } \\ \varpi ^{r(n-1)+\kappa }g_1&\in \varpi ^{m + 1}b\sigma (g_1) {\mathcal {O}}+ \dots + \varpi ^{m + 1} b\sigma (g_{n-1}){\mathcal {O}}+ b\sigma (g_n) {\mathcal {O}}^{\times }. \end{aligned}$$

This shows that $g = g_{b,r}(g_1)$, and hence the claimed surjectivity. Lemma 6.6 shows that the lower map in part (ii) is an isomorphism. Exactly as in the proof of (i), one shows that the claim of (ii) is true if one replaces the upper left entry by $\left\{ x \in V_b^\mathrm {adm}:{\begin{matrix} \det (g_{b,r}(x))\, \mathrm{mod} \, \varpi ^{m+1} \\ \text {is fixed by } \sigma \end{matrix}} \right\}$. As $x\, {\dot{\sim }}_{b,m,r}\, xu$ for any $u \in 1 + {\mathfrak {p}}^{m+1}$, the original claim of (ii) follows from this modified claim along with the surjectivity of the map $1 + {\mathfrak {p}}^{m+1} \rightarrow 1 + {\mathfrak {p}}^{m+1}$, $u \mapsto \prod _{i=0}^{n-1} \sigma ^i(u)$, and the fact that $\det g_b(x) \in K^{\times } \Leftrightarrow \det g_{b,r}(x) \in K^{\times }$.

It remains to show that the vertical arrows in the diagram in (ii) are surjective. It suffices to handle the left arrow. Let $x \in V^{\mathrm{adm}}_b$. By definition of $\sim _{b,m,r}$, for any $\lambda \in {\mathcal {O}}^\times$ we have $\lambda x \sim _{b,m,r} x$. Now we have $\det g_b(\lambda x) = \varpi ^a \cdot \prod _{i=0}^{n-1}\sigma ^i(\lambda ) \cdot \det g_b(x)$ for an appropriate $a \in {\mathbb {Z}}$. Now the map $\lambda \mapsto \prod _{i=0}^{n-1}\sigma ^i(\lambda ) :{\mathcal {O}}^\times \rightarrow {\mathcal {O}}^\times$ is surjective, hence by rescaling x with an appropriate $\lambda \in {\mathcal {O}}^\times$ (thus not changing its class in $V_b^{\mathrm{adm}}/\sim _{b,m,r}$) we can arrange that $\det g_b(x) \in K^\times$, i.e., that $x\in V_b^{\mathrm{adm, rat}}$. $\square$

The natural projection maps $X_{\dot{w}_r}^{m+1}(b) \rightarrow X_{\dot{w}_r}^m(b)$ and $\dot{X}_{\dot{w}_r}^{m+1}(b) \rightarrow \dot{X}_{\dot{w}_r}^m(b)$ are obviously morphisms of schemes. However, Theorem 6.5 implies that there are G- and $G \times T_w({\mathcal {O}}_K/\varpi ^{m+1})$-equivariant maps of sets (on $\overline{{\mathbb {F}}}_q$-points)

$$\begin{aligned} X_{\dot{w}_{r+1}}^m(b) \rightarrow X_{\dot{w}_r}^m(b), \qquad \text {and} \qquad \dot{X}_{\dot{w}_{r+1}}^m(b) \rightarrow \dot{X}_{\dot{w}_r}^m(b) \end{aligned}$$

(6.4)

induced by $g_{b,r+1}(x)\mapsto g_{b,r}(x)$. In Sect. 6.4, we explicate the scheme structure on $X_{\dot{w}_r}^m(b)$, $\dot{X}_{\dot{w}_r}^m(b)$ and prove that these maps of sets are actually morphisms of schemes (Theorem 6.17). Taking Theorem 6.17 for granted at the moment, we have a notion of an affine Deligne–Lusztig variety at infinite level.

Definition 6.8

Define the (infinite-dimensional) ${{\overline{{\mathbb {F}}}}}_q$-scheme

$$\begin{aligned} {X_w^{\infty }(b) \,{:=}\,\varprojlim \limits _{r,m :r> m} X_{{\dot{w}}_r}^m(b) \qquad \text {and} \qquad {\dot{X}}_w^{\infty }(b) \,{:=}\,\varprojlim \limits _{r,m :r > m} {\dot{X}}_{{\dot{w}}_r}^m(b).} \end{aligned}$$

Both have actions by G and the natural G-equivariant map ${\dot{X}}_w^{\infty }(b) \rightarrow X_w^{\infty }(b)$ is a $T_w({\mathcal {O}}_K)$-torsor.

Passing to the infinite level in Theorem 6.5 gives the following result.

Theorem 6.9

There is a commutative diagram of sets with G-equivariant maps:

The upper horizontal maps are $T_w({\mathcal {O}}_K)$-equivariant. This extends the natural $T_w({\mathcal {O}}_K)$-action on $\dot{X}_w^{\infty }(b)$ to a $T_w(K)$-action.

Using the set-theoretic isomorphism in Theorem 6.9, we will see in Sect. 6.4 that by endowing $V_b^{\mathrm {adm}}$ with the natural scheme structure over ${{\overline{{\mathbb {F}}}}}_q$ coming from the lattice ${\mathscr {L}}_0$, we can view the semi-infinite Deligne–Lusztig sets $X_w^{DL}(b), \dot{X}_w^{DL}(b)$ as (infinite-dimensional) ${{\overline{{\mathbb {F}}}}}_q$-schemes. Moreover, every isomorphism in Theorem 6.9 is an isomorphism of $\overline{{\mathbb {F}}}_q$-schemes (Corollary 6.19).

8.3 Connected components

To “minimize” powers of the uniformizer, we define

$$\begin{aligned} {g_b^\mathrm {red}(v) \,{:=}\,\left( v \Bigm \vert \frac{1}{\varpi ^{\lfloor k_0/n_0 \rfloor }} b\sigma (v) \Bigm \vert \frac{1}{\varpi ^{\lfloor 2k_0/n_0 \rfloor }} (b\sigma )^2(v) \Bigm \vert \cdots \Bigm \vert \frac{1}{\varpi ^{\lfloor (n-1)k_0/n_0 \rfloor }} (b\sigma )^{n-1}(v) \right) } \end{aligned}$$

(6.5)

to be the $n \times n$ matrix whose ith column is $\frac{1}{\varpi ^{\lfloor (i-1)k_0/n_0 \rfloor }} \cdot (b\sigma )^{i-1}(v)$ for $v \in V$. Observe that

$$\begin{aligned} g_b(v) = g_b^\mathrm {red}(v) \cdot D_{k,n}, \end{aligned}$$

where $D_{k,n}$ is the diagonal matrix whose (i, i)th entry is $\varpi ^{\lfloor (i-1)k_0/n_0\rfloor }$.

Definition 6.10

For any basic b (with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$) which is integrally $\sigma$-conjugate to the special representative as in Sect. 5.2.2, we define

$$\begin{aligned} {\mathscr {L}}_{0,b}^{\mathrm {adm}}&\,{:=}\,\left\{ v \in {\mathscr {L}}_0 : \det g_b^{\mathrm {red}}(v) \in {\mathcal {O}}^\times \right\} , \\ {\mathscr {L}}_{0,b}^{\mathrm {adm}, \mathrm {rat}}&\,{:=}\,\left\{ v \in {\mathscr {L}}_0 : \det g_b^{\mathrm {red}}(v) \in {\mathcal {O}}_K^\times \right\} , \\ {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat},\dot{w}_0}&\,{:=}\,\left\{ v \in \mathscr {L}_0 : \sigma (\det g_b^{\mathrm {red}}(v)) = \det (\dot{w}_0) \det (b)^{-1} \det g_b^{\mathrm {red}}(v) \in {\mathcal {O}}^\times \right\} . \end{aligned}$$

As in (6.1), note that ${\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \cong {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}}$ by rescaling appropriately by an element of ${\mathcal {O}}^\times$.

Let now b be the special representative with $\kappa _G(b) = \kappa$. As $G_{{\mathcal {O}}} \subseteq {{\,\mathrm{GL}\,}}_n({\mathcal {O}}) = \mathrm{Stab}({\mathscr {L}}_0)$ inside ${{\,\mathrm{GL}\,}}_n(\breve{K})$, we see that ${\mathscr {L}}_{0,b}^{\mathrm{adm, rat}}, \, {\mathscr {L}}_{0,b}^{\mathrm{adm}}$ are stable under $G_{{\mathcal {O}}} \times T_w({\mathcal {O}}_K)$. We have

$$\begin{aligned} {\mathscr {L}}_{b,0}^{\mathrm {adm}} {=} \left\{ v {=} \sum _{i=1}^n a_i \mathbf {e}_i \in {\mathscr {L}}_0 :\begin{aligned} a_i \in {\mathcal {O}}\text { for }1 \le i \le n; \{ a_i \mathbf {e}_i \!\!\!\!\pmod \varpi \}_{i \equiv 1 \!\!\!\!\pmod {n_0}} \\ \text {generate the }{{\overline{{\mathbb {F}}}}}_q\text {-vector space }{{\overline{V}}} \end{aligned} \right\} ,\nonumber \\ \end{aligned}$$

(6.6)

where ${{\overline{V}}}$ is as in Sect. 5.6 (compare [32, Lemma 4.8]). For $x \in {\mathscr {L}}_{b,0}^{\mathrm {adm}}$ with reduction-modulo-$\varpi$ ${{\overline{x}}}$, define $\overline{g_b}({\bar{x}}) \in {{{\,\mathrm{GL}\,}}}_{n'}({\overline{{\mathbb {F}}}}_q)$ to be the matrix from reducing every entry of $g_b^{\mathrm{red}}(x)$ modulo $\varpi$ and deleting the ith row and jth column for all $(i,j) \not \equiv (1,1)$ modulo $n_0$.

Lemma 6.11

We have a disjoint decomposition

$$\begin{aligned} V_b^{\mathrm{adm}} = \coprod _{g \in G/G_{\mathcal {O}}} g({\mathscr {L}}_{0,b}^{\mathrm{adm}}) \end{aligned}$$

Proof

Let c, d be as in Lemma 5.8. On V we have the operators considered in [32, 4.1]: $b\sigma$, $\varpi (b\sigma )^{-1}$, $\varpi ^d(b\sigma )^c$, $\varpi ^{-\kappa _0}(b\sigma )^{n_0} = \sigma ^{n_0}$ (in [32], these operators are denoted $F,V,\pi _1,\sigma _1$ respectively). For $v \in V_b^\mathrm {adm}$ we may consider the smallest ${\mathcal {O}}$-submodule P(v) of V, containing v and stable under these four operators (this is a indeed lattice: for $\kappa >0$ see [32, p. 354, paragraph before Lemma 4.10]; for $\kappa = 0$, Lemma 6.1 shows that this is the lattice generated by $\{\sigma ^i(v)\}_{i=0}^{n-1}$). Further we have

$$\begin{aligned} {\mathscr {L}}_{0,b}^{\mathrm{adm}} = \left\{ v \in {\mathscr {L}}_0 :P(v) = {\mathscr {L}}_0 \right\} . \end{aligned}$$

This follows from the explicit description of both sides: (6.6) above and [32, Lemma 4.8 and beginning of §4.4]. Next, the set of lattices in V stable under the four operators above is in bijection with $G/G_{\mathcal {O}}$ via $gG_{\mathcal {O}}\mapsto g{\mathscr {L}}_0$. Indeed, for $\kappa > 0$ this follows from Lemma 4.8 and 4.10 of [32] (note that there Viehmann only considers bi-infinitesimal p-divisible groups, so that the slope(s) of V must be strictly between 0 and 1); and for $\kappa = 0$, this is clear from the description of the affine Grassmannian of ${{\,\mathrm{GL}\,}}_n$ in terms of lattices.

Any $g \in G$ commutes with the four operators above, hence $P(gv) = gP(v)$ and hence $g({\mathscr {L}}_{0,b}^{\mathrm{adm}}) = \{v \in {\mathscr {M}} :P(v) = {\mathscr {M}}\}$ if ${\mathscr {M}} = g({\mathscr {L}}_0)$. Finally, $\bigcup _{{\mathscr {M}}} \{v \in {\mathscr {M}} :P(v) = {\mathscr {M}}\}$ (where ${\mathscr {M}}$ runs through all lattices stable under the four operators) is disjoint and equal to $V_b^\mathrm {adm}$. $\square$

For each $h \in G/G_{\mathcal {O}}$, let $X_{\dot{w}_r}^m(b)_{h({\mathscr {L}}_0)}$ be the subset of $X_{\dot{w}_r}^m(b)$ consisting of all points which under the isomorphism $X_{\dot{w}_r}^m(b)({{\overline{{\mathbb {F}}}}}_q) \cong V_b^\mathrm {adm}/\sim _{b,m,r}$ of Theorem 6.5 correspond to $h({\mathscr {L}}_{0,b}^\mathrm {adm})$.

The Iwahori level variety $X_{\dot{w}_r}^0(b)$ is known to be locally closed in the ind-scheme ${{\,\mathrm{GL}\,}}_n(\breve{K})/I$ and locally of finite type over ${{\overline{{\mathbb {F}}}}}_q$. The following result (as well as the preceeding lemma) is based on ideas from [32], which were explained to the authors by E. Viehmann.

Proposition 6.12

Let $r > 0$. For any $h\in G$, $X_{\dot{w}_r}^0(b)_{h({\mathscr {L}}_0)}$ is a closed and open subset of $X_{\dot{w}_r}^0(b)$. In other words, $X_{\dot{w}_r}^0(b) = \coprod _{h \in G/G_{\mathcal {O}}} X_{\dot{w}_r}^0(b)_{h({\mathscr {L}}_0)}$ is a scheme-theoretic disjoint union decomposition.

Proof

The proof follows along the same lines as [32, Lemma 4.16]. First we show that $X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0} \subseteq X_{\dot{w}_r}^0(b)$ is closed. To this end, recall that points of ${{\,\mathrm{GL}\,}}_n(\breve{K})/I$ can be interpreted as complete chains of ${\mathcal {O}}$-lattices in $\breve{K}^n$. Let ${\mathscr {L}}_\bullet = \{{\mathscr {L}}_0 \supseteq {\mathscr {L}}_1 \supseteq \dots \supseteq {\mathscr {L}}_{n-1} \supseteq \varpi {\mathscr {L}}_0\}$ be the standard chain (stabilized by I). Then gI corresponds to the lattice chain $g{\mathscr {L}}_\bullet = \{g{\mathscr {L}}_i\}_{i=0}^{n-1}$. We claim that there is an integer $C > 0$ only depending on $n,\kappa ,r$ such that

$$\begin{aligned} X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0} = \{ {\mathscr {M}}_\bullet = ({\mathscr {M}}_i)_{i=0}^{n-1} \in X_{\dot{w}_r}^0(b) :{\mathscr {M}}_0 \subseteq {\mathscr {L}}_0 \text { and } {{\,\mathrm{vol}\,}}({\mathscr {M}}_0) = C \}. \end{aligned}$$

(6.7)

Let ${\mathscr {M}}_\bullet \in X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0}$. By construction, there is some $v \in {\mathscr {L}}_{0,b}^{\mathrm{adm}}$ such that ${\mathscr {M}}_\bullet = g_{b,r}(v){\mathscr {L}}_\bullet$. Then ${\mathscr {M}}_0 = g_{b,r}(v)({\mathscr {L}}_0)$ is the lattice generated by $\{\varpi ^{ri}(b\sigma )^i(v)\}_{i=0}^{n-1}$, which is contained in ${\mathscr {L}}_0$. Moreover,

$$\begin{aligned} {{\,\mathrm{vol}\,}}({\mathscr {M}}_0) = {{\,\mathrm{vol}\,}}(g_{b,r}(v)({\mathscr {L}}_0)) = {{\,\mathrm{ord}\,}}\det g_{b,r}(v) = C + {{\,\mathrm{ord}\,}}\det g_b^{\mathrm{red}}(v) = C, \end{aligned}$$

with $C > 0$ some explicit constant depending on $n,\kappa ,r$. Conversely, let ${\mathscr {M}}_\bullet \in X_{\dot{w}_r}^0(b)$ be such that ${\mathscr {M}}_0 \subseteq {\mathscr {L}}_0$ and ${{\,\mathrm{vol}\,}}({\mathscr {M}}_0) = C$ with the same C as above. By Theorem 6.5, there is some $v\in V_b^{\mathrm {adm}}$ with ${\mathscr {M}}_\bullet = g_{b,r}(v){\mathscr {L}}_\bullet$. Then ${\mathscr {M}}_0 = g_{b,r}(v){\mathscr {L}}_0$ is the lattice generated by $\{\varpi ^{ri}(b\sigma )^{i}(v)\}_{i=0}^{n-1}$. In particular, we must have $v \in {\mathscr {M}}_0 \subseteq {\mathscr {L}}_0$ and

$$\begin{aligned} {{\,\mathrm{ord}\,}}\det (g_b^{\mathrm{red}}(v)) = {{\,\mathrm{ord}\,}}\det (g_{b,r}(v)) - C = {{\,\mathrm{vol}\,}}({\mathscr {M}}_0) - C = 0. \end{aligned}$$

This proves claim (6.7). From this claim it follows that $X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0}$ is the intersection in ${{\,\mathrm{GL}\,}}_n(\breve{K})/I$ of $X_{\dot{w}_r}^0(b)$ with the preimage under

$$\begin{aligned} {{\,\mathrm{GL}\,}}_n(\breve{K})/I \rightarrow {{\,\mathrm{GL}\,}}_n(\breve{K})/\mathrm{Stab ({\mathscr {L}}_0)} \cong \{{\mathcal {O}}\text {-lattices in }\breve{K}^n \}, \quad {\mathscr {M}}_\bullet = \{\mathscr {M_i}\}_{i=0}^{n-1} \mapsto {\mathscr {M}}_0 \end{aligned}$$

of the closed (see [32, Remark 4.15]) subset of lattices with fixed volume and contained in ${\mathscr {L}}_0$. Hence $X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0}$ is closed in $X_{\dot{w}_r}^0(b)$.

Applying the G-action on $X_{\dot{w}_r}(b)$ we deduce that also $X_{\dot{w}_r}^0(b)_{h({\mathscr {L}}_0)}$ is closed in $X_{\dot{w}_r}^0(b)$ for each $h \in G$. Now the closed subvarieties $X_{\dot{w}_r}^0(b)_{h({\mathscr {L}}_0)}$ form a disjoint cover of $X_{\dot{w}_r}^0(b)$, as this holds on geometric points by Lemma 6.11 and Theorem 6.5. As $X_{\dot{w}_r}^0(b)$ is locally of finite type, this disjoint union is locally finite. Hence $X_{\dot{w}_r}^0(b)_{h({\mathscr {L}}_0)}$ is also open. $\square$

Remark 6.13

We explain the differences between our setting and that of [32, §4]. Viehmann proved a similar decomposition for an open subset ${\mathcal {S}}_1$ of some minuscule affine Deligne–Lusztig varieties at the hyperspecial level (in particular, in the bi-infinitesimal case, which in our notation corresponds to $\kappa > 0$). A point of ${\mathcal {S}}_1$ corresponds to a Dieudonné lattice ${\mathscr {M}}$ in V, that is a lattice stable by the operators $b\sigma$ and $p(b\sigma )^{-1}$. Such a lattice also possesses a single generator $v \in V_b^\mathrm {adm}$, but the difference between ${{\,\mathrm{vol}\,}}({\mathscr {M}})$ and ${{\,\mathrm{vol}\,}}(P({\mathscr {M}}))$ (where $P({\mathscr {M}})$ is the smallest lattice containing ${\mathscr {M}}$ and stable under the four operators as in the proof of Lemma 6.11), is quite inexplicit, and it is a complicated task [32, Theorem 4.11(ii)] to show that this difference is constant. In our situation the lattice (chain) corresponding to a point of $X_{\dot{w}_r}^0(b)$ is completely explicit, and the difference of volumes is immediate to compute. Note also that we work with the cocharacter $(-r,\ldots , -r,(n-1)r)$ for $r \ge 1$, and since this is never minuscule, there is no direct comparison between our setting and the varieties from [32]. $\Diamond$

Corollary 6.14

Let $b \in \breve{G}$ be integrally $\sigma$-conjugate to the special representative attached to $\kappa$. Then the conclusion of Proposition 6.12 holds for this b.

Proof

If $h \in {{\,\mathrm{GL}\,}}_n({\mathcal {O}})$ is such that $b = h^{-1}b_{sp}\sigma (h)$, where $b_{sp}$ is the special representative, then $g \mapsto h^{-1}g$ defines an isomorphism $X_{\dot{w}_r}^m(b_{sp}) {\mathop {\longrightarrow }\limits ^{\sim }} X_{\dot{w}_r}^m(b)$. Further, $g_b^{\mathrm {red}}(v) = h^{-1}g_{b_{sp}}^{\mathrm {red}}(hv)$ and the corollary follows from the commutativity of the obvious diagram. $\square$

By Lemma 5.6, Corollary 6.14 applies to the Coxeter-type representatives from Sect. 5.2.1.

8.4 The structure of $X_{\dot{w}}^m(b)$

Let b be the special representative with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$. Let $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$ be as defined before Proposition 6.12. The following auxiliary elements of ${{\,\mathrm{GL}\,}}_n(\breve{K})$ will be used in this subsection only. For $r\ge 1$, put $\mu _r = (1,r,2r,\dots ,(n-1)r) \in X_{*}(T_{\mathrm{diag}})$. For an integer a, let $0\le [a]_{n_0}<n_0$ denote its residue modulo $n_0$. Let $v_1 \in {{\,\mathrm{GL}\,}}_{n_0}(\breve{K})$ be the permutation matrix whose only non-zero entries are concentrated in the entries $(1 + [(i-1)k_0]_{n_0}, i)$ and are all equal to 1. Let $v \in \mathrm{GL}_n(\breve{K})$ denote the block-diagonal matrix, whose diagonal $n_0 \times n_0$-blocks are each equal to $v_1$. We begin with the following key proposition.

Proposition 6.15

For $r\ge 1$, the Iwahori level variety $X_{\dot{w}_r}^0(b)_{{\mathscr {L}}_0}$ is contained in the Schubert cell $Iv D_{\kappa ,n}\mu _rI/I \subseteq {{\,\mathrm{GL}\,}}_n(\breve{K})/I$. In particular, $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0} \subseteq Iv D_{\kappa ,n}\mu _r I/I^m \subseteq \mathrm{GL}_n(\breve{K})/I^m$.

Proof

We have to show that for $x \in {\mathscr {L}}_0^{\mathrm{adm}}$ one has $Ig_{b,r}(x)I = IvD_{\kappa ,n}\mu _rI$, i.e., that by successively multiplying by elements from I on the left and right side we can bring $g_{b,r}(x) = g_b^{{{\,\mathrm{red}\,}}}(x)D_{\kappa ,n}\mu _r$ to the form $vD_{\kappa ,n}\mu _r$. For $1\le i \le n'$, we call a matrix in ${{\,\mathrm{GL}\,}}_n(\breve{K})$ i-nice, if the following two conditions hold:

• (i) each of its $n^{\prime 2}$ blocks of size $n_0 \times n_0$ has the following shape: in its $\ell$th column ($1\le \ell \le n_0$), the entries above the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry lie in ${\mathfrak {p}}$ and the other entries lie in ${\mathcal {O}}$;

• (i) for $1\le \ell \le n_0$, the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry of the (i, i)th $(n_0\times n_0)$-block lies in ${\mathcal {O}}^{\times }$.

The inductive algorithm to prove the lemma is as follows: put ${A_1 \,{:=}\,g_b^{{{\,\mathrm{red}\,}}}(x)}$ and let $1 \le i \le n'$. Assume that by modifying $g_b^{{{\,\mathrm{red}\,}}}(x)D_{\kappa ,n}\mu _r$ (by multiplication from left and right with I) we have constructed the i-nice matrix $A_i$, such that $Ig_b^{{{\,\mathrm{red}\,}}}(x)D_{\kappa ,n}\mu _rI = I A_iD_{\kappa ,n}\mu _r I$ and such that the first $i-1$ rows and $i-1$ columns of $n_0 \times n_0$-blocks of $A_iD_{\kappa ,n}\mu _r$ coincide with $vD_{\kappa ,n}\mu _r$ up to ${\mathcal {O}}^{\times }$-multiplies of the non-zero entries. Now we do the following steps:

• (1) Annihilate the entries of the(i, i)th $n_0 \times n_0$-block of$A_i$ lying over$(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry (for each$1 \le \ell \le n_0$). By assumption, the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry lies in ${\mathcal {O}}^{\times }$. By multiplying upper triangular unipotent elements from I (with non-diagonal entries in ${\mathfrak {p}}$) from the left to $A_iD_{\kappa ,n}\mu _r$ (i.e., performing elementary row operations on matrices), we obtain a nice matrix $A_i'$ (uniquely determined by $A_i$) whose entries have the same images in ${\mathcal {O}}/{\mathfrak {p}}$ as those of $A_i$. Moreover, $IA_iD_{\kappa ,n}\mu _rI = IA_i'D_{\kappa ,n}\mu _rI$.

Put ${A_{i,0}' \,{:=}\,A_i'}$. For $\ell = 1, 2, \dots , n_0$ do successively the following step:

(2)${}_{\ell }$:

Annihilate the $(n_0(i-1)+\ell )$th column and $(n_0(i-1)+1 + [(\ell -1)k_0]_{n_0})$th row of $A_{i,\ell - 1}'$. By assumption, the $(n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}, n_0(i-1)+\ell )$th entry of the i-nice matrix $A_{i,\ell -1}'$ lies in ${\mathcal {O}}^{\times }$. By multiplying $A_{i,\ell -1}'D_{\kappa ,n}\mu _r$ successively from the left by lower triangular matrices from I which have 1’s on the main diagonal and only further non-zero entries in the $n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}$th column, we can kill all entries of the $n_0(i-1) + \ell$th column of $A_{i,\ell -1}'$ except for the $(n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}, n_0(i-1)+\ell )$th entry itself, which remains unchanged. After this we can, using the $(n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}, n_0(i-1)+\ell )$th entry, easily eliminate all entries $n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}$th row except for $(n_0(i-1)+1 + [(\ell -1)k_0]_{n_0}, n_0(i-1)+\ell )$th entry itself, which remains unchanged (by multiplying $A_{i,\ell -1}'D_{\kappa ,n}\mu _r$ from the right with unipotent upper triangular matrices in I). This does not change the rest of the matrix, because $n_0(i-1) + \ell$th column contains precisely one non-zero entry.

As an output we obtain the matrix ${A_{i+1} \,{:=}\,A_{i,n_0}'}$ which we claim is $(i+1)$-nice. Assume for now that this is true. Proceeding the described algorithm for all $1\le i\le n'$, we obtain the matrix $A_{n'+1}$, which differs from v only by some diagonal matrix with entries in ${\mathcal {O}}^{\times }$, so that $IA_{n'+1}D_{\kappa ,n}\mu _rI = IvD_{\kappa ,n}\mu _rI$ is now clear.

Observe that when looking modulo ${\mathfrak {p}}$, the step (2)${}_{\ell }$ in the algorithm for a single $\ell$ affects the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry of the $(i+1,i+1)$th $n_0\times n_0$-block, but does not affect the entries $(1 + [(\ell '-1)k_0]_{n_0}, \ell ')$th ($\forall \ell ' \ne \ell$) of the same block. In particular, the steps (2)${}_{\ell }$ can be applied in any order of the $\ell$’s, and when the (2)${}_{\ell _0}$ is applied first to $A_i'$ (to kill its $(n_0(i-1)+\ell _0)$th column and $(n_0(i-1)+1 + [(\ell _0-1)k_0]_{n_0})$th row) giving the matrix $A_{i,\ell _0}''$, then the $(1 + [(\ell _0 -1)k_0]_{n_0}, \ell _0)$th entry of $(i+1,i+1)$th $n_0\times n_0$-block of $A''_{i,\ell _0}$ already coincides modulo ${\mathfrak {p}}$ with the same entry of $A_{i+1}$.

We now show that for $1 \le i \le n$, the matrix $A_i$ appearing in the algorithm is i-nice. (By induction we may assume that $A_{i'}$ is $i'$-nice for $1\le i' < i$, which is sufficient to run the first $i-1$ steps of the algorithm to obtain $A_i$). For $1 \le j \le i' \le n$, $1\le \ell \le n'$, let $\alpha _{i',j,\ell } \in {\mathcal {O}}/{\mathfrak {p}}$ denote the residue modulo ${\mathfrak {p}}$ of the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry of the (j, j)th $n_0\times n_0$-block of $A_{i'}$. Note that $\alpha _{i',j,\ell } = \alpha _{i'',j,\ell }$ for all $1\le j \le i' \le i''$. Indeed, if $j<i'$, this is obvious as the first $i'-1$ diagonal blocks of $A_{i'}$ and $A_{i''}$ coincide. If $j=i'$ observe that the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entries (for all $1\le \ell \le n_0$) of the $(i',i')$th $n_0 \times n_0$-block of $A_{i'}$ can only be affected by step (1) of the algorithm, which does not change the residue modulo ${\mathfrak {p}}$.

Recall the image ${{\bar{x}}} = ({{\bar{x}}}_1, \dots , {{\bar{x}}}_{n'})^T$ of x in ${\overline{V}}$ and the corresponding matrix $\overline{g_b}({\bar{x}}) \in {{{\,\mathrm{GL}\,}}}_{n'}({\overline{{\mathbb {F}}}}_q)$ defined in Sect. 6.3. For $1\le i \le n'$, let $m_i \in {\overline{{\mathbb {F}}}}_q$ denote the determinant of the upper left $i\times i$-minor of $\overline{g_b}({\bar{x}})$. By Lemma 6.16, $m_i \in {\overline{{\mathbb {F}}}}_q^{\times }$ for all i. We claim that for $1\le \ell \le n_0$,

$$\begin{aligned} \alpha _{i,j,\ell } = {\left\{ \begin{array}{ll} \sigma ^{\ell - 1}(m_1) &{}\quad \text {if }j=1 \\ \sigma ^{\ell -1}(\frac{m_j}{m_{j-1}}) &{}\quad \text {if }2 \le j \le i \end{array}\right. } \end{aligned}$$

(6.8)

By induction we may assume that this holds for all $1 \le i' < i$, from which (6.8) follows for all $j<i$. It thus remains to compute $\alpha _{i,i,\ell }$. Note that for $1\le \ell \le n_0$, the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$-entry of $A_1 = g_b^{{{\,\mathrm{red}\,}}}(x)$ is equal to is equal to $\sigma ^{\ell -1}(x_{1,0}) = \sigma ^{\ell -1}({{\bar{x}}}_1)$. This finishes the case $i=1$. Assume $i \ge 2$ and fix some $1 \le \ell \le n_0$. By the observation above, $\alpha _{i,i,\ell }$ is equal to the residue modulo $\mathfrak p$ of the $(1 + [(\ell -1)k_0]_{n_0}, \ell )$th entry of the (i, i)th $n_0\times n_0$-block of the matrix $A_{i-1,\ell }''$, obtained from $A_{i-1}'$ by directly applying step (2)${}_{\ell }$.

For $X \in {{\,\mathrm{GL}\,}}_n(\breve{K})$, let M(X) denote the $(n_0(i-1) + 1) \times (n_0(i-1) + 1)$-minor of X obtained by removing from X all columns with numbers $\{j :j > n_0(i-1) \text { and } j \ne n_0(i-1) + \ell \}$ and all rows with numbers $\{s :s > n_0(i-1) \text { and } s \ne n_0(i-1) + 1 + [(\ell -1)k_0]_{n_0} \}$. We compute:

$$\begin{aligned} \alpha _{i,i,\ell }\prod _{\lambda = 1}^{n_0} \sigma ^{\lambda - 1}(m_{i-1}) \equiv \det M(A_{i-1,\ell }'') = \det M(A_{i-1}') = \det M(g_b^{{{\,\mathrm{red}\,}}}(x)) \mod \mathfrak {p}. \end{aligned}$$

The first equality follows from the explicit form of $A_{i-1,\ell }''$ and by the induction hypothesis on the $\alpha _{i,j,\ell }$’s. The remaining equalities are true as every operation in the algorithm does not change the determinant of the matrices. On the other side, a simple calculation shows that

$$\begin{aligned} \det M(g_b^{{{\,\mathrm{red}\,}}}(x)) \equiv \frac{\sigma ^{\ell }(m_i)}{\sigma ^{\ell }(m_{i-1})} \prod _{\lambda = 1}^{n_0} \sigma ^{\lambda - 1}(m_{i-1}) \mod \mathfrak {p}. \end{aligned}$$

This finishes the proof of (6.8), and thus of the proposition. $\square$

Lemma 6.16

Let $x \in {\mathscr {L}}_{0,b}^{\mathrm{adm}}$ and let ${{\bar{x}}} \in {\overline{V}}$ denote its image. For $1\le i \le n'$, let $m_i$ denote the upper left $(i \times i)$-minor of $\overline{g_b}({{\bar{x}}}) \in {{\,\mathrm{GL}\,}}_{n'}({\overline{{\mathbb {F}}}}_q)$. Then $m_i \in {\overline{{\mathbb {F}}}}_q^{\times }$ for all i.

Proof

Replacing ${\mathbb {F}}_{q^{n_0}}$ by ${\mathbb {F}}_q$ we may assume that $n_0 = 1$, $n' = n$. We have $\overline{g_b}({{\bar{x}}}) = ({\bar{x}}_i^{q^{j-1}})_{1\le i,j \le n}$ and $\det \overline{g_b}({{\bar{x}}}) \in {\overline{{\mathbb {F}}}}_q^{\times }$. Clearly, $m_1 = {\bar{x}}_1 \ne 0$. Let $2 \le i \le n$. By induction we may assume that $m_{i'} \in {\overline{{\mathbb {F}}}}_q^{\times }$ for all $1\le i' < i$. Suppose $m_i = 0$. This means that the i vectors $v_j = (x_j^{q^{k-1}})_{k=1}^i \in {\overline{{\mathbb {F}}}}_q^i$ ($1\le j \le i$) are linearly ${\overline{{\mathbb {F}}}}_q$-dependent. Note that the first $i-1$ of these vectors are ${\overline{{\mathbb {F}}}}_q$-independent, as already the vectors $(x_j^{q^{k-1}})_{k=1}^{i-1} \in {\overline{{\mathbb {F}}}}_q^{i-1}$ ($1\le j\le i-1$) are ${\overline{{\mathbb {F}}}}_q$-independent, which in turn follows from the induction hypothesis $m_{i-1} \ne 0$. This shows that there exist $\lambda _1, \dots , \lambda _{i-1} \in {\overline{{\mathbb {F}}}}_q$ with $\sum _{j = 1}^{i-1} \lambda _j v_j = v_i$. From this we deduce two systems of linear equations which uniquely determine the $\lambda _j$’s: (1) $\sum _{j=1}^{i-1} \lambda _j (x_j^{q^{k-1}})_{k=1}^{i-1} = (x_i^{q^{k-1}})_{k=1}^{i-1}$ as well as (2) $\sum _{j=1}^{i-1} \lambda _j (x_j^{q^{k-1}})_{k=2}^i = (x_i^{q^{k-1}})_{k=2}^i$. Note that (2) is obtained from (1) by raising all coefficients to the qth power. For $1\le j\le i-1$ let $m_{i-1}^{(j)}$ denote the minor $m_{i-1}$, in which jth row is replaced by $(x_i^{q^{k-1}})_{k=1}^{i-1}$. Then (1) gives $\lambda _j = m_{i-1}^{-1} m_{i-1}^{(j)}$, whereas (2) gives $\lambda _j = (m_{i-1}^{-1} m_{i-1}^{(j)})^q$ for each $1\le j \le i-1$. Thus $\lambda _j \in {\mathbb {F}}_q$. This gives a non-trivial ${\mathbb {F}}_q$-relation between the $x_1,\dots , x_i$, and hence also between the first i rows of $\overline{g_b}({{\bar{x}}})$, i.e., $\det \overline{g_b}({{\bar{x}}}) = 0$, contradicting the assumption. $\square$

Let

$$\begin{aligned} {\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \,{:=}\,{\mathbb {P}}({\overline{V}}) {\,\smallsetminus \,}\bigcup _{\begin{array}{c} H \subseteq {\overline{V}} \\ {\mathbb {F}}_{q^{n_0}}-\text {rational hyperplane} \end{array}} H} \end{aligned}$$

(6.9)

be $n'-1$-dimensional Drinfeld’s upper half-space over ${\mathbb {F}}_{q^{n_0}}$.

Theorem 6.17

Let b be the special representative with $\kappa _{{{\,\mathrm{GL}\,}}_n}(b) = \kappa$. Let $r > m \ge 0$. Then we have a decomposition of ${\mathbb {F}}_q$-schemes

$$\begin{aligned} X_{\dot{w}_r}^m(b) \cong \bigsqcup _{G/G_{{\mathcal {O}}}} \Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \times {\mathbb {A}}, \end{aligned}$$

where ${\mathbb {A}}$ is a finite dimensional affine space over ${\mathbb {F}}_q$ (with dimension depending on r, m). The morphism $\dot{X}_{{\dot{w}}_r}^m(b) \rightarrow X_{\dot{w}_r}^m(b)$ is a finite étale $T_w({\mathcal {O}}_K/\varpi ^{m+1})$-torsor. In particular, all these schemes are smooth.

Proof

To prove the first statement of the theorem it suffices, by applying Proposition 6.12, to show that $X_{{\dot{w}}_r}^m(b)_{{\mathscr {L}}_0}$ is a locally closed subset of ${{\,\mathrm{GL}\,}}_n(\breve{K})/I^m$ isomorphic to $\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \times {\mathbb {A}}$. By Proposition 6.15, $X_{{\dot{w}}_r}^m(b)_{{\mathscr {L}}_0} \subseteq IvD_{\kappa , n}\mu _r(\varpi )I/I^m$. So, it suffices to show that as a subset of $IvD_{\kappa , n}\mu _r(\varpi ) I/I^m$, $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$ is locally closed and with its induced reduced sub-scheme-structure isomorphic to $\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \times {\mathbb {A}}$. For simplicity, we treat the case that $\kappa = 0$ or 1, so that $v= D_{\kappa ,n} = 1$. The general case is done in exactly the same way, but is slightly more technical due to the presence of the permutation matrix v (the corresponding technical details are very similar to those appearing in the proof of Proposition 6.15, which we proved in full generality).

First, by Lemma 4.7, $I\mu _r(\varpi )I/I^m$ is isomorphic to an affine space and we fix the following coordinates on it: let $\alpha _{ij}$ ($1\le i\ne j \le n$) denote the root of $T_{\mathrm{diag}}$ corresponding to (i, j)th matrix entry. Then

$$\begin{aligned} \psi :I \mu _r(\varpi ) I/I^m {\mathop {\rightarrow }\limits ^{\sim }} C:= \underbrace{\prod _{i=2}^n L_{[0,(i-1)r)} U_{\alpha _{i1}}}_{A:=} \times \underbrace{\prod _{n \ge i> j > 1} L_{[0,(i-j)r)}U_{\alpha _{ij}}}_{B:=} \times I/I^m\nonumber \\ \end{aligned}$$

(6.10)

(the products can be taken in any fixed order; each factor – including $I/I^m$ – is an affine space over ${\overline{{\mathbb {F}}}}_q$) is a parametrization of $I\mu _r(\varpi )I/I^m$, whose inverse sends $(a_{i1})_{i=2}^n, (a_{ij})_{i>j\ne 1}, g$ to $\prod _{i=2}^n a_{i1} \cdot \prod _{i,j} a_{ij} \cdot {{\dot{\mu }}}_r(\varpi ) \cdot g I^m$. It suffices to show that there is an open subset $U \subseteq A$, isomorphic to $\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \times {\mathbb {A}}$, such that $X_{\dot{w}_r}(b)_{{\mathscr {L}}_0} \subseteq I \mu _r(\varpi ) I/I^m$ is the graph of some morphism $f :U \rightarrow B \times I/I^m$. Indeed, then it follows that $X_{\dot{w}_r}(b)_{{\mathscr {L}}_0}$ is a locally closed subset of $I \mu _r(\varpi ) I/I^m$, which (endowed with the induced reduced sub-scheme structure) gets isomorphic to U via the projection $p :C \cong A \times B \times I/I^m \rightarrow A$ to the first factor. First, we define U. Therefore, consider the natural projection

$$\begin{aligned} A \twoheadrightarrow \textstyle \prod \limits _{i=2}^{n'} L_{[0,1)}U_{\alpha _{1 + n_0(i-1),1}} \cong \{ [v] \in {\mathbb {P}}({\overline{V}}) :v = \sum _i v_i e_{1 + n_0(i-1)} \in {\overline{V}}, v_1 \ne 0\}\nonumber \\ \end{aligned}$$

(6.11)

where the latter isomorphism is $(v_i)_{i=2}^{n'} \mapsto [1:v_2: \dots :v_{n'}]$ and let U be the preimage of $\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1}$, which is a subspace of the right hand side via (6.9). (If $n'=1$, ${\overline{V}}$ is one-dimensional, and the right hand side of (6.11) as well as $\Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1}$ is a point). It is clear that $U \cong \Omega _{{\mathbb {F}}_{q^{n_0}}}^{n'-1} \times {\mathbb {A}}$.

Next, we determine the image of $X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$ under $\psi$. Let $g_{b,r}(x)I^m = g_b^{{{\,\mathrm{red}\,}}}(x)\mu _r(\varpi ) I^m \in X_{\dot{w}_r}(b)_{{\mathscr {L}}_0}$, i.e., $x \in {\mathscr {L}}_0^{\mathrm{adm}}$. This point does not change if we multiply $g_{b,r}(x)$ by an element of $I^m$ from the right, or equivalently, if we multiply $g:= g_b^{{{\,\mathrm{red}\,}}}(x)$ by an element of

$$\begin{aligned} {}^{\mu _r(\varpi )}I^m = \mu _r(\varpi ) I^m \mu _r(\varpi )^{-1} = \begin{pmatrix} {\mathcal {O}}^{\times } &{}\quad {\mathfrak {p}}^{m+1-r} &{}\quad \cdots &{}\quad \cdots &{}\quad {\mathfrak {p}}^{m+1-(n-1)r} \\ *&{}\quad {\mathcal {O}}^{\times } &{}\quad {\mathfrak {p}}^{m+1-r} &{}\quad \cdots &{}\quad {\mathfrak {p}}^{m+1 - (n-2)r} \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ *&{}\quad \cdots &{}\quad *&{}\quad {\mathcal {O}}^{\times }&{}\quad {\mathfrak {p}}^{m+1-r} \\ *&{}\quad \cdots &{}\quad \cdots &{}\quad *&{}\quad {\mathcal {O}}^{\times }\end{pmatrix} \end{aligned}$$

(6.12)

from the right (the entries marked with $*$ are uninteresting for us). First, we multiply g by the diagonal matrix $i_1 = {{\,\mathrm{diag}\,}}(x_1, \sigma (x_1), \dots ,\sigma ^{n-1}(x_1))^{-1} \in {}^{\mu _r(\varpi )}I^m$ (note that $x_1$ invertible by (6.6); see also Lemma 6.16), achieving that all entries of $gi_1$ are of the form $\sigma ^i(\frac{x_j}{x_1})$ resp. $\varpi \sigma ^i(\frac{x_j}{x_1})$ and, in particular, the first column of $gi_1$ has the entries $1,\frac{x_2}{x_1}, \dots ,\frac{x_n}{x_1}$. Next, using that $r > m$, so that all ${\mathfrak {p}}^{m+1-r}\supseteq {\mathcal {O}}$ in (6.12), we may eliminate all (1, j)th ($2\le j \le n$) entries of $gi_1$, i.e., we find some $i_1' \in {}^{\mu _r(\varpi )}I^m$ (with entries different from 0 and 1 only in the first row), such that $gi_1i_1'$ has the same first column as $gi_1$ and 0’s in all entries of the first row except the first one. Also, all entries of $gi_1i_1'$ lie in ${\mathcal {O}}$ and are some functions in $\sigma ^i(\frac{x_j}{x_1})$ (as the same is true for $gi_1$). Moreover, the (2, 2) entry of $gi_1i_1'$ must now be in ${\mathcal {O}}^\times$ (otherwise $g\mu _r(\varpi )I^m \not \in I\mu _r(\varpi )I/I^m$), and we can iterate the procedure: rescale the second column such that (2, 2)th entry equals 1, then kill all entries (2, j) with $3\le j \le n$, etc. At the end we obtain a matrix $g' = gi_1i_1'i_2i_2' \dots i_{n-1}i_{n-1}'$, such that $g'\mu _r(\varpi )I^m = g\mu _r(\varpi )I^m$ and

$$\begin{aligned} g'= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \frac{x_2}{x_1} &{}\quad 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \frac{x_3}{x_1} &{}\quad *&{}\quad 1 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \frac{x_{n-1}}{x_1} &{}\quad *&{}\quad \dots &{}\quad *&{}\quad 1 &{}\quad 0 \\ \frac{x_n}{x_1} &{}\quad *&{}\quad \dots &{}\quad *&{}\quad *&{}\quad 1 \end{pmatrix} = \begin{pmatrix} 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \frac{x_2}{x_1} &{}\quad 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \frac{x_3}{x_1} &{}\quad 0 &{}\quad 1 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \frac{x_{n-1}}{x_1} &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ \frac{x_n}{x_1} &{}\quad 0 &{}\quad \dots &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}\\&\begin{pmatrix} 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ 0 &{}\quad *&{}\quad 1 &{}\quad \dots &{}\quad \dots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad *&{}\quad \dots &{}\quad *&{}\quad 1 &{}\quad 0 \\ 0 &{}\quad *&{}\quad \dots &{}\quad *&{}\quad *&{}\quad 1 \end{pmatrix} \end{aligned}$$

where the entries marked by $*$ all lie in ${\mathcal {O}}$ and are functions of $\frac{x_2}{x_1}$, $\dots$, $\frac{x_n}{x_1}$. We can regard the first matrix in the product as an element of A (as in (6.10)), and moreover from (6.6) it follows that it lies in the open subset $U \subseteq A$. It gets clear now that with respect to the parametrization in (6.10), $\psi (X_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0})$ consists of points of the form $(u,f_0(u), 1\cdot I^m)$ with $u \in U \subseteq A$ and $f_0(u) \in B$, where $f_0 :U \rightarrow B$ is some morphism (which determines the entries $*$ in terms of $\frac{x_2}{x_1}, \dots , \frac{x_n}{x_1}$). Thus $f :U \rightarrow B \times I/I^m$, defined by $u \mapsto (f_0(u), 1\cdot I^m)$ is the required morphism we wished to construct. This finishes the proof of the first claim of the theorem.

For the second claim in the theorem, we could repeat the above arguments with $I\mu _r(\varpi )I/\dot{I}^m$ replacing $I\mu _r(\varpi )I/I^m$. Alternatively we can argue as follows: by Theorem 4.9 (see Remark 6.3 and Lemma 6.4), $\dot{X}_{\dot{w}_r}^m(b)$ is locally closed in $G(\breve{K})/\dot{I}^m$, and hence a scheme locally of finite type over $\overline{{\mathbb {F}}}_q$ (Corollary 4.10), and by Proposition 4.2(iii) the morphism $G(\breve{K})/\dot{I}^m \rightarrow G(\breve{K})/I^m$ is representable and has sections étale-locally. It thus follows that $\dot{X}_{\dot{w}_r}^m(b) \rightarrow X_{w_r}^m(b)$ is a honest morphism of schemes locally of finite type over $\overline{{\mathbb {F}}}_q$. Moreover, by the explicit description on geometric points in Theorem 6.5 it is surjective and a torsor under $T_w({\mathcal {O}}_K/\varpi ^{m+1})$. $\square$

Corollary 6.18

Let $r'> m' > 0$, $r> m > 0$ be two pairs of integers with $r' \ge r$, $m' \ge m$. Then all maps $X_{\dot{w}_{r'}}^{m'}(b) \rightarrow X_{\dot{w}_r}^m(b)$, $\dot{X}_{\dot{w}_{r'}}^{m'}(b) \rightarrow \dot{X}_{\dot{w}_r}^m(b)$, $\dot{X}_{\dot{w}_{r'}}^{m'}(b) \rightarrow X_{\dot{w}_r}^m(b)$ induced by $g_{b,r'}(x) \mapsto g_{b,r}(x)$ are morphisms of schemes. In particular, $X_w^{\infty }(b)$ and $\dot{X}_w^{\infty }(b)$ are schemes over ${\mathbb {F}}_q$.

Proof

With respect to the coordinates on $X_{\dot{w}_r}^m(b)$, $\dot{X}_{\dot{w}_r}^m(b)$ in the proof of Theorem 6.17, these maps are simply induced by the natural projections $L_{[0,\nu ')}U_{\alpha _{j,1}} \rightarrow L_{[0,\nu )}U_{\alpha _{j,1}}$ for $\nu ' \ge \nu$ and $L_{[0,m'+1)}{\mathbb {G}}_m \rightarrow L_{[0,m+1)}{\mathbb {G}}_m$ for $m' \ge m$. $\square$

We are now ready to endow all objects in the diagram in Theorem 6.9 with scheme structures and compare them. The set ${\mathscr {L}}_{0,b}^{\mathrm{adm, \mathrm {rat}}}$ has an obvious scheme structure as a closed subset of the infinite dimensional affine space ${\mathscr {L}}_0$ over ${\mathbb {F}}_q$. Analogously, the natural embedding ${\mathscr {L}}_0^{\mathrm{adm}}/{\mathcal {O}}^{\times } \subseteq {\mathscr {L}}_0/{\mathcal {O}}^{\times } = L^+{\mathbb {P}}({\mathscr {L}}_0)({\overline{{\mathbb {F}}}}_q)$, where $L^+{\mathbb {P}}({\mathscr {L}}_0)$ is an infinite-dimensional ${\mathbb {F}}_q$-scheme, endows ${\mathscr {L}}_0^{\mathrm{adm}}/{\mathcal {O}}^{\times }$ with the structure of an open subscheme. We endow $V_b^{\mathrm{adm, rat}}$ and $V_b^{\mathrm{adm}}/{\mathcal {O}}^{\times }$ with the scheme structure of a disjoint union:

$$\begin{aligned} V_b^{\mathrm{adm, rat}} = \bigsqcup _{g \in G/G_{{\mathcal {O}}}} g.{\mathscr {L}}_{0,b}^{\mathrm{adm,rat}} \qquad \text {and} \qquad V_b^{\mathrm {adm}}/{\mathcal {O}}^{\times } = \bigsqcup _{g \in G/G_{{\mathcal {O}}}} g.\left( {\mathscr {L}}_{0,b}^{\mathrm{adm}}/{\mathcal {O}}^{\times }\right) . \end{aligned}$$

Since the action of $\varpi$ on $V_b^{\mathrm {adm}}/{\mathcal {O}}^{\times }$ just permutes the connected components, the quotient $V^{\mathrm {adm}}/\breve{K}^{\times }$ inherits the scheme structure $V^{\mathrm {adm}}/\breve{K}^{\times } = \bigsqcup _{G/Z(G)G_{{\mathcal {O}}}} g.\left( {\mathscr {L}}_{0,b}^{\mathrm {adm}}/{\mathcal {O}}^{\times }\right)$.

Corollary 6.19

The maps of sets $V_b^{\mathrm{adm, rat}} {\mathop {\rightarrow }\limits ^{\sim }} \dot{X}_w^{\infty }(b)$, $V_b^{\mathrm{adm}}/{\mathcal {O}}^{\times } {\mathop {\rightarrow }\limits ^{\sim }} X_w^{\infty }(b)$ from Theorem 6.9 are isomorphisms of ${\mathbb {F}}_q$-schemes. We endow $X_w^{DL}(b)$, $\dot{X}_w^{DL}(b)$ with the scheme structure via the isomorphisms in the diagram in Theorem 6.9.

Proof

To show the first isomorphism, it suffices to prove that for the special representative b, we have an isomorphism of schemes ${\mathscr {L}}_{0,b}^{\mathrm{adm, rat}} {\mathop {\rightarrow }\limits ^{\sim }} \dot{X}_w^{\infty }(b)_{{\mathscr {L}}_0}$. Rescaling by an appropriate element of ${\mathcal {O}}^\times$, we may replace ${\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}}$ by ${\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat},\dot{w}_0}$. With notation as in the proof of Theorem 6.17, the coordinates on the inverse limit $\dot{X}_w^{\infty }(b)_{{\mathscr {L}}_0}$ are given by $((a_{\alpha _{j,1}})_{j=2}^n,c_1) \in L^+U_{\alpha _{j,1}} \times L^+{\mathbb {G}}_m$ and the map ${\mathscr {L}}_{0,b}^{\mathrm {adm}, \mathrm {rat}, \dot{w}_0} \rightarrow \dot{X}_w^\infty (b)_{{\mathscr {L}}_0}$ is given by $(x_i)_{i=1}^n \mapsto (\frac{x_j}{x_1})_{j=2}^n, x_1$. This is an isomorphism. The second isomorphism is proven similarly. $\square$

8.5 Example $\mathrm{SL}_2$, w Coxeter, $b = 1$

It is instructive to explicate the scheme structure on $X_w^{DL}(1)$ from Remark 3.3(ii) and compare it to the one obtained via affine Deligne–Lusztig varieties (a similar description applies in a number of further cases, in particular for $\mathrm{GL}_n$ or $\mathrm{GSp}_{2n}$ and w Coxeter). We have ${{\,\mathrm{SL}\,}}_2/B = {\mathbb {P}}^1$ and

$$\begin{aligned} X_w^{DL}(1) = {\mathbb {P}}^1(\breve{K}) {\,\smallsetminus \,}{\mathbb {P}}^1(K). \end{aligned}$$

It is thus given by the open condition $\det \left( {\begin{matrix} x &{} \sigma (x) \\ y &{} \sigma (y) \end{matrix}}\right) = x \sigma (y) - \sigma (x) y \not = 0$ inside

$$\begin{aligned} L{\mathbb {P}}^1_K({\overline{{\mathbb {F}}}}_q) = L^+{\mathbb {P}}^1_{{\mathcal {O}}_K}({\overline{{\mathbb {F}}}}_q) = {\mathbb {P}}^1({\mathcal {O}}) = \{ [x:y] :x,y \in {\mathcal {O}}, \text {at least one of }x,y\text { lies in }{\mathcal {O}}^{\times } \} \end{aligned}$$

(where $[x:y] = [x^{\prime }:y^{\prime }]$ if and only if there exists $a \in {\mathcal {O}}^{*}$ with $ax = x^{\prime }$, $ay = y^{\prime }$) and

$$\begin{aligned} X_w^{DL}(1)_r = \{ [x:y] \in L^+{\mathbb {P}}^1_{{\mathcal {O}}_K}({\overline{{\mathbb {F}}}}_q) :\sigma (x) y - x \sigma (y) \not \equiv 0 \mod \mathfrak {p}^r \}. \end{aligned}$$

It is clear (from the version of Theorem 6.5 for ${{\,\mathrm{SL}\,}}_2$) that if $g \in {{\,\mathrm{SL}\,}}_2(K) {\,\smallsetminus \,}{{\,\mathrm{SL}\,}}_2({\mathcal {O}})$, then $g.X_w^{DL}(1)_1 \cap X_w^{DL}(1)_1 = \varnothing$. Moreover, $X_w^{DL}(1)_1 \subseteq X_w^{DL}(1)$ is dense open. This means that g maps a dense open subset of $X_w^{DL}(1)$ onto a subset which lies in its boundary and hence cannot be dense. Thus g cannot be an automorphism of the scheme $X_w^{DL}(1)$, and the action of G on $X_w^{DL}(1)$ with the above scheme structure is not algebraic.

The subsets $Y_r$ of $L^+_r{\mathbb {P}}^1_{{\mathcal {O}}_K}({\overline{{\mathbb {F}}}}_q) = {\mathbb {P}}^1({\mathcal {O}}/{\mathfrak {p}}^r)$ can easily be computed to be

$$\begin{aligned} Y_1&= \Omega _{{\mathbb {F}}_q} \\ Y_2&= (\Omega _{{\mathbb {F}}_q} \times {\mathbb {A}}^1) \,\, \sqcup \,\, \bigsqcup _{\lambda \in {\mathbb {P}}^1({\mathbb {F}}_q)} \Omega _{{\mathbb {F}}_q}, \\&\;\; \vdots \\ Y_r&= (Y_{r-1} \times {\mathbb {A}}_{{\mathbb {F}}_q}^1) \,\, \sqcup \,\, \bigsqcup \,\, \Omega _{{\mathbb {F}}_q}, \end{aligned}$$

where the last union is taken over all hyperspecial vertices in the Bruhat–Tits building of $\mathrm{SL}_2$ over K such that the minimal gallery connecting this vertex to the one stabilized by ${{\,\mathrm{SL}\,}}_2({\mathcal {O}}_K)$ has length $2r-1$. The unions are disjoint set-theoretically but not scheme-theoretically, since for example the preimage of $Y_1$ in $Y_2$ is open and not closed.

On the other hand, we can explicate the way in which $X_w^{DL}(1)$ is built from finite-dimensional pieces as dictated by Theorems 6.5, 6.17. In fact, $X_w^{DL}(1)$ is an inverse limit of the affine Deligne–Lusztig varieties of increasing level

$$\begin{aligned} X_{{\dot{w}}_m}^m(1) \cong \bigsqcup _{{{\,\mathrm{SL}\,}}_2(K)/{{\,\mathrm{SL}\,}}_2({\mathcal {O}}_K)} \Omega _{{\mathbb {F}}_q}^1 \times {\mathbb {A}}, \end{aligned}$$

where $\Omega _{{\mathbb {F}}_q}^1 = {\mathbb {P}}^1_{{\mathbb {F}}_q} {\,\smallsetminus \,}{\mathbb {P}}^1({\mathbb {F}}_q)$ is the Drinfeld upper half-plane over ${\mathbb {F}}_q$, ${\dot{w}}_m$ are lifts of w whose length in the affine Weyl group has to grow with m, and ${\mathbb {A}}$ is some finite dimensional affine space over ${\mathbb {F}}_q$, whose dimension depends on m and ${\dot{w}}_m$ and goes to $\infty$ when $m \rightarrow \infty$.

9 A family of finite-type varieties $X_h$

In this section, we study the geometry of a family of finite-type varieties $X_h$ for $h \ge 1$ which have natural projection maps $X_h \rightarrow X_{h-1}$. These varieties are more tractable than (components of) the affine Deligne–Lusztig varieties $\dot{X}_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0}$, but we can see that after passing to the limit, these two families at infinite level are the same:

$$\begin{aligned} \varprojlim _{r,m :r > m} \dot{X}_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0} = {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat},\dot{w}_0} \cong {\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}} = \varprojlim _h X_h. \end{aligned}$$

(7.1)

Our work in this section will prepare us for Part 3, where we will study the cohomology of $X_h$ as representations of $G_h \times T_h$.

We remark that $X_h$ will depend on whether we choose b to be the Coxeter-type representative or the special representative, but they are isomorphic as ${\mathbb {F}}_{q^n}$-schemes for the same reason as in Corollary 6.14. The flexibility of choosing this representative b allows us to use a wide range of techniques to understand $X_h$ and its cohomology. We will see this theme throughout Part 3.

9.1 Ramified Witt vectors

Recall the schemes ${\mathbb {W}}$, ${\mathbb {W}}_h$ from Sect. 2 (see [18, 18.6.13, 25.3.18] for more details on the construction of ramified Witt vectors). We will need to coordinatize ${\mathbb {W}}$ in order to make an explicit computations about the variety $X_h$. If A is a perfect ${\mathbb {F}}_q$-algebra, the elements of ${\mathbb {W}}(A)$ can be written in the form $\sum _{i \ge 0} [x_i] \varpi ^i$, where $[x_i]$ is the Teichmüller lift of $x_i \in A$ if ${{\,\mathrm{char}\,}}K = 0$ and $[x_i] = x_i$ if ${{\,\mathrm{char}\,}}K > 0$. (Note that the perfectness assumption is only necessary when ${{\,\mathrm{char}\,}}K = 0$.) We identify ${\mathbb {W}}$ with ${\mathbb {A}}^{{\mathbb {Z}}_{\ge 0}}$ and identify ${\mathbb {W}}_h$ with ${\mathbb {A}}^h$ under this choice of coordinates. We recall the following lemma about the ring structure of ${\mathbb {W}}$ with respect to these coordinates.

Lemma 7.1

Let A be a perfect ${\mathbb {F}}_q$-algebra.

• (i) The coefficient of $\varpi ^i$ in $(\sum _{i \ge 0} [a_i] \varpi ^i) + (\sum _{i \ge 0} [b_i] \varpi ^i)$ is

  $$\begin{aligned}{}[a_i + b_i + c_i], \qquad \text {where }c_i \in A[a_j^{1/q^N}, b_j^{1/q^N} : j < i, \, N \in {\mathbb {Z}}_{\ge 0}]. \end{aligned}$$

• (ii) The coefficient of $\varpi ^i$ in $(\sum _{i \ge 0} [a_i] \varpi ^i)(\sum _{i \ge 0} [b_i] \varpi ^i)$ is

  $$\begin{aligned} \left[ \textstyle \sum \limits _{j = 0}^i a_j b_{i-j} + c_i \!\right] \!, \quad \text {where }c_i \!\in \! A[a_{i_1}^{e_1/q^N}b_{i_2}^{e_2/q^N} : i_1+i_2 < i, \, e_1, e_2, N \in {\mathbb {Z}}_{\ge 0}]. \end{aligned}$$

In both cases, we call $c_i$ the “minor contribution.” Note that if ${{\,\mathrm{char}\,}}K > 0$, then the minor contribution is identically zero. In particular, for any given i, the ith minor contribution does only depend on $a_j, b_j$ with $j<i$.

This lemma says that up to “minor contributions”, working in coordinates with the Witt vectors is the same as working in coordinates in ${\mathbb {F}}_q[\![t]\!]$. This allows us to uniformly perform calculations in the mixed and equal characteristic settings. We will implicitly use Lemma 7.1 in Sects. 7.4 and 9.

Remark 7.2

Note in particular that by Lemma 7.1(ii), the coefficient of $\varpi ^i$ in the product $(\sum _{i \ge 0}[a_i] \varpi ^i)(\sum _{i \ge 0} [b_i] \varpi ^i)$ is of the form $[a_0 b_i + \mathbf {e}_i]$ where $\mathbf {e}_i$ is independent of $b_i$. For this reason, the minor contributions never play a role in our formulae as we study $X_h$ as a subvariety of $X_{h-1} \times {\mathbb {A}}^N$ (for some N), and so the minor contributions only contribute to unspecified “constant” terms (see c in Proposition 7.6).

We also point out a case where the minor contribution vanishes (this is used in Proposition 7.7). Let A be a perfect ${\mathbb {F}}_q$-algebra and pick an integer $h \ge 1$. Then the product $(1 + \sum _{i \ge h} [a_i] \varpi ^i)(\sum _{i \ge 0} [b_i] \varpi ^i) \in [b_0] + [b_1]\varpi + \dots + [b_{h-1}]\varpi ^{h-1} + [a_h + a_0 b_h]\varpi ^h + \varpi ^{h+1} {\mathbb {W}}(A)$. Indeed, it suffices to compute modulo $\varpi ^{h+1}$ (that is, in the $(h+1)$-truncated ramified Witt vectors ${\mathbb {W}}_{h+1}(A)$), where we have

$$\begin{aligned} (1 + \varpi ^h[a_h])\cdot \sum _{i=0}^h [b_i]\varpi ^i&= \sum _{i=0}^{h-1} [b_i]\varpi ^i + \varpi ^h([b_h] + [b_0 a_h]) = \sum _{i=0}^{h-1} [b_i]\varpi ^i + [b_h + b_0 a_h]\varpi ^h. \end{aligned}$$

9.2 The scheme $X_h$

Fix a $0 \le \kappa < n$ and let b be either the Coxeter-type or special representative with $\kappa _G(b) = \kappa$ as in Sect. 5.2. Define the ${\mathcal {O}}$-submodule of ${\mathscr {L}}_0$,

$$\begin{aligned} {{\mathscr {L}}_0^{(h)} \,{:=}\,\bigoplus _{\begin{array}{c} 1 \le i \le n \\ i \equiv 1 \!\!\!\! \pmod {n_0} \end{array}} \varpi ^h{\mathscr {L}}_0 \oplus \bigoplus _{\begin{array}{c} 1 \le i \le n \\ i \not \equiv 1 \!\!\!\! \pmod {n_0} \end{array}} \varpi ^{h-1}{\mathscr {L}}_0.} \end{aligned}$$

Under the conventions set in Sect. 7.1, any $x \in {\mathscr {L}}_0/{\mathscr {L}}_0^{(h)}$ can be written as

$$\begin{aligned} x = \sum _{\begin{array}{c} 1\le i \le n \\ i \equiv 1 \!\!\!\! \pmod {n_0} \end{array}} \sum _{\ell =0}^{h-1} [x_{i,\ell }]\varpi ^{\ell } \mathbf {e}_i + \sum _{\begin{array}{c} 1\le i \le n \\ i \not \equiv 1 \!\!\!\!\pmod {n_0} \end{array}} \sum _{\ell =0}^{h-2} [x_{i,\ell }]\varpi ^{\ell } \mathbf {e}_i \qquad (x_{i,\ell } \in \overline{{\mathbb {F}}}_q). \end{aligned}$$

(7.2)

This identifies ${\mathscr {L}}_0/{\mathscr {L}}_0^{(h)}$ with ${\mathbb {A}}^{n(h-1) + n'}_{{\mathbb {F}}_{q^n}}$. Observe that if b is Coxeter-type, then although ${\mathscr {L}}_0^{(h)}$ is stable under $(b\sigma )^{n_0}\varpi ^{-k_0}$, the ${\mathbb {F}}_{q^{n_0}}$-rational structure given by this Frobenius on ${\mathscr {L}}_0/{\mathscr {L}}_0^{(h)}$ does not agree with the ${\mathbb {F}}_{q^{n_0}}$-rational structure on ${\mathbb {A}}^{n(h-1)+n'}$ given by the standard ${\mathbb {F}}_{q^{n_0}}$-Frobenius.

Definition 7.3

For $h \ge 1$, define

$$\begin{aligned} {X_h({{\overline{{\mathbb {F}}}}}_q) \,{:=}\,{\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}} / {\mathscr {L}}_0^{(h)} = \text {image of }{\mathscr {L}}_{0,b}^{\mathrm {adm}, \mathrm {rat}}\text { in} {\mathscr {L}}_0/{\mathscr {L}}_0^{(h)}} \end{aligned}$$

and let $X_h \subset {\mathbb {A}}^{n(h-1)+n'}$ be the ${\mathbb {F}}_{q^n}$-subscheme whose ${\mathbb {F}}_{q^n}$-rational structure comes from the standard ${\mathbb {F}}_{q^n}$-Frobenius on ${\mathbb {A}}^{n(h-1)+n'}$.

As $\det (g_b^{\mathrm {red}}(\cdot )) :X_h \rightarrow ({\mathcal {O}}_K/\varpi ^h)^{\times }$ is a morphism onto a discrete scheme, we have the scheme-theoretic disjoint decomposition

$$\begin{aligned} X_h = \bigsqcup _{a \in ({\mathcal {O}}_K/\varpi ^h)^{\times }} g_a.X_h^{\det \equiv 1}, \end{aligned}$$

(7.3)

where $X_h^{\det \equiv 1}$ consists of all $x \in X_h$ with $\det g_b^{\mathrm {red}}(x) \equiv 1 \pmod {\varpi ^h}$, and $g_a \in G_h$ is any matrix with determinant a.

Proposition 7.4

$X_h$ is a smooth affine scheme of dimension $(n-1)(h-1) + (n'-1)$.

Proof

The proof is very similar to that of [12, Proposition 3.10]. Choose b to be the Coxeter-type or special representative. Write $\det (g_b^{\mathrm{red}}(x_1, \ldots , x_n)) = [g_s]_{0 \le s \le h-1}$. It is enough to prove the assertions for the open and closed subset $X_h^{\det \equiv 1}$, which is defined by the equations $g_0 = 1$ and $g_s = 0$ for $1 \le s \le h-1$.

To prove that $X_h^{\det \equiv 1}$ is a smooth affine scheme of dimension $(n-1)(h-1)+n'-1$, it suffices to show that for any point $X_h^{\det \equiv 1}$, there exists a nonsingular $h \times h$ submatrix of the Jacobian matrix J. First let $g_b^{\mathrm{red}}(x_1, \ldots , x_n) \in X_h^{\det \equiv 1}$. Then for some $x_r$, the determinant of the $(n-1) \times (n-1)$ minor obtained by deleting the 1st column and the rth row is nonzero modulo $\varpi$—denote by $d[x_r]$ the reduction of this determinant. From (6.5), observe that $x_{r,i}$ only contributes to $g_s$ if $i \le s$,

$$\begin{aligned} g_s = d[x_r] x_{r,s} + (\text {terms w/ }q\text {th powers of }x_{r,s}, \text { and }x_{i,j}\text { for }(i,j) \ne (r,s)). \end{aligned}$$

Reorder the rows of J so that the first h rows correspond to the coordinates $x_{r,0}, \ldots , x_{r,h-1}$ of $x_r \in {\mathbb {W}}_h$. Since we are working in characteristic p, we have

$$\begin{aligned} \frac{\partial g_s}{\partial x_{1,i}} = {\left\{ \begin{array}{ll} d[x_r] \ne 0 &{}\quad \text {if }i = s, \\ 0 &{}\quad \text {if }i > s, \\ \text {?} &{}\quad \text {if }i < s. \end{array}\right. } \end{aligned}$$

This submatrix of J is an upper triangular matrix with nonzero determinant. Hence we have shown that $X_h^{\det \equiv 1}$ is a smooth complete intersection of dimension $(n-1)(h-1) + n'-1$. $\square$

9.3 Relation to classical Deligne–Lusztig varieties

Recall that for ${{\overline{V}}} = {\mathscr {L}}_0/{\mathscr {L}}_0^{(1)}$ we have that ${\mathbb {G}}_1 = \mathrm{Res}_{{\mathbb {F}}_{q^{n_0}}/{\mathbb {F}}_q}{{\,\mathrm{GL}\,}}({{\overline{V}}})$ (see Sects. 5.3, 5.6). The scheme $X_1$ is a classical Deligne–Lusztig variety corresponding to the maximal nonsplit torus ${\mathbb {F}}_{q^n}^\times$ in ${\mathbb {G}}_1({\mathbb {F}}_q) = {{\,\mathrm{GL}\,}}_{n'}({\mathbb {F}}_{q^{n_0}})$. We get a commutative diagram

where $\Omega _{{\overline{V}}}$ is isomorphic to the Drinfeld upper half-space ${\mathbb {P}}({\overline{V}}) {\,\smallsetminus \,}{\mathbb {P}}({\overline{V}})({\mathbb {F}}_{q^{n_0}})$ and $X_1$ is a ${\mathbb {F}}_{q^n}^\times$-torsor over $\Omega _{{{\overline{V}}}}$. (If b is the special representative, $\Omega _{{{\overline{V}}}}$ is literally the Drinfeld upper half-space.)

For $v \in {\overline{V}}$ define $\overline{g_b}(v)$ to be the $(n' \times n')$-matrix whose ith column is $\overline{\sigma _b}^{i-1}(v)$ (written with respect to the basis $\{\mathbf {e}_i\}_{i \equiv 1 \pmod {n_0}}$ of ${\overline{V}}$ from Lemma 5.8). Then

$$\begin{aligned} X_1 = \{ v \in {\overline{V}} :\det \overline{g_b}(v) \in {\mathbb {F}}_{q^{n_0}}^{\times } \}. \end{aligned}$$

Example 7.5

If $\kappa = 0$, then ${\overline{V}} = {\mathscr {L}}_0/\varpi {\mathscr {L}}_0$, $\overline{\sigma _b}^{i-1} = b\sigma$ and $X_1$ is the Deligne–Lusztig variety for ${{\,\mathrm{GL}\,}}_n({\mathbb {F}}_q)$ associated to the maximal nonsplit torus ${\mathbb {F}}_{q^n}^\times$. If $\kappa ,n$ are coprime, then ${\overline{V}}$ is one-dimensional and $X_1$ is a finite set of points and can be identified with ${\mathbb {F}}_{q^n}^\times$.

9.4 The projection $X_h \rightarrow X_{h-1}$ and its fibers

Let $h \ge 2$. We will actually work with an intermediate scheme: $X_h \twoheadrightarrow X_{h-1}^+ \twoheadrightarrow X_{h-1}$. By Sects. 7.1, 7.2, the quotient ${\mathscr {L}}_0/\varpi ^{h-1} {\mathscr {L}}_0$ can be identified with the affine space ${\mathbb {A}}^{n(h-1)}$. Define $X_{h-1}^+$ to be the ${\mathbb {F}}_{q^n}$-subscheme of ${\mathbb {A}}^{n(h-1)}$ defined by

$$\begin{aligned} {X_{h-1}^+({{\overline{{\mathbb {F}}}}}_q) \,{:=}\,{\mathscr {L}}_{0,b}^{\mathrm {adm}, \mathrm {rat}}/\varpi ^{h-1} {\mathscr {L}}_0 = \text {image of }{\mathscr {L}}_{0,b}^{\mathrm {adm},\mathrm {rat}}\text { in} {\mathscr {L}}_0/\varpi ^{h-1} {\mathscr {L}}_0.} \end{aligned}$$

Observe that

$$\begin{aligned} X_{h-1}^+ = X_{h-1} \times {\mathbb {A}}^{n-n'}, \end{aligned}$$

(7.4)

since the coordinates $x_{i,h-2}$ for $i \not \equiv 1 \pmod {n_0}$ do not contribute to $\det (g_b^{{{\,\mathrm{red}\,}}}(x))$ modulo $\varpi ^{h-1}$. Furthermore, $X_h$ is a closed subscheme of $X_{h-1}^+ \times {\mathbb {A}}^{n'}$, and under this embedding

$$\begin{aligned} X_h \hookrightarrow X_{h-1}^+ \times {\mathbb {A}}^{n'}, \end{aligned}$$

we may write $x = ({{\widetilde{x}}}, x_{1,h-1}, x_{n_0+1,h-1}, \ldots , x_{n_0(n'-1)+1,h-1})$ for $x \in X_h$ and its image ${{\tilde{x}}} \in X_{h-1}^+$. More precisely, we have the following technical proposition, which will be used in Sect. 9.

Proposition 7.6

Let $h \ge 2$.

• (i) $X_h$ is the closed subscheme of $X_{h-1}^+ \times {\mathbb {A}}^{n'}$ cut out by the polynomial

  $$\begin{aligned} {P \,{:=}\,P_0^q - P_0,} \end{aligned}$$

  where $[P_0]$ is the coefficient of $\varpi ^{h-1}$ in $\det (g_b^{{{\,\mathrm{red}\,}}}(\cdot ))$.

• (ii) Let b be the special representative. Then

  $$\begin{aligned} P_0(x) = c({{\widetilde{x}}}) + \sum _{i=0}^{n_0 - 1} P_1(x)^{q^i} \end{aligned}$$

  where $\sum _{i=0}^{n_0 - 1} P_1^{q^i}$ exactly consists of all terms of $P_0$ that depend on the coordinates $x_{1,h-1}, x_{n_0 + 1, h-1}, \ldots , x_{n_0(n'-1)+1,h-1}$ and c is a morphism $X_{h-1}^+ \rightarrow {\mathbb {A}}^1$. In particular, $X_h$ is the closed subscheme of $X_{h-1}^+ \times {\mathbb {A}}^{n'}$ cut out by the equation

  $$\begin{aligned} P_1^{q^{n_0}} - P_1 = c - c^q. \end{aligned}$$

• (iii) Let b be the special representative. Explicitly, the polynomial in (ii) is given by

  $$\begin{aligned} P_1 = \sum _{1 \le i,j \le n^{\prime }} m_{ji} x_{1 + n_0(i-1),h-1}^{q^{(j-1)n_0}}, \end{aligned}$$

  where ${m \,{:=}\,(m_{ji})_{j,i}}$ is the adjoint matrix of $\overline{g_b}({\bar{x}})$ and ${{\bar{x}}}$ denotes the image of x in ${\overline{V}} = {\mathscr {L}}_0/{\mathscr {L}}_0^{(1)}$. Explicitly, $m \cdot \overline{g_b}({\bar{x}}) = \det \overline{g_b}({\bar{x}}) \cdot 1_{n'}$ and the (j, i)th entry of m is $(-1)^{i+j}$ times the determinant of the $(n^{\prime }-1)\times (n^{\prime }-1)$ matrix obtained from $\overline{g_b}({\bar{x}})$ by deleting the ith row and jth column.

Proof

An explicit calculation shows that $P_0 = c + \sum _{i=0}^{n_0 - 1} \sigma ^i(P_1)$, with $P_1$ as claimed if b is the special representative. Note that in the mixed characteristic setting, we use Lemma 7.1(ii) to see that minor contributions only appear in the $c({{\widetilde{x}}})$ term. From this the proposition easily follows. $\square$

9.5 Level compatibility on the cohomology of $X_h$

Proposition 7.7

Let $h \ge 2$. The action of $\ker (T_h \rightarrow T_{h-1}) = {\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ on $X_h$ preserves each fiber of the map $X_h \rightarrow X_{h-1}$, the induced morphism $X_h/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n}) \rightarrow X_{h-1}$ is smooth, and each of its fibers is isomorphic to ${\mathbb {A}}^{n-1}$.

Proof

Let b be the special representative and let $x \in X_h$ be coordinatized as in Sect. 7.2. Then $x_{i,0} \ne 0$ for $i \equiv 1 \pmod {n_0}$. By (a slight variant of) Proposition 7.6, $X_h$ is the closed subscheme of $X_{h-1} \times {\mathbb {A}}^n$ given by $P = 0$, where ${\mathbb {A}}^n$ has the coordinates $\{y_i\}_{i=1, \ldots , n}$, where $y_i = x_{i,h-1}$ if $i \equiv 1 \pmod {n_0}$ and $y_i = x_{i,h-2}$ if $i \not \equiv 1 \pmod {n_0}$. Note that the natural ${\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$-action on $X_h$ extends to the action on $X_{h-1} \times {\mathbb {A}}^n$ over $X_{h-1}$ given by

$$\begin{aligned} 1 + [\lambda ]\varpi ^{h-1} :{\left\{ \begin{array}{ll} x_{i,h-1} \mapsto x_{i,h-1} + x_{i,0} \lambda &{}\quad \text {if }i \equiv 1 \pmod {n_0}, \\ x_{i,h-2} \mapsto x_{i,h-2} &{}\quad \text {otherwise,}\end{array}\right. } \end{aligned}$$

where $\lambda \in {\mathbb {F}}_{q^n}$. (Note that we use Remark 7.2 here.) Consider the morphism

$$\begin{aligned} f :X_{h-1} \times {\mathbb {A}}^n \rightarrow X_{h-1} \times {\mathbb {A}}^n, \qquad y_i \mapsto {\left\{ \begin{array}{ll} \left( \frac{y_1}{x_{1,0}}\right) ^{q^n} - \frac{y_1}{x_{1,0}} &{}\quad \text {if }i = 1, \\ y_i - \frac{x_{i,0} y_1}{x_{1,0}} &{} \quad \text {if }i > 1, i \equiv 1 \pmod {n_0}, \\ y_i &{}\quad \text {if }i \not \equiv 1 \pmod {n_0}. \end{array}\right. } \end{aligned}$$

This morphism factors through the surjection $X_{h-1} \times {\mathbb {A}}^n \rightarrow X_{h-1} \times {\mathbb {A}}^n/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ so that it is a composition

$$\begin{aligned} X_{h-1} \times {\mathbb {A}}^n \rightarrow X_{h-1} \times {\mathbb {A}}^n/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n}) {\mathop {\rightarrow }\limits ^{\sim }} X_{h-1} \times {\mathbb {A}}^n, \end{aligned}$$

where the second map must in fact be an isomorphism. Since ${\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ is a p-group, [11, Proposition 3.6] implies that $P((y_i)_{i=1,\ldots , n}) = P'(f(y_i)_{i=1,\ldots ,n})$ for some $P' :X_{h-1} \times {\mathbb {A}}^n \rightarrow {\mathbb {A}}^1$. Now $X_h/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ is the closed subscheme of $X_h \times {\mathbb {A}}^n/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ defined by $P' = 0$. We therefore have a commutative diagram

Since P is a degree-$q^n$ polynomial in $x_{1,h-1}$, we know that $P^{\prime }$ must be at most degree one in $y_1$. A calculation shows that the coefficient of $y_1$ is the function on $X_{h-1}$ given by $x \mapsto \det \overline{g_b}({\bar{x}})$, where ${\bar{x}}$ is the image of $x \in X_{h-1}$ in $X_1$ (notation as in Sect. 7.3). This function is constant on connected components of $X_{h-1}$, taking values in ${\mathbb {F}}_q^{\times }$. In particular, the coefficient of $y_1$ in $P'$ over any point in $X_{h-1}$ is nonzero, so it follows that each fiber of $X_h/{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n}) \rightarrow X_{h-1}$ is isomorphic to ${\mathbb {A}}^{n-1}$. $\square$

Corollary 7.8

There is a natural isomorphism

$$\begin{aligned} H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )^{{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})} \cong H_c^{i + 2(n-1)}(X_{h-1}, {{\overline{{\mathbb {Q}}}}}_\ell )(n-1), \end{aligned}$$

where $(n-1)$ denotes the Tate twist.

This corollary allows to define a direct limit of the homology groups for $X_h$ (see Sect. 11).

9.6 $X_h$ as a subscheme of ${\mathbb {G}}_h$

Let b be a Coxeter-type representative. Let $1 \le l \le n$ be an integer satisfying $e_{\kappa ,n} l \equiv 1 \pmod n$. For $x = \sum _{i=1}^n x_i \mathbf {e}_i \in {\mathscr {L}}_0$ where $x_i \in {\mathcal {O}}$, define

$$\begin{aligned} {\lambda (x) \,{:=}\,\sum _{i=1}^n \frac{1}{\varpi ^{\lfloor k_0(i-1)/n_0 \rfloor }} \cdot b^{i-1} \cdot D(x_i),} \end{aligned}$$

where $D(a) = {{\,\mathrm{diag}\,}}(a, \sigma ^l(a), \ldots , \sigma ^{[(n-1)l]}(a))$. Let $\gamma$ be the inverse of the permutation of the set $\{1, 2, \dots , n\}$ defined by $1 \mapsto 1$ and $i \mapsto [(i-1)e_{\kappa ,n}] + 1$ for $2 \le i \le n$. Let $\gamma \in {{\,\mathrm{GL}\,}}_n(K)$ also denote the matrix given by $\gamma (\mathbf {e}_i) = e_{\gamma (i)}$.

Lemma 7.9

We have

$$\begin{aligned} \lambda (x) = g_b^{\mathrm {red}}(\gamma ^{-1}(x)) \cdot \gamma . \end{aligned}$$

In particular, $\det \lambda (x) = \det g_b^{\mathrm {red}}(x)$. Moreover, we have $\gamma b_0^{e_{\kappa ,n}}\gamma ^{-1} = b_0$.

Proof

This is a direct computation. $\square$

Example 7.10

• (i) For $n = 3$, $\kappa = e_{\kappa ,n} = 1$, we have $b = \left( {\begin{matrix} 0 &{} 0 &{} \varpi \\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{matrix}}\right)$ and for $x = \left( {\begin{matrix} x_1\\ x_2 \\ x_3\end{matrix}}\right)$,

  $$\begin{aligned} \lambda (x) = g_b^{\mathrm {red}}(x) = g_b(x) = \left( {\begin{matrix} x_1 &{} \varpi \sigma (x_3) &{} \varpi \sigma ^2(x_2) \\ x_2 &{} \sigma (x_1) &{} \varpi \sigma ^2(x_3) \\ x_3 &{} \sigma (x_2) &{} \sigma ^2(x_1) \end{matrix}}\right) . \end{aligned}$$

  We have $F(\lambda (x)) \ne \lambda (\sigma (x))$. Thus $\lambda$ is not an ${\mathbb {F}}_q$-morphism.

• (ii) For $n=3$, $\kappa = 2$, $e_{\kappa ,n} = 2$, we have $b = \left( {\begin{matrix} 0 &{} \varpi &{} 0 \\ 0 &{} 0 &{} \varpi \\ 1 &{} 0 &{} 0 \end{matrix}}\right)$ and

  $$\begin{aligned} g_b^{\mathrm {red}}(x) = \left( {\begin{matrix} x_1 &{}\quad \varpi \sigma (x_2) &{}\quad \varpi \sigma ^2(x_3) \\ x_2 &{}\quad \varpi \sigma (x_3) &{}\quad \sigma ^2(x_1) \\ x_3 &{}\quad \sigma (x_1) &{}\quad \sigma ^2(x_2) \end{matrix}}\right) \qquad \text { and } \qquad \lambda (x) = \left( {\begin{matrix} x_1 &{}\quad \varpi \sigma ^2(x_2) &{}\quad \varpi \sigma (x_3) \\ x_3 &{}\quad \sigma ^2(x_1) &{}\quad \varpi \sigma (x_2) \\ x_2 &{}\quad \sigma ^2(x_3) &{}\quad \sigma (x_1) \end{matrix}}\right) \in \breve{G}_{\mathbf{{x}},0}. \end{aligned}$$

Proposition-Definition 7.11

The assignment $\lambda$ defines an embedding,

$$\begin{aligned} {\mathscr {L}}_0 \hookrightarrow M_{n^{\prime }}({\mathcal {O}}_{D_{k_0/n_0}}), \end{aligned}$$

which restricts to

$$\begin{aligned} \lambda :{\mathscr {L}}_{0,b}^{\mathrm{adm}} \hookrightarrow \breve{G}_{{\mathbf {x}},0}, \end{aligned}$$

Moreover, $\det (\lambda (x)) \in {\mathcal {O}}_K^\times$ if and only if $x \in {\mathscr {L}}_{b,0}^{\mathrm {adm},\mathrm {rat}}$. The reduction modulo $\varpi ^{h}$ of $\lambda$ induces an ${\mathbb {F}}_{q^n}$-rational embedding

$$\begin{aligned} {\mathscr {L}}_{0,b}^{\mathrm{adm, \mathrm rat}}/{\mathscr {L}}_0^{(h)} = X_h \hookrightarrow {\mathbb {G}}_h. \end{aligned}$$

We denote its image again by $X_h$. This is an ${\mathbb {F}}_{q^n}$-subscheme of ${\mathbb {G}}_h$.

Proof

It is easy to see that $\lambda (\mathbf {e}_i) \in M_{n^{\prime }}({\mathcal {O}}_{D_{k_0/n_0}})$ for $i = 1, \dots , n$. This implies that $\lambda ({\mathscr {L}}_0) \subseteq M_{n^{\prime }}({\mathcal {O}}_{D_{k_0/n_0}})$. By Lemma 7.9 it is immediate that $\det (\lambda (x)) \in {\mathcal {O}}^{\times }$ if and only if $\det (g_b^{\mathrm{red}}(x)) \in {\mathcal {O}}^{\times }$ and similarly $\det (\lambda (x)) \in {\mathcal {O}}_K^{\times }$ if and only if $\det (g_b^{\mathrm{red}}(x)) \in {\mathcal {O}}_K^{\times }$. Finally, note that $\lambda$ is a ${\mathbb {F}}_{q^n}$-morphism since $\lambda (\sigma ^n(x)) = \sigma ^n(\lambda (x)) = F^n(\lambda (x))$. $\square$

The natural $(\breve{G}_{{\mathbf {x}},0}^F \times {\mathcal {O}}_L^\times )$-action on ${\mathscr {L}}_{0,b}^{\mathrm{adm, \mathrm rat}}$ induces a left action of $(G_h \times T_h)$-action on $X_h \subseteq {\mathbb {G}}_h$, given by left-multiplication by $G_h = {\mathbb {G}}_h({\mathbb {F}}_q)$ and right-multiplication by $T_h = {\mathbb {T}}_h({\mathbb {F}}_q)$:

$$\begin{aligned} {(g,t) \cdot x \,{:=}\,g x t, \qquad \text {for }g \in G_h, \, t \in T_h, \, x \in X_h.} \end{aligned}$$

9.7 Relation to Deligne–Lusztig varieties for finite rings

Let b be the Coxeter-type representative. The following proposition gives a description of $X_h$ reminiscent of Deligne–Lusztig varieties for reductive groups over finite rings [26, 31]. Let $U_{up}$ and $U_{low}$ denote the $\breve{K}$-subgroups of upper and lower triangular unipotent matrices in $J_b$. Consider the unipotent radicals ${U \,{:=}\,\gamma ^{-1}U_{up}\gamma }$, $U^- = \gamma ^{-1}U_{low}\gamma$ of opposite Borels (over $\breve{K}$) in $J_b$ containing the diagonal torus T. Let ${\mathbb {U}}$ and ${\mathbb {U}}^-$ denote the smooth subgroup schemes of ${\mathbb {G}}$ whose ${\overline{{\mathbb {F}}}}_q$-points are $U(\breve{K}) \cap \breve{G}_{\mathbf{x},0}$ and $U^-(\breve{K}) \cap \breve{G}_{\mathbf{x},0}$, and let ${\mathbb {U}}_h$ and ${\mathbb {U}}^-_h$ be the corresponding subgroups of ${\mathbb {G}}_h$.

Proposition 7.12

The subgroup ${\mathbb {U}}_h^- \cap F({\mathbb {U}}_h) \subseteq {\mathbb {G}}_h$ consists of matrices with 1’s along the main diagonal and 0’s outside the first column. We have

$$\begin{aligned} X_h({{\overline{{\mathbb {F}}}}}_q)&= \left\{ g \in {\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q) : g^{-1} F(g) \in {\mathbb {U}}_h^- \cap F({\mathbb {U}}_h) \right\} \\&= \left\{ g \in {\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q) : g^{-1} F(g) \in {\mathbb {U}}_h^-\right\} /({\mathbb {U}}_h^- \cap F^{-1}({\mathbb {U}}_h^-)). \end{aligned}$$

Proof

Using $\gamma b_0^{e_{\kappa ,n}} \gamma ^{-1} = b_0$ and $\gamma t_{\kappa ,n} \gamma ^{-1} = t_{\kappa ,n}$ from Lemma 7.9, we compute

$$\begin{aligned} U^- \cap F(U)&= \gamma ^{-1} U_{low} \gamma \cap F(\gamma ^{-1}U_{up}\gamma ) = \gamma ^{-1} U_{low} \gamma \cap b_0^{e_{\kappa ,n}}t_{\kappa ,n} \gamma ^{-1}U_{up} t_{\kappa ,n}^{-1} b_0^{-e_{\kappa ,n}} \gamma \\&= \gamma ^{-1} (U_{low} \cap b_0 U_{up} b_0^{-1} ) \gamma \end{aligned}$$

and (using $\gamma (e_1) = e_1$) the claim about ${\mathbb {U}}_h^- \cap F({\mathbb {U}}_h)$ follows easily. For any $a \in {\mathbb {W}}_h({{\overline{{\mathbb {F}}}}}_q)$, we have that

$$\begin{aligned} F({{\,\mathrm{diag}\,}}(a, \sigma ^{[l]}(a), \ldots , \sigma ^{[(n-1)l]}(a))) = {{\,\mathrm{diag}\,}}(\sigma ^n(a), \sigma ^{[l]}(a), \ldots , \sigma ^{[(n-1)l]}(a)). \end{aligned}$$

Thus for any $v = (v_i)_{i=1}^n$ with $v_i \in {\mathbb {W}}_h(\overline{{\mathbb {F}}}_q)$ ($i \equiv 1 \pmod {n_0}$) and $v_i \in {\mathbb {W}}_{h-1}(\overline{{\mathbb {F}}}_q)$ ($i \not \equiv 1 \pmod {n_0}$),

$$\begin{aligned} F(\lambda (x)) = \sum _{i=1}^n \frac{1}{\varpi ^{\lfloor k_0(i-1)/n_0 \rfloor }} \cdot b^{i-1} \cdot {{\,\mathrm{diag}\,}}(\sigma ^n(x_i), \sigma ^{[l]}(x_i), \ldots , \sigma ^{[(n-1)l]}(x_i)) \end{aligned}$$

differs from $\lambda (x)$ in only the first column. Thus for $x \in {\mathscr {L}}_0$, we see that $\lambda (x)^{-1}F(\lambda (x))$ can differ from an element of ${\mathbb {U}}_h^- \cap F({\mathbb {U}}_h)$ only in the left upper entry, and this entry is equal to $\det (\lambda (x)^{-1}F(\lambda (x))) = \det (g_b^{\mathrm {red}}(x)^{-1}\sigma (g_b(x)))$ (Lemma 7.9). Now for $x \in {\mathscr {L}}_0^{\mathrm {adm}, \mathrm {rat}}$, $\det g_b^{\mathrm {red}}(x) \in {\mathcal {O}}_K^{\times }$. This proves

$$\begin{aligned} X_h \subset \left\{ g \in {\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q) : g^{-1} F(g) \in {\mathbb {U}}_h^- \cap F({\mathbb {U}}_h)\right\} . \end{aligned}$$

To see the other inclusion, observe that if $F(g) = g \cdot u$ for some $u \in {\mathbb {U}}_h^- \cap F({\mathbb {U}}_h)$, then comparing the jth column for $j \ge 2$ shows that g must necessarily be of the form $\lambda (v)$ for some $v \in {\mathscr {L}}_0^{\mathrm {adm}}$. The determinant condition then follows from $\det (u) = 1$. The last equality in the proposition follows from Lemma 7.13. $\square$

Lemma 7.13

The morphism

$$\begin{aligned} ({\mathbb {U}}^-_h \cap F^{-1} {\mathbb {U}}^-_h) \times ({\mathbb {U}}^-_h \cap F {\mathbb {U}}_h) \rightarrow {\mathbb {U}}^-_h, \qquad (x,g) \mapsto x^{-1} g F(x). \end{aligned}$$

is an isomorphism.

Proof

We can consider the ${\overline{{\mathbb {F}}}}_q$-scheme $\gamma {\mathbb {G}}\gamma ^{-1}$, whose ${\overline{{\mathbb {F}}}}_q$-points are $\gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}$, together with a Frobenius isomorphism

$$\begin{aligned} F_0 :\gamma {\mathbb {G}}\gamma ^{-1} {\mathop {\rightarrow }\limits ^{\sim }} \gamma {\mathbb {G}}\gamma ^{-1}, \quad F_0(x) = b_0 (\gamma t_{\kappa ,n}\gamma ^{-1}) \sigma (x) (b_0(\gamma t_{\kappa ,n}\gamma ^{-1}))^{-1} \end{aligned}$$

By Lemma 7.9, $\gamma b_0^{e_{\kappa ,n}} t_{\kappa ,n} \gamma ^{-1} = b_0(\gamma t_{\kappa ,n}\gamma ^{-1})$. Thus if $c_{\gamma } :{\mathbb {G}}{\mathop {\rightarrow }\limits ^{\sim }} \gamma {\mathbb {G}}\gamma ^{-1}$, $x \mapsto \gamma x \gamma ^{-1}$ denotes the conjugation by $\gamma$, we have $c_{\gamma } \circ F = F_0 \circ c_{\gamma }$ (this in particular shows that $F_0$ is an isomorphism).

We will first show that $({\mathbb {U}}^- \cap F^{-1} {\mathbb {U}}^-) \times ({\mathbb {U}}^- \cap F {\mathbb {U}}) \rightarrow {\mathbb {U}}^-$, $(x,g) \mapsto x^{-1} g F(x)$ is bijective. We have ${\mathbb {U}}^-({\overline{{\mathbb {F}}}}_q) = \gamma ^{-1}(\breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1})\gamma$ and ${\mathbb {U}}({\overline{{\mathbb {F}}}}_q) = \gamma ^{-1}(\breve{U}_{up} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1})\gamma$. Applying $c_{\gamma }$, we thus have to show that the map

$$\begin{aligned}&\big (( \breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}) \cap F_0(\breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}) \big ) \nonumber \\&\quad \times \big ((\breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}) \cap F_0(\breve{U}_{up} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1})\big ) \nonumber \\&\qquad \rightarrow \breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}, \end{aligned}$$

(7.6)

$(x,g) \mapsto x^{-1}gF_0(x)$ is bijective. We first show that the following is an isomorphism:

$$\begin{aligned} (\breve{U}_{low} \cap b_0^{-1} \breve{U}_{low} b_0) \times (\breve{U}_{low} \cap b_0 \breve{U}_{up} b_0^{-1}) \rightarrow \breve{U}_{low}, \qquad (x, g) \mapsto x^{-1} g F_0(x).\nonumber \\ \end{aligned}$$

(7.7)

To do this, it is equivalent to prove that given any $A \in \breve{U}_{low}$, there exists a unique element $(x,g) \in (\breve{U}_{low} \cap b_0^{-1} \breve{U}_{low} b_0) \times (\breve{U}_{low} \cap b_0 \breve{U}_{up} b_0^{-1})$ such that $x A = g F_0(x)$. We now compute explicitly and write

$$\begin{aligned} x = \left( \begin{matrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \\ b_{21} &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \\ b_{31} &{}\quad b_{32} &{}\quad 1 &{}\quad \ddots &{}\quad &{}\quad \vdots \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad 0 &{}\quad \vdots \\ b_{n-1,1} &{}\quad b_{n-1,2} &{}\quad \cdots &{}\quad b_{n-1,n-2} &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{matrix}\right) , \qquad g = \left( \begin{matrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ c_1 &{}\quad 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ c_2 &{}\quad 0 &{}\quad 1 &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ c_{n-1} &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 1 \end{matrix}\right) . \end{aligned}$$

Let $\gamma t_{\kappa ,n} \gamma ^{-1} = {{\,\mathrm{diag}\,}}(t_1, t_2, \ldots , t_n)$ so that we have

$$\begin{aligned} b_0 t_{\kappa ,n} \sigma (x) t_{\kappa ,n}^{-1} b_0^{-1} = \left( \begin{matrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad \sigma (b_{21}) t_2/t_1 &{}\quad 1 &{}\quad 0 &{}\quad &{}\quad 0 \\ 0 &{}\quad \sigma (b_{31}) t_3/t_1 &{}\quad \sigma (b_{32}) t_3/t_2 &{}\quad 1 &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad \sigma (b_{n-1,1}) t_{n-1}/t_1 &{}\quad \sigma (b_{n-1,2}) t_{n-1}/t_2 &{}\quad \cdots &{}\quad \sigma (b_{n-1,n-2}) t_{n-1}/t_{n-2} &{}\quad 1 \end{matrix}\right) . \end{aligned}$$

We therefore see that the (i, j)th entry of $g F_0(x)$ is

$$\begin{aligned} (g F_0(x))_{i,j} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }i = j, \\ 0 &{}\quad \text {if }i < j, \\ c_{i-1} &{} \quad \text {if }i> j = 1, \\ \sigma (b_{i-1,j-1}) t_{i-1}/t_{j-1} &{}\quad \text {if }i> j > 1. \end{array}\right. }. \end{aligned}$$

(7.8)

We also compute the (i, j)th entry of xA when $A = (a_{i,j})_{i,j} \in \breve{U}_{low}$:

$$\begin{aligned} (xA)_{i,j} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }i = j, \\ 0 &{}\quad \text {if }i< j, \\ b_{ij} + \sum _{k=j+1}^{i-1} b_{ik} a_{kj} + a_{ij} &{}\quad \text {if }j< i \le n-1, \\ a_{nj} &{}\quad \text {if }j < i = n. \end{array}\right. } \end{aligned}$$

(7.9)

We now have $n^2$ equations given by (7.8) $=$ (7.9), viewed as equations in the variables $b_{ij}$ and $c_i$. First look at the equations corresponding to $(n,2), (n,3), \ldots , (n,n-1).$ This gives

$$\begin{aligned} \sigma (b_{n-1,j-1}) t_{n-1}/t_{j-1} = a_{nj} \qquad \text {for }1< j < n. \end{aligned}$$

which uniquely determines $b_{n-1,1}, b_{n-1,2}, \ldots , b_{n-1,n-2}$. Proceeding inductively, let $1<i\le n-1$, and suppose that all $b_{i',j}$ for all $i'\ge i$ and $1 < j \le i'$ are uniquely determined. Then look at the equations corresponding to $(i-1,2), (i-1,3), \ldots , (i-1,i-2)$. This gives

$$\begin{aligned} \sigma (b_{i-1,j-1}) t_{i-1}/t_{j-1} = b_{i,j} + \sum _{k=j+1}^{i-1} b_{i,k} a_{kj} + a_{i,j} \qquad \text {for }1< j < i, \end{aligned}$$

(7.10)

which uniquely determines $b_{i-1,1}, b_{n-2,2}, \ldots , b_{i-1,i-2}$. This uniquely determines x. Finally, by looking at the equations corresponding to $(2,1), (3,1), \ldots , (n,1)$, it is immediately clear that the $c_i$’s are also uniquely determined, so g is as well. This shows the isomorphism (7.7).

Now we deduce (7.6) from this. Using the same notation as above, assume that $A \in \breve{U}_{low} \cap \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q)\gamma ^{-1}$. Let $\tau _i := {{\,\mathrm{ord}\,}}(t_i)$ ($1\le i \le n$) and $\lambda _{i,j}$ denote the minimum of valuations of all elements of $\gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1} \cap \breve{U}_{\alpha _{i,j}}$, where $\breve{U}_{\alpha _{i,j}}$ is the root subgroup corresponding to the (i, j)th entry ($1 \le i\ne j \le n$). Then $\tau _i,\lambda _{ij} \in \{0, 1\}$ for all i, j. Moreover, the fact that $F_0$ is an isomorphism shows

$$\begin{aligned} \lambda _{i,j} = \lambda _{i-1,j-1} + \tau _{i-1} - \tau _{j-1}. \end{aligned}$$

(7.11)

To establish (7.6), we have to show that for all $2\le j < i \le n$, we have ${{\,\mathrm{ord}\,}}(b_{i-1,j-1}) \ge \lambda _{i-1,j-1}$ and ${{\,\mathrm{ord}\,}}(c_{i-1}) \ge \lambda _{i-1,1}$.

We first prove the assertion about the b’s. As in the proof of (7.7) above, we may proceed inductively on i: assuming that the assertion holds for all $i' > i$, we will show that the assertion holds for i. (The basic induction step $i=n$ follows from the same argument as below.) Observe that if $\tau _{i-1} = 0$ and $\tau _{j-1} = 1$, then we are done by formula (7.10).

Assume that $\tau _{i-1} = \tau _{j-1}$. If $\lambda _{i-1,j-1} = 0$ then by (7.10) there is again nothing to show. Thus we may assume $\lambda _{i-1,j-1} = 1$. By (7.10) we have to check that $\lambda _{i,j} = 1$ and that for each $j+1 \le k \le i-1$, either $\lambda _{i,k}=1$ or $\lambda _{k,j}=1$. First, $\lambda _{i,j} = 1$ follows from (7.11). Second, $\alpha _{i,k} + \alpha _{k,j} = \alpha _{i,j}$ ($\alpha _{i,j}$ is the root of the diagonal torus of ${{\,\mathrm{GL}\,}}_n$ corresponding to (i, j)th entry). Thus the fact that $\gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q)\gamma ^{-1}$ is a group implies that $\lambda _{i,k} + \lambda _{k,j} \ge \lambda _{i,j}$ (for all k), so $\lambda _{i,k} = 1$ or $\lambda _{k,j} = 1$.

Finally, assume that $\tau _{i-1} = 1$, $\tau _{j-1} = 0$. Then (7.11) implies $\lambda _{i-1,j-1} = 0$ and $\lambda _{i,j} = 1$. Then by (7.10) we have to show that $\lambda _{i,j} = 1$ (which we already know) and that for each $j+1\le k \le i-1$, we have $\lambda _{i,k} = 1$ or $\lambda _{k,j} = 1$ (which holds for the same reason as above). This completes the proof of the assertion about the b’s.

Analogously, one proves the assertion about the $c_{i-1}$’s. Since (7.10) and the equations corresponding to $(2,1), (3,1), \ldots , (n,1)$ uniquely determine the b’s and the c’s, this establishes bijectivity of (7.6).

To finish the proof of the lemma, it suffices to check that if $A_1, A_2 \in \gamma {\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \gamma ^{-1}$ differ by some element in the normal subgroup $\gamma \ker ({\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \rightarrow {\mathbb {G}}_h({\overline{{\mathbb {F}}}}_q)) \gamma ^{-1}$, then the corresponding pairs $(x_1,g_1)$ and $(x_2,g_2)$ with $x_i^{-1}g_iF_0(x_i) = A_i$ ($i=1,2$) satisfy $x_1^{-1}x_2, g_1^{-1}g_2 \in \ker ({\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \rightarrow {\mathbb {G}}_h({\overline{{\mathbb {F}}}}_q))$. Let $\lambda _{i,j}^h \in \{h-1,h\}$ be the smallest possible valuation of an element in $\gamma \ker ({\mathbb {G}}({\overline{{\mathbb {F}}}}_q) \rightarrow {\mathbb {G}}_h({\overline{{\mathbb {F}}}}_q)) \gamma ^{-1} \cap \breve{U}_{\alpha _{i,j}}$. As $F_0$ induces an isomorphism of ${\mathbb {G}}_h$, we again have a formula

$$\begin{aligned} \lambda _{i,j}^h = \lambda _{i-1,j-1}^h + \tau _{i-1} - \tau _{j-1}. \end{aligned}$$

We can once again proceed inductively to deduce that the $b_{i-1,j-1}$ and $c_{i-1}$ are uniquely determined as elements in ${\mathfrak {p}}^{\lambda _{i-1,j-1}}/{\mathfrak {p}}^{\lambda _{i-1,j-1}^h}$ by the elements $a_{i,j} \in {\mathfrak {p}}^{\lambda _{i,j}}/{\mathfrak {p}}^{\lambda _{i,j}^h}$. $\square$

10 Part 3. Alternating sum of cohomology of $X_h$

In this part, we study the virtual $G_h$-representations

$$\begin{aligned} {R_{T_h}^{G_h}(\theta ) \,{:=}\,\sum _{i \ge 0} (-1)^i H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ],} \end{aligned}$$

where $\theta$ is a character of $T_h \cong {\mathcal {O}}_L^\times /U_L^h = {\mathbb {W}}_h^\times ({\mathbb {F}}_{q^n})$.

In Sect. 8, we prove that if $\theta$ is primitive, then $R_{T_h}^{G_h}(\theta )$ is (up to a sign) an irreducible $G_h$-representation (Theorem 8.1). Our strategy is to extend ideas of Lusztig, who proves the analogous result in the context of division algebras [25] and split groups [26] (see [31] for the mixed characteristic analogue). This is done in Sect. 8.4. We note that the main result there, Proposition 8.7, is more general than Theorem 8.1 in that it works for any Frobenius F on ${\mathbb {G}}_h$ and the F-fixed points of any F-stable maximal torus in ${\mathbb {G}}_h$. For example, if we take F to be the twisted Frobenius coming from the Coxeter-type representative, then the F-fixed points of the diagonal torus forms the group ${\mathbb {W}}_h^\times ({\mathbb {F}}_{q^n})$, which exactly gives Theorem 8.1. On the other hand, if we take F to be the twisted Frobenius coming from the special representative, then the F-fixed points of the diagonal torus forms the $n'$-fold product of ${\mathbb {W}}_h^\times ({\mathbb {F}}_{q^{n_0}})$, which corresponds to the maximally split unramified torus in $G_h$.

In Sect. 8, we also give a character formula for $R_{T_h}^{G_h}(\theta )$ on certain elements of $T_h$ (Proposition 8.3) and give a geometric interpretation of determinant-twisting on the cohomology groups (Lemma 8.4). Keeping in mind the remarks in the preceding paragraph, the methods in Sect. 8 primarily use the Coxeter-type representative b (Sect. 5.2).

In Sect. 9, we prove an analogue of a cuspidality result for $R_{T_h}^{G_h}(\theta )$ when $\theta$ is primitive (Theorem 9.1). To do this, we perform a character calculation using the geometry of $X_h$. Our approach is a (far-reaching) generalization of the proof in [21] in the special case $G = {{\,\mathrm{GL}\,}}_2(K)$. We use the special representative b (Sect. 5.2) as F-stable parahoric subgroups are more well-behaved for this choice. We note that although there is no notion of cuspidality for $G_h$-representations, we will see later that Theorem 9.1 implies the supercuspidality of the corresponding G-representation (Theorem 12.5).

11 Deligne–Lusztig varieties for Moy–Prasad quotients for ${{\,\mathrm{GL}\,}}_n$

We say that a character $\theta :T_h \cong {\mathbb {W}}_h^\times ({\mathbb {F}}_{q^n}) \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ is primitive if the restriction of $\theta$ to ${\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ does not factor through any nontrivial norm maps ${\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n}) \rightarrow {\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^r})$ for $r \mid n$, $r < n$.

11.1 Irreducibility of $R_{T_h}^{G_h}(\theta )$

Theorem 8.1

Let $\theta , \theta ' :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be two characters and assume $\theta$ is primitive. Then

$$\begin{aligned} \left\langle R_{T_h}^{G_h}(\theta ), R_{T_h}^{G_h}(\theta ') \right\rangle _{G_h} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }\theta = \theta ', \\ 0 &{} \quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

In particular, the virtual $G_h$-representation $R_{T_h}^{G_h}(\theta )$ is (up to a sign) irreducible.

Let ${\mathbb {U}}_h,{\mathbb {U}}_h^- \subseteq {\mathbb {G}}_h$ be as in Sect. 7.7. Put

$$\begin{aligned} {S_h \,{:=}\,\{x \in {\mathbb {G}}_h :x^{-1}F(x) \in {\mathbb {U}}_h^-\}.} \end{aligned}$$

This has an action of $G_h \times T_h$ by $(g,t) :x \mapsto gxt$. Recalling from Proposition 7.12 that $X_h = \{x \in {\mathbb {G}}_h : x^{-1} F(x) \in {\mathbb {U}}_h^-\}/({\mathbb {U}}_h^- \cap F({\mathbb {U}}_h^-))$, we immediately have the following lemma.

Lemma 8.2

The morphism $X_h \times ({\mathbb {U}}_h^- \cap F{\mathbb {U}}_h^-) {\mathop {\rightarrow }\limits ^{\sim }} S_h$ given by $(x,h) \mapsto xh$ is a $(G_h \times T_h)$-equivariant isomorphism, where the action on the left-hand side is given by $(g,t) :(x,h) \mapsto (gxt,t^{-1}ht)$. As ${\mathbb {U}}_h^- \cap F{\mathbb {U}}_h^-$ is isomorphic to an affine space, for any character $\theta$ of $T_h$, we have $R_{T_h}^{G_h}(\theta ) = \sum _i (-1)^i {H}_c^i(S_h, \overline{{\mathbb {Q}}}_\ell )[\theta ]$ as virtual $G_h$-representations.

We show how to reduce Theorem 8.1 to a calculation of the cohomology of

$$\begin{aligned} {\Sigma \,{:=}\,\{(x, x', y) \in {\mathbb {U}}_h^- \times {\mathbb {U}}_h^- \times {\mathbb {G}}_h : x F(y) = y x'\},} \end{aligned}$$

and postpone the study of $\Sigma$ to Sect. 8.4. Taking for granted Proposition 8.7, we give the proof of the main theorem:

Proof of Theorem 8.1

Let F be the twisted Frobenius given by the Coxeter-type representative b of Sect. 5.2. Consider the action of $G_h \times T_h \times T_h$ on $S_h \times S_h$ given by $(g, t_1, t_2) :(x_1, x_2) \mapsto (g x_1 t_1, g x_2 t_2)$. The map

$$\begin{aligned} (g,g') \mapsto (x,x',y), x = g^{-1}F(g), x' = g^{\prime -1}F(g'), y = g^{-1} g' \end{aligned}$$

defines an $T_h \times T_h$-equivariant isomorphism $G_h \backslash S_h \times S_h \cong \Sigma$. We denote by $H_c^i(S_h \times S_h)_{\theta ^{-1}, \theta '}$ and $H_c^i(\Sigma )_{\theta ^{-1}, \theta '}$ the subspace where $T_h \times T_h$ acts by $\theta ^{-1} \otimes \theta '$. We have

$$\begin{aligned} \langle R_{T_h}^{G_h}(\theta ), R_{T_h}^{G_h}(\theta ') \rangle _{G_h}&= \sum _{i,i' \in {\mathbb {Z}}} (-1)^{i+i'} \dim (H_c^i(X_h, \overline{{\mathbb {Q}}}_{\ell })[\theta ^{-1}] \otimes H_c^{i'}(X_h, \overline{{\mathbb {Q}}}_{\ell })[\theta '])^{G_h} \\&= \sum _{i,i' \in {\mathbb {Z}}} (-1)^{i+i'} \dim (H_c^i(S_h, \overline{{\mathbb {Q}}}_{\ell })[\theta ^{-1}] \otimes H_c^{i'}(S_h, \overline{{\mathbb {Q}}}_{\ell })[\theta '])^{G_h}&\text {(by Lemma }8.2)\\&= \sum _{i \in {\mathbb {Z}}} (-1)^i \dim H_c^i(G_h\backslash (S_h \times S_h), \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '} \\&= \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i(\Sigma , \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '} \\&= \# \{ \gamma \in {{\,\mathrm{Gal}\,}}(L/K) :\theta \circ \gamma = \theta ' \}&\text {(by Proposition }8.7) \end{aligned}$$

where in the final equality, we use the fact that $\theta$ is primitive if and only if $\theta$ is regular in the sense of Lusztig [26, 1.5] with respect to the F coming from the Coxeter-type representative b. Finally, since the primitivity of $\theta$ implies that the stabilizer of $\theta$ in ${{\,\mathrm{Gal}\,}}(L/K)$ is trivial, the desired conclusion of Theorem 8.1 now follows. $\square$

11.2 Traces of very regular elements

In Part 4, where we study $R_{T_h}^{G_h}(\theta )$ from the perspective of automorphic induction, we will need to know the trace of very regular elements of ${\mathcal {O}}_L^\times$; i.e. elements $x \in {\mathcal {O}}_L^\times$ whose image in the residue field generates the multiplicative group ${\mathbb {F}}_{q^n}^\times$. In fact, we can explicate the character on elements of ${\mathcal {O}}_L^\times$ whose image in the residue field has trivial ${{\,\mathrm{Gal}\,}}({\mathbb {F}}_{q^n}/{\mathbb {F}}_q)$-stabilizer.

Proposition 8.3

Let $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be any character. Then for any element $x \in {\mathcal {O}}_L^\times /U_L^h \cong T_h$ in $G_h$ whose image in the residue field has trivial ${{\,\mathrm{Gal}\,}}({\mathbb {F}}_{q^n}/{\mathbb {F}}_q)$-stabilizer,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; R_{T_h}^{G_h}(\theta )\right) = \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)[n']} \theta ^\gamma (x), \end{aligned}$$

where ${{\,\mathrm{Gal}\,}}(L/K)[n']$ is the unique order $n'$ subgroup of ${{\,\mathrm{Gal}\,}}(L/K)$.

Proof

Let $\zeta _1, \zeta _2 \in T_h$ be $(q^n-1)$th roots of unity, let $t_1, t_2 \in T_h^1$, and assume that the image of $\zeta _1$ modulo $\varpi$ has trivial ${{\,\mathrm{Gal}\,}}({\mathbb {F}}_{q^n}/{\mathbb {F}}_q)$-stabilizer. Note that $(\zeta _1 t_1, \zeta _2 t_2) \in G_h \times T_h$ and therefore acts on $X_h$. By Proposition 7.4, $X_h$ is a separated, finite-type scheme over ${\mathbb {F}}_{q^n}$. Since $(\zeta _1, \zeta _2) = (\zeta _1 t_1, \zeta _2 t_2)^{q^{n(h-1)}}$ has order prime-to-p and $(t_1, t_2) = (\zeta _1 t_1, \zeta _2 t_2)^N$ (where $N \equiv 1 \pmod {q^{n(h-1)}}$ and $(q^n-1) \mid N$) has order a power of p, by the Deligne–Lusztig fixed-point formula [13, Theorem 3.2],

$$\begin{aligned} \sum _i (-1)^i {{\,\mathrm{Tr}\,}}\left( (\zeta _1 t_1, \zeta _2 t_2)^* ; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )\right) = \sum _i (-1)^i {{\,\mathrm{Tr}\,}}\left( (t_1, t_2)^* ; H_c^i(X_h^{(\zeta _1, \zeta _2)}, {{\overline{{\mathbb {Q}}}}}_\ell )\right) . \end{aligned}$$

By definition, if $\lambda (x) \in X_h$ corresponds to $x = (x_1, \ldots , x_n) \in {\mathscr {L}}_{0,b}^{\mathrm{adm, \mathrm rat}}/{\mathscr {L}}_0^{(h)}$, then $(\zeta _1, \zeta _2) x$ corresponds to the tuple $(\zeta _1 \zeta _2 x_1, \sigma ^l(\zeta _1) \zeta _2 x_2, \ldots , \sigma ^{(n-1)l}(\zeta _1) \zeta _2 x_n)$, where l is the inverse of $e_{\kappa ,n}\pmod n$. In particular, we see that if $\zeta _1$ has trivial stabilizer in ${{\,\mathrm{Gal}\,}}({\mathbb {F}}_{q^n}/{\mathbb {F}}_q)$, then the set $X_h^{(\zeta _1, \zeta _2)}$ is nonzero if and only if $\zeta _2^{-1}$ is one of the n distinct elements $\zeta _1, \sigma (\zeta _1), \ldots , \sigma ^{n-1}(\zeta _1)$.

Assume $\zeta _2^{-1} = \sigma ^{jl}(\zeta _1)$ with $0 \le j \le n-1$, then the elements of $X_h^{(\zeta _1, \zeta _2)}$ correspond to vectors of the shape $x = (0, \ldots , 0, x_{j+1}, 0, \ldots , 0)$. If $n_0$ does not divide j, then $\det \lambda (x) \equiv 0 \pmod \varpi$, which contradicts $\det \lambda (x) \in {\mathcal {O}}_K^{\times }$. Thus in this case we have $X_h^{(\zeta _1,\zeta _2)} = \varnothing$. Assume $n_0$ divides j. Then $x=(0, \ldots , 0, x_{j+1}, 0, \ldots , 0)$ with $x_{j+1} \in {\mathbb {W}}_h({\overline{{\mathbb {F}}}}_q)$ lies in $X_h$ if and only if $\det \lambda (x) = \prod _{i=0}^{n-1} \sigma ^i(x_{j+1}) \in ({\mathcal {O}}_K/\varpi ^h)^{\times }$. Thus $X_h^{(\zeta _1,\zeta _2)} = \{x = (0, \ldots , 0, x_{j+1}, 0, \ldots , 0) :x_{j+1} \in ({\mathcal {O}}_L/\varpi ^h)^\times = T_h \}$ is zero-dimensional, and the action of $(t_1,t_2)$ is given by $x_{j+1} \mapsto \sigma ^{jl}(t_1) t_2 x_{j+1}$. Thus

$$\begin{aligned} {{\,\mathrm{Tr}\,}}((t_1,t_2)^{*}, {H}_c^0(X_h^{(\zeta _1,\zeta _2)})) = {\left\{ \begin{array}{ll} \# T_h &{}\quad \text {if }t_2 = \sigma ^{jl}(t_1)^{-1}, \\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

From this, we see that

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( (\zeta _1 t_1, 1)^*; R_{T_h}^{G_h}(\theta )\right)&= \frac{1}{\# T_h} \sum _{\zeta _2 \in {\mathbb {F}}_{q^n}^\times } \sum _{t_2 \in T_h^1} \theta (\zeta _2)^{-1} \theta (t_2)^{-1} {{\,\mathrm{Tr}\,}}\left( (t_1, t_2)^* ; H_c^0(X_h^{(\zeta _1, \zeta _2)}, {{\overline{{\mathbb {Q}}}}}_\ell )\right) \\&= \sum _{\begin{array}{c} 0 \le j \le n - 1 \\ n_0 \mid j \end{array}} \theta (\sigma ^{jl}(\zeta _1)) \theta (\sigma ^{jl}(t_1)) = \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)[n']} \theta ^\gamma (\zeta _1 t_1). \end{aligned}$$

$\square$

11.3 Behavior under twisting of $\theta$

Lemma 8.4

Let $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be a character with trivial ${{\,\mathrm{Gal}\,}}(L/K)$-stabilizer and let $\chi :{\mathbb {W}}_h^\times ({\mathbb {F}}_q) \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be any character. Then as $G_h$-representations,

$$\begin{aligned} H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}})] \cong H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] \otimes (\chi \circ \det ), \qquad \text {for all }i \ge 0. \end{aligned}$$

Proof

Let $\Gamma _h$ denote the kernel of the natural homomorphism $G_h \times T_h \rightarrow {\mathbb {W}}_h^\times ({\mathbb {F}}_q)$ given by $(g,t) \mapsto \det (t) {{\,\mathrm{Nm}\,}}(t)$. Recall from (7.3) that we have a scheme-theoretic morphism $X_h \rightarrow {\mathbb {W}}_h^\times ({\mathbb {F}}_q)$. Write $X_h^{\det \equiv 1}$ for the preimage of the identity. First observe that as $G_h \times T_h$-representations,

$$\begin{aligned} \bigoplus _{\begin{array}{c} \theta ' :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell \\ \theta '|_{T_h^\circ } = \theta |_{T_h^\circ } \end{array}} H_c^i(X_h, \overline{{\mathbb {Q}}}_\ell )[\theta '] \cong {{\,\mathrm{Ind}\,}}_{\Gamma _h}^{G_h \times T_h} \left( H_c^i(X_h^{\det \equiv 1}, \overline{{\mathbb {Q}}}_\ell )[\theta |_{T_h^\circ }]\right) . \end{aligned}$$

Since the number of summands on the left-hand side is equal to the index of $\Gamma _h$ in $G_h \times T_h$, it follows that as representations of $\Gamma _h$,

$$\begin{aligned} H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta '] \cong H_c^i(X_h^{\det \equiv 1}, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta |_{T_h^\circ }] \end{aligned}$$

(8.1)

for any $\theta ' :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ with $\theta '|_{T_h^\circ } = \theta |_{T_h^\circ }$. In particular, as $\Gamma _h$-representations,

$$\begin{aligned} H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}})] \cong H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]. \end{aligned}$$

Now observe that the subgroup of $G_h \times T_h$ generated by $\Gamma _h$ and $1 \times T_h$ is the whole group. For any $g \in G_h$, let $t_g \in T_h$ be any element such that $\det (g) {{\,\mathrm{Nm}\,}}(t_g) = 1$. Then $(g,t_g) \in \Gamma _h$, and we have

$$\begin{aligned}&{{\,\mathrm{Tr}\,}}((g,1)^*; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}})]) \\&\quad = {{\,\mathrm{Tr}\,}}((g,t_g)^* ; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}})]) \cdot \theta (t_g^{-1}) \cdot \chi ({{\,\mathrm{Nm}\,}}(t_g^{-1})) \\&\quad = {{\,\mathrm{Tr}\,}}((g,t_g)^* ; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]) \cdot \theta (t_g^{-1}) \cdot \chi ({{\,\mathrm{Nm}\,}}(t_g^{-1})) \\&\quad = {{\,\mathrm{Tr}\,}}((g,1)^* ; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]) \cdot \theta (t_g) \cdot \theta (t_g^{-1}) \cdot \chi ({{\,\mathrm{Nm}\,}}(t_g^{-1})) \\&\quad = {{\,\mathrm{Tr}\,}}((g,1)^* ; H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]) \cdot \chi (\det (g)). \end{aligned}$$

$\square$

Observe that by Lemma 8.4, we have that $R_{T_h}^{G_h}(\theta )$ is (up to sign) irreducible if and only if $R_{T_h}^{G_h}(\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}}))$ is, where $\chi :{\mathbb {W}}_h({\mathbb {F}}_q)^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$. Recall that by Proposition 7.7, if $\theta$ is a character of $T_h$ that factors through the natural surjection $T_h \rightarrow T_{h'}$ for some $h' < h$, then $R_{T_h}^{G_h}(\theta ) = R_{T_{h'}}^{G_{h'}}(\theta ).$ Thus we can strengthen Theorem 8.1 to obtain that $R_{T_h}^{G_h}(\theta \otimes (\chi \circ {{\,\mathrm{Nm}\,}}))$ is (up to sign) irreducible for any primitive $\theta :T_{h'} \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ and any $\chi :{\mathbb {W}}_h({\mathbb {F}}_q)^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$. Such characters exactly correspond to minimal admissible characters of $L^\times$ of level h (see Part 4). This argument will be appear again in the proof of Theorem 12.5.

11.4 Lusztig’s theorem

This is a generalization of [26, 31] to non-reductive groups over ${\mathcal {O}}$. The Iwahori case (which corresponds to the division algebra setting over K) was done in [25] (see also [12, Section 6.2]) and is a simpler incarnation of these ideas. We keep our notation as close as possible to that of [26, 31] as most of the arguments are the same.

11.4.1 Set-up

Let $T, T'$ be two maximal F-stable tori of $J_b$, split over $\breve{K}$ and let $(U, U^-)$ and $(U', U'{}^-)$ be two pairs of (possibly not F-stable) unipotent radicals of opposite Borels containing T and T, respectively. (Outside Sect. 8.4T always denotes a maximal elliptic torus of G, but here we want the notation to coincide with [26]). Consider the intersections of $\breve{K}$-points of $T,T',U,U^-,U',U^{'-}$ with $\breve{G}_{{\mathbf {x}},0}$ (Sect. 5.3) and denote the corresponding subgroup schemes in ${\mathbb {G}}_h$ by ${\mathbb {T}}_h, {\mathbb {T}}_h', {\mathbb {U}}_h, {\mathbb {U}}_h^-, {\mathbb {U}}_h', {\mathbb {U}}_h'{}^-$. For $1 \le a \le h$, let ${{\mathbb {G}}_h^a \,{:=}\,\ker ({\mathbb {G}}_h \rightarrow {\mathbb {G}}_a)}$ be the kernel of the natural projection, and analogously define ${\mathbb {T}}_h^a, {\mathbb {U}}_h^a,$ and so forth. We set ${\mathbb {G}}_h^{a,*} = {\mathbb {G}}_h^a \smallsetminus {\mathbb {G}}_h^{a+1}$, and analogously for ${\mathbb {T}}_h^{a,*}, {\mathbb {U}}_h^{a,*}$, and so forth. We use the shorthand ${{\mathcal {T}}\,{:=}\,{\mathbb {T}}_h^{h-1}}$.

Let $N({\mathbb {T}}, {\mathbb {T}}') = \{g \in \breve{G}_{{\mathbf {x}},0} : g^{-1} {\mathbb {T}}g = {\mathbb {T}}'\}$ and $N({\mathbb {T}}_h, {\mathbb {T}}_h') = \{g \in {\mathbb {G}}_h : g^{-1} {\mathbb {T}}_h g = {\mathbb {T}}_h'\}$, and define

$$\begin{aligned} {W(T, T') \,{:=}\,{\mathbb {T}}\backslash N({\mathbb {T}}, {\mathbb {T}}') = {\mathbb {T}}_h \backslash N({\mathbb {T}}_h, {\mathbb {T}}_h').} \end{aligned}$$

Observe that $W(T, T')$ is a principal homogeneous space under the Weyl group of the torus ${\mathbb {T}}_1$ in the reductive quotient ${\mathbb {G}}_1$ of $G_{{\mathcal {O}}}$.

11.4.2 Roots and regularity

Let $\Phi = \Phi (T,J_b)$ denote the set of roots of T in $J_b$. It carries a natural action of F. For $\alpha \in \Phi$, let ${\mathbb {G}}_h^{\alpha }$ denote the subgroup of ${\mathbb {G}}_h$ coming from the root subgroup of $J_b(\breve{K}) = {{\,\mathrm{GL}\,}}_n(\breve{K})$ corresponding to $\alpha$. For $\alpha \in \Phi$, let $T^{\alpha } \subseteq T$ be the image of the coroot of T in ${{\,\mathrm{GL}\,}}_n(\breve{K})$ corresponding to $\alpha$. It is an one-dimensional subtorus of T. We denote by ${\mathbb {T}}_h^{\alpha }$ the corresponding subgroup of ${\mathbb {G}}_h$. We write ${\mathcal {T}}^{\alpha } \subseteq {\mathcal {T}}$ for the one-dimensional subgroup $({\mathbb {T}}_h^{\alpha })^{h-1}$ of ${\mathbb {T}}_h^{\alpha }$.

Following [26, 1.5], a character $\chi :{\mathcal {T}}^F \rightarrow \overline{{\mathbb {Q}}}_{\ell }^{\times }$ is called regular if for any $\alpha \in \Phi$ and any $m\ge 1$ such that $F^m({\mathcal {T}}^{\alpha }) = {\mathcal {T}}^{\alpha }$, the restriction of $\chi \circ N_F^{F^m} :{\mathcal {T}}^{F^m} \rightarrow \overline{{\mathbb {Q}}}_{\ell }^{\times }$ to $({\mathcal {T}}^{\alpha })^{F^m}$ is non-trivial. Here, $N_F^{F^m} :{\mathcal {T}}^{F^m} \rightarrow {\mathcal {T}}^F$ is the map $t \mapsto t F(t) \cdots F^{m-1}(t)$. A character $\chi$ of ${\mathbb {T}}_h^F$ is called regular if its restriction $\chi |_{{\mathcal {T}}^F}$ is regular.

Remark 8.5

In our situation, when b is a Coxeter-type representative and T is the elliptic diagonal torus of $J_b$, let $\chi$ be a character of $T(K) \cong L^{\times }$ of level h. Then the restriction of $\chi$ to ${\mathcal {O}}_L^\times$ can be viewed as a character $\chi _h$ of ${\mathbb {T}}_h^F \cong ({\mathcal {O}}_L/\varpi ^h)^{\times }$. A straightforward computation shows: $\chi _h$ is regular in the above sense if and only if it is primitive, i.e. the restriction of $\chi _h$ to ${\mathcal {T}}^F \cong {\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})$ does not factor through any of the norm maps ${\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n}) \rightarrow {\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^r})$ for $r \mid n$, $r < n$. We use this in the proof of Theorem 8.1. $\Diamond$

11.4.3 Bruhat decomposition

For each $w \in W(T,T')$ choose a representative ${\dot{w}} \in N(T,T')$. We have the Bruhat decomposition ${\mathbb {G}}_1 = \bigsqcup _{w\in W(T,T')} {\mathbb {G}}_{1,w}$ of the reductive quotient, where ${\mathbb {G}}_{1,w} = {\mathbb {U}}_1{\dot{w}}{\mathbb {T}}_1'{\mathbb {U}}_1'$. Define ${\mathbb {G}}_{h,w}$ to be the pullback of ${\mathbb {G}}_{1,w}$ along the natural projection ${\mathbb {G}}_h \twoheadrightarrow {\mathbb {G}}_1$. Thus ${\mathbb {G}}_h = \bigsqcup _{w \in W(T,T')} {\mathbb {G}}_{h,w}$. Let ${{\mathbb {K}}_h \,{:=}\,{\mathbb {U}}_h^- \cap \dot{w} {\mathbb {U}}_h^{\prime -} \dot{w}^{-1}}$ and ${{\mathbb {K}}_h^1 \,{:=}\,{\mathbb {K}}_h \cap {\mathbb {G}}_h^1}$.

Lemma 8.6

${\mathbb {G}}_{h,w} = {\mathbb {U}}_h {\mathbb {K}}_h^1 {\dot{w}} {\mathbb {T}}_h'{\mathbb {U}}_h'$.

Proof

Indeed, we compute

$$\begin{aligned} {\mathbb {G}}_{h,w}&= {\mathbb {U}}_h \dot{w} {\mathbb {T}}_h' {\mathbb {G}}_h^1 {\mathbb {U}}_h' = {\mathbb {U}}_h \dot{w} {\mathbb {T}}_h' \left( ({\mathbb {G}}_h^1 \cap {\mathbb {T}}_h') ({\mathbb {G}}_h^1 \cap {\mathbb {U}}_h^{\prime -}) ({\mathbb {G}}_h^1 \cap {\mathbb {U}}_h')\right) {\mathbb {U}}_h' \\&= {\mathbb {U}}_h \dot{w} {\mathbb {T}}_h' ({\mathbb {G}}_h^1 \cap {\mathbb {U}}_h^{\prime -}) {\mathbb {U}}_h' = {\mathbb {U}}_h \left( \dot{w} ({\mathbb {G}}_h^1 \cap {\mathbb {U}}_h^{\prime -}) \dot{w}^{-1}\right) {\dot{w}} {\mathbb {T}}_h' {\mathbb {U}}_h' \\&= {\mathbb {U}}_h \left( {\mathbb {U}}_h^- \cap \dot{w} ({\mathbb {G}}_h^1 \cap {\mathbb {U}}_h^{\prime -}) \dot{w}^{-1}\right) \dot{w} {\mathbb {T}}_h' {\mathbb {U}}_h' = {\mathbb {U}}_h {\mathbb {K}}_h^1 \dot{w} {\mathbb {T}}_h' {\mathbb {U}}_h'. \end{aligned}$$

$\square$

11.4.4 The scheme $\Sigma$

Define

$$\begin{aligned} \Sigma&= \{ (x,x',y) \in F({\mathbb {U}}_h) \times F({\mathbb {U}}_h') \times {\mathbb {G}}_h :xF(y) = yx' \} \\ \Sigma _w&= \{ (x,x',y) \in F({\mathbb {U}}_h) \times F({\mathbb {U}}_h') \times {\mathbb {G}}_h :xF(y) = yx', y \in {\mathbb {G}}_{h,w} \} \subseteq \Sigma , \end{aligned}$$

for $w \in W(T,T')$. Set-theoretically, $\Sigma$ is the disjoint union of the locally closed subschemes $\Sigma _w$. The group ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$ acts on $\Sigma$ by $(t,t') :(x,x',y) \mapsto (txt^{-1}, t'x't^{\prime -1}, tyt^{\prime -1})$ and $\Sigma _w$ is stable under this action for any $w\in W(T,T')$.

Proposition 8.7

Let $\theta$ and $\theta '$ be characters of ${\mathbb {T}}_h^F$ and ${\mathbb {T}}_h^{\prime F}$ respectively and assume that $\theta$ is regular. Then

$$\begin{aligned} \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i(\Sigma , \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '} = \# \{ w \in W(T,T')^F :\theta \circ Ad(\dot{w}) = \theta ' \}. \end{aligned}$$

Proof

Using $\Sigma = \bigcup _w \Sigma _w$, it is enough to show that $\sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i(\Sigma , \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '}$ is 1 if $w \in W(T,T')^F$ and $\theta \circ Ad(\dot{w}) = \theta '$, and is 0 otherwise. Fix a $w \in W(T,T')$. Let

$$\begin{aligned} {{\widehat{\Sigma }}}_w&= \{ (x,x',u,u',z,\tau ') \in F({\mathbb {U}}_h) \times F({\mathbb {U}}_h') \times {\mathbb {U}}_h \times {\mathbb {U}}_h' \times {\mathbb {K}}_h^1 \times {\mathbb {T}}_h' :\\&\quad xF(uz{\dot{w}} \tau ' u') = uz{\dot{w}} \tau ' u' x' \}. \end{aligned}$$

We have the morphism ${{\widehat{\Sigma }}}_w \rightarrow \Sigma _w$, $(x,x',u,u',z,\tau ') \mapsto x,x',uz{\dot{w}}\tau 'u'$, which by Lemma 8.6 is surjective. Moreover, this map is ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$-equivariant, when we endow ${{\widehat{\Sigma }}}_w$ with the ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$-action

$$\begin{aligned} (t,t') :(x,x',u,u',z,\tau ') \mapsto (txt^{-1}, t'x't^{\prime -1}, tut^{-1}, t'u't^{\prime -1}, tzt^{-1}, {\dot{w}}^{-1}t{\dot{w}}\tau ' t^{\prime -1}).\nonumber \\ \end{aligned}$$

(8.2)

As the projection ${{\widehat{\Sigma }}}_w \rightarrow \Sigma _w$ is locally trivial fibration, the cohomology does not change if we pass from $\Sigma _w$ to ${{\widehat{\Sigma }}}_w$. Thus to finish the proof the proposition it is enough to show that

$$\begin{aligned} \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i({{\widehat{\Sigma }}}, \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '} {=} {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }w \in W(T,T')^F\text { and }\theta \circ Ad(\dot{w}) = \theta ', \\ 0 &{}\quad \text {otherwise.} \end{array}\right. }\nonumber \\ \end{aligned}$$

(8.3)

We make the change of variables replacing xF(u) by x and $x'F(u')^{-1}$ by $x'$, and rewrite ${{\widehat{\Sigma }}}_w$ as

$$\begin{aligned} {{\widehat{\Sigma }}}_w = \{ (x,x',u,u',z,\tau ') \in F({\mathbb {U}}_h) \times F({\mathbb {U}}_h') \times {\mathbb {U}}_h \times {\mathbb {U}}_h' \times {\mathbb {K}}_h^1 \times {\mathbb {T}}_h' :xF(z{\dot{w}} \tau ') = uz{\dot{w}} \tau ' u' x' \}, \end{aligned}$$

and the torus action is still given by (8.2). Define a partition ${{\widehat{\Sigma }}}_w = {{\widehat{\Sigma }}}_w' \sqcup \widehat{\Sigma }_w^{\prime \prime }$ by

$$\begin{aligned} {{\widehat{\Sigma }}}_w'&= \{ (x,x',u,u',z,\tau ') \in {{\widehat{\Sigma }}}_w :z \ne 1 \}, \\ {{\widehat{\Sigma }}}_w^{\prime \prime }&= \{ (x,x',u,u',z,\tau ') \in {{\widehat{\Sigma }}}_w :z = 1 \}. \end{aligned}$$

Both subsets are stable under the ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$-action. By Sect. 8.4.5,

$$\begin{aligned}&\sum _{i \in {\mathbb {Z}}} (-1)^i \dim H_c^i({{\widehat{\Sigma }}}_w'', \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1}, \theta '} \nonumber \\&\quad = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }w \in W(T, T')^F\text { and }\theta \circ Ad(\dot{w}) = \theta ', \\ 0 &{}\quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

(8.4)

and by Sect. 8.4.8, under the assumption that $\theta$ is regular,

$$\begin{aligned} \sum _{i \in {\mathbb {Z}}} (-1)^i \dim H_c^i({{\widehat{\Sigma }}}_w', \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1}, \theta '} = 0, \end{aligned}$$

(8.5)

so (8.3) holds. $\square$

11.4.5 Cohomology of ${{\widehat{\Sigma }}}_w^{\prime \prime }$

We prove (8.4). This works exactly as in [26] (see the proof of Lemma 1.9, specifically the proof of claim (b) in op. cit. beginning on page 8). For convenience of the reader, we recall the arguments. Consider the closed subgroup

$$\begin{aligned} {\widetilde{H}} = \{ (t,t') \in {\mathbb {T}}_h \times {\mathbb {T}}_h' :tF(t)^{-1} = F({\dot{w}}) t'F(t')^{-1} F({\dot{w}}^{-1}) \} \subseteq {\mathbb {T}}_h \times {\mathbb {T}}_h'. \end{aligned}$$

Note that ${{\widetilde{H}}}$ contains ${\mathbb {T}}_h^F \times {\mathbb {T}}_h'{}^F$ and (8.2) containing ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$. The action of ${\mathbb {T}}_h^F \times {\mathbb {T}}_h^{\prime F}$ on ${{\widehat{\Sigma }}}_w^{\prime \prime }$ extends to an action of ${{\widetilde{H}}}$, still given by (8.2). Let ${\mathbb {T}}_{h,*}$ and ${\mathbb {T}}_{h,*}'$ be the reductive part of ${\mathbb {T}}_h$ and ${\mathbb {T}}_h'$ respectively. Set ${{\widetilde{H}}_{*} \,{:=}\,{\widetilde{H}} \cap ({\mathbb {T}}_{h,*} \times {\mathbb {T}}_{h,*}')}$ and let ${\widetilde{H}}_{*}^0$ be the connected component of ${\widetilde{H}}_{*}$. Then ${\widetilde{H}}_{*}^0$ is a torus acting on ${{\widehat{\Sigma }}}_w^{\prime \prime }$. By [14, 4.5 (and 11.2) and 10.15] (compare the similar computation in the proof of [31, Theorem 3.1]), we have

$$\begin{aligned} \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i({{\widehat{\Sigma }}}_w^{\prime \prime }, \overline{{\mathbb {Q}}}_{\ell })_{\theta ^{-1},\theta '} = \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i\left( ({{\widehat{\Sigma }}}_w^{\prime \prime })^{{{\widetilde{H}}}_{*}^0}, \overline{{\mathbb {Q}}}_{\ell } \right) _{\theta ^{-1},\theta '}. \end{aligned}$$

Let $(x,x',u,u',1,\tau ') \in ({{\widehat{\Sigma }}}_w^{\prime \prime })^{{{\widetilde{H}}}_{*}^0}$. By Lang’s theorem, ${{\widetilde{H}}}_{*} \rightarrow {\mathbb {T}}_{h,*}$ is surjective and hence (as ${\mathbb {T}}_{h,*}$ is connected) also ${\widetilde{H}}_{*}^0 \rightarrow {\mathbb {T}}_{h,*}$ is surjective. Similarly, ${\widetilde{H}}_{*}^0 \rightarrow {\mathbb {T}}_{h,*}'$ is surjective. Thus for any $t \in {\mathbb {T}}_{h,*}$, $t' \in {\mathbb {T}}_{h,*}'$, we have

$$\begin{aligned} txt^{-1} = x, \,\, t'x't^{\prime -1} = x', \,\, tut^{-1} = u, \,\, t'u't^{\prime -1} = u'. \end{aligned}$$

This implies $x = x' = u = u' = 1$ since ${\mathbb {T}}_{h,*}$ acts non-trivially on all affine roots subgroups contained in ${\mathbb {U}}_h$ (and similarly for ${\mathbb {T}}'_h$, ${\mathbb {U}}'_h$). Thus

$$\begin{aligned} ({{\widehat{\Sigma }}}_w^{\prime \prime })^{{{\widetilde{H}}}_{*}^0} \subseteq \{(1,1,1,1,1,\tau ') :\tau ' \in {\mathbb {T}}_h', \, F(\dot{w} \tau ') = \dot{w} \tau ' \}, \end{aligned}$$

and we deduce

$$\begin{aligned} \sum _{i\in {\mathbb {Z}}} (-1)^i \dim H_c^i\left( ({{\widehat{\Sigma }}}_w^{\prime \prime })^{{{\widetilde{H}}}_{*}^0}, \overline{{\mathbb {Q}}}_{\ell } \right) _{\theta ^{-1},\theta '} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }F(w) = w\text { and }\theta \circ Ad(\dot{w}) = \theta ', \\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

11.4.6 Some preparations

In the next two sections, we make the necessary preparations in order to carry out Lusztig’s argument for (8.5) in Sect. 8.4.8. Let $N, N^-$ be unipotent radicals of opposite Borel subgroups of $J_b(\breve{K}) = {{\,\mathrm{GL}\,}}_n(\breve{K})$ containing T, and for $h \ge 1$, let ${\mathbb {N}}_h$, ${\mathbb {N}}_h^-$ be the corresponding subgroups of ${\mathbb {G}}_h$. Let $\Phi ^+ = \{ \alpha \in \Phi :{\mathbb {G}}_h^{\alpha } \subseteq {\mathbb {N}}_h\}$ and $\Phi ^- = \Phi {\,\smallsetminus \,}\Phi ^+ = \{\alpha \in \Phi :{\mathbb {G}}_h^{\alpha } \subseteq {\mathbb {N}}_h^-\}$. For $\alpha \in \Phi ^+$ let $\mathrm{ht}(\alpha )$ denote the largest integer $m \ge 1$, such that $\alpha = \sum _{i=1}^m \alpha _i$ with $\alpha _i \in \Phi ^+$.

We call the roots $\alpha \in \Phi$ for which ${\mathbb {G}}_1^{\alpha } \ne 1$ reductive and the other roots non-reductive. Equivalently, a root $\alpha \in \Phi$ is reductive if and only if $\langle \alpha , {\mathbf {x}}\rangle \in {\mathbb {Z}}$, where ${\mathbf {x}}$ is as in Sect. 5.3.

To make explicit calculations, we may assume that T is the diagonal torus in ${{\,\mathrm{GL}\,}}_n(\breve{K})$. For $1\le i \ne j \le n$, let $\alpha _{i,j}$ denote the root corresponding to the (i, j)th entry of an $n\times n$ matrix. For $1\le i \le n$, let $1\le [i]_{n_0} \le n_0$ denote its residue modulo $n_0$. Define ${\mathrm{ht}_{n_0}(\alpha _{i,j}) \,{:=}\,[i]_{n_0} - [j]_{n_0}}$. Then $\alpha \in \Phi$ is reductive if and only if $\mathrm{ht}_{n_0}(\alpha ) = 0$. If $\mathrm{ht}_{n_0}(\alpha ) > 0$ (resp. $\mathrm{ht}_{n_0}(\alpha ) < 0$), we call $\alpha$ non-reductive of type 1 (resp. of type 2). For any $\alpha = \alpha _{i,j} \in \Phi$ and $1\le a\le h$, we have

$$\begin{aligned} \left( {\mathbb {G}}_h^{\alpha }\right) ^a \cong {\left\{ \begin{array}{ll} {\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1} &{}\quad \text {if }\mathrm{ht}_{n_0}(\alpha ) > 0, \\ {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad \text {if }\mathrm{ht}_{n_0}(\alpha ) \le 0, \end{array}\right. } \end{aligned}$$

(8.6)

in the sense that $\left( {\mathbb {G}}_h^{\alpha }\right) ^a$ consists of $n\times n$ matrices with 1’s on the main diagonal, an element of the subgroup ${\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1}$ (resp. ${\mathfrak {p}}^a/{\mathfrak {p}}^h$) sitting in the (i, j)th entry, and 0’s everywhere else.

Example 8.8

Let $n= 4$, $\kappa = 2$. Then if ${\mathcal {A}}$ is the apartment of ${\mathcal {B}}^{\mathrm{red}}({{\,\mathrm{GL}\,}}_4, \breve{K})$ corresponding to the diagonal torus, then ${\mathbf {x}}$ is the unique fixed point under the action of $b = b_0\cdot {{\,\mathrm{diag}\,}}(1,\varpi ,1,\varpi ) = \left( {\begin{matrix} &{} &{} &{} \varpi \\ 1 &{} &{} &{} \\ &{} \varpi &{} &{} \\ &{} &{} 1 &{} \end{matrix}}\right)$. Computing, the matrix of inner products for $\alpha _{i,j} \in \Phi$ is

$$\begin{aligned} (\langle \alpha _{i,j}, {\mathbf {x}}\rangle )_{1 \le i,j \le 4} = \left( {\begin{matrix} * &{}\quad -\frac{1}{2} &{}\quad 0 &{}\quad -\frac{1}{2} \\ \frac{1}{2} &{}\quad * &{}\quad \frac{1}{2} &{}\quad 0 \\ 0 &{}\quad -\frac{1}{2} &{}\quad * &{}\quad -\frac{1}{2} \\ \frac{1}{2} &{}\quad 0 &{}\quad \frac{1}{2} &{}\quad * \end{matrix}}\right) . \end{aligned}$$

Hence for $h \ge 1$, we have

$$\begin{aligned} \breve{G}_{{\mathbf {x}},0} = \left( {\begin{matrix} {\mathcal {O}}&{}\quad {\mathfrak {p}} &{}\quad {\mathcal {O}}&{}\quad {\mathfrak {p}} \\ {\mathcal {O}}&{}\quad {\mathcal {O}}&{}\quad {\mathcal {O}}&{}\quad {\mathcal {O}}\\ {\mathcal {O}}&{}\quad {\mathfrak {p}} &{}\quad {\mathcal {O}}&{}\quad {\mathfrak {p}} \\ {\mathcal {O}}&{}\quad {\mathcal {O}}&{}\quad {\mathcal {O}}&{}\quad {\mathcal {O}}\end{matrix}}\right) ^{\times } \twoheadrightarrow {\mathbb {G}}_h(\overline{{\mathbb {F}}}_q) = \left( {\begin{matrix} {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h \\ {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h \\ {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}/{\mathfrak {p}}^h \\ {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h &{}\quad {\mathcal {O}}/{\mathfrak {p}}^{h-1} &{}\quad {\mathcal {O}}/{\mathfrak {p}}^h \end{matrix}}\right) ^{\times }, \end{aligned}$$

where the $\times$ superscript means the group of invertible matrices, and for $1 \le a \le h$,

$$\begin{aligned} {\mathbb {G}}_h^a({{\overline{{\mathbb {F}}}}}_q) = \left( {\begin{matrix} 1 + {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h \\ {\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1} &{}\quad 1 + {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1} &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h \\ {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad 1 + {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h \\ {\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1} &{}\quad {\mathfrak {p}}^a/{\mathfrak {p}}^h &{}\quad {\mathfrak {p}}^{a-1}/{\mathfrak {p}}^{h-1} &{}\quad 1 + {\mathfrak {p}}^a/{\mathfrak {p}}^h \end{matrix}}\right) . \end{aligned}$$

For two elements $z,\xi \in {\mathbb {G}}_h$, we write $[\xi ,z] = \xi ^{-1}z^{-1}\xi z$.

Lemma 8.9

Let $\alpha \in \Phi$. Let $1 \le a \le h-1$.

• (i) If $\alpha$ is non-reductive, then $[{\mathbb {G}}_h^{a+1}, ({\mathbb {G}}_h^{\alpha })^{h-a}] = 1$.

• (ii) If $\alpha$ is reductive, then $[{\mathbb {G}}_h^a, ({\mathbb {G}}_h^{\alpha })^{h-a}] = 1$.

Proof

The computation to show (i) and (ii) is nearly the same. We prove (i). It suffices to check that $[{\mathbb {T}}_h^{a+1},({\mathbb {G}}_h^{\alpha })^{h-a}] = 1$ and that $[({\mathbb {G}}_h^{\beta })^{a+1},({\mathbb {G}}_h^{\alpha })^{h-a}] = 1$ for any $\beta \in \Phi$. This is an immediate computation using the explicit description of ${\mathbb {G}}_h$ and (8.6). The only critical case is when $\alpha$, $\beta$ are both non-reductive of type 1. Here, it suffices to observe that if $\alpha + \beta$ is again a root, then it is again non-reductive of type 1. $\square$

Let $({\mathbb {N}}_h^1)^{\le 0}$ denote the subgroup of ${\mathbb {N}}_h^1$ generated by ${\mathbb {N}}_h^2$ and all $({\mathbb {G}}_h^\beta )^1$ with $\beta \in \Phi ^+$ satisfying $\mathrm{ht}_{n_0}(\beta ) \le 0$. Obviously ${\mathbb {N}}_h^2 \subseteq ({\mathbb {N}}_h^1)^{\le 0} \subseteq {\mathbb {N}}_h^1$.

Lemma 8.10

Let $1 \le a \le h-1$ and $z \in {\mathbb {N}}_h^{a,*}$. Write $z = \prod _{\beta \in \Phi ^+} x_{\beta }^z$ with $x_{\beta }^z \in ({\mathbb {G}}_h^{\beta })^a$ for a fixed (but arbitrary) order on $\Phi ^+$. For $\beta \in \Phi ^+$, let $a \le a(\beta ,z) \le h$ be the integer such that $x_{\beta }^z \in ({\mathbb {G}}_h^{\beta })^{a(\beta ,z),*}$.

• (i) If $z \in {\mathbb {N}}_h^{a,*} \cap ({\mathbb {N}}_h^1)^{\le 0}$, then the set

  $$\begin{aligned} {A_z \,{:=}\,\{\beta \in \Phi ^+ :a(\beta ,z) = a\}} \end{aligned}$$

  is independent of the chosen order on $\Phi ^+$.

• (ii) If $z \in {\mathbb {N}}_h^1 \smallsetminus ({\mathbb {N}}_h^1)^{\le 0}$, then the set

  $$\begin{aligned} {A_z \,{:=}\,\{\beta \in \Phi ^+ : \mathrm{ht}_{n_0}(\beta ) \text { is minimal among those with }\mathrm{ht}_{n_0} > 0\text { and }a(\beta , z) = 1\}} \end{aligned}$$

  does not depend on the chosen order on $\Phi ^+$.

Proof

(i) First let $2 \le a \le h-1$. From the explicit description of the root subgroups it follows that the quotient ${\mathbb {N}}_h^a/{\mathbb {N}}_h^{a+1}$ is abelian (for $a=2$ one needs to use that the sum of two non-reductive roots of type 1 is again of type 1 if it is a root), thus its elements are simply tuples $(x_{\beta })_{\beta \in \Phi ^+}$ with $x_{\beta } \in ({\mathbb {G}}_h^{\beta })^a/({\mathbb {G}}_h^{\beta })^{a+1}$ with entry-wise multiplication. If ${\bar{z}}= ({\bar{x}}_{\beta }^z)$ is the image of z in this quotient, then $A_z$ identifies with the set of those $\beta$ for which ${\bar{x}}_{\beta }^z \ne 1$ (which is obviously independent of the order). Now let $a = 1$. Then $z \in ({\mathbb {N}}_h^1)^{\le 0} {\,\smallsetminus \,}{\mathbb {N}}_h^2$ and the same arguments apply to the abelian quotient $({\mathbb {N}}_h^1)^{\le 0}/{\mathbb {N}}_h^2$.

(ii) The group ${\mathbb {N}}_h^1/({\mathbb {N}}_h^1)^{\le 0}$ is not abelian, but is generated by its subgroups $({\mathbb {G}}_h^{\beta })^1/({\mathbb {G}}_h^{\beta })^2$ for $\beta \in \Phi ^+$ non-reductive of type 1. For $m\ge 1$, let $H_m$ be the subgroup generated by all $({\mathbb {G}}_h^{\beta })^1/({\mathbb {G}}_h^{\beta })^2$ with $\mathrm{ht}_{n_0}(\beta ) \ge m$. Since the function $\mathrm{ht}_{n_0}$ is additive on $\Phi$, the $H_m$ form a filtration of ${\mathbb {N}}_h^1/({\mathbb {N}}_h^1)^{\le 0} = H_1$ with abelian quotients $H_m/H_{m+1} \cong \prod \nolimits _{\begin{array}{c} \beta \text { non-red. type 1} \\ \mathrm{ht}_{n_0}(\beta ) = m \end{array}} ({\mathbb {G}}_h^{\beta })^1/({\mathbb {G}}_h^{\beta })^2$. Since $z \not \in ({\mathbb {N}}_h^1)^{\le 0}$, there is an $m \ge 1$ such that the image of z in ${\mathbb {N}}_h^1/({\mathbb {N}}_h^1)^{\le 0}$ lies in $H_m {\,\smallsetminus \,}H_{m+1}$. Denote by ${\bar{z}} = ({\bar{x}}_{\beta }^z)_{\begin{array}{c} \beta \text { non-red. type 1} \\ \mathrm{ht}_{n_0}(\beta ) = m \end{array}}$ the image of z in $H_m/H_{m+1}$. Now $A_z$ is the set of all $\beta \in \Phi ^+$ non-reductive of type 1 with $\mathrm{ht}_{n_0}(\beta ) = m$ such that ${\bar{x}}_{\beta }^z \ne 1$. This does not depend on the chosen order. $\square$

11.4.7 Stratification of ${\mathbb {K}}_h^1$

Lemma 8.11

Let $1 \le a \le h-1$, $z \in {\mathbb {N}}_h^{a,*}$ and $A_z$ as in Lemma 8.10.

• (i) If $A_z$ contains a non-reductive root, let $-\alpha \in A_z$ be a non-reductive root of maximal height and $\alpha \in \Phi ^-$ its opposite. Then for any $\xi \in ({\mathbb {G}}_h^{\alpha })^{h-a}$, we have $[\xi ,z] \in {\mathcal {T}}^{\alpha }({\mathbb {N}}_h^-)^{h-1}$. Moreover, projecting $[\xi ,z]$ into ${\mathcal {T}}^{\alpha }$ induces an isomorphism

  $$\begin{aligned} \lambda _z :({\mathbb {G}}_h^{\alpha })^{h-a}/({\mathbb {G}}_h^{\alpha })^{h-a+1} {\mathop {\rightarrow }\limits ^{\sim }} {\mathcal {T}}^{\alpha } \end{aligned}$$

• (ii) If $A_z$ contains only reductive roots, let $-\alpha \in A_z$ be a root of maximal height and $\alpha \in \Phi ^-$ its opposite. Then for any $\xi \in ({\mathbb {G}}_h^{\alpha })^{h-a-1}$, we have $[\xi ,z] \in {\mathcal {T}}^{\alpha }({\mathbb {N}}_h^-)^{h-1}$. Moreover, projecting $[\xi ,z]$ into ${\mathcal {T}}^{\alpha }$ induces an isomorphism

  $$\begin{aligned} \lambda _z :({\mathbb {G}}_h^{\alpha })^{h-a-1}/({\mathbb {G}}_h^{\alpha })^{h-a} {\mathop {\rightarrow }\limits ^{\sim }} {\mathcal {T}}^{\alpha } \end{aligned}$$

Proof

We first prove (i) when $z \in ({\mathbb {N}}_h^1)^{\le 0}$. Assume first that $A_z$ contains a non-reductive root and let $-\alpha$ be such a root of maximal height and $\alpha \in \Phi ^-$ its opposite. By Lemma 8.9 (applied three times), the commutator map ${\mathbb {N}}_h^a \times ({\mathbb {G}}_h^{\alpha })^{h-a} \rightarrow {\mathbb {G}}_h$ induces a pairing of abelian groups,

$$\begin{aligned} {\mathbb {N}}_h^a/{\mathbb {N}}_h^{a+1} \times ({\mathbb {G}}_h^{\alpha })^{h-a}/({\mathbb {G}}_h^{\alpha })^{h-a+1} \rightarrow {\mathbb {G}}_h^{h-1}, \quad {\bar{x}},{\bar{\xi }} \mapsto [{\bar{\xi }},{\bar{x}}]. \end{aligned}$$

(If $a=1$, one has to replace ${\mathbb {N}}_h^a/{\mathbb {N}}_h^{a+1}$ by $({\mathbb {N}}_h^1)^{\le 0}/{\mathbb {N}}_h^2$.) This is bilinear in ${\bar{x}}$: if $x_1,x_2 \in {\mathbb {N}}_h^a$, then

$$\begin{aligned}{}[\xi ,x_1x_2]&= \xi ^{-1} x_2^{-1}x_1^{-1}\xi x_1 x_2 = \xi ^{-1} x_1^{-1} x_2^{-1} \xi x_2 x_1 \\&= \xi ^{-1} x_1^{-1} \xi [\xi ,x_2] x_1 = [\xi ,x_1] [\xi ,x_2], \end{aligned}$$

where the second equality follows from Lemma 8.9 and ${\mathbb {N}}_h^a/{\mathbb {N}}_h^{a+1}$ (resp. $({\mathbb {N}}_h^1)^{\le 0}/{\mathbb {N}}_h^2$ if $a=1$) being abelian, and the fourth follows from Lemma 8.9 as $[\xi ,x_2] \in {\mathbb {G}}_h^{h-1}$.

Now let ${\bar{\xi }} \in ({\mathbb {G}}_h^{\alpha })^{h-a}/({\mathbb {G}}_h^{\alpha })^{h-a+1}$ and ${{\bar{z}}} \in {\mathbb {N}}_h^a/{\mathbb {N}}_h^{a+1}$ be the images of $\xi$ and z respectively. Write

$$\begin{aligned} {\bar{z}} = {\bar{x}}_{-\alpha }^z \prod _{\beta \in \Phi ^+ \text { red.}} {\bar{x}}_{\beta }^z \cdot \prod _{\begin{array}{c} \beta \in \Phi ^+ \text { non-red., } \beta \ne -\alpha \\ \mathrm{ht}(\beta ) \le \mathrm{ht}(-\alpha ) \end{array}} {\bar{x}}_{\beta }^z. \end{aligned}$$

Then $[\xi ,z]$ is the product of $[{\bar{\xi }},{\bar{x}}_{-\alpha }]$ with all the $[{\bar{\xi }},{\bar{x}}_{\beta }^z]$ in any order. Let $x_{\beta }^z$ be any lift of ${\bar{x}}_{\beta }^z$ to $({\mathbb {G}}_h^{\beta })^a$. If $\beta$ is reductive and $\alpha$ is (non-reductive) of type 1, then either $\xi$, $x_{\beta }^z$ commute anyway or $\alpha + \beta$ is again a root (necessarily non-reductive of type 1) and (8.6) shows that $[\xi , x_{\beta }^z] = 1$. If $\beta$ is reductive and $\alpha$ is (non-reductive) of type 2, then (8.6) shows that $\xi ,x_{\beta }^z$ commute. If $\beta \ne -\alpha$ is non-reductive, then by assumption $\mathrm{ht}(\beta ) \le \mathrm{ht}(-\alpha )$. Then $[\xi ,x_\beta ^z] = 1$ unless $\alpha + \beta$ is a root, in which case $[\xi ,x_{\beta }^z]\in ({\mathbb {G}}_h^{\alpha + \beta })^{h-1}$ by (8.6). But the height condition implies that $\alpha + \beta \in \Phi ^{-}$. Following this case-by-case examination, the claim about $\lambda _z$ in (i) when $z \in ({\mathbb {N}}_h^1)^{\le 0}$ is then established once we make the following observation: If $\xi$ has $[y] \varpi ^{h-a}$ (resp. $[y] \varpi ^{h-a-1}$, if $a = 1$) and $x_{-\alpha }^z$ has $[u]\varpi ^{a-1}$ (resp. $[u] \varpi ^a$) in their only non-trivial entries, then $[\xi , x_{-\alpha }^z]$ is a diagonal matrix with only two nontrivial entries: $1 \pm [uy] \varpi ^{h-1}$.

In (ii), it is automatic that $z \in ({\mathbb {N}}_h^1)^{\le 0}$, and this case can be proven in exactly the same way as above (and is slightly easier) and we omit the details.

It remains to prove (i) in the case that $z \in {\mathbb {N}}_h^1 {\,\smallsetminus \,}({\mathbb {N}}_h^1)^{\le 0}$. In particular, $\xi \in ({\mathbb {G}}_h^\alpha )^{h-1}$ since $a = 1$. By construction, $A_z$ consists of non-reductive roots of type 1, so $\alpha$ must be non-reductive of type 2. Modulo $({\mathbb {N}}_h^{1})^{\le 0}$ (which commutes with $\xi$) we may write

$$\begin{aligned} z = \left( \prod _{\begin{array}{c} \gamma \in \Phi ^+ \\ \mathrm{ht}_{n_0}(\gamma ) > \mathrm{ht}_{n_0}(-\alpha ) \end{array}} x_{\gamma }^z \right) \left( \prod _{\beta \in A_z {\,\smallsetminus \,}\{-\alpha \}} x_{\beta }^z \right) x_{-\alpha }^z. \end{aligned}$$

Recall that $A_z {\,\smallsetminus \,}\{-\alpha \}$ consists of (necessarily non-reductive, type 1) roots with $\mathrm{ht}_{n_0}(\beta ) = \mathrm{ht}_{n_0}(-\alpha )$. By construction $\mathrm{ht}(\gamma ), \mathrm{ht}(\beta ) \le \mathrm{ht}(-\alpha )$, and so in particular,

$$\begin{aligned} {s \,{:=}\,\prod _{\beta } [\xi ^{-1},(x_{\beta }^z)^{-1}] \in ({\mathbb {N}}_h^-)^{h-1}.} \end{aligned}$$

We claim:

$$\begin{aligned} \xi z&= \xi \left( \prod _{\gamma }x_{\gamma }^z \right) \left( \prod _{\beta } x_{\beta }^z \right) x_{-\alpha }^z \nonumber \\&= \left( \prod _{\gamma }x_{\gamma }^z \right) \xi \left( \prod _{\beta } x_{\beta }^z \right) x_{-\alpha }^z \end{aligned}$$

(8.7)

$$\begin{aligned}&= \left( \prod _{\gamma }x_{\gamma }^z \right) \left( \prod _{\beta } [\xi ^{-1},(x_{\beta }^z)^{-1}] x_{\beta }^z \right) x_{-\alpha }^z \xi [\xi ,x_{-\alpha }^z] \nonumber \\&= \left( \prod _{\gamma }x_{\gamma }^z \right) \left( \prod _{\beta } x_{\beta }^z \right) x_{-\alpha }^z s \xi [\xi ,x_{-\alpha }^z] \end{aligned}$$

(8.8)

$$\begin{aligned}&= z s \xi [\xi ,x_{-\alpha }^z] \nonumber \\&= z \xi [\xi , x_{-\alpha }^z] s \end{aligned}$$

(8.9)

Here (8.7) holds as $\alpha + \gamma$ (if it is a root) must be non-reductive of type 1, and hence $\xi$ and $x_{\gamma }^z$ commute by (8.6). To justify (8.8), let $\beta \in A_z {\,\smallsetminus \,}\{-\alpha \}$. If $\alpha + \beta$ is not a root, then $[\xi ,x_{\beta }^z] = 1$. If $\alpha + \beta$ is a root, then $\alpha + \beta$ is reductive (since $\mathrm{ht}_{n_0}(\beta ) = \mathrm{ht}_{n_0}(-\alpha )$) and $[\xi ,x_{\beta }^z] \in ({\mathbb {G}}_h^{\alpha + \beta })^{h-1} \subseteq ({\mathbb {N}}_h^-)^{h-1}$ (since $\mathrm{ht}(\beta ) \le \mathrm{ht}(-\alpha )$ by definition of $\alpha$). But every $\beta ' \in A_z$ is non-reductive of type 1, so we must also have $\mathrm{ht}_{n_0}(\beta ' + (\alpha + \beta )) > 0$, and (8.6) shows that $[\xi ,x_{\beta }^z]$ commute with $x_{\beta '}^z$ for all $\beta ' \in A_z$. Finally, (8.9) follows from the fact that $s \in ({\mathbb {N}}_h^-)^{h-1}$ commutes with $\xi \in ({\mathbb {N}}_h^-)^{h-1}$ and with $[\xi , x_{-\alpha }^z] \in {\mathcal {T}}^{\alpha }$. But now we have shown $[\xi ,z] = [\xi ,x_{-\alpha }^z] s \in {\mathcal {T}}^{\alpha }({\mathbb {N}}_h^-)^{h-1}$, which finishes the proof of the last remaining assertion of the lemma. $\square$

Let ${\mathbb {K}}_h = {\mathbb {U}}_h^- \cap {\mathbb {N}}_h$. Let $\Phi ' = \{\beta \in \Phi ^+ :{\mathbb {G}}_h^{\beta } \in {\mathbb {K}}_h\}$. Let ${\mathcal {X}}$ denote the set of all non-empty subsets $I \subseteq \Phi '$, on which $\mathrm{ht} :\Phi ^+ \rightarrow {\mathbb {Z}}_{>0}$ is constant. To $z \in {\mathbb {K}}_h^1 {\,\smallsetminus \,}\{1\}$ we attach a pair $(a_z,I_z)$ with $1 \le a_z \le h-1$ and $I_z \in {\mathcal {X}}$. Define $a_z$ by $z \in {\mathbb {K}}_h^{a_z,*}$. If $A_z$ contains a non-reductive root, let $I_z \subseteq A_z$ be the subset of all non-reductive roots of maximal height. (Note that if $a=1$, then $I_z$ contains only roots of type 1 if $z \notin ({\mathbb {N}}_h^1)^{\le 0}$ and only contains roots of type 2 if $z \in ({\mathbb {N}}_h^1)^{\le 0}$.) If $A_z$ contains only reductive roots, let $I_z \subseteq A_z$ be the subset of all roots of maximal height. We have a stratification into locally closed subsets

$$\begin{aligned} {\mathbb {K}}_h^1 {\,\smallsetminus \,}\{1\} = \bigsqcup _{a,I} {\mathbb {K}}_h^{a,*,I} \qquad \text {where }{\mathbb {K}}_h^{a,*,I} = \{z \in {\mathbb {K}}_h^1 {\,\smallsetminus \,}\{1\} :(a_z,I_z) = (a,I)\}.\nonumber \\ \end{aligned}$$

(8.10)

11.4.8 Cohomology of ${{\widehat{\Sigma }}}_w'$

We are now ready to prove (8.5) using the same arguments as in the proof of [26, Lemma 1.9]. To do this, it is enough to show that $H^j_c({{\widehat{\Sigma }}}'_w)_{\theta ,\theta '} = 0$ for all $j \ge 0$. For a ${\mathcal {T}}^{\prime F}$-module M and a character $\chi$ of ${\mathcal {T}}^{\prime F}$, write $M_{(\chi )}$ for the $\chi$-isotypic component of M. Note that ${\mathcal {T}}^{\prime F}$ acts on ${{\widehat{\Sigma }}}'_w$ by

$$\begin{aligned} t' :(x,x',u,u',z,\tau ') \mapsto (x, t'x't^{\prime -1}, u, t'u't^{\prime -1}, z, \tau 't^{\prime -1}). \end{aligned}$$

Hence $H^j_c({{\widehat{\Sigma }}}'_w)$ is a ${\mathcal {T}}^{\prime F}$-module. It is enough to show that $H^j_c(\widehat{\Sigma }'_w)_{(\chi )} = 0$ for any regular character $\chi$ of ${\mathcal {T}}^{\prime F}$. Fix such a $\chi$. Define $N = \dot{w} U^{\prime -} \dot{w}^{-1}$, $N^- = \dot{w} U^{\prime } \dot{w}^{-1}$. Then with notation as in Sects. 8.4.6 and 8.4.7, the stratification of ${\mathbb {K}}_h^1 \smallsetminus \{1\}$ given in (8.10) induces a stratification of ${{\widehat{\Sigma }}}'_w$ indexed by $1\le a\le h-1$ and $I \in {\mathcal {X}}$:

$$\begin{aligned} {{\widehat{\Sigma }}}'_w = \bigsqcup _{a,I} {{\widehat{\Sigma }}}_w^{\prime ,a,I} \qquad \text {where }{{\widehat{\Sigma }}}_w^{\prime ,a,I} = \{(x,x',u,u',z,\tau ') \in {{\widehat{\Sigma }}}'_w :z\in {\mathbb {K}}_h^{a,*,I} \}. \end{aligned}$$

Note that each ${{\widehat{\Sigma }}}_w^{\prime , a, I}$ is stable under ${\mathcal {T}}^{\prime F}$. Thus to show (8.5), it is enough to show

$$\begin{aligned} H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I}, \overline{{\mathbb {Q}}}_{\ell })_{(\chi )} = 0 \qquad \text {for any fixed }a,I. \end{aligned}$$

(8.11)

Choose a root $\alpha$ such that $-\alpha \in I$. Then ${\mathbb {G}}_h^{\alpha } \subseteq {\mathbb {U}}_h \cap {\dot{w}} {\mathbb {U}}_h' {\dot{w}}^{-1}$. For any $z \in {\mathbb {K}}_h^{a,*,I}$, Lemma 8.11 grants us an isomorphism

$$\begin{aligned} \lambda _z&:({\mathbb {G}}_h^\alpha )^{h-a}/({\mathbb {G}}_h^\alpha )^{h-a+1} {\mathop {\longrightarrow }\limits ^{\sim }} {\mathcal {T}}^\alpha ,&\text {if }\alpha \text { is non-reductive,} \\ \lambda _z&:({\mathbb {G}}_h^\alpha )^{h-a-1}/({\mathbb {G}}_h^\alpha )^{h-a} {\mathop {\longrightarrow }\limits ^{\sim }} {\mathcal {T}}^\alpha ,&\text {if }\alpha \text { is reductive.} \end{aligned}$$

Let $\pi$ denote the natural projection $({\mathbb {G}}_h^{\alpha })^{h-a} \rightarrow ({\mathbb {G}}_h^{\alpha })^{h-a}/({\mathbb {G}}_h^{\alpha })^{h-a+1}$ if $\alpha$ is non-reductive and the natural projection $({\mathbb {G}}_h^{\alpha })^{h-a-1} \rightarrow ({\mathbb {G}}_h^{\alpha })^{h-a-1}/({\mathbb {G}}_h^{\alpha })^{h-a}$ if $\alpha$ is reductive. Let $\psi$ be a section to $\pi$ such that $\pi \psi = 1$ and $\psi (1) = 1$. Let

$$\begin{aligned} {{\mathcal {H}}' \,{:=}\,\{t' \in {\mathcal {T}}' :t^{\prime -1} F(t') \in {\dot{w}}^{-1} {\mathcal {T}}^{\alpha } {\dot{w}} \}.} \end{aligned}$$

This is a closed subgroup of ${\mathcal {T}}'$. For any $t' \in {\mathcal {H}}'$ define $f_{t'} :{{\widehat{\Sigma }}}_w^{\prime ,a,I} \rightarrow {{\widehat{\Sigma }}}_w^{\prime ,a,I}$ by

$$\begin{aligned} f_{t'}(x,x',u,u',z,\tau ') = (xF(\xi ), {\hat{x}}^{\prime }, u, F(t')^{-1} u' F(t'), z, \tau 'F(t')), \end{aligned}$$

where

$$\begin{aligned} \xi = \psi \lambda _z^{-1}({\dot{w}}F(t')^{-1}t'{\dot{w}}^{-1}) \in ({\mathbb {G}}_h^{\alpha })^{h-a-1} \subseteq {\mathbb {U}}_h \cap {\dot{w}}{\mathbb {U}}_h'{\dot{w}}^{-1} \end{aligned}$$

($({\mathbb {G}}_h^\alpha )^{h-a-1}$ should be replaced by $({\mathbb {G}}_h^\alpha )^{h-a}$ if $\alpha$ is non-reductive), and ${\hat{x}}' \in {\mathbb {G}}_h$ is defined by the condition that

$$\begin{aligned} xF(\xi z {\dot{w}} \tau ' F(t')) \in u z {\dot{w}} \tau ' F(t')F(t')^{-1}u'F(t'){\hat{x}}'. \end{aligned}$$

To check that this is well-defined one needs to show ${\hat{x}}' \in F({\mathbb {U}}_h')$. This is done with exactly the same computation as in the proof of [26, Lemma 1.9], and we omit this. It is clear that $f_{t'} :{{\widehat{\Sigma }}}_w^{\prime ,a,I} \rightarrow {{\widehat{\Sigma }}}_w^{\prime ,a,I}$ is an isomorphism for any $t' \in {\mathcal {H}}'$. Moreover, since ${\mathcal {T}}^{\prime F} \subseteq {\mathcal {H}}'$ and since for any $t' \in {\mathcal {T}}^{\prime F}$ the map $f_{t'}$ coincides with the action of $t'$ in the ${\mathcal {T}}^{\prime F}$-action on ${{\widehat{\Sigma }}}_w^{\prime ,a,I}$ (we use $\psi (1) = 1$ here), it follows that we have constructed an action f of ${\mathcal {H}}'$ on ${{\widehat{\Sigma }}}_w^{\prime ,a,I}$ extending the ${\mathcal {T}}^{\prime F}$-action.

If a connected group acts on a scheme, the induced action in the cohomology is constant. Thus for any $t' \in {\mathcal {H}}^{\prime 0}$, the induced map $f_{t'}^{*} :H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I}, \overline{{\mathbb {Q}}}_{\ell }) \rightarrow H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I}, \overline{{\mathbb {Q}}}_{\ell })$ is constant when $t'$ varies in ${\mathcal {H}}^{\prime 0}$. Hence the restriction of the ${\mathcal {T}}^{\prime F}$-action on $H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I}, \overline{{\mathbb {Q}}}_{\ell })$ to ${\mathcal {T}}^{\prime F} \cap {\mathcal {H}}^{\prime ,0}$ is trivial.

Now we can find some $m\ge 1$ such that $F^m({\dot{w}}^{-1}{\mathcal {T}}^{\alpha }{\dot{w}}) = {\dot{w}}^{-1}{\mathcal {T}}^{\alpha } {\dot{w}}$. Then

$$\begin{aligned} t' \mapsto t'F(t')F^2(t') \cdots F^{m-1}(t') \end{aligned}$$

defines a morphism ${\dot{w}}^{-1}{\mathcal {T}}^{\alpha }{\dot{w}} \rightarrow {\mathcal {H}}'$. Since ${\mathcal {T}}^{\alpha }$ is connected, its image is also connected and hence contained in ${\mathcal {H}}^{\prime 0}$. If $t' \in ({\dot{w}}^{-1}{\mathcal {T}}^{\alpha }{\dot{w}})^{F^m}$, then $N_F^{F^m}(t') \in {\mathcal {T}}^{\prime F}$ and hence also $N_F^{F^m}(t') \in {\mathcal {T}}^{\prime F} \cap {\mathcal {H}}^{\prime 0}$. Thus the action of $N_F^{F^m}(t') \in {\mathcal {T}}^{\prime F}$ on $H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I})$ is trivial for any $t' \in ({\dot{w}}^{-1}{\mathcal {T}}^{\alpha }{\dot{w}})^{F^m}$.

Finally, observe that if $H_c^j({{\widehat{\Sigma }}}_w^{\prime ,a,I}, \overline{{\mathbb {Q}}}_{\ell })_{(\chi )} \ne 0$, then the above shows that $t' \mapsto \chi (N_F^{F^m}(t'))$ is the trivial character, which contradicts the regularity assumption on $\chi$. This establishes (8.11), which establishes (8.5), which was the last outstanding claim in the proof of Proposition 8.7.

12 Cuspidality

The next theorem (proved in Sect. 9.1) concerns the “cuspidality” of the representation $R_{T_h}^{G_h}(\theta )$ for primitive $\theta$. This is the higher-level analogue of Deligne–Lusztig’s theorem [13, Theorem 8.3] required to prove that the induced representation ${{\,\mathrm{c-Ind}\,}}_{Z \cdot G_{{\mathcal {O}}}}^G(|R_{T_h}^{G_h}(\theta )|)$ is irreducible and supercuspidal (Theorem 12.5). A proof that this induced representation is irreducible supercuspidal when $h = 1$ can be found in [27, Proposition 6.6], and when $G = {{\,\mathrm{GL}\,}}_2(K)$ and h arbitrary it was done by the first author in [21].

We work with a special representative b as in Sect. 5.2.2.

Let $N'$ be the unipotent radical of any standard parabolic subgroup of ${{\,\mathrm{GL}\,}}_{n'}$ and let $\breve{N}$ denote the subgroup of ${{\,\mathrm{GL}\,}}_n(\breve{K})$ consisting of unipotent matrices such that any $(n_0 \times n_0)$-block consists of a diagonal matrix and the (i, j)th block can have nonzero entries if and only if the (i, j)th entry of an element of $N'$ is nonzero. For each $h \ge 1$, let $\breve{N}_h$ denote the image of $\breve{N} \cap \breve{G}_{{\mathbf {x}},0}$ in ${\mathbb {G}}_h({{\overline{{\mathbb {F}}}}}_q)$. Define ${N_h \,{:=}\,\breve{N}_h^F}$ and ${N_h^{h-1} \,{:=}\,\ker (N_h \rightarrow N_{h-1})}$.

Theorem 9.1

Assume $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ is primitive. Then the restriction of $|R_{T_h}^{G_h}(\theta )|$ to $N_h^{h-1}$ does not contain the trivial representation.

12.1 Proof of Theorem 9.1

12.1.1 9.1.1.

We retain notation as in the statement of the Theorem and the set-up directly proceeding it. Let ${J \,{:=}\,\{\alpha = (i,j) : U_\alpha \subset N'\}}$ be the set of roots of the diagonal torus in ${{\,\mathrm{GL}\,}}_{n'}$ occurring in $N'$. Let l be the inverse of $k_0$ modulo $n_0$ and let $[a]_{n_0}$ denote the residue of $a \in {\mathbb {Z}}$ in $1 \le [a] \le n_0$. The elements of $N_h^{h-1}$ consist of $n\times n$-matrices, whose (i, j)th $(n_0 \times n_0)$-block is the identity matrix if $i = j$, is zero if $i\ne j$ and $(i,j) \not \in J$, and is of the form ${{\,\mathrm{diag}\,}}(\varpi ^{h-1}u, \varpi ^{h-1}\sigma ^{[l]_{n_0}}(u), \varpi ^{h-1}\sigma ^{[2l]_{n_0}}(u), \dots , \varpi ^{h-1}\sigma ^{[(n_0-1)l]_{n_0}}(u))$ for some $u \in {\mathbb {F}}_{q^{n_0}}$ if $(i,j) \in J$. Observe that it is sufficient to show that the theorem holds under the assumption that $N'$ is the unipotent radical of a maximal proper parabolic; that is,

$$\begin{aligned} J = \{(i,j):1\le i \le n' -\ell , \, n'-\ell +1 \le j \le n, \} \qquad \text {for some }1\le \ell \le n'. \end{aligned}$$

(This will be used only in the proof of Lemma 9.6.)

12.1.2 9.1.2.

Our main tool will be a close variant of [5, Lemma 2.12]. The set-up and proof of Lemma 9.2 is nearly the same as the proof of op. cit. verbatim. Assume that X is a separated scheme of finite type over ${\mathbb {F}}_q$ and we are given an automorphism $\varphi$ of X and a right action of a finite group A on X that commute with $\varphi$. For each character $\chi :A \rightarrow \overline{{\mathbb {Q}}}_\ell ^\times$, we write $H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )[\chi ]$ for the subspace of $H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )$ on which A acts by $\chi$. Note that this subspace is invariant under the action of $\varphi ^* :H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )[\chi ] {\mathop {\rightarrow }\limits ^{\cong }} H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )[\chi ]$.

Lemma 9.2

Let $\chi :A \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be a character. Assume that ${{\,\mathrm{Fr}\,}}_q$ acts on $\sum _i (-1)^i H_c^i(X, \overline{{\mathbb {Q}}}_\ell )[\chi ]$ by a scalar $\lambda$. Then

$$\begin{aligned}&{{\,\mathrm{Tr}\,}}\left( \varphi ^*; \textstyle \sum \limits _i (-1)^i(X, \overline{{\mathbb {Q}}}_\ell )[\chi ]\right) \\&= \frac{1}{\lambda \cdot \#A} \cdot \sum _{a \in A} \chi (a) \cdot \#\{x \in X({{\overline{{\mathbb {F}}}}}_q) : \varphi ({{\,\mathrm{Fr}\,}}_q(x))= x \cdot a\}. \end{aligned}$$

Proof

For each $a \in A$, let $\rho _a :X \rightarrow X$ denote the automorphism $x \mapsto x \cdot a$ and write $\varphi _a = \varphi \circ \rho _a$. Then $\rho _a$ is a finite-order automorphism of X and (as in the proof of [13, Proposition 3.3])

$$\begin{aligned} \textstyle \sum \limits _i (-1)^i {{\,\mathrm{Tr}\,}}({{\,\mathrm{Fr}\,}}_q \circ \, \varphi _a^*; H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )) = \#\{x \in X({{\overline{{\mathbb {F}}}}}_q) : \varphi ({{\,\mathrm{Fr}\,}}_q(x)) = x \cdot a^{-1}\}. \end{aligned}$$

Hence averaging over $\chi ^{-1}(a)$, we have

$$\begin{aligned}&\frac{1}{\# A} \cdot \sum _{a \in A} \chi ^{-1}(a) \cdot \#\{x \in X({{\overline{{\mathbb {F}}}}}_q) : \varphi ({{\,\mathrm{Fr}\,}}_q(x)) = x \cdot a^{-1}\}\\&\quad = \textstyle \sum \limits _i (-1)^i {{\,\mathrm{Tr}\,}}\left( {{\,\mathrm{Fr}\,}}_q \circ \, \varphi ^* ; H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )[\chi ]\right) \\&\quad = \lambda {{\,\mathrm{Tr}\,}}\left( \varphi ^* ; \textstyle \sum \limits _i (-1)^i H_c^i(X, {{\overline{{\mathbb {Q}}}}}_\ell )[\chi ]\right) . \end{aligned}$$

$\square$

12.1.3 9.1.3.

Now fix a character $\theta :T_h \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ as in the theorem. Recall from (7.3) that

$$\begin{aligned}&X_h = \bigsqcup _{a \in ({\mathcal {O}}_K/\varpi ^h)^{\times }} g_a.X_h^{\det \equiv 1}, \qquad \text {where }X_h^{\det \equiv 1}\\&= \{x \in X_h : \det g_b^{\mathrm{red}}(x) \equiv 1 \!\!\!\! \pmod {\varpi ^h}\}. \end{aligned}$$

Note that $T_h$ transitively permutes the components $g_a.X_h^{\det \equiv 1}$ ($a \in ({\mathcal {O}}_K/\varpi ^h)^{\times }$) and let $T_h^\circ \subseteq T_h$ denote the stabilizer of a (any) component. Since the composition $H_c^i(X_h^{\det \equiv 1})[\theta |_{T_h^\circ }] \hookrightarrow H_c^i(X_h)[\theta |_{T_h^\circ }] \twoheadrightarrow H_c^i(X_h)[\theta ]$ is bijective, it must be an isomorphism of $N_h^{h-1}$-representations (see also (8.1)). Hence to show the theorem, it is enough to show that the trivial character of $N_h^{h-1}$ does not occur in $\sum _i (-1)^i H_c^i(X_h^{\det \equiv 1})[\theta |_{T_h^\circ }]$; that is,

$$\begin{aligned}&\left\langle \mathrm{triv}, \textstyle \sum _i (-1)^i H_c^i(X_h^{\det \equiv 1}, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta |_{T_h^\circ }] \right\rangle _{N_h^{h-1}} \nonumber \\&\quad = \frac{1}{\# N_h^{h-1}}\sum _{g \in N_h^{h-1}} {{\,\mathrm{Tr}\,}}\left( g ; \textstyle \sum _i (-1)^i H_c^i(X_h^{\det \equiv 1}, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta |_{T_h^\circ }]\right) = 0. \end{aligned}$$

(9.1)

We now apply Lemma 9.2 to the ${\mathbb {F}}_{q^n}$-scheme $X_h^{\det \equiv 1}$ with $A = T_h^\circ$ and $\varphi :X_h^{\det \equiv 1} \rightarrow X_h^{\det \equiv 1}$ given by $x \mapsto g \cdot x$ for some $g \in N_h^{h-1}$. We see that to show (9.1), we must show

$$\begin{aligned} {\sum _{g \in N_h^{h-1}} \sum _{t \in T_h^\circ } \theta (t) \cdot \# S_{g,t} = 0, \qquad \text {where }S_{g,t} \,{:=}\,\{x \in X_h^{\det \equiv 1}({{\overline{{\mathbb {F}}}}}_q) : g \cdot {{\,\mathrm{Fr}\,}}_{q^n}(x) = x \cdot t\}.} \end{aligned}$$

Lemma 9.3

Let $g \in N_h^{h-1}$ and $t \in T_h^\circ$ such that $S_{g,t} \ne \varnothing$. Then $t \equiv (-1)^{n'-1} \pmod {\varpi ^{h-1}}$ and $\sigma ^n(x) \equiv (-1)^{n'-1}x \pmod {\varpi ^{h-1}}$ for all $x \in S_{g,t}$.

Proof

An element $y \in {\mathscr {L}}_0$ lies in ${\mathscr {L}}_{0,b}^{\mathrm{adm,rat}}$ if and only if $\det g_b^{{{\,\mathrm{red}\,}}}(y) \in {\mathcal {O}}_K^{\times }$, or equivalently, ${{\,\mathrm{ord}\,}}\det g_b(y) = {{\,\mathrm{ord}\,}}\det (D_{\kappa ,n}) =: c$ and $\sigma (\det g_b(y)) = \det g_b(y)$. Multiplying by b on both sides, we see that these conditions are equivalent to

$$\begin{aligned} \det (b\sigma (y) \,|\, (b\sigma )^2(y) \,|\, \dots \,|\, (b\sigma )^n(y)) = \det (b) \det (g_b(y))\in \varpi ^{c + \kappa } {\mathcal {O}}^{\times }.\nonumber \\ \end{aligned}$$

As b is the special representative, $\det (b) = ((-1)^{(n_0 - 1)k_0} \varpi ^{k_0})^{n'} = (-1)^{\kappa (n_0 - 1)} \varpi ^{\kappa }$, and moreover, $b^n = \varpi ^{\kappa }$. Thus the above is equivalent to

$$\begin{aligned} \varpi ^{\kappa } \det (b\sigma (y) \,|\, (b\sigma )^2(y) \,|\, \dots \,|\, \sigma ^n(y)) = (-1)^{\kappa (n_0 - 1)} \varpi ^{\kappa } \det (g_b(y)) \in \varpi ^{c + \kappa } {\mathcal {O}}^{\times }, \end{aligned}$$

An elementary computation shows $(-1)^{n-1 - \kappa (n_0 - 1)} = (-1)^{n' - 1}$, thus the above is equivalent to

$$\begin{aligned} (-1)^{n'-1} \det (\sigma ^n(y) \,|\, b\sigma (y) \,|\, (b\sigma )^2(y) \,|\, \dots \,|\, (b\sigma )^{n-1}(y)) = \det (g_b(y)) \in \varpi ^c {\mathcal {O}}^{\times }.\nonumber \\ \end{aligned}$$

(9.2)

Let now $x \in S_{g,t} \subseteq X_h$. Denote by $y \in {\mathscr {L}}_0^\mathrm{adm,rat}$ a lift of x. As $g \equiv 1 \pmod {\varpi ^{h-1}}$, we by assumption have $\sigma ^n(y) \equiv yt \pmod {\varpi ^{h-1}}$. Thus replacing in (9.2) $\sigma ^n(y)$ by $ty + \varpi ^{h-1}*$ for some $*\in {\mathscr {L}}_0$, using the linearity of the determinant in the first column, and the fact that each entry of the ith column ($2 \le i \le n$) of the matrix on the left hand side of (9.2) is in ${\mathcal {O}}$ divisible by $\varpi ^{\left\lfloor \frac{(i-1)\kappa _0}{n_0} \right\rfloor }$ (and $\sum _{i=2}^n \left\lfloor \frac{(i-1)\kappa _0}{n_0} \right\rfloor = c$), we deduce that

$$\begin{aligned} (-1)^{n' - 1}t \equiv 1 \pmod {\varpi ^{h-1}}. \end{aligned}$$

If ${{\tilde{x}}} \in X_{h-1}^+$ denotes the image of x modulo $\varpi ^{h-1}$, we obtain $\sigma ^n({{\tilde{x}}}) = (-1)^{n'-1}\tilde{x}$. $\square$

Thus for g, t as in the lemma, $S_{g,t} \ne \varnothing$ implies

$$\begin{aligned} t \in (-1)^{n'-1}T_h^{h-1} \cap T_h^\circ = \{(-1)^{n'-1}(1 + \varpi ^{h-1}[a]) :a \in {\mathbb {F}}_{q^n}, \mathrm{tr}_{{\mathbb {F}}_{q^n/{\mathbb {F}}_q}}(a) = 0 \}. \end{aligned}$$

so that, after factoring out the constant $\theta (-1)^{n'-1}$, it remains to show:

$$\begin{aligned} \sum _{g \in N_h^{h-1}} \sum _{a \in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_q)} \theta (1 + \varpi ^{h-1}[a]) \cdot \# S_{g,(-1)^{n'-1}(1 + \varpi ^{h-1} [a])} = 0. \end{aligned}$$

(9.3)

12.1.4 9.1.4.

Before we can prove (9.3), we need some preparations. Recall from Sect. 7.4 that one has an intermediate scheme $X_h \twoheadrightarrow X_{h-1}^+ \twoheadrightarrow X_{h-1}$. Define $X_{h-1}^{+,\det \equiv 1}$ to be the subscheme of $X_{h-1}^+$ consisting of $x \in X_{h-1}^+$ with $\det (g_b^{{{\,\mathrm{red}\,}}}(x)) \equiv 1$ modulo $\varpi ^{h-1}$. Then we have a surjection

$$\begin{aligned} f :X_h^{\det \equiv 1} \rightarrow X_{h-1}^{+, \det \equiv 1} \end{aligned}$$

and by Proposition 7.6, $X_h^{\det \equiv 1} \hookrightarrow X_{h-1}^{+, \det \equiv 1} \times {\mathbb {A}}^{n'}$ is the (relative) hypersurface given by

$$\begin{aligned} \sum _{i=0}^{n_0-1} \sigma ^i(P_1) + c = 0, \end{aligned}$$

where $c :X_h \rightarrow {\mathbb {A}}^1$ factors through f and $P_1$ is a polynomial over $X_{h-1}^+$ in the variables $x_{i,h-1}$ for $i \equiv 1 \pmod {n_0}$.

12.1.5 9.1.5.

By Lemma 9.3, for $g \in N_h^{h-1}$ and $t \in (-1)^{n'-1}(T_h^{h-1} \cap T_h^\circ )$ with $S_{g,t} \ne \varnothing$, we have $S_{g,t} \subseteq f^{-1}(S_{h-1})$, where

$$\begin{aligned} {S_{h-1} \,{:=}\,\left\{ {{\widetilde{x}}} \in X_{h-1}^{+, \det \equiv 1}: \sigma ^n({{\widetilde{x}}}) = (-1)^{n'-1} \widetilde{x}\right\} \subset X_{h-1}^{+, \det =1}} \end{aligned}$$

is a finite set of points. Regard $S_{h-1}$ as a (zero-dimensional, reduced) subscheme of $X_{h-1}^{+,\det \equiv 1}$. Consider the $S_{h-1}$-morphism $S_{h-1} \times {\mathbb {A}}^{n'} {\mathop {\rightarrow }\limits ^{\sim }} S_{h-1} \times {\mathbb {A}}^{n'}$, which is the linear change of variables defined by

$$\begin{aligned} (x_{1,h-1}, x_{n_0+1,h-1}, \dots , x_{n_0(n'-1)+1,h-1})^{\intercal } = \overline{g_b}({{\bar{x}}}) (z_1, z_2, \ldots , z_{n'})^{\intercal }, \end{aligned}$$

where ${\bar{x}}$ is the image of ${\tilde{x}} \in S_{h-1}$ in $X_1$ and $\overline{g_b}({{\bar{x}}})$ is as in Sect. 7.3.

Claim

$X_h^{\det \equiv 1}$ is a (relative) hypersurface over $X_{h-1}^{+,\det \equiv 1}$ defined by an equation $\sum _{i=0}^{n-1} z_1^{q^i} = c$.

It is enough to show that in the new coordinates $z_1, \ldots , z_{n'}$, the polynomial $P_1$ as in Proposition 7.6 takes the form $P_1 = \sum _{i=0}^{n'-1} z_1^{q^{n_0i}}$. We prove this now.

Recall the $n'$-dimensional ${\mathbb {F}}_{q^{n_0}}$-vector space ${\overline{V}}$ with its distinguished basis $\{\bar{e}_{n_0(i-1)+1}\}_{1\le i \le n'}$ and the ${\mathbb {F}}_{q^{n_0}}$-linear morphism $\overline{\sigma _b}$ of ${\overline{V}}$ from Lemma 5.8. To simplify notation, we write ${\bar{x}}_j$ instead of $x_{n_0(j-1)+1,0}$ for $x \in X_h$ and $1\le j \le n'-1$ in what follows (i.e., the image of $x \in X_h$ in ${\overline{V}}$ is ${\bar{x}} = ({\bar{x}}_i)_{i=1}^{n'}$). Recall from Sect. 7.3 that for ${{\bar{x}}} \in {\overline{V}}$ the ith column of the $(n' \times n')$-matrix $\overline{g_b}({\bar{x}})$ is $\overline{\sigma _b}^{i-1}({{\bar{x}}})$. Let $m_i$ denote the ith row of the adjoint matrix $(m_{ij})$ of $\overline{g_b}({{\bar{x}}})$. Then the above change of variables gives

$$\begin{aligned} P_1&= (m_1 \cdot {\bar{x}})z_1 + (m_2 \cdot {\bar{\sigma }}_b({{\bar{x}}}))z_1^{q^{n_0}} + (m_3 \cdot {{\bar{\sigma }}}_b^2({{\bar{x}}})) z_1^{q^{2n_0}} + \dots + (m_{n'} \cdot {{\bar{\sigma }}}_b^{n'-1}({{\bar{x}}})) z_1^{q^{n_0(n'-1)}} \\&\quad + (m_1 \cdot {{\overline{\sigma }}}_b({{\bar{x}}})) z_2 + (m_2 \cdot \overline{\sigma _b}^2({{\bar{x}}})) z_2^{q^{n_0}} + (m_3 \cdot {{\bar{\sigma }}}_b^3({{\bar{x}}})) z_2^{q^{2n_0}} + \dots + (m_{n'} \cdot {{\bar{\sigma }}}_b^{n'}({{\bar{x}}})) z_2^{q^{n_0(n'-1)}} \\&\quad + \cdots + (m_1 \cdot \overline{\sigma _b}^{n'-1}({{\bar{x}}})) z_{n'} + (m_2 \cdot \overline{\sigma _b}^{n'}({{\bar{x}}})) z_{n'}^{q^{n_0}} + \dots + (m_n \cdot \overline{\sigma _b}^{2n'-2}({{\bar{x}}})) z_{n'}^{q^{n_0(n'-1)}}. \end{aligned}$$

(Here $\cdot$ denotes the matrix product.) But $\sigma ^n({{\bar{x}}}) = (-1)^{n'-1} {{\bar{x}}}$ (where $\sigma ^n$ is applied entry-wise), and hence from the explicit form of $\overline{\sigma _b}$ we deduce that $\overline{\sigma _b}^{n'}({{\bar{x}}}) = (-1)^{n'-1}{\bar{x}}$. As $(m_{ij})$ is adjoint to $\overline{g_b}({{\bar{x}}})$ and $\det (\overline{g_b}({{\bar{x}}})) = 1 \in {\mathbb {F}}_q^{\times }$, we have

$$\begin{aligned} m_i \cdot \overline{\sigma _b}^j({{\bar{x}}}) = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }j = i-1, \\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

This shows that all coefficients are equal to 1 in the first line of the above expression and vanish in lines $2, \dots , n'$. This completes the proof of the claim.

12.1.6 9.1.6.

Note that $N_h^{h-1} \times (T_h^{h-1} \cap T_h^\circ )$ stabilizes $S_{h-1}$ and acts trivially on it. We describe the action of $N_h^{h-1} \times (T_h^{h-1} \cap T_h^\circ )$ on the new coordinates $z_1, \ldots , z_{n'}$.

Let $g \in N_h^{h-1}$ and for $(i,j) \in J$ as in Sect. 9.1.1, let $[u_{i,j}]\varpi ^{h-1}$ denote the upper left entry of the (i, j)th $n_0\times n_0$-block of g. Recall that the action of g on $f^{-1}(S_{h-1})$ in the old coordinates $x_{1,h-1}, \ldots , x_{n_0(n'-1) + 1, h-1}$ is given by

$$\begin{aligned} g.(x_{n_0(i-1),h-1})_{i=1}^{n'} = \left( x_{n_0(i-1),h-1} + \textstyle \sum \limits _{\begin{array}{c} 1\le j \le n' \\ (i,j) \in J \end{array}} u_{i,j} {{\bar{x}}}_j \right) _{i=1}^{n'}. \end{aligned}$$

Since $\det (\overline{g_b}({{\overline{x}}})) = 1$ by assumption, the adjoint matrix $(m_{ij})_{ij}$ of $\overline{g_b}({{\overline{x}}})$ is in fact the inverse, so that $z_i = \sum _{j=1}^{n'} m_{ij}x_{n_0(j-1) + 1,h-1}$. Thus the action of g on the new coordinates is given by

$$\begin{aligned} z_i \mapsto z_i + \textstyle \sum \limits _{\begin{array}{c} 1\le k,j\le n' \\ (k,j) \in J \end{array}} m_{ik} u_{kj} {{\bar{x}}}_j. \end{aligned}$$

We now describe the action of $(T_h^{h-1} \cap T_h^\circ ) = \{1 + [a] \varpi ^{h-1} :{{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_q}(a) = 0\}$. For $a \in \ker ({{\,\mathrm{Tr}\,}}:{\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_q)$, the action of $1 + [a] \varpi ^{h-1}$ on the old coordinates is given by

$$\begin{aligned} x_{n_0(i-1) + 1,h-1} \mapsto x_{n_0(i-1) + 1,h-1} + a {{\bar{x}}}_i. \end{aligned}$$

Since $\sum _{k=1}^n m_{ik} {{\bar{x}}}_k$ is equal to 1 when $i = 1$ and equal to 0 when $i > 1$, the action of $1 + [a] \varpi ^{h-1}$ on the new coordinates is given by

$$\begin{aligned} z_i \mapsto {\left\{ \begin{array}{ll} z_1 + a &{}\quad \text {if }i = 1, \\ z_i &{}\quad \text {if }i = 2, \ldots , n'. \end{array}\right. } \end{aligned}$$

Moreover, $x \mapsto \sigma ^n(x) \cdot (-1)^{n'-1}$ defines an isomorphism of each fiber $f^{-1}({{\tilde{x}}})$, and one computes that in coordinates $z_i$ it is given by $z_i \mapsto \sigma ^n(z_i)$. Thus for $t = (-1)^{n'-1}(1+\varpi ^{h-1}[a]) \in (-1)^{n'-1}(T_h^{h-1} \cap T_h^\circ )$, the assignment $x \mapsto \sigma ^n(x)\cdot t$ defines an isomorphism of $f^{-1}({{\tilde{x}}})$ which in the coordinates $z_i$ is given by $z_1 \mapsto \sigma ^n(z_1) + a$, $z_i \mapsto \sigma ^n(z_i)$ for $2 \le i \le n'$.

12.1.7 9.1.7.

We next claim that $c({{\widetilde{x}}}) \in {\mathbb {F}}_q$ for ${\tilde{x}} \in S_{h-1}$. Consider the “extension by zero” morphism ${\mathbb {W}}_{h-1} \rightarrow {\mathbb {W}}$ given by $\sum _{i=0}^{h-2} [a_i] \varpi ^i \mapsto \sum _{i=0}^{h-2} [a_i] \varpi ^i$. It defines a map ${\mathscr {L}}_0/\varpi ^{h-1} {\mathscr {L}}_0 \rightarrow {\mathscr {L}}_0$, $y \mapsto [y,0]$. To show the claim it is sufficient to show that $[{{\tilde{x}}}, 0]$ lies in ${\mathscr {L}}_{0,b}^{\mathrm{adm, rat}}$. Obviously, $\det g_b^{{{\,\mathrm{red}\,}}}([{{\tilde{x}}}, 0]) \in {\mathcal {O}}$. Now, note that as ${{\tilde{x}}} \in X_{h-1}^+$, there exists some lift $z \in {\mathscr {L}}_{0,b}^{\mathrm{adm, rat}}$ of ${{\tilde{x}}}$. This gives in particular $\det g_b^{{{\,\mathrm{red}\,}}}(z) \equiv \det g_b^{{{\,\mathrm{red}\,}}}([{{\tilde{x}}}, 0]) \pmod {\varpi ^{h-1}}$. We deduce $\det g_b^{{{\,\mathrm{red}\,}}}([{{\tilde{x}}}, 0]) \in {\mathcal {O}}^{\times }$. It remains to show that $\det g_b^{{{\,\mathrm{red}\,}}}([{{\tilde{x}}}, 0]) \in K$. To do this, it suffices to prove that $\det g_b([{{\tilde{x}}}, 0]) \in K$, as $\det g_b^{{{\,\mathrm{red}\,}}}(\cdot )$ and $\det g_b(\cdot )$ differ only by a power of $\varpi$. But as $\sigma ^n({{\widetilde{x}}}) = (-1)^{n'-1} (\widetilde{x})$, we have $\sigma ^n([{{\widetilde{x}}},0]) = (-1)^{n'-1} [\widetilde{x},0]$. Using this and $\det (b) = (-1)^{\kappa (n_0-1)}\varpi ^k$ we compute:

$$\begin{aligned}&(-1)^{\kappa (n_0-1)}\varpi ^k \sigma (\det g_b([{{\tilde{x}}}, 0]))\\&= \det b\sigma (g_b([{{\tilde{x}}}, 0])) \\&= \det \left( b\sigma ([{{\tilde{x}}}, 0]) \, | \, (b\sigma )^2([{{\tilde{x}}}, 0]) \, | \, \dots \, | \, \varpi ^k \sigma ^n([{{\tilde{x}}}, 0])\right) \\&= (-1)^{(n-1) + (n'-1)} \varpi ^{\kappa } \det g_b([{{\tilde{x}}}, 0]). \end{aligned}$$

But as in the proof of Lemma 9.3, we have $(-1)^{\kappa (n_0-1)} = (-1)^{(n-1) + (n'-1)}$. This shows the claim.

12.1.8 9.1.8.

Fix ${{\tilde{x}}} \in S_{h-1}$ and $t = (-1)^{n'-1}(1+ \varpi ^{h-1} [a])$ with ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_q}(a) = 0$ (as in Eq. (9.3)). We see that a point $x \in f^{-1}({{\tilde{x}}})$ with coordinates $(z_i)_{i=1}^{n'}$ as in Sect. 9.1.5 lies in $S_{g,t} \cap f^{-1}({{\widetilde{x}}})$ if and only if

$$\begin{aligned} g \cdot \sigma ^n(x) \cdot t^{-1} = x \qquad \text {and} \qquad z_1 + z_1^q + \cdots + z_1^{q^{n-1}} = c({{\widetilde{x}}}). \end{aligned}$$

By Sect. 9.1.6, the first equation is equivalent to (use that $\sigma ^n(m_{i,k}) = -m_{i,k}$, $\sigma ^n({\bar{x}}_j) = (-1)^{n'-1}{\bar{x}}_j$)

$$\begin{aligned} z_1^{q^n} + \sum _{(k,j) \in J} m_{1k}u_{kj} {{\bar{x}}}_j = z_1 + a, \end{aligned}$$

along with similar equations for the $(z_i)_{i=2}^{n'}$ (of the form $z_i^{q^n} + \text {(sum of terms)} = z_i$). Since $c({{\widetilde{x}}}) \in {\mathbb {F}}_q$ by Sect. 9.1.7, the second equation implies $z_1 = z_1^{q^n}$, which eliminates $z_1$ from the first equation. Therefore $S_{g,t} \cap f^{-1}({{\widetilde{x}}}) \ne \varnothing$ if and only if

$$\begin{aligned} {\psi ({{\widetilde{x}}},g) = a, \qquad \text {where }\psi ({{\widetilde{x}}},g) \,{:=}\,\textstyle \sum _{(k,j) \in J} m_{1k}u_{kj} {{\bar{x}}}_j.} \end{aligned}$$

(9.4)

Moreover, since the $n'-1$ equations for $(z_i)_{i=2}^{n'}$ is a separable polynomial in $z_i$, each gives precisely $q^n$ choices for $z_i$, $2 \le i \le n'$, with no further conditions. Thus

$$\begin{aligned} S_{g,t} \cap f^{-1}({{\widetilde{x}}}) \ne 0 \quad&\Longleftrightarrow \quad (9.4)\text { holds} \\&\Longleftrightarrow \quad \#(S_{g,t} \cap f^{-1}({{\widetilde{x}}})) = \underbrace{q^{n-1}}_{\text {for }z_1}(\underbrace{q^n}_{\text {for } z_i, 2 \le i \le n'})^{n'-1} = q^{nn'-1}. \end{aligned}$$

This shows the following lemma.

Lemma 9.4

For $g \in N_h^{h-1}$, $t = (-1)^{n'-1} (1 + \varpi ^{h-1}[a])$ with ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_q}(a) = 0$, and ${\tilde{x}} \in S_{h-1}$,

$$\begin{aligned} \# S_{g,t} \cap f^{-1}({{\tilde{x}}}) = {\left\{ \begin{array}{ll} q^{nn' - 1} &{}\quad \text {if }\psi (g, {{\tilde{x}}}) = a, \\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

For $a \in \ker ({{\,\mathrm{Tr}\,}}:{\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_q)$, put

$$\begin{aligned} {B_{g,a} \,{:=}\,\{{{\tilde{x}}} :\psi (g,{{\tilde{x}}}) = a \} \subseteq S_{h-1}.} \end{aligned}$$

As $S_{g,t} = \bigsqcup _{{{\widetilde{x}}} \in S_{h-1}} S_{g,t} \cap f^{-1}({{\widetilde{x}}})$, Lemma 9.4 implies that

$$\begin{aligned} \# S_{g,(-1)^{n'-1}(1 + \varpi ^{h-1}[a])} = q^{nn' - 1} \cdot \# B_{g,a}. \end{aligned}$$

Thus the left hand side of (9.3) is

$$\begin{aligned} q^{nn'-1} \cdot \sum _{a \in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_q)} \sum _{g \in N_h^{h-1}} \theta (1 + \varpi ^{h-1}[a]) \cdot \# B_{g,a}. \end{aligned}$$

(9.5)

12.1.9 9.1.9.

We have the following lemma.

Lemma 9.5

Let $g \in N_h^{h-1}$ and let $t = (-1)^{n'-1}(1 + \varpi ^{h-1}[a])$ with ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_q}(a) = 0$. We have $S_{g,t} = \varnothing$, unless ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}(a) = 0$.

Proof

It is enough to show that if ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}(a) \ne 0$, then $S_{g,t} \cap f^{-1}({{\tilde{x}}}) = \varnothing$ for all ${{\tilde{x}}} \in S_{h-1}$. By Lemma 9.4, it is enough to show that for all $g \in N_h^{h-1}$ and ${{\tilde{x}}} \in S_{h-1}$, we have $\psi ({{\tilde{x}}}, g) \in \ker ({{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}})$. Fix such g and ${{\tilde{x}}}$ and let $\varpi ^{h-1} u_{k,j}$ ($(k,j) \in J$) denote the entries of g (as in beginning of Sect. 9.1.6). As $u_{k,j} \in {\mathbb {F}}_{q^{n_0}}$, and as $k\ne j$ holds for all pairs $(k,j) \in J$, it suffices to show that $m_{1,k}{{\bar{x}}}_j \in \ker ({{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}})$ if $k \ne j$. Since ${\tilde{x}} \in S_{h-1}$, one computes $m_{k,l} = m_{k-1,l}^{q^{n_0}}$. Thus ${{\,\mathrm{Tr}\,}}(m_{1,k}{{\bar{x}}}_j)$ is precisely the (j, k)th entry of the matrix $\overline{g_b}({\bar{x}}) \cdot m$, which is equal 0. $\square$

By Lemma 9.5 and (9.5), we have reduced showing (9.3) to showing

$$\begin{aligned} \sum _{a \in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})} \sum _{g \in N_h^{h-1}} \theta (1 + \varpi ^{h-1}[a]) \cdot \# B_{g,a} = 0 \end{aligned}$$

(9.6)

12.1.10 9.1.10.

For ${{\tilde{x}}} \in S_{h-1}$, consider the ${\mathbb {F}}_{q^{n_0}}$-vector subspace ${W({\tilde{x}}) := \langle m_{1,i} {\bar{x}}_j | (i,j) \in J \rangle \subseteq \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})}$. The left hand side of (9.6) is

$$\begin{aligned}&\sum _{a \in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})} \sum _{g \in N_h^{h-1}} \theta (1 + \varpi ^{h-1}[a]) \cdot \# B_{g,a} \nonumber \\&\qquad = \sum _{a\in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})} \sum _{{{\tilde{x}}} \in S_{h-1}} \theta (1 + \varpi ^{h-1}[a]) \cdot \# \{ g \in N_h^{h-1} :\psi (g,{{\tilde{x}}}) = a \} \nonumber \\&\qquad = \sum _{a\in \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})} \sum _{ W \subseteq \ker ({\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}})} \sum _{{{\tilde{x}}} :W({\tilde{x}}) = W} \theta (1 + \varpi ^{h-1}[a]) \cdot \# \{ g \in N_h^{h-1} :\psi (g,{{\tilde{x}}}) = a \}. \end{aligned}$$

(9.7)

Now fix some W and ${\tilde{x}} \in S_{h-1}$ such that $W({{\tilde{x}}}) = W$. Then $\{m_{1,i}{\bar{x}}_{j}\}_{(i,j) \in J}$ span the ${\mathbb {F}}_{q^{n_0}}$-vector space W, and from the explicit form (9.4) of $\psi (g,a)$, it is clear that

$$\begin{aligned} \#\{g \in N_h^{h-1} :\psi (g,{\tilde{x}}) = a \} = {\left\{ \begin{array}{ll} q^{n_0(\# J - \dim W)} &{}\quad \text {if }a \in W,\\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

Note that $\#\{g \in N_h^{h-1} : \psi (g, {{\tilde{x}}}) = a\}$ depends only on $W({{\tilde{x}}})$ and not on ${{\tilde{x}}}$ itself. Thus, if we set ${S_{h-1,W} \,{:=}\,\{{{\tilde{x}}} \in S_{h-1} :W({\tilde{x}}) = W\}}$, then (9.7) is equal to

$$\begin{aligned} \sum _W \#S_{h-1,W} \cdot q^{n_0(\#J - \dim W)} \cdot \sum _{a \in W} \theta (1 + \varpi ^{h-1}[a]). \end{aligned}$$

But as $\theta$ is assumed to be primitive in the theorem, this expression is equal to 0 once we show the following lemma:

Lemma 9.6

Let ${{\tilde{x}}} \in S_{h-1}$. Then there is some $r \mid n'$, $r < n'$ such that $W({{\tilde{x}}}) = \ker ({{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0r}}})$.

Proof

Write $W = W({{\tilde{x}}})$. Consider the perfect symmetric ${\mathbb {F}}_{q^{n_0}}$-bilinear trace pairing

$$\begin{aligned} {\mathbb {F}}_{q^n} \times {\mathbb {F}}_{q^n} \rightarrow {\mathbb {F}}_{q^{n_0}}, \qquad (x,y) \mapsto {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}(xy). \end{aligned}$$

It is an immediate computation that $\ker ({{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0r}}})^\perp = {\mathbb {F}}_{q^{n_0r}}$ for any divisor r of $n'$, so we need to show that $W^{\perp }$ is of the form ${\mathbb {F}}_{q^{n_0r}}$ for some $r<n'$. For this, it suffices to show that $W^{\perp }$ is an ${\mathbb {F}}_{q^{n_0}}$-algebra, which is properly contained in ${\mathbb {F}}_{q^n}$.

First of all note that $W^{\perp }$ contains 1 since for all $(i,j) \in J$, $m_{1,i} {\bar{x}}_j \in \ker ({{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}})$ (as in the proof of Lemma 9.5). Since $W^\perp$ is an ${\mathbb {F}}_{q^{n_0}}$-vector space and contains 1, it must contain ${\mathbb {F}}_{q^{n_0}}$. It remains to show that $W^{\perp }$ is closed under multiplication. We now use that J is of the form

$$\begin{aligned} J = \{(i,j):1\le i \le n' -\ell , \, n'-\ell +1 \le j \le n, \} \end{aligned}$$

for some $1\le \ell \le n'$ (see Sect. 9.1.1). For a fixed $n'-\ell +1 \le j \le n'$, let

$$\begin{aligned} {L_j \,{:=}\,\mathrm{span}_{{\mathbb {F}}_{q^{n_0}}} \left\langle m_{1,i} {\bar{x}}_j :1\le i \le n'-\ell \right\rangle ^{\perp }.} \end{aligned}$$

Observe that the $m_{1,i}$ are all ${\mathbb {F}}_{q^{n_0}}$-linearly independent (since b is the special representative) and hence $L_j$ has dimension $n'-\ell$. For $1 \le i \le n' - \ell$ and $n' - \ell + 1 \le i' \le n'$ we have

$$\begin{aligned} {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}} \left( m_{1,i}{{\bar{x}}}_j \cdot \frac{{{\bar{x}}}_{i'}}{{{\bar{x}}}_j} \right) = {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}( m_{1,i}{{\bar{x}}}_{i'}) = 0, \end{aligned}$$

as in the proof of Lemma 9.5. This implies the inclusion “$\supseteq$” in the formula

$$\begin{aligned} L_j = \mathrm{span}_{{\mathbb {F}}_{q^{n_0}}} \left\langle \frac{{\bar{x}}_{i'}}{{\bar{x}}_j} :n' -\ell + 1 \le i' \le n' \right\rangle . \end{aligned}$$

The other inclusion follows by dimension reasons. As W is generated by all $L_j^\perp$ ($n' - \ell + 1\le j \le n'$), we have $W^{\perp } = \bigcap _{j=n-\ell + 1}^n L_j$. Let $v,w \in W^{\perp }$. We need to show that $vw \in W^{\perp }$, i.e., that for all $(i_0,j_0) \in J$ we have ${{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}(m_{1,i_0}{\bar{x}}_{j_0} v w) = 0$. As $v\in L_{j_0}$, we may write $v = \sum _{(a,j_0) \in J} v_a \cdot \frac{{{\bar{x}}}_i}{{{\bar{x}}}_{j_0}}$ with $v_a \in {\mathbb {F}}_{q^{n_0}}$. Then

$$\begin{aligned} {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}(m_{1,i_0}{\bar{x}}_{j_0} v w)&= {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}} \left( m_{1,i_0}{\bar{x}}_{j_0} \left( \textstyle \sum \limits _{(a,j_0) \in J} v_a \cdot \frac{{{\bar{x}}}_a}{{{\bar{x}}}_{j_0}} \right) w \right) \\&= \textstyle \sum \limits _{(a,j_0) \in J} v_a \cdot {{\,\mathrm{Tr}\,}}_{{\mathbb {F}}_{q^n}/{\mathbb {F}}_{q^{n_0}}}\left( m_{1,i_0} {{\bar{x}}}_a w \right) = 0, \end{aligned}$$

where the last equality holds since $w \in W^{\perp }$ is orthogonal to each $L_a^{\perp }.$ $\square$

13 Part 4. Automorphic induction and the Jacquet–Langlands correspondence

In this part, we use the results of Parts 2 and 3 to study the $\ell$-adic homology groups of the semi-infinite Deligne–Lusztig variety $\dot{X}_{\dot{w}}^{DL}(b)$, which by Theorem 6.9 along with Corollary 6.19 is isomorphic to the affine Deligne–Lusztig variety at infinite level $\dot{X}_w^\infty (b)$ constructed in Sect. 6. In Sect. 10, we recall methods of Henniart characterizing certain representations by considering the action of very regular elements. In Sect. 11, we define the homology of $\dot{X}_w^\infty (b) \cong X_w^{DL}$ and give a representation-theoretic description of

$$\begin{aligned} {R_T^G(\theta ) \,{:=}\,\sum _{i \ge 0} (-1)^i H_i(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] \qquad \text {for }\theta :T = L^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times \text { smooth}} \end{aligned}$$

in terms of the cohomology of the finite-type variety $X_h$ studied in the previous two parts of the paper. Using methods of Henniart as reviewed in Sect. 10, we prove Theorem 11.3: if $|R_T^G(\theta )|$ is irreducible supercuspidal, then the assignment $\theta \mapsto |R_T^G(\theta )|$ realizes automorphic induction. To finish, we prove in Sect. 12 that when $\theta :L^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ is minimal admissible, then $|R_T^G(\theta )|$ is irreducible supercuspidal.

We now give some basic definitions which we will use throughout the next few sections. Recall that for any smooth character $\theta :L^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$, there exists an integer $h \ge 1$ such that $\theta$ is trivial on $U_L^h = 1 + \varpi ^h {\mathcal {O}}_L$. We call the smallest such h the level of $\theta$. We say that $\theta$ is in general position if its stabilizer in ${{\,\mathrm{Gal}\,}}(L/K)$ is trivial. Let ${\mathscr {X}}$ denote the set of such characters.

We say that an element x of $L^\times$ is very regular if $x \in {\mathcal {O}}_L^\times$ and its image in the residue field ${\mathbb {F}}_{q^n}$ generates its multiplicative group ${\mathbb {F}}_{q^n}^{\times }$.

We say that a virtual representation is a genuine representation if it is a nonnegative linear combination of irreducible representations. If R is a virtual representation that is $\pm \pi$, where $\pi$ is a genuine representation, we write $|R| = \pi$.

14 Results of Henniart on the local Langlands correspondence

In this section, we review the methods of Henniart [19, 20] characterizing certain cases of automorphic induction by considering the action of very regular elements. We give a generalization of the discussions of [6] to all inner forms of ${{\,\mathrm{GL}\,}}_n(K)$. There are no technical difficulties in doing this, but we provide it for completeness of our paper.

Fix a character $\epsilon$ of $K^\times$ with $\ker (\epsilon ) = {{\,\mathrm{Nm}\,}}_{L/K}(L^\times )$, and let ${\mathcal {G}}_K^\epsilon (n)$ denote the set of irreducible n-dimensional representations $\sigma$ of the Weil group ${\mathcal {W}}_K$ such that $\sigma \cong \sigma \otimes (\epsilon \circ \mathrm{rec}_K^{-1})$, where $\mathrm{rec}_K :K^{\times } \rightarrow {\mathcal {W}}_K^{ab}$ is the reciprocity isomorphism from local class field theory. It is known that every element of ${\mathcal {G}}_K^\epsilon (n)$ is of the form ${{\,\mathrm{Ind}\,}}_{{\mathcal {W}}_L}^{{\mathcal {W}}_K}(\theta )$ for some character $\theta \in {\mathscr {X}}$. However, it is also known that automorphic induction is not compatible with induction on Weil groups in the sense that the Langlands parameter may have a twist by a rectifying character. Hence the approach we take is via the $\chi$-datum of Langlands–Sheldstad [24, Section 2.5]. Because L/K is unramified, there is a canonical choice of $\chi$-datum, and this gives rise to a bijection

$$\begin{aligned} {\mathscr {X}}/{{\,\mathrm{Gal}\,}}(L/K) \rightarrow {\mathcal {G}}_K^\epsilon (n), \qquad \theta \mapsto \sigma _\theta . \end{aligned}$$

See [11, Section 7.2] for an exposition and an explicit discussion of the unramified setting. Note that $\sigma _\theta$ differs from the notation of [6] by a rectifying character.

Let ${\mathcal {A}}_K^\epsilon ({{\,\mathrm{GL}\,}}_n)$ denote the set of isomorphism classes of irreducible supercuspidal representations $\pi$ of ${{\,\mathrm{GL}\,}}_n(K)$ such that $\pi \cong \pi \otimes (\epsilon \circ \det )$. There is a canonical bijection

$$\begin{aligned} {\mathcal {G}}_K^\epsilon (n) {\mathop {\longrightarrow }\limits ^\mathrm{LLC}} {\mathcal {A}}_K^\epsilon ({{\,\mathrm{GL}\,}}_n), \qquad \sigma _\theta \mapsto \pi _\theta \end{aligned}$$

satisfying certain properties. By work of Henniart, the character of $\pi _\theta$ is very nicely behaved on certain elements of ${{\,\mathrm{GL}\,}}_n(K)$.

Now let G be an inner form of ${{\,\mathrm{GL}\,}}_n(K)$ so that $G \cong {{\,\mathrm{GL}\,}}_{n'}(D_{k_0/n_0})$, where $D_{k_0/n_0}$ is the division algebra of dimension $n_0^2$ over K with Hasse invariant $k_0/n_0$. Let ${\mathcal {A}}_K^\epsilon (G)$ denote the set of isomorphism classes of irreducible supercuspidal representations $\pi '$ of G such that $\pi ' \cong \pi ' \otimes (\epsilon \circ \det )$. By the Jacquet–Langlands correspondence, there is a canonical bijection

$$\begin{aligned} {{\mathcal {A}}_K^\epsilon ({{\,\mathrm{GL}\,}}_n) {\mathop {\longrightarrow }\limits ^\mathrm{JLC}} {\mathcal {A}}_K^\epsilon (G), \qquad \pi \mapsto \pi ' \,{:=}\,{{\,\mathrm{JL}\,}}(\pi )} \end{aligned}$$

such that the central characters of $\pi$ and $\pi '$ match and such that their characters on regular semisimple elements differs by $(-1)^{n-n'}$.

Remark 10.1

We remark that the notation $\pi _\theta$ agrees with the $\pi (\theta )$ of [20], but with the $\pi '(\theta )$ (rather than the $\pi (\theta )$) of [19]. When n is odd, there is no discrepancy, but when n is even, our $\pi _\theta$ is the representation $\pi _{\theta \omega } = \pi '(\theta )$ in [19], where $\omega$ is the unique unramified character of $L^\times$ of order 2. $\Diamond$

The following theorem can be found in [19, Section 3.14].

Theorem 10.2

(Henniart) For each $\theta \in {\mathscr {X}}$, there exists a constant $c_\theta = \pm 1$ such that

$$\begin{aligned} {{\,\mathrm{Tr}\,}}{{\,\mathrm{JL}\,}}(\pi _\theta )(x) = c_\theta \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x) \end{aligned}$$

for every very regular element $x \in L^\times \subset {{\,\mathrm{GL}\,}}_n(K)$.

As we will see momentarily, one can even go the other direction: the trace of $\pi \in {\mathcal {A}}_K^\epsilon ({{\,\mathrm{GL}\,}}_n)$ on very regular elements of $L^\times$ characterizes $\pi$. Furthermore, $c_\theta$ can be pinpointed for ${{\,\mathrm{GL}\,}}_n(K)$ by [19, Theorem 3.14] and extended to any inner form of ${{\,\mathrm{GL}\,}}_n(K)$ via the character condition of the Jacquet–Langlands correspondence. For each positive integer r and each $\theta \in {\mathscr {X}}$, consider the subgroup of ${{\,\mathrm{Gal}\,}}(L/K)$ given by ${{\mathscr {G}}_{\theta ,r} \,{:=}\,\{\gamma \in {{\,\mathrm{Gal}\,}}(L/K) : a(\gamma ) \le r\}}$, where $a(\gamma )$ is the level of $\theta /\theta ^\gamma$.

Theorem 10.3

(Henniart) The constant $c_\theta$ of Theorem 10.2 satisfies

$$\begin{aligned} (-1)^{n-n'} c_\theta = {\left\{ \begin{array}{ll} + 1 &{}\quad \text {if }n\text { is odd,} \\ + 1 &{}\quad \text {if }n\text { is even and }s\text { is even,} \\ - 1 &{}\quad \text {if }n\text { is even and }s\text { is odd,} \end{array}\right. } \end{aligned}$$

where s is such that ${\mathscr {G}}_{\theta ,s} \smallsetminus {\mathscr {G}}_{\theta ,s-1}$ contains the unique element of order 2 in ${{\,\mathrm{Gal}\,}}(L/K)$.

Lemma 10.4

(Henniart) Let $\theta \in {\mathscr {X}}$ and suppose that there exists a character $\theta '$ of $L^\times$ (a priori, not necessarily in ${\mathscr {X}}$) such that $\theta (\varpi ) = \theta '(\varpi )$ and

$$\begin{aligned} c \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x) = c' \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta '{}^\gamma (x) \end{aligned}$$

(10.1)

for all very regular elements of $x \in L^\times$. Assume in addition that $c = c'$ in the special case $n = 2$, $q = 3$, and $\theta |_{U_L^1}$ factors through the norm $U_L^1 \rightarrow U_K^1$ (i.e. $\theta \in {\mathscr {X}}^0$ with notation from Sect. 12). Then

$$\begin{aligned} \theta ' = \theta ^\gamma \qquad \text {for some }\gamma \in {{\,\mathrm{Gal}\,}}(L/K). \end{aligned}$$

Proof

We provide the proof in the case that $\theta |_{U_L^1}$ has trivial ${{\,\mathrm{Gal}\,}}(L/K)$-stabilizer, following [20, Section 5.3] (see also [6, Lemma 1.7]). This is the simplest setting. In [20, Section 5.3], Henniart proves the lemma for $\theta \in {\mathscr {X}}$ in the case [L : K] is prime by essentially the arguments presented here. A significantly more involved incarnation of these arguments is used in [19, Identity (2.5), Sections 2.6–2.12] to prove the lemma in full generality as stated.

We first show that the conclusion holds on $U_L^1$. Fix a very regular element $x \in L^\times$. Since every element of $x U_L^1 \subset L^\times$ is a very regular element, the assumption implies that we have an equation of linear dependence between the 2n characters of $U_L^1$ given by the restrictions of the ${{\,\mathrm{Gal}\,}}(L/K)$-translates of $\theta$ and $\theta '$. Explicitly: on $U_L^1$, we have

$$\begin{aligned} \theta ' = c'{}^{-1} \theta '(x)^{-1} \cdot \left( \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} c\theta ^\gamma (x) \cdot \theta ^\gamma - \sum _{1 \ne \gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta '(x)^{-1} \theta '{}^\gamma (x) \cdot \theta '{}^\gamma \right) . \end{aligned}$$

Considering the character inner product of $\theta '$ with $\theta ^{\gamma '}$ on $U_L^1$ for some fixed $\gamma ' \in {{\,\mathrm{Gal}\,}}(L/K)$, we have:

$$\begin{aligned} \langle \theta ', \theta ^{\gamma '} \rangle = \frac{c \cdot \theta ^{\gamma '}(x)}{c' \cdot \theta '(x)} - c' \cdot \sum _{1 \ne \gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta '{}^\gamma (x) \langle \theta '{}^\gamma , \theta ^{\gamma '} \rangle . \end{aligned}$$

If $\langle \theta '{}^\gamma , \theta ^{\gamma '} \rangle = 1$ for some $1 \ne \gamma \in {{\,\mathrm{Gal}\,}}(L/K)$, then we are done. Otherwise, we must have $c' \theta '(x) = c \theta ^{\gamma '}(x)$ and $\theta ' = \theta ^{\gamma '}$ on $U_L^1$ since $\theta , \theta '$ agree on $K^\times$.

We have now shown that there exists a $\gamma \in {{\,\mathrm{Gal}\,}}(L/K)$ such that $\theta '(x) = \theta ^\gamma (x)$ for any very regular element $x \in L^\times$. But now it follows that $\theta ' = \theta ^\gamma$ on ${\mathcal {O}}_L^\times$ since any very regular element together with $U_L^1$ generate ${\mathcal {O}}_L^\times$. The desired conclusion now follows by the assumption $\theta (\pi ) = \theta '(\pi )$ since $\langle \varpi \rangle \cdot {\mathcal {O}}_L^\times = L^\times$. $\square$

From Lemma 10.4, we obtain the following result:

Proposition 10.5

(Henniart, Boyarchenko–Weinstein) Let $\theta \in {\mathscr {X}}$ and let G be any inner form of ${{\,\mathrm{GL}\,}}_n(K)$. Assume that $\pi$ is an irreducible supercuspidal representation of G with central character $\theta |_{K^\times }$ satisfying:

• (i) $\pi \cong \pi \otimes (\epsilon \circ \det )$,

• (ii) there exists a constant $c \ne 0$ satisfying ${{\,\mathrm{Tr}\,}}\pi (x) = c \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x)$ for each very regular element $x \in L^\times$.

If $n = 2$, $q = 3$, and $\theta |_{U_L^1}$ factors through the norm $U_L^1 \rightarrow U_K^1$ (i.e. $\theta \in {\mathscr {X}}^0$ with notation from Sect. 12), assume in addition that $c = {\left\{ \begin{array}{ll} -1 &{} \text {if }G \cong {{\,\mathrm{GL}\,}}_2(K) \\ +1 &{} \text {if }G \cong D_{1/2}^\times \end{array}\right. }$. Then $\pi$ corresponds to $\theta$ under automorphic induction and the Jacquet–Langlands correspondence:

$$\begin{aligned} \pi \cong {{\,\mathrm{JL}\,}}(\pi _\theta ). \end{aligned}$$

Proof

This is [6, Proposition 1.5] (combined with the remarks of Section 1.4 of op. cit.) when $G \cong {{\,\mathrm{GL}\,}}_n(K)$ or $G \cong D_{1/n}^\times$. The proof extends to the general situation with no complications. $\square$

15 Homology of affine Deligne–Lusztig varieties at infinite level

We explain how the results of Part 3 on the cohomology of the finite-type of ${\mathbb {F}}_{q^n}$-schemes $X_h$ for $h \ge 1$ (Proposition-Definition 7.11, Proposition 7.12) allows one to define and determine homology groups of the schemes $\dot{X}_w^\infty (b)$.

15.1 Definition of the homology groups

Following [25], for any smooth ${{\overline{{\mathbb {F}}}}}_q$-scheme S of pure dimension d, we set

$$\begin{aligned} {H_i(S, {{\overline{{\mathbb {Q}}}}}_\ell )\,{:=}\,H_c^{2d-i}(S, \overline{{\mathbb {Q}}}_\ell )(d),} \end{aligned}$$

where (d) denotes the dth Tate twist. Recall from Proposition 7.4 that for any $h \ge 1$, the ${\mathbb {F}}_{q^n}$-scheme $X_h$ is smooth of pure dimension $(n-1)(h-1) + (n'-1)$.

By Proposition 6.12, Corollary 6.19 and (7.1), we have

$$\begin{aligned} \dot{X}_w^\infty (b) = \bigsqcup _{g \in G/G_{\mathcal {O}}} \varprojlim _{r > m \ge 0} g \cdot \dot{X}_{\dot{w}_r}^m(b)_{{\mathscr {L}}_0} = \bigsqcup _{g \in G/G_{\mathcal {O}}} \varprojlim _h X_h. \end{aligned}$$

By Proposition 7.7, we have the natural inclusion

$$\begin{aligned} H_i(X_{h-1}, {{\overline{{\mathbb {Q}}}}}_\ell ) = H_i(X_h, \overline{{\mathbb {Q}}}_\ell )^{{\mathbb {W}}_h^{h-1}({\mathbb {F}}_{q^n})} \subseteq H_i(X_h, \overline{{\mathbb {Q}}}_\ell ). \end{aligned}$$

We may therefore define

$$\begin{aligned} H_i \left( \dot{X}_w^\infty (b)_{{\mathscr {L}}_0}, {{\overline{{\mathbb {Q}}}}}_\ell \right)&= H_i \left( \varprojlim _h X_h, {{\overline{{\mathbb {Q}}}}}_\ell \right) \,{:=}\,\varinjlim _{h} H_i\left( X_h, {{\overline{{\mathbb {Q}}}}}_\ell \right) , \\ H_i\left( \dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell \right)&= \bigoplus _{G/G_{{\mathcal {O}}}} H_i\left( g \cdot \dot{X}_w^\infty (b)_{{\mathscr {L}}_0}, {{\overline{{\mathbb {Q}}}}}_\ell \right) . \end{aligned}$$

Recall that in Theorem 6.9 we extended the action of ${\mathcal {O}}_L^{\times }$ on $\dot{X}_w^\infty (b)$ to an action of $T=L^{\times }$.

Definition 11.1

For any (smooth) character $\theta :T \rightarrow \overline{{\mathbb {Q}}}_\ell ^\times$, define the virtual G-representation

$$\begin{aligned} {R_T^G(\theta ) \,{:=}\,\sum _{i \ge 0} (-1)^i H_i(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ],} \end{aligned}$$

where $[\theta ]$ denotes the subspace where T acts by $\theta$.

Let Z denote the center of G.

Theorem 11.2

Let $\theta :T = L^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be a character of level $h \ge 1$. Then as G-representations,

$$\begin{aligned} R_T^G(\theta ) \cong {{\,\mathrm{c-Ind}\,}}_{Z \cdot G_{\mathcal {O}}}^G\left( R_{T_h}^{G_h}(\theta )\right) , \end{aligned}$$

(11.1)

where we view the (virtual) $G_h$-representation $R_{T_h}^{G_h}(\theta )$ as a $G_{\mathcal {O}}$-representation by pulling back along the natural surjection $G_{\mathcal {O}}\rightarrow G_h$ and then extend to Z by letting $\varpi$ act by $\theta (\varpi )$. Furthermore, for any very regular element $x \in L^\times$,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; R_T^G(\theta )\right) = \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x). \end{aligned}$$

Proof

The stabilizer of $\dot{X}_w^{\infty }(b)_{{\mathscr {L}}_0} \subseteq \dot{X}_w^{\infty }(b)$ in G is $G_{{\mathcal {O}}}$. Let $T_{{\mathcal {O}}}$ be the preimage of ${\mathcal {O}}_L^{\times }$ under $T \cong L^{\times }$. It is easy to see that the stabilizer of $\dot{X}_w^{\infty }(b)_{{\mathscr {L}}_0} \subseteq \dot{X}_w^{\infty }(b)$ in $G\times T$ is the subgroup $\Gamma$ generated by $G_{\mathcal {O}}\times T_{\mathcal {O}}$ and $(\varpi , \varpi ^{-1})$. Hence as representations of $G \times T$, we have

$$\begin{aligned} \sum (-1)^i H_i(\dot{X}_w(b), {{\overline{{\mathbb {Q}}}}}_\ell ) \cong {{\,\mathrm{c-Ind}\,}}_{\Gamma }^{T \times G}\left( \sum (-1)^i H_i(\dot{X}_w(b)_{{\mathscr {L}}_0}, {{\overline{{\mathbb {Q}}}}}_\ell )\right) . \end{aligned}$$

Now let ${{\widetilde{\Gamma }}}$ be the subgroup of $G \times T$ generated by $\Gamma$ and $\{1\} \times T$. Note that $\widetilde{\Gamma }\cong Z G_{\mathcal {O}}\times T$. The isomorphism (11.1) follows from the above together with the definition of the homology groups of $\dot{X}_w(b)_{{\mathscr {L}}_0}$ in terms of the cohomology of $X_h$ (remembering that $\theta$ has level h by assumption).

It remains to determine the character on very regular elements of $L^\times .$ We use (11.1) together with the corresponding character formula result for $X_h$ (Proposition 8.3). By Lemma 5.7, we know that for each $\varphi \in {{\,\mathrm{Gal}\,}}(L/K)$, there exists an element $g_\varphi \in N_G(G_{\mathcal {O}})$ satisfying $g_\varphi x g_\varphi ^{-1} = \varphi (x)$ for all $x \in L^\times$ and that if $\varphi \in {{\,\mathrm{Gal}\,}}(L/K)[n']$, one can choose $g_\varphi \in G_{\mathcal {O}}$. By Sect. 5.5, we know that $N_G(G_{\mathcal {O}})/G_{\mathcal {O}}\cong {\mathbb {Z}}/n_0 {\mathbb {Z}}$, and therefore using the fact that

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; R_{T_h}^{G_h}(\theta )\right) = \sum _{\varphi \in {{\,\mathrm{Gal}\,}}(L/K)[n']} \theta (g_\varphi x g_\varphi ^{-1}) \end{aligned}$$

by Proposition 8.3, we have:

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; R_T^G(\theta )\right) = \sum _{\begin{array}{c} g \in G/Z G_{\mathcal {O}}\\ g x g^{-1} \in Z G_{\mathcal {O}} \end{array}} {{\,\mathrm{Tr}\,}}\left( x^* ; R_{T_h}^{G_h}(\theta )\right) = \sum _{\varphi \in {{\,\mathrm{Gal}\,}}(L/K)} \theta (g_\varphi x g_\varphi ^{-1}). \end{aligned}$$

$\square$

Theorem 11.3

Let $\theta \in {\mathscr {X}}$. If $|R_T^G(\theta )|$ is irreducible supercuspidal, then the assignment $\theta \mapsto |R_T^G(\theta )|$ is a geometric realization of automorphic induction and the Jacquet–Langlands correspondence. That is,

$$\begin{aligned} |R_T^G(\theta )| \cong {{\,\mathrm{JL}\,}}(\pi _\theta ), \end{aligned}$$

where ${{\,\mathrm{JL}\,}}$ denotes the Jacquet–Langlands transfer of the ${{\,\mathrm{GL}\,}}_n(K)$-representation $\pi _\theta$ to the (possibly split) inner form G of ${{\,\mathrm{GL}\,}}_n(K)$. Moreover, writing $|R_T^G(\theta )| = c_\theta ' R_T^G(\theta )$ for $c_\theta ' \in \{\pm 1\}$, we have $c_\theta ' = c_\theta$.

Remark 11.4

If $|R_T^G(\theta )|$ is irreducible supercuspidal, then $R_T^G(\theta ) = (-1)^{r_\theta } \pi$, where $\pi$ is an irreducible supercuspidal representation occurring in $H_{r_\theta }(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$ for some $r_\theta \in {\mathbb {Z}}$. (There may be other degrees where $\pi$ contributes, but they all cancel out. In particular, there may be more than one choice of $r_\theta$, but the parity of $r_\theta$ is invariant.) Then by Theorem 11.3 implies that $c_\theta = (-1)^{r_\theta }$, which gives a geometric interpretation of Henniart’s sign $c_\theta$ in terms of the surviving cohomological degree in the alternating sum $R_T^G(\theta )$. $\Diamond$

Proof

Write $|R_T^G(\theta )| = c_\theta ' R_T^G(\theta )$ for some $c_\theta ' = \pm 1$. If we can show that $|R_T^G(\theta )|$ satisfies the hypotheses of Proposition 10.5, then we are done. By assumption, $|R_T^G(\theta )|$ is an irreducible cuspidal representation and by definition of the $G \times T$ action on $R_T^G(\theta )$, the central character of $|R_T^G(\theta )|$ must be $\theta |_{K^\times }$.

To see that (i) of Proposition 10.5 holds, note that since L/K is unramified we have $\langle \varpi ^n \rangle {\mathcal {O}}_K^\times = {{\,\mathrm{Nm}\,}}_{L/K}(L^\times ) = \ker (\epsilon )$. In particular, we see that $\epsilon \circ \det$ is trivial on $Z G_{\mathcal {O}}$ and so by Theorem 11.2, we have $|R_T^G(\theta )| \cong |R_T^G(\theta )| \otimes (\epsilon \circ \det )$.

We now establish (ii) of Proposition 10.5 and the additional assumption in the special case $n=2$ and $q=3$. By Theorem 11.2, we have that for any very regular element $x \in L^\times$,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}(x^* ; |R_T^G(\theta )|) = c_\theta ' \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x). \end{aligned}$$

If $n=2$, $q = 3$, and $\theta \in {\mathscr {X}}^0$, then by Theorem 12.2, we know in addition that

$$\begin{aligned} c_\theta ' = (-1)^{n'-1} = {\left\{ \begin{array}{ll} -1 &{}\quad \text {if }G \cong {{\,\mathrm{GL}\,}}_2(K), \\ +1 &{}\quad \text {if }G \cong D_{1/2}^\times . \end{array}\right. } \end{aligned}$$

We have now established all the conditions required by Proposition 10.5 to conclude that $c_\theta ' = c_\theta$ and $|R_T^G(\theta )| \cong {{\,\mathrm{JL}\,}}(\pi _\theta ).$ $\square$

16 A geometric realization of automorphic induction and Jacquet–Langlands

In this section, we write down the cases in which we can prove Theorem 11.3 unconditionally. To this end, we consider the following two subsets of ${\mathscr {X}}$:

$$\begin{aligned} {\mathscr {X}}^0&\,{:=}\,\{\theta \in {\mathscr {X}}: \theta |_{U_L^1}\text { factors through the norm map }U_L^1 \rightarrow U_K^1\} \\ {\mathscr {X}}^{\mathrm{min}}&\,{:=}\,\{\theta \in {\mathscr {X}}: \theta \text { is minimal admissible}\} \\&= \{\theta \in {\mathscr {X}}: \text {the }\theta /\theta ^\gamma \text { have the same level for any }1 \ne \gamma \in {{\,\mathrm{Gal}\,}}(L/K)\} \end{aligned}$$

Note that ${\mathscr {X}}^0 \subseteq {\mathscr {X}}^{\mathrm{min}}$ is the “depth zero” part of ${\mathscr {X}}^{\mathrm{min}}$.

Remark 12.1

Let $\theta \in L^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$ be a smooth character with trivial ${{\,\mathrm{Gal}\,}}(L/K)$-stabilizer. Then its restriction to ${\mathcal {O}}_L^\times$ must have trivial ${{\,\mathrm{Gal}\,}}(L/K)$-stabilizer. For the reader’s convenience, we summarize the relation between minimal admissibility and similar notions in the literature:

$\cdot$:

$\theta$ is minimal admissible if and only if $(L/K, \theta )$ form a minimal admissible pair, which happens if and only if $\theta$ has only one “jump” in the sense of Bushnell–Henniart [9, Section 1.1].

$\cdot$:

$\theta$ is minimal admissible if and only if it can be written in the form $\theta _{\mathrm{prim}} \cdot (\chi \circ {{\,\mathrm{Nm}\,}}_{L/K})$ for some smooth $\chi :K^\times \rightarrow {{\overline{{\mathbb {Q}}}}}_\ell ^\times$, where $\theta _{\mathrm{prim}}$ is primitive in the sense of Boyarchenko–Weinstein [7, Section 7.1] (see also Sect. 8 of the present paper).

$\cdot$:

Let h be such that $\theta |_{U_L^h} = 1$ and $\theta |_{U_L^{h-1}} \ne 1$. Then $\theta$ is primitive if and only if $\theta$ is regular as a character of ${\mathcal {O}}_L^\times /U_L^h$ in the sense of Lusztig [26, Section 1.5], when ${\mathcal {O}}_L^\times /U_L^h$ is the F-fixed points of a maximal torus (see Remark 8.5). $\Diamond$

16.1 Depth zero representations

In this section we only consider characters $\theta \in {\mathscr {X}}^0$ and give a nonvanishing result for the individual cohomology groups $H_i(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$. Since each $\theta \in {\mathscr {X}}^0$ is of the form $\theta _0 \cdot (\chi \circ {{\,\mathrm{Nm}\,}}_{L/K})$, where $\theta _0 \in {\mathscr {X}}^0$ and $\theta _0|_{U_L^1} = 1$, determining when $H_i(\dot{X}_w^\infty (b), \overline{{\mathbb {Q}}}_\ell )[\theta ] \ne 0$ can be reduced to the corresponding question for the cohomology of classical Deligne–Lusztig varieties. Recall from Proposition 7.4 that $\dim X_h = (n-1)(h-1)+(n'-1)$.

Theorem 12.2

Fix $\theta \in {\mathscr {X}}^0$ of level h and write $\theta = \theta _0 \cdot (\chi \circ {{\,\mathrm{Nm}\,}}_{L/K})$ for some $\theta \in {\mathscr {X}}^0$ of level 1 and some character $\chi$ of $K^\times$ of level h. Then:

• (i) the cohomology groups $H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$ are concentrated in a single degree and

  $$\begin{aligned} |R_{T_h}^{G_h}(\theta )| = H_c^{2(n-1)(h-1) + n'-1}(X_h, \overline{{\mathbb {Q}}}_\ell )[\theta ] \cong H_c^{n'-1}(X_1, \overline{{\mathbb {Q}}}_\ell )[\theta _0] \otimes (\chi \circ \det ) \end{aligned}$$

• (ii) the homology groups $H_i(\dot{X}_w^\infty (b), \overline{{\mathbb {Q}}}_\ell )[\theta ]$ are concentrated in a single degree and

  $$\begin{aligned} |R_T^G(\theta )| = H_{n'-1}(\dot{X}_w^\infty (b), \overline{{\mathbb {Q}}}_\ell )[\theta ] \cong {{\,\mathrm{c-Ind}\,}}_{Z \cdot {{\,\mathrm{GL}\,}}_{n'}({\mathcal {O}}_{D_{k_0/n_0}})}^{{{\,\mathrm{GL}\,}}_{n'}(D_{k_0/n_0})}\left( \rho _\theta \right) \end{aligned}$$

  (12.1)

  is an irreducible supercuspidal representation of G. Here $\rho _\theta$ is the extension of the ${{\,\mathrm{GL}\,}}_{n'}({\mathcal {O}}_{D_{k_0/n_0}})$-representation $H_c^{n'-1}(X_1, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta _0] \otimes (\chi \circ \det )$ obtained by letting $\varpi \in Z = K^\times$ act by $\theta (\varpi )$.

Moreover, $|R_{T_h}^{G_h}(\theta )| = (-1)^{n'-1} R_{T_h}^{G_h}(\theta )$ and $|R_T^G(\theta )| = (-1)^{n'-1} R_T^G(\theta ).$

Proof

By Lemma 8.4 and Proposition 7.7, we have, as $G_h$-representations

$$\begin{aligned} H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta _0 \circ (\chi \circ {{\,\mathrm{Nm}\,}}_{L/K})] \cong H_c^i(X_h, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta _0] \otimes (\chi \circ \det ) \cong H_c^{i-2(n-1)(h-1)}(X_1, \overline{{\mathbb {Q}}}_\ell )[\theta _0] \end{aligned}$$

for all $i \ge 2(n-1)(h-1)$. This reduces the cohomology calculation to a statement about $X_1$, which is a classical Deligne–Lusztig variety attached to the maximal torus ${\mathbb {F}}_{q^n}^\times$ in ${{\,\mathrm{GL}\,}}_{n'}({\mathbb {F}}_{q^{n_0}})$. By [13, Corollary 9.9],

$$\begin{aligned} H_c^i(X_1, {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] \ne 0 \qquad \Longleftrightarrow \qquad i = n' - 1. \end{aligned}$$

This proves (i). Since $\dim X_h = (n-1)(h-1) + n'-1$ by Proposition 7.4, we now also see the nonvanishing assertion of (ii) and $H_{n'-1}(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$ has the form 12.1 by Theorem 11.2. It is well known that this representation is irreducible and supercuspidal (see also Theorem 12.5). For example, one can show by hand (by the first part of the proof of Theorem 12.5) that the induction to the normalizer of $Z G_{\mathcal {O}}$ is irreducible, and then the conclusion follows from [27, Proposition 6.6]. $\square$

Theorem 12.3

For $\theta \in {\mathscr {X}}^0$, the assignment $\theta \mapsto H_{n'-1}(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ]$ is a geometric realization of automorphic induction and the Jacquet–Langlands correspondence. That is,

$$\begin{aligned} H_{n'-1}(\dot{X}_w^\infty (b), {{\overline{{\mathbb {Q}}}}}_\ell )[\theta ] = (-1)^{n'-1} R_T^G(\theta ) = |R_T^G(\theta )| \cong {{\,\mathrm{JL}\,}}(\pi _\theta ). \end{aligned}$$

Proof

By Theorem 12.2, we know that $|R_T^G(\theta )| = (-1)^{n'-1} R_T^G(\theta )$ is an irreducible supercuspidal representation, and by Theorem 11.2, we know that for any very regular element $x \in L^\times$,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}(x^* ; |R_T^G(\theta )|) = (-1)^{n'-1} \cdot \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)} \theta ^\gamma (x). \end{aligned}$$

By definition $\epsilon$ is a finite-order character of $K^\times$ with $\ker (\epsilon ) = {{\,\mathrm{Nm}\,}}_{L/K}(K^\times )$. Since L/K is unramified, $\ker (\epsilon )$ contains ${\mathcal {O}}_K^\times$, and therefore $\epsilon \circ \det$ is trivial on $Z \cdot {{\,\mathrm{GL}\,}}_{n'}({\mathcal {O}}_{D_{k_0/n_0}})$. Hence $|R_T^G(\theta )| \otimes (\epsilon \circ \det ) \cong |R_T^G(\theta )|$. We can now apply Proposition 10.5, noting that in the case $n=2,$ $q=3$, we have the correct sign $c_\theta$ (compare with Theorem 10.3) as required by the proposition. $\square$

Remark 12.4

Observe that as in Remark 11.4, the nonvanishing degree $n'-1$ of the homology of $\dot{X}_w^\infty (b)$ gives a geometric interpretation of Henniart’s sign $c_\theta$ from Theorem 10.3. $\Diamond$

16.2 Representations corresponding to minimal admissible characters

We now prove the supercuspidality of $|R_T^G(\theta )|$ for $\theta \in {\mathscr {X}}^{\mathrm{min}}$. The main technical inputs are the irreducibility of $|R_{T_h}^{G_h}(\theta )|$ (Sect. 8) and a “cuspidality” result for $|R_{T_h}^{G_h}(\theta )|$ (Theorem 9.1).

Theorem 12.5

If $\theta \in {\mathscr {X}}^{\mathrm{min}}$, then $|R_T^G(\theta )|$ is irreducible supercuspidal.

Proof

We first establish some notation. If $\pi :H \rightarrow {{\,\mathrm{GL}\,}}(V)$ is a representation of a subgroup $H \subset G$, then for any $\gamma \in G$, we define ${}^\gamma \pi :\gamma H\gamma ^{-1} \rightarrow {{\,\mathrm{GL}\,}}(V)$ by ${{}^\gamma \pi (g) \,{:=}\,\pi (\gamma ^{-1} g \gamma )}$. Assume that $\theta$ is minimal admissible of level h. By definition, we can write $\theta = \theta ' \otimes (\chi \circ {{\,\mathrm{Nm}\,}})$, where $\theta '$ is a primitive character of $L^\times$ of level $h' \le h$, $\chi$ is any character of $K^\times$ of level h, and ${{\,\mathrm{Nm}\,}}:L^\times \rightarrow K^\times$ is the usual norm. Denoting by $\theta , \theta ', \chi$ the corresponding restrictions to the unit groups, by Proposition 7.7 and Lemma 8.4, we have

$$\begin{aligned} R_{T_h}^{G_h}(\theta ) = R_{T_h}^{G_h}(\theta ' \otimes (\chi \circ {{\,\mathrm{Nm}\,}})) \cong R_{T_h}^{G_h}(\theta ') \otimes (\chi \circ \det ) \cong R_{T_{h'}}^{G_{h'}}(\theta ') \otimes (\chi \circ \det ). \end{aligned}$$

In particular, by Theorem 11.2, we see that

$$\begin{aligned} R_T^G(\theta ) \cong R_T^G(\theta ') \otimes (\chi \circ \det ). \end{aligned}$$

Since twists of irreducible supercuspidal representations are again irreducible supercuspidal, it suffices to prove the theorem for primitive characters $\theta$.

Assume now that $\theta$ is a primitive character of level h. By Theorem 8.1, $|R_{T_h}^{G_h}(\theta )|$ is irreducible. Recall that there is a natural surjection $G_{\mathcal {O}}\rightarrow G_h$ so that we may view $|R_{T_h}^{G_h}(\theta )|$ as a representation of $G_{\mathcal {O}}$. We extend this to a representation of $Z \cdot G_{\mathcal {O}}= \langle \varpi \rangle \cdot G_{\mathcal {O}}$ by letting $\varpi$ act on $|R_{T_h}^{G_h}(\theta )|$ by $\theta (\varpi )$. We first claim that

$$\begin{aligned} {\rho _\theta \,{:=}\,{{\,\mathrm{c-Ind}\,}}_{Z \cdot G_{{\mathcal {O}}}}^{Z \cdot N_{G}(G_{{\mathcal {O}}})}\left( |R_{T_h}^{G_h}(\theta )|\right) } \end{aligned}$$

is irreducible. Recall from Sect. 5.5 that $\# N_G(G_{{\mathcal {O}}})/G_{{\mathcal {O}}} = n_0$ and let $\{1, \varphi _2, \ldots , \varphi _{n_0}\}$ denote a complete set of coset representatives of ${{\,\mathrm{Gal}\,}}(L/K)/{{\,\mathrm{Gal}\,}}(L/K)[n']$. By Lemma 5.7, there exists $g_{\varphi _i} \in N_{G}(G_{{\mathcal {O}}})$ such that $g_{\varphi _i}^{-1} x g_{\varphi _i} = \varphi _i(x)$ for all $x \in {\mathcal {O}}_L^\times$. By Mackey’s irreducibility criterion, it suffices to show that

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{G_{{\mathcal {O}}}}\left( |R_{T_h}^{G_h}(\theta )|, {}^{g_{\varphi _i}}|R_{T_h}^{G_h}(\theta )|\right) = 0, \qquad \text {for }i = 2, \ldots , n_0. \end{aligned}$$

(12.2)

Fix some i with $2 \le i \le n_0$. By Proposition 8.3, for any very regular element $x \in {\mathcal {O}}_L^\times$,

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; {}^{g_{\varphi _i}} R_{T_h}^{G_h}(\theta )\right) = {{\,\mathrm{Tr}\,}}\left( (g_{\varphi _i}^{-1} x g_{\varphi _i})^* ; R_{T_h}^{G_h}(\theta )\right) = \sum _{\gamma \in {{\,\mathrm{Gal}\,}}(L/K)[n']} \theta ^\gamma (\varphi _i(x)). \end{aligned}$$

Applying Lemma 10.4 to the case when $\theta ' = \theta ^{\varphi _i}$ and the base field K is replaced by the unique subfield of index $n'$ in L containing K, we see that

$$\begin{aligned} {{\,\mathrm{Tr}\,}}\left( x^* ; {}^{g_{\varphi _i}}R_{T_h}^{G_h}(\theta )\right) \ne {{\,\mathrm{Tr}\,}}\left( x^* ; R_{T_h}^{G_h}(\theta )\right) . \end{aligned}$$

But now ${}^{g_{\varphi _i}}R_{T_h}^{G_h}(\theta )$ and $R_{T_h}^{G_h}(\theta )$ are irreducible representations of $G_{{\mathcal {O}}}$ whose characters differ from each other, and so necessarily (12.2) holds and $\rho _\theta$ is irreducible.

We now fix $\gamma \in G \smallsetminus N_G(Z \cdot G_{{\mathcal {O}}})$. Once again by Mackey’s criterion, to complete the proof we must show that

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{\gamma Z G_{{\mathcal {O}}} \gamma ^{-1} \cap Z G_{{\mathcal {O}}}} \left( |R_{T_h}^{G_h}(\theta )|, {}^\gamma |R_{T_h}^{G_h}(\theta )|\right) = 0. \end{aligned}$$

(12.3)

At this point, let b be a special representative. By Sect. 5.5, we may assume that $\gamma = \Pi _0^\nu$, where $\nu = (\nu _1, \ldots , \nu _1, \nu _2, \ldots , \nu _2, \ldots , \nu _{n'}, \ldots , \nu _{n'})$ (each $\nu _i$ repeated $n_0$ times) for $0 = \nu _1 \le \nu _2 \le \cdots \le \nu _{n'}$, and $\Pi _0^\nu$ is the block-diagonal matrix whose ith $n_0 \times n_0$ block is given by $\left( {\begin{matrix} 0 &{} \varpi \\ 1_{n_0 - 1} &{} 0 \end{matrix}}\right) ^{\nu _i}$. Observe that if $(A_{i,j})_{1 \le i, j \le n'} \in {{\,\mathrm{GL}\,}}_n(\breve{K})$, where each $A_{i,j}$ is a $(n_0 \times n_0)$-matrix, then

$$\begin{aligned} \Pi _0^{-\nu } \cdot (A_{i,j})_{1 \le i, j \le n'} \cdot \Pi _0^\nu = (\Pi _0^{-\nu _i} A_{i,j} \Pi _0^{\nu _j})_{1 \le i, j \le n'}. \end{aligned}$$

(12.4)

For a parabolic subgroup $P'$ of ${{\,\mathrm{GL}\,}}_{n'}$ containing the upper triangular matrices, let $\breve{N}_{P'}$ be its unipotent radical. Let $\breve{N}_P$ denote the subgroup of ${{\,\mathrm{GL}\,}}_n(\breve{K})$ such that each $(n_0 \times n_0)$-block consists of a diagonal matrix and the (i, j)th block is nonzero if and only if the (i, j)th entry of an element of $\breve{N}_{P'}$ is nonzero. Write $N_P = \breve{N}_P^F \cap G_{\mathcal {O}}$. For $h\ge 1$ let $N_P^h = N_P \cap \ker (G_{\mathcal {O}}\rightarrow G_h)$.

We claim that there exists a parabolic $P' \subseteq {{\,\mathrm{GL}\,}}_{n'}$ as above, such that $\Pi _0^{-\nu } N_P^{h-1} \Pi _0^\nu \subset \ker (G_{\mathcal {O}}\rightarrow G_h)$. Let $1 \le i_0 \le n'$ be the last $\nu _{i_0} = 0$ so that $\nu _{i_0} < \nu _{i_0+1}$, and let $P'$ be the minimal parabolic corresponding to the partition $i_0 + (n'-i_0)$. Let $(A_{i,j})_{1 \le i,j \le n'} \in N_P^{h-1}$ so that each $A_{i,j}$ is a diagonal $n_0 \times n_0$ matrix whose entries all lie in ${\mathbb {W}}_h^{h-1}({{\overline{{\mathbb {F}}}}}_q)$. By (12.4), we see that the (i, j)th block of $\Pi _0^{-\nu } \cdot (A_{i,j})_{1 \le i,j \le n'} \Pi _0^{\nu }$ is $\Pi _0^{-\nu _i} A_{i,j} \Pi _0^{\nu _j}$, so that in particular, if $1 \le i \le i_0$ and $i_0 + 1 \le j \le n'$, then $\nu _j - \nu _i > 0$. By definition of $G_h$ (Sect. 5.3), we now have that $\Pi _0^{-\nu } \cdot (A_{i,j})_{1 \le i,j \le n'} \cdot \Pi _0^{\nu } \in \ker (G_{\mathcal {O}}\rightarrow G_h)$.

The above implies that the restriction of ${}^{\Pi _0^{\nu }} |R_{T_h}^{G_h}(\theta )|$ to $N_P^{h-1}$ is trivial. On the other hand, by Theorem 9.1, the restriction of $|R_{T_h}^{G_h}(\theta )|$ to $N_P^{h-1}$ does not contain the trivial representation. Therefore:

$$\begin{aligned}&\dim {{\,\mathrm{Hom}\,}}_{\gamma Z G_{{\mathcal {O}}} \gamma ^{-1} \cap Z G_{{\mathcal {O}}}} (|R_{T_h}^{G_h}(\theta )|, {}^\gamma |R_{T_h}^{G_h}(\theta )|) \\&\quad \le \dim {{\,\mathrm{Hom}\,}}_{N_P^{h-1}}(|R_{T_h}^{G_h}(\theta )|, {}^\gamma |R_{T_h}^{G_h}(\theta )|) \\&\quad \le \dim {{\,\mathrm{Hom}\,}}_{N_P^{h-1}}(|R_{T_h}^{G_h}(\theta )|, \text {triv}) = 0. \end{aligned}$$

$\square$

Combining Theorems 11.3 and 12.5 proves:

Theorem 12.6

If $\theta \in {\mathscr {X}}^{\mathrm{min}}$, then the assignment $\theta \mapsto |R_T^G(\theta )|$ is a geometric realization of automorphic induction and the Jacquet–Langlands correspondence.