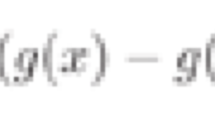$L^p$-independence of spectral radius for generalized Feynman–Kac semigroups

Abstract

Under mild conditions on measures used in the perturbation, we establish the $L^p$-independence of spectral radius for generalized Feynman–Kac semigroups without assuming the irreducibility and the boundedness of the function appeared in the continuous additive functionals locally of zero energy in the framework of symmetric Markov processes. These results are obtained by using the gaugeability approach developed by the first named author as well as the recent progress on the irreducible decomposition for Markov processes proved by the third author and on the analytic characterizations of gaugeability for generalized Feynman–Kac functionals developed by the second and third authors.

1 Introduction and main results

It is well known that Schrödinger operator ${\mathcal {L}}:= -\frac{1}{2} \Delta +V$, where V is a Kato class function on $\mathbb {R}^d$, is self-adjoint in $L^2(\mathbb {R}^d; \mathrm{d}x)$ and so it can be represented by its spectral family. The Schrödinger operator generates a strongly continuous semigroup $\{P_t^V =e^{-t {\mathcal {L}}}; t\ge 0\}$ in $L^2(\mathbb {R}^d; \mathrm{d}x)$. This Schrödinger semigroup admits a probabilistic representation (cf. [17, 41]): for $f\in C_c^2(\mathbb {R}^d)$, the space of $C^2$-smooth functions on $\mathbb {R}^d$ with compact support,

$$\begin{aligned} P_t^V f (x) = \mathbb {E}_x \left[ \exp \left( -\int _0^t V(X_s) \mathrm{d}s\right) f(X_t) \right] , \quad t\ge 0, \ x\in \mathbb {R}^d, \end{aligned}$$

where $\mathbf{X}=\{X_t; t\ge 0, \mathbb {P}_x, x\in \mathbb {R}^d\}$ is a d-dimensional Brownian motion. Hence $(P_t^V)_{t\ge 0}$ is also called a Feynman–Kac semigroup of Brownian motion. This semigroup can be extended to a strongly continuous symmetric semigroup in $L^p(\mathbb {R}^d; \mathrm{d}x)$ for any $p\in [1, \infty [$, and a bounded semigroup on $L^{\infty }(\mathbb {R}^d;\mathrm{d}x)$ (cf. [40]). We denote the $L^p$-Schrödinger semigroup by $(P_t^V)_{t\ge 0}$. There is a spectral family associated with the infinitesimal generator ${\mathcal {L}}^{(p)}$ of $(P_t^V)_{t\ge 0}$ in $L^p(\mathbb {R}^d; \mathrm{d}x)$ when $1\le p<\infty$. When $p=\infty$, ${\mathcal {L}}^{(\infty )}$ on $L^{\infty }(\mathbb {R}^d; \mathrm{d}x)$ is defined to be the dual of ${\mathcal {L}}^{(1)}$ on $L^{\infty }(\mathbb {R}^d; \mathrm{d}x)$, whose domain $D({\mathcal {L}}^{(\infty )})$ may not be dense in $L^{\infty }(\mathbb {R}^d; \mathrm{d}x)$. Let $\tilde{L}^{\infty }$ be the closure of $D({\mathcal {L}}^{(\infty )})$ in $L^{\infty }(\mathbb {R}^d; \mathrm{d}x)$. Then the spectrum of $-{\mathcal {L}}^{(\infty )}$ can be defined for the densely defined closed operator ${\mathcal {L}}^{(\infty )}: \tilde{L}^{\infty }\rightarrow \tilde{L}^{\infty }$. Note that the semigroup $(\tilde{P}_t^V)_{t\ge 0}$ on $\tilde{L}^{\infty }$ defined by the restriction $\tilde{P}_t^V:=P_t^V|_{\tilde{L}^{\infty }}$ is strongly continuous on $\tilde{L}^{\infty }$. Moreover, we can deduce $\Vert \tilde{P}_t^V\Vert _{\infty ,\infty }\le \Vert {P}_t^V\Vert _{\infty ,\infty }\le M \Vert \tilde{P}_t^V\Vert _{\infty ,\infty }$. Here M is the positive constant appeared in $\Vert {P}_t^V\Vert _{\infty ,\infty }\le Me^{Ct}$, $(C>0)$ under the Kato class condition for V. So the bottom of the spectrum of $-{\mathcal {L}}^{(\infty )}$ coincides with the spectral radius $\lambda _{\infty }:=-\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert {P}_t^V\Vert _{\infty ,\infty }$. An interesting but challenging question is when the $L^p$-spectral family of ${\mathcal {L}}^{(p)}$ is independent of $p\in [1,\infty ]$ (see Remarks 2 after Theorem 1.3 of [40]). When V is in certain function space, Simon [40, Theorem 1.3] showed that the bottom of the spectrum (also called spectral radius) of ${\mathcal {L}}^{(p)}$ is independent of $p\in [1,\infty ]$; in other words, $\lambda _p:=- \lim _{t\rightarrow \infty } \frac{1}{t} \log \Vert P_t^V\Vert _{p, p}$ is independent of $p\in [1,\infty ]$. This result has been extended in Hempel and Voigt [23, 24] to a larger class of V with $V^-$ being in an extended Kato class of Brownian motion and $V^+$ locally integrable. Moreover, it is shown in [23, 24] that the $L^p$-spectral family for the Schrödinger operator $-\frac{1}{2} \Delta +V$ is independent of $p\in [1,\infty ]$ for a subclass of V. Inspired by [23, 24, 40, 41], Sturm [44] later obtained $L^p$-independence of the spectrum of uniformly elliptic operators on Riemannian manifolds under a sub-exponential volume growth condition.

Note that $\int _0^t V(X_s) \mathrm{d}s$ in the Feynman–Kac representation of the Schrödinger semigroup $(P_t^V)_{t\ge 0}$ above is a continuous additive functional of the Brownian motion $\mathbf{X}$ having finite variation and signed Revuz measure $\mu (\mathrm{d}x)=V(x)\mathrm{d}x$. On the other hand, Brownian motion $\mathbf{X}$ has many continuous continuous additive functionals of finite variation but whose signed Revuz measure can be singular with respect to the Lebesgue measure. Local time of Brownian motion on the unit sphere is such an example. In this case, the corresponding Revuz measure $\mu$ is the surface measure on the unit sphere. Moreover, for any $u\in W^{1,2}(\mathbb {R}^d)$, the space of $L^2$-integrable functions on $\mathbb {R}^d$ whose distributional gradients are also $L^2$-integrable, it admits a quasi-continuous version $\widetilde{u}$ and there is a Fukushima’s decomposition (cf. [8, 22])

$$\begin{aligned} \widetilde{u}(X_t)-\widetilde{u}(X_0)= M^u_t +N^u_t, \quad t\ge 0, \end{aligned}$$

where $M^u_t$ is a continuous martingale additive functional of $\mathbf{X}$ having finite energy and $N^u$ is a continuous additive functional of $\mathbf{X}$ having zero energy. Hence it is natural to consider generalized Feynman–Kac semigroup defined by

$$\begin{aligned} P_t^{u,\mu } f (x) := \mathbb {E}_x \left[ \exp ( N^u_t+A^{\mu }_t ) f(X_t)\right] \end{aligned}$$

where $A^\mu$ is a continuous continuous additive functionals of finite variation with signed Revuz measure $\mu$ and $u\in W^{1,2}(\mathbb {R}^d)$. Intuitively, its corresponding Schrödinger operator is

$$\begin{aligned} -\frac{1}{2} \Delta - \left( \mu +\frac{1}{2} \Delta u\right) \end{aligned}$$

where $\Delta u$ should be understood in a distributional sense (cf. [16]). Furthermore, if $\mathbf{X}$ is a discontinuous symmetric strong Markov process on $\mathbb {R}^d$ such as an isotropic $\alpha$-stable Lévy process, $\mathbf{X}$ has discontinuous additive functionals as well. For example, for a bounded function F(x, y) on $\mathbb {R}^d \times \mathbb {R}^d$ that vanishes along the diagonal in certain rate, $t\mapsto A^F_t:=\sum _{0<s\le t} F(X_{s-}, X_s)$ is a purely discontinuous additive functional of an isotropic $\alpha$-stable Lévy process $\mathbf{X}$. This gives arise a non-local generalized Feynman–Kac semigroup

$$\begin{aligned} P_t^{u,\mu ,F} f (x) := \mathbb {E}_x \left[ \exp \left( N^u_t+A^{\mu }_t+A^F_t \right) f(X_t)\right] . \end{aligned}$$

The infinitesimal generator of $(P_t^{u,\mu ,F})_{t\ge 0}$ is

$$\begin{aligned} (-\Delta )^{\alpha /2} - \left( \mu + (-\Delta )^{\alpha /2} u\right) + \hbox {a non-local perturbation involving } F, \end{aligned}$$

where again $(-\Delta )^{\alpha /2} u$ should be interpreted in a distributional sense.

Using the large deviation principle for occupation time distribution, Takeda [45, 46] proved the $L^p$-independence of the spectral radius of symmetric Markov semigroups whose symmetrizing measure satisfies the tightness condition. After that, Takeda [49] extended the results on $L^p$-independence of the spectrum radius in [45, 46] to the case of Feynman–Kac semigroup under the tightness condition for the symmetrizing measures of the Markov processes. Meanwhile, Takeda [47] proved a characterization of $L^p$-independence of spectral radius of Feynman–Kac semigroup without assuming the tightness condition for the symmetrizing measures. The results in [47, 49] was extended to the case of generalized Feynman–Kac semigroups in [19, 31, 50, 51]. The method of the proofs in [19, 31, 45,46,47, 49,50,51] are all based on the large deviation principle for occupation time distribution. The results on the $L^p$-independence of spectral radius in [45,46,47, 49,50,51] are summarized in the survey paper [48].

In [4, 5] (see also [2, Theorem 2.12]), the first named author developed a new approach to study $L^p$-independence of spectral radius for generalized Feynman–Kac semigroups generated not only by continuous additive functionals but also by discontinuous additive functionals in the context of symmetric Markov processes. The new approach is based on the following two ingredients: (i) the analytic characterization of gaugeability for continuous and discontinuous Feynman–Kac functionals obtained in [2, 3], respectively; (ii) Chen and Zhang’s approach [16] to generalized Feynman–Kac transform $e^{N^u}$, where $N^u$ is the continuous additive functional of zero energy for bounded u in the associated Dirichlet space, by realizing it as a combination of Doob’s h-transform, a Girsanov transform and a Feynman–Kac transform by continuous additive functional of finite variation. This new approach, which does not use large deviation, has the advantage that it not only extends earlier results in [47,48,49,50,51] to a larger class of symmetric Markov processes but also gives several new criteria; see, e.g., [2, Remarks 4.10 and 5.6]. In [5], for generalized Feynman–Kac transform, u is assumed to be bounded. However, when the symmetric Markov process is a Feller process having strong Feller property, using a large deviation approach, the function u can be allowed to be any continuous function in $\mathcal {F}_{\mathrm{loc}}$ as in Theorem 1.2 of [19, 31]. Given the importance of Schrödinger semigroups and Feynman–Kac transforms in analysis and in probability theory, it is desirable to establish these results for general u and general strong Markov processes.

The main purpose of this paper is to study $L^p$-independence of spectral radius for generalized (possibly non-local) Feynman–Kac semigroups for a large class of symmetric strong Markov processes and for general u locally in the domain of the corresponding Dirichlet spaces. This paper adopts the gaugeability approach of the first named author in [4, 5] but with refinements. We do not require the underlying symmetric Markov process to be irreducible, nor do we assume the symmetric Markov process to have doubly Feller property or strong Feller property. Using the recent refinements from [27, 28] by the second and third named authors on the analytic characterization for the gaugeability of generalized Feynman–Kac functionals, we are able to extend results in both [4, 5] and [19, 31] (see Theorems 1.1, 1.2, 1.3 below).

Gärtner–Ellis theorem provides a useful way to establish large deviation principle. One of the conditions of the Gärtner–Ellis theorem is the existence of logarithmic moment generating function ([18, Sect. 2.3]). We point out that the $L^p$-independence of spectral radius of the generalized Feynman–Kac semigroups implies the existence of logarithmic moment generating function of the generalized Feynman–Kac semigroup.

We now state the setting of this paper. Let E be a Lusin metric space (i.e., a space that is homeomorphic to a Borel subset of a compact metric space) and $\mathfrak {m}$ a $\sigma$-finite Borel measure on E with full topological support. Let $E_{\partial }$ be a one point compactification of E with a point $\partial \notin E$ if E is a locally compact separable metric space. Otherwise we add $\partial$ as an isolated point to E. Let $\mathbf{X}=(\Omega ,\mathscr {F}_{\infty },\mathscr {F}_t,X_t, \mathbb {P}_x, x\in E_{\partial })$ be an $\mathfrak {m}$-symmetric right process on E with lifetime $\zeta :=\inf \{t >0 : X_t =\partial \}$. The transition function $P_t(x,\mathrm{d} y)$ is defined to be $P_t(x,\mathrm{d} y):=\mathbb {P}_x(X_t\in \mathrm{d} y)$ and set

$$\begin{aligned} P_{t}f(x):=\mathbb {E}_x[f(X_t) : t<\zeta ]=\mathbb {E}_x[f(X_t)]= \int _{\Omega }f(X_t(\omega ))\mathbb {P}_x(\mathrm{d} \omega ) \end{aligned}$$

for bounded or non-negative Borel function f on E. Let $(\mathcal {E}, \mathcal {F})$ be the Dirichlet form on $L^2(E;\mathfrak {m})$ associated with $\mathbf{X}$. Then $(\mathcal {E},\mathcal {F})$ is automatically quasi-regular (cf. [8, 39]). We further assume that $\mathbf{X}$ satisfies the absolute continuity condition (AC) (see Sect. 2 for its definition).

Suppose $\mu$ is a signed smooth measure, that is, $\mu$ is $\sigma$-finite and its total variation measure $|\mu |$ is a smooth measure (see [22, Sect. 2.2] for the definition of smooth measures). Let $\mu ^+$ and $\mu ^-$ denote the positive and negative variation measure of $\mu$ in its the Jordan decomposition, which are smooth measures Let $A^{\mu ^{+}}$ (resp. $A^{\mu ^{-}}$) be the positive continuous additive functional associated to $\mu ^{+}$ (resp. $\mu ^-$) (see (2.1) below or [22, Theorem 5.1.4]). We define $A^\mu :=A^{\mu ^+}-A^{\mu ^-}$. Let $\dot{\mathcal {F}}_{\mathrm{loc}}$ be the family of all functions locally in $\mathcal {F}$ in the broad sense, i.e., $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ if and only if there exist an increasing sequence $\{O_n\}$ of finely open nearly Borel sets satisfying $\bigcup _{n=1}^{\infty }O_n=E$ and $\{u_n\}\subset \mathcal {F}$ such that $u=u_n$$\mathfrak {m}$-a.e. on $O_n$. Since $(\mathcal {E},\mathcal {F})$ is quasi-regular, every $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ admits an $\mathcal {E}$-quasi-continuous $\mathfrak {m}$-version $\tilde{u}$, and we omit tilde from $\tilde{u}$, i.e., we always assume $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is represented by its $\mathcal {E}$-quasi-continuous version. Every $f\in \mathcal {F}$ admits the Beurling–Deny decomposition and LeJan formulae (see [22, Theorem 3.2.1 and Lemmas 3.2.3, 3.2.4 and 3.2.5]):

$$\begin{aligned} \mathcal {E}(f,g)=\frac{1}{2}\mu _{{\langle }f{\rangle }}^c(E)+\int _{E\times E{\setminus } {\mathsf {diag}}}(f(x)-f(y))^2J(\mathrm{d}x\mathrm{d}y)+\int _Ef(x)^2\kappa (\mathrm{d}x), \end{aligned}$$

where $\mu _{{\langle }f{\rangle }}^c$ is called the energy measure of continuous part, J is called the jumping measure, and $\kappa$ is called the killing measure. Hereafter, we fix a $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$. We may and do assume $u(\partial )=0$ because we can always take u as $u(x)-u(\partial )$ whenever we need. The energy measure $\mu _{{\langle }u{\rangle }}^c$ of the continuous part is well-defined by setting $\mu _{{\langle }u{\rangle }}^c:=\mu _{{\langle }u_n{\rangle }}^c$ on $O_n$. The energy measure $\mu _{{\langle }u{\rangle }}^j$ of the jumping part is defined by $\mu _{{\langle }u{\rangle }}^j(\mathrm{d}x)=2\int _E(u(x)-u(y))^2J(\mathrm{d}x\mathrm{d}y)$ and the energy measure $\mu _{{\langle }u{\rangle }}^{\kappa }$ of the killing part is defined by $\mu _{{\langle }u{\rangle }}^{\kappa }(\mathrm{d}x)=\int _E u(x)^2\kappa (\mathrm{d}x)$. We define the energy measure $\mu _{{\langle }u{\rangle }}$ of $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ by $\mu _{{\langle }u{\rangle }}:=\mu _{{\langle }u{\rangle }}^c+\mu _{{\langle }u{\rangle }}^j+\mu _{{\langle }u{\rangle }}^{\kappa }$. This definition is consistent with the definition of energy measure $\mu _{{\langle }u{\rangle }}$ for $u\in \mathcal {F}$ with $u(\partial )=0$.

Let $N^u$ be the continuous additive functional of zero quadratic variation appeared in a Fukushima decomposition of $u(X_t)-u(X_0)$ up to the lifetime (see (2.3) below). Note that $N^u$ is not necessarily of bounded variation in general. Let F be a bounded symmetric function on $E\times E$ which is extended to a function defined on $E_\partial \times E_\partial$ so that $F(x,\partial )=F(\partial ,x)=F(x,x)=0$ for $x\in E_{\partial }$ (actually there is no need to define the value $F(\partial ,y)$ for $y\in E$). Then $A^F_t:=\sum _{0<s\le t}F(X_{s-},X_s)$ (whenever it is summable) is an additive functional of $\mathbf{X}$. It is natural to consider the following generalized non-local Feynman–Kac transforms by the additive functionals $A:=N^u + A^\mu + A^F$ of the form

$$\begin{aligned} e_{A}(t):=\exp (A_t), \quad t \in [0,\zeta [, \end{aligned}$$

(1.1)

because the process $\mathbf{X}$ admits many continuous additive functionals which do not have bounded variations, and many discontinuous additive functionals. We define $Q_tf(x):=\mathbb {E}_x[e_A(t)f(X_t)]$ for any Borel function f whenever $Q_tf$ makes sense. In this case, $Q_tf$ is also Borel measurable under $\mathbf{(AC)}$. Owing to $\mathbf{(AC)}$, $Q_tf(x)=0$ for all $x\in E$ if $f=0$$\mathfrak {m}$-a.e. So $Q_t$ can act on any non-negative $\mathfrak {m}$-measurable function. Let (N, H) be a Lévy system of $\mathbf{X}$ (see (2.2) below for the definition). Let $\mathcal {Q}$ be the quadratic form defined by

$$\begin{aligned} \mathcal {Q}(f,g):={\mathcal {E}}(f,g)+{\mathcal {E}}(u,fg) - \mathcal {H}(f,g), \end{aligned}$$

(1.2)

where

$$\begin{aligned} \mathcal {E}(u,fg)&:=\frac{1}{2}\int _Ef\,\mathrm{d} \mu _{{\langle }u,g{\rangle }}+ \frac{1}{2}\int _Eg\,\mathrm{d} \mu _{{\langle }u,f{\rangle }},\\ \mathcal {H}(f,g)&:=\int _{E}f(x)g(x)\mu (\mathrm{d}x)+\int _E\int _Ef(x)g(y)(e^{F(x,y)}-1)N(x,\mathrm{d}y)\mu _{H}(\mathrm{d}x). \end{aligned}$$

In view of Stollmann-Voigt’s inequality, $\mathcal {Q}(f,g)$ is well-defined for $f,g\in \mathcal {F}$ provided $|\mu | +N(|F|)\mu _H+\mu _{{\langle }u{\rangle }}\in S_{D}^1(\mathbf{X})$. Here $S_{D}^1(\mathbf{X})$ denotes the class of smooth measures in the strict sense of Dynkin class (see Sect. 2 below for the definition of $S_{D}^1(\mathbf{X})$). For $p\in [1,\infty ]$, we define $\Vert Q_t\Vert _{p,p}$ by

$$\begin{aligned} \Vert Q_t\Vert _{p,p}:=\sup _{f\in L^p(E;\mathfrak {m}){\setminus }\{0\}}\frac{\Vert Q_tf\Vert _p}{\Vert f\Vert _p}(\le \infty ), \end{aligned}$$

(1.3)

where $\Vert \cdot \Vert _p$ is the $L^p$-norm of the measure space $(E,\mathscr {B}(E),\mathfrak {m})$. Note here that the supremum can run over $f\in L^p_+(E;\mathfrak {m})\cap \mathscr {B}(E){\setminus }\{0\}$ since $|Q_tf|\le Q_t|f|$. One can define the $L^p$-spectral radius $\lambda _p(\mathbf{X},u,\mu ,F)\in [-\infty ,\infty ]$ by

$$\begin{aligned}&\lambda _p(\mathbf{X},u,\mu ,F)\\&\quad :=\sup \{\alpha \in \mathbb {R}: \exists \gamma \in [0,\infty [ \text { such that }\Vert Q_t\Vert _{p,p}\le \gamma e^{-\alpha t}\text { for any }t\ge 0\}, \end{aligned}$$

with the convention $\sup \emptyset = -\infty$. By (1.3), the semigroup property of $(Q_t)_{t>0}$ yields the subadditivity of $t\mapsto \log \Vert Q_t\Vert _{p,p}$. So one has

$$\begin{aligned} \lambda _p(\mathbf{X},u,\mu ,F)=-\downarrow \lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t\Vert _{p,p}=-\inf _{t>0}\frac{1}{t}\log \Vert Q_t\Vert _{p,p}. \end{aligned}$$

(1.4)

If $(\mathcal {Q},\mathcal {F})$ is bounded below on $L^2(E;\mathfrak {m})$ under $|\mu | +N(|F|)\mu _H+\mu _{{\langle }u{\rangle }}\in S_{D}^1(\mathbf{X})$, then $(Q_t)_{t\ge 0}$ forms a symmetric $C_0$-semigroup on $L^2(E;\mathfrak {m})$ associated to $(\mathcal {Q},\mathcal {F})$ (see [6, Theorem 3.1], [7, Theorem 1.4]), in particular, $(Q_t)_{t\ge 0}$ is an analytic $C_0$-semigroup on $L^2(E;\mathfrak {m})$. Consequently, by [20, Chapter IV Corollary 3.12] with [20, Chapter II Definition 4.13], the spectral bound equal growth bound condition (see [20, Chapter IV Definition 2.1] for the definitions of spectral bound and growth bound) is satisfied under the lower boundedness of $(\mathcal {Q},\mathcal {F})$ on $L^2(E;\mathfrak {m})$ and $|\mu | +N( |F| )\mu _H+\mu _{{\langle }u{\rangle }}\in S_{D}^1(\mathbf{X})$, that is, $\lambda _2(\mathbf{X},u,\mu ,F)$ is the largest lower bound of the quadratic form $(\mathcal {Q},\mathcal {F})$ on $L^2(E;\mathfrak {m})$, i.e.,

$$\begin{aligned} \lambda _2(\mathbf{X},u,\mu ,F)=\inf \left\{ \mathcal {Q}(f,f): \ f\in \mathcal {F}\hbox { with } \int _Ef^2\mathrm{d}\mathfrak {m}=1\right\} . \end{aligned}$$

(1.5)

Using the symmetry of $(Q_t)_{t\ge 0}$ and interpolation, it is easy to deduce (cf. [4, (4.2)]) that

$$\begin{aligned} \Vert Q_t\Vert _{2,2}\le \Vert Q_t\Vert _{p,p}\le \Vert Q_t\Vert _{\infty ,\infty }\quad \text { for all }p\in [1,\infty ] \end{aligned}$$

and therefore

$$\begin{aligned} \lambda _2(\mathbf{X},u,\mu ,F)\ge \lambda _p(\mathbf{X},u,\mu ,F)\ge \lambda _{\infty }(\mathbf{X},u,\mu ,F)\quad \text { for all } p\in [1,\infty ]. \end{aligned}$$

(1.6)

Thus to establish the $L^p$-independence of spectral radius, it suffices to show $\lambda _2(\mathbf{X},u,\mu ,F) \le \lambda _{\infty }(\mathbf{X},u,\mu ,F)$. For $\alpha >0$, denote by $\mathbf{X}^{(\alpha )}$ the $\alpha$-subprocess of $\mathbf{X}$. Let $S_{EK}^1(\mathbf{X})$ (resp. $S_{K}^1(\mathbf{X})$, $S_{LK}^1(\mathbf{X})$) denote the class of smooth measures in the strict sense of extended Kato class (resp. Kato class, local Kato class) with respect to $\mathbf{X}$. Let $S_{NK_{\infty }}^1(\mathbf{X})$ (resp. $S_{NK_1}^1(\mathbf{X})$) be the family of natural Green-tight measures of Kato class (resp. natural semi-Green-tight measures of extended Kato class) with respect to ${\mathbf {X}}$ and $S_{D_0}^1(\mathbf{X})$ the family of Green-bounded smooth measures with respect to $\mathbf{X}$ (see Sect. 4 for the definitions of these families). It follows directly from the definition that for $\beta > \alpha \ge 0$, $S_{NK_1}^1(\mathbf{X}^{(\alpha )}) \subset S_{NK_1}^1(\mathbf{X}^{(\beta )})$. Such monotone property holds for other Kato classes as well.

Throughout this paper, we assume the following condition:

Under (A), $(\mathcal {Q},\mathcal {F})$ on $L^2(E;\mathfrak {m})$ is well-defined and lower bounded and $(Q_t)_{t\ge 0}$ is a $C_0$-semigroup associated to $(\mathcal {Q},\mathcal {F})$, and so (1.5) always holds. Moreover, $(Q_t)_{t\ge 0}$ forms a strongly continuous semigroup on $L^2(E;\mathfrak {m})$ and there exists $C_2>0$ such that $\Vert Q_t\Vert _{2,2}\le C_2e^{C_2t}$ for all $t>0$, hence $\lambda _2(\mathbf{X},u,\mu ,F)\ge -C_2>-\infty$ always holds (see [29, Lemma 2.1 and Remark 2.1]).

Our main results are the following:

Theorem 1.1

Suppose that

$$\begin{aligned} \text {there is a }t_0>0\text { so that }P_{t_0}\text { is a bounded operator from } L^1(E;\mathfrak {m}) \text { to }L^{\infty }(E;\mathfrak {m}). \end{aligned}$$

(1.7)

Then $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$.

Theorem 1.1 extends [4, Theorem 5.3], in which $\mathfrak {m}(E)<\infty$, $u=0$, $\mu ^++N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $\mu ^-\in S_D^1(\mathbf{X})$ are assumed. Theorem 1.1 extends also [5, Theorem 4.1], in which $\mathfrak {m}(E)<\infty$, the boundedness of $u\in \mathcal {F}_e$, $|\mu |+N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $\mu _{{\langle }u{\rangle }}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ are assumed.

Theorem 1.2

Suppose that $\mu ^+ +N(e^{F^+}-1)\mu _H\in \cap _{\alpha >0} S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ and $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Then the following holds.

• 1. $\lambda _{\infty }(\mathbf{X},u,\mu ,F)\ge \min \{\lambda _2(\mathbf{X},u,\mu ,F),0\}$. Consequently, $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$ provided $\lambda _2(\mathbf{X},u,\mu ,F)\le 0$.

• 2. Assume that X is conservative. Suppose one of the following holds:

  • (i) X is transient and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$. Assume one of the following:

    • (a) $u^-:=\max \{-u,0\}\in L^p(E;\mathfrak {m})$ for some $p\in [1,\infty ]$.

    • (b) $\mu _{{\langle }u{\rangle }}\in S_{D_0}^1(\mathbf{X})$ and $\mathfrak {m}(E)<\infty$.

    • (c) $\mu _{{\langle }u{\rangle }}(E)<\infty$.

  • (ii) $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a bounded function and ${\mu ^-}+N(F^-)\mu _H\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$.

  Then $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=0$ if $\lambda _2(\mathbf{X},u,\mu ,F)>0$. Hence $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$ if and only if $\lambda _2(\mathbf{X},u,\mu ,F)\le 0$.

Note that the conditions of Theorem 1.2 are satisfied if $\mathbf{X}$ is transient, $\mu ^+ +N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X})$, $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X})$, and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$. The first condition in Theorem 1.2 is satisfied if $\mu ^+ +N(e^{F^+}-1)\mu _H\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Theorem 1.2(1) extends [4, Theorem 5.4], in which $u=0$, $\mu ^++N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $\mu ^-\in S_D^1(\mathbf{X})$ are assumed. Moreover [4, Theorem 5.4] requires the irreducibility condition (I) for the use of the gauge theorems developed in [2, 3] (see Sect. 2 for the definition of (I)). Theorem 1.2(1) extends also [5, Theorem 4.2], in which the boundedness of $u\in \mathcal {F}_e$, $|\mu |+N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $\mu _{{\langle }u{\rangle }}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ are assumed. Theorem 1.2 extends also [47, Theorem 3.1], in which the transience and the conservativeness of $\mathbf{X}$, $u=0$, $F=0$, $|\mu | \in S_{CK_{\infty }}^1(\mathbf{X})$ are assumed (see also [50, 51]). Here [47, Theorem 3.1] requires the irreducibility condition (I) for the use of large deviation principle. Our Theorem 1.2 does not require condition (I).

Theorem 1.3

Assume $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Then $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$.

The condition (A) is satisfied if $|\mu |+N(|F|)\mu _H+\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Theorem 1.3 extends [4, Theorem 5.5], in which $u=0$, $\mathfrak {m}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $|\mu |+N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ are assumed. Theorem 1.3 extends also [5, Theorem 4.3], in which the boundedness of $u\in \mathcal {F}_e$, $\mathfrak {m}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$, $|\mu |+N(|F|)\mu _H\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ and $\mu _{{\langle }u{\rangle }}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ are assumed. Moreover, Theorem 1.3 extends [31, Theorem 1.2(1)], in which the doubly Feller property of X, $u\in \mathcal {F}_{\mathrm{loc}}\cap C(E_{\partial })$, $\mathfrak {m}\in S_{K_{\infty }}^1(\mathbf{X}^{(1)})$, $\mu ^+ +N(e^{F^+}-1)\mu _H\in S_{LK}^1(\mathbf{X})\cap S_{EK}^1(\mathbf{X})$ and ${\mu ^-}+N(F^-)\mu _H\in S_{LK}^1(\mathbf{X})\cap S_{D}^1(\mathbf{X})$ are assumed. As noted above, [5, Theorem 4.3] and [31, Theorem 1.2(1)] require the irreducibility condition (I). Our Theorem 1.3 does not require (I).

We emphasize again that Theorems 1.1, 1.2 and 1.3 are new even if we consider the case of Feynman–Kac semigroup $P_t^{\mu }f(x):=\mathbb {E}_x[e^{A_t^{\mu }}f(X_t)]$ without assuming the irreducibility condition $\mathbf{(I)}$. For readers’ understanding, we summarize the simplified versions below. Let $\lambda _p(\mathbf{X},\mu ):=\lambda _p(\mathbf{X},0,\mu ,0)$ be the $L^p$-spectral radius of Feynman–Kac semigroup $(P_t^{\mu })_{t\ge 0}$. Assume $\mu ^+\in S_{EK}^1(\mathbf{X})$ and $\mu ^-\in S_D^1(\mathbf{X})$. Then we have the following:

Theorem 1.4

(Simplified version of Theorem 1.1) Suppose that (1.7) holds. Then $\lambda _p(\mathbf{X},\mu )$ is independent of $p\in [1,\infty ]$.

Theorem 1.5

(Simplified version of Theorem 1.2) Suppose that $\mu ^+ \in \cap _{\alpha >0} S_{NK_1}^1 (\mathbf{X}^{(\alpha )})$. Then we have the following.

• (1) $\lambda _{\infty }(\mathbf{X},\mu )\ge \min \{\lambda _2(\mathbf{X},\mu ),0\}$. Consequently, $\lambda _p(\mathbf{X},\mu )$ is independent of $p\in [1,\infty ]$ provided $\lambda _2(\mathbf{X},\mu )\le 0$.

• (2) Assume that X is conservative. Suppose one of the following holds:

  • (i) X is transient and ${\mu ^-}\in S_{D_0}^1(\mathbf{X})$.

  • (ii) ${\mu ^-}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$.

  Then $\lambda _{\infty }(\mathbf{X},\mu )=0$ if $\lambda _2(\mathbf{X},\mu )>0$. Hence $\lambda _p(\mathbf{X},\mu )$ is independent of $p\in [1,\infty ]$ if and only if $\lambda _2(\mathbf{X},\mu )\le 0$.

Theorem 1.6

(Simplified version of Theorem 1.3) Assume $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Then $\lambda _p(\mathbf{X},\mu )$ is independent of $p\in [1,\infty ]$.

Of course, all assumptions for $\mu$ in Theorems 1.4, 1.5 and 1.6 are satisfied when $|\mu |$ belongs to $S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ (denoted by $\mathbf{K}_{\infty }({X}^{(1)})$ in [2]), a class of 1-order Green-tight smooth measures of Kato class in the strict sense. Moreover, Theorems 1.1, 1.2 and 1.3 are new without assuming the irreducibility condition $\mathbf{(I)}$ even if we treat the case of $L^p$-spectral radius for Markov semigroup $(P_t)_{t\ge 0}$, which are the special cases of Theorems 1.4, 1.5 and 1.6.

Finally, we expose a new example in the framework of Brownian motion on Riemannian manifold. For the details, see Example 7.4 below. Let (M, g) be a d-dimensional complete smooth Riemannian manifold with lower Ricci bound. Let $\mathfrak {m}:={\mathrm{vol}}_g$ be the volume measure of (M, g) and $\Delta _g$ the Laplace-Bertrami operator of (M, g). In this case, the Brownian motion $\mathbf{X}$ associated to $\frac{1}{2}\Delta _g$ is conservative. Assume $\inf _{x\in M}\mathfrak {m}(B_1(x))>0$ and $p\in [1,\infty [$. Take $V\in L^p(M;\mathfrak {m})$ and set $\mu =V\mathfrak {m}$. Suppose $p>d/2$ (resp. $p\ge 1$) for $d\ge 3$ (resp. $d=1,2$), or $p=1$ with $|\mu |\in S_K^1(\mathbf{X})$. Then $|\mu |\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ (see Propositions 7.5 and 7.7 below). Let $\lambda _p(\mathbf{X},\mu )$ be the $L^p$-spectral radius of Feynman–Kac semigroup $(P_t^{\mu })_{t\ge 0}$ associated to the Schrödinger operator $-\frac{1}{2}\Delta _g-\mu$. Then $\lambda _p(\mathbf{X},\mu )$ is $L^p$-independent provided one of the following conditions holds:

• $P_{t_0}$ maps $L^1(M;\mathfrak {m})$ to $L^{\infty }(M;\mathfrak {m})$ as a bounded operator for some $t_0>0$.

• $\lambda _2(\mathbf{X},\mu )\le 0$.

• $\mathfrak {m}\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$.

The rest of the paper is organized as follows. In Sect. 2, we summarize some basics of Dirichlet forms that will be used in this paper. In Sect. 3, we present some results on Girsanov transform in connection with the generalized Feynman–Kac transform by $e^{N^u_t}$ for bounded $u \in \dot{\mathcal {F}}_{\mathrm{loc}}$. The results of this section are slight extension of some earlier results and will be used to reduce to the case of $u=0$ by applying the approach of Chen and Zhang [16] to realize the transformation $e^{N^u_t}$ as a combination of a Girsanov transform and a Feynman–Kac transform by continuous additive functional of finite variation followed by a Doob’s h-transform. In Sect. 4, we recall the definition of natural (semi-)Green tight measures of (extended) Kato class from [28], which are the extensions of the various Kato class measures introduced in [2]. and summarize the results on the characterization for the gaugeability of non-local Feynman–Kac functionals. In Sect. 5, we prove main theorems for the case that $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a finely continuous nearly Borel bounded function. In Sect. 6, we prove the main results of this paper in the general case. In Sect. 7, we give several examples on measures that are in various Kato classes used in the main results of this paper.

In this paper, we use $:=$ as a way of definition. For $a,b\in \mathbb {R}$, $a\vee b:=\max \{a,b\}$, $a\wedge b:=\min \{a,b\}$.

2 Preliminary

Let E be a Lusin metric space and $\mathfrak {m}$ a $\sigma$-finite Borel measure on E with full topological support. Let $\partial$ be a point added to E as an isolated point of $E_\partial :=E\cup \{\partial \}$ (it is added to E as the one-point compactification of E provided E is a locally compact separable metric space). The point $\partial$ also serves as the cemetery point for E. Let $\mathbf{X}=(\Omega ,\mathscr {F}_{\infty },\mathscr {F}_t,X_t, \mathbb {P}_x, x\in E_{\partial })$ be an $\mathfrak {m}$-symmetric special standard process on E with lifetime $\zeta :=\inf \{t >0 : X_t =\partial \}$ and $(\mathcal {E},\mathcal {F})$ the associated symmetric Dirichlet form which is quasi-regular on $L^2(E;\mathfrak {m})$. An increasing sequence $\{F_k\}$ of closed set is said to be an $\mathcal {E}$-nest if $\bigcup _{k=1}^{\infty }\mathcal {F}_{F_k}$ is dense in $\mathcal {F}$ with respect to $\mathcal {E}_1^{1/2}$-norm. A subset N of E is said to be $\mathcal {E}$-polar or$\mathcal {E}$-exceptional if there exists an $\mathcal {E}$-nest $\{F_k\}$ such that $N\subset \bigcap _{k=1}^{\infty }(E{\setminus } F_k)$. It is known that a subset N of E is $\mathcal {E}$-polar if and only if it is $\mathbf{X}$-exceptional, i.e., there exists a Borel set $\tilde{N}$ containing N such that $\mathbb {P}_{\mathfrak {m}}(\sigma _{\tilde{N}}<\zeta )=0$ (see [39, Chapter IV Theorem 5.29(i)], cf. [22, pp. 152]). For a statement P(x) depending on $x\in E$, we say that P(x) holds q.e. $x\in E$ if the set $\{x\in E : P(x)\text { does not holds}\}$ is $\mathcal {E}$-polar. A function f on E is said to be $\mathcal {E}$-quasi-continuous onE if there exists an $\mathcal {E}$-nest $\{F_k\}$ such that $f|_{F_k}$ is continuous on each $F_k$. A set $B(\subset E_{\partial })$ is called nearly Borel if there exist Borel subsets $B_1,B_2$ of $E_{\partial }$ such that $B_1\subset B\subset B_2$ and $\mathbb {P}_{\nu }(X_t\in B_2{\setminus } B_1, \exists t\in [0,\infty [)=0$ for all $\nu \in \mathcal {P}(E_{\partial })$. Here $\mathcal {P}(E_{\partial })$ denotes the family of all probability measures on $E_{\partial }$ and $\mathbb {P}_{\nu }(\mathrm{d}\omega ):=\int _{E_{\partial }}\mathbb {P}_x(\mathrm{d}\omega )\nu (\mathrm{d} x)$. Denote by $\mathscr {B}^n(E_{\partial })$ (resp. $\mathscr {B}^n(E)$) the family of nearly Borel subsets of $E_{\partial }$ (resp. E). A set A is called finely open if for each $x\in A$, there exists a $B\in \mathscr {B}^n(E)$ such that $E{\setminus } A\subset B$ and $\mathbb {P}_x(\sigma _B>0)=1$. The family of finely open sets defines a topology on E which is called the fine topology of X. An increasing sequence $\{G_n\}$ of finely open nearly Borel sets is said to be a nest if $\mathbb {P}_x (\lim _{n\rightarrow \infty } \tau _{G_n}=\zeta )=1$ for q.e. $x\in E$. Denote by $\Xi$ the family of nests $\{G_n\}$ of finely open nearly Borel sets. Note that for an $\mathcal {E}$-nest $\{F_n\}$ of closed sets, $\{G_k\}\in \Xi$ by setting $G_k :=F_k^{{f\text {-}int}}$, $k\in \mathbb {N}$, where $F_k^{{f\text {-}int}}$ means the fine interior of $F_k$. A set $B\subset E$ is said to be $\mathbf{X}$-invariant if $B\in \mathscr {B}^n(E)$ and

$$\begin{aligned} \mathbb {P}_x(X_t\in B\text { for all }t\in [0,\zeta [,\; X_{t-}\in B\text { for all }t\in ]0,\zeta [)=1, \quad \ x\in B. \end{aligned}$$

By definition, any $\mathbf{X}$-invariant set is finely open. A set $N\subset E$ is called properly exceptional if N is a nearly Borel $\mathfrak {m}$-negligible set and $E{\setminus } N$ is X-invariant. We say that $(\mathcal {E},\mathcal {F})$ (or $\mathbf{X}$) is irreducible ((I) in abbreviation) if any $(T_t)_{t>0}$-invariant set B satisfies $\mathfrak {m}(B)=0$ or $\mathfrak {m}(B^c)=0$. We do not assume the irreducibility condition $\mathbf{(I)}$ in this paper, but we use it in the proof by reducing the case in which $\mathbf{(I)}$ is satisfied. Here $(T_t)_{t>0}$ is the strongly continuous semigroup on $L^2(E;\mathfrak {m})$ associated with $(\mathcal {E},\mathcal {F})$. The transition kernel of $\mathbf{X}$ is denoted by $P_t(x,\mathrm{d}y)$, $t>0$. The correspondence between $\mathbf{X}$ and $(\mathcal {E},\mathcal {F})$ is given by $T_tf(x)=P_tf(x)$$\mathfrak {m}$-a.e. $x\in E$, where

$$\begin{aligned} P_tf(x):=\mathbb {E}_x[f(X_t): t <\zeta ]:=\int _Ef(y)P_t(x,\mathrm{d}y)\quad x\in E,~t>0. \end{aligned}$$

(Here and in the sequel, unless mentioned otherwise, we use the convention that a function defined on E takes the value 0 at $\partial$). The process $\mathbf{X}$ is said to satisfy the absolute continuity condition with respect to $\mathfrak {m}$ ((AC) in abbreviation) if for any $x \in E$ and $t>0$, $\mathfrak {m}(A)=0$ implies $P_t(x,A)=0$ for all $A \in \mathscr {B}(E)$. Throughout this paper, we assume $\mathbf{(AC)}$. For $\alpha >0$, there exists an $\alpha$-order resolvent kernel $R_{\alpha }(x,y)$ which is defined for all $x,y\in E$ (see Lemma 4.2.4 in [22]). Since $\alpha \mapsto R_{\alpha }(x,y)$ is decreasing for each $x,y\in E$, we can define 0-order resolvent kernel $R(x,y):=R_0(x,y):=\lim _{\alpha \rightarrow 0}R_{\alpha }(x,y)$ provided X is transient. R(x, y) is called the Green function of $\mathbf{X}$. For a non-negative Borel measure $\nu$, we write $R_{\alpha }\nu (x):=\int _ER_{\alpha }(x,y)\nu (\mathrm{d}y)$ and $R\nu (x):=R_0\nu (x)$. Note that $R_{\alpha }f(x)=R_{\alpha }(f\mathfrak {m})(x)$ for any $f\in \mathscr {B}_+(E)$ or $f\in \mathscr {B}_b(E)$. The space of bounded continuous functions on E will be denoted as $C_b(E)$. The process $\mathbf{X}$ is said to have resolvent strong Feller property ((RSF) in abbreviation) if $R_{\alpha }(\mathscr {B}_b(E))\subset C_b(E)$ for any/some $\alpha >0$. A measure $\nu$ on $(E,\mathscr {B}(E))$ is said to be smooth if $\nu$ charges no $\mathcal {E}$-exceptional set and there exists an $\mathcal {E}$-nest $\{F_n\}$ of compact sets such that $\nu (F_n)<\infty$ for each $n\in \mathbb {N}$. Let $S(\mathbf{X})$ be the family of positive smooth measures on E. We say that a positive continuous additive functional (PCAF in abbreviation) $A^{\nu }$ of $\mathbf{X}$ and a positive measure $\nu \in S(\mathbf{X})$ are in the Revuz correspondence if they satisfy for any $t >0$, $f \in \mathscr {B}_{+}(E)$,

$$\begin{aligned} \int _{E}f(x)\nu (\mathrm{d}x) =\, \uparrow \lim _{t \downarrow 0}\frac{1}{t}\mathbb {E}_{\mathfrak {m}}\left[ \int _0^tf(X_s)\mathrm{d}A_s^{\nu }\right] . \end{aligned}$$

(2.1)

$\nu \in S(\mathbf{X})$ is said to be of finite energy integral provided $\mathcal {F}\subset L^1(E;\nu )$ in the sense that for any $f\in \mathcal {F}$, its $\mathcal {E}$-quasi-continuous $\mathfrak {m}$-version $\tilde{f}$ belongs to $L^1(E;\nu )$. For simplicity, we always assume that any $f\in \mathcal {F}$ (or more generally $f\in \dot{\mathcal {F}}_{\mathrm{loc}}$) is taken to be $\mathcal {E}$-quasi-continuous. Denote by $S_0(\mathbf{X)}$ the family of measures of finite energy integrals. For $\nu \in S_0(\mathbf{X})$ and $\alpha >0$, there exists a unique $U_{\alpha }\nu \in \mathcal {F}$ such that $\mathcal {E}_{\alpha }(U_{\alpha }\nu ,v)=\int _E\tilde{v}\mathrm{d}\nu$ for any $v\in \mathcal {F}$. $U_{\alpha }\nu$ for $\nu \in S_0(\mathbf{X})$ is called the $\alpha$-potential of $\nu$. $\nu \in S_0(\mathbf{X})$ if and only if there exists an $\mathcal {E}$-nest $\{F_n\}$ such that $\mathbf{1}_{F_n}\nu \in S_0(\mathbf{X})$ for each $n\in \mathbb {N}$. It can be proved that for $\nu \in S_0(\mathbf{X})$, $R_{\alpha }\nu$ is an $\mathcal {E}$-quasi-continuous $\mathfrak {m}$-version of $U_{\alpha }\nu$, hence ${\langle }\nu ,R_{\alpha }\nu {\rangle }=\mathcal {E}_{\alpha }(U_{\alpha }\nu ,U_{\alpha }\nu )<\infty$. We define $S_{00}(\mathbf{X}):=\{\nu \in S_0(\mathbf{X}): \nu (E)<\infty \text { and }U_{\alpha }\nu \in L^{\infty }(E;\mathfrak {m})\}$. In the same way of the proof of [22, Theorem 5.1.6], for $\nu \in S_{00}(\mathbf{X})$, there exists a PCAF $A_t^{\nu }$ in the strict sense such that $R_{\alpha }\nu (x)=\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right]$ for $x\in E$. We say that $\nu \in S(\mathbf{X})$ is a smooth measure in the strict sense if there exists an $\mathcal {E}$-nest $\{F_n\}$ of compact sets such that $\mathbf{1}_{F_n}\nu \in S_{00}(\mathbf{X})$ for each $n\in \mathbb {N}$. Denote by $S_1(\mathbf{X})$ the family of positive smooth measures in the strict sense. For any $\nu \in S_1(\mathbf{X})$, $\nu$ is associated to a PCAF $(A_t^{\nu })_{t\ge 0}$ of $\mathbf{X}$ in the strict sense under Revuz correspondence, in particular, $R_{\alpha }\nu (x)=\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right]$ for $x\in E$. $S_1(\mathbf{X})$ is the subclass of $S(\mathbf{X})$ associated to the PCAFs in the strict sense under Revuz correspondence (see [22] for the case of locally compact separable state space). These statement are shown in the framework of regular Dirichlet forms ([22]), whose proof remains valid in our general setting. A measure $\nu \in S_1(\mathbf{X})$ is said to be in the Dynkin class (resp. Green-bounded) of $\mathbf{X}$ if $\sup _{x\in E}R_{\alpha }\nu (x)<\infty$ for some $\alpha >0$ (resp. $\sup _{x\in E}R\nu (x)<\infty$ and X is transient). A measure $\nu \in S_1(\mathbf{X})$ is said to be in the Kato class (resp. extended Kato class) with respect to $\mathbf{X}$ if $\lim _{\alpha \rightarrow \infty } \sup _{x\in E}R_{\alpha }\nu (x)=0$ (resp. $\lim _{\alpha \rightarrow \infty } \sup _{x\in E}R_{\alpha }\nu (x)<1$). A measure $\nu \in S_1(\mathbf{X})$ is said to be in the local Kato class if for any compact subset K of E, $\mathbf{1}_K\nu$ is of Kato class. Denote by $S_D^1(\mathbf{X})$ (resp. $S_{D_0}^1(\mathbf{X})$) the family of measures of Dynkin class (resp. Green-bounded), and by $S_K^1(\mathbf{X})$ (resp. $S_{EK}^1(\mathbf{X})$, $S_{LK}^1(\mathbf{X})$) the family of measures of Kato class (resp. extended Kato class, local Kato class). Clearly, $S_K^1(\mathbf{X})\subset S_{EK}^1(\mathbf{X})\subset S_{D}^1(\mathbf{X})$, $S_K^1(\mathbf{X})\subset S_{LK}^1(\mathbf{X})$ and $S_{D_0}^1(\mathbf{X}) \subset S_D^1(\mathbf{X})$. In view of Theorem 3.1 in [42], any $\nu \in S_D^1(\mathbf{X})$, in particular any $\nu \in S_{D_0}^1(\mathbf{X})$, is a Radon measure on E, because of the regularity of the Dirichlet form.

It is known that the family of equivalence classes of the set of PCAFs in the strict sense and the family of positive measures belonging to $S_1(\mathbf{X})$ are in one to one correspondence under the Revuz correspondence ([22, Theorem 5.1.4]).

Let $(N(x, \mathrm{d}y), H_t)$ be a Lévy system for X, that is, $N(x, \mathrm{d}y)$ is a kernel on $(E_{\partial }, {\mathscr {B}}(E_{\partial }))$ and $H_t$ is a PCAF with bounded 1-potential such that for any nonnegative Borel function $\phi$ on $E_{\partial }\times E_{\partial }$ vanishing on the diagonal and any $x\in E_{\partial }$, non-negative Borel function g on $[0,\infty [$ and $(\mathscr {F}_t)$-stopping time T,

$$\begin{aligned} \mathbb {E}_x \left[ \sum _{s\le T}g(s) \phi (X_{s-}, X_s)\right] =\mathbb {E}_x \left[ \int ^T_0\int _{E_{\partial }} g(s)\phi (X_s, y)N(X_s,\mathrm{d}y)\mathrm{d}H_s \right] \end{aligned}$$

(2.2)

(see [8, A.3.33]). To simplify notation, we will write

$$\begin{aligned} N \phi (x):= \int _{E_{\partial }} \phi (x, y) N(x, \mathrm{d}y). \end{aligned}$$

Let $\mu _H$ be the Revuz measure of the PCAF H. Then the jumping measure J and the killing measure $\kappa$ of X are given by

$$\begin{aligned} J(\mathrm{d}x\mathrm{d}y)=\frac{1}{2}N(x, \mathrm{d}y)\mu _H (\mathrm{d}x)\quad \text { and }\quad \kappa (\mathrm{d}x)=N(x, \{\partial \})\mu _H(\mathrm{d}x). \end{aligned}$$

These measures appear in the Beurling–Deny decomposition of $\mathcal {E}$ (cf. [8, 22]): for $f, g\in {\mathcal {F}}_e$,

$$\begin{aligned} {\mathcal {E}}(f, g)= & {} {\mathcal {E}}^{c}(f, g)+\int _{E\times E {\setminus } {\mathsf {diag}}}(f (x)- f(y))(g(x)- g(y))J(\mathrm{d}x\mathrm{d}y)\\&+\int _E f(x)g(x)\kappa (\mathrm{d}x), \end{aligned}$$

where ${\mathcal {E}}^{c}$ is the strongly local part of ${\mathcal {E}}$.

As noted before, $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is represented by its $\mathcal {E}$-quasi-continuous version. So u is finely continuous q.e. (cf. [22, Theorem 4.2.2]), i.e., there exists a properly exceptional set N such that u is nearly Borel measurable and finely continuous on $E{\setminus } N$, more strongly, for any $x\in E{\setminus } N$,

$$\begin{aligned} \mathbb {P}_x\left( u(X_t)\text { is right continuous at }t\in [0,\zeta [\text { and }\lim _{s\uparrow t}u(X_s)=u(X_{t-})\text { at }t\in ]0,\zeta [\right) =1. \end{aligned}$$

If we replace the state space E with $E{\setminus } N$, there is no essential change of $L^p$-spectral radius of $(Q_t)_{t\ge 0}$. So we may and do assume that $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is always finely continuous and nearly Borel on E. For $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ with $\mu _{{\langle }u{\rangle }}\in S(\mathbf{X})$, the additive functional $u(X_t)-u(X_0)$ admits the following decomposition ([33, Theorem 4.2], [34, Theorem 1.2]):

$$\begin{aligned} u(X_t)-u(X_0)=M_t^u+N_t^u \end{aligned}$$

(2.3)

holds for all $t \in [0,\zeta [$${\mathbb {P}}_x$-a.s. for q.e. $x\in E$, where $M^u$ is a locally square integrable martingale additive functional, and $N^u$ is a continuous additive functional (CAF in abbreviation) which is locally of zero energy. Moreover, if $\mu _{{\langle }u{\rangle }}\in S_D^1(\mathbf{X})$, then we can construct $M_t^u$ as a square integrable martingale additive functional according to the proof of [31, Theorem 6.2(2)], precisely, $M^u$ can be constructed as the sum

$$\begin{aligned} M_{t}^{u}=M_{t}^{u,c} + M_{t}^{u,j} + M_{t}^{u,\kappa } \end{aligned}$$

(2.4)

under $\mu _{{\langle }u{\rangle }}\in S_D^1(\mathbf{X})$, where $M_{t}^{u,j}$, $M_{t}^{u,\kappa }$ and $M_{t}^{u,c}$ are the jumping, killing and continuous part of $M^{u}$ respectively. Those are defined for all $t\in [0,\infty [$ under the law $\mathbb {P}_x$ for all $x\in E$ (see the proof of [31, Theorem 6.2(2)]). Note that we do not assert that (2.3) holds beyond the lifetime $\zeta$. If u is strictly $\mathcal {E}$-quasi-continuous, i.e., there exists an increasing sequence $\{F_n\}$ of closed sets such that $\mathbb {P}_x(\lim _{n\rightarrow \infty }\sigma _{E{\setminus } F_n}=\infty )=1$ for all $x\in E$ and $u|_{F_n\cup \{\partial \}}$ is continuous on $F_n\cup \{\partial \}$ for each $n\in \mathbb {N}$, then $N_t:=u(X_t)-u(X_0)-M_t^u$ is continuous at all $t\in [0,\infty [$ under $\mathbb {P}_x$ for all $x\in E$, consequently (2.3) holds for all $t\in [0,\infty [$ under $\mathbb {P}_x$.

Let $\mu _{{\langle } u{\rangle }}$, $\mu ^{c}_{{\langle } u{\rangle }}$, $\mu ^{j}_{{\langle } u{\rangle }}$ and $\mu ^{\kappa }_{{\langle } u{\rangle }}$ be the smooth Revuz measures in the strict sense associated with the quadratic variational processes (or the sharp bracket PCAFs in the strict sense) ${\langle } M^u{\rangle }$, ${\langle } M^{u,c}{\rangle }$, ${\langle } M^{u,j}{\rangle }$ and ${\langle } M^{u,\kappa }{\rangle }$ respectively. Then

$$\begin{aligned} \mu _{{\langle } u{\rangle }}(\mathrm{d}x)=\mu ^{c}_{{\langle } u{\rangle }}(\mathrm{d}x)+\mu ^{j}_{{\langle } u{\rangle }}(\mathrm{d}x)+\mu ^{\kappa }_{{\langle } u{\rangle }}(\mathrm{d}x). \end{aligned}$$

Note that $\mathcal {E}(f,f)=\frac{1}{2}\nu _{{\langle }f{\rangle }}(E)$ with $\nu _{{\langle }f{\rangle }}:=\mu _{{\langle }f{\rangle }}^c+\mu _{{\langle }f{\rangle }}^j+2\mu _{{\langle }f{\rangle }}^{\kappa }$ provided $f\in \mathcal {F}_e$.

3 Girsanov transforms

Throughout this section, we fix $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ which is s bounded finely continuous function $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ and the convention $u(\partial )=0$. In particular, we always have $N(U^2)\mu _H\in S_K^1(\mathbf{X})$ and $N(e^U-U-1)\mu _H\in S_K^1(\mathbf{X})$, where $U(x,y): =u(x)-u(y)$ for $x,y\in E_{\partial }$. From this, we have the generalized Fukushima’s decomposition in the strict sense:

$$\begin{aligned} u(X_t)-u(X_0)=M_t^{u,c}+M_t^{u,j}+M_t^{u,\kappa }+N_t^u, \quad t\in [0,\zeta [ \end{aligned}$$

$\mathbb {P}_x$-a.s. for all $x\in E$. Note that $M^{u,c}$, $M^{u,j}$, $M^{u,\kappa }$ are defined as square integrable martingale additive functionals for all time under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ (see the proof of [31, Theorem 6.2(2)]). We set $M^U$ by

$$\begin{aligned} M^{U}_{t}= M_{t}^{-u,j} + M_{t}^{-u,\kappa }. \end{aligned}$$

(3.1)

There also exists a purely discontinuous square integrable martingale additive functional $M^{e^U-1}$ such that $\Delta M^{e^U-1}_{t}=e^{U(X_{t-},X_{t})}-1$, $t\in [0,\infty [$$\mathbb {P}_x$-a.s. for all $x\in E$. $M^{e^U-1}_{t}$ is given by

$$\begin{aligned} M_{t}^{e^U-1}=M_{t}^{U}+\sum _{0<s\le t}(e^U-U-1)(X_{s-},X_{s}) - \int _{0}^{t}N(e^U-U-1)(X_{s})\mathrm{d}H_{s}, \quad t \in [0,\infty [ \nonumber \\ \end{aligned}$$

(3.2)

Put $M_{t}:=M_{t}^{e^U-1} + M_{t}^{-u,c}$ and let

$$\begin{aligned} U_{t}:=\mathrm{Exp} (M)_{t},\quad t\in [0,\infty [ \end{aligned}$$

(3.3)

be the solution of the SDE

$$\begin{aligned} U_{t}=1+\int _{0}^{t}U_{s-}\mathrm{d}M_{s}, \quad t \in [0,\infty [,~~{\mathbb {P}}_{x}\text {-a.s.} \end{aligned}$$

(3.4)

Note that $U_{t}$ is positive and a local martingale. Therefore it is a supermartingale. Moreover, $\{U_t\}_{t\in [0,\infty [}$ is a martingale with respect to $\mathbf{X}$ for any starting point under the boundedness of u and $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. This was proved in [16, Lemma 4.1] when u is a bounded function in $\mathcal {F}_e$ with $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ but its proof remains valid under the present generality.

Let $\mathbf{U}=(\Omega , \widetilde{\mathscr {F}}_{\infty }, \widetilde{\mathscr {F}}_{t}, \widetilde{X}_{t}, {\mathbb {P}}_{x}^U, \zeta )$ be the Girsanov transformed process of $\mathbf{X}$ by $U_{t}$. The transition semigroup $\{{P}_{t}^U\}_{t\ge 0}$ of $\mathbf{U}$ is defined by

$$\begin{aligned} {P}_{t}^Uf(x):={{\mathbb {E}}}_{x}^U[f(X_t)]={\mathbb {E}}_{x}[U_{t}f(X_t)]. \end{aligned}$$

The following proposition is an extension of [5, Theorem 3.1] and [28, Theorems 3.1 and 3.2].

Proposition 3.1

We have the following:

• 1. $U_{t}$ can be represented as follows:

  $$\begin{aligned} U_{t}= & {} \exp \left( M_{t}^{U}+M_{t}^{-u,c}-\int _{0}^{t}N(e^U-U-1)(X_{s})\mathrm{d}H_{s}-\frac{1}{2}\langle M^{u,c}\rangle _{t}\right) ,\nonumber \\&\quad t\in [0,\infty [. \end{aligned}$$

  (3.5)

• 2. $\mathbf{U}$ is an $e^{-2u}\mathfrak {m}$-symmetric Markov process on E.

• 3. Let $A_t$ be a PCAF of $\mathbf{X}$ with Revuz measure $\nu$, then the Revuz measure for A as a PCAF of $\mathbf{U}$ is $e^{-2u}\nu$.

• 4. The Dirichlet form $(\mathcal {E}^U,\mathcal {F}^U)$ on $L^2(E;e^{-2u}\mathfrak {m})$ associated to $\mathbf{U}$ satisfies that $\mathcal {F}^U=\mathcal {F}$ and for any $f\in \mathcal {F}^U$

  $$\begin{aligned} \begin{aligned} {\mathcal {E}}^U(f,f)&=\frac{1}{2}\int _{E}e^{-2u(x)}\mu _{{\langle } f{\rangle }}^{c}(\mathrm{d}x)\\&\quad +\int _{(E\times E){\setminus }{\mathsf {diag}}} (f(x)-f(y))^{2}e^{-u(x)-u(y)}J(\mathrm{d}x\mathrm{d}y) \\&\quad + \int _{E}f(x)^{2}e^{-u(x)}\kappa (\mathrm{d}x). \end{aligned} \end{aligned}$$

• (5) A Lévy system $(N^U,H^U)$ of $\mathbf{U}$ is given by $N^U(x,\mathrm{d}y):=e^{-u(y)}N(x,\mathrm{d}y)$ and $H^U_t:=\int _0^te^{u(X_s)}{ \mathrm d}H_s$. That is, $\mu _{H^U}=e^{-u}\mu _H$.

• (6) $\{U_t\}_{t\in [0,\infty [}$ is a uniformly integrable martingale with respect to $\mathbf{X}^{(\alpha )}$ for any $\alpha >0$ and any starting point. Moreover, if $\mathbf{X}$ is transient and $\mu _{{\langle }u{\rangle }}\in S_{D_0}^1(\mathbf{X})$, then $\{U_t\}_{t\in [0,\infty [}$ is a uniformly integrable martingale with respect to $\mathbf{X}$ for any starting point.

Proof

The proof of (1) is easy. The proofs of (2) and (4) were done in [28, Theorems 3.1 and 3.2], whose proofs are mimics of the proofs of [16, Lemma 3.1, Theorem 3.4]. (3) also holds in the same way by the proof of [16, Theorem 3.3], which was not directly stated in [28] but needed for the proofs of (4) and (5). Note that in [28, Theorems 3.1 and 3.2], strict $\mathcal {E}$-quasi-continuity of u was assumed, but this condition was not used in the proof. The assertion (5) is noted in [5] after its Theorem 3.1. It remains to prove (6). By [4, Theorem 3.2], it suffices to check $\sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ [M]_{\infty } \right] <\infty$ and $\Delta M_t\ge \delta -1$ for some $\delta \in ]0,1[$. Here $\mathbb {E}_x^{(\alpha )}$ is the expectation with respect to $\mathbf{X}^{(\alpha )}$. Indeed, $\Delta M_t=e^{U(X_{t-},X_t)}-1\ge e^{-2\Vert u\Vert _{\infty }-1}-1$ and

$$\begin{aligned} \sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ [M]_{\infty } \right]&=\sup _{x\in E}\mathbb {E}_x^{(\alpha )}[{\langle }M{\rangle }_{\infty }]\\&=\sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ {\langle }M^{-u,c}{\rangle }_{\infty }+\sum _{0<t<\infty }(\Delta M_t)^2\right] \\&=\sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ {\langle }M^{-u,c}{\rangle }_{\infty }+\sum _{0<t<\infty }( e^{U(X_{t-},X_t)}-1)^2\right] \\&\le \sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ {\langle }M^{-u,c}{\rangle }_{\infty }+e^{2\Vert u\Vert _{\infty }}\sum _{0<t<\infty }U(X_{t-},X_t)^2\right] \\&=\sup _{x\in E}\mathbb {E}_x^{(\alpha )}\left[ {\langle }M^{-u,c}{\rangle }_{\infty }+e^{2\Vert u\Vert _{\infty }}\int _0^{\infty }N(U^2)(X_t)\mathrm{d}H_t\right] \\&=\sup _{x\in E}\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}{\langle }M^{-u,c}{\rangle }_t+e^{2\Vert u\Vert _{\infty }}\int _0^{\infty }e^{-\alpha t}N(U^2)(X_t)\mathrm{d}H_t\right] \\&<\infty . \end{aligned}$$

The proof for the transient case is similar. $\square$

Remark 3.2

The boundedness of $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ in Proposition 3.1 is needed to establish (3.5).

4 (Semi-)Green-tight measures of (extended) Kato classes and gaugeability

Let $\mu$ be a signed smooth measure in the strict sense whose associated CAF of $\mathbf{X}$ is $A^{\mu }:=A^{\mu ^+}-A^{\mu ^-}$. Here $A^{\mu ^+}$ and $A^{\mu ^-}$ are the PCAFs of $\mathbf{X}$ with Revuz measures $\mu ^+\in S_1(\mathbf{X})$ and $\mu ^-\in S_1(\mathbf{X})$, respectively. Now we start with the notion of Green-tight measures of (extended) Kato class in the strict sense given in [2, Definition 2.2].

Definition 4.1

(Green-tight Kato class measures) Let $\nu \in S_1(\mathbf{X})$ and take an $\alpha \ge 0$. When $\alpha =0$, we always assume the transience of X.

• 1. $\nu$ is said to be an $\alpha$-order Green-tight measure of Kato class with respect to$\mathbf{X}$ if $\nu \in S_{K}^1(\mathbf{X})$ and for any $\varepsilon >0$ there exists a compact subset $K=K(\varepsilon )$ of E such that

  $$\begin{aligned} \sup _{x\in E}R_{\alpha }(\mathbf{1}_{K^c}\nu )(x)=\sup _{x\in E}\int _{K^c}R_{\alpha }(x,y)\nu (\mathrm{d}y)<\varepsilon . \end{aligned}$$

• 2. $\nu$ is said to be a $\alpha$-order semi-Green-tight measure of extended Kato class with respect to$\mathbf{X}$ if $\nu \in S_{EK}^1(\mathbf{X})$ and there exists a compact subset K of E such that

  $$\begin{aligned} \sup _{x\in E}R_{\alpha }(\mathbf{1}_{K^c}\nu )(x)=\sup _{x\in E}\int _{K^c}R_{\alpha }(x,y)\nu (\mathrm{d}y)<1. \end{aligned}$$

• 3. $\nu$ is said to be an $\alpha$-order Green-tight measure of Kato class with respect to$\mathbf{X}$in the sense of [2] if for any $\varepsilon >0$ there exists a Borel subset $K=K(\varepsilon )$ of E with $\nu (K)<\infty$ and a constant $\delta >0$ such that for all $\nu$-measurable set $B \subset K$ with $\nu (B) < \delta$,

  $$\begin{aligned} \sup _{x\in E}R_{\alpha }(\mathbf{1}_{B\cup K^{c}}\nu )(x)=\sup _{x \in E}\int _{B\cup K^{c}}R_{\alpha }(x,y)\nu (\mathrm{d}y) < \varepsilon . \end{aligned}$$

  (4.1)

• 4. $\nu$ is said to be a $\alpha$-order semi-Green-tight measure of extended Kato class with respect to$\mathbf{X}$in the sense of [2] if there exists a Borel subset K of E with $\nu (K)<\infty$ and a constant $\delta >0$ such that for all $\nu$-measurable set $B \subset K$ with $\nu (B) < \delta$,

  $$\begin{aligned} \sup _{x\in E}R_{\alpha }(\mathbf{1}_{B\cup K^{c}}\nu )(x)=\sup _{x \in E}\int _{B\cup K^{c}}R_{\alpha }(x,y)\nu (\mathrm{d}y) < 1. \end{aligned}$$

  (4.2)

In view of the resolvent equation, for positive $\alpha$, the $\alpha$-order Green-tightness of Kato class is independent of the choice of $\alpha >0$. Let denote by $S_{K_{\infty }^{+}}^1(\mathbf{X})$ (resp. $S_{CK_{\infty }^{+}}^1(\mathbf{X})$) the family of positive order Green-tight measures of Kato class (resp. the family of positive order Green-tight measures of Kato class in the sense of [2]) with respect to $\mathbf{X}$. The class $S_{K_{\infty }}^1(\mathbf{X})$ (resp. $S_{K_1}^1(\mathbf{X})$) is then denoted as the family of 0-order Green-tight measures of Kato class (resp. 0-order semi-Green-tight measures of extended Kato class), and the class $S_{CK_{\infty }}^1(\mathbf{X})$, (resp. $S_{CK_{1}}^1(\mathbf{X})$) is then denoted as the family of the family of 0-order Green-tight measures of Kato class in the sense of [2], (resp. the family of 0-order semi-Green-tight measures of extended Kato class in the sense of [2]) with respect to $\mathbf{X}$. Clearly, $S_{CK_{\infty }^{+}}^1(\mathbf{X}) =S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$. Note that since a Green kernel is invariant under time change by PCAF associated to a non-negative smooth measure with full quasi support, the definitions of $S_{CK_{\infty }}^1(\mathbf{X})$ and $S_{CK_{1}}^1(\mathbf{X})$ are invariant under such time change in contrast to the Kato class $S_K^1(\mathbf{X})$. It is known in [2] that $S_{CK_{\infty }}^1(\mathbf{X}) \subset S_{CK_{1}}^1(\mathbf{X}) \subset S_{D_0}^1(\mathbf{X})\cap S_{EK}^1(\mathbf{X})$, $S_{CK_{\infty }^+}^1(\mathbf{X}) \subset S_K^1(\mathbf{X})$ and $S_{CK_{\infty }}^1(\mathbf{X}) \subset S_K^1(\mathbf{X})$. Since any measure $\nu$ in Definition 4.1 belongs to $S_{D_0}(\mathbf{X})$, it is a Radon measure, the Borel set K in Definition 4.1(3), (4) can be taken to be a closed set or an open set (see [2, remark after Definition 2.2]). Moreover, such closed set K can be taken to be a compact set, in particular, we always have $S_{CK_{\infty }^+}^1(\mathbf{X})\subset S_{K_{\infty }^+}^1(\mathbf{X})$, $S_{CK_{\infty }}^1(\mathbf{X})\subset S_{K_{\infty }}^1(\mathbf{X})$ and $S_{CK_{1}}^1(\mathbf{X})\subset S_{K_{1}}^1(\mathbf{X})$. Indeed, take $\nu \in S_{CK_{\infty }^+}^1(\mathbf{X})$, $\varepsilon >0$, and a closed set K such that (4.1) holds. Then there exists a compact subset $C\subset K$ with $\nu (K{\setminus } C)<\delta$ for a given $\delta >0$, because $\nu \in S_{D_0}^1(\mathbf{X})$ is a Radon measure on E. Since $\nu \in S_{CK_{\infty }^+}^1(\mathbf{X})$, we have $\sup _{x\in E}R_{\alpha }\mathbf{1}_{C^c}\nu (x)=\sup _{x\in E}R_{\alpha }\mathbf{1}_{K^c\cup (K{\setminus } C)}\nu (x)<\varepsilon$.

Let $\nu \in S_1(\mathbf{X})$ and denote by $A_t^{\nu }$ PCAF in the strict sense associated to $\nu$ in Revuz correspondence. Denote by ${\mathsf {S}}_{o}^{\nu }$ the support of $A^{\nu }$ defined by ${\mathsf {S}}_o^{\nu }:=\{x\in E : \mathbb {P}_x(R=0)=1\}$, where $R(\omega ):=\inf \{t>0 : A_t^{\nu }(\omega )>0\}$. ${\mathsf {S}}_{o}^{\nu }$ is nothing but the fine support of $\nu$, i.e., the topological support of $\nu$ with respect to the fine topology of X. Let $(\check{\mathbf{X}}, \nu )$ be the time changed process of X by $A_t^{\nu }$ and $(\check{\mathcal {E}},\check{\mathcal {F}})$ the associated Dirichlet form on $L^2({\mathsf {S}}^{\nu };\nu )$, where ${\mathsf {S}}^{\nu }$ is the support of $\nu$. It is known that $(\check{\mathcal {E}},\check{\mathcal {F}})$ is a quasi-regular Dirichlet form and ${\mathsf {S}}^{\nu }{\setminus } {\mathsf {S}}_o^{\nu }$ is $\check{\mathcal {E}}$-polar, i.e., 1-capacity 0 set with respect to $(\check{\mathcal {E}},\check{\mathcal {F}})$. The lifetime of $(\check{\mathbf{X}}, \nu )$ is given by $A_{\zeta }^{\nu }$. Let $C^{\nu }:2^E\rightarrow [0,\infty ]$ be the weighted 1-capacity with respect to $(\check{\mathcal {E}},\check{\mathcal {F}})$, i.e., for an open subset G of E, we define

$$\begin{aligned} C^{\nu }(G):=\inf \{\check{\mathcal {E}}_1(f,f) : f\in \check{\mathcal {F}},\; f\ge \check{R}_1\varphi \quad \nu \text {-a.e.}~\text {on }G\} \end{aligned}$$

and for arbitrary subset A of E

$$\begin{aligned} C^{\nu }(A):=\inf \{C^{\nu }(G) : A\subset G,\;G\text { is an open subset of }E\}, \end{aligned}$$

where $\check{R}_1\varphi (x):=\mathbb {E}_x[\int _0^{\infty }e^{-A_t^{\nu }}\varphi (X_t)\mathrm{d}A_t^{\nu }]$ is the 1-order resolvent of a $\nu$-a.e. strictly positive bounded function $\varphi \in L^1(E;\nu )$ under $(\check{\mathbf{X}}, \nu )$ and $\check{\mathcal {E}}_1(f,f):=\check{\mathcal {E}}(f,f)+\int _Ef^2\mathrm{d}\nu$. We emphasize that $C^{\nu }$ is defined to be an outer capacity on E. By definition, $C^{\nu }(E{\setminus } {\mathsf {S}}^{\nu })=0$. Note that $C^{\nu }(E)\le \check{\mathcal {E}}_1(\check{R}_1\varphi ,\check{R}_1\varphi )= \int _E\varphi (x) \check{R}_1\varphi (x)\nu (\mathrm{d}x) <\infty$ always holds. Note also that $C^{\nu }$ is tight in the sense that there exists an increasing sequence $\{K_n\}$ of compact subsets of ${\mathsf {S}}^{\nu }$ such that $\lim _{n\rightarrow \infty }C^{\nu }({\mathsf {S}}^{\nu }{\setminus } K_n)=0$ equivalently $\lim _{n\rightarrow \infty }C^{\nu }(E{\setminus } K_n)=0$. Hence any quasi closed set with respect to $C^{\nu }$ is quasi compact in the sense of Fuglede [21, Lemma 2.2]. By [21, Theorem 2.10], any decreasing sequence $\{A_n\}$ of quasi closed subsets of E with respect to $C^{\nu }$ satisfies

$$\begin{aligned} C^{\nu }\left( \bigcap _{n=1}^{\infty }A_n\right) =\inf _{n\in \mathbb {N}}C^{\nu }(A_n). \end{aligned}$$

(4.3)

Now we introduce the following new classes of (semi-)Green-tight measures of (extended) Kato class by replacing the $\nu$-measure smallness condition “$\nu (B)<\delta$” in Definition 4.1 with the capacity smallness condition “$C^\nu (B)<\delta$” for the time changed process induced by the measure $\nu$.

Definition 4.2

(Natural (semi-)Green-tight measures of (extended) Kato class) Let $\alpha \ge 0$ and $\nu \in S_1(\mathbf{X})$.

• 1. $\nu$ is said to be an $\alpha$-order natural Green-tight measure of Kato class with respect to$\mathbf{X}$ if $\nu \in S_{D}^1(\mathbf{X})$ ($\nu \in S_{D_0}^1(\mathbf{X})$ for $\alpha =0$) and for any $\varepsilon >0$ there exists a closed subset $K=K(\varepsilon )$ of E and a constant $\delta >0$ such that for all $\nu$-measurable subset $B \subset K$ with $C^{\nu }(B) < \delta$,

  $$\begin{aligned} \sup _{x\in E}\mathbb {E}_x\left[ \int _0^{\tau _{B\cup {K^c}}}e^{-\alpha t}\mathrm{d}A_t^{\nu } \right] < \varepsilon . \end{aligned}$$

• 2. $\nu$ is said to be a 0-order natural semi-Green-tight measure of extended Kato class with respect to$\mathbf{X}$ if $\nu \in S_{D_0}^1(\mathbf{X})$ and there exists a closed subset K of E and a constant $\delta >0$ such that for all $\nu$-measurable subset $B \subset K$ with $C^{\nu }(B) < \delta$,

  $$\begin{aligned} \sup _{x\in E}\mathbb {E}_x\left[ A_{\tau _{B\cup {K^c}}}^{\nu } \right] < 1. \end{aligned}$$

In view of the resolvent equation, for positive $\alpha$, the $\alpha$-order natural Green-tightness is independent of the choice of $\alpha >0$. We use $S_{NK_{\infty }^{+}}^1(\mathbf{X})$ to denote the family of positive order natural Green-tight measures of Kato class with respect to $\mathbf{X}$. The class $S_{NK_{\infty }}^1(\mathbf{X})$ (resp. $S_{NK_{1}}^1(\mathbf{X})$) is then denoted as the family of 0-order natural Green-tight measures of Kato class (resp. the family of 0-order natural semi-Green-tight measures of extended Kato class) with respect to $\mathbf{X}$. Similarly, as we remarked after Definition 4.1, the closed set K appeared in Definition 4.2 can be taken to be compact, because the weighted 1-capacity $C^{\nu }$ is tight. Clearly, $S_{NK_{\infty }^{+}}^1(\mathbf{X}) =S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Since $\int _Bg\,\mathrm{d}\nu \le C^{\nu }(B)$ holds for the $\nu$-a.e. strictly positive bounded function $g:=(\check{R}_1\varphi )^2\in L^1(E;\nu )$, by [28, Lemma 4.2], we have $S_{CK_{\infty }}^1(\mathbf{X})\subset S_{NK_{\infty }}^1(\mathbf{X})$ and $S_{CK_{1}}^1(\mathbf{X})\subset S_{NK_{1}}^1(\mathbf{X})$, hence $S_{CK_{\infty }^+}^1(\mathbf{X})\subset S_{NK_{\infty }^+}^1(\mathbf{X})$. It is shown in [27, Proposition 4.1] that $S_{K_{\infty }}^1(\mathbf{X}^{(1)})= S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ ($S_{K_{\infty }}^1(\mathbf{X})= S_{CK_{\infty }}^1(\mathbf{X})=S_{NK_{\infty }}^1(\mathbf{X})$ under the transience of X) provided X is a (resolvent) doubly Feller process.

Let G be a non-empty finely open nearly Borel subset of E. The cemetery point $\partial$ is also an isolated point of $G\cup \{\partial \}$. Let $\mathbf{X}^G :=(\Omega , X_t,\mathbb {P}_x^G)=(\Omega ,X_t^G,\mathbb {P}_x)$ the part process of X on G defined by

$$\begin{aligned} X_t^G:=\left\{ \begin{array}{cc}X_t &{}\quad t<\tau _G, \\ \partial &{}\quad t\ge \tau _G\end{array}\right. \text { under }\mathbb {P}_x \end{aligned}$$

We consider the lifetime $\zeta _G$ of ${\mathbf{X}^G}$ defined by $\zeta _G:=\inf \{t>0 : X_t^G=\partial \}$ under $\mathbb {P}_x^G$. Of course, the distribution of $\zeta _G$ under $\mathbb {P}_x^G$ coincides with the distribution of $\tau _G$ under $\mathbb {P}_x$.

Lemma 4.3

Let G be a finely open nearly Borel subset of E. Suppose that (1.7) holds for X. Then (1.7) holds for ${\mathbf{X}^G}$.

Proof

It is easy to see $\Vert P_t\Vert _{1,\infty }=\sup \{\Vert P_tf\Vert _{\infty } : f\in L^1_+(E;\mathfrak {m}),\Vert f\Vert _1=1\}$. Then the assertion is clear from

$$\begin{aligned} \Vert P_t\Vert _{1,\infty }&\ge \sup \{\Vert P_tf\Vert _{\infty }: f\in L^1_+(E;\mathfrak {m}),f=0\;\mathfrak {m}\text {-a.e.}~\text {on }E{\setminus } G,\;\Vert f\Vert _1=1\}\\&\ge \sup \{\Vert P_t^Gf\Vert _{\infty } : f\in L^1_+(G;\mathfrak {m}),\Vert f\Vert _1=1\}=\Vert P_t^G\Vert _{1,\infty }. \end{aligned}$$

$\square$

It is known that the Dirichlet form $(\mathcal {E}_G,\mathcal {F}_G)$ on $L^2(G;\mathfrak {m})$ associated to ${\mathbf{X}^G}$ is quasi-regular. So we can consider several notions on $(\mathcal {E}_G,\mathcal {F}_G)$. For example, the family $S_0({\mathbf{X}^G})$ of measures of finite energy with respect to ${\mathbf{X}^G}$ and so on. For a Borel measure on E, denote by $\nu |_G$ the restriction of $\nu$ on G defined by $\nu |_G(A):=\nu (A)$ for $A\in \mathscr {B}(G)$. For the proof of main theorems, we need the following lemma.

Lemma 4.4

Let G be a finely open nearly Borel set. Then we have

• 1. $\nu \in S_0(\mathbf{X})$ (resp. $\nu \in S_{00}(\mathbf{X})$) implies $\nu |_G\in S_0({\mathbf{X}^G})$ (resp. $\nu |_G\in S_{00}({\mathbf{X}^G})$).

• 2. $\nu \in S(\mathbf{X})$ (resp. $\nu \in S_1(\mathbf{X})$) implies $\nu |_G\in S({\mathbf{X}^G})$ (resp. $\nu |_G\in S_1({\mathbf{X}^G})$).

• 3. $\nu \in S_D^1(\mathbf{X})$ implies $\nu |_G\in S_D^1({\mathbf{X}^G})$.

• 4. $\nu \in S_K^1(\mathbf{X})$ implies $\nu |_G\in S_K^1({\mathbf{X}^G})$.

• 5. $\nu \in S_{EK}^1(\mathbf{X})$ implies $\nu |_G\in S_{EK}^1({\mathbf{X}^G})$.

Suppose further that X is transient. Then

• 6. $\nu \in S_{D_0}^1(\mathbf{X})$ implies $\nu |_G\in S_{D_0}^1({\mathbf{X}^G})$.

• 7. $\nu \in S_{CK_{\infty }}^1(\mathbf{X})$ implies $\nu |_G\in S_{CK_{\infty }}^1({\mathbf{X}^G})$.

• 8. $\nu \in S_{CK_1}^1(\mathbf{X})$ implies $\nu |_G\in S_{CK_1}^1({\mathbf{X}^G})$.

• 9. $\nu \in S_{NK_{\infty }}^1(\mathbf{X})$ implies $\nu |_G\in S_{NK_{\infty }}^1({\mathbf{X}^G})$.

• 10. $\nu \in S_{NK_1}^1(\mathbf{X})$ implies $\nu |_G\in S_{NK_1}^1({\mathbf{X}^G})$.

Proof

The proof of the first assertion in (1) is easy, because $\mathcal {F}\subset L^1(E;\nu )$ implies $\mathcal {F}_G\subset L^1(G;\nu )$. (2) easily follows from (1). The assertions of the second part of (1) and (3)–(5) follow from the estimate:

$$\begin{aligned} R^G_{\alpha }\nu |_G(x)&:=\mathbb {E}_x^G\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] =\mathbb {E}_x\left[ \int _0^{\tau _G}e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] \le \mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] \\&=R_{\alpha }\nu (x). \end{aligned}$$

Here $\mathbb {P}_x^G$ is the law for the part process ${\mathbf{X}^G}$. The assertion (6) follows the estimate $R^G\nu |_G(x)\le R\nu (x)$. The proof of (7) follows the following: For any ${\varepsilon }>0$, take a Borel set $K=K({\varepsilon })$ with $\nu (K)<\infty$ and a subset B of K, we see for $B_G:=B\cap G$ and $K_G:=K\cap G$ that

$$\begin{aligned} \sup _{x\in G}R^G\mathbf{1}_{B_G\cup (G{\setminus } K_G)}\nu |_G(x)\le \sup _{x\in E}R\mathbf{1}_{B\cup (E{\setminus } K)}\nu (x)<{\varepsilon }. \end{aligned}$$

The proof of (8) is similar. We now prove (9) and (10). By [28, Lemma 4.4], for any decreasing sequence $\{D_n\}$ of Borel subsets of G, it suffices to prove $\lim _{n\rightarrow \infty }C_G^{\nu }(D_n)=0$ implies $\lim _{n\rightarrow \infty }C^{\nu }(D_n)=0$. Here $C^{\nu }$ (resp. $C_G^{\nu }$) denotes the 1-weighted capacity with respect to $(\check{\mathbf{X}},\nu )$ (resp. $(\check{\mathbf{X}}^G,\nu |_G)$). Recall that these 1-weighted capacities has the continuity for decreasing sequence of quasi-closed sets by (4.3). Denote by $\overline{D_n}^{\check{\mathcal {E}}_G}$ the $\check{\mathcal {E}}_G$-quasi-closure of $D_n$. Then we have

$$\begin{aligned} C_G^{\nu }\left( \bigcap _{n=1}^{\infty } \overline{D_n}^{\check{\mathcal {E}}_G}\right) =\lim _{n\rightarrow \infty }C_G^{\nu }(\overline{D_n}^{\check{\mathcal {E}}_G})=0, \end{aligned}$$

that is, $\bigcap _{n=1}^{\infty }\overline{D_n}^{\check{\mathcal {E}}_G}$ is an $\check{\mathcal {E}}_G$-polar set. Applying [32, Lemma 3.5(ii)] to the Dirichlet form $(\check{\mathcal {E}},\check{\mathcal {F}})$ on $L^2({\mathsf {S}}^{\nu };\nu )$ associated to the time changed process $(\check{\mathbf{X}},\nu )$, we have the $\check{\mathcal {E}}$-polarity of $\bigcap _{n=1}^{\infty }\overline{D_n}^{\check{\mathcal {E}}_G}$, i.e., $C^{\nu }\left( \bigcap _{n=1}^{\infty }\overline{D_n}^{\check{\mathcal {E}}_G} \right) =0$. Applying [32, Lemma 3.5(iv)] to $(\check{\mathcal {E}},\check{\mathcal {F}})$ again, we see the $\check{\mathcal {E}}$-quasi-closedness of $\overline{D_n}^{\check{\mathcal {E}}_G}$. Hence

$$\begin{aligned} \lim _{n\rightarrow \infty }C^{\nu }(D_n)\le \lim _{n\rightarrow \infty }C^{\nu }(\overline{D_n}^{\check{\mathcal {E}}_G})=C^{\nu }\left( \bigcap _{n=1}^{\infty }\overline{D_n}^{\check{\mathcal {E}}_G} \right) =0. \end{aligned}$$

We see that for any $C\in \mathscr {B}(E)$,

$$\begin{aligned} \mathbb {E}_x^G[A_{\tau _{C}}^{\nu }]=\mathbb {E}_x[A_{\tau _C\wedge \tau _G}^{\nu }]\le \mathbb {E}_x[A_{\tau _{C}}^{\nu }]. \end{aligned}$$

Now the assertions follow from this estimate. $\square$

Let (N, H) be a Lévy system of X. Consider a finely open nearly Borel set G. Define $N^G(x,\mathrm{d}y):=\mathbf{1}_G(y)N(x,\mathrm{d}y)+N(x,E_{\partial }{\setminus } G)\delta _{\partial }(\mathrm{d}y)$ and let $H^G_t$ be the PCAF of ${\mathbf{X}^G}$ under $\mathbb {P}_x^G$ associated to the Revuz measure $\mu _H|_G$. Then $H^G_t$ under $\mathbb {P}_x^G$ has the same distribution as $H_{t\wedge \tau _G}$ under $\mathbb {P}_x$ for $x\in G$. The following lemma follows immediately from the definition of Lévy system (2.2).

Lemma 4.5

$(N^G, H^G)$ is the Lévy system of ${\mathbf{X}^G}$.

Let $\phi$ be a bounded non-negative symmetric function defined on $E\times E$ satisfying $\phi (x,x)=0$ for $x\in E$. We further assume that $\phi$ is extended to be a function on $E_{\partial }\times E_{\partial }$ with $\phi (x,\partial )=\phi (\partial ,x)=0$ for $x\in E_{\partial }$. Then we see $N^G(\phi )(x)=\int _G\phi (x,y)N(x,\mathrm{d}y)$.

Lemma 4.6

Let $\phi$ be the function as above and G a finely open nearly Borel set. If $N(\phi )\mu _H\in S_{NK_1}^1(\mathbf{X})$ (resp.  $N(\phi )\mu _H\in S_{EK}^1(\mathbf{X})$, $N(\phi )\mu _H\in S_{D}^1(\mathbf{X})$, $N(\phi )\mu _H\in S_{D_0}^1(\mathbf{X})$), then $N^G(\phi )\mu _H\in S_{NK_1}^1({\mathbf{X}^G})$ (resp. $N^G(\phi )\mu _H\in S_{EK}^1({\mathbf{X}^G})$, $N(\phi )\mu _H\in S_{D}^1({\mathbf{X}^G})$, $N^G(\phi )\mu _H\in S_{D_0}^1({\mathbf{X}^G})$).

Proof

First we prove that $N(\phi )\mu _H\in S_{EK}^1(\mathbf{X})$ (resp.  $N(\phi )\mu _H\in S_{D}^1(\mathbf{X})$, $N(\phi )\mu _H\in S_{D_0}^1(\mathbf{X})$) implies $N^G(\phi )\mu _H\in S_{EK}^1({\mathbf{X}^G})$ (resp.  $N(\phi )\mu _H\in S_{D}^1({\mathbf{X}^G})$, $N^G(\phi )\mu _H\in S_{D_0}^1({\mathbf{X}^G})$). For $\alpha \ge 0$, we see that

$$\begin{aligned} R^G_{\alpha }N^G(\phi )\mu _H(x)&=\mathbb {E}_x^G\left[ \int _0^{\infty }e^{-\alpha s} N^G(\phi )(X_s)\mathrm{d}H_s\right] \\&=\mathbb {E}_x\left[ \int _0^{\tau _G}e^{-\alpha s}\int _G\phi (X_s,y)N(X_s,\mathrm{d}y)\mathrm{d}H_s\right] \\&\le \mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha s}\int _E\phi (X_s,y)N(X_s,\mathrm{d}y)\mathrm{d}H_s\right] \\&= \mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha s} N(\phi )(X_s)\mathrm{d}H_s\right] =R_{\alpha }N(\phi )\mu _H(x) \end{aligned}$$

implies the assertions by Lemma 4.4(5), (6). Next we prove that $N(\phi )\mu _H\in S_{NK_1}^1(\mathbf{X})$ implies $N^G(\phi )\mu _H\in S_{NK_1}^1({\mathbf{X}^G})$. This follows from that for $C\in \mathscr {B}(G)$

$$\begin{aligned} \mathbb {E}_x^G\left[ \int _0^{\tau _C}N^G(\phi )(X_s)\mathrm{d}H_s \right]&=\mathbb {E}_x\left[ \int _0^{\tau _C\wedge \tau _G}N^G(\phi )(X_s)\mathrm{d}H_s \right] \\&\le \mathbb {E}_x\left[ \int _0^{\tau _C}N(\phi )(X_s)\mathrm{d}H_s \right] \end{aligned}$$

with Lemma 4.4(8). $\square$

For a finely open nearly Borel set G, $(Q_t^{G})_{t\ge 0}$ denotes the Feynman–Kac semigroup obtained from the part process ${\mathbf{X}^G}$, which is defined by $Q_t^Gf(x):=\mathbb {E}_x[e_A(t)f(X_t):t<\tau _G]$. Under $\mathbf{(A)}$, we see that $(Q_t^{G})_{t\ge 0}$ is a $C_0$-semigroup on $L^2(G;\mathfrak {m})$ associated to the quadratic form $(\mathcal {Q},\mathcal {F}_G)$ on $L^2(G;\mathfrak {m})$.

For an AF A, we say that $(\mathbf{X},A)$ is gaugeable if

$$\begin{aligned} \sup _{x\in E}\mathbb {E}_x\left[ \exp (A_{\zeta })\right] <\infty . \end{aligned}$$

From here to the end of Theorem 4.10, we assume the transience of $\mathbf{X}$ and irreducibility condition (I) for the characterization of gaugeability of Feynman–Kac functionals. The following lemmas and theorem are proved in [27] under the assumption that E is a locally compact separable metric space and $\mathfrak {m}$ is a positive Radon measure with full support, which are modifications of Lemmas 2.7, 2.14, Theorems 2.8, 2.15, Corollaries 2.9, 2.16 and Theorems 2.10, 2.11 in [2]. Those proofs remain valid in the framework of this paper and they are quite similar as those in [2].

Lemma 4.7

(cf. [27, Lemma 4.2]) Set $A:=A^{\mu }+A^{F}$ and $e_A(t):=\exp (A_t)$. Suppose that $\mu ^+ +N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X})$ and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$ hold. Then we have the following:

• 1. If $(\mathbf{X},A)$ is gaugeable, then for any $\delta >0$ there is a constant $c(\delta )>0$ such that

  $$\begin{aligned} \Vert g_{A}\Vert _{\infty }^{-1}g_{A}(x)\le \sum _{n=0}^{\infty }\mathbb {E}_x\left[ e_A(\tau _{n\delta }^p):\tau _{n\delta }^p<\zeta \right] \le c(\delta )<\infty \quad \text { for all }x\in E. \end{aligned}$$

  Here $\tau _t^p:=\inf \{s>0 : A_s^{\eta _p}>t\}$ is the right continuous inverse of $A_t^{\eta _p}$ with $\eta _p=\mu ^+ +\frac{1}{p}N(e^{pF^+}-1)\mu _H$ and $g_{A}(x):=\mathbb {E}_x[e_A(\zeta )]$ is the gauge function for $A=A^{\mu }+A^{F}$.

• 2. The following are equivalent:

  • (a) $(\mathbf{X},A)$ is gaugeable.

  • (b) $\mathbb {E}_x\left[ \int _0^{\zeta }e_A(t)\mathrm{d} (A_t^{\mu ^+}+A_t^{F^+}) \right] <\infty$ for some $x\in E$.

  • (c) $\sup _{x\in E}\mathbb {E}_x\left[ \int _0^{\zeta }e_A(t)\mathrm{d} (A_t^{\mu ^+}+A_t^{F^+}) \right] <\infty$.

  • (d) $\mathbb {E}_x\left[ \sup _{t\in [0,\zeta ]}e_A(t)\right] <\infty$ for some $x\in E$.

  • (e) $\sup _{x\in E}\mathbb {E}_x\left[ \sup _{t\in [0,\zeta ]}e_A(t)\right] <\infty$.

  • (f) $(\mathbf{X}^*, A^{\mu ^+} +A^{F^+})$ is gaugeable. Here $\mathbf{X}^*$ is the killed process of X by $e^{-A_t^{{\mu ^-}}-A_t^{F^-}}$.

Remark 4.8

(cf. [27, Remark 4.1]) If $\mathfrak {m}\in S_{D_0}^1(\mathbf{X})$, under the same condition as in Lemma 4.7, without using time change, we have the following: Suppose that $(\mathbf{X},A)$ is gaugeable with $A=A^{\mu }+A^F$ and $e_A(t):=\exp (A_t)$. Then, for any $\delta >0$, there is a constant $c(\delta )>0$ such that

$$\begin{aligned} \Vert g_{A}\Vert _{\infty }^{-1}g_{A}(x)\le \sum _{n=0}^{\infty }\mathbb {E}_x\left[ e_A(n\delta ):n\delta<\zeta \right] \le c(\delta )<\infty \quad \text { for all }x\in E. \end{aligned}$$

By Remark 4.8, we can prove the following:

Lemma 4.9

(cf. [27, Lemma 4.3]) Suppose $\mathfrak {m}\in S_{D_0}^1(\mathbf{X})$, $\mu ^+ +N(e^{F^+}-1)\mu _H\in S_{NK_{1}}^1(\mathbf{X})$ and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$. Set $A:=A^{\mu }+A^{F}$ and $e_A(t):=\exp (A_t)$. Then the following are equivalent:

• 1. $(\mathbf{X},A)$ is gaugeable.

• 2. For some $\delta >0$ and some $x\in E$,

  $$\begin{aligned} \sum _{n=1}^{\infty }\mathbb {E}_x\left[ e_A(n\delta ):n\delta<\zeta \right] <\infty . \end{aligned}$$

  (4.4)

• 3. For all $\delta >0$ and all $x\in E$, (4.4) is true.

• 4. For some $x\in E$, $\mathbb {E}_x\left[ \int _0^{\zeta }e_A(t)\mathrm{d}t\right] <\infty$.

• 5. $\sup _{x\in E}\mathbb {E}_x\left[ \int _0^{\zeta }e_A(t)\mathrm{d}t\right] <\infty$.

• 6. There exists some $t>0$ such that $\sup _{x\in E}\mathbb {E}_x\left[ e_A(t):t<\zeta \right] <\infty$.

• 7. There are constants $C>0$ and $b>0$ such that $\sup _{x\in E}\mathbb {E}_x\left[ e_A(t):t<\zeta \right] \le Ce^{-bt}$ for all $t>0$.

Recall that the quadratic form $(\mathcal {Q},\mathcal {F})$ defined in (1.2). We consider the case $u=0$. Using Lemma , we can prove the following theorem, whose proof is similar to that of [2, Theorem 2.12].

Theorem 4.10

(cf. [27, Theorem 4.2]) Suppose that $\mathfrak {m}\in S_{D_0}^1(\mathbf{X})$ with $\mathfrak {m}(E)<\infty$ and $u=0$. Assume ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_{1}}^1(\mathbf{X})$ and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$. Set $A:=A^{\mu }+A^{F}$ and $e_A(t):=\exp (A_t)$. Then $(\mathbf{X},A)$ is gaugeable if and only if

$$\begin{aligned} \lambda ^{\mathcal {Q}}(\mathfrak {m}):=&\inf \left\{ \mathcal {Q}(f,f): f\in \mathcal {C}\hbox { with } \int _Ef^2\mathrm{d}\mathfrak {m}=1\right\} >0. \end{aligned}$$

Consider the non-local Feynman–Kac transforms by the additive functionals $A:=N^u +A^\mu +A^F$ of the form (1.1) under (A) for finely continuous nearly Borel $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$. If such u is a bounded function and $\mu _{{\langle }u{\rangle }}\in S_{K}^1(\mathbf{X})$, then $\{U_t\}_{t\in [0,\infty [}$ forms a uniformly integrable martingale on $[0,\infty [$ under $\mathbf{X}^{(1)}$ by Proposition 3.1(6). We have that for all $t\in [0,\zeta [$,

$$\begin{aligned} e_A(t) =U_te^{u({X}_t)-u(X_0)}\exp \left( A_t^{\bar{\nu }}+A_t^F\right) , \end{aligned}$$

(4.5)

where $\bar{\nu }=\bar{\nu }_1-\bar{\nu }_2$ and $\bar{\nu }_1:={\mu ^+}+N(e^U-U-1)\mu _H+\frac{1}{2}\mu _{{\langle }u{\rangle }}^c$ and $\bar{\nu }_2:={\mu ^-}$. Hence for $x\in E$ and $f\in \mathscr {B}_+(E)$,

$$\begin{aligned} \left. \begin{array}{cl} \mathbb {E}_x\left[ e_A(t)f(X_t)\right] =e^{-u(x)}{\mathbb {E}}_x^U[\exp \left( A_t^{\bar{\nu }}+A_t^F\right) (e^uf)(\widetilde{X}_t)].\end{array}\right. \end{aligned}$$

(4.6)

Recall that ${\mathsf {S}}_o^{\nu }$ is the fine support of $A_t^{\nu }$ for a smooth measure $\nu \in S_1(\mathbf{X})$. We have the following:

Lemma 4.11

(cf. [28, Lemma 4.5], [27, Lemma 4.1]) Suppose that $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a bounded finely continuous nearly Borel function and $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. Then the following hold:

• 1. For $\nu \in S_D^1(\mathbf{X})$, $e^{-2u}\nu \in {S}_D^1(\mathbf{U})$.

• 2. For $\nu \in S_K^1(\mathbf{X})$, $e^{-2u}\nu \in {S}_K^1(\mathbf{U})$.

• 3. For $\nu \in S_{EK}^1(\mathbf{X})$, $e^{-2u}\nu \in {S}_{EK}^1(\mathbf{U})$.

• 4. For $\nu \in S_{K_{\infty }}^1(\mathbf{X}^{(1)})$, $e^{-2u}\nu \in {S}_{K_{\infty }}^1(\mathbf{U}^{(1)})$.

• 5. For $\nu \in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$, $e^{-2u}\nu \in {S}_{CK_{\infty }}^1(\mathbf{U}^{(1)})$.

• 6.

  • (a) Assume $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. For $\nu \in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, $e^{-2u}\nu \in {S}_{NK_{\infty }}^1(\mathbf{U}^{(1)})$.

  • (b) Assume that $\mathbf{X}$ is transient and $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X})$. For $\nu \in S_{NK_{\infty }}^1(\mathbf{X})$, $e^{-2u}\nu \in {S}_{NK_{\infty }}^1(\mathbf{U})$.

• (7)

  • (a) Assume $\mu _{{\langle }u{\rangle }} \in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. For $\nu \in S_{NK_1}^1(\mathbf{X}^{(1)})$, we have $e^{-2u}\nu \in {S}_{NK_1}^1(\mathbf{U}^{(1)})$.

  • (b) Assume that $\mathbf{X}$ is transient and $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X})$. For $\nu \in S_{NK_1}^1(\mathbf{X})$, we have $e^{-2u}\nu \in {S}_{NK_1}^1(\mathbf{U})$.

Proof

The proofs of (1)–(5), (6)(a) and (7)(a) are essentially done in [27, Lemma 4.1]. The continuity of u is assumed in [28, Lemma 4.5], [27, Lemma 4.1], but its proof does not depend on it. Moreover, the strict $\mathcal {E}$-quasi-continuity of u is also assumed in [28, Lemma 4.5], [27, Lemma 4.1] instead of the uniform integrability of $\{U_t\}_{t\in [0,\infty [}$ under $\mathbf{X}^{(\alpha )}$. The assertion of [27, Lemma 4.1] is a special case of [28, Lemma 4.5]. Both of them require the irreducibility condition $\mathbf{(I)}$. But the proof of [28, Lemma 4.5] does not use $\mathbf{(I)}$. So we can apply [27, Lemma 4.1] without $\mathbf{(I)}$. Though the transience of X is also assumed in [27], the proofs of (1)–(5), (6)(a) and (7)(a) remain valid without assuming it. The statements of (6) and (7) are improvements of [27, Lemma 4.1(6), (7)]. It suffices to prove (6)(b), because the proof of (7)(b) is similar. Suppose that $\mathbf{X}$ is transient and $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X})$. Then $\{U_t\}_{t\in [0,\infty [}$ is a uniformly integrable martingale with respect to $\mathbf{X}$. By Hölder’s inequality,

$$\begin{aligned} \mathbb {E}_x^{U}\left[ A_{\tau _{D_n}}^{\nu } \right] =\mathbb {E}_x\left[ U_{\tau _{D_n}}A_{\tau _{D_n}}^{\nu } \right] \le \mathbb {E}_x[U_{\tau _{D_n}}^p]^{\frac{1}{p}}q^{\frac{1}{q}} \sup _{x\in E}\mathbb {E}_x\left[ A_{\tau _{D_n}}^{\nu } \right] , \end{aligned}$$

it suffices to prove that for $p>1$

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x\in E}\mathbb {E}_x[U_{\tau _{D_n}}^p]<\infty . \end{aligned}$$

(4.7)

Take $\nu \in S_{NK_{\infty }}^1(\mathbf{X})$ and assume ${\mathsf {S}}_0^{\nu }\supset {\mathsf {S}}_0^{\mu _{{\langle }u{\rangle }}^c+N(e^U-U-1)\mu _H}$ q.e. In this case, for $p\in ]1,\infty [$ and $q=\frac{p}{p-1}$, the measure $\mu _p$ defined by

$$\begin{aligned} \mu _p:=\frac{q}{p}N(e^{p^2U}-p^2U-1)\mu _H+\frac{pq}{2}(p^2-1)\mu _{{\langle }u{\rangle }}^c \end{aligned}$$

satisfies $\mu _p\in S_{NK_{\infty }}^1(\mathbf{X})$, hence for any decreasing sequence $\{D_n\}$ of Borel subsets satisfying $\mathbb {P}_x(\lim _{n\rightarrow \infty }\sigma _{D_n}\ge \zeta )=1$ q.e. $x\in {\mathsf {S}}_0^{\nu }\supset {\mathsf {S}}_0^{\mu _p}$ q.e., we have $\lim _{n\rightarrow \infty }\sup _{x\in E} \mathbb {E}_x[A_{\tau _{D_n}}^{\mu _p}]=0$. Thus we can obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x\in E} \mathbb {E}_x[U_{\tau _{D_n}}^p]&\le \lim _{n\rightarrow \infty }\sup _{x\in E} \mathbb {E}_x\left[ \exp \left( A_{\tau _{D_n}}^{\mu _p}\right) \right] ^{\frac{1}{q}} \le \left( \frac{1}{1-\lim \limits _{n\rightarrow \infty }\sup \limits _{x\in E}\mathbb {E}_x\left[ A_{\tau _{D_n}}^{\mu _p} \right] } \right) ^{\frac{1}{q}}\\&=1. \end{aligned}$$

Therefore we have $e^{-2u}\nu \in S_{NK_{\infty }}^1(\mathbf{X})$ under ${\mathsf {S}}_o^{\nu }\supset {\mathsf {S}}_o^{\mu _{{\langle }u{\rangle }}+N(e^U-U-1)\mu _H}$ q.e. It is easy to see ${\mathsf {S}}_o^{\nu +\mu _{{\langle }u{\rangle }}}\supset {\mathsf {S}}_o^{\mu _{{\langle }u{\rangle }}^c+N(e^U-U-1)\mu _H}$ q.e. so that $e^{-2u}(\nu +\mu _{{\langle }u{\rangle }})\in S_{NK_{\infty }}^1(\mathbf{U})$, hence $e^{-2u}\nu \in S_{NK_{\infty }}^1(\mathbf{U})$. $\square$

Lemma 4.12

Suppose that E is a locally compact separable metric space with one point compactification $E_{\partial }$ , $\mathfrak {m}$ is a positive Radon measure with full support, and $(\mathcal {E},\mathcal {F})$ is a regular Dirichlet form on $L^2(E;\mathfrak {m})$. Let v be a function defined on $E_{\partial }$. Suppose that $v\in \mathcal {F}$, $v(\partial )=0$ and v is finely continuous q.e. on E. Then v is strictly $\mathcal {E}$-quasi-continuous on $E_{\partial }$.

Proof

By [22, Theorem 2.1.3], v admits a strictly $\mathcal {E}$-quasi-continuous $\mathfrak {m}$-version $\tilde{v}$ with $\tilde{v}(\partial )=0$. Then $\tilde{v}$ itself is finely continuous q.e. by [22, Theorem 4.2.2]. Since $v=\tilde{v}$$\mathfrak {m}$-a.e., we can conclude from [22, Lemma 4.1.5] that there exists a capacity zero set N such that $v=\tilde{v}$ on $E{\setminus } N$. Taking a common strict $\mathcal {E}$-nest $\{F_n\}$ of closed sets such that $N\subset \bigcap _{n=1}^{\infty }(E{\setminus } F_n)$ and $\tilde{v}$ is continuous on each $F_n\cup \{\partial \}$, we see that v coincides with $\tilde{v}$ on each $F_n\cup \{\partial \}$. This implies the strict $\mathcal {E}$-quasi-continuity of v on $E_{\partial }$. $\square$

Remark 4.13

Lemma 4.12 is a refinement of [22, Lemma 4.2.2(i)].

Lemma 4.14

For $\nu \in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, we have $\inf _{x\in E}\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] =0$ for every $\alpha >0$, that is, $R_{\alpha }\nu$ is an $\alpha$-potential.

Proof

We may assume that E is a locally compact separable metric space, $\mathfrak {m}$ is a positive Radon measure on E with full support, and $(\mathcal {E},\mathcal {F})$ is a regular Dirichlet form on $L^2(E;\mathfrak {m})$. Indeed, (see [39, Chapter IV Theorems 1.2, 1.6 and Corollary 1.4]), by replacing E with $\bigcup _{k=1}^{\infty }E_k$ for some $\mathcal {E}$-nest $\{E_k\}$ of compact sets, there exists a locally compact separable metric space $E^{\sharp }$ such that

• (i) E is a dense subset of $E^{\sharp }$ and $\mathscr {B}(E)=\{A\in \mathscr {B}(E^{\sharp }): A\subset E\}$.

• (ii) The relative topologies on $E_k$ induced by E, $E^{\sharp }$ coincide for every $k\in \mathbb {N}$.

• (iii) The image $(\mathcal {E}^{\sharp },\mathcal {F}^{\sharp })$ of $(\mathcal {E},\mathcal {F})$ under inclusion map $i:E\rightarrow E^{\sharp }$ is a Dirichlet form on $L^2(E^{\sharp };\mathfrak {m}^{\sharp })$, where $\mathfrak {m}^{\sharp }:=\mathfrak {m}\circ i^{-1}$ is a positive Radon measure with full support.

• (iv) $\{F_k\}$ is an $\mathcal {E}^{\sharp }$-nest, then $\{F_k\cap E_k\}$ is an $\mathcal {E}$-nest. Conversely, if $\{F_k\cap E_k\}$ is an $\mathcal {E}$-nest, then $\{F_k\}$ is an $\mathcal {E}^{\sharp }$-nest.

• (v) $N^{\sharp }$ is $\mathcal {E}^{\sharp }$-polar if and only if $N^{\sharp }\cap E$ is $\mathcal {E}$-polar. In particular, $E^{\sharp }{\setminus } E$ is $\mathcal {E}^{\sharp }$-polar.

• (vi) A function $u^{\sharp }:E^{\sharp }\rightarrow \mathbb {R}$ is $\mathcal {E}^{\sharp }$-quasi-continuous if and only if $u^{\sharp }|_E$ is $\mathcal {E}$-quasi-continuous.

• (vii) Let $\mathbf{X}=(\Omega , X_t, \mathbb {P}_x)_{x\in E_{\partial }}$ be a Borel right process properly associated to the quasi-regular Dirichlet form $(\mathcal {E},\mathcal {F})$. Then there exists an $\mathcal {E}$-polar set N such that $E{\setminus } N$ is $\mathbf{X}$-invariant and if $\mathbf{X}^{\sharp }$ is the trivial extension to $E^{\sharp }$ (cf. [39, Chapter IV 3.23(i)]) of $\mathbf{X}$ restricted to $E{\setminus } N$, then $\mathbf{X}^{\sharp }$ is a Hunt process properly associated to $(\mathcal {E}^{\sharp },\mathcal {F}^{\sharp })$ on $L^2(E^{\sharp };\mathfrak {m}^{\sharp })$, where $E^{\sharp }_{\partial }$ is taken as the one point copactification of $E^{\sharp }$.

As noted in the proof of [39, Chapter IV Theorem 2.4], we can see that every PCAF $(A_t)_{t\ge 0}$ of $\mathbf{X}$ in the strict sense can be extended (e.g.  by 0) to a PCAF $(A_t^{\sharp })_{t\ge 0}$ of $\mathbf{X}^{\sharp }$ in the strict sense. In particular, for every $\nu \in S_1(\mathbf{X})$, its trivial extension $\nu ^{\sharp }$ defined by $\nu ^{\sharp }(A)=\nu (A\cap E)$ for $A\in \mathscr {B}(E^{\sharp })$ belongs to $S_1(\mathbf{X}^{\sharp })$. The following are easily confirmed:

• 1. For the PCAF $(A_t)_{t\ge 0}$ of $\mathbf{X}$ in the strict sense associated to $\nu \in S_1(\mathbf{X})$, we have $\mathbb {E}_x\left[ \int _0^{\tau _B}e^{-\alpha t}\mathrm{d}A_t\right] =\mathbb {E}_{i(x)}^{\sharp }\left[ \int _0^{\tau _{i(B)}^{\sharp }}e^{-\alpha t}\mathrm{d}A_t^{\sharp }\right]$. Here $\tau _{i(B)}^{\sharp }$ is the first exit time from i(B) with respect to $\mathbf{X}^{\sharp }$. In particular, $\inf _{x\in E}\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t\right] =\inf _{x^{\sharp }\in E^{\sharp }}\mathbb {E}_{x^{\sharp }}^{\sharp }\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\sharp }\right]$, because $\mathbb {P}_{x^{\sharp }}(A^{\sharp }=0)=1$ for $x^{\sharp }\in E^{\sharp }{\setminus } E$.

• 2. $\nu \in S_D^1(\mathbf{X})$ (resp. $\nu \in S_K^1(\mathbf{X})$, $\nu \in S_{EK}^1(\mathbf{X})$) implies $\nu ^{\sharp }\in S_D^1(\mathbf{X}^{\sharp })$ (resp. $\nu ^{\sharp }\in S_K^1(\mathbf{X}^{\sharp })$, $\nu ^{\sharp }\in S_{EK}^1(\mathbf{X}^{\sharp })$).

• 3. $\nu \in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ (resp. $\nu \in S_{NK_1}^1(\mathbf{X}^{(1)})$) implies $\nu ^{\sharp }\in S_{NK_{\infty }}^1(\mathbf{X}^{\sharp ,(1)})$ (resp. $\nu ^{\sharp }\in S_{NK_1}^1(\mathbf{X}^{\sharp ,(1)})$).

So we can and do assume the local compactness of E and so on in the present proof. By definition of $\nu \in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, for any ${\varepsilon }>0$, there exists a Borel subset K and a constant $\delta >0$ so that for every Borel subset $B\subset K$ with $C^{\nu }(B)<\delta$,

$$\begin{aligned} \sup _{x\in E}\mathbb {E}_x\left[ \int _0^{\tau _{B\cup K^c}}e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] <{\varepsilon }. \end{aligned}$$

We may assume such Borel set K can be taken to be compact. On the other hand, by [22, Theorem 2.3.15] there exists an increasing sequence of $\mathcal {E}$-nest $\{F_k\}$ of closed sets such that $\nu (F_k)<\infty$ and $\mathbf{1}_{F_k}\nu \in S_0(\mathbf{X})$ for each $k\in \mathbb {N}$. Let $j\ge 1$ be large enough so that $C^{\nu }(K{\setminus } F_j)<\delta$. Let $u_1(x):=R_{\alpha }\mathbf{1}_{F_j\cap K}\nu (x)$ and $u_2(x):=\mathbb {E}_x[e^{-\alpha \sigma _{K\cap F_j}}]$. Then $u_1\in \mathcal {F}$. Moreover, $u_2\in \mathcal {F}$ due to the regularity of $(\mathcal {E},\mathcal {F})$. It is easy to see $u_1(\partial )=u_2(\partial )=0$. Then we have the strict $\mathcal {E}$-quasi-continuity of $u_1+u_2$ on $E_{\partial }$ by Lemma 4.12. Let $\{K_n\}$ be a strict $\mathcal {E}$-nest of closed sets such that $(u_1+u_2)|_{K_n\cup \{\partial \}}$ is continuous on each $K_n\cup \{\partial \}$. Hence $\inf _{x\in E}(u_1+u_2)(x)\le (u_1+u_2)(x)\rightarrow (u_1+u_2)(\partial )=0$ as $K_n\ni x\rightarrow \partial$. It follows that

$$\begin{aligned}&\inf _{x\in E}R_{\alpha }\nu (x)=\inf _{x\in E}\left( R_{\alpha }\mathbf{1}_{K\cap F_j}\nu (x)+R_{\alpha }\mathbf{1}_{K^c\cup (K{\setminus } F_j)}\nu (x) \right) \\&\quad \le \inf _{x\in E}\left( R_{\alpha }\mathbf{1}_{K\cap F_j}\nu (x)+\mathbb {E}_x\left[ \int _0^{\tau _{K^c\cup (K{\setminus } F_j)}}e^{-\alpha t}\mathrm{d}A_t^{\nu } \right] +\mathbb {E}_x\left[ e^{-\alpha \sigma _{K\cap F_j}}R_{\alpha } \nu (X_{\sigma _{K\cap F_j}}) \right] \right) \\&\quad \le \inf _{x\in E}\left( R_{\alpha }\mathbf{1}_{K\cap F_j}\nu (x)+\mathbb {E}_x\left[ \int _0^{\tau _{K^c\cup (K{\setminus } F_j)}}e^{-\alpha t}\mathrm{d}A_t^{\nu } \right] + \Vert R_{\alpha }\nu \Vert _{\infty } \mathbb {E}_x\left[ e^{-\alpha \sigma _{K\cap F_j}}\right] \right) \\&\quad \le \inf _{x\in E}(u_1(x)+{\varepsilon }+ \Vert R_{\alpha }\nu \Vert _{\infty }u_2(x))\\&\quad \le {\varepsilon }+\max \{\Vert R_{\alpha }\nu \Vert _{\infty },1\}\inf _{x\in E}(u_1(x)+u_2(x))={\varepsilon }. \end{aligned}$$

Since ${\varepsilon }>0$ is arbitrary, we have $\inf _{x\in E}R_{\alpha }\nu (x)=0$. $\square$

Remark 4.15

In [4, Lemma 4.6], the first author proved $\inf _{x\in E}\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}A_t^{\nu }\right] =0$$(\alpha >0)$ for $\nu \in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ under the condition that X is transient and has no killing inside. Since $S_{CK_{\infty }}^1(\mathbf{X}^{(1)})\subset S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ (see [28, before Proposition 4.2]), Lemma 4.14 extends [4, Lemma 4.6].

5 $L^p$-independence of spectral radius for generalized Feynman–Kac semigroups with bounded u

Throughout this section, we assume condition (A) holds and that $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a bounded finely continuous and nearly Borel function and $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. We do not assume $\mathbf{(I)}$. Note that under (A), $(Q_t)_{t\ge 0}$ associated with the generalized Feynman–Kac transform (1.1) is a bounded semigroup in $L^\infty (E; m)$. Indeed there exists $p_0>1$ sufficiently close to 1 such that $p{\mu ^+}+N(e^{pF^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$ for any $p\in [1,p_0[$. Indeed,

$$\begin{aligned}&\sup _{x\in E}\mathbb {E}_x[A_t^{p\mu ^+}+A_t^{N(e^{pF^+}-1)\mu _H}]\\&\quad \le \sup _{x\in E}\mathbb {E}_x\left[ A_t^{\mu ^+}+A_t^{N(e^{F^+}-1)\mu _H}\right] +\sup _{x\in E}\mathbb {E}_x\left[ (p-1)A_t^{\mu ^+}+A_t^{N(e^{pF^+}-e^{F^+})\mu _H}\right] \\&\quad \le \sup _{x\in E}\mathbb {E}_x\left[ A_t^{\mu ^+}+A_t^{N(e^{F^+}-1)\mu _H}\right] \\&\qquad +(p-1)\sup _{x\in E}\mathbb {E}_x[A_t^{\mu ^+}]+ (p-1)e^{2\Vert F^+\Vert _{\infty }}\sup _{x\in E} \mathbb {E}_x\left[ \int _0^tN(F^+)(X_s)\mathrm{d}H_s\right] \end{aligned}$$

yields the assertion, because of $\mu ^++N(F^+)\mu _H\in S_D^1(\mathbf{X})$. Here we use the estimate

$$\begin{aligned} e^{pF^+}-e^{F^+}\le e^{\Vert F^+\Vert _{\infty }}(e^{(p-1)F^+}-1)\le (p-1)e^{2\Vert F^+\Vert _{\infty }}F^+. \end{aligned}$$

Let $q:=p/(p-1)$ be the conjugate exponent of $p\in ]1,p_0[$. We then see that for small $t>0$

$$\begin{aligned} \left. \begin{array}{rl} \mathbb {E}_x[\exp (pA_t^{{\mu ^+}}+pA_t^{F^+})]&{}=\mathbb {E}_x[{\mathrm{Exp}}(A^{p{\mu ^+}}+A^{e^{pF^+}-1})_t]\\ &{}\le \frac{1}{1-\sup _{x\in E}\mathbb {E}_x[A_t^{p{\mu ^+}}+A_t^{e^{pF^+}-1}]}<\infty \end{array}\right. \end{aligned}$$

(5.1)

and

$$\begin{aligned}&\mathbb {E}_x[\exp (q N_t^u)]\\&\quad =e^{-qu(x)}\mathbb {E}_x^{U_q}\left[ \exp \left( \int _0^tN(e^{qU}-qU-1)(X_s)\mathrm{d}H_s+\frac{q^2}{2}{\langle }M^{-u,c}{\rangle }_t\right) e^{qu(X_t)} \right] \\&\quad \le \frac{e^{2q\Vert u\Vert _{\infty }}}{1-\sup _{x\in E}\mathbb {E}_x^{U_q}\left[ \int _0^tN(e^{qU}-qU-1)(X_s)\mathrm{d}H_s+\frac{q^2}{2}{\langle }M^{-u,c}{\rangle }_t\right] }<\infty . \end{aligned}$$

Here $\mathbf{U}_q:=(\Omega , X_t,\mathbb {P}_x^{U_q})$ is the Girsanov transformed process by $U_t^q:={\mathrm{Exp}}(M^{e^{qU-1}}+M^{-qu,c})_t$ and $qU(x,y):=qu(x)-qu(y)$. $\mathbf{U}_q$ is an $e^{-2qu}\mathfrak {m}$-symmetric Markov process. Note here that $e^{-2qu}(N(e^{qU}-qU-1)\mu _H+\frac{q^2}{2}\mu _{{\langle }u{\rangle }}^c)\in S_K^1(\mathbf{U}_q)$ holds by Lemma 4.11(2), because of the boundedness of u and $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. Thus, for sufficiently small $t>0$ we have

$$\begin{aligned} \Vert Q_t\Vert _{\infty ,\infty }=\Vert Q_t1\Vert _{\infty }&\le \sup _{x\in E}\mathbb {E}_x[\exp (N_t^u+A_t^{\mu }+A_t^F)]\\&\le \sup _{x\in E}\mathbb {E}_x[\exp (qN_t^u)]^{\frac{1}{q}}\sup _{x\in E}\mathbb {E}_x[\exp (pA_t^{{\mu ^+}}+pA_t^{F^+})]^{\frac{1}{p}}<\infty . \end{aligned}$$

By use of the Markov property, there is $C_{\infty }\in ]0,\infty [$ depending on $\Vert u\Vert _{\infty }$ such that $\Vert Q_t\Vert _{\infty ,\infty }\le C_{\infty }e^{C_{\infty }t}$ for all $t>0$, hence $\lambda _{\infty }(\mathbf{X},u,\mu ,F)\ge -C_{\infty }>-\infty$. Thus we have

$$\begin{aligned} -C_\infty \le \lambda _{\infty }(\mathbf{X},u,\mu ,F)\le \lambda _p(\mathbf{X},u,\mu ,F)\le \lambda _2(\mathbf{X},u,\mu ,F)\quad \text { for }\quad p\in [1,\infty ] . \end{aligned}$$

(5.2)

In this section and the next, we will adopt the approaches from [4, 5] to establish the $L^p$-independence of spectral radius $\lambda _p(\mathbf{X},u,\mu ,F)$ .

Lemma 5.1

We have the following:

• 1. ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$ is equivalent to ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H\in S_{EK}^1(\mathbf{X})$ provided $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$.

• 2. Fix $\alpha \ge 0$ and assume the transience of $\mathbf{X}$ if $\alpha =0$. ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{CK_1}^1(\mathbf{X}^{(\alpha )})$ is equivalent to ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H\in S_{CK_1}^1(\mathbf{X}^{(\alpha )})$ provided $\mu _{{\langle }u{\rangle }}\in S_{CK_{\infty }}^1(\mathbf{X}^{(\alpha )})$.

• 3. Fix $\alpha \ge 0$ and assume the transience of $\mathbf{X}$ if $\alpha =0$. ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ is equivalent to ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ provided $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(\alpha )})$.

Proof

Since $e^U(e^{F^+}-1)=(e^U-1)(e^{F^+}-1)+(e^{F^+}-1)$ and $|e^U-1|(e^{F^+}-1)\le e^{\Vert U\Vert _{\infty }}|U|(e^{F^+}-1)$, it suffices to show that $N(|U|(e^{F^+}-1)) \mu _H\in S_K^1(\mathbf{X})$ (resp. $\in S_{CK_{\infty }}^1(\mathbf{X}^{(\alpha )})$, $\in S_{NK_{\infty }}^1(\mathbf{X}^{(\alpha )})$) under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ (resp. $\in S_{CK_{\infty }}^1(\mathbf{X}^{(\alpha )})$, $\in S_{NK_{\infty }}^1(\mathbf{X}^{(\alpha )})$). This can be easily confirmed because of $N(U^2)\mu _H\in S_K^1(\mathbf{X})$ (resp. $\in S_{CK_{\infty }}^1(\mathbf{X}^{(\alpha )})$, $\in S_{NK_{\infty }}^1(\mathbf{X}^{(\alpha )})$) under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ (resp. $\in S_{CK_{\infty }}^1(\mathbf{X}^{(\alpha )})$, $\in S_{NK_{\infty }}^1(\mathbf{X}^{(\alpha )})$) and $N((e^{F^+}-1)^2)\mu _H\le (e^{\Vert F^+\Vert _{\infty }}-1)e^{\Vert F^+\Vert _{\infty }}N(F^+)\mu _H \in S_{D}^1(\mathbf{X})$. $\square$

Theorem 5.2

Suppose that (1.7) as well as condition (A) holds. Then $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$.

Proof

Step 1: First we prove the assertion under $u=0$ and $\mathfrak {m}(E)<\infty$. We write $\lambda _p(\mathbf{X},\mu ,F):=\lambda _p(\mathbf{X},0,\mu ,F)$ for $p\in [1,\infty ]$. Note that $\lambda _2 (\mathbf{X},\mu ,F)<\infty$ holds under (A) by (1.5). Suppose first $\lambda _2(\mathbf{X},\mu ,F)>0$. Then for any ${\varepsilon }\in ]0,\lambda _2(\mathbf{X},\mu ,F)[$, there is $\delta ({\varepsilon })>0$ such that

$$\begin{aligned} \Vert Q_t\Vert _{2,2}\le e^{-t(\lambda _2(\mathbf{X},\mu ,F)-{\varepsilon })}\quad \text { for }t\ge \delta ({\varepsilon }). \end{aligned}$$

(5.3)

Assume that (1.7) and (A) hold. On the other hand, since ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$, there exists $p>1$ sufficiently close to 1 such that $p{\mu ^+}+N(e^{pF^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$. By Markov property of $\mathbf{X}$ and (5.1), there exists $C=C(p)>0$ such that

$$\begin{aligned} \sup _{x\in E}\mathbb {E}_x\left[ \exp \left( pA_t^{{\mu ^+}}+pA_t^{F^+} \right) \right] \le Ce^{Ct}\quad \text { for all }\quad t>0. \end{aligned}$$

Thus for every $f\in L^q(E;\mathfrak {m})$ with $q=\frac{p}{p-1}$ and $x\in E$, by Hölder’s inequality,

$$\begin{aligned} |Q_{t_0}f(x)|= & {} \mathbb {E}_x\left[ \exp \left( A_{t_0}^{\mu }+A_{t_0}^{F}\right) f(X_{t_0}) \right] \nonumber \\\le & {} \left( \mathbb {E}_x\left[ \exp \left( pA_{t_0}^{{\mu ^+}}+pA_{t_0}^{F^+}\right) \right] \right) ^{{1}/{p}} \left( \mathbb {E}_x\left[ f(X_{t_0})^q\right] \right) ^{{1}/{q}}\nonumber \\\le & {} \left( Ce^{Ct_0}\right) ^{{1}/{p}}\Vert P_{t_0}\Vert _{1,\infty }^{{1}/{q}}\Vert f\Vert _{q}. \end{aligned}$$

(5.4)

Under $\lambda _2(\mathbf{X},\mu ,F)>0$, for any ${\varepsilon }\in ]0,\lambda _2(\mathbf{X},\mu ,F)[$, there is $\delta ({\varepsilon })>0$ so that (5.3) holds. Then for $t>\delta ({\varepsilon })+t_0$, by (5.4) and (5.3),

$$\begin{aligned} \Vert Q_t\Vert _{\infty ,\infty }&=\Vert Q_t1\Vert _{\infty }= \Vert Q_{t_0}(Q_{t-{t_0}}1)\Vert _{\infty } \le \left( Ce^{Ct_0}\right) ^{\frac{1}{p}} \Vert P_{t_0}\Vert _{1,\infty }^{\frac{1}{q}}\Vert Q_{t-t_0}1\Vert _{q}\\&\le \left( Ce^{Ct_0}\right) ^{\frac{1}{p}} \Vert P_{t_0}\Vert _{1,\infty }^{\frac{1}{q}} \Vert Q_{t-t_0}1\Vert _{\infty }^{1-\frac{2}{q}} \Vert Q_{t-t_0}1\Vert _{2}^{\frac{2}{q}}\\&\le \left( Ce^{Ct_0}\right) ^{\frac{1}{p}}\Vert P_{t_0}\Vert _{1,\infty }^{\frac{1}{q}} \Vert Q_{t-t_0}1\Vert _{\infty }^{1-\frac{2}{q}} \left( \sqrt{\mathfrak {m}(E)}e^{-(t-t_0)(\lambda _2(\mathbf{X},\mu ,F)-{\varepsilon })}\right) ^{\frac{2}{q}} \end{aligned}$$

This implies $\lambda _{\infty }(\mathbf{X},\mu ,F)\ge \lambda _2(\mathbf{X},\mu ,F)-{\varepsilon }$ and so $\lambda _{\infty }(\mathbf{X},\mu ,F)\ge \lambda _2(\mathbf{X},\mu ,F)$. Hence $\lambda _{\infty }(\mathbf{X},\mu ,F)= \lambda _2(\mathbf{X},\mu ,F)= \lambda _p(\mathbf{X},\mu ,F)$ for $p\in [1,\infty ]$ under $\lambda _2(\mathbf{X},\mu ,F)>0$. The condition (A) implies ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{EK}^1(\mathbf{X}^{(\alpha )})$ and (1.7) remains valid under $\mathbf{X}^{(\alpha )}$. Moreover, $\{Q_t\}_{t\ge 0}$ is still well-defined as a strongly continuous semigroup in $L^2(E;\mathfrak {m})$, because (A) for $\mathbf{X}^{(\alpha )}$ holds under (A) for $\mathbf{X}$. Thus, we can apply the above argument with respect to $\mathbf{X}^{(\alpha )}$. By taking $\alpha >0$ so large with the relation

$$\begin{aligned} \lambda _p(\mathbf{X}^{(\alpha )},\mu ,F)=\alpha +\lambda _p(\mathbf{X},\mu ,F),\quad p\in [1,\infty ], \end{aligned}$$

we see $\lambda _2(\mathbf{X}^{(\alpha )},\mu ,F)>0$ for such $\alpha >0$, consequently $\lambda _{\infty }(\mathbf{X}^{(\alpha )},\mu ,F)=\lambda _2(\mathbf{X}^{(\alpha )},\mu ,F)$, that is, $\lambda _p(\mathbf{X},\mu ,F)=\lambda _2(\mathbf{X},\mu ,F)$ for $p\in [1,\infty ]$.

Step 2: Next we prove the assertion under $u=0$ without assuming $\mathfrak {m}(E)<\infty$. Let $\{G_n\}$ be a nest of finely open Borel sets satisfying $\mathfrak {m}(G_n)<\infty$ for each $n\in \mathbb {N}$. Such a $\{G_n\}$ always exists. Indeed, for $f\in L^1(E;\mathfrak {m})\cap L^{\infty }(E;\mathfrak {m})$ with $f>0$ on E, the set $G_n:=\{x\in E : R_1f(x)>1/n\}$ does the job. We consider the part process $\mathbf{X}^{G_n}$ on $G_n$. Note that (1.7) holds for $\mathbf{X}^{G_n}$ by Lemma 4.3. Moreover, condition (A) holds for each $\mathbf{X}^{G_n}$ by Lemma 4.6. For $p\in [1,\infty ]$, let $\lambda _p^{(n)}:=\lambda _p(\mathbf{X}^{G_n},\mathbf{1}_{G_n}\mu ,\mathbf{1}_{G_n\times G_n}F)$ be the $L^p$-spectral radius for the Feynman–Kac semigroup $(Q_t^{(n)})_{t\ge 0}$ defined by $Q_t^{(n)}f(x):=\mathbb {E}_x[e^{A_t^{\mu }+A_t^F}f(X_t):t<\tau _{G_n}]$ for each $n\in \mathbb {N}$. Recall that $(Q_t^{(n)})_{t\ge 0}$ is associated to $(\mathcal {Q},\mathcal {F}_{G_n})$. Applying Step 1 for $\mathbf{X}^{G_n}$, we have the $L^p$-independence of $\lambda _p^{(n)}$:

$$\begin{aligned} \lambda _{\infty }^{(n)}=\lambda _2^{(n)}. \end{aligned}$$

(5.5)

Since $E=\bigcup _{n=1}^{\infty }G_n$$\mathfrak {m}$-a.e. (i.e. $\bigcap _{n=1}^{\infty }(E{\setminus } G_n)$ is $\mathfrak {m}$-negligible) and $Q^{(n)}_t 1(y)$ increases to $Q_t 1(y)$ on $\bigcup _{n=1}^{\infty }G_n$, we have

$$\begin{aligned} \Vert Q_t\Vert _{\infty ,\infty }=\mathfrak {m}\text {-}\sup \limits _{y\in E}Q_t1(y) =\sup _{n\in \mathbb {N}}\left( \mathfrak {m}\text {-}\sup \limits _{y\in G_n}Q_t^{(n)}1(y)\right) =\sup _{n\in \mathbb {N}}\Vert Q_t^{(n)}\Vert _{\infty ,\infty }. \end{aligned}$$

Here $\mathfrak {m}$-sup denotes the $\mathfrak {m}$-essentially supremum. From this, we can deduce $\lambda _{\infty }(\mathbf{X},\mu ,F)=\inf _{n\in \mathbb {N}}\lambda _{\infty }^{(n)}$. Indeed, define $f_n(t):=\frac{1}{t}\log \Vert Q_t^{(n)}\Vert _{\infty ,\infty }$. For $t>0$, by Fatou’s lemma,

$$\begin{aligned} \mathbb {E}_y[e^{A_t^{\mu }+A_t^F}:t<\tau _{G_n}]&=\mathbb {E}_y[\varliminf _{s\rightarrow t}e^{A_s^{\mu }+A_s^F}\mathbf{1}_{\{s<\tau _{G_n}\}}]\\&\le \varliminf _{s\rightarrow t}\mathbb {E}_y[e^{A_s^{\mu }+A_s^F}\mathbf{1}_{\{s<\tau _{G_n}\}}]\\&\le \varliminf _{s\rightarrow t}\Vert Q_s^{(n)}\Vert _{\infty ,\infty }. \end{aligned}$$

Here in the equality we used the fact that for each fixed $t>0$, $\mathbb {P}_x(X_t=X_{t-})=1$ holds for all $x\in E$. It follows that $\Vert Q_t^{(n)}\Vert _{\infty ,\infty }\le \mathop {{\varliminf }}_{s\rightarrow t} \Vert Q_s^{(n)}\Vert _{\infty ,\infty }$, and so $f_n(t)$ is lower semi continuous in t. Let $X:=[1,\infty ]$ which is compact, and define

$$\begin{aligned} f_n(\infty ):=\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t^{(n)}\Vert _{\infty ,\infty }=\inf _{t>0}\frac{1}{t}\log \Vert Q_t^{(n)}\Vert _{\infty ,\infty }. \end{aligned}$$

Then $t\mapsto f_n(t)$ is a lower semi continuous function on the compact set X. By the minimax theorem (see [52, Corollary in pp. 407]), we have

$$\begin{aligned} \sup _{n\in \mathbb {N}}(-\lambda _{\infty }^{(n)})&=\sup _{n\in \mathbb {N}}\inf _{t\in X}f_n(t)\nonumber \\&=\inf _{t\in X}\sup _{n\in \mathbb {N}}\frac{1}{t}\log \Vert Q_t^{(n)}\Vert _{\infty ,\infty }\nonumber \\&=\inf _{t\in X}\frac{1}{t}\log \Vert Q_t\Vert _{\infty ,\infty }= -\lambda _{\infty }(\mathbf{X},\mu ,F). \end{aligned}$$

(5.6)

On the other hand,

$$\begin{aligned} \lambda _2(\mathbf{X},\mu ,F)&=\inf \left\{ \mathcal {Q}(f,f): f\in \mathcal {F}\hbox { with } \int _Ef^2\mathrm{d}\mathfrak {m}=1 \right\} \\&\le \inf \left\{ \mathcal {Q}(f,f): f\in \mathcal {F}_{G_n} \hbox { with } \int _{G_n}f^2\mathrm{d}\mathfrak {m}=1 \right\} =\lambda _2^{(n)}. \end{aligned}$$

Consequently, we have from (5.5) that

$$\begin{aligned} \lambda _{\infty }(\mathbf{X},u,\mu ,F)=\inf _{n\in \mathbb {N}}\lambda _{\infty }^{(n)} = \inf _{n\in \mathbb {N}}\lambda _{2}^{(n)} \ge \lambda _2(\mathbf{X},u,\mu ,F) \end{aligned}$$

and so $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=\lambda _{2}(\mathbf{X},u,\mu ,F)$ in view of (1.6).

Step 3: Finally we prove the assertion without assuming $u=0$. By Lemma 5.1(1), the condition (A) implies ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H \in S_{EK}^1(\mathbf{X})$ under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ because of the boundedness of u and $F^+$. Note that $\lambda _2(\mathbf{X}, u,\mu ,F)<\infty$ under (A) by (1.5). By assumption, we have $e^{-2u}\mathfrak {m}(E)<\infty$ and $e^{-2u}(\bar{\nu }_1+N(e^U(e^{F^+}-1))\mu _H)\in S_{EK}^1(\mathbf{U})$ and $e^{-2u}(\bar{\nu }_2+N(e^UF^-)\mu _H)\in S_D^1(\mathbf{U})$ by Lemma 4.11(1), (3), equivalently we have $e^{-2u}\bar{\nu }_1+N^U(e^{F^+}-1)\mu _{H^U}\in S_{EK}^1(\mathbf{U})$ and $e^{-2u}\bar{\nu }_2+N^U(F^-)\mu _{H^U}\in S_D^1(\mathbf{U})$, where $(N^U,H^U)$ is a Lévy system of $\mathbf{U}$. Here $\bar{\nu }_1:={\mu ^+}+N(e^U-U-1)\mu _H+\frac{1}{2}\mu _{{\langle }u{\rangle }}^c$ and $\bar{\nu }_2:={\mu ^-}$. We set $\bar{\nu }:=\bar{\nu }_1-\bar{\nu }_2$. By (1.7), $P_{t_0}$ is a bounded operator from $L^1(E;\mathfrak {m})$ to $L^{\infty }(E;\mathfrak {m})$. Then we see that for $f\in L^2(E;e^{-2u}\mathfrak {m})$

$$\begin{aligned} \Vert P_{t_0}^Uf\Vert _{\infty }&=\sup _{x\in E}\mathbb {E}_x\left[ U_{t_0}f(X_{t_0}) \right] \nonumber \\&\le \sup _{x\in E}\mathbb {E}_x[U_{t_0}^2]^{1/2}P_{t_0}f^2(x)^{1/2}\nonumber \\&\le \sup _{x\in E}\mathbb {E}_x[U_{t_0}^2]^{1/2}\Vert P_{t_0}\Vert _{1,\infty }^{1/2}\Vert f\Vert _{L^2(E;\mathfrak {m})}\nonumber \\&\le \sup _{x\in E}\mathbb {E}_x[U_{t_0}^2]^{1/2}\Vert P_{t_0}\Vert _{1,\infty }^{1/2}e^{2\Vert u\Vert _{\infty }}\Vert f\Vert _{L^2(E;e^{-2u}\mathfrak {m})}. \end{aligned}$$

(5.7)

Since $\sup _{x\in E}\mathbb {E}_x[U_{t_0}^2]<\infty$ under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$, $P_{t_0}^U$ is a bounded operator from $L^2(E;e^{-2u}\mathfrak {m})$ to $L^{\infty }(E;e^{-2u}\mathfrak {m})$. From this, $P_{2t_0}^U$ is a bounded operator from $L^1(E;e^{-2u}\mathfrak {m})$ to $L^{\infty }(E;e^{-2u}\mathfrak {m})$, because of the $e^{-2u}\mathfrak {m}$-symmetry of $(P_t^U)_{t\ge 0}$. Thus (1.7) holds for $(P_t^U)_{t\ge 0}$. Then one can apply Step 2 to U so that $\lambda _p(\mathbf{U},e^{-2u}\bar{\nu }, F)$ is independent of $p\in [1,\infty ]$, in particular, $\lambda _{\infty }(\mathbf{U},e^{-2u}\bar{\nu }, F)=\lambda _2(\mathbf{U},e^{-2u}\bar{\nu }, F)$. Since $\lambda _p(\mathbf{X},u,\mu , F)=\lambda _p(\mathbf{U},e^{-2u}\bar{\nu }, F)$ for $p\in [1,\infty ]$, we have $\lambda _{\infty }(\mathbf{X},u,\mu , F)=\lambda _2(\mathbf{X},u,\mu , F)$. Thus we obtain that $\lambda _p(\mathbf{X},u,\mu , F)$ is independent of $p\in [1,\infty ]$, because $\lambda _{\infty }(\mathbf{X},u,\mu , F)\le \lambda _p(\mathbf{X},u,\mu , F)\le \lambda _2(\mathbf{X},u,\mu , F)$ always holds for $p\in ]1,\infty [$. $\square$

Theorem 5.3

Consider the following conditions:

• (i) X is transient. ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X})$, $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X})$ and ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X})$ hold.

• (ii) Suppose that ${\mu ^+}+N(e^{F^+}-1)\mu _H\in \bigcap _{\alpha >0} S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ holds and $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ holds.

Then we have the following:

• (i) Suppose that (i) or (ii) holds. Then $\lambda _{\infty }(\mathbf{X},u,\mu ,F)\ge \min \{\lambda _2(\mathbf{X},u,\mu ,F),0\}$. Consequently, $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$ provided $\lambda _2(\mathbf{X},\mu ,F)\le 0$.

• (ii) Suppose that (i), or (ii) with ${\mu ^-}+N(F^-)\mu _H\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ holds and assume that X is conservative. Then $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=0$ if $\lambda _2(\mathbf{X},u,\mu ,F)>0$. Hence $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$ if and only if $\lambda _2(\mathbf{X},u,\mu ,F)\le 0$.

Proof

Step 1: First we prove the assertion under $u=0$ and the irreducibility condition $\mathbf{(I)}$. We write $\lambda _p(\mathbf{X},\mu ,F)= \lambda _p(\mathbf{X},u,\mu ,F)$ for $p\in [1,\infty ]$.

(1): Under $\mathbf{(A)}$, we see $\lambda _2(\mathbf{X},\mu ,F)<\infty$ by (1.5). Note that (i) implies (ii). So it suffices to prove the assertion under (ii). Take any $\lambda <\min \{\lambda _2(\mathbf{X},\mu ,F),0\}$. Clearly, for every $0<\alpha < \lambda _2(\mathbf{X},\mu ,F) -\lambda$,

$$\begin{aligned}&\inf \biggl \{\mathcal {E}_{\alpha }(f,f)-\int _Ef(x)^2(\mu +\lambda \mathfrak {m})(\mathrm{d}x)\\&\quad -\int _{E\times E {\setminus } {\mathsf {diag}}}f(x)f(y)(e^{F(x,y)}-1)N(x,\mathrm{d}y)\mu _H(\mathrm{d}x):\\&\quad f\in \mathcal {F}\hbox { with } \int _Ef(x)^2\mathfrak {m}(\mathrm{d}x)=1 \biggr \}= \lambda _2(\mathbf{X},\mu ,F)-(\lambda -\alpha ) >0. \end{aligned}$$

By assumption, we have ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$, ${\mu ^-}-\lambda \mathfrak {m}+N(F^-)\mu _H\in S_D^1(\mathbf{X})=S_{D_0}^1(\mathbf{X}^{(\alpha )})$. Applying [29, Corollary 1.2] to $\mathbf{X}^{(\alpha )}$, we have that $(\mathbf{X}^{(\alpha )}, A^{\mu +\lambda \mathfrak {m}}+A^{F})$ is gaugeable, where we use $\mathbf{(I)}$. Then

$$\begin{aligned} \sup _{t\ge 0}e^{(\lambda -\alpha ) t}\Vert Q_t1\Vert _{\infty }&=\sup _{t\ge 0}\left( e^{-\alpha t}\sup _{x\in E} \mathbb {E}_x\left[ e^{A_t^{\mu +\lambda \mathfrak {m}}+A_t^F}:t<\zeta \right] \right) \nonumber \\&=\sup _{t\ge 0}\sup _{x\in E} \mathbb {E}_x^{(\alpha )}\left[ e^{A_t^{\mu +\lambda \mathfrak {m}}+A_t^{F}}:t<\zeta \right] \nonumber \\&\le \sup _{x\in E}\mathbb {E}_x^{(\alpha )} \left[ \sup _{t<\zeta }e^{A_t^{\mu +\lambda \mathfrak {m}}+A_t^{F}}\right] <\infty , \end{aligned}$$

(5.8)

where the last inequality is due to [27, Lemma 4.2(2)] with respect to $\mathbf{X}^{(\alpha )}$. Since $\alpha >0$ can be taken to be arbitrarily close to 0, the estimate (5.8) under (ii) implies that

$$\begin{aligned} \lambda _{\infty }(\mathbf{X},\mu ,F)=-\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t1\Vert _{\infty }\ge \lambda . \end{aligned}$$

This inequality holds for any $\lambda <\min \{\lambda _2(\mathbf{X},\mu ,F),0\}$. Thus we can conclude $\lambda _{\infty }(\mathbf{X},\mu ,F)\ge \min \{\lambda _2(\mathbf{X},\mu ,F),0\}$. In particular, $\lambda _2(\mathbf{X},\mu ,F)\le 0$ implies $\lambda _{\infty }(\mathbf{X},\mu ,F)\ge \lambda _2(\mathbf{X},\mu ,F)$. This together with (5.2) yields that $\lambda _p(\mathbf{X},\mu ,F)$ is independent of $p\in [1,\infty ]$ when $\lambda _2(\mathbf{X},\mu ,F)\le 0$.

(2): Since $\lambda _2(\mathbf{X},\mu ,F)>0$, we have from (1) that $\lambda _{\infty }(\mathbf{X},\mu ,F)\ge 0$. Assume now that $\mathbf{X}$ is conservative. Under (i), we have that

$$\begin{aligned} x\mapsto \mathbb {E}_x[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]&=\mathbb {E}_x\left[ A_{\infty }^{{\mu ^-}}+A_{\infty }^{N(F^-)\mu _H}\right] \\&= R({\mu ^-}+N(F^-)\mu _H)(x) \end{aligned}$$

is bounded. Then

$$\begin{aligned} \Vert Q_t1\Vert _{\infty }&=\sup _{x\in E}\mathbb {E}_x[\exp (A_t^{\mu }+A_t^{F})]\ge \sup _{x\in E}\mathbb {E}_x[\exp (-A_t^{{\mu ^-}}-A_t^{F^-})]\\&\ge \sup _{x\in E}\mathbb {E}_x[\exp (-A_{\infty }^{{\mu ^-}}-A_{\infty }^{F^-})]\\&\ge \exp \left( -\sup _{x\in E}\mathbb {E}_x[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]\right) \ge \exp (-\Vert R({\mu ^-}+N(F^-)\mu _H)\Vert _{\infty }). \end{aligned}$$

Under (ii) with ${\mu ^-}+N(F^-)\mu _H\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, we have

$$\begin{aligned} x\mapsto \mathbb {E}_x^{(\alpha )}[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]&=\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}(A_t^{{\mu ^-}}+A_t^{N(F^-)\mu _H})\right] \\&= R_{\alpha }({\mu ^-}+N(F^-)\mu _H)(x) \end{aligned}$$

is bounded and is an $\alpha$-potential, i.e., $\inf _{x\in E}\mathbb {E}_x^{(\alpha )}[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]=0$ by Lemma 4.14. Then

$$\begin{aligned} \Vert Q_t1\Vert _{\infty }&=\sup _{x\in E}\mathbb {E}_x[\exp (A_t^{\mu }+A_t^{F})]\ge \sup _{x\in E}\mathbb {E}_x[\exp (-A_t^{{\mu ^-}}-A_t^{F^-})]\\&\ge \sup _{x\in E}\left[ \exp \left( -e^{\alpha t}\mathbb {E}_x\left[ \int _0^{\infty }e^{-\alpha t}\mathrm{d}(A_t^{{\mu ^-}}+A_t^{N(F^-)\mu _H})\right] \right) \right] \\&\ge \exp \left( -e^{\alpha t}\inf _{x\in E}\mathbb {E}_x^{(\alpha )}[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]\right) =1. \end{aligned}$$

In either cases, we have

$$\begin{aligned} \lambda _{\infty }(\mathbf{X},\mu ,F)=-\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t1\Vert _{\infty }\le 0. \end{aligned}$$

Therefore $\lambda _{\infty }(\mathbf{X},\mu ,F)=0<\lambda _2(\mathbf{X},\mu ,F)$.

Step 2: Next we prove the assertion under the irreducibility condition $\mathbf{(I)}$ only without assuming $u=0$. Note that $\mathbf{U}$ also satisfies $\mathbf{(I)}$.

(1): By Lemma 5.1(3), the condition ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ implies ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ under $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$ because of the boundedness of u and $F^+$. By assumption, $e^{-2u}(\bar{\nu }_2+N(e^UF^-)\mu _H)\in S_{D_0}^1(\mathbf{U}^{(1)})$ and $e^{-2u}(\bar{\nu }_1+N(e^U(e^{F^+}-1))\mu _H)\in S_{NK_1}^1(\mathbf{U}^{(\alpha )})$ for any $\alpha >0$. Applying Step 1 for (1) under (ii) to $\mathbf{U}$, we have $\lambda _{\infty }(\mathbf{U},e^{-2u}\bar{\nu },F)\ge \min \{\lambda _2(\mathbf{U},e^{-2u}\bar{\nu },F),0\}$. Hence we have the conclusion as above.

(2): First note that U is conservative under the conservativeness of X, because $\{U_t\}_{t\in [0,\infty [}$ is a $\mathbb {P}_x$-martingale under $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. Assume (i). Then $e^{-2u}(\bar{\nu }_1+N(e^U(e^{F^+}-1))\mu _H)\in S_{NK_1}^1(\mathbf{U})$ and $e^{-2u}(\bar{\nu }_2+N(e^UF^-)\mu _H)\in S_{D_0}^1(\mathbf{U})$ by Lemmas 5.1(3) and 4.11(7)(b), equivalently, $e^{-2u}\bar{\nu }_1+N^U(e^{F^+}-1)\mu _{H^U}\in S_{NK_1}^1(\mathbf{U})$ and $e^{-2u}\bar{\nu }_2+N^U(F^-)\mu _{H^U}\in S_{D_0}^1(\mathbf{U})$. Applying Step 1 for (2) under (i) to $\mathbf{U}$, we have $\lambda _{\infty }(\mathbf{U},e^{-2u}\bar{\nu },F)=0$ if $\lambda _2(\mathbf{U},e^{-2u}\bar{\nu },F)>0$. Since $\lambda _2(\mathbf{X},u,\mu , F)=\lambda _2(\mathbf{U},e^{-2u}\bar{\nu }, F)$ and $\lambda _{\infty }(\mathbf{X},u,\mu , F)=\lambda _{\infty }(\mathbf{U},e^{-2u}\bar{\nu }, F)$, we have $\lambda _{\infty }(\mathbf{X},u,\mu , F)=0$ if $\lambda _2(\mathbf{X},u,\mu , F)>0$.

Finally we assume (ii). By assumption, we have $e^{-2u}(\bar{\nu }_1+N(e^U(e^{F^+}-1))\mu _H)\in S_{NK_1}^1(\mathbf{U}^{(\alpha )})$ for all $\alpha >0$ and $e^{-2u}(\bar{\nu }_2+N(e^UF^-)\mu _H)\in S_{NK_{\infty }}^1(\mathbf{U}^{(1)})$ by Lemmas 5.1(3) and 4.11(7)(a), equivalently, $e^{-2u}\bar{\nu }_1+N^U(e^{F^+}-1)\mu _{H^U}\in S_{NK_1}^1(\mathbf{U}^{(\alpha )})$ for $\alpha >0$ and $e^{-2u}\bar{\nu }_2+N^U(F^-)\mu _{H^U}\in S_{NK_{\infty }}^1(\mathbf{U}^{(1)})$. Applying Step 1 for (2) under (ii) to $\mathbf{U}$, we have $\lambda _{\infty }(\mathbf{U},e^{-2u}\bar{\nu },F)=0$ if $\lambda _2(\mathbf{U},e^{-2u}\bar{\nu },F)>0$. Hence we have the conclusion as above.

Step 3: Finally, we prove the assertion without assuming $\mathbf{(I)}$. By [36], under $\mathbf{(AC)}$, for each $x\in E$ there exists an $\mathbf{X}$-invariant set $E_x$ such that $E=\bigcup _{x\in E}E_x$, $E_x\cap E_y\ne \emptyset$ implies $E_x=E_y$, and each $\mathbf{X}^{E_x}$ satisfies (I). Moreover, there exists at most countable sets $\{x_i\}_{i\in I}$ such that $E=\bigcup _{i\in I}E_{x_i}$ forms a disjoint union. We set $Q_t^if(x):= \mathbb {E}_x[e_A(t)f(X_t):t<\tau _{E_{x_i}}]$ for $f\in \mathscr {B}_b(E)$ and define the $L^p(E_{x_i};\mathfrak {m})$-spectral radius $\lambda _p^i:=\lambda _p(\mathbf{X}^{E_{x_i}},u,\mu ,F)$ for $(Q_t^i)_{t\ge 0}$. We see that the condition (i) (resp. (ii)) for $\mathbf{X}^{E_{x_i}}$ holds under (i) (resp. (ii)). So we can apply the result of Step 2 to $\mathbf{X}^{E_{x_i}}$. Since $Q_t1(y)=Q_t^i1(y)$ for $y\in E_{x_i}$, we see $\Vert Q_t\Vert _{\infty ,\infty }=\sup _{y\in E}Q_t1(y)=\sup _{i\in I}\sup _{y\in E_{x_i}}Q_t^i1(y)=\sup _{i}\Vert Q_t^i\Vert _{\infty ,\infty }$. From this we can deduce $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=\inf _{x\in E}\lambda _{\infty }^i$ by use of the minimax theorem (see [52, Corollary in pp. 407]) and $\lambda _2(\mathbf{X},u,\mu ,F)\ge \lambda _2^i$ as done in the Step 2 of the proof of Theorem 5.2. Consequently, we have $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=\inf _{i\in I}\lambda _{\infty }^i$ and $\lambda _2(\mathbf{X},u,\mu ,F)\le \lambda _2^i$ for each $i\in I$. Thus we can obtain (1) and (2) without assuming (I). Note that each irreducible component $\mathbf{X}^{E_{x_i}}$ is conservative if $\mathbf{X}$ is conservative. $\quad \square$

Theorem 5.4

Assume $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. Then $\lambda _p(\mathbf{X},u,\mu ,F)$ is independent of $p\in [1,\infty ]$.

Proof

Step 1: First we prove the assertion under $u=0$. From (A), ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$. Then there exists a sufficiently large $\beta >0$ such that ${\mu ^+}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\beta )})$ by [30, Lemma 4.5]. Recall that $\lambda _2(\mathbf{X}^{(\beta )},\mu ,F)<\infty$ always holds under (A) by (1.5). Then there exists $\gamma >0$ such that $\lambda _2(\mathbf{X}^{(\beta )},\mu ,F)<\gamma$, equivalently $\lambda _2(\mathbf{X}^{(\beta )},\mu +\gamma \mathfrak {m},F)<0$. Note here that $\mathbf{X}^{(\beta )}$ is a transient process, hence ${\mu ^-}+N(F^-)\mu _H\in S_{D_0}^1(\mathbf{X}^{(\beta )})$. Since $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(\beta )})$, we have ${\mu ^+}+\gamma \mathfrak {m}+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\beta )})$. Applying Theorem 5.3(1) under (i) to $\mathbf{X}^{(\beta )}$, $\lambda _p(\mathbf{X}^{(\beta )},\mu +\gamma \mathfrak {m},F)=\lambda _2(\mathbf{X}^{(\beta )},\mu +\gamma \mathfrak {m},F)$ for all $p\in [1,\infty ]$. Since

$$\begin{aligned} \lambda _p(\mathbf{X}^{(\beta )},\mu +\gamma \mathfrak {m},F)=\beta -\gamma +\lambda _p(\mathbf{X},\mu ,F)\quad \text { for }p\in [1,\infty ], \end{aligned}$$

we obtain the $L^p$-independence of $\lambda _p(\mathbf{X},\mu ,F)$.

Step 2: Next we prove the assertion without assuming $u=0$. By Lemma 5.1, ${\mu ^+}+N(e^U(e^{F^+}-1))\mu _H\in S_{EK}^1(\mathbf{X})$. Since $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$ and u is bounded, we get $\bar{\nu }_1+N(e^U(e^{F^+}-1))\mu _H\in S_{EK}^1(\mathbf{X})$. Then

$$\begin{aligned} e^{-2u}\bar{\nu }_1+N^U(e^{F^+}-1)\mu _{H^U}\in S_{EK}^1(\mathbf{U}) \end{aligned}$$

from Lemma 4.11(3). Since $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, we have $e^{-2u}\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{U}^{(1)})$ by Lemma 4.11(6). Moreover, $e^{-2u}{\mu ^-}+N^U(F^-)\mu _{H^U}\in S_{D}^1(\mathbf{U})$. We can apply the result from Step 1 to $\mathbf{U}$ so that $\lambda _{\infty }(\mathbf{U}, e^{-2u}\bar{\nu }, F)= \lambda _2(\mathbf{U}, e^{-2u}\bar{\nu }, F)$. Thus we have $\lambda _{\infty }(\mathbf{X},u,\mu ,F)= \lambda _{\infty }(\mathbf{U}, e^{-2u}\bar{\nu }, F)= \lambda _2(\mathbf{U}, e^{-2u}\bar{\nu }, F)=\lambda _2(\mathbf{X}, u,\mu , F)$. $\square$

6 Proof of Theorems 1.1, 1.2 and 1.3

In this section, we removed boundedness assumption on u imposed in the last section and consider general $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ which is finely continuous and nearly Borel measurable on E. We do not assume the irreducibility of $\mathbf{X}$. The $L^p$-spectral radius $\lambda _p(\mathbf{X},u,\mu ,F)$ is defined by

$$\begin{aligned} \lambda _p(\mathbf{X},u,\mu ,F):=-\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t\Vert _{p,p}. \end{aligned}$$

Recall that

$$\begin{aligned} \lambda _{\infty }(\mathbf{X},u,\mu ,F)\le \lambda _p(\mathbf{X},u,\mu ,F)\le \lambda _2(\mathbf{X},u,\mu ,F) \end{aligned}$$

(6.1)

always holds for $p\in [1,\infty ]$.

Proof of Theorem 1.1

The proof is based on Theorem 5.2. For simplicity, write $\lambda _p$ for $\lambda _p(\mathbf{X},u,\mu ,F)$ for $p\in [1,\infty ]$. Since $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a finely continuous nearly Borel function and it satisfies $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$, we see $N(\mathbf{1}_{E\times E}|U|\mathbf{1}_{\{|U|>1\}})\mu _H\in S_K^1(\mathbf{X})$ Consequently the quantity

$$\begin{aligned} \int _0^t\int _E|u(y)-u(X_s)|\mathbf{1}_{\{1<|u(y)-u(X_s)|\}}N(X_s,\mathrm{d}y)\mathrm{d}H_s \end{aligned}$$

is a PCAF of Kato class in the strict sense. We define

$$\begin{aligned}&K_t^{u,2}:=\sum _{0<s\le t}\mathbf{1}_{\{s<\zeta \}}(u(X_s)-u(X_{s-}))\mathbf{1}_{\{1<|u(X_s)-u(X_{s-})|\}}\\&\quad -\int _0^t\int _E(u(y)-u(X_s))\mathbf{1}_{\{1<|u(y)-u(X_s)|\}}N(X_s,\mathrm{d}y)\mathrm{d}H_s. \end{aligned}$$

Then $K_t^{u,2}$ is a purely discontinuous square integrable local martingale with $\Delta K_t^{u,2}:=K_t^{u,2}-K_{t-}^{u,2}=\mathbf{1}_{\{t<\zeta \}}(u(X_t)-u(X_{t-}))\mathbf{1}_{\{|u(X_t)-u(X_{t-})|>1\}}$, because $\mu _{{\langle }u{\rangle }}\in S_K^1(\mathbf{X})$. Applying [14, Lemma 3.1] to $\phi (x,y):=\mathbf{1}_{E\times E}(x,y)(u(y)-u(x))\mathbf{1}_{\{|u(x)-u(y)|\le 1\}}$, there exists a purely discontinuous locally square integrable local martingale $K_t^{u,1}$ with

$$\begin{aligned} \Delta K_t^{u,1}:=K_t^{u,1}-K_{t-}^{u,1}=\mathbf{1}_{\{t<\zeta \}}(u(X_t)-u(X_{t-}))\mathbf{1}_{\{|u(X_t)-u(X_{t-})|\le 1\}}. \end{aligned}$$

It is shown in [14, Lemma 3.1] that

$$\begin{aligned} K_t^{u,1}&=\lim _{n\rightarrow \infty }\left( \sum _{0<s\le t}\mathbf{1}_{\{s<\zeta \}}(u(X_s)-u(X_{s-}))\mathbf{1}_{\{1/n<|u(X_s)-u(X_{s-})|\le 1\}}\right. \\&\left. \quad -\int _0^t\int _E(u(y)-u(X_s))\mathbf{1}_{\{1/n<|u(y)-u(X_s)|\le 1\}}N(X_s,\mathrm{d}y)\mathrm{d}H_s \right) . \end{aligned}$$

We set $G_k{:=} \{x\in E : |u(x)|<k\}$. Then $\{G_k\}$ is a nest of finely open nearly Borel sets. We set $u_k:=(-k)\vee u\wedge k$ for $k\in \mathbb {N}$. Then $u=u_k$ on $G_k$. Clearly, $K_t^{u,1}=K_t^{u_{k+1},1}$ for $t<\tau _k:=\tau _{G_k}$. By definition for $K_t^{u,2}$ and $K_t^{u_{k+1},2}$, we see that for $t<\tau _k$

$$\begin{aligned} K_t^{u,2}-K_t^{u_{k+1},2}&=\int _0^t\int _E(u_{k+1}(y)-u_{k+1}(X_s)) \mathbf{1}_{\{|u_{k+1}(y)-u_{k+1}(X_s)|>1\}}N(X_s,\mathrm{d}y)\mathrm{d}H_s \\&\quad -\int _0^t\int _E(u(y)-u(X_s)) \mathbf{1}_{\{|u(y)-u(X_s)|>1\}}N(X_s,\mathrm{d}y)\mathrm{d}H_s. \end{aligned}$$

Define the smooth measure $\mu _k$ in the strict sense by

$$\begin{aligned} \mu _k(\mathrm{d}x)&:=\mathbf{1}_{G_k}(x)\int _E (u_{k+1}(y)-u_{k+1}(x)) \mathbf{1}_{\{|u_{k+1}(y)-u_{k+1}(x)|>1\}}N(x,\mathrm{d}y)\mu _H(\mathrm{d}x)\\&\quad -\mathbf{1}_{G_k}(x)\int _E (u(y)-u(x)) \mathbf{1}_{\{|u(y)-u(x)|>1\}}N(x,\mathrm{d}y)\mu _H(\mathrm{d}x). \end{aligned}$$

Then the total variation $|\mu _k|$ of $\mu _k$ is estimated by

$$\begin{aligned} |\mu _k|(\mathrm{d}x)\le 2\mathbf{1}_{G_k}(x)\int _E(u(y)-u(x))^2N(x,\mathrm{d}y)\mu _H(\mathrm{d}x) \le 2\mathbf{1}_{G_k}(x)\mu _{{\langle }u{\rangle }}(\mathrm{d}x). \end{aligned}$$

Thus we have $|\mu _k|\in S_{K}^1(\mathbf{X})$ from $\mu _{{\langle }u{\rangle }}\in S_{K}^1(\mathbf{X})$. In particular, $\mu _k$ is a signed smooth measure in the strict sense belonging to $S_{K}^1(\mathbf{X})-S_{K}^1(\mathbf{X})$. Consider the generalized Fukushima’s decomposition up to lifetime for finely continuous nearly Borel $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ with $\mu _{{\langle }u{\rangle }}\in S_{K}^1(\mathbf{X})\subset S_1(\mathbf{X})$:

$$\begin{aligned} u(X_t)-u(X_0)=M_t^u+N_t^u,\quad t\in [0,\zeta [\quad \mathbb {P}_x\text {-a.s.} \end{aligned}$$

for all $x\in E$. Here $M_t^u$ is locally square integrable local MAF in the strict sense and $N_t^u$ is a CAF in the strict sense locally of zero energy. From this, $u_{k+1}|_{G_k}$ admits the following generalized Fukushima’s decomposition

$$\begin{aligned} u_{k+1}(X_t)-u_{k+1}(X_0)=M_t^{u_{k+1}}+N_t^{u_{k+1}},\quad t\in [0,\tau _k[\quad \mathbb {P}_x\text {-a.s.} \end{aligned}$$

for all $x\in G_k$. It follows from that on $\{t<\tau _k\}$

$$\begin{aligned} M_t^u-M_t^{u_{k+1}}&=M_t^{u,c}+M_t^{u,d}-M_t^{u_{k+1},c}-M_t^{u_{k+1},d}\\&=K_t^{u,2}-K_t^{u_{k+1},2}=A_t^{\mu _k}, \end{aligned}$$

where $A_t^{\mu _k}$ is a CAF of bounded variation associated to the signed smooth measure $\mu _k$ in the strict sense. Hence for $t<\tau _k$

$$\begin{aligned} N_t^u&=u(X_t)-u(X_0)-M_t^u =u_{k+1}(X_t)-u_{k+1}(X_0)-M_t^{u_{k+1}}-A_t^{\mu _k}\\&=N_t^{u_{k+1}}-A_t^{\mu _k}. \end{aligned}$$

Define $(Q_t^{(k)})_{t\ge 0}$ by

$$\begin{aligned} Q_t^{(k)}f(x)&:=\mathbb {E}_x[e_A(t)f(X_t):t<\tau _k]\\&=\mathbb {E}_x[\exp (N_t^u+A_t^{\mu }+A_t^F)f(X_t):t<\tau _k]\\&=\mathbb {E}_x[\exp (N_t^{u_{k+1}}+A_t^{\mu -\mu _k}+A_t^F)f(X_t):t<\tau _k]. \end{aligned}$$

Let $\mathbf{U}_{k+1}$ be the Girsanov transformed process defined by $u_{k+1}$ just as we define $\mathbf{U}$ for u. Denote by $U_t^{k+1}$ its Girsanov density. Since $u_{k+1}\in \dot{\mathcal {F}}_{\mathrm{loc}}$ is a bounded finely continuous nearly Borel function having a finite value at $\partial$ and $\mu _{{\langle }u_{k+1}{\rangle }}\in S_{K}^1(\mathbf{X})$, $\{U_t^{k+1}\}_{t\in [0,\infty [}$ is a uniformly integrable martingale under $\mathbf{X}^{(\alpha )}$ by Proposition 3.1(6). Then one can apply Lemma 4.11 to $\mathbf{U}_{k+1}$. From Proposition 3.1(1), we have

$$\begin{aligned} Q_t^{(k)}f(x)=e^{-u_{k+1}}(x)\mathbb {E}_x^{U^{k+1}}\left[ \exp \left( A_t^{\bar{\nu }^k}+A_t^F \right) (fe^{u_{k+1}})(X_t):t<\tau _k \right] . \end{aligned}$$

Here $\bar{\nu }^k:=\bar{\nu }_1^k-\bar{\nu }_2^k$, $\bar{\nu }_1^k:={\mu ^+}+\mu _k^-+ N(e^{U_{k+1}}-U_{k+1}-1)\mu _H+\frac{1}{2}\mu _{{\langle }u_{k+1}{\rangle }}^c$ and $\bar{\nu }_2^k:={\mu ^-}+\mu _k^+$. We will apply Theorem 5.2 for $(\mathbf{U}^{G_k}_{k+1},\mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$, where $\mathbf{U}^{G_k}_{k+1}$ is the part process of $\mathbf{U}_{k+1}$ on $G_k$. For this, we further need to check conditions. By assumption, $\bar{\nu }_1^k+N(e^{F^+}-1)\mu _H\in S_{EK}^1(\mathbf{X})$. From Lemmas 4.11(3) and 5.1, we have

$$\begin{aligned} e^{-2u_{k+1}}\bar{\nu }_1^k+\widetilde{N}(e^{F^+}-1)\mu _{\widetilde{H}}\in S_{EK}^1(\mathbf{U}_{k+1}). \end{aligned}$$

Here $(\widetilde{N},\widetilde{H})$ is a Lévy system of $\mathbf{U}_{k+1}$. By Lemmas 4.4(5) and 4.6,

$$\begin{aligned} \mathbf{1}_{G_k}(e^{-2u_{k+1}}\bar{\nu }_1^k+\widetilde{N}^{G_k}(e^{F^+}-1)\mu _{\widetilde{H}}) \in S_{EK}^1(\mathbf{U}_{k+1}^{G_k}). \end{aligned}$$

Similarly, we can obtain $\mathbf{1}_{G_k}(\bar{\nu }_2^k+\widetilde{N}^{G_k}(F^-)\mu _{\widetilde{H}})\in S_{D}^1(\mathbf{U}_{k+1}^{G_k})$ by use of Lemmas 4.11 and 4.4. Moreover, the condition (1.7) holds for $\mathbf{U}_{k+1}^{G_k}$, which can be similarly proved by a similar estimate with (5.7) obtained by replacing U with $U_{k+1}$. Thus one can apply Theorem 5.2 for $(\mathbf{U}^{G_k}_{k+1},\mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$ so that

$$\begin{aligned} \lambda _{\infty }^{(k)}=\lambda _2^{(k)}, \end{aligned}$$

(6.2)

where $\lambda _p^{(k)}:=\lambda _p(\mathbf{U}^{G_k}_{k+1}, \mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$ is the $L^p$-spectral radius for the Feynman–Kac semigroup $(Q_t^{(k)})_{t\ge 0}$ for $p\in [1,\infty ]$. In the same way of Step 3 in the proof of Theorem 5.3 without assuming $\mathbf{(I)}$, we can prove $\lambda _2\le \lambda _2^{(k)}$ and $\lambda _{\infty }=\inf _{k\in \mathbb {N}}\lambda _{\infty }^{(k)}$ by use of Terkelsen’s minimax theorem. Hence $\lambda _2(\mathbf{X},u,\mu ,F)\le \lambda _{\infty }(\mathbf{X},u,\mu ,F)$. Therefore, we obtain $\lambda _{\infty }(\mathbf{X},u,\mu ,F)=\lambda _2(\mathbf{X},u,\mu ,F)$ by (1.6). $\square$

Proof of Theorem 1.2

(1): It suffices to prove the assertion under (ii). Let $\{G_k\}$, $u_k$, $\mu _k$, $\bar{\nu }^k$ and $\mathbf{U}_{k+1}$ be the notions constructed in the proof of Theorem 1.1. Recall that $\lambda _p^{(k)}:=\lambda _p(\mathbf{U}^{G_k}_{k+1}, \mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$ is the $L^p$-spectral radius for the Feynman–Kac semigroup $(Q_t^{(k)})_{t\ge 0}$ for $p\in [1,\infty ]$. As in the proof of Theorem 1.1, (A) holds for $(\mathbf{U}_{k+1}^{G_k}, \mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$. We prove

$$\begin{aligned} \lambda _{\infty }^{(k)}\ge \min \{\lambda _2^{(k)},0\}. \end{aligned}$$

(6.3)

The proof is based on Theorem 5.3. Under the condition, $|\mu _k|\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. By assumption, we have $\bar{\nu }_1^k+N(e^{F^+}-1)\mu _H\in S_{NK_1}^1(\mathbf{X}^{(\alpha )})$ for all $\alpha >0$. By Lemmas 4.11(7) and 5.1, we have $e^{-2u_{k+1}}\bar{\nu }_1^k+\widetilde{N}(e^{F^+}-1)\mu _{\widetilde{H}}\in S_{NK_1}^1((\mathbf{U}_{k+1})^{(\alpha )})$ for all $\alpha >0$. Here $(\widetilde{N},\widetilde{H})$ is a Lévy system of $\mathbf{U}_{k+1}$. From Lemmas 4.4(10) and 4.6, we have $\mathbf{1}_{G_k}(\bar{\nu }_1^k+\widetilde{N}^{G_k} (e^{F^+}-1)\mu _{\widetilde{H}})\in S_{NK_1}^1((\mathbf{U}_{k+1}^{G_k})^{(\alpha )})$ for all $\alpha >0$. Similarly,

$$\begin{aligned} \mathbf{1}_{G_k}(\bar{\nu }_2^k+\widetilde{N}^{G_k}( F^-)\mu _{\widetilde{H}})\in S_D^1(\mathbf{U}_{k+1}^{G_k}). \end{aligned}$$

One can apply Theorem 5.3(1)(ii) to the case $(\mathbf{U}_{k+1}^{G_k}, \mathbf{1}_{G_k}\bar{\nu }^k, \mathbf{1}_{G_k\times G_k}F)$ so that (6.3) holds. The rest of the proof is the same after (6.2) in the proof of Theorem 1.1. Therefore, we have $\lambda _{\infty }(\mathbf{X},u,\mu ,F)\ge \min \{\lambda _2(\mathbf{X},u,\mu ,F),0\}$.

(2): Since $\lambda _2(\mathbf{X},u,\mu ,F)>0$, we have from (1) that $\lambda _{\infty }(\mathbf{X},u,\mu ,F)\ge 0$. Assume now that $\mathbf{X}$ is conservative. The proof for (ii) is already done in Theorem 5.3(2). We prove the assertion for (i). By Jensen’s inequality,

$$\begin{aligned} \Vert Q_t1\Vert _{\infty }&=\sup _{x\in E}\mathbb {E}_x[\exp (N_t^u+A_t^{\mu }+A_t^{F})]\ge \sup _{x\in E}\mathbb {E}_x[\exp (N_t^u-A_t^{{\mu ^-}}-A_t^{F^-})]\\&\ge \sup _{x\in E}\mathbb {E}_x[\exp (N_t^u-A_{\infty }^{{\mu ^-}}-A_{\infty }^{F^-})]\\&\ge \exp \left( \sup _{x\in E}\mathbb {E}_x[N_t^u]-\sup _{y\in E}\mathbb {E}_y[A_{\infty }^{{\mu ^-}}+A_{\infty }^{F^-}]\right) \\&=\exp \left( \sup _{x\in E}\mathbb {E}_x[N_t^u]-\Vert R({\mu ^-}+N(F^-)\mu _H)\Vert _{\infty }\right) . \end{aligned}$$

Then we see that

$$\begin{aligned} \lambda _{\infty }(\mathbf{X},u,\mu ,F)=-\lim _{t\rightarrow \infty }\frac{1}{t}\log \Vert Q_t1\Vert _{\infty }\le -\mathop {{\varlimsup }}_{t\rightarrow \infty }\frac{1}{t}\sup _{x\in E}\mathbb {E}_x[N_t^u]. \end{aligned}$$

(6.4)

Now suppose (a). Since

$$\begin{aligned} N_t^u&=u(X_t)-u(X_0)-M_t^u\ge -u^-(X_t)-u^+(X_0)-M_t^u, \end{aligned}$$

(6.5)

we have $\mathbb {E}_x[N_t^u]\ge -\mathbb {E}_x[u^-(X_t)]-u^+(x),$ because $M^u$ is a square integrable martingale when $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})\subset S_K^1(\mathbf{X})$. So it suffices to prove that

$$\begin{aligned} \mathop {{\varliminf }}_{t\rightarrow \infty }\frac{1}{t}\inf _{x\in E}(\mathbb {E}_x[u^-(X_t)]+u^+(x))=\mathop {{\varliminf }}_{t\rightarrow \infty }\frac{1}{t}\inf _{x\in E}(P_tu^-(x)+u^+(x)) \le 0. \end{aligned}$$

(6.6)

Take $g\in L^1(E;\mathfrak {m})$ with $0<g\le 1$$\mathfrak {m}$-a.e. on E such that $u\in L^1(E;g\mathfrak {m})$. Under (a), we have

$$\begin{aligned} {\langle }g\mathfrak {m}, P_tu^-{\rangle }&\le {\langle }g\mathfrak {m}, (P_t|u^-|^p)^{1/p}{\rangle }\\&\le \left\{ \begin{array}{lc} \Vert u^-\Vert _1 &{} (p=1), \\ \Vert u^-\Vert _p\Vert g\Vert _1^{\frac{p-1}{p}} &{} (1<p<\infty ),\\ \Vert u^-\Vert _{\infty }\Vert g\Vert _1 &{} (p=\infty ). \end{array}\right. \end{aligned}$$

Then

$$\begin{aligned} \Vert g\Vert _1\lim _{t\rightarrow \infty } \frac{1}{t}\inf _{x\in E}(P_tu^-(x)+u^+(x))\le \lim _{t\rightarrow \infty }\frac{1}{t}\left( {\langle }g\mathfrak {m},P_tu^-{\rangle }+\int _Eu^+g\mathrm{d}\mathfrak {m}\right) =0. \end{aligned}$$

Therefore, we obtain the assertion in this case. Next suppose (b) or (c). From (6.5), we see $\mathbb {E}_x[N_t^u]\ge -\mathbb {E}_x[(u(X_t)-u(X_0))^2]^{\frac{1}{2}}$. So it suffices to prove

$$\begin{aligned} \mathop {{\varliminf }}_{t\rightarrow \infty }\frac{1}{t}\inf _{x\in E}\mathbb {E}_x[(u(X_t)-u(X_0))^2]^{\frac{1}{2}}\le 0. \end{aligned}$$

(6.7)

Since $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})\subset S_K^1(\mathbf{X})$, $\mu _{{\langle }u{\rangle }}$ is a smooth measure in the strict sense. Consider the Lyons-Zheng’s decomposition for $u\in \dot{\mathcal {F}}_{\mathrm{loc}}$ satisfying $\mu _{{\langle }u{\rangle }}^j\in S_1(\mathbf{X})$ (see [35, Corollary 5.3]):

$$\begin{aligned} u(X_t)-u(X_0)=\frac{1}{2}M_t^{u}-\frac{1}{2}M_t^{u}\circ r_t \end{aligned}$$

under $\mathbb {P}_{\mathfrak {m}}$. Here $r_t$ is the time reverse operator defined by $X_T(r_t\omega ):=X_{(T-t)-}(\omega )$ for $t<T$. It is known that $\mathbb {E}_{\mathfrak {m}}[G\circ r_t]=\mathbb {E}_{\mathfrak {m}}[G]$ for non-negative $\mathscr {F}_t$-measurable G. We then see that

$$\begin{aligned} \mathbb {E}_{\mathfrak {m}}[(u(X_t)-u(X_0))^2]&\le \mathbb {E}_{\mathfrak {m}}\left[ \frac{1}{2}(M_t^{u})^2+\frac{1}{2} (M_t^{u}\circ r_t)^2\right] \\&\le \mathbb {E}_{\mathfrak {m}}[{\langle }M^{u}{\rangle }_t]\le \mathbb {E}_{\mathfrak {m}}[{\langle }M^{u}{\rangle }_{\infty }]\\&= \int _ER\mu _{{\langle }u{\rangle }}\mathrm{d}\mathfrak {m}\le \Vert R\mu _{{\langle }u{\rangle }}\Vert _{\infty }\mathfrak {m}(E)<\infty \end{aligned}$$

when $\mu _{{\langle }u{\rangle }}\in S_{D_0}^1(\mathbf{X})$ and $\mathfrak {m}(E)<\infty$. If $\mu _{{\langle }M^u{\rangle }}(E)<\infty$, we see

$$\begin{aligned} \mathbb {E}_{\mathfrak {m}}[(u(X_t)-u(X_0))^2]&\le \mathbb {E}_{\mathfrak {m}}[{\langle }M^{u}{\rangle }_t]\le 2t\mu _{{\langle }M^{u}{\rangle }}(E). \end{aligned}$$

Then we have $M:=\mathop {{\varlimsup }}_{t\rightarrow \infty }\frac{1}{t}\mathbb {E}_{\mathfrak {m}}[(u(X_t)-u(X_0))^2]<\infty$ in either case.

Take $g\in L^1(E;\mathfrak {m})$ with $0<g\le 1$$\mathfrak {m}$-a.e. Then

$$\begin{aligned}&\Vert g\Vert _1 \lim _{t\rightarrow \infty }\frac{1}{t}\inf _{x\in E}\mathbb {E}_x[(u(X_t)-u(X_0))^2]^{\frac{1}{2}}\\&\quad \le \lim _{t\rightarrow \infty }\frac{1}{t}\mathbb {E}_{\mathfrak {m}}[(u(X_t)-u(X_0))^2]^{\frac{1}{2}}\Vert g\Vert _1^{\frac{1}{2}}\\&\quad = \lim _{t\rightarrow \infty }\frac{1}{\sqrt{t}}\left( \frac{1}{t} \mathbb {E}_{\mathfrak {m}}[ (u(X_t)-u(X_0))^2]\right) ^{\frac{1}{2}}\Vert g\Vert _1^{\frac{1}{2}}=0. \end{aligned}$$

Thus we have (6.7). Therefore, we obtain $\lambda _{\infty }(\mathbf{X},\mu ,F)=0<\lambda _2(\mathbf{X},\mu ,F)$. $\square$

Proof of Theorem 1.3

Let $\{G_k\}$, $u_k$, $\mu _k$, $\bar{\nu }^k$ and $\mathbf{U}_{k+1}$ be the notions constructed in the proof of Theorem 1.1. Recall that $\lambda _p^{(k)}:=\lambda _p(\mathbf{U}^{G_k}_{k+1}, \mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$ is the $L^p$-spectral radius for the Feynman–Kac semigroup $(Q_t^{(k)})_{t\ge 0}$ for $p\in [1,\infty ]$. As in the proof of Theorem 1.1, (A) holds for $(\mathbf{U}_{k+1}^{G_k}, \mathbf{1}_{G_k}\bar{\nu }^k,\mathbf{1}_{G_k\times G_k}F)$. Since $\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$, we have $e^{-2u_{k+1}}\mathfrak {m}\in S_{NK_{\infty }}^1((\mathbf{U}_{k+1})^{(1)})$ by Lemma 4.11(6). Then one can apply Theorem 5.3 to $\mathbf{U}^{G_k}$ to the case $(\mathbf{U}_{k+1}^{G_k}, \mathbf{1}_{G_k}\bar{\nu }^k, \mathbf{1}_{G_k\times G_k}F)$ so that

$$\begin{aligned} \lambda _{\infty }^{(k)}=\lambda _2^{(k)}. \end{aligned}$$

(6.8)

The rest of the proof is similar to that of Theorem 1.1. $\square$

7 Examples

In this section, we give three examples on measures that are in various Kato classes used in the main results of this paper.

Example 7.1

(Brownian motion) Let $\mathbf{X}=(\Omega , X_t, {\mathbb {P}}_x)$ be a d-dimensional Brownian motion. X is a typical irreducible doubly Feller process on $\mathbb {R}^d$. The associated Dirichlet form on $L^2(\mathbb {R}^d;\mathrm{d}x)$ is $(H^1(\mathbb {R}^d),\frac{1}{2}{} \mathbf{D})$, where $H^1(\mathbb {R}^d):=\{f\in L^2(\mathbb {R}^d;\mathrm{d}x): |\nabla f|\in L^2(\mathbb {R}^d;\mathrm{d}x)\}$ and $\mathbf{D}(f,g):=\int _{\mathbb {R}^d}\nabla f(x)\cdot \nabla g(x)\,\mathrm{d}x$. Fix a $u\in H^1(\mathbb {R}^d)_{\mathrm{loc}}\cap C(\mathbb {R}^d)$. For a signed Borel measure $\mu$ on $\mathbb {R}^d$, $\mu$ is said to be of Kato class with respect to $\mathbf{X}$ if and only if

$$\begin{aligned} \lim _{r\rightarrow 0}\sup _{x\in \mathbb {R}^d}\int _{|x-y|<r}\frac{|\mu |(\mathrm{d}y)}{|x-y|^{d-2}}&=0 \quad \text { for }\quad d\ge 3, \\ \lim _{r\rightarrow 0}\sup _{x\in \mathbb {R}^d}\int _{|x-y|<r}(\log |x-y|^{-1})|\mu |(\mathrm{d}y)&=0 \quad \text { for }\quad d=2, \\ \sup _{x\in \mathbb {R}^d}\int _{|x-y|\le 1}|\mu |(\mathrm{d}y)&<\infty \quad \text { for }\quad d=1. \end{aligned}$$

Denote by ${K}_{d}$ the family of non-negative measures of Kato class with respect to X. Then we have ${K}_{d}=S_K^1(\mathbf{X})$ by [1]. Under $d\ge 3$, $\mu \in K_d$ is said to be Green-tight if

$$\begin{aligned} \lim _{R\rightarrow \infty }\sup _{x\in \mathbb {R}^d}\int _{B_R(0)^c}\frac{\mu (\mathrm{d}y)}{|x-y|^{d-2}}=0. \end{aligned}$$

Denote by $K_d^{\infty }$ the family of Green-tight measures of Kato class under $d\ge 3$. Then $K_d^{\infty }=S_{K_{\infty }}^1(\mathbf{X})= S_{CK_{\infty }}^1(\mathbf{X})=S_{NK_{\infty }}^1(\mathbf{X})$ under $d\ge 3$. It is proved in [53, Proposition 1] that $f\in L^1(\mathbb {R}^d;\mathrm{d}x)$ satisfying $|f(x)|\mathrm{d}x\in K_d$, then $|f(x)|\mathrm{d}x\in K_d^{\infty }$ provided $d\ge 3$. It is shown in [19, Lemma 5.1(2)] that for $f\in L^1(\mathbb {R}^d;\mathrm{d}x)$ satisfying $|f(x)|\mathrm{d}x\in S_K^1(\mathbf{X})$, then $|f(x)|\mathrm{d}x\in S_{K_{\infty }}^1(\mathbf{X}^{(1)})= S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$. The following is proved in [5, Lemma 5.2].

Proposition 7.2

([5, Lemma 5.2], see Proposition 7.5 below)

• 1. Assume $p>d/2$ (resp. $p\ge 1$) for $d\ge 3$ (resp. $d=1,2$). Let $f\in L^p(\mathbb {R}^d;\mathrm{d}x)$. Then $|f(x)|\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

• 2. Suppose that $u\in L^2_{\mathrm{loc}}(\mathbb {R}^d;\mathrm{d}x)$ is bounded with $|\nabla u|\in L^2(\mathbb {R}^d;\mathrm{d}x)\cap L^p(\mathbb {R}^d;\mathrm{d}x)$ for some $p>d$ (resp. $p\ge 2$) under $d\ge 3$ (resp. $d=1,2$). Then $u\in H^1(\mathbb {R}^d)_e$ with $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

Proposition 7.2(1) partially extends [1, Theorem 1.4(iii)]. We shall point out that the condition in Proposition 7.2(2) can be relaxed in the following Proposition 7.3(2), whose proof is similar to that of [5, Lemma 5.1(2)].

Proposition 7.3

The following holds.

• 1. Suppose that $u\in L^2_{\mathrm{loc}}(\mathbb {R}^d;\mathrm{d}x)$ satisfies $|\nabla u|\in L^2(\mathbb {R}^d;\mathrm{d}x)$ and $|\nabla u(x)|^2\mathrm{d}x\in S_K^1(\mathbf{X})$. Then $u\in H^1(\mathbb {R}^d)_e$ with $|\nabla u(x)|^2\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

• 2. Suppose that $u\in L^2_{\mathrm{loc}}(\mathbb {R}^d;\mathrm{d}x)$ satisfies $|\nabla u|\in L^2_{\mathrm{loc}}(\mathbb {R}^d;\mathrm{d}x)\cap L^p(\mathbb {R}^d;\mathrm{d}x)$ for some $p>d$ (resp. $p\ge 2$) under $d\ge 3$ (resp. $d=1,2$). Then $u\in H^1(\mathbb {R}^d)_{\mathrm{loc}}$ with $|\nabla u(x)|^2\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

Let $\phi \in C^{\infty }([0,\infty [)$ satisfy $\phi (0)=0$ and $\phi (t)=\log t$ for $t>1$. Set $u(x):=\phi (|x|)$. Then u is an unbounded function on $\mathbb {R}^d$ and satisfies $u\in H^1(\mathbb {R}^d)_{\mathrm{loc}}\cap C^{\infty }(\mathbb {R}^d;\mathrm{d}x)$ and $|\nabla u|\in L^2_{\mathrm{loc}}(\mathbb {R}^d;\mathrm{d}x)\cap L^p(\mathbb {R}^d;\mathrm{d}x)$ for any $p>d$. In this case, we have $|\nabla u(x)|^2\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

Example 7.4

(Diffusion process on Riemannian manifold) Let (M, g) be a d-dimensional complete smooth Riemannian manifold. We assume that Ricci curvature of (M, g) has a lower bound $\kappa (d-1)$ with $\kappa \in \mathbb {R}$, that is, ${\mathrm{Ric}}_g\ge \kappa (d-1)$. Let $\mathfrak {m}:={\mathrm{vol}}_g$ be the volume measure of (M, g) and $\Delta _g$ the Laplace-Bertrami operator of (M, g). Then, it is known that the $\frac{1}{2}\Delta _g$ admits a smooth heat kernel $p_t(x,y)$ admitting following estimates (see [26]): for any ${\varepsilon }>0$, there exists positive constants $C_1({\varepsilon }), C_2({\varepsilon })$ depending on $\kappa$, d such that for all $x,y\in M$ and $t>0$

$$\begin{aligned}&\frac{C_1({\varepsilon })^{-1}}{V_{\sqrt{t}}(x)} \exp \left( -C_2({\varepsilon })t-\frac{d(x,y)^2}{ (2-{\varepsilon })t}\right) \le p_t(x,y)\nonumber \\&\quad \le \frac{C_1({\varepsilon })}{V_{\sqrt{t}}(x)} \exp \left( C_2({\varepsilon })t-\frac{d(x,y)^2}{(2+{\varepsilon })t}\right) . \end{aligned}$$

(7.1)

Here $V_r(x):=\mathfrak {m}(B_{r}(x))$ is the volume of the r-ball. Moreover, $C_2({\varepsilon })$ can be taken to be zero provided $\kappa \ge 0$ or $d=1$. Let $\mathbf{X}$ be the diffusion process associated to $\frac{1}{2}\Delta _g$. Then $\mathbf{X}$ is a doubly Feller $\mathfrak {m}$-symmetric conservative process on (M, g). It is proved in [38, Example 5.3] that for any $f\in L^p(M;\mathfrak {m})$ with $p\in [1,\infty [$ we have $|f|\mathfrak {m}\in S_K^1(\mathbf{X})$ provided $p>d/2$ (resp. $p\ge 1$) for $d\ge 2$ (resp. $d=1$) and $\inf _{x\in M}V_1(x)>0$. Though the positivity of injectivity radius is assumed in [38, Example 5.3], this assertion remains valid under $\inf _{x\in M}V_1(x)>0$ because

$$\begin{aligned} \bar{V}_{\kappa }(r)\frac{V_1(x)}{\bar{V}_{\kappa }(1)}\le V_r(x)\le \bar{V}_{\kappa }(r) \quad \text { for }\quad r\in ]0,1[ \end{aligned}$$

and $\bar{V}_{\kappa }(r)\approx \omega _dr^d/d$ for small $r>0$. Here $\omega _d$ is the area of the unit sphere $\mathbb {S}^{d-1}$ in the Euclidean space $\mathbb {R}^d$ and $\bar{V}_{\kappa }(r):=\omega _d\int _0^r{\mathsf {s}}_{\kappa }(t)^{d-1}\mathrm{d}t$ is the volume of r-ball in the d-dimensional space form $\mathbb {M}_d^{\kappa }$ of constant curvature $\kappa$. Here ${\mathsf {s}}_{\kappa }(t):=\frac{\sin {\sqrt{\kappa }t}}{\sqrt{\kappa }}$ for $\kappa >0$, ${\mathsf {s}}_{\kappa }(t):=t$ for $\kappa =0$, ${\mathsf {s}}_{\kappa }(t):=\frac{\sinh {\sqrt{-\kappa }t}}{\sqrt{-\kappa }}$ for $\kappa <0$. We summarize this in the following.

Proposition 7.5

Suppose $\inf _{x\in M}V_1(x)>0$ and take $p\in [1,\infty [$. Assume $p>d/2$ (resp. $p\ge 1$) for $d\ge 3$ (resp. $d=1,2$). Let $f\in L^p(M;\mathfrak {m})$. Then $|f|\mathfrak {m}\in S_{K}^1(\mathbf{X})$.

Moreover, we have the following stronger assertion:

Proposition 7.6

Suppose $\inf _{x\in M}V_1(x)>0$ and take $p\in [1,\infty [$. Assume $p>d/2$ (resp. $p\ge 1$) for $d\ge 3$ (resp. $d=1,2$). Let $f\in L^p(M;\mathfrak {m})$. Then $|f|\mathfrak {m}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

Proof of Proposition 7.6

By Proposition , $|f|\mathfrak {m}\in S_K^1(\mathbf{X})$ under $\inf _{x\in M}V_1(x)>0$. It is proved in [27, Proposition 4.1] that $S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$ under the doubly Feller property of $\mathbf{X}$. By (7.1), we have that for $x,y\in M$ and $t>0$

$$\begin{aligned} p_t(x,y)\le \frac{C_1}{V_{\sqrt{t}}(x)}\exp \left( C_2t- \frac{r_x(y)^2}{Ct}\right) , \end{aligned}$$

where $r_x(y):=d(x,y)$. We may assume $f\ge 0$. It suffices to show that for any $t_0\in ]0,1]$ and any increasing sequence $\{K_{\ell }\}$ of compact sets with $\bigcup _{\ell =1}^{\infty }K_{\ell }=M$

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x\in M}\mathbb {E}_x\left[ \int _0^{t_0}e^{-\alpha s}\mathbf{1}_{K_{\ell }^c}f(X_s)\mathrm{d}s \right] =0 \end{aligned}$$

(7.2)

for sufficiently large $\alpha >C_2$ in view of the proof of [19, Lemma 2.3]. We define

$$\begin{aligned} S_{\alpha }^{t_0}(x,y)&:=\int _0^{t_0}e^{-\alpha t}p_t(x,y)\mathrm{d}t \le C_1 \int _0^{t_0}e^{-\alpha t} \frac{1}{V_{\sqrt{t}}(x)}\exp \left( C_2t-\frac{r_x(y)^2}{Ct}\right) \mathrm{d}t. \end{aligned}$$

By Bishop-Gromov inequality and $\bar{V}_{\kappa }(1)/\bar{V}_{\kappa }(\sqrt{t})\le c_1/t^{d/2}$ for $t\in ]0,1]$,

$$\begin{aligned}&\int _0^{t_0}e^{-\alpha t}\frac{1}{V_{\sqrt{t}}(x)}\exp \left( C_2t-\frac{r^2}{Ct}\right) \mathrm{d}t \\&\quad \le \frac{1}{V_1(x)} \int _0^{t_0} \frac{\bar{V}_{\kappa }(1)}{\bar{V}_{\kappa }(\sqrt{t})} \exp \left( -(\alpha -C_2)t-\frac{r^2}{Ct}\right) \mathrm{d}t\\&\quad \le \frac{1}{\inf _{x\in M}V_1(x)} \int _0^{t_0} \frac{c_1}{t^{\frac{d}{2}}} \exp \left( -(\alpha -C_2)t-\frac{r^2}{Ct}\right) \mathrm{d}t\\&\quad =\frac{c_1 r^{2-d}}{\inf _{x\in M}V_1(x)} \int _0^{t_0/r^2}\frac{1}{u^{\frac{d}{2}}} \exp \left( -(\alpha -C_2)r^2u-\frac{1}{Cu}\right) \mathrm{d}u\\&\quad \le \frac{c_1 r^{2-d}}{\inf _{x\in M}V_1(x)} \int _0^{\infty }\frac{1}{u^{\frac{d}{2}}} \exp \left( -(\alpha -C_2)r^2u-\frac{1}{Cu}\right) \mathrm{d}u\\&\quad \le \frac{c_1c_2 r^{2-d}}{\inf _{x\in M}V_1(x)} \int _0^{\infty }\left( \frac{1}{u^{\frac{d}{2}+1}} \wedge 1\right) \exp \left( -\frac{(\alpha -C_2)r^2u}{2}-\frac{1}{2Cu}\right) \mathrm{d}u\\&\quad \le \frac{c_1c_2 r^{2-d}e^{-\sqrt{(\alpha -C_2)/C}r}}{\inf _{x\in M}V_1(x)} \int _0^{\infty }\left( \frac{1}{u^{\frac{d}{2}+1}}\wedge 1\right) \mathrm{d}u, \end{aligned}$$

where we use that there is $c_2>0$ such that $\frac{1}{u^{d/2}}\le c_2\left( \frac{1}{u^{\frac{d}{2}+1}}\wedge 1\right) \exp \left( \frac{1}{2Cu}+\frac{(\alpha -C_2) r^2u}{2}\right)$. Consequently, there are positive constants $C_1(\alpha ,d),C_2(\alpha ,d)$ such that

$$\begin{aligned} S_{\alpha }^{t_0}(x,y)\le C_1(\alpha ,d)d(x,y)^{2-d}\exp (-C_2(\alpha ,d)d(x,y)). \end{aligned}$$

Note here that $C_2(\alpha ,d)$ can be taken to be large for sufficient large $\alpha$. From this, we can calculate that for $q:=\frac{p}{p-1}$ under $p>d/2$ (resp. $p>1$) with $d\ge 3$ (resp. $d=1,2$)

$$\begin{aligned} \sup _{x\in M}\int _MS_{\alpha }^{t_0}(x,y)^q\mathfrak {m}(\mathrm{d}y)&=\sup _{x\in M}\sum _{k=-\infty }^{\infty }\int _{2^{k-1}<d(x,y)\le 2^k}S_{\alpha }^{t_0}(x,y)^q\mathfrak {m}(\mathrm{d}y)<\infty . \end{aligned}$$

Indeed,

$$\begin{aligned}&\sum _{k=-\infty }^0\int _{2^{k-1}<d(x,y)\le 2^k}d(x,y)^{q(2-d)}e^{-C_2(\alpha ,d)qd(x,y)}\mathfrak {m}(\mathrm{d}y)\\&\quad =\sum _{k=0}^{\infty }\int _{\frac{1}{2^{k-1}}<d(x,y)\le \frac{1}{2^k}}d(x,y)^{q(2-d)}\mathfrak {m}(\mathrm{d}y)\\&\quad \le \frac{c_3\omega _d}{d2^{q(d-2)}}\sum _{k=0}^{\infty }\left( \frac{1}{2^k} \right) ^{d-q(d-2)}= \frac{c_3\omega _d}{d2^{q(d-2)}}\sum _{k=0}^{\infty }\left( \frac{1}{2^k} \right) ^{\frac{2p-d}{p-1}} <\infty \end{aligned}$$

and

$$\begin{aligned}&\sum _{k=1}^{\infty }\int _{2^{k-1}<d(x,y)\le 2^k}d(x,y)^{q(2-d)}e^{-C_2(\alpha ,d)qd(x,y)}\mathfrak {m}(\mathrm{d}y)\\&\quad \le \sum _{k=1}^{\infty }\int _{2^{k-1}<d(x,y)\le 2^k}e^{-C_2(\alpha ,d)qd(x,y)}\mathfrak {m}(\mathrm{d}y)\\&\quad \le \sum _{k=1}^{\infty }e^{-C_2(\alpha ,d)q2^{k-1}}\bar{V}_{\kappa }(2^k)<\infty \end{aligned}$$

provided $\kappa \ge -\left( \frac{C_2(\alpha ,d)q}{2(d-1)}\right) ^2$. This condition holds for sufficiently large $\alpha >0$. Note here that $\bar{V}_{\kappa }(r)\le \omega _dr^d/d$ when $\kappa \ge 0$, and $\bar{V}_{\kappa }(r)\le \frac{\omega _d}{(2\sqrt{-\kappa })^{d-1}}\exp ((d-1)\sqrt{-\kappa }r)$ when $\kappa <0$. Therefore, we obtain that for $p>1$

$$\begin{aligned} \sup _{x\in M}\mathbb {E}_x\left[ \int _0^{t_0}e^{-\alpha t}(\mathbf{1}_{K_{\ell }^c}f)(X_t)\mathrm{d}t \right]&=\sup _{x\in M} \int _{K_{\ell }^c}S_{\alpha }^{t_0}(x,y)f(y)\mathfrak {m}(\mathrm{d}y)\\&\le \left( \sup _{x\in M}\int _MS_{\alpha }^{t_0}(x,y)^q\mathfrak {m}(\mathrm{d}y) \right) ^{\frac{1}{q}}\left( \int _{K_{\ell }^c}|f|^p\mathrm{d}\mathfrak {m}\right) ^{\frac{1}{p}} , \end{aligned}$$

which tends to 0 as $\ell \rightarrow \infty$. If $p=1$ and $d=1,2$, $S_{\alpha }^{t_0}(x,y)$ is bounded above. This proves the desired assertion. $\square$

The following proposition can not be directly obtained from [19, Lemma 5.1(2)], because the large time upper estimate for heat kernel like [19, (5.1)] can not be obtained for complete smooth Riemmanian manifolds even if its Ricci curvature is non-negative.

Proposition 7.7

Suppose $\inf _{x\in M}V_1(x)>0$. Assume $f\in L^1(M;\mathfrak {m})$ and $|f|\mathrm{d}\mathfrak {m}\in S_K^1(\mathbf{X})$. Then $|f|\mathrm{d}\mathfrak {m}\in S_{K_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$.

Proof

The assumption $\inf _{x\in M}V_1(x)>0$ is used for the short time heat kernel estimates. Fix a sufficiently small $t_0\in ]0,1[$. We already obtain $S_{\alpha }^{t_0}(x,y)\le C_1(\alpha ,d)d(x,y)^{2-d}e^{-C_2(\alpha ,d)d(x,y)}$. We may assume $d\ge 3$, because $S_{\alpha }^{t_0}(x,y)$ is bounded if $d=1,2$. Since $|f|\mathrm{d}\mathfrak {m}\in S_K^1(\mathbf{X})$, for given ${\varepsilon }>0$, there exists a sufficiently small $r>0$ such that

$$\begin{aligned} \sup _{x\in M}\int _{d(x,y)<r}S_{\alpha }^{t_0}(x,y)|f(y)|\mathfrak {m}(\mathrm{d}y)\le \sup _{x\in M}\int _{d(x,y)<r}R_{\alpha }(x,y)|f(y)|\mathfrak {m}(\mathrm{d}y) <{\varepsilon }\end{aligned}$$

by [38, Theorem 3.1] under $d\ge 3$ and $\inf _{x\in M}V_1(x)>0$. Note here that the assumption (A2.3) in [38] is satisfied under $\inf _{x\in M}V_1(x)>0$ with the help of Bishop and Bishop-Gromov inequalities. Then

$$\begin{aligned} \sup _{x\in M}\int _{K_{\ell }^c}S_{\alpha }^{t_0}(x,y)|f(y)|\mathfrak {m}(\mathrm{d}y)&<{\varepsilon }+\sup _{x\in M}\int _{K_{\ell }^c\cap \{d(x,y)\ge r\}}S_{\alpha }^{t_0}(x,y)|f(y)|\mathfrak {m}(\mathrm{d}y)\\&\le {\varepsilon }+C(\alpha ,d, r)\int _{K_{\ell }^c}|f(y)|\mathfrak {m}(\mathrm{d}y), \end{aligned}$$

where $C(\alpha ,d, r):=\sup _{s\ge r}C_1(\alpha ,d)s^{2-d}e^{-C_2(\alpha ,d)s}$. Letting $\ell \rightarrow \infty$ and ${\varepsilon }\rightarrow 0$, we obtain

$$\begin{aligned} \lim _{\ell \rightarrow \infty }\sup _{x\in M}\int _{K_{\ell }^c}S_{\alpha }^{t_0}(x,y)|f(y)|\mathfrak {m}(\mathrm{d}y)=0. \end{aligned}$$

Thus we obtain the assertion. $\square$

Remark 7.8

• 1. It is still open if $|f|\mathrm{d}\mathfrak {m}\in S_{K_{\infty }}^1(\mathbf{X})=S_{CK_{\infty }}^1(\mathbf{X})=S_{NK_{\infty }}^1(\mathbf{X})$ for $f\in L^1(M;\mathfrak {m})$ satisfying $|f|\mathrm{d}\mathfrak {m}\in S_K^1(\mathbf{X})$ when X is transient.

• 2. The assertions of Propositions 7.5 and 7.7 remain valid for RCD${}^*(K,N)$-space $(X,d,\mathfrak {m})$ for $K\in \mathbb {R}$ and $N\in ]1,\infty [$ satisfying $\sup _{x\in X}\mathfrak {m}(B_r(x))\le \bar{V}_{\kappa }^N(r)$ with $\kappa :=K/(N-1)$ and $\inf _{x\in X}\mathfrak {m}(B_1(x))>0$ (see [26] for the definition of RCD${}^*(K,N)$-space). Here $\bar{V}_{\kappa }^N(r):=\omega _N\int _0^r{\mathsf {s}}_{\kappa }^{N-1}(s)\mathrm{d}s$ ($\omega _N:=\frac{\pi ^{N/2}}{\Gamma \left( 1+N/2\right) }$), which is the volume of r-ball in $\mathbb {M}_{\kappa }^N$ provided $N\in \mathbb {N}$.

Example 7.9

(Relativistic symmetric stable process) Take $0<\alpha <2$ and $m\ge 0$. Let $\mathbf{X}=(\Omega ,X_t,\mathbb {P}_x)$ be a Lévy process on $\mathbb {R}^d$ with

$$\begin{aligned} \mathbb {E}_{0}\left[ e^{\sqrt{-1}{\langle } \xi , X_{t} {\rangle }}\right] = \exp \left( -t\left\{ (|\xi |^2+m^{2/\alpha })^{\alpha /2}-m\right\} \right) . \end{aligned}$$

If $m>0$, it is called the relativistic$\alpha$-stable process with mass m (see [12]). In particular, if $\alpha =1$ and $m>0$, it is called the relativistic free Hamiltonian process (see [25])). When $m=0$, $\mathbf{X}$ is nothing but the usual (rotationally) symmetric$\alpha$-stable process. It is known that $\mathbf{X}$ is transient if and only if $d>2$ under $m>0$ or $d>\alpha$ under $m=0$, and X is a doubly Feller conservative process.

Let $(\mathcal {E},\mathcal {F})$ be the Dirichlet form on $L^2(\mathbb {R}^d;\mathrm{d}x)$ associated with $\mathbf{X}$. Using Fourier transform $\hat{f}(x):=\frac{1}{(2\pi )^{d/2}}\int _{\mathbb {R}^d}e^{i{\langle }x,y{\rangle }}f(y)\mathrm{d}y$, it follows from Example 1.4.1 of [22] that

$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {F}:=\displaystyle {\left\{ f\in L^2(\mathbb {R}^d;\mathrm{d}x) : \int _{\mathbb {R}^d} |\hat{f}(\xi )|^2\left( (|\xi |^2+m^{2/\alpha })^{\alpha /2} -m \right) \mathrm{d}\xi <\infty \right\} }, \\ \mathcal {E}(f,g):=\displaystyle {\int _{\mathbb {R}^d} \hat{f}(\xi )\bar{\hat{g}}(\xi )\left( (|\xi |^2+m^{2/\alpha })^{\alpha /2} -m \right) \mathrm{d}\xi \quad \text { for }f,g\in \mathcal {F}. } \end{array}\right. \end{aligned}$$

It is shown in [15] that the corresponding jumping measure J of $(\mathcal {E},\mathcal {F})$ satisfies

$$\begin{aligned} J(\mathrm{d}x\mathrm{d}y)=J_m(x,y)\mathrm{d}x\mathrm{d}y \quad \text { with }~~J_m(x,y)=A(d,-\alpha ) \frac{\Psi (m^{1/\alpha }|x-y|)}{|x-y|^{d+\alpha }}, \end{aligned}$$

where $A(d,-\alpha )=\frac{\alpha 2^{d+\alpha }\Gamma (\frac{d+\alpha }{2})}{2^{d+1}\pi ^{d/2}\Gamma (1-\frac{\alpha }{2})}$, and $\Psi (r):=I(r)/I(0)$ with

$$\begin{aligned} I(r):=\int _0^{\infty }s^{\frac{d+\alpha }{2}-1}e^{-\frac{s}{4}-\frac{r^2}{s}}\mathrm{d}s \end{aligned}$$

is a decreasing function satisfying $\Psi (r)\asymp e^{-r}(1+r^{(d+\alpha -1)/2})$ near $r=\infty$, and $\Psi (r)=1+\Psi ''(0)r^2/2+o(r^4)$ near $r=0$. In particular,

$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {F}=\displaystyle {\left\{ f\in L^2(\mathbb {R}^d;\mathrm{d}x): \int _{\mathbb {R}^d\times \mathbb {R}^d}|f(x)-f(y)|^2J_m(x,y)\mathrm{d}x\mathrm{d}y<\infty \right\} }, \\ \mathcal {E}(f,g): =\displaystyle {\frac{1}{2}\int _{\mathbb {R}^d\times \mathbb {R}^d} (f(x)-f(y))(g(x)-g(y))J_m(x,y)\mathrm{d}x\mathrm{d}y \quad \text { for }f,g\in \mathcal {F}}. \end{array}\right. \end{aligned}$$

For a signed Borel measure $\mu$ on $\mathbb {R}^d$, $\mu$ is said to be of Kato class with respect to $\mathbf{X}$ if and only if

$$\begin{aligned} \lim _{r\rightarrow 0}\sup _{x\in \mathbb {R}^d}\int _{|x-y|<r}\frac{|\mu |(\mathrm{d}y)}{|x-y|^{d-\alpha }}&=0 \quad \text { for }\quad d>\alpha , \\ \lim _{r\rightarrow 0}\sup _{x\in \mathbb {R}^d}\int _{|x-y|<r}(\log |x-y|^{-1})|\mu |(\mathrm{d}y)&=0 \quad \text { for }\quad d=1=\alpha , \\ \sup _{x\in \mathbb {R}^d}\int _{|x-y|\le 1}|\mu |(\mathrm{d}y)&<\infty \quad \text { for }\quad d=1<\alpha . \end{aligned}$$

Denote by ${K}_{d,\alpha }$ the family of non-negative measures of Kato class with respect to X. Then we have ${K}_{d,\alpha }=S_K^1(\mathbf{X})$ by [38, Theorem 3.2, Example 5.1]. It is shown in [37, Theorem 2.1] that for any $f\in L^p(\mathbb {R}^d;\mathrm{d}x)$, $|f(x)|\mathrm{d}x\in S_K^1(\mathbf{X})$ provided $p>d/\alpha$ (resp. $p\ge 1$) for $d\ge \alpha$ (resp. $d<\alpha$). More strongly, under $m=0$, it is shown in [5, Lemma 5.1] that for any $f\in L^p(\mathbb {R}^d;\mathrm{d}x)$, $|f(x)|\mathrm{d}x\in S_{CK_{\infty }}^1(\mathbf{X}^{(1)})$ provided $p>d/\alpha$ (resp. $p\ge 1$) for $d\ge \alpha$ (resp. $d<\alpha$).

Let $p_t(x,y)$ be the heat kernel of X. The following global heat kernel estimates were proved in [11, Theorem 2.1]: There exists $C_1,C_2>0$ such that

$$\begin{aligned} C_2^{-1}\Phi ^m_{1/C_1}(t,x,y)\le p_t(x,y)\le C_2\Phi ^m_{C_1}(t,x,y), \end{aligned}$$

(7.3)

where

$$\begin{aligned}&\Phi ^m_C(t,x,y)\\&\quad :=\left\{ \begin{array}{lc}t^{ -d/\alpha } \wedge tJ_m(x, y), &{} t\in ]0,1/m], \\ m^{d/\alpha -d/2} t^{-d/2} \exp \left( -C^{-1}\left( m^{1/\alpha }|x - y| \wedge m^{2/\alpha -1}\frac{|x-y|^2}{t}\right) \right) , &{} t\in ]1/m,\infty [.\end{array}\right. \end{aligned}$$

It is shown in [13, Theorem 1.2 and Example 2.4] or [9, 10, Theorem 1.2] that $p_t(x,y)$ is jointly continuous in $(t,x,y)\in ]0,\infty [\times \mathbb {R}^d\times \mathbb {R}^d$.

The following proposition extends [5, Lemma 5.1] for general $m\ge 0$:

Proposition 7.10

Let $0<\alpha <2$ and $\mathbf{X}$ be a relativistic symmetric $\alpha$-stable process on $\mathbb {R}^d$.

• 1. Assume $p>\frac{d}{\alpha }$ (resp. $p\ge 1$) if $d\ge \alpha$ (resp. $d<\alpha$). Let $f\in L^p(\mathbb {R}^d;\mathrm{d}x)$. Then $|f(x)|\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

• 2. Assume $p>\frac{d}{\alpha }$ (resp. $p\ge 1$) if $d\ge \alpha$ (resp. $d<\alpha$). For $u\in \mathcal {F}_{\mathrm{loc}}\cap C(\mathbb {R}^d)$, $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$ if $f_u(x):=\int _{\mathbb {R}^d}(u(x)-u(y))^2J_m(x,y)\mathrm{d}y$ is in $L^p(\mathbb {R}^d;\mathrm{d}x)$. In particular, if $u\in C_c^1(\mathbb {R}^d)$, then $\mu _{{\langle }u{\rangle }}\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

• 3. If F is a bounded symmetric function on $\mathbb {R}^d\times \mathbb {R}^d$ with

  $$\begin{aligned} |F(x,y)|\le c|x-y|^{\gamma }\quad \text { for }x,y\in \mathbb {R}^d\quad \text { and } F(x,y)=0\quad \text { for }(x,y)\in \mathbb {R}^d\times K^c, \end{aligned}$$

  where K is a compact subset of $\mathbb {R}^d$, c and $\gamma$ are two positive constants such that $\gamma >\alpha$, then for $f(x):=\int _{\mathbb {R}^d}|F(x,y)|J_m(x,y)\mathrm{d}y$, $|f(x)|\mathrm{d}x\in S_{NK_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{K_{\infty }}^1(\mathbf{X}^{(1)})$.

Proof

(1): Take $t_0<\frac{1}{m}\wedge 1$ so small and set $S_1^{t_0}(x,y):=\int _0^{t_0}e^{-t}p_t(x,y)\mathrm{d}t$. In view of the proof of [19, Lemma 2.3], it suffices to prove

$$\begin{aligned} c:=\sup _{x\in \mathbb {R}^d}\int _{\mathbb {R}^d}S_1^{t_0}(x,y)^q\mathrm{d}y<\infty , \end{aligned}$$

(7.4)

for $q:=p/(p-1)\in ]1,\infty [$ under $p>\frac{d}{\alpha }$, and $\sup _{x,y\in \mathbb {R}^d}S_1^{t_0}(x,y)<\infty$ under $p=1$ with $d=1<\alpha$, because

$$\begin{aligned} \sup _{x\in \mathbb {R}^d}\int _{B\cup K^c}S_1^{t_0}(x,y)|f(y)|\mathrm{d}y&\le \left( \sup _{x\in \mathbb {R}^d}\int _{\mathbb {R}^d}S_1^{t_0}(x,y)^q\mathrm{d}y \right) ^{\frac{1}{q}}\left( \int _{B\cup K^c}|f(y)|^p\mathrm{d}y \right) ^{\frac{1}{p}}\\&\le c\left( \int _{B\cup K^c}|f(y)|^p\mathrm{d}y \right) ^{\frac{1}{p}}. \end{aligned}$$

For this, we show

$$\begin{aligned}&\sup _{x\in \mathbb {R}^d}\int _{\{|x-y|^{\alpha }\le t_0\}}S_1^{t_0}(x,y)^q\mathrm{d}y<\infty , \end{aligned}$$

(7.5)

$$\begin{aligned}&\sup _{x\in \mathbb {R}^d}\int _{\{|x-y|^{\alpha }>t_0\}}S_1^{t_0}(x,y)^q\mathrm{d}y<\infty . \end{aligned}$$

(7.6)

For $|x-y|^{\alpha }\le t_0$, we have from (7.3)

$$\begin{aligned} C_2^{-1}S_1^{t_0}(x,y)&\le \int _0^{|x-y|^{\alpha }}e^{-t}\left( t^{-d/\alpha }\wedge tJ_m(x,y)\right) \mathrm{d}t\\&\quad +\int _{|x-y|^{\alpha }}^{t_0}e^{-t}\left( t^{-d/\alpha }\wedge tJ_m(x,y)\right) \mathrm{d}t\\&\le c_1\frac{e^{-|x-y|^{\alpha }}}{|x-y|^{d-\alpha }} +\mathrm{II}, \end{aligned}$$

where

$$\begin{aligned} \mathrm{II}:=\int _{|x-y|^{\alpha }}^{1/m}e^{-t}t^{-d/\alpha }\mathrm{d}t\le \left\{ \begin{array}{cc}\frac{\alpha }{d-\alpha }\cdot \frac{e^{-|x-y|^{\alpha }}}{|x-y|^{d-\alpha }} &{} d>\alpha , \\ e^{-|x-y|^{\alpha }} \left( -\log m|x-y|^{\alpha } \right) &{} d=1=\alpha , \\ e^{-|x-y|^{\alpha }}\cdot \frac{\alpha }{\alpha -d}\left( m^{\frac{d-\alpha }{\alpha }}-|x-y|^{\alpha -d} \right) &{} d=1<\alpha . \end{array}\right. \end{aligned}$$

From these estimates, we can easily deduce (7.5).

For $|x-y|^{\alpha }> t_0$, we have from (7.3)

$$\begin{aligned} C_2^{-1}S_1^{t_0}(x,y)&\le \int _0^{\frac{1}{m}}e^{-t}\left( t^{-d/\alpha }\wedge tJ_m(x,y)\right) \mathrm{d}t \le \frac{1}{|x-y|^{d+\alpha }}\int _0^{\frac{1}{m}} te^{-t}\mathrm{d}t. \end{aligned}$$

From this estimate, we can easily deduce (7.6). When $p=1$ under $d=1<\alpha$, we easily confirm the boundedness of $S_1^{t_0}(x,y)$.

(2): The first statement is clear from (2). Note that $C_c^1(\mathbb {R}^d)\subset \mathcal {F}$. We next show that for $u\in C_c^1(\mathbb {R}^d)$, $f_u\in L^p(\mathbb {R}^d;\mathrm{d}x)$ for every $p\ge 1$. Clearly,

$$\begin{aligned} f_u(x)\le \int _{\{y\in \mathbb {R}^d:|x-y|<1\}}\frac{\Vert \nabla u\Vert _{\infty }^2}{|x-y|^{d+\alpha -2}}\mathrm{d}y+\int _{\{y\in \mathbb {R}^d:|x-y|\ge 1\}}\frac{2\Vert u\Vert _{\infty }^2}{|x-y|^{d+\alpha }}\mathrm{d}y \end{aligned}$$

and so $f_u$ is bounded above by $\omega _d\left( \frac{\Vert \nabla u\Vert _{\infty }^2}{2-\alpha }+ \frac{2\Vert u\Vert _{\infty }^2}{\alpha }\right)$. Here $\omega _d$ is the area of the $(d-1)$-dimensional unit sphere $\mathbb {S}^{d-1}$ in $\mathbb {R}^d$. Let K be the support of u. Then for $x\in K^c$,

$$\begin{aligned} f_u(x)\le \int _Ku(y)^2\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y\le \Vert u\Vert _{\infty }^2 \int _K\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y. \end{aligned}$$

Thus for some $C>1$, $|f_u|$ is bounded above by C and estimated by $C\int _K\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y$ on $K^c$. Taking a relatively compact open set G containing K, we see that for any $p\ge 1$

$$\begin{aligned} \int _{\mathbb {R}^d}|f_u(x)|^p\mathrm{d}x&\le C^p\left( |G|+\int _{G^c}\left| \int _K\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y\right| ^p\mathrm{d}x\right) \\&\le C^p\left( |G|+|K|^{p-1}\int _{G^c}\int _K\frac{1}{|x-y|^{p(d+\alpha )}}\mathrm{d}y\mathrm{d}x\right) \\&= C^p\left( |G|+|K|^{p-1}\int _{K}\int _{G^c}\frac{1}{|x-y|^{p(d+\alpha )}}\mathrm{d}x\mathrm{d}y\right) \\&\le C^p\left( |G|+|K|^{p-1}\frac{\omega _d}{p(d+\alpha )-d} \int _{K}\frac{1}{d(y,G^c)^{p(d+\alpha )-d}}\mathrm{d}y\right) \\&<\infty . \end{aligned}$$

(3): By assumption,

$$\begin{aligned} |f(x)|\le \int _{\{y\in K:|y-x|<1\}}\frac{c}{|x-y|^{d+\alpha -\gamma }}\mathrm{d}y+\int _{\{y\in K:|y-x|\ge 1\}}\frac{\Vert F\Vert _{\infty }}{|x-y|^{d+\alpha }}\mathrm{d}y \end{aligned}$$

is bounded above by $\frac{c\omega _d}{\gamma -\alpha }+\Vert F\Vert _{\infty }|K|$ from $\gamma >\alpha$ and estimated by $(c\vee \Vert F\Vert _{\infty })\int _K\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y$. Thus $|f(x)|\le C\left( 1\wedge \int _K\frac{1}{|x-y|^{d+\alpha }}\mathrm{d}y \right)$ for some $C>1$. Then one can confirm the p-th integrability of f for any $p\ge 1$ as in the proof of (2). $\square$

Applying [19, Lemma 5.1(2)], it can be shown that for $f\in L^1(\mathbb {R}^d;\mathrm{d}x)$ satisfying $|f(x)|\mathrm{d}x\in S_K^1(\mathbf{X})$, we have $|f(x)|\mathrm{d}x\in S_{K_{\infty }}^1(\mathbf{X})=S_{CK_{\infty }}^1(\mathbf{X})=S_{NK_{\infty }}^1(\mathbf{X})$ provided X is transient, that is, $d>\alpha$ (resp. $d\ge 3$) holds for $m=0$ (resp. $m>0$) (for $m>0$ see [19, Example 6.2 ]). The following Proposition can be similarly proved as for Proposition 7.7. We omit its proof.

Proposition 7.11

Assume $f\in L^1(\mathbb {R}^d;\mathrm{d}x)$ and $|f(x)|\mathrm{d}x\in S_K^1(\mathbf{X})$. Then $|f(x)|\mathrm{d}x\in S_{K_{\infty }}^1(\mathbf{X}^{(1)})=S_{CK_{\infty }}^1(\mathbf{X}^{(1)})=S_{NK_{\infty }}^1(\mathbf{X}^{(1)})$.