1 Introduction

Renewable energy is a long-term and potentially sustainable strategy for reducing green house gas emissions significantly. Due to environmental concerns, economic expansion, and the energy crisis problem, incorporating renewable energy sources into the power system is now getting accelerated. The transition from centralized to distributed generation (DG) has enhanced the desirability and suitability of micro-grids for integrating renewable energy sources [1]. Micro-grid is a small-scale integrated energy system with multifarious distribution configuration consisting of several interconnected distributed energy resources and loads situated within a specific local area and operating within a well-defined electrical boundary [2].

Microgrids may be viewed as a more developed form of distributed generation system with minimal influence from the stochastically distributed generations through efficient management of the storage systems and dispatched loads [3]. Generally, a microgrid operates in grid-connected mode or autonomous mode. However, due to their lower equivalent inertia compared to the main grid, the management and controls of autonomous microgrids are often more complex than those of grid-connected ones. Consequently, even moderate or minor disruptions in the power supply can cause issues in power quality and stability, specifically, a deterioration in the quality of the voltage and frequency [4]. Incorporating energy storage systems into microgrids can maintain the instantaneous power balance and enhance the microgrid’s dynamic performance, which is crucial in is-land operation mode. The integration of multiple energy storage devices, such as batteries and flywheel, has the potential to enhance the stability of microgrids. However, this integration also introduces increased complexity of control issues.

Frequency regulation is a significant challenge in autonomous microgrids due to the low inertia of the system and the large share of intermittent renewable sources [5]. Renewable energy sources and energy storage systems must co-ordinate in autonomous microgrids to limit the frequency deviations by minimizing the mismatch between generation and demand [6,7,8]. When there is an imbalance between generated power and demand power, different control strategies are needed to maintain the frequency stability of the system [9]. To stabilize the system, primary droop controllers are widely employed. Still, frequency deviations from the nominal value are observed in the steady state. Consequently, a secondary control strategy is employed to reach optimal frequency synchronization. Generally, the primary droop and secondary frequency control are called automatic generation control (AGC). In generally, it is also known as load frequency control (LFC). This paper mainly focuses on the automatic generation control of micro-grid supported by renewable energy and storage systems.

Demand response, grid integration of electric vehicles, smart homes, presence of noise on the sensor, etc. increase the unpredictability in the power system operation [10]. Huge integration of renewable energy sources increases the uncertainty of the system due to their intermittent in nature. During the parameter measurement of the microgrid, the value of internal parameters of the system may deviate in a small range from their nominal values. The presence of parameter uncertainties and load disruptions introduces unpredictability and uncertainty into the power system [11]. Due to the aforementioned reasons, the dynamics of the power system varies with time, and an accurate simulation model cannot always be found. Conventional controllers such as Proportional-Integral-Derivative (PID), Linear Matrix Inequality (LMI), Sliding Mode Control (SMC), and Model Predictive Control (MPC) are developed using model-based techniques to obtain the optimal control performance. These model-based control techniques guarantee optimal the performance when applied to a precise system model with no uncertainty. However, the interest of this paper is to design of controller for unknown system dynamics.

Reinforcement learning (RL) and adaptive dynamic programming (ADP) can solve the optimal control problem from data without having the knowledge of the system dynamics [12,13,14]. RL and ADP fill the gap between conventional optimal control and adaptive control techniques. The optimal solution is obtained by learning online the solution to the Hamilton–Jacobi–Bellman (HJB) equation [15]. The HJB equation reduces to an algebraic Recati equation (ARE) for linear systems. RL adopts the temporal difference (TD) approach. TD method can learn directly from the raw experience without having a model of the environment dynamics. TD method implements mainly two steps [15, 16]: (1) to solve the temporal difference equation (known as policy evaluation), (2) to find the optimal control strategy (known as policy improvement). These steps are analogous in solving Hamilton–Jacobi–Bellman (HJB) equation for the optimal control problem. Policy and value iteration methods determine the sequence in which the TD equations can be solved, and the corresponding optimal policies can be obtained.

In recent years, extensive research on RL-based AGCs has been conducted, including DQN-based AGC [17], DDQN based AGC [18], DDPG-based AGC [19, 20], SAC-based AGC [21], and others. However, these controllers often require multiple neural networks for designing the control strategy. Each algorithm presents its unique advantages; however, increased use of neural networks increases the complexity of the design. Considering the challenges associated with design complexity and popularity of PID controllers for AGC, authors of [22] propose RL-based adaptive PID for AGC. The above discussion reveals that adaptive control strategies to reduce design complexity have room for AGC. In [23, 24], the authors present an integral reinforcement learning (IRL) algorithm-based optimum control method for automatic generation control in power systems. Papers [23] present two different implementations of online IRL controllers, each employing separate neural networks for actor and critic networks, it lacks discussion on the neural network configurations, raising concerns about the complexity of the controller design. Conversely, the recursive least square-based IRL [25] approach offers a solution to the optimal control problem without relying on neural networks. The authors in [23] utilized the gradient method to update neural network parameters by computing the cost function gradient for each parameter. However, using the recursive least square method, the parameters of the IRL-based optimal controller can be evaluated directly, eliminating the need for a gradient descent approach [25]. This approach effectively eradicates suboptimal control policies arising from local optima.

Table 1 Comparison of recent research on energy management
Full size table

The integration of renewable energy sources poses a significant challenge to traditional power system control methods, necessitating innovative approaches to ensure efficient and reliable operation. While the integral reinforcement learning (IRL) algorithm-based optimum control method proposed by [23] and [24] shows promise in addressing uncertainties and unknown dynamics in power systems, its efficacy in the context of renewable energy sources remains largely unexplored. Furthermore, IRL-based AGC needs to investigate the impact of uncertainty and unpredictability resulting from parameter uncertainty and external disturbances such as renewable integration and electric vehicle (EV) integration. Moreover, it is crucial to emphasize that the application of IRL controller for AGC of microgrids is still limited, and further research is needed in this area. This is because the IRL-based optimal controller offers notable advantages: (1) similar to value-based model-free RL algorithms, it does not rely on the discretization of action and state spaces, and (2) akin to deep RL algorithms, it avoids the necessity of training multiple neural networks. The proposed work can be viewed as an energy management problem. A comparison table of the proposed method with traditional methods is provided in Table 1.

The main contributions of the paper are as follows:

  • This paper investigates the automatic generation control of an isolated microgrid. The investigation focuses on the impact of an EV aggregator, parameter uncertainty, and the uncertainty associated with renewable energy sources on the frequency stability of the system.

  • This paper introduces an adaptive optimal control technique for secondary frequency control using the integral reinforcement learning algorithm. Like other model-free RL algorithms, it can learn the system without prior knowledge of the system dynamics. During pre-learning, the recursive least square (RLS) method is implemented to estimate the controller parameters.

  • For comparison purposes, the effectiveness of the IRL controller is compared with the performance of deep Q-learning (DQN) techniques and PI controller.

The rest parts of the paper are organized as follows. Section 2 describes the dynamic model of the system components. In Sect. 3, the mathematical formulation of the proposed control strategy is provided, followed by Sect. 4. Section 4 presents the simulation results. Finally, Sect. 5 concludes the paper.

2 Dynamic model of autonomous microgrid understudy

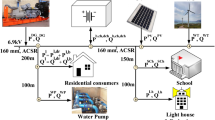
The proposed microgrid is comprised of various system components, including photovoltaic (PV) and wind power generation, a diesel engine system, an electric vehicle (EV) aggregator, and energy storage systems such as flywheel energy storage systems (FESS) and battery energy storage systems (BESS). This section presents the dynamic model of these components and the microgrid’s state-space representation. Figure 1 illustrates the schematic diagram of the system.

Fig. 1
figure 1

General schematic of proposed micro-grid

Full size image

2.1 Diesel generator system

Diesel generators can provide reliable and stable power to remote areas. The dynamic model of the diesel generator can be expressed as follows [35]:

$$\begin{aligned} \begin{aligned}&\Delta {\dot{X}}_{g}(t)=-\frac{1}{T_{g}}\left( \Delta X_{g}(t)+\frac{1}{R} \Delta f(t)-\Delta I(t)-u(t)\right) \\&\Delta {\dot{P}}_{g}(t)=-\frac{1}{T_{t}}\left( \Delta P_{g}(t)-\Delta X_{g}(t)\right) \\&\Delta {\dot{f}} (t)=-\frac{1}{T_{p}}\left( \Delta f(t)-K_{p} \Delta P_{g}(t)+K_{p} \Delta P_{d}(t)\right) \\&\Delta {\dot{I}}(t)=K_I \Delta f(t) \end{aligned} \end{aligned}$$
(1)

where \(\Delta X_{g}(t)\), \(\Delta P_{g}(t)\), \(\Delta f(t)\), \(\Delta I(t)\) and \(\Delta P_d\) denote deviation in governor position, deviation in generator power, deviation in frequency, incremental change in integral control and change in load disturbance, respectively.

2.2 Renewable energy sources

The renewable energies integrated to the micro-grid are PV and wind power. The first-order dynamic equations of PV and wind are given in Eqs. 2 and 3, respectively [40,41,42].

$$\begin{aligned} \Delta {\dot{P}}_{\textrm{PV}}(t)=-\frac{1}{T_{\textrm{PV}}} \Delta P_{\textrm{PV}}(t)+\frac{1}{T_{\textrm{PV}}} \Delta P_{\textrm{Solar}}(t) \end{aligned}$$
(2)
$$\begin{aligned} \Delta {\dot{P}}_{\textrm{W}}(t)=-\frac{1}{T_{\textrm{WT}}} \Delta P_{\textrm{W}}(t)+\frac{1}{T_{\textrm{WT}}} \Delta P_{\textrm{Wind}}(t) \end{aligned}$$
(3)

2.3 Storage systems

In the proposed micro-grid energy storage systems, battery energy storage system and flywheel energy storage systems (BESS and FESS) are used. The capacity of the BESS should reach a certain scale to significantly influence the system frequency [36]. However, the capital cost of a large BESS is relatively high. To get a large-scale BESS, aggregated multiple small-scale BESS is implemented in [37] for LFC. In this study, multiple small-scale BESS are aggregated for primary frequency control of the micro-grid. The first-order dynamic equations of ith BESS and FESS are given in Eqs. 4, and 5, respectively [38, 39]. \(\alpha _i\) represents the participation factor of each BESS and \(i=\)1, 2, 3.

$$\begin{aligned} \Delta {\dot{P}}_{\textrm{BESSi}}(t)=-\frac{1}{T_{\textrm{BESSi}}} \Delta P_{\textrm{BESSi}}(t)+\frac{\alpha _i}{T_{\textrm{BESSi}}} \Delta f(t) \end{aligned}$$
(4)
$$\begin{aligned} \Delta {\dot{P}}_{\textrm{FESS}}(t)=-\frac{1}{T_{\textrm{FESS}}} \Delta P_{\textrm{FESS}}(t)+\frac{1}{T_{\textrm{FESS}}}\Delta f(t) \end{aligned}$$
(5)

2.4 EV Aggregrator

Assuming that all EVs participating in the EV aggregator have same time constant (\(T_e\)), the first-order dynamic model of the EV aggregator is expressed in Eq. 6 [43].

$$\begin{aligned} \Delta {\dot{P}}_{\textrm{e}}(t)=-\frac{1}{T_{\textrm{e}}} \Delta P_{\textrm{e}}(t)+\frac{K_{\textrm{e}}}{T_{\textrm{e}}} \alpha P_{\textrm{ce}}(t) \end{aligned}$$
(6)

where \(K_e=\sum _{i=1}^N K_{{ei}} / N, i=1, \ldots , N\). \(K_{ei}\) is the gain of the ith EV. \(\alpha \) is the the participation factor of EV aggregator. N is the total number of EVs. The gain \((K_e)\) depends on the SOC of battery. An EV can take part in LFC with SOC controllable mode or SOC idle mode. In SOC idle mode, an EV can absorb or discharge power without considering its battery SOC. The gain (\(K_{ei}\)) of the ith EV is considered as \({\bar{K}}_{e}=1\) in SOC idle mode. When SOC is considered ,the gain of ith EV can be modified as \(K_{\textrm{ei}}={\bar{K}}_e-{\bar{K}}_e g_i(t)\), where

$$\begin{aligned} g_i(t)=\left( \frac{{SOC}_i-{SOC}_{\text{ low } (\textrm{high}), i}}{{SOC}_{\max (\min ), i}-{SOC}_{\text{ low } (\textrm{high}), i}}\right) ^{2} \end{aligned}$$
(7)

When the \({SOC}_i\) \(\ge \) \({SOC}_{\text{ high } ,i}\), the ith EV will only deliver power with \(K_{{ei}}={\bar{K}}_e\). When the \({SOC}_i\) \(\le \) \({SOC}_{\text{ low } ,i}\), the ith EV will only absorb power with \(K_{{ei}}=0\). For other cases, \(K_{ei}\) is calculated using Eq. 7.

Assume that among N EVs, \(N_1\) and \(N_{2}\) (\(=N-N_{1}\)) are participating in LFC with SOC idle mode and SOC controllable mode, respectively. Then the gain of the aggregated EVs can be written as

$$\begin{aligned} \begin{aligned} K_e&=\sum _{i=1}^N K_{\textrm{ei}} / N\\&=\frac{N_1}{N} {\bar{K}}_e+\frac{1}{N} {\bar{K}}_e\left( N_2-\sum _{i=N_1+1}^N g_i(t)\right) \\&={\bar{K}}_e +\Delta K_e\\&={\bar{K}}_e -\eta _2 g_0(t) {\bar{K}}_e \\&={\bar{K}}_e(1-\eta g(t)) \end{aligned} \nonumber \\ \end{aligned}$$
(8)

where \(\eta _2\) is \(N_2/N\), \(\eta =max(\eta _2)\), \(g_0(t)=\) \(\sum _{i=N_1+1}^N\) \(g_i(t)/N_2\) and \(g(t)=(\eta _2/\eta )g_0(t)\). N, \(N_1\) and \(N_2\) are varying with time. Figure 2a–c represents the number of plug-in EVs participating in LFC. The maximum and minimum numbers for the total number of available EVs (N) have been set at 650 and 900, respectively. The value of N, depicted in Fig. 2a, is determined randomly between the minimum and maximum values. Figure 2b presents the number of vehicles in idle mode. Similarly, Fig. 2c depicts the number of EVs in SOC controllable mode and it is set in such way that the \(\eta _2\) value should be less than given \(\eta \). Given \(\eta \) is 0.5, Fig. 2d shows \(\eta \) and \(\eta _2=N_2/N\). Based on these variables, \(g_0(t)\) and g(t) of Eq. 8 are shown in Fig. 3a and b. The time-dependent gain (\(K_e\)) is illustrated in Fig. 3c.

Fig. 2
figure 2

EV aggregator parameter a total number of EVs, b number of EVs in Idle mode, c number of EVs in SOC controllable mode, and, d \(\eta _2 \) and its maximum value

Full size image
Fig. 3
figure 3

EV aggregator parameter: a \(g_0\), b g, and c \(K_e\)

Full size image

Remark

In [43], the total number of EVs of the aggregator is experiencing rapid fluctuations with time between the minimum and maximum values. However, maintaining such variation during all times may not be feasible in practice. Therefore, in this paper, the total number of EVs is adjusted slowly over time and fluctuates within the minimum and maximum values. A wide range of variations in total number of EVs, including slow and fast variations and constant fluctuations, are considered.

The complete state space model of the proposed micro-grid is

$$\begin{aligned} {\dot{x}}=[A_1\vdots A_2] x+B u+\Gamma \Delta P_{d} \end{aligned}$$
(9)

where \( x=[\Delta X_{g }, \Delta P_{t }, \Delta f, \Delta I, \Delta P_{PV }, \Delta P_{W }, \Delta P_{BESS1 },\) \(\Delta P_{BESS2}, \Delta P_{BESS3 }, \Delta P_{FESS }, \Delta P_{e} ]^T\). u is the output of the controller. \(\Delta P_{d}=[\Delta P_{Solar }, \Delta P_{Wind }]^T\). \(A_1\), \(A_2\), B, and \(\Gamma \) are as follows:

\(A_1\)=\(\begin{bmatrix} -\frac{1}{ T_{g} } & 0 & \frac{-1}{R{Tg}}& \frac{-1}{T_{g}}& 0& 0\\ \frac{1}{T_{t}} & \frac{-1}{T_{t}} & 0 & 0 & 0 & 0 \\ 0 & \frac{K_{P}}{T_{P}} & \frac{-1}{T_{p}} & 0 & \frac{K_{P}}{T_{P}} & \frac{K_{P}}{T_{P}} \\ 0 & 0 & 0 & K_I & 0 & 0 \\ 0 & 0 & 0 & 0 & -\frac{1}{T_{PV}} & 0 \\ 0 & 0 & 0 & 0 & 0 & -\frac{1}{T_{WT}}\\ 0& 0& \frac{\alpha _1}{T_{BESS1}}& 0& 0& 0\\ 0& 0& \frac{\alpha _2}{T_{BESS1}}& 0& 0& 0\\ 0& 0& \frac{\alpha _3}{T_{BESS1}}& 0& 0& 0\\ 0& 0& \frac{1}{T_{FESS}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ \end{bmatrix}\)

\(A_2\)=\(\begin{bmatrix} 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \frac{K_{P}}{T_{P}}& \frac{K_{P}}{T_{P}}& \frac{K_{P}}{T_{P}}& \frac{K_{P}}{T_{P}}& \frac{K_{P}}{T_{P}}\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ -\frac{1}{T_{BESS1}}& 0& 0& 0& 0\\ 0& -\frac{1}{T_{BESS2}}& 0& 0& 0\\ 0& 0& -\frac{1}{T_{BESS3}}& 0& 0\\ 0& 0& 0& -\frac{1}{T_{FESS}}& 0\\ 0& 0& 0& 0& -\frac{1}{T_{e}}\\ \end{bmatrix}\)

figure b
figure c

This paper aims to design a controller that can effectively determine the u value, as per Eq. 9, for the above system.

Fig. 4
figure 4

Pictorial view of training process of DQN at time step t

Full size image

3 Adaptive controller design

3.1 IRL controller

In this section, an adaptive control strategy based on the IRL algorithm is presented. The IRL is an online learning technique of internal system dynamics [25]. In this article, the IRL algorithm is used for secondary frequency control. Consider the linear continuous-time system

$$\begin{aligned} {\dot{x}}=A x+B u \end{aligned}$$
(10)

with the Q-value function

$$\begin{aligned} \begin{aligned} Q\left( x(t),u(t)\right)&=\int _t^{\infty } J(x(t),u(t)) d \tau \\&=\int _t^{t+T} J(x(t),u(t)) d \tau \\&\quad +Q\left( x(t+T),u(t+T)\right) \end{aligned} \end{aligned}$$
(11)

where \(x \in R^n\) is the system state, \(u\in R^m\) is the control input, \(A \in {\mathbb {R}}^{n \times n}\) and \( B \in {\mathbb {R}}^{n \times m}\). J(x, u) is the quadratic cost function. It is assumed that (A, B) is controllable. The cost function J(x, u) is defined as \(J(x, u)=x^T {\textbf {Q}} x+u^T {\textbf {R}} u. ~{\textbf {Q}}={\textbf {Q}}^T \ge 0 \in {\mathbb {R}}^{n \times n}\) and \({\textbf {R}}={\textbf {R}}^T>0 \in {\mathbb {R}}^{m \times m}\) are time-invariant weight matrices. By the Belllman’s optimal principle [15], the Kvalue can be found as

$$\begin{aligned} K={\textbf {R}}^{-1} B^T P \end{aligned}$$
(12)

where P is the unique positive definite solution of the algebric Reccati equation(ARE)

$$\begin{aligned} A^T P+P A+{\textbf {Q}}-P B {\textbf {R}}^{-1} B^T P=0. \end{aligned}$$
(13)

The optimal continuous time Q-value function can be presented in quadratic form [44] as shown in Eq. 14.

$$\begin{aligned} \begin{aligned} Q^*(x, u)&=\left[ \begin{array}{ll} x^T&u^T \end{array}\right] \left[ S^*\right] \left[ \begin{array}{l} x \\ u \end{array}\right] \\&=\left[ \begin{array}{ll} x^T&u^T \end{array}\right] \left[ \begin{array}{ll} S_{11}^* & S_{12}^* \\ S_{21}^* & S_{22}^* \end{array}\right] \left[ \begin{array}{l} x \\ u \end{array}\right] \\&=\left[ \begin{array}{ll} x^T&u^T \end{array}\right] \left[ \begin{array}{cc} A^T P^*+P^* A+{\textbf {Q}} & P^* B \\ B^T P^* & {\textbf {R}} \end{array}\right] \left[ \begin{array}{l} x \\ u \end{array}\right] \end{aligned} \nonumber \\ \end{aligned}$$
(14)

It can be noticed that the \(S^*\) is associated with \(P^*\) in ARE. By minimizing \(Q^*(x,u)\) with respect to u, the optimal solution \(u^*\) can be found as follows:

$$\begin{aligned} \begin{aligned} u^*&=-K^* x \\&=-\left( S_{22}^*\right) ^{-1}\left( S_{12}^*\right) ^T x \end{aligned} \end{aligned}$$
(15)

Problem Statement: Solving the value function (Eq. 14) yields the optimal policy (u); however, the system matrix B is involved in this case, and it is unknown. The final objective is to implement the online adaptive IRL algorithm to get the optimal policy \(u^*\) (as per Eq. 15) without involving matrix B.

Pseudo code of pre-learning of IRL algorithm:

  1. 1.

    Initialize Time step (t), Step size (T), K(t), W(t), \( W(t - T )\) and x(t)

  2. 2.

    Calculate \(u(t) = - K(t)x(t)\). Apply the current policy to the system and observe the next state \(x(t+T )\). Then calculate \(u(t + T ) = - K(t)x(t + T )\). Collect dataset (x(t), \(x(t + T )\), u(t), \(u(t + T )\) and compute \(\phi (z(t))\), \(\phi (z(t + T )\))

  3. 3.

    Define the value function in parametric form as \(Q(x(t), u(t)) =W^T\phi (z(t))\), where W is weight matrix, \( \phi (z(t)) \) is the quadratic polynomial basis set, z(t) is the vector \([x(t)^T~u(t)^T]\). \(\phi (z(t))=z(t) \bigotimes z(t)\) and \(\bigotimes \) represents the Kronecker product [45]. The number of elements of W is \(n(n+1)/2\), where n represents the number of elements in z(t).

  4. 4.

    Calculate the weight matrix as follows

    $$\begin{aligned} W(t+T)^T=\Delta \phi ^{-1} \int _t^{t+T} J(x, u) d \tau \end{aligned}$$
    (16)

    where \(\Delta \phi =\phi (z(t))-\phi (z(t+T))\). The inverse of \(\Delta \phi \) cannot be found directly as it is a vector. In this study, the inverse is determined using the recursive least square (RLS) method [46]. So, \(\Delta \phi ^{-1}=\Delta \phi ^T\left( \Delta \phi \Delta \phi ^T\right) ^{-1}\).

  5. 5.

    Unpack the vector \(W(t+T)\) into matrix S (shown in Eq. 14) and find \(K=\left( S_{22}\right) ^{-1}\left( S_{12}\right) ^T\).

  6. 6.

    Check condition \(||W (t+T) - W (t )|| < \zeta \) (Tolerance). If not so, set \(W(t)\leftarrow W(t+T)\), \(t\leftarrow t+T\). Go to Step 2. Else Go to Step 7.

  7. 7.

    Get the final K.

  8. 8.

    STOP

3.2 Deep Q-learning Controller

The DQN [47] uses two networks, namely the current (Q) and target (\(Q^-\)) networks. These networks are the same in structure. \(\theta \) and \(\theta ^-\) are the parameter of the current network and target network, respectively. The current network selects the action (\({\arg \max }\hspace{0.1cm} Q(s,u;\theta )\)) associated with the highest Q value. The target network evaluates the Q value (\(Q(s_t^\prime , u_t^\prime \)) of the target state (\(s_t^\prime \)). In this paper, these networks are three-layer backpropagation neural networks, with an input layer of four dimensions and an output layer of seven.

DQN employs a replay buffer to collect the experiences at each time step of pre-learning. At each time step (t), a mini-batch of samples is drawn from the buffer and passed through the current neural network. The optimal action, obtained from greedy policy, is then executed in the environment, leading to the observation of next state (\(s^\prime \)) and the calculation of reward (\(R_{l_t}\)). These experiences are stored as tuples containing the current state, action taken, reward obtained, and resulting next state. For example, the tuple for the ith sample is (\(s_i,u_i,R_{l_i},s_{i}^\prime \)). Subsequently, the immediate next state is provided to the target network to determine the maximum \(Q^-\)-value. The pictorial view of pre-learning of DQN at time step (t) is shown in Fig. 4. After pre-learning the current network is used as controller.

The loss function of ith sample of the mini-batch is expressed in Eq. 17.

$$\begin{aligned} L_i\left( \theta \right) =\left[ \left( R_{l_i}+\gamma \max Q_i^-\left( s^{\prime }, u^{\prime }; \theta ^{-}\right) -Q_i\left( s, u; \theta \right) \right) ^2\right] \nonumber \\ \end{aligned}$$
(17)

Here, \(R_l\) and \(\gamma \) are reward function and discount factor, respectively. The reward (R) is chosen using Eq. 10.

$$\begin{aligned} R_l= -10 \hspace{0.2cm} \Delta f^2 \end{aligned}$$
(18)

The parameters \(\theta \) are updated using Eq. 19, where N is the number of samples in a mini-batch.

$$\begin{aligned} \theta _{t+1} =\theta _t+\alpha _l \frac{1}{N} \sum _{i} \nabla _{\theta _t} L_i\left( \theta _t\right) \end{aligned}$$
(19)

where \(\nabla _{\theta _t} L\left( \theta _t\right) \) is the gradient of loss function with respect to parameter of current network \(\theta \) at time step t. After each c time step, the critic network’s parameters are modified to match the actor network’s. \(\theta ^-\) is updated using Eq. 20. \(\theta _{t+c}\) is the critic parameter

$$\begin{aligned} \theta _t^{-} =\theta _{t+c} \end{aligned}$$
(20)

4 Simulation

This section demonstrates the performance of the proposed control technique for automatic generation control of the proposed micro-grid subject to unpredictability and uncertainty associated with load disturbances and an EV aggregator. Table 2 displays the parameters related to the micro-grid.

Table 2 Parameters of the micro-grid
Full size table
Table 3 Initial K value
Full size table
Fig. 5
figure 5

Convergence Curves: a \(||W_{t+T}-W_t||\), b) \(||K_{t+T}-K_t||\)

Full size image
Fig. 6
figure 6

Convergence Curves: a \(K_1\), b \(K_2\), c \(K_3\), d \(K_4\)

Full size image
Fig. 7
figure 7

Convergence Curves: a W1, b W2, c W3, d W4, e W5, f W6, g W7, h W8, i W9, j W10, k W11, l W12, m W13, n W14, and o W15

Full size image

Pre-learning of proposed technique: Algorithm 1 depicts the pre-learning procedure of the IRL controller. It is assumed that the states (\(x=\left[ \Delta X_{g }, \Delta P_{t }, \Delta f, \Delta I(t) \right] ^T\)) are observable. Q and R, involved in cost function J, are chosen as \(0.001 I_{4\times 4}\) and 0.08, respectively. The initial state \(x_0\) is \([0.1,0,0,0]^T\). Step size (T) is chosen as 0.1 s. Four different initial K values are chosen to show the convergence of the controller. The values are given in Table 3. The corresponding convergence curves are shown in Fig. 7, 5, and 6. Figure 7 shows the 2- norm of difference of weight matrix (W) and the 2-norm of difference of K over consecutive time steps. The convergence of elements of K are illustrated in Fig. 5a–d. Figure 6a–o illustrates the convergence of elements of weight matrix (W). Step size (T) is chosen as 0.1 s. Based on algorithm 1, the kernel matrix S and optimal K values are found and expressed in Eqs. 21 and 22, respectively. Likewise, Fig. 8 depicts the convergence curve of the DQN in response to the sinusoidal load disturbance, as illustrated in Fig. 9.

$$\begin{aligned} {\textbf {S}}= & \begin{bmatrix} -0.16104& 0.03718& -0.012587 & 0.00035414& 0.13471\\ 0.03718& -0.0085838& 0.002906 & -8.1762e-05& -0.031099 \\ -0.012587 & 0.002906& -0.00098383& 2.768e-05 & 0.010529\\ 0.00035414& -8.1762e-05& 2.768e-05& -7.788e-07& -0.00029623\\ 0.13471 & -0.031099 & 0.010529& -0.00029623 & -0.20515 \end{bmatrix} \end{aligned}$$
(21)
$$\begin{aligned} K= & \begin{bmatrix} -0.6566&0.1516&-0.0513&0.0014 \end{bmatrix} \end{aligned}$$
(22)

4.1 Case 1: Performance comparison under step load disturbance

This case study aims to investigate the performance of the proposed controller under step load disturbance. Notably, this analysis does not consider the uncertainties corresponding to the PV and wind systems. To appraise the effectiveness and adaptive performance of the proposed control strategy, a step load disturbance of 0.01pu is applied to the system. Figure 10 depicts the outcomes of the simulation. The numerical values of the peak and peak time of the controllers are provided in Table 4. The peak value of the proposed method is reduced by 6\(\%\) and 14\(\%\) compared to DQN and PI controllers. From the simulation result, it is observed that the proposed control enhances the transient performance by reducing the peak of the frequency deviation. The proposed controller shows a faster response compared to the DQN and PI controller.

4.2 Case 2: Performance comparison under multiple step load change

This case study evaluates the performance of the IRL controller under step frequent load changes. The effect of PV and wind power is not considered. The system is applied to multi-step load perturbations, and the corresponding change in frequency is illustrated in Fig. 11. The numerical value of applied step load disturbances is given in Table 5.

Fig. 8
figure 8

Convergence curve for DQN

Full size image
Fig. 9
figure 9

Change in load for pre-learning of DQN

Full size image
Fig. 10
figure 10

Performance under step load disturbance: change in frequency (\(\Delta f\)) in pu

Full size image

The result demonstrates that the proposed controller helps the system to reach its steady state faster despite frequent disturbances. For performance evaluation, this case study considers three performance indices: mean squared error (MSE), integral absolute error (IAE), and integral time absolute error (ITAE) [48]. Tracking accuracy is evaluated using the MSE index. The IAE index evaluates the system’s overall overshoot. The ITAE index is used to assess the transient response time. The numerical results for these indices of frequency deviation are given in Table 6. The MSE for the proposed controller is decreased by 28% and 42% compared to the DQN and PI controller, respectively. Similarly, the IAE and ITAE for the proposed controller are approximately decreased by 21% and 35% percent compared to the DQN and PI controller, respectively. From these numerical performance values, it is observed that the proposed controller achieves better tracking performance with smaller tracking errors, smaller overshoots, and faster responses than other controllers.

Table 4 Step response of the system
Full size table
Fig. 11
figure 11

\(\Delta f\) (pu) Under multi-step load disturbances

Full size image
Table 5 Applied step load to system
Full size table

4.3 Case 3: Performance comparison under renewable sources

This case study investigates the robustness of the proposed controller towards the PV and wind power uncertainty under random load disturbances. The system subjected to random load disturbances (\(\Delta P_d\) \( \in \) [0.04,0.08] pu), as depicted in Fig. 12a. The perturbations in wind and solar power applied to the system are illustrated in Fig. 12b and c. The dynamic performances of the system are shown in Fig. 13. For performance evaluation, this case study considers the normal distribution of the frequency deviation. Figure 14 illustrates this. The proposed controller reduces the standard deviation in the frequency curve by 17\(\%\) and 23\(\%\) compared to DQN and PI controller. It is observed that the proposed controller exhibits a lower standard deviation compared to others, indicating less deviation frequency from the mean value. Furthermore, compared to other controllers, the mean value of frequency deviation for the proposed controller is closer to zero, which signifies a performance improvement. Therefore, it is observed that the probability of getting the frequency deviation close to zero is highest for the proposed controller. From the above discussion, it is concluded that the proposed controller effectively minimizes frequency deviations against the uncertainties imposed by PV and wind power.

4.4 Case 4: Sensitivity analysis

Table 6 Numerical performance results
Full size table
Fig. 12
figure 12

a Change in Load (pu), b Change in PV power (in pu) and c Change in Wind power (in pu)

Full size image
Fig. 13
figure 13

\(\Delta f\) (pu) Under renewable sources

Full size image

Theoretical examinations indicate that in cases where the power system exhibits inherent stability, variations in frequency remain relatively minor and constrained across varying load-damping coefficients. Conversely, within an unstable power system, disturbances can lead to amplified frequency deviations over time [49]. To demonstrate the robustness and efficacy of the proposed IRL controller in a more challenging condition, some critical parameters of the power system are varied and corresponding deviation in frequency (\(\Delta f\)) is illustrated in Fig. 15. The change in parameters are shown in Table 7. At a time of 2 s in this case study, a step load disturbance of 0.02 per unit is applied. Figure 15 unveils the adaptability and robustness of the IRL controller to the variations in system parameters. Case 3 corresponds to no change in parameters. Despite changes to the system parameters, the desired outputs are bounded with small fluctuations.

Based on the analysis of case studies 1 and 2, it has been determined that the controller proposed is highly effective in reducing frequency deviations when faced with step load disturbances, even in the presence of EV uncertainties. Similarly, in case study 3, the proposed controller has demonstrated effectiveness in minimizing frequency deviations despite the uncertainties introduced by PV and wind power. The controller has also been shown to be robust against parameter changes, which further highlights its reliability and efficiency.

In the given study, the target network of DQN updates its parameters without requiring the gradient of the loss function; instead, it directly copies parameters from the current network. In contrast, the current network requires the gradient of the loss function to update its parameters. As shown in Fig. 4, the current networks employ gradient ascent to update 77 (weights of the current network) parameters at each time step. However, the proposed controller adopts the RLS method, requiring only 15 parameter updates. In this paper, the simulation results show that the proposed controller performs better than the DQN algorithm. However, DQN may achieve enhanced performance, particularly with deep neural networks featuring more hidden layers and a larger discretized action set. However, the complexity of the controller will increase, causing an increase in the number of parameter updates and learning time. Moreover, the proposed controller needs no discretization of action set.

Fig. 14
figure 14

Probability density of \(\Delta f\)

Full size image
Fig. 15
figure 15

\(\Delta f\) (pu) under step load disturbance

Full size image
Table 7 Change in parameters of the power system
Full size table

5 Conclusion

An optimal control technique that uses integral reinforcement learning has been successfully implemented for automatic generation control of EV, renewable, and storage system integrated is-landed micro-grid. The proposal includes four case studies that analyze the robustness of the controller against uncertainties due to load disturbances, EV aggregator, renewable integration, and parameter uncertainty. The case studies show that the proposed IRL controller effectively minimizes the frequency deviation. The proposed controller markedly enhances performance metrics relative to the DQN and PI controllers. Specifically, it achieves a reduction in peak frequency deviation by 6\(\%\) and 14\(\%\) compared to the DQN and PI controllers, respectively. Under multiple-step load disturbances, the controller decreases the mean square error by 28\(\%\) and 42\(\%\), respectively, while reducing both the integral absolute error and the integral time absolute error by 21\(\%\) and 35\(\%\) in comparison to the DQN and PI controllers. Furthermore, in scenarios involving renewable energy sources, the proposed controller lowers the standard deviation in frequency deviation by 17\(\%\) compared to the DQN controller and by 23\(\%\) compared to the PI controller. The proposed method is a policy iteration-based algorithm. The main limitation of the proposed method is it needs permissible initial conditions, which have been determined based on human expertise in this study. This paper applies the method to a single-area microgrid, but future work could potentially expand to interconnected multi-microgrids.