1 Introduction

Environmental protection and global warming, the main causes of which are industry and the production of electricity from nonrenewable energy sources, have influenced the increasing use of renewable energy sources in recent decades [1]. Renewable energy sources are the keys to green transitions, the keys to energy independence, and the keys to preserving the environment. According to IRENA data, the share of renewable sources in the production of electricity is constantly increasing [2]. This is due to numerous political and energy crises, as well as the increasing cost of energy production from nonrenewable energy sources [3].

Solar energy has been the most interesting form of renewable energy source in recent years [4]. The price of solar panels and inverters has drastically declined, which has led to the expansion of solar power plant installations and small solar plants. On the other hand, the large production of electricity from solar power plants affects the prices of electricity on the market.

The conversion of electric solar energy into electricity is performed in solar cells, which are the basic components of solar panels [5]. However, the efficiency of solar panels is strongly influenced by the degree of insolation and temperature, as well as by the occurrence of clouds, rain, and soiling [6]. Therefore, it is necessary to pay special attention to the conditions under which solar panels work. Additionally, to use the maximum possible production from solar panels, they must be regulated. Specifically, DC-DC converters, which are used to control the operation of solar panels at the point of maximum power (application of maximum power point tracking—MPPT regulation), must be used [7]. These issues were the main reasons why research in science in this area was directed toward the development of solar cells with a higher degree of efficiency.

The new generation of solar cells is perovskite solar cells [8], named after the nickname for their crystal structure. These cells have begun to be intensively researched in the last decade and have shown exceptional performance in terms of efficiency [9]. Furthermore, the efficiency of these solar cells is more than 22% [10], while simulation studies have shown an efficiency of more than 30% [11]. On the other hand, these cells are made from different perovskite materials that are quite cheap, which makes this technology extremely attractive for research [12]. Moreover, it is important to emphasize that there is a large amount of research dealing with materials for new types of solar cells [13,14,15,16,17].

As with other solar cells, the most important characteristic of PSCs is their current–voltage characteristic [18, 19]. In the mathematical sense, the current–voltage characteristics of PS are extremely nonlinear. However, numerous studies in recent years have addressed this area and proposed the application of the Lambert W equation for the analytical solution of current as a function of voltage and voltage as a function of the current of these solar cells [18,19,20]. In [20], simplified PSC models were proposed and modified, which neglects some of the resistances used to describe these solar cells.

The Lambert W equation represents an equation of the type x = β*exp(− x), where x is a variable and β is a real number. The solution of this equation is denoted by W(β), where β is the argument of the function [21]. Numerous iterative methods [22], as well as analytical approaches [23, 24], can be used to solve the abovementioned equation. Moreover, as this equation is extensively used in the scientific literature, software packages, such as MATHEMATICA, MATLAB, Maple, and Python, have built-in functions for solving this problem [23]. However, the accuracy of solving this equation depends on the value of the argument β. Namely, for large values of the argument β, there is no possibility of their analytical solution through either the Taylor series [23] or the application of the Theory of Special Tran Functions (STFT) [23, 24]. Moreover, both approaches in their mathematical form imply the scaling of the argument of the Lambert W function with some natural number, which means that the already sufficiently large value of the argument β increases even more. On the other hand, for large values of parameter β on the order of more than approximately 10309, the computational possibility of solving the Lambert W equation in software packages is impossible [25]. This large value of the Lambert W function argument appears for PSC no-load and low-load currents, which will be discussed and demonstrated in this paper.

In this paper, the application of the g-function, i.e., the LogWright function, for mathematical modeling of PSCs is proposed [25,26,27,28]. The application of this function solves problems related to the high values of numbers that exist in the application of the Lambert W function. Therefore, the primary goal is to develop a new analytical model of the current–voltage characteristics of PSCs that has solutions for all voltage and current values. Second, it is important to point out that the available literature uses the procedure described in [26] to solve the g-function. The proposed procedure is based on the application of Halley's method [25, 26] or Newton–Raphson's iterative procedure [29]. A discussion about the disadvantages of these methods will also be presented in this paper. In contrast to existing methods, a new original iterative procedure for solving the proposed g-function is presented in this paper. The proposed iterative procedure overcomes problems of initial values, as well as other mathematical requirements of the existing methods. Furthermore, based on the presented iterative procedure, a few approximate solutions for the g-function are proposed and tested in this article.

Therefore, the main contributions of this paper can be summarized as follows:

  • A discussion about the applicability of the Lambert W function for solving the invertible current–voltage characteristics of PSCs is given.

  • Mathematical formulations of the invertible current–voltage characteristics of PSCs will be established.

  • For the first time, in the literature, the application of the g-function in PSC modeling is proposed.

  • A new original iterative method for solving the g-function is proposed.

  • A few approximate g-function solutions will be proposed.

  • The application of all the well-known and proposed expressions to three different PSCs will be tested.

To effectively present the research, the work itself is organized into several sections. In the second chapter, the PSC equivalent circuit is described, and the basic PSC current–voltage equations are given. In the third section, the g-function is described. Additionally, in this section, iterative and approximate solutions for the g-function are proposed. In the fourth section, new, original, inverse current–voltage relations for PSCs are presented and tested on three PSCs. The main contributions of the work are presented in the Conclusion section.

2 Perovskite solar cells: PSCs

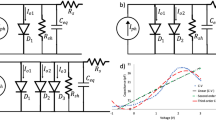
The equivalent circuit of the PSC is shown in Fig. 1 [18,19,20]. This circuit consists of a current source Ipv (photocurrent generated in the cell when light falls on it), two diodes D1 and D2, connected in series, and two resistances RP and RS—one connected in parallel with the diodes and the other in series with the connecting end. Resistances RS and RP represent losses in PSCs (internal and due to a reverse saturation current, respectively), while diodes represent active junctions due to sunlight absorption. Note that the simplest model of standard solar cells has one diode [30, 31].

Fig. 1
figure 1

PSC equivalent circuit

Full size image

Based on PSC physics [18], the reverse saturation currents of the diodes are equal (I01 = I02), while the voltage ratio on the diodes is proportional to the ratio of the ideal factors of the diodes (n1 and n2). Therefore, the current–voltage equation (I–U) of a PSC has the following form [13,14,15, 26]:

$$ I = I_{pv} - I_{0} \left( {e^{{\frac{{U + IR_{S} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{{{\text{th}}}} }}}} - 1} \right) - \frac{{U + IR_{S} }}{{R_{P} }} $$
(1)

where I0 = I01 = I02 and Vth = KBT/q is the thermal voltage, KB is the Boltzmann constant, T is the temperature, and q is the charge of the electron.

Analytical solutions for the current and voltage of the previous equation represented by the Lambert W equation have the following forms [20, 32]:

$$ \begin{aligned} & I = \frac{{R_{P} \left( {I_{pv} + I_{0} } \right) - U}}{{R_{S} + R_{P} }} - \frac{{n \cdot V_{th} }}{{R_{S} }} \cdot W\left( {\beta_{{\text{U}}} } \right) \\ & \beta_{{\text{U}}} = \frac{{I_{01} R_{P} R_{S} }}{{n \cdot V_{th} \left( {R_{S} + R_{P} } \right)}}{\text{e}}^{{\frac{{R_{P} \left( {R_{S} I_{pv} + R_{S} I_{01} + U} \right)}}{{n \cdot V_{th} \left( {R_{S} + R_{P} } \right)}}}} , \\ \end{aligned} $$
(2)
$$ \begin{aligned} & U = R_{P} \left( {I_{pv} + I_{0} } \right) - I\left( {R_{S} + R_{P} } \right) - \left( {n_{1} + n_{2} } \right)V_{th} \cdot W\left( {\beta_{{\text{I}}} } \right) \\ & \beta_{{\text{I}}} = \frac{{I_{0} R_{P} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}{\text{e}}^{{\frac{{R_{P} \left( {I_{pv} + I_{0} - I} \right)}}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}}} , \\ \end{aligned} $$
(3)

where W is the Lambert W function.

2.1 Numerical results

Table 1 shows the data for three PSCs taken from [18, 32]. Based on the data from this table (PSC parameters), the values of the arguments of the functions βI and βU were determined by using Eqs. 2 and 3 for different values of the PSC current and voltage, respectively. The obtained results are presented in Fig. 2.

Table 1 PSC parameters
Full size table
Fig. 2
figure 2

βI = f(U) (upper graph), and βU = f(I) (lower graph)

Full size image

Due to the relatively small value of the argument, the values of βI can be calculated for all voltage values, which is not the case for βU (for the no-load operation, as well as for small loads, βU exceeds the value of 10309). Therefore, it is clear that the expression for the voltage as a function of the PSC current, Eq. 3, expressed through the Lambert W function, is not applicable for all current values. However, the expression for the current as a function of voltage, Eq. 2, is applicable for all voltage values.

3 g-function: description, iterative and approximate solutions

In this section, we briefly introduce the g-function. Additionally, a novel iterative procedure for solving the g-function is proposed, as are its approximate solutions.

3.1 g-function

The problem of solving the Lambert W function for large values of the argument was studied in [25,26,27,28]. Namely, the g-function, or the so-called LogWright function [28], which represents the logarithm of the basic Lambert W equation, was proposed as a potential solution for solving this type of equation. Therefore, starting from the basic Lambert W equation:

$$ W = \beta \cdot \exp ( - W) $$
(4)

and if we express β = exp(α), the g-function has the form [20]:

$$ g = \log \left( W \right) = \alpha - W $$
(5)

In this way, the value of the argument of the g-function (α) has the logarithmic value of β.

To solve the g-function, the approach described in [26] is used in most of the available literature. The proposed principle is based on the well-established Halley's method [25, 26] or Newton–Raphson's method [29], which therefore includes the search for the first derivative of the function. Moreover, the proposed procedure requires limiting the starting value of the iterative procedure as a function of the argument or interpolating the starting value within a certain range. Additionally, to speed up the calculation, the authors suggest using the calculated value of the exponential value in two adjacent iterations. For more details, please see [25].

3.2 Proposed iterative procedure for solving the g-function

In this paper, a new iterative procedure for solving the g-function is proposed. The proposed iterative procedure starts with an arbitrary value of W (denoted by (0)W). After that, the next value of W (denoted by (1)W) is calculated according to the following form:

$$^{\left( 1 \right)} W = \alpha - \log (^{\left( 0 \right)} W). $$
(6)

If it is

$$ \left| {^{\left( 1 \right)} W -^{\left( 0 \right)} W} \right| > \varepsilon , $$
(7)

where ε is the iteration criterion. The initial value of W is calculated as follows:

$$^{\left( 0 \right)} W = \alpha - \log (^{\left( 1 \right)} W). $$
(8)

The entire procedure is repeated until the needed accuracy is achieved. Finally, after k iterations, the g-function value is:

$$^{\left( k \right)} g = \alpha -^{{\left( {k - 1} \right)}} W. $$
(9)

The proposed iterative procedure, called g-IP, was tested for different values of α, different initial values of (0)W, and different iteration criteria ε (see Fig. 3 and Table 2). In Table 2, the RNI represents the number of iterations needed to achieve the desired accuracy. A part of the realized MATLAB code is given in Appendix 1.

Fig. 3
figure 3

Convergence curve of W for α = 50

Full size image
Table 2 Numerical results for g-IP
Full size table

Based on the presented results,

  • it is clear that the proposed iterative procedure does not depend on the initial value (0)W,

  • the proposed iterative procedure converges efficiently for all initial values (0)W,

  • g-IP operates effectively for all values of α and

  • for large values of the argument α, g-IP converges to a solution extremely quickly, even in a few iterations.

Therefore, the applicability of the g-IP for solving the g-function is clear. Note that the g-IP is applicable for α > 1; for α ≤ 1, it is efficient to use the method proposed in [25] for g-function solving or to use voltage–current modeling expressed via the Lambert W function (see Eq. 2).

3.3 Proposed approximate solution for solving the g-function

Based on the previous conclusions and g-IP observations, approximate expressions for solving the g-function can be derived. Namely, the approximate expressions (gapp) have the form:

$$ g_{{{\text{app1}}}} = \log \left( {\alpha - \log \left( {\alpha - \log \left( \alpha \right)} \right)} \right) $$
(10)
$$ g_{{{\text{app2}}}} = \log \left( {\alpha - \log \left( {\alpha - \log \left( {\alpha - \log \left( \alpha \right)} \right)} \right)} \right) $$
(11)
$$ g_{{{\text{app3}}}} = \log \left( {\alpha - \log \left( {\alpha - \log \left( {\alpha - \log \left( {\alpha - \log \left( \alpha \right)} \right)} \right)} \right)} \right) $$
(12)

The accuracy of the approximate solution for different values of α is given in Fig. 4. Figure 4 represents the difference between the exact solution of the g-function and its approximate solutions, Eqs. 10–12, for different values of the argument α. Clearly, the best approximation is provided by gaap3, and the maximum value of the difference compared to the exact solution, in the entire range, is less than 5 × 10–5. Moreover, for α > 50, the maximum difference is less than 10–7. The second approximate function, gapp2, also has good accuracy (for α > 100, the maximum difference is less than 10–8), while the first approximate function, gapp1, is the least accurate (for α > 500, the difference compared to the exact solution is less than 10–8). Therefore, for α > 500, the approximate solutions of the g-function have a high level of accuracy.

Fig. 4
figure 4

Accuracy of the g-function calculation

Full size image

4 PSC voltage–current characteristics

With simple mathematical manipulations, the voltage–current characteristic of the PSC expressed through the g-function takes the following form:

$$ \begin{aligned} & U = \left( {n_{1} + n_{2} } \right) \cdot g\left( {\alpha_{I} } \right) - \left( {n_{1} + n_{2} } \right) \cdot \log \left( {\frac{{I_{0} R_{P} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}} \right) - I \cdot R_{S} \\ & \alpha_{I} = \log \left( {\frac{{I_{0} R_{P} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}} \right) + \frac{{R_{P} \left( {I_{pv} + I_{0} - I} \right)}}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }} \\ \end{aligned} $$
(13)

Equation 13 represents an original and novel analytical solution for the voltage–current dependencies of the PSC. Therefore, the current–voltage characteristics of PCSs can be represented via the Lambert W function, while the voltage–current characteristics must be represented via the g-function approach. The U-I g-function approach for solar cells is given in [25].

Figure 5 shows the αI-current characteristics for all the observed PSCs. The value of the argument α is approximately 1000 when the current is low. Additionally, it is evident that the value of the coefficient α, in the whole observed range, has a higher value of 1, which confirms that we can use the proposed iterative procedure.

Fig. 5
figure 5

The value of coefficient αI for all the current values

Full size image

The current–voltage and power–voltage PSC characteristics of all three observed PSCs are presented in Fig. 6. The corresponding numerical results for certain current values are given in Table 3. In this figure, the proposed approach is compared with the approaches based on the application of the Lambert W function in Eq. 2. The match between characteristics is obvious. Additionally, according to the results presented in Table 3, the g-IP requires a small number of iterations for a high level of calculation accuracy. All these results confirm the feasibility, accuracy, and originality of the g-function in modeling the voltage–current characteristics of PSC cells.

Fig. 6
figure 6

Current–voltage (upper graph) and power–voltage (lower graph) characteristics

Full size image
Table 3 Numerical results for certain values of currents
Full size table

4.1 PSC no-load expression

Based on the previous analysis, it is clear that the most “problematic” point for voltage–current calculations via the Lambert W function is the no-load voltage. Therefore, this point can be only adequately modeled by using the g-function approach proposed previously. Observing the voltage–current characteristics in Eq. 13 and taking I = 0, the original expression for the no-load voltage has the following form:

$$ \begin{aligned} & U_{{\text{no - load}}} = \left( {n_{1} + n_{2} } \right) \cdot \left( {g\left( {\alpha_{{I - {\text{no - load}}}} } \right) - \log \left( {\frac{{I_{0} R_{P} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}} \right)} \right) \\ & \alpha_{{I - {\text{no - load}}}} = \frac{{R_{P} \left( {I_{pv} + I_{0} } \right)}}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }} + \log \left( {\frac{{I_{0} R_{P} }}{{\left( {n_{1} + n_{2} } \right) \cdot V_{th} }}} \right) \\ \end{aligned} $$
(14)

The numerical results, calculated by using Eq. 14, for the no-load voltage calculation for all three observed PSCs are given in Table 4. It is clear that achieving a high level of calculation accuracy requires a small number of iterations. Therefore, it is more than evident that we can use any of the proposed approximate solutions for no-load PSC voltage calculations.

Table 4 Numerical results for no-load voltage calculation
Full size table

Additionally, observing Eq. 14, we can see that the dominant effect on the value of αI-no-load has the value of the parallel resistance. A higher parallel resistance influences a higher value of the argument αI-no-load. Note that in [20], other PSCs can also be found. The value of the no-load voltage for all of them can also be determined by using the proposed equation as well as the proposed approximate functions for solving the g-function.

4.2 PSC modeling around the maximum power point

During operation, the PSC, similar to any solar cell/panel, needs to operate within a certain range around the maximal power point [33]. Namely, as the operating conditions change, the DC-DC converter, which regulates the operation of the PSC, "moves" the operating point around the point of maximum power so that the power obtained from the PSC is maximized. For that reason, in Fig. 7, we present the current–voltage and power–voltage curves expressed by using Eq. 2 as well as the corresponding characteristics determined by using the proposed approximate functions for solving the g-function for PSC #1. The numerical results for certain current values are presented in Table 5. For the voltage around the maximum power point, the differences between the proposed approximate solutions and the corresponding ones determined by using Eq. 2 are presented in the mentioned figure.

Fig. 7
figure 7

Current–voltage, power–voltage (upper graph), and voltage error-current (lower graph) characteristics

Full size image
Table 5 Numerical results for approximate solutions
Full size table

Based on the presented results, it is evident that the proposed approximate solution for the g-function has very good accuracy. Furthermore, the difference between the exact and approximate solution errors confirms this conclusion. For that reason, it is more than clear that we can use approximate solutions for g-function solving for very accurate PSC operation around the maximum power point.

5 Conclusion

The well-known approach for PSC invertible current–voltage modeling, based on the application of the Lambert W function, cannot be applied for whole voltage ranges, especially for no-load and low-load values. Therefore, this paper fills this research gap and proposes novel PSC invertible current–voltage characteristics based on the application of the g-function. Furthermore, in this paper, the original iterative procedure and approximate solutions for this equation are proposed and tested. The proposed iterative procedure does not depend on the initial conditions and does not require searching for the derivative of the observed function. The application of the proposed solutions is tested on three different PSCs, especially for no-load conditions and for regions about the maximum power point. The proposed mathematical modeling of the PSC invertible current–voltage characteristics is confirmed to be possible, accurate, and original with the application of the g-function in the whole voltage range.

In future work, attention will be given to the application of the proposed function for solving other nonlinear engineering problems in the fields of induction machines, storage devices, power inductors, etc. Additionally, we will research the novel iterative procedure for g-function solving to improve the convergence for lower values of the arguments.