Torque ripple minimization in SRM drive using second-order-generalized-integrator-based FLL equivalent PR current controller

Abstract

A second-order-generalized-integrator (SOGI)-based frequency-locked-loop (FLL) equivalent proportional-resonant (PR) current controller is introduced in this paper to minimize torque ripple in switched reluctance motor (SRM) drive system. The typical cascaded closed-loop speed control of SRM comprises a speed controller giving desired torque, a static look-up table mapping the desired torque to desired/reference phase currents of SRM, and a current controller to track the reference phase currents. It is often seen that conventional current controllers like hysteresis controllers, proportional-integral (PI) controllers, and even intelligent controllers such as fuzzy logic controllers and model predictive direct torque controllers (MPDTC) are not very effective in minimizing the torque pulsations for a wide range of operating scenarios. The proposed SOGI-FLL-PR-based current control strategy is aimed at improving torque control under a wide range of operations of SRM. The performance of the proposed current controller has been compared to that of traditional current controllers like the hysteresis controller, the proportional-integral controller, the fuzzy logic current controller (FLCC), and MPDTC; and has shown to be superior in both simulation and experimental studies. Our study details a systematic approach to the dynamic modeling of SRMs, control strategy formulation, dynamic analysis, and experimental verification.

1 Introduction

Switched reluctance motors (SRMs) are becoming increasingly popular due to their low cost, extended lifespan, outstanding resilience, and exceptional electromagnetic features [1, 2]. In contrast, the SRM has issues including weaker power and torque strength, large torque ripple, vibrations, and noise concerns [2, 3] because of its discontinuous method of energization and doubly salient structure. The nonlinear electromagnetic features of SRM also make it difficult to achieve more efficient modeling and high-performance control [4,5,6]. Because of its high dependability and error tolerance capability, the SRM is an appealing solution for various adaptable drive applications [7, 8]. At below-base speeds, control techniques exist to reduce torque ripple [9]. As the rotor speed raises, the stator phase winding excitations have better turn-on and off angles, resulting in higher T/A and, finally, operating in a single pulse mode [10, 11]. Several methods have been developed to address torque ripple control at various rotational speeds. The necessity of torque sharing and control in the conduction zone has been disregarded in favor of a more sophisticated speed and position control method for providing reference torque [12]. Reference [13] suggest a method of instantaneous torque regulation called direct torque control (DITC). As the control strategy needs to be modified when the motor speed increases, this strategy achieves reduced torque ripple; but it has a limited working speed range. The authors of [14] offered a design method to increase SRM's practical application. However, this approach ignores the prospect of reducing torque ripple beyond the rated speed, where current regulation is conceivable.

In this study, a SOGI-FLL-PR current controller is proposed to enhance high-speed performance. A 6/4, 3-phase, 1 hp, 1500 r/min SRM is used for both simulation study and experimental testing. The proposed SOGI-FLL-PR controller offers good SRM performance at a maximum rotational speed of 2000 r/min. Existing conventional and planned current controllers for the SRM drive system have been briefly analyzed in terms of their ability to reduce torque ripple. In this study, we introduce a second-order-generalized-integrator (SOGI) equivalent proportional-resonant (PR) current controller for effective SRM drive system operation using a frequency-locked loop (FLL). Justifications for adopting the proposed control approach are provided below. Traditional PI controllers can only achieve zero steady-state error at zero frequency because their transfer functions have a pole there. Because of this, the PI current controller's current tracking is subpar throughout a broad range of speeds. To solve this challenge, we construct a proportional-resonant current controller employing a SOGI to obtain maximal gain at the resonant frequency. The reference current's instantaneous frequency is determined using an FLL. The proposed current controller for high-speed performance has been carefully compared to the performance of conventional current controllers to confirm its efficacy (including a fuzzy logic-based controller).

The paper's format is consistent. Chapter 2 models the SRM motor drive system. Section 3 discusses the proposed current control method for the SRM drive and the cascaded closed-loop speed control system. The simulation and hardware findings in Sects. 4 and 5 demonstrate the improved performance of the proposed current controller. Section 6 concludes the paper.

2 Switched reluctance motor drive model

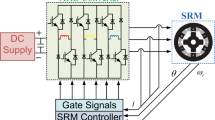
The stator and rotor of the SRM both contain laminated salient poles, resulting in a fairly straightforward doubly salient structure. The rotor is devoid of magnets and windings. On its poles, only the stator has concentrated windings. One phase of the motor is made up of each pair of opposite windings on the stator [15]. The rotor is constructed of laminations to reduce eddy current losses. A 3-phase, 6/4 SRM and its power converter circuit for a single-phase winding are in Fig. 1. The stator magnetic field is produced by the sequential excitation of the stator windings, and it is in this field that the rotor poles attempt to align themselves to obtain the lowest possible reluctance.

Fig. 1

Cross-sectional view of a 3-phase, 6/4 SRM (along with power converter circuit of a typical phase winding

2.1 SRM dynamic model

The complete dynamic model of a 3-phase SRM is given below.

$$ \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \omega $$

(1)

$$ J\frac{{{\text{d}}\omega }}{{{\text{d}}t}} + B\omega = T_{m} - T_{L} = \sum\limits_{q = 1}^{3} {T_{q} - } T_{L} $$

(2)

$$ \frac{{{\text{d}}\lambda_{q} }}{{{\text{d}}t}} = v_{q} - Ri_{q} \quad ,q = 1,2,3 $$

(3)

$$ \begin{gathered} T_{q} \left( {\theta ,I_{q} } \right) = \left. {\frac{{{\text{d}}W_{c} \left( {\theta ,i_{q} } \right)}}{{{\text{d}}\theta }}} \right|_{{i_{q} = I_{q} }} ; \hfill \\ W_{c} \left( {\theta ,I_{q} } \right) = \int\limits_{0}^{{I_{q} }} {\lambda_{q} } \left( {\theta ,i_{q} } \right){\text{d}}i_{q} \hfill \\ \hfill \\ \end{gathered} $$

(4)

where $\theta$ is rotor position, $\omega$ is motor speed,$v$ is phase voltage,$T_{m}$ is electromagnetic torque generated by SRM, $T_{l}$ is load torque,$\lambda$ is phase flux linkage, $q$ is phase index, $W_{c}$ is co-energy, $R$ is phase resistance, $i$ is phase current, $B$ is viscous friction coefficient, and $J$ is total inertia of the SRM drive. The mechanical parameters $J$ and $B$ of the SRM drive system used in this study are obtained experimentally [16].

2.2 Static electromagnetic characteristics

Most flux-linkage measurements in SRM are performed using the dc-excitation method [17]. When the rotor has been properly fastened mechanically, a dc voltage is applied to the stator, and the phase voltage ($v$) and current ($i$) are measured and recorded immediately. Utilizing Eq. 5, we can calculate the flux linkage.

$$ \lambda \left( {\theta ,I} \right) = \lambda \left( 0 \right) + \int\limits_{0}^{{t_{I} }} {\left( {v - Ri} \right){\text{d}}t;} \;\theta \;{\text{is}}\;{\text{fixed}}. $$

(5)

where $\lambda \left( 0 \right)$ denotes the initial flux linkage (at zero current) and $t_{l}$ is the time instant when the current magnitude reaches $I$. Due to the absence of permanent magnets in SRM, $\lambda \left( 0 \right) = 0$.

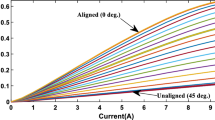
The static flux-linkage characteristics obtained for one phase of the experimental 3-phase, 1 hp, 6/4 SRM are displayed in Fig. 2. We have derived the static torque profiles from the flux-linkage data using Eq. 4, which is based on the concept of co-energy. Figure 3 is a plot of the computed torque characteristics. As can be shown in Fig. 3, if an excitation current is passed through the phase, the rotor will be attracted, resulting in positive torque, much before the rotor pole has attained its aligned condition.

Fig. 2

Experimentally measured static flux linkage vs. rotor position vs. current characteristics for the experimental 6/4, 3-phase, 1 H.P. SRM

Fig. 3

Computed static torque vs. rotor position vs. current characteristics for the experimental 6/4, 3-phase SRM

2.3 Simulation model of SRM

The phase current as a function of rotor position and flux linkage should be derived from the look-up table{$\lambda_{{{\text{ph}}}} (i_{{{\text{ph}}}} ,\theta_{{{\text{elec}}}} )$} created from the measured flux-linkage data, which is required for the dynamic simulation research of SRM.

Each phase's dynamic voltage equation in SRM can be expressed as follows:

$$ v_{{{\text{ph}}}} = R_{{{\text{ph}}}} i_{{{\text{ph}}}} + \frac{{{\text{d}}\lambda_{{{\text{ph}}}} (i_{{{\text{ph}}}} ,\theta_{{{\text{elec}}}} )}}{{{\text{d}}t}} $$

(6)

where $v_{{{\text{ph}}}}$ is phase voltage, $i_{{{\text{ph}}}}$ is phase current, $\lambda_{{{\text{ph}}}}$ is phase flux linkage,$R_{{{\text{ph}}}}$ is phase resistance, and $\theta_{{{\text{elec}}}}$ is rotor angle (electrical). Equation 6 can be solved for flux linkage to obtain the phase flux as:

$$ \lambda_{{{\text{ph}}}} (t) = \int {[v_{{{\text{ph}}}} (t) - R_{{{\text{ph}}}} i_{{{\text{ph}}}} (t)]{\text{d}}t} $$

(7)

$i_{{{\text{ph}}}}$ is dependent on the flux linkage and rotor electrical angle. The flux-linkage look-up table {$\lambda_{{{\text{ph}}}} (i_{{{\text{ph}}}} ,\theta_{{{\text{elec}}}} )$} is inverted into another look-up table $i_{{{\text{LUT}}}} \{ \lambda_{{{\text{ph}}}} (t),\theta_{{{\text{elec}}}} (t)\}$ and $i_{{{\text{ph}}}}$ is obtained from the look-up table $i_{{{\text{LUT}}}} \{ \lambda_{{{\text{ph}}}} (t),\theta_{{{\text{elec}}}} (t)\}$, by using linear interpolation. Subsequently, in the iterative simulation study, the flux linkage $\lambda_{{{\text{ph}}}}$ is computed iteratively using this $i_{{{\text{ph}}}}$ by using Eq. 8:

$$ \lambda_{{{\text{ph}}}} (t) = \int {[v_{{{\text{ph}}}} (t) - R_{{{\text{ph}}}} i_{{{\text{LUT}}}} (\lambda_{{{\text{ph}}}} (t),\theta_{{{\text{elec}}}} (t))]{\text{d}}t} $$

(8)

In the dynamic simulation, Eq. 8 is implemented in a discretized form given by:

$$ \lambda_{{{\text{ph}}}} (k) = \lambda_{{{\text{ph}}}} (k - 1) + [v_{{{\text{ph}}}} (k) - R_{{{\text{ph}}}} i_{{{\text{LUT}}}} (\lambda_{{{\text{ph}}}} (k - 1),\theta_{{{\text{elec}}}} (k - 1))]T_{s} $$

(9)

where $T_{s}$ is sampling time used to solve the discrete-time integration and $k$ is the discrete step number. Figure 4 depicts a fully dynamic model of the SRM in the discrete-time domain. While both continuous and discrete representations of the model are possible, discrete models with a set time step are typically used in practice because they are more amenable to digital controller implementation. Because the look-up table (LUT) represents the nonlinear electromagnetic properties of SRM, the dynamic current waveform may be calculated using the voltage equation.

Fig. 4

Complete dynamic simulation model of an SRM drive

3 Proposed current control strategy SRM drive system

A closed-loop speed control method can be implemented by the SRM drive system using the second-order (SO)-SOGI-FLL-PR current controller, as shown in Fig. 5. The system is made up of SRM, rotor position sensor, reference current generator, commutation logic system, speed controller, torque sharing function (TSF), and SO-SOGI-FLL-PR current controller. The operation of the control system is as follows. The derivative of the rotor position yields the actual rotor speed ($\omega_{{{\text{actual}}}}$), which is then compared to the reference/desired speed ($\omega_{{{\text{ref}}}}$). The proportional-integral (PI) speed controller receives the speed error ($\omega_{{{\text{error}}}}$) as input and provides the desired torque ($T_{d}$) as output. Each phase's current reference is also generated using the cubic TSF.

Fig. 5

The closed-loop speed control scheme of the SRM drive system using the proposed current control scheme

The following is a description of the computations used in the proposed controller for control purposes. The reference torque ($T_{{{\text{ref}}}}$) for each phase of SRM is calculated using the demand torque ($T_{d}$), cubic TSFs, the turn-on angle ($\theta_{{{\text{on}}}}$), the turn-off angle ($\theta_{{{\text{off}}}}$), and the overlap angle ($\theta_{{{\text{ov}}}}$). For a given rotor position ($\theta_{{{\text{elec}}}}$) and phase, a reference current ($i_{{{\text{ref}}}}$) can be calculated by linearly interpolating a look-up table of current as a function of torque (created using experimentally collected static toque characteristics data). The SO-SOGI-FLL-PR controller provides the appropriate control signal for generating the phase voltages. The phase voltages generated by SRM are used to power an asymmetric bridge converter attached to the stator windings.

To improve the SRM drive system's current tracking performance, a second-order-generalized-integral-based frequency-locked-loop (SOGI-FLL) equivalent proportional-resonant (PR) current controller is provided.

The SOGI-PR controller is used since PI fails to match the reference current at any frequency other than zero. As a result, the PI current controller has inadequate current tracking throughout a broad range of operating speeds. A proportional-resonant current controller based on a second-order-generalized integrator has been offered as a solution to the problem. Maximum gain is provided at the resonant frequency ($\omega_{0}$), which coincides with the instantaneous frequency of the current reference, for efficient current tracking. Using an FLL, one may determine the reference current's instantaneous frequency.

As the SOGI-PR controller is a low-pass filter; it will produce tracking errors if the actual current contains unknown frequencies due to sudden dynamic changes. The error may further cause failures in the frequency-locked loop implemented by the SOGI-PR control. Thus, better filtering is required to remove the unknown harmonics. So, the use of higher-order filters is required. Accordingly, a second-order (SO)-SOGI-PR control has been proposed to further improve SOGI-PR control execution. Simulation and experimental experiments confirm the proposed control strategy's superior current tracking performance.

3.1 Cubic torque sharing function

A torque sharing function (TSF) divides the constant torque demand (desired torque) among phases using a reference torque profile. Equation 10 in Ref. [18] provides a straightforward example of how to define a torque sharing function for a specific SRM phase. The commutation zone phase torque commitment is found by squaring the transitional sharing function (TSF).

$$ T_{{{\text{ref}}}} \left( n \right) = \left\{ \begin{gathered} 0,0 \le \theta_{{{\text{elec}}}} < \theta_{{{\text{on}}}} \hfill \\ T_{{{\text{ref}}}} \chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right),\theta_{{{\text{on}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} \hfill \\ T_{{{\text{ref}}}} ,\theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{off}}}} \hfill \\ T_{{{\text{ref}}}} \chi_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right),\theta_{{{\text{off}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{off}}}} + \theta_{{{\text{ov}}}} \hfill \\ 0,\theta_{{{\text{of}}f}} + \theta_{{{\text{ov}}}} \le \theta_{{{\text{elec}}}} < \theta_{p} \hfill \\ \end{gathered} \right. $$

(10)

This is shown in Fig. 6 and the formulae $\chi_{{{\text{rise}}}} \left( \theta \right)$ are expressed as in Eq. 11 with the coefficient $\gamma_{0}$, $\gamma_{1}$, $\gamma_{2}$, and $\gamma_{3}$.

$$ \chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \gamma_{0} + \gamma_{1} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} ) + \gamma_{2} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} )^{2} + \gamma_{3} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} )^{3} $$

(11)

Fig. 6

Cubic torque sharing functions (TSFs)

To guarantee that this TSF is continuous for all rotor locations, boundary constraints are established:

$$ \chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \left\{ \begin{gathered} 0,\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} } \right) \hfill \\ 1,\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} } \right) \hfill \\ \end{gathered} \right\};\;\frac{{{\text{d}}\chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right)}}{{{\text{d}}\theta_{{{\text{elec}}}} }} = \left\{ \begin{gathered} 0,\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} } \right) \hfill \\ 0,\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} } \right) \hfill \\ \end{gathered} \right\} $$

(12)

Equations 11 and 12 give the cubic TSF coefficients (given in Eq. 13). Now we have cubic TSF (Eq. 14).

$$ \gamma_{0} = 0,\gamma_{1} = 0,\gamma_{2} = \frac{3}{{\theta_{{{\text{ov}}}}^{2} }},\gamma_{3} = \frac{ - 2}{{\theta_{{{\text{ov}}}}^{3} }} $$

(13)

The phases' contribution to the motor's torque during phase commutation with cubic TSF varies nonlinearly with rotor position. To graphically depict this nonlinearity, a cubic polynomial is employed.

$$ \begin{gathered} \chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \frac{3}{{\theta_{{{\text{ov}}}}^{2} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} } \right)^{2} - \frac{2}{{\theta_{{{\text{ov}}}}^{3} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} } \right)^{3} \hfill \\ \chi_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right) = 1 - \chi_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} + \theta_{{{\text{on}}}} - \theta_{{{\text{off}}}} } \right) \hfill \\ \chi_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right) = 1 - \frac{3}{{\theta_{{{\text{ov}}}}^{2} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} } \right)^{2} - \frac{2}{{\theta_{{{\text{ov}}}}^{3} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} } \right)^{3} \hfill \\ \end{gathered} $$

(14)

The majority of earlier research on offline TSFs focused on optimizing the performance of these algorithms following one or two secondary objectives. This article examines and analyses a variety of well-known TSFs, including linear, cubic, sinusoidal, and exponential TSFs.

While the TSF for the leaving phase linearly falls from 1 to 0 during commutation, the linear TSF (15) for the arriving phase climbs linearly from 0 to 1. Reference current tracking becomes challenging when SRM enters single pulse mode.

$$ \begin{gathered} \chi_{{{\text{rise}}}} = \frac{1}{{\theta_{{{\text{ov}}}} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} } \right) \hfill \\ \chi_{{{\text{fall}}}} (\theta ) = 1 - \chi_{{{\text{rise}}}} (\theta_{{{\text{elec}}}} + \theta_{{{\text{on}}}} - \theta_{{{\text{off}}}} ) \hfill \\ = 1 - \frac{1}{{\theta_{{{\text{ov}}}} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{of}}f}} } \right) \hfill \\ \end{gathered} $$

(15)

As seen in (16), the torque in the commutation zone is specified by an exponential function, which is reflected in the exponential TSF. Exhibit 8 illustrates an illustration of the exponential TSF.

$$ \begin{gathered} \chi_{{{\text{rise}}}} (\theta ) = 1 - exp\left( {\frac{{ - (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} )^{2} }}{{\theta_{{{\text{ov}}}} }}} \right) \hfill \\ \chi_{{{\text{fall}}}} (\theta ) = 1 - \chi_{{{\text{rise}}}} (\theta_{{{\text{elec}}}} + \theta_{{{\text{on}}}} - \theta_{{{\text{off}}}} ) \hfill \\ = exp\left( {\frac{{ - (\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} )^{2} }}{{\theta_{{{\text{ov}}}} }}} \right) \hfill \\ \end{gathered} $$

(16)

Expressions for the $\chi_{{{\text{rise}}}} (\theta )$ and $\chi_{{{\text{fall}}}} (\theta )$ of cosinusoidal TSF are expressed as (17):

$$ \begin{gathered} \chi_{{{\text{rise}}}} (\theta ) = 0.5 - 0.5*cos\left( {\pi \tfrac{{\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} }}{{\theta_{{{\text{ov}}}} }}} \right) \hfill \\ \chi_{{{\text{fall}}}} (\theta ) = 0.5 + 0.5*cos\left( {\pi \tfrac{{\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} }}{{\theta_{{{\text{ov}}}} }}} \right) \hfill \\ \end{gathered} $$

(17)

3.2 SOGI-based proportional-resonant current controller

Figure 7 is a simplified block diagram depicting a typical implementation of the first-order integrator with a closed loop. The high gain at zero frequency [19] allows the closed loop to precisely follow the dc input. On the other hand, it can only accurately follow the input reference current signal at a single frequency. To get around this, it is recommended [20] to use proportional resonators (PR) to create a SOGI-quadrature signal generator (QSG). A glance at Fig. 8 reveals that the SOGI-QSG-PR controller operates on a basic but powerful principle. The SOGI, a crucial component of the PR controller, is based on the generalized integrator (GI) structure shown in Eq. 18. The heart of the SOGI- QSG system is the SOGI itself. Equation 19 provides a form for the SOGI transfer function.

$$ {\text{GI}}(s) = \left[ {\frac{2s}{{s^{2} + \omega_{0}^{2} }}} \right] $$

(18)

$$ {\text{SOGI}}(s) = \left[ {\frac{{\omega_{0} s}}{{s^{2} + \omega_{0}^{2} }}} \right] $$

(19)

Fig. 7

Closed-loop diagram of the first-order integral controller

Fig. 8

Block diagram of SOGI-QSG based PR current controller

The SOGI can integrate the magnitude of the sinusoidal input signal, per Eq. 19. This signal resembles the correct dc input integration pretty closely. Consequently, a first-order system that can recognize sinusoidal signals can forecast the SOGI-QSG characteristic. Since this is the case, dc signals are often followed using a first-order system (FOS). If the SOGI-QSG is applied to sinusoidal signals, it can be thought of as a form of FOS. The SOGI-QSG-PR controller has significant advantages over its resonant frequencies.

Thus, the interrelated components in the control output, given in Eq. 20, are meant for the tracking of the reference current with instantaneous frequency $\omega_{0}$.

$$ u(s) = K_{p} + \frac{{K_{1} \omega_{0} s}}{{s^{2} + K_{1} \omega_{0} s + \omega_{0}^{2} }}*K_{r} $$

(20)

where SOGI gain $K_{1}$ is related to the damping ratio of the band-pass filter transfer function designated by: $\xi = \frac{{K_{1} }}{2}$. It is often useful to set $\xi \ge 0.5$ to get a reasonably well-damped response. The values of $K_{p}$ and $K_{r}$ are chosen to provide high-performance current tracking.

3.2.1 Structure of second-order (SO) SOGI-QSG-based PR controller

Equation 20 demonstrates that the SOGI-QSG generates outcomes similar to those of a low-pass filter. Due to its low-pass filter design, the SOGI-QSG is prone to dc offset and subharmonics. It can cause SOGI-QSG signal distortion and errors. Unknown input harmonic frequencies present another difficulty for the SOGI-QSG. Distortion of the SOGI-QSG output might occur when the input signal contains frequencies that are not known to the controller. Therefore, strong harmonic reduction skills are required for SOGI-QSG, i.e., good filtering is required to remove unknown harmonics. To overcome this problem, higher-order filters have been used. A second-order (SO)-SOGI-QSG is used in this work (Fig. 9) to further develop SOGI-QSG execution [19].

Fig. 9

Structure of the SO-SOGI-QSG-based PR current controller

3.2.2 SO-SOGI-QSG-based PR controller parameter design

The method used to develop the SO-SOGI-QSG parameters is described below [19]:

• First, choose the required settling time $t_{s}$ for the SO-SOGI-QSG.

• The overshoot $\sigma$ which is derived from the damping ratio $\zeta$ can be calculated as:

  $$ \sigma = {\text{exp}}\left( { - \frac{\pi \zeta }{{\sqrt {1 - \zeta^{2} } }}} \right)\;,\;0 \le \zeta \le 1 $$

  (21)

• Considering the standard second-order system settling time equation, the undamped natural frequency ($\omega_{n}$) can be expressed as:

  $$ \omega_{n} = \frac{4}{{\zeta t_{s} }} $$

  (22)

• The gains $K_{1}$ and $K_{2}$ of the SO-SOGI-QSG can then be formulated by Eq. 23.

  $$ K_{1} = \frac{{\omega_{n} }}{{\omega_{0} \xi }}\;{\text{and}}\;K_{2} = \frac{{4\xi \omega_{n} }}{{\omega_{0} }} $$

  (23)

3.2.3 SOGI based on frequency-locked loop

The FLL is an effective modification of the SOGI-QSG to determine the resonant frequency $\omega_{0}$ [21] as shown in Fig. 10. The two in-quadrature output signals $i_{{{\text{error}}}}^{^{\prime}}$ and $qi_{{{\text{error}}}}^{^{\prime}}$, are defined by Eqs. 24 and 25:

$$ X(s) = \frac{{i_{{{\text{error}}}}^{^{\prime}} }}{{i_{{{\text{error}}}} }} = \frac{{k\omega_{0} s}}{{s^{2} + k\omega_{0} s + \omega_{0}^{2} }} $$

(24)

$$ Y(s) = \frac{{qi_{{{\text{error}}}}^{^{\prime}} }}{{i_{{{\text{error}}}} }} = \frac{{k\omega_{0}^{2} }}{{s^{2} + k\omega_{0} s + \omega_{0}^{2} }} $$

(25)

Fig. 10

Second-order-generalized-integrator (SOGI)-based frequency-locked loop

The transfer function between the current tracking error $i_{{{\text{error}}}}$ to the error signal $\varepsilon_{{i_{{{\text{error}}}} }}$, i.e., $E(s)$, is given by

$$ E(s) = \frac{{\varepsilon_{{i_{{{\text{error}}}} }} }}{{i_{{{\text{error}}}} }} = \frac{{s^{2} + \omega_{0}^{2} }}{{s^{2} + k\omega_{0} s + \omega_{0}^{2} }} $$

(26)

The Bode plots of the transfer function $Y(s)$ and $E(s)$ are shown in Fig. 11. It is observed that the signals $qi_{{{\text{error}}}}^{^{\prime}}$ and $\varepsilon_{{i_{{{\text{error}}}} }}$ are in phase when ($\omega_{i/p} < \omega_{0}$); and $qi_{{{\text{error}}}}^{^{\prime}}$ and $\varepsilon_{{i_{{{\text{error}}}} }}$ are in counter phase when ($\omega_{i/p} > \omega_{0}$). So, a frequency error variable $\varepsilon_{f}$ is used as the multiplication of $qi_{{{\text{error}}}}^{^{\prime}}$ by $\varepsilon_{{i_{{{\text{error}}}} }}$.

Fig. 11

Bode diagrams of the frequency-locked-loop transfer functions

As per the Bode plot, the average value $\varepsilon_{f}$ will be positive when $\omega_{i/p} < \omega_{0}$, zero when $\omega_{i/p} = \omega_{0}$, and negative when $\omega_{i/p} > \omega_{0}$. A negative gain $- \lambda$ integral component is utilized to eliminate the dc part of the frequency error by matching the SOGI resonant frequency $\omega_{0}$ to the input signal frequency $\omega_{i/p}$. Knowing the approximate fundamental frequency $\omega_{ff}$ reduces FLL startup time.

4 Simulation result analysis

The proposed SO-SOGI-FLL-PR current controller's performance in closed-loop speed regulation for the 3-phase, 1 hp, 6/4 SRM has been evaluated using MATLAB/SIMULINK. 1 microsecond is the simulation step time. Intelligent fuzzy logic, PI current, and hysteresis current controllers are compared to SO-SOGI-FLL-PR. An asymmetric power converter uses a unipolar pulse-width-modulation (PWM) switching method to supply electricity to the motor. The phase excitation angles $\theta_{{{\text{on}}}}$, $\theta_{{{\text{off}}}}$, and $\theta_{{{\text{ov}}}}$ are chosen as $10^\circ$, $130^\circ$, and $35^\circ$, respectively, ($0^\circ$ and $180^\circ$ are represented as the aligned and unaligned positions, respectively) in all the simulation experiments. At the most, two phases can be energized simultaneously (tow-phase-on scheme). The control technique determines the phases to be energized depending on the rotor position. The performances are compared and analyzed based on current tracking capability and torque ripple.

4.1 Hysteresis current controller

Figure 12 shows the performance of the hysteresis current controller, where $\theta_{{\text{on,elec}}} = 10^\circ$, $\theta_{{\text{off,elec}}} = 130^\circ$, and load torque ($T_{l}$) = 1 Nm. The reference current is used as the hysteresis band's setting of 2%. Between turn-on angle ($\theta_{{{\text{on}}}}$) and turn-off angle ($\theta_{{{\text{off}}}}$), the regulation of phase current is shown in Fig. 12. In the freewheeling mode, the phase winding is short circuited and only one switch is activated. Furthermore, the phase current decays more slowly at full negative DC link voltage ($- V_{{{\text{dc}}}}$) due to high phase inductance near the aligned position. It is critical to notice from Eq. 34 (mentioned in appendix) that the hysteresis control is only operational when the reference current signal is bigger than zero. If the current is not being dissipated, the phase should be turned off and the applied voltage should be zero.

Fig. 12

Hysteresis current control for SRM demonstrating current chopping with phase current and phase voltage at 2000 r/min. (zone1 = $0\parallel {\text{ref}}{\text{.current}} > 0 \cap i_{{{\text{ph}}}} \ge i_{{{\text{upper}}}}$ and zone 2 = $- V_{{{\text{dc}}}} \parallel ... \cap i_{{{\text{ph}}}} > 0$)

Figure 13a, b, and c, which demonstrate the current tracking inaccuracy, respectively, show the phase current, reference current, and total torque at 750, 1500, and 2000 r/min. The phase current is directly chopped into the hysteresis controller. The torque ripple is found to be more severe across the commutation region and this increases with motor speed. The torque ripples are 55.94%, 56.25%, and 57.05% at respective speeds of 750 r/min, 1500 r/min, and 2000 r/min. Additionally, the average motor torque values at 750, 1500, and 2000 r/min are 1.153, 1.278, and 1.358 Nm, respectively. The average torque and torque ripple both climb as the speed does.

Fig. 13

Simulation results with hysteresis current controller (load torque = 1 Nm): a 750 r/min, b 1500 r/min, and c 2000 r/min

4.2 PI current controller

Figure 14 shows the performance of the PI current controller, where $\theta_{{\text{on,elec}}} = 10^\circ$, $\theta_{{\text{off,elec}}} = 130^\circ$, and load torque ($T_{l}$) = 1 Nm.

Fig. 14

Simulation results with PI current controller (load torque = 1 Nm): a 750 r/min, b 1500 r/min, and c 2000 r/min

Figure 14a, b, and c shows the phase current, reference current, and total torque at 750, 1500, and 2000 r/min, respectively, highlighting the current tracking error. Due to a phase current tracking issue, the toque ripple is 17.02% at 750 r/min. Figure 14b shows that at 1500 r/min, the motor experiences a torque ripple of 21.66%, which leads to a worsening of the current tracking error. Since the rate of change of flux linkage for high-speed operation is constrained, the phase current in the demagnetization area cannot decay as quickly as that of the reference current. As a result, the phase generates a negative torque, which causes a significant torque ripple. Finally, given the flux-linkage rate is quite low, it can be shown in Fig. 14c that the current tracking inaccuracy is most pronounced at 2000 r/min. Torque ripple amounts to 28.88% because of the presence of negative torque.

4.3 Proposed SO-SOGI-FLL-PR current controller with cubic TSF

The performances with the SO-SOGI-FLL-PR current controller are shown in Fig. 15 with $\theta_{{\text{on,elec}}} = 10^\circ$, $\theta_{{\text{off,elec}}} = 130^\circ$, and load torque ($T_{l}$) = 1 Nm. Figure 15a, b, and c depicts current and total torque at 750, 1500, and 2000 r/min, respectively. Torque ripples are 7.89, 10.2, and 12.38% at 750, 1500, and 2000 r/min, respectively. The performance is much better with the proposed SO-SOGI-FLL-PR current controller compared to the other current controllers, without creating an unexpectedly high current rise. Also, the proposed current controller eliminates the need for rapid adjustment of excitation angles ($\theta_{{{\text{on}}}}$ and $\theta_{{{\text{off}}}}$) for reducing torque ripple and it prevents the gradual decrease of outgoing current in the demagnetization zone, respectively.

Fig. 15

Simulation results with the proposed SO-SOGI-FLL-PR current controller ($T_{l}$ = 1Nm): a 750 r/min, b 1500 r/min, and c 2000 r/min

Figure 16 depicts dynamic simulation results for the proposed SOGI-FLL-PR current controller at 1000 r/min and 2 Nm torque load, demonstrating that the current references have good tracking capability. Figure 17 depicts the proposed current controller results at 2000 r/min and a load torque of 3 Nm. In Fig. 17a, the proposed current controller tracks the current reference with a substantial tracking error in the demagnetization zone. As illustrated in Fig. 17b, this causes a considerable torque ripple. Figure 16a shows that the current tracking error for the 1000 r/min is reduced, resulting in a substantially smoother torque profile Fig. 16b. In this situation, the proposed current control reduces torque ripple by decreasing current tracking errors. This example demonstrates that, despite the large induced voltage in the phase, the SOGI-FLL-PR current controller may be used up to the base speed. Due to their shared conduction time, Figs. 16a and 17a show that the true phase current profile is very similar in both circumstances. The current reference at the lower speed in Fig. 16a more correctly portrays the true current dynamics because the current references are dispersed more appropriately. As a result, torque ripple is decreased and tracking performance is improved. The reason for this improvement is that the optimization problem now includes the flux-linkage features, allowing for a more precise computation of the slope of the current profile in the commutation zone. As a result, at an operating point where the traditional control approach might not be successful, the proposed control method can be employed to reduce the torque ripple. For reference, Table 1 lists the average torque values, RMS values for current and torque ripple, and other relevant data for the proposed control approach.

Fig. 16

Dynamic simulation using the proposed TSF at 1000 r/min and $T_{l}$ = 2 Nm showing a phase current and reference, b torque and phase torque, and c flux linkage

Fig. 17

Dynamic simulation using the proposed TSF at 2000 r/min and $T_{l}$ = 3 Nm showing a phase current and reference, b torque and phase torque, and c flux linkage

Table 1 Performance of the proposed current control method

The rising time of SOGI-FLL-PR is 0.112 s, as displayed in Fig. 18. The proposed control system responds more quickly. Furthermore, the control approach has an overshoot of 0.505%. Because of phase current regulation, the RMS and peak current in the proposed control system are reduced, implying that the SOGI-FLL-PR control system has a lower copper loss. SOGI-FLL-PR has a maximum torque of 3.818 Nm and a minimum torque of 3.215 Nm. Furthermore, SOGI-FLL-PR has a torque ripple of 18.05%. This means that the SOGI-FLL-PR can decrease torque ripples and control torque values around 3 Nm. Table 2 summarizes the performance of the SOGI-FLL-PR control approach. It proves that the SOGI-FLL-PR control strategy provides greater torque per amp and reduced torque ripple. When the speed is adjusted from 1500 to 2000 rpm in 0.25 s while the load torque (2 Nm) remains constant, the speed and torque are shown in Fig. 18. When the speed varies, the SOGI-FLL-PR control method takes 0.04 s to reach the steady state, as demonstrated. As a result, the proposed control method provides a faster speed response.

Fig. 18

The simulation results when speed changes from 1500 to 2000 r/min a Rotor speed and b Total torque

Table 2 Summary of simulation results of the SOGI-FLL-PR current control method

4.3.1 Proposed SO-SOGI-FLL-PR current controller performance with different TSFs

The simulation results at 2000 r/min and a 2 Nm load torque are shown in Fig. 19. Given that the sample period is set to 1 microsecond, the torque ripples for the linear, cubic, exponential, and cosine TSFs, respectively, exhibit higher torque ripples of 15.80%, 10.48%, 54.53%, and 16.20%. To compare the TSFs fairly, the turn-on angle, turn-off angle, and overlap angle are kept constant for each of these cases. At 2000 r/min, exponential TSF torque ripples are nearly five times larger than cubic TSF torque ripples. Notably, the cubic TSF displays a slight reduction in torque ripple at a higher speed as a result of the proposed SOGI-FLL-PR current controller's improved tracking capability. Torque ripple at higher speeds can be further decreased by better tuning of control parameters.

Fig. 19

Simulation result of torque ripple for different TSFs (speed = 2000 r/min, $T_{l}$ = 2 Nm)

4.4 Fuzzy logic current controller (FLCC)

Using fuzzy logic, a simple intelligent current controller has been created and tested for SRM's closed-loop speed regulation. Figures 20 and 21 show simulation results with the FLCC, where $\theta_{{\text{on,elec}}} = 10^\circ$,$\theta_{{\text{off,elec}}} = 130^\circ$, and load torque ($T_{l}$) = 1 Nm. The torque ripple is found to be more severe in the commutation region and it further increases with speed.

Fig. 20

Reference and actual phase current waveforms (for one phase of SRM) with the fuzzy logic current controller at different rotor speeds ($T_{l}$ = 1Nm): a 750 r/min, b 1000 r/min, c 1500 r/min, and d 2000 r/min

Fig. 21

Total motor torque with the fuzzy logic current controller at different rotor speeds ($T_{l}$ = 1Nm): a 750 r/min, b 1000 r/min, c 1500 r/min, and d 2000 r/min

The quantitative results from these simulation experiments with hysteresis current controller, PI current controller, and FLCC are summarized and compared with those obtained with the proposed current control strategy in Table 3. The proposed current control method is superior in terms of performance. We find that the proposed controller yields the least amount of torque ripple. Further, the performance comparisons of the proposed controller based on torque ripple are done with some of the existing approaches reported in the literature [25, 26] and it is summarized in Table 4.

Table 3 Simulation results summary with three different current control strategies ($T_{{{\text{avg}}}}$ = average torque, $T_{{{\text{ripple}}}}$ = torque ripple)

Table 4 Torque ripple (simulation results) comparison with existing control strategies

4.5 Dynamic operation with the proposed current controller

The SRM drive's closed-loop dynamic operation is carried out by the proposed current controller while being sensitive to parameter changes and load torque disturbances.

4.5.1 Load torque disturbance

Figure 22 shows the SO-SOGI-FLL-PR controller's planned SRM drive's response to an abrupt change in load torque. Figure 22 shows the SRM in its default operating condition, with a load torque of 2 Nm and a rotational speed of 1500 r/min. A torque of 3 Nm is delivered abruptly to the SRM shaft at t = 0.5 s. The rotor slows down by 20 r/min as a result of this abrupt rise in load torque. As a consequence, the torque ripple increases from 9.39 to 11.607%.

Fig. 22

Total torque response of SRM drive system with SO-SOGI-FLL-PR controller during load torque disturbance

4.5.2 Parameter sensitivity effect

The effects of parameter changes are illustrated in Fig. 23 by varying the inertia (J) and phase winding resistance (R) of SRM. Initially, the motor is running with nominal values of J and R. The changes in values of J and R are considered at t = 0.5 s, where the value of J is doubled and the value of R is increased to five times the nominal value. The corresponding changes in inertia and phase resistance have minimal influence on torque output using the proposed current controller, as observed in Fig. 23. Even under parameter variations, the proposed controller performs satisfactorily without causing major degradation in drive performance.

Fig. 23

Total torque response of SRM drive system with SO-SOGI-FLL-PR controller during parameter variation

5 Experimental result analysis

Experimental testing of the proposed SOGI-FLL-PR current controller was done on a 1 hp, 1500 r/min, 6/4 SRM. The incremental encoder was utilized for rotor position sensing. The dSPACE system was used to implement the proposed current controller. The experimental setup is shown in Fig. 24. The proposed SRM drive system used an inner and an outer loop, as shown in Fig. 5.

Fig. 24

Experimental setup of the SRM drive system

While the PI speed controller functioned in the outer loop, the SOGI-FLL-PR current controller did so in the inner loop. Switching frequencies for pulse width modulation were limited to 5 kHz. Experimental work was done using the proposed current controller, which is based on the cubic torque sharing function. A look-up table (LUT) that took into account the impacts of mutual torque was used to determine the torque. The precision of the experiment-based simulation was comparable to the calculated torque from the LUT. The experiment's data were gathered in dSPACE and plotted in MATLAB. The real-time simulation and experiment test configuration for the SRM drive system is depicted in block diagram form in Fig. 25.

Fig. 25

Block diagram model of a test bench for real-time experiments on SRM drive system

The SRM drive system concentrates on an exact testing setup with a torque transducer and mechanical load. The SRM driving system is under the control of an asymmetric bridge converter. Mechanical inertia polling is employed as a mechanical load. MATLAB's hardware integration with the dSPACE-DS1104 is used to implement the proposed control schemes. Table 5 shows the components used in the controller and converter. For sensing and feedback of the three-phase currents and voltages, LA-55P and LV25-P current and voltage sensors were utilized, and a speed incremental encoder has linked to the machine shaft to acquire the speed. In a digital storage oscilloscope, a four-channel METRIX OX 9304 is interfaced with the dSPACE to produce the hardware findings.

Table 5 Experimental SRM specifications and details of other components used in the experimental setup

The electromagnetic torque's maximum ($T_{\max }$), minimum ($T_{\min }$), and $T_{{{\text{avg}}{.}}}$ average values for a certain period are used to determine the torque ripple in (27). One electrical cycle or more must be used as the calculation period. The accuracy of the electromagnetic torque estimation directly affects the accuracy of the real-time torque estimation. Thus, an electromagnetic torque estimate function was developed using the same static electromagnetic torque characteristics $T\left( {i_{{{\text{phase}}}} ,\theta } \right)$ look-up table (LUT) that was utilized in the simulation modeling [22,23,24,25]. Using the measured phase currents and rotor location, the LUT is searched to estimate the required motor torque.

$$ T_{{{\text{ripple}}}} (\% ) = \frac{{T_{\max } - T_{\min } }}{{T_{{{\text{avg}}}} }}*100 $$

(27)

5.1 Hysteresis and PI current controller performance

Figure 26 shows the experimental results with hysteresis and PI current control strategies, which $\theta_{{\text{on,elec}}}$ and $\theta_{{\text{off,elec}}}$ are set to 10° and 130°, respectively, and the load torque is set at 0.5 Nm. The following are the test conditions. The SRM is initially operating at 1500 revs per minute, then after some time, the reference speed is modified to 2000 revs per minute. Figure 26b displays the tracking performance of the hysteresis current controller (hysteresis band = 2%) at a speed of 1500 r/min, and Fig. 26d displays the corresponding motor torque profile. Figure 26c displays the tracking performance of the PI current controller at a speed of 2000 r/min, and Fig. 26e displays the matching motor torque profile. With two consecutive phases conducted during the switching region, a low level of inductance change will result in the production of insufficient torque by the concerned phase resulting in a higher torque ripple. Considering the SRM operation, negative torque is produced at higher speeds, which will eventually lead to high torque pulsations in the case of both hysteresis and PI current controllers.

Fig. 26

Experimental test results of laboratory SRM drive system: a speed profile, b current waveforms with hysteresis current controller (speed = 1500 r/min), c current waveforms with PI current controller (speed = 2000 r/min), d total motor torque with hysteresis current controller (speed = 1500 r/min), and e total motor torque with PI current controller (speed = 2000 r/min)

5.2 Fuzzy logic current controller performance

Figure 27 shows the hardware's experimental results at 2000 r/min and 0.5 Nm of load torque. High torque ripple results from a considerable tracking error in the current waveform. Due to a misalignment between the reference current and the incoming and outgoing phases, the latter are improperly magnetized and the former are demagnetized. This is because of the restrictions imposed by the flux linkage at higher speeds on the rate of change.

Fig. 27

Experimental results of SRM drive system with the fuzzy logic current controller ($T_{l}$ = 0.5 Nm, speed = 2000 r/min): a current waveforms, b motor speed, and c total torque

5.3 Proposed current control method with cubic TSF performance

The outcomes of tests using the proposed SO-SOGI-FLL-PR current controller at a 0.5 Nm load torque are shown in Fig. 28. The SRM's operating speed is initially set to 1500 r/min; however, as time goes on, the reference speed is raised to 2000 r/min. Figure 28b shows the proposed current controller's current racking performance at a speed of 1500 r/min, and Fig. 28d shows the motor torque profile at the same speed. Figure 28c shows the proposed current controller's tracking performance at 2000 r/min, and Fig. 28e shows the motor torque profile corresponding to that speed. The current waveforms show that the incoming and outgoing phases are magnetized and demagnetized properly relative to the reference current. The proposed controller achieves a smoother torque profile even when the torque production exceeds the torque reference, which reduces torque ripple. Notably, the proposed controller has reduced the torque ripple to 39.09 and 40.30%. By comparing the conduction regions in Fig. 26b and c, the whole performance range is more effective and the phase current stays inside the range using the proposed control technique. The negative torque production is enormously diminished. Consequently, the proposed control method makes full use of the available torque-generating capacity in each phase, hence lowering torque ripple.

Fig. 28

Experimental results of SRM drive system with SO-SOGI-FLL-PR current controller: a speed profile, b current waveforms (speed = 1500 r/min), c current waveforms (speed = 2000 r/min), d total motor torque (speed = 1500 r/min), and e total motor torque (speed = 2000 r/min)

5.4 Proposed current control method with different TSFs performance

Figure 29 displays the experiment's outcomes at 2000 revolutions per minute with a 0.5 Nm load torque. According to Fig. 29, the comparable values in the simulation results are 15.80%, 10.48%, 54.53%, and 16.20%, whereas the torque ripples of the linear, cubic, cosine, and exponential TSF are around 46.24, 40.70, 52, and 62%, respectively, in hardware experimental results. A larger-than-expected torque ripple is obtained in the experimental results compared to the simulation due to sensor noise in the commutation zone (see Fig. 29). As a consequence, in terms of torque ripples and torque response, the modeling findings and the experimental results of TSFs agree under the same operating conditions. Better tracking and nearly flat output torque at 2000 r/min are both achieved with the cubic TSF, which disregards the torque ripple introduced by the existing hysteresis, PI, and fuzzy current controller. Due to the current tracking inaccuracy, torque ripples in the linear, cosine, and exponential TSFs are substantially bigger than in the cubic TSF.

Fig. 29

Experimental result of torque ripple for different TSFs (speed = 2000 r/min, $T_{l}$ = 2 Nm)

5.5 Model predictive direct torque control method performance

According to the model proposed in the appendix, the MPDTC method's control block is shown in Fig. 34. Reference values of 1500 r/min, 2000 r/min, and 0.5 Nm have been selected for the rotor speed and load torque, respectively. In addition, 10 kHz is used for sampling. The control sampling time is set to 400 microseconds. Figure 30 shows the motor torque, and current of MPDTC methods under 1500 r/min and 2000 r/min at 0.5 Nm. Compared to the MPDTC system's 0.34 Nm and 0.32 Nm, SOGI-FLL-PR's average torques are 0.37 Nm and 0.35 Nm, respectively. Moreover, the MPDTC control method has a 48.12% and 54.20% torque ripple while SOGI-FLL-PR only has a 39.09% and 49.70% ripple. This indicates that the SOGI-FLL-PR control method is 6–7% more effective than the MPDTC method at damping torque ripple, and that torque levels are easily tunable to within 0.5 Nm. Under both SOGI-FLL-PR and MPDTC, the current trajectory of SRM looks very much like similar. MPDTC may significantly lower the torque ripple and the peak phase current. With the MPDTC, dSPACE takes 400 microseconds to compute while the proposed SOGI-FLL-PR takes 100 microseconds.

Fig. 30

Experimental test results of laboratory SRM drive system at $T_{l}$ = 0.5 Nm: a current waveforms with MPDTC controller (speed = 1500 r/min and 2000 r/min) and b total motor torque with MPDTC controller (speed = 1500 r/min, and 2000 r/min)

As the load increases, the overshoot in speed for both SOGI-FLL-PR and MPDTC is unavoidable. The speed vibration when using MPDTC is more pronounced than when using SOGI-FLL-PR, and the speed vibration is also more sensitive to changes in torque when using MPDTC. However, the drawback of SOGI-FLL-PR is its constrained working range and cubic TSF between two phases during commutation. The operating speed affects both the commuter schedule and the sharing feature. The machine's EMF grows with speed, which restricts the controller's capacity to change the current. Accurate tracking of the reference current is impossible when SRM switches to single pulse mode. Table 6 compares the average torque and torque ripple of the implemented controllers (hysteresis control, PI control, FLCC, MPDTC, and the proposed SO-SOGI-FLL-PR controller). Table 7 summarizes the results of comparing the proposed current controller to various methods of SRM for reducing torque ripple.

Table 6 Experimental results in comparison of the proposed control strategy ($T_{{{\text{avg}}}}$ = average torque, $T_{{{\text{ripple}}}}$ = torque ripple)

Table 7 Experimental performance comparison of the proposed current controller with other current controllers reported in the literature

5.6 Dynamic performance of SOGI-FLL-PR current control method

The dynamic performance of the proposed current control method is further assessed, with experimental findings displayed in Fig. 31. By displaying the waveforms of the phase current, rotor speed, and the generated torque, we can see how the motor responds to a sudden shift in the speed references. As shown in Fig. 31a, the motor reference speed is increased from 750 to 1500 r/min and then to 2000 r/min. As the reference speed changes, the closed-loop torque and stator currents adapt correspondingly. The increase in phase current corresponding to the reference speed is observed to be normal and the magnitude of the phase current does not exceed the limiting value as seen in Fig. 31b. The torque ripples during the reference speed changes are observed to be 28.45, 38.54, and 42.24%, respectively.

Fig. 31

Experimental results of SRM drive system with proposed current controller under variation motor speed: a motor speed, b current waveform, and c total torque

Figure 32 depicts the dynamic performance of the SRM with the proposed current controller as the load torque varies from 0.5 to 0.7 Nm and the SRM speed is 1500 r/min. As a consequence of the load change, the torque ripple increases from 43.33 to 48.52% as seen in Fig. 32c. Torque insufficiency at the commutation region might occur when the motor is operating under high load conditions and is unable to generate the required torque. Nonetheless, the proposed current control technique significantly reduces torque ripple as compared to the hysteresis controller, PI controller, FLCC, and MPDTC. Furthermore, the motor's stability is preserved despite load variations. As a result, the proposed control approach achieves both loading and acceleration stability.

Fig. 32

Experimental results of SRM drive system under variation load torque: a motor speed, b current waveform, and c total torque

Four successive speed command steps (1000 r/min, 2200 r/min, 3000 r/min, and 1250 r/min with defined time intervals between the commands) are now used in the experimental evaluation. The motor speed responses are shown in Fig. 33, showing satisfactory performance.

Fig. 33

Experimental results of SRM drive system with proposed current controller for step changes in reference speed

6 Conclusion

This paper proposes a PR current controller based on SOGI with FLL to decrease torque ripple in SRM across a wide range of speeds. A complete theoretical and experimental investigation was performed to demonstrate the efficacy of the current controller based on the pure integrator, the single SOGI, and the two in-series SOGIs with FLL. The second-order SOGI-FLL-based current controller performs well at low speeds, but the slower rate of change of flux linkage has a major impact on current tracking at higher speeds. Furthermore, the cubic TSF is used to allocate total torque to each phase. Simulation results for a 6/4, 1 hp, 3-phase SRM show the effectiveness of the proposed cubic TSF at the machine's nominal speed. According to simulations, this TSF could be employed at speeds greater than the basic speed (i.e., 1500 r/min) depending on machine dynamics and the availability of current control. At 1500 r/min and 2000 r/min, the proposed SOGI-FLL-PR current controller reduced torque ripple to 39.09 and 40.30%, respectively. The results demonstrate the proposed current control system's effectiveness in tracking current and reducing torque ripple. The proposed control approach is adaptable enough to be applied in any SRM phase configuration.

Fig. 34

The control block of the MPDTC method

Fig. 35

The voltage vectors of the asymmetric bridge converter

Table 8 Space voltage vectors state table of the SRM

Appendix

1.1 Model predictive direct torque control (MPDTC) method

SRM ought to investigate model predictive direct torque control (MPDTC) to lessen torque ripple in the low-speed range given that the switching frequency will be high at higher speed and result in a larger torque ripple. In this study, MPDTC [27] replaces conventional direct torque control (DTC) with double hysteresis control to eliminate torque pulsation and boost SRM performance. To reduce torque ripple, traditional MPDTC cost functions include total torque. To minimize torque ripple, this torque control strategy distributes the total electromagnetic torque to each phase using a cubic torque sharing function. Figure 34 shows the MATLAB/Simulink architecture used to create the MPDTC control system for the SRM drive experimental verification platform.

1.2 Voltage vector selection

Phases A, B, and C are the voltage vector's operational states. Figure 35 shows the eight sectors V0-V7 that make up the space voltage vectors area, with the basic space voltage vectors represented by N1–N8. The suitable space voltage vectors can control the flux linkage and torque. Additionally, Table 8 has a listing of the voltage vectors in space that are shown in Fig. 35.

1.3 Torque predictive model for SRM

The standard equation for the phase voltage is as follows:

$$ v_{q} = Ri_{q} + \frac{{{\text{d}}\lambda_{q} \left( {i_{q} ,\theta_{q} } \right)}}{{{\text{d}}t}};\quad q = 1,\,2,\,3,\, \ldots $$

(28)

where $v_{q}$, $R$, $i_{q}$, and $\theta_{q}$ are denoted as phase voltage, phase resistance, phase current, and phase rotor position, respectively. $\lambda_{q}$ is the phase flux, which depends on the phase current and the rotor position.

The dynamic model (28) could be modified in the following ways to facilitate the development of a torque predictive model:

$$ \frac{{{\text{d}}i_{q} }}{{{\text{d}}t}} = \frac{1}{{{\text{d}}\lambda_{q} /{\text{d}}i_{q} }}\left( {v_{q} - Ri_{q} - \frac{{{\text{d}}\lambda_{q} }}{{{\text{d}}\theta_{q} }}\omega } \right) $$

(29)

$$ \frac{{{\text{d}}\theta_{q} }}{{{\text{d}}t}} = \omega $$

(30)

where $\omega$ is the rotor speed. The digital device operates in discrete time. As a result, the continuous-time model must be transformed into a discrete-time model.

$$ \begin{gathered} i_{k + 1} = i_{k} + \frac{{T_{s} }}{{{\text{d}}\lambda /{\text{d}}i_{k} }}\left[ {v_{k + 1} - Ri_{k} - \frac{{{\text{d}}\lambda }}{{{\text{d}}\theta_{k} }}\omega_{k} } \right] \hfill \\ \theta_{k + 1} = \theta_{k} + \omega_{k} T_{s} \hfill \\ T_{e,k + 1} = \sum T_{{{\text{ph}},k + 1}} \hfill \\ \end{gathered} $$

(31)

We can determine the phase torque at the (k + 1) instant by predicting the phase current and rotor position at the kth step. Once the cost function is defined, it may be used to pick the best vector for controlling the voltage.

$$ {\text{Min}}\,J\left( {u_{k} } \right) = \left( {T_{e,k + 1} - T_{d} } \right)^{2} ;\;u_{k} \in \left\{ {N1,\,N2,\, \ldots \,,\,N8} \right\} $$

(32)

1.4 Hysteresis current control

The full negative DC link voltage ($- V_{{{\text{dc}}}}$), chosen based on motor voltage rating, is applied by the hysteresis current controller across a phase winding during turn-off. The hysteresis current controller generates switching signals, which are fed to the asymmetric bridge converter to switch the DC link voltage for regulating the phase currents. To maintain the phase current at the computed $i_{{{\text{ref}}{.}}}$, a hysteresis band is defined by $i_{{{\text{upper}}}}$ and $i_{{{\text{lower}}}}$. These values are calculated based on $i_{{{\text{ref}}{.}}}$ and a tolerance band $\alpha$, as shown in (Eq. 33). Generally, $\alpha$ is given as a percentage of the current reference, $i_{{{\text{ref}}{.}}}$.

$$ \begin{gathered} i_{{{\text{upper}}}} = i_{{{\text{ref}}}} (1 + \alpha ) \hfill \\ i_{{{\text{lower}}}} = i_{{{\text{ref}}}} (1 - \alpha ) \hfill \\ \end{gathered} $$

(33)

Hysteresis control of phase current is implemented using soft (unipolar) switching strategy [15], at time step k, as shown in Eq. 34.

$$ V_{{{\text{ph}}}} \left( k \right) = \left\{ \begin{gathered} 0\parallel {\text{ref}}{\text{.current}} \le 0 \cap i_{{{\text{ph}}}} \le 0 \hfill \\ - V_{{{\text{dc}}}} \parallel ... \cap i_{{{\text{ph}}}} > 0 \hfill \\ 0\parallel {\text{ref}}{\text{.current}} > 0 \cap i_{{{\text{ph}}}} \ge i_{{{\text{upper}}}} \hfill \\ + V_{{{\text{dc}}}} \parallel ... \cap i_{{{\text{ph}}}} < i_{{{\text{lower}}}} \hfill \\ V_{{{\text{ph}}}} (k - 1)\parallel ... \cap i_{{{\text{upper}}}} > i_{{{\text{ph}}}} \ge i_{{{\text{lower}}}} \hfill \\ 0\parallel ... \cap {\text{otherwise}} \hfill \\ \end{gathered} \right. $$

(34)

where the sign “$\parallel$”denotes provided and the symbol “$\cap$” represents logical.