Second-Order Generalized Integrator-Based Proportional-Resonant Current Controller for Torque Ripple Minimization in Switched Reluctance Motors

Abstract

In this paper, a second-order generalized integrator (SOGI)-based proportional-resonant (PR) current controller is proposed to minimize the torque ripple in switched reluctance motor (SRM) drives. The reference current for each phase of SRM is generated based on smooth torque sharing functions (TSFs). The TSF is dependent upon turn-on angle, turn-off angle, overlap angle, and demand torque. The SOGI-based PR current controller is implemented to track the reference current. Ideally, the SOGI-PR controller has an infinite gain at a resonant frequency, which should be the same as the frequency of the reference current which changes with the rotor position. The short-time Fourier transform (STFT) is employed to determine the frequency of reference current which varies with the rotor position. The simulation study on a 3-phase, 1-hp SRM shows efficient tracking performance by the proposed current controller to reduce the torque ripple.

1 Introduction

The torque ripple is an inherent disadvantage of switched reluctance motor (SRM) drives. The main reasons for torque pulsation are due to its doubly salient structure and operation in the commutation period where the torque generation is shifted from one phase winding to another. The issue of torque ripple reduction has been addressed by many researchers [1,2,3]. The instantaneous torque control is picking up enthusiasm for torque ripple minimization; this is done by changing the phase current profile with rotor position. This includes greater adaptability in torque ripple minimization [4]. Phase current profiling has been a widely proposed technique to minimize torque ripple, and these current profile defining techniques are called torque sharing functions (TSFs) [3]. For torque ripple minimization, the reference currents must be loyally followed by the particular stator phase windings. Torque sharing function (TSF) is a powerful way to deal with executing the control of torque ripple reduction in SRM drives [5,6,7,8,9].

This paper proposes a novel current controller for a 1-hp, 3-phase, 6/4 SRM. The reference current for various phases is generated by cubic TSFs. The proposed current controller is essentially a second-order generalized integrator (SOGI)-based proportional-resonant (PR) control. Theoretically, a proportional-integral (PI) controller has a pole at zero frequency, thereby not being able to eliminate steady-state error at any specific frequency $\omega_{0}$. The SOGI-based PR controller introduces an infinite gain at the resonant frequency ($\omega_{0}$), which is equal to the instantaneous frequency of the reference current to achieve a good tracking effect [10, 11]. The frequency of the reference current in each time-window is determined by the short-time Fourier transform (STFT) algorithm [12]. The proposed control structure is evaluated, by simulation studies, on an SRM drive. The current controller tracking performance is noted to be very effective, and thus, the torque ripple is significantly reduced. The proof-of-concept is verified by the simulation studies. The results and analysis are presented.

The paper is organized as follows. In Sect. 2, the static electromagnetic characteristics of the SRM used in this study are discussed. Section 3 presents the detailed torque control of SRM using the proposed current controller. The simulation results are provided in Sect. 4. Section 5 concludes the paper.

2 Static Electromagnetic Characteristics of Switched Reluctance Motor

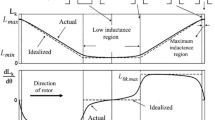
The doubly salient structure (for both stator and rotor) of an SRM is fundamental to its torque generation mechanism [3]. The mutual coupling between phase of SRM is negligible. The rotating motion of SRM is due to the production of reluctance torque. To get flux-linkage characteristics, a constant current is applied to one of the stator phases at a fixed rotor position for one electrical cycle. Repeating similar experiments with various current levels shows how the flux characteristics change as the SRM saturates magnetically. Figure 1 shows the flux-linkage characteristics obtained for the 1-hp SRM, used in this study, at various rotor positions (unaligned position = 0° elect.; aligned position = 180° elect.).

Fig. 1

Static flux-linkage characteristics of the 1-hp SRM for one electrical cycle

The electromagnetic torque characteristics can also be experimentally for various constant current excitations at various rotor positions, and they are shown in Fig. 2 for the 1-hp SRM. It can be seen that the torque is positive when the rotor movement is from the unaligned to aligned position, and the produced torque is negative when the rotor moves from the aligned to unaligned position.

Fig. 2

Static torque characteristics for the 1-hp SRM

3 Proposed Current Controller for Torque Control of SRM

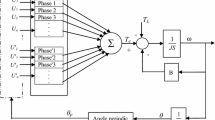
A 1-hp, 3-phase, 6/4 SRM is used for this study. The dynamic block diagram model used for the torque control studies using the proposed current controller is shown in Fig. 3. A two-phase-on excites scheme is used. The control algorithm operates as follows. The reference torque $T_{{{\text{ref}}}}$ for each phase of SRM is calculated from the demand/desired torque $T_{{\text{d}}}$ using the cubic TSFs, turn-on angle $\theta_{{{\text{on}}}}$, turn-off angle $\theta_{{{\text{off}}}}$, and overlap angle $\theta_{{{\text{ov}}}}$. By using linear interpolation of the lookup table of experimental data with current as a function of rotor position and torque, the reference current $i_{{{\text{ref}}}}$ is obtained for the reference torque $T_{{{\text{ref}}}}$ and specific rotor position $\theta_{{{\text{elec}}}}$. The SOGI-PR controller is used to produce the control signal (phase voltage) as shown. The SOGI-PR controller is used instead of the proportional integral (PI) current controller because the PI controller provides infinite gain only at zero frequency, and thus, it is not able to track the reference current at any other frequency. The frequency $\omega_{0}$ of reference current for SOGI is computed by the STFT algorithm for each sliding time window. The generated phase voltages are utilized to drive the asymmetric bridge converter connected to stator windings of SRM.

Fig. 3

Complete dynamic model for SRM torque control

3.1 Dynamic Modeling of Switched Reluctance Motor

The dynamic behavior of SRM is analyzed by its dynamic model [3]. The torque generation ability essentially improves under magnetic saturation. This must be viewed in modeling the SRM. The SRMs are not energized with sinusoidal current. The SRM requires a distinctive modeling procedure for its dynamic evaluation. Figure 4 shows the complete dynamic model of switched reluctance motor in the discrete domain. Although it is possible in both continuous and discrete forms, the discrete form is helpful for digital controller implementation. The voltage equation in Fig. 4 can be used to calculate the dynamic current waveform. Once the current waveform is calculated, it can be applied to the torque lookup-table to calculate the dynamic torque magnitude for each phase (λ = flux-linkage).

Fig. 4

Dynamic model of SRM used for toque control studies

3.2 Torque Sharing Function

A torque sharing function (TSF) cleverly partitions a steady torque demand among various phases by characterizing a reference current profile for each phase [3]. A basic method of characterizing a torque sharing function for mth phase is represented as follows:

$$T_{{{\text{ref}}}} \left( n \right) = \left\{ {\begin{array}{*{20}l} {0,} & {0 \le \theta_{{{\text{elec}}}} < \theta_{{{\text{on}}}} } \\ {T_{{{\text{ref}}}} f_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right),} & {\theta_{{{\text{on}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} } \\ {T_{{{\text{ref}}}} ,} & {\theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{off}}}} } \\ {T_{{{\text{ref}}}} f_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right),} & {\theta_{{{\text{off}}}} \le \theta_{{{\text{elec}}}} < \theta_{{{\text{off}}}} + \theta_{{{\text{ov}}}} } \\ {0,} & {\theta_{{{\text{off}}}} + \theta_{{{\text{ov}}}} \le \theta_{{{\text{elec}}}} < \theta_{{\text{p}}} } \\ \end{array} } \right.$$

(1)

With cubic TSF, the torque delivered by the phases during phase commutation changes nonlinearly with the rotor position. This nonlinearity is expressed by a cubic polynomial. The cubic TSF determines the phase torque commitment in the commutation area as a cubic function. This is shown in Fig. 5, and the formulae for $f_{{{\text{rise}}}} \left( \theta \right)$ is expressed as in Eq. (2) with the coefficients $\beta_{0} ,\beta_{1} ,\beta_{2} ,\,{\text{and}}\,\beta_{3}$.

$$f_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \beta_{0} + \beta_{1} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} ) + \beta_{2} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} )^{2} + \beta_{3} (\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} )^{3}$$

(2)

Fig. 5

Cubic torque sharing functions (TSFs)

To ensure that this TSF is continuous for all rotor positions, the imperatives are set as follows:

$$f_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \left\{ {\begin{array}{*{20}l} {0,} & {\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} } \right)} \\ {1,} & {\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} } \right)} \\ \end{array} } \right\}\,\,\,\frac{{{\text{d}}f_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right)}}{{{\text{d}}\theta_{{{\text{elec}}}} }} = \left\{ {\begin{array}{*{20}l} {0,} & {\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} } \right)} \\ {0,} & {\left( {\theta_{{{\text{elec}}}} = \theta_{{{\text{on}}}} + \theta_{{{\text{ov}}}} } \right)} \\ \end{array} } \right\}$$

(3)

Then, by substituting Eq. (2) in Eq. (3), the coefficients of the cubic TSF can be derived as in Eq. (4), and the cubic TSF can be obtained as given in Eq. (5).

$$\beta_{0} = 0,\,\,\beta_{1} = 0,\,\,\beta_{2} = \frac{3}{{\theta_{{{\text{ov}}}}^{2} }},\,\,\beta_{3} = \frac{ - 2}{{\theta_{{{\text{ov}}}}^{3} }}$$

(4)

$$\begin{gathered} f_{{{\text{rise}}}} \left( {\theta_{{{\text{elec}}}} } \right) = \frac{3}{{\theta_{{{\text{ov}}}}^{2} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} } \right)^{2} - \frac{2}{{\theta_{{{\text{ov}}}}^{3} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{on}}}} } \right)^{3} , \hfill \\ f_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right) = 1 - f_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} + \theta_{{{\text{on}}}} - \theta_{{{\text{off}}}} } \right) \hfill \\ f_{{{\text{fall}}}} \left( {\theta_{{{\text{elec}}}} } \right) = 1 - \frac{3}{{\theta_{{{\text{ov}}}}^{2} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} } \right)^{2} - \frac{2}{{\theta_{{{\text{ov}}}}^{3} }}\left( {\theta_{{{\text{elec}}}} - \theta_{{{\text{off}}}} } \right)^{3} \hfill \\ \end{gathered}$$

(5)

3.3 SOGI-Based PR Controller

The typical structure of a first-order integral controller structure is shown in Fig. 6. The system precisely follows the applied DC (constant reference) signal because of the infinite gain of at zero frequency. This is the basis of the proportional integral (PI) controller. Thus, it cannot faithfully track a reference signal (phase current) at some other frequency.

Fig. 6

Typical structure of standard first-order integral controller

To overcome this, a SOGI-quadrature signal generator (QSG)-based proportional-resonant (PR) controller is used by the researchers. The standard structure of the SOGI-quadrature signal generator-based proportional-resonant controller is shown in Fig. 7. The SOGI is derived from the generalized integrator (GI) as represented in Eq. (6), which is the main component of the proportional-resonant (PR) controller. The second-order generalized integrator is the principal block of the SOGI-quadrature signal generator whose transfer function is given in Eq. (7).

$${\text{GI}}\,(s) = \left[ {\frac{2s}{{s^{2} + \omega_{0}^{2} }}} \right]$$

(6)

$${\text{SOGI}}\,(s) = \left[ {\frac{{\omega_{0} s}}{{s^{2} + \omega_{0}^{2} }}} \right]$$

(7)

Fig. 7

Structure of SOGI-QSG-based PR current controller

According to Eq. (7), the SOGI has magnitude integration qualities for the input sinusoidal signal. This trademark is very much like the ideal integrator for input dc-signal integration. Thus, the attributes of the SOGI-QSG are predictable with the first-order system which can assess the sinusoidal sign. Taking that into account, the structure shown in Fig. 6 is a first-order system (FOS) for DC assessment. The SOGI-quadrature signal generator would thus be able to be taken as a magnitude FOS for sinusoidal signal assessment. The SOGI-QSG-based PR controller, shown in Fig. 7, has high gains at its resonant frequencies (frequency of interest). Thereby, the corresponding term in control output given by Eq. (8) is responsible for tracking the signal (phase current) component at the instantaneous frequency $\omega_{0}$.

$$u\,(s) = K_{{\text{p}}} + \frac{{K_{1} \omega_{0} s}}{{s^{2} + K_{1} \omega_{0} s + \omega_{0}^{2} }}*K_{{\text{r}}}$$

(8)

where SOGI gain $K_{1}$ compares to the band-pass filter transfer function damping ratio as indicated by: $\xi = \frac{{K_{1} }}{2}$. It is typically helpful to set $\xi \ge 0.5$ to achieve a reasonably well-damped response. The numerical values of the control parameters $K_{{\text{p}}}$ and $K_{{\text{r}}}$ are providing optimum performance in the current tracking.

3.4 Short-Time Fourier Transform

The frequency $\omega_{0}$ of the reference current in each time-window is determined by the short-time Fourier transform (STFT) algorithm. The STFT breaks a long signal data into small segments, alternatively covered as well as windowed, and finds the discrete Fourier transform of each (windowed) fragment independently to record the nearby spectra in a matrix with frequency-time lists [12] and expressed in Eq. (9).

$$\begin{gathered} {\text{STFT}}\left\{ {x\left[ n \right]} \right\} = X\left[ {k,n} \right] = \sum\limits_{m = 0}^{N - 1} {x\left[ {m + n} \right]} w\left[ m \right]W_{N}^{km} \hfill \\ \quad \quad \mathop = \limits^{m \to m - n} \sum\limits_{m = n}^{n + N - 1} {x\left[ m \right]} w\left[ {m - n} \right]W_{N}^{k(m - n)} \quad {\text{for}}\,k = 0,1, \ldots ,N - 1 \hfill \\ \end{gathered}$$

(9)

where the window w[m] is used to select a finite-length reference current data segment from the sliding sequence x [m + n] and possibly to reduce the spectral leakage.

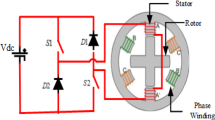
3.5 Asymmetric Bridge Converter

The asymmetric bridge converter for one phase of SRM is shown in Fig. 8. The bridge converter provides current to the stator windings of the switched reluctance motor. The torque generated in the SRM is not dependent on the course/sign of the current in the stator phase windings. The asymmetric bridge converter has two free-wheeling diodes and two semiconductor switches for each phase. Based on the torque generation principle, the most popular unipolar switching strategy is implemented in this type of converter to provide both ± phase voltages [13]. The implementation method for unipolar switching is presented in Eq. (10).

$$v_{{\text{a}}} = \left\{ {\begin{array}{*{20}l} {V_{{{\text{dc}}}} ,} & {i_{{{\text{ref}}}} > 0,\,v_{{\text{c}}} \ge v_{{{\text{ramp}}}} \,{\text{and}}\, - v_{{\text{c}}} < v_{{{\text{ramp}}}} } \\ { - V_{{{\text{dc}}}} ,} & {i_{{{\text{ref}}}} > 0,\,v_{{\text{c}}} < v_{{{\text{ramp}}}} \,{\text{and}}\, - v_{{\text{c}}} \ge v_{{{\text{ramp}}}} } \\ {0,} & {{\text{elsewhere}}} \\ \end{array} } \right.$$

(10)

Fig. 8

Asymmetric bridge converter for phase 1 of SRM

where $v_{{\text{c}}}$ is the control signal, $v_{{{\text{ramp}}}}$ is the carrier signal, and $v_{{\text{a}}}$ is the phase voltage provided by the asymmetric bridge converter.

4 Simulation Results and Discussion

The proposed SOGI-PR current controller has been evaluated by simulations on 3-phase, 1-hp, 6/4 SRM. The SRM is assumed to be rotating at a constant speed. The simulation results for $\theta_{{{\text{on}}}} = 10^{\circ } ,\,\theta_{{{\text{off}}}} = 130^{\circ } ,\,\theta_{{{\text{ov}}}} = 35^{\circ }$, and $T_{{\text{d}}} = 2\,{\text{Nm}}$ are presented below. The reference current $i_{{{\text{ref}}}}$ for each phase is computed by the cubic TSFs. The various frequency components of the reference current are calculated by the STFT algorithm. The other parameters of the controller are $K_{{\text{p}}}$ = 2 and $K_{{\text{r}}}$ = 0.05. The phase reference current and its spectrogram are shown in Fig. 9. From the spectrogram analysis, the frequency of the higher magnitude component in each time-window is fed to the SOGI-PR controller. For a speed of 1500 rpm, the phase current and torque tracking performances are shown in Fig. 10. It can be seen that the tracking performance of the phase current waveform is very good leading to a smooth torque profile with 28.97% torque ripple. Figures 11 and 12 show the output torque and phase currents for two different speed conditions. At a low speed of 750 rpm, the SOGI-PR controller shows good performance because the current controller can track the reference command with very less tracking error due to the smooth current reference waveform. At a higher speed of 1500 rpm, the bandwidth of the current control loop is not sufficient to track the reference command because of higher induced emf.

Fig. 9

a Reference current; b spectrogram of reference current for phase 1 at $T_{{\text{d}}} = 2\,{\text{Nm}},\,{\text{speed}} = 1500\,{\text{rpm}}$

Fig. 10

Reference current and torque tracking for $\theta_{{{\text{on}}}} = 10^{\circ } ,\,\theta_{{{\text{off}}}} = 130^{\circ } ,\,\theta_{{{\text{ov}}}} = 35^{\circ } ,\,T_{{\text{d}}} = 2\,{\text{Nm}}$ and speed = 1500 rpm

Fig. 11

Total torque produced and current waveform at speed of 750 rpm and demand torque of 2 Nm

Fig. 12

Total torque produced and current waveform at speed of 1500 rpm and demand torque of 2 Nm

5 Conclusion

A novel SOGI-PR current controller structure to reduce the torque ripple in switched reluctance motor has been presented in this paper. The dynamic model of SRM is modeled based on the measured flux-linkage and torque characteristics data of a 1-hp 3-phase SRM. The SOGI-based PR controller has been implemented with cubic TSF to analyze the tracking performance of both the current and torque command. The STFT is used to obtain the time variations in the frequency of the phase reference current. The MATLAB/SIMULINK simulation results show that the proposed current control structure can be effectively used to achieve the torque ripple reduction in SRM drives.