1 Introduction

Induction motors (IMs) are widely used in industrial applications and electrical vehicles that require high-performance variable speed and/or torque control because of their characteristic advantages such as high durability, reliability, and low cost. The dynamic performances of IM drives have remarkably improved with the introduction of vector control-based methods such as the direct torque control (DTC) and the field-oriented control (FOC) systems. Thus, IM drives have become suitable for the industrial applications and electric vehicles that require exact control. Nevertheless, the control performance of the IM drive depends directly on the performance of the estimation algorithms. The performances of estimation algorithms are affected by changes in both electrical and mechanical parameters of the IM. When the IM runs, the stator and rotor resistances (\(R_s\) and \(R_r\)) change with temperature and frequency (skin effect) [1, 2]. In addition, the magnetizing inductance (\(L_m\)) hence stator and rotor inductances (\(L_s\) and \(L_r\)) depends on the flux level changes in the field-weakening region of the IM. Also, changes in load torque can be described as mechanical uncertainties [3]. In order to obtain a reliable and correct knowledge of the flux angle and magnitude utilized in vector-based IM control methods such as FOC and DTC, these changing electrical parameters or mechanical uncertainties in the IM model need to be exactly known, estimated as online, or eliminated. To achieve higher estimation accuracy, numerous deterministic and stochastic-based observers and estimators algorithms for different state and/or parameter estimations are proposed in the literature [4]. Open-loop estimators [5, 6], artificial neural network (ANN) [7], extended Luenberger observer [8, 9], full-order observer (FOO) [10], adaptive flux observer, [11], sliding-mode observer (SMO) [12, 13], model reference adaptive system (MRAS) [14, 15], extended Kalman filters (EKF) [3, 16,17,18], and unscented Kalman Filter [19, 20] are main methods reported.

When the studies employing deterministic based methods for state or parameter estimation are examined, in [8], stator currents (\(i_{s\alpha }\) and \(i_{s\beta }\)) and stator fluxes (\(\varphi _{s\alpha }\) and \(\varphi _{s\beta }\)) are estimated using a Luenberger observer. In [10] estimation of the stator fluxes is performed by a FOO, where the stator current errors are fed-back to the FOO to improve the estimation of the stator fluxes. However, in [8, 10] the changes in motor parameters are ignored. In [12], the stator fluxes and rotor/stator resistance estimations are realized with the adaptive SMO. In [15], the estimations of \(R_r\) and \(L_m\) are realized by an MRAS utilizing the rotor fluxes provided by two SMOs. The results of the study show that the estimations of rotor resistance and magnetizing inductance are dependent on each other. Therefore, for better estimation performance a decoupling method is proposed, which is designed in [21]. In [22] are presented estimations of the rotor speed, the stator resistance, and the inverse rotor time constant by an MRAS-based ANN. In [23] estimation of the rotor time constant of IM is realized by the least-squares method.

Contrary to the other model-based estimation methods, EKF observes offer a stochastic approach in order to estimate the states and parameters of IM taking into account the system and measurement noises. Therefore, the EKF is a high-performance observer algorithm for estimations of states and/or parameters for noisy nonlinear systems [24]. In addition, the EKF is applicable to any IM at a wide speed range from very low to high speeds. Many researchers are focused on using an EKF observer for the state and parameter estimations. When EKF observer-based studies in the literature are examined, estimation of the stator fluxes and stator currents are presented in [16], where the changes in motor parameters are neglected. As well as the \(i_{s\alpha }\) and \(i_{s\beta }\) and \(\varphi _{s\alpha }\) and \(\varphi _{s\beta }\), \(R_r\) and \(R_s\) estimations are also presented in [25]. The authors of [25] state that the proposed EKF algorithm requires the correct magnetizing inductance value in the field-weakening region. [26] introduces a reduced-order EKF algorithm utilizing rotor flux-based motor model for estimations of the rotor flux, rotor resistance, and magnetizing inductance. In [3], the measurement matrix of the motor model used in the EKF observer is expanded by the measured rotor speed in addition to the measured stator currents, in order to make better the estimation performance of the rotor fluxes, rotor velocity (\(\omega _m\)), stator currents, magnetizing inductance, rotor resistance, and load torque. However, expanding the measurement matrix of the motor model used in the EKF has been increased execution time and design complexity. Moreover, there are other EKF-based studies concentrating on the increase in the number of estimated states and parameters, which are called bi-input EKF in [27,28,29]. In spite of increasing the number of states/parameters, these studies are required two different IM models in a single EKF. Therefore, their computational burden and memory requirement increase for the microprocessor together with making the design, as well as the tuning process difficult regarding the number of noise covariance matrices’ elements to be tuned, can be classified as their disadvantages.

The main contribution of this study is introducing an EKF-based estimator with a low computation burden that is not affected by changes in the \(R_r\), \(L_s\), \(L_r\), and \(L_m\), in order to estimate the \(\omega _m\), \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), and \(\tau _l\). For this aim:

  • The reduced IM model is constructed for the EKF observer by using the stator fluxes and the equation of motion from the traditional stator flux-based IM model equations.

  • In contrast to the previous studies [16,17,18, 25], the proposed reduced model does not use the stator current equations of the conventional IM model. Therefore, the reduced model used EKF observer is not included the \(R_r\), \(L_m\), \(L_s\), and \(L_r\) parameters of IM.

  • Since the reduced IM model used by the proposed EKF-based estimator does not include \(R_r\), \(L_m\), \(L_s\), and \(L_r\) from the motor parameters, the estimation performance of the EKF algorithm is not affected by changes in the \(R_r\), \(L_m\), \(L_s\), and \(L_r\).

  • In contrast to the previous studies that use the stator currents [17, 25] and the stator currents and rotor speed [3] in the measurement equations, the proposed EKF-based algorithm uses only the rotor angular velocity.

  • The average execution time of each iteration for the proposed EKF observer which uses the reduced IM model has been measured as \( 2.1 \mu s \).

The operation of matrix inversion that is necessary for the previous EKF algorithms utilizing the stator currents [17, 25] and the rotor speed and the stator currents [3] in the measurement equation is translated in the inverse of a real number in the proposed EKF. Therefore, the EKF observer using the proposed reduced IM model does not require matrix inversion. Likewise, the size of the measurement and system noise covariance matrices required to be determined for the EKF observer is reduced due to the use of the reduced IM model. Thus, in the EKF observer where matrix multiplications are made intensively, the element-based multiplication operations are also decreased. To confirm the performance of the EKF observer in DTC-based IM drive, challenging scenarios are produced under variations of the \(R_r\), \(L_m\), and \(\tau _l\) in a wide speed range including field-weakening zone and zero speed in the simulations. Simulation results obtained from EKF and DTC system show very high performance for both the estimation and the control. Finally, the correctness and the effectiveness of the EKF-based estimator are demonstrated by experimental results under variations in \(\omega _m\), \(\tau _l\), and \(R_s\) in a wide speed range.

The rest of this paper is organized as follows: Section 2 derives the mathematical model of IM. Section 3 gives the design stages of the EKF observer. Section 4 demonstrates the simulation results of the DTC-based drive system and EKF observer. Section 5 shows the hardware configuration. Section 6 presents the real-time experimental results of the EKF observer. Finally, Sect. 7 gives the conclusion.

2 Mathematical model of IM

The continuous-time differential expressions of the stator flux-based IM model in the stator stationary axis (\(\alpha \beta -\) axis) and the equation of motion can be expressed in the following equations: [18, 29]

$$\begin{aligned} \frac{di_{s\alpha }}{dt}= & {} -\left( \frac{R_s}{L_{\sigma }}+\frac{R_{r} L_{s}}{L_{r}L_{\sigma }}\right) i_{s\alpha } - p_p\omega _{m}i_{s\beta } \nonumber \\{} & {} + \frac{R_r}{L_{r}L_{\sigma }}\varphi _{s\alpha } + \frac{p_p\omega _{m}}{L_{\sigma }}\varphi _{s\beta } + \frac{v_{s\alpha }}{L_{\sigma }} \end{aligned}$$
(1)
$$\begin{aligned} \frac{di_{s\beta }}{dt}= & {} -\left( \frac{R_s}{L_{\sigma }}+\frac{R_{r} L_{s}}{L_{r}L_{\sigma }}\right) i_{s\beta } - p_p\omega _{m}i_{s\alpha } \nonumber \\{} & {} + \frac{R_r}{L_{r}L_{\sigma }}\varphi _{s\beta } - \frac{p_p\omega _{m}}{L_{\sigma }}\varphi _{s\alpha } + \frac{v_{s\beta }}{L_{\sigma }} \end{aligned}$$
(2)
$$\begin{aligned} \frac{d\varphi _{s\alpha }}{dt}= & {} -R_{s}i_{s\alpha } + v_{s\alpha } \end{aligned}$$
(3)
$$\begin{aligned} \frac{d\varphi _{s\beta }}{dt}= & {} -R_{s}i_{s\beta } + v_{s\beta } \end{aligned}$$
(4)
$$\begin{aligned} \frac{d\omega _{m}}{dt}= & {} \frac{3}{2}\frac{p_{p}}{J_{t}}(\varphi _{s\alpha }i_{s\beta } - \varphi _{s\beta }i_{s\alpha })\nonumber \\{} & {} - \frac{B_{t}}{J_{t}}\omega _{m} - \frac{\tau _{l}}{J_{t}} \end{aligned}$$
(5)

where \(v_{s\alpha }\) and \(v_{s\beta }\) are the stator voltages, \(p_{p}\) is the pole pairs, \(L_\sigma = L_{s} - L_{m}^{2}/L_{r}\) is the stator transient inductance, \(B_{t}\) and \(J_{t}\) are total viscous friction and inertia term of both load and motor, respectively. The continuous-time stator flux-based IM model in the stator stationary axis can be expressed in the following general form:

$$\begin{aligned} \dot{\textbf{x}}_{t}&=\textbf{f}(\textbf{x}_{t},\textbf{u}_{t})+\textbf{w}_{t}\nonumber \\&={\textbf {A}}({\textbf {x}}_{t}){\textbf {x}}_{t}+{\textbf {B}}{} {\textbf {u}}_{t}+{\textbf {w}}_t \end{aligned}$$
(6a)
$$\begin{aligned} \textbf{z}_{t}&=\textbf{h}(\textbf{x}_{t})+\textbf{v}_{t}~~ \text {(Measurement Equation)}\nonumber \\&={\textbf {H}}{} {\textbf {x}}_{t}+{\textbf {v}}_t \end{aligned}$$
(6b)

where \( \textbf{f} \) is the nonlinear function of states and inputs, and \( \textbf{x}_t \) and \( \textbf{u}_{t} \) are the state and the control input vector, respectively. \(\textbf{w}_{t}\) and \(\textbf{v}_{t}\) are the process and measurement noises, respectively. \(\textbf{h}\) is the function of outputs. \( \textbf{A} \), \( \textbf{B}, \) and \( \textbf{H} \) are the system matrix, the input matrix, and the measurement matrix, respectively.

The IM model, the general form of which is given in equation (6a), can be discretized by using the forward Euler approximation shown in (7).

$$\begin{aligned} \dot{\textbf{x}}_t \approx \frac{\textbf{x}_{k+1} - \textbf{x}_{k}}{T} \end{aligned}$$
(7)

3 Extended Kalman filter observer

In order to simultaneously estimate \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), \(\omega _{m}\), and \(\tau _{l}\), the reduced IM model given the discretized state equations in (8) and (9) is constructed for the EKF observer by using (3)–(5) from the traditional stator flux-based IM model equations. Since the model used in the EKF observer does not include the stator current equations (see (1) and (2)) of the conventional IM model, it is defined as the reduced-order motor model. Because EKF observer uses directly measured current information instead of stator current states given in (1) and (2), it is made independent from \(L_s\), \(L_r\), \(L_m\), and \(R_r\) parameters of IM. In the reduced IM model used in the EKF observer, \(\tau _{l}\) is considered a constant state, and the viscous friction term, \(B_{t}\omega _{m}\), is included in \({\hat{\tau }}_{l}\).

$$\begin{aligned}{} & {} \underbrace{\left[ \begin{array}{c} \varphi _{s\alpha ,k+1} \\ \varphi _{s\beta ,k+1} \\ \omega _{m,k+1} \\ \tau _{l,k+1} \end{array}\right] }_{{\textbf {x}}_{k+1}}=\underbrace{\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ \frac{3p_{p}i_{s\beta }T}{2J_{t}} &{} \frac{-3p_{p}i_{s\alpha }T}{2J_{t}} &{} 1 &{} \frac{-T}{J_{t}} \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] }_{\textbf {A}} \underbrace{\left[ \begin{array}{c} \varphi _{s\alpha ,k} \\ \varphi _{s\beta ,k} \\ \omega _{m,k} \\ \tau _{l,k} \end{array}\right] }_{{\textbf {x}}_{k}}\nonumber \\{} & {} \quad + \underbrace{\left[ \begin{array}{cc} T &{} 0 \\ 0 &{} T \\ 0 &{} 0 \\ 0 &{} 0 \end{array}\right] }_{{\textbf {B}}} \underbrace{\left[ \begin{array}{c} v_{s\alpha }-R_{s}i_{s\alpha } \\ v_{s\beta }-R_{s}i_{s\beta } \end{array}\right] }_{{\textbf {u}}_{k}}+{\textbf {w}} \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \underbrace{\left[ \begin{array}{c} \omega _{m,k} \end{array}\right] }_{{\textbf {z}}_{k}} = \underbrace{\left[ \begin{array}{cccc} 0&0&1&0 \end{array}\right] }_{{\textbf {H}}} \underbrace{\left[ \begin{array}{c} \varphi _{s\alpha ,k} \\ \varphi _{s\beta ,k} \\ \omega _{m,k} \\ \tau _{l,k} \end{array}\right] }_{{\textbf {x}}_{k}} +{\textbf {v}} \end{aligned}$$
(9)
Fig. 1
figure 1

DTC-based induction motor drive

Full size image

The general equations of the EKF observer used for the estimations of \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), \(\omega _{m}\), and \(\tau _{l}\) are as below:

1- Linearization:

$$\begin{aligned} \textbf{F}_{k+1\vert k}=\frac{\partial \textbf{f}(\textbf{x}_k,\textbf{u}_k)}{\partial \textbf{x}}\vert _{\textbf{x}=\textbf{x}_{k}} \end{aligned}$$
(10)

2- Time update:

$$\begin{aligned} \hat{\textbf{x}}^-_{k+1}= & {} \textbf{f}(\hat{\textbf{x}}_{k},\textbf{u}_{k+1}) \end{aligned}$$
(11)
$$\begin{aligned} \textbf{P}_{k+1}^{-}= & {} \textbf{F}_{k+1\vert k} \textbf{P}_{k}\textbf{F}_{k+1\vert k}^T+\textbf{Q}_{k} \end{aligned}$$
(12)

3- Measurement update:

$$\begin{aligned}{} & {} \textbf{K}_{k+1}=\textbf{P}^-_{k+1}\textbf{H}^T \left[ \textbf{H}\textbf{P}^-_{k+1}\textbf{H}^T+\textbf{R}_k \right] ^{-1} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \hat{\textbf{x}}_{k+1}=\hat{\textbf{x}}^-_{k+1}+\textbf{K}_{k+1}(\textbf{z}_{k+1}-\textbf{H}\hat{\textbf{x}}^-_{k+1}) \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \textbf{P}_{k+1}= (\textbf{I}-\textbf{K}_{k+1}\textbf{H})\textbf{P}^-_{k+1} \end{aligned}$$
(15)

where \( \textbf{F}_{k+1\vert k} \) is the function to linearize the nonlinear model; \( \textbf{K}_{k+1} \) is the Kalman gain; \( \textbf{P}_{k+1}^{-} \) and \( \textbf{P}_{k+1} \) are the priori and the posteriori covariance matrices, respectively; \( \textbf{Q}_{k} \) and \( \textbf{R}_{k} \) are the covariance matrices of the system noise and output noise, respectively.

The EKF algorithm used for state and parameter estimations of IM in this study is initialized with \( \hat{\textbf{x}}_{0|0}=0 \) and \( {\textbf {P}}={\textbf {P}}_0 \), where \( {\textbf {P}}_0 \) is the initial estimation error covariance.

Because the term of \( {\textbf {H}}{\textbf{P}}_{k+1}^-{\textbf {H}}^T+{\textbf {R}}_{k} \) in (13) is scalar, the proposed EKF algorithm does not require matrix inversion.

The operation of matrix inversion that is necessary for the previous EKF algorithms utilizing the stator currents [17, 25] and the rotor speed and the stator currents [3] in the measurement equation is translated in the inverse of a real number in the proposed EKF. In addition, the size of the matrices in the EKF algorithm is reduced by the use of the proposed reduced-order IM model. Thus, in the EKF algorithm where matrix multiplications are made intensively, the element-based multiplication operations are also decreased.

The stability analysis of an EKF observer was previously studied by [30] with the presumption that nonlinear system knowledge is known. In addition, the stability analysis for EKF using the IM model is studied by [31] in detail.

4 Simulation results

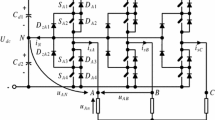
Simulation studies are arranged in two parts to demonstrate the effectiveness of EKF using the proposed reduced IM model that is independent of the \(R_r\), \(L_s\), \(L_r\), and \(L_m\) parameters of the IM. In the first part, while the open-loop estimation performance of the EKF observer is performed, in the second part, the closed-loop estimation performance of the EKF observer is presented. The diagram for the DTC-based IM drive is given in Figure 1. The IM has the parameters given in Table 1. In Figure 1, the switching table and the sector selector are built as in [32]. \( {\hat{\theta }}_{rf} \) is the sector position of the stator flux. The IM drive system, as the speed controller, employs a traditional PID controller. Also, the flux reference \(\vert \varphi _s\vert ^r \) shown in Figure 1 decreases with increasing speed reference in the field-weakening region on account of the voltage limit, also leading to increase in the magnetizing inductance [27]. Also, there is a switch (S1) changing the operation mode: S1 allows to test of the EKF observer in open loop or closed loop.

The relations between flux, speed, and magnetizing inductance are mathematically expressed as in equations (16) and (17).

$$\begin{aligned} \begin{aligned} \vert \varphi _s\vert ^r=\dfrac{n_b}{n_m^r}\vert \varphi _s\vert _{rated}^r~~~~\text {for}~~n_m^r>n_b \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned} \begin{aligned} L_m=\dfrac{\vert \varphi _s\vert _{rated}^r}{\vert \varphi _s\vert ^r}L_{mn}~~~~\text {for}~~n_m^r>n_b \end{aligned} \end{aligned}$$
(17)

where \( L_{mn} \) is the constant value of \( L_m \) obtained from the parameter experiments of IM for \( n_m^r\le n_b \), \( n_b \) is the base value of velocity and taken as 1000 r/min in simulations.

Table 1 Parameters of the IM
Full size table
Fig. 2
figure 2

References for the performance tests of the EKF observer and speed-sensored drive system

Full size image

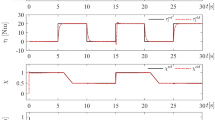
In order to test the open-loop or closed-loop performance of the EKF estimator which uses a reduced IM model, the scenarios including parameter variations shown in Figure 2 are generated. In the scenarios given with Figure 2;

  • The IM is operated in zero (0 r/min), low (50 r/min), rated speed (950 or \( -950 \) r/min), and field weakening zone (1500 or \( -1500 \) r/min) which is known as the high-speed zone above the rated speed.

  • The load torque applied to the IM is changed linearly or step-wise between 20 N.m and \(-15\) N.m at different speed zones.

  • The \(R_r\) is changed between the \(R_{rn}\) and \(2\times R_{rn}\), which is the nominal value of the rotor resistance, in zero speed (\(t=10\) s) and field weakening zone (\(t=18 \) s).

  • The \(L_m\) is changed between the \(L_{mn}\) and \(1.5\times L_{mn}\) with the decreasing stator flux reference in the field-weakening region.

In order to obtain both open-loop and closed-loop estimation performances from the proposed EKF observer in simulations, the sampling time (T) is taken as 100 \(\mu \)s and covariance matrices (\({\textbf {Q}}\), \({\textbf {P}}\), and \({\textbf {R}}\)) used in the observer are determined by trial and error, as below:

$$\begin{aligned} {\textbf {Q}}= & {} \text {diag}\left\{ 10^{-15}~~10^{-15}~~ 10^{-7}~~ 10^{-6}\right\} \\ {\textbf {P}}_0= & {} \text {diag}\left\{ 10~~10~~ 10~~ 10\right\} \\ {\textbf {R}}= & {} \left\{ 10^{-3}\right\} \end{aligned}$$

To test the open-loop and closed-loop estimation performances of the EKF observer:

Fig. 3
figure 3

Open-loop estimation performance for EKF observer

Full size image
Fig. 4
figure 4

Open-loop estimation errors for the EKF observer

Full size image

  • Firstly, the information required for the DTC-based IM drive, such as rotor mechanical speed and rotor position, is obtained from the IM model, and thus the performance in the open-loop mode of EKF can be demonstrated. The open-loop simulation results of the EKF observer are given in Figures 3 and 4.

  • Secondly, the information required for the DTC-based IM drive, such as rotor mechanical speed and rotor position, is obtained from the EKF observer which uses the proposed reduced IM model, and thus the closed-loop estimation performance of EKF can be demonstrated. The closed-loop simulation results of the EKF observer are given in Figures 5 and 6.

Fig. 5
figure 5

The estimation and control performance of the EKF observer and speed-sensored drive system

Full size image
Fig. 6
figure 6

Estimation and tracking errors of the EKF observer and speed-sensored drive system

Full size image

When the estimation results, demonstrated in Figures 3–6, of the EKF algorithm are examined, the following inferences can be made:

  • The EKF observer is capable to estimate as both open loop and closed loop in a wide speed region including field weakening zone and zero speed under different load torques.

  • In spite of the initial values of the estimated \(\omega _m\), \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), and \(\tau _l\) by the EKF are selected as zero, the whole of the estimations abruptly converges to reference values.

  • Since the reduced IM model does not include \(R_r\), \(L_s\), \(L_r\), and \(L_m\), the performance of the EKF observer is not affected by their changes.

Fig. 7
figure 7

Experimental setup for the real-time experiments

Full size image
Fig. 8
figure 8

\(v_{s\alpha }\) and \(v_{s\beta }\) supplied to the induction motor through ac drive [17]

Full size image

In summary, the simulation results approve the performance of the proposed EKF observer which uses the reduced IM model for a wide speed region including field-weakening zone and very low speed, under parameter variations.

5 Hardware configuration

To indicate the real-time performance of the proposed EKF-based estimator, the experimental test setup demonstrated in Figure 7 is used. In the experimental tests, an IM (squirrel-cage) of 3-phase is used, the specifications of which are given in Table. 1. In order to test the EKF observer which uses reduced IM under load torque variations, a Foucault brake able to provide max 30 N.m load is used. Variations in load torque apply to the motor are generated by changes in the rotor angular speed \( \omega _m \) (\( n_m \) r/min) of the IM or manually by a step-like variable DC source. An encoder of 5000  lines/rev is used to confirm estimation of \( n_m \). A torque transducer of 50  N.m to approve estimation of \( \tau _l \) is used; the measured torque information is not used by the estimation algorithm. To actualize the EKF observer which uses a reduced IM model derived in C / C ++ language in MATLAB S-function block is used PC-based dSPACE DS1104 controller board, connector panel, and ControlDesk software. The dSPACE DS1104 controller board has capable of processing floating-point operations at a rate of 250 MHz. Only the real-time open-loop performances of the EKF observer are tested in this paper, due to the nonexistence of the inverter module. However, for a realistic assessment, the IM is driven by an AC drive providing the pulse-width modulated voltages shown in Figure 8 and also the currents. The AC drive is had a field weakening feature in the constant power region, that is, in the speed region above the rated speed.

Fig. 9
figure 9

Estimation results for the velocity and load torque reversals

Full size image

6 Real-time experiments

The estimation performance of the proposed EKF observer which realizes the estimations of the \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), and \(\tau _l\) in this paper is tested with different scenarios such as \(\omega _m\) and \(\tau _l\) reversals, \(\tau _l\) variations, the transition of speed, in the field-weakening zone studies, and \(R_s\) variations. For this purpose, the following compelling scenarios are produced.

  • Performance of the EKF observer under \(\omega _m\) and \(\tau _l\) reversal at the nominal speed.

  • Performance of the EKF observer under different torque at the nominal speeds.

  • Performance of the EKF observer in the field weakening zone.

  • Performance the EKF observer at the different speeds including the low speed.

  • Performance of the EKF observer under the \(R_s\) variations.

In order to obtain high estimation performances from the proposed EKF observer in real-time experiments, covariance matrices used in the observer are determined by trial and error, as below:

$$\begin{aligned} {\textbf {Q}}= & {} \text {diag}\left\{ 10^{-13}~~10^{-13}~~ 10^{-14}~~ 50^{-14}\right\} \\ {\textbf {P}}_0= & {} \text {diag}\left\{ 10~~10~~ 10~~ 10\right\} \\ {\textbf {R}}= & {} \left\{ 10^{-9}\right\} \end{aligned}$$

6.1 Real-time performance of the EKF observer under speed and load torque reversals

In this scenario, the proposed EKF observer is tested under \( \omega _m \) and \( \tau _l \) reversals. To this end, while the motor is rotating at rated speed (950 r/min) with the torque of 20 N.m, the velocity and hence the load torque are linearly reversed by the AC drive at 5.5 s. Then, while the IM is operating at \(-950\) r/min with the torque of \(-20\) N.m, velocity and load torque are reversed at 23.3 s. The estimation results for this scenario are displayed in Figure 9. The obtained results represent that the whole of estimations right away converges to the measured ones. The change that occurs in \( \tau _l \) in Figure 9 is on account of the conventional speed–torque characteristics of the Foucault brake [28].

6.2 Real-time performance of the EKF observer under different load torque at the nominal speeds

In this scenario, the estimation results present the performance of the EKF observer under \( \tau _l \) variations at high speeds. Estimation results are demonstrated in Figure 10. Firstly, when the motor is running at 998 r/min, the \( \tau _l \) is increased from 1 N.m to 8.5 N.m at 5.2 s and the IM’s speed goes down to 982 r/min. Next, the \( \tau _l \) is increased from 8.5 N.m to 18 N.m at 25.5 s. As a results, the IM speed decreased to 955.5 r/min. Finally, the \( \tau _l \) is reduced from 18 N.m to 1 N.m and the IM velocity goes back up to 998 r/min. The performance of the EKF observer, which is tested with the stepwise-generated changes in the load torque, is quite high.

Fig. 10
figure 10

Estimation results for different load torque at rated speed

Full size image

6.3 Real-time performance of the EKF observer in the field weakening zone

In this scenario, the performance of the EKF observer is tested in the field weakening zone. To this end, while the motor is running at 987 r/min with the load torque of 6 N.m, the velocity is increased to 1498 r/min by the AC drive at 12 s. Next, the velocity is linearly reversed at 28.2 s. Finally, while the motor is running at \(-1498\) r/min, the velocity is decreased to \(-987\) r/min. The estimation results of the proposed estimation algorithm including the field weakening region performance are demonstrated in Figure 11. It is known that rotor resistance changes with rotor/slip frequency (skin effect) [33]. In addition, the magnetizing inductance is changed due to the flux level in the field weakening region [34, 35]. In the field weakening region, the values of \( R_r \) and \( L_m \) naturally change with operating conditions. The EKF observer has high performance in the field weakening zone because it has a model independent from \( R_r \) and \( L_m \).

Fig. 11
figure 11

Estimation results for the field weakening zone

Full size image

6.4 Real-time performance of the EKF observer at the different speeds including the low speed

This scenario demonstrates the performance of the EKF observer in the course of the transition from very low speed to nominal speed. To this end, while the motor is operated at 65 r/min with the \( \tau _l \) of 3 N.m, firstly, the velocity is linearly increased to 460 r/min at 10 s. Later the speed rumps up from 460 to 960 r/min at 24 s. As a result, the motor is also almost linearly loaded to 10 and 15 N.m, respectively. The estimation results obtained from the EKF observer in this scenario are shown in Figure 12. Even though the \( \tau _l \) is described as a constant parameter in the proposed reduced motor model, in order to test the EKF observer, an almost linear \( \tau _l \) is applied to the IM during the transition. Despite this stringent scenario, the proposed EKF observer satisfactorily estimates the \(\omega _m\), \(\varphi _{s\alpha }\), \(\varphi _{s\beta }\), and \(\tau _l\) without being affected by the rotor frequency-dependent rotor resistance changes [33].

Fig. 12
figure 12

Estimation results for the different speed regions

Full size image

6.5 Real-time performance of the EKF observer under the stator resistance variations

The last test examining \(R_s\) changes is performed at 87 r/min, and the performances of the EKF observer under \(R_s\) changes are shown in Figure 13. In this scenario, the stator resistance is first increased to \(R_{sn}+1.5~\Omega \) at 7 s and then to \(R_{sn}+2.5~\Omega \) at 13 s. Finally, it is reduced to \(R_{sn}\) at 19 s. The proposed EKF observer in this paper estimates other states and parameters according to the error between the measured velocity and the estimated velocity. The equation of motion used in the observer requires the stator fluxes and load torque information that can be obtained either by measurement or by estimating. Due to the fact that the IM model includes the \(R_s\) parameter, it is possible for the observer performance to be affected by temperature and frequency changes. Therefore, as it can be from Figure 13 since the proposed EKF observer accepts that \(R_s\) is equal to \(3.03~\Omega \), there is a dc bias between the estimated and measured load torque for \(R_s\) variations. This dc bias emerges at the estimated load torque due to the fact that the proposed EKF observer optimizes the error between estimated and measured speed. As it can be seen from Figure 13, the proposed EKF algorithm is affected by \(R_s\) changes at low speeds. To achieve high estimation performance, \(R_s\) changes should be updated in the EKF observer.

Fig. 13
figure 13

Estimation results for \(R_s\) variations at the very low speed

Full size image

When the results given in Figures 9–13 are examined, the performance of the proposed algorithm for estimations of \( \omega _m \), \( \tau _l \), \( \varphi _{s\alpha } \), and \( \varphi _{s\beta } \) is quite high. The experimental setup shown in Figure 7 for the real-time tests of the proposed EKF observer is not suitable for the measurement of \( \varphi _{s\alpha } \), and \( \varphi _{s\beta } \). But, estimation of the stator fluxes is indirectly confirmed by the equation of motion used for the rotor velocity estimation because the equation of motion includes the stator current, rotor speed, and load torque together with the stator fluxes. The proposed estimation algorithm has high performance in the field weakening zone because it has an observer model independent from \( R_r \), \( L_r \), \( L_s \), and \( L_m \). In summary, the obtained real-time results from different scenarios demonstrate the applicability of the estimator.

In addition to the estimation performance of the EKF observer, the computational time of the estimation algorithm is also measured. The average execution times of each iteration for the proposed estimation algorithm are measured as \(2.1\mu s\). This time (\(2.1\mu s\)) is quite small compared to previous studies using \( i_{s\alpha } \), \( i_{s\beta } \) [25] and \( i_{s\alpha } \), \( i_{s\beta } \) with \( \omega _m \) [3] in the measurement equation for state and parameter estimations.

7 Conclusion

In this paper, \( \omega _m \), \( \varphi _{s\alpha } \), \( \varphi _{s\beta } \), and \(\tau _l \) estimations are realized by the EKF observer which uses a reduced IM model that does not include \( R_r \) \( L_r \), \( L_s \), and \( L_m \). The proposed EKF observer estimates using the rotor angular velocity, as opposed to the previous studies that use the stator current components and the stator current components with rotor angular speed in the measurement equation. The proposed EKF observer which uses a reduced motor model presents an easier design and lower computational burden than the previous studies [3, 26]. The estimation performance of the proposed EKF observer is tested with real-time experiments and simulations for wide ranges of speeds. When the experimental and simulation results are considered, the performance of the proposed estimation algorithm in a wide speed range including the field weakening zone and very low speed is quite satisfactory. On the other hand, the proposed EKF algorithm is especially affected by \(R_s\) changes at low speeds. Therefore, to achieve high estimation performance, \(R_s\) changes should be updated in the EKF observer. In addition, in future studies, it is planned to accelerate the torque response by feed-forward control of the estimated load torque to the control system.