Condorcet domains, median graphs and the single-crossing property

Abstract

Condorcet domains are sets of linear orders with the property that, whenever the preferences of all voters of a society belong to this set, their majority relation has no cycles. We observe that, without loss of generality, every such domain can be assumed to be closed in the sense that it contains the majority relation of every profile with an odd number of voters whose preferences belong to this domain. We show that every closed Condorcet domain can be endowed with the structure of a median graph and that, conversely, every median graph is associated with a closed Condorcet domain (in general, not uniquely). Condorcet domains that have linear graphs (chains) associated with them are exactly the preference domains with the classical single-crossing property. As a corollary, we obtain that a domain with the so-called ‘representative voter property’ is either a single-crossing domain or a very special domain containing exactly four different preference orders whose associated median graph is a 4-cycle. Maximality of a Condorcet domain imposes additional restrictions on the associated median graph. We prove that among all trees only (some) chains can be associated graphs of maximal Condorcet domains, and we characterize those single-crossing domains which are maximal Condorcet domains. Finally, using the characterization of Nehring and Puppe (J Econ Theory 135:269–305, 2007) of monotone Arrovian aggregation, we show that any closed Condorcet domain admits a rich class of strategy-proof social choice functions.

1 Introduction

The problem of finding and characterizing preference domains on which pairwise majority voting never admits cycles—the so-called Condorcet domains—has a long history in social choice theory. In their seminal contributions, Black (1948) and Arrow (1951) noticed that the domain of all linear preference orders that are single-peaked with respect to some underlying linear spectrum forms a Condorcet domain. Later, Sen (1966) provided a characterization of Condorcet domains in terms of the well-known condition of value restriction. Since this early work some progress has been made in understanding the structure of Condorcet domains; see Abello (1991, 2004), Chameni-Nembua (1989), Danilov et al. (2012), Danilov and Koshevoy (2013), Fishburn (1997, 2002) and Galambos and Reiner (2008) for important contributions, and Monjardet (2009) for an excellent survey. However, with the exception of Danilov and Koshevoy (2013), the bulk of the results established in the literature pertains only to the special case of connected domains.¹ The analysis of Danilov and Koshevoy (2013), on the other hand, is confined to the case of ‘normal’ Condorcet domains that contain at least one pair of completely reversed orders.

The present paper provides a unifying general approach by establishing a close connection between Condorcet domains and median graphs (see a comprehensive survey about these in Klavzar and Mulder 1999) on the one hand, and the well-studied class of single-crossing domains on the other hand; see Roberts (1977), Gans and Smart (1996) and Saporiti (2009), among others.

First, we observe that if a Condorcet domain of linear preference orders admits a profile with an odd number of voters whose (transitive) majority relation does not belong to this domain, then we can add this majority relation to the Condorcet domain and obtain a larger Condorcet domain. We may thus assume without loss of generality that Condorcet domains are closed in the sense that pairwise majority voting among an odd number of individuals always yields an order within the given domain. In particular, all maximal Condorcet domains are necessarily closed.

The concept of betweenness, introduced for linear orders by Kemeny (1959), plays a major role in our analysis. An order is between two orders, or intermediate, if it agrees with all binary comparisons on which the two linear orders agree (see also Kemeny and Snell 1960; Grandmont 1978). This allows us to associate a graph to any domain of linear orders by connecting two linear orders of this domain by an edge and calling them ‘neighbors’ if there are no other linear orders in this domain that are between them.

We show that (i) every closed Condorcet domain on a finite set of alternatives equipped with the neighborhood relation is isomorphic to a median graph,² and (ii) for every finite median graph there exists a set of alternatives and a closed Condorcet domain whose associated graph is isomorphic to the given median graph. Importantly, the median graph corresponding to a Condorcet domain is not always a subgraph of the permutohedron, which is the graph associated with the universal domain of all strict linear orders (see Sect. 3 below for detailed explanation).³

Our analysis is related to prior work by Nehring and Puppe (2007) and Demange (2012). Nehring and Puppe (2007) introduce a general notion of a median space and demonstrate its usefulness in aggregation theory. Since a closed Condorcet domain is a particular case of a median space, their results have immediate implications for our present analysis, and we comment on the relation to their work in more detail below. Demange (2012) starts with an exogenously given connected graph and assigns linear orders to its vertices so that, for any pair of orders, the intermediate orders (in Kemeny’s sense) are exactly those that lie on a shortest path in the given graph. She then proves that the domain of all these orders is a closed Condorcet domain if the given graph is a median graph. An important consequence of our results is that this procedure of constructing Condorcet domains is in fact universal, i.e., for every closed Condorcet domain there is an associated median graph with respect to which the domain satisfies the intermediateness property.

The close connection between Condorcet domains and median graphs established here allows one to apply results from the theory of median graphs to shed further light on the structure of Condorcet domains. For instance, as a simple corollary of our analysis we obtain that all closed Condorcet domains that contain two completely reversed linear orders are distributive lattices. This fact was first established for connected maximal Condorcet domains by Chameni-Nembua (1989) and Abello (1991), and then for all maximal Condorcet domains by Danilov and Koshevoy (2013) who used a different technique. Here we show this for the much larger class of all closed (but not necessarily maximal) Condorcet domains.

While all median graphs give rise to closed Condorcet domains, not all of them correspond to a maximal Condorcet domain. It turns out that in fact certain types of median graphs never enable maximality of the respective Condorcet domains. In particular, we prove that among all trees only (some) chains are associated with maximal Condorcet domains.

Condorcet domains, whose median graphs are chains, have been studied quite extensively in economics under the name of single-crossing domains. They are characterized by the single-crossing property which stipulates that the orders of the domain can be arranged in a chain so that, for any ordered pair of alternatives, the set of all orders that rank one alternative strictly above the other form an interval in this chain. It is well known that single-crossing domains have the representative voter property (cf. Rothstein 1991), i.e., in any profile with an odd number of voters whose preferences belong to the given domain there is one voter whose preference order coincides with the majority relation. We show here that the representative voter property essentially characterizes the class of single-crossing domains.⁴

A maximal single-crossing domain must obviously contain two completely reversed orders. Interestingly, not all maximal single-crossing domains are maximal Condorcet domains, i.e., typically it is possible to add further preference orders to a maximal single-crossing domain without generating cycles in the majority relation of any profile. Here, we provide a simple necessary and sufficient condition of when a maximal single-crossing domain is also a maximal Condorcet domain. The condition requires that the ‘switched’ pairs of alternatives associated with any two consecutive orders of the domain have one element in common.

As noted above, every closed Condorcet domain is a median space in the sense of Nehring and Puppe (2007). It thus follows from their results that closed Condorcet domains not only enable pairwise majority voting as a consistent aggregation method but in fact admit a wide range of further aggregation rules satisfying Arrow’s independence condition. We adapt their characterization of all monotone Arrovian aggregators to the case of Condorcet domains of linear orders and show that every monotone Arrovian aggregator on a closed Condorcet domain induces a strategy-proof social choice function on the same domain. For each Condorcet domain, we thus obtain a rich class of strategy-proof voting rules, of which the rules identified by Saporiti (2009) for single-crossing domains are special cases.

The remainder of the paper is organized as follows. In the following Sect. 2, we introduce the concept of a Condorcet domain and observe some of its fundamental properties. In particular, we show that closed Condorcet domains are exactly the domains such that any triple of linear orders from the domain admits a ‘median’ order within the domain. Section 3 introduces median graphs and states our main result establishing the correspondence between closed Condorcet domains and median graphs. Section 4 provides the characterization of single-crossing domains and discusses a weaker version of the single-crossing property, namely single-crossingness on trees. Section 5 addresses maximality of Condorcet domains, an issue that has already received attention in the literature (cf. Monjardet 2009). In particular, we prove that trees different from chains are never associated with maximal Condorcet domains, and we characterize the chains (i.e., single-crossing domains) that correspond to maximal Condorcet domains. Any maximal single-crossing domain necessarily contains two completely reversed orders; this does not hold for all maximal Condorcet domains as we show by means of an example. In Sect. 6, we adapt the characterization of all monotone Arrovian aggregators obtained in Nehring and Puppe (2007) to the case of (closed) Condorcet domains and show how it induces a large class of strategy-proof social choice functions on any such domain. An appendix briefly reviews the theory of geometric interval operators (see, e.g., van de Vel 1993) and contains the proof of the central Lemma 3.1 using the so-called triangle condition introduced by Bandelt and Chepoi (1996).

2 Condorcet domains and median domains

In this section, we show that the domains that are closed under taking the majority relation for all profiles with an odd number of voters are precisely the domains that admit a median order for any triple of its elements where the median order is defined relative to the Kemeny betweenness relation. Most of the results in this section are not original. In Theorem 1 we gather a number of classical characterizations of Condorcet domains (Monjardet 2009), and Theorem 2 can be derived from the analysis in Nehring and Puppe (2007) who investigated a more general class of median spaces. Nevertheless, we believe that our exposition and the short proof of the fundamental characterization result, Theorem 2 below, will help to clarify and unify several different approaches in the literature.

2.1 Condorcet domains

Consider a finite set of alternatives X and the set $\mathcal{R}(X)$ of all (strict) linear orders (i.e., complete, transitive and antisymmetric binary relations) on X which we will refer to as the universal domain. Any subset $\mathcal{D}\subseteq \mathcal{R}(X)$ will be called a domain of preferences or simply a domain. A profile$\rho =({R}_1,\ldots ,{R}_{n})$over$\mathcal{D}$ is an element of the Cartesian product $\mathcal{D}^n$ for some number $n\in {\mathbb {N}}$ of ‘voters’, where the linear order $R_i$ represents the preferences of the ith voter over the alternatives from X. A profile with an odd number of voters will simply be referred to as an odd profile. Frequently, we will denote linear orders simply by listing the alternatives in the order of decreasing preference, e.g., a linear order that ranks a first, b second, c third, etc., is denoted by $abc\ldots$.

The majority relation associated with a profile $\rho$ is the binary relation $P_{\rho }^\text {maj}$ on X such that $x P_{\rho }^\text {maj} y$ if and only if more than half of the voters rank x above y. Note that, according to this definition, the majority relation is asymmetric and, for any odd profile $\rho$ and any two distinct alternatives $x,y\in X$, we have either $x P_{\rho }^\text {maj} y$ or $y P_{\rho }^\text {maj} x$. An asymmetric binary relation P is acyclic if there does not exist a subset $\{ x_1,\ldots ,x_m\}\subseteq X$ such that $x_1 P x_2, x_2 P x_3, \ldots , x_{m-1} P x_m$ and $x_m P x_1$. The class of all domains $\mathcal{D}\subseteq \mathcal{R}(X)$ such that, for all n, the majority relation associated with any profile $\rho \in \mathcal{D}^n$ is acyclic has received significant attention in the literature, see the survey of Monjardet (2009) and the references therein. In the following, we will refer to any such domain as a Condorcet domain.⁵

The following result prepares the ground for our analysis, providing some well-known characterizations of Condorcet domains (cf. Monjardet 2009, p. 142). In particular, condition (d) below is Sen’s (1966) ‘value restriction’; condition (e) has been introduced by Ward (1965) as the ‘absence of a Latin square’ (in other terminology, it requires the absence of a ‘Condorcet cycle’; cf. de Condorcet 1785).

Theorem 1

Let X be finite, and let $\mathcal{D}\subseteq \mathcal{R}(X)$ be a domain. The following statements are equivalent:

• (a) Domain $\mathcal{D}$ is a Condorcet domain.

• (b) For every profile over $\mathcal{D}$, the corresponding majority relation is a strict partial order (i.e., transitive and asymmetric binary relation).

• (c) For every odd profile over $\mathcal{D}$, the corresponding majority relation is a linear order, i.e., an element of $\mathcal{R}(X)$.

• (d) For every triple $x,y,z \in X$ of pairwise distinct alternatives, there exists one element in $\{ x,y,z\}$ that is either never ranked first, or never ranked second, or never ranked third in all restrictions of the orders in $\mathcal{D}$ to the set $\{ x,y,z\}$.

• (e) For no triple $R_1, R_2, R_3\in \mathcal{D}$, and no triple $x,y,z\in X$ of pairwise distinct alternatives one has $x R_1 y R_1 z, y R_2 z R_2 x$ and $z R_3 x R_3 y$ simultaneously.

We will say that a Condorcet domain $\mathcal{D}$ is closed if the majority relation corresponding to any odd profile over $\mathcal{D}$ is again an element of $\mathcal{D}$, and we will say that a Condorcet domain $\mathcal{D}$ is maximal if no Condorcet domain (over the same set of alternatives) is a proper superset of $\mathcal{D}$. The following simple observation will be very useful.

Lemma 2.1

Let $\mathcal{D}$ be a Condorcet domain and $R\in \mathcal{R}(X)$ be the majority relation corresponding to an odd profile over $\mathcal{D}$. Then $\mathcal{D}\cup \{ R\}$ is again a Condorcet domain. In particular, every Condorcet domain is contained in a closed Condorcet domain.

Proof

By Theorem 1(e), it suffices to show that $\mathcal{D}\cup \{ R\}$ does not admit three orders $R_1, R_2, R_3$ and three elements $x,y,z\in X$ such that $xR_1 yR_1 z, yR_2 zR_2 x$ and $zR_3 xR_3 y$. Assume on the contrary that it does; then, evidently, not all three orders $R_1, R_2, R_3$ belong to $\mathcal{D}$. Thus, one of them, say $R_3$, is the majority relation of an odd profile $\rho \in \mathcal{D}^n$, i.e., $R_3=R$. Consider the profile $\rho ' =(nR_1, nR_2,\rho ) \in \mathcal{D}^{3n}$ that consists of n voters having the order $R_1, n$ voters having the order $R_2$ and the n voters of the profile $\rho$. Then the voters of the subprofile $(nR_1, nR_2)$ will unanimously prefer y to z, which forces the majority relation $P_{\rho ' }^\text {maj}$ corresponding to $\rho '$ to have the same ranking of y and z. At the same time, the voters of this subprofile are evenly split in the ranking of any other pair of alternatives from $\{x,y,z\}$. Hence, the majority relation $P_{\rho ' }^\text {maj}$ yields the cycle $z P_{\rho ' }^\text {maj} x P_{\rho ' }^\text {maj} y P_{\rho ' }^\text {maj} z$, in contradiction to the assumption that $\mathcal{D}$ is a Condorcet domain. $\square$

This observation allows us to concentrate our attention on closed Condorcet domains without loss of generality, and we do so for the rest of the paper. Note, in particular, that by Lemma 2.1 all maximal Condorcet domains are closed. The converse does not hold. For instance, all domains consisting of exactly two different orders are closed Condorcet domains; but these are never maximal Condorcet domains if $|X| \ge 3$. Another simple example is the following.

Example 1

(A closed but not maximal Condorcet domain). Consider on $X=\{ a,b,c\}$ the domain $\mathcal{D}= \{ abc, bca, cba\}$. By Theorem 1(d), $\mathcal{D}$ is a closed Condorcet domain. Indeed, consider any odd profile on $\mathcal{D}$: (i) if more than half of the voters have the preference order abc, that order evidently coincides with the majority relation; (ii) similarly, if more than half of the voters have the preference order cba, that order evidently coincides with the majority relation; (iii) in all other cases the majority relation coincides with the ‘middle’ order bca.

However, $\mathcal{D}$ is not a maximal Condorcet domain, since $\mathcal{D}\cup \{ bac\}$ is also Condorcet domain (indeed, a maximal one).

2.2 Betweenness and median domains

The universal domain $\mathcal{R}(X)$ can be endowed with the ternary relation of ‘Kemeny betweenness’ (Kemeny 1959). According to it, an order Q is between orders R and $R'$ if $Q\supseteq R\cap R'$, i.e., Q agrees with all binary comparisons on which R and $R'$ agree.⁶ The set of all orders that are between R and $R'$ is called the interval spanned by R and $R'$ and is denoted by $[R,R']$.

Given every triple of elements $R_1,R_2,R_3\in \mathcal{R}(X)$, an order $R^\text {med} = R^\text {med}(R_1,R_2,R_3)\in \mathcal{R}(X)$ is called the median order corresponding to $R_1,R_2,R_3$ if

$$\begin{aligned} R^\text {med}\in [R_1,R_2]\cap [R_1,R_3]\cap [R_2,R_3]. \end{aligned}$$

Proposition 2.1

The median order of a triple $R_1, R_2, R_3\in \mathcal{R}(X)$, if it exists, is unique.

Proof

If a triple $R_1, R_2, R_3$ admits two different median orders, say R and $R'$, these must differ on the ranking of at least one pair of alternatives. Suppose they disagree on the ranking of x and y. In this case, not all three orders of the triple agree on the ranking of x versus y. Hence, exactly two of them, say $R_1$ and $R_2$, must agree on the ranking of x versus y; but then, either R or $R'$ is not between $R_1$ and $R_2$, a contradiction. $\square$

A domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is called a median domain if every triple of elements in $\mathcal{D}$ admits a median order in $\mathcal{D}$. Evidently, not every subset of $\mathcal{R}(X)$ is a median domain; for instance, the universal domain $\mathcal{R}(X)$ itself is not a median domain whenever $|X|\ge 3$. This can be verified by considering any three orders of the form $R_1 = \ldots a \ldots b \ldots c \ldots , R_2 = \ldots b \ldots c \ldots a \ldots$, and $R_3 = \ldots c \ldots a \ldots b \ldots$. Since any linear order R in $[R_1,R_3]$ has aRb, any linear order R in $[R_1,R_2]$ has bRc, and any linear order R in $[R_2,R_3]$ has cRa, we obtain $[R_1,R_2]\cap [R_1,R_3]\cap [R_2,R_3] = \emptyset$ due to the transitivity requirement. Prominent examples of median domains include the well-studied single-crossing domains.

Example 2

(Classical single-crossing domains). There are several equivalent descriptions of single-crossing domains (see, e.g., Gans and Smart 1996; Saporiti 2009). The following will be useful for our purpose. A domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is said to have the single-crossing property if $\mathcal{D}$ can be linearly ordered, say according to $R_1> R_2> \cdots > R_m$, so that, for all pairs x, y of distinct elements of X, the sets $\{ R_j\in \mathcal{D}\mid xR_j y\}$ and $\{ R_j\in \mathcal{D}\mid yR_j x\}$ are connected in the order >. Thus, for each pair x, y of distinct elements, there is exactly one ‘cut-off’ order $R_k$ such that either (i) $xR_j y$ for all $j\le k$ and $yR_jx$ for all $j>k$, or (ii) $yR_j x$ for all $j\le k$ and $xR_jy$ for all $j>k$. Domains with the single-crossing property are referred to as single-crossing domains. It is easily verified that, for any triple with $R_i>R_j>R_k$ the median order exists and coincides with the ‘middle’ order, i.e., $R^\text {med}(R_i,R_j,R_k) =R_j$. Note that both the domain $\mathcal{D}=\{ abc, bca, cba\}$ and the augmented domain $\mathcal{D}\cup \{ bac\}$ considered in Example 1 are single-crossing domains.

The close connection between Condorcet domains and median domains to be established in Theorem 2 below stems from the following simple but fundamental observation (cf. Nehring and Puppe 2007, Sect. 4).

Observation. A triple $R_1, R_2, R_3\in \mathcal{R}(X)$ admits a median order if and only if the majority relation of the profile $\rho =(R_1, R_2, R_3)$ is acyclic, in which case the median order $R^\text {med}(R_1,R_2,R_3)$ and the majority relation of $\rho$ coincide.

Proof

If the majority relation $P_{\rho }^\text {maj}$ is acyclic, and hence is an element of $\mathcal{R}(X)$, it belongs to each interval $[R_i,R_j]$ for all distinct $i,j\in \{ 1,2,3\}$. Indeed, if both $R_i$ and $R_j$ rank x higher than y, then so does the majority relation. Conversely, if R is the median of the triple $R_1, R_2, R_3$, then for any pair $x,y\in X$, at least two orders from this triple agree on ranking of x and y. Then R must agree with them; hence, it is the majority relation for the profile $\rho =(R_1, R_2, R_3)$. $\square$

Corollary 2.1

Any closed Condorcet domain is a median domain.

Proof

Suppose $\mathcal{D}$ is a closed Condorcet domain, and let $R_1, R_2, R_3$ be any triple of orders from $\mathcal{D}$. The majority relation R corresponding to the profile $(R_1, R_2, R_3)\in \mathcal{D}^3$ by Theorem 1(c) is an element of $\mathcal{R}(X)$, and by the assumed closedness it is in fact an element of $\mathcal{D}$. By the preceding observation, R is the median order of the triple $R_1, R_2, R_3$. $\square$

A subset $\mathcal{C}\subseteq \mathcal{D}$ of a domain $\mathcal{D}\subseteq \mathcal{R}(X)$ will be called convex in$\mathcal{D}$ if $\mathcal{C}$ contains with any pair $R,R'\in \mathcal{C}$ all orderings of $\mathcal{D}$ that are between R and $R'$, that is, $\mathcal{C}$ is convex in $\mathcal{D}$ if

$$\begin{aligned} \{ R,R'\}\subseteq \mathcal{C}\Rightarrow \left( [ R, R'] \cap \mathcal{D}\right) \subseteq \mathcal{C}. \end{aligned}$$

A family ${\mathbb F}$ of subsets of a set is said to have the Helly property if the sets in any subfamily ${\mathbb F}'\subseteq {\mathbb F}$ have a non-empty intersection whenever their pairwise intersections are non-empty, i.e., if $\mathcal{C}\cap \mathcal{C}'\ne \emptyset$ for each pair $\mathcal{C},\mathcal{C}'\in {\mathbb F}'$ implies $\cap \, {\mathbb F}'\ne \emptyset$. For us this property will be important when ${\mathbb F}$ is the set of all subsets of a domain $\mathcal{D}\subseteq \mathcal{R}(X)$ that are convex in $\mathcal{D}$.

Proposition 2.2

(Helly property and median domains) A domain $\mathcal{D}$ is a median domain if and only if it has the Helly property for the family of all subsets that are convex in $\mathcal{D}$.

Proof

Let $\mathcal{D}$ be median domain and ${\mathbb F}$ be a family of subsets that are convex in $\mathcal{D}$ with pairwise non-empty intersection. We proceed by induction over $m=|{\mathbb F}|$. If $m=2$, there is nothing to prove, thus let $m=3$, i.e., ${\mathbb F} = \{ \mathcal{C}_1,\mathcal{C}_2,\mathcal{C}_3\}$. Choose any triple of orders $R_1\in \mathcal{C}_1\cap \mathcal{C}_2, R_2\in \mathcal{C}_2\cap \mathcal{C}_3$ and $R_3\in \mathcal{C}_3\cap \mathcal{C}_1$ and consider the median order $R = R^\text {med}(R_1,R_2,R_3)\in \mathcal{D}$. By convexity in $\mathcal{D}$ of the sets $\mathcal{C}_1,\mathcal{C}_2,\mathcal{C}_3$ we have $R\in \mathcal{C}_1\cap \mathcal{C}_2\cap \mathcal{C}_3$ which, in particular, shows that $\cap \, {\mathbb F}$ is non-empty. Now consider ${\mathbb F} = \{ \mathcal{C}_1,\ldots ,\mathcal{C}_m\}$ with $m>3$ elements and assume that the assertion holds for all families with less than m elements. Then, the family $\{ \mathcal{C}_1, \mathcal{C}_2, \mathcal{C}_3\cap \cdots \cap \mathcal{C}_m\}$ constitutes a family of three convex subsets with pairwise non-empty intersections. By the preceding argument, we thus have $\cap \, {\mathbb F}\ne \emptyset$.

Conversely, consider a domain $\mathcal{D}$ such that any family of convex subsets in $\mathcal{D}$ has the Helly property. Consider any three orders $R_1,R_2,R_3\in \mathcal{D}$. Since, evidently, all intervals are convex in $\mathcal{D}$, the Helly property applied to $[R_1,R_2]\cap \mathcal{D}, [R_1,R_3]\cap \mathcal{D}, [R_2,R_3]\cap \mathcal{D}$ implies the existence of a median. $\square$

For any domain $\mathcal{D}$ and any pair $x,y\in X$ of alternatives, denote by $\mathcal{V}^{\mathcal{D}}_{xy}$ the set of orders in $\mathcal{D}$ that rank x above y, i.e.,

$$\begin{aligned} \mathcal{V}^{\mathcal{D}}_{xy}:= \{ R\in \mathcal{D}\mid xRy\}. \end{aligned}$$

Note that, for all distinct $x,y\in X$, the sets $\mathcal{V}^{\mathcal{D}}_{xy}$ and $\mathcal{V}^{\mathcal{D}}_{yx}$ form a partition of $\mathcal{D}$. Also observe that the sets of the form $\mathcal{V}^{\mathcal{D}}_{xy}$ are convex in $\mathcal{D}$ for all pairs $x,y\in X$. We will now use the Helly property applied to this family to show that every median domain is a closed Condorcet domain. The following is the main result of this section.

Theorem 2

The classes of median domains and closed Condorcet domains coincide, i.e., a domain is a median domain if and only if it is a closed Condorcet domain.

Proof

In the light of Corollary 2.1, it suffices to show that every median domain is a closed Condorcet domain. Thus, let $\mathcal{D}$ be a median domain and consider an odd profile $\rho =({R}_1,\ldots ,{R}_{n})\in \mathcal{D}^n$. For any two alternatives $x,y\in X$, let $\mathcal{U}_{xy}=\{R_i \mid xR_iy \}$, and observe that obviously, $\mathcal{U}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{xy}$. Let z, w also be alternatives in X, not necessarily distinct from x and y. If $xP^\text {maj}_{\rho }y$ and $zP^\text {maj}_{\rho }w$, then $\mathcal{U}_{xy}\cap \, \mathcal{U}_{zw}\ne \emptyset$ and hence $\mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{zw}\ne \emptyset$. By Proposition 2.2 we have

$$\begin{aligned} \bigcap _{x,y\in X \, : \, xP^\text {maj}_{\rho }y} \mathcal{V}^{\mathcal{D}}_{xy}\ne \emptyset , \end{aligned}$$

hence there is a linear order in $\mathcal{D}$ which coincides with the majority relation of $\rho$. $\square$

Relation to Nehring and Puppe (2007). We conclude this section by commenting on the relation to the work of Nehring and Puppe (2007). They introduce the notion of a median (property) space and show, among other things, that these are exactly the spaces on which issue-wise majority voting with an odd number of voters is consistent (see their Corollary 5). Closed Condorcet domains are special cases of median domains in which issue-wise majority voting amounts to pairwise majority voting between alternatives and consistency amounts to transitivity. Theorem 2 can thus be derived from their results, and in fact the Helly property is implicit in their analysis.

3 Closed Condorcet domains and median graphs

The close relation between the majority relation and the median operator in closed Condorcet domains established in Theorem 2 suggests that there exists a corresponding relation between closed Condorcet domains and median graphs.⁷ The details of this connection are worked out in this section. We start in Sect. 3.1 with some basic facts about median graphs. In Sect. 3.2 we observe that every domain naturally induces a graph, and we prove that the graph associated with every median domain—hence by Theorem 2 also with every closed Condorcet domain—is a median graph. In Sect. 3.3 we show that, conversely, for every median graph one can construct a (non-unique) median domain whose associated graph is isomorphic to the given graph.

3.1 Median graphs

Let $\Gamma =(V,E)$ be a connected graph with V as the set of vertices and E as the set of edges.⁸ The distanced(u, v) between two vertices $u,v\in V$ is the smallest number of edges that a path connecting u and v may contain. While the distance is uniquely defined, there may be several shortest paths from u to v. We say that a vertex w is geodesically between the vertices u and v if w lies on a shortest path that connects u and v or, equivalently, if $d(u,v)=d(u,w)+d(w,v)$. A (geodesically) convex set in a graph $\Gamma =(V,E)$ is a subset $C\subseteq V$ such that for any two vertices $u,v\in C$ all vertices on every shortest path between u and v in $\Gamma$ lie in C. A connected graph $\Gamma =(V,E)$ is called a median graph if, for any three vertices $u,v,w\in V$, there is a unique vertex $\text {med} (u,v,w)\in V$ which lies simultaneously on some shortest paths from u to v, from u to w and from v to w.

To characterize the structure of an arbitrary median graph, we recall the concept of convex expansion. For any two subsets $S,T\subseteq V$ of the set of vertices of the graph $\Gamma$, let $E(S,T)\subseteq E$ denote the set of edges that connect vertices in S and vertices in T.

Definition 1

Let $\Gamma =(V,E)$ be a graph. Let $W_1,W_2\subset V$ be two subsets with a non-empty intersection $W_1\cap W_2\ne \emptyset$ such that $W_1\cup W_2=V$ and $E(W_1{\setminus } W_2,W_2{\setminus } W_1)=\emptyset$. The expansion of $\Gamma$ with respect to $W_1$ and $W_2$ is the graph $\Gamma '$ constructed as follows:

• each vertex $v\in W_1\cap W_2$ is replaced by two vertices $v^1, v^2$ joined by an edge;

• $v^1$ is joined to all the neighbors of v in $W_1{\setminus } W_2$ and $v^2$ is joined to all the neighbors of v in $W_2{\setminus } W_1$;

• if $v,w\in W_1\cap W_2$ and $vw\in E$, then $v^1$ is joined to $w^1$ and $v^2$ is joined to $w^2$;

• if $v,w\in W_1{{\setminus }} W_2$ or if $v,w\in W_2{\setminus } W_1$, they will be joined by an edge in $\Gamma '$ if and only if they were joined in $\Gamma$; if $v\in W_1{\setminus } W_2$ and $w\in W_2{\setminus } W_1$, they remain not joined in $\Gamma '$.

If $W_1$ and $W_2$ are (geodesically) convex, then $\Gamma '$ will be called a convex expansion of $\Gamma$.

Example 3

(Convex expansion). In the graph $\Gamma$ shown on the left of Fig. 1 we set $W_1=\{a,b,c,d\}$ and $W_2=\{c,d,e,f\}$. These are convex and their intersection $W_1\cap W_2=\{c,d\}$ is not empty. On the right we see the graph $\Gamma '$ obtained by the convex expansion of $\Gamma$ with respect to $W_1$ and $W_2$.

Fig. 1

Convex expansion of a median graph

The following important theorem about median graphs is due to Mulder (1978).

Theorem 3

(Mulder’s convex expansion theorem) A graph is median if and only if it can be obtained from a trivial one-vertex graph by repeated convex expansions.

3.2 Every closed Condorcet domain induces a median graph

As we already said in the introduction, with every domain $\mathcal{D}\subseteq \mathcal{R}(X)$ one can associate a graph $\Gamma _{\mathcal{D}}$ on $\mathcal{D}$ as follows. Two distinct orders $R,R'\in \mathcal{D}$ are said to be neighbors in$\mathcal{D}$, or simply $\mathcal{D}$-neighbors, if $[R,R']\cap \mathcal{D}=\{ R,R'\}$. Define $\Gamma _{\mathcal{D}}$ to be the (undirected) graph on $\mathcal{D}$ that connects each pair of $\mathcal{D}$-neighbors by an edge. We say that $\Gamma _{\mathcal{D}}$ is the associated graph of $\mathcal{D}$. We recall that the graph associated with the universal domain $\mathcal{R}(X)$ is called the permutohedron. Note that the graph $\Gamma _{\mathcal{D}}$ is always connected, i.e., any two orders in $\mathcal{D}$ are connected by a path in $\Gamma _{\mathcal{D}}$. Moreover, any two $\mathcal{R}(X)$-neighbors $R,R'$ are always $\mathcal{D}$-neighbors whenever $R,R'\in \mathcal{D}$. However, two $\mathcal{D}$-neighbors need not be $\mathcal{R}(X)$-neighbors, so, if $\mathcal{D}\ne \mathcal{R}(X)$, the associated graph $\Gamma _{\mathcal{D}}$ need not be a subgraph of the permutohedron, i.e., not every edge of $\Gamma _{\mathcal{D}}$ is necessarily also an edge of $\Gamma _{\mathcal{R}(X)}$. If it is, the domain $\mathcal{D}$ is called connected.⁹

We will now define another concept of betweenness, different from the Kemeny one. For any $\mathcal{D}\subseteq \mathcal{R}(X)$, the order $Q\in \mathcal{D}$ is $\Gamma _{\mathcal{D}}$-geodesically between the orders $R, R'\in \mathcal{D}$ if Q lies on a shortest $\Gamma _{\mathcal{D}}$-path that connects R and $R'$.

As a first example, consider Fig. 2 which depicts two single-crossing domains on the set $X=\{ a,b,c\}$ with their corresponding graphs. The domain on the left is $\mathcal{D}_1=\{ abc, acb, cab, cba\}$, the domain on the right is $\mathcal{D}_2=\{ abc, bac, bca, cba\}$. Note that the permutohedron is given by the entire 6-cycle, and that the graphs associated with the two single-crossing domains are linear subgraphs of the permutohedron. In particular, both domains are connected and the Kemeny betweenness relation on $\mathcal{D}_1$ and $\mathcal{D}_2$ translates into the geodesic betweenness of their associated graphs.

Fig. 2

Two single-crossing domains on $\{ a,b,c\}$ with their associated graphs

It is important to note that for an arbitrary domain $\mathcal{D}$ both of these properties may not be true: neither is $\Gamma _{\mathcal{D}}$ in general a subgraph of $\Gamma _{\mathcal{R}(X)}$, nor do the Kemeny betweenness on $\mathcal{D}$ and the geodesic betweenness on $\Gamma _{\mathcal{D}}$ correspond to each other. To illustrate this, consider the three domains with their associated graphs depicted in Fig. 3. Evidently, none of the three graphs is a subgraph of the permutohedron; hence, none of the corresponding domains is connected. As is easily verified, the domain $\{ abc, acb, cba, bca\}$ on the left of Fig. 3 is a median domain, but the two other domains are not; for instance, the domain $\{ abc, cab, cba, bca\}$ in the middle of Fig. 3 contains a cyclic triple of orders abc, bca and cab, and the 5-element domain $\{ acb, cab, cba, bca, bac\}$ on the right of Fig. 3 contains the cyclic triple acb, cba and bac.

Fig. 3

Three domains on $\{ a,b,c\}$ with their associated graphs

In case of the domain on the left-hand side, the Kemeny betweenness on $\mathcal{D}$ and the geodesic betweenness on the associated graph $\Gamma _{\mathcal{D}}$ agree. By contrast, for the domain in the middle we have $abc \not \in [cab,bca]$ but evidently abc is geodesically between the orders cab and bca in the associated graph. On the other hand, in this example the Kemeny betweenness implies geodesic betweenness. But this also does not hold in general, as the domain on the right of Fig. 3 shows: here, both orders cab and cba are elements of [acb, bca], but neither of them is geodesically between acb and bca.

For any domain $\mathcal{D}\subseteq \mathcal{R}(X)$, we now have two betweenness relations on $\mathcal{D}$: the Kemeny betweenness and the geodesic betweenness in the associated graph $\Gamma _\mathcal{D}$. We will show that in important cases they coincide, in which case for all $R,R',Q\in \mathcal{D}$, we have

$$\begin{aligned} Q\in [R,R'] \Leftrightarrow Q \text{ is } \Gamma _{\mathcal{D}}\text{-geodesically } \text{ between } R \text{ and } R'. \end{aligned}$$

(3.1)

The following lemma is central to our approach. It states that the Kemeny betweenness on a domain coincides with the geodesic betweenness of its associated graph for three natural classes of domains: (i) median domains, (ii) connected domains, and (iii) domains for which the associated graph is acyclic.

Lemma 3.1

The Kemeny betweenness on a domain $\mathcal{D}\subseteq \mathcal{R}(X)$ coincides with the geodesic betweenness of the associated graph $\Gamma _{\mathcal{D}}$, if one of the following conditions is satisfied:

• (i) $\mathcal{D}$ is a median domain,

• (ii) $\mathcal{D}$ is connected,

• (iii) $\Gamma _{\mathcal{D}}$ is acyclic (i.e., a tree).

The proof of this lemma is provided in the appendix and invokes a general result on ‘geometric interval operators’ satisfying the so-called triangle condition due to Bandelt and Chepoi (1996).

From Theorem 2 and Lemma 3.1(i), we immediately obtain the central result of this section.

Theorem 4

The associated graph $\Gamma _{\mathcal{D}}$ of any closed Condorcet domain $\mathcal{D}$ is a median graph. Moreover, the Kemeny betweenness relation on $\mathcal{D}$ coincides with the geodesic betweenness on $\Gamma _{\mathcal{D}}$.

We again stress that not all median domains are connected, as exemplified by the domain on the left-hand-side of Fig. 3. It is also worth noting that Lemma 3.1 does not imply that $\mathcal{D}$ is a median domain whenever the associated graph $\Gamma _{\mathcal{D}}$ is median graph. A counterexample is the domain $\mathcal{D}$ in the middle of Fig. 3, which is not a median domain despite the fact that its graph $\Gamma _{\mathcal{D}}$ is a median graph. However, we have the following corollary.

Corollary 3.1

Let $\mathcal{D}\subseteq \mathcal{R}(X)$ be a connected domain. Then, $\mathcal{D}$ is a median domain if and only if the associated graph $\Gamma _{\mathcal{D}}$ is a median graph.

Proof

The associated graph of any median domain is a median graph by Lemma 3.1(i). Conversely, if $\mathcal{D}$ is connected, the geodesic median of any triple of vertices with respect to $\Gamma _{\mathcal{D}}$ is also the median with respect to the Kemeny betweenness in $\mathcal{D}$ by Lemma 3.1(ii). Thus, if $\Gamma _{\mathcal{D}}$ is a median graph, $\mathcal{D}$ is a median domain. $\square$

As another important corollary of our analysis, we obtain that all closed Condorcet domains that contain two completely reversed orders have the structure of a distributive lattice. Say that two orders $\overline{R},\underline{R}\in \mathcal{R}(X)$ are completely reversed if $\overline{R}\cap \underline{R} =\{ (x,x) \mid x\in X\}$, i.e., if $\overline{R}$ and $\underline{R}$ agree on the ranking of no pair of distinct alternatives.

Corollary 3.2

Let $\mathcal{D}$ be a closed Condorcet domain. If $\mathcal{D}$ contains at least two completely reversed orders, then it is a distributive lattice.

Proof

By Theorem 4, the graph $\Gamma _{\mathcal{D}}$ associated with $\mathcal{D}$ is a median graph. Let $\overline{R},\underline{R}\in \mathcal{D}$ be two completely reversed orders, and define the join and meet operations on ${\mathcal{D}}$ by $R\vee R' := R^\text {med}(R,\overline{R},R')$ and $R\wedge R' := R^\text {med}(R,\underline{R},R')$, respectively. It is easy (though tedious) to verify that with these operations the space ${\mathcal{D}}$ has the structure of a distributive lattice. Another way to prove the corollary is by invoking a well-known result by Avann (1961) which states that a median graph is (the covering graph of) a distributive lattice if and only if it contains two vertices, say 1 and 0, such that every vertex is on a shortest path connecting 1 and 0. If one takes 1 to be $\overline{R}$ and 0 to be $\underline{R}$, it is easily seen using Lemma 3.1(i) that $\Gamma _{\mathcal{D}}$ satisfies all premises of Avann’s result. $\square$

Remark

Chameni-Nembua (1989) and Abello (1991) have shown that all maximal and connected Condorcet domains that contain at least two completely reversed orders have the structure of a distributive lattice. This result was generalized by Danilov and Koshevoy (2013) who showed that the connectedness is in fact not needed for the conclusion. Corollary 3.2 further generalizes this by showing that the condition of maximality can be substantially weakened to the condition of closedness. In fact, even without the closedness condition, one would still obtain that every Condorcet domain that contains two completely reversed orders can be embedded in a distributive lattice. On the other hand, the condition that the domain contain at least one pair of completely reversed orders cannot be dropped (an example illustrating this is given in Fig. 8 below).

3.3 Every median graph is associated with a closed Condorcet domain

Is every median graph induced by some closed Condorcet domain? The following result gives an affirmative answer. Interestingly, we will see later in Sect. 5, that the answer becomes negative if we insist on maximality of the Condorcet domain, i.e., there exist median graphs that cannot be associated with any maximal Condorcet domain.

Theorem 5

For every (finite) median graph $\Gamma = (V,E)$ there exists a closed Condorcet domain $\mathcal{D}\subseteq \mathcal{R}(Y)$ on a finite set of alternatives Y with $|Y| \le |V|$ such that $\Gamma _{\mathcal{D}}$ is isomorphic to $\Gamma$.

Proof

We apply Mulder’s theorem (Theorem 3). Since the statement is true for the trivial graph consisting of a single vertex, arguing by induction, we assume that the statement is true for all median graphs with k vertices or less. Let $\Gamma '= (V',E')$ be a median graph with $|V'| = k+1$. By Mulder’s theorem $\Gamma '$ is a convex expansion of some median graph $\Gamma = (V,E)$ relative to convex subsets $W_1$ and $W_2$, where $|V| =\ell \le k$. By induction there exists a closed Condorcet domain $\mathcal{D}\subseteq \mathcal{R}(X)$ with $|X| \le k$ such that $\Gamma _{\mathcal{D}}$ is isomorphic to $\Gamma$ with the mapping $R:v\mapsto R_v$ associating a linear order $R_v\in \mathcal{D}$ to a vertex $v\in V$.

To obtain a new domain $\mathcal{D}'$ such that $\Gamma _{\mathcal{D}'}$ is isomorphic to $\Gamma '$, we clone an arbitrary alternative $x\in X$ and introduce a clone¹⁰$y\notin X$ of x and denote $X'=X\cup \{y\}$. The mapping $R':v\mapsto R'_v$ that associates any vertex $v\in \Gamma '$ to a linear order $R'_v$ over $X'$ will be constructed as follows. If v is a vertex of $W_1{\setminus } W_2$, to obtain $R'_v$ we replace x with xy in $R_v$, placing x higher than y, and to obtain $R'_u$ for $u\in W_2{\setminus } W_1$ we replace x by yx in $R_u$, placing y higher than x. Let v now be in $W_1\cap W_2$. In the convex expansion this vertex is split into $v^1$ and $v^2$. To obtain $R'_ {v^1}$ we clone the linear order $R_v$ replacing x by xy and to obtain $R'_ {v^2}$ we clone the same linear order $R_v$ replacing x by yx. The number of alternatives has increased by one only, so it is not greater than $|V'|=\ell +1\le k+1$.

To prove that $\Gamma _{\mathcal{D}'}$ is isomorphic to $\Gamma '$ we must prove that $R'_u$ and $R'_v$ are neighbors in $\Gamma _{\mathcal{D}'}$ if and only if $u,v\in V'$ are neighbors in $\Gamma '$.

First, we need to show that there is no edge between $R'_u$ and $R'_v$ if $v\in W_1{\setminus } W_2$ and $u\in W_2{\setminus } W_1$ since u and v are not neighbors in $\Gamma '$. This follows from the fact that u and v were not neighbors in $\Gamma$ and hence $R_u$ and $R_v$ were not neighbors in $\Gamma _{\mathcal{D}}$. Hence there was a linear order $R_w\in [R_u,R_v]$ between them. In $\mathcal{D}'$ this linear order will be cloned to $R'_w$ and, no matter how we place x and y there, we obtain $R'_w\in [R'_u,R'_v]$ since $R'_u$ and $R'_v$ disagree on x and y. Hence $R'_u$ and $R'_v$ are not neighbors in $\Gamma _{\mathcal{D}'}$ as well. Secondly, we have to check that $R'_ {v^1}$ and $R'_ {v^2}$ are linked by an edge since $v^1$ and $v^2$ are neighbors in $\Gamma '$. This holds because these orders differ in the ranking of just one pair of alternatives, namely x and y; hence, they are neighbors in $\Gamma _{\mathcal{D}'}$. If $w\in W_1\cap W_2$ was a neighbor of $v\in W_1{\setminus } W_2$ in $\Gamma$, then $w^1$ is a neighbor of v in $\Gamma '$ but $w^2$ is not. We then have that $R_w$ is a neighbor of $R_v$ in $\Gamma _{\mathcal{D}}$. Then $R'_{w^1}$ will obviously be a neighbor of $R'_v$ in $\Gamma _{\mathcal{D}'}$ while $R'_{w^2}$ will not be a neighbor of $R'_v$ in $\Gamma _{\mathcal{D}'}$ since $R'_{w^1}$ will be between them. The remaining cases are considered similarly.

To complete the induction step, we need to prove that $\mathcal{D}'$ is a closed Condorcet domain. Let $\mathcal{D}' = \mathcal{V}'_{xy} \cup \mathcal{V}'_{yx}$ be a partition of $\mathcal{D}'$ into subsets of linear orders where x is preferred to y and y is preferred to x, respectively. Using Theorem 2, we prove that $\mathcal{D}'$ is a median domain. Consider a triple $R'_u, R'_v$ and $R'_w$, where $u,v,w\in X$, and denote by $R_u, R_v$ and $R_w$ these linear orders ‘decloned,’ i.e., obtained by the removal of y in $R'_u, R'_v$ and $R'_w$, respectively. Without loss of generality, we assume that $R'_u$ and $R'_v$ belong to $\mathcal{V}'_{xy}$. This means both u and v belong to $W_1$. Let $R_z=R^\text {med}(R_u,R_v,R_w)$ be the median of $R_u, R_v$ and $R_w$ in $\Gamma _{\mathcal{D}}$. Since $W_1$ is convex and $\Gamma _\mathcal{D}$ is isomorphic to $\Gamma$, we have $z\in W_1$ and hence $R'_z$ will have x above y. In this case $R'_z$ will be the median of $R'_u, R'_v$ and $R'_w$. $\square$

Among other things, Clearwater et al. (2015) showed that for a star-graph $S_k$ on k vertices the smallest cardinality of the set X for which there exists a closed Condorcet domain $\mathcal{D}\subset \mathcal{R}(X)$ with $\Gamma _\mathcal{D}$ isomorphic to $S_k$ is exactly k. Thus, in Theorem 5 the restriction $|Y| \le |V|$ cannot be strengthened.

Relation to Demange (2012). We conclude this section by commenting on the relation to Demange (2012). She introduces profiles of preferences that are parametrized by a median graph and derives the acyclicity of the majority relation from the requirement of intermediateness (cf. Grandmont 1978) of preferences. Specifically, she considers a median graph with set of vertices V (identified with the set of voters), and a collection $\{ R_v\in \mathcal{R}(X)\,{:}\,v\in V\}$ of linear orders and assumes that, for all $v,v',u\in V$, the following condition is satisfied:

$$\begin{aligned} R_u\in [R_v,R_{v'}] \text{ whenever } u \text{ is } \text{ on } \text{ a } \text{ shortest } \text{ path } \text{ between } v \text{ and } v'. \end{aligned}$$

(3.2)

Lemma 3.1(i) above shows that, for every median domain $\mathcal{D}$, the intermediateness condition (3.2) is always satisfied with respect to the geodesic betweenness of the underlying graph $\Gamma _{\mathcal{D}}$. Thus, Theorem 4 above implies that in fact all closed Condorcet domains are of the kind considered by Demange and demonstrates the existence of a ‘canonical parametrization’ of these domains (namely by the induced graph $\Gamma _{\mathcal{D}}$). Finally, Demange (2012) takes both the (median) graph and the corresponding profile as given. We show that this does not impose any restriction on the graph since, by Theorem 5, for every median graph there exists a domain satisfying the intermediateness requirement (3.2).¹¹

4 Characterizing and generalizing the single-crossing property

4.1 The representative voter property

A representative voter for a given profile of linear orders is a voter, present in this profile, whose preference coincides with the majority relation of the profile. We say that a domain $\mathcal{D}$ has the representative voter property if any odd profile composed of linear orders from $\mathcal{D}$ admits a representative voter. The representative voter property is a very simple way to guarantee consistency of pairwise majority voting since, if the majority relation coincides with the preference order of one voter, all rationality requirements on preferences are automatically transferred from individual preferences to the collective preference.

In this subsection, we prove that the single-crossing domains (cf. Example 2 above) are exactly the median domains whose associated graphs are chains. From this, we obtain that—with the exception of the Condorcet domains associated with the 4-cycle graph—the single-crossing domains are the domains that have the representative voter property.

Proposition 4.1

A domain $\mathcal{D}\subseteq \mathcal{R}(X)$ has the single-crossing property if and only if its associated graph $\Gamma _{\mathcal{D}}$ is a chain.

Proof

It is easily seen that, if $\mathcal{D}= \{ R_1,\ldots ,R_m \}$ is single-crossing with respect to the linear order $R_1> R_2> \cdots > R_m$, then the interval $[R_i,R_j]$ for $i<j$ consists of linear orders $R_i,R_{i+1},\ldots , R_j$. Hence, the graph $\Gamma _{\mathcal{D}}$ is given by the chain connecting $R_j$ and $R_{j+1}$ by an edge for all $j=1,\ldots ,m-1$.

Conversely, suppose that $\mathcal{D}=\{ R_1,\ldots ,R_m\}$ is such that the associated graph $\Gamma _{\mathcal{D}}$ is a chain, say the one that connects $R_j$ with $R_{j+1}$ by an edge for all $j=1,\ldots ,m-1$. We show that $\mathcal{D}$ is single-crossing with respect to the linear order $R_1> R_2> \cdots > R_m$. By Lemma 3.1(iii), the geodesic betweenness in $\Gamma _{\mathcal{D}}$ agrees with the Kemeny betweenness of $\mathcal{D}$ as a subset of $\mathcal{R}(X)$, hence, if $R_h,R_l\in \mathcal{D}$ with $l>h$ are such that $xR_h y$ and $xR_l y$, then we also have $xR_j y$ for all $j\in \{ h,\ldots , l\}$ and all $x,y\in X$. This implies that $\mathcal{D}$ has the single-crossing property relative to the specified order. $\square$

Rothstein (1991) proved the sufficiency of the single-crossing property for the validity of the representative voter property. The following result shows that the single-crossing property is in fact ‘almost’ necessary.

Theorem 6

Let $\mathcal{D}\subseteq \mathcal{R}(X)$ be a domain of linear orders on X. Then, $\mathcal{D}$ has the representative voter property if and only if $\mathcal{D}$ is either a single-crossing domain, or $\mathcal{D}$ is a closed Condorcet domain with exactly four elements such that the associated graph $\Gamma _{\mathcal{D}}$ is a 4-cycle.

Proof

Suppose that $\mathcal{D}$ has the representative voter property. Evidently, in this case $\mathcal{D}$ is a closed Condorcet domain. By Theorem 4, the associated graph $\Gamma _{\mathcal{D}}$ is median, and by Lemma 3.1(i) the geodesic betweenness in $\Gamma _{\mathcal{D}}$ agrees with the Kemeny betweenness on $\mathcal{D}$. We will show that all vertices of $\Gamma _{\mathcal{D}}$ have degree at most 2.¹² Suppose by way of contradiction, that $\Gamma _{\mathcal{D}}$ contains a vertex, say R, of degree at least 3. Consider any profile $\rho = (R_1,R_2,R_3)$ consisting of three distinct neighbors of R. The majority relation corresponding to $\rho$ is the median $R^\mathrm{med}(R_1, R_2, R_3)$. Since the median graph $\Gamma _{\mathcal{D}}$ does not have 3-cycles, $R_i$ and $R_j$ cannot be neighbors for all distinct $i,j\in \{ 1,2,3\}$, hence $R^\mathrm{med}(R_1, R_2, R_3) = R$. Since R is not an element of $\{R_1,R_2,R_3\}$ the representative voter property is violated, a contradiction. Since $\Gamma _{\mathcal{D}}$ is always connected (as a graph), the absence of vertices of degree 3 or more implies that $\Gamma _{\mathcal{D}}$ is either a cycle or a chain. It is well known that among all cycles, only 4-cycles are a median graphs.¹³ On the other hand, if $\Gamma _{\mathcal{D}}$ is a chain, then $\mathcal{D}$ has the single-crossing property by Proposition 4.1.

To prove the converse, suppose first that $\mathcal{D}$ is a single-crossing domain. Then $\Gamma _{\mathcal{D}}$ is a chain by Proposition 4.1 and, evidently, the preference of the median voter in any odd profile coincides with the corresponding majority relation; this is Rothstein’s theorem (Rothstein 1991). On the other hand, consider any odd profile over a domain $\mathcal{D}$ such that the induced graph is a 4-cycle. In that case, the representative voter property holds trivially if the profile contains all four different orders; if it contains at most three different orders, the representative voter property follows as in the case of a chain with at most three elements. $\square$

4.2 Generalizing the single-crossing property to trees

The classical single-crossing property (Mirrlees 1971; Gans and Smart 1996) naturally generalizes to trees. We rephrase the definition suggested by Kung (2015) and Clearwater et al. (2015) as follows.

Definition 2

A domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is single-crossing with respect to the tree$T=(V,E)$ if $|\mathcal{D}|=|V|$ and the linear orders of $\mathcal{D}$ can be parametrized by the vertices of T so that the intermediateness condition (3.2) is satisfied. Moreover, we say that a domain is generalized single-crossing if it is single-crossing with respect to some tree.

As is easily verified, a domain $\mathcal{D}$ is generalized single-crossing if and only if its associated graph $\Gamma _{\mathcal{D}}$ is a tree. Indeed, if a domain $\mathcal{D}$ is single-crossing with respect to the tree T, then $\Gamma _{\mathcal{D}}=T$. Conversely, if $\Gamma _{\mathcal{D}}$ is a tree, then by Lemma 3.1(iii), the preferences of $\mathcal{D}$ are intermediate on $\Gamma _{\mathcal{D}}$ so $\mathcal{D}$ is generalized single-crossing. In particular, every generalized single-crossing domain is a closed Condorcet domain by Lemma 3.1(iii) (cf. Demange 2012; Clearwater et al. 2015).

To justify our terminology of ‘generalized single-crossingness,’ let $\mathcal{D}\subseteq \mathcal{R}(X)$ be a generalized single-crossing domain and suppose not all orders in $\mathcal{D}$ agree on the ranking of $x,y\in X$, then the sets $\mathcal{V}^{\mathcal{D}}_{xy} := \{ R\in \mathcal{D}\mid xRy\}$ and $\mathcal{V}^{\mathcal{D}}_{yx} := \{ R\in \mathcal{D}\mid yRx\}$ are both non-empty. In the tree $\Gamma _\mathcal{D}$, there will be a unique edge QR such that $Q\in \mathcal{V}^{\mathcal{D}}_{xy}$ and $R\in \mathcal{V}^{\mathcal{D}}_{yx}$; moreover, both sets $\mathcal{V}^{\mathcal{D}}_{xy}$ and $\mathcal{V}^{\mathcal{D}}_{yx}$ are convex, and $\mathcal{V}^{\mathcal{D}}_{xy}\cup \mathcal{V}^{\mathcal{D}}_{yx}=\mathcal{D}$.

Example 4

(The single-crossing property on a tree). Consider domain $\mathcal{D}$ on the set $\{ a,b,c,d\}$ consisting of four orders: $\hat{R} = abcd, R_1 = acbd, R_2 = abdc$, and $R_3 = bacd$. As is easily seen, $\mathcal{D}$ is a closed Condorcet domain. The associated graph $\Gamma _{\mathcal{D}}$ connects $\hat{R}$ with each of the other three orders by an edge and the graph has no other edges (cf. Fig. 4). Thus, $\Gamma _{\mathcal{D}}$ is a tree and $\hat{R}$ is the median order of any triple of distinct elements of $\mathcal{D}$.

Fig. 4

A generalized single-crossing domain

The following result characterizes the single-crossing property and its generalization to trees directly in terms of the structure of the underlying domain, i.e., without explicit reference to the associated graph.

Proposition 4.2

(a) A domain $\mathcal{D}$ has the single-crossing property with respect to some linear order on $\mathcal{D}$ if and only if, for all $x,y,z,w\in X$ such that each of the sets $\mathcal{V}^{\mathcal{D}}_{xy}, \mathcal{V}^{\mathcal{D}}_{yx}, \mathcal{V}^{\mathcal{D}}_{zw}$, and $\mathcal{V}^{\mathcal{D}}_{wz}$ is non-empty, we have:

$$\begin{aligned} \mathcal{V}^{\mathcal{D}}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{zw}\quad \text{ or } \quad \mathcal{V}^{\mathcal{D}}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{wz}. \end{aligned}$$

(4.1)

(b) Let $|X|\ge 4$ and ${\mathbb F}=\{\mathcal{V}^{\mathcal{D}}_{xy}\mid x,y\in X\}$. A domain $\mathcal{D}$ has the generalized single-crossing property if and only if ${\mathbb F}$ has the Helly property and, for all distinct $x,y,z,w\in X$, at least one of the following four sets is empty:

$$\begin{aligned} \mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{zw},\quad \mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{wz},\quad \mathcal{V}^{\mathcal{D}}_{yx}\cap \mathcal{V}^{\mathcal{D}}_{zw},\quad \mathcal{V}^{\mathcal{D}}_{yx}\cap \mathcal{V}^{\mathcal{D}}_{wz}. \end{aligned}$$

(4.2)

Proof

(a) Evidently, every single-crossing domain satisfies (4.1). To prove the converse, we notice that this condition allows one to order the family of all sets of the form $\mathcal{V}^{\mathcal{D}}_{xy}$ so that, for an appropriate sequence of pairs of alternatives $(a_1,b_1), \ldots , (a_m,b_m)$,

$$\begin{aligned} \mathcal{V}^{\mathcal{D}}_{a_1 b_1}\subseteq \mathcal{V}^{\mathcal{D}}_{a_2 b_2}\subseteq \cdots \subseteq \mathcal{V}^{\mathcal{D}}_{a_m b_m}\quad \text{ and }\quad \mathcal{V}^{\mathcal{D}}_{b_1 a_1}\supseteq \mathcal{V}^{\mathcal{D}}_{b_2 a_2}\supseteq \cdots \supseteq \mathcal{V}^{\mathcal{D}}_{b_m a_m}. \end{aligned}$$

It is now easily verified that $\mathcal{D}$ has the single-crossing property with respect to any linear order of the members of $\mathcal{D}$ which lists the elements of $\mathcal{V}^{\mathcal{D}}_{a_1 b_1}$ first, then the elements of $\mathcal{V}^{\mathcal{D}}_{a_2 b_2}{\setminus } \mathcal{V}^{\mathcal{D}}_{a_{1} b_{1}}$ second, and further lists elements of $\mathcal{V}^{\mathcal{D}}_{a_j b_j}{\setminus } \mathcal{V}^{\mathcal{D}}_{a_{j-1} b_{j-1}}$ after listing $\mathcal{V}^{\mathcal{D}}_{a_{j-1} b_{j-1}}$.

(b) Suppose that $\mathcal{D}$ has the generalized single-crossing property. Then, $\Gamma _{\mathcal{D}}$ is a tree. By Lemma 3.1(iii), the betweenness on $\mathcal{D}$ coincides with the induced geodesic betweenness on $\Gamma _{\mathcal{D}}$. In particular, $\mathcal{D}$ is a median domain, and as such satisfies the Helly property for convex sets, and all elements of ${\mathbb F}$ are convex. To verify (4.2), assume by contradiction that

$$\begin{aligned} P\in \mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{zw},\quad Q\in \mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{wz},\quad R\in \mathcal{V}^{\mathcal{D}}_{yx}\cap \mathcal{V}^{\mathcal{D}}_{zw},\quad S\in \mathcal{V}^{\mathcal{D}}_{yx}\cap \mathcal{V}^{\mathcal{D}}_{wz}, \end{aligned}$$

for $P,Q,R,S\in \mathcal{D}$. Consider a shortest path between P and R and a shortest path between Q and S. The first path lies entirely in $\mathcal{V}^{\mathcal{D}}_{zw}$ and the second one lies entirely in $\mathcal{V}^{\mathcal{D}}_{wz}$; in particular, they do not intersect. But on each of them there is a switch from xy to yx, and thus there exist two pairs of neighboring orders such that one of them is in $\mathcal{V}^{\mathcal{D}}_{xy}$ and the other one in $\mathcal{V}^{\mathcal{D}}_{yx}$. This contradicts the generalized single-crossing property.

Conversely, suppose that a domain $\mathcal{D}$ satisfies the Helly property and condition (4.2). Proposition 2.2 then implies that $\mathcal{D}$ is a median domain; hence by Lemma 3.1(i), the betweenness in $\mathcal{D}$ coincides with the geodesic betweenness in $\Gamma _{\mathcal{D}}$. By (4.2), $\Gamma _{\mathcal{D}}$ is acyclic, hence a tree, which implies the generalized single-crossing property, as desired. $\square$

5 Maximal Condorcet domains revisited

The problem of characterizing maximal Condorcet domains has received considerable attention in the literature. Since every maximal Condorcet domain is closed, our analysis allows one to address this problem by studying the structure of the associated median graph. In particular, we will show that if the median graph associated with a maximal domain is acyclic, then it must, in fact, be a chain, i.e., among all trees only chains can be associated with maximal Condorcet domains. On the other hand, it is well known that single-crossing domains are in general not maximal Condorcet domains (see, e.g., Monjardet 2009). However, occasionally this happens, and we provide a simple necessary and sufficient condition for a single-crossing domain to be a maximal Condorcet domain. Finally, we demonstrate by means of an example that even though the induced median graph of a maximal Condorcet domain is never a tree different from a chain, it does not need to have the structure of a distributive lattice either (in view of Corollary 3.2 above, such maximal Condorcet domain cannot contain two completely reversed orders).

If X has three elements, all maximal Condorcet domains have four elements and are either of the type shown in Fig. 2 (connected and single-crossing) or of the type shown to the left of Fig. 3 (not connected and cyclic). If $|X| > 3$, not all maximal Condorcet domains on X have the same cardinality. Call a domain a maximum Condorcet domain on X if it achieves the largest cardinality among all Condorcet domains on X. Evidently, every maximum Condorcet domain is also maximal (and therefore closed), but not vice versa. If X has four elements, the cardinality of a maximum Condorcet domain is known to be nine, see Fig. 5 for a domain attaining this number.

Fig. 5

A connected maximum Condorcet domain on $\{ a,b,c,d\}$

The domain shown in Fig. 5 consists of the following nine orders on $\{ a,b,c,d\}$: abcd, abdc, bacd, badc, bdac, bdca, dbac, dbca, dcba. Note that this domain is connected. Indeed, most of the known general results about the size and the structure of maximal Condorcet domains pertain to connected Condorcet domains; for instance, the domains described in Abello (1991), Chameni-Nembua (1989), Danilov et al. (2012) and Galambos and Reiner (2008) are all connected. However, not all maximal Condorcet domains are connected, as we have already seen above. Figure 6 shows a maximal Condorcet domain with 8 elements on $\{ a,b,c,d\}$ that is not connected (and not maximum); in fact, it belongs to the class of the so-called ‘symmetric’ Condorcet domains studied in Danilov and Koshevoy (2013); a domain is called symmetric if it contains with any order also its completely reversed order.

Fig. 6

A non-connected maximal Condorcet domain on $\{ a,b,c,d\}$

All examples of maximal Condorcet domains that we have given so far are either single-crossing domains, or their associated graph contains at least one 4-cycle.¹⁴ As we will see, this is a general feature of all maximal Condorcet domains. To show this, we need to do some preliminary work.

Lemma 5.1

Suppose $\mathcal{D}$ is a generalized single-crossing domain and QR is an edge in $\Gamma _\mathcal{D}$. Suppose that $P\in [Q,R]$ is different from Q and R (thus $P\not \in \mathcal{D}$). Then $\mathcal{D}'=\mathcal{D}\cup \{P\}$ is also a generalized single-crossing domain and, in particular, $\mathcal{D}$ is not a maximal Condorcet domain.

Proof

We add P to the graph splitting the edge QR, placing P in the middle. The new graph will be still a tree and the preferences of $\mathcal{D}'=\mathcal{D}\cup \{P\}$ will be intermediate with respect to this tree, hence generalized single-crossing. In particular, $\mathcal{D}'=\mathcal{D}\cup \{P\}$ is a median domain and hence a closed Condorcet domain by Theorem 2. $\square$

We note that the lemma is specific to generalized single-crossing domains, i.e., when $\Gamma _{\mathcal{D}}$ is a tree; if $\Gamma _\mathcal{D}$ is a rectangle, the corresponding statement would not hold as the right-hand side of Fig. 3 shows.

Corollary 5.1

Any maximal generalized single-crossing domain on X is connected, i.e., is a subgraph of the permutohedron.

Now we can prove the first of the two main results of this section.

Theorem 7

Let $\mathcal{D}$ be a maximal Condorcet domain. If $\Gamma _{\mathcal{D}}$ is a tree, it is, in fact, a chain.

Proof

Let $\mathcal{D}$ be a maximal Condorcet domain, and assume that $\Gamma _{\mathcal{D}}$ is a tree but not a chain. Then there exists a vertex R in $\Gamma _{\mathcal{D}}$ of degree at least 3. Consider now any three neighbors of R in $\Gamma _{\mathcal{D}}$, say $R_1, R_2$ and $R_3$. Since, by Corollary 5.1, $\mathcal{D}$ is connected, there are three distinct ordered pairs $(x_i,y_i), i=1,2,3$, of alternatives such that $R_i=R{{\setminus }}\{(x_i,y_i)\}\cup \{(y_i,x_i)\}$. We will say that $R_i$ is obtained from R by switching the pair of adjacent alternatives $(x_i,y_i)$. Moreover, since in every pair $(x_i,y_i), i=1,2,3$, the alternatives are adjacent in R, there must exist at least two pairs that have no alternative in common, say $\{ x_1,y_1\} \cap \{ x_2,y_2\} = \emptyset$.

Now let $R'$ be the order that coincides with R except that both pairs $(x_1,y_1)$ and $(x_2,y_2)$ in $R'$ are switched, i.e., $y_1 R' x_1$ and $y_2 R' x_2$, and consider the domain $\mathcal{D}\cup \{ R'\}$. Since $x_1,y_1$ and $x_2,y_2$ are neighbors in each of the orders $R, R_1, R_2, R'$, for every three alternatives $\{a,b,c\}$ no new order among them appears in $R'$ which has not yet occurred in $R, R_1$, or $R_2$. Hence, by Theorem 1(d), $\mathcal{D}\cup \{ R'\}$ is a Condorcet domain. By the maximality of $\mathcal{D}$, this implies $R'\in \mathcal{D}$. But in this case, the graph $\Gamma _{\mathcal{D}}$ evidently contains the 4-cycle $\{ R,R_1,R',R_2\}$, contradicting the assumed acyclicity of $\Gamma _{\mathcal{D}}$. Hence, there cannot exist a vertex of degree 3 or larger, i.e., $\Gamma _{\mathcal{D}}$ is a chain. $\square$

Figure 4 (cf. Example 4 above) illustrates the proof of Theorem 7: one easily verifies that the order badc can be added to the depicted domain $\mathcal{D}$, creating a 4-cycle in the associated graph $\Gamma _{\mathcal{D}}$; in particular, $\mathcal{D}$ is not maximal.

As we will see some—but by far not all—maximal single-crossing domains are also maximal Condorcet domains. Figure 5, however, shows instances of non-maximality: the depicted maximal Condorcet domain contains four maximal single-crossing domains as proper subdomains; for instance, the seven orders abcd, abdc, badc, bdac, bdca, dbca, dcba form a maximal chain, i.e., a maximal single-crossing subdomain. The next result characterizes exactly when a maximal single-crossing domain is also a maximal Condorcet domain.

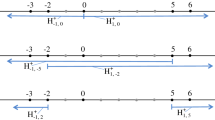
To formulate the result, we need the following definitions. Let $\mathcal{D}\subseteq \mathcal{R}(X)$ be a maximal single-crossing domain and $|X|=n$. Then we know that the associated graph $\Gamma _\mathcal{D}$ is a line. By Corollary 5.1, it is a subgraph of the permutohedron. Let us enumerate orders of $\mathcal{D}$ so that the edges of $\Gamma _\mathcal{D}$ are $R_1R_2, R_2R_3, \ldots , R_{m-1}R_m$. Then the sequence $\langle {R}_1,\ldots ,{R}_{m} \rangle$ will be called a maximal chain. Due to Lemma 5.1, each edge $R_iR_{i+1}$ in $\Gamma _\mathcal{D}$ has a unique switching pair of alternatives $(x_i,y_i)$ which are adjacent in $R_i$. Due to the (standard) single-crossing condition, once switched the pair is never switched back, so for a two-element subset of alternatives $\{x,y\}$ we cannot have both pairs (x, y) and (y, x) as switching pairs. Moreover, $R_1$ and $R_m$ are completely reversed. Indeed, if $R_m$ is not $\underline{R_1}$, which is completely reversed $R_1$, then we can add $\underline{R_1}$ at the end of the sequence $\langle {R}_1,\ldots ,{R}_{m} \rangle$ and add another vertex to our graph in contradiction to maximality of $\mathcal{D}$. Hence, $m=\frac{(n-1)n}{2}+1$, so, in particular, all maximal chains are of the same length.

Without loss of generality, we may assume that $X=\{1,2,\ldots , n\}$, that $\overline{R}=R_1=1\,2\ldots n-1\, n$ and that $\underline{R}=R_m=n\, {n-1}\ldots 2\, 1$. Traveling along the maximal chain $\langle {R}_1,\ldots ,{R}_{m} \rangle$ from $\overline{R}$ in direction of $\underline{R}$ the alternatives in every 2-element subset $\{x,y\}$, where $x<y$, switch exactly once from xy to yx. That is, for each pair $(x,y)\in X\times X$ there exists exactly one edge $R_j R_{j+1}$ such that $xR_1 y,\ldots , xR_j y$ and $yR_{j+1}x,\ldots , yR_m x$. We say that this maximal chain satisfies the pairwise concatenation condition if the switching pairs corresponding to any two adjacent edges have one alternative in common. Formally, a maximal chain $\langle {R}_1,\ldots ,{R}_{m} \rangle$ with the switching pairs $(x_j,y_{j})$ of the edges $R_jR_{j+1}, j=1,\ldots ,m-1$, satisfies the pairwise concatenation condition if

$$\begin{aligned} \{ x_j,y_j\} \cap \{ x_{j+1},y_{j+1}\} \ne \emptyset \end{aligned}$$

(5.1)

for all $j=1,\ldots ,m-1$. Note that the intersection in (5.1) then has exactly one element. We also note that the sequence of switching pairs $(x_1,y_1), \ldots , (x_{m-1},y_{m-1})$ determines the maximal chain $\langle {R}_1,\ldots ,{R}_{m} \rangle$ uniquely.

To illustrate the pairwise concatenation condition consider Fig. 7 which depicts a single-crossing domain on $X = \{ a,b,c,d\}$ with $m=7$. The maximal chain for this domain is:

$$\begin{aligned} R_1= & {} abcd, R_2=acbd, R_3=acdb, R_4=adcb, R_5=dacb, R_6=dcab,\\ R_7= & {} dcba, \end{aligned}$$

with the sequence of switching pairs (b, c), (b, d), (c, d), (a, d), (a, c), (a, b), which obviously satisfies the pairwise concatenation condition.

Fig. 7

A maximal chain constituting a maximal Condorcet domain on $\{ a,b,c,d\}$

We will now show that the pairwise concatenation condition is necessary and sufficient for a maximal single-crossing domain to be a maximal Condorcet domain.¹⁵

Definition 3

(Galambos and Reiner 2008) Two maximal chains are equivalent if their respective sequences of switching pairs can be transformed one to another by swapping adjacent non-intersecting pairs.

It is easily verified that this notion indeed defines an equivalence relation on the class of all maximal chains. To illustrate the definition, consider the maximum Condorcet domain $\mathcal{D}$ on the set $X=\{ a,b,c,d\}$ depicted in Fig. 5 above. The following sequence is one of its maximal chains:

$$\begin{aligned} \mathcal{C}_1 := \langle abcd, abdc, badc, bdac, dbac, dbca, dcba \rangle \end{aligned}$$

with the corresponding sequence of switching pairs

$$\begin{aligned} (d,c), (a,b), (a,d), (b,d), (a,c), (b,c). \end{aligned}$$

(5.2)

If one swaps the first two pairs in this sequence, i.e., (d, c) and (a, c), one obtains the sequence of switching pairs corresponding to the equivalent maximal chain:

$$\begin{aligned} \mathcal{C}_2 := \langle abcd, bacd, badc, bdac, dbac, dbca, dcba \rangle , \end{aligned}$$

which is also contained in the maximum domain $\mathcal{D}$. If in the sequence (5.2), one switches the fourth and fifth pair, i.e., (b, d) and (a, c), one obtains another equivalent maximal chain of $\mathcal{D}$:

$$\begin{aligned} \mathcal{C}_3 := \langle abcd, abdc, badc, bdac, bdca, dbca, dcba \rangle . \end{aligned}$$

Finally, if one switches both pairs in (5.2), first (d, c) against (a, b) and then (b, d) against (a, c), one obtains the equivalent maximal chain:

$$\begin{aligned} \mathcal{C}_4 := \langle abcd, bacd, badc, bdac, bdca, dbca, dcba \rangle . \end{aligned}$$

Evidently, the maximum Condorcet domain $\mathcal{D}$ is the union of the pairwise equivalent maximal chains $\mathcal{C}_1, \mathcal{C}_2, \mathcal{C}_3, \mathcal{C}_4$ that it contains. The following result due to (Galambos and Reiner 2008, Th. 2) shows that this is a general property of all maximal Condorcet domains that contain at least one maximal chain.

Theorem 8

(Galambos and Reiner 2008) Let $\mathcal{D}$ be a single-crossing domain and let $\langle {R}_1,\ldots ,{R}_{m}\rangle$ be its corresponding maximal chain. Then the maximal Condorcet domain containing $\mathcal{D}$ consists of all linear orders of all maximal chains equivalent to $\langle {R}_1,\ldots ,{R}_{m} \rangle$.

We can now state the second main result of this section.

Theorem 9

A maximal single-crossing domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is a maximal Condorcet domain if and only if the maximal chain corresponding to $\mathcal{D}$ satisfies the pairwise concatenation condition.

Proof

Let $\mathcal{D}$ be a maximal single-crossing domain and $\langle {R}_1,\ldots ,{R}_{m} \rangle$ be the corresponding maximal chain. To verify the necessity of the pairwise concatenation condition suppose, by contraposition, that for two consecutive switching pairs $(x_j,y_j)$ and $(x_{j+1},y_{j+1})$ one has $\{ x_j,y_j\}\cap \{ x_{j+1},y_{j+1}\}=\emptyset$. Without loss of generality assume that $x_jR_jy_j$ and $y_jR_{j+1}x_j$, as well as $x_{j+1}R_{j+1}y_{j+1}$ and $y_{j+1}R_{j+2}x_{j+1}$. Since $\{ x_j,y_j\}\cap \{ x_{j+1},y_{j+1}\}=\emptyset$, both pairs of alternatives $(x_j,y_j)$ and $(x_{j+1},y_{j+1})$ must be adjacent in all three orderings $R_j,R_{j+1},R_{j+2}$, respectively. In particular, these three orders agree in the ranking of all pairs except for the two pairs $(x_j,y_j)$ and $(x_{j+1},y_{j+1})$, respectively. Consider the order $R'$ that has $x_jR'y_j$ and $y_{j+1}R'x_{j+1}$ and agrees with each of $R_j,R_{j+1},R_{j+2}$ in the ranking of all other pairs. Clearly, $R'\not \in \mathcal{D}$, but the restriction of $R'$ to any triple of distinct alternatives coincides with the restriction of $R_j, R_{j+1}$, or $R_{j+2}$ to this triple. Hence, $\mathcal{D}\cup \{ R'\}$ is a Condorcet domain by Theorem 1(d), and thus $\mathcal{D}$ is not maximal. This demonstrates the necessity of the pairwise concatenation condition.

The sufficiency of the pairwise concatenation condition follows from Theorem 8. Indeed, it is easily seen that a maximal chain satisfying the pairwise concatenation condition has no other maximal chain equivalent to it, i.e., it forms an equivalence class of its own. By Theorem 8, the corresponding maximal single-crossing domain is a maximal Condorcet domain. $\square$

Theorems 7 and 9 can be combined into the following single statement.¹⁶

Corollary 5.2

A domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is a maximal Condorcet domain such that $\Gamma _{\mathcal{D}}$ admits no cycles if and only if $\mathcal{D}$ is a maximal single-crossing domain satisfying the pairwise concatenation condition.

In light of Theorem 7 and Corollary 3.2 above, a natural conjecture is that all maximal Condorcet domains are distributive lattices. However, this turns out not to be true, as the domain depicted in Fig. 8 shows. The domain consists of the following eight orders: abcd, bacd, bcad, bcda, cbad, cbda, bdca, dbca. This Condorcet domain is connected and maximal but not a distributive lattice; in view of Corollary 3.2 it clearly cannot contain a pair of completely reversed orders.

It seems to be an interesting and worthwhile subject for future research to characterize the class of median graphs that can arise as the associated graphs of maximal Condorcet domains. However, this approach has to be complemented by other considerations as well, since the graph alone does in general not contain information about maximality. For instance, we have already seen that chains may be the associated graphs of maximal Condorcet domains only if their length is one greater than a triangular number, i.e., $\frac{1}{2}(n-1)n +1$. Another example that illustrates this point quite drastically is the 4-cycle. We have already seen above that even non-median domains can induce a 4-cycle, albeit the betweenness structures of the domain and the 4-cycle will not be the same (see the domain in the middle of Fig. 3). But even if we insist on them being isomorphic, thus ensuring that the corresponding domain is a closed Condorcet domain, the 4-cycle may or may not yield a maximal Condorcet domain. For instance, all 4-cycles in Figs. 5, 6 and 8 evidently do not correspond to maximal Condorcet domains since they form proper subdomains. But Fig. 9 shows that the 4-cycle can also be the associated graph of a maximal Condorcet domain in $\mathcal{R}(\{ a,b,c,d\} )$, namely the domain consisting of the orders adbc, bacd, cbda, dcab. Such maximal Condorcet domain of size 4 can be found in $\mathcal{R}(X)$ for any cardinality of X, as shown by Danilov and Koshevoy (2013).

Fig. 8

A maximal Condorcet domain with no pair of completely reversed orders

Fig. 9

A maximal Condorcet domain on $\{ a,b,c,d\}$ with four elements

6 Arrovian aggregation and strategy-proof social choice on median preference domains

Closed Condorcet domains not only preclude intransitivities in pairwise majority voting, they are also endowed with a large class of further aggregation rules satisfying Arrow’s independence condition. This follows from the analysis of Nehring and Puppe (2007, 2010). Indeed, their main result entails a characterization of all Arrovian aggregators on such domains under an additional monotonicity condition. In the first subsection below, we apply their result to describe the class of all monotone Arrovian aggregators on closed Condorcet domains. The monotonicity condition plays then a crucial role in the construction of strategy-proof social choice functions on such domains in the second subsection. There, we demonstrate that the anonymous strategy-proof social choice functions identified by Moulin (1980) for single-peaked domains and by Saporiti (2009) for single-crossing domains share a common structure which, indeed, yields corresponding (anonymous, but also more generally, non-dictatorial) strategy-proof social choice functions on all closed Condorcet domains.

6.1 Characterization of all Arrovian aggregators

Let $N=\{ 1,2,\ldots ,n\}$ be the set of voters. An aggregator on a domain $\mathcal{D}\subseteq \mathcal{R}(X)$ is a mapping $f:\mathcal{D}^n\rightarrow \mathcal{D}$ that assigns an order in $\mathcal{D}$ to each profile of individual orders in $\mathcal{D}$. The following conditions on aggregators have been extensively studied in the literature.

Full Range. For all $R\in \mathcal{D}$, there exist $R_1,\ldots ,R_n$ such that $f(R_1,\ldots ,R_n)=R$.

Unanimity. For all $R\in \mathcal{D}, f(R,\ldots ,R)=R$.

Independence. For all $R_1,\ldots ,R_n, R'_1,\ldots ,R'_n\in \mathcal{D}$ and all pairs of distinct alternatives $x,y\in X$, if xRy and, for all $i\in N$, [$xR_iy\Leftrightarrow xR'_iy$], then $xR'y$, where $R=f(R_1,\ldots ,R_n)$ and $R'=f(R'_1,\ldots ,R'_n)$.

An aggregator is called Arrovian if it satisfies unanimity and independence. In what follows, we will be concerned with Arrovian aggregators that satisfy in addition the following monotonicity condition.

Monotonicity For all $R_1,\ldots ,R_n, R'_i\in \mathcal{D}$ and all pairs of distinct alternatives x, y, if $xR'y$ and $x R_i y$, then xRy, where $R' = f(R_1,\ldots ,R'_i,\ldots ,R_n)$ and $R=f(R_1,\ldots ,R_i,\ldots ,R_n)$.

The monotonicity condition can be rephrased as follows. An aggregator f is monotone if and only if, for all $R_i,R'_i\in \mathcal{D}$ and all $R_{-i}\in \mathcal{D}^{n-1}$,

$$\begin{aligned} f(R_i,R_{-i})\in \left[ R_i,f\left( R'_i,R_{-i}\right) \right] . \end{aligned}$$

(6.1)

This has the following interpretation. Consider any pair of distinct alternatives a and b, and suppose that $aR_i b$ according to agent i’s true order $R_i$. Then, if agent i can force the social order to rank a above b by submitting some order $R'_i$, the social order would also rank a above b if agent i submitted his true preference $R_i$. In other words, no agent can benefit in a pairwise comparison from any misrepresentation. The monotonicity condition thus has a clear ‘non-manipulability’ flavor which we will further exploit.

The conjunction of independence and monotonicity is equivalent to the following single condition.

Monotone Independence For all $R_1,\ldots ,R_n$ and for all pairs (x, y) of distinct alternatives $x,y\in X$, if xRy, where $R=f(R_1,\ldots ,R_n)$ and [$x R_i y\Rightarrow x R'_iy$] for all $i\in N$, then $xR'y$, where $R'=f(R'_1,\ldots ,R'_n)$.

Note also that under monotonicity, unanimity can be deduced from the full range condition, i.e., from the assumption that the aggregator is onto.

For every pair $(x,y)\in X\times X$ of distinct alternatives, let $\mathcal{W}_{xy}$ be a non-empty collection of non-empty subsets $W\subseteq N$ of voters (the winning coalitions for x against y ) satisfying

$$\begin{aligned} \left[ W\in \mathcal{W}_{xy}\,\, \text{ and } \,\,W'\supseteq W\right] \Rightarrow W'\in \mathcal{W}_{xy}. \end{aligned}$$

(6.2)

Definition 4

A collection $\mathcal{W}=\left\{ \mathcal{W}_{ab} \mid (a,b)\in X\times X, a\ne b \, \right\}$ is called a structure of winning coalitions if, for all distinct pairs of alternatives $(x,y)\in X\times X$,

$$\begin{aligned} W\in \mathcal{W}_{xy} \Leftrightarrow W^c\not \in \mathcal{W}_{yx}, \end{aligned}$$

(6.3)

where $W^c=N{\setminus } W$ denotes the complement of the coalition W.

Note that condition (6.3) is equivalent to the following condition:

$$\begin{aligned} W\in \mathcal{W}_{xy} \Leftrightarrow W\cap W'\ne \emptyset \quad \text{ for } \text{ all } \quad W'\in \mathcal{W}_{yx}. \end{aligned}$$

Examples. There are numerous examples of structures of winning coalitions. The simplest are the dictatorships which arise whenever there exists a voter i such that, for all distinct pairs (x, y), a coalition W belongs to $\mathcal{W}_{xy}$ if and only if $i\in W$. More generally, an oligarchy is characterized by the existence of a non-empty set M of voters such that, for all distinct pairs (x, y), either (i) $W\in \mathcal{W}_{xy}\Leftrightarrow M\subseteq W$, or (ii) $W\in \mathcal{W}_{yx}\Leftrightarrow M\subseteq W$. Note that, by (6.3), if (i) holds, then $\{i\}\in \mathcal{W}_{yx}$ for all $i\in M$; similarly, if (ii) holds, then $\{i\}\in \mathcal{W}_{xy}$ for all $i\in M$.

A structure of winning coalitions is anonymous if, for any fixed pair $(x,y)\in X\times X$, membership of a coalition W to $\mathcal{W}_{xy}$ depends only on the number of voters in W. A special case is pairwise majority voting which requires that for all pairs $(x,y)\in X\times X$ of distinct alternatives

$$\begin{aligned} W\in \mathcal{W}_{xy} \Leftrightarrow |W| > n/2. \end{aligned}$$

Note that this is jointly satisfiable with (6.3) only if n is odd.

Given a domain $\mathcal{D}\in \mathcal{R}(X)$, a structure of winning coalitions is said to be order preserving on$\mathcal{D}$ if, for every pair of distinct alternatives $(x,y)\in X\times X$ and every pair of distinct alternatives $(z,w)\in X\times X$,

$$\begin{aligned} \mathcal{V}^{\mathcal{D}}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{zw} \Rightarrow \mathcal{W}_{xy} \subseteq \mathcal{W}_{zw}. \end{aligned}$$

(6.4)

Observe that pairwise majority voting always defines an order preserving structure of winning coalitions (since $\mathcal{W}_{xy} = \mathcal{W}_{zw}$ for all distinct x, y and z, w in the case of pairwise majority voting).

The following result is due to Nehring and Puppe (2007).

Proposition 6.1

Let $\mathcal{D}$ be a closed Condorcet domain and let $\mathcal{W}$ be any order preserving structure of winning coalitions on $\mathcal{D}$. For all preference profiles $(R_1,\ldots ,R_n)\in \mathcal{D}^{n}$ there exists a unique order $R^*\in \mathcal{D}$ such that, for every pair of distinct alternatives ${(x,y)\in X\times X}$

$$\begin{aligned} xR^* y \Leftrightarrow \{ i\in N \mid xR_i y\}\in \mathcal{W}_{xy}\,. \end{aligned}$$

(6.5)

The aggregator defined by (6.5) is a monotone Arrovian aggregator. Conversely, every monotone Arrovian aggregator on $\mathcal{D}$ takes this form for some order preserving structure of winning coalitions $\mathcal{W}$.

Proof

The proof can be deduced from (Nehring and Puppe 2007, Prop. 3.4). For the sake of the paper being self-contained, we reproduce the argument here, again emphasizing the role of the Helly property on median domains as in the proof of Theorem 2 above.

For any profile $(R_1,\ldots ,R_n)\in \mathcal{D}^{n}$, define a binary relation $R^*$ by (6.5). First, we show that $R^*\in \mathcal{D}$. Consider distinct $x,y\in X$ and distinct $z,w\in X$ such that $xR^* y$ and $zR^*w$; we will show that $\mathcal{V}^{\mathcal{D}}_{xy}\cap \mathcal{V}^{\mathcal{D}}_{zw} \ne \emptyset$. By contradiction, suppose that this does not hold, then we would obtain $\mathcal{V}^{\mathcal{D}}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{wz}$, and in particular also $\{ i\in N \mid xR_i y\}\subseteq \{ i\in N \mid wR_i z\}$. At the same time, we would have $\mathcal{W}_{xy}\subseteq \mathcal{W}_{wz}$ because the structure of winning coalitions is order preserving. Thus, $\{ i\in N \mid xR_i y\}\in \mathcal{W}_{wz}$, hence also $\{ i\in N \mid wR_i z\}\in \mathcal{W}_{wz}$. But the latter contradicts $zR^*w$ using (6.3). Thus, the collection of convex sets $\{ \mathcal{V}^{\mathcal{D}}_{xy}\mid xR^*y\}$ has pairwise non-empty intersections. By the Helly property for convex sets in any Condorcet domain (Proposition 2.2), we obtain

$$\begin{aligned} \bigcap _{\{ x R^* y\} }\mathcal{V}^{\mathcal{D}}_{xy}\ne \emptyset , \end{aligned}$$

which means that $R^*$ is an element of $\mathcal{D}$. Thus, (6.5) indeed defines a mapping from $\mathcal{D}^n$ to $\mathcal{D}$. It is easily verified that it is onto, monotone and independent, i.e., an Arrovian aggregator.

Conversely, let f be a monotone Arrovian aggregator. By the monotonicity and independence conditions, it is easily seen that f can be defined in terms of a structure of winning coalitions as in (6.5). We thus have only to verify that the corresponding structure of winning coalitions must be order preserving. Thus, assume that, for distinct $(x,y)\in X\times X$ and distinct $(z,w)\in X\times X$, we have $\mathcal{V}^{\mathcal{D}}_{xy}\subseteq \mathcal{V}^{\mathcal{D}}_{zw}$, and $W\in \mathcal{W}_{xy}$. Then, if the profile $(R_1,\ldots ,R_n)$ is such that all voters in W prefer x to y, we must have xRy where $R=f(R_1,\ldots ,R_n)$. By assumption, all orders in $\mathcal{D}$ which rank x above y must also rank z above w, hence zRw. By independence, this holds for all profiles in which the agents in W rank x above y, hence also z above w, i.e., the agents in W are also winning for z versus w. $\square$

6.2 Strategy-proof social choice

It is well known that on domains on which pairwise majority voting with an odd number of voters is transitive, choosing the Condorcet winner yields a strategy-proof social choice function (see, e.g., Lemma 10.3 in Moulin 1988). In this final subsection, we use Proposition 6.1 and Property (6.1) which is entailed by monotonicity to construct a rich class of further strategy-proof social choice functions on any closed Condorcet domain.

A social choice function F that maps every profile $(R_1, \ldots ,R_n)\in \mathcal{D}^n$ to an element $F (R_1, \ldots ,R_n)\in X$ is strategy-proof if, for all $i\in N$, all $R_i,R'_i\in \mathcal{D}$ and all $R_{-i}\in \mathcal{D}^{n-1}$,

$$\begin{aligned}{}[F(R_i,R_{-i})] R_i \left[ F\left( R'_i,R_{-i}\right) \right] , \end{aligned}$$

i.e., if no voter can benefit by misrepresenting her true preferences.

For each order $R\in \mathcal{R}(X)$ denote by $\tau (R)\in X$ the top-ranked element of R. Let $\mathcal{D}\subseteq \mathcal{R}(X)$ be any closed Condorcet domain, and consider any order preserving structure of winning coalitions $\mathcal{W}$. For every profile $(R_1, \ldots ,R_n)\in \mathcal{D}^n$ let $R_{\mathcal{W}}\in \mathcal{D}$ be the unique order satisfying (6.5) for all distinct $x,y\in X$. Define a social choice function $F_{\mathcal{W}}:\mathcal{D}^n\rightarrow X$ by

$$\begin{aligned} F_{\mathcal{W}}(R_1,\ldots ,R_n) = \tau (R_{\mathcal{W}}). \end{aligned}$$

(6.6)

Theorem 10

Let $\mathcal{D}\subseteq \mathcal{R}(X)$ be any closed Condorcet domain. For every order preserving structure of winning of coalitions $\mathcal{W}$, the social choice function $F_{\mathcal{W}}$ defined by (6.6) is strategy-proof.

Proof

By Proposition 6.1, the aggregator $f_{\mathcal{W}}:\mathcal{D}^n\rightarrow \mathcal{D}$ that maps any profile $(R_1,\ldots ,R_n)$ to the social order $R_{\mathcal{W}}$ according to (6.5) is a monotone Arrovian aggregator; in particular, it satisfies (6.1). In other words, if we denote $R_{\mathcal{W}} = f_{\mathcal{W}} (R_i,R_{-i})$ and $R'_{\mathcal{W}} = f_{\mathcal{W}} (R'_i,R_{-i})$, we have for all $R_1,\ldots ,R_n$, all i, all $R'_i$, and all distinct pairs of alternatives $(x,y)\in X\times X$,

$$\begin{aligned} \left[ xR_i y\, \text{ and } \,xR'_{\mathcal{W}}y \right] \Rightarrow xR_{\mathcal{W}}y \end{aligned}$$

(6.7)

This implies at once the strategy-proofness of $F_{\mathcal{W}}$, by contraposition. Indeed, suppose that agent i could benefit by misreporting $R'_i$, i.e., suppose that $\tau (R'_{\mathcal{W}})R_i\tau (R_{\mathcal{W}})$, where $R_i$ is agent i’s true preference order. Then, since $\tau (R'_{\mathcal{W}})$ is the top element of the order $R'_{\mathcal{W}}$ we obtain from (6.7), $\tau (R'_{\mathcal{W}})R_{\mathcal{W}}\tau (R_{\mathcal{W}})$. Since $\tau (R_{\mathcal{W}})$ is the top element of $R_{\mathcal{W}}$ this implies $\tau (R'_{\mathcal{W}}) = \tau (R_{\mathcal{W}})$, i.e., the misrepresentation does not change the chosen alternative. $\square$

In case of the classical single-crossing property, the anonymous social choice functions defined by (6.6) are exactly the ones identified by Saporiti (2009). Thus, in this special case, the class of anonymous social choice functions considered in Theorem 10 exhausts all anonymous strategy-proof social choice functions. It is an open and interesting question whether this holds more generally on all closed Condorcet domains (and whether the anonymity assumption is really necessary for this conclusion).

Appendix: Remaining proofs

Lemma 3.1 is proven using a result by Bandelt and Chepoi (1996). The statement of this result requires some additional definitions, in particular the notion of a ‘geometric interval operator,’ as follows. An interval operator on a (finite) set V is a mapping that assigns to each pair $(v,w)\in V\times V$ a non-empty subset $[v,w]\subseteq V$, the interval spanned by v and w, such that, for all $v,w\in V, v\in [v,w]$ and $[v,w] = [w,v]$. An interval operator is called geometric if it satisfies in addition the following properties (cf. van de Vel 1993). For all $t,u,v,w\in V$,

$$\begin{aligned}{}[v,v]= & {} \{ v\}, \end{aligned}$$

(A.1)

$$\begin{aligned} u\in [v,w]\Rightarrow & {} [v,u]\subseteq [v,w], \end{aligned}$$

(A.2)

$$ \begin{aligned} t,u\in [v,w] \, \& \, t\in [v,u]\Rightarrow & {} u \in [t,w]. \end{aligned}$$

(A.3)

A pair v, w is called an edge if $v\ne w$ and $[v,w]=\{ v,w\}$. These edges form a graph $\Gamma$ on the vertex set V.

Lemma A.1

Consider a geometric interval operator on V, and let $u\in [v,w]$. Then, there exist pairwise distinct $t_1, \ldots , t_m \in [v,w]$ such that $t_1 = v, t_m =w, t_k = u$ for some $k\in \{ 1, \ldots , m\}$, and such that

$$\begin{aligned}{}[t_1, t_2]\subset [t_1,t_3]\subset \cdots \subset [t_1,t_m] \end{aligned}$$

forms a maximal chain. In particular, the graph induced by a geometric interval operator is connected.

Proof

The existence of a maximal chain of the required form follows at once from condition (A.2). The pairs $t_kt_{k+1}$ must form an edge for $k=1, \ldots , m-1$ by maximality of the chain. Thus, any two vertices are connected by a path. $\square$

An interval operator is called graphic if, for all $u,v,w\in V, u\in [v,w]$ if and only if u is geodesically between v and w in the induced graph $\Gamma$; note that this is exactly condition (3.1) in Lemma 3.1 above. An interval operator is said to satisfy the triangle condition if, for all triples $u,v,w\in V$ such that

$$\begin{aligned}{}[u,v] \cap [v,w] = \{ v\} \text{ and } [v,w] \cap [w,u] = \{ w\} \text{ and } [w,u] \cap [u,v] = \{ u\}, \end{aligned}$$

(A.4)

all three intervals are edges whenever one of them is. Observe that (A.4) can be satisfied only if either all three elements u, v, w coincide, or are pairwise distinct. The following result is due to (Bandelt and Chepoi 1996, Th. 1).

Proposition A.1

Any geometric interval operator satisfying the triangle condition is graphic.

We want to apply Proposition A.1 to prove Lemma 3.1. In order to do so, we first verify the geometricity of the natural interval operator induced by every subdomain of orders.

Lemma A.2

For any domain $\mathcal{D}\subseteq \mathcal{R}(X)$, the interval operator that assigns to every pair $R,R'\in \mathcal{D}$ the interval $[R,R']\cap \mathcal{D}$ is geometric.

Proof

Properties (A.1) and (A.2) are easily verified. To verify the so-called ‘inversion law’ (A.3), consider $T,U,V,W\in \mathcal{D}$ as required in the antecedent of (A.3). Let $x,y\in X$ be such that xTy and xWy. We have to show that then xUy. Since x, y were arbitrarily chosen, this would imply $U\in [T,W]$, as desired. Assume, by contradiction, that yUx; then, we must have xVy since by assumption $T\in [V,U]$. But this contradicts the assumption that $U\in [V,W]$. $\square$

The following proof of Lemma 3.1 shows that the triangle condition is a powerful sufficient condition for an interval operator to be graphic, since it is indeed satisfied in all three cases considered in Lemma 3.1 (sometimes vacuously).

Proof of Lemma 3.1

(i) In case of a median domain, the triangle condition is vacuously satisfied, since there can obviously be no triples of pairwise distinct elements satisfying (A.4) by the median property. By Proposition A.1 the equivalence (3.1) is satisfied for any median domain.

(ii) Next consider any connected domain $\mathcal{D}\subseteq \mathcal{R}(X)$. There can exist triples satisfying (A.4), but we shall show that in this case none of the three intervals can form an edge; hence, the triangle condition is again satisfied. Thus, suppose that the three pairwise distinct orders $U,V,W\in \mathcal{D}$ satisfy (A.4) and, by contradiction, that one of the three intervals is an edge, say $[U,V]=\{ U,V\}$. Since $\mathcal{D}$ is connected, there exists $x,y\in X$ such that U and V differ only in the ranking of x versus y, say xUy and yVx, while U and V agree in the ranking of all other pairs of alternatives. There are two possibilities: either xWy or yWx. In the first case, we have $U\in [V,W]$ and hence $([U,V] \cap [V,W]) \supseteq \{ U,V\}$; in the second case, $V\in [W,U]$ and hence $([W,U] \cap [U,V]) \supseteq \{ U,V\}$. In both cases, we thus obtain a contradiction to assumption (A.4). By Proposition A.1 the equivalence (3.1) is satisfied for $\mathcal{D}$.

(iii) Finally, assume that $\mathcal{D}$ is such that $\Gamma _{\mathcal{D}}$ is acyclic, i.e., a tree. As in part (i), we show that there cannot exist triples satisfying (A.4) hence again the triangle condition is satisfied vacuously.¹⁷ Assume, by way of contradiction, that the pairwise distinct orders $U,V,W\in \mathcal{D}$ satisfy (A.4). By Lemma A.1, there exists a path $\pi _{UV}$ in $\Gamma _{\mathcal{D}}$ connecting U and V that stays entirely in [U, V]; in particular, $\pi _{UV}$ does not contain W. Similarly, there exists a path $\pi _{VW}$ in $\Gamma _{\mathcal{D}}$ connecting V and W and staying entirely in [V, W], and a path $\pi _{WU}$ connecting W and U and staying entirely in [W, U]. But then the union $\pi _{UV}\cup \pi _{VW}\cup \pi _{WU}$ forms a cycle, which contradicts the assumed acyclicity of $\Gamma _{\mathcal{D}}$. Thus, again, by Proposition A.1 the equivalence (3.1) is satisfied for the domain $\mathcal{D}$. $\square$

Note that there do exist connected domains $\mathcal{D}$ and pairwise distinct orders $U,V,W\in \mathcal{D}$ satisfying condition (A.4). Examples are all triples of orders on a common 6-cycle with pairwise distance of two such as, for instance, abc, bca, cab in Fig. 2, or abcd, bcad, cabd in Fig. 5.