Abstract
We answer the question asked by Robert Aumann as to whether core equivalence depends on there being “many more agents than commodities.” We show that for a large class of commodity spaces, which might be infinite-dimensional and even non-separable, core equivalence is indeed equivalent to the presence of “many more agents than commodities” when allocations are Bochner integrable. By contrast, we show that in a classical model of an atomless economy with an infinite-dimensional commodity space, the model where the commodity space is \(L_\infty (\mu )\) with the Mackey topology and allocations are Gelfand integrable, core equivalence holds in full generality, even when there are “many more commodities than agents.” The assumptions we make on economies are much weaker than what is commonly used in core equivalence results for infinite-dimensional commodity spaces and reduce to Aumann’s original assumptions when there are finitely many commodities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
That in an economic environment with many insignificant agents all gains from trade are exhausted precisely at market outcomes is an idea going back to Edgeworth in the nineteenth century. The clearest and most natural formulation of this idea can be found in Aumann (1964). Taking an atomless measure space to represent the set of agents, so that in a mathematically precise sense there are many agents, each of them being negligible in the set of all agents, Aumann showed in his core equivalence theorem, under surprisingly weak assumptions, that the core allocations of an economy are exactly the Walrasian allocations. In Aumann’s model, the number of commodities is finite. Of course, with finitely many commodities, an atomless measure space of agents does not just mean “many agents,” but actually means “many more agents than commodities.” One may see “many more agents than commodities” as an assumption on top of that of “many agents” and may ask whether it is important for core equivalence that the former assumption holds in addition to the latter. The issue was raised by Aumann himself. As Mertens writes in the 1991 reprint of his core equivalence paper from 1970: “If I remember correctly that conversation with R. Aumann, he was stressing the importance of going beyond the separable case [...] to check whether equivalence did not depend on there being (many) more traders than commodities.”
It was first shown by Tourky and Yannelis (2001) that the “many more agents than commodities” aspect of Aumann’s model indeed matters for core equivalence, even when the space of agents is atomless. Assuming the generalized continuum hypothesis, Tourky and Yannelis showed that, given a vector space \(E\) whose algebraic dimension is at least the cardinal of the continuum, there are a vector order and a norm on \(E\), so that \(E\) becomes an ordered non-separable Hilbert space with positive cone having non-empty interior, and an economy with an atomless measure space of agents and \(E\) as commodity space such that—allocations taken to be Bochner integrable—all assumptions made in Aumann (1964) hold, but such that core equivalence fails. Extending the scope of the result in Tourky and Yannelis (2001), it was shown in Podczeck (2003) that core equivalence can fail whenever the commodity space is a non-separable Banach space.
Of course, the algebraic dimension of a linear space provides a natural way to extend the usual notion of “number of commodities” to infinite-dimensional commodity spaces. However, there is a problem. The algebraic dimension of every infinite-dimensional Banach space is at least the cardinal of the continuum, even without the continuum hypothesis.Footnote 1 On the other hand, there are (positive) core equivalence results for commodity spaces that are separable infinite-dimensional Banach spaces, e.g., Rustichini and Yannelis (1991). A main factor behind these results is that in a separable commodity space, trades among agents can be approximated by points in some countable subset, so that, with continuous preferences, all welfare gains through trading can be approximately achieved in a countable subset of the commodity space. From this perspective, a separable infinite-dimensional commodity space looks as if there were just countably many commodities. So, one may view an atomless economy where the commodity space is an infinite-dimensional but separable Banach space as an economy in which there are “many more agents than commodities,” even though the algebraic dimension of the commodity space is not smaller than the cardinal of the continuum. In particular, if one wants to interpret core equivalence as a manifestation of “many more agents than commodities,” one cannot use the algebraic dimension of a commodity space as the notion of the number of commodities.
In this paper, we formalize the idea of “many more agents than commodities” as a condition that is satisfied in an atomless economy whenever the commodity space is separable; see Sect. 4. In Sect. 5, we then consider the case in which the commodity space is an ordered Banach space whose positive cone has non-empty interior, and allocations are taken to be Bochner integrable (the setting treated in Tourky and Yannelis 2001; Podczeck 2003) and show that under assumptions on the primitives of an economy exactly as in Aumann (1964), core equivalence is indeed equivalent to the presence of “many more agents than commodities,” without any special set-theoretic assumptions in the background.
There are some subtleties, concerning the order of the commodity space and the fact that the assumptions in Aumann (1964) do not include transitivity of preferences. For a discussion of these points and for relevant results, see Sect. 5. In Sect. 6, we show that the identification of core equivalence with “many more agents than commodities” also holds for many economically relevant commodity spaces which are not covered by the previous results, in particular for the \(L_{p}\)-spaces, \(1\le p<\infty \).
In Sect. 7, we revisit the setting of Mertens’ (1970) core equivalence result. The commodity space is \(L_{\infty }(\mu )\) with the Mackey topology and feasibility is defined in terms of the Gelfand integral, viewing \(L_{\infty }(\mu )\) as the dual of \(L_{1}(\mu )\). In particular, continuity of preferences is required with respect to the Mackey topology. It is assumed in Mertens (1970) that \(L_{\infty }(\mu )\) with the Mackey topology is separable; thus, there are “many more agents than commodities.” We show, however, that core equivalence holds without this assumption. In fact, there might be many more commodities than agents. This also answers a question raised by Mertens. By weakening some assumptions made by Mertens, we actually get a core equivalence result that reduces to that of Aumann (1964) when the number of commodities is finite.
So, the notion of integral chosen to define feasibility of allocations matters for core equivalence. The crucial difference in this regard between the Gelfand and the Bochner integral is that with the latter integral, an allocation must be strongly measurable and therefore essentially separably valued. If the commodity space itself is not separable, this means that Bochner integrable allocations take values in thin subspaces of the commodity space, which, compared with the case of Gelfand integrable allocations, makes the blocking possibilities of any coalition rather limited.
The organization of this paper is as follows. The next section contains the principal definitions. Section 3 contains a restatement of Aumann’s (1964) core equivalence theorem, which is the point of reference for our results, which are stated in Sects. 5–7, after a Sect. 4 where our formalization of the notion of “many more agents than commodities” may be found. The proofs of our results are given in Sects. 8–11. In Appendix 1, connections between some of the assumptions we use and assumptions known from the literature are established, and in Appendix 2, some mathematical background information is provided.
2 Notation and terminology
(1) Let \(E\) be a linear topological space. Assume that some notion of integrability for functions from measure spaces to \(E\) is given. Now an economy \({\fancyscript{E}}\) with commodity space \(E\) is given by a list \({\fancyscript{E}}=[(T,{\fancyscript{T}} ,\nu ),\langle X_{t},\succ _{t},e (t)\rangle _{t\in T}]\) where
-
\((T,{\fancyscript{T}} ,\nu )\) is a complete probability space, representing the space of agents;
-
\(X_{t}\subseteq E\) is the consumption set of agent \(t\);
-
\(\succ _{t}\,\subseteq X_{t}\times X_{t}\) is the (strict) preference relation of agent \(t\);
-
\(e(t)\in E\) is the initial endowment of agent \(t\);
-
the endowment map \(e:T\rightarrow E\), given by \(t\mapsto e(t)\), is integrable.
The economy \({\fancyscript{E}}\) is said to be atomless if the probability space \((T,{\fancyscript{T}} ,\nu )\) of agents is atomless.
An allocation in the economy \({\fancyscript{E}}\) is an integrable function \(f:T\rightarrow E\) such that \(f(t)\in X_{t}\) for almost all \(t\in T\). An allocation \(f\) is said to be feasible if

Price systems are continuous linear functionals on the commodity space \(E\). A Walrasian equilibrium for the economy \(\mathcal E\) is a pair \((p,f)\), where \(f\) is a feasible allocation and \(p\) is a price system, such that for almost every \(t\in T\):
-
(i)
\(p{f(t)}\le p{e(t)}\) and
-
(ii)
if \(x\succ _t f(t)\) then \(px>pe(t)\).Footnote 2
A feasible allocation \(f\) is said to be a Walrasian allocation if there is a price vector \(p\) such that the pair \((p,f)\) is a Walrasian equilibrium. An allocation \(f\) is a core allocation if it is feasible and if it cannot be blocked by any non-negligible coalition, i.e., if there is no \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\) and no allocation \(g:T\rightarrow E\) such that
-
(i)
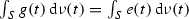 , i.e., \(g\) is feasible for \(S\), and
, i.e., \(g\) is feasible for \(S\), and -
(ii)
\(g(t)\succ _t f(t)\) for almost all \(t\in S\).
The core is the set of all core allocations.
(2) We need to fix some additional notation and terminology.
(a) If \(E\) is a linear topological space, \(E^*\) denotes the (topological) dual space, i.e., the space of all continuous linear functionals on \(E\).
(b) If \(E\) is an ordered linear space, we write \(\ge \) for the order of \(E\), and \(E_{+}\) for the positive cone; thus, \(E_{+}=\{{x\in E}:{x\ge 0}\}\). Elements of \(E_{+}\) are called positive. We write \(x>y\) to mean “\(x\ge y\) and \(x\ne y\).”
(c) If \(E\) is an ordered linear topological space, i.e., an ordered linear space endowed with a linear space topology such that the positive cone \(E_{+}\) is closed, then \(E^{*}\) is always viewed as being endowed with the dual order defined from \(E\); thus for any \(p\), \(q\in E^{*}\), \(p\ge q\) means \(px\ge qx\) for all \(x\in E_{+}\), so that, in particular, \(E_{+}^{*}=\{{p\in E^{*}}:{px\ge 0 \text { for all }x\in E_{+}}\}\).
(d) Let \(E\) be an ordered linear topological space.
(i) An element \(x\in E\) is called strictly positive if \(x\ge 0\) and \(px>0\) for every \(p\in E^{*}\) with \(p>0\). Of course, if \(E=\mathbb {R}^{\ell }\) with the usual topology and order, then this definition says nothing else than that a vector is strictly positive if it is larger than zero in each coordinate. A more general fact is that if \(E\) is locally convex and \(E_{+}\) has non-empty interior, then the strictly positive vectors in \(E\) are the interior points of \(E_{+}\) (see Aliprantis and Tourky 2007, Lemma 2.17, p. 73).
(ii) A linear functional on \(E\), in particular an element \(p\in E^{*}\), is called strictly positive if \(px>0\) for every \(x\in E\) with \(x> 0\).
(iii) Note that if \(E_{+}\) has non-empty interior, or if \(E\) is a Banach lattice, then any positive linear functional on \(E\) is continuous, i.e., belongs to \(E^{*}\).
(e) A convex subset \(H\) of a cone \({\varLambda }\) in a vector space \(E\) is a base of \({\varLambda }\) if for each \(x\in {\varLambda }\!\setminus \! \{0\}\), there is a unique \(h\in H\) and a unique \(\lambda >0\) such that \(x=\lambda h\); if \(E\) is a normed space, then such a set \(H\) is said to be a bounded base of the cone \({\varLambda }\) if \(H\) is a norm-bounded subset of \(E\).
Remark 1
Let \(E\) be an ordered normed space and suppose that \(E_+\) has a base \(H\). Then by Aliprantis and Tourky (2007, Theorem 1.47 and Exercise 2, p. 42), there is a strictly positive linear functional \(q\) on \(E\) such that \(H=\{{x\in E_{+}}:{qx=1}\}\). If \(E_+\) has an interior point, such a \(q\) must be continuous, i.e., must be an element of \(E^{*}_+\). It follows from these two facts that if \(E_+\) has a bounded base and an interior point, then the dual cone \(E^{*}_+\) must have non-empty interior for the dual norm.
Remark 2
The notion of “strictly positive” as stated in (d)(i) involves the topology of \(E\) in an essential way. For example, if \(({\varOmega },{\varSigma },\mu )\) is a \(\sigma \)-finite measure space, then for \(L_{\infty }(\mu )\) with the Mackey topology defined from the duality with \(L_{1}(\mu )\), an element \(p\in L_{\infty }(\mu )\) is strictly positive if (for any of its versions) \(p(\omega )>0\) a.e. in \({\varOmega }\), while for \(L_{\infty }(\mu )\) with the \(||\cdot ||_{\infty }\)-topology, a \(p\in L_{\infty }(\mu )\) is strictly positive if and only if there is an \(\varepsilon >0\) such that \(p(\omega ) >\varepsilon \) a.e. in \({\varOmega }\).
3 Aumann’s classical core equivalence result
In Aumann’s (1964) model, the commodity space \(E\) is \(\mathbb {R}^{\ell }\) (with the usual topology and order) and allocations are Lebesgue integrable functions. The following assumptions are made by Aumann (1964):
-
(P) (Positive consumption) For each \(t\in T\), \(X_{t}=E_{+}\).
-
(D) (Desirability) For each \(t\in T\), \(\succ _{t}\) is strictly monotone, i.e., if \(x\), \(y\in X_{t}\) and \(x>y\) then \(x\succ _{t} y\).
-
(C) (Continuity) For each \(t\in T\) and each \(x\in X_{t}\), the set \(\{{y\in X_{t}}:{y\succ _{t}x}\}\) is open in \(X_{t}\).
-
(AM) (Aumann measurability) If \(f\), \(g\) are allocations, then \(\{{t\in T}:{f(t)\succ _{t}g(t)}\}\) is a measurable set.
-
(EC) (Endowments are consumption vectors) For each \(t\in T\), \(e(t)\in X_{t}\).
-
(RA) (Resource availability) The aggregate endowment
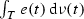 is strictly positive.
is strictly positive.
Here is Aumann’s (1964) classical core equivalence result.
Theorem 1
Let \({\fancyscript{E}}\) be an atomless economy with commodity space \(E=\mathbb {R}^{\ell }\). If (P), (D), (C), (AM), (EC), and (RA) are satisfied, then the core of the economy \({\fancyscript{E}}\) coincides with the set of Walrasian allocations.
A few remarks are in order. In Aumann (1964), the continuity assumption on preferences is stated in a form slightly stronger than (C); not only the upper sections of the preference relations are assumed to be open, but also the lower sections. However, in the proof given by Aumann, only the former assumption is used.
Instead of assuming (AM), several papers on core equivalence make a weaker measurability assumption in which only constant allocations are compared. We refer to Podczeck (2004) for a discussion of the relationship between these two measurability assumptions.
There is a growing literature on core equivalence in atomless economies with asymmetric information among agents; see, e.g., Einy et al. (2001), Angeloni and Martins-da Rocha (2009), and Hervés-Beloso et al. (2005). We will not investigate this context here.
4 Many more agents than commodities
In this section, we want to give the phrase “many more agents than commodities” a precise definition. For this, we need some more notation.
(a) We write \(\mathfrak c\) for the cardinal of the continuum, i.e., the cardinal of \(\mathbb {R}\).
(b) If \(E\) is a linear space, we write \({{\mathrm{dim^{a}}}}(E)\) for the algebraic dimension of \(E\), i.e., the least cardinal of any subset of \(E\) with a full linear span, and if \(E\) is actually a linear topological space, we write \(\dim (E)\) for the least cardinal of any subset of \(E\) with a dense linear span. As noted in the introduction, \({{\mathrm{dim^{a}}}}(E)\ge \mathfrak c\) if \(E\) is an infinite-dimensional Banach space.
(c) Given an atomless probability space \((T,{\fancyscript{T}},\nu )\), we write \(\mathcal {N}(\nu )\) for the ideal of null sets in \(T\), and \({{\mathrm{add}}}\mathcal {N}(\nu )\) for the least cardinal of any family in \(\mathcal {N}(\nu )\) whose union is not in \(\mathcal {N}(\nu )\). Note that \({{\mathrm{add}}}\mathcal {N}(\nu )\le \mathfrak c\). (To see this, let \(\langle {{\fancyscript{T}}_{n}}\rangle _{n\in \mathbb {N}}\) be a sequence of partitions of \(T\) into measurable subsets such that for each \(n\), \(\nu (A)=2^{-n}\) for each \(A\in {\fancyscript{T}}_{n}\). Then the non-empty sets of the form \(\bigcap _{n}A_{n}\), where \(A_{n}\in {\fancyscript{T}}_{n}\) for each \(n\), form a partition of \(T\) into no more that \(\mathfrak c\) null sets.) But of course, \({{\mathrm{add}}}\mathcal {N}(\nu )\) is uncountable because the union of countably many null sets is a null set.
Now let \((T,{\fancyscript{T}},\nu )\) be an atomless probability space of agents, and \(E\) a linear topological space, taken to be the commodity space. In Tourky and Yannelis (2001), \({{\mathrm{dim^{a}}}}(E)\) is the notion of number of commodities, and “many more agents than commodities” is formally expressed by saying that \({{\mathrm{add}}}\mathcal {N}(\nu )>{{\mathrm{dim^{a}}}}(E)\).Footnote 3 However, as pointed out in the introduction, one may well view an atomless economy where the commodity space is a separable infinite-dimensional Banach space as an economy with “many more agents than commodities.” But this is incompatible with the formalization above, because \({{\mathrm{add}}}\mathcal {N}(\nu )\le \mathfrak c\) but \({{\mathrm{dim^{a}}}}(E)\ge \mathfrak c\) if \(E\) is an infinite-dimensional Banach space.
A notion of the “number of commodities” which is more permissive than \({{\mathrm{dim^{a}}}}(E)\) is provided by \(\dim (E)\). Informally, while \({{\mathrm{dim^{a}}}}(E)\) amounts to a notion of the number of commodities in physical terms, \(\dim (E)\) amounts to a notion of the number of commodities in economic terms, incorporating certain substitutability relations among commodities. Of course, if \(E=\mathbb {R}^{\ell }\), then \(\dim (E)={{\mathrm{dim^{a}}}}(E)\), and \(\dim (E)\) is just the number of commodities in the usual sense. Here is our formalization of “many more agents than commodities,” following that in Tourky and Yannelis (2001) concerning the side of the agents, but with \(\dim (E)\) in place of \({{\mathrm{dim^{a}}}}(E)\) on the side of the commodities.
Definition 1
An atomless economy satisfies (MMATC) (has “many more agents than commodities”) if \({{\mathrm{add}}}\mathcal {N}(\nu )>\dim (E)\), where \(E\) is the commodity space of the economy and \(\nu \) is the measure on the set of agents.
Now according to this definition, there are “many more agents than commodities” in an atomless economy whenever the commodity space is separable. But it should be noted that (MMATC) may not imply separability of the commodity space. As an example of what is conceivable, take the unit interval with Lebesgue measure for the space of agents, and recall that under Martin’s axiom, \({{\mathrm{add}}}\mathcal {N}(\nu )=\mathfrak c\) if \(\nu \) is Lebesgue measure, and that Martin’s axiom is compatible with \(\mathfrak c\) being an arbitrarily large cardinal (see Jech 2003, Theorem 16.13 and Corollary 26.41, or Appendix 2). So, we can have plenty of uncountable cardinals \(\kappa \) for which (MMATC) holds with \(\dim (E)=\kappa \).
5 Core equivalence when the commodity space is an ordered Banach space whose positive cone has non-empty interior
In this section, we adopt the setting considered by Tourky and Yannelis (2001) to relate the core equivalence problem to the notion of “many more agents than commodities:” The commodity space \(E\) is an ordered Banach space with positive cone having non-empty interior, and allocations are taken to be Bochner integrable.
The first theorem in this section shows that, in this setting, Aumann’s classical core equivalence result carries over verbatim to an infinite-dimensional commodity space provided that there are “many more agents than commodities.” As this latter condition trivially holds if the commodity space is \(\mathbb {R}^{\ell }\), the theorem contains Aumann’s result as a special case. In particular, the theorem significantly strengthens the core equivalence result of Tourky and Yannelis (2001), showing that, as in Aumann’s result, transitivity and irreflexivity of preferences are not needed. Recall that (MMATC) may not imply that the commodity space is separable.
Theorem 2
Let \(E\) be an ordered Banach space whose positive cone \(E_{+}\) has non-empty interior and let \({\fancyscript{E}}\) be an atomless economy with commodity space \(E\) such that (P), (D), (C), (AM), (EC), (RA), and (MMATC) are satisfied. Then the core of the economy \({\fancyscript{E}}\) coincides with the set of Walrasian allocations.
In fact, in the context of Theorem 2, the assumption of “many more agents than commodities” is pivotal for core equivalence:
Theorem 3
Let \((T,{\fancyscript{T}},\nu )\) be an atomless probability space, and \(E\) an ordered Banach space such that \(E_{+}\) has non-empty interior and \(E^{*}\) has strictly positive elements. If \({{\mathrm{add}}}\mathcal {N}(\nu )\le \dim (E)\), then there is an economy \({\fancyscript{E}}\) with \((T,{\fancyscript{T}},\nu )\) as space of agents and \(E\) as commodity space such that (P), (D), (C), (AM), (EC), and (RA) are satisfied but such that there is a core allocation which is not Walrasian.
This remains true if all individual endowments are required to be strictly positive.
Together, Theorems 2 and 3 show that (MMATC) is essentially equivalent to core equivalence. In the proof of Theorem 3, strictly positive prices are used to construct strictly monotone preferences. Of course, if the commodity space is such that there are no strictly positive prices, then there can be no economies with strictly monotone preferences and a Walrasian equilibrium, and the question addressed by Theorem 3 becomes pointless.
In the context of Theorems 2 and 3, preferences need not be transitive. Transitivity may be seen as a reasonable property of preferences. So, let us state this property formally as an assumption.
-
(Tr) For each \(t\in T\), \(\succ _{t}\) is transitive.
The next theorem, together with the subsequent example, shows that if (Tr) is assumed, then, in the context of Theorem 2, “many more agents than commodities” need no longer be a prerequisite for core equivalence. As may be inferred from the proof, the reason is that the effects of strict monotonicity of preferences can be strengthened by transitivity, so that it becomes easier for any non-negligible group of agents to find common directions of improvement.
Theorem 4
Let \(K\) be a compact Hausdorff space and let the commodity space \(E\) be \(C(K)\) with the usual norm and order. Let \({\fancyscript{E}}\) be an atomless economy satisfying (P), (D), (C), (AM), (EC), (RA), and (Tr). Let \(M^{1}_{+}(K)\) be the set of tight Borel probability measures on \(K\). If \(M^{1}_{+}(K)\) is first countable in the \({\text {weak}}^{*}\)-topology, then the core of the economy \({\fancyscript{E}}\) coincides with the set of Walrasian allocations.
Example
Let \(E=C(I^{\sharp })\) where \(I^{\sharp }\) is the split interval (or “double arrow space”), i.e., \(I^{\sharp }=\left( 0,1\right] \times \left\{ 0\right\} \cup \left[ 0,1\right) \times \left\{ 1\right\} \subseteq \mathbb {R}^{2}\), endowed with the lexicographical order topology; see, e.g., Engelking (1989, 3.10.C, p. 212). The space \(I^{\sharp }\) is a separable compact Hausdorff space, and as shown in Pol (1982), the space \(M^{1}_{+}(I^{\sharp })\) of tight Borel probability measures on \(I^{\sharp }\) is \({\text {weak}}^{*}\)-first countable. Separability of \(I^{\sharp }\) implies that \(M^{1}_{+}(I^{\sharp })\) has elements with full support. Thus, the dual of \(C(I^{\sharp })\) has strictly positive elements, so Assumptions (P) and (D) are simultaneously satisfiable for \(C(I^{\sharp })\) as commodity space. Thus, economies satisfying the assumptions in Theorem 4 for \(C(I^{\sharp })\) as commodity space do exist. Now the order of \(I^{\sharp }\) has continuum many “jumps,” so the weight of \(I^{\sharp }\) is \(\mathfrak c\). This implies that \(\dim (C(I^{\sharp }))=\mathfrak c\) (use Engelking 1989, 3.2.I, p. 147, together with Fact 1 in Sect. 8). Hence, as \({{\mathrm{add}}}\mathcal {N}(\nu )\le \mathfrak c\) for any atomless probability measure, (MMATC) fails for any atomless economy with commodity space \(C(I^{\sharp })\).
Now in the results on failure of core equivalence presented in Tourky and Yannelis (2001) and Podczeck (2003), preferences actually have continuous utility representations and are, in particular, transitive. So, one may ask for the relationship between these results and Theorem 4. The point is that in the core non-equivalence results in Tourky and Yannelis (2001) and Podczeck (2003), the positive cone of the commodity space has a bounded base [see 2(2)(e)] in addition to having a non-empty interior. On the other hand, in Theorem 4 the commodity space is Banach lattice. It is a well-known fact that no infinite-dimensional Banach lattice can have simultaneously a non-empty interior and a bounded base,Footnote 4 and therefore there is no contradiction between Theorem 4 and the core non-equivalence results in Tourky and Yannelis (2001) and Podczeck (2003).
As noted in the introduction, in these non-equivalence results the continuum hypothesis is assumed.Footnote 5 Of course, if the continuum hypothesis holds, then our condition (MMATC) is equivalent to the commodity space being separable. In view of this, the continuum hypothesis is not just an innocent assumption, but imposes severe restrictions on the scope of our notion of “many more agents than commodities.” It is therefore desirable to avoid the continuum hypothesis. Our next theorem shows that if the positive cone of the commodity space has a bounded base, as in the above mentioned results of Tourky and Yannelis (2001) and Podczeck (2003), then Theorem 3 remains true for preferences with continuous utility representations, without any need for the continuum hypothesis.
-
(UR) For each \(t\in T\), \(\succ _{t}\) has a continuous utility representation.
Theorem 5
Let the commodity space \(E\) be an ordered Banach space such that \(E_{+}\) has non-empty interior. If \(E_{+}\) has a bounded base, then given an atomless economy \({\fancyscript{E}}\), conditions (P), (D), (C), (AM), (EC), (RA), and (UR) together imply core equivalence if and only if (MMATC) is satisfied.
This remains true if all individual endowments are strictly positive.
To compare Theorems 4 and 5, recall that if \(E\) is an ordered Banach space such that \(E_{+}\) has a bounded base and non-empty interior, then the dual cone \(E^{*}_{+}\) must have non-empty interior for the dual norm (see Remark 1), whereas if \(E\) is an infinite-dimensional Banach lattice such that \(E_+\) has non-empty interior, then \(E^{*}_{+}\) has empty interior. Thus, if preferences are strictly monotone, so that the members of \(E^{*}_{+}\) reflect the possible marginal rates of substitution, then the latter case may be seen as imposing more restrictions on the possible diversity of preferences than the former.
Remark 3
A vector order such that the positive cone has both a bounded base and a non-empty interior exists on every Banach space. For example, given a Banach space \(E\), let \({\varLambda }\) be an “ice cream cone” in \(E\), i.e., a closed convex cone of the form
where \(q\in E^{*}\) is of norm \(1\) and \(\varepsilon \) is a number with \(0<\varepsilon <1\) (see Aliprantis and Tourky 2007, p. 99). Setting \(x\ge y\) whenever \(x-y\in {\varLambda }\) defines a vector order on \(E\) such that \(E_{+}={\varLambda }\). The fact that \(q\) is of norm 1 and \(\varepsilon <1\) implies that \({\varLambda }\) has non-empty interior. Evidently the set \(H=\{{x\in {\varLambda }}:{qx=1}\}\) is a base of \({\varLambda }\). Moreover, if \(x\in H\), then \(||x||_{}\le 1/\varepsilon \), and thus \(H\) is bounded.
In view of this remark, we have the following corollary of Theorem 5, which parallels the statement of the core non-equivalence results in Tourky and Yannelis (2001) and Podczeck (2003) (but without the continuum hypothesis).
Corollary
Let \(E\) be a Banach space and \((T,{\fancyscript{T}},\nu )\) an atomless probability space. Suppose \(\dim (E)\ge {{\mathrm{add}}}\mathcal {N}(\nu )\). Then there is a vector order on \(E\), for which \(E\) is an ordered Banach space with \({{\mathrm{int}}}E_{+}\ne \emptyset \), and an economy \({\fancyscript{E}}\), with \((T,{\fancyscript{T}},\nu )\) as space of agents and \(E\) as commodity space, such that (P), (D), (C), (AM), (EC), (RA), and (UR) hold, but such that there is a core allocation which is not Walrasian.
This is the case even when all individual endowments are required to be strictly positive.
6 Core equivalence when the commodity space is an order-continuous Banach lattice
Infinite-dimensional commodity spaces arising in applications often require dealing with consumption sets having empty interior. Such contexts are not covered by the treatment in the previous section. In this section, we allow for consumption sets with empty interior. We will restrict attention to the framework where the commodity space is a Banach lattice with order-continuous norm (in short, an order-continuous Banach lattice). This framework is sufficiently general for the core equivalence problem to be of interest when consumption sets may have empty interior. Note that the \(L_{p}\)-spaces for \(1\le p<\infty \) are covered.
It is well known that if the commodity space is infinite-dimensional and consumption sets have empty interior, then continuity of preferences does not guarantee appropriate bounds on marginal rates of substitution in order for preferred sets to have supporting price vectors. As a consequence, core equivalence may fail through marginal rates of substitution that are not properly bounded; see Example 5.1 in Rustichini and Yannelis (1991). To avoid such a technical failure of core equivalence, which is unrelated to whether or not there are “many more agents than commodities,” we will employ the following assumption, which is a rephrasing of the notion of “extremely desirable commodity” used in the core equivalence result in Rustichini and Yannelis (1991).
-
(EDC) (Extremely desirable commodity) There are a \(v\in E_{+}\!\setminus \! \{0\}\) and a strictly positive \(q\in E^{*}\) such that for each \(t\in T\) and any number \(\lambda >0\), \(x+\lambda (v+u)\succ _{t} x\) whenever \(x\in X_{t}\) and \(u\in E\) are such that \(x+\lambda (v+u)\in X_{t}\) and \(q|u|_{}<1\).
Here \(|u|_{}\) is the absolute value of \(u\), i.e., the supremum of \(u\) and \(-u\). Actually, in Rustichini and Yannelis (1991) the notion of “extremely desirable commodity” is stated for the case in which the consumption sets of the agents are equal to the positive cone of the commodity space. In Appendix 1(A), we show that, in this case, the notion of “extremely desirable commodity” in the statement of (EDC) is indeed equivalent to that in Rustichini and Yannelis (1991). For us, the version we use is easier to operate with.
Another assumption that has been used in the context of core equivalence to deal with consumption sets with empty interior is as follows.
-
(US) (Uniform substitutability) There are strictly positive linear functionals \(a \) and \(b \in E^{*}\), with \(a \le b \), such that for each \(t\in T\), \(x+v-u\succ _{t} x\) whenever \(x\in X_{t}\) and \(u,v\in E_{+}\) are such that \(x+v-u\in X_{t}\) and \(a v>b u\).
This condition was developed by Zame (1986). In (B) in Appendix 1, we show that (US) implies (EDC). Observe that if \(E=\mathbb {R}^{\ell }\), then (EDC) is automatically satisfied if (P) and (D) are. This is not true of (US).
As in the previous section, allocations are taken to be Bochner integrable in the following theorem.
Theorem 6
Let the commodity space \(E\) be an order-continuous Banach lattice such that \(E_{+}\) has strictly positive elements. Then given an atomless economy \({\fancyscript{E}}\), Assumptions (P), (D), (C), (AM), (EC), (RA), (Tr), and (EDC) together imply core equivalence if and only if (MMATC) is satisfied.
This remains true if all individual endowments are strictly positive and if (EDC) is strengthened to (US), and (Tr) to (UR).
Remark 4
The sufficiency part of Theorem 6 remains true if the requirement that \(E\) be order-continuous is dropped; see the proof of this theorem. However, by Theorem 4 and the example following the statement of that theorem, the necessity part does not hold in all Banach lattices.
7 Core equivalence when the commodity space is \(L_{\,\infty }(\mu )\) with the Mackey topology
In this section, the commodity space \(E\) is taken to be \(L_{\infty }(\mu )\) endowed with the Mackey topology defined from the usual pairing of \(L_{\infty }(\mu )\) with \(L_{1}(\mu )\), the measure \(\mu \) being \(\sigma \)-finite, and allocations are taken to be Gelfand integrable, viewing \(L_{\infty }(\mu )\) as the (norm) dual of \(L_{1}(\mu )\). Recall that the usual pairing of \(L_{\infty }(\mu )\) and \(L_{1}(\mu )\) is given by integration, i.e.,  , \(p\in L_{1}(\mu )\), \(x\in L_{\infty }(\mu )\) and that the Mackey topology of \(L_{\infty }(\mu )\) for this pairing is the strongest locally convex topology on \(L_{\infty }(\mu )\) such that \(L_{1}(\mu )\) is the (topological) dual. In the sequel, we will refer to this topology simply as the Mackey topology of \(L_{\infty }(\mu )\).
, \(p\in L_{1}(\mu )\), \(x\in L_{\infty }(\mu )\) and that the Mackey topology of \(L_{\infty }(\mu )\) for this pairing is the strongest locally convex topology on \(L_{\infty }(\mu )\) such that \(L_{1}(\mu )\) is the (topological) dual. In the sequel, we will refer to this topology simply as the Mackey topology of \(L_{\infty }(\mu )\).
According to the definitions in Sect. 2, price vectors are taken to be elements of the topological dual of the commodity space, so, as in Mertens (1970), they are now required to be in \(L_{1}(\mu )\). Furthermore, assumptions (C) and (RA), which involve topological notions, have now to be interpreted in the Mackey topology of \(L_{\infty }(\mu )\). In particular, (RA) does not imply that the aggregate endowment of an economy is strictly positive for the \(||\cdot ||_{\infty }\)-topology of \(L_{\infty }(\mu )\).
Remark 5
It has been argued in Tourky and Yannelis (2001, Remark10.1) that weak integrals such as the Gelfand or Pettis integral may be inappropriate to define feasibility of allocations, because there could be functions with integral equal to zero that are everywhere positive and nonzero. (E.g., let \((T,{\fancyscript{T}},\nu )\) be the unit interval with Lebesgue measure, let \(E\) be the Hilbert space \(\ell _{2}([0,1])\), and define \(h:T\rightarrow E\) by setting \(h(t)=1_{\{t\}}\) for each \(t\in T\).) Under Assumptions (P) and (D), adding such a function to a given allocation improves every agent without affecting feasibility. As a consequence of this kind of free lunch, the core would be empty and core equivalence holds trivially. This is not a problem in the setting defined above. As the measure \(\mu \) is \(\sigma \)-finite, there is a strictly positive element \(p\in L_{1}(\mu )\). Now for \(x\in E_+\), \(px=0\) can happen only if \(x=0\). So, under Assumption (P), an allocation with Gelfand integral equal to zero must be zero almost everywhere in \(T\). See (D) of Appendix 1 for a more precise statement.
The following assumption, which is stronger than Assumption (RA) if \(L_{\infty }(\mu )\) is infinite-dimensional, is implied by the assumptions made in Mertens (1970) on the endowments in an economy [see (C) in Appendix 1].
-
(TAE) (Thick aggregate endowment) There is a non-decreasing sequence \(\langle {e_{n}}\rangle \) of \(||\cdot ||_{\infty }\)-Bochner integrable functions \(e_{n}:T\rightarrow E_{+}\) such that \(e_{n}(t)\rightarrow e(t)\) in the Mackey topology a.e. in \(T\) and such that
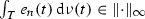 -\({{\mathrm{int}}}E_{+}\) for each \(n\).Footnote 6
-\({{\mathrm{int}}}E_{+}\) for each \(n\).Footnote 6
Observe that (TAE) does not imply the initial allocation to be \(||\cdot ||_{\infty }\)-Bochner integrable. In fact, the initial allocation need not even be \(||\cdot ||_{\infty }\)-strongly measurable. But of course, (TAE) implies that the aggregate endowment of an economy belongs to the \(||\cdot ||_{\infty }\)-interior of \(E_{+}\) and that there is a Mackey-separable subset of \(E_{+}\) which contains the individual endowment of almost all agents. In these latter two aspects, (TAE) is stronger than (RA).
In view of the fact that the indefinite Bochner integrals of the functions \(e_{n}\) are \(\nu \)-continuous, (TAE) says that small groups of agents can have no corner (i.e., monopoly power) on the market, in the sense that, for some \(\varepsilon >0\), if \(T'\subseteq T\) is such that \(\nu (T')<\varepsilon \), then  , i.e., the aggregate endowment of the complementary group \(T\!\setminus \! T'\) contains all commodities.
, i.e., the aggregate endowment of the complementary group \(T\!\setminus \! T'\) contains all commodities.
Note that (TAE) does not imply that the individual endowments \(e(t)\) are in the \(||\cdot ||_{\infty }\)-interior of \(E_{+}\). In this aspect, (TAE) is actually more general than the assumptions on endowments made in Mertens (1970). In fact, when \(E=\mathbb {R}^{\ell }\) and (EC) holds, then (TAE) is equivalent to (RA).
In the following core equivalence result, (MMATC) does not play any role; the “size” of the commodity space may be arbitrarily large, without any relation to properties of the space of agents. Note in this regard that for any cardinal \(\kappa \), there is a probability measure \(\mu \) such that least cardinal of any subset of \(L_{\infty }(\mu )\) whose linear span is dense in \(L_{\infty }(\mu )\) for the Mackey topology is larger than \(\kappa \). (Just look at the usual measure on \(\{0,1\}^{\kappa }\), where \(\kappa \) is an arbitrary cardinal.)
Theorem 7
Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space and let the commodity space \(E\) be \(L_{\infty }(\mu )\) with the Mackey topology. Let \({\fancyscript{E}}\) be an atomless economy with commodity space \(E\) such that (P), (D), (C), (AM), and (TAE) are satisfied. Then the core of the economy \({\fancyscript{E}}\) coincides with the set of Walrasian allocations.
As noted above, if \(E=\mathbb {R}^{\ell }\) and (EC) is satisfied, then (TAE) is equivalent to (RA), so Theorem 7 includes Aumann’s core equivalence result as a special case. In the core equivalence result of Mertens (1970), individual endowments are assumed to belong to \(||\cdot ||_{\infty }\text {-}{{\mathrm{int}}}E_{+}\); also, the desirability assumption includes a transitivity requirement. For these reasons, Merten’s result does not include that of Aumann.
As already noted in the introduction, in Mertens (1970) the commodity space is assumed to be separable for the Mackey topology. However, Mertens asked whether this assumption may be dropped. Our result above gives an affirmative answer.
As also noted above, assumption (TAE) is stronger than (RA). The next theorem shows that if the assumptions on preferences are strengthened so as to include (EDC) and (Tr), then core equivalence holds again with the standard assumptions (RA) and (EC), and (TAE) is not needed.Footnote 7
Theorem 8
Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space and let the commodity space \(E\) be \(L_{\infty }(\mu )\) with the Mackey topology. Let \({\fancyscript{E}}\) be an atomless economy with commodity space \(E\). If (P), (D), (C), (AM), (RA), (EC), (Tr), and (EDC) are satisfied, then the core of the economy \({\fancyscript{E}}\) coincides with the set of Walrasian allocations.
Note that, given some price system, optimal consumptions of agents, and hence their demands, reflect marginal rates of substitution. Assumption (EDC) imposes bounds on marginal rates of substitution, uniformly across the agents in an economy. Thus, this assumption may be seen as implying that small groups of agents cannot have monopsony power in the market. As remarked above, (TAE) may be seen as an assumption implying that small groups of agents cannot have monopoly power in the market. Thus, what drives the two core equivalence results in this section seems to be that the assumptions imply that there is some kind of “thickness” on at least one side of the market.
8 Preliminaries for the proofs
In this section, we introduce further notation, record two basic facts, and make some general preparing remarks for the proofs.
(1) (a) Given a measure space \((T,{\fancyscript{T}},\nu )\), we write \(\nu ^{*}\) for the outer measure defined from \(\nu \).
(b) If \(Z\) is a topological space and \(A\subseteq Z\), then \({{\mathrm{int}}}A\) denotes the interior of \(A\), and \({{\mathrm{c\ell }}}A\) or \(\overline{A}\) the closure of \(A\).
(c) If \(E\) is a linear topological space and \(A\subseteq E\), then \({{\mathrm{co}}}A\) denotes the convex hull of \(A\), and \({{\mathrm{\overline{co}}}}A\) the closed convex hull; further, \({{\mathrm{span}}}A\) denotes the linear span of \(A\), i.e., the set of all (finite) linear combinations of members of \(A\).
(d) For elements \(x\), \(y\) of a Riesz space \(X\), the expressions \(x^{+}\), \(x^{-}\), \(|x|_{}\), \(x\vee y\), \(x\wedge y\), and \(x\perp y\) have the usual lattice theoretic meaning; we refer to Aliprantis and Tourky (2007) for this as well as for the Riesz space-related facts that will be used in some of the proofs below.
(2) If \(Z\) is a topological space and \(A\subseteq Z\), then \({{\mathrm{dens}}}(A)\) denotes the density character of \(A\), i.e., the least cardinal of any subset of \(A\) which is dense in \(A\).
Recall that for a linear topological space \(E\), \(\dim (E)\) is defined to be the least cardinal of any set \(A\subseteq E\) such that \({{\mathrm{span}}}A\) is dense in \(E\). By the following fact, we may replace the cardinal \(\dim (E)\) in the definition of (MMATC) by \({{\mathrm{dens}}}(E)\).Footnote 8
Fact 1
If \(E\) is a linear topological space, then \({{\mathrm{dens}}}(E)=\dim (E)\) if \(\dim (E)\) is infinite.
(Indeed, it is clear that \(\dim (E)\le {{\mathrm{dens}}}(E)\). For the reverse inequality, note that if \(A\subseteq E\) and \({{\mathrm{span}}}A\) is dense in \(E\), then the subset of \({{\mathrm{span}}}A\) consisting of those linear combinations of members of \(A\) where the coefficients are rational is dense in \(E\), too.)
(3) It will be convenient to have the following definition.
Definition 2
Given a measurable space \((T,{\fancyscript{T}})\) and a linear space \(X\), we say that a set \(A\) of functions from \(T\) to \(X\) is decomposable if whenever \(f\), \(g\in A\) and \(S\in {\fancyscript{T}}\) then also \(1_{S}\times f+1_{T\!\backslash \!S}\times g\in A\).
The following fact may be inferred from the proof of Theorem 6.2 in Yannelis (1991, p. 22).
Fact 2
Let \((T,{\fancyscript{T}},\nu )\) be a totally finite measure space, and \(E\) a Banach space. Let \(A\) be a set of Bochner integrable functions from \(T\) to \(E\) and let  . If \(A\) is decomposable and \((T,{\fancyscript{T}},\nu )\) is atomless, then the norm-closure of \(B\) is convex.
. If \(A\) is decomposable and \((T,{\fancyscript{T}},\nu )\) is atomless, then the norm-closure of \(B\) is convex.
(4) The theorems to be proved contain the implication that a Walrasian allocation is a core allocation. That this is true is a standard and well-known fact, so in the proofs given below we will not look at this implication.
(5) According to the definition of economy as stated in Sect. 2, the probability space \((T,{\fancyscript{T}},\nu )\) of agents is complete. We will invoke this fact frequently without explicit reference.
(6) In the proofs below, it is assumed without loss of generality that \(E\ne \{0\}\) whenever this is needed for an argument but is not implied by the assumptions in force. Note that the assumption \(E\ne \{0\}\) means in particular that \(0\) cannot be an interior point of the positive cone \(E_{+}\).
9 Proofs of Theorems 2–4
9.1 Proof of Theorem 2
Let \(f\) be a core allocation of the given economy and let
Every \(h\in A\) is \(||\cdot ||_{\infty }\)-Bochner integrable; write  . Clearly, \(A\) is decomposable, so, as \(\nu \) is atomless, Fact 2 implies that \({{\mathrm{c\ell }}}B\) is convex. Moreover, \(0\in B\), so \({{\mathrm{c\ell }}}B\) is non-empty.
. Clearly, \(A\) is decomposable, so, as \(\nu \) is atomless, Fact 2 implies that \({{\mathrm{c\ell }}}B\) is convex. Moreover, \(0\in B\), so \({{\mathrm{c\ell }}}B\) is non-empty.
Note that \(({{\mathrm{c\ell }}}B)\cap {{\mathrm{int}}}(-E_{+})=\emptyset \). Otherwise, as \(0\notin {{\mathrm{int}}}E_{+}\), there are a \(v\in {{\mathrm{int}}}E_{+}\) and an \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\) such that  where \(g\) is as in the definition of \(A\). As the measure \(\nu \) is atomless and the indefinite Bochner integral of the function \(g-e\) is \(\nu \)-continuous, we may assume, shrinking the set \(S\) if necessary, that \(\nu (T\!\setminus \! S)>0\). For each \(n\in \mathbb {N}\), set \(T_{n}=\{{t\in T\!\setminus \! S}:{e(t)+nv\ge f(t)}\}\). Note that \(T_{n}\in {\fancyscript{T}}\) for each \(n\) because the map \(t\mapsto e(t)+nv-f(t)\), being Bochner integrable, is Borel measurable. Now because \(v\), belonging to \({{\mathrm{int}}}E_{+}\), is an order unit of \(E\), we have \(\bigcup _{n=0}^{\infty }T_{n}=T\!\setminus \! S\). Thus, as \(\nu (T\!\setminus \! S)>0\), there is an \(n_{1}\in \mathbb {N}\) such that \(\nu (T_{n_{1}})>0\). Choose \(n_{2}\in \mathbb {N}\) so that both \(n_{2}>n_{1}\) and \(\nu (T_{n_{1}})>1/n_{2}\). By Assumptions (D) and (P), \(e(t)+n_{2}v\succ _{t}f(t)\) for all \(t\in T_{n_{1}}\). Because \(\nu \) is atomless, we can choose an \(F\subseteq T_{n_{1}}\) with \(\nu (F)=1/n_{2}\). Define a function \(f':T\rightarrow E_{+}\) by setting \(f'(t)=g(t)\) for \(t\in S\), \(f'(t)=e(t)+n_{2}v\) for \(t\in F\), and \(f'(t)=0\) for \(t\in T\!\setminus \! (F\cup S)\). Then \(f'(t)\succ _{t} f(t)\) for almost all \(t\in F\cup S\). Moreover, \(f'\) is Bochner integrable and we have
where \(g\) is as in the definition of \(A\). As the measure \(\nu \) is atomless and the indefinite Bochner integral of the function \(g-e\) is \(\nu \)-continuous, we may assume, shrinking the set \(S\) if necessary, that \(\nu (T\!\setminus \! S)>0\). For each \(n\in \mathbb {N}\), set \(T_{n}=\{{t\in T\!\setminus \! S}:{e(t)+nv\ge f(t)}\}\). Note that \(T_{n}\in {\fancyscript{T}}\) for each \(n\) because the map \(t\mapsto e(t)+nv-f(t)\), being Bochner integrable, is Borel measurable. Now because \(v\), belonging to \({{\mathrm{int}}}E_{+}\), is an order unit of \(E\), we have \(\bigcup _{n=0}^{\infty }T_{n}=T\!\setminus \! S\). Thus, as \(\nu (T\!\setminus \! S)>0\), there is an \(n_{1}\in \mathbb {N}\) such that \(\nu (T_{n_{1}})>0\). Choose \(n_{2}\in \mathbb {N}\) so that both \(n_{2}>n_{1}\) and \(\nu (T_{n_{1}})>1/n_{2}\). By Assumptions (D) and (P), \(e(t)+n_{2}v\succ _{t}f(t)\) for all \(t\in T_{n_{1}}\). Because \(\nu \) is atomless, we can choose an \(F\subseteq T_{n_{1}}\) with \(\nu (F)=1/n_{2}\). Define a function \(f':T\rightarrow E_{+}\) by setting \(f'(t)=g(t)\) for \(t\in S\), \(f'(t)=e(t)+n_{2}v\) for \(t\in F\), and \(f'(t)=0\) for \(t\in T\!\setminus \! (F\cup S)\). Then \(f'(t)\succ _{t} f(t)\) for almost all \(t\in F\cup S\). Moreover, \(f'\) is Bochner integrable and we have

Thus, the coalition \(F\cup S\) can block \(f\) via \(f'\), contradicting the property of \(f\) being a core allocation. Thus, \(({{\mathrm{c\ell }}}B)\cap {{\mathrm{int}}}(-E_{+})=\emptyset \).
Now, as \({{\mathrm{int}}}E_{+}\) is non-empty, it follows from the separation theorem that there is a nonzero positive \(p\in E^{*}\) such that \(p z\ge 0\) for each \(z\in B\). For each \(x\in E_{+}\), let \(N_{x}=\{{t\in T}:{x\succ _{t}f(t),\ px<pe(t)}\}\). From Assumptions (P) and (AM), together with the fact that the map \(t\mapsto pe(t)\) is measurable, it follows that \(N_{x}\in {\fancyscript{T}}\) for each \(x\in E_{+}\). Hence, the fact that \(pB\ge 0\) implies that \(N_{x}\) is a null set for each \(x\in E_{+}\).
By (MMATC), \(E_{+}\) has a dense subset \(D\) such that \({{\mathrm{add}}}\mathcal {N}(\nu )>\#(D)\).Footnote 9 It follows that \(N=\bigcup _{x\in D}N_{x}\) is a null set, and by Assumptions (P) and (C), and continuity of \(p\):
-
(\(*\)) For all \(t\in T\!\setminus \! N\), if \(x\succ _{t}f(t)\), then \(px\ge pe(t)\).
It is now routine to verify that for almost all \(t\in T\),
-
(i)
\(pf(t)\le pe(t)\);
-
(ii)
if \(x\succ _{t}f(t)\), then \(px> pe(t)\).
Note first that by (P) and (D), (\(*\)) implies that \(pf(t)\ge pe(t)\) a.e. in \(T\). Consequently, since \(f\) is feasible, i.e., since  , (i) holds a.e. in \(T\). Let \(S=\{{t\in T}:{pe(t)>0}\}\). By (C) and (P), (\(*\)) implies that (ii) holds a.e. in \(S\). Now by (RA), the fact that \(p\) is nonzero and positive implies that \(\nu (S)>0\), so by (P) and (D) again, the fact that (ii) holds a.e. in \(S\) implies that \(p\) is strictly positive. Consequently, by (P) and (EC), for \(t\in T\!\setminus \! S\) a failure of (ii) implies that \(e(t)\succ _{t}f(t)\). By (AM), the set \(\{{t\in T}:{e(t)\succ _{t} f(t)}\}\) is measurable. Because \(f\) is a core allocation, this set must be a null set, so (ii) holds also a.e. in \(T\!\setminus \! S\). We may conclude that the pair \((p,f)\) is a Walrasian equilibrium. \(\square \)
, (i) holds a.e. in \(T\). Let \(S=\{{t\in T}:{pe(t)>0}\}\). By (C) and (P), (\(*\)) implies that (ii) holds a.e. in \(S\). Now by (RA), the fact that \(p\) is nonzero and positive implies that \(\nu (S)>0\), so by (P) and (D) again, the fact that (ii) holds a.e. in \(S\) implies that \(p\) is strictly positive. Consequently, by (P) and (EC), for \(t\in T\!\setminus \! S\) a failure of (ii) implies that \(e(t)\succ _{t}f(t)\). By (AM), the set \(\{{t\in T}:{e(t)\succ _{t} f(t)}\}\) is measurable. Because \(f\) is a core allocation, this set must be a null set, so (ii) holds also a.e. in \(T\!\setminus \! S\). We may conclude that the pair \((p,f)\) is a Walrasian equilibrium. \(\square \)
9.2 Proof of Theorem 3
Fix an interior point \(\bar{e}\) of \(E_{+}\) and a strictly positive \(q\in E^{*}\) such that \(q\bar{e}=1\). Let \(H=\{{x\in E_{+}}:{qx=1}\}\). Observe that \({{\mathrm{dens}}}(H)={{\mathrm{dens}}}(E)\).
Write \(\alpha ={{\mathrm{add}}}\mathcal {N}(\nu )\) and choose a family \(\langle {N_{\xi }}\rangle _{\xi <\alpha }\) of null sets in \(T\) such that \(\bigcup _{\xi <\alpha }^{}N_{\xi }\) is not a null set. Recall that in every metric space of density character \(\kappa \), there is a disjoint family of non-empty open subsets which has cardinal \(\kappa \) (see, e.g., Engelking 1989, 4.1.H, or Hodel 1984, Theorem 8.1). As \(\alpha \le {{\mathrm{dens}}}(H)\) by hypothesis, we can therefore find a family \(\langle {B_{\xi }}\rangle _{\xi <\alpha }\) of open balls in \(E\), each of them centered at some point \(x_{\xi }\in H\), such that the family \(\langle {B_{\xi }\cap H}\rangle _{\xi <\alpha }\) of intersections is disjoint. Using the fact that in a normed space the distance between the centers of two disjoint open balls cannot be smaller than the sum of the radii of these balls, we see that, in fact, the family \(\langle {B_{\xi }}\rangle _{\xi <\alpha }\) is disjoint.
Now for each agent \(t\in T\), let \(X_{t}=E_{+}\) and \(e(t)=\bar{e}\), so that (P) and (EC) are satisfied. In particular, the initial allocation \(t\mapsto e(t)\) is Bochner integrable and we have  , so (RA) is also satisfied.
, so (RA) is also satisfied.
As for preferences, for \(\xi <\alpha \) and \(t\in N_{\xi }\) let
and for \(t\in T\!\setminus \! \bigcup _{\xi <\alpha }^{}N_{\xi }\) let \(\succ _{t}=\bigl \{{(x,y)\in E_{+}\times E_{+}}:{qx>qy}\bigr \}\). As \(q\) is strictly positive, (D) is satisfied, and as each \(B_{\xi }\cap E_{+}\) is open in \(E_{+}\), (C) is satisfied, too.
Note that any separable subspace \(S\) of \(E\) can intersect only countably many members of the family \(\langle {B_{\xi }}\rangle _{\xi <\alpha }\) (by the choice of this family). Hence, given any such \(S\), we must have
for almost all \(t\in T\). As allocations are Bochner integrable, and Bochner integrable functions are essentially separably valued, it follows that given any two allocations \(f\), \(g:T\rightarrow E_{+}\), there is a null set \(N\subseteq T\) such that
This shows that (AM) is satisfied and also shows that the initial allocation is a core allocation.
Suppose there is a \(p\in E^{*}\) for which the initial allocation is Walrasian. Then \(q=\lambda p\) for some number \(\lambda \). Otherwise, by a well-known fact from linear algebra, there is a \(z\in E\) with \(pz=0\) and \(qz>0\), so that \(p(\bar{e}+z)=p\bar{e}\) but \(q(\bar{e}+z)>q\bar{e}\). As \(\bar{e}\in {{\mathrm{int}}}E_{+}\), we may assume that \(\bar{e}+z\in E_{+}\). But then by the choice of preferences, we have \(\bar{e}+z\succ _{t} \bar{e}\) for all \(t\in T\), thus getting a contradiction to the assumption that the initial allocation is Walrasian for \(p\). Now if \(q=\lambda p\), then for the points \(x_{\xi }\) from above, we have \(px_{\xi }=p\bar{e}\). But by the choice of preferences again, we have \(x_{\xi }\succ _{t}\bar{e}\) for each \(t\in N_{\xi }\) and each \(\xi <\alpha \). Because \(\bigcup _{\xi <\alpha }^{}N_{\xi }\) is non-negligible, we get a contradiction as before, and it follows that the initial allocation is not Walrasian. \(\square \)
9.3 Proof of Theorem 4
Lemma 1
Let \(E\) be an ordered Banach space whose positive cone \(E_{+}\) has a non-empty interior. Let \(p\in E^{*}_{+}\!\setminus \! \{0\}\), and let \(G\subseteq E\) be such that whenever \(q\in E^{*}_{+}\) satisfies \(qx=px\) for all \(x\in G\), then \(q=p\). Then there is an \(H\subseteq E_{+}\), with \(\#(H)\le \max \{\#(G),\omega \}\), such that whenever \(x\in E_{+}\) and \(c\in \mathbb {R}_{+}\) satisfy \(px<c\), then there is a \(y\in H\) with \(y> x\) and \(py< c\).
Proof
We may assume both that \(G\cap {{\mathrm{int}}}E_{+}\ne \emptyset \) and that \(pz=1\) for all \(z\in G\). Indeed, as \(p\in E^{*}_{+}\!\setminus \! \{0\}\), we may pick an \(e\in {{\mathrm{int}}}E_{+}\) with \(pe=1\). Now for each \(z\in G\), set \(\beta _z=1-pz\). Let \(G'=\{{z+\beta _{z}e}:{z\in G}\}\cup \{e\}\). Then \(qz=pz\) for all \(z\in G\) whenever \(q\in E^{*}_+\) is such that \(qy =py\) for all \(y\in G'\). Note that \(\max \{\#(G),\omega \}=\max \{\#(G'),\omega \}\). Thus, if necessary, we may replace \(G\) by \(G'\).
Let \(K\) be the affine hull of \(G\). In particular, \(K\) is convex and \(pz=1\) for all \(z\in K\). Let \(x\in E_{+}\) and suppose \(px< 1\). There must be a \(z\in K\) such that \(z\in \{x\}+{{\mathrm{int}}}E_{+}\). Otherwise, by the separation theorem, there is a nonzero \(q\in E^{*}\) such that \(qz\le qy\) for all \(z\in K\) and \(y\in \{x\}+{{\mathrm{int}}}E_{+}\). Now \(q\) must be positive, and because \(K\) is affine, there must be a number \(c\) such that \(qz=c\) for all \(z\in K\). As \(K\cap {{\mathrm{int}}}E_{+}\ne \emptyset \), we must have \(c>0\), so replacing \(q\) by a suitable scalar multiple, we may assume \(c=1\). But then \(qz=pz\) for all \(z\in G\), and on the other hand, \(qx\ge 1>px\), contradicting the hypothesis on \(G\).
Let \(L\) be the set of those members of \(K\) for which the coefficients in the representation as a linear combination of members of \(G\) are rational. Then \(L\) is dense in \(K\), and we have \(\#(L)\le \max \{\#(G),\omega \}\). Since \(L\) is dense in \(K\), and since for any \(x\in E\), \(K\cap (\{x\}+{{\mathrm{int}}}E_{+})\) is open in \(K\), it follows from the previous paragraph that given \(x\in E_{+}\) with \(px<1\), there is a \(z\in L\) such that \(z>x\).
Set \(H=\{{rz}:{z\in L,r\in \mathbb {Q}}\}\cap E_{+}\) where \(\mathbb {Q}\) is the set of rational numbers. Then \(\#(H)\le \omega \cdot \#(L)\le \max \{\#(G),\omega \}\). Suppose \(x\in E_{+}\) and \(c\in \mathbb {R}\) are such that \(px<c\). Pick an \(r\in \mathbb {Q}\) such that \(px<r<c\). Now \(p\frac{1}{r}x<1\), so there is a \(z\in L\) such that \(z> \frac{1}{r}x\); clearly \(rz> x\) and \(px\le prz= r<c\). Thus, \(H\) is as required. \(\square \)
Proof of Theorem 4 Let \(f\) be a core allocation of the given economy \({\fancyscript{E}}\). As in the proof of Theorem 2, it follows that there is a nonzero positive \(p\in E^{*}\) such that for each \(x\in E_{+}\) the set \(N_{x}=\{{t\in T}:{x\succ _{t}f(t),\ px<pe(t)}\}\) is a null set.
Write \(v=1_{K}\in C(K)\equiv E\) and let \({\varDelta }=\{{q\in E^{*}_{+}}:{qv=1}\}\). We may assume \(p\in {\varDelta }\). Since \({\varDelta }\) may be identified with the set of all tight Borel probability measures on \(K\), \({\varDelta }\) is \({\text {weak}}^{*}\)-first countable by hypothesis. By the definition of the \({\text {weak}}^{*}\)-topology, this means there is a countable set \(C\subseteq E\) such that whenever \(q\in {\varDelta }\) and \(qx=px\) for all \(x\in C\), then \(q=p\). Of course, we may assume that \(v\) is in \(C\), so that whenever \(q\in E^{*}_{+}\) is such that \(qx=px\) for all \(q\in C\), then \(q=p\).
By Lemma 1, it follows that there is a countable \(H\subseteq E_{+}\) such that whenever \(x\in E_{+}\) and \(c\in \mathbb {R}_{+}\) satisfy \(px<c\), there is a \(y\in H\) with \(y> x\) and \(py< c\). As \(H\) is countable, \(N=\bigcup _{x\in H}N_{x}\) is a null set. Now by Assumptions (P), (D), and (Tr), for any \(t\in T\), if there is an \(x\in E_{+}\) with \(x\succ _{t}f(t)\) and \(px<pe(t)\), then \(t\in N\). Thus, by (P) again, if \(t\in T\!\setminus \! N\) then \(px\ge pe(t)\) whenever \(x\succ _{t} f(t)\). As in the proof of Theorem 2, it follows that the pair \((p,f)\) is a Walrasian equilibrium. \(\square \)
9.4 Proof of Theorem 5
In view of Theorem 2, the following statement needs to be proved.
-
Let \(E\) be an ordered Banach space such that \(E_{+}\) has both a non-empty interior and a bounded base, and let \((T,{\fancyscript{T}},\nu )\) be an atomless probability space such that \({{\mathrm{add}}}\mathcal {N}(\nu )\le {{\mathrm{dens}}}(E)\). Then there is an economy \({\fancyscript{E}}\), with \((T,{\fancyscript{T}},\nu )\) as space of agents and \(E\) as commodity space, such that (P), (D), (C), (AM), (EC), (RA), and (UR) are satisfied, but such that there is a core allocation which is not Walrasian.
Let \(E\) and \((T,{\fancyscript{T}},\nu )\) be as in this statement. Let \(H\) be a bounded base of \(E_{+}\). By Remark 1, there is a strictly positive \(q\in E^{*}\) such that \(H=\{{x\in E_{+}}:{qx=1}\}\). Choose an interior point \(\bar{e}\) of \(E_{+}\) with \(\bar{e}\in H\).
Follow the proof of Theorem 3 down to the start of the construction of preferences. Now for \(t\in T\!\setminus \! \bigcup _{\xi <\alpha }^{}N_{\xi }\), define preferences exactly as in that proof (in particular, there is a continuous utility representation). For \(t\in N_{\xi }\), \(\xi <\alpha \), let preferences be given by the continuous utility function \(u_{t}:E_{+}\rightarrow \mathbb {R}\) defined by
where \(k>0\) is real number, common for all \(\xi <\alpha \) and all \(t\in N_{\xi }\). Note that for the points \(x_{\xi }\) from the proof of Theorem 3, we have \(u_{t}(x_{\xi })>u_{t}(\bar{e})\) for each \(t\in N_{\xi }\), \(\xi <\alpha \). Below we will show that the hypothesis that \(E_{+}\) has a bounded base implies that the number \(k\) can be chosen in such a way that the preferences given by the \(u_{t}\)’s are strictly monotone.
Supposing that has been done, we have, as in the proof of Theorem 3, an economy such that (P), (D), (C), (EC), and (RA) hold, and now also (UR) in addition. Observe that for any \(\xi <\alpha \) and \(t\in N_{\xi }\), and any \(x\in E_{+}\), if \(u_{t}(x)\ne qx \) then \(x+\lambda \bar{e}\in B_{\xi }\) for some number \(\lambda >0\), and that if \(S\) is a separable subspace of \(E\), then so is \(S+\{\lambda \bar{e}:\lambda \in \mathbb {R}\}\). Consequently, the fact that allocations are Bochner integrable and therefore essentially separably valued implies that given any two allocations \(f\), \(g:T\rightarrow E_{+}\), there is a null set \(N\subseteq T\) such that
Thus, as in the proof of Theorem 3, (AM) is satisfied and the initial allocation is a core allocation. As in that proof, it follows that this allocation is not Walrasian.
Finally, to see that there is a number \(k>0\) such that the preferences given by the functions \(u_{t}\) are strictly monotone for all \(t\in N_{\xi }\) and \(\xi <\alpha \), note first that the fact that \(H=\{{x\in E_{+}}:{qx=1}\}\) is a bounded base of \(E_{+}\) means that there is a number \(k'>0\) such that \(\left||y\right||_{}<k'qy\) for all \(y\in E_{+}\!\setminus \! \{0\}\), which implies that
for any \(y\in E_{+}\!\setminus \! \{0\}\). Thus, setting \(k=\bigl (k'+||\bar{e}||_{}\bigr )^{-1}\), we have \(qy>k\bigl ||y-(qy)\bar{e}\bigr ||_{}\) for such \(y\). Now for any \(x\), \(y\in E_{+}\), writing \(A\) for \(H\!\setminus \! B_{\xi }\),
and it follows that
for any \(x\), \(y\in E_{+}\) with \(y\ne 0\), showing that the preferences given by the \(u_{t}\)’s are indeed strictly monotone for the above choice of \(k\). \(\square \)
10 Proof of Theorem 6
Lemma 2
Let \(X\) be a Riesz space, with positive cone \(X_{+}\), let \(v\in X_{+}\), and suppose that \(q\) is a strictly positive linear functional on \(X\). Write \(U=\{{u\in X}:{q(|u|_{})<1}\}\). Let \(x_{i}\), \(i=0,\dots ,n\), and \(e\) be elements of \(X_{+}\), let \(\nu _{i}>0\), \(i=0,\dots ,n\), be real numbers, and suppose \(\sum _{i=0}^{n}\nu _{i} x_{i}+\lambda (v+u)=e\) for some \(u\in U\) and some real number \(\lambda >0\). Then there exist real numbers \(\lambda _{i}\ge 0\) and elements \(u_{i}\in U\), \(i=0,\dots ,n\), such that \(x_{i}+\lambda _{i}(v+u_{i})\in X_{+}\) for each \(i=0,\dots ,n\) and such that \(\sum _{i=0}^{n}\nu _{i}\bigl (x_{i}+\lambda _{i}(v+u_{i})\bigr )=e\).
Proof
Scaling the element \(e\) and the numbers \(\nu _{i}\) by some common factor, if necessary, we may assume \(\lambda =1\), so that \(v+u=e-\sum _{i=0}^{n}\nu _{i}x_{i}\).
Now if \(v\ge u^{-}\), we are done by setting \(u_{i}=u\) for all \(i=0,\dots ,n\), \(\lambda _{0}=1/\nu _{0}\), and \(\lambda _{i}=0\) for \(i=1,\dots ,n\).
Otherwise, note that we must have \(q(u^{-}-(v\wedge u^{-}))>0\) as \(q\) is strictly positive. Note also that \((v+u)^{-}=u^{-}-(v\wedge u^{-})\). Thus we must have \(u^{-}-(v\wedge u^{-})\le \sum _{i=0}^{n}\nu _{i}x_{i}\). By the Riesz decomposition theorem, we obtain elements \(b_{0},\dots ,b_{n}\in X_{+}\) such that \(\sum _{i=0}^{n}b_{i}=u^{-}-(v\wedge u^{-})\) and \(b_{i}\le \nu _{i}x_{i}\) for each \(i=0,\dots ,n\). Set \(d_{i}=(1/\nu _{i})b_{i}\), so that \(x_{i}-d_{i}\in X_{+}\), and set
Note that \(\sum _{i=0}^{n}\nu _{i}\lambda _{i}=1\). Set \(u_{i}=u^{+}-(v\wedge u^{-})-(1/\lambda _{i})d_{i}\) if \(\lambda _{i}>0\), and \(u_{i}=u\) otherwise. Then \(x_{i}+\lambda _{i}(v+u_{i})\in X_{+}\) for each \(i=0,\dots ,n\), because \(v-(v\wedge u^{-})\ge 0\). If \(\lambda _{i}>0\), then by the triangle inequality for the absolute value,
as the three summands involved are all in \(X_{+}\), so
Hence \(u_{i}\in U\) for each \(i=1,\dots ,n\), because \(u\in U\). Also, because \(\nu _{i}d_{i}=b_{i}\) for each \(i=1,\dots ,n\), and because \(\sum _{i=0}^{n}\nu _{i}\lambda _{i}=1\), we have
so \(\sum _{i=0}^{n}\nu _{i}\bigl (\lambda _{i}(v+u_{i})\bigr )=v+u\), and it follows that \(\sum _{i=0}^{n}\nu _{i}\bigl (x_{i}+\lambda _{i}(v+u_{i})\bigr )=e\), because we have assumed \(v+u=e-\sum _{i=0}^{n}\nu _{i}x_{i}\). \(\square \)
Lemma 3
Let \(E\) be an infinite-dimensional order-continuous Banach lattice such that \(E_{+}\) has strictly positive elements. Then there is a strictly positive \(p\in E^{*}\) such that given any cardinal \(\kappa \le {{\mathrm{dens}}}(E)\), there is a family \(\langle {p_{i}}\rangle _{i\in I}\) in the order interval \([-p,p]\), with \(\#(I)=\kappa \), such that \(p_{i}\ne 0\) for each \(i\in I\) but such that on any separable subspace of \(E\), \(p_{i}\) is zero for all but countably many \(i\in I\).
Proof
By the representation theorem for order-continuous Banach lattices in Lindenstrauss and Tzafriri (1979, p. 25, Theorem 1.b.14), we may assume that, for some probability space \(({\varOmega },{\varSigma },\mu )\), \(L_{\infty }(\mu )\subseteq E \subseteq L_{1}(\mu )\) and \(L_{\infty }(\mu ) \subseteq E^{*}\subseteq L_{1}(\mu )\), the inclusions being continuous and order preserving; in particular, \(1_{{\varOmega }}\) is a strictly positive element in \(E^{*}\). [Recall for the reference that in a normed Riesz space, strictly positive elements are weak order units; see Aliprantis and Burkinshaw (1985, p. 266, Theorem 4.85, and p. 267(b)).]
Now by Fabian et al (2001, p. 364, Theorem 11.12), there is a family \(\langle x_{i},p_{i}\rangle _{i\in I}\) in \(L_{1}(\mu )\times L_{\infty }(\mu )\), with \(\#(I)={{\mathrm{dens}}}(L_{1}(\mu ))\), such that
-
(1)
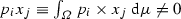 if and only if \(i= j\),
if and only if \(i= j\), -
(2)
\({{\mathrm{span}}}\{{x_{i}}:{i\in I}\}\) is dense in \(L_{1}(\mu )\).
Scaling the elements \(p_{i}\), if necessary, we may assume that all of them belong to \([-1_{{\varOmega }},1_{{\varOmega }}]\). Now (1) implies that if \(x\in {{\mathrm{span}}}\{{x_{i}}:{i\in I}\}\) then \(p_{i}x=0\) for all but finitely many \(i\in I\), and hence (2) implies that for any \(x\in L_{1}(\mu )\), \(p_{i}x=0\) for all but countably many \(i\in I\) (consider a sequence in \({{\mathrm{span}}}\{{x_{i}}:{i\in I}\}\) converging to \(x\)). It follows that if \(D\) is any countable subset of \(L_{1}(\mu )\) then \(p_{i}\) is zero on \(D\) for all but countably many \(i\in I\) (i.e., \(\{{i\in I}:{p_{i}d\ne 0 \text{ for } \text{ some } d\in D}\}\) is countable), and hence that if \(S\) is any separable subspace of \(E\), then \(p_{i}\) is zero on \(S\) for all but countably many \(i\in I\).
It remains to see that \({{\mathrm{dens}}}(E)\le {{\mathrm{dens}}}(L_{1}(\mu ))\). To this end, let \(A\subseteq [-1_{{\varOmega }},1_{{\varOmega }}]\) be dense in \([-1_{{\varOmega }},1_{{\varOmega }}]\) for the weak topology of \(L_{1}(\mu )\) and of minimal cardinal among the subsets of \([-1_{{\varOmega }},1_{{\varOmega }}]\) with this property. Note that since \(E\) is order-continuous, order intervals in \(E\) are weakly compact, so, as \(L_{\infty }(\mu )\subseteq E^{*}\), the weak topology of \(E\) agrees on \([-1_{{\varOmega }},1_{{\varOmega }}]\) with the weak topology of \(L_{1}(\mu )\). Hence \(A\) is dense in \([-1_{{\varOmega }},1_{{\varOmega }}]\) also for the weak topology of \(E\). Observe that \([-1_{{\varOmega }},1_{{\varOmega }}]\) separates the points of \(L_{1}(\mu )\) and therefore also those of \(E^{*}\). Thus \(A\), being dense in \([-1_{{\varOmega }},1_{{\varOmega }}]\) for the weak topology of \(E\), separates the points of \(E^{*}\), so \({{\mathrm{span}}}A\) is norm-dense in \(E\). Let \(B\) be the subset of \({{\mathrm{span}}}A\) consisting of those linear combinations of members of \(A\) in which the coefficients are rational. Then \(B\) is still norm-dense in \(E\); moreover, \(\#(B)=\#(A)\). Thus \({{\mathrm{dens}}}(E)\le \#(A)\). Now by the choice of \(A\), \( \#(A)\le ||\cdot ||_{1}\text {-}{{\mathrm{dens}}}{\big ([-1_{{\varOmega }},1_{{\varOmega }}]\big )}\le {{\mathrm{dens}}}(L_{1}(\mu ))\), and we conclude that \({{\mathrm{dens}}}(E)\le {{\mathrm{dens}}}(L_{1}(\mu ))\). \(\square \)
Proof of Theorem 6 (a) Sufficiency Let \(E\) be as in the statement of the theorem, and let \({\fancyscript{E}}\) be an atomless economy with commodity space \(E\) such that all the assumption listed in the theorem, including (MMATC), are satisfied. Let \(f\) be a core allocation of the economy \({\fancyscript{E}}\) and let
Every \(h\in A\) is Bochner integrable; write  . As in the proof of Theorem 2, we see that \({{\mathrm{c\ell }}}B\) is convex and non-empty.
. As in the proof of Theorem 2, we see that \({{\mathrm{c\ell }}}B\) is convex and non-empty.
Let \(v\in E_{+}\!\setminus \! \{0\}\) and \(q\in E^{*}\) be chosen according to Assumption (EDC). Write \(U=\{{u\in E}:{q|u|_{}<1}\}\) and note that \(U\) is convex. By the continuity of the lattice operations in \(E\), the map \(u\mapsto q|u|_{}:E\rightarrow \mathbb {R}\) is continuous, so \(U\) is an open subset of \(E\). Let
As \(U\) is open in \(E\) and convex, so is \({\varGamma }\). We may assume that \(0\notin {\varGamma }\), replacing \(q\) by a sufficiently large multiple if necessary.
We claim that \(({{\mathrm{c\ell }}}B)\cap -{\varGamma }=\emptyset \). Otherwise, \(B\cap -{\varGamma }\ne \emptyset \) because \({\varGamma }\) is open, and thus, as \(0\notin {\varGamma }\), there are an \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\), a \(u\in U\), and a \(\lambda >0\) such that  where \(g:T\rightarrow E_{+}\) is as in the definition of \(A\). Now by Lemma 2, there are measurable simple functions \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) and \(\tilde{u}:T\rightarrow U\) such that both
where \(g:T\rightarrow E_{+}\) is as in the definition of \(A\). Now by Lemma 2, there are measurable simple functions \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) and \(\tilde{u}:T\rightarrow U\) such that both  and \(g(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in E_{+}\) for every \(t\in S\). Define \(g':T\rightarrow E_{+}\) by setting \(g'(t)=g(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\) if \(t\in S\) and \(g'(t)=0\) otherwise. By Assumptions (P), (EDC), and (Tr), \(g'(t)\succ _{t}f(t)\) a.e. in \(S\), and we get a contradiction to the property of \(f\) being a core allocation.
and \(g(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in E_{+}\) for every \(t\in S\). Define \(g':T\rightarrow E_{+}\) by setting \(g'(t)=g(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\) if \(t\in S\) and \(g'(t)=0\) otherwise. By Assumptions (P), (EDC), and (Tr), \(g'(t)\succ _{t}f(t)\) a.e. in \(S\), and we get a contradiction to the property of \(f\) being a core allocation.
By the separation theorem, it follows that there is a nonzero \(p\in E^{*}\) such that \(pB\ge 0\). As in the proof of Theorem 2, we see that there is a null set \(N\subseteq T\) such that if \(t\in T\!\setminus \! N\), then \(px\ge pe(t)\) whenever \(x\succ _{t}f(t)\). In particular, \(p\) must be positive. Indeed, pick any \(a\in E_{+}\!\setminus \! \{0\}\). By Assumptions (P) and (D), \(f(t)+na\succ _{t} f(t)\) for each \(t\in T\) and each \(n\in \mathbb {N}\!\setminus \! \{0\}\), so \(p(f(t)+na)\ge p e(t)\) for each \(n\in \mathbb {N}\!\setminus \! \{0\}\) and \(t\in T\!\setminus \! N\), and it follows that \(pa\ge 0\).
Arguing as in the proof of Theorem 2, we can conclude that the pair \((p,f)\) is a Walrasian equilibrium.
(b) Necessity Let the commodity space \(E\) be an order-continuous Banach lattice whose positive cone has strictly positive elements, and let \((T,{\fancyscript{T}},\nu )\) be an atomless probability space of agents such that \({{\mathrm{add}}}\mathcal {N}(\nu )\le {{\mathrm{dens}}}(E)\). We will construct an economy such that (P), (D), (C), (AM), (EC), (RA), (UR), and (US) are satisfied, but such that there is a core allocation which is not Walrasian.
Fix a strictly positive element \(\bar{e}\) in \(E_{+}\). For each \(t\in T\), let \(X_{t}=E_{+}\) and \(e(t)=\bar{e}\), so that (P), (EC), and (RA) are satisfied.
As in the proof of Theorem 3, write \(\alpha ={{\mathrm{add}}}\mathcal {N}(\nu )\) and choose a family \(\langle {N_{\xi }}\rangle _{\xi <\alpha }\) of null sets in \(T\) such that \(\bigcup _{\xi <\alpha }^{}N_{\xi }\) is not a null set.
As \(\alpha \le {{\mathrm{dens}}}(E)\), we may apply Lemma 3 to find a strictly positive \(q\in E^{*}\) and a family \(\langle {q'_{\xi }}\rangle _{\xi <\alpha }\) in the order interval \([-q,q]\) such that \(q'_{\xi }\ne 0\) for each \(\xi <\alpha \) but such that on any separable subspace of \(E\), \(q'_{\xi }\) is zero for all but countably many \(\xi <\alpha \). For each \(\xi <\alpha \), set \(q_{\xi }=q+(1/2)q'_{\xi }\), so that \(q_{\xi }\) is strictly positive. Clearly, \(q_{\xi }\ne q\) for each \(\xi <\alpha \), but on any separable subspace \(S\) of \(E\), \(q_{\xi }\!\upharpoonright \!S =q\!\upharpoonright \!S\) for all but countably many \(\xi <\alpha \).
Now define preference relations \(\succ _{t}\) by setting
and \(\succ _{t}=\bigl \{{(x,y)\in E_{+}\times E_{t}}:{qx>qy}\bigr \}\) for \(t\in T\!\setminus \! \bigcup _{\xi <\alpha }^{}N_{\xi }\), so that (UR), (D), and (C) are satisfied. Set \(a=(1/2)q\) and \(b=(3/2)q\). Then for any \(u\), \(v\in E_{+}\) with \(av>bu\), and any \(q'\) in the order interval \([a,b]\), we have \(q'(v-u) \ge av-bu> 0\). Consequently, as \(q\) and each \(q_{\xi }\), \(\xi <\alpha \) are in \([a,b]\), (US) is also satisfied.
As allocations are Bochner integrable, and Bochner integrable functions are essentially separably valued, the choice of the preference relations implies that given any two allocations \(f\), \(g:T\rightarrow E_{+}\), there is a null set \(N\subseteq T\) such that
As in the proof of Theorem 3, we see from this that (AM) is satisfied and that the initial allocation is a core allocation.
Suppose there is a \(p\in E^{*}\) for which the initial allocation \(t\mapsto e(t)=\bar{e}\) is Walrasian. Write \(I_{\bar{e}}\) for the order ideal in \(E\) generated by \(\bar{e}\). Note that \(\bar{e}\) is an order unit of \(I_{\bar{e}}\). Thus, if the equilibrium conditions hold for a \(t\in N_{\xi }\), \(\xi <\alpha \), we must have \(q_{\xi }\!\upharpoonright \!I_{\bar{e}}=\lambda _{\xi }p\!\upharpoonright \!I_{\bar{e}}\) for some real number \(\lambda _{\xi }\) (see the end of the proof of Theorem 3). Since \(E\) is a Banach lattice, the fact that \(\bar{e}\) is strictly positive implies that \(I_{\bar{e}}\) is dense in \(E\) (Aliprantis and Burkinshaw 1985, Theorem 4.85), so we have \(q_{\xi }=\lambda _{\xi }p\) if \(q_{\xi }\!\upharpoonright \!I_{\bar{e}}=\lambda _{\xi }p\!\upharpoonright \!I_{\bar{e}}\). Hence, as \(N_{\xi }\) is a null set for each \(\xi <\alpha \), but \(\bigcup _{\xi <\alpha }^{}N_{\xi }\) is non-negligible, the assumption that the initial allocation is Walrasian for \(p\) implies that there is an uncountable set \(H\subseteq \alpha \) such that \(q_{\xi }\in {{\mathrm{span}}}\{p\}\) for each \(\xi \in H\). Now by construction, we have a \(q\in E^{*}\) such that \(q_{\xi }\ne q\) for all \(\xi \in H\), but such that for any \(z\in E\), \(q_{\xi }z=qz\) for all but countably many \(\xi \in H\). As \(H\) is uncountable, this implies that the set \(\{{q_{\xi }}:{\xi \in H}\}\) cannot be included in a one-dimensional subspace of \(E^{*}\). In particular, we cannot have \(q_{\xi }\in {{\mathrm{span}}}\{p\}\) for each \(\xi \in H\). We thus obtain a contradiction, proving that the initial allocation is not Walrasian.
11 Proofs of Theorems 7 and 8
11.1 Basic facts
Fact 3
(Cf. Zame 1986, Sect. 9, p.1) Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space with \(\mu ({\varOmega })=\infty \). Then there is a probability measure \(\bar{\mu }\) on \(({\varOmega },{\varSigma })\) such that:
-
(a)
\(L_{\infty }(\mu )=L_{\infty }(\bar{\mu })\), as Banach lattices, and in particular as sets, so that no distinction in notation is needed in (b) and (c) below.
-
(b)
The Mackey topology of \(L_{\infty }(\mu )\) under the pairing with \(L_{1}(\mu )\) is the same as that under the pairing with \(L_{1}(\bar{\mu })\).
-
(c)
Whenever \((T,{\fancyscript{T}},\nu )\) is a totally finite measure space, a function \(f:T\rightarrow L_{\infty }(\mu )\) is Gelfand integrable for the pairing of \(L_\infty (\mu )\) with \(L_{1}(\mu )\) if and only if it is Gelfand integrable for the pairing of \(L_\infty (\mu )\) with \(L_{1}(\bar{\mu })\), in which case both pairings yield the same Gelfand integral of \(f\) over any \(S\in {\fancyscript{T}}\).
Proof
Let \(\langle {B_{n}}\rangle _{n\in \mathbb {N}}\) be a partition of \({\varOmega }\) into measurable sets with \(0<\mu (B_{n})<\infty \) for each \(n\in \mathbb {N}\), and define \(\bar{\mu }:{\varSigma }\rightarrow \mathbb {R}_{+}\) by \(\bar{\mu }(A)=\sum _{n=0}^{\infty }2^{-(n+1)}\mu (B_{n})^{-1}\mu (A\cap B_{n})\) for each \(A\in {\varSigma }\). Then \(\bar{\mu }\) is a probability measure which gives the same null sets in \({\varOmega }\) as the measure \(\mu \) and thus \((a)\) holds.
Now for each \(p\in L_{1}(\mu )\), set \(\phi (p)=\sum _{n=0}^{\infty }2^{n+1}\mu (B_{n})1_{B_{n}}\times p\). This defines a bijection \(\phi \) from \(L_{1}(\mu )\) to \(L_{1}(\bar{\mu })\) such that for each \(x\in L_{\infty }(\mu )\),

and thus (c) must hold. In fact, \(\phi \) is an isomorphism for the norm-topologies of \(L_{1}(\mu )\) and \(L_{1}(\bar{\mu })\), therefore also for the weak topologies of these spaces, and thus (b) holds by the above equality because the Mackey topology of \(L_{\infty }(\mu )\) is the topology of uniform convergence on weakly compact subsets of \(L_{1}(\mu )\). \(\square \)
Fact 4
Let \(({\varOmega },{\varSigma },\mu )\) be a totally finite measure space, so that \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Then the Mackey topology of \(L_{\infty }(\mu )\) and the \(||\cdot ||_{1}\)-topology of \(L_{1}(\mu )\) agree on \(||\cdot ||_{\infty }\)-bounded subsets of \(L_{\infty }(\mu )\). (See Zame 1986, Lemma A).
Definition 3
Let \((T,{\fancyscript{T}},\nu )\) be a totally finite measure space, and \(({\varOmega },{\varSigma },\mu )\) a \(\sigma \)-finite measure space. A function \(\eta :T\rightarrow L_{\infty }(\mu )\) is called a \(weak ^*\) -null function if for each \(p\in L_{1}(\mu )\), \(p\eta (t)=0\) for almost all \(t\in T\).
The point of this definition is that the exceptional set of measure zero is allowed to vary with \(p\in L_{1}(\mu )\). Of course, if the measure space \(({\varOmega },{\varSigma },\mu )\) is separable, so that \(L_{1}(\mu )\) has a countable subset separating the points of \(L_{\infty }(\mu )\), then \(\eta :T\rightarrow L_{\infty }(\mu )\) is a \({\text {weak}}^{*}\)-null function if and only if \(\eta (t)=0\) a.e. in \(T\). In any case, given that \(\mu \) is \(\sigma \)-finite, so that \(L_{1}(\mu )\) has strictly positive elements, if \(\eta :T\rightarrow L_{\infty }(\mu )\) is a \({\text {weak}}^{*}\)-null function, there can be no non-negligible \(S\subseteq T\) such that \(\eta (t)>0\) for all \(t\in S\).
Lemma 4
Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space. Then there is a \(Q_{+}\subseteq L_{\infty }(\mu )_{+}\) such that:
-
(a)
\(Q_{+}\) is dense in \(L_{\infty }(\mu )_{+}\) for the Mackey topology.
-
(b)
If \((T,{\fancyscript{T}},\nu )\) is a totally finite measure space, \(S\) a subset of \(T\), with \(\nu ^{*}(S)>0\), and \(h:S\rightarrow Q_{+}\) a function, then there are a set \(S'\subseteq S\), with \(\nu ^{*}(S')>0\), and an element \(a\in L_{\infty }(\mu )_{+}\) such that \(h(t)=a+\eta (t)\) for all \(t\in S'\) where \(\eta :T\rightarrow L_{\infty }(\mu )\) is a \({\text {weak}}^{*}\)-null function.
Proof
In view of Fact 3, we may assume that \(\mu \) is a probability measure, so that, in particular, \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Then by the proof of Lemma 9 in Podczeck (2004), there is a family \(\langle x_{i},p_{i}\rangle _{i\in I}\) of elements of \(L_{\infty }(\mu )\times L_{\infty }(\mu )\) such that, writing \(Q\) for the set of all finite linear combinations of \(x_{i}\)’s with rational coefficients:
-
(1)
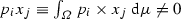 if and only if \(i= j\).
if and only if \(i= j\). -
(2)
The set \(\{{p_{i}}:{i\in I}\}\) separates the points of \(L_{\infty }(\mu )\).
-
(3)
\(Q\cap [0,1_{{\varOmega }}]\) is \(||\cdot ||_{1}\)-dense in \([0,1_{{\varOmega }}]\)
(where \([0,1_{{\varOmega }}]\) is the order interval \(\{{x\in L_{\infty }(\mu )}:{0\le x\le 1_{{\varOmega }}}\}\)).
By Fact 4, (3) implies that \(Q\cap [0,1_{{\varOmega }}]\) is actually Mackey dense in \([0,1_{{\varOmega }}]\). As \(L_{\infty }(\mu )_{+}=\bigcup _{n=1}^{\infty }[0,n1_{{\varOmega }}]\) and \(nQ=Q\) for each \(n\in \mathbb {N}\), it follows that \(Q\cap L_{\infty }(\mu )_{+}\) is Mackey dense in \( L_{\infty }(\mu )_{+}\). Set \(Q_{+}=Q\cap L_{\infty }(\mu )_{+}\).
Now let \((T,{\fancyscript{T}},\nu )\), \(S\), and \(h\) be as hypothesized in (b) of the lemma. For every \(t\in T\), let \(I_{t}=\{{i\in I}:{p_{i}h(t)\ne 0}\}\).
By (1) and the definition of \(Q_{+}\), \(I_{t}\) is finite for each \(t\in S\). By the fact that \(\nu ^{*}(S)>0\) and that the countable union of null set in \(S\) is a null set, we can choose an integer \(n\) and an \(S_{1}\subseteq S\) with \(\nu ^{*}(S_{1})>0\) such that \(\#(I_{t})=n\) for each \(t\in S_{1}\). Note that if \(F\subseteq I\) is such that \(\#(F)=0\), i.e., \(F=\emptyset \), then \(F\subseteq I_{t}\) for each \(t\in S_{1}\). There is therefore an integer \(\bar{k}\le n\) which is maximal among the integers \(k\le n\) such that there is an \(F\subseteq I\) with \(\#(F)=k\) and with the property that there is an \(S_{2}\subseteq S_{1}\) such that \(\nu ^{*}(S_{2})>0\) and \(F\subseteq I_{t}\) for each \(t\in S_{2}\). Choose and fix \(F\) and \(S_{2}\) corresponding in this sense to \(\bar{k}\). Note that for each \(i\in I\!\setminus \! F\), \(\{{t\in S_{2}}:{p_{i}h(t)\ne 0}\}\) is a null set.
As \(F\) is finite, the product of \(\#(F)\) copies of the set of rational numbers is countable. Thus, as \(\nu ^{*}(S_{2})>0\), there are rational numbers \(r_{i}\), \(i\in F\), and a set \(S'\subseteq S_{2}\) with \(\nu ^{*}(S')>0\) such that for each \(t\in S'\) and each \(i\in F\) the coefficient of \(x_{i}\) in \(h(t)\) as a member of \(Q\) is \(r_{i}\). Set \(a=\sum _{i\in F}r_{i}x_{i}\) (where \(a=0\) if \(F=\emptyset \)). Then (1) implies that \(p_{i}h(t)=p_{i}a\) for each \(t\in S'\) and each \(i\in F\), and that \(p_{i}a=0\) for \(i\in I\!\setminus \! F\). Define \(\eta :T\rightarrow L_{\infty }(\mu )\) by setting \(\eta (t)=h(t)-a\) if \(t\in S'\) and \(\eta (t)=0\) otherwise. As \(S'\subseteq S_{2}\), \(\{{t\in S'}:{p_{i}h(t)\ne 0}\}\) is a null set for each \(i\in I\!\setminus \! F\), and it follows that \(\{{t\in T}:{p_{i}\eta (t)\ne 0}\}\) is a null set for each \(i\in I\).
For each \(p\in L_{1}(\mu )\), let \(T_{p}=\{{t\in T}:{p\eta (t)\ne 0}\}\). Then \(T_{p_{i}}\) is a null set in \(T\) for each \(i\in I\). If \(p\in {{\mathrm{span}}}\{{p_{i}}:{i\in I}\}\), then \(T_{p}\subseteq \bigcup _{i\in I_{p}}T_{p_{i}}\) for some finite \(I_{p}\subseteq I\), and it follows that \(T_{p}\) is a null set. Let \(p\) be an arbitrary element of \(L_{1}(\mu )\). As we have \(L_{1}(\mu )^{*}=L_{\infty }(\mu )\subseteq L_{1}(\mu )\), (2) implies that \({{\mathrm{span}}}\{{p_{i}}:{i\in I}\}\) is dense in \(L_{1}(\mu )\) by the Hahn–Banach theorem, so there is a sequence \(\langle {p_{n}}\rangle \) in \({{\mathrm{span}}}\{{p_{i}}:{i\in I}\}\) with \(p_{n}\rightarrow p\). Now \(T_{p}\subseteq \bigcup _{n\in \mathbb {N}}T_{p_{n}}\), and thus \(T_{p}\) is a null set. As \(p\in L_{1}(\mu )\) was arbitrary, \(\eta \) is a \({\text {weak}}^{*}\)-null function.
It now also follows that the element \(a\in L_{\infty }(\mu )\) defined above is positive. Indeed, otherwise there is a \(p\in L_{1}(\mu )_{+}\) with \(pa<0\). As \(a=h(t)-\eta (t)\) for \(t\in S'\), and \(\eta \) is a \({\text {weak}}^{*}\)-null function, it follows that \(ph(t)<0\) for almost all \(t\in S'\). But this is impossible because \(h(t)\in Q_{+}\subseteq L_{\infty }(\mu )_{+}\) for all \(t\in S'\) and \(\nu ^{*}(S')>0\). Thus we must have \(a\in L_{\infty }(\mu )_{+}\). \(\square \)
11.2 Proof of Theorem 7
Let \(f\) be a core allocation of the given economy and let
Then every \(h\in A\) is \(||\cdot ||_{\infty }\)-Bochner integrable; write  where
where  is the Bochner integral of \(h\). Evidently, \(A\) is decomposable. Thus, as \(\nu \) is atomless, it follows from Fact 2 that \(||\cdot ||_{\infty }\)-\({{\mathrm{c\ell }}}B\) is a convex subset of \(L_{\infty }(\mu )\). Moreover, as \(0\in B\), \(||\cdot ||_{\infty }\)-\({{\mathrm{c\ell }}}B\) is non-empty.
is the Bochner integral of \(h\). Evidently, \(A\) is decomposable. Thus, as \(\nu \) is atomless, it follows from Fact 2 that \(||\cdot ||_{\infty }\)-\({{\mathrm{c\ell }}}B\) is a convex subset of \(L_{\infty }(\mu )\). Moreover, as \(0\in B\), \(||\cdot ||_{\infty }\)-\({{\mathrm{c\ell }}}B\) is non-empty.
Observe that \((||\cdot ||_{\infty }\text {-}{{\mathrm{c\ell }}}B)\cap ||\cdot ||_{\infty }\)-\({{\mathrm{int}}}(-L_{\infty }(\mu )_{+})=\emptyset \). Indeed, otherwise, because \(0\notin ||\cdot ||_{\infty }\)-\({{\mathrm{int}}}(-L_{\infty }(\mu )_{+})\), there are an \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\) and a \(v'\in ||\cdot ||_{\infty }\)-\({{\mathrm{int}}}L_{\infty }(\mu )_{+}\) such that  where \(g\) and \(e'\) are as in the definition of \(A\). Because the measure \(\nu \) is atomless and the indefinite Bochner integral of the function \(g-e'\) is \(\nu \)-continuous with respect to \(||\cdot ||_{\infty }\), we may assume, shrinking the set \(S\), if necessary, that \(\nu (T\!\setminus \! S)>0\). Now set
where \(g\) and \(e'\) are as in the definition of \(A\). Because the measure \(\nu \) is atomless and the indefinite Bochner integral of the function \(g-e'\) is \(\nu \)-continuous with respect to \(||\cdot ||_{\infty }\), we may assume, shrinking the set \(S\), if necessary, that \(\nu (T\!\setminus \! S)>0\). Now set  . As \(e'(t)\le e(t)\) a.e. in \(T\), we have \(v\ge v'\), and therefore \(v\in ||\cdot ||_{\infty }\)-\({{\mathrm{int}}}L_{\infty }(\mu )_{+}\). For each \(n\in \mathbb {N}\), set \(T_{n}=\{{t\in T\!\setminus \! S}:{e(t)+nv\ge f(t)}\}\). Then \(\bigcup _{n=0}^{\infty }T_{n}=T\!\setminus \! S\). Hence, as \(\nu (T\!\setminus \! S)>0\), there must be an \(n_{1}\in \mathbb {N}\) such that \(\nu ^{*}(T_{n_{1}})>0\).Footnote 10 Choose \(n_{2}\in \mathbb {N}\) so that both \(n_{2}>n_{1}\) and \(\nu ^{*}(T_{n_{1}})>1/n_{2}\). By Assumptions (P) and (D), \(e(t)+n_{2}v\succ _{t}f(t)\) for all \(t\in T_{n_{1}}\), and by (P) and (AM), \(\{{t\in T}:{e(t)+n_{2}v\succ _{t}f(t)}\}\in {\fancyscript{T}}\). Therefore, if \(G\) is a measurable envelope of \(T_{n_{1}}\), then \(e(t)+n_{2}v\succ _{t}f(t)\) for almost all \(t\in G\) and we have \(\nu (G)=\nu ^{*}(T_{n_{1}})>1/n_{2}\). As \(\nu \) is atomless, we can choose an \(F\subseteq G\) with \(\nu (F)=1/n_{2}\). Clearly we may assume that \(F\cap S=\emptyset \). Now according to (b) in the definition of \(A\), there is a \({\text {weak}}^{*}\)-null function \(\eta :T\rightarrow L_{\infty }(\mu )\) such that \(g(t)+\eta (t)\succ _{t}f(t)\) for almost all \(t\in S\). Define \(f':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(f'(t)=g(t)+\eta (t)\) for \(t\in S\), \(f'(t)=e(t)+n_{2}v\) for \(t\in F\), and \(f'(t)=0\) for \(t\in T\!\setminus \! (F\cup S)\). By construction, \(f'(t)\succ _{t} f(t)\) a.e. in \(F\cup S\). Also, being the sum of a Bochner integrable function and a \({\text {weak}}^{*}\)-null function, \(f'\) is Gelfand integrable and we have
. As \(e'(t)\le e(t)\) a.e. in \(T\), we have \(v\ge v'\), and therefore \(v\in ||\cdot ||_{\infty }\)-\({{\mathrm{int}}}L_{\infty }(\mu )_{+}\). For each \(n\in \mathbb {N}\), set \(T_{n}=\{{t\in T\!\setminus \! S}:{e(t)+nv\ge f(t)}\}\). Then \(\bigcup _{n=0}^{\infty }T_{n}=T\!\setminus \! S\). Hence, as \(\nu (T\!\setminus \! S)>0\), there must be an \(n_{1}\in \mathbb {N}\) such that \(\nu ^{*}(T_{n_{1}})>0\).Footnote 10 Choose \(n_{2}\in \mathbb {N}\) so that both \(n_{2}>n_{1}\) and \(\nu ^{*}(T_{n_{1}})>1/n_{2}\). By Assumptions (P) and (D), \(e(t)+n_{2}v\succ _{t}f(t)\) for all \(t\in T_{n_{1}}\), and by (P) and (AM), \(\{{t\in T}:{e(t)+n_{2}v\succ _{t}f(t)}\}\in {\fancyscript{T}}\). Therefore, if \(G\) is a measurable envelope of \(T_{n_{1}}\), then \(e(t)+n_{2}v\succ _{t}f(t)\) for almost all \(t\in G\) and we have \(\nu (G)=\nu ^{*}(T_{n_{1}})>1/n_{2}\). As \(\nu \) is atomless, we can choose an \(F\subseteq G\) with \(\nu (F)=1/n_{2}\). Clearly we may assume that \(F\cap S=\emptyset \). Now according to (b) in the definition of \(A\), there is a \({\text {weak}}^{*}\)-null function \(\eta :T\rightarrow L_{\infty }(\mu )\) such that \(g(t)+\eta (t)\succ _{t}f(t)\) for almost all \(t\in S\). Define \(f':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(f'(t)=g(t)+\eta (t)\) for \(t\in S\), \(f'(t)=e(t)+n_{2}v\) for \(t\in F\), and \(f'(t)=0\) for \(t\in T\!\setminus \! (F\cup S)\). By construction, \(f'(t)\succ _{t} f(t)\) a.e. in \(F\cup S\). Also, being the sum of a Bochner integrable function and a \({\text {weak}}^{*}\)-null function, \(f'\) is Gelfand integrable and we have

Thus, the coalition \(F\cup S\) can block \(f\) via \(f'\), contradicting the property of \(f\) being a core allocation.
As \(||\cdot ||_{\infty }\)-\({{\mathrm{int}}}L_{\infty }(\mu )_{+}\) is non-empty, the separation theorem implies that there is a nonzero positive linear functional \(\pi \) on \(L_{\infty }(\mu )\) such that \(\pi z\ge 0\) for each \(z\in B\). Now \(\pi \) can be identified with a finitely additive measure on \({\varSigma }\) so that  , \(x\in L_{\infty }(\mu )\); in particular, \(\pi (E)=0\) whenever \(\mu (E)=0\). Let \(\pi =\pi _{c}+\pi _{f}\) be the Yosida–Hewitt decomposition of \(\pi \), where \(\pi _{c}\ge 0\) is countably additive and \(\pi _{f}\ge 0\) is purely finitely additive, and choose a sequence \(\langle {C_{k}}\rangle _{k\in \mathbb {N}}\) in \({\varSigma }\) with \(\mu ({\varOmega }\!\setminus \! C_{k})\rightarrow 0\) such that \(\pi _{f}(C_{k})=0\) for each \(k\in \mathbb {N}\) (Yosida and Hewitt 1952, Theorems 1.23 and 1.22). We may view \(\pi _{c}\) as an element of \(L_{1}(\mu )\).
, \(x\in L_{\infty }(\mu )\); in particular, \(\pi (E)=0\) whenever \(\mu (E)=0\). Let \(\pi =\pi _{c}+\pi _{f}\) be the Yosida–Hewitt decomposition of \(\pi \), where \(\pi _{c}\ge 0\) is countably additive and \(\pi _{f}\ge 0\) is purely finitely additive, and choose a sequence \(\langle {C_{k}}\rangle _{k\in \mathbb {N}}\) in \({\varSigma }\) with \(\mu ({\varOmega }\!\setminus \! C_{k})\rightarrow 0\) such that \(\pi _{f}(C_{k})=0\) for each \(k\in \mathbb {N}\) (Yosida and Hewitt 1952, Theorems 1.23 and 1.22). We may view \(\pi _{c}\) as an element of \(L_{1}(\mu )\).
Now \(\pi _{c}\ne 0\). To see this, fix a \(||\cdot ||_{\infty }\)-Bochner integrable function \(e':T\rightarrow L_{\infty }(\mu )_{+}\) with  such that \(e'(t)\le e(t)\) for almost all \(t\in T\), as is possible by Assumption (TAE). The indefinite Bochner integral of \(e'\) is \(\nu \)-continuous, so there is an \(\bar{\varepsilon }\) such that
such that \(e'(t)\le e(t)\) for almost all \(t\in T\), as is possible by Assumption (TAE). The indefinite Bochner integral of \(e'\) is \(\nu \)-continuous, so there is an \(\bar{\varepsilon }\) such that  whenever \(\nu (T\!\setminus \! T')<\bar{\varepsilon }\). Now for each \(n\in \mathbb {N}\) let \(T_{n}=\{{t\in T}:{n1_{{\varOmega }}\succ _{t}f(t)}\}\). For each \(t\in T\), \(n1_{{\varOmega }}> f(t) \) if \(n\) is sufficiently large, so by Assumptions (P) and (D), we have \(\bigcup _{m\in \mathbb {N}}^{}\bigcap _{n\ge m}^{}T_{n}=T\). By Assumptions (P) and (AM), \(T_{n}\) is measurable for each \(n\), and it follows that there is an integer \(\bar{n}\) such that \(\nu (T\!\setminus \! T_{\bar{n}})<\bar{\varepsilon }\).
whenever \(\nu (T\!\setminus \! T')<\bar{\varepsilon }\). Now for each \(n\in \mathbb {N}\) let \(T_{n}=\{{t\in T}:{n1_{{\varOmega }}\succ _{t}f(t)}\}\). For each \(t\in T\), \(n1_{{\varOmega }}> f(t) \) if \(n\) is sufficiently large, so by Assumptions (P) and (D), we have \(\bigcup _{m\in \mathbb {N}}^{}\bigcap _{n\ge m}^{}T_{n}=T\). By Assumptions (P) and (AM), \(T_{n}\) is measurable for each \(n\), and it follows that there is an integer \(\bar{n}\) such that \(\nu (T\!\setminus \! T_{\bar{n}})<\bar{\varepsilon }\).
Consider the sequence \(\langle {\bar{n}1_{C_{k}}}\rangle _{k\in \mathbb {N}}\) in \(L_{\infty }(\mu )_{+}\), where the sets \(C_{k}\in {\varSigma }\) are those chosen above. By (P) and (AM) again, the set \(T_{k}=\{{t\in T_{\bar{n}}}:{\bar{n}1_{C_{k}}\succ _{t}f(t)}\}\) is measurable for each \(k\). Note that because \(\mu ({\varOmega }\!\setminus \! C_{k})\rightarrow 0\), \(\bar{n}1_{C_{k}}\rightarrow \bar{n} 1_{{\varOmega }}\) in the Mackey topology of \(L_{\infty }(\mu )\). Hence, by Assumption (C), we have \(\bigcup _{l\in \mathbb {N}}^{}\bigcap _{k\ge l}^{}T_{k}=T_{\bar{n}}\) and thus \(\nu (T_{\bar{n}}\!\setminus \! T_{k})\rightarrow 0\) as \(k\rightarrow \infty \). As \(\nu (T\!\setminus \! T_{\bar{n}})<\bar{\varepsilon }\), it follows that there is a \(\bar{k}\) such that \(\nu (T\!\setminus \! T_{\bar{k}})<\bar{\varepsilon }\). By the choice of \(\bar{\varepsilon }\),  , and thus we have
, and thus we have  , as \(\pi \) is nonzero and positive. On the other hand, consider the allocation \(g:T\rightarrow L_{\infty }(\mu )_{+}\) given by setting \(g(t)=\bar{n} 1_{C_{\bar{k}}}\) for each \(t\in T\). Note that
, as \(\pi \) is nonzero and positive. On the other hand, consider the allocation \(g:T\rightarrow L_{\infty }(\mu )_{+}\) given by setting \(g(t)=\bar{n} 1_{C_{\bar{k}}}\) for each \(t\in T\). Note that  and that
and that  . Thus would we have \(\pi =\pi _{f}\), then
. Thus would we have \(\pi =\pi _{f}\), then  , and we would get a contradiction to the fact that \(\pi z\ge 0\) for each \(z\in B\). Thus \(\pi _{c}\ne 0\) must be true.
, and we would get a contradiction to the fact that \(\pi z\ge 0\) for each \(z\in B\). Thus \(\pi _{c}\ne 0\) must be true.
Note that \(\pi _{c}z\ge 0\) for each \(z\in B\). Otherwise, for some \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\), and functions \(e'\), \(g\), and \(\eta \) as in the definition of the set \(A\), we have

but \(g(t)+\eta (t)\succ _{t} f(t)\) for almost all \(t\in S\). Set \(f'=1_{S}\times g+1_{S}\times \eta \) and note that by Assumption (P), \(f'\) takes values in \(L_{\infty }(\mu )_{+}\) a.e. in \(T\). For every \(k\in \mathbb {N}\), define \(g_{k}:T\rightarrow L_{\infty }(\mu )_{+}\) and \(\eta _{k}:T\rightarrow L_{\infty }(\mu )\) by setting \(g_{k}(t)=1_{C_{k}}\times g(t)\) and \(\eta _{k}(t)=1_{C_{k}}\times \eta (t)\) if \(t\in S\), the sets \(C_{k}\) being as before, and \(g_{k}(t)=\eta _{k}(t)=0\) if \(t\in T\!\setminus \! S\). Then for each \(k\), \(g_{k}\) is a measurable simple function and \(\eta _{k}\) is a \({\text {weak}}^{*}\)-null function. (For any \(q\in L_{1}(\mu )\), \(q\eta _{k}(t)=q(1_{C_{k}}\times \eta (t))=(1_{C_{k}}\times q)\eta (t)\) for all \(t\in S\). Thus, since \(\eta \) is \({\text {weak}}^{*}\)-null function, and since \(1_{C_{k}}\times q\in L_{1}(\mu )\) whenever \(q\in L_{1}(\mu )\), \(\eta _{k}\) is a \({\text {weak}}^{*}\)-null function as well.) For each \(k\in \mathbb {N}\), set \(f_{k}=g_{k}+\eta _{k}\). Note that \(f_{k}(t)=1_{C_{k}}\times f'(t)\) for each \(t\in T\). Thus, for each \(k\), \(f_{k}\) takes values in \(L_{\infty }(\mu )_{+}\) a.e. in \(T\), because \(f'\) does. Moreover, for each \(k\), \(f_{k}\) is Gelfand integrable, being the sum of a measurable simple function and a \({\text {weak}}^{*}\)-null function. Hence, by Assumptions (P) and (AM), for each \(k\) the set \(S_{k}=\{{t\in S}:{f_{k}(t)\succ _{t} f(t)}\}\) belongs to \({\fancyscript{T}}\). Arguing similarly as above, we see that \(\nu (S_{k})\rightarrow \nu (S)\) as \(k\rightarrow \infty \), so  . There must therefore be a \(\bar{k}\) such that
. There must therefore be a \(\bar{k}\) such that  . Now because \(\pi _{f}(C_{\bar{k}})=0\) (and \(\pi _{f}\ge 0\)), we have
. Now because \(\pi _{f}(C_{\bar{k}})=0\) (and \(\pi _{f}\ge 0\)), we have

But by construction,  belongs to \(B\), and we get a contradiction to the fact that \(\pi z\ge 0\) for all \(z\in B\). Thus, as claimed, \(\pi _{c}z\ge 0\) for all \(z\in B\).
belongs to \(B\), and we get a contradiction to the fact that \(\pi z\ge 0\) for all \(z\in B\). Thus, as claimed, \(\pi _{c}z\ge 0\) for all \(z\in B\).
Now by Assumption (TAE), there is a non-decreasing sequence \(\langle {e_{n}}\rangle _{}\) of Bochner integrable functions \(e_{n}:T\rightarrow L_{\infty }(\mu )_{+}\) such that \(e_{n}(t)\rightarrow e(t)\) in the Mackey topology for almost all \(t\in T\). As \(\pi _{c}\in L_{1}(\mu )\), we must have \(\pi _{c} e_{n}(t)\rightarrow \pi _{c} e(t)\) for almost all \(t\in T\). Consequently, for any \(S\in {\fancyscript{T}}\),  , just by the monotone convergence theorem, and thus
, just by the monotone convergence theorem, and thus  . It follows that whenever \(S\in {\fancyscript{T}}\) and \(g:T\rightarrow L_{\infty }(\mu )_{+}\) are such that the conditions in (b) of the definition of the set \(A\) are satisfied, so that
. It follows that whenever \(S\in {\fancyscript{T}}\) and \(g:T\rightarrow L_{\infty }(\mu )_{+}\) are such that the conditions in (b) of the definition of the set \(A\) are satisfied, so that  for each \(n\), then
for each \(n\), then  .
.
Write \(p=\pi _{c}\). We claim now that a.e. in \(T\) we have \(px\ge p e(t)\) whenever \(x\succ _{t}f(t)\). Otherwise, by Assumption (P), there is a map \(h:S\rightarrow L_{\infty }(\mu )_{+}\) where \(S\subseteq T\) with \(\nu ^{*}(S)>0\) such that for all \(t\in S\), \(h(t)\succ _{t}f(t)\) but \(ph(t)<pe(t)\). Let \(Q_+\subseteq L_{\infty }(\mu )_{+}\) be chosen according to Lemma 4. In particular, \(Q_+\) is Mackey dense in \(L_{\infty }(\mu )_{+}\). Therefore, as \(p\in L_{1}(\mu )\), Assumptions (P) and (C) imply that we may assume that \(h(t)\in Q_+\) for all \(t\in S\). Now by Lemma 4(b), there are an \(S_{1}\subseteq S\), with \(\nu ^{*}(S_{1})>0\), an \(a\in L_{\infty }(\mu )_{+}\), and a \({\text {weak}}^{*}\)-null function \(\eta :T\rightarrow L_{\infty }(\mu )\) such that \(h(t)=a+\eta (t)\) for all \(t\in S_{1}\). Define \(h':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(h'(t)=a+\eta (t)\) if \(t\in S_{1}\), and \(h'(t)=a\) otherwise. Note that \(h'\) is Gelfand integrable. Let \(S_{2}=\{{t\in T}:{h'(t)\succ _{t}f(t)}\}\). By Assumptions (P) and (AM), \(S_{2}\in {\fancyscript{T}}\). Let \(S_{3}=\{{t\in S_{2}}:{ph'(t)<pe(t)}\}\). Then also \(S_{3}\in {\fancyscript{T}}\). Note that \(S_{1}\subseteq S_{3}\). Therefore, as \(\nu ^{*}(S_{1})>0\), we have \(\nu (S_{3})>0\). Define \(g:T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(g(t)=a\) for all \(t\in T\). Observe that \(h'-g\) is a \({\text {weak}}^{*}\)-null function. Hence, relative to the set \(S_{3}\), \(g\) satisfies the conditions in (b) of the definition of \(A\), because \(h'(t)\succ _{t}f(t)\) for all \(t\in S_{3}\). On the other hand, we must have \(pg(t)=ph'(t)\) for almost all \(t\in T\). By the definition of \(S_{3}\), it follows that  , and we get a contradiction to what has been established in the previous paragraph.
, and we get a contradiction to what has been established in the previous paragraph.
Arguing as in the proof of Theorem 2, we can conclude that the pair \((p,f)\) is a Walrasian equilibrium, observing that (TAE) implies that  , because \(p\) is a positive and nonzero element of \(L_{1}(\mu )\). \(\square \)
, because \(p\) is a positive and nonzero element of \(L_{1}(\mu )\). \(\square \)
11.3 Additional facts for the proof of Theorem 8
Fact 5
Let \(({\varOmega },{\varSigma },\mu )\) be a totally finite measure space, so that \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Let \((T,{\fancyscript{T}},\nu )\) be a totally finite measure space, and \(f:T\rightarrow L_{\infty }(\mu )\) a function ; write \(f_{1}\) for \(f\) viewed as a function from \(T\) to \(L_{1}(\mu )\).
-
(a)
If \(f\) is Gelfand integrable, then \(f_{1}\) is Pettis integrable, and for any \(S\in {\fancyscript{T}}\), the Pettis integral of \(f_{1}\) over \(S\) agrees with the Gelfand integral of \(f\) over \(S\).
-
(b)
If \(f_{1}\) is Pettis integrable and \(||\cdot ||_{\infty }\)-bounded, then \(f\) is Gelfand integrable and for any \(S\in {\fancyscript{T}}\), the Pettis integral of \(f_{1}\) over \(S\) agrees with the Gelfand integral of \(f\) over \(S\).
Proof
By hypothesis, \(L_{1}(\mu )^{*}= L_{\infty }(\mu )\subseteq L_{1}(\mu )\) and thus (a) holds. Now suppose \(f_{1}\) is Pettis integrable, so that, in particular, the map \(t\mapsto pf_{1}(t)\) is measurable for each \(p\in L_{\infty }(\mu )\). But then \(t\mapsto pf(t)\) must be measurable for each \(p\in L_{1}(\mu )\), because \(L_{\infty }(\mu )\) is sequentially dense in \(L_{1}(\mu )\). Moreover, \(|pf(t)|_{}\le ||p||_{1}||f(t)||_{\infty }\) for all \(t\in T\) and all \(p\in L_{1}(\mu )\). Hence, if \(f\) is \(||\cdot ||_{\infty }\)-bounded, then \(t\mapsto |pf(t)|_{}\) is integrable for each \(p\in L_{1}(\mu )\) because \((T,{\fancyscript{T}},\nu )\) is totally finite, so \(f\) is Gelfand integrable, and by (a), for any \(S\in {\fancyscript{T}}\), the Pettis integral of \(f_{1}\) over \(S\) agrees with the Gelfand integral of \(f\) over \(S\). \(\square \)
Fact 6
Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space, \((T,{\fancyscript{T}},\nu )\) a totally finite measure space, and \(A\) a set of Gelfand integrable functions from \(T\) to \(L_{\infty }(\mu )\). Suppose that \((T,{\fancyscript{T}},\nu )\) is atomless and that \(A\) is decomposable. Write  and suppose that \(B\) is \(||\cdot ||_{\infty }\)-bounded, or, equivalently, that \(B\) is included in an order interval of \(L_{\infty }(\mu )\). Then the Mackey closure of \(B\) is convex.
and suppose that \(B\) is \(||\cdot ||_{\infty }\)-bounded, or, equivalently, that \(B\) is included in an order interval of \(L_{\infty }(\mu )\). Then the Mackey closure of \(B\) is convex.
Proof
Note first that, \(\mu \) being \(\sigma \)-finite, \(L_{1}(\mu )\) is weakly compactly generated and therefore measure compact.Footnote 11 By Fact 3 we may assume that \(\mu \) is actually totally finite, so that \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Now, as \(L_{1}(\mu )\) is measure compact, it follows from Podczeck (2004, proof of Lemma 6) together with Fact 5(a) that the \(||\cdot ||_{1}\)-closure of \(B\) is a convex subset of \(L_{1}(\mu )\). Observe that, \(\mu \) being totally finite, an order interval of \(L_{\infty }(\mu )\) is both a closed subset of \(L_{1}(\mu )\) and a Mackey closed subset of \(L_{\infty }(\mu )\). As \(B\) is included in an order interval of \(L_{\infty }(\mu )\), we now see from Fact 4 that the Mackey closure of \(B\) in \(L_{\infty }(\mu )\) is convex. \(\square \)
Fact 7
Let \((T,{\fancyscript{T}},\nu )\) be a totally finite measure space, and \(({\varOmega },{\varSigma },\mu )\) a \(\sigma \)-finite measure space. Let \(f:T\rightarrow L_{\infty }(\mu )_{+}\) be Gelfand integrable and let \(x\in L_{\infty }(\mu )\) be such that  . Suppose \({\fancyscript{T}}=2^{T}\) and that \(f\) is \(||\cdot ||_{\infty }\)-bounded. Then there is a Gelfand integrable function \(h:T\rightarrow L_{\infty }(\mu )_{+}\) such that
. Suppose \({\fancyscript{T}}=2^{T}\) and that \(f\) is \(||\cdot ||_{\infty }\)-bounded. Then there is a Gelfand integrable function \(h:T\rightarrow L_{\infty }(\mu )_{+}\) such that  and \(h(t)\le f(t)\) for all \(t\in T\).Footnote 12
and \(h(t)\le f(t)\) for all \(t\in T\).Footnote 12
Proof
By Fact 3, we may assume that \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Then \(x\) may be viewed as element of \(L_{1}(\mu )_+\), and by Fact 5(a), \(f\) may be viewed as a Pettis integrable function from \(T\) to \(L_{1}(\mu )_{+}\), with Pettis integral equal to the Gelfand integral; moreover, the assumption that \(f\) is \(||\cdot ||_{\infty }\)-bounded implies that \(f\) is \(||\cdot ||_{1}\)-bounded as well. Now \(L_{1}(\mu )\) is an order-continuous Banach lattice which, \(\mu \) being totally finite, is weakly compactly generated and thus has the PIP.Footnote 13 Hence by Podczeck (2004, Lemma 11), the hypothesis that \({\fancyscript{T}}=2^{T}\) and the facts that  and that \(f\) is \(||\cdot ||_{1}\)-bounded and has positive values imply the existence of a Pettis integrable \(h :T\rightarrow L_{1}(\mu )_{+}\) with Pettis integral equal to \(x\) such that \(h(t)\le f(t)\) for all \(t\in T\). As \(f\) is \(||\cdot ||_{\infty }\)-bounded and \(0\le h(t)\le f(t)\) for all \(t\in T\), \(h\) actually takes values in \(L_{\infty }(\mu )\) and is \(||\cdot ||_{\infty }\)-bounded. An appeal to Fact 5(b) concludes the proof. \(\square \)
and that \(f\) is \(||\cdot ||_{1}\)-bounded and has positive values imply the existence of a Pettis integrable \(h :T\rightarrow L_{1}(\mu )_{+}\) with Pettis integral equal to \(x\) such that \(h(t)\le f(t)\) for all \(t\in T\). As \(f\) is \(||\cdot ||_{\infty }\)-bounded and \(0\le h(t)\le f(t)\) for all \(t\in T\), \(h\) actually takes values in \(L_{\infty }(\mu )\) and is \(||\cdot ||_{\infty }\)-bounded. An appeal to Fact 5(b) concludes the proof. \(\square \)
Lemma 5
Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space, let \(v\in L_{\infty }(\mu )\), and let \(q\) be a strictly positive element of \(L_{1}(\mu )\). Write \(U=\{{u\in L_{\infty }(\mu )}:{q(|u|_{})<1}\}\). Let \((T,{\fancyscript{T}},\nu )\) be a totally finite measure space with \({\fancyscript{T}}=2^{T}\), let \(h\rightarrow L_{\infty }(\mu )_{+}\) be Gelfand integrable, and let \(e\in L_{\infty }(\mu )_{+}\). Suppose \(h\) is \(||\cdot ||_{\infty }\)-bounded and that for some \(u\in U\) and some number \(\lambda >0\),  . Then there are an integrable function \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) and a function \(\tilde{u}:T\rightarrow U\) such that \(h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in L_{\infty }(\mu )_{+}\) for almost all \(t\in T\) and such that the function \(t\mapsto h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\) is Gelfand integrable with
. Then there are an integrable function \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) and a function \(\tilde{u}:T\rightarrow U\) such that \(h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in L_{\infty }(\mu )_{+}\) for almost all \(t\in T\) and such that the function \(t\mapsto h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\) is Gelfand integrable with  .
.
Proof
Scaling \(e\) and the function \(h\), if necessary, we may assume \(\lambda =1\).
Suppose first that \(v\ge u^{-}\). In this case, set \(\tilde{u}(t)=u\) and \(\tilde{\lambda }(t)=1/(\nu (T))\) for all \(t\in T\), and we are done (clearly, we may assume \(\nu (T)>0\)).
Otherwise, note that \(q(u^{-}-(v\wedge u^{-}))>0\). Similarly as in the proof of Lemma 2, we see that  . By Fact 7, there is a Gelfand integrable function \(b:T\rightarrow L_{\infty }(\mu )_{+}\) such that
. By Fact 7, there is a Gelfand integrable function \(b:T\rightarrow L_{\infty }(\mu )_{+}\) such that  and \(b(t)\le h(t)\) for almost all \(t\in T\). Define \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) by setting
and \(b(t)\le h(t)\) for almost all \(t\in T\). Define \(\tilde{\lambda }:T\rightarrow \mathbb {R}_{+}\) by setting
and note that  . Now define the function \(\tilde{u}:T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(\tilde{u}(t)=u^{+}-(v\wedge u^{-})-(1/\tilde{\lambda }(t))b(t)\) if \(\tilde{\lambda }(t)>0\) and \(\tilde{u}(t)=u\) otherwise. As \(b(t)\le h(t)\) for almost all \(t\in T\) and \(v-(v\wedge u^{-})\ge 0\), we have \(h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in L_{\infty }(\mu )_{+}\) for almost all \(t\in T\), and similarly as in the proof of Lemma 2, it follows that \(\tilde{u}(t)\in U\) for almost all \(t\in T\).
. Now define the function \(\tilde{u}:T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(\tilde{u}(t)=u^{+}-(v\wedge u^{-})-(1/\tilde{\lambda }(t))b(t)\) if \(\tilde{\lambda }(t)>0\) and \(\tilde{u}(t)=u\) otherwise. As \(b(t)\le h(t)\) for almost all \(t\in T\) and \(v-(v\wedge u^{-})\ge 0\), we have \(h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\in L_{\infty }(\mu )_{+}\) for almost all \(t\in T\), and similarly as in the proof of Lemma 2, it follows that \(\tilde{u}(t)\in U\) for almost all \(t\in T\).
Note that \(\tilde{\lambda }(t)\tilde{u}(t)=\tilde{\lambda }(t)\bigl (u^{+}-(v\wedge u^{-})\bigr )-b(t)\) for each \(t\in T\). Consequently, the map \(t\mapsto h(t)+\tilde{\lambda }(t)(v+\tilde{u}(t))\) is Gelfand integrable (because the maps \(b\) and \(h\) and because the map \(\tilde{\lambda }\) is integrable), and because  and
and  , we get
, we get

\(\square \)
11.4 Proof of Theorem 8
Let \(f\) be a core allocation of the given economy. Recall for the following arguments that the probability space \((T,{\fancyscript{T}},\nu )\) of agents is complete.
(a) To start the proof that \(f\) is Walrasian, let \(v\in L_{\infty }(\mu )_{+}\!\setminus \! \{0\}\) and \(q\in L_{1}(\mu )\) be chosen according to Assumption (EDC). Write \(U=\{{u\in L_{\infty }(\mu )}:{q|u|_{}<1}\}\). Because the lattice operations in \(L_{\infty }(\mu )\) are continuous for the Mackey topology, the map \(u\mapsto q|u|_{}:L_{\infty }(\mu )\rightarrow \mathbb {R}\) is Mackey continuous, and thus \(U\) is an open neighborhood of \(0\) in \(L_{\infty }(\mu )\) for the Mackey topology. Let
As \(U\) is Mackey open, so is \({\varGamma }\). As in the proof of Theorem 6, \({\varGamma }\) is convex and we may assume that \(0\notin {\varGamma }\). Set
so that \(|pU|_{}\le 1\) whenever \(p\in K\). As the polars of the weakly compact subsets of \(L_{1}(\mu )\) form a local base at zero in \(L_{\infty }(\mu )\) for the Mackey topology, it follows from the bipolar theorem that \(K\) is a weakly compact set in \(L_{1}(\mu )\).
(b) Let
Because \(2^{\emptyset }=\{\emptyset \}\subseteq {\fancyscript{T}}\), there is an \(S_{n}\in {\fancyscript{T}}\) with \(2^{S_{n}}\subseteq {\fancyscript{T}}\) and \(\nu (S_{n})>\overline{r}-(1/n)\) for each integer \(n>0\). Set \(T_{1}=T\!\setminus \! \bigcup _{n>0}^{}S_{n}\) and \(T_{2}=\bigcup _{n>0}^{}S_{n}\). Then \(T_{1}\) and \(T_{2}\) belong to \({\fancyscript{T}}\) and \(2^{T_{2}}\subseteq {\fancyscript{T}}\); moreover, \(\nu (T_{2})=\overline{r}\), so every \(S\subseteq T_{1}\) with \(S\in {\fancyscript{T}}\) and \(\nu (S)>0\) has a non-measurable subset.
Note that if \(S\in {\fancyscript{T}}\) and \(g:S\cap T_{2}\rightarrow L_{\infty }(\mu )\) is any \(||\cdot ||_{\infty }\)-bounded function, then for every \(p\in L_{1}(\mu )\) the integral  is defined. Thus, for any such \(g\), the map \(1_{S\cap T_{2}}\times g:T\rightarrow L_{\infty }(\mu )\) is Gelfand integrable.
is defined. Thus, for any such \(g\), the map \(1_{S\cap T_{2}}\times g:T\rightarrow L_{\infty }(\mu )\) is Gelfand integrable.
(c) For each \(n\in \mathbb {N}\), let
For each \(n\), every \(h\in A_{n}\) is Gelfand integrable; let  where
where  is the Gelfand integral of \(h\). Note that \(A_{n}\) is decomposable for each \(n\) and that \(B_{n}\) is included in the order interval
is the Gelfand integral of \(h\). Note that \(A_{n}\) is decomposable for each \(n\) and that \(B_{n}\) is included in the order interval  . Hence, as \(\nu \) is atomless, Fact 6 implies that the Mackey closure of \(B_{n}\) is convex for each \(n\). Note that \(0\in B_{n}\) for each \(n\), so the Mackey closure of \(B_{n}\) is non-empty for each \(n\).
. Hence, as \(\nu \) is atomless, Fact 6 implies that the Mackey closure of \(B_{n}\) is convex for each \(n\). Note that \(0\in B_{n}\) for each \(n\), so the Mackey closure of \(B_{n}\) is non-empty for each \(n\).
Now \(B_{n}\cap -{\varGamma }=\emptyset \) for every \(n\). Otherwise, as \(0\notin {\varGamma }\), for some \(n\) there are an \(S\in {\fancyscript{T}}\) with \(\nu (S)>0\), a \(u\in U\), and a \(\lambda >0\) such that  where \(g:T\rightarrow L_{\infty }(\mu )_{+}\) is as in the definition of \(A_{n}\). Write \(g_{1}=g\!\upharpoonright \! T_{1}\), \(g_{2}=g\!\upharpoonright \! T_{2}\), and set \(S_{1}=S\cap T_{1}\) and \(S_{2}=S\cap T_{2}\), so that
where \(g:T\rightarrow L_{\infty }(\mu )_{+}\) is as in the definition of \(A_{n}\). Write \(g_{1}=g\!\upharpoonright \! T_{1}\), \(g_{2}=g\!\upharpoonright \! T_{2}\), and set \(S_{1}=S\cap T_{1}\) and \(S_{2}=S\cap T_{2}\), so that  . By Lemma 2, there are points \(u_{1}\), \(u_{2}\in U\) and \(e_{1}\), \(e_{2}\in L_{\infty }(\mu )_{+}\), and numbers \(\lambda _{1}\), \(\lambda _{2}\ge 0\), such that
. By Lemma 2, there are points \(u_{1}\), \(u_{2}\in U\) and \(e_{1}\), \(e_{2}\in L_{\infty }(\mu )_{+}\), and numbers \(\lambda _{1}\), \(\lambda _{2}\ge 0\), such that  , \(i=1,2\), and
, \(i=1,2\), and  . Now, \(g_{1}\) being a measurable simple function, another application of Lemma 2 yields measurable simple functions \(\tilde{\lambda }_{1}:T_{1}\rightarrow \mathbb {R}_{+}\) and \(\tilde{u}_{1}:T_{1}\rightarrow U\) such that
. Now, \(g_{1}\) being a measurable simple function, another application of Lemma 2 yields measurable simple functions \(\tilde{\lambda }_{1}:T_{1}\rightarrow \mathbb {R}_{+}\) and \(\tilde{u}_{1}:T_{1}\rightarrow U\) such that  and \(g_{1}(t)+\tilde{\lambda }_{1}(t)(v+\tilde{u}_{1}(t))\in L_{\infty }(\mu )_{+}\) for \(t\in T_{1}\). Applying Lemma 5 (with \(S_2\) substituted for \(T\)), we can find an integrable function \(\tilde{\lambda }_{2}:T_{2}\rightarrow \mathbb {R}_{+}\) and a function \(\tilde{u}_{2}:T_{2}\rightarrow U\) with the result that the function \(t\mapsto g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\) is Gelfand integrable, with
and \(g_{1}(t)+\tilde{\lambda }_{1}(t)(v+\tilde{u}_{1}(t))\in L_{\infty }(\mu )_{+}\) for \(t\in T_{1}\). Applying Lemma 5 (with \(S_2\) substituted for \(T\)), we can find an integrable function \(\tilde{\lambda }_{2}:T_{2}\rightarrow \mathbb {R}_{+}\) and a function \(\tilde{u}_{2}:T_{2}\rightarrow U\) with the result that the function \(t\mapsto g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\) is Gelfand integrable, with  , and \(g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\in L_{\infty }(\mu )_{+}\) for all \(t\in T_{2}\). Now define \(g':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(g'(t)=g_{1}(t)+\tilde{\lambda }_{1}(t)(v+\tilde{u}_{1}(t))\) if \(t\in T_{1}\), and \(g'(t)=g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\) if \(t\in T_{2}\). Then \(g'\) is Gelfand integrable and
, and \(g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\in L_{\infty }(\mu )_{+}\) for all \(t\in T_{2}\). Now define \(g':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(g'(t)=g_{1}(t)+\tilde{\lambda }_{1}(t)(v+\tilde{u}_{1}(t))\) if \(t\in T_{1}\), and \(g'(t)=g_{2}(t)+\tilde{\lambda }_{2}(t)(v+\tilde{u}_{2}(t))\) if \(t\in T_{2}\). Then \(g'\) is Gelfand integrable and  . By Assumptions (P), (EDC), and (Tr), \(g'(t)\succ _{t}f(t)\) a.e. in \(S\), and we get a contradiction to the fact that \(f\) is a core allocation.
. By Assumptions (P), (EDC), and (Tr), \(g'(t)\succ _{t}f(t)\) a.e. in \(S\), and we get a contradiction to the fact that \(f\) is a core allocation.
Note that since \({\varGamma }\) is Mackey open, the fact that \(B_{n}\cap -{\varGamma }=\emptyset \) implies that also the Mackey closure of \(B_{n}\) does not intersect \(-{\varGamma }\).
(d) Using the separation theorem, it follows that for each \(n\in \mathbb {N}\), there is a nonzero \(p_{n}\in L_{1}(\mu )\) such that \(p_{n}B_{n}\ge 0\ge p_{n}(-{\varGamma })\). Note that we must have \(p_{n}v>0\) for each \(n\). Hence, by the facts noted in (b), we may assume that there is a nonzero \(p\in L_{1}(\mu )\) such that \(p_{n}\rightarrow p\) weakly in \(L_{1}(\mu )\) as \(n\rightarrow \infty \) (recall that in any Banach space, “weakly compact” implies “weakly sequentially compact” by the Eberlein–Šmulian theorem). As the sequence \(\langle {B_{n}}\rangle _{n\in \mathbb {N}}\) is non-decreasing, it follows that \(pB_{n}\ge 0\) for each \(n\).
Note that because the map \(t\mapsto pe(t):T\rightarrow \mathbb {R}\) is measurable, Assumptions (P) and (AM) imply that the set \(\{{t\in T_{1}}:{x\succ _{t}f(t),\ px<pe(t)}\}\) is a measurable set in \(T\) for each \(x\in L_{\infty }(\mu )_{+}\). Therefore, the fact that \(pB_{n}\ge 0\) for each \(n\) implies the following:
-
(i)
For every \(x\in L_{\infty }(\mu )_{+}\), the set \(\{{t\in T_{1}}:{x\succ _{t}f(t),\ px<pe(t)}\}\) is a null set.
As for \(T_{2}\), note that the fact that \(pB_{n}\ge 0\) for each \(n\) implies that if \(g:T\rightarrow L_{\infty }(\mu )_{+}\) is \(||\cdot ||_{\infty }\)-bounded and there is a non-negligible \(S\subseteq T_{2}\) such that \(g(t)\succ _{t}f(t)\) for almost all \(t\in S\), then there is a non-negligible \(S'\subseteq S\) such that \(pg(t)\ge e(t)\) for all \(t\in S'\). Note also that if \(S\subseteq T_{2}\) is non-negligible and \(g:T\rightarrow L_{\infty }(\mu )_{+}\) is any function, there is a non-negligible \(S'\subseteq S\) such that \(g\) is \(||\cdot ||_{\infty }\)-bounded on \(S'\). Consequently:
-
(ii)
If \(S\subseteq T_{2}\) is non-negligible and \(g:S\rightarrow L_{\infty }(\mu )_{+}\) satisfies \(g(t)\succ _{t}f(t)\) a.e. in \(S\), then there is a non-negligible \(S'\subseteq S\) such that \(pg(t)\ge pe(t)\) for all \(t\in S'\).
(e) Suppose there is an \(S\subseteq T\) with \(\nu ^{*}(S)>0\) and a function \(h:S\rightarrow L_{\infty }(\mu )_{+}\) such that for all \(t\in S\), \(h(t)\succ _{t}f(t)\) and \(ph(t)<pe(t)\). Note that by (d)(ii), \(S\cap T_{2}\) is a null set. We may therefore assume that \(S\subseteq T_{1}\). Arguing as in the proof of Theorem 7, we may assume that there are an \(S_{1}\subseteq S\) with \(\nu ^{*}(S_{1})>0\), an \(a\in L_{\infty }(\mu )_{+}\), and a \({\text {weak}}^{*}\)-null function \(\eta :T\rightarrow L_{\infty }(\mu )\) such that for every \(t\in S_{1}\), \(h(t)=a+\eta (t)\). According to (b), there is a non-measurable set \(S_{2}\subseteq S_{1}\). Define \(h':T\rightarrow L_{\infty }(\mu )_{+}\) by setting \(h'(t)=a+\eta (t)\) if \(t\in S_{2}\) and \(h'(t)=a\) otherwise. Then \(h'\) is Gelfand integrable. By Assumptions (P) and (AM), the set \(\{{t\in T}:{h'(t)\succ _{t} f(t)}\}\) is measurable, and hence so is the set
Let \(S_{4}=\{{t\in T}:{a\succ _{t} f(t),\ pa<pe(t)}\}\). Observe that \(S_{3}=S_{2}\cup S_{4}\). By (d)(i) and (d)(ii), \(S_{4}\) is a null set. As \(S_{2}\) is a non-measurable, it follows that \(S_{3}\) is non-measurable, and we get a contradiction.
(f) By Assumption (P), it follows that for almost all \(t\in T\), \(px\ge p e(t)\) whenever \(x\succ _{t}f(t)\). In particular, \(p\) must be positive. Indeed, consider any \(a\in L_{\infty }(\mu )_{+}\!\setminus \! \{0\}\). By Assumptions (P) and (D), \(f(t)+na\succ _{t} f(t)\) for each \(t\in T\) and each \(n\in \mathbb {N}\!\setminus \! \{0\}\). It follows that \(p(f(t)+na)\ge p e(t)\) for each \(n\in \mathbb {N}\!\setminus \! \{0\}\) and almost all \(t\in T\) and hence that \(pa\ge 0\). Arguing as in the proof of Theorem 2, we can conclude that the pair \((p,f)\) is a Walrasian equilibrium. \(\square \)
Notes
To avoid unnecessary clutter of parentheses, we frequently write \(qx\), rather than \(q(x)\), for the value of a linear functional \(q\) at a point \(x\) in its domain when no confusion can arise.
Actually, to give the “number of agents” a formal expression, Tourky and Yannelis (2001) define a cardinal for a probability space, which they call the “weight” of this space. Now if a probability space \((T,{\fancyscript{T}},\nu )\) is atomless, this cardinal is the same as \({{\mathrm{add}}}\mathcal {N}(\nu )\). We will use this latter expression because it is standard terminology in measure theory and has a more compact definition.
To see this, use Remark 1 and the fact that if \(E\) is an infinite-dimensional Banach lattice such that \(E_+\) has non-empty interior, then the dual cone \(E_+^{*}\) has empty norm-interior.
Actually, in Tourky and Yannelis (2001), GCH (the generalized continuum hypothesis) is assumed, and in addition, it is assumed that the algebraic dimension of the commodity space is a regular cardinal. But this excludes many possible commodity spaces from the analysis. For example, let \(A\) be a set such that \(\#(A)\) is a singular cardinal with uncountable cofinality, such as \(\omega _{\omega _1}\). Then \(\#(A)\ge \mathfrak {c}\) by CH. Let \(E=\ell _2(A)\). Then \(\#(A)\le {{\mathrm{dim^{a}}}}(E)\le \#(E)\le \mathfrak {c}^\omega \cdot \#(A)^\omega =\#(A)^\omega \). Since \({{\mathrm{cf}}}(\#(A))>\omega \), GHC implies that \(\#(A)^\omega =\#(A)\), so \({{\mathrm{dim^{a}}}}(E)=\#(A)\), a singular cardinal. Note that it is relatively consistent that GCH holds and every uncountable limit cardinal is singular, i.e., is not weakly inaccessible (Kunen 2011, Corollary II.6.26).
Bochner integrability of the maps \(e_{n}\) implies that they are also Gelfand integrable; moreover, the integrals according to these two notions of integrability agree. Thus, the statement of (TAE) is consistent with the present setting where allocations are taken to be Gelfand integrable.
In the statement of (EDC), the functional \(q\) is required to be in the topological dual of the commodity space, which now means that this functional must be an element of \(L_{1}(\mu )\).
As the cardinal \({{\mathrm{add}}}\mathcal {N}(\nu )\) is uncountable, this replacement leaves the condition in (MMATC) the same also when \(\dim (E)\) is finite because in this case \({{\mathrm{dens}}}(E)\) is of course countable.
Recall that if \(Z\) is a metric space and \(Y\subseteq Z\), then \({{\mathrm{dens}}}(Y)\le {{\mathrm{dens}}}(Z)\).
Actually, the sets \(T_{n}\) can be shown to be measurable, but we don’t need this property here.
See Edgar (1979) for the definition of “measure compact” and the fact that a weakly compactly generated Banach space has this property.
This fact and Lemma 5 below are needed only if there exists an atomless probability space with no non-measurable subset. Recall that it is (relatively) consistent with ZFC that no such measure space exists. However, it is not known whether the existence of such a measure space is inconsistent with ZFC, and for this reason, we do not want to exclude such a measure space. See the brief discussion in Appendix 2(B).
See Edgar (1979) for the definition of “PIP” (Pettis integral property) and the fact that a weakly compactly generated Banach space has this property.
Solidity of \(U\) is assumed by Rustichini and Yannelis (1991) in the proof of their Theorem 6.1.
References
Aliprantis, C.D., Burkinshaw, O.: Positive Operators. No. 119 in Pure and Applied Mathematics Series. Academic Press, London (1985)
Aliprantis, C.D., Tourky, R.: Cones and Duality, Graduate Studies in Mathematics, vol. 84. American Mathematical Society, Providence (2007)
Angeloni, L., Martins-da Rocha, V.F.: Large economies with differential information and without free disposal. Econ. Theory 38(2), 263–286 (2009)
Aumann, R.J.: Markets with a continuum of traders. Econometrica 32, 39–50 (1964)
Diestel, J., Uhl Jr, J.J.: Vector Measures, Mathematical Surveys and Monographs, vol. 15. American Mathematical Society, Providence (1977)
Edgar, G.A.: Measurability in a Banach space, II. Indiana Univ. Math. J. 28(4), 559–579 (1979)
Einy, E., Moreno, D., Shitovitz, B.: Competitive and core allocations in large economies with differential information. Econ. Theory 18(2), 321–332 (2001)
Engelking, R.: General Topology, Sigma Series in Pure Mathematics, vol. 6. Heldermann Verlag, Berlin (1989)
Fabian, M., Habala, P., Hájek, P., Montesinos Santalucía, V., Pelant, J., Zizler, V.: Functional Analysis and Infinite-Dimensional Geometry. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, vol. 8. Springer, New York (2001)
Hervés-Beloso, C., Moreno-García, E., Yannelis, N.C.: Characterization and incentive compatibility of Walrasian expectations equilibrium in infinite dimensional commodity spaces. Econ. Theory 26(2), 361–381 (2005)
Hodel, R.E.: Cardinal functions I. In: Kunen, K., Vaughan, J.E. (eds.) Handbook of Set-Theoretic Topology, chap. 1. North-Holland, Amsterdam (1984)
Jech, T.: Set Theory, Springer Monographs in Mathematics, 3rd edn. Springer, Berlin (2003)
Kunen, K.: Set Theory, Studies in Logic, vol. 34. College Publications, London (2011)
Lacey, H.E.: The Hamel dimension of any infinite dimensional separable Banach space is \(c\). Am. Math. Mon. 80, 298 (1973)
Lindenstrauss, J., Tzafriri, L.: Classical Banach Spaces II. Springer, New York (1979)
Mackey, G.W.: On infinite-dimensional linear spaces. Trans. Am. Math. Soc. 57, 155–207 (1945)
Mertens, J.F.: An equivalence theorem for the core of an economy with commodity space \(L_{\infty }-\tau (L_\infty , L_1)\). In: Ali Khan, M., Yannelis, N.C. (eds.) Equilibrium Theory in Infinite Dimensional Spaces. Springer, New York, 1991, pp 189–196, reprint of CORE DP 7028 (1970)
Podczeck, K.: Core and Walrasian equilibria when agents’ characteristics are extremely dispersed. Econ. Theory 22, 699–725 (2003)
Podczeck, K.: On core-Walras equivalence in Banach spaces when feasibility is defined by the Pettis integral. J. Math. Econ. 40, 429–463 (2004)
Pol, R.: Note on the spaces \(P(S)\) of regular probability measures whose topology is determined by countable subsets. Pac. J. Math. 100(1), 185–201 (1982)
Rustichini, A., Yannelis, N.C.: Edgeworth’s conjecture in economies with a continuum of agents and commodities. J. Math. Econ. 20, 307–326 (1991)
Tourky, R., Yannelis, N.C.: Markets with many more agents than commodities: Aumann’s “hidden” assumption. J. Econ. Theory 101, 189–221 (2001)
Yannelis, N.C.: Integration of Banach-valued correspondences. In: Ali Khan, M., Yannelis, N.C. (eds.) Equilibrium Theory in Infinite Dimensional Spaces, pp. 2–35. Springer, New York (1991)
Yosida, K., Hewitt, E.: Finitely additive measures. Trans. Am. Math. Soc. 72, 46–66 (1952)
Zame, W.R.: Markets with a continuum of traders and infinitely many commodities. Working paper, SUNY at Buffalo (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
We wish to thank Manfred Nermuth, Rabeè Tourky, and Nicholas Yannelis for helpful conversations on the topic of this paper. Thanks also to an anonymous referee for valuable suggestions.
Appendices
Appendix 1
(A) Let \(E\) be a Banach lattice and let \({\fancyscript{E}}\) be an economy with commodity space \(E\). Suppose the consumption set of every agent is \(E_{+}\). Now the statement of the notion of “extremely desirable commodity” in Rustichini and Yannelis (1991) says that there are a \(v\in E_{+}\!\setminus \! \{0\}\) and a convex solid open neighborhood \(U\) of zero in \(E\) such that
-
(a)
for each \(t\in T\) and any number \(\lambda >0\), \(x+\lambda (u+v)\succ _{t} x\) whenever \(x\in E_{+}\) and \(u\in U\) are such that \(x+\lambda (u+v)\in E_{+}\);
-
(b)
whenever \(\delta _{1},\dots ,\delta _{n}\) are positive real numbers and \(x_{1},\dots ,x_{n}\) are elements of \(E_{+}\) such that \(\sum _{i=1}^{n}\delta _{i}=1\) and \(x_{i}\notin \delta _{i}U\), \(i=1,\dots ,n\), then \(\sum _{i=1}^{n}x_{i}\notin U\).Footnote 14
Suppose this condition holds. Let \(\rho \) be the gauge of \(U\). By the properties of \(U\), \(\rho \) is a Riesz seminorm on \(E\), and \(U=\{{x\in E}:{\rho (x)<1}\}\). Pick any \(x\), \(y\in E_{+}\), and set \(\alpha =\rho (x)\) and \(\beta =\rho (y)\). If \(\alpha =0\), then \(\rho (x)+\rho (y)=\rho (y)\le \rho (x+y)\), since \(\rho \) is a Riesz seminorm. Similarly, if \(\beta =0\), then \(\rho (x)+\rho (y)\le \rho (x+y)\). Assume that \(\alpha \) and \(\beta \) are both larger than 0, and set \(x_{1}=\frac{1}{\alpha +\beta }x\) and \(y_{1}=\frac{1}{\alpha +\beta }y\). Then \(x_{1}\notin \frac{\alpha }{\alpha +\beta }U\) and \(y_{1}\notin \frac{\beta }{\alpha +\beta }U\). Now by (b), \(x_{1}+y_{1}\notin U\), so \(\rho (x+y)\ge \alpha +\beta \), and we see again that \(\rho (x)+\rho (y)\le \rho (x+y)\). Thus the seminorm \(\rho \) is additive on \(E_{+}\). There is therefore a positive linear functional \(q_{1}\) on \(E\) which agrees with \(\rho \) on \(E_{+}\). By the fact that \(U\) is solid, we see that \(U=\{{u\in E}:{q_{1}|u|_{}<1}\}\). Moreover, since \(E\) is a Banach lattice, the fact that the linear functional \(q_{1}\) is positive implies that \(q_{1}\) is continuous, i.e., \(q_{1}\in E^{*}\). Now it is assumed in Rustichini and Yannelis (1991) that \(E\) is separable, so \(E^{*}\) has a strictly positive element, \(q_{2}\) say (see, e.g., Lindenstrauss and Tzafriri 1979, p. 25). Set \(q=q_{1}+q_{2}\). Then \(q\) is strictly positive, and \(q_{1}|u|_{}<1\) whenever \(u\in E\) is such that \(q|u|_{}<1\). Hence, by (a), (EDC) must hold.
The other direction, i.e., that (EDC) implies the notion of “extremely desirable commodity” in Rustichini and Yannelis (1991) is immediate.
(B) Let \(E\) be a Banach lattice, and let \(a\) and \(b\) be as in the statement of (US). Choose any \(v\in E_{+}\) with \(a v>1\). Let \(x\in X_{t}\), \(u\in E\), and a number \(\lambda >0\) be given so that \(b|u|_{}<1\) and \(x+\lambda (v+u)\in X_{t}\). We may write
Now as \(a\) and \(b\) are positive, we have
Thus, (US) implies (EDC).
(C) Let \(({\varOmega },{\varSigma },\mu )\) be a \(\sigma \)-finite measure space, and let the commodity space be \(L_{\infty }(\mu )\) with the Mackey topology. Let \({\fancyscript{E}}\) be an economy with probability space of agents \((T,{\fancyscript{T}},\nu )\) (and recall that the measure \(\nu \) is complete according to our definition of economy). The assumption in Mertens (1970) on endowments is that the endowment map \(e:T\rightarrow L_{\infty }(\mu )_{+}\) is Gelfand integrable (as in (TAE)) and that
-
(i)
\(e(t)\in ||\cdot ||_{\infty }\text {-}{{\mathrm{int}}}L_{\infty }(\mu )_{+}\) for almost all \(T\);
-
(ii)
there is a non-decreasing sequence \(\langle {e_{n}}\rangle _{}\) of measurable countably valued functions \(e_{n}:T\rightarrow L_{\infty }(\mu )_{+}\) such that \(e_{n}(t)\rightarrow e(t)\) in the Mackey topology for almost all \(t \in T\).
We will show now that this assumption implies (TAE). Note first that as \((T,{\fancyscript{T}},\nu )\) is a probability space, the property of \(e_{n}\) being measurable and countably valued implies that we can find a set \(S_{n}\in {\fancyscript{T}}\) with \(\nu (T\!\setminus \! S_{n})<2^{-n}\) such that \(1_{S_{n}}\times e_{n}\) is a simple function, i.e., takes only finitely many values. Set \(T_{n}=\bigcap _{m\ge n}S_{m}\) for each \(n\), so that the sequence \(\langle {T_{n}}\rangle _{}\) is non-decreasing with \(\nu (T_{n})\rightarrow \nu (T)\). Now for each \(n\), \(1_{T_{n}}\times e_{n}\) is a measurable simple function, and the sequence \(\langle 1_{T_{n}}\times e_{n}\rangle _{}\) is non-decreasing such that \((1_{T_{n}}\times e_{n})(t)\rightarrow e(t)\) in the Mackey topology a.e. in \(T\).
We may therefore assume that each \(e_{n}\) is a simple function. By Fact 3, we may also assume that \(({\varOmega },{\varSigma },\mu )\) is a probability space, so that \(L_{\infty }(\mu )\subseteq L_{1}(\mu )\). Observe that for almost all \(t\in T\), \(e_{n}(t)\) is an element of the order interval \([0,e(t)]\) for all \(n\). Hence, by Fact 4, we have \(e_{n}(t)\rightarrow e(t)\) in \(L_{1}(\mu \)) for almost all \(t\in T\). Thus, as a map from \(T\) to \(L_{1}(\mu )\), \(e\) is strongly measurable, therefore Borel measurable as \((T,{\fancyscript{T}},\nu )\) is complete. Now for each number \(r\), the set \(\{{x\in L_{1}(\mu )}:{x\ge r1_{{\varOmega }}}\}\) is a closed subset of \(L_{1}(\mu )\), and it follows that the set \(\{{t\in T}:{e(t)\ge r1_{{\varOmega }}}\}\) is a measurable subset of \(T\) for each number \(r\).
Note that (i) means that for almost every \(t\in T\) there is an integer \(n>0\) such that \(e(t)\ge (1/n)1_{{\varOmega }}\). By the previous paragraph, we can therefore find a number \(r>0\) and a set \(H\in {\fancyscript{T}}\) with \(\nu (H)\ge r\) such that \(e(t)\ge r1_{{\varOmega }}\) for each \(t\in H\). For each \(n\in \mathbb {N}\), define \(e'_{n}:T\rightarrow L_{\infty }(\mu )\) by setting \(e'_{n}(t)=e_{n}(t)\vee r1_{{\varOmega }}\) if \(t\in H\), and \(e'_{n}(t)=e_{n}(t)\) if \(t\in T\!\setminus \! H\). Then for each \(n\), \(e'_{n}\) is a measurable simple function; in particular, \(e'_{n}\) is Bochner integrable. Observe that  . Thus
. Thus  for each \(n\). Moreover, the sequence \(\langle {e'_{n}}\rangle _{}\) is non-decreasing, and using the fact that the lattice operations in \(L_{\infty }(\mu )\) are continuous for the Mackey topology, we see that \(e'_{n}(t)\rightarrow e(t)\) in the Mackey topology for almost all \(t\in T\). Thus (TAE) holds.
for each \(n\). Moreover, the sequence \(\langle {e'_{n}}\rangle _{}\) is non-decreasing, and using the fact that the lattice operations in \(L_{\infty }(\mu )\) are continuous for the Mackey topology, we see that \(e'_{n}(t)\rightarrow e(t)\) in the Mackey topology for almost all \(t\in T\). Thus (TAE) holds.
(D) The following two lemmata show that in the context of Sect. 7, the Gelfand integral does not exhibit pathological features. With \(S=T\) and \(B={\varOmega }\), Lemma 6 below amounts to a translation of Remark 5 into formal language. Lemma 7 shows that if Assumption (P) holds, and an allocation \(f\) is feasible for a coalition \(S\in {\fancyscript{T}}\), i.e.,  , then the agents belonging to \(S\) cannot get commodities that are not available in the aggregate endowment of \(S\).
, then the agents belonging to \(S\) cannot get commodities that are not available in the aggregate endowment of \(S\).
Lemma 6
Let \((T,{\fancyscript{T}},\nu )\) be a probability space, \(({\varOmega },{\varSigma },\mu )\) a \(\sigma \)-finite measure space, and \(f:T\rightarrow L_{\infty }(\mu )_{+}\) Gelfand integrable. Let \(S\in {\fancyscript{T}}\) and write  for the Gelfand integral of \(f\) over \(S\). If a set \(B\in {\varSigma }\) is such that \(1_{B}\times v=0\), then the set \(N=\{t\in S:1_{B}\times f(t)\ne 0\}\) is a null set.
for the Gelfand integral of \(f\) over \(S\). If a set \(B\in {\varSigma }\) is such that \(1_{B}\times v=0\), then the set \(N=\{t\in S:1_{B}\times f(t)\ne 0\}\) is a null set.
Proof
Choose a strictly positive \(q\in L_{1}(\mu )\) (as is possible because \(\mu \) is \(\sigma \)-finite). Note that

As \((1_{B}\times q)(f(t))\ge 0\) for all \(t\in S\), it follows that \((1_{B}\times q)(f(t))=0\) for almost all \(t\in S\). Consequently, as \((1_{B}\times q)(f(t))=q(1_{B}\times f(t))\) and \(q\) is strictly positive, we must have \(1_{B}\times f(t)=0\) for almost all \(t\in S\). \(\square \)
Lemma 7
Let \((T,{\fancyscript{T}},\nu )\), \(({\varOmega },{\varSigma },\mu )\), \(f\), \(S\), and, \(v\) be as in the previous lemma. Let \(C=\{{\omega \in {\varOmega }}:{v(\omega )>0}\}\), identifying \(v\) with any of its versions. Then there is a null set \(N\subseteq S\) such that \(f(t)=1_{C}\times f(t)\) for all \(t\in S\!\setminus \! N\).
Proof
Set \(B={\varOmega }\!\setminus \! C\), so that \(1_{B}\times v=0\). By the previous lemma, there is a null set \(N\subseteq S\) such that \(1_{B}\times f(t)=0\) for all \(t\in S\!\setminus \! N\), which implies that \(f(t)=1_{C}\times f(t)\) for all \(t\in S\!\setminus \! N\), because \(f(t)=1_{B}\times f(t)+1_{C}\times f(t)\). \(\square \)
Appendix 2
In this appendix, we provide some mathematical background information, collecting some basics on vector integrals and on set theory.
(A) Let \((T,{\fancyscript{T}},\nu )\) be a nontrivial complete and totally finite measure space, and \(E\) a Banach space, with norm \(\Vert \cdot \Vert \). A measurable function \(f{:}\;T\rightarrow E\) is called a simple function if \(f(T)\) is finite. The integral of a simple function \(f\) is given by

A function \(f{:}\;T\rightarrow E\) is strongly measurable if there exists a sequence \(\langle f_n\rangle \) of simple functions such that
for \(\nu \)-almost all \(t\). Every strongly measurable function is Borel measurable. Since for \(\nu \)-almost all \(t\), \(f(t)\in {{\mathrm{c\ell }}}\big (\bigcup _n f_n(T)\big )\), a strongly measurable function takes values in a separable subspace of \(E\) outside a \(\nu \)-null set. A strongly measurable function \(f{:}\;T\rightarrow E\) is Bochner integrable if there exists a sequence of simple functions \(\langle f_n\rangle \) such that

In that case, the Bochner integral of \(f\) is

This limit exists and is independent of the particular approximating sequence \(\langle f_n\rangle \). A strongly measurable function \(f\) is Bochner integrable if and only if the function \(t\mapsto \Vert f(t)\Vert \) is Lebesgue integrable (Diestel and Uhl 1977, Theorem II.2.2). Bochner integrals inherit many convenient properties of the Lebesgue integral. If \(f\) is Bochner integrable, we call the function from \({\fancyscript{T}}\) to \(E\) given by

the indefinite Bochner integral. The indefinite Bochner integral is a \(\nu \)-continuous countably additive vector measure; \(\nu \)-continuity meaning that if \(\lim _{n\rightarrow \infty }\nu (A_n)=0\), then  (Diestel and Uhl 1977, Theorem II.2.4(i)).
(Diestel and Uhl 1977, Theorem II.2.4(i)).
In order to be able to integrate functions with values that do not essentially lie in a separable subspace, one can use weak integrals. Let \(E^*\) be the topological dual of \(E\). A function \(f{:}\;T\rightarrow E\) is weakly measurable if \(t\mapsto x^*f(t)\) is measurable for all \(x^*\in E^*\). A function \(f{:}\;T\rightarrow E^*\) is weak*-measurable if \(t\mapsto xf(t)\) is measurable for all \(x\in E\). By Pettis’ measurability theorem, a function is strongly measurable exactly when it is weakly measurable and there is a separable subspace of \(E\) containing almost all values (Diestel and Uhl 1977, Theorem II.1.2). A weak*-measurable function need not be weakly measurable and a weakly measurable function need not be strongly measurable (Diestel and Uhl 1977, Examples II.1.5 and II.1.6). Let \(f{:}\;T\rightarrow E\) be weakly measurable. If for each \(A\in {\fancyscript{T}}\), there is an \(x_{A}\in E\) such that  for all \(x^*\in E^*\), \(f\) is called Pettis integrable and
for all \(x^*\in E^*\), \(f\) is called Pettis integrable and

the Pettis integral of \(f\) over \(A\). It agrees with the Bochner integral if the latter is well defined, so this notation is unambiguous. It is possible for a weakly measurable function that \(t\mapsto x^*f(t)\) is integrable for all \(x^*\in E^*\) without \(f\) being Pettis integrable (Diestel and Uhl 1977, Example II.3.3). Better behaved in that respect is the Gelfand integral. If \(f{:}\;T\rightarrow E^*\) is weak*-measurable and \(t\mapsto xf(t)\) is integrable for all \(x\in E\), then \(f\) is Gelfand integrable and there is a unique \(x^*\in E^*\) such that  for all \(x\in E\) (Diestel and Uhl 1977, Lemma II.3.1). We call
for all \(x\in E\) (Diestel and Uhl 1977, Lemma II.3.1). We call

the Gelfand integral of \(f\). It follows that whenever \(f\) is Gelfand integrable and \(A\in {\fancyscript{T}}\), there is an \(x_{A}^*\in E^*\) such that  for all \(x\in E\).
for all \(x\in E\).
(B) We now collect some set-theoretic results. Many of the results will not be used in proofs, but in discussing how certain results fit into the literature. All results of this paper are derivable from the usual axioms of set theory, i.e., Zermelo–Fraenkel set theory with the axiom of choice (ZFC).
Recall that a partially ordered set is well-ordered if every non-empty subset has a minimum. An ordinal is a set well-ordered by the relation “\(\in \) or \(=\)” and such that every element of the set is also a subset. If \(\alpha \) and \(\gamma \) are ordinals, we write \(\alpha \le \gamma \) if \(\alpha \in \gamma \) or \(\alpha =\gamma \). Every set of ordinals is well-ordered by \(\le \) and each ordinal equals the set of strictly smaller ordinals. In particular, we can use notation such as \(\langle x_\xi \rangle _{\xi <\alpha }\) to denote a transfinite sequence indexed by the ordinal \(\alpha \). There is no set containing all ordinals.
For each set \(X\), there is a smallest ordinal \(\kappa \) such that there is a bijection from \(\kappa \) onto \(X\). We call \(\kappa \) the cardinal of \(X\) and write \(\kappa =\#(X)\). Finite cardinals can be identified with the natural numbers \(0,1,2,3,\ldots \) In particular, \(2=\{0,1\}\). The set of all finite cardinals is a cardinal itself, the first infinite cardinal \(\omega \). The next larger cardinal is \(\omega _1\), the first uncountable cardinal. The cardinal of \(\mathbb {R}\) is of special importance and is denoted by \(\mathfrak {c}\) and called the cardinal of the continuum. If \(\kappa \) is a cardinal, we let \(\kappa ^+\) be the smallest cardinal strictly larger than \(\kappa \). For example, \(\omega ^+=\omega _1\). A cardinal of the form \(\kappa ^+\) is a successor cardinal and every other cardinal is a limit cardinal. The continuum hypothesis (CH) says that \(\omega _1=\mathfrak {c}\).
If \(\kappa \) and \(\lambda \) are cardinals, we let \(\kappa ^\lambda \) be the cardinal of the set of functions from \(\lambda \) to \(\kappa \). Since one can identify subsets with indicator functions, \(2^\kappa \) is the cardinal of the set of all subsets of \(\kappa \). For every cardinal \(\kappa \), we have \(\kappa <2^\kappa \). We have \(\mathfrak {c}=2^\omega \). CH can be written as \(\omega ^{+}=2^\omega \). The generalized continuum hypothesis (GCH) says that \(\kappa ^+=2^\kappa \) for every cardinal \(\kappa \). There are other operations one can do with the cardinals \(\kappa \) and \(\lambda \). We let \(\kappa +\lambda \) be the cardinal of the disjoint union of \(\kappa \) and \(\lambda \) and \(\kappa \cdot \lambda \) be the cardinal of their Cartesian product. If \(\kappa \) or \(\lambda \) is infinite and both are nonzero, these operations are trivial and one has \(\kappa +\lambda =\kappa \cdot \lambda =\max \{\kappa ,\lambda \}\).
An axiom A is relatively consistent with ZFC if every proof of a contradiction from ZFC together with A can be turned into a proof of a contradiction from ZFC alone. Clearly, everything is relatively consistent with ZFC if there is a contradiction provable from ZFC. So, we assert our faith in mathematics and assume this is not possible. The generalized continuum hypothesis, and therefore also the continuum hypothesis, is relatively consistent with ZFC (Kunen 2011, Theorem II.6.24). A weakening of the continuum hypothesis is provided by Martin’s axiom. The original statement of Martin’s axiom is slightly intricate, but Martin’s axiom is equivalent to the following statement: If \(X\) is a compact Hausdorff topological space in which every disjoint family of non-empty open subsets is countable, then the intersection of less than \(\mathfrak {c}\) open dense subsets is non-empty (Kunen 2011, Lemma III.3.17). A consequence of Martin’s axiom is that the additivity of Lebesgue measure is \(\mathfrak {c}\), that is, the union of less than \(\mathfrak {c}\) Lebesgue null sets is again a null set (Kunen 2011, Lemma III.3.28). Baire’s category theorem for compact Hausdorff spaces shows that Martin’s axiom in its topological version is implied by the continuum hypothesis. However, Martin’s axiom is much weaker; in fact, there is a precise sense in which Martin’s axiom is consistent with the cardinal of the continuum being arbitrarily large (Kunen 2011, Theorem V.4.1).
There are axioms that are widely used and widely taken to be consistent even though their relative consistency cannot be established. For example, one cannot prove the relative consistency of the existence of an atomless probability space in which every subset is measurable. By a result of Ulam, if such a probability space exists, a so-called weakly inaccessible cardinal must exist too (Jech 2003, Theorem 10.1). Such weakly inaccessible cardinals are known to imply the consistency of ZFC (Kunen 2011, Corollary II.6.26 and Theorem II.6.23). But by Gödels second incompleteness theorem, an axiom system strong enough to prove the consistency of ZFC is not relatively consistent with ZFC.
Rights and permissions
About this article
Cite this article
Greinecker, M., Podczeck, K. Edgeworth’s conjecture and the number of agents and commodities. Econ Theory 62, 93–130 (2016). https://doi.org/10.1007/s00199-015-0866-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-015-0866-y



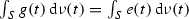 , i.e.,
, i.e., 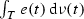 is strictly positive.
is strictly positive.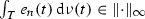 -
-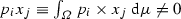 if and only if
if and only if 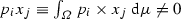 if and only if
if and only if