1 Introduction

Traditional gas turbine combustors, which are widely used in both the power and propulsion industries, operate on constant pressure, deflagrative combustion. In recent years, detonation-based combustion has gained significant attention due to its potential for increased thermal efficiencies in power cycles [1]. Zel’dovich [2] showed that the detonation process results in less entropy generation than deflagration combustion. Additionally, a benefit of the detonation process is the rapid energy release, as the chemical reactions occur much faster than the surrounding gas expansion, which prevents sufficient time for pressure to equilibrate, leading to the overall process being thermodynamically closer to a constant volume process rather than constant pressure process. This characteristic enables the design of a relatively compact and efficient combustor, which makes it attractive for propulsion applications even if the overall system pressure gain is not achieved. However, if the overall system pressure gain can be achieved, detonation-based cycles can improve thermal efficiency by 5% to 10% over the traditional constant pressure combustor. This improvement is substantially higher than any other technological advancement in the propulsion and power generation industry [3]. However, utilizing the benefits of detonation involves challenges, such as efficient injection system design, the ability to operate over a wide range of conditions, the turbulent mixing effect on wave stability, and managing heat loss from the combustor [4].

Fig. 1
figure 1

Temperature contour with flow features: A wave front, B high-pressure region behind wave front, C secondary shock wave, D slip line, E oblique shock, F mixing of reactant and product, and G refill zone

Full size image

Initial development in the field of pressure gain combustion (PGC), namely, pulse detonation engine (PDE), was carried out by Nicholls [5] in 1957. PDE involves a pulsating detonation wave in a linear tube with a frequency of 20 to 100 Hz. The study was initiated to understand the feasibility of an engine operating on intermittent detonation combustion. The drawback of a PDE is the intermittent-based detonation rather than a continuous mode, making it difficult to couple with a downstream turbine or to provide a quasi-steady source of thrust. Due to these challenges, rotating detonation combustor (RDC) has emerged as an attractive alternative to PDE, as it provides a quasi-steady source of thrust/power and does not require repeated initiation of detonation. In an RDC, fuel and air are injected axially at the bottom of an annular combustor, and a steady detonation wave, once initiated, propagates circumferentially within the annulus provided a continuous fuel/oxidizer mixture is supplied. The frequency of wave propagation ranges from 1 to 10 kHz depending on the mixture composition and the size of the combustor. The simple and compact design of an RDC and quasi-steady mode of operation makes it well suited for propulsion and power-generating applications.

A prolific amount of research has been carried out by Bykovskii et al. [6, 7] and Voitsekhovskii [8] in the study of RDC for different fuels, injection schemes, and geometries, showcasing the versatility of RDCs. Moreover, they developed a design guideline that correlates combustor dimensions to a detonation cell size for stable operation. In recent times, various research groups have studied the concept of RDC using numerical and experimental techniques to understand flow physics, the effect of geometry, and fuel injection design on its performance [9,10,11,12]. These RDC studies identified difficulties, such as detonation-turbulence interaction, injector design, structural integrity of the components, cooling strategies, and their effects on the overall performance. Another critical parameter that impacts the performance of an RDC is the distribution of the fuel–oxidizer mixture in the combustion domain.

Fig. 2
figure 2

2-D domain of RDC with monitoring probes

Full size image

Several numerical investigations are conducted to understand the fundamental physics of an RDC [12,13,14,15]. Early numerical simulations were conducted by the authors with perfectly premixed fuel/oxidizer injection to understand the flow field and flow features within the combustor, as shown in Fig. 1. In premixed combustion, a uniform mixture composition is present, which provides higher combustion efficiency [16]. However, a high-pressure region is present behind the detonation wave front (as represented by B in Fig. 1), which may cause product backflow into the injection plenum [6]. The injection plenum in a perfectly premixed system will be prone to flashback due to the backflow of hot products [17]. One method to mitigate this problem is to design the system such that the plenum pressure is higher than the detonation pressure to prevent product backflow [18]. However, by doing so, the benefit of pressure gain is negated. Therefore, most RDCs are designed with separate fuel–oxidizer injection systems. Separate injection of fuel and oxidizer creates an inhomogeneous mixture within the combustion domain, creating regions of varying equivalence ratio. This varying fuel/oxidizer composition can cause a reduction in wave speed, skewed wave front [19], irregular detonation cell structure [20], and loss in performance such as thrust/power [21] compared to a premixed mixture. Most experimental studies are performed with discrete fuel–oxidizer injection. Previous studies showed that inhomogeneous mixing of fuel and oxidizer affects the wave structure, peak static pressure, wave velocities, and pressure gain [22,23,24] in an RDC; however, due to the large number of physical variables present, it is not possible to isolate the effects of inhomogeneous mixing from other variables.

More recent numerical studies have investigated RDCs with full-scale 3D simulations, incorporating discrete fuel/oxidizer injection systems, to understand the effects of mixture inhomogeneity [6, 9,10,11, 16,17,18,19,20,21,22,23, 25, 26] on RDC performance. However, one of the challenges associated with these numerical simulations is the computational resources required to simulate the large difference in length and time scales associated with the chemical reactions and the flow field. To resolve the detailed flow structures in an RDC, very fine grid cells of the order of 10 to 100 microns and time steps of the order of 10 ns are required, which makes these simulations computationally expensive. To mitigate these effects, 2D numerical simulations are often utilized to gain a basic and qualitative understanding of an RDC system. The 2D domain is obtained by unwrapping the annular geometry because the radial dimension is typically small compared to the azimuthal and axial dimensions [27]. The gradient of flow parameters along the radial direction is similar in both 3D and 2D simulations [28]. Initially, 2D numerical simulations of RDC were performed [27, 29] to study the effect of varying injection parameters such as inlet stagnation pressure, temperature, injection area ratio, chamber diameter, and length. Rankin et al. [30] used a combination of both numerical simulation and experimental data to compare the values of pressure, thrust, and wave speed. However, most of the early 2D RDC simulations [31, 32] studies utilize premixed injection and thus do not account for mixture inhomogeneity arising from discrete fuel/oxidizer injection.

Fuji et al. [33] used the numerical source terms to model the mixture inhomogeneity in a 2D simulation. The model assumes that the inlet boundary of the 2D domain consists of imaginary converging injection nozzles set at a constant interval (discrete points), along with an adiabatic slip wall condition for the remaining portion of the boundary. The model is used to predict the detonation velocity and a reduction in wave speed due to inadequate mixing. Subramanian and Meadows [34] developed a new technique to induce mixture inhomogeneity in a 2D simulation by incorporating a Probability Density Function (PDF) extracted from a non-reacting, 3D RDC simulation with discrete fuel–oxidizer injection. Their study showed the contrast in performance between a premixed and 2D non-premixed simulation. The present study utilizes a similar approach [34]; however, a predefined lognormal distribution is used to investigate the effects of unmixedness. The objective of the present study is to analyze the effects of varying mixture inhomogeneity on detonation performance, including wave propagation velocity, pressure gain at the combustor exit, wave dynamics, and wave stability. A lognormal distribution is chosen as it is a close approximation of the non-reacting fuel–oxidizer distribution obtained by Subramanian and Meadows [34] based on the RDE geometry and injection scheme in Rankin et al. [23]. The distribution of fuel and oxidizer within the combustor is dependent on the geometry, and it is closely coupled to the injector design, fluid properties, dynamic injector response, and injection pressures, which makes it nearly impossible to alter the degree of inhomogeneity without altering the distribution. Therefore, the predefined distribution provides the flexibility to vary mixture inhomogeneity while keeping all other parameters constant and closely approximates the distribution obtained from [34]. By varying the standard deviation of the PDF while maintaining constant mean values, the impact of inhomogeneous mixing on detonation performance, including wave propagation, pressure gain, cell size, and wave stability, is independently assessed.

2 Methodology

2.1 Geometry

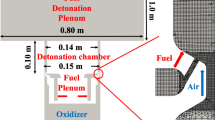
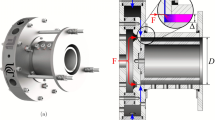
The 2D RDC domain (see Fig. 2) is obtained by unwrapping the 3D combustion chamber design based on the experimental test setup presented by Rankin et al. [23]. The length of the 2D domain is equal to the mean circumference (\({l} = 459.6\) mm) of the annular combustor (see Fig. 2). The height of the 2D domain (\(h=101.6\) mm) is equal to the height of the combustor in the experimental setup (see Fig. 2). The effects of fuel–oxidizer inhomogeneity are modeled using numerical source terms at the inlet boundary, presented in Sect. 2.3. Multiple probe points are placed at different axial locations to analyze the flow parameters, such as detonation wave speeds, peak pressures, and temperatures. Four sets (90° apart in the circumferential direction) of 11 axial probe points are created. Each probe point is 6.35 mm apart, and the first probe point is located 6.35 mm from the inlet.

2.2 Solver

The reacting flow field is predicted by solving the Unsteady Reynolds-Averaged Navier Stokes (URANS) equations. The governing equations of mass, momentum, energy, and species conservation are:

$$\begin{aligned} \frac{\partial {\varvec{W}}}{\partial t}+ {\varvec{\nabla }} \cdot ({\varvec{F}}-{\varvec{G}})={0}, \end{aligned}$$
(1)
$$\begin{aligned} \textrm{where}\, {\varvec{W}}= & \, \left[ {\begin{array}{*{20}c} \rho \\ \rho {\varvec{v}}\\ \rho E\\ \end{array} } \right] \quad , \quad {\varvec{F}}= \, \left[ {\begin{array}{*{20}c} \rho {\varvec{v}}\\ \rho {\varvec{vv}}+p{\varvec{I}}\\ \rho {\varvec{v}}H\\ \end{array} } \right] , \quad \\ {\varvec{G}}= & \, \left[ {\begin{array}{*{20}c} 0\\ \bar{\tau }\mathbf {+}{\varvec{T}}_{\textrm{RANS}}\\ \left( \bar{\tau }\mathbf {+}{\varvec{T}}_{\textrm{RANS}} \right) \cdot {\varvec{v}}-{\varvec{q}}_{\textrm{e}}^{\prime \prime }\\ \end{array} } \right] , \textrm{and} \end{aligned}$$
$$\begin{aligned} \frac{\partial \rho Y_{i}}{\partial t}+{\varvec{\nabla }}\cdot (\rho {\varvec{v}}Y_{i})= \, {\varvec{\nabla }}\cdot \left( {\varvec{J}}_{i}+\frac{\mu _{\textrm{t}}}{\sigma _{\textrm{t}}}{\varvec{\nabla }}Y_{i}\right) +S_{\textrm{species}} \end{aligned}$$
(2)

The above equations are solved using the commercial software Star-CCM+, which uses the finite volume discretization method. The overall fluid density is \(\rho \). From Dalton’s law of partial pressure, the pressure of a mixture is the summation of the partial pressures of each of the species \(p=\sum _{i}^{N_{\textrm{s}}} p_{i} =\sum _{i}^{N_{\textrm{s}}} {\rho _{i}R_{i}T} (\textrm{where} \, R_{i}=R_{\textrm{u}}/{\textrm{MW}}_{\textrm{i}}\) and \(R_{\textrm{u}}\) is the universal gas constant). The continuum velocity of the fluid is \({\varvec{v}}\), and E is the specific total energy calculated as \(E=H-p/\rho \). The specific heat capacities and specific enthalpies are obtained as a function of temperature using the NASA polynomials from the GRI-MECH 3.0 thermodynamic data file [35]. The mixture averaged approach is used to obtain the specific heat and specific enthalpy of the mixture. The terms \(p{\varvec{I}}\) and \(\bar{{\varvec{\tau }}}\) represent mean normal and shear stresses, and \({\varvec{T}}_{\textrm{RANS}}\) is the shear stress due to the turbulent fluid flow, which is obtained by:

$$\begin{aligned} {\varvec{T}}_{\textrm{RANS}}=2\mu _{\textrm{t}}{\varvec{S}}_{\textrm{t}}-\frac{2}{3}k{\varvec{{\delta }}}_{ij} \end{aligned}$$
(3)

The turbulent eddy viscosity is \(\mu _{\textrm{t}}\), k is the turbulent kinetic energy, \({\varvec{S}}_{\textrm{t}}\) is the mean strain tensor, and \({\varvec{{\delta }}}_{ij}\) is the Kronecker delta function. To obtain the value of \(\mu _{\textrm{t}}\) and k, the two-equation SST \(k-\omega \) model [36] is used. The quantity \({\varvec{q}}_{\textrm{e}}^{\prime \prime }\) represents heat flux due to the thermal conduction and diffusion of the species:

$$\begin{aligned} {\varvec{q}}_{\textrm{e}}^{\prime \prime }=k_{\textrm{cond}}{\varvec{\nabla }}T-\rho \sum \limits _{i=1}^{N_{\textrm{s}}} {h_{i}D_{i,\textrm{m}}{\varvec{\nabla }}Y_{i}}, \end{aligned}$$
(4)

where \(k_{\textrm{cond}}\) is the mixture thermal conductivity, and \(D_{i,\textrm{m}}\) is the mass diffusivity of species i to the mixture. These properties are obtained from the transport data file (GRI-Mech 3.0) [35]. The mixture transport properties are approximated from species properties using the mixture-averaged approach. In (2), \(Y_{i}\) represents the species mass fraction, and \({\varvec{J}}_{i}\) represents the laminar diffusive flux of the species calculated using Fick’s law of diffusion, given by \({\varvec{J}}_{i}=\rho D_{i,\textrm{m}}{\varvec{\nabla }}Y_{i}\). The quantity \(D_{i,\textrm{m}}\) represents molecular diffusivity of the component, and \(\sigma _{\textrm{t}}\) is the turbulent Schmidt number obtained from the SST k–\(\omega \) model. Furthermore, to include the creation and destruction of species in the species equation (see (2)), the source term \(S_{\textrm{species}}={\dot{\omega }_{{i}}}\) (species production rate) of each species i is given by:

$$\begin{aligned} {\dot{\omega }_{{i}}} = \sum \limits _{k{=}1}^{N_{\textrm{r}}} \left( \nu _{ik}^{\prime \prime }-\nu _{ik}^{\prime } \right) \left[ k_{\textrm{f},k}\prod \limits _{j{=}1}^{N_{\textrm{s}}} {C_{j}^{\nu _{ik}^{\prime }}{-}k_{\textrm{r},k}\prod \limits _{j{=}1}^{N_{\textrm{s}}} C_{j}^{\nu _{ik}^{\prime \prime }} } \right] , \nonumber \\ \end{aligned}$$
(5)

where the molar concentration of the species i is represented by \(C_{i}\) and \(C_{i}=\rho _{i}/\textrm{MW}_{i}\). In the above equation, the indices i and k denote species and reactions, respectively. The quantity \(\nu _{ik}^{\prime }\) indicate the stoichiometric coefficients for the reactant, while \(\nu _{ik}^{\prime \prime }\) indicate the stoichiometric coefficient of the products. The forward reaction rate constant \(k_{\textrm{f},k}\) is calculated using the Arrhenius rate equation:

$$\begin{aligned} k_{\textrm{f},k}=A_{\textrm{f}}T^{\beta }\exp \left( -\frac{E_{\textrm{a}}}{R_{\textrm{u}}T} \right) , \end{aligned}$$
(6)

where \(A_{\textrm{f}}\) is the pre-exponential factor, \(\beta \) is the temperature exponent, and \(E_{\textrm{a}}\) is the activation energy. The reverse rate constant \(k_{\textrm{r},k}\) is determined by the forward rate constant and the equilibrium constant \(K_{\textrm{c},k}\) (calculated from the thermodynamic properties of the species):

$$\begin{aligned} k_{\textrm{r},k}=k_{\textrm{f},k}/K_{\textrm{c},k} \end{aligned}$$
(7)
Table 1 Grid Convergence Index (GCI) analysis
Full size table

The turbulent flow is modeled using the SST k-\(\omega \) model [36], and the laminar flame concept (LFC) is selected for turbulence-chemistry interaction [34]. The LFC considers the turbulence effects on combustion implicitly through increased turbulent diffusivity provided by the turbulence model. The finite volume scheme used for the spatial discretization of the 2D domain is the third-order MUSCL scheme (Monotonic Upstream-Centered Scheme for Conservation Laws) [37]. This scheme was selected because it is a hybrid scheme that switches between third-order upwind (in the presence of steep gradients, such as shock waves) and third-order central difference scheme (in the remainder of the domain). Note, that a second-order implicit backward differencing scheme is used for temporal discretization, and this scheme is neutrally stable for all Courant numbers. A chemical mechanism with 9 species and 23 reactions [38] is used to model the combustion chemistry of the \(\hbox {H}_{{2}}\)/air mixture. A time step of \({2.5\times }{{10}}^{{-8}}\)s is used for all the simulations in this study

A grid convergence study is performed with three different mesh sizes: 50, 75, and 100 microns (\(N_{{1}}, N_{{2}}, \textrm{and}\,\, N_{{3}})\). The mass fraction of \(\hbox {H}_{{2}}\hbox {O}\) (product), temperature, and pressure were selected as the variables of interest to measure the numerical error (GCI). These variables indicate species transport in the flow field after combustion, following a method presented in detail in [39, 40]. The grid convergence analysis is presented in Table 1, with equations explained in [41]. In Table 1, X represents the variable of interest, which includes \(Y_{\textrm{H}_{{2}}\textrm{O}}\), temperature, and pressure; r is the refinement ratio; N is the cell size of the mesh. The subscripts 1, 2, and 3 correspond to values for the mesh size of 50, 75, and 100 microns, respectively. The GCI shows that the error due to numerical uncertainty in \(Y_{\textrm{H}_{{2}}\textrm{O}}\), temperature, and pressure is less than 0.75, 0.42, and 0.25% (as shown in Table 1). The GCI study indicates that the discretization error among these meshes is relatively low, and given the computational cost of the simulation, a 100-micron mesh is chosen.

Based on the grid independence study, the current work uses a structured mesh grid with a grid size, up to the height of the detonation wave front, of 0.1 mm, and it gets progressively coarser towards the exit plane, up to a maximum of 0.15 mm. An HPC cluster with parallel processing is utilized for running the 2D reacting numerical simulations, and about 1600 core hours are used per revolution of the detonation wave. All the analyses and post-processing are carried out once the detonation wave reaches a quasi-steady state.

2.3 Boundary conditions

The 2D numerical analyses are conducted under a specific operating condition corresponding to case 2.2.1.3 mentioned in [23], where the inlet plenum pressure is held constant at 4.12 bar. The mass flow rates of fuel and air injected into the 2D domain are 0.0093 kg/s and 0.32 kg/s, respectively, resulting in a mean global equivalence ratio (\(\phi \)) of unity. To replicate the flow through the nozzle geometry, the fuel–oxidizer injection into the 2D simulation is modeled as a numerical source term and applied to the first row of the computational domain. The fresh \(\hbox {H}_{{2}}\)-air mixture is injected at the inlet boundary using the compressible isentropic flow equations for calorically perfect gases. The injection of the fresh reactant mixture depends on the local pressure. In the absence of the detonation wave, the mass flow rate entering the 2D domain is calculated using the isentropic relation:

$$\begin{aligned} \dot{m}=\frac{P_{{\textrm{o}}}A_{\textrm{th}}\sqrt{\gamma }}{\sqrt{RT_{{\textrm{o}}}} }M\left( 1+\frac{\gamma -1}{2}M^{2} \right) ^{ -\frac{\gamma +1}{2(\gamma -1)} }, \end{aligned}$$
(8)

where total pressure (\(P_{\textrm{o}})\) and total temperature (\(T_\textrm{o}\)) at the inlet of the 2D simulation are set to 4.12 bar and 300 K, respectively. The throat area \(A_{\textrm{th}}\) in (8) is determined from the RDC geometry presented in [23] and is 3.793\( {\textrm{cm}}^{{2}}\). The total cross-sectional area of the combustor is 34.93 \(\textrm{cm}^{{2}}\). To determine the local mass flux for each cell, the Mach number M, as defined in (8), is dependent on the cell static pressure \(P_\textrm{local}\) at the inlet of the domain and is calculated by:

$$\begin{aligned} M=\sqrt{\frac{2}{\gamma -1}\left[ \left( \frac{P_{\textrm{local}}}{P_\textrm{o}} \right) ^{-\frac{\gamma -1}{\gamma }}-1 \right] }, \end{aligned}$$
(9)

where local mass flux, \(\dot{m}^{\prime \prime }_{\textrm{local}}\), for each cell, is defined as the mass flow rate in the cell divided by the cell width (\(N_{{3}} =100\,\upmu \hbox {m}\)) and unit dimension in the third coordinate. The equation for it is as follows:

$$\begin{aligned} \dot{m}_{\textrm{local}}^{\prime \prime }=\frac{\dot{m}}{N_{{3}}} \end{aligned}$$
(10)

The cell static pressure \(P_{\textrm{local}}\) near the inlet of the 2D domain determines the flow conditions for each cell, and if \(P_{\textrm{local}}\le P_{\textrm{cr}}\), a choked flow condition is assumed and the local static pressure \(P_{\textrm{local}}\) in (9) takes a value of \({P}_{\textrm{cr}}\), where \(P_{\textrm{cr}}\) represents the critical pressure of the nozzle at the sonic condition. The value of \(P_{\textrm{cr}}\) is obtained using:

$$\begin{aligned} P_{\textrm{cr}}=P_{\textrm{o}}\left( \frac{\gamma +1}{2} \right) ^{-\frac{\gamma }{\gamma -1}} \end{aligned}$$
(11)

However, if \(P_{\textrm{cr}}<P_{\textrm{local}}<P_{\textrm{o}}\), the flow is not choked, and thus the value of \(P_{\textrm{local}}\) in (9) is the actual static pressure of the cell obtained from the solver. From this, the local Mach number M is obtained, which is further employed to calculate the local mass flux, denoted as \(\dot{m}^{\prime \prime }_{\textrm{local}}\), for each cell at the inlet. Finally, if \(P_{\textrm{local}}>P_{\textrm{o}}\), the cell static pressure exceeds the plenum pressure, and the flow rate is zero in that cell. The present study does not consider the effects of product backflow, which occurs when the downstream pressure exceeds the inlet total pressure. The mass flux source term at the inlet boundary of the 2D domain is \(S_{\textrm{mass}}=\dot{m}_{\textrm{local}}^{\prime \prime }\). Similarly, momentum and energy source terms are \(S_{\textrm{mom}}=\dot{m}_{\textrm{local}}^{\prime \prime }u\) and \(S_{\textrm{e}}=\dot{m}_{\textrm{local}}^{\prime \prime }C_{{p}}\left( T_{\textrm{isen}}-T_{\textrm{local}} \right) \), respectively. The term u in momentum source term denotes the flow velocity in the first row of the grid cell and is calculated using:

$$\begin{aligned} u=\sqrt{2C_{p}T_{\textrm{o}}\left[ 1-\left( \frac{P_{\textrm{local}}}{P_{\textrm{o}}} \right) ^{\frac{\gamma -1}{\gamma }} \right] } \end{aligned}$$
(12)

Similarly, the term \(T_{\textrm{local}}\) in the energy source term represents the local static temperature near the first row of the cells. The term \(T_{\textrm{isen}}\) denotes the value of temperature obtained using the isentropic flow equation and is given by:

$$\begin{aligned} \frac{T_{\textrm{isen}}}{T_{\textrm{o}}}=\left( 1+\frac{\gamma -1}{2}M^{2} \right) ^{-1} \end{aligned}$$
(13)
Fig. 3
figure 3

Distribution plots of hydrogen mass fraction for varying level of unmixedness (q) at the RDC inlet

Full size image

In an experimental setup, fuel and air are injected from separate plenums, producing an inhomogeneous mixture in the chamber. The effects of mixture inhomogeneity are studied using a predefined lognormal distribution with a mean equivalence ratio of one. As explained in Sect. 1, a predefined PDF is selected to independently investigate the impact of mixture inhomogeneity, while keeping all other operating conditions constant, which is not possible with experiments. The lognormal distribution is selected for three reasons: the PDF obtained from the 3D non-reacting simulation presented in [34] is positively skewed, the lognormal distribution is a close approximation of the distribution obtained from 3-D non-reacting simulation of the RDC geometry from Rankin et al. [23], and to ensure positive values of equivalence ratio. To generate a spatially/temporally varying mixture composition based on the lognormal PDF, a Java macro was developed to randomly generate a lognormal distribution of fuel mass fractions every three time-steps. Using this approach, the degree of inhomogeneity, referred to as unmixedness (q), can be systematically investigated. The assigned random numbers, and consequently, the fuel–air mass fraction at the inlet, are updated every three time-steps to account for the spatial and temporal variation of the fuel/oxidizer mass fraction. The degree of inhomogeneity of fuel/oxidizer mixing varies by changing the standard deviation of the PDF while maintaining the mean value (the global \(\phi \)) as unity. The outlet boundary condition is set to atmospheric condition (see Fig. 2), and the other two boundaries of the 2D domain are periodic (see Fig. 2). To generate the appropriate distribution of fuel mass fractions, the predefined lognormal PDF is divided into bins with a bin width of 0.02 and are stored in an array along with the corresponding weights (whose sum is 1). The weight of a bin is multiplied by the number of grid cells (4596 cells) to generate the required random numbers. The following expression is looped based on the number of bins and the weight of each bin to replicate the given lognormal PDF under consideration:

$$\begin{aligned} R_{\textrm{n}}=B_{\mathrm {left-edge}}+\left[ \left( B_{\mathrm {right-edge}}-B_{\mathrm {left-edge}} \right) \psi \right] \end{aligned}$$
(14)

The random number, \(R_{\textrm{n}}\), is generated, and its value lies between the left and the right edge values of its corresponding bin (B), and \(\psi \) represents a uniformly distributed random number generator bounded between 0 and 1. The number of random numbers generated equals the number of cells in the first row of the computational domain (4596 cells). Each cell is then assigned a fuel mass fraction, ensuring that the distribution at the inlet follows a lognormal distribution. The mass fractions of \(\hbox {O}_{{2}}\) and \(\hbox {N}_{{2}}\) are calculated assuming air as the oxidizer and ensuring that the sum of mass fractions at each cell is unity. Unmixedness (q), defined as the standard deviation of the equivalence ratio divided by the mean global equivalence ratio (which is unity in this case), represents the degree of inhomogeneous mixture, as expressed by:

$$\begin{aligned} q=\frac{\sqrt{\frac{\sum \left( \phi _{i}-\phi _{\textrm{global}} \right) ^{2}}{N}}}{\phi _{\textrm{global}}} \end{aligned}$$
(15)

It is important to note that the distribution of fuel and oxidizer within an RDC is tightly coupled with the injector design, operating conditions, and fluid properties. This tight coupling makes it difficult to modify the unmixedness without simultaneously changing the shape of the distribution. Six cases are considered to represent varying unmixedness (\(q =0.3\), 0.5, 0.6, 0.7, 0.9, and 1.0) with a constant mean (\(\phi _{\textrm{global}}= 1.0\)) (see Fig. 3). Simulation results indicate wave failure for the case of \(q= 1.0\). The flow is governed by the pressure difference between the first-row cells of the chamber and the plenum pressure at a given time-step. Figure 4 shows the variation in the local equivalence ratio resulting from the introduction of unmixedness in a non-reacting flow field, along with a perfectly premixed case. This figure provides a zoomed-in view of a small section of a 2D RDC domain before combustion (non-reacting). The contour plot of the equivalence ratio illustrates how mixture inhomogeneity creates localized pockets of rich and lean fuel–air mixture regions in the detonation chamber.

3 Results and discussion

The present study investigates the effect of an inhomogeneous fuel/oxidizer mixture on detonation wave propagation in an RDC for six different levels of unmixedness. The impact of unmixedness on detonation wave velocity, mean and peak static pressures, detonation wave structure, detonation efficiency, and cell structure are presented and discussed.

Fig. 4
figure 4

Contour of equivalence ratio in a non-reacting flow: a premixed, b \(q=0.3\), c \(q=0.5\), d \(q=0.6\), e \(q=0.7\), and f \(q=0.9\)

Full size image

3.1 Detonation wave velocity

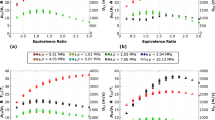
The theoretical Chapman–Jouguet (CJ) velocity is determined using the analytical method outlined in [34], where a system of non-linear equations is solved for the \(\hbox {H}_{{2}}\)-air mixture. The detonation velocities for different levels of unmixedness are obtained using the multiple probe points shown in Fig. 2 at different time-steps. With the distance between the probe points known, the time between peak static pressures at these points provides the necessary information for calculating the local detonation velocity in the domain. Data is collected over three revolutions after the wave reaches a quasi-steady state. Figure 5 presents the mean detonation velocity for the perfectly premixed case, theoretical CJ velocity, experimental wave velocity obtained from Rankin et al. [23], and five cases of varying unmixedness. It is important to note that the unmixedness (q) value of 1.0 is not presented in Fig. 5, as wave instability/failure is observed which is discussed in Sect. 3.6.

Figure 5 illustrates the trend of mean detonation velocity for varying unmixedness conditions. It is apparent from Fig. 5 that as the effect of unmixedness increases, the mean wave speed reduces, indicating an inverse relationship between mixture inhomogeneity and detonation wave speeds. The inclusion of the experimental detonation velocity (see Fig. 5) provides a perspective between simulated wave velocity and the experimental value, given the geometry and operating conditions are the same. For the case of \(q=0.9\) the mean detonation velocity shows approximately a 12% lower wave speed compared to the CJ value. While the fuel distribution at \(q=0.9\) may not be identical to that in the experiments, the distribution shape and predicted mean wave speeds are similar, suggesting similar levels of unmixedness. However,other factors that can impact detonation wave speed, such as dynamic injector response, fuel-product stratification, and heat loss, are not considered in the present study. Subramanian and Meadows [34] analysis revealed that both fuel-product stratification and heat loss reduce the detonation velocity, with the impact of fuel-product stratification being much more significant than that of heat loss.

Fig. 5
figure 5

Trend of mean detonation velocity and % of theoretical CJ velocity as a function of unmixedness (q)

Full size image

The distribution plot of detonation velocities for non-premixed simulations (see Fig. 6), measured at different time steps, clearly indicates that localized patches of varying equivalence ratio (as shown in Fig. 4) cause a significant change in the wave speed distribution. In the case of \(q=0.3\) (the least inhomogeneous condition), one can observe that the detonation velocity is close to the theoretical CJ velocity, and the span of the velocity distribution is also narrow, indicating a more uniformly mixed fuel–air mixture compared to the other cases. However, for the case \(q=0.9\) (most inhomogeneous condition), due to a higher degree of mixture inhomogeneity, there are larger variations in wave velocity, as observed in Fig. 6, resulting in a reduction in mean detonation velocity.

Fig. 6
figure 6

Distribution plots of detonation velocity for varying unmixedness: a \(q = 0.3\), b \(q = 0.5\), c \(q = 0.6\), d \(q = 0.7\), and e \(q = 0.9\)

Full size image
Fig. 7
figure 7

Comparison between premixed and unmixedness (q) cases: a mean peak static pressure, b time-averaged total pressure

Full size image

The significant variation in local wave velocities results from differences in chemical time scales between fuel-rich and fuel-lean regions. These localized patches of fuel-rich and fuel-lean regions cause the wave to accelerate or decelerate. When the wave travels through a region close to stoichiometric conditions, it accelerates due to a reduction in the induction time behind the wave front. Conversely, in the lean region, the wave decelerates due to an increased induction time, leading to delayed reactions relative to the shock wave.

3.2 Pressure profile

Peak static pressures are obtained at multiple probe points over three revolutions of wave propagation (after a quasi-steady state is achieved) to compare the mean peak pressure profile for all cases. Figure 7a shows the mean peak pressure comparison for varying unmixedness conditions. Figure 7a shows that as the effect of unmixedness increases, the mean peak pressure decreases. Additionally, as unmixedness increases, the variation in peak pressure increases, as shown by the error bar in Fig. 7a. Equivalence ratio data are obtained at the physical locations/times corresponding to the peak pressures. This data is used for a linear regression analysis on the peak pressure with equivalence ratio, revealing that the equivalence ratio is only lightly correlated (\(R_{\textrm{m}}\cong 0.3)\) with the peak pressures. Peak pressures in a detonation wave occur immediately after the shock wave and before the chemical reactions start, known as the von Neumann pressure. The von Neumann pressure depends on the wave speed, which is a function of the local equivalence ratio ahead of the wave front. The von Neumann pressure depends on the shock Mach number, which depends on the detonation velocity (solely governed by the energy released) and the speed of sound of the fresh mixture. As the fresh mixtures compress across the shock wave, a change in equivalence ratio can cause the wave to accelerate or decelerate. The effect of local wave speed due to variations in equivalence ratio would be delayed by the induction/ignition time after the mixture is compressed across the shock. Therefore, there is not a strong correlation between peak pressures and equivalence ratios.

A similar comparison is made for the time-averaged total pressure (shown in Fig. 7b). Time-averaged total pressure is obtained from multiple probe points (see in Fig. 2) at different time steps (over three wave cycles) for the least, most inhomogeneous, and perfectly premixed cases. Figure 7b shows a decreasing trend in time-averaged total pressure as mixture inhomogeneity increases. Also, it is evident that for the least case of unmixedness (\(q=0.3\)) time-averaged total pressures fall within the uncertainty limits of the total pressure obtained in premixed simulation. Furthermore, Fig. 7b shows that the difference in time-averaged total pressures between a perfectly premixed and \(q= 0.9\) is significant, as the error bars (in Fig. 7b) of the time-averaged total pressure for the two cases do not coincide for most axial locations. This effect is more prominent near the inlet and decreases with an increase in axial distance due to the downstream mixing and diffusion.

Fig. 8
figure 8

Mean equivalent available pressure (EAP) for varying unmixedness cases (q)

Full size image
Fig. 9
figure 9

Wave structure and features comparison between premixed and varying condition of unmixedness: a premixed, b \(q=0.3\), c \(q=0.5\), d \(q=0.6\), e \(q=0.7\), and f \(q=0.9\)

Full size image

The PGC system promises to provide improved thermodynamic performance; however, due to the high speed, compressible, and unsteady flow field, it is difficult to quantify pressure gain and compare it with conventional propulsion/power devices. To address this issue, Kaemming and Paxson [42] proposed a method to determine and quantify the pressure gain in an RDC using Equivalent Available Pressure (EAP), representing the ability to do work or provide thrust if the flow expanded isentropically to ambient pressure. Employing the methodology defined by Kaemming and Paxson [42], EAP is determined for each unmixedness condition. The EAP values are collected over three revolutions of the wave propagation after it reaches a quasi-steady state. Figure 8 shows the time-averaged EAP values for varying unmixedness conditions.

Figure 8 illustrates that as the influence of unmixedness increases, the mean EAP value decreases, indicating a reduction in pressure gain. Additionally, the variance in EAP value increases with higher unmixedness, as shown by the error bars in Fig. 8. Figure 8 also demonstrates that the mean EAP values are lower than the inlet total pressure (\(P_{\textrm{o}}\)) condition imposed in the simulation, which is 4.12 bar. The Air Force Research Lab (AFRL) RDC geometry (Rankin et al. [23]) was designed with an excessive pressure drop across the injectors to study the fundamental aspect of the detonation wave in an RDC, which prevents realizable pressure gain. However, despite the limitations in obtaining significant pressure gain, the relative performance of EAP due to unmixedness provides insights into the effect of mixture inhomogeneity on pressure gain.

3.3 Detonation wave structure

The detonation wave structure is visualized using numerical schlieren imaging function. The following expression from [43] is used to generate the numerical schlieren images:

$$\begin{aligned} \textrm{Sc} = {c}\left\{ \textrm{exp}\left[ -\frac{{d}(|{\varvec{\nabla }}{{\uprho }}|-|{\varvec{\nabla }}{{\uprho }}|_\textrm{min})}{|{\varvec{\nabla }}{{\uprho }}|_\textrm{max}-|{\varvec{\nabla }}{{\uprho }}|_\textrm{min}}\right] \right\} \end{aligned}$$
(16)

The density gradient between grid cells is given by \({\varvec{\nabla }}\rho \), and c and d are the scaling constants (\({c} = 0.8\) and \({d} = 1000\) for this study), employed to enhance flow visualization even for small density gradients in the flow field. The height of the detonation wave front is similar for both the premixed and the unmixedness cases, as observed in Fig. 9. The height of the detonation wave front is a function of inlet stagnation pressure, which agrees with Schwer and Kailasanath [44], and it remains unaffected by changes in mixture inhomogeneity. A distinct slip line is visible in Fig. 9, attributed to differences in gas state and velocity across the slip line. A double-layer vortex structure develops across the slip line, leading to the formation of a distinct wake profile (denoted by \(\alpha \) in Fig. 9). This shear layer region, identified to reduce the thrust or combustor performance [45], shows a moderate effect on lower levels of unmixedness. However, for cases \(q =0.7\) and 0.9, a more dominant shear region is observed, particularly for \(q=0.9\) (as shown in Fig. 9), indicating a greater performance loss for higher levels of mixture inhomogeneity.

Another feature in Fig. 9 is the variance in flow features within the fill zone (denoted by the red bracket in Fig. 9). These variations result from varying density gradients arising from inhomogeneous fuel/oxidizer injection. As unmixedness increases, there is a corresponding rise in the density gradients within the fill zone. Additionally, a weak reflected shock wave is visible in the refill zone (denoted by an arrow in Fig. 9), consistent with findings by Schwer et al. [31], who showed that these weak shock waves are a function of the inlet stagnation and back pressure in the combustor.

Figure 9 illustrates that the structure of the detonation wave front is highly influenced by the fuel/air mixture inhomogeneity. As the detonation wave travels through regions of varying equivalence ratio, these localized variations in the fuel–air mixture distort the wave front. The presence of randomly distributed pockets of fuel-rich and lean regions within the domain induces additional shear stress between adjacent pockets of varying fuel composition leading to distortion in the wave front curvature as the wave propagates. Moreover, unmixedness generates vortical structures behind the wave front. Figure 10 shows the distribution of vorticity in the region behind the detonation front. The distribution plot for vorticity is obtained by creating a threshold region behind the wave front (shown with a dashed rectangle in the bottom middle of Fig. 9) and the data is collected over several time steps. Figure 10 clearly shows that as the effect of mixture inhomogeneity increases, both the mean and the variance of vorticity increase (see Fig. 10). These large vortical structures are less efficient in facilitating the mixing of residual and post-detonation gas mixture and induce viscous losses, resulting in reduced combustion efficiency and lower peak pressure behind the wave front.

Fig. 10
figure 10

Vorticity distribution behind the detonation wave front: a \(q=0.3\), b \(q=0.5\), c \(q=0.6\), d \(q=0.7\), and e \(q=0.9\)

Full size image
Fig. 11
figure 11

Numerical shadowgraph contour showing wave front corrugation between different cases of unmixedness and premixed: a premixed, b \(q=0.3\), c \(q=0.5\), d \(q=0.6\), e \(q=0.7\), and f \(q=0.9\)

Full size image

The flame front corrugation increases with an increase in mixture inhomogeneity. To further understand the effect of mixture inhomogeneity on wave front structure a numerical shadowgraph contour for varying unmixedness is shown in Fig. 11. The numerical shadowgraph plot is created using \(\textrm{Sh} = {\varvec{{\nabla }}} \cdot {\varvec{{\nabla }}}\rho \). Flows involving shock waves produce strong higher-order derivates of density. Thus, the numerical shadowgraph can capture the salient features of the shock front compared to numerical schlieren. However, numerical schlieren is more sensitive and captures weaker disturbances and gradients within the flow field, which are often downplayed in the numerical shadowgraph technique.

As illustrated in Fig. 11, detonation wave front corrugation intensifies with an increase in mixture inhomogeneity. This effect is particularly pronounced in the case of \(q=0.9\), as indicated by the arrow in Fig. 11f. The periodic passage of the wave through regions of lean and rich mixtures, each with varying chemical timescales, leads to increased resistance to wave motion and separation of the shock wave and the reaction zone. This generates distortion in the wave front, and the distance between the triple point collisions increases (see Fig. 11). The collision of triple points induces corrugation in the wave front, and as the distance between triple points collision increases, higher distortion is observed. Due to the presence of localized pockets of fuel-rich and fuel-lean regions, as the detonation wave passes through a fuel-rich region, the mixture ignites and allows the onset of the triple points, which propagate along the detonation wave. The collision of triple points recouples the shock and the reaction zone, sustaining detonation locally with high temperature, pressure, and heat release at the point of collision, which further accelerates the detonation wave. However, when the wave passes through a fuel-lean region, the shock and the reaction front begin to decouple as the detonation loses strength. Consequently, the unreacted mixture imposes an increased drag force, resulting in a reduction of wave speeds.

Fig. 12
figure 12

Detonation cell structure for varying unmixedness conditions and premixed case: a premixed, b \(q=0.3\), c \(q=0.5\), d \(q=0.6\), e \(q=0.7\), and f \(q=0.9\)

Full size image
Fig. 13
figure 13

Contour of cell size (left) and corresponding equivalence ratio (right): a and b \(q = 0.3\), c and d \(q = 0.7\)

Full size image
Fig. 14
figure 14

Distribution of cell size for varying levels of unmixedness and perfectly premixed condition: a premixed, b \(q=0.3\), c \(q=0.5\), d \(q=0.6\), e \(q=0.7\), and f \(q = 0.9\)

Full size image
Fig. 15
figure 15

Comparison of heat release as a function of chamber pressure for varying level of unmixedness (q)

Full size image
Fig. 16
figure 16

Comparison of heat release at different equivalence ratio for varying level of unmixedness (q)

Full size image
Fig. 17
figure 17

Temperature contour at different time steps for \(q =1.0\), showing wave failure (bottom right figure)

Full size image

3.4 Detonation cell size

Detonation cell size is a critical parameter for estimating the geometric dimensions of an RDC, as it is influenced by the fuel composition, pressure, temperature, and equivalence ratio. The cell size \(\lambda \), is defined as the distance between triple points moving in the same direction, located at the point of intersection of the detonation front, the transverse wave, and the reflected shock wave. Bykovskii et al. [6] proposed a criterion for geometric dimensions of an RDC based on \(\lambda \). The minimum diameter of the combustor is estimated to be \(d=30\lambda \), and the width of the annulus is estimated to be \(\Delta =2.5\lambda \). In addition, Bykovskii estimated the height of the fresh mixture entering the annulus of the detonation combustor as \({h}_{\textrm{f}}=\left( 12\pm 5 \right) \lambda \). These empirical correlations provide a good estimate to calculate the size of an RDC for different fuel propellants. The detonation cell size for a \(\hbox {H}_{{2}}\)-air mixture is much smaller than for the hydrocarbon fuels [46], which is why \(\hbox {H}_{{2}}\)-air is typically used in RDC studies [47,48,49,50]. To obtain the detonation cell sizes for all cases, the maximum pressure at each computational cell over a finite period is recorded. Analyzing the detonation cell structure for varying unmixedness (as shown in Fig. 12) indicates that the structure becomes distorted and staggered. The impact of mixture inhomogeneity is evident on the cell pattern (shown in Fig. 12), especially for the cases of \(q=0.7\) and \(q=0.9\), where the cells deform from a diamond shape to a parallelogram shape due to mixture concentration gradients within the domain.

Figure 13 shows a plot of the equivalence ratio obtained at the corresponding maximum pressure (cell structure) for the case of \(q= 0.3\) and 0.7. The variation in local equivalence ratio is significantly higher for the higher unmixedness condition (\(q = 0.7\)) compared to the lower unmixedness condition (\(q = 0.3\)). A prior study [51] showed that the smallest induction lengths are located in regions immediately after the collision of two triple points, as the shock front and reaction zone reattach. After the collision, the induction length increases by nearly an order of magnitude as the shock and reaction front separate in the direction of wave propagation. In the present study, as unmixedness increases, the triple point passes through regions of a non-detonable mixture, causing it to fail, and it re-initiates when it passes through conditions near stoichiometry or slightly rich. The intermittent phenomenon of failure and reforming of triple points in the flow field leads to irregular and staggered cell size patterns. The probability of the triple point passing through a non-detonable mixture is much higher as unmixedness increases. The intermittent behavior of extinguishing and re-igniting of triple points is more prominent with higher mixture inhomogeneity, leading to a discontinuous cellular pattern. Additionally, in a non-detonable mixture, the wave front decouples from the reaction zone, leading to the onset of turbulent deflagration mode within the reaction zone [52], causing a reduction in pressure gain and detonation efficiency of the RDC.

The individual cell size is calculated from the plot in Fig. 12 using the commercial software package called ImageJ The mean value with the corresponding distribution is calculated for all the cases and is presented in Fig. 14. The data for the distribution plot is obtained over three revolutions. The lower cases of unmixedness (\(q= 0.3\) and 0.5) show a similar mean cell size, but the variance in cell size is higher for the premixed condition. In the lower unmixedness cases, strong shock structures are observed farther from the inlet, forming relatively large and uniform cell patterns further downstream. On the other hand, in the premixed case, cell sizes further from the inlet are smaller and less predominant due to relatively weaker shock structures. This leads to a narrower cell size distribution for the lower cases of unmixedness. However, as the influence of unmixedness increases, the cell size pattern becomes more distorted. For conditions of \(q = 0.7\) and 0.9, the cell size pattern is highly staggered and elongated (see Fig. 12e and f). The higher unmixedness conditions show significantly larger mean cell size and a greater degree of variance (see Fig. 14). Several past studies have shown [20, 53] that the variation in equivalence ratio affects the cell shape and cell structure. Similar features are observed in Fig. 12, where the detonation cellular pattern for an inhomogeneous mixture differs from that of a perfectly premixed mixture.

3.5 Variation in heat release with pressure and equivalence ratio

In RDCs, both detonation and deflagration-type combustion can occur, with the latter occurring at much lower pressures. To investigate the variations in local heat release as a function of static pressure and equivalence ratio (\(\phi \)), data are extracted from a narrow region behind the detonation wave (see Fig. 9e) at different time steps and compared between the cases of varying unmixedness. The fraction of heat release is grouped under each pressure bin to determine the fraction of heat release occurring through detonation. A threshold of five bar pressure is considered as the lower limit for detonation combustion [16]. To maximize the advantages of high-pressure heat release due to detonation, it is desired to limit the amount of low-pressure heat release. Figure 15 shows that the amount of low-pressure heat increases as unmixedness increases. The lowest inhomogeneous condition (\(q= 0.3\)) has 7.5% heat release in the low-pressure region (below 5 bars), whereas, for the case of \(q= 0.9\), 25% of heat release occurs below the threshold limit reducing the pressure gain of the system. High-pressure heat release due to detonation generates less entropy (at constant volume) compared to low-pressure heat release due to deflagration (at constant pressure). Therefore, the detonation efficiency decreases as unmixedness increases.

Figure 16 shows the overall heat release as a function of the equivalence ratio. Heat release is gathered into bins depending on the local equivalence ratio, and the total in each bin is plotted as a fraction of overall heat release. The deviation of heat release from stoichiometric conditions increases as the effect of mixture inhomogeneity increases. As unmixedness increases, the fraction of heat release occurring on the rich side and its variances also increases. The biasing of the heat release towards a richer mixture increases the amount of unburnt fuel that penetrates through the detonation wave, leading to a decrease in combustion efficiency.

3.6 Detonation wave failure at higher unmixedness

While performing the sweeps of varying unmixedness, unstable wave propagation, and wave failure are observed as unmixedness is increased to \(q = 1.0\) (see Fig. 17). As mentioned previously, as the effect of mixture inhomogeneity increases, the probability of the triple points passing through a non-detonable mixture increase, which can lead to the decoupling of the reaction zone from the wave front. This decoupling can result in unstable wave propagation and wave failure, if it becomes significant enough.

Figure 17 highlights this phenomenon, starting with premixed wave propagation. Soon after, the unmixedness boundary condition is initiated. After a finite time, the high-temperature region behind the wave detaches (top right Fig. 17), and the separation distance between the shock wave and reaction front increases until complete wave failure occurs. Furthermore, the adjacent layers of mixture concentrations generate additional shear stress, further promoting the detachment of the shock wave from the reaction front.

4 Conclusions

Understanding the impact of unmixedness is critical for the successful design of an efficient fuel/oxidizer injection system. In the present study, a computationally efficient 2D CFD simulation of an RDC is used to investigate the effect of unmixedness on detonation wave propagation and structure. Results indicate that variations in local equivalence ratio significantly impact the detonation wave speeds, pressure gain, cellular structure, and detonation efficiency. An inverse relationship is observed between EAP and unmixedness. In regions of locally lean fuel/air ratios, the induction time increases, causing wave speed reduction. If sufficiently low, these lean pockets can extinguish the local detonation front resulting in a highly irregular detonation cell structure and separation of the reaction front from the shock wave. Re-attachment of the reaction zone to the shock front will periodically occur as fresh reactants near stoichiometry enter the induction zone. In regions of locally rich fuel/air ratios, unburnt fuel penetrates the detonation wave and mixes with post-detonation products resulting in an increase in low-pressure heat release and reduction in detonation efficiency. If unmixedness is further increased, detachment of the reaction zone will lead to wave instability and subsequently wave failure.