Abstract
A detached bow shock wave is strongest where it is normal to the upstream velocity. While the jump conditions across the shock are straightforward, many properties, such as the shock’s curvatures and derivatives of the pressure, along and normal to a normal shock, are indeterminate. A novel procedure is introduced for resolving the indeterminacy when the unsteady flow is three-dimensional and the upstream velocity may be nonuniform. Utilizing this procedure, normal shock relations are provided for the nonunique orientation of the flow plane and the corresponding shock’s curvatures and, e.g., the downstream normal derivatives of the pressure and the velocity components. These algebraic relations explicitly show the dependence of these parameters on the shock’s shape and the upstream velocity gradient. A simple relation, valid only for a normal shock, is obtained for the average curvatures. Results are also obtained when the shock is an elliptic paraboloid shock. These derivatives are both simple and proportional to the average curvature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A curved shock wave with a point (or line) where it is normal to the upstream velocity is ubiquitous in supersonic flows. For instance, a Mach stem may have a point where the shock is normal. The most frequent occurrence, however, is with a detached bow shock.
The analytical treatment at a normal shock is straightforward and benefits from having a 90\({^{\circ }}\) shock wave angle. Many properties, however, are indeterminate ([1], Subsect. 10.8.2). These include the shock wave curvatures, as well as derivatives along and normal to the shock of the pressure, density, etc. Shock wave curvatures are important, in part, because of their impact on shock-generated vorticity. In curved shock theory [2, 3], the curvatures are central to the analysis.
A flow plane is undefined at a normal shock location. In general, a unique flow plane is defined by the shock’s upstream and downstream velocities when the two velocities are not aligned. A vector normal to the shock can also be used instead of the downstream velocity; the three vectors are coplanar. At a normal shock, the velocities are aligned, and relations for the curvatures, along with other properties, are indeterminate. For a simple shock shape, the indeterminacy is readily resolved, as demonstrated in [1], Subsect. 10.8.2. This is not the case for an unsteady, three-dimensional flow with a nonuniform freestream.
A novel approach is introduced that partially resolves the indeterminacies. The formulation in Sect. 2 is general, i.e., the unsteady, three-dimensional flow may have a nonuniform, nonhomenergetic freestream, and a gas model is not prescribed. In the vicinity of the normal shock location, the curved shock may be convex, concave, or may have a saddle point. Steady flow of a perfect gas, however, is assumed in the normal derivative analysis in Sect. 3.
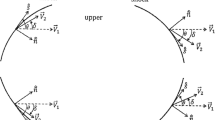
In contrast to a regular shock point, a normal shock does not have a unique flow plane, as evident when the flow is axisymmetric. When the flow is two-dimensional, there is a unique flow plane. Nevertheless, in the general case, an arbitrary flow plane can be defined with corresponding shock curvatures, shock-based basis vectors, and flow derivatives.
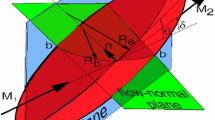
The formulation in Sect. 2 is first utilized to obtain the shock-based, right-handed, orthonormal basis, \(\hat{\tilde{s}}_o, \,\hat{\tilde{n}}_o, \,\hat{\tilde{b}}_o,\) where \(\hat{\tilde{s}}_o\) is tangent to the shock in the flow plane, \({\hat{\tilde{n}}} _o \) is normal to the shock in the downstream direction, \({\hat{\tilde{b}}} _o \) is orthogonal to \({\hat{\tilde{s}}} _o \) and \({\hat{\tilde{n}}} _o \), and the “o” subscript denotes the normal shock location.
Two curvatures are considered that, by definition, are in orthogonal planes. The \(S_a \) curvature is in the flow plane, while \(S_b \) is in a plane that is normal to the shock and the flow plane. A by-product of the analysis is a simple formula for the average curvature, an important surface property in differential geometry [4]. The third section contains a normal shock analysis for selected normal derivatives. Normal derivatives, compared to tangential ones, are independent of the flow plane’s orientation. The fourth section is an analysis, at the normal shock location, of an elliptic paraboloid shock for \(S_{{ ao}} \), \(S_{{ bo}} \), and the normal derivatives of various properties, such as the pressure and entropy, just downstream of the shock. These derivatives are also shown to be proportional to the average curvature. The final section is a brief summary.
2 Formulation, flow plane, and curvatures
Since the curvature analysis holds at an instant of time, time itself is an arbitrary, fixed parameter. The normal shock point is located at \(x_{io} \), \(i=\) 1, 2, 3, where \(x_i \) are Cartesian coordinates. The shock’s shape is represented by
while \(\vec {V}(x_{i},t)\) is the velocity just upstream of the shock. Subscripts 1 and 2, respectively, represent conditions just upstream and downstream of the shock. Both F and \(V_1 \) are considered to be analytic at \(x_{io} \) and therefore can be expanded in a Taylor series, as will be done shortly. The current analysis only requires these two expansions. Extension of the formulation, e.g., to certain downstream tangential derivatives along the shock, also requires expansions for the upstream pressure and density.
Without loss of generality, the \(x_i \) coordinates can be translated and solid-body-rotated. A translation is utilized such that \(x_{io} =0\). A rotation is introduced in order that \(\vec {V}_{1o}\) is parallel to \(x_1 \), i.e.,
where the \({\hat{|}} _i \) are corresponding orthonormal basis vectors. An arbitrary point, \(x_i^*\), on the shock very near the origin is chosen, where the shock wave angle in the well-defined \(x_i^*\) flow plane, \(\theta ^{*}\), measured relative to \(\vec {V}_{1}^{*}\), is not 90\({^{\circ }}\). It is convenient to utilize the flow-plane formalism in [1], Sect. 10.2. Toward this end, it is convenient to introduce another solid-body rotation about \(x_1 \) such that \(x_3^*=0\). While there is no loss in generality, the second rotation yields a flow plane with an arbitrary orientation. The choice of \(x_i^*\) and the two rotations fix the Cartesian coordinate system, centered at the normal shock state, and greatly simplify the subsequent analysis. Any further coordinate rotation is unwarranted.
A Cartesian coordinate system is centered at a point where the shock is normal, \(x_1 \) is along \(\vec {V}_{1o}\), and the \(x_i^*\) are given by
where \(\varepsilon \) is a small parameter. Conditions at the normal shock location are obtained by setting \(\varepsilon \rightarrow 0\), or, as is often the case, by \(\varepsilon \) cancelling. As will be apparent, the final results at the normal shock location are well defined and are independent of the \(x_i^*\) location.
In view of the above, F is written as
where higher-order \(x_i \) terms are neglected. Since \(x_1 \) is normal to the shock, its coefficient is nonzero. Moreover, the \(x_i\) are nondimensionalized such that the \(x_1 \) coefficient is unity, as shown in (4).
With the upstream velocity written as
its components are
and
where
Higher-order terms in (7) are also neglected. It should be noted that the coefficients in the F and \(\vec {V}_1\) expansions depend on the orientation chosen for the flow plane. With a uniform freestream, the \(e_{{ ij}} \) are equal to zero.
Let \({\hat{n}} \) be a unit vector that is normal to the shock and points in the downstream direction, i.e.,
The normal shock condition
results in
or
The \(F=0\) relation in (3) becomes a quadratic equation for \(x_1^*\)
and yields
Expand the square root term for small \(\varepsilon \), to obtain
Since \(x_1^*=0\) when \(\varepsilon =0\), the plus sign is used, resulting in, to leading order,
This is of higher-order than \(x_2^*\left( {=\varepsilon } \right) \), since \(x_1 \) is normal to the shock.
The \(\hat{\tilde{s}}\) and \(\hat{\tilde{b}}\) vectors, along with other parameters, are to be evaluated at \(x_i^*\). To order \(\varepsilon \), except in (18), the \(F^{*}\) derivatives and the \(v_{1,i}^*\) are
Section (10.2) in [1] is utilized to obtain relations for \(\hat{\tilde{b}}_o\) and \(\hat{\tilde{s}}_o\). Toward this end, introduce the parameters
With the foregoing, to order \(\varepsilon \), one obtains
where \(k_2 \) and \(k_3 \) are defined by (25).
General relations for \(\hat{\tilde{s}} \) and \(\hat{\tilde{b}} \) are
where \(\hat{\tilde{s}}, \, \hat{\tilde{n}}, \, \hat{\tilde{b}}\) is a right-handed, orthonormal basis. At \(x_i^*\), these become
where the \(\varepsilon \) in \(K_j^*\) and \(L_j^*\) cancel the \(\varepsilon \) in \(\chi ^{*}\). Equation (9) readily yields
Equations (29a) and (30) define a nonunique flow plane that is dependent on the arbitrarily chosen shock point \(x_i^*\). These equations also provide the dependence of the flow plane’s orientation on the shock’s shape and upstream velocity profile through \(k_2 \) and \(k_3 \), where the k coefficients depend on two \(c_{{ ij}} \) and two \(e_{{ ij}} \) parameters. Continued dependence on \(k_2 \) and \(k_3 \) will be apparent in the subsequent analysis.
The two orthogonal curvatures are given in [1], Sect. 10.4
and are defined such that they are positive when the shock is convex relative to the upstream flow. These curvatures depend on more than the \(c_{{ ij}} \), because the flow-plane definition involves the upstream velocity. To order \(\varepsilon ^{2}\), \(S_a^*\) and \(S_b^*\) require
The above are substituted into (31), the \(\varepsilon \) terms again cancel, with the curvature result
Of course, planar normal shocks occur, as in shock tube flow. It is analytically possible, however, to have a normal shock flat spot, i.e.,
on an otherwise curved shock wave. This could occur, e.g., when
The average curvature is
In contrast to \(S_{{ ao}} \) and \(S_{{ bo}} \), which depend on the \(e_{{ ij}} \), the average curvature is independent of \(\vec {V}_{1}\). An average curvature, at a regular shock point, is readily obtained from (31), but this result simplifies to (36) only at a normal shock location.
Let \(S_1 \) be the curvature in a plane rotated from the \(S_a \) plane by an angle \(\alpha \). Then by Euler’s theorem [4],
Let \(S_2 \) be the curvature in a plane rotated 90\({^{\circ }}\) from \(S_1 \). We then obtain
and, consequently,
Thus, the average curvature, at any point on the shock, is invariant to a rotation about a line normal to the shock providing the two planes are orthogonal to each other.
3 Normal derivatives
The state 2 derivatives
are to be explicitly evaluated in the general case, but for a steady flow of a perfect gas. Here, v is the velocity component normal to the shock, and p and \(\rho \) are the pressure and density. The n coordinate is normal to the shock and equals \(x_1 \) when the shock is a normal shock, and normal derivatives then coincide with streamline derivatives. The normal derivatives, at any point on the shock, are given in [1], App. H
The right-hand sides are evaluated at state 2, \(M_1 \) is the variable upstream Mach number, and
The s coordinate is tangent to the shock in the flow plane, u is the velocity component tangent to the shock, just downstream of the shock in the flow plane, and \(h_3 \) is the scale factor for the coordinate that is tangent to the shock and normal to the flow plane. Both s and u are positive when aligned with \({\hat{s}} \). In the foregoing relations, s, n, \(1/S_a \), and \(1/S_b \) are viewed as normalized lengths. On the right-hand sides of (38) and (40), p, \(\rho \), and u and v are normalized with \(p_1 \), \(\rho _1 \), and \(V_1 \). (This does not imply that \(p_1 \), \(\rho _1 \), or \(V_1 \) are constants.)
At state 2, the \(u,v_o ,\ldots ,\) parameters are
where \(\theta \) is the shock wave angle in the flow plane, \(m_o =M_{1o}^2 \), and \(\gamma \) is the ratio of specific heats of a perfect gas. Since \(u_o =0\), the u in (41) is devoid of the “o” subscript, and \(A_{co} \) and \(A_{eo} \hbox {}\) are both zero. The scale factor term in (40a), however, is indeterminate; it will be shown that \(\left[ {\left( {1/h_3 } \right) \left( {\partial h_3 /\partial s} \right) } \right] _o \) is infinite. This is the reason for including the rightmost term in (41). The denominator in (38) becomes
and the normal derivative relations simplify to
where
The first two terms on the right-hand side of \(A_{{ ao}} \) are evaluated in the next two subsections.
3.1 Scale factor derivative term
From [1], Sect. 10.7, write the b-coordinate scale factor, \(h_3 \), as
which is to be evaluated at \(x_i^*\). To leading order, the various factors are
and \(\chi ^{*}\) is given by (27). By substituting the above into (46), the \(h_3 \) derivative result is obtained
which demonstrates the infinity value when \(\varepsilon \rightarrow 0\). From (27), (41), and (47a), \(u^{*}\) is
and the sought after result is
3.2 Tangential velocity derivative term
From [1], App. H, the u derivative is
To leading order, this simplifies to
In view of (41), \(\hbox {sin}\,\theta ^{*}\), to order \(\varepsilon \), is
and the \(\theta _{x_i } \) derivative is given in [1], Sect. 10.5,
The preceding formulation provides, to order \(\varepsilon \), the summations that appear in \(G_i^*\) and \(H_i^*\):
With the above, (54b) and (54c) become
which yields
The summation in (52) becomes
and the u flow-plane tangential derivative is
If the freestream is uniform, this simplifies to
3.3 Derivative results
As a result of cancellation and the use of (36), (45) has the simple form
where the importance of the average curvature is evident. Equations (44) are now relatively simple relations for the normal derivatives. When the freestream is uniform and the shock is two-dimensional or axisymmetric, (44) simplify to
where r is the shock wave’s nose radius, and \(\sigma =0/1\) for a two-dimensional/axisymmetric flow.
4 Elliptic paraboloid shock derivatives
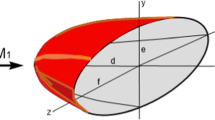
To avoid undue complexity, the analysis is limited to a convex, elliptic paraboloid (EP) shock with a uniform freestream
where \(r_2 \) is the radius of curvature at the origin in the \(x_3 =0\) plane and \(r_3 \) is the radius of curvature at the origin in the \(x_2 =0\) plane. From (29), (30), and (33), one readily obtains
When \(\sigma =1\) and \(r_2 \ne r_3 \), the case of interest, the shock has an elliptical shape in an \(x_1 \) plane. If \(r_2 >r_3 \), the major axis corresponds to \(S_a \), while the minor axis corresponds to \(S_b \), with \(S_b>S_a >0\). As noted in [4], the minimum (min) and maximum (max) curvatures of a surface are in orthogonal planes. It is evident that \(S_a \) and \(S_b \) are either max/min or min/max curvatures depending on whether or not \(r_2 >r_3 \).
A variety of normal derivatives, at state 2, are evaluated
where S is the entropy. It is expected that for an isentropic flow
The subsequent analysis is based on [1], App. J. From this reference, one obtains
where
Equation (66) holds at any point on the EP shock. In the limit, as \(x_i^*\rightarrow 0\), the derivative becomes
The pressure derivative is
where
The A coefficients are the EP shock version of (40). At the normal shock location, (71) reduces to
The \(A_{co} \) and \(A_{eo} \) parameters are readily evaluated:
The \(A_a \) parameter becomes
The terms on the right-hand side are each indeterminate, since \({\psi }_o =0\). When \(\sigma =0\), however, one readily obtains
When \(\sigma =1\), the two terms combine to yield
The above \(A_{{ ao}} \) equations combine to yield
Substitute the \(A_o \) equations into (75) with the result
By normalizing with \(p_2 \), instead of \(p_1 \), as is done in curved shock theory [2, 3], the above simplifies to
Thus, the normalized, by \(p_2 \), pressure derivative depends only on \(\gamma \) and the average curvature, but not on \(M_1 \). The \(S_{{ ao}} +S_{{ bo}} \) factor stems from \(A_a \), which, in turn, stems directly from continuity. As the average curvature increases, the corresponding radius of curvature decreases and the magnitude of the derivatives increases.
The next objective is to evaluate \(\left( {\partial S/\partial n} \right) _o \). The entropy is given by
where R is the gas constant. This yields
From App. J in [1], the density derivative is
With the aid of the \(A_o \) parameters, this becomes
which can be written as
This result is similar to the \(\left( {1/p_2 } \right) \left( {\partial p/\partial n} \right) _o \) relation. For the state 2, nondimensional coefficients in (81), one obtains
Combining the above yields
again as expected for an isentropic flow.
The normal derivative of the velocity component normal to the shock is given by
With the foregoing results, this becomes
In contrast to the normalized pressure and density normal derivatives, \(\left( {\partial v/\partial n} \right) _o \) also depends on \(M_1^2 \).
5 Summary
Even though the orientation of the flow plane is arbitrary, a general formulation is provided for the shock-based basis vectors and the orthogonal curvatures, \(S_{{ ao}} \) and \(S_{{ bo}} \), that hold when a curved shock is a normal shock. An especially simple result is obtained for the average curvature.
Several normal derivatives are evaluated when the flow is steady and three-dimensional. Explicit, algebraic, nondimensional results in Sects. 2 and 3 are obtained that depend on \(\gamma \), \(M_{1o} \), \(V_{1o} \), \(c_{11} ,c_{23} ,c_{33} ,e_{22} ,e_{23} ,e_{32}\), and \(e_{33} \), where the \(c_{{ ij}} \) control the shock’s shape and the \(e_{{ ij}} \) specify the local upstream velocity profile. A number of the \(c_{{ ij}} \) and \(e_{{ ij}} \) parameters are thus superfluous. Final results for the normal derivatives, however, are independent of the flow plane’s orientation. Of special note for the upstream tangential velocity derivatives are \(e_{22} \) and \(e_{33} \) that appear in (60) and directly contribute to the magnitude of the downstream normal shock derivatives.
Normal derivatives, (64), are evaluated for an elliptic paraboloid shock. The tangential velocity component derivative, in the flow plane, and the entropy derivative are both zero. The pressure and density derivatives, when normalized with \(p_2 \) and \(\rho _2 \), respectively, depend only on the ratio of specific heats and the average curvature. On the other hand, the velocity component that is normal to the shock has a derivative that also depends on \(M_1^2 \).
Abbreviations
- \(A_a ,A_c ,A_e \) :
-
Defined by (40)
- \(\tilde{b}\) :
-
Coordinate normal to the flow plane
- \(\hat{\tilde{b}}\) :
-
Unit vector normal to the flow plane
- \(c_i ,c_{{ ij}} \) :
-
Coefficient defining the shock’s configuration
- \(e_{{ ij}} \) :
-
Coefficient defining the upstream velocity gradient
- F :
-
\(F=0\) provides the shock’s configuration
- \(G_i, H_i \) :
- \(h_3\) :
-
\(\tilde{b}\)-coordinate scale factor
- \({\hat{|}} _i \) :
-
Cartesian coordinate basis
- \(K_i \) :
-
Defined by (20)
- \(k_2 ,k_3 \) :
-
Defined by (25)
- \(L_i \) :
-
Defined by (21)
- M :
-
Mach number
- m :
-
\(M_1^2 \)
- \(\tilde{n}\) :
-
Coordinate normal to the shock, positive in the downstream direction
- \(\hat{\tilde{n}}\) :
-
Unit vector normal to the shock, oriented in the downstream direction
- p :
-
Pressure
- r :
-
Nose radius of the shock when the shock is two-dimensional or axisymmetric
- R :
-
Gas constant
- \(\tilde{s}\) :
-
Arc length along the shock in the flow plane
- \(\hat{\tilde{s}}\) :
-
Unit vector tangent to the shock in the flow plane
- S :
-
Entropy
- \(S_a \) :
-
Shock curvature in the flow plane
- \(S_b \) :
-
Shock curvature in a plane normal to the shock and the flow plane
- \(S_1 ,S_2 \) :
-
Orthogonal shock curvatures
- t :
-
Time
- u :
-
Velocity component tangent to the shock in the flow plane, just downstream of the shock
- v :
-
Velocity component normal to the shock, just downstream of the shock
- \(\vec {V}\) :
-
Velocity
- w :
-
\(M_1^2 \hbox {sin}^{2}\beta \)
- \(x_i \) :
-
Cartesian coordinates centered at a point on the shock, where \(x_i \) is parallel to \(\vec {V}_1\)
- X :
-
\(1+\frac{\gamma -1}{2}w\)
- Y :
-
\(\gamma w-\frac{\gamma -1}{2}\)
- Z :
-
\(w-1\)
- \(\alpha \) :
-
Angle between planes containing \(S_1 \) and \(S_a \)
- \(\gamma \) :
-
Ratio of specific heats
- \(\theta \) :
-
Shock wave angle measured relative to \(\vec {V}_1\) in the flow plane
- \(\varepsilon \) :
-
Small parameter
- \(\rho \) :
-
Density
- \(\sigma \) :
-
\(=0/1\) for a two-dimensional/axisymmetric flow
- \(\chi \) :
-
Defined by (22)
- \({\psi }\) :
-
Defined by (67)
- 1:
-
Flow state just upstream of the shock
- 2:
-
Flow state just downstream of the shock
- o :
-
Location where the shock is a normal shock
- ( )\(^*\) :
-
Location where the shock is not a normal shock
- (\(\,\hat{\,}\,\)):
-
Denotes a unit vector
References
Emanuel, G.: Analytical Fluid Dynamics, 3rd edn. CRC Press, Boca Raton (2016). doi:10.1201/b19392
Mölder, S.: Curved aerodynamic shock waves. PhD Dissertation. McGill University (2012)
Mölder, S.: Curved shock theory. Shock Waves 26, 337–353 (2016). doi:10.1007/s00193-015-0589-9
Struik, D.J.: Differential Geometry, p. 81. Addison-Wesley Press, Cambridge (1950)
Acknowledgements
The author acknowledges the helpful comments of S. Mölder.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by D. Zeitoun and A. Higgins.
Rights and permissions
About this article
Cite this article
Emanuel, G. Flow derivatives and curvatures for a normal shock. Shock Waves 28, 427–435 (2018). https://doi.org/10.1007/s00193-017-0742-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-017-0742-8