Observations on the normal reflection of gaseous detonations

Abstract

Experimental results are presented examining the behavior of the shock wave created when a gaseous detonation wave normally impinges upon a planar wall. Gaseous detonations are created in a 7.67-m-long, 280-mm-internal-diameter detonation tube instrumented with a test section of rectangular cross section enabling visualization of the region at the tube-end farthest from the point of detonation initiation. Dynamic pressure measurements and high-speed schlieren photography in the region of detonation reflection are used to examine the characteristics of the inbound detonation wave and outbound reflected shock wave. Data from a range of detonable fuel/oxidizer/diluent/initial pressure combinations are presented to examine the effect of cell-size and detonation regularity on detonation reflection. The reflected shock does not bifurcate in any case examined and instead remains nominally planar when interacting with the boundary layer that is created behind the incident wave. The trajectory of the reflected shock wave is examined in detail, and the wave speed is found to rapidly change close to the end-wall, an effect we attribute to the interaction of the reflected shock with the reaction zone behind the incident detonation wave. Far from the end-wall, the reflected shock wave speed is in reasonable agreement with the ideal model of reflection which neglects the presence of a finite-length reaction zone. The net far-field effect of the reaction zone is to displace the reflected shock trajectory from the predictions of the ideal model, explaining the apparent disagreement of the ideal reflection model with experimental reflected shock observations of previous studies.

1 Introduction

Gaseous detonation waves are a potential safety concern for piping systems or pressure vessels that may contain a detonable gaseous mixture. When a detonation impinges upon a hard surface like the interior of a metal pipe or pressure vessel, a reflected shock wave is created. Depending on the angle of incidence of the detonation wave, a range of reflected wave configurations are possible, for example, regular or Mach reflection for obliquely incident waves. In the present study, we consider the simplest case of the reflection of a detonation normal to the wall such as would occur if a detonation propagating in a tube reached a closed valve or dead end.

Fig. 1

Space–time diagram of a reflecting detonation and attached Taylor–Zel’dovich expansion wave. The detonation reflects off the wall located at $x = L$, and the reflected shock wave passes through the expansion

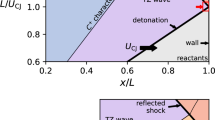
A schematic illustrating the primary features of one-dimensional detonation reflection is given in Fig. 1. The detonation propagates from the ignition location $x = 0$ at the constant theoretical Chapman–Jouguet (CJ) speed $U_\mathrm {CJ}$ into the unburned reactants at state 1; the CJ speed may be calculated a priori to determine both the expected detonation speed and the fluid conditions behind the detonation reaction zone (state 2). Behind the detonation, the Taylor–Zel’dovich (TZ) expansion gradually slows the fluid from state 2 to zero-velocity state 3. The fluid properties in this region may be calculated using the method of characteristics and the assumption that the gas is calorically perfect using realistic chemistry to determine the fluid properties. With this method, the conditions are everywhere known until the reflected shock wave arrives. When the detonation impinges upon the reflecting end-wall at $x = L$, a reflected shock wave is created to stagnate the flow. The speed of this reflected shock, $U_\mathrm {R}$, will change as it propagates first through the reaction zone behind the detonation and second through the TZ expansion. It is the speed and behavior of the reflected shock that is the focus of this study.

The speed of the reflected shock before it is affected by the TZ wave may be calculated ignoring the reaction zone as the shock strength necessary to stagnate flow at the CJ state (state 2), and the effect of the TZ expansion on the wave speed may be estimated by supposing the spatial gradients are zero for locations between the reflecting end-wall and the reflected shock [1]. This calculation neglects the detonation’s cellular structure, boundary layer, and finite thickness of the reaction zone. With these assumptions, and with the CJ detonation conditions known, the speed and strength of the reflected shock wave near the end-wall are determined by the conservation equations with a zero fluid speed boundary condition at the end-wall to predict the shock conditions. This process allows for the calculation of the reflected shock speed, $U_{\mathrm {R,CJ}}$, predicted from an incident CJ detonation. In performing these calculations, realistic chemical properties are determined using Cantera as described by [2]; gas properties are computed on the basis of chemical equilibrium as described in [3]. The situation shown in Fig. 1 is idealized and ignores important effects, including the boundary layer induced on the side-walls of the pipe or channel, the finite reaction zone thickness behind the detonation front, and the known instability of the combustion zone in detonations. This idealized model was considered in the previous work by [4] who examined the interaction of the reflected shock wave with the Taylor expansion and the reverberation of the shock wave within the vessel or channel. The structure of the detonation wave and possible role of the reaction zone were not considered in that study. In the present study, we instead focus on the near-wall behavior of the reflected shock as it interacts with the detonation structure and do not consider the subsequent interaction with the Taylor expansion.

Fig. 2

An overview of the GDT experimental facility, with inset showing test section details. Detonation initiation occurred on the left-hand side of the image, and detonation reflection occurred at the reflecting end-wall located on the right-hand side of the image

This investigation builds upon previous studies into gaseous detonation behavior performed in the Explosion Dynamics Laboratory studying the gasdynamics of reflecting detonations and detonation-driven deformation. Multiple regimes have been investigated that result in varying degrees of deformation. Depending on the pressure, deformation will be purely elastic (as described by [1] and [5]), a combination of elastic and plastic [6] as produced by normally reflected detonation waves, or will result in tube rupture [7]. One of the motivations for the present study was the findings by [6], a discrepancy in the speed of the reflected wave as measured at the tube side-walls was discovered. A possible explanation for this discrepancy was that the reflected wave was undergoing reflected shock wave–boundary layer interaction in the form of reflected shock bifurcation; the potential for this was explored in two-dimensional computations [8]. Reflected shock wave bifurcation has been extensively studied as it pertains to shock tube performance [9,10,11,12,13], ignition [14, 15], and DDT [16]; however, it had not been studied in the case of reflected detonation waves. Gaseous detonations create temperatures that are much larger than those observed in shock tube experiments. Additionally, detonations are intrinsically three-dimensional with transverse shocks propagating behind the detonation front (for examples of the cellular structure of detonation waves, see [17]). The large temperature variation through the boundary layer and presence of transverse shocks and associated disturbances to the boundary layer distinguish the case of reflected detonations from otherwise analogous shock tube studies.

The present work used the GALCIT Detonation Tube to experimentally examine the behavior of reflected gaseous detonations. Dynamic pressure measurements and schlieren images were gathered to examine the strength and speed of the inbound detonation wave and outbound reflected shock wave in the vicinity of normal detonation reflection. These data are compared to models of normal detonation and shock wave reflection with the goal of gaining fundamental understanding into the behavior of normally reflected gaseous detonation waves.

2 Experimental setup

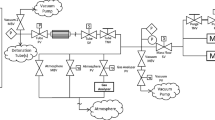
Experiments were performed in the GALCIT detonation tube (GDT). The GDT is a 7.67-m-long, 280-mm-inner-diameter detonation tube equipped with a 152.4-mm-wide test section of rectangular cross section and two quartz windows to provide optical access. A complete description of this facility is given in [18] and [19], and an expanded description of the experimental setup is given in [20]. The possibility of shock wave–boundary layer interaction motivated the design and construction of a splitter plate that raised the effective floor of the test section to the center of the windows. This allowed any interaction of the shock wave with the boundary layer to be observed. The relevant geometry of the GDT, test section, and splitter plate is illustrated in Fig. 2.

Fig. 3

Schematic of schlieren visualization system and GDT test section as viewed from above

In addition to raising the test section floor to the center of the windows, the splitter plate housed a suite of pressure gauges. Twelve PCB 113B26 piezoelectric pressure transducers were located in a line running parallel to the detonation tube axis 12.7 mm from the center of the plate with 12.7 mm gauge center-to-center spacing. Additionally, three PCB 113A24 pressure sensors were mounted in the GDT to record the speed and strength of the detonation before entering the test section. In plots of the pressure data (e.g., Fig. 4), the gauge locations are included as one axis. Pressure signals were recorded at a rate of 2.5 MHz. All pressure gauges have a 6.4 mm diameter and maximum error of 1.3% as determined from calibration data.

Table 1 Measured detonation speeds ($U_\mathrm {det}$) compared to the theoretical Chapman–Jouguet speed ($U_\mathrm {CJ}$)

A two-lens Z-type schlieren system was used to visualize the detonation and reflected shock behavior. The schematic of this system is shown in Fig. 3. The purpose of the visualization system was to record high-resolution images of the incident detonation and reflected shock wave, with an emphasis on precisely determining the speed of the reflected shock wave in the immediate vicinity of detonation reflection. The schlieren system used a Photogenics PL1000DRC flash lamp with flash duration (1 ms) of sufficient length so as to be illuminating for the entire time that the detonation and reflected shock were in the field of view. Images were recorded using a Specialised Imaging SIMD16 Ultra Fast Framing Camera. The SIMD16 recorded 16 1280 $\times$ 960 pixel 12 bit images for each experiment using intensified CCD sensors. The image magnification resulted in a field of view of 29.1 mm by 21.8 mm, or equivalently 43.9 pixels/mm. A USAF 1951 target was used to quantify the resolving power of this system to be 223 $\upmu$m horizontally and 125 $\upmu$m vertically as measured with the target at the center of the test section. The exposure time was set to 20 ns for all experiments to freeze the flow (all detonations studied had speed less than 3000 m/s corresponding to less than 60 $\upmu$m of motion over the 20 ns exposure, less than half what could be resolved), and a frame rate was chosen based on the wave speeds as predicted using Cantera [21] and the Shock and Detonation Toolbox [2]. The camera has a monitor signal that was recorded using the same data acquisition system that recorded the pressure signals, so that it was known precisely when the camera was imaging relative to the pressure signals. After the experiment, the recorded schlieren images were grayscale balanced to account for differences between the intensified CCD sensors. Multiple examples of detonation images captured with this system are included below (e.g., Fig. 7). The circle-of-confusion diameter is calculated from the aperture angle to be 250$~\upmu$m for a depth of focus equal to the 76 mm half-width of the test section [22]. Since this diameter is smaller than the features of interest and comparable to the resolving power, we can approximate that all disturbances in the density field across the test section are integrated equally and will uniformly influence the resulting schlieren image.

Before each experiment, the GDT was evacuated and filled via the method of partial pressures to the desired initial pressure and composition. The gas was circulated with a pump to ensure complete mixing. Detonations were initiated using a process developed by [18]. A volume of acetylene–oxygen was injected into the ignition end of the GDT. Then, a blast wave was created by vaporizing an 80-$\upmu$m-diameter copper wire with 2 $\upmu$F of capacitance charged to 9 kV. This blast wave initiated a detonation in the acetylene–oxygen that propagated into the test mixture toward the opposite end of the tube.

Fig. 4

Pressure measurements for shots 2152 and 2179. The initial composition for both experiments was stoichiometric hydrogen–oxygen at fill pressure 25 kPa. Arrival times $t_{5\%}$ and $t_{95\%}$ for shot 2152 are shown as dashed black lines

Test mixtures of stoichiometric hydrogen–oxygen, ethylene–oxygen, and hydrogen–nitrous oxide were examined at different fill pressures, diluents, and diluent percentages. Nineteen detonations are described herein with test conditions included in Table 1. These tests explored the effect of initial pressure, fuel, and dilution on the incident detonation and reflected shock waves.

3 Analysis

The pressure and video data were processed so as to determine the speeds of the detonation and reflected shock waves. Figure 4 shows pressure signals obtained for two different experiments, shot numbers 2152 and 2179. Both of these experiments were detonations of stoichiometric hydrogen–oxygen at fill pressure 25 kPa. Two shots with identical fill conditions are shown to illustrate the repeatability of the pressure measurements. This plot shows features present in all detonation measurements and will serve as a representative case in describing how the waves were analyzed. In Fig. 4, the detonation first arrives at the gauge located 127 mm from the end-wall as observed by the pressure jump shortly after 50 $\upmu$s. The detonation propagates toward the end-wall producing pressure increases in each subsequent gauge. Shortly after the detonation arrives at the pressure gauge nearest the end-wall (12.7 mm from the point of reflection), a second pressure increase is observed in this gauge marking the arrival of the reflected shock wave. The shock travels back toward the point of ignition, causing a second increase in each pressure measurement. Data spikes in shot 2179 in the gauges located 38.1 and 127 mm from the end-wall are due to cabling loosened by the detonation.

The raw image file for shot 2152 is shown in Fig. 5. The 16 frames are tiled left-to-right, top-to-bottom, so as to view the entire recording. Counting the frames sequentially from left-to-right, top-to-bottom, the first 6 frames show the detonation propagating from the left to the reflecting end-wall located at the right-most edge of each frame; the floor of the splitter plate is barely visible along the bottom edge of each frame. The detonation is seen to impinge upon the end-wall at the approximate time of the 7th frame. Frames 8 to 16 then show the reflected shock wave propagating back to the left.

Fig. 5

Schlieren images of the incident detonation and reflected shock for shot 2152. The initial composition was stoichiometric hydrogen–oxygen at initial pressure 25 kPa. The exposure time was 20 ns, the intra-frame time was 1.27 $\upmu$s, and each frame is approximately 29 mm wide. Images are placed chronologically left-to-right, top-to-bottom

Analogous pressure profiles and images were observed for all detonation experiments (a complete set of data for all experiments performed is given in [20]). It was desired to use the pressure and image data to precisely calculate the wave speeds in a manner that accounted for the signal rise time in the pressure data, the apparent wave thickness in the images, and the non-uniform sampling rate across the two measurement types. The pressure signals exhibited a rise time of several microseconds. The pressure signals from shot 2152 (as seen in Fig. 4), for example, had a mean rise time of 1.0 $\upmu$s for the incident detonation and 5.1 $\upmu$s for the reflected shock. In order to systematically account for the finite rise time, a time interval $[t_{5\%},t_{95\%}]$ was determined for both the detonation and reflected shock corresponding to the pressure signal increasing by 5 and 95% of the maximum pressure rise produced by the associated wave. Figure 4 shows the $t_{5\%}$ and $t_{95\%}$ arrival times given in dashed black lines. To account for the finite size of the pressure gauges, the gauge radius of 3.2 mm was used as a maximum uncertainty in gauge location for all pressure measurements. The location of the gauge centers relative to the reflecting end-wall was known to within 0.1 mm, and thus the finite gauge size dominated the overall gauge-location uncertainty. In contrast to the pressure measurements, the time of measurement for each image is known with great accuracy given by the 20-ns exposure, but the wave location in each image must now be determined. The procedure for doing this was as follows. First, if applicable, each frame was rotated and cropped so that the end-wall was straight and just visible at the right-edge of the image. Second, the mean transverse grayscale value was determined as a function of distance from the end-wall by taking a vertical average of the image intensity. Third, $x_{5\%}$ and $x_{95\%}$ values were determined based on the vertical mean image intensity analogously to the method used to determine the wave time of arrival from the pressure data. In this manner, the position of the detonation and shock waves as a function of time was measured with uncertainty for each experiment.

In this manner, wave arrival data were recorded for each initial condition given in Table 1. With these data, we constructed location-time diagrams describing the motion of the incident detonation and reflected shock wave. An example of this is shown in Fig. 6 for representative shot 2152; here we observe the detonation propagating toward the end-wall and the reflected shock propagating away from the end-wall. The time axis has been shifted such that the detonation impinges on the end-wall at time $t = 0$ (as determined by time $t_0$ below), and the lengths of the lines equate to the signal rise times and measurement uncertainties.

Fig. 6

x–t diagram showing detonation and shock arrivals, with uncertainties, for representative shot 2152. The detonation propagates toward the end-wall at the right, and the reflected shock propagates back. The points clustered near the end-wall correspond to arrivals taken from the image files, and the points farther away correspond to arrivals taken from the pressure measurements

Examining the space–time diagrams revealed that the reflected shock speed was not constant over the observed region with the shock propagating faster near the end-wall. To quantify this effect, we fit the arrival data to a piecewise-continuous linear function:

$$\begin{aligned} X_{\mathrm {wave}} (t)&= {\left\{ \begin{array}{ll} \displaystyle U_{\mathrm {det}}\left( t_0-t\right) &{} t< t_0\\ \displaystyle U_{\mathrm {rs,w}}(t-t_0) &{} \displaystyle t_0< t<\frac{x_\mathrm{t}}{U_{\mathrm {rs,w}}}\\ \displaystyle U_{\mathrm {rs,\infty }}\left( t-t_0\right) + x_\mathrm{t}\left( 1-r\right) &{} \displaystyle t>\frac{x_\mathrm{t}}{U_{\mathrm {rs,w}}} \end{array}\right. }\nonumber \\ \end{aligned}$$

(1)

where

$$\begin{aligned} r&=\frac{U_{\mathrm {rs,\infty }}}{U_{\mathrm {rs,w}}}. \end{aligned}$$

(2)

This functional form is used to analyze the limit behaviors of the reflected shock wave near and far from the wall. This equation fits the detonation and shock arrival data using five fit parameters: the detonation speed $U_{\mathrm {det}}$, the time the detonation impinges on the end-wall $t_0$, the speed of the reflected shock near the wall $U_{\mathrm {rs,w}}$, far from the wall $U_{\mathrm {rs,\infty }}$, and the distance from the end-wall where the shock speed transitions $x_\mathrm{t}$. Fitting was performed using weighted nonlinear least squares regression with the weighting set in a manner to incorporate the non-uniform sampling rate and measurement uncertainties. Specifically, the weighting of the ith point was given by $w_i = \left( \chi _i/\epsilon _i\right) ^2$ such that $\chi _i$ accounts for the non-uniform sampling and $\epsilon _i$ accounts for differing measurement uncertainties. $\chi _i$ is the physical length which is nearest the ith data point (in the trivial case of spatially uniform sampling, $\chi _i$ would be constant and equal to the physical distance separating each sample). $\epsilon _i$ is related to the location and time uncertainties of the ith point $e_{{x,}i}$ and $e_{{t,}i}$ by

$$\begin{aligned} \epsilon _i&= e_{{x,}i} + e_{{t,}i}U_{\mathrm {theory}}. \end{aligned}$$

(3)

$U_{\mathrm {theory}}$ equals the Chapman–Jouguet detonation speed $U_{\mathrm {CJ}}$ for measurements of the detonation and the calculated shock speed required to stagnate the flow behind a CJ detonation $U_{\mathrm {R,CJ}}$ calculated as described in [2] for measurements of the reflected shock. Note that ideally the true speeds would be used to relate the uncertainties in time to corresponding uncertainties in position, however using the fit speeds could not be done directly since the speeds were themselves an output of the fit and performing the fit iteratively had negligible effect on the overall results. The 95% confidence intervals on the fit outputs were used to examine fit uncertainties. Note that this is a different procedure for determining the wave speeds than has been performed in the previous work (e.g., [24]) in order to more completely account for the non-uniform measurements and the different degrees of uncertainties.

Fig. 7

Schlieren images of incident detonation and reflected shock wave for shots a 2164, b 2161, and c 2170. The initial mixture was stoichiometric hydrogen–oxygen with 50% argon dilution at fill pressure 10, 25, and 50 kPa, respectively

4 Discussion

4.1 Detonation and reflected shock wave behavior

Before examining the wave speeds in detail, it is enlightening to use the data to inspect the qualitative behavior of the incident detonation and reflected shock waves. Figures 7 and 8 show images from six detonations, and five of the 16 total frames are included for each experiment. A complete set of images is given in [20]. Figure 7 contains hydrogen–oxygen detonations with 50% argon dilution at fill pressures of 10, 25, and 50 kPa . In these mixtures, we see a nearly planar detonation front propagating toward the wall (frame 1) and a nearly planar reflected shock exiting (frames 2–5). Although the three-dimensional structures of the detonation waves are partially concealed in these images due to the schlieren integration through the width of the test section, the transverse waves behind the detonations are still visible. These waves appear as horizontal stripes across the images. These transverse waves propagate behind the detonation with speeds in the lab-frame that are affected by the local fluid motion. After the reflected shock wave passes through the transverse waves, the mean lateral fluid velocity is zero, and therefore we observe the motion of the transverse waves freeze and slowly dissipate. This effect is particularly visible in the 25 and 50 kPa fill pressure cases shown in Fig. 7b, c. Figure 8 shows the effect of carbon dioxide dilution on the incident detonation and reflected shock waves. Carbon dioxide dilution produces an irregular detonation structure [25] as is visible in these images. In cases such as these, it was especially important to consider the finite rise times in determining an axial wave location.

Fig. 8

Schlieren images of incident detonation and reflected shock wave for shots a 2168, b 2158, and c 2181. The initial mixture was stoichiometric hydrogen–oxygen with 33% carbon dioxide dilution at fill pressure 10, 25, and 50 kPa, respectively

Although it is not the focus of this report, it is of interest to note that the reflected shock wave did not bifurcate in any experiment performed. The strong thermal boundary layer present behind the detonation inhibits bifurcation by increasing the reflected shock Mach number in the boundary layer. The increase in Mach number serves to increase the stagnation pressure in the boundary layer in the reflected shock-fixed frame; this stagnation pressure increase prevents flow separation and, in turn, bifurcation.

Fig. 9

Pressure measurements for shot 2162. The initial composition was stoichiometric hydrogen–oxygen with 80% argon dilution at fill pressure 25 kPa

Fig. 10

Pressure measurements for shot 2166. The initial composition was stoichiometric hydrogen–oxygen with 80% argon dilution at fill pressure 10 kPa

Figure 9 shows pressure measurements taken during shot 2162. As in the experiments shown in Fig. 4, the flammable mixture was at fill pressure 25 kPa, but the mixture was stoichiometric hydrogen–oxygen with 80% argon dilution. The detonation cell size is increased by adding a diluent and lowering the pressure [26, 27]. The pressure signals look similar to the data for shots 2152 and 2179 shown above. The primary differences were slower wave speeds and a lower frequency content as caused by the larger cell size. As the transverse waves behind the detonation front impinge upon the side-walls, they create pressure spikes. When the cell size is larger, the transverse waves impinge on the side-wall less frequently. This effect is exaggerated when the cell size is further increased, as seen in Fig. 10, which shows shot 2166 with the fill pressure lowered to 10 kPa.

4.2 Wave speeds

Using the method outlined in Sect. 3, wave speeds were determined for each initial condition given in Table 1. Next, we compare the speeds from the experimental measurements to theoretical speeds for the detonation and reflected shock.

Fig. 11

Measured detonation speed compared to the theoretical CJ detonation speed. The dashed line corresponds to $U_{\mathrm {det}} = U_{\mathrm{CJ}}$

4.2.1 Detonation speeds

The detonation wave may be modeled by one-dimensional CJ theory which neglects the finite size of the reaction zone to predict the speed of the detonation. Table 1 gives the experimentally determined detonation speeds, $U_{\mathrm {det}}$, compared to the theoretical CJ detonation speed, $U_\mathrm {CJ}$, for every experiment performed; these data are also plotted in Fig. 11 with the case of $U_{\mathrm {det}} = U_\mathrm {CJ}$ included for reference. The CJ detonation speeds were calculated using the Shock and Detonation Toolbox [2] with the GRI30 chemical mechanism [23].

We observe the experimental measurements are overall in good alignment with CJ theory. The only experiments with deviations above 5% are shots 2168 and 2189 with relative differences of the CJ speeds to the measured speeds of 7.3 and 10.2%, respectively. The source of these discrepancies is the large irregular cellular structure caused by low pressure (in the case of shot 2168) and carbon dioxide dilution (shots 2168 and 2189); this structure is poorly approximated by a one-dimensional model. Hence, moderate differences exist between the measured detonation speed and the Chapman–Jouguet theory in these cases. Generally, the measured detonation speed is extremely close to the theoretical CJ speed corroborating extensive previous detonation research wherein the CJ theory accurately predicted global properties, such as the average detonation speed (see, for example, [25]).

4.2.2 Reflected shock speeds

Analyzing the location-time data of the reflected shock wave revealed that the shock did not propagate at a constant speed for the 300 mm proximate to the end-wall. This behavior may be observed in Fig. 12 where the same location-time data shown in Fig. 6 are plotted with the addition of the piecewise continuous linear fit to the wave arrival data using the fit speeds $U_{\mathrm {det}}$, $U_{\mathrm {rs,w}}$, and $U_{\mathrm {rs,\infty }}$ given in Tables 1 and 2. For this particular shot, we see the wall speed was 38% faster than the speed far from the wall.

Fig. 12

x-t Diagram showing detonation and shock arrivals for representative shot 2152 with initial composition of stoichiometric hydrogen–oxygen at fill pressure 25 kPa. The detonation is modeled with constant speed, $U_{\mathrm {det}}$, and the reflected shock is modeled as having constant speeds $U_{\mathrm {rs,w}}$ for $x<x_\mathrm{t}$ and $U_{\mathrm {rs,\infty }}$ for $x>x_\mathrm{t}$

Additional wave arrival data with associated fits are included in Fig. 13a, b for shots 2163 and 2180, respectively. The measured reflected shock wave speeds for all experiments performed determined from the bilinear fit are tabulated in Table 2 and compared to the idealized value $U_{\mathrm {R,CJ}}$ in Fig. 14. Large uncertainties in the near-wall shock speed are found in shots 2186 and 2188. In the case of shot 2186, images were recorded at 5 times the frame rate of other experiments recording an image every 360 ns; the small overall distance traveled by the reflected shock wave during when images were recorded resulted in the large uncertainty. Shot 2188 predicted a transition location within 5 mm of the end-wall in which only a few data points could be applied to determine the speed; this resulted in the large uncertainty and implies that the two-speed effect observed in other experiments was not pronounced in this experiment. Referencing Fig. 14, we see that the far-field speed, $U_{\mathrm {rs,\infty }}$, is closely approximated by $U_{\mathrm {R,CJ}}$ with the 10 and 25 kPa initial pressures H$_2$–O$_2$ experiments (shots 2163 and 2152, respectively) being possible exceptions with absolute relative differences in excess of 10%.¹ Conversely, the speed near the wall, $U_{\mathrm {rs,w}}$, is greater than $U_{\mathrm {R,CJ}}$ in every experiment performed. This suggests the reflecting CJ detonation model is lacking a fundamental element of the gasdynamics of detonation reflection near the location of reflection. In order to explain the origin of the discrepancy between the measured reflected shock speed at the wall and the speed expected from a reflecting CJ detonation, we examined the assumptions inherent to the model. Three possible sources were considered that may be affecting the speed of the reflected shock: (1) the TZ expansion, (2) multi-dimensional effects, and (3) the chemical induction zone. Each of these possibilities is addressed below.

• 1. The TZ expansion creates an unsteady flow field behind the detonation that will affect the speed of the reflected shock as it propagates through the expansion wave. This effect is included in Fig. 1. Given the 7.6 m detonation tube length, we did not expect the TZ expansion to substantially influence the shock in the observed region, but we include the analysis here for completeness. To quantify the effect of the TZ wave on the reflected shock, [1] developed a semi-empirical model wherein it is assumed that no spatial gradient exists in fluid velocity or thermodynamic properties between the reflected shock and the reflecting end-wall. With this assumption, it is only necessary to determine the pressure at the end-wall as a function of time to calculate the speed and strength of the reflected shock. The pressure ratio across the shock wave at the time of reflection is calculated using the method described above, and the final pressure is the pressure in state 3. An exponential decay in pressure is then assumed with a time constant fit to experimental data. The predicted pressures from this model are plotted in Fig. 15 alongside pressure measurements for shots 2152 and 2179. We observe that incorporating the TZ expansion into the reflecting CJ detonation model still results in the reflected shock speed being under predicted near the end-wall, even when we consider the experimental uncertainties. Therefore, we conclude that the TZ expansion is not the source of the discrepancy in the reflected wave speed.

• 2. The flow field predicted using CJ theory combined with the TZ wave (such as shown in Fig. 1) is one-dimensional and does not consider multi-dimensional effects. In approaching this problem, we initially hypothesized that the reflected wave may be interacting with the boundary layer induced by the flow behind the incident detonation to create a bifurcated foot analogous to experiments performed in shock tubes (e.g., [10]). Such a foot would precede the main front of the reflected wave and make the apparent speed of the shock faster when measured at the wall than in the center of the channel. However, as noted above, in no experiment was bifurcation of the reflected wave observed in the schlieren images.

  Alternatively, the cellular detonation structure was a second potential source of introducing multi-dimensional effects into the reflected shock wave. The detonation cellular structure is clearly visible in the schlieren images (see Fig. 7), but does not appear to have a systematic effect on the reflected wave. Therefore, we conclude that the one-dimensional flow assumption is not the cause of the discrepancy in the reflected wave speed.

• 3. The finite size of the chemical induction zone in the detonation is neglected in CJ theory. Here, we consider the effect of relaxing this assumption to allow for a reflecting detonation with a finite-length reaction zone. An idealized version of the reaction zone is the ZND model in which a one-dimensional region of chemical reaction exists behind a planar non-reactive shock wave. The shocked gas will continuously react as it passes through the reaction zone; a further idealization is to consider the reaction zone to have a definite extent and consist of an induction zone of shocked but unreacted gas followed by an extremely short region of rapid reaction. The scenario of this idealized detonation impinging upon an end-wall is shown in Fig. 16 with Fig. 16a showing the profile of the incident detonation propagating toward the wall. When the detonation impinges upon the end-wall, the reflected shock will first pass through this unreacted induction zone creating an overdriven detonation as shown in Fig. 16b; the reaction zone is consumed in time $\Delta /\left( U_\mathrm {rs}^*+U_\mathrm {CJ}\right) \sim 1$ $\upmu$s, this transient is too short-lived to resolve $U_\mathrm {rs}^*$ in the experiments presented herein. The state when the reflected shock precisely reaches the end of the reaction zone is sketched in Fig. 16c. After the reaction zone is consumed, the shock wave continues to propagate into gas at the CJ state as shown in Fig. 16d. A contact surface separates the gas processed by the overdriven detonation from the gas processed in the incident detonation. This layer of high-pressure gas begins to expand into the gas at state 7 creating an expansion wave that propagates toward the end-wall. The expansion fan reflects from the end-wall and chases the shock wave causing it to decay as shown in Fig. 16e.

Table 2 Measured reflected shock speeds at the wall ($U_{\mathrm {rs},\mathrm{w}}$) and in the far field ($U_{\mathrm {rs,\infty }}$) compared to the theoretical reflected Chapman–Jouguet speed ($U_{\mathrm {R,CJ}}$)

Fig. 13

x-t diagram showing detonation and shock arrivals for shots a 2163 and b 2180 with initial composition of stoichiometric hydrogen–oxygen at fill pressure 10 and 50 kPa, respectively. The detonation is modeled with constant speed, $U_{\mathrm {det}}$, and the reflected shock is modeled as having constant speeds $U_{\mathrm {rs,w}}$ for $x<x_\mathrm{t}$ and $U_{\mathrm {rs,\infty }}$ for $x>x_\mathrm{t}$

The final situation considered is when the gas between the reflected shock and the end-wall has equilibrated in pressure to create a region of stationary gas between the shock and the end-wall; this is shown in Fig. 16f. Figure 17 shows the same physical process as Fig. 16 in the format of a space–time diagram. As illustrated, following the detonation front impinging on the end-wall there is an overdriven detonation propagating back toward the point of ignition. This produces a reflected shock wave that is initially driven by the reaction zone explosion, but eventually decays to the equilibrium reflected shock speed. Additional details and computed thermodynamic conditions for a representative case are included in the Appendix.

Fig. 14

Measured reflected shock speed at the wall $U_{\mathrm {rs,w}}$, and in the far field $U_{\mathrm {rs,\infty }}$, compared to the idealized reflected shock speed $U_{\mathrm {R,CJ}}$. The dashed black line corresponds to $U_{\mathrm {measured}} = U_\mathrm {R,CJ}$

Fig. 15

Pressure measurements for shots 2152 and 2179 compared to a one-dimensional infinitesimal-length reaction zone pressure model that incorporates the TZ expansion. The initial composition was stoichiometric hydrogen–oxygen at fill pressure 25 kPa

Fig. 16

Simplified model of the fluid mechanics present in a reflecting detonation with finite-length reaction zone of width $\Delta$. As sketched, for times soon after reflection, the reflecting wave is an overdriven detonation

Fig. 17

Space–time diagram of the simplified reflecting detonation model with finite-length reaction zone. The transition region where the reflected expansion wave catches the reflected shock is condensed in the blank region of the schematic to allow greater detail of the reaction zone

The net effect of the overdriven detonation propagating through the induction zone is to create a region of high pressure which generates a one-dimensional planar blast wave. This initially accelerates the shock away from the end-wall, and then the blast wave begins to decay once the reactants have been consumed and the expansion wave catches the shock front. The speed and decay of the reflected shock near the wall are a function of the pressure in state 5 and the unsteady gasdynamics associated with the interaction of the blast wave with the expansions ahead of and behind the wave. A quantitative predictor of the near-wall reflected shock behavior is not possible with our simplified model, and numerical simulations will be needed to make quantitative predictions. By analyzing the interaction process shown in Fig. 16d, we are able to determine the initial value of $U_\mathrm {rs}$. Correlating the predicted speed $U_\mathrm {rs}$ with the measured speeds $U_\mathrm {rs,w}$, we find a correlation coefficient of 0.80; this correlation improves to 0.84 if the two experiments with a greater than 10% uncertainty in the fit $U_\mathrm {rs,w}$ values (shots 2186 and 2188) are removed. However, these idealized values of $U_\mathrm {rs}$ are approximately a factor of 2 higher than the measured wave speeds $U_\mathrm {rs,w}$. We believe that this difference is due to the small dimensions of the high-pressure region leading to the rapid deceleration which we are unable to resolve with our experimental technique, and the considerable simplification inherent to the square-wave detonation model.

A further refinement of this model would be to carry out numerical simulations of the reflection process using a model reaction mechanism and the associated ZND structure behind a propagating wave, similar to the results of [28] for obliquely reflecting detonations. The results of such simulations will depend strongly on the extent of the reaction zone compared to the time for observations with non-equilibrium effects being most observable for reaction times that are long compared to the time between observations. Just as in the Mach reflection case, we anticipate a reactive and frozen regime in agreement with the present observations. We also expect that the time-dependent decay of the initial blast wave should scale with the induction time behind the incident wave, similar to the results of [28] for the scaling of Mach stem height trajectories for the obliquely incident waves. From an experimental point of view, using the detonation cell width as a scaling parameter rather than induction time is in line with previous efforts in scaling detonation behavior. An alternative scaling would be to use the detonation hydrodynamic thickness discussed by [29]. In comparing the present results to the hydrodynamic thickness, the relevant distance is the transition location in the detonation-fixed frame of reference. The span of time $t'_\mathrm{t}$ between the detonation wave arriving at the transition location $x_\mathrm{t}$ and the reflected shock wave returning to the same location may be calculated using the detonation speed $U_{\mathrm {det}}$ and the speed of the reflected shock near the wall $U_{\mathrm {rs,w}}$:

$$\begin{aligned} t'_\mathrm{t}&= \frac{x_\mathrm{t}}{U_{\mathrm {det}}} + \frac{x_\mathrm{t}}{U_{\mathrm {rs,w}}}. \end{aligned}$$

(4)

Using this time, we calculate a detonation-fixed transition location $x'_\mathrm {t}$ from

$$\begin{aligned} x'_\mathrm{t}&= t'_\mathrm{t}U_{\mathrm {det}} = x_\mathrm{t}\left( 1 + \frac{U_{\mathrm {det}}}{U_{\mathrm {rs,w}}}\right) . \end{aligned}$$

(5)

This value is reported in Table 2 using the measured wave speeds, but comparing the transition location to the hydrodynamic thickness was not performed in the present work. Note that although the existence of an abrupt transition location is assumed in the analysis in order to model the apparent wave behavior, this behavior is likely an artifact of the measurement point sparsity. We did not carry out sufficient experiments to test any of these scaling ideas with statistical reliability; the variation in reaction zone length or cell size was quite modest except for the highly unstable cases.

Sufficiently far from the wall, $x>x_\mathrm{t}$, the reflected wave speed approaches the ideal value predicted by the infinitesimal-length reaction zone model. As shown in Table 2 and Fig. 14, the difference between measured and calculated speeds has a mean absolute difference of 5.0% for the cases considered. The largest discrepancies were observed in shots 2163 and 2152.

Another way to interpret the effect of the finite reaction zone on the reflection process is that it results in an offset of the reflected wave location for $x>x_\mathrm{t}$. The offset distance, $x_{\mathrm {off}}$, can be calculated from the transition distance $x_\mathrm{t}$ and the speed of the shock at the wall and far field:

$$\begin{aligned} x_{\mathrm {off}}&= x_\mathrm{t} \left( 1 - \frac{U_{\mathrm {rs,\infty }}}{U_{\mathrm {rs,w}}}\right) . \end{aligned}$$

(6)

Using values given in Table 2, we see that the scale of $x_{\mathrm {off}}$ is one to two orders of magnitude larger than the lengths of the reaction zone that created this offset.²

5 Conclusions

Pressure data and high-speed schlieren images were used together with a regression analysis to quantify the wave speed of incident gaseous detonation waves and the reflected shock waves created when the detonation normally impinged upon an end-wall. The incident detonation wave speeds agree with CJ theory within 4% for the majority of cases. The speed of the reflected shock was observed to change in the 100 mm nearest the end-wall with the speed at the end-wall being substantially faster than expected from a reflecting CJ detonation using the idealized model [4] which neglects the presence of a finite-length reaction zone. After examining various possibilities, we propose that the finite extent of the reaction zone of the detonation wave plays an essential role in accounting for our observations.

Considering the reaction zone structure, we observe that the reflection of the leading shock front will result in an overdriven detonation and very high pressure region near the end-wall. The interaction of the overdriven detonation with the end of the reaction zone and the expansion of the high-pressure near-wall region creates a blast wave with a high-speed close to the wall. The blast wave is followed by an expansion wave resulting in the decay of the wave speed as the wave propagates away from the wall. This theory was qualitatively consistent with the measured wave speeds, but the simplified nature of the model makes it impractical to analytically predict the near-wall wave speeds. After the reflected shock wave passes through the reaction zone and sufficiently far from the end-wall, the speed decays to the values predicted when the finite-length reaction zone is not considered. The net far-field effect of the increased speed through the reaction zone is to displace the reflected shock wave from the location predicted by the idealized model that does not consider reaction zone structure. The maximum calculated offset distance was 26.9 mm.

We expect that these results are applicable to the experiments described in [6] and explain the inconsistency they noted between the experimental observations of the reflected wave and the idealized model neglecting the reaction zone length.

Appendix: Computation of reflected detonations

The computation of reflected shock waves into an idealized detonation reaction zone relies on the usual principles of applying mass, momentum, and energy conservation across the incident and reflected waves. To accomplish this while taking into account realistic thermodynamic properties of reacting mixtures, we performed the computation using the Shock and Detonation Toolbox [2].

The first step is to compute the Chapman–Jouguet (CJ) state in order to obtain the incident detonation speed $U_\mathrm {CJ}$ for each mixture. Next, we consider the idealized model of a “square-wave” detonation structure which consists of a leading shock wave moving at speed $U_\mathrm {S}$ = $U_\mathrm {CJ}$ followed by an induction zone of high-pressure and high-temperature reactants which is terminated by rapid energy release zone followed by combustion products at chemical equilibrium. The thermodynamic state within the induction zone is assumed to be the “von Neumann” (VN) state obtained by computing the post-shock conditions assuming a “frozen”, i.e., unreactive, composition across the leading shock wave. As discussed in the main text, when the leading shock front reflects from the end-wall of the detonation test section, the temperature and pressure behind the reflected wave are so high that combustion reactions are initiated and proceed to completion immediately and can be treated as being in chemical equilibrium. The reflected wave is therefore a type of detonation propagating into the shocked but unreacted gas within the induction zone.

Fig. 18

Reflection of the leading shock wave into reaction zone of incident detonation

Table 3 Results of reflected detonation interaction computations for shot number 2152

Referring to Fig. 18 for the state definitions, the conservation relations that apply across the reflected detonation wave propagating into the induction zone are:

$$\begin{aligned}&\rho _\mathrm {VN}(U^*_\mathrm {rs}+u_\mathrm {VN}) = \rho _{5} U^*_\mathrm {rs} \end{aligned}$$

(7)

$$\begin{aligned}&P_\mathrm {VN} + \rho _\mathrm {VN}(U^*_\mathrm {rs}+u_\mathrm {VN})^2 = P_{5} + \rho _{5}U^{*2}_\mathrm {rs} \end{aligned}$$

(8)

$$\begin{aligned}&h_\mathrm {VN} + \dfrac{1}{2}(U^*_\mathrm {rs}+u_\mathrm {VN})^2 = h_{5} + \dfrac{1}{2}U^{*2}_\mathrm {rs}. \end{aligned}$$

(9)

where state VN is the post-shock state behind the incident detonation and state 5 is the detonation product state behind the reflected wave moving at speed $U_\mathrm {rs}^*$. The composition of state VN is that of reactants and for state 5, equilibrium products. In formulating the conservation relations, we have set the flow speed (in the laboratory frame) equal to zero consistent with the boundary condition at the end-wall of the detonation test section $u_{5} = 0$. We are making the further assumption that the region between the end-wall and reflected wave is uniform and subsonic. Although not obvious, this will turn out to be the case due to the combination of the high-speed flow $u_\mathrm {VN}$ of reactants into the wave and the zero flow speed behind, resulting in the reflected wave being a highly overdriven detonation wave in order to satisfy these boundary conditions.

An example of the results of this computation as well as the wave speeds is given in Table 3 for case 2152, a stoichiometric mixture of H$_2$ and O$_2$.