Mach reflection of a ZND detonation wave

Abstract

The Mach reflection of a ZND detonation wave on a wedge is investigated numerically. A two-step chain-branching reaction model is used giving a thermally neutral induction zone followed by a chemical reaction zone for the detonation wave. The presence of a finite reaction zone thickness renders the Mach reflection process non-self-similar. The variation of the height of the Mach stem with distance of propagation does not correspond to a straight curve from the wedge apex as governed by self-similar three-shock theory. However, the present results indicate that in the near field around the wedge apex, and in the far field where the reaction zone thickness is small compared to the distance of travel of the Mach stem, the behavior appears to be self-similar. This corresponds to the so-called frozen and equilibrium limit pointed out by Hornung and Sanderman for strong discontinuity shock waves and by Shepherd et al. for cellular detonations. The critical wedge angle for the transition from regular to Mach reflection is found to correspond to the value determined by self-similar three-shock theory, but not by reactive three-shock theory for a discontinuous detonation front.

1 Introduction

The study of Mach reflection of detonation waves from a wedge has been carried out by many investigators in the past few decades [1–10]. Similar to shock waves, the wave configuration of a Mach reflection of a detonation wave consists of an incident detonation wave, an overdriven reactive Mach stem and a reflected shock intersecting at the triple point. In the case of a shock wave, there is no characteristic length scale in the problem as the shock thickness is in general vanishingly small. This results in the Mach reflection of a shock wave being self-similar and the trajectory of the triple point to be a straight line from the wedge apex [11–13]. On the other hand, a detonation front has a finite thickness which is not negligible. Hence, Mach reflection of a detonation wave is not self-similar, but may become self-similar when the distance of propagation is large compared to the detonation front thickness. Note that besides the above two cases of Mach reflection, there could exist other configurations which agree with all conservation laws and thermodynamics. Vysk and Smirnov [14] reported a case where a plane incident shock wave reflected from a solid wall in a detonating gas mixture. They found a formation of a triple-wave configuration with a reflected detonation wave and a Mach stem in the form of a shock wave in this case. However, in the present study, we are not concerned with this special case.

In the previous studies of Ong [2], Meltzer et al. [5], Akbar [15], Li et al. [4], the thickness of the detonation fronts (incident wave and Mach stem) were assumed to be negligible, and the detonation front was treated as a discontinuity across which the reactive jump conditions can be applied. The reflected wave is still treated as a non-reactive shock. Without a characteristic length scale, the reactive three-shock theory was applied to determine the triple-point trajectory angle as well as the critical wedge angle for the transition from Mach to regular reflection. However, results based on treating the detonation front as a discontinuity are not in agreement with experimental observations in general.

The presence of a characteristic length scale on the Mach reflection of a shock wave has been investigated by Ben-Dor and Takayama [16–18] and Lau-Chapdelaine and Radulescu [19]. In their studies, the characteristic length scale arises from the geometry of the wedge. In Ben-Dor and Takayama’s work, a double wedge was considered and the length of the first wedge presented a length scale to the problem. In the study of Lau-Chapdelaine and Radulescu, the characteristic length scale is the radius of curvature introduced at the tip of the wedge. These investigators found that the presence of a characteristic length scale renders the Mach reflection non-self-similar. However, the Mach reflection approaches self-similarity asymptotically when the geometrical length scale becomes insignificant as compared to the distance traveled by the Mach stem. Ben-Dor and Takayama [16] also reported that Mach reflection of the shock wave over the second surface of the double wedge approaches one that would have been obtained by the same shock wave reflecting over a single wedge. This suggests that the Mach reflection process tends to “forget” certain aspects of the initial conditions in the far field. On the other hand, they also found that the critical wedge angle for the transition from regular reflection to Mach reflection was changed due to the initial non-similar nature of the propagation. The critical wedge angle was found to increase for a concave double wedge, but to decrease for a convex double wedge. For a shock of $M=6.6$ and $\gamma =1.2$, Lau-Chapdelaine and Radulescu [19] also found that the critical wedge angle was increased by about $13^{\circ }$ for an initially curved wedge with a certain radius of curvature compared to a sharp abrupt straight wedge. The influence of a length scale on the critical wedge angle suggests that the asymptotic self-similar behavior retains some information of the initial non self-similar process.

A characteristic length scale can also arise from the physical and chemical processes in the shock front. For strong shock waves where ionization and dissociation occur, the thickness of the shock front may not be negligible due to the finite rate of the relaxation. Sandeman et al. [20] demonstrated that self-similarity was lost due to the presence of a relaxation length at the shock front. However, Hornung et al. [21] reported that self-similarity can be still obtained in two limiting cases: when the relaxation length is very small or very large as compared to the distance of shock propagation. These two limits are referred to as the equilibrium and frozen limits, respectively. When the relaxation zone is very small, equilibrium is reached immediately behind the shock and this corresponds to a negligible shock thickness. When the relaxation zone is very large, the shocked state is essentially frozen and a characteristic length is also absent.

Shepherd et al. [22] and Akbar [15] discussed the Mach reflection of detonation waves according to the two limits mentioned by Hornung et al. [21] and Sandeman et al. [20]. The characteristic length scale of the detonation front can be the reaction zone thickness $\Delta$ of a ZND detonation wave (or the cell size $\lambda$ for the case of a cellular detonation). For the ZND detonation, one can speak of a frozen state in the thermally neutral induction zone behind the shock prior to the onset of chemical reaction. However, for a cellular detonation it is no longer possible to separate frozen and equilibrium states, since the cellular structure is three dimensional and transient. In spite of this, an overall length scale for the cellular detonation of the order of a cell length can still be defined.

Recent studies [23–25] also discussed the Mach reflection of a ZND detonation numerically. Mach et al. [23] and Radulescu et al. [24] addressed the mechanism of new cell formation in irregular structure detonations by studying the reflection of the ZND detonation wave on a wedge and the bifurcation phenomenon of the Mach stem front. Ziegler et al. [25] conducted some high-resolution numerical simulations of the Mach reflection of a ZND detonation wave. The detailed structures near the triple point of a Mach reflection can be clearly observed in the numerical results. However, they did not focus on the self-similarity problem and the effect of detonation thickness on Mach reflection of the ZND detonation wave.

The breakdown of self-similarity due to finite thickness of the detonation wave was not taken into consideration in many of the previous studies on Mach reflection of detonation waves, and three-shock theory was generally used to determine the triple-point trajectory and the critical wedge angle. Comparisons of the experimental observation with the three-shock theory showed poor agreement in general. Two-dimensional numerical simulations of Mach reflection of cellular detonation waves have also been carried out by a number of investigators [6, 8]. Apart from reproducing some qualitative features of the Mach reflection, such as an overdriven Mach stem where the cell size is small, little information was obtained on the detailed complex processes of the interactions of the transverse waves of cellular instability with the reflected shock and the shear layer at the triple point of the Mach reflection. The past numerical simulation of Trotsyuk [26] also indicates that there can exist a relaxation region before the overdriven Mach stem is established.

The present paper investigates the effect of the finite thickness of a detonation front on the Mach reflection phenomenon. A planar ZND detonation wave is considered rather than a cellular detonation. It is felt that a simple two-dimensional detonation structure would permit the effect of a finite length scale on the breakdown of self-similarity to be investigated in more detail. In particular, the asymptotic approach to self-similarity in the far field, when the distance traveled is large compared to the detonation thickness, can also be examined.

2 Problem formulations and numerical methodology

2.1 Problem definition

The governing equations used to simulate the inviscid, two-dimensional propagation of a detonation wave are the two-dimensional reactive Euler equations. All flow variables are dimensionalized with respect to the unburned mixture states ahead of the detonation front as follows:

$$\begin{aligned} \rho =\frac{\tilde{\rho }}{\tilde{\rho }_o}, p=\frac{\tilde{p}}{\tilde{p}_o}, T=\frac{\tilde{T}}{\gamma \tilde{T}_o}, u=\frac{\tilde{u}}{\sqrt{R \tilde{T}_o}}, v=\frac{\tilde{v}}{\sqrt{R \tilde{T}_o}}, \end{aligned}$$

(1)

where the symbol ( $\tilde{}$ ) denotes dimensional quantities and subscript ($o$) indicates quantities ahead of the detonation front. The variables $\rho$, $u$, $v$, $p$ and $T$ are the density, velocity in $x$-direction, velocity in $y$-direction, pressure and temperature, respectively. $R$ is the universal gas constant and $\gamma$ is the specific heat ratio.

The non-dimensionalized two-dimensional reactive Euler equations have the following form:

$$\begin{aligned}&\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y} =0 \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial (\rho u)}{\partial t}+\frac{\partial (\rho u^2 +p)}{\partial x}+\frac{\partial (\rho uv)}{\partial y} =0 \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial (\rho v)}{\partial t}+\frac{\partial (\rho uv )}{\partial x}+\frac{\partial (\rho v^2 +p)}{\partial y} =0\end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial E}{\partial t}+\frac{\partial ((E+p)u)}{\partial x}+\frac{\partial ((E+p)u)}{\partial y} =0. \end{aligned}$$

(5)

The total energy $E$ per unit volume is given by

$$\begin{aligned} E=\frac{p}{\gamma -1}+ \frac{\rho (u^2+v^2)}{2}-q, \end{aligned}$$

(6)

where $q$ is the local heat release per unit volume (non-dimensionalized with $R \tilde{T}_o$) and a perfect gas equation of state is used, i.e.,

$$\begin{aligned} p=\rho T \end{aligned}$$

(7)

The physical coordinates $x$ and $y$ are both non-dimensionalized with the induction length $\Delta _\mathrm{I}$.

The above reactive Euler equations are coupled with a two-step chain-branching reaction model as in [27]. The first step represents a thermally neutral induction zone, with a temperature-sensitive Arrhenius form of the reaction rate given by:

$$\begin{aligned}&\frac{\partial (\rho y_1)}{\partial t}+ \frac{\partial (\rho u y_1)}{\partial x}+\frac{\partial (\rho v y_1)}{\partial y} \nonumber \\&\quad = H(1-y_1)\rho k_\mathrm{I} \exp {\bigg (E_\mathrm{I} \bigg (\frac{1}{T_\mathrm{S}}-\frac{1}{T} \bigg ) \bigg )}, \end{aligned}$$

(8)

where $k_\mathrm{I}$, $E_\mathrm{I}$ and $T_\mathrm{S}$ are the induction rate constant, the activation energy for the induction period and the temperature jump across the leading shock, respectively. $y_1$ is the reaction progress variable in the induction period and $H(1-y_1)$ is a step function which can be defined as

$$\begin{aligned} H(1-y_1)= \left\{ \begin{array}{ll} 1 \,\,\,\,\mathrm{if}\,\, y_1<1\\ 0 \,\,\,\,\mathrm{if}\,\, y_1\ge 1 \\ \end{array}\right. \end{aligned}$$

(9)

Here, the reference length scale $x_\mathrm{ref}$ is chosen such that the one-dimensional ZND detonation induction length is unity (i.e., $k_\mathrm{I}=-u_{vn}$). $u_{vn}$ is the particle velocity behind the shock front in the shock-fixed frame for the CJ detonation. The reference time scale is therefore set to the reference length scale divided by the initial sound speed of the reactant (i.e., $t_{\mathrm{ref}}=\frac{x_{\mathrm{ref}}}{c_0}$). At the end of induction period, the second step describes the rapid energy release after the branched-chain thermal explosion and the slow heat release in the radical recombination stage. The reaction rate equation for this step is given by:

$$\begin{aligned}&\frac{\partial (\rho y_2)}{\partial t}+ \frac{\partial (\rho u y_2)}{\partial x}+\frac{\partial (\rho v y_2)}{\partial y} \nonumber \\&\quad = (1-H(1-y_1))\rho k_\mathrm{R} (1-y_2) \exp \left( {\frac{E_\mathrm{R}}{T}} \right) , \end{aligned}$$

(10)

where $k_\mathrm{R}$ and $E_\mathrm{R}$ denote the chain-recombination reaction rate constant and activation energy for the heat release process. $y_2$ is the chemical reaction progress variable. Similar to the previous study [27], the reaction rate constant $k_\mathrm{R}$ is used as a parameter to control the ratio of the reaction length to the induction length. Consistent with the previous study, we also introduce dimensionless activation energies:

$$\begin{aligned} \varepsilon _\mathrm{I}= \frac{E_\mathrm{I}}{T_\mathrm{S}}, \quad \varepsilon _\mathrm{R}= \frac{E_\mathrm{R}}{T_\mathrm{S}}. \end{aligned}$$

(11)

Since the present study only limits itself to stable ZND detonations, a very low activation energy $\varepsilon _\mathrm{I}$ is chosen for the numerical simulation to suppress cellular instability (i.e., $\varepsilon _\mathrm{I}=0.1, \varepsilon _\mathrm{R}=1.0$).

Fig. 1

Structure of a ZND detonation wave

The ZND detonation structure based on the present two-step chain-branching reaction model is illustrated in Fig. 1. The induction zone width $\Delta _\mathrm{I}$ is controlled by the induction rate constant $k_\mathrm{I}$, and the reaction rate constant $k_\mathrm{R}$ determines the width of reaction zone $\Delta _\mathrm{R}$. In the present study, we keep the induction zone width constant and vary the reaction zone width to obtain different overall thicknesses of the detonation front, $\Delta =\Delta _\mathrm{I} + \Delta _\mathrm{R}$.

To define the reaction zone width, we choose

$$\begin{aligned} \Delta _\mathrm{R}=\frac{u_\mathrm{CJ}}{\dot{\sigma }_\mathrm{max}}, \end{aligned}$$

(12)

where $u_\mathrm{CJ}$ is the particle velocity at the CJ plane in shock-fixed coordinates. The thermicity $\dot{\sigma }$ denotes the normalized chemical energy release rate and has a dimension of 1/time. Hence, the inverse of maximum thermicity $\dot{\sigma }_\mathrm{max}$ can be taken as a characteristic time scale for the heat release. For the present two-step chemical reaction model of ideal gases with constant specific heat ratio, the thermicity is expressed as [28]:

$$\begin{aligned} \dot{\sigma }_\mathrm{max}=(\gamma -1)\frac{Q}{c^2}\frac{\mathrm{d}y_2}{\mathrm{d}t}. \end{aligned}$$

(13)

Figure 2 shows the definition of the overall detonation thickness $\Delta$ considered in the present two-step chain-branching reaction model.

Fig. 2

Definition of the overall detonation thickness $\Delta$

2.2 Numerical methods

The unsteady two-dimensional reactive Euler equations are solved numerically using a fifth-order high-resolution weighted essentially non-oscillatory (WENO) finite difference scheme and a third-order TVD Runge–Kutta scheme [29]. In the present work, a parallel calculation technique is also adopted for saving computation time. The wedge boundary is implemented using the embedded boundary [30]. This permits the use of a Cartesian grid where the boundary geometry is mapped. The boundary is defined as a level-set function. Slip solid wall boundary conditions are imposed on the upper and the bottom boundary and the wedge surface as well. Inlet and outlet boundary conditions are also imposed on the left and right boundary, respectively. The initial conditions are given by placing stable ZND detonation waves with different reaction thicknesses (changing from $1.5\Delta _\mathrm{I}$ to $20\Delta _\mathrm{I}$) upstream of the wedge.

In the present study, a constant isentropic exponent of $\gamma =1.44$ and an incident detonation Mach number of $M=6.5$ are used throughout all simulations. The wedge angle is $\theta _w=30^{\circ }$ except in Sect. 3.2.3 where the wedge angle varies around $50^{\circ }$ to determine the critical wedge angle between regular and Mach reflection. The wedge length can be up to 400 $\Delta$.

To obtain a non-reactive shock wave, the simplest way is to just reduce the induction rate constant $k_\mathrm{R}$ to obtain a very large induction zone. The induction zone is thermally neutral and the ZND detonation corresponds in essence to a non-reactive shock. Thus the isentropic exponent $\gamma$ and the Mach number $M$ of the shock wave are essentially the same as that for detonation waves.

2.3 Grid resolution study

To test the convergence of the results in the present study, different resolutions were considered for the Mach reflection of ZND detonations on a wedge of $30^{\circ }$. Sharpe [13] claimed that more than 20 points per half reaction zone length are required to ensure convergence in the simulation of a cellular detonation with a second-order Godunov scheme and a one-step reaction model. The sufficient resolution depends on not only the numerical schemes applied, but also on the phenomenon studied.

Figure 3 shows the density gradient of the Mach reflection in the case of ZND detonations at the same position. The results for resolutions of 20, 10, 5 and 2 Pts/$\Delta _\mathrm{I}$ are shown. It can be observed that there is a convergence of the features of the flow field as the resolution increases. Similar resolution convergence can also be seen in Fig. 4 which shows the triple-point trajectory of Mach reflection. For 10 Pts/$\Delta _\mathrm{I}$, the triple-point trajectory is in good agreement with that for the higher resolution of 20 Pts/$\Delta _\mathrm{I}$.

Fig. 3

Schlieren plots of the density gradient for different grid resolutions

Fig. 4

Triple-point trajectory of Mach reflection in the case of ZND detonation waves for different grid resolutions

Hence, considering the high accuracy of numerical schemes and that we do not need to resolve the cellular detonation wave, a fixed numerical resolution of ten points per induction zone length is used to ensure that the detailed features of the ZND detonation wave are properly resolved.

3 Numerical results and discussions

3.1 Shock reflection

It is of interest to first consider the Mach reflection of a shock wave to serve as a reference. This also serves to indicate the accuracy of the present numerical scheme. Figure 5a shows four positions of the shock wave as it propagates up a wedge of $30^{\circ }$. Note that the Mach stem is not straight, but slightly convex due to the “piston effect” of the wall jet. The triple points at different instants were found to give a straight trajectory, as would be the case if the Mach reflection was self-similar. Although there is always a “numerical thickness” associated with the shock front, this is vanishingly small to be of consequence.

Fig. 5

Mach reflection of a shock wave. a Density gradient; b pressure distribution behind the Mach stem along the wedge surface

The triple-point trajectory angle obtained from the numerical simulation for a $30^{\circ }$ wedge is $9.8^{\circ }$ and is about $2^{\circ }$ higher than the theoretical value of $7.8^{\circ }$ using von Neumann three-shock theory. A possible reason for this difference is that the Mach stem is assumed to be straight according to the three-shock theory, whereas a convex Mach stem is obtained in the numerical simulation (Fig. 5a). Ben-Dor [11] pointed out that this assumption could result in under-prediction of the triple-point trajectory angle by 1–$3^{\circ }$.

The pressure distribution behind the Mach stem is shown in Fig. 5b. The contours of pressure and density of the Mach reflection at position 3 in Fig. 5a are illustrated in Fig. 6. As shown in Fig. 5b, the pressure along the wedge surface increases behind the Mach stem (from $a$ to $b$). Inside the region of the vortex structure of the wall jet, the pressure drops as shown in Fig. 5 (behind b). There is a local pressure peak at point $c,$ just behind the wall jet. Further back from the complex flow field of the wall jet region, the pressure gradually increases to a peak value at the tip of the wedge. Hornung [12] pointed out that the pressure to the left of the slip line must be higher than the pressure to the right, since the slip line curves forward toward the Mach stem. The higher pressure is analogous to the stagnation point flow in the pseudo-steady frame of reference of the triple point.

Fig. 6

Pressure and density contours for Mach reflection of the shock wave

As can be observed in Fig. 5b, the amplitude of the Mach stem remains constant as the Mach stem propagates along the wedge. Regarding the strength of the Mach stem, von Neumann three-shock theory predicts a pressure ratio of $\frac{p_1}{p_0}=60$. This is slightly lower than the value obtained from the present numerical simulation of $\frac{p_1}{p_0}=63$.

3.2 Mach reflection of ZND detonation wave

3.2.1 Reactive Mach stem

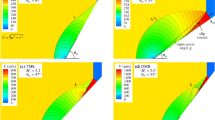
The Mach reflection of a planar ZND detonation wave with a reaction zone thickness $\Delta =7.96$ propagating on a wedge of $30^{\circ }$ is shown in Fig. 7. Compared to the Mach stem structure of the shock wave with the same shock Mach number (Fig. 5a), it is observed that the Mach stem is now slightly concave instead of being convex. In addition, the slip line does not seem to curve rapidly toward the Mach stem as in the case of a shock wave, but approaches the wedge surface gradually far behind the Mach stem. Thus there is no wall jet for the case of Mach reflection of a ZND detonation wave. However, for very early times near the apex of the wedge (Fig. 8), a wall jet curling toward the Mach stem can still be observed. In Fig. 8, a finer resolution of 50 points per $\Delta _I$ is used (instead of the normal resolution of 10 points per $\Delta _I$) to reveal the detailed structure of the reactive Mach stem. The evolution of the slip layer observed in Figs. 7, 8 suggests that the Mach reflection of the ZND detonation wave is not pseudo-steady and self-similar as in the case of the shock wave where the shape of the shear layer does not change and its length grows linearly with time.

Fig. 7

Mach reflection of a ZND detonation wave

Fig. 8

Mach reflection configuration of a ZND detonation wave at the early time near the wedge tip

Enlarged sketches of the detailed structure of the Mach stem are shown in Fig. 7 for various positions along the wedge. It can be observed that the Mach stem structure does not change significantly with time. In a previous study of the reactive Mach stem by Strehlow [31], he defined two types of Mach stem structures, a weak and a strong one. The results obtained in the present numerical simulation appear to correspond to the weak reactive Mach stem structure of Strehlow (Fig. 9a). The difference between the two types of the reactive Mach stem defined by Strehlow is that for the weak one, the reflected wave is straight within the induction zone, whereas for the strong one the reflected wave within the induction zone is kinked and there exists a second triple point with respect the first one ahead of it. Since only a very stable ZND detonation wave is considered in the present study, no strong reactive Mach stem structure is observed.

Fig. 9

Two types of reactive Mach stem by Strehlow [31]. I incident wave, M Mach stem, R reflected wave, SS Slip stream

3.2.2 Triple-point trajectory

The triple-point trajectory of the Mach reflection of a ZND detonation wave is illustrated in Fig. 10. The Mach stem height is defined as the vertical distance from the triple point to the wedge surface since the Mach stem is curved. The Mach stem travel is the distance measured from the wedge tip to the Mach stem along the wedge surface.

Fig. 10

Triple-point trajectory of a ZND detonation wave. Dashed line triple-point trajectory for non-reactive shock; dotted line triple-point trajectory for discontinuous detonation front; solid line triple-point trajectory for ZND detonation wave

The triple-point trajectory of a shock wave with the same shock Mach number from three-shock theory is shown in Fig. 10 for comparison. It can be observed that the overall triple-point trajectory of the ZND detonation wave is not a straight line; hence the Mach reflection process is not self-similar. However near the tip of the wedge, the initial triple-point trajectory seems to coincide with that of the non-reactive shock wave. This is because in the initial process near the wedge tip, the thermally neutral induction zone dominates and the Mach reflection tends toward that of a non-reactive shock. However, when the detonation has traveled some distance away from the wedge tip, the effect of the length scale due to the reaction zone thickness becomes important and the triple-point trajectory deviates from that of a shock wave. The triple-point trajectory is observed to asymptotically approach a straight line with a slope corresponding to that of the triple-point trajectory calculated from the reactive three-shock theory for a discontinuous detonation front. This indicates the Mach reflection process becomes self-similar asymptotically when the detonation thickness $\Delta$ becomes small compared to the distance traveled by the Mach stem $L$ (i.e., $L\gg \Delta$). Between the initial and the final self-similar behavior is a non-self-similar region of propagation. The length of the non-self-similar region would depend on the overall detonation thickness $\Delta$.

The pressure behind the Mach stem of the ZND detonation wave at the wall for different times is shown in Fig. 11. The strength of the Mach stem is found to decay with time as it propagates away from the wedge tip, but eventually approaches asymptotically a constant value. This differs from the Mach reflection of a shock wave where the strength of the Mach stem remains constant throughout as the shock is propagating away from the wedge tip. The asymptotic amplitude of the Mach stem is found to be higher than the V–N pressure of the incident C–J detonation wave. Thus, the Mach stem corresponds to an overdriven detonation wave.

Fig. 11

Pressure profile of the Mach stem at different times

We define the degree of overdrive of the reactive Mach stem, $f=\frac{M_{s}}{M_{i}}$ (where $M_{s}$ and $M_{i}$ represent the Mach number of the Mach stem and incident detonation wave, respectively). The reactive three-shock theory gives a degree of overdrive of $f=1.2$ (for a $30^{\circ }$ wedge). Meanwhile, the Mach reflection of the shock wave from the non-reactive three-shock theory gives a value of $f=1.28$ for the Mach stem for the same wedge.

In the present numerical simulations, the degree of overdrive of the Mach stem is not available directly in the form of Mach number ratio. However, it is easy to obtain the V–N pressure ratio of Mach stem to incident wave from Fig. 11. Thus, we can rewrite the degree of overdrive, $f=\frac{M_{s}}{M_{i}}=\sqrt{\frac{p_{vns}}{p_{vni}}}$ ( where $p_{vns}$ and $p_{vni}$ represent the V–N pressures of Mach stem and incident wave, respectively). From the numerical simulation, the degree of overdrive is found to be 1.3 initially near the apex of the wedge and to have a value of $f=1.19$ in the far field, when the Mach stem has propagated a long distance from the apex. The numerical results agree well with the values from the non-reactive and reactive three-shock theories. This is in accord with the frozen limit and equilibrium limit as discussed by Shepherd and Akbar [10, 15].

In Fig. 12, the Mach stem height versus the distance traveled by the Mach stem for different detonation thicknesses $\Delta$ are shown. Note that the distance of the Mach stem travel and the Mach stem height are both non-dimensionalized with respect to the detonation thickness $\Delta$. Comparisons are made with triple-point trajectories predicted by self-similar non-reactive and reactive three-shock theories, respectively. It can be observed that the triple-point trajectories asymptotically approach a straight line when the detonation thickness $\Delta$ is small compared to the distance of Mach stem travel $L$.

Fig. 12

Triple-point trajectory of the ZND detonation wave with different reaction thickness $\Delta$. Dashed line triple-point trajectory for non-reactive shock, dotted line triple-point trajectory for discontinuous detonation front

As shown in Fig. 13, the transition length $L_\mathrm{tr}$ increases as the detonation thickness $\Delta$ increases. A reason for this is that for a detonation wave with larger characteristic length scale, more distance is required to allow the characteristic length scale to become “small” as compared to the distance traveled by the Mach stem. However, as shown in Fig. 13, the scaled transition length $\frac{L_\mathrm{tr}}{\Delta }$ is found to decrease as the detonation thickness $\Delta$ increases.

Fig. 13

Variation of the transition length with $\Delta$

Note that in the present numerical simulation, as discussed in Sect. 2, different detonation thicknesses $\Delta _\mathrm{R}$ are obtained by changing the chemical reaction rate, but keeping the induction rate constant and with $\Delta =\Delta _\mathrm{I}+\Delta _\mathrm{R}$. This allows to model detonation waves with the same induction zone thickness $\Delta _\mathrm{I},$ but different chemical reaction thickness $\Delta _\mathrm{R}$. Thus, there exist two characteristic length scales, $\Delta _\mathrm{R}$ and $\Delta _\mathrm{I}$, within the detonation front. Scaling the transition length with the characteristic length scale $\Delta$ means eliminating its effect on the Mach reflection process. However, the effect of the other characteristic length scale $\Delta _\mathrm{I}$ can still influence the Mach reflection process. That is why the scaled transition length $\frac{L_\mathrm{tr}}{\Delta }$ is found to decrease as the detonation thickness $\Delta$ increases in Fig. 13.

3.2.3 Critical wedge angle

The critical wedge angle for a shock wave ($M$=6.5, $\gamma =1.44$) from the numerical simulation is found to be between $\theta _w=50^{\circ }$ and $\theta _w=51^{\circ }$ in Fig. 14 where a Mach reflection is observed at $\theta _w=50^{\circ }$ and a regular reflection is observed when $\theta _w=51^{\circ }$. Thus, in this case the critical wedge angle is $\theta _{w,\mathrm{crit}}=50.5^{\circ }\pm 0.5^{\circ }$. This critical wedge angle is almost identical to the one predicted by the non-reactive three-shock theory of $50^{\circ }$.

Fig. 14

Reflection of a shock wave at a $\theta _w=50^{\circ }$ and b $\theta _w=51^{\circ }$

The numerical results for the Mach reflections of the ZND detonation wave are shown in Fig. 15. The transition wedge angle was found to be as in the case of a shock wave. Furthermore, the critical wedge angle is found to be not sensitive to the reaction zone thickness of the detonation wave. However, the critical wedge angle predicted by the reactive three-shock theory is found to be only about $35^{\circ },$ which is about $15^{\circ }$ lower than the result from the present numerical simulation of $50.5^{\circ }\pm 0.5^{\circ }$.

Fig. 15

Reflection of a ZND detonation wave at a $\theta _w=50^{\circ }$ and b $\theta _w=51^{\circ }$

This suggests that for the Mach reflection of a ZND detonation wave, the critical wedge angle is determined by the non-reactive three-shock theory rather than the reactive three-shock theory. In previous experimental studies, the critical wedge angle is observed to be 6–10$^{\circ }$ higher than the predicted value by applying the reactive three-shock theory [5], but close to the frozen limit of the shock. This is probably because the critical wedge angle depends only on the thermally neutral induction zone which is essentially a frozen shock front. Hornung [12] pointed out in his study that the transition from regular to Mach reflection occurs when the flow behind the reflected shock is subsonic with respect to the reflection point of a regular reflection. This transition criterion can be applied to the case of ZND detonation wave. Since for the regular reflection of a ZND detonation wave, the flow in the thermally neutral induction zone before and behind the reflected shock is supersonic, the chemical reaction zone and the flow state far behind it cannot influence the induction zone and the transition.

4 Conclusion

In this paper, the problem of Mach reflection of a ZND detonation wave using a two-step chain-branching reaction model has been investigated. The present study shows that the overall Mach reflection process of a ZND detonation wave is not self-similar due to the presence of a characteristic length scale presented by the reaction thickness $\Delta$. However, from the triple-point trajectory, it appears that at the early times near the wedge tip, the Mach reflection corresponds to that of a shock which agrees with the frozen limit. In the far field, the Mach reflection approaches self-similarity in accordance with the equilibrium limit. From the degree of overdrive of the Mach stem, the present numerical results also indicate the existence of the two limits of frozen and equilibrium.

The critical wedge angle of the transition from regular reflection to Mach reflection is found to be the same as that in the case of a shock and can be predicted by the non-reactive rather than the reactive three-shock theory assuming a discontinuous detonation front. This result is consistent with some previous experimental studies [3, 10], even though a cellular detonation was investigated. This is probably because the critical wedge angle depends only on the thermally neutral induction zone which is essentially a frozen shock front.

The present study is based on a planar ZND detonation wave. In reality, cellular instability occurs at the detonation front and the structure is more complicated. The finding of the present study may therefore be invalid for cellular detonations.