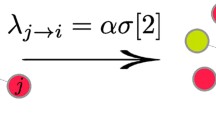Strategic diffusion in networks through contagion

Abstract

This paper studies the diffusion of products and behaviour with coordination effects through social networks when agents are myopic best responders. We develop a new network measure, the contagion threshold, that determines when a p-dominant action—an action that is a best response when adopted by at least proportion p of an agent’s opponents—spreads to the whole population starting from a group of players whose size is smaller than half and independent of the population size. We show that a p-dominant action spreads to the whole network whenever the contagion threshold of that network is greater or equal to p. We then show that in settings where agents regularly or occasionally experiment and choose non-optimal actions, there exists a threshold level of experimentation below which a p-dominant action is chosen with the highest probability in the long run. This result implies that targeted contagion, a network-wide diffusion of actions initiated by targeting agents, is justified even in settings where agents’ decisions are noisy.

1 Introduction

The adoption of new products and behaviour through social influence is a well-documented phenomenon.¹ This phenomenon provides a justification for targeted contagion, a process by which a firm initiates a cascading adoption of a product from a relatively small group (compared to the population size) of consumers, called initial adopters, to the whole population. The feasibility of targeted contagion depends on the structure of interactions and payoffs, and the behavioural assumptions that underlie individual decision processes.²

This paper studies how the interaction structure and payoffs interactively determine the feasibility of targeted contagion of products and behaviour with coordination effects (i.e. where individuals benefit from coordinating their activities by making the same decisions).³ The existing literature in this topic focuses on examining contagion in unbounded networks (Morris 2000; Oyama and Takahashi 2015). However, most social interactions are best described by finite networks, and most of the simplifying assumptions that are applicable to contagion dynamics in unbounded networks do not hold for finite networks.⁴ Moreover, the literature does not address the question of whether targeted contagion is economically reasonable in settings where individuals regularly or occasionally experiment with their choices (see for example McKelvey and Palfrey (1995), Anderson et al. (2001) and Ellison (2006) for evidence of noisy decision making). In such settings, targeted contagion is economically reasonable if the level of experimentation does not prevent actions from spreading through contagion. To address these gaps in the literature, we examine the following two questions: For a diffusion process on networks where agents are best responders and payoffs exhibit coordination effects, which actions are contagious and when is contagion feasible? In situations where individuals experiment with their choices, when is it economically reasonable to engage in targeted contagion?

To address these questions, we consider two related evolutionary game models. In Model 1, evolution with best response, we consider a diffusion process where agents, who are myopic best responders, interact through a finite network and revise their actions over time (Morris 2000; Oyama and Takahashi 2015). Here, myopia means that agents choose best responses to the most recent actions taken by their network neighbours. It captures the notion of bounded rationality; that is, in the real world, individuals have short memories and do not worry about the long-run consequences of their actions (Egidi et al. 1992).

In Model 2, evolution with best response and mutations, we consider a diffusion process where agents follow the structural and behavioural assumptions of Model 1, but in addition, they regularly or occasionally make mistakes and choose actions that are not best responses (Young 1993; Ellison 2000). Individual mistakes are either due to deliberate experimentation where agents try-out new actions (possibly because of lack of complete information about the game), or due to random errors in action implementation leading agents to choose unintended actions.

We use Model 1 to examine which actions (of a coordination game) are contagious and when contagion is feasible, and Model 2 to examine when targeted contagion is economically reasonable in settings where agents’ decisions are noisy. Formally, an action is contagious on a finite network if: (i) it can spread from a small group of initial adopters, whose size is less than half and independent of the population size, to the whole population; (ii) it is uninvadable – it can spread from a strictly smaller group (of initial adopters) than is needed to leave a state where it is adopted by the whole population. In Model 2, individual mistakes ensure that every configuration of actions is played with a positive probability at any period. We define the long-run equilibrium of this model as the configuration of actions that is played with the highest probability in the long run. Targeted contagion is then said to be economically reasonable if the contagious action in Model 1 is also the long-run equilibrium of Model 2 (i.e. if the long-run equilibrium is a configuration containing only the contagious action).

We develop a new network measure – the contagion threshold – that determines when contagion is feasible in finite networks. Let a_j be the p-dominant action/strategy of a coordination game (i.e. a strategy that is a best response when played by at least proportion p of an agent’s neighbours). The contagion threshold of a finite network is the maximum value of p such that action a_j spreads contagiously in that network starting from the second-neighbourhood (i.e. the set of all agents within two steps away from a given agent, with that agent included) of any agent. This definition is similar to the definition of the contagion threshold for unbounded networks and 2 × 2 coordination games in Morris (2000) — the contagion threshold of an unbounded network is the maximum p such that a_j spreads contagiously from a finite group of agents. The difference arises because for contagion dynamics in finite networks, it is necessary to have knowledge of the size and identity of the initial adopters that trigger the contagious spread of a p-dominant action.

We show, for Model 1, that a p-dominant action of a coordination game, if it exists, is contagious on any sufficiently large and strongly connected network (i.e. a network where every pair of agents is connected through some path) with the contagion threshold greater or equal to p. The set of initial adopters that trigger the contagious spread of a p-dominant action corresponds to the smallest second-neighbourhood of the network. The smallest second-neighbourhood of any network is independent of the population size and it can be as small as three agents. More generally, the smallest second-neighbourhood is smaller for networks with a lower density of connections.⁵ This result suggests that the cost of targeted contagion, measured as the number of initial adopters that trigger the contagious spread of a p-dominant action, is lower for sparsely connected than highly connected networks. We discuss this and other implications of these results in more detail in Section 3.

For Model 2, we show that there exists a threshold level of noise below which targeted contagion is economically reasonable. Specifically, below the threshold level of noise, a configuration containing only a p-dominant action is the unique long-run equilibrium in a strongly connected network with the contagion threshold greater or equal to p. Above the threshold level of noise, noisy dynamics becomes more prominent relative to best response dynamics, which makes contagion a less relevant means of spreading an action to the whole population. Targeting therefore becomes economically unreasonable because targeted agents will ultimately switch to other actions through experimentation.

This paper is closely related to the literature that examines how the network structure affects the contagious spread of actions that exhibit coordination effects (Morris 2000; Alós-Ferrer and Weidenholzer 2008; Oyama and Takahashi 2015).⁶ Morris (2000) shows that, for best response dynamics on unbounded networks, a p-dominant strategy of a 2 × 2 coordination game is contagious if p is less or equal to the contagion threshold. Alós-Ferrer and Weidenholzer (2008) consider a model of imitation dynamics and show that, with some restrictions on the information structure, a Pareto-dominant equilibrium of a 2 × 2 coordination game is contagious on any network that is strongly connected. Oyama and Takahashi (2015) consider a model of best response dynamics on unbounded networks and show that either a risk-dominant or a Pareto-dominant strategy is contagious in the presence of a third dominated strategy. Like Oyama and Takahashi (2015), we generalize the analysis in Morris (2000) to multiple strategy coordination games. However, Oyama and Takahashi (2015), focus on two types of networks – linear and non-linear networks – so that a strategy is contagious if it can spread contagiously in either of these two networks. Our analysis is richer in that we establish the conditions under which a strategy is contagious on any given network. A more fundamental difference between our analysis and Morris (2000) and Oyama and Takahashi (2015) is that we examine contagion in finite networks and provide steps for computing the smallest number of initial adopters needed to trigger contagion.

Our analysis and results from Model 2 are related to the literature on stochastic evolutionary game dynamics in networks (Ellison 1993, 2000; Blume 1995; Berninghaus and Schwalbe 1996; Young 1998; Lee and Valentinyi 2000; Lee et al. 2003; Alós-Ferrer and Weidenholzer 2007; Peski 2010; Opolot 2018, 2020). Except for Peski (2010) and Opolot (2018, 2020), these papers focus on identifying the stochastically stable states (i.e. states that are played with a positive probability at the limit of noise) by considering specific network structures, such as a ring and 2-dimensional grid networks. Peski (2010) considers a model of evolution with best response and mutations and shows that a p-dominant strategy is uniquely stochastically stable in networks with the smallest odd degree k₀ (i.e. the size of the smallest odd first-order neighbourhood) satisfying the condition $p\leq \frac {1}{2}(1-1/k_{0})$. Following the same framework, Opolot (2018) shows that a p-best response set (i.e. a subset of strategies of a coordination game that are best responses when adopted by at least proportion p of an agent’s neighbours) is uniquely stochastically stable in any strongly connected network with the contagion threshold greater or equal to p; and Opolot (2020) generalizes these results by establishing the conditions under which the smallest iterated p-best response set is uniquely stochastically stable. In contrast, we establish the conditions under which a p-dominant strategy is not only stochastically stable, but also played with the highest probability in evolutionary models with high noise levels. We then use this result as a justification for targeted contagion in diffusion environments where agents’ decisions are not strictly optimal.

The remainder of the paper is organized as follows. In Section 2, we introduce Model 1 and Model 2. Section 3 derives our main results on contagion. In Section 4 we derive the main results of Model 2 and discuss their implications for targeted contagion. Sections 5 and Appendix A offer concluding remarks and the implications of our results for the speed of learning respectively. All lengthy proofs are contained in the Appendix.

2 The model

2.1 Network, actions and payoffs

We model the diffusion of strategies (representing actions or products) of a coordination game in social networks using an evolutionary game theory framework. We consider a finite set of players, N = {1, ⋯ , i, ⋯ , n}, connected through a social network represented by a graph G(N, E), where E is the set of edges connecting players in N. Let G be an n × n interaction matrix representing all connections in G(N, E), where G_ik = 1 if a link exists from i to k, and zero otherwise. We place the following restrictions on G:

• (i) G is undirected and unweighted, that is, either G_ik = G_ki = 1, or G_ik = G_ki = 0.

• (ii) G is strongly connected, that is, for every pair of agents i, k ∈ N, there exists a path of (undirected) links from i to k.

Both restrictions are simplifications that ensure that the evolutionary process (described below) converges. Directed and/or non-strongly connected networks can lead to cyclic interactions and/or isolated nodes, which inhibits convergence. Let N_i be the set of direct neighbours of i, that is, N_i = {k∣G_ik = 1}; and let n_i be the cardinality of N_i, also commonly referred in the social networks literature as the degree of i.

Every player plays a coordination game with each neighbor. A coordination game consists of a set of strategies, A = {a₁, ⋯ , a_j, ⋯ , a_m}, which we assume to be identical for all players, and an m × m payoff matrix, U. Let u(a_j, a_l) be the payoff of playing strategy a_j against an opponent playing strategy a_l. The double, (A, U), is a coordination game if for each a_j ∈ A, u(a_j, a_j) ≥ u(a_l, a_j) for all a_l≠a_j. We focus on strict symmetric coordination games where u(a_j, a_l), for all a_j, a_l ∈ A, is identical for all players, and for each a_j ∈ A, u(a_j, a_j) > u(a_l, a_j) for all a_l≠a_j.

Let Σ be the set of all mixed strategies over A so that, for any σ ∈ Σ, σ(a_j) is the mass that σ places on a_j. For player i, we write σ_i = (σ_i(a₁), ⋯ , σ_i(a_m)) for the distribution over A representing the proportion of i’s neighbours playing each pure strategy. We consider linear payoffs where the total payoff that i receives from playing strategy a_j against σ_i is

$$ U_{i}(a_{j}\mid \sigma_{i})= \underset{a_{l}\in A}{\sum}\sigma_{i}(a_{l})u(a_{j}, a_{l}). $$

(1)

We refer to the quadruple (A, U, N, G) as a local interaction symmetric coordination game.

2.2 Behaviour and dynamics

Given the local interaction symmetric coordination game (A, U, N, G), we consider an evolutionary process where players simultaneously and independently revise their strategies at discrete times t = 1, 2, ⋯ . This evolutionary process suitably models the diffusion of products where agents can replace the old, spoilt or no longer preferred products with new ones of the same type/brand, or with different competing products. We consider two related evolutionary models that capture realistic behavioural assumptions about how people react to observed behaviour:

• (i) Model 1: evolution with best response, where players choose strategies that are best responses to the strategy profile of their direct neighbours.

• (ii) Model 2: evolution with best response and mutations (BRM), where, in addition to the best response behaviour of Model 1, players make mistakes with a positive probability and choose strategies that are not best responses. Individual mistakes can be thought of as deliberate experimentation with new strategies (i.e. trying-out new strategies possibly due to lack of complete information about the game), or random errors in strategy implementation leading a player to choose an unintended strategy.

As customary in the literature of evolutionary game theory, we assume that players are myopic best responders. That is, at every period, t, each player chooses a strategy that is a best response to the distribution of strategies in her neighbourhood at period t − 1. The assumption of myopia captures the notion that, in the real world, individuals have short memories and are incapable of keeping track of the entire history of play, and that they do not worry about the long run consequences of their strategy choices (Egidi et al. 1992).

To formalize these ideas, let lowercase bold letters (e.g. x, y, z,⋯) denote vectors representing profiles (configurations) of strategies. Let xⁱ (i.e. the i th element of configuration x) be the strategy that player i ∈ N plays in configuration x. Given the local interaction symmetric coordination game (A, U, N, G), we write X for the set of all possible strategy configurations. The cardinality of X is mⁿ, where m is the number of strategies. Let σ_i(a_l; x) be the proportion of i’s neighbours playing a_l in configuration x, and let σ_i(x) = (σ_i(a₁; x), ⋯ , σ_i(a_m; x)) be the distribution over A representing the proportion of i’s neighbours playing each strategy under configuration x. Let x_t be the strategy configuration at period t. Then, following (1), the payoff to i for playing strategy a_j against distribution σ_i(x_t) is $U_{i}(a_{j},\mathbf {x}_{t})= {\sum }_{a_{l}\in A}\sigma _{i}(a_{l};\mathbf {x}_{t})u(a_{j}, a_{l})$. The set of strategies that are best responses to σ_i(x_t) is defined as

$$ BR_{i}(\mathbf{x}_{t}) = \left\{a_{j}: U_{i}(a_{j},\mathbf{x}_{t})\geq U_{i}(a_{l},\mathbf{x}_{t}), \forall a_{l}\neq a_{j}\right\} $$

Associated with each BR_i(x_t) is BR_i(a_j; x_t), which is the probability that i chooses a_j through best response given configuration x_t. The following assumption places structure on these probabilities.

Assumption 1

For any x ∈ X, if the cardinality of BR_i(x) is greater than one for some i ∈ N, then there exists some tie-breaking rule where BR_i(a_j; x) = 1 for some a_j ∈ BR_i(x) and BR_i(a_l; x) = 0 for all other a_l ∈ BR_i(x) and a_l≠a_j.

Assumption 1 implies that whenever a player is indifferent between two or more strategies, some tie-breaking rule ensures that only one of the strategies is played with probability one. This assumption is a simplification that, although not necessary for Model 1, is used to derive the equilibrium conditions for Model 2.⁷

A tie-breaking rule in the context of Assumption 1 means that, when indifferent between a set of strategies, a player chooses one strategy among this set based on some strategy characteristics. There are several examples of tie-breaking rules that satisfy the conditions in Assumption 1. First, we could let players choose a strategy within BR_i(x) that is also contained in configuration x and is played by the highest proportion of neighbours: that is, given configuration x and the respective distribution σ_i(x), player i plays a strategy a_j ∈ BR_i(x) for which σ_i(a_j; x) > σ_i(a_l; x) for all a_l ∈ BR_i(x)∖a_j.

Second, we can let players choose some strategy in BR_i(x) that dominates other strategies within BR_i(x) under some criteria. For example, we can choose pairwise domination where a_j ∈ BR_i(x) is chosen over a_l ∈ BR_i(x) if its average payoff is higher than for a_l whenever it is played by at least half of neighbours and the rest play a_l: that is, a_j ∈ BR_i(x) is chosen over a_l ∈ BR_i(x) if U_i(a_j, σ) > U_i(a_l, σ) for all σ with $\sigma (a_{j})\geq \frac {1}{2}$ and σ(a_l) = 1 − σ(a_j). Such a relationship between any pair of strategies is called pairwise risk-dominance (i.e. a_j is pairwise risk-dominant relative to a_l). Thus, a player chooses a_j from BR_i(x) if it is pairwise risk-dominant relative to all other strategies in BR_i(x). Overall, to generate the conditions in Assumption 1, we can apply one or a combination of tie-breaking rules.

Model 1::

Given the above definitions and assumptions, the probability that configuration x is followed by configuration y at period t + 1, denoted by P(x, y), is given by

$$ P(\mathbf{x}, \mathbf{y})=\prod\limits_{i=1}^{n} BR_{i}\left( y^{i}; \mathbf{x}_{t} = \mathbf{x}\right) $$

(2)

where the product on the right hand side of Eq. 2 follows because players revise strategies simultaneously and independently.

Model 2::

The probability, $\mathbb {P}_{i}(a_{j}; \mathbf {x}_{t})$, that player i chooses a_j (in period t + 1) given configuration x_t, is

$$ \mathbb{P}_{i}(a_{j}; \mathbf{x}_{t}) = \frac{1}{m}\exp(-\beta) + (1-\exp(-\beta))BR_{i}(a_{j}; \mathbf{x}_{t}) $$

(3)

The first term on the right hand side of Eq. 3, $\frac {1}{m}\exp (-\beta )$, captures individual choices due to mistakes/mutations, and the second term captures best response dynamics. Specifically, a player follows a best response behaviour with probability $(1-\exp (-\beta ))$, and with probability $\exp (-\beta )$, a player mutates and randomly picks any strategy (i.e. with a uniform probability $\frac {1}{m}$).

A closer examination of Eq. 3 reveals that as β increases to infinity, players choose best responses with higher probability, and as β tends to zero, players’ choices become more random. The exact value of β may depend on the interaction environment, and may also vary across players. For the former, our analysis examines the effects of varying β on equilibrium behaviour. However, for simplicity, we assume that β is identical across players.

Analogously to Eq. 2, the probability, P_β(x, y), that configuration x is followed by configuration y in Model 2 is given by

$$ P_{\beta}(\mathbf{x}, \mathbf{y})= \prod\limits_{i=1}^{n}\mathbb{P}_{i}\left( y^{i}; \mathbf{x}_{t} = \mathbf{x}\right) $$

(4)

The dynamics defined by the transition probabilities in Eqs. 2 and 4 both follow a stationary Markov chain on the configuration space X. Let P and P_β denote the respective Markov transition matrices with P(x, y) and P_β(x, y) as typical elements of P and P_β respectively. We refer to (A, U, N, G, P) and (A, U, N, G, P_β) as the best response diffusion process and best response with mutation diffusion process corresponding to Model 1 and Model 2 respectively. Given these two models, we seek to:

• (i) use Model 1 to establish conditions under which contagion occurs on a given network;

• (ii) establish conditions under which targeting is economically reasonable in a framework where agents experiment with their choices.

2.3 Equilibrium behaviour

The equilibrium behaviour of Model 1 is represented by its limit (absorbing) sets. A subset $L\subseteq \mathbf {X}$ of states (strategy configurations) is an absorbing set of a Markov chain if, once entered, is never exited. If an absorbing set is a singleton set, then it is called an absorbing state or a convention; that is, any state x ∈ X for which P(x, x) = 1 is an absorbing state. If an absorbing set contains more than one state, then it is referred to as an absorbing cycle. For example, a pair of states x and y form an absorbing cycle if P(x, y) = 1 and P(y, x) = 1.

Let L be a set of all absorbing sets (i.e. all absorbing states and absorbing cycles) of P. The composition of L depends on the payoff and network structures. Since (A, U) is a strict symmetric coordination game, L consists of all monomorphic configuration (i.e. where all players coordinate on the same strategy). But depending on the network structure, L may also contain absorbing cycles and configurations where strategies co-exist. For each a_l ∈ A, we write a_l for the monomorphic absorbing configuration where all players coordinate on a_l. Associated with each L ⊂L is the basin of attraction, D(L), which is the set of all configurations from which (A, U, N, G, P) converges to L.

For Model 1, the contagion analysis involves examining the stability of monomorphic absorbing configurations (i.e. examining the costs, measured in terms of the number of mutations, of reaching and leaving monomorphic absorbing configurations) to determine which configuration contains a contagious strategy. In doing so, we also establish the conditions under which contagion is feasible.

For Model 2, the presence of mutations ensures that every strategy configuration is visited multiple times in the long run. That is, unlike Model 1 where (A, U, N, G, P) eventually settles in some absorbing set, in Model 2, each configuration is reached with a positive probability at any given time. The a suitable measure of equilibrium behaviour in Model 2 is therefore the stationary distribution, denoted by π_β. The stationary distribution of a Markov chain, if it exists, describes the fractional amount of time the chain spends in each configuration in the long run, or equivalently, the probability with which each configuration is visited in the long run.

Formally, let q₀ be an mⁿ-row vector, where mⁿ is the size of the state space X of (A, U, N, G, P_β), representing an initial distribution of the Markov chain of Model 2. For example, if the chain starts from configuration x, then q₀ is a vector of all zeros except a one in configuration x. Since the transition matrix P_β is homogeneous (i.e. independent of time), the distribution of the Markov chain corresponding to (A, U, N, G, P_β) after t iterations is $\mathbf {q}_{t} = \mathbf {q}_{0}P_{\beta }^{t}$. The stationary distribution π_β is then an mⁿ-vector defined as $\pi _{\beta }=\lim _{t\rightarrow \infty }\mathbf {q}_{0}P_{\beta }^{t}$. This limit exists and is unique because the Markov chain associated with (A, U, N, G, P_β) is ergodic (i.e. (A, U, N, G, P_β) has a unique absorbing set since every configuration is visited with a positive probability).

Thus, for Model 2, we use the notion of long-run equilibrium, which is the set of strategy configurations that are visited most often in the long run by the Markov chain associated with (A, U, N, G, P_ε). Specifically, a subset L^∗⊂L is the long-run equilibrium of (A, U, N, G, P_β) if π_β(L^∗) ≥ π_β(L) for all $L\subseteq \mathbf {L}\backslash L^{*}$. Our definition of long-run equilibrium is more general than the notion of stochastic stability often used in evolutionary game models. A subset L^∗⊂L is stochastically stable if $\lim _{\beta \rightarrow \infty }\pi _{\beta }(L^{*})>0$. This implies that there exists a threshold value of β above which the long-run equilibria of (A, U, N, G, P_β) are stochastically stable. We show that this threshold value of β also corresponds to the value above which best response dynamics dominates noisy dynamics, so that targeting players is economically reasonable.

3 Diffusion through contagion

We aim to generalize the notion of contagion defined by Morris (2000) for 2 × 2 coordination games played on unbounded networks to multiple-strategy coordination games played on finite networks. For a 2 × 2 symmetric coordination game with strategies a_j and a_l played on an unbounded network, strategy a_l is contagious if: (i) starting from a strategy profile where all players play a_j, a_l spreads contagiously from a finite group of initial adopters; (ii) it is uninvadable – once a convention where all players play a_l is established, it should not be possible to leave it with a finite group of deviants. These concepts can be extended to multiple-strategy coordination games and finite networks through the following series of conceptual definitions.

Definition 1

A sequence of strategy profiles $\left \{\mathbf {x}_{t} \right \}_{t=0}^{\bar {t}}$ of (A, U, N, G, P), for some $\bar {t}\geq 2$, is a best response sequence if it satisfies the following properties: (i) for all $1\leq t<\bar {t}$, there exists at least one i ∈ N such that ${x_{t}^{i}}\neq x_{t-1}^{i}$; (ii) if ${x_{t}^{i}}\neq x_{t-1}^{i}$, then ${x_{t}^{i}}\in BR(\sigma _{i}(\mathbf {x}_{t-1}))$.⁸

Property (i) of Definition 1 requires that at least one player must switch a strategy at each period – this follows because we consider a dynamic process with a simultaneous revision protocol. Property (ii) requires players to switch strategies through best response dynamics.

Definition 2

Let (A, U, N, G, P) start from some a ∈ L∖a_l. Strategy a_l spreads contagiously from a subset of players, $N(\mathbf {a}\rightarrow \mathbf {a}_{l})\subset N$, if there exists some $\bar {t}\geq 2$ such that every best response sequence $\left \{\mathbf {x}_{t} \right \}_{t=0}^{\bar {t}}$ with x₀ = a and ${x_{1}^{i}}=a_{l}$ for all $i\in N(\mathbf {a}\rightarrow \mathbf {a}_{l})$ satisfies $x_{\bar {t}}^{i}=a_{l}$ for all i ∈ N.

Let $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ be the cardinality of $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$. According to Definition 2, when (A, U, N, G, P) starts from a, strategy a_l spreads contagiously from a subset of players, $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$, if it spreads to the whole network through best response. If $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$ is the smallest set from which a_l can spread contagiously, then we refer to it as the set of initial adopters of a_l needed to trigger a network-wide adoption of a_l starting from a.

Definition 3

A Strategy, a_l, spreads contagiously on network G if for every a ∈ L∖a_l, there exists some $N(\mathbf {a}\rightarrow \mathbf {a}_{l})\subset N$ with $n(\mathbf {a}\rightarrow \mathbf {a}_{l})<\frac {n}{2}$, and independent of n, such that a_l spreads contagiously from $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$.

For unbounded networks considered by Morris (2000) and Oyama and Takahashi (2015), it is sufficient to require $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ to be finite. However, for finite networks, an equivalent requirement is for $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ to be relatively small (i.e. less than half the population size) and independent of the population size. This implies that as n grows, $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ stays finite. One of the objectives of this paper is to define a network measure that determines when a strategy can spread contagiously on a given network. Once such a measure is defined, it is then possible to derive an upper bound for $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$, for all a ∈ L∖a_l.

Definition 4

Let r(a_l) be the number of mutations required to leave convention a_l. Convention a_l is uninvadable if, for every a ∈ L∖a_l, there exists a subset of initial adopters, $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$, such that $r(\mathbf {a}_{l})>n(\mathbf {a}\rightarrow \mathbf {a}_{l})$, and that r(a_l) is an increasing function of n.

Definition 4 ensures that once strategy a_l has spread contagiously to the whole network, convention a_l should not be easily replaced by another convention through a few mutations. The second condition for uninvadability in Definition 4, (i.e. r(a_l) must be an increasing function of n) ensures that as n grows, it becomes harder (i.e. many mutations are required) to leave convention a_l; and in unbounded networks, $\lim _{n\rightarrow \infty }r(\mathbf {a}_{l})=\infty$, so that it is not possible to leave a_l with a finite number of mutations.

Definition 5

Given a strict symmetric coordination game (A, U), strategy a_l is contagious on network G(N, E) if it spreads contagiously on G(N, E) and is uninvadable.

From Definition 5, we see that strategy a_l is contagious in a finite network if, for all a ∈ L∖a_l, $n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ is independent of the population size, n, and r(a_l) is an increasing function of n. As the population size becomes infinitely large, we then have an equivalent definition for contagion in unbounded networks where $\lim _{n\rightarrow \infty }n(\mathbf {a}\rightarrow \mathbf {a}_{l})<\infty$ and $\lim _{n\rightarrow \infty }r(\mathbf {a}_{l})=\infty$.

Given a network G and any subset of players S ⊂ N, let N_i(S) = N_i ∩ S be the set of i’s direct neighbours within G that belong to subgroup S. Let n_i(S) be the corresponding cardinality of N_i(S) and $\alpha _{i}(S) = \frac {n_{i}(S)}{n_{i}}$ be the proportion of i’s neighbours in S.

Now, let (A, U, N, G, P) start from some a ∈ L∖a_l. Then from Definitions 1 and 2, strategy a_l spreads contagiously from subgroup $N(\mathbf {a}\rightarrow \mathbf {a}_{l})$ if the following two conditions hold. First, a_l must be a p-dominant strategy, where, following Morris et al. (1995), a strategy is p-dominant if it is a best response to all distributions that place on it a mass of at least p. That is, for a strict symmetric coordination game (A, U), strategy a_l is (strictly) p-dominant if for all a_k ∈ A, and all σ ∈ Σ with σ(a_l) ≥ p,

$$ \underset{a_{k}\in A}{\sum}\{\sigma(a_{k})u(a_{l},a_{k})>\underset{a_{k}\in A}{\sum}\sigma(a_{k})u(a_{j},a_{k}) \quad \text{ for all $a_{j}\neq a_{l}$} $$

In the context of the local interaction symmetric coordination game, a strategy is p-dominant if it is a best response whenever it is played by at least proportion p, or a total of at least ⌈pn_i⌉, of a player’s neighbours, where ⌈x⌉ is the least integer greater than or equal to x.

Second, there must exist a sequence of sets of players, S₁, S₂, ⋯ , S_J, with $S_{1}=N(\mathbf {a}\rightarrow \mathbf {a}_{l})$ and $\bigcup _{j=1}^{J}S_{j}=N$, whereby for each i ∈ S_j, and all j = 2, 3, ⋯ , J, α_i(S_j− 1) ≥ p. That is, for each player i ∈ S_j, the proportion of i’s neighbours that belong to S_j− 1 is greater than p. This inequality ensures that once all players in $S_{1}=N(\mathbf {a}\rightarrow \mathbf {a}_{l})$ play strategy a_l from period t = 1 onward, then at t = 2, a_l is a best response to all i ∈ S₂, so that all players in S₁ ∪ S₂ play a_l; at t = 3, a_l is a best response to all i ∈ S₃, so that all players in S₁ ∪ S₂ ∪ S₃ play a_l; and so on, until t = J at which all players play strategy a_l.

Example 1

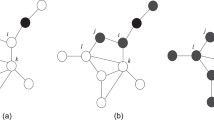
Consider the 2 × 2 coordination game in Fig. 1 with strategy a₂ as a p-dominant strategy, for $p>\frac {1}{1+\beta }$. First consider a scenario where β = 1.01, so that a₂ is a $\frac {1}{2}$-dominant strategy. When this game is played on network G₂ of Fig. 2a, strategy a₂ is a best response whenever it is played by at least $\lceil {\frac {1}{2}\times 2}\rceil =1$ neighbour. If (A, U, N, G, P) starts from a monomorphic configuration a₁, strategy a₂ will spread contagiously from any pair of two adjacently placed players. This is because, for any pair of adjacently placed players, say $N(\mathbf {a}_{1}\rightarrow \mathbf {a}_{2})=\{1, 2\}$, there exists a sequence of sets of players, S₁ = {1, 2}, S₂ = {3, 12}, S₃ = {4, 11}⋯ , S₆ = {7, 8}, whereby for each i ∈ S_j, $\alpha _{i}(S_{j-1})=\frac {1}{2}=p$. That is, if all players in S₁ play a₂ from period t = 1 onward, then at t = 2, all players in S₁ ∪ S₂ play a₂; at t = 3, all players in S₁ ∪ S₂ ∪ S₃ play a₂; and so on, until t = 6 at which all players play a₂.

Fig. 1

A 2 × 2 strict coordination game where a₂ is a p-dominant strategy, for $p>\frac {1}{1+\beta }$. That is, a₂ is a best response when played by more than proportion $\frac {1}{1+\beta }$ of neighbours

Fig. 2

Examples of undirected regular cyclic networks, regular in that each player has the same number of neighbours: (a) A regular cyclic network of degree two (i.e., each player has two neighbours), denoted by G₂; (b) A regular cyclic network of degree three, denoted by G₃

However, for network G₃ of Fig. 2b, when β = 1.01, strategy a₂ is a best response only when played by at least $\lceil {\frac {1}{2}\times 3}\rceil =2$ neighbours. This implies that for any sequence, S₁, S₂, ⋯ , S_J, of players in G₃ where the size of S₁ is less than $\frac {n}{2}$, there exists at least one i in some S_j with $\alpha _{i}(S_{j-1})=\frac {1}{3}<p=\frac {1}{2}$.⁹ Thus, $n(\mathbf {a}_{1}\rightarrow \mathbf {a}_{2})\geq \frac {n}{2}$ and increases with the population size, and according to Definitions 2 and 3, strategy a₂ does not spread contagiously on G₃. Strategy a₂ spreads contagiously on G₃ only when β ≥ 2.01 so that a₂ is $\frac {1}{3}$-dominant.

We define a new network measure – the contagion threshold – for finite networks that captures the second condition above. This measure not only determines when a p-dominant strategy can spread contagiously, but also when it is uninvadable. For each i ∈ N, let $B_{i_{r}}$ be the r th neighbourhood of i, the set of all players within distance r (i.e. r steps) from i, with i included, and $N_{i_{r}}$ be the r th-order neighbours of i (i.e. all players at distance r from i). We write $B_{i_{r}}$ and $N_{i_{r}}$ for the respective cardinalities of $B_{i_{r}}$ and $N_{i_{r}}$. We then define and compute the contagion threshold of a finite network as follows.

Definition 6

Given G(N, E):

• (i) pick any i ∈ N and the corresponding $B_{i_{1}}$;

• (ii) for each r ≥ 2 and $j\in N_{i_{r}}$, compute $\alpha _{j}(B_{i_{r-1}})$ and $\displaystyle \alpha _{i_{r}}^{*}=\underset {j\in N_{i_{r}}}{\min \limits }\alpha _{j}(B_{i_{r-1}})$;

• (iii) given i ∈ N, compute $\displaystyle \alpha _{i}^{*}=\underset {r\geq 2}{\min \limits }\alpha _{i_{r}}^{*}$.

The contagion threshold of G(N, E), η(G), is given by $\displaystyle \eta (G)=\underset {i\in N}{\min \limits }\alpha _{i}^{*}$.

The definition of the contagion threshold builds on the notion of sequences of sets of players discussed above. For each i with a corresponding first neighbourhood $B_{i_{1}}$, Definition 6 requires that along a sequence of the r-order neighbours of i, $N_{i_{2}}, N_{i_{3}},\cdots ,N_{i_{d_{i}}}$, where d_i is the shortest distance from i to the furthest player, $\alpha _{j}(B_{i_{r-1}})\geq \eta (G)$ for every $j\in N_{i_{r}}$ and all r = 2, 3, ⋯ , d_i. For the two networks in Fig. 2, the contagion thresholds are $\eta (G_{2})=\frac {1}{2}$ and $\eta (G_{3})=\frac {1}{3}$.

Following the above discussion and Example 1, when p ≤ η(G), a p-dominant strategy can spread contagiously from the set $B_{i_{2}}$ of any i. Consider the game of Fig. 1, and let β = 1.01 so that a₂ is a $\frac {1}{2}$-dominant strategy. Consider an evolutionary process (A, U, N, G, P) on a strongly connected network G with $\eta (G)=p=\frac {1}{2}$. Then, starting from a₁, strategy a₂ will spread contagiously from $N(\mathbf {a}_{1}\rightarrow \mathbf {a}_{2})=B_{i_{2}}$ of any i ∈ N. This is because along the sequence $N_{i_{3}}, N_{i_{4}},\cdots ,N_{i_{d_{i}}}$, $\alpha _{j}(B_{i_{r-1}})\geq \eta (G)=\frac {1}{2}=p$ for every $j\in N_{i_{r}}$ and all r = 3, 4, ⋯ , d_i, so that once all players in $B_{i_{2}}$ play a₂ at some period t, all players in $N_{i_{3}}$ will switch to a₂ at t + 1 (because each has at least proportion p of neighbours play a₂ at t); followed by all players in $N_{i_{4}}$ at t + 2; and so on, until the entire network eventually switches to a₂.

Our definition of the contagion threshold for finite networks is closely related to the definition of the contagion threshold for unbounded networks according to Morris (2000). For a 2 × 2 symmetric coordination game with strategies a₁ and a₂, let strategy a₂ be a p-dominant strategy. Morris (2000) defines the contagion threshold of an unbounded network as the maximum p such that a₂ can spread contagiously in that network. This definition ensures that the contagious spread of a₂ can be triggered from some finite group of players. The similarity with Definition 6 is that η(G) is the maximum p above which a p-dominant strategy of an m × m symmetric coordination game can spread contagiously on a finite G.

However, the definition of the contagion threshold for unbounded networks in Morris (2000) does not directly carry-on to finite networks. This is because unlike unbounded networks where it is sufficient to know that contagion can be triggered from some finite group of players, for finite networks, it is necessary to have knowledge of the size and the identity of the smallest group of players from which contagion can be triggered. From Definition 6 and the discussion that follows, the contagious spread of a p-dominant strategy can be triggered from within the smallest second-neighbourhood of the network. We further discuss the bounds for the size of the smallest group that triggers the contagious spread of a p-dominant strategy below. But first, the following theorem establishes the conditions for a p-dominant strategy to be contagious on a given network.

Theorem 1

Given the diffusion process (A, U, N, G, P) on a strongly connected network G, if a^∗∈ A is a p-dominant strategy of (A, U), then it is contagious on G if p ≤ η(G) and $b^{*}_{2}\leq n^{\frac {3}{5}}$, where $b^{*}_{2}=\min \limits _{i\in N}b_{i_{2}}$. For all a ∈ L∖a^∗, $n(\mathbf {a}\rightarrow \mathbf {a}^{*})\leq b^{*}_{2}\leq n^{\frac {3}{5}}$.

Proof

See Appendix B□

The proof of Theorem 1 follows in two steps. Let a^∗ be a monomorphic absorbing state where all players coordinate on strategy a^∗. We first show that if a^∗ is a p-dominant strategy of (A, U), and p ≤ η(G), then starting from any state a ∈ L∖a^∗, the size of the subgroup from which a^∗ spreads contagiously in G is bounded from above by $b^{*}_{2}$.

Let (A, U, N, G, P) start from some a ∈ L∖a^∗, and pick any i ∈ N. If all players in $B_{i_{2}}$ mutate to a^∗ at t = 1, then from t = 2 onward, a^∗ is a best response to all players in $B_{i_{2}}\cup N_{i_{3}}=B_{i_{3}}$ since $\alpha _{j}(B_{i_{2}})\geq \eta (G)\geq p$ for each $j\in B_{i_{3}}$. That is, since each $j\in B_{i_{3}}$ has at least proportion p of their interactions with players in $B_{i_{2}}$, all of whom play a^∗ at t = 1, and a^∗ is a best response whenever it is played by at least proportion p of neighbours, it follows that a^∗ is a best response for each $j\in B_{i_{3}}$. From t = 3 onward, a^∗ is a best response to all $B_{i_{3}}\cup N_{i_{4}}=B_{i_{4}}$ since $\alpha _{j}(B_{i_{3}})\geq \eta (G)\geq p$ for each $j\in B_{i_{4}}$; and so on, until t = d_i − 1 when the entire network eventually plays a^∗.

Now, let $b^{*}_{2}$ be the second-neighbourhood of player i for whom $b_{i_{2}}=b_{2}^{*}$ (i.e. the cardinality of $b^{*}_{2}$ is $b_{2}^{*}$), and let d^∗ be the shortest distance from the player for whom $b_{i_{2}}=b_{2}^{*}$ to any other player (i.e. $d^{*}=d_{i^{*}}$, where i^∗ is some player for whom $b_{i^{*}_{2}}=b_{2}^{*}$). Then the above iterative process implies that, for every a ∈ L∖a^∗, there exists a best response sequence $\left \{\mathbf {x}_{t} \right \}_{t=0}^{d^{*}-1}$ with x₀ = a and ${x_{1}^{j}}=a^{*}$ for all $j\in B^{*}_{2}$ satisfying $x_{d^{*}-1}^{j}=a^{*}$ for all j ∈ N. Thus, a^∗ spreads contagiously on any strongly connected network G whenever p ≤ η(G). The size of the subgroup from which a^∗ spreads contagiously is bounded from above by $b^{*}_{2}$.

Note that $b^{*}_{2}$ is an upper bound for the minimum number of mutations needed for a^∗ to spread contagiously on a given network because the exact number of mutations can be much smaller than $b^{*}_{2}$. The exact number of initial adopters of a^∗ needed to trigger its contagious spread can be computed in two steps:

• (i) identify $b^{*}_{2}$ by computing $B_{i_{2}}$ for each i ∈ N and then picking the one with the smallest cardinality;

• (ii) within $b^{*}_{2}$, identify the smallest set of players that should play a^∗ so that all players in $b^{*}_{2}$ eventually switch to play a^∗ through best response. The cardinality of this subset of $b^{*}_{2}$ is then the number of initial adopters.

The second step of the proof of Theorem 1 shows that if a^∗ is the p-dominant strategy, and p ≤ η(G), then the number of mutations needed to leave (the basin of attraction of) convention a^∗ is greater than $n^{\frac {3}{5}}$. The intuition behind this result is that since each $j\in N_{i_{r}}$ has $\alpha _{j}(B_{i_{r-1}})\geq \eta (G)\geq p$ for all r ≥ 2, and that $p\leq \frac {1}{2}$, players within a given $B_{i_{2}}$ will switch to a strategy different from a^∗ if each has more than proportion $(1-p)>\frac {1}{2}$ of neighbours playing a strategy different from a^∗. Thus, to leave convention a^∗, the set of mutants, R(a^∗), must be selected in such a way that, for each i ∈ N, each $j\in B_{i_{2}}$ has more than half of their neighbours in R(a^∗). This implies that the identification of R(a^∗) is equivalent to the graph theory problem of identifying monopolies (i.e. sets of vertices of a graph containing at least half of the direct and/or indirect interactions of every player). Using the well established results in graph theory (e.g. Bermond et al. (1996, Proposition 4)), it follows that the cardinality of R(a^∗) is greater than $n^{\frac {3}{5}}$.

Since the number of mutations needed to leave convention a^∗ is a function of n, it follows that a^∗ is uninvadable whenever $b^{*}_{2}\leq n^{\frac {3}{5}}$. Thus, a p-dominant strategy, a^∗, is contagious on a strongly connected network G whenever p ≤ η(G) and $b^{*}_{2}\leq n^{\frac {3}{5}}$. The following example illustrates a direct application of Theorem 1 to two networks with different contagion thresholds.

Example 2

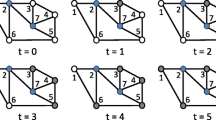
Consider the network structures in Fig. 3. Network G_a of Fig. 3a has a contagion threshold of $\eta (G_{a})=\frac {2}{7}$.¹⁰ According to Theorem 1, a p-dominant strategy a^∗ spreads contagiously in G_a if $p\leq \frac {2}{7}$. To identify the minimum number of mutations needed to trigger the contagious spread of a^∗ in this network, we follow the two steps outlined above. First, we identify the $b^{*}_{2}$ sets. There are six $b^{*}_{2}$ sets in G_a and we pick the one centred around player 1, $B^{*}_{2}=B_{1_{2}}=\{1, 2, 7, 8, 15, 16, 17, 18\}$.

Fig. 3

(a) An example of a network, denoted by G_a, with a contagion threshold of η(G_a) = 2/7; (b) An example of a network, denoted by G_b, with a contagion threshold of η(G_b) = 1/6

Second, we identify the subset of players of $b^{*}_{2}$ that must mutate to a^∗ so that all players in $b^{*}_{2}$ eventually play a^∗ through best response. Consider the case where $p=\frac {2}{7}$ so that, for players {1, 2}, a^∗ is a best response (BR) when played by at least $\lceil {\frac {2}{7}\times 2}\rceil =1$ neighbour; for player 7, a^∗ is a BR when played by at least $\lceil {\frac {2}{7}\times 5}\rceil =3$ neighbours; and for players {8, 15, 16, 17, 18}, a^∗ is a BR when played by at least $\lceil {\frac {2}{7}\times 6}\rceil =2$ neighbours. For this scenario, if players {1, 2, 7, 8} simultaneously mutate to a^∗, then all players in $B_{1_{2}}$ will eventually switch to a^∗ through best response. Any other combinations of less than four mutations by players within $B_{1_{2}}$ may lead to an absorbing cycle containing a^∗ and other strategies but not convention a^∗. Thus, the number of initial adopters that trigger the contagious spread of a^∗ is four, a small number that is independent of the population size.

For network G_b of Fig. 3b, the contagion threshold is $\eta (G_{b})=\frac {1}{6}$. Pick $B^{*}_{2}=B_{1_{2}}=\{1, 7, 13, 14\}$. For each $j\in B_{1_{2}}$, a^∗ is a BR when played by at least one neighbour. Thus, all players in $B_{1_{2}}$ will switch to a^∗ within three steps of iteration once one player, player {7}, switches to a^∗. The corresponding number of initial adopters is thus one, which is a very small number compared to the population size.

For both networks, a^∗ is uninvadable since the cardinality of $b^{*}_{2}$ is less than r(a^∗). Specifically, for $p\leq \frac {1}{2}$, R(a^∗) must at the least consist of R(a^∗) = {7, 8, 9, 10, 11, 12, 13, 14, 23, 24, 25, 26} for network G_a, and R(a^∗) = {13, 14, 15, 16, 17, 18, 19, 20, 29, 30, 31, 32} for network G_b. Thus, r(a^∗) ≥ 12 for both networks.

The above example helps to highlight two interactive aspects of our results which a firm/planner aiming to diffuse a product/behaviour must consider: the contagion threshold versus the number of initial adopters needed to trigger the contagious spread of a strategy. Consider a new firm contemplating to enter a market (or an existing firm aiming to introduce a new product) where two or more products (exhibiting coordination effects) already exist. To diffuse her product through contagion, the firm would first determine the contagion threshold of the network of consumers. The contagion threshold in turn determines the value of p (i.e. the extent to which a new product should dominate the existing alternative products) that ensures that the product can spread contagiously. If the contagion threshold of the network is much smaller than $\frac {1}{2}$, then the firm must incur large initial costs to ensure that p is sufficiently smaller (i.e. the new product must be highly beneficial compared to existing products) than the contagion threshold. The upside is that the smaller p, the smaller the number of initial adopters needed to trigger the contagious spread of a p-dominant strategy, and hence, a firm need not incur large costs on targeting. Conversely, if the contagion threshold is close to $\frac {1}{2}$, then p can also be close to $\frac {1}{2}$ so that the new product only needs to be slightly better than the existing product for it to spread contagiously. The downside is that the firm may have to invest more resources on targeting initial adopters. A firm’s objective is thus to evaluate these two types of costs.

Overall, low-density networks (i.e. networks with sparse connection) have lower contagion thresholds. This is because the smallest possible value for the contagion threshold of any strongly connected network G is $\frac {1}{\bar {n}(G)}$, where $\bar {n}(G)$ is the size of the smallest first-order neighbourhood in G. Moreover, low-density networks also have smaller $b^{*}_{2}$, and hence, a small number of initial adopters needed to trigger contagion. This implies that it is relatively less costly to diffuse new products and behaviour to low-density networks. One possible evidence of this implication of our results is in the observed discrepancy between the dynamics in the market for messaging and chat apps (e.g. AOL Instant Messenger, Google talk, VOIP, skype, Kik., whatsapp, snapchat, HipChat and slack), where there is a high turnover and entry rate, versus social networking apps (e.g. Friendster, Myspace and Facebook), where turnover and entry rate is relatively low. Specifically, messaging and chat apps consist of low-density networks where individual interact with (speak, chat or message to) a few others (family and close friends). Social network apps on the other hand consist of large number of connections where some individuals may have as many as tens of thousands of friends. Thus, to invade a network of messaging and chat apps, a new product need not be much more beneficial than those existing in the market. Invading a Facebook-type network, however, requires a new product to be far better, or simply to offer a different but related services.

Like Oyama and Takahashi (2015), our results extend Morris (2000) who examines contagion for 2 × 2 coordination games to multiple strategy coordination games. However, in Oyama and Takahashi (2015), a strategy is contagious if it is contagious in some unbounded network. As such, it is sufficient to check whether a strategy spreads contagiously in any of two types of networks, linear and non-linear networks. Our analysis is richer in that we establish conditions under which a strategy (i.e. a p-dominant strategy) is contagious on any given network. In doing so, we also provide steps for computing the smallest number of initial adopters needed to trigger contagion.

A more fundamental difference between our analysis and Morris (2000) and Oyama and Takahashi (2015) is that we study contagion in finite networks. In particular, Morris (2000) provides bounds for the contagion threshold in unbounded networks but computing the exact contagion threshold of an unbounded network is not a straightforward matter. Ideally, one would select some finite group of players in some region of the network and then iterate over the entire network following similar steps in Definition 6 above. The problem with using this method when the network is unbounded is that there is no obvious means of knowing how many iterations are sufficient for computing the contagion threshold. One would have to assume some form of uniformity across the unbounded network, and hence, the contagion threshold can feasibly be determined for only unbounded regular or close to regular networks (i.e. networks where all players have the same neighbourhood size).

Finally, Alós-Ferrer and Weidenholzer (2008) examine contagion in both bounded and unbounded network but focuses on establishing conditions under which a Pareto-dominant strategy spreads under imitation dynamics – where players play strategies that earned the highest payoff in their neighbourhood in the previous period. Imitation dynamics does not, in most cases, generate intermediate absorbing states where strategies co-exist as best response dynamics does. Thus, the network structure does not affect contagion under imitation dynamics in the same way it does under best response dynamics. Consequently, the network measures that affect contagion under best response dynamics, such as contagion thresholds, are not necessarily relevant for contagion under imitation dynamics.

4 Contagion and best response dynamics with mutations

In Section 3, we established the conditions for contagion in a framework where players strictly follow best response dynamics. The question we ask in this section is the following: is contagion relevant in a framework of noisy best response dynamics? There is plenty of empirical evidence showing that individual decision processes are best described by probabilistic models (McKelvey and Palfrey 1995; Anderson et al. 2001; Ellison 2006).

Naturally, the level of noise in individual decisions may vary across settings and it is possible that, in some settings, the amount of noise affects the relevance of the process of contagion. That is, if players frequently make mistakes and play strategies that are not best responses, then the evolutionary process will frequently deviate from paths corresponding to contagion dynamics (i.e. the evolutionary process frequently deviates from best response sequences defined in Definition 1). This may in turn imply that contagious strategies are not played with the highest probability in the long run. In such a scenario, it will not be economically reasonable to target specific players to aid network-wide diffusion.

To examine the above question, we establish conditions under which a convention corresponding to a contagious strategy is a long-run equilibrium in Model 2. We show that, indeed, under Model 2, there exists a threshold value, β^∗ > 0, of the noise parameter β, above which the convention corresponding to the p-dominant strategy is the long-run equilibrium. Above β^∗, best response dynamics, and hence, contagion, dominates experimentation and targeting is economically reasonable; conversely, below β^∗, players’ choices are too noisy and targeting is not economically reasonable. The following definition and notations are used to state the main results of this section.

Definition 7

Let g ⊂X ×X be any oriented graph defined within the configuration space X. Then for a subset W ⊂X and its complement $\bar {W}$, we denote by Γ(W) a set of all oriented graphs satisfying two conditions: (i) no arrows start from W and exactly one arrow starts from each configuration outside of W, (ii) each g ∈ Γ(W) has no loops.

From Definition 7, if W is a singleton set, say W = {x}, then Γ({x}) is a set of all spanning trees of x (i.e. x-trees). Consider an example where X = {a, b, c, d, e, f, g, h}; Fig. 4 presents two examples of g-trees.

Fig. 4

Examples of g-trees, that is Γ({g}) graphs and in which the configuration space X = {a, b, c, d, e, f, g, h}

From the definition of Γ(x) graphs, every g ∈ Γ(x) spans the entire state space, except for x. Each y ∈ X has only one arrow emanating from it so that each g ∈ Γ(x) has a total of mⁿ − 1 directed edges, where mⁿ is the cardinality of X. Thus, if we let γ(x) = #Γ(x) be the cardinality of Γ(x), then γ(x) is identical for any pair of configurations x, y ∈ X; that is, γ(x) = γ(y) = γ.

The cardinality of Γ(x), γ, is a multiple of, and not an exponential function of the cardinality of the state space, mⁿ. For example, when the size of the state space is 2, γ = 1; when it is 3, γ = 3; when it is 4, γ = 15;¹¹ and when it is 5, γ = 51. Thus, the natural logarithm of γ, $\ln (\gamma )$, is a linear function of n.

Proposition 1

For a diffusion model (A, U, N, G, P_β), let Assumption 1 hold. If a^∗ is contagious on network G, then there exists some $\beta ^{*}\in \left (0, \ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})\right ]$ such that for all β ≥ β^∗, $\pi _{\beta }(\mathbf {a}^{*})>\pi _{\beta }(\mathbf {a})$ for all a ∈ L∖a^∗.

Proof

See Appendix C□

The proof of Proposition 1 follows in two steps. First, we characterise the structure of stationary distributions using a graph theoretic method of Freidlin and Wentzell (1984). This method represents the stationary distribution of any configuration x in terms of the probabilities of Γ(x) graphs. Let c(y, z) be the number of mutations involved in the direct transition from y to z. The total cost ϕ(x; g) of some g ∈ Γ(x) is the sum of costs of all transitions in g. That is, $\phi (\mathbf {x};g)={\sum }_{(\mathbf {y},\mathbf {z})\in g} c(\mathbf {y},\mathbf {z})$. This quantity captures the total cost of reaching x from every other configuration through paths of graph g.

These costs are directly related to the transition probabilities. The probability that c(y, z) players simultaneously mutate to play strategies that are not best responses to y is $\left (e^{-\beta }/m\right )^{c(\mathbf {y},\mathbf {z})}$. Thus, if the probability of mistakes is relatively small, then the larger c(y, z) the smaller the probability of the transition from y to z. The same argument extends to any g ∈ Γ(x): if the probability of mistakes is small, then the higher the cost ϕ(x; g) associated with g, the smaller the probability of reaching x through paths in g. Using the relationship between stationary distributions and the probabilities of Γ(x) graphs provided by Freidlin and Wentzell (1984, Lemma 3.1) we derive bounds for stationary distributions as functions of costs of Γ(x) graphs and model parameters.

Second, we show that under Assumption 1, there exists some $\beta ^{*}\in \left (0, \ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})\right ]$ such that for all β ≥ β^∗, the long-run equilibrium is the strategy configuration with the minimal cost Γ(x) graph: that is, for all β ≥ β^∗, x ∈ argmin_{x∈ X, g∈ Γ(x)}ϕ(x; g) is the long-run equilibrium; and that convention a^∗, corresponding to a contagious strategy a^∗, has the minimal cost graph.

As discussed above, the intuition behind Proposition 1 is that when the level of experimentation is very high (i.e. β is small and between 0 and β^∗), the evolutionary process frequently deviates from the contagion paths (i.e. paths of best response sequences) so that the convention containing only the contagious strategy need not be the long-run equilibrium. For example, when β = 0, every strategy configuration is visited with equal probability. The upper bound for β^∗, $\ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})$, increases with n. Specifically, $\ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})$ is of order $\mathcal (O)(n^{2/5})$ because $\ln \gamma$ is a linear function of n.

The findings of Proposition 1 suggest that targeting is indeed economically reasonable even in settings where players make mistakes and play strategies that are not best responses. More broadly, Proposition 1 suggests that the predictions in evolutionary game theory that employ stochastic stability as a solution concept are admissible for relatively high levels of experimentation. Recall that a configuration x is stochastically stable if $\lim _{\beta \rightarrow \infty }\pi _{\beta }(\mathbf {x})>0$ (Foster and Young 1990; Kandori et al. 1993; Young 1993). Proposition 1 states that the level of experimentation need not be very small (i.e. β need not be asymptotically large); it is sufficient that β ≥ β^∗. And in evolutionary models with a finite and small population size, the level of experimentation can be admissibly large because the upper bound for β^∗, which is a linear function of the population size, is small.

5 Concluding remarks

We examined the diffusion of products and practices with coordination effects through contagion using evolutionary game theory framework. Evolutionary game theory captures many realistic aspects of individual decision making and interactions, most notably, myopia (i.e. the inability to remember the entire history of play in complex social interactions); the tendency to experiment or make mistakes on optimal choices; and the locality of social interactions. We consider two related models that capture these structural and behavioural properties of social interactions: evolution with best response, and evolution with best response and mutations.

Using these two models, we show that a p-dominant strategy of a symmetric coordination game, if it exists, is contagious in networks with the contagion threshold equal or greater than p. We defined a measure of the contagion threshold for finite networks that is easily computable. We then examined the effects of noise on contagion, showing that there exists a threshold level of noise below which contagious choices are long-run equilibrium of an evolutionary process where agents make mistakes.

Our results have broader implications for targeted contagion. First, we provide steps for identifying the smallest set of agents that sufficiently trigger the contagious spread of a p-dominant action. We find that this set can be as small as three agents, and is independent of the population size. Second, our results imply that targeted contagion is economically reasonable even in settings where agents experiment with their choices.

Finally, our results have implications for convergence rates of evolutionary dynamics in networks. One of the common criticisms of the evolutionary game models is that the convergence rates to equilibrium tend to increase with the population size, so that in very large populations, equilibrium is not reached in timescales of economic relevance. In the analysis that we have relegated to Appendix A, we show that if a contagious strategy exist, then equilibrium is reached fast.

Appendices

Appendix A: Expected waiting time

This section focuses on Model 2 to examine how the process of contagion affects the expected waiting time from any state to the state with the highest long-run probability. The problem of slow diffusion does not arise in situations where the level of experimentation is sufficiently high. Kreindler and Young (2013) and Kreindler and Young (2014) show that when β is sufficiently small, convergence is fast. Here, we examine the case where β is very large (i.e. $\beta \rightarrow \infty$).

We show that when β is large, the expected waiting time to the monomorphic convention corresponding to the contagious strategy is independent of the population size. The direct implication of this result is that even in large networks and with low levels of experimentation, the diffusion process converges fast to the long-run equilibrium. The expected waiting time is formally defined as follows.

Definition 8

Let W ⊂X be a subset of the configuration space and $\bar {W}$ its complement. Define $T(W)=\inf \{t\geq 0 |\mathbf {x}_{t}\in W\}$ to be the first time W is reached. The expected waiting time from some configuration $\mathbf {x}\in \bar {W}$ to W is then defined as $\mathbb {E}\left [T(W) |\mathbf {x}_{0}=\mathbf {x}\right ]$.

Let a^∗ be a p-dominant strategy of (A, U), and assume that p ≤ η(G) so that a^∗ is contagious on G. We aim to show that (A, U, N, G, P_ε) converges to a^∗ fast (i.e. the expected waiting time to a^∗ is independently of the population size). To do so, we show that if a^∗ is contagious on G, then there exists a function F(β) that is independent of n so that $\mathbb {E}\left [T(\mathbf {a}^{*}) |\mathbf {x}_{0}=\mathbf {x}\right ]\leq F(\beta )$ for all initial configurations $\mathbf {x}_{0}\neq \mathbf {a}^{*}$.

Proposition 2

Let a^∗ be a p-dominant strategy of (A, U) and assume that a^∗ is contagious on a strongly connected network G so that a^∗ is the long-run equilibrium of the diffusion process (A, U, N, G, P_β). Then there exists some $b^{*}\in (0,b^{*}_{2})$ such that

$$ \lim_{\beta\rightarrow\infty}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})]}{\beta} = b^{*} $$

(5)

Proof

See Appendix A□

Proposition 2 shows that the expected waiting time to the equilibrium configuration of the evolutionary process with mutations from any other configuration takes the form

$$ \mathbb{E}[T(\mathbf{a}^{*})] \leq \exp\left[\beta b^{*} + g(\beta)\right]=F(\beta) $$

(6)

where g(β) is a decreasing function of noise parameter β. As the level of experimentation tends to zero (i.e. $\beta \rightarrow \infty$), $g(\beta )\rightarrow 0$ and the expected waiting time increases at an exponential rate of b^∗, which is independent of the population size.

Compared to existing results on convergence rates of evolutionary processes such as Ellison (1993), Young (2011), Kreindler and Young (2013) and Kreindler and Young (2014), the result in Proposition 2 is driven more by contagion and less by noise. Kreindler and Young (2014) also find that learning is fast in networks, but they consider a 2 × 2 coordination game with random sampling and with deterministic dynamics. Moreover, they define fast learning as the case in which noise is large to the extent that only one unique equilibrium exists. On a contrary, Proposition 2 shows that contagion makes learning fast in stochastic evolutionary game dynamics for m × m coordination games.

Appendix B: Proof of Theorem 1

The proof of Theorem 1 follows in two steps. The first step, which is already discussed in detail in Section 3, demonstrates that if a^∗∈ A is a p-dominant strategy of (A, U) and p ≤ η(G), then a^∗ spreads contagiously on G, and that the size of the set of initial adopters is bounded from above by $b^{*}_{2}$. The second step demonstrates that if a^∗∈ A is a p-dominant strategy and p ≤ η(G), then the number of mutations needed to leave convention a^∗ is greater than $n^{\frac {3}{5}}$.

Strategy a ^∗ spreads contagiously on G

Given the diffusion process (A, U, N, G, P) on a strongly connected network G, and a p-dominant strategy a^∗∈ A, let p ≤ η(G). Let also A₁ = A∖a^∗. Since a^∗ is p-dominant, it is a best response when played by at least proportion p of a player’s neighbours and the rest play strategies in A₁. This implies that if all players in a given subgroup Z ⊂ N play a^∗, then a^∗ is a unique best response to any i ∈ N for whom α_i(Z) ≥ p.

Let the evolutionary process start from any state a ∈ L∖a^∗, where a can consist of only strategies in A₁ or both a^∗ and strategies in A₁. Pick any i ∈ N and the respective $B_{i_{2}}$, and at period t = 1, let all players in $B_{i_{2}}$ mutate to play a^∗. The evolutionary process will evolve through best response from t = 1 onward as follows, where we write $\bar {B}_{i_{r}}=N\backslash B_{i_{r}}$ for the complement of $B_{i_{r}}$, $i\rightarrow A_{l}$ to mean that i plays a strategy in A_l, $Z\rightarrow A_{l}$ to mean that each j ∈ Z plays a strategy in A_l:

Table 1

We see from the above iterative process that after t = d_i − 1 iterations, the evolutionary process converges to convention a^∗. Thus, starting from any a ∈ L∖a^∗, there exists a best response sequence $\left \{\mathbf {x}_{t} \right \}_{t=0}^{d_{i}-1}$ with x₀ = a and ${x_{1}^{j}}=a^{*}$ for all $j\in N(\mathbf {a}\rightarrow \mathbf {a}^{*})=B_{i_{2}}$, for any i ∈ N, satisfying $x_{d_{i}-1}^{l}=a^{*}$ for all l ∈ N. Since this holds for $B_{i_{2}}$ of any i ∈ N, it follows that the size of the smallest set of initial adopters is $b^{*}_{2}= \operatorname *{arg min}_{i\in N}b_{i_{2}}$.

Since $b^{*}_{2}$ is independent of the population size, n, we conclude that when p ≤ η(G), strategy a^∗ spreads contagiously on G with $n(\mathbf {a}\rightarrow \mathbf {a}^{*})\leq b^{*}_{2}$ for all a ∈ L∖a^∗. Note that the upper bound for $n(\mathbf {a}\rightarrow \mathbf {a}^{*})$ follows because although $b^{*}_{2}$ mutations to a^∗ guarantee that a^∗ spreads contagiously, it is possible, in most networks, to find a smaller set than $b^{*}_{2}$ that sufficiently triggers the contagious spread of a^∗.

Uninvadability of a ^∗

Recall that convention a^∗ is uninvadable if $r(\mathbf {a}^{*})>n(\mathbf {a}\rightarrow \mathbf {a}^{*})$ for all a ∈ L∖a^∗, and that r(a^∗), which is the number of mutations required to leave the basin of attraction of convention a^∗, is a function of n. We first show that if a^∗ spreads contagiously on a strongly connected network G, then $r(\mathbf {a}^{*})\geq n^{\frac {3}{5}}$.

Let R(a^∗) ⊂ N be the smallest set of players that should mutate to strategies in A₁ for the evolutionary process to leave the basin of attraction of a^∗, where r(a^∗) is the cardinality of R(a^∗). We see from the preceding analysis that if there exists a player i in G for whom all players in $B_{i_{2}}$ play a^∗, then a^∗ spreads contagiously, and hence, the evolutionary process converges to a^∗ regardless of the strategy configuration of other players not in $B_{i_{2}}$. Thus, to leave a^∗, no such player must exist, and that each player must be at most two steps away from R(a^∗); that is, for each i, a sufficiently large proportion of players in $B_{i_{2}}$ are in R(a^∗). Since a^∗ is p-dominant, where $p\leq \frac {1}{2}$, strategies in A₁ are best responses only when more than proportion $(1-p)>\frac {1}{2}$ of neighbours play strategies in A₁. For strategies in A₁ to become best responses to players within $B_{i_{2}}$, more than $\frac {1}{2}$ of the interactions of players in $B_{i_{2}}$ must be in R(a^∗); and R(a^∗) must be chosen to satisfy this condition for each i ∈ N.

The identification of the smallest R(a^∗) is then equivalent to the problem of identifying the smallest 2-monopolies in graph theory, defined as follows. A player i in network G is said to be 2-controlled by the set Z ⊂ N of players if at least half of the players in $B_{i_{2}}$ are in Z. The set Z is called a 2-monopoly if it 2-controls every player in the network. Bermond et al (1996, Proposition 4) show that the minimum size of a 2-monopoly on any undirected and strongly connected network of size n is $n^{\frac {3}{5}}$ (see Peleg (2002) for a review of the literature on monopolies and local majorities in networks), and hence, $r(\mathbf {a}^{*})>n^{\frac {3}{5}}$. Note that the inequality follows because we require R(a^∗) to contain more than half of interactions of $B_{i_{2}}$ for all i ∈ N while the definition of a 2-monopoly requires R(a^∗) to contain at least half of the interactions of $B_{i_{2}}$.

Since $r(\mathbf {a}^{*})>n^{\frac {3}{5}}$ is an increasing function of n, it follows that convention a^∗ is uninvadable whenever $n^{\frac {3}{5}}\geq n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ for all a ∈ L∖a^∗. And since $n(\mathbf {a}\rightarrow \mathbf {a}_{l})\leq b^{*}_{2}$ for all a ∈ L∖a^∗, convention a^∗ is uninvadable, and hence, also contagious, whenever $b^{*}_{2}\leq n^{\frac {3}{5}}$.

Appendix C: Proof of Proposition 1

To prove Proposition 1, we first characterize the structure of stationary distributions, and in particular, the ratio, $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {y})}$, of stationary distributions of any pair of configurations x, y ∈ X. We use the following results from Freidlin and Wentzell (1984).

Lemma 1

(Lemma 3.1 ; Freidlin and Wentzell 1984). Given a diffusion process P_β, the stationary distribution π_β(x) of some configuration x ∈ X is given by

$$ \pi_{\beta}(\mathbf{x})=\left( \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g)\right)\left( \underset{\mathbf{y}\in \mathbf{X}}{\sum}\underset{g\in {{\varGamma}}(\{\mathbf{y}\})}{\sum}P_{\beta}(g)\right)^{-1} $$

(7)

where the total probability P_β(g) associated with each graph g is $\displaystyle P_{\beta }(g)=\underset {(\mathbf {z},\mathbf {y})\in g}{\prod }P_{\beta }(\mathbf {z},\mathbf {y})$ and Γ(x) graphs are defined in Definition 7.

To fully characterise the structure of π_β, we first characterise the structure of transition probabilities P_β(x, y) between pairs of states x, y ∈ X. Recall that c(x, y) is the number of mutations involved in the direct transition from x to y. That is, the number of players who choose different strategies in state y than those chosen in state x, and that their choices are a result of mutations. Employing Assumption 1, the transition probability P_ε(x, y) can directly be expressed in terms of c(x, y) as

$$ P_{\beta}(\mathbf{x},\mathbf{y}) = \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{x}, \mathbf{y})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n-c(\mathbf{x}, \mathbf{y})} $$

(8)

The right hand side of Eq. 8 follows because, first, if yⁱ (i.e. the strategy i plays in configuration y) is not a best response to x so that BR_i(yⁱ; x) = 0, then from Eq. 3, the probability that i plays yⁱ is $\frac {e^{-\beta }}{m}$. Consequently, the probability that c(x, y) players simultaneously play strategies that are not best responses to x in configuration y is $\left (\frac {e^{-\beta }}{m}\right )^{c(\mathbf {x}, \mathbf {y})}$.

Second, if yⁱ is instead a best response to x, so that, from Assumption 1, BR_i(yⁱ; x) = 1, then i plays yⁱ with probability

$$\frac{e^{-\beta}}{m} + (1-e^{-\beta}) = \frac{m+(1-m)e^{-\beta}}{m} $$

Thus, the probability that the remaining n − c(x, y) players simultaneously play strategies that are best responses to x is $\left (\frac {m+(1-m)e^{-\beta }}{m}\right )^{n-c(\mathbf {x}, \mathbf {y})}$.

Next, we characterise the probabilities of Γ(x) graphs. From the definition of Γ(x) graphs, every g ∈ Γ(x) spans the entire state space except x, which is the root of the graph. Each y ∈ X∖x has only one arrow emanating from it. Thus, each g ∈ Γ(x) contains a total of mⁿ − 1 directed edges, where mⁿ is the cardinality of X. Similarly, if we let d(L_j) be the cardinality of D(L_j) (the basin of attraction of L_j), then there are d(L_j) directed edges that originate from states in D(L_j).

Now, let g(D(L)) be a subgraph of g consisting of all d(L_j) directed edges that originate from states in D(L_j). Since D(L_j) for all L_j ⊂L are non-overlapping sets, we can rewrite P_β(g) as

$$ P_{\beta}(g)=\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod}P_{\beta}(\mathbf{y},\mathbf{z}) $$

(9)

We can further subdivide the set of edges of g(D(L_j)) into those that involve at least one mutation, denoted by g(D(L_j); β), and those whose dynamics are governed solely by best response, denoted by $\overline {g(D(L_{j});\beta )}$. That is, for each x ∈ D(L_j) and some y≠x, a directed edge (x, y) ∈ g(D(L_j); β) if c(x, y) > 0, and $(\mathbf {x},\mathbf {y})\in \overline {g(D(L_{j});\beta )}$ if c(x, y) = 0. Using these definitions and notation, P_β(g) can be rewritten as

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=&\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod} P_{\beta}(\mathbf{y},\mathbf{z})\\ &=&\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod} \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{y}, \mathbf{z})}{\prod}_{i=1}^{n-c(\mathbf{y}, \mathbf{z})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)\\ &=& \underset{L_{j}\in \mathbf{L}}{\prod}\left[\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}{\prod} \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{y}, \mathbf{z})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n-c(\mathbf{y}, \mathbf{z})} \right.\\ &&\left.\times\underset{(\mathbf{y},\mathbf{z})\in \overline{g(D(L_{j});\beta)}}{\prod} \left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n}\right] \end{array} $$

(10)

Let n(g; L_j; β) be the cardinality of subgraph g(D(L_j); β) (i.e. the number of directed edges in subgraph g(D(L_j); β)) so that the cardinality of $\overline {g(D(L_{j});\beta )}$ is d(L_j) − n(g; L_j; β). Then Eq. 10 can be rewritten as

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=&\! \underset{L_{j}\in \mathbf{L}}{\prod}\left[\left( \!\frac{e^{-\beta}}{m}\!\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}c(\mathbf{y}, \mathbf{z})}\left( \!\frac{m + (1 - m)e^{-\beta}}{m}\!\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}(n-c(\mathbf{y}, \mathbf{z}))}\right.\!\! \\ &&\times\left.\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n[d(L_{j})-n(g;L_{j};\beta)]}\right]\\ &=&\underset{L_{j}\in \mathbf{L}}{\prod}\left( \frac{e^{-\beta}}{m}\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}c(\mathbf{y}, \mathbf{z})}\\&&\times\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n[d(L_{j})-n(g;L_{j};\beta)]+{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}(n-c(\mathbf{y}, \mathbf{z}))} \end{array} $$

(11)

The summation $c(L_{j};g)={\sum }_{(\mathbf {y},\mathbf {z})\in g(D(L_{j});\beta )}c(\mathbf {y}, \mathbf {z})$ on the exponent of the expressions of P_β(g) in Eq. 11 is the total cost of leaving the basin of attraction of each L_j under graph g ∈ Γ(x). Using this definition, we can simplify $n[d(L_{j})-n(g;L_{j};\beta )]+{\sum }_{(\mathbf {y},\mathbf {z})\in g(D(L_{j});\beta )}(n-c(\mathbf {y}, \mathbf {z}))$ as follows:

$$ \begin{array}{@{}rcl@{}} n[d(L_{j})-n(g;L_{j};\beta)]+\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}{\sum}(n-c(\mathbf{y}, \mathbf{z})) &=& n[d(L_{j})-n(g;L_{j};\beta)]\\&&+n(g;L_{j};\beta)n - c(L_{j};g)\\ &=&nd(L_{j})-c(L_{j};g) \end{array} $$

Eq. 11 then simplifies to

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=& \underset{L_{j}\in \mathbf{L}}{\prod}\left( \frac{e^{-\beta}}{m}\right)^{c(L_{j};g)}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{nd(L_{j})-c(L_{j};g)}\\ &=& \exp\left[-\underset{L_{j}\in \mathbf{L}}{\sum}\left( c(L_{j};g)\beta_{m} + (nd(L_{j})-c(L_{j};g))\beta_{m}^{\prime} \right)\right]\\ & =& \exp\left[-\underset{L_{j}\in \mathbf{L}}{\sum}\left( c(L_{j};g)(\beta_{m}-\beta_{m}^{\prime}) + nd(L_{j})\beta_{m}^{\prime} \right)\right] \end{array} $$

(12)

where $\beta _{m} =\beta -\ln m^{-1}$ and $\beta _{m}^{\prime }= -\ln \left [\frac {m+(1-m)e^{-\beta }}{m}\right ]$.

Recall the definition of the long-run equilibrium of (A, U, N, G, P_ε) as configurations that maximize the stationary distribution. So, to compute the long-run equilibrium, we take ratios of probabilities and identify configurations for which the ratio is less than one. Specifically, configuration a^∗ is a long-run equilibrium if $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {a}^{*})}\leq 1$ for all x≠a^∗. From π_β(x) in Eq. 7, the expression for the ratio of stationary distribution, $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$ of any pair of configurations x, w ∈ X is given by

$$ \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}=\frac{{\sum}_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{{\sum}_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} $$

(13)

where the quantity $\left ({\sum }_{\mathbf {y}\in \mathbf {X}}{\sum }_{g\in {{\varGamma }}(\{\mathbf {y}\})}P_{\beta }(g)\right )^{-1}$ cancels out since it is identical for all configurations.

Let γ(x) = #Γ(x) be the cardinality of Γ(x). Since for any x ∈ X every g ∈ Γ(x) spans the entire state space except for one configuration (i.e. the number of edges in any g ∈ Γ(x) is equal to mⁿ − 1), the cardinality of Γ(x) is the same for any pair of configurations x, y ∈ X; that is, γ(x) = γ(y) = γ. Using this notation, the following bounds hold:

$$\underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g)\leq \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}\max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)=\gamma \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)$$

$$\underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g) \geq \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)$$

Thus, the ratio $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$ is bounded from below and above by

$$ \frac{\max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{\gamma \max_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} \leq \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}\leq \frac{\gamma \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{\max_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} $$

(14)

Substituting for P_β(g) from Eq. 12 into the ratios of stationary distributions in Eq. 14 yields the following expression.

$$ \begin{array}{@{}rcl@{}} \frac{\max_{g\in {{{\varGamma}}}(\{\mathbf{x}\})}P_{\beta}(g)}{\max_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}P_{\beta}(g)} &=& \frac{\max_{g\in {{{\varGamma}}}(\{\mathbf{x}\})}\exp\left[-{\sum}_{L_j\in \mathbf{L}}\left( c(L_j;g)(\beta_m-\beta_m^{\prime}) + nd(L_j)\beta_m^{\prime} \right)\right]}{\max_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}\exp\left[-{\sum}_{L_j\in \mathbf{L}}\left( c(L_j;g)(\beta_m-\beta_m^{\prime}) + nd(L_j)\beta_m^{\prime} \right)\right]}\\ &=&\exp\left[\min_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)(\beta_m-\beta_m^{\prime}) - \underset{g\in {{{\varGamma}}}(\{\mathbf{x}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)(\beta_m-\beta_m^{\prime})\right]\\ &=&\exp\left[-(\beta_m-\beta_m^{\prime}) \left( \underset{g\in {{{\varGamma}}}(\{\mathbf{x}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)- \underset{g\in {{{\varGamma}}}(\{\mathbf{w}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)\right)\right] \end{array} $$

(15)

whereby, due to the negative in the exponents, the expressions for P_β(g) are maximized when the costs of exiting the basins of attractions of absorbing sets are minimized. Substituting Eq. 15 into Eq. 14 yields the following lower and upper bounds for $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$

$$ \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}= \exp\left[-(\beta_{m}-\beta_{m}^{\prime}) \left( \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)- \underset{g\in {{\varGamma}}(\{\mathbf{w}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)\right)\pm \ln\gamma \right] $$

(16)

Now, notice that for all β ≥ 0, $(\beta _{m}-\beta _{m}^{\prime })\geq 0$: that is,

$$ \begin{array}{@{}rcl@{}} (\beta_{m}-\beta_{m}^{\prime})&=& \beta-\ln m^{-1} + \ln \left[\frac{m+(1-m)e^{-\beta}}{m}\right]\\&=& \beta-\ln m^{-1} + \ln \left[m+(1-m)e^{-\beta}\right]+\ln m^{-1}\\ &=& \beta + \ln \left[m+(1-m)e^{-\beta}\right] \end{array} $$

(17)

Since m + (1 − m)e^−β ≥ 1 for all β ≥ 0, it follows from the right hand side of Eq. 17 that $(\beta _{m}-\beta _{m}^{\prime })\geq 0$ for all β ≥ 0. Let Φ(x, w) denote the difference between costs of graphs (i.e. the expression in the exponent of Eq. 16). That is,

$${{{\varPhi}}}(\mathbf{x},\mathbf{w})= \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)- \underset{g\in {{\varGamma}}(\{\mathbf{w}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)$$

It then follows from Eq. 16 that $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}\leq 1$ if Φ(x, w) ≥ 0 and that

$$ \begin{array}{@{}rcl@{}} -(\beta_{m}-\beta_{m}^{\prime}) {{{\varPhi}}}(\mathbf{x},\mathbf{w})+ \ln\gamma \leq0 \end{array} $$

(18)

Substituting for the values of β_m and $\beta _{m}^{\prime }$ in Eq. 18 yields

$$ \beta \geq \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})}-\ln \left[m+(1-m)e^{-\beta}\right] $$

(19)

Let β^∗ be the solution to

$$ \beta = \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})}-\ln \left[m+(1-m)e^{-\beta}\right] $$

(20)

By comparison β^∗ is smaller than $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$. To see why, notice that the function $\ln \left [m+(1-m)e^{-\beta }\right ]$ increases from 0 to the upper bound $\ln m$ as $\beta \rightarrow \infty$, which implies that $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln \left [m+(1-m)e^{-\beta }\right ]$ decreases from $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$ to $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln m$. This implies that the equilibrium value of β in Eq. 20, that is, the value of β at which the 45-degree line depicting β = β meets $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln \left [m+(1-m)e^{-\beta }\right ]$, is less than $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$, and hence,

$$ \beta^{*} \leq \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})} $$

(21)

It then follows that configuration a^∗ is the long-run equilibrium for all β ≥ β^∗ if it hase the least cost a^∗-tree, that is, Φ(x, a^∗) ≥ 0 for all x≠a^∗.

We now show that if a p-dominant strategy, a^∗, is contagious in a given network, then convention a^∗ has the minimum cost Γ(a^∗) graph. Note that configurations with the minimum cost graph belong to some absorbing state, and hence, it suffices to focus on examining the costs of graphs for configurations within L. Let ϕ(a, g) denote the total cost of some g ∈ Γ(a) for any a ∈ L; that is,

$$ \phi(\mathbf{a};g)= \underset{g\in {{\varGamma}}(\{\mathbf{a}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g) $$

(22)

We can see from Eq. 22 that ϕ(a; g) is identical to the cost derived from a reduced form of Γ(a), denoted by ${{\varGamma }}^{\prime }(\mathbf {a})$, on a state space L ×L (i.e. where vertices are absorbing sets). For any $g\in {{\varGamma }}^{\prime }(\mathbf {a})$ the cost of an arrow originating from some L_j ∈ L is c(L_j; g).

We deduce from the proof of Theorem 1 in Appendix B that for convention a^∗, the minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$ involves direct transitions from every $\mathbf {a}\in L_{j}\subset \mathbf {L}\backslash \mathbf {a}^{*}$ to a^∗, and each has a cost bounded from above by $c(\mathbf {a};g)\leq b^{*}_{2}$. Note that if $c(\mathbf {a};g)\leq b^{*}_{2}$ for all a ∈ L_j, then $c(L_{j};g)\leq b^{*}_{2}$. Thus, if we let ζ^∗(L) be the number of independent absorbing sets in L (i.e. all L_j ⊂L) with a^∗ excluded, then

$$ \phi(\mathbf{a}^{*})= \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g) \leq b^{*}_{2}\zeta^{*}(\mathbf{L}) $$

(23)

Now, consider any other a ∈ L ⊂L∖a^∗. The minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a})$ will consist of an arrow $\mathbf {a}^{*}\rightarrow \mathbf {a}^{\prime }$ starting from a^∗ to some $\mathbf {a}^{\prime }\neq \mathbf {a}^{*}$. The minimum cost $g\in {{\varGamma }}^{\prime }(\mathbf {a})$ can thus be constructed from the minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$ by deleting $\mathbf {a}\rightarrow \mathbf {a}^{*}$ and replacing it with $\mathbf {a}^{*}\rightarrow \mathbf {a}^{\prime }$, so that

$$ \phi(\mathbf{a})= \phi(\mathbf{a}^{*}) - \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}c(\mathbf{a};g)+\min_{g\in {{\varGamma}}^{\prime}(\mathbf{a})}c(\mathbf{a}^{*};g) $$

(24)

And hence,

$$ \phi(\mathbf{a})-\phi(\mathbf{a}^{*}) = \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a})}{\min}c(\mathbf{a}^{*};g)- \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}c(\mathbf{a};g) > \left( n^{\frac{3}{5}}-b^{*}_{2}\right) $$

(25)

where the second inequality is because the minimum cost of leaving a^∗ is greater than $n^{\frac {3}{5}}$ mutations (see Appendix B) and that $c(\mathbf {a};g)\leq b^{*}_{2}$ for all $\mathbf {a}\in L_{j}\subset \mathbf {L}\backslash \mathbf {a}^{*}$.

Since $n^{\frac {3}{5}}\geq b^{*}_{2}$ is a condition for strategy a^∗ to be contagious, it follows that ϕ(a) − ϕ(a^∗) > 0 for all a ∈ L∖a^∗, and hence, a^∗ has the minimum cost a^∗-tree. The inequality, $\phi (\mathbf {a})-\phi (\mathbf {a}^{*})>n^{\frac {3}{5}}-b^{*}_{2}$, also implies that ${{{\varPhi }}}(\mathbf {a},\mathbf {a}^{*})> n^{\frac {3}{5}}-b^{*}_{2}$ for all a ∈ L∖a^∗. Thus,

$$\frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{a},\mathbf{a}^{*})}< \frac{\ln \gamma}{n^{\frac{3}{5}}-b^{*}_{2}} \quad \text{for all $\mathbf{a}\in\mathbf{L}\backslash\mathbf{a}^{*}$}$$

It then follows that there exists some $\beta ^{*}\in \left (0, \ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})\right ]$ such that for all β ≥ β^∗, convention a^∗ has the least cost tree, and hence, the long-run equilibrium.

Appendix D: Proof of Proposition 2

The following definitions are used in the next steps of the proof. Given transition probabilities P_β(x, y) in Eq. 8, the cost function c(x, y) can be rewritten as follows

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{-\ln P_{\beta}(\mathbf{x},\mathbf{y})}{\beta} = c(\mathbf{x},\mathbf{y}) $$

(26)

The following definition is for Γ_{x, y}(W) graphs, which are a special form of Γ(W) graphs defined in Definition 7.

Definition 9

For any $\mathbf {x}\in \bar {W}$ and y ∈ W where x≠y, Γ_{x, y}(W) is a set of all Γ(W)-graphs which link x to y. For any two configurations $\mathbf {x}, \mathbf {y}\in \bar {W}$, Γ_{x, y}(W ∪{y}) is the set of Γ(W)-graphs in which x is joined to some point y possibly itself and not to W, and that all other points of $\bar {W}$ are joined to either the same point or to W.

Consider a configuration space X = {a, b, c, d, e, f, g, h} with examples of g-trees depicted in Fig. 4. Let W = {d, e, f, g, h}, with examples of Γ(W) graphs depicted in Fig. 5. Then examples of ${{\varGamma }}_{\mathbf {a},\mathbf {c}}\left (W\cup \{\mathbf {c}\}\right )$ graphs based on Γ(W) graphs in Fig. 5 are: $\{\mathbf {a}\rightarrow \mathbf {c}, \mathbf {b}\rightarrow W \}$ for the graph on the left, $\{\mathbf {c}\rightarrow W, \mathbf {b}\rightarrow W \}$ for the middle graph, and $\{\mathbf {a}\rightarrow \mathbf {b}, \mathbf {c}\rightarrow W \}$ for the graph on the right.

Fig. 5

Examples of Γ(W) graphs, where $\bar {W}=\{\mathbf {a}, \mathbf {b}, \mathbf {c}\}$

Recall the definition of ϕ(W; g) for some W ⊂X and g ∈ Γ(W) from Appendix C as $\phi (W;g)={\sum }_{(\mathbf {x},\mathbf {y})\in g}c(\mathbf {x},\mathbf {y})$. The following result is derived in Catoni (1999, Proposition 4.2).

Lemma 2

For any W ⊂X, W ≠ ∅ and $\bar {W}=\mathbf {X}\backslash W$, for any $\mathbf {x},\mathbf {y}\in \bar {W}$

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(W)| \mathbf{x}_{0}=\mathbf{x}]}{\beta} = \underset{g\in {{\varGamma}}(W)}{\min}\phi(W;g)-\underset{\mathbf{y}\in \bar{W}}{\min}\underset{g\in {{\varGamma}}_{\mathbf{x}, \mathbf{y}}(W\cup\{\mathbf{y}\})}{\min}\phi(W;g) $$

(27)

We are interested in the expected waiting time for convention a^∗ associated with the contagious strategy a^∗. Thus, we can substitute W = {a^∗} into Eq. 27. That is,

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})| \mathbf{x}_{0}=\mathbf{x}]}{\beta} = \underset{g\in {{\varGamma}}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g)-\underset{\mathbf{y}\in \mathbf{L}\backslash\mathbf{a}^{*}}{\min}\underset{g\in {{\varGamma}}_{\mathbf{x}, \mathbf{y}}(\mathbf{a}^{*}\cup\{\mathbf{y}\})}{\min}\phi(\mathbf{a}^{*};g) $$

(28)

Recall from the analysis in Appendices B and C for the minimum cost graph g ∈ Γ(a^∗), the costs are bounded from above as $c(\mathbf {a};g)\leq b^{*}_{2}$ for all a ∈ L∖a^∗, and from Eq. 23, $\phi (\mathbf {a}^{*})=\min \limits _{g\in {{\varGamma }}(\mathbf {a}^{*})}\phi (\mathbf {a}^{*};g) \leq b^{*}_{2}\zeta ^{*}(\mathbf {L})$. Focusing on reduced form graphs, ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$, it follows from the definition of ${{\varGamma }}^{\prime }_{\mathbf {a}, \mathbf {a}^{\prime }}(\mathbf {a}^{*}\cup \{\mathbf {a}^{\prime }\})$ graphs that $\min \limits _{\mathbf {a}^{\prime }\in \mathbf {L}\backslash \mathbf {a}^{*}}\min \limits _{g\in {{\varGamma }}^{\prime }_{\mathbf {a}, \mathbf {a}^{\prime }}(\mathbf {a}^{*}\cup \{\mathbf {a}^{\prime }\})}\phi (\mathbf {a}^{*};g)\leq b^{*}_{2}(\zeta ^{*}(\mathbf {L})-1)$. Thus, there exists some $b^{*}\in (0,b^{*}_{2})$ such that

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})| \mathbf{x}_{0}=\mathbf{a}]}{\beta} = \underset{g\in {{\varGamma}}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g) - \min_{\mathbf{a}^{\prime}\in \mathbf{L}\backslash\mathbf{a}^{*}}\underset{g\in {{\varGamma}}^{\prime}_{\mathbf{a}, \mathbf{a}^{\prime}}(\mathbf{a}^{*}\cup\{\mathbf{a}^{\prime}\})}{\min}\phi(\mathbf{a}^{*};g) =b^{*} $$

(29)